SSM CA Spanish Fifth Grade Sample

GRADO 5

CALIFORNIA

Muestra de la edición para el maestro

Muestra de la edición para maestros Grado 5

Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.

Para obtener más información, visítenos en www.stemscopes.com.

GRADO 5 NÚMEROS Y OPERACIONES: FRACCIONES

MULTIPLICACIÓN DE MODELOS DE FRACCIONES

ESTÁNDARES CLAVE

Aplicar y ampliar conocimientos previos de multiplicación y división para multiplicar y dividir fracciones.

• Aplicar y ampliar conocimientos previos de multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpretar el producto (a/b) × q como una parte de una partición de q en b partes iguales; equivalentemente, como el resultado de una secuencia de operaciones a × q ÷ b. Por ej., utilice un modelo visual de fracción para mostrar (2/3) × 4 = 8/3, y cree un contexto de historia para esta ecuación. Haga lo mismo con (2/3) x (4/5)= 8/15. (En general, (a/b) x (c/d) = (ac/bd).

• Interpretar la multiplicación como una escala (cambio de tamaño), al:

a. Comparar el tamaño de un producto con el tamaño de un factor a partir del tamaño del otro factor, sin realizar la multiplicación indicada.

b. Explicar por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado (reconociendo la multiplicación por números enteros mayores que 1 como un caso familiar); explicando por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionar el principio de equivalencia de fracciones a/b = (n x a)/(n x b) con el efecto de multiplicar a/b por 1.

ESTÁNDARES DE CONEXIÓN

Utilizar fracciones equivalentes como estrategia para sumar y restar fracciones.

• Sumar y restar fracciones con denominadores distintos (incluyendo números mixtos) sustituyendo fracciones dadas por fracciones equivalentes de manera que se produzca una suma o diferencia equivalente de fracciones con denominadores iguales. Por ejemplo: 2/3 + 5/4 = 8/12 + 15/12 = 23/12. Por lo general, a/b + c/d = (ad+bc) / bd.

ACTIVIDADES DE PARTICIPACIÓN

ACCESO A CONOCIMIENTOS PREVIOS

Los estudiantes explorarán y representarán la multiplicación de una fracción unitaria por un número entero para profundizar en su comprensión de las fracciones.

• Los estudiantes utilizarán una cuadrícula para crear un modelo visual de fracción que represente la multiplicación de una fracción unitaria por un número entero.

• Colaborarán con sus compañeros para proponer y describir sus modelos y soluciones.

• Los estudiantes usarán una recta numérica para identificar el rango entre números enteros donde se encuentra el producto de la multiplicación.

• La actividad enfatiza la comprensión de que multiplicar por una fracción propia resulta en un producto menor que el número entero.

CAPTAR INTERÉS: MULTIPLICAR FRACCIONES (UN PEDAZO DE PASTEL)

Los estudiantes exploran el concepto de multiplicar un número entero por una fracción para comprender el tamaño del producto en relación con los factores.

• Los estudiantes trabajan en grupos para representar la multiplicación de un número entero por una fracción utilizando un modelo de pastel.

• Visualizan y resuelven un problema del mundo real que implica estimar el número de pasteles necesarios para una fiesta.

• Los estudiantes utilizan pizarras blancas para dibujar modelos de fracciones, escribir ecuaciones y explicar su razonamiento.

• La actividad fomenta el pensamiento crítico sobre la multiplicación y sus efectos cuando se trata de números menores, iguales o mayores que uno.

ACTIVIDADES DE EXPLORAR

EXPLORACIÓN 1: MULTIPLICAR FRACCIONES POR NÚMEROS ENTEROS

Los estudiantes exploran el concepto de multiplicar una fracción por un número entero a través de modelos prácticos y razonamiento.

• Los estudiantes trabajan en grupos para completar tareas en diferentes estaciones, utilizando fichas de fracciones, contadores de dos colores y líneas numéricas para representar escenarios de multiplicación.

• Participan en conversaciones guiadas para conectar la adición repetida y la multiplicación, y para entender la relación entre el tamaño del producto y sus factores.

• Los estudiantes documentan sus modelos y razonamientos en un diario del estudiante y participan en un debate en clase para reflexionar sobre su aprendizaje y sus estrategias.

• La actividad concluye con una papeleta de salida para evaluar la comprensión y con oportunidades para que los estudiantes compartan y perfeccionen sus estrategias y puntos de vista.

EXPLORACIÓN 2: MULTIPLICAR FRACCIONES POR FRACCIONES

Los estudiantes exploran el concepto de multiplicar fracciones por fracciones a través del modelado y el razonamiento sobre el tamaño del producto en relación con los factores.

• Los estudiantes trabajan en pequeños grupos para representar la multiplicación de fracciones utilizando fichas de fracciones, reglas y tiras de frases.

• Crean modelos de áreas y rectas numéricas para visualizar y resolver problemas relacionados con las distancias de los senderos.

• Los estudiantes desarrollan ecuaciones de multiplicación para cada escenario y comparan el producto con los factores originales.

• La actividad fomenta la discusión y el razonamiento sobre por qué el producto de dos fracciones es menor que los factores, desafiando las suposiciones previas sobre la multiplicación.

EXPLORACIÓN 3: RELACIÓN DE ESCALA

Los estudiantes exploran el concepto de cambio de tamaño y su impacto en el área de un espacio a través del razonamiento colaborativo y el modelado.

• Los estudiantes trabajan en parejas para comparar y contrastar los planes de negocio de una granja, centrándose en cómo el cambio de tamaño de las dimensiones afecta al área.

• Utilizan dibujos, modelos o manipulativos para justificar su razonamiento y explorar diferentes estrategias.

• Las parejas conversan y registran sus hallazgos en los diarios del estudiante, identificando similitudes y diferencias en sus enfoques.

• La actividad concluye con una charla de matemáticas para compartir observaciones y reforzar la comprensión de la multiplicación como escala.

ALCANCE:IDEAS FUNDAMENTALES

SHAPES ON A PLANE

MODELING

CONCEPTOS CLAVE

• Puedo utilizar modelos de áreas, diagramas de cinta y rectas numéricas para dar sentido al proceso de multiplicación de dos fracciones o de multiplicación de una fracción por un número entero.

• Puedo razonar sobre cómo cambian los números cuando se multiplican por fracciones.

• Puedo reconocer que al multiplicar por una fracción mayor que 1, el número aumenta, y al multiplicar por un número menor que uno, el número disminuye.

Los estudiantes dividen cuadrículas e interpretan la multiplicación de fracciones en el contexto del área que cubre un espacio bidimensional, lo que les ayuda a conectar la multiplicación de fracciones con conceptos geométricos. También aplicarán esta comprensión fundamental para graficar valores de fracción en un plano de coordenadas más adelante en el año.

Los estudiantes usan modelos de áreas, rectas numéricas y fichas de fracciones para representar la multiplicación de fracciones en contextos reales. Justifican su razonamiento demostrando visualmente cómo la multiplicación de fracciones afecta al tamaño del producto.

Los estudiantes exploran la relación entre fracciones y multiplicación resolviendo problemas que implican escalas, áreas y grupos repetidos de cantidades de fracción. Analizan cómo la multiplicación por fracciones mayores o menores que uno afecta al producto.

PREGUNTAS FUNDAMENTALES

• ¿Qué estrategias puedo utilizar para representar la multiplicación de dos fracciones o de una fracción y un número entero?

• ¿Cómo cambian los números cuando se multiplican por fracciones?

• ¿Cómo depende la magnitud de un producto del tamaño de las fracciones que se multiplican?

INICIO: CALENDARIO SUGERIDO

PLANIFICACIÓN

Internalización de la lección

Alcance

• Revise los estándares abordados en el alcance.

• Familiarícese con la forma en que se evalúan los estándares y lo que demuestra el dominio de la materia.

• Revise el documento «Secuencia de aprendizaje» que se encuentra en el elemento «Visión general del alcance» para comprender la secuencia de los conceptos.

• Determine qué recursos se utilizarán para la práctica y la evaluación. Lección

• Revise las instrucciones para el maestro y los documentos asociados.

• Familiarícese con los modelos, herramientas y estrategias que los estudiantes utilizarán en la actividad.

• Considere el propósito de la lección dentro del alcance e identifique lo que los estudiantes deben saber y ser capaces de hacer como resultado.

• Identifique las áreas en las que los estudiantes pueden necesitar apoyo o enriquecimiento y planifique cómo responder.

Contenido de apoyo

Contenido desglosado

Visión general del alcance

Manipulativos/materiales

DÍA 1

Se presenta a los estudiantes una actividad que consiste en reconocer y explicar por qué al multiplicar un número dado por una fracción menor que uno se obtiene un producto menor que el número original dado. Los estudiantes volverán a realizar la actividad después de haber completado las exploraciones correspondientes.

Los estudiantes expresan opiniones, ideas y sentimientos sobre un problema utilizando frases como «yo noto . . .» y «me pregunto si . . .»

DÍA 2

Los estudiantes modelan la multiplicación de una fracción y un número entero y razonan sobre el tamaño del producto en relación con ambos factores.

Exploración 1

• 6 cubos o contenedores (por clase)

• 14 juegos de fichas de fracciones (por clase)

• 2 juegos de contadores de dos colores (por clase)

• 36 tiras de papel manila de 3 × 18 pulgadas (por clase)

• 2 rollos de cinta adhesiva (por clase)

Exploración 2

• 1 juego de fichas de fracciones (por grupo)

• 2 tiras de oraciones (por grupo)

Exploración 3

• 1 juego de bloques de base diez (por estación)

Acceso a conocimientos previos (~15 minutos)

• Completar la semana anterior a este alcance.

Carta para llevar a casa

• Imprimir y enviar a casa la semana anterior a este alcance.

DÍA 3

Los estudiantes modelan la multiplicación de una fracción y un número entero y razonan sobre el tamaño del producto en relación con ambos factores.

DÍA 4

Los estudiantes modelan la multiplicación de una fracción por una fracción y razonan sobre el tamaño del producto en relación con ambos factores.

Los estudiantes utilizan apoyos como dibujos, modelos y gestos para mejorar su comunicación verbal.

Los estudiantes comparten ideas y escuchan a los demás durante las actividades de aprendizaje cooperativo.

Enunciado diario de aritmética Ciencia de datos

Enunciado diario de aritmética Ciencia de datos

Enunciado diario de aritmética Ciencia de datos

Captar interés (parte 1): Exploración previa

Comience la «Exploración 1: Multiplicar fracciones por números enteros»

Continúe la «Exploración 1: Multiplicar fracciones por números enteros»

Charla de matemáticas

Libreta interactiva: Multiplicar fracciones por números enteros

Los estudiantes conversan y resumen textos en pequeños grupos para demostrar comprensión y entendimiento.

Práctica independiente (del alcance o nivel de grado anterior)

Constructor de fluidez

Práctica interactiva

Práctica guiada

Constructor de bases fundamentales

Conversaciones estructuradas

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Lista de verificación de la observación

Preguntas de facilitación

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Parte I: Intervención en grupos pequeños

Exploración 1: Boleto de salida

Muestra lo que sabes (parte 1)

Lista de verificación de observación

Preguntas de facilitación

Enunciado diario de aritmética Ciencia de datos

Esquema de anclaje: Exploración 1

Comience la «Exploración 2: Multiplicar fracciones por fracciones»

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Lista de verificación de la observación

Preguntas de facilitación

PRÁCTICA

Práctica independiente

Todos los estudiantes

• Fluidez en los hechos matemáticos: Suma y resta (15-30 minutos)

• Fluidez en los hechos matemáticos: Multiplicación y división (15-30 minutos)

• Explicar: Vocabulario ilustrado (15-30 minutos)

• Explicar: Mis pensamientos de matemáticas (15-30 minutos)

• Elaborar: Conexiones profesionales (15-30 minutos)

• Elaborar: Revisión en espiral (1530 minutos)

Los que dominan

• Aceleración: Matemáticas de hoy (15-30 minutos)

• Aceleración: Crea el tuyo (30-45 minutos)

DÍA 5

Los estudiantes representan la multiplicación de una fracción por una fracción y razonan sobre el tamaño del producto en relación con ambos factores.

• Aceleración: Tablero de opciones (15-30 minutos)

Los que cumplen

• Elaborar: Cuento de matemáticas (30-45 minutos)

• Elaborar: Tarea basada en problemas (30-45 minutos)

• Elaborar: Constructor de fluidez(15-30 minutos)

Los deficientes

• Elaborar: Práctica interactiva(15-30 minutos)

• Evaluar: Prueba de habilidades (30-45 minutos)

Práctica guiada

• Intervención: Intervención en grupos pequeños (15-30 minutos)

• Explicar: Conexiones lingüísticas (15-30 minutos)

• Inicio: Guía de instrucción andamiada (30-45 minutos)

DÍA 6

Los estudiantes crean un organizador gráfico que compara y describe los productos al multiplicar un número entero por una fracción mayor que uno, menor que uno e igual a uno.

Los estudiantes repiten el lenguaje nuevo aprendido en clase para practicar su uso apropiado.

Los estudiantes usan palabras y frases de vocabulario verbalmente y por escrito para demostrar su comprensión.

Enunciado diario de aritmética Ciencia de datos

Enunciado diario de aritmética Ciencia de datos

Esquema de anclaje: Exploración 2

Continúe la «Exploración 2: Multiplicar fracciones por fracciones»

Math Chat

Libreta interactiva: Multiplicar fracciones por fracciones

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Parte II: Intervención en grupos pequeños

Exploración 2: Boleto de salida

Muestra lo que sabes (parte 2)

Lista de verificación de la observación

Preguntas de facilitación

Habilidades básicas: Compara el tamaño de los productos

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Lista de verificación de la observación

Preguntas de facilitación

Habilidades básicas: Folleto del estudiante

INICIO: CALENDARIO SUGERIDO

EVALUACIONES

Acceso a conocimientos previos (D)

Breve actividad de sondeo para evaluar los conocimientos previos antes de abordar el contenido del alcance.

Boleto de salida (F)

Evaluación rápida sobre lo que aprendieron en esta exploración.

Muestra lo que sabes (F)

Tarea de práctica independiente que permite a los estudiantes demostrar su aprendizaje.

Decide y defiende (F)

Evaluación abierta que pide a los estudiantes que razonen matemáticamente y apoyen sus ideas con pruebas.

Lista de verificación de la observación (D, F)

Lista de conceptos y habilidades que el maestro y el estudiante pueden usar para reflexionar sobre el progreso del estudiante y establecer objetivos.

Prueba de habilidades (F, S)

Evaluación basada en estándares para determinar la habilidad para resolver problemas matemáticos de manera eficiente

y precisa.

Evaluación basada en estándares (S)

Evaluación basada en estándares de opción múltiple en la que los estudiantes demuestran el dominio del contenido

Intervención en grupos pequeños: Revisión (F)

Tarea de práctica independiente para evaluar el dominio del contenido después de la intervención en grupos pequeños.

Evaluaciones de referencia (D, S)

Evaluaciones de principio, mitad y final de año que ofrecen datos significativos que pueden informar la instrucción.

Evaluaciones de medición del crecimiento (D, S)

Evaluaciones previas y posteriores diseñadas para realizar un seguimiento del crecimiento de los estándares de nivel de grado desde el principio hasta el final del año.

DÍA 7 DÍA 8

Los estudiantes razonan sobre el tamaño del producto basándose en el cambio de tamaño de uno o ambos factores. Los estudiantes justifican sus razonamientos con dibujos, modelos o manipulativos. Los estudiantes comparan o contrastan sus estrategias con sus compañeros.

Los estudiantes usan apoyos como modelos e imágenes para mejorar su comprensión de vocabulario y conceptos nuevos.

Los estudiantes repiten una actividad que consiste en reconocer y explicar por qué al multiplicar un número dado por una fracción menor que uno se obtiene un producto menor que el número original dado. Resolverán el problema original ahora que han completado las exploraciones correspondientes.

Los estudiantes intercambian ideas, proporcionan retroalimentación y modifican su trabajo según sea necesario.

Enunciado diario de aritmética Ciencia de datos

Enunciado diario de aritmética Ciencia de datos

Exploración 3: Relación de escala

Charla de matemáticas

Esquema de anclaje: Exploración3

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Parte III: Intervención en grupos pequeños

Exploración 3: Boleto de salida

Muestra lo que sabes (parte 3)

Lista de verificación de la observación

Preguntas de facilitación

Captar interés (parte 2): Posexploración

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Comprobación de la intervención en grupos pequeños

Evaluación de habilidades

INICIO: CALENDARIO SUGERIDO

DÍA 9

Los estudiantes demuestran su dominio de los conceptos y habilidades clave del alcance de aplicación a través de una evaluación basada en estándares.

Los estudiantes emplean habilidades de lectura y escritura utilizando lenguaje académico para demostrar su comprensión de los conceptos clave.

Enunciado diario de aritmética Ciencia de datos

Práctica independiente

Refiérase a la sección de «Práctica»

Práctica guiada

Refiérase a la sección de «Práctica»

Decidir y defender Evaluación basada en estándares

INICIO: CALENDARIO SUGERIDO

GRADO 5: MODELO DE MULTIPLICACIÓN DE FRACCIONES

INICIO: CONTENIDO DE APOYO

¿QUÉ ESTOY ENSEÑANDO?

CONTENIDO DE APOYO

Aplicar y ampliar conocimientos previos de multiplicación y división para multiplicar y dividir fracciones.

• Aplicar y ampliar conocimientos previos de multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpretar el producto (a/b) × q como a partes de una partición de q en b partes iguales; equivalentemente, como el resultado de una secuencia de operaciones a × q ÷ b. Por ejemplo, utilice un modelo visual de fracción para mostrar (2/3) × 4 = 8/3, y cree un contexto de historia para esta ecuación. Haga lo mismo con (2/3) x (4/5)= 8/15. (En general, (a/b) x (c/d) = (ac/bd).

• Interpretar la multiplicación como una escala (cambio de tamaño), al:

a. Comparar el tamaño de un producto con el tamaño de un factor a partir del tamaño del otro factor, sin realizar la multiplicación indicada.

b. Explicar por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado (reconociendo la multiplicación por números enteros mayores que 1 como un caso familiar); explicando por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionar el principio de equivalencia de fracciones a/b = (n x a)/(n x b) con el efecto de multiplicar a/b por 1.

CONOCIMIENTOS PREVIOS

Las habilidades fundamentales para usar representaciones visuales de fracciones y con operaciones de fracciones comienzan con el trabajo previo en los dominios del número, la medida y la geometría. Los estudiantes de primer y segundo grado entienden el sistema de base diez y usan el lenguaje de las fracciones para describir formas divididas en partes iguales (mitades, tercios y cuartos). En tercero, miden con reglas marcadas con mitades y cuartos de pulgada. Utilizan la notación de fracciones y modelos visuales (diagramas de cinta, rectas numéricas y modelos de área) para representar y comparar fracciones. En cuarto grado, consolidan su comprensión de las fracciones equivalentes, suman y restan fracciones y números mixtos con denominadores iguales y multiplican fracciones por números enteros. En quinto, los estudiantes suman y restan fracciones y números mixtos con denominadores distintos, resuelven problemas de multiplicación de fracciones, dividen números enteros entre fracciones unitarias y dividen fracciones unitarias entre números enteros.

CONCEPTOS ERRÓNEOS Y OBSTÁCULOS

• Los estudiantes pueden pensar que la multiplicación siempre da como resultado una cantidad mayor. El uso de modelos visuales para multiplicar fracciones puede ayudar a los estudiantes a hacer mejores generalizaciones acerca de los productos de fracciones.

• Los estudiantes podrían dividir un entero en partes que son desiguales. Los estudiantes deben practicar el uso de una variedad de modelos de fracciones para que entiendan cómo representar partes iguales dentro de un todo.

EN ESTE ALCANCE

Los estudiantes utilizan modelos de área, diagramas de cinta y rectas numéricas para dar sentido al proceso de multiplicación de dos fracciones o de multiplicación de una fracción por un número entero. Los estudiantes crean contextos de historias que representan la multiplicación de fracciones y escriben ecuaciones para representar las soluciones. Los estudiantes interpretan la multiplicación como un cambio de escala o de tamaño. Los estudiantes razonan sobre cómo cambian los números cuando se multiplican por fracciones considerando el tamaño de un producto en relación con los tamaños de cada factor. Reconocen, que al multiplicar una fracción mayor que uno, el número aumenta, y al multiplicar por un número menor que uno el número disminuye.

TÉRMINOS CLAVE

• modelo de área: un modelo rectangular de multiplicación o división que representa el total como el área; los factores o cociente y divisor están representados por las longitudes de los lados

• división: el proceso de compartir o dividir equitativamente

• ecuación: una oración matemática que usa números, uno o más símbolos de operación y un signo igual

• equivalente: que tiene la misma cantidad o valor

• factor: un número que se multiplica por otro número para obtener un producto

• fracción: una parte de un grupo de objetos, un número o un entero

• multiplicación: una forma de crear un producto haciendo grupos iguales, repitiendo la suma o formando matrices

• recta numérica: una línea con marcas espaciadas uniformemente para mostrar la posición de un número en relación con otros números

• operaciones: procesos matemáticos, como la suma, la resta, la multiplicación y la división

• parte: un trozo de algo

• producto: el resultado de multiplicar dos o más números juntos

• escala: comparación del tamaño del producto con el tamaño de un factor en función del otro factor; predicción de productos en función de factores

• diagrama de cinta: modelo utilizado para resolver problemas de palabras que muestra la relación entre cantidades conocidas y desconocidas

• número entero: valor numérico sin parte decimal ni de fracción

INICIO: CONTENIDO DE APOYO

APLICAR LAS PRÁCTICAS MATEMÁTICAS

• MP.1 Dar sentido a los problemas y perseverar en su resolución: Los estudiantes trabajan a través de escenarios de multiplicación de fracciones del mundo real, tales como la planificación de inversiones empresariales, la medición de distancias de senderos, y el escalado de áreas agrícolas, lo que requiere que analicen e interpreten las relaciones entre los valores fraccionarios.

• MP.2 Razonan abstracta y cuantitativamente: Los estudiantes dan sentido a la multiplicación de fracciones considerando cómo el producto se compara con los factores. Entienden cómo el producto se comparará con el primer factor en función del tamaño del segundo factor.

• MP.3 Construir argumentos viables y criticar el razonamiento de los demás: Los estudiantes justifican sus estrategias de multiplicación de fracciones explicando su razonamiento usando modelos de áreas, líneas numéricas y notación simbólica mientras comparan estrategias con sus compañeros.

• MP.4 Modelan con matemáticas: Los estudiantes usan modelos visuales de fracciones, rectas numéricas, modelos de áreas y manipulativos como fichas de fracciones para representar la multiplicación de fracciones, demostrando comprensión a través de representaciones concretas y pictóricas.

• MP.5 Usan herramientas apropiadas estratégicamente: Los estudiantes seleccionan herramientas tales como tiras de fracciones, papel cuadriculado, bloques de base diez, rectas numéricas y pizarras de borrado en seco para representar la multiplicación de fracciones de manera efectiva, ajustando sus estrategias según sea necesario.

• MP.6 Prestan atención a la precisión: Los estudiantes dividen cuidadosamente enteros en partes de fracción iguales, asegurando el etiquetado preciso de las fracciones y utilizando consistentemente notación matemática como ecuaciones.

• MP.7 Buscar y hacer uso de la estructura: Los estudiantes reconocen patrones en la multiplicación de fracciones, comprendiendo cómo la multiplicación por una fracción menor que 1 reduce un valor, mientras que la multiplicación por una fracción mayor que 1 lo aumenta.

• MP.8 Buscan y expresan regularidad en razonamientos repetidos: Los estudiantes generalizan el proceso de multiplicación de fracciones aplicando consistentemente el mismo razonamiento a diferentes tipos de problemas, observando patrones en modelos concretos, modelos de área y escalamiento.

LOS

ESTUDIANTES APLICAN Y AMPLÍAN

SUS CONOCIMIENTOS PREVIOS DE MULTIPLICACIÓN PARA MULTIPLICAR UNA FRACCIÓN O UN NÚMERO ENTERO POR UNA FRACCIÓN

A medida que los estudiantes multiplican fracciones, piensan en la operación de más de una manera. Utilizan modelos visuales para representar e interpretar un producto y crean un contexto narrativo para la ecuación correspondiente.

Ejemplo: Había 40 estudiantes en 5.º grado. Tres cuartas partes de los estudiantes iba en autobús a la escuela. Este diagrama de cinta representa la cantidad de estudiantes que viajaron en autobús. ¿Cuántos estudiantes viajaron en autobús? Explica tu razonamiento.

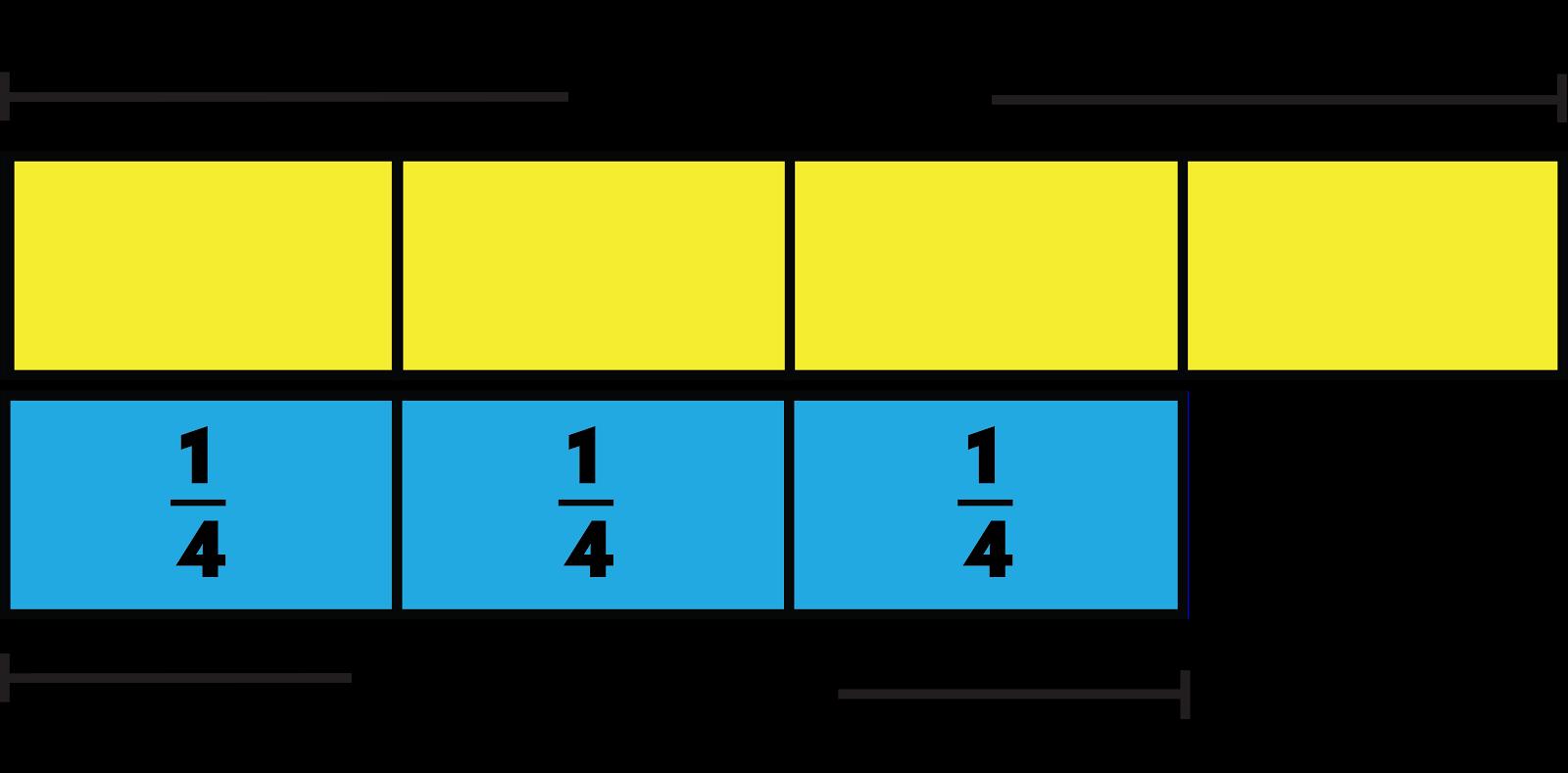
30 estudiantes viajaron en autobús. Ejemplo de razonamiento: 40 ÷ 4 = 10, por lo que cada unidad dentro de la población total de estudiantes tiene un valor de 10. 1/4 de 40 es 10, y 10 × 3 = 30

Ejemplo: ¿Cuál de las siguientes ecuaciones tiene el mismo valor que 2/3 × 4?

a 2 × (4 ÷ 3)

b 2 × 3/4

c 2 × 4/3

d (2 × 4) ÷ 3

Las respuestas correctas son a, c, y d.

a. Si multiplicamos esto por 2, nos queda dos y dos tercios, que es el valor de la expresión de la pregunta.

c. 2 × 4/3 es correcta porque cuatro tercios dos veces da un total de ocho tercios. Esta fracción puede entonces simplificarse a dos y dos tercios.

d. (2 × 4) ÷ 3 es correcta porque al multiplicar 2 y 4, el producto es 8. Ocho se divide entonces por 3, lo que nos da ocho tercios. Esta fracción se reduce entonces a dos y dos tercios.

GRADO

INICIO: CONTENIDO DE APOYO

Ejemplo: ¿Cuál de los siguientes contextos argumentales puede resolverse multiplicando 2/3 por 4?

a Hay 4 pizzas en una fiesta y se han comido 2/3 de las pizzas. ¿Cuántas pizzas quedan?

b ¿Cuántas tazas de 2/3 se pueden servir con 4 tazas de jugo?

c Todos los días paso 2/3 de hora leyendo. ¿Cuánto leo al cabo de 4 días?

d Hay 4 yardas de hilo. Se cortan dos tercios del hilo para hacer un pompón. ¿Cuánto hilo queda?

Las respuestas correctas son a y c

• a es correcta porque hay un total de cuatro enteros. En cada uno de ellos se han comido 2 de los 3 trozos iguales. Para hallar la porción total de los trozos que se han ido, tendríamos que combinar 2/3 cuatro veces.

• c es correcto porque una hora, que representa el todo en este caso, se está dividiendo en 3 partes iguales. De estas tres partes de una hora, dos se dedican a la lectura, lo que resulta en 2/3 de una hora de lectura cada día. Si esto se repite cuatro veces, la fracción debe multiplicarse por cuatro para obtener el número total de horas dedicadas a la lectura.

Ejemplo: Este modelo de fracción muestra el producto de 4 y 2/3. ¿Cuánto es 2/3?

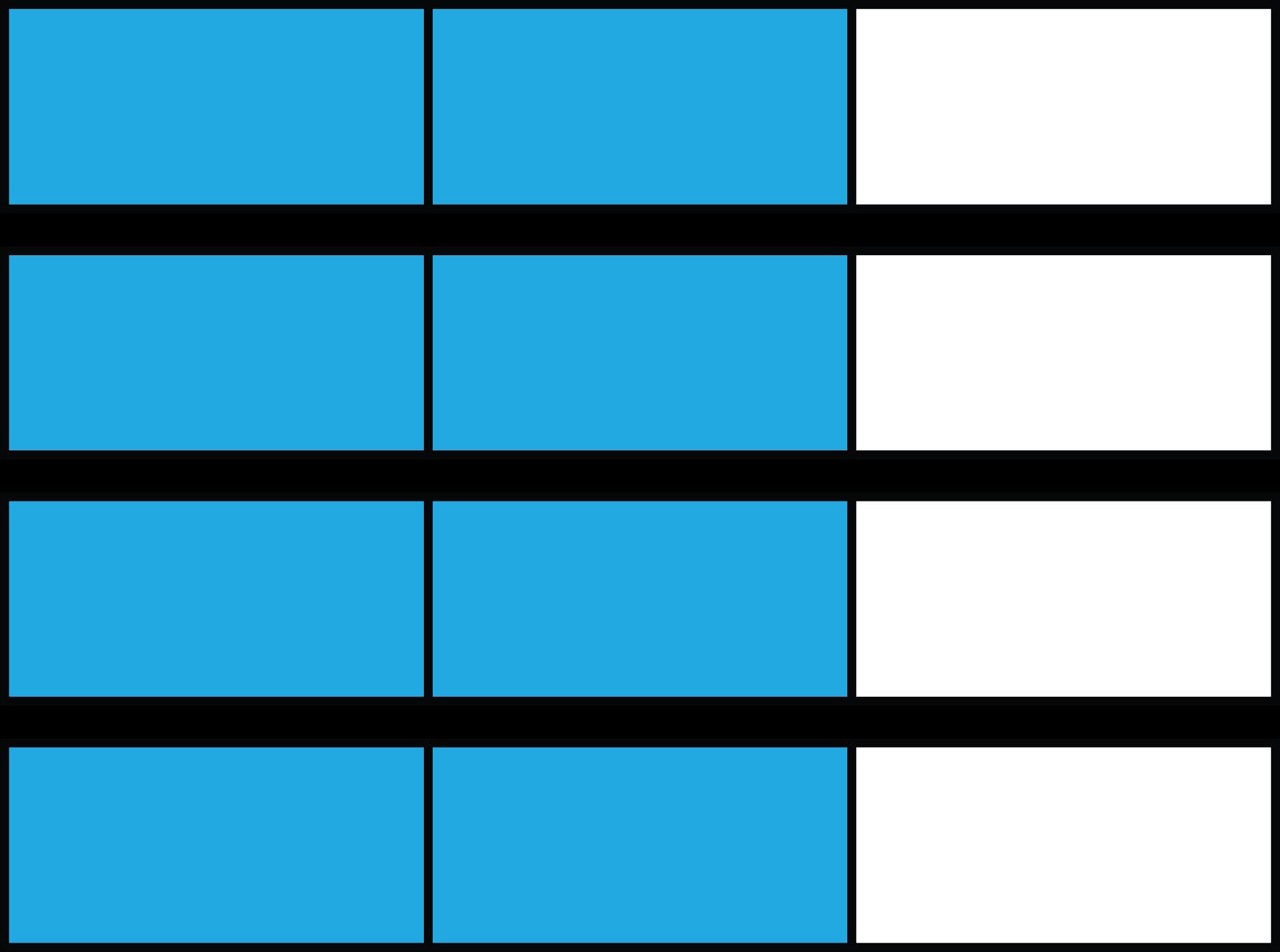
La respuesta es 8/3, ó 2 2/3. El modelo muestra 4 enteros divididos en tercios. En cada uno de los cuatro enteros, dos de las tres partes iguales están sombreadas, 2 x 4 = 8. Esto significa que hay un total de 8 tercios individuales sombreados. Simplificado, ocho tercios da como resultado 2 enteros 2/3

LOS ESTUDIANTES INTERPRETAN LA MULTIPLICACIÓN COMO UNA ESCALA

Los estudiantes examinan la magnitud de los productos observando la relación entre los dos factores del problema. Ven que los números cambian cuando se multiplican por fracciones. Al multiplicar una fracción mayor que uno, el número aumenta, y al multiplicar una fracción menor que uno, el número disminuye.

Ejemplo: ¿El producto de 3/4 × 5 es menor que 5 o mayor que 5? Usa un modelo visual para explicar tu razonamiento. El producto es menor que 5.

Ejemplo de razonamiento A: Este diagrama de cinta muestra que 3/4 de 5 es menor que 5.

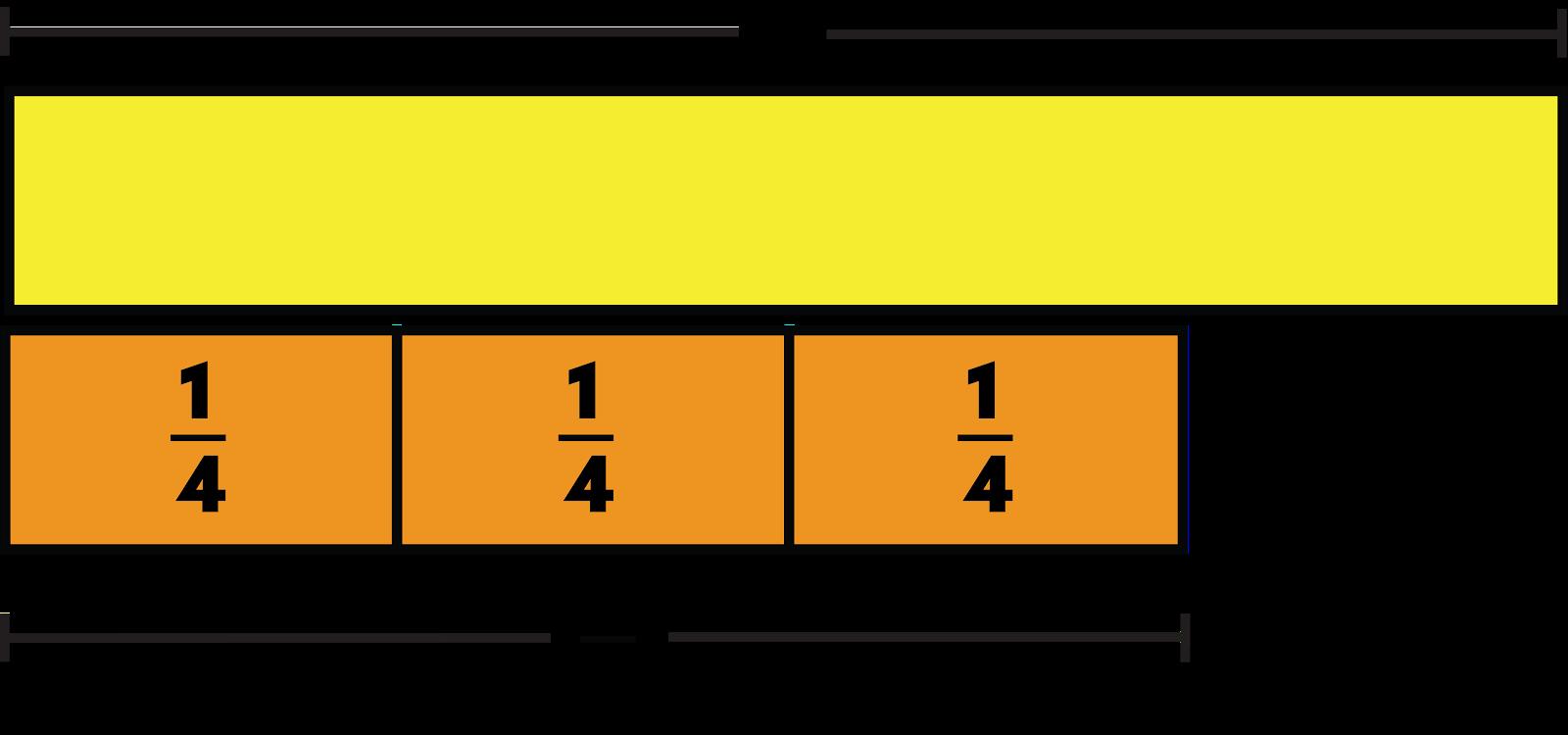
Ejemplo de razonamiento B: Este modelo de fracción muestra que el producto de 5 y 3/4 es menor que 5.

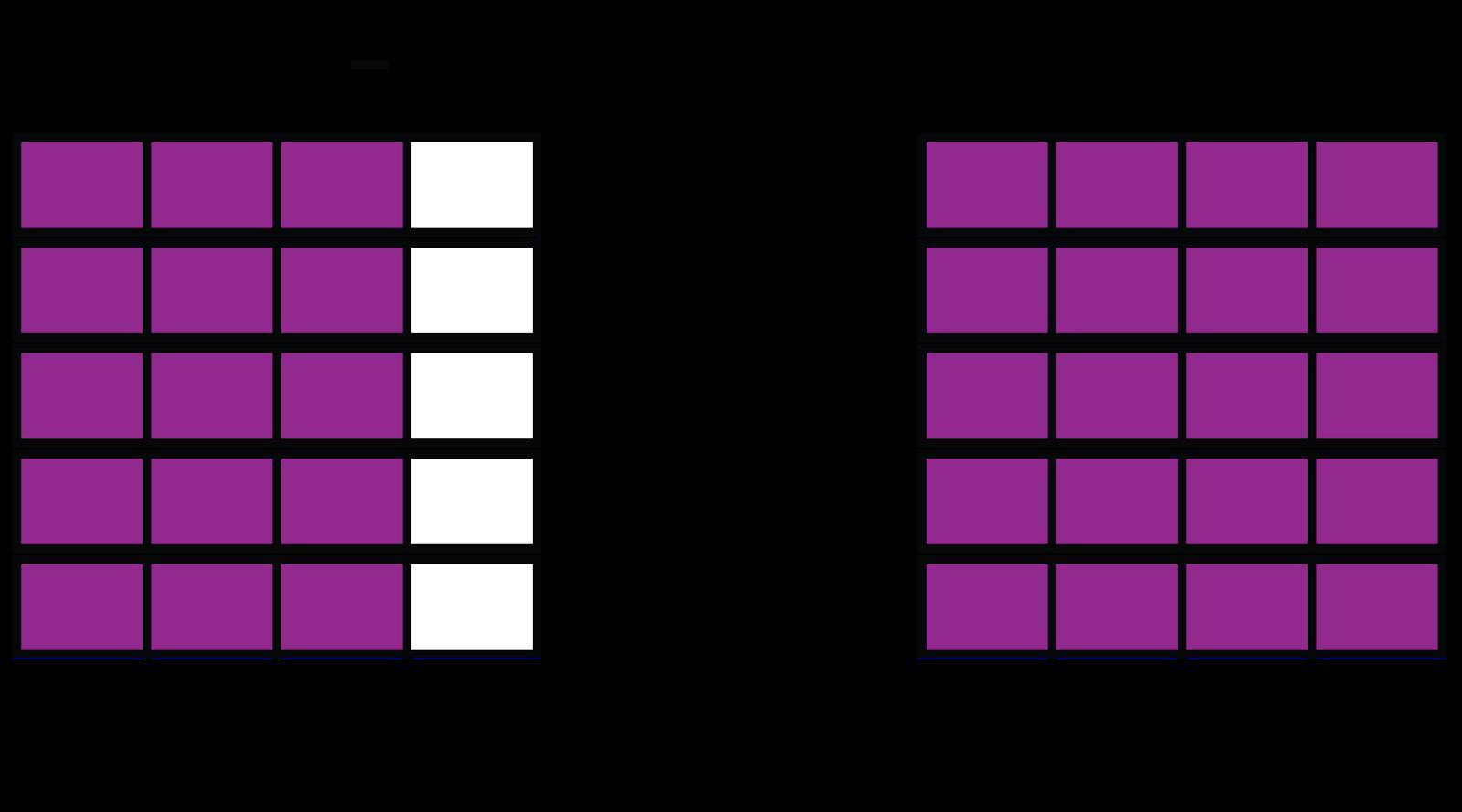
Ejemplo: ¿Cuál de las siguientes afirmaciones es cierta?

a 5/4 × 2 es mayor que 2.

b 5/4 × 2 es menor que 2.

c 3/4 × 2 es menor que 2.

d 4/4 × 2 es igual a 2.

Las respuestas correctas son a, c, y d.

• a es cierto porque dos grupos de cinco cuartos nos dan un total de 10 cuartos. Simplificado, diez cuartos es 2 2/4 ó 2 1/2, que es mayor que 2.

• c es verdadero porque dos grupos de tres cuartos dan un total de 6 cuartos. Simplificado, 2/4 ó 1 1/2 , que es mayor que 2.

• d es cierto porque 4/4 equivale al entero. Si hay dos 4/4s, eso es equivalente a tener 2 enteros.

AVANCES

En grados posteriores, las fracciones se consideran números racionales. En sexto grado, los estudiantes usan la recta numérica para dar sentido al orden, magnitud y valor absoluto de los números racionales. Los estudiantes resuelven problemas que implican la división de fracciones y números mixtos. En sexto grado, adquieren fluidez con procedimientos más abstractos para la división y explican por qué funcionan los algoritmos de división de fracciones. En séptimo grado, los estudiantes amplían la notación de fracciones para incluir los números racionales negativos. En sexto y séptimo grado, los estudiantes usan su comprensión de las fracciones para razonar sobre las razones. Los estudiantes de sexto analizan razones, tasas y porcentajes usando tablas de razones equivalentes y grafican pares de razones equivalentes en el plano de coordenadas. Los estudiantes de séptimo grado identifican la constante de proporcionalidad y usan ecuaciones y gráficas para representar y analizar relaciones proporcionales. En octavo grado, los estudiantes usan relaciones proporcionales para resolver problemas de razones y porcentajes de varios pasos. Los estudiantes han utilizado tablas para representar y comparar valores desde cuarto grado, pero en octavo grado se introduce el dominio funciones. Es entonces cuando las funciones se trabajan formalmente como un algoritmo para la pendiente; los estudiantes definen, evalúan y comparan funciones lineales.

ESTÁNDARES

Aplicar y ampliar conocimientos previos de multiplicación y división para multiplicar y dividir fracciones.

• Aplicar y ampliar conocimientos previos de multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpretar el producto (a/b) × q como a partes de a partición de q en b partes iguales; equivalentemente, como el resultado de una secuencia de operaciones a × q ÷ b. Por ejemplo, utilice un modelo visual de fracción para mostrar (2/3) × 4 = 8/3, y cree un contexto de cuento para esta ecuación. Haga lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = ac/bd).

• Interpretar la multiplicación como una escala (cambio de tamaño) mediante:

a. Comparar el tamaño de un producto con el tamaño de un factor a partir del tamaño del otro factor, sin realizar la multiplicación indicada.

b. Explicar por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado (reconociendo la multiplicación por números enteros mayores que 1 como un caso familiar); explicanr por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionar el principio de equivalencia de fracciones a/b = (n×a)/(n×b) con el efecto de multiplicar a/b por 1.

DESGLOSAR EL ESTÁNDAR

VERBOS: ¿QUÉ DEBERÍAN HACER LOS ESTUDIANTES?

• aplicar: utilizar

• ampliar: aumentar el alcance.

• multiplicar: crear un producto haciendo grupos iguales, repitiendo sumas o formando matrices.

• interpretar: explicar; dar o proporcionar significado.

• utilizar: emplear o utilizar para un fin.

• crear: generar o producir algo.

• comparar: determinar semejanzas o diferencias entre dos o más objetos o números.

• particionar: dividir en partes iguales.

• realizar: llevar a cabo una tarea.

• explicar: explicar o aclarar; decir cómo o por qué algo ocurre o funciona de determinada manera.

• reconocer: identificar a partir de un conocimiento o experiencia previos.

• relacionar: establecer una conexión.

INICIO: CONTENIDO DE APOYO

ANÁLISIS PROFUNDO DE LOS ESTÁNDARES

CONTENIDO DESGLOSADO

SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS DEBEN CONOCER LOS ESTUDIANTES?

• comprensión: comprensión

• multiplicación: una forma de crear un producto haciendo grupos iguales, repitiendo la suma o formando conjuntos.

• división: el proceso de repartir o dividir en partes iguales.

• fracción: parte de un grupo de objetos, un número o un entero.

• número entero: valor numérico sin parte decimal ni de fracción.

• producto: el resultado de multiplicar dos o más números juntos.

• parte: parte de algo.

• secuencia: números o formas en un orden determinado.

• operaciones: procesos matemáticos, como la suma, la resta, la multiplicación y la división.

• modelo: una representación

• problema escrito (contexto de la historia): una situación hipotética y una pregunta que requieren conocimientos matemáticos, estrategias y una ecuación que hay que resolver.

• ecuation: una oración matemática que usa números, uno o más símbolos de operación y un signo igual.

• escalar: comparar el tamaño del producto con el tamaño de un factor basado en el otro factor; predecir productos basados en factores.

• factor: un número que se multiplica por otro número para encontrar un producto.

• tamaño: qué tan grande es algo.

• número: palabra o símbolo que se utiliza para indicar una cantidad.

• principio: una idea que explica cómo hacer algo.

• equivalente: tener la misma cantidad o valor.

IMPLICACIONES PARA LA ENSEÑANZA

• En grados anteriores, los estudiantes han multiplicado números enteros por fracciones, específicamente fracciones unitarias. En este grado, multiplican fracciones propias e impropias, así como números mixtos.

• Los estudiantes deben usar modelos de fracciones para ayudar a construir la comprensión conceptual de lo que sucede con las fracciones a medida que se multiplican. Estos pueden incluir modelos pictóricos, tiras de fracciones, rectas numéricas, modelos de área y diagramas de cinta.

• El uso de estos modelos también ayuda a los estudiantes con la comprensión de lo que sucede cuando se multiplica un número entero por una fracción.

◦ Cuando se multiplica un número entero por una fracción mayor que 1, el producto es mayor que el factor del número entero.

◦ Cuando se multiplica un número entero por una fracción menor que 1, el producto es menor que el factor del número entero.

INICIO: CONTENIDO DESGLOSADO

ALINEACIÓN VERTICAL

GRADO

1

2

ESTÁNDAR

Divida círculos y rectángulos en dos y cuatro partes iguales, describa las partes utilizando las palabras mitades, cuartos, y cuartos, y utilice las frases mitad de, cuarto de, y cuarto de. Describa el todo como dos de, o cuatro de las partes. Comprender para estos ejemplos que la descomposición en partes más iguales crea partes más pequeñas.

Partir círculos y rectángulos en dos, tres o cuatro partes iguales, describir las partes utilizando las palabras mitades, tercios, mitad de, un tercio de, etc., y describir el todo como dos mitades, tres tercios, cuatro cuartos. Reconocer que partes iguales de enteros idénticos no tienen por qué tener la misma forma.

3 Interpretar productos de números enteros, por ejemplo, interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos pueda expresarse como 5 × 7

3

4

5

Entender una fracción 1/b como la cantidad formada por 1 parte cuando un todo se divide en b partes iguales; entender una fracción a/b como la cantidad formada por a partes de tamaño 1/b.

Aplicar y ampliar conocimientos previos de multiplicación para multiplicar una fracción por un número entero.

a. Entender una fracción a/b como un múltiplo de 1/b. Por ejemplo, utilice un modelo de fracción visual para representar 5/4 como el producto 5 × (1/4), registrando la conclusión mediante la ecuación 5/4 = 5 × (1/4).

b. Comprender un múltiplo de a/b como un múltiplo de 1/b, y usar esta comprensión para multiplicar una fracción por un número entero. Por ejemplo, utilizar un modelo visual de fracciones para expresar 3 × (2/5) como 6 × (1/5), reconociendo este producto como 6/5. (En general, n × (a/b) = (n × a)/b).

c. Resolver problemas escritos que impliquen la multiplicación de una fracción por un número entero; por ej., con modelos visuales de fracciones y ecuaciones para representar el problema. Por ejemplo, si cada persona en una fiesta comerá 3/8 de libra de carne asada, y habrá 5 personas en la fiesta, ¿cuántas libras de carne asada se necesitarán? ¿Entre qué dos números enteros se encuentra tu respuesta?

Aplicar y ampliar los conocimientos previos sobre la multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpretar el producto (a/b) × q como a partes de una partición de q en b partes iguales; de manera equivalente, como el resultado de una secuencia de operaciones: a × q ÷ b. Por ejemplo, utilizar un modelo visual de fracciones para mostrar que (2/3) × 4 = 8/3, y crear un contexto narrativo para esta ecuación. Hacer lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = ac/bd).

Interpretar la multiplicación como una escala (cambio de tamaño), mediante:

a. Comparar el tamaño de un producto con el tamaño de uno de los factores en función del tamaño del otro factor, sin realizar la multiplicación indicada.

5

b. Explicar por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado (reconociendo la multiplicación por números enteros mayores que 1 como un caso familiar); explicar por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionar el principio de equivalencia de fracciones a/b = (n×a)/(n×b) con el efecto de multiplicar a/b por 1.

Interpretar y calcular cocientes de fracciones, y resolver problemas verbales que involucren la división de fracciones entre fracciones, por ejemplo, utilizando modelos visuales de fracciones y ecuaciones para representar el problema.

6

7

7

Por ejemplo, crear un contexto narrativo para (2/3) ÷ (3/4) y usar un modelo visual de fracciones para mostrar el cociente; usar la relación entre la multiplicación y la división para explicar que (2/3) ÷ (3/4) = 8/9 porque 3/4 de 8/9 es 2/3. (En general, (a/b) ÷ (c/d) = ad/bc.)

¿Cuánta chocolate recibirá cada persona si 3 personas comparten 1/2 libra de chocolate en partes iguales?

¿Cuántas porciones de 3/4 de taza hay en 2/3 de taza de yogur?

¿Cuál es el ancho de una franja rectangular de terreno con una longitud de 3/4 de milla y un área de 1/2 milla cuadrada?

Comprender que la multiplicación se extiende de las fracciones a los números racionales exigiendo que las operaciones sigan satisfaciendo las propiedades de las operaciones, en particular la propiedad distributiva, dando lugar a productos como (-1)(-1) = 1 y las reglas para multiplicar números con signo. Interpretar productos de números racionales describiendo contextos del mundo real.

Resolver problemas de la vida real y matemáticos de varios pasos que involucren números racionales positivos y negativos en cualquier forma (números enteros, fracciones y decimales), utilizando herramientas de manera estratégica. Aplicar las propiedades de las operaciones para calcular con números en cualquier forma; convertir entre formas según sea apropiado; y evaluar la razonabilidad de las respuestas usando el cálculo mental y estrategias de estimación.

Por ejemplo: Si una mujer que gana $25 por hora recibe un aumento del 10%, ganará 1/10 adicional de su salario por hora, es decir, $2.50 más, para un nuevo salario de $27.50.

Si se desea colocar una barra para toallas de 9 3/4 pulgadas de largo en el centro de una puerta que mide 27 1/2 pulgadas de ancho, será necesario colocar la barra aproximadamente a 9 pulgadas de cada borde; esta estimación puede usarse como verificación del cálculo exacto.

8 Realizar operaciones con números expresados en notación científica, incluyendo problemas en los que se utilicen tanto la notación decimal como la científica. Utilizar notación científica y elegir unidades de tamaño apropiado para mediciones de cantidades muy grandes o muy pequeñas (por ejemplo, utilizar milímetros por año para la extensión del fondo marino). Interpretar notación científica que ha sido generada por la tecnología.

HS Utilizar unidades como una forma de entender problemas y para guiar la solución de problemas de varios pasos; elegir e interpretar unidades consistentemente en fórmulas; elegir e interpretar la escala y el origen en gráficos y visualizaciones de datos.

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

GUÍA DE INSTRUCCIÓN ANDAMIADA

La guía de instrucción andamiada se proporciona para que los maestros puedan planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.

Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes.

Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance.

La guía se divide en cuatro rangos de percentiles para cada estándar.

Refuerzo del grado anterior Nivel de grado con apoyos Nivel de grado Ampliación del nivel de grado

Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.

Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.

Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.

Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.

Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:

1 Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.

2 Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.

3 Haga clic en el enlace directo al material elegido para el estudiante.

Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:

1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.

2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.

3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.

4. Haga clic en el enlace directo al material recomendado para el estudiante.

La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.

Área de instrucción: Operaciones y pensamiento algebraico

Todos los estudiantes:

• Captar interés

• Exploración

• Muestra lo que sabes

• Prueba de habilidades

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

Aplicar y ampliar los conocimientos previos sobre la multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpretar el producto (a/b) × q como una parte de una partición de q en b partes iguales; equivalentemente, como el resultado de una secuencia de operaciones a × q

÷ b. Por ejemplo, utilice un modelo visual de fracción para mostrar (2/3) × 4 = 8/3, y cree un contexto de historia para esta ecuación. Haga lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = ac/bd.)

0 %25 % (Nivel de grado anterior con apoyo)

25 %50 % (Nivel de grado con apoyo)

4 - Multiplicar fracciones por números enteros

Intervención en grupos pequeños

Práctica interactiva

• Recarga de robots

Prueba de habilidades

Mis pensamientos de matemáticas

5 - Representar multiplicación de fracciones

Acceso a conocimientos previos

Constructor de fluidez

Intervención en grupos pequeños

• Partes 1-3

5 - Aprendizaje virtual Números y operaciones

• Fracciones de un grupo y modelos de área

5 - Representar multiplicación de fracciones

Vocabulario ilustrado

Libreta interactiva

50 %80 % (Nivel de Grado)

80 % -

100 % (Ampliando el Nivel de Grado)

Mis pensamientos de matemáticas

Práctica interactiva

• Recarga de robots

Constructor de fluidez

• Multiplicar fracciones con modelos y ecuaciones

Ciencia de datos

Conexiones de lenguaje

5 - Representar multiplicación de fracciones

Tarea basada en problemas

Conexiones profesionales

Matemáticas de hoy

Cuento de matemáticas

Crea el tuyo

Tablero de opciones

Interpretar la multiplicación como una escala (cambio de tamaño), mediante:

d. Comparar el tamaño de un producto con el tamaño de un factor a partir del tamaño del otro factor, sin realizar la multiplicación indicada.

e. Explicar por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado. Reconocier la multiplicación por números enteros mayores que 1 como un caso familiar; explicar por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionar el principio de equivalencia de fracciones a/b = (n×a) / (n×b) para efecto de multiplicar a/b por 1.

0 %25 % (Nivel de grado anterior con apoyo)

25 %50 % (Nivel de grado con apoyo)

50 %80 % (Nivel de Grado)

4 - Multiplicar fracciones por números enteros

Intervención en grupos pequeños

Práctica interactiva

• Recarga de robots

Prueba de habilidades

Mis pensamientos de matemáticas

5 - Representar multiplicación de fracciones

Acceso a conocimientos previos

Constructor de fluidez

Intervención en grupos pequeños

• Partes 1-3

5 - Representar multiplicación de fracciones

Vocabulario ilustrado

Libreta interactiva

Mis pensamientos de matemáticas

Práctica interactiva

• Recarga de robots

Ciencia de datos

Conexiones de lenguaje

80 %100 % (Ampliando el Nivel de Grado)

5 - Representar multiplicación de fracciones

Tarea basada en problemas

Conexiones profesionales

Matemáticas de hoy

Cuento de matemáticas

Crea el tuyo

Tablero de opciones

Multiplicación de modelos de fracciones

PREPARACIÓN

• Haga una copia del folleto del estudiante para cada estudiante o grupo.

• También puede mostrar el folleto del estudiante y pedirles que resuelvan usando sus propios diarios.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya o muestre el folleto del estudiante.

2. Pida a los estudiantes que describan la expresión «4 x 1/3».

◦ Cuatro grupos de 1/3, 1/3 de 4 enteros, 1/3 repetidos 4 veces, 4 veces 1 divididos

3. Para la parte 1, los estudiantes utilizarán la cuadrícula para crear un modelo de fracción que represente la expresión. Pida a los estudiantes que compartan su modelo con un miembro del grupo y que describan la solución.

◦ Muestre 4 grupos de un tercio, para un total de 4 tercios. Cuando se reagrupan, 4/3 es equivalente a 1 1/3.

ATRAER: ACCESO A CONOCIMIENTOS PREVIOS

EVALUAR PREVIAMENTE EL CONOCIMIENTO DE LOS ESTUDIANTES

ACCESO A CONOCIMIENTOS PREVIOS

DESCRIPCIÓN

En esta actividad, el estudiante describirá y representará un problema de multiplicación de una fracción unitaria y un número entero. Esta actividad pretende evaluar el dominio del siguiente estándar:

• a. Comprender una fracción a/b como múltiplo de 1/b. Por ejemplo, use un modelo visual de fracción para representar 5/4 como el producto de 5 x (1/4). Registre la conclusión con la ecuación 5/4 = 5 x (1/4).

• b. Entender un múltiplo de a/b como un múltiplo de 1/b, y utilizar esta comprensión para multiplicar una fracción por un número entero. Por ejemplo, use un modelo visual de fracción para expresar 3 × (2/5) como 6 × (1/5), reconociendo este producto como 6/5. (En general, n × (a/b) = (n × a)/b).

MATERIALES

IMPRESOS

• 1 folleto del estudiante (por alumno, por grupo o por clase)

4. Pida a los estudiantes que hablen con su grupo sobre el hecho de que el producto sea más pequeño que el todo. Pregunte a los estudiantes cómo pueden predecir cuándo ocurrirá esto.

◦ Cuando multiplicamos por una fracción propia, el producto es menor que el número entero. Estamos encontrando una parte del número entero; «4 × 1/3» sería menor que 4 porque es menor que el grupo entero.

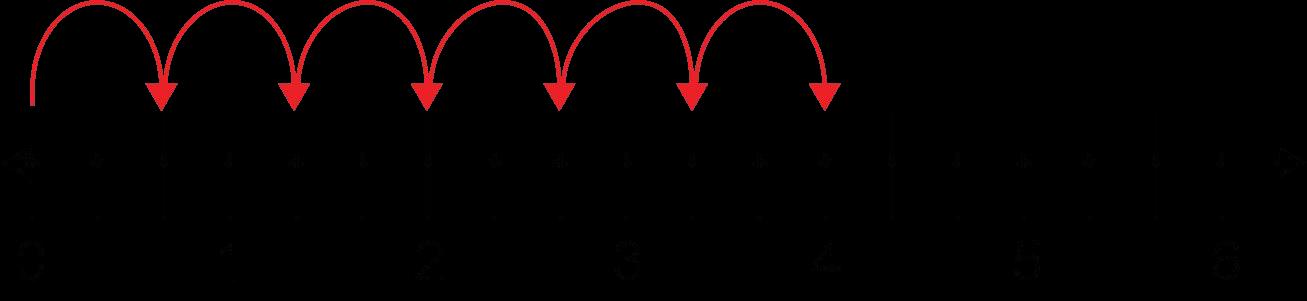
5. Para la parte 2, los estudiantes representarán la expresión en una recta numérica para mostrar entre qué dos números enteros estará el producto. El estudiante mostrará las partes de fracción para los tercios y mostrará 4 saltos de 1/3

6. Si los estudiantes tienen dificultades para completar esta tarea, pase al constructor de bases fundamentales para llenar este vacío de conocimientos previos antes de pasar a otras partes del alcance.

Parte 1: Utiliza la siguiente cuadrícula para delinear y sombrear el modelo

ATRAER: CAPTAR INTERÉS

LECCIÓN PARA CAPTAR INTERÉS

CAPTAR INTERÉS: MULTIPLICAR FRACCIONES (UN PEDAZO DE PASTEL)

DESCRIPCIÓN

Los estudiantes modelan la multiplicación de un número entero por una fracción y razonan sobre el tamaño del producto en relación con los factores.

MATERIALES

IMPRESO

• 1 modelo de pastel (por grupo)

REUTILIZABLE

• 1 fenómeno (por clase)

• 1 pizarra blanca (por estudiante)

• 1 marcador de borrado en seco (por estudiante)

• 1 protector de hojas (por grupo)

PREPARACIÓN

• Planee mostrar los fenómenos.

• Planifique que los estudiantes trabajen en grupos de 3-4 para completar esta actividad.

• Imprima un «modelo de pastel» por grupo y colóquelo en un protector de hojas para crear una superficie que se pueda borrar.

• Reúna una pizarra blanca y un marcador de borrado en seco para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: EXPLORACIÓN PREVIA

1. Presente esta actividad hacia el comienzo del alcance. La clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades explorar correspondientes.

2. Muestre los fenómenos. Formule a los estudiantes las siguientes preguntas: «¿Qué observas? ¿Dónde puedes ver matemáticas en esta situación?». Permita que los estudiantes compartan todas sus ideas.

3. Narre este escenario a la clase: «Escuchas a tus amigos Gabriella y Marcos hablando sobre el postre que Gabriella quiere servir en su fiesta de graduación. Gabriella cree que cada uno de sus 100 invitados comerá aproximadamente 1/10 de su pastel de chocolate favorito de la pastelería que más le gusta. Gabriella y Marcos están de acuerdo en que si ella multiplica el número de invitados por la fracción de pastel que comerán, se hará una idea de cuántas pasteles necesita encargar. Gabriella dice que calcula 10 pasteles, pero que podría pedir un par más para asegurarse de tener suficientes. Marcos no está de acuerdo y dice que serán cientos de pasteles porque cuando multiplicas 100 por cualquier número, el producto será mayor que 100. Marcos y Gabriella te preguntan quién tiene razón. ¿Qué les dices?

Modelo de pastel (Corta en déc mos)

MODELO DE PASTEL

4. Permita que los estudiantes cuestionen y aclaren el contexto según sea necesario. Anímeles a compartir sus ideas y experiencias con la clase usando las siguientes preguntas:

a. ¿Cuál es su tipo de pastel favorito?

b. ¿Ha estado alguna vez en una fiesta en la que se sirva un postre a los invitados?

c. ¿Por qué es importante pedir la cantidad adecuada de comida para una fiesta?

5. Muestre a los estudiantes el modelo de pastel y explíqueles que utilizarán el modelo para ayudar a visualizar la situación. A continuación, haga las siguientes preguntas con la clase:

a. DOK-1 «¿Qué información tenemos?» Tenemos la cantidad estimada de pastel redonda de chocolate (en una fracción) que comerá cada invitado, que es 1/10. Sabemos que habrá aproximadamente 100 invitados.

b. DOK-2 «¿Qué necesitamos averiguar? ¿Podemos reformular la pregunta como un enunciado de solución con un espacio en blanco». El problema pregunta cuántos pasteles tendrá que encargar Gabriella para su fiesta. Gabriella debería encargar ____ pasteles.

c. DOK-2 «¿Qué pasos habrá que dar para resolver el problema?». Necesitaremos usar el modelo y una ecuación para determinar cuántos pasteles necesita comprar Gabriella. Podemos utilizar la pastel dividida para representar los trozos de pastel que se comerá cada persona. Luego explicaremos nuestra solución a Gabriella y a Marcos.

6. Continúa con las actividades de exploración.

PARTE II: DESPUÉS DE LA EXPLORACIÓN

1. Después de que los estudiantes hayan completado las actividades de exploración para este tema, muestre de nuevo los fenómenos y repita el escenario.

2. Haga las siguientes preguntas con la clase:

a. DOK-1 «¿Qué información tenemos?». Tenemos la cantidad estimada de pastel redondo de chocolate (en una fracción) que comerá cada invitado, que es 1/10. Sabemos que habrá aproximadamente 100 invitados.

b. DOK-2 «¿Qué necesitamos averiguar? ¿Podemos reformular la pregunta como un enunciado de solución con un espacio en blanco?». El problema pregunta cuántos pasteles tendrá que encargar Gabriella para su fiesta. Gabriella debería encargar ____ pasteles.

c. DOK-2 «¿Qué pasos habrá que dar para resolver el problema?». Necesitaremos usar el modelo y una ecuación para determinar cuántos pasteles necesita comprar Gabriella. Podemos utilizar la pastel dividida para representar los trozos de pastel que se comerá cada persona. A continuación, explicaremos nuestra solución a Gabriella y Marcos.

3. Coloque a los estudiantes en grupos de 3 ó 4 y entrega un modelo de pastel a cada grupo.

4. Entregue una pizarra y un marcador de borrado en seco a cada estudiante.

5. De a los grupos unos 10 minutos para determinar cuántas pasteles creen que Gabriella debería encargar para su fiesta de graduación.

6. Los estudiantes deben usar el modelo de pastel para ayudar a visualizar la situación.

7. Luego, los estudiantes deben usar sus pizarras blancas para dibujar modelos de fracciones, escribir una ecuación que represente el escenario y resolver.

8. Haga las siguientes preguntas con la clase:

a. DOK-1 «¿Cuál fue la solución al problema?». Las respuestas variarán. La mayoría de los estudiantes dirán 10 pasteles porque 100 × 1/10 = 10. Sin embargo, algunos grupos dirán 11 o 12 pasteles en caso de que algunas personas coman más de un trozo, de modo que tengan sobras para la familia, o en caso de que aparezcan más invitados de lo esperado.

i. Siempre que un grupo obtenga la ecuación correcta, la solución puede variar según la lógica de cada uno. Acepte una variedad de respuestas correctas.

b. DOK-2 «¿Era Gabriella o Marcos más razonable en su estimación del número de pasteles necesarios? Explica». Gabriella fue más razonable. Cada pastel entera puede alimentar a unas 10 personas, por lo que 10 pasteles podrían alimentar a unas 100 personas. La predicción de Marcos de que se necesitarían más de 100 pasteles no es razonable porque hay 100 invitados que comen cada uno menos de 1 pastel entera.

c. DOK-3 «¿Qué ocurre cuando multiplicas un número dado (como 100) por 1? ¿Por qué? Pon un ejemplo relacionado con el postre». El producto del número dado y 1 da como resultado un producto que es igual al número dado. Esto se debe a que el número dado ocurre exactamente 1 todo el tiempo. Los ejemplos variarán. Por ejemplo, 100 × 1 = 100. Si 100 personas comieran 1 galleta cada una, se necesitarían 100 galletas para tener suficientes. Ese número de galletas es igual al número de personas.

d. DOK-3 «¿Qué sucede cuando multiplicas un número dado (como 100) por un número mayor que 1? ¿Por qué? Pon un ejemplo relacionado con el postre». El producto del número dado y el número mayor que 1 resulta en una solución mayor que el número dado. Esto se debe a que el número dado es mayor que 1 todo el tiempo. Esto se puede ver con la propiedad distributiva. Los ejemplos pueden variar. Por ejemplo, 100 × 1 ½ = 150; 100 × 1 = 100 y 100 × ½ = 50, so 100 + 50 = 150. Si 100 personas comieran cada una 1 1/2 de brownies, entonces necesitarías 150 brownies para tener suficientes.

e. DOK-3 ¿Qué ocurre cuando multiplicas un número dado (como 100) por un número menor que 1? ¿Por qué? Pon un ejemplo relacionado con un postre. El producto del número dado y el número menor que 1 da como resultado una solución menor que el número dado. Esto ocurre porque el número dado ocurre menos que 1 entero. La multiplicación por una fracción menor que 1 también se puede considerar como una división porque estás hallando una fracción del número dado. Los ejemplos varían. Por ejemplo: 100 × 1/10 = (100 × 1) / 10 = 100/10 = 100 ÷ 10 = 10. Si 100 personas come 1/10 de pastel cada una, entonces vas a necesitar 10 pasteles para que te alcance.

1. Esta actividad podría ampliarse desafiando a los estudiantes a considerar un número diferente de invitados a la fiesta que comieran cada uno otra cantidad de fracción de pastel. ¿Cuántos pasteles tendría que encargar Gabriella si espera 50 invitados que comerán cada uno 1/8 de un pastel?

EXPLORAR: EXPLORACIÓN 1

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 1: MULTIPLICAR FRACCIONES POR NÚMEROS ENTEROS ENTEROS

Estándar(es)

• Aplicar y ampliar conocimientos previos de multiplicación y división para multiplicar y dividir fracciones. Aplicar y ampliar conocimientos previos de multiplicación para multiplicar una fracción o un número entero por una fracción. Interpretar el producto (a/b) × q como a partes de a partición de q en b partes iguales; equivalentemente, como el resultado de una secuencia de operaciones a × q ÷ b. Por ejemplo, utilice un modelo visual de fracción para mostrar (2/3) × 4 = 8/3, y cree un contexto de cuento para esta ecuación. Haga lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = ac/bd).

• Aplicar y ampliar los entendimientos previos de la multiplicación y la división para multiplicar y dividir fracciones. Interpretar la multiplicación como escalado (ajuste), comparar el tamaño de un producto con el tamaño de uno de los factores, basándose en el tamaño del otro factor, sin realizar la multiplicación indicada.

• Aplicar y ampliar los conocimientos previos sobre multiplicación y división para multiplicar y dividir fracciones. Interpretar la multiplicación como un escalado (ajuste), mediante: explicro por qué al multiplicar un número dado por una fracción mayor que 1 se obtiene un producto mayor que el número dado. Reconocer la multiplicación por números enteros mayores que 1 como un caso familiar; explicar por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionar el principio de equivalencia de fracciones a/b = (n×a/n×b) al effecto de multiplicación a/b por 1.

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.2 Razonar abstracta y cuantitativamente.

MP.3 Construir argumentos viables y criticar el razonamiento de otros.

MP.4 Representar con matemáticas

MP.7 Buscar y hacer uso de la estructura.

MP.8 Buscar y expresar regularidad en razonamientos repetidos.

DESCRIPCIÓN

Los estudiantes modelan la multiplicación de una fracción y un número entero y razonan sobre el tamaño del producto en relación con ambos factores.

CC2 Explorar cantidades cambiantes

CC3 Desmontar el todo, unir las partes

CC4 Descubrir la forma y el espacio

DI1 Dar sentido al mundo (Comprender y explicar)

DI2 Predecir lo que podría ocurrir (Predecir)

DI3 Impactar en el futuro (Afectar)

MATERIALES

IMPRESOS

• 1 diario del estudiante (por estudiante)

• 2 juegos de tarjetas de estación (por clase)

• 1 boleto de salida (por estudiante)

REUTILIZABLES

• 6 cubos o contenedores (por clase)

• 14 juegos de fichas de fracciones (por clase)

• 2 juegos de contadores de dos colores (por clase)

• 2 reglas (por clase)

CONSUMIBLES

• 3 tiras de papel manila, de 3 × 18 pulgadas (por estudiante)

• 2 rollos de cinta adhesiva (por clase)

PREPARACIÓN

• Planee que los estudiantes trabajen en 6 grupos para completar esta actividad.

• Imprima un diario del estudiante y un boleto de salida por alumno.

• Imprima y recorte dos juegos de tarjetas de estación, en cartulina para mayor durabilidad, para la clase.

• Reúna seis cubos o recipientes para crear estaciones.

• Prepare seis estaciones alrededor de la sala: la «Estación 1» tendrá dos recipientes idénticos, la «Estación 2» tendrá dos recipientes idénticos y la «Estación 3» tendrá dos recipientes idénticos.

◦ Cada recipiente de la «Estación 1» debe tener los siguientes materiales:

• Tres juegos de fichas de fracciones

• Tarjeta de la estación 1

◦ Cada recipiente de la «Estación 2» debe tener los siguientes materiales:

• 1 juego de fichas de dos colores (12 o más)

• Tarjeta de estación 2

◦ Cada recipiente de la «Estación 3» debe tener los siguientes materiales:

• Cuatro juegos de fichas de fracciones

• Regla

• Cinta

• 18 tiras de papel nanila

• Tarjeta de estación 3

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen: tiras de fracciones, círculos de fracciones y recta numérica abierta en la sección de «Intervención».

• Digitalízate ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes.(Círculos de fracciones y rectas numéricas).

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Lea el siguiente escenario a la clase: «Hoy, serás el gerente de producción de la empresa de bebidas Fresh Sips. Un jefe de producción tiene bastantes responsabilidades. A medida que avanza por la fábrica, es su responsabilidad asegurarse de que todo funcione correctamente. En la sala 1, también conocida como “Estación 1”, ayudará a los trabajadores del ponche Sassy de fresa y limón a usar los ingredientes adecuados para completar el pedido. En la sala 2, o “Estación 2”, los trabajadores del área de suministros necesitan ayuda para determinar la cantidad de suministros necesarios para el gran pedido de cumpleaños. Por último, en la sala 3, o “Estación 3”, tendrán que resolver algunos problemas que están teniendo los contables con los totales de producción semanales».

2. Ayude a los estudiantes a acceder a la tarea planteándoles las siguientes preguntas orientadoras:

a. ¿Crees que las habilidades matemáticas son importantes a la hora de gestionar un negocio?

b. ¿Cuál es tu bebida favorita?

c. ¿Qué sabes ya sobre la conexión entre la suma y la multiplicación repetidas?

3. Explique a los estudiantes que habrá diferentes modelos en cada estación. En la «Estación 1», los usarán fichas de fracciones. En la «Estación 2», usarán fichas de dos colores. Por último, en la «Estación 3», usarán rectas numéricas.

4. Asigne grupos de estudiantes a su primera estación. Pídales que revisen la ficha de su estación. Haga las siguientes preguntas: (Las respuestas variarán dependiendo de la estación.)

a. DOK-1 ¿Qué información sabes? Sabemos que hay un pedido de 5 galones de ponche, y que cada galón requiereres 2/5 de un galón de jugo de limón.

b. DOK-1 ¿Qué les pide el problema que determinen? Necesitamos determinar la cantidad total de jugo de limón necesaria para el pedido.

c. DOK-2 ¿Qué operación se puede usar para resolver? Podemos multiplicar o usar la suma repetida.

i. Para los grupos de la estación 2, aclare que encontrar una fracción de un grupo también puede resolverse usando la multiplicación, y por lo tanto también la suma repetida.

5. Haga que debatan en grupo cómo pueden representar los escenarios y trabajar juntos dentro de su estación usando los materiales provistos para representar y resolver los problemas. A medida que los estudiantes trabajen, pase de un grupo a otro y ayúdelos según sea necesario. Recuérdeles que dibujen sus modelos y anoten sus ideas en el diario del estudiante de cada estación.

6. Para la «Estación 1», monitoree y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía: (Las respuestas variarán dependiendo del problema.)

a. DOK-1 Háblame de las partes de tu modelo. Usé las fichas de fracciones para representar la fracción en el escenario, y luego repetí esta representación de fracción tantas veces como sea necesario en el escenario.

b. DOK-2 ¿Qué expresión de adición se puede usar para representar este escenario? Podríamos utilizar 2/5 + 2/5 + 2/5 + 2/5 + 2/5 porque había 5 galones de ponche que usaron cada uno 2/5 de un galón de jugo de limón.

c. DOK-2 ¿Qué expresión de multiplicación se puede usar para representar este escenario? Podríamos usar 2/5 × 5 porque había 5 galones de ponche que usaron cada uno 2/5 de un galón de jugo de limón.

d. DOK-1 Explica tu proceso para calcular el total. Calculé el total usando manipulativos de fracciones para representar el escenario, y luego escribí una expresión para representar mi modelo y usé esa expresión para resolver.

e. DOK-2 ¿Cómo se relaciona el modelo con las expresiones de suma y multiplicación? El modelo representa el ingrediente que se repite en partes de fracción y podemos usar esa representación para escribir y resolver una expresión de multiplicación.

f. DOK-2 ¿Cómo usaste tu modelo para determinar la solución? Miré el modelo completado para ver cuántos enteros y cuántas partes adicionales estaban sombreados en total. Luego, escribí eso como un número mixto o una fracción mayor que 1.

7. Para la estación 2, monitoree y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía: (Las respuestas variarán dependiendo del problema.)

a. DOK-1 Cuéntame sobre las partes de tu modelo. Utilicé los contadores para mostrar el número entero. Los organicé en columnas según mi denominador. Por ejemplo, al encontrar 3/4 de 12, organicé 12 fichas en 4 columnas iguales. A continuación, rodeé con un círculo o di la vuelta a 3 de las 4 columnas de fichas para representar la parte de fracción del grupo.

i. Los estudiantes también pueden optar por hacer 4 filas iguales. Permítales descubrir que cualquiera de los dos métodos funciona, y enfatice la flexibilidad de las estrategias resaltando una variedad de representaciones precisas.

b. DOK-2 ¿Notaron una relación entre el número en cada grupo, el número de grupos seleccionados y la solución? Notamos que la solución puede hallarse tomando el total y dividiéndolo por el número de grupos para hallar la cantidad en cada grupo, y luego multiplicando el número de grupos por la cantidad en cada grupo.

Bebidas Sorbos Frescos

Estación 1: Refresco de l món y fresa

Jugo de l món

________ grupos de ________

Modelo: La fábrica necesita __________ galones de jugo de limón para 5 tandas.

Expresión de multiplicación:

Fresas ________ grupos de ________

Modelo:

La fábrica necesita _______________ libras de fresas para el martes.

Expresión de multiplicación:

Estac ón 2 Orden para el gran cumpleaños

Popotes para el refresco de uva ________ de los ________

Modelo:

Model Fraction Multiplication Explore 1

Sorbos Frescos tiene __________ cajas de popotes para los envases de refresco Uva Divertida.

Expresión de multiplicación:

Ga ones de galones ________ de los ________

Modelo: La fábrica tiene recipientes de __________ galones para el refresco Kiwi Loco.

Expresión de multiplicación:

DIARIO DEL ESTUDIANTE

Estación 3 Producc ón de Sorbos Frescos V ruta de emba aje ________ de los ________

Modelo:

Sorbos Frescos usa _____________ libras de viruta de embalaje para envíos.

Expresión de multiplicación: Sand a Loca ________ grupos de ________

Modelo:

El refresco Sandía Loca usa __________ galones de sandía fresca.

Expresión de multiplicación:

Reflex ona

1. ¿Qué conexiones hiciste durante esta actividad?

2. ¿Por qué el producto no siempre es mayor que los factores?

3. ¿Por qué el producto es mayor que el factor de la fracción?

4. Explica por qué el denominador no cambió.

EXPLORAR: EXPLORACIÓN 1

c. DOK-3 ¿En qué parte de este proceso puedes encontrar representada cada una de las cuatro operaciones? En el escenario de las pajitas, vemos la suma porque podemos contar la cantidad en cada grupo para determinar el número de cajas que tiene el factor (3 + 3 + 3), o podríamos usar la multiplicación para determinar el total (3 × 3). Vemos la división porque el modelo tiene 12 divididos en grupos de igual tamaño (12 ÷ 4). Vemos la resta porque podemos restar la cantidad que no está marcada con un círculo para determinar la cantidad de cajas de pajitas que tiene la fábrica (12 - 3).

8. Para la «Estación 3», supervise y hable con los estudiantes según sea necesario para comprobar la comprensión utilizando las siguientes preguntas orientadoras: (Las respuestas variarán dependiendo del problema.)

a. DOK-1 ¿Cómo puedes establecer una recta numérica utilizando los materiales proporcionados? Podemos unir las tiras con cinta adhesiva y utilizar una regla para dibujar una línea recta en el centro de cada tira.

i. Pida a los estudiantes que utilicen tres tiras de papel manila cada una y las unan con cinta adhesiva por los extremos cortos para formar una tira más larga.

ii. A continuación, pida a los estudiantes que utilicen la regla para dibujar una recta numérica sin etiquetar en el centro de la tira, a lo largo de toda ella.

b. DOK-2 ¿Cómo puedes representar un entero utilizando una recta numérica? Puede utilizar una de las fichas de fracción entera.

Fraction Multiplication Explore 1 DIARIO DEL ESTUDIANTE

i. Pida a los estudiantes que coloquen una marca cerca del lado izquierdo de la recta para el 0.

ii. Pídales que utilicen la ficha de fracción entera para marcar los intervalos de números enteros en la recta colocando la ficha de 1 entero debajo de la recta numérica, empezando en el 0 y utilizando el otro extremo para marcar el 1.

c. DOK-1 ¿Cómo puedes usar las fichas de fracciones para marcar la recta numérica? Puedes poner la ficha debajo de la recta numérica, colocando el extremo izquierdo en 0. El extremo derecho es la ubicación del intervalo entero. Pueden marcarlo en la recta numérica.

i. Pueden mover el extremo izquierdo de la ficha de fracción entera a 1 y marcar 2, etc.

ii. Pida a los estudiantes que continúen hasta que tengan al menos 5 unidades enteras. Utilice las fichas de fracción para marcar las partes de fracción de la recta numérica.

d. DOK-2 ¿Cómo se puede mostrar una cantidad si es menor que un entero? Puedes usar los otros modelos de fichas de fracciones, como las mitades, y poner marcas a lo largo de la recta. O puedes ponerlas a lo largo de la parte superior de la recta numérica.

e. DOK-2 ¿Cómo puedes representar el escenario en la recta numérica? Se puede pensar en el escenario como una multiplicación o una suma repetida. Así que mostraré el salto basado en la cantidad fraccionaria y luego el número de saltos se basará en el número entero.

9. Cuando los estudiantes dibujen un modelo, busque estrategias de reagrupación. El enfoque debe ser que hay grupos repetidos de fracciones. Algunos estudiantes también empezarán a relacionar que en realidad están multiplicando las fracciones. Los estudiantes deben anotar las expresiones utilizadas para hallar el producto.

EXPLORAR: EXPLORACIÓN 1

10. Después de que los grupos hayan completado sus estaciones, haga las siguientes preguntas en clase:

a. DOK-1 ¿Qué notaste acerca de los productos relativos a los números enteros en las expresiones de multiplicación en esta exploración? El producto siempre fue menor que el número entero.

b. DOK-2 ¿Por qué crees que es así? Cuando multiplicamos cualquier número por 1, el producto siempre es ese número porque estamos repitiendo ese número una vez. Cuando multiplicamos cualquier número por un número que es menor que 1, el producto tiene que ser menor que el otro factor porque lo estamos repitiendo menos de una vez. Sólo estamos tomando una parte.

c. DOK-3 ¿Cómo puedes demostrarlo? Cuando construimos un modelo, primero dibujamos el número entero, pero luego sólo sombreamos una parte, no la cantidad completa.

d. DOK-1 ¿Qué notaste acerca de los productos en relación con las fracciones en las expresiones de multiplicación en esta exploración? El producto era mayor que la fracción.

e. DOK-2 ¿Por qué crees que es así? Al multiplicar cualquier número por 1, el producto es igual a ese número. Al multiplicar un número que es mayor que 1, se repite más de una vez, por lo que hay un número mayor de esa cantidad.

f. DOK-3 ¿Cómo puedes probarlo? Crea el modelo de la fracción. Luego repite la fracción la cantidad de veces que indica el número entero. El producto tiene que ser mayor que el factor ya que lo estás repitiendo más de una vez.

g. DOK-2 Antes de empezar a modelizar o multiplicar, ¿qué puedes predecir sobre el producto al multiplicar una fracción y un número entero? El producto será mayor que la fracción pero menor que el número entero.

11. Pídales que trabajen con su grupo para responder las preguntas de reflexión al final del diario del estudiante.

12. Pídales que compartan sus estrategias y anímelos a que se hagan preguntas entre ellos y establezcan conexiones. Anímelos a notar las similitudes y diferencias entre las estrategias usadas para multiplicar números enteros por fracciones.

13. Después de la exploración, invite a la clase a una charla de matemática para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• Elija una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-3 ¿Qué conexiones hiciste durante esta exploración? Las formas en que puedo representar estos problemas son similares a representar otros problemas de multiplicación. Puedo usar la adición repetida o un modelo visual, como una recta numérica.

• DOK-2 ¿Por qué el producto es menor que el factor del número entero? Al multiplicar un número entero por una fracción, la respuesta será menor que el factor del número entero porque sólo estamos tomando una parte. No lo estamos repitiendo una vez. Estamos multiplicando un número entero por una fracción, que es menor que 1.

Multiplicación de modelos de fracciones

Boleto de salida

Lee el siguiente problema. Crea un modelo y una expresión para representar la situación. Luego responde la pregunta.

4 5

La fábrica de bebidas Sorbos Frescos usa de galón de jugo natural de manzana para producir un galón de su sidra Manzanas Deliciosas. Producen 7 galones de sidra por día.

S dra Manzanas De c osas

________ grupos de ________

Modelo:

La fábrica necesita __________ galones de jugo natural de manzana para producir 7 galones de su sidra.

Expresión de multiplicación:

El tamaño del producto es __________________ que el factor de número entero y _________ que la fracción multiplicada porque _________________

BOLETO DE SALIDA

• DOK-2 ¿Por qué el producto es mayor que el factor de la fracción? Cuando multiplicamos la fracción por un número mayor que 1, entonces estamos repitiendo la fracción más de una vez por lo que el producto será mayor que el factor con el que empezamos.

• DOK-3 ¿Serían los contadores de dos colores un modelo útil para representar 2/3 de 20? ¿Por qué sí o por qué no? No funcionaría bien utilizar contadores si el denominador y el número total de elementos no fueran números compatibles. Por ejemplo, si hay 20 elementos y necesitamos encontrar 2/3 de los elementos, no podríamos usar contadores para dividir 20 en 3 grupos iguales porque 3 no es un factor de 20.

• DOK-3 ¿Qué notaste sobre el denominador al multiplicar una fracción y un número entero? Explique. Noté que el denominador no cambió. Creo que esto se debe a que el tamaño de la parte, o fracción, es el mismo en todo el problema. Además, podemos pensar en la multiplicación como una suma repetida, y sé que el denominador no cambia al sumar fracciones. Por ejemplo, al calcular el número total de galones cuando 2/5 de un galón se repite 5 veces, estamos encontrando el número total de quintos. Por lo tanto, la respuesta es 10/5, que equivale a 2 galones enteros.

EXPLORAR: EXPLORACIÓN 1

Multiplicación de modelos de fracciones

Parte 1 Mu tipl car fracc ones por números enteros

● Lee cada escenario con cuidado.

● Crea un modelo para representar la situación.

● Registra la solución (valor total representado).

● Escribe la ecuación de multiplicación que corresponda al modelo que creaste.

● Explica tu razonamiento sobre el valor del producto: ¿es el valor del producto mayor o menor que el valor de los factores y por qué?

Escenario

Margo, la hermana de Sara, invitó a Sara a su fiesta de té. Sara se sirvió a ella, a Marga y al oso de peluche de Margo de taza de té. ¿Cuántas tazas de té sirvió Sara en total?

Modelo

Solución:

Ecuación de multiplicación Valor del producto

Escenario

Jeremy tuvo una fiesta de cumpleaños con sus 3 mejores amigos. Cada uno de sus amigos tenía diferentes restricciones de alimentación, por lo que su mamá pidió para cada niño una pizza individual. Cada pizza era del mismo tamaño y fue cortada en 8 porciones iguales. Cada niño comió 3 porciones. Si fueras a combinar las porciones que comieron los 4 niños, ¿cuántas pizzas habrían comido entre todos?

Modelo

Solución: _____________________________

Ecuación de multiplicación Valor del producto

Escenario

Sam tenía 12 canicas. Accidentalmente, tiró de ellas por una grieta cerca del ascensor de la oficina de su madre. ¿Cuántas canicas perdió Sam?

Modelo

Solución: _____________________________

Ecuación de multiplicación Valor del producto

DESPUÉS DE LA EXPLORACIÓN

1. Pida a los estudiantes que completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completen el esquema de anclaje como clase.

3. Pida a cada estudiante que complete su libreta interactiva.

APOYOS PEDAGÓGICOS

1. Si los estudiantes necesitan apoyo adicional para crear sus modelos, pídales que primero representen la fracción dada en el problema. En el primer problema de la «Estación 1», ¿son capaces de usar fichas de fracciones para representar 1/5? Si no es así, revisa el concepto de fracciones como partes iguales de un todo y el uso de múltiples formas de representar una fracción.

2. Si los estudiantes necesitan apoyo adicional para convertir una fracción impropia en un número mixto, recuérdales que los números mixtos tienen dos componentes: una parte entera y una parte de fracción. Pregúntales cuántas partes enteras hay en su modelo y escríbelo. Pregúntales cuántas partes quedan en su modelo que no sean enteras y escríbelas junto al número entero. Esto también puede relacionarse con la división mostrando que un ejemplo como 25/8 (en la tarjeta de estación 3) significa 25 ÷ 8. Con 25 se pueden hacer tres enteros grupos de 8, por lo que 3 es el número entero y el resto es 1 octavo sobrante: 25/8 = 3 1/8.

3. Si los estudiantes necesitan ayuda para dibujar los modelos en sus Diarios del estudiante, considere la posibilidad de proporcionarles Papel cuadriculado, que está disponible como elemento de Ayudas complementarias en la sección Intervención. Los estudiantes pueden dibujar sus enteros, dividirlos y sombrear las partes de fracción más fácilmente utilizando las líneas del papel cuadriculado.

4. Si necesitan apoyo adicional para comprender por qué el denominador no cambia, recuérdeles que al sumar fracciones, el denominador permanece igual. Ayúdeles a comprender esta idea explicando cómo la multiplicación de una fracción por un número entero puede representarse con la suma repetida. El denominador te dice el tamaño de las piezas, y eso no cambia cuando multiplican una fracción por un número entero; sólo tienen más piezas.

5. Algunos estudiantes pueden preferir representar los problemas usando la suma repetida, y otros pueden preferir usar rectas numéricas. Permítales utilizar su método preferido para todos los problemas.

6. Haga hincapié en que el objetivo de la Exploración no es obtener la respuesta de inmediato. Se trata de desafiar a sus cerebros para que crezcan y aprendan algo nuevo.

7. Como extensión, pida a los estudiantes que modelen los problemas de la estación de más de una manera y busquen relaciones entre sus modelos.

EXPLORAR: EXPLORACIÓN 1

APOYOS LINGÜÍSTICOS

Antes de la exploración, proporcione ejemplos de lo que significa que algo esté repetido.

Aclare el significado de cualquier palabra no matemática que afecte la comprensión de las tarjetas de estación, como suministros y envíos. Proporcione elementos visuales cuando sea posible para mejorar la comprensión.

Aclare que el denominador indica el número de partes iguales en un todo y puede considerarse como el sustantivo que indica el nombre de las piezas. Utilice la siguiente ilustración: «Así como yo diría “tengo 3 gatos”, cuando dices “tengo 3 cuartos”, estás diciendo de que tienes 3». Pida a los estudiantes que compartan otros ejemplos de sustantivos que podrían seguir a un número en clase de matemáticas, como 3 lados o 5 dígitos.

Ayude a los estudiantes a practicar la pronunciación correcta de los términos clave de este alcance (multiplicación, grupos iguales, expresión, y suma repetida) dividiendo las palabras más largas en sílabas y haciendo que los estudiantes repitan después de usted.

Muestre estructuras de frases para que los estudiantes las utilicen a lo largo de la exploración, como los siguientes ejemplos:

• La multiplicación y la adición repetida son similares porque ________.

• Para modelizar la situación, voy a ________, y luego voy a ________.

• La multiplicación puede utilizarse cuando ________.

• Hay ____ contadores divididos en ____ grupos iguales, con ____ en cada grupo.

• ____ (fracción) de ____ (número entero) es ____.

Después de que los estudiantes respondan a las preguntas de la Reflexión, pídales que compartan sus respuestas con un compañero e intercambien comentarios constructivos. Pueden revisar sus respuestas según sea necesario.

Una vez que hayan completado sus Diarios del estudiante, pídales que hagan una búsqueda del tesoro con sus diarios del estudiante para practicar el nuevo vocabulario. Mencione palabras o números del folleto y pídales que señalen esos elementos tan rápido como puedan. Por ejemplo: «señala un modelo que muestre tercios» o «señala la palabra expresión».

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 2: MULTIPLICAR FRACCIONES POR FRACCIONES

Estándar(es)

• Aplicar y ampliar los entendimientos previos de la multiplicación y la división para multiplicar y dividir fracciones. Aplicar y ampliar los entendimientos previos de la multiplicación para multiplicar una fracción o un número entero por una fracción. Interpretar el producto (a/b) × q como partes de una partición de q en b partes iguales; equivalente a la secuencia de operaciones a × q ÷ b. Por ej., usar un modelo visual de fracciones para mostrar (2/3) × 4 = 8/3, y crear un contexto narrativo para esta ecuación. Hacer lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = ac/bd.)

• Aplicar y ampliar los entendimientos previos de la multiplicación y la división para multiplicar y dividir fracciones. Interpretar la multiplicación como escalado (redimensionamiento), comparando el tamaño de un producto con el tamaño de uno de los factores, basándose en el tamaño del otro factor, sin realizar la multiplicación indicada.

• Aplicar y ampliar los entendimientos previos de la multiplicación y la división para multiplicar y dividir fracciones. Interpretar la multiplicación como escalado (redimensionamiento), explicando por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado (reconociendo que multiplicar por números enteros mayores que 1 es un caso familiar); explicando por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionando el principio de equivalencia de fracciones a/b = (n×a/n×b) con el efecto de multiplicar a/b por 1.

Estándares para la práctica matemática

MP.2 Razonar abstracta y cuantitativamente.

MP.3 Construir argumentos viables y criticar el razonamiento de otros.

MP.4 Representar con matemáticas.

MP.7 Buscar y hacer uso de la estructura.

CC2 Explorar cantidades cambiantes

CC3 Desmontar el todo, unir las partes

CC4 Descubrir la forma y el espacio

DESCRIPCIÓN

Los estudiantes modelan la multiplicación de una fracción por una fracción y razonan sobre el tamaño del producto en relación con ambos factores.

MATERIALES

IMPRESO

• 1 diario del estudiante (por estudiante)

• 2 juegos de «Rutas de senderismo» (por clase)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 1 juego de fichas de fracciones (por grupo)

• 1 regla (por grupo)

• 1 marcador de borrado en seco (por estudiante)

• 1 pizarra blanca (por estudiante, opcional)

CONSUMIBLE

• 2 tiras de frases (por grupo)

DI1 Dar sentido al mundo (Comprender y explicar)

DI2 Predecir lo que podría ocurrir (Predecir)

DI3 Impactar en el futuro (Afectar)

PREPARACIÓN

• Prevea que los estudiantes trabajen en grupos de 2 ó 3 para completar esta actividad.

• Imprima el diario del estudiante y un boleto de salida para cada estudiante.

• Recoja un marcador borrablepara cada estudiante. Los estudiantes pueden utilizar sus pupitres como superficie para el marcador o una pizarra blanca.

• Imprima y recorta 2 grupos de «Rutas de senderismo» Proyecte una lista y coloca las otras tres por la sala para que todos los grupos puedan verlas y consultarlas fácilmente.

• Prepare los siguientes elementos para cada grupo:

◦ 1 juego de fichas de fracciones

◦ 1 regla

◦ 2 tiras de oraciones

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen: tiras de fracciones, recta numérica abierta y papel cuadriculado en la sección de «Intervención».

• Digitalízate ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Tiras de fracciones y recta numérica).

EXPLORAR: EXPLORACIÓN 2

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Ayude a los estudiantes a acceder a la tarea formulando las siguientes preguntas orientadoras:

a. ¿Han hecho alguna vez senderismo o han estado en un sendero?

b. ¿Qué suministros o habilidades se necesitan para tener éxito en un sendero difícil?

c. ¿Qué podrías ver en un sendero o durante una excursión?

2. Lea la siguiente situación a la clase: «Tú y tus amigos quieren ir de excursión por algunos de los senderos locales este verano. Como hay muchos senderos, tu grupo ha decidido recorrer sólo una parte de cada sendero la primera semana. Luego, más adelante en el verano, tu grupo elegirá tu sendero favorito y lo recorrerán en su totalidad».

3. Entregue el diario del estudiante a cada uno. Explíqueles que deben determinar la distancia que recorrieron en cada uno de los cuatro senderos de los escenarios en sus diarios del estudiante.

4. Entregue el juego de fichas de fracciones, una regla y 2 tiras de frases a cada grupo.

5. Anime a los estudiantes a dibujar un modelo para ayudar a resolver la distancia recorrida.

a. Para los escenarios 1 y 3, invite a los estudiantes a crear modelos de área con sus marcadores de borrado en seco en sus escritorios o pizarras blancas. Para los escenarios 2 y 4, invítelos a utilizar sus tiras de frases para crear líneas numéricas. Recuerde a los estudiantes que primero deben representar la longitud del camino dividiéndola en función del denominador y sombreando las secciones en función del numerador. A continuación, dividan la longitud del sendero en secciones más pequeñas en función del denominador de la fracción que el grupo recorrió. Los modelos ayudarán a los estudiantes a determinar el denominador común y la distancia recorrida antes de dibujarla en sus Diarios del estudiante.

b. Además de cada modelo, los grupos desarrollarán una ecuación de multiplicación para cada ruta de senderismo.

c. Pide a los grupos que observen y comparen la distancia total recorrida (producto) con la longitud total del sendero y la fracción que recorrieron. Razonen juntos por qué el producto es mayor o menor que cada factor. Revise las suposiciones previas que los estudiantes pueden haber hecho sobre la multiplicación, como que el producto siempre es mayor que ambos factores, y si esas "reglas" siguen siendo válidas.

Caminatas felices

Modelo:

Ecuación de multiplicación: Distancia recorrida:

Aderezo Fino

El martes, el grupo decidió caminar por el sendero Aderezo Fino. Recorrieron del camino.

Modelo:

Ecuación de multiplicación: Distancia recorrida:

Monte Cisco

El jueves, el grupo caminó por el monte Cisco. Recorrieron del camino.

Modelo:

Ecuación de multiplicación: Distancia recorrida:

Sendero Retorcido

El viernes, el grupo caminó por el sendero Retorcido. Recorrieron del camino.

Modelo:

Ecuación de multiplicación: Distancia recorrida:

DIARIO DEL ESTUDIANTE

Cam no Gal eta Salada

El lunes, el grupo decidió caminar por el camino Galleta Salada. Recorrieron del camino.

1. ¿Qué conexiones hiciste durante esta actividad?

que es así?

3. Explica por qué cambió el denominador en el producto.

6. Si los estudiantes necesitan apoyo adicional para crear modelos de área, utilice las siguientes preguntas orientadoras para trabajar juntos en el primer escenario:

a. DOK-1 ¿Cuál es la longitud total del sendero camino Pretzel? ¿Cómo puedes representar esta cantidad usando un rectángulo dividido? El sendero camino Pretzel tiene 7/9 de milla de longitud. Podemos representar esto dividiendo un rectángulo en 9 secciones y sombreando 7 de ellas.

b. DOK-2 ¿Cuánto camino recorrió el grupo? ¿Cómo puedes representar esta cantidad usando el mismo rectángulo dividido? Caminaron 1/3 del sendero. Podemos representar esto dividiendo el rectángulo en 3 secciones iguales, yendo en la dirección opuesta a la primera fracción, y sombreando 1 sección.

c. DOK-2 ¿Cuál es la distancia total recorrida? ¿Dónde puedes ver la solución en el modelo? La distancia total recorrida es 7/27 de milla. Esto se muestra en el modelo por el área donde las 2 fracciones sombreadas se superponen.

d. DOK-1 ¿Qué ecuación de multiplicación representa este escenario? 1/3 × 7/9 = 7/27

7. Si un grupo necesita apoyo adicional para crear rectas numéricas, entonces haga las siguientes preguntas guía para trabajar juntos en el segundo escenario:

a. DOK-1 ¿Cuál es la longitud total del sendero Salsa delicada? ¿Cómo puedes representar esta cantidad usando una recta numérica? Salsa delicada tiene 1/4 de milla de longitud. Podemos representar esto dividiendo una recta numérica en 4 secciones y sombreando o marcando 1 de ellas.

b. DOK-2 ¿Cuánto camino recorrió el grupo? ¿Cómo puedes representar esto usando la misma recta numérica? Caminaron 5/6 del sendero. Podemos representar esto dividiendo cada cuarto en 6 secciones porque el denominador de la fracción caminada es 6.

c. DOK-2 ¿Qué es 5/6 de 1/4? Explica. 5/6 de 1/4 es 5/24 porque ahora hay 24 secciones en total ya que cada cuarta parte se dividió en 6 partes iguales y estamos tomando 5 de las 6 partes entre 0 y 1/4

d. DOK-2 ¿Cuál es la distancia total recorrida? ¿Dónde puedes ver la solución en el modelo? La distancia total recorrida es 5/24 de milla. Esto se muestra en el modelo por la quinta marca de verificación de un total de 24 secciones entre 0 y 1.

e. DOK-1 ¿Qué ecuación de multiplicación representa este escenario? 5/6 × 1/4 = 5/24

8. Monitorea y habla con los estudiantes según sea necesario para verificar que comprendan la ecuación.

a. DOK-1 ¿Qué observas en la distancia recorrida y en la longitud total del sendero? La distancia recorrida es menor que la longitud del sendero.

b. DOK-2 ¿Por qué? Cuando multiplicamos cualquier número por 1, el producto es siempre ese número porque estamos repitiendo ese número 1 vez. Cuando multiplicamos cualquier número por un número que es menor que 1, el producto tiene que ser menor que el otro factor porque lo estamos repitiendo menos de 1 vez. Sólo estamos tomando una parte. En este caso, recorrimos una parte de un sendero, por lo que recorrimos menos de la longitud total.

c. DOK-3 ¿Cómo puedes probar tu solución? Cuando construimos un modelo, primero dibujamos la fracción que representa la longitud del sendero, pero cuando sombreamos la parte fraccionaria que caminamos, sólo cubrió parte de la sección que ya estaba sombreada.

d. DOK-2 Antes de comenzar a resolver, ¿cómo puedes estimar el producto al multiplicar una fracción por una fracción? El producto será menor que la primera fracción porque estamos resolviendo un trozo de una fracción de milla.

2. ¿Qué observaste sobre el producto al multiplicar una fracción por una fracción? ¿Por qué crees

EXPLORAR: EXPLORACIÓN 2

9. Pídale que compartan sus estrategias y anímales a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para multiplicar fracciones por fracciones.

10. Después de la exploración, invite a la clase a una charla de matemática para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-2 ¿Aprendiste algo nuevo sobre la multiplicación durante esta Exploración? Aprendí que se puede multiplicar una fracción por una fracción usando modelos como las rectas numéricas o los modelos de área. Antes pensaba que la multiplicación siempre daba como resultado un producto mayor que 1 o que ambos factores, pero ahora aprendí que la multiplicación puede dar como resultado un producto menor que ambos factores.

• Elija una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-2 ¿Por qué el producto es menor que la longitud de fracción del sendero? Al multiplicar 2 fracciones que son menores que 1 entero, la respuesta será menor que los factores porque sólo estamos tomando una parte de cada uno. No estamos repitiendo el primer factor 1 vez; lo estamos repitiendo menos de 1 entero. Al multiplicar una fracción por otra fracción, cada parte de fracción se corta en trozos fraccionarios más pequeños. En este caso, caminamos una porción de un sendero, así que caminamos menos de la longitud total.

• DOK- 2 Sin usar ningún número, ¿qué pregunta podría hacerle a un compañero de clase para determinar si entiende cómo multiplicar fracciones? Podría preguntar: "Cuando multiplicas fracciones, ¿cómo se compara el producto con los 2 factores?" o "¿Cómo puedes representar un problema de multiplicación de fracciones?"

• DOK-2 ¿Por qué cambia el denominador cuando se multiplica una fracción por una fracción? Estamos separando la fracción original en grupos más iguales de partes de fracción. Debido a que el denominador nos dice cuántas partes se necesitan para hacer 1 entero, el denominador cambiará porque estamos cambiando las partes de fracción en pedazos más pequeños.

DESPUÉS DE LA EXPLORACIÓN

1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completen un esquema de anclaje como clase.

3. Haga que cada estudiante complete su libreta interactiva.

Sendero del Lago Cristal

Boleto de salida

El sábado, el grupo decidió ir a caminar por el sendero del Lago Cristal. El sendero tenía de milla de largo. Tu grupo recorrió del sendero.

3 2 3

● Dibuja un modelo para mostrar la distancia que recorrió tu grupo.

● Escribe una ecuación de multiplicación y la distancia recorrida.

● Escribe el razonamiento para el tamaño del producto.

Ecuación de multiplicación: _______________________________

Distancia recorrida: _______________________________

Explica la distancia recorrida en comparación con la distancia del sendero. Explica tu razonamiento.

BOLETO DE SALIDA

APOYOS PEDAGÓGICOS

1. Antes de esta exploración, puede ser útil repasar la multiplicación de un número entero por una fracción y de una fracción por un número entero.

2. Si los estudiantes necesitan apoyo adicional para crear un modelo de recta numérica, proporcióneles rectas numéricas previamente marcadas con incrementos a escala y números de referencia. Guíe a los estudiantes haciéndoles las siguientes preguntas «¿Cuál es el rango de valores para esta recta numérica? ¿Qué valor es el más pequeño y está situado más a la izquierda? ¿Qué valor es el mayor y está situado más a la derecha? ¿Qué valores fraccionarios debemos mostrar entre cada número entero? ¿Cuántas marcas de graduación debemos dibujar entre cada número entero?».

3. Permita a los estudiantes flexibilidad a la hora de elegir qué tipo de modelo utilizar. Si necesitan ayuda para dibujar los modelos en sus Diarios del estudiante, considere la posibilidad de proporcionarles Papel cuadriculado, que está disponible como elemento de Ayudas complementarias en la sección Intervención. Los estudiantes pueden dibujar sus enteros, dividirlos y sombrear las partes fraccionarias más fácilmente utilizando las líneas del papel cuadriculado.

Multiplicar fracciones

Parte 2: Mu t p icar fracciones por fracciones

● Lee cada escenario con cuidado.

● Crea un modelo para representar la situación.

● Registra la solución (valor total representado).

● Representa tu respuesta con una ecuación.

● Explica tu razonamiento sobre el valor del producto: ¿es el valor del producto mayor o menor que el valor de los factores y por qué?

Escenario

Eugenia le enseñó a su hermana pequeña Juana a andar en bicicleta. Juana lo hizo tan bien que Eugenia le prometió llevarla a andar en bicicleta y a un picnic esa tarde. Planearon andar por de mila al parque, pero a de camino hacia allí, una rueda de Juana se desinfló y su mamá tuvo que ir a buscarlas y poner sus bicicletas en el maletero. ¿Qué tan lejos habían andado?

Modelo

Solución: _________________

Ecuación de multiplicación Valor del producto

Escenario

Julián había estado enfermo durante la celebración del cumpleaños de su mamá, por lo que no pudo comer pastel. Al día siguiente se sentía mejor y su madre le dejó comer un poco de lo que sobró. Julián vio que quedaba del pastel. Comió de lo que quedaba. ¿Qué parte del pastel entero comió Julián?

Modelo

Solución: ________________

Ecuación de multiplicación Valor del producto

¿Por qué cambió el denominador en las soluciones de estos problemas? 1 2 3 8

4. Los estudiantes pueden beneficiarse de una explicación adicional sobre por qué la multiplicación de dos fracciones propias da como resultado una fracción menor que ambos factores. Para explicarlo, hable de la multiplicación de una fracción por un número entero y pida a los estudiantes que revisen qué expresión tiene un valor mayor, 10 × 1 or 10 × 1/2. Para demostrar la respuesta, prepare una recta numérica dividida por mitades del 1 al 10. Si saltas por unos 10 veces, entonces caes en 10, pero si saltas por 1/2 diez veces, entonces caes en 5. Para demostrarlo con más detalle, pide a 10 estudiantes que se pongan de pie. Ahora haga que 1/2 de ellos se sienten. Los estudiantes verán que el número original de estudiantes es la mitad de lo que era. A través de la práctica repetida, ven que multiplicar por una fracción reduce el producto.

5. Como extensión, desafíe a los estudiantes a considerar contextos en el aula en los que puedan ver que una fracción de una fracción da como resultado un producto menor que los factores fraccionarios. Por ejemplo, si te queda por leer 1/2 de tu libro y lees 1/3 de las páginas restantes, entonces ¿qué fracción del libro leíste? Invite a los estudiantes a presentar situaciones similares a la clase.

APOYOS LINGÜÍSTICOS

Aclare el significado de cualquier palabra no matemática que afecte a la comprensión de las situaciones por parte de los estudiantes, como distancia, sendero, camino, y caminata. Proporcione elementos visuales siempre que sea posible para mejorar la comprensión.

Antes de que los estudiantes trabajen en la resolución de un problema, anímeles a dibujar un modelo que represente el escenario. Permítales señalar el modelo y utilizarlo como referencia cuando expliquen su razonamiento a sus grupos. Además, puede permitir que los estudiantes respondan oralmente y utilicen sus Diarios del estudiante como referencia cuando respondan a las preguntas Reflexionar.

Puede ser útil proporcionar una ayuda visual, como un gráfico de anclaje, que muestre las formas numéricas y escritas de fracciones comunes, como un tercio = 1/3. Anima a los estudiantes a utilizar verbos en sus respuestas sobre cada pista durante la charla de matemáticas y mientras interactúan con sus grupos. Ayúdeles a identificar estos verbos en sus respuestas. Cree tallos de oraciones para ayudar a los estudiantes a expresar sus respuestas usando verbos, como los siguientes:

• Noté ____.

• Sé ____.

• Pienso ____.

• Usé ____.

• Dibujé ____.

EXPLORAR: EXPLORACIÓN 3

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 3: RELACIÓN DE ESCALA

Antes de completar esta Exploración, pida a los estudiantes que completen Skill Basics - Compare the Size of Products para que puedan aplicar la habilidad a este concepto.

Estándar(es)

• Aplicar y ampliar los entendimientos previos de la multiplicación y la división para multiplicar y dividir fracciones. Aplicar y ampliar los entendimientos previos de la multiplicación para multiplicar una fracción o un número entero por una fracción. Interpretar el producto (a/b) × q como partes de una partición de q en b partes iguales; equivalente a la secuencia de operaciones a × q ÷ b. Por ejemplo, usar un modelo visual de fracciones para mostrar (2/3) × 4 = 8/3, y crear un contexto narrativo para esta ecuación. Hacer lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = (ac)/(bd).)

• Aplicar y ampliar los entendimientos previos de la multiplicación y la división para multiplicar y dividir fracciones. Interpretar la multiplicación como escalado (ajuste), comparando el tamaño de un producto con el tamaño de uno de los factores, basándose en el tamaño del otro factor, sin realizar la multiplicación indicada.

• Aplicar y ampliar los entendimientos previos de la multiplicación y la división para multiplicar y dividir fracciones. Interpretar la multiplicación como escalado (redimensionamiento), explicando por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado (reconociendo que multiplicar por números enteros mayores que 1 es un caso familiar); explicando por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado; y relacionando el principio de equivalencia de fracciones a/b = (n×a)/(n×b) con el efecto de multiplicar a/b por 1.

Ideas fundamentales Estándares para la práctica matemática Conexiones de contenido Motores de investigación

Estándares para la práctica matemática

MP.2 Razonar abstracta y cuantitativamente.

MP.3 Construir argumentos viables y criticar el razonamiento de otros.

MP.7 Buscar y hacer uso de la estructura.

MP.8 Buscar y expresar regularidad en razonamientos repetidos.

DESCRIPCIÓN

Los estudiantes razonan sobre el tamaño del producto basándose en el cambio de tamaño de uno o ambos factores. Los estudiantes justifican sus razonamientos con dibujos, modelos o manipulativos. Los estudiantes comparan o contrastan sus estrategias con sus compañeros.

MATERIALES

IMPRESO

• 1 diario del estudiante (por alumno)

• 3 juegos de tarjetas de estación (por clase)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 1 juego de bloques de base diez (por estación)

CC2 Explorar cantidades cambiantes

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

DI1 Dar sentido al mundo (Comprender y explicar)

DI2 Predecir lo que podría suceder (Predecir)

DI3 Impactar en el futuro (Afectar)

PREPARACIÓN

• Planifique que los estudiantes trabajen en parejas para completar esta actividad.

• Imprima un diario del estudiante y una hoja de salida por alumno.

• Imprima y recorte tres juegos de tarjetas de estación y colóquelas por la clase. Asigna varias parejas a cada juego de tarjetas. Puede imprimir cada conjunto en cartulinas de diferentes colores.

• Decida en qué estación comenzará cada pareja.

• Prepare cada estación con el juego de bloques de base diez.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen bases de diez y papel cuadriculado disponibles en la sección «Intervención».

• ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Bloques de base diez)

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Lea el siguiente escenario a la clase: Usted y su socio empresarial han invertido en una finca y tienen que planificar dónde irá todo. Los dos tenéis planes e ideas diferentes para la nueva propiedad.

2. Ayude a los estudiantes a acceder a la tarea utilizando las siguientes preguntas orientadoras:

a. ¿Qué es un negocio? ¿Conoces a alguien que tenga un negocio?

b. ¿Qué es un socio comercial?

c. Fuera de la escuela, ¿alguna vez has trabajado con un socio para completar una tarea o resolver un problema?

3. Continúa leyendo el escenario a la clase: Hoy compartirás tus planes con tu socio comercial y compararás cómo quiere usar el espacio cada uno. No están tratando de encontrar las medidas exactas; simplemente están comparando cuál sería ese espacio para uno u otro plan de negocios.

4. Explique que los estudiantes trabajarán con un socio de negocios mientras viajan a las diferentes partes de su granja.

5. Enfatice que no están resolviendo el área; simplemente están comparando planes de negocios para su nueva inversión.

6. Desafíe a las parejas a pensar, revisar y compartir sus pensamientos sobre lo siguiente:

a. DOK-2 ¿Qué pasaría con el área si la longitud de uno de los lados disminuyera? ¿Por qué lo crees? El área disminuiría. La longitud y la anchura de un rectángulo afectan al espacio del área. Si cambiara la longitud de uno de los lados, también lo haría el área.

b. DOK-2 ¿Y si la longitud de uno de los lados aumentara? ¿Por qué lo crees? El área aumentaría. La longitud y el ancho de un rectángulo afectan el espacio del área. Si cambiara la longitud de uno de los lados, también lo haría el área.

c. DOK-2 ¿Cómo sabes que ocurriría esto? ¿Qué entiendes por área? Cuando resolvemos el área, multiplicamos largo × ancho. Si éstas cambian, también lo hace el área. Si hiciera un arreglo, esto significa que el número de columnas y/o filas cambiaría, lo que afectaría el número total de elementos en el arreglo.

d. DOK-2 Si un lado disminuye en una fracción, como 1/2, ¿qué crees que le pasaría al área? ¿Por qué crees eso? El área total también se reduce a la mitad. Esto se debe a que se quita la mitad de la longitud o de la anchura. Si lo comparamos con una matriz, la mitad de los elementos de la matriz se eliminan.

e. DOK-2 ¿Qué pasaría con el área si se redimensionaran ambos lados? ¿Qué crees que pasaría si disminuyera el largo o el ancho a la mitad? El área disminuiría porque ambas dimensiones disminuyeron. Tenemos que multiplicar cómo se redimensionan, 1/2 × 1/2, y eso será cuánto se redimensiona el área total.

7. Explique que en cada área de la granja, las parejas compararán cómo cada socio comercial quiere utilizar el espacio para el propósito determinado.

8. Anime a los estudiantes a razonar individualmente (con un dibujo, modelos o manipulativos) sobre cómo el espacio que utilizarán es diferente y cómo lo saben basándose en la relación de las medidas de cada plano. Pida a los estudiantes que utilicen un tipo de modelo específico si necesitan ayuda para empezar.

9. Anímeles a que muestren su razonamiento de forma diferente en función del escenario y a que anoten su razonamiento en sus Diarios del estudiante. Siga insistiendo en la importancia de disponer de múltiples estrategias entre las que elegir y de aplicarlas cuando sea pertinente.

10. Invite a las parejas a comparar sus estrategias utilizando sus diarios del estudiante.

11. Reta a las parejas a encontrar similitudes y diferencias en las estrategias de los demás y a anotar sus conclusiones en los diarios del estudiante.

12. Supervise a los estudiantes y hable con ellos según sea necesario para comprobar su comprensión utilizando las siguientes preguntas orientadoras:

a. DOK-2 Ambos pensasteis en dibujar un rectángulo escribiendo las medidas. ¿Cuál podría ser otra forma? Uno de nosotros podría hacer un rectángulo pero con bloques de valor posicional y luego quitar algunos de ellos para hacer el otro rectángulo.

b. DOK-2 ¿Cómo se pueden usar los bloques de valor posicional? Por ejemplo, el maíz y los pimientos: hice un rectángulo y utilicé 2 varillas de diez y 2 cubos de unidad para hacer 22. Luego utilicé 1 varilla de diez y 2 cubos de unidad para hacer 22. Luego usé 1 barra de diez y 2 cubos unitarios para hacer 12. Cuando tuve que hacer el siguiente rectángulo, dejé los 22, pero añadí otra barra de diez y 2 cubos unitarios a los 12 que ya tenía para hacer 24. Esto me demostró que, como había duplicado el número de cubos unitarios, había duplicado el número de cubos unitarios. Esto me demostró que como duplicaba el ancho, duplicaría el área.

13. Ayude a los estudiantes a encontrar similitudes y diferencias con las 2 estrategias utilizando las siguientes preguntas guía: (Las respuestas variarán.)

a. DOK-1 ¿Los dos dibujaron lo mismo? No, uno dibujó el primero y el otro dibujó el segundo.

b. DOK-1 ¿Qué permaneció igual en ambas estrategias? El largo o el ancho.

c. DOK-1 ¿Cómo cambiaron las medidas? 1/2, 1/4, 1/3, etc. de la

d. DOK-1 ¿Están de acuerdo con el tamaño del área? Sí.

14. Si observa que los estudiantes multiplican los números, aléjelos de esa estrategia y recuérdeles que esta actividad es sólo para razonar. Explíqueles que lo que buscan no es el producto real, sino la comparación de tamaños. Puede ser beneficioso incluso tapar los números según sea necesario para demostrar cómo razonar sobre el área sin números reales.

15. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para interpretar la multiplicación como escalamiento.

16. Después de la exploración, invite a la clase a una charla de matemática para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-2 ¿Qué habilidades matemáticas previamente aprendidas pudiste aplicar durante esta Exploración? Apliqué mis conocimientos sobre el área de rectángulos y la multiplicación de números enteros y fracciones.

• DOK-2 ¿Era necesario multiplicar para averiguar cómo se vería afectada el área? ¿Por qué? No, porque el razonamiento es siempre el mismo al aumentar o disminuir. El área aumentará o disminuirá según lo que ocurra con uno o ambos lados.

• Elige una rutina de Conversación Estructurada para facilitar la siguiente pregunta:

◦ DOK-3 ¿Cómo determinaste el cambio de tamaño del área de cada espacio? Si el largo o el ancho disminuyeron en 1/2, 1/4, o cualquier fracción, entonces el área también disminuyó en esa misma cantidad. Si era la mitad del tamaño, entonces sabía que tenía que dividir por 2. Si era 1/4 el tamaño, entonces dividía por 4. Si se duplicaba, entonces sabía que tenía que multiplicar por 2. Si ambos lados se redujeron, entonces tenía que multiplicar ambas fracciones juntas para determinar cómo se redujo el área.

Ovejas y aves

Boleto de salida

Yo quería un lugar donde las aves pudieran encontrar refugio, hacer sus nidos, comer y bañarse. Planifiqué un área para casas, comederos y aseo para aves. Mi socio comercial quería un redil rectangular para ovejas que midiera 26 yardas de ancho por 10 yardas de largo. Yo solo necesitaba un espacio rectangular que tuviera la mitad de ancho, pero la misma longitud.

❏ Compara los dos espacios. Halla similitudes y diferencias entre las áreas. ❏ Usa un modelo o imágenes para justificar tu razonamiento.

BOLETO DE SALIDA

• DOK-3 ¿Cuál es una estrategia que usaste para representar cómo se compararían las dos áreas? ¿Cómo sabe que su estrategia fue efectiva y precisa? Las respuestas pueden variar. 1

DESPUÉS DE LA EXPLORACIÓN

1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completen la esquema de anclaje como clase.

3. Haga que cada estudiante complete su libreta interactiva.

4. Regrese a la sección «captar interés» e instruya a los estudiantes a usar sus habilidades recién adquiridas para completar exitosamente la actividad.

APOYOS PEDAGÓGICOS

1. Si los estudiantes necesitan apoyo adicional con escenarios en los que no encuentran respuestas exactas, entonces pídales que cuenten de un momento en sus vidas en el que estimaron una solución. Pídales que compartan sus ejemplos con la clase.

2. Antes de la exploración, puede ser beneficioso hacer algunos ejemplos sencillos en los que se resuelve y ver qué patrones emergen. Puede pedir a los estudiantes que primero determinen el área de un rectángulo de 10 de largo y 5 de ancho. Pídales que predigan qué ocurriría con el área si un rectángulo tuviera la mitad de longitud pero la misma anchura. Pida a los estudiantes que resuelvan y observen lo que observan. Haga algunos ejemplos más con números sencillos y explique que podemos utilizar estos patrones para hacer generalizaciones y predicciones sobre un área sin necesidad de calcular.

¿Cómo se comparan ambos planes de negocios? ¿Cómo lo sabes? Explica las similitudes y diferencias entre tu razonamiento y estrategia y los de tu socio.

se comparan ambos planes de negocios? ¿Cómo lo sabes? Explica las similitudes y diferencias entre tu razonamiento y estrategia y los de tu socio.

Corra vs ch quero

¿Cómo se comparan ambos planes de negocios? ¿Cómo lo sabes?

Explica las similitudes y diferencias entre tu razonamiento y estrategia y los de tu socio.

DIARIO DEL ESTUDIANTE

¿Cómo

Modelo:

EXPLORAR: EXPLORACIÓN 3

3. Si los estudiantes necesitan apoyo adicional para comprender el concepto de comparando áreas, pídales que dibujen un diagrama de cada parte de la granja como ayuda visual para empezar a resolver. Esto resulta especialmente útil en el caso de los animales frente a los cultivos. Para visualizar la relación entre las dos áreas, los estudiantes pueden dibujar el área de los animales y luego trazar líneas que muestren la longitud cortada por la mitad y la anchura cortada por la mitad. Considere la posibilidad de proporcionar Papel cuadriculado, que está disponible como elemento de Ayudas complementarias en la sección de Intervención, para ayudar a dibujar los modelos.

4. Como extensión, pida a los estudiantes que resuelvan problemas similares con fracciones no unitarias.

APOYOS LINGÜÍSTICOS

Tómese el tiempo necesario para desentrañar el contexto de la exploración proporcionando explicaciones adicionales o elementos visuales para conceptos como la agricultura o la creación de un plan de negocios.

Antes de que los estudiantes trabajen en la resolución de un problema, anímelos a dibujar un modelo que represente el escenario. Permítales señalar el modelo y utilizarlo como referencia cuando expliquen sus ideas a sus grupos. Además, puede permitir que los estudiantes respondan oralmente y utilicen sus Diarios del estudiante como referencia cuando respondan a las preguntas de reflexión.

Puede ser útil proporcionar una ayuda visual, como un gráfico de anclaje, que muestre las formas numéricas y escritas de fracciones comunes, como un tercio = 1/3.

Aclare el significado de la palabra redimensionar y del prefijo re-. Pregunte a los estudiantes si conocen otras palabras que empiecen por re- y qué creen que significa.

Para ayudar a los estudiantes a comunicar su trabajo, proporcione las siguientes estructuras de frases:

• El área de ____________ es mayor que _____________ porque

• El área de ____________ es menor que ______________ porque

• El área de ____________ es ___________ del tamaño del área de ____________.

Proporcione las siguientes estructuras de oraciones para las preguntas de conversación matemática y reflexión:

• Una conexión que hice durante esta exploración es ________.

• Determiné el cambio de tamaño por ________.

Multiplicar fracciones

Parte 3: Hacer una escala

● Lee con cuidado cada escenario.

● Crea un modelo para representar la situación.

● Registra tu solución.

● Representa tu respuesta con una ecuación.

● Explica tu razonamiento sobre tu solución.

● Crea un nuevo plan que funcione.

Escenario

La perra de Sara, Diablilla, duerme en el granero por la noche. Cuando Diablilla tuvo cachorros el año pasado, su casita tenía 12 pies de largo y 8 pies de ancho. Ahora sus cachorros han ido a hogares felices. Sara hace un plan para darle a Diablilla una casita que tiene un área que es de pies cuadrados que la actual. Sara dice que hará esto dándole una casita de larga y de ancha. Su hermano le dice que la casita elegida no será del tamaño de la anterior.

¿Quién tiene razón? ¿Sara o su hermano?

Modelo

Solución y razonamiento

Explica tu razonamiento

Ayuda a Sara a crear un nuevo plano para una casita de la mitad del tamaño de la original.

MUESTRA LO QUE SABES (PARTE 3)

EXPLICAR: ESQUEMA DE ANCLAJE

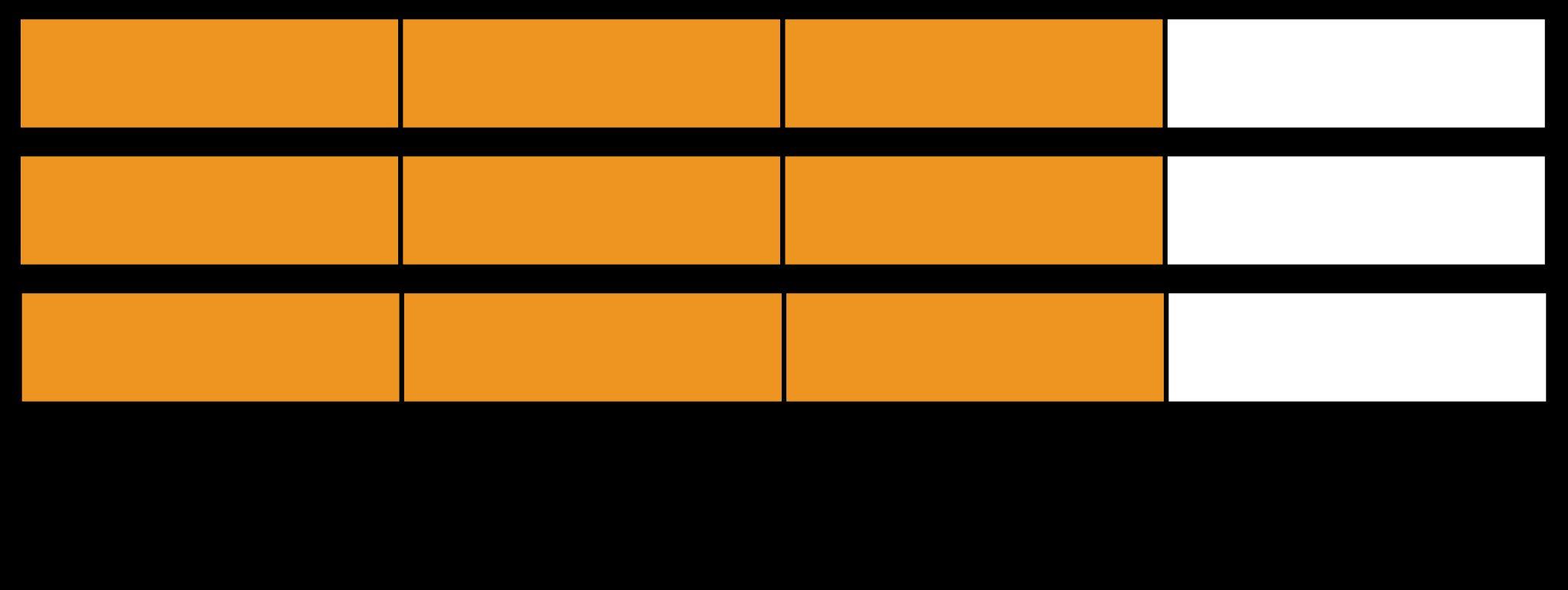
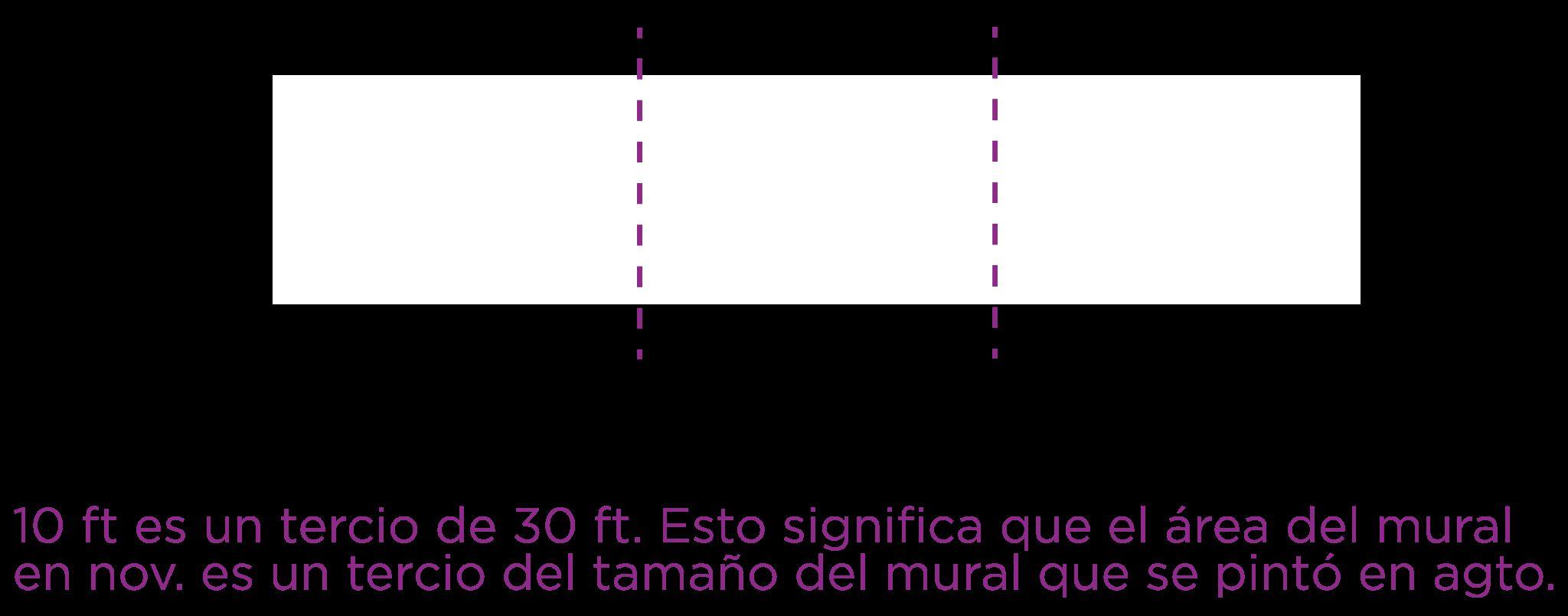
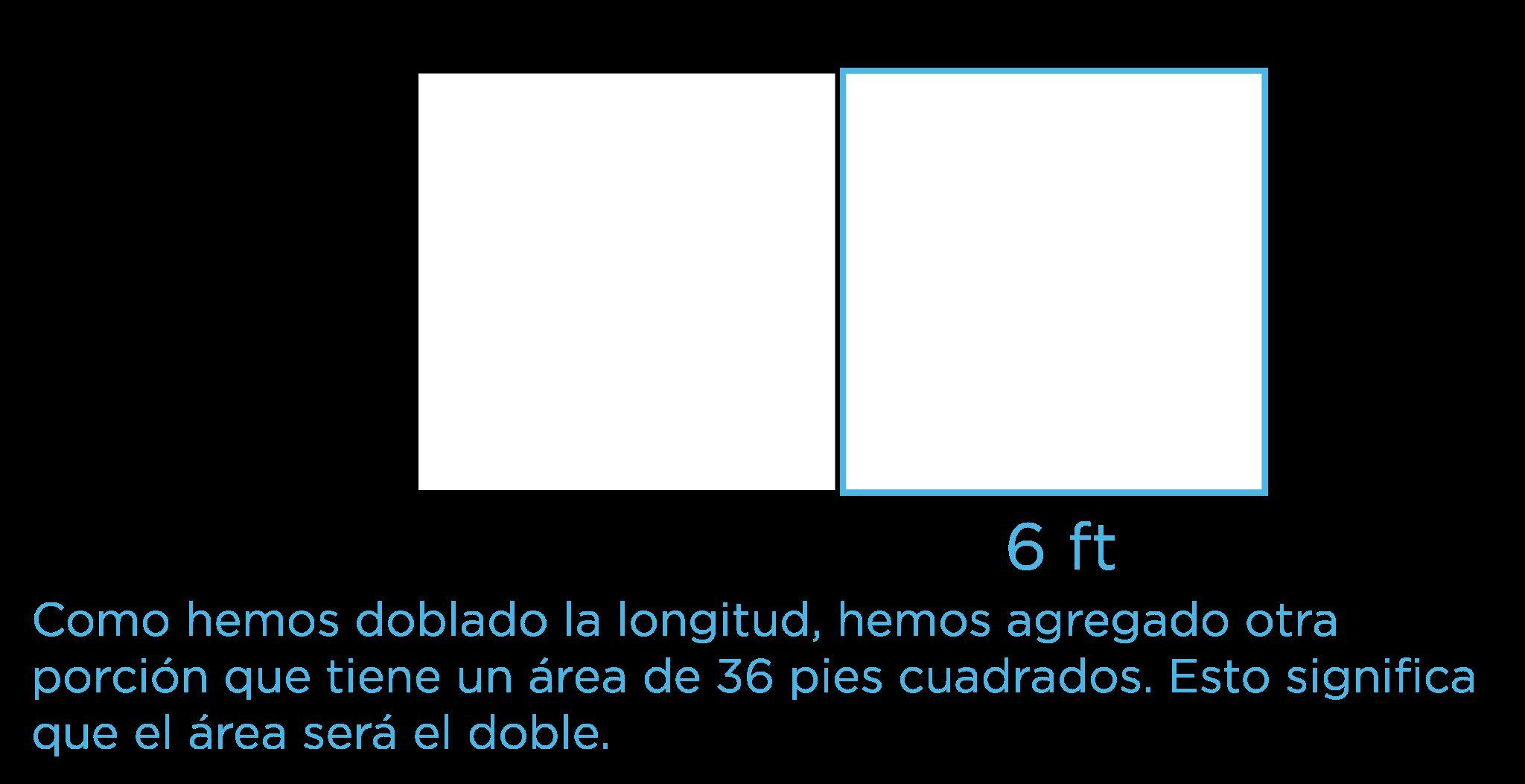
CONSOLIDAR EL APRENDIZAJE DEL ESTUDIANTE

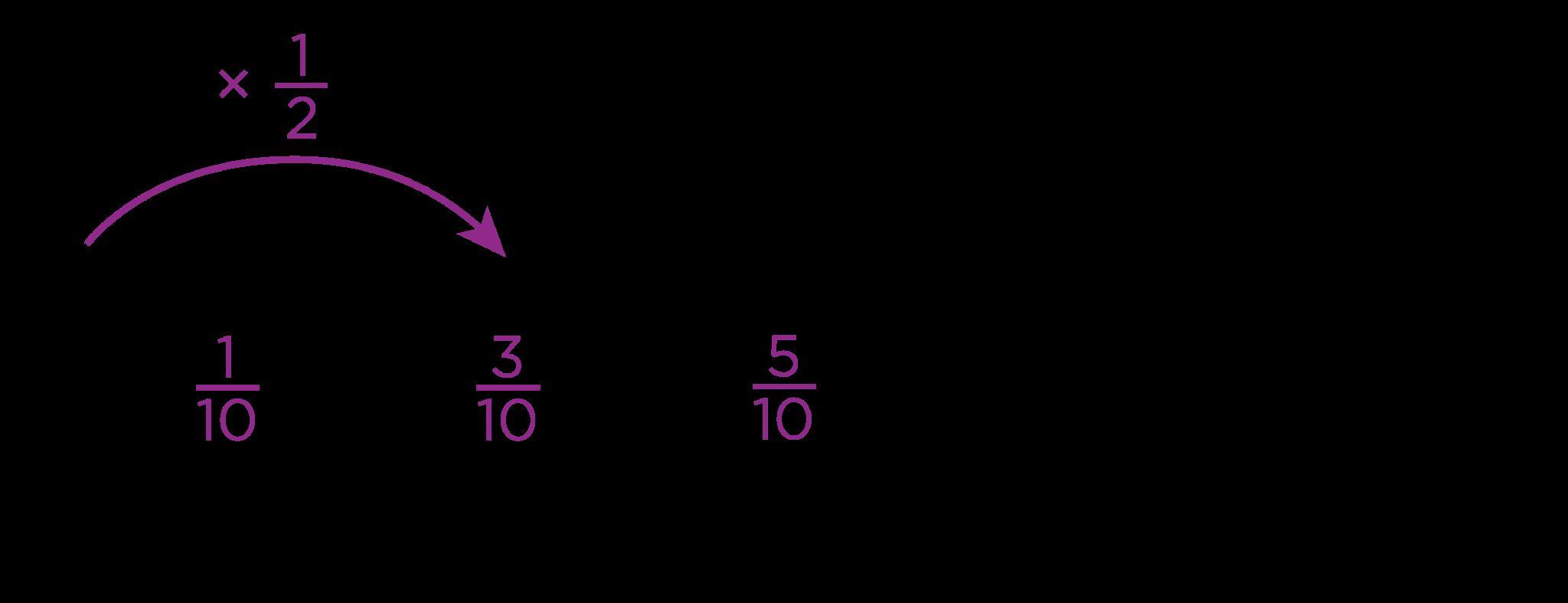
DESCRIPCIÓN

ESQUEMA DE ANCLAJE

Esta esquema de anclaje destaca la resolución de problemas de multiplicación que implican multiplicar fracciones por números enteros, multiplicar fracciones por fracciones y el uso de escalas.

EXPLORACIÓN 1: MULTIPLICAR FRACCIONES POR NÚMEROS ENTEROS

1. Prepare el esquema de anclaje dibujando una tabla de dos columnas y titulando la primera parte como «Fracciones Unitarias × Números Enteros». Escriba una expresión de multiplicación que multiplique una fracción unitaria por un número entero.

2. Después de que los estudiantes completen la exploración, remítalos a la expresión. Dé tiempo a los estudiantes para que piensen en el problema y, a continuación, pregunte lo siguiente:

a. ¿Qué representa cada uno de los factores de esta expresión? El número entero representa el número de grupos (3), y la fracción en este caso representa la cantidad en cada grupo.

3. Pida a los estudiantes que trabajen con un compañero. Proporcióneles pizarras blancas o papel y pídales que creen un modelo para representar este problema. Reúnanse para compartir las representaciones de los estudiantes. Elija una representación para adjuntarla al gráfico de anclaje (ver ejemplo) y a lo siguiente:

a. ¿Qué representa cada entero? 1 entero

b. ¿Cuántas unidades tiene cada entero y por qué? Cada entero tiene 4, porque un entero se divide en cuatro partes iguales.

c. ¿Cuántos cuartos se sombrearon en total? 9/4

d. ¿Es esta fracción mayor que un entero, y cómo lo sabes? Sí, suma 2 y 1/4, porque hacen falta 8 cuartos para tener 2 enteros, y además tenemos 1/4 sombreado.

e. ¿Cómo se relaciona el proceso de multiplicar una fracción por un número entero con la suma repetida? Sumamos 3/4 tres veces: 3/4 + 3/4 + 3/4. Esto es lo mismo que 3/4 × 3.

f. Al multiplicar fracciones, ¿por qué no cambia el denominador? Estás combinando grupos iguales de partes fraccionarias. El denominador te dice cuántas partes se necesitan para hacer un entero, que no cambia porque siempre hay cuatro cuartos en un entero.

EXPLICAR:

EXPLORACIÓN 2: MULTIPLICAR FRACCIONES

POR FRACCIONES

1. Prepare el esquema de anclaje dibujando una tabla de dos columnas y titulando la primera parte como «Multiplicar fracciones por fracciones» y registre una expresión que multiplique una fracción por una fracción (ver ejemplo).

2. Después de que los estudiantes completen la exploración, remítalos a la expresión. Dé tiempo para que piensen en el problema y, a continuación, pregunte lo siguiente:

a. ¿Qué sabemos y qué necesitamos averiguar? Buscamos la mitad de tres quintos.

3. Pida a los estudiantes que trabajen con un compañero. Proporcióneles pizarras blancas o papel y pídales que creen un modelo para representar este problema. Reúnanse para compartir las representaciones de los estudiantes. Destaque las distintas representaciones, como el uso de un modelo de área y/o una recta numérica. Elija una representación para adjuntar a la esquema de anclaje (ver ejemplo) y a lo siguiente:

a. ¿Por qué es útil dividir el todo en 10 partes? Cuando dividimos quintos en mitades, obtenemos décimos porque cada parte igual se divide en dos partes iguales.

b. ¿Por qué el producto es menor que el valor original?

Cuando multiplicamos una fracción por otra fracción, estamos hallando una parte de la fracción original, lo que da como resultado un valor más pequeño.

EXPLORACIÓN 3: RELACIÓN DE ESCALA

1. Prepare el esquema de anclaje con una sección titulada «Escala». Divida esta sección por la mitad. A la izquierda, registre un problema escrito que implique un escenario que reduzca la escala de un área y, a la derecha, registre un problema de palabras que aumente la escala de un área (véa el ejemplo).

2. Después de que los estudiantes completen la exploración, revise los problemas escritos con toda la clase. Pida que trabajen con un compañero. Proporcióneles pizarras blancas o papel y deje tiempo para que los estudiantes creen modelos para representar y resolver cada problema.

3. Comparta el trabajo de los estudiantes con toda la clase y destaque las diferentes estrategias usadas. Anote ejemplos en el esquema de anclaje mientras pregunta lo siguiente:

a. ¿Cómo podemos predecir el tamaño del área sin multiplicar? Podemos comparar el tamaño de los factores.

b. ¿Cuándo la multiplicación da como resultado un producto que es mayor que el número por el que se multiplica? Cuando se multiplica por un factor mayor que uno, el producto es mayor.

c. ¿Cuándo la multiplicación da lugar a un producto menor que el número por el que se multiplica? Cuando se multiplica por un factor menor que uno, el producto es menor.

d. ¿Cómo nos ayuda un modelo de área rectangular o de área a dar sentido a la escala? El área de un rectángulo aumentará o disminuirá en función de lo que ocurra con uno o ambos lados. Si un lado aumenta, el área aumenta. Si uno de los lados disminuye, el área disminuye.

4. Debajo de los modelos, anota el razonamiento de los estudiantes sobre cada uno de los problemas.

5. En la parte inferior de la tabla, escriba dos enunciados que describan lo que ocurre al multiplicar un número dado por un factor mayor que uno y al multiplicar un número dado por un factor menor que uno (ver ejemplo).

USO DE STEMSCOPES MATH

PUNTOS DE REFERENCIA

Desde jardín de infancia hasta álgebra I, STEMscopes Math ofrece potentes evaluaciones de referencia para controlar al principio, a mediados y al final del año. Elaboradas por expertos de STEMscopes Math, estas evaluaciones están diseñadas con el mismo aspecto que los exámenes estatales estandarizados, lo que proporciona a los estudiantes una práctica auténtica y a los maestros la información que necesitan.

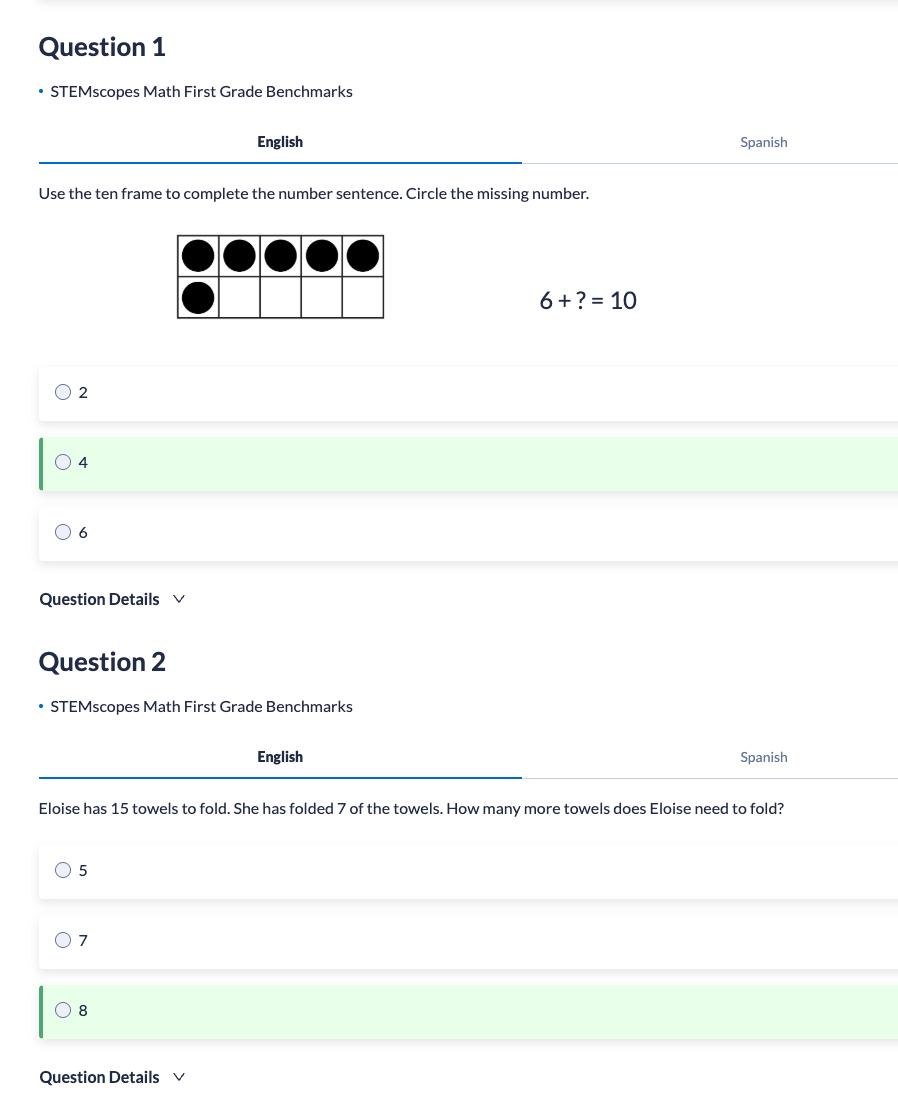
Instrucciones para el maestro:

● Recorte (o pida a los estudiantes que recorten) cada folioscopio.

Asegúrese de recortar las solapas

● Pida a los estudiantes que pongan pegamento en el reverso de la sección gris y que peguen en su cuaderno cada folioscopio.

● Pida a los estudiantes que levanten cada solapa y que resuelvan cada ecuación al usar el modelo indicado en la solapa. 1 3

24 × Multiplicar fracciones por números enteros

Modelo de área 24 ×

Diagrama de cintas

24 × Recta numérica

Modelo de área

Diagrama de cintas

FOLLETO DEL ESTUDIANTE

EXPLICAR: LIBRETA INTERACTIVA

DOCUMENTAR EL APRENDIZAJE DEL ESTUDIANTE

LIBRETA INTERACTIVA

DESCRIPCIÓN

Los estudiantes toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y el cuaderno.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por alumno)

PREPARACIÓN

• Imprime una copia del folleto del estudiante para cada uno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Prepara un libreta interactiva utilizando un cuaderno de espiral o de composición para cada estudiante. Los estudiantes pueden utilizar las primeras páginas para crear un índice con números de página para llevar un registro de las actividades.

2. Recorte previamente o deje que los estudiantes recorten las piezas de cada material para el estudiante según las instrucciones del maestro que aparecen en el recuadro de la primera página.

3. Deje tiempo a los estudiantes para que completen la actividad y luego peguen las piezas en su libreta interactiva.

4. Las libretas interactivas pueden utilizarse como referencia de los estudiantes durante el trabajo independiente y pueden enviarse a casa al final del año como registro de su aprendizaje.

EXPLICAR: CONEXIONES LINGÜÍSTICAS

APOYO PARA ESTUDIANTES MULTILINGÜES

CONEXIONES LINGÜÍSTICAS

DESCRIPCIÓN

Los estudiantes tienen la oportunidad de utilizar sus conocimientos lingüísticos y culturales previos para apoyar las conexiones con nuevas destrezas, vocabulario y conceptos en sus niveles de competencia.

MATERIALES

IMPRESOS

• 1 folleto del estudiante a nivel de competencia (por alumno)

REUTILIZABLES

• 1 juego de fichas de fracciones (por estudiante)

PREPARACIÓN

• Determine el nivel de competencia en inglés de cada estudiante.

• Imprima un folleto del estudiante para cada estudiante según su nivel de inglés.

• Permita que los estudiantes tengan acceso al vocabulatio ilustrado para este alcance.

• Permita que los estudiantes tengan acceso a las fichas de fracciones.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un folleto del estudiante del nivel de inglés apropiado a cada estudiante.

2. Utilice las indicaciones para las partes de comprensión auditiva, expresión oral, lectura y escritura. Utilice gestos, señale objetos y elementos visuales según proceda. Consulte las indicaciones para obtener sugerencias.

3. Conceda tiempo a los estudiantes para que piensen con sus vecinos antes de responder.

4. Anime a los estudiantes a perseverar en su pensamiento y a utilizar herramientas y modelos matemáticos.

5. Invite a los estudiantes a responder adecuadamente a cada dominio lingüístico.

PRINCIPIANTE

Disponga de fichas de fracciones para que los estudiantes las utilicen. Lee las siguientes instrucciones de una en una:

• Escucha mientras leo el siguiente problema:

◦ Aisha está haciendo pasteles para su reunión familiar. Cada pastel necesita 5/6 de una taza de harina. ¿Cuántas tazas de harina necesitará para hacer 4 pasteles?

• Vuelve a leer el problema de la historia pero más despacio, y haz una pausa entre las frases.

• Escribe (escribe con el gesto) el número de pasteles. Escribe la cantidad de harina necesaria para cada pastel. Vuelve a leer el problema de la historia si es necesario.

• Completa los espacios en blanco(lee y señala «____ grupos de ____»).

• Utiliza tus fichas de fracciones(sujeta las fichas) para crear un modelo.

• Dibuja(dibuja con el gesto) tu modelo en tus folletos(señala).

• Asegúrate de rodear con un círculo tu solución en tu modelo.

• Escribe la ecuación de multiplicación que representa tu modelo (señala la sección de ecuaciones).

• Escucha mientras leo el enunciado de la solución. Escribe la respuesta correcta en el espacio en blanco. Lea el enunciado de la solución:

◦ Aisha necesita ___ tazas de harina para hacer 4 pasteles.

PRINCIPIANTE

Lea la historia en grupo, dividiéndola en frases. Pida a los estudiantes que señalen cada palabra mientras leen e invíteles a rodear con un círculo las palabras que no conozcan. Discuta las palabras en grupo.

• Lea la primera pregunta. Señale la respuesta en el cuento antes de contestar. Rodea con un círculo tu respuesta.

• Usa el espacio proporcionado para representar el escenario. (Señala la sección de modelos.)

• ¿Cuántos vestidos tiene Sakura en total? ¿Dónde está representado esto en tu modelo?

• ¿Cuántos de los vestidos de Sakura son verdes? ¿Dónde está representado en tu modelo?

• ¿Cuántos vestidos tiene Sakura que no son verdes? ¿Dónde están representados en tu modelo?

• Lee la última afirmación de la hoja de registro para el estudiante. Rodea con un círculo si la afirmación es verdadera o falsa.

INTERMEDIO

Tenga fichas de fracciones disponibles para que los estudiantes las usen. Lea las siguientes instrucciones de una en una:

• Escuche mientras leo el siguiente problema de la historia:

◦ Aisha está horneando pasteles para su reunión familiar. Cada pastel necesita 5/6 de una taza de harina. ¿Cuántas tazas de harina necesitará para hacer 4 pasteles?

• Vuelve a leer el problema de la historia pero más despacio, y haz una pausa entre las frases.

• Escribe el número de pasteles y la cantidad de harina necesaria para cada pastel en tus hojas.

• Vuelve a leer el problema de la historia si es necesario.

• Completa los espacios en blanco (lee y señala «____ grupos de ____»).

• Usa tus fichas de fracciones para crear un modelo.

• Dibuja tu modelo en tus folletos.

• Asegúrate de encerrar en un círculo tu solución en tu modelo.

• Escribe la ecuación de multiplicación que representa tu modelo (señala la sección de ecuaciones).

• Escucha mientras leo el enunciado de la solución. Escribe la respuesta correcta en el espacio en blanco. Lea el enunciado de la solución:

◦ Aisha necesita ___ tazas de harina para hacer 4 pasteles.

AVANZADO

Tenga fichas de fracciones a mano para que los estudiantes las usen. Lea las siguientes instrucciones de una en una:

• Escuche mientras leo el siguiente problema de la historia:

◦ Aisha está horneando pasteles para su reunión familiar. Cada pastel necesita 5/6 de una taza de harina. ¿Cuántas tazas de harina necesitará para hacer 4 pasteles?

• Escribe el número de pasteles y la cantidad de harina necesaria para cada pastel en tus hojas. Vuelve a leer el problema de la historia si es necesario.

• Completa los espacios en blanco (lee y señala «____ grupos de ____»).

• Usa tus fichas de fracciones para crear un modelo.

• Dibuja tu modelo en tus folletos y encierra tu respuesta en un círculo.

• Escribe la ecuación de multiplicación que representa tu modelo.

• Completa el enunciado de la solución.

INTERMEDIO

Coral: lee la historia en grupo. Haz que los estudiantes señalen cada palabra mientras leen e invítales a rodear con un círculo las palabras que no conozcan. Haz que comenten las palabras con sus compañeros.

• Comparte con tus compañeros dos cosas que sepas sobre el problema de la historia. Señala dónde puedes encontrar esas cosas en el párrafo.

• Modela el escenario. ¿Cómo representa su modelo cada parte del problema?

• Coral: lea las instrucciones y afirmaciones bajo la historia de uno en uno.

• Anime a los estudiantes a consultar la historia con sus compañeros para encontrar las respuestas.

AVANZADO

Haga que los estudiantes lean la historia con sus compañeros. Pídales que señalen cada palabra mientras leen e invíteles a rodear las palabras que no conozcan y a comentarlas con sus compañeros.

• ¿Qué información tienes sobre el problema? Señala dónde puedes encontrarla en el párrafo.

• ¿Qué pide el problema? ¿Cómo lo sabes?

• Modela el escenario. ¿Cómo representa tu modelo cada parte del problema?

• Haz que los estudiantes lean la pregunta y los enunciados con sus compañeros. Anímales a que hagan referencia a la historia.

HABLAR

PRINCIPIANTE

Lea las siguientes preguntas de una en una:

• ¿Cuántos pasteles va a hacer Aisha? Pida a los estudiantes que utilicen el siguiente marco de frases:

◦ Aisha va a hornear ____ pasteles.

• ¿Cuánta harina utilizará Aisha para cada pastel? Pida a los estudiantes que usen el siguiente marco de oraciones:

◦ Aisha usará ______ tazas de harina para cada pastel.

• ¿Cómo creaste un modelo usando tus fichas de fracciones? Pida a los estudiantes que usen el siguiente marco de oraciones:

◦ Hice ____ grupos de ____ usando mis fichas de fracciones.

• ¿Cuánta harina necesita Aisha para hacer los cuatro pasteles? Pida a los estudiantes que usen el siguiente marco de oraciones:

◦ Aisha necesita ____ tazas de harina.

• ¿Qué observas en el producto de un número entero y una fracción? ¿El producto es mayor o menor que un entero? Pida a los estudiantes que usen el siguiente marco de oraciones:

◦ El producto de un número entero y una fracción es ______ un entero.

ESCRIBIR

PRINCIPIANTE

Lee y comenta las palabras del banco de palabras. Defina y proporcione ejemplos según sea necesario.

• Observe la expresión en la parte superior de la página.

• ¿Qué nota acerca de la expresión? Pida a los estudiantes que utilicen la siguiente estructura de frase:

◦ Me doy cuenta de que es multiplicar un _____ por un _____.

• Lea la pregunta del banco de palabras a los estudiantes: Explicar cómo se resuelve.

• Escuchen mientras leo cada frase y elijan la mejor palabra del banco de palabras para ponerla en el espacio en blanco.

• Dé tiempo a los estudiantes para que completen los espacios en blanco y ayúdeles a definir el vocabulario según sea necesario.

INTERMEDIO

Lea las siguientes instrucciones una a la vez:

• Diga a sus compañeros dos cosas que sabe sobre el escenario.

• ¿Cuántos pasteles va a hornear Aisha?

• ¿Cuánta harina usará para hornear cada pastel?

• ¿Cómo creó un modelo usando sus fichas de fracciones? Pida a los estudiantes que utilicen los siguientes enunciados:

◦ Primero, yo...

◦ Después, yo...

• ¿Cuánta harina necesita Aisha para hacer los cuatro pasteles? Pida a los estudiantes que utilicen el siguiente marco de frases:

◦ Aisha necesita ____ tazas de harina.

• ¿Qué observas en el producto de un número entero y una fracción? Pida a los estudiantes que usen el siguiente marco de oraciones:

◦ El producto de un número entero y una fracción es ______ un entero.

AVANZADO

Lea las siguientes instrucciones una a la vez:

• Diga a sus compañeros dos cosas que sabe sobre el escenario.

• ¿Cuántos pasteles va a hornear Aisha?

• ¿Cuánta harina usará para hornear cada pastel?

• ¿Cómo creó un modelo usando sus fichas de fracciones? Pida a los estudiantes que utilicen los siguientes enunciados:

◦ Primero, yo...

◦ Después, yo...

• ¿Cuánta harina necesita Aisha para hacer los cuatro pasteles?

• ¿Qué observas en el producto de un número entero y una fracción?

INTERMEDIO

Lectura coral y pida a los estudiantes que revisen el significado de las palabras con sus compañeros. Defina y proporcione ejemplos según sea necesario.

• Observe la expresión en la parte superior de la página.

• Haga la siguiente pregunta con sus compañeros:

◦ ¿Qué notan acerca de esta expresión?

• Lea a los estudiantes la pregunta debajo del banco de palabras: Explica cómo resolver.

• Trabaja con tus compañeros y utiliza palabras del banco de palabras para ayudarte a completar las frases.

• Deja tiempo para que los estudiantes conversen al respecto.

AVANZADO

Lectura coral o invita a los estudiantes a leer las preguntas bajo la expresión.

• Haz la siguiente pregunta a tus compañeros:

◦ ¿Qué notas sobre esta expresión?

• Responde a cada pregunta con una frase completa.

• Comparte lo que has escrito con tus compañeros. Dígales una cosa que hayan hecho bien y una forma en la que pueden mejorar una de sus respuestas.

• Deje tiempo a los estudiantes para debatir y revisar sus respuestas basándose en los comentarios de sus compañeros.

EXPLICAR: MIS PENSAMIENTOS DE MATEMÁTICAS

Model Fraction Multiplication

Usa un modelo para demostrar cómo se resuelve esta expresión.

MIS PENSAMIENTOS DE MATEMÁTICAS

DESCRIPCIÓN

Los estudiantes tendrán la oportunidad de escribir sus pensamientos e ideas matemáticas utilizando las siguientes tres vías diferentes:

Imagen Tipo

Descripción

De acuerdo con el modelo, ¿cuánto es de ? Explica por qué esta respuesta es razonable.

¿De qué manera te ayuda un modelo visual a entender la multiplicación de una fracción por otra fracción?

Contenido

Proceso

Afectivo

Escritura sobre conceptos y relaciones matemáticas

Escritura centrada en la resolución de problemas, estrategias y procedimientos

Escritura sobre la actitud, experiencia o mentalidad de un estudiante hacia las matemáticas

Fraction Multiplication

Crea un problema escrito que requiera multiplicar una fracción por un número entero en el espacio a continuación.

¿De qué manera te ayuda un modelo visual a entender la multiplicación de una fracción por otra fracción?

FOLLETO DEL ESTUDIANTE

Los iconos de arriba se proporcionan en cada actividad con el fin de darle orientación en cuanto a qué tipo de escritura se utilizará. Los tres tipos se entrelazarán a lo largo del programa para garantizar un enfoque equilibrado de la escritura en matemáticas.

MATERIALES

IMPRESOS

• 1 folleto del estudiante (por estudiante)

REUTILIZABLES

• Acceso a herramientas y modelos matemáticos (por clase)

PREPARACIÓN

• Permita que los estudiantes tengan acceso a una variedad de herramientas matemáticas como bloques de valor posicional y círculos de fracciones, y modelos matemáticos como tablas de valor posicional, muros de fracciones, rectas numéricas, etc.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Permita que los estudiantes planteen sus ideas a un compañero antes de escribir sus pensamientos en papel.

2. Anímelos a perseverar en su pensamiento y a usar herramientas y modelos matemáticos según sea necesario.

3. Invite a los estudiantes a escribir sus respuestas en oraciones completas utilizando ortografía, gramática y puntuación correctas.

EXPLICAR: VOCABULARIO ILUSTRADO

PALABRAS QUE HAY QUE CONOCER

VOCABULARIO ILUSTRADO

Adición

Combinar dos o más números para obtener una suma o total

Comparar

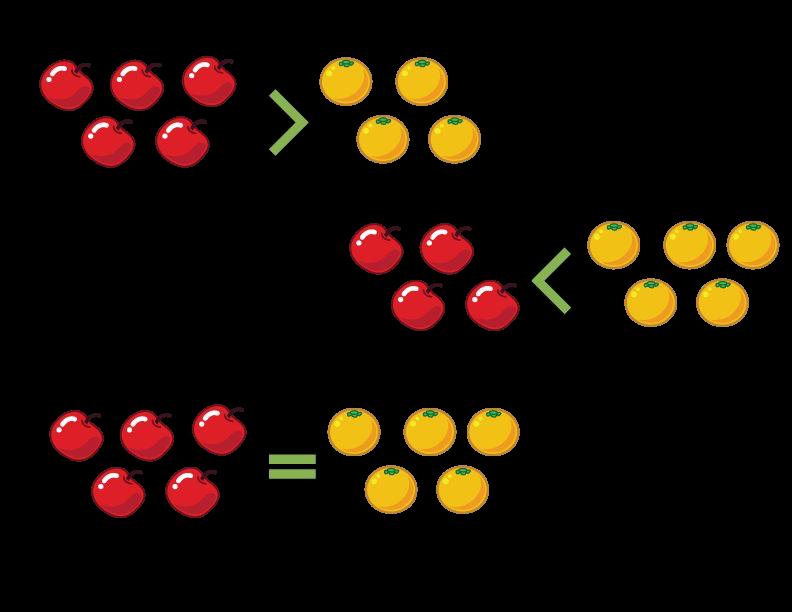
Determinar similitudes o diferencias entre dos o más objetos o números

Grupos iguales

Conjuntos de objetos que tienen la misma cantidad o número, o que tienen el mismo valor

Fracción

Una parte de un grupo de objetos, de un número o de un entero

Área

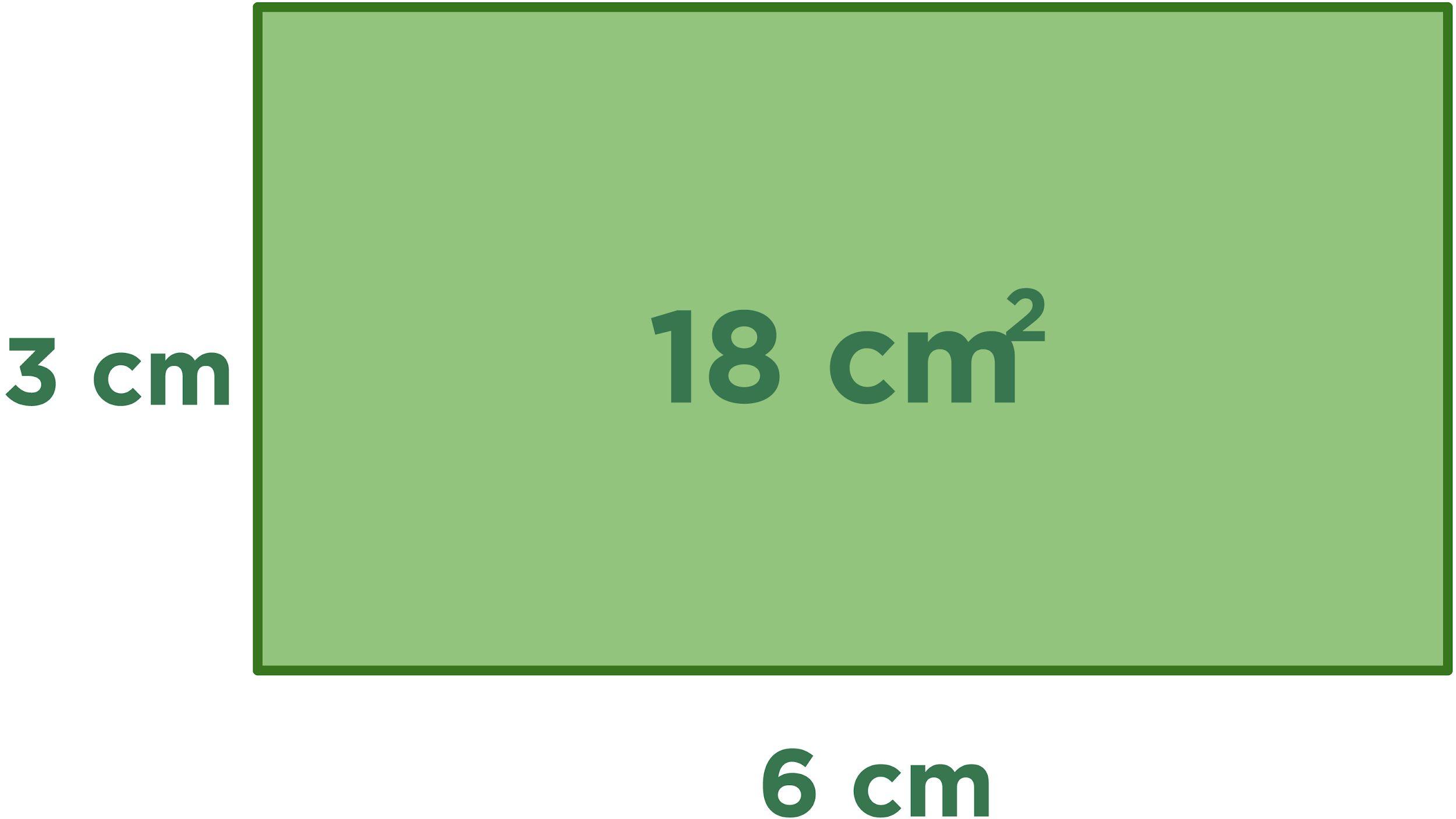
Medida de un espacio dentro de las líneas de límite; medido en unidades cuadradas

Modelo del área

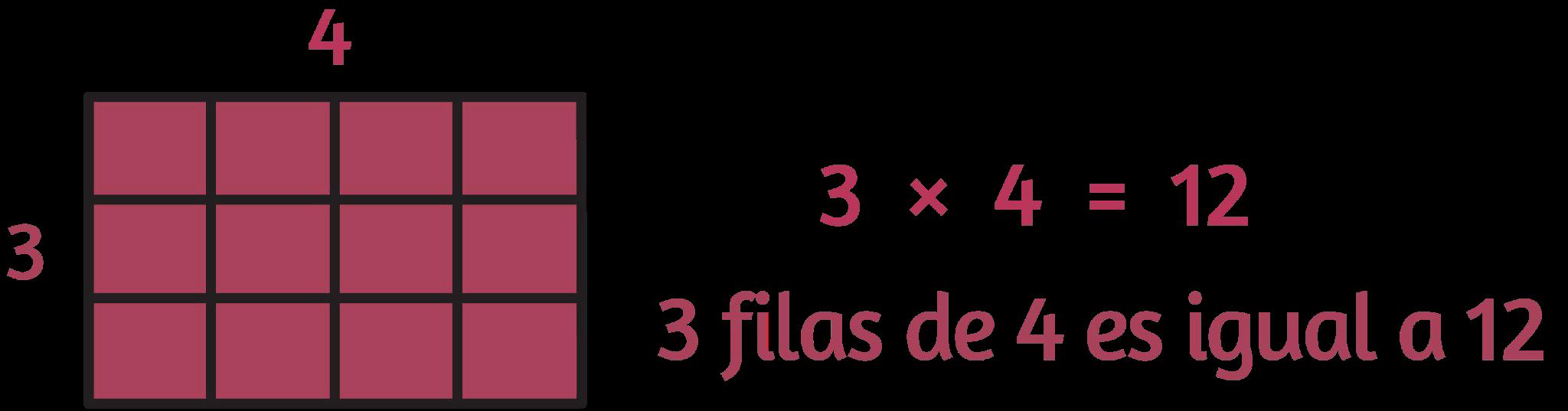
Modelo rectangular de multiplicación o división que representa el área total; los factores, el cociente y el divisor están representados por las longitudes laterales

Denominador

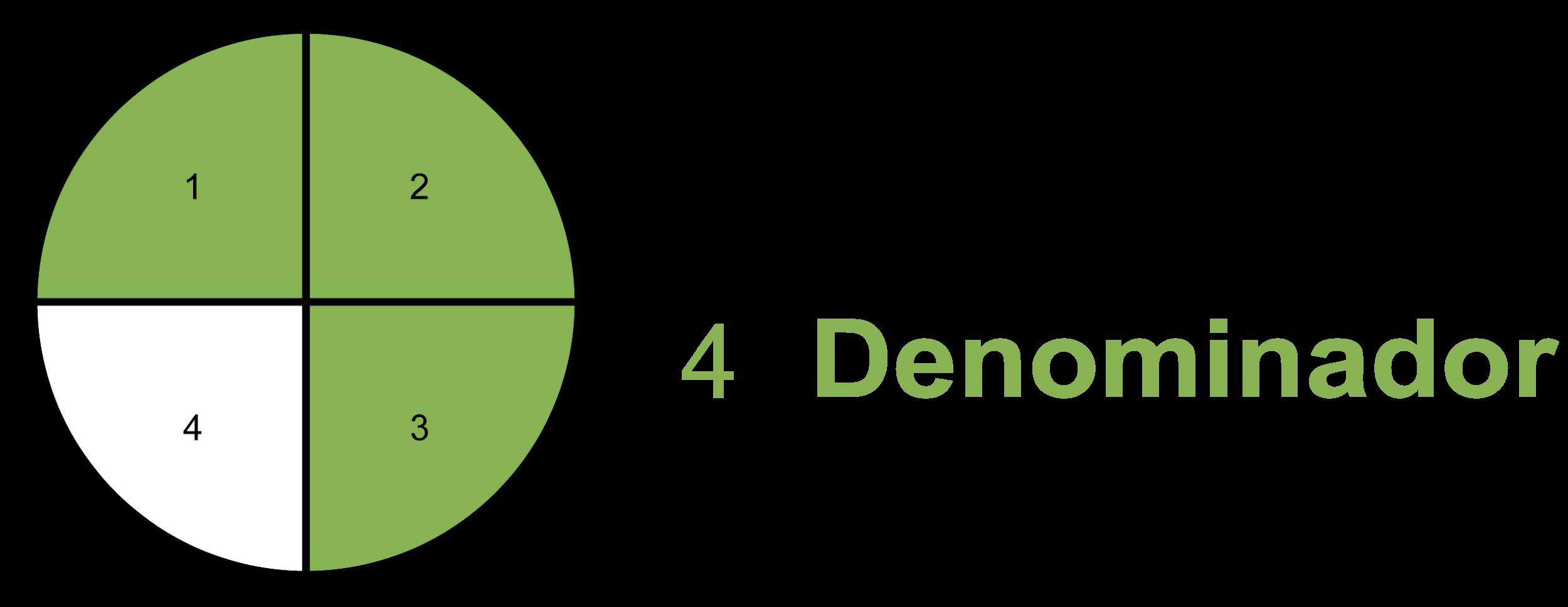
Número inferior de una fracción; representa el número total de partes iguales en un todo

Ecuación

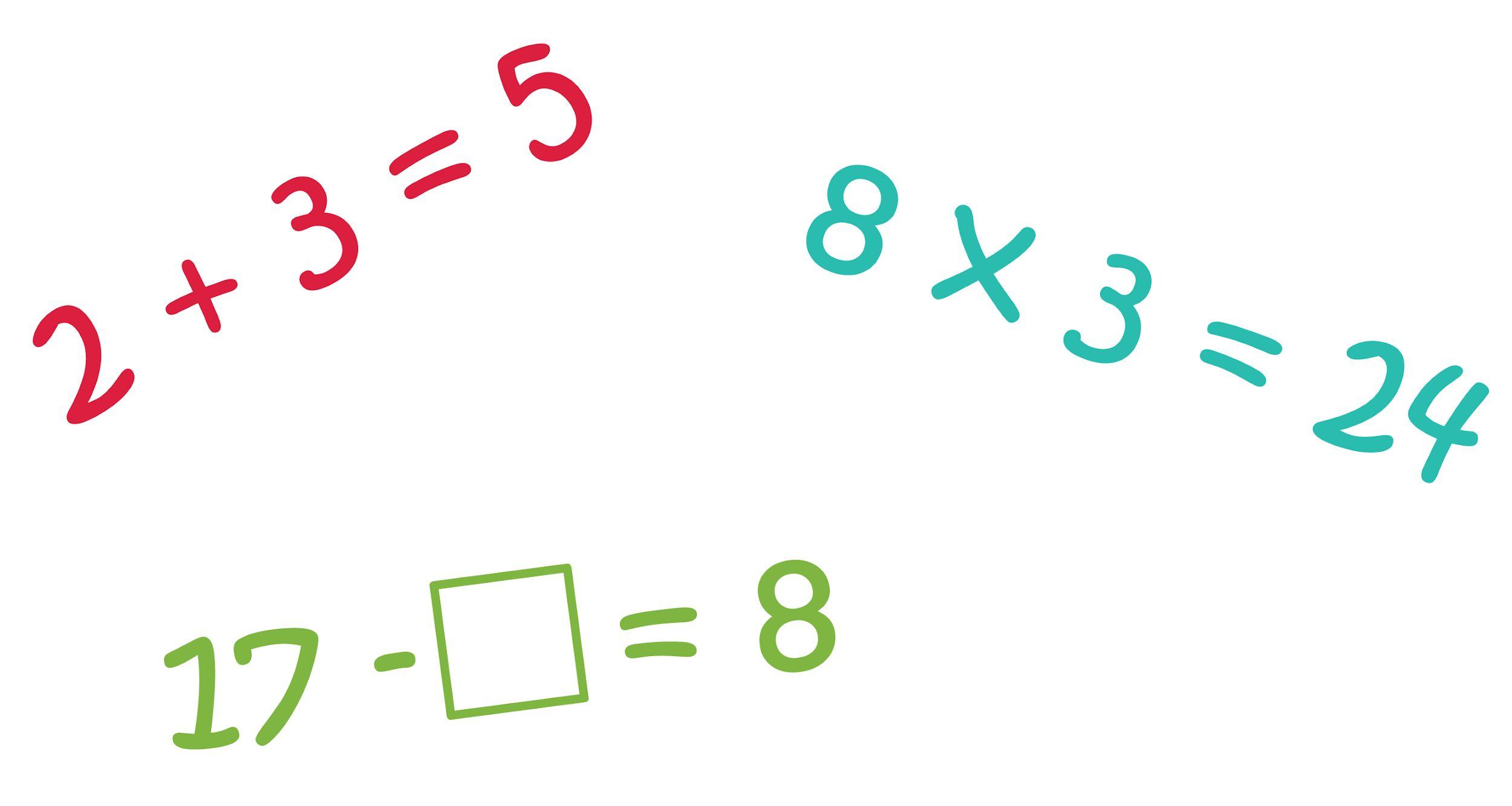
Operación matemática que utiliza números, uno o más símbolos de operación y un signo de igual

Expresión

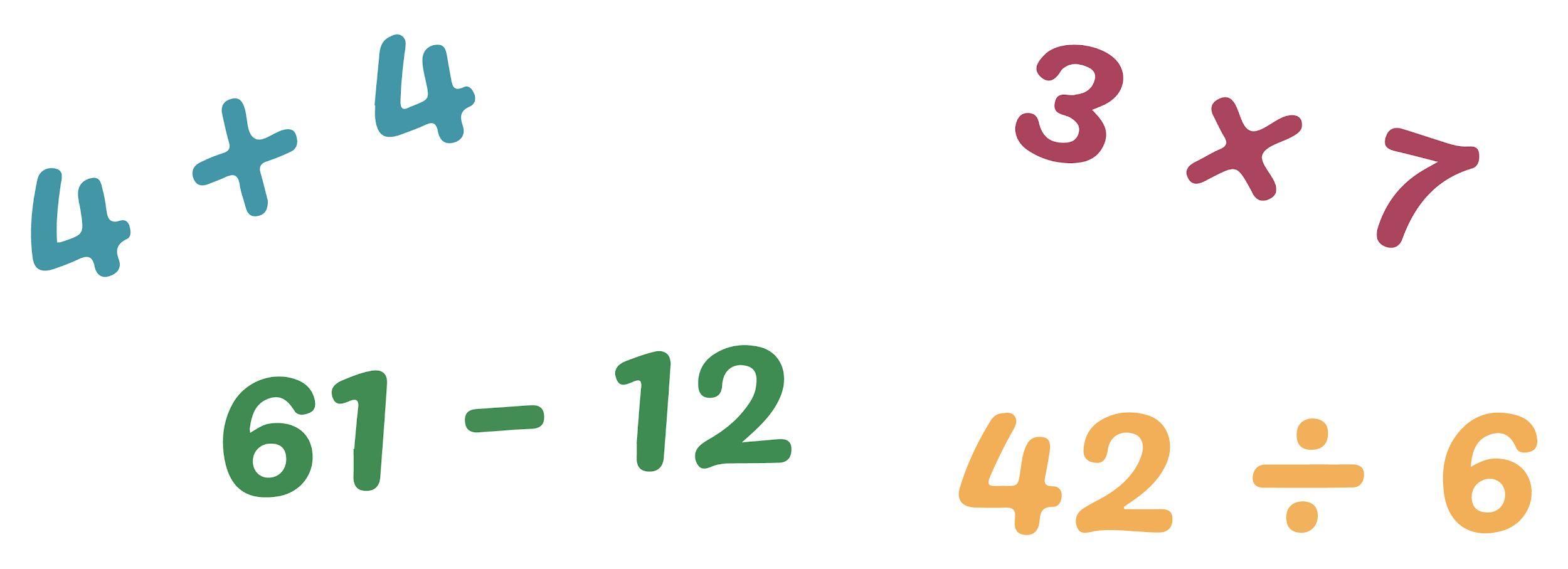
Grupo de números y símbolos de operaciones sin signo igual

Factor

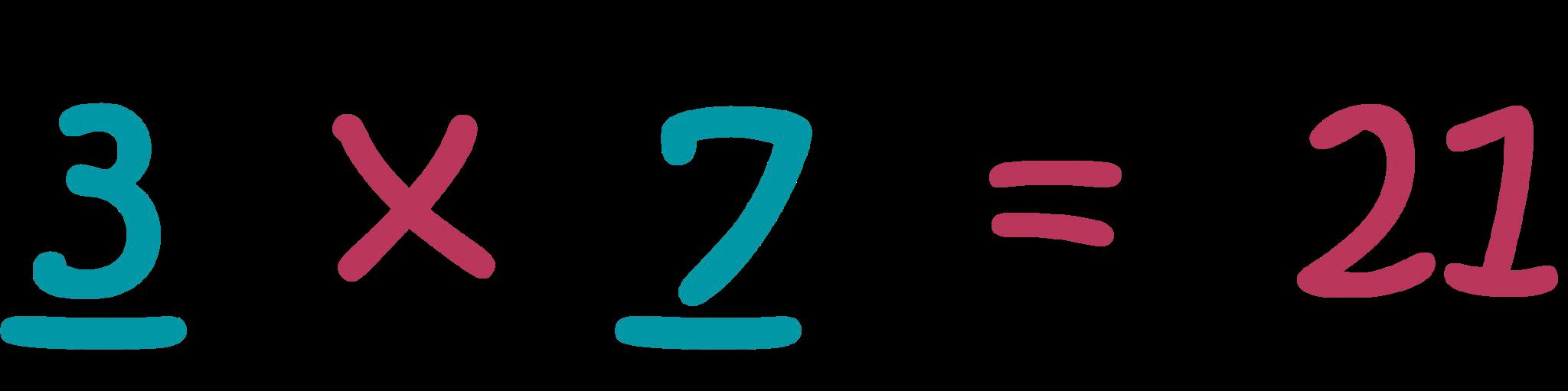
Número que se multiplica por otro número para encontrar un producto

Mayor que

Más que; que muestra una relación entre números; >

Fracción impropia

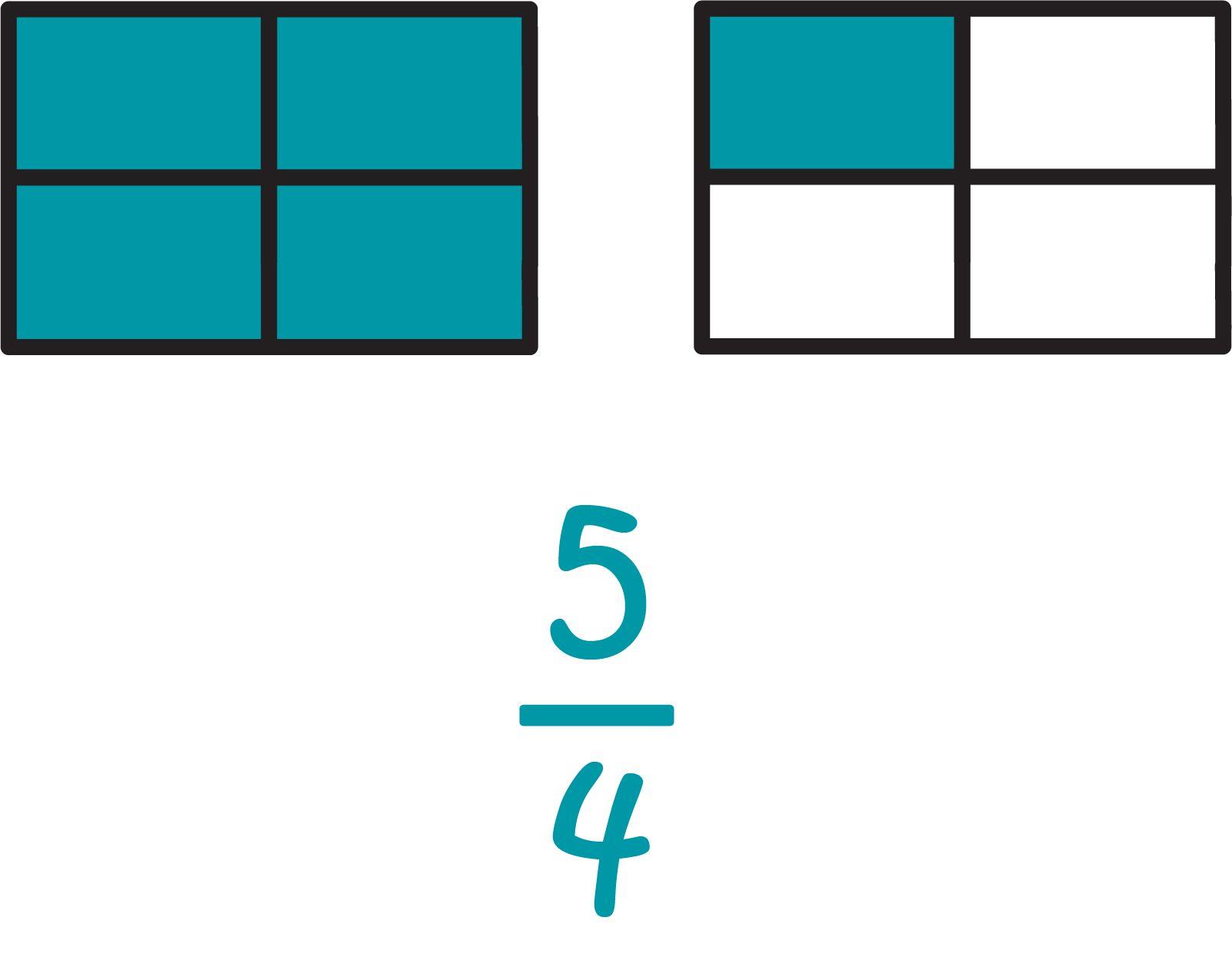
Fracción en la cual el numerador es mayor que el denominador; representa un valor mayor que un entero

EXPLICAR: VOCABULARIO ILUSTRADO

Menos que

Menor que; que muestra una relación entre números; <

Numerador

Número superior en una fracción; representa parte de un todo

Razonabilidad

Número mixto

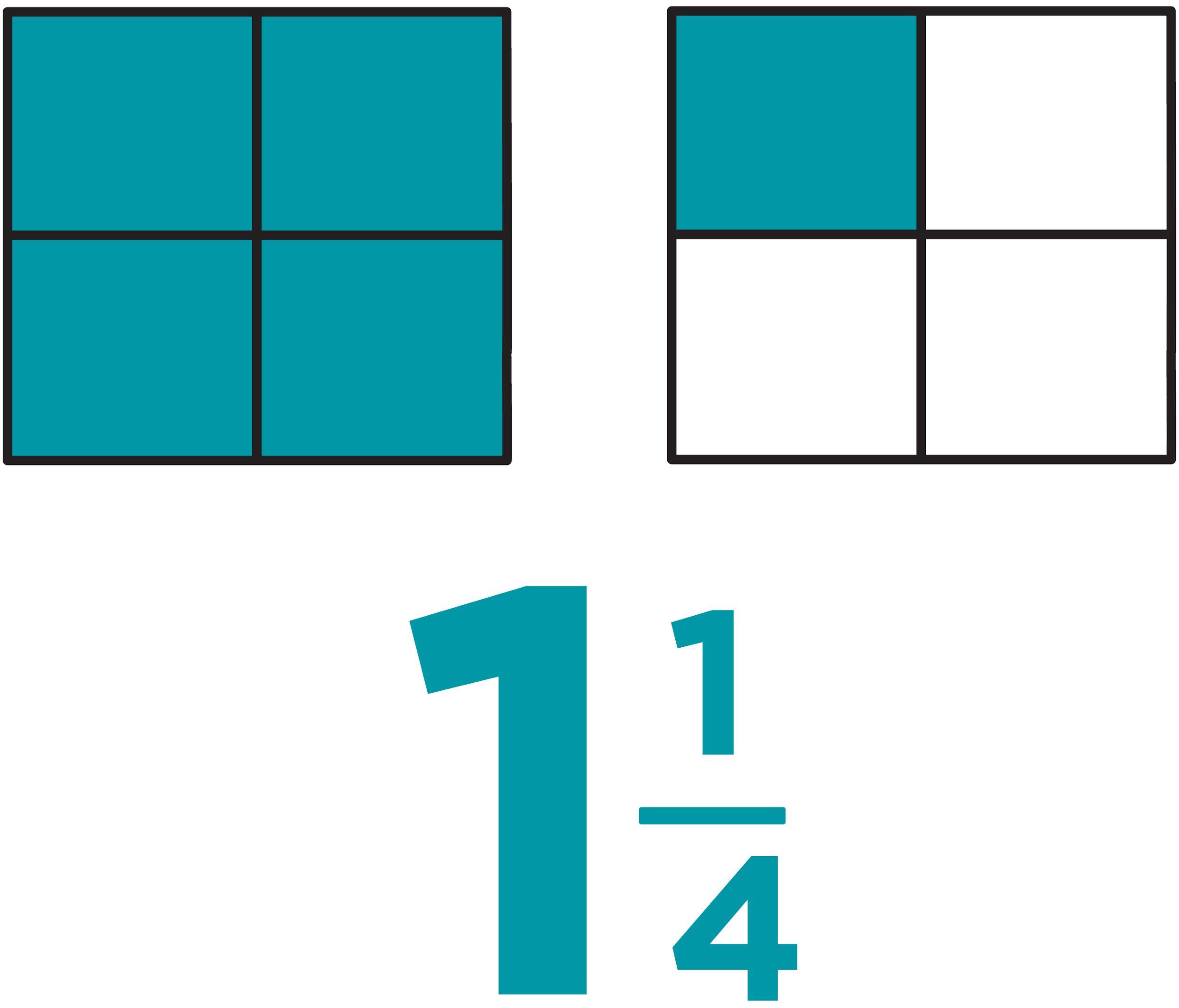
Número formado por un número entero y una fracción propia

Separar

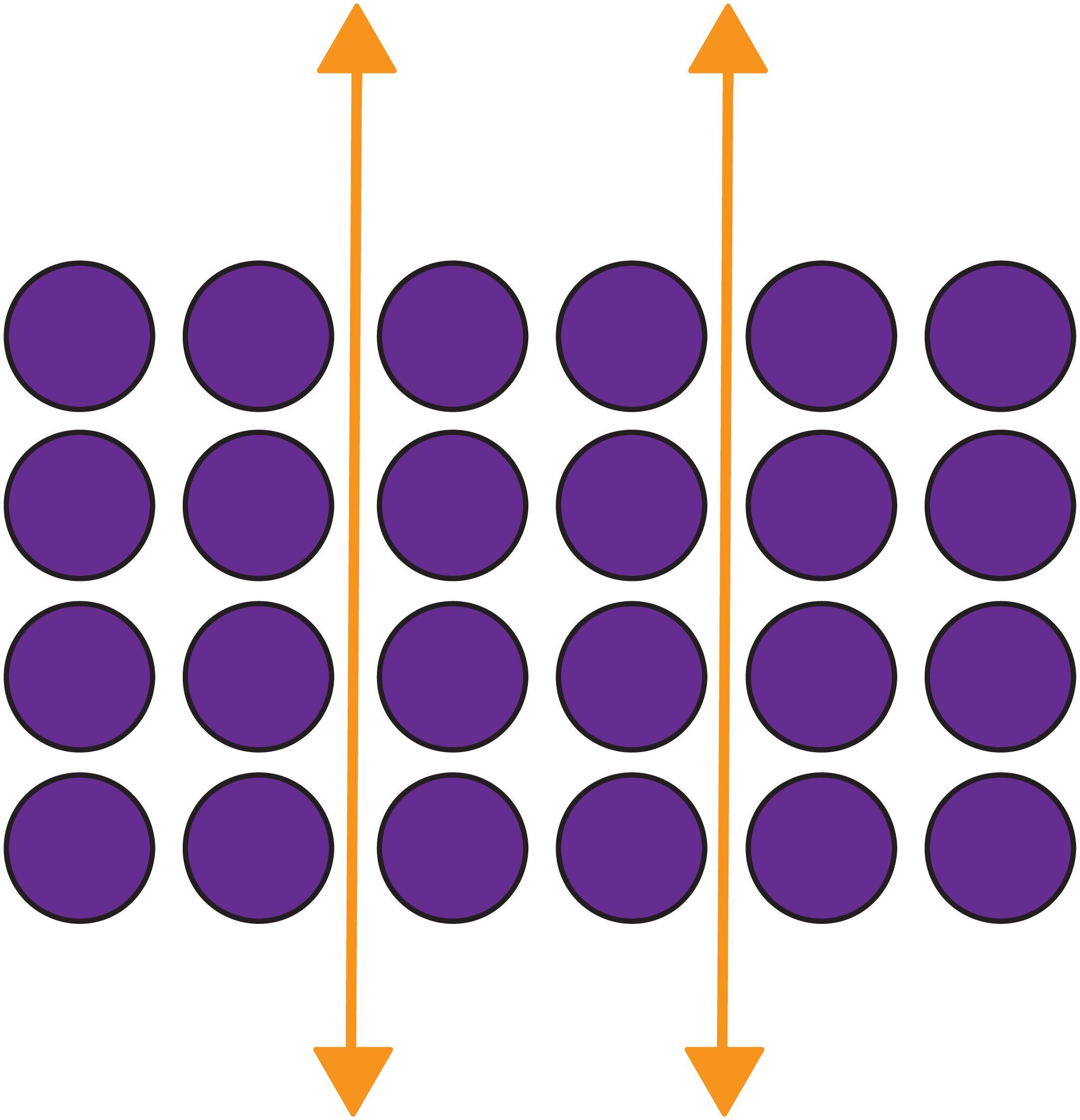
Dividir en partes iguales

Multiplicación

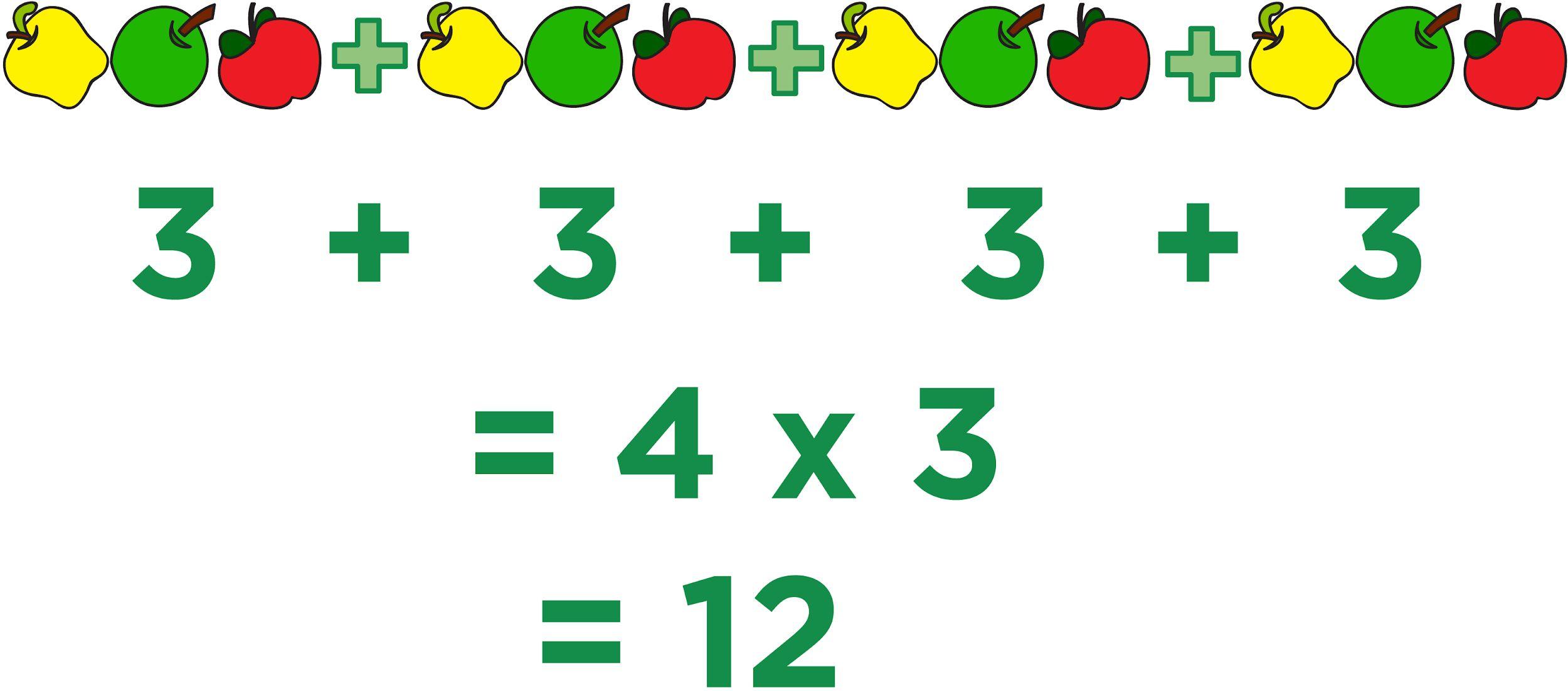
Forma de crear un producto al hacer grupos iguales, sumar repetidamente o formar matrices

Producto

El resultado de multiplicar dos o más números

Reagrupar

Solución a un problema tiene sentido y puede verificarse con una estimación

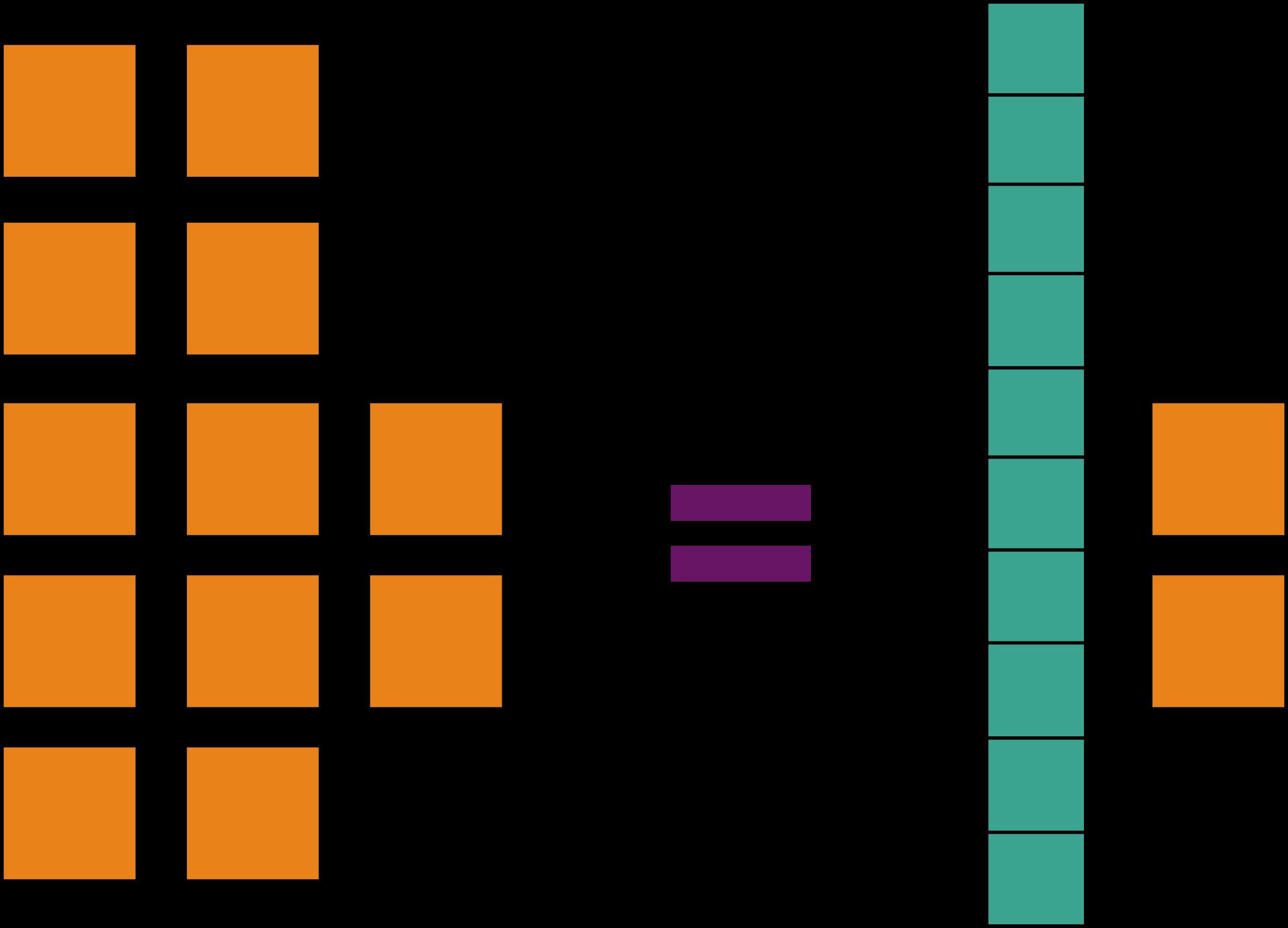
Cambiar grupos de un valor posicional en uno diferente para ayudar a sumar o restar

Hacer una escala

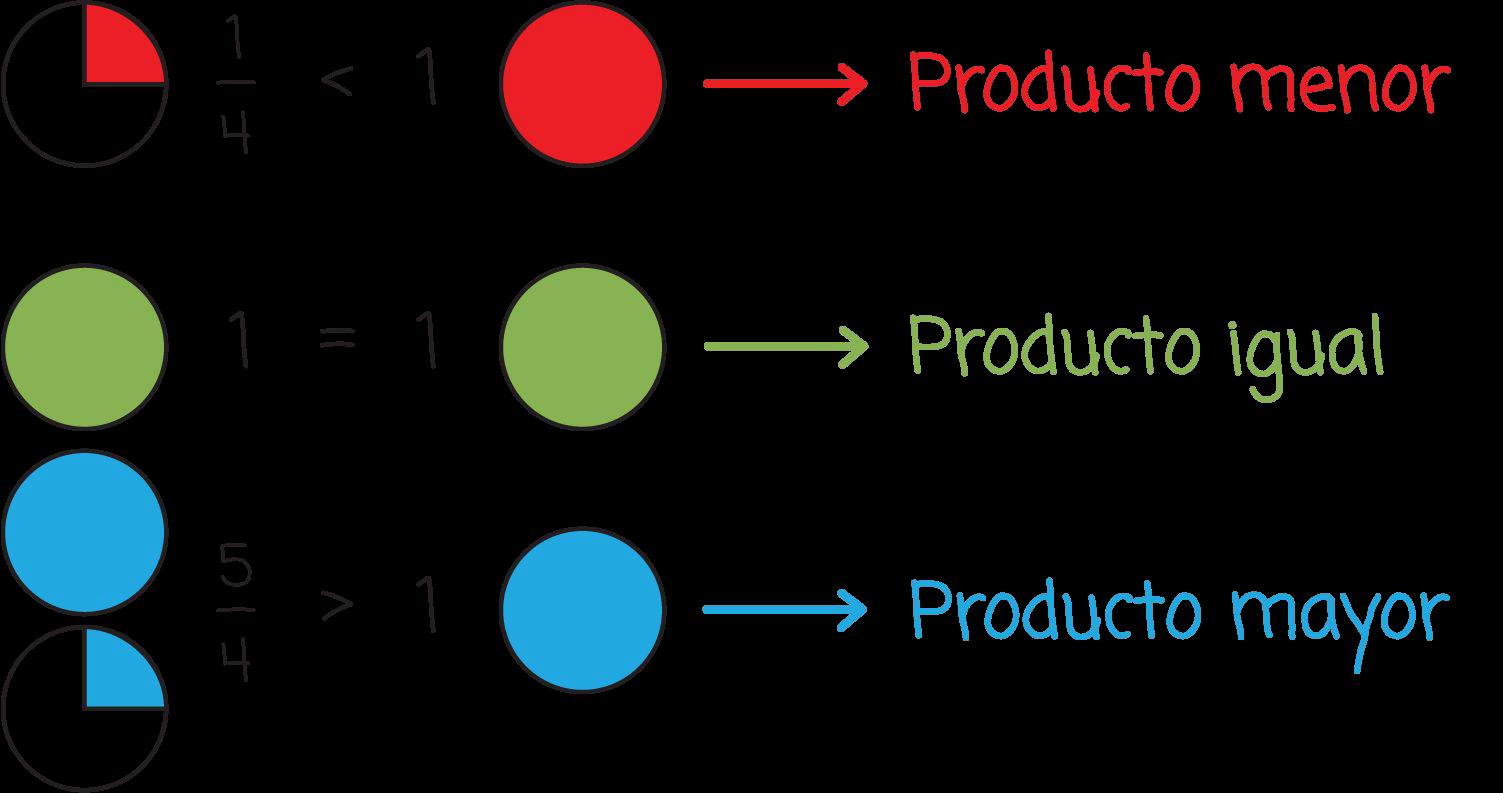
Comparar el tamaño del producto con el tamaño de un factor con respecto al otro factor; predecir productos en base a factores

Número entero

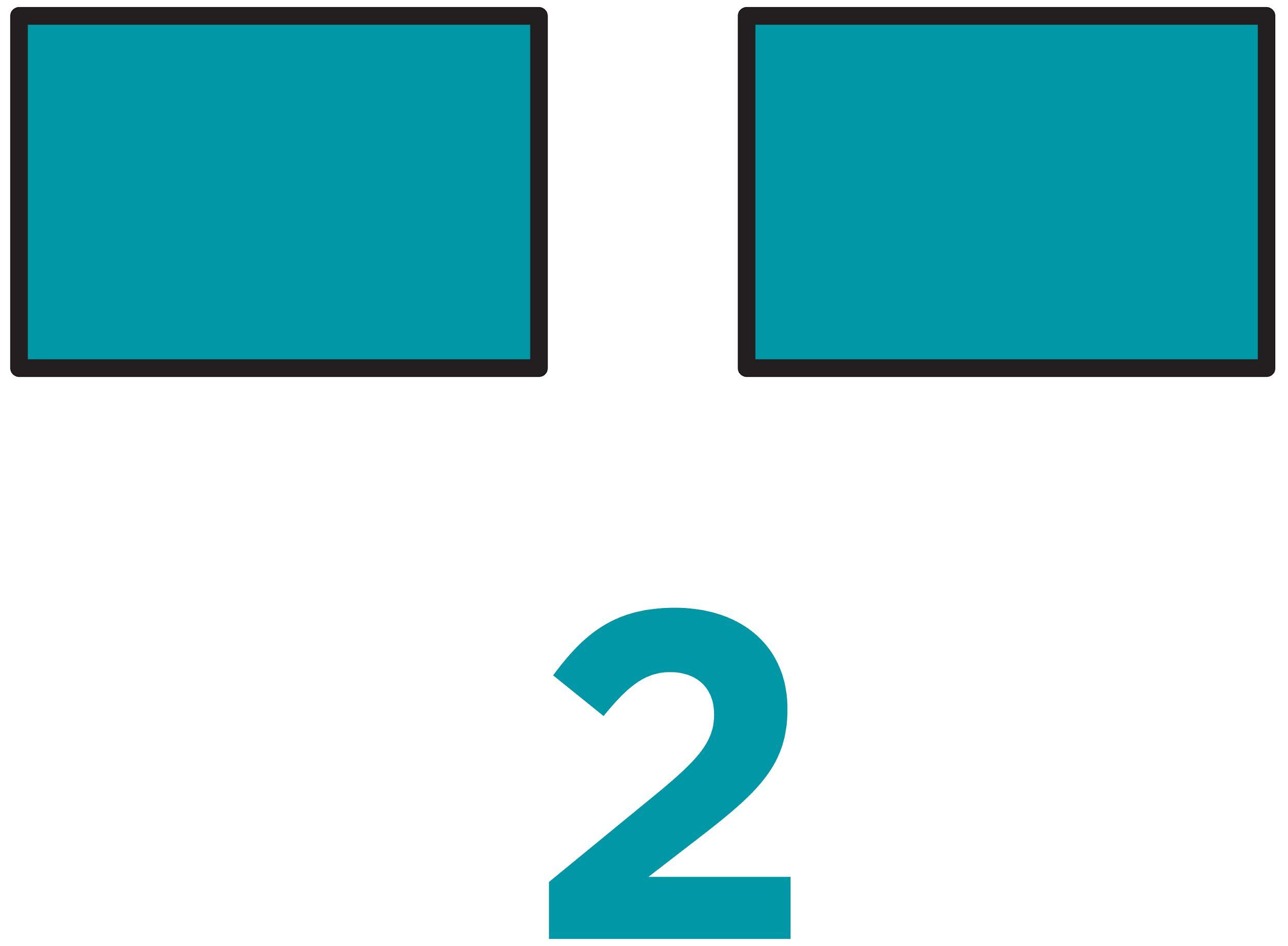
Valor numérico sin partes decimales o fraccionarias

ELABORAR: CONSTRUCTOR DE FLUIDEZ

DESARROLLAR LA FLUIDEZ CONCEPTUAL

CONSTRUCTOR DE FLUIDEZ:

MULTIPLICAR FRACCIONES CON MODELOS Y ECUACIONES

DESCRIPCIÓN

Los estudiantes dan la vuelta a dos tarjetas y buscan la correspondencia entre las imágenes, los números y/o las palabras.

MATERIALES

IMPRESO

• 1 hoja de instrucciones (por pareja)

• 1 juego de tarjetas de correspondencias (por pareja)

• 1 hoja de registro del estudiante (por estudiante)

REUTILIZABLE

• 1 sobre o bolsa con cierre (por pareja)

PREPARACIÓN

• Imprima y recorta un juego de tarjetas de correspondencias para cada pareja. Asegúrate de imprimirlas por las dos caras para que el logotipo del juego aparezca en una cara de cada tarjeta.

• Imprima una hoja de instrucciones para cada juego de tarjetas.

• Considere plastificar todos los materiales impresos, excepto la hoja de registro del estudiante, para que puedan usarse por mucho tiempo. Puede colocar las piezas más pequeñas en sobres o bolsas con cierre.

• Imprima la hoja de registro del estudiante por alumno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Muestre a los estudiantes cómo barajar las cartas y colocarlas boca abajo en una matriz de 4 × 6.

2. Haga una demostración del juego con un estudiante.

a. El primer jugador voltea dos cartas para intentar encontrar una coincidencia.

b. Si el jugador encuentra dos coincidencias, se queda con el conjunto coincidente y vuelve a jugar.

c. Si el jugador no encuentra ninguna coincidencia, vuelve a colocar las cartas boca abajo y es el turno del siguiente jugador.

d. Los jugadores continúan turnándose hasta que se hayan encontrado todas las coincidencias.

e. Gana el jugador que reúna más cartas.

3. Distribuya los materiales.

4. Pida a los estudiantes que jueguen.

5. Al final del juego, pida a cada jugador que anote dos de las coincidencias que haya encontrado en la Hoja de registro del estudiante. Pida a los estudiantes que expliquen por qué las 2 cartas coinciden. Anime a los estudiantes a compartir sus respuestas con sus compañeros.

Pareo

Hoja de registro del estudiante

Al final del juego, selecciona dos parejas hechas por ti. Dibuja las parejas en los recuadros de abajo.

Tarjeta 1 Tarjeta 2 ¿Por qué son parejas?

HOJA DE REGISTRO DEL ESTUDIANTE

Par 1 Par 2

ELABORAR: REVISIÓN EN ESPIRAL

Un paseo a circo

El sábado por la mañana, Lola acababa de despertarse cuando Miles, su hermano pequeño, irrumpió en su habitación. Al principio ella estaba molesta, pero luego vio que él sonreía, saltaba y agitaba unos boletos en el aire. Ella tomó uno y lo leyó con atención. Entonces comprendió su entusiasmo. ¡Ellos iban a ir al circo!

Lola había ido al circo cuando era más chica, pero Miles nunca había ido. ¡Miles estaba obsesionado con el circo! Le encantaban los payasos, los elefantes, las rositas de maíz, los maníes e incluso la música de circo. Lola sonrió al recordar cómo Miles había jugado al «circo» todo el verano pasado. Él había sido el maestro de ceremonias de una compañía de circo imaginaria. En Halloween, incluso se había disfrazado de domador de leones, con todo y un compañero de león feroz.

Lola le dio a Miles un gran abrazo y se apresuró a prepararse. Este iba a ser un día divertido para todos, pero especialmente para Miles. ¡Y ella sentía mucha emoción de verlo pasar el mejor día de su vida!

1. Había 1,284 trabajadores en el circo. Su tren se averió a 20 millas del circo, por lo que tomaron camionetas.

En cada camioneta cabían 11 trabajadores. ¿Cuántas camionetas necesitaban? Muestra tu trabajo y explica tu razonamiento.

3. Lola compró una bolsa grande de maníes. Ella se comió de la bolsa y su mamá se comió de la bolsa. Cuando se la dio a Miles, él exclamó: — ¡Te comiste más de la mitad!

¿Fue razonable la estimación de Miles? ¿Cuánto comieron realmente Lola y su mamá?

REPASAR CONCEPTOS PREVIOS

REVISIÓN EN ESPIRAL: UN PASEO AL CIRCO

DESCRIPCIÓN

Los estudiantes repasan el contenido del grado anterior o actual basándose en el trabajo principal establecido para cada grado.

PREPARACIÓN

• Imprima una copia de la hoja de repaso en espiral por estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Es posible que necesite ayudar con la lectura para que algunos estudiantes completen esta actividad.

2. Antes de que el circo comenzara, Miles quería ir de compras a la tienda de regalos. Él quería comprar unos coloridos zapatos de payaso que fueran rojos o amarillos. Lola se dio cuenta que de los zapatos eran rojos y de los zapatos eran amarillos.

¿Cuántos zapatos eran rojos o amarillos?

4. Después de comer maníes, Miles y Lola les dio sed. Ellos vieron paquetes de 12 latas de refrescos en unas hieleras transparentes. ¡Mientras esperaba en la fila, Miles contó 231 paquetes de refrescos!

Le preguntó a Lola cuántas latas de refresco había. ¿Qué le dijo ella?

2. Lea la historia en la primera página para despertar el interés de los estudiantes antes de pasar a las preguntas.

3. Use este repaso en espiral como calentamiento en clase o envíelo a casa como deberes, pero asegúrese de comentar las respuestas y las estrategias con toda la clase.

4. Consulte la norma que aparece en la esquina inferior derecha de cada cuadro de preguntas para evaluar los conocimientos de contenido de los estudiantes o la necesidad de una mayor intervención.

REPASO EN ESPIRAL ENFOQUE POR PREGUNTA

• Pregunta 1

◦ Grado 5: Encontrar cocientes de números enteros con dividendos de hasta cuatro dígitos y divisores de dos dígitos, usando estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre multiplicación y división. Ilustrar y explicar el cálculo utilizando ecuaciones, matrices rectangulares y/o modelos de áreas.

• Pregunta 2

◦ Grado 5: Sumar y restar fracciones con denominadores diferentes (incluyendo números mixtos) reemplazando fracciones dadas con fracciones equivalentes de tal manera que se produzca una suma o diferencia equivalente de fracciones con denominadores similares. Por ejemplo 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (En general, a/b + c/d = (ad + bc)/bd.)

• Pregunta 3

◦ Grado 5 - Resolver problemas de palabras que involucren sumas y restas de fracciones referidas al mismo entero, incluyendo casos de denominadores diferentes, por ej., con modelos visuales de fracciones o ecuaciones para representar el problema. Utilizar fracciones de referencia y el sentido numérico de las fracciones para estimar mentalmente y evaluar la razonabilidad de las respuestas. Por ejemplo 2/5 + 1/2 = 3/7, observando que 3/7 < 1/2.

• Pregunta 4

◦ Grado 5: Multiplicar con fluidez números enteros de varias cifras utilizando el algoritmo estándar.

ELABORAR: TAREA BASADA EN PROBLEMAS

DESARROLLAR HABILIDADES PARA RESOLVER PROBLEMAS

TAREA BASADA EN

PROBLEMAS:

DISEÑAR UN ÁRBOL

DESCRIPCIÓN

Los estudiantes trabajan en colaboración para aplicar los conocimientos y habilidades que han aprendido a un desafío abierto del mundo real.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Permita que los estudiantes trabajen en grupos.

2. Anime a los estudiantes a revisar sus diarios del estudiante de las actividades explorar si necesitan repasar las habilidades que han aprendido.

3. Si los estudiantes están atascados, utilice preguntas orientadoras para ayudarles a pensar sin decirles qué pasos deben dar a continuación. Si el tiempo lo permite, permite que cada grupo comparta su solución con la clase.

4. Revise cómo los distintos grupos abordaron el reto de maneras diferentes.

3

2

1

Comprensión Cálculo Razonamiento Producto

El estudiante no comprende lo que el problema le pide que haga y no aborda el problema. Las estrategias utilizadas no son adecuadas para el problema.

El estudiante comprende algo de lo que el problema le pide que haga y aborda la mayoría de las partes del problema. Las estrategias utilizadas para resolver el problema son algo apropiadas.

El estudiante comprende completamente lo que el problema le pide que haga, aborda todas las partes del problema y es capaz de emplear estrategias para resolver el problema.

El estudiante no resuelve el problema correctamente. El estudiante no apoya su respuesta con trabajo.

El estudiante no apoya su razonamiento. El estudiante no usa lenguaje matemático.

El estudiante resuelve algunas partes del problema, pero puede tener algunos errores. El estudiante apoya algunas de sus respuestas con trabajo.

El estudiante apoya un poco su razonamiento con algunos errores. El estudiante usa un poco el lenguaje matemático con algunos errores.

El estudiante no crea un producto que sea apropiado para la tarea.

El estudiante crea una solución para algunas partes del problema, pero puede tener algunos errores.

El estudiante resuelve todas las partes del problema correctamente y es capaz de respaldar su respuesta con trabajo.

El estudiante apoya de manera clara y precisa el razonamiento detrás de su respuesta. El estudiante usa un lenguaje matemático preciso de manera consistente.

El estudiante crea una solución al problema correctamente y es capaz de respaldar su respuesta con trabajo.

Diseñar un árbol

A muchos diseñadores les gusta usar losas para el salpicadero de la cocina, las paredes de las duchas y las paredes de las escuelas. Algunos usan el mismo tipo de losa en todo el proyecto y otros incluyen lo que llaman detalles o acentos. Los acentos son losas al azar que se ven diferentes al resto. Dicha diferencia llama la atención y las hace resaltar.

Eres un diseñador de interiores y te han pedido que remodeles una pared del baño. Eres famoso por la creatividad de tus diseños. Usa losas de colores para diseñar tu pared.

El cliente te ha pedido que la pared tenga en su mayor parte un color; sin embargo, quieren que del diseño tenga acentos.

Usa losas de goma Eva de colores para diseñar la pared. Haz tu diseño en la cuadrícula como un ejemplo para tu cliente. No tienes que llenar toda la cuadrícula.

Especificaciones para el cliente:

1. ¿Cuántas losas en total tiene el diseño?

2. ¿Cuántas losas son acentos?

3. Si el cliente decide usar tu diseño en cuatro paredes, ¿cuántas losas de acento necesitarás?

DIAPOSITIVA DEL CHEF

ELABORAR: CONEXIONES PROFESIONALES

MATEMÁTICAS EN EL TRABAJO

CONEXIONES PROFESIONALES: CHEF

Las conexiones profesionales pretenden ser una vía que introduzca a sus estudiantes en las carreras matemáticas y en las habilidades del siglo XXI necesarias para tener éxito en diversos campos. Éstas incluyen, entre otras, la creatividad y la innovación, el pensamiento crítico, la resolución de problemas y las habilidades tecnológicas.

DESCRIPCIÓN

Este alcance destaca la carrera de un chef. Los estudiantes considerarán la profesión, las matemáticas utilizadas y el impacto que esta carrera ha tenido en su comunidad.

MATERIALES

IMPRESOS

• diapositivas del chef (por clase o por estudiante)

REUTILIZABLES

• Proyector (por clase)

PREPARACIÓN

• Agrupa a los estudiantes para una rica colaboración y discurso.

• Prepárate para proyectar la diapositiva del chef a la clase. Si no dispone de proyector, puede imprimir las diapositivas para que las utilicen los estudiantes.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Proyecte la presentación de diapositivas del chef e invite a un estudiante a leer la información proporcionada sobre la profesión.

2. Organice una conversación con los estudiantes, formulando preguntas como las siguientes:

a. ¿Cómo utiliza diariamente un chef sus conocimientos sobre la multiplicación de fracciones?

b. ¿Te parece difícil o fácil utilizar las matemáticas de esta forma?

c. ¿Habías pensado alguna vez en las matemáticas de esta forma?

d. ¿Por qué crees que esta carrera es importante para nuestra sociedad cotidiana?

e. ¿Es una carrera que te interesa? ¿Por qué o por qué no?

f. ¿Cómo utiliza un chef sus habilidades para resolver problemas?

ELABORAR: CIENCIA DE DATOS

ANÁLISIS DE DATOS

CIENCIA DE DATOS

La ciencia de datos consiste en un breve debate en clase sobre un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los estudiantes a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los estudiantes en contexto.

DESCRIPCIÓN

Los estudiantes analizan, interpretan y generan conjuntos de datos, además de responder a preguntas basadas en los datos.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por estudiante)

• 1 conjunto de datos (por clase)

REUTILIZABLE

• 1 proyector o cámara de documentos (por clase)

• 1 marcador de borrado en seco (por clase)

CONSUMIBLE

• 1 trozo de papel milimetrado (por clase)

PREPARACIÓN

• Prepárese para proyectar el conjunto de datos en la clase.

• Reúna un trozo de papel milimetrado y un marcador de borrado en seco.

• Imprima el folleto del estudiante para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los estudiantes.

2. Plantee las siguientes preguntas:

a. ¿Qué observas en este conjunto de datos?

b. ¿Qué representa este conjunto de datos?

c. ¿Qué categorías se incluyen en este conjunto de datos?

d. Al seguir una receta, ¿qué cosas importantes hay que recordar?

e. ¿Puedes contarnos alguna vez que hayas seguido una receta para preparar una bebida?

f. ¿Qué preguntas tienes sobre los datos?

Mi conjunto de datos

Recopila datos que incluyan fracciones y crea una representación visual de los datos. Responde las preguntas con el uso de los datos recopilados.

1. ¿Qué representa tu conjunto de datos?

2. Multiplica una fracción de tu conjunto de datos por un número entero. ¿Puedes crear un modelo para representar la multiplicación?

3. Multiplica una fracción de tu conjunto de datos por otra fracción. ¿Es el producto mayor o menor que la fracción de tu conjunto de datos?

4. Crea un problema escrito que pueda resolverse con el uso de los datos de tu conjunto de datos. ¿Cuál es la solución?

FOLLETO DEL ESTUDIANTE

PARTE II

1. Repase el modelo de multiplicación de fracciones y escriba lo que los estudiantes recuerden en el papel milimetrado.

2. Haga las siguientes preguntas:

a. ¿Cuántas raciones rinde la receta de limonada tropical? ¿Cómo lo sabes? La receta rinde 2 porciones porque dice "sirve para 2".

b. Si quisieras hacer 4 porciones de limonada tropical, ¿cuántas tazas de jugo de piña usarías? ¿Jugo de papaya? Necesitarías 1 1/3 tazas de zumo de piña. Necesitarías 1 1/2 tazas de zumo de papaya.

c. Dibuja un modelo para representar cuántas tazas de zumo de piña utilizarías para hacer 4 raciones. Las respuestas variarán.

d. ¿Cuál es un modelo diferente para representar cuántas tazas de jugo de papaya usarías para hacer 4 porciones? Las respuestas variarán.

e. Si preparas 4 raciones, ¿la cantidad de zumo de naranja que utilizarías sería mayor o menor que 3/4 taza? La cantidad de zumo de naranja sería mayor que 3/4 taza

f. Si quieres preparar 6 raciones de limonada tropical, ¿qué tipos de zumo utilizarías en cantidades enteras? Utilizarías cantidades enteras de zumo de piña, limón y lima.

g. Si preparas 1 ración, ¿la cantidad de zumo de mango que utilizarías sería mayor o menor que 1/2 taza? La cantidad de zumo de mango sería inferior a 1/2 taza

h. Dibuja un modelo para representar cuánto zumo de mango se utilizaría para preparar 1 ración. Las respuestas variarán.

PARTE III

1. Entregue una copia del folleto del estudiante por alumno.

2. Lea las instrucciones y responda a las preguntas que puedan tener los estudiantes.

3. Conceda tiempo para que completen el folleto el estudiante en clase o la envíen a casa como tarea. Anime a los estudiantes a compartir sus datos con la clase.

EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN

Habilidad o concepto clave ¿Cómo podrías demostrar que sabes esto? ¿Cómo te calificarías a ti mismo?

Puedo aplicar y ampliar mi conocimiento de la multiplicación para multiplicar un número entero por una fracción. Puedo interpretar el producto a/b) × q como parte de una repartición de q en partes iguales de b y como resultado de una secuencia de operaciones, a × q ÷ b

Puedo aplicar y ampliar mi conocimiento de la multiplicación para multiplicar una fracción por otra fracción. Puedo utilizar un modelo visual y generalizar que (a/b) × (c/d = ac/bd

Puedo interpretar la multiplicación como hacer una escala, o redimensionamiento, al comparar el tamaño de un producto con el tamaño de un factor en función del tamaño del otro factor, sin realizar la multiplicación indicada.

❏ Represéntalo.

❏ Dibújalo.

❏ Aplícalo.

❏ Habla sobre esto.

❏ Escribe sobre esto.

❏ Represéntalo.

❏ Dibújalo.

❏ Aplícalo.

❏ Habla sobre esto.

❏ Escribe sobre esto.

❏ Represéntalo.

❏ Dibújalo. ❏ Aplícalo.

❏ Habla sobre esto.

❏ Escribe sobre esto.

¡Lo tengo!

¡Ya casi!

¡Todavía no!

¡Lo tengo!

¡Ya casi!

¡Todavía no!

¡Lo tengo!

¡Ya casi!

¡Todavía no!

Habilidad o concepto clave

Puedo interpretar la multiplicación como hacer una escala, o redimensionamiento, y explicar por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado y por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado. Puedo relacionar mi conocimiento de la equivalencia de fracciones, a/b = (n×a)/(n×b), con el efecto de multiplicar a/b por 1.

¿Cómo podrías demostrar que sabes esto?

❏ Represéntalo.

❏ Dibújalo.

❏ Aplícalo.

❏ Habla sobre esto.

❏ Escribe sobre esto.

¿Cómo te calificarías a ti mismo?

¡Lo tengo!

¡Ya casi! ¡Todavía no!

LISTA

DESCRIPCIÓN

EVALUACIÓN DE HABILIDADES

DE VERIFICACIÓN DE LA OBSERVACIÓN

Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestros y como autoevaluación para los estudiantes.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por estudiante)

• 1 materiales para el maestro (por estudiante)

PREPARACIÓN

• Imprima los materiales para el maestro y un folleto del estudiante para cada alumno.

PROCEDIMIENTO Y PUNTOS DE APOYO

1. Distribuya un folleto del estudiante por alumno.

2. A medida que los estudiantes trabajen en las actividades explorar y explicar del alcance, evalúe formativamente su progreso tomando notas sobre cómo se observaron los conceptos y habilidades clave. Se pueden plantear preguntas de reflexión para medir el impacto de las actividades tanto en grupo completo como en pequeño grupo.

3. Pida a los estudiantes que reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan tanto en grupo completo como en pequeño grupo.

Práctica matemática ¿Cómo te calificarías a ti mismo?

Puedo dar sentido a los problemas y resolverlos sin rendirme.

Puedo pensar en números y problemas de muchas formas diferentes.

Puedo explicar mi pensamiento y evaluar el pensamiento de los demás.

Puedo mostrar mi trabajo de muchas maneras y resolver problemas con modelos, números y símbolos.

Puedo utilizar las herramientas matemáticas adecuadas y explicar por qué las he elegido.

Puedo trabajar con cuidado y comprobar la exactitud de mis respuestas.

Puedo encontrar patrones y utilizar conocimientos previos para resolver problemas nuevos.

Puedo ver en qué se parecen algunos problemas y utilizar lo que sé para resolverlos.

Reflexiona sobre tu pensamiento, aprendizaje y trabajo en este alcance.

¿Qué objetivos te has propuesto? ¿En qué has mejorado en este alcance?

¿Tienes nuevos objetivos? ¿Dónde quieres mejorar en el próximo alcance? FOLLETO PARA

4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado y establecer nuevas metas de aprendizaje.

5. Quienes brindan apoyo pedagógico a los estudiantes pueden estar equipados con las adaptaciones y modificaciones anotadas en los materiales para el maestro

6. Las notas anecdóticas proporcionadas en las instrucciones del maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.

7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la guía de instrucción andamiada en la sección «Inicio» de este alcance para diferenciar la instrucción para cada estudiante.

ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN

MAPA DE CALOR

DESCRIPCIÓN

Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.

MATERIALES

• 1 mapa de calor (por estudiante)

• 1 crayón rojo (por estudiante)

• 1 crayón verde (por estudiante)

PREPARACIÓN

• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.

• Imprima un mapa de calor para cada estudiante.

• Reúna un crayón rojo y un crayón verde para cada estudiante.

ROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un mapa de calor a cada estudiante junto con los crayones rojo y verde. Los estudiantes deben tener a mano su(s) evaluación(es) corregida(s).

2. Los estudiantes utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Por cada pregunta contestada correctamente, colorean de verde la casilla correspondiente. Para cada pregunta contestada incorrectamente, los estudiantes colorean la casilla correspondiente en rojo.

3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.

4. Consulte la guía de instrucción andamiadas que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.

Consulta tus respuestas en la tabla «Prueba de habilidades». Al lado de cada estándar, colorea el cuadro de preguntas de verde si tu respuesta es correcta. Colorea el cuadro de preguntas de rojo si tu respuesta es incorrecta.

Prueba de hab dades

Estándares Preguntas

Aplica y amplía conocimientos previos sobre la multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpreta el producto (a/b) × q como una parte de una repartición de q en partes iguales de b; equivalentemente, el resultado de una secuencia de operaciones a × q ÷ b Por ejemplo, usa un modelo visual de fracción para mostrar (2/3) × 4 = 8/3 y crea un contexto de historia para esta ecuación. Haz lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = ac/bd).

Interpreta la multiplicación como hacer una escala (redimensionamiento) al: a. Comparar el tamaño de un producto con el tamaño de un factor en función del tamaño del otro factor, sin realizar la multiplicación indicada.

9 10 11 12 6 7

Prueba de hab dades

Estándares Preguntas

Interpreta la multiplicación como hacer una escala (redimensionamiento) al: b. Explica por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado ( al reconocer la multiplicación por números enteros mayores que 1 como un caso familiar); explicar por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado, y relacionar el principio de equivalencia de fracciones a/b = n × a)/(n × b) con el efecto de multiplicar a/b por 1.

Preguntas de ref ex ón

1. ¿Con qué habilidad te has sentido más seguro? ¿Por qué?

2. ¿Qué habilidad te ha parecido más desafiante? ¿Por qué?

3. ¿Qué tipo de error cometiste con más frecuencia?

4. ¿Cómo puedes evitar esos errores en el futuro?

Consulta tus respuestas en la tabla «Evaluación basada en estándares». Al lado de cada estándar, colorea el cuadro de preguntas de verde si tu respuesta es correcta. Colorea el cuadro de preguntas de rojo si tu respuesta es incorrecta.

Eva uac ón basada en estándares

Estándares Preguntas

Aplica y amplía conocimientos previos sobre la multiplicación para multiplicar una fracción o un número entero por una fracción. a. Interpreta el producto (a/b) × q como una parte de una repartición de q en partes iguales de b equivalentemente, el resultado de una secuencia de operaciones a × q ÷ b Por ejemplo, usa un modelo visual de fracción para mostrar (2/3) × 4 = 8/3 y crea un contexto de historia para esta ecuación. Haz lo mismo con (2/3) × (4/5) = 8/15. (En general, (a/b) × (c/d) = ac/bd).

Interpreta la multiplicación como hacer una escala (redimensionamiento) al: a. Comparar el tamaño de un producto con el tamaño de un factor en función del tamaño del otro factor, sin realizar la multiplicación indicada.

3 4 1 2 5 6 7 9

Eva uac ón basada en estándares

Estándares Preguntas

Interpreta la multiplicación como hacer una escala (redimensionamiento) al:

b. Explicar por qué multiplicar un número dado por una fracción mayor que 1 da como resultado un producto mayor que el número dado ( al reconocer la multiplicación por números enteros mayores que 1 como un caso familiar); explicar por qué multiplicar un número dado por una fracción menor que 1 da como resultado un producto menor que el número dado, y relacionar el principio de equivalencia de fracciones a/b = (n × a)/(n × b con el efecto de multiplicar a/b por 1. 8 10

Preguntas de ref ex ón

1. ¿Con qué habilidad te has sentido más seguro? ¿Por qué?

2. ¿Qué habilidad te ha parecido más desafiante? ¿Por qué?

3. ¿Qué tipo de error cometiste con más frecuencia?

4. ¿Cómo puedes evitar esos errores en el futuro?

Model Fraction Multiplication 4

Instrucciones: Resuelve los siguientes problemas.

receso o actividades especiales.

Parte A. Escribe en el recuadro de abajo una expresión que sea equivalente a × 8:

Parte B. Completa el enunciado de comparación de este escenario:

Parte C. ¿Cuánto tiempo pasan los estudiantes en el salón de clases? Explica tu razonamiento. Anota tu respuesta en el recuadro.

2. Coloca un símbolo de comparación entre cada conjunto de valores:

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

REFORZAR

INTERVENCIÓN EN PEQUEÑOS GRUPOS

DESCRIPCIÓN

Los estudiantes representan la multiplicación de una fracción por un número entero, de un número entero por una fracción y de una fracción por una fracción, y razonan sobre el tamaño del producto en relación con ambos factores. También debaten sobre el tamaño de un producto basándose en el cambio de tamaño de uno o ambos factores.

MATERIALES

IMPRESO

• 1 lista de control del maestro (por maestro)

• 1 ficha de control (por estudiante)

• 1 juego de tarjetas de situación (por pareja)

3. Una tienda de ropa ha reservado de la tienda para vender ropa de hombre. De esa sección, es para vender camisas de hombre. ¿Qué sección de la tienda de ropa es para vender camisas de hombre? Crea un modelo y escribe tu respuesta en el recuadro de abajo. Modelo

Respuesta: 1 3 1 2

4. Kevin usó el modelo de abajo para encontrar el producto de una fracción y un número entero.

Escribe en el recuadro de abajo una expresión que represente el modelo de Kevin:

EVALUACIÓN DE CONTROL

• 1 tapete de trabajo para multiplicar fracciones (por pareja)

REUTILIZABLE

• 1 juego de fichas de colores (por pareja)

• 3 protectores de hojas (por pareja)

• 1 marcador de borrado en seco (por pareja)

• 2 marcadores borrables de diferentes colores (por pareja)

• 3 bolsas resellables (por pareja)

PREPARACIÓN

• Planee que los estudiantes trabajen en parejas para completar esta actividad.

• Imprima la lista de control del maestro.

• Imprima una ficha de control por estudiante.

• Prepare un juego de fichas de colores por pareja.

Parte I

• Imprima en cartulina un conjunto de tarjetas de situación de la parte I por cada pareja, córtelas por las líneas de puntos y colóquelas en una bolsa resellable con la etiqueta «Parte I».

• Imprima la parte I del tapete de trabajo para multiplicar fracciones en cartulina para que dure y colóquela en un protector de hojas para que se pueda borrar.

• Entregue un marcador de borrado en seco a cada pareja de estudiantes.

Parte II

• Imprima en cartulina un conjunto de tarjetas de situaciones de la parte II, recórtelas a lo largo de las líneas de puntos y colóquelas en una bolsa resellable etiquetada como «Parte II».

• Imprima en cartulina la parte II del tapete de trabajo para multiplicar fracciones por pareja y colóquela en un protector de hojas para que la superficie se pueda borrar.

• Entregue dos marcadores borrables de diferentes colores a cada pareja.

Parte III

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

• Imprima en cartulina un conjunto de tarjetas de situación de la parte III por pareja, córtelas a lo largo de las líneas punteadas y colóquelas en una bolsa resellable rotulada «Parte III».

• Imprima en cartulina la parte III del tapete de trabajo para multiplicar fracciones por pareja y colóquela en un protector de hojas para que se pueda borrar.

• Entregue dos marcadores borrables de diferentes colores a cada pareja.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: MULTIPLICAR FRACCIONES POR NÚMEROS ENTEROS

1. Entregue un tapete de trabajo para multiplicar fracciones de la parte I, un juego de fichas de colores, una bolsa de tarjetas de situaciones hipotéticas de la parte I y un marcador borrable a cada pareja de estudiantes.

2. Pida a las parejas que separen sus tarjetas de situaciones hipotéticas en tres pilas: una con las situaciones hipotéticas, otra con las expresiones y otra con las soluciones.

3. Diga a los estudiantes que cuando las personas se encuentran con problemas matemáticos del mundo real, no siempre tratan con números enteros. También pueden tratar con fracciones. Pídales ejemplos de problemas con fracciones en la vida real. Las respuestas pueden variar: recetas de comida, medidas, etc.

4. Explique a los estudiantes que van a leer varios escenarios que implican la multiplicación de números enteros y fracciones, y pídales que seleccionen la tarjeta del escenario que dice lo siguiente: Hannah tenía 2 horas en el gimnasio para hacer ejercicio. Pasó 2/3 de cada hora levantando pesas. ¿Qué fracción del tiempo que Hannah pasó en el gimnasio dedicó a levantar pesas?

5. Pida a los estudiantes que coloquen la tarjeta del escenario en la parte superior de sus tapetes de trabajo para multiplicar fracciones.

6. Explíqueles que usarán sus fichas de colores para representar el escenario, anime a cada pareja a trabajar juntos para crear un modelo que represente el escenario y formule las siguientes preguntas orientadoras mientras trabajan:

a. ¿Qué información sabemos del escenario? Sabemos que Hannah hizo ejercicio durante dos horas y pasó 2/3 de cada hora levantando pesas.

b. ¿Cómo podemos representar el número entero utilizando las fichas de colores? Las respuestas variarán. Podemos dividir cada hora en tercios porque la fracción en el denominador es un 3. Podemos hacer esto para ambas horas, así que tendremos dos filas de tres fichas en cada fila para un total de seis fichas de color.

c. ¿Cómo podemos representar la fracción usando fichas de color? Las respuestas pueden variar. Sabemos que levantó pesas durante 2/3 de cada hora, así que podemos hacer que dos baldosas de color de cada fila sean del mismo color y que la tercera baldosa de color de cada fila sea de un color diferente.

Se muestra un modelo de baldosas de color como ejemplo:

a. ¿Deberíamos pensar en esta multiplicación como una fracción de un conjunto o como una suma repetida? Este escenario es como una adición repetida porque la fracción se repite dos veces.

7. Haga que los estudiantes encierren con un círculo la palabra «adición repetida» en sus tapetes de trabajo de multiplicar fracciones. Recuérdeles que ambos tipos de escenarios pueden resolverse usando la multiplicación; sólo están pensando en el tipo de pregunta para dar sentido al escenario y ayudarles a representarlo.

8. Después de que los estudiantes hayan creado sus modelos utilizando sus fichas de colores, anímelos a compartir sus modelos y a explicar cómo representan el escenario.

9. Indique a los estudiantes que utilicen sus tapetes de trabajo para multiplicar fracciones para representar un modelo de sus fichas de colores y formule las siguientes preguntas orientadoras mientras trabajan.

a. ¿Cómo podemos representar el número entero a partir de nuestro modelo? Las respuestas pueden variar. Podemos usar nuestro marcador de borrado en seco para dibujar dos barras de fracción para representar las dos horas.

b. ¿Cómo podemos representar la fracción a partir de nuestro modelo? Las respuestas pueden variar. Podemos sombrear dos tercios de cada fila para representar la fracción que ella levantó pesas en cada hora.

Se muestra un modelo de ejemplo:

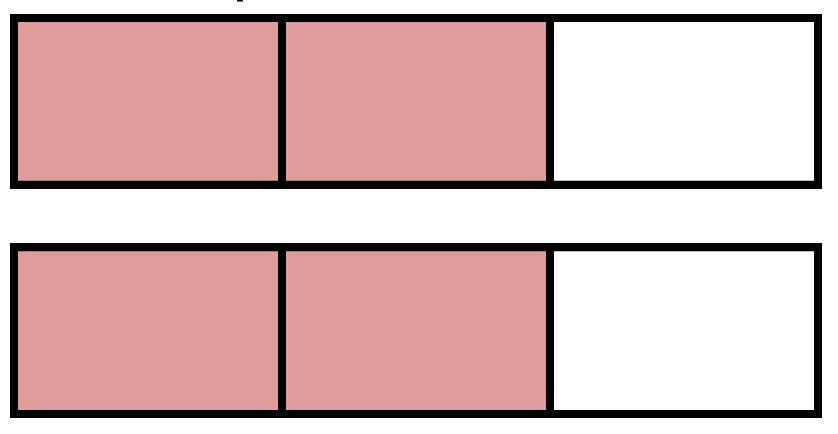
10. Revise el modelo en los tapetes de trabajo para multiplicar fracciones de los estudiantes para verificar su exactitud y corrija cualquier malentendido.

11. Pida a los estudiantes que encuentren la tarjeta de expresión correspondiente, determinen una estimación y encuentren la tarjeta de solución para colocar en sus tapetes de trabajo para multiplicar fracciones, y haga las siguientes preguntas guía:

a. ¿Qué operación estamos usando para resolver nuestro escenario? Multiplicación

b. ¿Cómo sabes que estamos resolviendo con esa operación? Las respuestas pueden variar. Estamos multiplicando porque tenemos cantidades fraccionarias que se repiten y estamos buscando un total.

c. ¿Cuáles son los factores de nuestra ecuación? 2/3 y 2

e. ¿Cómo podemos estimar el producto basándonos en el valor de los factores? 2 es un número entero, y lo estamos multiplicando por una cantidad menor que 1 entero, por lo que el producto será menor que 2.

f. ¿Es el factor fraccionario mayor o menor que la mitad? ¿Cómo afecta esto a tu estimación? 2/3 es mayor que 1/2. Por lo tanto, sabemos que el producto será mayor que la mitad de 2, que es 1.

g. ¿Cómo puedes completar los espacios en blanco para crear un enunciado estimativo en tu carpeta de trabajo Multiplicar fracciones? El producto estará entre 1 y 2.

i. Pide a los estudiantes que completen el enunciado de estimación en sus tapetes de trabajo.

h. ¿Cómo podemos usar nuestro modelo para ayudarnos a determinar una solución? 2/3 + 2/3 de nuestro modelo para determinar que nuestra respuesta es 4/3.

i. Podemos sumar 4/3 o 1 1/3

j. ¿Es razonable nuestro producto? Explícalo. Nuestra respuesta es menor que nuestro número entero porque nuestro número entero era 2 y nuestro producto era 1 1/3. Sabemos que esto es razonable porque estimamos que el producto estaría entre 1 y 2, y cuando multiplicas por una fracción, el producto será menor que el número entero.

12. Comprueba la correspondencia de las tarjetas, los modelos y las estimaciones de cada pareja en sus Tapetes de trabajo para multiplicar fracciones y corrige cualquier malentendido.

13. Pide a las parejas que vuelvan a colocar las tarjetas que acaban de utilizar en sus bolsas con cierre y borra sus Tapetes de trabajo para multiplicar fracciones.

14. Pida a los estudiantes que seleccionen la tarjeta del escenario que dice lo siguiente: Una tienda de comestibles encargó 8 cajas de productos agrícolas. Hasta ahora, la tienda ha recibido 3/4 de su envío. ¿Cuántas cajas de productos ha recibido la tienda?

15. Pida a los estudiantes que coloquen la tarjeta del escenario en la parte superior de sus Tapetes de trabajo para multiplicar fracciones.

16. Anime a cada pareja a trabajar juntos para crear un modelo que represente el escenario utilizando sus fichas de colores, y haga las siguientes preguntas guía mientras trabajan:

a. ¿Qué información sabemos del escenario? Sabemos que la tienda pidió 8 cajas y ha recibido 3/4 de su envío.

b. ¿Cómo podemos representar el número entero utilizando las fichas de color? Las respuestas variarán. Podemos utilizar 8 fichas de colores y ordenarlas en dos filas de 4 porque el denominador del factor fraccionario es 4.

c. ¿Cómo podemos representar la fracción utilizando fichas de colores? Las respuestas pueden variar. Debido a que la tienda ha recibido 3/4 de su envío, podemos utilizar una baldosa de color diferente

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

d. para tres de las cuatro columnas. Se muestra un modelo de azulejo de color de ejemplo:

e. ¿Deberíamos pensar en esta multiplicación como una fracción de un conjunto o como una suma repetida? Este escenario modela una fracción de un conjunto porque se ha recibido una parte del envío.

7. Pida a los estudiantes que marquen con un círculo la «fracción de un conjunto» en sus tapetes de trabajo multiplicar fracciones. Recuérdeles que ambos tipos de escenarios pueden resolverse con la multiplicación; sólo están pensando en el tipo de pregunta para dar sentido al escenario y ayudarles a representarlo.

8. Después de que los estudiantes hayan creado sus modelos utilizando sus fichas de colores, anímelos a compartir sus modelos y a explicar cómo representan el escenario.

9. Indique a los estudiantes que utilicen las tapetes de trabajo para multiplicar fracciones para representar un modelo con sus fichas de colores y formule las siguientes preguntas orientadoras mientras trabajan:

a. ¿Cómo podemos representar el número entero a partir de nuestro modelo? Las respuestas pueden variar. Podemos usar nuestro marcador de borrado en seco para dibujar un rectángulo dividido en dos filas de 4 para mostrar las 8 casillas totales en el orden.

b. ¿Cómo podemos representar la fracción a partir de nuestro modelo? Las respuestas variarán. Podemos sombrear tres de las cuatro columnas para mostrar que se han recibido tres cuartas partes del pedido.

Se muestra un modelo de ejemplo:

10. Compruebe la exactitud del modelo en las tapetes de trabajo para multiplicar fracciones de los estudiantes y corrija cualquier malentendido.

11. Pida a los estudiantes que encuentren la tarjeta de expresión correspondiente, determinen una estimación y encuentren la tarjeta de solución para colocarla en sus tapetes de trabajo para multiplicar fracciones y formule las siguientes preguntas orientadoras:

a. ¿Qué operación estamos utilizando para resolver nuestra situación? Multiplicación

b. ¿Cómo sabes que estamos resolviendo con esa operación?

Las respuestas pueden variar. Estamos multiplicando porque estamos hallando una fracción de un conjunto.

c. ¿Cuáles son los factores de nuestra ecuación? 3/4 y 8

d. ¿Cómo podemos estimar el producto basándonos en el valor de los factores? 8 es un número entero y lo estamos multiplicando por una cantidad menor que 1 entero, por lo que el producto será menor que 8.

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

d. ¿El factor fraccionario es mayor o menor que la mitad? ¿Cómo afecta esto a tu estimación? 3/4 es mayor que 1/2; por lo tanto, sabemos que el producto será mayor que 1/2 de 8m que es 4.

e. ¿Cómo puedes completar los espacios en blanco para crear un enunciado estimativo en tu carpeta de trabajo multiplicar fracciones? El producto estará entre 4 y 8.

i. Pide a los estudiantes que completen el enunciado de estimación en sus tapetes de trabajo.

f. ¿Cómo podemos usar nuestro modelo para ayudarnos a determinar una solución? Cada sección del modelo representa 1 caja en el pedido, y 6 cajas están sombreadas. Por lo tanto, se han recibido 6 cajas.

g. ¿Cuál es el producto de nuestra expresión? 6

h. ¿Es razonable nuestro producto? Explícalo. Nuestra respuesta es menor que nuestro número entero porque nuestro número entero era 8 y nuestro producto era 6. Sabemos que esto es razonable porque estimamos que el producto estaría entre 4 y 8, y cuando multiplicas por una fracción, el producto será menor que el número entero.

17. Revisa las correspondencias de las tarjetas de cada pareja, los modelos y las estimaciones en sus tapetes de trabajo para multiplicar fracciones, y corrige cualquier malentendido.

18. Pide a las parejas que coloquen las tarjetas que acaban de usar en sus bolsas resellables y borren sus tapetes de trabajo para multiplicar fracciones. A continuación, pídales que seleccionen otra tarjeta de escenario y la coloquen en la parte superior de sus tapetes de trabajo.

19. Pídales que continúen trabajando con sus compañeros para representar los dos escenarios restantes utilizando sus fichas de colores, dibujen modelos en las tapetes de trabajo multiplicar fracciones, calculen los productos y encuentren las tarjetas de expresión y las tarjetas de solución correspondientes.

20. Compruebe el trabajo de los estudiantes a medida que completan cada escenario y formule preguntas orientadoras similares a las utilizadas anteriormente. Asegúrate de documentar su progreso y comprensión.

21. Después de que los estudiantes hayan completado todos los escenarios, haga las siguientes preguntas:

a. ¿Qué notas sobre el producto cuando multiplicas un número entero por una fracción? El producto es menor que el número entero.

b. ¿Por qué? Cuando multiplicamos cualquier número por 1, el producto es siempre ese número. Cuando multiplicas por cualquier número que es menor que 1, el producto tiene que ser menor que el factor del número entero porque sólo estamos tomando una parte del número entero.

c. ¿Qué notas sobre el producto cuando multiplicas un número entero por una fracción impropia? El producto será mayor que el número entero.

d. ¿Por qué? Cuando multiplicamos cualquier número por 1, el producto siempre es ese número. Cuando multiplicas por cualquier número que es mayor que 1, el producto tiene que ser mayor que el factor del número entero porque estamos repitiendo el número entero más de una vez.

22. Pide a los estudiantes que organicen y devuelvan sus materiales.

PARTE II: MULTIPLICAR FRACCIONES POR FRACCIONES

1. Entregue a cada pareja un tapete de trabajo de la parte II multiplicar fracciones, un juego de fichas de colores, dos marcadores borrables de diferentes colores y una bolsa de tarjetas de escenarios de la parte II.

2. Indique a las parejas que separen sus tarjetas de escenarios en tres montones: uno con los escenarios, otro con las expresiones y otro con las soluciones.

3. Pida que seleccionen la tarjeta de escenario que dice lo siguiente: Jorge posee 7/8 de un acre de tierra. Quiere utilizar 2/3 de ese acre para construir un granero. ¿Cuánto de un acre se utilizará para construir un granero?

4. Indique a los estudiantes que coloquen la tarjeta del escenario en la parte superior de sus tapetes de trabajo para multiplicar fracciones.

5. Anímelos a trabajar con sus compañeros para crear un modelo que represente ese escenario usando sus fichas de colores, y formule las siguientes preguntas:

a. ¿Qué información sabemos de nuestro problema? Sé que George posee 7/8 de un acre de tierra y quiere usar 2/3 de ese acre para construir un granero.

b. ¿Cómo podemos representar las fracciones usando fichas de colores? Las respuestas pueden variar. Sé que Jorge quiere usar 2/3 de su 7/8 acre de tierra para construir un granero, así que empezaré colocando siete fichas de un color en una fila y una ficha de color diferente como octava ficha para representar 7/8 de un acre de tierra.

Como estamos multiplicando 7/8 por 2/3 , hacemos 3 filas d 7/8 y contamos el número de 7 fichas en dos de tres filas.

Ejemplo de modelo de fichas de colores:

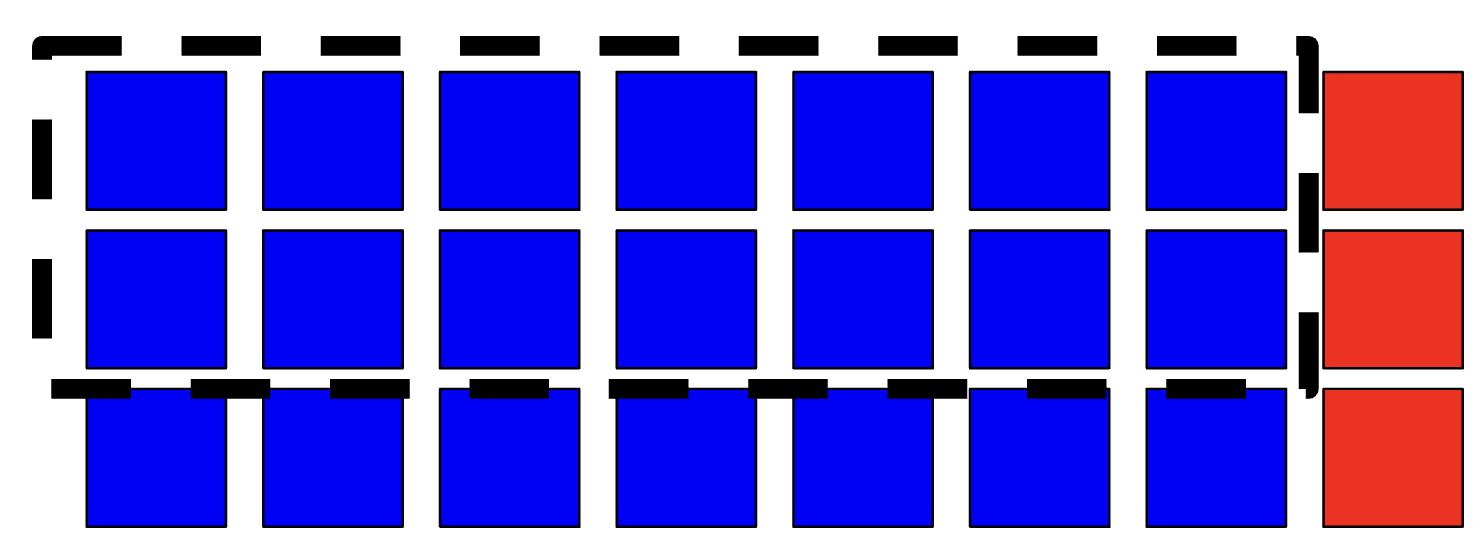
El número total de baldosas es nuestro denominador, y el número de 7 baldosas en 2 filas es nuestro numerador.

c. ¿Cuántas baldosas hay en total? 24 baldosas

d. ¿Cuál es el número de 7 baldosas en dos filas? 14 baldosas

e. ¿Qué es 7/8 × 2/3? 14/24

f. ¿Puede simplificarse 14/24? Sí, 14/24 es equivalente a 7/12.

12. Después de que los estudiantes hayan creado sus modelos utilizando sus fichas de colores, anímelos a compartir sus modelos y a explicar cómo representan el escenario.

13. Indíqueles que utilicen sus tapetes de trabajo para multiplicar fracciones para representar un modelo de sus fichas de colores y formule las siguientes preguntas orientadoras mientras trabajan:

a. ¿Cómo podemos representar 7/8 de nuestro modelo? Las respuestas variarán. Podemos hacer un modelo de área dibujando un rectángulo dividido en 8 partes y sombrear 7 de las 8 columnas con un marcador de un color.

b. ¿Cómo podemos representar 2/3 de nuestro modelo? Las respuestas variarán. Podemos hacer 2 filas más de 7/8 para que haya 3 filas con 7 de las 8 partes sombreadas de un color y luego sombrear 2 de las 3 filas con el marcador del otro color. Las partes donde los colores se superponen son el numerador del producto, y el número total de partes es el denominador del producto.

Se muestra un modelo de área de ejemplo:

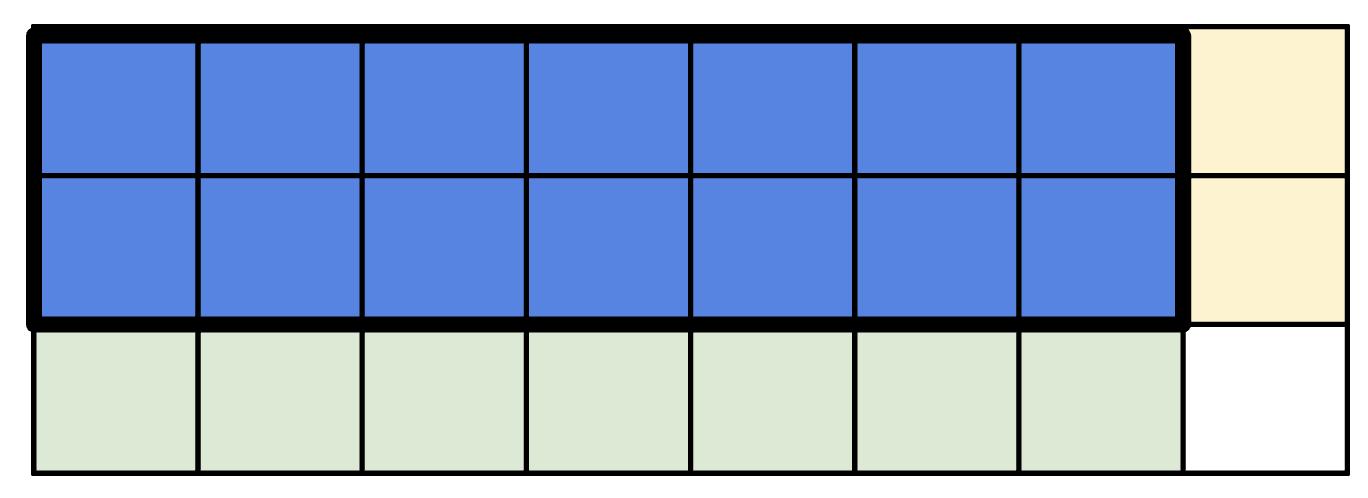
c. ¿Qué parte del acre se utilizará para construir el granero? 14/24, or 7/12, de un acre.

14. Pida a los estudiantes que encuentren la ecuación correspondiente y las tarjetas de solución para el escenario, y formule las siguientes preguntas guía:

a. ¿Qué operación estamos usando para resolver nuestro escenario? Multiplicación

b. ¿Cómo sabes que estamos resolviendo con esa operación? Estoy multiplicando porque estoy tomando una parte de una parte.

c. ¿Cuáles son los factores de nuestra ecuación? 2/3 y 7/8

d. ¿Cómo podemos estimar el producto basándonos en los valores de los factores? Ambos factores son menores que un entero, por lo que el producto será menor que ambas fracciones. 2/3 es menor que 7/8 y el producto será menor que cualquiera de los factores, por lo que el factor será menor que 2/3.

e. ¿Cómo puedes completar los espacios en blanco para crear un enunciado estimativo en tu carpeta de trabajo Multiplicar fracciones? El producto estará entre 0 y 2/3.

i. Pide a los estudiantes que completen el enunciado estimativo en sus tapetes de trabajo.

f. ¿Cómo se multiplica una fracción por otra fracción? Multiplicamos los numeradores juntos y los denominadores juntos.

g. ¿Cómo podemos representar la multiplicación de dos fracciones como una fracción? (7×2)/(8×3)

h. ¿Cuál es el producto de nuestra ecuación? 14/24 or 7/12

6. Compruebe las correspondencias de las tarjetas de cada pareja, los modelos y las estimaciones en sus tapetes de trabajo para multiplicar fracciones y corrige cualquier malentendido.

7. Pide a las parejas que vuelvan a colocar las tarjetas que acaban de usar en las bolsas resellables y que borren sus tapetes de trabajo para multiplicar fracciones. Pide a los estudiantes que seleccionen otra tarjeta de escenario y la coloquen en la parte superior de sus tapetes de trabajo.

8. Pídales que continúen trabajando con sus compañeros para representar los escenarios utilizando sus fichas de colores, que dibujen modelos en sus tapetes de trabajo para multiplicar fracciones, que calculen las respuestas y que encuentren las tarjetas de expresión y las tarjetas de solución correspondientes.

9. Compruebe el trabajo de los estudiantes a medida que completan cada escenario y formule preguntas similares a las utilizadas anteriormente. Asegúrate de documentar su progreso y comprensión.

10. Después de que los estudiantes hayan completado todos los escenarios, haga las siguientes preguntas:

a. ¿Qué notas sobre el producto cuando multiplicas una fracción por otra fracción? Al multiplicar una fracción por otra fracción, el producto será menor que cualquiera de los factores porque sólo estamos tomando una parte. No lo estamos repitiendo una vez; estamos multiplicando una fracción por otra fracción, que es menor que 1.

b. ¿Por qué cambia el denominador cuando multiplicamos fracciones? Estás separando la fracción original en grupos más iguales de partes de fracción. El denominador te dice cuántas partes hacen falta para formar un todo. Las partes totales cambian porque los denominadores originales se están dividiendo en partes más pequeñas.

c. Antes de empezar a representar o multiplicar, ¿cómo puedes estimar cuál será el producto al multiplicar una fracción por una fracción? Sé que puedo estimar que el producto será menor que cualquiera de las fracciones porque sólo estoy multiplicando una parte de una parte.

11. Pida a los estudiantes que organicen y devuelvan sus materiales.

PARTE III: RELACIÓN DE ESCALA

1. Entregue un tapete de trabajo para multiplicar fracciones de la parte III, un juego de fichas de colores, dos marcadores borrables de diferentes colores y una bolsa de tarjetas de escenario de la parte III a cada par de estudiantes.

2. Pida a los estudiantes que seleccionen la tarjeta de escenario que dice lo siguiente: «David tiene un jardín de 10 pies de largo y 5 pies de ancho. Diane tiene un jardín que es la mitad de largo que el de David pero tiene el mismo ancho. Sin multiplicar, compare las áreas de los jardines de David y Diane».

3. Explique a los estudiantes que trabajarán con sus compañeros para conversar y razonar sobre cómo los tamaños de los jardines son similares y diferentes y cómo lo saben, basándose en la relación de las medidas de cada elemento.

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

4. Pídales que trabajen con sus compañeros para crear un modelo concreto de cada parte del escenario utilizando sus fichas de colores.

5. Pida a los estudiantes que anoten sus modelos en sus tapetes de trabajo para multiplicar fracciones. Cada modelo de jardín en su tapete de trabajo debe dibujarse utilizando marcadores borrables de diferentes colores para que puedan identificar fácilmente cada modelo y revisar las similitudes y diferencias en los modelos.

6. Haga las siguientes preguntas guía mientras los estudiantes crean un modelo de cada jardín:

a. ¿Cómo puedes representar el modelo para el jardín de David? Las respuestas variarán. Podemos utilizar las baldosas de colores y hacer un modelo que tenga 10 baldosas de largo y cinco de ancho. Podemos dibujar una matriz que tenga cinco filas con 10 cuadrados en cada fila. Podemos dibujar un rectángulo y etiquetar la longitud como 10 pies y la anchura como 5 pies.

b. ¿Qué sabemos sobre el jardín de Diane? Su longitud es la mitad de la de David, pero tiene la misma anchura.

c. ¿Crees que el área del jardín de Diane será mayor o menor que el área del jardín de David? Las respuestas pueden variar. Creo que la superficie del jardín de Diane será menor.

d. ¿Por qué crees que será mayor/menor? Las respuestas pueden variar. Creo que será menor porque uno de los lados es igual pero el otro es más pequeño.

e. ¿Cómo podemos representar el modelo del jardín de Diane? Las respuestas pueden variar. Podemos utilizar las baldosas de colores y hacer una maqueta que tenga cinco baldosas de largo y cinco de ancho. Podemos dibujar una matriz que tenga cinco filas con cinco cuadrados en cada fila. Podemos dibujar un rectángulo y etiquetar la longitud con 5 pies y la anchura con 5 pies.

f. ¿Qué notas acerca de las longitudes y anchuras de cada jardín? Observo que las anchuras son iguales, pero la longitud del jardín de Diane es la mitad que la del jardín de David.

7. Haga hincapié en que los estudiantes no están resolviendo el área; simplemente están comparando los jardines. Si los estudiantes están multiplicando los números, aléjelos de esa estrategia y recuérdeles que esta actividad es sólo para razonar. Explíqueles que lo que buscan no es el producto real, sino la comparación de tamaños.

8. Después de que los estudiantes hayan modelado los jardines, desafíe a las parejas a comparar cada modelo y a encontrar similitudes y diferencias entre los modelos, y luego formule las siguientes preguntas orientadoras:

a. ¿Qué permaneció igual en ambos modelos? El ancho es la mismo.

b. ¿Cómo cambiaron las medidas? La longitud del jardín de Diane era la mitad de la longitud del jardín de David.

c. ¿Qué puedes concluir acerca de cómo se compara el área del jardín de David con el área del jardín de Diane? El jardín de David es el doble de grande que el jardín de Diane porque la longitud del jardín de Diane es la mitad de la longitud del jardín de David.

i. Pide a los estudiantes que anoten sus conclusiones sobre la comparación en sus tapetes de trabajo para multiplicar fracciones.

9. Revisa el trabajo y razonamiento de los estudiantes para asegurarte de que entienden las similitudes y diferencias de escala entre los modelos, y corrige cualquier malentendido.

10. Pida a los estudiantes que borren sus Tapetes de trabajo Multiplicar fracciones, seleccionen otra Tarjeta de situación y continúen modelando y razonando a través de las similitudes y diferencias entre los modelos.

11. Supervise mientras continúan trabajando juntos y haga preguntas de orientación según sea necesario.

12. Una vez que los estudiantes hayan completado todas las tarjetas de situación, formule las siguientes preguntas a la clase:

a. ¿Qué sucedería con el área si disminuyera la longitud de uno de los lados? ¿Por qué lo crees? El área también disminuiría. La longitud y la anchura de un rectángulo afectan al espacio del área. Si cambiara la longitud de uno de los lados, también lo haría el área.

b. ¿Y si aumentara la longitud de uno de los lados? ¿Por qué lo crees? El área también aumentaría. La longitud y la anchura de un rectángulo afectan al espacio del área. Si cambiara la longitud de uno de los lados, también lo haría el área.

c. ¿Era necesario multiplicar para calcular el área redimensionada? ¿Por qué? No, porque el área será mayor o menor en función de lo que ocurra con uno o ambos lados.

d. Explica cómo has determinado el redimensionamiento. Si el largo o el ancho disminuyeron en 1/2, 1/4, o cualquier otra fracción, entonces el área también disminuyó en esa misma cantidad. Si era la mitad, entonces sabíamos que teníamos que dividir por dos. Si era 1/4 del tamaño, entonces teníamos que dividir por 4. Si se duplicaba, entonces sabíamos que teníamos que multiplicar por 2. Si ambos lados se redujeron, entonces teníamos que multiplicar ambas fracciones juntas para determinar cómo se redujo el área.

13. Pida a los estudiantes que organicen y devuelvan sus materiales.

14. Después, dé tiempo para que los estudiantes completen la comprobación individualmente.

ACELERACIÓN: MATEMÁTICAS DE HOY

CONEXIONES CON EL MUNDO REAL Una casa para las abejas

En Maine se le recomienda a las personas que construyan en su patio casas nido para las abejas. Esto ayudará al crecimiento de la población de las abejas, y a que continúen su importante labor de transportar polen para que podamos tener arándanos rojos, arándanos azules y otras deliciosas frutas. Las dimensiones en pulgadas de una casa nido para abejas se muestran a continuación.

in 6 in

1. Se perforarán agujeros en la parte delgada de la casa para abejas para que las abejas entren y salgan. ¿Cuál es el área de este lado? Usa un modelo y escribe una expresión para resolver.

MATEMÁTICAS DE HOY: UN HOGAR PARA LAS ABEJAS

DESCRIPCIÓN

Los estudiantes explorarán las conexiones y aplicaciones de las matemáticas y otros contenidos transversales a través de interacciones con medios auténticos del mundo real proporcionados por Associated Press.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Permita que los estudiantes vean el vídeo. Explique brevemente que los abejorros pueden acceder a las flores de ciertas plantas que otros insectos no pueden. Esto permite a las abejas transportar el polen de una planta a otra para que puedan seguir creciendo y produciendo más frutos.

2. Conversación:

a. Deje que los estudiantes compartan con ellos las afirmaciones «me doy cuenta...» y «me pregunto...». Pregunte a los estudiantes cómo se utilizan las matemáticas en esta situación.

Model Fraction Multiplication

2. ¿Cuál es el área del frente de la casa? Usa un modelo y escribe una expresión para resolver.

3. Una de los voluntarias corta las tablas para la parte de atrás de la casa nido. Tiene que cortar cada tabla de 5 pulgadas de largo. Corta 15 paneles en la siguiente hora. ¿Cuántas pulgadas de madera usó? Usa un modelo y escribe una expresión para mostrar tu solución.

FOLLETO DEL ESTUDIANTE

b. Ciento seis voluntarios se han apuntado para ayudar con el censo de abejas. Alrededor de 3/4 de esos voluntarios han podido capturar abejas y recoger datos sobre ellas. Aproximadamente, ¿cuántos voluntarios han capturado abejas? (Redondea al número entero más próximo.)

n = 106 × 3/4

n = 106/1 × 3/4 = 318/4 = 79.5

Unos 80 voluntarios han capturado abejas.

c. Un grupo de voluntarios capturó 1/8 del total de abejas recolectadas. Si se recogieron 248 abejas, ¿cuántas capturó este grupo?

n = 248 × 1/8

n = 248/1 × 1/8 = 248/8 = 31 abejas

3. Los estudiantes deben completar la hoja del estudiante de forma independiente o con un compañero.

ACELERACIÓN: CREA EL TUYO

ESTABLECER CONEXIONES RELEVANTES

CREA EL TUYO

DESCRIPCIÓN

Crea el tuyo es una actividad enriquecedora para que los estudiantes puedan crear sus propios inventos, obras de teatro, canciones, aplicaciones tecnológicas, ¡y mucho más!

MATERIALES

IMPRIMIR

• 1 material «crea el tuyo» para el estudiante (por estudiante)

• 1 material «crea el tuyo» (para el maestro)

REUTILIZABLE

• Herramientas y modelos matemáticos (por clase) CONSUMIBLE

• Materiales para crear juegos, obras de teatro e inventos

PREPARACIÓN

Ninguna

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un material «crea el tuyo» por estudiante.

2. Deles tiempo para que sean lo más creativos posible. No hay límites para su creatividad en esta actividad.

3. Invite a cada estudiante a presentar o representar su producto ante la clase o el pequeño grupo.

El padre de tu amiga tiene varios empleados. Necesita un programa de computadora que le sirva para determinar sus salarios cuando trabajan durante una fracción del día. ¿Puedes ayudar?

Genera tus ideas.

Haz una lista de los materiales que necesitas.

Dibuja tu programa de computadora aquí o desarróllalo en una computadora.

Crea una presentación digital para convencer al padre de tu amigo de que use el programa de computadora que tú diseñaste.

FOLLETO DEL ESTUDIANTE

ACELERACIÓN: TABLERO DE OPCIONES

Model Fraction Multiplication

Multiplicación de modelos de fracciones

Elige una o varias actividades de ampliación de la tabla a continuación.

Conex ón con la ectura Conex ón con el arte

Cuento de matemáticas

Completa la actividad para el cuento de matemáticas «Los bomberos y su cena de panqueques». Crea 5 preguntas sobre el cuento, incluida una clave de respuestas, que impliquen multiplicar fracciones para resolverlas. Intercambia tus preguntas con un compañero.

Conexión profes ona

Chef

Completa la actividad conexiones profesionales. Busca tu receta favorita. Calcula y reescribe la receta para servir 5 veces la cantidad original.

Conex ón con a tecnolog a

Recarga de robots

Haz el juego de la práctica interactiva Recarga de robots. Resuelve cada problema en una hoja de papel. ¿Qué patrones observaste?

Tira cómica

Dibuja o crea digitalmente una tira cómica en la que se multipliquen fracciones por fracciones. Incluye fracciones mayores que un entero. Utiliza modelo pictóricos para mostrar cómo resolver los productos. Comparte tu tira cómica con la clase.

Conexión en casa

Fracciones de un grupo

Escribe afirmaciones de «Si..., entonces...» sobre tu casa o tu escuela que impliquen fracciones de un grupo. Por ejemplo, podrías darte cuenta de que tu edificio de apartamentos tiene 18 apartamentos, así que podrías escribir: «Si dos tercios de los 18 apartamentos tuvieran tapetes, entonces habría 12 tapetes».

Conex ón con a ngeniería

Hacer nudos

Investiga formas de hacer nudos. Luego corta un trozo de cuerda o hilo a una longitud fraccionaria en pulgadas. Practica diferentes nudos. ¿Cuánta cuerda o hilo necesitarías si 3 amigos también quisieran practicar nudos? ¿Y 8 amigos? Muestra cómo calcular la longitud total necesaria con tu estrategia favorita.

TABLERO DE OPCIONES

OPCIONES PARA EL APRENDIZAJE CONTINUO

TABLERO DE OPCIONES

DESCRIPCIÓN

Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.

MATERIALES

IMPRESO

• 1 tablero de opciones (por estudiante)

REUTILIZABLE

• Tecnología (si procede)

PREPARACIÓN

• Imprima un tablero de opciones por estudiante.

• Planifique con antelación el uso de la tecnología. Es posible que se necesite acceso a otras actividades dentro del alcance para algunas variaciones del tablero de opciones.

• Esta actividad se puede completar en clase o en casa.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un tablero de opciones a cada estudiante.

2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.

3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.

4. Si el tiempo lo permite, pida a los estudiantes que compartan las conexiones que hicieron al completar las actividades que eligieron.