

GRADO 8

CALIFORNIA
Muestra de la edición para el maestro
Muestra de la edición para maestros Grado 8
Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.
Para obtener más información, visítenos en www.stemscopes.com.
TEOREMA DE PITÁGORAS
ESTÁNDARES CLAVE
Comprender y aplicar el teorema de Pitágoras.
• Explicar una demostración del teorema de Pitágoras y su recíproco.
• Aplicar el teorema de Pitágoras para determinar longitudes laterales desconocidas en triángulos rectángulos en problemas matemáticos y del mundo real en dos y tres dimensiones.
• Aplicar el teorema de Pitágoras para encontrar la distancia entre dos puntos en un sistema de coordenadas.
ESTÁNDARES DE CONEXIÓN
Trabajar con radicales y exponentes enteros.
• Conocer y aplicar las propiedades de los exponentes enteros para generar expresiones numéricas equivalentes. Por ej., 32 × 3-5 = 3-3 = 1/ 33 = 1/27 .
• Utilizar los símbolos de raíz cuadrada y raíz cúbica para representar soluciones a ecuaciones de la forma x² = p y x³ = p, donde p es un número racional positivo. Evaluar raíces cuadradas de pequeños cuadrados perfectos y raíces cúbicas de pequeños cubos perfectos. Saber que √ 2 es irracional.
ACTIVIDADES DE PARTICIPACIÓN
ACCESO A CONOCIMIENTOS PREVIOS: ACUERDO O DESACUERDO
Los estudiantes se involucran en el pensamiento crítico evaluando las respuestas de sus compañeros a una pregunta matemática y articulando su razonamiento.
• Los estudiantes evalúan de forma independiente si están de acuerdo o en desacuerdo con las respuestas dadas por los estudiantes y explican su razonamiento.
• Utilizan transportadores y reglas para apoyar sus evaluaciones.
• Los estudiantes participan en una discusión dinámica en clase, formando parejas para compartir y discutir sus respuestas con sus compañeros.
• La actividad concluye con una discusión en clase para abordar los conceptos erróneos y reforzar la comprensión de las propiedades y clasificaciones de los triángulos.
CAPTAR INTERÉS
Los estudiantes exploran el teorema de Pitágoras para resolver problemas reales relacionados con triángulos rectángulos.
• Los estudiantes empiezan observando un escenario de golf y discutiendo los conceptos matemáticos implicados en el juego.
• Se les presenta el teorema de Pitágoras y lo aplican para determinar los lados que faltan en triángulos rectángulos.
• Después de completar las actividades exploratorias, los estudiantes vuelven a visitar el escenario para aplicar sus nuevos conocimientos.
• Como ampliación, los estudiantes diseñan sus propios hoyos del campo de golf utilizando el teorema de Pitágoras para incorporar obstáculos y calcular distancias.
ACTIVIDADES DE EXPLORAR
EXPLORACIÓN 1: REPRESENTAR EL TEOREMA DE PITÁGORAS Y EL RECÍPROCO
Los estudiantes exploran el teorema de Pitágoras a partir de la representación y la aplicación prácticas. Trabajarán en parejas para profundizar su comprensión de los triángulos rectángulos y el recíproco del teorema.
• Usan modelos para demostrar el teorema de Pitágoras hallando el área de cuadrados conectados a triángulos rectángulos.
• Aplican la inversa del teorema de Pitágoras para identificar triángulos rectángulos sin utilizar un transportador.
• La actividad consiste en recortar y ordenar formas para representar visualmente conceptos matemáticos, fomentando el aprendizaje colaborativo.
• Participan en debates para compartir estrategias y observaciones, mejorando su comprensión a través de la interacción entre iguales.
EXPLORACIÓN 2: ENCONTRAR UNA LONGITUD DE LADO DESCONOCIDA EN TRIÁNGULOS RECTÁNGULOS
Los estudiantes aplican el teorema de Pitágoras para resolver las longitudes laterales que faltan en triángulos rectángulos utilizando herramientas prácticas y la resolución de problemas en colaboración.
• Los estudiantes trabajan en parejas utilizando tableros geométricos para recrear triángulos rectángulos y calcular la hipotenusa midiendo y aplicando el teorema de Pitágoras.
• Participan en debates guiados para profundizar en la comprensión y compartir estrategias para encontrar las longitudes de los lados que faltan.
• Los estudiantes utilizan tarjetas para determinar los catetos que faltan en los triángulos rectángulos, aplicando la resta en el teorema de Pitágoras.
• La actividad concluye con una charla de matemáticaspara reflexionar sobre el aprendizaje y una ficha de salida para evaluar la comprensión.
EXPLORACIÓN 3: EL TEOREMA DE PITÁGORAS EN PRISMAS RECTANGULARES
Los estudiantes exploran la aplicación del teorema de Pitágoras a prismas rectangulares tridimensionales.
• Los estudiantes trabajan en parejas para construir prismas rectangulares utilizando los materiales proporcionados y calculan la longitud de la diagonal utilizando el teorema de Pitágoras.
• Participan en discusiones guiadas y ejercicios de resolución de problemas para profundizar en su comprensión de los conceptos geométricos y sus aplicaciones en el mundo real.
• La actividad incluye la construcción práctica, reflexiones en el diario y un chat de matemáticas para facilitar el aprendizaje colaborativo y el intercambio de estrategias.
• Los estudiantes completan un boleto de salida para evaluar su comprensión de los conceptos clave de la lección.
EXPLORACIÓN 4: EL TEOREMA DE PITÁGORAS EN UNA CUADRÍCULA DE COORDENADAS
Los estudiantes exploran la aplicación del teorema de Pitágoras para determinar distancias en una cuadrícula de coordenadas.
• Los estudiantes trabajan en parejas para trazar puntos y formar triángulos rectángulos en una cuadrícula de coordenadas, utilizando cubos numéricos para generar pares ordenados.
• Calculan las longitudes de los lados de los triángulos utilizando el teorema de Pitágoras, con la ayuda de calculadoras.
• La actividad incluye preguntas guiadas para facilitar la comprensión y la reflexión, seguidas de una charla de matemáticas para discutir observaciones y estrategias.
• Los alumnos completan un diario del estudiante y un boleto de salida para evaluar su comprensión y aplicar su aprendizaje a un escenario del mundo real.
ALCANCE: IDEAS FUNDAMENTALES

TRANSFORMATIONAL GEOMETRY

SHAPE, NUMBER & EXPRESSIONS

CYLINDRICAL INVESTIGATIONS









Los estudiantes aplican el teorema de Pitágoras para resolver problemas del mundo real que implican calcular las distancias o diagonales en formas tridimensionales. Por ej., al trabajar con prismas rectangulares, usan el teorema para hallar la longitud de la diagonal aplicando la fórmula a2 + b2 = c2, que ayuda a determinar si un objeto cabe en un espacio o a comprender cómo se relacionan ciertas dimensiones con la estructura general. Esta conexión entre el teorema de Pitágoras y las formas tridimensionales es esencial para resolver problemas relacionados con el volumen y la superficie de objetos cilíndricos y otras figuras geométricas.






PYTHAGOREAN EXPLORATIONS


CONCEPTOS CLAVE
• Puedo explicar utilizando una demostración con un modelo del teorema de Pitágoras.
• Puedo usar mis habilidades de razonamiento para determinar que la inversa del teorema de Pitágoras también debe ser cierta.
• Puedo aplicar el teorema de Pitágoras para determinar el valor de un lado desconocido de un triángulo rectángulo bidimensional o tridimensional en problemas matemáticos o del mundo real.
• Puedo usar el teorema de Pitágoras para calcular la distancia entre dos puntos en un plano de coordenadas.
Los estudiantes se comprometen con los conceptos fundamentales de transformación geométrica mediante el desarrollo de habilidades esenciales para la comprensión de las relaciones geométricas en el plano de coordenadas. Aprenden a determinar las distancias entre puntos con el teorema de Pitágoras, que permite trazar figuras en el plano de coordenadas. Esta habilidad fundamental es crucial para analizar posteriormente movimientos como traslaciones y rotaciones dentro del marco de la geometría transformacional. Al relacionar las propiedades de los cuadrados con los triángulos rectángulos, los estudiantes se inician en el razonamiento proporcional. La aplicación de estos conceptos en contextos tridimensionales mejora el razonamiento espacial, necesario para visualizar transformaciones complejas en varias dimensiones. Esta comprensión apoya su capacidad para mantener las propiedades de congruencia o semejanza, esenciales para los principios de la transformación geométrica.
Los estudiantes usan el teorema de Pitágoras para calcular la diagonal de un cuadrado o un prisma rectangular y aplican estos cálculos al analizar problemas geométricos del mundo real relacionados con la forma, el área y el volumen.
Los estudiantes realizan investigaciones en el plano de coordenadas para comprender la aplicación del teorema de Pitágoras a los triángulos rectángulos. Con herramientas como las pizarras geométricas y las calculadoras gráficas, exploran cómo los cuadrados de los catetos de un triángulo rectángulo suman el cuadrado de la hipotenusa, reforzando el concepto de relaciones geométricas. Esto se aplica a situaciones del mundo real, en las que resuelven las longitudes de los lados que faltan en los triángulos rectángulos y trabajan con números irracionales al tratar con raíces cuadradas. Este enfoque práctico profundiza su comprensión del teorema de Pitágoras y los prepara para resolver problemas geométricos más complejos.
PREGUNTAS FUNDAMENTALES
• Define el teorema de Pitágoras.
• Explica cómo sabes que la inversa del teorema de Pitágoras también debe ser cierta.
• Explica el proceso de aplicación del teorema de Pitágoras.
• Describe el proceso de utilización del teorema de Pitágoras para hallar la distancia entre dos puntos de un plano de coordenadas.
INICIO: CONTENIDO DE APOYO
¿QUÉ ESTOY ENSEÑANDO?
CONTENIDO DE APOYO
Comprender y aplicar el teorema de Pitágoras.
• Explicar una demostración del teorema de Pitágoras y su inversa.
• Aplicar el teorema de Pitágoras para determinar longitudes desconocidas de lados en triángulos rectángulos en problemas matemáticos y del mundo real en dos y tres dimensiones.
• Aplicar el teorema de Pitágoras para encontrar la distancia entre dos puntos en un sistema de coordenadas.
CONOCIMIENTOS PREVIOS
En 6.ºgrado, los estudiantes aprendieron a calcular la distancia entre dos puntos en el plano de coordenadas. Hallaron la distancia de rectas horizontales y verticales mediante el conteo. En 7.º grado, descubrieron los triángulos singulares, explorando cómo los ángulos y lados de los triángulos representan su clasificación. Los estudiantes comprenden los números irracionales y racionales y han conocido las raíces cuadradas y su significado. Estos conceptos serán importantes cuando descubran el teorema de Pitágoras y su inverso.
CONCEPTOS ERRÓNEOS Y OBSTÁCULOS
• Los estudiantes deberán tener confianza en su conocimiento de los números racionales e irracionales.
• Pueden tener la impresión de que todos los triángulos rectángulos darán como resultado longitudes enteras. Deben practicar la resolución de problemas con longitudes racionales e irracionales, enteras y no enteras.
• Mientras que las longitudes a y b son intercambiables, la longitud c debe ser la hipotenusa y no puede ser cualquiera de los tres números.
• Pueden creer que el teorema de Pitágoras es válido para todos los triángulos. Deben recordar que sólo sirve para triángulos con un ángulo recto.
• Hay que distinguir bien entre el teorema de Pitágoras y su inverso. La inversa invierte la idea de cualquier teorema. Por ejemplo, si llueve, jugaré dentro. Inverso: Si juego dentro, llueve.
EN ESTE ALCANCE
En este alcance, los estudiantes serán capaces de explicar el teorema de Pitágoras y su inverso. Definirán el teorema de Pitágoras como dado un triángulo rectángulo con lados a y b e hipotenusa c, entonces a2 + b2 = c2. Comprenderán que su inversa es si un triángulo con lados a y b e hipotenusa c satisface la ecuación a2 + b2 = c2, entonces el triángulo es rectángulo. Utilizarán estos teoremas para calcular los lados desconocidos de un triángulo rectángulo, así como para hallar la distancia entre dos puntos en una cuadrícula de coordenadas. Los estudiantes serán capaces de expresar los lados de los triángulos en forma radical cuando sea necesario.
TÉRMINOS CLAVE
• figuras congruentes: figuras con el mismo tamaño y forma.
• inversa del teorema de Pitágoras: teorema que establece que si el cuadrado de la longitud del lado más largo de un triángulo es igual a la suma de los cuadrados de los otros dos lados, entonces el triángulo es rectángulo; si c2 = a2 + b2, entonces es un triángulo rectángulo.
• distancia: medida de la longitud entre dos puntos.
• exponente: notación matemática que indica el número de veces que el número base se multiplica por sí mismo; también se llama potencia.
• altura: distancia perpendicular de un vértice al lado opuesto de una figura.
• hipotenusa: el lado más largo del triángulo rectángulo, el lado opuesto al ángulo recto.
• número irracional: un número decimal que no puede expresarse como fracción, no es imaginario y no se repite ni termina.
• cateto: cualquiera de los dos lados de un triángulo rectángulo que forman el ángulo recto y son opuestos a los ángulos agudos.
• cuadrado perfecto: un número entero que es el resultado de otro número entero multiplicado por sí mismo.
• teorema de Pitágoras: teorema que establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados de un triángulo rectángulo; a2 + b2 = c2.
• número racional: un número que puede escribirse como fracción de enteros a/b donde b ≠ 0; Un número que puede escribirse como cociente utilizando dos enteros.
• ángulo recto: un ángulo que mide 90º.
• triángulo rectángulo: un triángulo con un ángulo de 90º.
• figuras similares: dos o más figuras que tienen la misma forma pero tamaños diferentes.
• raíz cuadrada: un número que, al multiplicarse por sí mismo, produce el número dado.
INICIO: CONTENIDO DE APOYO
APLICAR LAS PRÁCTICAS MATEMÁTICAS
• MP.1 Dar sentido a los problemas y perseverar en su resolución: Los estudiantes son capaces de identificar los dos catetos y la hipotenusa de un triángulo rectángulo basándose en la longitud de cada lado. Cuando falta la longitud de uno de los lados del triángulo rectángulo, usan el teorema de Pitágoras para resolver el cateto o la hipotenusa que falta.
• MP.2 Razonar abstracta y cuantitativamente: Los estudiantes descontextualizan problemas para usar el teorema de Pitágoras para hallar las diagonales en prismas rectangulares. Una vez halladas, aplican lo encontrado al contexto del problema.
• MP.3 Construir argumentos viables y criticar el razonamiento de otros: Los estudiantes construyen argumentos sobre la búsqueda de diagonales en prismas rectangulares. Aplican lo aprendido sobre diagonales de prismas rectangulares a otras situaciones y justifican su proceso de pensamiento.
• MP.4 Representar con matemáticas: Los estudiantes analizan cajas dadas en forma de prismas rectangulares tridimensionales y calculan la longitud de la diagonal del prisma. Usan ese conocimiento para determinar qué puede caber en las cajas.
• MP.5 Utilizar estratégicamente las herramientas adecuadas: Los estudiantes usan tableros geométricos para explorar la construcción de triángulos rectángulos. Con geotableros, siempre crean un ángulo de 90 grados con dos de los catetos del triángulo.
• MP.6 Prestar atención a la precisión: Los estudiantes necesitan ser precisos a la hora de determinar si sus respuestas son racionales o irracionales. Son capaces de escribir números irracionales de diferentes formas, como radicales y símbolos como π. Encuentran la longitud precisa del lado de un triángulo prestando atención a teoremas y fórmulas.
• MP.7 Buscar y hacer uso de la estructura: Los estudiantes hacen uso de la estructura del teorema de Pitágoras e identifican si los triángulos son rectángulos o no basándose en este teorema. También comprenden la diferencia entre los catetos y la hipotenusa para mantener la estructura de la fórmula.
• MP.8 Buscar y expresar regularidades en razonamientos repetidos: Los estudiantes buscan regularidades al encontrar patrones en los triángulos pitagóricos. Observan la relación entre los cuadrados de los catetos y los cuadrados de la hipotenusa en un triángulo rectángulo. Determinan patrones que son válidos para triángulos rectángulos frente a triángulos no rectángulos.
DEMOSTRAR EL TEOREMA DE PITÁGORAS
Los estudiantes modelizarán la demostración del teorema de Pitágoras. Razonarán que la inversa del teorema de Pitágoras también es cierta.
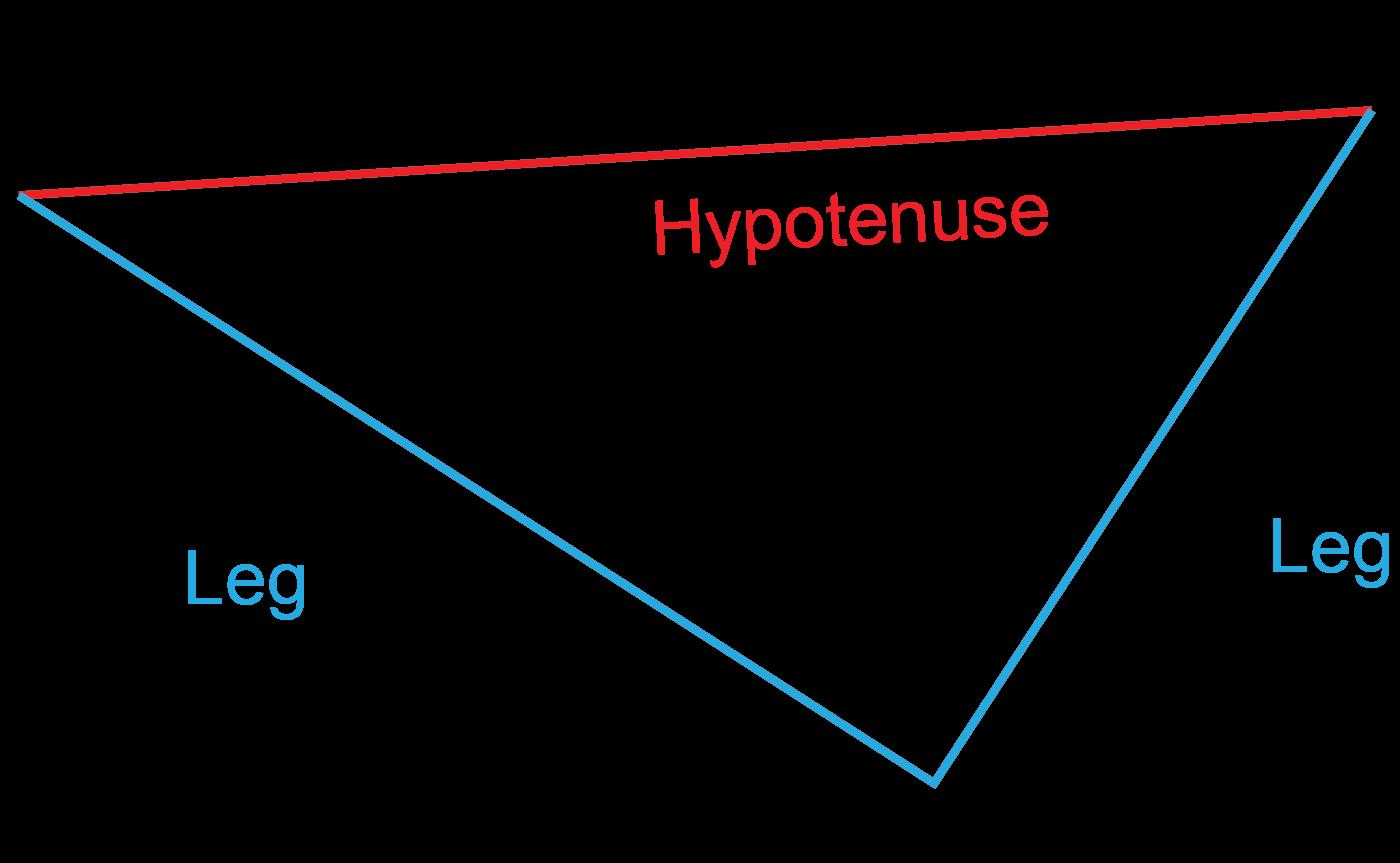
La siguiente figura muestra un triángulo rectángulo con lados j, k, y m

¿Cuál de las siguientes relaciones entre j, k, y m es verdadera?
a j2 + k2 = m2
b m2 + j2 = k2
c j2 = m2 + k2
d k2 = j2 + m2
La respuesta correcta es la opción C. Los estudiantes deben saber que la hipotenusa es el lado que está al otro lado del ángulo recto. Entonces deben seguir el teorema de Pitágoras colocando la suma del cuadrado de los dos catetos (m y k) en un lado de la ecuación con el cuadrado de la hipotenusa (j) en el otro lado.
INICIO: CONTENIDO DE APOYO
Ejemplo 2: Existe un triángulo cuyos catetos miden 4 y 8 y cuya hipotenusa mide √ 80. ¿Es un triángulo rectángulo? Explica tu respuesta.
La respuesta correcta es la siguiente: sí, se trata de un triángulo rectángulo porque satisface el teorema de Pitágoras. (Ten en cuenta que las razones pueden variar.) Los estudiantes deben reconocer esto como la inversa pitagórica. Si los números cumplen el teorema de forma que a2 + b2 = c2 entonces es un triángulo rectángulo. Introduciendo a = 4, b = 8 y c = √80, los estudiantes encontrarán que 42 + 82 =( √80)2; 16 + 64 = 80; 80 = 80. Debido a que ambos lados de la ecuación son iguales, el teorema se cumple; por lo tanto, el triángulo es un triángulo rectángulo.
LONGITUD DESCONOCIDA
Los estudiantes encontrarán una longitud desconocida en triángulos rectángulos. Usarán el teorema de Pitágoras para determinar la longitud que falta.
Ejemplo: ¿Cuál es el valor de x en la figura de abajo?

a 8 b 4
c 64 d √ 8
La respuesta correcta es la opción A. Como este es un triángulo rectángulo, los estudiantes necesitarán usar el teorema de Pitágoras para encontrar el lado faltante del triángulo. Sustituyendo a = 6, b = x, y c = 10, en la fórmula encontrarán que 62 + x2 =102 ; 36 + x2 =100. Después de restar 36 de ambos lados y sacar la raíz cuadrada, encontrarán que x2 = 64; x = 8.
TRIÁNGULOS SEMEJANTES
Los estudiantes usarán el teorema de Pitágoras para resolver problemas de semejanza de triángulos.
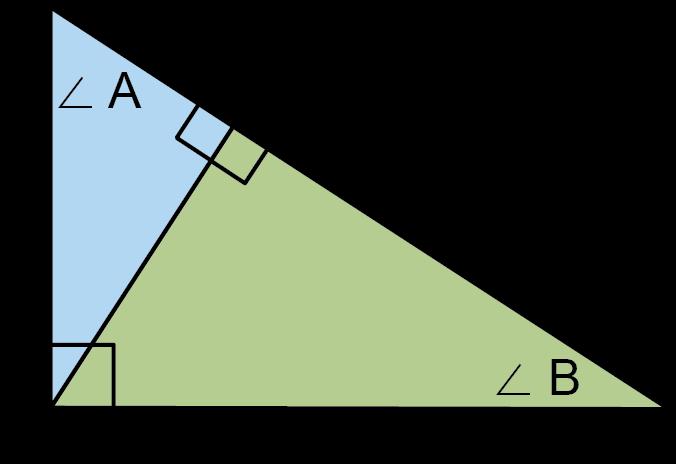
Ejemplo: Crea un triángulo que sea semejante al triángulo de abajo. (Pista: Usa el teorema de Pitágoras.)

Las respuestas pueden variar. Los estudiantes usarán el teorema de Pitágoras para determinar que el cateto que falta en el triángulo original es 9. (92 + 122 = 152). Un triángulo rectángulo con una hipotenusa igual al cateto de otro triángulo con un ángulo igual proporcionará dos ángulos semejantes mediante el Teorema de Semejanza Ángulo-Ángulo. Puedes ver a continuación que tanto el triángulo original como el nuevo triángulo comparten ∠A. Al compartir un ángulo y tener ambos triángulos un ángulo recto, se demuestra que estos triángulos son semejantes. Los estudiantes también podrían haber mostrado un triángulo con hipotenusa 12 (el triángulo verde) con ∠B compartido.
ENCONTRAR LA ALTURA OBLICUA
Los estudiantes usarán el teorema de Pitágoras para encontrar las alturas oblicuas faltantes en figuras tridimensionales.
Ejemplo: Halla la altura oblicua de la pirámide cuadrada con una longitud de 4 unidades y una altura de 10 unidades.

DISTANCIA ENTRE PUNTOS
Los estudiantes hallarán la distancia entre dos puntos en un gráfico usando el teorema de Pitágoras.
Ejemplo: ¿Cuál es la distancia entre los dos puntos de la siguiente gráfica?

a 4 b 5 c √ 29 d 29
La respuesta correcta es la opción C Para encontrar la distancia entre los puntos A y B, los estudiantes necesitarán crear un triángulo rectángulo. A continuación, utilizarán el teorema de Pitágoras para hallar la hipotenusa del triángulo. Ésta será la distancia entre los puntos A y B. Después de crear el triángulo, pueden contar una distancia de dos para el cateto horizontal y una distancia de 5 para el cateto vertical. Sustituyendo esto en la fórmula encontrarán que 22 + 52 = c2; 4 + 25 = c2; 29 = c2; √29 = c

AVANCES
Los estudiantes usarán estos conceptos en los próximos alcances de 8.º grado cuando determinen el volumen de figuras tridimensionales. El teorema de Pitágoras también establece la base para la congruencia de triángulos que se ampliará en la escuela secundaria. Los estudiantes usarán esta entrada en las raíces cuadradas a medida que continúan trabajando con radicales y raíces cuadradas a medida que se extienden en la simplificación de radicales en álgebra 1
ESTÁNDARES
Comprender y aplicar el teorema de Pitágoras.
• Explicar una demostración del teorema de Pitágoras y su inversa.
• Aplicar el teorema de Pitágoras para determinar longitudes laterales desconocidas en triángulos rectángulos en problemas matemáticos y de la vida real en dos y tres dimensiones.
• Aplicar el teorema de Pitágoras para hallar la distancia entre dos puntos en un sistema de coordenadas.
DESGLOSAR EL ESTÁNDAR
VERBOS: ¿QUÉ DEBERÍAN HACER LOS ESTUDIANTES?
• aplicar: utilizar
• determinar: resolver; averiguar
• explicar: explicar acciones o sucesos explicando por qué.
• encontrar: descubrir; resolver.
• comprender: entender el significado de.
SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS DEBEN CONOCER LOS ESTUDIANTES?
• teorema de Pitágoras inverso: el teorema que afirma que si el cuadrado de la longitud del lado más largo de un triángulo es igual a la suma de los cuadrados de los otros dos lados, entonces el triángulo es rectángulo; si c2 = a2 + b2, entonces es un triángulo rectángulo.
• sistema de coordenadas: un sistema que usa uno o más números, o coordenadas, para determinar unívocamente la posición de los puntos.
• distancia: una medida de la longitud entre dos puntos
• problema matemático: un problema que puede ser representado, analizado, y posiblemente resuelto, con los métodos de las matemáticas.
• punto: punto que representa un punto específico en una recta numérica o en un plano de coordenadas; objeto geométrico sin dimensión que se utiliza para indicar un lugar.
• prueba: prueba o argumento que establece un hecho o la verdad de una afirmación.
• teorema de Pitágoras: teorema que establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados de un triángulo rectángulo; a2 + b2 = c2.
• problema del mundo real: un problema contextual que puede interpretarse, representarse y analizarse mediante la aplicación de las matemáticas.
• triángulo rectángulo: un triángulo con un ángulo de 90º.
INICIO: CONTENIDO DESGLOSADO
ANÁLISIS PROFUNDO DE LOS ESTÁNDARES
CONTENIDO DESGLOSADO
• figura tridimensional: un sólido que tiene tres dimensiones medibles.
• figura bidimensional: una figura plana con dos dimensiones medibles.
• longitud desconocida de un lado: un lado que no tiene su longitud etiquetada con un número.
IMPLICACIONES PARA LA ENSEÑANZA
• En grados anteriores, los estudiantes han encontrado el área de triángulos, han representado objetos tridimensionales con triángulos y rectángulos, y han resuelto problemas del mundo real que involucran área, volumen y superficie. Los estudiantes han dibujado polígonos en un plano de coordenadas.
• En este nivel de grado, se espera que los estudiantes expliquen una prueba del teorema de Pitágoras y su inversa. Los estudiantes aplican el teorema de Pitágoras para encontrar longitudes laterales desconocidas en triángulos rectángulos en problemas del mundo real. Los estudiantes exploran las longitudes laterales de triángulos rectángulos para comprender la fórmula a2 + b2 = c2 .
INICIO: CONTENIDO DESGLOSADO
ALINEACIÓN VERTICAL
GRADO
6
ESTÁNDAR
Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
6 Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.
6 Representar figuras tridimensionales utilizando redes formadas por rectángulos y triángulos, y utilizar las redes para hallar la superficie de dichas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.
7 Resolver problemas matemáticos y de la vida real relacionados con el área, el volumen y la superficie de objetos bidimensionales y tridimensionales compuestos por triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.
8 Explicar una demostración del teorema de Pitágoras y su inversa.
8 Aplicar el teorema de Pitágoras para determinar longitudes laterales desconocidas en triángulos rectángulos en problemas matemáticos y del mundo real en dos y tres dimensiones.
8 Aplicar el teorema de Pitágoras para encontrar la distancia entre dos puntos en un sistema de coordenadas.
HS Demostrar teoremas sobre triángulos. Los teoremas incluyen: una línea paralela a un lado de un triángulo divide a los otros dos proporcionalmente, y a la inversa; el Teorema de Pitágoras probado usando la semejanza de triángulos.
HS Usar razones trigonométricas y el teorema de Pitágoras para resolver triángulos rectángulos en problemas aplicados.
HS Usar triángulos especiales para determinar geométricamente los valores del seno, coseno y tangente de π/3, π/4, and π/6 y usa la circunferencia unitaria para expresar los valores del seno, coseno y tangente para π – x, π + x, and 2π – x en términos de sus valores para x, donde x es cualquier número real.
HS Demostrar la identidad pitagórica sen² (θ) + cos² (θ) = 1 y utilizarla para hallar sen(θ), cos(θ) o tan(θ) dados sen(θ), cos(θ) o tan(θ) y el cuadrante del ángulo.
HS Derivar la ecuación de una circunferencia de centro y radio dados utilizando el teorema de Pitágoras; completar el cuadrado para hallar el centro y radio de una circunferencia dada por una ecuación.
HS Deducir la ecuación de una parábola dados un foco y una directriz.
HS (+) Deducir las ecuaciones de elipses e hipérbolas dados los focos, utilizando el hecho de que la suma o diferencia de distancias desde los focos es constante.
HS Usar coordenadas para demostrar algebraicamente teoremas geométricos similares.
HS Usar coordenadas para calcular perímetros de polígonos y áreas de triángulos y rectángulos, por ejemplo, utilizando la fórmula de la distancia.
INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA
GUÍA DE INSTRUCCIÓN
ANDAMIADA
La guía de instrucción andamiada se proporciona para que los maestros puedan planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.
Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes. Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance. La guía se divide en cuatro rangos de percentiles para cada estándar.
Refuerzo del grado anterior Nivel de grado con apoyos Nivel de grado
Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.
Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.
Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.
Ampliación del nivel de grado
Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.
Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:
1 Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.
2 Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.
3 Haga clic en el enlace directo al material elegido para el estudiante.
Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:
1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.
2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.
3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.
4. Haga clic en el enlace directo al material recomendado para el estudiante.
La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.
Área de instrucción: Operaciones y pensamiento algebraico
Todos los estudiantes:
• Captar interés
• Exploración
• Muestra lo que sabes
• Prueba de habilidades
INICIO:
Explica una demostración del teorema de Pitágoras y su inverso.
7 - Propiedades de los triángulos
Repaso y práctica de destrezas
Constructor de fluidez
0 %25 % (Nivel de grado anterior con apoyo)
• Propiedades de los triángulos
Práctica interactiva
• Entrega de drones
Prueba de habilidades
7 - Área, superficie y volumen
Repaso y práctica de habilidades
Constructor de fluidez
• Área de figuras compuestas
Práctica interactiva
• Hábitats de criaturas
Prueba de habilidades
25 %50 % (Nivel de grado con apoyo)
8 - Teorema de Pitágoras
Acceso a conocimientos previos
Constructor de bases fundamentales
Repaso y práctica de habilidades
• Evaluación rápida (preguntas 1, 2)
• Repaso: sección «El teorema de Pitágoras», «El teorema de Pitágoras inverso»
• Revisión (preguntas 1-4)
50 %80 % (Nivel de Grado)
80 %100 % (Ampliando el Nivel de Grado)
8 - Teorema de Pitágoras
Vocabulario ilustrado
Vocabulario interactivo
Libreta interactiva
Conexiones lingüísticas
8 - Teorema de Pitágoras
Tareas de modelado matemático
Tablero de opciones
Aplicar el teorema de Pitágoras para determinar longitudes laterales desconocidas en triángulos rectángulos en problemas matemáticos y del mundo real en dos y tres dimensiones.
7 - Propiedades de triángulos
Repaso y práctica de destrezas
Constructor de fluidez
0 %25 % (Nivel de grado anterior con apoyo)
• Propiedades de los triángulos
Práctica interactiva
• Entrega de drones
Prueba de habilidades
7 - Área, superficie y volumen
Repaso y práctica de habilidades
Constructor de fluidez
• Área de figuras compuestas
Práctica interactiva
• Hábitats de criaturas
Prueba de habilidades
25 %50 % (Nivel de grado con apoyo)
8 - Teorema de Pitágoras
Acceso a conocimientos previos
Constructor de bases fundamentales
Repaso y práctica de habilidades
• Evaluación rápida (preguntas 3, 4)
• Repaso: sección «Hallar un lado desconocido», y «El teorema de Pitágoras», en la sección 3D
• Revisión (preguntas 5-8)
8 - Teorema de Pitágoras
Vocabulario ilustrado
50 %80 % (Nivel de Grado)
80 % -
100 % (Ampliando el Nivel de Grado)
Vocabulario interactivo
Libreta interactiva
Constructor de fluidez
• Teorema de Pitágoras
Ciencia de datos
Conexiones lingüísticas
8 - Teorema de Pitágoras
¿Qué prefieres?
Tablero de opciones
INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA
Aplica el teorema de Pitágoras para encontrar la distancia entre dos puntos en un sistema de coordenadas.
7 - Propiedades de los triángulos
Repaso y práctica de habilidades
Constructor de fluidez
0 %25 % (Nivel de grado anterior con apoyo)
• Propiedades de los triángulos
Práctica interactiva
• Entrega de drones
Prueba de habilidades
6 - Resolución de problemas en el plano de coordenadas
Repaso y práctica de habilidades
Constructor de fluidez
• Resolución de problemas en el plano de coordenadas
Práctica interactiva
• Lluvia de gnomos
Prueba de habilidades
25 %50 % (Nivel de grado con apoyo)
8 - Teorema de Pitágoras
Acceso a conocimientos previos
Constructor de bases fundamentales
Repaso y práctica de habilidades
• Evaluación rápida (pregunta 5)
• Repaso: sección «Hallar la distancia entre puntos en un plano de coordenadas»
• Revisión (preguntas 9-10)
8 - Teorema de Pitágoras
50 %80 % (Nivel de Grado)
Vocabulario ilustrado
Vocabulario interactivo
Libreta interactiva
Práctica interactiva
• Entrega de drones
Conexiones lingüísticas
80 %100 % (Ampliando el Nivel de Grado)
8 - Teorema de Pitágoras
Tareas de modelado matemático
Tablero de opciones
ATRAER: ACCESO A CONOCIMIENTOS PREVIOS
EVALUAR PREVIAMENTE EL CONOCIMIENTO DE LOS ESTUDIANTES
ACCESO A CONOCIMIENTOS PREVIOS:
ACUERDO O DESACUERDO
ESTÁNDAR PREVIO
Dibujar (a mano alzada, con regla y transportador, y con tecnología) formas geométricas con condiciones dadas. Enfocarse en construir triángulos a partir de tres medidas de ángulos o lados, notando cuando las condiciones determinan un triángulo único, más de un triángulo o ningún triángulo.
DESCRIPCIÓN
Los estudiantes leerán diferentes respuestas a una pregunta sobre el estándar previo, decidirán si están de acuerdo o en desacuerdo y explicarán su razonamiento.
MATERIALES
IMPRESO
• 1 documento de «Acuerdo o desacuerdo» (por estudiante)
REUTILIZABLE
• 1 transportador (por estudiante)
• 1 regla (por estudiante)
PREPARACIÓN
● Si no asigna el archivo de «Acceso a conocimientos previos» digitalmente, imprima udocumento de «Acuerdo o desacuerdo» por estudiante.
● Reúna los transportadores y las reglas.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Pida a los estudiantes que completen el documento de «Acuerdo o desacuerdo» de forma independiente.
2. Una vez que lo hayan completado, pídales que se pongan de pie.
3. Los estudiantes deben caminar por el aula con la mano levantada en posición de chocar los cinco.
4. A su señal, pídales que se detengan y choquen los cinco con la persona más cercana. Ésta será su pareja.
5. Conceda a un par de minutos para que acuerden juntos sus respuestas y justificaciones.
6. Luego, puede continuar tantas veces como quiera con diferentes parejas.
7. Converse las respuestas en clase. Permita que los estudiantes expliquen sus razonamientos para cada problema. Luego proporcione una clave de respuestas.
a De acuerdo con Samantha
b En desacuerdo con Kyle
c De acuerdo con Danté

ACUERDO O DESACUERDO
8. Si los estudiantes tienen dificultades para completar esta tarea, pasen a realizar el constructor de cimientos para llenar este vacío de conocimientos previos antes de pasar a otras partes del alcance.
IDENTIFICACIÓN DE CONCEPTOS ERRÓNEOS
• Puede ser útil recordar a los estudiantes que las medidas de tres ángulos en un triángulo suman 180°.
• Repasar la clasificación de los triángulos por sus ángulos (agudo, recto y obtuso) y por sus lados (escaleno, isósceles y equilátero).

TEOREMA DE PITÁGORAS
DESCRIPCIÓN
ATRAER: CAPTAR INTERÉS
LECCIÓN PARA CAPTAR INTERÉS
Los estudiantes determinan los lados que faltan en los triángulos rectángulos utilizando el teorema de Pitágoras.
MATERIALES
IMPRESOS
• 1 teorema de Pitágoras (por clase)
REUTILIZABLES
• 1 fenómenos (por clase)
PREPARACIÓN
• Planee mostrar los fenómenos.
• Prepárese para proyectar la diapositiva teorema de Pitágoras para que la vea toda la clase.
• Prepárese para presentar el escenario y anime a los estudiantes a pensar en cómo resolverlo. Prepárese para pasar a las actividades de exploración, regresando a la actividad para captar interés con los nuevos conocimientos adquiridos después de que se hayan completado las exploraciones.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I: EXPLORACIÓN PREVIA
1. Presente esta actividad hacia el comienzo del alcance. La clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades explorar correspondientes.
2. Muestre los fenómenos. Formule a los estudiantes las siguientes preguntas: ¿Qué observas? ¿Dónde puedes ver matemáticas en esta situación? Permita que los estudiantes compartan todas sus ideas.
3. Explique el escenario a la clase: «Oliver está jugando al golf con su familia. Lleva años jugando al minigolf y espera que sus habilidades se trasladen al campo grande. Lo primero que nota es lo lejos que está el hoyo de donde empieza. Sabe que tiene que golpear la bola en el menor número de golpes posible, así que tiene que decidir qué estrategia debe usar. Intenta elegir entre dos opciones. Puede ir a lo seguro y golpearla corta hacia la calle, o puede intentar golpearla por encima de los árboles hacia el green».
4. Deje que los estudiantes hagan preguntas y aclaren el contexto si es necesario. Anímeles a compartir sus ideas y experiencias con la clase con las siguientes preguntas:
a. ¿Has jugado alguna vez al golf?
b. ¿Qué significa un golpe en golf?
c. ¿Cuáles son las ventajas o desventajas de las dos opciones de Oliver?
5. Proyecte la diapositiva del teorema de Pitágoras.
6. Explique que el padre de Oliver le sugirió que intentara golpear la pelota por encima de los árboles hasta el green. Plantee las siguientes preguntas a la clase:
a DOK-1 ¿Dónde ves las matemáticas en el golf?
Permita que los estudiantes compartan sus ideas. Las respuestas de los estudiantes variarán.
Ejemplo de respuesta de un estudiante: Puedes medir la distancia desde la zona del tee hasta el hoyo para determinar el menor número de golpes hasta el hoyo.
b DOK-1 ¿Qué representa esta frase? Permita que los estudiantes compartan sus ideas. Las respuestas de los estudiantes variarán. Este enunciado incluye variables, por lo que podemos identificar la información que ya conocemos y sustituir las variables para resolver el problema.
7. Continúe para completar las actividades de explorar. PARTE II: DESPUÉS DE LA EXPLORACIÓN
1. Después de que los estudiantes hayan completado las actividades de explorar para este tema, muestre nuevamente fenómenos y repita el escenario.
2. Consulte la diapositiva teorema de Pitágoras y haga las siguientes preguntas a la clase:
a DOK-1 ¿Dónde ves las matemáticas en el golf? Permita que los estudiantes compartan sus ideas. Las respuestas de los estudiantes variarán. Ejemplo de respuesta de un estudiante: Se puede medir la distancia desde la zona del tee hasta el hoyo para determinar el menor número de golpes hasta el hoyo.
b DOK-1 ¿Qué representa esta frase? Permita que los estudiantes compartan sus ideas. Las respuestas de los estudiantes variarán. Esta frase incluye variables, por lo que podemos identificar la información que ya conocemos y sustituir las variables para resolver el problema.
c DOK-1 ¿Tiene más sentido este enunciado matemático después de las explicaciones? Sí, se llama Teorema de Pitágoras.
d DOK-1 ¿Qué estrategias utilizarías para resolver la distancia desde la zona del tee hasta el hoyo? Podemos ver el dogleg izquierdo del campo de golf como un triángulo rectángulo desde la zona del tee hasta el hoyo. Podemos medir la distancia de cada lado del triángulo rectángulo. Cada lado representaría la distancia. La distancia desde la zona del tee hasta el hoyo representaría la hipotenusa en un triángulo rectángulo. Podemos utilizar la distancia de los catetos de un triángulo rectángulo para hallar la hipotenusa.
e DOK-1 ¿Consideras que comprendes bien el uso del teorema de Pitágoras? Las respuestas variarán en función del éxito de los estudiantes durante la actividad y de su nivel de confianza.
3. Si el tiempo lo permite, pida a los estudiantes que utilicen el teorema de Pitágoras para diseñar los hoyos de su propio campo de golf. Pueden añadir trampas de arena, árboles y otros obstáculos si lo desean.
EXPLORAR: EXPLORACIÓN 1
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 1: REPRESENTAR EL TEOREMA DE PITÁGORAS Y EL RECÍPROCO DEL TEOREMA DE PITÁGORAS
Estándar(es)
• Comprender y aplicar el Teorema de Pitágoras. Explicar una prueba del teorema de Pitágoras y su inverso.
Grandes Ideas
Investigaciones cilíndricas
Forma, número y expresiones
Transformación geométrica
DESCRIPCIÓN
Estándares para la Práctica Matemática
MP.1 Dar sentido a los problemas y perseverar en resolverlos.
MP.3 Construir argumentos viables y criticar el razonamiento de otros.
MP.4 Representar con matemáticas.
MP.6 Prestar atención a la precisión.
Los estudiantes demuestran el teorema de Pitágoras utilizando modelos y hallarán el área de tres cuadrados conectados. Los estudiantes identifican triángulos rectángulos con la inversa del teorema de Pitágoras.
MATERIALES
IMPRESO
• 1 diario del estudiante (por estudiante)
• 1 boleto de salida (por estudiante)
• 1 tarjetas de la inversa del teorema de Pitágoras (por pareja)
• 1 tapete de trabajo del modelando del teorema de Pitágoras (por pareja)
• 1 documento «Demostrando el teorema de Pitágoras Trivia de Triángulos» (por pareja)
REUTILIZABLE
• 1 tijeras (por pareja)
• 1 pegamento en barra (por pareja)
• 1 calculadora (por pareja)
PREPARACIÓN
• Planee que los estudiantes trabajen en grupos de dos para completar esta actividad.
• Imprime un diario del estudiante y una hoja de salida para cada estudiante.
• Imprime un tapete de trabajo del modelando del teorema de Pitágoras y un documento «Demostrando el teorema de Pitágoras Trivia de Triángulos» por pareja.
Conexiones de Contenido Motores de Investigación
CC3 Desarmar el todo, armar las partes
CC4 Descubrir la forma y el espacio
DI1 Dar sentido al mundo (comprender y explicar)
• Imprima un tarjetas de la inversa del teorema de Pitágoras por pareja.
• Reúna suficientes pares de tijeras, barras de pegamento y calculadoras para que cada pareja de estudiantes utilice una de cada para la parte II.
• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen papel cuadriculado en la sección de «Intervención».
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I: REPRESENTAR DEL TEOREMA DE PITÁGORAS
1. Lea el siguiente escenario a la clase: «Mason planea abrir un campo de minigolf dentro de unos meses. Comienza a planificar su nuevo campo investigando varios diseños en Internet. Mason observa que la mayoría de los 18 hoyos de cada campo tienen forma de triángulo rectángulo. Mason observa que hay un pequeño borde a lo largo del perímetro de cada uno de estos hoyos en forma de triángulo rectángulo. Después de observar el borde a lo largo de cada hoyo en forma de triángulo rectángulo, Mason siente curiosidad por saber si existe una relación entre los tres lados de un triángulo rectángulo. Ayudemos a Mason a determinar la relación entre los 3 lados de un triángulo rectángulo mientras comienza a planificar su campo de minigolf».
2. Ayude a los estudiantes a acceder a la tarea haciéndoles las siguientes preguntas:
a. ¿Qué sabes sobre los triángulos rectángulos?
b. ¿Has jugado alguna vez al mini golf?
c. ¿Qué tipo de matemáticas se podrían utilizar al jugar al mini golf?
3. Entregue un diario del estudiante por alumno.
4. Entregue un tapete de trabajo del modelando del teorema de Pitágoras y un documento «Demostrando el teorema de Pitágoras Trivia de Triángulos» por pareja.
5. Pida a los estudiantes que usen el tapete de trabajo del modelando del teorema de Pitágoras y un documento «Demostrando el teorema de Pitágoras Trivia de Triángulos». Los estudiantes deben recortar los triángulos de la hoja de trabajo «Demostrando el teorema de Pitágoras Trivia de Triángulos» y usar esos triángulos para colocarlos en trabajo del modelando del teorema de Pitágoras
6. Indique a los estudiantes que usen un documento «Demostrando el teorema de Pitágoras Trivia de Triángulos» para demostrar el teorema de Pitágoras. Colocarán esos triángulos enel tapete de trabajo. Después de colocar los triángulos en lel tapete de trabajo del modelando del teorema de Pitágoras, los estudiantes pueden dibujar un cuadrado para cada longitud lateral, con las longitudes laterales de cada triángulo elevado al cuadrado, y recortar cada cuadrado para representar el lado². Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión mediante las siguientes preguntas orientativas:
a DOK-1 ¿Qué es el teorema de Pitágoras? Las respuestas pueden variar. El teorema de Pitágoras describe una relación especial entre los lados de un triángulo rectángulo. Al aplicar el teorema de Pitágoras, cada lado de los triángulos rectángulos es también un lado de un cuadrado que está unido al triángulo.
b DOK-1: ¿Cómo puedes determinar el área de un cuadrado? Las respuestas pueden variar. El área de un cuadrado es cualquier lado multiplicado por sí mismo. (Por ejemplo, a × a = a2).
c DOK-1: ¿Cómo puedes usar los triángulos abc, def y mno para demostrar el teorema de Pitágoras? Las respuestas pueden variar. Haz tres cuadrados con lados iguales a cada lado del triángulo. Recorta cada cuadrado para colocarlo en cada lado del triángulo.

d DOK-1: Dada el área del cuadrado a, ¿qué operación permite determinar la longitud lateral del cuadrado a?
Las respuestas pueden variar. La raíz cuadrada permite hallar la longitud lateral de un cuadrado dada el área del cuadrado.
e DOK-2: ¿Es a2 + b2 = c2, lo mismo que b2 + a2 = c2? ¿Por qué sí o por qué no? Las respuestas pueden variar. Sí, debido a la propiedad conmutativa de la suma, 2 + 4 da la misma respuesta que 4 + 2.
7. Conceda a los estudiantes tiempo suficiente para registrar todo su trabajo de la parte I de la exploración en el diario del estudiante.
8. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anímelos a notar las similitudes y diferencias entre las estrategias usadas para representar el teorema de Pitágoras.


DIARIO DEL ESTUDIANTE
9. Después de la parte I de la exploración, invite a la clase a un charla de matemáticas para compartir sus observaciones y aprendizajes.
CHARLA DE MATEMÁTICAS
• DOK-1 Usando el área de cada cuadrado, describe el teorema de Pitágoras. El área de los cuadrados a y b juntos es igual al área del cuadrado c
• DOK-1 ¿Cómo puedes determinar la longitud del lado de un cuadrado dada su área? Tendríamos que hallar la raíz cuadrada (√) del área para determinar la longitud de uno de los lados del cuadrado.
• DOK-2 ¿Qué has observado en la suma del cuadrado a y del cuadrado b en comparación con el cuadrado c? La suma del número de fichas que se necesitan para llenar el cuadrado a y el cuadrado b es la misma cantidad de fichas que se necesitan para llenar el cuadrado c
• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:
◦ DOK-2 ¿Crees que el teorema de Pitágoras sólo se aplica a los triángulos rectángulos? ¿Qué pasa con los triángulos no rectángulos? Creo que el teorema de Pitágoras se aplica a todos los triángulos, incluidos los triángulos no rectángulos.
PARTE II: EL RECÍPROCO DEL TEOREMA DE PITÁGORAS
1. Lea la siguiente situación a la clase: «Al investigar en Internet, Mason se da cuenta de que muchos de los campos de golf contienen hoyos en forma de triángulo rectángulo, pero no está 100% seguro de que cada uno de estos hoyos sea un triángulo rectángulo. Sin un transportador, no sabe cómo demostrar qué hoyos son triángulos rectángulos y cuáles no. Ayudemos a Mason a decidir si un triángulo es rectángulo aplicando el teorema de Pitágoras».
2. Entregue a cada pareja las tarjetas del teorema de Pitágoras, un par de tijeras y una barra de pegamento. También se puede darles una calculadora cuando evalúen el cuadrado de números más grandes.
3. Indique a los estudiantes que empiecen por identificar si el «Agujero 7» y el «Agujero 12» son triángulos rectángulos aplicando el teorema de Pitágoras. Pida a los estudiantes que rellenen los espacios en blanco con los catetos y la hipotenusa supuesta de cada triángulo. Pida a los estudiantes que resuelvan la ecuación simplificando los cuadrados. Indique a los estudiantes que encierren en con un círculo Sí si la ecuación es cierta, y que encierren con un círculo No si la ecuación no es cierta.
4. Pida a los estudiantes que dividan en dos la página de tarjetas del teorema de Pitágoras, de modo que cada estudiante reciba un juego de tarjetas. Indique a la clase que cada estudiante recortará su propio juego de 6 tarjetas. A continuación, pida a los estudiantes que trabajen juntos y apliquen el teorema de Pitágoras a cada triángulo y determinen si el triángulo es un ejemplo de triángulo rectángulo. Cuando los estudiantes lleguen a un consenso sobre cada triángulo, pegarán cada tarjeta en la columna correspondiente.
5. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión haga las siguientes preguntas:
a DOK-1: ¿Cómo sabes qué medidas utilizar al aplicar el teorema de Pitágoras? Las respuestas pueden variar. Necesitamos conocer las longitudes de los lados de ambos catetos para sustituir los valores de las variables, a y b. Luego sustituiremos la longitud de la hipotenusa por la variable c
b DOK-2: ¿Qué sucede cuando el teorema de Pitágoras crea un enunciado verdadero? Las respuestas pueden variar. Cuando la ecuación creada usando el teorema de Pitágoras genera un enunciado verdadero, entonces las tres longitudes de los lados forman un triángulo rectángulo.
c DOK-2: ¿Qué ocurre cuando el teorema de Pitágoras genera una afirmación falsa? Las respuestas pueden variar. Cuando la ecuación creada usando el teorema de Pitágoras no genera un enunciado verdadero, entonces las tres longitudes laterales no forman un triángulo rectángulo. Sin embargo, las tres longitudes laterales podrían crear otro tipo de triángulo.
6. Conceda tiempo a los estudiantes para que completen la parte II del diario del estudiante, incluidas las preguntas de reflexión.
7. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anímelos a notar las similitudes y diferencias entre las estrategias utilizadas para determinar si un triángulo es rectángulo.
8 Después de la parte II de la exploración, invita a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.
CHARLA DE MATEMÁTICAS
• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:
◦ DOK-2 ¿Cómo puedes determinar si un triángulo es rectángulo, dadas sólo las longitudes de cada lado? Podemos aplicar el teorema de Pitágoras utilizando las longitudes de los lados del triángulo. Si el teorema de Pitágoras forma un enunciado verdadero, el triángulo es un triángulo rectángulo.
• DOK-2 En tus propias palabras, describe el teorema de Pitágoras inverso. Se genera una afirmación verdadera cuando se utiliza el teorema de Pitágoras y las longitudes de los tres lados de un triángulo rectángulo. Si se genera una afirmación falsa, entonces el triángulo no es rectángulo.
• DOK-2 Un triángulo tiene longitudes laterales de 7, 9 y 10. ¿Es un triángulo rectángulo? ¿Es un triángulo rectángulo?
a2 + b2 = c2
72 + 92 = 102
49 + 81 = 100
130 ≠ 100
Estas longitudes laterales no forman un triángulo rectángulo.
EXPLORAR: EXPLORACIÓN 1



DIARIO DEL ESTUDIANTE GRADO
EXPLORAR: EXPLORACIÓN 1

BOLETO DE SALIDA
DESPUÉS DE LA EXPLORACIÓN
1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.
2. Completen el esquema de anclaje como clase.
3. Haga que cada estudiante complete su libreta interactiva.
APOYOS PEDAGÓGICOS
1. Proporcione flexibilidad a los estudiantes que necesitan tareas reducidas haciéndoles completar sólo dos triángulos en la parte I y/o completar sólo un juego de tarjetas del del teorema de Pitágoras inverso en la parte II.
2. Proporcione flexibilidad a los estudiantes que tienen diferentes niveles de destreza permitiéndoles completar la parte I sin recortar los triángulos y proporcionándoles cuadrados precortados y/o precortando las tarjetas del teorema de Pitágoras inverso en la parte II.
3. Ancle la instrucción vinculando y activando el conocimiento previo relevante, incluyendo triángulos rectángulos, área, cuadrados y raíces cuadradas.
4. Algunos estudiantes pueden describir el proceso para determinar el área de un cuadrado usando la multiplicación. Cuando vea o escuche a los estudiantes usar esta descripción, recuérdeles que multiplicar un número por sí mismo se llama elevar el número al cuadrado.
5. Como extensión, pida a cada estudiante que cree su propio triángulo en su tapete de trabajo que muestre el teorema de Pitágoras.
APOYOS LINGÜÍSTICOS
Aclare que en matemáticas, el término área se refiere al espacio dentro de una figura bidimensional y no significa un espacio genérico.
Proporcione elementos visuales con frecuencia para reiterar la definición de términos clave como triángulo, área, cuadrado, raíz cuadrada, y hipotenusa.
Lea la boleto de salida en voz alta a los estudiantes y luego pídales que la reformulen con sus propias palabras.
Proporcione estructuras de frases para apoyar a los estudiantes mientras comparten sus ideas verbalmente y por escrito.
• La longitud del lado ____ (letra) es ______.
• El cuadrado del lado ____ (letra) da un área de ______.
• El área de ____ (letra) al cuadrado y el área de ____ (letra) al cuadrado juntas tienen un área total de ______.
• Esto es lo mismo que el área de ____ (letra) al cuadrado.
Anime a los estudiantes a participar en una charla matemática durante el trabajo en grupo. Pídales que discutan cómo hallar el área de un cuadrado antes de responder a la segunda pregunta de reflexión en el diario del estudiante.

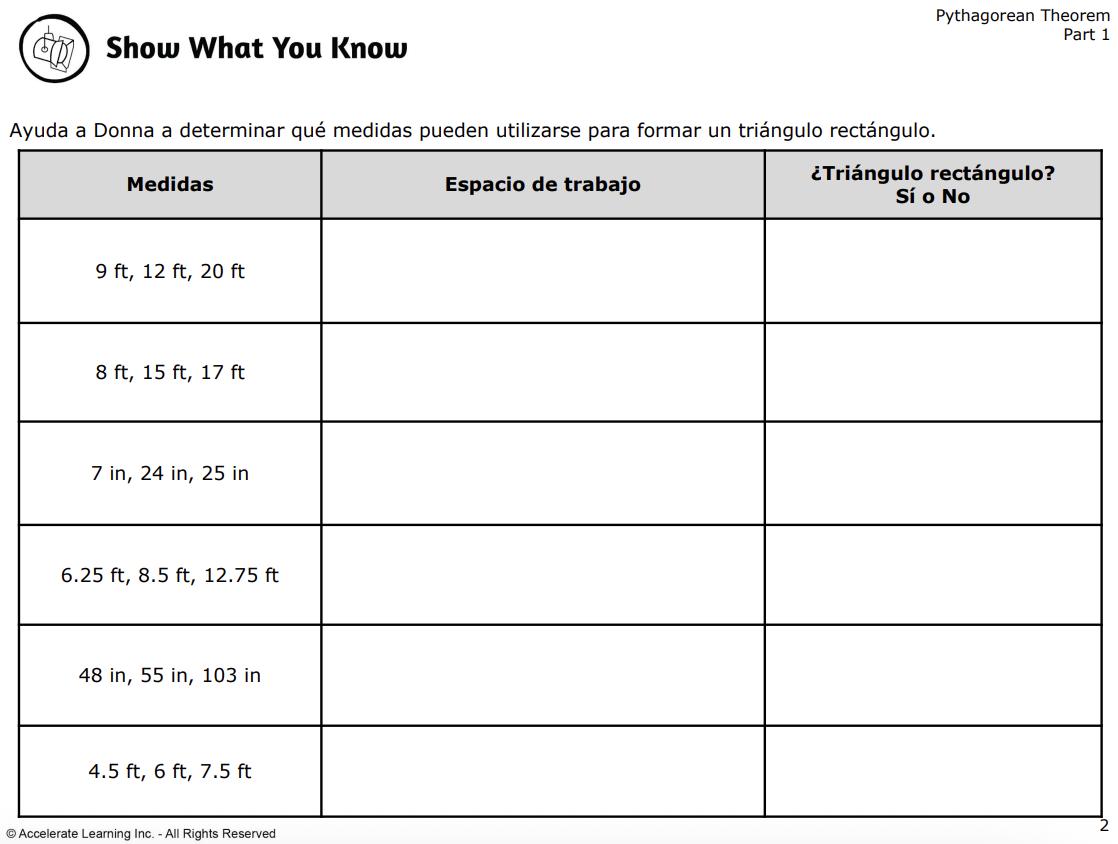
MUESTRA LO QUE SABES (PARTE 1)
EXPLORAR: EXPLORACIÓN 2
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 2: ENCONTRAR UNA LONGITUD DE LADO
DESCONOCIDA EN TRIÁNGULOS RECTÁNGULOS RECTÁNGULOS
Estándar(es)
• Comprender y aplicar el teorema de Pitágoras. Aplicar el teorema de Pitágoras para determinar longitudes laterales desconocidas en triángulos rectángulos en problemas matemáticos y del mundo real en dos y tres dimensiones.
Grandes Ideas Estándares para la Práctica Matemática Conexiones de Contenido Motores de Investigación
Investigaciones cilíndricas
Exploraciones Pitagóricas
Forma, número y expresiones
Transformación geométrica
DESCRIPCIÓN
MP.1 Dar sentido a los problemas y perseverar en su resolución.
MP.4 Representar con matemáticas.
MP.5 Usar herramientas apropiadas estratégicamente.
MP.6 Atender a la precisión.
Los estudiantes usan el teorema de Pitágoras para determinar la longitud del lado faltante de un triángulo rectángulo, cuando se dan ambos catetos o un cateto y la hipotenusa.
MATERIALES
IMPRESO
• 1 diario del estudiante (por estudiante)
• 1 boleto de salida (por estudiante)
• 1 geotablero (por pareja)
• 1 tarjetas para encontrar el cateto que falta en un triángulo rectángulo (por pareja)
REUTILIZABLE
• 1 calculadora (por pareja)
• 1 pegamento en barra (por pareja)
• 1 tijeras (por pareja)
CC3 Desarmar el todo, armar las partes
CC4 Descubrir la forma y el espacio
DI1 Dar sentido al mundo (Comprender y explicar)
DI2 Predecir lo que podría suceder (Predecir)
PREPARACIÓN
• Planee que los estudiantes trabajen en grupos de dos para completar esta actividad.
• Imprime un diario del estudiante y un boleto de salida para cada estudiante.
• Imprima un juego de tarjetas para encontrar el cateto que falta en un triángulo rectángulo por pareja.
• Imprima un geotablero para cada pareja de estudiantes para la parte I.
• Reúna una calculadora, un par de tijeras y una barra de pegamento para cada pareja.
• Para los estudiantes que necesiten más ayuda para recordar la información, consulta los elementos de ayuda complementaria del papel cuadriculado en la sección Intervención.
• ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Geotablero)
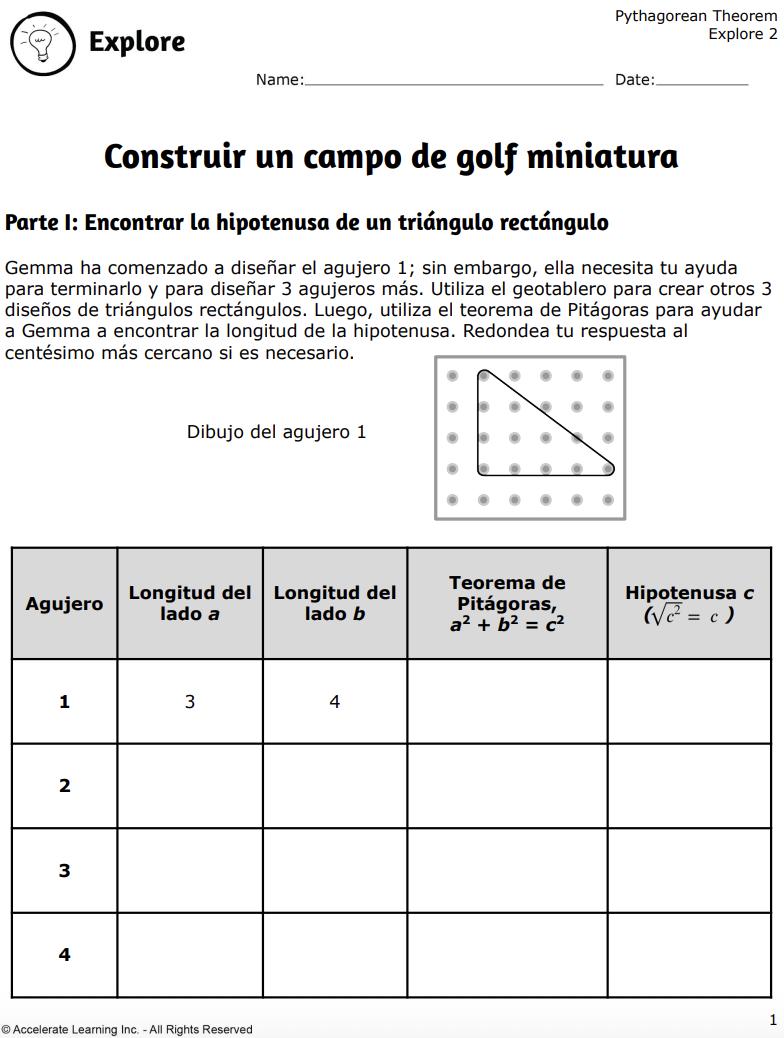

DIARIO DEL ESTUDIANTE
EXPLORAR: EXPLORACIÓN 2
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I: HALLAR LA HIPOTENUSA DE UN TRIÁNGULO RECTÁNGULO
1. Lea la siguiente situación a la clase: «Gemma está construyendo un nuevo campo en Pacific Putt-Putt inspirado en su película de ciencia ficción favorita. Cada uno de los 18 hoyos del nuevo campo tiene forma de triángulo rectángulo y presentará varios obstáculos. Se colocará un fino borde a lo largo del perímetro de cada hoyo. Ayudemos a Gemma a crear varios diseños de triángulos rectángulos utilizando un geotablero. A continuación, utilicemos el teorema de Pitágoras y el geotablero para calcular la longitud de cada lado».
2. Entregue un diario del estudiante por alumno.
3. Entregue un geotablero a cada pareja de estudiantes.
4. Pida a los estudiantes que recreen el «Agujero 1» utilizando el geotablero. Los estudiantes medirán la distancia vertical y horizontal entre las clavijas para determinar las longitudes de ambos catetos. Los estudiantes aplicarán el teorema de Pitágoras para resolver la hipotenusa. También pueden utilizar una calculadora para evaluar la raíz cuadrada.
5. Explique a los estudiantes que crearán tres triángulos rectángulos adicionales y resolverán la hipotenusa de cada uno. (Nota: los 3 triángulos rectángulos adicionales deben caber en el geotablero.)
6. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión mediante el uso de las siguientes preguntas guía:
a DOK-1: ¿Cómo se puede determinar el valor de c, cuando se da c2? Necesitaríamos determinar la raíz cuadrada (√) de c2
b DOK-2: ¿Cuál crees que es el triángulo rectángulo más pequeño que puedes crear en el geoboard? El triángulo más pequeño que puedo crear es un triángulo con catetos que miden 1 unidad cada uno.
c DOK-3: ¿Cómo sabes que has creado un ángulo recto usando los dos catetos de un triángulo rectángulo en el geoboard? Los catetos de un triángulo rectángulo deben ser perpendiculares, por lo que uno de los catetos del geoboard debe incluir clavijas verticales y el otro cateto debe formarse utilizando clavijas horizontales.
7. Conceda tiempo a los estudiantes para que completen la parte I del diario del estudiante, incluidas las preguntas de reflexión.
8. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para encontrar la longitud de la hipotenusa de un triángulo rectángulo.
9. Después de la Parte I, invite a la clase a una Charla de matemáticaspara compartir sus observaciones y aprendizajes.
EXPLORAR: EXPLORACIÓN 2
CHARLA DE MATEMÁTICAS
• DOK-3 ¿Cómo usaste el teorema de Pitágoras para resolver la hipotenusa que falta? Identifiqué los valores de ambos catetos y los sustituí en el teorema de Pitágoras como las variables a y b. Luego elevé ambos números al cuadrado y los sumé. Luego encontré la raíz cuadrada de este total para resolver la hipotenusa que faltaba.
• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:
◦ DOK-2 ¿Qué notas sobre la hipotenusa del agujero 1, cuando la comparas con los agujeros 2-4? La hipotenusa del agujero 1 es un número entero, mientras que los agujeros 2-4 tienen hipotenusas que son números irracionales que involucran decimales.
• DOK-2 ¿Eres capaz de crear un triángulo rectángulo con medidas de catetos que involucren fracciones o decimales usando el geoboard? ¿Por qué sí o por qué no? No, porque la distancia entre los geoboards representa una unidad, cada línea dibujada en el geoboard tiene que conectarse con cada clavija y no estar entre las clavijas para representar un número racional.
• DOK-2 Un triángulo rectángulo tiene catetos que miden 10 pies y 17 pies. ¿Cuál es la longitud de la hipotenusa? Redondea tu respuesta a la centésima más cercana, si es necesario.
102 + 172 = c2
100 + 289 = c2
389 = c2
√ 389 = c
c
≈ 19,72 pies
PARTE II: ENCONTRAR EL CATETO QUE FALTA EN UN TRIÁNGULO RECTÁNGULO
1. Lee la siguiente situación a la clase: «Gemma tiene espacio para algunos hoyos más en su campo de minigolf. Crea tres diseños más pero se olvida de incluir una medida clave en cada uno de los tres diseños en forma de triángulo rectángulo. Utilicemos el teorema de Pitágoras para ayudar a Gemma a determinar la longitud de cada uno de los catetos que faltan».
2. Ayude a los estudiantes a acceder a la tarea planteándoles las siguientes preguntas:
a. ¿Qué recuerdas sobre la determinación de las longitudes de los lados de los triángulos rectángulos?
b. ¿Ha habido alguna ocasión en la que hayas olvidado anotar algo importante? ¿Cómo remediaste la situación?
3. Distribuye las tarjetas para encontrar el cateto que falta en un triángulo rectángulo, un par de tijeras y una barra de pegamento a cada pareja de estudiantes. También se puede proporcionar una calculadora a los estudiantes cuando evalúen la raíz cuadrada de los números.
4. Pida a los estudiantes que dividan en dos la página de tarjetas para encontrar el cateto que falta en un triángulo rectángulo, de modo que cada estudiante reciba un juego de tarjetas. Cada estudiante recortará su propio juego de 12 tarjetas. Los estudiantes trabajarán juntos e identificarán el cateto y la hipotenusa dados de cada agujero en forma de triángulo rectángulo. (Nota: Sólo se utilizarán 9 de las 12 tarjetas. Cada tarjeta representa un cateto o una hipotenusa). A continuación, los estudiantes aplicarán el teorema de Pitágoras a cada triángulo para determinar el cateto que falta. Cuando los estudiantes lleguen a un consenso sobre cada triángulo, pegarán cada tarjeta en el espacio correspondiente.
5. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión mediante las siguientes preguntas orientativas:
a DOK-1 ¿Cuáles son algunas de las diferencias en el uso del teorema de Pitágoras cuando se resuelve un cateto que falta en lugar de una hipotenusa que falta? La mayor diferencia es usar la resta para resolver un cateto faltante en lugar de usar la suma para resolver una hipotenusa faltante.
b DOK-2 Aparte del valor de la raíz cuadrada, ¿cuál es la diferencia entre la raíz cuadrada de 16 y la raíz cuadrada de 20? La raíz cuadrada de 16 es 4. 4 es un número entero. La raíz cuadrada de 20 es un número irracional, sin embargo podemos redondearlo a 4,47.
c DOK-3 Dado que a y b son las medidas de ambos catetos y c es la medida de la hipotenusa, ¿es c2a2 = b2 lo mismo que c2 - b2 = a2? Sí, puesto que el valor de un cateto puede ser a o b siempre que el otro cateto sea la otra variable, ambas ecuaciones pueden utilizarse para resolver el cateto que falta.
6. Conceda tiempo a los estudiantes para que completen la parte II del diario del estudiante, incluidas las preguntas de reflexión.
7. Pida a los estudiantes que compartan sus estrategias y anímelos a hacerse preguntas y establecer conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias usadas para encontrar las longitudes de los lados faltantes de los triángulos rectángulos.
8. Después de la parte II, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.


EXPLORAR: EXPLORACIÓN 2
CHAT DE MATEMÁTICAS
• Elija una rutina de conversación estructurada para facilitar la siguiente pregunta:
◦ DOK-2 Has calculado el valor de un cateto que falta. Este valor es mayor que la longitud de la hipotenusa. ¿Es esto posible? No, la hipotenusa debe ser la mayor longitud de los tres lados de un triángulo. Si esto ocurre, comprueba tu trabajo.
• DOK-2 Un triángulo rectángulo tiene un cateto que mide 11 pulgadas y una hipotenusa que mide 20 pulgadas. ¿Cuál es la longitud del cateto que falta?
c2 - a2 = b2
202 – 112 = b2
400 – 121 = b2
279 = b2
√279 = b
b
≈ 16.70 pulgadas
• DOK-3 ¿Por qué crees que no se utilizó un geoboard para modelizar la resolución del cateto que falta en un triángulo rectángulo? Es mucho más difícil crear y medir las diagonales de las líneas en un geoboard que las medidas verticales y horizontales para cada cateto.
DESPUÉS DE LA EXPLORACIÓN
1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.
2. Complete el esquema de anclaje en clase.
3. Haga que cada estudiante complete su libreta interactiva.

EXPLORAR: EXPLORACIÓN 2
APOYOS PEDAGÓGICOS
1. Proporcione flexibilidad a los estudiantes que necesiten tareas reducidas pidiéndoles que completen dos agujeros para la tabla en la parte I y/o dos juegos de tarjetas de triángulos en la parte II.
2. Diferencie el grado de dificultad para la parte I, pregunta de reflexión 1, proporcionando las siguientes cuatro ecuaciones a los estudiantes. Pida a los estudiantes que determinen la ecuación que tiene un número entero como longitud de la hipotenusa.
a. 4 + 4 = 8
b. 9 + 16 = 25
c. 16 + 16 = 32
d. 25 + 4 = 29
3. Proporcione tarjetas precortadas para los estudiantes con diferentes niveles de destreza.
4. Para los estudiantes que tienen problemas para crear un triángulo utilizando las tres tarjetas, explique que cada hipotenusa se ha simplificado en la tarjeta y que la hipotenusa es siempre el lado más largo de un triángulo rectángulo.
5. Algunos estudiantes pueden tener dificultades para encontrar el lado que falta del triángulo cuando no es la hipotenusa. Proporcione un esquema de anclaje que muestre una familia de hechos que los estudiantes puedan consultar.
6. Como desafío adicional, pida a los estudiantes que encuentren dos ejemplos de triángulos rectángulos en los que los tres lados sean números enteros.
APOYOS LINGÜÍSTICOS
Aclare que el término piernas se refiere a los dos lados más cortos de un triángulo rectángulo y no se refiere a las piernas de una persona, animal o mueble.
Mientras los estudiantes trabajan y discuten ideas con sus grupos, resuma lo que escucha y repita las ideas clave y el vocabulario a través de la entonación, el habla más lenta y las señales visuales. Las ideas y palabras que se deben escuchar incluyen triángulo, área, cuadrado, raíz cuadrada, catetos, y hipotenusa
Pida a los estudiantes que se turnen para leer en voz alta el escenario y las instrucciones para la parte II antes de que trabajen juntos para construir un modelo y resolverlo.
Para la parte II, facilite una conversación estructurada entre parejas. Use las estructuras de frases proporcionadas para ayudar a los estudiantes a formular y responder preguntas. Permita que los estudiantes se turnen para ser el compañero A y el compañero B.
• Compañero A: ¿Qué lado falta?
• Compañero B: Falta el lado _______.
• Compañero A: ¿Es el lado _______ la hipotenusa?
• Compañero B: ____ (Sí/No).
• Compañero A: ¿Qué proceso podemos utilizar para encontrar el lado que falta?
Al responder a las preguntas de reflexión, haga que los estudiantes se turnen primero para decir sus respuestas en voz alta a sus compañeros, para recibir comentarios de sus compañeros y luego para escribir sus respuestas en sus diarios del estudiante. Los estudiantes pueden hacer las correcciones necesarias.


MUESTRA LO QUE SABES (PARTE 2) CLAVE DE RESPUESTAS
3
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 3: EL TEOREMA DE PITÁGORAS EN PRISMAS RECTANGULARES
Estándar(es)
● Comprender y aplicar el teorema de Pitágoras. Aplicar el teorema de Pitágoras para determinar longitudes laterales desconocidas en triángulos rectángulos en problemas matemáticos y del mundo real en dos y tres dimensiones.
Grandes Ideas
Investigaciones cilíndricas
Exploraciones Pitagóricas
Forma, número y expresiones
Transformación geométrica
DESCRIPCIÓN
Estándares para la Práctica Matemática Conexiones de Contenido Motores de Investigación
MP.1 Dar sentido a los problemas y perseverar en su resolución.
MP.4 Representar con matemáticas.
MP.5 Usar herramientas apropiadas estratégicamente.
MP.6 Atender a la precisión.
Los estudiantes aplican el teorema de Pitágoras a prismas rectangulares tridimensionales.
MATERIALES
IMPRESO
• 1 diario del estudiante (por estudiante)
• 1 boleto de salida (por estudiante)
• 1 cajas de putter (por pareja)
REUTILIZABLE
• 1 calculadora (por pareja)
• 1 tijera (por estudiante)
CONSUMIBLE
• 1 rollo de cinta adhesiva (por pareja) PREPARACIÓN
• Planifique que los estudiantes trabajen en grupos de dos para completar esta actividad.
• Imprima un diario del estudiante y un boleto de salida ppor alumno.
• Imprime un documento de «cajas de putter» por pareja de estudiantes.
• Reúne suficientes calculadoras y rollos de cinta adhesiva para que cada pareja tenga uno de cada.
• Reúne suficientes pares de tijeras para que cada estudiante tenga uno.
• Para quienes necesiten más apoyo para recordar información, consulte nuestros elementos complementarios como: papel cuadriculado y objetos tridimensionales con líneas de puntos en la sección «Intervención».
CC3 Desarmar el todo, armar las partes
CC4 Descubrir la forma y el espacio
DI1 Dar sentido al mundo (Comprender y explicar)
DI2 Predecir lo que podría suceder (Predecir)
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Lea la siguiente situación a la clase: «Kyle vende palos de minigolf, conocidos como "putters", a propietarios y gerentes de campos de minigolf. Los putters vienen en una variedad de longitudes dependiendo de la altura del cliente. Kyle utiliza cajas de cartón en forma de prismas rectangulares para enviar sus putters a los clientes. Ayudemos a Kyle a determinar la longitud máxima de un putter que puede colocar en la caja si el putter se coloca en la caja en diagonal».
2. Ayude a los estudiantes a acceder a la tarea planteándoles las siguientes preguntas orientadoras:
a. ¿Qué sabes ya sobre los prismas rectangulares?
b. ¿Qué cosas de tu vida compras adaptadas a tu estatura?
3. Entregue un diario del estudiante a cada estudiante.
4. Pídales que utilicen el prisma rectangular para rellenar los espacios en blanco de los pasos 1 y 2 con el fin de determinar la longitud diagonal desde la esquina delantera inferior izquierda hasta la esquina trasera superior derecha. Si lo desea, puede proporcionar a sus estudiantes calculadoras para que las utilicen cuando apliquen el teorema de Pitágoras.
5. Distribuye las cajas de putter y los rollos de cinta adhesiva a las parejas de estudiantes.
6. Entregue un par de tijeras a cada estudiante.
7. Pídales que usen la hoja de trabajo de las cajas de putter para recortar las dos redes de las cajas Putter, A y B, y que usen la cinta para unir los lados de cada una y formar dos prismas rectangulares. Los estudiantes utilizarán las medidas de cada prisma para responder a las preguntas de la página 2 de su diario del estudiante. Pueden usar una calculadora cuando apliquen el teorema de Pitágoras.
8. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión utilizando las siguientes preguntas orientadoras:
a DOK-1 ¿Qué medidas se necesitan para determinar la longitud de la diagonal de un prisma rectangular? Necesitaría conocer la longitud, anchura y altura del prisma rectangular para resolver la longitud de la diagonal.
b DOK-1 ¿Cómo sabes que se puede aplicar el teorema de Pitágoras al resolver la longitud de la diagonal de un prisma rectangular dado el tipo de ángulo que se forma entre la base del prisma y uno de sus lados laterales? Las dos caras son perpendiculares entre sí y forman un ángulo de 90 grados. El teorema de Pitágoras sólo se puede aplicar a un triángulo con un ángulo de 90 grados.
c DOK-2 Cuando se proporcionan las medidas de la longitud y anchura de un prisma rectangular, ¿cuántas veces será necesario aplicar el teorema de Pitágoras al resolver la diagonal del prisma? Tendremos que utilizar el teorema de Pitágoras dos veces, una para la diagonal de la base del prisma y otra para determinar la longitud de la diagonal del prisma.
9. Dé tiempo a los estudiantes para que completen el diario del estudiante, incluidas las preguntas de reflexión.
10. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para encontrar las medidas que faltan en los prismas rectangulares utilizando el teorema de Pitágoras.

11. Después de que los estudiantes hayan completado el diario del estudiante, invita a la clase a una charla de matemáticaspara compartir sus observaciones y aprendizajes.
CHARLA DE MATEMÁTICA
• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:
◦ DOK-2 ¿Cómo se aplica el teorema de Pitágoras a las figuras tridimensionales? Podemos aplicar el teorema de Pitágoras para determinar la distancia de una de las esquinas inferiores del prisma a la esquina superior del lado opuesto.
• DOK-2 ¿Cuál es la longitud diagonal de un prisma rectangular con una longitud de 12 pulgadas, un ancho de 5 pulgadas y una altura de 7 pulgadas? Redondea tu respuesta a la centésima más cercana, si es necesario.
Diagonal de la base, d
122 + 52 = d2
169 = d2
√169 = d
d = 13 pulgadas
Prisma diagonal, x
13 2 + 7 2 = x 2
169 + 49 = x 2
√218 = x
x ≈ 14.76 pulgadas
• DOK-2 Dada la caja de putter A o la caja de putter B, ¿qué prisma rectangular tiene mayor longitud diagonal y en cuánto? Redondea tu respuesta a la pulgada más cercana. La caja de putter B tiene una diagonal mayor en aproximadamente 3 pulgadas.
(32.20 - 29.07 = 3.13)
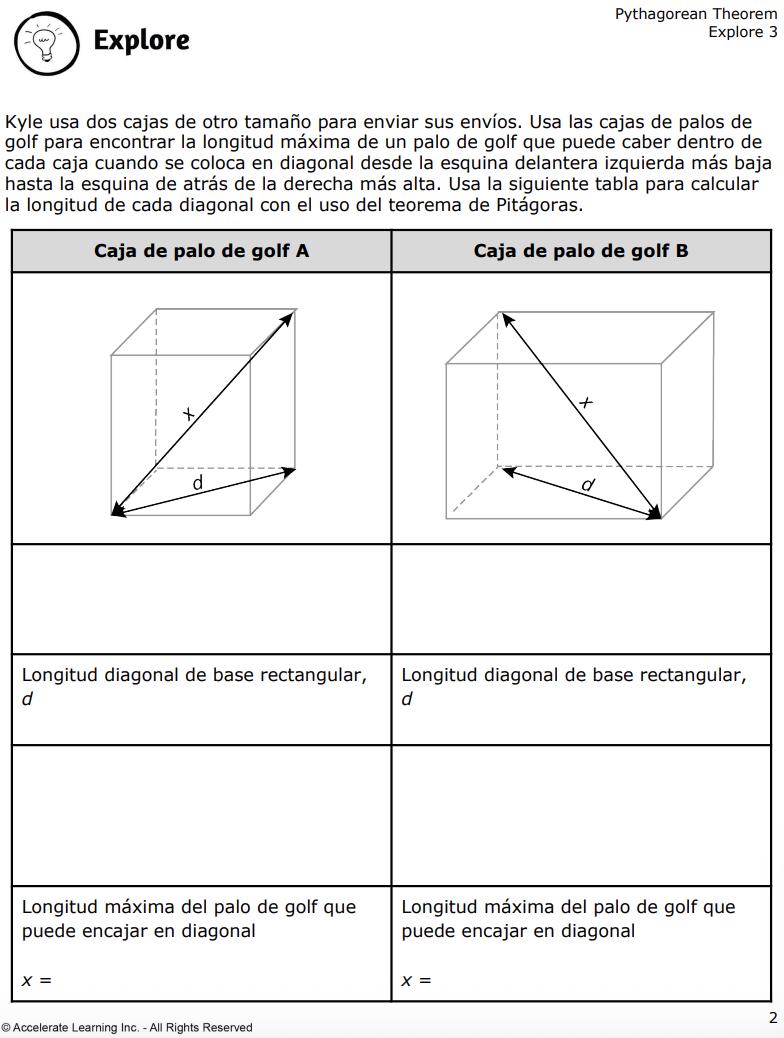

DIARIO DEL ESTUDIANTE
EXPLORAR: EXPLORACIÓN 3

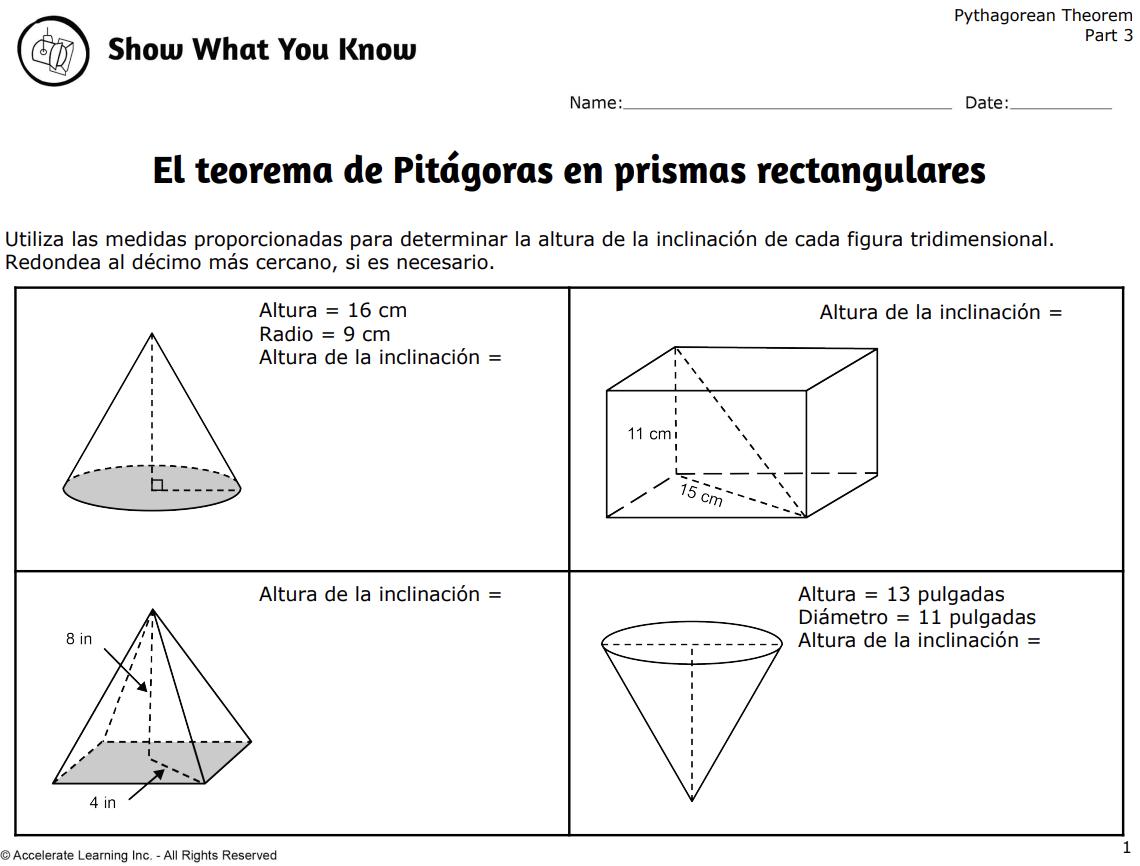
DESPUÉS DE LA EXPLORACIÓN
1. Pida a los estudiantes que completen el boleto de salida para evaluar formativamente su comprensión del concepto.
2. Completen el esquema de anclaje como clase.
3. Pida a cada estudiante que llene su libreta interactiva.
APOYOS DIDÁCTICOS
1. Algunos estudiantes pueden tener problemas para visualizar lo que se está midiendo. Tenga a mano una caja y un palo o una barra para demostrar qué se está midiendo y cómo.
2. Proporcione prismas rectangulares precortados para estudiantes con diferentes niveles de destreza.
3. Algunos pueden sentirse abrumados con la conversión de un triángulo a un prisma rectangular. Haga que se centren en el rectángulo de la primera sección. Puede ser beneficioso tener los lados previamente etiquetados para que los estudiantes sólo tengan que preocuparse de encontrar la hipotenusa que falta.
4. Diferencie el grado de dificultad para la pregunta de reflexión 1 proporcionando las siguientes opciones para el mejor lugar para utilizar este conocimiento fuera del aula de matemáticas:
a. Ir a la tienda
b. Practicar un deporte
c. Moverse
d. Bajar por un tobogán
5. Como extensión, pida a los estudiantes que creen una caja en la que quepa un putter de tamaño medio de 34 pulgadas.
APOYOS LINGÜÍSTICOS
Al repasar cada paso de la página 1, invite a los estudiantes a que se giren hacia un compañero y repitan lo que han oído utilizando lenguaje matemático.
Aclare los significados de los términos matemáticos prisma rectangular y diagonal y del término no matemático putter, y proporcione ejemplos visuales.
Lea las preguntas del diario del estudiante en voz alta mientras los estudiantes señalan las palabras que están leyendo. Haga hincapié en los términos diagonal, rectángulo, y prisma rectangular.
Invite a los estudiantes a presentar uno de sus prismas a la clase y a explicar verbalmente qué pasos siguieron para resolverlo.
Llame la atención sobre el verbo girar en la pregunta de reflexión 2. Use un recuadro para mostrar las distintas formas en que se puede girar y, a continuación, formule la pregunta.
Proporcione ejemplos visuales y aclare los términos matemáticos prisma rectangular y diagonal y el término no matemático putter.
BOLETO DE SALIDA
MUESTRA LO QUE SABES (PARTE 3)
EXPLORAR: EXPLORACIÓN 4
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 4: EL TEOREMA DE PITÁGORAS EN UNA CUADRÍCULA DE COORDENADAS
Estándar(es)
• Comprender y aplicar el teorema de Pitágoras. Aplicar el teorema de Pitágoras para encontrar la distancia entre dos puntos en un sistema de coordenadas.
Grandes Ideas
Investigaciones cilíndricas
Exploraciones Pitagóricas
Forma, número y expresiones
Transformación geométrica
DESCRIPCIÓN
Estándares para la Práctica Matemática Conexiones de Contenido Motores de Investigación
MP.1 Dar sentido a los problemas y perseverar en su resolución.
MP.4 Representar con matemáticas.
MP.5 Usar herramientas apropiadas estratégicamente.
MP.6 Atender a la precisión.
Los estudiantes determinan la distancia entre dos puntos en una cuadrícula de coordenadas utilizando el teorema de Pitágoras.
MATERIALES
IMPRESO
• 1 diario del estudiante (por estudiante)
• 1 boleto de salida (por estudiante)
REUTILIZABLE
• 1 calculadora (por pareja)
• 1 cubo numérico (por pareja)
PREPARACIÓN
• Planifique que los estudiantes trabajen en grupos de dos para completar esta actividad.
• Imprima un diario del estudiante y un boleto de salida para cada estudiante.
• Reúna suficientes calculadoras y cubos numéricos para cada pareja.
• Para los estudiantes que necesiten más ayuda para recordar la información, consulte nuestros elementos de ayuda complementaria de Papel cuadriculado en la sección de «Intervención».
PROCEDIMIENTO Y PUNTOS DE
FACILITACIÓN
1. Lea el siguiente escenario a la clase: «La diseñadora de campos de golf en miniatura Yvette está añadiendo varios hoyos en forma de triángulo rectángulo al campo de golf existente. Comienza la planificación usando una cuadrícula de coordenadas para determinar el trazado de cada hoyo. Ayudemos a Yvette trazando varios esquemas que pueda utilizar para sus adiciones».
CC3 Desarmar el todo, armar las partes
CC4 Descubrir la forma y el espacio
DI1 Dar sentido al mundo (Comprender y explicar)
DI2 Predecir lo que podría suceder (Predecir)
2. Ayude a los estudiantes a acceder a la tarea planteándoles las siguientes preguntas:
a. ¿Qué recuerdas sobre el uso de una cuadrícula de coordenadas?
b. ¿Qué otra profesión podría necesitar conocer o usar el teorema de Pitágoras?
3. Entregue un diario del estudiante a cada estudiante.
4. De una calculadora y un cubo numérico por pareja.
5. Explique a los estudiantes que van a crear la suma 1. Indique que empiecen trazando el punto A en la cuadrícula de coordenadas. A continuación, pídales que usen el cubo numérico para generar los pares ordenados de los puntos B y C. Pídales que formen un triángulo con estos tres puntos. Pide a los estudiantes que anoten las medidas de cada lado utilizando la tabla proporcionada. Permita que los estudiantes utilicen calculadoras cuando apliquen el teorema de Pitágoras. A continuación, pida a los estudiantes que repitan este proceso creando la adición 2, un segundo triángulo rectángulo.
6. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión con las siguientes preguntas:
a DOK-1: ¿Cuántos pares ordenados se necesitan para crear un triángulo rectángulo en una cuadrícula de coordenadas? Se necesitaron tres pares ordenados para crear los triángulos rectángulos.
b DOK-1: ¿Cómo se miden los dos catetos perpendiculares de un triángulo rectángulo en una cuadrícula de coordenadas? Podríamos contar el número de espacios de la cuadrícula entre los dos puntos que forman cada cateto.
c DOK-2: ¿Qué tipos de números utilizaste al lanzar el cubo numérico para generar pares ordenados? Números enteros y números enteros. Como el cubo numérico tiene números enteros del 1 al 6, no había forma de generar un par ordenado con fracciones o decimales.
7. Deje tiempo para que los estudiantes completen el diario del estudiante, incluidas las preguntas de reflexión.
8. Pida a los estudiantes que compartan sus estrategias y anímelos a hacerse preguntas y establecer conexiones. Indique que anoten las similitudes y diferencias entre las estrategias usadas para encontrar la distancia en una cuadrícula de coordenadas usando el teorema de Pitágoras.
9. Después de que hayan completado el diario del estudiante, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizaje.
CHARLA DE MATEMÁTICAS
• Elija una rutina de conversación estructurada para facilitar la siguiente pregunta:
◦ DOK-3 ¿Cómo es útil usar la cuadrícula de coordenadas al crear triángulos rectángulos? La cuadrícula de coordenadas es una guía útil cuando se dibujan líneas rectas, especialmente para los dos catetos de un triángulo rectángulo. Las líneas de la cuadrícula en el plano de coordenadas también nos ayudan a determinar las longitudes de ambos catetos.

• DOK-2 Se dibuja el triángulo rectángulo XYZ en una cuadrícula de coordenadas. El punto X está situado en (5, 5), el punto Y está situado en (10, 5), y el punto Z está situado en (5, 6). ¿Cuál es la distancia entre los puntos Y y Z?
Distancia del punto X al punto Y = 5 unidades
Distancia del punto X al punto Z = 1 unidad
Distancia del punto Y al punto Z =
52 + 12 = c2
25 + 1 = c2
26 = c2
√26 = c
c ≈ 5.10 unidades
• DOK-2 ¿Cuál de las dos sumas de tu grupo tenía la hipotenusa más pequeña? ¿Y cuánto más pequeña? Redondea tu respuesta a la centésima más próxima. Las respuestas pueden variar.
La adición 2 tenía la hipotenusa más pequeña en 0,23 aproximadamente.


DIARIO DEL ESTUDIANTE
EXPLORAR: EXPLORACIÓN 4
DESPUÉS DE LA EXPLORACIÓN
1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.
2. Completen el esquema de anclaje como clase.
3. Haga que cada estudiante complete su libreta interactiva.
4. Regrese la sección «captar interés» e instruya a los estudiantes a usar sus habilidades recién adquiridas para completar exitosamente la actividad.
APOYOS PEDAGÓGICOS
1. Proporcione flexibilidad a los estudiantes que necesitan tareas reducidas eliminando la segunda pregunta.
2. Algunos pueden tener problemas para contar los bloques entre puntos en el plano de coordenadas. Pídales que tracen la línea entre los puntos, contando cada cuadrado a medida que avanzan.
3. Para quines no conozcan la diferencia entre horizontal y vertical, cree un esquema de anclaje. Utilice la brújula para etiquetar esas direcciones.
4. Diferencie el grado de dificultad para la pregunta de reflexión 2 haciendo referencia al esquema de anclaje con horizontal y vertical etiquetadas en la brújula.
5. Como extensión, haga que los estudiantes creen un campo de golf de nueve hoyos donde cada hoyo tenga un hoyo de forma triangular diferente.
APOYOS LINGÜÍSTICOS
Aclare que el término adición en esta exploración se refiere al trazado de los hoyos de golf que están añadiendo al campo y no al proceso de sumar números.
Recuerde a los estudiantes que el término piernas se refiere a los dos lados más cortos de un triángulo rectángulo y no se refiere a las piernas de una persona, animal o mueble.
La palabra brújula tiene múltiples significados en inglés. Haga referencia a la brújula en el diario del estudiante o cree un gráfico de anclaje que pueda mostrarse cuando se hable de la brújula.
Para los estudiantes hispanohablantes, haga hincapié en la similitud entre el término las coordinadas y el término inglés coordinates.
Durante la charla de matemáticas, muestre los tallos de las oraciones para que los estudiantes los utilicen:
• Observé _______.
• Me di cuenta _______.
Permita que los estudiantes expliquen sus pensamientos verbalmente y que un compañero lo escriba en el papel por ellos. A continuación, pida al compañero que lea en voz alta lo que ha escrito. A continuación, el estudiante puede decidir si su mensaje se ha transmitido con claridad y hacer los ajustes necesarios.
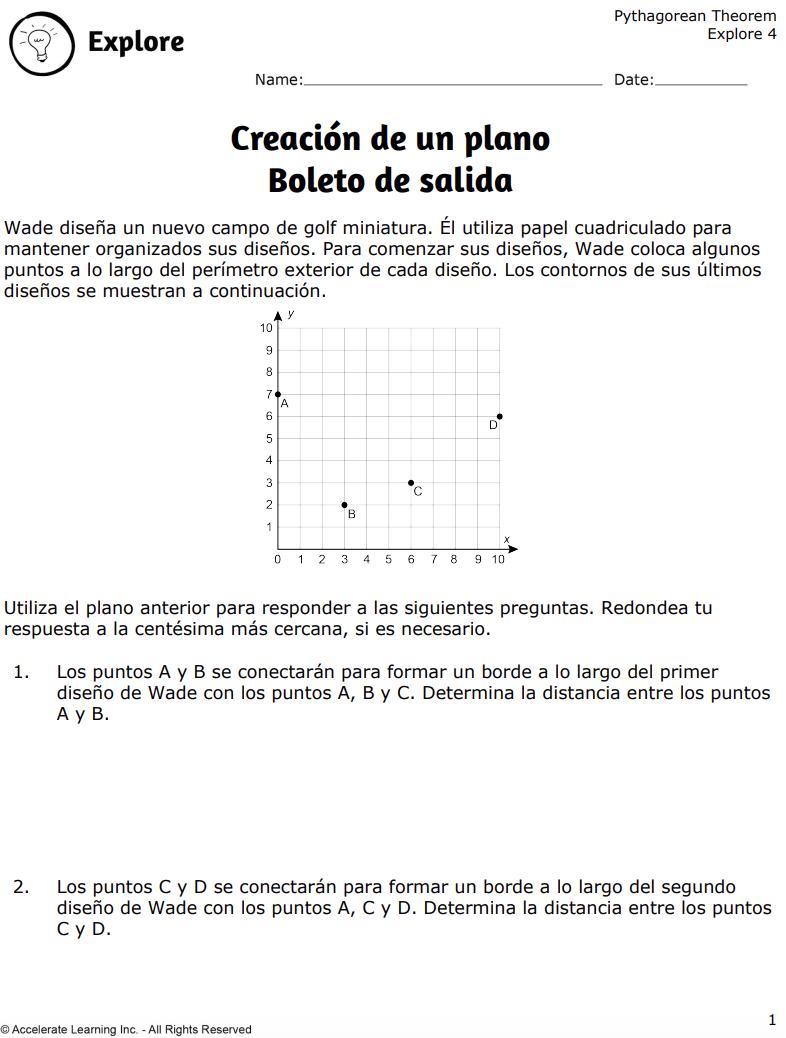

BOLETO DE SALIDA
MUESTRA LO QUE SABES (PARTE 4)
EXPLICAR: ESQUEMA DE ANCLAJE

EJEMPLO DE ESQUEMA DE ANCLAJE
CONSOLIDAR EL APRENDIZAJE DEL ESTUDIANTE
ESQUEMA DE ANCLAJE
DESCRIPCIÓN
Este gráfico de anclaje destaca las ideas principales del alcance. Esta es una herramienta para apoyar la instrucción y anclar el aprendizaje de los estudiantes a lo largo del alcance.
MATERIALES
• 1 hoja de papel cuadriculado
• 1 juego de marcadores multicolores
PREPARACIÓN
● Imprima el ejemplo de esquema de anclaje (opcional).
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. El ejemplo de esquema de anclaje puede usarse como referencia antes de crear el esquema de anclaje de la clase con los estudiantes. La creación de un esquema de anclaje debe estar dirigida por los estudiantes para promover que se apropien de su aprendizaje.
2. A medida que los estudiantes trabajen en el alcance, colaboren para añadir piezas al esquema de anclaje. Formule las siguientes preguntas:
a. ¿Qué estrategia utilizamos para resolver este problema?
b. ¿Qué vocabulario necesitamos conocer para poder resolver este problema?
3. Continúe añadiendo habilidades o estrategias importantes aprendidas después de cada exploración para resaltar el contenido importante.
4. Explique a los estudiantes que pueden utilizar este esquema como herramienta de apoyo para su aprendizaje. Los estudiantes también pueden pegar una copia del esquema de anclaje en sus cuadernos para utilizarla como referencia durante todo el año.
5. Algunos esquema de anclaje sólo se mostrarán durante ese alcance o grupo de alcances, mientras que otras permanecerán expuestas durante todo el año escolar.
EXPLICAR: LIBRETA INTERACTIVA
DOCUMENTAR EL APRENDIZAJE DEL ESTUDIANTE
LIBRETA INTERACTIVA
DESCRIPCIÓN
Los estudiantes toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y el cuaderno.
MATERIALES
IMPRESO
● 1 folleto del estudiante (por estudiante)
PREPARACIÓN
● Imprime una copia del folleto del estudiante por alumno.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Prepara una libreta interactiva con un cuaderno de espiral o de composición para cada estudiante. Los estudiantes pueden utilizar las primeras páginas para crear una tabla de contenidos con números de página para realizar un seguimiento de las actividades.
2. En el folleto del estudiante se ofrecen instrucciones para cada actividad.
3. Dé tiempo a los estudiantes para que completen la actividad y peguen las piezas en sus cuadernos interactivos.
4. Las libretas ineractivas pueden utilizarse como referencia para los estudiantes durante el trabajo independiente y pueden enviarse a casa al final del año como registro de su aprendizaje.


DESCRIPCIÓN
Los estudiantes tienen la oportunidad de utilizar sus conocimientos lingüísticos y culturales previos para apoyar las conexiones con nuevas destrezas, vocabulario y conceptos en sus niveles de competencia.
MATERIALES
IMPRESO
• 1 folleto del estudiante según su nivel de competencia (por estudiante)
REUTILIZABLE
• 1 calculadora (por estudiante, opcional)
PREPARACIÓN
• Prepárese para que los estudiantes trabajen con compañeros cuando sea necesario.
• Determine el nivel de competencia en inglés de cada estudiante.
• Imprima un folleto del estudiante para cada estudiante según su nivel de competencia en inglés.
• Permita que los estudiantes tengan acceso al vocabulario ilustrado para este alcance.


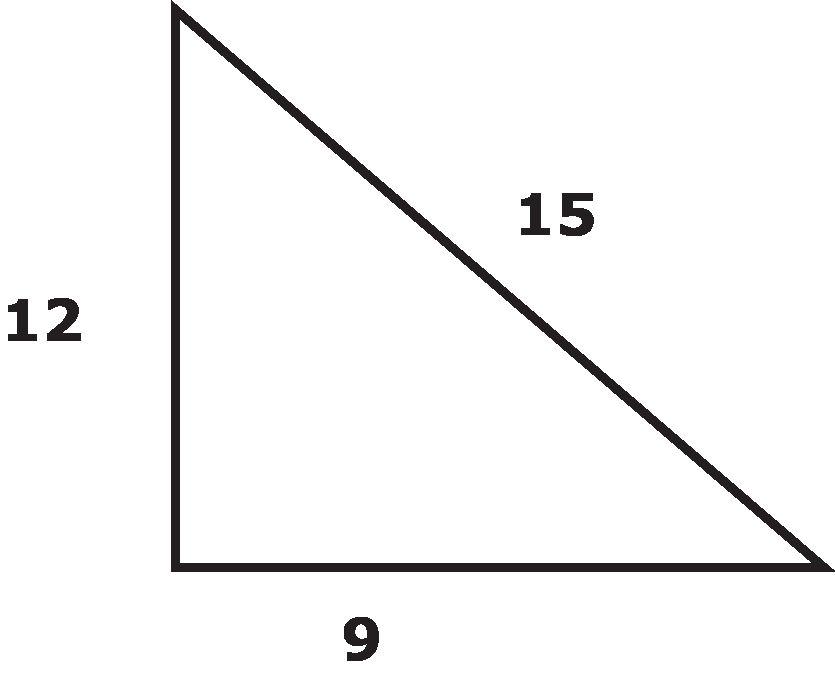
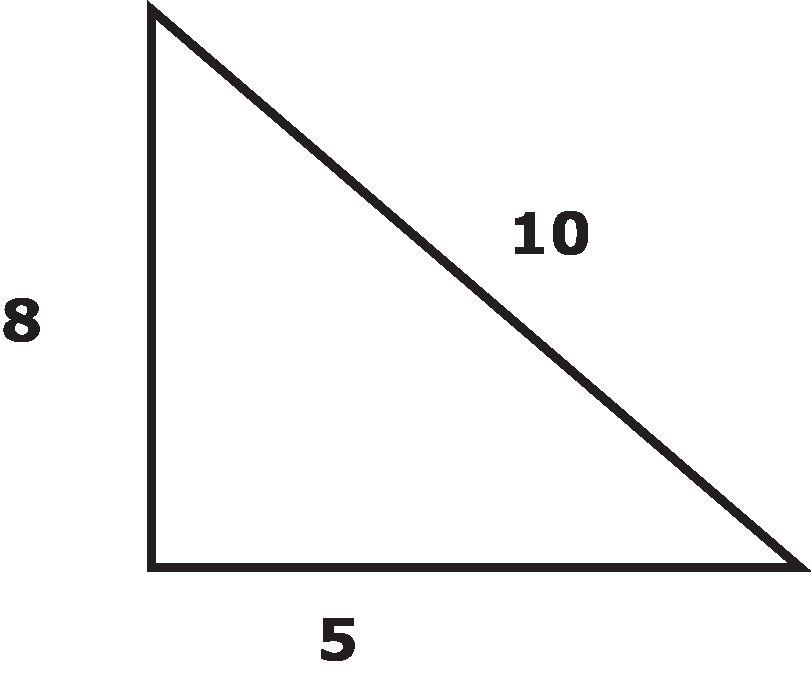



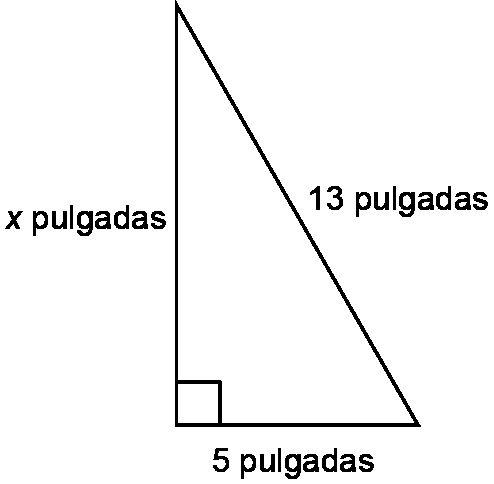









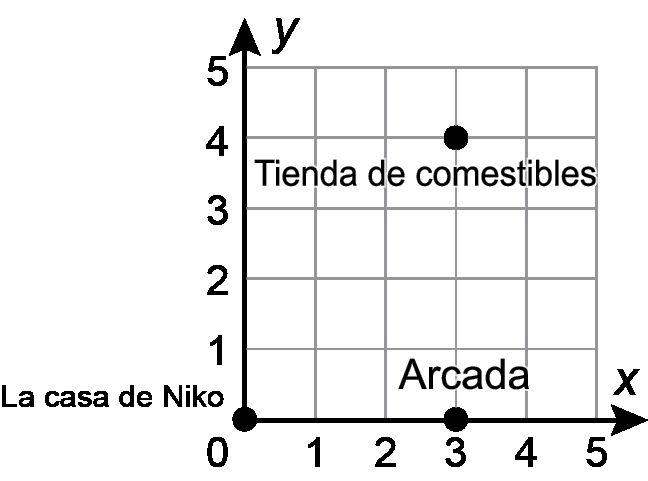















CONEXIONES
LINGÜÍSTICAS
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1 Distribuya a cada estudiante un folleto con el nivel de competencia adecuado.
2 Utilice las instrucciones para las partes de comprensión oral, expresión oral, lectura y escritura. Utilice gestos, señale objetos y elementos visuales, según proceda. Consulte las sugerencias en las instrucciones.
3 Deje tiempo a los estudiantes para que piensen con sus vecinos antes de responder.
4 Anime a los estudiantes a perseverar en su pensamiento y a utilizar herramientas y modelos matemáticos.
5 Invite a los estudiantes a responder adecuadamente a cada dominio lingüístico.
6 Pida a los estudiantes que utilicen la página final del folleto del estudiante para establecer conexiones entre los conceptos matemáticos y el mundo real.
















AVANZADO FOLLETO DEL ESTUDIANTE
ESCUCHAR Y HABLAR
PRINCIPIANTE
Tenga a mano el vocabulario con imágenes para que los estudiantes lo utilicen. Lea las siguientes frases de una en una:
• Señale la hipotenusa del primer triángulo.
• ¿Cómo sabe que es la hipotenusa?
• Pida a los estudiantes que utilicen la siguiente secuencia de frases:
◦ Sé que es la hipotenusa porque _____.
• Señale los catetos del primer triángulo.
• ¿Cómo sabe que son los catetos?
• Pida a los estudiantes que utilicen la siguiente raíz de frase:
◦ Sé que son los catetos porque _____.
• ¿Cómo podemos determinar si el primer triángulo es rectángulo? Utilice el teorema de Pitágoras que se ha resuelto aquí (señale la página) para explicarlo.
• Pida a los estudiantes que utilicen la siguiente raíz de frase:
◦ Podemos determinar que el primer triángulo es un triángulo rectángulo porque ____.
• Veamos el siguiente ejemplo. ¿Qué observas en este ejemplo que sea similar o diferente del primer ejemplo?
• Pida a los estudiantes que utilicen la siguiente secuencia de oraciones:
◦ He observado en el segundo triángulo que ____.
• Sí, el segundo triángulo no es un triángulo rectángulo porque el teorema de Pitágoras no describe la relación de los catetos con la hipotenusa.
• ¿Es el tercer triángulo un triángulo rectángulo? Utiliza el teorema de Pitágoras para demostrar si lo es. Escribe "sí" o "no" en el recuadro.
LEER Y HABLAR
PRINCIPIANTE
Lea la historia en grupo. Divida la historia en frases. Pida a los estudiantes que señalen cada palabra mientras leen. Pídales que rodeen con un círculo las palabras que no conozcan. Discuta las palabras con todo el grupo.
• ¿A dónde va Niko primero?
◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciones: Niko va a _______.
• ¿Has estado antes en un salón recreativo?
◦ Pida a los estudiantes que utilicen el siguiente marco oracional: Yo _____ he estado antes en un salón recreativo.
INTERMEDIO
Ponga a disposición de los estudiantes un vocabulario ilustrado. Lea las siguientes instrucciones de una en una:
• Señale la hipotenusa del primer triángulo.
• ¿Cómo sabes que es la hipotenusa?
◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciónSé que es la hipotenusa porque _____.
• Señale los catetos del primer triángulo.
• ¿Cómo sabes que son los catetos?
◦ Pida a los estudiantes que utilicen la siguiente secuencia de oración: Sé que son los catetos del triángulo porque _____.
• ¿Es el primer triángulo un triángulo rectángulo? ¿Cómo lo sabes?
◦ Pida a los estudiantes que utilicen la siguiente raíz de frase: El primer triángulo es un triángulo rectángulo porque _____.
• Escribe tu respuesta, sí o no, en el recuadro.
• ¿Es el segundo triángulo un triángulo rectángulo? ¿Cómo lo sabes?
◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciones: El segundo triángulo es/no es un triángulo rectángulo porque _____.
• Escribe tu respuesta, sí o no, en el recuadro.
• ¿Es el tercer triángulo un triángulo rectángulo?
Utiliza el teorema de Pitágoras para demostrar si lo es. Escribe sí o no en el recuadro.
• ¿Cómo puedes saber si un triángulo es rectángulo o no?
◦ Pide a los estudiantes que utilicen el siguiente enunciado: Puedes saber si un triángulo es rectángulo o no si ____.
INTERMEDIO
Coro: lea la historia en grupo. Pida a los estudiantes que señalen cada palabra mientras leen. Pídales que rodeen con un círculo las palabras que no conozcan. Discuta las palabras con sus compañeros.
• Comparta con sus compañeros de qué trataba la historia.
• Comparta con sus compañeros lo que sabe sobre la sala de juegos.
• Pregunte a su compañero: "¿Qué lugares te gusta visitar en tu barrio?"
◦ Pida a los estudiantes que utilicen el siguiente marco de frases: Me gusta visitar el _______ de mi barrio.
AVANZADO
Ponga a disposición de los estudiantes vocabulario con imágenes. Lea las siguientes preguntas de una en una:
• Señala la hipotenusa del primer triángulo.
• ¿Cómo sabes que es la hipotenusa?
• Señala los catetos del primer triángulo.
• ¿Cómo sabes que son los catetos?
• ¿Cómo sabes si un triángulo es rectángulo o no?
• Determina si cada uno de estos triángulos es un triángulo rectángulo. Muestra tu trabajo. Escribe tu respuesta, sí o no, en las casillas.
• Comenta con tus compañeros qué triángulos son rectángulos.
AVANZADO
Pida a los estudiantes que lean la historia con sus compañeros y que señalen cada palabra mientras leen. Invite a los estudiantes a rodear con un círculo las palabras que no conozcan y a comentarlas con sus compañeros.
• Explique a sus compañeros de qué trataba el pasaje.
• Explique a sus compañeros cada uno de los puntos del plano de coordenadas.
• Explique a sus compañeros cómo determinar la distancia entre dos puntos de un plano de coordenadas.
• Lea cada enunciado y comente sus respuestas con sus compañeros.
LEER Y HABLAR (CONTINUACIÓN)
PRINCIPIANTE
• ¿Adónde va Niko después de ir a los recreativos? ¿Por qué?
◦ Pida a los estudiantes que utilicen el siguiente marco de frases: Niko va a la _______ a por un _______.
• ¿Cuál es tu merienda favorita?
◦ Pida a los estudiantes que utilicen el siguiente marco oracional: Mi tentempié favorito es ________.
• Pida a los estudiantes que rodeen con un círculo sus respuestas para las dos primeras afirmaciones.
• Haga eco de la tercera afirmación antes de pedir a los estudiantes que respondan.
• ¿Cómo encontrarías la distancia de la sala de máquinas recreativas desde la casa de Niko utilizando el plano de coordenadas?
◦ Pida a los estudiantes que utilicen la siguiente raíz de oración: Encontraría la distancia de la sala de juegos a la casa de Niko mediante _____.
• Encuentra la distancia. Encierre en un círculo su respuesta.
• Lea el cuarto enunciado antes de que los estudiantes respondan. Encuentra la distancia. Rodea con un círculo tu respuesta. Lea el quinto enunciado antes de que los estudiantes respondan.
• Dibuje una línea desde la casa de Niko hasta la sala de juegos.
• Dibuje una línea desde la sala de juegos hasta la tienda de comestibles.
• Dibuje una línea desde la tienda de comestibles hasta la casa de Niko.
• ¿Qué forma se forma?
◦ Pida a los estudiantes que usen la siguiente raíz de oración: La forma que se forma es un ________.
• ¿Qué tipo de triángulo es?
◦ Pida a los estudiantes que utilicen el siguiente marco oracional: Es un _______ triángulo.
• ¿Qué puedes hacer para encontrar la distancia desde la tienda de comestibles hasta la casa de Niko? ¿Qué fórmula podrías utilizar? Encierra en un círculo la fórmula correcta que usarías.
◦ Haz que los estudiantes usen el siguiente marco de oración: Para hallar la distancia desde la tienda de comestibles hasta la casa de Niko, yo ___.
• Coral-lea el siguiente enunciado. ¿Qué letra de la fórmula representaría la distancia desde la tienda de comestibles hasta la casa de Niko? Encierra en un círculo la letra correcta.
• Ahora completa la ecuación para encontrar el lado que falta.
• Encuentra la distancia desde la tienda de comestibles hasta la casa de Niko.
• Encierra en un círculo tu respuesta.
INTERMEDIO
• Eco-lee la primera afirmación. Señala la respuesta en la historia antes de marcar la afirmación como verdadera o falsa.
• Lee la segunda afirmación. Señala la respuesta en la historia antes de marcar la afirmación como verdadera o falsa.
• Lee la tercera afirmación. Señala la información útil de la historia.
• Explica a tus compañeros cómo determinarías el número de manzanas que hay entre la sala de juegos y la casa de Niko.
• Rodea con un círculo verdadero o falso.
• Coro: lee la cuarta afirmación. Muestra a tus compañeros información útil de la historia.
• Explica a tus compañeros cómo determinarías el número de manzanas a las que se encuentra la sala de máquinas recreativas de la tienda de comestibles.
• Encierra en un círculo verdadero o falso.
• Compañero-lee el quinto enunciado. Explica a tus compañeros qué fórmula utilizarías para hallar la longitud que falta. Explique cómo encontrará las respuestas.
◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciones cuando compartan su estrategia con sus compañeros:
◦ Encontraré la respuesta en _____.
• Coro: lea la sexta afirmación. Discuta con sus compañeros para decidir si es verdadero o falso.
• Discuta con sus compañeros cómo rellenar los espacios en blanco para resolver el teorema de Pitágoras, y luego resuelva.
◦ Haga que los estudiantes usen las siguientes estructuras de oraciones:
• Para el primer espacio en blanco, usaremos el __________ de ______ a ____.
• Para el segundo espacio en blanco, usaremos el __________ de ______ a ____.
• El tercer espacio en blanco nos dirá el __________ de ______ a ____.
• Coro-lea la última afirmación. Discute con tus compañeros para decidir si es verdadera o falsa.
ESCRIBIR
PRINCIPIANTE
Disponga de tarjetas de vocabulario con imágenes para los estudiantes. Lea y comente las palabras del banco de palabras. Defina y ponga ejemplos según las necesidades de los estudiantes. Discuta las siguientes preguntas mientras lee:
• Eco-lectura de las instrucciones.
• Discuta las partes de un triángulo rectángulo con los estudiantes:
◦ ¿Qué valor tiene la longitud de la hipotenusa?
◦ ¿Cómo sabes que es la hipotenusa?
◦ Señala los catetos del triángulo.
◦ ¿Cómo sabes que son los catetos?
◦ ¿Cuál es la fórmula del teorema de Pitágoras?
• Eco-lea cada enunciado y pida a los estudiantes que consulten el banco de palabras antes de escribir su respuesta.
INTERMEDIO
Ponga a disposición de los estudiantes tarjetas de vocabulario con imágenes. Coro: lee y comenta las palabras del banco de palabras. Defina y proporcione ejemplos según las necesidades de los estudiantes. Discuta las siguientes preguntas mientras lee:
• Haga que los estudiantes discutan cada palabra del banco de palabras con sus compañeros.
• Doble la mitad inferior del papel para que sólo se vea el banco de palabras. Por turnos, señale cada palabra del banco de palabras y explíquela a sus compañeros.
• Tome nota de los estudiantes que proporcionan explicaciones matemáticamente precisas de las palabras del banco de palabras.
• A continuación, señale una palabra del banco de palabras cuyo significado necesite aclarar.
• En función de los estudiantes que haya oído dar explicaciones matemáticamente precisas, pida a los estudiantes que ayuden a aclarar las palabras seleccionadas a sus compañeros: Veo que nos vendría bien una aclaración sobre la palabra ___. (Nombre del estudiante) pudo dar una explicación clara sobre la palabra ________ a su compañero. _____, ¿podrías compartir tu explicación?
• Lee los enunciados con tus compañeros y utiliza las palabras del banco de palabras para completar cada enunciado. Tenga en cuenta que algunas palabras pueden utilizarse más de una vez o no utilizarse en absoluto.
• Recuerde a los estudiantes que consulten el banco de palabras cuando rellenen los espacios en blanco.
AVANZADO
Ponga a disposición de los estudiantes las tarjetas de vocabulario con imágenes. Los estudiantes deben leer en coro las palabras del banco de palabras con sus compañeros. Pídales que comenten el significado de las palabras con sus compañeros. Defina y proporcione ejemplos según las necesidades de los estudiantes. Mientras los estudiantes leen, pídales que discutan las siguientes preguntas con sus compañeros:
• Pídales que discutan las palabras del banco de palabras con sus compañeros.
• Discutan las palabras del banco de palabras con sus compañeros. Cada persona debe dar una explicación o descripción de una palabra y luego pedir a su compañero que parafrasee el significado de la palabra. Continúa este proceso hasta que hayas discutido todas las palabras del banco de palabras.
• Lee las instrucciones con tus compañeros. ¿Qué plan seguirás para asegurarte de que utilizas el mayor número posible de palabras del banco de palabras en tu redacción? Si no estás seguro de cómo utilizar una palabra, enciérrala en un círculo en el banco de palabras. Los estudiantes no deben empezar a escribir todavía.
• Presta atención a los estudiantes que tengan dificultades para crear un plan o que encierren palabras en un círculo en el banco de palabras. Ofrezca apoyo y permita que los estudiantes que hayan podido crear un plan lo compartan con la clase.
◦ Veo que varios de nosotros necesitamos aclaraciones sobre la palabra _______. Diríjase a alguien cercano que no sea su compañero y pídale que aclare o defina la palabra
◦ Veo que varios de nosotros necesitamos ayuda para diseñar un plan que utilice palabras del banco de palabras. Acércate a alguien que no sea tu compañero y pídele que explique cómo piensa utilizar el mayor número posible de palabras del banco de palabras.
• Pide a los estudiantes que escriban sus explicaciones una vez que se hayan aclarado todas las palabras y se hayan compartido los planes.
• Ahora, escribid vuestras explicaciones utilizando al menos cinco de las palabras del banco de palabras. Cuando terminen de escribir, compártanlas con sus compañeros.
Figuras congruentes

Figuras del mismo tamaño y forma


Teorema de pitágoras

Teorema que establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados de un triángulo rectángulo; a² + b² = c²
Ángulo que mide 90° Ángulo recto


Triángulo rectángulo
Triángulo con un ángulo de 90º (triángulo recto)

Raíz cuadrada
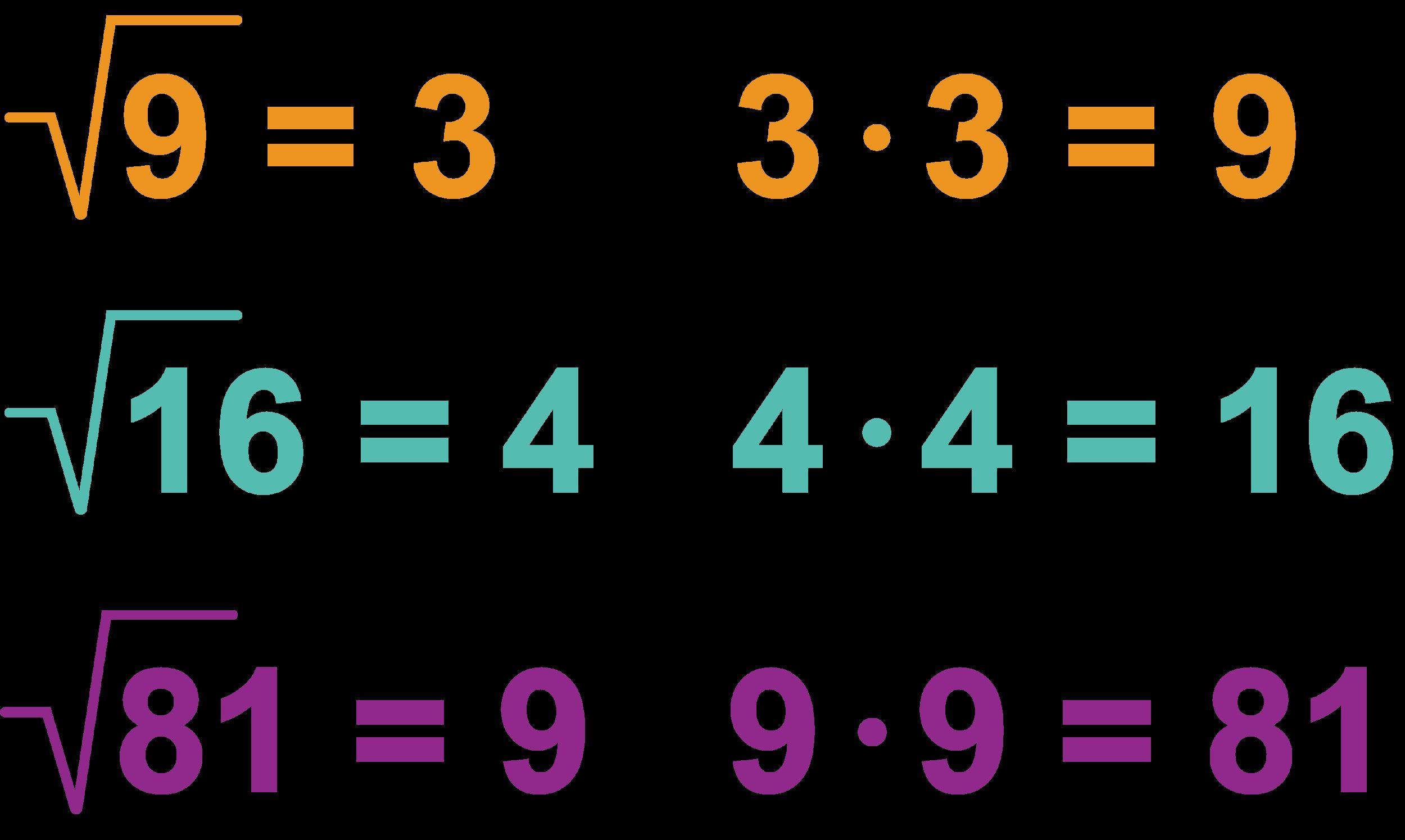
Número que, cuando se multiplica por sí mismo, produce el número dado

Notación matemática que indica el número de veces que el número base se multiplica por sí mismo; también llamado potencia Exponente


Número irracional

Número decimal que no puede expresarse como fracción, no es imaginario y no se repite ni termina


Teorema que establece que si el cuadrado de la longitud del lado mayor de un triángulo es igual a la suma de los cuadrados de los otros dos lados, entonces el triángulo es un triángulo rectángulo; si c² = a² + b², entonces es un triángulo rectángulo.


Distancia perpendicular de un vértice al lado opuesto de una figura


PALABRAS QUE HAY QUE CONOCER
VOCABULARIO ILUSTRADO

Número racional

Número que puede escribirse como una fracción de los números enteros a/b, donde b ≠ 0; número que se puede escribir como una razón con dos números enteros

Dos o más figuras que tienen la misma forma, pero diferentes tamaños


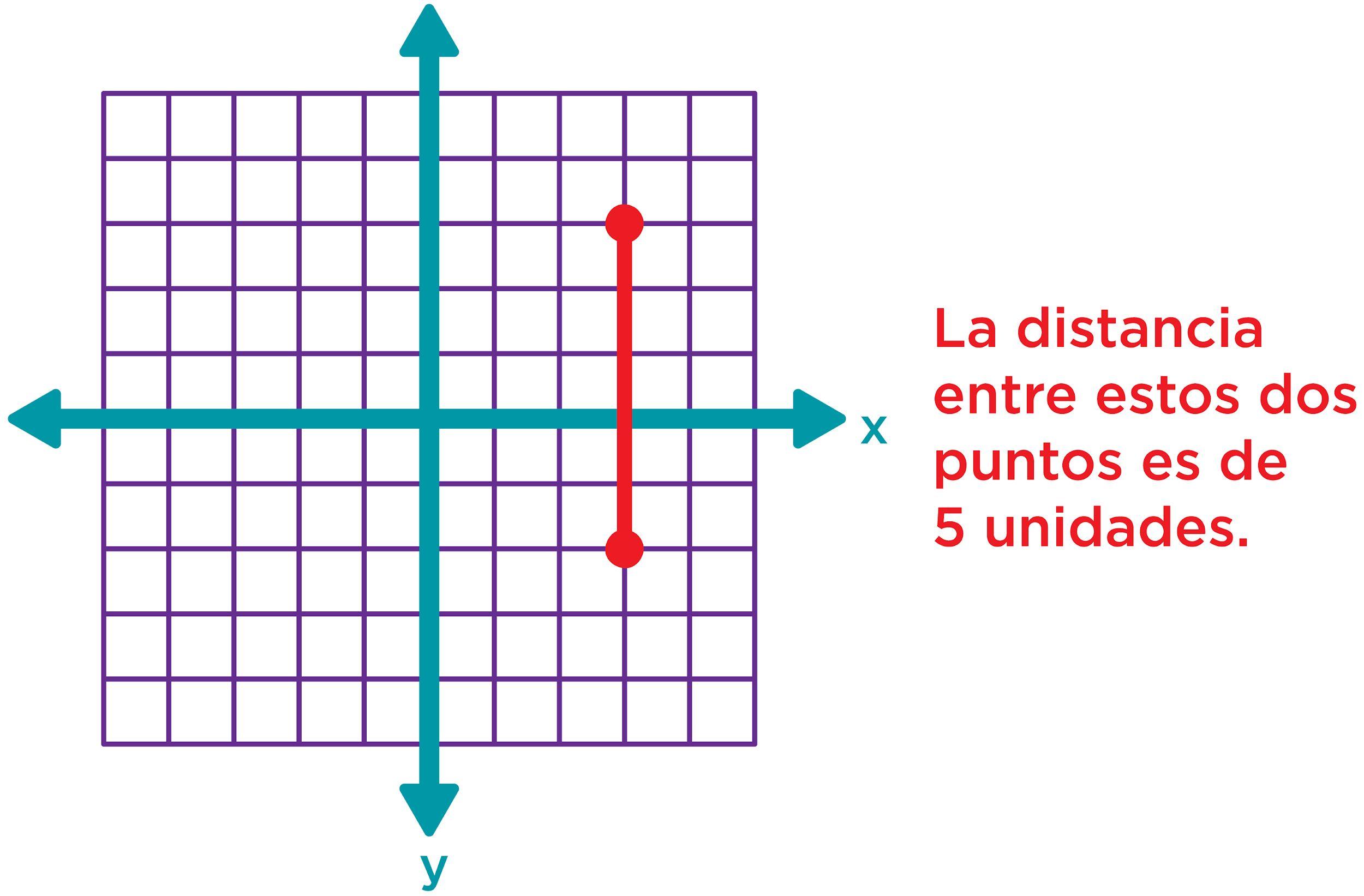
Medida de la longitud entre dos puntos

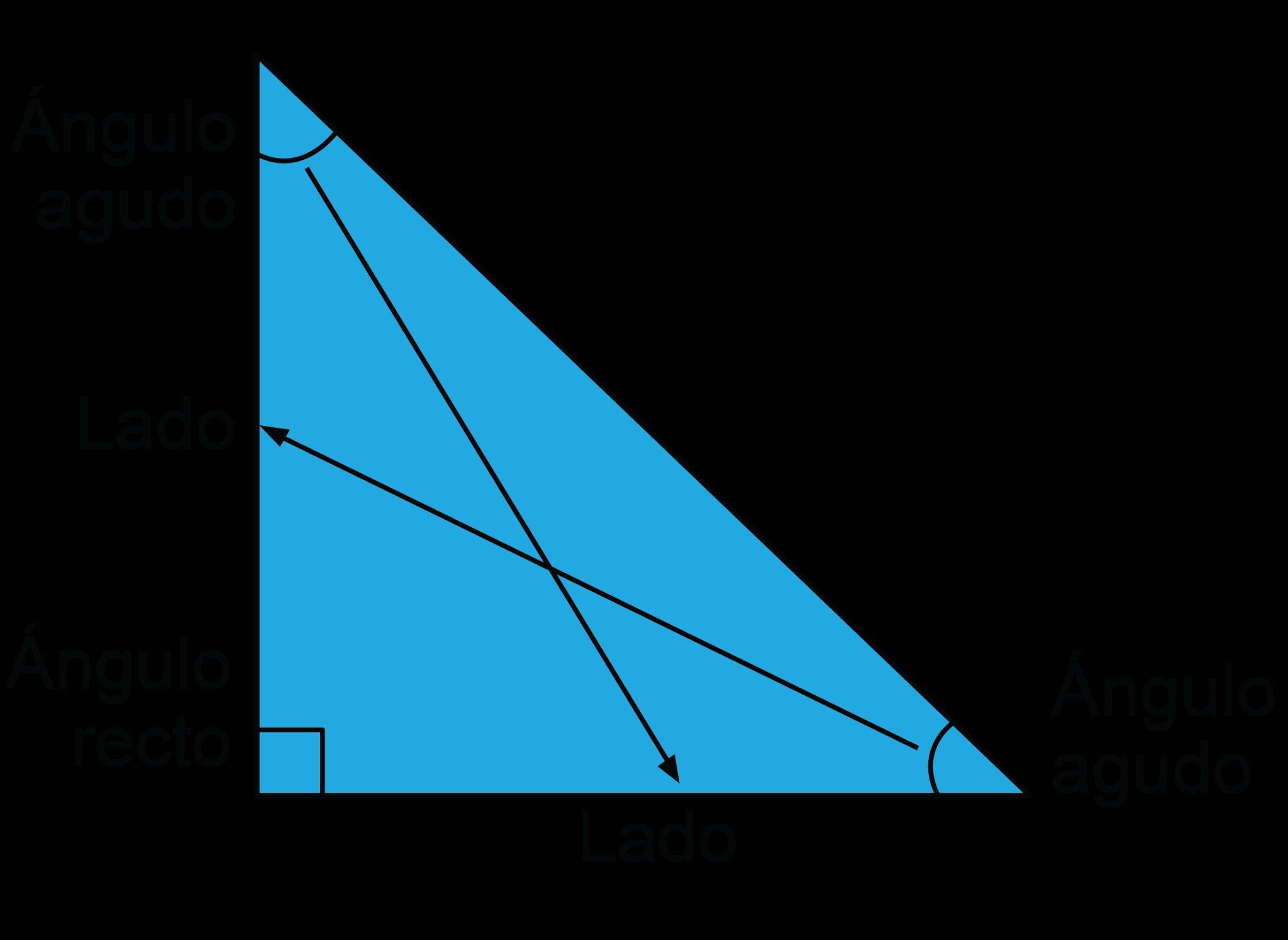
Cualquiera de los dos lados en un triángulo rectángulo que forman el ángulo recto y son opuestos a los ángulos agudos
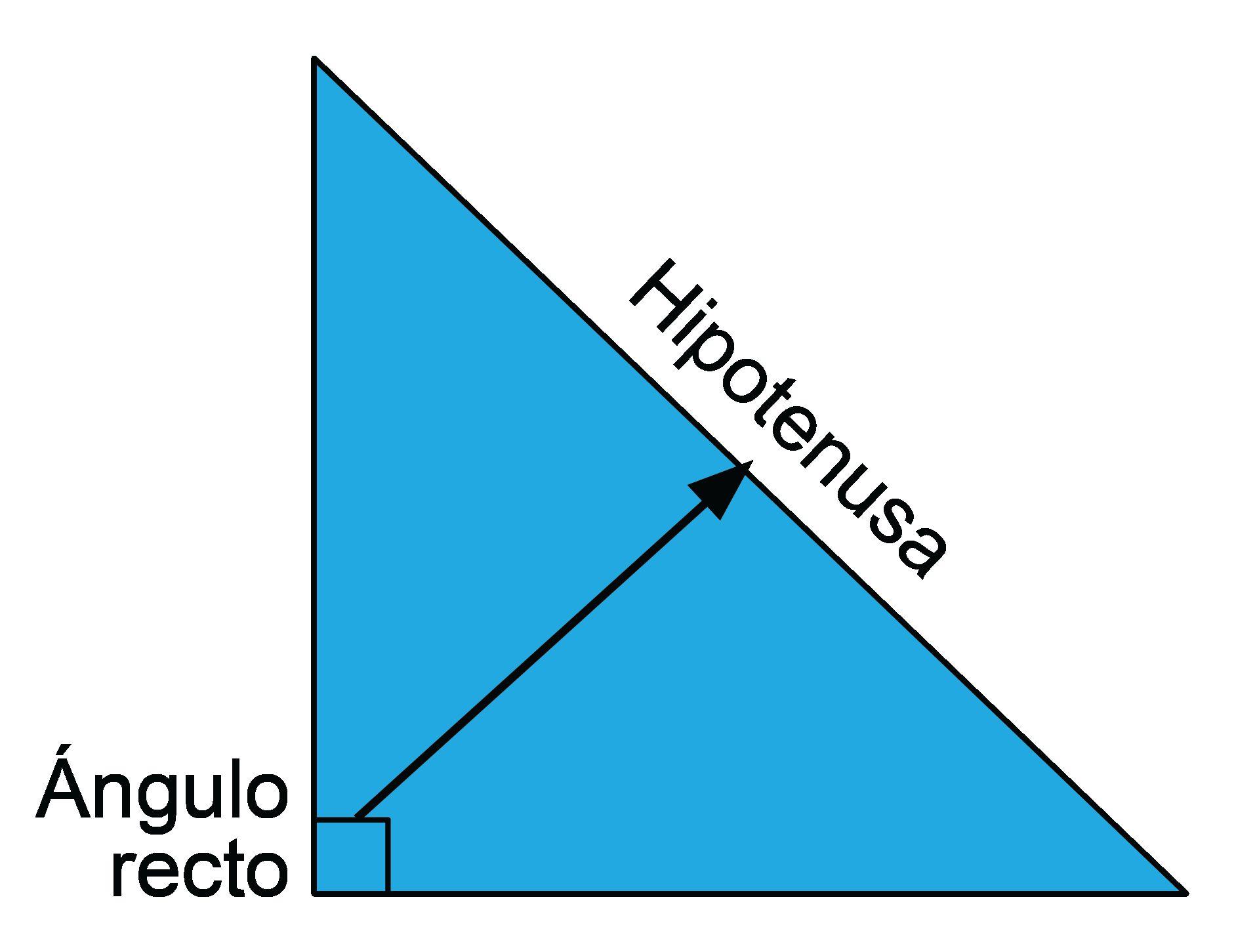
Lado más largo del triángulo rectángulo, opuesto al ángulo recto


Número entero que es el resultado de otro número entero por sí mismo Cuadrado perfecto
ELABORAR: CONSTRUCTOR DE FLUIDEZ
DESARROLLAR LA FLUIDEZ CONCEPTUAL
CONSTRUCTOR DE FLUIDEZ:
TEOREMA DE PITÁGORAS
¡DESCRIPCIÓN
En esta actividad, los estudiantes se turnan para sacar tarjetas de problemas de un tarro y adivinar la respuesta.
MATERIALES
IMPRESOS
• 1 hoja de instrucciones de ¡Bam! (por pareja)
• 1 juego de ¡Bam! ¡(por pareja)
REUTILIZABLES
• 1 tarro u otro recipiente (por pareja)
• 1 cronómetro (por profesor)
PREPARACIÓN
• Haga copias a doble cara de las tarjetas de ¡Bam! Si lo desea, puedes imprimirlas en cartulina para que duren más.
• Recorte las tarjetas individuales.
• Ponga a los estudiantes en parejas.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Muestre a los estudiantes cómo doblar las tarjetas y colocarlas en el frasco.
2. Explique cómo jugar el juego con un estudiante.
a. El jugador 1 saca una tarjeta del frasco y se la entrega al jugador 2.
b. El jugador 2 leerá la pregunta en voz alta para que el jugador 1 la resuelva.
c. El jugador 2 puede comprobar la respuesta del jugador 1 en la parte inferior de la tarjeta.
d. Si un jugador acierta un problema, se queda con la tarjeta. ¡Si es incorrecta, el otro jugador se queda con la tarjeta!
e. Nota: Si la tarjeta contiene una imagen, como un gráfico o una recta numérica, el jugador que hace la pregunta puede mostrar la imagen mientras tapa la respuesta con la mano.
f. Si un jugador saca una tarjeta ¡Bam! todas las cartas de ese jugador vuelven al tarro.
g. Se turnan para sacar cartas del tarro y responder a las preguntas hasta que se acabe el tiempo.
h. Deben intentar conseguir tantas cartas como puedan antes de que se acabe el tiempo.
i. El jugador con más cartas gana.
3. Establezca un límite de tiempo. Cuando se acabe, ganará el estudiante que tenga más tarjetas.
4. Distribuya los materiales e indique a los estudiantes que comiencen cuando empiece el cronómetro.
5. Supervise a los estudiantes para asegurarse de que resuelven los problemas correctamente.
Hoja de instrucciones ¡Bum!
Este juega es para jugar en pareja.
Necesitarás
1 conjunto de tarjetas del juego ¡Bum! (por pareja)
1 frasco u otro recipiente (por par)
Instrucciones del juego

1. Dobla las tarjetas por la mitad y colócalas en el frasco.
2. El jugador 1 saca una tarjeta del frasco y se la entrega al jugador 2.
3. El jugador 2 leerá la pregunta en voz alta para que la resuelva el jugador 1.
4. El jugador 2 puede verificar la respuesta del jugador 1 en la parte inferior de la tarjeta.
5. Si un jugador acierta un problema, se queda con la tarjeta. Si son incorrectos, el otro jugador se queda con la tarjeta.
6. Nota: Si la tarjeta contiene una imagen, como un gráfico o una recta numérica, el jugador que hace la pregunta puede mostrar la imagen mientras cubre la respuesta con la mano.
7. Si un jugador saca una tarjeta de ¡Bum! ilustrada, todas las tarjetas de ese jugador se devuelven al frasco.
8. Los jugadores toman turnos para sacar tarjetas del frasco y responder preguntas hasta que se agote el tiempo.
9. Los jugadores deben intentar obtener la mayor cantidad de tarjetas como puedan antes de que se agote el tiempo.
10. El jugador que termine con más tarjetas ganará el juego.

CONSTRUCTOR DE FLUIDEZ HOJA DE INSTRUCCIONES
ELABORAR: REVISIÓN EN ESPIRAL
El juego final
¿Quién ganará el juego de campeonato hoy? Ha estado en la mente de todos durante la última semana. Ambos equipos han trabajado muy duro para llegar a este juego. Los Dragones están 12-1, mientras que los Espartanos invictos están 13-0. Los jugadores trabajan noche y día en los entrenamientos para mejorar aún más. Los entrenadores elaboran estrategias para hacer las mejores jugadas para su equipo. ¡Va a ser un gran juego!
El juego comenzó con cada equipo en la ejecución de sus propias jugadas a la perfección. Los Espartanos tuvieron 4 tiros de 3 puntos seguidos. Los Dragones regresaron con algunos contraataques. Los entrenadores de los Espartanos hicieron jugadas que los Dragones no pudieron defender.
Dos minutos para el final del partido, el marcador estaba empatado. La defensa de los Espartanos era tan fuerte que a los Dragones les costaba anotar. Se pasaban el balón por todos lados. El defensa de los Espartanos robó el balón y corrió por la cancha. Él hizo un movimiento en zigzag alrededor de los jugadores y anotó cuando sonó la bocina. ¡Los Espartanos ganan por 2!



1. Los Espartanos realizaron una jugada que puso a 4 de los jugadores en forma de trapecio. La jugada se llamaba TRAMPA. En la siguiente mitad, los Espartanos hicieron la misma jugada, pero fue un reflejo de TRAMPA. Si el ángulo en la posición M era de 47°, ¿cuál sería la medida del ángulo en la posición reflejada de M?
3. Los jugadores de los Espartanos se pasaban el balón como profesionales. El entrenador dibujó un diagrama de la forma que crearon los pases. El entrenador notó que su equipo lo volvió a hacer más tarde, pero en un lugar diferente. Encierra con un círculo la(s) transformación(es) que describen lo que sucedió con la primera figura para crear la segunda figura.

Reflexión Rotación Traslación Dilatación
2. Los Dragones ejecutaron una defensa de zona que se muestra a continuación. Dibuje la zona defensiva rotada 90° en sentido contrario a las manecillas del reloj.
4. El club de matemáticas Dragón veía el partido. Vieron al base driblar el balón en un triángulo isósceles. TJ le preguntó a Jaxon cuál era la medida del ángulo exterior d de ese triángulo.
FOLLETO DEL ESTUDIANTE CLAVE DE RESPUESTAS
REPASAR CONCEPTOS PREVIOS
REVISIÓN
DESCRIPCIÓN
Los estudiantes repasan el contenido previo o actual del grado para ayudar a apoyar su trabajo en el alcance actual y fortalecer las habilidades necesarias para alcances posteriores.
PREPARACIÓN
• Imprima un folleto del estudiante por alumno.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Entregue un folleto del estudiante a cada alumno.
2. Anime a los estudiantes a tratar de responder a las preguntas de forma independiente sin utilizar recursos externos para ver lo que saben. Invite a los estudiantes a anotar ideas o fragmentos que recuerden sobre los temas que han aprendido previamente. Reconozca que los errores son bienvenidos en esta actividad y en la clase de matemáticas.
3. Utilice las preguntas de repaso en espiral como calentamiento en clase, o envíelas a casa como deberes. Proporcione a los estudiantes comentarios y oportunidades para corregir su trabajo y consolidar aún más sus conocimientos previos.
4. Consulte la sección «Revisión en espiral centrada en la pregunta» para evaluar los conocimientos de contenido de los estudiantes o su necesidad de una mayor intervención. Si es necesario repasar más, utilice los Constructores de fluidez en los alcances apropiados.
5. Capstone incluye una parte del alcance actual para que los estudiantes vean la conexión y relevancia de su aprendizaje previo con el alcance actual.
ELABORAR: CIENCIA DE DATOS
ANÁLISIS DE DATOS
CIENCIA DE DATOS
La ciencia de datos consiste en un breve debate en clase sobre un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los estudiantes a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los estudiantes en contexto.
DESCRIPCIÓN
Los estudiantes analizan, interpretan y generan conjuntos de datos, además de responder a preguntas basadas en los datos.
MATERIALES
IMPRESOS
• 1 conjunto de datos (por clase)
REUTILIZABLES
• 1 proyector o cámara de documentos (por clase)
• 1 marcador de borrado en seco (por clase)
CONSUMIBLES
• 1 trozo de papel milimetrado (por clase)
PREPARACIÓN
• Prepárese para proyectar el conjunto de datos en la clase.
• Reúna un trozo de papel milimetrado y un marcador de borrado en seco.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I
1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los estudiantes.
2. Plantee las siguientes preguntas:
a. «¿Qué observas en este conjunto de datos?».
b. «¿Qué representa este conjunto de datos?».
c. «¿Qué categorías se incluyen en este conjunto de datos?».
a. «¿Por qué podría ser útil conocer la medida diagonal, la anchura o la altura de la pantalla de un televisor?».
b. «¿Qué tiendas de tu zona venden televisores con tamaños de pantalla adecuados para ti?».
c. «¿Qué preguntas tiene sobre los datos?».

¿Qué tan grande es la pantalla de tu televisor?

CONJUNTO DE DATOS
PARTE II
1. Repasa el teorema de Pitágoras y escribe lo que los estudiantes recuerden en el papel milimetrado.
2. Discuta las siguientes preguntas:
a ¿Cuál es la altura de la pantalla de televisión de 50"? 502 - 43,62 = b2, por lo que 2,500 - 1,900.96 = 599.04.
b2 = 599.04, por lo que √599.04 = 24,48".
b ¿Cómo se puede usar el teorema de Pitágoras para determinar la altura de una pantalla de televisión? El teorema de Pitágoras se puede utilizar para hallar la altura de la pantalla de televisión elevando al cuadrado el tamaño de la pantalla desde una esquina hasta la esquina opuesta (el lado más largo de un triángulo) y restando el cuadrado de la longitud conocida del lado (la parte inferior de la pantalla).
c ¿Por qué alguien compraría una pantalla de televisión de 70" en lugar de una de 80"? Las respuestas pueden variar. Alguien podría querer una pantalla de televisión de 70" en lugar de una de 80" si el soporte de su televisor no es lo suficientemente grande como para sostener la pantalla más grande.
d ¿Cuál es la diferencia de altura entre una pantalla de televisión de 40" y una de 50"? 402 - 34.92 = b2, por lo que 1,600 – 1,218.01 = b2.
b2 = 381.99, por lo que √381.99 = 19,54".
24.48 - 19.54 = 4,94
e Hay una diferencia de 4,94" entre la pantalla de 40" y la de 50".
f Según estos datos, ¿cuál sería el tamaño de la pantalla de televisión si la anchura de un televisor fuera de 37,5" y la altura de 21.1"?
37,52 + 21,12 = c2, por lo que 1,406.25 + 445.21 = c2
c2 = 1.851.46, por lo que √1,851.46 = 43.03".
La pantalla del televisor mediría 43.03".
Pythagorean Theorem
Skill or Key Concept How was the skill or concept observed? Notes and Feedback
Explain a proof of the Pythagorean Theorem and its converse.

Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
❏ Physical modeling
❏ Pictorial modeling
❏ Problem solving
❏ Discussion
❏ Written explanation
❏ Physical modeling
❏ Pictorial modeling
❏ Problem solving
❏ Discussion
❏ Written explanation
❏ Physical modeling
Pictorial modeling
Problem solving
❏ Discussion ❏ Written explanation
EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN
EVALUACIÓN DE HABILIDADES
LISTA DE VERIFICACIÓN DE LA OBSERVACIÓN
DESCRIPCIÓN
Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestros y como autoevaluación para los estudiantes.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por alumno)
• 1 materiales para el maestro (por estudiante)
PREPARACIÓN
• Imprima los materiales para el maestro y un folleto del estudiante para cada alumno.
PROCEDIMIENTO Y PUNTOS DE APOYO
1. Distribuya un folleto del estudiante a cada alumno.
Standards for Mathematical Practice Notes and Feedback
Make sense of problems and persevere in solving them
Reason abstractly and quantitatively
Construct viable arguments and critique the reasoning of others
Model with mathematics
Use appropriate tools strategically
Attend to precision
Look for and make use of structure
Look for and express regularity in repeated reasoning
Consider these reflection questions in this scope.
● Is this student proficient in the skills addressed in this scope?
○ If so, what is next for them?
○ If not, how can I support them?
● What activities worked well for this student, and what would I do differently next time?

MATERIAL PARA EL MAESTRO
2. A medida que los estudiantes trabajen en las actividades explorar y explicar del alcance, evalúe formativamente su progreso tomando notas sobre cómo se observaron los conceptos y habilidades clave. Se pueden plantear preguntas de reflexión para medir el impacto de las actividades tanto en grupo completo como en pequeño grupo.
3. Pida a los estudiantes que reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan tanto en grupo completo como en pequeño grupo.
4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado y establecer nuevas metas de aprendizaje.
5. Quienes brindan apoyo pedagógico a los estudiantes pueden estar equipados con las adaptaciones y modificaciones anotadas en los materiales para el maestro.
6. Las notas anecdóticas proporcionadas en las instrucciones del maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.
7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la guía de instrucción andamiada en la sección «Inicio» de este alcance para diferenciar la instrucción para cada estudiante.
Pythagorean Theorem
EVALUAR: MAPA DE CALOR
ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN
MAPA DE CALOR
DESCRIPCIÓN
Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.
MATERIALES
• 1 mapa de calor (por estudiante)
• 1 lápiz rojo (por estudiante)
• 1 lápiz azul (por estudiante)
• 1 lápiz naranja (por estudiante)
PREPARACIÓN
• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.
• Imprima un mapa de calor para cada estudiante.
• Reúna lápices de color rojo, azul y naranja para cada estudiante.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un mapa de calor a cada estudiante junto con los lápices de color rojo, azul y naranja. Los estudiantes deben tener a mano su(s) evaluación(es) corregida(s).
2. Los estudiantes utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Para cada pregunta no contestada por error de cálculo, los estudiantes colorean de azul la casilla correspondiente. Para cada pregunta no contestada por una explicación, los estudiantes colorean la casilla correspondiente de naranja. Para cada pregunta omitida por un concepto erróneo, colorean el cuadro correspondiente de rojo.
3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.
4. Consulte la guía de instrucción andamiadas que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.
Consulta tus respuestas en la tabla «Prueba de habilidades». Colorea de verde los cuadros de preguntas correctas y colorea según la siguiente clave los cuadros de preguntas incorrectas.
Prueba de habilidades
Estándares Preguntas
Explica una demostración del teorema de Pitágoras y su inversa.
Aplica el teorema de Pitágoras para determinar las longitudes desconocidas de los lados de triángulos rectángulos en problemas matemáticos y de la vida real en dos y tres dimensiones.
Aplica el teorema de Pitágoras para encontrar la distancia entre dos puntos en un sistema de coordenadas.

Pythagorean Theorem 1 5 7 4 10 1 3 8 2 6 9
Preguntas de reflexión
1. ¿Con qué habilidad te has sentido más seguro? ¿Por qué? 2. ¿Qué habilidad te ha parecido más desafiante? ¿Por qué?
3. ¿Qué tipo de error cometiste con más frecuencia?

4. ¿Cómo puedes evitar esos errores en el futuro?
Consulta tus respuestas en la tabla «Prueba de habilidades». Colorea de verde los cuadros de preguntas correctas y colorea según la siguiente clave los cuadros de preguntas incorrectas. Azul: Error de cálculo Naranja: Explicación Rojo: Error de concepto
Evaluación basada en estándares
Estándares Preguntas
Explica una demostración del teorema de Pitágoras y su inversa.
Aplica el teorema de Pitágoras para determinar las longitudes desconocidas de los lados de triángulos rectángulos en problemas matemáticos y de la vida real en dos y tres dimensiones.
Azul: Error de cálculo Naranja: Explicación Rojo: Error de concepto MAPA DE CALOR
Pythagorean Theorem 4a
Aplica el teorema de Pitágoras para encontrar la distancia entre dos puntos en un sistema de coordenadas. 3 5 7 4b 10 1 3 8 2 6 9

DESCRIPCIÓN
Esta actividad está diseñada para repasar los conceptos clave del alcance. Utilícela como repaso o para intervención.
MATERIALES
IMPRESOS
• 1 evaluación rápida (por estudiante)
• 1 repaso (por estudiante)
• 1 evaluación de control (por estudiante)
• 1 lista de verificación para el maestro (por profesor)
PREPARACIÓN
• Imprima una copia de la evaluación rápida, el repaso y la evaluación de control por estudiante.
• Si lo desea, coloque a los estudiantes en grupos de 3 o 4 para completar la revisión.
• Si lo desea, imprima un ejemplo del esquema de anclaje de la sección «Explicar» o pida a los estudiantes que usen la libreta interactiva como recurso.
• Opcionalmente, imprima cualquiera de los materiales de ayuda complementarios para que los estudiantes los utilicen mientras trabajan.
INTERVENCIÓN: REVISIÓN Y PRÁCTICA DE HABILIDADES
REFORZAR Y VOLVER A ENSEÑAR
REVISIÓN Y PRÁCTICA DE HABILIDADES
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. De una copia de la evaluación rápida a cada estudiante.
2. Cada uno debe completarla de forma independiente.
3. Use la rúbrica de habilidades al final de la evaluación rápida para identificar qué estudiantes necesitan ayuda adicional en las habilidades.
4. Distribuya una copia del repaso a cada estudiante.
5. Cada uno debe completar el repaso como actividad de intervención o como actividad independiente.
a. Si lo desea, reúna a los estudiantes en pequeños grupos para trabajar en las destrezas de repaso. Use el repaso como ayuda para la reenseñanza.
6. Distribuya una copia de la evaluación de control a cada estudiante.
7. Cada estudiante debe completarla de forma independiente.
8. Analice los resultados de la evaluación de control utilizando la lista de verificación para el maestro para identificar a quienes necesitan un repaso adicional y quienes han alcanzado el dominio de los conceptos.
Revisión
Usa el teorema de Pitágoras para determinar si las longitudes de los lados formarán un triángulo rectángulo.
Longitudes de los lados a2 + b2 c2 ¿Es a2 + b2 = c2? ¿Triángulo rectángulo?
1. 8, 14, 17
2. 20, 99, 101
Cada conjunto de números de las preguntas 3 y 4 representa las longitudes de los lados de un triángulo. Encierra con un círculo el conjunto de números que forman un triángulo rectángulo. Muestra tu trabajo.
3. 48, 55, 72
4. 15, 36, 39
5. ¿Cuál es la distancia más corta entre la casa de Jamal y la arcada?


Pythagorean Theorem
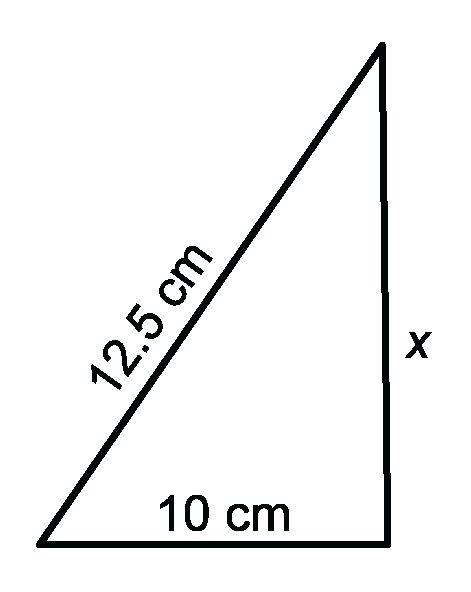

inferior derecha del prisma? Redondea al décimo más cercano.





ACELERACIÓN: ¿QUÉ PREFIERES?
RAZONAMIENTO MATEMÁTICO
¿QUÉ PREFIERES? RAMPA PARA MONOPATÍN
DESCRIPCIÓN
Los estudiantes utilizan el razonamiento matemático y la creatividad para justificar una respuesta.
MATERIALES
IMPRESORA
• 1 folleto del estudiante (por alumno)
• 1 rúbrica (por maestro)
PREPARACIÓN
• Imprima un folleto del estudiante por alumno.
• Planifique que los estudiantes trabajen en parejas para completar esta actividad, si lo desea.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Entregue un folleto del estudiante a cada alumno.
2. Anime a los estudiantes a mirar sus folletos del estudiante de las exploraciones si necesitan repasar habilidades.
3. Invite a los estudiantes a compartir respuestas y justificaciones con sus compañeros.
4. Utilice la rúbrica proporcionada para evaluar las habilidades de comprensión, cálculo y razonamiento de los estudiantes.
Skateboard Ramp
Use mathematical reasoning and creativity to justify your answer to the Would You Rather question.




FOLLETO DEL ESTUDIANTE CLAVE DE RESPUESTAS
Pythagorean Theorem
ACELERACIÓN: TABLERO DE OPCIONES
Teorema de Pitágoras
Selecciona una o más actividades de extensión de la siguiente tabla.
Conexión profesional Matemáticos en primer plano
Arquitecto
Investiga la profesión de arquitectura. La investigación debe responder las preguntas proporcionadas. Crea una presentación para compartir la investigación con tu clase.

Pitágoras
Investiga el trabajo de Pitágoras.
Crea un póster informativo, un diorama o un discurso para presentar el trabajo de este matemático relacionado con el teorema de Pitágoras.
Conexión con las ciencias Crear algo nuevo
Travesía por el océano
Utilizar el teorema de Pitágoras para determinar medidas es una habilidad muy útil en ciencias. Completa la actividad para aplicar tu comprensión del uso del teorema de Pitágoras.
Arte pitagórico
Crea tu propio trabajo de arte al usar triángulos rectángulos para demostrar el teorema de Pitágoras.
Conexión con el arte Analogías
Revisión de arte
Muchos artistas han usado sus obras de arte para demostrar el teorema de Pitágoras. Completa esta actividad para comprender la influencia que Pitágoras ha tenido en el arte.
Analogía desafiante
Una analogía es un tipo de comparación. Completa la actividad de analogías al usar tu conocimiento del teorema de Pitágoras.
TABLERO DE OPCIONES
OPCIONES PARA EL APRENDIZAJE CONTINUO
TABLERO DE OPCIONES
DESCRIPCIÓN
Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.
MATERIALES
IMPRESOS
• 1 tablero de opciones (por estudiante)
• 1 juego de hojas de actividades (por estudiante)
• 1 autoevaluación del tablero de opciones (por estudiante)
REUTILIZABLE
• Tecnología (si corresponde)
PREPARACIÓN
• Imprima un tablero de elección y un juego de hojas de actividades para cada estudiante.
• Imprime una autoevaluación del tablero para cada estudiante.
• Planifica con antelación el uso de la tecnología. Puede ser necesario investigar para algunas actividades del tablero de opciones.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un tablero de opciones a cada estudiante.
2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.
3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.
4. Distribuya las hojas de actividades correspondientes según las elecciones de los estudiantes.
5. Al finalizar cada actividad del tablero de opciones, haga que los estudiantes completen una autoevaluación del tablero para revisar su propio pensamiento matemático y sus esfuerzos en su proyecto.
Pythagorean Theorem
