SSM CA Spanish Algebra 1 Sample

A1 ÁLGEBRA

CALIFORNIA

Muestra de la edición para el maestro

Muestra de la edición para maestros Álgebra 1

Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.

Para obtener más información, visítenos en www.stemscopes.com.

PROPIEDADES DE LAS FUNCIONES

ESTÁNDARES CLAVE

Comprender el concepto de función y utilizar la notación de función.

• Comprender que una función de un conjunto (llamado dominio) a otro conjunto (llamado rango) asigna a cada elemento del dominio exactamente un elemento del rango. Si f es una función y x es un elemento de su dominio, entonces f(x) denota la salida de f correspondiente a la entrada x. La gráfica de f es la gráfica de la ecuación y = f(x).

• Usar notación de funciones, evaluar funciones para entradas en sus dominios e interpretar enunciados que usan notación de funciones en términos de un contexto.

Interpretar funciones que surgen en aplicaciones en términos del contexto.

• Relacionar el dominio de una función con su gráfica y, cuando sea aplicable, con la relación cuantitativa que describe. Por ejemplo, si la función h da el número de horas-persona que se necesitan para montar n motores en una fábrica, entonces los números enteros positivos serían un dominio apropiado para la función.

• Calcular e interpretar la tasa de variación media de una función (presentada simbólicamente o en forma de tabla) en un intervalo especificado. Estimar la tasa de cambio a partir de una gráfica.

*Este alcance se centra en la linealidad.

ACTIVIDADES DE PARTICIPACIÓN

ACCESO A CONOCIMIENTOS PREVIOS: ENCUENTRA LAS PAREJAS EN EL SALÓN

Los estudiantes participarán en una actividad de emparejamiento de tarjetas para evaluar su comprensión de un estándar matemático previo e identificar cualquier concepto erróneo.

• Los estudiantes escribirán números en un papel y los utilizarán para emparejar tarjetas numeradas con tarjetas con letras alrededor de la habitación.

• Caminarán por el aula para encontrar y emparejar las tarjetas correspondientes.

• Los estudiantes discutirán su razonamiento y emparejamientos con un compañero.

CAPTAR INTERÉS

Los estudiantes explorarán la notación de funciones relacionándola con un escenario real que implique la carga de un teléfono.

• Presenta el escenario con un vídeo y guía a los estudiantes para que observen y cuestionen los aspectos matemáticos de la carga de un teléfono.

• Facilita un debate sobre la notación de funciones y su aplicación al escenario, animando a los estudiantes a interpretar enunciados matemáticos.

• Guía a los estudiantes a través de las actividades de Exploración para profundizar en su comprensión de la notación de funciones.

ACTIVIDADES DE EXPLORAR

EXPLORACIÓN 1: RELACIONES Y FUNCIONES

Los estudiantes explorarán las propiedades de las funciones y no funciones a través de representaciones algebraicas para desarrollar una definición de función y distinguir entre funciones continuas y discretas.

• Los estudiantes analizarán las entradas y salidas de máquinas widget para identificar las que funcionan mal.

• Colaborarán en grupos para justificar su razonamiento para determinar las máquinas que funcionan y las que no.

• Los estudiantes participarán en charlas matemáticas para discutir las observaciones y refinar su comprensión de las funciones.

• Completarán un boleto de salida para evaluar su comprensión del concepto de funciones.

EXPLORACIÓN 2: EVALUAR FUNCIONES

Los estudiantes evaluarán e interpretarán funciones lineales y cuadráticas usando la notación de funciones en varios contextos.

• Los estudiantes analizarán gráficas y datos para completar reportes sobre la migración de las tortugas, usando la notación de funciones para completar la información faltante.

• Los estudiantes colaborarán en grupos para evaluar funciones para valores dados y determinar entradas para salidas específicas.

• Los estudiantes participarán en Charlas de Matemáticas para discutir observaciones y profundizar su comprensión de la notación de funciones y sus aplicaciones.

• Los estudiantes completarán un Boleto de Salida para demostrar su comprensión de la evaluación de funciones y la interpretación de la notación de funciones.

EXPLORACIÓN 3: TASA DE CAMBIO PROMEDIO

Los estudiantes calcularán e interpretarán las tasas promedio de cambio en intervalos específicos, conectarán estas tasas a través de diferentes representaciones y harán generalizaciones sobre los comportamientos de las funciones en el tiempo.

• Los estudiantes analizarán datos de ventas para calcular los cambios en el tiempo y registrarán sus hallazgos en sus Diarios del Estudiante.

• Los estudiantes colaborarán en grupos para comparar datos y hacer recomendaciones basadas en las tasas de cambio promedio calculadas.

• Los estudiantes participarán en charlas de matemáticas para discutir observaciones y compartir ideas sobre las tasas de cambio promedio.

• Los estudiantes completarán un boleto de salida para demostrar su comprensión del concepto de tasas de cambio promedio.

EXPLORACIÓN 4: DOMINIO Y RANGO

Los estudiantes explorarán y determinarán los dominios y rangos de funciones, diferenciarán entre datos discretos y continuos, y aplicarán estos conceptos a escenarios del mundo real.

• Analizarán tablas y gráficas para identificar entradas y salidas, usando este análisis para hacer recomendaciones para la planeación de eventos.

• Colaborar en grupos para clasificar y emparejar gráficos con los dominios y rangos correspondientes, utilizando tijeras y pegamento para organizar la información.

• Participar en charlas de matemáticas para discutir las observaciones y profundizar la comprensión de los conceptos de dominio y rango.

• Completar un boleto de salida para demostrar la comprensión y aplicar las habilidades recién adquiridas para resolver problemas.

CONCEPTOS CLAVE

• Puedo determinar si una relación es una función.

• Puedo identificar y explicar que cada función tiene un dominio y un rango correspondiente.

• Puedo utilizar la notación de funciones.

• Puedo determinar un dominio y un rango razonables para situaciones del mundo real.

• Puedo evaluar funciones cuando la entrada se da como un valor numérico, una expresión algebraica o un gráfico.

• Puedo interpretar funciones y relacionarlas con contextos del mundo real.

• Puedo calcular la tasa de variación media de una función (presentada simbólicamente o en forma de tabla) a lo largo de un intervalo especificado.

• Puedo utilizar la tasa de variación media y relacionarla con la determinación de la pendiente.

• Puedo interpretar la tasa de variación media de una función (presentada simbólicamente o en forma de tabla) a lo largo de un intervalo especificado basándome en el contexto.

ALCANCE GRANDES IDEAS

CUESTIONES FUNDAMENTALES

• ¿Qué información se necesita para determinar si una relación es una función?

• ¿Cómo se determina si cada elemento del dominio corresponde exactamente a un elemento del rango?

• ¿Cómo puede utilizarse la notación de función para identificar los elementos del dominio y/o del rango?

• ¿Sobre qué valores de entrada es la función creciente, decreciente o constante?

INICIO: CONTENIDO DE APOYO

¿QUÉ ESTOY ENSEÑANDO?

CONTENIDO DE APOYO

Comprender el concepto de función y utilizar la notación de función.

• Comprender que una función de un conjunto (llamado dominio) a otro conjunto (llamado rango) asigna a cada elemento del dominio exactamente un elemento del rango. Si f es una función y x es un elemento de su dominio, entonces f(x) denota la salida de f correspondiente a la entrada x. La gráfica de f es la gráfica de la ecuación y = f(x).

• Utilizar notación de funciones, evaluar funciones para entradas en sus dominios e interpretar enunciados que utilizan notación de funciones en términos de un contexto.

Interpretar funciones que surgen en aplicaciones en términos del contexto.

• Relacionar el dominio de una función con su gráfica y, en su caso, con la relación cuantitativa que describe. Por ejemplo, si la función h da el número de horas-persona que se necesitan para montar n motores en una fábrica, entonces los números enteros positivos serían un dominio apropiado para la función.

• Calcular e interpretar la tasa de variación media de una función (presentada simbólicamente o en forma de tabla) en un intervalo especificado. Estimar la tasa de cambio a partir de una gráfica.

Este alcance se enfoca en lo lineal.

CONOCIMIENTOS PREVIOS

En grados anteriores, los estudiantes utilizaron relaciones funcionales para crear modelos lineales y determinar la tasa de cambio. Los estudiantes han reconocido y explicado una función como cada valor de entrada devuelve exactamente un valor de salida, y el par ordenado representa la entrada y la salida.

CONCEPTOS ERRÓNEOS Y OBSTÁCULOS

• Los estudiantes a los que se les enseña la notación de funciones en forma aislada no siempre entienden que esta notación representa un par ordenado y tiene significado en términos del contexto. Del mismo modo, los estudiantes a los que se les enseñan funciones continuas y discretas en contexto desarrollan una mejor comprensión de cuándo y por qué se utilizan los tipos.

• Los estudiantes confunden con frecuencia «cada valor de entrada devuelve exactamente un valor de salida» con el significado de «cada valor de salida devuelve exactamente un valor de entrada».

• Con frecuencia, los estudiantes confunden f(x) con "f veces x" . Esta interpretación incorrecta puede llevar a conclusiones falsas utilizando la propiedad distributiva. Por ejemplo, un estudiante puede llegar a la falsa conclusión de que f(x - 2) es lo mismo que f(x) - f(2).

• Los estudiantes suelen pensar que todas las funciones utilizan f, x, y y. Cuando se encuentran por primera vez con una representación como d(t) = 3t, no les resulta familiar.

EN ESTE ALCANCE

En este nivel de grado, los estudiantes ampliarán su comprensión de las funciones como entrada y salida a conjuntos que representan el dominio y el rango. Los estudiantes serán capaces de crear ejemplos de lo que es y lo que no es una función usando una variedad de representaciones, como una tabla, una gráfica, símbolos o una descripción verbal. Los estudiantes serán capaces de determinar la tasa media de cambio a partir de un gráfico, una tabla o una representación algebraica. Dado el contexto, los estudiantes interpretarán el significado de los enunciados en notación de función.

Términos clave

• función: una relación especial entre valores; cada valor de entrada devuelve exactamente un valor de salida.

• conjunto: una colección de hechos organizados, normalmente en forma numérica, pero también puede darse en palabras, medidas o descripciones.

• dominio: el conjunto de todas las posibles entradas (x valores) de una función.

• rango: el conjunto de todas las posibles salidas, o y valores, de una relación o función.

• elemento: cualquier número o valor distinto que forme parte de un conjunto.

• salida: el resultado de la entrada colocada en la función.

• entrada: conjunto de valores suministrados a una función.

• ecuación: enunciado matemático que muestra que dos expresiones son iguales entre sí.

• notación de función: forma de representar y, el valor dependiente en una relación, como f(x), léase "f de x" donde f nombra la función.

• tasa media de cambio: cambio total de los valores de la función (valores de salida) dividido por el cambio en los valores de entrada.

• simbólicamente: compuesto de símbolos numéricos y algebraicos para formar una ecuación

• intervalo: cantidad de tiempo que pasa de un período de tiempo al siguiente; distancia entre dos puntos.

INICIO: CONTENIDO DE APOYO

APLICAR LAS PRÁCTICAS MATEMÁTICAS

• MP.1 Dar sentido a los problemas y perseverar en su resolución: Los estudiantes dan sentido a descripciones verbales de funciones e identifican sus gráficas representativas, dominios y rangos con base en la información dada.

• MP.2 Razonar abstracta y cuantitativamente: Los estudiantes utilizan datos del mundo real de tablas y gráficos para encontrar tasas promedio de cambio y luego utilizan esta información para hacer recomendaciones y predicciones sobre la situación.

• MP.3 Construir argumentos viables y criticar el razonamiento de los demás: Los estudiantes critican la afirmación de otro estudiante usando su comprensión de encontrar la tasa promedio de cambio para justificar y apoyar su argumento.

• MP.4 Modelar con matemáticas: Los estudiantes utilizan ecuaciones y gráficas para modelar descripciones verbales de funciones y evalúan las funciones para representar los datos y hacer predicciones sobre valores futuros.

• MP.5 Utilizar estratégicamente las herramientas adecuadas: Los estudiantes usan gráficas, tablas y descripciones escritas para escribir y analizar funciones. También tienen en cuenta todos los datos proporcionados para escribir funciones que representen los datos con precisión.

• MP.6 Prestar atención a la precisión: Los estudiantes atienden a la precisión cuando encuentran el dominio y el rango de una función dada. Analizan descripciones escritas, tablas y gráficas para encontrar el dominio y el rango más precisos.

• MP.7 Buscar y utilizar la estructura: Los estudiantes aplican sus conocimientos sobre la evaluación de una expresión para evaluar una función, reconociendo que el proceso es el mismo y que la notación f(x) es el nombre de la función y no una operación.

• MP.8 Buscan y expresan regularidades en razonamientos repetidos: Los estudiantes generalizan sobre qué tipos de funciones son discretas y continuas y reconocen el tipo de función a partir de la información dada. Por ej., al ver los valores de dominio y rango listados, concluyen que una función es discreta.

RELACIONES Y FUNCIONES

Los estudiantes aprenderán que una función es una relación especial entre valores en la que cada elemento del dominio corresponde exactamente a un elemento del rango. Serán capaces de determinar si una relación es una función a través de múltiples representaciones, incluyendo verbalmente, por tabla, por gráfica o simbólicamente. Los estudiantes deben centrarse en que cada entrada produzca exactamente una salida, independientemente de la representación de la función. Los estudiantes explorarán las representaciones y crearán reglas para definir una función. Evite la enseñanza directa de atajos como la prueba de la línea vertical. En su lugar, permita que los estudiantes desarrollen primero esa teoría para promover una comprensión más profunda.

Diagrama de Mapeo

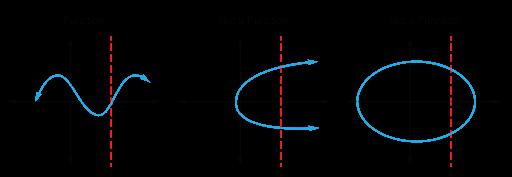
Gráfico

Tabla

INICIO: CONTENIDO DE APOYO

DESCRIPCIÓN VERBAL

a. Función: Dominic registra la cantidad de nieve caída, en centímetros, durante un periodo de cuatro horas.

b. No es una función: Pinton Middle School registra la cantidad de tiempo que tardan 40 estudiantes en llegar a la escuela y la distancia a la que viven de la escuela.

Los estudiantes también determinarán si las funciones son continuas o discretas. Las variables continuas pueden tomar cualquier valor en cualquier punto del intervalo. Las variables discretas sólo pueden tomar ciertos valores a lo largo del intervalo.

Discreta Continua

Número de niños en una clase Cantidad de lluvia

Número de votos en unas elecciones Velocidad del viento

Número de coches en el aparcamiento Peso de tu perro

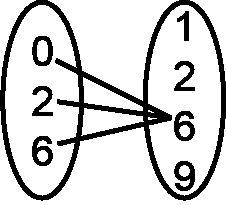
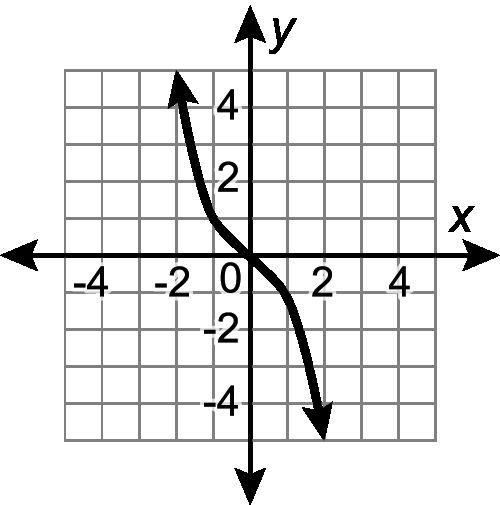
Ejemplo: ¿Cuál de las siguientes relaciones representa una función?

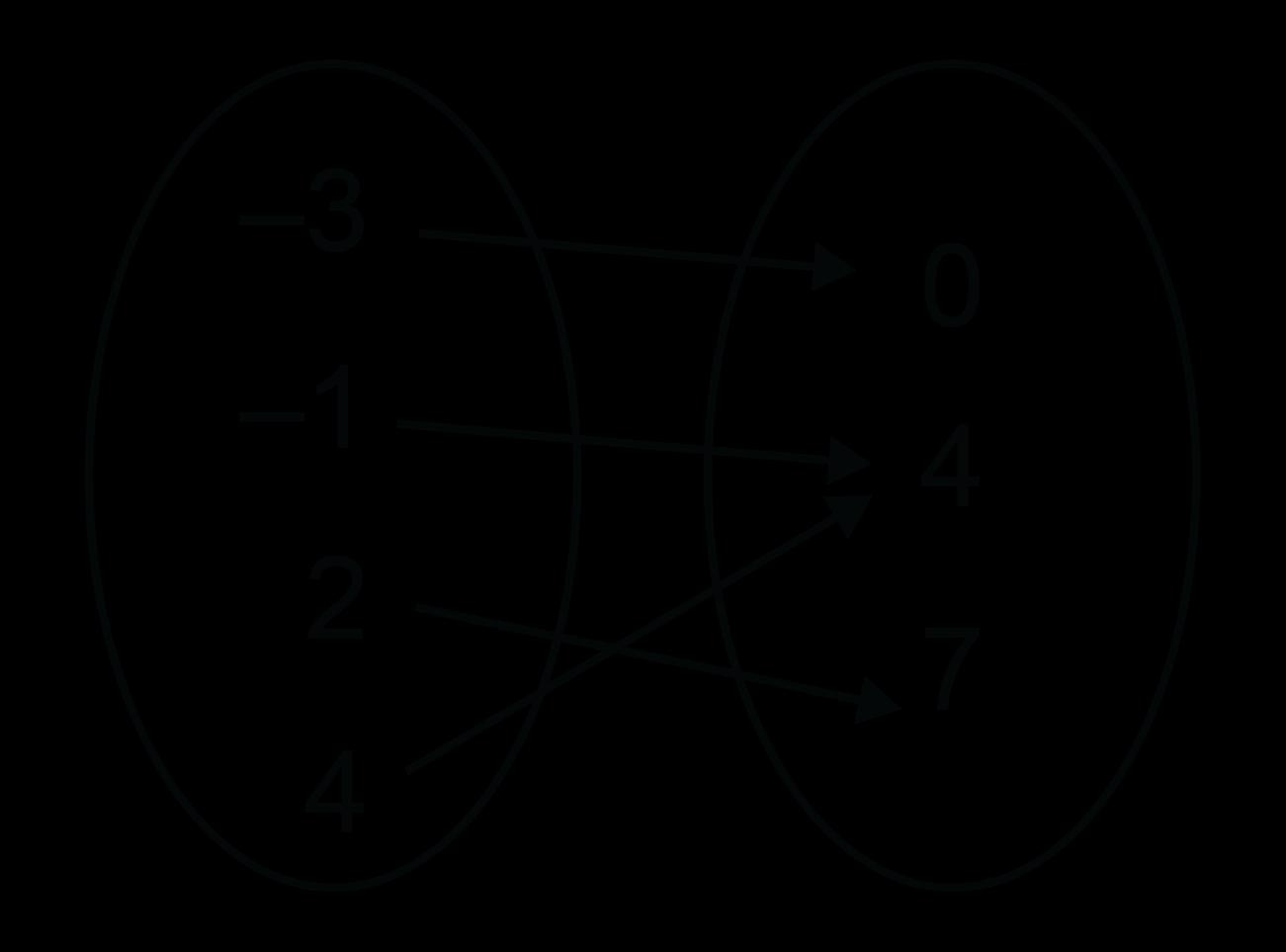
D. Todas las relaciones anteriores son funciones. La respuesta correcta es A. Cada valor de x sólo tiene un valor de y. La opción de respuesta B no es una función porque el valor x de 5 se repite. La opción de respuesta C no es una función porque es una línea vertical con valores x que se repiten.

Ejemplo: La función h = 4.000 - 600m da la altura, h, de una paracaidista en pies después de haber estado cayendo durante m minutos. ¿Es este un ejemplo de discreto o continuo?

Esto es continuo. La entrada debe utilizarse para determinar si una situación puede representarse mediante una función discreta o continua. La entrada m representa minutos. El tiempo es continuo y será ininterrumpido mientras dure la caída del paracaidista.

INICIO: CONTENIDO DE APOYO

EVALUACIÓN DE FUNCIONES

Una ventaja fundamental de la notación de funciones es que la conexión entre el dominio y el rango está incorporada en la notación. Por ejemplo, la notación g(3) significa "el valor de salida de g cuando el valor de entrada es 3". Los estudiantes evaluarán funciones lineales y cuadráticas, en notación de funciones, dados uno o más elementos en el dominio. Los estudiantes sustituirán un valor dado por la variable en una función y simplificarán utilizando el orden de las operaciones. Es posible que los estudiantes no estén familiarizados con el formato de estos problemas. Los estudiantes están acostumbrados a sustituir con la variable igual a un número, como x = 5. Se entiende la intención cuando alguien dice "la función f(x)". Sin embargo, para discutir o llamar a la función por su nombre, deberíamos decir "la función f, donde f(x) = 2x - 5" o simplemente "la función f." Los estudiantes también interpretarán la notación de función en contextos.

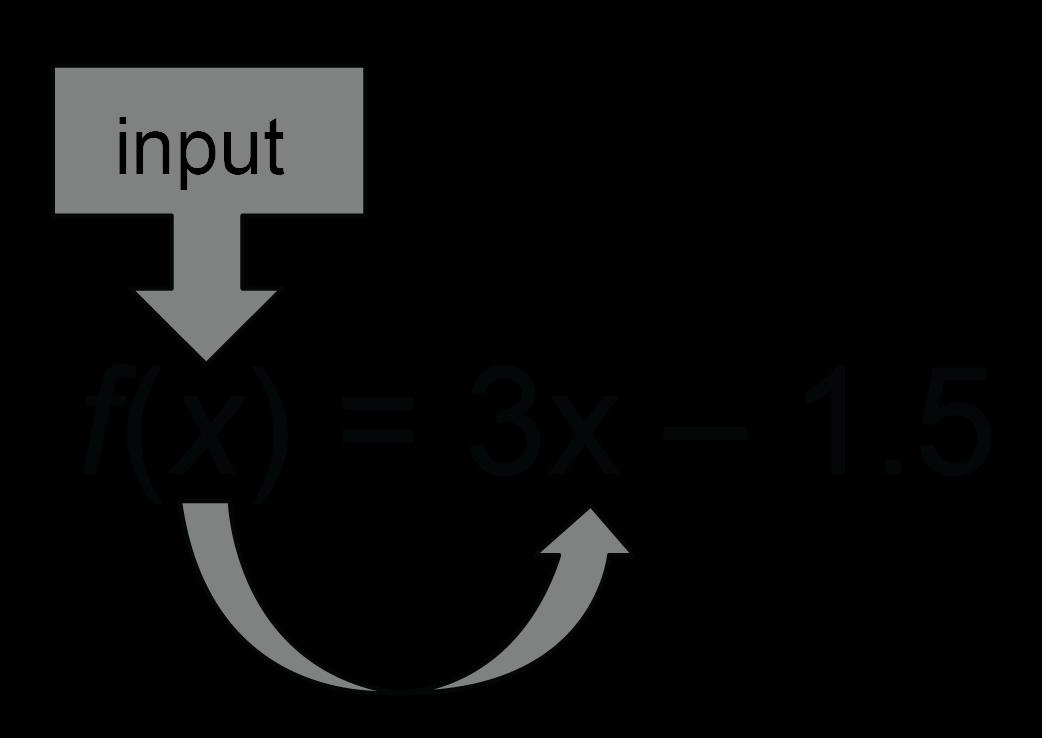
Ejemplo: La función w relaciona la altura en centímetros de Guillermo con su edad en meses. ¿Qué significa w(18) = 80? ¿Qué significa w(12)? ¿Qué significa w(x) = 66?

w(18) = 80 significa que William medía 80 cm cuando tenía 18 meses.

w(12) significa la altura que tenía William cuando tenía 12 meses.

w(x) = 66 significa la edad que tenía William cuando medía 66 cm.

Ejemplo: Dado que f(x) = 3x + 4 y g(x) = x2-7x + 2, halla f(1) + g(1).

La respuesta correcta es 3.

Para f(1), los estudiantes sustituirían 1 en la ecuación f(x) = 3x + 4. Así, 3(1) + 4 significa la edad de William cuando tenía 66 cm de altura. Por tanto, 3(1) + 4 = 7.

Para g(1), los estudiantes sustituirían 1 en la ecuación g(x) = x2 - 7x + 2. Entonces, (1)2 - 7(1) + 2 = -4. A continuación, los estudiantes sumarán 7 + -4 para obtener la respuesta final de 3.

TASA DE CAMBIO PROMEDIO

La pendiente es una característica física de un gráfico. La tasa de cambio describe cómo cambia la función y no está conectada a ninguna representación específica. Los estudiantes calcularán e interpretarán la tasa de cambio promedio en intervalos específicos. El objetivo es relacionar la tasa de cambio con las distintas representaciones y con el contexto. En el caso de las funciones no lineales, las tasas de cambio no son constantes, por lo que podemos usar las tasas de cambio promedio a lo largo de un intervalo para discutir cómo cambian las funciones no lineales a lo largo de un intervalo específico o para hacer una generalización acerca del comportamiento a lo largo del tiempo.

Tasa de cambio promedio = f(b)-f(a)/b-a

Ejemplo: El Servicio Meteorológico Nacional registró la temperatura en Albuquerque, Nuevo México, durante varias horas y mostró lo que encontró en la siguiente tabla.

Horas después de medianoche Temperatura en ℉

¿En qué intervalo de tiempo disminuye la temperatura más rápidamente?

a Entre la medianoche y las 3:00 a. m.

b Entre las 3:00 a. m. y las 4:00 a. m.

c Entre las 4:00 a. m. y las 6:00 a. m.

La respuesta correcta es B. Entre las 3:00 a. m. y las 4:00 a. m. , la tasa media de cambio es -3, lo que significa que la temperatura bajó tres grados por hora. De medianoche a las 3:00 a. m. , la temperatura descendió dos grados por hora, y de las 4:00 a. m. a las 6:00 a. m., la temperatura descendió un grado por hora.

INICIO: CONTENIDO DE APOYO

Ejemplo: ¿En qué intervalo tiene la función h(x) una tasa de variación media negativa?

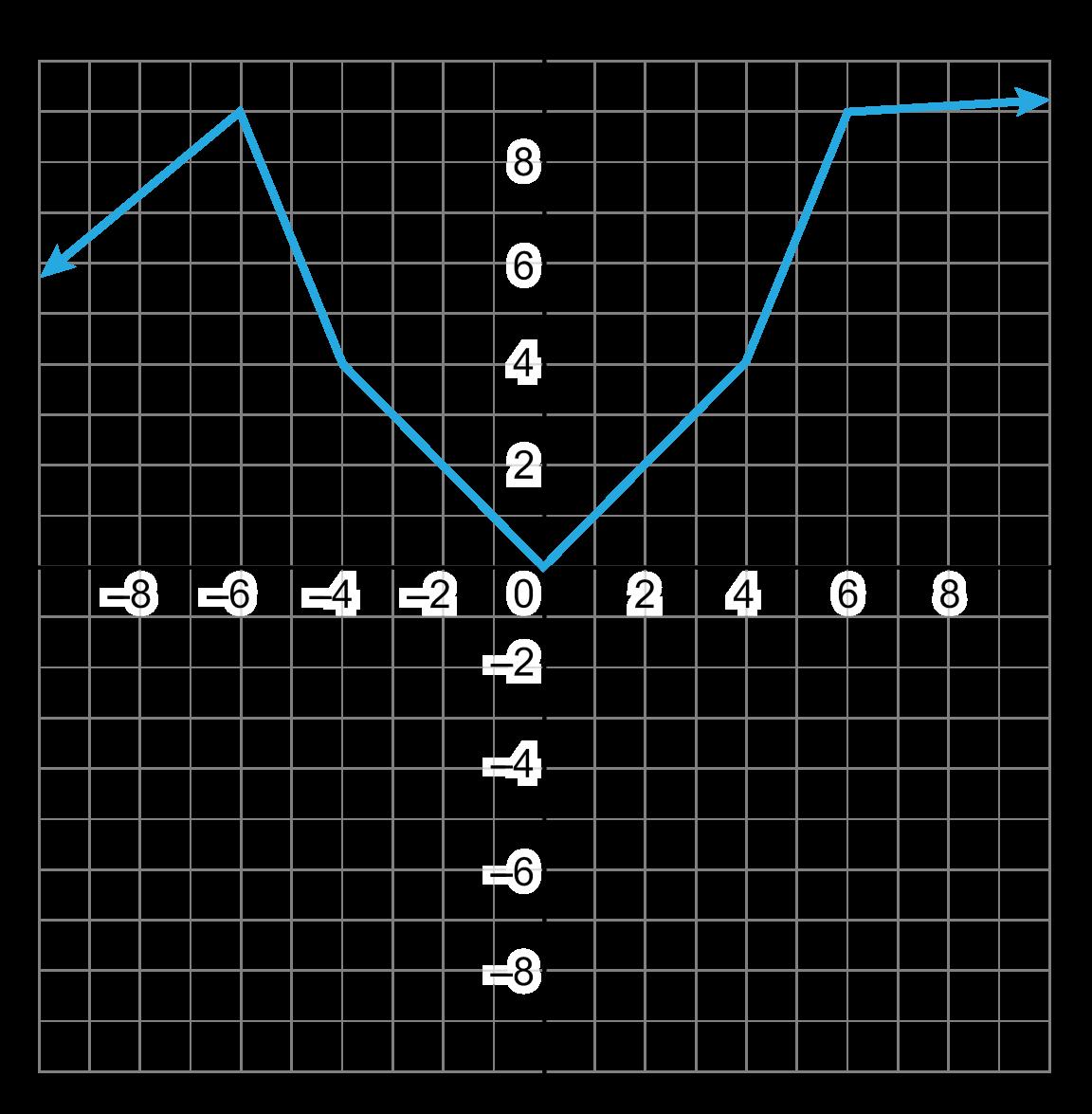
a De -9 a -6

b De -6 a -4

c De -2 a 4

d De 3 a 6

La respuesta correcta es B. La tasa de variación media se calcula utilizando dos puntos: (-6, 9) y (-4, 4). cambio en y/cambio en x = 4 - 9/-4 - (-6) = -5/2 = -2.5

DOMINIO Y RANGO

Los estudiantes determinarán el dominio y rango de funciones lineales y escribirán esos valores usando desigualdades. Los estudiantes también determinarán el dominio y el rango en relación con el contexto de un problema. El dominio es el conjunto de todos los valores de entrada y el rango es el conjunto de todos los valores de salida. Utilizar un contexto simple para discutir la noción de dominio de una función permite a los estudiantes reconocer que las limitaciones en el conjunto de números que representan el dominio son relativas al contexto, no a la función. Por ej., si la función g(x) = 11x representa el coste de las entradas de un cine local, el dominio se limita a números enteros. La limitación del dominio se debe a la situación, no a la función.

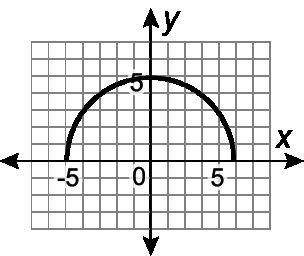
Ejemplo: ¿Cuál es el rango de la gráfica de abajo?

a -6 < y ≤ 3

b -6 ≤ y < 3

c -2 < y ≤ 6

d -2 ≤ y < 6

La respuesta correcta es C. Los valores de las opciones de respuesta A y B representan los valores usados para describir el dominio de la gráfica, así que podemos eliminar esas opciones. La opción de respuesta D tiene las desigualdades cambiadas. -2 es un círculo abierto, por lo que es menor que y. 6 es un círculo cerrado, por lo que es mayor o igual que y

Ejemplo: Paolo cobra $25 la hora por dar clases particulares de matemáticas. ¿Cuál es el dominio de cuánto dinero puede ganar Paolo dando clases particulares de matemáticas?

a El conjunto de todos los números reales

b El conjunto de todos los números enteros positivos

c El conjunto de todos los números reales mayores o iguales que 0

d El conjunto de todos los números enteros mayores o iguales que 0

La respuesta correcta es C. La variable independiente, o input, es el tiempo dando clases particulares. El tiempo es continuo y no negativo. Paolo puede ganar 0$ si trabaja 0 horas. Las opciones A y B no se ajustan al contexto porque incluyen números negativos, y Paolo no puede trabajar horas negativas. La opción D no funciona porque Paolo podría trabajar fracciones de hora y ganar valores que no son enteros.

AVANCES

Los estudiantes continuarán explorando el dominio y el rango con funciones cuadráticas y exponenciales más adelante en Álgebra I. En Álgebra II, los estudiantes continuarán desarrollando estas habilidades escribiendo el dominio y el rango de una función en notación de intervalo, desigualdades y notación de conjunto. También describirán y analizarán la relación entre una función y su inversa (cuadrática y raíz cuadrada, logarítmica y exponencial), incluyendo la(s) restricción(es) sobre el dominio, que restringirá(n) su rango. En grados posteriores, los estudiantes estudiarán la tasa instantánea de cambio.

ESTÁNDARES

Comprender el concepto de función y utilizar la notación de función.

• Comprender que una función de un conjunto (llamado dominio) a otro conjunto (llamado rango) asigna a cada elemento del dominio exactamente un elemento del rango. Si f es una función y x es un elemento de su dominio, entonces f(x) denota la salida de f correspondiente a la entrada x. La gráfica de f es la gráfica de la ecuación y = f(x).

• Usar notación de funciones, evaluar funciones para entradas en sus dominios e interpretar enunciados que usan notación de funciones en términos de un contexto.

Interpretar funciones que surgen en aplicaciones en términos del contexto.

• Relacionar el dominio de una función con su gráfica y, en su caso, con la relación cuantitativa que describe. Por ejemplo, si la función h da el número de horas-persona que se necesitan para montar n motores en una fábrica, entonces los números enteros positivos serían un dominio apropiado para la función.

• Calcular e interpretar la tasa de variación media de una función (presentada simbólicamente o en forma de tabla) en un intervalo especificado. Estimar la tasa de cambio a partir de un gráfico.

Nota: Este alcance se centra en la linealidad.

DESGLOSAR EL ESTÁNDAR VERBOS: ¿QUÉ DEBERÍAN HACER LOS ESTUDIANTES?

• comprender: captar el significado de.

• utilizar: aplicar una estrategia.

• evaluar: determinar o calcular el valor numérico de algo.

• interpretar: explicar el significado de.

• relacionar: encontrar o mostrar la conexión entre dos o más cosas.

• calcular: determinar la cantidad de algo matemáticamente.

• estimar: predecir un tamaño, cantidad o valor aproximado de algo; estrategia utilizada a menudo para resolver un problema.

INICIO: CONTENIDO DESGLOSADO

ANÁLISIS PROFUNDO DE LOS ESTÁNDARES

CONTENIDO DESGLOSADO

SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS

DEBEN CONOCER LOS ESTUDIANTES?

• función: una relación especial entre valores; cada valor de entrada devuelve exactamente un valor de salida.

• conjunto: un grupo de números u objetos únicos llamados miembros o elementos.

• dominio: el conjunto de todos los posibles valores de entrada, o x, de una relación o función.

• rango: el conjunto de todos los posibles valores de salida, o y , de una relación o función.

• elemento: cualquier número o valor distinto que forma parte de un conjunto.

• salida: el resultado de la entrada colocada en la función.

• entrada: conjunto de valores suministrados a una función.

• gráfico: una representación visual de los datos.

• ecuación: un enunciado matemático que muestra que dos expresiones son iguales entre sí.

• relación cuantitativa: la relación entre magnitudes.

• notación de funciones: una forma de representar y, el valor dependiente en una relación, como f(x), léase "f de x" donde f nombra la función.

• tasa media de cambio: cambio total de los valores de la función (valores de salida) dividido por el cambio en los valores de entrada.

• simbólicamente: consistente en símbolos numéricos y algebraicos para formar una ecuación.

• tabla: una tabla que contiene datos que se muestran en columnas y filas.

• intervalo: la cantidad de tiempo que pasa de un periodo de tiempo al siguiente; la distancia entre dos puntos.

IMPLICACIONES PARA LA ENSEÑANZA

• En grados anteriores, los estudiantes usaron relaciones funcionales para crear modelos lineales y determinar la tasa de cambio. Reconocieron y explicaron una función como "cada valor de entrada devuelve exactamente un valor de salida", y el par ordenado representa la entrada y la salida.

• En este nivel, ampliarán su comprensión de las funciones como entrada y salida a conjuntos que representan el dominio y el rango.

• En este nivel de grado, los estudiantes deben ser capaces de crear ejemplos de lo que es y lo que no es una función utilizando una variedad de representaciones tales como una tabla, un gráfico, símbolos o una descripción verbal.

INICIO: CONTENIDO DESGLOSADO

• Los estudiantes a los que se les enseña la notación de funciones de forma aislada no siempre entienden que esta notación representa un par ordenado y tiene un significado en función del contexto. Del mismo modo, los estudiantes a los que se les enseñan funciones continuas y discretas en contexto desarrollan una mejor comprensión de cuándo y por qué se utilizan los tipos.

• Los estudiantes confunden con frecuencia "cada valor de entrada devuelve exactamente un valor de salida" con el significado de "cada valor de salida devuelve exactamente un valor de entrada".

• Los estudiantes confunden con frecuencia f(x) con el significado de "f times x.". Los estudiantes suelen pensar que todas las funciones utilizan f, x, y y. Cuando se encuentran por primera vez con una representación como d(t) = 3t, no les resulta familiar.

ALINEACIÓN VERTICAL

GRADO

8

Álgebra

ESTÁNDAR

Entender que una función es una regla que asigna a cada entrada exactamente una salida. La gráfica de una función es el conjunto de pares ordenados formados por una entrada y la salida correspondiente.

Comparar propiedades de dos funciones representadas cada una de una manera diferente (algebraicamente, gráficamente, numéricamente en tablas o mediante descripciones verbales). Por ejemplo, dada una función lineal representada por una tabla de valores y una función lineal representada por una expresión algebraica, determinar qué función tiene la mayor tasa de cambio.

Construir una función para modelar una relación lineal entre dos cantidades. Determinar la tasa de variación y el valor inicial de la función a partir de la descripción de una relación o de dos (x,y) valores, incluso leyéndolos en una tabla o en una gráfica. Interpretar la tasa de cambio y el valor inicial de una función lineal en términos de la situación que modela, y en términos de su gráfica o de una tabla de valores.

Describir cualitativamente la relación funcional entre dos cantidades analizando una gráfica (por ejemplo, si la función es creciente o decreciente, lineal o no lineal). Dibujar una gráfica que muestre las características cualitativas de una función que se ha descrito verbalmente.

Entender que una función de un conjunto (llamado dominio) a otro conjunto (llamado rango) asigna a cada elemento del dominio exactamente un elemento del rango. Si f es una función y x es un elemento de su dominio, entonces f(x) denota la salida de f correspondiente a la entrada x. La gráfica de f es la gráfica de la ecuación y = f(x).

Utilizar notación de funciones, evaluar funciones para entradas en sus dominios e interpretar enunciados que utilicen notación de funciones en términos de un contexto.

Relacionar el dominio de una función con su gráfica y, en su caso, con la relación cuantitativa que describe. Por ejemplo, si la función h da el número de horas-persona que se necesitan para montar n motores en una fábrica, entonces los números enteros positivos serían un dominio apropiado para la función.

Calcular e interpretar la tasa de variación media de una función (presentada simbólicamente o en forma de tabla) en un intervalo especificado. Estimar la tasa de cambio a partir de una gráfica.

Reconocer que las secuencias son funciones, a veces definidas recursivamente, cuyo dominio es un subconjunto de los números enteros. Por ejemplo, la sucesión de Fibonacci se define recursivamente por f(0) = f(1) = 1, f(n + 1) = f(n) + f(n - 1) para n ≥ 1.

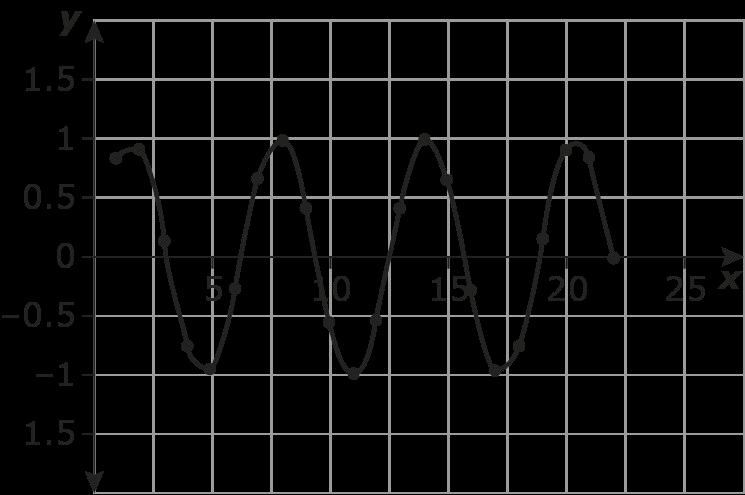
En el caso de una función que modela una relación entre dos magnitudes, interpreta las características principales de gráficas y tablas en términos de las magnitudes, y dibuja gráficas que muestren las características principales a partir de una descripción verbal de la relación. Las características clave incluyen: interceptos; intervalos en los que la función es creciente, decreciente, positiva o negativa; máximos y mínimos relativos; simetrías; comportamiento final; y periodicidad.

Graficar funciones expresadas simbólicamente y mostrar las características clave de la gráfica, a mano en casos sencillos y utilizando tecnología para casos más complicados.

Graficar funciones lineales y cuadráticas y mostrar interceptos, máximos y mínimos.

Graficar funciones de raíz cuadrada, raíz cúbica y funciones definidas a trozos, incluyendo funciones escalonadas y funciones de valor absoluto.

Graficar funciones exponenciales y logarítmicas, mostrando interceptos y comportamiento final, y funciones trigonométricas, mostrando período, línea media y amplitud.

Comparar propiedades de dos funciones representadas cada una de una manera diferente (algebraicamente, gráficamente, numéricamente en tablas o por descripciones verbales). Por ejemplo, dada una gráfica de una función cuadrática y una expresión algebraica para otra, decir cuál tiene el máximo mayor.

Identificar el efecto en la gráfica de sustituir f(x) por f(x) + k, kf(x), f(kx), y f(x + k) para valores concretos de k (tanto positivos como negativos); hallar el valor de k dadas las gráficas. Experimentar con casos e ilustrar una explicación de los efectos en la gráfica utilizando la tecnología. Incluir el reconocimiento de funciones pares e impares a partir de sus gráficas y expresiones algebraicas para ellas.

Construir funciones lineales y exponenciales, incluyendo secuencias aritméticas y geométricas, dada una gráfica, una descripción de una relación o dos pares de entrada-salida (incluir la lectura de éstas a partir de una tabla).

Álgebra

INICIO:

GUÍA DE INSTRUCCIÓN ANDAMIADA

MONITOREAR Y AJUSTAR

GUÍA DE INSTRUCCIÓN ANDAMIADA

La guía de instrucción andamiada se proporciona para que el maestro pueda planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.

Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes.

Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance.

La guía se divide en cuatro rangos de percentiles para cada estándar.

Refuerzo del grado anterior Nivel de grado con apoyos

Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.

Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.

Nivel de grado Ampliación del nivel de grado

Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.

Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.

Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:

1 Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.

2 Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.

3 Haga clic en el enlace directo al material elegido para el estudiante.

Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:

1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.

2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.

3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.

4. Haga clic en el enlace directo al material recomendado para el estudiante.

La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.

Área de instrucción: Operaciones y pensamiento algebraico

Todos los estudiantes:

• Captar interés

• Exploración

• Muestra lo que sabes

• Prueba de habilidades

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

Entender que una función de un conjunto (llamado dominio) a otro conjunto (llamado rango) asigna a cada elemento del dominio exactamente un elemento del rango. Si f es una función y x es un elemento de su dominio, entonces f(x) denota la salida de f correspondiente a la entrada x. La gráfica de f es la gráfica de la ecuación y = f(x).

0 %25 % (Nivel de grado anterior con apoyo)

8 - Funciones

Repaso y Práctica de Habilidades

Generador de Fluidez

• ¡Bam!

Prueba de Habilidades

Usar notación de funciones, evaluar funciones para entradas en sus dominios e interpretar enunciados que usan notación de funciones en términos de un contexto.

0 %25 % (Nivel de grado anterior con apoyo)

8 - Funciones

Repaso de Habilidades y Práctica

Constructor de Fluidez

• ¡Bam!

Examen de Habilidades

25 %50 % (Nivel de grado con apoyo)

Alg.I: Propiedades de las Funciones

APK

Foundation Builder

Repaso y Práctica de Habilidades

• Revisión Rápida (Preguntas 1, 2)

• Repaso (Sección Determinar si una Relación es una Función)

• Revisión (Preguntas 1, 3, 4)

25 %50 % (Nivel de grado con apoyo)

Alg.I: Propiedades de las Funciones

APK

Foundation Builder

Repaso y Práctica de Habilidades

• Revisión Rápida (Preguntas 3, 4)

• Repaso (Sección Evaluar Valores de Funciones)

• Revisión (Preguntas 5, 6)

80 % -

50 %80 % (Nivel de Grado)

100 % (Ampliando el Nivel de Grado)

Alg.I: Propiedades de las funciones

Vocabulario con imágenes

Vocabulario interactivo

Libreta interactiva

Generador de fluidez

• Concentración

Alg.I: Propiedades de las funciones

Tablero de opciones

50 %80 % (Nivel de Grado)

80 %100 % (Ampliando el Nivel de Grado)

Alg.I: Propiedades de las funciones

Vocabulario con imágenes

Vocabulario interactivo

Libreta interactiva

Generador de fluidez

• Concentración

Ciencia de datos

Alg.I: Propiedades de las funciones

Tablero de opciones

Relaciona el dominio de una función con su gráfica y, en su caso, con la relación cuantitativa que describe. Por ejemplo, si la función h(n) da el número de horas-persona que toma ensamblar n motores en una fábrica, entonces los números enteros positivos serían un dominio apropiado para la función.*

0 %25 % (Nivel de grado anterior con apoyo)

25 %50 % (Nivel de grado con apoyo)

8 - Funciones

Repaso de Habilidades y Práctica

Constructor de Fluidez

• ¡Bam!

Prueba de Habilidades

Alg.I: Propiedades de las Funciones

APK

Foundation Builder

Repaso y Práctica de Habilidades

• Revisión Rápida (Pregunta 1)

• Repaso (sección Determinar Dominio y Rango de Funciones)

• Revisión (Preguntas 2, 9, 10)

Alg.I: Propiedades de las funciones

Vocabulario con imágenes

50 %80 % (Nivel de Grado)

80 %100 % (Ampliando el Nivel de Grado)

Vocabulario interactivo

Práctica interactiva

• ¡Atrapa ese robot!

Generador de fluidez

• Concentración

Ciencia de datos

Alg.I: Propiedades de las funciones

Preferirías

Tablero de opciones

1: PROPIEDADES DE LAS FUNCIONES

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

Calcular e interpretar la tasa de cambio promedio de una función (presentada simbólicamente o como una tabla) en un intervalo específico. Estimar la tasa de cambio a partir de una gráfica.

8 - Tasa de Cambio

0 %25 % (Nivel de grado anterior con apoyo)

Repaso y Práctica de Habilidades

Constructor de Fluidez

• ¡A Pescar!

Práctica Interactiva

• Primer Contacto

Examen de Habilidades

25 %50 % (Nivel de grado con apoyo)

Alg.I: Propiedades de Funciones

Repaso de Habilidades y Práctica

• Revisión Rápida (Pregunta 5)

• Repaso (Calcular la Tasa de Cambio Promedio de la sección de Funciones)

• Revisión (Preguntas 7, 8)

Alg.I: Propiedades de las funciones

Vocabulario con imágenes

Vocabulario interactivo

50 %80 % (Nivel de Grado)

80 %100 % (Ampliando el Nivel de Grado)

Práctica interactiva

• ¡Atrapa ese robot!

Generador de fluidez

• Concentración

Ciencia de datos

Alg.I: Propiedades de las funciones

Preferirías

Tablero de opciones

ÁLGEBRA

ATRAER: ACCESO A CONOCIMIENTOS PREVIOS

EVALUAR PREVIAMENTE EL CONOCIMIENTO DE LOS ESTUDIANTES

ACCESO A CONOCIMIENTOS PREVIOS: ENCUENTRA

LAS PAREJAS EN EL SALÓN

ESTÁNDAR PREVIO

Entender que una función es una regla que asigna a cada entrada exactamente una salida. La gráfica de una función es el conjunto de pares ordenados que consisten en una entrada y la salida correspondiente.

DESCRIPCIÓN

Los estudiantes emparejarán tarjetas numeradas con tarjetas con letras colocadas alrededor del salón para demostrar su conocimiento del estándar previo. Este elemento está diseñado para descubrir los conceptos erróneos de los estudiantes; no debe tomarse para una calificación.

MATERIALES

IMPRESOS

• 1 tarjetas de Emparejar alrededor del salón (por clase)

PREPARACIÓN

• Imprime una copia de las tarjetas de emparejar alrededor del salón.

• Cuelga las tarjetas en un orden aleatorio alrededor del salón.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

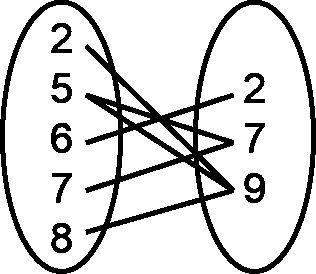
1. Pida a los estudiantes que escriban los números 1, 2, 3 y 4 en una hoja de papel.

2. Pida a los estudiantes que caminen por la sala con sus papeles. Mientras caminan por la sala, deben ver las tarjetas numeradas y emparejarlas con las tarjetas con letras.

3. Permita que los estudiantes compartan su pensamiento con un vecino.

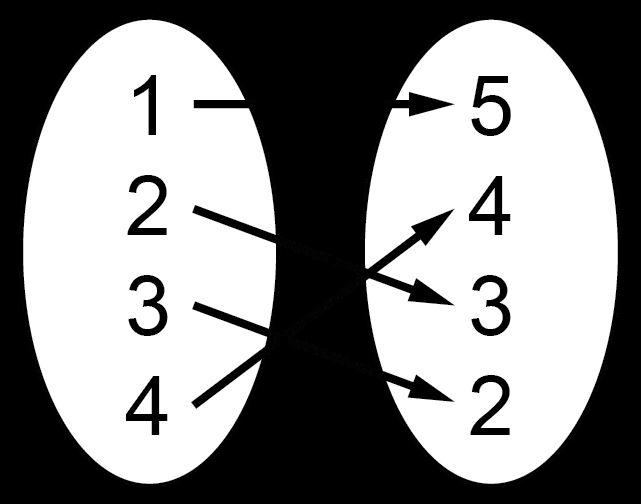
a. La tarjeta 1 coincide con la tarjeta B

b. La tarjeta 2 coincide con la tarjeta A

c. La tarjeta 3 coincide con la tarjeta D

d. La tarjeta 4 coincide con la tarjeta C

4. Si los estudiantes tienen dificultades para completar esta tarea, pase al Constructor de Fundamentos con el fin de llenar este vacío en el conocimiento previo antes de pasar a otras partes del alcance.

IDENTIFICACIÓN DE CONCEPTOS ERRÓNEOS

• Los estudiantes pueden tener dificultades para recordar cómo identificar funciones. Es beneficioso permitir que los estudiantes investiguen los patrones que ven cuando observan juntos tablas, gráficos y ecuaciones.

EMPAREJA LAS TARJETAS

DESCRIPCIÓN

Los estudiantes relacionarán la notación de funciones con una situación del mundo real.

MATERIALES

IMPRESOS

• 1 propiedades de las funciones (por clase)

REUTILIZABLES

• 1 video de Fenómenos (por clase)

PREPARACIÓN

• Planee mostrar el video.

• Prepárese para proyectar Propiedades de las Funciones para que toda la clase lo vea.

• Prepárese para presentar el escenario y para animar a los estudiantes a pensar en cómo resolverlo. Prepárese para pasar a las actividades de Exploración, regresando a la actividad Gancho con los nuevos conocimientos adquiridos una vez que se hayan completado las Exploraciones.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: EXPLORACIÓN PREVIA

1. Presente esta actividad hacia el comienzo del alcance. La clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades Explorar correspondientes.

2. Explique la situación mientras muestra el vídeo que tiene detrás. Mark está cargando su teléfono después de que se apagara. Está pensando en cómo modelar la cantidad de carga que tiene el teléfono a medida que pasa el tiempo.

3. Haga las siguientes preguntas a los estudiantes: ¿Qué observas? W¿qué te preguntas? ¿Dónde puedes ver matemáticas en esta situación? Permita que los estudiantes compartan todas sus ideas. Las respuestas de los estudiantes variarán. Creo que la cantidad de carga aumenta a un ritmo constante. Creo que la carga se estabilizará cuando se acerque al 100%. Creo que tardará dos horas en cargarse completamente. Me pregunto cuánto tardará el teléfono en cargarse al 80%. Me pregunto cuánto tardará en encenderse el teléfono muerto.

4. Proyecto Propiedades de las funciones.

ATRAER: CAPTAR INTERÉS

LECCIÓN PARA CAPTAR INTERÉS

CAPTAR INTERÉS

Propiedades de las funciones

Las siguientes afirmaciones sobre el teléfono de Mark son verdaderas, donde f(t) es la cantidad de carga en el teléfono después de t minutos.

1. f(100) – f(90) < f(30) – f(20)

2. f(150) – f(115) = 0

PROPIEDADES DE LAS FUNCIONES

5. Explique a los estudiantes que Mark hizo un seguimiento de la carga de su teléfono y escribió un par de enunciados para describir lo que estaba ocurriendo. Discuta las siguientes preguntas:

a. DOK-1 ¿Por qué el primer enunciado matemático tiene un símbolo de desigualdad? Permita que los estudiantes compartan sus ideas. Las respuestas de los estudiantes variarán. La cantidad de carga durante un intervalo es menor que otra cantidad de carga.

b. DOK-1 ¿Qué representa la parte "f(100) - f(90)" de esta oración matemática? La carga después de 100 minutos menos la carga después de 90 minutos.

6. Comparta con los estudiantes que la siguiente pregunta guía será utilizada a lo largo del tema: ¿Cómo desarrollamos una taquigrafía matemática?

7. Completa las actividades de Exploración.

PARTE II: DESPUÉS DE LA EXPLORACIÓN

1. Vuelve a mostrar el video Fenómenos y replantea el problema.

2. Consulta Propiedades de las funciones y discute las siguientes preguntas:

a. DOK-1 ¿Tienen más sentido estos enunciados con notación de funciones después de las Exploraciones? Sí, puedo interpretar esta notación en el contexto del teléfono que se carga.

b. DOK-2 ¿Qué estrategias utilizarías para explicar por qué estos enunciados tienen sentido?

Escribiría cada enunciado matemático como una frase completa y averiguaría cómo tiene sentido teniendo en cuenta lo que sé sobre la carga del teléfono.

c. DOK-2 ¿Qué significa f(100) - f(90) < f(30)f(20)? El teléfono aumenta su cantidad de carga menos entre los minutos 90 y 100 que entre los minutos 20 y 30.

d. DOK-2 ¿Qué significa para f(150) - f(115) = 0? Es probable que el teléfono ya haya alcanzado la carga completa después de 115 minutos.

EXPLORAR: EXPLORACIÓN 1

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 1:

RELACIONES Y FUNCIONES

DESCRIPCIÓN

Los estudiantes analizarán las propiedades de las funciones y no funciones a través de diversos tipos de representaciones algebraicas con el fin de desarrollar la definición de una función. Los estudiantes también serán capaces de descifrar entre funciones continuas y discretas.

ESTÁNDARES DE PRÁCTICA MATEMÁTICA

• MP.3 Construir argumentos viables y criticar el razonamiento de otros: Los estudiantes analizarán problemas y utilizarán supuestos matemáticos, definiciones y resultados establecidos para construir argumentos.

• MP.4 Modelar con matemáticas: Los estudiantes aplicarán las matemáticas que conocen para resolver problemas de la vida cotidiana.

• MP.8 Buscar y expresar regularidades en razonamientos repetidos: Los estudiantes comprenderán la aplicación más amplia de los patrones y verán la estructura en situaciones similares.

MATERIALES

IMPRESO

• 1 Diario del estudiante (por estudiante)

• 1 Juego de tarjetas Widget (por estudiante)

• 1 Ticket de salida (por 2 estudiantes)

REUTILIZABLE

• 1 Par de tijeras (por estudiante)

• 1 Barra de pegamento (por estudiante)

PREPARACIÓN

• Separe la clase en grupos de 2 o 3 estudiantes.

• Imprime un Diario del estudiante para cada estudiante.

• Imprime un juego de Tarjetas Widget para cada estudiante.

• Imprime un documento de Boleto de salida para cada 2 estudiantes. Recorta los boletos de salida de media página para que cada estudiante tenga uno.

• Reúne tijeras y barras de pegamento para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Lea el siguiente escenario a la clase: ¡Felicidades! Te acaban de contratar a tiempo parcial en la nueva fábrica de widgets de tu ciudad. Es tu primer día de trabajo. El empleado del turno de noche te ha dejado una nota en la que te dice que una de las tres máquinas de widgets que tienes a tu cargo funciona mal y no produce widgets según los estándares de la fábrica, ¡pero no te ha dicho cuál! Analice las entradas y salidas de cada máquina para identificar la máquina de widgets que funciona mal y así poder apagarla para repararla.

2. Entregue un Diario del estudiante a cada estudiante.

3. Explique a los estudiantes que trabajarán con sus grupos para analizar las entradas y salidas de cada máquina de widgets para determinar cuáles son las dos máquinas que funcionan y cuál es la máquina que no funciona correctamente.

4. A medida que los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas guía para evaluar la comprensión de los estudiantes:

a. DOK-1 ¿Qué se entiende por el término entrada? Significa el conjunto de valores suministrados a una función. También representa el dominio de una función.

b. DOK-1 ¿Qué significa el término output? Significa el conjunto resultante de valores basados en la entrada de la función. También representa el rango de una función.

c. DOK-2 ¿Qué patrones puedes identificar en las máquinas que funcionan correctamente? Cada entrada se corresponde con una sola salida.

5. Evite confirmar las elecciones de los grupos para las máquinas que funcionan y las que no. Permita que los grupos tomen sus propias decisiones y justificaciones basándose en sus observaciones. Está bien que los estudiantes diagnostiquen mal las máquinas en este punto. La idea errónea se aclarará durante la Charla de matemáticas.

6. Conceda a los estudiantes tiempo suficiente para completar la Parte I y responder a las preguntas que siguen.

7. Después de completar la Parte I, invite a la clase a una Charla de matemáticas para compartir sus observaciones y lo aprendido hasta el momento.

¿Qué widgets (artilugios) funcionan?

Parte I

Analiza las máquinas de artilugios a continuación para determinar qué dos máquinas funcionan y qué características se requieren para que un artilugio sea aprobado por los estándares de fábrica.

A Máquina B

Entrada Salida 2 gotas 1 artilugio 5 gotas 9 artilugios 7 gotas 13 artilugios

Máquina C

Entrada Salida 1 gota 1 artilugio 3 gotas 1 artilugio 9 gotas 14 artilugios

Entrada Salida 3 gotas 1 artilugio 3 gotas 5 artilugios 8 gotas 2 artilugios

1. ¿Qué dos máquinas crees que funcionan correctamente? ¿Qué patrones encontraste entre esas dos máquinas?

2. ¿Qué máquina no funciona correctamente y debe apagarse?

3. ¿Qué tiene de diferente la máquina que no funciona correctamente?

DIARIO DEL ESTUDIANTE

CHARLA DE MATEMÁTICAS

• DOK-1 ¿Cómo determinó tu grupo la máquina que no funcionaba correctamente? Nos dimos cuenta de que la máquina B era la única que tenía la misma entrada (3 blobs) resultando en diferentes salidas (1 widget y 5 widgets). No tenía sentido que pusieras la misma entrada en la máquina pero los resultados fueran diferentes.

• DOK-2 ¿Qué condiciones deben cumplirse para que se considere que una máquina funciona?La máquina funciona si cada valor de entrada devuelve exactamente un valor de salida.

PARTE II

7. Lee el siguiente escenario a la clase: Ahora que la máquina B se ha parado, tu supervisor sospecha que otras máquinas de widgets de la fábrica también pueden estar funcionando mal. Te ha pedido que analices el resto de las máquinas de widgets para determinar si es necesario parar alguna más por no funcionar correctamente. Asegúrate de justificar tu razonamiento de por qué funciona o no cada máquina para informar a tu supervisor.

1. Entregue un juego de tarjetas Widget a cada estudiante.

2. Explique a los estudiantes que trabajarán con sus grupos para analizar la información dada sobre cada máquina para decidir si las máquinas funcionan correctamente o no. También justificarán su elección en cada tarjeta.

3. Anime a los estudiantes a analizar, clasificar y colaborar con sus grupos antes de pegar las tarjetas en sus columnas correspondientes.

4. Mientras los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas orientativas para evaluar la comprensión de los estudiantes:

a. DOK-1 En la tarjeta etiquetada como "Máquina H", ¿qué representan las dos flechas que salen del 1 en la columna Dominio? Las dos flechas representan que el valor 1 aparece dos veces.

b. DOK-1 En la tarjeta etiquetada "Máquina D", ¿cuántos valores de salida se muestran cuando x = 2? Hay dos valores de salida cuando x = 2. Los valores son 1 y -1. Los valores son 1 y -1.

c. DOK-1 En las tarjetas etiquetadas como "Máquina F" y "Máquina G", ¿dónde ves los valores de entrada y salida? Los valores de entrada están representados por la coordenada x, y los valores de salida están representados por la coordenada y

d. DOK-1 ¿Cuál es la regla que creamos para identificar las máquinas que funcionan? Cada entrada debe corresponderse exactamente con una salida.

5. Concede a los estudiantes tiempo suficiente para completar la Parte II y responder a las preguntas que siguen.

6. Después de la Exploración, invita a la clase a una Charla de matemáticas para compartir sus observaciones y aprendizajes.

Máquina

EXPLORAR: EXPLORACIÓN 1

CHARLA DE MATEMÁTICAS

Properties of Functions Explore 1

y determina si cada máquina funciona correctamente o no. Indica tu razonamiento en el lado derecho de cada tarjeta. Recorta las

y

en las columnas correspondientes a

Máquinas de artilugios que funcionan Máquinas de artilugios que no funcionan

Pega aquí las tarjetas de artilugios que funcionan.

Pega aquí las tarjetas de artilugios que no funcionan.

Reflexiona

1. Resume tus hallazgos generales sobre las máquinas de artilugios que funcionaban correctamente.

2. Resume tus hallazgos generales sobre las máquinas de artilugios que no funcionaban correctamente.

3. ¿Es posible que una máquina de artilugios en funcionamiento tenga solo un valor de salida? Explica.

• DOK-1 ¿Cómo pudiste determinar las entradas y salidas para las máquinas D y E?Miré los pares ordenados de las coordenadas en cada gráfico. La x-coordenada representa la entrada, y la y-coordenada representa la salida.

• DOK-1 Encuentra la Tarjeta Widget para la máquina D. ¿Cuáles son dos puntos en la gráfica que te indican que ésta no es una máquina widget que funciona?

◦ Recoge todas las respuestas.

◦ (-1, 1) y (-1, -1)

◦ (0, 1) y (0, -1)

◦ (1, 1) y (1, -1)

◦ (2, 1) y (2, -1)

• DOK-2 ¿Qué notas sobre la ubicación de cada par de coordenadas? ¿Qué te dice esto sobre las gráficas de las funciones?Cada par de coordenadas está situado en la misma recta vertical. Si una gráfica contiene dos puntos en la misma línea vertical, entonces los datos no pueden ser una función.

• DOK-1 ¿Qué estrategias usaste para determinar qué máquinas estaban funcionando?Para cada máquina, miré las entradas. Si ninguna de las entradas se repetía, entonces la máquina funcionaba correctamente. Si las entradas se repetían, comprobaba las salidas. Cada entrada tenía que estar emparejada exactamente con una salida.

8. Cuando los estudiantes hayan terminado, pídales que completen la Boleta de Salida para evaluar formativamente su comprensión del concepto.

ESQUEMA DE ANCLAJE Y LIBRETA INTERACTIVA

• Asegúrese de completar la Esquema de anclaje como clase. Una vez que la clase haya completado el Esquema de anclaje, haga que cada estudiante complete su Libreta interactiva.

APOYOS PEDAGÓGICOS

1. Los estudiantes pueden confundir si deben analizar entradas o salidas al determinar si una expresión es una función. Crear un gráfico básico de entradas mapeadas a salidas o graficar coordenadas puede ayudarlos.

2. Los estudiantes pueden no prestar atención a los números negativos y positivos cuando evalúan y/o grafican entradas y sus correspondientes salidas. Refuerce este concepto reflejando el trabajo de los

en gráficos para ayudarlos a confrontar cualquier inconsistencia.

3. Los estudiantes pueden tener problemas graficando puntos en un sistema de coordenadas y pueden necesitar que se les recuerden las convenciones usadas para graficar correctamente.

estudiantes

Parte II

Analiza cada tarjeta de artilugio del documento «Tarjetas de artilugios»

tarjetas

pégalas

continuación.

APOYOS PARA LA ADQUISICIÓN DEL LENGUAJE

La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad Explorar. Consulte las estrategias siguientes para saber cómo apoyar el desarrollo lingüístico de los estudiantes. Se proporcionará a los estudiantes apoyos previos a la lectura (organizadores gráficos, diagramas de formas y vocabulario preenseñado) para ayudarles en la comprensión lectora.

Principiante: Antes de la lección, proporcione a los estudiantes una lista del vocabulario nuevo que encontrarán en la lección junto con imágenes que indiquen el significado de los términos. Anime a los estudiantes a subrayar los términos y a releer sus definiciones a medida que los vayan encontrando en sus diarios del estudiante. Los términos clave que deben incluirse son entrada, salida, dominio, rango, relación, función, continua, y discreta

Intermedia: Antes de la lección, proporcione a los estudiantes notas guiadas que incluyan imágenes y diagramas junto con definiciones incompletas de los nuevos términos que encontrarán en la Exploración. A medida que los estudiantes avancen en la lección, anímeles a completar las definiciones. Los términos clave a incluir son entrada, salida, dominio, rango, relación, función, continua

Relaciones y funciones Completar los espacios en blanco para que cada tabla represente una función. 1. 2. 3.

Avanzada: Antes de la lección, proporcione a los estudiantes notas guiadas que incluyan imágenes y diagramas junto con definiciones incompletas de los nuevos términos que encontrarán en la Exploración. A medida que los estudiantes avancen en la lección, anímeles a completar las definiciones. Los términos clave a incluir son entrada, salida, dominio, rango, relación, función, continua

Relaciones y funciones Boleto de salida

1. A continuación, encierra con un círculo todas las imágenes que representen funciones.

(3, 4) (5, 3) (5, 5) (5, 6)

2. Alyssa y Maura discutían sobre las dos imágenes a continuación. Maura cree que ambas imágenes representan funciones, ya que la imagen B es solo el círculo completo de la imagen A. ¿Estás de acuerdo con el razonamiento de Maura?

¿Por qué sí o por qué no?

Imagen A Imagen B

Relaciones y funciones Boleto de salida

1. A continuación, encierra con un círculo todas las imágenes que representen funciones.

(3, 4) (5, 3) (5, 5) (5, 6)

2. Alyssa y Maura discutían sobre las dos imágenes a continuación. Maura cree que ambas imágenes representan funciones, ya que la imagen B es solo el círculo completo de la imagen A. ¿Estás de acuerdo con el razonamiento de Maura? ¿Por qué sí o por qué no?

Imagen A Imagen B

BOLETO DE SALIDA

LO QUE SABES (PARTE 1)

EXPLORAR: EXPLORACIÓN 2

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 2: EVALUAR

FUNCIONES

DESCRIPCIÓN

Los estudiantes evaluarán funciones lineales y cuadráticas en notación de funciones e interpretarán la notación de funciones dentro de varios contextos.

ESTÁNDARES DE PRÁCTICA MATEMÁTICA

• MP.3 Construir argumentos viables y criticar el razonamiento de otros: Los estudiantes analizarán problemas y utilizarán supuestos matemáticos, definiciones y resultados establecidos para construir argumentos.

• MP.4 Modelar con matemáticas: Los estudiantes aplicarán las matemáticas que conocen para resolver problemas de la vida cotidiana.

• MP.8 Buscar y expresar regularidades en razonamientos repetidos: Los estudiantes comprenderán la aplicación más amplia de los patrones y verán la estructura en situaciones similares.

PREPARACIÓN VÍDEO

MATERIALES

IMPRESOS

• 1 Diario del estudiante (por estudiante)

• 1 Boleto de salida (por cada 2 estudiantes)

PREPARACIÓN

• Separa la clase en grupos de 2 o 3 estudiantes.

• Imprime un Diario del estudiante para cada estudiante.

• Imprime un Boleto de salida para cada 2 estudiantes. Corta los boletos de salida de media página para que cada estudiante tenga uno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Lea el siguiente escenario a la clase: Recientemente ha obtenido un puesto de asistente de zoólogo en el zoológico de su localidad. El zoólogo jefe, el Dr. Angola, le ha asignado su primer proyecto de investigación, en el que debe averiguar más información sobre el comportamiento migratorio de las tortugas laúd. El equipo del Dr. Angola ha recopilado datos para seguir la distancia recorrida por un nido de tortugas laúd a lo largo del tiempo. Los datos se muestran en un gráfico, pero usted debe interpretar el gráfico y utilizar la información para completar el informe sobre la migración de las tortugas laúd.

2. Entregue un Diario del estudiante a cada estudiante.

3. Explique a los estudiantes que trabajarán con sus grupos para analizar la información relativa a la migración de las tortugas en el gráfico. Los estudiantes idearán una estrategia para completar los datos que faltan en el informe sobre la migración de las tortugas laúd y responderán a las preguntas que siguen en la Parte I en sus Diarios del estudiante.

4. Mientras los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas orientativas para evaluar la comprensión de los estudiantes:

a. DOK-1 ¿Cómo puedes utilizar f(5) = 50 para ayudarte a rellenar el espacio en blanco de f(___) = 80? En la fila A, el 5 representa los días que se tardó en recorrer 50 millas. Así que en la fila B, 8 debe ir en el espacio en blanco porque tardó 8 días en recorrer 80 millas. El número entre paréntesis debe representar los días.

b. DOK-1 ¿Qué representa la coordenada (8, 80) en la gráfica? La coordenada (8, 80) significa que las tortugas viajaron 80 millas en 8 días.

5. Conceda a los estudiantes suficiente tiempo para completar la Parte I y responder a las preguntas que siguen.

6. Después de completar la Parte I, invite a la clase a una Charla de matemáticas para compartir sus observaciones y lo aprendido hasta el momento.

Parte

Rastreador de tortugas

gráfica y los datos para completar el informe de la Dra. Angola.

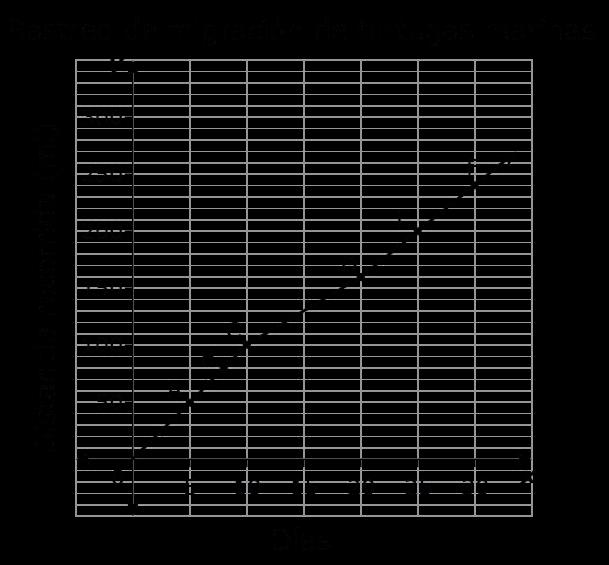
Informe: Migración de la tortuga laúd

A (5, 50) f(5) = 50 Después de 5 días, las tortugas habían viajado 50 millas.

B (8, 80) f(___) = 80 Después de ____ días, las tortugas habían viajado 80 millas.

C (10, 100) f(10) = ____ Después de 10 días, las tortugas habían viajado ____ millas.

D Después de ____ días, las tortugas habían viajado ____ millas.

E Después de ____ días, las tortugas habían viajado ____ millas.

F Después de ____ días, las tortugas habían viajado ____ millas.

DIARIO DEL ESTUDIANTE

CHARLA DE MATEMÁTICAS

• DOK-1 Normalmente, un número junto a un paréntesis representa una multiplicación. ¿Es ése el caso aquí? Explica.Aquí, el número dentro del paréntesis nos está diciendo la entrada, o x-coordenada.

• DOK-2 ¿Cuál es la diferencia entre f(20) y f(x) = 20?f(20) nos pide encontrar la distancia recorrida después de 20 días, mientras que f(x) = 20 nos pide encontrar el número de días en que las tortugas recorrieron 20 millas.

• DOK-1 Al considerar la función de la pregunta 1, f(x) = 8x, ¿cuál es la variable dependiente (salida) y cuál es la variable independiente (entrada)?La variable dependiente es f(x), que representa la distancia recorrida. Este es el valor de la salida. La variable independiente es x, que representa el número de días. Esto representa el valor de la entrada.

• DOK-2 ¿En qué se diferencia f(x) = 8x de y = 8x? ¿En qué se parecen?Ambos representan el mismo patrón y pueden utilizarse indistintamente.

PARTE II

1. Lea el siguiente escenario a la clase: Las tortugas laúd no son la única especie de tortuga marina que el equipo de la Dra. Angola ha estado siguiendo. La Dra. Angola quedó tan satisfecha con su informe sobre las tortugas laúd que les ha pedido que completen el informe sobre la migración multiespecie. El equipo ha desarrollado funciones para representar las distancias recorridas durante cualquier cantidad de tiempo para cada especie estudiada.

2. Explique a los estudiantes que trabajarán con sus grupos para evaluar funciones para el valor dado o encontrar la entrada para una salida dada. Los estudiantes utilizarán estos cálculos para completar el informe sobre la migración multiespecífica en la Parte II de sus Diarios del Estudiante.

3. Mientras los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas guía para evaluar la comprensión de los estudiantes:

a. DOK-1 ¿Qué significa f(14)? Significa evaluar la función dada con una entrada de 14.

b. DOK-1 Una vez que calculas que f(14) = 576, ¿cómo determinas qué número representa los días y qué número representa las millas recorridas? Sé que 14 es la variable de entrada o independiente, y 576 es la variable de salida o dependiente. En este escenario, el número de días es la variable independiente, y el número de millas recorridas es la variable dependiente.

c. DOK-1 ¿Cómo evalúas una función que tiene más de una x (por ejemplo, g(x) = (x + 4)(x2))? Sustituyo la entrada dada por cada aparición de x y luego utilizo el orden de las operaciones para simplificar.

d. DOK-2 Si f(14) representa la distancia recorrida por flatbacks en 14 días y g(14) representa la distancia recorrida por greens en 14 días, ¿qué representaría f(14) + g(14)? Esto representaría la distancia combinada recorrida por flatbacks y greens en 14 días.

4. Concede a los estudiantes tiempo suficiente para completar la Parte II y responder a las preguntas que siguen.

5. Después de la Exploración, invita a la clase a una Charla de matemáticas para compartir sus observaciones y aprendizajes.

I Analiza la siguiente gráfica que muestra los datos recopilados por el equipo de la Dra. Angola. Usa la

EXPLORAR: EXPLORACIÓN 2

CHARLA DE MATEMÁTICAS

Properties of Functions Explore 2

1. La Dra. Angola está más interesada en la sección de la gráfica que contiene los puntos D, E y F, ya que cree que las tortugas continuarán con esta tendencia durante los próximos días. Completa la siguiente función para representar la relación entre la cantidad de días y la distancia recorrida en esta sección de la gráfica.

f(x) = _______

2. Usa tu ecuación de la pregunta 1 para predecir la distancia recorrida por las tortugas después de 36 días.

Parte II

Evalúa las funciones para el valor dado o encuentra la entrada para una salida dada. Completa el informe de múltiples especies para la Dra. Angola.

Informe: Migración de múltiples especies

Tortugas planas

f(x) = 4(x – 2)2 f(14) = ____ Después de ____ días, las tortugas planas habían viajado ____ millas.

Tortugas marinas

a(x) = 7x a(x) = 126 x = ____ Después de ____ días, las tortugas marinas habían viajado ____ millas.

Tortugas bobas

l(x) = x2 + 5x l(9) = ____ Después de ____ días, las tortugas bobas habían viajado ____ millas.

Tortugas carey

h(x) = 18x h(x) = 54 x = ____

Tortugas verdes

Después de ____ días, las tortugas carey habían viajado ____ millas.

g(x) = (x + 4)(x – 2) g(6) = ____ Después de ____ días, las tortugas verdes habían viajado ____ millas.

Tortugas loras

k(x) = 16x + 10 k(x) = 170 x = ____

Después de ____ días, las tortugas loras habían viajado ____ millas.

Reflexiona

1. Considera la función t(x) = x2 + 8x − 4. a. Encuentra t(−4).

b. Si t(x) representa la distancia recorrida por las tortugas espalda de diamante a lo largo del tiempo, ¿tiene sentido t(−4)? Explica.

2. La Dra. Angola explicó que las tortugas marinas y las tortugas bobas a menudo nadan durante 3 días y luego se toman un descanso. Ella quiere saber la distancia total recorrida por estas dos especies después de 3 días. Utiliza las funciones del informe sobre la migración de múltiples especies, evalúa a(3) + l(3).

3. ¿Por qué un estudiante podría pensar que f(x) significa multiplicar f por x?

4. Explica qué significa «evalúa g(5)» con tus propias palabras.

5. ¿En qué se diferencia resolver la ecuación f(x) = 10 de evaluar la expresión f(10)?

• DOK-2 Para las tortugas de espalda plana, f(20) > f(15). Explica qué significa esto en contexto y qué te dice esta información sobre la gráfica de f(x).Puesto que f(20) > f(15), las tortugas de lomo plano han viajado más lejos después de 20 días que después de 15 días. En una gráfica, la salida, o el valor de y, cuando x = 20 sería mayor que el valor de y cuando x = 15.

• DOK-2 ¿Es posible evaluar una función usando un número negativo? ¿Tiene sentido en este caso? Explica.Sí, es posible. Sustituirías y simplificarías igual que lo harías con un número positivo. Sin embargo, no tiene sentido en este escenario porque nuestras entradas representan días, y las tortugas no pueden viajar por una cantidad negativa de días.

• DOK-2 ¿Cuáles son algunas ventajas de usar notación de funciones?La notación de funciones es más flexible que usar "y = ." Es más fácil seguir la pista de diferentes funciones en el mismo escenario usando notación de funciones: f(x), g(x), h(x), etc.

6. Cuando los estudiantes terminen, pídales que completen el Boleto de Salida para evaluar formativamente su comprensión del concepto.

ESQUEMA DE ANCLAJE Y LIBRETA INTERACTIVA

• Asegúrese de completar la Esquema de anclaje como clase. Una vez que la clase haya completado el Esquema de anclaje, haga que cada estudiante complete su Libreta interactiva.

APOYOS PEDAGÓGICOS

1. Los estudiantes pueden tener dificultades para entender cómo evaluar funciones para un valor dado de x. Puede ser útil resaltar (o subrayar/usar un color diferente) para escribir x y luego, al sustituir el valor de x, usar ese mismo color para cada instancia de x.

2. Los estudiantes pueden tener dificultades para entender que f(x) puede representarse por y. Refuerce que son lo mismo.

3. Los estudiantes pueden no entender que x representa la "entrada" y y representa la "salida" de la Exploración 1. Refuerce la conexión entre la entrada y la salida. Refuerce la conexión entre la entrada de la función como representación del valor x y la salida como representación del valor y en el plano de coordenadas. Luego revise la prueba de la línea vertical para mostrar qué es o no es una función.

4. Los estudiantes pueden suponer, basándose en la comprensión de entrada/salida de la Exploración 1, que f(x) representa una función discreta. Refuerce que f(x) es realmente sólo y y que, en estos casos, x y y pueden ser todos números reales y son continuos para estos propósitos.

Evaluar funciones

Boleto de salida

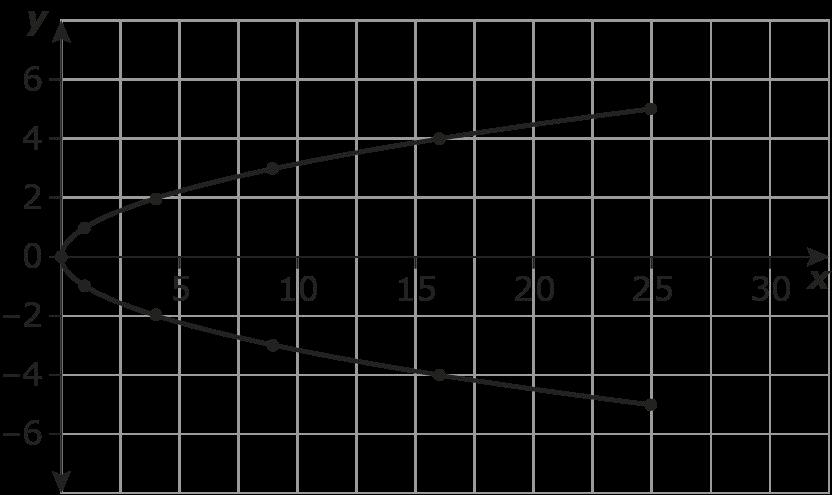
1. Usa la gráfica para determinar los siguientes valores:

a. h(2) = _____

b. h(7) = _____

c. h(x) = −3, x = _____

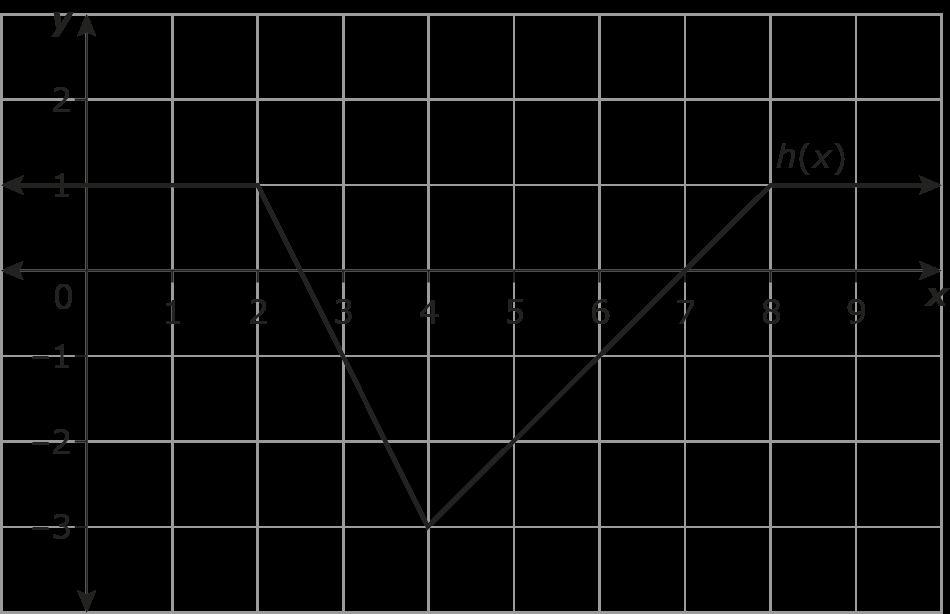
2. Dado que f(x) = 3x y g(x) = x2 − 7x + 2, encuentra los siguientes valores:

a. f(2) = _____

b. g(−1) = _____

c. f(2) + g(−1) = _____

Evaluar funciones

Boleto de salida

1. Usa la gráfica para determinar los siguientes valores:

a. h(2) = _____

b. h(7) = _____

c. h(x) = −3, x = _____

2. Dado que f(x) = 3x y g(x) = x2 − 7x + 2, encuentra los siguientes valores:

a. f(2) = _____

b. g(−1) = _____

c. f(2) + g(−1) = _____ BOLETO DE SALIDA

del uso de los teléfonos celulares. Encontró esta gráfica de datos sobre la cantidad de usuarios de teléfonos inteligentes en EE. UU.

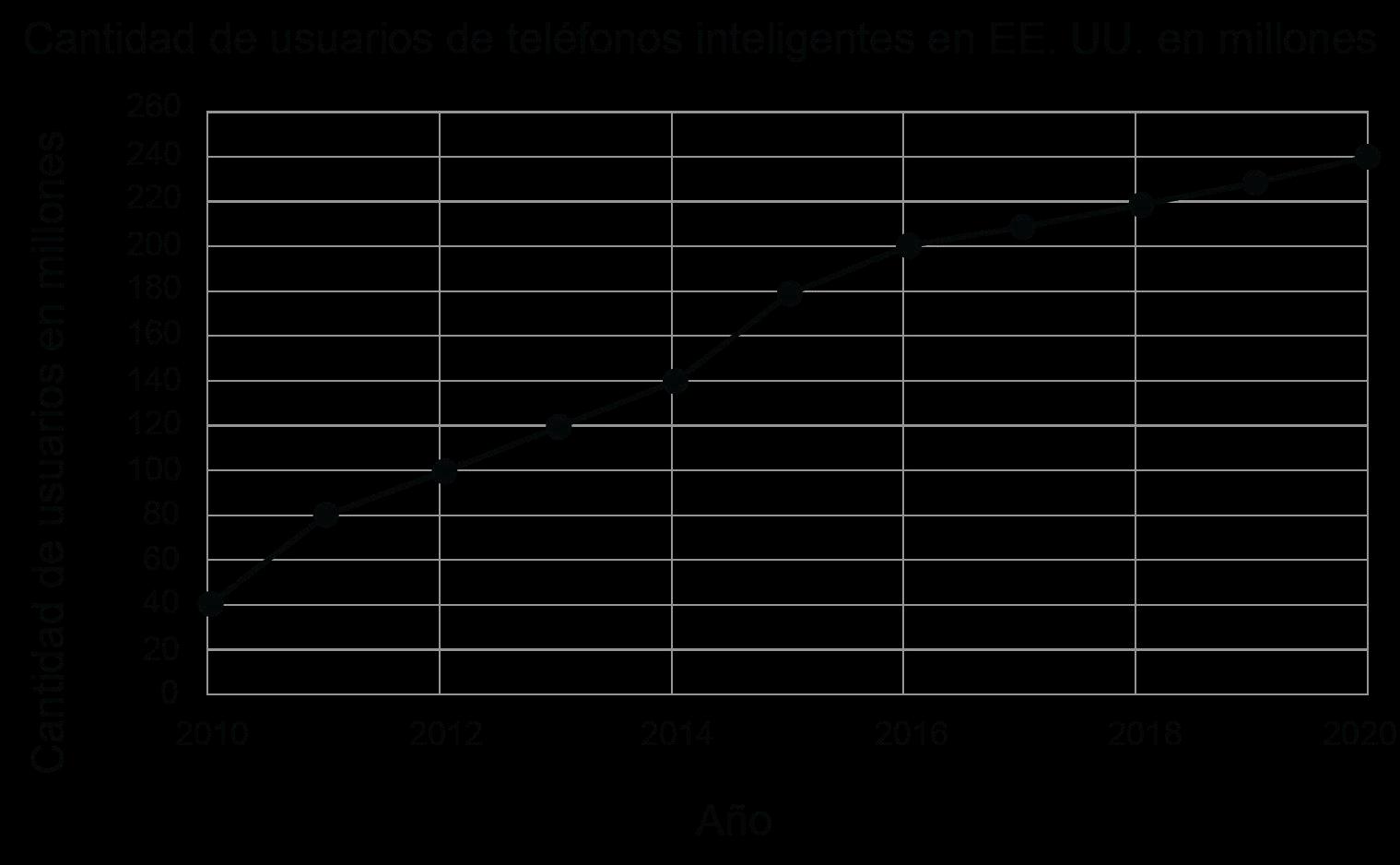
1. Si usamos f(x) para describir estos datos como una función, ¿qué variable representa x?

2. f(2012) = __________

3. f(2016) = __________

4. Si f(x) = 140 millones, entonces x = _________.

5. Evalúa f(2020) – f(2010) y describe lo que representa en su contexto.

APOYOS A LA ADQUISICIÓN DEL LENGUAJE

La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad de Explorar. Consulte las estrategias que siguen para encontrar formas de apoyar el desarrollo lingüístico de los estudiantes.

Los estudiantes utilizarán técnicas de aprendizaje como la elaboración de mapas conceptuales, el dibujo, la comparación, el contraste, la memorización y el repaso para adquirir vocabulario básico y de nivel de grado.

Principiante: Como actividad posterior a la clase, guíe a los estudiantes en la creación de cuadros de vocabulario para los términos función y evaluar. Completa en clase las siguientes secciones de los cuadros de vocabulario: Definición, Ejemplo (problema matemático) y Ausencia de ejemplo. Pida a los estudiantes que creen su propia imagen para cada término.

Intermedio: Como actividad posterior a la clase, pide a los estudiantes que creen cuadrados de vocabulario para los términos función y evaluar. Los cuadrados de vocabulario deben incluir las siguientes secciones: Definición, Ejemplo (problema matemático), Sin ejemplo e Imagen. Proporcione a los estudiantes las definiciones y los ejemplos, pero anímelos a reescribir las definiciones con sus propias palabras.

Avanzado: Como actividad posterior a la lección, pida a los estudiantes que creen cuadrados de vocabulario para los términos función y evaluar. Los cuadros de vocabulario deben incluir las siguientes secciones: Definición, Ejemplo (problema matemático), Sin ejemplo e Imagen. Proporcione a los estudiantes las definiciones, pero anímelos a reescribirlas con sus propias palabras.

Dado que a(x) = x ² + 5x + 6 y b(x) = 4x – 10, encuentra

9. Crea una gráfica que represente el siguiente escenario de mareas. Deja que x = 0 represente la medianoche cuando la marea está en un punto alto de 9 pies en el puerto. A las 3 a. m., la marea está en su punto medio de 5 pies y a las 6 a. m., la marea

EXPLORAR: EXPLORACIÓN 3

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 3: TASA DE CAMBIO PROMEDIO

DESCRIPCIÓN

Los estudiantes calcularán e interpretarán las tasas de cambio promedio en intervalos especificados. Los estudiantes conectarán las tasas de cambio a través de representaciones y harán generalizaciones acerca de los comportamientos de las funciones a través del tiempo.

ESTÁNDARES DE PRÁCTICA MATEMÁTICA

• MP.3 Construir argumentos viables y criticar el razonamiento de otros: Los estudiantes analizarán problemas y utilizarán supuestos matemáticos, definiciones y resultados establecidos para construir argumentos.

• MP.4 Modelar con matemáticas: Los estudiantes aplicarán las matemáticas que conocen para resolver problemas de la vida cotidiana.

• MP.8 Buscar y expresar regularidades en razonamientos repetidos: Los estudiantes comprenderán la aplicación más amplia de los patrones y verán la estructura en situaciones similares.

MATERIALES

IMPRESOS

• 1 Diario del estudiante (por estudiante)

• 1 Juego de tarjetas de opciones de comida y bebida (por grupo)

• 1 Boleto de salida (por estudiante)

PREPARACIÓN

• Separa la clase en grupos de 2 o 3 estudiantes.

• Imprime un Diario del estudiante y un Boleto de salida para cada estudiante.

• Imprime un juego de tarjetas de opciones de comida y bebida, en cartulina para mayor durabilidad, para cada grupo de estudiantes. No corte las tarjetas, ya que los estudiantes compararán las dos opciones de cada categoría.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Lee el siguiente escenario a la clase: Usted forma parte del comité de planificación de eventos estudiantiles de su centro de enseñanza. Este comité se encarga de planificar las Jornadas de Celebración Estudiantil que tendrán lugar periódicamente a lo largo del curso escolar. Tu equipo se encarga de encargar la comida para los eventos y quieres asegurarte de elegir alimentos que hayan demostrado ser populares entre los estudiantes durante las épocas en las que tendrán lugar las Jornadas de Celebración Estudiantil. Para planificar qué artículos comprar, necesita analizar las ventas de alimentos del año anterior e identificar los cambios promedio en las ventas para períodos específicos.

2. Entregue un Diario del estudiante a cada estudiante.

3. Explique a los estudiantes que trabajarán con sus grupos para analizar los datos provistos para las ventas de hamburguesas y porciones de pizza. Los estudiantes calcularán los cambios en las ventas a lo largo del tiempo y completarán la información para cada tipo de alimento. Los estudiantes registrarán su trabajo en sus Diarios del estudiante.

4. Mientras los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas guía para evaluar la comprensión de los estudiantes:

a. DOK-2 ¿Qué significaría obtener un número negativo para la columna de cambio en las ventas por mes? Un número negativo en esa columna significaría que la tasa de ventas estaría disminuyendo durante ese período de tiempo.

b. DOK-1 ¿Qué aspecto tendría la pendiente de esa línea cuando se representa gráficamente? La línea tendría una pendiente negativa. La pendiente iría cuesta abajo al graficar de izquierda a derecha.

c. DOK-2 Si estuvieras hallando el promedio de 4 números, dividirías el total entre 4. ¿Cómo se relaciona esto con hallar el cambio promedio en las ventas? Divido el cambio total por el número de meses en el intervalo. Esto es exactamente como calcular el promedio.

d. DOK-2 En la gráfica de ventas de rebanadas de pizza, ¿qué información necesita saber para poder calcular un cambio promedio en las ventas por mes del mes 3 al mes 5? Miraría el cambio en ventas y el cambio en meses. Dividiría el cambio en las ventas por el cambio en los meses para obtener el cambio promedio en las ventas por mes.

5. Conceda a los estudiantes suficiente tiempo para completar la Parte I y responder a las preguntas que siguen.

6. Después de completar la Parte I, invite a la clase a una Charla de matemáticas para compartir sus observaciones y lo aprendido hasta el momento.

Parte I

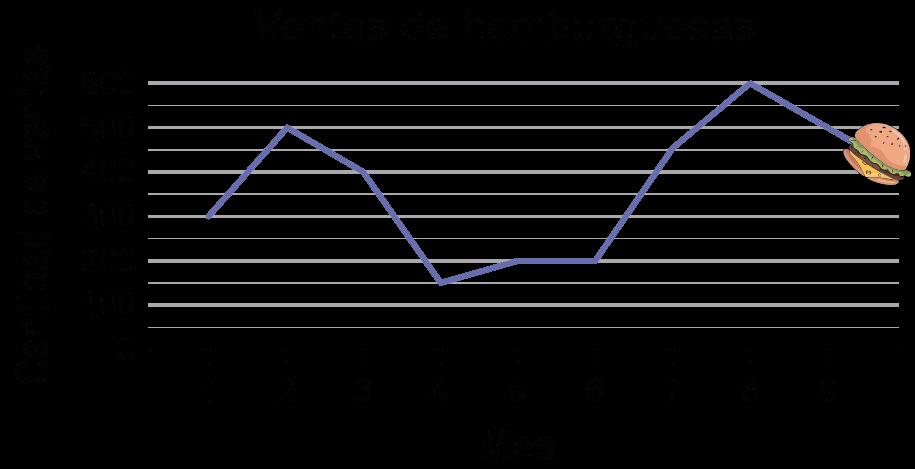
Ventas de hamburguesas

Período de tiempo Cambio en las ventas Cambio en meses Cambio promedio en ventas por mes

Del mes 1 al mes 2 200 1 200 hamburguesas por mes

Del mes 2 al mes 3 ______ hamburguesas por mes

Del mes 3 al mes 4 ______ hamburguesas por mes

Del mes 4 al mes 7 ______ hamburguesas por mes

Del mes 5 al mes 9 ______ hamburguesas por mes

Gráfica de ventas de rebanadas de pizza

Mes

Ventas de rebanadas de pizza

Período de tiempo Cambio en las ventas Cambio en meses Cambio promedio en ventas por mes

Del mes 2 al mes 3 ______ rebanadas de pizza por mes

Del mes 3 al mes 5 ______ rebanadas de pizza por mes

Del mes 5 al mes 9 ______ rebanadas de pizza por mes

1. El primer Día de Celebración Estudiantil ocurrirá después del tercer mes de clases. ¿Qué alimento tuvo las mayores ventas promedio por mes del mes 2 al mes 3?

2. El último Día de Celebración Estudiantil ocurrirá hacia el final del año escolar y se basará en el cambio promedio en las ventas por mes del mes 5 al mes 9. ¿Qué alimento se debe comprar? Explica.

CHARLA DE MATEMÁTICAS

• DOK-3 Al calcular el cambio en el número de ventas cada mes, ¿qué cosas necesitas tener en cuenta?Necesito tener en cuenta el período de tiempo. Si no estoy calculando el cambio promedio en las ventas de un mes al mes siguiente, entonces necesitaré dividir por el número de meses. También necesito prestar atención a la escala de los ejes.

• DOK-2 ¿En qué se parece el cambio promedio en las ventas a la pendiente?Calculé el cambio promedio en las ventas exactamente como calcularía la pendiente. Encontré el cambio en las salidas y lo dividí entre el cambio en las entradas.

• DOK-2 ¿En qué se diferencia el cambio promedio en las ventas de la pendiente?Una función lineal tiene la misma pendiente sin importar el intervalo que esté observando. Los datos de ventas de porciones de pizza y de hamburguesas no eran lineales porque no tenían una tasa de cambio constante. Pude encontrar el cambio promedio en las ventas cuando me dieron intervalos específicos.

PARTE II

1. Lee el siguiente escenario a la clase: Para todos los Días de Celebración Estudiantil, el comité quiere ofrecer una opción de comida saludable, un postre y una bebida. Se le han proporcionado datos para estas tres categorías basados en las ventas del año pasado. Analice los datos y realice los cálculos necesarios para hacer su recomendación para cada una de las tres categorías.

2. Entregue un juego de tarjetas de opciones de comida y bebida a cada grupo de estudiantes.

3. Explique a los estudiantes que trabajarán con sus grupos para comparar los datos de las dos opciones de cada categoría. Los estudiantes seguirán las instrucciones de la página 3 de sus Diarios del estudiante, realizarán los cálculos necesarios y harán una recomendación para cada categoría.

Comida divertida de viernes

EXPLORAR: EXPLORACIÓN 3

4. Mientras los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas orientativas para evaluar la comprensión de los estudiantes:

a. DOK-2 ¿Cómo puedes determinar qué opción de comida saludable tuvo el mayor índice medio de cambio del mes 1 al mes 5 con sólo mirar los gráficos? Como los intervalos de tiempo son los mismos y la escala de los gráficos es la misma, puedo comparar los gráficos. Puedo decir que la gráfica de Salad tiene un mayor incremento en ventas del mes 1 al mes 5.

b. DOK-2 ¿En qué se parece el cálculo de la tasa de cambio promedio al cálculo de la pendiente de una línea? Son similares porque estoy viendo el cambio en el valor y dividido por el cambio en el valor x. Con una función lineal, no importa qué parte de la gráfica observe, la pendiente es consistente. Con gráficas no lineales, debo prestar mucha atención a los intervalos.

c. DOK-1 ¿Cómo se calcula la tasa unitaria cuando se da una tasa? Tengo que dividir la cantidad asociada con la variable dependiente entre la cantidad asociada con la variable independiente.

d. DOK-2 ¿En qué se parece esto al cálculo de la tasa de cambio promedio? Es lo mismo que calcular la tasa de variación media. Sé que los costes de la bebida serán lineales.

e. DOK-1 ¿Qué meses debería analizar para el intervalo 2 ≤ x ≤ 9? Esta notación me dice que debo analizar el cambio en las ventas del mes 2 al mes 9.

5. Conceda a los estudiantes tiempo suficiente para completar la Parte II y responder a las preguntas que siguen.

6. Después de la exploración, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

Parte II Usa las tarjetas de opciones de alimentos y bebidas del documento «Tarjetas de opciones de alimentos y bebidas» para analizar las ventas del año anterior para las siguientes opciones. Realiza los cálculos correspondientes y luego selecciona la opción para tu recomendación.

Opciones saludables

Basa tu recomendación en la tasa de cambio promedio más alta del mes 1 al mes 5.

Tasa de cambio promedio durante el período de tiempo especificado:

a. Ventas de ensalada: b. Ventas de enrollado de pollo:

Recomendación:

Opciones de postre

Basa tu recomendación en la tasa de cambio promedio más alta del intervalo

2 ≤ x ≤ 9.

Tasa de cambio promedio durante el período de tiempo especificado:

a. Ventas de brownies de chocolate: b. Ventas de paletas heladas:

Recomendación:

Opciones de bebidas

Basa tu recomendación en el costo total más bajo de 50 galones de bebida.

Usa el costo promedio por galón para completar los valores que faltan en la tabla.

Galones de limonada que se necesitan Costo total ($)

Galones de jugo de

Recomendación:

Reflexiona

1. ¿En qué se parecen la pendiente y la tasa de cambio promedio? ¿En qué se diferencian?

2. Kamille analizaba los datos de ventas de sodas vendidas durante el año anterior. Los datos de las ventas se muestran en la siguiente gráfica.

Kamille afirmó que la tasa promedio de cambio del mes 8 al mes 10 fue de 50 sodas por mes. ¿Es precisa su afirmación? Justifica tu respuesta.

3. Dibuja el segmento de recta que muestra la tasa de cambio promedio de los meses 2 a 10 y luego encuentra el valor y explícalo en contexto.

CHARLA DE MATEMÁTICAS

• DOK-2 ¿Por qué es útil usar tasas de cambio promedio en gráficas no lineales?Las gráficas no lineales no tienen tasas de cambio constantes, así que usar el promedio sobre un intervalo puede ayudar a generalizar el comportamiento de la función.

• DOK-2 ¿Cómo calculaste la tasa de cambio promedio dentro de cada conjunto de datos? ¿Qué regla general se te ocurre que podría ayudar en cualquier escenario?Calcula el cambio en las salidas a lo largo de un intervalo específico, y divide ese número por el cambio en las entradas a lo largo del mismo intervalo.

7. Cuando los estudiantes hayan terminado, pídeles que completen el Boleto de Salida para evaluar formativamente su comprensión del concepto.

ESQUEMA DE ANCLAJE Y LIBRETA INTERACTIVA

• Asegúrate de completar la Esquema de anclaje como clase. Una vez que la clase haya completado el Esquema de anclaje, haga que cada estudiante complete su Libreta interactiva.

APOYOS PEDAGÓGICOS

1. Los estudiantes pueden olvidar calcular tasas de cambio como una razón de dos números y pueden olvidar el denominador. Refuerce la idea de una tasa dando ejemplos de unidades (por ejemplo, millas por hora, ciclos por minuto) donde una medida divide a otra.

2. Es posible que los estudiantes no presten atención a los signos negativos o positivos frente a las pendientes cuando grafican. Anime a los estudiantes a pensar en lo que significa cada número antes de graficarlo para que puedan verificarlo ellos mismos después de terminar.

3. Los estudiantes pueden no entender la diferencia entre tasa de cambio promedio y tasa de cambio instantánea. Anime a los estudiantes a pensar en coches que circulan por una carretera y que cambian constantemente de velocidad en función de lo que ocurre a su alrededor. Una velocidad instantánea podría oscilar entre 0 mph y su velocidad máxima, mientras que una velocidad media no sería ni 0 ni su velocidad máxima.

4. Los estudiantes pueden tener dificultades para interpretar gráficos para determinar tasas medias de cambio. Anímeles a elegir puntos que puedan ayudarles a evaluar estas tasas de cambio y asegúrese de que cualquier número que calculen tiene sentido basándose en el gráfico. En particular, asegúrese de que el valor calculado tiene el signo correcto.

APOYOS A LA ADQUISICIÓN DEL LENGUAJE

La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad de Explorar. Consulte las estrategias que siguen para encontrar formas de apoyar el desarrollo lingüístico de los estudiantes.

Los estudiantes utilizarán técnicas de aprendizaje como mapas conceptuales, dibujar, comparar, contrastar, memorizar y repasar para adquirir vocabulario básico y de nivel de grado.

Principiante: Como actividad posterior a la lección, guíe a los estudiantes en la creación de un cuadrado de vocabulario para el término tasa media de cambio Completa en clase las siguientes secciones del cuadrado de vocabulario: Definición, Ejemplo (problema matemático) y Ausencia de ejemplo. Haz que los estudiantes creen su propia imagen para el término. Intermedio: Como actividad posterior a la clase, pide a los estudiantes que creen un cuadrado de vocabulario para el término tasa media de variación. Los cuadros de vocabulario deben incluir las siguientes secciones: Definición, Ejemplo (problema matemático), No-ejemplo e Imagen. Proporcione a los estudiantes la definición y el ejemplo, pero anímelos a reescribir la definición con sus propias palabras.

Avanzado: Como actividad posterior a la lección, pida a los estudiantes que creen un cuadrado de vocabulario para el término promedio tasa de cambio. Los cuadros de vocabulario deben incluir las siguientes secciones: Definición, Ejemplo (problema matemático), Sin ejemplo e Imagen. Proporcione a los estudiantes la definición, pero anímelos a reescribirla con sus propias palabras.

Tasa de cambio promedio

Boleto de salida

1. La función g(x) se representa en la siguiente tabla. ¿Cuál es la tasa de cambio promedio de esta función en el intervalo −1 ≤ x ≤ 1?

2

2. ¿Qué intervalo a continuación daría como resultado una tasa de cambio promedio de −2.5?

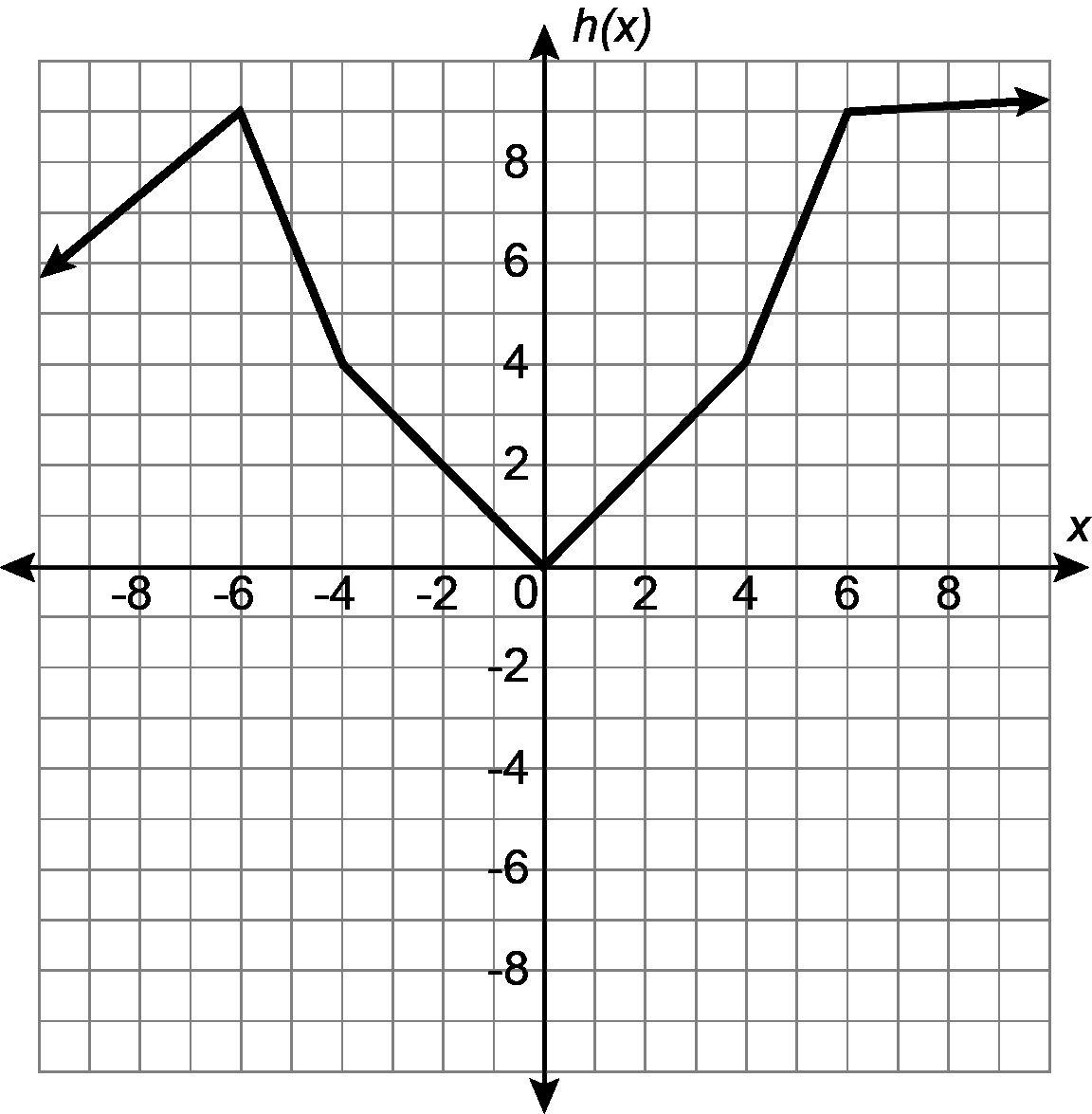
Tasa promedio de cambio

Tanya ha conseguido un nuevo trabajo como entrenadora de la liga de verano de natación para un grupo de edad más joven. Ella planifica los entrenamientos para sus chicos; a continuación aparecen sus objetivos generales para la cantidad promedio de yardas que ellos deben nadar cada semana. Utiliza los datos para completar la tabla y responde las preguntas de abajo.

Período Semanas 1 a 3 Semanas 3 a 4 Semanas 1 a 5 Semanas 3 a 8 Semanas 8 a 10

Tasa promedio de cambio en yardas por semana

1. ¿Qué significa que la tasa de cambio sea negativa en este escenario?

2. ¿Qué intervalo de una semana tiene el mayor aumento de yardas si observamos la gráfica? ¿Cuál es la tasa de cambio para ese intervalo?

3. Elige dos semanas entre las que la tasa promedio de cambio sea 0.

Usa las siguientes gráficas para responder las preguntas 7–9.

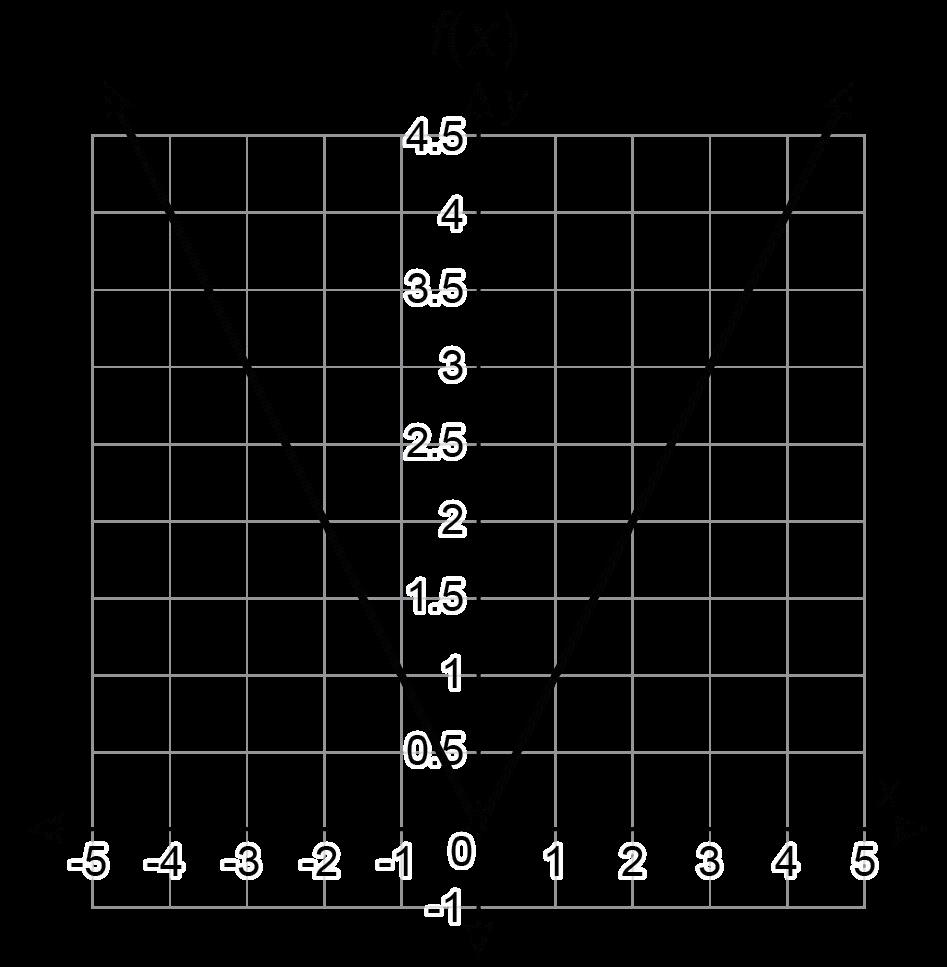
Al final de la temporada, Tanya puso las tasas promedio de tiempo de los nadadores y se sintió muy orgullosa de los progresos que habían hecho. Utiliza los datos de abajo para responder las preguntas.

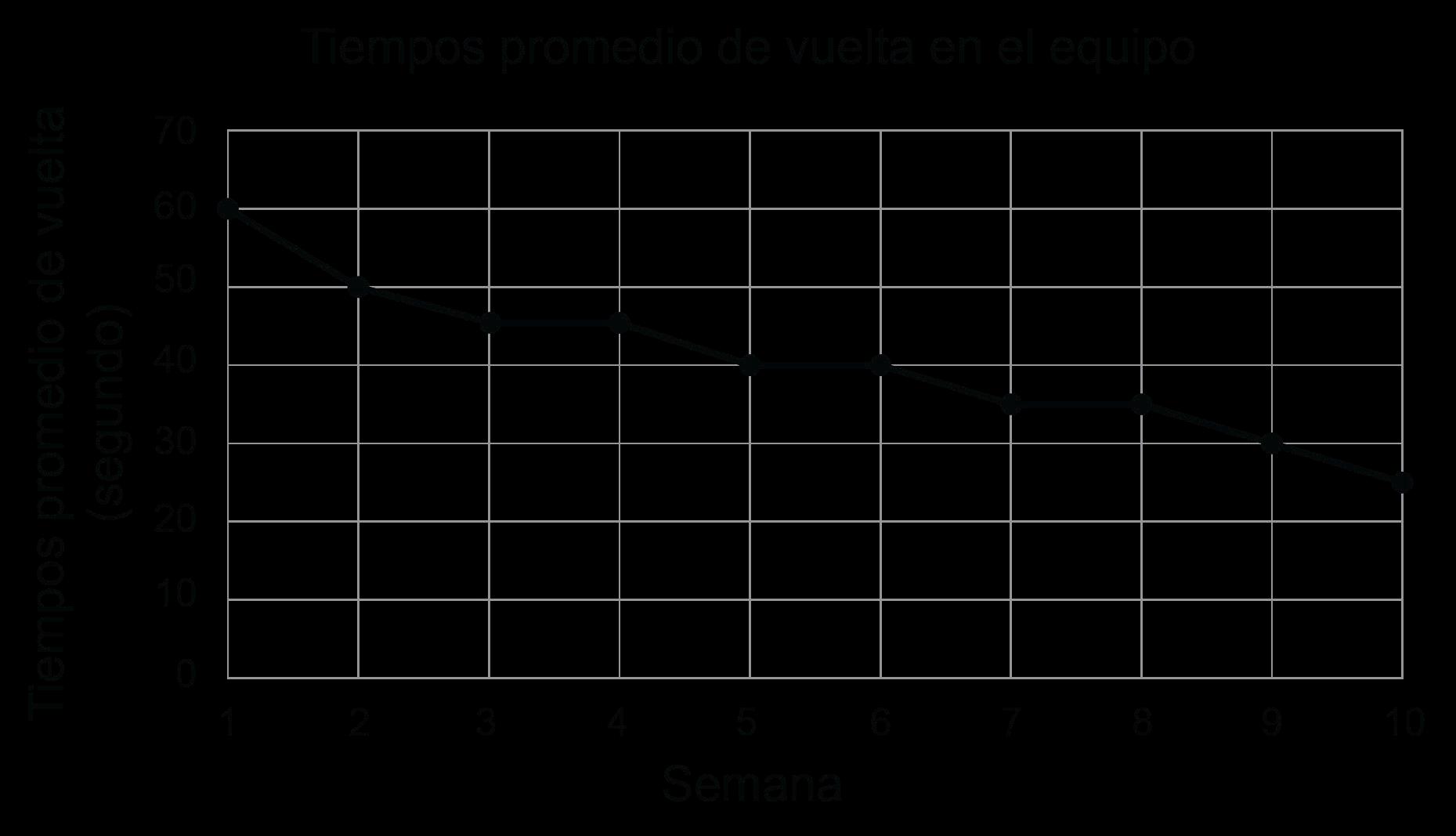
4. ¿Durante qué período la tasa promedio de cambio fue de −10 segundos por semana?

A. Entre las semanas 1 y 2

B. Entre las semanas 4 y 5

C. Entre las semanas 7 y 8

D. Entre las semanas 6 y 9

5. ¿Cuál fue la tasa de cambio entre las semanas 8 y 10?

A. 5 segundos por semana

B. −5 segundos por semana

C. 10 segundos por semana

D. −10 segundos por semana

6. ¿Parece razonable que si la temporada se prolongara durante otras 10 semanas, la tasa de cambio podría ser la misma que entre las semanas 8 y 10? Explica por qué sí o por qué no.

7. ¿Cuál función tiene la mayor tasa promedio de cambio de x = 0 a x = 4?

A. f(x)

B. g(x)

C. h(x)

8. ¿Cuál de las siguientes opciones tiene el menor valor?

A. Tasa promedio de cambio de f(x) de x = 3 a x = 4

B. Tasa promedio de cambio de g(x) de x = 1 a x = 2

C. Tasa promedio de cambio de g(x) de x = −4 a x = 3

D. Tasa promedio de cambio de h(x) de x = −3 a x = 0

9. Selecciona todos los escenarios siguientes en los que la tasa promedio de cambio es 0.

A. Tasa promedio de cambio de f(

B. Tasa promedio de cambio de f(

Tasa promedio de cambio de

D. Tasa promedio de cambio de

E. Tasa promedio de cambio de h

F. Tasa promedio de cambio de

DEMUESTRA LO QUE SABES PARTE 3

DESCRIPCIÓN

Los estudiantes determinarán los dominios y rangos de funciones y escribirán esos valores usando formatos apropiados. Los estudiantes también determinarán el dominio y el rango en relación con el contexto de un problema y serán capaces de diferenciar entre situaciones discretas y continuas.

ESTÁNDARES DE PRÁCTICA

MATEMÁTICA

• MP.3 Construir argumentos viables y criticar el razonamiento de otros: Los estudiantes analizarán problemas y utilizarán supuestos matemáticos, definiciones y resultados establecidos para construir argumentos.

• MP.4 Modelar con matemáticas: Los estudiantes aplicarán las matemáticas que conocen para resolver problemas de la vida cotidiana.

• MP.8 Buscar y expresar regularidades en razonamientos repetidos: Los estudiantes comprenderán la aplicación más amplia de los patrones y verán la estructura en situaciones similares.

MATERIALES

IMPRESO

• 1 Diario del estudiante (por estudiante)

• 1 Juego de tarjetas de eventos (por estudiante)

• 1 Boleto de salida (por 2 estudiantes)

REUTILIZABLE

• 1 Par de tijeras (por estudiante)

• 1 Barra de pegamento (por estudiante)

PREPARACIÓN

• Separe la clase en grupos de 2 o 3 estudiantes.

• Imprime un diario del estudiante y un juego de tarjetas de sucesos para cada estudiante.

• Imprime una tarjeta de salida para cada 2 estudiantes. Recorta los boletos de salida de media página para que cada estudiante tenga uno.

• Reúne tijeras y pegamento para cada estudiante.

LECCIÓN PEDAGÓGICA

EXPLORACIÓN

4:

DOMINIO Y RANGO

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Lea la siguiente situación a la clase: El comité de planificación de eventos estudiantiles tiene un evento más que planificar para el año, la fiesta de fin de curso. Usted está a cargo del seguimiento de la venta de entradas durante los 7 días previos al evento para poder informar sobre la asistencia prevista al evento. Este número es necesario para que el comité pueda estar seguro de tener suficiente comida y premios. También te encargas de hacer un seguimiento de la asistencia de estudiantes durante las 4 horas que dura el evento, de modo que puedas ayudar al comité a determinar si la fiesta del año que viene debe ampliarse. Los datos que has recopilado se representan en tablas y gráficos. Utiliza los datos para hacer tus recomendaciones al comité de planificación del evento estudiantil.

2. Entrega un Diario del estudiante a cada estudiante.

3. Explica a los estudiantes que trabajarán con sus grupos para analizar las tablas y los gráficos y luego responderán a las preguntas sobre entradas y salidas. Utilizarán este análisis para apoyar sus recomendaciones sobre la venta de entradas y la asistencia en sus Diarios del estudiante.

4. Mientras los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas orientativas para evaluar la comprensión de los estudiantes:

a. DOK-1 ¿Cuál es la variable independiente? La variable x es la variable independiente.

b. DOK-1 ¿Qué variable es la variable dependiente? La variable y es la variable dependiente.

c. DOK-3 ¿Querrías conectar los puntos de la gráfica para la venta de entradas? ¿Por qué sí o por qué no? No, no quiero conectar los puntos en este gráfico porque sólo recogí datos para días específicos, y no hay nada que indique que las ventas fueron continuas.

d. DOK-3 ¿Por qué estaría bien conectar los puntos en el gráfico para el número de estudiantes que asistieron al evento? Esta gráfica muestra el número de personas en el evento durante un intervalo de tiempo específico. Dado que el tiempo está en constante movimiento, conectar los puntos está bien.

5. Concede a los estudiantes tiempo suficiente para completar la Parte I y responder a las preguntas que siguen.

6. Después de completar la Parte I, invita a la clase a una Charla de matemáticas para compartir sus observaciones y lo aprendido hasta ahora.

EXPLORAR: EXPLORACIÓN 4

CHARLA DE MATEMÁTICAS

¡Fiesta de fin de año!

Parte I Ventas de boletos La venta de boletos comenzó lenta, pero aumentó en un margen mayor cada día. Los datos que recopilaste se organizaron en una tabla y una gráfica. Analiza los datos para responder las preguntas y haz tu recomendación al comité. Properties of Functions Explore 4

Día Cantidad de ventas de boletos

1 10

2 12

3 16 4 21

5 38

6 72

7 140

1. ¿Cuáles son las posibles entradas para esta situación?

2. ¿Tienen sentido los decimales en esta situación? ¿Por qué sí o por qué no?

3. ¿Cuáles son los valores de las salidas de la situación? ¿Qué representan?

4. ¿Serían posibles valores negativos en esta situación? ¿Por qué sí o por qué no?

5. Con base en los datos recopilados, ¿cuántos estudiantes deberían anticipar en este evento? ¿Cuál es tu recomendación para la comida y los premios? 1

• DOK-2 ¿Qué palabra usamos para describir los posibles valores x?Los valores x también se llaman entradas.

◦ Explica lo siguiente a la clase: En álgebra, definimos el conjunto de entradas como el dominio. Cuando te preguntan por el dominio de una función, estás buscando los posibles valores x, o entradas.

• DOK-2 ¿Qué palabra usamos para describir los posibles valores y?Los valores y también se llaman salidas.

◦ Explica lo siguiente a la clase: En álgebra, definimos el conjunto de salidas como el rango. Cuando te preguntan por el rango de una función, estás buscando los posibles valores y, o salidas.

• DOK-2 Diríamos que el dominio de la venta de entradas es discreto y el dominio de la asistencia al evento es continuo. ¿Qué podrían significar estas palabras? Piensa en las diferencias de los gráficos de estos dos conjuntos de datos.Continuo significaría que el dominio podría ser cualquier valor entre los puntos de datos (por ejemplo, 1,5 horas). Los puntos de datos del gráfico se conectaron con una línea. Discreto debe significar que el dominio está restringido a puntos de datos específicos. Los puntos de datos en la gráfica no estaban conectados.

Asistencia La cantidad de estudiantes en la fiesta de fin de año aumentó continuamente hasta la hora 2, cuando la cantidad de asistentes alcanzó su punto máximo. Después de la hora 2, la cantidad de estudiantes en el evento disminuyó continuamente hasta el final del evento en la hora 4. Los datos que recopilaste se organizaron en una tabla y una gráfica. Analiza los datos para responder las preguntas y haz tu recomendación al comité. Properties of Functions Explore 4

Hora Cantidad de estudiantes

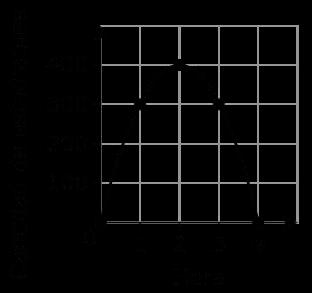
6. ¿Pueden describirse las posibles entradas al enumerar todos los valores posibles? ¿Por qué sí o por qué no?

7. Describe las posibles entradas con el uso de las desigualdades.

8. ¿Describir los posibles resultados al enumerar todos los valores posibles es la forma más eficiente de describir los posibles resultados? ¿Por qué sí o por qué no?

9. Describe las posibles salidas con el uso de las desigualdades.

10. Según los datos recopilados, ¿recomendarías que la fiesta de fin de año del próximo año se extienda a 5 horas de duración? Explica.

DIARIO DEL ESTUDIANTE

• DOK-3 ¿Qué significa que el dominio de una función puede estar restringido si la función representa una situación del mundo real? Da un ejemplo.Es un recordatorio de que tengo que considerar lo que es razonable para una situación. Cuando una función sólo representa una relación y no está en contexto, las únicas restricciones son las restricciones matemáticas. Un ejemplo de un dominio restringido podría ser un estudiante caminando a casa desde la escuela a un ritmo constante. Vive a 1 milla de la escuela. Si representamos la distancia como una función del tiempo, el tiempo estaría limitado. El mínimo es 0 porque el tiempo negativo no tiene sentido, y el máximo estaría limitado porque su casa está a una distancia fija y viaja a un ritmo constante. Si consideráramos la representación algebraica sin un contexto, el dominio no estaría limitado.

• DOK-3 ¿Qué puede ser útil para identificar si una función es discreta o continua?Si hay una gráfica, observe si los puntos están conectados o no. Si el dominio y el rango están escritos sin gráfica, mire si los valores están enumerados o escritos usando desigualdades.

PARTE II

1. Lee la siguiente situación a la clase: Gracias a tu magnífico trabajo y a tus recomendaciones sobre la fiesta de fin de curso, el comité de planificación de eventos estudiantiles te ha elegido como presidente para organizar todos los actos del año que viene. En la última reunión del año, los miembros del comité se estaban repartiendo las tarjetas de datos de los eventos de este año. Torpemente, las tarjetas de eventos se mezclaron mientras los miembros las pasaban por la mesa. Utiliza tus conocimientos para clasificar la información y organizarla para el comité.

2. Distribuye un juego de tarjetas de eventos, tijeras y pegamento a cada estudiante.

3. Haz que los estudiantes recorten las tarjetas.

4. Explica a los estudiantes que trabajarán con sus grupos para clasificar las tarjetas y emparejar cada gráfico con un dominio y rango correspondientes. Los estudiantes pegarán sus propias tarjetas en sus Diarios del estudiante.

5. Mientras los estudiantes colaboran, supervise su trabajo y utilice las siguientes preguntas guía para evaluar la comprensión de los estudiantes:

a. DOK-1 ¿Qué significa cuando ves un círculo abierto en un punto específico de la función?

Un círculo abierto significa que ese valor en particular no está incluido en su dominio o rango.

b. DOK-1 ¿Qué significa cuando ves un círculo cerrado en un punto específico de la función?

Un círculo cerrado significa que ese valor en particular está incluido en su dominio o rango.

También significa que ese valor es el último valor del conjunto.

6. Concede a los estudiantes tiempo suficiente para completar la parte II y responder a las preguntas que siguen.

7. Después de la exploración, invita a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-2 ¿En qué se diferencia el dominio de una representación algebraica del dominio de una situación?El dominio de una representación algebraica sólo está limitado por el álgebra o la representación. El dominio de una situación está limitado por la situación y el álgebra utilizada para representar la situación.

• DOK-3 ¿Es posible tener un dominio restringido y un rango no restringido? ¿Por qué o por qué no?No, el rango son las restricciones de la variable dependiente. Puesto que la variable independiente está restringida, las variables dependientes correspondientes también estarían restringidas.

• DOK-2 ¿Cómo se puede saber si el valor de un punto final se va a incluir en un conjunto solución cuando se observan desigualdades?Si la desigualdad es menor que (<) o mayor que (>), entonces el valor no se incluirá. Si la desigualdad es menor o igual que (≤) o mayor o igual que (≥), entonces el valor se incluirá.

8. Cuando los estudiantes terminen, pídeles que completen el Boleto de salida para evaluar formativamente su comprensión del concepto.

9. Regresa a la sección de «Captar interés» e instruye a los estudiantes para que usen sus habilidades recién adquiridas para completar exitosamente la actividad.

EXPLORAR: EXPLORACIÓN 4

Parte II

Recorta las tarjetas de eventos del documento «Tarjetas de eventos», mira la información de cada tarjeta y decide a qué evento pertenece. Una vez que hayas decidido, pega cada tarjeta en el lugar apropiado a continuación.

El comité de planificación de eventos estudiantiles vende caramelos la última semana de clases. La ecuación y = 2.5x se usa para calcular la ganancia. Se ha determinado que necesitan vender entre 55 y 60 gramos de caramelos para cumplir con su meta de ganancias.

Gramos de caramelo

Pega el dominio y rango aquí. Pega la gráfica aquí.

El evento de lanzamiento de huevo resultó en que el huevo del ganador alcanzó una altura de 150 pies y aterrizó a una distancia de 8 pies de la plataforma de inicio.

Lanzamiento de huevo

Pega el dominio y rango aquí. Pega la gráfica aquí.

Se ha reservado un tanque de agua para la fiesta en el patio. Debe llenarse a una velocidad de 2.5 pulgadas por segundo. Se usa la ecuación y = 2.5x y se ha determinado que tomará 60 segundos llenar el tanque.

Fiesta en el patio

Pega el dominio y rango aquí. Pega la gráfica aquí.

Empareja cada una de las gráficas restantes con su dominio y rango correctos. Luego, pega las tarjetas de eventos en los espacios a continuación.

Pega la gráfica aquí.

Pega la gráfica aquí.

Pega el dominio y rango aquí.

Reflexiona

1. ¿Qué tipos de situaciones serían discretas? Enumera algunos ejemplos.

2. ¿Qué tipos de situaciones serían continuas? Enumera algunos ejemplos.

3. ¿Por qué hacemos una lista cuando escribimos el dominio y rango de situaciones discretas?

4. ¿Por qué escribimos el dominio y el rango de una situación continua con el uso de una desigualdad? 5. Dibuja una gráfica cuyo dominio sea

cuyo rango

DIARIO DEL ESTUDIANTE

Pega el dominio y rango aquí. Pega la gráfica aquí.

Pega el dominio y rango aquí.

ESQUEMA DE ANCLAJE Y LIBRETA INTERACTIVA

• completado, pida a cada estudiante que complete

Dominio y rango

Boleto de salida

Aditya estaba parado en una plataforma con vista a un lago que estaba ubicada a 10 metros sobre la superficie del agua. Lanzó una roca desde su ubicación al agua de abajo. Usa la gráfica para responder las siguientes preguntas.

1. ¿Cuál es el dominio de esta función?

2. ¿Cuál es el rango de esta función?

3. ¿Cuántos segundos tardó la roca en caer al agua?

4. ¿Esta función es continua o discreta? Explica.

Dominio y rango Boleto de salida

EXPLORAR: EXPLORACIÓN 4

1. Es posible que los estudiantes no tengan cuidado con los puntos finales de círculos cerrados y abiertos al determinar el dominio y el rango. Anímelos a practicar tanto la escritura del dominio y el rango basándose en ejemplos graficados como el uso de un dominio y rango dados para crear un gráfico apropiado.

Aditya estaba parado en una plataforma con vista a un lago que estaba ubicada a 10 metros sobre la superficie del agua. Lanzó una roca desde su ubicación al agua de abajo. Usa la gráfica para responder las siguientes preguntas.

1. ¿Cuál es el dominio de esta función?

2. ¿Cuál es el rango de esta función?

3. ¿Cuántos segundos tardó la roca en caer al agua?

4. ¿Esta función es continua o discreta? Explica.

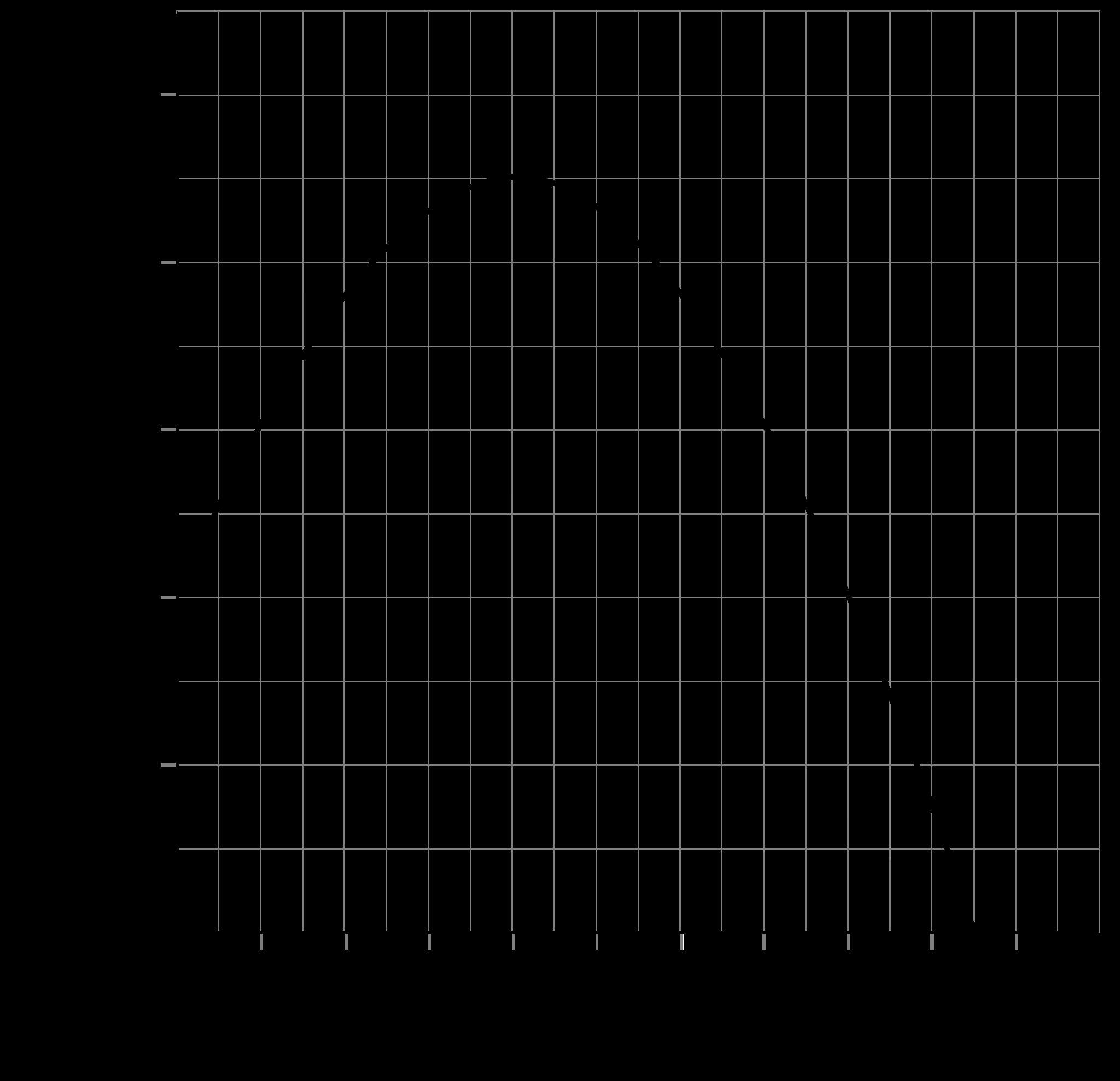
2. Los estudiantes pueden tener dificultades para determinar si los puntos finales deben incluirse en las desigualdades. Anima a los estudiantes a introducir esos puntos finales para comprobar si crean un enunciado verdadero.

APOYOS PARA LA ADQUISICIÓN DEL LENGUAJE

La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad de Explora. Consulte las estrategias que siguen para encontrar formas de apoyar el desarrollo del lenguaje de los estudiantes.

BOLETO DE SALIDA

APOYOS DIDÁCTICOS

Se proporcionará a los estudiantes apoyos previos a la lectura (organizadores gráficos, diagramas de formas y vocabulario preenseñado) para ayudarlos en la comprensión de la lectura.

3. Los estudiantes pueden tener dificultades para nombrar el dominio y el rango de una gráfica que es discreta. Anime a los estudiantes a considerar los tramos de la gráfica que son continuos y luego a escribir el dominio y el rango para ellos individualmente.

4. Los estudiantes pueden no entender que las expresiones pueden tener un dominio y un rango independientemente de si son funciones. Use el ejemplo x = 1, que no es una función, donde el dominio es sólo x = 1, y el rango son todos los números reales.

Principiante: Como actividad previa a la lección, guíe a los estudiantes en la creación de cuadrados de vocabulario para los términos dominio y rango. Completa en clase las siguientes secciones de los cuadrados de vocabulario: Definición, Ejemplo (problema matemático) y Ausencia de ejemplo. Pida a los estudiantes que creen sus propias imágenes para los términos.

Intermedio: Como actividad previa a la clase, pide a los estudiantes que creen cuadrados de vocabulario para los términos dominio y rango

Los cuadrados de vocabulario deben incluir las siguientes secciones: Definición, Ejemplo (problema matemático), No-ejemplo e Imagen. Proporcione a los estudiantes las definiciones y los ejemplos, pero anímelos a reescribir las definiciones con sus propias palabras.

Avanzado: Como actividad previa a la lección, pida a los estudiantes que creen cuadrados de vocabulario para los términos dominio y rango

Los cuadrados de vocabulario deben incluir las siguientes secciones: Definición, Ejemplo (problema matemático), No-ejemplo e Imagen. Proporcione a los estudiantes las definiciones y los ejemplos, pero anímelos a reescribir las definiciones con sus propias palabras.

EXPLORAR: EXPLORACIÓN 4

Dominio y rango

Samuel trabaja en la oficina de un veterinario, un cliente tiene dos cachorros de 18 meses, Polly y Teo. Usa la tabla y el diagrama de sus pesos para responder las preguntas.

2 5 3 11 4 15 6 18

1. ¿Es viable enumerar todas las entradas posibles de esta función? Explícalo.

2. ¿Es el peso de Polly una función continua o discreta?

3. ¿Cuál es el dominio del peso de Polly?

4. ¿Cuál es el rango del peso de Polly?

5. ¿Cuál es el dominio del peso de Teo?

6. ¿Cuál es el rango del peso Teo? Properties of Functions Part 4 Edad en meses Peso de Polly

A Samuel se le encargó la tarea de analizar la cantidad de mascotas que tiene cada cliente. Él hizo una tabla con la cantidad de clientes y la cantidad de mascotas que cada uno tiene. Responde las preguntas de abajo con sus datos.

Cantidad de mascotas Cantidad de clientes 1 45 2 89 3 62 4 23 5 15 6 4

7. ¿Es viable enumerar todas las entradas posibles de esta función? De ser así, escríbelas.

8. ¿Tendría sentido tener números negativos o números decimales para los valores de entrada? Explícalo.

9. ¿Cuál es el dominio de esta función?

10. ¿Cuál es el rango de esta función?

Properties of Functions Part 4

11. Empareja las siguientes gráficas con la expresión de rango adecuada.

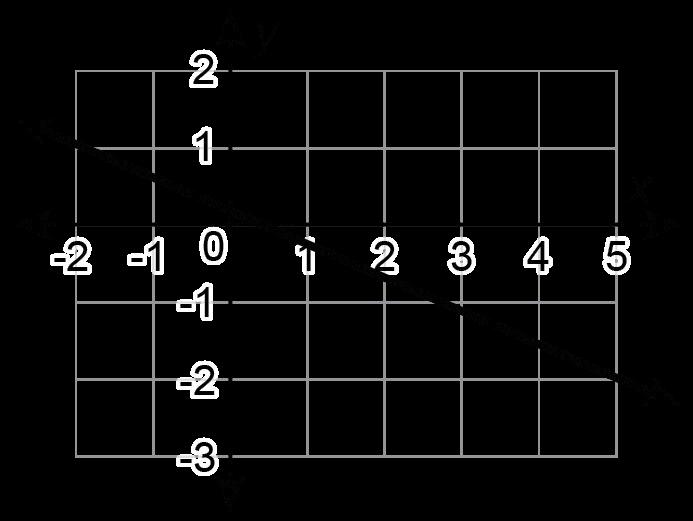
Rango:

Rango: Rango:

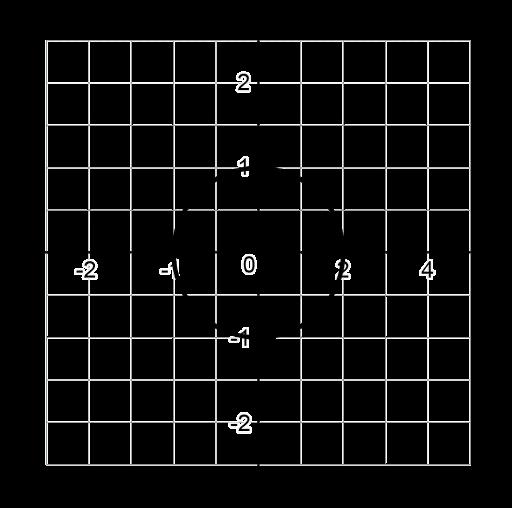
Rango:

Rango:

Propiedades de las funciones

Una función es una relación especial entre valores, donde cada valor de entrada corresponde exactamente a un valor de salida.

f de x es igual a x menos uno y cinco décimos.”

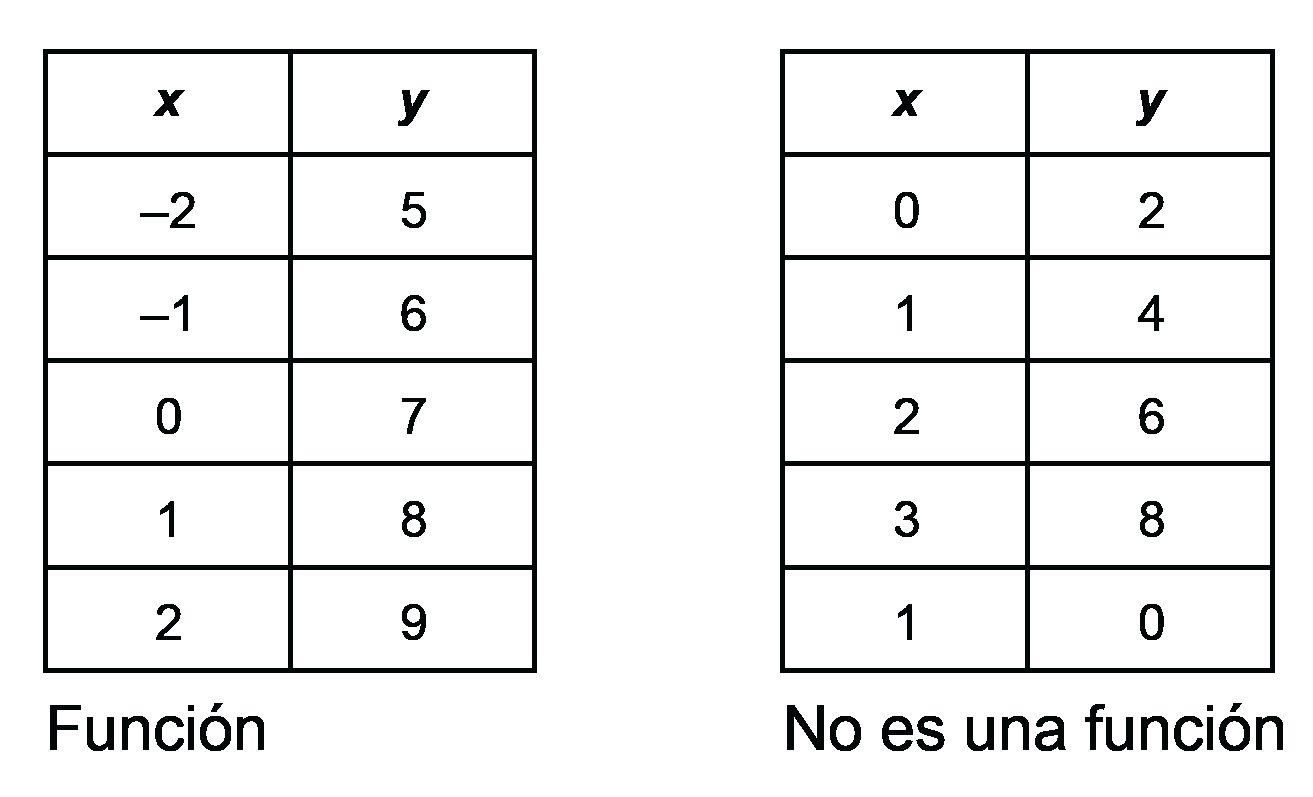
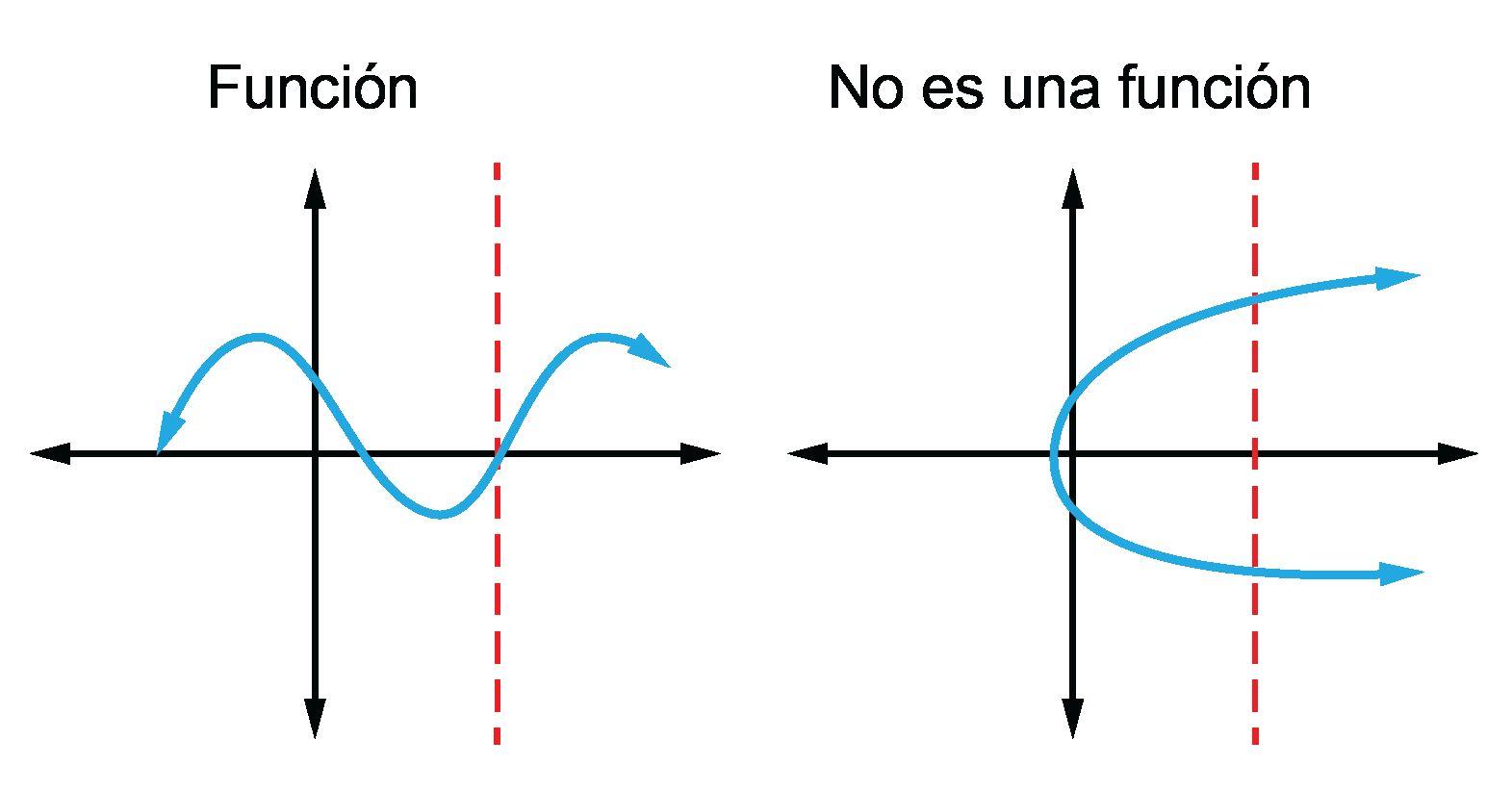
¡En una función, cada valor de x tiene un solo valor de y!

DOMINIO: Conjunto de todos los valores de entrada

RANGO: Conjunto de todos los valores de salida

El DOMINIO de esta gráfica es −6 < x ≤ 3.

El RANGO de esta gráfica es −2 < y ≤ 6.

Tasa promedio de cambio = cambio en y cambio en x

EJEMPLO DE ESQUEMA DE ANCLAJE

EXPLICAR: ESQUEMA DE ANCLAJE

CONSOLIDAR EL APRENDIZAJE DEL ESTUDIANTE

ESQUEMA DE ANCLAJE

DESCRIPCIÓN

Este gráfico de anclaje destaca las ideas principales del alcance. Esta es una herramienta para apoyar la instrucción y anclar el aprendizaje de los estudiantes a lo largo del alcance.

MATERIALES

• 1 hoja de papel cuadriculado

• 1 juego de marcadores multicolores

PREPARACIÓN

● Imprima el ejemplo de esquema de anclaje (opcional).

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. El ejemplo de esquema de anclaje puede usarse como referencia antes de crear el esquema de anclaje de la clase con los estudiantes. La creación de un esquema de anclaje debe estar dirigida por los estudiantes para promover que se apropien de su aprendizaje.

2. A medida que los estudiantes trabajen en el alcance, colaboren para añadir piezas al esquema de anclaje. Formule las siguientes preguntas:

a. ¿Qué estrategia utilizamos para resolver este problema?

b. ¿Qué vocabulario necesitamos conocer para poder resolver este problema?

3. Continúe añadiendo habilidades o estrategias importantes aprendidas después de cada exploración para resaltar el contenido importante.

4. Explique a los estudiantes que pueden utilizar este esquema como herramienta de apoyo para su aprendizaje. Los estudiantes también pueden pegar una copia del esquema de anclaje en sus cuadernos para utilizarla como referencia durante todo el año.

5. Algunos esquema de anclaje sólo se mostrarán durante ese alcance o grupo de alcances, mientras que otras permanecerán expuestas durante todo el año escolar.

EXPLICAR: LIBRETA INTERACTIVA

DOCUMENTAR EL APRENDIZAJE DEL ESTUDIANTE

LIBRETA INTERACTIVA

DESCRIPCIÓN

Los estudiantes toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y el cuaderno.

MATERIALES

IMPRESO

● 1 folleto del estudiante (por estudiante)

PREPARACIÓN

● Imprima una copia del folleto del estudiante por alumno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Prepare una libreta interactiva con un cuaderno de espiral o de composición para cada estudiante. Los estudiantes pueden utilizar las primeras páginas para crear una tabla de contenidos con números de página para realizar un seguimiento de las actividades.

2. En el folleto del estudiante se ofrecen instrucciones para cada actividad.

3. Dé tiempo a los estudiantes para que completen la actividad y peguen las piezas en sus cuadernos interactivos.

4. Las libretas ineractivas pueden utilizarse como referencia para los estudiantes durante el trabajo independiente y pueden enviarse a casa al final del año como registro de su aprendizaje.

Instrucciones

● Recorta el plano cartesiano y la tabla, y pega en tu cuaderno.

● Llena la tabla con tres pares coordinados para la función h(x) = 2x

● Grafica los tres puntos en el plano cartesiano y conecta para formar una línea.

Instrucciones

x h(x)

● Contesta las preguntas en la página de notas a continuación.

● Recorta la página de notas y pega en tu cuaderno.

¿Es h(x) = 2x una función? ¿Por qué sí o por qué no?

Si h(x) = 2x representa la cantidad de dinero que Pedro recibe al perder x dientes.

● ¿Cuál es el dominio de la función?

● ¿Cuál es el rango de la función?

FOLLETO DEL ESTUDIANTE

EXPLICAR: VOCABULARIO ILUSTRADO

PALABRAS QUE HAY QUE CONOCER

VOCABULARIO ILUSTRADO

Relación especial entre valores; cada valor de entrada devuelve exactamente un valor de salida Función

Función lineal

Relación que cuando se grafica es una línea recta

Función exponencial

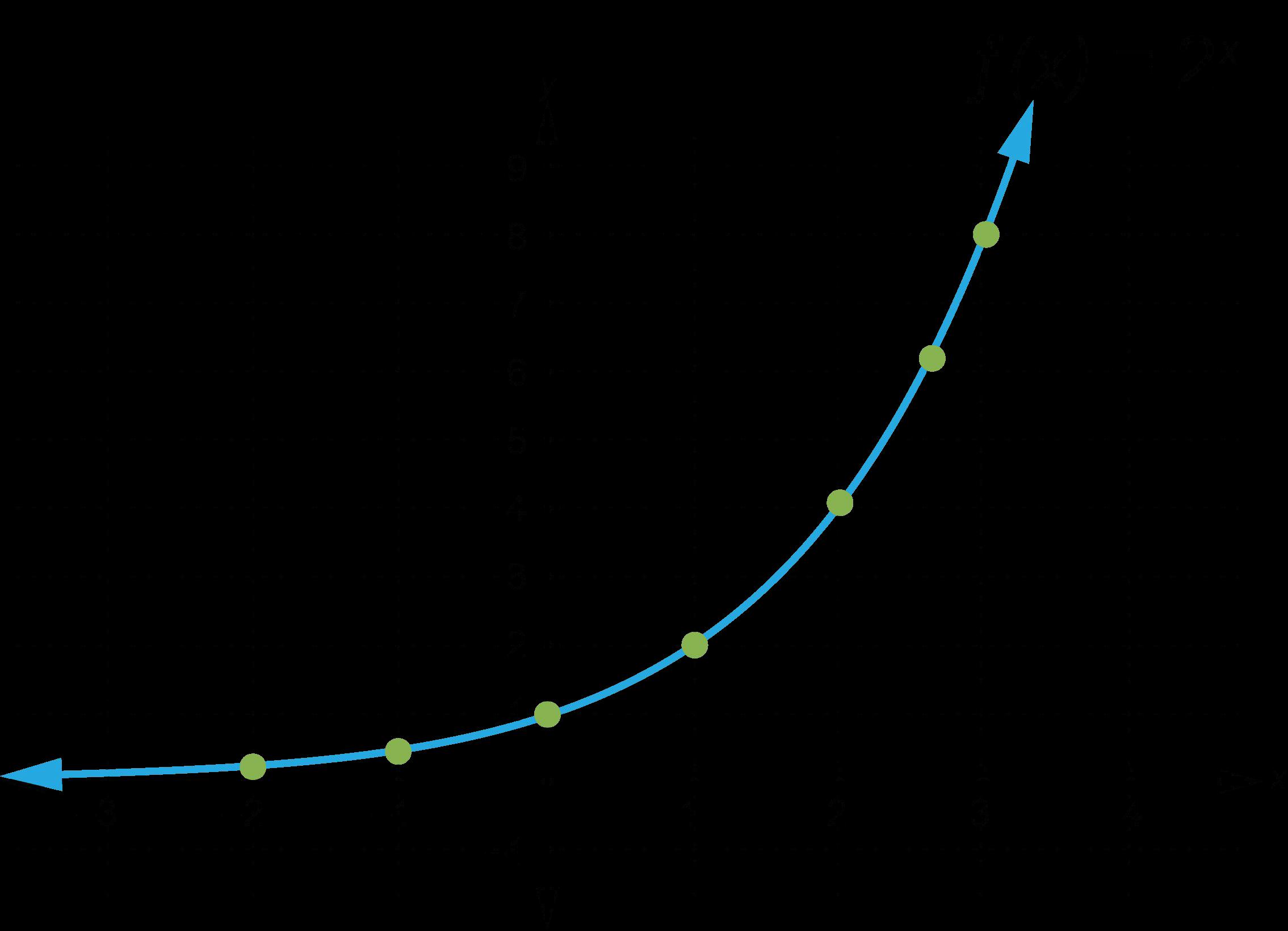
Función en la forma de f(x) = abˣ donde a y b son números reales y a ≠ 0, b ≠ 1, y b > 0

Notación de función

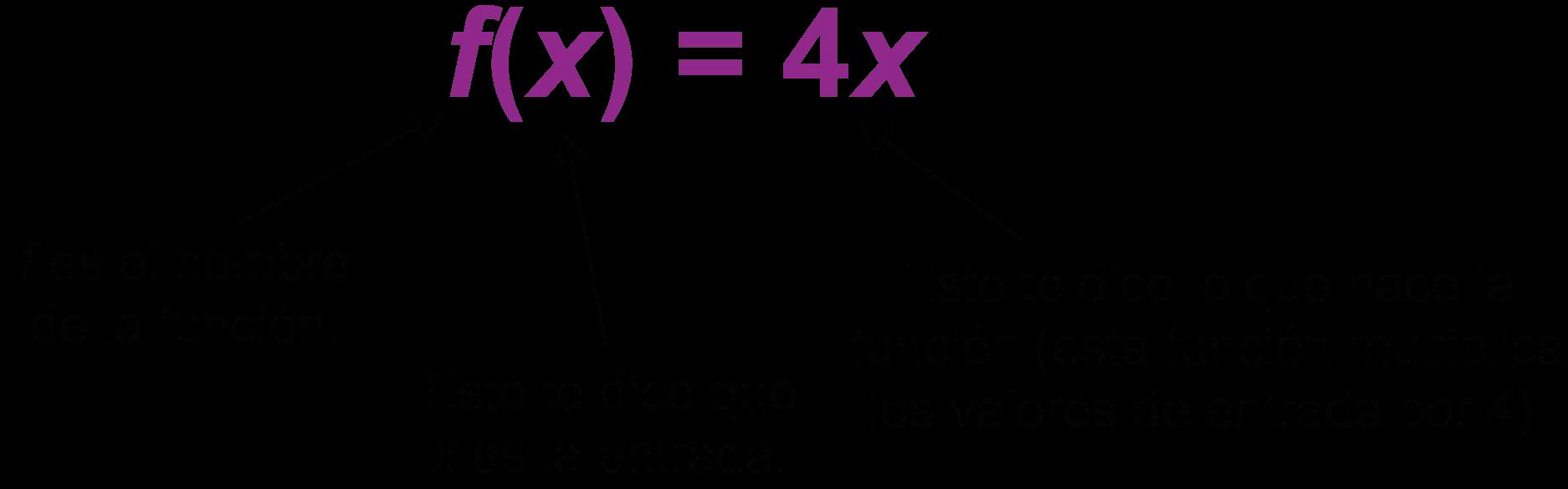
Forma de representar y, el valor dependiente en una relación, como f(x), leer «f de x» donde f nombra la función

Desigualdad

Oración matemática que usa símbolos como <, ≤, > o ≥ para comparar dos cantidades

Relación cuantitativa

Relación entre magnitudes

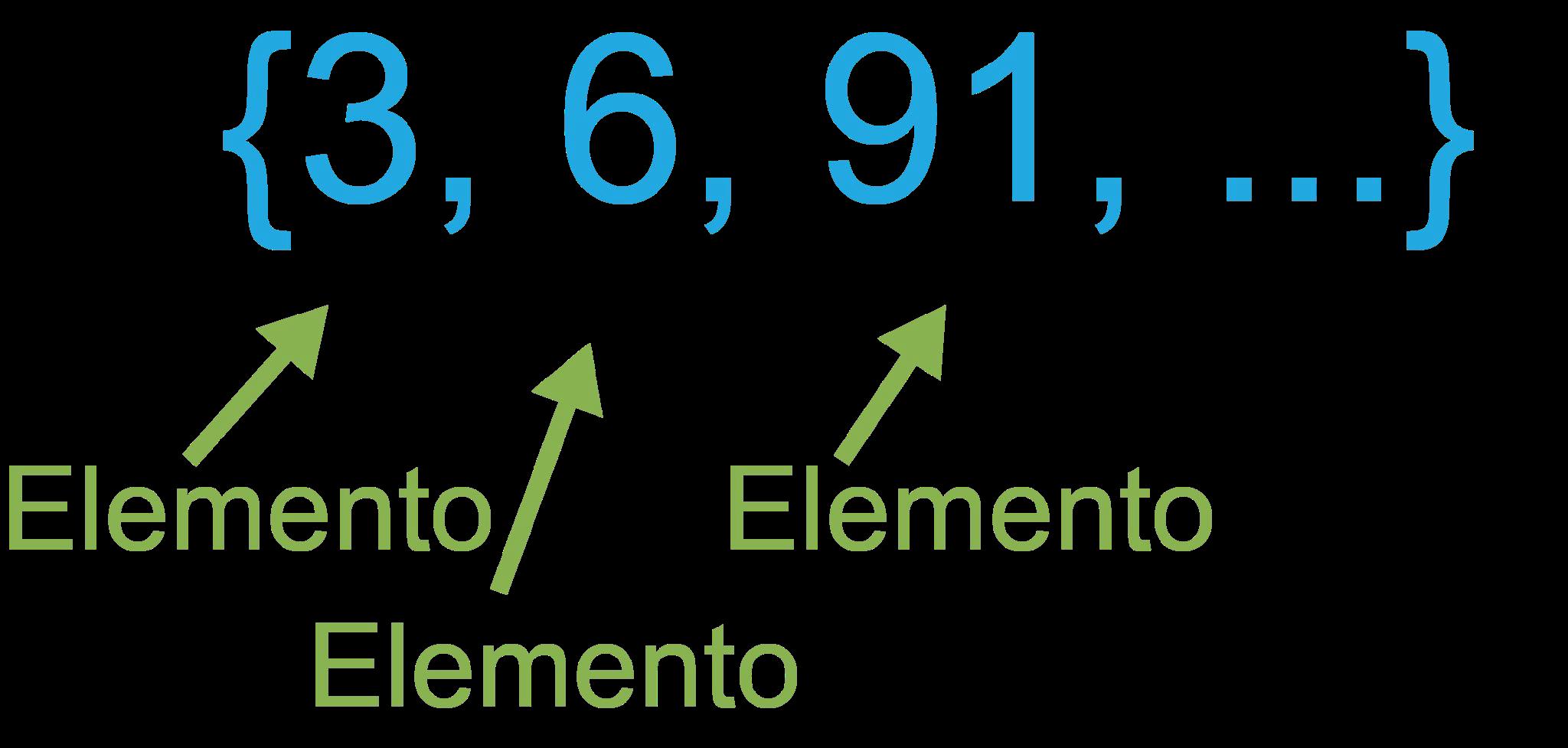
Cualquier número o valor distinto que es parte de un conjunto Elemento Grupo de números únicos u objetos llamados miembros o elementos Conjunto

Desigualdad lineal

Desigualdad que implica una función lineal

Tasa de cambio

Tasa que muestra cómo cambia una cantidad en relación con otra

Función cuadrática

Intervalo

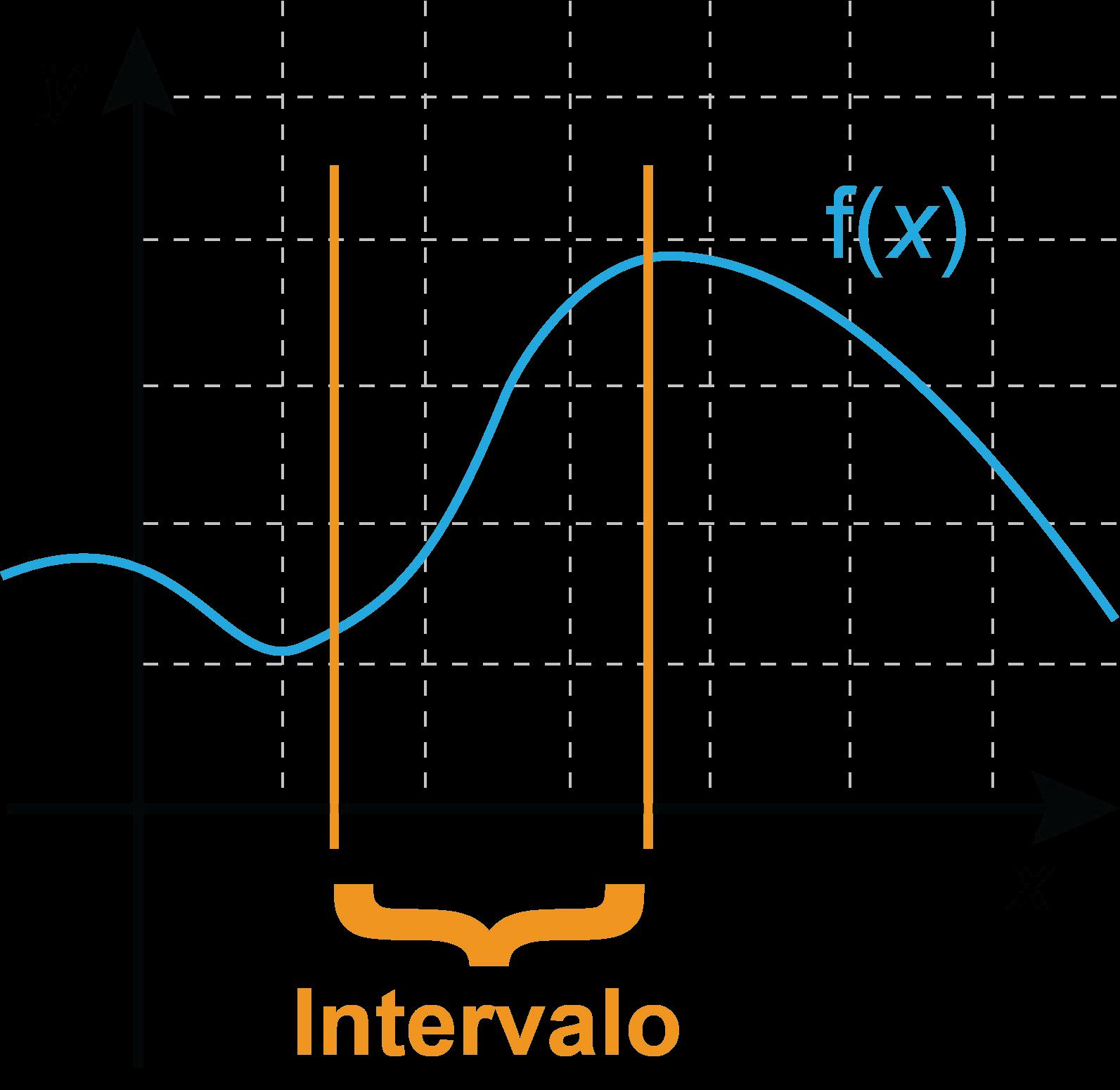
El conjunto de valores de entrada continuo en el cual los datos de salida de una función pueden incrementarse, decrementarse o ser constantes

Dos rectas numéricas perpendiculares, llamadas eje X y eje Y, que se intersecan en el punto (0, 0) y crean cuatro cuadrantes; también llamado gráfico, cuadrícula de coordenadas o plano de coordenadas Plano cartesiano 14

Punto central de un plano de coordenadas, donde el eje X y el eje Y se cruzan, ubicado en (0, 0) Origen

Recta numérica horizontal en un plano de coordenadas Eje X 15

Ubicación de un solo punto en un plano de coordenadas donde el primer y segundo valor representan la posición relativa al eje X y al eje Y, respectivamente (x, y); conocido también como par de coordenadas Par ordenado

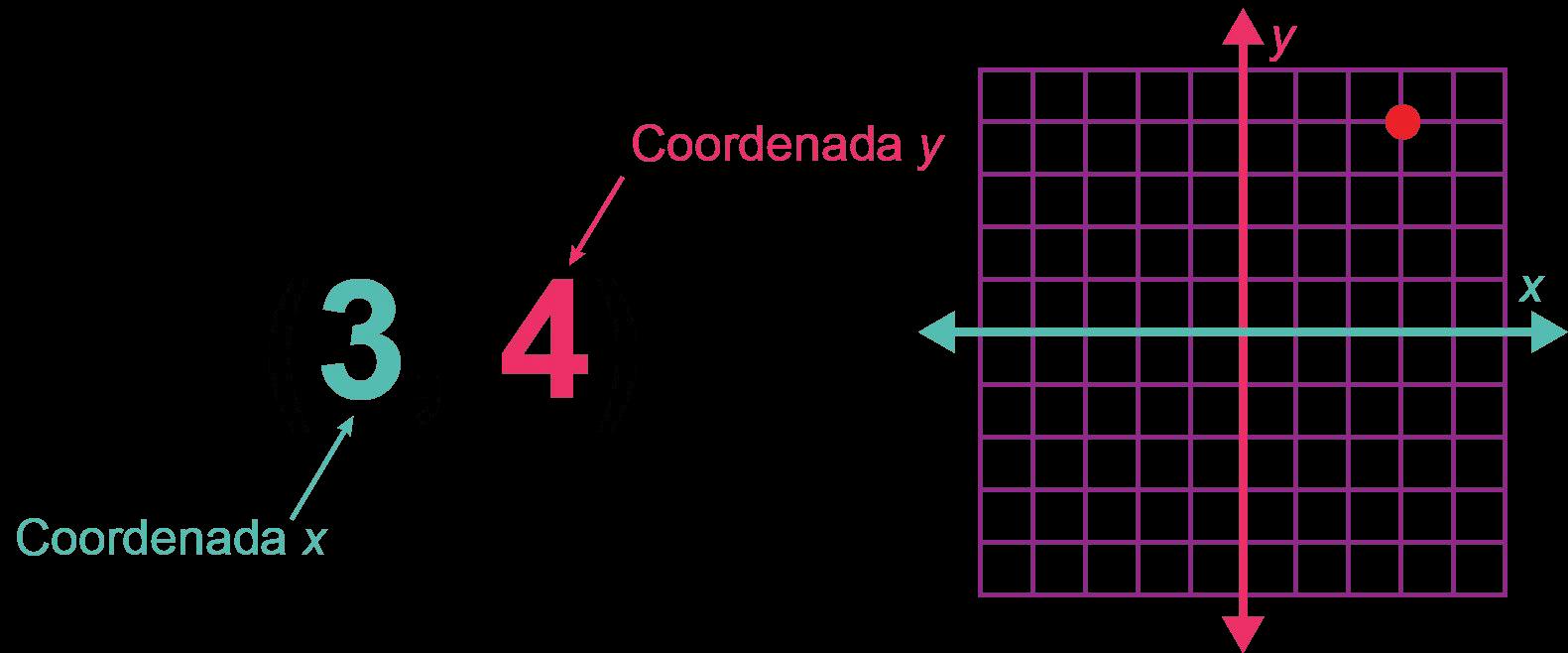
Recta numérica vertical en un plano de coordenadas Eje Y 16

Coordenada X

Primer término en un par ordenado; proporciona la ubicación a lo largo del eje X dentro del plano de coordenadas

Una de las cuatro secciones del plano de coordenadas, formada por la intersección del eje X y el eje Y Cuadrante 17

Coordenada Y

Segundo término en un par ordenado; proporciona la ubicación a lo largo del eje Y dentro del plano de coordenadas

EXPLICAR: VOCABULARIO ILUSTRADO

Discreto

Datos que no pueden contener los valores de números reales entre puntos de datos; los puntos de datos no están conectados

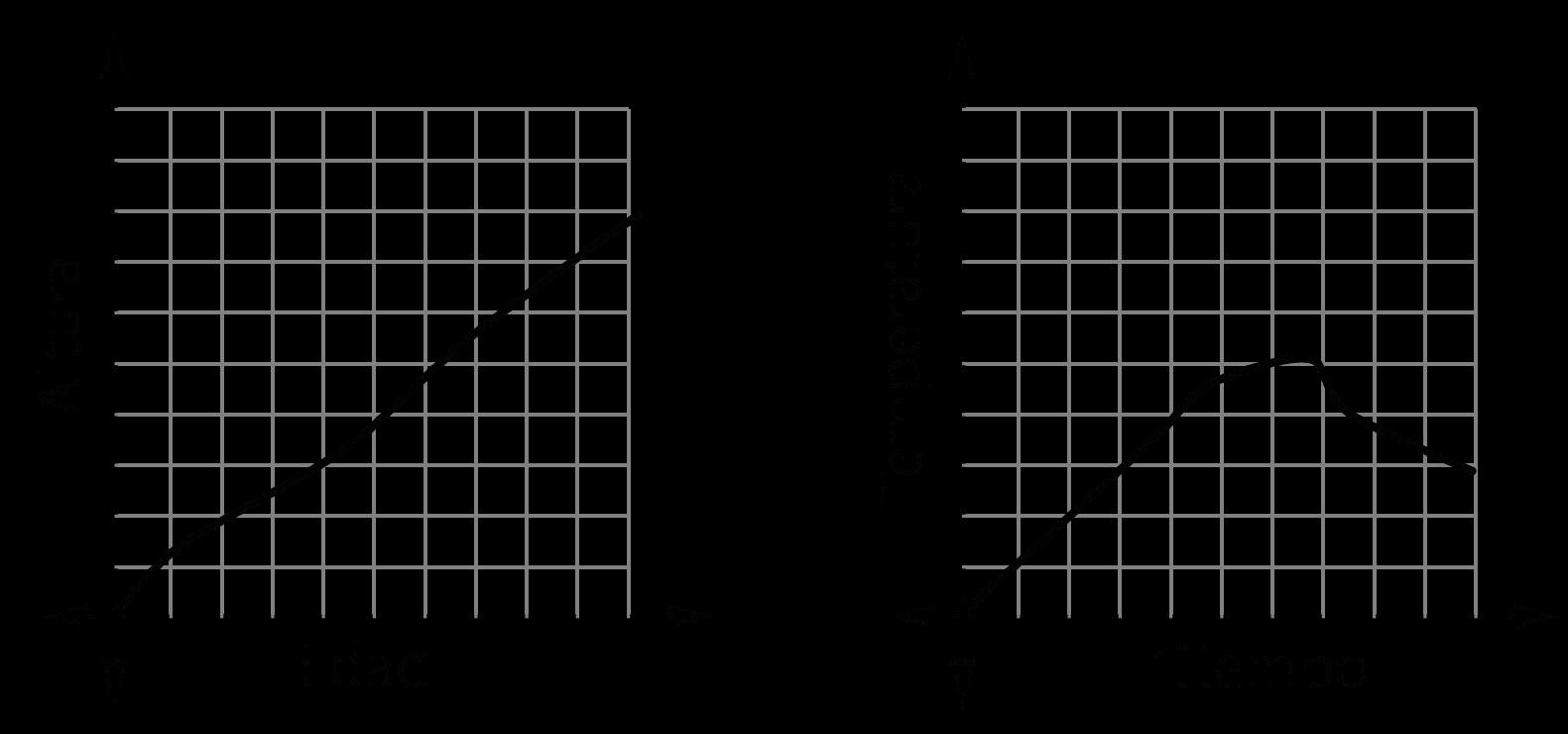
Datos que pueden contener cualquier valor numérico real entre puntos de datos. Los puntos de datos se pueden conectar

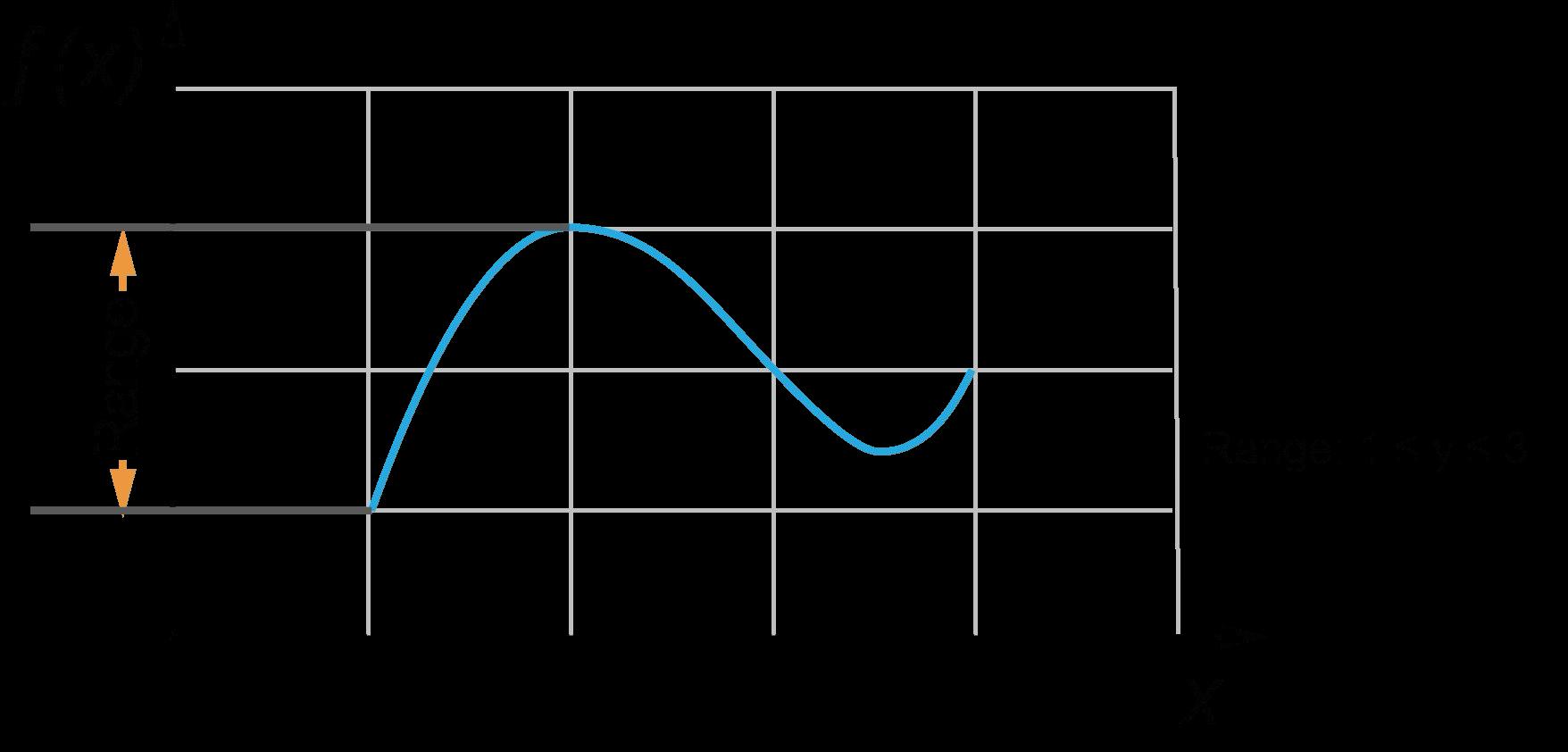
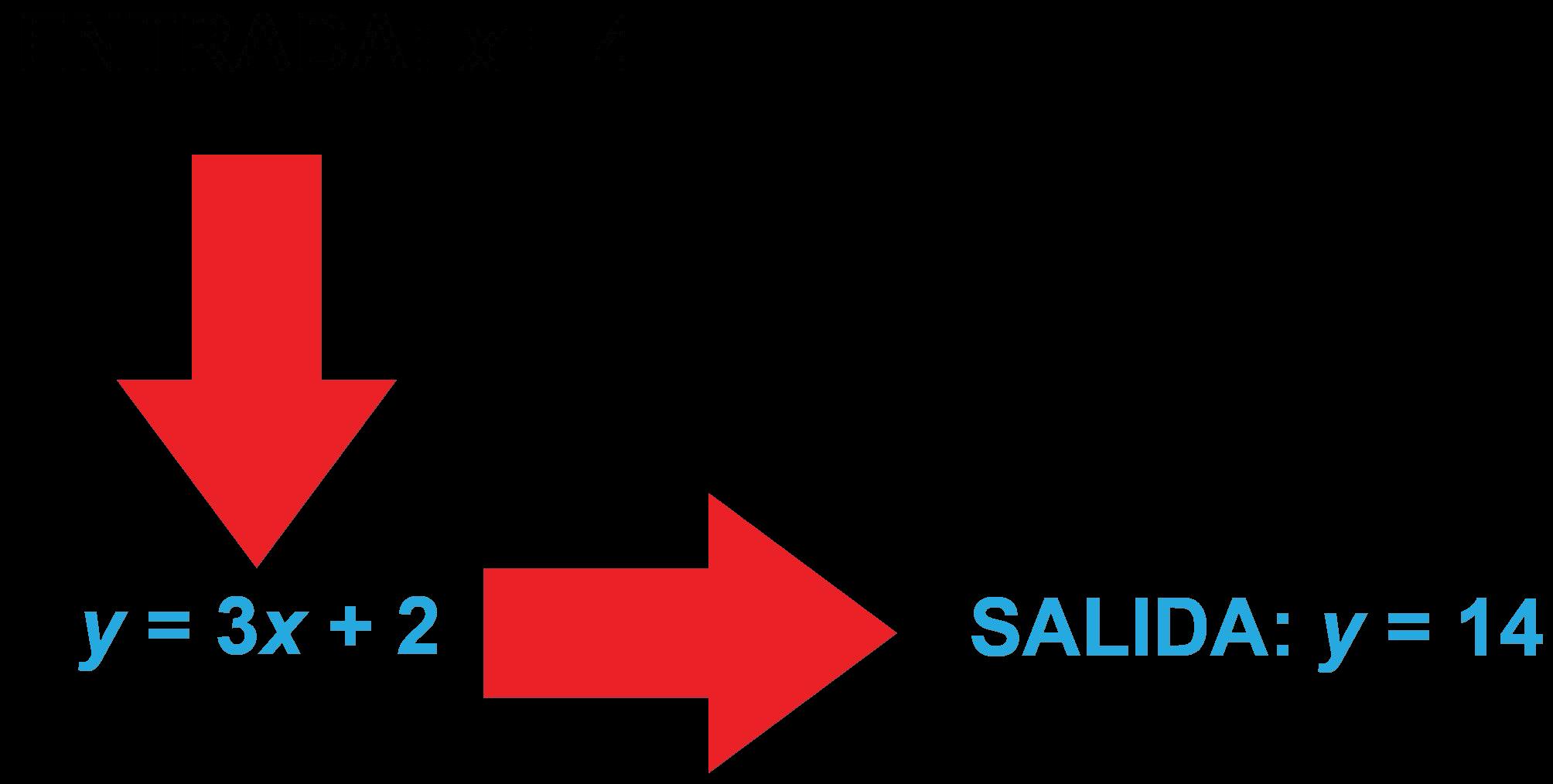
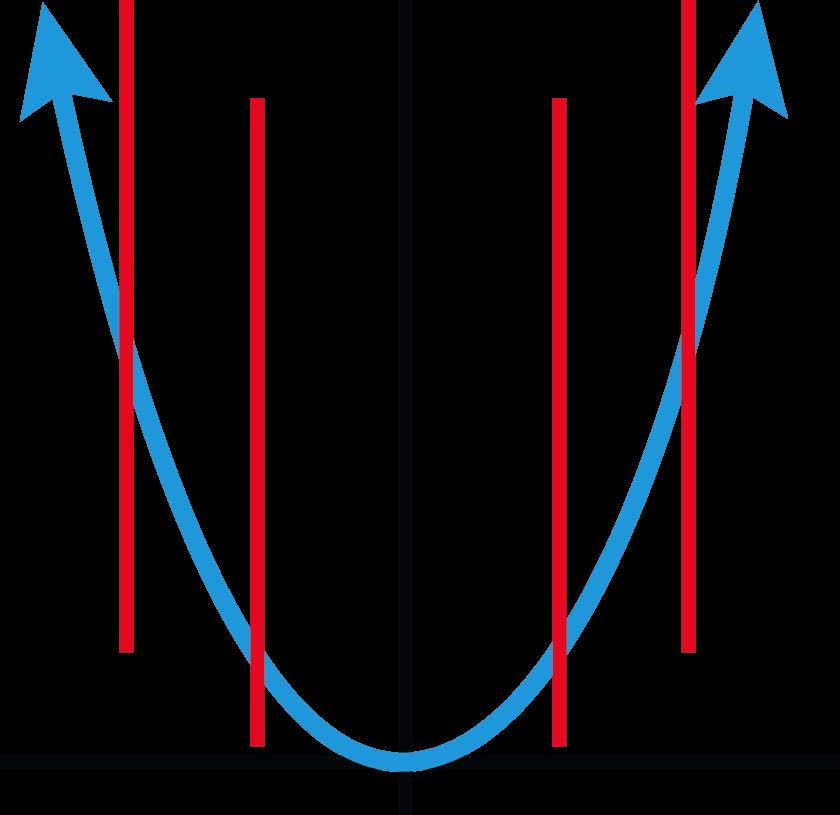
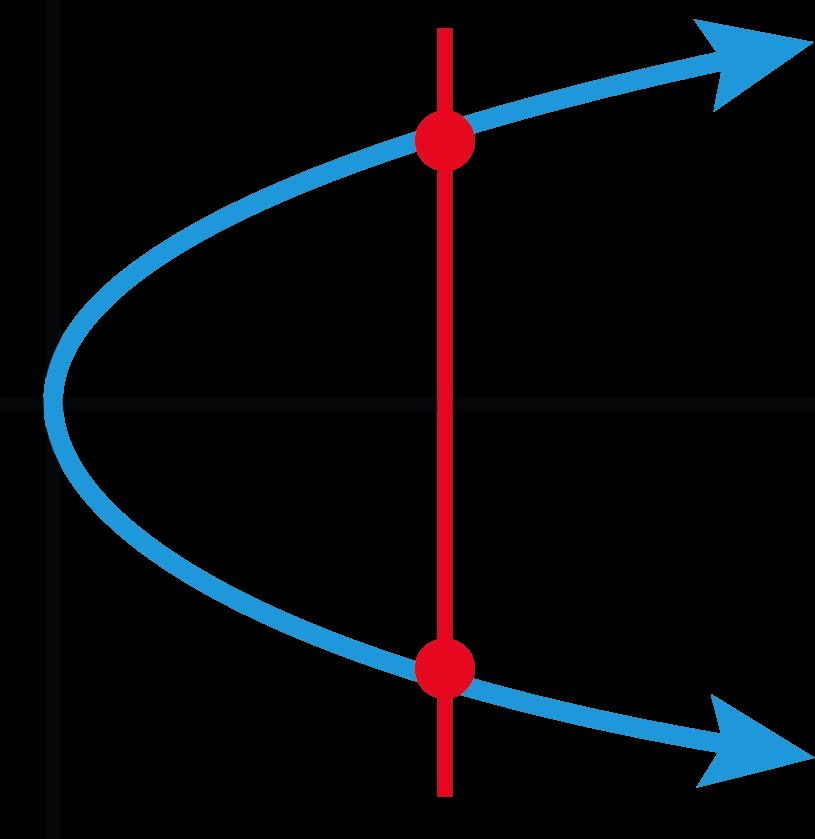
ELABORAR: CONSTRUCTOR DE FLUIDEZ

Hoja de instrucciones de Concentración

Este juega es para jugar en pareja.

Necesitarás 1 conjunto de tarjetas del juego Concentración (por pareja)

Instrucciones del juego

2. Barajea las tarjetas y colócalas boca abajo para formar una matriz de 4 × 6.

3. El jugador 1 voltea dos tarjetas para tratar de encontrar un pareo. Un pareo es un problema con su respuesta correcta. Los problemas deberán resolverse para determinar que respuestas respuestas se parean.

4. Si el jugador 1 empareja un problema con la respuesta correcta, entonces el jugador 1 se queda con el conjunto emparejado y toma otro turno.

5. Si el jugador 1 no encuentra ningún pareo, vuelve a colocar las tarjetas boca abajo y es el turno del siguiente jugador.

6. Los jugadores continúan tomando turnos hasta que se hayan encontrado todas los pareos.

7. El jugador que termine con más tarjetas ganará el juego.

HOJA DE INSTRUCCIONES

DESARROLLAR LA FLUIDEZ CONCEPTUAL

CONSTRUCTOR DE FLUIDEZ: PROPIEDADES DE LAS FUNCIONES

DESCRIPCIÓN

En esta actividad, los estudiantes jugarán a un juego de Concentración.

MATERIALES

IMPRESOS

• 1 hoja de instrucciones de concentración (por pareja)

• 1 Juego de tarjetas de concentración (por pareja)

REUTILIZABLES

• 1 Sobre o bolsa (por pareja)

PREPARACIÓN

• Haga copias a doble cara de las tarjetas de concentración.

• Lamínalas para que duren más.

• Recorta las tarjetas individuales y colócalas en un sobre o bolsa para facilitar su distribución y limpieza.

• Coloque a los estudiantes en parejas.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Muestre a los estudiantes cómo barajar las tarjetas y colocarlas boca abajo en una matriz de 4 × 6.

2. Modele cómo jugar el juego con un estudiante.

a. El jugador 1 voltea 2 tarjetas para tratar de encontrar una coincidencia. Una coincidencia es un problema con su respuesta correcta. Será necesario resolver los problemas para determinar las respuestas que coinciden.

b. Si el jugador 1 encuentra un problema con la respuesta correcta, entonces el jugador 1 se queda con el conjunto coincidente y toma otro turno.

c. Si el jugador 1 no encuentra una coincidencia, entonces vuelve a colocar las tarjetas boca abajo y es el turno del siguiente jugador.

d. Los jugadores continúan tomando turnos hasta que se hayan encontrado todas las coincidencias.

e. Gana el jugador que reúna la mayor cantidad de tarjetas.

3. Distribuya los materiales. A continuación, pida a los estudiantes que barajen las cartas y las coloquen boca abajo.

4. Vigile a los estudiantes para asegurarse de que encuentran las parejas correctas.

ELABORAR: REVISIÓN EN ESPIRAL

REPASAR CONCEPTOS PREVIOS

REVISIÓN EN ESPIRAL: EXPLORACIÓN DEL ESPACIO

DESCRIPCIÓN

Los estudiantes repasan contenidos de grados anteriores o actuales para ayudar a apoyar su trabajo en el alcance actual y fortalecer las habilidades necesarias para alcances posteriores.

REPASO EN ESPIRAL ENFOQUE POR PREGUNTA

• Pregunta 1

◦ Grado 8: Identificar funciones a partir de representaciones múltiples.

• Pregunta 2

◦ Grado 7: Usar la comprensión de las operaciones para resolver problemas que involucran números racionales.

• Pregunta 3

◦ Grado 7: Determinar si un valor dado hace que una ecuación o desigualdad sea verdadera.

• Pregunta 4

◦ Grado 8: Resolver ecuaciones de una variable.

PREPARACIÓN

• Imprima un folleto del estudiante para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Entregue un folleto del estudiante a cada estudiante.

2. Anime a los estudiantes a tratar de responder a las preguntas de forma independiente sin utilizar regrados externos para ver lo que saben. Invite a los estudiantes a anotar ideas o fragmentos que recuerden sobre los temas que han aprendido previamente. Reconozca que los errores son bienvenidos en esta actividad y en la clase de matemáticas.

3. Utilice las preguntas de repaso en espiral como calentamiento en clase, o envíelas a casa como deberes. Proporcione a los estudiantes comentarios y oportunidades para corregir su trabajo y consolidar aún más sus conocimientos previos.

4. Consulte la sección enfoque por pregunta del repaso en espiral para evaluar los conocimientos de contenido de los estudiantes o su necesidad de una mayor intervención. Si es necesario repasar más, utilice los constructores de fluidez en los alcances apropiados.

5. El capstone incluye una parte del alcance actual para que los estudiantes vean la conexión y relevancia de su aprendizaje previo con el alcance actual.

Exploración del espacio

El ser humano siempre ha querido descubrir los misterios del espacio. ¿Hasta dónde llega el universo? ¿Pueden los humanos vivir en otro planeta? ¿Cómo sabemos si la estrella sigue ahí si su luz tarda tanto en llegar hasta nosotros? Los humanos han desarrollado una tecnología increíble que nos ha permitido aprender sobre el espacio al enviar humanos, robots, naves espaciales y más al espacio para su exploración. Sus tareas son desarrollar un nuevo casco espacial, lanzar un cohete al espacio, navegar un dron espacial y calcular el tiempo que tarda la luz en alcanzar varios objetos en el espacio. ¡Abróchate el cinturón y ponte las botas espaciales!

1. Vuelas de forma remota un dron espacial en Marte desde la Estación Espacial Internacional. Al navegar con el dron, debe seguir un camino que represente y en función de x. ¿Qué gráfica muestra esta relación?

3. Venus está a 6 minutos luz del Sol. Si x = 6, ¿cuál desigualdad es verdadera?

A. 2x + 7 > 20

B. 5x – 12 > 17

C. −10x + 50 > 10

D. x + 4 > 14

2. La visera protectora del casco tiene una superficie de 120 centímetros cuadrados. Es demasiado angosto para que los astronautas tengan una buena visión periférica, por lo que debe aumentar el área del visor a . ¿Cuál será el área de la nueva visera?

1

4. Cohete Sombra Z usa la siguiente fórmula para calcular una salida segura de la atmósfera de la Tierra al espacio: 4(x – 6) = 20. ¿Qué valor de x hace que esta ecuación sea verdadera?

Ciencia de datos es un breve debate en clase basado en un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los estudiantes a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los estudiantes en contexto.

DESCRIPCIÓN

Los estudiantes analizarán, interpretarán y generarán conjuntos de datos, además de responder a preguntas basadas en los datos.

MATERIALES

IMPRESOS

• 1 Conjunto de datos (por clase)

REUTILIZABLES

• 1 Proyector o cámara de documentos (por clase)

• 1 Marcador (por clase)

CONSUMIBLES

• 1 Trozo de papel milimetrado (por clase)

PREPARACIÓN

• Prepárese para proyectar el conjunto de datos para la clase.

• Reúna un trozo de papel milimetrado y un marcador.

PROCEDIMIENTO Y PUNTOS DE APOYO

PARTE I

1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los estudiantes.

2. Discuta las siguientes preguntas:

a. ¿Qué observa acerca de este conjunto de datos?

b. ¿Qué representa este conjunto de datos?

c. ¿Qué categorías se incluyen en este conjunto de datos?

d. ¿Qué representa la expresión f(x)?

e. ¿Qué tan bien parece modelar la curva los puntos de datos?

f. ¿Qué preguntas tiene acerca de los datos?

ELABORAR: CIENCIA DE DATOS

ANÁLISIS DE DATOS

CIENCIA DE DATOS

PARTE II

1. Repasa cómo evaluar una función para un valor en su dominio, y escribe lo que los estudiantes recuerden en el papel cuadriculado.

2. Discute las siguientes preguntas:

a. La función mostrada en la gráfica es f(x) = -60/ x+0.5 + 120.

Define las variables de la función. x es el tiempo, en horas, que ha estado cargando el teléfono, y f(x) es el porcentaje de carga de la batería.

b. ¿Qué dominio tiene sentido dado el contexto del problema? Explica. x ≥ 0; el número de horas no puede ser negativo, pero puede ser un valor decimal.

c. ¿Qué rango tiene sentido dado el contexto del problema? Explícalo. 0 ≤ y ≤ 100; La carga de la batería no puede ser negativa, ni puede superar el 100%.

d. Halla la tasa de cambio en la carga de la batería entre x = 0 y x = 1. Muestre su trabajo. m = f(1)-f(0)/1-0 f(1) = -60/1+0.5 + 120 = -60/1.5 + 120 = -40 + 120 = 80; f(0) = -60/0+0.5 + 120 = -60/0.5 + 120 = -120 + 120 = 0;

m = 80-0/1-0 = 80% por hora

e. Explique visualmente cómo sabe que la tasa media de variación es mayor en el intervalo entre x = 0,5 y x = 1,5 que en el intervalo entre x = 1,5 y x = 2,5. La gráfica aumenta a un ritmo mayor durante el primer intervalo, y el cambio en la duración de la batería es mayor al principio del proceso de carga.

f. Halla el ritmo de cambio en la carga de la batería entre x = 1 y x = 2. Redondea a la centésima más próxima. Muestra tu trabajo.

m = f(2)-f(1)/2-1; f(2) = -60/2+0,5 + 120 = -60/2,5 + 120 = -24 + 120 = 96;

f(1) = -60/1+0,5 + 120 = -60/1.6 + 120 = -40 + 120 = 80;

m = 96-80/2-1 = 16/1 = 16% por hora

g. ¿A qué porcentaje esperas que esté la carga de la batería después de 45 minutos? Redondea a la centésima más cercana. Muestra tu trabajo. 45 minutos = 0,75 hora;

f(0,75) = -60/0,75+0,5 + 120 = -60/1,25 + 120 = -48 + 120 = 72%

h. ¿Cuánto tiempo esperas que tarde la carga de la batería en alcanzar el 90%? Muestra tu trabajo.

90 = -60/x+0,5 + 120

-30 = -60/x+0,5

-30(x + 0,5) = -60

-30x - 15 = -60

-30x = -45

x = 1,5 horas

EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN

EVALUACIÓN DE HABILIDADES

LISTA DE VERIFICACIÓN DE LA OBSERVACIÓN

Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestroes y como autoevaluación para los estudiantes.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por alumno)

• 1 material para el maestro (por estudiante)

PREPARACIÓN

• Imprima un material para el maestro y un folleto del estudiante para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un folleto del estudiante a cada estudiante.

2. A medida que los estudiantes trabajen en las actividades de «Explorar» y «Explicar» del alcance, evalúe formativamente su progreso tomando notas anecdóticas sobre cómo se observaron los conceptos y habilidades clave. Pueden plantearse preguntas de reflexión para medir el impacto de las actividades tanto en grupo como en pequeño grupo.

Propiedades de las funciones

Habilidad o concepto clave ¿Cómo podrías demostrar que sabes esto?

Puedo entender que una función de un conjunto (llamado dominio) a otro conjunto (llamado rango) asigna a cada elemento del dominio exactamente un elemento del rango.

Puedo utilizar la notación de funciones para evaluar funciones para entradas en sus dominios e interpretar enunciados que utilizan la notación de funciones en relación con un contexto.

Puedo relacionar el dominio de una función con su gráfica y, cuando corresponda, con la relación cuantitativa que describe.

Puedo calcular e interpretar la tasa promedio de cambio de una función (presentada simbólicamente o en forma de tabla) a lo largo de un intervalo especificado. Puedo estimar la tasa de cambio a partir de una gráfica.

❏ Represéntalo.

❏ Dibújalo.

❏ Aplícalo.

❏ Habla sobre esto.

❏ Escribe sobre esto.

❏ Represéntalo.

❏ Dibújalo. ❏ Aplícalo. ❏ Habla sobre esto. ❏ Escribe sobre esto.

❏ Represéntalo. ❏ Dibújalo. ❏ Aplícalo. ❏ Habla sobre esto. ❏ Escribe sobre esto.

❏ Represéntalo. ❏ Dibújalo. ❏ Aplícalo. ❏ Habla sobre esto. ❏ Escribe sobre esto.

¿Cómo te calificarías a ti mismo?

¡Lo tengo!

¡Ya casi!

¡Todavía no!

¡Lo tengo!

¡Ya casi!

¡Todavía no!

¡Lo tengo!

¡Ya casi!

¡Todavía no!

¡Lo tengo!

¡Ya casi!

3. Haga que los estudiantes reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan en las actividades tanto en grupo como en pequeño grupo.

4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado; y establecer nuevos objetivos de aprendizaje.

5. Los colegas que proporcionan apoyo de instrucción a los estudiantes pueden estar equipados con las adaptaciones y modificaciones señaladas en el Manual del maestro.

6. Las notas anecdóticas proporcionadas en la hoja para el maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.

7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la Guía de instrucción de andamiaje en la sección Inicio de este alcance para diferenciar la instrucción para cada estudiante.

Properties of Functions 1

Estándares para la práctica matemática ¿Cómo te calificarías a ti mismo?

Puedo dar sentido a los problemas y perseverar en resolverlos.

Puedo razonar de forma abstracta y cuantitativa.

Puedo construir argumentos viables y criticar el razonamiento de otros.

Puedo representar con matemáticas.

Puedo utilizar estratégicamente las herramientas adecuadas.

Puedo prestar atención a la precisión.

Puedo buscar y utilizar estructuras.

Puedo buscar y expresar regularidad en razonamientos repetidos.

Reflexiona sobre tu pensamiento, aprendizaje y trabajo en este alcance.

¿Qué objetivos te has propuesto? ¿En qué has mejorado en este alcance?

¿Tienes nuevos objetivos? ¿Dónde quieres mejorar en el próximo alcance?

Properties of Functions

¡Todavía no! 2

FOLLETO DEL ESTUDIANTE

DESCRIPCIÓN

Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.

MATERIALES

• 1 mapa de calor (por estudiante)

• 1 lápiz rojo (por estudiante)

• 1 lápiz azul (por estudiante)

• 1 lápiz naranja (por estudiante)

PREPARACIÓN

• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.

• Imprima un mapa de calor para cada estudiante.

• Reúna lápices de color rojo, azul y naranja para cada estudiante.

EVALUAR: MAPA DE CALOR

ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN

MAPA DE CALOR

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un mapa de calor a cada estudiante junto con los lápices de color rojo, azul y naranja. Los estudiantes deben tener a mano su(s) evaluación(es) corregida(s).

2. Los estudiantes utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Para cada pregunta no contestada por error de cálculo, los estudiantes colorean de azul la casilla correspondiente. Para cada pregunta no contestada por una explicación, los estudiantes colorean la casilla correspondiente de naranja. Para cada pregunta omitida por un concepto erróneo, colorean el cuadro correspondiente de rojo.

3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.

4. Consulte la guía de instrucción andamiada que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.

Consulta tus respuestas en la tabla «Prueba de habilidades». Colorea de verde los cuadros de preguntas correctas y colorea según la siguiente clave los cuadros de preguntas incorrectas. Azul: Error de cálculo Naranja: Explicación Rojo: Error de concepto

Prueba de habilidades

Estándares Preguntas

Comprende que una función de un conjunto (llamado el dominio) a otro conjunto (llamado el rango) asigna a cada elemento del dominio exactamente un elemento del rango. Si f es una función y x es un elemento de su dominio, entonces f(x) denota la salida de f correspondiente a la entrada x. La gráfica de f es la gráfica de la ecuación y = f(x).

Utiliza la notación de funciones, evalúa funciones para entradas en sus dominios e interpreta declaraciones que utilizan la notación de funciones en términos de un contexto.

Relaciona el dominio de una función con su gráfica y, cuando corresponda, con la relación cuantitativa que describe. Calcula e interpreta la tasa de cambio promedio de una función (presentada simbólicamente o en una tabla) en un intervalo específico. Estima la tasa de cambio de una gráfica. 7 4 10 1 3 5 8 2 6 9

1

Preguntas de reflexión

1. ¿Con qué habilidad te has sentido más seguro? ¿Por qué?

2. ¿Qué habilidad te ha parecido más desafiante? ¿Por qué?

3. ¿Qué tipo de error cometiste con más frecuencia?

4. ¿Cómo puedes evitar esos errores en el futuro?

Consulta tus respuestas en la tabla «Evaluación basada en estándares». Colorea de verde los cuadros de preguntas correctas y colorea según la siguiente clave los cuadros de preguntas incorrectas. Azul: Error de cálculo Naranja: Explicación Rojo: Error de concepto

Evaluación basada en estándares

Estándares Preguntas

Comprende que una función de un conjunto (llamado el dominio) a otro conjunto (llamado el rango) asigna a cada elemento del dominio exactamente un elemento del rango. Si f es una función y x es un elemento de su dominio, entonces f(x) denota la salida de f correspondiente a la entrada x. La gráfica de f es la gráfica de la ecuación y = f(x).

Utiliza la notación de funciones, evalúa funciones para entradas en sus dominios e interpreta declaraciones que utilizan la notación de funciones en términos de un contexto.

Relaciona el dominio de una función con su gráfica y, cuando corresponda, con la relación cuantitativa que describe.

Calcula e interpreta la tasa de cambio promedio de una función (presentada simbólicamente o en una tabla) en un intervalo específico. Estima la tasa de cambio de una gráfica. 7 4 10 1 3 5 8 2 6 9 Properties of Functions 3

INTERVENCIÓN: REVISIÓN Y PRÁCTICA DE HABILIDADES

REFORZAR Y VOLVER A ENSEÑAR

REPASO Y PRÁCTICA DE HABILIDADES

DESCRIPCIÓN

Esta actividad está diseñada para repasar los conceptos clave del alcance. Utilícela como repaso o para intervención.

MATERIALES

IMPRESOS

• 1 evaluación rápida (por estudiante)

• 1 repaso (por estudiante)

• 1 evaluación de control (por estudiante)

• 1 lista de verificación para el maestro (por profesor)

PREPARACIÓN

• Imprima una copia de la evaluación rápida, el repaso y la evaluación de control por estudiante.

• Si lo desea, coloque a los estudiantes en grupos de 3 o 4 para completar la revisión.

• Si lo desea, imprima un ejemplo del esquema de anclaje de la sección «Explicar» o pida a los estudiantes que usen la libreta interactiva como regrado.

• Opcionalmente, imprima cualquiera de los materiales de ayuda complementarios para que los estudiantes los utilicen mientras trabajan.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. De una copia de la evaluación rápida a cada estudiante.

2. Cada uno debe completarla de forma independiente.

3. Use la rúbrica de habilidades al final de la evaluación rápida para identificar qué estudiantes necesitan ayuda adicional en las habilidades.

4. Distribuya una copia del repaso a cada estudiante.

5. Cada uno debe completar el repaso como actividad de intervención o como actividad independiente.

a. Si lo desea, reúna a los estudiantes en pequeños grupos para trabajar en las destrezas de repaso. Use el repaso como ayuda para la reenseñanza.

6. Distribuya una copia de la evaluación de control a cada estudiante.

7. Cada estudiante debe completarla de forma independiente.

8. Analice los resultados de la evaluación de control utilizando la lista de verificación para el maestro para identificar a quienes necesitan un repaso adicional y quienes han alcanzado el dominio de los conceptos.

Revisión

4.

1. ¿Es una función? ¿Por qué sí o por qué no?

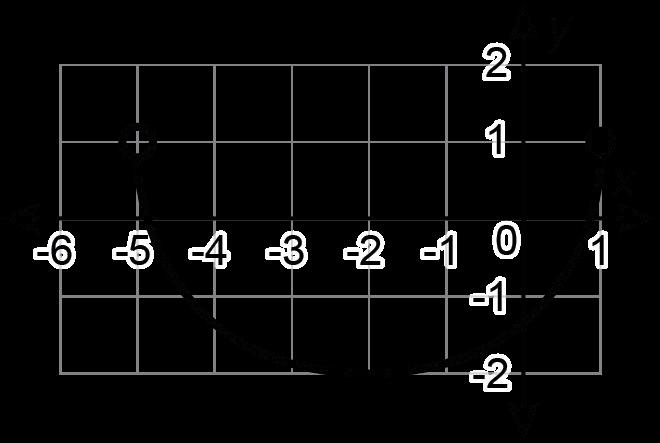
2. Determina el dominio y rango de la función graficada en la pregunta 1.

Dominio:

Rango:

3.La función g contiene 5 pares ordenados en un conjunto que describe la función.

Función g

{(1, 4), (5, 1), (6, 1), (9, 3), (x, y)}

¿Cuál de los siguientes pares ordenados no puede ser incluido en el conjunto?

A.(2, 6)

B.(6, 5)

C.(3, 4)

D.(7, 2)

5.Para la función h(x) = –7x + 9, determina el valor de x cuando h(x) = 2.

6.La función t está definida por t(x) = –1.3x2 – 2x + 5.71. Evalúa t(4).

7. Cuál es el promedio de la tasa de cambio de la función f sobre el intervalo –1 ≤ x ≤ 2?

8. La gráfica muestra el número de visitantes que recibe un museo durante 6 días. De acuerdo con la gráfica, ¿Cuál es la tasa promedio de cambio entre el día 2 y el día 5?

9. Un lugar para acampar tiene un cargo por servicio de $10, y $12 por noche por alquiler de las tiendas. Si x representa el número de noches, y el costo total por acampar es representado por c(x) = 12x + 10. ¿Cuál es un dominio razonable para esta situación?

A. Múltiplos de 12

B. Enteros positivos

C. Número racionales

D. Números enteros

10. Los 3 hijos de la señora Jones vienen por el descanso de la primavera, y ella desea llevarlos al parque de diversiones. Hay un cargo familiar de $35 para tener un acceso rápido al parque y el boleto por persona cuesta $90. Si x representa el número de boletos comprados y el costo total es representado por f(x) = 90x + 35. ¿Cuál es un rango razonable para esta situación?

A. {1, 2, 3, 4, 5}

B. {125, 215, 305, 395}

C. 3 ≤ x ≤ 7

D. 35 ≤ y ≤ 395

Proyecto de Historia

Usa razonamiento matemático y la creatividad para justificar tu respuesta a la pregunta, ¿qué prefieres?

En su clase de Historia, a Carolina se le asigna un proyecto que debe entregarse exactamente en dos semanas. Ella estima que el proyecto le tomará aproximadamente 7 horas para completarlo. Carolina delibera si tratará de completar una cierta cantidad de trabajo todos los días hasta terminar el proyecto (Opción A) o si esperará hasta el día anterior a la fecha de entrega del proyecto y se queda despierta hasta tarde hasta que finalice el proyecto (Opción B). ¿ Preferirías elegir la Opción A o la Opción B? Justifica tu razonamiento con matemáticas.

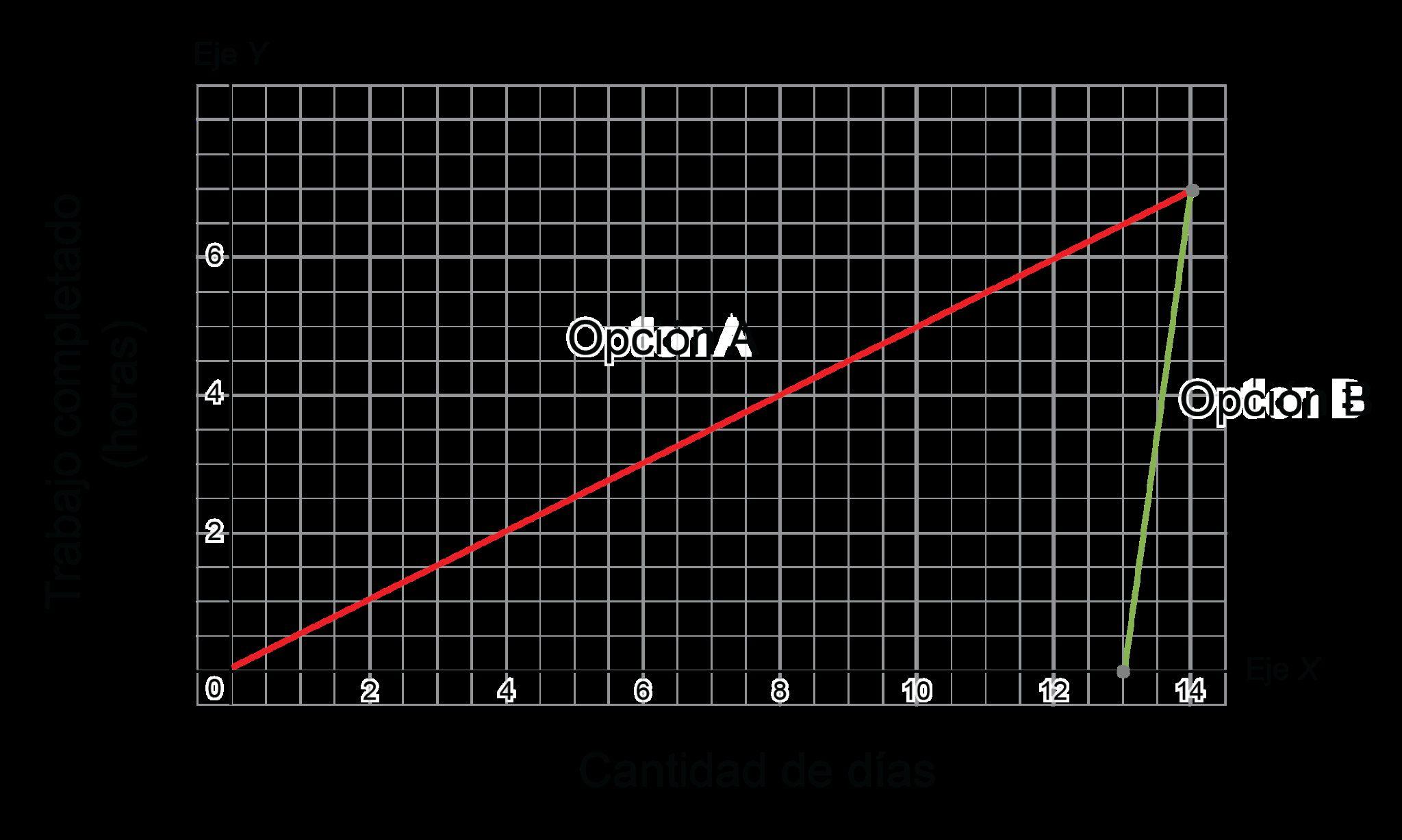
ACELERACIÓN: ¿QUÉ PREFIERES?

RAZONAMIENTO MATEMÁTICO

PROYECTO DE HISTORIA

DESCRIPCIÓN

Los estudiantes utilizan el razonamiento matemático y la creatividad para justificar una respuesta.

MATERIALES

IMPRESORA

• 1 folleto del estudiante (por alumno)

• 1 rúbrica (por maestro)

PREPARACIÓN

• Imprima un folleto del estudiante por alumno.

• Planifique que los estudiantes trabajen en parejas para completar esta actividad, si lo desea.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Entregue un folleto del estudiante a cada alumno.

2. Anime a los estudiantes a mirar sus folletos del estudiante de las exploraciones si necesitan repasar habilidades.

3. Invite a los estudiantes a compartir respuestas y justificaciones con sus compañeros.

4. Utilice la rúbrica proporcionada para evaluar las habilidades de comprensión, cálculo y razonamiento de los estudiantes.

ACELERACIÓN: TABLERO DE OPCIONES

OPCIONES PARA EL APRENDIZAJE CONTINUO

TABLERO DE OPCIONES

DESCRIPCIÓN

Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.

MATERIALES

IMPRESOS

• 1 tablero de opciones (por estudiante)

• 1 juego de hojas de actividades (por estudiante)

• 1 autoevaluación del tablero de opciones (por estudiante)

REUTILIZABLE

• Tecnología (si corresponde)

PREPARACIÓN

• Imprima un tablero de elección y un juego de hojas de actividades para cada estudiante.

• Imprime una autoevaluación del tablero para cada estudiante.

• Planifica con antelación el uso de la tecnología. Puede ser necesario investigar para algunas actividades del tablero de opciones.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un tablero de opciones a cada estudiante.

2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.

3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.

4. Distribuya las hojas de actividades correspondientes según las elecciones de los estudiantes.

5. Al finalizar cada actividad del tablero de opciones, haga que los estudiantes completen una autoevaluación del tablero para revisar su propio pensamiento matemático y sus esfuerzos en su proyecto.

Propiedades de las funciones

Elige una o varias actividades de extensión de la siguiente tabla.

Conexión profesional

Científicos de control climático

Investiga el campo profesional de la ciencia de control climático. Tu investigación debe responder las preguntas proporcionadas. Crea una presentación para compartir tu investigación con la clase.

Conexión financiera

Tienda de emparedados

Utilizamos las matemáticas cada día en nuestro mundo financiero. Completa el folleto para explorar cómo nuestro tema de matemáticas actual se relaciona con nuestro mundo financiero.

Conexión matemática

Explorar funciones

Explora las funciones claves de dos nuevos tipos de funciones a través de tablas y gráficas antes de estudiarlas a profundidad en futuros grados.

Properties of Functions

Conexión con el arte

Estrellita dónde estás

Utiliza una función matemática para transponer una pieza musical de una tonalidad a otra.

Conexión con las ciencias

Migración de patos

Relaciona las matemáticas y las ciencias al interpretar una gráfica que muestra la relación entre la distancia y el tiempo durante la migración de patos.

Matemáticos en primer plano

Leonhard Euler

Busca varios artículos de noticias o investigaciones que incluyan el trabajo de Leonhard Euler. Crea un cartel informativo, un diorama o un discurso para presentar el trabajo de este matemático relacionado con las funciones

TABLERO DE OPCIONES

ÁLGEBRA 1: PROPIEDADES DE LAS FUNCIONES