BY ACCELERATE LEARNING

8


8

The program is structured by course, unit, and lesson. Each unit includes formative checkpoints throughout and an end-of-unit assessment. Lessons are approximately 45–50 minutes long. They are intentionally designed to fit within the calendar year, so teachers have pacing flexibility. Here is a breakdown by course of the number of units and lessons.

* Scopes and sequences are intentionally designed for Florida’s accelerated and honors courses.
**The time estimates in these materials refer to instructional time. Some lessons contain optional activities that provide additional practice for teachers to use at their discretion. Additional Centers and Activities are also available to differentiate instruction.

Math Nation Florida is built exclusively for Florida’s B.E.S.T. Standards, providing teachers with a highquality, standards-aligned curriculum that ensures all students can succeed in mathematics.
The design emphasizes:
• Student-centered, inquiry-based learning that builds from what students know.
• Scaffolded instruction within and across lessons, ensuring accessibility for all learners.
• Balanced development: conceptual understanding, procedural fluency, and realworld application.
• Multiple representations to deepen understanding and connect math to authentic contexts.
• Collaboration: students learn together and view mistakes as learning opportunities.
• Transfer learning: spiraling and connecting content across courses to highlight the beauty and interconnectedness of mathematics.
• Mathematical Thinking & Reasoning Standards (MTRs): embedded throughout for deeper engagement.
• Communication skills: consistent opportunities for oral and written mathematical reasoning.
Instruction draws on John Hattie’s Visible Learning research and incorporates:
• Practices with the highest impact on student growth.
• Classroom discourse and rich discussion opportunities.
• Clear strategies and content knowledge support in the Teacher Edition.
Teachers also have access to:
• Progress monitoring tools within a MultiTiered System of Support (MTSS): embedded assessments, reports, and analytics aligned to Florida’s B.E.S.T. Standards.
• Differentiation supports: remediation, intervention, and enrichment at both unit and lesson levels.
• Professional learning: point-of-use digital resources and a teacher community for continuous support.
Math Nation Florida’s Unit and Lesson Guides serve as a companion to our dynamic curriculum. The Unit and Lesson Guides accompany the curriculum for Grades 6–12, acting as an extension and planning partner for further clarification of the purpose, intent, coherence, and language of the lessons.
Each unit includes a Unit Guide that offers additional planning support for the unit as a whole. Florida’s B.E.S.T. Standards are designed to ensure vertical alignment across grade levels and horizontal alignment within each course. In the Unit Guide, the Unit Narrative section describes the content of the unit, including horizontal connections to other units. The Vertical Alignment section of the Unit Guide provides the vertical alignment for the benchmarks taught in the unit.
Each Unit Guide also incorporates instructional strategies for differentiating, enriching, and implementing lessons throughout the unit.
The narrative captures the story of the unit, its progression, and connections to other units and courses. This section also includes a Unit-ata-Glance that gives an overview of the lessons included in the unit.
The differentiation section includes recommendations for incorporating Universal Design for Learning (UDL)™ and information for English Language Learners (ELLs). UDL from CAST© 2008 prioritizes strategies for differentiating instruction that seek to eliminate barriers of entry so that all students can learn. Each Unit Guide offers techniques specific to that unit content through the lens of UDL.
This section offers visual coherence with benchmarks aligned to lessons and clarifications to inform planning and instruction.
This section provides the vertical alignment of the benchmarks taught in the unit by noting the benchmarks from prior courses that are being built upon, and the benchmarks in future courses that students are working toward.
Every lesson includes a Lesson Guide that provides insight into the math thinking and reasoning for effective implementation.
Each Lesson Guide begins with an introduction that captures a snapshot of the lesson content for purposeful preparation. The Lesson Introduction includes the benchmarks and learning targets found in each student lesson. Teacher planning supports include vertical benchmark coherence, essential questions, a brief lesson narrative, a component summary for pacing and adaptation, and resources, including materials and vocabulary.
Each Lesson Guide includes additional planning support, such as:
• Mathematical Thinking and Reasoning (MTR) Standards: one is highlighted for each lesson for intentional focus when planning, though a lesson may integrate several MTRs.
• Common Misconceptions
• Things to Consider
• Literacy and Language Routines
• Differentiation Suggestions: found here and also incorporated throughout the lesson components.
In the Lesson Guide, specific guidance incorporating instructional strategies is provided for each component of a lesson. This support is shown in line with the answer key of the student lesson for point-of-use implementation in the classroom. These recommendations include teacher moves, additional questions to consider asking, differentiation ideas related to the component, and possible enrichment ideas.
Student lessons across all courses feature the same structure. The lessons include several components, each with a specific icon associated with it.

Focus benchmarks are indicated on the first page of each student lesson.
Learning Target(s)
Learning Targets are clearly defined at the beginning of each lesson so student and families have clear expectations.

Every lesson begins with a Warm-Up. The Warm-Ups are designed to vary so that all students have access and a positive start to each lesson. WarmUps include bell work, STEM career profiles, critical thinking, and more.

Every lesson ends with a short Wrap-Up. Wrap-Ups include student reflection, cool downs, error analysis, and tickets out the door that can be used for formative assessment.
Lessons also include some combination of the components indicated below. Green lesson components identify student-led components that are intentionally designed for students to explore, discover, and practice concepts either independently or collaboratively with peers. These activities promote active engagement and deepen understanding of the content.

Explorations are student-led discovery, often involving student collaboration and discussion. The topics explored in these components may not yet be formalized.

Activities include gallery walks, data collection, and games.


Students collaborate in pairs or small groups.
Students may not have reached mastery when completing Try It. These problems are an opportunity to apply previously learned skills to more formal practice problems.
Blue lesson components indicate that lesson components are intended to be teacher-led. These provide opportunities for direct instruction and teacher facilitation of learning and are intended to be rich in student collaboration.

Instruction should be studentcentered during Guided Instruction, but may require more support from the teacher.

Guided Practice presents an opportunity for students to learn new concepts through practice problems.

Bring it Together components formalize concepts explored in the lesson.

Vocabulary and concepts learned in previous units or courses are reviewed in Refresher components.

Your Turn! provides students with the opportunity for independent practice. These problems may also be used for homework.

Lesson Activities serve as the core learning experience in every Math Nation Florida lesson. These engaging tasks:
• Encourage collaborative, student-led discovery through guided investigation, reasoning, and communication of mathematical ideas
• Replace front-loaded instruction with problem-solving, pattern recognition, and strategy development
• Foster a discovery-based approach where students actively construct mathematical understanding
• Purposefully integrate horizontal and vertical alignment, helping students connect concepts deeply and meaningfully
• Include built-in supports in the Teacher Edition for effective student questioning, discourse, exploration, and conceptual clarity

Each lesson includes multiple opportunities for student practice. Here are some examples of meaningful practice and targeted supports in Math Nation Florida:
Your Turn! provides students with a chance for true independent practice of the concepts they are learning in a given lesson.
Math Nation Florida is packed with practice that is designed to have students working collaboratively to solve problems, develop solutions, discover new ideas and strategies, engage in error analysis and much more. With peer-to-peer practice embedded throughout the program, students are provided with ongoing, meaningful collaboration opportunities.


Students may not have reached mastery when completing Try It. These problems are an opportunity to apply skills learned in previous components to more formal practice problems.
Check Your Understanding are a set of three digital practice problems available for students at the end of each lesson to inform and check for understanding.
The Guided Practice components provide opportunities for students to practice their skills in a structured, teacher-led setting. The intention is to practice together with guidance to maximize retention and understanding.
Activities include gallery walks, data collection, and games that allow the students to get additional practice in practical, engaging ways to leverage their critical and creative thinking skills.
Each lesson has a set of additional practice questions to provide another opportunity for students to independently practice what they learned in the lesson. These can be utilized in class or for homework.
Each lesson has a set of digital practice questions called Stepping Stones. These give students targeted practice that moves them toward mastery of lesson-level expectations. They can be used flexibly before or after the main lesson to reinforce understanding.
An additional Florida Independent Skills Practice Book helps students solidify and refine their skills, either in class or for homework. Practice books include embedded tutorial videos in English and Spanish so students and families have 24/7 support.
5.8.5
1.



Math Nation Florida is designed to extend support into the home for student success. To help families, we provide:
Helpful take-home letters explain how to navigate and use the Math Nation Florida platform effectively. They provide families with specific guidance on how to leverage all of the resources available to best support their student in their math journey.
Families also gain unlimited access to a comprehensive library of multilingual Study Expert videos that can be downloaded on our iOS and Android mobile apps, ensuring access anytime, anywhere, to a math tutor. The videos:
• Come in English, Spanish, and Haitian Creole
• Allow families to see how a math concept is taught to better support their student at home
• Help students who miss school due to illness or vacation keep up with their studies











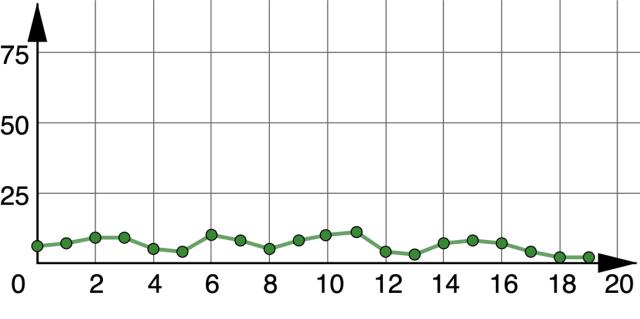
Each graph represents the number of wins for the Arkansas Razorbacks football team for the 2000-2019 seasons, where the ���� -axis represents the number of years since 2000.
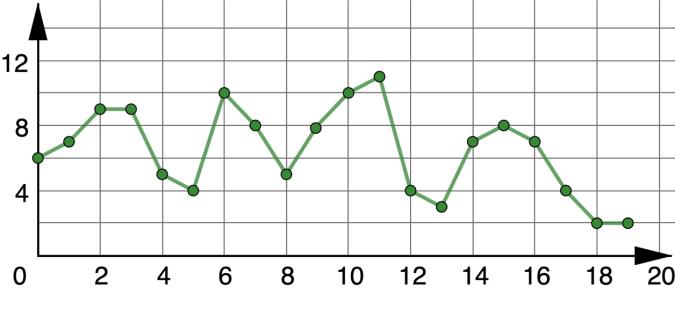
1. What do you wonder about the two graphs?
2. What do you notice about the two graphs?
3. In what years did the team win at least 10 games?
4. Explain how the scale of the ���� -axis impacts the graphs.
A gameboard is shown on the coordinate grid, along with the number of points earned for landing in each area. Each coordinate grid axis is scaled at 1.
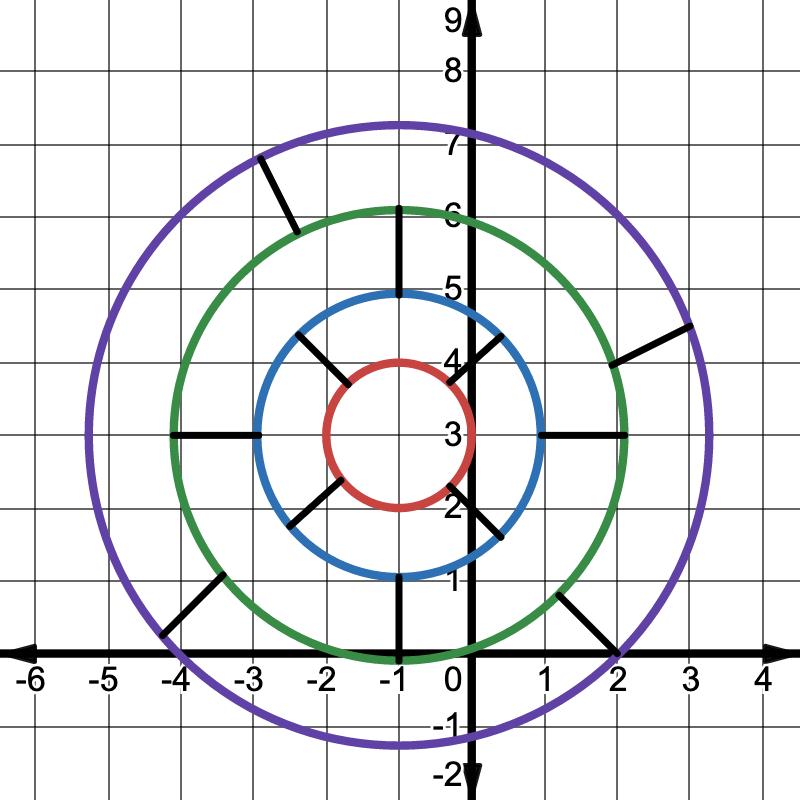












1. Several points are given in the table. Locate each point on the coordinate grid. Complete the table by writing the score value for landing at each point. Calculate the game score by finding the sum of all the points. Verify your answer with your teacher.
Point
Score Value ( 3, 4.9) (4 5 , 1 3 4) (0, 2 2) ( 3.8, 4.9) (1.5, 4.4) ( 1 2 3 , 2) (5 4 , 11 2 )
Game Score: ____________
There are six shapes on the coordinate grid shown. Each partner will select one shape as their game piece. The object of the game is to guess which shape your partner selected before they guess yours. A hit means the point you guessed is inside their shape. A miss means that it is not. Keep your gameboard hidden from your partner duri ng the game.
2. Record the coordinates of each guess in the table below. Then, plot the point on the coordinate grid gameboard.
or miss?
1. The temperature in Princeton, New Jersey was recorded at various times during the day. The times relative to midnight, ���� , and temperatures in degrees Celsius (°���� ) are shown in the table.
a. Plot the points that represent the data.
b. In the town of New Haven, Connecticut, the temperature at midnight was 2 10 °���� . Plot and label this point on the same grid. Label the point C.
c. Label the point that represents the temperature in Princeton at midnight ���� . Which town was warmer at midnight, Princeton or New Haven?
d. Explain how to determine which town you selected in Part C is warmer at midnight.
2. The average NBA player scores 9.7 points per game. The table below lists six players, along with their average points per game and their difference from the average.
Graph the points from the table on the coordinate grid.
Think about what you have learned in the past four lessons about plotting points. As you read each statement, consider which best describes your understanding right now.
1. I need help plotting points. I’m not sure where to begin.
2. I can plot points with integers on a coordinate grid with a scale of 1, but I still need help with rational numbers and different scales.
3. I can plot points with decimals on a coordinate grid with a tenths scale, but I still need help with points that are fractions.
4. I can plot points with rational numbers that are decimals or fractions using any scale.
1. Explain which number from the list best describes you.
2. Write a plan for what you can do to either move to number 4 or to help a classmate move to number 4.
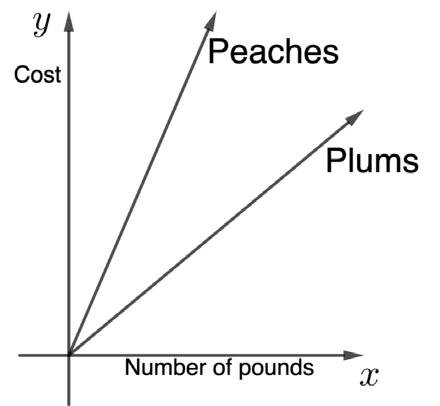
The graphs below show the cost, ���� , of buying ���� pounds of fruit. One graph shows the cost of buying ���� pounds of peaches, and the other shows the cost of buying ���� pounds of plums.
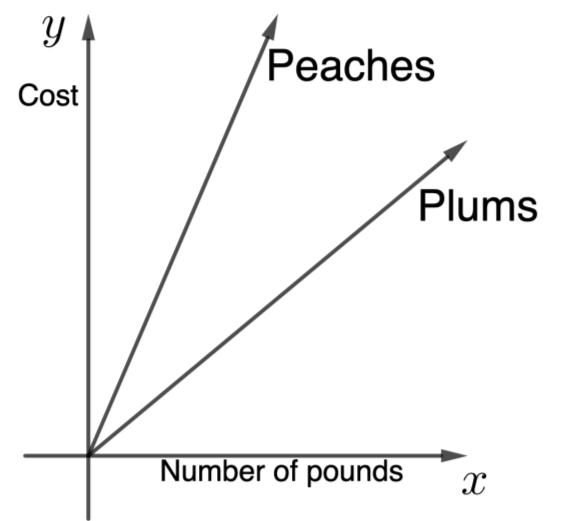
1. After looking at the relationships graphed, complete the table with one thing you notice and one thing you wonder.
2. Explain which fruit you think costs more per pound.
Several scenarios are described in the chart. Your teacher will give you two sets of cards showing tables and graphs.
1. Work with your partner to match a table of values and graph to each scenario. Write the matching table number and letter of the graph in the chart.
a. T-shirts are priced $10 each at a store. There is a sale posted that says, “Buy two T-shirts, get the second one half-price.” The table and graph show the total cost, ���� , of ���� T-shirts.
b. A movie streaming service costs $8.49 each month. The table and graph show the total cost, ���� , for ���� months of the subscription.
c. A recipe uses 2 tablespoons of honey, ���� , for every 8 cups of flour, ���� .
d. Camping fees, ���� , at Blue Springs State Park in Volusia, FL include a $6 70 reservation fee and $24 per night, ���� .
e. Rachel ran 6 laps in 18 minutes around the track at Riverview High School in Sarasota, FL. She notes the average number of minutes, ���� , that have passed after each lap, ���� .
f. Kenneth is filling his fish tank with water at a flow rate of 1.6 gallons per minute. The table and graph show the number of gallons of water, ���� , after ���� minutes.
2. Complete the statements using the words from the bank.
constant equivalent line ordered origin table
When two quantities are in a proportional relationship, the graph will include the , (0, 0) and the points on the graph will form a straight . The pairs of the points on the graph match the pairs of values in the representing the same relationship. The ordered pairs in a proportional relationship are ratios. The value of the ratio is called the of proportionality.
3. Work with your partner to determine which scenarios from the card sort represent proportional relationships using the matching tables and graphs. Write the letter P next to the written description in the chart for each relationship that is proportional.
4. Use Graph D and the context it represents to complete the following parts with your partner.
a. Discuss why, for this context, it makes sense that every point on the line shown is possible.
b. Explain whether you think the graph representing this relationship will continue increasing every minute that passes.
5. Use Graph E and the table it matches to complete the following parts with your partner.
a. The points on Graph E form a straight line, but the situation does not represent a proportional relationship. Explain why it does not represent a proportional relationship.
b. Use at least two ordered pairs from the table of values that matches Graph E to show why this relationship is not proportional.
11.4.3 Bring it Together: Determining if a Relationship is Proportional


Graphs representing proportional relationships have the following in common.
• The points that satisfy the relationship lie on a straight line.
• The line they lie on passes through the origin, (0, 0).


Tables representing proportional relationships have the following in common.


• Each row in the table shows a ratio of the two quantities in the relationship.
• All of the ratios in the relationship are equivalent.
11.4.4 Your Turn!
1. A graph is shown.
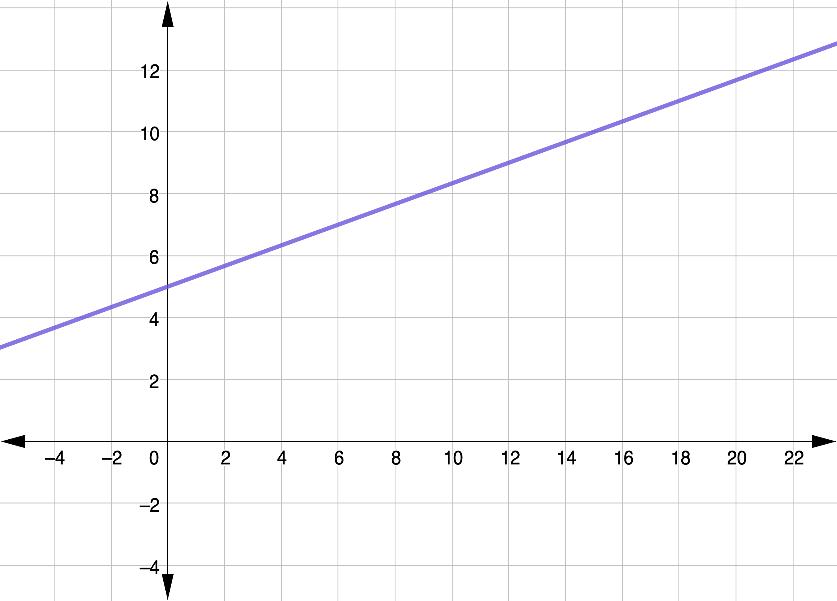
a. Complete the statement.
The graph a proportional relationship between two quantities.
b. Explain your selection for Part A.
2. Fountain drinks at Wawa are priced by size. The volume in fluid ounces (fl . oz.) and price in dollars ($), before tax, for each size is shown in the table.
a. Complete the statement.
The table a proportional relationship between two quantities.
o represents o does not represent o represents o does not represent
b. Explain your selection for Part A.
11.4.5 Wrap-Up: Cool Down
1. Your friend is absent today and will need the notes from class. Write a quick note to help them understand how to determine if two quantities have a proportional relationship.
7.5.1 Warm-Up: Which One Doesn’t Belong?
The graphs of four linear relationships are shown.
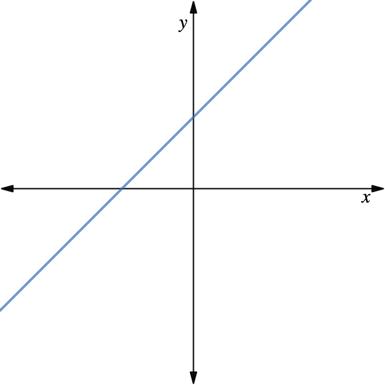
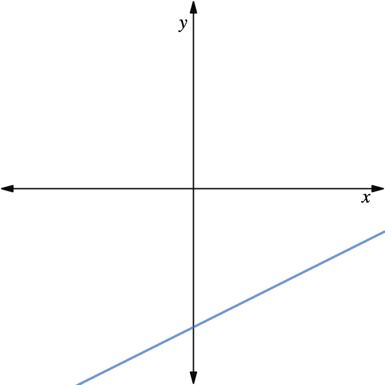
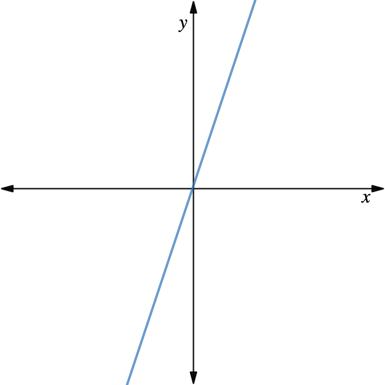
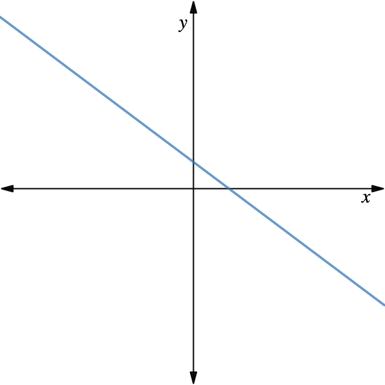
1. Circle the graph that doesn’t belong. Explain your reasoning.
1. When plugged into a USB charger, cell phones charge at a constant rate until they get closer to being fully charged.
When Michaela plugged in her phone, the battery was at 16%. After charging for 15 minutes, the battery level was at 41%.
This linear relationship can be represented by a graph where ���� represents the number of minutes the phone was plugged in, and ���� represents the percentage of the battery charged.
Harry said there is enough information from this context to find two points on the graph of this relationship.
a. Work with your partner to determine the coordinates of the two points.
Which point represents the phone’s charge when Michaela plugged it in?
Which point represents the phone’s charge 15 minutes after Michaela plugged it in?
( , ) ( , )
b. Graph the linear relationship.

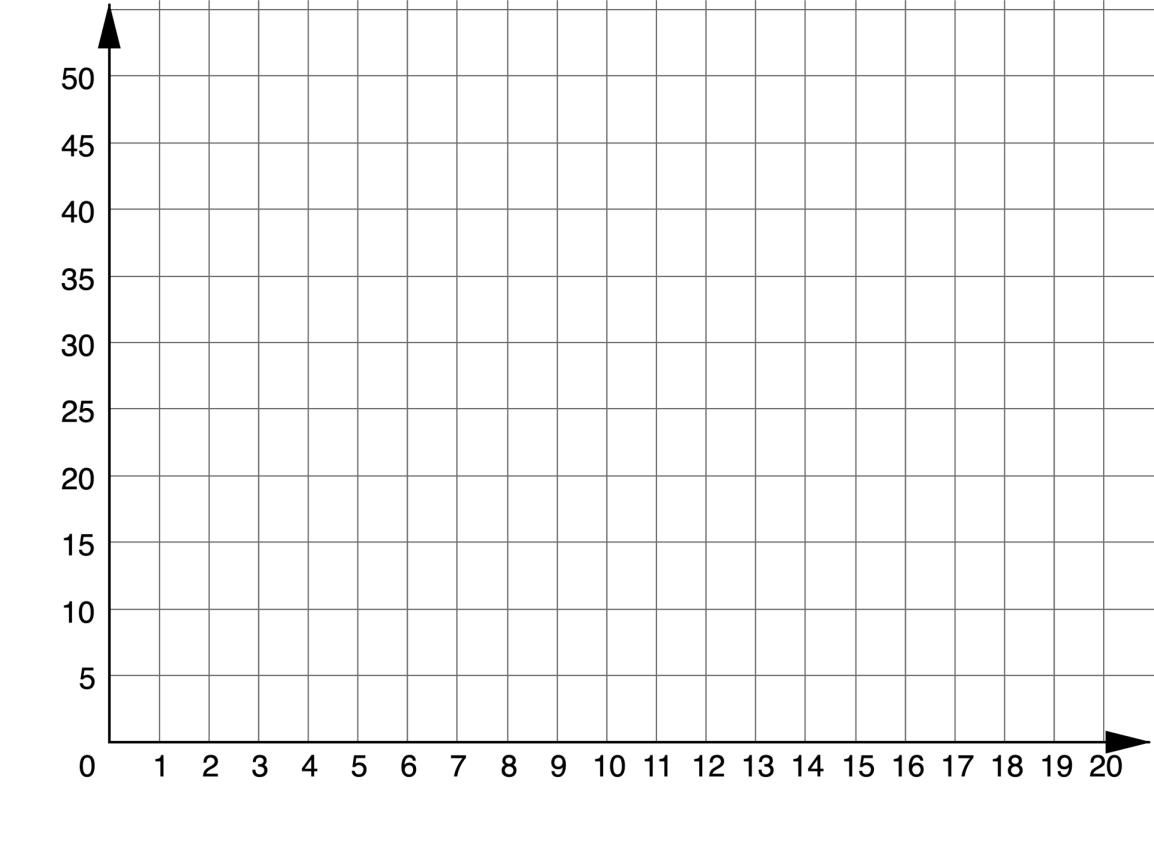
c. What information was used to graph the relationship?
d. Explain why the slope was not needed to graph this relationship.
2. The body length, ���� , of a milk snake in inches can be represented by the equation ���� = 6.5 + 2���� , where ���� is the age of the snake in months for the first two years of its life.

a. Graph the relationship between ���� and ���� .
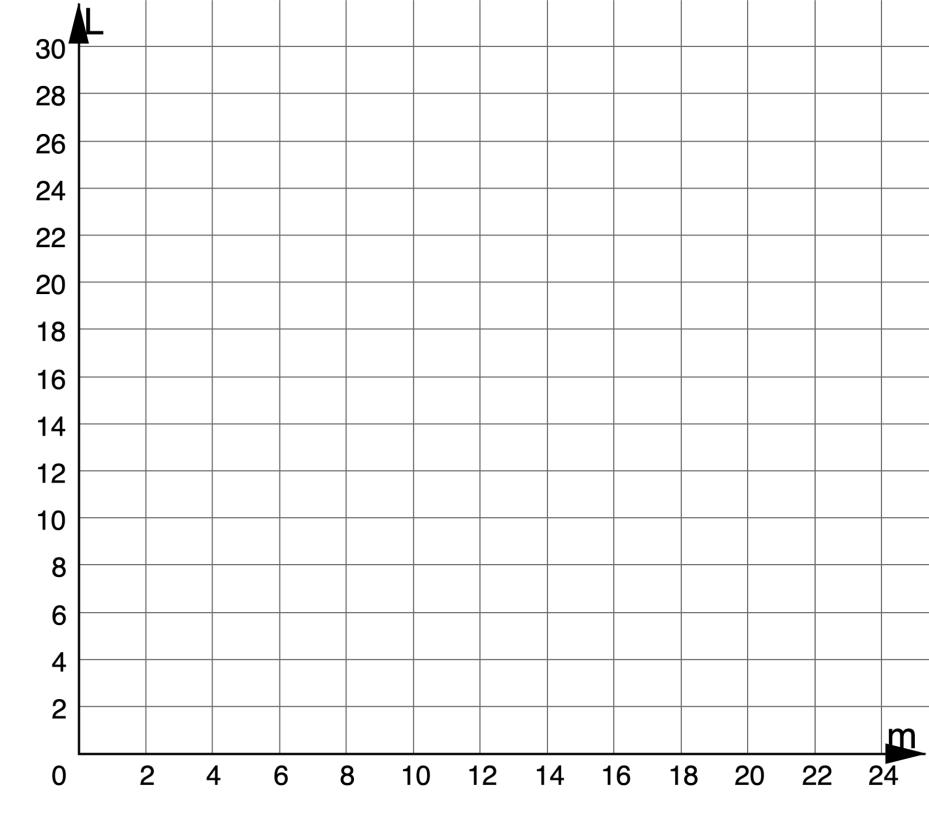
b. What information was used to graph the relationship?
c. Discuss with your partner how to determine from the equation which value represents the slope and which value represents the ���� -intercept. Write a brief summary of your discussion.
7.5.3 Bring it Together: Graphing Relationships from
For each context, different information was used to graph the linear relationships.
To graph a linear relationship given a real-world context, the information that is necessary to know is either or
o the slope only
o the ���� -intercept only
o the slope and ���� -intercept
o two ordered pairs.
o a table of values with five ordered pairs.
7.5.4 Guided
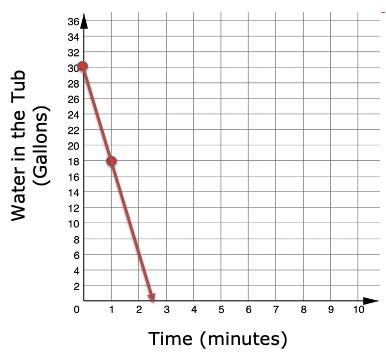
1. A bathtub drains at a constant rate. There are 30 gallons of water in the tub when Camille opens the drain. The bathtub drains at 12 gallons per minute.
a. Which information about the relationship can be determined from the situation?
o the slope and ���� -intercept of the graph o at least two ordered pairs on the graph
b. What are the slope and ���� -intercept, or at least two of the ordered pairs?
c. Graph the linear relationship between time, in minutes, ���� , and the number of gallons in the bathtub, ���� .

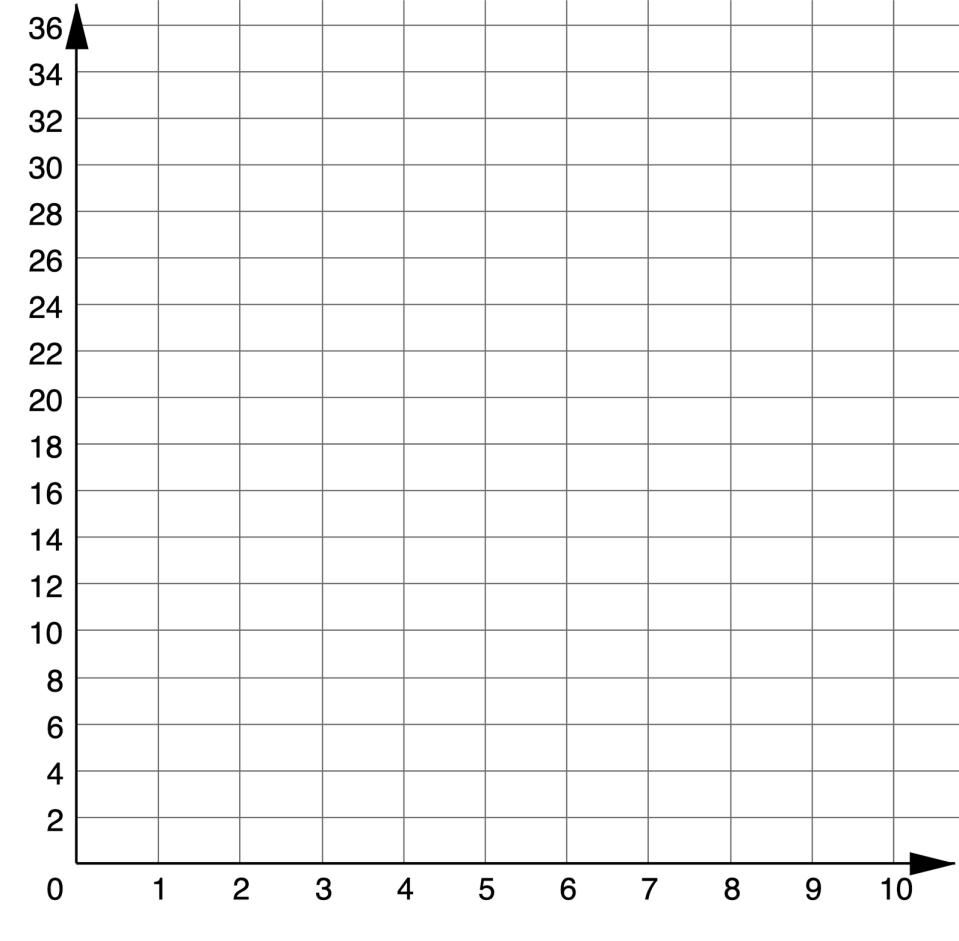
Time (minutes)
2. Scuba divers wear protective equipment when diving because the pressure placed on the body increases as they dive, due to the weight of the water. At sea level, a diver experiences 1 atmosphere of pressure (atm). The table shows the pressure on a scuba diver at various diving depths.
a. Graph the linear relationship between depth in feet, ���� , and pressure, in number of atmospheres of pressure (atm), exerted on the diver, ���� .
Pressure (atm)
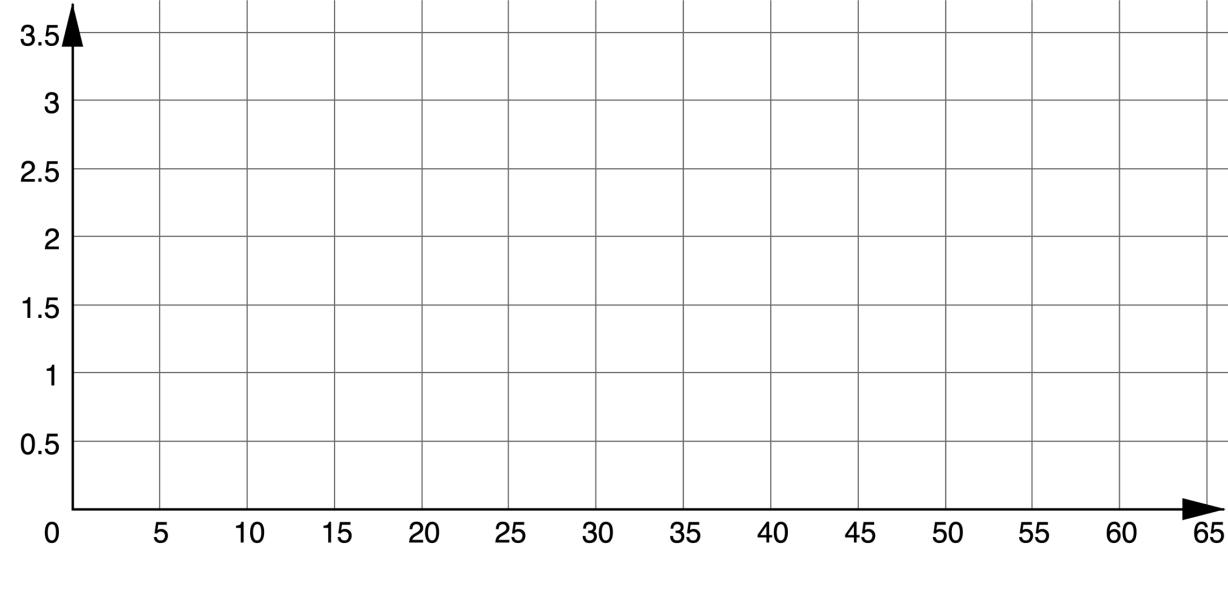
Depth (feet)
b. What is the slope of the line?
7.5.5 Your Turn!
1. A candle is 10 inches long. Ximena lights the candle and records the length of the candle, ���� , in inches (in.) over ���� hours (hrs). The table shows Ximena’s recordings.
Graph the relationship between candle height and time.
Candle Height (inches)

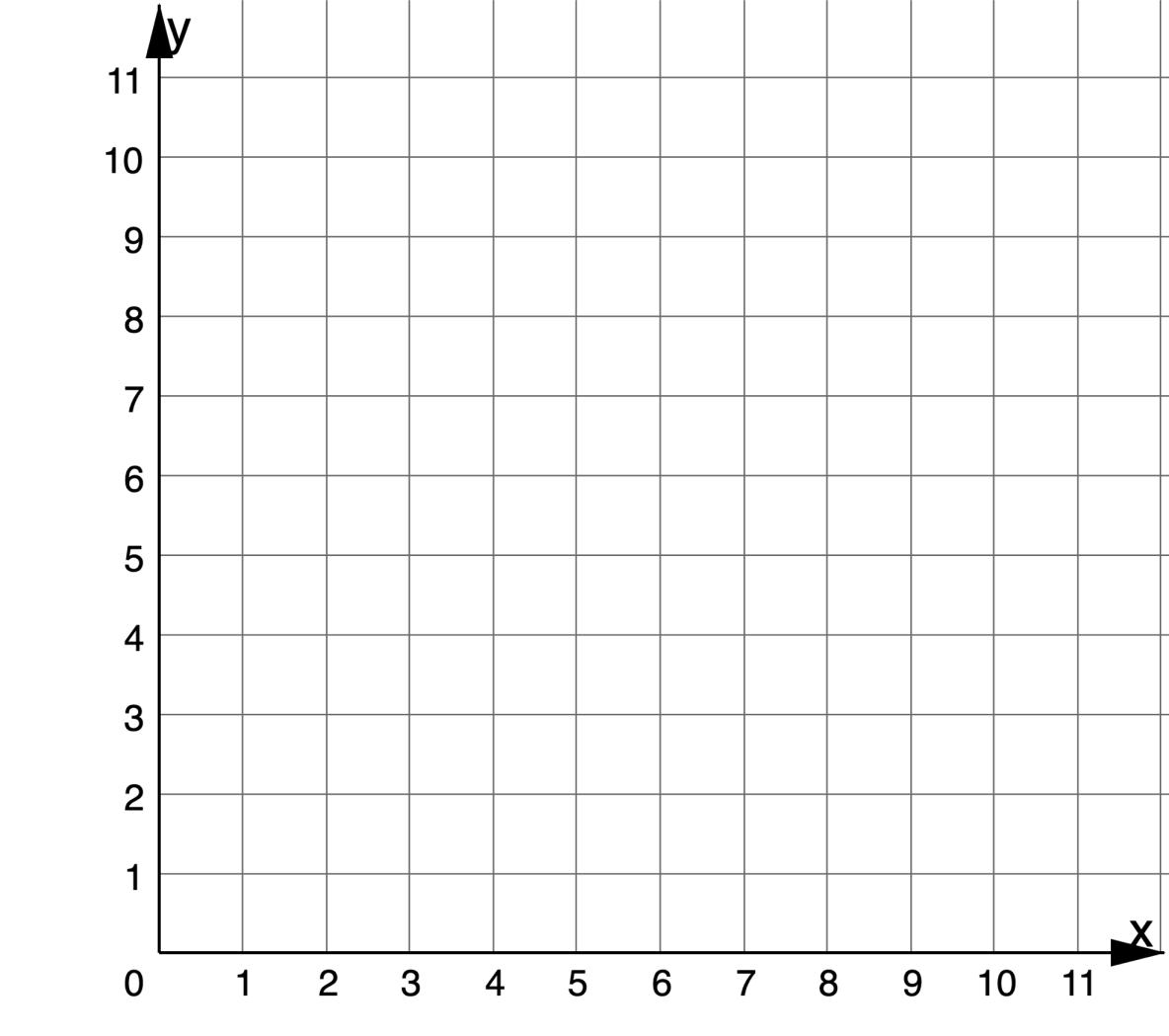
Time (hrs)
2. Gabriel planted a Leyland Cypress tree in his front yard. The tree was 11.5 feet tall when he planted it. It reached a height of 13 feet after 6 months.
Graph the linear relationship between the height of the tree in feet, ���� , and the number of months since it was planted in Gabriel’s yard, ���� .

Height (feet) Time


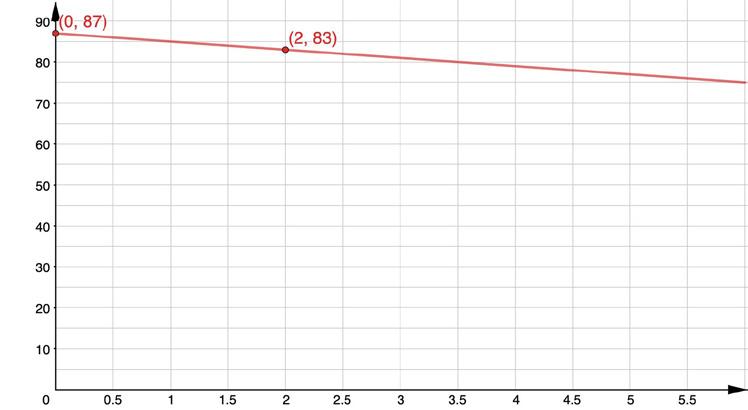
The Johnstons turned their air conditioner off while they were out of town. When they returned home, the internal temperature of the house was 87℉. They turned the air conditioner back on and after 2 hours, the temperature had dropped to 83℉. The internal temperature of the house decreased at a constant rate until reaching 75℉.
1. Graph the linear relationship.
Time (in hours)






MA.6.GR.1.1 Extend previous understanding of the coordinate plane to plot rational number ordered pairs in all four quadrants and on both axes. Identify the x- or y-axis as the line of reflection when two ordered pairs have an opposite x- and y-coordinate.
● I can plot rational numbers using a scale of 1.
BENCHMARK COHERENCE
BUILDING ON
MA.5.GR.4.1 Identify the origin and axes in the coordinate system. Plot and label ordered pairs in the first quadrant of the coordinate plane.
WORKING TOWARD
N/A
ESSENTIAL QUESTIONS
● How can you plot decimal coordinates on a graph with a whole-number scale?
● How can you plot fractional coordinates on a graph with a whole-number scale?
LESSON NARRATIVE
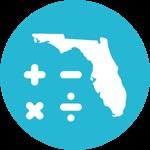
Students continue plotting coordinates with rational numbers in this second part of a two-part lesson series. Students apply what they have learned in engaging, game-like contexts in addition to real-world examples. Students will need to analyze the data to determine the range of values and the best location of the axes and plot rational numbers with a scale of one.
COMPONENT SUMMARY
5.4.1 WARM-UP (~5 MIN.)
Compare different graphs of the same data
5.4.3 COLLABORATION (15-20 MIN.)
Pinpoint coordinates playing a graphing game
5.4.5 WRAP UP (~5 MIN.)
5.4.2 TRY IT (10 MIN.)
Graph rational numbers
5.4.4 YOUR TURN! (10-15 MIN.)
Graph rational numbers and compare coordinates
Reflect on understanding of past four lessons and discuss next steps
GLOSSARY
Key Terms: N/A
Additional Terms:
● Coordinate
COMMON MISCONCEPTIONS
MATERIALS
● (Optional) Computer
ADDITIONAL PREPARATION
● The gameboard in 5.4.2 Try It is pre-made and available to print.
● Students may struggle with estimating the location of rational ordered pairs. When graphing negative fractions and decimals on a whole-number scale, students may struggle with which number to graph closer to.
● Improper fractions may be incorrectly graphed.
THINGS TO CONSIDER
● Students are still grasping negative numbers and may need vertical and horizontal number lines to aid their thinking.
● Students may struggle with converting improper fractions to mixed numbers, which may cause a roadblock to graphing. Consider having students convert all mixed numbers before beginning to graph.
LITERACY AND LANGUAGE ROUTINES
Notice and Wonder
Students participate in a Notice and Wonder routine during this lesson’s Warm-Up. This positions students to consider how the scales of graphs impact the way data is presented visually and encourages students to draw conclusions about a data set from a graph.
MATHEMATICAL THINKING AND REASONING (MTR) STANDARD
MA.K12.MTR.7.1 Real-World Contexts
5.4.4 Your Turn! positions students to consider how information in the real world can be represented using graphs and coordinate planes. Students graph data relating to temperature in two cities and then NBA player statistics. Encourage students to draw conclusions about the significance of graphing data in the real world.
Throughout this lesson, students engage with the content in a variety of ways. As students graph data points on the coordinate plane, they visually represent the data. The 5.4.2 Try It and 5.4.3 Collaboration activities encourage partner discussion for students to process the learning verbally, providing auditory entry points for learners as well.
Notice and Wonder
Engage the class in a Notice and Wonder routine. Position students to discuss what they see on each graph, ensuring they understand both graphs represent the same data set and information. Students should begin to draw conclusions about the impact of scale on the graphs and consider which graph displays the data in a more understandable way.

Each graph represents the number of wins for the Arkansas Razorbacks football team for the 2000-2019 seasons, where the �������� -axis represents the number of years since 2000.
Graph A Graph B
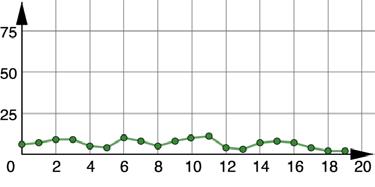
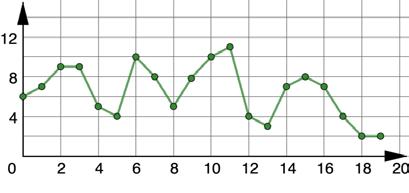
1. What do you wonder about the two graphs? Answers will vary. I wonder why the changes between the points in Graph A don’t seem as big as they are in Graph B.
2. What do you notice about the two graphs? The scale for the ��������-axis is different between the two graphs.
3. In what years did the team win at least 10 games?
Years 6, 10, and 11
4. Explain how the scale of the ��������-axis impacts the graphs. Answers will vary. The scale of the ��������-axis can make the data more or less clear. If the scale used is too big, like in Graph A, it is hard to get exact data and to see the trends of the data

A gameboard is shown on the coordinate grid, along with the number of points earned for landing in each area. Each coordinate grid axis is scaled at 1













1. Several points are given in the table. Locate each point on the coordinate grid. Complete the table by writing the score value for landing at each point. Calculate the game score by finding the sum of all the points. Verify your answer with your teacher.
( 3, 4 9)
(4 5 , 1 3 4)
(0, 2 2) 6
( 3 8, 4 9) 8
(1 5, 4 4) 5 2
( 1 2 3 , 2) 1 19
(5 4 , 11 2 ) 11 5 Game Score: ____36 26
Consider providing additional visual support for students, as the graph may be difficult to read given the number of point values and the scales on the x- and y-axes. It may be helpful to project the game board for the class so students can more clearly see where each point value is in relation to the scales, and/or to color-code each point value with the associated region of the gameboard.
If students are struggling to plot rational numbers on the gameboard, consider further scaffolding through questioning like:
• How can you plot decimal coordinates on a graph that uses a whole-number scale? How can you plot fractions on a graph that uses a whole-number scale?
• Do the coordinates need to be plotted accurately in this activity? Why?
Encourage partners to engage in mathematical discussion regarding their strategies.
• Who won? Was their strategy the same as yours?
• Did you have any issues plotting points or coming up with ordered pairs? Why?
• How did your knowledge of graphing points help you in this game?
• How did the scale of the axes impact the guessing game?

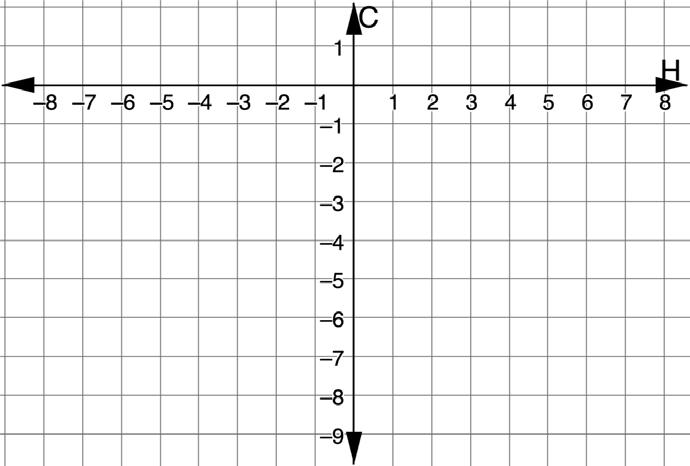
5.4.3 Collaboration: Hit or Miss
There are six shapes on the coordinate grid shown. Each partner will select one shape as their game piece. The object of the game is to guess which shape your partner selected before they guess yours. A hit means the point you guessed is inside their shape. A miss means that it is not. Keep your game board hidden from your partner during the game. Game Board
1. The shape of the region I am picking is a ______________. Answers will vary.
2. Record the coordinates of each guess in the table below. Then, plot the point on the coordinate grid game board. Answers will vary. See example below

5.4.4 Your Turn!
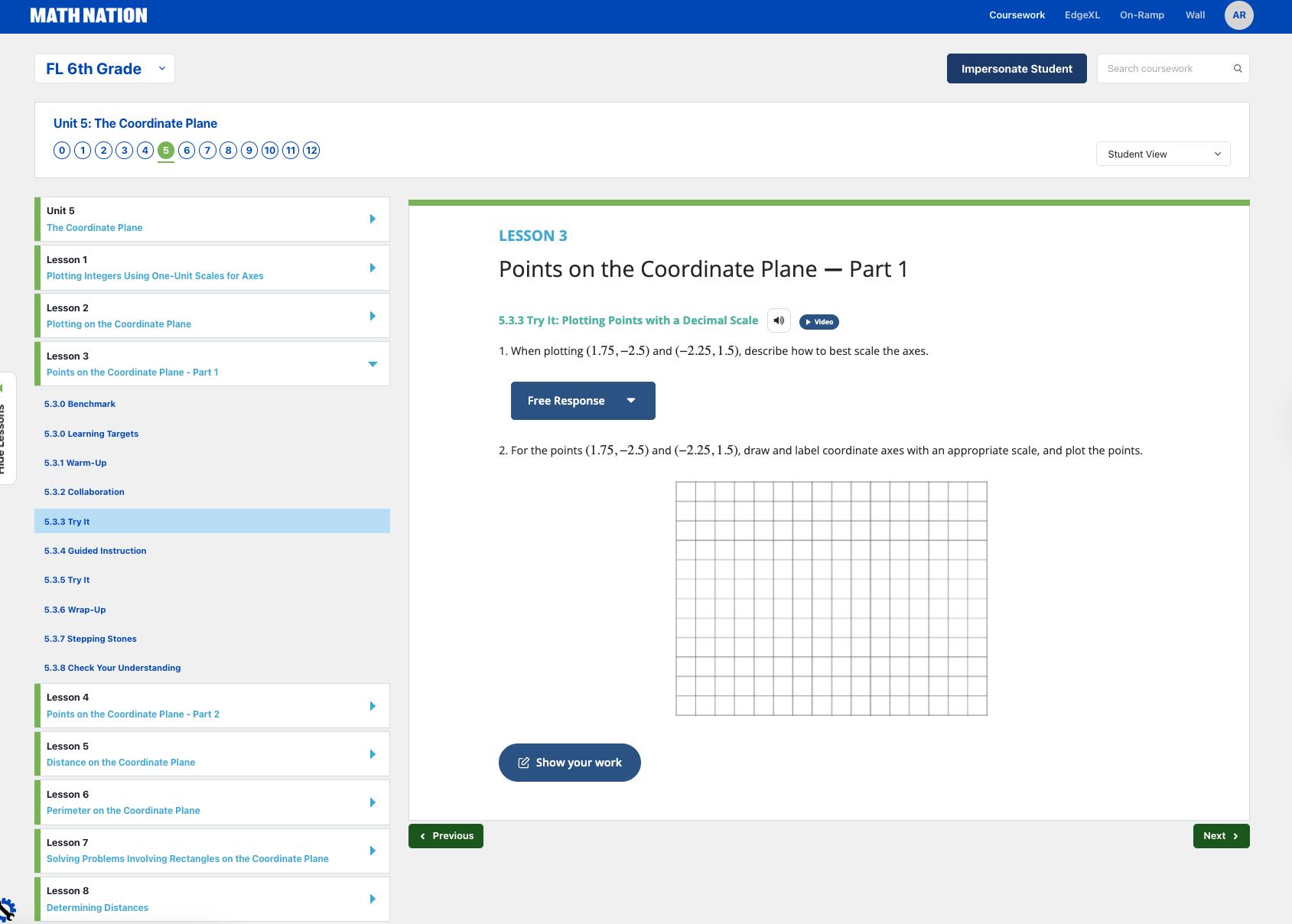
1. The temperature in Princeton, New Jersey was recorded at various times during the day. The times relative to midnight, �������� , and temperatures in degrees Celsius (°�������� ) are shown in the table.
Time (hours before or after midnight, �������� ) Temperature (°��������
a. Plot the points that represent the data.
P
b. In the town of New Haven, Connecticut, the temperature at midnight was 2 10 °�������� Plot and label this point on the same grid. Label the point C
c. Label the point that represents the temperature in Princeton at midnight �������� . Which town was warmer at midnight, Princeton or New Haven? New Haven is warmer.
Students may graph negative fractions and mixed numbers. Consider posing questions to help students reason about where to plot the points, such as:
• How did you know where to plot the fractions whose denominators were more or less than halfway?
• If the time is in hours before or after midnight, what time is zero?
• Why is 2 the highest number on the y-axis?
If students struggle to answer questions 1c and 1d, consider asking the following to provide scaffolding:
• Which coordinates should be compared to determine the warmer town?
• Is a negative mixed number greater or less than a negative fraction?
• As temperatures go further negative, are they getting hotter or colder?
Students can label each column “x” and “y” or write out ordered pairs to help remember which axis each number is on.
MA.K12.MTR.7.1: Mathematics in Real-World Context
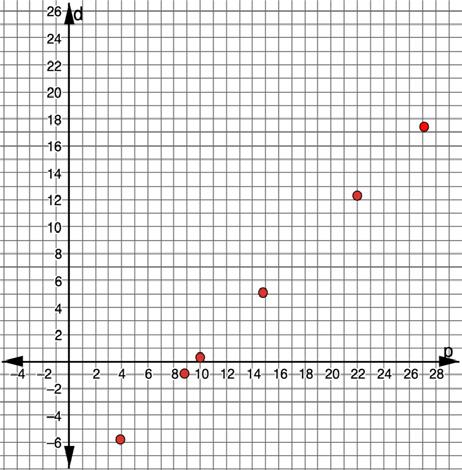
Students are graphing specific NBA players’ average points per game and how much they deviate from the average of the rest of the league. Consider asking:
• What does it mean when a coordinate is close to the x-axis on the graph?
• What does it mean when a player’s coordinates are higher on the graph?
• What does it mean when a player’s coordinates are lower on the graph?
Have students who finish early answer the following:
• What jobs do you think use this type of data?
• How would this graph be helpful to them?
• Are they jobs that you are interested in?
d. Explain how to determine which town you selected in Part C is warmer at midnight. Using the ��������-coordinate of both points, 2 10 is further up or greater than 7 2 meaning that it is warmer the other number.
2. The average NBA player scores 9 7 points per game. The table below lists six players, along with their average points per game and their difference from the average.

Think about what you have learned in the past four lessons about plotting points. As you read each statement, consider which best describes your understanding right now.
1. I need help plotting points. I’m not sure where to begin.
2. I can plot points with integers on a coordinate grid with a scale of 1, but I still need help with rational numbers and different scales.
3. I can plot points with decimals on a coordinate grid with a tenths scale, but I still need help with points that are fractions.
4. I can plot points with rational numbers that are decimals or fractions using any scale.
1. Explain which number from the list best describes you. Answers will vary.
2. Write a plan for what you can do to either move to number 4 or to help a classmate move to number 4. Answers will vary. I will practice labeling and plotting ordered pairs on a graph to increase my understanding and accuracy
Students may need to put either a checkmark or an “X” by each statement they agree or disagree with to help frame their thinking. When answering question 2, consider giving students a sticky note to write their answer on and place on their desk to help remind themselves how to achieve their goal.
MA.7.AR.4.1 Determine whether two quantities have a proportional relationship by examining a table, graph, or written description.
LEARNING TARGETS
● I can determine if two quantities have a proportional relationship.
● I can relate tables and graphs that represent the same relationship between two quantities in a real-world context.
BENCHMARK COHERENCE BUILDING ON N/A
WORKING TOWARD
MA.8.AR.3.1 Determine if a linear relationship is also a proportional relationship.
ESSENTIAL
● How do you determine if two quantities have a proportional relationship?
● How can you use a table or graph to represent a proportional relationship?
LESSON NARRATIVE
Students will be introduced to using tables and graphs to determine if a relationship is proportional or not. Students relate different representations of relationships, including written descriptions, tables, and graphs, before determining if the relationship is proportional. Students learn to determine whether a relationship is proportional from a table or graph, including explaining how they know.
11.4.1 WARM-UP (~5 MINS)
Notice and wonder with graphs of two different relationships
11.4.3 BRING IT TOGETHER (5-10 MINS)
Synthesize how to determine if a relationship is proportional
11.4.5 WRAP-UP (5 MINS)
Explaining proportional relationships
11.4.2 ACTIVITY (15-20 MINS)
Relate written descriptions of proportional relationships to graphs and tables of values
11.4.4 YOUR TURN! (~5-10 MINS)
Identifying whether relationships are proportional
GLOSSARY
Key Terms: N/A
Additional Terms: N/A
● Cards for card sort
ADDITIONAL PREPARATION
● Consider using the Five Practices for Orchestrating Productive Class Discussion when planning for the 11.4.2 Activity and 11.4.3 Bring It Together.
COMMON MISCONCEPTIONS
● Students may struggle to recognize proportional relationships from graphs or tables.
● Students may not recognize how to use the ordered pairs from a table of values to determine if a relationship is proportional.
THINGS TO CONSIDER
● Consider having students make one stack of cards from 11.4.2 Activity that shows proportional relationships and another stack of cards that does not show proportional relationships. Work with students to either create a T-chart or a Venn diagram noting the characteristics of each group of cards.
LITERACY AND LANGUAGE ROUTINES
Clarify, Critique, Correct
11.4.2 Activity and 11.4.4 Your Turn! require students to provide analysis and explanation of their responses. Allow students to swap their responses with another student. Students will then ask their partner for clarification and additional analysis as needed. This process allows students to think more analytically and to provide more detailed mathematical explanations.
MATHEMATICAL THINKING AND REASONING (MTR) STANDARD
MA.K12.MTR.5.1 Patterns and Structure
11.4.2 Activity allows students to use visual and mathematical patterns to identify common features of proportional relationships. Students analyze the tables and graphs to look for evidence of a constant ratio between each coordinate pair. Support students as they use their observations of patterns to generalize about proportional relationships.
Read and discuss the problems and scenarios aloud to assist students who benefit from auditory entry points. Emphasize the visual nature of the proportions for students who prefer visual learning methods.
Consider using the Five Practices for Orchestrating Productive Class Discussion to plan for how to facilitate a discussion that highlights various students’ voices and understanding as they further explore these relationships.
Notice and Wonder
Engage students in a Notice and Wonder routine to draw conclusions about the cost of peaches and plums based on the graph. After students complete the Warm-Up independently, consider asking questions like:
• How would you describe the cost-to-pound ratio of plums/ peaches?
• Why do you think cost is shown on the y-axis?
• What does this tell you about the relationship of the cost of an item to its weight?
If time allows during the debrief, suggest students mark where x=1 could be along the x-axis and then discuss with a partner what they notice about the y-values when x=1. Ask if they all had to use the same location for x=1 for this relationship to be true.

The graphs below show the cost, ��������, of buying �������� pounds of fruit. One graph shows the cost of buying �������� pounds of peaches, and the other shows the cost of buying �������� pounds of plums.
1. After looking at the relationships graphed, complete the table with one thing you notice and one thing you wonder.
One thing I notice is… One thing I wonder is… Answers will vary. Answers will vary.
2. Explain which fruit you think costs more per pound. Peaches cost more per pound because the line is steeper, meaning the price for 1 pound of peaches is higher on the �������� axis than for 1 pound of plums.

Several scenarios are described in the chart. Your teacher will give you two sets of cards showing tables and graphs.
1. Work with your partner to match a table of values and graph to each scenario. Write the matching table number and letter of the graph in the chart.
Written Description Table of Values Graph
a. T-shirts are priced $10 each at a store. There is a sale posted that says, “Buy two T-shirts, get the second one half-price.” The table and graph show the total cost, ��������, of �������� T-shirts.
b. A movie streaming service costs $8 49 each month. The table and graph show the total cost, ��������, for �������� months of the subscription.
c. A recipe uses 2 tablespoons of honey, �������� , for every 8 cups of flour, ��������.
d. Camping fees, ��������, at Blue Springs State Park in Volusia, FL include a $6 70 reservation fee and $24 per night, ��������
e. Rachel ran 6 laps in 18 minutes around the track at Riverview High School in Sarasota, FL. She notes the average number of minutes, �������� , that have passed after each lap, ��������
f. Kenneth is filling his fish tank with water at a flow rate of 1 6 gallons per minute. The table and graph show the number of gallons of water, ��������, after �������� minutes.
This activity is scaffolded to allow students to engage with it with their partner rather than be guided through by the teacher. There will be an opportunity to summarize and synthesize in the next component. Students may revise their thinking throughout the activity as they engage with each new question.
Observe and listen as students work with their partners. Make note of student ideas that you can ask them to share in the whole group for 11.4.3 Bring It Together. Additional scaffolding questions are provided, if needed, but this should be a primarily student-directed activity.
Support students as they analyze the tables and graphs by encouraging them to use their observations of patterns to form generalizations about proportional relationships.
2. Complete the statements using the words from the bank.
constant equivalent line ordered origin table
When two quantities are in a proportional relationship, the graph will include the , (0, 0) and the points on the graph will form a straight . The
pairs of the points on the graph match the pairs of values in the representing the same relationship. The ordered pairs in a proportional relationship are ratios. The value of the ratio is called the of proportionality.
3. Work with your partner to determine which scenarios from the card sort represent proportional relationships using the matching tables and graphs. Write the letter P next to the written description in the chart for each relationship that is proportional. Labeled in chart. The written descriptions for b, c, e, and f represent proportional relationships.
4. Use Graph D and the context it represents to complete the following parts with your partner.
a. Discuss why, for this context, it makes sense that every point on the line shown is possible.
b. Explain whether you think the graph representing this relationship will continue increasing every minute that passes.
The relationship should not continue increasing because a fish tank can only h old a set amount of water. Eventually, it would overflow. origin line ordered table equivalent constant
Question 4 and its parts provide an opportunity for the teacher to listen to students’ discussions, to observe whether they understand why the graph is continuous, and if they make connections to constraints on real-world contexts, which they explored in Unit 10. The intention of this question is to provide students with an opportunity to discuss and share their current thinking, not necessarily that they will all get this correct at this point.
The teacher can then use these observations from listening to the discussions about this question (along with the previous ones) to determine which areas may need more emphasis in the remainder of this lesson and Lesson 5, as students continue working on this benchmark.
*Note: It is not expected that students use the vocabulary of “continuous/discrete” or “constraint.” Students can use their own words to describe these concepts as they consider the real-world context.
If students are struggling with question 5, consider asking:
• If a relationship is proportional, what do we know about the ratios formed from each pair of values? (They are equivalent. (Point back to question 2.))
If students are still stuck, ask:
• If the ratios of each pair of values are equivalent for a proportional relationship, how will the ratios compare to each other if the relationship is not proportional? (They will not be equivalent.)
If the majority of the class is struggling with this, consider going over this question before or after the 11.4.3 Bring It Together.
5. Use Graph E and the table it matches to complete the following parts with your partner.
a. The points on Graph E form a straight line, but the situation does not represent a proportional relationship. Explain why it does not represent a proportional relationship. The ordered pairs in the table do not form equivalent ratios. Also, the line does not pass through the origin.
b. Use at least two ordered pairs from the table of values that matches Graph E to show why this relationship is not proportional.
Answers will vary.
This component is intended to be teacher-led and to summarize the key take-aways from the activity in 11.4.2 Activity.
Consider using observations from the activity to determine which key ideas need to be solidified or clarified. This could include discussing specific questions the student worked on. It should not be the teacher going through each question and telling the correct answer. Instead, the teacher might consider calling on students to share their thinking and respond to one another or restating something they heard while observing and asking students to discuss as the teacher leads the conversation toward solidifying these ideas.
Consider incorporating the Five Practices for Orchestrating Productive Class Discussion.


11.4.3 Bring it Together: Determining if a Relationship is Proportional Graphs representing proportional relationships have the following in common.
• The points that satisfy the relationship lie on a straight line.



• The line they lie on passes through the origin, (0, 0) Tables representing proportional relationships have the following in common.
• Each row in the table shows a ratio of the two quantities in the relationship.


• All of the ratios in the relationship are equivalent

11.4.4 Your Turn!
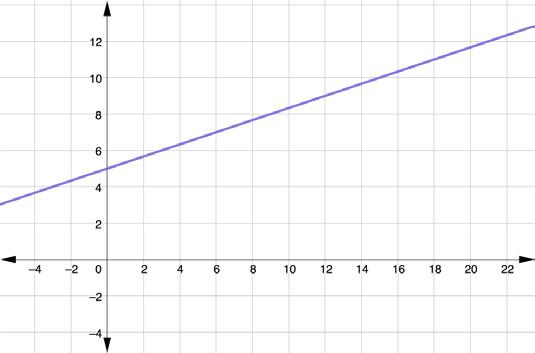
1. A graph is shown.
a. Complete the statement.
Clarify, Critique, Correct
Consider having students analyze the responses of a partner. Students will then ask their partner for clarification and additional analysis as needed. This process allows students to think more analytically and to provide more detailed mathematical explanations.
The graph a proportional relationship between two quantities
b. Explain your selection for Part A
The line does not pass through the origin.
2. Fountain drinks at Wawa are priced by size. The volume in fluid ounces (fl oz ) and price in dollars ($), before tax, for each size is shown in the table.
Volume (fl oz ) 16 21 30 Cost ($) 1 49 1 59 1 89
a. Complete the statement.
o represents o does not represent o represents o does not represent
The table a proportional relationship between two quantities
b. Explain your selection for Part A.
The ratios of the two quantities from the table are not equivalent.

11.4.5 Wrap-Up: Cool Down
1. Your friend is absent today and will need the notes from class. Write a quick note to help them understand how to determine if two quantities have a proportional relationship.
Two quantities have a proportional relationship if:
#1 – the line passes through the origin and #2 – the ratios formed from the ordered pairs, �������� �������� , are all equivalent.
11.4.5 WRAP-UP: COOL DOWN 11.4.4 YOUR TURN!
Allow students to complete the Wrap-Up verbally if they struggle to explain their thoughts in writing. Students may also prefer to draw and label an example to demonstrate a proportional relationship.
Use the information provided by students to inform future instructional approaches as well as decisions about differentiating instruction in future lessons.
MA.8.AR.3.4 Given a mathematical or real-world context, graph a two-variable linear equation from a written description, a table, or an equation in slope-intercept form.
● I can graph a two-variable linear equation from an equation, table, or written description given a real-world context.
BUILDING ON
MA.7.AR.4.3 Given a mathematical or real-world context, graph proportional relationships from a table, equation, or a written description.
WORKING TOWARD
MA.912.AR.2.4 Given a table, equation, or written description of a linear function, graph that function and determine and interpret its key features.
● How can I use the information given from a written description to graph a linear relationship?
● How can I use a linear equation or table of values to graph a linear relationship?
Students make connections between graphing two-variable linear equations and real-world situations. Students graph lines given linear relationships represented as equations, tables, and written descriptions in a real-world context.
7.5.1 WARM-UP (~5 MIN.)
Determine which graph does not belong with the others and justify their reasoning
7.5.3 BRING IT TOGETHER (5 MIN.)
Determine what information is needed to graph a linear relationship from a real-world context
7.5.5 YOUR TURN! (10 MIN.)
Additional practice graphing lines from written descriptions and tables of values of real-world linear relationships
7.5.2 EXPLORATION (10-15 MIN.)
Explore how to graph lines from written descriptions of realworld linear relationships
7.5.4 GUIDED PRACTICE (10-15 MIN.)
Practice graphing lines from written descriptions and tables of values of real-world linear relationships
7.5.6 WRAP-UP (~5 MIN.)
Demonstrate understanding of graphing linear relationships from a real-world context
GLOSSARY
Key Terms: N/A
Additional Terms:
● Slope-intercept form
● Linear relationship
● Two-variable linear equation
● Slope
● y-intercept
COMMON MISCONCEPTIONS
MATERIALS
● Straightedge
● (Optional) Desmos or graphing calculators
ADDITIONAL PREPARATION
● N/A
● Students may struggle deciding how to label the axes when graphing real-world relationships.
● Students may not know what information they need from the written description to graph the line.
THINGS TO CONSIDER
● Graphs are limited to Quadrant 1 for this lesson. The teacher can facilitate discussion on why the x- and y- values are both positive based on the contexts addressed. This will be developed further in the next lesson.
● Emphasize the importance of always including units. Thinking in terms of the units throughout the problem-solving process will help students understand the context of the relationship.
LITERACY AND LANGUAGE ROUTINES
Which One Doesn’t Belong?
The 7.5.1 Warm-Up provides students with the opportunity to choose which graph they believe does not belong with the others. All of the options can be selected, so there is no wrong answer. This encourages all students to participate. The focus is having students justify why the graph they selected does not belong.
MATHEMATICAL THINKING AND REASONING (MTR) STANDARD
MA.K12.MTR.7.1 Real-World Contexts
Students graph linear representations of real-world contexts. They determine what information they need from written descriptions to graph the line. For example, in the 7.5.2 Exploration, students must determine the two points given in a written description and then graph the points and connect them to represent the linear relationship.
7.5.2 Exploration, 7.5.4 Guided Practice, and 7.5.5 Your Turn! require students to determine what information they need in a written description to graph the linear relationship. Have students underline, circle, or label the key information. Consider adding scaffolding questions to the 7.5.5 Your Turn! activity, similar to what is included in the 7.5.4 Guided Practice, to help students who are struggling determine the important information. Also, consider having students check their graphs using Desmos or graphing calculators.
Encourage students to use mathematical vocabulary when justifying their choice. Involve several students, ideally students who rarely participate. Participating has the potential to improve students’ efficacy and agency.
• Who used slope as the criteria to determine which graph doesn’t belong? (Call on a student to share.)
• Who used the y-intercept as the criteria to determine which graph doesn’t belong? (Call on a student to share.)
• What other criteria can you use to mathematically justify which one does not belong with the others?
Challenge students who finish early to think of a reason (and even multiple reasons) that would justify why each of the options do not belong. This will keep all students engaged while students who work at a slower pace determine one response.

The graphs of four linear relationships are shown.




1. Circle the graph that doesn’t belong. Explain your reasoning.
Answers will vary. An example would be the bottom right does not belong because it is the only one with a negative slope.

1. When plugged into a USB charger, cell phones charge at a constant rate until they get closer to being fully charged.
When Michaela plugged in her phone, the battery was at 16%. After charging for 15 minutes, the battery level was at 41%
This linear relationship can be represented by a graph where represents the number of minutes the phone was plugged in, and represents the percentage of the battery charged.
Harry said there is enough information from this context to find two points on the graph of this relationship.
a. Work with your partner to determine the coordinates of the two points.
Which point represents the phone’s charge when Michaela plugged it in?
Which point represents the phone’s charge 15 minutes after Michaela plugged it in?
( __0__ ,_16__ ) ( _15__ ,__41 )
b. Graph the linear relationship.
Consider encouraging students to highlight, underline, circle, or label the key information as a form of annotation while they read. Also, use a Think Aloud to help students understand how you determined the key information and used it to graph the line.
How did you determine the points on question 1? How do you know which quantity is x and which is y? Besides being a point on the line, what does (0,16) represent?

Battery Charge (Percentage)
Number of Minutes
c. What information was used to graph the relationship?
The two points from the context were used to graph the relationship.
d. Explain why the slope was not needed to graph this relationship.
The slope between any two points on a line is the same, only two points were needed.
2. The body length, , of a milk snake in inches can be represented by the equation = 6 5 + 2 , where is the age of the snake in months for the first two years of its life.

a. Graph the relationship between and .
b. What information was used to graph the relationship?
The slope and -intercept.
c. Discuss with your partner how to determine from the equation which value represents the slope and which value represents the -intercept. Write a brief summary of your discussion. The slope is being multiplied by the independent variable. The -intercept is the constant value.
Consider asking students who finish early to estimate how many minutes it would take to fully charge the battery based on the information provided.
Compare the information used to create each graph. Discuss what specific information provided would lead to using a specific method for graphing. These discussions will improve student understanding and provide auditory entry points.
Consider having students record this information on a reference card to use in subsequent components.

7.5.3 Bring It Together: Graphing Relationships from Real-World Contexts
For each context, different information was used to graph the linear relationships.
To graph a linear relationship given a real-world context, the information that is necessary to know are either or o the slope only
o the -intercept only
o the slope and -intercept
o two ordered pairs.
o a table of values with five ordered pairs.

7.5.4 Guided Practice: Graphing Linear Relationships for Real-World Contexts
1. A bathtub drains at a constant rate. There are 30 gallons of water in the tub when Camille opens the drain. The bathtub drains at 12 gallons per minute.
a. Which information about the relationship can be determined from the situation?
o the slope and �-intercept of the graph
o at least two ordered pairs on the graph
b. What are the slope and �-intercept, or at least two of the ordered pairs?
slope = 12 ������� 1 ������ and y-intercept = 30 gallons
c. Graph the linear relationship between time, in minutes, � , and the number of gallons in the bathtub, �
How did you know that context provided information about the slope and y-intercept for question 1?
Ask students to interpret the meaning of the slope, y-intercept, and a point based on the context.
2. Scuba divers wear protective equipment when diving because the pressure placed on the body increases as they dive, due to the weight of the water. At sea level, a diver experiences 1 atmosphere of pressure (atm). The table shows the pressure on a scuba diver at various diving depths.
• On question 2, did you use all the points provided?Why or why not?
• Which points did you choose to graph and why?
a. Graph the linear relationship between depth in feet, � , and pressure, in number of atmospheres of pressure (atm), exerted on the diver, �


b. What is the slope of the line? Slope= 1 6−1
Consider having students record this information on a reference card to use in subsequent components.

7.5.3 Bring It Together: Graphing Relationships from Real-World Contexts
For each context, different information was used to graph the linear relationships.
To graph a linear relationship given a real-world context, the information that is necessary to know are either or o the slope only
o the -intercept only
o the slope and -intercept
o two ordered pairs.
o a table of values with five ordered pairs.

The Johnstons turned their air conditioner off while they were out of town. When they returned home, the internal temperature of the house was 87℉. They turned the air conditioner back on and after 2 hours, the temperature had dropped to 83℉. The internal temperature of the house decreased at a constant rate until reaching 75℉
1. Graph the linear relationship.

DIFFERENTIATE INSTRUCTION
Consider allowing students to use an audio recorder to respond to question 1.



















































































































































I can find and position pairs of integers or other rational numbers on a coordinate plane.
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
1
A town used a coordinate plane to map its landmarks. Plot the location of the town hall at the origin.
y x
Use these if you need help.
• The origin is located where the x-axis and y-axis intersect.
• The coordinates of the origin are (0, 0).
I can find and position pairs of integers or other rational numbers on a coordinate plane.
Solve the following questions.
Three locations are shown on the coordinate plane.
The gas station is located at ( 3, 2). Which point represents the gas station?
The police station is located at (3.5, 2). Plot the location of the police station on the coordinate plane.
The bakery is located at (2 1 2, 5). Plot the location of the bakery on the coordinate plane.
Three locations are shown on the coordinate plane.
The park is located at ( 5.5, 5.5). Plot the location of the park on the coordinate plane.
The location of the school is ( 6, 4). Which point represents the location of the school?
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
I can determine whether two quantities are in a proportional relationship by graphing on a coordinate plane and observing whether the graph is a straight line through the origin. 1
The table shows the relationship between money earned, y, in dollars, and number of days worked, x.
Use these if you need help.
• Graphs of proportional relationships include the origin, (0, 0)
• Graphs of proportional relationships form a straight line.
a. Graph the relationship on the coordinate plane.
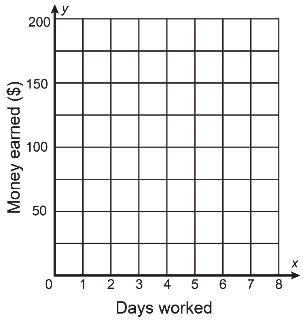
b. Explain whether the relationship is proportional.
• The ratio y x for every point on the graph of a proportional relationship except for (0, 0) is equivalent.
A video about how to solve
Solve the following questions. I can determine whether two quantities are in a proportional relationship by graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
The set of ordered pairs represents the relationship between the number of lines on a family cell phone plan, x, and the cost of the plan, y, in dollars.
(1, 100), (2, 125), (3, 150), (4, 175)
a. Graph the relationship on the coordinate plane.
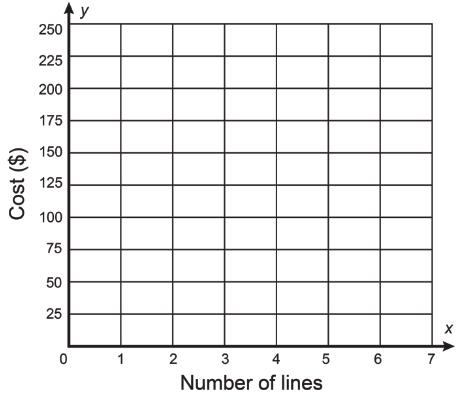
b. Explain whether the relationship is proportional.
The temperature of an ice cube is 32° Fahrenheit (°F). As the ice cube melts into water, the water temperature gradually increases over time, in minutes (min.). After 5 min., the ice is completely melted, and the water temperature is 70°F.
a. Graph the relationship on the coordinate plane.
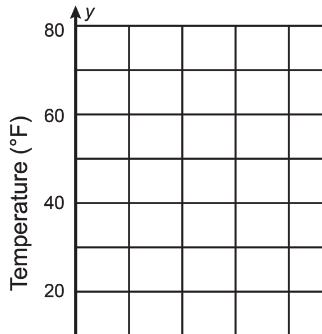
b. Explain whether the relationship is proportional.
The graph shows the relationship between the number of centimeters, x, and the number of millimeters, y, that a length measures.
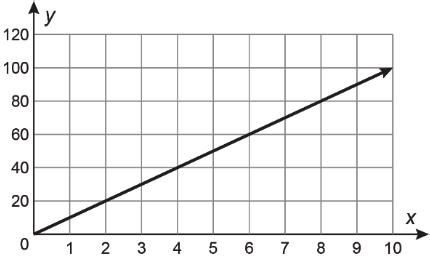
Explain whether the relationship is proportional.
The graph shows the relationship between the number of stickers, x, and their cost, y, in dollars.
Explain whether the relationship is proportional.
The graph shows the relationship between time, in months, x, and the cost of membership at a warehouse club, y, in dollars.
Explain whether the relationship is proportional.
Date:
I can gr ze a linear function expressed as
I caph and analyze I c can graph expr functiessed analyz onfuncti e a v tion, a table, and an equation with and a verbal description, equa t tion with and on descripable, able, descrip echnology. . without t. 1
I can graph a linear relationship given as an equation or verbal description.
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
Graph a linear function that has an x-intercept of (2, 0) and a y-intercept of (0, 7).
Use these if you need help.
• Linear functions can be graphed using any two points on the line, or using the slope and any single point on the line.
•Slope-intercept form of a linear function is expressed as y = mx + b, where m is the slope and the y-intercept is (0, b)
•Point-slope form of a linear function is expressed as y k = m(x h), where m is the slope and (h, k) is a point on the line.
VIDEO TUTORIAL
A video about how to solve
I can graph a linear relationship given as an equation or verbal description.
Solve the following questions. I can gr on expressed as a verbal description, a table, and an equation with ze a linear function I caph and analyze I c can graph analyz v on, tion, exprerbal functi erbal expr e essed functiessed xpressed equati t tion with descripti descripable, equa and without t. echnology.t
Graph the function y = 3x + 1.
Use the equation y = 2 1x to answer questions 3 and 4.
Complete the statement describing the key features of the line.
The graph has a slope of _____ and passes through the point (5, ____).
Use the equation y = − 3x − 7 to answer questions 5 and 6.
Complete the statement describing the key features of the line.
The graph has a slope of _______ and a y-intercept of _______.
Graph the linear function.
Graph the linear function.
BY
