BY ACCELERATE LEARNING




The program is structured by course, unit, and lesson. Each unit includes formative checkpoints throughout, centers resources, and an end-of-unit assessment. Lessons are approximately 50–60 minutes long. They are intentionally designed to fit within the calendar year, so teachers have pacing flexibility. Here is a breakdown by course of the number of units and lessons.

9–11 Units per Course (13 Units per Accelerated Course)
50–60 Min.**
* Scopes and sequences are intentionally designed for Florida’s accelerated courses.
**The time estimates in these materials refer to instructional time. Some lessons contain optional activities that provide additional practice for teachers to use at their discretion. Additional Centers and Activities are also available to differentiate instruction.

Math Nation Florida is built exclusively for Florida’s B.E.S.T. Standards, providing teachers with a highquality, standards-aligned curriculum that ensures all students can succeed in mathematics.
The design emphasizes:
• Student-centered, inquiry-based learning that builds from what students know.
• Scaffolded instruction within and across lessons, ensuring accessibility for all learners.
• Balanced development: conceptual understanding, procedural fluency, and realworld application.
• Multiple representations to deepen understanding and connect math to authentic contexts.
• Collaboration: students learn together and view mistakes as learning opportunities.
• Transfer learning: spiraling and connecting content across courses to highlight the beauty and interconnectedness of mathematics.
• Mathematical Thinking & Reasoning Standards (MTRs): embedded throughout for deeper engagement.
• Communication skills: consistent opportunities for oral and written mathematical reasoning.
Instruction draws on John Hattie’s Visible Learning research and incorporates:
• Practices with the highest impact on student growth.
• Classroom discourse and rich discussion opportunities.
• Clear strategies and content knowledge support in the Teacher Edition.
Teachers also have access to:
• Progress monitoring tools within a MultiTiered System of Support (MTSS): embedded assessments, reports, and analytics aligned to Florida’s B.E.S.T. Standards.
• Differentiation supports: remediation, intervention, and enrichment at both unit and lesson levels.
• Professional learning: point-of-use digital resources and a teacher community for continuous support.
Each unit includes a Unit Overview, or Unit 0, that offers additional planning support for the unit as a whole. Florida’s B.E.S.T. Standards are designed to ensure vertical alignment across grade levels and horizontal alignment within each course. In the Unit Overview, the Unit Narrative section describes the content of the unit, including connections to other units. The Vertical Progression section of the Unit Overview provides the vertical alignment for the benchmarks taught in the unit. Each Unit Overview also incorporates instructional strategies for differentiating, enriching, and implementing lessons throughout the unit.
The narrative captures the story of the unit, its progression, and connections to other units and courses. The overview also includes a Lessonsat-a-Glance that gives an overview of the lessons included in the unit.





This section offers specific content support for teachers to inform planning and instruction. It includes recommended strategies and models specific to the content of the unit.
The Language Supports and Instructional Supports section includes recommendations for incorporating Universal Design for Learning (UDL)™ and information for English Language Learners (ELLs). UDL from CAST© 2008 prioritizes strategies for differentiating instruction that seek to eliminate barriers of entry so that all students can learn. Each Unit Guide offers techniques specific to that unit content through the lens of UDL.
This section provides the vertical alignment of the benchmarks taught in the unit by noting the benchmarks from prior grades that are being built upon, and the benchmarks in future grades that students are working toward.
Every lesson includes a Lesson Guide that provides insight into the math thinking and reasoning for effective implementation.
Each Lesson Guide begins with an introduction that captures a snapshot of the lesson content for purposeful preparation. The Lesson Introduction includes the benchmarks and learning targets found in each student lesson. Teacher planning supports include a brief lesson narrative, key vocabulary, and lesson resource and preparation information.
Each Lesson Guide includes additional planning support, such as:
• Mathematical Thinking and Reasoning (MTR) Standards: specific MTRs are highlighted for each lesson for intentional focus when planning, though a lesson may integrate additional MTRs.
• Specific Questioning Strategies
• Math Chats
• Facilitation Suggestions: found here and also incorporated throughout the lesson components.
In the Lesson Guide, specific guidance incorporating instructional strategies is provided for each component of a lesson. This support is shown in line with the answer key of the student lesson for point-of-use implementation in the classroom. These recommendations include teacher moves, additional questions to consider asking, and differentiation ideas related to the component.

Each unit includes special lessons that wrap around the main lessons in the unit. Each unit begins with a Unit Opener and concludes with a Bring It Together, followed by a Unit Closer.
The Unit Opener is designed around a vertically aligned benchmark from the prior grade level, providing teachers with an opportunity to formatively assess students’ readiness for the unit material. The activities in these lessons are intentionally designed to be accessible to all learners, giving every student an entry point and helping teachers gauge where support may be needed as the unit begins. Following the Unit Opener, students engage in lessons that address the grade-level benchmarks for the unit.
This lesson follows the main lessons that address the grade-level benchmarks for the unit. During the Bring It Together, students revisit and apply several benchmarks taught throughout the unit. These opportunities for integrated practice not only reinforce learning but also help students build connections between mathematical concepts, deepening their understanding and skill set.
The Unit Closer presents open-ended tasks that encourage students to engage with authentic, real-world scenarios as they apply the content benchmarks from the unit. By presenting challenges that require creative problem solving and thoughtful application of mathematical concepts, these lessons support deeper learning and nurture flexible thinking. The activities in these lessons invite multiple approaches and solutions.

The main lessons that follow the Unit Opener feature the same structure. Each of these lessons includes several components.
#1 Warm-up / 5–7 minutes
The warm-up aims to engage and activate students’ existing knowledge.
Exploration Activity / 20 minutes
Each Exploration Activity gives students the opportunity to explore concepts independently or in groups, allowing them to actively engage with the material. These activities provide an entry point that enables all students to connect with new content. Guidance primarily comes through thoughtful questioning that encourages inquiry and deeper understanding.
#3
Guided Activity / 20–25 minutes
During the Guided Activity, students may work on their own or with their classmates. This is when the teacher can provide direct instruction, model useful strategies, and explain any new vocabulary to help support students’ understanding.
#4
Practice Problems / 10 minutes
Practice Problems consist of exercises that tie in the work from this lesson or spiral back to a previous day. These are designed for independent work.
Wrap-Up / 5–10 minutes
The Wrap-Up provides an opportunity for students to close out the lesson by demonstrating their understanding.
Exploration and Guided Activities serve as the core learning experience in every Math Nation Florida lesson. These engaging tasks:
• Encourage collaborative, student-led discovery through guided investigation, reasoning, and communication of mathematical ideas
• Replace front-loaded instruction with problem-solving, pattern recognition, and strategy development
• Foster a discovery-based approach where students actively construct mathematical understanding
• Purposefully integrate horizontal and vertical alignment, helping students connect concepts deeply and meaningfully
• Include built-in supports in the Teacher Edition for effective student questioning, discourse, exploration, and conceptual clarity

An additional Florida Independent Skills Practice Book (ISP) helps students solidify and refine their skills, either in class or for homework. Practice books include embedded tutorial videos in English and Spanish so students and families have 24/7 support.

Each lesson includes a set of Practice Problems. These problems are intended for independent practice.

Activity Kits provide resources for hands-on stations that reinforce Math Nation Florida concepts, allowing students to collaborate, practice skills, and apply strategies in interactive ways. Each center activity is designed to deepen understanding of Florida standards through problemsolving, discussion, and benchmark-aligned tasks.


Math Nation Florida is designed to extend support into the home for student success. To help families, we provide:
Helpful take-home letters explain how to navigate and use the Math Nation Florida platform effectively. They provide families with specific guidance on how to leverage all of the resources available to best support their student in their math journey.
Families also gain unlimited access to a comprehensive library of multilingual Study Expert videos that can be downloaded on our iOS and Android mobile apps, ensuring access anytime, anywhere, to a math tutor. The videos:
• Come in English, Spanish, and Haitian Creole
• Allow families to see how a math concept is taught to better support their student at home
• Help students who miss school due to illness or vacation keep up with their studies Dear Parent or Guardian,
● MATH NATION is an all-inclusive, comprehensive math resource created for Florida's B.E.S.T. Standards for Mathematics.
● MATH NATION IS AVAILABLE ONLINE, AND CAN BE DOWNLOADED ON IPHONES, ANDROID PHONES, AND IPADS Your student can access and engage on their own time in a familiar, comfortable, pressure-free environment.
● Fun, highly-interactive instructional videos help your student review the material they learn in class. And best yet, there are several Study Experts to choose from for each video, including Spanish and Haitian Creole speaking Study Experts.
● Digital workbook lessons align with every video and can be translated into multiple languages. Your student can also use the printed, color workbook to follow along with the videos.
● Accessibility features empower students and ensure that all students have the resources they need to be successful.
● Auto-graded practice is available for your student via the Stepping Stones and Check Your Understanding tools for each lesson. They can also engage in the Test Yourself! auto practice tool at the end of each unit.
What can I do to help my student succeed?
● Go to best.MathNation.com and have your student show you how they sign in.
● Ask your student to watch MATH NATION videos to help with homework, to review for a test, or to get caught up if they are absent from class.
● Your student can also use Stepping Stones and Check Your Understanding at the end of a lesson and the Test Yourself! Practice Tool at the end of each unit to identify which parts of the material they understood and which videos and topics they need to review.
● Visit the Family Area to watch the Welcome Video, which should help you navigate the resource-rich environment. You can access the Family Area in the lower left corner of the digital workbook or from the Menu in the top right corner.
● Watch the Family Support Videos which are provided for each and every lesson. These will tell you exactly what your student is learning in each unit and how their learning connects to how you may have learned the very same concepts.
● Take advantage of after school and weekend tutoring by having your Algebra 1, Geometry, or Algebra 2 student post their questions on the Student Wall.
● We know that education is not one-size-fits-all, so if you worry that your student needs some help getting caught up or is not being challenged, we have solutions! While our On Ramp Personalized Learning Tool is available at 5 different course levels to help students fill any gaps they might have, we also provide enrichment opportunities at the end of each unit.
● You can track your student’s performance at any time by clicking the Student Progress tab at the top of the page!



















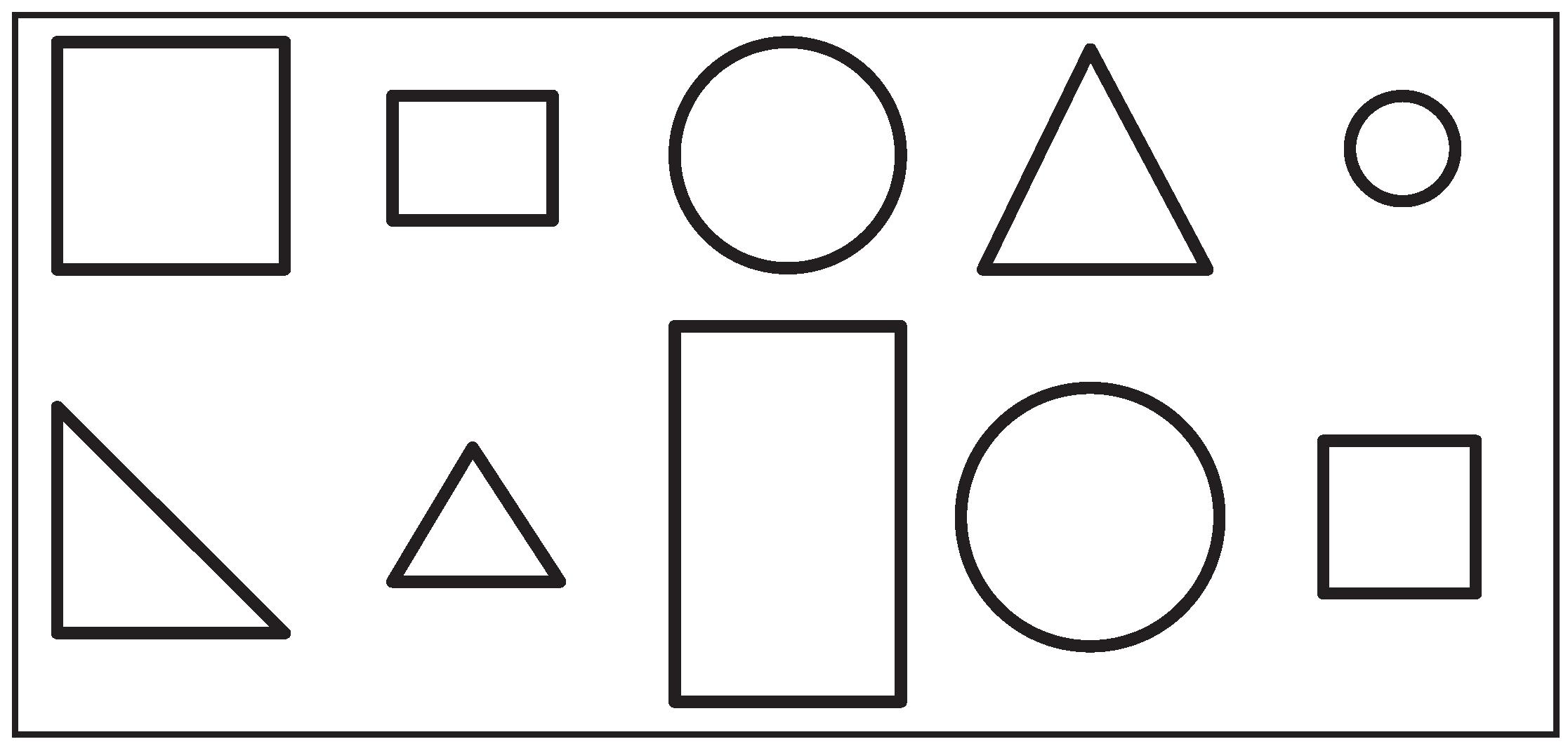
SORTING 2-D FIGURES
An image is shown.

Color each figure using a color shown in the key. Color carefully, and try to find them all!




1. Look at each figure in your bag. Can you find ways to sort them into groups? Try grouping them more than one way. Then, tell your partner what you see.
Try sorting by:
• Figures with straight sides
• Figures with corners
• Figures with curves
2. Draw two figures from each group you made.
Group 1
Pick 8 different figures. Take turns choosing with your partner. Then, sort your figures into 2–4 groups and ask your partner to check your work. Glue them in the boxes shown.
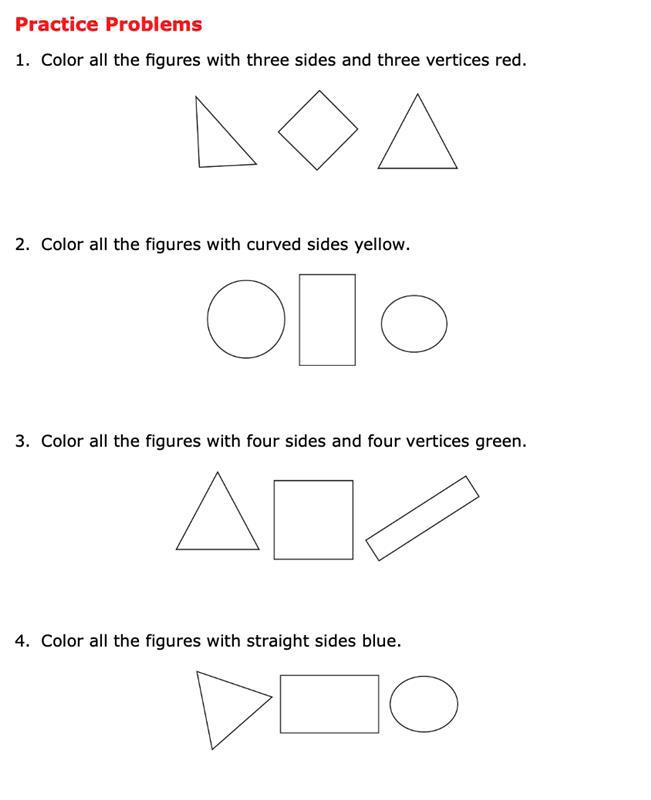
1. Color in all the figures that have 4 sides.
2. Color in all the figures that have 3 sides.
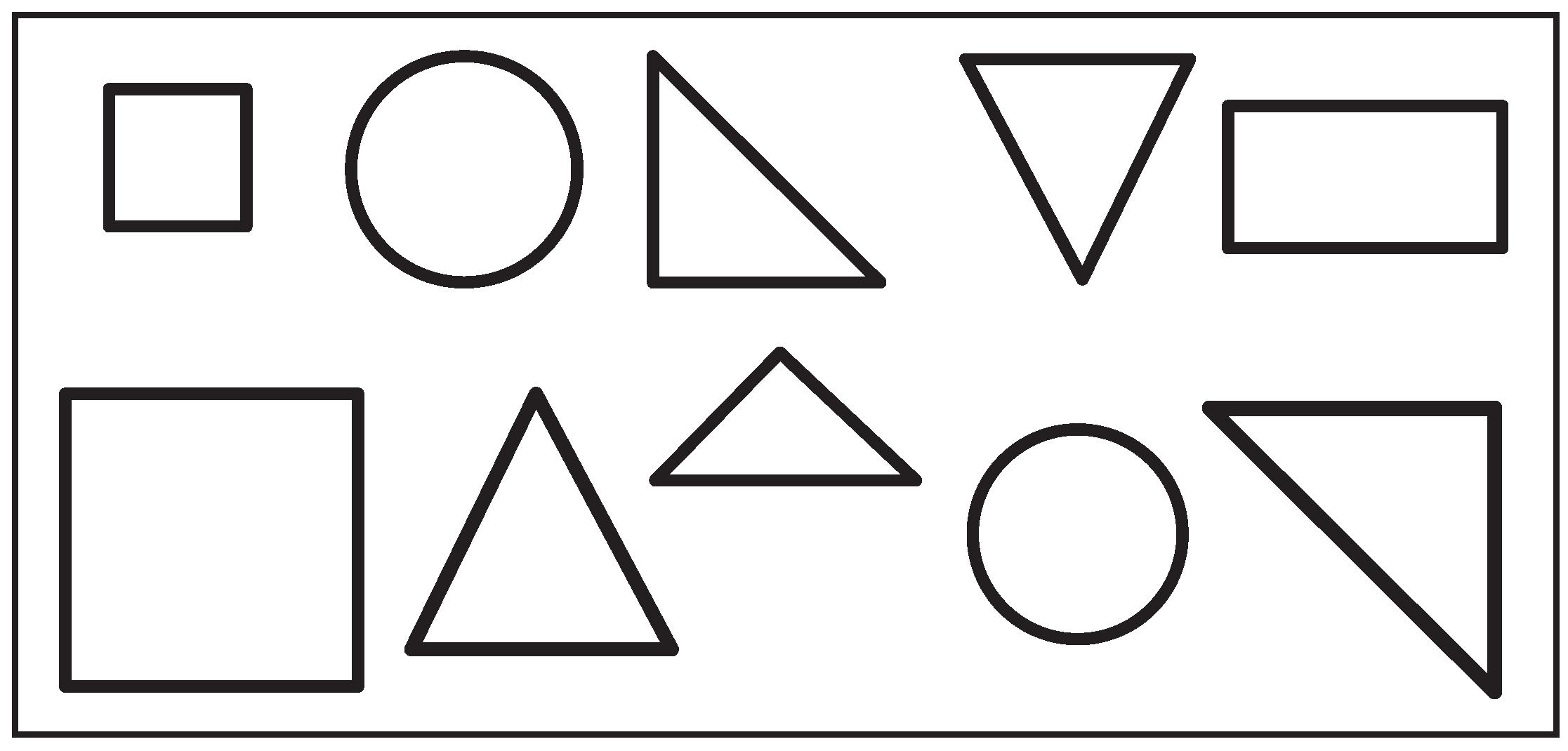
1. Look at the figures in group 1.
Circle which of the two figures shown belongs in group 1.

2. Look at the figures in group 2.
Circle which of the two figures shown belongs in group 2.

Group 1

Group 2





Unit 1, Lesson 9: Putting Together/Taking Apart –Unknown in All Positions (to 10)
TOGETHER/TAKING APART –UNKNOWN IN ALL POSITIONS (TO 10)
When you are writing a subtraction number sentence, does it matter which number you place first? Use the numbers 3, 5, and 8 to show your thinking.
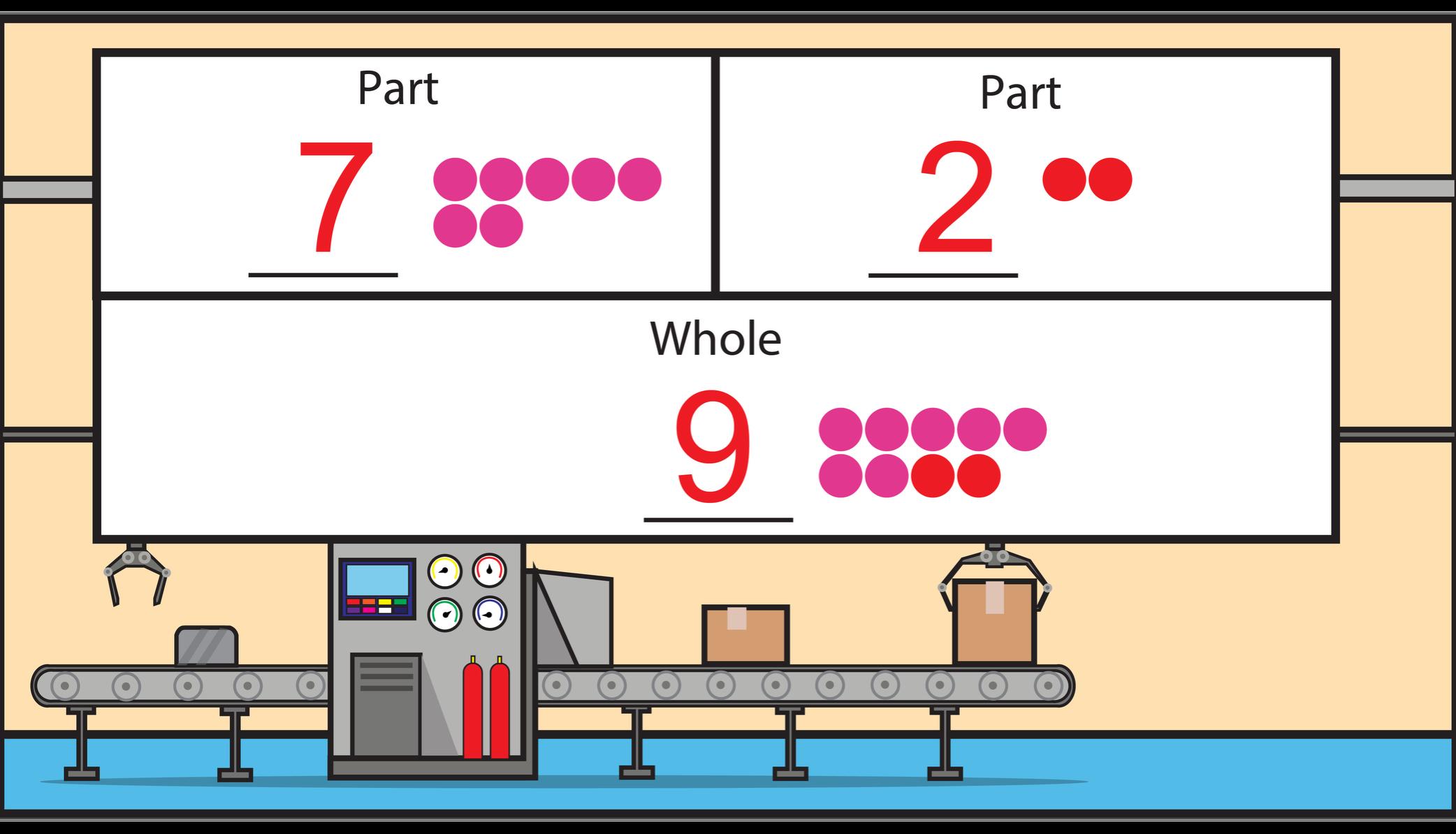
The Nail Polish Factory has decided to treat their customers to surprise boxes of free bottles of nail polish. Before the boxes can ship, the manager needs to record how many bottles of each color are in each box. Can you help the manager solve the word problems to find out how many bottles of each color are in the surprise boxes?
1. A surprise box has just been filled. There are 2 green bottles of nail polish and some purple bottles of nail polish. There are 9 total bottles of nail polish in the box.
a. Use a purple crayon and a green crayon to draw circles in the partpart-whole model to help you solve the problem.
b. Complete the number sentence to match your box of nail polish.
______ green + _______ purple = 9 bottles of nail polish
c. Complete the sentence.
There are ________ bottles of purple nail polish in the box.



1. Surprise Box 1: This box has 7 pink bottles ( ) and some red bottles ( ) of nail polish. There are 9 bottles of nail polish altogether. How many red bottles of nail polish are in the box?
a. What information do you have?
b. What do you think you are trying to find out?

c. Model this problem using the Part-Part-Whole Mat.

d. Record your answer in the ten frame.

e. Write two number sentences to represent the problem.
f. Complete the sentence.
There are ________ bottles of red nail polish in the box.
2. Read through the problem, and use manipulatives to solve it.

Surprise Box 2: This box has 3 orange bottles ( ) and 4 blue bottles ( ) of nail polish. How many bottles of nail polish are in the box?



Number of Nail Polish Bottles
Surprise Box 2
Part-Part-Whole Model
Sentences 3 Orange 4 Blue
Read through each problem and use the manipulatives to solve.

1. Surprise Box 3: This box has some blue bottles ( ) and 5 red bottles ( ) of nail polish. There are 8 bottles of nail polish in all. How many blue bottles of nail polish are in the box?






2. Surprise Box 4: This box has some pink bottles and some orange bottles of nail polish. There are 10 bottles in total. How many bottles of pink and orange nail polish could be in the box?




Surprise Box 4
Number of Nail Polish Bottles Part-Part-Whole Model Number Sentences Pink Orange 10 Total bottles Part Part Whole + = _____ There could be pink bottles and ______ orange bottles. ? ?

3. Surprise Box 5: This box has 6 red bottles ( ) and 1 orange bottle ( ) of nail polish. How many bottles of nail polish are in the box?



Surprise Box 5
Number of Nail Polish Bottles Part-Part-Whole Model Number Sentences 6 Red 1 Orange Total bottles Part Part Whole _____ + _____ = There are ______ total bottles. ?



4. Surprise Box 6: This box has some blue bottles and some pink bottles of nail polish. There are 6 bottles in total. How many bottles of blue and pink nail polish could be in the box?



Number of Nail Polish Bottles
Surprise Box 6
Part-Part-Whole Model
Number Sentences Blue Pink 6 Total bottles Part Part Whole + = _____ There could be blue bottles and ______ pink bottles. ? ?
If a new color of nail polish was added to the boxes, do you think you and your partner could use 3 numbers to put together a full box of 10? Could you also take apart 10 using three or more addends? Write an example of each.
1. Put together 3 numbers for a full box of 10.
2. Take apart 10 using 3 or more numbers.
o r k M a t
Two lists of addition expressions are shown. Draw a line to match each expression from list A with an equivalent expression in list B.
For each problem, three numbers are given. Use these numbers to create a true equation and a false equation.
1. 34, 52, 18
2. 62, 27, 35
For each equation, determine whether the equation is true or false. Then, explain your reasoning.
1. 45 + 20 = 50 + 15
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning.
2. 76 + 24 = 80 + 20
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning.
3. 18 + 25 = 20 + 13
a. Is the equation true or false?
¡ True ¡ False
b. Explain your reasoning.
For each equation, determine whether the equation is true or false. Explain your reasoning.
1. 36 + 24 = 40 + 20
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning.
2. 28 + 19 = 30 + 18
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning.
3. 50 + 25 = 45 + 30
a. Is the equation true or false?
¡ True ¡ False
b. Explain your reasoning.
4. 25 + 15 = 20 + 20
a. Is the equation true or false?
¡ True ¡ False
b. Explain your reasoning.
1. Which equation is false?
A. 18 + 19 = 20 + 17
B. 41 + 22 = 43 + 20
C. 54 + 39 = 49 + 34
D. 37 + 56 = 40 + 53
Warm-Up: Which One Doesn’t Belong?
Four different representations of numbers are shown.
3,402 2 thousands 14 hundreds 2 ones Three thousand forty-two 34 hundreds 2 ones
1. Which representation doesn’t belong?
2. Explain your thinking to your partner.
3. Draw a model to justify your thinking.
Your class decides to collect signatures from people living in your city to show support for updating the zoo. You place signature sheets at three different businesses in your city. The total number of signatures collected at each business is shown.
For each location, draw a visual representation of the amount of signatures in two different ways. Then, write an expression for each of the amounts you drew. Challenge yourself to think of two different ways to show the given amount.
The table shows the signatures that your class collected from three more businesses. Write two different expressions for each amount that was collected.
Number of Signatures Six thousand six hundred sixty-five
Expression 1 Expression 2
Restaurant
Number of Signatures 56 hundreds 121 ones
Expression 1 Expression 2
Toy Store
Number of Signatures 9,942
Expression 1 Expression 2
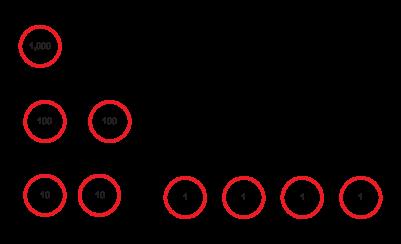
1. Complete the chart to represent the number 3,125.
Place Thousands Hundreds Tens Ones
2. Complete the chart to represent the number described.
4 thousands 11 hundreds 4 ones
Place Thousands Hundreds Tens Ones
3. Select all the expressions that represent the number 4,712.
o 47,000 + 12
o 4,000 + 700 + 10 + 2
o 47 hundreds + 12 tens
o 47 thousands + 12 ones
o 40 hundreds + 7 tens + 12 ones
Write two different expressions to represent the number 6,203.
Unit 3, Lesson 8: Remainders as Fractional Parts
Warm-Up: What Is the Question?
When all the juice is shared equally among 3 people, each person will receive a glass containing 1 ! " cups of juice.
Choose one question stem or create one of your own to help you write a question. • What is the total ___________________________________
How many
Make sense of the scenario, and respond to the problems.
The Howard family decided to take a Voyager of the Waters cruise. Their vacation will cover 2,026 miles in 5 days. The cruise ship travels at the same pace each day before docking for the night. How many miles will the Howard family be at sea each day?
1. Draw a model to represent the scenario.
2. Fill in the blanks to complete each statement.
a. The Howard family will travel ______ whole mile(s) per day, with a remainder of ______ mile(s).
b. The remainder expressed as a fraction of the divisor is , which represents the additional part of a mile the Howard family will travel per day.
3. Write an equation that represents the scenario.
4. Write a solution statement.
Make sense of each scenario, and respond to the problems.
1. The Sánchez family decided to travel across the country on motorcycles. Their vacation will span 547 miles in 6 days. They will travel the same number of miles each day. How many miles will the Sánchez family travel each day?
a. Draw a model to represent the scenario.
b. Fill in the blanks to complete each statement.
i. The Sánchez family will travel ______ whole mile(s) per day, with a remainder of ______ mile(s).
ii. The remainder expressed as a fraction of the divisor is ______, which represents the additional part of a mile the Sánchez family will travel per day.
c. Write an equation that represents the scenario.
d. Write a solution statement.
2. The Chen family decides to take a train to 7 different destinations. The train will travel the same distance to each destination, amounting to 2,144 miles in total. How many miles will the Chen family ride the train between destinations?
a. Draw a model to represent the scenario.
b. Fill in the blanks to complete each statement.
i. The Chen family will travel ______ whole mile(s) to each destination, with a remainder of ______ mile(s).
ii. The remainder expressed as a fraction of the divisor is ______, which represents the additional part of a mile the Chen family will travel to each destination.
c. Write an equation that represents the scenario.
d. Write a solution statement.
3. The Ingersoll family decides to rent a luxury car for their road trip. They plan to cover 487 miles in 4 days. They will travel the same distance each day. How many miles will the Ingersoll family drive each day?
a. Draw a model to represent the scenario.
b. Fill in the blanks to complete each statement.
i. The Ingersoll family will travel ______ whole mile(s) per day, with a remainder of ______ mile(s).
ii. The remainder expressed as a fraction of the divisor is ______, which represents the additional part of a mile the Ingersoll family will travel per day.
c. Write an equation that represents the scenario.
d. Write a solution statement.
1. Emma is keeping track of her fitness steps. Yesterday, she walked the same number of steps each hour, and that amounted to 2,225 steps in 3 hours.
a. Draw a model to represent this scenario.
b. How many steps did Emma fully complete each hour?
c. What is the remainder? Express this as a fraction, and explain what it represents in relation to the context of the situation.
d. Complete the statement with a mixed number. Emma’s step rate is steps per hour.
2. Express the remainder of the following division problem as a fraction, and explain your reasoning.
36 ÷ 5 = 7 R1
3. Which part of a division equation represents the denominator when the remainder is expressed as a fractional part?
A. Divisor
B. Dividend
C. Quotient
D. Remainder
The Welch family is on a road trip. Their goal is to travel a total distance of 1,342 miles in one week. If they space the distance out equally each day, how many miles will the Welch family travel each day?
1. Draw a model to represent the scenario.
2. Fill in the blanks to complete each statement.
a. The Welch family will travel ______ whole mile(s) per day, with a remainder of ______ mile(s).
b. The remainder expressed as a fraction of the divisor is ______, which represents the additional part of a mile the Welch family travels per day.
3. Write an equation that represents the scenario.
4. Write a solution statement.
Unit 6, Lesson 12: Divide a Unit Fraction by a Whole Number – Part 2
Warm-Up: What’s the Word? Two fraction problems are shown.
Problem A Problem B ! " ÷ 4 4 ÷ ! "
Ramsey and her friend Julisa were discussing the problems. Ramsey said that problems A and B will result in the same quotient. Explain whether you agree with Ramsey. Show your thinking or work.
Mr. Cooper made a pan of brownies. He has ! # of the pan left, and he wants to pack the leftovers into containers to share. An image representing the brownie pan is shown.
The containers Mr. Cooper has come in 3 different sizes:
• There are 6 small containers he can use if he divides the remaining brownies into 6 equal pieces.
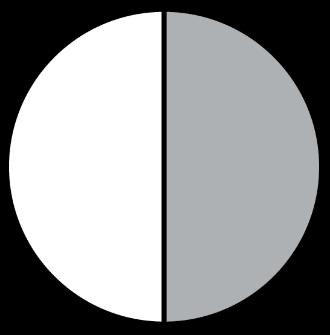
• There are 3 medium containers he can use if he divides the remaining brownies into 3 equal pieces.
• There are 2 large containers he can use if he divides the remaining brownies into 2 equal pieces.
Help Mr. Cooper determine the size of each piece of brownie depending on which set of containers he uses to share with his coworkers.
1. Complete the table. Divide each circle into equal sections. Draw a star on one of the shaded sections. Write an expression to represent the model. Determine the fractional size of each brownie in the container.
Fractional Size of Each Brownie Compared to the Whole Pan
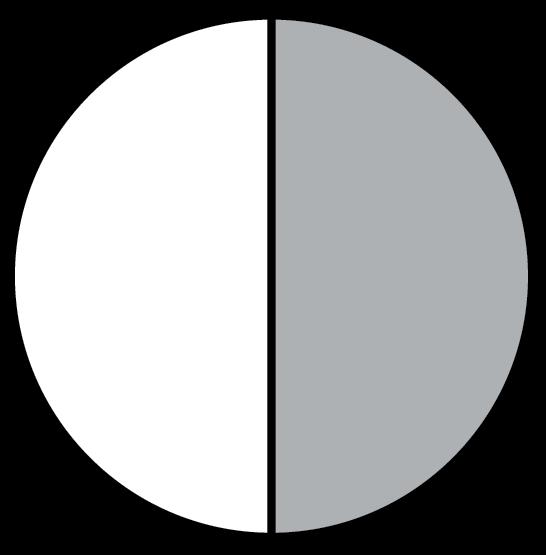


2. What do the lines you drew represent?
3. After dividing the ! # of a pan of brownies, what do the small, shaded parts represent?
4. Complete the statements.
a. The _______________ containers hold the biggest brownies. Each of these containers holds a piece that is _____ of the brownie pan.
b. The _______________ containers hold the smallest brownies. Each of these containers holds a piece that is _____ of the brownie pan.
Sew-It-All Fabrics has ! " of a square yard of their best-selling fabric left over after making a tablecloth. A scale drawing of the fabric is shown, with the remaining fabric shaded gray.
Sew-It-All Fabrics wants to make some napkins out of the remaining fabric, but they have multiple options:
• They could divide the remaining fabric into 3 equal pieces.
• They could divide the remaining fabric into 5 equal pieces.
• They could divide the remaining fabric into 7 equal pieces.

Help Sew-It-All Fabrics determine the size of each napkin they could make.
1. Complete the table. Use the number line to represent how to divide the remaining fabric into equal sections. Draw a star on one of the sections. Write an expression to represent each model, and determine the fractional size of each napkin.
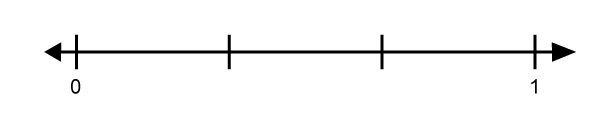


2. What does one whole represent in this scenario?
3. Complete the statement.
Each napkin size represents a fraction of ___________________.
4. How are the problems from the Exploration Activity and Guided Activity similar?
5. Complete the statements.
a. When dividing a unit fraction by a whole number, the result is a fraction.
smaller ¡ larger
b. The greater the divisor is, the each piece is and the pieces there are.
Draw a representation of the expression using a model or a number line. Then, write the resulting quotient.
5. Choose one of the problems 1–4, and use a different model to represent your answer.
1. What is ! " ÷ 2?
A. ! $
B. # "
C. ! %
D. ! !
2. What is ! & ÷ 5?
A. % & B. ! #'
C. ! (
D. & %
3. What is ! $ ÷ 5?
A. ! !!
B. # !'
C. ! "'
D. # $












Kindergarten Mathematics • Unit 7, Lesson 3
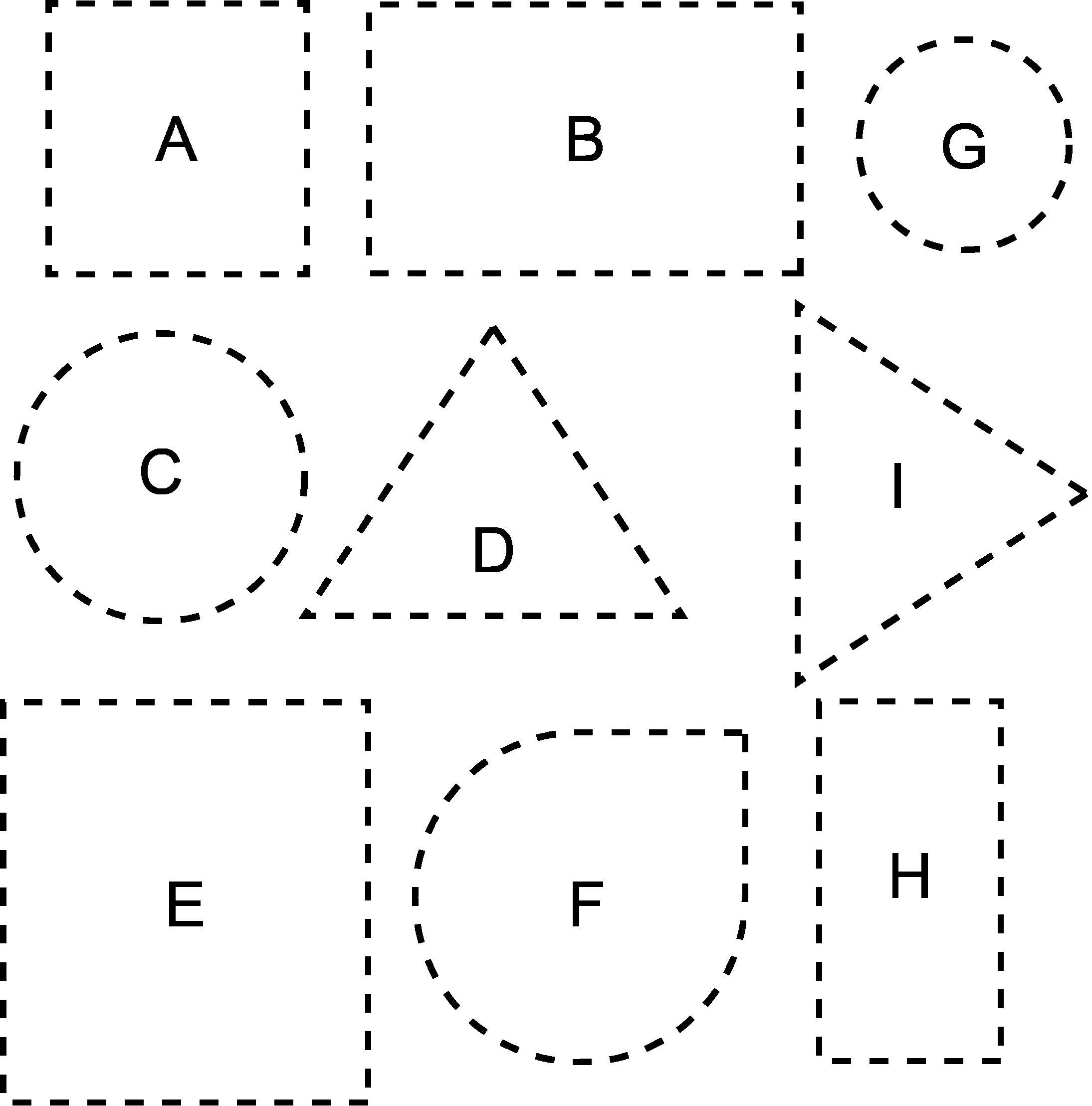
Students will sort regular and irregular two-dimensional figures into groups based on their observations.
Benchmark/MTRs
• MA.K.GR.1.2 Compare twodimensional figures based on their similarities, differences and positions. Sort two-dimensional figures based on their similarities and differences. Figures are limited to circles, triangles, rectangles and squares.
• MA.K12.MTR.1.1 Actively participate in effortful learning both individually and collectively.
• MA.K12.MTR.2.1 Demonstrate understanding by representing problems in multiple ways.
• MA.K12.MTR.4.1 Engage in discussions that reflect on the mathematical thinking of self and others.
Students explore and sort two-dimensional figures by identifying similarities and differences. They develop a conceptual understanding of attributes such as sides and vertices while learning that color and size are not defining attributes of figures.
• attribute: a characteristic or feature of an object, typically used to describe the size, shape, or color of objects in a group or pattern
• circle: a perfectly round two-dimensional figure, where all points on the circle are equidistant from the center
• compare: to examine the similarities and differences between items
• rectangle: a quadrilateral containing four right angles
• side: a straight line segment or curved segment that joins two vertices in a figure
• sort: to group or arrange according to specific characteristics
• square: a quadrilateral with four right angles and four equal-length sides
• triangle: a polygon with exactly three sides and three vertices
• two-dimensional figure: a flat figure that has only two dimensions, such as length and width; examples include circles, triangles, rectangles, and squares
• vertex (of a figure): the point at which the rays or sides of an angle, the sides of a twodimensional figure, or the edges of a three-dimensional figure meet (the plural form is vertices.)
Printed
• 1 Set of 2-D Figure Cutouts (per pair) Reusable
• 1 Green crayon (per student)
• 1 Red crayon (per student)
• 1 Blue crayon (per student)
• 1 Purple crayon (per student)
PREPARATION
Consumable
• 1 Resealable bag (per pair)
• 1 Glue stick (per pair)
• Plan for students to work in pairs for the Exploration and Guided Activities.
• Print the 2-D Figure Cutouts on different-colored paper. (Consider printing in different colors and mixing the colors to show that color is not an attribute used to classify the figures.)
• Cut out the 2-D Figure Cutouts, and place one of each figure into a resealable bag for each pair. (Do not put all the figures that are the same color in one bag.)
• Gather crayons for each student.
• Gather a glue stick for each pair.
Procedure and Facilitation
• Display the image from the Warm-Up. Then, ask the following questions:
o What do you see? Answers will vary: a building, trees, a fence, etc.
o What do you wonder? Answers will vary. Why are some of the figures white?
• Explain that students will color in some of the figures in the image based on the type of figure they are.
• Call on a few students to share what they know about each type of figure (triangles, squares, rectangles, and circles). Note that observations can be informal as students develop the language to describe attributes of the figures.
• Distribute crayons to each student.
• Students should work independently to complete the Warm-Up.
• Monitor students as they work to check for understanding. Provide assistance as needed.
• After the activity, use the following guiding questions to facilitate a discussion:
o How did you know the difference between a square and a rectangle? Answers will vary. A square has sides that are all the same length. A rectangle has two long sides and two short sides.
o Were there other figures in the picture? Answers will vary. Yes, there were figures that weren’t in the key.
o How many of each figure did you see? Answers will vary. I found and colored 3 triangles, 4 squares, 1 rectangle, and 1 circle. (The clock is a circle, so some students may have colored it purple also.)
Student-Facing Activity and Answer Key
An image is shown.

Color each figure using a color shown in the key. Color carefully, and try to find them all!




Procedure and Facilitation
• Read the following scenario to the class: My family and I dropped off some bags of donations at a local secondhand store. When they received our bags, the workers poured out the contents and started to sort the objects into groups. Although the objects in each bag were not exactly alike, the workers were able to find something about them that was the same. Can you help the workers sort the objects in the bags they didn’t get to?
• Arrange students in pairs to complete the activity.
• Give a set of 2-D Figure Cutouts to each pair.
• Direct students’ attention to the figures. Allow them a few moments to discover the objects and experience how they work with their partners.
• Read problem 1 to students. Encourage them to sort in several different ways.
• Circulate to monitor students as they work with their partners, and check for understanding using the following guiding questions. As students respond, repeat their responses to incorporate the formal vocabulary they are learning:
o How did you sort your figures? Answers will vary. These figures have straight sides, and these figures do not.
o What do the figures in this group have in common? Answers will vary. These figures all have curved lines.
o Is there another way you can sort your figures? Answers will vary. I can sort them by how many vertices/corners each figure has.
• After the activity, ask a few pairs to share a group they created and the attribute they used to sort the figures into that group. As students respond, repeat their responses to incorporate the formal vocabulary they are learning.
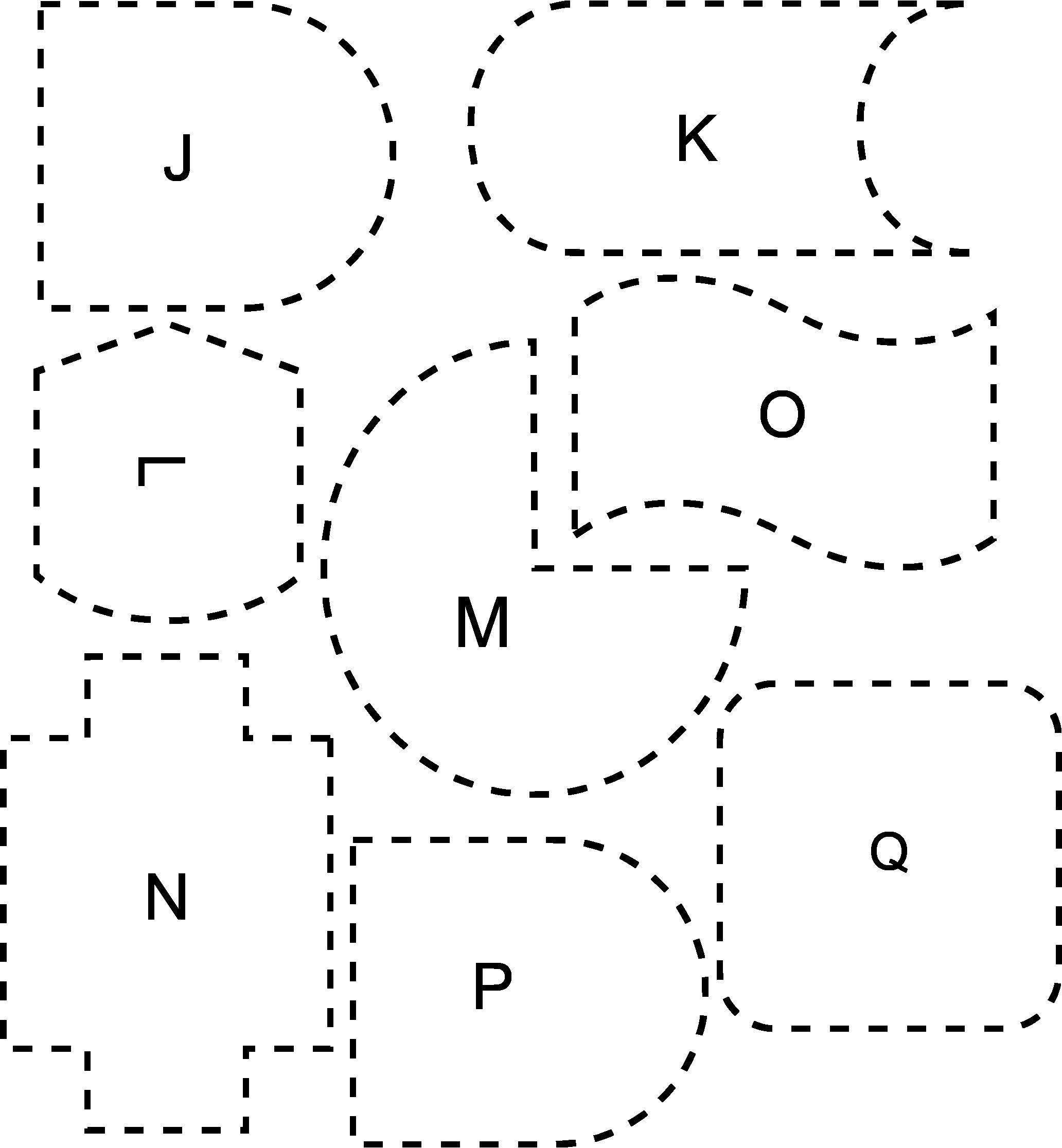
1. Look at each figure in your bag. Can you find ways to sort them into groups? Try grouping them more than one way. Then, tell your partner what you see.
Try sorting by:
• Figures with straight sides
• Figures with corners
• Figures with curves
2. Draw two figures from each group you made. Answers will vary. Students may sort figures with straight lines, corners, or curves.
Procedure and Facilitation
• Students will continue working in pairs for this activity.
• Read the instructions in the Student-Facing Activity.
• Clarify that each student will select their own 8 figures. Pairs should take turns picking from the figures in their bag until each student has chosen 8 figures. Each student sorts their own selected figures. They get to choose the way they want to sort the objects and how many groups they want to use (up to 4 different groups).
• Continue using the guiding questions from the Exploration Activity as you monitor students while they work.
• Give a glue stick to each pair.
• Prompt students to explain to their partners how they sorted their figures. If their partners approve of how the figures were sorted, instruct students to glue the figures into the boxes in their workbooks Remind them that they can make up to 4 groups.
• After the activity, invite the class to a Math Chat to share their observations and learning.
o If we put all these figures together in a group, how could you describe something they all have in common? Answers will vary. All of these figures are flat. They are all two-dimensional.
o How did you and your partner sort the objects in your bag? Answers will vary: curved sides and straight sides; 1 side, 3 sides, 4 sides, more than 4 sides.
o Is there another way to sort the figures in the bag? Explain. Answers will vary. We could have sorted by how many vertices/corners the figures have.
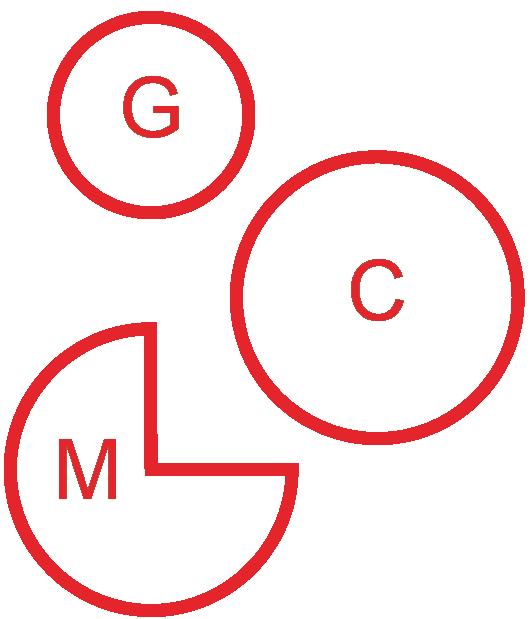
o Were there some objects in your bag that didn’t seem to fit in any categories? Why? Answers will vary. Figure F was hard for me to sort because it had a point (vertex/corner) but no sides.
o What do figures A and B have in common? Answers will vary. They both have four sides. They both have four vertices/corners.
o Can you draw a new figure that would fit into each of your groups? Answers will vary. Students can draw a new figure and share their reasoning with their partners or with the whole class.
o How are figures C and F different? Answers will vary. Figure F has a vertex, but figure C does not.
o How are figures C and M similar? How are they different? Answers will vary. Figures C and M both have a curved side Figure M has vertices/corners, but figure C does not.
o What are two-dimensional figures? Answers will vary: figures that are flat and can be measured in only two ways (length and width).
Pick 8 different figures. Take turns choosing with your partner. Then, sort your figures into 2–4 groups and ask your partner to check your work. Glue them in the boxes shown.
Answers will vary. Possible groups include the following:
• Straight and curved lines
• Points and no points (vertices/corners)
• Number of sides
• Number of points (vertices/corners)
• Same shape of figure
Sample group:
Sample group:
Read each problem aloud one at a time, and give students time to complete the problem. They should complete the practice problems independently.
Student-Facing Activity and Answer Key
1. Color in all the figures that have 4 sides.
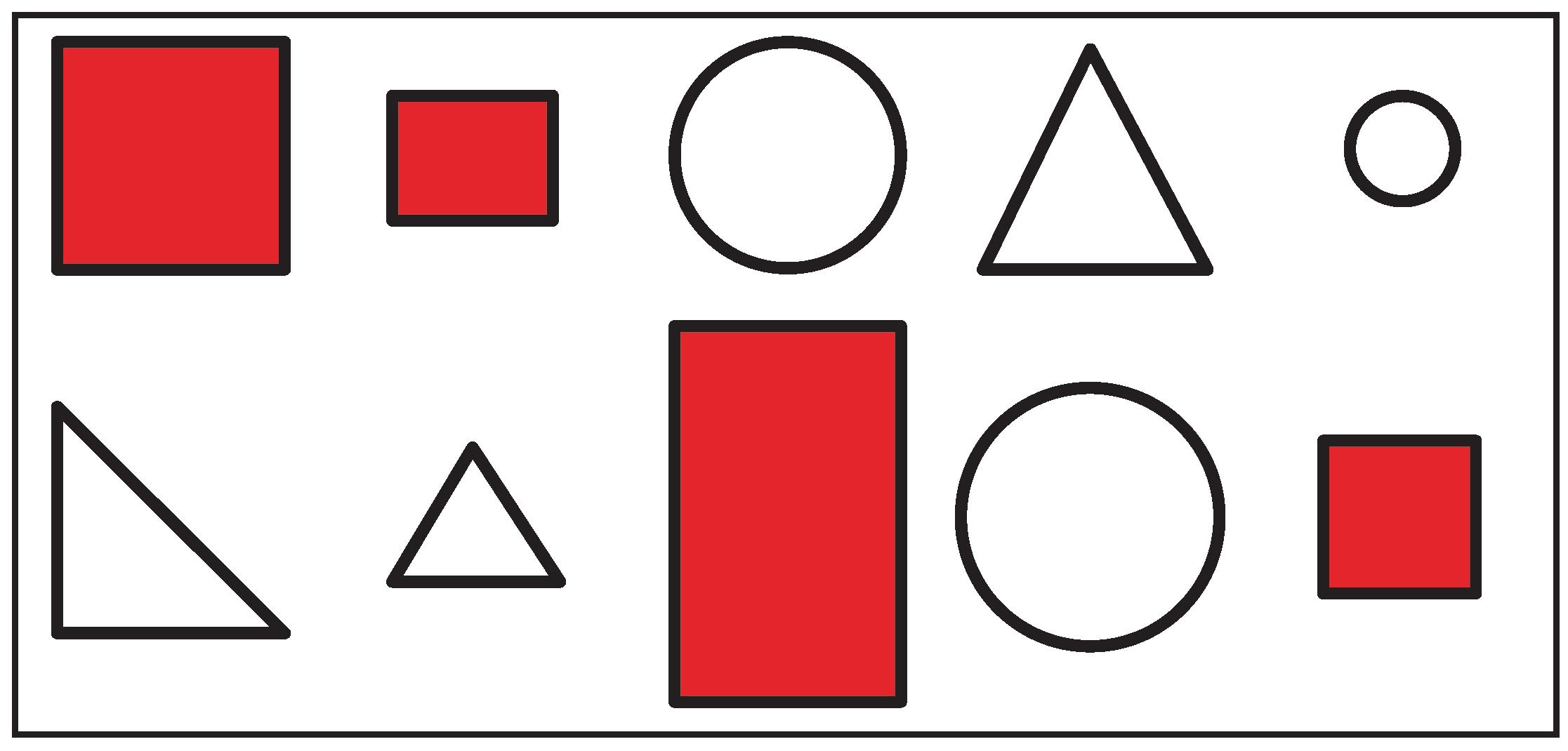
2. Color in all the figures that have 3 sides.
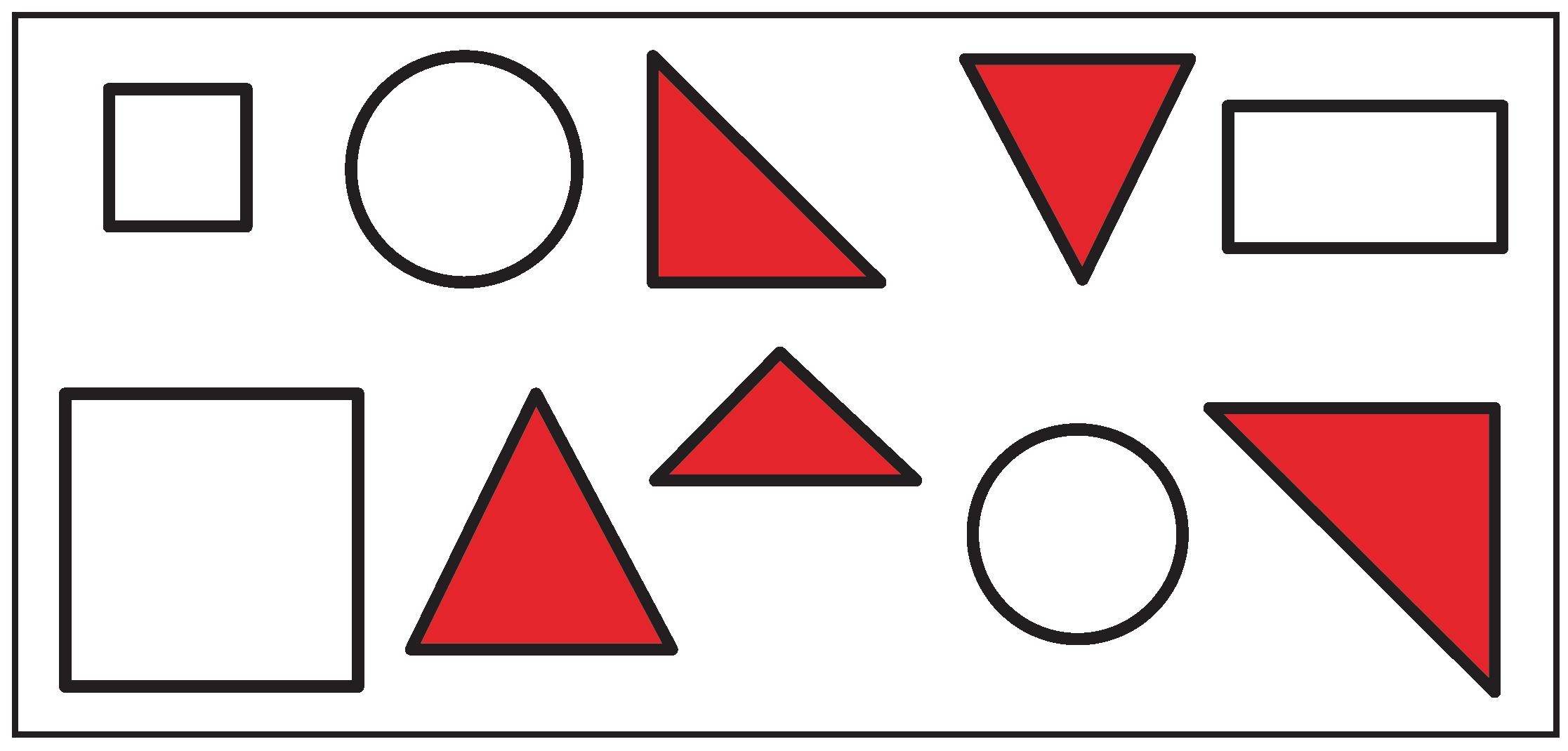
Allow students to complete the Wrap-Up independently to assess their understanding of how figures can be sorted based on attributes such as number of sides or corners.
Student-Facing Activity and Answer Key
1. Look at the figures in group 1.
Circle which of the two figures shown belongs in group 1.
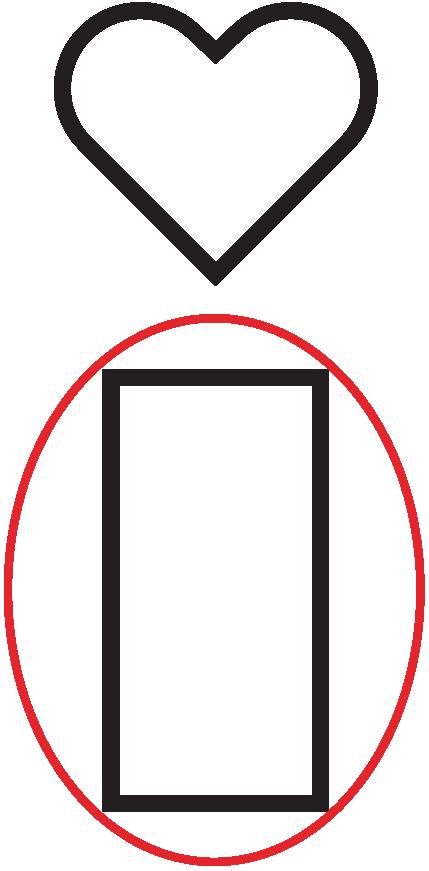
2. Look at the figures in group 2.
Circle which of the two figures shown belongs in group 2.
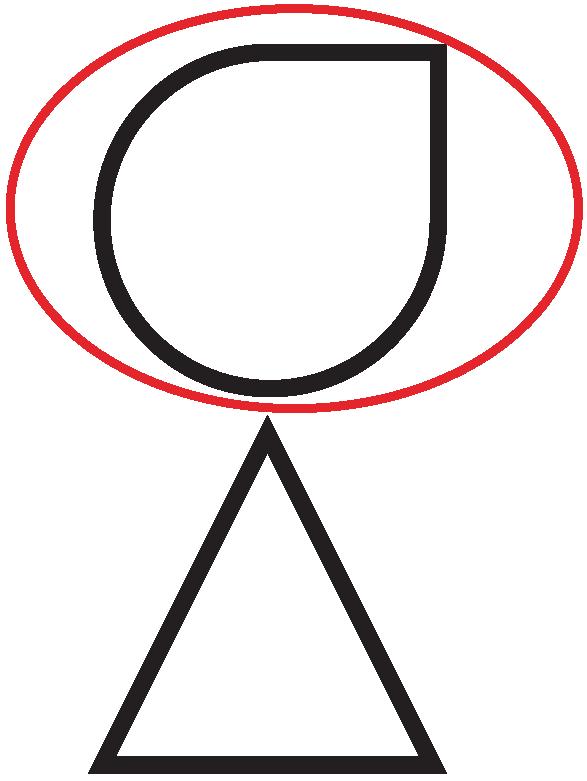
1

2

Students will use objects and pictorial models to solve put-together and take-apart problem types where the unknowns may be in any position.
Benchmarks / MTRs
• MA.1.NSO.2.2 Add two whole numbers with sums from 0 to 20 and subtract using related facts with procedural reliability.
• MA.1.AR.1.2 Solve addition and subtraction real-world problems using objects, drawings or equations to represent the problem.
• MA.1.AR.2.3 Determine the unknown whole number in an addition or subtraction equation, relating three whole numbers, with the unknown in any position.
• MA.K12.MTR.1.1 Actively participate in effortful learning both individually and collectively.
• MA.K12.MTR.4.1 Engage in discussions that reflect on the mathematical thinking of self and others.
• MA.K12.MTR.7.1 Apply mathematics to real-world contexts.
Students use objects and pictorial models to solve put-together and take-apart problem types where the unknowns may be in any position. Students learn through a scenario in which they must find how many bottles of each color of nail polish are in each surprise box. Once solved, students share their learning.
• add: to combine two or more numbers to get a sum, or total
• compare: to determine similarities or differences between two or more objects or numbers
• compose: to put pieces together
• decompose: to break apart
• difference: the distance between two numbers; the result of subtracting one number from another
• equal: same or balanced
• join: to put together
• part-part-whole model: a visual model for showing the relationship among numbers in addition and subtraction situations
• separate: to take apart or remove
• solve: to find an answer or solution to a problem
• subtract: to take away an amount from a larger amount; to find the difference between two numbers
• sum: the total amount; the result in addition
• total: how many there are in all
Printed
• 1 Work Mat (optional, per pair)
Reusable
• 1 Purple crayon (per student)
• 1 Green crayon (per student)
• 10 Two-color counters (optional, per student)
• Prepare to have students work with partners to complete the Exploration Activity.
• Either print a Work Mat for each pair of students or have them work in their workbooks.
• Prepare to have students work individually to complete the Guided Activity.
Procedure and Facilitation
• Give students quiet time to think about the problem and work on it individually.
• Then, have students share their responses or progress with a partner.
• Once these partner conversations have taken place, select students to share their thoughts with the class.
Student-Facing Activity and Answer Key
When you are writing a subtraction number sentence, does it matter which number you place first? Use the numbers 3, 5, and 8 to show your thinking. Answers will vary. Yes. Usually, the largest number comes first. The second number also matters because 8 – 5 = 3 is different from 8 – 3 = 5.
Procedure and Facilitation
• Read the introduction of the activity to the students.
• Instruct students to begin by reading the problem or provide reading assistance if needed. Monitor students as they use crayons to create a drawing to model the problem. Students can draw the model in their workbooks or by using the provided Work Mat.
• Ask students to write the number of each color of nail polish from the problem in the partpart-whole model. Then, have them solve for the missing number represented with an empty box.
• Monitor and talk with students as needed to check for understanding by using the following guiding questions:
o Can you put this problem into your own words? Answers will vary. There are 9 bottles of nail polish in a box, and 7 of them are purple. The rest are green, but we have to figure that part out.
o What information do you have? Answers will vary. There were 7 purple bottles in the box. Some green bottles were in the box. There were 9 total bottles in the box.
o What do you think you are trying to find out? Answers will vary. How many green bottles of nail polish were in the box
o How could you model this problem using the Work Mat? Answers will vary. We drew 2 green circles in one part section of the Work Mat. We drew purple circles into the other part section until we got to a total of 9. Then, we drew all the circles from each part in the whole section to check to see if the total equaled 9 bottles.
o Optional How could you model this problem using a Rekenrek? Answers will vary. I could move 9 beads to the left to show the total bottles in the box and then move 2 of those beads back to the right and see that there are 7 left over on the left. Those 7 are how many purple bottles are in the box.
o How could you prove your solution using a number sentence to find the missing number? Answers will vary. 7 + 2 = 9 or 9 – 7 = 2
o What does the empty box in the last sentence represent? The missing number that we were trying to find, our solution.
The Nail Polish Factory has decided to treat their customers to surprise boxes of free bottles of nail polish. Before the boxes can ship, the manager needs to record how many bottles of each color are in each box. Can you help the manager solve the word problems to find out how many bottles of each color are in the surprise boxes?
1. A surprise box has just been filled. There are 2 green bottles of nail polish and some purple bottles of nail polish. There are 9 total bottles of nail polish in the box.
a. Use a purple crayon and a green crayon to draw circles in the part-part-whole model to help you solve the problem.
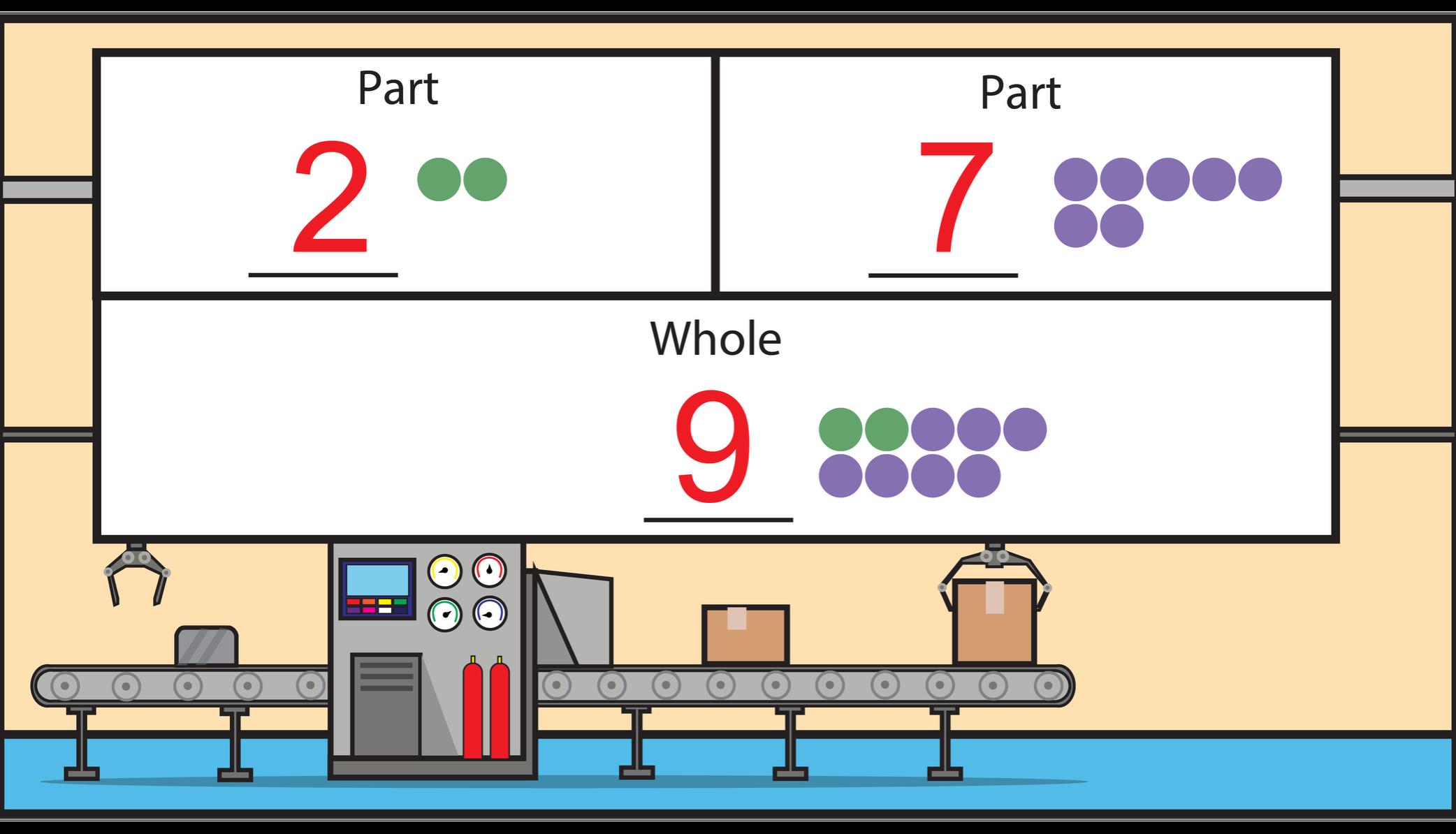
b. Complete the
c. Complete the sentence.
There are 7 bottles of purple
Procedure and Facilitation
• Guide students as they answer the questions for surprise box 1. If needed, consider providing students with two-color counters that they can use to model the problem on the ten frame.
• Facilitate a class discussion to answer the guiding questions for surprise box 1 by randomly selecting students (craft sticks, flash cards, popcorn) to share their thinking.
• Repeat the discussion for surprise box 2, and model where the answers should be recorded in the chart while students record their answers in their workbook
Student-Facing Activity and Answer Key



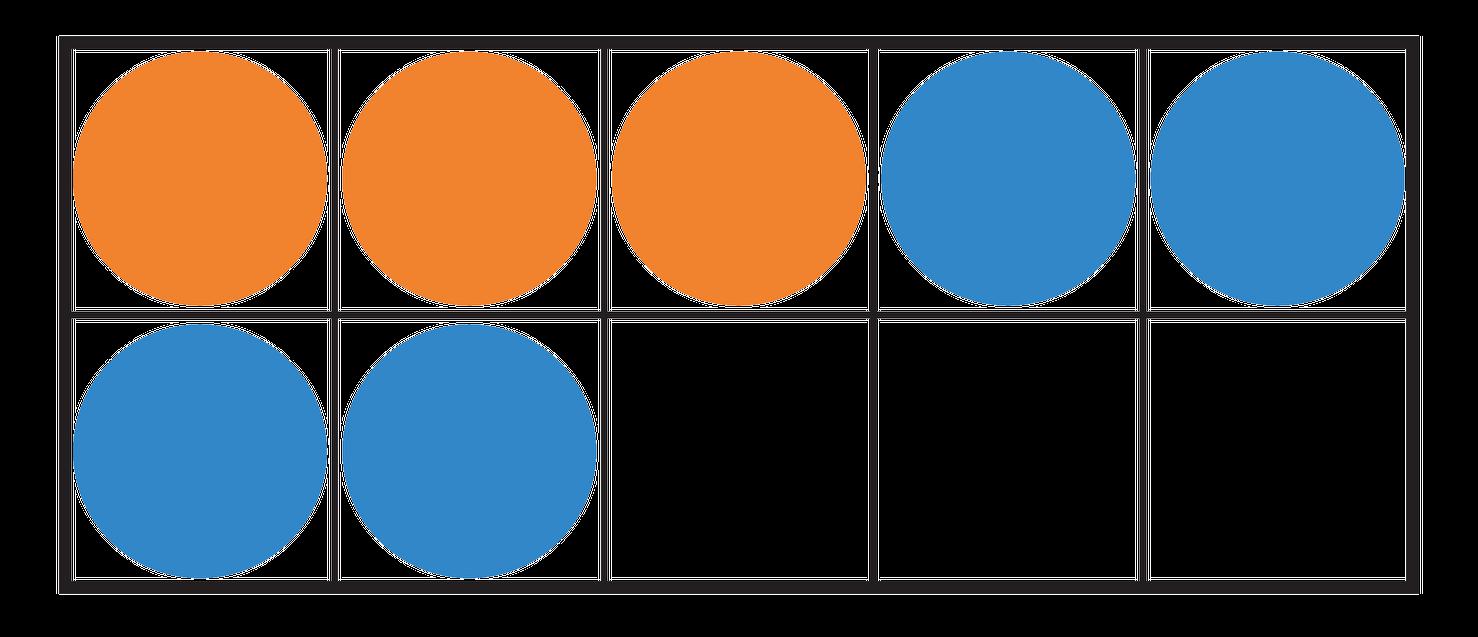
1. Surprise Box 1: This box has 7 pink bottles ( ) and some red bottles ( ) of nail polish. There are 9 bottles of nail polish altogether. How many red bottles of nail polish are in the box?

a. What information do you have? There are 9 total bottles of nail polish; 7 of them are pink.
b. What do you think you are trying to find out? How many red bottes of nail polish are in the box
c. Model this problem using the Part-Part-Whole Mat
d. Record your answer in the ten frame

2. Write two number sentences to represent the problem.
3. Read through the problem and use the manipulatives to solve it.


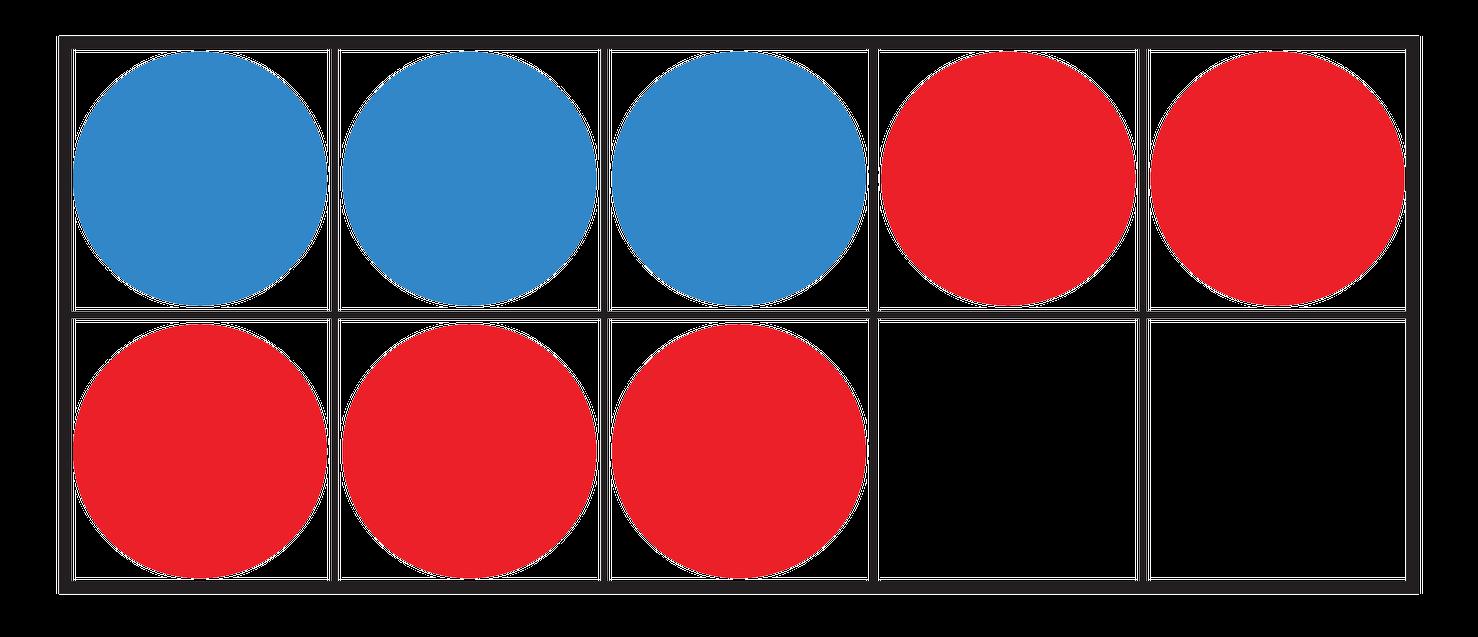
Surprise Box 2: This box has 3 orange bottles ( ) and 4 blue bottles ( ) of nail polish. How many bottles of nail polish are in the box?
Surprise Box 2

Read through each problem, and encourage students use the manipulatives to solve it
There are multiple correct answers for problems 2 and 4. Consider facilitating a Math Chat about the different answers students found for each problem.
Student-Facing Activity and Answer Key


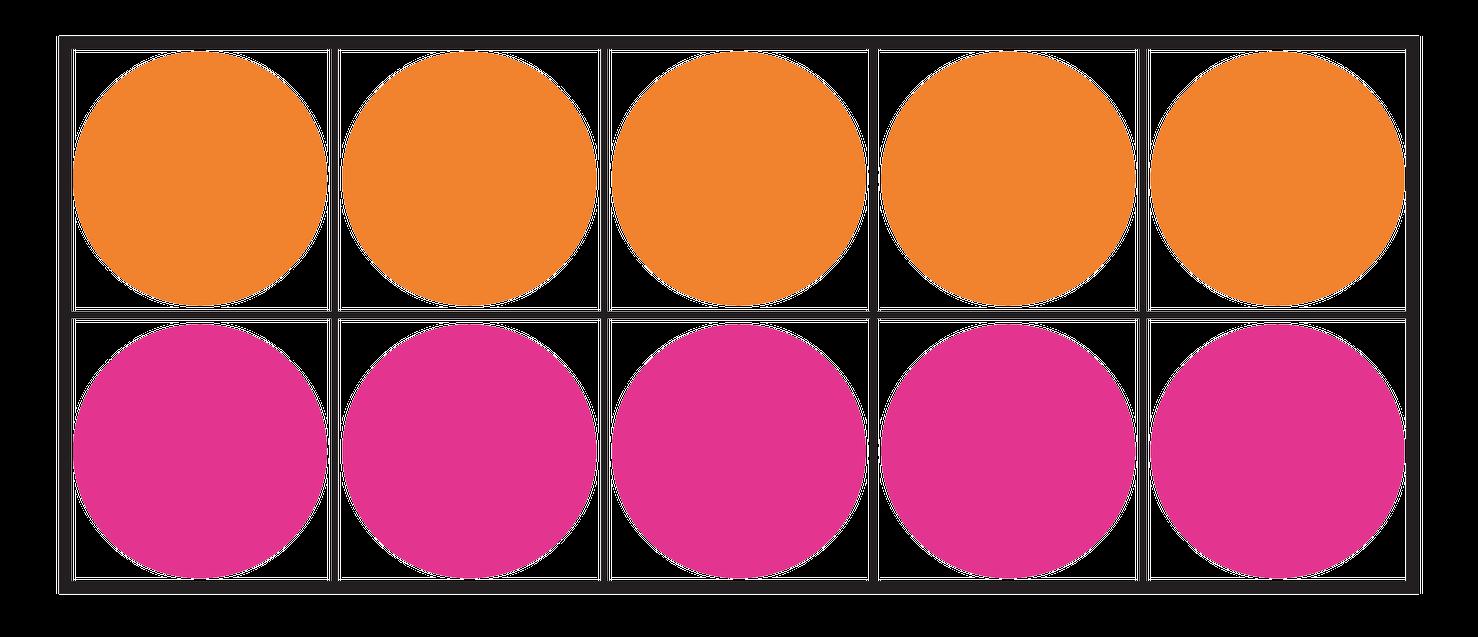
1. Surprise Box 3: This box has some blue bottles ( ) and 5 red bottles ( ) of nail polish. There are 8 bottles of nail polish in all. How many blue bottles of nail polish are in the box?




2. Surprise Box 4: This box has some pink bottles and some orange bottles of nail polish. There are 10 bottles in total. How many bottles of pink and orange nail polish could be in the box?



Number of Nail Polish Bottles Part-Part-Whole Model Number Sentences


3. Surprise Box 5: This box has 6 red bottles ( ) and 1 orange bottle ( ) of nail polish. How many bottles of nail polish are in the box?




4. Surprise Box 6: This box has some blue bottles and some pink bottles of nail polish. There are 6 bottles in total. How many bottles of blue and pink nail polish could be in the box?
Surprise Box 6


Number of Nail Polish Bottles
Part-Part-Whole Model Number Sentences
This Wrap-Up is designed to assess students’ current understanding before the next lesson in which they will solve problems with 3 addends. Allow students to complete the Wrap-Up independently to assess their understanding.
Then, ask students to share their responses or progress with a partner. Once these partner conversations have taken place, select students to share their thoughts with the class.
Student-Facing Activity and Answer Key
If a new color of nail polish was added to the boxes, do you think you and your partner could use 3 numbers to put together a full box of 10? Could you also take apart 10 using three or more addends? Write an example of each.
1. Put together 3 numbers for a full box of 10: Answers will vary. 2 + 1 + 7 = 10
Take apart 10 using 3 or more numbers: Answers will vary. 10 – 5 – 3 – 2
Students will use their understanding of the equal sign to determine whether given addition equations are true or false.
Benchmark/MTRs
• MA.2.AR.2.1 Determine and explain whether equations involving addition and subtraction are true or false.
• MA.K12.MTR.1.1 Actively participate in effortful learning both individually and collectively.
• MA.K12.MTR.5.1 Use patterns and structure to help understand and connect mathematical concepts.
• MA.K12.MTR.6.1 Assess the reasonableness of solutions.
Students explore the relationships between numbers in addition equations to determine whether the equations are true or false. By understanding how the placement and combination of numbers affect the balance of an equation, students develop a deeper comprehension of mathematical equality. This understanding helps them recognize the meaning and importance of the equal sign as they confidently assess the truthfulness of equations.
VOCABULARY TERMS
• addition: combining two or more numbers to get a sum, or total
• equal: same or balanced
• ones: the right-most place value unit in a whole number; a one has a value of 1.
• place value: how much a digit is worth based on its location in a number
• sum: the total amount; the result in addition
• tens: the place value that is one place to the left of the ones place; a ten has a value of 10; a ten has the same value as 10 ones.
Printed
• N/A
Reusable
• 1 Whiteboard (per student)
• 1 Dry-erase marker (per student)
• 1 Set of base-ten blocks (per student, optional)
• Plan for students to work in pairs during the Exploration and Guided Activities.
Procedure and Facilitation
• Before beginning the activity, review the meaning of the word equivalent with students. Say, “Expressions are equivalent if they have the same value.”
• To check for understanding, ask a few students to share simple expressions they believe are equivalent. For example, 7 + 3 and 5 + 5 are equivalent because they both have the same value, 10.
• Give students a few minutes of quiet work time to complete the activity independently.
• Display the Student-Facing Activity. Invite two students to share which expression they selected as equivalent to the first expression in list A, 20 + 60. Ask the class to vote on whether or not they agree with the match. Encourage students to explain their reasoning, or pose additional questions as needed. Repeat this routine for each expression in list A.
• Consider modeling with a place value chart or a number line to show the sum of each expression as a way to justify the equivalence between expressions.
Student-Facing Activity and Answer Key
Two lists of addition expressions are shown. Draw a line to match each expression from list A with an equivalent expression in list B.
Procedure and Facilitation
• Begin the activity by reviewing the meanings of the words true, false, and equal with students.
o True = correct
o False = incorrect
o Equal = the same or balanced
• Give a whiteboard and dry-erase marker to each student.
• Write the equation 27 + 13 = 40 on the board, and ask students to write the equation on their whiteboards. Ask them how they can determine whether the equation is true or false. Answers will vary. I can add the numbers 27 + 13 to see whether the sum is 40.
• Allow students time to add the numbers, and ask the following questions:
o Is the equation true or false? How do you know? Answers will vary. I know the equation is true because I added 27 and 13 and it is equal to 40.
• Write the equation 99 = 37 + 52 on the board.
• Allow students time to consider whether the equation is true or false. Then, ask these questions:
o Does it matter that 99 is to the left of the equal sign? Answers will vary. No. It is still an addition equation no matter which side the equal sign is on. The equal sign indicates the relationship between the two expressions, so here, it is stating that 99 has the same value as 37 + 52.
o Is this equation true or false? Answers will vary. The equation is false because it is incorrect. I added 37 and 52, and the sum is 89, not 99.
• Direct students to their workbooks, and say, “You will work with a partner for this activity. For each problem, three numbers are given. You will need to use the three values to create one number sentence that is true and one number sentence that is false. Make sure to pay attention to where the equal sign is located in your equations.”
• Tell students to write their true and false equations on their whiteboards. Then, have them swap whiteboards with their partners to determine whether they agree or disagree with their partners’ equations before recording them in their workbooks.
• As students work, rotate around the classroom and ask the following questions:
o What combination of these numbers would give you a false equation? Answers will vary. If I add two numbers and they don’t equal the third number, that’s a false equation.
o How did you and your partner decide on the true and false equations? Answers will vary. We tried adding the numbers together to see whether any could be used to create a true equation.
• Invite 2–3 students to share a true equation and a false equation for problems 1 and 2 As the problems are discussed, record students’ equations in two lists true equations and false equations. Encourage them to make observations about the shared equations. Some things they may notice include the following:
o The order of the addends is different, but the true equation is the same for all examples.
o The false equations were easier to create than the true equations.
For each problem, three numbers are given. Use these numbers to create a true equation and a false equation.
1. 34, 52, 18 Answers will vary.
True equation: 18 + 34 = 52
False equation: 34 + 52 = 18
2. 62, 27, 35 Answers will vary.
True equation: 62 = 35 + 27
False equation: 35 = 27 + 62
Procedure and Facilitation
• Explain to students that they will now work with equations that include four terms, or numbers. Remind them that the equal sign indicates that the sum on both sides of it must be the same for the equation to be true.
• Write the equation 58 + 26 = 58 + 26 on the board, and ask the following questions:
o What do you notice about the addends on each side of the equal sign? Answers will vary. They are the same.
o Before we do any adding, do you think this equation is true or false? Why? Answers will vary. It is true because the numbers are the same on each side of the equal sign, so the sum will be the same on each side. It is true to say that one side of the equation has the same value as the other side.
• Prompt students to use any strategy they would like to complete the problem on their whiteboards and confirm the equation is true and that 84 is the sum on both sides of the equation.
• Change the equation to 57 + 26 = 58 + 26, and ask the following questions:
o Is the equation still true? Explain. No. It is no longer true that the sum on the left side of the equation is the same as the sum on the right side.
o What will happen to the sum on the left side of the equal sign? It will be one less than it was before because the number 57 is one less than 58.
o How would we need to change the other side of the equation to make the two sums equivalent again? We would need to subtract 1 from one of the numbers.
• Change the equation to 57 + 26 = 58 + 25, and ask whether the equation is now equal. Yes. It is equal because we took 1 away from 25. Now, both sides have the same value.
• Allow students time to work out the problem on their whiteboards to confirm that the sum on both sides of the equal sign is 83.
• Write the problem 17 + 83 = 16 + 84 on the board, and ask the following questions:
o What do you notice about the addends on each side of the equal sign? Answers will vary. The numbers on both sides of the equal sign are close to each other. 17 is one more than 16, and 83 is one less than 84.
o How can we determine whether the equation is true? We can add the numbers on both sides of the equal sign to see whether they are the same.
o Is there a way we can determine whether the equation is true without adding both sides? Yes Because 16 is one less than 17, I know that I would need one more than 83, which is 84, to make both sides equal.
o Is this equation true? Yes.
• Give students time to work through the problems in their workbooks with their partners. Encourage them to consider the relationships between the numbers instead of simply adding the expressions on each side of the equal sign.
• Ask students to share their answers for each problem and explain their reasoning. Encourage them to ask clarifying questions or explain a different way to verify whether the equations are true or false.
For each equation, determine whether the equation is true or false. Then, explain your reasoning.
1. 45 + 20 = 50 + 15
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning. Answers will vary. 50 can be rewritten as 45 + 5 and 15 + 5 is 20, so both sides of the equation are equal to 45 + 20.
2. 76 + 24 = 80 + 20
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning. Answers will vary. 76 + 24 can be rewritten as 76 + 4 + 20, or 80 + 20, which is the same as the right side of the equation.
3. 18 + 25 = 20 + 13
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning. Answers will vary. 18 + 25 can be rewritten as 18 + 2 + 23, which is equal to 20 + 23, but that is not the same as 20 + 13.
Students should complete the practice problems independently.
Student-Facing Activity and Answer Key
For each equation, determine whether the equation is true or false. Explain your reasoning.
1. 36 + 24 = 40 + 20
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning. Answers will vary. 36 + 24 can be rewritten as 36 + 4 + 20, or 40 + 20, which is the same as the right side of the equation.
2. 28 + 19 = 30 + 18
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning. Answers will vary. 28 + 19 can be rewritten as 18 + 10 + 19, or 18 + 29, which is not the same as 30 + 18.
3. 50 + 25 = 45 + 30
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning. Answers will vary. 50 + 25 = 75, which is equal to 45 + 30.
4. 25 + 15 = 20 + 20
a. Is the equation true or false?
¡ True
¡ False
b. Explain your reasoning. Answers will vary. 25 + 15 is equal to 40, and 20 + 20 is also equal to 40. If 5 is taken from 25 and added to 15, the result is 20 and 20.
Allow students to complete the Wrap-Up independently to assess their understanding. After students have had time to complete the Wrap-Up, poll the class to determine which answer choices they selected. Then, facilitate a discussion in which students share their reasoning for which equations are true and which one is false. Encourage them to use relationships between the quantities to justify their thinking rather than simply finding the sum of each side.
1. Which equation is false?
A. 18 + 19 = 20 + 17
B. 41 + 22 = 43 + 20
C. 54 + 39 = 49 + 34
D. 37 + 56 = 40 + 53
Students will compose and decompose four-digit whole numbers in multiple ways. They use place value disks, drawings, expressions, and equations to represent numbers.
Benchmark / MTRs
• MA.3.NSO.1.2 Compose and decompose four-digit numbers in multiple ways using thousands, hundreds, tens, and ones. Demonstrate each composition or decomposition using objects, drawings and expressions or equations.
• MA.K12.MTR.2.1 Demonstrate understanding by representing problems in multiple ways.
• MA.K12.MTR.5.1 Use patterns and structure to help understand and connect mathematical concepts.
Using place value understanding, students explore a real-world scenario as they decompose numbers in different ways. Students create varied visual representations and expressions to show a given amount in different ways. Students engage in collaborative discussion to understand and explain when it is necessary to regroup a place value.
• compose: to put pieces together
• digit: a single symbol used to create a numeral; The digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
• expanded form: a way to write a number as a sum of each digit according to its place value
• model: a representation of something
• place value: how much a digit is worth based on its location in a number
• standard form: the most common way to write a number; a number shown in digits
• word form: a way to write a number using words
Reusable
• Place value disks or base-ten blocks (for support)
• Organize students in pairs or small groups for the Exploration and Guided Activities.
• Provide access to place value disks or base-ten blocks for student support.
Procedure and Facilitation
• Display the prompt from the Warm-Up.
• Ask students to consider which representation doesn’t belong.
• Give students a few minutes to quietly think and then signal when they have an answer.
• Ask students to explain their rationale for deciding which option doesn’t belong.
• After a few students have shared, encourage students to determine a reason why each of the representations doesn’t belong with the others. Sample reasons are given in the Answer Key.
Student-Facing Activity and Answer Key
Different representations of numbers are shown.
3,402 2 thousands 14 hundreds 2 ones Three thousand forty-two 34 hundreds 2 ones
1. Which one doesn’t belong? Answers will vary.
• Number A doesn’t belong because it’s the only number written in standard form.
• Number B doesn’t belong because it’s the only representation that begins with 2 thousands.
• Number C doesn’t belong because it’s the only number that has a 4 in the tens place instead of the hundreds place. It’s the only number not equal to the other numbers.
• Number D doesn’t belong because it’s the only number with only two place values.
2. Explain your thinking to your partner.
3. Draw a model to justify your thinking. Models will vary.

Procedure and Facilitation
• Read the following scenario to students: On a recent field trip to the zoo, your class noticed that the zoo needed some updating. Some of the animals needed new enclosures and some of the enclosures were empty. You want to convince your city to update the zoo with newer animal enclosures and more animals.
• Explain to students that your class collected signatures from three different businesses in the city. The students’ job is to represent the total number of signatures collected at each business.
• For each business, instruct students to draw a visual representation in two different ways, followed by writing two different expressions for each model.
• Remind students that an expression is a meaningful string of numbers and operation symbols.
• Instruct students to use place value disks or base-ten blocks to support them in making a visual representation. Students may exchange their place value disks to show when a place value has been composed.
• Tell students to challenge themselves to create two or more expressions for each model. These can vary within the group, but group members should check each other for accuracy.
• Monitor and assess students as they work together by asking guiding questions such as the following:
o What do you notice about how the numbers of signatures are represented? The numbers are shown in different forms. I notice that some numbers have more than 10 of a place value. For example, the Clothing Shop shows 21 tens and 14 ones.
o If you have a group of 10 in one place value, what do you need to do? We need to regroup the 10 to create 1 of the next highest place value.
o How can you model 423 in two different ways? I can draw 4 hundreds, 2 tens, and 3 ones. I can also draw 4 hundreds, 1 ten, and 13 ones.
o What is another way we could describe 15 hundreds? We can regroup 15 hundreds into 1 thousand and 5 hundreds.
o What is another way we could describe 12 ones? We can regroup 12 ones into 1 ten and 2 ones.
o What is another way we could describe 21 tens? We can regroup 21 tens into 2 tens and 1 one.
o What is another way we could describe 14 ones? We can regroup 14 ones into 1 ten and 4 ones.
o What is another way to write the expression 10 + 2? 10 + 2 is the same as 12. It is also equivalent to 5 + 5 + 2.
• Invite students to share their thinking and observations.
Your class decides to collect signatures from people living in your city to show support for updating the zoo. You place signature sheets at three different businesses in your city. The total number of signatures collected at each business is shown.
For each location, draw a visual representation of the amount of signatures in two different ways. Then, write an expression for each of the amounts you drew. Challenge yourself to think of two different ways to show the given amount.
1. Hardware store Answers will vary. Sample responses are shown.

Expression 1
400 + 20 + 3
Expression 2
300 + 110 + 13

Expression 1
300 + 100 + 20 + 3
Expression 2
200 + 200 + 23
2. Grocery store Answers will vary. Sample responses are shown.

Expression 1
1,000 + 500 + 12
Expression 2
500 + 500 + 500 + 12

Expression 1 1,500 + 10 + 2
Expression 2
1,000 + 100 + 100 + 100 + 100 + 100 + 10 + 2
3. Clothing shop Answers will vary. Sample responses are shown.
Model 1
Expression 1
1,000 + 200 + 20 + 4
Expression 2
500 + 500 + 10 + 10 + 4
Model 2

Expression 1 1,000 + 210 + 10 + 4
Expression 2 1,200 + 24
Procedure and Facilitation
• Explain to students that their class collected more signatures from three more businesses. The number of signatures collected at these locations are given in different forms.
• Remind students to compose each place value as necessary.
• Prompt students to record two different expressions for each amount.
• After students complete the table, invite them to share the expressions they created for each location as you write them in a location visible to all students.
• Compile the list of expressions for one location at a time. Once a list has been created for a location, ask students to discuss similarities, differences, and other observations they notice in the variety of expressions the class generated.
• After the activity, invite the class to a Math Chat to share their observations and learning using the following questions and prompt:
o Why did some place values need to be regrouped? Answers will vary. In some place values, we had more than 10 disks. If you have a group of 10 or more, you must regroup to create one unit of the next highest place value.
o If you look at the standard form of a number, how can you know the value of a specific digit within that number? Answers will vary. If you know the place value of the digit, you can figure out the value. For example, if you have a 3 in the hundreds place, then you have three groups of 100, which equals 300.
o Describe the process of decomposing a number. Answers will vary. We are used to composing by place value, but we know that we can regroup the digits in any place to make lots of new expressions. For example, 923 could be written as 900 + 20 + 3, 900 + 23, 800 + 123, and so on.
The table shows the signatures that your class collected from three more businesses. Write two different expressions for each amount that was collected. Expressions will vary.
Bakery Number of Signatures Six thousand six hundred sixty-five Expression 1 6,000 + 600 + 65 Expression 2 6,000 + 500 + 165
Number of Signatures 56 hundreds 121 ones Expression 1
+ 600 + 100 + 21
+
Students complete the practice problems independently
Student-Facing Activity and Answer Key
1. Complete the chart to represent the number 3,125. Place Thousands Hundreds Tens Ones
Model

Standard Form



3, 1 2 5
Expression 1 Answers vary. 3,000 + 100 + 20 + 5
Expression 2 Answers vary. 31 hundreds + 25 ones
2. Complete the chart to represent the number described: 4 thousands 11 hundreds 4 ones



Expression 1 Answers vary. 5,000 + 100 + 4
Expression 2 Answers vary. 4,000 + 1,100 + 4
3. Select all the expressions that represent the number 4,712.
o 47,000 + 12
o 4,000 + 700 + 10 + 2
o 47 hundreds + 12 tens
o 47 thousands + 12 ones
o 40 hundreds + 7 tens + 12 ones
Allow students to complete the Wrap-Up independently to assess their understanding.
Student-Facing Activity and Answer Key
Write two different expressions to represent the number 6,203.
Answers will vary. 6,000 + 200 + 35,000 + 1,000 + 100 + 100 + 3
Students will interpret remainders as fractional parts.
Benchmarks/MTRs
• MA.4.NSO.2.4 Divide a whole number up to four digits by a one-digit whole number with procedural reliability. Represent remainders as fractional parts of the divisor.
• MA.4.AR.1.1 Solve real-world problems involving multiplication and division of whole numbers including problems in which remainders must be interpreted within the context.
• MA.K12.MTR.2.1 Demonstrate understanding by representing problems in multiple ways.
• MA.K12.MTR.3.1 Complete tasks with mathematical fluency.
• MA.K12.MTR.4.1 Engage in discussions that reflect on the mathematical thinking of self and others.
• MA.K12.MTR.5.1 Use patterns and structure to help understand and connect mathematical concepts.
• MA.K12.MTR.6.1 Assess the reasonableness of solutions.
Students solve division problems involving the distances traveled per day during family vacations and interpret the remainder as a fractional part in relation to the context.
• area model: a rectangular diagram that utilizes the decomposition of side lengths by place value to multiply numbers using the distributive property
• array: an arrangement of objects or symbols in rows and columns; all rows have an equal number and all columns have an equal number.
• difference: the answer to a subtraction problem
• distributive property of multiplication over addition: Multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together; a × (b + c) = (a × b) + (a × c)
• divide: to separate or group a number into equal parts or fair shares
• dividend: a quantity that is to be divided
• divisor: the number by which another number is divided
• equation: a mathematical relation statement where two equivalent expressions and values are separated by an equal sign
• quotient: the answer to a division problem
• represent: to describe or depict a concept
• strategy: a plan of action to find a solution
• sum: the answer to an addition problem
• whole numbers: the natural numbers and zero
MATERIALS
Reusable
• 1 Sheet of chart paper (per class)
• 1 Set of markers (per class)
PREPARATION
• Prepare to display the prompt during the Warm-Up.
• Arrange students in pairs for the Exploration Activity.
• Prepare to display the Voyager of the Waters prompt during the Exploration Activity.
• Prepare to showcase student work under a document camera or on a piece of chart paper during the Guided Activity.
Student-Facing Activity
The answer is:
When all the juice is shared equally among 3 people, each person will receive a glass containing 1 ! " cups of juice.
Choose one question stem or create one of your own to help you write a question.
• What is the total ______________________________________________ ___________________________________________________________? • How many ___________________________________________________ ___________________________________________________________?
___________________________________________________________?
Preparation and Facilitation
• Gather students in a whole group, and prepare a piece of chart paper and a marker.
• Display the prompt, and give students a minute to examine it independently.
• Depending on the needs of your students, model how to generate a question.
• Allow students to work with a partner to generate a question that would lead to the answer.
• Invite student pairs to share their questions, and record them on the chart paper.
Sample question: There is a pitcher containing 4 cups of juice. When all the juice is shared equally among 3 people, how much juice will each person get?
• Discuss the following questions:
o Explain the meaning of a remainder. It is a quantity left over when two numbers are divided.
o How much juice was there to start with, and how do you know? 4 cups because 1 + 1 + 1 + ! " + ! " + ! " = 4
o What is 4 ÷ 3? 1 R1
o Invite students to work with their partners to discuss how the remaining 1 cup could be equally shared among the 3 people. Each person would get another ! " of a cup because ! " + ! " + ! " = " ", or one whole (1).
• Ask students to recall their work from the previous lesson, in which they determined whether they would need to account for a remainder in a problem’s solution. Explain that in this lesson, remainders will be accounted for, but instead of rounding the whole number up, the remainder will be expressed as a fractional part of the whole amount.
Preparation and Facilitation
• Students should work with a partner for this activity.
• Read the following scenario to the class: Cruise ships and airplane trips are just two options people like to use when traveling for vacation. Both options can cover many miles in a short amount of time while offering travelers different locations to visit. Several families have decided to go on vacation next year. Each vacation will last several days and will cover many miles. During this activity and the next, you will help each family figure out how many miles they will travel each day.
• Display the prompt, direct students to their workbooks, and discuss the following questions:
o What information do we know? We know the total distance the Howard family will travel (2,026 miles) and the number of days it will take (5 days).
o What do we need to find out? We need to find out how many miles per day they will travel.
o What operation is needed to solve this problem? Division
o Which number will be divided by the other? 2,026 will be divided by 5.
o What division strategies could you use to solve this problem? Equal groups, arrays, area models, or partial products
• Invite student pairs to select a strategy and model the quotient.
• Call on students to share their strategies with the class.
• Feature each strategy under a document camera, and discuss the similarities and differences between strategies. Consider displaying these examples for students to reference during the Guided Activity.
• Discuss the following questions as students record their answers to problem 2 in their workbooks:
o How many whole miles will they travel each day? 405
o What is the remainder, and what does it represent? The remainder is 1, and it represents 1 extra mile that needs to be evenly spread over the 5 days.
o What fractional part of the extra mile does the remainder represent? Explain your reasoning. ! # of a mile because when 1 is divided into 5 equal groups, each group is one-fifth in value
• Draw a number line ranging from 0 to 1 with increments of fifths. Use this to illustrate that there are # # in one whole. Therefore, when splitting 1 mile across 5 days, the Howards will travel ! # of a mile more than 405 miles each day.
• Invite students to write the equation and solution statement.
• Confirm students’ answers, and address misconceptions as needed.
Make sense of the scenario, and respond to the problems.
The Howard family decided to take a Voyager of the Waters cruise. Their vacation will cover 2,026 miles in 5 days. The cruise ship travels at the same pace each day before docking for the night. How many miles will the Howard family be at sea each day?
1. Draw a model to represent the scenario. Models will vary.

2. Fill in the blanks to complete each statement.
a. The Howard family will travel 405 whole mile(s) per day, with a remainder of 1 mile(s).
b. The remainder expressed as a fraction of the divisor is ! #, which represents the additional part of a mile the Howard family will travel per day.
3. Write an equation that represents the scenario. 2,026 ÷ 5 = 405! #
4. Write a solution statement.
The Howard family will be at sea for 405! # miles each day.
Preparation and Facilitation
• Direct students to the Guided Activity. Thell them that if they get stuck, they can refer to their prior work in the Exploration Activity.
• Prompt students to begin the problem-solving process.
• Select a student group to showcase each scenario, and have those students explain their model and interpretation of the remainder as a fraction, equation, and solution. Clarify misconceptions as needed.
• After the activity, invite the class to a Math Chat to share their observations and learning:
o Why were the remainders for these scenarios expressed as fractions? In these scenarios, the leftover amount was a distance that had been traveled during the trip, so that distance is expressed as a fraction to show the extra part of a whole mile included in the distance traveled each day.
o Would it be appropriate to round the remainder up like we did for some problems in the previous lesson? Explain. No. That would mean we’re saying they traveled farther each day than they actually did. It is possible to travel part of a mile.
o Would it be appropriate to ignore or drop off the remainder like we did for some problems in the previous lesson? Explain. No because we would be reporting an answer that wouldn’t cover the total distance traveled over that number of days
• Challenge students to think of other situations that would involve expressing the remainder as a fraction, and record their ideas on the chart paper. Sample situation: If I had a deadline for completing a project, I might have to set aside a certain amount of time each day to work on it, and that amount of time might involve a fractional part, such as working 1 " $ hours each day.
Student-Facing Activity and Answer Key
Make sense of each scenario, and respond to the problems.
1. The Sánchez family decided to travel across the county on motorcycles. Their vacation will span 547 miles in 6 days. They will travel the same number of miles each day. How many miles will the Sánchez family travel each day?
a. Draw a model to represent the scenario. Models will vary.

b. Fill in the blanks to complete each statement.
i. The Sánchez family will travel 91 whole mile(s) per day, with a remainder of 6 mile(s).
ii. The remainder expressed as a fraction of the divisor is ! %, which represents the additional part of a mile the Sánchez family will travel per day.
c. Write an equation that represents the scenario. 547 ÷ 6 = 91! %
d. Write a solution statement.
The Sánchez family will travel 91! % miles each day.
2. The Chen family decides to take a train to 7 different destinations. The train will travel the same distance to each destination, amounting to 2,144 miles in total. How many miles will the Chen family ride the train between destinations?
a. Draw a model to represent the scenario. Models will vary.
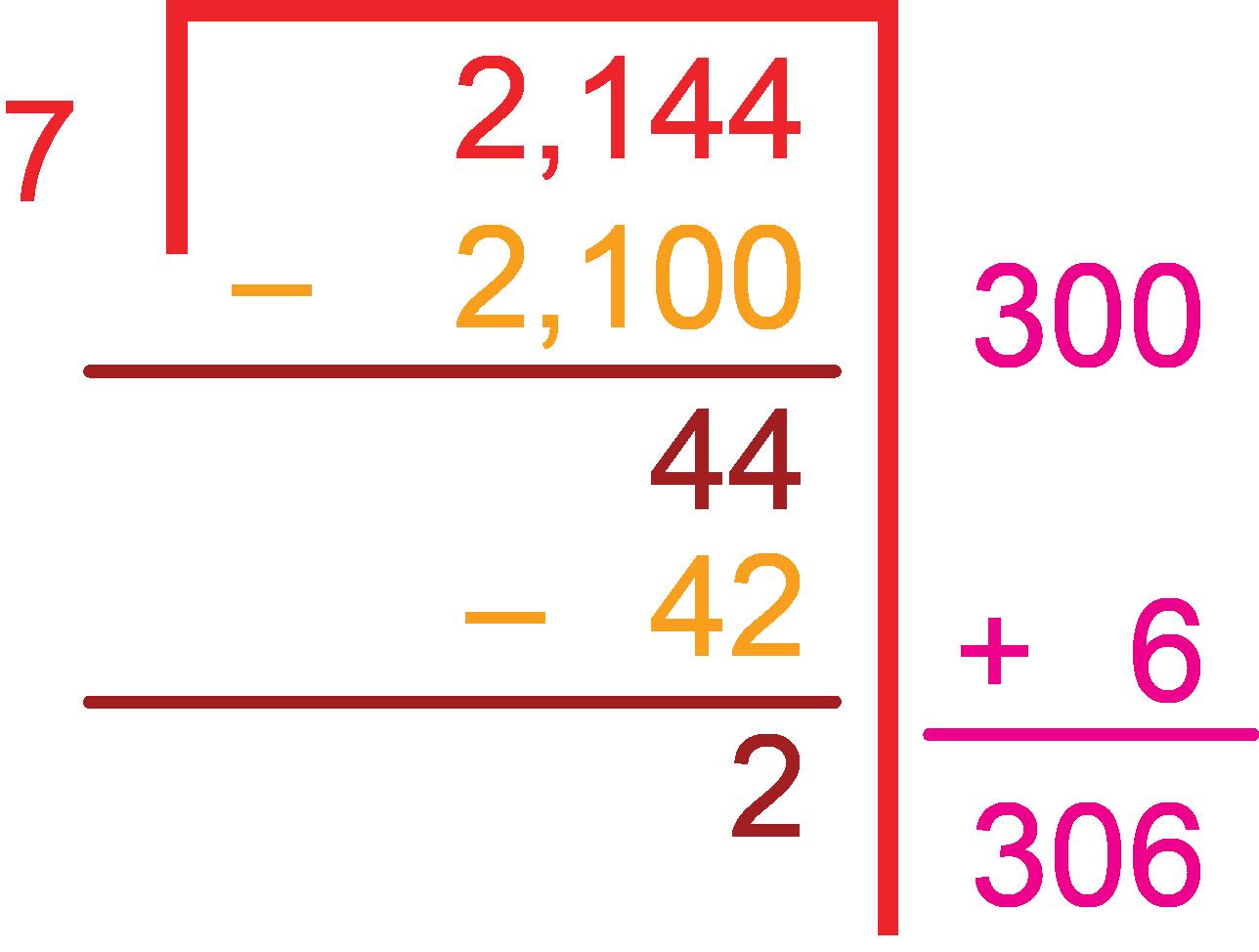
b. Fill in the blanks to complete each statement.
i. The Chen family will travel 306 whole mile(s) to each destination, with a remainder of 2 mile(s).
ii. The remainder expressed as a fraction of the divisor is & ', which represents the additional part of a mile the Chen family will travel to each destination.
c. Write an equation that represents the scenario. 2,144 ÷ 7 = 306& '
d. Write a solution statement.
The Chen family will ride 306& ' miles between destinations.
3. The Ingersoll family decides to rent a luxury car for their road trip. They plan to cover 487 miles in 4 days. They will travel the same distance each day. How many miles will the Ingersoll family drive each day?
a. Draw a model to represent the scenario. Models will vary.
b. Fill in the blanks to complete each statement.
i. The Ingersoll family will travel 121 whole mile(s) per day, with a remainder of 3 mile(s).
ii. The remainder expressed as a fraction of the divisor is " $, which represents the additional part of a mile the Ingersoll family will travel per day.
c. Write an equation that represents the scenario. 487 ÷ 4 = 121" $
d. Write a solution statement.
The Ingersoll family will ride 121" $ miles each day.
Students complete the practice problems independently.
Students-Facing Activity and Answer Key
1. Emma is keeping track of her fitness steps. Yesterday, she walked the same number of steps each hour, and that amounted to 2,225 steps in 3 hours.
a. Draw a model to represent this scenario. Models will vary.

b. How many steps did Emma fully complete each hour?
Emma fully completed 741 steps per hour.
c. What is the remainder? Express this as a fraction, and explain what it represents in relation to the context of this situation.
The remainder is 2. This means that she walked another & " of a step each hour.
d. Complete the statement with a mixed number.
Emma’s step rate is 741& " steps per hour.
2 Express the remainder of the following division problem as a fraction, and explain your reasoning.
36 ÷ 5 = 7 R1
7 ! # because 7 groups of 5 is 35, and when ! # more is added to each group, that amounts to another whole
3. Which part of a division equation represents the denominator when the remainder is expressed as a fractional part?
A. Divisor
B. Dividend
C. Quotient
D. Remainder
Students complete the Wrap-Up independently.
The Welch family is on a road trip. Their goal is to travel a total distance of 1,342 miles in one week. If they space the distance out equally each day, how many miles will the Welch family travel each day?
1. Draw a model to represent the scenario. Models will vary.

2. Fill in the blanks to complete each statement.
a. The Welch family will travel 191 whole mile(s) per day, with a remainder of 5 mile(s).
b. The remainder expressed as a fraction of the divisor is # ', which represents the additional part of a mile the Welch family travels per day.
3. Write an equation that represents the scenario. 1,342 ÷ 7 = 191# '
4. Write a solution statement.
The Welch family traveled 191# ' miles each day.
Students will divide a unit fraction by a whole number using models and number lines.
Benchmarks/MTRs
• MA.5.FR.2.4 Extend previous understanding of division to explore the division of a unit fraction by a whole number and a whole number by a unit fraction.
• MA.5.AR.1.3 Solve real-world problems involving division of a unit fraction by a whole number and a whole number by a unit fraction
• MA.K12.MTR.1.1 Actively participate in effortful learning both individually and collectively.
• MA.K12.MTR.7.1 Apply mathematics to real-world contexts.
Students explore how to divide a unit fraction by a whole number using visual models, including fraction circles and number lines. These visual models help students develop a conceptual understanding of how dividing a small part into even smaller parts results in a smaller fraction.
VOCABULARY TERMS
• divide: to separate or group a number into equal parts or fair shares
• dividend: a quantity that is to be divided
• divisor: the number by which another number is divided
• quotient: the answer to a division problem
• unit fraction: a fraction that represents only one part of the whole or set
Reusable
• 1 Set of fraction tiles (per pair, optional)
• Optionally, gather a set of fraction tiles for each pair of students.
• Plan for students to work in pairs for the Warm-Up.
• Plan for students to work in groups of 3–4 for the Exploration and Guided Activities.
Procedure and Facilitation
• Group students into pairs.
• Optionally, give a set of fraction tiles to each pair.
• Direct students to their workbooks, and read the problem
• Give students time to analyze the problem independently as they decide whether they agree with Ramsey.
• Prompt students to turn and talk to discuss whether they agree with Ramsey and then work with their partners to explain why and show their thinking. Explain that they can use models or manipulatives to help them decide.
• As students work with their partners, monitor and assess their understanding using the following questions:
o What are the dividends in problems A and B? The dividend in problem A is ! " . The dividend in problem B is 4.
o How do they differ? The dividend in problem A is a fraction. The dividend in problem B is a whole number. The answer to problem A will represent the number of pieces, and the answer to problem B will represent the size of the piece.
o How would you represent the dividends in problem A and problem B? For problem A, I would draw one whole, split it into 3 parts, and shade in one of the parts. For problem B, I would draw 4 wholes.
o How would you represent the divisors in problem A and problem B? For problem A, I would split each third into 4 parts. In problem B, I would split each whole into thirds.
o How does the quotient compare to the dividend in problem A? The quotient has a larger denominator than the dividend. That means the quotient is a smaller value than the dividend because it is divided into even smaller parts.
o How does the quotient compare to the dividend in problem B? The quotient is larger than the dividend. The 4 wholes are divided into smaller parts. That means there will be smaller parts, but there will be more of them.
• After students have had some time to complete the activity, bring them back together to discuss their answers and reasoning. Call on 2–3 students to share. Consider using the previous questions to probe student thinking during the whole-class discussion.
Student-Facing Activity and Answer Key
Two fraction problems are shown.
Ramsey and her friend Julisa were discussing the problems. Ramsey said that problems A and B will result in the same quotient.
Explain whether you agree with Ramsey. Show your thinking or work.
Answers will vary. I do not agree with Ramsey because the problems are not the same. In problem A, you are dividing a small piece, ! ", into 4 parts, so the quotient will be a smaller fraction. In problem B, you are determining how many ! " pieces fit into 4, so the quotient will be a whole number. The quotients will be different.
Procedure and Facilitation
• Organize students into groups of 4.
• Ask students the following question:
o What do you remember about dividing unit fractions by whole numbers from yesterday’s lesson? Answers will vary. They might remember that when they divide a unit fraction by a whole number, the resulting fraction is smaller than the dividend. The quotient represents the size of the piece compared to the whole. They may also recall that they can draw a model to help them see the pieces and that the value in the denominator gets bigger because they’re splitting the fraction into more parts.
• Direct students to their workbooks, and read the scenario to the class.
• Say, “Mr. Cooper is planning to share the remaining brownies with his coworkers. He wants to make sure anyone he shares with gets an equal-sized piece, but he needs to determine how many people he will share with using his containers. You will work in groups to help Mr. Cooper decide.”
• Ask students to work with their groups on problem 1.
• As students work, monitor and assess their understanding using questions such as the following:
o How can you show that the remaining half of the pan is being divided into equal pieces? We can draw lines through the brownie pan model to show that it is being divided.
o How can you show that each ! # of the pan is being divided into 2 groups? Draw one line to split each ! # into 2 equal parts.
o What is the dividend? The dividend is ! # .
o What is the divisor? The divisor is 2.
o What does the divisor tell us in this context? It tells us how many parts to divide something into or how many groups to make
o What is the fractional size of each brownie after ! # ÷ 2? ! $ of the whole pan
o What do you notice about the denominators when you divide a unit fraction by a whole number? When I divide a unit fraction by a whole number, the denominator gets bigger. I’m splitting the fraction into more pieces, so each unit piece is smaller
• After students have completed the activity, bring the class back together for a wholegroup discussion. Ask 2–3 students to share their work.
• Highlight key points and address any misconceptions before proceeding to the Guided Activity.
Mr. Cooper made a pan of brownies. He has ! # of the pan left, and he wants to pack the leftovers into containers to share. An image representing the brownie pan is shown.
The containers Mr. Cooper has come in 3 different sizes:
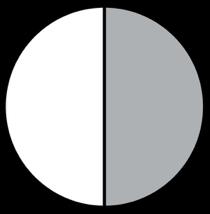
• There are 6 small containers he can use if he divides the remaining brownies into 6 equal pieces.
• There are 3 medium containers he can use if he divides the remaining brownies into 3 equal pieces.
• There are 2 large containers he can use if he divides the remaining brownies into 2 equal pieces.
Help Mr. Cooper determine the size of each piece of brownie depending on which set of containers he uses to share with his coworkers.
1. Complete the table. Divide each circle into equal sections. Draw a star on one of the shaded sections. Write an expression to represent the model. Determine the fractional size of each brownie in the container.

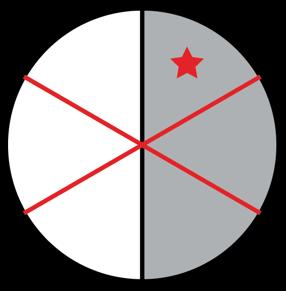
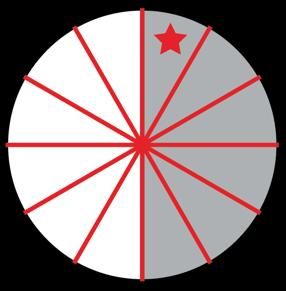
2. What do the lines you drew represent?
They represent dividing the leftover brownies into equal pieces.
3. After dividing the ! # of a pan of brownies, what do the small, shaded parts represent?
They represent the smaller pieces of brownie that would fit into the containers.
4. Complete the statements.
a. The large containers hold the biggest brownies. Each of these containers holds a piece that is ! $ of the brownie pan.
b. The small containers hold the smallest brownies. Each of these containers holds a piece that is ! !# of the brownie pan.
Procedure and Facilitation
• Keep students in groups.
• Explain to students that the concepts discussed in the Exploration Activity are going to assist them in solving the scenario in this activity.
• Then, direct students to their workbooks, and read the scenario.
• Explain to students, “For this next scenario, we will be modeling how to divide unit fractions by whole numbers using a number line.”
• Ask students the following questions:
o In problem 1, what is the problem asking us to solve? It’s asking us to model a number line that represents one third being divided into 3 equal parts.
o How can I show thirds on a number line? Split the number line into 3 equal parts.
o How would I label the number line? 0, ! ", # ", 1
o How could I represent one-third on the number line? By shading in a third on the number line
• Use the first row in the table in problem 1 to model for students. Instruct them on how to take their number line, split it into 3 equal parts, label each third, and shade the first third.
• Then, ask students this question:
o What are we splitting equally? Each third into 3 equal parts
• Model how to split each third into 3 equal parts with a Think-Aloud using the following questions:
o How many parts did we create when we split each third into 3 equal parts? We created 9 equal parts.
o What fraction is each of these parts? Each of them is ! % .
o Draw a star in the first ninth. What fraction of the whole represents the shaded portion with the star? ! %
o What equation could we use to represent this model? ! " ÷ 3 = ! % . Write ! " ÷ 3 for the expression in the first row.
o What do you notice about the denominator after you divided the unit fraction by the whole number? I notice that the denominator got bigger after dividing. That’s because we’re splitting the fraction into more parts, so each part is smaller.
o What is the fractional size of each napkin if Sew-It-All Fabrics divides the remaining ! " of a square yard into 3 napkins? ! % of a square yard
• Write ! % for the fractional size of each napkin in the first row.
• Have students complete the rest of the activity with their groups.
• After students have completed the activity, bring the class back together and allow student groups to share their work.
• Review the responses to all the problems. Then, invite the class to a Math Chat to share their observations and learning.
o In this lesson and the previous lesson, we have used different models to divide unit fractions by whole numbers. Which model do you prefer to use? Answers may vary. I like using number lines because I can see the jumps and how many equal parts fit into the whole. Bar models are also helpful because I can see the pieces clearly. Sometimes I use fraction circles when I want to see what the parts look like in a round shape.
o What patterns have you noticed about dividing unit fractions by whole numbers between the previous lesson and today’s lesson? I noticed that when we divide a unit fraction by a whole number, the denominator gets bigger and the fraction gets smaller. I saw that you can multiply the denominator by the whole number to find the new fraction. I also realized that the more people you share with, the smaller each piece is. Using the bar models, number lines, and fraction circles helped me see the same idea in different ways.
Student-Facing Activity and Answer Key
Sew-It-All Fabrics has ! " of a square yard of their best-selling fabric left over after making a tablecloth. A scale drawing of the fabric is shown, with the remaining fabric shaded gray.
Sew-It-All Fabrics wants to make some napkins out of the remaining fabric, but they have multiple options:
• They could divide the remaining fabric into 3 equal pieces.
• They could divide the remaining fabric into 5 equal pieces.
• They could divide the remaining fabric into 7 equal pieces.
Help Sew-It-All Fabrics determine the size of each napkin they could make.

1. Complete the table. Use the number line to represent how to divide the remaining fabric into equal sections. Draw a star on one of the sections. Write an expression to represent each model, and determine the fractional size of each napkin.
of Pieces



2. What does one whole represent in this scenario?
The whole represents the original square yard of fabric.
3. Complete the statement.
Each napkin size represents a fraction of a square yard.
4. How are the problems from the Exploration Activity and Guided Activity similar?
Answers will vary. In both problems, a unit fraction is being divided by a whole number. We found the size of each part after dividing the original fraction into that many equal parts. The quotients were all less than the dividends. The quotients were all fractions.
5. Complete the statements
a. When dividing a unit fraction by a whole number, the result is a fraction.
¡ smaller ¡ larger ¡ smaller ¡ larger ¡ fewer ¡ more
b. The greater the divisor is, the each piece is and the pieces there are.
Students complete the practice problems independently.
Student-Facing Activity and Answer Key
Draw a representation of the expression using a model or a number line. Then, write the resulting quotient 1.


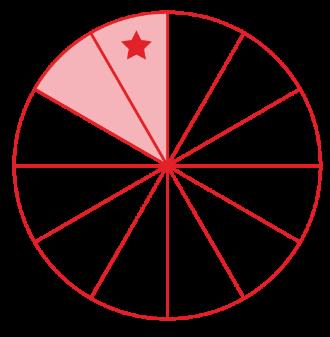

5. Choose one of the problems 1–4, and use a different model to represent your answer. Representations will vary.
Allow students to complete the Wrap-Up independently to assess their understanding of dividing a unit fraction by a whole number.
Student-Facing Activity and Answer Key
1. What is ! " ÷ 2? A. ! & B. # " C. ! ' D. ! !
2. What is ! $ ÷ 5?
A. ' $ B. ! #( C. ! % D. $ '
3. What is ! & ÷ 5? A. ! !! B. # !(
# &






















































































































































































































































































































I can sort two-dimensional figures based on their similarities and differences.
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
1
Circle the figure that belongs to group 1.
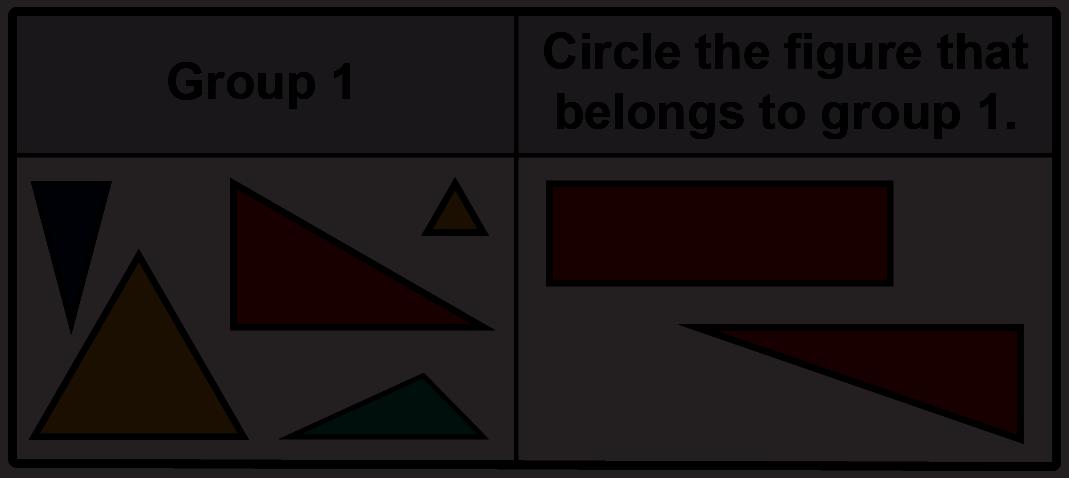
Use these if you need help.
• Two-dimensional figures can be sorted based on their attributes such as number of sides and vertices or corners.
• For example, squares have four equal sides and four vertices.
• Some figures you may not be familiar with; count the number of sides or vertices to compare the figures.
A video about how to solve
I can sort two-dimensional figures based on their similarities and differences.
Solve the following questions.
2
Circle the figure that belongs to group 2.
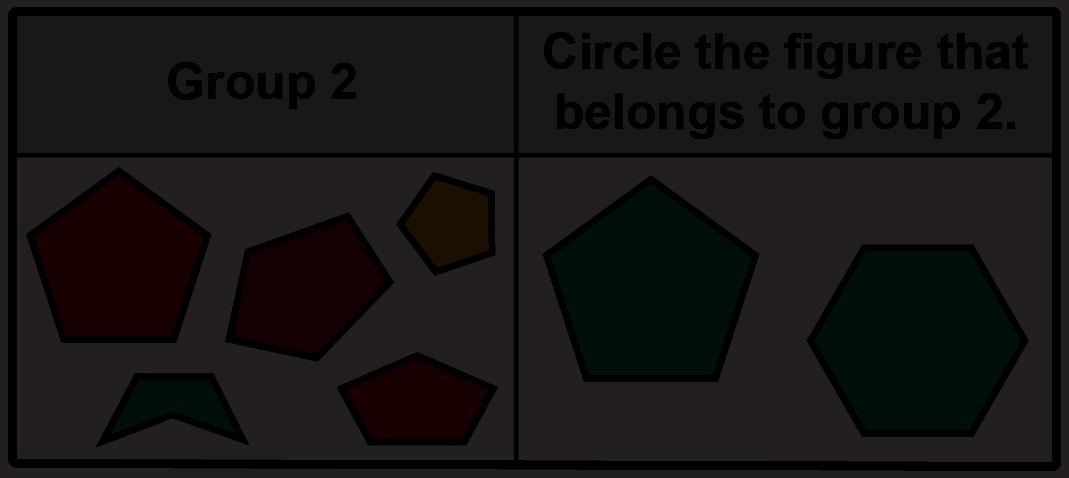
Group 2
3
Circle the figure that belongs to group 3.
Circle the figure that belongs to group 2.
Group 3
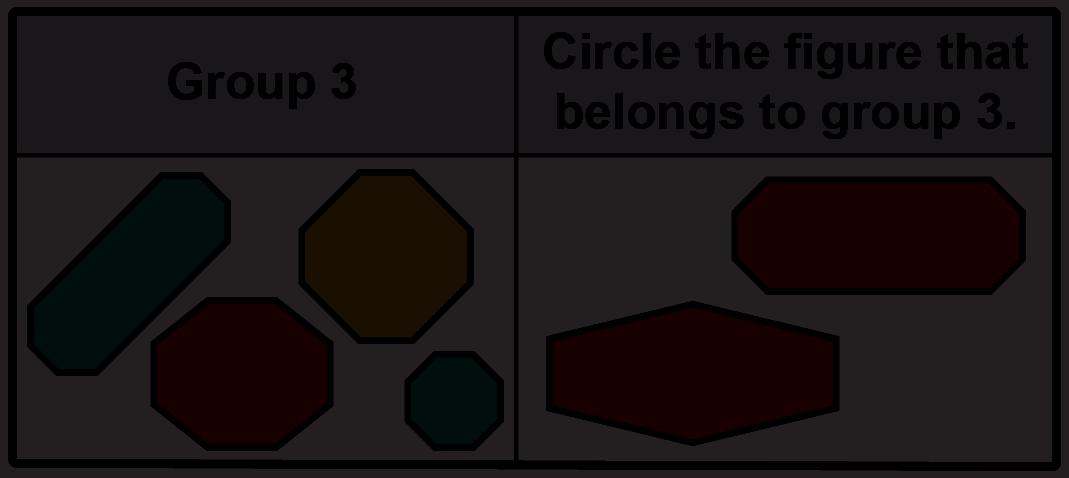
Circle the figure that belongs to group 3.
I can sort two-dimensional figures based on their similarities and differences.
4
5 Circle the figure that belongs to group 4.
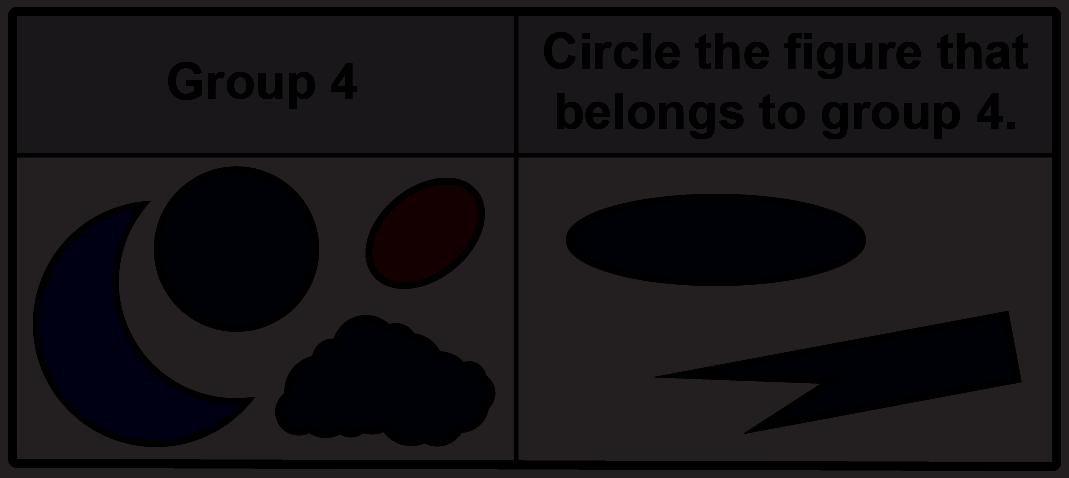
Circle the figure that belongs to group 4.
Draw the figures shown into two groups. Tell how you sorted the figures based on their attributes.
I can sort two-dimensional figures based on their similarities and differences.
6 Draw the figures shown into two groups. Tell how you sorted the figures based on their attributes.
Date:
I can use the relationship between addition and subtraction to restate a subtraction problem as a missing addend problem.
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
1
Emily had 4 erasers.
Emily bought more at the bookfair, and now she has 10 erasers. Use the ten frame and complete the number sentence to determine how many erasers Emily bought at the bookfair.
Use these if you need help.
• Use the ten frame to help you count on.
• How many empty spaces are on the ten frame?
4 + ? = 10
VIDEO
A video about how to solve
Solve the following questions. I can use the relationship between addition and subtraction to restate a subtraction problem as a missing addend problem.
2 3 Tina had 8 stuffed penguins.

Ted gave Tina more stuffed penguins, and now she has 10. Use the ten frame and complete the number sentence to determine how many stuffed penguins her friend gave her.
8 + ? = 10
Sophia has a box of crayons with 3 green crayons and some pink ones. There are 9 total crayons in the box. Use the part-part-whole model and complete the number sentence to determine the number of pink crayons in Sophia’s box.
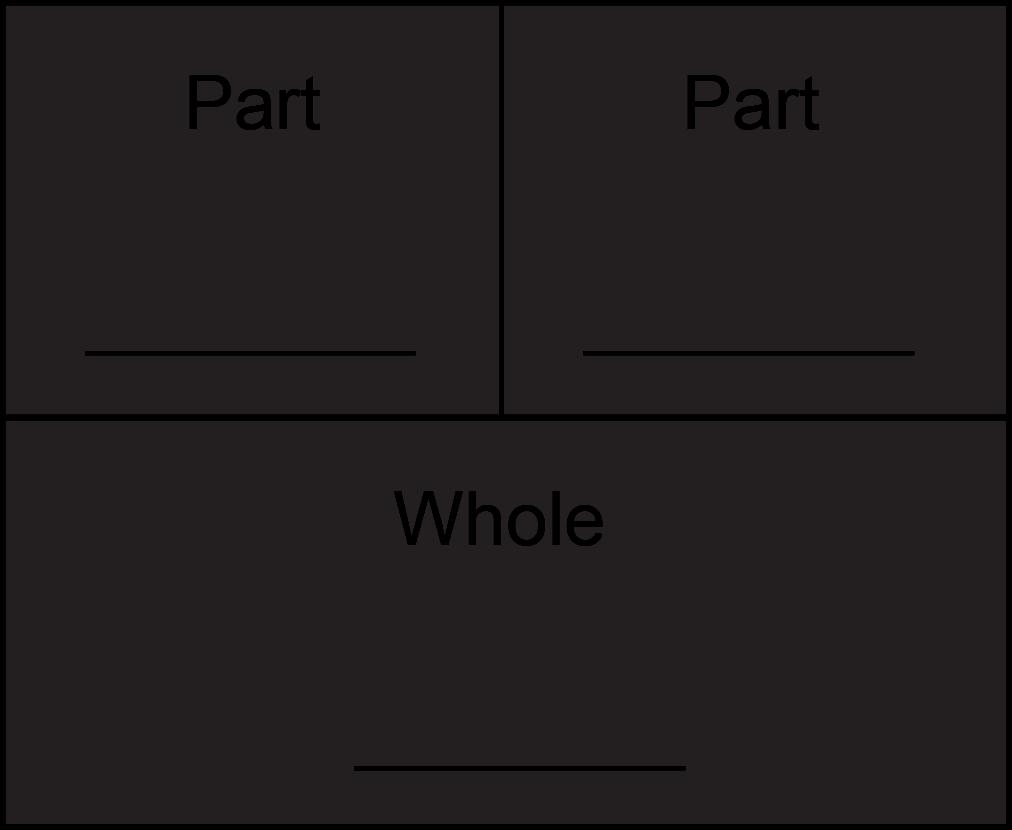
3 + ? = 9
I can use the relationship between addition and subtraction to restate a subtraction problem as a missing addend problem.
4 5 Byron has a bag of 7 dog treats. There are 4 bone-shaped snacks, and the rest are paw-shaped. Use the part-part-whole model and complete the number sentence to determine the number of paw-shaped bones in the bag.

Mark had 7 gumballs. His friend gave him some more. Now Mark has 10 gumballs. Use the ten frame and complete the number sentence to determine how many gumballs his friend gave him.

+ ? = 10
I can use the relationship between addition and subtraction to restate a subtraction problem as a missing addend problem.
6 Ricky has 8 sports stickers on his folder. There are 2 football stickers, and the rest are baseball stickers. Use the part-part-whole model and complete the number sentence to determine the number of baseball stickers on Ricky’s folder.

Date:
I can determine and explain whether equations involving addition and subtraction are true or false within 100 in equations with three or four terms with the unknown on either side of the equal sign.
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
1
Determine if the equation is true or false, and provide evidence to support your answer.
44 + 16 = 50 + 10
Use these if you need help.
• First, solve for one side, and then compare the other side to see if they are equal.
• Look to compare the values of the two sets of numbers in relationship to the other set of numbers. Both sides of the equation have to balance each other to be true.
A video about how to solve VIDEO TUTORIAL
I can determine and explain whether equations involving addition and subtraction are true or false within 100 in equations with three or four terms with the unknown on either side of the equal sign.
Solve the following questions.
Determine if the equation is true or false, and provide evidence to support your answer.
Determine if the equation is true or false, and provide evidence to support your answer.
I can determine and explain whether equations involving addition and subtraction are true or false within 100 in equations with three or four terms with the unknown on either side of the equal sign.
4 5 Elise adds two sets of numbers she believes are equal.
Is the equation true or false? _______________
Explain your answer. ________________________________________________________
Look at each pair of number sentences. Write true if they are equal or false if they are not equal.
I can determine and explain whether equations involving addition and subtraction are true or false within 100 in equations with three or four terms with the unknown on either side of the equal sign.
6 Look at each pair of number sentences. Write true if they are equal or false if they are not equal.
Date:
I can compose and decompose four-digit numbers in multiple ways using thousands, hundreds, tens, and ones using expressions or equations.
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
1
Which expressions represent the number 7,564? Select all that apply.
A. 7,000 + 500 + 6 + 4
B. 700 + 50 + 6 + 4
C. 7,000 + 500 + 60 + 4
D. 7,000 + 564
Use these if you need help.
• Decompose the number by place value.
• If you get stuck, use place value blocks and a place value mat to model the problem.
A video about how to solve
Solve the following questions. I can compose and decompose four-digit numbers in multiple ways using thousands, hundreds, tens, and ones using expressions or equations.
Which expression represents the number 5,603?
A. 5,000 + 600 + 10 + 3
B. 5,000 + 600 + 3
C. 5,000 + 600 + 30
D. 500 + 60 + 3
Complete the information in the table to represent the number shown.
1,235
Pictorial Model (Use circles showing values of 1,000, 100, 10, and 1.):
Write the number 8,462 in expanded and word forms.
Expression 1:
1,000 + 200 + ______ +
Expression 3: 12 hundreds + ______ ones
Expression 2: 12 hundreds + ______ tens + ______ ones
Expression 4: 1 thousand + ______ ones
There are 4,398 books in your school library. Write this value in expanded and word forms.
The expanded form of a number is shown: 5,000 + 700 + 20
What is the number in standard form?
A. 5,072
B. 5,712
C. 5,072
D. 5,720
Date:
I can find quotients that result in whole numbers and remainders, which are represented as fractional parts of the divisor.
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
1
What is 196 ÷ 5? Express the remainder as a fractional part of the divisor.
Use these if you need help.
• Use an array, area model, or partial quotients to find the quotient.
• The amount left over is the numerator, and the divisor, 5, is the denominator.
Solve the following questions. I can find quotients that result in whole numbers and remainders, which are represented as fractional parts of the divisor.
A cruise ship offers a 7-day tour and covers 1,034 kilometers. The ship travels the same number of miles each day. How many kilometers will the cruise ship travel each day? Express the remainder as a fractional part of the divisor.
What is 2,071 ÷ 2? Express the remainder as a fractional part of the divisor.
What is 2,896 ÷ 10? Express the remainder as a fractional part of the divisor.
The cafeteria has 328 fluid ounces of juice and needs to separate it into 5 equal-size dispensers. How much juice will be in each dispenser?
Blaise has a 329-page book. He sets a goal of finishing the book in 5 days. If he reads the same number of pages each day, how many pages will he read each day if he meets his goal?
Date:
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
I can interpret and compute a quotient when dividing a unit fraction by a whole number. 1
Ms. Smith used 1 3 of a gallon of paint to fill 5 paint bottles.

What fraction of all the paint went into each paint bottle?
Use these if you need help.
• The quotient is a fraction that is less than the dividend.
• What fraction of the model is filled in?
I can interpret and compute a quotient when dividing a unit fraction by a whole number.
Solve the following questions.
Mr. Johnson had 1 2 of a liter of juice. He poured the juice into 6 evenly sized servings. What fraction of a liter was each serving size? Explain your reasoning.
What is the value of 1 7 ÷ 14 ?
5 6
Draw a representation of the expression using an area model or a number line, and then write the quotient.
Expression: 1 5 ÷ 5 Model: Quotient:
Draw a representation of the expression using an area model or a number line, and then write the fraction size represented.
Expression: 1 3 ÷ 8 Model: Fraction size:
What is the value of 1 3 ÷ 5 ?
