BY ACCELERATE LEARNING
Program Architecture
Program Structure
The program is structured by course, unit, and lesson. Each unit includes formative checkpoints throughout and an end-of-unit assessment. Lessons are approximately 45–50 minutes long. They are intentionally designed to fit within the calendar year, so teachers have pacing flexibility. Here is a breakdown by course of the number of units and lessons.
13–15 Units per Course
* Scopes and sequences are intentionally designed for Florida’s accelerated and honors courses.
***The time estimates in these materials refer to instructional time. Some lessons contain optional activities that provide additional practice for teachers to use at their discretion. Additional Centers and Activities are also available to differentiate instruction.
Instructional Design
Math Nation Florida is built exclusively for Florida’s B.E.S.T. Standards, providing teachers with a highquality, standards-aligned curriculum that ensures all students can succeed in mathematics.
The design emphasizes:
• Student-centered, inquiry-based learning that builds from what students know.
• Scaffolded instruction within and across lessons, ensuring accessibility for all learners.
• Balanced development: conceptual understanding, procedural fluency, and realworld application.
• Multiple representations to deepen understanding and connect math to authentic contexts.
• Collaboration: students learn together and view mistakes as learning opportunities.
• Transfer learning: spiraling and connecting content across courses to highlight the beauty and interconnectedness of mathematics.
• Mathematical Thinking & Reasoning Standards (MTRs): embedded throughout for deeper engagement.
• Communication skills: consistent opportunities for oral and written mathematical reasoning.
Instruction draws on John Hattie’s Visible Learning research and incorporates:
• Practices with the highest impact on student growth.
• Classroom discourse and rich discussion opportunities.
• Clear strategies and content knowledge support in the Teacher Edition.
Teachers also have access to:
• Progress monitoring tools within a MultiTiered System of Support (MTSS): embedded assessments, reports, and analytics aligned to Florida’s B.E.S.T. Standards.
• Differentiation supports: remediation, intervention, and enrichment at both unit and lesson levels.
• Professional learning: point-of-use digital resources and a teacher community for continuous support.
Math Nation Florida’s Unit and Lesson Guides serve as a companion to our dynamic curriculum. The Unit and Lesson Guides accompany the curriculum for Grades 6–12, acting as an extension and planning partner for further clarification of the purpose, intent, coherence, and language of the lessons.
Unit Guides
Each unit includes a Unit Guide that offers additional planning support for the unit as a whole. Florida’s B.E.S.T. Standards are designed to ensure vertical alignment across grade levels and horizontal alignment within each course. In the Unit Guide, the Unit Narrative section describes the content of the unit, including horizontal connections to other units. The Vertical Alignment section of the Unit Guide provides the vertical alignment for the benchmarks taught in the unit.
Each Unit Guide also incorporates instructional strategies for differentiating, enriching, and implementing lessons throughout the unit.
Unit Narrative
The narrative captures the story of the unit, its progression, and connections to other units and courses. This section also includes a Unit-ata-Glance that gives an overview of the lessons included in the unit.
Differentiation
The differentiation section includes recommendations for incorporating Universal Design for Learning (UDL)™ and information for English Language Learners (ELLs). UDL from CAST© 2008 prioritizes strategies for differentiating instruction that seek to eliminate barriers of entry so that all students can learn. Each Unit Guide offers techniques specific to that unit content through the lens of UDL.
Section Overview
This section offers visual coherence with benchmarks aligned to lessons and clarifications to inform planning and instruction.
Vertical Alignment
This section provides the vertical alignment of the benchmarks taught in the unit by noting the benchmarks from prior courses that are being built upon, and the benchmarks in future courses that students are working toward.
Lesson Guides
Every lesson includes a Lesson Guide that provides insight into the math thinking and reasoning for effective implementation.
Lesson Introduction
Each Lesson Guide begins with an introduction that captures a snapshot of the lesson content for purposeful preparation. The Lesson Introduction includes the benchmarks and learning targets found in each student lesson. Teacher planning supports include vertical benchmark coherence, essential questions, a brief lesson narrative, a component summary for pacing and adaptation, and resources, including materials and vocabulary.
Each Lesson Guide includes additional planning support, such as:
• Mathematical Thinking and Reasoning (MTR) Standards: one is highlighted for each lesson for intentional focus when planning, though a lesson may integrate several MTRs.
• Common Misconceptions
• Things to Consider
• Literacy and Language Routines
• Differentiation Suggestions: found here and also incorporated throughout the lesson components.
Component Guidance
In the Lesson Guide, specific guidance incorporating instructional strategies is provided for each component of a lesson. This support is shown in line with the answer key of the student lesson for point-of-use implementation in the classroom. These recommendations include teacher moves, additional questions to consider asking, differentiation ideas related to the component, and possible enrichment ideas.
TARGETS
BENCHMARK COHERENCE
BUILDING
ESSENTIAL QUESTIONS
Student Lesson Design
Student lessons across all courses feature the same structure. The lessons include several components, each with a specific icon associated with it.
Benchmark(s)
Focus benchmarks are indicated on the first page of each student lesson.
Learning Target(s)
Learning Targets are clearly defined at the beginning of each lesson so student and families have clear expectations.
Warm-Up
Every lesson begins with a Warm-Up. The Warm-Ups are designed to vary so that all students have access and a positive start to each lesson. WarmUps include bell work, STEM career profiles, critical thinking, and more.
Wrap-Up
Every lesson ends with a short Wrap-Up. Wrap-Ups include student reflection, cool downs, error analysis, and tickets out the door that can be used for formative assessment.
Green lesson components identify student-led components that are intentionally designed for students to explore, discover, and practice concepts either independently or collaboratively with peers. These activities promote active engagement and deepen understanding of the content.
Explorations
Explorations are student-led discovery, often involving student collaboration and discussion. The topics explored in these components may not yet be formalized.
Activity
Activities include gallery walks, data collection, and games.
Collaboration
Students collaborate in pairs or small groups.
Try It
Students may not have reached mastery when completing Try It. These problems are an opportunity to apply previously learned skills to more formal practice problems.
Blue lesson components indicate that lesson components are intended to be teacher-led. These provide opportunities for direct instruction and teacher facilitation of learning and are intended to be rich in student collaboration.
Guided Instruction
Instruction should be studentcentered during Guided Instruction, but may require more support from the teacher.
Guided Practice
Guided Practice presents an opportunity for students to learn new concepts through practice problems.
Bring it Together
Bring it Together components formalize concepts explored in the lesson.
Refresher
Vocabulary and concepts learned in previous units or courses are reviewed in Refresher components.
Your Turn!
Your Turn! provides students with the opportunity for independent practice. These problems may also be used for homework.
DAILY LESSON STRUCTURE
Instruction and Practice to Meet Rigor
Lesson Activities
Lesson Activities serve as the core learning experience in every Math Nation Florida lesson. These engaging tasks:
• Encourage collaborative, student-led discovery through guided investigation, reasoning, and communication of mathematical ideas
• Replace front-loaded instruction with problem-solving, pattern recognition, and strategy development
• Foster a discovery-based approach where students actively construct mathematical understanding
• Purposefully integrate horizontal and vertical alignment, helping students connect concepts deeply and meaningfully
• Include built-in supports in the Teacher Edition for effective student questioning, discourse, exploration, and conceptual clarity
Student Practice
Each lesson includes multiple opportunities for student practice. Here are some examples of meaningful practice and targeted supports in Math Nation Florida:
Your Turn!
Your Turn! provides students with a chance for true independent practice of the concepts they are learning in a given lesson.
Collaborative Peer-to-Peer Practice
Math Nation Florida is packed with practice that is designed to have students working collaboratively to solve problems, develop solutions, discover new ideas and strategies, engage in error analysis and much more. With peer-to-peer practice embedded throughout the program, students are provided with ongoing, meaningful collaboration opportunities.
Try It
Students may not have reached mastery when completing Try It. These problems are an opportunity to apply skills learned in previous components to more formal practice problems.
Check Your Understanding
Check Your Understanding are a set of three digital practice problems available for students at the end of each lesson to inform and check for understanding.
Guided Practice
The Guided Practice components provide opportunities for students to practice their skills in a structured, teacher-led setting. The intention is to practice together with guidance to maximize retention and understanding.
Hands-On Practice
Activities include gallery walks, data collection, and games that allow the students to get additional practice in practical, engaging ways to leverage their critical and creative thinking skills.
Additional Lesson Practice
Each lesson has a set of additional practice questions to provide another opportunity for students to independently practice what they learned in the lesson. These can be utilized in class or for homework.
Stepping Stones
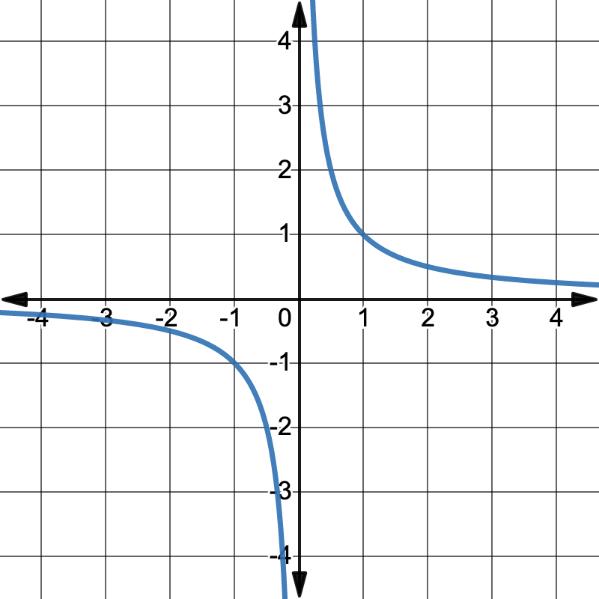
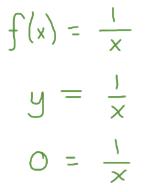
Each lesson has a set of digital practice questions called Stepping Stones. These give students targeted practice that moves them toward mastery of lesson-level expectations. They can be used flexibly before or after the main lesson to reinforce understanding.
Florida Independent Skills Practice Book
An additional Florida Independent Skills Practice Book helps students solidify and refine their skills, either in class or for homework. Practice books include embedded tutorial videos in English and Spanish so students and families have 24/7 support.
Home Support Resources
Math Nation Florida is designed to extend support into the home for student success. To help families, we provide:
Take-home Letters
Helpful take-home letters explain how to navigate and use the Math Nation Florida platform effectively. They provide families with specific guidance on how to leverage all of the resources available to best support their student in their math journey.
Study Expert Videos
Families also gain unlimited access to a comprehensive library of multilingual Study Expert videos that can be downloaded on our iOS and Android mobile apps, ensuring access anytime, anywhere, to a math tutor. The videos:
• Come in English, Spanish, and Haitian Creole
• Allow families to see how a math concept is taught to better support their student at home
• Help students who miss school due to illness or vacation keep up with their studies
SOLVING QUADRATICS BY FACTORING
9.7.1 Warm-Up: Satellite Dishes
Valerie Thomas is a scientist and inventor. In 1980, she received a patent for inventing the illusion transmitter. This was an integral piece of technology in developing the digital media formats needed for today’s video games, movies, and 3D television.
Thomas worked at NASA from 1964 -1995, where she helped develop real -time computer data systems to support satellite operations. She oversaw the creation of the Landsat program there, which supported the first satellite to transmit images from outer space.
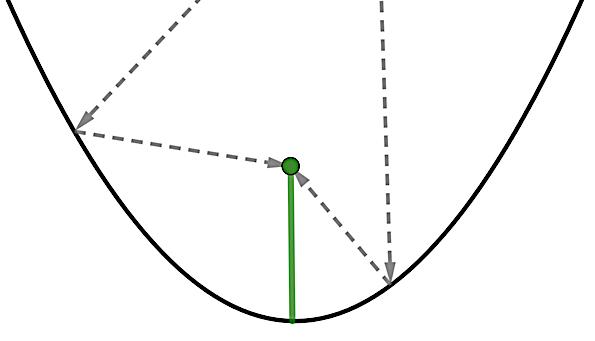
Today, satellite dishes are everywhere. Satellite dishes are designed using a parabolic curve.
1. What key feature of a parabola is the bottom of the dish?
2. The arrows show how signals bounce off a satellite dish to the receiver. The receiver is always located at a parabola’s focus. What key feature does the focus lie on?
9.7.2 Activity: Card Sort
1. Work with your partner to match the cards.
2. Factor each expression.
3.
Work with your partner to match the factored expressions to the ���� -intercepts.
4. Discuss with your partner how the factored expression reveals the ���� -intercepts. Make a conjecture about the connection.
9.7.3 Guided Instruction: Solving Quadratic Equations by Factoring
1. In the equation ���� ∙ ���� ∙ ���� = 0, which variable has to equal 0 so that the product is equal to 0?
o ���� o ���� o ����
o At least one of ���� , ���� , or ����
Zero Product Property
If the product of two numbers is , then at least one of the numbers is .
2. For each expression, use the zero product property to determine the values of ���� for which the expression would equal 0.
Expression (���� + 7)(���� 2) (2���� + 7)(���� 6) ( 3���� + 11)(4���� + 18) ����-values
Each of these expressions could have been written as quadratic equations that are set equal to 0 such as ���� 2 + 5���� 14 = 0.
3. When solving a quadratic equation set the equation equal to 0, the solution(s) will be the value(s) of ���� when ���� =_____. Explain how this relates to your conjecture from the card sort.
Another method of solving quadratics is by factoring. When solving by factoring the quadratic must be set equal to 0. Once the quadratic is factored, the zero product property is applied.
4. Solve ℎ2 10ℎ + 25 = 0 by factoring.
5. Solve 10���� 2 + 13���� 3 = 0 by factoring.
To solve by factoring, the quadratic equation should be in standard form and set equal to zero.
6. Solve ����2 + 36 = 13���� for ���� by factoring.
7. Solve 40���� 2 18���� = 12���� + 135 for ���� by factoring.
9.7.4 Try It: Factoring
Solve each by factoring. Show your work.
1. ���� 2 10���� 15 = 9
2. 3���� 2 + 6���� + 22 = 2 5����
9.7.5 Wrap-Up: Error Analysis
The work of two students who solved 2���� 2 12���� + 14 = 2���� 6 is shown.
Ruchelle
2���� 2 12���� + 14 = 2���� 6
2(���� 2 6���� + 7) = 2(���� 3)
2(���� 2 6���� + 7) 2 = 2(���� 3) 2
Quinyang
5)(���� 4) = 0 ���� = 5 2 or ���� = 4
1. Both Ruchelle and Quinyang made one mistake. Circle each mistake.
ALGEBRAIC
DESCRIPTIONS FOR REFLECTIONS
4.2.1 Warm-Up: Moving Circles
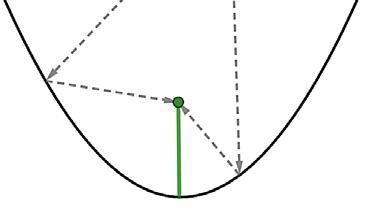
1. Move any three circles so that the pyramid points down.
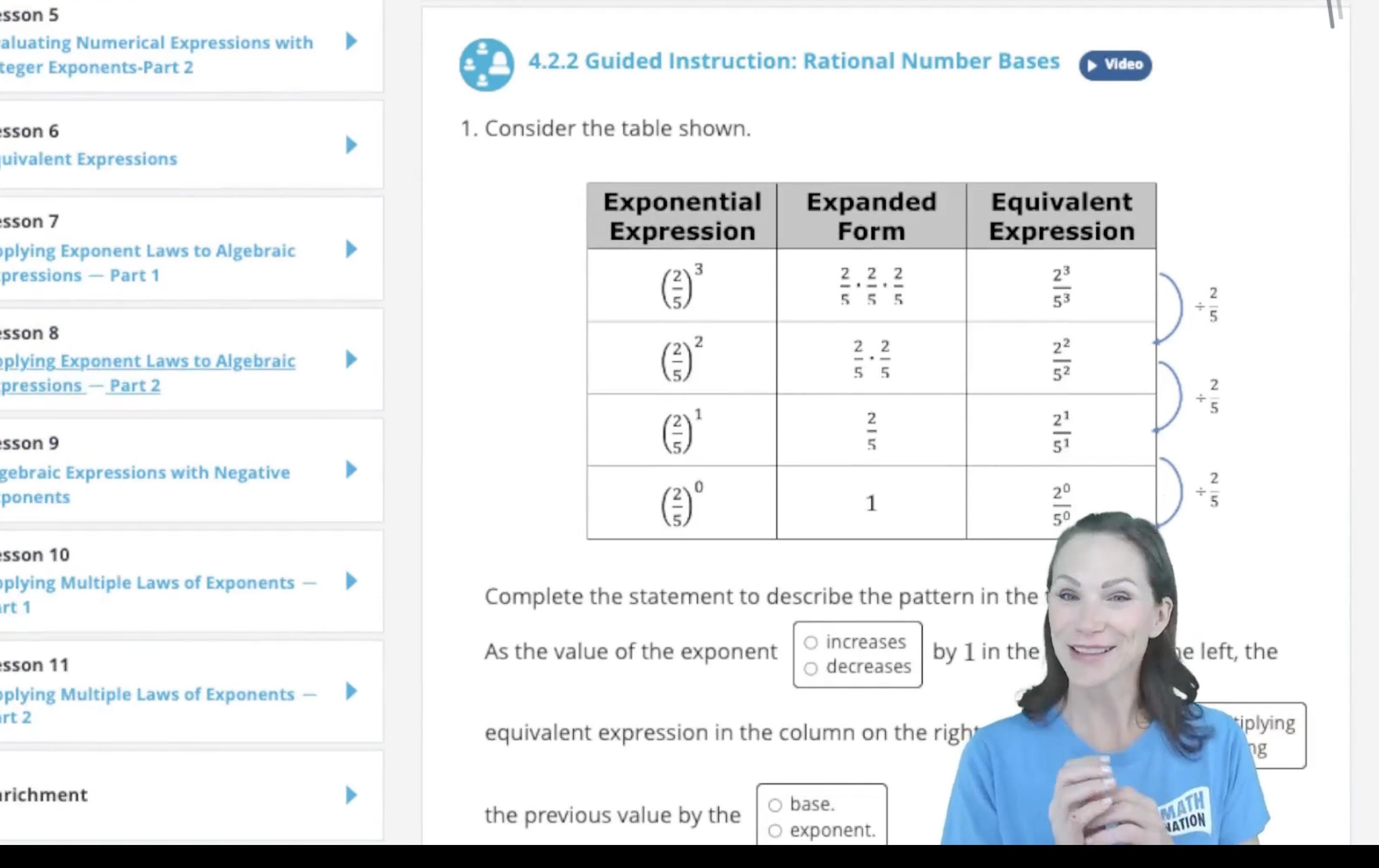
4.2.2
Exploration: Discovering Algebraic Descriptions for Reflections
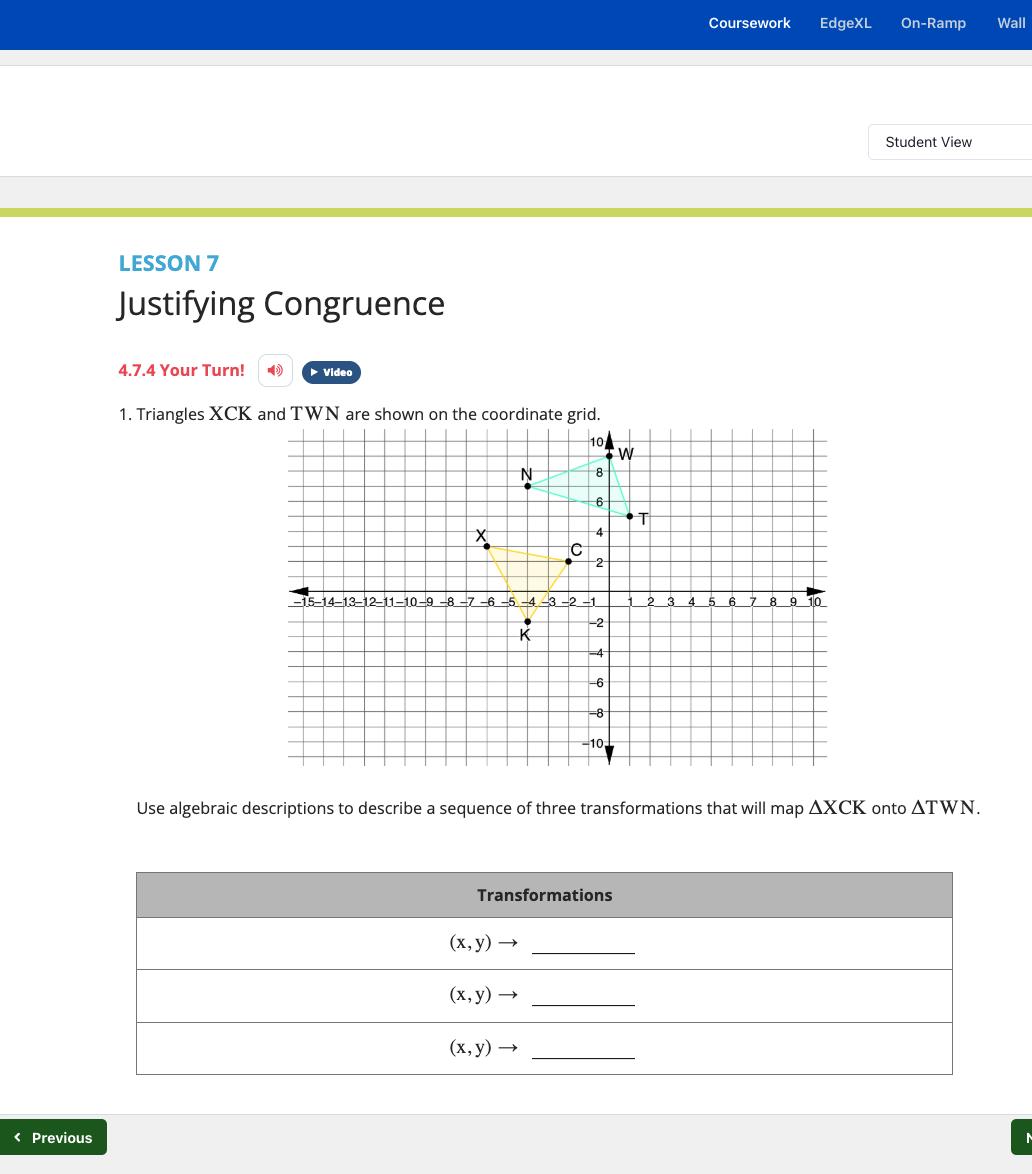
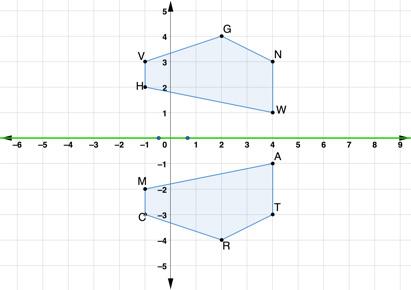
1. Quadrilaterals ���������������� and ���������������� are shown on the coordinate grid. Quadrilateral ���������������� was reflected across the ���� -axis to create quadrilateral ���������������� .
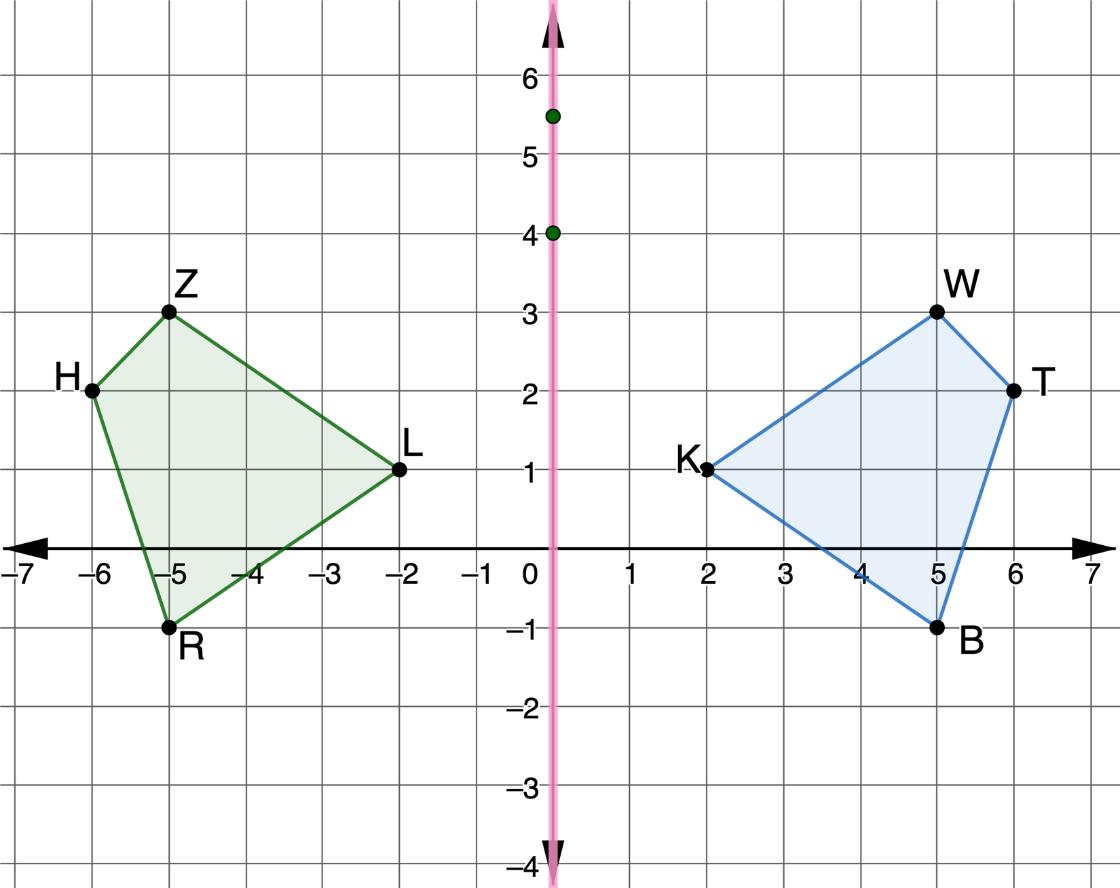
a. Draw a line segment between each set of corresponding vertices.
b. Describe how the line segments between the vertices are related to the ���� -axis.
c. Complete the table.
Ordered Pair of the Midpoint
d. What do you notice about the midpoints?
e. The table shows the coordinates of each vertex.
Work with your partner to describe how the coordinates of the preimage, quadrilateral ���������������� , are related to the coordinates of the image, quadrilateral ���������������� .
f. Write a conjecture that you and your partner think will work for the algebraic description of a reflection.
(���� , ����) → ( , )
g. Discuss with your partner if the algebraic description will work for any reflection. Summarize your conclusion.
2. Polygons �������������������� and �������������������� are shown on the coordinate grid. Polygon �������������������� was reflected across the ���� -axis to create polygon �������������������� .
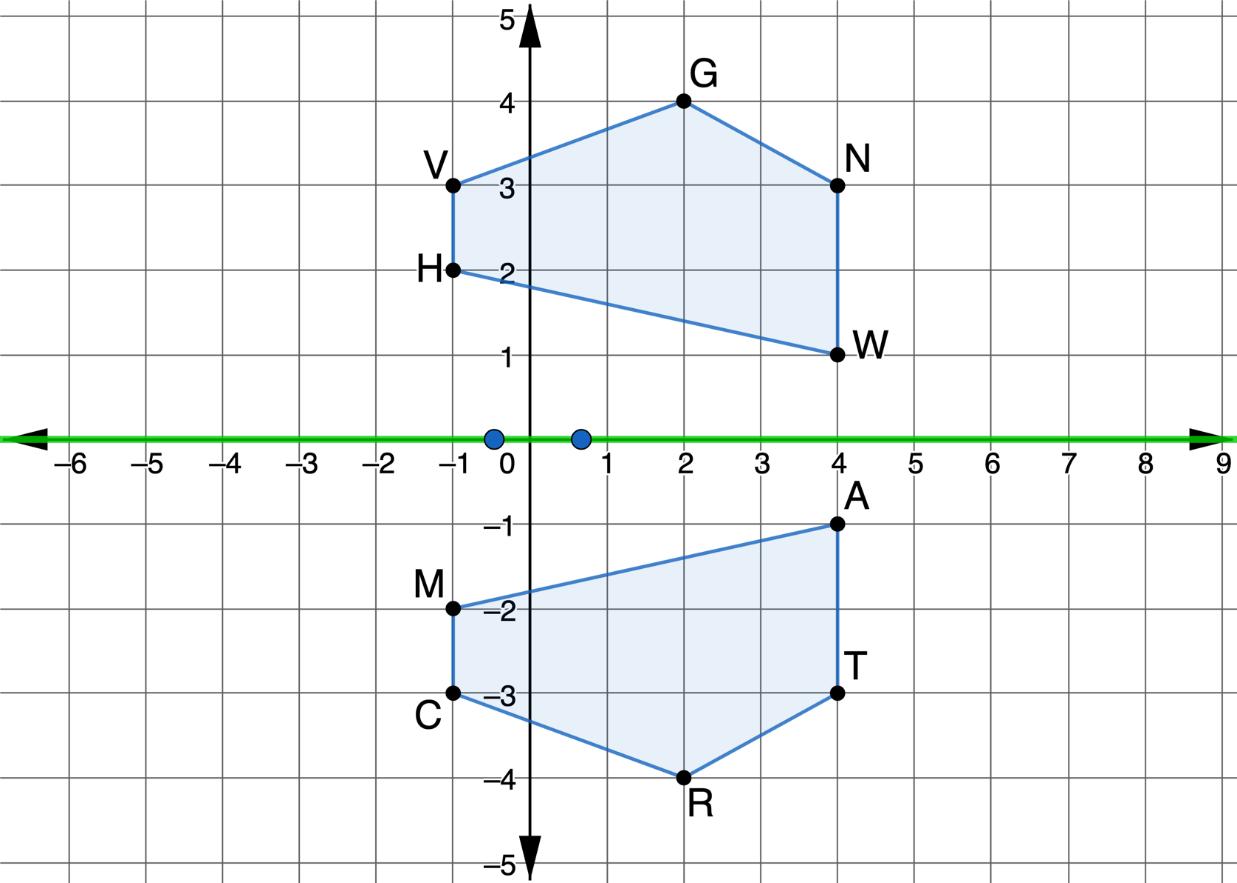
a. Describe the relationship that the line segments between each set of corresponding vertices have with the ���� -axis.
b. Wendall and Samah were working together on writing an algebraic description for reflections across the ���� -axis. Each student’s algebraic description and explanation of their thinking is shown in the table.
Samah (����, ����) → ( ����, ����) (���� , ����) → (���� , ����)
Because the polygon flipped over the ���� -axis, the ���� becomes its opposite.
Because above the ���� -axis all ���� -values are positive and below the ���� -axis all ���� -values are negative, the ���� becomes its opposite.
Discuss with your partner which, if any, algebraic description is correct. Use at least two ordered pairs from polygons �������������������� and �������������������� to defend your choice.
Wendall
3. Triangles ������������ and ����′����′����′ are shown on the coordinate grid. Triangle ������������ was reflected across the origin to create ∆����′����′����′.
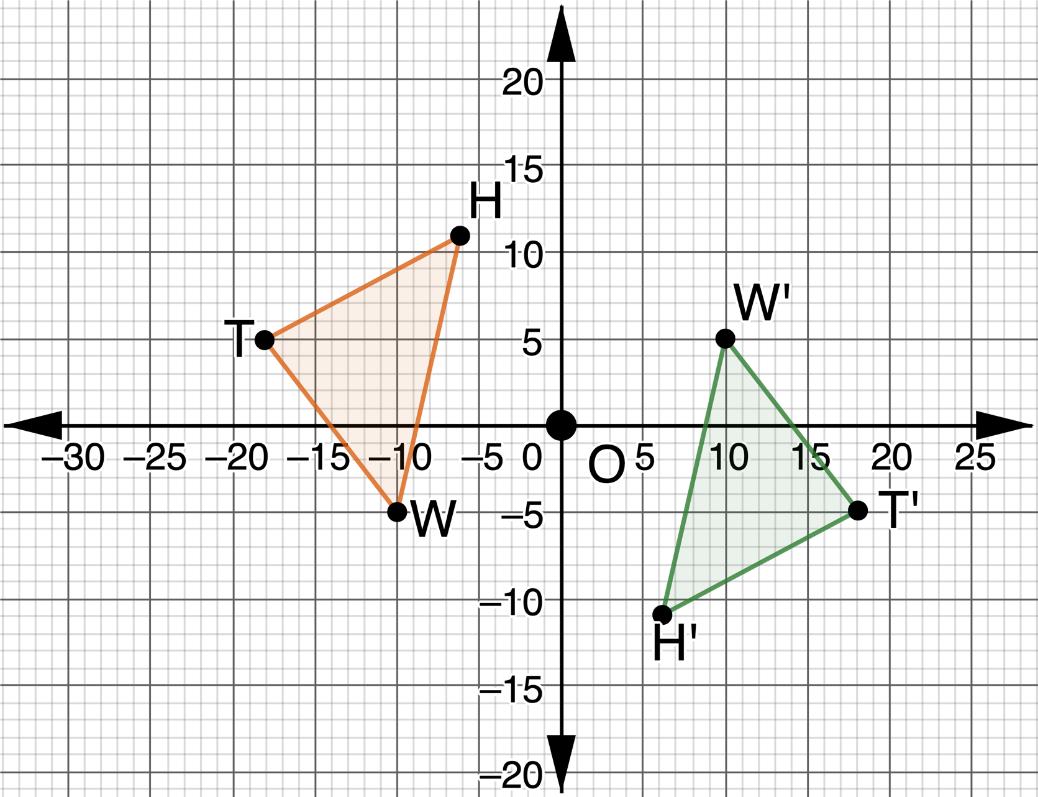
a. Discuss with your partner how to write the algebraic description for a reflection across the origin.
(���� , ����) → ( , )
b. Re-examine the algebraic descriptions of rotations. Which rotation is similar to a reflection across the origin?
4. Triangles ������������ and ����′����′����′ are shown on the coordinate grid. Triangle ������������ was reflected across the line ���� = ���� to create ∆����′����′����′.
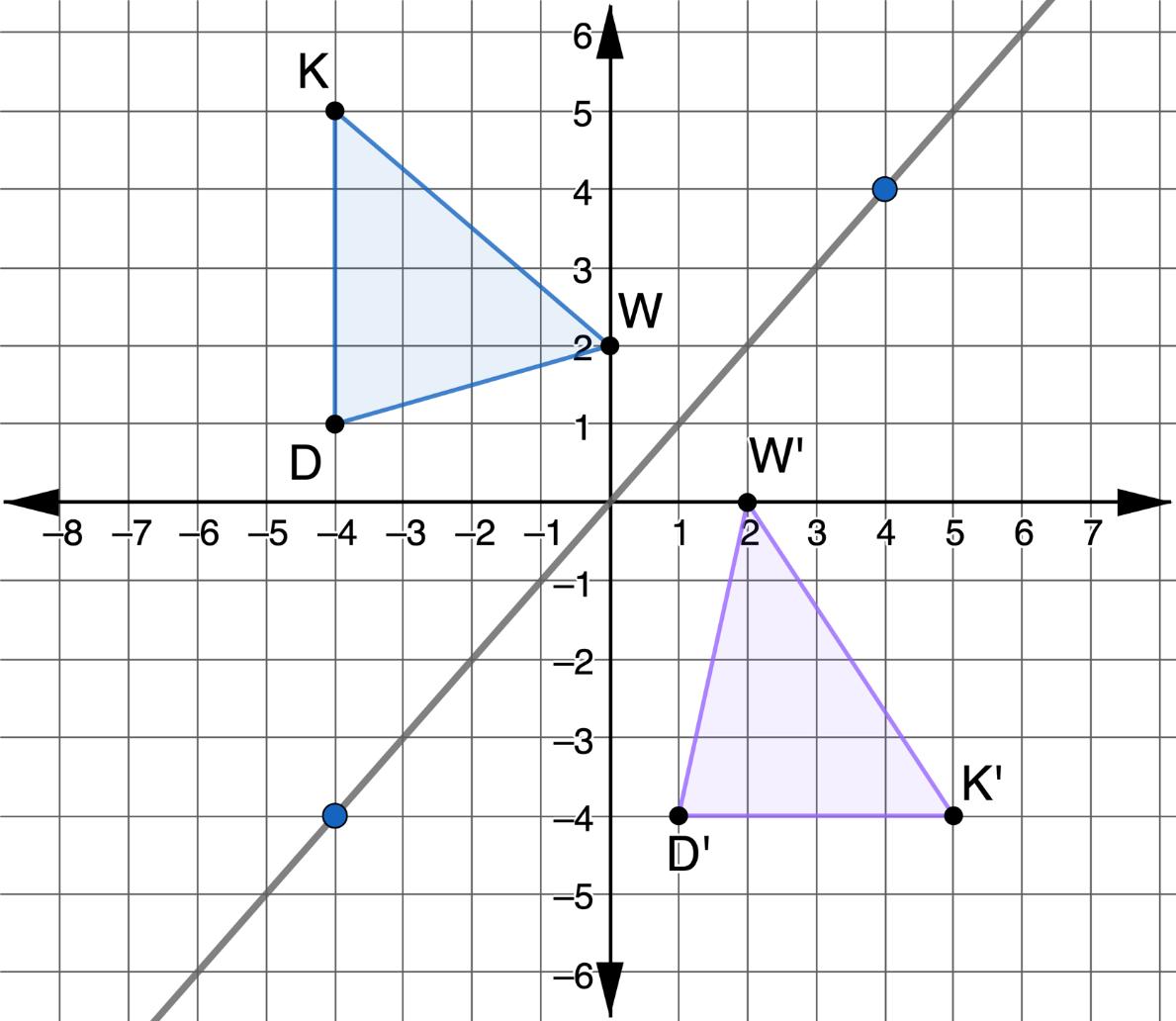
Use the coordinates to determine the algebraic description for a reflection across the line ���� = ���� . (���� , ����) → ( , )
5. Triangles ������������ and ������������ are shown on the coordinate grid. Triangle ������������ was reflected across the line ���� = ���� to create ∆������������ .
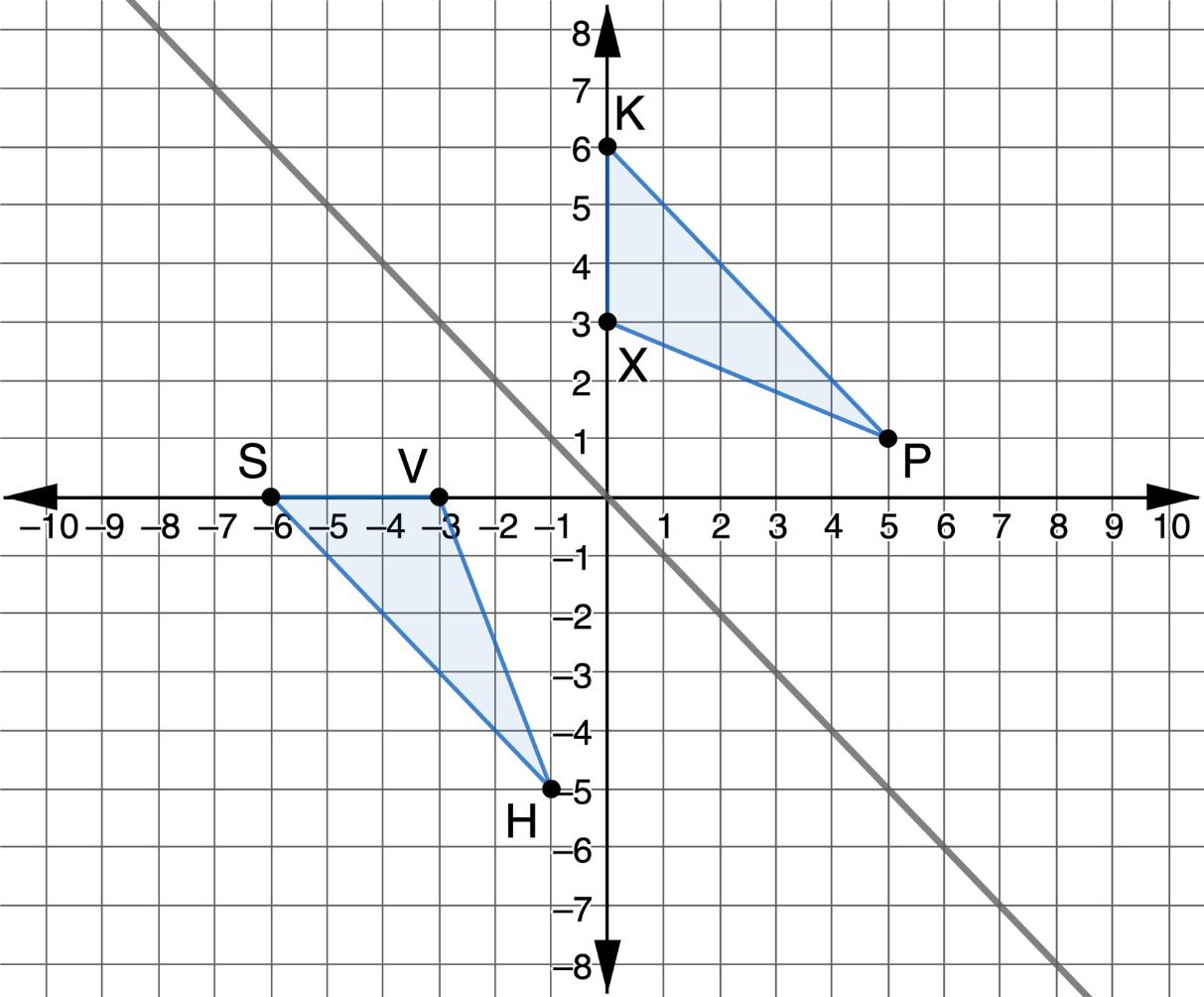
Use the coordinates to determine the algebraic description for a reflection across the line ���� = ���� .
(���� , ����) → ( , )
4.2.3 Bring It Together: Algebraic Descriptions for Reflections
Reflections
The coordinate changes to its
The coordinate changes to its
4.2.4 Wrap-Up: Cool Down
A reflection can be thought of as folding or "flipping" an object over the line of reflection. A squish painting is a fun application of a line of reflection.
To make a squish painting , a large sheet of construction paper is folded in half then opened up. Paint is dotted along one side of the fold. T he paper is folded, and the folded paper is rubbed, pounded, and squished to move the paint around. The paper is then opened up to reveal the squish painting.
1. How does a squish painting show that in a reflection, each point of the original figure and its image are the same distance away from the line of reflection?
DETERMINING ZEROS WITHIN A REAL-WORLD CONTEXT
3.2.1 Warm-Up: Would You Rather?
1. Which deal would you rather choose – buy 1, get 2 free for $120, or buy 1 pair that is already 60% off for $48?
2. Justify your answer mathematically.
3.2.2 Collaboration: Using Quadratics in the Music Business
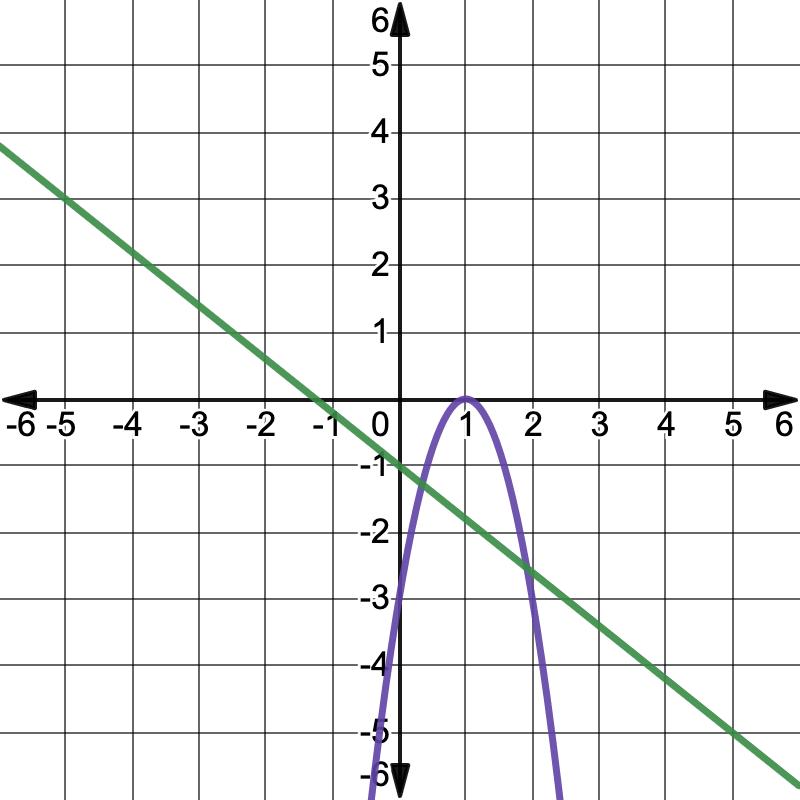
1. Organizers of a music festival charge $60 for admission. The organizers polled the attendees to determine how increasing the price would affect attendance. The equation ���� (����) = 20,000���� 2 20,000���� + 600,000 models profit as a function of ���� , where ���� is each $1 increase in the admission fee.
a. Discuss with your partner which factors would affect your attendance at a music festival. List your top three factors.
b. What admission fee would you consider to be too high?
c. If ���� = 2, what is the admission fee to the festival?
d. Solve 20,000���� 2 20,000���� + 600,000 = 0 by factoring. Show your work.
e. Interpret the solutions in terms of the context.
f. Ask two other classmates for their interpretations of the solutions to 20,000���� 2 20,000���� + 600,000 = 0. Write a summary of their interpretations of the solutions. You are the only person who should write in the first column of the table. Have each person initial next to your summary stating that your summary was accurate.
My Summary of Their Interpretation of the Solutions in Terms of the Context Initials
g. Review your classmates’ interpretations with your partner. If necessary, adjust your interpretation.
2. The compact disc (CD) was invented in 1979, many years before online music existed. At the time it was the most sophisticated way to store and play music. In 1982, CDs were made available to the public. CDs quickly became the most efficient way of storing music, which replaced vinyl records and cassette tapes.
The function ���� (���� ) = 2���� 2 + 38���� + 40 models the sales, in hundreds of millions of dollars, of compact discs in the years since 1990.
a. Solve 2���� 2 + 38���� + 40 = 0 by factoring.
b. Interpret the year that each zero represents.
c. Discuss the interpretation of each zero with your partner. Then, determine whether or not the interpretation makes sense. Summarize your discussion.
d. In 2001, iTunes was launched by Apple. For the first time, people could buy songs online and store them on mp3 players , iPods, or on a computer. Then, in 2008, the music streaming site Spotify was started.
Discuss with your partner why one of the zeros shows that online access to music may have led to CD sales eventually reaching zero. Summarize your discussion.
3.2.3 Guided Instruction: Finding Zeros
1. A landscape designer is adding a garden to a client’s backyard. One side of the garden will be alongside an existing fence. The client has 180 feet of fencing that is left over from another project. The client would like the garden to use all of the fencing.
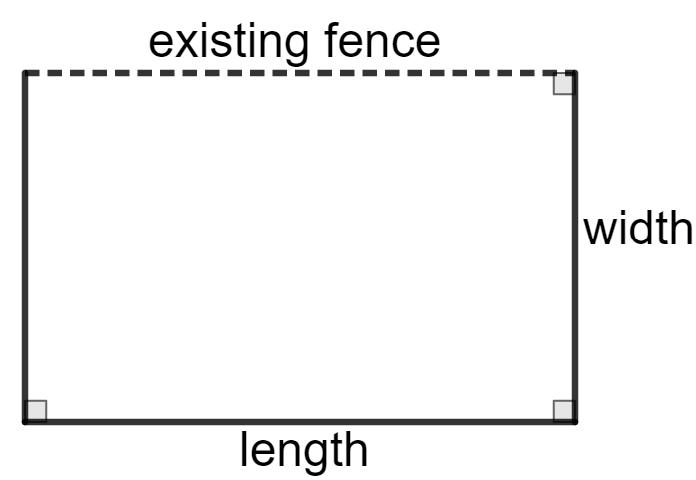
The equation ���� = 180���� 2���� 2 can be used to find the area of the garden, where ���� is the garden’s width, in feet.
a. Find the zeros of the equation ���� = 180���� 2���� 2 .
b. Interpret both of the zeros in terms of the context.
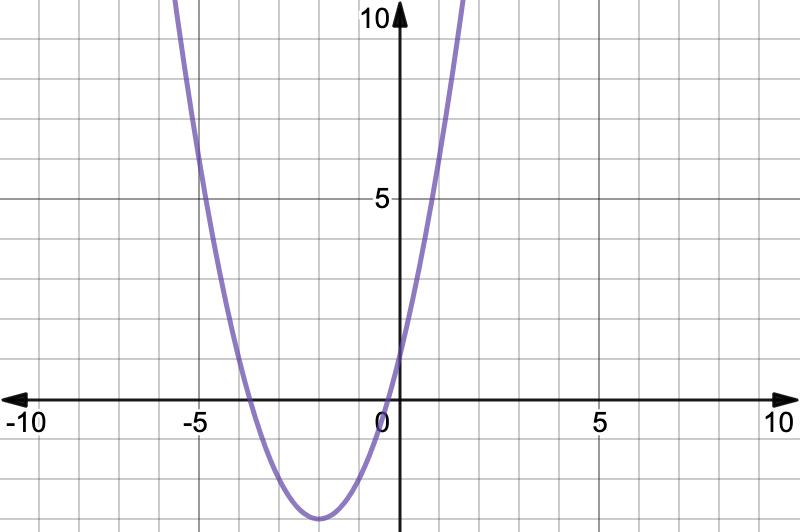
2. A statistician gathers data over several years, starting in 1995, on the average number of trips a household makes to run errands. The statistician uses the data to find the equation, ���� (���� ) = 2���� 2 + 68���� + 480, which models the average annual number of trips for errands per household for years since 1995. The graph of the equation is shown.
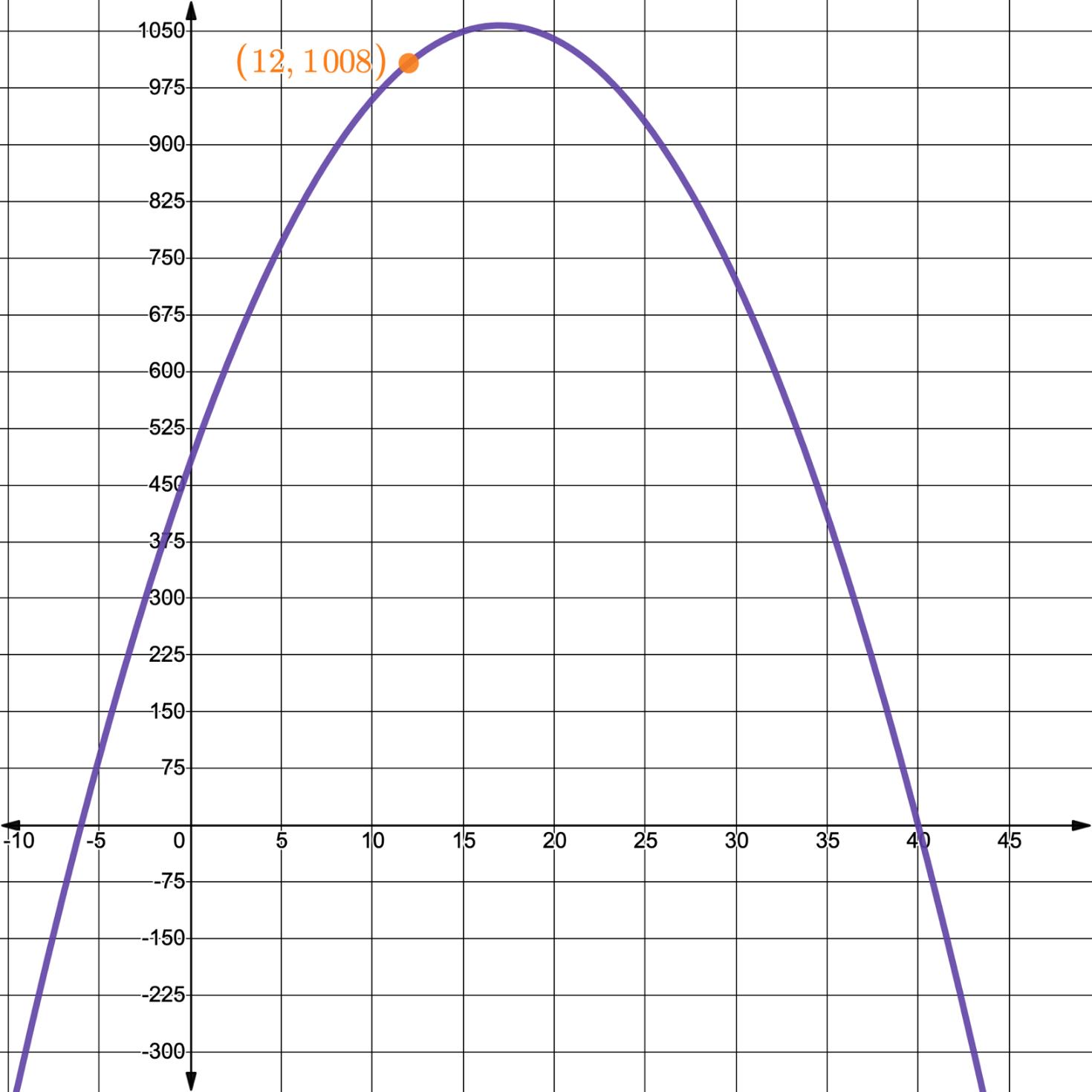
a. Interpret ���� (12). Include units.
b. Determine the zeros of the function. Show your work.
c. Interpret both of the zeros in terms of the context.
d. Discuss with your partner whether or not both zeros are viable. If a zero is non-viable, explain why.
3.2.4 Your Turn!
1. The equation ���� (����) = 16���� 2 + 64���� + 192 models the height, ���� , in feet, of a toy rocket after ���� seconds that it is launched from the top of a 16 -story building.
a. Determine the zeros of the function. Show your work.
b. Interpret both of the zeros in terms of the context.
c. Determine whether or not both zeros are viable. If a zero is no n-viable, explain why.
3.2.5 Wrap-Up: Ticket Out the Door
A firework is launched from a hill that is 80 feet (ft) above a lake. The firework will descend into the lake after it has exploded at its maximum height. The firework’s height, in ft, above the lake’s surface is given by ℎ(����) = 16���� 2 + 64���� + 80, where ���� is the time in seconds.
1. Determine the zeros of the function. Show your work.
2. Determine the viable solution and interpret in terms of the context.
LESSON 9.7
SOLVING QUADRATICS BY FACTORING
SOLVING QUADRATICS BY FACTORING
LESSON INTRODUCTION
MA.912.AR.3.1 Given a mathematical or real-world context, write and solve one-variable quadratic equations over the real number system.
LEARNING TARGETS
● I can solve a quadratic by factoring.
BENCHMARK COHERENCE
BUILDING ON
MA.8.AR.2.3 Given an equation in the form of x2 = p and x3 = q, where p is a whole number and q is an integer, determine the real solutions.
WORKING TOWARD
MA.912.AR.3.2 Given a mathematical or real-world context, write and solve one-variable quadratic equations over the real number system.
ESSENTIAL QUESTIONS
● How can my knowledge of factoring help solve quadratic equations?
● When is factoring an appropriate method for solving quadratic equations?
LESSON NARRATIVE
In this lesson, students will apply their knowledge of factoring polynomial expressions to solving quadratic equations. Students will be introduced to the zero-product property and learn how their ability to factor can help solve certain quadratic equations.
COMPONENT SUMMARY
9.7.1 WARM-UP (~5 MIN.)
Reading a passage about Valerie Thomas and relating satellite dishes to parabolas
9.7.3 GUIDED INSTRUCTION (10 MIN.)
Introduction to solving a quadratic equation by factoring
9.7.5 WRAP-UP (~5 MIN.)
Error Analysis activity on solving a quadratic by factoring.
9.7.2 ACTIVITY (15 MIN.)
Matching equations, graphs, intercepts, and factored expressions Card Sort
9.7.4 TRY IT (10 MIN.)
Solving quadratic equations by factoring practice
GLOSSARY
Key Terms:
● Zero product property
Additional Terms:
● Factoring
MATERIALS
● Cards for Card Sort Activity
ADDITIONAL PREPARATION
● Work through each of these questions prior to teaching. After each question, highlight where students may have misconceptions during the factoring process.
TEACHER TIPS
COMMON MISCONCEPTIONS
● Students may choose the wrong factors.
● Students may use the wrong sign of the factors.
● Students may make calculation errors when factoring.
● Students may forget to find both solutions after factoring.
THINGS TO CONSIDER
● Students have already learned how to factor in earlier lessons. Some students may need additional support for factoring, and not as much on using the zero-product property. Consider your student population when designing your lesson.
LITERACY AND LANGUAGE ROUTINES
Notice and Wonder
The 9.7.1 Warm-Up for this lesson contains a passage about Valerie Thomas and her role in developing satellite dishes. Students can discuss what they notice and wonder about the relationship between the satellite dish and the parabola.
MATHEMATICAL THINKING AND REASONING (MTR) STANDARD
MA.K12.MTR.4.1 Discussion and Reflection
In the 9.7.5 Wrap-Up, students will be provided with two work samples from two different students solving the same question. Students will be asked to determine the error in each work sample and provide an explanation of how to correctly solve the question.
DIFFERENTIATE INSTRUCTION
9.7.4 Try It provides students with an opportunity for solving quadratic equations by factoring. Students will be able to show mastery of multiple components of the question, allowing for more easily identifiable differentiation opportunities.
9.7.2 Activity provides students with an opportunity to engage in a card sort. Consider having students do all three questions with real cards for kinesthetic learners to connect to the content.
9.7.1 WARM-UP: SATELLITE DISHES
TEACHER MOVES
Consider a Notice and Wonder learning routine for this Warm-Up. Have students share out everything they notice and wonder as a class. Then release the students to work with a partner or group to answer the remaining questions. Position students to analyze the relationship between the key features of a parabola and the satellite dish. Probe student thinking about other objects in the real-world that may have also been designed using a parabolic curve.
ENRICHMENT
What are other objects in the real-world that are shaped as a parabola?
9.7.1 Warm-Up: Satellite Dishes
Valerie Thomas is a scientist and inventor. In 1980, she received a patent for inventing the illusion transmitter. This was an integral piece of technology in developing the digital media formats needed for today’s video games, movies, and 3D television.
Thomas worked at NASA from 1964-1995, where she helped develop real-time computer data systems to support satellite operations. She oversaw the creation of the Landsat program there, which supported the first satellite to transmit images from outer space.
Today, satellite dishes are everywhere. Satellite dishes are designed using a parabolic curve.
1. What key feature of a parabola is the bottom of the dish? vertex
2. The arrows show how signals bounce off a satellite dish to the receiver. The receiver is always located at a parabola’s focus. What key feature does the focus lie on?
Axis of symmetry
ALGEBRA 1 Teacher Guide
9.7.2 ACTIVITY: CARD SORT
9.7.2 Activity: Card Sort
1. Work with your partner to match the cards.
Equation Graph ��������-intercept ��������-intercept
2. Factor each expression.
3. Work with your partner to match the factored expressions to the �������� -intercepts.
4. Discuss with your partner how the factored expression reveals the �������� -intercepts. Make a conjecture about the connection.
Answers will vary. The �������� -intercept is the opposite sign of each factor. The �������� -intercepts are the numbers inside the parenthesis, but with different signs.
DIFFERENTIATE INSTRUCTION
Consider having students do all three questions with real cards and then posting them on a large visual like chart paper for kinesthetic and visual learners to connect to the content. In the interest of time, it would be beneficial to have the cards cut out and ready prior to the lesson, to allow more time to be spent on the activity.
TEACHER MOVES
Consider making each question an instructional event in the classroom.
• Review the instructions for a question
• Set a time to complete
• Call time
• Select groups to share their response
• Poll class for agree/disagree
• Move to next activity
DIFFERENTIATE INSTRUCTION
Try having students switch groups/partners for each question to have different experiences and conversations.
ENRICHMENT
What is the relationship between the factored form and the x-intercepts?
9.7.3 GUIDED INSTRUCTION: SOLVING QUADRATIC EQUATIONS BY FACTORING
TEACHER MOVES
Make a connection to what students learned about factoring in a previous unit. Highlight key differences, including that in this scenario they are working with equations, not expressions.
9.7.3 Guided Instruction: Solving Quadratic Equations by Factoring
1. In the equation �������� �������� �������� = 0, which variable has to equal 0 so that the product is equal to 0?
�������� o
o
o at least one of �������� , ��������, or ��������
Zero Product Property
If the product of two numbers is 0, then at least one of the numbers is 0.
2. For each expression, use the zero product property to determine the values of �������� for which the expression would equal 0.
Each of these expressions could have been written as quadratic equations that are set equal to 0 such as �������� 2 + 5�������� 14 = 0.
3. When solving a quadratic equation set the equation equal to 0, the solution(s) will be the value(s) of �������� when �������� = 0 Explain how this relates to your conjecture from the card sort. Answers will vary. This would be similar to finding the �������� -intercepts during the card sort activity. I set the �������� equal to zero during the card sort activity.
Another method of solving quadratics is by factoring. When solving by factoring the quadratic must be set equal to 0 Once the quadratic is factored, the zero product property is applied.
4. Solve ℎ2 10ℎ + 25 = 0 by factoring.
(ℎ 5)(ℎ 5) = 0 (ℎ 5) = 0 (ℎ 5) = 0
ℎ = 5 ℎ = 5
5. Solve 10�������� 2 + 13�������� 3 = 0 by factoring.
(2�������� + 3)(5�������� 1) = 0 (2�������� + 3) = 0 (5�������� 1) = 0 �������� = 3 2 �������� = 1 5
To solve by factoring, the quadratic equation should be in standard form and set equal to zero.
6. Solve ��������2 + 36 = 13�������� for �������� by factoring.
��������2 13�������� + 36 = 0 (�������� 9)(�������� 4) = 0 (�������� 9) = 0 (�������� 4) = 0 �������� = 9 �������� = 4
7. Solve 40�������� 2 18�������� = 12�������� + 135 for �������� by factoring.
40�������� 2 30�������� 135 = 0
5(8�������� 2 6�������� 27) = 0
5(4�������� 9)(2�������� + 3) = 0 (4�������� 9) = 0 (2�������� + 3) = 0 �������� = 9 4 �������� = 3 2
9.7.3 GUIDED INSTRUCTION: SOLVING QUADRATIC
EQUATIONS BY FACTORING (CONTINUED)
TEACHER MOVES
Have students relate what they did in their 9.7.2 Activity to what they are experiencing now. Students will begin making the connection between their knowledge of factoring and their ability to solve quadratic equations. Help students build their understanding of the zero-product property by naming the property when setting each factor equal to 0.
DIFFERENTIATE INSTRUCTION
Differentiation may be necessary at this stage if students did not do well with the factoring pieces of the 9.7.2 Activity. If students struggle with factoring, this additional step may add too much complexity for the student.
ENRICHMENT
• How do questions 6 and 7 looks different than questions 4 and 5?
• What would we need to do before factoring?
• How does this relate to applying the zero-product property?
9.7.4 TRY IT: FACTORING
DIFFERENTIATE INSTRUCTION
Consider grouping students together who have a deficit in factoring. Evidence from their performance on the factoring unit and their performance on the 9.7.2 Activity and 9.7.3 Guided Instruction in this lesson should be used to determine which students will need support. Work with these students on the factoring component so that they can complete the work of this concept.
ENRICHMENT
To factor, what must the equation be set equal to? Ask students their strategies for question 2. Students may need to be reminded that the polynomial on the left side of the equation could be moved to the right side of the equation, resulting in a positive leading coefficient.
9.7.4 Try It: Factoring
Solve each by factoring. Show your work.
ALGEBRA
9.7.5 Wrap-Up: Error Analysis
The work of two students who solved
is shown.
Quinyang 2��������
9.7.5 WRAP-UP: ERROR ANALYSIS
DIFFERENTIATE INSTRUCTION
This activity will provide differentiation data for which students need additional supports in which component of the process. The component the students miss and/or get correct in the error analysis could determine what a student understands to provide differentiation and support if necessary.
QUESTIONING
For an additional challenge, have students explain or correct the mistake in the process.
1. Both Ruchelle and Quinyang made one mistake. Circle each mistake.
ALGEBRAIC DESCRIPTIONS FOR REFLECTIONS
LESSON INTRODUCTION
LESSON 4.2 ALGEBRAIC DESCRIPTIONS FOR
REFLECTIONS
MA.912.GR.2.1 Given a preimage and image, describe the transformation and represent the transformation algebraically using coordinates.
LEARNING TARGETS
● I can relate a reflection on the coordinate plane to an algebraic notation of the transformation.
BENCHMARK COHERENCE
BUILDING ON
MA.8.GR.2.1 Given a preimage and image generated by a single transformation, identify the transformation that describes the relationship.
WORKING TOWARD
N/A
ESSENTIAL
QUESTIONS
● What is a reflection?
● How can reflections be represented algebraically?
LESSON NARRATIVE
The main part of the lesson, 4.2.2 Exploration, immerses students in an in-depth exploratory discovery of the effects of reflections across a variety of lines. Students focus on the ordered pairs of the vertices and the midpoint of line segments that connect corresponding vertices across the line of reflection. Students engage in language routines and math thinking and reasoning to draw conclusions leading toward generating algebraic descriptions of reflections.
COMPONENT SUMMARY
4.2.1 WARM-UP (~5 MIN.)
Critical thinking problem
4.2.3 BRING IT TOGETHER (5-10 MIN.)
Students summarize and synthesize their findings from the Exploration
4.2.2 EXPLORATION (25-30 MIN.)
Exploration of reflections across a variety of lines of reflection
4.2.4 WRAP-UP (~5 MIN.)
Students relate elements of reflections to a squish painting
GLOSSARY
Key Terms:
● N/A
Additional Terms:
● N/A
MATERIALS
● (Optional) Integer chips or other chips for 4.2.1 Warm-Up
● (Optional) Squish painting
ADDITIONAL PREPARATION
● N/A
TEACHER TIPS
COMMON MISCONCEPTIONS
● Students may struggle differentiating between axes, values in an ordered pair, and their opposites.
● Students who struggle in spatial reasoning might find it difficult to navigate the visual elements of reflections.
THINGS TO CONSIDER
● Consider using sentence stems to actively convert student verbal descriptions into mathematical language. For example, when students are describing the effects of reflection like, “They are in the same place,” provide scaffolded phrases like, “Vertex __ is the same distance away from __ as Vertex __.”
LITERACY AND LANGUAGE ROUTINES
Notice and Wonder
4.2.2 Exploration questions 1c-f provide two opportunities for students to make sense of their observations in mathematically meaningful ways. Encourage students to utilize Notice and Wonder techniques for each element to help each other discover and produce algebraic descriptions based on the Exploration.
MATHEMATICAL THINKING AND REASONING (MTR) STANDARD
MA.K12.MTR.4.1 Discussion and Reflection
4.2.2 Exploration question 2b provides an opportunity for students to engage in mathematical discussion by analyzing and critiquing the thinking of others. Use this as an opportunity to provide students with practice analyzing the thinking of others and then articulating their own thinking in response.
DIFFERENTIATE INSTRUCTION
For a kinesthetic entry point, consider using physical manipulatives such as patty paper or cut-outs for students to explore the reflections in 4.2.2 Exploration.
4.2.1 WARM-UP: MOVING CIRCLES
TEACHER MOVES
The arrows provided here are for answer key purposes. Students will only have the blue dots visible.
ENRICHMENT
Consider prompting questions to target specific actions of Growth Mindset.
• Was the puzzle a struggle, or was it easy for you?
• What did you look for first when making pyramid point down?
• What did you try first? What strategy or different way of looking at the pyramid helped you know what to do next?
DIFFERENTIATE INSTRUCTION
Do you have integer chips or similar manipulatives? Students could interact with this pyramid prompt for a kinesthetic learning experience. This could also be done with digital manipulatives.
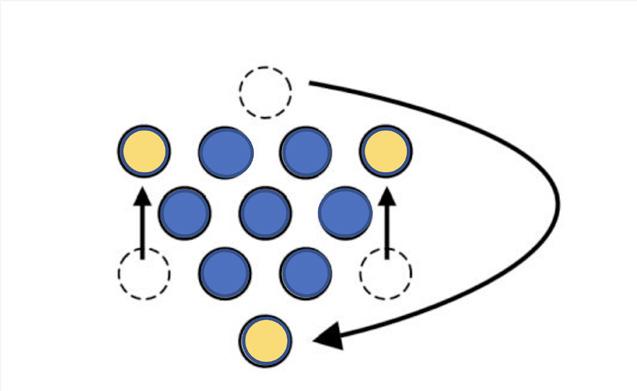
1. Move any three circles so that the pyramid points down.
4.2.1 Warm-Up: Moving Circles
4 2 2 Exploration: Discovering Algebraic Descriptions for Reflections
1. Quadrilaterals �������������������������������� and �������������������������������� are shown on the coordinate grid. Quadrilateral �������������������������������� was reflected across the ��������-axis to create quadrilateral
a. Draw a line segment between each set of corresponding vertices. Shown on figure.
b. Describe how the line segments between the vertices are related to the ��������-axis. Answers will vary. Each vertex is the same distance from the ��������-axis as its corresponding vertex. The ��������-axis bisects each line segment. The line segments between the vertices are perpendicular to the ��������-axis.
4.2.2 EXPLORATION: DISCOVERING ALGEBRAIC DESCRIPTIONS FOR REFLECTIONS
TEACHER MOVES
This Exploration is scaffolded to allow students to engage with it with their partner rather than being guided through by the teacher. There will be an opportunity to summarize and synthesize what is discovered in the next component. Students may revise their thinking throughout the exploration as they engage with each new reflection.
Observe and listen as students work with their partners. Make note of student ideas that you can ask them to share in the whole group Bring it Together.
Additional scaffolding questions are provided, if needed, but this should be a primarily student-directed exploration.
TEACHER MOVES
During the exploration, allow students to describe relationships using their own words first. Students informally experienced reflections in Unit 1, so the exploration helps them recall that information. For students who are struggling with descriptions, refer them to Unit 1. As you circulate, if student descriptions show misunderstanding, then ask probing questions like:
• What is the relationship (ZW) ̅has with the y-axis?
• Is that relationship the same for the other line segments?
4.2.2 EXPLORATION: DISCOVERING ALGEBRAIC DESCRIPTIONS FOR REFLECTIONS (CONTINUED)
TEACHER MOVES
Notice and Wonder Routine
Notice the intentional scaffolding of language routine elements embedded within the Exploration. Questions
1c-1d and 1e-1f provide the space and opportunity for students to discover how the ordered pairs of the vertices after a reflection can be used to generate algebraic descriptions. Students may not be engaging in a formal Notice and Wonder routine, but they can be prompted to notice and wonder about what they see for additional entry points when stuck in parts like question 1e.
Emphasize the word “opposite” in student discussion, as this word is seen in later questions of this lesson.
TEACHER MOVES
MA.K12.MTR.5.1: Patterns and Structure
The exploration provides students the opportunity to use patterns and structure to help understand and connect previously learned concepts (reflections) to new concepts (representing them with algebraic descriptions).
c. Complete the table
d. What do you notice about the midpoints? Answers will vary. All �������� -values are zero. All of the midpoints are on the ��������-axis.
e. The table shows the coordinates of each vertex.
Work with your partner to describe how the coordinates of the pre-image, quadrilateral
, are related to the coordinates of the image, quadrilateral
Answers will vary. The �������� -values are opposites and the ��������-values are the same.
f. Write a conjecture that you and your partner think will work for the algebraic description of a reflection.
Answers will vary. Since the polygon is reflecting over the ��������-axis, the �������� -values change to their opposite sign. (��������, ��������) → ( ��������, ��������)
g. Discuss with your partner if the algebraic description will work for any reflection. Summarize your conclusion.
Answers will vary. The point or line of reflection matters. Reflections over the ��������-axis will follow that description, but if the line of reflection is not the ��������axis, then a new algebraic description would be needed.
2. Polygons ���������������������������������������� and ���������������������������������������� are shown on the coordinate grid. Polygon ���������������������������������������� was reflected across the �������� -axis to create polygon ����������������������������������������
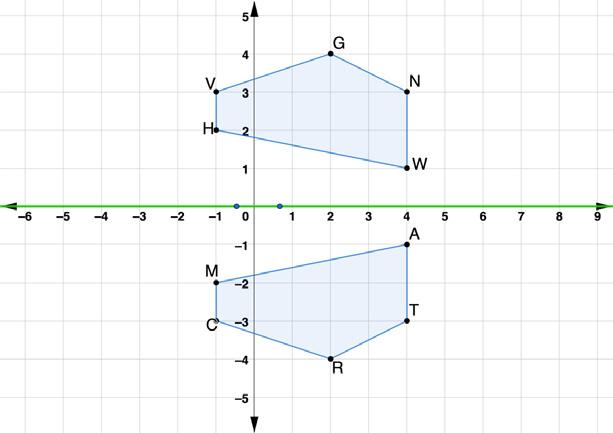
a. Describe the relationship that the line segments between each set of corresponding vertices have with the �������� -axis.
Answers will vary. Each vertex is the same distance from the �������� -axis as its corresponding vertex. The line segments between corresponding vertices are perpendicular to the �������� -axis.
b. Wendall and Samah were working together on writing an algebraic description for reflections across the �������� -axis. Each student’s algebraic description and explanation of their thinking is shown in the table.
Wendall Samah (��������, ��������) → ( ��������, ��������) (��������, ��������) → (��������, ��������)
Because the polygon flipped over the �������� -axis, the �������� becomes its opposite.
Because above the �������� -axis all ��������-values are positive and below the �������� -axis all ��������-values are negative, the �������� becomes its opposite.
4.2.2 EXPLORATION: DISCOVERING ALGEBRAIC DESCRIPTIONS FOR REFLECTIONS (CONTINUED)
ENRICHMENT
Monitor student discussion for question 2a. If necessary, prompt students to use the scaffolding from question 1 similarly in question 2. Draw line segments between each set of corresponding vertices from polygon MCRTA to polygon HVGNW.
Prompting questions could include the following:
• What do you notice about the midpoints of the line segments?
• What do you notice about the coordinates of each ordered pair?
• What do you notice about the line of reflection and the line segments?
• How are these relationships similar to and different from the previous reflection?
TEACHER MOVES
MA.K12.MTR.4.1: Discussion and Reflection
Students have the opportunity to critique the reasoning and thinking of others. Consider having students or their partners read this passage out loud for others to listen and respond to in conversation. The error analysis of question 2b has students look at the common misconception of a reflection across the x-axis resulting in the x-value changing.
4.2.2
EXPLORATION: DISCOVERING
ALGEBRAIC DESCRIPTIONS FOR REFLECTIONS (CONTINUED)
QUESTIONING
Question 3b seeks to build a conceptual connection to the previous lesson. Consider how to best engage students with the two elements of question 3 by beginning with a question like, “Does this look familiar? Why or why not?” and suggest they start with question 3b before finishing on question 3a.
Discuss with your partner which, if any, algebraic description is correct. Use at least two ordered pairs from polygons ���������������������������������������� and ���������������������������������������� to defend your choice. Write a summary of your discussion.
Samah is correct.
Answers will vary Samah is correct because ��������(4, 1) becomes ��������(4,1) and ��������(2, 4) becomes ��������(2 4). You can see that the �������� -values remained the same but the ��������-values are now the opposite sign
3. Triangles ������������������������ and ��������′��������′��������′ are shown on the coordinate grid. Triangle ������������������������ was reflected across the origin to create ∆��������′��������′��������′.
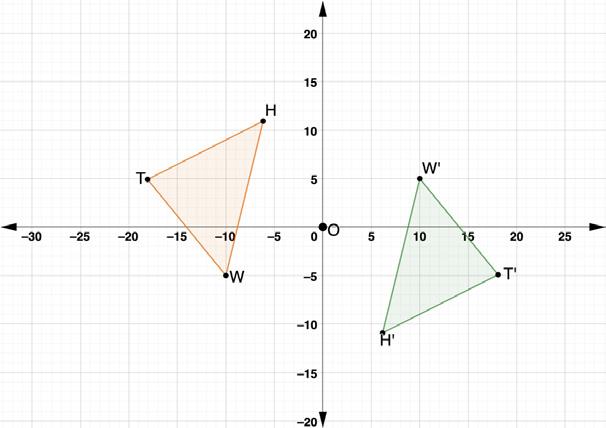
a. Discuss with your partner the algebraic description for a reflection across the origin. (��������, ��������) → (
b. Re-examine the algebraic descriptions of rotations. Which rotation is similar to a reflection across the origin? 180° rotation
QUESTIONING
If time permits, transform your classroom into a coordinate plane and challenge students to create a mathematically accurate reflection using elements like desks, chairs, bags, and more!
4. Triangles
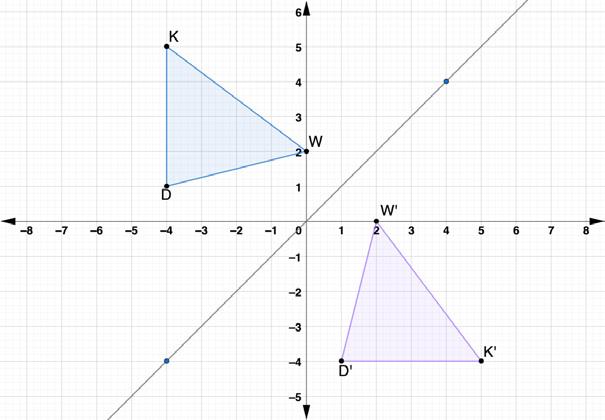
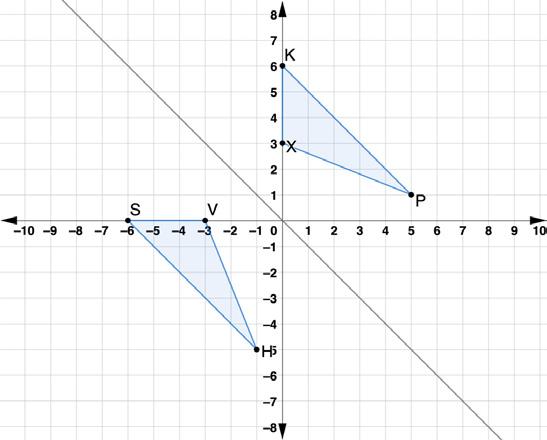
4.2.3 Bring It Together: Algebraic Descriptions for Reflections Reflections
Across the ��������-axis Across the ��������-axis
The �������� coordinate changes to its opposite The �������� coordinate changes to its opposite
Across
The coordinates switch places. The coordinates switch places and become opposite
4.2.3 BRING IT TOGETHER: ALGEBRAIC DESCRIPTIONS FOR REFLECTIONS
TEACHER MOVES
Use this section to encourage synthesis, not memorization. Call on students to share their ideas following the exploration to highlight student voice and solidify takeaways from the Exploration.
4.2.4 Wrap-Up: Cool Down
A reflection can be thought of as folding or "flipping" an object over the line of reflection. A squish painting is a fun application of a line of reflection.
To make a squish painting, a large sheet of construction paper is folded in half then opened up. Paint is dotted along one side of the fold. The paper is folded, and the folded paper is rubbed, pounded, and squished to move the paint around. The paper is then opened up to reveal the squish painting.
1. How does a squish painting show that in a reflection, each point of the original figure and its image are the same distance away from the line of reflection?
4.2.4 WRAP-UP: COOL DOWN
QUESTIONING
Consider what this Cool Down might look like as a performance task or interdisciplinary project with an art class. Students could be immersed into an exploration of reflections in art to establish a strong foundation for key elements of reflections, while the 4.2.2 Exploration can serve to quantify and make mathematical sense of their findings of reflections in art.
Answers will vary. In a squish painting, you can see how close each part of the painting is to the crease in the paper. You can see that the picture is a mirror image. The fold is the line of reflection.
MODELING WITH QUADRATIC EQUATIONS AND
MODELING WITH QUADRATIC EQUATIONS AND FUNCTIONS
LESSON 3.2
LESSON
DETERMINING ZEROS WITHIN A REAL-WORLD CONTEXT
DETERMINING ZEROS WITHIN A REAL-WORLD CONTEXT
LESSON INTRODUCTION
MA.912.AR.3.2 Given a mathematical or real-world context, write and solve one-variable quadratic equations over the real- and complex number systems.
LEARNING TARGETS
● I can solve a quadratic by factoring when given a real-world context.
● I can interpret solutions as viable or non-viable options given a real-world context.
BENCHMARK COHERENCE
BUILDING ON
MA.912.AR.3.1 Given a mathematical or real-world context, write and solve one-variable quadratic equations over the real-number system.
WORKING TOWARD
N/A
ESSENTIAL QUESTIONS
● How can the validity of solutions be identified when solving quadratic equations by factoring within a real-world context?
● How can a quadratic equation be solved by factoring within a real-world context?
LESSON NARRATIVE
In this lesson, students extend their knowledge of solving quadratic equations by factoring from Lesson 1 to real-world contexts. Given a real-world context, students will apply their knowledge of factoring and the zero-product property to solve quadratic equations. Students will interpret the solutions to quadratic equations within the given context and will further analyze the validity of solutions.
COMPONENT SUMMARY
3.2.1 WARM-UP (~5 MIN)
“Would You Rather?” activity on sale prices
3.2.3 GUIDED INSTRUCTION (10-15 MIN)
Solving real-world quadratic equations by factoring and interpreting solutions
3.2.5 WRAP-UP (~5 MIN)
Solving a quadratic equation to model fireworks
3.2.2 COLLABORATION (20-15 MIN)
Solving real-world quadratic equations by factoring and interpreting solutions
3.2.4 YOUR TURN! (5-10 MIN)
Analyzing the flight path of a toy rocket modeled by a quadratic equation
RESOURCES
GLOSSARY
Key Terms:
● N/A
Additional Terms:
● Roots
● Zeros
● Zero-product property
MATERIALS
● (optional) Graphing utility
ADDITIONAL PREPARATION
● Consider creating a review of factoring techniques, including factoring out the greatest common factor, to aid struggling students.
TEACHER TIPS
COMMON MISCONCEPTIONS
● Students may believe that quadratic equations set equal to zero must always have the zero on the right side of the equation, causing confusion with function notation.
THINGS TO CONSIDER
● Although factoring is a review skill, students still struggle. Consider reviewing all forms of factoring to aid struggling students. It may also benefit students to utilize multiple methods, such as algebra tiles, area model, grouping, etc.
LITERACY AND LANGUAGE ROUTINES
Three Reads
Consider a Three Reads strategy for 3.2.3 Guided Instruction (struggling students may benefit from utilizing this strategy throughout the entire lesson). Students often struggle with word problems, so the use of this strategy will ensure that students know what they are being asked to do. This strategy supports reading comprehension of questions and negotiating information in a text with a partner in a mathematical conversation.
MATHEMATICAL THINKING AND REASONING (MTR) STANDARD
MA.K12.MTR.7.1 Real-World Contexts
This lesson extends student understanding of solving quadratic functions by factoring to modeling and solving real-world problems. In this way, students are connecting the idea of solving quadratic equations by factoring to real-world experiences. Given a realworld context, students are applying the zero-product property to solve quadratic equations and interpreting solutions as viable or nonviable in terms of the given context.
DIFFERENTIATE INSTRUCTION
Continue to expose students to the vocabulary by connecting the terms “solutions,” “x-intercepts,” “roots,” and “zeros” of what is being found when solving quadratics. It may benefit struggling students to utilize a graphing utility to draw the connection between zeros and x-intercepts. Students who struggle to understand the zeros of a quadratic equation may benefit from interacting with the corresponding graph.
3.2.1 WARM-UP: WOULD YOU RATHER?
ENRICHMENT
Based on the pricing, what do you think the sale items may be?
TEACHER MOVES
Turn and Talk
Engage students in a Turn and Talk after completing the Warm-Up. Position students to consider the mathematics behind the sale pricing when making their decision. A Turn and Talk routine will allow students to think individually about the questions and then discuss their thoughts with a partner.
Warm-Up: Would You Rather?
1. Which deal would you rather choose – buy 1, get 2 free for $120 or buy pair that is already off for $48? Answers will vary.
2. Justify your answer mathematically. Answers will vary. Sample response – I would choose option 1 because if you are buying 3 items for $120, each item would be $40 each, which is cheaper than option 2
3 2.2 Collaboration: Using Quadratics in the Music Business
1. Organizers of a music festival charge $60 for admission The organizers polled the attendees to determine how increasing the price would affect attendance. The equation ��������(��������) = 20,000�������� 2 20,000�������� + 600,000 models profit as a function of �������� , where �������� is each $1 increase in the admission fee.
a. Discuss with your partner which factors would affect your attendance at a music festival. List your top three factors
Answers will vary. Sample response – Cost of festival, location, and type of music.
b. What admission fee would you consider to be too high?
Answers will vary.
c. If �������� = 2, what is the admission fee to the festival?
$62
d. Solve 20,000�������� 2 20,000�������� + 600,000 = 0 by factoring. Show your work.
20,000(�������� 5)(�������� + 6) = 0
�������� = 6, �������� = 5
e. Interpret the solutions in terms of the context. If the price increases $5 or decreases $6, then the profit will be $0
3.2.2 COLLABORATION: USING QUADRATICS IN THE MUSIC BUSINESS
TEACHER MOVES
Students may see the negative zero in question 1 parts d and e and immediately think that a negative would not work in terms of the given context. Position students to connect negative x-values to a decrease in price.
If x strictly represented the actual price of a ticket, would it still be viable for x to be negative?
TEACHER MOVES
Students who struggle to identify the greatest common factor may not recognize the need to factor out -20,000 in question 1 part d. Consider facilitating a brief class discussion to review the process of identifying the greatest common factor.
f. Ask two other classmates for their interpretations of the solutions to 20,000�������� 2 20,000�������� + 600,000 = 0 Write a summary of their interpretations of the solutions You are the only person who should write in the first column of the table. Have each person initial next to your summary stating that your summary was accurate
My Summary of Their Interpretation of the Solutions in Terms of the Context Initials Answers will vary.
g. Review your classmates’ interpretations with your partner If necessary, adjust your interpretation.
Answers will vary.
ENRICHMENT
Position students to see the relationship between the validity of solutions and the given context.
• What key factors make a negative root okay or not okay?
• Can you think of an example where a negative root would not be okay?
TEACHER MOVES
2. The compact disc (CD) was invented in 1979, many years before online music existed. At the time it was the most sophisticated way to store and play music. In 1982, CDs were made available to the public. CDs quickly became the most efficient way of storing music, which replaced vinyl records and cassette tapes.
The function ��������(��������) = 2�������� 2 + 38�������� + 40 models the sales, in hundreds of millions of dollars, of compact discs in the years since 1990.
a. Solve 2�������� 2 + 38�������� + 40 = 0 by factoring.
2(�������� 20)(�������� + 1) = 0
�������� = 20, �������� = 1
Students may struggle with negative leading coefficients when factoring. Position students to factor out a negative when the leading coefficient is negative.
DIFFERENTIATE INSTRUCTION
Continue to expose students to the vocabulary by connecting the terms “solutions,” “x-intercepts,” “roots,” and “zeros” of what is being found when solving quadratics. It may benefit struggling students to utilize a graphing utility to draw the connection between zeros and x-intercepts.
3.2.2 COLLABORATION: USING QUADRATICS
IN THE MUSIC BUSINESS (CONTINUED)
ENRICHMENT
Do you know anyone who still uses CDs? How does this impact your answer for question 2 part d?
b. Interpret the year that each zero represents.
Zero Year
�������� = 20 2010
�������� = 1 1989
c. Discuss the interpretation of each zero with your partner. Then, determine whether or not the interpretation makes sense. Summarize your discussion.
Answers will vary. Sample response - �������� = 20 means that in 2010 the sales of compact discs was 0 and �������� = 1 means that in 1989, the sales was also 0
d. In 2001, iTunes was launched by Apple. For the first time, people could buy songs online and store them on mp3 players, iPods, or on a computer. Then, in 2008, the music streaming site Spotify was started.
Discuss with your partner why one of the zeros shows that online access to music may have led to CD sales eventually reaching zero. Summarize your discussion.
Answers will vary. Sample Response – when �������� = 20, the year was 2010, which was 9 years after Apple launched iTunes so it would make sense that the sales of CDs would be 0
ALGEBRA 2 Teacher Guide
3.2.3 Guided Instruction: Finding Zeros
1. A landscape designer is adding a garden to a client’s backyard. One side of the garden will be alongside an existing fence. The client has 180 feet of fencing that is left over from another project. The client would like the garden to use all of the fencing.
The equation �������� = 180�������� 2�������� 2 can be used to find the area of the garden, where �������� is the garden’s width.
a. Find the zeros of the equation �������� = 180�������� 2�������� 2 2��������(�������� 90) = 0 �������� = 0 and �������� = 90
b. Interpret both of the zeros in terms of the context. A width of 0 feet is not realistic in the context. If the landscaper creates the garden with a width of 90 feet, there will not be enough left over fencing material for any length for the garden.
3.2.3 GUIDED INSTRUCTION: FINDING ZEROS
TEACHER MOVES
Three Reads
Consider a Three Reads strategy for the questions in 3.2.3 Guided Instruction. Students who struggle with interpreting word problems and making sense of the given context may benefit from using this strategy throughout the entire lesson. Students should first read through the word problems to make sense of the context. Then they should reread the problem to make sense of the mathematics involved. Students will then read the problem a third time to design a strategy for solving the problem.
ENRICHMENT
Which zero makes more sense in terms of the given context?
TEACHER MOVES
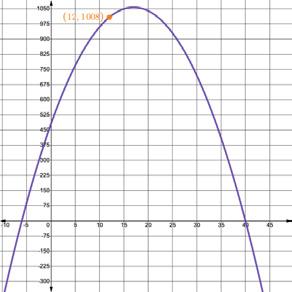
2. A statistician gathers data over several years, starting in 1995, on the average number of trips a household makes to run errands. The statistician uses the data to find the equation, ��������(��������) = 2�������� 2 + 68�������� + 480, which models the average annual number of trips for errands per household for years since 1995. The graph of the equation is shown.
a. Interpret ��������(12). Include units. In 2007, 12 years after 1995, the average number of trips to run errands a household makes per year is 1008
b. Determine the zeros of the function. Show your work.
�������� = 40, 6
c. Interpret both of the zeros in terms of the context. The zero of �������� = 40 means that in 2035, 40 years after 1995, and the zero �������� = 6 means that in 1989, 6 years before 1995; households are expected to make an annual average of 0 trips to run errands.
d. Discuss with your partner whether or not both zeros are viable. If a zero is non-viable, explain why. Both zeros are not viable. The zero �������� = 6 is not viable because people were running errands in 1989 before this data was collected. Also, �������� = 40 is unlikely to be viable as it is unrealistic that the average number of trips to run errands for a household is zero
Students who struggle with function notation may struggle with question 2 part a. Position students to connect the notation E(12) to evaluating the function for x=12.
TEACHER MOVES
Though this lesson largely utilizes the standards in MA.K12. MTR.7.1 (real-world contexts), students are also utilizing the standards in MA.K12.MTR.6.1 (reasonableness of solutions). For instance, in question 2 part d, students are asked to interpret the reasonableness of the solutions.
3.2.2 COLLABORATION: USING QUADRATICS
IN THE MUSIC BUSINESS (CONTINUED)
ENRICHMENT
Do you know anyone who still uses CDs? How does this impact your answer for question 2 part d?
b. Interpret the year that each zero represents.
Zero Year
�������� = 20 2010
�������� = 1 1989
c. Discuss the interpretation of each zero with your partner. Then, determine whether or not the interpretation makes sense. Summarize your discussion.
Answers will vary. Sample response - �������� = 20 means that in 2010 the sales of compact discs was 0 and �������� = 1 means that in 1989, the sales was also 0
d. In 2001, iTunes was launched by Apple. For the first time, people could buy songs online and store them on mp3 players, iPods, or on a computer. Then, in 2008, the music streaming site Spotify was started.
Discuss with your partner why one of the zeros shows that online access to music may have led to CD sales eventually reaching zero. Summarize your discussion.
Answers will vary. Sample Response – when �������� = 20, the year was 2010, which was 9 years after Apple launched iTunes so it would make sense that the sales of CDs would be 0
ALGEBRA 2 Teacher Guide
3.2.5 Wrap-Up: Ticket Out the Door
A firework is launched from a hill that is 80 feet (ft) above a lake. The firework will descend into the lake after it has exploded at its maximum height. The firework’s height , in ft, above the lake’s surface is given by ℎ(��������) = 16�������� 2 + 64�������� + 80, where �������� is the time in seconds
1. Determine the zeros of the function. Show your work. �������� = 1, �������� = 5
3.2.5 WRAP-UP: TICKET OUT THE DOOR
QUESTIONING
Consider using the Ticket Out the Door as a formative assessment to gather data on student progress and understanding from this lesson.
2. Determine the viable solution and interpret in terms of the context. The viable solution is �������� = 5 because it means that it takes 5 seconds for the rocket to touch the lake after take off.
I can solve quadratics by factoring.
GUIDED PRACTICE
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
Solve each quadratic equation by factoring. Show your work.
a. x 2 3x 28 = 0
GUIDING TIPS
Use these if you need help.
• To solve a quadratic equation by factoring, the quadratic equation must first be written in standard form, a x 2 + bx + c = 0
• A quadratic equation can be solved by factoring using the zero product property.
• The zero product property states that if the product of two numbers is 0, then one of the numbers is 0
b. x 2 12x = 20
c. 2 x 2 3x = 10x + 15
VIDEO TUTORIAL
A video about how to solve
I can solve quadratics by factoring.
INDEPENDENT PRACTICE
Solve the following questions.
Use the following information to answer questions 2 and 3.
Whitman solved the quadratic equation
x 2 + 11x + 28 = 54 by factoring, but he made an error. His work is shown. Step Work
1 x 2 + 11x + 28 = 54
2 (x + 4)(x + 7) = 54
3 x + 4 = 0 x + 7 = 0
4 x = 4, 7
Explain where Whitman made his first error.
Serenity started solving the quadratic equation 7 x 2 12 = x 2 x by factoring, but she got stuck. Her partial work is shown.
Find the correct solution(s) of the quadratic equation by factoring. Show your work.
Help Serenity solve the equation by completing the steps to solve by factoring.
Select all of the solutions to the equation 2x 2 + 6x 80 = 0
Solve the quadratic equation 12x 2 81x = 21 by factoring. Show your work.
SKILL
I can relate a reflection on the coordinate plane to an algebraic notation of the transformation.
GUIDED PRACTICE
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
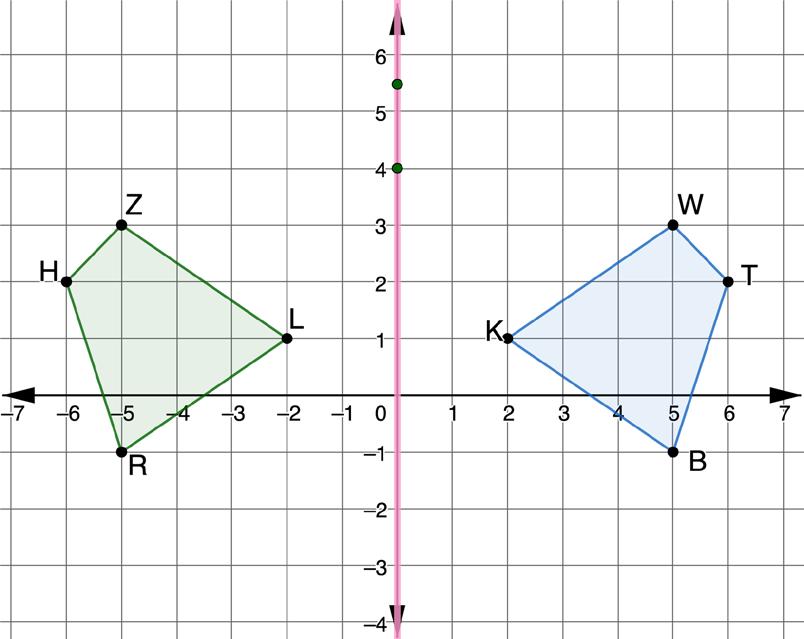
Polygons PFCG, SZWV, LTDH, and KBRM are shown on the coordinate plane.
GUIDING TIPS
Use these if you need help.
• The algebraic description for reflecting a point across the x-axis is (x, y) → (x, y)
• The algebraic description for reflecting a point across the y-axis is (x, y) → ( x, y)
• The algebraic description for reflecting a point across the line y = x is (x, y) → (y, x).
• The algebraic description for reflecting a point across the line y = x is (x, y) → ( y, x)
a. What is the line of reflection that maps polygon PFCG to polygon KBRM?
b. Write an algebraic description for this reflection.
c. Which polygon is the reflection of polygon LTDH across y = x?
d. Write an algebraic description for this reflection.
e. What is the line of reflection that maps polygon KBRM to polygon SZWV?
f. Write an algebraic description for this reflection.
I can relate a reflection on the coordinate plane to an algebraic notation of the transformation.
INDEPENDENT PRACTICE
Solve the following questions.
Use the following information for questions 2–4.
Parallelogram KPSR, with vertices K( 9, 0), P( 2, 0), S( 2, 10), and R( 9, 10), undergoes the transformation (x, y) → (x, y).
Write the coordinates of the vertices of the image that results from the transformation.
Use the following information to answer questions 5 and 6.
Describe the transformation that occurred on parallelogram KPSR
Triangles HRB and TLX are shown on the coordinate plane. Write the algebraic description for the reflection that maps ∆ HRB to ∆ TLX
Pentagon LXRBN is shown on the coordinate plane.
What are the coordinates of Bʹ and Lʹ after pentagon LXRBN is reflected across the y-axis?
Write the algebraic description for the transformation of pentagon LXRBN
I can solve a quadratic equation by factoring when given a real-world context, interpreting solutions as viable or nonviable.
GUIDED PRACTICE
Use the guiding tips to solve the problem. Scan the QR code to watch a video tutorial.
A student club is selling raffle tickets for a fundraiser. The profit function for ticket sales is represented by P(x) = x 2 + 3x 10, where x is the number of tickets sold.
a. Determine the zero(s) of the function. Show your work.
GUIDING TIPS
Use these if you need help.
• When solving a quadratic equation by factoring, look for common factors, and apply the zero-product property.
• Always consider the real-world context when interpreting solutions; some solutions may not make sense in context.
b. Determine whether the zero(s) is viable in this context. If a zero is nonviable, explain why.
c. Interpret the viable zero(s) in context.
INDEPENDENT PRACTICE
Solve the following questions. I can solve a quadratic equation by factoring when given a real-world context, interpreting solutions as viable or nonviable.
A splash pad shoots a stream of water into the air such that the height of the water stream in meters (m) can be modeled by the quadratic equation h(t) = 3t² + 9t, where t is time in seconds.
a. Determine the zero(s) of the function. Show your work.
A manufacturer’s cost function for producing a certain item is C(x) = 2x² 9x + 9, where x is the number of items produced.
a. Determine the zero(s) of the function. Show your work.
b. Interpret the zero(s) in terms of the context.
c. Determine whether the zero(s) is (are) viable. If a zero is nonviable, explain why.
A landscape architect is designing a rectangular garden. The length of the garden is represented by x, and the width is represented by 10 x.
a. Determine the zero(s) of the function that represents the area of the garden. Show your work.
b. Determine whether the zero(s) is viable. If a zero is nonviable, explain why.
Use the following information to answer questions 5 and 6.
A local movie theater charges $12 for a regular movie ticket. The theater management is considering changing the ticket prices. They want to know how potential price changes could affect their total profit. The equation P(x) = 1,500x 2 + 1,500x + 9,000 models the total weekly profit as a function of x, where x is the potential change in the ticket price in dollars.
Determine the zero(s) of the function. Show your work.
b. Determine whether the zero(s) is (are) viable. If a zero is nonviable, explain why.
Interpret the solution(s) in terms of the context.
BY ACCELERATE LEARNING
