

Muestra de la edición para el maestro



Muestra de la edición para el maestro
Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).
La plataforma de recursos curriculares en línea que se ofrece en "mathnation.com", incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.
La marca comercial "Math Nation" es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.
Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.
Objetivos de aprendizaje de la unidad
• Los estudiantes representan y resuelven problemas de multiplicación a través del contexto de gráficos de imágenes y de barras que representan datos categóricos.
En esta unidad, los estudiantes interpretan y representan datos en gráficos de imágenes a escala y en gráficos de barras a escala. Luego, aprenden el concepto de multiplicación.
Esta es la primera de cuatro unidades que se centran en la multiplicación. En esta unidad, los estudiantes exploran gráficos de imágenes a escala y gráficos de barras como punto de entrada para aprender sobre grupos de igual tamaño y multiplicación.
En el grado 2, los estudiantes analizaron gráficos de imágenes en los que una imagen representaba un objeto y gráficos de barras que se escalaban por unidades individuales. En este caso, los estudiantes se encuentran con gráficos en los que cada imagen representa más de un objeto y gráficos de barras con escalas de 2 o 5 unidades. La idea de que una imagen puede representar varios objetos ayuda a introducir la idea de grupos de igual tamaño.
Los estudiantes aprenden que la multiplicación puede significar encontrar el número total de objetos en �� grupos de �� objetos cada uno, y puede representarse por �� × ��. A continuación, relacionan la idea de grupos iguales y la expresión �� × �� con las filas y columnas de una matriz. Al trabajar con matrices, los estudiantes empiezan a darse cuenta de la propiedad conmutativa de la multiplicación.
En todos los casos, los estudiantes dan sentido al significado de las expresiones de multiplicación antes de hallar su valor y antes de escribir ecuaciones que relacionan dos factores y un producto.
Más adelante en la unidad, los estudiantes ven situaciones en las que se conoce el número total de objetos pero se desconoce el número de grupos o el tamaño de cada grupo. Los problemas con un factor faltante ofrecen a los estudiantes una vista previa a la división.
A lo largo de la unidad, proporcione acceso a cubos de conexión o contadores, ya que los estudiantes pueden optar por usarlos para representar y resolver problemas.
Sección A: Interpretar y representar datos en gráficos a escala
Alineación de estándares
Abordaje de
• 3.MD.3
Sección de los objetivos de aprendizaje
• Interpretar dibujos a escala y gráficos de barras.
• Representar datos usando dibujos a escala y gráficos de barras.
• Resolver problemas de historias de uno y dos pasos usando sumas y restas.
En esta sección, los estudiantes interpretan y dibujan gráficos de imágenes y gráficos de barras para representar datos, con base en su experiencia con la representación de datos y con el conteo saltado por 2, 5 y 10 en el grado 2.
Los estudiantes ven que cada imagen en un gráfico de imágenes y cada línea o incremento en un gráfico de barras puede representar más de un objeto. Trabajan con escalas numéricas familiares de 2, 5, y 10
©Accelerate Learning Inc. - Todos los derechos reservados
Gráfico de barras
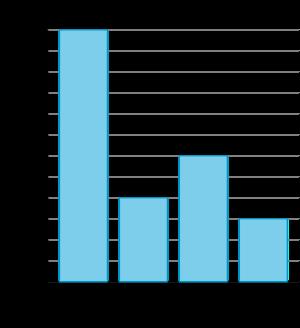

Grado 3 . Matemáticas . Unidad 1
Gráfico de barras a escala
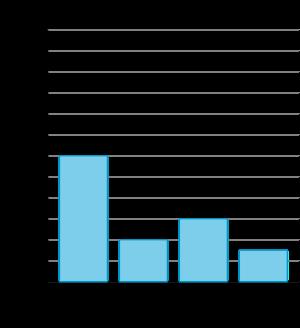
Los estudiantes utilizan la información de los gráficos de barras a escala para resolver problemas de «cuántos más» y «cuántos menos» de uno y dos pasos en 100. Este trabajo permite a los profesores evaluar formativamente la fluidez de los estudiantes con la suma y la resta dentro de 100, una expectativa de grado 2.
PLC: Lección 3, actividad 1: Tantas respuestas
Sección B: De las gráficas a la multiplicación
Alineación de estándares
Abordando
• 3.OA.1
• 3.OA.3
• 3.OA.4
• 3.OA.9
Sección de los objetivos de aprendizaje
• Representar y resolver problemas de multiplicación que involucren grupos iguales.
• Comprender la multiplicación en términos de grupos iguales.
En esta sección, los estudiantes dan sentido a la multiplicación en términos de grupos iguales de objetos. Utilizan dibujos discretos y diagramas de cinta que muestran grupos iguales para representar la multiplicación, y luego relacionan estas representaciones con expresiones como 3 × 2, interpretándolas como "3 grupos de 2."
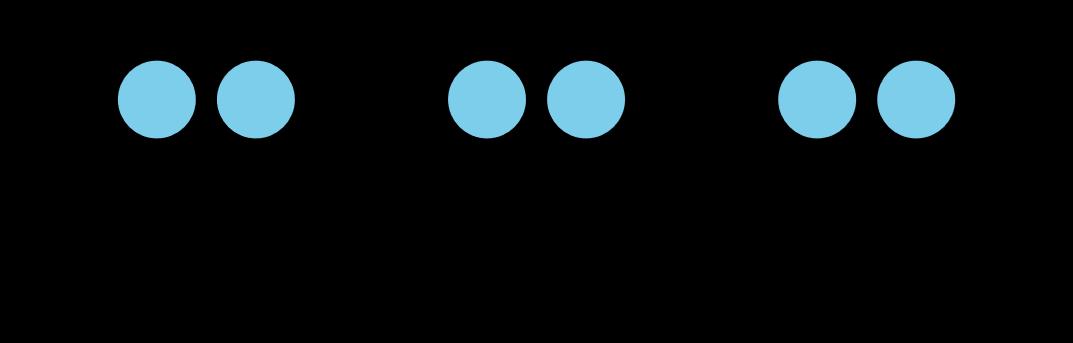
Tenga en cuenta que expresiones de la forma �� × �� podrían interpretarse como �� grupos de �� o �� grupos de a. Sin embargo, como tendemos a decir " grupos de " cuando nos referimos a grupos iguales, en estos materiales escribimos las expresiones de multiplicación en ese orden: número de grupos × tamaño de cada grupo
No es necesario que los estudiantes utilicen esta convención siempre que puedan explicar lo que representa cada número en su expresión.
Más adelante, los estudiantes escriben ecuaciones para representar situaciones de multiplicación y encontrar productos o factores desconocidos. Al razonar sobre estos últimos, empiezan a dar sentido a la relación entre multiplicación y división, sin utilizar formalmente el lenguaje de la división.
PLC: Lección 10, actividad 2, tarjetas de clasificación: grupos iguales
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

Sección C: Representar la multiplicación con matrices y la propiedad conmutativa
Alineación de estándares
Abordaje
• 3.MD.3
• 3.OA.1
• 3.OA.3
• 3.OA.4
• 3.OA.5
• 3.OA.9
Sección de los objetivos de aprendizaje
• Representar y resolver problemas de multiplicación que involucren arreglos.
En esta sección, los estudiantes relacionan la idea de grupos iguales con la estructura de un arreglo, una representación introducida en el grado 2.
Los estudiantes ven que las filas y columnas de un arreglo representan grupos iguales. El número de filas (o columnas), el número de elementos de cada fila (o columna) y el número total de objetos de un conjunto pueden representarse con una ecuación de multiplicación. Las ecuaciones pueden incluir un valor desconocido, ya sea uno de los factores o el producto. A medida que los estudiantes razonan sobre las matrices, también se dan cuenta de que la multiplicación es conmutativa.
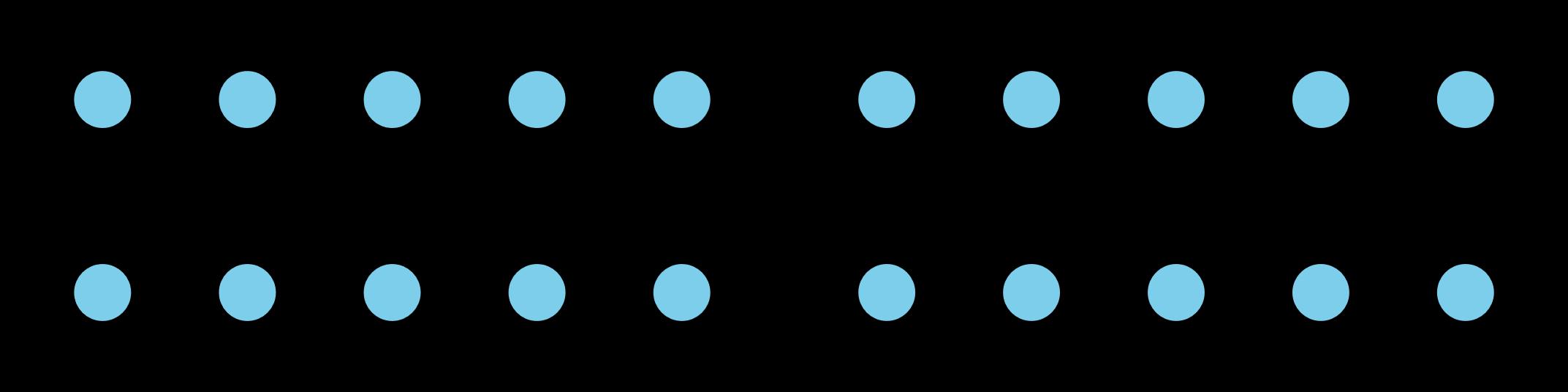
PLC: Lección 20, actividad 1, aprende más sobre la multiplicación
Días estimados: 20 - 21
Grado 3 . Matemáticas . Unidad 1
Enfoque en ideas fundamentales
• Representar datos multivariables
• Flexibilidad numérica hasta 100 para las cuatro operaciones
• Patrones en cuatro operaciones
ESTÁNDARES POR LECCIÓN
Lección

Estándar(es) abordado(s)
3.1.1 3.MD.3
3.1.2 3.MD.3
3.1.3 3.MD.3
3.1.4 3.MD.3
3.1.5 3.MD.3
3.1.6 3.MD.3
3.1.7 3.MD.3
3.1.8 3.MD.3
3.1.9 3.OA.1
3.1.10 3.OA.1
3.1.11 3.OA.1
3.1.12 3.OA.1, 3.OA.3
3.1.13 3.OA.1, 3.OA.3
3.1.14
3.OA.1, 3.OA.3, 3.OA.4, 3.OA.9
3.1.15.1.15 3.OA.3, 3.OA.4, 3.OA.9
3.1.16 3.OA.1
3.1.17 3.OA.1
3.1.18 3.OA.1
3.1.19
3.OA.1, 3.OA.3, 3.OA.9
3.1.20 3.OA.5
3.1.21
3.MD.3, 3.OA.3, 3.OA.4
Nation California - Grado 3 ©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.MD.3 Dibuja un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Construir
2.MD.10
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
Estándares ELD de California
I.A.1
I.B.5
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo razonar abstracta y cuantitativamente razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo interpretar gráficos de imágenes y gráficos de barras.
• Puedo comparar un gráfico de imágenes y un gráfico de barras.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Interpretar gráficos de imágenes y gráficos de barras para generar preguntas (oralmente y por escrito) sobre los datos.
PREGUNTA DE REFLEXIÓN PARA EL MAESTRO
La lección de hoy le ha brindado la oportunidad de aprender de sus estudiantes. ¿Cómo has podido incorporar a la lección la experiencia vivida por tus estudiantes?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Notar y maravillarse (calentamiento)
Objetivos de aprendizaje para el estudiante
• Leamos y hagamos preguntas sobre los datos.
Narrativa de la lección
El objetivo de esta lección es obtener los conocimientos previos de los estudiantes sobre los gráficos de barras y los gráficos de barras a escala de una sola unidad como preparación para el próximo trabajo con gráficos de barras a escala.
En segundo grado, los estudiantes aprendieron a dibujar y rotular gráficos de barras y gráficos de barras a escala de una sola unidad y utilizaron datos categóricos presentados en gráficos para resolver problemas simples.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado . Matemáticas . Unidad 1
problemas. En esta lección, los estudiantes repasan la estructura de los gráficos de imágenes y de barras, las características de los gráficos que ayudan a comunicar la información con claridad y la información que pueden aprender analizando un gráfico. Los estudiantes aprenden que la clave es la parte de un gráfico que indica lo que representa cada imagen. Los estudiantes contextualizan y dan sentido a los datos basándose en el título, los valores dados y sus propias experiencias (MP2).
Prepara un espacio, como un trozo de papel para carteles, titulado "Comunidad matemática" y un gráfico en forma de T con los encabezados "Haciendo matemáticas" y "Normas". Divide cada una de las columnas en dos secciones: estudiantes y maestro. Las dos secciones animan a los estudiantes y a los maestroes a ser conscientes de que ambas partes son responsables de la forma en que se hacen las matemáticas en el aula.
Comunidad matemática
Haciendo matemáticas
Estudiantes

Normas
Estudiantes
Maestro Maestro
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo
Descripción breve
Calentamiento En parejas 10 min. Los estudiantes hacen observaciones sobre un gráfico.
Actividad de exploración 1 En parejas 15 min.
Actividad de exploración 2 En parejas 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Math Nation California - Grado 3
Los estudiantes activan sus conocimientos previos sobre las partes esenciales de un gráfico describiendo las categorías que podrían encajar en el gráfico.
Los estudiantes comparan un gráfico de imagen y un gráfico de barras que representan la misma información y escriben preguntas a las que podrían responder los gráficos.
Los estudiantes discuten las similitudes y diferencias entre los gráficos de imagen y los gráficos de barras y discuten cómo representan los datos.
Los estudiantes analizan un gráfico de barras para escribir un hecho y una pregunta sobre el contexto de la situación.
Apoyo:
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de imagen o de barras
• Capturar cuadrados (1-3), Etapa 3: Sumar dentro de 20
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Notar y preguntarse
El objetivo de este calentamiento es obtener los conocimientos previos de los estudiantes sobre las representaciones de datos categóricos, que serán útiles cuando los estudiantes trabajen con gráficos de barras e imágenes a escala de una unidad en actividades posteriores. Aunque los estudiantes pueden notar y preguntarse muchas cosas sobre este gráfico, es importante prestar atención a las formas en que los estudiantes dan sentido a un gráfico de imagen, las preguntas que tienen sobre los datos categóricos y los contextos que tienen sentido para los datos categóricos mostrados. Para todas las rutinas de calentamiento, considere establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, u otra señal sutil. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se precipiten al levantar las manos por toda la clase. Como se trata del primer calentamiento del año, asignamos 15 minutos, en lugar de 10, para establecer la estructura de una rutina.
• Grupos de 2
• Muestre el gráfico.
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "¿Qué notan? ¿Qué te preguntas?"
• 1 minuto: tiempo para pensar en silencio
• "Comenta lo que has pensado con tu compañero."
• 1 minuto: debate entre compañeros
• Comparte y anota las respuestas.
¿Qué notas? ¿Qué te preguntas?
RESPUESTAS POSIBLES
Los estudiantes pueden observar:
• Parece un gráfico.
• No hay título.
• Las categorías están ocultas.
• Hay personas de palo en cada columna.
Los estudiantes pueden preguntarse:
• ¿De qué trata este gráfico?
• ¿Qué representan las personas de palo?
• ¿Por qué hay tantas personas de palo en las dos últimas columnas?
• ¿Dónde está el título?
SÍNTESIS DE LA ACTIVIDAD

Grado . Matemáticas . Unidad 1
• "¿Qué situaciones podría representar el gráfico?". (Día favorito de la semana. Tipo de comida favorita. Tipos de animales que la gente vio en el parque.)
• Comunidad matemática: Pida a los estudiantes que reflexionen sobre las acciones individuales y de grupo mientras se plantean la pregunta "¿Cómo es y cómo suena hacer matemáticas juntos como una comunidad matemática? ¿Qué hago yo? (Hablamos entre nosotros y con el maestro. Reflexionamos en silencio. Compartimos nuestras ideas. Pensábamos en las ideas y palabras matemáticas que conocíamos. Escribías nuestras respuestas. Estabas esperando a que diéramos las respuestas.)
• Registra y muestra sus respuestas bajo el encabezado "Haciendo matemáticas".
15 minutos
El objetivo de esta actividad es obtener los conocimientos previos de los estudiantes sobre las partes esenciales de un gráfico. El gráfico de esta actividad es el mismo que el del calentamiento, pero incluye un título. Se anima a los estudiantes a pensar qué categorías podrían aparecer en el gráfico. Los estudiantes contextualizan y dan sentido a los datos basándose en el título, los valores dados y sus propias experiencias (MP2). Esta es una oportunidad para que los estudiantes conecten su experiencia vivida con las matemáticas, apoyando el desarrollo de sus identidades matemáticas.
Apoyo para estudiantes con discapacidad
Representación: Desarrollar el lenguaje y los símbolos. Active o proporcione conocimientos previos para ayudar a los estudiantes a recordar los términos "gráfico de imagen" y "clave". Pregunte: "¿Por qué llamamos a este gráfico un gráfico de imagen?", "¿Qué tipo de información muestra una clave?"
Apoya la accesibilidad para: Memoria, Lenguaje
• Grupos de 2
• Mostrar el gráfico.
• "¿En qué se diferencia este gráfico del primero que discutimos?" (Tiene un título. Sabemos de qué trata el gráfico.)
• 30 segundos: tiempo de reflexión en silencio
• Comparta las respuestas.
INTRODUCCIÓN
ACTIVIDAD
Math Nation California - Grado 3
• "El título del gráfico nos ayuda a dar sentido a los datos que se muestran en el gráfico."
• Según sea necesario, recuerde a los estudiantes que los datos son información sobre las cosas o las personas de un grupo.
• "¿Cómo regresan a casa de la escuela tú y otros estudiantes de nuestra comunidad?"
• Comparta las respuestas.
• "Este es un gráfico de imágenes que representa cómo regresan a casa de la escuela los estudiantes. Un gráfico de imágenes muestra cuántos hay en cada grupo o categoría utilizando imágenes de los objetos o símbolos. Los gráficos de imágenes tienen claves que indican lo que representa cada imagen."
• "¿Cuáles podrían ser las categorías en este gráfico de imágenes? Prepárate para explicar tu razonamiento."
• 2-3 minutos: tiempo de trabajo en pareja
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
¿Cuáles podrían ser las categorías de este gráfico de imágenes?
Prepárate para explicar tu razonamiento.
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Ejemplos de respuestas:
• Coche, porque así es como llego a casa desde la escuela.
• Autobús, porque algunos estudiantes de nuestra clase toman el autobús para volver a casa.
• Muestre el gráfico.
• Invite a los estudiantes a compartir posibles categorías para el gráfico.
• Considere preguntar: "¿Cuántas categorías habrá para este gráfico? ¿Cómo puedes saberlo?"
20 minutos
El propósito de esta actividad es preparar a los estudiantes para trabajar con gráficos de barras a escala en las próximas lecciones. Ahora que los estudiantes han razonado sobre las partes de un gráfico de imagen, observan en qué se parecen y en qué se diferencian los gráficos de imagen y los gráficos de barras. Los estudiantes utilizan la información presentada en los ejes del gráfico de barras para leer el gráfico, interpretar los datos categóricos presentados en los gráficos y generar preguntas que puedan responderse utilizando los gráficos.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Por cada observación que se comparta, invite a los estudiantes a que se dirijan a un compañero y reafirmen lo que han oído utilizando un lenguaje matemático preciso.
Avances: Escuchar, hablar
INTRODUCCIÓN
©Accelerate Learning Inc. - Todos los derechos reservados
• Grupos de 2
• Visualice el gráfico de imágenes y el gráfico de barras.
• "La segunda imagen es un gráfico de barras. Un gráfico de barras muestra cuántos hay en cada grupo o categoría utilizando la longitud de los rectángulos. ¿En qué se parecen los gráficos? ¿En qué se diferencian?"
• 2 minuto: debate por parejas
• Compartir y mostrar las respuestas.
California - Grado 3
Math
ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
FOMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
Nation California - Grado 3
Grado . Matemáticas . Unidad 1
• "¿Qué podrías aprender de los gráficos sobre cómo llegan los estudiantes a casa? Escribe dos preguntas a las que podrían responder los gráficos."
• 7-10 minutos: tiempo de trabajo en pareja
Se preguntó a un grupo de estudiantes: "¿Cómo llegas a casa?". Sus respuestas se muestran en un gráfico de imágenes y en un gráfico de barras.
1. ¿En qué se parecen los gráficos? ¿En qué se diferencian?
2. ¿Qué podemos aprender sobre cómo llegan los estudiantes a casa basándonos en los gráficos?
3. Escriba dos preguntas que podría hacer sobre cómo llegan los estudiantes a casa basándose en los gráficos.
1. Ejemplos de respuestas:
• Ambos tienen un título en la parte superior y categorías en la parte inferior.
• El gráfico de imágenes tiene dibujos para mostrar el número en cada categoría, pero el gráfico de barras utiliza barras.
• El gráfico de barras tiene etiquetas en la parte inferior y en el lateral para ayudarte a saber qué significan las barras.
• El gráfico de imágenes tiene una clave, pero el gráfico de barras tiene los números en el lateral del gráfico.
2. Ejemplos de respuestas:
• 7 los estudiantes vuelven a casa en autobús.
• Hay más estudiantes que vuelven a casa en autobús o tren que de cualquier otra forma.
3. Ejemplos de respuestas:
• ¿Cuántos estudiantes vuelven a casa andando?
• ¿Cuántos estudiantes más vuelven a casa en autobús que en bicicleta?
Si los estudiantes escriben preguntas que no pueden responderse con los gráficos, considere preguntar:
• "¿Cómo se te ocurrió tu pregunta?"
• "¿Cómo podríamos plantear una pregunta que pudiera responderse con el gráfico?"
• Muestra los gráficos.
• "¿Qué podemos aprender sobre cómo llegan los estudiantes a casa desde el colegio basándonos en los gráficos completos?"
• "¿Qué preguntas podrías hacer sobre cómo llegan los estudiantes a casa desde el colegio basándote en los gráficos?"
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
"¿Qué hemos aprendido hoy sobre los diagramas y los gráficos de barras?" (Los diagramas y los gráficos de barras nos muestran datos. En un gráfico, una imagen representa un objeto o una persona. En un gráfico de barras, la escala indica cuántos objetos o personas hay. Podemos hacer y responder preguntas sobre los datos de los gráficos).
Si no surgen estas ideas, plantéate hacer las siguientes preguntas:
• "¿Qué partes de los gráficos nos ayudan a comunicar los datos del gráfico a los demás?"
• "¿En qué se parecen los gráficos de imágenes y los gráficos de barras? ¿En qué se diferencian?"
5 minutos

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
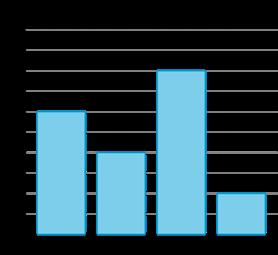
Se preguntó a un grupo de estudiantes: "¿Cómo llegas a casa desde la escuela cada día?" Sus respuestas se muestran en este gráfico de barras: Basándote en los datos que se muestran en el gráfico:
1. Escribe un hecho que hayas aprendido sobre cómo los estudiantes llegan a casa.
2. Escribe una pregunta que podrías hacer sobre cómo vuelven los estudiantes de la escuela a casa.
RESPUESTAS POSIBLES
Reflexiones:
Ejemplos de respuestas:
1. Hay más estudiantes que vuelven a casa en autobús que en bicicleta. Ocho estudiantes vuelven a casa en autobús. Dos estudiantes vuelven en coche.
2. ¿Cuántos estudiantes más vuelven a casa en autobús que andando? ¿Cuántos estudiantes vuelven a casa en bicicleta?


IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.MD.3 Dibuja una gráfica de imagen a escala y una gráfica de barra a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Construir
2.MD.10 2.OA.3
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP6 Atender a la precisión.
Estándares ELD de California
I.A.1 I.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo
razonar abstracta y cuantitativamente y atender a la precisión razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo crear un gráfico de barras.
• Puedo utilizar un gráfico de barras para resolver problemas.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Representar datos utilizando gráficos de barras y gráficos de imágenes.
• Resolver problemas de uno y dos pasos utilizando sumas y restas dentro de 20
Piensa en quién ha participado hoy en la clase de matemáticas. ¿Qué suposiciones estás haciendo sobre los que no participaron? ¿Cómo puedes aprovechar las ideas de cada uno de tus estudiantes para ayudarles a ser vistos y escuchados en la clase de matemáticas de mañana?
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
¿Cuántos ves? (Calentamiento)
Materiales para reunir
Notas adhesivas: Actividad 1
Objetivos de aprendizaje para el alumno
• Vamos a crear gráficos y a responder preguntas.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes resuelvan problemas de uno y dos pasos sobre datos representados en gráficos de barras.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
Los estudiantes resolvieron problemas de un paso sobre datos en 2º curso. En esta lección, los estudiantes crean primero un gráfico y un diagrama de barras que representan cómo vuelven a casa del colegio. A continuación, resuelven problemas de uno y dos pasos del tipo "cuántos más" y "cuántos menos" utilizando datos presentados en un gráfico de barras. Considere iniciar la lección con una lectura en voz alta de Last Stop on Market Street de Matt de la Peña y Christian Robinson.
Comunidad matemática
Diga a los estudiantes que tendrán la oportunidad de revisar sus ideas de comunidad matemática al final de esta lección. Mientras trabajan hoy, deben pensar en las acciones que pueden faltar en la lista actual.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo
Calentamiento Parejas 10 min.
Actividad de exploración 1 Parejas 15 min.
Actividad de exploración 2 Parejas 20 min.
Síntesis Todo el Grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional

Math Nation California - Grado 3
Descripción breve
Los estudiantes explican las estrategias utilizadas para determinar el número de puntos mostrados.
Los estudiantes crean un gráfico de barras utilizando los datos de un gráfico de imágenes.
Los estudiantes interpretan el gráfico de barras de la Actividad de Exploración 1 para responder preguntas de un paso y de dos pasos "cuántos más" sobre el conjunto de datos.
Los estudiantes discuten cómo utilizar un gráfico de barras para interpretar el gráfico y sus datos respondiendo preguntas adicionales de un paso y de dos pasos.
Los estudiantes analizan un gráfico de barras para resolver problemas sobre los datos.
Apoyo:
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de imagen o de barras
• Capturar cuadrados (1-3), Etapa 3: Sumar dentro de 20
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
¿Cuántos ves?
El objetivo de este Cuántos ves es que los estudiantes subitiicen o utilicen estrategias de agrupación para describir el número de puntos que ven. También establecen conexiones entre las imágenes para determinar el número de puntos. Las estrategias de agrupación y el recuento por saltos de 2, 5, y 10 ofrecen un repaso del trabajo de 2º curso y contribuyen a la multiplicación en futuras lecciones. En la síntesis, los estudiantes revisan el lenguaje de "cuántos más" para prepararlos a usar datos de un gráfico de barras para resolver problemas de "cuántos más" a lo largo de esta lección.
• Grupos de 2
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "¿Cuántos ves? ¿Cómo los ves?"
• Muestra la imagen.
• 30 segundos: tiempo para pensar en silencio
• Muestra la imagen.
• "Discute tus ideas con tu compañero."
• 1 minuto: discusión en pareja
• Registra las respuestas.
• Repite para cada imagen.
¿Cuántos ves? ¿Cómo los ve?
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
• 6: Veo 2 filas de 3
• 8: Veo 2 grupos de 4
• 10: Veo 5 grupos de 2
• "¿Cuántos puntos más había en la tercera imagen que en la segunda? ¿Qué ecuación coincide con tu pensamiento?" (Había 2 puntos más en la imagen. 8 + 2 = 10.)
Materiales a reunir
Notas adhesivas
15 minutos
Preparación necesaria
Crea una presentación visual con un gráfico de barras en blanco que sea lo suficientemente grande como para que quepa una columna de notas adhesivas en cada categoría.
El propósito de esta actividad es que los estudiantes creen un gráfico de barras que incluya características que ayuden a comunicar los datos con claridad. Se crea un gráfico de imágenes de la clase y los estudiantes elaboran un gráfico de barras utilizando esos datos. Durante la síntesis, centre la atención en las similitudes y diferencias entre los gráficos de imágenes y de barras. Al crear el gráfico de barras en blanco de las "formas de llegar a casa" para el Introducción, siéntete libre de
Grado 3 . Matemáticas . Unidad 1
Ajuste las categorías en función de cómo lleguen sus estudiantes del colegio. Cuando los estudiantes etiquetan sus gráficos, incluyendo un título, una clave y números si hacen un gráfico de barras, se están comunicando de forma clara y precisa (MP6).
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Algunos estudiantes pueden beneficiarse de la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.
Avances: Expresión oral

INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 2
• Muestra un gráfico vacío con etiquetas en el eje inferior para bicicleta, a pie, furgoneta, autobús, coche y tren.
• Entrega a cada alumno una pequeña nota adhesiva.
• Pide a cada alumno que dibuje una carita sonriente en su nota adhesiva.
• "Pon tu carita sonriente en el gráfico según cómo vuelves a casa desde el colegio".
• "¿Qué hay que añadir al gráfico de la clase para comunicar los datos con claridad?". (Un título. Una clave para saber qué representa cada cara sonriente.)
• Facilite la adición del título y la clave al gráfico de la clase.
• "Representa los datos mostrados en el gráfico de la clase en un gráfico de barras con tu compañero. Asegúrate de incluir las partes del gráfico que ayudarán a otra persona a leerlo."
• 5-7 minutos: tiempo de trabajo en pareja
1. Sigue las instrucciones de tu maestro para organizar y representar los datos de la clase en un gráfico de barras.
2. Representa los mismos datos que muestran cómo llega nuestra clase a casa en un gráfico de barras.

Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES
Ejemplos de respuestas: 1. 2.

AUMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
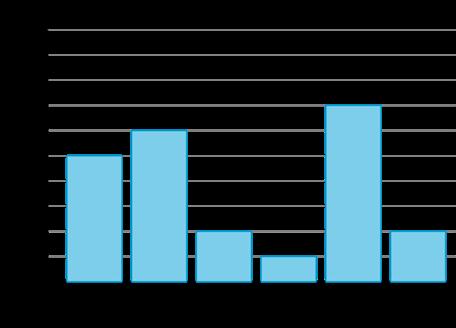
Si los estudiantes crean gráficos de barras que no coinciden con los datos del gráfico de la imagen de la clase, considere preguntar:
• "Cuéntenme cómo hicieron su gráfico de barras".
• "¿Cómo podríamos usar los datos del gráfico de la imagen de la clase para ayudar a hacer el gráfico de barras?"
• "¿En qué se parecen nuestro gráfico de imagen y nuestro gráfico de barras?" (Ambos muestran los mismos datos. Tienen las mismas categorías.)
• "¿En qué se diferencian nuestro gráfico de imagen y nuestro gráfico de barras?" (El gráfico de imagen tiene una clave, pero el gráfico de barras tiene una escala. Para el gráfico de imágenes, tienes que contar cada imagen, pero en el gráfico de barras, puedes utilizar los números del lateral para saber cuántas).
20 minutos
El objetivo de esta actividad es que los estudiantes respondan a preguntas de uno y dos pasos del tipo "cuántos más" utilizando datos representados en un gráfico de barras. Los estudiantes deciden si las afirmaciones sobre los datos del gráfico de barras de la actividad anterior son verdaderas o falsas y, a continuación, responden a las preguntas sobre los datos. Cuando los estudiantes utilizan expresiones, ecuaciones o describen sumas o restas para hallar cuántos más o cuántos menos, demuestran que pueden descontextualizar y recontextualizar los datos para dar sentido y resolver los problemas (MP2). Usted generará las preguntas que los estudiantes responden en esta tarea a partir del gráfico de la clase.
Apoyo para estudiantes con discapacidad
Representación: Acceso para la percepción. Lee las instrucciones y los enunciados en voz alta. Los estudiantes que escuchen y lean a la vez la información se beneficiarán de un tiempo de procesamiento adicional.
Apoya la accesibilidad para: Lenguaje
INTRODUCCIÓN
ACTIVIDAD
• Grupos de 2
• "Ahora vas a utilizar tu gráfico de barras para decidir si las afirmaciones son verdaderas o falsas."
• 1-2 minutos: tiempo de trabajo independiente
• 3-5 minutos: discusión por parejas
ACTIVIDAD CONTINUACIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
AVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
Grado 3 . Matemáticas . Unidad 1
• Mientras los estudiantes trabajan, decida qué categorías irán en los esquemas de preguntas para el siguiente problema.
• Considere proporcionar estos esquemas de oraciones si los estudiantes necesitan apoyo para explicar su razonamiento:
• "Sabía que la afirmación era falsa porque..."
• "Sabía que la afirmación era verdadera porque..."
• "¿Cómo sabías si cada afirmación era verdadera o falsa?"
• Comparta las respuestas.
• Guíe a toda la clase para que rellene los espacios en blanco de las preguntas utilizando las categorías previamente identificadas.
• "Utiliza los datos de tu gráfico de barras para responder a las preguntas"
• 3-5 minutos: tiempo de trabajo en pareja
1. Decide si cada afirmación es verdadera o falsa sobre cómo llega nuestra clase a casa. Explica tu razonamiento a tu compañero.
A. Hay más estudiantes que vuelven a casa andando que de cualquier otra forma.
B. Hay más estudiantes que vuelven a casa en autobús que en coche.
C. Hay menos estudiantes que vuelven a casa andando que en bicicleta.
D. Hay más estudiantes que vuelven a casa andando o en bicicleta que en furgoneta.
2. Rellena los espacios en blanco como te indique tu maestro y luego responde a cada pregunta.
A. "¿Cuántos estudiantes más que ?"
B. "¿Cuántos estudiantes más o que ?"
1. Ejemplo de respuesta: Sé que la primera afirmación es falsa porque hay más estudiantes que van en bicicleta que los que van andando a casa.
2. Por ejemplo, si una pregunta se completa como "¿Cuántos estudiantes más van en bicicleta que andando?" y 6 estudiantes van en bicicleta y 4 estudiantes van andando, los estudiantes deben explicar cómo saben 2 más estudiantes van en bicicleta que andando.
Si los estudiantes encuentran diferencias que no coinciden con los datos del gráfico, considere preguntar:
• "¿Cómo respondiste a las preguntas?"
• "¿Cómo podrías utilizar los gráficos para responder a las preguntas?"
• Pida a los estudiantes que compartan sus respuestas a cada problema de comparación.
• "¿Tenéis alguna pregunta pendiente sobre cómo responder a estas preguntas del gráfico de barras?".
• Considere preguntar: "¿Qué ecuación coincide con tu razonamiento?"
10 minutos
Muestre un gráfico de barras creado por los estudiantes.
Genere algunas preguntas para que los estudiantes respondan sobre cómo llegan a casa utilizando el gráfico de barras. Por ejemplo, puede preguntar:
• "¿Cuántos estudiantes más que ?"
• "¿Cuántos estudiantes menos _______________ que ?"
• "¿Cuántos estudiantes más o que ?"
Pida a los estudiantes que respondan a las preguntas y compartan sus razonamientos.
California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

Comunidad matemática
Después del enfriamiento, dé a los estudiantes 2-3 minutos para discutir cualquier revisión de las acciones "Haciendo matemáticas" en pequeños grupos. Comparte las ideas con todo el grupo y anota las revisiones.
5 minutos
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Reflexiones:
Se preguntó a un grupo de estudiantes: "¿Cuál es tu lugar favorito para leer?"
Sus respuestas se muestran en este gráfico de barras:
1. ¿Cuántos estudiantes más eligieron el parque que su casa como su lugar favorito para leer?
2. Verdadero o falso: A más estudiantes les gusta leer en el colegio o la biblioteca que en el parque. Explica o muestra tu razonamiento.
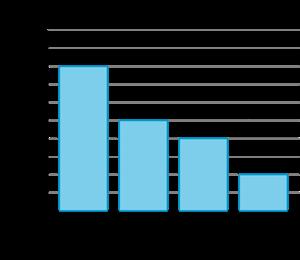
• 3 más estudiantes
• Falso. Ejemplo de respuesta: A seis estudiantes (4 + 2) les gusta leer en la escuela o en la biblioteca, y a 8 estudiantes les gusta leer en el parque.


IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.MD.3 Dibuja un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Construir
2.NBT.5
Enfoque SMPs
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué?
Para...
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo buscar y utilizar la estructura razonar con datos.
META(S) DE APRENDIZAJE
• Puedo interpretar y hacer preguntas acerca de una gráfica ilustrada.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Interpretar gráficas ilustradas a escala para generar preguntas (oralmente y por escrito) acerca de los datos.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
En esta lección, los estudiantes dan sentido al hecho de escalar un gráfico por un número distinto de 1. ¿Cómo apoya esto el trabajo que los estudiantes harán con la multiplicación más adelante en esta unidad?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Hablar de números (calentamiento)
Objetivos de aprendizaje para el estudiante
• Exploremos las gráficas de imágenes a escala.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes lean y respondan preguntas sobre gráficas de imágenes a escala.
En lecciones anteriores, los estudiantes revisaron cómo crear e interpretar gráficas de imágenes a escala de una sola unidad. En esta lección, los estudiantes aprenden que una gráfica de imagen a escala es una imagen
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
gráfico en el que cada imagen representa una cantidad distinta de 1. Leen, interpretan y responden preguntas sobre gráficos de imágenes a escala con una escala de 2 y 5, y generan preguntas que pueden responderse con estos gráficos.
Comunidad matemática
Diga a los estudiantes que, al final de la lección, se les pedirá que identifiquen acciones específicas de su lista "Haciendo matemáticas" (tanto de la sección del maestro como de la del alumno) que hayan experimentado personalmente.
Componente de la lección Estructura Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 Pares 15 min.
Actividad de exploración 2 En parejas 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional

Math Nation California - Grado 3
Descripción breve
Los estudiantes calculan mentalmente la suma de expresiones de adición y comparten las estrategias que utilizaron.
Los estudiantes leen y comparan gráficos de imágenes con diferentes escalas que representan los mismos datos.
Los estudiantes interpretan gráficos de imágenes a escala determinando la cantidad en cada categoría y escribiendo preguntas que los gráficos podrían responder.
Los estudiantes discuten la importancia de los gráficos de imágenes a escala y los comparan con un gráfico de imágenes que tiene una escala de 1
Los estudiantes interpretan un gráfico de imágenes a escala para responder preguntas sobre los datos.
Apoyo:
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de imagen o de barras
• Capturar cuadrados (1-3), Etapa 3: Sumar dentro de 20
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
minutos

Rutinas didácticas
Hablar de números
El propósito de esta Charla sobre números es obtener estrategias y conocimientos de los estudiantes para sumar dentro de 100 Estos conocimientos ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección, cuando los estudiantes necesiten sumar el número total de estudiantes representados en un gráfico. Cuando los estudiantes usan estrategias basadas en el valor posicional para sumar, buscan y hacen uso de la estructura (MP7).
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Mostrar una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste."
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra el valor de cada expresión mentalmente.
• 50 + 10
• 50 + 12
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
• 60 + 13
• 65 + 13
• 60: Cinco decenas y 1 diez hacen 6 decenas, que es 60
• 62: Es como el primero, pero hay 2 unos, así que sería 62
• 73: Es como el segundo problema, pero hay 1 más diez y 1 más uno. Así que cada uno sube por 1 por lo que es 73
• 78: Hay 7 decenas y 8 unidades por lo que es 78.
• "¿Cómo te ayudó el valor posicional al sumar estos números?" (Pude usar decenas y unidades para ayudarme a encontrar la suma.)
• Considere preguntar:
• "¿Quién puede replantear el razonamiento de de una manera diferente?"
• "¿Alguien tuvo la misma estrategia pero la explicaría de manera diferente?"
• "¿Alguien planteó el problema de una manera diferente?"
• "¿Alguien quiere añadir algo a la estrategia de 's?"
15 minutos
El propósito de esta actividad es que los estudiantes lean un gráfico de imágenes a escala. Se utiliza una escala de 5 para fomentar el conteo saltado, ya que los estudiantes contaron saltado 5 en 2º curso. Las preguntas de la tarea se centran en la estructura de un gráfico de imagen a escala y en las estrategias para leerlos.
• Grupos de 2
INTRODUCCIÓN
• "¿Cuál es tu deporte o actividad favorita fuera del colegio?"
• Comparte las respuestas.
• Muestra la primera imagen del gráfico a escala de una unidad.
INTRODUCCIÓN
CONTINUÓ

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Math Nation California - Grado 3
Grado 3 . Matemáticas . Unidad 1
• "¿Qué notas? ¿Qué te preguntas?" (Los estudiantes pueden darse cuenta: El gráfico trata de los deportes favoritos de los estudiantes. Hay muchas caritas sonrientes. Cada cara sonriente representa 1 estudiante. Lleva mucho tiempo contar los estudiantes de cada categoría. Los estudiantes pueden preguntarse ¿Cuántas respuestas de estudiantes se muestran en todo el gráfico? ¿Cómo podríamos hacer que el gráfico ocupara menos espacio?)
• 1 minuto: tiempo para pensar en silencio
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Comparte y registra las respuestas.
• "Trabaja con tu compañero para averiguar cuántos estudiantes están representados en el gráfico."
• 3-5 minutos: tiempo de trabajo en pareja
• Vigile a los estudiantes que agrupan las caritas sonrientes por 2, 5, o 10 para que sea más fácil contarlas.
• Pida a los estudiantes que agruparon las caritas sonrientes que compartan sus estrategias sobre cómo hallaron el número total de estudiantes representados en el gráfico.
• Si ningún estudiante utiliza esta estrategia, pregunte: "¿Cómo podría ser más fácil contar las imágenes agrupadas en el gráfico?". (Podríamos rodear las decenas para poder contar de diez en diez. Sería más fácil llevar la cuenta que contando de uno en uno.)
• Muestre la segunda imagen del gráfico de imágenes a escala.
• "¿Cómo podríamos contar el número total de estudiantes en este gráfico?"
• 2 minutos: tiempo de trabajo en parejas
• Comunidad matemática: Mientras los estudiantes trabajan, monitoree para ver ejemplos de las acciones de "Haciendo Matemáticas".
1. A un grupo de estudiantes se les preguntó: "¿Cuál es tu deporte favorito?". Sus respuestas se muestran en este gráfico:
2. Sus respuestas también se muestran en este gráfico:
¿Cuántos estudiantes están representados en el gráfico?
¿En qué se diferencia contar el número total de estudiantes en este gráfico de contar el número total de estudiantes en el primer gráfico?
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

POSIBLE RESPUESTAS
AUMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
1. 65 estudiantes.
2. Contamos por 5 para hallar el total en lugar de contar por 1. Podemos contar para hallar el total mucho más rápido.
Si los estudiantes cuentan a los estudiantes en el gráfico del dibujo a escala y obtienen un total distinto de 65, considere preguntar:
• "¿Cómo hallaste el número total de estudiantes representados en el gráfico?"
• "¿Cómo podrías usar el conteo por 5 para hallar el número total de estudiantes representados en el gráfico?"
• "En un gráfico en el que hay muchos datos podemos ajustar la escala para que cada imagen represente más de 1 objeto. Cuando cada imagen representa algo distinto de 1, decimos que se trata de un gráfico de imágenes a escala. La clave nos dice que en este gráfico, cada cara sonriente representa a 5 estudiantes".
20 minutos
El propósito de esta actividad es que los estudiantes interpreten un gráfico de imágenes a escala y escriban preguntas que puedan formularse basándose en los datos representados en un gráfico de imágenes a escala.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Utilizar ejemplos multimodales para mostrar el significado de un símbolo. Utilizar descripciones verbales junto con gestos, dibujos u objetos concretos para mostrar cómo cada flor del gráfico es un símbolo que representa cinco flores que se vieron en el parque.
Avances: Escuchar, Representar
INTRODUCCIÓN
Representación: Interiorizar la comprensión. Síntesis: Invite a los estudiantes a identificar qué detalles eran necesarios para resolver el problema. Muestre el marco de la frase: "La próxima vez que lea un gráfico con imágenes a escala prestaré atención a..."
Apoya la accesibilidad para: Procesamiento conceptual
ACTIVIDAD
• Grupos de 2
• Muestra los gráficos para que todos los vean.
• "¿Cuáles son algunas estrategias que podrías usar para leer los gráficos?" (En el gráfico Flores que vi camino a casa podría contar cada categoría por 5 ya que cada dibujo representa 5 flores.)
• 1 minuto: tiempo para pensar en silencio
• Comparte y anota las respuestas.
• "Ahora vamos a responder a algunas preguntas sobre los gráficos de dibujos a escala. También tendrás la oportunidad de escribir tu propia pregunta que se puede hacer en base a cada gráfico."
• 8-10 minutos: tiempo de trabajo en pareja
• Si hay tiempo, haz que los grupos intercambien libros y respondan a las preguntas de los demás.
• Comunidad matemática: Mientras los estudiantes trabajan, observe si hay ejemplos de las acciones de "Haciendo Matemáticas".
Grado 3 . Matemáticas . Unidad 1

Math
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. André recogió datos para ver cuántas de cada tipo de flor vio de camino a casa. Los datos se muestran en este gráfico de imágenes:
2. Se preguntó a un grupo de estudiantes: "¿Cuál es tu tipo de libro favorito?". Sus respuestas se muestran en este gráfico:
A. ¿Cuántas flores de cada tipo vio Andre de camino a casa? rosas tulipanes margaritas violetas
B. Escribe 2 preguntas que podrías hacer sobre las flores que Andre vio de camino a casa.
1.
2.
RESPUESTAS POSIBLESS
AUMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
Nation California - Grado 3
A. ¿A cuántos estudiantes les gustó cada tipo de libro? ¿Cómo lo sabe?
B. Escriba 2 preguntas que podría hacer sobre los tipos de libros favoritos de los estudiantes basándose en el gráfico.
A. 10, 5, 25, 15
B. Ejemplos de respuestas: ¿Cuántas rosas más vio André que tulipanes? ¿Cuántas violetas menos vio André que margaritas?
A. 8 le gustaban los libros de chistes, 2 le gustaban los libros de cómics, 8 le gustaban los libros de ciencia, y 6 le gustaban los libros de misterio. Ejemplo de respuesta: Cada cara sonriente representa a 2 estudiantes, así que para hallar el número en cada categoría conté por 2
B. Respuestas de muestra: ¿A cuántos estudiantes les gustan más los libros de ciencia que los de misterio? ¿A cuántos estudiantes les gustan los libros de chistes o los cómics?
Si los estudiantes responden a las preguntas sobre el gráfico con números que no coinciden con el gráfico, considere preguntarles:
• "¿Cómo respondiste a las preguntas sobre el gráfico?"
• "¿Qué nos dice la clave sobre cada imagen del gráfico?"
• Pida a los estudiantes que compartan las respuestas a las preguntas que respondieron y que expliquen su razonamiento.
• Considere preguntar:
• "¿Cómo utilizó la escala para responder a las preguntas?" (Yo conté por el número que representaba cada dibujo, como por 5 para las flores y por 2 para los estudiantes.)
• Comparta una variedad de preguntas escritas por los estudiantes.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN
• Considere preguntar:
• "¿Cómo sabías que tu pregunta podía responderse con el gráfico?" (Los datos que necesitabas para responder a la pregunta estaban en el gráfico.)
• Si hay tiempo pregunte: "¿Qué preguntas no pueden responderse con este gráfico?" (¿El tipo de libro favorito de cuántos estudiantes son las novelas gráficas?)
10 minutos
Muestra las imágenes de los dos gráficos de "Deportes favoritos".
"Hoy hemos aprendido sobre gráficos de imágenes a escala. (Cuando hay muchos datos que representar, es más rápido usar una escala.)
"¿En qué se diferencia la lectura de gráficos de imágenes a escala de la lectura de gráficos que tienen una escala de 1?" (Cada imagen no representa 1 cosa, por lo que necesitas mirar la escala. En un gráfico de imágenes a escala puedes contar por la escala para encontrar el total en cada categoría en lugar de contar por 1.)
Comunidad matemática
Después del enfriamiento, pide a los estudiantes que reflexionen individualmente sobre la pregunta "¿Qué acción de 'Hacer Matemáticas' sentiste que fue más importante en tu trabajo de hoy, y por qué?". Pide a los estudiantes que escriban sus respuestas en la parte inferior de su papel de reflexión, en una hoja aparte o en un diario de matemáticas.
Recoge y lee sus respuestas después de clase. Estas respuestas le ofrecerán una idea de cómo se sienten los estudiantes sobre su propio trabajo matemático y le ayudarán a establecer conexiones personales con las normas que crearán durante los días 4-6
5 minutos
Jada recopiló datos para ver cuántos de cada tipo de pájaro vio de camino a casa. Los datos se muestran en este gráfico: Basándose en los datos del gráfico:
1. ¿Cuántos gorriones vio Jada de camino a casa?
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
2. Escriba una pregunta que podría hacer sobre los pájaros que Jada vio de camino a casa.

1. 10 gorriones
2. Ejemplos de respuestas: ¿Cuántos pájaros vio Jada de camino a casa? ¿Cuántos arrendajos azules y cardenales vio Jada de camino a casa?


IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Alineación de estándares y principios de Abordar
3.MD.3 Dibuja un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP6 Atender a la precisión.
Estándares CA ELD
I.A.3 I.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo razonar abstracta y cuantitativamente razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo crear un gráfico de imagen a escala.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Representar datos utilizando gráficos de imágenes a escala.
PREGUNTA DE REFLEXIÓN DEL MAESTRO
¿Cuál ha sido la mejor pregunta que has hecho hoy a los estudiantes? ¿Por qué la consideras la mejor basándote en lo que han dicho o hecho los estudiantes?
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
¿Cuántos ves? (Calentamiento)
Objetivos de aprendizaje para el estudiante
• Hagamos un gráfico de imagen a escala.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes creen un gráfico de imagen a escala para representar datos categóricos.
En una lección anterior, los estudiantes interpretaron y respondieron preguntas sobre gráficos de imagen a escala. En esta lección, reúnen y organizan datos sobre las formas en que a los estudiantes les gustaría viajar y representan los datos en un gráfico de imagen a escala con una escala de 2. Los estudiantes entienden cómo representar a un solo estudiante en un gráfico de imagen a escala que tiene una escala de 2
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1

Comunidad matemática
Explique a los estudiantes que las normas son expectativas que ayudan a que todos en el aula se sientan seguros, cómodos y productivos haciendo matemáticas juntos. Diga a los estudiantes que algunas de estas normas pueden aplicarse tanto a ustedes como a mí, sin embargo, puede haber cosas que ustedes necesiten que yo haga para apoyarlos al hacer matemáticas cada día. Ofrezca un ejemplo, como "Puede ayudarnos a compartir nuestras ideas como toda la clase si tenemos la norma 'Escuchar mientras los demás comparten sus ideas'". Diga a los estudiantes que hará una pausa en dos momentos diferentes de la lección para identificar las normas que ayudan a todos a hacer matemáticas.
Componente de la lección Estructura Tiempo
Calentamiento En parejas 10 min.
Descripción breve
Los estudiantes explican cómo determinar el número de puntos que aparecen en las imágenes.
Actividad de exploración 1 Grupos pequeños 15 min. Los estudiantes recogen y organizan los datos de su clase.
Actividad de exploración 2 Por parejas 20 min.
Síntesis Grupo completo 10 min.
Los estudiantes crean un gráfico de imagen con una escala de 2 que representa los datos recogidos de la clase.
Los estudiantes discuten las estrategias utilizadas para crear un gráfico de imagen a escala y cómo representar un dato más añadido al gráfico.
Enfriamiento Independiente 5 min. Los estudiantes añaden datos a un gráfico de imagen a escala.
Centro(s) sugerido(s) Grupos pequeños Opcional
Apoyo:
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de imagen o de barras
• Capturar cuadrados (1-3), Etapa 3: Añadir dentro de 20
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
¿Cuántos ves?
El objetivo de esta actividad es que los estudiantes subitizen o utilicen estrategias de agrupación para describir el número de puntos que ven. Aunque los puntos se han agrupado deliberadamente por 5 para provocar el conteo por 5 como estrategia, los estudiantes pueden ver 2 grupos de 5 como 10. Las estrategias de agrupación y el conteo saltado por 2, 5, y 10 ofrecen un repaso del trabajo del grado 2 y construyen hacia la multiplicación en lecciones futuras.
• Grupos de 2
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "¿Cuántos ves? ¿Cómo los ves?"
• Muestra la imagen.
• 30 segundos: tiempo para pensar en silencio
• Muestra la imagen.
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Registra las respuestas.
• Repite para cada imagen.
¿Cuántos ves? ¿Cómo los ves?
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
• 15: Vi 3 grupos de 5.
• 25: Vi 5 grupos de 5
• "¿Qué patrón viste primero y cómo te ayudó esto a calcular el total?" (Vi que los puntos estaban en grupos de 5. Esto me ayudó porque sé contar por 5.)
• Considera preguntar:
• "¿Alguien vio los puntos de la misma forma pero lo explicaría de otra manera?"
• "¿Alguien quiere añadir una observación a la forma en que vio los puntos?"
Grado 3 . Matemáticas . Unidad 1
15 minutos
El objetivo de esta actividad es que los estudiantes recopilen y organicen datos categóricos sobre sus compañeros de clase. Los estudiantes registran la forma preferida de viajar de sus compañeros y discuten las ventajas y desventajas de mostrar los datos categóricos en una tabla.
Para que el proceso de recogida de datos sea más rápido, los estudiantes pueden recoger primero sus respuestas dentro de su grupo y luego cada grupo puede repartirse cuántos estudiantes eligieron cada forma de viajar. Los nombres pueden estar preimpresos en una tabla para ellos o pueden escribir solo el nombre de la persona y la abreviatura de la forma de viajar (dada en el enunciado de la tarea) en la tabla. En la siguiente actividad, los estudiantes crean un gráfico a escala para estos datos categóricos.
INTRODUCCIÓN

ACTIVIDAD
FRENTE AL ALUMNO ENUNCIADO DE LA TAREA
• Grupos de 4
• "Hoy encuestarás a tus compañeros de clase. Empezaréis con vuestro grupo y luego recopilaremos los datos del grupo como clase".
• Indique a los estudiantes cómo deben recopilar los datos categóricos (véanse las sugerencias en la narración).
• 10 minutos: los estudiantes registran las respuestas de sus compañeros
¿Cómo te gustaría viajar?
• coche (C)
• tren (T)
• barco (B)
• globo (Bal)
• avión (P)
• helicóptero (H)
Nombre del alumno Forma de viajar

RESPUESTAS POSIBLES Las respuestas varían.
• "¿Qué tiene de útil tener estos datos en forma de lista? ¿Qué no es útil?" (Sabemos el camino que le gustaría recorrer a cada persona. Es difícil ver cuántas personas querrían viajar en cada sentido).
SÍNTESIS DE LA ACTIVIDAD
Math Nation California - Grado 3
• Math Community: Pide a los estudiantes que reflexionen sobre las acciones individuales y de grupo mientras se plantean la pregunta "¿Qué normas, o expectativas, hemos tenido en cuenta mientras hacíamos matemáticas juntos en nuestra comunidad matemática?"
• Registra y muestra sus respuestas en el apartado "Normas".
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
20 minutos
El propósito de esta actividad es que los estudiantes apliquen lo comprendido en lecciones anteriores para crear un gráfico de imagen con una escala de 2 a partir de los datos categóricos que recogieron. Se guía a los estudiantes para que utilicen una escala de 2 pero pueden elegir su propio símbolo. Dependiendo de los datos, puede que los estudiantes necesiten utilizar la mitad del símbolo para representar un número impar de estudiantes que eligen un método específico de desplazamiento. Esta idea se discute en la síntesis. Los estudiantes volverán a utilizar sus gráficos de imágenes a escala en la próxima lección.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Cuando los estudiantes comparen gráficos, muestre los siguientes marcos de oraciones: "El símbolo que elegí para representar es , porque . . . ", "One way our graphs are the same is . . .", y "One way our graphs are different is . . ."
Advances: Hablar, representar

Apoyo para estudiantes con discapacidad
Representación: Interiorizar la comprensión. Invite a los estudiantes a comenzar creando un modelo físico de un gráfico. Proporcione acceso a objetos físicos, como cubos de conexión, que los estudiantes puedan utilizar para representar a cada persona y, a continuación, organícelos en grupos de 2
Apoya la accesibilidad para: Procesamiento visual-espacial, Procesamiento conceptual
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 2
• "¿Cómo podemos representar los datos de nuestra encuesta en un gráfico de imágenes sin tener que hacer un dibujo para cada alumno de nuestra clase?" (Podemos hacer que cada símbolo represente a más de un estudiante para no tener que dibujar tanto.)
• "Representa los datos que has recogido en tu propio gráfico de imágenes a escala en el que cada imagen represente a 2 estudiantes."
• 10 minutos: tiempo de trabajo independiente
• Circula mientras los estudiantes trabajan:
• Anímales a incluir un título, etiquetas de categorías y una clave.
• Presta atención a cómo los estudiantes están agrupando por 2
• Apoye a los estudiantes con las preguntas que puedan tener (especialmente en torno a la representación de cantidades impares).
• "Compara tu gráfico con tu compañero".
• 2 minutos: discusión por parejas
• Vigile si hay un gráfico que utilice una media imagen para mostrar un número impar de estudiantes en una de las categorías para compartirlo durante la síntesis de la actividad.
Represente los datos de nuestra encuesta en un gráfico de imágenes a escala en el que cada imagen represente 2 estudiantes.
RESPUESTAS POSIBLES

AUMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
Grado 3 . Matemáticas . Unidad 1
Los gráficos de los estudiantes deben coincidir con los datos de la clase. Ejemplo de respuesta:
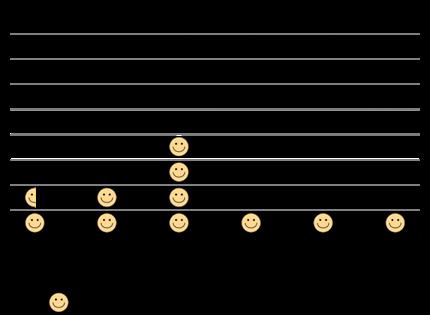
Si los estudiantes eligen símbolos que llevan mucho tiempo dibujar, considere preguntar:
• "¿Cómo elegiste el símbolo para usar en tu gráfico?"
• "¿Cómo podrías hacer que tu símbolo fuera más fácil de dibujar?"
• Muestre los trabajos seleccionados de los estudiantes.
• "¿Cómo representa este gráfico los datos de la encuesta de nuestra clase?"
• "¿Cómo representó el número de estudiantes que eligieron una forma de viajar cuando era un número impar?"
• "¿Qué preguntas tienen sobre la creación de un gráfico de imágenes a escala?" (¿Podría una cara representar 3 estudiantes o 5 estudiantes? ¿Puedes utilizar la imagen que quieras para representar a 2 estudiantes?)
10 minutos
Muestre un gráfico a escala de la lección de hoy. "¿Qué pasaría si 2 más estudiantes eligieran viajar en globo? ¿Cómo podríamos representarlo en este gráfico?" (Añade 1 imagen más en esa categoría.)
"¿Qué pasaría si 1 más estudiantes eligieran viajar en coche? ¿Cómo podríamos representarlo en este gráfico?" (Añade la mitad de la imagen de esa categoría).
Comunidad matemática
Repasa la lista de "Normas". Pide a los estudiantes que comenten con un compañero cuándo una norma les resultó útil mientras hacían matemáticas. Añada las ideas que falten o revise las anteriores.
Math
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
minutos

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Se preguntó a un grupo de estudiantes: "¿Cómo te gustaría viajar?" Sus respuestas se muestran en este gráfico de imágenes:

Cuatro estudiantes estaban ausentes cuando se recogieron estos datos. Les gustaría viajar en avión. Añade sus datos al gráfico.
RESPUESTAS POSIBLES Los estudiantes dibujan otras dos caritas sonrientes en la columna del avión.
Reflexiones:


IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
3.MD.3 Dibuja un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Enfoque SMPs
MP6 Prestar atención a la precisión.
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares CA ELD
I.A.1
I.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo
atender a la precisión y buscar y expresar la regularidad en razonamientos repetidos razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo crear un gráfico de barras a escala.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Representar datos utilizando gráficos de barras a escala.
Basándose en el trabajo previo de los estudiantes con gráficos de imágenes a escala, ¿qué estrategia anticipó hoy? ¿Qué estrategia no anticipó?
Rutinas didácticas
Conversación sobre números (calentamiento)
Materiales para reunir
Materiales de una lección anterior: Actividad 2
Materiales necesarios
Actividad 2:
Cada alumno necesita el gráfico que creó en la lección anterior.
Objetivos de aprendizaje para el alumno
• Vamos a hacer un gráfico de barras a escala.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes creen un gráfico de barras a escala.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
En una lección anterior, los estudiantes recogieron datos categóricos de la clase y aprendieron a crear un gráfico de imagen a escala. Ahora, los estudiantes hacen conexiones entre gráficos de imágenes a escala y gráficos de barras a escala, y amplían la idea de una escala que es más de uno a gráficos de barras. En esta lección, los estudiantes eligen una escala de 2 o 5 para su gráfico de barras.
Comunidad matemática
Diga a los estudiantes que, al final de la lección, se les pedirá que identifiquen ejemplos específicos de normas que experimentaron mientras hacían matemáticas.
Componente de la lección Estructura Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 En parejas 10 min.
Actividad de exploración 2 En parejas 25 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.

Centro(s) sugerido(s) Grupos pequeños Opcional
Descripción breve
Los estudiantes encuentran mentalmente la suma de expresiones de adición repetidas y comparten las estrategias que utilizaron.
Los estudiantes comparan un gráfico de barras con una escala de una unidad con un gráfico de barras con una escala de 2 que representa los mismos datos.
Los estudiantes crean un gráfico de barras con una escala de 2 o 5 que representa los datos y luego explican su elección de escala.
Los estudiantes debaten cómo crear un gráfico de barras con una escala distinta de 1
Los estudiantes completan un gráfico de barras con una escala de 5
Abordar:
• Ordenar y mostrar (1-3), Etapa 3: Gráficos a escala Apoyo:
• Cinco en raya: Suma y resta (1-2), Etapa 6. Sumar dentro de 100 Sumar dentro de 100 con Composición
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Charla sobre números
El propósito de esta Charla sobre Números es obtener estrategias que los estudiantes tienen para contar de 2 y 5. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y se utilizarán más adelante en esta lección cuando los estudiantes necesiten ser capaces de escalar gráficos de barras.
Cuando los estudiantes notan que el número de sumandos iguales se duplica en la segunda expresión, están buscando y dando sentido a la estructura (MP7). Cuando notan que el patrón se repite en el segundo par de expresiones y usan el patrón para encontrar el valor de la suma, también están buscando y expresando regularidad en razonamientos repetidos (MP8).
• Mostrar una expresión.
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS
POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste".
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada expresión.
• 2 + 2 + 2 + 2
• 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2
• 5 + 5 + 5 + 5
• 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5
• 8: Había cuatro 2s así que conté por 2 cuatro veces como 2, 4, 6, 8.
• 16: Sabía que 4 dos era 8 y ahora hay dos grupos de 8, así que doblé 8 para obtener 16.
• 20: Sabía que 2 cincos es 10 y hay 4 cincos, así que doblé 10
• 40: Sabía que cuatro cincos era 20 y ahora hay 2 grupos de 20, así que doblé 20 para obtener 40.
• "¿Cómo te ayudaron las dos primeras expresiones a resolver la tercera y la cuarta?" (Si observas que hay el doble de doses o cincos, puedes simplemente duplicar la suma.)
• Considera preguntar:
• "¿Quién puede replantear el razonamiento de 'de una manera diferente?"
• "¿Alguien tuvo la misma estrategia pero la explicaría de otra manera?"
• "¿Alguien planteó el problema de una manera diferente?"
• "¿Alguien quiere añadir algo a la estrategia de 's?"
Grado 3 . Matemáticas . Unidad 1
10 minutos
El propósito de esta actividad es presentar a los estudiantes un gráfico de barras a escala. Los estudiantes consideran un gráfico de barras con escala de una sola unidad junto a un gráfico de barras con escala de 2, ambos representando el mismo conjunto de datos categóricos. Discuten las similitudes y diferencias entre un gráfico de barras a escala de una sola unidad y un gráfico de barras con una escala de 2
INTRODUCCIÓN • Grupos de 2
• Mostrar las imágenes.
• "¿En qué se parecen estos gráficos de barras? ¿En qué se diferencian?"

Math
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• 1 minuto: tiempo para pensar en silencio
• 4 minutos: discusión por parejas
Se preguntó a una clase: "¿Cómo llegas a casa desde el colegio?". Sus respuestas se muestran en estos dos gráficos de barras:
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Nation California - Grado 3
Discute con tu compañero: ¿En qué se parecen los dos gráficos? ¿En qué se diferencian?
• Ambos tienen barras, las mismas categorías, etiquetas, etc.
• Uno cuenta por unos para la escala y el otro cuenta por dos (llama a esto "escalar").
• El 12 en el primer gráfico es más alto que el 12 en el segundo gráfico.
• "¿Qué era igual? ¿Qué era diferente?"
• Comparte y anota las respuestas.
• Si no surge, suscita la idea de que la escala del segundo gráfico cuenta de 2
• "Cuando cada salto de la escala es algún número distinto de 1, decimos que es un gráfico de barras a escala."
• "¿Por qué sería útil hacer un gráfico de barras a escala?" (Si no querías contar de uno en uno. Si quisieras mostrar números más grandes en tu gráfico).
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
Materiales a reunir
Materiales de una lección anterior

25 minutos
Preparación necesaria
Cada estudiante necesita el gráfico que creó en la lección anterior.
El objetivo de esta actividad es que los estudiantes creen un gráfico de barras a escala. Los estudiantes deciden una escala de 2 o 5, por lo que será importante preguntar a los estudiantes por qué eligieron su escala y con qué precisión pueden decir el número exacto que representa la barra (MP6). En la síntesis de la actividad, los estudiantes discuten cómo representaron un número impar de estudiantes con una escala de 2 y un número de estudiantes que no era múltiplo de 5 en una escala de 5. Esta pregunta debe ajustarse en función de los datos que recoja tu clase.
Apoyo para estudiantes de inglés
MLR7 Compare and Connect. Síntesis: Dé tiempo a los estudiantes para estudiar los trabajos de los estudiantes expuestos con ambas escalas. Durante la discusión de toda la clase, pregunte a los estudiantes: "¿Qué tienen en común los gráficos?", "¿En qué se diferencian?", "¿Por qué los diferentes gráficos conducen al mismo resultado?"
Avances: Representar, hablar
INTRODUCCIÓN
• Grupos de 2
ACTIVIDAD
Apoyo para estudiantes con discapacidad
Engagement: Desarrollar el esfuerzo y la persistencia. Divide esta tarea en partes más manejables. Revisa con los estudiantes para darles retroalimentación y ánimo después de que hayan representado un método de viaje en un gráfico.
Apoya la accesibilidad para: Organización, Atención
• Asegúrate de que cada alumno tiene su gráfico a escala de la lección anterior.
• "Hoy representaremos los datos que recogimos ayer sobre las formas en que nos gustaría viajar en un gráfico de barras a escala"
• "Decide con tu compañero si quieres utilizar una escala de 2 o 5. Prepárate para explicar tu elección. Si tienes tiempo, intenta hacer un gráfico con una escala de 2 y otro con una escala de 5."
• 12 minutos: tiempo de trabajo en pareja
• Considera preguntar: "¿Cómo te ayudó tu gráfico de imagen a escala a hacer tu gráfico de barras a escala?"
1. Representa los datos que recogimos anteriormente en un gráfico de barras a escala .
2. Utiliza el gráfico con una escala de 2 o el gráfico con una escala de 5. Si tienes tiempo, puedes hacer gráficos de 2. Asegúrate de etiquetar el título y las categorías.
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
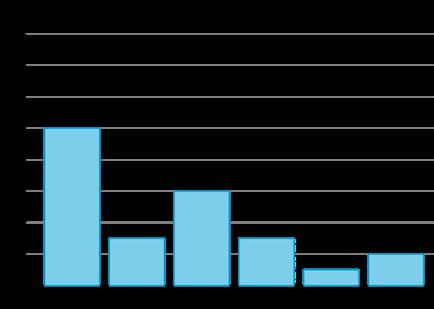
AVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD
Grado 3 . Matemáticas . Unidad 1
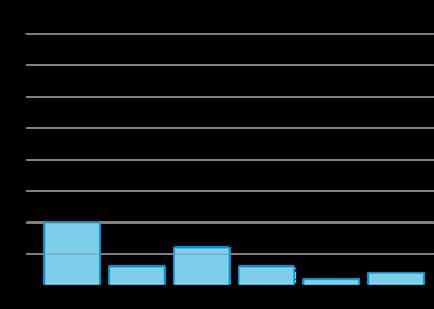
Si los estudiantes dibujan la parte superior de la barra en un lugar que no se corresponde con las formas en que nos gustaría recorrer los datos, considere preguntar:
• "¿Cómo decidiste dónde terminaría la parte superior de la barra?"
• "¿Cómo podrías usar el conteo por 2 (o 5) para ayudarte a decidir dónde debería terminar la parte superior de la barra?"
• "¿Qué escala elegisteis tú y tu compañero? ¿Por qué?"
• Muestre el trabajo de los estudiantes con ambas escalas.
• "¿Cómo representaste una forma de viajar que no caía justo en los números de la escala?" (Estaba entre los números de 2, así que tuve que adivinar dónde debía parar la barra.)
• "¿Qué diferencias notas cuando el gráfico está con una escala de 2 y cuando el gráfico está con una escala de 5?" (Ejemplos de respuestas: Las barras parecen más altas cuando la escala es 2. Es difícil saber qué número representan algunas barras cuando la escala es 5. Era más fácil contar hasta cantidades mayores cuando la escala era 5).
10 minutos
Muestra un gráfico de barras a escala de la lección.
"Hemos estado aprendiendo cómo hacer gráficos de barras a escala. Si fueras a ayudar a un amigo a crear un gráfico de barras a escala, ¿qué consejo le darías?". (Les diría que significa que la escala sube por números distintos de 1. Deberían fijarse en el número de personas de cada categoría y pensar si esos números son fáciles de contar por 2 o 5 o algún otro número.)
Asegúrese de resaltar las ideas sobre el uso de escalas de 2 o 5
Comunidad matemática
Después del enfriamiento, dé a los estudiantes 2-3 minutos para debatir en pequeños grupos cualquier revisión de la sección
"Normas". Recoge y anota las revisiones.
California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
5 minutos

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
A los estudiantes que visitaron el zoológico se les preguntó: "¿Cuál es tu animal favorito en el zoológico?" Sus respuestas se muestran en esta tabla:
Animal Número de estudiantes elefante 17
10
14
4
RESPUESTAS POSIBLES
Utilice los datos de la tabla para completar el gráfico de barras a escala.
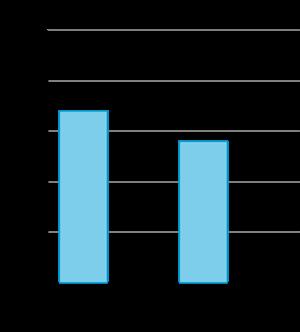
Los gráficos de barras de los estudiantes deben mostrar 10 estudiantes eligieron tigres y 4 estudiantes eligieron nutrias.
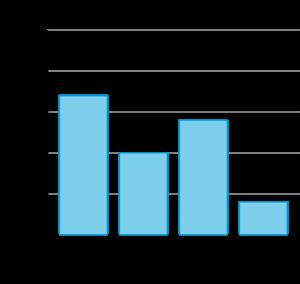
Reflexiones:


IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.MD.3 Dibujar un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
Estándares ELD de California
I.A.3 I.B.5 I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo
construir argumentos viables y criticar el razonamiento de otros razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo elegir una escala adecuada para un gráfico de barras.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Elegir una escala adecuada para un gráfico de barras que represente un conjunto de datos dado.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
En la lección de mañana, los estudiantes resolverán problemas de uno y dos pasos de "cuántos más" y "cuántos menos" utilizando datos presentados en gráficos de barras a escala. Basándose en el trabajo que ha visto hacer a los estudiantes en lecciones anteriores, ¿qué estrategias prevé que utilizará cada estudiante para resolver estos problemas? ¿Cómo animará a cada alumno a compartir sus conocimientos y a escuchar las estrategias de los demás?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Notar y maravillarse (calentamiento)
Objetivos de aprendizaje para el alumno
• Elijamos una escala para nuestro gráfico de barras.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes consideren las ventajas y desventajas de varias escalas de gráficos de barras.
©Accelerate Learning Inc. - Todos los derechos reservados

Grado 3 . Matemáticas . Unidad 1
En lecciones anteriores, los estudiantes crearon gráficos de barras e imágenes a escala con una escala dada de 2 o 5. Esta lección amplía este trabajo para permitir a los estudiantes elegir la escala de su gráfico de barras y reflexionar sobre las ventajas o desventajas de sus elecciones. A través del trabajo de la lección, los estudiantes se dan cuenta de que pueden elegir una escala basándose en los números del conjunto de datos y que la escala puede hacer que un gráfico sea más fácil o más difícil de leer (MP6).
Comunidad de matemáticas
Diga a los estudiantes que reflexionarán sobre sus normas identificadas al final de esta lección.
Componente de la lección
Estructura
Tiempo
Calentamiento Pares 10 min.
Actividad de exploración 1 En parejas 20 min.
Actividad de exploración 2 Grupos pequeños 15 min.
Síntesis Todo el Grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Descripción breve
Los estudiantes hacen observaciones sobre tres gráficos de barras que tienen diferentes escalas.
Los estudiantes analizan tres escalas para un gráfico de barras para determinar cuál representa mejor los datos y, a continuación, crean un gráfico de barras utilizando esa escala.
Los estudiantes eligen una escala adecuada para los datos y, a continuación, crean un gráfico de barras a escala.
Los estudiantes revisan las estrategias utilizadas para determinar las escalas apropiadas para dibujar gráficos de barras a escala.
Los estudiantes describen cómo su comprensión de los gráficos de barras a escala puede ayudarles a crear gráficos de barras a escala en el futuro.
Abordar:
• Ordenar y mostrar (1-3), Etapa 3: Gráficos a escala
Apoyo:
• Cinco en raya: Suma y resta (1-2), Etapa 6. Sumar dentro de 100 Suma dentro de 100 con Composición
Math
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
minutos

Rutinas didácticas
Notar y preguntarse
El propósito de este calentamiento es provocar la idea de que ajustar la escala cambia el tamaño de las barras en un gráfico de barras y puede hacerlo más fácil o más difícil de interpretar. Si bien los estudiantes pueden notar y preguntarse muchas cosas sobre estos gráficos, las diferentes escalas en los gráficos de barras son los puntos de discusión más importantes.
• Grupos de 2
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Muestre los gráficos.
• "¿Qué notan? ¿Qué te preguntas?"
• 1 minuto: tiempo para pensar en silencio
• "Comenta lo que has pensado con tu compañero."
• 1 minuto: debate entre compañeros
• Comparte y anota las respuestas.
¿Qué observas? ¿Qué te preguntas?
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Los estudiantes pueden notar:
• Los datos son los mismos.
• Los saltos en las escalas son diferentes. El número más alto de los gráficos es diferente.
• Es más difícil distinguir el número de cobayas en el último gráfico.
Los estudiantes pueden preguntarse:
• ¿Por qué los saltos en las escalas son diferentes?
• ¿Por qué las líneas son iguales en cada gráfico?
• "¿En qué se diferencian los tres gráficos?" (Muestran los mismos datos, pero las barras tienen alturas diferentes. Tienen escalas diferentes).
Grado 3 . Matemáticas . Unidad 1
20 minutos
El propósito de esta actividad es que los estudiantes analicen una escala y creen un gráfico de barras a escala. Los estudiantes consideran una gran colección de bloques de patrones y deciden qué escala funcionará mejor para representar los datos categóricos. Consideran las ideas de tres estudiantes, eligen una escala de 2, 5, o 10, y crean un gráfico de barras a escala para representar los datos categóricos. Los estudiantes deben justificar por qué están de acuerdo en que una escala determinada sería la mejor. Durante la actividad y el debate en clase, los estudiantes comparten sus ideas y tienen la oportunidad de escuchar y criticar el razonamiento de sus compañeros (MP3). Ofrecer una variedad de escalas para que los estudiantes elijan permite debatir sobre las ventajas de utilizar escalas mayores para grupos de objetos más grandes y sobre el efecto de una escala en la facilidad de lectura e interpretación de los datos en un gráfico.
Apoyo para estudiantes con discapacidad
Representación: Acceso para la percepción. Proporcionar acceso a bloques de patrones para Representar la colección de bloques de patrones en el enunciado de la tarea orientada al alumno.
Apoya la accesibilidad para: Organización, Procesamiento Visual-Espacial
• Grupos de 2
• Muestre la imagen.
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "Tómese un minuto para considerar estos bloques de patrones y piense cómo podría representarlos en un gráfico de barras a escala."
• 30 segundos: tiempo para pensar en silencio
• "Ahora responda a las preguntas sobre la organización y representación de los bloques de patrones en un gráfico de barras con su compañero. Prepárate para justificar tu elección de escala."
• 12 minutos: trabajo en parejas
• Supervisa a los estudiantes que utilizaron cada una de las escalas para crear su gráfico de barras.
Aquí tienes una colección de bloques de patrones.
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE LA TAREA PARA EL ESTUDIANTE
CONTINUACIÓN
RESPUESTAS POSIBLESS
FOMENTAR EL PENSAMIENTO DEL ALUMNO
SÍNTESIS DE LA ACTIVIDAD
Mai, Noah y Priya quieren hacer un gráfico de barras para representar el número de triángulos, cuadrados, trapecios y hexágonos de la colección.
• Mai dice que la escala del gráfico de barras debería ser 2.
• Noah dice que la escala del gráfico de barras debería ser 5.
• Priya dice que la escala del gráfico de barras debería ser 10.
1. ¿Con quién estás de acuerdo? Explica tu razonamiento.
2. Utiliza la escala que hayas elegido para crear un gráfico de barras a escala que represente la colección de bloques de patrones.
1. Estoy de acuerdo con Mai porque hay muchos bloques y contar por 2 es fácil. Mi compañera está de acuerdo con Priya porque sería muy rápido contar de 10.
2. Ejemplo de respuesta:
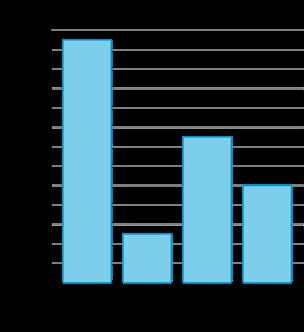
Si los estudiantes utilizan una escala de 2, considere preguntar:
• "¿Cómo decidiste la escala que utilizarías en tu gráfico?"
• "¿Cómo afectaría a tu gráfico utilizar una escala de 5 o 10?"
• Muestre los trabajos seleccionados de los estudiantes que muestren cada una de las escalas.
• "¿Qué escala utilizaste para tu gráfico de barras? ¿Por qué elegiste esa escala?" (Utilicé una escala de 5 porque cada cantidad se puede contar por 5. Utilicé una escala de 10 para no tener que hacer tantas marcas en la escala).
15 minutos
El objetivo de esta actividad es que los estudiantes representen datos en un gráfico de barras a escala. En esta actividad, los datos categóricos se presentan en una tabla. Los estudiantes eligen una escala y hacen un gráfico de barras a escala de los datos categóricos. Los estudiantes tienen experiencia previa con escalas de 2, 5, y 10, y no se les indica una escala específica en esta actividad. Sin embargo, debido a los grandes números, es probable que los estudiantes elijan una escala de 5 o 10. Si a los estudiantes les cuesta empezar, puede sugerir una escala de 5 o 10. En el debate de toda la clase, los estudiantes comparten cómo su elección de escala afectó a su gráfico.
Los estudiantes volverán a utilizar sus gráficos de barras a escala en la próxima lección.
Grado 3 . Matemáticas . Unidad 1

Apoyo para estudiantes de inglés
MLR8 Discussion Supports. Durante la discusión en pequeños grupos, invite a los estudiantes a compartir sus respuestas por turnos. Pida a los estudiantes que repitan lo que han oído utilizando un lenguaje matemático preciso y sus propias palabras. Muestre el marco de frases: "Te he oído decir...". Los interlocutores originales pueden estar de acuerdo o aclarar para su compañero.
Avances: Escuchar, hablar
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 4
• "¿Cuál es tu época favorita del año?"
• 30 segundos: tiempo para pensar en silencio
• Comparte las respuestas.
• "Vamos a hacer un gráfico de barras a escala para representar las épocas favoritas del año de algunos estudiantes de 3º de primaria"
• "Representa los datos de la tabla en un gráfico de barras a escala. Piensa en una escala que tenga sentido con el número de estudiantes."
• 5-7 minutos: tiempo de trabajo independiente
• "Comparte tus gráficos con tu pequeño grupo. Discute las escalas que elegiste usar."
• 2-3 minutos: discusión en grupos pequeños
A todos los estudiantes de tercer grado de la escuela se les preguntó: "¿Cuál es tu época favorita del año?" Sus respuestas se muestran en esta tabla: época favorita del año número de estudiantes invierno 24 primavera 13 verano 40 otoño 22
Utilice los datos de esta tabla para crear un gráfico de barras a escala.
Ejemplos de respuestas:
RESPUESTAS POSIBLES
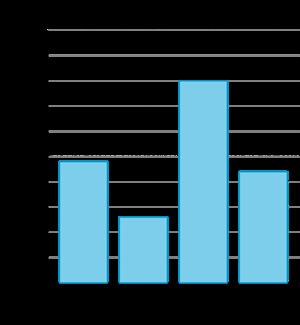
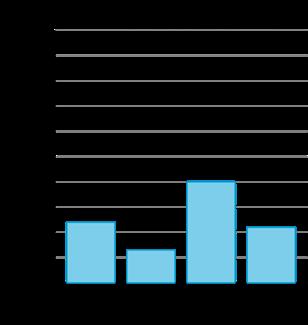
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• "¿Cómo afectó la escala que elegiste para tu gráfico la forma en que tu gráfico se vio al final?" (Ciertas escalas facilitan o dificultan la lectura de los datos. Por ejemplo, con una escala de 10, podría ser más difícil leer los valores exactos del gráfico.)
10 minutos
Muestra los gráficos de barras de la lección de hoy.
"¿Qué has aprendido hoy que te ayudará a tomar decisiones sobre cómo crear gráficos a escala en el futuro?" (Puedes elegir escalas que se ajusten a los datos. Si la mayoría son números grandes, puedes elegir una escala como 5 o 10. La escala puede ayudar a que el gráfico sea más fácil de leer).
Comunidad de matemáticas
Después del enfriamiento, pide a los estudiantes que reflexionen individualmente sobre la siguiente pregunta: "¿Cuál de las normas te ha parecido más importante en tu trabajo de hoy y por qué?". Los estudiantes pueden escribir sus respuestas en la parte inferior de su papel de enfriamiento, en una hoja separada o en un diario de matemáticas.
Diga a los estudiantes que a medida que su comunidad matemática trabaje junta en el transcurso del año, el grupo agregará y revisará continuamente sus acciones y expectativas de "Hacer matemáticas" y "Normas".
Y ESCALA 5 minutos
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Reflexiones:
1. ¿Cómo decidiste la escala para tu gráfico en la última actividad?
2. ¿Qué fue lo más importante que aprendiste hoy que te ayudará cuando hagas tu próximo gráfico de barras a escala?
1. Ejemplo de respuesta: Elegí una escala de 5 para tener menos números que escribir en mi escala.
2. Respuesta de muestra: Aprendí a pensar en los números de mi gráfico para ayudarme a elegir una escala.


IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.MD.3 Dibuja un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Construir
2.OA.3
Enfoque SMPs
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.B.5 II.C.6
A PREGUNTAS SOBRE
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo buscar y utilizar la estructura razonar con datos.
• Puedo leer e interpretar un gráfico de barras a escala para resolver problemas de un solo paso.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Resolver problemas de un paso de "cuántos más" y "cuántos menos" dentro de 100, con base en los datos presentados en gráficas de barras a escala.
PREGUNTA DE REFLEXIÓN PARA EL MAESTRO
Piensa en una ocasión en la que te hayas equivocado recientemente durante la clase de matemáticas. ¿Cómo aprovechó su error para mostrar a los estudiantes que los errores no son más que aprendizaje en proceso?
Rutinas didácticas ¿Cuántos ves? (Calentamiento)
Materiales a reunir
Materiales de una lección anterior: Actividad 1
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 1:
Los estudiantes necesitarán sus gráficos de la época favorita del año de la lección anterior.
Grado 3 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Resolvamos problemas basados en datos representados en gráficas de barras.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes resuelvan problemas de un solo paso de "cuántos más" y "cuántos menos" basados en datos presentados en una gráfica de barras a escala.
En segundo grado, los estudiantes resolvieron problemas sencillos de armar, desarmar y comparar usando datos representados en una gráfica de barras a escala de una sola unidad.
En esta lección, los estudiantes resuelven problemas de comparar de un paso usando datos representados en gráficas de barras a escala.
RESUMEN DE LA LECCIÓN
Componente de la lección

Estructura Tiempo
Calentamiento Pares 10 min.
Actividad de exploración 1 Parejas 15 min.
Actividad de exploración 2 En parejas 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Descripción breve
Los estudiantes explican cómo determinaron el número de puntos en las imágenes proporcionadas.
Los estudiantes analizan un gráfico de barras a escala para resolver problemas de un paso y luego representan matemáticamente su pensamiento.
Los estudiantes interpretan un gráfico de barras con una escala de 10 para responder a preguntas sobre "cuántos más" y "cuántos menos" y luego explican matemáticamente sus respuestas.
Los estudiantes resumen las estrategias utilizadas para resolver problemas sobre "cuántos más" y "cuántos menos" basándose en los datos representados en un gráfico de barras a escala.
Los estudiantes interpretan un gráfico de barras a escala y luego explican matemáticamente sus respuestas.
Abordar:
• Ordenar y mostrar (1-3), Etapa 3: Gráficos a escala
Apoyo:
• Cinco en raya: Adición y sustracción (1-2), Etapa 6: Suma dentro de 100 con Composición
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
¿Cuántos ves?
El propósito de este ¿Cuántos ves? es que los estudiantes subitizen o utilicen estrategias de agrupación para describir las imágenes que ven.
Cuando los estudiantes se dan cuenta de que algunos de los puntos están en grupos iguales y saltan a contar para encontrar el número total de puntos están buscando y haciendo uso de la estructura (MP7).

ACTIVIDAD
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
• Grupos de 2
• "¿Cuántos ves? ¿Cómo los ves?"
• Muestre la imagen.
• 30 segundos: tiempo para pensar en silencio
• Muestre la imagen.
• "Discute tus ideas con tu compañero."
• 1 minuto: discusión en pareja
• Registra las respuestas.
• Repite para cada imagen.
¿Cuántos ves? ¿Cómo los ves?
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Ejemplos de respuestas:
• 7: Veo 3 grupos de 2 y uno más.
• 22: Conté por 5 para los 4 grupos de 5 para obtener 20, luego agregué 2 más para los puntos del medio.
• "¿Cómo te ayudó pensar en los grupos a encontrar el número total de puntos?" (Algunos de los puntos estaban en grupos y otros no. Utilicé el conteo por saltos para contar los grupos que eran del mismo tamaño y luego sumé el resto de los puntos).
• Considere preguntar:
• "¿Quién puede volver a expresar la forma en que vio los puntos con palabras diferentes?"
• "¿Alguien vio los puntos de la misma forma pero lo explicaría de manera diferente?"
Grado 3 . Matemáticas . Unidad 1
Materiales a reunir
Materiales de una lección anterior

15 minutos
Preparación requerida
Los estudiantes necesitarán sus gráficas de la Época del Año Favorita de la lección anterior.
El objetivo de esta actividad es que los estudiantes utilicen los datos presentados en gráficos de barras a escala para resolver problemas de un paso de "cuántos más" y "cuántos menos". Los estudiantes utilizan los gráficos de barras a escala que crearon en la lección anterior y que contienen datos sobre la época favorita del año. Responder a preguntas sobre un gráfico con el que están familiarizados les prepara para la siguiente tarea, en la que responderán a preguntas sobre un nuevo gráfico. Esta actividad ofrece una oportunidad para la evaluación formativa de los métodos de suma y resta de los estudiantes. En el grado 2, se espera que los estudiantes sumen y resten con fluidez dentro de 100
• Grupos de 2
• Asegúrese de que los estudiantes tengan sus gráficas de la Época del Año Favorita de una lección anterior.
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "Dedica un minuto a repasar las preguntas que responderás utilizando el gráfico de la Época del Año Favorita de una lección anterior"
• 1 minuto: tiempo para pensar en silencio
• "Trabaja con tu compañero para responder a las preguntas."
• 7-10 minutos: tiempo de trabajo en pareja
• Controla las diferentes estrategias que usan los estudiantes para sumar o restar, en particular las estrategias que usan decenas y unidades.
Usa tu gráfico de la época favorita del año para responder las preguntas. Muestre su pensamiento utilizando expresiones o ecuaciones.
1. ¿Cuántos estudiantes están representados en el gráfico?
2. ¿Cuántos estudiantes eligieron la primavera o el otoño como su estación favorita?
3. ¿Cuántos estudiantes más eligieron el verano que el invierno?
4. ¿Cuántos estudiantes menos eligieron la primavera que el otoño?
1. 99 estudiantes. Respuesta de muestra:
24 + 13 = 37
37 + 40 + 77
77 + 22 = 99
RESPUESTAS POSIBLES
AMPLIACIÓN DEL PENSAMIENTO DE LOS ESTUDIANTES
2. 16 estudiantes más. Respuesta de muestra:
40 - 24
40 - 20 = 20
20 - 4 = 16
3. 35 estudiantes. Respuesta de muestra:
13 + 22 = ?
13 + 2 = 15
15 + 20 = 35
4. 9 estudiantes menos. Respuesta de muestra:
13 + ? = 22
13 + 7 = 20
20 + 2 = 22
7 + 2 = 9
Si los estudiantes encuentran la suma de las cantidades en los problemas de comparación o no encuentran un valor, considere preguntar:
• "¿De qué se trata este problema?"
• "¿Cómo describirías dos categorías en el gráfico usando la frase, 'más que' o 'menos que'?"
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• Pida a los estudiantes que compartan las respuestas a las últimas 2 preguntas.
• "¿En qué se parecen estas preguntas? ¿En qué se diferencian?" (Ambas preguntan sobre la diferencia entre 2 categorías. En la primera pregunta se utiliza "más" y en la segunda "menos").
• Cuando los estudiantes compartan sus respuestas, aproveche para destacar las estrategias de suma y resta en las que los estudiantes utilizan decenas y unidades.
20 minutos
El objetivo de esta actividad es que los estudiantes utilicen los datos presentados en gráficos de barras a escala para resolver problemas de un paso de "cuántos más" y "cuántos menos". El gráfico de la actividad anterior era familiar para los estudiantes, ya que lo habían creado en la lección anterior, pero el gráfico utilizado en esta actividad es nuevo para ellos. Dado que el gráfico tiene una escala de 10, los estudiantes deben estimar valores que no muestren un múltiplo exacto de 10. Como resultado, las respuestas pueden variar ligeramente. Acepte todas las respuestas que se ajusten a estimaciones razonables.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Invite a ambos estudiantes a compartir su respuesta con toda la clase. Mientras un alumno habla, invite al otro a seguirle y a señalar las partes correspondientes del gráfico de barras en la pantalla.
Avances: Hablar, representar, escuchar
• Grupos de 2
INTRODUCCIÓN
ACTIVIDAD
Apoyo para estudiantes con discapacidad
Representación: Interiorizar la comprensión. Comience preguntando: "¿A alguien le recuerda esta situación a algo que hayamos visto, leído o hecho antes?"
Apoya la accesibilidad para: Funcionamiento socioemocional
• "Mira el gráfico de barras a escala y dile a tu compañero una cosa que notes"
• 1 minuto: discusión por parejas
• "Trabaja con tu compañero para usar los datos del gráfico de barras para completar los primeros cuatro problemas"."
• 7-10 minutos: tiempo de trabajo en pareja
• Observa las diferentes estrategias que utilizan los estudiantes para sumar o restar, en particular las estrategias que utilizan decenas y unidades.
• "Ahora, intercambia las preguntas que escribiste para la cuarta pregunta con otro grupo y responde a sus preguntas."
• 2-3 minutos: tiempo de trabajo en pareja
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Se recogieron datos para ver cuántos bichos de cada tipo había en un jardín. Los datos se muestran en este gráfico de barras:
Grado 3 . Matemáticas . Unidad 1

Utiliza el gráfico de barras para responder a las preguntas. Muestra tu pensamiento usando expresiones o ecuaciones.
1. ¿Cuántos bichos había en el jardín?
2. ¿Cuántas hormigas más había en el jardín que arañas?
3. ¿Cuántas mariquitas menos había que hormigas?
4. Trabaja con tu compañero para escribir 2 preguntas que se podrían hacer sobre los bichos del jardín.
5. Intercambia con otro grupo y responde a las preguntas de los demás.

1. 99 errores. Ejemplo de respuesta:
62 + 11 + 19 + 7 = ?
11 + 19 = 30
30 + 62 = 92
92 + 7 = 99
RESPUESTAS POSIBLES
AVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
2. 53 más. Respuesta de muestra: 61 - 8 es 61 - 1 - 7, que es 53
3. 51 menos. Respuesta de muestra: 62 - 11 = 51
4. Respuesta de muestra: ¿Cuántos de los bichos eran arañas o escarabajos?
5. Respuesta de muestra: 26 de los bichos eran arañas o escarabajos. 7 + 19 = 6 + 1 + 19, que es 26
Si los estudiantes encuentran sumas para comparar problemas o no encuentran una solución, considere preguntar:
• "Cuéntame cómo empezaste este problema"
• "¿Cómo podrías usar la información del gráfico para resolver el problema?"
• Haz que los estudiantes compartan las respuestas para los tres primeros problemas. Asegúrese de compartir una variedad de estimaciones razonables para los valores de cada categoría para que los estudiantes sepan que no pasa nada si no conocen el valor exacto con seguridad.
• Haga que los grupos 2-3 compartan una pregunta que hayan escrito y que toda la clase la resuelva. Mientras los estudiantes comparten, aproveche esta oportunidad para destacar las estrategias de suma y resta en las que los estudiantes utilizan decenas y unidades.
10 minutos
Muestre el gráfico de barras de la última actividad de la lección de hoy. "¿Cuáles fueron algunas estrategias que te resultaron útiles hoy al responder preguntas sobre los datos representados en los gráficos de barras?" (Usé el gráfico de barras para obtener los números antes de sumar o restar. Utilicé el gráfico de barras para encontrar las respuestas mirando una de las barras y contando hasta la otra barra del problema).
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Reflexiones:
Se preguntó a un grupo de estudiantes: "¿Cuál es tu deporte favorito?"
Sus respuestas se muestran en este gráfico de barras: Utilice el gráfico para responder a las preguntas.
1. ¿Cuántos estudiantes más eligieron el fútbol que el fútbol americano? Demuestra lo que piensas utilizando expresiones o ecuaciones.
2. ¿Cuántos estudiantes menos eligieron hockey que baloncesto? Muestre su razonamiento utilizando expresiones o ecuaciones.
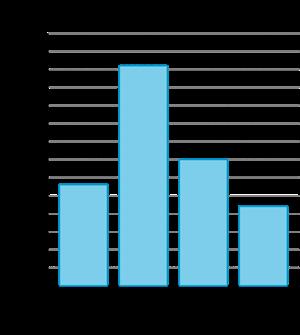
1. 33 estudiantes. Ejemplo de respuesta: 28 + 2 = 30, 30 + 31 = 61, y 2 + 31 = 33
2. 13 estudiantes. Respuesta de muestra: 35 - 22 = 13


IDEA(S) FUNDAMENTAL(ES)
• Representar datos multivariables
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
3.MD.3 Dibuja un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en resolverlos.
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.1
I.B.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo y predecir lo que podría ocurrir
dar sentido a los problemas y perseverar en su resolución razonar con datos.
META(S) DE APRENDIZAJE
• Puedo estimar valores en una gráfica de barras a escala para resolver problemas.
• Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" dentro de 100, basados en los datos presentados en gráficas de barras a escala.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿Quién ha podido hacer matemáticas hoy en clase y cómo lo sabes? Identifica las normas o rutinas que permitieron a esos estudiantes dedicarse a las matemáticas. ¿Cómo puede ajustar estas normas y rutinas para que todos los estudiantes hagan matemáticas mañana?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR6 Tres lecturas (Actividad 1)
Hablar de números (Calentamiento)
Metas de aprendizaje para el estudiante
• Resolvamos problemas usando datos mostrados en gráficas de barras.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes resuelvan problemas de uno y dos pasos de "cuántos más" y "cuántos menos", basados en datos presentados en una gráfica de barras a escala.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
Esta lección introduce Tres Lecturas (MLR 6) para ayudar a los estudiantes a dar sentido y resolver situaciones. En esta lección los estudiantes continúan interpretando gráficos que representan cantidades que no son múltiplos exactos de la escala y requieren que los estudiantes estimen valores. Como resultado, las respuestas pueden variar ligeramente. Acepte todas las respuestas que se ajusten a estimaciones razonables.
Esta lección tiene un Resumen de la sección del estudiante.
Componente de la lección

Estructura Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 Pares 20 min.
Actividad de exploración 2 En parejas 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Descripción breve
Los estudiantes calculan mentalmente las sumas de expresiones de adición repetidas y luego comparten las estrategias que utilizaron.
Los estudiantes analizan un gráfico de barras a escala para resolver un problema de dos pasos sobre "cuántos más"."
Los estudiantes estiman las alturas de las barras en un gráfico de barras a escala para resolver problemas de dos pasos sobre "cuántos más" y "cuántos menos".
Los estudiantes resumen estrategias que pueden usarse para responder preguntas sobre gráficos de barras a escala.
Los estudiantes aplican lo que han aprendido sobre gráficos de barras a escala para responder preguntas sobre "cuántos más" y "cuántos menos".
Abordar:
• Ordenar y mostrar (1-3), Etapa 3: Gráficos a escala
Apoyo:
• Cinco en raya: Adición y sustracción (1-2), Etapa 6: Suma dentro de 100 con Composición
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
REPETIDA 15 minutos
Rutinas didácticas
Conversación sobre números
El propósito de esta Charla sobre números es obtener estrategias y conocimientos de los estudiantes para sumar grupos de 2 y grupos de 5. Estos conocimientos ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten utilizar datos en gráficos de barras a escala para resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos". Los estudiantes utilizan la estructura de las expresiones y el razonamiento repetido cuando emplean métodos basados en el conteo saltado de 2 o 5 o en el conteo de 2 o 5 a partir de un valor previo conocido (MP7, MP8).
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• Mostrar una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste".
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada expresión.
• 2 + 2 + 2 + 2 + 2
• 2 + 2 + 2 + 2 + 2 + 2
• 5 + 5 + 5 + 5 + 5 + 5 + 5
• 5 + 5 + 5 + 5 + 5 + 5 + 5
• 10: Me salté la cuenta 2 cinco veces: 2, 4, 6, 8, 10.
• 12: Es uno más 2 que el primer problema, 10 + 2 = 10.
• 30: Conté por 5.
• 35: Es uno más 5 que el problema anterior a éste.
• "¿Cuál es una estrategia que no habías utilizado antes y que podrías utilizar en el futuro?" (Pensar en un grupo más si ya conozco parte del problema. Omitir el conteo.)
• Considere preguntar:
• "¿Quién puede replantear 'el razonamiento de una manera diferente?"
• "¿Alguien tuvo la misma estrategia pero la explicaría de manera diferente?"
• "¿Alguien resolvió el problema de una manera diferente?"
• "¿Está de acuerdo o en desacuerdo? ¿Por qué?"
ESCOLAR 20 minutos
Rutinas didácticas
MLR6 Tres lecturas

Grado 3 . Matemáticas . Unidad 1
ACTIVIDAD
ENUNCIADO DE LA TAREA DE CARA AL ESTUDIANTE
• Grupos de 2
MLR6 Tres lecturas
• "Mantengan sus libros cerrados."
• Muestre solo el gráfico, sin revelar la pregunta.
• "Vamos a leer este gráfico 3 veces."
• 1ª lectura: "Tómense un momento para leer los datos que muestra este gráfico"
• "¿De qué trata este gráfico?" (Trata de cómo se sienten los estudiantes con respecto al nuevo año.)
• 1 minuto: debate por parejas
• Escuche y aclare cualquier duda sobre el contexto.
• 2ª lectura: "Lee e interpreta el gráfico por segunda vez. ¿Qué cantidades están representadas? ¿Qué se puede contar o medir en esta situación?". (Podemos contar el número de estudiantes en cada categoría.)
• 30 segundos: tiempo para pensar en silencio
• 2 minutos: discusión en parejas
• Registrar las cantidades en una pantalla para que todos las vean.
• Revelar la pregunta.
• 3ª lectura: Leer la pregunta en voz alta.
• "¿Qué estrategias podemos utilizar para resolver este problema?" (Podríamos sumar los 24 más 25 para ver cuántos estudiantes están nerviosos o sienten curiosidad. Podríamos restar cuántos estudiantes están nerviosos o curiosos del número de estudiantes que están entusiasmados.)
• 30 segundos: tiempo para pensar en silencio
• 1-2 minutos: discusión en pareja
• 5-7 minutos: tiempo de trabajo en pareja
• Vigile a los estudiantes que:
• suman 25 + 23 y luego restan 55 - 48
• restan 55 - 23 y luego restan 32 - 25
• restan 55 - 25 y luego restan 30 - 23
Se preguntó a un grupo de estudiantes: "¿Cómo te sientes sobre el nuevo año escolar?" Sus respuestas se muestran en este gráfico de barras: ¿Cuántos estudiantes más están entusiasmados con el nuevo año escolar que nerviosos o curiosos?
RESPUESTAS POSIBLES 7 estudiantes
• Haga que 1-2 estudiantes seleccionados compartan su solución y estrategia.
SÍNTESIS DE LA ACTIVIDAD
Math Nation California - Grado 3
• Muestre los pasos de la rutina de Tres lecturas y manténgalos expuestos para la siguiente actividad.
• "¿Cómo le ayudó leer el problema tres veces a darle sentido?" (Me sentía más cómodo con el problema cada vez que lo leía. Tenía más sentido cada vez que leía el problema. Noté detalles diferentes cada vez que lo leí).
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
El propósito de esta actividad es que los estudiantes practiquen por su cuenta la rutina de lenguaje matemático Three Reads y utilicen los datos presentados en un gráfico de barras a escala para resolver una situación de "cuántos más" de dos pasos. La rutina de las Tres Lecturas hace que los estudiantes lean un problema tres veces con diferentes propósitos para apoyarlos a darle sentido al problema y perseverar en su resolución (MP1).
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Algunos estudiantes pueden beneficiarse de la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.
Avances: Escuchar, Hablar

Apoyo para estudiantes con discapacidad
Engagement: Proporcionar acceso captando el interés. Ofrezca opciones. Invita a los estudiantes a decidir por qué problema empezar o a decidir el orden para completar la tarea.
Apoya la accesibilidad para: Funcionamiento socioemocional
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE LA TAREA PARA EL ESTUDIANTE
• Grupos de 2
• "¿Qué tipos de plantas ves en tu camino a casa desde la escuela?" (Árboles. Arbustos. Flores. Enredaderas.)
• Comparte las respuestas.
• Muestra el gráfico.
• "Trabaja independientemente para usar el gráfico para resolver los problemas. Puedes usar la rutina de las Tres Lecturas si te resulta útil"
• 7-10 minutos: tiempo de trabajo independiente
• Monitorear a los estudiantes que resuelven los problemas de un paso:
• usando las barras del gráfico para contar hacia arriba o hacia atrás de un número a otro.
• usando ecuaciones para mostrar la suma o resta por lugar.
• Controle a los estudiantes que resuelven problemas de dos pasos:
• sumando dos números y luego restando la suma de otro número.
• restando un número y luego restando nuevamente la diferencia.
El gráfico de barras muestra cuántos árboles de cada tipo vio Clara en el camino a casa. Utiliza el gráfico para responder a las preguntas. Muestra tu razonamiento usando expresiones o ecuaciones.
1. ¿Cuántos pinos más vio Clara que abetos?
2. ¿Cuántos pinos más vio Clara que robles o arces?
3. ¿Cuántos robles menos vio Clara que pinos?
4. ¿Cuántos arces o robles menos vio Clara que abetos?
Learning Inc. - Todos los derechos reservados
RESPUESTAS POSIBLES

AVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
1. 24 más. Ejemplos de respuestas:
• 82 - 20 = 62
62 - 4 = 58
• 58 + 2
60 + 20
80 + 2
2 + 20 + 2
3. 53 menos. Respuestas de muestra:
• 82 - 20 = 62
62 - 2 = 60
60 - 7 = 53
• 29 + 1
30 + 50
80 + 2
1 + 50 + 2
Grado 3 . Matemáticas . Unidad 1
2. 38 más. Respuestas de muestra: 20 + 10 = 30
• 9 + 5 = 14
30 + 14 = 44
82 - 40 = 42
42 - 4 = 38
• 82 - (29 + 15)
4. 14 menos. Ejemplo de respuesta:
• 20 + 10 = 30
9 + 5 = 14
30 + 14 = 44
58 - 44 = 14
• 58 - (15 + 29)
Si los estudiantes encuentran la suma de todas las categorías o no encuentran una solución a los problemas, considere preguntar:
• "Cuéntame cómo empezaste este problema"."
• "¿Cómo podrías usar la información del gráfico para resolver el problema?"
• Haz que 1-2 estudiantes compartan el método, incluidas las expresiones o ecuaciones que utilizaron para resolver el primer problema.
• Haz que 2-3 estudiantes compartan las expresiones o ecuaciones que utilizaron para resolver el último problema.
• "¿En qué se parecen estos métodos? ¿En qué se diferencian? (Algunas personas sumaron los arces y los robles y luego lo restaron del número de abetos. Algunas personas restaron el número de arces de los abetos y luego restaron el número de robles. De ambas formas se obtuvo el mismo número de árboles).
10 minutos
Muestre las ecuaciones del primer problema de la última actividad.
"¿Cómo usaste lo que sabes sobre decenas y unidades para resolver los problemas?" (Algunas preguntas vi que solo podía contar por 10 en la gráfica porque la escala era 10. No restamos todo a la vez. Restábamos las decenas y luego las unidades. Pensábamos en cómo llegar a la siguiente decena para que sumar las decenas fuera más fácil).
"En el futuro, ¿cómo podrías utilizar la estrategia de las tres lecturas por tu cuenta, sin un compañero?" (Podríamos utilizarla en cualquier momento pensando de qué trata el problema. Podemos leer el problema para buscar qué se puede medir o contar en el problema. Podemos leerlo para pensar en las estrategias que podríamos utilizar para resolver el problema.)
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
minutos
Se preguntó a un grupo de estudiantes: "¿Cuál es tu hora favorita para leer?". Sus respuestas se muestran en este gráfico de barras: Utilice el gráfico para responder a las preguntas.

ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
1. ¿A cuántos estudiantes menos les gusta leer por la mañana que por la tarde? Demuestra tu pensamiento utilizando expresiones o ecuaciones.
2. ¿A cuántos estudiantes más les gusta leer por la noche que por la mañana o a la hora de comer ? Muestra tu razonamiento usando expresiones o ecuaciones.
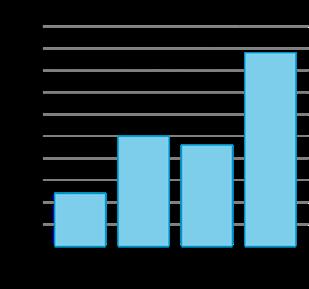
1. 12. Ejemplos de respuestas: 23 - 11 = 12
2. 7. Respuestas de muestra:
• 44 - (12 + 25)
• 44 - 10 - 20 = 14
• 14 - 2 - 5 = 7
Resumen de la sección del estudiante
En esta sección, creamos gráficos de imágenes a escala y gráficos de barras a escala.
Hicimos y respondimos preguntas que podían ser contestadas por los gráficos.
• ¿Cuántas margaritas más se vieron que violetas?
• ¿Cuántos estudiantes menos caminan a casa que en bicicleta?
• ¿Cuántos estudiantes más van en bicicleta a casa que caminan o van en auto?


IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.OA.1 Interpretar productos de números enteros.
Construir
2.NBT.5
Enfoque SMPs
MP4 Representar con matemáticas.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1 I.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo e inciden en el futuro
buscan y hacen uso de la estructura y representan con matemáticas explorando cantidades cambiantes.
• Puedo describir la relación entre los grupos iguales y la multiplicación.
• Puedo Representar situaciones que involucran grupos iguales.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Comprender la multiplicación como grupos iguales.
• Representar una situación que involucre grupos iguales de manera que tenga sentido para los estudiantes.
¿Cómo ha preparado el trabajo de los estudiantes con los gráficos a escala y los gráficos de barras la introducción de la multiplicación en la lección de hoy?
Rutinas didácticas
Conversación sobre números (calentamiento)
Materiales para reunir
Cubos o fichas para conectar: Actividad 1, Actividad 2
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 1:
Cada alumno necesita 20 cubos o fichas de conexión.
Actividad 2:
Cada alumno necesita 20 cubos o fichas de conexión.
Grado 3 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Trabajemos con grupos iguales de cosas.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes utilicen gráficos de imágenes a escala como una introducción a la multiplicación como grupos iguales.
Los gráficos de imágenes a escala proporcionan un contexto de agrupación igual que naturalmente provoca multiplicación. Las expresiones de multiplicación no se introducen en esta lección para que los estudiantes pasen más tiempo con representaciones concretas de la multiplicación antes de ser introducidos a la representación más abstracta. Las siguientes lecciones se centran en el significado y las representaciones de la multiplicación, no en el producto. Aunque es posible que los estudiantes quieran ir directamente a encontrar el producto, es importante centrarse en el significado de la multiplicación como grupos iguales y en las formas en que puede representarse en las discusiones.
A lo largo de esta sección, ponga cubos o fichas de conexión a disposición de los estudiantes que los necesiten.
Componente de la lección Estructura Tiempo Descripción breve
Calentamiento Independiente 10 min.
Actividad de Exploración 1 Pares 15 min.
Actividad Exploratoria 2 Pares 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes calculan mentalmente las sumas de expresiones de adición y luego comparten las estrategias que utilizaron.
Los estudiantes hacen conexiones entre gráficos de imágenes a escala y escenarios que involucran grupos iguales.
Los estudiantes representan enunciados verbales que involucran grupos iguales en contexto.
Los estudiantes establecen conexiones entre situaciones que implican grupos iguales y la multiplicación.
Los estudiantes representan un escenario del mundo real que implica grupos iguales.
Apoyo:
• Capturar cuadrados (1-3), Etapa 4: Restar dentro de 20
• Cinco en raya: Suma y resta (1-2), Etapa 6. Sumar dentro de 100 Suma dentro de 100 con Composición

Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Charla sobre números
El objetivo de esta Charla sobre números es obtener estrategias y conocimientos de los estudiantes para sumar dentro de 100 También brinda una oportunidad para observar las estrategias de los estudiantes a medida que trabajan para adquirir fluidez en la suma dentro de 1.000
Cuando los estudiantes usan estrategias basadas en el valor posicional para sumar, buscan y hacen uso de la estructura (MP7).
• Muestre una expresión.
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste".
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra el valor de cada expresión mentalmente.
• 40 + 35
• 45 + 35
• 45 + 36
• 34 + 58
• 75: Hay 7 decenas y 5 unidades, que es 75
• 80: Hay 7 decenas y 5 más 5 hacen otra decena, que sería 80
• 81: Es como el anterior, pero hay 1 más, lo que haría 81.
• 92: Hay 8 decenas y 12 unidades. Si descompongo los 12 en una decena y 2 unos, entonces tengo 9 decenas y 2 unos, lo que es 92.
• "¿Cómo compusiste nuevas decenas al resolver estos problemas?". (En el segundo problema compuse una decena a partir de los 2 cincos. En el tercer problema compuse una nueva decena a partir de los 5 y los 6 y aún me sobró 1.)
• Considera preguntar:
• "¿Quién puede replantear el razonamiento de de otra manera?"
• "¿Alguien tenía la misma estrategia pero la explicaría de otra manera?"
• "¿Alguien planteó el problema de otra manera?"
• "¿Alguien quiere añadir algo a la estrategia de ?"
Grado 3 . Matemáticas . Unidad 1
Materiales a reunir
Cubos o fichas de conexión

15 minutos
Preparación necesaria
Cada estudiante necesita 20 cubos o fichas de conexión.
El objetivo de esta actividad es que los estudiantes relacionen gráficos de imágenes a escala con situaciones que impliquen grupos iguales. La escala del gráfico se utilizará para ayudar a los estudiantes a pensar en una categoría del gráfico como una situación que involucra grupos iguales.
El inicio de la actividad es una oportunidad para que los estudiantes compartan sus experiencias y hagan preguntas sobre el gráfico para asegurar que cada estudiante tenga acceso al contexto. Si resulta útil, muestre algunas imágenes de diferentes tipos de señales que los estudiantes puedan ver en su comunidad.
Apoyo para estudiantes con discapacidad
Representación: Interiorizar la comprensión. Síntesis: Invite a los estudiantes a identificar qué detalles fueron importantes o más útiles para resolver el problema. Muestre el marco de la frase: "La próxima vez que lea un gráfico con imágenes a escala, prestaré atención a. . . "
Apoya la accesibilidad para: Procesamiento visual-espacial
• Grupos de 2
• Dar a los estudiantes acceso a cubos de conexión o fichas.
ACTIVIDAD
Math Nation California - Grado 3
• "Vamos a ver un gráfico a escala sobre señales que Elena vio de camino a casa. ¿Qué tipos de señales ves en la comunidad?". (señales de stop, señales de límite de velocidad, señales de tráfico, vallas publicitarias)
• 30 segundos: tiempo para pensar en silencio
• 1 minuto: discusión por parejas
• Compartir las respuestas.
• Mostrar el gráfico.
• "Trabaja de forma independiente para representar el número de señales de límite de velocidad que Elena vio de camino a casa."
• 1 minuto: tiempo de trabajo independiente.
• Vigila a los estudiantes que creen dibujos de grupos iguales similares al mostrado en el último problema para mostrarlos durante la síntesis.
• 1 minuto: discusión por parejas
• "Trabaja con tu pareja para completar el siguiente problema."
• 1 minuto: tiempo para pensar en silencio
• 2 minutos: discusión por parejas
• "¿Cómo supiste qué enunciado describía las señales de límite de velocidad que Elena vio de camino a casa?" (Había 3 dibujos en el gráfico. Cada dibujo representa 2 señales.)
• Comparte las respuestas.
• "Tómate unos minutos para completar el último problema por tu cuenta."
• 3 minutos: tiempo de trabajo independiente
• "Comparte tus respuestas con tu compañero."
• 1 minuto: discusión en pareja
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Elena recopiló datos sobre el tipo de señales que vio de camino a casa. Los datos se muestran en este gráfico de imágenes:
1. Representa el número de señales de límite de velocidad que Elena vio de camino a casa.
2. ¿Qué afirmación describe el número de señales de límite de velocidad que vio Elena? Explica tu razonamiento.
A. Hay 3 dibujos y cada dibujo representa 1 señal de límite de velocidad .
B. Hay 3 dibujos y cada dibujo representa 2 señales de límite de velocidad.
C. Hay 2 dibujos y cada dibujo representa 2 señales de límite de velocidad.
3. ¿Cómo podría representar este dibujo las señales de tráfico que Elena vio de camino a casa?
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
1. Respuesta de muestra:
2. B. Respuesta de muestra: B describe 6 señales y ese es el número de señales de límite de velocidad que Elena vio de camino a casa. Además, había 3 dibujos en el gráfico y cada dibujo representa 2 señales.
3. Respuestas de muestra: Hay 5 imágenes en el gráfico y hay 5 grupos. Cada imagen representa 2 signos y hay 2 puntos en cada grupo. Hay 10 puntos en los grupos y 10 signos en el gráfico.
• Muestre un dibujo de grupos iguales creado por el alumno que represente las señales de límite de velocidad que Elena vio de camino a casa y el dibujo del último problema.
• "Estos dibujos muestran grupos iguales. ¿Cómo te ayudaron estos dibujos a representar los datos en el gráfico de imágenes?" (La clave nos decía que cada imagen representaba 2 señales y los dibujos nos ayudaban a ver las 2 señales. Cada grupo mostró 2 signos.)
20 minutos
Materiales para reunir
Cubos conectores o fichas
Preparación requerida
Cada estudiante necesita 20 cubos conectores o fichas.
El propósito de esta actividad es que los estudiantes representen situaciones que involucran grupos iguales de una manera que tenga sentido para ellos. Disponga de cubos de conexión para que los estudiantes los utilicen para representar la situación, si lo desean. Los estudiantes también pueden hacer un dibujo. Un compañero podría utilizar los objetos mientras otro dibuja y luego cambiar para cada problema. La discusión se centra en las cantidades importantes de cada situación y en cómo los estudiantes utilizaron su representación para modelizar cada cantidad (MP4).
En el inicio de la actividad, puede ser útil pedir a los estudiantes que cuenten a su compañero una historia rápida o que hagan cualquier pregunta sobre el enfoque de cada uno de los tres contextos para asegurarse de que cada alumno tiene acceso. También puede ser útil mostrar imágenes para que los estudiantes puedan consultarlas.
Grado 3 . Matemáticas . Unidad 1

Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Invite a ambos compañeros a compartir su respuesta con toda la clase. Mientras un alumno habla, invite al otro a seguirle y a señalar dónde están los números en sus representaciones.
Avances: Representar, Escuchar
• Grupos de 2
• Da a los estudiantes acceso a cubos o fichas de conexión.
• "¿Cuáles son algunos lugares en los que ves grupos de 2 en la comunidad? Grupos de 5? Grupos de 10?" (Zapatos. Calcetines. Alas. Las manos tienen 5 dedos. Las flores pueden tener 5 pétalos. Los rotuladores vienen en paquetes de 10. Diez personas en un autobús.)
• 30 segundos: tiempo para pensar en silencio
• 1 minuto: discusión por parejas
• Compartir y anotar las respuestas.
INTRODUCCIÓN
ACTIVIDAD
FRENTE AL ALUMNO ENUNCIADO DE LA TAREA
• Elegir un ejemplo generado por los estudiantes con números pequeños o mostrar esta situación: "Hay 3 flores. Cada flor tiene 5 pétalos."
• "¿Cómo podrías representar esta situación?"
• 30 segundos: tiempo de reflexión en silencio
• 1-2 minutos: tiempo de trabajo en pareja
• Compartir y registrar las respuestas. Concéntrate en cómo la representación se conecta con el problema.
• Considera preguntar:
• "¿Cómo representaste las 3 flores?"
• "¿Cómo representaste los 5 pétalos en cada flor?"
• "¿Alguien representó esto de manera diferente?"
• "Ahora vas a representar algunas situaciones más que involucren grupos iguales con tu compañero."
• 5-7 minutos: tiempo de trabajo en pareja
• Si algunos estudiantes terminan antes que otros, anímelos a escribir su propia situación e intercambiarla con su compañero.
Represente cada situación.
1. Hay 4 personas que llevan zapatos. Cada persona lleva 2 zapatos.
2. Hay 2 cajas de rotuladores. Cada caja tiene 10 marcadores.
3. Hay 3 equipos de baloncesto. Cada equipo tiene 5 jugadores.
Ejemplos de respuestas:
1.
RESPUESTAS POSIBLES
Math Nation California - Grado 3
2.
3.
• 4 grupos de 2 cubos conectores
• Un dibujo de 4 grupos con 2 puntos en cada grupo
• 2 grupos de 10 fichas
• Un dibujo de 2 grupos con 10 puntos en cada grupo
• 3 grupos de 5 cubos de conexión
• Un dibujo de 3 grupos con 5 fichas en cada grupo
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• Pida a los estudiantes 2-3 que compartan su trabajo para cada problema. Asegúrese de compartir una variedad de representaciones diferentes.
• En cada uno, pregunte cómo se representan los números en la situación en su trabajo.
• "¿Cómo te ayudan las representaciones a imaginar la situación?". (Puedo simular que los objetos son las cosas del cuento, como los zapatos. El dibujo es como una imagen de lo que ocurre en la historia.)
Muestre una representación de grupos iguales de la lección.
10 minutos
"Las situaciones que vimos hoy fueron todas multiplicaciones. La multiplicación es la forma en que representamos el número total de objetos cuando tenemos un cierto número de grupos iguales. Por ejemplo, en este dibujo, diríamos que tenemos 5 grupos de 2."
"Describe una situación con grupos iguales que podrías representar como multiplicación". (Paquetes de lápices, cubos o cestas con el mismo número de cosas en cada uno, pares de zapatos, filas de asientos en el autobús).
5 minutos
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Jada tiene 3 bolsas. Cada bolsa tiene 5 pulseras. Representar la situación.
Ejemplos de respuestas:
• Los estudiantes hacen 3 grupos de 5 fichas o 3 grupos de 5 cubos de conexión.
• Los estudiantes crean un dibujo de 3 grupos con 5 objetos en cada uno.
RESPUESTAS POSIBLES

Reflexiones:


IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.OA.1 Interpretar productos de números enteros.
Construir
2.NBT.5
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Prestar atención a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de CA
I.A.3 I.B.5 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo y repercuten en el futuro razonan abstracta y cuantitativamente explorando cantidades cambiantes.
• Puedo utilizar un diagrama de cinta para representar la multiplicación.
• Puedo dibujar diagramas de cinta para representar problemas.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Interpretar una situación que implique grupos iguales y representarla con un diagrama.
• Dar sentido a los diagramas de cinta que representan la multiplicación.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿De qué manera la conexión de diferentes representaciones de la multiplicación durante la clasificación de las tarjetas ayudó a los estudiantes a desarrollar su comprensión de la multiplicación?
Rutinas didácticas
Card Sort (Actividad 2)
Notice and Wonder (Warm-up)
Materiales para copiar
Card Sort Equal Groups (grupos de 2): Actividad 2
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 2:
Crea un juego de tarjetas a partir del patrón de líneas negras para cada grupo de 2
Grado 3 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Representemos grupos iguales.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes conecten situaciones que involucran grupos iguales con diagramas de cinta.
Esta lección introduce los diagramas de cinta como una forma de representar grupos iguales y la multiplicación, basándose en el trabajo de los estudiantes con gráficos de imágenes a escala y dibujos discretos de grupos iguales. Los estudiantes profundizan su comprensión de la multiplicación a medida que relacionan los diagramas de cinta con situaciones que involucran grupos iguales. A continuación, se les presentan las expresiones de multiplicación como forma de representar las cantidades y situaciones encontradas en la lección. Esto ocurre al final para permitir a los estudiantes trabajar con otras representaciones de la multiplicación antes de aprender sobre los símbolos abstractos que representan la multiplicación.
Componente de la lección Estructura Tiempo

Descripción breve
Calentamiento Pares 10 min. Los estudiantes hacen observaciones sobre grupos de 2.
Actividad de exploración 1 Parejas 15 min.
Actividad de exploración 2 Pares 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes exploran los diagramas de cinta comparándolos con un gráfico ilustrado con una escala de 2 y luego dibujan una representación de una categoría diferente en el gráfico ilustrado.
Los estudiantes relacionan situaciones que implican grupos iguales con dibujos y diagramas de cinta. Luego, crean dibujos o diagramas para representar situaciones que involucran grupos iguales.
Los estudiantes discuten cómo los diagramas de cinta representan la multiplicación y cómo las expresiones de multiplicación pueden escribirse para representar diagramas de cinta.
Los estudiantes analizan un diagrama de cinta para determinar si representa un escenario dado.
Apoyo:
• Capturar cuadrados (1-3), Etapa 4: Restar dentro de 20
• Cinco en fila: Suma y resta (1-2), Etapa 7: Sumar dentro de 1.000 sin componer
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Notar y preguntarse
El objetivo de este calentamiento es suscitar diferentes estrategias para contar objetos dispuestos en grupos de 2, que serán útiles cuando los estudiantes multipliquen por 2 en una actividad posterior. Aunque los estudiantes pueden notar y preguntarse muchas cosas sobre estas imágenes, las formas flexibles de ver los grupos y las estrategias para encontrar el número total de objetos son los puntos de discusión importantes.
Cuando los estudiantes ven que los calcetines están agrupados por 2 y usan eso para encontrar el total, están buscando y haciendo uso de la estructura (MP7).
• Grupos de 2
INTRODUCCIÓNR

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Mostrar la imagen.
• "¿Qué notas? ¿Qué te preguntas?"
• 1 minuto: tiempo para pensar en silencio
• "Discute tu pensamiento con tu compañero"
• 1 minuto: discusión en pareja
• Comparte y registra las respuestas.
¿Qué notas? ¿Qué te preguntas?
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Los estudiantes pueden notar:
• Los calcetines están en pares.
• Hay 12 calcetines.
• Podrías contar por 2 para encontrar el número total de calcetines.
Los estudiantes pueden preguntarse:
• ¿Cuántos calcetines hay?
• ¿Cuántos pares de calcetines hay?
• ¿Por qué hay 6 pares de calcetines?
• "¿Cómo se relaciona este problema con lo que sabemos sobre la multiplicación?" (Hay grupos iguales de calcetines, podemos decir que hay 6 grupos de 2.)
Grado 3 . Matemáticas . Unidad 1
minutos
El propósito de esta actividad es que los estudiantes se basen en el trabajo que han realizado con los gráficos de imagen a escala para utilizar el diagrama de cinta como una nueva representación de la multiplicación. La escala del gráfico de imagen se utilizará para ayudar a los estudiantes a pensar en una categoría del gráfico como una situación en la que intervienen grupos iguales.
Para añadir movimiento a esta actividad, los estudiantes podrían encontrar a alguien de la clase que representara una categoría diferente a la suya o que representara la misma categoría de forma diferente. Cuando encuentren a una persona, pueden describir en qué se parecen y en qué se diferencian sus representaciones.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Cuando los estudiantes comparen el diagrama y el gráfico de imagen a escala, muestre marcos de oraciones para apoyar la discusión de toda la clase: " y son iguales porque...", y " y son diferentes porque..."
Avances: Hablar, representar

INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 2
• Muestra el gráfico y el diagrama de cinta.
• "¿Qué notas? ¿Qué te preguntas?" (La clave dice que cada cuadrado representa 2 signos. El diagrama muestra 3 grupos de 2. Me pregunto si representan lo mismo.)
• 1 minuto: tiempo para pensar en silencio
• 1 minuto: tiempo para discutir en pareja
• "¿Cómo muestra el diagrama las señales de límite de velocidad que Elena vio de camino a casa?"
• Comparte las respuestas.
• "Ahora representa independientemente los datos de otra categoría en el gráfico con tu propio dibujo o diagrama."
• 1-2 minutos: tiempo de trabajo independiente
• "Comparte con tu compañero cómo representaste los datos en tu dibujo o diagrama."
• 2-3 minutos: discusión por parejas
• Supervise a los estudiantes que crean un diagrama de cinta para representar una de las otras categorías para usar durante la síntesis.
1. ¿Cómo muestra el diagrama las señales de límite de velocidad que Elena vio en el camino a casa?
2. Representa los datos de otra categoría en el gráfico con tu propio dibujo o diagrama.
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

RESPUESTAS
POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
1. Ejemplo de respuesta: Hay 3 imágenes (cuadrados) en el gráfico y 3 secciones del diagrama. El gráfico nos dice que cada imagen (cuadrado) representa 2 signos. En el diagrama, cada sección está etiquetada con un 2.
2. Ejemplos de respuestas para las señales de tráfico:

• Pida a los estudiantes que compartan las diferentes formas en que representaron una categoría en el gráfico.
• Muestre un diagrama de cinta creado por los estudiantes o haga un bosquejo rápido de uno para representar los carteles de las calles que Elena vio camino a casa.
• "¿Qué categoría representa este diagrama de cinta? ¿Cómo lo sabes?"
• "¿En qué se parece el diagrama al gráfico de imágenes a escala?" (Cada imagen y cada parte del diagrama de cinta representa 2 señales.)
• "¿En qué se diferencia el diagrama del gráfico de imágenes a escala?" (En el gráfico, tienes que leer la clave para saber que cada imagen muestra dos señales. En el diagrama, cada parte está etiquetada con un 2.)
Rutinas didácticas
Clasificación de tarjetas
20 minutos
Materiales para copiar
Clasificación de tarjetas Grupos iguales (grupos de 2)
Preparación necesaria
Cree un conjunto de tarjetas a partir del patrón de líneas negras para cada grupo de 2
El propósito de esta actividad es que los estudiantes conecten situaciones que involucran grupos iguales con dibujos y diagramas de cinta. Una tarea de clasificación ofrece a los estudiantes la oportunidad de analizar detenidamente representaciones, enunciados y estructuras y de establecer conexiones (MP2, MP7). Los estudiantes explican por qué dos tarjetas coinciden y tienen la oportunidad de criticar y cuestionar el razonamiento de sus compañeros (MP3). Al explicar, los estudiantes tienen la oportunidad de revisar su lenguaje para que sus explicaciones sean más precisas y claras (MP6). Después de clasificar y describir su clasificación, los estudiantes observan que todas las representaciones refuerzan el significado de la multiplicación como una forma de expresar grupos iguales.
Los estudiantes dedicarán toda la próxima lección a trabajar con expresiones. Guarde las tarjetas de grupos iguales para la próxima lección.
Engagement: Desarrollar el esfuerzo y la persistencia. Divida esta tarea en partes más manejables. Dé a los estudiantes un subconjunto de tarjetas para empezar y presente las tarjetas restantes una vez que los estudiantes hayan completado su serie inicial de emparejamientos.
Apoya la accesibilidad para: Atención, Organización
• Grupos de 2
• Entrega a cada grupo de 2 estudiantes un juego de tarjetas.
INTRODUCCIÓN
• "Este juego de tarjetas incluye dibujos, situaciones y diagramas. Tómense un poco de tiempo para pensar cómo podrían coincidir algunas de las tarjetas."
• 1 minuto: tiempo para pensar en silencio
INTRODUCCIÓN CONTINUACIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Math Nation California - Grado 3
Grado 3 . Matemáticas . Unidad 1
• "Busca las cartas que coincidan. Trabaja con tu compañero para justificar tus elecciones. Prepárate para explicar tu razonamiento."
• 5 minutos: tiempo de trabajo en pareja
• Pida a los estudiantes que compartan las parejas que han encontrado y cómo saben que esas tarjetas van juntas.
• Preste atención al lenguaje que utilizan los estudiantes para describir sus parejas. Si los estudiantes solo hacen referencia a los números que coinciden, considere preguntar:
• "¿Qué quieres decir cuando dices ?"
• "¿Cómo podrías usar las palabras 'grupos iguales' para explicarlo?"
• "Ahora vas a crear un dibujo o diagrama para representar dos situaciones diferentes."
• 3-5 minutos: tiempo de trabajo independiente
• Supervise a los estudiantes que dibujan grupos iguales y a los estudiantes que dibujan un diagrama de cinta.
1. Su maestro le dará un conjunto de tarjetas que muestran dibujos, situaciones y diagramas. Busca las tarjetas que correspondan. Prepárate para explicar tu razonamiento.
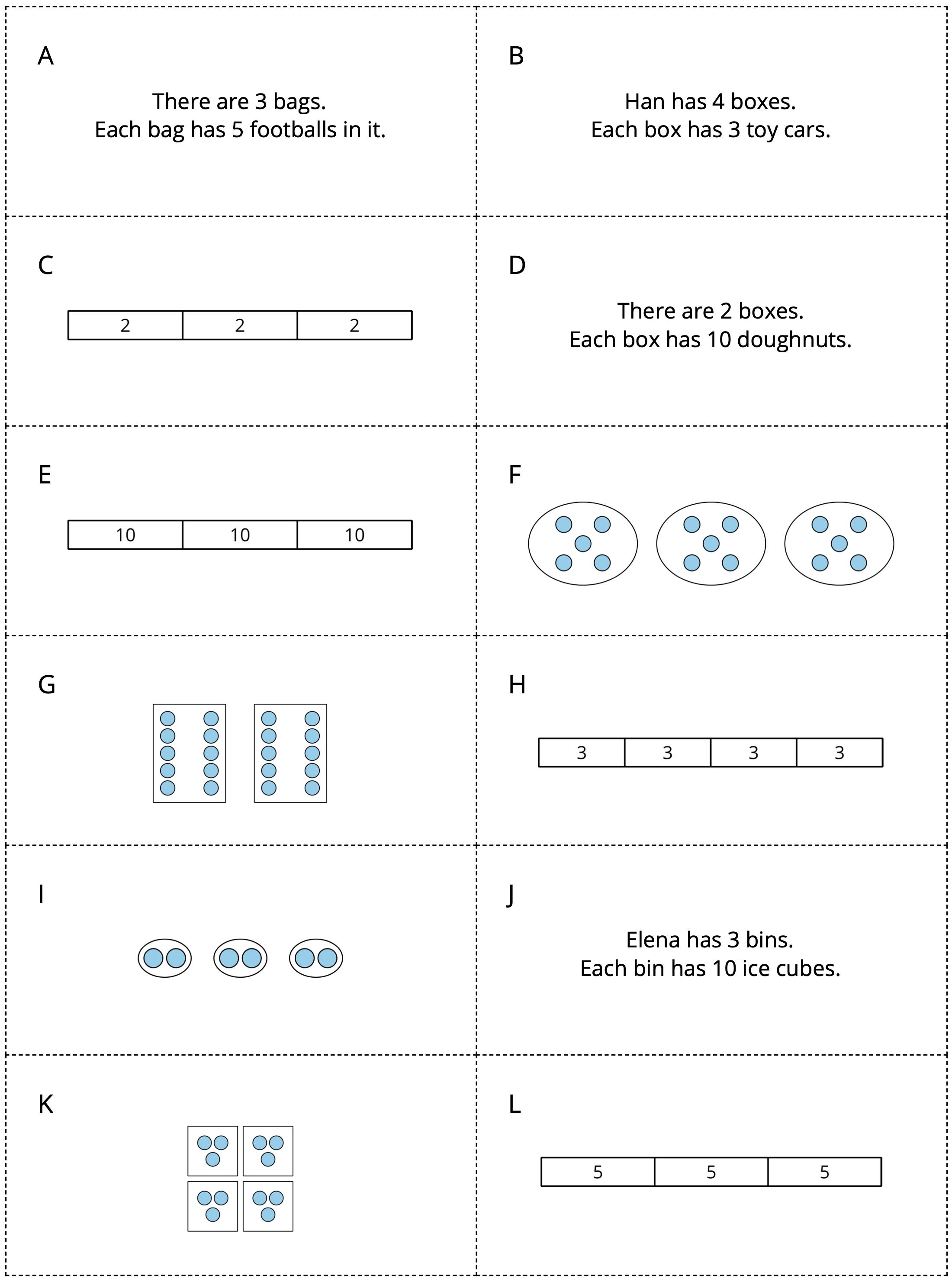
2. Crea un dibujo o diagrama para cada situación.
A. Hay 4 bolsas. Cada bolsa tiene 2 fresas.
B. Hay 4 manos. Cada mano tiene 5 dedos.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES
1.
AUMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
• A, F y L
• B, H y K
• C e I
• D y G
• E y J
Ejemplo de respuesta: E y J van juntos porque los recipientes son como las secciones del diagrama y los números son como los cubitos de hielo.
2. A. Ejemplo de respuesta: B. Ejemplo de respuesta:
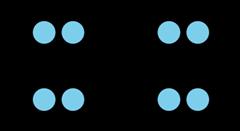
Si los estudiantes crean representaciones que no coinciden con el número de grupos o el tamaño de los grupos en las situaciones, considere preguntar:
• "¿Cómo representaste la situación?"
• "¿Cómo podrías mostrar los grupos en la situación? ¿Cómo podrías mostrar los objetos de cada grupo?"
• Para cada situación de los últimos 2 problemas, muestre 2-3 representaciones de los estudiantes, al menos un dibujo de grupos iguales y un diagrama de cinta. Déjelas expuestas.
• "¿Qué tienen en común todas estas representaciones?" (Todas muestran grupos iguales. Todas tienen grupos. Cada grupo tiene la misma cantidad.)
• "¿Dónde están las 4 bolsas y 2 fresas en cada dibujo o diagrama?"
• "¿Dónde están las 4 manos y 5 dedos en cada dibujo o diagrama?"
10 minutos
Muestra el diagrama de cinta.
"La lección de hoy trataba sobre la multiplicación. ¿Cómo puede un diagrama mostrar la multiplicación?" (Un diagrama puede mostrar la multiplicación porque puedes dibujar el número de grupos y escribir cuántos hay en cada grupo. Puedes ver que hay 4 partes en este diagrama, así que hay 4 grupos y el 5 te dice que hay 5 cosas en cada grupo.
Muestra:
4 grupos y 5 en cada grupo 4 × 5
"Puedes recordar que una expresión tiene al menos 2 números y al menos una operación matemática. Una expresión de multiplicación es cómo representamos el número de grupos y el número en cada grupo en una situación. Por ejemplo, la expresión de multiplicación 4 × 5 representaría este diagrama porque tenemos 4 grupos y 5 en cada grupo." Señala los 4 y 5 en el diagrama y la expresión mientras explicas.
"El símbolo en medio de la expresión es el símbolo de multiplicación. 4 × 5 puede leerse como '4 grupos de 5.'"
Grado 3 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE

5 minutos
La tienda tiene 4 cajas. Cada caja tiene 10 camisas. ¿Coincide este diagrama con la situación? Explica tu razonamiento.

RESPUESTAS POSIBLES Sí, porque las 4 partes representan las 4 cajas y las 10 de cada parte representan las 10 camisas de cada caja.
Reflexiones:
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Alineación de estándares y principios de Abordar
3.OA.1 Interpretar productos de números enteros.
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares CA ELD
I.A.4
I.C.11
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
dar sentido al mundo e incidir en el futuro
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
razonar abstracta y cuantitativamente y buscar y hacer uso de la estructura explorar cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo escribir una expresión de multiplicación para representar grupos iguales.
• Puedo crear representaciones de expresiones de multiplicación.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Escribo expresiones de multiplicación para representar situaciones que involucran grupos iguales y diagramas.
PREGUNTA DE REFLEXIÓN DEL MAESTRO
¿Qué dijo, hizo o preguntó durante la síntesis de la lección que ayudó a los estudiantes a tener claro el aprendizaje del día? ¿De qué manera te ayudó a sintetizar el aprendizaje la comprensión de la lección cool-down antes de comenzar a enseñar hoy?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Recuento coral (calentamiento)
Materiales para reunir
Materiales de una lección anterior:
Actividad 1
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 1:
Cada grupo de 2 necesita 1 tarjeta de la clasificación de tarjetas de la lección anterior.
Coloca estas expresiones por la clase:
• 3 × 5
• 4 × 3
• 3 × 2
• 2 × 10
• 3 × 10
Grado 3 . Matemáticas . Unidad 1
• Escribamos expresiones de multiplicación.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes usen expresiones de multiplicación para representar grupos iguales.
En lecciones anteriores, los estudiantes representaron situaciones que involucraban grupos iguales con dibujos y diagramas de cinta. También se les mostró cómo representar grupos iguales como una expresión. En esta lección, los estudiantes conectan la estructura de los dibujos, los diagramas de cinta y las situaciones de multiplicación con la estructura de las expresiones de multiplicación (MP7). Los estudiantes crean diagramas y dibujos para representar expresiones de multiplicación y, en última instancia, escriben sus propias expresiones para representar dibujos, diagramas y situaciones (MP2).
Al generar expresiones de multiplicación, considere utilizar la convención del número de grupos como primer factor y el tamaño de los grupos como segundo factor. Sin embargo, no es necesario que los estudiantes escriban los factores en este orden. Es importante que los estudiantes relacionen sus expresiones con las situaciones y representaciones correspondientes. Deben ser capaces de explicar correctamente lo que representa cada factor en sus expresiones. Si los estudiantes hacen preguntas sobre la idea de conmutatividad, considere la posibilidad de registrar las preguntas públicamente para futuras investigaciones.
Para dar tiempo a que los estudiantes se centren en el significado de la multiplicación, no se espera que los estudiantes encuentren el producto de cada expresión en esta lección. En lecciones posteriores, los estudiantes trabajarán estrategias para hallar el producto. Si los estudiantes mencionan el producto en la lección de hoy, está bien anotarlo, pero trate de mantener el enfoque en las conexiones entre la expresión y los diagramas.
Componente de la lección

Estructura Tiempo
Descripción breve
Calentamiento Todo el grupo 10 min. Los estudiantes cuentan de 5 en 5 y de 2 en 2 y luego identifican patrones que ayudan a contar.
Actividad de exploración 1
Parejas 10 min. Los estudiantes relacionan dibujos, diagramas de cinta y situaciones con expresiones de multiplicación.
Actividad de exploración 2 Parejas 15 min. Los estudiantes crean y justifican dibujos o diagramas que representan expresiones de multiplicación.
Actividad de exploración 3 Parejas 10 min.
Síntesis Todo el grupo 10 min.
Los estudiantes analizan diferentes representaciones que involucran grupos iguales para escribir una expresión de multiplicación para cada situación.
Los estudiantes hacen conexiones entre dibujos de grupos iguales, diagramas de cinta, situaciones y expresiones de multiplicación.
Enfriamiento Independiente 5 min. Los estudiantes escriben una expresión de multiplicación para representar un escenario que involucre grupos iguales.
Centro(s) sugerido(s) Grupos pequeños Opcional
Math Nation California - Grado 3
Apoyo:
• Capturar cuadrados (1-3), Etapa 4: Restar dentro de 20
• Cinco en fila: Suma y resta (1-2), Etapa 7: Sumar dentro de 1.000 sin componer
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Conteo coral
El propósito de este conteo coral es que los estudiantes practiquen contar por 5 y 2 y noten patrones en el conteo. Estos conocimientos ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes escriban expresiones de multiplicación.
Cuando los estudiantes notan patrones en el conteo, como en el conteo por 5 que el lugar de las unas alterna entre 0 y 5, buscan y expresan regularidad en el razonamiento repetido (MP8).
• "Cuenta por 5, comenzando en 0."

INTRODUCCIÓN
ACTIVIDAD
• Registra mientras los estudiantes cuentan. Véase Respuestas de los estudiantes para la estructura de registro.
• Deje de contar y registrar en 50
• "¿Qué patrones ven?"
• 1-2 minutos: tiempo para pensar en silencio
• Registre las respuestas.
• Repita la actividad. Contar por 2, empezar en 0 y parar en 20.
SÍNTESIS DE LA ACTIVIDAD
• "¿Cómo podrían ayudarte algunos de los patrones con c (Sé que la siguiente cuenta por 5 debe terminar en 5. Sé que la siguiente cuenta por 2 debe tener un 2 en el lugar de los).
• Considera preguntar:
• "¿Quién puede replantear el patrón en diferentes palabras?"
• "¿Alguien quiere agregar una observación sobre por qué ese patrón está sucediendo aquí?"
• "¿Estás de acuerdo o en desacuerdo? ¿Por qué?"
Grado 3 . Matemáticas . Unidad 1
Materiales para reunir
Materiales de una lección anterior

Preparación necesaria
Cada grupo de 2 necesita 1 tarjeta de la clasificación de tarjetas de la lección anterior.
Coloca estas expresiones en el aula:
• 3 × 5
• 4 × 3
• 3 × 2
• 2 × 10
• 3 × 10
El objetivo de esta actividad es que los estudiantes emparejen dibujos, diagramas de cinta y situaciones con expresiones de multiplicación (MP2). Los estudiantes se basan en su comprensión de cómo la estructura de los dibujos, diagramas de cinta y situaciones de multiplicación muestran grupos iguales y conectan esto a la estructura de una expresión de multiplicación (MP7). Esto será útil más adelante en la lección cuando los estudiantes creen dibujos o diagramas para emparejar expresiones y escriban expresiones que representen dibujos, diagramas y situaciones.
INTRODUCCIÓN
ACTIVIDAD
• Grupos de 2
• Entrega a cada grupo de 2 estudiantes 1 tarjeta de la cartulina maestra.
• "Trabaja con tu compañero para encontrar la expresión que coincide con tu tarjeta.
• 2 minutos: tiempo de trabajo en parejas
Tu maestro te dará una tarjeta que muestre un dibujo, un diagrama o una situación.
Emparéjala con una de las expresiones expuestas en la sala. Prepárate para explicar tu razonamiento.
Math
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Nation California - Grado 3

• A, F y L: 3 × 5
• B, H y K: 4 × 3
• C e I: 3 × 2
• D y G: 2 × 10
• E y J: 3 × 10
• Pide a los estudiantes que están cerca de cada expresión que compartan cómo saben que su tarjeta coincide con la expresión.
• Considere preguntar:
• "¿Dónde ves cada número de la expresión en tu tarjeta?".
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
15 minutos
El propósito de esta actividad es que los estudiantes demuestren una comprensión conceptual de las expresiones de multiplicación mediante la creación de dibujos de grupos iguales o diagramas de cinta que coincidan con las expresiones. Los dibujos de grupos iguales y los diagramas de cinta son representaciones familiares para los estudiantes de lecciones anteriores y les ayudan a dar sentido a las expresiones de multiplicación.
Se dan tres expresiones, pero el objetivo de la síntesis es la segunda expresión, 3 × 4. Esto ofrece la oportunidad de ayudar a los estudiantes en el primer problema mientras usted supervisa y luego les deja probar la segunda y la tercera expresión por su cuenta. Para mantener las cosas sencillas y permitir que las ideas sobre la conmutatividad se desarrollen con el tiempo, en esta actividad sugerimos que muestres las respuestas de los estudiantes siguiendo la convención de los grupos como primer factor y el tamaño de los grupos como segundo factor.
Si hay tiempo y quieres incluir más movimiento, esta actividad podría realizarse como un paseo por la galería.
Apoyo para estudiantes de inglés
MLR2 Collect and Display. Recoger el lenguaje que los estudiantes utilizan para describir los diagramas de cada una de las expresiones. Mostrar palabras y frases como: "5 grupos de 2", "hay 5 grupos, y 2 en cada grupo", y "hay 5 grupos iguales". Durante la síntesis, invite a los estudiantes a sugerir formas de actualizar la visualización y a tomar prestado el lenguaje de la visualización según sea necesario.
Avances: Conversar, leer

Acción y Expresión: Desarrolla la expresión y la comunicación. Proporcionar acceso a una variedad de herramientas: mini-pizarras y mostradores.
Apoya la accesibilidad para: Procesamiento Conceptual, Procesamiento Visual-Espacial
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 2
• Repasar los conceptos clave de la multiplicación:
• "La multiplicación es la forma en que expresamos grupos iguales"
• "Utilizamos el símbolo de la multiplicación para crear una expresión como 5 × 10 que representa el número total de objetos en '5 grupos de 10' o '5 decenas.'"
• Muestra las expresiones.
• "Piensa en los dibujos o diagramas que podrías hacer para estas expresiones."
• 30 segundos: tiempo para pensar en silencio
• "Trabaja con tu compañero para crear un dibujo o diagrama para cada expresión. Después, escribe tu propia expresión y el diagrama correspondiente. Explica tu razonamiento."
• 5-7 minutos: tiempo de trabajo en pareja
• Supervisa los dibujos creados por los estudiantes y los diagramas de cinta adhesiva para compartirlos durante la síntesis.
1. Crea un dibujo o diagrama para cada expresión. Explica tu razonamiento.
A. 5 × 2
B. 3 × 4
C. 3 × 10
2. Escribe tu propia expresión y el diagrama correspondiente. Explica tu razonamiento.
RESPUESTAS POSIBLES

Grado 3 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
1. Ejemplos de respuestas: A. Mostré 5 grupos de 2

B. Hay 3 grupos y 4 en cada grupo.

C. Es 3 grupos de 10.

2. Las respuestas varían.
• Para la expresión 3 × 4, muestre 2 diferentes representaciones una al lado de la otra (un dibujo de grupos iguales y un diagrama de cinta).
• "¿En qué se parecen? ¿En qué se diferencian?"
• Si hay tiempo, considere preguntar:
• "¿Cómo cambiaría el diagrama si la expresión fuera 5 × 4?" (Habría 5 secciones en lugar de 3.)
• "¿Cómo cambiaría el diagrama si la expresión fuera 3 × 5?" (Cada sección sería 5 en lugar de 4.)
10 minutos
El propósito de esta actividad es que los estudiantes escriban expresiones para representar dibujos de grupos iguales, diagramas de cinta y situaciones de multiplicación. A medida que los estudiantes trabajen, pregúnteles continuamente dónde se encuentra cada número de la expresión en el dibujo, diagrama o situación.
Si los estudiantes terminan antes, pídales que encuentren algo en el aula que puedan representar con una expresión de multiplicación. Pídales que anoten lo que representaron y su expresión.
• Grupos de 2
INTRODUCCIÓN
ACTIVIDAD
• "Ahora vas a escribir expresiones de multiplicación para representar un dibujo, un diagrama y una situación. Tómate un minuto para mirarlas antes de empezar a trabajar."
• 1 minuto: tiempo para pensar en silencio
• "Trabaja con tu compañero para escribir una expresión de multiplicación que se corresponda con cada representación. Explica tu razonamiento."
• 3-5 minutos: trabajo en parejas
Escribe una expresión de multiplicación que corresponda a cada representación. Explica tu razonamiento.
3.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Math Nation California - Grado 3
4.
5. Había 2 paquetes de agua. Cada paquete tenía 6 botellas de agua.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES
AVANZAR EL PENSAMIENTO DEL ESTUDIANTE
SÍNTESIS DE LA ACTIVIDAD
1. 3 × 3: Hay 3 grupos de 3.
2. 2 × 4 o 4 × 2: Había 2 partes y cada parte tenía 4 en ella.
3. 2 × 6 o 6 × 2: Hay 2 grupos con 6 en cada grupo.
Si un estudiante escribe una expresión de multiplicación que no coincide con la representación dada, considere preguntarle:
• "¿Cómo podrías describir los grupos iguales en este dibujo/diagrama/situación?"
• "¿Cómo podrías convertir tu enunciado en una expresión de multiplicación?"
• Compartir respuestas.
• "¿Por qué cada una de las representaciones muestra multiplicación?" (Todas muestran grupos en los que hay el mismo número de cosas en cada grupo.)
10 minutos
Muestre el dibujo de los grupos iguales, el diagrama de cinta, la situación y la expresión de la Actividad 2.
"Hemos aprendido sobre diferentes formas de representar la multiplicación. Comparte con tu compañero algo que hayas aprendido hoy sobre la multiplicación". (La multiplicación se puede representar con dibujos de grupos iguales o con diagramas. La multiplicación puede consistir en situaciones del mundo real en las que intervienen grupos iguales. La multiplicación puede expresarse utilizando el símbolo de multiplicación (×). Una expresión como 4 × 5 significa el número total de objetos en 4 grupos de 5).
5 minutos
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
Reflexiones:
Había 6 sobres. Cada sobre tenía 2 billetes dentro.
Escribe una expresión de multiplicación para representar la situación. Explica o muestra tu razonamiento. Haz un dibujo o un diagrama si te resulta útil.
6 × 2 o 2 × 6. El 6 representa los 6 sobres. El 2 representa los 2 billetes de cada sobre.


IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.OA.1 Interpretar productos de números enteros.
3.OA.3 Usar la multiplicación y división dentro de 100 para resolver problemas de palabras en situaciones que involucren grupos iguales, arreglos y cantidades medidas.
Enfoque SMPs
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1
I.B.5
I.C.10
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo e inciden en el futuro buscan y hacen uso de la estructura explorando cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo representar grupos iguales de diferentes maneras.
• Puedo usar representaciones para resolver problemas de grupos iguales.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Representar y resolver problemas de multiplicación.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿Qué estrategia le ha parecido más cómoda a cada alumno para encontrar productos hoy?
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
¿Cuántos ves? (Calentamiento)
MLR5 Preguntas de co-construcción (Actividad 1)
Objetivos de aprendizaje para el estudiante
• Representemos y resolvamos problemas que involucran grupos iguales.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes representen y resuelvan problemas de multiplicación.
En lecciones anteriores, los estudiantes aprendieron diferentes formas de representar situaciones de grupos iguales con dibujos, diagramas de cinta y expresiones. El objetivo de esta lección es que los estudiantes resuelvan problemas que involucran grupos iguales con una representación de su elección.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
Componente de la lección Estructura Tiempo
Calentamiento Pairs 10 min.
Exploration Activity 1 Pairs 15 min.
Actividad de Exploración 2 Pares 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.

Centro(s) sugerido(s) Grupos pequeños Opcional
Math Nation California - Grado 3
Descripción breve
Los estudiantes aplican estrategias de agrupación para determinar el número de puntos en imágenes.
Los estudiantes representan un escenario de grupos iguales con diagramas, dibujos o expresiones.
Los estudiantes resuelven problemas que involucran grupos iguales y luego justifican su pensamiento con representaciones.
Los estudiantes reflexionan sobre la lección identificando y explicando qué representación de grupos iguales les resultó más útil.
Los estudiantes representan y resuelven un problema que involucra grupos iguales.
Abordar:
• Capturar cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
Apoyo:
• Cinco en raya: Suma y resta (1-2), Etapa 7: Sumar dentro de 1.000 sin componer
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos

Rutinas didácticas
¿Cuántas ves?
El objetivo de este calentamiento es que los estudiantes subitizen o utilicen estrategias de agrupación para describir las imágenes que ven. Cuando los estudiantes descomponen las imágenes en grupos de 10 para contar de manera eficiente, están buscando y haciendo uso de la estructura (MP7). Para estas imágenes, los estudiantes pueden necesitar que se muestren durante más tiempo para poder ver la estructura.
• Grupos de 2
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "¿Cuántas ves? ¿Cómo los ves?"
• Muestra la imagen.
• 30 segundos: tiempo para pensar en silencio
• Muestra la imagen.
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Registra las respuestas. Use expresiones de multiplicación cuando los estudiantes compartan explicaciones que involucren grupos iguales.
• Repita para cada imagen.
¿Cuántos ves? ¿Cómo los ves?
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Ejemplos de respuestas:
• 40: Conté por 5 (o 2 o 10) hasta 40
• 30: Vi que cada paso tenía 10 así que conté por 10 hasta 30
• "¿Qué patrón fue útil para encontrar el número total de puntos?"
• Considere preguntar:
• "¿Quién puede replantear la forma en que vio los puntos con palabras diferentes?"
• "¿Alguien vio los puntos de la misma forma pero lo explicaría de otra manera?"
• "¿Alguien quiere añadir una observación a la forma en que vio los puntos?"
Grado 3 . Matemáticas . Unidad 1
15 minutos
Rutinas didácticas
MLR5 Preguntas de co-creacións
El propósito de esta actividad es que los estudiantes utilicen la rutina de lenguaje matemático de las Preguntas Co-craft para dar sentido a una situación de multiplicación antes de resolverla. Primero se pide a los estudiantes que generen preguntas que podrían hacer sobre parte de un problema. A continuación, se les da el problema completo y se les pide que lo resuelvan. Al final de la actividad, los estudiantes reflexionan sobre las representaciones que han utilizado. En esta actividad, los estudiantes tendrán que ver el problema completo para resolverlo. Antes de la lección, registre el problema y manténgalo oculto hasta el momento apropiado de la lección o escríbalo para que todos lo vean en ese momento de la actividad.
Esta actividad utiliza las preguntas de co-craft de la RML5. Avances: escribir, leer, representar
• Grupos de 2
MLR5 Preguntas de co-creación
• Muestre solo la raíz del problema, "Tyler tiene 3 cajas." sin revelar la pregunta.

INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE LA TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Math Nation California - Grado 3
• "Escriba una lista de preguntas matemáticas que podrían hacerse sobre esta situación." (¿Qué hay en las cajas? ¿Cuántas cosas hay en las cajas? ¿Cuántas cosas tiene en total?)
• 2 minutos: tiempo de trabajo independiente
• 2-3 minutos: discusión por parejas
• Invite a varios estudiantes a compartir una pregunta con la clase. Anote las respuestas.
• "¿Qué tienen en común estas preguntas? ¿En qué se diferencian?"
• Revele la tarea (los estudiantes abren los libros), e invite a realizar conexiones adicionales.
• "Piensen cómo resolverán el problema"
• 30 segundos: tiempo para pensar en silencio
• 2-3 minutos: tiempo de trabajo en parejas
Tyler tiene 3 cajas. Tiene 5 pelotas de béisbol en cada caja. ¿Cuántas pelotas de béisbol tiene en total? Muestra tu pensamiento usando diagramas, símbolos u otras representaciones.

15. Ejemplos de respuestas:

• • Tyler tiene 15 pelotas de béisbol porque conté por 5.
• Tyler tiene 15 pelotas de béisbol. 3 × 5 o 5 × 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• Muestre el trabajo de los estudiantes con diferentes representaciones del problema, de una en una (dibujos de grupos iguales, diagramas de cinta y expresiones). Si ningún estudiante escribe una expresión, escriba una para que los estudiantes la analicen.
• "¿Cómo nos ayuda cada representación a ver lo que está sucediendo en el problema?"
20 minutos
El propósito de esta actividad es que los estudiantes utilicen lo que han aprendido sobre la multiplicación para resolver y representar situaciones que involucran grupos iguales. Los estudiantes tienen ahora experiencia con múltiples representaciones y tienen la oportunidad de elegir qué representación es más útil para representar situaciones de multiplicación.
El inicio de la actividad es una oportunidad para que los estudiantes compartan sus experiencias y hagan preguntas sobre los objetos para asegurar que cada estudiante tenga acceso al contexto. Si resulta útil, muestre imágenes de los objetos para que los estudiantes puedan consultarlos.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Mientras los estudiantes describen sus representaciones de los problemas, utilice gestos para enfatizar el número de grupos y cuántos hay en cada grupo. Por ejemplo, trace con el dedo alrededor de cada grupo y señale cada objeto de cada grupo para mostrar cuántos hay.
Avances: Escuchar, representar
INTRODUCCIÓN
Apoyo para estudiantes con discapacidad
Representación: Acceso para la percepción Proporcione acceso a cubos de conexión. Pida a los estudiantes que identifiquen correspondencias entre la representación concreta y la visual utilizadas.
Apoya la accesibilidad para: Procesamiento conceptual
ACTIVIDAD
• Grupos de 2
• Escriba la lista de objetos ("equipos, pendientes, lápices, trozos de vidrio, zanahorias") en una pantalla para que todos los estudiantes la vean.
• "Tómense un minuto para leer esta lista. Cuando terminen, discutan los objetos que conocen o sobre los que tienen preguntas".
• 3 minutos: discusión por parejas
• Compartan algunas respuestas.
• "Ahora vamos a representar y resolver más problemas con grupos iguales. Tómense un par de minutos para empezar a trabajar en los problemas antes de trabajar en parejas."
• 2-3 minutos: tiempo de trabajo independiente
• "Trabaja con tu pareja para resolver cada problema."
• 5-7 minutos: trabajo en pareja
• Identifica a los estudiantes que utilizan diferentes representaciones como dibujos de grupos iguales o diagramas de cinta mientras resuelven los problemas.
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE

RESPUESTAS
POSIBLESS
AVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
Grado 3 . Matemáticas . Unidad 1
Resuelve cada problema. Muestra tu razonamiento utilizando diagramas, símbolos u otras representaciones.
1. Hay 4 campos de fútbol. Hay dos equipos en cada campo. ¿Cuántos equipos hay en total?
2. Hay 7 ventanas. Cada ventana tiene 2 cristales. ¿Cuántos cristales hay en las ventanas?
3. Jada tiene 5 bolsas. Cada bolsa tiene 10 pendientes. ¿Cuántos pendientes tiene Jada?
4. Kiran tiene 4 cajas. Cada caja tiene 5 lápices. ¿Cuántos lápices tiene Kiran?
5. Andre tiene 3 bolsas de zanahorias. Cada bolsa tiene 10 zanahorias. ¿Cuántas zanahorias tiene Andre?
1. 8 equipos. Ejemplo de respuesta:

Utilicé los grupos para contar los puntos. Cada punto representa un equipo.
2. 14 trozos de vidrio. Respuesta de muestra: 7 × 2. Conté por 2 siete veces porque cada ventana tenía 2 trozos de vidrio.
3. 50 pendientes. Respuesta de muestra:
Usé un diagrama para mostrar 5 grupos de 10, luego conté por 10 para encontrar el total.
4. 20 lápices. Respuesta de muestra:

Utilicé un dibujo para mostrar 4 cajas con 5 en cada caja.
5. 30 zanahorias. Respuesta de muestra: Conté las 3 bolsas de 10 como 10, 20, 30.
Si los estudiantes suman o restan en lugar de multiplicar para resolver los problemas, considere preguntarles:
• "Cuéntame cómo resolviste este problema".
• "¿De qué manera el problema involucra grupos iguales?"
• Para cada problema, muestre diferentes representaciones, una a la vez.
• "¿Cómo nos ayuda esta representación a ver lo que está sucediendo en el problema?" (Puedes ver que hay 4 grupos para los campos y 2 puntos en cada grupo para los equipos. El diagrama está dividido en 5 partes para las 5 bolsas, y cada sección tiene un 10 en ella para el número de pendientes.)
• "¿Cómo podría ayudarnos cada representación a resolver el problema?" (Contando los puntos. Contando por 10.)
• Si es necesario, "¿Qué expresión podríamos escribir para representar esta situación?"
10 minutos
Exhiba muestras del trabajo de los estudiantes con diferentes representaciones (dibujos de grupos iguales, diagramas de cinta y ecuaciones).
"¿Qué representación te pareció más útil hoy y por qué?" (Dibujos de grupos iguales porque pude ver lo que sucedía en el problema. Diagramas porque me ayudaron a entender el problema, pero no tuve que dibujar todos los puntos.)
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Hay 4 estanques. En cada estanque hay 5 patos. ¿Cuántos patos hay en total? Utiliza diagramas, símbolos u otras formas de mostrar tu pensamiento.
20 patos. Ejemplos de respuestas:
• 4 × 5
• 5, 10, 15, 20
RESPUESTAS POSIBLES


Reflexiones:


IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.OA.1 Interpretar productos de números enteros.
3.OA.3 Usar la multiplicación y división dentro de 100 para resolver problemas de palabras en situaciones que involucren grupos iguales, arreglos y cantidades medidas.
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP6 Atender a la precisión.
Estándares ELD de California
I.A.2 I.C.12 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo y repercuten en el futuro razonan abstracta y cuantitativamente explorando cantidades cambiantes.
META(S) DE APRENDIZAJE
• Puedo escribir una ecuación de multiplicación para representar una situación, diagrama o dibujo.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Relacionar ecuaciones con situaciones y diagramas de multiplicación.
• Escribir ecuaciones para situaciones y diagramas de multiplicación usando un símbolo para el número desconocido.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿En qué medida fueron útiles los términos factor y producto cuando los estudiantes empezaron a trabajar con ecuaciones de multiplicación?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
¿Cuál no pertenece? (Calentamiento)
Objetivos de aprendizaje para el estudiante
• Aprendamos sobre ecuaciones de multiplicación.
Narrativa de la lección
En lecciones anteriores los estudiantes representaron situaciones y diagramas con expresiones de multiplicación. En esta lección, los estudiantes aprenden el significado de factor y producto. Los estudiantes no tienen que usar el vocabulario en esta lección ya que seguirán teniendo
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
oportunidades para hacerlo a lo largo del año. En futuras lecciones, los estudiantes representarán situaciones y diagramas con ecuaciones que utilicen un símbolo para el número desconocido, que puede ser un factor o el producto.
Considere la posibilidad de seguir utilizando la convención de los grupos como primer factor y el tamaño de los grupos como segundo factor al escribir ecuaciones. Sin embargo, no es necesario que los estudiantes escriban los factores en este orden. Es importante que los estudiantes relacionen sus ecuaciones con las situaciones y representaciones correspondientes (MP2). Deben ser capaces de explicar correctamente lo que representa cada factor en sus ecuaciones. Si los estudiantes hacen preguntas sobre la idea de conmutatividad, considere la posibilidad de registrar las preguntas públicamente para futuras investigaciones.
Componente de la lección

Estructura
Tiempo
Descripción breve
Calentamiento Pairs 10 min. Students explain which mathematical representation does not belong.
Actividad de exploración 1 Parejas o Grupos pequeños 20 min.
Actividad de exploración 2 Parejas 15 min.
Síntesis Grupo Entero 10 min.
Enfriamiento Independiente 5 min.
Centro(s)
Sugerido(s) Grupos Pequeños Opcional
Los estudiantes emparejan ecuaciones de multiplicación dadas con modelos y situaciones basándose en su comprensión de factores, grupos iguales, diagramas y situaciones.
Los estudiantes escriben ecuaciones de multiplicación que representan situaciones, diagramas o dibujos.
Los estudiantes revisan las similitudes y diferencias entre una expresión y una ecuación de multiplicación.
Los estudiantes identifican todas las representaciones que coinciden con una ecuación.
Abordar:
• Capturar Cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
Apoyo:
• Cinco en raya: Suma y resta (1-2), Etapa 7: Sumar dentro de 1.000 sin componer
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
REPRESENTACIONES 10 minutos
Rutinas didácticas
¿Cuál no pertenece?
Este calentamiento incita a los estudiantes a analizar y comparar cuidadosamente las características de expresiones y ecuaciones. Cuando los estudiantes comparan el dibujo, la expresión y las ecuaciones, deben utilizar el lenguaje con precisión para describir en qué es igual o diferente cada uno (MP6). Escuche el lenguaje que utilizan los estudiantes para describir las diferentes características de cada expresión y ecuación y conecte el lenguaje de los estudiantes con los nuevos términos, factor y producto, que se introducen en la síntesis.
• Grupos de 2
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Muestre la imagen, la expresión y las ecuaciones.
• "Elija una que no pertenezca. Prepárate para compartir por qué no pertenece."
• 1 minuto: tiempo para pensar en silencio
• "Discute tu pensamiento con tu compañero."
• 2-3 minutos: discusión en pareja
• Comparte y registra las respuestas.
¿Cuál no pertenece?
A. C. 2 × 5 = 10
Ejemplos de respuestas:
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
D. 3 × 5
D. 7 + 8 = 15
• A es la única que no muestra ningún número.
• B es la única que no muestra el total.
• C es la única que no muestra 15
• D es la única que no trata sobre la multiplicación y no trata sobre grupos de 5.
• "¿Qué patrón fue útil para encontrar el número total de puntos?"
• "¿En qué se diferencia C de las otras formas en que hemos representado grupos iguales antes?" (Tiene un signo igual. Es una ecuación.)
• "C es una ecuación de multiplicación porque contiene un símbolo de multiplicación y el signo igual."
• "Hay palabras que nos ayudan a hablar de las diferentes partes de la ecuación de multiplicación. Los factores son los números que se multiplican. El producto es el resultado de multiplicar unos números. En la ecuación en C, los números 2 y 5 son los factores. El producto es 10. Ten en cuenta estas palabras hoy cuando trabajemos con otras ecuaciones de multiplicación."
Grado 3 . Matemáticas . Unidad 1
minutos
El propósito de esta actividad es que los estudiantes emparejen ecuaciones de multiplicación con situaciones y representaciones. Los estudiantes establecen conexiones explícitas entre los factores y el número de grupos o el número de objetos de cada grupo y entre el producto y el número total de objetos. Estas conexiones se ponen de manifiesto explícitamente durante la síntesis. Cuando los estudiantes establecen conexiones explícitas entre las situaciones de multiplicación y las ecuaciones, están razonando de forma abstracta y cuantitativa (MP2).
INTRODUCCIÓN

ACTIVIDAD
• Grupos de 2 o 4
• "Piensa cómo podrías emparejar estas ecuaciones con una situación o diagrama."
• 1 minuto: tiempo para pensar en silencio
• "Por turnos, encuentra una situación o diagrama que coincida con cada ecuación. Explica tu razonamiento a tu compañero."
• 5-7 minutos: discusión por parejas
• Supervise a los estudiantes que hagan conexiones directas entre cada factor que representa el número en cada grupo o el número de grupos y el producto que representa el número total de objetos para compartir durante la síntesis.
• "Reúnanse con otro grupo para discutir las correspondencias que hicieron".
• 3-5 minutos: discusión en grupos pequeños
Encuentre una ecuación de la lista que pueda representar cada situación, diagrama o dibujo. Anota la ecuación. Prepárate para explicar tu razonamiento.
• 3 × 5 = 15
• 4 × 10 = 40
• 2 × 10 = 20
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
4. 6 manos estaban sobre la mesa. Cada mano tenía 5 dedos.
• 10 = 5 × 2
• 30 = 6 × 5
• 4 × 2 = 8
Andre tenía 5 pares de calcetines.
• 16 = 8 × 2
• 4 × 5 = 20
• 50 = 5 × 2
9. Había 4 cajas de rotuladores. Cada caja tenía 10 marcadores.
RESPUESTAS POSIBLES
Math Nation California - Grado 3
1. 2 × 10 = 20
2. 10 = 5 × 2
3. 16 = 8 × 2
4. 30 = 6 × 5
5. 3 × 5 = 15 6. 4 × 5 = 20
7. 50 = 5 × 10
8. 4 × 2 = 8
9. 4 × 10 = 40
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• "¿Hubo alguna correspondencia en la que no estuvieron de acuerdo? ¿Cómo llegasteis a un acuerdo?" (Volvimos a contar los puntos juntos.)
• Para la primera, cuarta y séptima parejas que coincidan pregunte: "¿Cómo representa la ecuación la situación (o diagrama)?" (El 2 representa las partes 2 en el diagrama. El 5 representa los 5 dedos de cada mano. El 50 representa cuántos puntos había en total en los grupos).
15 minutos
El propósito de esta actividad es que los estudiantes escriban ecuaciones que correspondan a situaciones y diagramas. Los estudiantes usan lo que aprendieron en la última actividad para usar ecuaciones de multiplicación para representar situaciones y diagramas. En la síntesis de la lección, utilice las palabras factor y producto para ayudar a los estudiantes a relacionar el vocabulario con los conceptos.
MLR7 Compare and Connect. Síntesis: Invite a los grupos a preparar una presentación visual que muestre su razonamiento para una de las ecuaciones utilizando detalles como diferentes colores, flechas, etiquetas, diagramas o dibujos. Dé tiempo a los estudiantes para que investiguen el trabajo de los demás. Pregunte: "¿Qué detalles o lenguaje les ayudó a entender las exposiciones?", "¿Alguien creó la misma ecuación, pero la explicaría de manera diferente?"
Avances: Representar, conversar
INTRODUCCIÓN • Grupos de 2
Engagement: Facilitar el acceso captando el interés Ofrecer opciones. Invita a los estudiantes a decidir por qué problema empezar o a decidir el orden para completar la tarea.
Apoya la accesibilidad para: Funcionamiento socioemocional
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "Trabaja con tu compañero para escribir una ecuación que represente cada situación y diagrama."
• 5-7 minutos: tiempo de trabajo en pareja
• Supervisa a los estudiantes que puedan justificar las ecuaciones que escribieron explicando el significado de los factores y productos en sus ecuaciones.
Escribe una ecuación que represente cada situación, dibujo o diagrama. Prepárate para explicar tu razonamiento.
1. Un paquete tiene 6 par de calcetines.
2.
3. Diego tiene 7 secciones en su cuaderno. Cada sección tiene 10 páginas.
Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA
PARA EL ESTUDIANTE CONTINUACIÓN 1. 2.
3. Elena tiene 4 bolsas de naranjas. Cada bolsa tiene 5 naranjas.
4.
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
1. 6 × 2 = 12 o 2 × 6 = 12. Ejemplo de respuesta: Hay 6 grupos de calcetines con 2 calcetines en cada grupo. Esto hace 12 calcetines.
2. 7 × 2 = 14 o 2 × 7 = 14. Respuesta de ejemplo: Hay 7 partes y cada parte tiene 2 en ella. Si cuentas por 2 siete veces, obtienes 14
3. 7 × 10 = 70 o 10 × 7 = 70. Respuesta de ejemplo: Hay 7 secciones y cada sección tiene 10 páginas, por lo que hay 70 páginas en total.
4. 9 × 2 = 18 o 2 × 9 = 18. Respuesta de ejemplo: Hay 9 círculos y cada círculo tiene 2 puntos en él. Esto hace un total de 18 círculos.
5. 6 × 10 = 60 o 10 × 6 = 60. Respuesta de ejemplo: Hay 6 partes con 10 en cada parte. Esto hace 60
6. 4 × 5 = 20 o 5 × 4 = 20. Respuesta de ejemplo: Hay 4 bolsas y cada bolsa tiene 5 naranjas. Esto es 20 naranjas.
• Para cada problema pida a un estudiante que comparta su ecuación. Considere preguntar:
• "¿Cómo tiene sentido esta ecuación para esta situación, dibujo o diagrama?"
• "¿Qué partes de la situación, dibujo o diagrama fueron especialmente útiles mientras escribías la ecuación?"
Visualización:
10 minutos
Expresión: 3 × 5
Ecuación: 3 × 5 = 15
"Hoy hemos aprendido sobre ecuaciones y cómo podemos usarlas para representar multiplicaciones. En esta ecuación, 3 y 5 son los factores y 15 es el producto."
"¿En qué se parecen las expresiones de multiplicación y las ecuaciones?" (Ambas usan el símbolo de multiplicación. Ambas tienen factores.)
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

"¿En qué se diferencian las expresiones de multiplicación y las ecuaciones?". (Las ecuaciones tienen un signo igual. Las ecuaciones de multiplicación tienen números a ambos lados del signo igual.)
"¿Cuándo sería útil cada una?" (Las expresiones son útiles cuando quieres describir una situación. Las ecuaciones son útiles si estás tratando de encontrar el producto).
5 minutos
Selecciona todos los dibujos, diagramas y situaciones que podrían representar la ecuación.
80 = 8 × 10
A.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
B. Andre tiene 8 cajas. Cada caja tiene 10 coches dentro. Tiene 80 coches en total.
C.
D.
E. Andre tiene 8 cajas. Luego, encontró 10 cajas más. ¿Cuántas cajas tiene André? F.
RESPUESTAS POSIBLES A, B y D
Reflexiones:
Learning Inc. - Todos los derechos reservados


IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica hasta 100 para las cuatro operaciones
• Patrones en cuatro operaciones
Abordar
3.OA.1 Interpretar productos de números enteros.
3.OA.3 Usar la multiplicación y la división dentro de 100 para resolver problemas de palabras en situaciones que involucren grupos iguales, arreglos y cantidades medidas.
Alineación de estándares y principios de California
3.OA.4 Determinar el número entero desconocido en una ecuación de multiplicación o división que relacione tres números enteros.
3.OA.9 Identificar patrones aritméticos (incluyendo patrones en la tabla de sumas o en la tabla de multiplicación) y explicarlos usando las propiedades de las operaciones.
Construir
3.OA.7
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP4 Representar con matemáticas.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California I.A.3
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo y predecir lo que podría ocurrir
razonar abstracta y cuantitativamente y modelizar con matemáticas explorar cantidades cambiantes.
META(S) DE APRENDIZAJE
• Puedo escribir una ecuación de multiplicación que contenga un símbolo para un número desconocido para representar situaciones, dibujos y diagramas.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Relacionar ecuaciones con situaciones y diagramas de multiplicación usando un símbolo para el número desconocido.
• Escribir ecuaciones para situaciones y diagramas de multiplicación usando un símbolo para el número desconocido.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿Cómo ayudan los diagramas de cinta a los estudiantes a dar sentido a las ecuaciones en las que el número desconocido se encuentra en diferentes posiciones?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Hablar de números (Calentamiento)
Materiales para copiar
Clasificar números desconocidos con tarjetas
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Cree un juego de tarjetas a partir del patrón de líneas negras para cada grupo de 2
Grado 3 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Trabajemos con ecuaciones con números desconocidos.
Narrativa de la lección
Los estudiantes han trabajado con ecuaciones de suma y resta con un símbolo para representar el número desconocido en los grados 1º y 2º. Los estudiantes se basan en ese trabajo y en el trabajo con ecuaciones de multiplicación de la lección anterior cuando encuentran ecuaciones de multiplicación que tienen un símbolo para el número desconocido por primera vez.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo

Descripción breve
Calentamiento Independiente 10 min. Usando la matemática mental, los estudiantes encuentran los productos de expresiones de multiplicación.
Actividad de exploración 1 Parejas 15 min.
Actividad de exploración 2 En parejas 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Los estudiantes emparejan ecuaciones de multiplicación con números desconocidos con las situaciones o diagramas de multiplicación correspondientes.
Los estudiantes representan y resuelven problemas de multiplicación escribiendo ecuaciones que contienen un símbolo para una cantidad desconocida.
Los estudiantes discuten las diferencias entre encontrar un factor desconocido y encontrar un producto desconocido.
Los estudiantes escriben y resuelven una ecuación de multiplicación que representa un diagrama.
Abordar:
• Capturar Cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
Centro(s) Sugerido(s) Grupos Pequeños Opcional
Apoyo:
• Cinco en raya: Suma y resta (1-2), Etapa 8: Sumar dentro de 1.000 con Componer
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos

Rutinas didácticas
Hablar de números
El propósito de esta Charla sobre Números es obtener estrategias y comprensiones que los estudiantes tienen para multiplicar por 5. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes representen y resuelvan un problema que involucra grupos de 5
Cuando los estudiantes razonan por qué a medida que un factor aumenta en 1, el producto aumenta en 5, están buscando y expresando la regularidad que notan en las expresiones (MP8).
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Mostrar una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste"
• 1 minuto: tiempo para pensar en silencio
• Registrar respuestas y estrategia.
• Mantén las expresiones y el trabajo a la vista.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada expresión.
• 1 × 5
• 2 × 5
• 5: Es solo 1 grupo de 5
• 10: Añadí 5 más a la primera respuesta.
• 3 × 5
• 4 × 5
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
• : Sumé 5 + 5 + 5
• 20: Conté por 5
• "¿Qué patrón observas al mirar todos los problemas? ¿Por qué ocurre esto?" (El factor que no es 5 aumenta en 1 cada vez. Los productos aumentan en 5. Agregamos otro grupo de 5.)
Rutinas didácticas
Clasificación de tarjetas
15 minutos
Materiales para copiar
Clasificación de tarjetas de números desconocidos
Preparación necesaria
Crea un conjunto de tarjetas a partir del patrón de líneas negras para cada grupo de 2
El objetivo de esta actividad es que los estudiantes relacionen ecuaciones con situaciones y diagramas de multiplicación utilizando un símbolo para el número desconocido. Una tarea de ordenación ofrece a los estudiantes la oportunidad de analizar detenidamente representaciones, enunciados y estructuras y establecer conexiones (MP2, MP7). Los estudiantes explican sus correspondencias a sus compañeros y revisan su lenguaje para que sea más preciso y claro cuando describen cómo los números y los símbolos de las ecuaciones coinciden con las representaciones (MP3, MP6). En la síntesis, los estudiantes explican el significado de los factores y los productos, y lo que representa un símbolo en una ecuación.
Grado 3 . Matemáticas . Unidad 1
MLR8 Discussion Supports. Invite a los estudiantes a turnarse para encontrar una coincidencia y explicar su razonamiento a su compañero. Muestre los siguientes marcos de oraciones para que todos los vean: "Me he fijado en , así que he emparejado...". Anime a los estudiantes a rebatirse cuando no estén de acuerdo.
Avances: Conversar, representar

INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 2
• Visualiza: 4 × 5 = ?
• "¿Qué puede significar esta ecuación?" (Hay 4 grupos de 5. Hay un número en la ecuación que no conocemos. No sabemos el total.)
• 2 minutos: discusión por parejas
• Compartir respuestas.
• "Se pueden utilizar diferentes símbolos para representar el número desconocido en una ecuación. Algunos que son comunes son los signos de interrogación, los espacios en blanco y los recuadros".
• "Por ejemplo, en la ecuación 80 = 8 × 10, si no conociéramos el producto podríamos escribir ? = 8 × 10." Muestra estas ecuaciones mientras explicas.
• "Si no conociéramos uno de los factores, ¿qué ecuación podrías escribir utilizando un símbolo para el número desconocido?". (80 = × 10, 80 = ? × 10)
• Distribuya un juego de tarjetas precortadas a cada grupo de estudiantes.
• Este juego de tarjetas incluye ecuaciones, situaciones y diagramas. Relaciona cada ecuación con una situación o diagrama. Trabaja con tu compañero para justificar tus elecciones."
• 5-7 minutos: tiempo de trabajo en pareja
• Supervisa a los estudiantes que explican el significado de los factores y el producto, específicamente que el símbolo es para un número que falta que representa una cantidad que falta en el diagrama o situación.
Tu maestro te dará un conjunto de tarjetas. Empareja cada ecuación con una situación o diagrama.
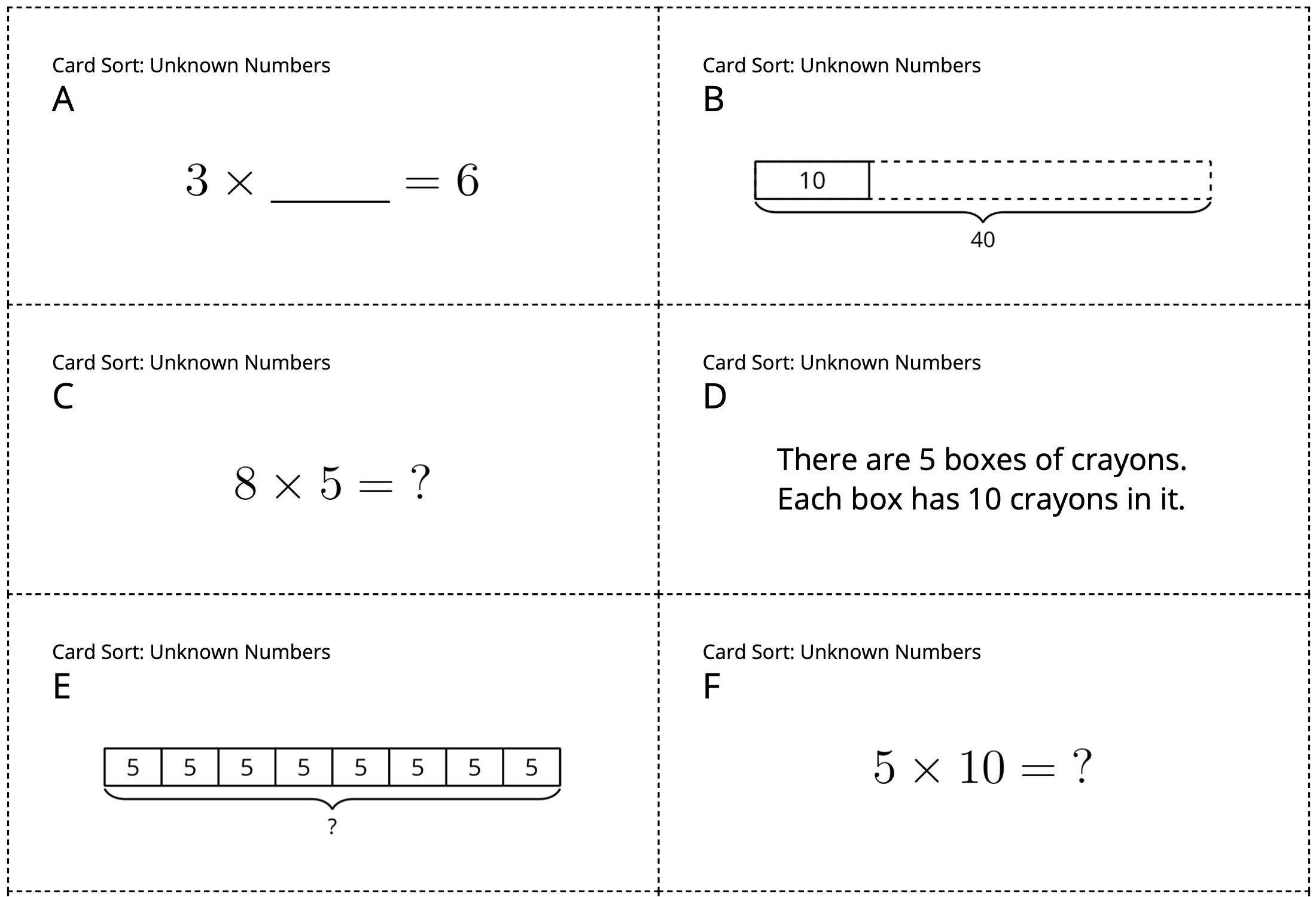
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA
PARA EL ESTUDIANTE CONTINUACIÓN
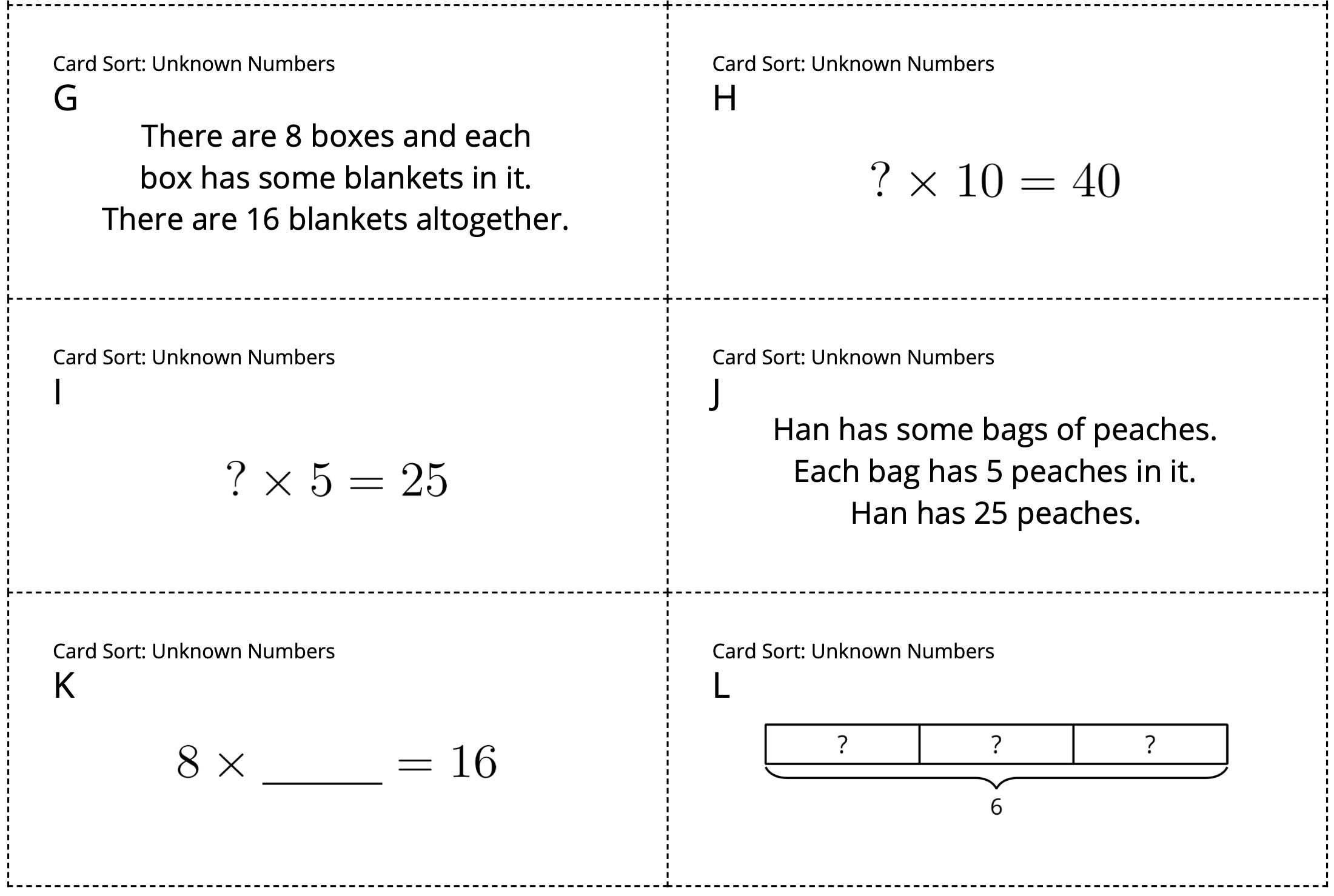
• A y L
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• B y H
• C y E
• D y F
• G y K
• I y J
Ejemplo de respuesta: Sé que A y L van juntas porque hay 3 grupos que juntos hacen 6, pero no sabemos el tamaño de cada grupo.
• Haga que los estudiantes compartan sus coincidencias y cómo saben que esas tarjetas van juntas.
• Elija 1-2 ecuaciones (al menos una con un factor que falta) y pregunte:
• "¿Qué representa cada número en la ecuación?"
• "¿Qué representa cada signo de interrogación (o espacio en blanco o recuadro)?"
• "¿Cómo podemos averiguar qué número va en el espacio en blanco para que la ecuación sea verdadera?"
• Escuche el lenguaje que utilizan los estudiantes para describir sus correspondencias y las ecuaciones, diagramas y situaciones de forma clara y precisa. Cuando sea necesario, pregunte:
• "¿Qué quieres decir cuando dices ?"
• "¿La incógnita era el producto o uno de los factores? Explique".
• "¿Qué representaba el factor desconocido? Explique".
• Resalte términos como "factor" y "producto".
20 minutos
El propósito de esta actividad es que los estudiantes escriban ecuaciones para situaciones y diagramas de multiplicación usando un símbolo para el número desconocido. Cuando los estudiantes escriben una ecuación para representar una situación, incluyendo un símbolo para el número desconocido, representan una situación con matemáticas (MP4).
Los estudiantes encuentran un factor desconocido o un producto desconocido en problemas de multiplicación. En esta tarea, los diagramas de factores desconocidos y las situaciones solo incluyen el tipo de problema "cuántos grupos" y los factores 2, 5, y 10. Esto prepara a los estudiantes para saltar la cuenta y encontrar el número desconocido.
Grado 3 . Matemáticas . Unidad 1
Este tipo de problema se volverá a tratar ampliamente en futuras lecciones y se relacionará con la división. No es necesario establecer ahora la relación con la división. En la síntesis, los estudiantes explican cómo las ecuaciones que han escrito representan el diagrama o la situación.
Representación: Interiorizar la comprensión. Síntesis: Invite a los estudiantes a identificar qué detalles fueron importantes o más útiles para prestarles atención. Muestre el marco de la frase: "La próxima vez que escriba una ecuación con un número desconocido, yo..."
Apoya la accesibilidad para: Procesamiento visual-espacial
INTRODUCCIÓN • Grupos de 2
• "Ahora practicarás escribiendo tus propias ecuaciones con un símbolo para la incógnita."
• 2-3 minutos: tiempo de trabajo independiente
• "Comparte tus ecuaciones con tu compañero. Discute cómo sabes que cada ecuación coincide con el diagrama o la situación."
• 2-3 minutos: discusión por parejas
• Ten una discusión con toda la clase enfocada en cómo las ecuaciones coinciden con las diferentes representaciones.

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Considera preguntar:
• "¿Cómo usaste las representaciones para escribir una ecuación con un símbolo para la incógnita?" (Busqué lo que faltaba en el diagrama. Pensé en la situación para averiguar si lo que faltaba era el número en cada grupo, el número de grupos o el total.)
• "Ahora encuentra el número que falta en cada ecuación y escribe una nueva ecuación que incluya la solución."
• 3-5 minutos: tiempo de trabajo en pareja
• Escribe una ecuación para representar cada diagrama o situación. Utiliza un símbolo para la incógnita. Prepárate para compartir tu razonamiento.
• Encuentra el número que hace que cada ecuación sea verdadera. Vuelve a escribir la ecuación con la solución.
Diagrama o situación
Jada tiene algunos paquetes de tarjetas deportivas. Cada paquete tiene 5 tarjetas. Si Jada tiene 45 tarjetas, ¿cuántas barajas tiene?
Ecuación con símbolo
Ecuación con solución
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE LA TAREA PARA EL ESTUDIANTE CONTINUACIÓN
Diagrama o situación
Ecuación con símbolo
Ecuación con solución
RESPUESTAS POSIBLES
La escuela tiene 6 bolsas. Cada bolsa tiene 10 pelotas de baloncesto. ¿Cuántas pelotas de baloncesto tiene la escuela?
Diagrama o situación
Jada tiene algunos paquetes de tarjetas deportivas. Cada paquete tiene 5 tarjetas. Si Jada tiene 45 tarjetas, ¿cuántas barajas tiene?
Ecuación con símbolo Ecuación con solución
AVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
La escuela tiene 6 bolsas. Cada bolsa tiene 10 pelotas de baloncesto. ¿Cuántas pelotas de baloncesto tiene la escuela?
Si los estudiantes escriben una ecuación sin un símbolo para el número desconocido, considera preguntar:
1. "¿Cómo representa tu ecuación el diagrama (o situación)?"
2. "¿Cómo podrías mostrar el número desconocido con un símbolo?"
• "¿Qué estrategias usaste para encontrar los números desconocidos?" (Conté por 2 para obtener el total. Conté por diferentes números hasta encontrar un número que me diera el producto)
• "¿Cómo cambió cada ecuación a medida que encontrabas el número desconocido?" (El símbolo fue reemplazado por el número).
Grado 3 . Matemáticas . Unidad 1
Visualización:

10 minutos
6 × 5 = ?
6 × ? = 30
? × 5 = 30
"Hoy hemos encontrado el número desconocido en ecuaciones de multiplicación."
"¿En qué se diferencia encontrar un factor desconocido de encontrar un producto desconocido?" (Si no conociéramos el producto, podríamos saltarnos la cuenta por el número el número correcto de veces, como 5, 10, 15, 20, 25, 30. Si no conociéramos uno de los factores, tendríamos que saltarnos el número suficientes veces para llegar al producto. Si no conociéramos uno de los factores, podríamos no saber por qué saltar-cuenta, solo el número de cuentas).
5 minutos
1. Escribe una ecuación que coincida con el diagrama. Usa un símbolo para la incógnita.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Reflexiones:
2. Encuentra el número que hace que la ecuación sea verdadera. Reescribe la ecuación con ese número. Explica tu razonamiento.
1. 4 × ? = 40 o ? × 4 = 40
2. 4 × 10 = 40 o 10 × 4 = 40. Ejemplo de respuesta: Si cuento de diez en diez 4 veces obtengo 40, por lo que sé que el número que falta es 10
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
3.OA.3 Usar la multiplicación y la división dentro de 100 para resolver problemas de palabras en situaciones que involucren grupos iguales, arreglos y cantidades medidas.
3.OA.4 Determinar el número entero desconocido en una ecuación de multiplicación o división que relaciona tres números enteros.
3.OA.9 Identificar patrones aritméticos (incluyendo patrones en la tabla de sumas o multiplicaciones) y explicarlos utilizando propiedades de las operaciones.
Construir
3.OA.7
Enfoque SMPs
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.1
I.B.5
I.C.11
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo y predecir lo que podría ocurrir
buscar y expresar regularidad en razonamientos repetidos explorar cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo escribir una ecuación de multiplicación con un valor desconocido para resolver problemas.
OBJETIVOS DE APRENDIZAJE
• Resolver problemas de multiplicación.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
Mientras los estudiantes trabajaban hoy en sus pequeños grupos, ¿las ideas de quién fueron escuchadas, valoradas y aceptadas? ¿Cómo puedes ajustar la estructura del grupo mañana para garantizar que las ideas de cada alumno formen parte del aprendizaje colectivo?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Hablar de números (Calentamiento)
Objetivos de aprendizaje para el estudiante
• Resolvamos más problemas de multiplicación.
Narrativa de la lección
Los estudiantes escriben ecuaciones con un símbolo para la incógnita para representar problemas de multiplicación y luego resuelven los problemas. Como en la lección anterior, algunos problemas son de factor desconocido que los estudiantes no relacionan con la división hasta una unidad futura. Los estudiantes unen lo que han aprendido sobre dibujos, diagramas, expresiones y ecuaciones para resolver problemas de multiplicación.
©Accelerate Learning Inc. - Todos los derechos reservados
Resumen de la lección Componente de la Lección Estructura Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 En parejas 15 min.
Actividad de exploración 2 En parejas 20 min.
Síntesis Grupo Entero 10 min.
Enfriamiento Independiente 5 min.

Centro(s) Sugerido(s) Grupos Pequeños Opcional
Math Nation California - Grado 3
Grado 3 . Matemáticas . Unidad 1
Descripción breve
Los estudiantes calculan mentalmente los productos de expresiones de multiplicación que utilizan 10 y luego discuten las estrategias que utilizaron.
Los estudiantes escriben y resuelven una ecuación con un símbolo para el valor desconocido que representa cada situación.
Los estudiantes resuelven problemas de multiplicación del mundo real que tienen un factor desconocido o un producto desconocido y luego justifican sus soluciones.
Los estudiantes resumen las estrategias utilizadas para resolver problemas de multiplicación.
Los estudiantes utilizan estrategias o representaciones para resolver problemas de multiplicación con un factor o producto desconocido.
Abordar:
• Captura de Cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10 Apoyo:
• Cinco en raya: Suma y resta (1-2), Etapa 8: Sumar dentro de 1.000 con Componer
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas instruccionales
Charla sobre números
El propósito de esta Charla sobre Números es obtener estrategias y comprensiones que los estudiantes tienen para multiplicar por 10. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de representar y resolver un problema que involucre grupos de 10
Cuando los estudiantes razonan por qué a medida que un factor aumenta en 1, el producto aumenta en 10, buscan y expresan la regularidad que notan en las expresiones (MP8).
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• Muestre una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste".
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada expresión.
• 1 × 10
• 2 × 10
• 10: Es solo 1 grupo de 10
• 20: Añadí 10 más a la primera respuesta.
• 30: Sumé 10 + 10 + 10
• 40: Conté 10
• 3 × 10
• 4 × 10
• "¿Qué patrón vemos al mirar todos los problemas? ¿Por qué ocurre esto?" (El factor que no es 10 aumenta en 1 cada vez. Los productos aumentan en 10 porque tengo un grupo más de 10.)
• Considera preguntar:
• "¿Alguien usó una estrategia diferente?"
• "¿Alguien tuvo la misma estrategia pero la explicaría de manera diferente?"
15 minutos
El propósito de esta actividad es que los estudiantes representen una situación con una ecuación de multiplicación que incluya un símbolo para la incógnita, y encuentren el número que hace que la ecuación sea verdadera. Los estudiantes pueden utilizar una representación anterior para resolver el problema; sin embargo, algunos pueden simplemente escribir la ecuación y omitir el conteo para hallar el producto. Cualquiera de las dos opciones es válida. En la síntesis, comparta las diferentes formas en que los estudiantes representaron el problema más allá de la ecuación. Si los estudiantes utilizan la suma repetida, evite decir "la multiplicación es la suma repetida" porque, aunque la suma repetida es una forma de hallar el producto, no es el significado de la multiplicación.
Para añadir movimiento a esta actividad, los estudiantes pueden trabajar en grupos de 4 para hacer un cartel para uno de los problemas. Después de que cada grupo haya terminado, pueden hacer un recorrido por la galería para buscar cosas iguales o diferentes en los carteles.
Grado 3 . Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad
Engagement: Desarrollar el esfuerzo y la persistencia. Divida esta tarea en partes más manejables. Comprueba con los estudiantes que reciben comentarios y ánimos después de cada parte.
Apoya la accesibilidad para: Atención, Memoria
• "Vamos a resolver algunos problemas sobre grupos iguales que podrías ver cuando estás haciendo o comiendo una comida."
• "¿Cuáles son algunos grupos iguales que podrías ver cuando estás haciendo o comiendo una comida?"
INTRODUCCIÓN
• Comparte las respuestas.
• "Piensa en cómo podrías representar estos problemas de manera que te ayude a escribir una ecuación con un número desconocido para cada problema."
• 1 minuto: tiempo para pensar en silencio
• 1 minuto: discusión por parejas
• "Ahora, trabaja de forma independiente en estos problemas."
• 5-7 minutos: tiempo de trabajo independiente
ACTIVIDAD
• Mientras circula, considere preguntar:
• "¿Cómo podrías representar esta situación?"
• "¿Qué información falta en la situación?"
Para cada problema:
• Escribe una ecuación con un símbolo para la incógnita que represente la situación.
• Encuentra el número que hace que la ecuación sea verdadera. Muestra tu razonamiento.
1. Hay 15 platos. Han colocó 5 platos en cada mesa. ¿Cuántas mesas tienen platos?
A. ecuación:
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
B. solución:
2. Lin preparó 6 sándwiches. Utilizó 2 rebanadas de pan para cada sándwich. ¿Cuántas rebanadas de pan utilizó?
A. ecuación:
B. solución:
3. Han tiene 60 cubitos de hielo. Los cubitos están en bandejas de 10. ¿Cuántas bandejas de cubitos de hielo tiene Han?
A. ecuación:
B. solución:
1.
RESPUESTAS POSIBLESS
Math Nation California - Grado 3
A. ? × 5 = 15 o 5 × ? = 15
B. 3 × 5 = 15 o 5 × 3 = 15
Respuesta de ejemplo:
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

1.
RESPUESTAS
POSIBLESS
CONTINUACIÓN
SÍNTESIS DE LA ACTIVIDAD
A. 6 × 2 = o 2 × 6 =
B. 6 × 2 = 12 o 2 × 6 = 12
Ejemplo de respuesta: He contado 2, 4, 6, 8, 10, 12. 2.
A. ? × 10 = 60 o 10 × ? = 60
B. 6 × 10 = 60 o 10 × 6 = 60
Ejemplo de respuesta:
• Exponga muestras del trabajo de los estudiantes para cada problema uno al lado del otro, incluyendo una muestra de un dibujo de grupos iguales y una muestra de un diagrama de cinta.
• "¿Dónde vemos las partes del problema en el dibujo y en el diagrama?" (El número de objetos en cada grupo son los puntos en el dibujo, pero el número está escrito en cada parte del diagrama.)
• "¿Cómo usaste los factores en cada ecuación para encontrar el producto?" (Los factores me dijeron cuántos grupos había y cuántos había en cada grupo.)
• "¿Cómo son útiles los dibujos y los diagramas para encontrar la solución del problema?" (Puedes contar los puntos del dibujo. El diagrama se puede utilizar para contar por 10.)
MEZCLA 20 minutos
El objetivo de esta actividad es que los estudiantes practiquen la resolución de problemas de multiplicación en los que la incógnita puede ser el número de grupos, el número de cada grupo o el total. Los tres primeros problemas tienen la incógnita en cada uno de esos lugares. La secuencia de estos problemas, el contexto y el uso de los mismos factores y producto anima a los estudiantes a utilizar un dato conocido para hallar la incógnita en el problema "cuántos hay en cada grupo". Los estudiantes harán la conexión entre este tipo de problema y la división en una unidad futura. Los estudiantes pueden elegir la representación que utilizan para representar y resolver los problemas.
Apoyo para estudiantes de inglés
MLR8 Discussion Supports. Supervise y aclare cualquier duda sobre el contexto. Mientras los estudiantes repasan los problemas, pregunte: "¿Hay alguna palabra que no os resulte familiar o sobre la que tengáis dudas?"
Avances: Lectura, representación
INTRODUCCIÓN
ACTIVIDAD
• Grupos de 2
• "Tómate un minuto para repasar estos problemas. ¿Qué representaciones o estrategias podrían serte útiles para resolver estos problemas?"
• 1 minuto: tiempo para pensar en silencio
• Comparte y registra las respuestas.
• "Ahora practicarás escribiendo tus propias ecuaciones con un símbolo para la incógnita"
• "Trabaja con tu compañero para resolver cada problema"
• 8-10 minutos: tiempo de trabajo en pareja
ACTIVIDAD CONTINUACIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES:
SÍNTESIS DE LA ACTIVIDAD
Grado 3 . Matemáticas . Unidad 1
• Circule y considere las siguientes preguntas para centrar a los estudiantes en la estructura de las situaciones:
• "¿Qué información falta en la situación?"
• "¿Cómo podrías representar esta situación?"
Resuelva cada problema. Explica o muestra tu razonamiento.
1. Clara tiene 16 calcetines. Los pone en montones de 2 ¿Cuántos montones puede hacer?
2. Diego tiene 8 montones de calcetines. Cada montón de calcetines tiene 2 calcetines. ¿Cuántos calcetines tiene Diego?
3. André tiene 16 calcetines. Los pone en 8 grupos del mismo tamaño. ¿Cuántos calcetines hay en cada grupo?
4. La tienda tiene 9 cajas. Cada caja tiene 5 camisas. ¿Cuántas camisas hay?
5. Una tienda tiene 80 jerséis. Hay 8 jerséis en cada pila de una estantería. ¿Cuántas pilas de jerséis hay en la estantería?
1. 8 pilas. Respuesta de ejemplo:

2. 16 calcetines. Respuesta de ejemplo: Son 8 grupos de 2. He contado los montones de dos como 2, 4, 6, 8, 10, 12, 14, 16.
3. 2 calcetines. Respuesta de muestra:

4. 45 camisas. Respuesta de muestra: 5 + 5 = 10, 10 + 10 = 20, 20 + 20 = 40. Son 8 cajas. Una más es 40 + 5 = 45
5. 10 pilas. Respuesta de muestra: 80 = ? × 8. Sé que 10 × 8 = 80 es 80. Así que 10 grupos de 8 deben ser 80.
1. Comparta el trabajo de los estudiantes para cada problema y pídales que expliquen su razonamiento. Asegúrese de compartir una variedad de estrategias y representaciones. 2. Mientras los estudiantes comparten, considere preguntar a la clase:
• "¿Por qué tiene sentido esta estrategia?"
• "¿Por qué tiene sentido esta representación?"
• "¿Alguien resolvió este problema de una manera diferente?"
• "¿Qué notan que es lo mismo sobre las representaciones y estrategias que estamos usando para resolver estos problemas?"
10 minutos
"Hoy hemos resuelto problemas de multiplicación utilizando cualquier estrategia o representación que hayamos querido."
"¿Qué estrategia o representación te resulta más útil cuando resuelves este tipo de problemas? ¿Por qué?" (A mí me gusta dibujar grupos iguales para poder ver cuántos grupos hay y cuántos hay en cada grupo. Creo que es mejor dibujar un diagrama porque no tengo que dibujar todas las cosas, pero puedo ver los grupos. Me gusta usar una ecuación para poder ver dónde está el número desconocido).
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

"¿Cuáles son las cosas más importantes que hay que recordar cuando se resuelven problemas de multiplicación?". (Siempre hay grupos del mismo tamaño. Podrías buscar el número de grupos, cuántas cosas hay en cada grupo o el número total de cosas en todos los grupos).
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
minutos
Resuelve cada problema. Explica o muestra tu razonamiento.
1. Hay 4 cajas. Cada caja tiene 10 juguetes. ¿Cuántos juguetes hay?
2. Elena tiene 10 calcetines. Ella los pone en pilas de 2 ¿Cuántas pilas hace?
1. 40 juguetes. Respuesta de muestra:
2. 5 pilas. Respuesta de ejemplo: 10 = ? × 2 Sé que 5 × 2 es 10.
Resumen de la sección del estudiante
En esta sección, aprendimos sobre grupos iguales. Creamos dibujos y diagramas para representar situaciones que involucran grupos iguales.
Situación
Diego tiene 8 montones de calcetines. Cada pila de calcetines tiene 2 calcetines.

Escribimos expresiones y ecuaciones de multiplicación para representar grupos iguales. expresión

8 × 2 ecuación
8 × 2 = 16
Aprendimos que los números que se multiplican se llaman factores y que el número que resulta de multiplicar se llama producto. En la ecuación 8 × 2 = 16, los números 8 y 2 son los factores y 16 es el producto.
Reflexiones:
Learning Inc. - Todos los derechos reservados


IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.OA.1 Interpretar productos de números enteros.
Construir
2.OA.4
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1
I.B.5
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo e inciden en el futuro buscan y hacen uso de la estructura explorando cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo organizar objetos en arreglos.
• Puedo explicar cómo los arreglos se relacionan con la multiplicación y los grupos iguales.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Construir arreglos con objetos físicos y describirlos en términos de multiplicación.
• Describir un arreglo como un arreglo de objetos en filas con un número igual de objetos en cada fila y en columnas con un número igual en cada columna.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
En cursos anteriores, los estudiantes vieron ejemplos de matrices, como 10-marcos, y contaron objetos dispuestos en matrices. ¿Cómo apoya esa experiencia previa su trabajo con grupos iguales en matrices en esta lección?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Notar y maravillarse (Calentamiento)
Materiales a reunir
Conectar cubos
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 2:
• Cada grupo de 2 necesita 60 cubos.
Grado 3 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Hagamos algunas matrices.
Narrativa de la lección
En segundo grado, los estudiantes conocieron los arreglos y los relacionaron con expresiones de suma y ecuaciones. En esta lección, los estudiantes profundizan su comprensión de los arreglos a medida que organizan objetos físicos y relacionan los arreglos con la multiplicación y los grupos iguales. Los estudiantes utilizan cubos de conexión para representar arreglos en la Actividad 2 y en el enfriamiento.
Al trabajar con situaciones de arreglos, los estudiantes pueden ver los grupos iguales en un arreglo ya sea en las filas o en las columnas. Por ejemplo, al representar 3 filas de 5 sillas, pueden crear una matriz 3 por 5 o una matriz 5 por 3. Esto está bien siempre y cuando los estudiantes puedan describir correctamente dónde están las "3 filas de 5 sillas" en su matriz. Los estudiantes aprenderán sobre la conmutatividad en la última lección de esta sección, así que si surgen preguntas sobre la conmutatividad, anótalas públicamente para discutirlas en esa lección.
Componente de la lección Estructura Tiempo
Calentamiento Parejas 10 min.
Actividad de exploración 1 Parejas 15 min.
Actividad de exploración 2 Parejas 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional

Math Nation California - Grado 3
Descripción breve
Los estudiantes hacen observaciones sobre objetos dispuestos en una matriz del mundo real.
Los estudiantes comparan la disposición de puntos en grupos iguales en un dibujo con la disposición de los mismos puntos en una matriz y luego explican si ambas disposiciones muestran grupos iguales.
Los estudiantes utilizan cubos para construir matrices y luego explican cómo se relacionan con grupos iguales.
Los estudiantes resumen cómo se pueden organizar los cubos en matrices.
Los estudiantes construyen un arreglo con cubos y luego explican cómo el arreglo se relaciona con la multiplicación.
Dirección:
• Capturar cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
• Cinco en raya: Multiplicación (3-5), Etapa 1: Factores 1-5 y 10
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Observación y asombro
El objetivo de este calentamiento es suscitar las ideas que los estudiantes tienen sobre los objetos dispuestos en una matriz, que serán útiles cuando los estudiantes organicen grupos iguales en matrices en una actividad posterior. Aunque los estudiantes pueden observar y preguntarse muchas cosas sobre esta imagen, las ideas sobre la disposición y los grupos iguales son los puntos de debate importantes. Cuando los estudiantes se fijan en la disposición de los huevos, buscan y utilizan la estructura (MP7).
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 2
• Mostrar la imagen.
• "¿Qué observas? ¿Qué te sorprende?"
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Comparte y registra las respuestas.
¿Qué notas? ¿Qué te preguntas?
Los estudiantes pueden observar:
• Hay 12 huevos.
• Hay 2 grupos de 6
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
• Veo 6 grupos de 2. Los estudiantes pueden preguntarse:
• ¿Cuántos huevos habría en dos cartones?
• ¿Hay otros grupos iguales que no veo?
• "¿Cómo te ayuda tener los huevos en un cartón a ver grupos iguales?" (Puedo ver cómo se podrían dividir en grupos iguales. Puedo ver 6 huevos en cada fila. Puedo ver 6 grupos de 2.)
• "Los huevos están dispuestos en una matriz. Una matriz es una disposición de objetos en filas y columnas. Cada columna debe contener el mismo número de objetos que las otras columnas, y cada fila debe tener el mismo número de objetos que las otras filas."
Grado 3 . Matemáticas . Unidad 1
IGUALES Y MATRICES 15 minutos
El objetivo de esta actividad es que los estudiantes describan una matriz como una disposición de objetos en filas con un número igual de objetos en cada fila y en columnas con un número igual en cada columna. Esto será útil en la siguiente actividad, cuando los estudiantes organicen los objetos en matrices y describan las matrices en términos de multiplicación.
Cuando los estudiantes decidan si están o no de acuerdo con Noah en ver grupos iguales en la matriz y expliquen su razonamiento, construirán un argumento viable y criticarán el razonamiento de los demás (MP3).
• Grupos de 2
• Muestre las imágenes.
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "Considere estos dibujos. A la izquierda hay un dibujo que muestra grupos iguales. A la derecha hay un conjunto. ¿En qué se parecen los dibujos? ¿En qué se diferencian?" (Parecidos: Ambos tienen 20 puntos. Ambos tienen grupos de 5. Diferentes: Los puntos están dispuestos de forma diferente. El segundo grupo tiene los puntos en filas. El primer dibujo tiene los puntos en círculos.)
• 1-2 minutos: tiempo para pensar en silencio
• Comparte y anota las respuestas.
• "Trabaja con tu compañero para describir cómo la disposición de los puntos en una matriz afecta a cómo ves el número."
• 2-3 minutos: tiempo de trabajo en pareja
• Comparte las respuestas.
• "Lee lo que Noé dice sobre los puntos y decide si estás de acuerdo o en desacuerdo. Prepárate para compartir tu razonamiento."
• 1 minuto: tiempo de trabajo independiente
• "Ahora discute si estás de acuerdo o en desacuerdo con Noah con tu compañero."
• 2-3 minutos: discusión por parejas
1. ¿Cómo afecta la disposición de los puntos en una matriz a cómo ves el número?
2. Noah dice que ve grupos iguales en el dibujo con 4 círculos y 5 puntos en cada círculo, pero dice que no hay grupos iguales en la matriz. ¿Estás de acuerdo con Noah? Explica tu razonamiento.
1. Ejemplo de respuesta: La matriz permite ver diferentes números dentro de los 20, como 2 grupos de 10 o 5 grupos de 4.
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Math Nation California - Grado 3
2. Respuesta de muestra: No, hay 5 puntos en cada fila, así que cada fila es un grupo igual.
• "¿Cómo se relacionan las matrices con los grupos iguales?" (Hay el mismo número de puntos en cada fila, por lo que las filas son grupos iguales. Hay el mismo número de puntos en cada columna, por lo que las columnas son grupos iguales).
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
20 minutos
Materiales a reunir
Cubos conectores

Preparación requerida
Cada grupo de 2 necesita 60 cubos.
El propósito de esta actividad es que los estudiantes construyan matrices con objetos físicos y describan las matrices en términos de multiplicación. Los estudiantes se centran en dónde pueden verse grupos iguales en las matrices. En futuras lecciones, los estudiantes escribirán expresiones y ecuaciones para representar matrices. En la actividad, se pide a los estudiantes que creen diferentes matrices con 24 cubos. No es una expectativa del grado 3 que los estudiantes encuentren todos los arreglos para un número dado.
Cuando los estudiantes notan que las filas o columnas en un arreglo tienen el mismo número de objetos y relacionan esto con grupos iguales, buscan y hacen uso de la estructura (MP7).
Mantenga los cubos conectores fuera para el enfriamiento.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Cree una presentación visual de las distintas matrices creadas por los estudiantes. A medida que los estudiantes discutan cada matriz, anote la visualización con el lenguaje utilizado, como "matriz", "filas", "columnas" y "grupos iguales".
Avances: Hablar, representar
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE LA TAREA
RESPUESTAS POSIBLES
• Grupos de 2
Representación: Interiorizar la comprensión. Síntesis: Invite a los estudiantes a identificar a qué es importante o más útil prestar atención. Muestre el marco de la frase: "La próxima vez que ordene objetos en una matriz, me acordaré de..."
Apoya la accesibilidad para: Procesamiento conceptual, Procesamiento visual-espacial, Memoria
• Entregue a cada grupo de 2 estudiantes al menos 60 cubos de conexión.
• 7-10 minutos: tiempo de trabajo en pareja
• Supervise a los estudiantes que relacionan el mismo número de objetos en cada fila y columna de una matriz con la forma en que la multiplicación expresa grupos iguales de objetos.
1. Utilice cubos para formar 6 grupos de 5
• Organícelos en una matriz.
• Explica o muestra cómo se relaciona la matriz con los grupos de ecuaciones.
2. Cuenta 20 cubos.
• Organízalos en una matriz.
• Explica o muestra cómo se relaciona la matriz con los grupos de ecuaciones.
3. Cuenta 24 cubos.
• Organícelos en un arreglo.
• Explique o muestre cómo se relaciona el arreglo con los grupos de ecuaciones.
1. Los estudiantes pueden organizar los cubos en un arreglo 5 por 6, 6 por 5, 3 por 10, 10 por 3, 15 por 2, o 2 por 15
Ejemplo de respuesta: El array está relacionado con la multiplicación porque hay 5 en cada fila, que es como tener grupos iguales, y eso es lo que representa la multiplicación.
Grado 3 . Matemáticas . Unidad 1

RESPUESTAS
POSIBLESS
CONTINUACIÓN
SÍNTESIS DE LA ACTIVIDAD
1. Los estudiantes pueden ordenar los cubos en un conjunto 2 por 10, 10 por 2, 5 por 4, o 4 × 5.
Respuesta de ejemplo: El array está relacionado con la multiplicación porque veo 2 cubos en cada fila. Las filas son como grupos iguales.
2. Los estudiantes pueden ordenar los cubos en una matriz 4 por 6, 6 por 4, 3 por 8, 8 por 3, 12 por 2, o 2 por 12
Ejemplo de respuesta: El array está relacionado con la multiplicación porque veo 4 cubos en cada columna. Las columnas son como grupos iguales.
1. Pida a los estudiantes que compartan los diferentes arreglos que hicieron para el último problema.
2. "¿Por qué pudiste crear diferentes arreglos con 24 objetos?" (Hay muchas maneras de poner 24 cosas en grupos iguales.)
10 minutos
"Hoy organizamos objetos en matrices y describimos cómo las matrices se relacionan con los grupos iguales."
"¿En qué pensaste cuando organizaste cubos en matrices?" (Repartí los cubos en grupos iguales y luego los organicé en un arreglo. Pensé en grupos iguales que podría usar para hacer el total e hice de cada grupo una fila con el mismo número de cosas en cada fila. Los ordené hasta que hubo el mismo número de cubos en cada fila y el mismo número de cubos en cada columna).
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Reflexiones:
5 minutos
Organice 12 cubos en un arreglo. Explique o muestre cómo el arreglo está relacionado con la multiplicación.
Ejemplo de respuesta: Está relacionado con la multiplicación porque hay 4 cubos en cada fila, que es como 3 grupos iguales.
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
3.OA.1 Interpretar productos de números enteros.
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
Estándares CA ELD
I.A.3
I.B.5 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo atienden a la precisión explorando cantidades cambiantes.
• Puedo crear un arreglo para representar grupos iguales y explicar cómo se relaciona con la multiplicación.
METAS DE APRENDIZAJE PARA EL MAESTRO
• El propósito de esta lección es que los estudiantes relacionen los arreglos con dibujos de grupos iguales y describan los arreglos en términos de multiplicación.
PREGUNTA DE REFLEXIÓN PARA EL MAESTRO
¿Qué pregunta desearías haber formulado hoy? ¿Cuándo y por qué deberías haberla hecho?
DE LA LECCIÓN
Rutinas didácticas
¿Cuál no pertenece? (Calentamiento)
Materiales para reunir
Cubos de conexión o fichas
Materiales para copiar
Listas para ordenar tarjetas
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 1:
• Crea un juego de tarjetas a partir del patrón de líneas negras para cada grupo de 2 o 4 estudiantes.
Grado 3 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Emparejemos matrices con grupos iguales y dibujemos matrices.
Narrativa de la lección
Los estudiantes primero emparejan matrices con dibujos de grupos iguales. Luego, redibujan dibujos de grupos iguales como matrices. El trabajo de esta lección se conecta con las lecciones siguientes cuando los estudiantes representen arreglos con expresiones y ecuaciones. Ponga cubos o fichas de conexión a disposición de los estudiantes que los necesiten.
Siga recopilando las ideas que surjan sobre la conmutatividad.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo

Descripción breve
Calentamiento Parejas 10 min. Los estudiantes explican qué disposición de puntos no pertenece.
Actividad de exploración 1 Parejas o Grupos pequeños 20 min.
Actividad de exploración 2 Pares 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes emparejan matrices con dibujos de grupos iguales que representan el mismo número y luego justifican sus emparejamientos.
Los estudiantes dibujan matrices para representar disposiciones de puntos y luego explican cómo se relaciona cada matriz con la multiplicación.
Los estudiantes repasan cómo dibujar una matriz para representar grupos iguales.
Los estudiantes dibujan un arreglo para representar un diagrama de grupos iguales y luego explican cómo se relacionan el arreglo y los grupos iguales.
Dirección:
• Capturar cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
• Cinco en raya: Multiplicación (3-5), Etapa 1: Factores 1-5 y 10
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
¿Cuál no pertenece?
El propósito de este calentamiento es que los estudiantes comparen cuatro arreglos de puntos para elicitar los atributos, o estructura, de un arreglo. Da a los estudiantes un motivo para utilizar el lenguaje con precisión (MP6). Da al maestro la oportunidad de escuchar cómo los estudiantes utilizan la terminología y hablan de las características de los elementos en comparación unos con otros. Durante la síntesis, pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como filas, esquinas, grupos y matriz.
• Grupos de 2
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Muestre la imagen.
• "Elige uno que no pertenezca. Prepárate para compartir por qué no pertenece."
• 1 minuto: tiempo para pensar en silencio
• "Discute tu pensamiento con tu compañero."
• 2-3 minutos: discusión en pareja
• Comparte y registra las respuestas.
¿Cuál no pertenece?
RESPUESTAS POSIBLES
• A es el único en el que los grupos iguales no están en línea recta.
• B es el único en el que los grupos iguales y los puntos de los grupos iguales no están siempre uno al lado del otro.
• C es el único en el que los grupos iguales no están organizados en filas.
• D es el único que no tiene 15 puntos.
Learning Inc. - Todos los derechos reservados
SÍNTESIS DE LA ACTIVIDAD

Grado 3 . Matemáticas . Unidad 1
• "¿Por qué B no es una matriz?" (Tiene el mismo número de puntos en cada fila, pero no el mismo en cada columna. Una de las columnas solo tiene 3 puntos. Falta la 3ª fila.)
• Considera preguntar:
• "Encontremos al menos una razón por la que cada uno no pertenece."
20 minutos
Rutinas didácticas
Ordenar tarjetas
MLR1 Cada vez más fuerte y más claro
Materiales a reunir
Ordenar tarjetas matrices
Preparación necesaria
Crea un conjunto de tarjetas a partir del patrón de líneas negras para cada grupo de 2 o 4 estudiantes.
El objetivo de esta actividad es que los estudiantes relacionen dibujos de grupos iguales con matrices. En concreto, los estudiantes buscan matrices que tengan el mismo número de objetos en cada fila o columna que el que tiene cada dibujo en cada grupo. En algunas matrices, los grupos iguales del dibujo se representan en filas y, en otras, en columnas. Los estudiantes tienen la oportunidad de explicar las conexiones que ven entre los dibujos y las matrices, recibir comentarios de sus compañeros y revisar su explicación para que sea más precisa y clara (MP3, MP6). Esto será útil en futuras lecciones cuando los estudiantes registren expresiones de multiplicación y ecuaciones para representar matrices.
Esta actividad utiliza MLR1 Cada vez más fuerte y más claro. Avances: lectura, escritura.
Apoyo para estudiantes con discapacidad
Engagement: Desarrollar el esfuerzo y la persistencia. Divida esta tarea en partes más manejables. Dé a los estudiantes un subconjunto de tarjetas para empezar y presente las tarjetas restantes una vez que los estudiantes hayan completado su serie inicial de emparejamientos.
Apoya la accesibilidad para: Atención, Organización
INTRODUCCIÓN
ACTIVIDAD
Math Nation California - Grado 3
• Grupos de 2 o 4
• Distribuya un juego de tarjetas precortadas a cada grupo de estudiantes.
• "Este juego de tarjetas incluye dibujos de grupos y matrices iguales. Relaciona cada dibujo con una matriz. Trabaja con tu compañero para justificar tus elecciones."
• 8 minutos: tiempo de trabajo en pareja
• "Elige independientemente una correspondencia que hayáis hecho tú y tu compañero. Escribe cómo sabes que el dibujo coincide con la matriz."
• 2 minutos: tiempo de trabajo independiente
MLR1 Cada vez más fuerte y más claro
• "Comparte con tu compañero tu respuesta a por qué tus tarjetas coinciden. Túrnense para hablar y para escuchar. Si eres el orador, comparte tus ideas y lo que has escrito hasta ahora. Si eres el oyente, haz preguntas y da tu opinión para ayudar a tu compañero a mejorar su trabajo."
• 3-5 minutos: debate estructurado entre compañeros
• Repite con 2-3 compañeros diferentes.
• "Revisa tu borrador inicial basándote en la opinión que recibiste de tus compañeros."
• 2-3 minutos: tiempo de trabajo independiente
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. Empareja el dibujo de grupos iguales y matrices que sean semejantes. Prepárate para explicar tu razonamiento.
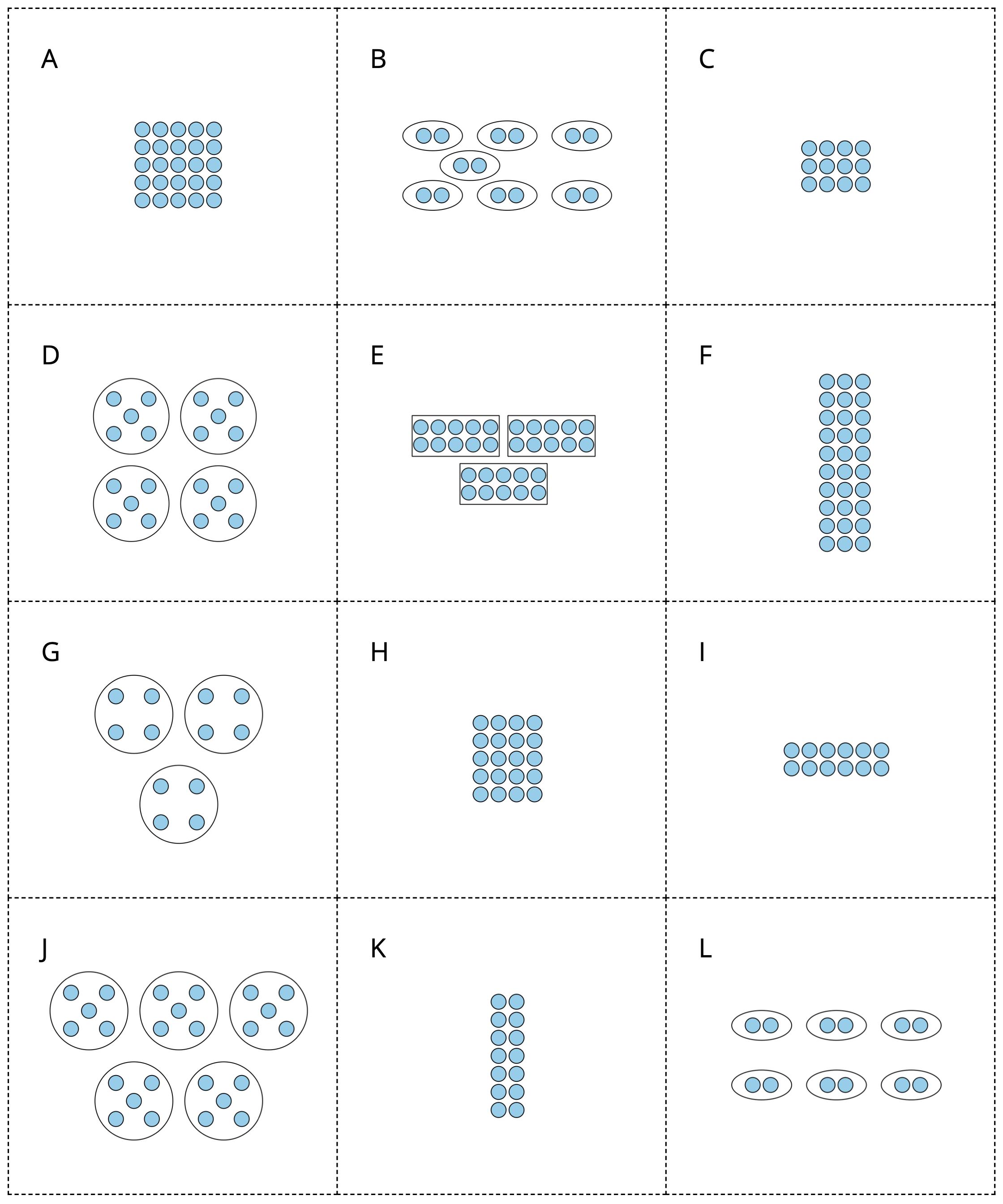
2. Elige un emparejamiento que hayáis hecho tú y tu compañero. Escribe cómo sabes que el dibujo coincide con esa matriz.
1.
RESPUESTAS POSIBLESS
• A y J
• B y K
• C y G
• D y H
• E y F
• I y L
2. Ejemplo de respuesta: I y L coinciden porque la matriz tiene 2 puntos en cada columna y el dibujo tiene 2 puntos en cada grupo. Además, el dibujo tiene 6 grupos y la matriz tiene 6 columnas. Ambos tienen 12 puntos.
SÍNTESIS DE LA ACTIVIDAD

Grado 3 . Matemáticas . Unidad 1
• Pida a los estudiantes que compartan las combinaciones que han hecho y que describan cómo saben que esas cartas van juntas. En esta actividad sería útil disponer de cubos o fichas para que los estudiantes los reordenen físicamente.
• "¿Se ha puesto de acuerdo tu grupo sobre las combinaciones? (Sí, buscamos grupos iguales que tuvieran el mismo número de puntos en un grupo que en una de las filas de la matriz).
• Preste atención al lenguaje que utilizan los estudiantes para describir sus parejas y la estructura de las matrices. Cuando sea necesario, pregunte:
• "¿Qué quieres decir con ?"
• "¿Qué otra cosa podríamos llamar ?"
• "¿Cómo podrías usar 'grupos iguales' para explicar tu emparejamiento?"
• Resalte el uso de términos como fila, columna y grupos iguales.
15 minutos
Materiales para reunir
Cubos o fichas de conexión
El objetivo de esta actividad es que los estudiantes dibujen matrices a partir de una disposición dada de puntos. Los estudiantes dibujan una matriz a partir de puntos en grupos iguales para reforzar la definición de matriz y, a continuación, dibujan tantas matrices como puedan a partir de 16 puntos colocados al azar.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Para apoyar la discusión en parejas, muestre los siguientes marcos de oraciones: "This array matches the diagram because...", y "This array shows multiplication because..."
Avances: Conversar, representar
INTRODUCCIÓN
• Grupos de 2
• Dé a los estudiantes acceso a cubos de conexión o fichas.
• "Trabaja de forma independiente para dibujar una forma en que el primer grupo de puntos del problema 1 podría organizarse en una matriz"."
• 2 minutos: tiempo de trabajo independiente
• "Discute con tu compañero cómo organizaste tus puntos y cómo el arreglo se relaciona con la multiplicación"
• 1 minuto: discusión en parejas
ACTIVIDAD
Math Nation California - Grado 3
• "¿Cómo reorganizaste los puntos para hacer un arreglo?" (Como había 3 en cada grupo, puse 3 puntos en cada fila. Vi 2 grupos de 6, así que hice 2 filas de 6.)
• Considera preguntar:
• "¿Alguien creó un arreglo diferente?"
• "Ahora vas a hacer tantos arreglos como puedas a partir de 16 puntos."
• 2-3 minutos: tiempo de trabajo independiente
• "Comparte con tu compañero cómo reorganizaste los puntos en arreglos. A ver si se os ocurre alguna otra disposición"
• 3-5 minutos: trabajo en parejas
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1.
A. Dibuje una forma en la que los puntos se pueden reorganizar en una matriz.
B. Explique o muestre cómo se relaciona la matriz con la multiplicación. 2.
A. Dibuja maneras de reorganizar los puntos en una matriz. Dibuja tantas como puedas.
B. Explique o muestre cómo se relaciona la matriz con la multiplicación.
RESPUESTAS POSIBLES
SÍNTESIS DE ACTIVIDAD
1. Ejemplos de respuestas:
A. Matriz de 4 x 3, matriz de 3 x 4, matriz de 6 x 2, matriz de 2 x 6
B. La matriz muestra multiplicación porque cada fila tiene 3 puntos, que es un grupo igual.
2. Ejemplos de respuestas:
A. Matriz de 2 x 8, matriz de 8 x 2, matriz de 4 x 4
B. La matriz muestra multiplicación porque cada columna tiene 2 puntos, que es un grupo igual.
• “¿Qué tipos de grupos iguales hiciste con 16 puntos? ¿Cómo puedes ver los grupos iguales en las matrices que hiciste?” (Puedo hacer 2 grupos de 8. Lo dibujé como 2 filas de 8 puntos).
10 minuts
Hoy hicimos dibujos que mostraban cómo los grupos de puntos se podían reorganizar en matrices.
¿Qué hay que tener en cuenta al dibujar una matriz? (Asegúrate de que las filas y las columnas tengan el mismo número de puntos. Haz que el número de grupos sea igual al número de columnas o filas de la matriz y luego dibuja cuántos hay en cada grupo de cada columna o fila. Se deben usar todos los puntos).
Grado 3 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES
Reflexiones:
1. Vuelve a dibujar los grupos iguales como una matriz.
2. Describe cómo se relacionan el diagrama y la matriz.
1. Ejemplo de respuesta: Los estudiantes crean una matriz 4 × 5, 5 × 4, 2 × 10, o 10 × 2
2. Respuesta de ejemplo: Hay 5 puntos en cada grupo y hay 5 puntos en cada fila. Hay 4 grupos y hay 4 filas. Ambos tienen 20 puntos.
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
3.OA.1 Interpretar productos de números enteros.
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo razonan abstracta y cuantitativamente explorando cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo crear una matriz y escribir una expresión para representar una situación de multiplicación.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Representar situaciones de multiplicación con matrices y expresiones de multiplicación.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
En una próxima lección, los estudiantes aprenderán sobre la propiedad conmutativa de la multiplicación. ¿Qué observas en su trabajo de la lección de hoy que podrías aprovechar en esa futura lección?
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
¿Cuántos ves? (Calentamiento)
Materiales para reunir
Cubos de conexión o fichas
Objetivos de aprendizaje para el estudiante
• Representemos situaciones con arreglos y expresiones.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes representen situaciones de multiplicación con arreglos y expresiones de multiplicación.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
En una lección anterior, los estudiantes organizaron objetos en matrices y describieron las matrices en términos de grupos iguales. En esta lección, los estudiantes escriben expresiones para representar matrices para conectar aún más las matrices y la multiplicación (MP2).
A medida que los estudiantes conectan matrices con expresiones, pueden escribir 3 × 5 o 5 × 3 para representar 3 filas de 5 sillas. Esto está bien siempre que los estudiantes puedan describir correctamente dónde están las "3 filas de 5 sillas" en su matriz o expresión. Siga recogiendo las ideas que surjan sobre la conmutatividad.
RESUMEN DE LA LECCIÓN
Componente de la lección
Calentamiento Pares 10 min.
Actividad de exploración 1 Pares 20 min.
Actividad de exploración 2 Pares 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes explican cómo determinar el número de triángulos en una imagen.
Los estudiantes crean matrices y luego escriben expresiones de multiplicación para representar situaciones de multiplicación.
Los estudiantes dibujan matrices que representan expresiones de multiplicación.
Los estudiantes discuten cómo su comprensión de los grupos iguales les ayuda a crear matrices y escribir expresiones para representar situaciones de multiplicación.
Los estudiantes representan una situación de multiplicación usando un arreglo y una expresión.
Abordar:
• Capturar cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
• Cinco en raya: Multiplicación (3-5), Etapa 1: Factores 1-5 y 10

Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
¿Cuántos ves?
El propósito de este Cuántos ves es que los estudiantes subitiicen o utilicen estrategias de agrupación para describir las imágenes que ven. Cuando los estudiantes utilizan la estructura de la matriz para averiguar cuántos objetos se muestran, buscan y hacen uso de la estructura (MP7).
• Grupos de 2
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• "¿Cuántos ves? ¿Cómo los ves?"
• Imagen flash.
• 30 segundos: tiempo para pensar en silencio
• Mostrar imagen.
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Registrar respuestas.
¿Cuántos ves? ¿Cómo los ves?
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Ejemplos de respuestas:
• 20: Vi 4 grupos de 5 o 5 grupos de 4.
• 20: Veo 2 grupos de 10 o 10 grupos de 2
• "¿Cómo te ayudó ver los grupos iguales a saber cuántos triángulos había en la matriz?"
• Considere preguntar:
• "¿Quién puede replantear la forma en que vio los triángulos con palabras diferentes?"
• "¿Alguien vio los triángulos de la misma forma pero lo explicaría de manera diferente?"
Grado 3 . Matemáticas . Unidad 1
Materiales a reunir
Cubos de conexión o fichas

20 minutos
Preparación necesaria
Cada grupo de 2 necesitará 20 cubos de conexión o fichas.
El propósito de esta actividad es que los estudiantes representen situaciones de multiplicación con matrices y expresiones de multiplicación. Los estudiantes deben tener la opción de utilizar herramientas matemáticas, como fichas o cubos conectores, para crear las matrices antes de dibujarlas. La conexión de situaciones, matrices y expresiones refuerza la idea de que la multiplicación se puede utilizar para expresar el número total de objetos en grupos iguales (MP2).
MLR2 Collect and Display. Ampliar el lenguaje utilizado para describir matrices. En una pantalla visible, registre palabras, frases y expresiones como: fila, columna, cada, para cada, 3 por 5, 5 por 3, 5 × 3, y 3 × 5. Incluya diagramas y anotaciones. Invite a los estudiantes a tomar prestado el lenguaje de la pantalla según sea necesario y actualícelo a lo largo de la lección.
Avances: Representar, leer, hablar
INTRODUCCIÓN
ACTIVIDAD
Math Nation California - Grado 3
• Grupos de 2
Representación: Interiorizar la comprensión. Haga visibles las conexiones entre las representaciones. Invite a los estudiantes a utilizar gestos o dibujos mientras describen verbalmente las correspondencias entre sus matrices y expresiones. Por ejemplo, "El 4 en mi expresión 4 × 5, muestra el número de filas, y el 5 muestra que hay 5 coches en cada fila."
Apoya la accesibilidad para: Procesamiento conceptual, Memoria
• Dé a los estudiantes acceso a cubos de conexión o fichas.
• Muestre la primera situación.
• "Tómense un minuto para representar esta situación con una matriz. Puedes utilizar dibujos u objetos."
• 2 minutos: tiempo de trabajo independiente
• "Discute tus ideas con tu compañero."
• 2 minutos: discusión en pareja
• Comparte las respuestas. Destaque las formas en que los estudiantes utilizaron grupos iguales para crear sus matrices.
• "Trabaja con tu compañero para representar las siguientes tres situaciones con una matriz. Prepárate para compartir cómo ves los grupos iguales en tu matriz."
• 5 minutos: tiempo de trabajo en pareja
• Haz que los estudiantes compartan una matriz para los problemas 2-4. Intenta mostrar tanto dibujos como matrices. Intente mostrar tanto dibujos como matrices hechas con objetos.
• "¿Cómo veis los grupos iguales en vuestras matrices?" (Las filas pueden mostrar el número de grupos, y luego se pone el número que hay en cada grupo a lo largo de la fila).
• Muestre de nuevo la primera situación.
• "Volvamos a la primera situación. ¿Qué expresión de multiplicación representaría esta situación?"
• 30 segundos: tiempo para pensar en silencio
• Comparte las respuestas. Haga hincapié en cómo los estudiantes utilizan grupos iguales para escribir la expresión.
• "Trabaja con tu compañero para escribir expresiones de multiplicación para las otras tres situaciones."
• 2 minutos: tiempo de trabajo en pareja
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
Utilice objetos o dibujos para representar cada situación con una matriz.
1. Hay 3 filas de sillas. Cada fila tiene 5 sillas.
2. Hay 4 filas de coches. Cada fila tiene 5 coches.
3. Hay 2 filas de huevos. Cada fila tiene 6 huevos.
4. Hay 2 equipos de estudiantes en fila. Cada equipo tiene 10 estudiantes. Escribe una expresión de multiplicación para representar cada situación.
1. 3 por 5 o 5 por 3 matriz dibujada o construida, 3 × 5 o 5 × 3
2. 4 por 5 o 5 por 4 matriz dibujada o construida, 4 × 5 o 5 × 4
3. 6 por 2 o 2 por 6 array dibujado o construido, 2 × 6 o 6 × 2
4. 10 por 2 o 2 por 10 array dibujado o construido, 2 × 10 o 10 × 2
• "¿Cómo usaste grupos iguales para escribir tu expresión de multiplicación?" (Pensé en cuántos grupos había en la situación y luego cuántas cosas había en cada grupo. Por ejemplo, sé que 2 equipos de 10 estudiantes es 2 grupos de 10, así que puedo escribir 2 × 10.)
CON EXPRESIONES 15 minutos
El objetivo de esta actividad es que los estudiantes apliquen sus conocimientos de actividades anteriores para dibujar matrices que coincidan con expresiones de multiplicación. Disponga de cubos conectores o fichas para los estudiantes que los necesiten. En el Introducción, los estudiantes utilizan sus cuerpos para hacer un arreglo para la expresión 4 × 6. Siéntete libre de ajustar esta expresión para que se adapte mejor al número de estudiantes de tu clase.
• Grupos de 2
• Muestra 4 × 6
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS
POSIBLESS
• "Trabajen juntos como clase para usar sus cuerpos para crear una matriz para esta expresión de multiplicación."
• Si el número de estudiantes no coincide exactamente con el producto, pida a los estudiantes adicionales que controlen la matriz y estén preparados para explicar dónde ven partes de la expresión en la matriz.
• 3-5 minutos: tiempo de trabajo de toda la clase
• "Trabaja con tu compañero para dibujar una matriz para cada expresión de multiplicación. Prepárate para compartir las conexiones que observes entre las expresiones de multiplicación y las matrices."
• 2-3 minutos: tiempo de trabajo por parejas
Dibuja una matriz para cada expresión de multiplicación. Prepárate para compartir tu razonamiento.
1. 2 × 3
2. 5 × 2
3. 4 × 4
1. 3 por 2 o 2 por 3 matriz
2. 2 por 5 o 5 por 2 matriz
3. 4 por 4 matriz
AVANZANDO EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD

Grado 3 . Matemáticas . Unidad 1
Si los estudiantes dibujan grupos iguales que no son matrices, considere preguntar:
• "¿Cómo usaron la expresión para crear su dibujo?"
• "¿Cómo podríamos reorganizar su dibujo en una matriz?"
• Comparte una o dos matrices para cada expresión.
• "¿Qué conexiones vieron tú y tu compañero entre las expresiones de multiplicación y las matrices?" (Los factores nos dicen cuántas cosas hay en cada fila y columna. Para 2 × 3, dibujamos una matriz con 2 columnas que tienen 3 cosas en cada columna. Para 2 × 3, dibujamos una matriz con 2 filas que tienen 3 cosas en cada fila.)
10 minutos
Muestre una situación de la primera actividad, y una matriz y una expresión que represente la situación.
"Aprendimos que la multiplicación es la forma en que expresamos el número total de objetos en grupos iguales."
"¿Cómo te ayudó tu conocimiento de los grupos iguales a crear arreglos y escribir expresiones para situaciones de multiplicación?" (Pensé en cuántos grupos había y dibujé los grupos como cada fila [o columna]. Entonces el número de grupos me dice cuántas filas [o columnas] hay. El array y la expresión representan el número total de objetos del problema).
5 minutos
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Hay 2 filas de plantas. Cada fila tiene 5 plantas.
1. Dibuja una matriz para representar la situación.
2. Escribe una expresión para representar la situación.
1. Ejemplo de respuesta:
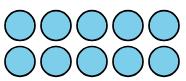
2. 2 × 5 o 5 × 2
Respondiendo al pensamiento de los estudiantes
Los estudiantes no escriben una expresión de multiplicación que coincida con la matriz que crearon.
Apoyo para el día siguiente
• Utilice el Introducción de la actividad del día siguiente para que los estudiantes discutan cómo escribir una expresión que represente un arreglo.
Reflexiones:
Math
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica hasta 100 para las cuatro operaciones
• Patrones en cuatro operaciones
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
3.OA.1 Interpretar productos de números enteros.
3.OA.3 Usar la multiplicación y la división dentro de 100 para resolver problemas de palabras en situaciones que involucren grupos iguales, arreglos y cantidades medidas.
3.OA.9 Identificar patrones aritméticos (incluyendo patrones en la tabla de sumas o en la tabla de multiplicación) y explicarlos usando propiedades de las operaciones.
Enfoque SMPs
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.1
I.B.5
II.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo y predecir lo que podría ocurrir buscar y expresar regularidad en razonamientos repetidos explorar cantidades cambiantes.
• Puedo representar una situación de matriz con una ecuación de multiplicación y usar un símbolo para el valor desconocido.
• Puedo describir la relación entre ecuaciones de multiplicación y matrices.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Representar una situación de matriz con una ecuación con un símbolo para el número desconocido.
• Resolver problemas de multiplicación que involucren matrices.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿Quién ha compartido sus ideas en clase últimamente? Toma nota de los estudiantes cuyas ideas no hayan sido compartidas y busca una oportunidad para que compartan su pensamiento en la lección de mañana.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Charla sobre números (calentamiento)
MLR5 Preguntas de co-creación (Actividad 1)
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
Metas de aprendizaje para el estudiante
• Resolvamos problemas que involucren arreglos.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes representen una situación de arreglo usando una ecuación con un símbolo para el número desconocido y resuelvan.
En lecciones anteriores, los estudiantes representaron situaciones de multiplicación usando arreglos y expresiones de multiplicación con énfasis en grupos iguales. Los grupos iguales continúan siendo enfatizados en esta lección a medida que los estudiantes aprenden que encontrar el producto en una ecuación de multiplicación da el número total de objetos en el arreglo relacionado.
A medida que los estudiantes conectan los arreglos con las ecuaciones, pueden escribir 3 × 5 = 15 o 5 × 3 = 15 para representar 3 filas de 5 sillas. Esto está bien siempre que los estudiantes puedan describir correctamente dónde están las "3 filas de 5 sillas" en su matriz o ecuación. Siga recogiendo las ideas que surjan sobre la conmutatividad.
Componente de la lección

Estructura Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 En parejas 25 min.
Actividad de exploración 2 Parejas 10 min.
Síntesis Grupo completo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Descripción breve
Los estudiantes calculan mentalmente expresiones de multiplicación y luego describen las estrategias que utilizaron para encontrar los productos.
Los estudiantes resuelven un problema de multiplicación y luego representan la situación con una matriz y una ecuación con un símbolo para el valor desconocido.
Los estudiantes escriben y resuelven ecuaciones de multiplicación con un símbolo para el valor desconocido que representan situaciones de multiplicación.
Los estudiantes discuten cómo las ecuaciones con símbolos para valores desconocidos pueden representarse en matrices.
Los estudiantes representan una situación de multiplicación con una ecuación usando un símbolo para el valor desconocido y luego determinan la solución.
Abordar:
• Capturar cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
• Cinco en raya: Multiplicación (3-5), Etapa 1: Factores 1-5 y 10
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Conversación sobre números
El propósito de esta Charla sobre números es obtener estrategias y conocimientos que los estudiantes tienen sobre grupos iguales en expresiones de multiplicación y ver un patrón a medida que se disminuye un factor. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de usar la multiplicación para responder preguntas sobre situaciones de conjuntos.
Cuando los estudiantes notan que a medida que el número que se multiplica por 2 disminuye, el producto disminuye en un grupo de 2, buscan y expresan regularidad en razonamientos repetidos (MP8).
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• Muestre una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste".
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada expresión.
• 10 × 2
• 9 × 2
• 20: 2 grupos de 10 es 20
• 18: Conté por 2 (2, 4, 6, 8, 10, 12, 14, 16, 18).
• 8 × 2
• 7 × 2
• 16: Conté por 2 o es un grupo de 2 menos que la última ecuación.
• 14: Conté por 2 o es un grupo de 2 menos que la última ecuación.
• "¿Qué notas sobre los productos a medida que trabajamos en esta serie de problemas?" (Disminuyen en 2.)
• "¿Por qué el producto disminuye en 2 cada vez?" (El número de grupos disminuyó en 1.)
25 minutos
Rutinas didácticas
MLR5 Preguntas de Co-elaboración
El propósito de esta actividad es que los estudiantes usen la rutina de lenguaje matemático Co-craft para escribir preguntas que se pueden hacer sobre situaciones de matrices y para relacionar situaciones de matrices con ecuaciones. Se anima a los estudiantes a utilizar cualquier estrategia o representación que consideren adecuada. Dadas sus experiencias previas, pueden representar la situación con una matriz y saltar la cuenta o considerar grupos iguales de otras maneras para encontrar el total.
Esta actividad utiliza MLR5 Preguntas de co-creación. Avances: escribir, leer, representar.
INTRODUCCIÓN

Grado 3 . Matemáticas . Unidad 1
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• Grupos de 2
MLR5 Preguntas co-elaboradas
• "Mantenga sus libros cerrados."
• Visualice: "Hay 7 filas".
• "Escribe una lista de preguntas matemáticas que podrían hacerse sobre esta situación". (¿Qué hay en las filas? ¿Cuántas cosas hay en cada fila? ¿Cuántas cosas hay en total?)
• 2 minutos: tiempo de trabajo independiente
• 2-3 minutos: discusión por parejas
• Invite a varios estudiantes a compartir una pregunta con la clase. Anote las respuestas.
• "¿Qué tienen en común estas preguntas? ¿En qué se diferencian?" (Todas tienen que ver con las filas. Tienen que ver con más detalles sobre las filas, como qué hay en las filas y cuántos hay en cada fila.)
• Revele la tarea (los estudiantes abren los libros), e invite a realizar conexiones adicionales.
• "Completa el primer problema resolviendo esta situación de cualquier manera que tenga sentido para ti."
• 3-4 minutos: tiempo de trabajo independiente
• 1-2 minutos: discusión en parejas
• Comparte una variedad de representaciones y estrategias de solución de los estudiantes.
• "Piensa en la situación que hemos estado considerando. ¿Cómo podrías representar la situación utilizando una ecuación con un símbolo para la incógnita?"
• 2 minutos: tiempo para pensar en silencio
• "Comparte tu ecuación con tu compañero. Juntos, reescribid la ecuación con la solución que habéis encontrado en lugar del símbolo."
• 2 minutos: trabajo en pareja
Hay 7 filas. Cada fila tiene 5 lápices de colores. ¿Cuántos lápices de colores hay?
1. Resuelve este problema. Explica o muestra tu razonamiento.
2. Representa la situación con una matriz y una ecuación con un símbolo para la incógnita.
1. Ejemplo de respuesta: Hay 35 crayones porque conté por 5.
2. Un arreglo 7 por 5 o un arreglo 5 por 7 7 × 5 = ? o 5 × 7 = ?
• "¿Qué ecuación(es) escribiste?"
• Muestre una ecuación con un símbolo y una con la solución.
• "¿Cómo se conecta cada parte de la ecuación con la situación?" (El 7 es el número de filas. El 5 es el número de crayones en cada fila. El 35 representa el número total de crayones, pero era un signo de interrogación cuando no sabíamos cuántos había).
TYLER 10 minutos
El propósito de esta actividad es que los estudiantes escriban una ecuación con un símbolo para la incógnita que represente una situación de matriz. Luego, responden la pregunta en la situación de multiplicación. Anime a los estudiantes a utilizar cualquier estrategia o representación que les parezca adecuada. Dadas sus experiencias previas, podrían representar la situación con una matriz y omitir el conteo o considerar grupos iguales de otras maneras para encontrar el total.
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

En el Introducción de la actividad, puede ser útil pedir a los estudiantes que cuenten a su compañero una historia rápida o que hagan alguna pregunta sobre el contexto del primer problema. Para garantizar que todos los estudiantes tengan acceso, también puede ser útil mostrarles imágenes de referencia sobre los cocoteros o México.
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Si es necesario, invite a los estudiantes a repetir su pregunta utilizando lenguaje matemático. Por ejemplo: "¿Puedes repetirlo utilizando la palabra array?"
Avances: Escuchar, Hablar
Apoyo a Estudiantes con Discapacidad
Acción y Expresión: Desarrollar la Expresión y la Comunicación. Actividad: Invita a los estudiantes a mostrar su pensamiento utilizando cubos conectores o fichas.
Apoya la accesibilidad para: Procesamiento Conceptual
ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Grupos de 2
• Mostrar la imagen.
• "Los cocoteros se cultivan en climas cálidos y tienen muchos usos. A veces se cultivan en hileras. ¿Cuáles son otros cultivos que se dan en hileras?" (Maíz. Fresas. Zanahorias.)
• "Ahora vas a practicar lo que acabamos de aprender sobre resolver situaciones de conjuntos y escribir una ecuación con un símbolo para la incógnita."
• 5-7 minutos: tiempo de trabajo independiente
• Mientras circulas, considera preguntar:
• "¿Cómo se conecta cada número o símbolo en tu ecuación con la situación?"
• "¿Cómo estás usando grupos iguales para encontrar la solución al problema?"
• "Comparte tu estrategia con tu compañero. Haz cualquier pregunta que tengas sobre las ideas de tu compañero."
• 2 minutos: discusión entre compañeros
Para cada problema:
• Escribe una ecuación con un símbolo para la incógnita que represente la situación.
• Resuelve el problema. Muestra tu razonamiento.
1. Un campo de cocoteros en México tiene 5 filas de árboles. Cada hilera tiene 9 árboles. ¿Cuántos árboles hay?
2. Después de aprender sobre el cultivo de cocos en México, Tyler quiere plantar cocoteros en su patio de Florida. Su madre solo le deja plantar 2 filas de 4 árboles en su patio. ¿Cuántos árboles plantará Tyler?
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
1. Ecuación con incógnita: 5 × 9 = o 9 × 5 = . Solución: 45 árboles. Ejemplo de respuesta: Conté de cinco en cinco 9 veces. 5, 10, 15, 20, 25, 30, 35, 40, 45
2. Ecuación con incógnita: 2 × 4 = ? o 4 × 2 = ? Solución: 8 árboles. Ejemplo de respuesta: Sé que 2 grupos de 4 es 8
• "¿Qué preguntas tienes todavía sobre la resolución de problemas de conjuntos o la escritura de una ecuación con un símbolo para la incógnita?"
Grado 3 . Matemáticas . Unidad 1
10 minutos
Muestra la información del primer problema de la Actividad 2. Un campo de cocoteros en México tiene 5 filas de 5 × 9 = ? 5 × 9 = 45 árboles.
Cada fila tiene 9 árboles. ¿Cuántos árboles hay?
"¿Cómo representa cada una de estas ecuaciones la situación de la matriz?" (La ecuación con el símbolo representa las 5 filas de árboles y los 9 árboles de cada fila en la situación anterior a que supiéramos que había 45 árboles. La ecuación con el 45 incluye la solución al problema porque había 45 árboles.)
Considera preguntar: "¿Qué representa en la situación el signo de interrogación de la primera ecuación? ¿Qué representa en la situación el 45 de la segunda ecuación?".
5 minutos
Clare tiene 3 filas de tarjetas de béisbol. Cada fila tiene 10 tarjetas. ¿Cuántas cartas tiene?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. Escribe una ecuación con un símbolo para el número desconocido para representar la situación.
2. Encuentra el número que hace que la ecuación sea verdadera. Explica o muestra tu razonamiento.
1. 3 × 10 = ? o 10 × 3 = ?
RESPUESTAS POSIBLES
2. 30. Ejemplo de respuesta: 30 porque 3 filas de 10 es 10, 20, 30
Respondiendo al pensamiento de los estudiantes
Los estudiantes escriben una ecuación que no usa un símbolo para el número desconocido.
Apoyo para el día siguiente
• Antes del calentamiento, haga que los estudiantes discutan cómo pueden representar el problema con una ecuación antes de conocer la solución, y cómo pueden representar el problema con una ecuación una vez que conocen la solución.
Reflexiones:
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica para 100 para las cuatro operaciones
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
3.OA.5 Aplicar propiedades de las operaciones como estrategias para multiplicar y dividir.
Construir
2.NBT.5
Construyendo hacia
3.NBT.2
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.3
I.C.12
II.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo e inciden en el futuro
buscan y hacen uso de la estructura explorando cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo escribir 2 ecuaciones que representan el mismo arreglo.
• Puedo usar arreglos para describir la propiedad conmutativa de la multiplicación.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Describir la propiedad conmutativa de la multiplicación usando arreglos.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿Qué parte de la lección ha ido realmente bien hoy en términos de aprendizaje de los estudiantes? ¿Qué has hecho para que esa parte haya ido bien?
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
Charla sobre números (calentamiento)
MLR1 Cada vez más fuerte y claro (Actividad 2)
Objetivos de aprendizaje para el estudiante
• Aprendamos sobre la propiedad conmutativa.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes describan la propiedad conmutativa de la multiplicación usando arreglos.
En lecciones anteriores, los estudiantes usaron dibujos de grupos iguales y arreglos para representar situaciones de multiplicación. También relacionaron expresiones y ecuaciones de multiplicación
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 3 . Matemáticas . Unidad 1
a estas representaciones. En esta lección, se presenta a los estudiantes la propiedad conmutativa. Los estudiantes se darán cuenta de que el mismo producto puede representarse mediante diferentes situaciones, matrices o ecuaciones. Reorganizar las matrices o invertir el orden de los factores en una expresión de multiplicación no cambia el número total de objetos. Es importante que los estudiantes relacionen sus ecuaciones con las situaciones y representaciones correspondientes. Deben ser capaces de explicar correctamente lo que representa cada factor y el producto en sus ecuaciones.
Tenga en cuenta que no se espera que los estudiantes utilicen el nombre de la propiedad. Sin embargo, deben ser capaces de basarse en su comprensión conceptual de la multiplicación para explicar por qué el producto no cambia cuando cambia el orden de los factores.
Componente de la lección

Estructura
Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1
Pares 20 min.
Actividad de exploración 2 Pares 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Descripción breve
Los estudiantes encuentran mentalmente las diferencias de números dentro de 100
Los estudiantes exploran la propiedad conmutativa comparando y estableciendo conexiones entre situaciones de matrices y ecuaciones que representan matrices con el mismo valor total.
Los estudiantes escriben dos ecuaciones de multiplicación para representar un conjunto dado y luego explican por qué ambas ecuaciones representan el conjunto.
Los estudiantes discuten informalmente la propiedad conmutativa examinando cómo el orden de los factores en una ecuación de multiplicación o la disposición de filas y columnas en una matriz no cambia el producto o el número total de objetos.
Los estudiantes demuestran su comprensión resumiendo lo que han aprendido de la lección sobre la multiplicación.
Abordar:
• Capturar cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
• Cinco en raya: Multiplicación (3-5), Etapa 1: Factores 1-5 y 10
Math Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1
10 minutos

Rutinas didácticas
Conversación sobre números
El propósito de esta Charla sobre Números es obtener estrategias y comprensiones que los estudiantes tienen para restar dentro de 100. También brinda una oportunidad para observar las estrategias de los estudiantes a medida que trabajan para adquirir fluidez en la suma dentro de 1.000
Cuando los estudiantes usan estrategias basadas en el valor posicional para restar, buscan y hacen uso de la estructura (MP7).
• Muestre una expresión.
INTRODUCCIÓN
ACTIVIDAD
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste".
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra el valor de cada expresión mentalmente.
• 70 - 10
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• 68 - 10
• 70 - 12
• 68 - 12
• 60: Siete decenas menos 1 decena sería 6 decenas, que es 60
• 58: Es como el primero, pero el número al que le estás restando es 2 menos, así que la diferencia sería 2 menos.
• 58Este es como el primer problema, pero estás restando 2 más de 70, así que en lugar de 60, sería 58.
• 56: Es como el primer problema, pero estás empezando con 2 menos y tomando 2 más, así que sería 4 menos que la primera respuesta. Resté decenas de decenas y unidades de unidades y terminé con 5 decenas y 6 unidades.
• "¿Cómo te ayudó el valor posicional a encontrar la diferencia en estos problemas?" (Primero resté las decenas y luego ajusté mi respuesta cada vez. Resté decenas de decenas y unidades de unidades.)
• Considere preguntar:
• "¿Quién puede replantear el razonamiento de de una manera diferente?"
• "¿Alguien tuvo la misma estrategia pero la explicaría de manera diferente?"
• "¿Alguien abordó el problema de una manera diferente?"
• "¿Alguien quiere agregar algo a la estrategia de ?"
Grado 3 . Matemáticas . Unidad 1
20 minutos
El propósito de esta actividad es introducir la propiedad conmutativa. Los estudiantes escriben situaciones de matrices para un par de matrices y discuten las similitudes y diferencias. Aunque las situaciones tendrán el mismo número total de objetos, la forma de agruparlos será diferente. A continuación, los estudiantes escriben ecuaciones para las matrices y las situaciones, y establecen conexiones entre las representaciones (MP2). Los estudiantes observan que, aunque cambia el orden de los factores en la ecuación de multiplicación, el producto no cambia (MP7).
Apoyo para estudiantes que aprenden inglés
MLR8 Discussion Supports. Síntesis: Crear una presentación visual de las ecuaciones y las matrices correspondientes. A medida que los estudiantes describen sus conexiones entre las ecuaciones y las situaciones, anote la visualización para ilustrar las conexiones. Por ejemplo, debajo de cada número, escriba filas, columnas o total.
Avances: Hablar, representar

Apoyo para estudiantes con discapacidad
Representación: Acceso para la percepción. Los estudiantes pueden beneficiarse de la oportunidad de observar una demostración que muestre la agrupación de puntos en las matrices. Por ejemplo, prepare una visualización de la Imagen A y la Imagen B mostrando solo los puntos. A continuación, invite a los estudiantes a que observen cómo usted rodea los grupos según corresponda.
Apoya la accesibilidad para: Procesamiento conceptual, Procesamiento visual-espacial
INTRODUCCIÓN
ACTIVIDAD
Math Nation California - Grado 3
• Grupos de 2
• Visualiza la imagen.
• "¿Qué notas? ¿Qué te preguntas?" (Los estudiantes pueden observar: Ambos grupos de puntos están dispuestos como matrices. Ambos tienen 10 puntos. Una matriz tiene grupos de 2. Una matriz tiene grupos de 5. Los estudiantes pueden preguntarse ¿Por qué los puntos están agrupados de forma diferente? ¿Son las matrices iguales?)
• 1 minuto: tiempo de reflexión en silencio
• "Comenta lo que has pensado con tu compañero"
• 1 minuto: debate en pareja
• Comparte y anota las respuestas.
• "Analicemos estas dos matrices con más detalle. Escribe una situación para cada matriz."
• 3-5 minutos: tiempo de trabajo independiente
• "Comparte tus situaciones con tu compañero. Juntos, consideren cómo las situaciones que escribieron para el primer arreglo son iguales y diferentes de las situaciones que escribieron para el segundo arreglo."
• 3 minutos: tiempo de trabajo en pareja
• "¿Qué era igual y qué era diferente en las situaciones que escribieron?"
• Compartan las respuestas.
• "Ahora, escribe una ecuación para cada situación que acabas de escribir para que coincida con las matrices."
• 1 minuto: tiempo de trabajo independiente
• "Comparte tus ecuaciones con tu compañero y discute cómo cada número en tus ecuaciones se conecta con tus situaciones y la matriz."
• 2 minutos: discusión en pareja
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
¿Qué observa? ¿Qué te preguntas?
Imagen A
1.
A. Escribe una situación de matriz para cada matriz.
Imagen A
Imagen B
B. ¿En qué se parecen las situaciones? ¿En qué se diferencian?
Ejemplos de respuestas: 1.
RESPUESTAS POSIBLES
2.
SÍNTESIS DE LA ACTIVIDAD
Imagen B
A. Escribe una ecuación para cada situación.
Imagen A
Imagen B
B. ¿Cómo se relaciona tu ecuación con la situación y el array?
Imagen A
Imagen B
A. Hay 2 filas de estudiantes. Cada fila tiene 5 estudiantes. Hay 5 grupos de estudiantes. Cada grupo tiene 2 estudiantes. o Hay 2 bolsas con 5 manzanas en cada bolsa. Hay 5 bolsas con 2 manzanas en cada bolsa.
B. La primera situación es 2 filas de 5, pero la segunda situación es 5 columnas de 2 Ambas situaciones describen 10 objetos.
A. 2 × 5 = 10 y 5 × 2 = 10
B. Las 5 y las 2 se intercambian en la segunda ecuación igual que se intercambian las filas y las columnas. El producto es el mismo.
• "Escribamos las ecuaciones que se nos ocurrieron."
• Muestra 2 × 5 = 10 y 5 × 2 = 10
• "¿Cómo se conecta cada uno de los números en las ecuaciones con la situación que escribiste?" (5 es el número de columnas en una situación, pero es cuántos puntos hay en cada fila en la otra situación. 2 es el número de grupos en una situación, pero es cuántos hay en cada grupo en la otra situación. 10 es el número total de objetos en ambas situaciones.)
15 minutos
Rutinas didácticas
MLR1 Cada vez más fuerte y más claro
El propósito de esta actividad es reforzar la idea de la propiedad conmutativa. En esta actividad, los estudiantes escriben dos ecuaciones que se ajustan a un arreglo para mostrar nuevamente que invertir el orden de los factores no cambia el producto. Si los estudiantes no ven inmediatamente cómo podrían escribir ecuaciones diferentes para la matriz, anímelos a considerar diferentes formas de agrupar los puntos en la matriz, de forma similar a la actividad anterior. Los estudiantes utilizan el vocabulario que han aprendido para describir matrices y multiplicaciones para explicar por qué ambas ecuaciones corresponden a una matriz con su compañero. La rutina "Cada vez más fuerte y más claro" permite a los estudiantes recibir comentarios y revisar su explicación para que sea más clara (MP3, MP6).
Grado 3 . Matemáticas . Unidad 1
Si los estudiantes terminan antes, considere la posibilidad de dibujar otra matriz. Pida a los estudiantes que escriban dos ecuaciones para el array y que consideren cómo pueden pensar en las filas o columnas como grupos iguales. Esta actividad utiliza MLR1 Cada vez más fuerte y más claro. Avances: lectura, escritura
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE LA TAREA PARA EL ALUMNO
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
• Grupos de 2
• "Habla con tu compañero sobre ecuaciones que podrían representar este array."
• 1 minuto: discusión en pareja
• "Escribe dos ecuaciones para este array. Si te sirve de ayuda, puedes imaginarte agrupando los puntos como en la actividad anterior. Luego escribe por qué ambas ecuaciones pueden representar el array."
• 5 minutos: tiempo de trabajo independiente
1. Escribe 2 ecuaciones de multiplicación que representen el array.
2. Explique por qué ambas ecuaciones pueden representar el arreglo.
1. 3 × 6 = 18 y 6 × 3 = 18
2. Ejemplo de respuesta: Ambas ecuaciones pueden representar el mismo arreglo porque podríamos pensar en el arreglo mostrando 6 grupos de 3 o 3 grupos de 6. Si pensamos en las columnas como grupos de 3, hay 6 de los grupos. Si pensamos en las filas como grupos de 6, hay 3 de los grupos. En cualquier caso, la matriz tiene 18 puntos, por lo que ambas ecuaciones tienen un total de 18
• "Escribamos las ecuaciones que se nos ocurrieron".
• Muestra las ecuaciones 3 × 6 = 18 y 6 × 3 = 18
MLR1 Cada vez más fuerte y más claro
• "Comparte con tu compañero por qué ambas ecuaciones pueden representar la matriz. Túrnense para hablar y para escuchar. Si eres el orador, comparte tus ideas y lo que has escrito hasta ahora.
• 3-5 minutos: debate estructurado por parejas.
• Repite con 2-3 parejas diferentes.
• "Revisa tu borrador inicial basándote en los comentarios que recibiste de tus compañeros"
• 2-3 minutos: tiempo de trabajo independiente
• Haz que los estudiantes compartan las revisiones que hicieron a su borrador inicial.
10 minutos
Muestra una matriz 3 por 4 y las ecuaciones 3 × 4 = 12 y 4 × 3 = 12
"(El orden de los factores no cambia el producto ni el número total de objetos en el arreglo o la situación). Relacionar los números de las ecuaciones con matrices y situaciones ayuda a aclarar lo que significa cada número).
Muestra 3 × 4 = 4 × 3
Math
Nation California - Grado 3
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Matemáticas . Unidad 1

"Como 3 × 4 = 12 y 4 × 3 = 12, podemos escribir 3 × 4 = 4 × 3."
"La idea de que podemos multiplicar dos números en cualquier orden y obtener el mismo producto se llama propiedad conmutativa."
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
5 minutos
Resume lo que aprendiste sobre la multiplicación hoy.
Ejemplo de respuesta: Si cambiamos el orden de los números que estamos multiplicando, obtenemos el mismo producto.
Resumen de la sección del estudiante
En esta sección, aprendimos cómo los grupos iguales están relacionados con los arreglos y cómo representar arreglos con expresiones y ecuaciones. dibujo de grupos iguales matriz expresión
3 × 5 ecuación
3 × 5 = 15
También aprendimos que podemos multiplicar números en cualquier orden y obtener el mismo producto. 3 × 5 = 15 5 × 3 = 15
Reflexiones:
Learning Inc. - Todos los derechos reservados


IDEA(S) FUNDAMENTAL(ES)
• Flexibilidad numérica hasta 100 para las cuatro operaciones
• Representar datos multivariables
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
3.MD.3 Dibujar un gráfico de imagen a escala y un gráfico de barras a escala para representar un conjunto de datos con varias categorías. Resolver problemas de uno y dos pasos de "cuántos más" y "cuántos menos" usando información presentada en gráficas de barras a escala.
3.OA.3 Usar multiplicación y división dentro de 100 para resolver problemas de palabras en situaciones que involucran grupos iguales, arreglos y cantidades medidas.
3.OA.4 Determinar el número entero desconocido en una ecuación de multiplicación o división que relaciona tres números enteros.
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP4 Representar con matemáticas.
Estándares CA ELD
I.A.2
I.C.11
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo y predicen lo que podría ocurrir representan con matemáticas explorando cantidades cambiantes.
• Puedo utilizar agrupaciones iguales para resolver problemas del mundo real.
• Puedo crear un gráfico de barras a escala para representar información sobre una situación del mundo real.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Tomar decisiones y hacer suposiciones.
• Representar datos usando gráficas de barras a escala para comunicar resultados.
• Resolver problemas del mundo real que involucren grupos iguales.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
¿Cómo ha ayudado la tarea de modelado a la colaboración entre los estudiantes?
Rutinas didácticas
Notar y maravillarse (calentamiento)
Materiales para reunir
Cubos o fichas para conectar
Baldosas de una pulgada
Herramientas para crear una exposición visual
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales para copiar
Papel cuadriculado centimétricoEstándar
Preparación requerida
Actividad 2:
• Cada estudiante necesita una hoja de papel cuadriculado.
Grado 3 . Matemáticas . Unidad 1
Metas de aprendizaje para el estudiante
• Planeemos una noche de juegos.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes utilicen su comprensión de grupos iguales para resolver un problema de diseño. Información de la lección
Esta lección es opcional porque no aborda ningún nuevo estándar de contenido matemático.
En las lecciones anteriores, los estudiantes crearon gráficos de barras a escala y resolvieron problemas que involucraban grupos iguales. En esta lección, utilizan estas ideas para organizar los asientos.
En primer lugar, los estudiantes examinan un diagrama que muestra grupos iguales y consideran las situaciones que podría representar. Al enterarse de que el diagrama representa una distribución de asientos, consideran la información necesaria para establecer la distribución de asientos para una noche de juegos. A continuación, los estudiantes planifican una disposición de los asientos teniendo en cuenta algunas restricciones -el número total de mesas de juego y una combinación de juegos que implican cada uno un determinado número de jugadores- y crean una pantalla para presentar su solución. Por último, los estudiantes crean un gráfico de barras a escala para representar el número de jugadores que pueden jugar a cada juego en su solución de asientos. A lo largo de la lección, los estudiantes dan sentido a los problemas y perseveran en su resolución (MP1).
Los estudiantes representan con matemáticas mientras definen cantidades y variables que son relevantes en la situación, comunican su solución y traducen una solución matemática de nuevo al contexto (MP4).
Componente de la lección Estructura Tiempo
Calentamiento En parejas 10 min.
Actividad de exploración 1 Por parejas o Grupos pequeños 25 min.
Actividad de exploración 2 Parejas o Grupos reducidos 10 min.
Síntesis Todo el Grupo 10 min.
Centro(s) sugerido(s) Grupos pequeños Opcional

Math Nation California - Grado 3
Descripción breve
Los estudiantes describen las cosas que observan y se preguntan sobre una imagen que incluye una disposición de cuadrados y círculos.
Los estudiantes crean y presentan una disposición de asientos con grupos iguales que cumpla unos requisitos dados.
Los estudiantes crean un gráfico de barras a escala para representar el número de jugadores de cada juego de la actividad anterior.
Los estudiantes discuten las decisiones que tomaron cuando crearon sus arreglos.
Dirección:
• Capturar cuadrados (1-3), Etapa 5: Multiplicar con 2, 5, y 10
• Cinco en raya: Multiplicación (3-5), Etapa 1: Factores 1-5 y 10
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Grado Matemáticas . Unidad 1
10 minutos
Rutinas didácticas
Observar y preguntarse
Este calentamiento tiene dos objetivos: suscitar observaciones sobre grupos iguales en la disposición de los asientos e identificar variables que pueden ser importantes a la hora de resolver un problema del mundo real en el que se da información limitada. Estas conversaciones preparan a los estudiantes para diseñar la distribución de los asientos teniendo en cuenta algunas limitaciones más adelante en la lección.
Durante la síntesis, destaque las observaciones sobre los grupos iguales y revele que la imagen muestra un diagrama de asientos. Pida a los estudiantes que identifiquen la información que podrían necesitar si tuvieran que encargarse de planificar la disposición de los asientos para una noche de juegos. A medida que los estudiantes plantean preguntas que les ayuden a reunir la información necesaria y a aclarar el problema, participan en aspectos de la modelización matemática (MP4).
• Grupos de 2
INTRODUCCIÓN

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• Muestra la imagen.
• "¿Qué observas? ¿Qué te preguntas?"
• 1 minuto: tiempo para pensar en silencio
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Comparte y registra las respuestas.
¿Qué notas? ¿Qué te preguntas?
RESPUESTAS POSIBLES
Los estudiantes pueden observar:
• Hay 6 cuadrados.
• Hay 4 círculos alrededor de cada cuadrado.
• Hay 24 círculos.
• Los cuadrados están dispuestos como una matriz con 2 filas y 3 cuadrados en cada fila.
Los estudiantes pueden preguntarse:
• ¿Por qué hay círculos alrededor de los cuadrados?
• ¿Hay algo dentro de los cuadrados?
• ¿Qué situación podría representar esto?
• ¿Los cuadrados representan mesas? ¿Los círculos representan sillas?
• ¿Es un tablero de juego?
Grado 3 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• "Alguien dibujó el diagrama para ilustrar una situación del mundo real. ¿Cuál podría ser esa situación?" (Disposición de las mesas. Tablero de juego. Disposición de los deportes.)
• "La imagen muestra la disposición de las mesas para una noche de juegos."
• "Si estuvieras a cargo de planificar la disposición de los asientos para una noche de juegos, ¿qué preguntas necesitarías hacer para tener suficiente información para planificar?" (¿Cuántas mesas hay? ¿Cuántas personas pueden jugar a cada juego? ¿Cuántas personas pueden sentarse en cada mesa? ¿Cuántas sillas hay? ¿Cuántos invitados asistirán a la noche de juegos? ¿De qué tamaño son las mesas?)
• Comparte y anota las respuestas. Mantén esto visible para la próxima actividad.
• "En la próxima actividad crearás un diagrama de asientos para una noche de juegos. Obtendrás respuestas a algunas de estas preguntas. Para otras preguntas, tendrás que tomar algunas decisiones."
Materiales para reunir
Cubos o fichas para conectar
Baldosas de pulgadas
Herramientas para crear una presentación visual
25 minutos
Materiales para copiar
Papel de cuadrícula centimétrica - Estándar
El objetivo de esta actividad es que los estudiantes planifiquen la disposición de los asientos. A los estudiantes solo se les da la información del número de jugadores necesarios para cada juego y el número total de mesas. Los números 2, 4, 5, y 10 se han elegido para reflejar el trabajo de multiplicación que los estudiantes han realizado en lecciones anteriores. Los estudiantes toman sus propias decisiones sobre otros aspectos de la situación antes de planificar su disposición de asientos y también eligen cómo representar su disposición de asientos (MP4).
Es posible que los estudiantes quieran respuestas del maestro antes de hacer la disposición. Anímeles a hacer sus propias suposiciones siempre que no contradigan la información dada.
Apoyo para estudiantes de inglés
MLR8 Discussion Supports. Aclare cualquier duda sobre el contexto. Dé a los estudiantes 1-2 minutos para leer y dar sentido a la tarea. Pregunte: "¿Hay alguna palabra con la que no estén familiarizados o sobre la que tengan dudas?"
Avances: Leer, representar
Math Nation California - Grado 3
Apoyo para estudiantes con discapacidad
Engagement: Desarrollar el Esfuerzo y la Persistencia. Diferencia el grado de dificultad o complejidad. Algunos estudiantes pueden beneficiarse de la oportunidad de completar la tarea con menos tipos de juego.
Apoya la accesibilidad para: Organización, Atención
• Grupos de 2 o 4
• Da a cada grupo herramientas para crear una presentación visual y acceso a fichas en pulgadas, papel cuadriculado y cubos o fichas de conexión.
• "La primera parte de la tarea responde a algunas de nuestras preguntas, como el número de personas necesarias para cada juego y el número total de mesas. Puedes decidir la información que no se da. En el póster que hagas, incluye la información que has supuesto y explica qué información nueva has obtenido como resultado. Incluye también cuántas personas pueden jugar en la sala con tu plan de asientos".
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Grado Matemáticas . Unidad 1

ACTIVIDAD
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
• 20 minutos: tiempo de trabajo en grupos pequeños
• Supervise a los grupos que:
• Describan sus suposiciones y expliquen cómo su suposición afectó el arreglo. Por ejemplo, si querían organizar 6 partidas del Juego A, entonces necesitan espacio para 12 personas.
• Hagan suposiciones sobre el número total de personas.
• "Trabaja con tu compañero para escribir expresiones de multiplicación para las otras tres situaciones"
• 2 minutos: tiempo de trabajo en pareja
Tu club está planeando una noche de juegos. Los invitados pueden jugar a uno de cuatro juegos diferentes que requieren un número distinto de jugadores:
• Juego A - 2 jugadores
• Juego B - 4 jugadores
• Juego C - 5 jugadores
• Juego D - 10 jugadores
La sala de juegos tiene 16 mesas cuadradas idénticas, en las que puede sentarse una persona a cada lado.
1. Haz un plan de asientos que muestre la disposición de las mesas para que cada invitado pueda jugar a uno de los juegos.
2. Haz un póster que incluya: A. un plano de asientos
B. una explicación sobre cómo decidiste tu plan de asientos C. cuántas personas pueden jugar en la sala con tu plan de asientos
Ejemplo de respuesta:
RESPUESTAS POSIBLES
AUMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES
Nos aseguramos de que hubiera mesas para cada juego. Utilizamos 4 mesas para el juego D, lo que nos dejó 12 mesas. Decidimos utilizar 4 mesas para cada uno de los otros juegos. Así que 8 personas podrían jugar al juego A, 16 personas podrían jugar al juego B, 10 personas podrían jugar al juego C, y 10 personas podrían jugar al juego D. Sumamos 8 + 16 + 10 + 10 para averiguar que 44 personas podrían jugar a juegos en la sala si utilizáramos esta distribución de asientos.
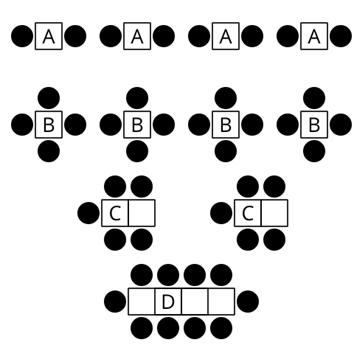
Si a los estudiantes les resulta difícil tomar decisiones sobre información desconocida, puede preguntarles:
• "Háblame de cómo has diseñado tu distribución de asientos hasta ahora"
• "¿Se da información en el problema sobre lo que estás eligiendo? ¿Qué opciones tienes sobre ? ¿Cómo afectaría a tu plano de asientos si ?"
SÍNTESIS DE LA ACTIVIDAD

Grado 3 . Matemáticas . Unidad 1
• Invite a los estudiantes previamente seleccionados a mostrar sus carteles para que todos los vean.
• "¿Qué nos dice este arreglo sobre la situación?" (Nos muestra cuántos de cada juego se juegan. Nos muestra cuántas personas pueden jugar a cada juego. Nos muestra cuántas personas pueden jugar a los juegos en la sala si está dispuesta así).
• "¿Qué expresión de multiplicación representa el número de personas que pueden jugar al juego A? B? C? D?"
10 minutos
Materiales para copiar
Papel cuadriculado de centímetros - Estándar
Materiales necesarios
Cada estudiante necesita una hoja de papel cuadriculado.
El objetivo de esta actividad es que los estudiantes representen sus planes para la noche de juegos en un gráfico de barras a escala. En la síntesis, los estudiantes consideran cómo su gráfico comunica información sobre su plan para la noche de juegos.
• Grupos de 2 o 4
• Entrega a cada estudiante papel cuadriculado.
INTRODUCCIÓN
ACTIVIDAD
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
• "Ahora vas a hacer un gráfico de barras a escala que muestre cuántas personas pueden jugar a cada juego con la disposición de tu sala."
• "Discutid qué escala utilizarán vuestros grupos para vuestro gráfico."
• 1 minuto: discusión en pequeños grupos
• "Podéis trabajar con vuestro grupo, pero cada uno de vosotros hará su propio gráfico. También pueden elegir una escala diferente a la del resto de su grupo."
• 5-7 minutos: tiempo de trabajo en grupos pequeños
Haz un gráfico de barras a escala que muestre el número de invitados que pueden jugar a cada uno de los juegos A, B, C y D.
Asegúrate de incluir:
• un título y otras etiquetas
• una escala que cuente por un número distinto de
Respuesta de ejemplo:
RESPUESTAS POSIBLESS
Math Nation California - Grado 3
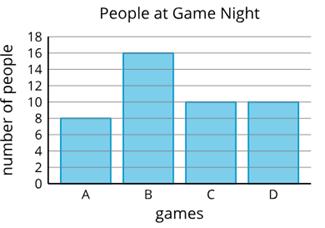
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 3 . Grado Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• Muestra los gráficos que utilizaron diferentes escalas.
• "¿Cómo afectó a los gráficos la elección de diferentes escalas?" (Algunos de los gráficos tienen barras más cortas porque cada salto en el gráfico vale más. Algunos de los gráficos son más fáciles de leer que otros.)
• "¿Qué información nos da este gráfico de barras sobre la situación?" (El número de personas en cada partido, los tipos de partidos. Podemos averiguar el número total de personas si los sumamos todos).
10 minutos
"Hoy hemos organizado los asientos basándonos en una información dada y en otras cosas que hemos decidido nosotros."
"¿Qué decisiones afectaron a tu organización? ¿Hubo alguna decisión que no afectó su arreglo?" (Decidimos que habría 2 de juegos A, B y C jugados al mismo tiempo. Esto afectó al número de personas que podían jugar al juego D.)
Reflexiones:
