




Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).
La plataforma de recursos curriculares en línea que se ofrece en "mathnation.com", incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.
La marca comercial "Math Nation" es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.
Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.
El trabajo con el área en 6.º grado se basa en el trabajo previo con la geometría y la medida geométrica. Los estudiantes empezaron a aprender sobre formas bidimensionales y tridimensionales en el jardín de infancia y continuaron este trabajo en 1.º y 2.º grado, componiendo, descomponiendo e identificando formas. El trabajo de los estudiantes con las medidas geométricas comenzó con la longitud y continuó con el área. Los estudiantes aprendieron a estructurar el espacio bidimensional, es decir, a ver un rectángulo con longitudes laterales de números enteros como compuesto por un conjunto de cuadrados unitarios o compuesto por filas iteradas o columnas iteradas de cuadrados unitarios. En 3.º grado, los estudiantes distinguen entre perímetro y área. Relacionaron el área de un rectángulo con la multiplicación, entendiendo por qué (para longitudes laterales enteras) multiplicando las longitudes laterales de un rectángulo se obtiene el número de cuadrados unitarios que forman el rectángulo. Utilizaron diagramas de área para representar casos de la propiedad distributiva. En 4.º grado, los estudiantes aplicaron las fórmulas de área y perímetro de rectángulos para resolver problemas matemáticos y de la vida real y aprendieron a utilizar transportadores. En 5.º grado, los estudiantes ampliaron la fórmula del área de rectángulos a rectángulos con lados de longitud fraccionaria.
En 6.º grado, los estudiantes amplían su razonamiento sobre el área para incluir formas que no están compuestas por rectángulos. Para ello, aprovechan las habilidades desarrolladas en grados anteriores para componer y descomponer formas, por ejemplo, para ver un rectángulo como compuesto de dos triángulos rectángulos congruentes. Mediante actividades diseñadas y secuenciadas para permitir a los estudiantes dar sentido a los problemas y perseverar en su resolución (MP1), los estudiantes aprovechan estas habilidades y su conocimiento de las áreas de los rectángulos para hallar las áreas de los polígonos descomponiéndolos y reordenándolos para hacer figuras cuyas áreas pueden determinar (MP7). Aprenden estrategias para hallar áreas de paralelogramos y triángulos, y usan la regularidad en razonamientos repetidos (MP8) para desarrollar fórmulas para estas áreas, usando propiedades geométricas para justificar la corrección de estas fórmulas. Utilizan estas fórmulas para resolver problemas. Comprenden que cualquier polígono puede descomponerse en triángulos y utilizan este conocimiento para hallar áreas de polígonos. Calculan las áreas de poliedros con superficies triangulares y rectangulares. Estudian, ensamblan y dibujan redes de poliedros y las utilizan para determinar sus áreas superficiales. A lo largo de todo el proceso, discuten sus ideas matemáticas y responden a las ideas de los demás (MP3, MP6).
Dado que los estudiantes de 6.º grado escribirán expresiones algebraicas y ecuaciones en las que interviene la letra X y Y se confunde fácilmente con x, estos materiales utilizan la notación «punto», por ejemplo: 2 ⋅, para la multiplicación en lugar de la «cruz», p. ej., 2 × La notación de punto será nueva para muchos estudiantes y necesitarán orientación explícita para utilizarla.
Grado 6 . Matemáticas . Unidad 1
Muchas de las lecciones de esta unidad piden a los estudiantes que trabajen con figuras geométricas que no están situadas en un contexto real. Esta elección de diseño respeta el importante trabajo intelectual que supone razonar sobre el área. Las tareas establecidas en contextos del mundo real que implican áreas de polígonos suelen ser artificiosas y dificultan la comprensión en lugar de ayudarla. Además, los contextos matemáticos son contextos legítimos que merecen ser estudiados. Al final de la unidad, los estudiantes tienen la oportunidad de abordar una aplicación en el mundo real (MP2, MP4).
En sexto grado es probable que los estudiantes necesiten herramientas físicas para comprobar que una figura es una copia idéntica de otra, donde «copia idéntica» se define de la siguiente manera:
Una figura es una copia idéntica de otra si se puede colocar una encima de la otra de manera que coincidan exactamente.
En octavo grado los estudiantes entenderán «copia idéntica de» como «congruente con» y comprenderán la congruencia en términos de movimientos rígidos, es decir, movimientos como la reflección, la rotación y la traslación. En 6.º grado, los estudiantes no tienen otra forma de comprobar la congruencia que la inspección, pero no es práctico recortar y apilar cada par de figuras que se ven. El papel de calco es una herramienta excelente para verificar que las figuras «coinciden exactamente» y los estudiantes deben tener acceso a esta y otras herramientas en todo momento en esta unidad. Por lo tanto, cada plan de lección sugiere que cada estudiante tenga acceso a un juego de herramientas de geometría, que contiene papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha para usar como regla o para marcar ángulos rectos. Proporcionar a los estudiantes estos juegos de herramientas les da la oportunidad de desarrollar habilidades para seleccionar las herramientas adecuadas y utilizarlas estratégicamente para resolver problemas (MP5). Tenga en cuenta que incluso los estudiantes en un aula mejorada digitalmente deben tener acceso a estas herramientas; las aplicaciones y simulaciones deben considerarse adiciones a sus juegos de herramientas, no reemplazos de herramientas físicas. En este grado, todas las figuras se dibujan y etiquetan de modo que las figuras que parecen congruentes realmente lo sean; en grados posteriores, cuando los estudiantes tengan las herramientas para razonar sobre figuras geométricas con mayor precisión, tendrán que aprender que la inspección visual no es suficiente para determinar la congruencia. Obsérvese también que todos los argumentos expuestos en esta unidad pueden (y deben) hacerse más precisos en grados posteriores, a medida que se profundiza en la comprensión geométrica de los estudiantes.
En esta unidad, los maestros pueden anticipar que los estudiantes utilizarán el lenguaje con fines matemáticos, como comparar, explicar y describir. A lo largo de la unidad, los estudiantes se beneficiarán de rutinas diseñadas para desarrollar un lenguaje disciplinar sólido, tanto para su propia construcción de sentido como para construir un entendimiento compartido con sus compañeros. Los maestros pueden evaluar formativamente cómo los estudiantes utilizan el lenguaje de estas maneras, en particular cuando los estudiantes utilizan el lenguaje para:
Comparar
• patrones y formas geométricas (lección 1)
• estrategias para finir áreas de formas (lección 3) y polígonos (lección 11)
• las características de prismas y pirámides (lección 13)
• las medidas y unidades de atributos de 1, 2 y 3 dimensiones (lección 16)
• representaciones de área y volumen (lección 17)
Explicar
• cómo hallar áreas componiendo (lección 3)
• estrategias utilizadas para hallar áreas de paralelogramos (lección 4) y triángulos (lección 8)
• cómo determinar el área de un triángulo con su base y altura (lección 9)
• estrategias para hallar áreas de superficie de poliedros (lección 14)
Describir
• observaciones sobre la descomposición de paralelogramos (lección 7)
• información necesaria para definir el área superficial de prismas rectangulares (lección 12)
• las características de los poliedros y sus redes (lección 13)
• las características de los poliedros (lección 15)
• relaciones entre las características de una tienda de campaña y la cantidad de tela necesaria para la tienda (lección 19)
Además, se espera que los estudiantes justifiquen afirmaciones sobre la base, la altura o el área de formas, generalicen sobre las características de paralelogramos y polígonos, interpreten información relevante para hallar el área superficial de prismas rectangulares y representen las medidas y unidades de figuras de 2 y 3 dimensiones. A lo largo de la unidad, los maestrps pueden apoyar la comprensión matemática de los estudiantes ampliando (no simplificando) el lenguaje utilizado para todos estos propósitos a medida que los estudiantes demuestran y desarrollan ideas.

California . Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

La tabla muestra las lecciones en las que se introduce por primera vez la nueva terminología, incluido cuándo se espera que los estudiantes comprendan la palabra o frase de forma receptiva y cuándo se espera que produzcan la palabra o frase en su propia expresión oral o escrita. Los términos del glosario aparecen en negrita. Los maestros deben seguir apoyando a los estudiantes en el uso de un término nuevo en las lecciones siguientes a aquella en la que se introdujo por primera vez.
Lección
Nueva terminología
Receptivo Productivo
6. Terminología de la lengua1.1 área región plano brecha
6.1.2 componer descomponer reordenar bidimensional
6.1.3 sombreado estrategia
6.1.4 paralelogramo opuesto (lados o ángulos) cuadrilátero
6.1.5
base (de un paralelogramo o triángulo) altura correspondiente expresión representar
6.1.6 horizontal vertical
6.1.7 idéntico paralelogramo
6.1.8
6.1.9 vértice opuesto (lados o ángulos) 1.9
base (de un paralelogramo o triángulo) altura componer descomponer reordenar
vértice opuesto
6.1.10 vértice arista
6.1.11 polígono horizontal vertical
6.1.12 cara superficie área región
6.1.13 poliedro red prisma pirámide base (de un prisma o pirámide) tridimensional polígono vértice arista cara
6.1.15 prisma pirámide
6.1.16 volumen apropiado cantidad bidimensional tridimensional
6.1.17 al cuadrado al cubo exponente longitud de arista
6.1.18 valor (de expresión)1.17

al cuadrado al cubo exponente longitud de arista
6.1.18 valor (de una expresión) al cuadrado al cubo neto
6.1.19 estimación descripción superficie volumen


Grado 6 . Matemáticas . Unidad 1
Enfoque en ideas fundamentales
• Graficar figuras
• Desarrollo plano y área de superficie
• Generalziaciones con representacionesmúltiples
ESTÁNDARES POR LECCIÓN
Lección
6.1.1
6.1.2

Estándar(es) abordado(s)
Prerrequisito para 6.G.1
Prerrequisito para 6.G.1
6.1.3 6.G.1
6.1.4 6.G.1
6.1.5
6.1.6
6.EE.2a, 6.EE.2c, 6.G.1
6.EE.2c, 6.G.1
6.1.7 6.G.1
6.1.8 6.G.1
6.1.9
6.EE.2a, 6.EE.2c, 6.G.1
6.1.10 6.EE.2c, 6.G.1
6.1.11 6.G.1
6.1.12 6.G.4
6.1.13 .1.13 6.G.4
6.1.14 6.G.4
6.1.15
6.G.2, 6.G.4
6.1.16 6.G.4
6.1.17
6.1.18
6.1.19
6.EE.1, 6.G.2
6.EE.1, 6.EE.2a, 6.G.2, 6.G.4
6.G.1, 6.G.4


IDEA(S) FUNDAMENTAL(ES)
• Graficar formas
• Redes y superficie
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP5 Usar herramientas apropiadas estratégicamente.
Estándares ELD de California
I.A.1
I.A.3
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dar sentido al mundo y predecir lo que podría ocurrir.
construir argumentos viables y argumentar sobre el razonamiento de los demás.
OBJETIVO(S) DE APRENDIZAJE
desmontan enteros, unir piezas y descubrir la forma y el espacio.
• Observar los patrones de teselado y pensemos en el área.
OBJETIVO(S) DE APRENDIZAJE
• Explicar el significado de área.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comparar (oralmente) las áreas de las formas que componen un patrón geométrico.
• Comprender que la palabra "área" (oralmente y por escrito) se refiere a la parte del plano que cubre una forma.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
¿Cuál no pertenece?
Anticipar, supervisar, seleccionar, secuenciar, conectar
Pensar, compartir en parejas
MLR2: Reunir y mostrar
Materiales necesarios
Enfriamiento
Materiales de geometría (papel vegetal, papel cuadriculado, lápices de colores, tijeras y una tarjeta índice).
PREPARACIÓN DE LA LECCIÓN (CONTINUACIÓN)
Preparación necesaria
Prepare los juegos de materiales de geometría (papel vegetal, papel cuadriculado, lápices de colores, tijeras y una tarjeta índice). Lo mejor sería que los estudiantes tuvieran acceso a estos materiales en todo momento a lo largo de la unidad. juegos de materiales incluyen papel vegetal, papel cuadriculado, lápices de colores, tijeras y una tarjeta índice para usar como regla o para marcar ángulos rectos.
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
Los estudiantes comienzan la primera lección del año escolar recordando lo que saben sobre área (tenga en cuenta que los estudiantes estudiaron las áreas de rectángulos con longitudes laterales de números enteros en tercer grado y con longitudes laterales fraccionarias en quinto grado). Las matemáticas que exploran no son complicadas, por lo que ofrecen un umbral de entrada bajo. Sin embargo, la lección pone de manifiesto dos ideas importantes:
• Si dos figuras pueden colocarse una encima de la otra de manera que coincidan exactamente, entonces tienen la misma área.
• El área de una región no cambia cuando la región se descompone y se reorganiza.
Al final de esta lección, se pide a los estudiantes que escriban su mejor definición de área. Es importante dejar que formulen su definición con sus propias palabras. En el caso de los estudiantes de inglés, es especialmente importante animarles a utilizar sus propias palabras y también las de sus compañeros. En la siguiente lección, los estudiantes retomarán la definición de área como el número de unidades cuadradas que cubren una región sin huecos ni solapamientos.
Como primer conjunto de problemas de un plan de estudios basado en problemas, los estudiantes también comenzarán su trabajo de un año sobre cómo dar sentido a los problemas y perseverar en su resolución (MP1). Esta lección de apertura deja espacio para que los maestroes comiencen a establecer las rutinas de clase y sus expectativas para el discurso matemático (MP3).
En todas las lecciones de esta unidad, los estudiantes deben tener acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), que deben contener papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha. Es posible que los estudiantes no necesiten todas (ni siquiera ninguna) de estas herramientas para resolver un problema concreto. Sin embargo, para tomar decisiones estratégicas sobre cuándo utilizar qué herramientas (MP5), los estudiantes deben tener la oportunidad de tomar esas decisiones. Las aplicaciones y las simulaciones deben complementar a las herramientas físicas, no sustituirlas.
Notas sobre terminología. En estos materiales, cuando hablamos de una figura como un rectángulo, un triángulo o un círculo, normalmente nos referimos al límite de la figura (por ejemplo, los lados del rectángulo), sin incluir la región interior. Sin embargo, también utilizamos un lenguaje abreviado como "el área de un rectángulo" para referirnos al "área de la región dentro del rectángulo". El término figura puede referirse a una figura con o sin su interior. Aunque los términos figura, región y forma se utilizan sin definirlos con precisión para los estudiantes, ayúdeles a comprender que a veces nos centramos en el límite (que en esta unidad siempre estará compuesto por segmentos de línea negra) y otras veces en la región interior (que en esta unidad siempre se mostrará en color y se denominará "la región sombreada").
Componente de la lección Estructura Tiempo

Descripción breve
Calentamiento Grupos pequeños 10 min Dados cuatro patrones, los estudiantes razonan basándose en sus propias determinaciones cuál no pertenece.
Los estudiantes analizan patrones compuestos de diferentes formas para determinar qué forma cubre la mayor parte del área del patrón más grande y justifican sus respuestas.
Actividad de exploración En parejas 25 min
Hay disponible un applet digital interactivo para permitir a los estudiantes explorar las áreas de las formas en los patrones utilizando la tecnología.
Hay disponible una extensión de exploración para desarrollar una comprensión más profunda de las áreas equivalentes de las formas en los patrones.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
Componente de la lección

Estructura Tiempo
Síntesis Todo el grupo 5 min
Descripción breve
Los estudiantes discuten el uso de herramientas matemáticas y repasan las áreas equivalentes y no equivalentes de las formas.
Enfriamiento Independiente 5 min Los estudiantes escriben una definición de área en sus propias palabras.
Práctica Independiente 10 min
El componente de práctica independiente incluye 6 problemas de la lección.
10 minutos
Rutinas didácticas
¿Cuál no pertenece?
Este calentamiento anima a los estudiantes a comparar cuatro patrones geométricos, explicar su razonamiento y mantener conversaciones matemáticas. Permite escuchar cómo los estudiantes utilizan la terminología al describir las características geométricas.
La observación de patrones ofrece a cada estudiante un punto de partida. Cada figura tiene al menos una razón por la que no encaja. Los patrones también instan a los estudiantes a pensar en formas que cubren el plano sin huecos ni solapamientos, lo que apoya futuras conversaciones sobre el significado de área.
Antes de que los estudiantes empiecen, considere establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, u otra señal sutil. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se precipiten al levantar las manos por toda la clase.
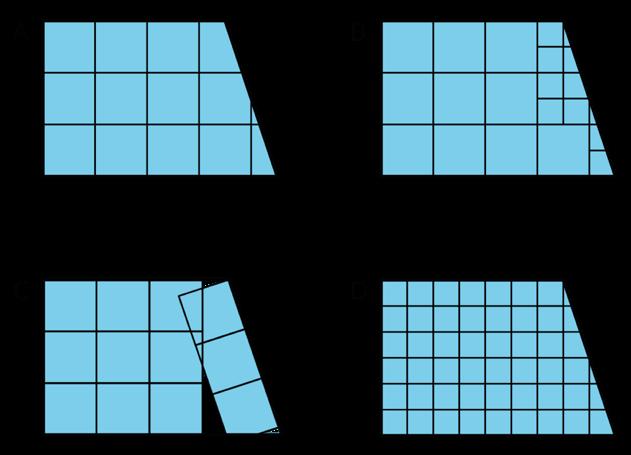
Anticipe que los estudiantes describirán los patrones en términos de:
• Colores (azul, verde, amarillo, blanco o sin color)
• Tamaño de las formas u otras medidas
• Formas geométricas (polígonos, cuadrados, pentágonos, hexágonos, etc.))
• Relaciones de las formas (si cada lado de los polígonos se encuentra con el lado de otro polígono, qué polígono está unido a cada lado, si hay un hueco entre los polígonos, etc.)
INSTRUCCIÓN
Organice a los estudiantes en grupos de 2-4. Exponga los cuatro patrones para que todos los vean. Conceda a los estudiantes 1 minuto de reflexión en silencio y pídales que indiquen cuándo han observado un patrón que no encaja y que expliquen por qué. Anímeles a pensar en más de una posibilidad. Cuando se acabe el minuto, dé a los estudiantes 2 minutos para que compartan su respuesta con su grupo y, a continuación, encuentren juntos al menos una razón, si es posible, por la que cada patrón no pertenece.
¿Qué patrón no pertenece?

Grado 6 . Matemáticas . Unidad 1

Las respuestas varían. Ejemplos de respuestas:
A. No tiene amarillo. Los grupos de cuatro pentágonos forman hexágonos que se entrelazan sin espacios.
B. No tiene azul. Grupos de seis pentágonos forman flores que se entrelazan sin espacios.
C. No tiene pentágonos. Tiene octógonos y cuadrados. Los polígonos que forman los patrones son de tamaños muy diferentes.
D. Tiene huecos entre las formas. No todos los polígonos de color se encuentran con otro polígono de color en todos sus lados. Tiene formas blancas (o sin relleno) que son más complejas que otras formas de color. Es el único en el que todos los polígonos tienen la misma longitud lateral.
Después de que los estudiantes hayan compartido sus observaciones en grupos, invita a cada grupo a compartir una razón por la que una figura en particular podría no pertenecer. Anota y muestra las respuestas para que todos las vean. Después de cada respuesta, sondea al resto de la clase para ver si los demás han hecho la misma observación.
Puesto que no hay una única respuesta correcta a la pregunta de qué figura no pertenece, presta atención a las explicaciones de los estudiantes y asegúrate de que las razones dadas son correctas. Pida a los estudiantes que expliquen el significado de la terminología que utilicen (nombres de polígonos o ángulos, partes de polígonos, área, etc.) y que fundamenten sus afirmaciones. Por ejemplo, un estudiante puede afirmar que el modelo D no pertenece porque todos sus polígonos tienen la misma longitud lateral. Pregúnteles cómo saben que es así y si es cierto para el polígono blanco (o sin relleno).
Explique a los estudiantes que cubrir una región bidimensional con copias de la misma forma o formas de manera que no haya huecos ni solapamientos se denomina "teselar" el plano. Los patrones A, B y C son ejemplos de mosaico. Diga a los estudiantes que exploraremos más mosaicos en las próximas actividades.
25 minutos
Rutinas didácticas
Anticipar, monitorear, seleccionar, secuenciar, conectar
Pensar, compartir, compartir en pareja
MLR2: Recoger y mostrar


Grado 6 . Matemáticas . Unidad 1

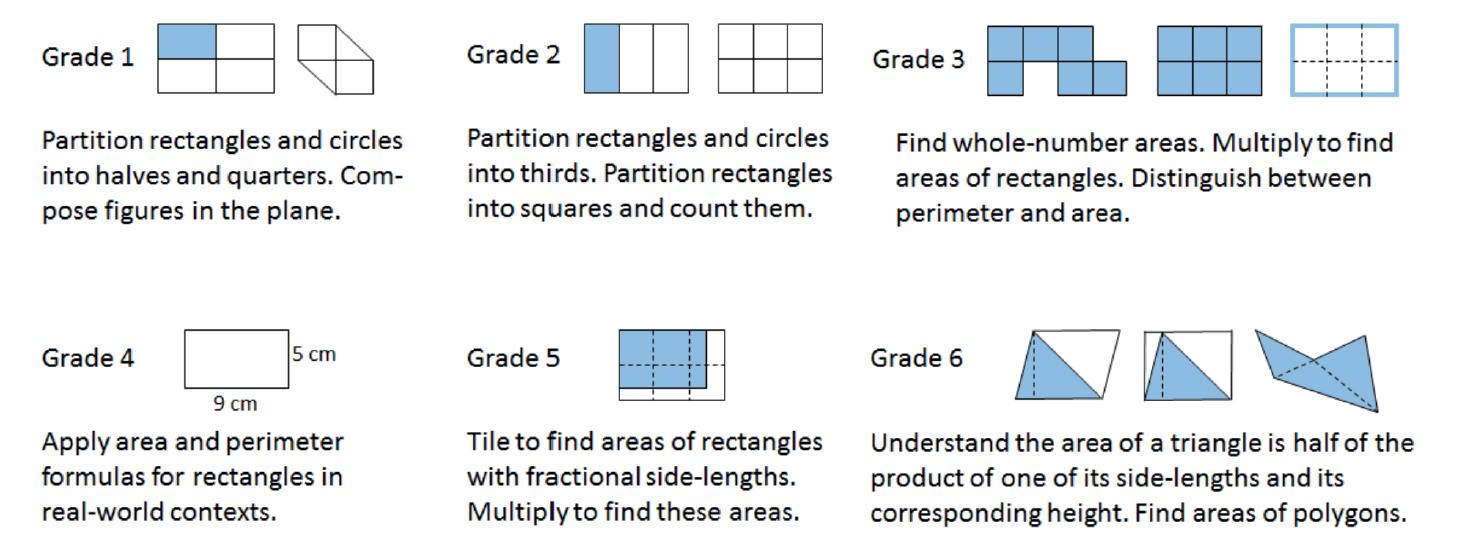
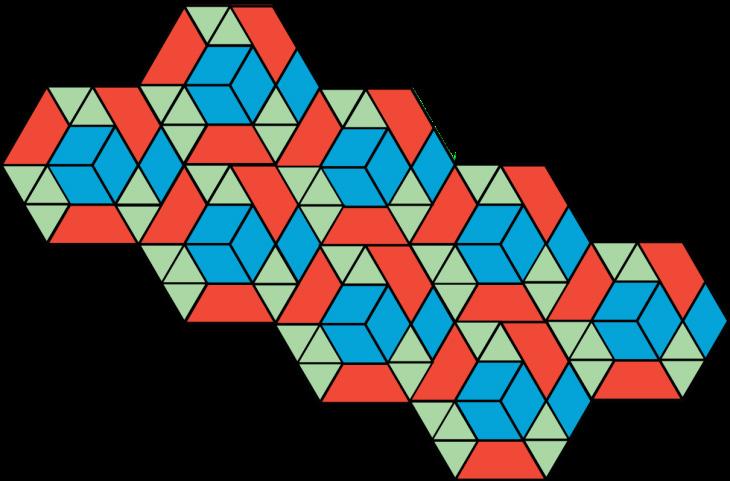
En esta actividad se pide a los estudiantes que comparen la superficie del plano cubierta por dos patrones de mosaico, con el fin de apoyar dos grandes ideas de la unidad:
• Si dos figuras pueden colocarse una encima de la otra de modo que coincidan exactamente, entonces tienen la misma superficie.
• Una región puede descomponerse y reordenarse sin que cambie su superficie.
Es probable que los estudiantes observen que en cada patrón:
• Se utilizan como baldosas los mismos tres polígonos (triángulos, rombos y trapecios).
• Todo el patrón de baldosas está compuesto por estos hexágonos.
• Las figuras están dispuestas sin huecos ni superposiciones, pero su disposición es diferente.
• Un determinado conjunto de baldosas más pequeñas forma un hexágono más grande. Cada hexágono tiene 3 trapezoides, 4 rombos y 7 triángulos.
Se espera que algunos estudiantes comiencen su comparación contando cada forma, ya sea dentro de un hexágono o de todo el patrón. Sin embargo, para comparar eficazmente qué parte del plano cubre cada forma, deben ser conscientes de las relaciones entre las formas. Por ejemplo, se pueden colocar dos triángulos verdes encima de un rombo azul de forma que coincidan exactamente, lo que nos indica que dos triángulos verdes cubren la misma superficie del plano que un rombo azul. Observe si los estudiantes son conscientes de ello. (No es necesario que los estudiantes utilicen la palabra "área" en sus explicaciones. En este punto, basta con frases como "coinciden" o "dos triángulos forman un rombo").
Si los estudiantes no están seguros de cómo plantear las preguntas, anímeles a pensar si alguna de las herramientas de su equipo de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) podría ayudarles. (Por ejemplo, podrían utilizar papel de calco para trazar patrones enteros o determinadas formas para hacer comparaciones, o utilizar una regla para extender las líneas dentro del patrón. Algunos estudiantes pueden inclinarse por recortar y comparar las formas). También se pueden ofrecer fichas de patrones, si se dispone de ellas.
Durante la discusión por parejas, vigile a los grupos que discuten las siguientes ideas para que puedan compartirlas más tarde, en esta secuencia:
• Relaciones entre dos formas: Por ejemplo, 2 triángulos forman un rombo, y 3 triángulos forman un trapecio.
• Cantidades globales relativas: Por ejemplo, hay 64 triángulos verdes, 32 rombos azules (que tienen la misma área que 64 triángulos), y 24 trapezoides rojos (que tienen la misma área que 72 triángulos), por lo que hay más rojo.
• Cantidades relativas en un hexágono: Por ejemplo, en cada hexágono hay 7 triángulos verdes, 4 rombos (que tienen la misma área que 8 triángulos), y 3 trapezoides (que tienen la misma área que 9 triángulos).
Las aulas que utilicen la actividad digital tienen la opción de que los estudiantes utilicen un applet que permite aislar el patrón y también enmarcarlo. Esto podría ayudar a los estudiantes a centrarse en cuántas formas de cada tipo componen el patrón.
Organice a los estudiantes en grupos de 2. Pida a un compañero que analice el patrón A y al otro que analice el patrón B. Diga a los estudiantes que su trabajo consiste en comparar la cantidad de plano cubierto por cada forma del patrón.
Antes de que los estudiantes comiencen, presénteles los juegos de materiales de geometría (papel vegetal, papel cuadriculado, lápices de colores, tijeras y una tarjeta índice) y explíqueles que pueden usarlos para obtener ayuda, si la necesitan. Conceda a los estudiantes 7-8 minutos de reflexión en silencio. A continuación, pídeles que compartan sus respuestas con sus compañeros y, después, discute con toda la clase.
Apoyo para estudiantes que aprenden el idioma inglés
Conversar, Hablar, Escuchar: Rutina 2 del Lenguaje Matemático, Recoger y Mostrar. Esta es la primera vez que se sugiere la Rutina 2 del Lenguaje Matemático como apoyo en este curso. En esta rutina, el maestro circula y escucha a los estudiantes hablar mientras anota las palabras, frases o dibujos que los estudiantes producen. El lenguaje recogido se expone visualmente para que toda la clase lo utilice a lo largo de la lección y la unidad. Por lo general, la exposición contiene diferentes ejemplos de estudiantes que utilizan características de las funciones lingüísticas disciplinares, como interpretar, justificar o comparar. El propósito de esta rutina es capturar una variedad de palabras y frases de los estudiantes en una pantalla a la que los estudiantes puedan referirse, basarse o con la que puedan establecer conexiones durante futuras discusiones, y aumentar la conciencia de los estudiantes sobre el lenguaje utilizado en las conversaciones sobre matemáticas.
Principio(s) de diseño: Apoyar la creación de sentido
Grado 6 . Matemáticas . Unidad 1
Procesamiento conceptual: Manipulativos. Para los estudiantes que se benefician de las actividades prácticas, proporcione fichas de patrones (o recorte previamente una copia extra de cada patrón) para que los estudiantes comparen las formas.
Tu maestro te asignará el patrón A o B.

En tu patrón, ¿qué formas cubren más el plano: rombos azules, trapecios rojos o triángulos verdes? Explica cómo lo sabes.
Patrón A
POSIBLES
Patrón B
Tanto en el patrón A como en el B, hay más trapezoides rojos que triángulos verdes o rombos azules en el plano. Posibles explicaciones:
• Los patrones A y B están formados cada uno por 56 triángulos verdes, 32 rombos azules, 24 trapezoides rojos.
• Un trapezoide rojo cubre la misma cantidad de plano que 3 triángulos verdes, por lo que 24 trapezoides rojos cubren la misma cantidad de plano que 72 triángulos verdes, que son más que los 56 triángulos verdes.
• Cada rombo azul cubre la misma superficie del plano que 2 triángulos verdes, por lo que los 32 rombos cubren la misma superficie del plano que 64 triángulos verdes, que también son más que los 56 triángulos verdes.
• Cada patrón está compuesto por 8 hexágonos. En cada hexágono hay 3 trapezoides rojos, 4 rombos azules, y 7 triángulos verdes.
• Dos trapezoides rojos pueden disponerse en un hexágono pequeño. También se pueden formar tres rombos en el mismo hexágono pequeño. Esto significa que 2 trapezoides cubren la misma superficie del plano que 3 rombos.
• Cada hexágono grande tiene 3 trapezoides rojos y 4 rombos azules. Como 2 trapezoides son iguales a 3 rombos, podemos simplemente comparar 1 trapezoide y 1 rombo. Podemos ver que 1 trapezoide rojo cubre más parte del plano que 1 rombo.
• Cada hexágono grande tiene 3 trapezoides rojos y 7 triángulos verdes. Un trapezoide cubre la misma cantidad del plano que 3 triángulos, por lo que 3 trapezoides cubren la misma cantidad del plano que 9 triángulos, que son más que 7 triángulos verdes.
Los estudiantes pueden decir que hay más superficie cubierta por el color que ven más en cada imagen, diciendo, por ejemplo: "Es que parece que hay más rojo." Pregunte a estos estudiantes si hay alguna forma de demostrar sus observaciones.
Es posible que los estudiantes sólo cuenten el número de triángulos verdes, trapecios rojos y rombos azules, pero que no tengan en cuenta la superficie cubierta por cada forma. Si sugieren que la forma con el mayor número de piezas cubre la mayor cantidad del plano, pídales que comprueben su hipótesis. Por ejemplo, pregunte: "¿Cubren más superficie del plano los triángulos 2 que el trapecio 1?".
Es posible que los estudiantes no recuerden los términos trapezoide, rombo y triángulo. Considere la posibilidad de repasar los términos, aunque no es necesario que conozcan las definiciones formales para trabajar en la tarea.
- Grado 6
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Seleccione a los estudiantes o grupos previamente identificados para que compartan sus respuestas y explicaciones. Secuencie las explicaciones en el orden indicado en la Narrativa de la Actividad. Para aclarar la idea de comparar formas colocándolas una encima de la otra y viendo si coinciden o cómo, considere hacer una demostración utilizando el applet digital.
Luego, haga explícito que cuando preguntamos "¿Qué tipo de forma cubre más del plano?" les estamos pidiendo que comparen las áreas cubiertas por los diferentes tipos de formas. Para reformular las comparaciones de las formas en términos de área, formule preguntas como:
• "¿Cómo se compara el área del trapecio con el área del triángulo?" (El área del trapecio es tres veces el área del triángulo).)
• "¿Cómo se compara el área del rombo con el área del triángulo?" (El área del rombo es el doble del área del triángulo.)
• "¿Es posible comparar el área de los rombos en el patrón A y el área de los triángulos en el patrón B? ¿Cómo?" (Sí, podemos contar el número de rombos de A y el número de triángulos de B. Como los triángulos de 2 tienen la misma área que los rombos de 1, dividimos el número de triángulos por 2 para compararlos).
¿Estás listo para más?
En papel cuadriculado, crea un patrón de baldosas de manera que:
El patrón tenga al menos dos formas diferentes.
Cada tipo de forma cubra la misma cantidad del plano.
"¿Estás listo para más?" Respuesta del estudiante
Hay infinitas posibilidades. Aquí tienes una:

5 minutos
En esta lección, hemos empezado a razonar sobre lo que significa que dos formas tengan la misma área. Hemos empezado a hacer cálculos matemáticos y a pensar en herramientas que pueden ayudarnos. Pregunta a los estudiantes:
• "¿Cuáles son algunas de las herramientas del juego de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y para qué se utilizan?"
• "Dibuja dos formas que sepas que no tienen la misma área. ¿Cómo puedes saberlo?"
Diga a los estudiantes que seguiremos pensando en el área, haciendo y hablando de matemáticas y aprendiendo a utilizar las herramientas de forma estratégica.
Grado 6 . Matemáticas . Unidad 1
5 minutos
El propósito de este enfriamiento es comprobar cómo piensan los estudiantes sobre el área después de realizar las actividades. Aunque la tarea invita a los estudiantes a reflexionar sobre el trabajo de esta lección, también pueden surgir ideas sobre el área de trabajos anteriores de los estudiantes de 3º a 5º curso. Conocer el rango de pensamiento de los estudiantes ayudará a informar la lección del día siguiente.
Piensa en tu trabajo de hoy y escribe tu mejor definición de área.

RESPUESTAS POSIBLES
Las respuestas varían. Ejemplos de respuestas:
• La cantidad de espacio dentro de una forma bidimensional
• La medida del interior de un polígono
• El número de unidades cuadradas dentro de una forma
PROBLEMA 1
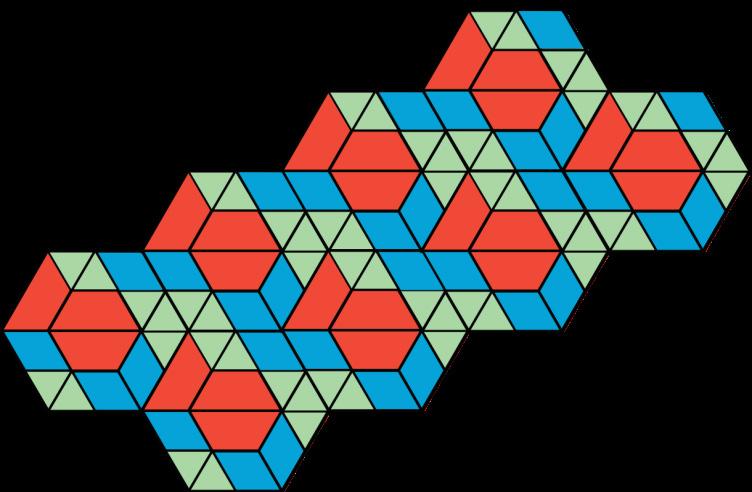
¿Qué cuadrado -grande, mediano o pequeño- cubre más superficie del plano? Explica tu razonamiento.
Soluciones posibles
El cuadrado grande cubre más superficie del plano. El razonamiento varía. Ejemplo de razonamiento: En un cuadrado grande caben exactamente 9 cuadrados pequeños. En un cuadrado mediano caben exactamente 4 cuadrados pequeños. Hay 5 cuadrados grandes, que cubren la misma superficie del plano que 45 cuadrados pequeños. Hay 10 cuadrados medianos, que cubren la misma superficie del plano que 40 cuadrados pequeños. Sólo hay 10 cuadrados pequeños.
- Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 2
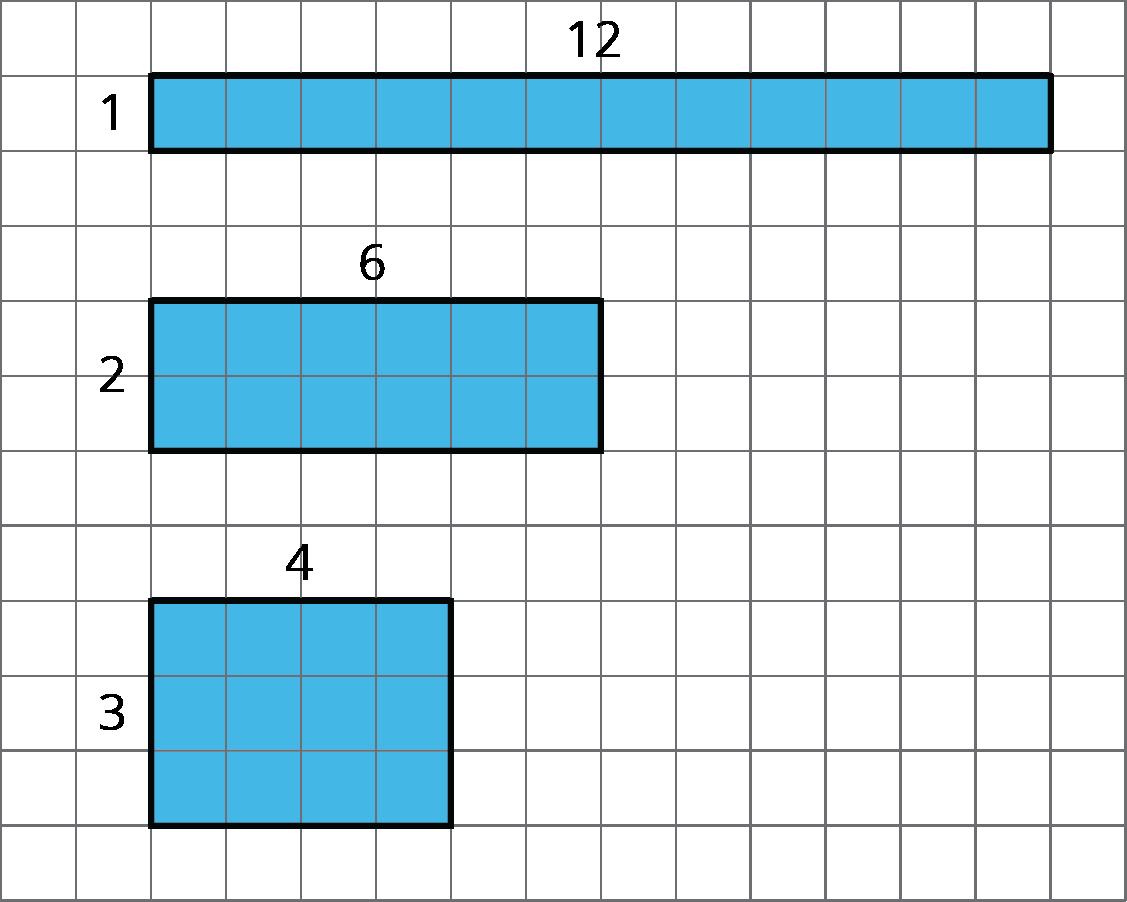
Dibuja tres cuadriláteros diferentes, cada uno con un área de 12 unidades cuadradas.

PROBLEMA 3
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta:
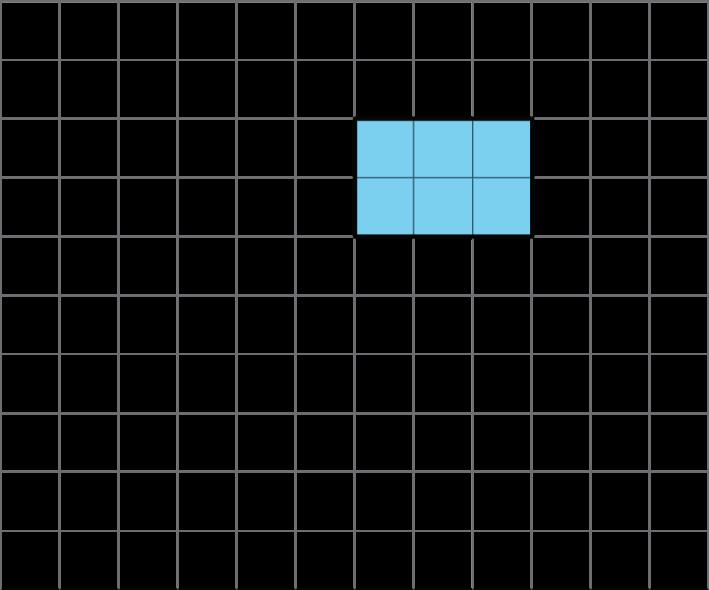
Utiliza copias del rectángulo para mostrar cómo un rectángulo podría:
A. teselar el plano.
Soluciones posibles
B. no teselar el plano.
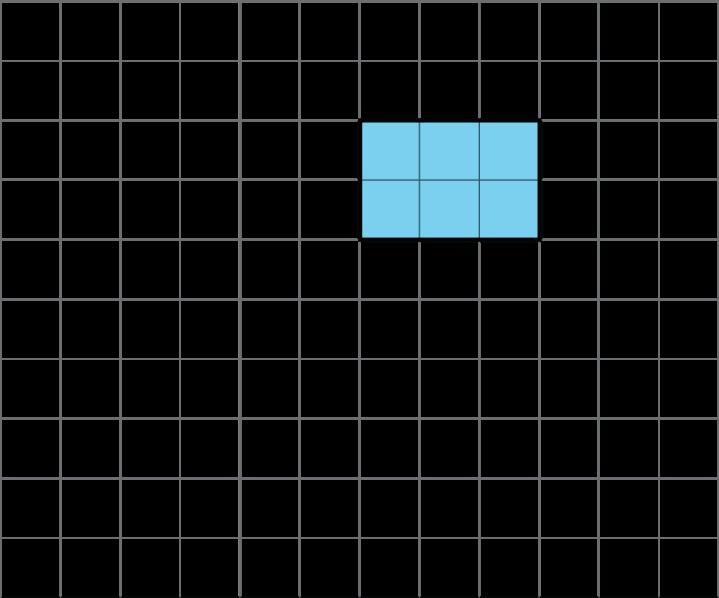
A. Las respuestas varían. Respuesta de ejemplo: B. Las respuestas varían. Ejemplo de respuesta:

PROBLEMA 4
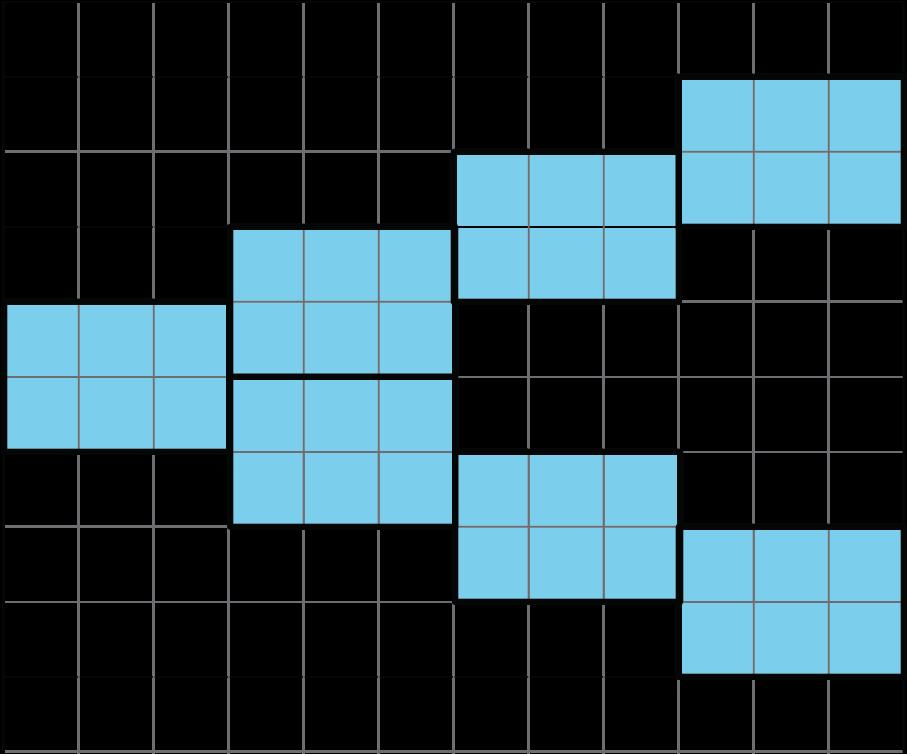
El área de esta figura es 24 unidades cuadradas. ¿Cuál de estas afirmaciones es cierta sobre el área? Seleccione todas las que correspondan.
El área se puede hallar contando el número de cuadrados que tocan el borde de la forma.
Se necesitan 24 cuadrados de cuadrícula para cubrir la forma sin huecos ni superposiciones.
El área se puede hallar multiplicando las longitudes de los lados que son 6 unidades y 4 unidades.
El área se puede hallar contando los cuadrados de la cuadrícula dentro de la forma.
El área se puede hallar sumando 4 × 3 y 6 × 2
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 6 . Matemáticas . Unidad 1

Soluciones posibles
El área de esta figura es 24 unidades cuadradas. ¿Cuál de estas afirmaciones es cierta sobre el área? Selecciona todas las que se apliquen.
El área se puede encontrar contando el número de cuadrados que tocan el borde de la forma.
Se necesitan 24 cuadrados de cuadrícula para cubrir la forma sin huecos ni solapamientos.
El área se puede hallar multiplicando las longitudes de los lados que son 6 unidades y 4 unidades.
El área se puede hallar contando los cuadrados de la cuadrícula dentro de la figura.
El área se puede hallar sumando 4 × 3 y 6 × 2
PROBLEMA 5
Aquí hay dos copias de la misma figura. Muestra dos formas diferentes de hallar el área de la región sombreada. Todos los ángulos son rectos.
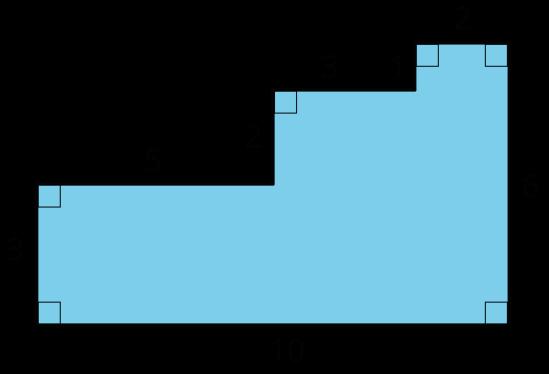

Soluciones posibles
Las respuestas varían. Estrategias de ejemplo:
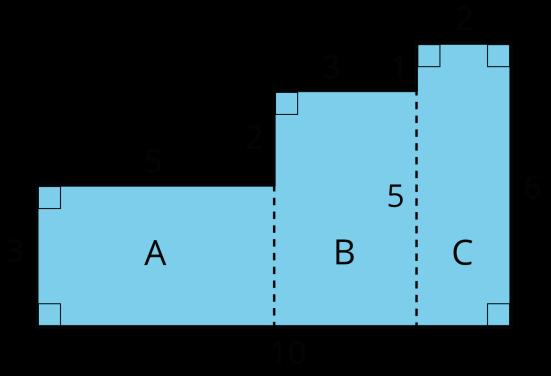
El área de A es 15 unidades cuadradas. El área de B es 15 unidades cuadradas. El área de C es 12 unidades cuadradas. El área de toda la región es 15 + 15 + 12 o 42 unidades cuadradas.
Nation California - Grado 6
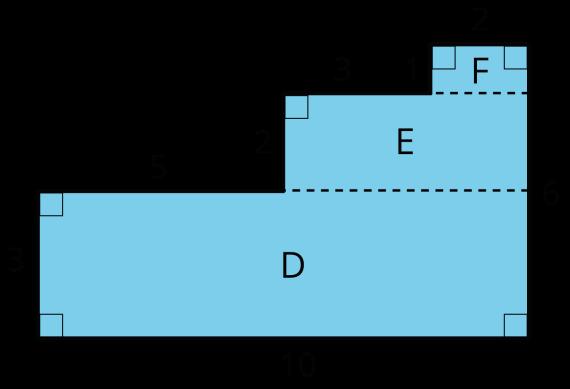
El área de D es 30 unidades cuadradas. El área de E es 10 unidades cuadradas. El área de F es 2 unidades cuadradas. El área de toda la región es 30 + 10 + 2 o 42 unidades cuadradas.

El área de F es 2 unidades cuadradas. El área de G es el área de el 10-por-5 rectángulo restado por el área de un 5-por-2 rectángulo en la parte superior izquierda. (10 × 5) - (5 × 2) = 50 - 10 = 40, por lo que el área de G es 40 unidades cuadradas. El área total es 40 + 2 o 42 unidades cuadradas.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 6
¿Qué forma tiene un área mayor: un rectángulo que mide 7 pulgadas por 3 4 pulgadas, o un cuadrado con una longitud lateral de 2 1 2 pulgadas? Muestra tu razonamiento.
Soluciones posibles
El cuadrado es más grande. Su área es 2
pulgadas cuadradas. El rectángulo tiene un área de 5 1 4 pulgadas cuadradas porque 7 × 3 4 = 21 4
Reflexiones:
Learning Inc. - Todos los derechos reservados


IDEA(S)
FUNDAMENTAL(ES)
• Graficar formas
• Redes y superficie
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
Estándares ELD de California
I.A.1
I.B.5
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dan sentido al mundo e influyen en el futuro. atienden a la precisión.
OBJETIVO(S) DE APRENDIZAJE
• Crear figuras y a encontrar sus áreas.
OBJETIVO(S)
desmontando enteros, juntando piezas y descubriendo la forma y el espacio.
• Explicar cómo encontrar el área de una figura que está compuesta de otras figuras.
• Saber cómo encontrar el área de una figura descomponiéndola y reordenando las partes.
• Saber lo que significa que dos figuras tengan la misma área.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Calcular el área de una región descomponiéndola y reordenando las piezas, y explicar (oralmente y por escrito) el método de solución.
• Reconocer y explicar (oralmente) que si dos figuras pueden colocarse una encima de otra de forma que coincidan exactamente, deben tener la misma área.
• Demostrar que el área es aditiva componiendo polígonos con un área dada.
Rutinas didácticas
Piensa, comparte, en En parejas
MLR2: Recopilar y mostrar
MLR8: Apoyo a la discusión
Materiales necesarios
Patrón de líneas negras para la actividad
2.2
Grado 6 . Matemáticas . Unidad 1
Preparación necesaria
Prepare 1 juego de tángrams que contenga 1 cuadrado, 4 pequeño, 1 mediano y 2 triángulos rectángulos grandes para cada 2 estudiantes. Imprima y recorte el patrón de líneas negras (se recomienda imprimirlo en cartulina) o utilice tángrams disponibles en el mercado. Tenga en cuenta que el conjunto de piezas de tángrama utilizado aquí difiere de un conjunto estándar en que se utilizan dos triángulos pequeños adicionales en lugar de un paralelogramo.
Se incluye un applet de tángram para las aulas que utilicen los materiales digitales, pero también se puede dar a los estudiantes la opción de utilizar tángrams físicos en lugar de la herramienta digital.
Asegúrate de que los estudiantes tienen acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), que deben incluir papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha para utilizar como regla o para marcar ángulos rectos.
Narrativa de la lección
Esta lección comienza repasando las definiciones de área que los estudiantes aprendieron en cursos anteriores. El objetivo aquí es refinar sus definiciones (MP6) y llegar a una que pueda ser utilizada por la clase durante el resto de la unidad. También aprenden a razonar con flexibilidad sobre figuras bidimensionales para hallar sus áreas y a comunicar su razonamiento con claridad (MP3). El área de figuras bidimensionales puede determinarse de múltiples maneras. Podemos componer una figura utilizando piezas más pequeñas con áreas conocidas. Podemos descomponer una figura en formas cuyas áreas podemos determinar y sumar las áreas de esas formas. También podemos descomponerla y reorganizar las piezas en una figura diferente pero conocida, de modo que podamos encontrar su área. Los dos principios clave de esta lección son:
• Las figuras que coinciden exactamente tienen áreas iguales. Si dos figuras pueden colocarse una encima de la otra de forma que coincidan exactamente, entonces tienen la misma área.
• Una figura puede descomponerse y sus piezas reordenarse sin que cambie su área. La suma de las áreas de las piezas es igual al área de la figura original. Del mismo modo, si una figura se compone de piezas no superpuestas, su área es igual a la suma de las áreas de las piezas. En otras palabras, el área es aditiva.
Los estudiantes han utilizado estos principios desde el tercer curso, pero principalmente para descomponer cuadrados, rectángulos y sus compuestos (por ejemplo, una forma de L) y reorganizarlos para formar otras figuras similares. En esta lección, descomponen triángulos y los reorganizan para formar figuras cuyas áreas saben calcular.
Una nota sobre "dos figuras que coinciden exactamente": En 8º curso, los estudiantes aprenderán a referirse a tales figuras como congruentes y a describir la congruencia en términos de movimientos rígidos (reflexiones, rotaciones y traslaciones). En estos materiales, la palabra congruente no se utiliza en 6º curso. Una posibilidad es utilizar un término informal como "idéntico", para que los estudiantes puedan hablar de que una figura es una "copia idéntica" de otra. Sin embargo, también podría ser necesario aclarar qué significa "idéntico" (por ejemplo, que es independiente del color y la orientación).
Componente de la lección Estructura Tiempo
Calentamiento En parejas 10 min

Nation California - Grado 6
Descripción breve
Los estudiantes recuerdan cómo calcular el área usando cuadrados dentro de formas y luego escriben una definición de área.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
Componente de la lección

Actividad de exploración
Estructura Tiempo
Actividad de exploración (opcional)
En parejas 25 min
En parejas 15 min
Síntesis Grupo completo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Descripción breve
Los estudiantes reorganizan triángulos y cuadrados para crear figuras compuestas con áreas específicas.
Un applet digital interactivo está disponible para permitir a los estudiantes explorar el área mediante la composición y descomposición de figuras utilizando la tecnología.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la composición de figuras para determinar el área.
Los estudiantes determinan y justifican las áreas de los triángulos en un conjunto tángram utilizando el área de la pieza tángram cuadrada y las figuras compuestas.
Hay disponible un applet digital interactivo que permite a los estudiantes explorar el área de las figuras tángram utilizando la tecnología.
Los estudiantes demuestran que el área es aditiva componiendo y descomponiendo triángulos para determinar las áreas de las figuras compuestas.
Los estudiantes calculan el área de una figura compuesta dada el área de una de las formas de la figura compuesta.
El componente de práctica independiente incluye 3 en la lección y 2 problemas de repaso en espiral.
10 minutos
Rutinas didácticas
Pensar, compartir
Este calentamiento activa y afina los conocimientos previos de los estudiantes sobre área. Se pide a los estudiantes que articulen una definición de área que pueda utilizarse durante el resto de la unidad. Esta definición de área no es nueva, sino que reitera lo que los estudiantes aprendieron en los cursos 3º a 5º.
Antes de esta lección, los estudiantes exploraron el embaldosado y los patrones de embaldosado. Aquí, analizan cuatro formas en que una región se dispone en mosaico o de otro modo con cuadrados. Deciden qué disposiciones de cuadrados pueden utilizarse para hallar el área de la región y por qué, y utilizan su análisis para escribir una definición de área. Al identificar los aspectos más importantes que deben incluirse en la definición, los estudiantes prestan atención a la precisión (MP6).
Las definiciones iniciales de los estudiantes pueden estar incompletas. Durante las discusiones por En parejas, anote a los estudiantes que mencionen estos componentes para que puedan compartirlos más tarde:
• Región plana o bidimensional
• Unidades cuadradas
• Cubrir una región completamente sin huecos ni solapamientos
Limite la discusión de toda la clase a 5-7 minutos para dejar tiempo suficiente para el trabajo que sigue.
Grado 6 . Matemáticas . Unidad 1

Organice a los estudiantes en grupos de 2. Conceda a los estudiantes 2 minutos de tiempo de reflexión en silencio para la primera pregunta y pídales que estén preparados para explicar su decisión. A continuación, dé a los compañeros 3-4 minutos para compartir sus respuestas y completar juntos la segunda pregunta.
Funcionamiento socioemocional: Tutores. Empareje a los estudiantes con sus tutores previamente identificados. ENUNCIADO
Recordarás que el término área nos dice algo sobre el número de cuadrados que hay dentro de una forma bidimensional.
1. Aquí tienes cuatro dibujos que muestran cuadrados dentro de una forma. Selecciona todos los dibujos cuyos cuadrados podrían utilizarse para hallar el área de la forma. Prepárate para explicar tu razonamiento.
2. Escribe una definición de área que incluya toda la información que consideres importante.
RESPUESTAS POSIBLESS
1. A y D. B podría considerarse si se distinguen los cuadrados más grandes y los más pequeños al determinar el área.
2. Las respuestas varían, pero la definición de trabajo debería contener todos estos componentes: "El área de una región bidimensional (en unidades cuadradas) es el número de cuadrados unitarios que cubren la región sin huecos ni solapamientos."
Los estudiantes pueden centrarse en cómo han hallado típicamente el área de un rectángulo -multiplicando las longitudes de sus lados- en lugar de pensar en lo que significa "el área de cualquier región". Pídeles que piensen qué nos dice realmente el producto de las longitudes de los lados de un rectángulo. (Por ejemplo, si dicen que el área de un rectángulo 5-por-3 es 15, pregúnteles qué significa 15.)
Algunos estudiantes pueden pensar que ninguna de las opciones, incluyendo A y D, podría usarse para hallar el área porque involucran cuadrados parciales, o porque los cuadrados parciales no parecen ser partes fraccionarias familiares. El uso de fracciones de referencia puede ayudar a los estudiantes a ver que el área de una región podría ser un número no entero. Por ejemplo, pregunte a los estudiantes si el área de un rectángulo podría ser, digamos, 8 1 2 o 2 1 4 unidades cuadradas.
- Grado
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Para cada dibujo de la primera pregunta, pida a los estudiantes que indiquen si creen que los cuadrados podrían o no utilizarse para hallar el área. A partir de su trabajo en cursos anteriores, es probable que los estudiantes vean que el número de cuadrados de A y D puede indicarnos el área. Teniendo en cuenta el trabajo reciente sobre el embaldosado, los estudiantes pueden decidir que C no es útil. Discuta las decisiones de los estudiantes y pregunte:
• "¿Qué tienen A y D que pueda ayudarnos a hallar el área?". (Los cuadrados son todos del mismo tamaño. Son cuadrados unitarios).
• "¿Qué tiene C que puede hacer que no sea útil para encontrar el área?". (Los cuadrados se superponen y no cubren toda la región, por lo que contar los cuadrados no nos dará el área.)
• "Si crees que B no se puede utilizar para hallar el área, ¿por qué no?" (No podemos contar el número de cuadrados y decir que el número es el área porque los cuadrados no son todos del mismo tamaño.)
• "Si crees que se puede usar B para hallar el área, ¿cómo?" (Cuatro cuadrados pequeños forman un cuadrado grande. Si contamos el número de cuadrados grandes y el número de cuadrados pequeños por separado, podemos convertir uno en el otro y encontrar el área en términos de cualquiera de ellos.)
Si el tiempo lo permite, discuta:
• "¿En qué se diferencian A y D?" (A utiliza cuadrados unitarios más grandes y D más pequeños. Cada tamaño representa una unidad diferente.)
• "¿Nos darán áreas diferentes?" (Nos darán áreas en unidades diferentes, como pulgadas cuadradas y centímetros cuadrados.)
Selecciona algunos grupos para que compartan sus definiciones de área o lo que piensan que debería incluirse en la definición de área de la clase. El debate debe conducir a una definición que transmita los aspectos clave del área: El área de una región bidimensional (en unidades cuadradas) es el número de unidades cuadradas que cubren la región sin huecos ni superposiciones.
Muestre la definición de la clase y vuelva a consultarla cuando sea necesario a lo largo de esta unidad. Diga a los estudiantes que ésta será una definición de trabajo que puede ser revisada a medida que continúen su trabajo en la unidad.
Rutinas didácticas
Piensa, comparte (en parejas)
MLR2: Recopilar y mostrar
25 minutos
Materiales requeridos
Maestro de línea negra
En tercer curso, los estudiantes reconocieron que el área es aditiva. Aprendieron a hallar el área de una figura rectilínea descomponiéndola en rectángulos no superpuestos y sumando sus áreas. Aquí los estudiantes amplían este conocimiento a formas no rectangulares. Componen piezas de tángram -que constan de triángulos y un cuadrado- en formas con áreas determinadas. El cuadrado sirve de cuadrado unidad. Como los estudiantes sólo tienen un cuadrado, deben utilizar estos principios en su razonamiento:
• Si dos figuras pueden colocarse una encima de la otra de forma que coincidan exactamente, entonces tienen la misma área.
• Si una figura se descompone y se reorganiza para componer otra figura, entonces su área es la misma que la de la figura original.
Cada pregunta de la tarea pretende suscitar debates sobre estos dos principios. Aunque puedan parecer obvios, estos principios deben enunciarse explícitamente (al final de la lección), ya que de ellos depende una comprensión más avanzada del área de las figuras complejas.
Los términos componer, descomponer, y reorganizar se formalizarán en una próxima lección, pero a lo largo de esta lección, busca oportunidades para demostrar su uso cuando los estudiantes describan su trabajo con las piezas del tángram. Cuando los estudiantes utilicen "hacer" o "construir", "romper" y "desplazar", reformule sus términos cotidianos utilizando los más formales.
Mientras los estudiantes trabajan, fíjese en cómo componen las piezas para crear formas con determinadas áreas. Busque estudiantes cuyo razonamiento ilustre las ideas expuestas en la Síntesis de la actividad.
Demuestre el uso de la palabra "componer" repitiendo el uso del lenguaje cotidiano por parte de los estudiantes y, a continuación, refunda utilizando los términos formales que aparecen aquí.
Grado 6 . Matemáticas . Unidad 1

Entregue a cada grupo de 2 estudiantes el siguiente conjunto de piezas de tángram del patrón de líneas negras o de conjuntos disponibles comercialmente. Tenga en cuenta que el conjunto de piezas de tángram utilizado aquí difiere de un conjunto estándar en que se utilizan dos triángulos pequeños adicionales en lugar de un paralelogramo.
• cuadrado: 1
• triángulos pequeños: 4
• triángulo mediano: 1
• triángulos grandes: 2
Es importante no darles más de estas piezas.
Dé a los estudiantes 2-3 minutos de tiempo de reflexión en silencio para las tres primeras preguntas. Pídeles que después hagan una pausa y comparen sus soluciones con las de sus compañeros. Si han creado la misma figura para cada pregunta, pídeles que creen una figura diferente que tenga la misma área dada antes de continuar. A continuación, pídeles que trabajen juntos para responder a las preguntas restantes. Las aulas que utilicen las actividades digitales pueden utilizar piezas físicas de tángram o un applet con las mismas formas para determinar las relaciones entre las áreas. El applet es una adaptación del trabajo de en GeoGebra.Harry Drew
Harblar, conversar: MLR2 Recopilar y mostrar. Mientras los estudiantes trabajan, circule y escúchelos hablar sobre las formas en que describen la composición, descomposición y reorganización de las formas. Anote las frases comunes que escuche sobre cada una de ellas (por ej., "construir", "descomponer", "mover"). Escriba las palabras en una pantalla visual, incluyendo cualquier imagen o dibujo. Esto los ayudará a usar el lenguaje matemático durante sus debates por En parejas y en grupo.
Principio(s) de diseño: Maximizar la metaconciencia
Apoyo a estudiantes con discapacidades
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus compañeros tutores previamente identificados.
Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una pregunta a la vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.
Este applet tiene un cuadrado y algunos triángulos rectángulos pequeños, medianos y grandes. El área del cuadrado es 1 unidad cuadrada.
Haz clic en una forma y arrastra para moverla. Coge el punto del vértice y arrastra para girarlo.
1. Observa que puedes juntar dos triángulos pequeños para formar un cuadrado. ¿Cuál es el área del cuadrado formado por dos triángulos pequeños? Prepárate para explicar tu razonamiento.
2. Utiliza tus formas para crear una nueva forma con un área de 1 unidad cuadrada que no sea un cuadrado. Dibuja tu figura en un papel y rotúlala con su área.
3. Utiliza tus figuras para crear una nueva figura con un área de 2 unidades cuadradas. Dibuja tu figura y rotúlala con su área.
4. Utiliza tus figuras para crear otra figura con un área de 2 unidades cuadradas. Dibuja tu figura y etiquétala con su área.
5. Utiliza tus figuras para crear una nueva figura con un área de 4 unidades cuadradas. Dibuja tu figura y rotúlala con su área.
- Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

1. El área del cuadrado formado por dos triángulos pequeños es una unidad cuadrada porque es idéntico al cuadrado dado con área 1 unidad cuadrada. "Idéntico" significa que puedes poner uno encima del otro y coinciden exactamente.
2. Cualquier compuesto de dos triángulos pequeños.

3. Cualquier compuesto de cuatro triángulos pequeños o dos triángulos pequeños y un triángulo mediano. Ejemplos de respuestas:
4. Cualquier compuesto de cuatro triángulos pequeños o dos triángulos pequeños y un triángulo mediano.
5. Cualquier compuesto con un área de 4 unidades cuadradas. Ejemplos de respuestas:

Los estudiantes pueden considerar que el área es el número de piezas de las composiciones, en lugar del número de unidades cuadradas. Recuérdeles el significado de área o pídales que repasen la definición de área discutida en la actividad de calentamiento.
Dado que los 2 triángulos grandes del conjunto tángram pueden disponerse para formar un cuadrado, los estudiantes pueden considerar que ese cuadrado es la unidad cuadrada en lugar del cuadrado más pequeño compuesto por 2 triángulos pequeños. Pida a los estudiantes que repasen el Enunciado de tarea para el estudiante y verifiquen el tamaño del cuadrado unidad.
Invite a los estudiantes previamente identificados (cuyo trabajo ilustra las ideas que se muestran aquí) a compartir. Nombre estos movimientos explícitamente a medida que surjan: componer, descomponer, y reordenar.
• Primera pregunta: Dos triángulos pequeños pueden componerse en un cuadrado que coincida exactamente con la pieza cuadrada dada. Esto significa que los dos cuadrados -el compuesto y el cuadrado unidad- tienen la misma área.
Di a los estudiantes: "Decimos que si una región puede colocarse encima de otra región de modo que coincidan exactamente, entonces tienen la misma área".
• Segunda pregunta: Dos triángulos pequeños pueden reorganizarse para componer una figura diferente, pero el área de ese compuesto sigue siendo 1 unidad cuadrada. Estas tres figuras -cada una compuesta por dos triángulos- tienen la misma área. Si giramos la primera figura, puede colocarse encima de la segunda para que coincidan exactamente. La tercera tiene una forma diferente a las otras dos, pero como está formada por los mismos dos triángulos, tiene la misma área.

Grado 6 . Matemáticas . Unidad 1
Subraye: "Si una figura se descompone y se reordena como una nueva figura, el área de la nueva figura es la misma que el área de la figura original".
• Tercera y cuarta preguntas: Las figuras compuestas podrían formarse de varias maneras: con sólo 4 triángulos pequeños, con dos triángulos pequeños y un triángulo mediano, o con dos triángulos pequeños y un cuadrado.
• Última pregunta: Aquí se necesita un triángulo grande. Para hallar su área, necesitamos o bien componer 4 triángulos más pequeños en un triángulo grande, o bien ver que el triángulo grande puede descomponerse en 4 triángulos más pequeños, que a su vez pueden componerse en 2 cuadrados unitarios.
Apoyo a los estudiantes con discapacidad
Pida a los estudiantes que creen una red de palabras o un organizador gráfico.
¿Estás listo para más?
Encuentra una forma de utilizar todas tus piezas para componer un único cuadrado grande. ¿Cuál es el área de este cuadrado grande?
"¿Estás listo para más?" Respuesta del estudiante
El área es 8 unidades cuadradas. Ejemplo de respuesta:

15 minutos
Rutinas didácticas
Pensar Compartir MLR8: Apoyos para el debate
En esta actividad, los estudiantes utilizan las áreas de las formas compuestas de la actividad anterior para razonar sobre el área de cada forma tángram. Los estudiantes pueden haber reconocido previamente que el área de un triángulo pequeño es 1 2 unidad cuadrada, el área de un triángulo mediano es 1 unidad cuadrada y el área de un triángulo grande es 2 unidades cuadradas. Aquí practican cómo saben que estas observaciones son ciertas (MP3). Las explicaciones pueden escribirse con palabras o como ilustraciones claramente etiquetadas que apoyen sus respuestas.
Mientras los compañeros discuten, busque dos formas de pensar sobre el área de cada triángulo asignado: componiendo copias del triángulo en un cuadrado o un triángulo más grande, o descomponiendo el triángulo o el cuadrado unitario en piezas más pequeñas y reorganizando las piezas. Identifique al menos a un estudiante que utilice cada enfoque.



Organice a los estudiantes en grupos de 2. Asigne la primera y la segunda pregunta a un compañero y la segunda y la tercera pregunta al otro compañero. Dé a cada grupo acceso a los juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y el mismo conjunto de piezas de tángram que se utilizó en la actividad anterior.
Dé a los estudiantes 3-4 minutos de tiempo tranquilo para encontrar las áreas de sus triángulos asignados y construir sus explicaciones, seguidos de unos minutos para compartir sus respuestas con su compañero. Diga a los estudiantes que mientras un compañero explica, el otro debe escuchar atentamente y estar de acuerdo o en desacuerdo con la explicación. A continuación, deben llegar a un acuerdo sobre las respuestas y las explicaciones.
Las aulas que utilicen las actividades digitales pueden utilizar un applet como ayuda para determinar las áreas de los triángulos.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar, escribir: MLR8 Apoyos para el debate. Utilice esta rutina cuando los estudiantes comparen las áreas de triángulos y cuadrados para apoyar el uso del lenguaje matemático. Mientras los estudiantes comparten sus respuestas con su compañero, circule y anime a los oyentes a que empujen a los hablantes a utilizar el lenguaje "componer", "descomponer" o "reorganizar" en sus explicaciones.
Busque estudiantes que nombren el cuadrado o los triángulos más grandes como "figuras compuestas" y amplíe este lenguaje. Anime a los estudiantes a tomar prestadas palabras y frases de los demás y a utilizar este lenguaje en sus respuestas escritas.
Principio(s) de diseño: Cultivar la conversación; Optimizar el rendimiento (para la explicación)
Apoyo a estudiantes con discapacidades
Funcionamiento socioemocional: Tutores. Empareje a los estudiantes con sus tutores previamente identificados.
Recuerda que el área del cuadrado que has visto antes es 1 unidad cuadrada. Completa cada enunciado y explica tu razonamiento.
1. El área del triángulo pequeño es unidades cuadradas. Lo sé porque . . .
2. El área del triángulo mediano es de unidades cuadradas. Lo sé porque . . .
3. El área del triángulo grande es de unidades cuadradas. Lo sé porque . . .
1. 1 2 unidad cuadrada. Ejemplos de explicaciones:
• Dos triángulosl pequeños se pueden juntar para formar un cuadrado, que tiene un área de una unidad cuadrada. Como esta forma compuesta coincide exactamente con el cuadrado unitario, sus áreas deben ser iguales. Esto significa que el área de cada triángulo pequeño es la mitad del área del cuadrado unitario.
• Un cuadrado can descomponerse exactamente en dos triángulos pequeños, por lo que el área de cada triángulo pequeño debe ser la mitad de la del cuadrado.
2. 1 unidad cuadrada. Explicaciones de ejemplo:
• Se pueden juntar dos triángulos pequeños para formar un triángulo mediano. También se pueden juntar dos triángulos para formar un cuadrado con un área de 1 unidad cuadrada. Como dos triángulos pequeños forman un triángulo mediano y un cuadrado, el área del triángulo mediano debe ser 1 unidad cuadrada.
• Un triángulo mediano puede descomponerse en dos triángulos pequeños. Estos pueden reordenarse en un cuadrado cuya área es 1 unidad cuadrada, por lo que el área del triángulo mediano es también 1 unidad cuadrada.
1. 2 unidades cuadradas. Algunos ejemplos:
• Dos triángulos medianos pueden disponerse en un triángulo grande. Como el área del triángulo mediano es 1 unidad cuadrada, una figura compuesta por dos de ellos tiene un área 2 unidades cuadradas.
Grado 6 . Matemáticas . Unidad 1 RESPUESTAS POSIBLES ( CONT.)
Si al principio los estudiantes tienen problemas para determinar las áreas de las figuras, pregúnteles cómo razonaron sobre las áreas en la actividad anterior. Ten a mano muestras de figuras compuestas y descompuestas que formen una unidad cuadrada para que los estudiantes puedan consultarlas.
• Un triángulo grande puede descomponerse en 4 triángulos pequeños, que a su vez pueden reorganizarse en dos cuadrados. El área combinada de los dos cuadrados es 2 unidades cuadradas. CONCEPTOS ERRÓNEOS PREVISTOS

Después de que los compañeros hayan compartido y acordado las áreas y explicaciones correctas, discute con la clase:
• "¿Utilizasteis tú y tu compañero la misma estrategia para encontrar el área de cada triángulo?"
• "¿En qué se parecían vuestras explicaciones? ¿En qué se diferenciaron?"
Seleccione a dos estudiantes previamente identificados para que compartan sus explicaciones: uno que razonó en términos de componer copias de su triángulo asignado en otra forma, y otro que razonó en términos de descomponer su triángulo o el cuadrado unitario en piezas más pequeñas y reordenarlas. Si los estudiantes no plantean estos enfoques, asegúrese de explicitarlos al final de la clase.
5 minutos
Hay dos principios que nos pueden ayudar a razonar sobre el área:
1. Si dos figuras se pueden colocar una encima de la otra de forma que coincidan exactamente, entonces tienen la misma área.
2. El área de una figura se puede encontrar sumando las áreas de sus partes. Si componemos (juntamos) una nueva figura a partir de piezas más pequeñas sin superponerlas, la suma de las áreas de las piezas es el área de la nueva figura. Del mismo modo, si descomponemos (cortamos o rompemos) una figura dada en trozos, el área de la figura dada es la suma de las áreas de los trozos. Aunque reordenemos las piezas, el área total no cambia.
He aquí un ejemplo. Supongamos que conocemos el área de un triángulo pequeño y queremos hallar el área de un triángulo grande. Demuestra lo siguiente (utilizando las piezas del tángram, si es posible):
• Podemos utilizar 4 triángulos pequeños para componer un triángulo grande. Aquí tienes dos formas de hacerlo. Si colocamos un triángulo grande encima de una composición de 4 triángulos pequeños y coinciden exactamente, sabemos que el área del triángulo grande es igual al área combinada de 4 triángulos pequeños.

- Grado
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

• Podemos descomponer el triángulo grande en 4 triángulos pequeños. De nuevo, podemos razonar que el área de un triángulo grande es igual al área combinada de 4 triángulos pequeños.
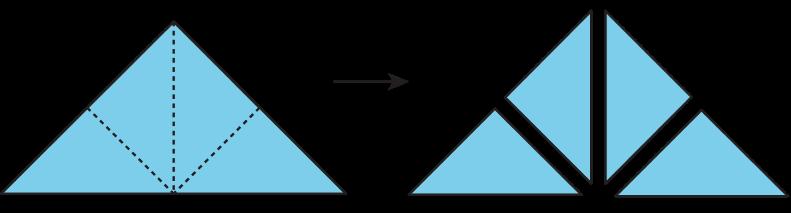
• Supongamos que no conocemos el área de un triángulo pequeño, pero sí conocemos el área de un cuadrado compuesto por 2 triángulos pequeños. Podemos descomponer el triángulo grande en 4 triángulos pequeños y luego reorganizarlos en 2 cuadrados. Podemos razonar que el área del triángulo grande es igual al área combinada de 2 cuadrados. Esto se debe a que cuando los 4 triángulos pequeños reordenados se colocan encima de dos cuadrados, coinciden exactamente.
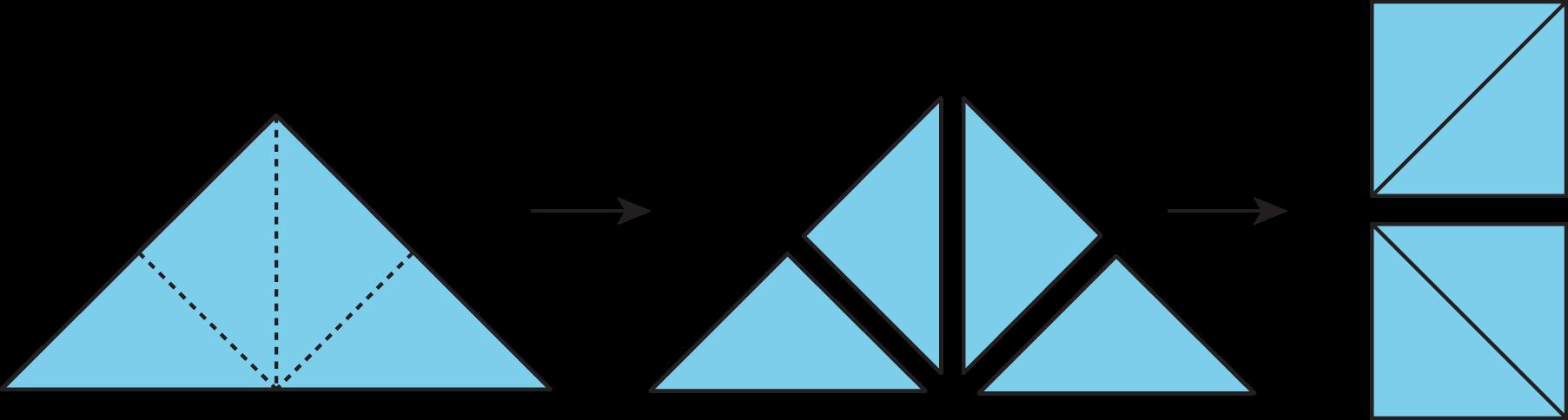
Profundizaremos en estas estrategias en la próxima lección.
5 minutos
INSTRUCCIÓN
Da a los estudiantes acceso a las formas del tángram y a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Diga a los estudiantes que esta figura se compone de dos triángulos rectángulos pequeños, dos triángulos rectángulos medianos y un cuadrado, igual que los que utilizaron antes.
Tenga en cuenta que, al principio, puede que los estudiantes no vean el "cuadrado del medio" como un cuadrado, o que piensen que es un rombo (con ángulos desiguales). Asegúrate de que todos entienden que la cuadratura no depende de cómo giremos el papel: Un cuadrado es un rectángulo (con los cuatro ángulos rectos) que tiene 4 lados iguales.
El cuadrado del centro tiene un área de 1 unidad cuadrada.
¿Cuál es el área de todo el rectángulo en unidades cuadradas? Explica tu razonamiento.

El área es 4 unidades cuadradas. Posibles estrategias:
• Junta los dos triángulos pequeños para formar un cuadrado. Su área es 1 unidad cuadrada. Descomponer cada triángulo mediano en dos triángulos pequeños que puedan disponerse como un cuadrado. Cada uno de estos cuadrados tiene un área de 1 unidad cuadrada. Junto con el cuadrado del centro, la suma de las áreas de estas piezas es 4 unidades cuadradas.
• Un triángulo pequeño tiene un área de 1 2 unidad cuadrada, y un triángulo mediano tiene un área de 1 unidad cuadrada.
1 + 1 + 1 + 1 2 + 1 2 = 4
Learning Inc. - Todos los derechos reservados
Grado 6 . Matemáticas . Unidad 1
PROBLEMA 1
Se muestra la diagonal de un rectángulo.
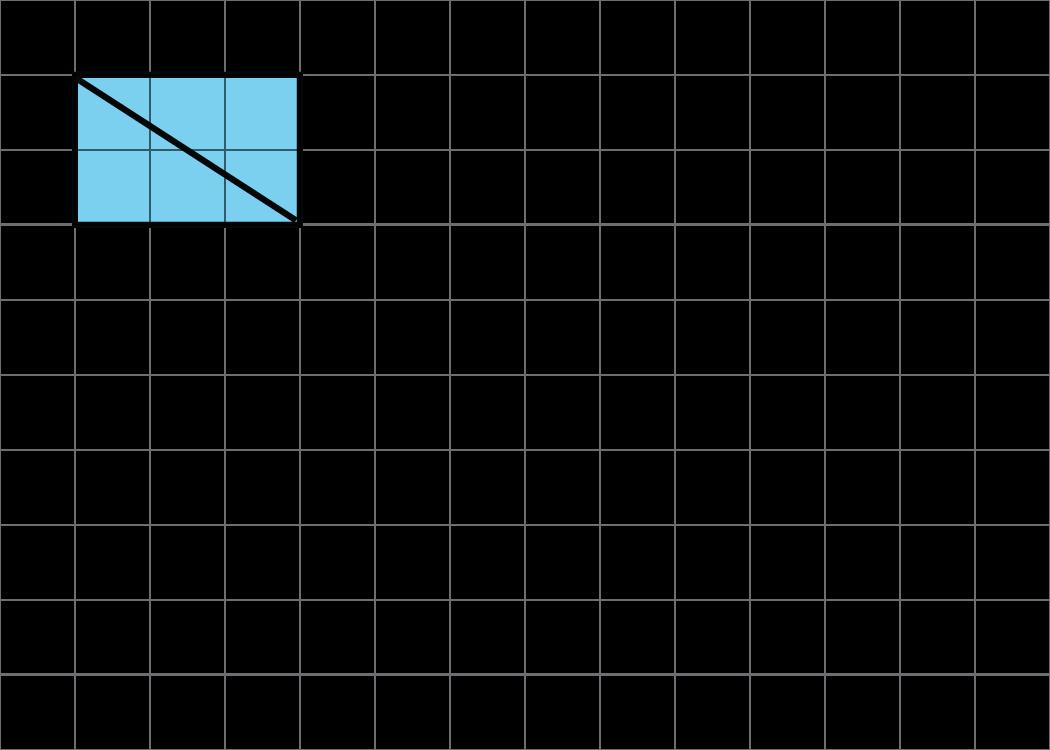
A. Descomponga el rectángulo a lo largo de la diagonal, y recomponga las dos piezas para hacer una forma diferente.
B. ¿Cómo se compara el área de esta nueva forma con el área del rectángulo original? Explica cómo lo sabes.
PROBLEMA 2

Soluciones posibles
A. Las respuestas varían. Se muestran cinco formas diferentes
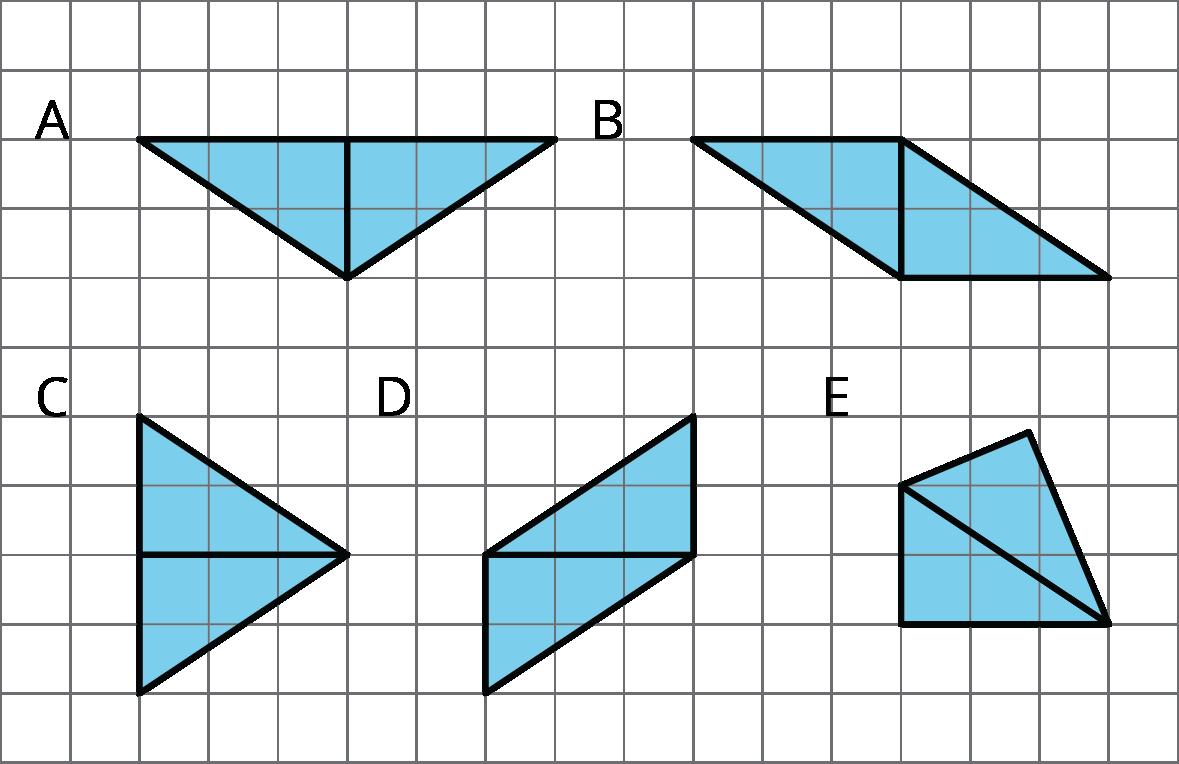
B. Las áreas son las mismas ya que todas las formas están compuestas por dos copias del mismo triángulo.
Priya descompuso un cuadrado en 16 cuadrados más pequeños de igual tamaño y luego recortó 4 de los cuadrados pequeños y los unió alrededor del exterior del cuadrado original para hacer una nueva figura.
¿Cómo se compara el área de su nueva figura con la del cuadrado original?
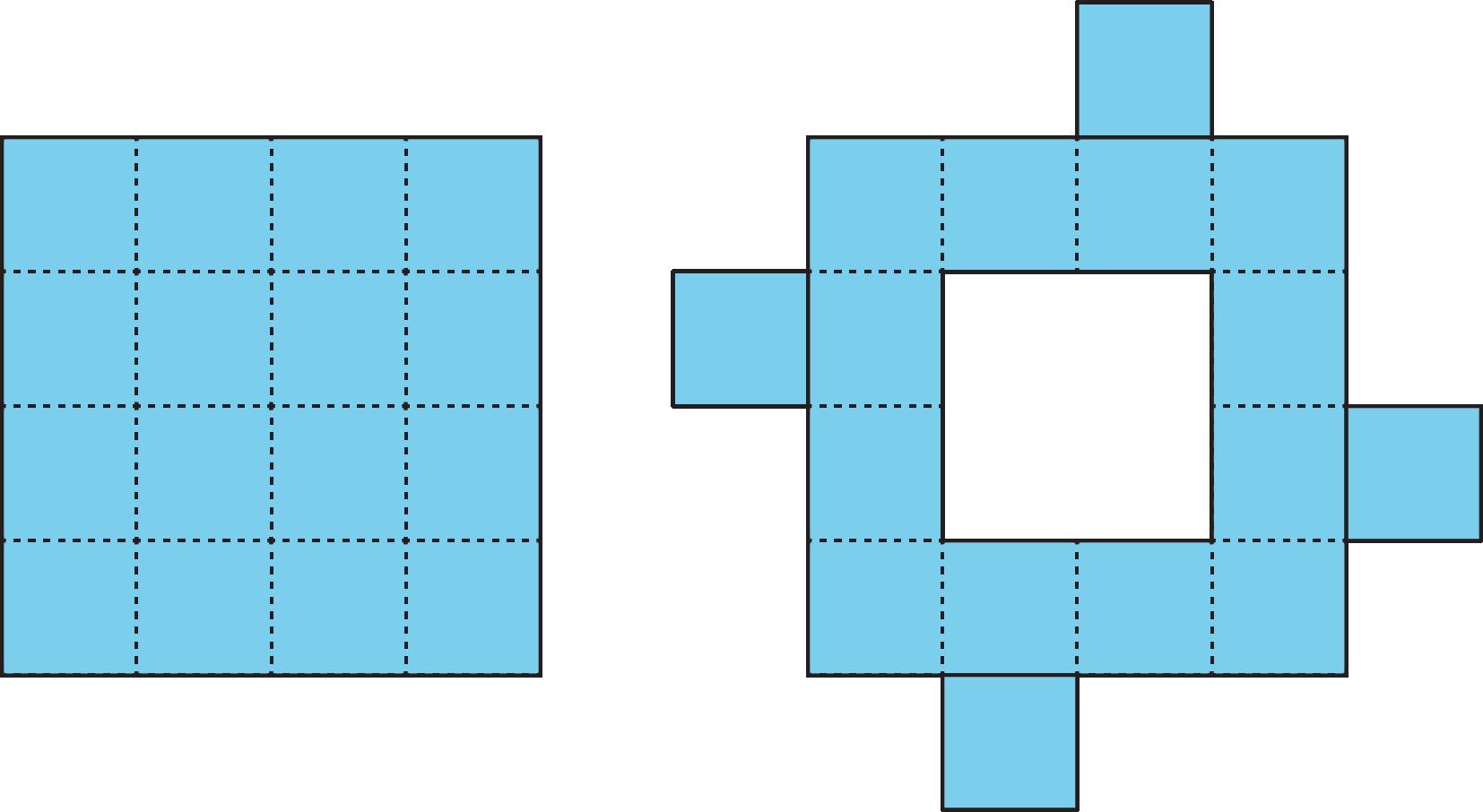
1. El área de la nueva figura es mayor.
2. Las dos figuras tienen la misma área.
3. El área del cuadrado original es mayor.
4. No lo sabemos porque no conocemos ni la longitud de los lados ni el área del cuadrado original.
Soluciones posibles
B


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 3
El área del cuadrado es 1 unidad cuadrada. Dos triángulos pequeños se pueden juntar para formar un cuadrado o para formar un triángulo mediano.
¿Qué figura también tiene un área de 1 1 2 unidades cuadradas? Selecciona todas las que correspondan.
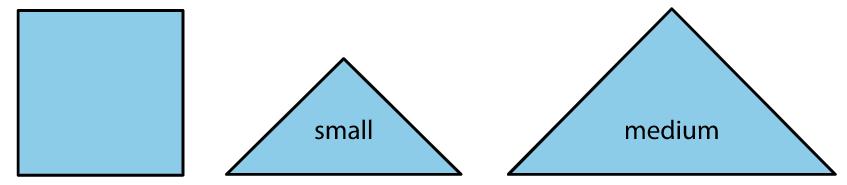

Figura A Figura B
Soluciones posibles
Figura A Figura B
PROBLEMA 4
Del Grado 6, Unidad 1, Lección 1
El área de un patio de recreo rectangular es 78 metros cuadrados. Si la longitud del patio de recreo es 13 metros, ¿cuál es su anchura?
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 1
Un estudiante dijo: "No podemos encontrar el área de la región sombreada porque la forma tiene muchas medidas diferentes, en lugar de sólo una longitud y una anchura que podríamos multiplicar."
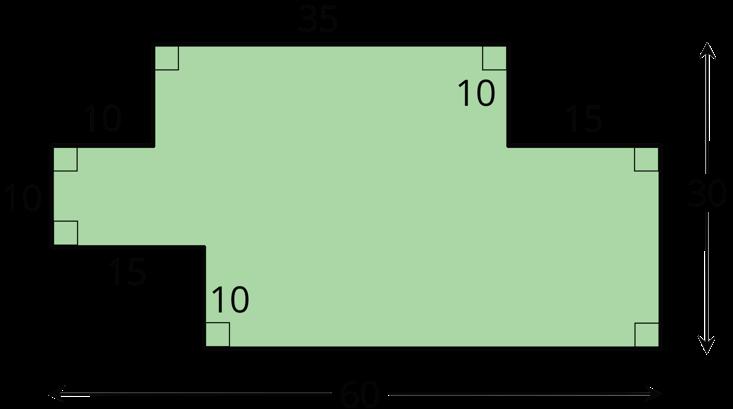
Explique por qué la afirmación del estudiante sobre el área es incorrecta.
Figura C Figura D
Figura C Figura D
Soluciones posibles 6 metros.
Soluciones posibles
Las respuestas varían. Ejemplo de explicación: El área mide cuántos cuadrados unitarios cubren una región sin huecos ni superposiciones. Multiplicamos una longitud y una anchura cuando hallamos el área de un rectángulo porque ese producto nos dice el número de cuadrados unitarios que hay en él. Podemos hallar el área de una figura como se muestra, pero primero tendremos que dividirla en rectángulos cuyas áreas podamos hallar y luego hallar el área total. También podemos encerrar la región 30-por-60 con un rectángulo, hallar su área y restar las áreas de las partes no sombreadas.


• Graficar formas
• Redes y superficie
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.3
I.C.9
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dan sentido al mundo e influyen en el futuro.
buscan y hacen uso de la estructura.
OBJETIVO(S) DE APRENDIZAJE
• Descomponer y reorganizar formas para hallar sus áreas.
OBJETIVO(S) DE APRENDIZAJE
desmontando enteros, juntando piezas y descubriendo la forma y el espacio.
• Utilizar diferentes estrategias de razonamiento para hallar las áreas de las formas.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comparar y contrastar (oralmente) diferentes estrategias para calcular el área de un polígono.
• Encontrar el área de un polígono descomponiendo, reordenando, restando o encerrando formas, y explicar (oralmente y por escrito) el método de solución.
• Incluir unidades apropiadas (en lenguaje oral y escrito) al enunciar el área de un polígono.
Rutinas didácticas
Pensar, compartir, pares
Anticipar, controlar, seleccionar, secuenciar, conectar
MLR3: clarificar, criticar, corregir
MLR2: Recoger y mostrar
MLR7: Comparar y conectar
Materiales necesarios
Lápiz negro para la actividad 3.1
Enfriamiento
Copias del lápiz negro
Materiales de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Grado 6 . Matemáticas . Unidad 1
Preparación requerida
Asegúrate de que los estudiantes tengan acceso a los elementos de sus juegos de materiales de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) para usar como regla o para marcar ángulos rectos.
Para la actividad de calentamiento, prepara varias copias del par de figuras en el patrón de líneas negras, en caso de que los estudiantes propongan recortarlas para comparar las áreas.
Narrativa de la lección
Esta lección es la tercera de tres lecciones que utilizan los siguientes principios de razonamiento sobre figuras para hallar el área:
• Si dos figuras pueden colocarse una encima de la otra de forma que coincidan exactamente, entonces tienen la misma área.
• Si una figura está compuesta por piezas que no se superponen, la suma de las áreas de las piezas es el área de la figura. Si una figura dada se descompone en piezas, entonces el área de la figura dada es la suma de las áreas de las piezas.
Siguiendo estos principios, los estudiantes pueden utilizar varias estrategias para hallar el área de una figura. Pueden:
• Descomponerla en figuras cuyas áreas puedan calcular.
• Descomponerla y reorganizarla en figuras cuyas áreas puedan calcular.
• Considerarla como una figura a la que le faltan una o más piezas, calcular el área de la figura y, a continuación, restar las áreas de las piezas que faltan.
• Encerrarlo con una figura cuya área puedan calcular, considerar el resultado como una región a la que le faltan piezas y hallar su área utilizando la estrategia anterior.
El uso de estas estrategias implica buscar y hacer uso de la estructura (MP7); explicarlas implica construir argumentos lógicos (MP3). Por ahora, los rectángulos son las únicas figuras cuyas áreas los estudiantes saben calcular, pero las estrategias serán más potentes a medida que crezca el repertorio de los estudiantes. Esta lección incluye una figura para la que la estrategia de "encerrar" es apropiada, sin embargo, esa estrategia no es el foco principal de la lección y no se incluye en la lista de estrategias al final.
Tenga en cuenta que estos materiales utilizan la notación "punto" (por ejemplo 2 ⋅ 3) para representar la multiplicación en lugar de la notación "cruz" (por ejemplo 2 × 3). Esto se debe a que los estudiantes escribirán muchas expresiones algebraicas y ecuaciones en este curso, a veces con la letra x como variable. Esta notación será nueva para muchos estudiantes y necesitarán una guía explícita para utilizarla.
DE LA LECCIÓN
Componente de la lección Estructura Tiempo Descripción breve
Calentamiento Independiente 5 min Los estudiantes comparan y justifican las áreas de dos figuras.
Dadas cuatro figuras en cuadrículas, los estudiantes encuentran el área de cada región sombreada usando estrategias de descomposición.

Actividad de exploración En parejas 20 min
- Grado 6
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la composición y descomposición de figuras en una cuadrícula.
Learning Inc. - Todos los derechos reservados


6 . Matemáticas . Unidad 1
Componente de la lección

Estructura Tiempo
Actividad de exploración Grupos pequeños 15 min
Síntesis Grupo completo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Descripción breve
Los estudiantes calculan las áreas de las regiones sombreadas de figuras que no están en una cuadrícula aplicando estrategias de descomposición y reordenamiento.
Los estudiantes resumen estrategias para encontrar áreas de regiones para varias formas y composiciones.
Los estudiantes descomponen una figura para determinar el área de una región sombreada.
El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.
5 minutos
Materiales necesarios
Plantilla para fotocopiar
Esta actividad lleva a los estudiantes a utilizar estrategias de razonamiento de lecciones anteriores para comparar las áreas de dos figuras. También es una oportunidad para utilizar (o introducir) el papel de calco como una forma de ilustrar la descomposición y reordenación de una figura.
A medida que los estudiantes trabajan, busque estudiantes que sean capaces de explicar o mostrar cómo saben que las áreas son iguales. Algunos estudiantes simplemente miran las figuras y dicen, sin justificación, que tienen la misma área. Pídales que piensen en una forma de demostrar que su conclusión es cierta.
Dé a los estudiantes acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y concédales 2 minutos de tiempo para pensar en silencio. Pídeles que estén preparados para apoyar su respuesta y recuérdales que utilicen las herramientas que tienen a su disposición. Tenga preparadas copias del esquema para los estudiantes que propongan recortar las figuras para compararlas o como forma de diferenciar la actividad.
¿Es el área de la figura A mayor, menor o igual que el área de la región sombreada de la figura B? Prepárate para explicar tu razonamiento.
Las áreas son iguales. Estrategias posibles:
• Medir: Mide las longitudes laterales del rectángulo pequeño sin relleno y del rectángulo pequeño del lado de la Figura B. Ambos rectángulos tienen las mismas longitudes laterales, por lo que sus áreas son iguales. Esto significa que el rectángulo del lado rellena el agujero del centro. Mide las longitudes de los lados del cuadrado grande sombreado en la Figura A y luego en la Figura B. Ambos tienen las mismas longitudes de lado, por lo que sus áreas son iguales.
• Utiliza unas tijeras: Corta el cuadrado pequeño del lado de la figura B y utilízalo para rellenar el agujero del centro de la figura B. De este modo obtendrás un cuadrado que coincide exactamente con el de la figura A.
• Utiliza papel de calco: Traza el límite del cuadradito en el lado de la figura B, mueve el papel de calco sobre el agujero sin sombrear y podrás ver que el cuadradito sombreado es exactamente del mismo tamaño que el agujero. Si movieras ese cuadradito sombreado para rellenar el agujero sin sombrear, obtendrías un cuadradito sombreado grande. Si trazas el límite de ese cuadrado sombreado grande y pones el papel de calco sobre la Figura A, puedes mostrar que el límite de ese cuadrado coincide exactamente con la Figura A.
Los estudiantes pueden interpretar el área de la Figura B como toda la región dentro del límite exterior, incluido el cuadrado sin rellenar. Aclare que sólo queremos comparar las áreas de las partes sombreadas de la Figura B y de la Figura A.

SÍNTESIS DE LA ACTIVIDAD
Inicie el debate pidiendo a los estudiantes que indiquen cuál de las tres respuestas posibles -área de la Figura A es mayor, área de la Figura B es mayor o las áreas son iguales- eligen. Seleccione a los estudiantes previamente identificados para que compartan sus explicaciones. Si ningún estudiante mencionó el uso de papel vegetal, demuestre lo siguiente.
• Descomponer y reordenar la Figura B: Coloque un trozo de papel de calco sobre la Figura B. Dibuje el límite del cuadrado pequeño, haciendo una línea auxiliar punteada para mostrar su separación del cuadrado grande. Mueve el papel de calco para que el cuadrado pequeño coincida exactamente con el cuadrado de la figura B. Dibuja el cuadrado grande. Explica que el cuadrado pequeño coincide exactamente con el agujero, por lo que sabemos que el cuadrado pequeño sombreado y el agujero tienen la misma superficie.
• Empareja las dos figuras: Mueva el papel de calco sobre la figura A de modo que el límite de la figura B reorganizada coincida exactamente con el de la figura A. Diga: "Cuando dos figuras superpuestas coinciden exactamente, sus áreas son iguales".
Destaque las estrategias y los principios fundamentales de esta unidad. Diga a los estudiantes: "Acabamos de descomponer y reordenar la figura B para que coincida exactamente con la figura A. Cuando dos figuras que se superponen una sobre otra coinciden exactamente, podemos decir que sus áreas son iguales".
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.


6 . Matemáticas . Unidad 1
20 minutos

Rutinas didácticas
Pensar compartir en par
Anticipar, monitorear, seleccionar, secuenciar, conectar
MLR3: clarificar, criticar, corregir
MLR2: recopilar y exhibir
Esta actividad ofrece a los estudiantes la oportunidad de encontrar áreas de regiones utilizando diversas estrategias. Al trabajar con una cuadrícula, los estudiantes pueden empezar contando cuadrados, como habían hecho en cursos anteriores. Sin embargo, las figuras se han elegido para suscitar las estrategias enumeradas en la Narrativa de la lección.
• La figura A puede descomponerse fácilmente en rectángulos.
• La figura B puede descomponerse en rectángulos. O, más eficazmente, puede verse como un cuadrado al que le falta una pieza, y el área del cuadrado interior sin sombrear puede restarse del área del cuadrado mayor.
• La figura C también puede verse como si le faltara una pieza, pero restar el área de la forma sin sombrear no funciona porque se desconocen las longitudes de los lados del cuadrado interior. En su lugar, los triángulos sombreados pueden descomponerse y reorganizarse en rectángulos.
• La figura D puede descomponerse y reorganizarse en rectángulos. También puede verse como el cuadrado interior de la figura C. Mientras los estudiantes trabajan, identifique a los que utilicen estas estrategias y puedan ilustrarlas o explicarlas claramente. Pídales que las compartan después. Busque al menos dos estrategias usadas para cada figura (una estrategia como se muestra en la Respuesta del Estudiante y al menos otra).
Diga a los estudiantes que van a encontrar las áreas de varias figuras en una cuadrícula. Para animar a los estudiantes a utilizar una estrategia más apropiada para su grado para encontrar áreas, muéstreles una estrategia de grados anteriores. En clase, hallen el área de la figura A contando los cuadrados uno a uno en voz alta. Confirme que hay 24 unidades cuadradas y, a continuación, pida a los estudiantes que piensen en otras formas de hallar el área de la Figura A y de otras figuras además de contar cada cuadrado. Organice a los estudiantes en grupos de 2. Pida a un compañero que empiece con las Figuras A y C, y al otro con B y D. Dé a los estudiantes 4-5 minutos de tiempo para pensar en silencio y facilíteles acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). A continuación, dales unos minutos para que compartan sus respuestas con sus compañeros. Haz hincapié en que mientras un compañero explica, el otro debe escuchar atentamente y ver si está de acuerdo o en desacuerdo con la respuesta y las explicaciones.
Apoyo para estudiantes que aprenden inglés
Hablar: MLR2 Recoger y mostrar. Mientras las parejas trabajan, circule y recoja las conversaciones sobre los enfoques para determinar el área de cada región sombreada. En algún lugar donde todos puedan verlo, anote frases comunes o importantes que oiga sobre cada representación (por ej., "descompuse el área" o "reorganicé los triángulos"). Esto ayudará al uso de lenguaje matemático durante sus debates por parejas y en clase.
Principio(s) de diseño: Apoyar la creación de sentido; Cultivar la conversación
Apoyo a estudiantes con discapacidades
Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (es decir, componer, descomponer, reorganizar) para mostrar públicamente definiciones, reglas, fórmulas o conceptos importantes para futuras referencias.
Habilidades motoras finas: Tutores. Empareje a los estudiantes con sus compañeros tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten cómo descomponer las figuras según sea necesario.
Grado 6 . Matemáticas . Unidad 1 ENUNCIADO
Cada cuadrado de la cuadrícula es 1 unidad cuadrada. Halla el área, en unidades cuadradas, de cada región sombreada sin contar cada cuadrado. Prepárate para explicar tu razonamiento.
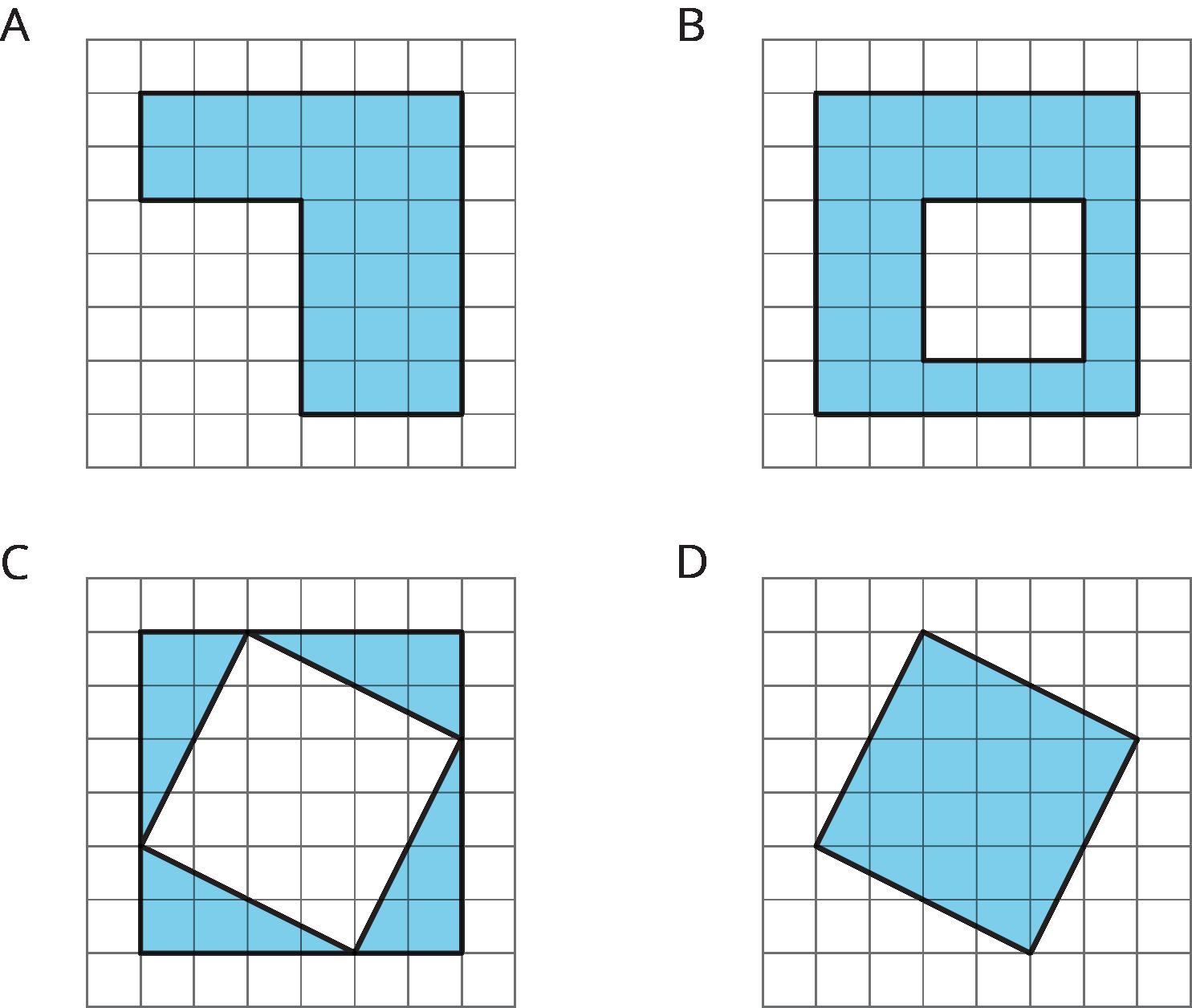

POSIBLES
RESPUESTAS
Las estrategias varían.
A. 24 unidades cuadradas. Ejemplo de estrategia: Descomponga la figura en rectángulos. Aquí se muestra una forma. (2 ⋅ 6) + (4 ⋅ 3) = 24
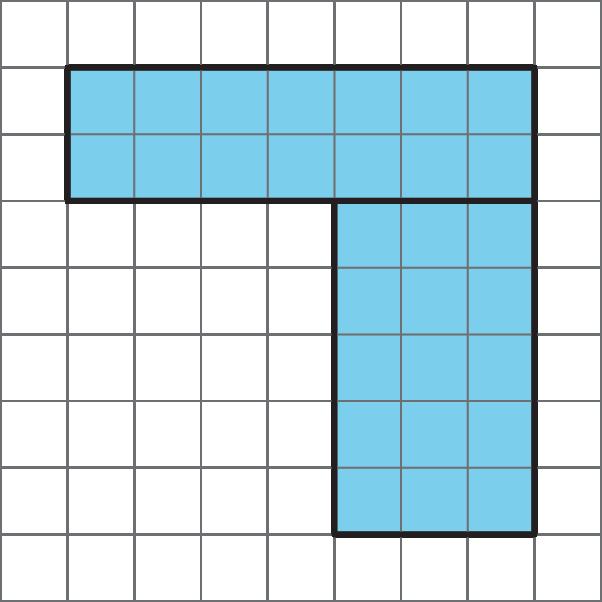
B. 27 unidades cuadradas. Estrategias de ejemplo:
• Descomponer la figura en cuatro rectángulos.
• Restar el área del cuadrado interior al cuadrado mayor. (6 ⋅ 6) - (3 ⋅ 3) = 27
C. 16 unidades cuadradas. Estrategias de ejemplo:
• Descomponer en triángulos rectángulos y reorganizar en rectángulos. (2 ⋅ 4) + (4 ⋅ 2) = 16
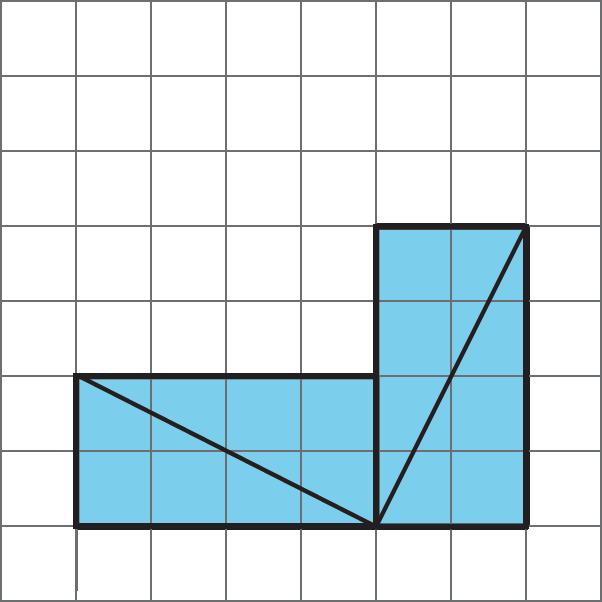
• Halla primero el área de la figura D y luego réstala del cuadrado 6-por-6
D. 20 unidades cuadradas. Estrategias de ejemplo:
• Descompone el cuadrado sombreado en cuatro triángulos rectángulos y un 2-por2 cuadrado. Reorganiza los triángulos rectángulos en dos rectángulos que sean cada uno 2 unidades por 4 unidades, con un área combinada de 16 unidades cuadradas. Sumando el área del cuadrado pequeño (4 unidades cuadradas) se obtiene un total de 20 unidades cuadradas.
• Observa que el cuadrado sombreado es el cuadrado interior de la figura C, enciérralo en un cuadrado como en la figura C y resta las áreas de los cuatro triángulos rectángulos (es decir, el área de la figura C) del área del cuadrado que lo encierra. (6 ⋅ 6) - 16 = 20
- Grado 6
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Es posible que algunos estudiantes cuenten cuadrados completos y parciales de la cuadrícula en lugar de buscar formas de descomponer y reorganizar formas más grandes. Pregúnteles si pueden encontrar una forma de hallar el área descomponiendo y reordenando piezas más grandes. La discusión del final, durante la cual todos ven una variedad de estrategias, es especialmente importante para estos estudiantes.
La discusión debe centrarse en cómo se utilizan las diferentes estrategias -descomponer, reorganizar, restar y encerrar- para hallar el área. Para cada figura, seleccione a dos estudiantes con estrategias diferentes para que compartan su trabajo, si es posible. Ordene las presentaciones de los estudiantes de modo que, para cada figura, la estrategia de sustracción sea la última, ya que suele ser la más difícil.
Antes de empezar a compartir, explique a los estudiantes que deben observar las similitudes y diferencias en las estrategias compartidas y estar preparados para explicarlas. Cuando los estudiantes compartan sus estrategias, considere la posibilidad de anotar los movimientos en cada figura para que todos puedan verlos. Después de que cada persona comparta, nombra la estrategia y sondea a la clase para ver si alguien más razonó de la misma manera. Si alguna de estas estrategias no aparece en el trabajo de los estudiantes, ilústrala para la clase.
• Descomponiendo (A y B)
• Descomponiendo y reordenando (C y D)
• Restando (B)
• Encerrando, luego restando (D)
Si el tiempo lo permite, dales a los estudiantes un minuto para hablar con sus compañeros sobre las similitudes y diferencias que vieron en las estrategias utilizadas para encontrar las áreas de las cuatro figuras. Considere la posibilidad de mostrar iniciadores de frases como:
• Las estrategias utilizadas para hallar las áreas de las figuras y se parecen en que. .
• Las estrategias utilizadas para hallar las áreas de las figuras y se diferencian en que. . . .
Apoyo para estudiantes que aprenden inglés
Conversación: MLR2 Recoger y mostrar.
Hablar: Rutina 3 del lenguaje matemático 3: aclarar, criticar, corregir: Esta es la primera vez que se sugiere la «Rutina 3 del lenguaje matemático 3» como apoyo en este curso. En esta rutina, los estudiantes reciben un trabajo matemático incorrecto o incompleto. Puede ser en forma de enunciado escrito, dibujo, pasos de resolución de problemas u otra representación matemática. Por parejas, analizan, reflexionan y mejoran el trabajo escrito corrigiendo errores y aclarando el significado. Las preguntas típicas son: "¿Hay algo que no esté claro?" o "¿Hay algún error de razonamiento?". El propósito de esta rutina es hacer que los estudiantes analicen el pensamiento matemático que no es el suyo y consoliden sus conocimientos mediante la comunicación sobre errores conceptuales y ambigüedades en el lenguaje.
Principio(s) de diseño: Maximizar la metaconciencia
Cómo se lleva a cabo:
1. En la conversación en clase para la Figura C de esta actividad, proporcione la siguiente explicación "en borrador": "Corté un cuadrado en el medio, luego vi que era un montón de triángulos, así que los calculé para obtener mi respuesta".
Pida a los estudiantes que identifiquen la ambigüedad de esta respuesta. Pregunte a los estudiantes: "¿Qué creéis que intenta decir esta persona? ¿Qué es lo que no está claro? ¿Utilizó el autor alguna de las estrategias que hemos estado utilizando para encontrar el área?"
Grado 6 . Matemáticas . Unidad 1

Apoyo para estudiantes que aprenden inglés (Continuación)
2. Dé a los estudiantes 1 minuto de tiempo individual para responder a las preguntas por escrito y, a continuación, 3 minutos para debatir con un compañero. Mientras discuten en parejas, proporcione estos marcos de oraciones para el andamiaje: "Creo que el autor intenta utilizar la estrategia _ porque....", "Creo que lo que el autor quiso decir con 'lo descubrió' fue....", y "La parte que me resulta más confusa es... porque....". Anime al oyente a insistir en los detalles haciendo preguntas de seguimiento para aclarar el significado de la afirmación. Permita que cada miembro de la pareja haga por turnos de hablante y oyente.
3. Invite a los estudiantes a mejorar el "borrador" de respuesta utilizando el vocabulario y las estructuras objetivo. El vocabulario objetivo incluye los nombres de las estrategias (descomponer, reordenar, restar, encerrar o cualquier combinación de ellas) y otros términos de esta lección como "igual", "diferente", "área" y "polígono". Las estructuras objetivo de la respuesta deben incluir una explicación de cada paso, palabras de transición de orden/tiempo (primero, siguiente, luego, etc.), y/o razones de las decisiones tomadas durante los pasos. He aquí un ejemplo de respuesta mejorada: "Primero, recorté el cuadrado en medio de las regiones sombreadas. Después, me di cuenta de que todas las regiones sombreadas eran un montón de triángulos rectángulos. A continuación, he transformado los triángulos en rectángulos. Por último, calculé el área de cada rectángulo y los sumé para obtener mi respuesta".
4. Pide a cada pareja de estudiantes que aporte su respuesta mejorada en un cartel, en la pizarra o en una proyección digital. Pida a 2-3 parejas de estudiantes que presenten su respuesta a toda la clase e invite a la clase a hacer comparaciones entre las respuestas compartidas y sus propias respuestas. Preste atención a las respuestas que incluyan la estrategia de descomponer y luego reorganizar los triángulos. Haga hincapié en que ésta es una forma de calcular el área de la región sombreada.
5. Comparta una respuesta mejorada más, discuta para llegar a una comprensión general y, a continuación, pase a la Figura D.
¿Estás listo para más?
Reordena los triángulos de la Figura C para que quepan dentro de la Figura D. Dibuja y colorea un diagrama de tu trabajo en la cuadrícula.

"¿Estás listo para más?" Respuesta del estudiante
Los triángulos caben dentro del cuadradore, con un cuadrado más pequeño 2-por-2 en el centro.
Este arreglo muestra que el área de la Figura D es 4 unidades cuadradas más que el área de la Figura C.


6 . Matemáticas . Unidad 1
15 minutos
Rutinas didácticas
MLR7: Comparar y conectar
En esta actividad, los estudiantes aplican las estrategias aprendidas para hallar las áreas de figuras que no están en una cuadrícula.
• La figura A puede descomponerse y reordenarse fácilmente.
• La figura B puede descomponerse y reordenarse en rectángulos de la misma forma que la figura C de la tarea anterior. Los estudiantes no pueden utilizar la estrategia de restar el área del cuadrado interior de la del cuadrado exterior porque se desconocen las longitudes de los lados del cuadrado interior.
• Para la Figura C, los estudiantes deben restar el área del cuadrado interior de la del cuadrado exterior porque no hay suficiente información para descomponer y reorganizar las regiones sombreadas en rectángulos.
Mientras los estudiantes discuten sus planteamientos en grupos, ayúdeles a nombrar las estrategias y a hacer preguntas aclaratorias. Fíjese en los grupos que puedan estar en desacuerdo sobre el área de una figura concreta. Identifique a los estudiantes que hayan observado que las mismas estrategias de razonamiento del área pueden aplicarse tanto dentro como fuera de la cuadrícula.
Es posible que los estudiantes no recuerden de cursos anteriores que si las medidas de las longitudes de los lados de un rectángulo se dan en una unidad determinada, entonces el área se da en unidades cuadradas. Busque estudiantes que tengan problemas para dar las unidades de área apropiadas (centímetros cuadrados) para estas figuras.

Diga a los estudiantes que ahora encontrarán áreas de figuras que no están en una cuadrícula. Dé a los estudiantes acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a 6-7 minutos de silencio para encontrar las tres áreas.
Luego, organice a los estudiantes en grupos de 4, y pida a cada grupo que discuta sus respuestas y estrategias, utilizando estas preguntas orientadoras:
1. ¿Qué unidades utilizaron para cada área?
2. Comparen sus respuestas y estrategias para hallar el área de cada figura.
• ¿En qué coinciden sus estrategias? ¿En qué se diferencian?
• ¿Qué estrategias son similares a las que utilizaron en la actividad anterior?
Apoyo para estudiantes con
Funcionamiento socio-emocional: Tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados. Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una pregunta a la vez), lo que ayudará a los estudiantes que se benefician del apoyo con habilidades de organización en la resolución de problemas.
Halla el área de la(s) región(es) sombreada(s) de cada figura. Explica o muestra tu razonamiento.
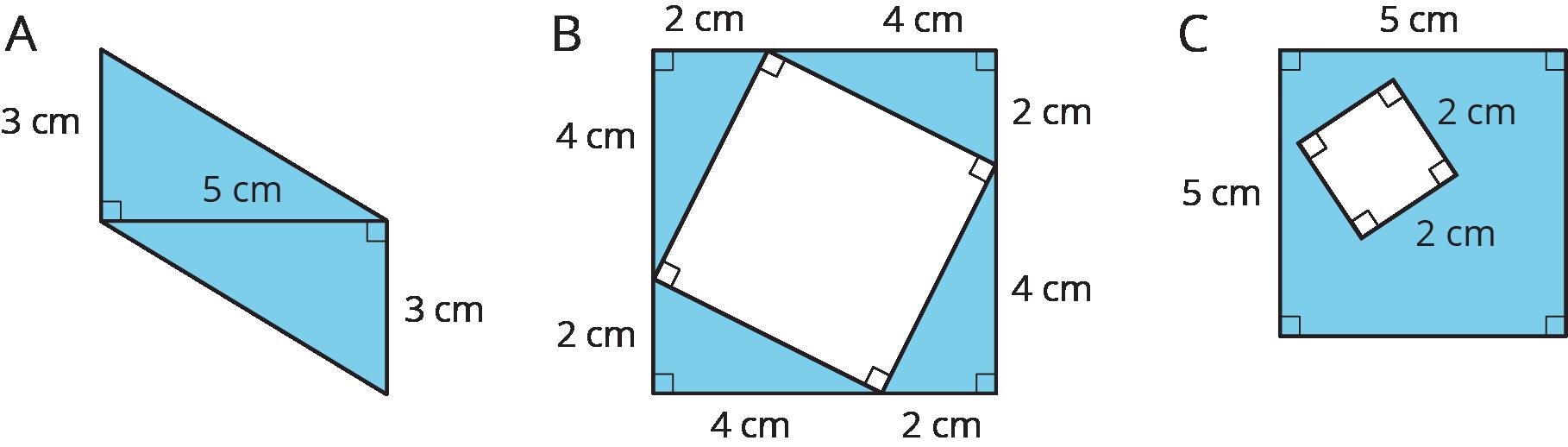
Grado 6 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
El razonamiento varía.
Figura A: El área es 15 centímetros cuadrados. Ejemplo de razonamiento: Descomponga los dos triángulos y reordénelos para formar un rectángulo con longitudes laterales de 5 centímetros y 3 centímetros.
Figura B: El área es 16 centímetros cuadrados. Ejemplo de razonamiento: Descomponga los triángulos y reordénelos para formar dos rectángulos con longitudes laterales de 4 centímetros y 2 centímetros.
Figura C: El área es 21 centímetros cuadrados. Ejemplo de razonamiento: Resta el área del cuadrado interior al área del cuadrado exterior. 25 - 4 = 21
En la figura B, los estudiantes pueden estimar las longitudes de los lados del cuadrado interior para poder restar su área de la del cuadrado exterior. Es posible que les cueste ver cómo se pueden reordenar los triángulos. Sugiérales que utilicen papel de calco para ayudarles a pensar.
En las figuras B y C, los estudiantes pueden confundir el cálculo del área con el del perímetro. Recuérdales que el área se refiere al número de unidades cuadradas que se necesitan para cubrir una región sin huecos ni solapamientos.
Puede que los estudiantes no estén familiarizados con los símbolos que indican ángulos rectos y piensen que estos símbolos indican unidades cuadradas. Recuérdeles que esos símbolos indican ángulos de 90 grados.
Vuelva a reunirse brevemente como clase para discutir la pregunta: "¿Qué estrategias son similares a las que utilizó en la actividad anterior?"
Seleccione 1-2 estudiantes previamente identificados para compartir (aquellos que notaron que descompusieron, reordenaron, encerraron y restaron en ambas actividades). Enfatice que se pueden utilizar las mismas estrategias para hallar el área tanto si utilizamos las medidas indicadas por una cuadrícula, como si las medidas se dan directamente (sin cuadrícula).
Apoyo para estudiantes que aprenden inglés
Hablar: Rutina del Lenguaje Matemático 7 Compara y Conecta. Esta es la primera vez que se sugiere la Rutina 7 del Lenguaje Matemático como apoyo en este curso. En esta rutina, se da a los estudiantes un problema que puede abordarse utilizando múltiples estrategias o representaciones, y se les pide que preparen una muestra visual de su método. A continuación, los estudiantes investigan las estrategias (mediante un recorrido guiado por el maestro, un intercambio entre compañeros, una presentación en grupo, etc.), comparan enfoques e identifican correspondencias entre distintas representaciones. Un tema de debate típico es: "¿Qué es lo mismo y qué es diferente?" en relación con su propia estrategia y la de los demás. El propósito de esta rutina es permitir a los estudiantes dar sentido a las estrategias matemáticas identificando, comparando, contrastando y conectando otros enfoques con el suyo propio, y desarrollar la conciencia de los estudiantes sobre el lenguaje utilizado a través de conversaciones constructivas.
Principios de diseño: Maximizar la metaconciencia
Cómo se lleva a cabo:
A. Identifique qué Figura (A, B o C) generó la mayor variedad entre las estrategias de los estudiantes. Invite a los estudiantes a crear una presentación visual en la que muestren cómo le han dado sentido a esta figura. Los estudiantes deben incluir estas características en su exhibición:
• el dibujo de la figura
• unidades apropiadas
• una representación de cómo se calculó el área
• el nombre de la estrategia utilizada para encontrar el área (descomponer, reordenar, restar, encerrar, o cualquier combinación de ellas)


Grado 6 . Matemáticas . Unidad 1

Apoyo para estudiantes que aprenden inglés (Continuación)
B. Organice a los estudiantes en grupos de 4, e invítelos a investigar el trabajo de los demás. Conceda 1 minuto a cada exposición y señale cuándo es el momento de cambiar. A continuación, dé a cada estudiante la oportunidad de añadir detalles a su propia exposición durante 1-2 minutos.
C. Circule por la clase e invite a los estudiantes de 2-3 a presentar su exposición a toda la clase. Asegúrese de seleccionar una variedad de estrategias.
D. Cuando los estudiantes preseleccionados hayan terminado de presentar sus exposiciones, dirija un debate en el que se comparen, contrasten y relacionen los distintos enfoques.
Considere la posibilidad de utilizar estas indicaciones para ampliar el lenguaje de los estudiantes mientras comparan y contrastan los diferentes enfoques:
• "¿Por qué los diferentes enfoques de la figura _ condujeron al mismo resultado?"
• "¿Qué funcionó bien en este enfoque de la figura _? ¿Qué no funcionó bien?"
• "¿Qué haría que esta estrategia para la Figura _ fuera más completa o fácil de entender?"
Considere la posibilidad de utilizar estas indicaciones para ampliar el lenguaje de los estudiantes mientras conectan los diferentes enfoques:
• "¿Puedes encontrar alguna conexión entre las representaciones?"
• "¿Dónde se utilizan las unidades en cada estrategia?"
• "¿Es posible utilizar la estrategia de descomponer para esta figura?"
• "¿Qué características matemáticas ves presentes en todas las representaciones?"
E. Cierra el debate invitando a 3 los estudiantes a que vuelvan a expresar las estrategias utilizadas en las presentaciones y, a continuación, pasa de nuevo a la Síntesis y enfriamiento de la lección.
5 minutos
Esta lección ha consistido en identificar estrategias para hallar el área y aplicarlas a diversas figuras. Hemos razonado sobre el área de una figura dentro y fuera de una cuadrícula:
• descomponiéndola en formas familiares;
• descomponiéndola y reorganizando las piezas en formas familiares; o
• considerándola como una forma a la que le faltan piezas, y restando las áreas de las piezas que faltan del área de la forma.
Pida a los estudiantes que repasen las actividades y encuentren problemas en los que se hayan utilizado estas estrategias, una estrategia cada vez. Diles que tendremos muchas oportunidades de utilizar estas estrategias en las próximas lecciones.
5 minutos
En esta tarea no se pide explícitamente a los estudiantes que indiquen las unidades de área porque uno de los propósitos de la tarea es evaluar si los estudiantes entienden qué unidades son apropiadas dada la información presentada.
Dé a los estudiantes acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Grado 6 . Matemáticas . Unidad 1
POSIBLES

Se muestra una bandera marítima. ¿Cuál es el área de la parte sombreada de la bandera? Explique o muestre su razonamiento.
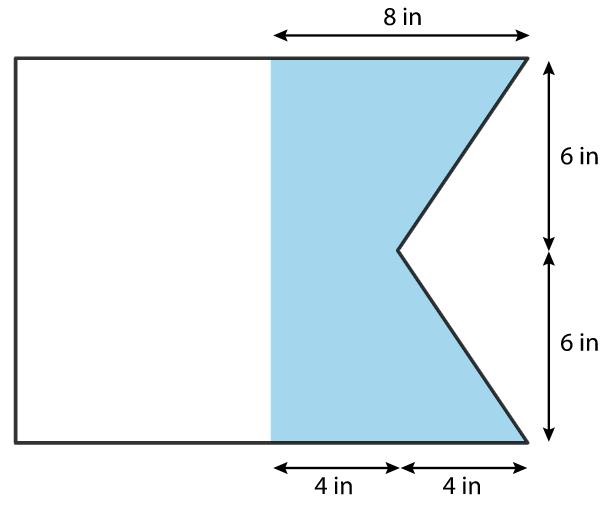
72 pulgadas cuadradas. El razonamiento varía. Ejemplo de razonamiento: Si trazamos una línea por el centro de la zona sombreada, tendríamos un 4 pulgadas-por12 pulgadas rectángulo a la izquierda y dos triángulos a la derecha. El rectángulo 4-por-12 tiene un área de 48 pulgadas cuadradas. Los dos triángulos de la derecha pueden componerse en un rectángulo de 4 pulgadas por6 pulgadas, por lo que su área combinada es de 24 pulgadas cuadradas. 48 + 24 = 72.
PROBLEMA 1
Encuentre el área de cada región sombreada. Muestra tu razonamiento.
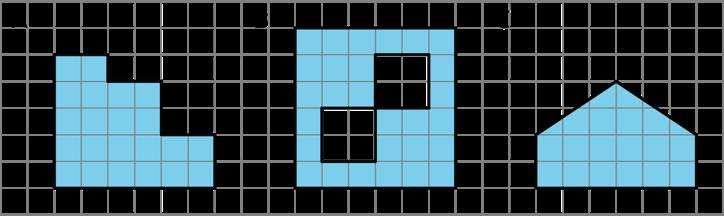
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta:
Forma A: 22 unidades cuadradas. La región sombreada puede dividirse en rectángulos. Una forma de hacerlo es la que se muestra arriba. El rectángulo 1 mide 2 unidades por 5 unidades, por lo que su área es de 10 unidades cuadradas. El Rectángulo 2 es de 2 por 4 unidades, por lo que su área es de 8 unidades cuadradas. El área del rectángulo 3 es de 4 unidades cuadradas. El área sombreada total es de 22 unidades cuadradas, ya que 10 + 8 + 4 = 22.
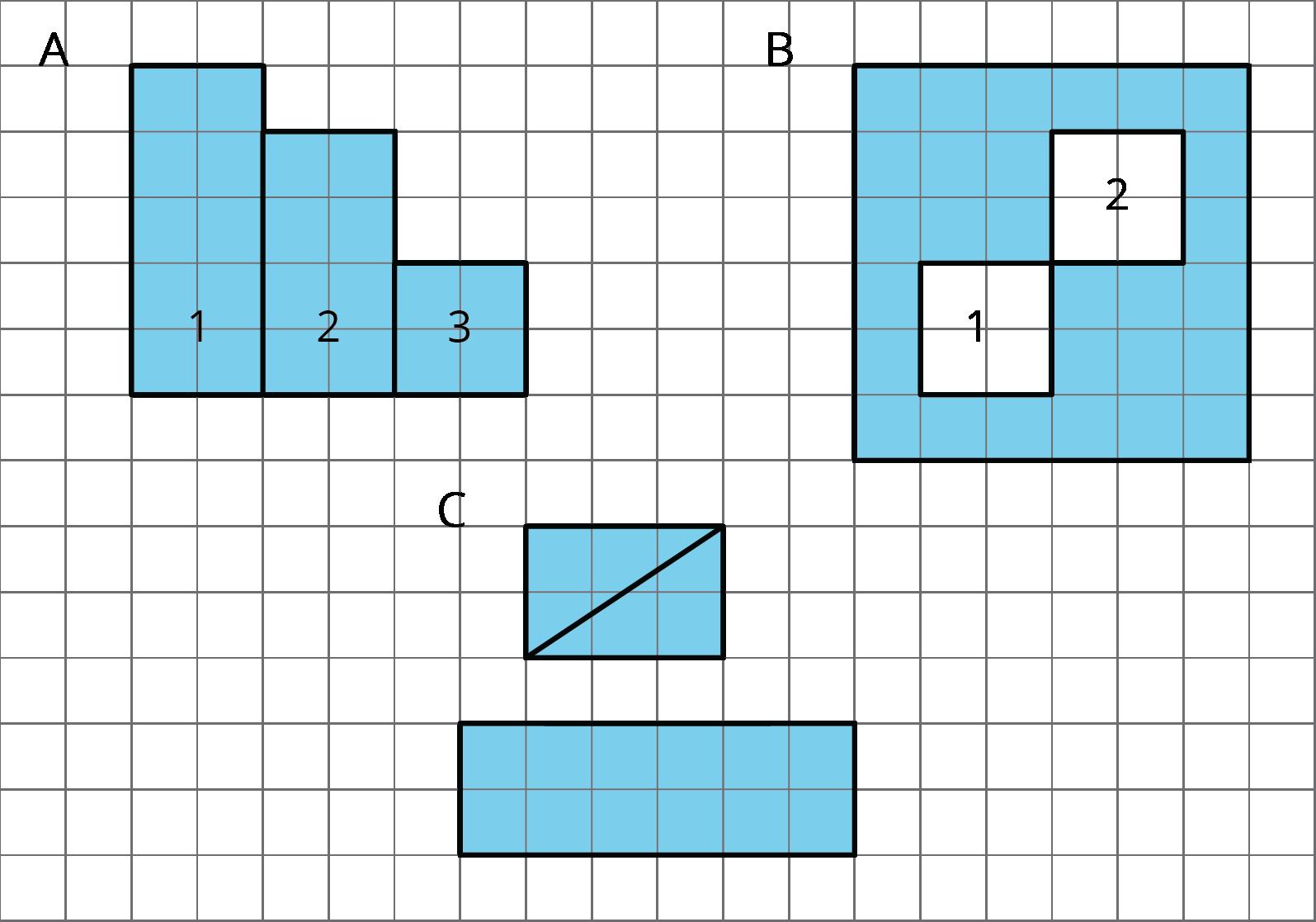
Forma B: 28 unidades cuadradas. El cuadrado exterior mide 6 unidades por 6 unidades, por lo que su área es de 36 unidades cuadradas. Dentro hay dos cuadrados más pequeños. El cuadrado 1 y el cuadrado 2 se han eliminado. Cada cuadrado pequeño tiene un área de 4 unidades cuadradas. Para obtener el área sombreada, calcula 36-4-4, que es igual a 28
Forma C: 18 unidades cuadradas. La región se puede recomponer para formar un rectángulo de 2 por 6 y otro de 2 por 3 (2 ⋅ 6) + (2 ⋅ 3) = 18
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 2
Halla el área de cada región sombreada. Muestra o explica tu razonamiento.
Soluciones posibles
El razonamiento varía. Ejemplos de respuestas:
A: 28 cm2. Un corte horizontal lo divide en un cuadrado de 2 cm por 2 cm (4 cm2) y un rectángulo de 4 cm por 6 cm (24 cm2).
B: 34 cm2. El rectángulo exterior tiene un área de 40 cm2 , mientras que el rectángulo interior tiene un área de 6 cm2 40 - 6 = 34
C: 96 cm2. El rectángulo exterior tiene un área de 150 cm2 , mientras que el rectángulo interior tiene un área de 54 cm2 150 - 54 = 96.
D: 40 cm2. Los dos triángulos rectángulos pueden unirse para formar un rectángulo de 5 cm por 8 cm.
PROBLEMA 3
Dos terrenos tienen formas muy diferentes. Noé dice que ambos terrenos tienen la misma superficie.
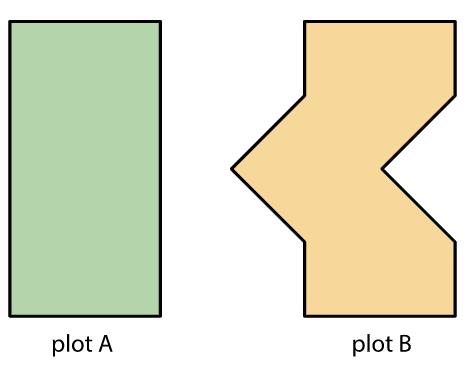
¿Estás de acuerdo con Noé? Explica tu razonamiento.
Soluciones posibles
De acuerdo. Las respuestas varían. Ejemplo de razonamiento: La forma triangular que sobresale del lado izquierdo de la parcela B se puede cortar y trasladar al lado derecho de la parcela B. La forma resultante es un rectángulo que coincide exactamente con la forma de la parcela A. Podemos utilizar papel de calco para verificarlo. Diagramas de ejemplo:
Grado 6 . Matemáticas . Unidad 1

PROBLEMA 4
Del Grado 6, Unidad 1, Lección 2
La dueña de una casa está decidiendo el tamaño de los azulejos que usará para embaldosar completamente una pared rectangular en su baño que mide 80 por 40 pulgadas. Los azulejos son cuadrados y vienen en tres longitudes de lado: 8 pulgadas, 4 pulgadas y 2 pulgadas. Diga si está de acuerdo con cada una de las afirmaciones sobre los azulejos. Explica tu razonamiento.
A. Independientemente del tamaño que elija, necesitará el mismo número de azulejos.
B. Independientemente del tamaño que elija, la superficie de la pared que se va a alicatar es la misma.
C. Necesitará dos 2 azulejos para cubrir la misma superficie que un 4 azulejo.
D. Necesitará cuatro 4-pulgadas para cubrir la misma superficie que con una 8-pulgada.
E. Si elige las 8-pulgadas, necesitará una cuarta parte de las baldosas que necesitaría con 2-pulgadas.
Las explicaciones varían. Ejemplos de explicaciones y diagrama:
A. En desacuerdo. Necesitará menos baldosas grandes y más baldosas pequeñas.
B. De acuerdo. La región cubierta no cambia independientemente de las baldosas que elija.
C. En desacuerdo. Necesitará cuatro baldosas de 2 pulgadas para cubrir la misma superficie que una baldosa de 4 pulgadas.
D. De acuerdo. Dos filas de dos baldosas 4-pulgadas cubren la misma superficie que una baldosa 8-pulgadas.
E. En desacuerdo. Como una baldosa 8-pulgadas cubre la misma superficie que cuatro baldosas 4-pulgadas, necesitará 1 16 tantas baldosas 8-pulgadas como 2-pulgadas.
Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Graficar formas
• Redes y superficie
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Construir sobre 5.G
Enfoque SMPs
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.1
I.B.5 I.C.11
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dan sentido al mundo.
buscan y expresan regularidades en razonamientos repetidos.
OBJETIVO(S) DE APRENDIZAJE
desmontan el todo, juntan las partes y descubren la forma y el espacio.
• Vamos a investigar las características y el área de los paralelogramos.
• Puedo utilizar estrategias de razonamiento y lo que sé sobre el área de un rectángulo para hallar el área de un paralelogramo.
• Sé describir las características de un paralelogramo utilizando vocabulario matemático.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comparar y contrastar (oralmente) diferentes estrategias para determinar el área de un paralelogramo.
• Describir (oralmente y por escrito) observaciones sobre los lados opuestos y los ángulos opuestos de los paralelogramos.
• Explicar (oralmente y por escrito) cómo encontrar el área de un paralelogramo reordenándolo o encerrándolo en un rectángulo.
Rutinas didácticas
Notar y preguntar
MLR2: recopilar y mostrar
Anticipar, monitorear, seleccionar, hacer secuenciasy connectar
MLR3: clarificar, criticar, corregir
Materiales necesarios
Enfriamiento
Materiales de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
de Matemáticas . Unidad 1
Narrativa de la lección
Los estudiantes conocieron las líneas paralelas en 4º curso. Aunque los estándares no establecen explícitamente que los estudiantes deben trabajar con paralelogramos en los grados 3-5, los estándares de geometría en esos grados invitan a los estudiantes a aprender y explorar cuadriláteros de todo tipo. La progresión de la geometría K-6 da ejemplos de los tipos de trabajo que los estudiantes pueden hacer en este dominio, incluyendo el trabajo con paralelogramos.
En esta lección, los estudiantes analizan los atributos definitorios de paralelogramos, observan otras propiedades que se derivan de esa definición, y utilizan estrategias de razonamiento de las lecciones anteriores para encontrar las áreas de los paralelogramos.
Al descomponer y reorganizar los paralelogramos en rectángulos, y al encerrar un paralelogramo en un rectángulo y luego restar el área de las regiones adicionales, los estudiantes comienzan a ver que los paralelogramos tienen rectángulos relacionados que se pueden utilizar para encontrar el área.
A lo largo de la lección, los estudiantes encuentran varios paralelogramos que, debido a su forma, fomentan el uso de ciertas estrategias. Por ejemplo, algunos pueden descomponerse fácilmente y reorganizarse en un rectángulo. Otros -como los que son estrechos y alargados- pueden animar a los estudiantes a encerrarlos en rectángulos y restar las áreas de las piezas sobrantes (dos triángulos rectángulos).
Después de trabajar con una serie de paralelogramos, los estudiantes intentan generalizar (informalmente) el proceso de hallar el área de cualquier paralelogramo (MP8).
Obsérvese que estos materiales utilizan la notación "punto" (por ejemplo 2 ⋅ 3) para representar la multiplicación en lugar de la notación "cruz" (por ejemplo 2 × 3). Esto se debe a que los estudiantes escribirán muchas expresiones algebraicas y ecuaciones en este curso, a veces con la letra x como variable. Esta notación será nueva para muchos estudiantes y necesitarán una guía explícita para utilizarla.
RESUMEN DE LA LECCIÓN
Componente Estructura Tiempo Breve descripción
Calentamiento En parejas 10 min

Actividad de exploración Grupos pequeños 15 min
Actividad de exploración Grupos Pequeños 15 min
Síntesis Grupo Entero 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Los estudiantes hacen observaciones sobre las características que definen los paralelogramos analizando ejemplos y no ejemplos de paralelogramos.
Un applet digital interactivoLos estudiantes determinan las áreas de paralelogramos en cuadrículas utilizando diferentes estrategias de descomposición y encerramiento. está disponible para permitir a los estudiantes explorar la descomposición y encerramiento de figuras para encontrar el área utilizando la tecnología.
Los estudiantes aplican estrategias para encontrar las áreas de paralelogramos dentro y fuera de la cuadrícula.
Los estudiantes repasan las características de los paralelogramos y las estrategias usadas para encontrar sus áreas.
Los estudiantes describen una estrategia que podría usarse para encontrar el área de un paralelogramo en una cuadrícula.
El componente de práctica independiente incluye 4 en la lección y 2 problemas de repaso en espiral.
California - Grado 6
Learning Inc. - Todos los derechos reservados


PARALELOGRAMO 10 minutos
Rutinas didácticas
Notar y preguntar
Antes del sexto grado, los estudiantes aprendieron que las líneas son paralelas si nunca se cruzan. En esta actividad, los estudiantes observan los atributos que definen a los paralelogramos-un cuadrilátero cuyos lados opuestos son paralelos. Observan otras propiedades que se derivan de esa definición: que los lados opuestos de un paralelogramo tienen la misma longitud y que los ángulos opuestos tienen la misma medida.
La investigación inicial de los paralelogramos por parte de los estudiantes debe incluir muchos ejemplos y no ejemplos, dándoles la oportunidad de buscar y expresar regularidad en razonamientos repetidos (MP8) y buscar y hacer uso de la estructura (MP7). Esta actividad asume que los estudiantes han tenido alguna exposición a los paralelogramos, pero también es accesible para los estudiantes que no la han tenido.
Muestre la imagen de las figuras A-F para que todos la vean. Conceda a los estudiantes un minuto para que la observen y se preparen para compartir al menos una cosa que observen y otra que se pregunten. Cuando termine el minuto, invite a los estudiantes a compartir sus respuestas con la clase.
Los estudiantes pueden notar que:
• todas las figuras excepto una (E) son cuadriláteros.
• las figuras C y E tienen lados que son todos iguales en longitud.
• las figuras A y B tienen dos pares de lados iguales.
• las figuras B y C son rectángulos.

• ninguno de los lados de D es paralelo.
• dos de los lados de F son paralelos.
Puede que se pregunten:
• por qué hay un hexágono en el conjunto.
• si los lados de la figura A son todos iguales.
• si la figura C es un paralelogramo. Es probable que uno o más estudiantes mencionen "paralelogramo" en sus observaciones o preguntas. Diga a los estudiantes que en esta lección van a estudiar detenidamente los paralelogramos. Lea en voz alta las frases iniciales del enunciado de la tarea. Aclare que A, B y C son ejemplos de paralelogramos, y que D, E y F no son ejemplos (es decir, no son paralelogramos).
Organice a los estudiantes en grupos de 2 y entrégueles herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a los estudiantes 3 minutos de reflexión en silencio para realizar la tarea. Después, dales un minuto para que comenten sus respuestas y observaciones con su compañero.
Apoyo para estudiantes con discapacidad
Funcionamiento ejecutivo:
• Organizadores gráficos. Proporcione un gráfico en forma de T para que los estudiantes anoten lo que observan y se preguntan antes de compartir estas ideas con los demás.
• Ayudas visuales. Añada el paralelogramo al cuadro de vocabulario de la clase.
6º de Matemáticas . Unidad 1

CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
Las figuras A, B y C son paralelogramos. Las figuras D, E y F son no paralelogramos.
Estudia los ejemplos y los no-ejemplos. ¿Qué notas acerca de:
1. el número de lados que tiene un paralelogramo?
2. lados opuestos de un paralelogramo?
3. ángulos opuestos de un paralelogramo?
1. Los paralelogramos tienen cuatro lados.
2. Los lados opuestos de los paralelogramos son paralelos y tienen la misma longitud.
3. Los ángulos opuestos de los paralelogramos tienen el mismo tamaño.
Los estudiantes pueden tener problemas para ver a C como un cuadrado debido a su orientación. También pueden pensar que los cuadrados y los rectángulos no son paralelogramos. Explique que la definición que utilizamos para los paralelogramos es: un cuadrilátero en el que ambos pares de lados opuestos son paralelos. Según esta definición, los rectángulos y los cuadrados son tipos especiales de paralelogramos. Si los estudiantes se preguntan cómo pueden saber si dos lados son paralelos, explíqueles que una consecuencia de que "nunca se crucen" es que la longitud de un segmento de recta perpendicular entre ellos siempre tiene la misma longitud. Los estudiantes pueden utilizar una ficha para comprobarlo en las figuras A y C.
Pida a algunos estudiantes que compartan sus respuestas a las preguntas. Después de cada respuesta, pida a los estudiantes que indiquen si están de acuerdo. Si un estudiante no está de acuerdo, discuta el desacuerdo. Registre las respuestas acordadas para que todos las vean y destaque que:
• Un paralelogramo es un polígono con cuatro lados, y ambos pares de lados opuestos son paralelos.
• Los lados opuestos tienen la misma longitud.
• Los ángulos opuestos tienen la misma medida.
Diga a los estudiantes que por ahora sólo tomaremos las propiedades sobre los paralelogramos como hechos, y que más adelante en su escolaridad aprenderán algunas formas de demostrar que siempre son verdaderas.
Si el tiempo lo permite, vuelva a revisar las figuras D, E y F. Pida a los estudiantes que expliquen por qué no son ejemplos y vea si los estudiantes conectan sus explicaciones con las propiedades de los paralelogramos.
• "¿Por qué la figura D no es un paralelogramo?"
• "¿Por qué la figura E no es un paralelogramo? ¿Y la figura F?"


15 minutos

Rutinas didácticas
MLR2: recopilar y mostrar
Anticipar, monitorear, seleccionar, hacer secuencia y conectar
En esta actividad, los estudiantes exploran diferentes métodos para descomponer un paralelogramo y reorganizar las piezas para encontrar su área. La presentación de los paralelogramos en una cuadrícula facilita que los estudiantes vean que el área no cambia a medida que descomponen y reorganizan las piezas.
Esta investigación sienta las bases para el trabajo posterior con el área de triángulos y otros polígonos. Estos son los dos enfoques clave para hallar el área de los paralelogramos:
• Descomponga el paralelogramo, reorganice las partes en un rectángulo y multiplique las longitudes de los lados del rectángulo para hallar el área.
• Encierre el paralelogramo en un rectángulo y reste el área combinada de las regiones adicionales.
Mientras los estudiantes trabajan y discuten, controle estos enfoques. Identifique a los estudiantes cuyo razonamiento pueda resaltar la utilidad de un rectángulo relacionado para hallar el área de un paralelogramo.
Algunos estudiantes pueden comenzar contando cuadrados porque es una estrategia utilizada en grados anteriores. Esta estrategia no se refuerza aquí. En su lugar, anime a los estudiantes a escuchar y probar métodos más sofisticados, apropiados para su grado, compartidos durante la discusión en clase.
En la versión digital de la actividad, los estudiantes reciben rectángulos y triángulos rectángulos como herramientas para visualizar su razonamiento (descomposición, reordenamiento y encierro).
Organice a los estudiantes en grupos de 2-4. Pida a los estudiantes que calculen el área del paralelogramo utilizando las estrategias y herramientas aprendidas recientemente. Prepare copias adicionales de la tarea por si los estudiantes desean recortar el paralelogramo.
Conceda a los estudiantes 5 minutos de tiempo de reflexión en silencio y acceso a sus juegos de herramientas. Pídales que compartan sus estrategias con su grupo después.
Para animar a los estudiantes a ser conscientes de sus estrategias y para plantar la semilla para la discusión de toda la clase, muestre y lea en voz alta las siguientes preguntas de reflexión antes de que los estudiantes comiencen a trabajar.
• ¿Por qué descompusiste el paralelogramo de la manera que lo hiciste?
• ¿Por qué reorganizaste las piezas de la manera que lo hiciste?
Para las aulas digitales, proyecte el applet para presentarlo. Pida a los estudiantes que experimenten con los polígonos dados para hallar el área de los paralelogramos. Para la segunda pregunta, se da a los estudiantes el mismo paralelogramo inicial que en la primera pregunta. Tendrán que mover los vértices para convertirlo en un paralelogramo diferente antes de hallar su área.
Apoyo para estudiantes que aprenden inglés
Hablar y escuchar: MLR2 Recoger y mostrar. Mientras las parejas trabajan, circule y escuche a los estudiantes hablar sobre las similitudes y diferencias entre los dos enfoques para encontrar el área. Anote las frases comunes o importantes que escuche decir a los estudiantes sobre cada enfoque utilizando una pantalla visual con las etiquetas "Descomponer, Reorganizar, Encerrar". Esto ayudará a los estudiantes a utilizar el lenguaje matemático durante sus debates por parejas y en grupo.
Principio(s) de diseño: Apoyar la creación de sentido; Maximizar la metaconciencia
de Matemáticas . Unidad 1

Halla el área de cada paralelogramo. Muestra tu razonamiento.
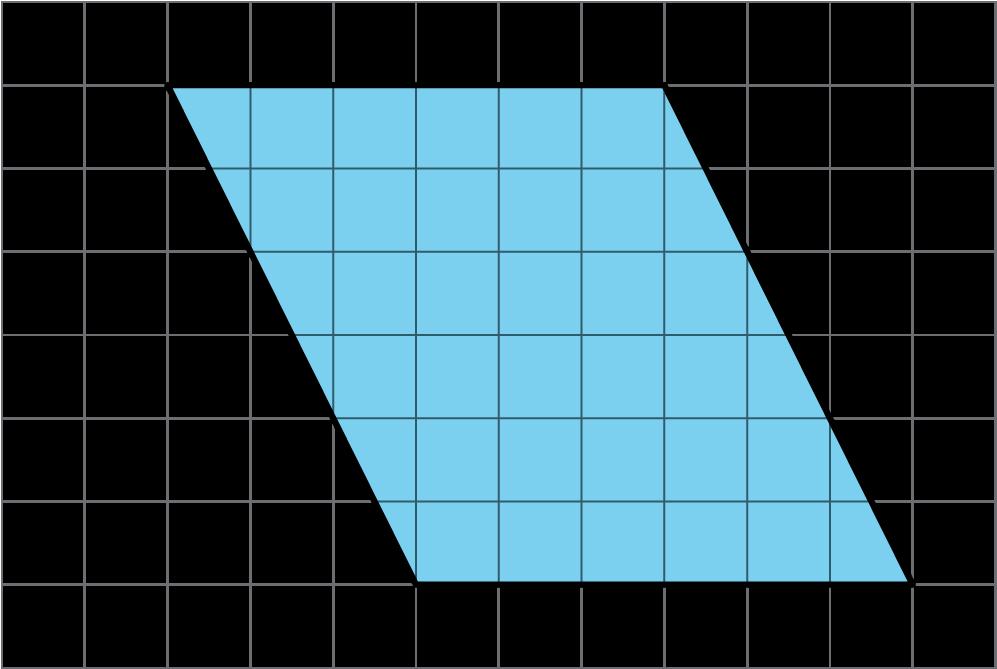
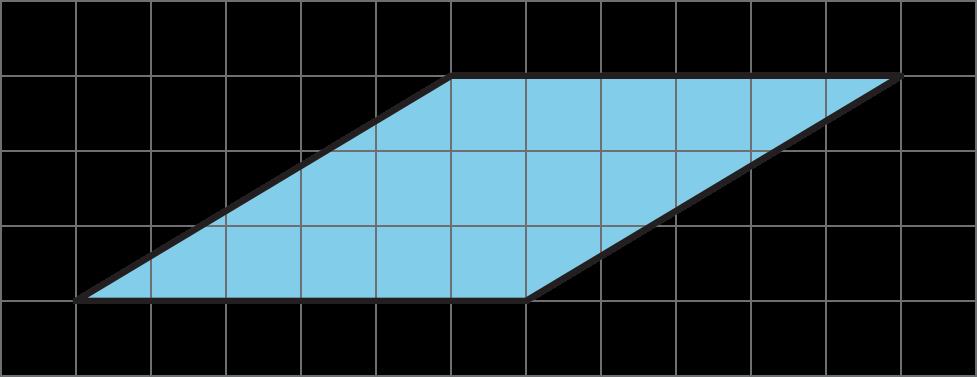
1. 36 unidades cuadradas. Estrategias posibles:
• Contar los cuadrados. Esta estrategia no se fomenta ni debe compartirse, pero puede surgir.
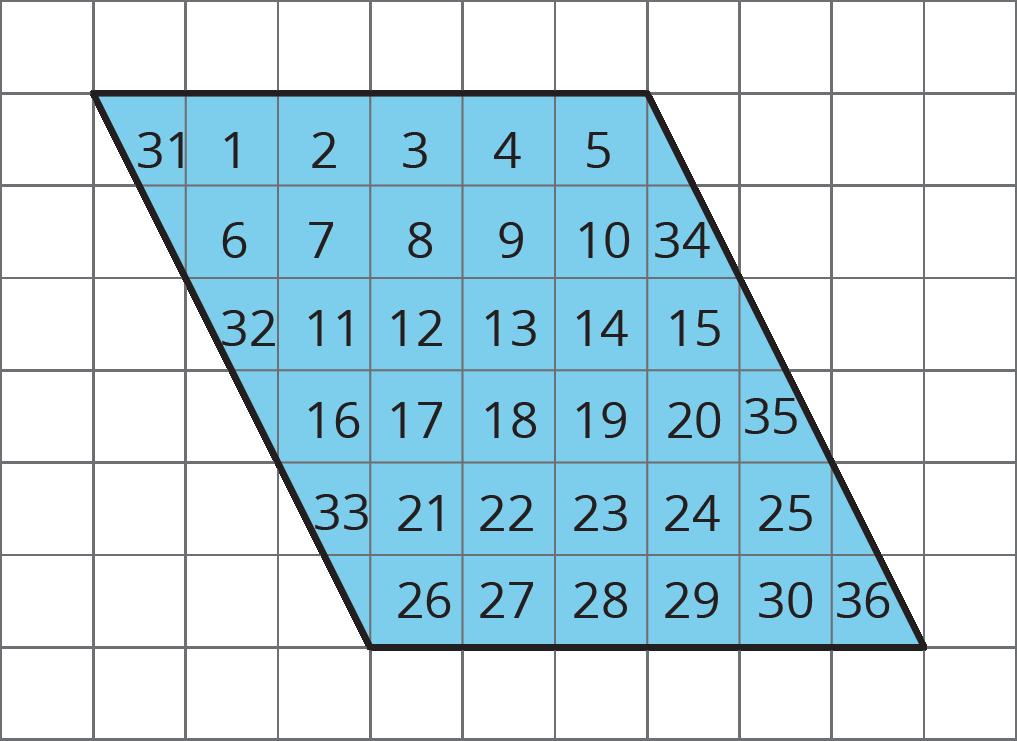
• Encierra el paralelogramo dentro de un rectángulo y resta los trozos sobrantes. Para restar el área de los dos triángulos rectángulos, los estudiantes pueden contar los cuadrados o juntarlos para formar un rectángulo. (6 ⋅ 9)-(6 ⋅ 3) = 36.
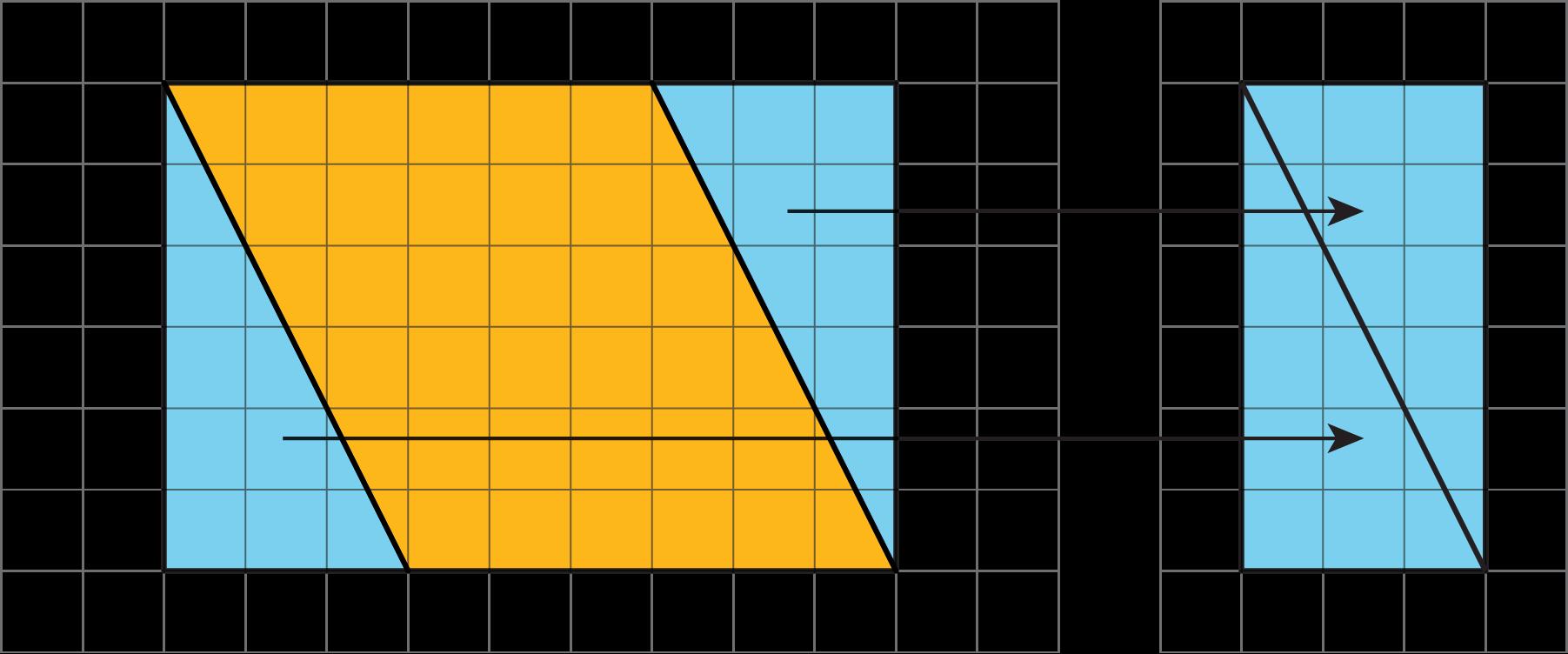
• Descompone el paralelogramo como se muestra y mueve el triángulo rectángulo para formar un rectángulo. 6 ⋅ 6 = 36
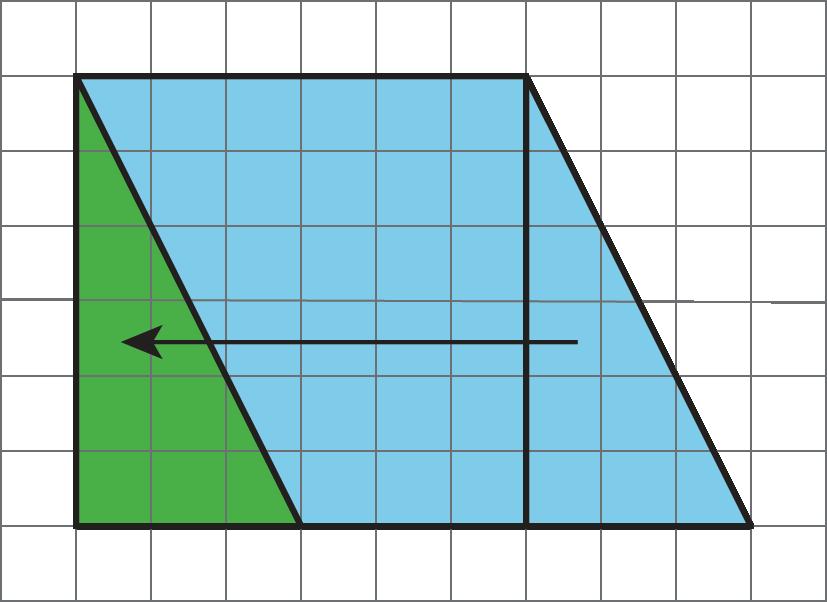
• Descompone el paralelogramo como se muestra y mueve el triángulo rectángulo para formar un rectángulo. 6 ⋅ 6 = 36
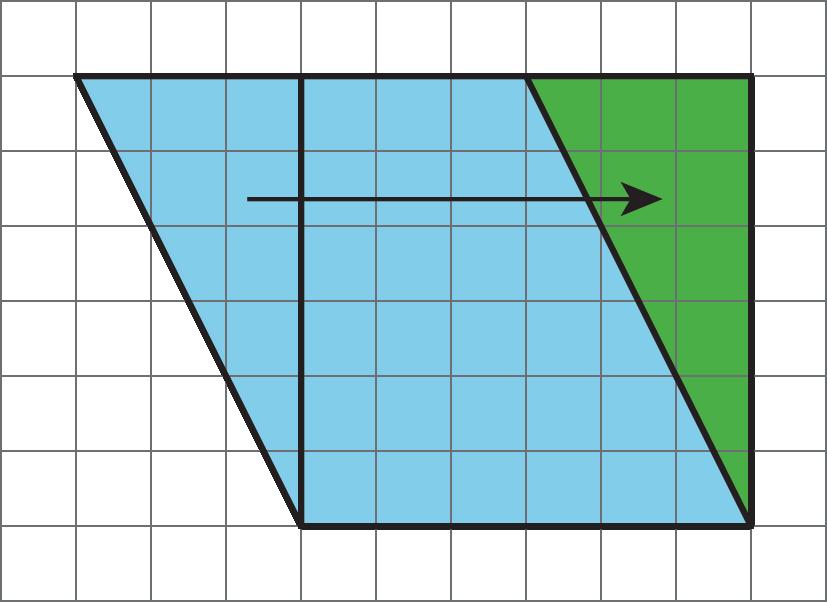
2. 18 unidades cuadradas. Los razonamientos varían, pero deben implicar descomposición y reordenación, u otras estrategias de razonamiento de áreas.
Nation California - Grado 6
Learning Inc. - Todos los derechos reservados



Invite a los estudiantes seleccionados a compartir cómo hallaron el área del primer paralelogramo. Comience con los estudiantes que descompusieron el paralelogramo de diferentes maneras. Siga con los estudiantes que cerraron el paralelogramo y reorganizaron los triángulos rectángulos adicionales. Mientras los estudiantes comparten, muestre y enumere las estrategias para que todos las vean. (Repítelas en términos de descomponer, reordenar y encerrar, según sea necesario). La lista servirá de referencia para los próximos trabajos. Si no se menciona una de las estrategias clave, ilústrala y añádela a la lista.
Utiliza las preguntas de reflexión del Instrucción para ayudar a destacar la utilidad de los rectángulos para hallar el área de los paralelogramos. Considere la posibilidad de utilizar el applet para ilustrar este punto
PARALELOGRAMOS 15 minutos
Rutinas didácticas
Anticipar, monitorizar, seleccionar, secuenciar, conectar MLR3: clarificar, criticar, corregir
En esta actividad, los estudiantes continúan razonando sobre las áreas de los paralelogramos, tanto dentro como fuera de la cuadrícula.
Aunque no hay una única forma correcta de hallar el área de un paralelogramo, cada paralelogramo aquí está diseñado para provocar una estrategia particular. Los paralelogramos A y C animan a descomponer y reorganizar los paralelogramos en un rectángulo. El paralelogramo B no es tan fácil de descomponer y reorganizar (aunque es probable que algunos estudiantes lo intenten primero), y puede incitar a los estudiantes a encerrar los paralelogramos y restar las áreas de las piezas adicionales. La cuadrícula y su ausencia permiten a los estudiantes razonar de forma concreta y abstracta, respectivamente, sobre las medidas que necesitan para hallar el área.
A medida que los estudiantes trabajan, vigile el uso de las dos estrategias principales: descomponer y reorganizar y encerrar y restar. Las tres medidas del paralelogramo C pueden dar que pensar a los estudiantes. Fíjese en los estudiantes que son capaces de razonar por qué el lado que mide 4.5 pulgadas no es necesario para hallar el área del paralelogramo.
Con razonamientos repetidos, los estudiantes pueden empezar a ver los segmentos y las medidas que tienden a ser útiles para hallar el área (MP8). No hay referencias a bases o alturas en esta lección, pero resaltar los segmentos y medidas que ayudaron a los estudiantes a razonar sobre el área aquí puede ayudar a apoyar el trabajo futuro de los estudiantes. En la próxima lección, se formalizará el conocimiento de las medidas que afectan al área de un paralelogramo.
Mantenga a los estudiantes en grupos de 2-4 y pídales que encuentren las áreas de varios paralelogramos más. Concédales 7-8 minutos para pensar en silencio, seguidos de un par de minutos para compartir sus estrategias con sus grupos. Pide a los estudiantes que intenten resolver al menos las dos primeras preguntas individualmente antes de discutirlas con su grupo. Proporcióneles acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Para preparar la discusión de toda la clase, considere pedir a los estudiantes que piensen, a medida que trabajan en los problemas, sobre qué medidas del paralelogramo parecen ser útiles para encontrar su área.
Encuentre el área de los siguientes paralelogramos. Demuestra tu razonamiento.
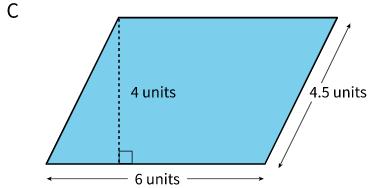
de Matemáticas . Unidad 1

Paralelogramo A: 15 unidades cuadradas. Posible estrategia: Descomponer y reorganizar las piezas para formar un rectángulo y multiplicar las longitudes de los lados del rectángulo para hallar el área. 5 ⋅ 3 = 15
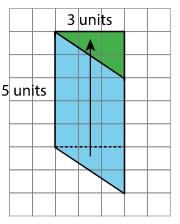
Paralelogramo B: 12 unidades cuadradas. Posible estrategia: Encierra el paralelogramo y resta el área de los trozos sobrantes. El área de los trozos sobrantes se halla reordenando los triángulos para formar un rectángulo. 6 ⋅ 8 - 6 ⋅ 6 = 12.
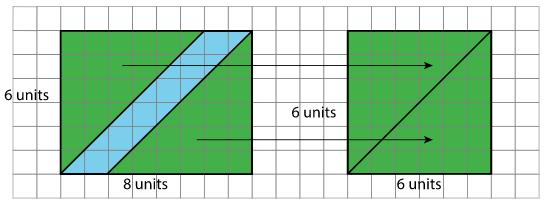
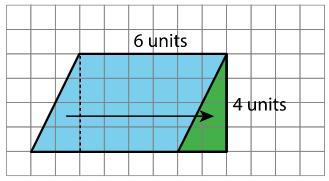
Algunos estudiantes pueden pensar que no es posible descomponer y reordenar el paralelogramo A porque tiene un par de lados verticales en lugar de un par de lados horizontales. Girar su papel 90 grados y volver atrás podría ayudarles a ver que aún podrían utilizar la misma estrategia de razonamiento. O puede resultarles útil razonar primero sobre el área con el paralelogramo girado 90 grados y luego girarlo de nuevo a su orientación original.
Paralelogramo C: 24 unidades cuadradas. Posible estrategia: Descompone el paralelogramo y reordénalo formando un rectángulo. Multiplica las longitudes de los lados del rectángulo. 6 ⋅ 4 = 24. CONCEPTOS ERRÓNEOS
Para cada paralelogramo, seleccione 1-2 estudiantes con estrategias diferentes para que compartan su trabajo con la clase, empezando por la estrategia menos eficiente. Si no se menciona una estrategia importante, menciónala e ilústrala. Sondea brevemente a la clase para ver cómo abordaron el problema los demás. Después de escuchar a los estudiantes sobre cada problema, considera la posibilidad de hacer preguntas como las siguientes. Centre el debate en los paralelogramos B y C.
• "¿Es el paralelogramo A diferente de otros que ha visto hasta ahora? ¿En qué sentido?" (Los estudiantes pueden responder sí o no, pero algunos pueden considerarlo diferente porque tiene un par de lados verticales). "¿Aún puede descomponerse y reordenarse en una forma cuya área sepamos calcular?". (Sí.)



• "¿Qué estrategia -descomponer y reordenar, o encerrar y restar- parece más práctica para hallar el área de un paralelogramo como B? ¿Por qué?" (Encerrar y restar, porque se puede hacer en menos pasos. Descomponer la figura en trozos pequeños podría resultar confuso y dar lugar a errores).
• "Si descompusieras C en un triángulo rectángulo y otra figura, ¿cómo sabes que el trozo recortado encaja realmente en el otro lado, dado que no hay una cuadrícula que verificar?" (Los dos lados opuestos de un paralelogramo son paralelos, por lo que el lado más largo (inclinado) del triángulo rectángulo que se reordena coincidiría perfectamente con el segmento del otro lado. Disponga de papel de calco o de una copia del dibujo para cortar y reordenar físicamente para que los estudiantes puedan comprobarlo).
• "Se muestran tres medidas para el paralelogramo C. ¿Cuáles utilizaste? ¿Cuáles no utilizaste? ¿Por qué sí y por qué no?" (Las 4 unidades y 6 unidades son longitudes de los lados de un rectángulo que tiene la misma área que el paralelogramo. Si descomponemos el paralelogramo con un corte vertical y movemos la pieza de la izquierda a la derecha para hacer un rectángulo, la 4.5-unidad de longitud ya no es relevante.)
• "¿Por qué tu estrategia tenía más sentido para ti para este paralelogramo?"
Para ayudar a los estudiantes a hacer conexiones y generalizar sus observaciones, haz preguntas como:
• "Cuando descompusiste y reorganizaste el paralelogramo en otra forma, ¿cambió el área?". (No.)
• "¿Por qué usar un rectángulo?"(Sabemos cómo encontrar el área de un rectángulo; podemos multiplicar las dos longitudes de los lados.)
• "Para aquellos de ustedes que encerraron el paralelogramo con un rectángulo, ¿cómo les ayudaron los dos triángulos rectángulos?" (Se pueden combinar en un rectángulo, cuya área podemos hallar y restar del área de un rectángulo grande.)
• "¿Qué medidas o longitudes fueron útiles para hallar el área del paralelogramo?" (La longitud de un lado del paralelogramo y la longitud de un segmento perpendicular entre ese lado y el lado opuesto). ¿Qué longitudes no utilizaste?" (La longitud del otro lado.)
Escribir, hablar: MLR3 Aclarar, Criticar, Corregir. Antes de que los estudiantes compartan su trabajo, presente a la clase la siguiente afirmación incorrecta: "Para calcular el área del paralelogramo A, conté 3 unidades en el lado diagonal y 5 unidades en el lado vertical. Luego, multipliqué 3 × 5 para obtener 15 unidades cuadradas". Conceda a los estudiantes unos minutos para corregir esta afirmación por escrito, antes de compartir sus mejoras con un compañero. Identifique a los estudiantes que puedan explicar por qué la longitud de un segmento diagonal no puede utilizarse fácilmente para hallar el área de un paralelogramo. Selecciónelos para que compartan su razonamiento con la clase y destaque cómo describen las medidas que pueden ser útiles para hallar el área. Esto ayudará a los estudiantes a utilizar el lenguaje matemático cuando la clase discuta las dos estrategias principales: descomponer y reorganizar y encerrar y restar.
Principio(s) de diseño: Optimizar el resultado (para la explicación); Maximizar la metaconciencia
5 minutos
Repasa con los estudiantes la definición de paralelogramo: Un paralelogramo tiene cuatro lados. Los lados opuestos de un paralelogramo son paralelos. Recuérdeles que, como resultado de que los lados sean paralelos, también es cierto que:
• Los lados opuestos de un paralelogramo tienen la misma longitud.
• Los ángulos opuestos de un paralelogramo tienen la misma medida
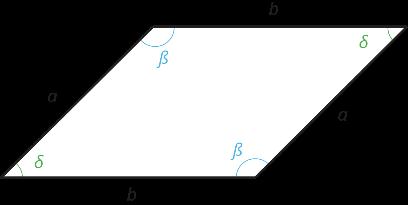
Dígales a los estudiantes que, si bien por ahora sólo estamos tomando estas propiedades como hechos, en grados posteriores podrán demostrarlas por sí mismos.
Repase brevemente la última tarea, mostrando para que todos vean las estrategias de áreas múltiples que los estudiantes utilizaron. Señale que, en algunos casos, los estudiantes optaron por descomponer y reorganizar las partes y, en otros, por encerrar el paralelogramo con un rectángulo y restar el área de las piezas adicionales del área del rectángulo. Pregunte sobre un par de los paralelogramos: "¿Qué tenía ese paralelogramo que motivó esa elección en particular?".
de Matemáticas . Unidad 1
5 minutos
Esta actividad prepara el terreno para la siguiente lección, que formaliza cómo hallar el área de cualquier paralelogramo. Fíjate en las estrategias que los estudiantes están utilizando para hacer conexiones con la expresión algebraica b ⋅ h que verán en la próxima lección.
¿Cómo hallarías el área de este paralelogramo? Describe tu estrategia.

RESPUESTAS POSIBLES
Las respuestas varían. Ejemplos de respuestas:
• Descomponga un triángulo de un lado del paralelogramo y muévalo al otro lado para formar un rectángulo. Multiplica las longitudes de los lados del rectángulo.
• Dibuja un rectángulo alrededor del paralelogramo, multiplica las longitudes de los lados del rectángulo para hallar el área del rectángulo y réstale el área combinada de los triángulos que no pertenecen al paralelogramo.
• Cuenta cuántos cuadrados hay en la parte inferior del paralelogramo y cuántos cuadrados tiene de alto y multiplícalos.
PROBLEMA 1
Selecciona todos los paralelogramos. Para cada figura que no seleccionada, explica cómo sabes que no es un paralelogramo.
Figura A
Figura B
Figura C
Figura D
Figura E
California - Grado 6
Posibles soluciones
Figura A
Figura B
Figura C
Figura D
Figura E
B y C son paralelogramos (C también es un rectángulo). A es un trapecio (dos lados opuestos no son paralelos y dos no tienen la misma longitud), D es un pentágono y E es un triángulo (rectángulo).
Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

PROBLEMA 2
A. Descomponga y reorganice este paralelogramo para formar un rectángulo.
B. ¿Cuál es el área del paralelogramo? Explica tu razonamiento.
PROBLEMA 3
Halla el área del paralelogramo.

PROBLEMA 4
Explica por qué este cuadrilátero no es un paralelogramo.
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 3
Halla el área de cada forma. Muestra tu razonamiento.

PROBLEMA 6
Del Grado 6, Unidad 1, Lección 1
Halla las áreas de los rectángulos con las siguientes longitudes laterales.
1. 5 en y 1 3 en 2. 5 en y 4 3 en
3. 5 2 en y 4 3 en 4. 7 6 en y 6 7 en
Learning Inc. - Todos los derechos reservados
Posibles soluciones
1. Las respuestas varían. Ejemplo de respuesta: El diagrama muestra que obtenemos un rectángulo que es 5 unidades por 9 unidades descomponiendo y reordenando.
2. El área del paralelogramo es la misma que el área del rectángulo, que es 45 unidades cuadradas.
Posibles soluciones
30 cm cuadrados
Posibles soluciones
Las explicaciones varían. Ejemplo de explicación: Los lados opuestos no son paralelos y no tienen la misma longitud. Los ángulos opuestos no son iguales.
Posibles soluciones
12 unidades cuadradas, 19 unidades cuadradas. El razonamiento varía.
Posibles soluciones
1. 5 3 pulgadas cuadradas 2. 20 3 pulgadas cuadradas
3. 10 3 pulgadas cuadradas 4. 1 pulgadas cuadradas


• Graficar formas
• Generalizar con representaciones múltiples
ALINEACIÓN
Abordar
6.EE.2a Escribir expresiones que registren operaciones con números y con letras que representan números.
Alineación de estándares y principios de California
6.EE.2c Evaluar expresiones en valores específicos de sus variables. Incluir expresiones que surjan de fórmulas utilizadas en problemas del mundo real. Realizar operaciones aritméticas, incluyendo aquellas que involucran exponentes de números enteros, en el orden convencional cuando no hay paréntesis para especificar un orden particular (Orden de Operaciones).
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales, y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de resolver problemas matemáticos y del mundo real.
Enfocar SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.3
I.B.5
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué?
Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dan sentido al mundo e influyen en el futuro buscan y hacen uso de la estructura
OBJETIVO(S) DE APRENDIZAJE
descubren la forma y el espacio y exploran las cantidades cambiantes.
• Investiguemos un poco más el área de los paralelogramos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo identificar los pares de base y altura de un paralelogramo.
• Puedo escribir y explicar la fórmula del área de un paralelogramo.
• Sé a qué se refieren los términos "base" y "altura" en un paralelogramo.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comprender los términos "base" y "altura" para referirse a un lado de un paralelogramo y a la distancia perpendicular entre ese lado y el lado opuesto.
• Generalizar (oralmente) un proceso para encontrar el área de un paralelogramo, usando la longitud de una base y la altura correspondiente.
• Identificar una base y la altura correspondiente para un paralelogramo y comprender que hay dos pares base-altura diferentes para cualquier paralelogramo.
Rutinas didácticas
Piensa, comparte en parejas
Observa y maravíllate
MLR8: Apoyos para el debate
MLR7: Comparar y conectar
Materiales necesarios
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
de Matemáticas . Unidad 1
Narrativa de la lección
Los estudiantes comienzan esta lección comparando dos estrategias para hallar el área de un paralelogramo. Esta comparación prepara el terreno tanto para definir formalmente los términos base y altura como para escribir una fórmula general para el área de un paralelogramo. Ser capaz de identificar correctamente un par base-altura para un paralelogramo requiere buscar y hacer uso de la estructura (MP7).
Los términos base y altura son potencialmente confusos porque a veces se utilizan para referirse a segmentos de línea particulares, y a veces a la longitud de un segmento de línea o a la distancia entre líneas paralelas. Además, siempre hay dos pares base-altura para cualquier paralelogramo, por lo que pedir la base y la altura no es, técnicamente, una pregunta bien planteada. En su lugar, es más apropiado preguntar por una base y su altura correspondiente. Cuando los estudiantes aclaran el significado que pretenden al utilizar estos términos, están atendiendo a la precisión del lenguaje (MP6). En estos materiales, las palabras "base" y "altura" significan los números a menos que quede claro por el contexto que se refieren a un segmento y que no hay confusión potencial.
Al final de la lección, los estudiantes buscan un patrón que pueden generalizar a la fórmula para el área de un rectángulo (MP8) y hacen argumentos que explican por qué esto funciona para todos los paralelogramos (MP3).
Componente de la lección Estructura Tiempo Breve descripción
Los estudiantes comparan muestras de paralelogramos descompuestos y reordenados.

Calentamiento Pares 10 min.
Un applet digital interactivo está disponible para permitir a los estudiantes explorar la descomposición y reordenación de paralelogramos utilizando la tecnología.
Los estudiantes descubren la relación entre la base y la altura en paralelogramos a través de ejemplos y no ejemplos.
Actividad de Exploración Pares 20 min.
Actividad de Exploración Pares 15 min.
Síntesis Grupo completo 3 min.
Una extensión de exploración está disponible con un applet digital interactivo para desarrollar una comprensión más profunda de la identificación de la base y la altura correspondiente de un paralelogramo.
Los estudiantes analizan patrones para generalizar una expresión que representa el área de un paralelogramo.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la relación entre el área de un paralelogramo y su altura y base.
Los estudiantes resumen las relaciones entre la altura, la base y el área de un paralelogramo.
Enfriamiento Independiente 5 min. Los estudiantes identifican las bases y las alturas de los paralelogramos para determinar sus áreas.
Práctica Independiente 8-10 min.
El componente de práctica independiente incluye 5 problemas de repaso de la lección y 2 problemas de repaso en espiral.
California - Grado 6
Learning Inc. - Todos los derechos reservados


minutos

Rutinas didácticas
Pensar Compartir
En este calentamiento, los estudiantes comparan y contrastan dos formas de descomponer y reordenar un paralelogramo en una cuadrícula para poder hallar su área. Esto tiene varios propósitos: reforzar el trabajo realizado en la lección anterior; permitir a los estudiantes practicar la comunicación de sus observaciones; y arrojar luz sobre las características de un paralelogramo que son útiles para encontrar el área: una base y una altura correspondiente.
El flujo de ideas clave -que se irán descubriendo durante la discusión y gradualmente a lo largo de la lección- es el siguiente:
• Hay múltiples formas de descomponer un paralelogramo (con un corte) y reorganizarlo en un rectángulo cuya área podemos determinar.
• El corte se puede hacer en diferentes lugares, pero para componer un rectángulo, el corte tiene que estar en un ángulo recto con dos lados opuestos del paralelogramo.
• La longitud de un lado de este rectángulo recién compuesto es la misma que la longitud de un lado del paralelogramo. Utilizamos el término base para referirnos a este lado.
• La longitud del otro lado del rectángulo es la longitud del corte que hemos hecho al paralelogramo. Llamamos a este segmento una altura que corresponde a la base elegida.
• Utilizamos estas dos longitudes para determinar el área del rectángulo y, por tanto, también el área del paralelogramo.
A medida que los estudiantes trabajan y discuten, identifique a aquellos que hacen comparaciones en términos de los dos primeros puntos para que puedan compartirlas más tarde. Asegúrese de dejar suficiente tiempo para discutir los primeros cuatro puntos como clase.
Organice a los estudiantes en grupos de 2. Dé a los estudiantes 2 minutos de tiempo para pensar en silencio y acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Pídales que después compartan sus respuestas con un compañero.
Si utiliza la actividad digital, pida a los estudiantes que exploren el applet durante 3 minutos individualmente y que después lo comenten con un compañero. Los estudiantes podrán ver los cortes arrastrando el punto sobre el segmento bajo el paralelogramo.
Apoyo a estudiantes con discapacidad
Habilidades motoras finas: Eliminar barreras. Proporcionar una versión ampliada de lo visual. Procesamiento conceptual: Tiempo de procesamiento. Comience con una demostración física de cómo Elena descompuso el paralelogramo, lo que proporcionará acceso a los estudiantes que se benefician de contextos concretos.
Elena y Tyler estaban hallando el área de este paralelogramo:

Así lo hizo Elena:
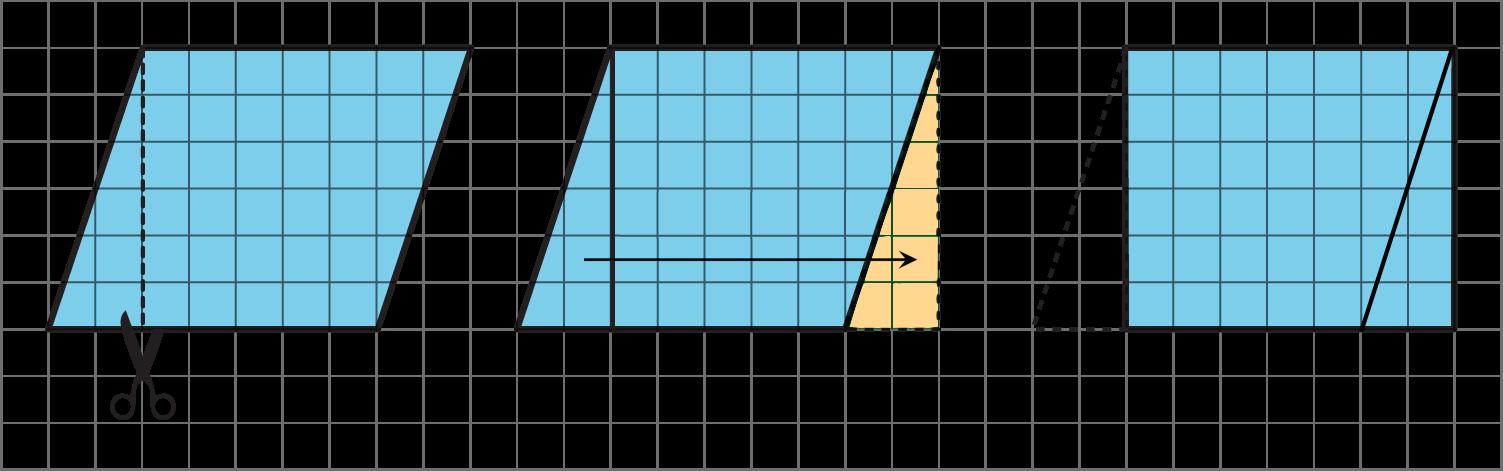
Matemáticas
Unidad
Así lo hizo Tyler:
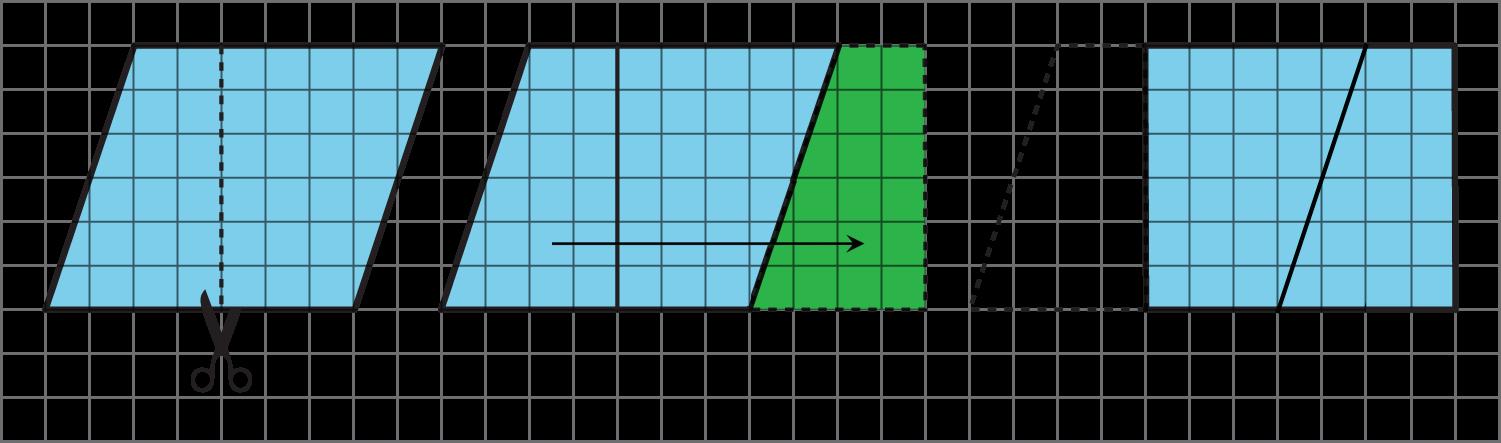
¿En qué se parecen las dos estrategias para hallar el área de un paralelogramo? ¿En qué se diferencian?
Las respuestas varían. Ejemplos de respuestas:
• Similares: Ambos cortaron un pedazo de la izquierda del paralelogramo y lo movieron hacia la derecha para hacer un rectángulo. Los rectángulos que hicieron son idénticos.
• Diferentes: Cortaron el paralelogramo en lugares diferentes. Elena cortó un triángulo rectángulo del lado izquierdo y Tyler cortó un trapecio. Los rectángulos que hicieron no están en el mismo lugar.
Pida a algunos estudiantes que compartan lo que era igual y lo que era diferente en los métodos que observaron.
Destaque los siguientes puntos sobre cómo los enfoques de Elena y Tyler son iguales, aunque no espere que los estudiantes utilicen el lenguaje. En su lugar, señale y gesticule para dejar claro lo que se quiere decir. Si los estudiantes no mencionan alguno de estos puntos, compártalos.
• Los rectángulos son idénticos; tienen las mismas longitudes laterales. (Rotula las longitudes de los lados de los rectángulos.)
• Los cortes se hicieron en lugares diferentes, pero la longitud de los cortes era la misma. (Rotula las longitudes de los cortes verticales.)
• Los lados horizontales del paralelogramo tienen la misma longitud que los lados horizontales del rectángulo. (Señala cómo ambos segmentos tienen la misma longitud.)
• La longitud de cada corte es también la distancia entre los dos lados horizontales del paralelogramo. También es la longitud del lado vertical del rectángulo. (Señala cómo esa distancia se mantiene igual en toda la longitud horizontal del paralelogramo.)
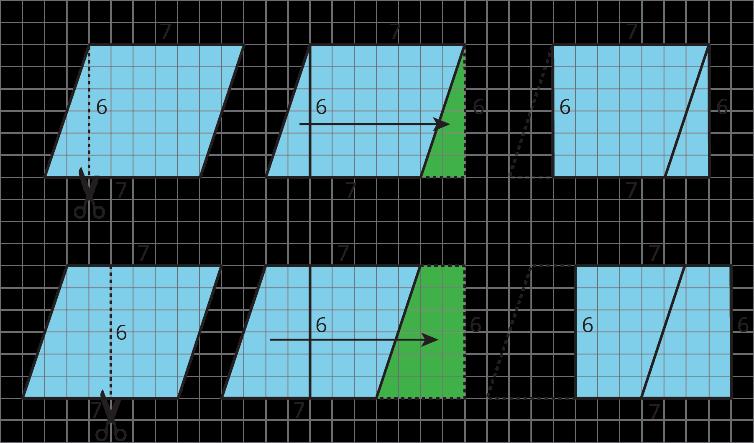
Empieza a relacionar las observaciones con los términos base y altura. Por ejemplo, explique:
• "Las dos medidas que vemos aquí tienen nombres especiales. La longitud de un lado del paralelogramo -que es también la longitud de un lado del rectángulo- se llama base. La longitud del segmento de corte vertical -que es también la longitud del lado vertical del rectángulo- se llama altura que corresponde a esa base."
• "Aquí, el lado del paralelogramo que tiene 7 unidades de longitud también se llama base. En otras palabras, la palabra base se utiliza tanto para el segmento como para la medida."
Diga a los estudiantes que exploraremos las bases y las alturas de un paralelogramo en esta lección.


20 minutos

Rutinas didácticas
Piensa en pareja Comparte
Observa y maravíllate
MLR8: Apoyos para la discusión
Anteriormente, los estudiantes vieron ejemplos numéricos de la base y la altura de un paralelogramo. Esta actividad desarrolla aún más la idea de base y altura mediante ejemplos y no ejemplos y análisis de errores.
Algunas ideas importantes a descubrir aquí:
• En un paralelogramo, el término "base" se refiere a la longitud de un lado y "altura" a la longitud de un segmento perpendicular entre ese lado y el lado opuesto.
• Cualquier lado de un paralelogramo puede ser una base.
• Siempre hay dos pares de base-altura para un paralelogramo dado.
Muestra la imagen de ejemplos y no ejemplos de bases y alturas para que todos la vean. Lee en voz alta la descripción de ejemplos y no ejemplos. Conceda a los estudiantes un minuto para observarla y para prepararse a compartir al menos una cosa que observen y otra que se pregunten. Cuando haya transcurrido el minuto, invite a los estudiantes a compartir sus respuestas con la clase y anótelas para que todos puedan verlas. No es necesario responder a sus preguntas en este momento.
Los estudiantes pueden observar:
• Ambos conjuntos de diagramas muestran los mismos 2 pares de paralelogramos y los mismos lados etiquetados como "base".
• Todos los ejemplos muestran una marca de ángulo recto, un segmento discontinuo y un lado etiquetado como "base".
• Sólo uno de los no-ejemplos muestra una marca de ángulo recto, pero todos ellos muestran un segmento discontinuo.
• Tanto en los ejemplos como en los no-ejemplos, hay un paralelogramo con un segmento discontinuo y un ángulo recto que se muestra fuera de él.
• Si los segmentos discontinuos se utilizan para cortar los tres primeros paralelogramos de los ejemplos, las piezas cortadas podrían reorganizarse para formar un rectángulo. No se puede hacer lo mismo con los segmentos discontinuos en los no-ejemplos.
Pueden preguntarse:
• Por qué algunos segmentos discontinuos están dentro del paralelogramo y otros están fuera.
• Cuál podría ser la regla para que un segmento discontinuo se considere una altura.
• Qué tienen que ver las bases y las alturas con el área.
Organice a los estudiantes en grupos de 2. Dé a los estudiantes 4-5 minutos para completar la primera pregunta con su compañero. Pídales que hagan una pausa para debatir en clase después de la primera pregunta. Seleccione a un maestro o a un grupo para que defienda si cada afirmación es verdadera o falsa. Si uno o varios estudiantes no están de acuerdo, pídales que expliquen su razonamiento y discutan para llegar a un consenso. Antes de pasar a la siguiente pregunta, asegúrese de que los estudiantes anotan las afirmaciones verificadas como verdaderas para que puedan utilizarlas como referencia más adelante.
Conceda a los estudiantes 3-4 minutos de silencio para responder a la segunda pregunta y otros 2-3 minutos para compartir sus respuestas con un compañero. Pídales que centren las conversaciones en pareja en las siguientes preguntas, expuestas a la vista de todos:
• ¿Cómo sabes que el paralelogramo está etiquetado correcta o incorrectamente?
• ¿Hay otra forma de etiquetar una base y una altura en este paralelogramo?
Después de responder a las preguntas, los estudiantes que utilicen la actividad digital pueden explorar el applet y utilizarlo para verificar sus respuestas y avanzar en su comprensión de las bases y las alturas. El applet es un paralelogramo dinámico en el que se muestra una altura. Permite a los estudiantes ver la colocación de la altura en una variedad de paralelogramos y cuando se elige cualquier lado como base.
Apoyos para estudiantes
Listening, Speaking, Conversing: MLR8 Apoyos para la Discusión. Utilice este apoyo para practicar el uso verbal del lenguaje matemático "base" y "altura".
Mientras los estudiantes comparan paralelogramos y ejemplos/no ejemplos de alturas correctas, anímelos a volver a expresar el razonamiento de sus compañeros. Refuerce el significado de "perpendicular" utilizando elementos visuales (por ejemplo, manipulativos, dibujos, gestos) de ángulos rectos.
Principio(s) de diseño: Apoyar la adquisición de sentido

Apoyo a los estudiantes con discapacidad
Funcionamiento ejecutivo: Organizadores gráficos. Proporcione a los estudiantes un gráfico en forma de T para que anoten lo que notan y se preguntan antes de compartir estas ideas con los demás.
Procesamiento conceptual: Tiempo de procesamiento. Compruebe con cada estudiante, según sea necesario, la comprensión durante cada paso de la actividad.
Cada paralelogramo tiene un lado que se denomina "base".
Estudia los ejemplos y no ejemplos de bases y alturas de paralelogramos. Después, contesta a las preguntas que siguen.
Ejemplos: El segmento discontinuo de cada dibujo representa la altura correspondiente a la base dada.

No ejemplos: El segmento discontinuo en cada dibujo no representa la altura correspondiente para la base dada.

1. Selecciona todas las afirmaciones que son ciertas sobre bases y alturas en un paralelogramo. Sólo un lado horizontal de un paralelogramo puede ser una base. Cualquier lado de un paralelogramo puede ser una base.
Una altura se puede dibujar en cualquier ángulo con respecto al lado elegido como base. Una base y su correspondiente altura deben ser perpendiculares entre sí.
Una altura sólo se puede dibujar dentro de un paralelogramo. Una altura se puede dibujar fuera de un paralelogramo, siempre que forme un ángulo de 90-grado con la base.
Una base no se puede extender para encontrarse con una altura.
2. Cinco estudiantes etiquetaron una base �� y una altura correspondiente h para cada uno de estos paralelogramos.
¿Están todos los dibujos correctamente etiquetados? Explica cómo lo sabes.
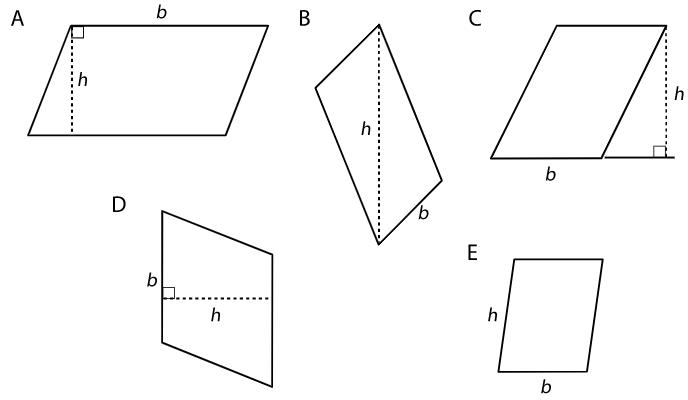



1. Las afirmaciones B, D y F son ciertas.
Sólo un lado horizontal de un paralelogramo puede ser una base.
Cualquier lado de un paralelogramo puede ser una base.
Se puede dibujar una altura con cualquier ángulo respecto al lado elegido como base.
Una base y su correspondiente altura deben ser perpendiculares entre sí.
Una altura sólo se puede dibujar dentro de un paralelogramo.
Una altura se puede dibujar fuera de un paralelogramo, siempre que forme un ángulo de 90-grado con la base.
Una base no se puede extender para encontrarse con una altura.
2. A, C y D son correctas. B y E no son correctas porque en cada una, el segmento etiquetado con una h no es perpendicular al lado etiquetado con una b.
Es posible que los estudiantes aún no interioricen que cualquier lado del paralelogramo puede ser una base (pueden pensar que una base debe ser el lado inferior, horizontal), o que la altura tiene que ser perpendicular a la base. Señale dónde se encuentran los símbolos de ángulo recto y cómo se relacionan con la altura. Los estudiantes pueden pensar que un segmento que muestre la altura no puede dibujarse fuera del paralelogramo (como en el Paralelogramo C).
Los estudiantes pueden relacionar cómo piensan sobre las longitudes de los lados de un rectángulo y aplicarlo incorrectamente al Paralelogramo E.
Sondea a la clase -con una rápida señal de acuerdo o desacuerdo- sobre si cada figura de la última pregunta está etiquetada correctamente con b y h. Después de cada sondeo, pide a un maestro que explique cómo sabe que es correcto o incorrecto.
Si un paralelogramo está etiquetado incorrectamente, pregunta dónde podría estar una altura correcta. Si está correctamente etiquetado, pregunte a los estudiantes si hay otra base y altura que podrían estar etiquetadas en este paralelogramo. Asegúrese de que los estudiantes entienden qué paralelogramos están etiquetados correctamente antes de avanzar en esta lección.
Un punto importante a destacar: "Podemos elegir cualquier lado de un paralelogramo como base. Para encontrar la altura que corresponde a esa base, dibuje un segmento que una la base y su lado opuesto; ese segmento tiene que ser perpendicular a ambos".
Considere la posibilidad de utilizar el applet para ilustrar con más detalle los posibles pares base-altura y reforzar la comprensión de los estudiantes sobre ellos.
¿Estás preparado para más?
En el applet, el paralelogramo está formado por segmentos de línea continua, y la altura y las líneas de apoyo están formadas por segmentos de línea discontinua. La base (b) y la altura correspondiente (h) están etiquetadas.
Experimenta arrastrando todos los puntos móviles por la pantalla. ¿Puedes cambiar el paralelogramo de modo que . . .
1. su altura esté en un lugar diferente?
2. tenga lados horizontales?
3. sea alto y delgado?
4. sea también un rectángulo?
5. sea no un rectángulo, y tenga �� = 5 y h = 3?
"¿Estás preparado para más?" Respuesta de los estudiantes
Las respuestas varían.

minutos

Rutinas didácticas
Piensa, comparte, en parejas
MLR7: Comparar y conectar
En lecciones anteriores, los estudiantes razonaron sobre el área de los paralelogramos descomponiéndolos, reordenándolos y encerrándolos y utilizando lo que saben sobre el área de los rectángulos. También identificaron pares base-altura en los paralelogramos. Aquí, utilizan lo que aprendieron para hallar el área de nuevos paralelogramos, generalizar el proceso y escribir una expresión para hallar el área de cualquier paralelogramo.
Mientras los estudiantes discuten su trabajo, monitoree las conversaciones para detectar cualquier desacuerdo entre los compañeros. Apóyeles haciendo preguntas aclaratorias:
• "¿Cómo elegiste una base? ¿Cómo puedes estar seguro de que esa es la altura?"
• "¿Cómo encontraste el área? ¿Por qué elegiste esa estrategia para este paralelogramo?"
• "¿Hay alguna otra forma de encontrar el área y comprobar nuestra respuesta?"
Mantén a los estudiantes en grupos de 2. Dar a los estudiantes acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y 5-7 minutos de tiempo de reflexión en silencio para completar las cuatro primeras filas de la tabla. Pídeles que estén preparados para compartir sus razonamientos. Si el tiempo es limitado, considere la posibilidad de dividir el trabajo: pida a un compañero que trabaje de forma independiente en los paralelogramos A y C, y al otro en B y D. Anime a los estudiantes a utilizar como referencia su trabajo de actividades anteriores (sobre bases y alturas).
Pida a los estudiantes que hagan una pausa después de completar las cuatro primeras filas y que compartan sus respuestas con su compañero. A continuación, deben discutir cómo escribir la expresión para el área de cualquier paralelogramo. Los estudiantes deben darse cuenta de que el área de cada paralelogramo es el producto de una base y su altura correspondiente.
Apoyos para estudiantes de inglés
Representar, conversar: MLR7 Comparar y conectar. Cuando los estudiantes compartan sus respuestas para las primeras cuatro filas de la tabla, pídales que identifiquen qué es igual y qué es diferente en la forma en que determinaron la base y la altura de cada paralelogramo. Escuche y amplíe las discusiones de los estudiantes que intentan explicar por qué sus diferentes enfoques condujeron a la misma área. A continuación, pregunte a los estudiantes si cualquier lado de un paralelogramo puede utilizarse como base. Esto ayudará a los estudiantes a comprender cómo el área de cada paralelogramo es el producto de la base y su altura correspondiente.
Principio(s) de diseño: Apoyar la adquisición de sentido
Apoyo a los estudiantes con discapacidad
Procesamiento conceptual: Ayudas visuales. Utilizar códigos de colores y anotaciones para resaltar conceptos importantes o conexiones entre representaciones en un problema.
Funcionamiento socioemocional: Tutores. Empareje a los estudiantes con sus compañeros tutores previamente identificados.



POSIBLES RESPUESTAS
Para cada paralelogramo:
• Identifique una base y una altura correspondiente y registre sus longitudes en la tabla que sigue.
• Encuentre el área y regístrela en la columna de más a la derecha.
En la última fila, escribe una expresión usando b y h para el área de cualquier paralelogramo.
Paralelogramo Base (Unidades) Altura (Unidades) Área (Sq. Unidades)
Cualquier paralelogramo �� h
Aunque hay dos posibles pares base-altura, éstos son los más fáciles de usar para los estudiantes dada la orientación de cada paralelogramo en la cuadrícula.
Paralelogramo Base (Unidades) Altura (Unidades) Área (Uq. Unidades)
Cualquier paralelogramo
Encontrar un segmento de altura fuera del paralelogramo puede ser todavía una idea poco familiar para los estudiantes. Tenga a la vista ejemplos de la sección "¿La altura correcta?" para que puedan servir de referencia a la hora de hallar alturas.
Los estudiantes pueden decir que no se puede determinar la base del paralelogramo D porque, tal como se muestra, no tiene un lado horizontal. Recuerda a los estudiantes que en una actividad anterior aprendimos que cualquier lado de un paralelogramo puede ser una base. Pide a los estudiantes que comprueben si hay algún lado cuya longitud se pueda determinar.
Muestre los paralelogramos y la tabla para que todos los vean. Selecciona a algunos estudiantes para que compartan las respuestas correctas de cada paralelogramo. A medida que los estudiantes comparten, resalte los pares base-altura en cada paralelogramo y registre las respuestas en la tabla. Aunque sólo se nombra un par base-altura para cada paralelogramo, reitere que hay otro par. Muestre el segundo par en el diagrama o pida a los estudiantes que lo señalen.
6º de Matemáticas . Unidad 1

Muestre los paralelogramos y la tabla para que todos los vean. Selecciona a algunos estudiantes para que compartan las respuestas correctas de cada paralelogramo. A medida que los estudiantes compartan, subraye los pares base-altura en cada paralelogramo y registre las respuestas en la tabla. Aunque sólo se nombra un par base-altura para cada paralelogramo, reitere que hay otro par. Muestre el segundo par en el diagrama o pida a los estudiantes que lo señalen.
Después de que se hayan compartido todas las respuestas para las primeras cuatro filas, discuta las siguientes preguntas, mostradas para que todos las vean:
• "¿Cómo determinaste la expresión para el área de cualquier paralelogramo?" (Las áreas de los paralelogramos A-D son cada una el producto de la base y la altura).
• "Supón que descompones un paralelogramo con un corte y lo reorganizas en un rectángulo. ¿Sigue funcionando esta expresión para hallar el área? ¿Por qué sí o por qué no?" (Sí. Un lado del rectángulo será igual a la base del paralelogramo. La altura del paralelogramo también es la altura del rectángulo: ambas son perpendiculares a la base).
• "¿Crees que esta expresión siempre funcionará?"
Asegúrate de que todos tengan la expresión correcta para hallar el área de un paralelogramo al final de la discusión. La segunda pregunta de la discusión está pensada para provocar conexiones con el rectángulo relacionado con el paralelogramo a medida que se descomponen y reordenan para hallar el área. La tercera pregunta (sobre si la expresión funcionará siempre) no pretende demostrarse aquí, por lo que se espera que los estudiantes especulen en este punto. Su objetivo es incitar a los estudiantes a pensar en otros paralelogramos de formas diferentes, además de los cuatro que se muestran aquí.
¿Estás preparado para más?
1. ¿Qué ocurre con el área de un paralelogramo si la altura se duplica, pero la base no cambia? ¿Si la altura se triplica? ¿Si la altura es 100 veces la original?
2. ¿Qué ocurre con el área si tanto la base como la altura se duplican? ¿Ambos se triplican? Ambas son 100 veces sus longitudes originales?
"¿Estás listo para más?" Respuesta del maestro
1. El área se duplica, se triplica, se multiplica por 100
2. El área se cuadruplica, es 9 veces el área original, es 10.000 veces el área original.
5 minutos
En esta lección, identificamos una base y una altura correspondiente en un paralelogramo, y luego escribimos una expresión algebraica para hallar el área de cualquier paralelogramo.
• "¿Cómo decides la base de un paralelogramo?" (Cualquier lado puede ser base. A veces un lado es preferible a otro porque su longitud es conocida o fácil de conocer).
• "Una vez elegida una base, ¿cómo podemos identificar una altura que le corresponda?". (Identifica un segmento perpendicular que una esa base y el lado opuesto; halla la longitud de ese segmento.)
• "¿De cuántas formas podemos identificar una base y una altura para un paralelogramo dado?" (Hay dos bases posibles. Para cada base, muchos segmentos posibles pueden representar la altura correspondiente.)
• "¿Cuál es la relación entre la base y la altura de un paralelogramo y su área?" (El área es el producto de la base y la altura.)
©Accelerate Learning Inc. - Todos los derechos reservados


ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Los paralelogramos S y T tienen cada uno una base y una altura correspondiente.
1. ¿Cuáles son los valores de b y h para cada paralelogramo?
• Paralelogramo S: �� = , h =
• Paralelogramo T: �� = , h =
2. Utiliza los valores de b y h para hallar el área de cada paralelogramo.
• Área del paralelogramo S:
• Área del paralelogramo T: POSIBLES RESPUESTASS
1.
2.

minutos
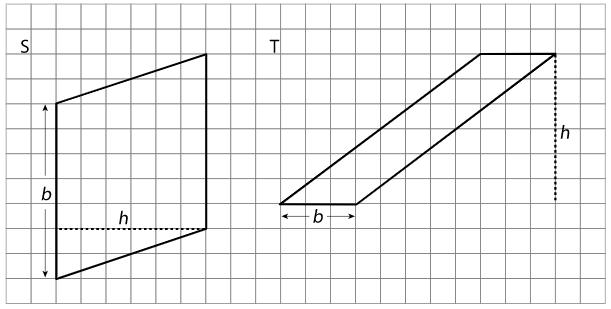
• Paralelogramo S: �� = 7, h = 6
• Paralelogramo T: �� = 3, h = 6
• Área del paralelogramo S: 42 unidades cuadradas. 7 ⋅ 6 = 42
• Área del paralelogramo T: 18 unidades cuadradas. 3 ⋅ 6 = 18
PROBLEMA 1
Selecciona todos los paralelogramos que tengan una altura correcta etiquetada para la base dada.
Posibles soluciones
(B es incorrecto porque la base y la altura no son perpendiculares.)
PROBLEMA 2
El lado etiquetado �� se ha elegido como base para este paralelogramo.

Dibuje un segmento que muestre la altura correspondiente a esa base.
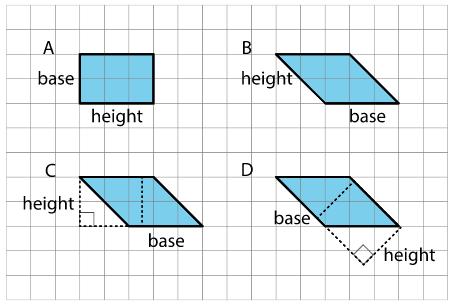
Posibles soluciones
Las respuestas varían. (La altura puede ser cualquier segmento perpendicular a la base que una la recta que contiene la base con la recta que contiene el lado opuesto a la base). Ejemplo de respuesta:
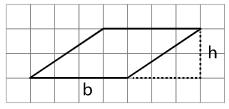
de Matemáticas . Unidad 1

PROBLEMA 3
Halla el área de cada paralelogramo.
PROBLEMA 4
Si el lado que mide 6 unidades es la base de este paralelogramo, ¿cuál es su altura correspondiente?

A. 6 unidades
B. 4.8 unidades
C. 4 unidades
D. 5 unidades
PROBLEMA 5
Halla el área de cada paralelogramo.
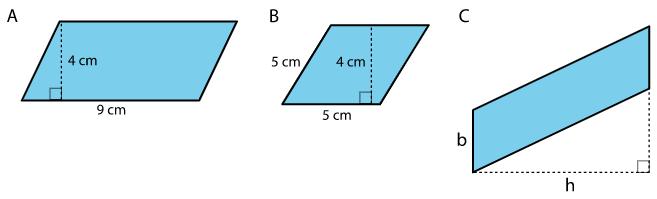
PROBLEMA 6
Del Grado 6, Unidad 1, Lección 4
Posibles soluciones
A: 8 unidades cuadradas. (Este es un 2-por-4 rectángulo.)
B: 10 unidades cuadradas. (El lado horizontal mide 5 unidades y puede ser la base. La altura para esta base es 2 unidades.)
C: 8 unidades cuadradas. (El lado vertical puede servir de base. La base es 2 unidades, y la altura para esta base es 4 unidades.)
Posibles soluciones C
Posibles soluciones
A: 36 cm2. (La base es 9 cm, y la altura para esta base es 4 cm.)
B: 20 cm2. (La base es 5 cm, y la altura para esta base es 4 cm.)
C: ��h. (La base es ��, y la altura correspondiente es h.)
¿Estás de acuerdo con cada una de estas afirmaciones? Explica tu razonamiento.
A. Un paralelogramo tiene seis lados.
B. Los lados opuestos de un paralelogramo son paralelos.
C. Un paralelogramo puede tener uno o dos pares de lados paralelos.
D. Todos los lados de un paralelogramo tienen la misma longitud.
E. Todos los ángulos de un paralelogramo tienen la misma medida.
Posibles soluciones
A. En desacuerdo. Un paralelogramo es un cuadrilátero.
B. De acuerdo. Por definición, los lados opuestos de un paralelogramo son paralelos.
C. En desacuerdo. Por definición, un paralelogramo tiene dos pares de lados paralelos.
D. En desacuerdo. A veces todos los lados de un paralelogramo tienen la misma longitud, pero no siempre. Los lados opuestos de un paralelogramo siempre tienen la misma longitud.
E. En desacuerdo. A veces todos los ángulos de un paralelogramo tienen la misma medida (cuando el paralelogramo es un rectángulo), pero no siempre. Los ángulos opuestos de un paralelogramo tienen la misma medida.
California - Grado 6
Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

PROBLEMA 7
Del Grado 6, Unidad 1, Lección 2
Un cuadrado con un área de 1 metro cuadrado se descompone en 9 cuadrados pequeños idénticos. Cada cuadrado pequeño se descompone en dos triángulos idénticos.
A. ¿Cuál es el área, en metros cuadrados, de 6 triángulos? Si te atascas, dibuja un diagrama.
B. ¿Cuántos triángulos se necesitan para componer una región de 1 1 2 metros cuadrados?
Posibles soluciones
A. 6 18 o 1 3 metros cuadrados.
B. 27 triángulos. Se necesitan 18 triángulos para hacer un área de 1 metro cuadrado y 9 triángulos para hacer un área de 1 2 metro cuadrado.
18 + 9 = 27
Reflejos:
Learning Inc. - Todos los derechos reservados


• Graficar formas
• Redes y superficie
• Generalizar con representaciones múltiples
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.EE.2c Evaluar expresiones en valores específicos de sus variables. Incluir expresiones que surgen de fórmulas utilizadas en problemas del mundo real. Realizar operaciones aritméticas, incluyendo aquellas que involucran exponentes de números enteros, en el orden convencional cuando no hay paréntesis para especificar un orden particular (Orden de Operaciones).
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales, y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de resolver problemas matemáticos y del mundo real.
Enfoque SMPs
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.B.7 I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dan sentido al mundo y predicen lo que podría ocurrir. atienden a la precisión.
OBJETIVO(S) DE APRENDIZAJE
descubriendo la forma y el espacio, desmontando enteros, juntando piezas y explorando el cambio de cantidades.
• Practiquemos cómo encontrar el área de paralelogramos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo usar la fórmula del área para encontrar el área de cualquier paralelogramo.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Aplicar la fórmula del área de un paralelogramo para hallar el área, la longitud de la base o la altura, y explicar (oralmente y por escrito) el método de solución.
• Elegir qué medidas utilizar para calcular el área de un paralelogramo cuando se da más de una medida de la base o de la altura, y explicar (oralmente y por escrito) la elección.
Rutinas de instrucción
MLR8: Apoyos para el debate
Materiales necesarios
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Narrativa de la lección
Esta lección permite a los estudiantes practicar el uso de la fórmula para el área de los paralelogramos, y elegir las medidas a utilizar como base y la altura correspondiente. Mediante razonamientos repetidos, ven que algunas medidas son más útiles que otras. Por ejemplo, si un paralelogramo en una cuadrícula tiene un lado vertical o un lado horizontal, tanto la base como la altura se pueden determinar más fácilmente si se utiliza el lado vertical u horizontal como base.
A lo largo del proceso, los estudiantes ven que los paralelogramos con la misma base y la misma altura tienen la misma área porque los productos de esos dos números son iguales, aunque los paralelogramos tengan un aspecto muy diferente. Esto nos da una forma de utilizar unas dimensiones dadas para encontrar otras.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 5 min

Actividad de Exploración Grupos Pequeños 25 min
Los estudiantes determinan el número de puntos mostrados y luego justifican su respuesta.
Los estudiantes construyen fluidez en encontrar las áreas y las longitudes de la base o la altura de paralelogramos.
Los applets digitales interactivos están disponibles para permitir a los estudiantes explorar la búsqueda y comparación de las áreas de los paralelogramos utilizando la tecnología.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la búsqueda de las áreas de los paralelogramos.
Síntesis Todo el grupo 5 min
Los estudiantes discuten qué medidas utilizar al calcular el área de un paralelogramo y luego comparan las dimensiones y áreas de diferentes paralelogramos.
Enfriamiento Independiente 5 min Los estudiantes encuentran el área de un paralelogramo dado.
Práctica Independiente 5-8 min
El componente de práctica independiente incluye 4 problemas de la lección y 2 problemas de repaso en espiral.


5 minutos

Rutinas didácticas
MLR8: Apoyos para la discusión
En este calentamiento, los estudiantes determinan el número de puntos de una imagen sin contarlos y explican cómo han llegado a esa respuesta. La actividad también da a los estudiantes la oportunidad de utilizar la descomposición y la estructura para cuantificar algo, en un escenario ligeramente diferente de lo que han visto en esta unidad. Para obtener el número total de puntos, los estudiantes tienen que visualizar y explicar cómo se descomponen los puntos y utilizar sus conocimientos sobre matrices, multiplicación y área para obtener el número que les interesa. Para animar a los estudiantes a referirse a la imagen en su explicación, pregúnteles cómo vieron los puntos en lugar de cómo hallaron el número de puntos. Como en un calentamiento anterior, considere establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, u otra señal sutil. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se apresuren al levantar las manos alrededor de la clase.
Dé a los estudiantes 1-2 minutos de tiempo para pensar en silencio y pídales que den una señal que muestre cuántas soluciones tienen. Anima a los estudiantes que hayan encontrado una forma de ver los puntos a que piensen en otra mientras esperan.
Apoyo a los estudiantes con discapacidad
Procesamiento visual-espacial: Ayudas visuales. Sugiera a los estudiantes que utilicen su propia copia de la tarea (en su cuaderno de trabajo, tableta, o proporcióneles una copia de la tarea) para dibujar o resaltar.
¿Cuántos puntos hay en la imagen?
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
POSIBLES RESPUESTAS
¿Cómo los ves?

30 puntos. Las estrategias varían. Ejemplos de estrategias:
• Descomponer la imagen en partes, luego multiplicar y sumar.
(2
6) + (3 ⋅ 4) + 6 = 30

2) + 6 = 30

RESPUESTAS ( CONTINUACIÓN)

6º de Matemáticas . Unidad 1
• Multiplica para hallar los puntos de toda la matriz y resta la matriz de puntos que falta.
• (6 ⋅ 6) - (2 ⋅ 3) = 30

Pide a los estudiantes que compartan cuántos puntos vieron y cómo los vieron. Registre y muestre las explicaciones de los estudiantes para que todos puedan verlas. Para involucrar a más estudiantes en la conversación, considere hacer algunas de las siguientes preguntas:
• "¿Quién puede reformular la forma en que vio los puntos con palabras diferentes?"
• "¿Alguien vio los puntos de la misma forma pero lo explicaría de otra manera?"
• "¿Alguien quiere añadir una observación a la forma en que vio los puntos?"
• "¿Estás de acuerdo o en desacuerdo? ¿Por qué?"
Apoyo para estudiantes de inglés
Speaking: MLR8 Apoyos para el debate. Proporcione marcos de frases para ayudar a los estudiantes a explicar sus estrategias. Por ejemplo: "I noticed that ." o "First, I because .". Cuando los estudiantes compartan sus respuestas con un compañero, pídales que ensayen lo que dirán cuando lo compartan con todo el grupo. Ensayar les brinda la oportunidad de aclarar sus ideas.
Principio(s) de diseño: Optimizar el resultado (para la explicación)
PARALELOGRAMOS
25 minutos
Rutinas didácticas
MLR8: Apoyo a la discusión
Esta actividad permite a los estudiantes practicar la búsqueda y el razonamiento sobre el área de varios paralelogramos dentro y fuera de una cuadrícula. Los estudiantes tienen que entender las medidas y relaciones de las figuras dadas, identificar un par apropiado de medidas de altura-base para utilizar y reconocer que dos paralelogramos con las mismas medidas de altura-base (o con diferentes medidas de altura-base pero el mismo producto) tienen la misma área.
Mientras trabajan individualmente, observa cómo los estudiantes determinan los pares de altura-base que van a utilizar. Mientras trabajan en grupos, escuche sus discusiones e identifique a aquellos que pueden explicar claramente cómo encontraron el área de cada uno de los paralelogramos.
Organice a los estudiantes en grupos de 4. Dé a cada estudiante acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y 5 minutos de tiempo tranquilo para encontrar las áreas de los paralelogramos en la primera pregunta. A continuación, asigna a cada maestro un paralelogramo (A, B, C o D). Pide a cada maestro que explique al grupo, de uno en uno, cómo ha hallado el área del paralelogramo asignado. Después de que cada maestro lo explique, compruebe si el resto del grupo está de acuerdo o en desacuerdo. Discuta cualquier desacuerdo y llegue a un consenso sobre la respuesta correcta antes de pasar al siguiente paralelogramo.
Después, dé a los estudiantes otros 5-7 minutos de tiempo de trabajo tranquilo para completar el resto de la actividad.
California - Grado 6
Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

Para las aulas que utilicen la actividad digital, organice a los estudiantes en grupos de 2. Pida a cada estudiante que explique a su compañero cómo encontró el área de cada paralelogramo. Cuando se utilice el segundo applet, cada estudiante debe encontrar un par de cuadriláteros con igual área.
Apoyo a estudiantes con discapacidad
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus tutores previamente identificados.
Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una pregunta cada vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.

de Matemáticas . Unidad 1
1. Encuentre el área de cada paralelogramo. 1. Halla el área de cada paralelogramo. Muestra tu razonamiento.
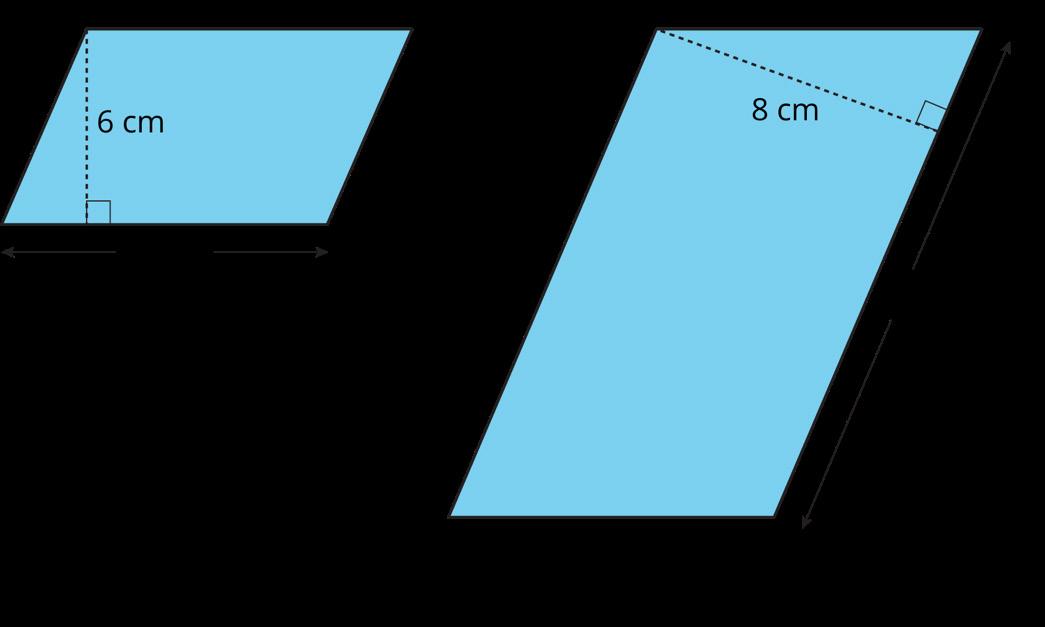
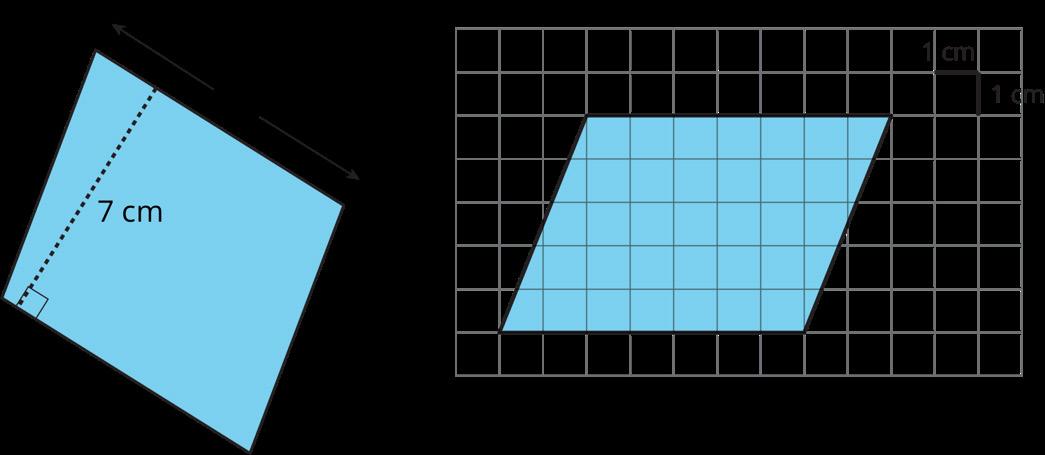
2. En el paralelogramo B de la primera pregunta, ¿cuál es la altura correspondiente para la base que mide 10 cm? Explica o muestra tu razonamiento.
3. Dos paralelogramos diferentes P y Q tienen ambos un área de 20 unidades cuadradas. Ninguno de los dos paralelogramos es un rectángulo. En la cuadrícula, dibuja dos paralelogramos que podrían ser P y Q.

Nation California - Grado 6
Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

Apoyo para estudiantes de inglés
Speaking: MLR8 Apoyo a la discusión. Use esta rutina para apoyar la discusión de toda la clase cuando los estudiantes explican cómo saben que crearon dos paralelogramos con igual área. Después de que los estudiantes hayan compartido sus explicaciones, pida a los demás estudiantes que repitan y/o repitan las descripciones de sus compañeros utilizando términos matemáticos (por ejemplo, área, producto, base, altura, etc.). Si los estudiantes no son capaces de reafirmar, deben pedir aclaraciones. De este modo, más estudiantes tendrán la oportunidad de producir el lenguaje necesario para describir el punto final.
¿Estás listo para más?
Aquí tienes un paralelogramo compuesto de paralelogramos más pequeños.
La región sombreada está compuesta por cuatro paralelogramos idénticos.
Todas las longitudes están en pulgadas.
¿Cuál es el área del paralelogramo no sombreado del centro? Explica o muestra tu razonamiento.
"¿Estás listo para más?" Respuesta del maestro
3.2 pulgadas cuadradas. Los razonamientos varían. Ejemplos de respuestas:
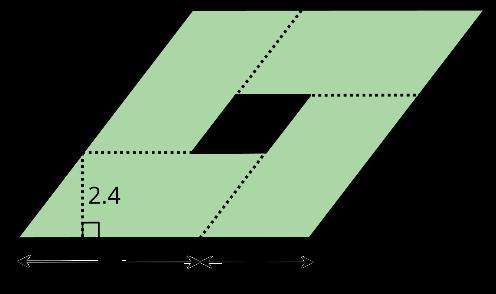
El área de un paralelogramo sombreado es 12 pulgadas cuadradas, porque una base mide 5 pulgadas y su altura correspondiente es 2.4 pulgadas (5 ⋅ (2.4) = 12). Esto significa que la altura correspondiente al lado que mide 3 pulgadas es 4 pulgadas (3 ⋅ 4 = 12). La altura del paralelogramo pequeño es la diferencia entre 4 pulgadas y 2.4 pulgadas, que es 1.6 pulgadas. El lado horizontal del paralelogramo sin sombrear, que puede ser una base, es 2 pulgadas (5 - 3 = 2). El área del paralelogramo sin sombrear es, por tanto, 2 ⋅ (1,6) o 3,2 pulgadas cuadradas.
La base del paralelogramo total es 8 pulgadas (5 + 3 = 8). Su altura es 6,4 pulgadas (4 + 2,4 = 6,4). Su área es, por tanto, 8 ⋅ (6,4) o 51,2 pulgadas cuadradas. El área de los cuatro paralelogramos sombreados es 4 ⋅ 12 o 48 pulgadas cuadradas. El área de la región no sombreada es, por tanto, 51,2 - 48 o 3,2 pulgadas cuadradas.
5 minutos
• Usamos la fórmula del área para practicar el cálculo del área de varios paralelogramos.
• "Cuando un paralelogramo está en una cuadrícula, ¿cómo sabemos qué lado elegir como base? ¿Podemos usar cualquier lado?" (Es útil utilizar un lado horizontal o vertical como base; sería más fácil saber la longitud de ese lado y de su altura correspondiente).
• "Fuera de una cuadrícula, ¿cómo sabemos qué medidas nos pueden ayudar a encontrar el área de un paralelogramo?" (Necesitamos la longitud de un lado del paralelogramo y de un segmento perpendicular que una ese lado con el lado opuesto).
• "¿Los paralelogramos que tienen la misma área tienen siempre el mismo aspecto?". (No.) "¿Puedes mostrar un ejemplo?"
6º de Matemáticas . Unidad 1
• "¿Los paralelogramos que tienen la misma base y la misma altura tienen siempre el mismo aspecto?" (No.) "¿Puedes mostrar un ejemplo?"
• "¿Cómo podemos dibujar dos paralelogramos diferentes con la misma área?" (Podemos encontrar dos pares cualesquiera de longitudes base-altura que tengan el mismo producto. También podemos usar el mismo par de números dibujando los paralelogramos de forma diferente).
5 minutos
Acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. Encuentra el área del paralelogramo. 1. Halla el área del paralelogramo. Explica o muestra tu razonamiento.
2. ¿Hubo alguna medida de longitud que no utilizaste para hallar el área? En caso afirmativo, explique por qué no la utilizó.

PROBLEMA 1
¿Cuáles de estos tres paralelogramos tienen la misma área entre sí?
Posibles soluciones
A, B, D. (Todos tienen un área de 15 unidades cuadradas.)
Nation California - Grado 6
Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

PROBLEMA 2
¿Cuál de los siguientes pares de base y altura produce la mayor área? Todas las medidas están en centímetros.
A. �� = 4, ℎ =3.5
B. �� = 0.8, ℎ =20
C. �� = 6, ℎ =2.25
D. �� = 10, ℎ =1.4
PROBLEMA 3
Aquí están las áreas de tres paralelogramos. Úsalos para encontrar la longitud que falta (etiquetada con un "?") en cada paralelogramo.
A. 10 unidades cuadradas
B. 21 unidades cuadradas
C. 25 unidades cuadradas

PROBLEMA 4
Posibles soluciones
B
Posibles soluciones
A. 2 unidades
B. 3 unidades
C. 5 unidades
El edificio Dockland de Hamburgo, Alemania, tiene forma de paralelogramo.
Si la longitud del edificio es 86 metros y su altura es 55 metros, ¿cuál es el área de esta cara del edificio?
Posibles soluciones
4.730 metros cuadrados (86 ⋅ 55 = 4.730)
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 5
Selige todos los segmentos que podrían representar una altura correspondiente si el lado m es la base. e f g h j k n


Learning Inc. - Todos los derechos reservados
Posibles soluciones e f g h j k n
PROBLEMA 6
Del Grado 6, Unidad 1, Lección 3 Halla el área de la región sombreada. Todas las medidas están en centímetros. Muestra tu razonamiento.
Posibles soluciones
80 centímetros cuadrados. Ejemplo de razonamiento: El área del rectángulo grande es 140 centímetros cuadrados, porque 14 ⋅ 10 = 140. Las áreas de los triángulos rectángulos pequeños sin sombrear son cada una 6 centímetros cuadrados, porque 6⋅2 ÷ 2 = 6. Las áreas de los triángulos rectángulos mayores sin sombrear son 24 centímetros cuadrados cada uno, porque 4 ⋅ 12 ÷ 2 = 24. Restando las áreas de los cuatro triángulos rectángulos sin sombrear del área del rectángulo grande se obtiene 80: 140-6-6-24-24=80
Reflexiones:

Nation California - Grado 6
Learning Inc. - Todos los derechos reservados

• Graficar formas
• Redes y superficie
ALINEACIÓN
Alineación de estándares y principios de Abordar
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfocar SMPs
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1
I.C.12
II.C.7
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? .
dar sentido al mundo y predecir lo que podría ocurrir.
OBJETIVO(S)
buscar y utilizar estructuras.
• Comparemos paralelogramos y triángulos.
OBJETIVO(S) DE APRENDIZAJE
. mientras . . .
desmontar enteros, unir partes y descubrir formas y espacios.
• Puedo explicar la relación especial entre un par de triángulos idénticos y un paralelogramo.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Describir (oralmente y por escrito) las formas en que dos triángulos idénticos pueden componerse, es decir, en un paralelogramo o en un rectángulo.
• Mostrar cómo cualquier paralelogramo puede descomponerse en dos triángulos idénticos trazando una diagonal y generalizar (por escrito) que esta propiedad se aplica a todos los paralelogramos, pero no a todos los cuadriláteros.
Rutinas didácticas
MLR2: Recoger y mostrar
MLR8: Apoyos para la discusión
Materiales necesarios
Patrón de líneas negras para la Actividad 7.3
Enfriamiento
Juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Fichas preimpresas, recortadas de copias del patrón de líneas negras
Reglas
Preparación necesaria
Imprime pares de triángulos del esquema de la Historia de dos triángulos (2ª parte). Si los estudiantes van a recortar los triángulos, utiliza sólo la primera página. Si los triángulos van a ser precortados por el maestro, imprime la segunda y la tercera página. Prepare suficientes juegos para que cada grupo de 3-4 estudiantes tenga un juego completo (2 copias de cada uno de los triángulos P-U).
Para las clases que utilicen la versión digital de la actividad, se proporciona un applet que puede utilizarse en lugar de, o además de, los triángulos recortados.
de Matemáticas . Unidad 1
Narrativa de la lección
Esta lección prepara a los estudiantes para aplicar lo que saben sobre el área de los paralelogramos para razonar sobre el área de los triángulos.
Destacar la relación entre triángulos y paralelogramos es un objetivo clave de esta lección. Las actividades utilizan tanto la idea de descomposición (de un cuadrilátero en triángulos) como la de composición (de dos triángulos en un cuadrilátero). El estudio bidireccional es deliberado y está diseñado para ayudar a los estudiantes a ver y razonar sobre el área de un triángulo de forma diferente. Los estudiantes ven que un paralelogramo siempre puede descomponerse en dos triángulos idénticos, y que dos triángulos idénticos cualesquiera siempre pueden componerse en un paralelogramo (MP7).
Como en esta lección ocurren muchas cosas y el tiempo puede ser escaso, es importante preparar todos los materiales y considerar la organización de los grupos con antelación.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 5 min

Actividad de exploración Grupos pequeños 15 min
Dados paralelogramos idénticos con diferentes combinaciones de base y altura correspondientes identificadas, los estudiantes encuentran el área y una longitud de base desconocida.
Hay disponible un applet digital interactivoLos estudiantes descubren que los paralelogramos pueden descomponerse en 2 triángulos idénticos. para permitir a los estudiantes explorar la descomposición de paralelogramos en triángulos utilizando la tecnología.
Hay disponible una extensión de exploración con un applet digital interactivo para desarrollar una comprensión más profunda de los cuadriláteros que pueden descomponerse en triángulos idénticos.
Los estudiantes exploran qué cuadriláteros pueden formarse utilizando pares de triángulos idénticos.
Actividad de exploración Grupos reducidos 15 min
Síntesis Grupo completo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Hay disponible un applet digital interactivo que permite a los estudiantes explorar formas que se forman utilizando pares de triángulos idénticos utilizando la tecnología.
Los estudiantes hacen conexiones entre pares de triángulos idénticos y paralelogramos.
Los estudiantes demuestran su comprensión de la relación entre pares de triángulos idénticos y paralelogramos.
El componente de práctica independiente incluye 4 problemas de repaso de la lección y 2 problemas de repaso en espiral.
California - Grado 6
Learning Inc. - Todos los derechos reservados


5 minutos
Este calentamiento refuerza la comprensión de los estudiantes de las bases y alturas de un paralelogramo. En lecciones anteriores, los estudiantes han calculado áreas de paralelogramos utilizando bases y alturas. También han determinado posibles bases y alturas de un paralelogramo dado un área entera. Vieron, por ejemplo, que encontrar posibles bases y alturas de un paralelogramo con un área de 20 unidades cuadradas significa encontrar dos números con un producto de 20. Los estudiantes amplían ese trabajo aquí trabajando con longitudes de lado y área decimales.
A medida que los estudiantes trabajan, observe a los estudiantes que entienden que los dos paralelogramos idénticos tienen igual área y que usan ese entendimiento para encontrar la base desconocida. Pídales que compartan más tarde.
Dé a los estudiantes 2 minutos de tiempo de trabajo tranquilo y acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Los estudiantes deben estar suficientemente familiarizados con las bases y las alturas para comenzar el calentamiento. Sin embargo, si es necesario, repase brevemente la relación de un par de base y altura en un paralelogramo, utilizando preguntas como:
• "¿Podemos utilizar cualquier lado de un paralelogramo como base?" (Sí.)
• "¿La altura es siempre la longitud de uno de los lados del paralelogramo?" (No.)
• "Una vez que hemos identificado una base, ¿cómo identificamos una altura?" (Puede ser cualquier segmento que sea perpendicular a la base y vaya de la base al lado opuesto.)
• "¿Se puede trazar un segmento de altura fuera de un paralelogramo?" (Sí.)
Procesamiento conceptual: Tiempo de procesamiento. Compruebe con cada maestro, según sea necesario, la comprensión durante cada paso de la actividad.
Lenguaje receptivo: Tiempo de procesamiento. Lea todos los enunciados en voz alta. Los estudiantes que escuchan y leen la información se beneficiarán de un tiempo de procesamiento adicional.

Aquíhay dos copias de un paralelogramo. Cada copia tiena un lado etiquetado como la base b y un segmento dibujado para altura correspondiente y etiquetado como h. .
1. La base del paralelogramo de la izquierda mide 2,4 centímetros; su altura correspondiente es 1 centímetro. Calcula su área en centímetros cuadrados.
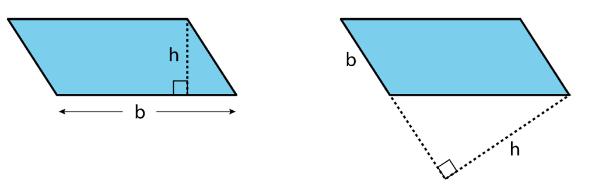
2. La altura del paralelogramo de la derecha mide 2 centímetros. ¿Cuánto mide la base de ese paralelogramo? Explica tu razonamiento.
1. El área del primer paralelogramo es de 2,4 centímetros cuadrados. (2,4) 1 = 2,4
2. El área del segundo paralelogramo también es de 2,4 centímetros cuadrados. Como la base y la altura deben multiplicarse para obtener la misma área de 2,4, la base debe ser de 1,2 centímetros porque (1,2) 2 = 2,4.
SÍNTESIS DE LA ACTIVIDAD

6º de Matemáticas . Unidad 1
Es posible que algunos estudiantes no sepan cómo empezar a responder a las preguntas porque las medidas no se muestran en los diagramas. Pida a los estudiantes que etiqueten los paralelogramos basándose en la información del ENUNCIADO DE TAREA PARA EL ESTUDIANTE.
Los estudiantes pueden decir que no hay suficiente información para responder a la segunda pregunta porque sólo se conoce un dato (la altura). Pregúnteles qué información adicional podrían necesitar. Pídales que revisen el ENUNCIADO DE TAREA PARA EL ESTUDIANTE y vean lo que dice sobre los dos paralelogramos. Pregúnteles qué saben sobre las áreas de dos figuras que son idénticas.
Los estudiantes pueden tener dificultades para encontrar la base desconocida en la segunda pregunta porque el área del paralelogramo es un decimal y no saben cómo dividir un decimal. Pídales que expliquen cómo razonarían si el área fuera un número entero. Si entienden que tienen que dividir el área por 2 (ya que la altura es 2 cm), vea si podrían razonar en términos de multiplicación (es decir, 2 veces ¿qué número es 2,4?) o si podrían razonar sobre la división utilizando fracciones (es decir, 2,4 puede verse como 2 4 10 o 24 10 ; ¿qué es 24 décimas dividido por 2?).
Seleccione 1-2 estudiantes previamente identificados para que compartan sus respuestas. Si los estudiantes aún no lo han explicado, haga hincapié en que sabemos que los paralelogramos tienen la misma área porque son idénticos, lo que significa que al colocar uno encima del otro, coincidirían exactamente.
Antes de continuar, pregunte a los estudiantes: "¿Cómo podemos verificar que la altura que encontramos es correcta, o que los dos pares de bases y alturas producen la misma área?". (Podemos multiplicar los valores de cada par y ver si ambos producen 2.4.)
minutos
Rutinas didácticas
MLR2: Recoger y mostrar
En lecciones anteriores, los estudiantes vieron que un cuadrado puede descomponerse en dos triángulos rectángulos isósceles idénticos. Concluyeron que el área de cada uno de esos triángulos es la mitad del área del cuadrado. Utilizaron esta observación para determinar el área de regiones compuestas.
Esta actividad ayuda a los estudiantes a ver que los paralelogramos distintos de los cuadrados también pueden descomponerse en dos triángulos idénticos trazando una diagonal. Lo comprueban trazando un triángulo en papel vegetal y girándolo para que coincida con la otra copia. Este proceso prepara a los estudiantes para ver cualquier triángulo como si ocupara la mitad de un paralelogramo y, en consecuencia, como si tuviera la mitad de su área. Para generalizar acerca de los cuadriláteros que pueden descomponerse en triángulos idénticos, los estudiantes deben analizar las características de las formas dadas y buscar su estructura (MP7).
Hay una serie de observaciones geométricas en esta unidad que deben darse por supuestas en este punto del estudio matemático de los estudiantes. Éste es uno de esos casos. Los estudiantes sólo han visto ejemplos de un paralelogramo que se descompone en dos copias del mismo triángulo, o sólo han verificado esta conjetura a través de la experimentación física, pero por el momento se puede considerar un hecho. A partir del grado 8, comenzarán a demostrar algunas de las observaciones que previamente han dado por ciertas.
Organizar a los estudiantes en grupos de 3-4. Dé a los estudiantes acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y permítales 2 minutos de tiempo de reflexión en silencio para las dos primeras preguntas. A continuación, les pide que compartan sus dibujos con su grupo y discutan cómo dibujaron sus líneas. Si los miembros del grupo no están de acuerdo sobre si un cuadrilátero puede descomponerse en dos triángulos idénticos, deben hacer constar el desacuerdo, pero no es necesario llegar a un acuerdo. Pronto tendrán la oportunidad de verificar sus respuestas.
California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


INSTRUCCIÓN ( CONTINUACIÓN)

A continuación, pida a los estudiantes que utilicen papel de calco para comprobar que los pares de triángulos que creen idénticos lo son realmente (es decir, que coincidirían exactamente si se colocaran uno encima del otro). Diga a los estudiantes que se repartan el trabajo de comprobación entre los miembros de su grupo para optimizar el tiempo.
Aunque los estudiantes hayan trabajado con papel de calco anteriormente en la unidad, puede que algunos no recuerden cómo utilizarlo para comprobar la congruencia de dos formas; puede que sea necesaria alguna orientación explícita. Anime a los estudiantes a trabajar con cuidado y precisión. Se puede utilizar una regla para trazar, pero no es imprescindible y puede ser un estorbo. Una vez que los estudiantes terminen de comprobar los triángulos de su lista y verifiquen que son idénticos (o corrijan su respuesta inicial), pídales que respondan a la última pregunta.
Los estudiantes que utilicen la actividad digital pueden descomponer las formas utilizando un applet. Anime a los estudiantes a utilizar la herramienta segmento en lugar de dibujar libremente un segmento para dividir las formas.
Apoyo para estudiantes de inglés
Conversar, representar: MLR2 Recoger y mostrar. Para ayudar a los estudiantes a razonar y utilizar el lenguaje matemático de descomponer, diagonal e idéntico, escuche a los estudiantes hablar sobre cómo están haciendo sus dibujos. Registre y muestre las frases comunes o importantes que escuche decir a los estudiantes, así como ejemplos de sus dibujos. Siga actualizando el lenguaje recogido de los estudiantes a lo largo de la lección y recuérdeles que tomen prestado el lenguaje de la pantalla cuando sea necesario.
Principio(s) de diseño: Apoyar la creación de sentido; Maximizar la metaconciencia
Dos polígonos son idénticos si coinciden exactamente cuando se colocan uno encima del otro.
1. Dibuje un segmento para descomponer cada uno de los siguientes polígonos en dos triángulos idénticos, si es posible. Si lo deseas, también puedes dibujar los triángulos.
Haz una pausa aquí para una discusión en pequeños grupos.
2. ¿Qué cuadriláteros pueden descomponerse en dos triángulos idénticos? Haz una pausa aquí para una discusión en pequeños grupos.
3. Estudia los cuadriláteros que eran, de hecho, descomponibles en dos triángulos idénticos. ¿Qué observas en ellos? Escribe un par de observaciones sobre lo que tienen en común estos cuadriláteros.
Apoyo a estudiantes con discapacidad
Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten cómo descomponer los cuadriláteros y utilicen el papel de calco según sea necesario.
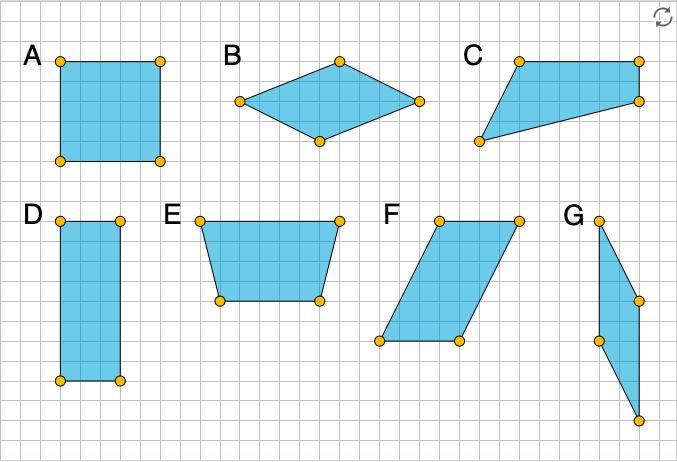
6º de Matemáticas . Unidad 1
1. Las respuestas varían. Las respuestas varían. Ejemplo de respuesta:

2. Las respuestas varían. c. Los cuadriláteros ��, ��, ��, ��, y �� pueden descomponerse en dos triángulos idénticos.
Sí, los triángulos que trazamos coinciden perfectamente.
3. Las respuestas varían. Ejemplos de respuestas: Tienen dos pares de lados paralelos y cada par tiene la misma longitud. Todos son paralelogramos.
Puede que a los estudiantes no se les ocurra girar los triángulos para comprobar la congruencia. Si es así, diga a los estudiantes que seguimos considerando idénticos dos triángulos aunque haya que girar uno para que coincida con el otro.
La discusión debe tener dos objetivos: poner de relieve cómo los cuadriláteros pueden descomponerse en triángulos y ayudar a los estudiantes a hacer generalizaciones sobre los tipos de cuadriláteros que pueden descomponerse en dos triángulos idénticos. Considera estas preguntas:
• ¿Cómo descompusiste los cuadriláteros en dos triángulos? (Une los vértices opuestos, es decir, dibuja una diagonal.)
• ¿Funcionó la estrategia de dibujar una diagonal para descomponer todos los cuadriláteros en dos triángulos? (Sí.) ¿Son todos los triángulos resultantes idénticos? (No.)
• ¿Qué tienen �� y �� que no se pueden descomponer en dos triángulos idénticos? (No tienen lados iguales ni ángulos iguales. Sus lados opuestos no son paralelos.)
• ¿Qué tienen ��, ��, y �� que no tengan �� y ��? ( ��, ��, y �� tienen dos pares de lados paralelos de igual longitud. Son paralelogramos.)
Pida a los estudiantes que completen este iniciador de frases: Para que un cuadrilátero sea descomponible en dos triángulos idénticos debe ser (o tener)...
Si el tiempo lo permite, discuta cómo verificaron los estudiantes la congruencia de los dos triángulos.
• ¿Cómo verificaron si los triángulos son idénticos? ¿Simplemente apilaron el triángulo trazado o hicieron algo más específico? (Pueden darse cuenta de que es necesario girar un triángulo -o reflejarlo dos veces- antes de poder emparejar los triángulos).
• ¿Alguien utilizó otra forma de comprobar la congruencia? (Los estudiantes también pueden pensar en términos de las partes o la composición de cada triángulo. Por ejemplo: "Ambos triángulos tienen las mismas longitudes de lado; ambos tienen un ángulo recto").
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

¿Estás listo para más?
Dibuja otros tipos de cuadriláteros que no estén ya representados. Intenta descomponerlos en dos triángulos iguales. ¿Puedes hacerlo? Inventa una regla general sobre lo que debe ser cierto si un cuadrilátero puede descomponerse en dos triángulos idénticos.
"¿Estás listo para más?" Respuesta de los estudiantes
Las respuestas varían.
Rutinas didácticas
MLR8: Apoyos para la discusión
15 minutos
Materiales necesarios
Maestro de línea negra
Anteriormente, los estudiantes descompusieron cuadriláteros en dos triángulos idénticos. Esta actividad les ha permitido familiarizarse con la idea de que un triángulo es la mitad de un cuadrilátero. Esta actividad les incita a pensar de la otra forma: componer cuadriláteros utilizando dos triángulos idénticos. Ayuda a los estudiantes a ver que dos triángulos idénticos de cualquier tipo siempre pueden unirse para producir un paralelogramo. Ambas exploraciones preparan a los estudiantes para hacer conexiones entre el área de un triángulo y la de un paralelogramo en la próxima lección.
Una comprensión clave a descubrir aquí es que dos copias idénticas de un triángulo se pueden unir a lo largo de cualquier lado correspondiente para producir un paralelogramo, y que se puede formar más de un paralelogramo.
A medida que los estudiantes trabajan, busque diferentes composiciones del mismo par de triángulos. Seleccione a los estudiantes que utilicen diferentes enfoques para compartirlos más tarde.
Al manipular los recortes, es probable que los estudiantes se den cuenta de que los triángulos rectángulos pueden componerse en rectángulos (y a veces en cuadrados) y que los triángulos no rectángulos producen paralelogramos que no son rectángulos. Es posible que los estudiantes no recuerden inmediatamente que los cuadrados y los rectángulos también son paralelogramos. Considere la posibilidad de preparar una referencia para que la consulten los estudiantes. He aquí un ejemplo:
Como antes, los estudiantes hacen aquí generalizaciones que aún no tienen las herramientas para justificar. Esto es apropiado en esta etapa. Más adelante, en su estudio de las matemáticas, aprenderán a verificar lo que ahora toman por hechos.
Para los estudiantes que utilicen la actividad digital, se puede utilizar un applet para componer triángulos en otras formas.

Mantener a los estudiantes en los mismos grupos. Entregue a cada grupo un conjunto de triángulos etiquetados ��- �� (dos copias de cada triángulo) del patrón de líneas negras y acceso a tijeras si los triángulos no están precortados. El juego incluye diferentes tipos de triángulos (isósceles rectángulos, escalenos rectángulos, obtusos, agudos y equiláteros). Pida a cada miembro del grupo que tome 1-2 pares de triángulos.
Reitere que los estudiantes aprendieron que ciertos tipos de cuadriláteros pueden descomponerse en dos triángulos idénticos. Explique que ahora van a ver si es posible componer cuadriláteros a partir de dos triángulos idénticos y, en caso afirmativo, averiguar qué tipos de cuadriláteros resultarían.
6º de Matemáticas . Unidad 1

Conceda a los estudiantes 1-2 minutos de tiempo de trabajo tranquilo y, a continuación, 5 minutos para discutir sus respuestas y contestar a la segunda pregunta con su grupo.
Apoyo para estudiantes de inglés
Conversing: MLR8 Apoyos para el debate. Para reforzar el uso del lenguaje que los estudiantes han aprendido previamente sobre los cuadriláteros, cree y muestre la tabla de referencia, como se describe, para que los estudiantes la consulten. Utilizar esta pantalla para ayudar a los estudiantes a visualizar los diferentes tipos de cuadriláteros. Pida a los estudiantes que comenten con un compañero: "¿En qué se parecen y en qué se diferencian los distintos tipos de cuadriláteros?". Diga a los estudiantes que se turnen para compartir lo que observan o recuerdan de lecciones anteriores y, a continuación, pida a diferentes grupos que compartan lo que observan con toda la clase. Cuando registre y muestre las observaciones de los estudiantes, preste atención a las oportunidades de volver a expresar los términos matemáticos que utilizaron los estudiantes.
Apoyo a los estudiantes con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Compruebe con cada maestro, según sea necesario, si ha comprendido cada paso de la actividad.
Este applet tiene ocho pares de triángulos. Cada miembro del grupo debe elegir 1-2 pares de triángulos. Utilízalos como ayuda para responder a las siguientes preguntas.
1. ¿Qué pareja(s) de triángulos tienes?
A. un rectángulo?
B. un paralelogramo?
¿Se puede componer cada par de triángulos en:
2. Discute tus respuestas a la primera pregunta con tu grupo. Después, completa cada una de las siguientes afirmaciones con todas, algunas o ninguna. Esboza 1-2 ejemplos para ilustrar cada afirmación completada.
A. de estos pares de triángulos idénticos pueden componerse en un rectángulo.
B. de estos pares de triángulos idénticos pueden componerse en un paralelogramo
POSIBLES RESPUESTAS
1.
California - Grado 6
A. Las respuestas varían. Sí para los triángulos ��, ��, ��, y ��. No para el resto.
B. Sí para todos los triángulos.
©Accelerate Learning Inc. - Todos los derechos reservados


2.

POSIBLES RESPUESTASS ( CONTINUACIÓN)
A. Algunos de estos pares de triángulos pueden componerse en un rectángulo.
B. Todos de estos pares de triángulos pueden componerse en un paralelogramo. Ejemplos:

Los estudiantes pueden llegar a conclusiones erróneas si algunas piezas de sus triángulos se dan la vuelta (para que queden boca abajo), o si no se les ocurrió que las piezas se podían mover. Pídales que prueben a manipular las piezas de diferentes maneras.
Al ver que dos copias de un triángulo siempre pueden componerse en un paralelogramo, los estudiantes podrían llegar a la conclusión errónea de que dos copias cualesquiera de un triángulo sólo pueden componerse en un paralelogramo (es decir, que no pueden formarse otros cuadriláteros a partir de la unión de dos triángulos idénticos). Mostrar un contraejemplo puede ser una forma sencilla de ayudar a los estudiantes a ver que esto no es así.
El objetivo de este debate sería aclarar si dos copias de cada triángulo pueden componerse o no en un rectángulo o un paralelogramo, y destacar las distintas formas en que dos triángulos pueden componerse en un paralelogramo.
Pida a algunos estudiantes que hayan compuesto paralelogramos diferentes a partir del mismo par de triángulos que lo compartan. Invita a la clase a que se fije en cómo estos estudiantes obtuvieron paralelogramos diferentes. Para ayudarles a ver que un triángulo puede unirse a lo largo de cualquier lado de su copia para producir un paralelogramo, haga preguntas como:
• Ésta es una forma de componer triángulos �� en un paralelogramo. ¿Alguien más lo ha hecho así?
¿Alguien ha obtenido un paralelogramo de otra forma?
• ¿Cuántos paralelogramos diferentes se pueden crear con dos copias cualesquiera de un triángulo? ¿Por qué? (3 maneras, porque hay 3 lados a lo largo de los cuales se podrían unir los triángulos.)
• ¿Qué tipos de triángulos se pueden utilizar para componer un rectángulo? ¿Cómo? (Triángulos rectángulos, uniendo dos copias a lo largo del lado opuesto al ángulo recto.)
• ¿Qué tipos de triángulos se pueden utilizar para componer un paralelogramo? ¿Cómo? (Cualquier triángulo, uniendo dos copias a lo largo de cualquier lado con la misma longitud).
de Matemáticas . Unidad 1
Exponga y vuelva a ver trabajos representativos de las dos actividades principales. Extrae las observaciones clave sobre las conexiones especiales entre triángulos y paralelogramos.
Primero, intentamos descomponer o separar cuadriláteros en dos triángulos idénticos.
• "¿Qué estrategia nos permitió hacerlo?". (Dibujar un segmento que uniera vértices opuestos.)
• "¿Qué tipos de cuadriláteros podrían descomponerse siempre en dos triángulos idénticos?". (Paralelogramos.)
• "¿Pueden descomponerse en triángulos los cuadriláteros que no son paralelogramos?" (Sí, pero los triángulos resultantes pueden no ser idénticos.)
A continuación, exploramos la relación entre triángulos y cuadriláteros a la inversa. Intentamos componer o crear cuadriláteros a partir de pares de triángulos idénticos.
• "¿Qué tipos de cuadriláteros pudiste componer con un par de triángulos idénticos?" (Paralelogramos-algunos de ellos son rectángulos.)
• "¿Importa qué tipo de triángulo se utilizó?" (No. Dos copias cualesquiera de un triángulo podrían componerse en un paralelogramo.)
• "¿Había algún lado en particular a lo largo del cual debían unirse los dos triángulos para formar un paralelogramo?" (No. Se puede utilizar cualquiera de los tres lados.)
Hemos visto cómo dos copias idénticas de un triángulo se pueden combinar para formar un paralelogramo. Esto es cierto para cualquier triángulo. Lo contrario también es cierto: cualquier paralelogramo puede dividirse en dos triángulos idénticos. En 8º curso adquiriremos algunas herramientas para demostrar estas observaciones. Por ahora, tomaremos las relaciones especiales entre triángulos y paralelogramos como un hecho. Las utilizaremos para hallar el área de cualquier triángulo en las próximas lecciones.
5 minutos
Dé a los estudiantes acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) si es necesario.

1. Aquí tienes algunos cuadriláteros.
A. Encierra en un círculo todos los cuadriláteros que creas que se pueden descomponer en dos triángulos idénticos utilizando sólo una línea.
B. ¿Qué características tienen en común los cuadriláteros que has rodeado con un círculo?
2. Aquí tienes un triángulo rectángulo. Muestra o describe brevemente cómo dos copias del mismo pueden componerse en un paralelogramo.

Learning Inc. - Todos los derechos reservados


1.

POSIBLES RESPUESTAS
A. Los cuadriláteros ��, ��, ��, y �� deben rodearse con un círculo.
B. Todos tienen dos pares de lados paralelos. Todos son paralelogramos.
2. Las respuestas varían. Ejemplo de respuesta: Unir dos copias del triángulo a lo largo de un lado que tenga la misma longitud (por ejemplo, el lado más corto de uno y el lado más corto del otro) formaría un paralelogramo. (Son posibles tres paralelogramos, ya que hay tres lados en los que se podrían unir los triángulos. Uno de los paralelogramos es un rectángulo.)
PROBLEMA 1
Para descomponer un cuadrilátero en dos formas idénticas, Clare dibujó una línea discontinua como se muestra en el diagrama.
A. Ella dijo que las dos formas resultantes tienen la misma área. ¿Estás de acuerdo? Explica tu razonamiento.
B. ¿Dividió Clara la figura en dos formas idénticas? Explica tu razonamiento.
Posibles soluciones
A. Sí, el rectángulo mide 2 unidades por 4 unidades, por lo que tiene un área de 8 unidades cuadradas. El triángulo es la mitad de un 4-por-4 cuadrado, por lo que su área es también 8 unidades cuadradas.
B. No, aunque las formas tienen la misma área, no son formas idénticas-una es un rectángulo y la otra un triángulo.
PROBLEMA 2
El triángulo �� es un triángulo rectángulo. ¿Podemos usar dos copias del triángulo �� para componer un paralelogramo que no sea un cuadrado?

Si es así, explica cómo o esboza una solución. Si no, explica por qué no.
Posibles soluciones
Sí, podemos usar dos triángulos rectángulos �� para componer un paralelogramo que no sea un cuadrado uniéndolos a lo largo de uno de los lados más cortos (los lados que forman el ángulo recto).
PROBLEMA 3
Se usan dos copias de este triángulo para componer un paralelogramo. ¿Qué paralelogramo no puede resultar de la composición? Si te atascas, considera usar papel de calco.
A. Paralelogramo A
B. Paralelogramo B
C. Paralelogramo C
D. Paralelogramo D
Posibles soluciones


C. El diagrama muestra cómo el triángulo original y su copia pueden componerse en A, B y D.
PROBLEMA 4
A. En la cuadrícula, dibuja al menos tres cuadriláteros diferentes que puedan descomponerse en dos triángulos idénticos con un único corte (muestra la línea de corte). Uno o más de los cuadriláteros deben tener ángulos no rectos.

B. Identifique el tipo de cada cuadrilátero.
Posibles soluciones
A. Las respuestas varían. Ejemplos de respuestas:
B. Los dos de arriba son paralelogramos. El de abajo a la izquierda es un cuadrado. El de abajo a la derecha es un rectángulo. (Todos son paralelogramos.)


de Matemáticas . Unidad 1

PROBLEMA 5
Del Grado 6, Unidad 1, Lección 6
A. Un paralelogramo tiene una base de 9 unidades y una altura correspondiente de 2 3 unidades. ¿Cuál es su área?
B. Un paralelogramo tiene una base de 9 unidades y un área de 1 2 unidades cuadradas. ¿Cuál es la altura correspondiente para esa base?
C. Un paralelogramo tiene un área de 7 unidades cuadradas. Si la altura que corresponde a una base es 1 4 unidades, ¿cuál es la base?
PROBLEMA 6
Del Grado 6, Unidad 1, Lección 5
Selecciona todos los segmentos que podrían representar una altura correspondiente si el lado �� es la base.

Reflexiones:
Posibles soluciones
A. 18 3 unidades cuadradas (o equivalente)
B. 12 9 unidades (o equivalente)
C. 28 unidades
Posibles soluciones

• Graficar formas
• Redes y superficie
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfocar SMPs
MP5 Usar herramientas apropiadas estratégicamente.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1
I.B.5
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dar sentido al mundo e influir en el futuro utilizar las herramientas adecuadas de forma estratégica desmontar enteros, unir piezas y descubrir la forma y el espacio.
OBJETIVO(S) DE APRENDIZAJE
• Utilicemos lo que sabemos sobre los paralelogramos para hallar el área de los triángulos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo utilizar lo que sé sobre los paralelogramos para razonar sobre las áreas de los triángulos.
OBJETIVOS
• Dibuja un diagrama para mostrar que el área de un triángulo es la mitad del área de un paralelogramo asociado.
• Explica (oralmente y por escrito) estrategias para utilizar la base y la altura de un paralelogramo asociado para determinar el área de un triángulo.
Rutinas instructivas
Observa y maravíllate
Piensa en pareja Comparte
Anticipa, controla, selecciona, secuencia, conecta
MLR2: Recoger y mostrar
MLR7: Comparar y conectar
Preparación necesaria
Los estudiantes necesitan tener acceso a cinta adhesiva o pegamento; no es necesario tener ambos. Cada copia del patrón de líneas negras contiene dos copias de cada uno de los paralelogramos A, B, C y D. Prepara suficientes copias para que cada estudiante reciba dos copias de un paralelogramo.
Materiales necesarios
Patrón de líneas negras para la Actividad 8.3
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Pegamento o barras de pegamento
Fichas preimpresas, recortadas de copias del patrón de líneas negras
Cinta adhesiva
6º de Matemáticas . Unidad 1
Narrativa de la lección
Esta lección se basa en el trabajo anterior de los estudiantes descomponiendo y reordenando regiones para hallar el área. Lleva a los estudiantes a ver que, además de usar los métodos de razonamiento de áreas de lecciones anteriores, pueden usar lo que saben que es cierto sobre los paralelogramos (es decir, que el área de un paralelogramo es �� ⋅ h) para razonar sobre el área de los triángulos.
Los estudiantes empiezan a ver que el área de un triángulo es la mitad del área del paralelogramo de la misma altura, o que es la misma que el área de un paralelogramo que tiene la mitad de su altura. Construyen esta intuición de varias maneras:
• recordando que dos copias de un triángulo pueden componerse en un paralelogramo;
• reconociendo que un triángulo puede recomponerse en un paralelogramo que tenga la mitad de la altura del triángulo; o
• razonando indirectamente, utilizando uno o más rectángulos con la misma altura que el triángulo.
Aplican esta intuición para hallar el área de triángulos tanto dentro como fuera de la cuadrícula.
LECCIÓN DE UN VISTAZO
Componente de lección Estructura Tiempo
Calentamiento Independiente 10 min
Actividad de exploración Grupos Pequeño 25 min
Actividad de Exploración Grupos Pequeños 25 min

Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Descripción breve
Los estudiantes determinan las alturas, las bases y las áreas de paralelogramos compuestos por dos triángulos.
Los estudiantes razonan y crean estrategias para encontrar las áreas de triángulos en una cuadrícula.
Los estudiantes comparan las áreas de dos paralelogramos en los que un paralelogramo se descompone en tres partes para explorar más profundamente las propiedades de los triángulos y su relación con los paralelogramos.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la descomposición de un triángulo para formar un rectángulo.
Los estudiantes resumen las relaciones entre las áreas y dimensiones de triángulos y paralelogramos.
Viendo el trabajo de muestra de los estudiantes, los estudiantes explican un proceso utilizado para determinar el área de un triángulo.
El componente de práctica independiente incluye 3 problemas de la lección y 2 problemas de repaso en espiral.
10 minutos
Rutinas instructivas
Notar y descubrir
Pensar en pareja Compartir
Nation California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Este calentamiento tiene dos objetivos: consolidar lo que los estudiantes han aprendido sobre la relación entre triángulos y paralelogramos y conectar sus nuevos conocimientos con el concepto de área.
Se da a los estudiantes un triángulo rectángulo y los tres paralelogramos que se pueden componer a partir de dos copias del triángulo. Aunque no se les pide que calculen el área del triángulo, pueden hacer algunas observaciones importantes. Es probable que vean que:
• El triángulo cubre la mitad de la región de cada paralelogramo.
• Las medidas base-altura de cada paralelogramo implican los números 6 y 4, que son las longitudes de dos lados del triángulo.
• Todos los paralelogramos tienen la misma área de 24 unidades cuadradas.
Estas observaciones les permiten razonar que el área del triángulo es la mitad del área de un paralelogramo (en este caso, cualquiera de los tres paralelogramos puede utilizarse para hallar el área del triángulo). En los próximos trabajos, los estudiantes pondrán a prueba y ampliarán esta conciencia, generalizándola para que les ayude a hallar el área de cualquier triángulo.
Muestre las imágenes del triángulo y de los tres paralelogramos para que todos las vean. Conceda a los estudiantes un minuto para que los observen. Pídales que estén preparados para compartir al menos una cosa que observan y una cosa que se preguntan. Dé a los estudiantes un minuto para que compartan sus observaciones y preguntas con un compañero.
Dé a los estudiantes 2-3 minutos de tiempo de silencio para completar la actividad, y facilíteles acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Continúe con un debate con toda la clase.

Apoyo
estudiantes
Habilidades motoras finas: Eliminar barreras. Proporcione una versión ampliada de la imagen.
Aquí está el Triángulo M.
Han hizo una copia del Triángulo M y compuso tres paralelogramos diferentes usando el M original y la copia, como se muestra aquí.
1. Para cada paralelogramo que Han compuso, identifique una base y una altura correspondiente, y escriba las medidas en el dibujo.
2. Encuentre el área de cada paralelogramo que Han compuso. Muestra tu razonamiento.
1. Primer paralelogramo: �� = 6 y h = 4, segundo paralelogramo : �� = 4 y h = 6, tercer paralelogramo: �� = 6 y h = 4
2. El área de todos los paralelogramos es 24 unidades cuadradas. Las medidas de base y altura de los paralelogramos son 4 unidades y 6 unidades, o 6 unidades y 4 unidades. 4 ⋅ 6 = 24 y 6 ⋅ 4 = 24
6º de Matemáticas . Unidad 1

Al identificar las bases y las alturas de los paralelogramos, algunos estudiantes pueden elegir un lado no horizontal o no vertical como base y esforzarse por hallar su longitud y la de su altura correspondiente. Pídeles que vean si hay otro lado que pueda servir de base y tenga una longitud que pueda determinarse más fácilmente.
Pida a un estudiante que identifique la base, la altura y el área de cada paralelogramo, así como la forma en que razonaron sobre el área. Si los estudiantes no lo han planteado ya en sus explicaciones, discuta las siguientes cuestiones:
• "¿Por qué todos los paralelogramos tienen la misma área a pesar de que todos tienen formas diferentes?" (Están formados por las mismas partes: dos copias de los mismos triángulos rectángulos. Tienen el mismo par de números para su base y altura. Todos pueden descomponerse y reorganizarse en un 6-por-4 rectángulo.)
• "¿Qué observas en las bases y alturas de los paralelogramos?" (Son el mismo par de números.)
• "¿Cómo se relacionan las medidas base-altura con el triángulo rectángulo?" (Son las longitudes de dos lados de los triángulos rectángulos.)
• "¿Podemos hallar el área del triángulo? ¿Cómo?" (Sí, el área del triángulo es 12 unidades cuadradas porque es la mitad del área de cada paralelogramo, que es 24 unidades cuadradas.)
25 minutos
Rutinas Instructivas
Anticipar, Monitorear, Seleccionar, Secuenciar, Conectar
MLR2: Recoger y Mostrar
En esta actividad, los estudiantes aplican lo que han aprendido para hallar el área de varios triángulos. Utilizan estrategias de razonamiento y herramientas que tengan sentido para ellos. No se espera que los estudiantes utilicen un procedimiento formal ni que presenten un argumento general. Pensarán en argumentos generales en una próxima lección.
Aquí se anticipan algunos caminos que pueden seguir los estudiantes, desde los más elaborados a los más directos. Esté atento también a otros enfoques.
• Dibuja dos rectángulos más pequeños que descompongan el triángulo dado en dos triángulos rectángulos. Halla el área de cada rectángulo y toma la mitad de su área. Suma las áreas de los dos triángulos rectángulos. (Es probable que esto se utilice para B y D.) Para el triángulo C, algunos estudiantes pueden optar por dibujar dos rectángulos alrededor y sobre el triángulo (como se muestra aquí), hallar la mitad del área de cada rectángulo y restar un área de la otra.
• Encerrar el triángulo con un rectángulo, hallar el área del rectángulo y restar la mitad de esa área. (Esto se usa probablemente para el triángulo rectángulo A.)
• Duplica el triángulo para formar un paralelogramo, halla el área del paralelogramo y toma la mitad de su área. (Probablemente se utiliza con cualquier triángulo.)
Supervisa las diferentes estrategias que utilizan los estudiantes. Considere la posibilidad de pedir a cada estudiante que utilice una estrategia única que cree una muestra visual de su trabajo y que la comparta con la clase más tarde.
©Accelerate Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

Diga a los estudiantes que ahora aplicarán sus observaciones de las últimas actividades para encontrar el área de varios triángulos. Organice a los estudiantes en grupos de 2-3. Dé a los estudiantes 6-8 minutos de tiempo de trabajo tranquilo y unos minutos más para discutir su trabajo con un compañero. Pídales que consulten con su grupo sólo después de que cada uno haya intentado hallar el área de al menos dos triángulos. Proporcióneles acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) (especialmente el papel de calco).
Procesamiento Conceptual: Eliminar Barreras. Ayudar a los estudiantes a ver las conexiones entre los nuevos problemas y el trabajo previo. Los estudiantes pueden beneficiarse de una revisión de diferentes representaciones para activar el conocimiento previo.
ENUNCIADO DE LA TAREA
Encuentra las áreas de al menos dos de los triángulos de abajo. Muestra tu razonamiento.
Los diagramas y las explicaciones varían. Ejemplos de respuestas:
A: 8 unidades cuadradas. 8 ⋅ 2 = 16, por lo que el área del rectángulo es 16 unidades cuadradas. El área del triángulo es la mitad de la del rectángulo, por lo que es 8 unidades cuadradas.
POSIBLES RESPUESTAS
B: 10,5 unidades cuadradas. 5 ⋅ 3 = 15, por lo que el área del rectángulo de la izquierda es 15 unidades cuadradas. El área del triángulo de la izquierda es entonces 7,5 unidades cuadradas. 2 ⋅ 3 = 6, por lo que el área del rectángulo derecho es 6 unidades cuadradas, por lo que el área del triángulo derecho es 3 unidades cuadradas. La suma de las áreas de los triángulos pequeños que forman el triángulo grande es 7,5 + 3 = 10,5, por lo que el triángulo grande tiene de área 10,5 unidades cuadradas.
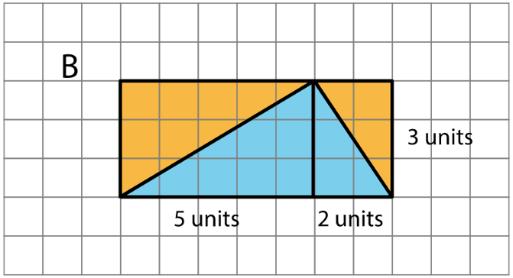
C: 10 unidades cuadradas. Si hacemos una copia del triángulo, lo giramos y los unimos por el lado más largo obtendríamos un paralelogramo. La longitud de la base es 5 unidades y la altura es 4 unidades, por lo que el área del paralelogramo es 20 unidades cuadradas. El área del triángulo es la mitad de esa área, por lo que es 10 unidades cuadradas.
D: 12 unidades cuadradas. Descompone el triángulo en un trapecio y un triángulo pequeño trazando una línea vertical 3 unidades desde el lado izquierdo. Gira el triángulo pequeño hasta alinearlo con el lado inferior del trapecio para crear un paralelogramo. Para obtener el área de ese paralelogramo 4 ⋅ 3 = 12.
6º de Matemáticas . Unidad 1

A estas alturas los estudiantes no deberían estar contando cuadrados para determinar el área. Si los estudiantes siguen utilizando este método, diríjalos en la dirección de las estrategias aprendidas recientemente (descomponer, reordenar, encerrar o duplicar).
Es posible que los estudiantes no reconozcan que el lado vertical del triángulo D podría ser la base e intenten medir las longitudes de los otros lados. Si es así, recuérdales que cualquier lado de un triángulo puede ser la base.
Aunque es posible que los estudiantes hayan consultado con uno o más compañeros durante la tarea, tómese unos minutos para reunirse como clase de modo que todos tengan la oportunidad de ver una gama más amplia de enfoques.
Seleccione a los estudiantes previamente identificados para que expliquen su enfoque y muestren su razonamiento para que todos lo vean. Empiece por la estrategia más elaborada (probablemente una estrategia que implique encerrar un triángulo) y avance hacia la más directa (probablemente duplicar el triángulo para componer un paralelogramo). Después de la presentación de cada estudiante, pregunte a la clase:
• "¿Alguien más razonó de la misma manera?"
• "¿Alguien más dibujó el mismo diagrama pero pensó en el problema de manera diferente?"
• "¿Es posible utilizar esta estrategia con otro triángulo de este conjunto? ¿Cuál?"
• "¿Hay algún triángulo para el que esta estrategia no sería útil? ¿Cuál, y por qué no?
Apoyo para estudiantes de inglés
Representar, conversar: MLR2 Recoger y mostrar. Utilice esta rutina para recoger el lenguaje inicial y las representaciones que los estudiantes producen al hallar el área de un triángulo antes de formalizar una fórmula. Mientras los estudiantes resuelven las preguntas, circule y observe las distintas estrategias que utilizan para hallar el área. Tome fotografías de las distintas estrategias o cópielas en una pantalla. Busque estudiantes que descompongan triángulos o que encierren triángulos en un rectángulo. Mientras los estudiantes hablan con un compañero, siga añadiendo ejemplos del lenguaje de los estudiantes a la pantalla. Durante el debate de toda la clase, invite a los estudiantes a tomar prestado el lenguaje de esta exposición para ayudarles a explicar su pensamiento.
PARALELOGRAMO 25 minutos
Rutinas Instructivas
MLR7: Comparar y Conectar
Materiales Requeridos
Maestro de línea negra
A estas alturas, los estudiantes ya tienen más de un camino para encontrar el área de un triángulo. Esta actividad opcional ofrece una perspectiva más para reflexionar sobre la relación entre triángulos y paralelogramos. Anteriormente, los estudiantes duplicaban triángulos para componer paralelogramos. Aquí ven que se puede crear un conjunto diferente de paralelogramos a partir de un triángulo, no duplicándolo, sino descomponiéndolo .
Se asigna a los estudiantes un paralelogramo que deben cortar en dos triángulos congruentes. Toman un triángulo y lo descomponen en trozos más pequeños cortando a lo largo de una línea que pasa por los puntos medios de dos lados. A continuación, utilizan estos trozos para componer un nuevo paralelogramo (es posible obtener dos paralelogramos) y hallar su área.
Los estudiantes observan que la altura de este nuevo paralelogramo es la mitad de la del paralelogramo original y que su área es también la mitad de la del paralelogramo original. Como el nuevo paralelogramo se compone de las mismas partes que un triángulo grande, el área del triángulo es también la mitad de la del paralelogramo original. Este razonamiento abre otra vía para entender la fórmula del área de los triángulos.
©Accelerate Learning Inc. - Todos los derechos reservados


De los cuatro paralelogramos dados, el paralelogramo B es probablemente el más manejable para los estudiantes. Cuando se descompone, sus piezas (cada una con un ángulo recto) se parecen a las vistas en trabajos anteriores sobre paralelogramos. Tenga esto en cuenta a la hora de asignar los paralelogramos a los estudiantes.

Diga a los estudiantes que van a investigar otra forma en la que los triángulos y los paralelogramos están relacionados. Organice a los estudiantes en grupos de 2-4. Asigne un paralelogramo diferente del esquema a cada estudiante del grupo. Dé a cada estudiante dos copias del paralelogramo y acceso a un par de tijeras y cinta adhesiva o pegamento.
Cada paralelogramo muestra algunas medidas y líneas de puntos para cortar. Para la primera pregunta, los estudiantes que tengan los paralelogramos C y D deben no cortar las medidas que se muestran fuera de las figuras.
Dé a los estudiantes 10 minutos para completar la actividad, seguidos de unos minutos para discutir su trabajo (especialmente las tres últimas preguntas). Pida a los estudiantes que terminen antes que busquen a alguien que tenga el mismo paralelogramo original y comparen sus trabajos.
Apoyo para Estudiantes con Discapacidades
Habilidades Motrices Finas: Tutores. Empareje a los estudiantes con sus compañeros tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten cómo cortar los paralelogramos según sea necesario.
Lenguaje receptivo: Tiempo de procesamiento. Lea todos los enunciados en voz alta. Los estudiantes que escuchen y lean la
información se beneficiarán de un tiempo de procesamiento adicional.
1. Su maestro les dará dos copias de un paralelogramo. Pega o pega con cinta adhesiva una copia de tu paralelogramo aquí y halla su área. Muestra tu razonamiento.
2. Descompone la segunda copia de tu paralelogramo cortando por las líneas de puntos. Toma sólo el triángulo pequeño y el trapecio y reorganiza estas dos piezas en un paralelogramo diferente. Pega el nuevo paralelogramo sobre el papel.
3. Calcula el área del nuevo paralelogramo que has formado. Muestra tu razonamiento.
4. ¿Qué notas acerca de la relación entre el área de este nuevo paralelogramo y el original?
5. ¿Cómo crees que se compara el área del triángulo grande con la del nuevo paralelogramo? ¿Es mayor, igual o menor? ¿A qué se debe?
6. Pega el triángulo grande que queda debajo. Utiliza cualquier parte del trabajo anterior para hallar su área. Muestra tu razonamiento.
Paralelogramo A:
1. 80 cm2. 10 ⋅ 8 = 80.

2. 3. 40 cm2. 10 ⋅ 4 = 40.
Paralelogramo B:
1. 60 cm2. 5 ⋅ 12 = 60.

2. 3. 30 cm2. 5 ⋅ 6 = 30
Paralelogramo C: 1. 60 cm2. 10 ⋅ 6 = 60.
2. 3. 30 cm2. 10 ⋅ 3 = 30
Paralelogramo D: 1. 40 cm2. 4 ⋅ 10 = 40
2. 3. 20 cm2. 4 ⋅ 5 = 20
6º de Matemáticas . Unidad 1

Todos los paralelogramos:
1. El área del nuevo paralelogramo es la mitad del área del original.
2. Las respuestas varían. Ejemplos de respuestas:
• El área del triángulo grande es la misma que la del nuevo paralelogramo. Lo sé porque el trapecio y el triángulo pequeño juntos pueden formar un triángulo idéntico al triángulo grande.
• El nuevo paralelogramo y el triángulo grande tienen la misma área porque son dos mitades del paralelogramo original.
3. Las respuestas varían. Ejemplos de respuestas:
• El triángulo grande del paralelogramo A tiene un área de 40 cm2 , ya que es el área del nuevo paralelogramo.
• El triángulo grande del paralelogramo D tiene un área de 20 cm2 , ya que es la mitad del paralelogramo original, que tiene un área de 40 cm2.
Los estudiantes pueden tener dificultades para formar un nuevo paralelogramo porque las dos piezas que lo componen no están orientadas hacia arriba (es decir, el triángulo o el trapecio están orientados hacia abajo).
Dígales que el lado sombreado de los recortes debe quedar hacia arriba.
Los estudiantes pueden tener dificultades para utilizar las medidas adecuadas necesarias para hallar el área del paralelogramo en la primera pregunta. Es posible que multipliquen más números de los necesarios porque las medidas están dadas. Si esto ocurre, recuérdeles que sólo se necesitan dos medidas (base y altura) para determinar el área de un paralelogramo.
Apoyo para estudiantes de inglés
Speaking, Listening: MLR7 Comparar y conectar. Seleccionar a los estudiantes que utilizan distintos enfoques para la última pregunta para que compartan su razonamiento con la clase y expongan sus trabajos para que todos los vean. Pregunte: "¿En qué se parecen y en qué se diferencian los distintos enfoques?". Escuche y amplíe el uso que hacen los estudiantes del lenguaje matemático (por ejemplo, triángulo, paralelogramo, trapecio) y de las relaciones (por ejemplo, "mitad de", "igual que"). Estos intercambios refuerzan el uso del lenguaje matemático y el razonamiento de los estudiantes.
Principio(s) de diseño: Optimizar la metaconciencia; Apoyar la creación de sentido


de Matemáticas . Unidad 1

¿Estás preparado para más?
¿Puedes descomponer este triángulo y reorganizar sus partes para formar un rectángulo? Describe cómo podría hacerse.
"¿Estás preparado para más?" Respuesta del estudiante
Las respuestas varían. Cortando el triángulo a la mitad de su altura, paralelo a la base, se crea un paralelogramo, luego otro corte ayuda a crear un rectángulo.


5 minutos
En esta lección, practicamos usando lo que sabemos sobre paralelogramos para razonar sobre áreas de triángulos. Duplicamos un triángulo para hacer un paralelogramo; descompusimos y reorganizamos un triángulo en un paralelogramo; o encerramos un triángulo con uno o más rectángulos.
• "¿Qué podemos decir sobre el área de un triángulo y la de un paralelogramo con la misma altura?" (El área del triángulo es la mitad del área del paralelogramo relacionado.)
• "En la segunda actividad, cortamos un triángulo a lo largo de una línea que pasa por los puntos medios de dos lados y reordenamos las piezas formando un paralelogramo. ¿Qué observamos sobre el área y la altura del paralelogramo resultante?" (Tiene la misma área que el triángulo original pero la mitad de su altura.)
• "¿Cómo podríamos empezar a hallar el área de cualquier triángulo, en general?" (Empieza por hallar el área de un paralelogramo afín cuya base sea también un lado del triángulo).
5 minutos
Los estudiantes han explorado varias formas de razonar sobre el área de un triángulo. Este enfriamiento les lleva a articular al menos una forma de hacerlo. No todos los métodos les resultarán igual de intuitivos o claros. Al escribir un comentario sobre al menos un método, los estudiantes pueden mostrar lo que tiene sentido para ellos en este momento.
Apoyo a estudiantes con discapacidad
Apoyo al lenguaje receptivo y expresivo. Permita múltiples métodos de articulación de la comprensión del estudiante (como: dibujo, oral, escrito, etc.)
Elena, Lin y Noah encontraron que el área del triángulo Q es 14 unidades cuadradas, pero razonaron de forma diferente, como se muestra en los diagramas. Explica al menos la forma de pensar de un estudiante y por qué su respuesta es correcta.
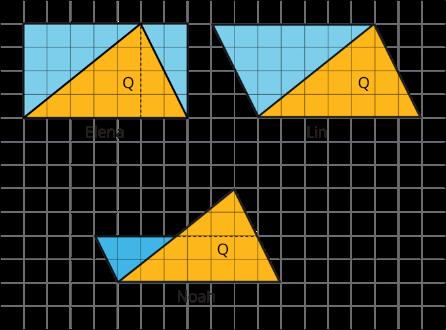
6º de Matemáticas . Unidad 1

Las explicaciones varían. Ejemplos de respuestas:
• Elena dibujó dos rectángulos que descomponían el triángulo en dos triángulos rectángulos. El área de cada triángulo rectángulo es la mitad del área del rectángulo que lo encierra. Esto significa que el área del triángulo original es la suma de la mitad del área del rectángulo de la izquierda y la mitad del área del rectángulo de la derecha. La mitad de (4 ⋅ 5) más la mitad de (4 ⋅ 2) es 10 + 4, por lo que el área es 14 unidades cuadradas.
• Lin lo vio como la mitad de un paralelogramo con base de 7 unidades y altura de 4 unidades (y por tanto un área de 28 unidades cuadradas). La mitad de 28 es 14
• Noah descompuso el triángulo cortándolo por la mitad de la altura del triángulo, dándole la vuelta al triángulo superior y uniéndolo con el trapecio inferior para formar un paralelogramo. Luego calculó el área de ese paralelogramo, que tiene la misma longitud de base pero la mitad de la altura del triángulo. 7 ⋅ 2 = 14, por lo que el área es 14 unidades cuadradas.
PROBLEMA 1
Para hallar el área de este triángulo rectángulo, Diego y Jada utilizaron diferentes estrategias. Diego trazó una línea a través de los puntos medios de los dos lados más largos, lo que descompone el triángulo en un trapecio y un triángulo más pequeño. A continuación, reorganizó las dos formas en un paralelogramo.
Jada hizo una copia del triángulo, lo giró y lo alineó contra un lado del triángulo original de modo que los dos triángulos forman un paralelogramo.
A. Explica cómo Diego podría utilizar su paralelogramo para encontrar el área del triángulo.
B. Explica cómo Jada podría utilizar su paralelogramo para encontrar el área del triángulo.
Posibles soluciones
Las respuestas varían. Ejemplos de explicaciones:
A. El paralelogramo de Diego tiene una base de 3 pies y una altura de 4 pies, por lo que su área es 12 pies cuadrados. Como el triángulo rectángulo original y el paralelogramo están formados por las mismas partes, tienen la misma área. El área del triángulo es también 12 pies cuadrados.
B. El paralelogramo de Jada tiene una base de 3 pies y una altura de 8 pies, por lo que su área es 24 pies cuadrados. Como está compuesto por dos copias del triángulo rectángulo, ella podría dividir 24 entre 2 para hallar el área del triángulo. 24 ÷ 2 = 12 o 12 pies cuadrados.
PROBLEMA 2
Halla el área del triángulo. Explica o muestra tu razonamiento.
©Accelerate Learning Inc. - Todos los derechos reservados


Posibles soluciones
A. 12 unidades cuadradas. El razonamiento varía. Ejemplo de razonamiento: Haz un corte horizontal y reorganiza las piezas para formar un rectángulo. El rectángulo mide 2 unidades por 6 unidades, por lo que su área es 12 unidades cuadradas.
B. 6 unidades cuadradas. El razonamiento varía. Ejemplo de razonamiento:
• Haz un corte horizontal y reorganiza las piezas para formar un paralelogramo. El paralelogramo tiene una base de 4 unidades y una altura de 112 unidades, por lo que su área es 6 unidades cuadradas.
• Descompone el triángulo con una línea de corte a medio camino entre la base y el vértice opuesto. Reordena el triángulo más pequeño para formar un paralelogramo. Este paralelogramo tiene una base horizontal de longitud 4 unidades y una altura de 1,5 unidades, por lo que su área es de 6 unidades cuadradas. Esto significa que el área del triángulo original es 6 unidades cuadradas.
PROBLEMA 3
¿Cuál de los tres triángulos tiene mayor área? Muestra tu razonamiento. Si te atascas, usa lo que sabes sobre el área de los paralelogramos para ayudarte.
Posibles soluciones
Los tres triángulos tienen la misma área de 10 unidades cuadradas. El razonamiento varía. Ejemplo de razonamiento: Dos copias idénticas de cada triángulo pueden componerse en un paralelogramo con una base de 5 unidades y una altura correspondiente de 4 unidades, lo que significa un área de 20 unidades cuadradas. El área de cada triángulo es la mitad de la del paralelogramo. 1 2 ⋅20 = 10
PROBLEMA 4
Del Grado 6, Unidad 1, Lección 7
Dibuja una copia idéntica de cada triángulo de modo que las dos copias juntas formen un paralelogramo. Si te atascas, considera usar papel de calco.
Posibles soluciones
Las respuestas varían. Ejemplo de respuesta:

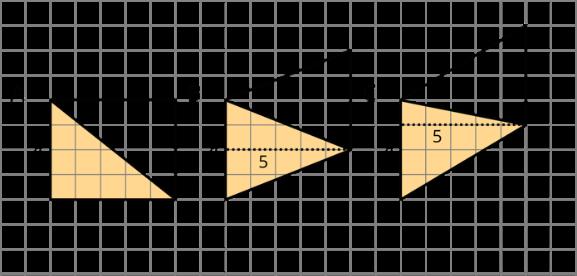
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 6
A. Un paralelogramo tiene una base de 3.5 unidades y una altura correspondiente de 2 unidades. ¿Cuál es su área?
B. Un paralelogramo tiene una base de 3 unidades y un área de 1.8 unidades cuadradas. ¿Cuál es la altura correspondiente a esa base?
C. Un paralelogramo tiene un área de 20,4 unidades cuadradas. Si la altura que corresponde a una base es 4 unidades, ¿cuál es la base?
Posibles soluciones
A. 7 unidades cuadradas
B. 0,6 unidades
C. 5,1 unidades

Reflexiones:
Nation California - Grado 6

• Graficar formas
• Redes y superficie
• Generalizar con representaciones múltiples
ALINEACIÓN
Abordar
6.EE.2a Escribir expresiones que registren operaciones con números y con letras que representen números.
CONEXIONES INTEGRADAS
Alineación de estándares y principios de California
6.EE.2c Evaluar expresiones con valores específicos de sus variables. Incluir expresiones que surjan de fórmulas utilizadas en problemas del mundo real. Realizar operaciones aritméticas, incluyendo aquellas que involucran exponentes de números enteros, en el orden convencional cuando no hay paréntesis para especificar un orden particular (Orden de Operaciones).
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales, y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de resolver problemas matemáticos y del mundo real.
Enfocar SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.3
I.B.5
I.C.12
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dan sentido al mundo
buscan y expresan regularidades en razonamientos repetidos
OBJETIVO(S) DE APRENDIZAJE
descubren la forma y el espacio, desmontan enteros, juntan partes y exploran cantidades cambiantes.
• Escribamos y utilicemos una fórmula para hallar el área de un triángulo.
OBJETIVO(S) DE APRENDIZAJE
• Puedo utilizar la fórmula del área para hallar el área de cualquier triángulo.
• Puedo escribir y explicar la fórmula del área de un triángulo.
• Sé a qué se refieren los términos "base" y "altura" en un triángulo.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comparar, contrastar y criticar (oralmente) diferentes estrategias para determinar el área de un triángulo.
• Generalizar un proceso para hallar el área de un triángulo y justificar (oralmente y por escrito) por qué puede abstraerse como 1 2 ⋅ �� ⋅ ℎ
• Reconocer que cualquier lado de un triángulo puede considerarse su base, elegir un lado para utilizarlo como base al calcular el área de un triángulo e identificar la altura correspondiente.
Rutinas instructivas
Notar y descubrir
MLR8: Apoyos para la discusión
MLR2: Recoger y mostrar
Materiales necesarios
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
6º de Matemáticas . Unidad 1

Narrativa de la lección
En esta lección los estudiantes comienzan a razonar sobre el área de triángulos de forma más metódica: generalizando sus observaciones hasta este punto y expresando el área de un triángulo en términos de su base y altura
Los estudiantes aprenden primero sobre bases y alturas en un triángulo estudiando ejemplos y contraejemplos. A continuación, identifican las medidas base-altura de los triángulos, las utilizan para determinar el área y buscan un patrón en su razonamiento que les ayude a escribir una fórmula general para hallar el área (MP8). Los estudiantes también tienen la oportunidad de construir un argumento informal sobre por qué la fórmula funciona para cualquier triángulo (MP3).
Componente de lección
Estructura Tiempo
Descripción breve
Calentamiento Pares 10 min Al observar una serie de imágenes similares, los estudiantes descifran un significado preciso de height y base en un triángulo.
Actividad de exploración Pequeños grupos 20 min Los estudiantes determinan las alturas, las bases y las áreas de triángulos en una cuadrícula para generalizar una expresión que represente el área de un triángulo.
Actividad de exploración Pequeños grupos 10 min
Los estudiantes calculan las áreas de triángulos aplicando la expresión generada en la actividad anterior.
Síntesis Todo el Grupo 5 min Los estudiantes resumen la relación entre la altura y la base de un triángulo y luego explican la expresión utilizada para encontrar el área de cualquier triángulo.
Enfriamiento Independiente 5 min Los estudiantes identifican las alturas y las bases de los triángulos para determinar las áreas.
Práctica Independiente 8-10 min
El componente de práctica independiente incluye 3 problemas de la lección y 3 problemas de repaso en espiral.
10 minutos
Rutinas instructivas
Notar y descubrir
En esta actividad, los estudiantes reflexionan sobre el significado de base y altura en un triángulo estudiando ejemplos y no ejemplos. El objetivo es que vean que en un triángulo:
• Cualquier lado puede ser una base.
• Un segmento que representa una altura debe trazarse en ángulo recto con la base, pero puede trazarse en más de un lugar. La longitud de este segmento perpendicular es la distancia entre la base y el vértice opuesto a ella.
• Un triángulo puede tener tres bases posibles y tres alturas correspondientes.
Los estudiantes pueden basarse en su experiencia con bases y alturas en un paralelogramo y observar similitudes. Anímelos a hacerlo, ya que les ayudará a conceptualizar los pares base-altura en los triángulos.
Mientras los estudiantes discuten con sus compañeros, escuche cómo justifican sus decisiones o cómo saben qué afirmaciones son verdaderas (MP3).
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


INSTRUCCIÓN

Muestre los ejemplos y no ejemplos de bases y alturas para que todos los vean. Conceda a los estudiantes un minuto para observarlos. Pídales que estén preparados para compartir al menos una cosa que observen y una cosa que se pregunten. Conceda a la clase un minuto para compartir algunas de sus observaciones y preguntas.
Diga a los estudiantes que ahora utilizarán los ejemplos y los no ejemplos para determinar qué es cierto sobre las bases y las alturas en un triángulo. Organice a los estudiantes en grupos de 2. Deles 2-3 minutos para pensar en silencio y luego un minuto para compartir su respuesta con un compañero.
Procesamiento visual-espacial: Ayudas visuales. Proporcione folletos de las representaciones para que los estudiantes las dibujen o las resalten.
• Estudia los ejemplos y no ejemplos de bases y alturas en un triángulo. Responde las preguntas siguientes.
• Estos segmentos discontinuos representan las alturas del triángulo.
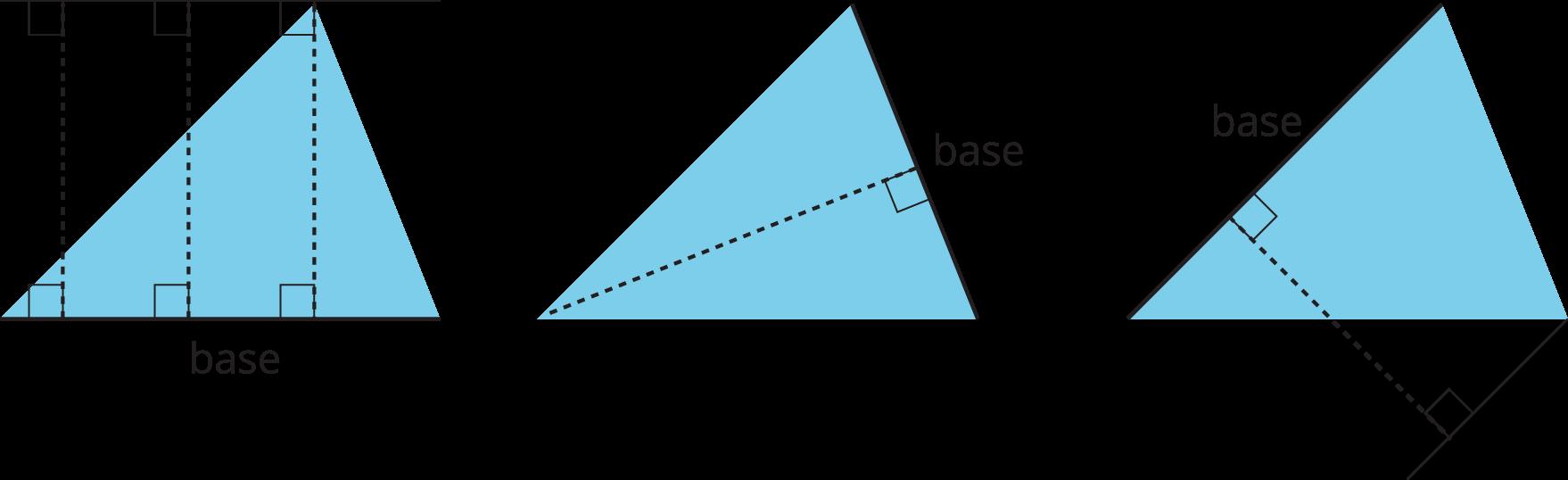
• Estos segmentos discontinuos no representan alturas del triángulo.
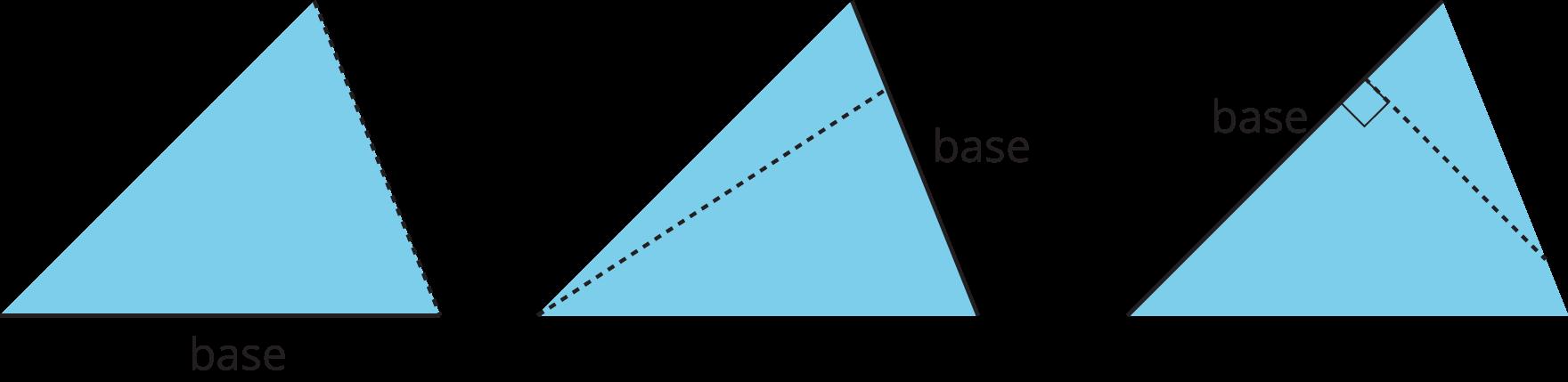
Seleccione todas las afirmaciones que sean verdaderas sobre las bases y las alturas en un triángulo.
Cualquier lado de un triángulo puede ser una base.
Solo hay una altura posible.
Una altura siempre es uno de los lados de un triángulo.
La altura correspondiente a una base debe dibujarse en ángulo agudo con respecto a ella.
La altura correspondiente a una base debe dibujarse en ángulo recto con respecto a ella.
Una vez elegida una base, solo hay un segmento que representa la altura correspondiente.
Un segmento que representa una altura debe pasar por un vértice. POSIBLES RESPUESTAS
Sólo las afirmaciones 1 y 5 son verdaderas.
Cualquier lado de un triángulo puede ser una base.
Solo hay una altura posible.
Una altura siempre es uno de los lados de un triángulo.
La altura correspondiente a una base debe dibujarse en ángulo agudo con respecto a ella.
La altura correspondiente a una base debe dibujarse en ángulo recto con respecto a ella
Una vez elegida una base, solo hay un segmento que representa la altura correspondiente
Un segmento que representa una altura debe pasar por un vértice.
6º de Matemáticas . Unidad 1

Algunos estudiantes pueden tener dificultades para interpretar los diagramas. Pídales que señalen las partes de los diagramas que puedan estar poco claras y aclárelas según sea necesario. Es posible que los estudiantes no recuerden de su experiencia con paralelogramos que una altura tiene que ser perpendicular a una base. Considera la posibilidad de colocar un diagrama de un paralelogramo -con su base y altura etiquetadas- en un lugar visible del aula para que pueda servir de referencia.
Para cada afirmación, pide a los estudiantes que indiquen si creen que es cierta. Para cada voto "verdadero", pida a uno o dos estudiantes que expliquen cómo lo saben (MP3). Haga lo mismo para cada voto "falso". Anime a los estudiantes a utilizar los ejemplos y contraejemplos para apoyar su argumento (por ejemplo: "La última afirmación no es cierta porque los ejemplos muestran segmentos discontinuos o alturas que no pasan por un vértice"), lo que significa más de una altura". Ponte de acuerdo sobre el valor de verdad de cada afirmación antes de continuar. Registre y muestre las afirmaciones verdaderas para que todos las vean. Los estudiantes deben ver que sólo las afirmaciones 1 y 5 son verdaderas: que cualquier lado de un triángulo puede ser una base, y que un segmento para la altura correspondiente debe dibujarse en ángulo recto con la base. Lo que falta -una laguna importante a rellenar durante la discusión- es la longitud de cualquier segmento que represente una altura. Pregunta a los estudiantes: "¿Qué longitud debe tener un segmento que represente una altura? Si trazamos una línea perpendicular desde la base, ¿dónde nos detenemos?". Solicite algunas ideas a los estudiantes. Explique que la longitud de cada segmento perpendicular es la distancia entre la base y el vértice opuesto a ella. El vértice opuesto es el vértice que no es un extremo de la base. Señala el vértice opuesto de cada base. Aclara que no es necesario que el segmento pase por el vértice (aunque ese sería un lugar natural para dibujarlo), siempre que mantenga esa distancia entre la base y el vértice opuesto. Es útil conectar esta idea con la de las alturas en un paralelogramo. Considera duplicar el triángulo y utilizar el original y la copia para componer un paralelogramo. La altura para una base elegida en el triángulo es también la altura del paralelogramo con la misma base. Los estudiantes tendrán muchas oportunidades de dar sentido a las bases y las alturas en esta lección y en una próxima, por lo que no necesitan saber cómo dibujar una altura correctamente en este momento.
20 minutos
Rutinas instructivas
MLR8: Apoyos para la discusión
Esta tarea culmina con la escritura de una fórmula para el área de triángulos. Es probable que los estudiantes ya hayan desarrollado la intuición de que el área de un triángulo es la mitad de la de un paralelogramo con la misma base y altura. Esta actividad resume ese trabajo en una expresión algebraica.
En primer lugar, los estudiantes calculan las áreas de varios triángulos a partir de las medidas de la base y la altura. A continuación, generalizan el trabajo numérico para llegar a una expresión que permita hallar el área de cualquier triángulo (MP8).
Si es necesario, recuerde a los estudiantes cómo razonaron sobre el área de los triángulos en la lección anterior (es decir, componiendo un paralelogramo, encerrándolo con uno o más rectángulos, etc.). Anímeles a consultar su trabajo anterior y a utilizar papel de calco si es necesario. Los estudiantes pueden escribir �� ⋅ ℎ ÷ 2 o �� ⋅ ℎ ⋅ ( 1 2 ) como expresión del área de cualquier triángulo. Debe celebrarse cualquier expresión equivalente.
©Accelerate Learning Inc. - Todos los derechos reservados


Al final de la actividad, considere la posibilidad de dar a los estudiantes la oportunidad de razonar de forma más abstracta y deductiva, es decir, de pensar por qué la expresión �� ⋅ ℎ ÷ 2 sería cierta para todos los triángulos. Consulte la actividad Síntesis para obtener indicaciones y diagramas que apoyen dicho razonamiento.

Organice a los estudiantes en grupos de 2-3. Explique que ahora van a encontrar el área de algunos triángulos utilizando lo que saben sobre los pares base-altura en triángulos y las relaciones entre triángulos y paralelogramos.
Dé a los estudiantes 5-6 minutos para completar la actividad y acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), especialmente el papel de calco. Pídeles que calculen el área de al menos un par de triángulos de forma independiente antes de discutirlo con su(s) compañero(s).
Apoyo a los estudiantes con discapacidad
Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una pregunta a la vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.
Funcionamiento ejecutivo: Ayudas visuales. Cree un gráfico de anclaje (por ejemplo, etiquetando la base y la altura de un triángulo y la fórmula para hallar el área) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para referencia futura.
• Para cada triángulo, etiqueta un lado que pueda utilizarse como base y un segmento que muestre su altura correspondiente.
• Registra las medidas de la base y la altura en la tabla y halla el área del triángulo. (La longitud lateral de cada cuadrado de la cuadrícula es 1 unidad.)
• En la última fila, escribe una expresión para el área de cualquier triángulo utilizando �� y ℎ
Triángulo
Base (Unidades) Altura (Unidades) Área (Unidades cuadradas)
Cualquier triángulo �� ℎ
de Matemáticas . Unidad 1

Triángulo Base (Unidades) Altura (Unidades) Área (Unidades Cuadradas)
Cualquier Triángulo �� ℎ �� ⋅ ℎ ÷ 2 (o equivalente)
2. Las explicaciones varían. Ejemplos de respuestas:
• Podemos hacer un paralelogramo a partir de cualquier triángulo utilizando la misma base y altura. El triángulo será la mitad del paralelogramo. El área de un paralelogramo es la longitud de la base por la longitud de la altura, así que el área del triángulo será �� ⋅ ℎ ÷ 2.
• Puedo cortar la mitad superior de un triángulo y girarla para hacer un paralelogramo. Ese paralelogramo tiene una base de b y una altura que es la mitad del triángulo original, que es 1 2 ⋅ ℎ, por lo que su área es �� ⋅ 1 2 ⋅ ℎ. Como el paralelogramo no es más que el triángulo reordenado, el área del triángulo es también 1 2 �� ⋅ ℎ
Puede que los estudiantes no se sientan inclinados a escribir una expresión utilizando las variables �� y ℎ y, en su lugar, sustituyan las variables por números de su elección. Pídeles que reflexionen sobre lo que hicieron con los números de los cuatro primeros triángulos. A continuación, anímeles a escribir las mismas operaciones pero utilizando las letras �� y ℎ en lugar de números.
Seleccione a algunos estudiantes para que compartan su expresión para hallar el área de cualquier triángulo. Anota cada expresión para que todos la vean. Para dar a los estudiantes la oportunidad de razonar lógica y deductivamente sobre su expresión, pregúnteles: "¿Pueden explicar por qué esta expresión es cierta para cualquier triángulo?" Muestre los siguientes diagramas para que todos los vean. Conceda a los estudiantes un minuto para observar los diagramas. Pídales que elijan uno que tenga sentido para ellos y que utilicen ese diagrama para explicar o mostrar por escrito que la expresión �� ⋅ ℎ ÷ 2 funciona para hallar el área de cualquier triángulo. (Considera la posibilidad de dar a cada estudiante una ficha o una hoja de papel en la que escribir su razonamiento para poder recoger sus respuestas, si lo deseas.



Cuando se trata sólo de las variables b y h y ningún número, es probable que los estudiantes encuentren los diagramas de Jada y Lin más intuitivos de explicar. Los que opten por utilizar el diagrama de Elena probablemente sugerirán mover uno de los triángulos adicionales y unirlo con el otro para formar un paralelogramo no rectangular con un área de �� ⋅ ℎ. Es de esperar que los estudiantes se sientan menos cómodos razonando en términos abstractos que en términos concretos. Prepárese para ayudarles a reconstruir un argumento lógico utilizando sólo variables. Si el tiempo lo permite, selecciona a los estudiantes que hayan utilizado diferentes diagramas para que compartan su explicación, empezando por el diagrama más utilizado (probablemente el de Jada). Pida a los demás estudiantes que apoyen, perfeccionen o discrepen de sus argumentos. Si el tiempo es limitado, considere la posibilidad de recoger ahora las respuestas escritas de los estudiantes y discutirlas en una próxima lección.
Apoyo para estudiantes de inglés
Speaking: MLR8 Apoyo a la discusión. Utilice esta rutina para apoyar el debate de toda la clase cuando los estudiantes compartan sus expresiones para hallar el área de cualquier triángulo. Proporcione a los estudiantes 1-2 minutos de tiempo de reflexión en silencio para que comiencen a considerar por qué su expresión es verdadera para cualquier triángulo, antes de que continúen trabajando con un compañero para completar su respuesta. Seleccione 1 o 2 parejas de estudiantes para compartir con la clase y, a continuación, pida a los estudiantes que repitan el razonamiento de sus compañeros. De este modo, más estudiantes tendrán la oportunidad de utilizar el lenguaje para interpretar y describir expresiones del área de triángulos.
10 minutos
Rutinas instructivas
MLR2: Recoger y Mostrar
En esta actividad, los estudiantes aplican la expresión que han generado previamente para hallar las áreas de varios triángulos. Cada diagrama está etiquetado con dos o tres medidas. Antes de calcular, los estudiantes piensan en qué longitudes se pueden utilizar para encontrar el área de cada triángulo.
Mientras los estudiantes trabajan, observe a los estudiantes que eligen diferentes bases para los triángulos B y D. Invítelos a contribuir a la discusión sobre cómo encontrar las áreas de triángulos rectángulos más adelante.
Explique a los estudiantes que ahora practicarán usando su expresión para encontrar el área de triángulos sin una cuadrícula. Para cada triángulo, pida a los estudiantes que estén preparados para explicar qué medida eligieron para la base y cuál para la altura correspondiente y por qué. Mantenga a los estudiantes en grupos de 2-4. Conceda a los estudiantes 5 minutos de reflexión en silencio, seguidos de 1-2 minutos para discutir sus respuestas en su grupo.
6º de Matemáticas . Unidad 1
Representar: MLR2 Recoger y mostrar. Mientras las parejas trabajan, circule y escuche la conversación de los estudiantes sobre la identificación de las bases y las alturas correspondientes para cada uno de los triángulos. Anote las frases comunes o importantes que escuche decir a los estudiantes sobre cada triángulo, centrándose específicamente en cómo los estudiantes dan sentido a la base y a la altura de cada triángulo. Anote las palabras que utilizan los estudiantes para referirse a cada triángulo y muéstrelas para que todos las vean durante el debate de toda la clase.
Principio(s) de diseño: Apoyar la creación de sentido; Maximizar la metaconciencia

POSIBLES RESPUESTAS
Para cada triángulo, rodea con un círculo una medida de la base que puedas utilizar para hallar el área del triángulo. A continuación, halla el área de tres triángulos cualesquiera. Muestra tu razonamiento.
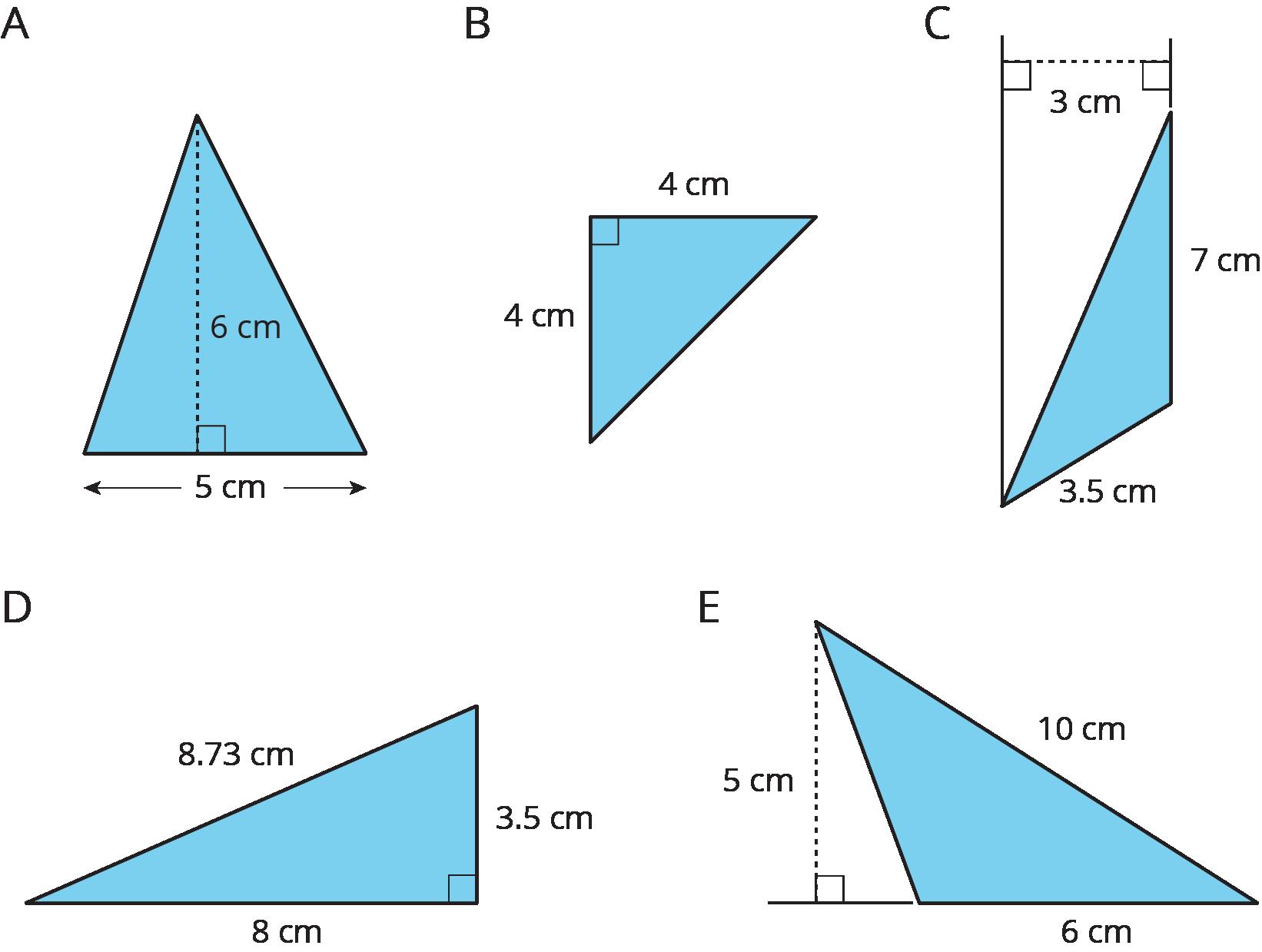
En B y D cualquiera de los pares de medidas dados puede ser la base.
Triángulo A: 15 cm cuadrados, �� = 5, ℎ = 6, �� = 5 ⋅ 6 ÷ 2 = 15
Triángulo B: 8 cm cuadrados, �� = 4, ℎ = 4, �� = 4 ⋅ 4 ÷ 2 = 8
Triángulo C: 10.5 cm cuadrados, �� = 7, ℎ = 3, �� = 7 ⋅ 3 ÷ 2 = 10,5
Triángulo D: 14 cm cuadrados, �� = 8, ℎ = 3.5, �� = 8 ⋅ (3,5) ÷ 2 = 14
Triángulo E: 15 cm cuadrados, �� = 6, ℎ = 5, �� = 6 ⋅ 5 ÷ 2 = 155
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados



La medida extra en los triángulos C, D y E puede confundir a algunos estudiantes. Si no están seguros de cómo decidir la medida a utilizar, pregúntales qué aprendieron que debe ser cierto sobre una base y una altura correspondiente en un triángulo. Pídeles que repasen el trabajo de la actividad de calentamiento.
El objetivo de este debate en clase es profundizar en el conocimiento de los estudiantes sobre la base y la altura de los triángulos. Discuta cuestiones como:
• Para el triángulo A, ¿podemos decir que el segmento 6-cm es la base y el segmento de 5 cm es la altura? ¿Por qué sí o por qué no? (No, la base de un triángulo es uno de sus lados.)
• ¿Y para el Triángulo C? ¿Puede el segmento 3-cm servir de base? ¿Por qué sí o por qué no? (No, ese segmento no es un lado del triángulo.)
• ¿Puede el lado de 3,5-cm del triángulo D servir de base? ¿Por qué sí o por qué no? (Sí, es un lado del triángulo, pero como no tenemos la altura que le corresponde, no es útil para hallar el área aquí.)
• Se dan más de dos medidas para los triángulos C, D y E. ¿Cuáles son útiles para hallar el área? (Necesitamos una base y una altura correspondiente, es decir, la longitud de un lado del triángulo y la longitud de un segmento perpendicular entre ese lado y el vértice opuesto).
• A la hora de hallar el área, ¿en qué son únicos los triángulos rectángulos -como B y D-? (Cualquiera de los dos lados que forman el ángulo recto podría ser la base o la altura. En los triángulos no rectángulos -como A, C y E- el segmento de altura no es un lado del triángulo; hay que trazar un segmento de línea diferente).
5 minutos
El área de un paralelogramo puede determinarse utilizando las medidas de la base y la altura. En esta lección aprendiste que podemos hacer lo mismo con triángulos.
• "¿Cómo ubicamos la base de un triángulo? ¿Cuántas bases posibles hay?" (Cualquier lado de un triángulo puede ser una base. Hay 3 bases posibles.)
• "¿Cómo localizamos la altura una vez que conocemos la base?" (Halla la longitud de un segmento perpendicular que una la base y su vértice opuesto.)
Podemos usar el par de medidas base-altura para hallar el área de un triángulo de forma bastante sencilla.
• "¿Qué expresión funciona para hallar el área de un triángulo?" ( 1 2 ⋅ �� ⋅ ℎ o �� ⋅ ℎ2)
• "¿Puedes explicar brevemente por qué funciona esta expresión o fórmula?" (El área de un triángulo es siempre la mitad del área de un paralelogramo afín que comparta la misma base y altura.)
Has aprendido que cualquier lado del triángulo puede ser la base, pero no todos los lados pueden ser la altura.
• "¿Hay casos en los que tanto la base como la altura son lados del triángulo? ¿Cuándo ocurre?" (Sí. En un triángulo rectángulo, tanto la base como la altura pueden ser lados del triángulo).
5 minutos
En este enfriamiento, los estudiantes aplican lo aprendido sobre la fórmula del área y sobre la base y la altura de un triángulo. Se dan varias medidas, por lo que los estudiantes deben estar atentos para elegir el par de medidas correcto que les permita calcular el área.
POSIBLES RESPUESTAS

Para cada triángulo, identifica una base y una altura correspondiente. Utilízalas para hallar el área. Muestre su razonamiento.
Las respuestas varían. Posibles respuestas:
Triángulo A:
• �� = 3, ℎ = 6, área: 9 pulgadas cuadradas, 1 2 ⋅ 3 ⋅ 6 = 9
• �� = 7,2, ℎ = 2,5, área: 9 pulgadas cuadradas, 1 2 ⋅ (7.2) ⋅ (2.5) = 9
Triángulo B:
• �� = 6, ℎ = 4, área: 1 2 pulgadas cuadradas, 1 2 ⋅ 6 ⋅ 4 = 12
• �� = 5, ℎ = 4.8, área: 1 2 pulgadas cuadradas, 1 2 ⋅ 5 ⋅ (4.8) = 12
PROBLEMA 1
Seleccione todos los dibujos en los que se identifique correctamente una altura correspondiente ℎ para una base dada ��
Posibles soluciones


de Matemáticas . Unidad 1

PROBLEMA 2
Para cada triángulo, se etiquetan una base y su correspondiente altura.
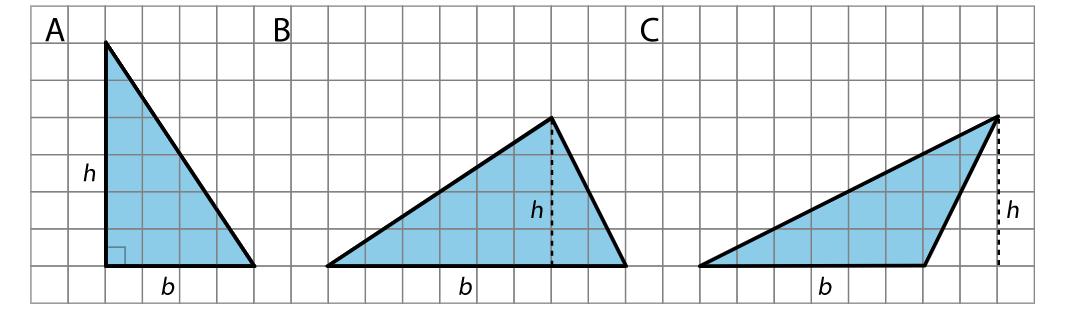
A. Halla el área de cada triángulo.
B. ¿Cómo se relaciona el área con la base y su correspondiente altura?
Posibles soluciones
A. Triángulo A: 12 unidades cuadradas, Triángulo B: 16 unidades cuadradas, Triángulo C: 12 unidades cuadradas
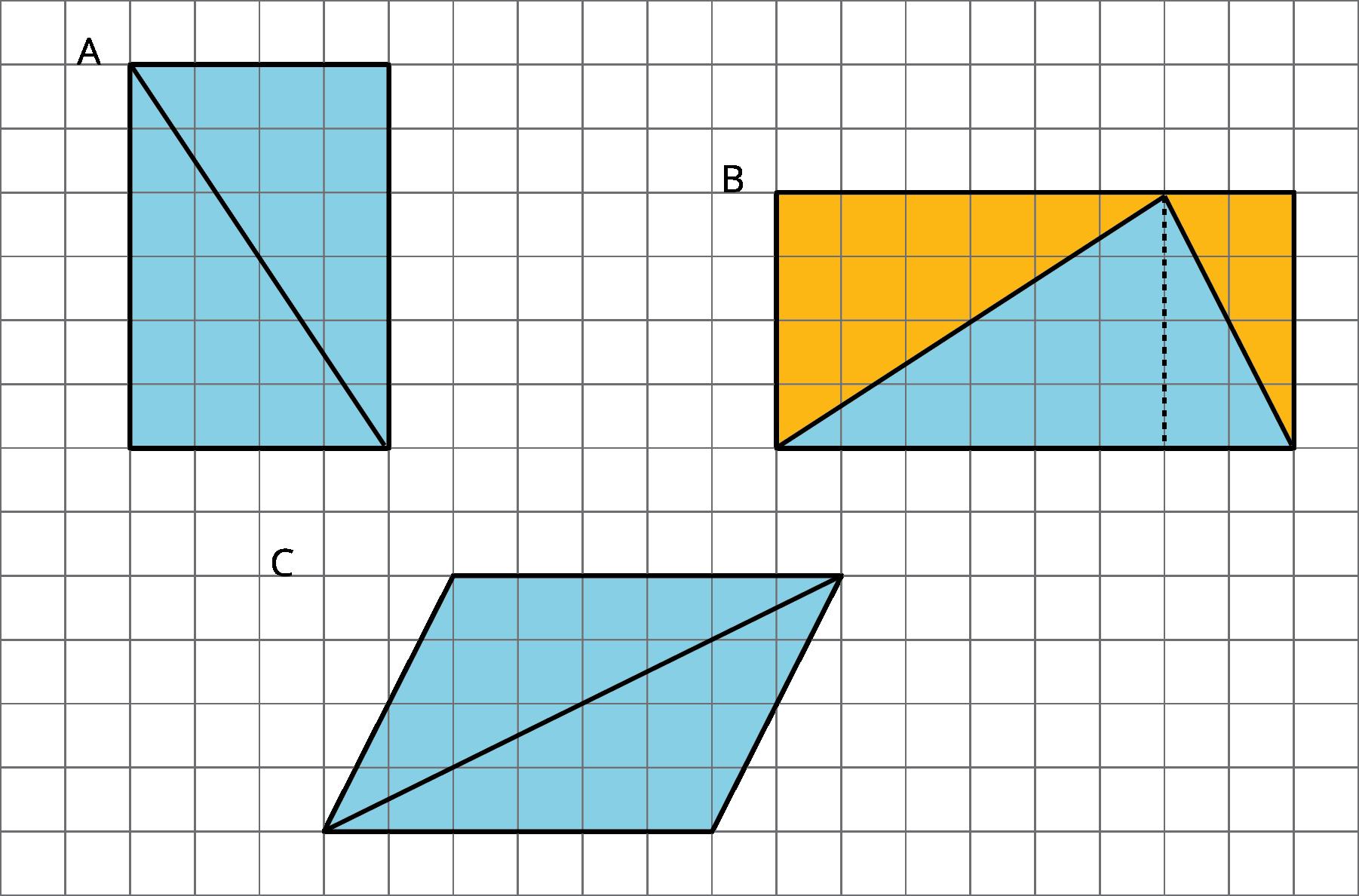
B. En cada caso, el área del triángulo, en unidades cuadradas, es la mitad de la base por su altura correspondiente, (��⋅ℎ) 2
PROBLEMA 3
He aquí un triángulo rectángulo. Nombra una altura correspondiente para cada base.
A. Lado ��
B. Lado ��
C. Lado ��
Learning Inc. - Todos los derechos reservados
Posibles soluciones
A. Segmento ��
B. Lado ��
C. Lado ��
6º de Matemáticas . Unidad 1

PROBLEMA 4
Del Grado 6, Unidad 1, Lección 8
Encuentra el área del triángulo sombreado. Muestra tu razonamiento.

Posibles soluciones
18 unidades cuadradas. El razonamiento varía. Una aproximación probable es descomponer el triángulo con una línea horizontal para formar dos rectángulos y dividir el triángulo en dos triángulos más pequeños. El triángulo superior es la mitad del rectángulo superior, por lo que su área es 1 2 ⋅ 6 ⋅ 2 = 6. El triángulo inferior es la mitad del rectángulo inferior, por lo que su área es 1 2 ⋅ 6 ⋅ 4 = 12. El área del triángulo original es 6 + 1 2 o 18 unidades cuadradas.
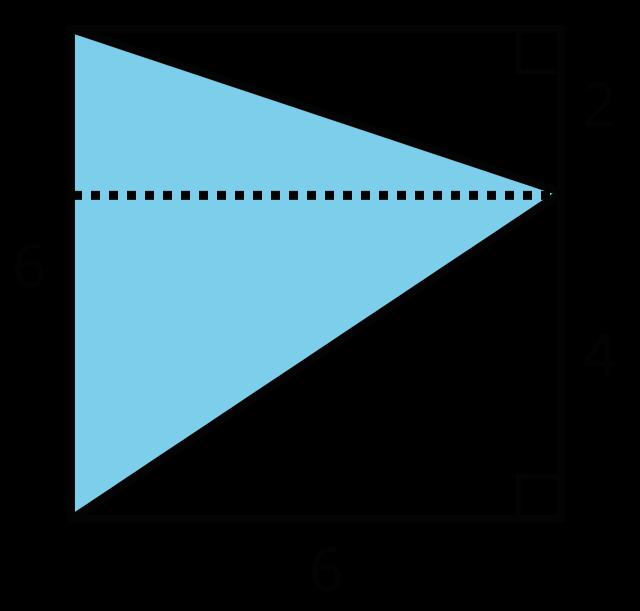
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 7
André dibujó una línea que une dos vértices opuestos de un paralelogramo. Selecciona todas las afirmaciones verdaderas sobre los triángulos creados por la línea que dibujó Andre.
Cada triángulo tiene dos lados que miden 3 unidades.
Cada triángulo tiene un lado que tiene la misma longitud que la línea diagonal.
Cada triángulo tiene un lado que mide 3 unidades.
Si colocamos un triángulo encima del otro y alineamos sus lados, veremos que un triángulo es mayor que el otro.
Los dos triángulos tienen la misma área el uno que el otro.
Posibles soluciones
Las respuestas varían. Ejemplos de estrategias:
Cada triángulo tiene dos lados que miden 3 unidades.
Cada triángulo tiene un lado que tiene la misma longitud que la línea diagonal.
Cada triángulo tiene un lado que mide 3 unidades.
Si colocamos un triángulo encima del otro y alineamos sus lados, veremos que un triángulo es mayor que el otro.
Los dos triángulos tienen la misma área.
California - Grado 6
Learning Inc. - Todos los derechos reservados


de Matemáticas . Unidad 1

PROBLEMA 6
Del Grado 6, Unidad 1, Lección 3
Aquí hay un octágono.
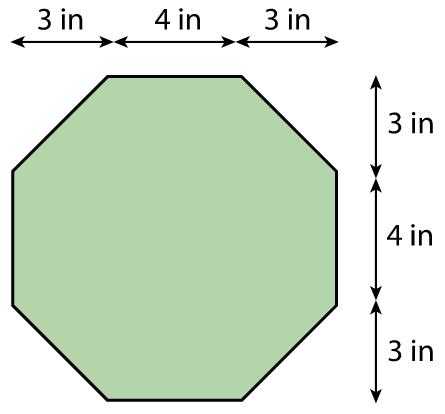
A. Al estimar el área del octágono, Lin razonó que debe ser menor que 100 pulgadas cuadradas. ¿Estás de acuerdo? Explica tu razonamiento.
B. Halla el área exacta del octógono. Muestre su razonamiento.
Posibles soluciones
A. Sí. Las explicaciones varían. Ejemplo de explicación: El octágono cabe en un cuadrado que mide 10 pulgadas por 10 pulgadas, pero sin las cuatro esquinas del cuadrado. El cuadrado tiene un área de 100 pulgadas cuadradas, así que el área del octágono debe ser menor que eso.
B. 82 pulgadas cuadradas. El razonamiento varía. Ejemplo de razonamiento: Un cuadrado de 10-pulgadas por10-pulgadas que encierra el octógono tiene un área de 100 pulgadas cuadradas. Dos triángulos de las esquinas componen un cuadrado de 3 pulgadas por3 pulgadas, por lo que su área combinada es de 9 pulgadas cuadradas. 100 - 2(3 ⋅ 3) = 100 - 18 = 82.
Reflexiones:
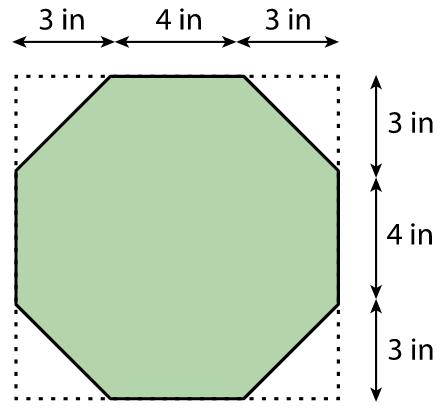


IDEAS FUNDAMENTALES
• Graficar formas
• Redes y superficie
• Generalizar con representaciones múltiples
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.EE.2c Evaluar expresiones en valores específicos de sus variables. Incluir expresiones que surgen de fórmulas utilizadas en problemas del mundo real. Realizar operaciones aritméticas, incluyendo aquellas que involucran exponentes de números enteros, en el orden convencional cuando no hay paréntesis para especificar un orden particular (Orden de Operaciones).
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfoque SMPs
MP5 Usar herramientas apropiadas estratégicamente.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué?
Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dan sentido al mundo e influyen en el futuro
buscan y hacen uso de la estructura
OBJETIVO(S) DE APRENDIZAJE
descubren la forma y el espacio, desmontan enteros, juntan piezas y exploran el cambio de cantidades.
• Utilicemos diferentes pares de base-altura para encontrar el área de un triángulo.
OBJETIVO(S)
• Puedo identificar los pares correspondientes de base y altura de cualquier triángulo.
• Cuando se me da información sobre la base de un triángulo, puedo identificar y dibujar la altura correspondiente.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Dibujar y rotular la altura que corresponde a una base dada de un triángulo, asegurándose de que es perpendicular a la base y de la longitud correcta.
• Evaluar (oralmente) la utilidad de diferentes pares base-altura para hallar el área de un triángulo dado.
Rutinas instructivas
Piensa, comparte, en parejas
MLR2: Recopilar y mostrar
MLR8: Apoyo a la discusión
Materiales necesarios
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
Esta lección fomenta la capacidad de los estudiantes para identificar y trabajar con una base y una altura en un triángulo de dos maneras:
1. Aprendiendo a dibujar (no sólo a reconocer) un segmento para mostrar la altura correspondiente para cualquier base dada, y 2. Aprendiendo a elegir los pares base-altura apropiados para permitir cálculos de área.
Los estudiantes han visto que el área de un triángulo se puede determinar de múltiples maneras. Utilizar las medidas de la base y la altura y la fórmula es un método práctico, pero como hay tres pares posibles de bases y alturas, hay que tener cuidado al identificar la combinación correcta de medidas. Algunos pares base-altura pueden ser más prácticos o eficientes que otros, por lo que conviene ser estratégico a la hora de elegir un lado para utilizarlo como base.
Componente de la lección

Estructura Tiempo
Calentamiento Parejas 5 min
Actividad de exploración Por parejas 25 min
Actividad de exploración opcional Grupos pequeños 10 min
Síntesis Grupo completo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Breve descripción
Los estudiantes dibujan un triángulo no rectángulo de su elección que tiene un área específica.
Un applet digital interactivoResumen de la lección está disponible para permitir a los estudiantes explorar el dibujo de triángulos dada un área.
Los estudiantes dibujan segmentos de línea para representar la altura correspondiente a la base predeterminada de varios triángulos.
Los estudiantes etiquetan y determinan las alturas y las bases de los triángulos y luego calculan el área de cada uno.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la determinación de la altura, la base y el área de un triángulo sin lados verticales u horizontales en una cuadrícula.
Los estudiantes resumen cómo identificar mejores opciones de base y altura correspondiente para determinar las áreas de triángulos y discuten las herramientas que ayudan a dibujarlos perpendiculares entre sí.
Los estudiantes dibujan las alturas correspondientes para las bases dadas de los triángulos y luego comparan las áreas de los triángulos en una cuadrícula.
El componente de práctica independiente incluye 4 problemas de la lección y 2 problemas de repaso en espiral.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
minutos

Rutinas instructivas
Pensar Compartir
Hasta ahora, los estudiantes han determinado el área a partir de un triángulo y algunas medidas. En este calentamiento, se invita a los estudiantes a invertir el proceso. Se les da una medida de área y se les pide que creen varios triángulos con esa área.
Se espera que los estudiantes se inclinen primero por los triángulos rectángulos (o que dividan por la mitad rectángulos que tengan factores de 12 como longitudes de sus lados). Este es un punto de partida natural y productivo. Animar a los estudiantes a crear triángulos no rectángulos les anima a aplicar los conocimientos adquiridos en sus experiencias con paralelogramos no rectángulos. Mientras los estudiantes trabajan solos y discuten con sus compañeros, observe las estrategias que utilizan para dibujar sus triángulos y comprobar sus áreas. Identifique a algunos estudiantes con estrategias diferentes para compartirlas más tarde.
Organice a los estudiantes en grupos de 2. Dé a los estudiantes 2-3 minutos de tiempo para pensar en silencio y 2 minutos para compartir sus dibujos con su compañero después. Anime a los estudiantes a que consulten su trabajo anterior cuando lo necesiten. Facilítales sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Diga a los estudiantes que dibujen otro triángulo con la misma área si terminan el primero antes de tiempo. Durante la discusión por parejas, cada uno debe convencer al otro de que el triángulo dibujado es efectivamente 12 unidades cuadradas.
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus tutores previamente identificados.
En la cuadrícula, dibuja un triángulo con un área de 12 unidades cuadradas. Intenta dibujar un triángulo no rectángulo. Prepárate para explicar cómo sabes que el área de tu triángulo es 12 unidades cuadradas.

Los dibujos y las explicaciones varían. Ejemplos de respuestas:
• Este triángulo rectángulo tiene una base de 8 unidades y una altura de 3 unidades.
El área es la mitad de 3 ⋅ 8 o la mitad de 24, que es 12
Grado 6 . Matemáticas . Unidad 1

• Este triángulo tiene un lado de 6 unidades. Esta puede ser la base. Dibuja un segmento de altura que sea perpendicular a la base y mida 4 unidades. El área del triángulo es b ⋅ h ÷ 2, por lo que es 6 ⋅ 4 ÷ 2, lo que es 12.
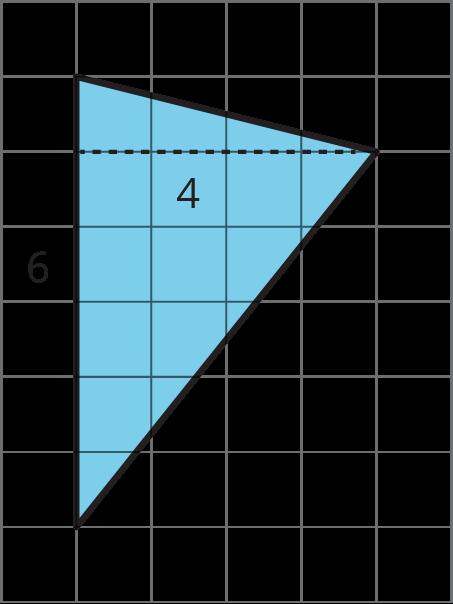
• Dibuja un paralelogramo con base 12 y altura 2, y luego traza una diagonal para crear dos triángulos idénticos. Cada uno de los triángulos tiene un área de 12 porque es la mitad de un paralelogramo con un área de 24
Si los estudiantes tienen problemas para empezar, pregúntales:
• "¿Puedes dibujar un cuadrilátero con un área de 12?"
• "¿Puedes usar lo que sabes sobre paralelogramos para ayudarte?"
• "¿Puedes utilizar alguna de las estrategias de área -descomponer, reordenar, encerrar, restar- para llegar a un área de 12?"
Los estudiantes que comienzan dibujando rectángulos y otros paralelogramos pueden utilizar factores de 12, en lugar de factores de 24, para la base y la altura. Si esto ocurre, pregúntales cuál es el área de su cuadrilátero y cómo se relaciona con el triángulo que intentan dibujar.
Invite a algunos estudiantes a compartir sus dibujos y formas de razonar con la clase. Para cada dibujo compartido, pregunte al creador por la base y la altura y anótelas para que todos las vean. Pregunte a la clase:
• "¿Alguien más dibujó un triángulo idéntico?"
• "¿Alguien dibujó un triángulo diferente pero con las mismas medidas de base y altura?"
Para reforzar la relación entre base, altura y área, discuta:
• "¿Cuál podría ser una mejor manera de dibujar un triángulo: empezando por la medida de la base o por la altura? ¿Por qué?"
• "¿Puedes nombrar otros pares base-altura que produzcan un área de 12 unidades cuadradas sin dibujar? ¿Cómo?"
25 minutos
Rutinas instructivas
MLR2: Recoger y Mostrar
Los estudiantes pueden ser capaces de reconocer una medida que se puede utilizar para la altura cuando la ven, pero identificar y dibujar un segmento apropiado es más desafiante. Esta actividad, y la demostración necesaria para iniciarla, proporciona a los estudiantes una estrategia concreta para identificar una altura con precisión. Cuando los estudiantes utilizan la estrategia de dibujar una recta auxiliar para resolver problemas, están buscando y haciendo uso de la estructura (MP7). A menudo es necesaria una instrucción explícita, como en esta actividad, antes de esperar que los estudiantes utilicen esta estrategia de forma espontánea.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Explique a los estudiantes que intentarán dibujar una altura que corresponda a cada lado de un triángulo. Organice a los estudiantes en grupos de 2. Dé a cada estudiante una ficha y 1-2 minutos para completar la primera pregunta. Recuérdeles que hay más de una forma correcta de dibujar la altura correspondiente a una base. Pídales que hagan una pausa después de la primera pregunta. Mientras los estudiantes trabajan, observe cómo utilizan las fichas (si es que lo hacen).
Después, solicite algunos comentarios rápidos sobre la exploración. Haga preguntas como:
• "¿Cómo supiste dónde dibujar los segmentos?"
• "¿Cómo los dibujaste?"
• "¿Por qué te dieron fichas? ¿Cómo podrían ayudar?"
Explique que ahora demostrará una manera de dibujar alturas eficazmente. (Si algún estudiante utilizó la ficha correctamente, reconozca que iba por buen camino).
Recuerde a los estudiantes que cualquier línea que tracemos para mostrar la altura de un triángulo debe dibujarse perpendicular a la base. Disponer de una herramienta con un ángulo recto y con bordes rectos puede ayudarnos a asegurarnos de que la línea que trazamos es recta y perpendicular a la base. Para eso está la ficha.
Pregunta: "¿Cómo sabemos dónde parar esta línea que estamos dibujando? ¿Qué longitud debe tener?"
Explica que lo más fácil es trazar la recta de forma que pase por el vértice opuesto a la base elegida. Dibuja o muestra un triángulo para que todos lo vean. Demuestra lo siguiente.
• Elige un lado del triángulo como base. Identifica el vértice opuesto.
• Alinea un borde de la tarjeta con esa base.
• Desliza la tarjeta a lo largo de la base hasta que un borde perpendicular de la tarjeta se encuentre con el vértice opuesto.
• Usa ese borde para dibujar un segmento de línea desde ese vértice hasta la base. La medida de ese segmento es la altura.
Pregunta: ¿Qué pasa si el vértice opuesto no está directamente sobre la base? Explique que a veces necesitamos extender la línea de la base y demuestre el proceso.
Demuestre el proceso con otro ejemplo en el que la tarjeta necesita deslizarse de derecha a izquierda (por ejemplo, girando el triángulo obtuso de arriba en el sentido de las agujas del reloj). Los estudiantes zurdos pueden encontrar esto particularmente útil.
Pida a los estudiantes que utilicen este método para comprobar las alturas que dibujaron en la primera pregunta, revisen los dibujos si eran incorrectos y compartan sus revisiones con sus compañeros. Circule y apoye a los estudiantes mientras dibujan. Los que terminen de verificar las alturas en la primera pregunta pueden pasar a completar el resto de la actividad con sus compañeros.

Grado 6 . Matemáticas . Unidad 1
Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina les dicten cómo utilizar la ficha para dibujar cada altura según sea necesario.
1. Aquí hay tres copias del mismo triángulo. El triángulo está girado de modo que el lado elegido como base está abajo y es horizontal. Dibuja una altura que corresponda a cada base. Utiliza una ficha para ayudarte.
Lado a como base: Lado b como base: Lado c como base:
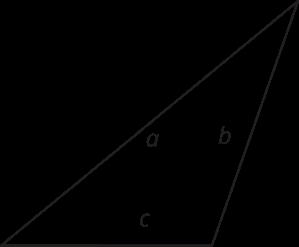
Espera las instrucciones de tu maestro antes de pasar a la siguiente pregunta.
2. Dibuja un segmento de línea para mostrar la altura correspondiente a la base elegida en cada triángulo.
1. Los dibujos varían. Dibujos de muestra: 2.


Grado 6 . Matemáticas . Unidad 1

Algunos estudiantes pueden utilizar la ficha simplemente como una regla y, por tanto, dibujar alturas que no sean perpendiculares a la base dada. Recuérdeles que una altura debe ser perpendicular o formar un ángulo recto con la base.
Los estudiantes pueden pensar erróneamente que una base debe ser un lado horizontal de un triángulo (o el más próximo a ser horizontal) y que una altura debe dibujarse dentro del triángulo. Señale algunos ejemplos de trabajos anteriores para recordar a los estudiantes que ninguna de las dos cosas es cierta. Recuérdeles que alineen su ficha con el lado denominado "base".
A algunos estudiantes les puede resultar incómodo dibujar segmentos de altura cuando la base no es horizontal. Anime a los estudiantes a rotar su papel según sea necesario para facilitar el dibujo.
Si el tiempo lo permite, considere seleccionar a un estudiante para que comparta el dibujo de la altura de cada triángulo, o muestre las soluciones en la Respuesta del estudiante para que todos las vean. Para ayudar a los estudiantes a reflexionar sobre su trabajo, discuta preguntas como:
• "¿Para qué triángulos fue fácil encontrar la altura correspondiente para la base dada?"
• "¿Para qué triángulos fue más difícil?"
• "¿En qué se diferenció el proceso de encontrar la altura del triángulo D del de los otros?" (La altura de un triángulo rectángulo ya está dibujada: es el otro segmento que enmarca el ángulo recto).
• "¿Cuándo podríamos necesitar extender la línea de la base, o dibujar una línea de altura fuera del triángulo?" (Cuando se trata de triángulos obtusos, o cuando el vértice opuesto no está directamente sobre la base).
Apoyo para estudiantes de inglés
Representar, Hablar, Escuchar: MLR2 Recoger y mostrar. Mientras los estudiantes trabajan, circule y recoja ejemplos de dibujos de segmentos de recta de los estudiantes que muestren la base y la altura. Para ello, tome fotografías digitales o copie los dibujos de los estudiantes en una pantalla visual. Busque ejemplos que muestren la altura dentro y fuera del triángulo, así como bases horizontales o verticales. Durante el debate con toda la clase, muestre los distintos ejemplos y pida a los estudiantes que comparen los diagramas preguntándoles: "¿Alguno de los dos diagramas tiene métodos similares para determinar la base o la altura?". Escuche y amplíe el lenguaje matemático que utilizan los estudiantes para apoyar su razonamiento.
15 minutos
Rutinas instructivas
MLR8: Apoyos a la discusión
Esta actividad permite a los estudiantes practicar la identificación de la base y la altura de los triángulos y su utilización para hallar áreas.
Como no hay indicaciones sobre qué base o altura utilizar, y como no todos los lados les permitirían calcular el área fácilmente, los estudiantes tienen que pensar estructuralmente y elegir estratégicamente. Todos los triángulos de los problemas tienen un lado vertical o uno horizontal. La elección de dicho lado como base facilita la identificación de la altura correspondiente.
En algunos casos, los estudiantes pueden optar por utilizar una combinación de estrategias de razonamiento del área en lugar de hallar la base y la altura de los triángulos sombreados y aplicar la fórmula. Por ejemplo, pueden encerrar un triángulo sombreado con un rectángulo y restar las áreas de los triángulos adicionales (con o sin utilizar la fórmula en esos triángulos adicionales). Fíjese en los estudiantes que utilicen tales estrategias para que puedan compartirlas más tarde.
Grado 6 . Matemáticas . Unidad 1

Mantenga a los estudiantes en grupos de 2. Explique que ahora van a practicar localizando o dibujando alturas y utilizándolas para hallar el área de triángulos. Conceda a los estudiantes 8-10 minutos para pensar en silencio y tiempo para compartir sus respuestas con un compañero después. Proporcione a los estudiantes sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) (especialmente fichas).
Si el tiempo es limitado, considere la posibilidad de pedir a los estudiantes que encuentren el área de dos o tres triángulos en lugar de los cuatro.
Habilidades motoras finas: Eliminar barreras. Proporcione una versión ampliada de la imagen. TAREAS
Para cada triángulo, identifica y etiqueta una base y una altura. Si es necesario, dibuja un segmento de línea para representar la altura.
Luego, calcula el área del triángulo. Explica tu razonamiento. (La longitud del lado de cada cuadrado en la cuadrícula es 1 unidad).
POSIBLES RESPUESTAS
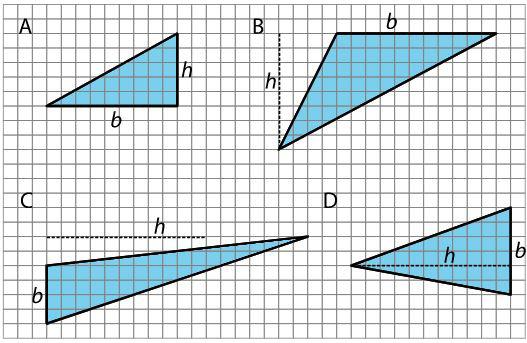
CONCEPTOS ERRÓNEOS ANTICIPADOS
Triángulo A: b = 9 and h = 5, 9 ⋅ 5 ÷ 2 = 22.5, área: 22.5 unidades cuadradas
Triángulo B: b = 11 and h = 8, 11 ⋅ 8 ÷ 2 = 44, área: 44 unidades cuadradas
Triángulo C: b = 4 and h = 18, 4 ⋅ 18 ÷ 2 = 36, área: 36 unidades cuadradas
Triángulo D: b = 6 and h = 11, 6 ⋅ 11 ÷ 2 = 33, área: 33 unidades cuadradas.
Los estudiantes pueden pensar que un lado vertical de un triángulo es la altura, independientemente del segmento usado como base. Si esto sucede, pídales que usen una ficha como regla para comprobar si los dos segmentos que usan como base y altura son perpendiculares. Algunos estudiantes pueden no comprender de inmediato que elegir un lado vertical u horizontal les permitiría calcular la altura correspondiente con mucha facilidad. Es posible que elijan un lado no vertical ni horizontal y no aprovechen la cuadrícula. Pregunte si un lado diferente facilitaría la determinación de las longitudes de la base y la altura sin tener que medir.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Enfoque el debate de toda la clase hacia cómo los estudiantes identificaron las bases y las alturas. Debate:
• "¿Qué lado elegiste como base del triángulo B? C? ¿Por qué?"
• "Aparte de elegir un lado vertical u horizontal como base, ¿hay otra forma de hallar el área de los triángulos sombreados sin utilizar sus bases y alturas?" (Invite a compartir a un par de estudiantes que utilicen el método de encerrar y restar para hallar el área de B, C o D.)
• "¿Qué estrategia prefieres o crees que es más eficiente?"
• "¿Se te ocurre algún ejemplo en el que sería preferible hallar la base y la altura del triángulo de interés?" (Los estudiantes pueden señalar cualquiera de los triángulos de la tarea.)
• "¿Se te ocurre un ejemplo en el que podría ser preferible encerrar el triángulo de interés y restar otras áreas?" (Los estudiantes pueden señalar el triángulo mostrado en "¿Estás preparado para más?", en el que ninguno de los lados del triángulo sombreado es horizontal o vertical).
Apoyo para estudiantes de inglés
Speaking, Representing: MLR8 Apoyos para el debate. Proporcione marcos de oraciones para ayudar a los estudiantes a producir enunciados que describan las estrategias que utilizan para identificar bases y alturas, y para hallar el área. Por ejemplo, "Para el triángulo , elegí el lado como base porque ." o "La próxima vez que necesite encontrar el área de un triángulo, la estrategia que usaré es , porque ."
Principio(s) de diseño: Apoyar la creación de sentido
¿Estás preparado para más?
Halla el área del triángulo de abajo. Muestra tu razonamiento.

"¿Estás listo para más?" Respuesta del estudiante
51, ya que podemos encerrar el triángulo dado en un cuadrado que tiene un área de 144(12 ⋅ 12 = 144), y luego restar el área de los triángulos rectángulos en cada esquina.
5 minutos
En esta lección, hemos estudiado detenidamente las alturas de un triángulo. Localizamos o dibujamos una altura para cualquier lado de un triángulo. También consideramos qué par de base y altura usar para hallar el área.
• "¿Qué debemos recordar sobre la relación entre la base de un triángulo y su altura correspondiente?" (La altura debe ser perpendicular a la base).
• "¿Qué herramientas podrían ayudarnos a dibujar un segmento de altura? ¿Qué tiene una ficha o una regla que nos ayude?" (Una herramienta con bordes rectos y un ángulo recto puede ayudarnos a dibujar segmentos perpendiculares).
Grado 6 . Matemáticas . Unidad 1
Cuando tenemos una base y su correspondiente altura, podemos hallar el área de forma bastante sencilla, pero para cada triángulo hay múltiples pares base-altura.
• "¿Importa qué lado elegimos como base? (Para la base, necesitamos un lado de longitud conocida. Para la altura, necesitamos un segmento que sea perpendicular a esa base y cuya longitud podamos determinar).
minutos
Proporcione acceso a los juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

1. Para cada triángulo de abajo, dibuje un segmento de altura que corresponda a la base dada, y rotúlelo h. Utilice una ficha si es necesario.
2. ¿Cuál triángulo tiene la mayor área? ¿El de menor área? Explica tu razonamiento.
1. Las respuestas varían. Hay muchas ubicaciones posibles para un segmento de altura. Los segmentos mostrados son los más sencillos.
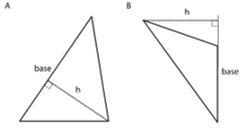
2. Todos los triángulos tienen la misma área: 4 unidades cuadradas. Todos tienen una base de 2 unidades y una altura de 4 unidades.


Grado 6 . Matemáticas . Unidad 1
PROBLEMA 1
Para cada triángulo, una base está etiquetada b. Dibuja un segmento de recta que muestre su altura correspondiente. Usa una ficha para ayudarte a dibujar una línea recta.

PROBLEMA 2
Selecciona todos los triángulos que tengan un área de 8 unidades cuadradas. Explica cómo lo sabes.
PROBLEMA 3
Halla el área del triángulo. Muestra tu razonamiento.

Si te atascas, considera cuidadosamente qué lado del triángulo usar como base.
Posibles soluciones
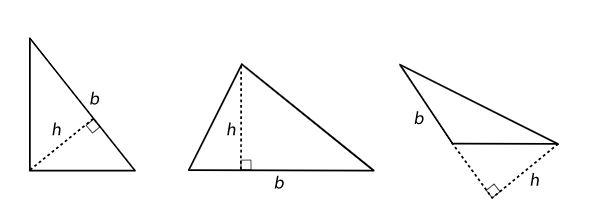
Posibles soluciones
A, B, D y E. Los triángulos A, B y D tienen una base horizontal de 4 unidades y una altura de 4 unidades. (4 ⋅ 4)2 = 8, por lo que el área de cada uno es 8 unidades cuadradas. El triángulo C tiene una base horizontal de 4 unidades y una altura de 5 unidades, por lo que su área es 10 unidades cuadradas. El triángulo E tiene una base horizontal de 8 unidades y una altura de 2 unidades, por lo que su área es 8 unidades cuadradas, ya que (8 ⋅ 2)2 = 8

Posibles soluciones
12 unidades cuadradas. Las explicaciones varían. Respuesta de ejemplo: El lado vertical mide 6 unidades, y este lado se puede utilizar como base. La altura correspondiente, mostrada en el diagrama, es 4 unidades. Por tanto, el área es 12 unidades cuadradas. Otro método consiste en rodear el triángulo con un rectángulo y luego restar las partes que no están en el triángulo.
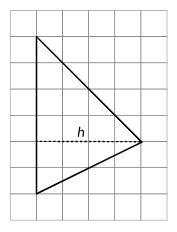
PROBLEMA 4
¿Puede ser el lado d la base de este triángulo? En caso afirmativo, ¿qué longitud sería la altura correspondiente? Si no, explica por qué no.
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 3
Halla el área de esta figura. Muestra tu razonamiento.

PROBLEMA 6
Del Grado 6, Unidad 1, Lección 6
En la cuadrícula, dibuja dos paralelogramos diferentes que tengan igual área. Rotula la base y la altura de cada uno y explica cómo sabes que las áreas son iguales.

Reflexiones:

Nation California - Grado 6
Grado 6 . Matemáticas . Unidad 1
Posibles soluciones
Sí, el lado d puede ser la base, porque es un lado del triángulo. La altura correspondiente es g
Posibles soluciones
18 unidades cuadradas. El razonamiento varía.
Posibles soluciones
Las respuestas varían.
Learning Inc. - Todos los derechos reservados

• Graficar formas
• Redes y superficie
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.G.1 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Construir sobre
5.G 4.G.2
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1
I.C.9
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dan sentido al mundo e influyen en el futuro
dan sentido a los problemas y perseveran en su resolución desmontando enteros, juntando piezas y descubriendo la forma y el espacio.
OBJETIVO(S) DE APRENDIZAJE
• Investiguemos los polígonos y sus áreas.
• Puedo describir las características de un polígono utilizando vocabulario matemático.
• Puedo razonar sobre el área de cualquier polígono descomponiéndolo y reordenándolo, y utilizando lo que sé sobre rectángulos y triángulos.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comparar y contrastar (oralmente) diferentes estrategias para hallar el área de un polígono.
• Describir (oralmente y por escrito) las características que definen a los polígonos.
• Hallar el área de un polígono, descomponiéndolo en rectángulos y triángulos, y presentar el método de solución (utilizando palabras y otras representaciones).
Rutinas instructivas
¿Cuál no pertenece?
MLR2: Recopilar y exhibir
Piensa, empareja, comparte
MLR8: Apoyo a la discusión
Materiales necesarios
Ejercicio maestro de línea negra para la Actividad 11.4
Enfriamiento
Preparación necesaria
Si va a realizar la actividad opcional del molinete, prepare una copia del esquema para cada grupo de 4 estudiantes.
Si se dispone de papel más grande (y de una fotocopiadora que pueda acomodarlo), sería útil disponer de copias de mayor formato.
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
Los estudiantes han trabajado con polígonos en grados anteriores y a lo largo de esta unidad. En esta lección, los estudiantes escriben una definición que caracteriza a los polígonos. Hay muchas definiciones precisas diferentes para un polígono . El objetivo de esta lección no es encontrar la definición más sucinta posible, sino articular las características que definen a un polígono de una manera que tenga sentido para los estudiantes.
Otra enseñanza clave para esta lección es que el área de cualquier polígono se puede encontrar descomponiéndolo en triángulos. La prueba de que todos los polígonos son triangulables (palabra que los estudiantes no necesitan conocer) es bastante sofisticada, pero los estudiantes pueden tomarla como un hecho por ahora. Al observar y utilizar este hecho, los estudiantes buscan y utilizan la estructura (MP7).
Componente de la lección

Estructura Tiempo Breve descripción
Calentamiento Grupos pequeños 5 min Los estudiantes determinan, basándose en sus observaciones y razonamientos, qué triángulo no pertenece.
Actividad de exploración Grupos pequeños 20 min
Actividad de Exploración
Grupos Pequeños 15 min
Actividad de Exploración Opcional Grupos Pequeños 30 min
Síntesis Todo el Grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Los estudiantes analizan ejemplos de polígonos y no polígonos para crear una definición informal de polígonos.
Los estudiantes aplican varias estrategias de descomposición y reordenamiento para encontrar las áreas de cuadriláteros en una cuadrícula.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la descomposición de un trapecio para escribir una fórmula para el área de un trapecio.
Los estudiantes encuentran el área de un polígono desconocido en una cuadrícula.
Los estudiantes solidifican sus definiciones de polígonos y cómo determinar las áreas de polígonos de forma irregular.
Los estudiantes justifican si las figuras son polígonos basándose en sus características y desarrollan un plan para encontrar el área de un polígono irregular en una cuadrícula.
El componente de práctica independiente incluye 4 problemas de la lección y 2 problemas de repaso en espiral.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
5 minutos

Rutinas instructivas
¿Cuál no pertenece?
Este calentamiento invita a los estudiantes a consolidar lo aprendido en las últimas lecciones y a hacer observaciones cuidadosas sobre los triángulos.
Espere que los estudiantes describan las diferencias en los triángulos en términos de:
• ángulos (agudo, recto u obtuso)
• orientación de los lados (vertical, horizontal)
• el lado que probablemente se elija como base
• longitud de la base o altura
Organice a los estudiantes en grupos de 2-4. Muestre la imagen de los triángulos para que todos la vean. Conceda a los estudiantes 1 minuto de reflexión en silencio y pídales que indiquen cuándo se han dado cuenta de que hay un triángulo que no encaja y que expliquen por qué. Anímeles a pensar en más de una posibilidad.
Cuando se acabe el minuto, dé a los estudiantes 2 minutos para que compartan su respuesta con su grupo y, a continuación, encuentren juntos al menos una razón, si es posible, por la que cada triángulo no pertenece.
Procesamiento conceptual: Manipulativos. Para los estudiantes que se benefician de las actividades prácticas, proporcione fichas de patrones (o corte previamente una copia extra de cada patrón) para que los estudiantes comparen las formas. Habilidades motoras finas: Eliminar barreras. Proporcione una versión ampliada de la imagen.
¿Cuál no pertenece?
Las respuestas varían. Ejemplos de respuestas:
• S: Es el único triángulo rectángulo. Es el único en el que se pueden elegir fácilmente dos lados como base y utilizarlos para hallar el área. Es el único en el que la base y la altura son ambos lados del triángulo.
• T: Es el único triángulo sin lado vertical. Es el único triángulo en el que el lado con más probabilidades de ser elegido como base es horizontal.
• U: Es el único triángulo agudo. Es el único triángulo que tiene más probabilidades de que su altura se dibuje en el interior del triángulo.
• V: Es el único que tiene una altura superior a 7 unidades.
Grado 6 . Matemáticas . Unidad 1

Después de que los estudiantes hayan compartido sus observaciones en grupos, invite a cada grupo a compartir una razón por la que un triángulo en particular podría no pertenecer. Registre y muestre las respuestas para que todos las vean. Después de cada respuesta, sondee al resto de la clase para ver si otros han hecho la misma observación.
Dado que no hay una única respuesta correcta a la pregunta de qué patrón no pertenece, preste atención a las explicaciones de los estudiantes y asegúrese de que las razones dadas son correctas. Pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen (partes de triángulos, tipos de ángulos, etc.) y que fundamenten sus afirmaciones.
20 minutos
Rutinas instructivas
MLR2: Recoger y exponer
Elaborar una definición útil y completa de polígono es más difícil de lo que parece. Una definición formal suele ser muy prolija o difícil de analizar. A menudo se hace referencia a los polígonos como figuras "cerradas", pero si se utiliza este término, es necesario definirlo, ya que el significado cotidiano de "cerrado" es diferente de su significado en un contexto geométrico.
Esta actividad pide a los estudiantes que desarrollen una definición práctica de polígono que tenga sentido para ellos, pero que también capture todos los aspectos necesarios que hacen que una figura sea un polígono (MP6). He aquí algunas características importantes de un polígono.
• Está compuesto por segmentos de línea. Los segmentos de línea son siempre rectos.
• Cada segmento de línea se encuentra con uno y sólo otro segmento de línea en cada extremo.
• Los segmentos de línea nunca se cruzan entre sí excepto en los puntos extremos.
• Es bidimensional.
Una consecuencia de la definición de polígono es que siempre hay tantos vértices como aristas. Los estudiantes pueden observar esto y querer incluirlo en su definición, aunque técnicamente es un resultado de la definición y no una característica definitoria.
Mientras los estudiantes trabajan, observe si hay definiciones correctas e incorrectas de un polígono. Preste atención a las descripciones claras y correctas, así como a las descripciones comunes pero inexactas (para poder discutirlas y refinarlas más adelante). Fíjese en los estudiantes con explicaciones precisas para que puedan compartirlas más tarde.
Organizar a los estudiantes en grupos de 2-4. Dar a los estudiantes 3-4 minutos de tiempo para pensar en silencio. Después, pídeles que compartan sus respuestas con su grupo y que completen juntos la segunda pregunta. Si hay desacuerdo sobre si una figura es un polígono, pídales que discutan cada punto de vista e intenten llegar a un acuerdo. A continuación, discuta con toda la clase.
Conversar, representar, escribir: MLR2 Recoger y mostrar. Mientras los estudiantes trabajan, escuche, recopile y muestre los términos y frases que los estudiantes utilizan para describir las características clave de los polígonos (por ejemplo, polígono, arista, vértices). Recuerde a los estudiantes que tomen prestado el lenguaje de la pantalla según sea necesario. Esto ayudará a los estudiantes a utilizar el lenguaje matemático al describir polígonos.
Principio(s) de diseño: Apoyar la creación de sentido; Maximizar la metaconciencia
Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (es decir, vértices, aristas, polígonos) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para referencia futura.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Aquí hay cinco polígonos:

Aquí hay seis figuras que no son polígonos:
POSIBLES RESPUESTASS

1. Encierra en un círculo las figuras que son polígonos.
2. ¿Qué tienen en común las figuras que has rodeado? ¿Qué características te ayudaron a decidir si una figura era un polígono?
1. B, E, F y G son polígonos.
2. Las respuestas varían. Características que los polígonos tienen en común: Son bidimensionales, están compuestos por segmentos de línea que nunca se cruzan entre sí, y cada segmento de línea se encuentra con uno y sólo otro segmento de línea en cada extremo.
ERRORES PREVISTOS
Los estudiantes pueden pensar que las figuras C e I son polígonos porque pueden ver varios triángulos o cuadriláteros en cada figura. Pida a los estudiantes que observen detenidamente los ejemplos y los no ejemplos y que comprueben si hay alguna figura compuesta por varios triángulos o cuadriláteros y, en caso afirmativo, que vean a qué grupo pertenece.
Muestre las figuras de la primera pregunta para que todos las vean. Para cada figura, pide al menos a un estudiante que explique por qué cree que es o no un polígono. (No pasa nada si las explicaciones de los estudiantes no son precisas en este punto.) A continuación, rodea con un círculo las figuras que sean polígonos en la pantalla.
A continuación, pida a los estudiantes que compartan sus ideas sobre las características de los polígonos. Anótalas para que todos las vean. Para cada una, pregunta a la clase si están de acuerdo o en desacuerdo. Si en general están de acuerdo, pregunte si hay algo que añadirían o ampliarían para que la descripción fuera más clara o precisa. Si no están de acuerdo, pídales una explicación.
Si los estudiantes no mencionan alguna de las características clave enumeradas en la descripción de la actividad, tráigala a colación y vuelva a tratarla al final de la clase.
Grado 6 . Matemáticas . Unidad 1

Diga a los estudiantes que llamamos a los segmentos de línea de un polígono aristas o lados , y que llamamos vértices a los puntos donde se encuentran las aristas. Señale los lados y los vértices de algunos de los polígonos identificados.
Señale que los polígonos siempre encierran una región, pero que la región no forma parte técnicamente del polígono. Cuando hablamos de hallar el área de un polígono, en realidad estamos hallando el área de la región que encierra. Así que "el área de un triángulo", por ejemplo, es en realidad la abreviatura de "área de la región encerrada por el triángulo".
15 minutos
Rutinas instructivas
Pensar Compartir
MLR8: Apoyos para la Discusión
Esta actividad tiene varios objetivos. Incita a los estudiantes a aplicar lo aprendido para hallar el área de cuadriláteros que no son paralelogramos, les anima a planificar antes de instruccionesse a un problema y les insta a reflexionar sobre las ventajas de los distintos métodos.
Los estudiantes empiezan pensando en los movimientos que harían para hallar el área de un cuadrilátero y explican sus preferencias a sus compañeros. A continuación, consideran y discuten las distintas estrategias adoptadas por otros estudiantes. A lo largo del proceso, pueden observar que algunas estrategias son más directas o eficaces que otras. Los estudiantes reflexionan sobre estas estrategias y utilizan sus conocimientos para planificar el trabajo de hallar el área de los polígonos en esta actividad y en las siguientes. Ten en cuenta que no es necesario que los estudiantes tomen el camino más eficiente. Es más importante que elijan un enfoque que tenga sentido para ellos, pero que tengan la oportunidad de ver los pros y los contras de los distintos caminos.
Pida a los estudiantes que recuerden la definición de cuadrilátero de grados anteriores, o diga a los estudiantes que un cuadrilátero es un polígono con 4 lados. Diga a los estudiantes que ahora vamos a pensar en cómo encontrar el área de los cuadriláteros.
Organice a los estudiantes en grupos de 4. Muestre la imagen de los cuadriláteros A-F para que todos los vean. Dirija su atención al cuadrilátero D.
Conceda a los estudiantes un minuto de silencio para pensar en los primeros 2-3 movimientos que harían para encontrar el área de D. Ofrezca algunos iniciadores de frases: "Primero, yo... A continuación, haría..., y después haría...". Anímeles a que muestren sus movimientos en el diagrama de su material. Haz hincapié en que sólo nos interesa el plan para encontrar el área y no el área en sí, por lo que no se espera que hagan cálculos. A continuación, deles 1-2 minutos para compartir sus movimientos con su grupo.
Pida a los estudiantes que indiquen cuál fue su primer movimiento. ¿Su primer movimiento consistió en:
• descomponer el cuadrilátero?
• encerrar el cuadrilátero?
• ¿otro movimiento?
Pregunte a los estudiantes cuyo primer movimiento consistió en descomponer la figura:
• "¿Cuántas piezas resultaron de la descomposición? ¿2 piezas? ¿3 piezas? ¿4 piezas? ¿Más?"
• "¿Cuál es el siguiente movimiento? ¿Reorganizar? ¿Duplicar una pieza? ¿Calcular el área de una pieza? ¿Algo más?"
Pregunte a los estudiantes cuyo primer movimiento es encerrar la figura:
• "¿Cuántos rectángulos has creado? ¿1 rectángulo? ¿2 rectángulos? ¿Más?"
• "¿Cuál es el siguiente movimiento? ¿Reorganizar las piezas sobrantes? ¿Calcular el área de una pieza extra? ¿Algo más?"
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

INSTRUCCIÓN CONTINUACIÓN
Para cada secuencia que mencionen los estudiantes, dibuje un diagrama rápido que la ilustre para que todos la vean.
Una vez que los estudiantes hayan tenido la oportunidad de ver una variedad de enfoques, pídeles que revisen su secuencia de movimientos. Conceda a los estudiantes 1-2 minutos para pensar en los pros y los contras de su plan original y en si había otra estrategia que les pareciera productiva. Invita a algunos estudiantes a compartir sus reflexiones.
A continuación, dé a los estudiantes un tiempo de silencio para completar la actividad y acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Pida a los estudiantes que tengan en cuenta las ventajas de las distintas estrategias que han visto a la hora de planificar su trabajo.
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus compañeros tutores previamente identificados.
Procesamiento conceptual: Eliminar Barreras. Ayudar a los estudiantes a ver las conexiones entre los nuevos problemas y el trabajo previo. Los estudiantes pueden beneficiarse de una revisión de diferentes representaciones para activar el
Encuentre el área de dos cuadriláteros de su elección. Muestra tu razonamiento.

POSIBLES RESPUESTAS
El razonamiento varía. Los estudiantes podrían descomponer el cuadrilátero en paralelogramos y triángulos para hallar el área, descomponer y reorganizar las piezas en una forma de la que puedan hallar fácilmente el área, o encerrar la figura en un rectángulo y restar el área de las piezas adicionales.
Figura A: 12 unidades cuadradas
Figura B: 18 unidades cuadradas
Figura C: 28 unidades cuadradas
Figura D: 14 unidades cuadradas
Figura E: 15 unidades cuadradas
Figura F: 18 unidades cuadradas SÍNTESIS DE LA ACTIVIDAD
Para concluir la actividad, pida a los estudiantes que elijan un cuadrilátero en el que hayan trabajado (que no sea el D) y que cuenten a su grupo el primer par de movimientos que hicieron para hallar su área y por qué. Anima a los demás miembros del grupo a que escuchen atentamente, comprueben que el razonamiento es válido y ofrezcan sus comentarios. Es posible que los estudiantes se hayan dado cuenta de que todas las aproximaciones implicaban descomponer una o más regiones en triángulos, rectángulos o ambos. Si los estudiantes no lo mencionan, señálelo. Haga hincapié en que podemos descomponer cualquier polígono en triángulos y rectángulos para hallar su área.
©Accelerate Learning Inc. - Todos los derechos reservados Math Nation California - Grade 6
Grado 6 . Matemáticas . Unidad 1

Apoyo para estudiantes de inglés
Speaking: MLR8 Apoyo a la discusión. Utilice esta rutina antes de que los grupos compartan el primer par de movimientos que hicieron para encontrar el área de uno de los cuadriláteros. Pregunte a la clase: "¿Cuáles son algunas palabras o frases importantes que pueden usar cuando describen los movimientos que hicieron?". Registre y muestre las respuestas de los estudiantes. Además de los términos matemáticos pertinentes, llame la atención de los estudiantes sobre el lenguaje que ayuda a comunicar el orden dentro de las aproximaciones. Recuerde a los estudiantes que utilicen la pantalla como recurso durante sus debates en grupo.
Principio(s) de diseño: Optimizar el resultado (para la explicación); Maximizar la metaconciencia
¿Estás preparado para más?
Aquí tienes un trapecio. a y b representan las longitudes de sus lados inferior y superior. El segmento denominado h representa su altura; es perpendicular a los lados superior e inferior.
Aplica estrategias de razonamiento de áreas -descomponer, reordenar, duplicar, etc.- en el trapezoide para que tengas una o más formas con áreas que ya sepas cómo hallar.
Utiliza las formas para ayudarte a escribir una fórmula para el área de un trapezoide. Muestra tu razonamiento.
Los estudiantes pueden cortar el trapezoide por la mitad horizontalmente, girar la pieza superior y unirla a la pieza inferior. Ven que pueden sumar las longitudes de los lados superior e inferior y multiplicarlas por la mitad de la altura original. Esto se construye sobre la comprensión previa de encontrar el área de un paralelogramo. 1 2 ⋅ �� ⋅ ( �� + ��)
Los estudiantes también pueden poner una copia idéntica del mismo trapezoide junto al original para formar un paralelogramo. A continuación, halla el área del paralelogramo y divídela entre 2 ( �� + ��) ⋅ �� ÷ 2
Otra forma de enfocar esto es trazar una diagonal y sumar las áreas de los dos triángulos resultantes. �� ⋅ �� ÷ 2 + �� ⋅ �� ÷ 2
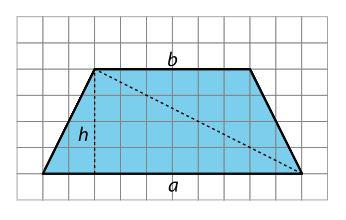
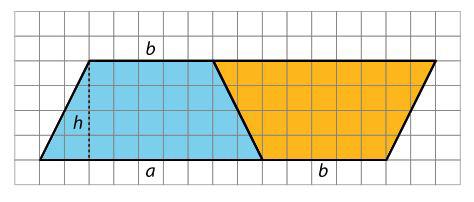
MOLINETE 30 minutos
Rutinas didácticas
MLR2: Recoger y exponer
Presentaciones en grupo
Materiales necesarios
Maestro de línea negra
En esta actividad, los estudiantes determinan el área de un polígono desconocido y piensan en varias formas de hacerlo. La tarea prepara a los estudiantes para hallar las áreas de otras formas desconocidas en contextos reales. También refuerza la práctica del razonamiento, la planificación y la perseverancia a la hora de resolver un problema (MP1). Los estudiantes razonan de forma independiente antes de discutir y registrar sus estrategias en grupos.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Dado que la forma del polígono es más compleja de lo que los estudiantes pueden haber visto hasta ahora, espere que los estudiantes experimenten con una o más estrategias. Considere la posibilidad de preparar copias adicionales del diagrama para que los estudiantes las utilicen, si es necesario.
A medida que los estudiantes trabajen, supervise los recorridos realizados por los distintos grupos y tome nota de las variaciones y complejidades. Si la variación de las estrategias es limitada, busque grupos que hayan registrado la misma estrategia de formas diferentes. Compruebe también si los estudiantes utilizan la estructura del molinete en sus razonamientos (MP7). ¿Se dan cuenta de que podría descomponerse en cuatro piezas (o conjuntos de piezas) idénticas? O, si encierran el molinete con un cuadrado, ¿utilizan el hecho de que las regiones adicionales son idénticas?
INSTRUCCIÓN
Organice a los estudiantes en grupos de 4. Dé a los estudiantes acceso a sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y 5 minutos de tiempo de silencio para planificar un enfoque para encontrar el área del molinete. A continuación, pídeles que compartan su plan con su grupo.
El grupo decide entonces qué estrategia o estrategias seguir, trabajan juntos para encontrar el área y crean una representación visual de la estrategia (o estrategias) utilizadas. Entrega a cada grupo una o varias copias del esquema para la presentación visual.
Habilidades motoras finas: Eliminar barreras. Proporcionar una versión ampliada de la imagen.
Funcionamiento socioemocional: Tutores. Empareje a los estudiantes con sus tutores previamente identificados.
ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS:
Halla el área de la región sombreada en unidades cuadradas. Muestra tu razonamiento.

El área es 40 unidades cuadradas.
Hay muchas maneras de descomponer esta figura. Ejemplos de respuestas:
Hay dos triángulos diferentes duplicados 4 veces. Ambos se pueden encontrar encerrando en rectángulos y restando las áreas de los triángulos rectángulos, o usando la fórmula para el área de un triángulo. 4 ⋅ 1 2 (3 ⋅ 4 + 2 ⋅ 4) = 40
El centro del molinete es un cuadrado con un área de 16 unidades cuadradas. Alrededor del cuadrado hay 4 trapezoides de los que los estudiantes pueden hallar el área encerrando y restando el área de las piezas sobrantes o descomponiéndolos y reordenándolos en un rectángulo con un área de 3 unidades cuadradas. Alrededor de cada trapezoide hay un triángulo cuya área los estudiantes pueden hallar utilizando la fórmula del área de un triángulo para hallar que cada uno tiene 3 unidades cuadradas.
©Accelerate Learning Inc. - Todos los derechos reservados Math Nation California - Grade 6
Grado 6 . Matemáticas . Unidad 1

Los estudiantes que superpongan un cuadrado girado sobre la figura de forma que los cuatro pivotes se muestren como cuatro triángulos rectángulos pueden utilizar longitudes laterales incorrectas para los triángulos (por ejemplo, suponiendo que una de las longitudes laterales es 2 unidades en lugar de 22⎯⎯√ unidades) o el cuadrado. Ayúdeles a ver que las diagonales de los cuadrados unitarios son más largas que la longitud de los lados midiéndolas.
Si los estudiantes tienen dificultades, sugiérales que utilicen una o más de las herramientas de su caja de herramientas para ayudarles a resolver el problema.
Pida a los grupos que visiten la exhibición visual de cada uno y discutan las siguientes preguntas mientras observan el trabajo de los demás:
• ¿Este grupo llegó a la misma área que nuestro grupo? Si no es así, ¿por qué?
• ¿En qué se parece su estrategia a la nuestra?
• ¿En qué se diferencia su estrategia de la nuestra?
Después del recorrido por la galería, pida a algunos estudiantes que comenten cómo se compara la estrategia de su grupo con la de otro grupo. Destaca las similitudes en el trabajo de los estudiantes en términos más generales. Por ejemplo, es probable que todos los grupos hayan utilizado uno de los siguientes enfoques:
• descompusieron el molinete en triángulos y utilizaron la fórmula para hallar el área de los triángulos
• descompusieron el molinete en triángulos y rectángulos, reorganizaron las piezas en rectángulos o paralelogramos y hallaron las áreas de esas regiones
• encerraron el molinete con un cuadrado, descompone las regiones sobrantes en triángulos y rectángulos, halla el área de las regiones sobrantes y réstalas de la del cuadrado
Refuerza que todos los enfoques implican descomponer un polígono en triángulos y rectángulos para hallar el área.
Apoyo para estudiantes de inglés
Conversar, representar: MLR2 Recoger y exponer. Durante el paseo por la galería, circule y escuche a los estudiantes hablar sobre las similitudes y diferencias entre las distintas estrategias. Preste atención a las frases comunes que escuche decir a los estudiantes sobre cada estrategia y anote las palabras de los estudiantes en una representación visual del molinete. Esto ayudará a los estudiantes a establecer conexiones entre las estrategias y también les proporcionará un lenguaje matemático que podrán utilizar durante el debate de toda la clase.
Principio(s) de diseño: Apoyar la adquisición de sentido
5 minutos
Para repasar las características definitorias de un polígono , vuelva a la imagen de la primera actividad (¿Qué son los polígonos?) y muestre la lista de características definitorias que los estudiantes generaron en esa actividad.
Repase cada figura que no sea un polígono y pida a los estudiantes que expliquen por qué no es un polígono. Anime a los estudiantes a utilizar su lista para apoyar sus explicaciones, así como para sugerir revisiones a su definición de trabajo.


Grado 6 . Matemáticas . Unidad 1

He aquí un polígono con 5 lados.

Pregunte a los estudiantes:
• "¿Cómo sabemos que esta figura es un polígono?". (Está compuesta por segmentos de recta. Cada segmento se encuentra sólo con otro segmento en cada extremo. Los segmentos no se cruzan. Es bidimensional.)
• "¿Qué significa hallar el área de este polígono?" (Significa hallar el área de la región dentro de él.)
• "¿Cómo podemos hallar el área de este polígono?" (Podemos descomponer la región dentro de él en triángulos y rectángulos.)
5 minutos
Este enfriamiento evalúa la comprensión de los estudiantes de las características que definen un polígono y las formas en que se puede descomponer.
INSTRUCCIÓN
ENUNCIADO DE LA TAREA
Dé a los estudiantes acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Diga a los estudiantes que sólo tienen que mostrar cómo se podría encontrar el área; no tienen que calcular realmente el área.
1. Aquí hay dos estrellas de cinco puntas. Un estudiante dice: "Ambas figuras A y B son polígonos. Ambas están compuestas por segmentos de línea y son bidimensionales. Ninguna tiene curvas". ¿Estás de acuerdo con la afirmación? Explica tu razonamiento.

2. Aquí tienes un polígono de cinco lados. Describe o muestra la estrategia que utilizarías para hallar su área. Marca y rotula el diagrama para mostrar tu razonamiento y que otros puedan seguirlo. (No es necesario calcular realmente el área.)

1. En desacuerdo. Sólo la figura B es un polígono. Las explicaciones varían. Ejemplo de explicación: Cada segmento de la figura A encuentra o cruza más de dos segmentos en sus extremos, por lo que no es un polígono. Cada segmento de la figura B se encuentra sólo con otro segmento en cada extremo.
2. Las respuestas varían. Ejemplos de diagramas y respuestas:
• El polígono puede descomponerse en tres triángulos: uno con una base de 6 unidades y una altura de 3, un segundo con una base de 7 y una altura de 6, y un tercero con una base de 4 y una altura de 6. Todas las áreas se pueden calcular utilizando la fórmula del área.

• El polígono se puede descomponer en dos triángulos y un rectángulo. Un triángulo tiene una base de 6 y una altura de 3, y el segundo tiene una base de 6 y una altura de 1. Sus áreas se pueden calcular con la fórmula del área. El rectángulo mide 6 por 4, por lo que su área es el producto de 6 y 4.
Grado 6 . Matemáticas . Unidad 1
PROBLEMA 1
Selecciona todos los polígonos.


PROBLEMA 2
Marca cada vértice con un punto grande. ¿Cuántas aristas y vértices tiene este polígono?

PROBLEMA 3
Halla el área de este trapecio. Explica o muestra tu estrategia.
Posibles soluciones
Posibles soluciones
Las siguientes figuras no son polígonos:
• Figura B, porque no tiene lados rectos
• Figura D, porque no es una figura cerrada
• Figura E, porque no tiene lados rectos
• Figura F, porque es una figura tridimensional
Posibles soluciones
12 aristas y 12 vértices

18 unidades cuadradas. Las estrategias varían. Posible estrategia: Encierra el trapezoide dentro de un rectángulo de 3-unidad por8-unidad. El área del rectángulo es 24 unidades cuadradas porque 8 ⋅ 3 = 24. El área de cada triángulo no sombreado dentro del rectángulo es 3 unidades cuadradas porque (2 ⋅ 3) ÷ 2 = 3. La suma de las áreas de los dos triángulos es 6 unidades cuadradas. 24 - 6 = 18, por lo que el área del trapecio es 18 unidades cuadradas.
PROBLEMA 4
Lin y Andre usaron métodos diferentes para hallar el área de un hexágono regular con 6-pulgadas de lado. Lin descompuso el hexágono en seis triángulos idénticos. André descompuso el hexágono en un rectángulo y dos triángulos.
Halla el área del hexágono usando el método de cada persona. Demuestra tu razonamiento.
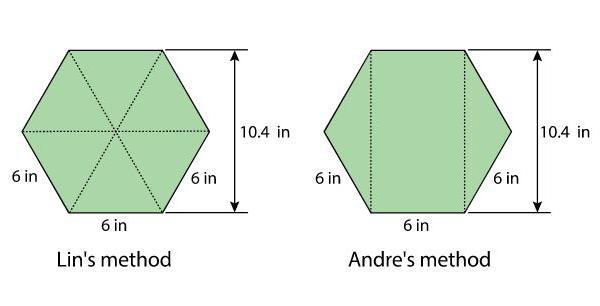
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Posibles soluciones
La altura de cada triángulo en el diagrama de Lin es la mitad de 10.4 pulgadas o 5.2 pulgadas. El área de cada triángulo es 15,6 pulgadas cuadradas.
1 2 ⋅ 6 ⋅ (5,2) = 15,6. El hexágono está formado por 6 triángulos, por lo que su área es 6 ⋅ (15 . 6) o 93.6 pulgadas cuadradas.
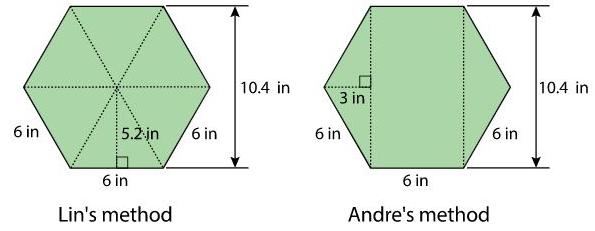
El rectángulo del diagrama de Andre es (10.4) ⋅ 6 o 62.4 pulgadas cuadradas. Cada triángulo tiene una base de 10.4 pulgadas y una altura de 3 pulgadas. (La distancia horizontal a través del centro del hexágono se compone de dos segmentos de 6-pulgadas. La línea vertical que dibujó André corta un segmento de 6-pulgadas por la mitad, por lo que el segmento de un lado mide 3 pulgadas). El área de cada triángulo es 1 2 ⋅ 10,4 ⋅ 3 o 15,6 pulgadas cuadradas. El área del hexágono es, por tanto, 62.4 + 15.6 + 15.6 o 93.6 pulgadas cuadradas.
PROBLEMA 5
Del 6º curso, Unidad 1, Lección 9
A. Identifica una base y una altura correspondiente que puedan usarse para hallar el área de este triángulo.
Rotula la base �� y la altura correspondiente ��.
B. Halla el área del triángulo. Muestra tu razonamiento.
PROBLEMA 6
Del Grado 6, Unidad 1, Lección 10
En la cuadrícula, dibuja tres triángulos diferentes con un área de 12 unidades cuadradas. Rotula la base y la altura de cada triángulo.

Reflexiones:
Posibles soluciones
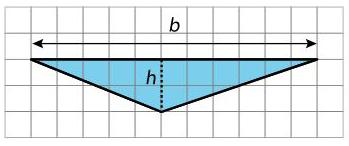
B. 11 unidades cuadradas. 1 2 ⋅ 11 ⋅ 2 = 11
Posibles soluciones
Las respuestas varían. Los dibujos deben mostrar triángulos con una base y una altura que se multipliquen para ser 24 unidades cuadradas (es decir, cada triángulo es la mitad de un paralelogramo con un área de 24 unidades cuadradas).
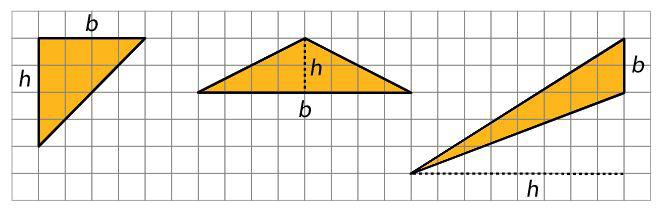


Redes y superficie
ALINEACIÓN
Alineación de estándares y principios de Abordar
6.G.4 Representar figuras tridimensionales utilizando redes formadas por rectángulos y triángulos, y utilizar las redes para hallar la superficie de estas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP6 Atender a la precisión.
Estándares ELD de California
I.A.3
I.C.12
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dar sentido al mundo
dar sentido a los problemas y perseverar en su resolución desarmar el todo, armar las partes y descubrir la forma y el espacio.
OBJETIVO(S) DE APRENDIZAJE
• Que's cubran las superficies de algunos objetos tridimensionales.
OBJETIVO(S) DE APRENDIZAJE
• Sé lo que significa la superficie de un objeto tridimensional.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Calcular la superficie de un prisma rectangular y explicar (oralmente y por escrito) el método de solución.
• Comprender que el término "superficie" (en lenguaje escrito y oral) se refiere a cuántas unidades cuadradas hacen falta para cubrir todas las caras de un objeto tridimensional.
Rutinas instructivas
Sondear a la clase
MLR8: Apoyos para la discusión
MLR7: Comparar y conectar
Pensar, compartir, en parejas
Materiales necesarios
Enfriamiento
Juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Cubos de chasquido
Preparación necesaria
Prepara 12 cubos por estudiante y copias adicionales de papel de puntos isométricos para la actividad Construir con cubos de presión.
Construye varios prismas rectangulares que sean cada uno 2 cubos por 3 cubos por 5 cubos para el enfriamiento.
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
Esta lección introduce a los estudiantes al concepto de área de superficie . Utilizan lo que han aprendido sobre el área de rectángulos para hallar el área superficial de prismas con caras rectangulares
Los estudiantes empiezan a explorar el área superficial en términos concretos, estimando y calculando después el número de notas adhesivas cuadradas que se necesitarían para cubrir un archivador. Dado que los estudiantes no reciben técnicas específicas de antemano, tienen que dar sentido al problema y perseverar en su resolución (MP1). La primera actividad pretende ser abierta y exploratoria. En la segunda actividad, aprenden que la superficie (en unidades cuadradas) es el número de unidades cuadradas que se necesitan para cubrir todas las superficies de una figura tridimensional sin huecos ni solapamientos (MP6).
Más adelante en la lección, los estudiantes utilizan cubos para construir prismas rectangulares y luego determinan sus superficies.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 5 min

Actividad de exploración Grupos reducidos 20 min
Los estudiantes determinan si la probabilidad indicada de diferentes sucesos hace que sea más o menos probable que ocurran.
Los miembros del grupo reciben cada uno distintas ruletas para realizar el mismo número de ensayos de un experimento.
Hay disponible un applet digital interactivoDespués, comparan los resultados para analizar cómo las diferencias en los espacios muestrales hacen que los experimentos no se ajusten a la probabilidad esperada. para que los estudiantes exploren los espacios muestrales no uniformes utilizando la tecnología.
Hay disponible una extensión de exploración para desarrollar una comprensión más profunda del efecto de los espacios muestrales en la probabilidad.
Actividad de exploración Grupos pequeños 10 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Los estudiantes se turnan para repetir un experimento y luego estiman la probabilidad de un suceso a partir de sus resultados.
Los estudiantes participan en un debate para consolidar su comprensión de la relación entre la probabilidad estimada y la probabilidad esperada.
Los estudiantes determinan qué probabilidad experimental es la más exacta y explican por qué ninguna de las probabilidades experimentales coincide con la probabilidad esperada.
El componente de práctica independiente incluye 3 en la lección y 2 problemas de repaso en espiral.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
Rutina didáctica
Sondeo de la clase
Notar y descubrirEsta actividad prepara a los estudiantes para pensar en la superficie, que explorarán en esta lección y en las siguientes. Los estudiantes ven un vídeo de un armario que se va embaldosando poco a poco con notas adhesivas que no se solapan. El armario se ha embaldosado sólo parcialmente, lo que plantea la cuestión del número de notas adhesivas necesarias para cubrir todo el prisma rectangular. Los estudiantes calculan la respuesta a esta pregunta.
Esta actividad fue inspirada por Andrew Stadel.
Organice a los estudiantes en grupos de 2. Muestre el vídeo de un maestro empezando a cubrir un gran armario con notas adhesivas o muestre las siguientes imágenes fijas para que todos las vean. Antes de empezar el vídeo o de mostrar la imagen, pide a los estudiantes que estén preparados para compartir una cosa que observan y una cosa que se preguntan. Conceda a los estudiantes un minuto para que compartan su observación y su pregunta con un compañero. Invita a algunos estudiantes a compartir sus preguntas con la clase. Si la pregunta "¿Cuántas notas adhesivas harían falta para cubrir todo el armario?" no se menciona, pregunte si alguien se pregunta cuántas notas adhesivas harían falta para cubrir todo el armario. Dé a los estudiantes un minuto para hacer una estimación. DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA


Las estimaciones varían. El número real de notas adhesivas es 935. Unas buenas estimaciones se sitúan en el intervalo 800-1.200.
Su maestro les mostrará un vídeo sobre un armario o algunas imágenes del mismo. Estime una respuesta a la pregunta: ¿Cuántas notas adhesivas harían falta para cubrir el armario, excluyendo el fondo? POSIBLES RESPUESTAS
Sondea a la clase para conocer las estimaciones de los estudiantes' y anótalas para que todos las vean. Invite a un par de estudiantes a compartir cómo han hecho su estimación. Explique a los estudiantes que ahora van a pensar cómo responder a esta pregunta.
Grado 6 . Matemáticas . Unidad 1
20 minutos
Rutinas instructivas
MLR7: Comparar y conectar
Después de hacer una estimación del número de notas adhesivas en un armario en el calentamiento, los estudiantes ahora hacen una lluvia de ideas para encontrar ese número con más precisión y luego calculan una respuesta. La actividad pide a los estudiantes que transfieran sus conocimientos sobre el área de los polígonos para hallar la superficie de un objeto tridimensional.
Los estudiantes aprenden que el área de la superficie de una figura tridimensional es el área total de todas sus caras. Dado que el área de una región es el número de unidades cuadradas que se necesitan para cubrir la región sin huecos ni solapamientos, el área de la superficie puede considerarse como el número de unidades cuadradas que se necesitan para cubrir todas las caras de un objeto sin huecos ni solapamientos. Las notas adhesivas cuadradas ilustran esta idea de forma concreta.
Mientras los estudiantes trabajan, observa los distintos enfoques adoptados para determinar el número de notas adhesivas necesarias para embaldosar las caras del armario (excluyendo la parte inferior). Identifique a los estudiantes con estrategias diferentes para compartirlas más tarde.
Organice a los estudiantes en grupos de 2-4. Dar a los estudiantes 1 minuto de silencio para pensar en la primera pregunta y otro minuto para compartir sus respuestas con su grupo. Pida a los estudiantes que hagan una pausa después.

Seleccione a algunos estudiantes para que compartan cómo harían para averiguar el número de notas adhesivas y qué información necesitarían. Los estudiantes pueden pedir algunas medidas:
• Las medidas del armario en términos de notas adhesivas: Diga a los estudiantes que el armario mide 24 por 12 por 6
• Las medidas del armario en pulgadas o centímetros: Diga a los estudiantes que no'dispone de esa información y pídales que piensen en otro dato que puedan utilizar.
• Las medidas de cada nota adhesiva: Comunique que mide 3 pulgadas por 3 pulgadas. Si ningún estudiante menciona que necesita las medidas de los bordes del armario en términos de notas adhesivas, deje que empiecen a trabajar en la segunda pregunta y proporcione la información cuando se den cuenta de que es necesaria. Conceda a los estudiantes entre 8 y 10 minutos para la segunda pregunta.
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus compañeros tutores previamente identificados.
Procesamiento conceptual: Ayudas visuales. Utilice una imagen del archivador con notas adhesivas a lo largo de los bordes,
Anteriormente, aprendiste acerca de un armario que se cubre con notas adhesivas.
1. ¿Cómo podrías encontrar el número real de notas adhesivas que se necesitarán para cubrir el armario, excluyendo la parte inferior? ¿Qué información necesitarías saber?
2. Utiliza la información que tienes para encontrar el número de notas adhesivas necesarias para cubrir el armario. Muestra tu razonamiento.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTASS
1. Halla el área de cada lado del armario, excluyendo la parte inferior, y súmalas. Información necesaria: medidas de las longitudes de los bordes del armario en notas adhesivas.
2. Las respuestas varían. Las estrategias pueden ser una combinación de las dos siguientes:
• Multiplica el número de notas adhesivas a lo largo de cada borde de cada lado. Suma todos los productos.
• Multiplica las longitudes de los bordes de cada lado del armario para hallar el área de cada lado. Suma todas las áreas.
Los estudiantes pueden tratar todos los lados como si fueran rectángulos congruentes. Es decir, encontrar el área de la parte frontal del armario y luego simplemente multiplicar por 5, o actuar como si la parte superior es el único lado que no es congruente con los demás. Si en el aula hay un armario real (o cualquier otro objeto grande con forma de prisma rectangular), considere la posibilidad de mostrar a los estudiantes que sólo los lados opuestos entre sí pueden suponerse idénticos.
Los estudiantes pueden pasar por alto el hecho de que la parte inferior del armario no estará cubierta. Señale que la parte inferior es inaccesible debido al suelo.
Invite a los estudiantes o grupos previamente identificados a compartir su respuesta y su estrategia. En una pantalla visual, registre cada respuesta y cada proceso distinto para determinar la superficie (es decir, multiplicar las longitudes de los lados de cada cara rectangular y sumar los productos). Después de cada presentación, pregunte a la clase si los demás han dado la misma respuesta o han seguido el mismo proceso.
Ponga el vídeo que revela el número real de notas adhesivas necesarias para cubrir el armario. Si las respuestas de los estudiantes' difieren de las mostradas en el vídeo, discuta las posibles razones de las diferencias. (Por ejemplo, es posible que los estudiantes no hayan tenido en cuenta los tiradores de las puertas del armario's . Algunos pueden haber cometido un error de cálculo).
Explica a los estudiantes que la pregunta que han intentado responder es sobre la superficie del armario. Explica que la superficie de una figura tridimensional es el área total de todas sus superficies. Llamamos a las superficies planas de una figura tridimensional sus caras.
El área de la superficie de un prisma rectangular sería entonces el área combinada de sus seis caras. En el contexto de este problema, excluimos la cara inferior, ya que está asentada sobre el suelo y no será embaldosada con notas adhesivas. Discute:
• "¿Qué unidad de medida estamos utilizando para representar la superficie del armario?" (Notas adhesivas cuadradas)
• "¿Cambiaría la superficie si utilizáramos notas adhesivas más grandes o más pequeñas? ¿Cómo?" (Sí, si utilizamos notas adhesivas más grandes, necesitaríamos menos. Si utilizamos notas adhesivas más pequeñas, necesitaríamos más).
Apoyo para estudiantes de inglés
Speaking, Listening: MLR7 Comparar y conectar. Mientras los estudiantes comparten sus estrategias para determinar el número de notas adhesivas que cubren el armario, pídales que establezcan conexiones entre las distintas estrategias. Algunos estudiantes calcularán el número de notas adhesivas que cubrirán cada una de las cinco caras del armario y las sumarán. Otros estudiantes pueden darse cuenta de que las caras opuestas del armario son congruentes, por lo que sólo es necesario calcular el área de tres caras del armario. Anime a los estudiantes a explicar por qué ambos métodos dan como resultado la misma respuesta. Esto fomentará en los estudiantes' el uso del lenguaje matemático a medida que van dando sentido a los distintos métodos para hallar el área de la superficie de un prisma rectangular.
Principios de diseño: Cultivar la conversación; Maximizar la metaconciencia
Grado 6 . Matemáticas . Unidad 1

¿Estás listo para más?
¿Cuántas notas adhesivas se necesitan para cubrir el exterior de 2 armarios empujados juntos (incluyendo la parte inferior)? ¿Y en 3 armarios? 20 armarios?
"¿Estás preparado para más?" Respuesta del estudiante
Dos armarios: 1.582 notas adhesivas. Tres armarios: 2.229 notas adhesivas. Veinte armarios: 13.228 notas adhesivas.
SNAP 20 minutos
Rutinas instructivas
MLR8: Apoyos para la discusión
Think Pair Share
Esta actividad anima a los estudiantes a aplicar estrategias para encontrar el área de polígonos para encontrar el área de superficie de prismas rectangulares. Los estudiantes utilizan 12 cubos para construir un prisma, piensan en su superficie y utilizan papel de puntos isométricos para dibujar su prisma.
A medida que los estudiantes construyen sus prismas, se fijan en los que tienen diseños diferentes y en los que tienen el mismo diseño pero diferentes enfoques para hallar la superficie (por ejemplo, contando cuadrados individuales, multiplicando las longitudes de las aristas de las caras rectangulares, etc.).
Lean juntos las dos primeras líneas del enunciado de la tarea. Recuerde a los estudiantes que nos referimos a las superficies planas de una figura tridimensional como caras Dé a los estudiantes un minuto para pensar cómo sabemos que el área de la superficie del prisma mostrado es 32 unidades cuadradas. Pida a 1-2 estudiantes que expliquen su razonamiento a la clase. Utilice las explicaciones de los estudiantes' para resaltar el significado de superficie, es decir, que hay que tener en cuenta el área de todas las caras, incluidas las que no podemos ver al mirar un dibujo bidimensional. Diga a los estudiantes que utilizarán 12 cubos para construir un prisma diferente, dibujarlo y hallar su superficie. Considere hacer una demostración rápida sobre cómo dibujar un prisma simple en papel de puntos isométricos. (Comience con un cubo y luego añada un cubo en cada dimensión.) Diga a los estudiantes que en esta actividad, llamamos a cada cara de un cubo, "1 unidad cuadrada."
Dé a cada estudiante 12 cubos para construir un prisma y 6-8 minutos de tiempo de trabajo tranquilo. Si los estudiantes utilizan cubos a presión, dígales que fingiremos que todas las caras son completamente lisas, por lo que no tendrán que preocuparse por los "entrantes y salientes" de los cubos a presión.
Mientras los estudiantes trabajan, considere la posibilidad de formar parejas con dos estudiantes con diseños o estrategias opuestos. Pídales que compartan sus respuestas, explicaciones y dibujos. Haga hincapié en que cada compañero debe centrar su explicación en cómo ha calculado la superficie. El oyente debe pensar si la explicación tiene sentido o si falta algo en el razonamiento.
Los estudiantes de aulas digitales pueden utilizar un applet para construir y dibujar prismas. No obstante, para construir las figuras se siguen recomendando y prefiriendo los cubos físicos.
Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina les dicten cómo dibujar la figura en el papel de puntos isométricos según sea necesario.
- Grado 6
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS
Aquí hay un prisma rectangular construido con 12 cubos::
Tiene seis caras, pero solo se ven tres en el boceto. Su superficie es de 32 unidades cuadradas. La aplicación también tiene 12 bloques. Todos están en el mismo punto de la pantalla, como una pila oculta de bloques. Siempre sabrás dónde está la pila porque se encuentra sobre un cuadrado gris. Para usar un bloque, arrastra el punto rojo para moverlo. Haz clic en los puntos rojos para cambiar de movimiento de izquierda a derecha a movimiento de arriba a abajo.
Usa los 12 cubos para construir un prisma rectangular diferente (con longitudes de aristas diferentes a las que se muestran en el prisma). Puedes girar la vista para ver todas las caras de tu figura.
1. ¿Cuántas caras tiene tu figura?
2. ¿Cuál es el área de la superficie de tu figura en unidades cuadradas?? Aquí se muestra un boceto de un prisma rectangular construido a partir de 12 cubos:
Tiene seis caras, pero solo se pueden ver tres de ellas en el boceto. Tiene una superficie de 32 unidades cuadradas.
Tienes 12 cubos encajables de tu maestro. Usa todos tus cubos encajables para construir un prisma rectangular diferente (con longitudes de aristas diferentes a las que se muestran en el prisma aquí).
1. ¿Cuántas caras tiene tu figura?
2. ¿Cuál es el área de la superficie de tu figura en unidades cuadradas?
3. Dibuja tu figura en papel punteado isométrico. Colorea cada cara de un color diferente.

• Hay 6 caras: frontal, posterior, izquierda, derecha, superior e inferior.
• Las respuestas varían según el diseño. Ejemplos de respuestas:
• Para un prisma de 12 unidades por 1 unidad por 1 unidad, el área superficial es de 50 unidades cuadradas. (4 ⋅ 12) + (2 ⋅ 1) = 50
• Para un prisma de 6 unidades por 2 unidades por 1 unidad, el área superficial es de 40 unidades cuadradas. (2 ⋅ 12) + (2 ⋅ 6) + (2 ⋅ 2) = 40
• Para un prisma de 4 unidades por 3 unidades por 1 unidad, el área superficial es de 38 unidades cuadradas. (2 ⋅ 12) + (2 ⋅ 4) + (2 ⋅ 3) = 40
Los estudiantes pueden contar las caras de los cubos individuales en lugar de las caras del prisma completo. Ayúdelos a comprender que las caras son las visibles en el exterior de la figura.
Grado 6 . Matemáticas . Unidad 1
Después de debatir en parejas, seleccione a un estudiante para que destaque ante la clase la estrategia (o estrategias) para hallar metódicamente el área de la superficie. Señale que, en esta actividad, cada cara de su prisma es un rectángulo y que podemos hallar el área de cada rectángulo multiplicando las longitudes de sus lados y sumando después las áreas de todas las caras. Explica que más adelante, cuando nos encontremos con prismas no rectangulares, podremos razonar sobre el área de cada cara del mismo modo que razonamos sobre el área de un polígono.
Apoyo para estudiantes de inglés
Speaking: MLR8 Apoyos para el debate. Utilice esta rutina para apoyar la discusión de toda la clase. Pida a los estudiantes que utilicen el lenguaje matemático (por ejemplo, cubos, caras, superficie, unidades cuadradas, etc.), para reafirmar y/o repetir la estrategia (o estrategias) presentada. Considere la posibilidad de dar tiempo a los estudiantes para que repitan lo que han oído a un compañero, antes de seleccionar a uno o dos estudiantes para que lo compartan con la clase. De este modo, más estudiantes tendrán la oportunidad de producir un lenguaje que describa las estrategias para hallar la superficie.
5 minutos
En esta lección, hemos hallado las áreas superficiales de un armario y de prismas rectangulares construidos con cubos.
• "¿Qué significa hallar la superficie de una figura tridimensional?" (Significa hallar el número de cuadrados unitarios que cubren toda la superficie del objeto sin huecos ni solapamientos.)
• "¿Cómo podemos hallar el número de cuadrados unitarios que cubren toda la superficie de un objeto?" (Podemos contarlos, o podemos hallar el área de cada cara del objeto y sumar las áreas de todas las caras.)
• "¿En qué se parecen hallar el área de la superficie y hallar el área? ¿En qué se diferencian?" (Ambas implican hallar el número de cuadrados unitarios que cubren una región por completo sin huecos ni solapamientos. Ambas tienen que ver con regiones bidimensionales. Para hallar la superficie se necesita un único polígono. Hallar la superficie significa hallar la suma de las áreas de múltiples polígonos (caras) de los que se compone una figura tridimensional).
5 minutos
Prepara varios prismas rectangulares que sean cada uno 2 cubos por 3 cubos por 5 cubos. Exponga uno para que todos lo vean y pase el resto para que los estudiantes lo examinen, si es necesario.
Un prisma rectangular mide 3 unidades de alto, 2 unidades de ancho y 5 unidades de largo. ¿Cuál es su superficie en unidades cuadradas? Explica o muestra tu razonamiento.


©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS
El área de la superficie es 2 ⋅ [(3 ⋅ 5) + (2 ⋅ 5) + (2 ⋅ 3)] = 62 (o 62 unidades cuadradas).
Los estudiantes pueden no incluir la cara inferior, ya que no es visible cuando el prisma está sentado sobre una mesa.
Los estudiantes pueden hallar el número de cubos en lugar de la superficie debido a su trabajo previo de volumen con prismas rectangulares en 5º curso.
PROBLEMA 1
¿Cuál es el área de la superficie de este prisma rectangular?
A. 16 unidades cuadradas
B. 32 unidades cuadradas
C. 48 unidades cuadradas
D. 64 unidades cuadradas
Soluciones posibles
D
PROBLEMA 2
¿Qué descripción puede representar el área de la superficie de este tronco?
A. El número de pulgadas cuadradas que cubren la parte superior del tronco.
B. El número de pies cuadrados que cubren todas las caras exteriores del tronco.
C. El número de pulgadas cuadradas de superficie horizontal dentro del tronco.
D. El número de pies cúbicos que pueden caber dentro del tronco.
Posibles soluciones
B
Learning Inc. - Todos los derechos reservados


PROBLEMA 3
¿Qué figura tiene una superficie mayor?
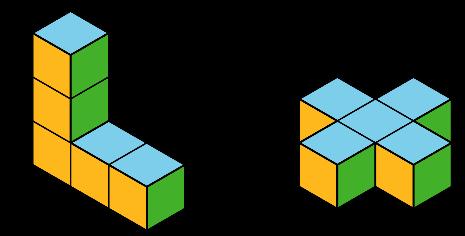
PROBLEMA 4
Un prisma rectangular tiene 4 unidades de alto, 2 unidades de ancho y 6 unidades de largo. ¿Cuál es su superficie en unidades cuadradas? Explica o muestra tu razonamiento.
Posibles soluciones
Grado 6 . Matemáticas . Unidad 1

PROBLEMA 5
Del Grado 6, Unidad 1, Lección 9
Dibuja un ejemplo de cada uno de los siguientes triángulos en la cuadrícula.

A. Un triángulo rectángulo con un área de 6 unidades cuadradas.
B. Un triángulo agudo con un área de 6 unidades cuadradas.
C. Un triángulo obtuso con un área de 6 unidades cuadradas.
PROBLEMA 6
Del Grado 6, Unidad 1, Lección 10
Encuentra el área del triángulo MOQ en unidades cuadradas. Muestra tu razonamiento.
California - Grado 6
La figura A y la figura B tienen la misma superficie de 22 unidades cuadradas.
Posibles soluciones
88 unidades cuadradas. Dos caras miden 4 unidades por 2 unidades, sumando 16 unidades cuadradas. Dos caras son 4 unidades por 6 unidades, sumando 48 unidades cuadradas. Dos caras son 2 unidades por 6 unidades, sumando 24 unidades cuadradas. 16 + 48 + 24 = 88
Posibles soluciones
Las respuestas varían. Ejemplo de respuesta:
Posibles soluciones
20 unidades cuadradas. El razonamiento varía. Ejemplo de razonamiento: El área del triángulo MOQ se puede hallar restando las áreas de los tres triángulos rectángulos del área del rectángulo MNPR.
• El área del rectángulo MNPR es 10 ⋅ 6 o 60 unidades cuadradas.
• El área del triángulo QRM es 1 2 ⋅ 6 ⋅ 5 o 15 unidades cuadradas.
• El área del triángulo MNO es 1 2 ⋅ 10 ⋅ 4 o 20 unidades cuadradas.
• El área del triángulo OPQ es 1 2 ⋅ 2 ⋅ 5 o 5 unidades cuadradas.
60 - (15 + 20 + 5) = 20
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 7
Del Grado 6, Unidad 1, Lección 3
Halla el área de esta figura. Muestra tu razonamiento.
Posibles soluciones
15 unidades cuadradas. El razonamiento varía. Ejemplo de razonamiento:
• La figura se puede descomponer en dos triángulos idénticos con un corte vertical en el medio. Cada triángulo tiene de base 3 unidades y de altura 5 unidades, por lo que su área es 1 2 ⋅ 3 ⋅ 5 o 7,5 unidades cuadradas. 2 ⋅ (7,5) = 15
• La figura puede descomponerse en dos triángulos idénticos y reorganizarse en un paralelogramo de base 3 unidades y altura 5 unidades. 3 ⋅ 5 = 15
Reflexiones:
Learning Inc. - Todos los derechos reservados


• Redes y superficie
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
6.G.4 Representar figuras tridimensionales usando redes formadas por rectángulos y triángulos, y usar las redes para encontrar el área de la superficie de estas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfocar SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.B.8
I.C.11
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dar sentido al mundo
construir argumentos viables y criticar el razonamiento de los demás
OBJETIVO(S) DE APRENDIZAJE
• Vamos a investigar los poliedros.
desmontar enteros, unir partes y descubrir la forma y el espacio.
• Puedo describir las características de un poliedro utilizando vocabulario matemático.
• Puedo explicar la diferencia entre prismas y pirámides.
• Comprendo la relación entre un poliedro y su red.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comparar y contrastar (oralmente y por escrito) características de prismas y pirámides.
• Comprender y utilizar las palabras "cara", "arista", "vértice" y "base" para describir poliedros (en lenguaje oral y escrito).
• Comprender que la palabra "red" se refiere a una figura bidimensional que puede ensamblarse en un poliedro, y crear una red para un poliedro dado.
Rutinas instructivas
Notar y descubrir
MLR2: recopilar y mostrar
MLR3: Aclarar, Criticar, Corregir
Materiales Requeridos
Patrón de líneas negras para la Actividad 13.1
Patrón de líneas negras para la Actividad 13.2
Patrón de líneas negras para la Actividad 13.3
Enfriamiento
Materiales necesarios Continuación
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Pegamento o barras de pegamento
Redes de poliedros
Poliedros premontados o producidos comercialmente
Tijeras
Cinta adhesiva
Grado 6 . Matemáticas . Unidad 1
Preparación necesaria
Reúne colecciones de figuras geométricas que contengan cada una al menos 2 poliedros conocidos, 2 poliedros desconocidos y 2 no poliedros. Prepare una colección para cada grupo de 3-4 estudiantes. Si no dispone de poliedros prefabricados, monte algunos a partir de las redes del patrón de líneas negras para el calentamiento.
Imprima y recorte previamente las redes y los polígonos del patrón de líneas negras para Prismas y pirámides. Prepara 1 juego de por grupo de 3-4 estudiantes, junto con cinta adhesiva para unir los polígonos en una red.
Para la actividad opcional de Ensamblaje de poliedros, imprime las redes a partir del mismo patrón de líneas negras que para el calentamiento. Prepara 2 copias de una red por estudiante, y cinta adhesiva o pegamento para ensamblar la red.
Narrativa de la lección
En esta lección, los estudiantes aprenden sobre poliedros y sus redes. También estudian prismas y pirámides como tipos de poliedros con ciertas características definitorias.
Los poliedros se pueden considerar como el análogo tridimensional de los polígonos.
He aquí algunos aspectos importantes de los polígonos:
• Están formados por segmentos de línea llamados aristas.
• Las aristas se encuentran en un vértice.
• Las aristas sólo se encuentran en los vértices.
• Los polígonos siempre encierran una región bidimensional.
He aquí una forma análoga de caracterizar los poliedros:
• Están formados por polígonos rellenos llamados caras.
• Las caras se encuentran en una arista.
• Las caras sólo se encuentran en las aristas.
• Los poliedros siempre encierran una región tridimensional.
No es necesario que los estudiantes memoricen una definición formal de poliedro, pero ayúdales a entender las redes y la superficie.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Grupos pequeños 10 min Los estudiantes descubren las características de los poliedros analizando ejemplos y no ejemplos y luego clasifican los objetos como poliedros o no poliedros.
Actividad de exploración Grupos pequeños 30 min
Actividad de Exploración Opcional

Independiente 20 min
Nation California - Grado 6
Los estudiantes analizan prismas y pirámides para determinar sus características y exploran redes de poliedros.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las caras de un poliedro.
Los estudiantes ensamblan una red de un poliedro y determinan el número de vértices, aristas y caras que tiene el poliedro.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
Componente de la lección Estructura Tiempo

Breve descripción
Síntesis Todo el grupo 5 min Los estudiantes resumen su comprensión de poliedros, prismas, pirámides y redes.
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Los estudiantes utilizan lenguaje académico para demostrar su comprensión de las características de los poliedros.
El componente de práctica independiente incluye 3 problemas de repaso en clase y 3 problemas de repaso en espiral.
10 minutos
Rutinas instructivas
Pensar Compartir en parejas
En este calentamiento, los estudiantes analizan ejemplos y contraejemplos de poliedros, observan las características que los definen y utilizan sus conocimientos para clasificar los objetos en poliedros y no poliedros. A continuación, empiezan a desarrollar una definición práctica de poliedro.
Prepare ejemplos físicos de poliedros y no poliedros para que los estudiantes los clasifiquen. Estos ejemplos deben ser figuras geométricas y no objetos del mundo real, como cajas de zapatos o botes. Si no se dispone de tales figuras, elabore algunas con antelación utilizando las redes del patrón de líneas negras.
Mientras los estudiantes trabajan y discuten, fíjese en aquellos que puedan articular las características definitorias de un poliedro. Invítelos a compartir más tarde.
INSTRUCCIÓN
Organice a los estudiantes en grupos de 3-4. Conceda a los estudiantes 1 minuto de tiempo de silencio para estudiar los ejemplos y los no-ejemplos del enunciado de la tarea. Pídales que estén preparados para compartir al menos una cosa en la que se hayan fijado y otra que se hayan preguntado. Concede a la clase un minuto para que compartan algunas de sus observaciones y preguntas.
A continuación, entregue a cada grupo un conjunto físico de figuras tridimensionales. El conjunto debe incluir algunos poliedros conocidos, otros desconocidos y algunos no poliedros.
Pida a los grupos que clasifiquen las figuras en poliedros y no poliedros (la primera pregunta). Si los miembros del grupo no están de acuerdo sobre si una figura es un poliedro, discútanlo. Cuando el grupo haya llegado a un acuerdo, déles 2-3 minutos de tiempo de silencio para completar la segunda pregunta.
Aquí hay imágenes que representan poliedros: Aquí hay imágenes que no representan poliedros:

1. Su maestro les dará algunas figuras u objetos. Clasifícalos en poliedros y no poliedros.
2. ¿Qué características te ayudaron a distinguir los poliedros de las otras figuras?
Grado 6 . Matemáticas . Unidad 1

1. No se requiere respuesta.
2. Las respuestas varían. Ejemplos de respuestas:
• Los poliedros están hechos de polígonos.
• Los poliedros no tienen aristas sueltas.
• Los no poliedros a veces tienen superficies curvas o redondas.
• Algunos no poliedros tienen una cara que no es un polígono.
Invite a los estudiantes a compartir los rasgos que creen que caracterizan a los poliedros. Anote sus respuestas para que todos las vean. Para cada una de ellas, pregunte a la clase si están de acuerdo o en desacuerdo. Si en general están de acuerdo, pregunte si hay algo que añadirían o ampliarían para que la descripción fuera más clara o precisa. Si no están de acuerdo, pida una explicación o un contraejemplo.
Los estudiantes tendrán la oportunidad de refinar su definición de poliedros más adelante en la lección, después de explorar los prismas y las pirámides y de aprender sobre las redes, por lo que no es importante recopilar un conjunto completo o preciso de descripciones o características.
Utilice un poliedro de muestra o un diagrama como el que se muestra a continuación para introducir o reforzar la terminología relativa a los poliedros.
A. Los polígonos que componen un poliedro se denominan caras
B. Los lugares donde se unen los lados de las caras se denominan aristas
C. Las "esquinas" se denominan vértices. (Aclarar que la forma singular es "vértice" y la forma plural es "vértices".)
30 minutos
Rutinas instructivas
MLR2: Recoger y exponer
Materiales necesarios
Maestro de línea negra
Esta actividad tiene dos objetivos: descubrir las características que definen los prismas y las pirámides así como introducir las redes como representaciones bidimensionales de los poliedros.
Los estudiantes analizan primero los prismas y las pirámides e intentan definir sus características. A continuación, aprenden sobre las redes y piensan en los polígonos necesarios para componer las redes de prismas y pirámides dados. A continuación, utilizan su experiencia con las redes de prismas y pirámides para afinar y refinar sus definiciones de estos poliedros.
Pida a los estudiantes que discutan las características de los prismas y las pirámides, anímeles a utilizar los términos cara, arista y vértice (vértices) en sus descripciones. INSTRUCCIÓN
Disponer a los estudiantes en grupos de 3-4
Para la primera pregunta:
• Decir a los estudiantes que los poliedros A-F son todos prismas y los poliedros P-S son todos pirámides. (Exponga y distribuya los prismas y pirámides del enunciado de la tarea, si dispone de ellos).
• Conceda a los estudiantes 2-3 minutos de silencio para la primera pregunta y 2-3 minutos para discutir sus observaciones en sus grupos. Pídales que hagan una pausa para debatir en clase antes de continuar.
• Solicite a los estudiantes sus ideas sobre las características que distinguen a los prismas de las pirámides. Anote las respuestas de los estudiantes en dos columnas: una para los prismas y otra para las pirámides. No es importante que las listas estén completas en este punto.
- Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

A continuación, diga a los estudiantes que vamos a utilizar redes para comprender mejor los prismas y las pirámides. Explique que una red es una representación bidimensional de un poliedro. Muestre un cubo ensamblado a partir de la red proporcionada en el patrón de líneas negras para el calentamiento, así como un recorte de una red desplegada (considere quitar las solapas). Demuestre cómo la red con cuadrados podría doblarse y ensamblarse en un cubo, o utilice este libro de applets digitales, Señale cómo el número y la forma de las caras en el cubo corresponden al número y la forma de los polígonos en la red.
Para la segunda pregunta:
• Dé a los grupos un minuto de tiempo para pensar en silencio y un minuto para discutir su respuesta.
• Para verificar su respuesta, entregue a cada grupo una de las tres redes de la primera página del patrón de líneas negras. Pídeles que intenten montar una pirámide triangular con su red.
• Invita a los grupos a compartir con la clase si es posible hacerlo. Discuta por qué la red 3 no se puede ensamblar en la Pirámide P (dos de los triángulos se solaparían).
Para la última pregunta, diga a los estudiantes que crearán una red de otro prisma o pirámide:
• Asigne a cada grupo un prisma o una pirámide del enunciado de la tarea (excepto el Prisma B y la Pirámide P).
• Entregue a cada grupo un conjunto de polígonos precortados de las dos últimas páginas del patrón de líneas negras.
• Pide a los estudiantes que elijan el tipo y el número de polígonos adecuados para formar su poliedro. A continuación, disponga los polígonos de modo que, al pegarlos y doblarlos, la disposición forme una red y pueda ensamblarse en su prisma o pirámide. Anímales a pensar en más de una red, si es posible.
Speaking, Conversing: MLR2 Recoger y mostrar. Mientras los estudiantes trabajan en la creación de una red de su poliedro asignado, circule y escuche el lenguaje que utilizan los estudiantes al hablar de los polígonos que componen sus poliedros, así como las características de sus poliedros (por ejemplo, triángulo, rectángulo, cuadrado, hexágono, pentágono, vértice, arista, cara). Recoja este lenguaje, con los dibujos correspondientes, y muéstrelo a todos los estudiantes. Recuerde a los estudiantes que tomen prestado el lenguaje de la exposición cuando describan las características de los prismas y las pirámides. Esto ayudará a los estudiantes a producir un lenguaje matemático para describir y definir las características de los poliedros.
Principio(s) de diseño: Apoyar la adquisición de sentido
Procesamiento conceptual: Manipulativos. Proporcionar manipulativos (por ejemplo, prismas y pirámides) para ayudar a los estudiantes que se benefician de las actividades prácticas.
Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (por ejemplo, poliedros, prisma, pirámide, base, cara, vértice, arista, etc.) para mostrar públicamente definiciones, reglas, fórmulas o conceptos importantes para referencia futura.
1. Aquí hay unos poliedros llamados prismas Aquí hay algunos poliedros llamados pirámides


A. Observa los prismas. ¿Cuáles son sus características?
B. Observa las pirámides. ¿Qué características tienen?
Grado 6 . Matemáticas . Unidad 1

1. ¿Cuál de las siguientes redes puede plegarse en la Pirámide P? Selecciona todas las que correspondan.
2. Tu maestro dará a tu grupo un conjunto de polígonos y asignará un poliedro.
A. Decide qué polígonos son necesarios para componer el poliedro asignado. Enumera los polígonos y cuántos de cada uno se necesitan.
B. Organiza los recortes en una red que, si se pega y se dobla, pueda ensamblarse en el poliedro. Dibuja la red. Si es posible, encuentra más de una forma de organizar los polígonos (muestra una red diferente para el mismo poliedro).
1. Las respuestas varían. Ejemplos de respuestas:
A. Un prisma tiene caras rectangulares. Algunas de las caras son paralelas entre sí. Un prisma puede tener dos caras que no sean rectángulos.
B. Una pirámide tiene un triángulo para todas o todas menos una de sus caras. Esa única cara puede ser un polígono diferente, y todos los triángulos comparten una arista con ella. Todos los triángulos también se encuentran en un único vértice.
2. Las redes 1 y 2 se pueden ensamblar en la pirámide P, pero la red 3 no.
3.
A. Las respuestas varían. Posibles respuestas:
Prisma A: 2 triángulos, 3 cuadrados
Prisma C: 2 triángulos, 3 rectángulos
Prisma D: 2 pentágonos, 5 rectángulos
Prisma E: 2 cuadrados, 4 rectángulos
Prisma F: 2 hexágonos, 6 rectángulos
Pirámide Q: 1 cuadrado, 4 triángulos
Pirámide R: 1 pentágono, 5 triángulos
Pirámide S: 1 hexágono, 6 triángulos
B. Los dibujos varían.
Selecciona grupos para que compartan sus disposiciones de polígonos. Si el tiempo lo permite y es posible, pida a los estudiantes que peguen con cinta adhesiva sus polígonos y doblen la red para comprobar que se puede ensamblar en el poliedro previsto. Debate:
• "¿Qué tienen en común las redes de los prismas?" (Todas tienen rectángulos. Tienen un par de polígonos que pueden no ser rectángulos.)
• "¿Qué tienen en común las redes de las pirámides?" (Todas tienen triángulos. Tienen un polígono que puede no ser un triángulo.)
• "¿Sólo hay una red posible para un prisma o una pirámide?" (No, los polígonos pueden disponerse de diferentes maneras y aún así ensamblarse en el mismo prisma o pirámide.)
Explica los siguientes puntos sobre prismas y pirámides:
• Un prisma tiene dos caras paralelas e idénticas llamadas bases y un conjunto de rectángulos que conectan las bases.
• Los prismas se llaman así por la forma de las bases. Por ejemplo, si la base de un prisma es un pentágono, entonces el prisma se llama "prisma pentagonal".
• Una pirámide tiene una cara llamada base que puede ser cualquier polígono y un conjunto de caras que son todas triángulos. Cada arista de la base se comparte con una arista de un triángulo. Todos estos triángulos se unen en un único vértice.
• Las pirámides reciben su nombre por la forma de su base. Por ejemplo, si la base de una pirámide es un cuadrado, entonces la pirámide se llama "pirámide cuadrada".
- Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

¿Estás preparado para más?
¿Cuál es el menor número de caras que puede tener un poliedro? Explica cómo lo sabes.
"¿Estás preparado para más?" Respuesta del estudiante
Cuatro caras (una pirámide triangular, también conocida como tetraedro). Las explicaciones varían. Ejemplo de explicación: El triángulo es el polígono con el menor número de lados. Si hay una cara triangular, debe haber otro polígono unido a cada uno de sus bordes, por lo que es imposible utilizar menos de cuatro caras. Es posible crear un poliedro con cuatro caras triangulares. (La pirámide P de esta actividad es un ejemplo.)
20 minutos
Rutinas didácticas
MLR3: Aclarar, Criticar, Corregir
Materiales necesarios
Blackline master
Esta actividad opcional proporciona a los estudiantes la experiencia de ensamblar poliedros a partir de redes. Contar los vértices, aristas y caras de un poliedro ayuda a reforzar la comprensión del vocabulario. Necesitará el mismo patrón de líneas negras que el proporcionado para el calentamiento. Es probable que los estudiantes necesiten ayuda para montar sus poliedros. Circule y ayude a los estudiantes según sea necesario.
INSTRUCCIÓN
Diga a la clase que van a ensamblar poliedros a partir de redes. Señale que la red tiene polígonos sombreados y no sombreados. Muestre un ejemplo y explique que sólo los polígonos sombreados de las redes se verán una vez que la red esté ensamblada. Los polígonos sin sombrear son "solapas" que facilitan el pegado de los polígonos; se colocan detrás de los polígonos sombreados y no forman parte del poliedro. Explica a los estudiantes que si primero pliegas todas las líneas, te resultará más fácil doblar la red y unir los distintos polígonos. Una regla puede ser muy útil para hacer los pliegues. Entrega a cada estudiante dos copias de una red para que puedan comparar la versión montada con la desplegada. Proporcione herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y pegamento o cinta adhesiva. Pida a los estudiantes que construyan sus figuras y completen la pregunta, y que después discutan sus respuestas con otro estudiante que tenga el mismo poliedro.
Apoyo a estudiantes con discapacidad
Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten cómo cortar, doblar y pegar la red según sea necesario.
1. Tu maestro te dará la red de un poliedro. Recorta la red y dóblala por las aristas para formar un poliedro. Pega las solapas con cinta adhesiva o pegamento para que no queden aristas sin unir.
2. ¿Cuántos vértices, aristas, y caras hay en tu poliedro?
ENUNCIADO
Grado 6 . Matemáticas . Unidad 1

1. No se requiere respuesta.
2. Las respuestas varían. Posibles respuestas:
A: 6 vértices, 9 aristas, 5 caras
B: 8 vértices, 12 aristas, 6 caras
C: 8 vértices, 12 aristas, 6 caras
D: 8 vértices, 12 aristas, 6 caras
E: 4 vértices, 6 aristas, 4 caras
F: 5 vértices, 8 aristas, 5 caras
G: 6 vértices, 10 aristas, 6 caras
H: 8 vértices, 14 aristas, 8 caras
J: 10 vértices, 20 aristas, 12 caras
K: 9 vértices, 15 aristas, 8 caras
Los estudiantes pueden tener problemas para obtener un recuento exacto de caras, aristas y vértices. Sugiérales que coloquen la figura sobre la mesa y luego cuenten por separado el número de caras superiores, inferiores y laterales de la figura. O recomiéndeles que etiqueten cada cara con un número o un nombre y que lleven la cuenta de las partes asociadas a cada cara, teniendo cuidado de no contar dos veces las aristas y los vértices.
Después de que los estudiantes hayan consultado con otro estudiante y se hayan puesto de acuerdo sobre el número de vértices, aristas y caras de su poliedro, diga a la clase que ahora compartirán con la clase sus poliedros completados y la versión desplegada de la red. Considere la posibilidad de pedir a los estudiantes que se pasen sus dos elementos o de dejar sus poliedros y redes expuestos mientras los estudiantes circulan por la clase para ver el trabajo de los demás.
Apoyo para estudiantes de inglés
Speaking, Conversing: MLR3 Aclarar, Criticar, Corregir. Para ayudar a los estudiantes a utilizar el lenguaje de los poliedros (por ejemplo, vértices, aristas, caras), ofrecer un enunciado incorrecto para el poliedro A que puedan mejorar. Presente el siguiente argumento incorrecto para el número de aristas: "Hay 18 aristas para el Poliedro A porque hay tres cuadrados (3 × 4 lados) y dos triángulos (2 × 3 lados)." Dé a los estudiantes 1-2 minutos para corregir o mejorar esta afirmación.
Pregunte: "¿Hay algún error en el razonamiento? ¿En qué creéis que estaba pensando el autor al medir las aristas?". Invite a los estudiantes a comparar sus críticas con un compañero antes de revisar su trabajo escrito.
Principio(s) de diseño: Cultivar la conversación; Optimizar el resultado (para la explicación)
5 minutos
Repase las características de los prismas y las pirámides seleccionando 1-2 poliedros utilizados en el calentamiento. Pida a los estudiantes que expliquen (utilizando la terminología aprendida, si es posible) por qué cada uno de ellos es o no es un prisma o una pirámide. Si es un prisma o una pirámide, pida a los estudiantes que le pongan nombre.
Revise la definición de trabajo de poliedros generada anteriormente en la lección y pida a los estudiantes que vean si se puede refinar o cómo. Pregúnteles si hay algo que deban añadir, eliminar o ajustar teniendo en cuenta su trabajo con prismas, pirámides y redes.
California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Destaque los siguientes puntos sobre los poliedros. Pida a los estudiantes que ilustren cada punto utilizando una figura o una red.
• Un poliedro es una figura tridimensional construida a partir de polígonos rellenos. Llamamos caras a los polígonos. (El plural de poliedro es poliedra.)
• Todas las aristas de los polígonos se encuentran con otro polígono a lo largo de una arista completa.
• Cada polígono se encuentra con uno y sólo un polígono en cada una de las aristas.
• Los polígonos encierran una región tridimensional.
Considera exponer en un lugar visible las ideas clave de la lista de los estudiantes y de esta discusión para que puedan servir de referencia más adelante.
5 minutos
Este enfriamiento mide si los estudiantes son capaces de conceptualizar números escritos como múltiplos de una potencia positiva de 10 en la recta numérica.
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
ERRORES ANTICIPADOS
1. Escribe tu mejor definición o descripción de un poliedro. Si es posible, utiliza los términos que has aprendido en esta lección.
2. Aquí hay dibujos de cinco poliedros.
A. ¿Cuáles de ellos son prismas?
B. ¿Cuáles de ellos son pirámides?

1. Las respuestas varían pero podrían incluir uno o más de estos elementos: Un poliedro es una figura tridimensional formada por caras que son polígonos rellenos. Cada cara se encuentra con una y sólo otra cara a lo largo de una arista completa. Los puntos de encuentro de las aristas se llaman vértices.
2.
A. A, C y D son prismas.
B. B y E son pirámides.
Algunos estudiantes pueden confundir un prisma triangular (especialmente uno que no está asentado sobre una de sus bases) con una pirámide porque tiene caras triangulares.
Grado 6 . Matemáticas . Unidad 1
PROBLEMA 1
Selecciona todos los poliedros.

PROBLEMA 2

Posibles soluciones
1. ¿Este poliedro es un prisma, una pirámide o ninguno de los dos? Explica cómo lo sabes.
2. ¿Cuántas caras, aristas y vértices tiene?
Posibles soluciones
1. Prisma. Tiene dos bases octogonales paralelas que coinciden exactamente. 2. 10 caras, 24 aristas, 16 vértices
PROBLEMA 3
Tyler dice que esta red no puede ser una red para un prisma cuadrado porque no todas las caras son cuadrados.
¿Estás de acuerdo con la afirmación de Tyler? Explique su razonamiento.
PROBLEMA 4
Del Grado 6, Unidad 1, Lección 8
Explica por qué cada uno de los siguientes triángulos tiene un área de 9 unidades cuadradas.

Posibles soluciones
En desacuerdo. Ejemplo de razonamiento: Un prisma cuadrado debe tener dos bases que sean cuadrados, pero las otras caras pueden ser rectángulos no cuadrados. Hay dos cuadrados en la red, y la red se puede doblar para formar un prisma cuadrado.
Posibles soluciones
Las respuestas varían. Ejemplo de explicación: Cada triángulo es la mitad de un paralelogramo con un área de 18 unidades cuadradas (es decir, con una base de 6 unidades y una altura de 3 unidades), como se muestra en estos diagramas.
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 5
Del Grado 6, Unidad 1, Lección 9
A. Un paralelogramo tiene una base de 12 metros y una altura de 1.5 metros. ¿Cuál es su área?
B. Un triángulo tiene una base de 16 pulgadas y una altura de 1 8 pulgadas. ¿Cuál es su área?
C. Un paralelogramo tiene un área de 28 pies cuadrados y una altura de 4 pies. ¿Cuál es su base?
D. Un triángulo tiene un área de 32 milímetros cuadrados y una base de 8 milímetros. ¿Cuál es su altura?
Posibles soluciones
A. 18 metros cuadrados
B. 1 pulgadas cuadradas
C. 7 pies
D. 8 milímetros
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 3 Halla el área de la región sombreada. Muestra o explica tu razonamiento.
Posibles soluciones
31 cm2. Ejemplo de razonamiento: Los dos triángulos rectángulos pueden unirse para formar un rectángulo de 7 cm por5 cm cuya área es 35 cm2. Sin embargo, se elimina un cuadrado de 2 cm-por2 cm. El área sombreada es 31 cm2.
Reflejos:
Learning Inc. - Todos los derechos reservados


• Redes y superficie
• Graficar formas
ALINEACIÓN
Alineación de estándares y principios de Abordar
6.G.4 Representarfiguras tridimensionalesusando redes formadas por rectángulos y triángulos, y usar las redes para encontrar el área de la superficie de estas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfocar SMPs
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dar sentido al mundo y predecir lo que podría ocurrir
buscar y utilizar estructuras desmontar enteros, unir partes y descubrir formas y espacios.
OBJETIVO(S) DE APRENDIZAJE
• Que's utilice redes para hallar la superficie de poliedros.
OBJETIVO(S) DE APRENDIZAJE
• Puedo relacionar poliedros con sus redes y explicar cómo lo sé.
• Cuando se me da una red de un prisma o una pirámide, puedo calcular su superficie.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Emparejar poliedros con sus redes y justificar (oralmente) que coinciden.
• Utilizar una red con cuadrículas para calcular la superficie de un prisma o pirámide y explicar (por escrito) el método de solución.
• Visualizar e identificar el poliedro que se puede ensamblar a partir de una red dada.
Rutinas instructivas
Pensar, Compartir, Pares
Anticipar, Controlar, Seleccionar, Secuenciar, Conectar
MLR2: Recoger y Mostrar
Materiales necesarios
Patrón de líneas negras para la Actividad 14.1
Patrón de líneas negras para la Actividad 14.2
Enfriamiento
Juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Redes de poliédricos
Cinta adhesiva
Grado 6 . Matemáticas . Unidad 1
Preparación Requerida
Prepara copias físicas de las redes en el calentamiento, en caso de ser necesario para apoyar a los estudiantes con la visualización. El patrón de líneas negras contiene una versión más grande de estas redes.
Haz copias de las redes en el patrón de líneas negras para la actividad principal. Prepare un juego de 3 redes (A, B y C) y pegamento o cinta adhesiva para cada grupo de 3 estudiantes.
Narrativa de la lección
Anteriormente, los estudiantes aprendieron sobre los poliedros, analizaron y definieron sus características e investigaron sus representaciones físicas. Los estudiantes también identificaron los polígonos que componen un poliedro; reconocieron una red como un arreglo de estos polígonos y como una representación bidimensional de una figura tridimensional.
Esta lección amplía la comprensión de los estudiantes' sobre los poliedros y sus redes. Practican visualizando los poliedros que podrían ensamblarse a partir de redes dadas y usan las redes para encontrar la superficie de los poliedros.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Por parejas 10 min Los estudiantes nombran y emparejan los poliedros con sus redes correspondientes.
Actividad de exploración Grupos pequeños 25 min Hay disponible una extensión de exploraciónLos estudiantes utilizan redes para identificar y hallar las áreas superficiales de varios poliedros. para desarrollar una comprensión más profunda de las redes y los poliedros que representan.
Síntesis Grupo completo 5 min

Los estudiantes discuten y comparan estrategias para calcular las áreas superficiales de los poliedros.
Enfriamiento Independiente 5 min Dada una red, los estudiantes clasifican y encuentran el área de la superficie de un poliedro.
Práctica Independiente 10 min
El componente de práctica independiente incluye 3 en la lección y 3 problemas de repaso en espiral.
10 minutos
Rutinas instructivas
Piensa en pareja y comparte
Este calentamiento pide a los estudiantes que emparejen redes con poliedros. Les invita a pensar en los polígonos que componen un poliedro y a manipular mentalmente las redes, lo que les ayuda a desarrollar sus habilidades de visualización.
Nation California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Dé a los estudiantes 3 minutos de tiempo de reflexión en silencio para emparejar las redes con los poliedros y luego otros 2 minutos para discutir su respuesta y razonamiento con un compañero. Anime a los estudiantes a utilizar la terminología que han aprendido en las lecciones anteriores.
Para ayudar a los estudiantes que necesiten más tiempo o ayuda en la visualización, prepare modelos físicos de los poliedros y copias de las redes del esquema. Recorte previamente las redes o disponga de tijeras para que los estudiantes puedan montar las redes y poner a prueba sus ideas.
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
ERRORES ANTICIPADOS
Cada una de las siguientes redes puede ensamblarse en un poliedro. Empareja cada red con su poliedro correspondiente y nombra el poliedro. Prepárate para explicar cómo sabes que la red y el poliedro van juntos.

La red A es una pirámide cuadrada (3). Tiene cinco caras: un cuadrado y cuatro triángulos, igual que la pirámide cuadrada (razonamiento similar para cada figura).
La red B es un prisma rectangular (2).
La red C es una pirámide triangular (4).
La red D es un prisma triangular (5).
La red E es un prisma cúbico o cuadrado (1).
Si los estudiantes tienen problemas para distinguir entre las figuras A, C y D, recuérdeles que tanto los prismas como las pirámides pueden contener caras que sean triángulos. En una pirámide, todas las caras triangulares que no son la base se encuentran en un vértice y tienen aristas compartidas. En un prisma, puede haber una base triangular, pero las demás caras son cuadriláteros.
ACTIVIDAD SÍNTESIS
Invite a algunos estudiantes a compartir con la clase sus decisiones de emparejamiento y sus razonamientos. Pregunte a los estudiantes: "¿Qué pistas utilizaste para ayudarte a emparejar? ¿Cómo habéis comprobado si estabais en lo cierto?" Si no hay acuerdo unánime sobre alguna de las redes, pide a los estudiantes con opiniones divergentes que expliquen su razonamiento. Discutid para llegar a un acuerdo.
Grado 6 . Matemáticas . Unidad 1
minutos

Rutinas Instructivas
Anticipar, Monitorizar, Seleccionar, Secuenciar, Conectar
MLR2: Recoger y Mostrar
En esta actividad, los estudiantes cortan y ensamblan redes en poliedros y aprenden a usar redes para encontrar el área de la superficie. La presencia de una cuadrícula ayuda a los estudiantes en sus cálculos. También refuerza la idea de área como el número de cuadrados de la unidad en una región y la conexión entre área y superficie. Los estudiantes aplican lo que aprendieron anteriormente sobre las áreas de triángulos y paralelogramos para hallar el área de la superficie.
A medida que los estudiantes realizan los cálculos, supervisa sus procesos. Fíjese en los que trabajan sistemáticamente para hallar la superficie (por ejemplo, organizando las medidas de cada cara, calculando el área de cada cara y sumando las áreas) y en los que no lo hacen'. Anime a los estudiantes con trabajos desorganizados o dispersos a adoptar un enfoque más sistemático. Demuestre estrategias como etiquetar tanto los polígonos en la red como las partes de su trabajo que se refieren a esas caras.
Fíjese también en los estudiantes que buscan y utilizan la estructura (MP7), por ejemplo, agrupando ciertos polígonos y hallando el área de la forma compuesta (por ejemplo, un grupo de rectángulos que tienen una longitud lateral común), o identificando múltiples copias del mismo polígono y calculando el área una vez. Seleccionarlos para compartir su trabajo más tarde.
Organiza a los estudiantes en grupos de 3. Entrega a cada grupo una de cada red (A, B y C), cinta adhesiva y acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) (especialmente las tijeras). Explique a los estudiantes que van a cortar algunas redes, montarlas en poliedros y calcular sus superficies. Recuerde a los estudiantes que la superficie de una figura tridimensional es la suma de las superficies de todas sus caras. Pida a los estudiantes que completen la primera pregunta antes de cortar nada.
Señale que la red tiene polígonos sombreados y no sombreados. Explique que, una vez montada la red, sólo se verán los polígonos sombreados. Los polígonos sin sombrear son "solapas" para que sea más fácil pegar los polígonos. Quedarán escondidos detrás de los polígonos sombreados y en realidad no forman parte del poliedro. Explica a los estudiantes que si primero pliegas todas las líneas, te resultará más fácil doblar la red y unir los distintos polígonos. Una regla puede ser muy útil para hacer los pliegues.
Di a los estudiantes que es fácil pasar por alto o contar dos veces el área de una cara cuando se calcula el área de la superficie. Pídeles que piensen detenidamente en cómo registrar sus cálculos para asegurarse de que se tienen en cuenta todas las caras, se utilizan las medidas correctas y se minimizan los errores. Cuando los estudiantes hayan completado sus cálculos, pídeles que comparen y discutan su trabajo con otro estudiante con el mismo poliedro.
Procesamiento conceptual: Eliminar barreras. Ayude a los estudiantes a ver las conexiones entre los nuevos problemas y el trabajo previo. Los estudiantes pueden beneficiarse de una revisión de diferentes representaciones para activar conocimientos previos.
- Grado 6
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Tu maestro te dará las redes de tres poliedros para recortar y ensamblar.
1. Nombra el poliedro que formaría cada red al ensamblarla.
A: B: C:
2. Recorta tus redes y úsalas para crear formas tridimensionales..
3. Calcula el área superficial de cada poliedro. Explica tu razonamiento claramente.
CONCEPTOS ERRÓNEOS ANTICIPADOS
1. A: prisma rectangular, B: pirámide cuadrada, C: prisma triangular
2. No se requiere respuesta
3. Las explicaciones varían. Ejemplos de respuestas:
• A: La superficie es de 82 unidades cuadradas.. 2(6 ⋅ 1) + 2(5 ⋅ 1) + 2(6 ⋅ 5) = 82
• B: La superficie es de 48 unidades cuadradas. (4 ⋅ 4) + 4� 1 2 ⋅ 4 ⋅ 4� = 48
• C: La superficie es de 48 unidades cuadradas. (3 ⋅ 5) + (3 ⋅ 3) + (3 ⋅ 4) + 2� 1 2 ⋅ 3 ⋅ 4� = 48
• C: El área combinada de las tres caras rectangulares es 36 unidades cuadradas. 3 ⋅ 12 = 36. El área combinada de los dos triángulos rectángulos es 12 unidades cuadradas. 2� 1 2 ⋅ 3 ⋅ 4� = 1 El área de la superficie es de 48 unidades cuadradas porque 36 + 12 = 48.
Si los estudiantes no identifican el tipo específico de prisma o pirámide, recuérdeles que también deben nombrar cada figura por la forma de su base.
• Para cada poliedro, seleccione al menos 2 estudiantes con cálculos correctos pero con diferentes enfoques para que compartan su trabajo, si es posible. Para el poliedro A, seleccione estudiantes que adoptaron los siguientes enfoques, en esta secuencia:
• Encontraron el área de cada rectángulo por separado.
• Encontraron las áreas de pares de rectángulos idénticos (3 pares en total).
• Calcularon el área de un grupo de rectángulos conectados con la misma longitud o ancho (por ejemplo, los cuatro rectángulos en el plano con una longitud de lado de 6 unidades).
• Para el poliedro B, seleccione estudiantes que:
• Encontraron el área de cada uno de los 5 polígonos por separado.
• Encontraron el área del cuadrado, reorganizaron los 4 triángulos en 2 paralelogramos y calcularon el área de cada paralelogramo.
• Calcularon el área del cuadrado y el área de 1 triángulo, y multiplicaron el área del triángulo por 4.
• Para el poliedro C, seleccione estudiantes que:
• Encontraron el área de cada uno de los 5 polígonos por separado.
• Reorganizaron los 2 triángulos rectángulos en un rectángulo y luego calcularon el área de cada rectángulo por separado.
• Calcularon el área de cada triángulo rectángulo. y lo duplicó, y encontró el área del grupo de rectángulos conectados con un ancho de 4 unidades.
Grado 6 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN
Señale que las estrategias de razonamiento que utilizamos anteriormente en la unidad siguen siendo válidas aquí. Aunque trabajemos con figuras tridimensionales, la superficie es una medida bidimensional. Destaque las ventajas de abordar los problemas de forma sistemática, por ejemplo, etiquetando las partes, enumerando las medidas y los cálculos en orden, etc.
Apoyo para estudiantes de inglés
Speaking, Representing: MLR2 Recoger y mostrar. Mientras los estudiantes trabajan, circule y observe cómo los estudiantes registran sus cálculos de superficie. Muestre estrategias comunes para registrar cálculos, utilizando palabras, imágenes y símbolos. Recuerde a los estudiantes que pueden utilizar el lenguaje de la exposición para describir su método. Esto ayudará a los estudiantes a conectar las representaciones de la red con las palabras y los cálculos utilizados para hallar la superficie.
¿Estás listo para más?
1. Para cada una de estas redes, decide si se puede ensamblar en un prisma rectangular.
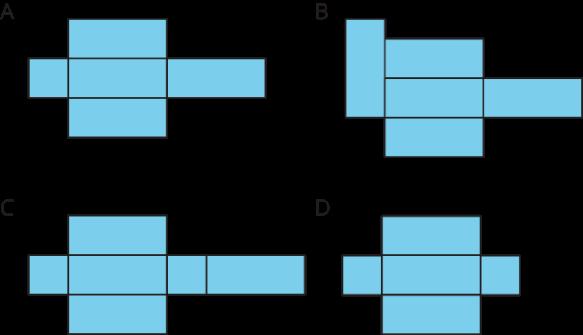
"¿Estás listo para más?" Respuesta del estudiante
1. Sólo C se puede doblar en un prisma rectangular.
2. C y D se pueden doblar en prismas triangulares.
2. Para cada una de estas redes, decide si se puede doblar en un prisma triangular.
5 minutos
En esta lección, emparejamos redes con los poliedros, armamos poliedros a partir de redes y usamos redes para encontrar área de superficie. Discute:
• "¿Cómo usamos una red para hallar el área de la superficie?" (Calculamos el área de cada polígono de la red y sumamos todas las áreas.)
• "¿En qué se diferencia hallar el área de la superficie utilizando una red de hallar el área de la superficie mirando una imagen de un poliedro - como habíamos hecho con el archivador, o estudiando el objeto real- como habíamos hecho con los cubos a presión?" (Una red nos permite ver todas las caras de un poliedro a la vez. Cuando trabajamos a partir de una imagen o un dibujo, necesitamos visualizar las caras ocultas. Trabajar con un poliedro real podría ayudar, pero de nuevo no estamos viendo todas las caras a la vez; tenemos que rotar el objeto y podríamos pasar por alto o contar dos veces una cara.)
• "Cuando usamos una red, ¿cómo hacemos un seguimiento de nuestros cálculos o nos aseguramos de que se tienen en cuenta todas las caras?" (Podemos etiquetar todos los polígonos y los cálculos.)
• "¿Hay formas de simplificar los cálculos? ¿O es mejor encontrar el área de cada polígono de uno en uno?" (A veces podemos simplificar el proceso combinando polígonos y hallando el área de la región combinada-por ejemplo, un grupo de rectángulos con la misma longitud lateral. Si hay varios polígonos que son idénticos, podemos hallar el área de un polígono y multiplicarla por el número de polígonos idénticos de la red).
California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
5 minutos
1. ¿Qué tipo de poliedro se puede ensamblar a partir de esta red?
2. Halla la superficie (en unidades cuadradas) del poliedro. Muestre su razonamiento. POSIBLES RESPUESTAS

1. Se ensamblaría formando un prisma rectangular.
2. La superficie sería 52 unidades cuadradas. 2(3 ⋅ 4) + 2(2 ⋅ 4) + 2(2 ⋅ 3) = 52
PROBLEMA 1
¿Se puede ensamblar la siguiente red para formar un cubo?
Explica cómo lo sabes. Etiqueta las partes de la red con letras o números si ayuda a tu explicación.

PROBLEMA 2
A. ¿Qué poliedro se puede ensamblar a partir de esta red? Explica cómo lo sabes.
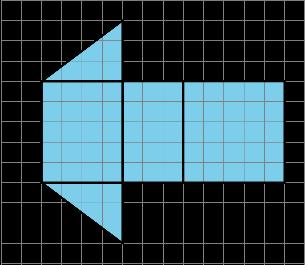
B. Halla la superficie de este poliedro. Muestra tu razonamiento.
Posibles soluciones
No. Ejemplo de explicación: Los cuatro cuadrados colocados uno al lado del otro sólo se pueden doblar de una manera para que se junten unos con otros, formando un cubo sin parte superior ni inferior. Uno de los dos cuadrados restantes se puede doblar para hacer la parte superior o inferior, pero el otro no se puede utilizar.

Posibles soluciones
A. Un prisma triangular. Ejemplo de explicación: Hay dos triángulos idénticos que son las bases. El resto de las caras son rectángulos.
B. 72 unidades cuadradas. Ejemplo de razonamiento: Las áreas de los tres rectángulos son 20, 15, y 25 unidades cuadradas. Las áreas de los dos triángulos son 2� 1 2 ⋅ 3 ⋅ 4� o 12 unidades cuadradas. 20 + 15 + 25 + 2(6) = 72
PROBLEMA 3
Aquí hay dos redes. Mai dice que ambas redes pueden ensamblarse en el mismo prisma triangular. ¿Estás de acuerdo? Explica o muestra tu razonamiento.
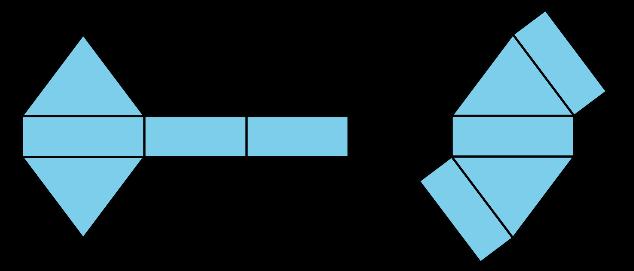
PROBLEMA 4
Del 6º Grado, Unidad 1, Lección 13
Aquí hay dos figuras tridimensionales.

Di si cada una de las siguientes afirmaciones describe la Figura A, la Figura B, ambas, o ninguna.
A. Esta figura es un poliedro.
B. Esta figura tiene caras triangulares.
C. Hay más vértices que aristas en esta figura.
D. Esta figura tiene caras rectangulares.
E. Esta figura es una pirámide.
F. Hay exactamente una cara que puede ser la base de esta figura.
G. La base de esta figura es un triángulo.
H. Esta figura tiene dos caras idénticas y paralelas que pueden ser la base.
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 12
Selecciona todas las unidades que se pueden usar para el área de superficie. Explique por qué las otras no pueden usarse para superficie.
metros cuadrados pies centímetros pulgadas cúbicas pulgadas cuadradas pies cuadrados

California - Grado 6
Grado 6 . Matemáticas . Unidad 1
Posibles soluciones
De acuerdo. Ejemplo de razonamiento: Ambas redes están compuestas por el mismo conjunto de polígonos. Las posiciones de una cara rectangular son diferentes, pero cuando se ensamblan, esa cara se encontrará con la misma arista de otros tres polígonos.
Posibles soluciones
A. Ambas
B. Ambas
C. Ninguna
D. Figura A
E. Figura B
F. Ninguna
G. Ambas
H. Figura A
Posibles soluciones
metros cuadrados pies centímetros pulgadas cúbicas pulgadas cuadradas pies cuadrados
Las opciones B (pies) y C (centímetros) son unidades de longitud. La opción D (pulgadas cúbicas) es una unidad de volumen.
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 6
Del Grado 6, Unidad 1, Lección 11 Halla el área de este polígono. Muestra tu razonamiento.
Posibles soluciones
33 unidades cuadradas. El razonamiento varía.
Reflexiones:
Learning Inc. - Todos los derechos reservados


• Redes y superficie
• Graficar formas
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.G.2 Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas �� = ����h y �� = ��h para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.
6.G.4 Representar figuras tridimensionales utilizando redes formadas por rectángulos y triángulos, y utilizar las redes para hallar la superficie de dichas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.
Construir sobre
5.MD.5
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP6 Atender a la precisión.
Estándares ELD de California
I.B.5
I.C.9
II.C.7
CONEXIONES INTEGRADAS
(DI) ¿Por qué?
Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dan sentido al mundo y predicen lo que podría ocurrir atienden a la precisión desmontando enteros, juntando piezas y descubriendo la forma y el espacio.
OBJETIVO(S) DE APRENDIZAJE
• Dibujemos redes y hallemos la superficie de poliedros.
OBJETIVO(S) DE APRENDIZAJE
• Puedo calcular las superficies de prismas y pirámides.
• Puedo dibujar las redes de prismas y pirámides.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Dibujar y montar una red para el prisma o pirámide que se muestra en un dibujo dado.
• Interpretar (utilizando palabras y otras representaciones) representaciones bidimensionales de prismas y pirámides.
• Utilizar una red sin cuadrículas para calcular la superficie de un prisma o pirámide y explicar (por escrito) el método de solución.
PREPARACIÓN DE LA LECCIÓN
Rutinas instructivas
Observa y maravíllate
MLR7: Compara y conecta
MLR8: Apoya el debate
Piensa, comparte en parejas
Preparación necesaria
Copia y recorta el esquema de la actividad
Construir prismas y pirámides. Haz una copia para cada 9 estudiantes, de forma que cada estudiante tenga un dibujo de un poliedro. Considera la asignación de los poliedros con antelación.
Materiales necesarios
Patrón de líneas negras para la actividad 15.2
Enfriamiento
Redes de demostración con y sin solapas
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Pegamento o barras de pegamento
Fichas preimpresas, recortadas de copias del patrón de líneas negras
Cinta adhesiva
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
Esta lección desarrolla aún más la habilidad de los estudiantes para visualizar la relación entre redes y poliedros y su capacidad para razonar sobre el área de la superficie.
Anteriormente, los estudiantes comenzaron con redes y visualizaron los poliedros que podrían ensamblarse a partir de las redes. Aquí van en la otra dirección: de los poliedros a las redes. Practican desplegando mentalmente formas tridimensionales, dibujando redes bidimensionales y utilizándolas para calcular la superficie. Los estudiantes también tienen la oportunidad de comparar y contrastar el área superficial y el volumen como medidas de dos atributos distintos de una figura tridimensional.
LECCIÓN
Componente de lección Estructura Tiempo Descripción breve
Calentamiento Pares 5 min Los estudiantes realizan observaciones de un prisma dado y sus medidas en contexto.
Actividad de Exploración Grupos Pequeños 30 min Los estudiantes dibujan la red de un poliedro y luego encuentran su área superficial.
Actividad de Exploración Grupos Pequeños 15 min

Los estudiantes analizan las redes de prismas rectangulares para comparar el área superficial y el volumen de cada prisma.
Una extensión de exploración n está disponible para desarrollar una comprensión más profunda de las redes de un cubo.
Síntesis Grupo Entero 5 min Los estudiantes resumen cómo encontrar el área de la superficie de un poliedro a partir de una imagen de un poliedro o de su red.
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Los estudiantes calculan el área de la superficie de un poliedro utilizando una red y luego identifican cómo se vería una vez ensamblado.
El componente de práctica independiente incluye 3 problemas de repaso de la lección y 2 problemas de repaso en espiral.
Rutinas instructivas
Notar y descubrir
5 minutos
Este calentamiento lleva a los estudiantes a pensar sobre un prisma y sus medidas en contexto y a considerar posibles preguntas que podrían plantearse y responderse.
Dado su trabajo reciente, es probable que los estudiantes se fijen y se pregunten sobre el área superficial, las redes y la altura que falta en la caja. También es posible que se pregunten por el volumen de la caja, teniendo en cuenta su trabajo geométrico de 5º curso.
Nation California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Cuando se les pregunte cómo hallar la superficie o el volumen de la caja, es probable que pregunten por la medida que falta. Esta es una oportunidad para que practiquen hacer una estimación razonable.
Organice a los estudiantes en grupos de 2. Conceda a los estudiantes un minuto de silencio para observar la imagen. Pídales que estén preparados para compartir al menos una cosa que les llame la atención y una cosa que se pregunten sobre la imagen. Pídales que hagan una señal cuando hayan observado o se hayan preguntado algo.
Apoyo para estudiantes con discapacidades
Funcionamiento ejecutivo: Organizadores gráficos. Proporcione a los estudiantes un gráfico en forma de T para que anoten lo que notan y se preguntan antes de compartir estas ideas con los demás.
CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
DE LA ACTIVIDAD
Kiran está envolviendo esta caja de cromos deportivos como regalo para un amigo.
¿Qué observas? ¿Qué te preguntas?
Las respuestas varían. Posibles respuestas:
• Observa: las longitudes de los lados de la caja, que la caja está cubierta con papel de regalo, que la caja es un prisma rectangular, que el área de las caras superior e inferior es 10 pulgadas cuadradas cada una
• Te preguntas: la longitud del lado que falta, cuántas cartas hay en la caja, el volumen de la caja, el área de la superficie de la caja, cuánto papel de regalo se necesitará para cubrir la caja
Invite a los estudiantes a compartir sus observaciones y preguntas. Registre las respuestas para que todos las vean. Si ningún estudiante se pregunta por la superficie, la cantidad de papel de regalo necesaria o el volumen de la caja, plantee estas cuestiones.
Pida a los estudiantes que elijan una pregunta sobre la superficie o una sobre el volumen y deles un minuto para que discutan con un compañero cómo encontrarían la respuesta a la pregunta. Si los estudiantes sugieren que no puede hacerse porque falta información, pídales que calculen la información que falta. Seleccione a un par de estudiantes para que compartan cómo encontrarían la superficie o el volumen de la caja dada. Después de cada respuesta, pregunte a la clase si están de acuerdo o en desacuerdo.
30 minutos
Rutinas instructivas
MLR7: Comparar y conectar
Anteriormente, los estudiantes utilizaron una red dada de un poliedro para hallar su área de superficie. Aquí utilizan un poliedro dado para dibujar una red y luego calcular su área superficial.

Grado 6 . Matemáticas . Unidad 1
Utiliza los poliedros proporcionados para diferenciar el trabajo para los estudiantes con diferentes grados de habilidades de visualización. Los prismas rectangulares (A y C), los prismas triangulares (B y D) y las pirámides cuadradas (F y G) pueden ser manejados por la mayoría de los estudiantes. El prisma triangular E requiere un poco más de trabajo interpretativo (es decir, las medidas de algunos lados pueden no ser inmediatamente evidentes para los estudiantes). El prisma trapezoidal H y el poliedro I (un compuesto de un cubo y una pirámide cuadrada) requieren interpretación y razonamiento adicionales.
A medida que los estudiantes trabajan, recuérdeles las estrategias de organización discutidas en lecciones anteriores, es decir, etiquetar los polígonos, mostrar las medidas en la red, etc.

Organice a los estudiantes en grupos de 2-3. Entregue a cada estudiante del grupo un poliedro diferente de la línea negra maestra y acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Los estudiantes necesitarán papel cuadriculado y una regla de sus kits de herramientas.
Explique a los estudiantes que van a dibujar una red, encontrar su área de superficie, y que su trabajo será revisado por un compañero. Conceda a los estudiantes 4-5 minutos de silencio para dibujar su red en papel cuadriculado y, a continuación, 2-3 minutos para compartir su red con su grupo y recibir comentarios. Cuando el grupo esté seguro de que cada red tiene sentido y de que se han tenido en cuenta todos los polígonos de cada poliedro, los estudiantes pueden continuar y utilizar la red para ayudar a calcular la superficie.
Si el tiempo lo permite, pida a los estudiantes que corten y ensamblen su red en un poliedro. Demuéstreles cómo añadir solapas a la red para poder pegarlas o pegarlas con cinta adhesiva. Debe haber tantas solapas como aristas tenga el poliedro. (Recuerde a los estudiantes que esto es diferente del número de aristas en los polígonos de la red).
Apoyo para estudiantes con discapacidades
Habilidades motoras finas: Tutores. Empareje a los estudiantes con sus compañeros tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten cómo dibujar la red para el poliedro dado según sea necesario.
Procesamiento conceptual: Eliminar Barreras. Comience con una demostración física de las acciones que se producen en una situación.
Tu maestro te dará el dibujo de un poliedro. Dibuja su red y calcula su superficie.
1. ¿Qué poliedro tienes?
2. Estudia tu poliedro. Después, dibuja su red en papel cuadriculado. Utiliza la longitud lateral de un cuadrado de la cuadrícula como unidad.
3. Etiqueta cada polígono de la red con un nombre o un número.
4. Calcula la superficie de tu poliedro. Muestra tu pensamiento de manera organizada para que pueda ser seguido por otros.
Cuando termines, haz una pausa para recibir instrucciones adicionales de tu maestro.
Nation California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

1. Las respuestas varían dependiendo del poliedro recibido. A y C son prismas rectangulares. B, D y E son prismas triangulares. F y G son pirámides cuadradas. H es un prisma trapezoidal. I es un compuesto de cubo y pirámide cuadrada.
2. Los dibujos netos varían. A y C deberían tener 6 rectángulos. B, D y E deben tener 5 polígonos: 2 triángulos rectángulos y 3 rectángulos. F y G deben tener 5 polígonos: 1 cuadrados y 4 triángulos. H debe tener 6 polígonos: 2 trapezoides y 4 rectángulos. I debería tener 9 polígonos: 5 cuadrados y 4 triángulos.
3. Las respuestas varían.
4. Las respuestas varían.
• A: 340 unidades cuadradas. 2(5 ⋅ 8) + 2(5 ⋅ 10) + 2(8 ⋅ 10) = 340
• B: 408 unidades cuadradas. 2(1/2 ⋅ 6 ⋅ 8) + (6 ⋅ 15) + (8 ⋅ 15) + (10 ⋅ 15) = 408
• C: 274 unidades cuadradas. 2(13 ⋅ 4) + 2(13 ⋅ 5) + 2(4 ⋅ 5) = 274
• D: 300 unidades cuadradas. 2(1/2 ⋅ 5 ⋅ 12) + (5 ⋅ 8) + (12 ⋅ 8) + (13 ⋅ 8) = 300
• E: 216 unidades cuadradas. 2(1/2 ⋅ 6 ⋅ 4) + (6 ⋅ 12) + 2(5 ⋅ 12) = 216
• F: 240 unidades cuadradas. 4(1/2 ⋅ 8 ⋅ 11) + (8 ⋅ 8) = 240
• G: 156 unidades cuadradas. 4(1/2 ⋅ 6 ⋅ 10) + (6 ⋅ 6) = 156
• H: 316 unidades cuadradas. La base trapezoidal puede descomponerse en un 5-por-4 rectángulo y un triángulo rectángulo de base 3 unidades y altura 4. 2(5 ⋅ 4) + 2(1/2 ⋅ 3 ⋅ 4) + (8 ⋅ 12) + 2(5 ⋅ 12) + (4 ⋅ 12) = 316
• I: 205 unidades cuadradas. 5(5 ⋅ 5) + 4(1/2 ⋅ 5 ⋅ 8) = 205
Los estudiantes pueden saber qué polígonos forman la red de un poliedro pero disponerlos incorrectamente en la red (es decir, al cortarlos y montarlos las caras se solapan en lugar de encontrarse en aristas compartidas, o las caras están orientadas incorrectamente o están en lugares equivocados). Proponga a los estudiantes que etiqueten algunas caras del dibujo del poliedro y trasladen las adyacencias que vean a la red. Si es necesario, demuestre el razonamiento (por ejemplo, "La cara 1 y la cara 5 comparten la arista que mide 7 unidades de largo, así que puedo dibujarlas como dos rectángulos adosados que comparten un lado que mide 7 unidades de largo.")
Puede que a los estudiantes no se les ocurra dibujar cada cara del poliedro a escala. Recuérdales que utilicen los cuadrados de la cuadrícula de su papel cuadriculado como unidades de medida. Si una red es imprecisa, esto se hace más evidente cuando se está doblando. Esto puede ayudar a los estudiantes a ver qué partes hay que ajustar y a decidir la mejor ubicación de las solapas. Tranquilice a los estudiantes diciéndoles que puede ser necesario hacer varios borradores de una red antes de que se resuelvan todos los detalles, y anímeles a perseverar (MP1).
Pida a los estudiantes que terminen su cálculo que encuentren a otra persona de la clase con el mismo poliedro y discutan las siguientes preguntas (expuestas a la vista de todos):
• ¿Coinciden sus cálculos? ¿Deberían?
• ¿Sus redes dan como resultado los mismos poliedros? ¿Deberían?
• ¿Coinciden tus modelos con la imagen que te dieron? ¿Por qué sí o por qué no?
Si el tiempo es limitado, considera la posibilidad de colocar la clave de respuestas en algún lugar del aula para que los estudiantes puedan comprobar rápidamente sus cálculos de superficie. Vuelve a reunirte brevemente para un debate con toda la clase. Invite a los estudiantes a reflexionar sobre el proceso de dibujar una red y calcular la superficie a partir de la imagen de un poliedro. Formule preguntas como las siguientes:
• ¿Cómo supiste que tu red mostraba todas las caras de tu poliedro?
• ¿Cómo supiste dónde colocar cada polígono o cómo disponer todos los polígonos de modo que, si se doblan, puedan ensamblarse en el poliedro del dibujo?
• ¿Cómo te ayudó la red a encontrar el área de la superficie?
Grado 6 . Matemáticas . Unidad 1

Apoyo para los estudiantes de inglés
Representar, conversar: MLR7 Comparar y conectar. Utilice esta rutina para ayudar a los estudiantes a tener en cuenta su audiencia a la hora de preparar una exposición visual de su trabajo. Pedir a los estudiantes que preparen una presentación visual que muestre sus dibujos netos y sus cálculos de superficie. Los estudiantes deben considerar cómo mostrar sus cálculos para que otro estudiante pueda interpretarlos. Algunos estudiantes pueden añadir notas o detalles a sus dibujos para ayudar a comunicar su pensamiento. Cuando los estudiantes encuentren a otra persona de la clase con el mismo poliedro, proporcione 2-3 minutos de tiempo de reflexión en silencio para que los estudiantes lean e interpreten los dibujos de los demás antes de debatir las cuestiones expuestas.
Principio(s) de diseño: Cultivar la conversación; Maximizar la metaconciencia
minutos
Rutinas Instructivas
MLR8: Apoyos para la Discusión
Think Pair Share
En esta actividad, los estudiantes comparan las áreas superficiales y los volúmenes de tres prismas rectangulares dadas las redes que no están en una cuadrícula. Para ello, deben ser capaces de visualizar las formas tridimensionales que adoptarían las redes bidimensionales al plegarse.
En 5º curso, los estudiantes habían aprendido a distinguir el área y el volumen como medidas de atributos diferentes. Esta actividad aclara y refuerza esa distinción.
Mantenga a los estudiantes en los mismos grupos de 2-3. Explique a los estudiantes que esta actividad implica trabajar tanto con el volumen como con la superficie. Para refrescar la comprensión del volumen de los estudiantes de 5º curso, pregunte a los estudiantes:
• "Cuando hallamos el volumen de un prisma, ¿qué estamos midiendo?"
• "¿En qué se diferencia el volumen de la superficie?"
• "¿Cómo podríamos hallar el volumen de un prisma rectangular?"
Reitere que el volumen mide el número de cubos unitarios que se pueden empaquetar en una forma tridimensional y que podemos encontrar el número de cubos unitarios en un prisma rectangular multiplicando las longitudes de los lados de un prisma.
Dé a los estudiantes 1-2 minutos para leer el enunciado de la tarea y las preguntas. Pídales que piensen cómo podrían responder a cada pregunta y que estén preparados para compartir sus ideas. Dales un minuto para que discutan sus ideas con su grupo. A continuación, pida a los grupos que colaboren: cada miembro debe realizar los cálculos para un prisma (A, B o C). Dé a los estudiantes 5-7 minutos de tiempo tranquilo para encontrar el área de la superficie y el volumen para su prisma y luego tiempo adicional para comparar sus resultados y responder a las preguntas.
Apoyo para Estudiantes con
Funcionamiento Ejecutivo: Eliminar Barreras. Proporcione una lista de comprobación de tareas que haga explícitos todos los componentes necesarios de la actividad.
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTASS
Aquí están las redes de tres cajas de cartón que are todos prismas rectangulares. Las cajas se embalarán con cubos de 1 centímetros. Todas las longitudes están en centímetros.
1. Compara las superficies de las cajas. ¿Qué caja utilizará menos cartón? Muestra tu razonamiento.
2. Compara ahora los volúmenes de estas cajas en centímetros cúbicos. ¿Qué caja contendrá más cubos de 1 centímetros? Muestra tu razonamiento.
1. La superficie de A es 42 centímetros cuadrados. ��: 4(2 ⋅ 3) + 2(3 ⋅ 3) = 42. La superficie de B y C es 54 centímetros cuadrados. ��: 2(3 ⋅ 6) + 2(3 ⋅ 1) + 2(6 ⋅ 1) = 54 ��: 6(3 ⋅ 3) = 54. La caja A es la que menos cartón utiliza. Las cajas B y C necesitan la misma cantidad de cartón, ambas más cartón que A.
2. El volumen de A y B es 18 centímetros cúbicos. ��: 3 ⋅2 ⋅ 3 = 18 ��: 6 ⋅ 1 ⋅ 3 = 18. El volumen de C es 27 centímetro cúbico. ��: 3 ⋅ 3 ⋅ 3 = 27. En la caja C caben el mayor número de 1-centimetros cúbicos. En A y B caben el mismo número de cubos, pero menos que en C.
Los estudiantes no deberían tener muchos problemas para hallar las áreas de los rectángulos, pero es posible que les cueste seguir la pista de los pares de medidas para multiplicar y acaben cometiendo errores de cálculo. Sugiérales que etiqueten cada polígono de la red y el trabajo escrito correspondiente y que vuelvan a comprobar sus cálculos para minimizar dichos errores.
Si los estudiantes tienen dificultades para hallar el volumen de su prisma utilizando la información de una red, sugiérales que hagan un boceto del prisma que puede ensamblarse a partir de la red y que etiqueten las aristas del prisma. Es posible que los estudiantes necesiten que se les recuerde que el área se mide en unidades cuadradas y el volumen en unidades cúbicas.
Selecciona a algunos estudiantes para que compartan el área de superficie y el volumen de cada prisma. Después de que cada persona comparta, pregunta a los que trabajaron en el mismo prisma si están de acuerdo o en desacuerdo. Anote los resultados en la pizarra.
Invite a los estudiantes a compartir algunas observaciones rápidas sobre la relación entre las superficies y los volúmenes de estos tres prismas, o entre las cantidades de material necesarias para construir las cajas y el número de cubos que pueden contener. Discute preguntas como:
• "Si estos prismas son cajas, ¿qué prisma -B o C- necesitaría más material para construirse? ¿En cuál caben más cubos unitarios?" (Es probable que B y C necesiten la misma cantidad de material para construirse, ya que sus superficies son iguales. C tiene mayor volumen que B, por lo que caben más cubos unitarios).
• "¿Qué prisma -A o B- necesitaría más material para construir? ¿En cuál caben más cubos unitarios?" (En A y B caben el mismo número de cubos unitarios, pero en B se necesitaría más material para construirlo.)
• "Si dos prismas tienen la misma superficie, ¿tendrían también el mismo volumen? ¿Cómo lo sabes?" (No, los prismas A, B y C son ejemplos de cómo dos figuras con el mismo volumen pueden no tener la misma superficie, y viceversa.)
Los estudiantes profundizarán en estas ideas cuando exploren los cuadrados, los cubos y los exponentes en las próximas lecciones. Si los estudiantes pudieran beneficiarse de un trabajo adicional para distinguir el área y los volúmenes como medidas diferentes, realice la lección opcional Distinguir entre área superficial y volumen.
Grado 6 . Matemáticas . Unidad 1

Apoyo para estudiantes de inglés
Representar, hablar: MLR8 Apoyos para el debate. Utilice esta rutina para apoyar el uso del lenguaje matemático al comparar la superficie y el volumen. Dé a los estudiantes 3-4 minutos para escribir una respuesta a la siguiente pregunta: "Si dos prismas tienen la misma superficie, su volumen siempre/algunas veces/nunca será el mismo porque...". Invite a los estudiantes a comentar sus respuestas con un compañero antes de seleccionar 1-2 estudiantes para compartirlas con toda la clase. Escuche y llame la atención de los estudiantes sobre cómo el uso de ejemplos y contraejemplos puede ayudar a justificar su razonamiento.
Principio(s) de diseño: Optimizar la salida (para la justificación); Apoyar la creación de sentido
¿Estás listo para más?
La figura C muestra una red de un cubo. Dibuja otra red de un cubo. Dibuja otra. Y otra más. ¿Cuántas redes diferentes se pueden dibujar y ensamblar en un cubo?
"¿Estás listo para más?" Respuesta del estudiante
Hay 11 redes diferentes para un cubo. Cualquier otra red sería congruente con una de éstas.
5 minutos

Para resaltar algunos puntos clave de la lección, muestre una imagen de un prisma o una pirámide y un dibujo de su red. Discute estas preguntas:
• "¿Puedes encontrar la superficie de un prisma o pirámide simple a partir de una imagen, si se dan todas las medidas necesarias?"
• "¿Puedes hallar la superficie a partir de una red, si se dan todas las medidas?"
• "¿Qué puede ser más útil para calcular la superficie: una imagen de un poliedro o una red?". (Si el poliedro es sencillo -por ejemplo, un cubo, una pirámide cuadrada, etc.- y no tiene caras ocultas con medidas diferentes ni requiere mucha visualización, puede funcionar una imagen o una red. De lo contrario, una red puede ser más útil porque podemos ver todas las caras a la vez y encontrar el área de cada polígono más fácilmente. Una red también puede ayudarnos a hacer un seguimiento de nuestros cálculos y a darnos cuenta de las áreas que faltan o sobran).
5 minutos
1. En esta red, los dos triángulos son triángulos rectángulos. Todos los cuadriláteros son rectángulos. ¿Cuál es su superficie en unidades cuadradas? Muestra tu razonamiento.
2. Si se ensambla la red, ¿cuál de los siguientes poliedros formaría?

Nation California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS
1. La superficie es 168 unidades cuadradas. Las explicaciones varían. Ejemplo de respuesta: Hay dos caras triangulares con área de 24 unidades cuadradas cada una. 1 2 ⋅ 6 ⋅ 8 = 24. Hay una cara rectangular con área de 50 unidades cuadradas.
10 ⋅ 5 = 50. Hay una cara rectangular con área de 40 unidades cuadradas. 5 ⋅ 8 = 40. Hay una cara rectangular con área 5 ⋅ 6 = 30 unidades cuadradas. 2 ⋅ 24 + 50 + 40 + 30 = 168
2. Prisma C
PROBLEMA 1
Jada dibujó una red para un poliedro y calculó su área superficial.
A. ¿Qué poliedro se puede formar a partir de esta red?
B. Jada cometió algunos errores en su cálculo del área.
¿Cuáles fueron los errores?
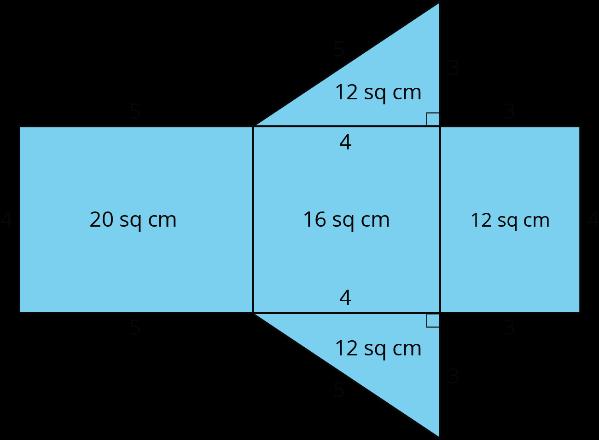
C. Halla la superficie del poliedro. Muestra tu razonamiento.
PROBLEMA 2
Posibles soluciones
A. Prisma triangular
B. Calculó mal las áreas de las dos caras triangulares. Los triángulos rectángulos tienen una base de 4 cm y una altura de 3 cm, por lo que el área de cada uno debería ser 1 2 ⋅ 4 ⋅ 3 o 6 cm cuadrados. Jada ha escrito "12 cm2" para el área de cada triángulo.
C. 60 cm2. Las caras triangulares deben medir 6 cm2 cada una, así que la superficie es 20 + 16 + 12 + 6 + 6, o 60
Una caja de cereales mide 8 pulgadas por 2 pulgadas por 12 pulgadas. ¿Cuál es su superficie? Razona. Si te atascas, considera dibujar un boceto de la caja o su red y etiquetar los bordes con sus medidas.
Posibles soluciones
272 pulgadas cuadradas. Ejemplo de razonamiento:
• Las caras superior e inferior miden 2 pulgadas por 8 pulgadas cada una, por lo que su área combinada es 2(2 ⋅ 8) o 32 pulgadas cuadradas.
• Las caras delantera y trasera miden 8 pulgadas por 12 pulgadas cada una, por lo que su área combinada es 2(8 ⋅ 12) o 192 pulgadas cuadradas.
• Las caras laterales miden 2 pulgadas por 12 pulgadas cada una, por lo que su área combinada es 2(2 ⋅ 12) o 48 pulgadas cuadradas.
• El área de la superficie es 32 + 192 + 48 o 272 pulgadas cuadradas.
PROBLEMA 3
Del Grado 6, Unidad 1, Lección 12
Se apilan doce cubos para formar esta figura.
A. ¿Cuál es su área de superficie?
B. ¿Cómo cambiaría el área de superficie si se quitan los dos cubos superiores?
Learning Inc. - Todos los derechos reservados

Grado 6 . Matemáticas . Unidad 1

Posibles soluciones
A. 36 unidades cuadradas
B. El área de superficie disminuiría en 6 unidades cuadradas.
PROBLEMA 4
Aquí hay dos poliedros y sus redes. Etiqueta todas las aristas de la red con las longitudes correctas.
Posibles soluciones
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 14
A. ¿Qué figura tridimensional puede ensamblarse a partir de la red?

B. ¿Cuál es el área superficial de la figura? (Un cuadrado de la red es 1 unidad cuadrada.)
Posibles soluciones
A. Pirámide cuadrada
B. 56 unidades cuadradas. El área de la base es 16 unidades cuadradas. Cada cara triangular tiene una base de 4 unidades y una altura de 5 unidades. Esto significa que cada cara triangular tiene un área de 10 unidades cuadradas. La superficie total es 56 unidades cuadradas, porque 16 + 10 + 10 + 10 + 10 = 56
Math Nation California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados

• Redes y superficie
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.G.2 Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = �� ��h y V = ��h para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.
6.G.4 Representar figuras tridimensionales utilizando redes formadas por rectángulos y triángulos, y utilizar las redes para hallar la superficie de dichas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.
Construyendo sobre
5.MD.3b 5.MD.4 5.MD.5a
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP6 Atender a la precisión.
Estándares ELD de California
I.A.1 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
dar sentido al mundo
dar sentido a los problemas y perseverar en su resolución desmontar el todo, unir las piezas y descubrir la forma y el espacio.
OBJETIVO(S) DE APRENDIZAJE
• Contrastemos área superficial y volumen.
OBJETIVO(S) DE APRENDIZAJE
• Puedo explicar cómo es posible que dos poliedros tengan la misma área superficial pero diferentes volúmenes, o que tengan diferentes áreas superficiales pero el mismo volumen.
• Sé cómo las medidas y unidades unidimensionales, bidimensionales y tridimensionales son diferentes.
OBJETIVOS DE APRENDIZAJE
• Comprender que la superficie y el volumen son dos atributos diferentes de los objetos tridimensionales y que se miden en unidades diferentes.
• Describir (oralmente y por escrito) formas construidas con cubos, incluyendo observaciones sobre su superficie y volumen.
• Determinar la superficie y el volumen de formas hechas con cubos.
Rutinas instructivas
Piensa, comparte, en parejas
Observa y maravíllate
Anticipa, monitoriza, selecciona, secuencia, conecta
MLR8: Apoyo a la discusión
Materiales necesarios
Lápiz negro para la actividad 11.4
Enfriamiento
Preparación requerida
Prepare las soluciones a la primera pregunta de 1-2-3 Actividad de atributos dimensionales en una pantalla visual grande.
Prepare juegos de 16 cubos a presión y dos notas adhesivas para cada estudiante.
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
En esta lección opcional, los estudiantes distinguen entre medidas de atributos unidimensionales, bidimensionales y tridimensionales y examinan más de cerca la distinción entre superficie y volumen (basándose en el trabajo de los estudiantes en grados anteriores). Utiliza esta lección para reforzar la idea de que la longitud es un atributo unidimensional de las figuras geométricas, la superficie es un atributo bidimensional y el volumen es un atributo tridimensional.
Al construir poliedros, dibujar representaciones de ellos y calcular tanto la superficie como el volumen, los estudiantes ven que diferentes figuras tridimensionales pueden tener el mismo volumen pero diferentes superficies, y viceversa. Esto es análogo al hecho de que las figuras bidimensionales pueden tener la misma área pero diferentes perímetros, y viceversa. Los estudiantes deben prestar atención a las unidades de medida durante toda la lección.
Nota: Los estudiantes deberán traer con antelación una colección personal de 10-50 objetos pequeños para la primera lección de la siguiente unidad. Por ejemplo, piedras, conchas, cromos o monedas.
RESUMEN DE LA LECCIÓN
Componente de la lección

Estructura Tiempo
Breve descripción
Calentamiento En parejas 10 min. Los estudiantes identifican qué unidades de medida tienen más sentido para varias cantidades.
Actividad de exploración opcional
Independiente o por parejas 25 min.
Actividad de Exploración Opcional Parejas 20 min.
Síntesis Todo el grupo 5 min.
Enfriamiento Independiente 5 min.
Los estudiantes construyen diferentes formas utilizando el mismo número de cubos y luego encuentran y comparan el volumen y la superficie de cada una.
Un applet digital interactivo está disponible para permitir a los estudiantes explorar la construcción de formas tridimensionales utilizando la tecnología.
Los estudiantes determinan y comparan las áreas superficiales y los volúmenes de prismas con la misma altura cuando se les dan dimensiones específicas de la base.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la construcción de prismas con la misma área superficial pero diferentes volúmenes.
Los estudiantes resumen las distinciones entre las áreas superficiales y los volúmenes de figuras tridimensionales mientras racionalizan cómo figuras con la misma área superficial pueden tener diferentes volúmenes y viceversa.
Los estudiantes eligen qué prismas tienen volúmenes diferentes pero la misma área superficial.
Práctica Independiente 5-8 min. El componente de práctica independiente incluye 3 problemas de repaso de la lección y 2 problemas de repaso en espiral.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Rutinas didácticas
Pensar Compartir en Pareja
Esta actividad refuerza la conciencia de los estudiantes sobre los atributos unidimensionales, bidimensionales y tridimensionales y las unidades que se utilizan habitualmente para medirlos. Los estudiantes deciden las unidades basándose en los atributos que se miden y en el tamaño de las unidades y en lo apropiadas que serían para describir cantidades dadas.
Mientras los estudiantes trabajan, seleccione a algunos para que compartan sus respuestas a las dos últimas preguntas de la actividad (sobre las cantidades que podrían medirse en millas y en metros cúbicos).
Considere un repaso rápido de las unidades métricas y estándar de medida antes de que los estudiantes comiencen a trabajar. Incluya algunos ejemplos concretos que puedan ayudar a ilustrar el tamaño de cada unidad.
A continuación, elija un objeto de la clase cuya superficie y volumen puedan medirse (por ejemplo, un escritorio). Pregunte a los estudiantes: "¿Qué unidades podríamos utilizar para medir la superficie del escritorio? ¿Qué unidades podríamos utilizar para medir el volumen de un cajón?".
Aclare los tamaños relativos de las distintas unidades que surjan en la conversación. Por ejemplo, discuta cómo un metro es un poco más de tres pies, una yarda es tres pies, un kilómetro es aproximadamente dos tercios de una milla, un milímetro es una décima parte de un centímetro, etc.
Dé a los estudiantes 4-5 minutos de tiempo para pensar tranquilamente y luego un par de minutos para compartir sus respuestas con un compañero. Prepárate para exponer las respuestas a las seis primeras preguntas.
Procesamiento conceptual: Ayudas visuales. Incluya imágenes que representen algunas de las cantidades descritas, lo que ayudaría a los estudiantes que se benefician de las vías múltiples para el procesamiento del lenguaje.
Para cada cantidad, elige una o más unidades de medida apropiadas.
Para las dos últimas filas, piensa en una cantidad que pueda medirse adecuadamente con las unidades dadas.
Cantidades
1. Perímetro de un estacionamiento:
2. Volumen de un camión de carga (tráiler):
3. Área superficial de un refrigerador:
4. Largo de una pestaña:
5. Área de un estado:
6. Volumen de un océano:
7. : millas
8. : metros cúbicos
i. milímetros (mm)
ii. pies (ft)
iii. metros (m)
iv. pulgadas cuadradas (pulg²)
v. pies cuadrados (ft²)
vi. millas cuadradas (mi²)
vii. kilómetros cúbicos (km³)
viii. yardas cúbicas (yd³)
Grado 6 . Matemáticas . Unidad 1

Dependiendo de la familiaridad de los estudiantes con las unidades métricas y estándar, puede haber cierta confusión sobre el tamaño de cada unidad. Considere la posibilidad de mostrar herramientas de medición o una hoja de referencia que muestre ejemplos concretos de elementos medidos en unidades de diferentes tamaños.
Muestre las soluciones a las seis primeras preguntas para que todos las vean y las utilicen para comprobarlas. A continuación, seleccione a algunos estudiantes para que compartan sus respuestas a las dos últimas preguntas.
Pregunte a los estudiantes qué les llama la atención sobre las unidades de superficie y las unidades de volumen. Si aún no lo han mencionado los estudiantes, destaque que el área siempre se mide en unidades cuadradas y el volumen en unidades cúbicas.
25 minutos
Rutinas instructivas
Notar y maravillarse
Anticipar, monitorear, seleccionar, secuenciar, conectar
MLR8: Apoyos para la discusión
Esta actividad aclara la distinción entre volumen y superficie e ilustra que dos poliedros pueden tener el mismo volumen pero diferentes superficies.
Los estudiantes construyen formas utilizando dos conjuntos de ocho cubos y determinan sus volúmenes y superficies. Como todos los diseños están formados por el mismo número de cubos, todos tienen el mismo volumen. A continuación, los estudiantes examinan todos los diseños y discuten qué distingue a las formas con superficies más pequeñas de las que tienen superficies mayores.
Mientras los estudiantes trabajan, controle el rango de superficies de las formas que han construido. Seleccione varios estudiantes cuyos diseños representen colectivamente esa gama.
Entregue a cada estudiante (o grupo de 2 estudiantes) 16 cubos a presión, dos notas adhesivas y 8-10 minutos de tiempo de trabajo.
Explíqueles que su trabajo consiste en diseñar y construir dos figuras -utilizando 8 cubos para cada una- y hallar el volumen y la superficie de cada figura. Pídales que den a cada figura un nombre o una etiqueta y que anoten el nombre, el área de superficie y el volumen en una nota adhesiva.
- Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTASS
Los diseños varían. Aquí tienes dos formas posibles:
Ambas tienen un volumen de 8 unidades cúbicas. La primera tiene una superficie de 24 unidades cuadradas. La segunda tiene una superficie de 28 unidades cuadradas. El área de superficie más pequeña posible para una construcción de 8 cubos es 24 unidades cuadradas, y la más grande es 34 unidades cuadradas.

Aunque los estudiantes están tratando sólo con 8 cubos a la vez, pueden cometer errores de conteo al omitir inadvertidamente o contar dos veces cuadrados o caras. Esto es especialmente probable en los diseños que no son prismas. Anime a los estudiantes a pensar en una forma sistemática de llevar la cuenta del número de unidades cuadradas que están contando.
Algunos estudiantes pueden asociar el volumen sólo con los prismas y afirmar que no se puede determinar el volumen de los diseños que no son prismas. Recuérdeles la definición de volumen.
Pida a todos los estudiantes que expongan sus diseños y sus notas adhesivas y deles un par de minutos para que circulen y vean el trabajo de los demás.
A continuación, pida a los estudiantes previamente identificados que ordenen sus diseños en función de su superficie, de menor a mayor, y que expongan sus diseños para que todos los vean. Anota la información sobre los diseños en una tabla, en el mismo orden. Expón la tabla a la vista de todos. Aquí tienes un ejemplo.
Concede a los estudiantes un minuto para que se fijen en los diseños y en la información de la tabla. Pida a los estudiantes que hagan una señal cuando hayan observado y se hayan preguntado al menos una cosa. Invite a algunos estudiantes a compartir sus observaciones y preguntas. A continuación, discuta las siguientes preguntas (si no las han mencionado ya los estudiantes):
• "¿Qué tienen en común todas las formas?" (Su volumen)
• "¿Por qué todos los volúmenes son iguales?" (El volumen mide el número de cubos unitarios que caben en una figura. Todos los diseños se construyen con el mismo número de cubos).
• "¿Por qué algunas figuras tienen mayor superficie que otras? ¿Qué aspecto tienen las formas con mayor superficie?" (Los cubos están más extendidos y tienen más caras al descubierto.)
• "¿Y las que tienen menor superficie?" (Son más compactas y tienen más caras ocultas o compartidas con otro cubo.)
• "¿Es posible construir una forma con un volumen diferente? ¿Cómo?" (Sí, pero implicaría utilizar menos o más cubos.)
Si los estudiantes tienen problemas para visualizar cómo cambia la superficie cuando cambia el diseño, demuestre lo siguiente:
• Haga un cubo hecho de 8 cubos más pequeños. Señala un cubo y pregunta cuántas de sus caras están expuestas (3).
• Quite ese cubo y muévalo a otro lugar.
• Señale que, en el "hueco" dejado por el cubo que fue movido, 3 las caras que antes eran interiores ahora contribuyen al área de la superficie. Al mismo tiempo, el cubo trasladado ahora tiene 5 caras expuestas.
Grado 6 . Matemáticas . Unidad 1

Apoyo para estudiantes de inglés
Speaking, Listening: MLR8 Apoyos para el debate. Para ayudar a los estudiantes a describir y explicar sus comparaciones, facilíteles el lenguaje que puedan utilizar (por ejemplo, extendido frente a compacto, expuesto/visible frente a oculto/ cubierto). Demuestre las comparaciones utilizando los diseños visuales de los cubos. Ofrezca a los estudiantes marcos de frases para ayudarles con sus explicaciones (por ejemplo, "La superficie de la forma es mayor (o menor) que la de la forma porque. . ."
Principio(s) de diseño: Optimizar el resultado (para la explicación)
20 minutos
Rutinas instructivas
MLR8: Apoyos para la discusión
Anteriormente, los estudiantes estudiaron formas con el mismo volumen pero diferentes áreas superficiales. Aquí ven que también es posible que las formas tengan la misma superficie pero volúmenes diferentes. Los estudiantes piensan en cómo se podría comparar visualmente el aspecto de estas formas.
Se dan a los estudiantes las longitudes de los lados de tres prismas rectangulares y se les pide que hallen la superficie y el volumen de cada uno. Algunos estudiantes pueden visualizarlos, pero otros pueden necesitar dibujar redes, esbozar las figuras en papel cuadriculado isométrico o construir prismas físicos. Prepare cubos para que los utilicen los estudiantes. Cada uno de los tres prismas puede construirse con 15 cubos o menos, pero se necesitan 40 cubos para construir los tres simultáneamente. (Si los cubos no son centimétricos, pida a los estudiantes que los traten como si la longitud de las aristas de cada cubo fuera 1 cm.)
Mientras los estudiantes trabajan, esté atento a los errores de cálculo de los estudiantes en la primera pregunta, que afectarán a las observaciones que hagan en la segunda pregunta. Seleccione algunos estudiantes que observen que los volúmenes de los prismas son todos diferentes pero las superficies son las mismas.
INSTRUCCIÓN
Organizar a los estudiantes en grupos de 2. Proporcionar acceso a cubos de presión y kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a los estudiantes 6-7 minutos de reflexión en silencio y, a continuación, 2-3 minutos para comentar sus respuestas con su compañero. Pídeles que se pongan de acuerdo sobre una observación clave para compartirla con toda la clase.
Apoyo para estudiantes de inglés
Writing, Speaking: MLR8 Apoyo a la discusión. Para ayudar a los estudiantes a comparar los volúmenes y las superficies de las figuras, ofrezca algunos marcos de frases. Por ejemplo: "Una cosa que noto sobre los volúmenes y las áreas superficiales de los prismas es...".
Principio(s) de diseño: Maximizar la
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus compañeros tutores previamente identificados.
Procesamiento conceptual: Manipulativos. Proporcionar manipulativos (por ejemplo, cubos de presión) para ayudar a los estudiantes que se benefician de las actividades prácticas.


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS
ANTICIPATED MISCONCEPTIONS
Tres prismas rectangulares tienen una altura de 1 cm cada uno.
• El prisma A tiene una base de 1 cm por 11 cm.
• El prisma B tiene una base de 2 cm por 7 cm.
• El prisma C tiene una base de 3 cm por 5 cm.
1. Calcula el área superficial y el volumen de cada prisma. Usa el papel punteado para dibujar los prismas, si es necesario.
2. Analiza los volúmenes y las áreas superficiales de los prismas. ¿Qué observas? Escribe una o dos observaciones sobre ellos.

1. Superficies:
• Prisma A: 4(11 ⋅ 1) + 2(1 ⋅ 1) = 46 centímetros cuadrados
• Prisma B: 2(7 ⋅ 2) + 2(7 ⋅ 1) + 2(2 ⋅ 1) = 46 centímetros cuadrados
• Prisma C: 2(5 ⋅ 3) + 2(5 ⋅ 1) + 2(3 ⋅ 1) = 46 centímetros cuadrados
Volúmenes:
• Prisma A: 11 centímetros cúbicos (11 ⋅ 1 ⋅ 1 = 11)
• Prisma B: 14 centímetros cúbicos (7 ⋅ 2 ⋅ 1 = 14)
• Prisma C: 15 centímetros cúbicos (5 ⋅ 3 ⋅ 1 = 15)
2. Las respuestas varían. Ejemplos de respuestas:
• Las áreas superficiales de los prismas son todas iguales, pero sus volúmenes son diferentes.
• Los polígonos que conforman las caras de cada prisma son rectángulos de diferentes tamaños, pero sus áreas suman la misma cantidad de centímetros cuadrados.
• El prisma C tiene capacidad para la mayor cantidad de cubos de un centímetro, pero como los cubos encajarían de forma compacta, algunos solo tendrían dos centímetros cuadrados de caras expuestas.
• El prisma A tiene capacidad para la menor cantidad de cubos de un centímetro, pero como los cubos estarían más dispersos, más caras quedarían expuestas.
Los estudiantes podrían omitir o contar dos veces una o más caras de los prismas y calcular mal las áreas superficiales. Anime a los estudiantes a ser sistemáticos en sus cálculos y a usar las estrategias de organización que aprendieron al calcular el área superficial a partir de redes.
Es posible que se les recuerde usar unidades cuadradas para el área y unidades cúbicas para el volumen.
Pida a los estudiantes que compartan sus observaciones en respuesta a la segunda pregunta. Regístrelas para que todos las vean. Por cada observación única, sondee a la clase para ver si otros notaron lo mismo. Resalte las siguientes observaciones o señálelas si aún no las han mencionado los estudiantes:
• Los volúmenes de los prismas son todos diferentes, pero las áreas superficiales son las mismas.
• El volumen se describe en términosde cubos unitarios y el áreasuper ficial en términos de las caras expuestas de esos cubos unitarios.. Explique que, en una actividad anterior, vimos cómo diferentes formas pueden tener el mismo volumen (es decir, estar compuestas por la misma cantidad de cubos unitarios) pero diferentes áreas de superficie. Ahora vemos que también es posible que formas con diferentes volúmenes (es decir, compuestas por diferentes cantidades de cubos unitarios) tengan la misma área de superficie.
Grado 6 . Matemáticas . Unidad 1
Si los estudiantes tienen problemas para conceptualizar la idea de que figuras con volúmenes diferentes tienen la misma superficie, remítanse a la actividad del archivador de la primera lección sobre la superficie. El número de notas adhesivas cuadradas necesarias para cubrir todas las caras del archivador es su superficie. Si utilizamos todas esas notas cuadradas (ni más ni menos) para cubrir completamente (sin superponer notas adhesivas) un archivador que tiene un volumen diferente, podemos decir que los dos muebles tienen la misma superficie y volúmenes diferentes.
¿Estás listo para más?
¿Puedes encontrar más ejemplos de prismas que tengan las mismas áreas superficiales pero diferentes volúmenes? ¿Cuántos puedes encontrar?
"¿Estás preparado para más?" Respuesta del estudiante
Las respuestas varían. Ejemplo de respuesta: Un prisma que es 4 unidades por 5 unidades por 1 unidad y uno que es 2 unidades por 9 unidades por 1 unidad tienen la misma área superficial pero diferentes volúmenes. Genera ejemplos encontrando diferentes pares de factores del mismo número y restando 1 de cada factor. Sin embargo, hay otras formas. Por ejemplo, 60 = 6 ⋅ 10 y 60 = 5 ⋅ 12. Los prismas 5-por-9-por-1 y 4-por-11-por-1 tienen la misma superficie pero distinto volumen.
5 minutos
En esta lección, hemos refrescado nuestra memoria sobre las medidas de atributos unidimensionales, bidimensionales y tridimensionales. Reitera que la longitud es un atributo unidimensional atributo de las figuras geométricas, el área es un atributo bidimensional y el volumen es un atributo tridimensional. Repase algunos ejemplos de unidades de longitud, área y volumen.
También exploramos las áreas de superficie y los volúmenes de los poliedros y observamos que dos figuras pueden tener los mismos volúmenes pero diferentes áreas de superficie, y viceversa.
• "¿Cómo podrían dos figuras con un volumen de 4 unidades cúbicas tener un área de superficie de 16 unidades cuadradas y 18 unidades cuadradas?" (La superficie y el volumen miden atributos diferentes de una forma tridimensional.)
• "¿Qué tipo de medida es la superficie? ¿Qué tipo de medida es el volumen?" (La superficie es un atributo bidimensional; la medimos en unidades cuadradas. El volumen es un atributo tridimensional; lo medimos en unidades cúbicas).
• "¿Están relacionadas ambas medidas? ¿Un mayor volumen implica necesariamente una mayor superficie, y viceversa?". (No, una medida no afecta a la otra. Una figura que tiene un volumen mayor que otra no tiene por qué tener necesariamente una superficie mayor.)
5 minutos
Anime a los estudiantes a consultar la lista de observaciones de la clase de la actividad anterior.

California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
POSIBLES RESPUESTAS

Elige dos figuras que tengan la misma superficie pero volúmenes diferentes. Muestra tu razonamiento.
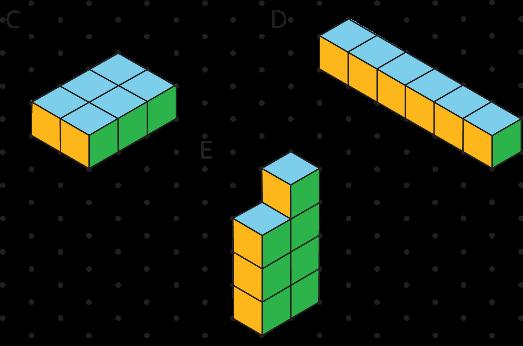
Las figuras D y E tienen ambas un área de superficie de 26 unidades cuadradas, pero D tiene un volumen de 6 unidades cúbicas, y E tiene un volumen de 7 unidades cúbicas.
PROBLEMA 1
Empareja cada cantidad con una unidad de medida apropiada.
A. La superficie de una caja de pañuelos
B. La cantidad de tierra en una jardinera
C. La superficie de un aparcamiento
D. La longitud de un campo de fútbol
E. El volumen de una pecera
Posibles soluciones
A. 5
B. 3, 4
C. 1
PROBLEMA 2
He aquí una figura construida a partir de cubos de encaje.
A. Halla el volumen de la figura en unidades cúbicas.
B. Halla la superficie de la figura en unidades cuadradas.
C. Verdadero o falso: Si duplicamos el número de cubos apilados, tanto el volumen como la superficie se duplicarán. Explica o muestra cómo lo sabes.
Learning Inc. - Todos los derechos reservados
i. Metros cuadrados
ii. Yardas
iii. Pulgadas cúbicas
iv. Pies cúbicos
v. Centímetros cuadrados
D. 2
E. 3, 4
Posibles soluciones
A. 4 unidades cúbicas. (1 ⋅ 1 ⋅ 4) = 4
B. 18 unidades cuadradas. (4 ⋅ 4) + (2 ⋅ 1) = 18
C. Falso. Ejemplo de razonamiento: El volumen se duplicará a 8 unidades cúbicas, pero no así la superficie. Sólo se duplicará el área de las caras laterales, hasta (4 ⋅ 8) o 32 unidades cuadradas, pero las caras superior e inferior no se duplicarán, por lo que el área de la superficie será 34, no 36, unidades cuadradas.
PROBLEMA 3
Lin dijo: "Dos figuras con el mismo volumen también tienen la misma superficie."
A. ¿Qué dos figuras sugieren que su afirmación es cierta?
B. ¿Qué dos figuras podrían mostrar que su afirmación no es cierta?
Posibles soluciones
A. B y C
B. A y B, o A y C
PROBLEMA 4
Del Grado 6, Unidad 1, Lección 11

Grado 6 . Matemáticas . Unidad 1
Dibuja un pentágono (polígono de cinco lados) que tenga un área de 32 unidades cuadradas. Rotula todos los lados o segmentos relevantes con sus medidas y demuestra que el área es 32 unidades cuadradas.
Posibles soluciones
Las respuestas varían. Ejemplos de respuestas:
El primer pentágono está formado por un cuadrado y un triángulo rectángulo. El cuadrado tiene un área de 16 unidades cuadradas. El triángulo tiene una base de 4 y una altura de 8, por lo que su área es 16 unidades cuadradas. El área combinada es 16 + 16 o 32 unidades cuadradas.
El segundo pentágono está formado por un paralelogramo de base 6 y altura 3, y un triángulo de base 7 y altura 4. El área del paralelogramo es 6 ⋅ 3 o 18 unidades cuadradas. El área del triángulo es 12 ⋅ 7 ⋅ 4 o 14 unidades cuadradas. El área combinada es 18 + 14 o 32 unidades cuadradas.
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 15
A. Dibuja una red para este prisma rectangular.
B. Halla el área de la superficie del prisma rectangular.

California - Grado 6
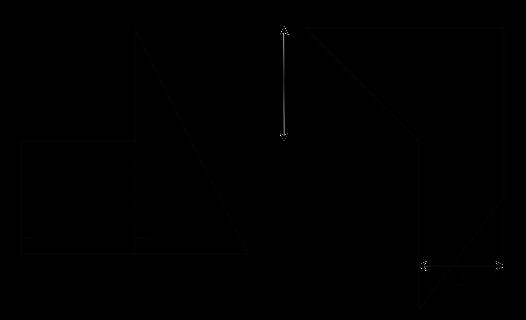
Posibles soluciones
Las respuestas varían. Estrategias de muestra:
A. Los diagramas varían. Aquí hay un ejemplo de red
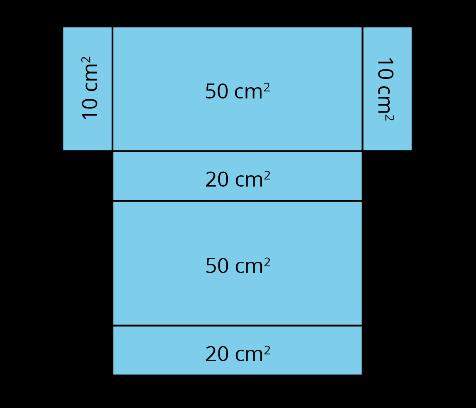
B. 160 unidades cuadradas. (Hay dos caras con un área de 50 cm cuadrados, dos caras con un área de 20 cm cuadrados, y dos caras con un área de 10 cm cuadrados).
Learning Inc. - Todos los derechos reservados

• Redes y superficie
ALINEACIÓN
Abordar
6.EE.1 Escribir y evaluar expresiones numéricas que involucren exponentes de números enteros.
Alineación de estándares y principios de California
6.G.2 Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empacándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = ����h y V = bh para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.
Construyendo sobre
5.MD.5a
Enfocar SMPs
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.1
II.A.2
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dar sentido al mundo y predecir lo que podría ocurrir
buscar y utilizar estructuras desmontar enteros, unir partes y descubrir formas y espacios.
OBJETIVO(S) DE APRENDIZAJE
• Investiguemos los cuadrados perfectos y los cubos perfectos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo escribir y explicar la fórmula para el volumen de un cubo, incluyendo el significado del exponente.
• Cuando conozco la longitud de la arista de un cubo, puedo encontrar el volumen y expresarlo usando las unidades apropiadas.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Generalizar un proceso para hallar el volumen de un cubo y justificar (oralmente) por qué se puede abstraer como s3
• Incluir unidades apropiadas (oralmente y por escrito) al informar sobre longitudes, áreas y volúmenes, por ejemplo cm, cm2, cm3
• Interpretar y escribir expresiones con exponentes 2 y 3 para representar el área de un cuadrado o el volumen de un cubo.
Rutinas instructivas
Anticipar, controlar, seleccionar, secuenciar, conectar
MLR2: Recopilar y exhibir
MLR8: Apoyo para la discusión
Piensa, empareja, comparte
MLR3: Clarificar, Criticar, Corregir
Materiales necesarios
Enfriamiento
cubos de chasquido
Preparación necesaria
Prepare juegos de 32 cubos de chasquido para cada grupo de 2 estudiantes.
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
En esta lección, los estudiantes aprenden sobre los cuadrados perfectos y los cubos perfectos. Ven que estos nombres provienen de las áreas de cuadrados y los volúmenes de cubos con longitudes laterales de números enteros. Los estudiantes encuentran longitudes desconocidas de los lados de un cuadrado dada el área o longitudes desconocidas de las aristas de un cubo dado el volumen. Para ello, utilizan la estructura de las expresiones para el área y el volumen (MP7).
Los estudiantes también utilizan los exponentes de 2 y 3 y ven que, en este contexto geométrico, los exponentes ayudan a expresar eficientemente la multiplicación de las longitudes laterales de cuadrados y cubos. Los estudiantes aprenden que las expresiones con exponentes de 2 y 3 se llaman cuadrados y cubos y ven la motivación geométrica de esta terminología. (El término "exponente" no se define de forma más general en este momento. Los estudiantes trabajarán con exponentes en mayor profundidad en una unidad posterior).
Al trabajar con longitud, área y volumen a lo largo de la lección, los estudiantes deben prestar atención a las unidades. Para escribir la fórmula del volumen de un cubo, los estudiantes buscan y expresan regularidades en razonamientos repetidos (MP8).
Nota: Los estudiantes deberán traer con antelación una colección personal de 10-50 objetos pequeños para la primera lección de la siguiente unidad. Por ejemplo, piedras, conchas, cromos o monedas.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 5 min.

Actividad de exploración opcional En parejas 15 min.
Actividad de Exploración Pares 10 min.
Actividad de Exploración Pares 15 min.
Los estudiantes exploran el concepto de cuadrados perfectos y lo relacionan con las áreas y las longitudes de los lados de los cuadrados.
Los estudiantes repasan los volúmenes de los prismas rectangulares utilizando cubos a presión para hallar el volumen de un cubo.
Un applet digital interactivo está disponible para permitir a los estudiantes construir cubos utilizando la tecnología.
Una extensión de exploración está disponible con un applet digital interactivo para desarrollar una comprensión más profunda de la construcción de cubos dentro de ciertos parámetros utilizando la tecnología.
Los estudiantes encuentran los volúmenes de cubos cuando se les dan varias longitudes de lado y luego generalizan una expresión para encontrar el volumen de cualquier cubo.
Los estudiantes expresan las áreas y volúmenes de cuadrados y cubos usando expresiones exponenciales.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de cuadrados perfectos y cubos perfectos.
Síntesis Todo el grupo 5 min. Los estudiantes establecen conexiones entre expresiones con exponentes y la expresión de áreas y volúmenes de cuadrados y cubos.
Enfriamiento Independiente 5 min.
Los estudiantes usan expresiones con exponentes de 2 y 3 para resolver problemas matemáticos.
Práctica Independiente 10 min. El componente de práctica independiente incluye 4 problemas de repaso de la lección y 3 espiral.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
5 minutos
Esta actividad introduce el concepto de cuadrados perfectos. También incluye oportunidades para practicar el uso de unidades de medida, lo que ofrece una visión de los conocimientos de los estudiantes de las lecciones anteriores.
Proporcione fichas cuadradas, si dispone de ellas. Algunos estudiantes pueden beneficiarse del uso de fichas físicas para razonar sobre los cuadrados perfectos.
A medida que los estudiantes trabajan, observe si utilizan las unidades apropiadas para la segunda y tercera preguntas.
Diga a los estudiantes: "Algunos números se llaman cuadrados perfectos. Por ejemplo, 9 es un cuadrado perfecto. Nueve copias de un cuadrado pequeño pueden formar un cuadrado grande". Muestre un cuadrado como éste para que todos lo vean:


Explique que 10, sin embargo, no es un cuadrado perfecto. Muestre imágenes como las siguientes, haciendo hincapié en que 10 cuadrados pequeños no se pueden organizar en un cuadrado grande (de la forma en que 9 cuadrados pequeños sí pueden).

Diga a los estudiantes que en este calentamiento encontrarán más números que son cuadrados perfectos. Conceda a los estudiantes 2 minutos de tiempo de reflexión para completar la actividad.
Apoyo a estudiantes con discapacidad
Procesamiento conceptual: Manipulativos. Proporcionar manipulativos (por ejemplo, fichas de una pulgada) para ayudar a los estudiantes que se benefician de las actividades prácticas.
1. El número 9 es un cuadrado perfecto. Encuentra cuatro números que sean cuadrados perfectos y dos que no lo sean..
2. Un cuadrado tiene un lado de 7 pulgadas. ¿Cuál es su área?
3. El área de un cuadrado es de 64 cm². ¿Cuál es la longitud de su lado?

Grado 6 . Matemáticas . Unidad 1

1. Las respuestas varían. Por ejemplo, aquí hay algunos cuadrados: 9, 25, 4, 49, 100 y no cuadrados: 1 2 , 2, 3, 10.
2. El cuadrado tiene una superficie de 49 kilómetros cuadrados.
3. La longitud del lado es 8 centímetros.
Si los estudiantes no recuerdan qué significan las abreviaturas km, cm y sq, proporcióneles esa información. Los estudiantes pueden dividir 64 entre 2 para la tercera pregunta. Si los estudiantes tienen problemas con esto, pídales que lo comprueben trabajando al revés, es decir, multiplicando las longitudes de los lados para ver si el producto da la medida de área dada.
Invite a los estudiantes a compartir los ejemplos y no ejemplos que encontraron para los cuadrados perfectos. Solicite algunas ideas sobre cómo decidieron si un número es o no un cuadrado perfecto. Si un estudiante pregunta si 0 es un cuadrado perfecto, espere hasta el final de la lección, cuando se introduce la notación de exponentes. 0 es un cuadrado perfecto porque 02 = 0 Discuta brevemente las respuestas de los estudiantes a las dos últimas preguntas, la última en particular. Si aún no se ha descubierto en la discusión, resalte que, dado que el área de un cuadrado se encuentra multiplicando las longitudes de los lados entre sí, encontrar las longitudes de los lados de un cuadrado con un área conocida significa averiguar si esa medida de área es un producto de dos del mismo número.
minutos
Rutinas instructivas
Anticipar, Monitorizar, Seleccionar, Secuenciar, Conectar
MLR2: Recoger y Mostrar
Esta actividad ofrece a los estudiantes una forma concreta de repasar el trabajo sobre volumen de 5º curso. Hace que los estudiantes recuerden que el volumen de un prisma rectangular se puede calcular de dos formas diferentes: contando los cubos unitarios que se pueden empaquetar en el prisma y multiplicando las longitudes de las aristas del prisma. Los estudiantes también se familiarizan con dos cubos perfectos, 27 y 64, antes de que la siguiente actividad introduzca este término.
A medida que los estudiantes trabajan, controle las diferentes rutas que siguen para hallar el volumen del cubo construido. Pueden contar todos los cubos a presión individualmente, contar el número de cubos a presión por capa y luego multiplicarlo por el número de capas, o simplemente multiplicar las longitudes de las aristas. Seleccione a un estudiante que utilice cada método para compartirlo más tarde.
California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Organice a los estudiantes en grupos de 2. Entregue 32 cubos de encaje a cada grupo. Si se dispone de cubos centimétricos, pida a los estudiantes que trabajen en centímetros en lugar de las unidades genéricas que se indican aquí.
Dé a los estudiantes entre 8 y 10 minutos para construir el cubo más grande que puedan con 32 cubos y para responder a las preguntas.
Para los grupos que terminen antes, considere la posibilidad de pedirles que combinen sus cubos y construyan el cubo individual más grande que puedan con 64 cubos. A continuación, pídales que respondan a las mismas cuatro preguntas que se muestran en el enunciado del problema.
Los estudiantes de aulas digitales pueden utilizar el applet para construir el cubo con 32 cubos. Para los estudiantes que terminen antes, pueden encontrar otro applet con 64 cubos en Extensión digital.
Apoyo para estudiantes de inglés
Conversar, representar: MLR2 Recoger y mostrar. Mientras los estudiantes trabajan en grupos, circule, escuche y recoja el vocabulario y las frases que utilizan al describir el proceso de construcción del cubo más grande y de averiguar su volumen y superficie. Escriba las palabras o frases y los dibujos correspondientes en una pantalla. Consulte esta lista cuando los estudiantes realicen las actividades restantes.
Principio(s) de diseño: Apoyar la adquisición de
DE CARA AL ESTUDIANTE ENUNCIADO DE LA
RESPUESTAS POSIBLES
Tu maestro te dará 32 cubos a presión. Utilízalos para construir el cubo individual más grande que puedas. Cada cubo pequeño tiene una longitud de arista de 1 unidad.
1. ¿Cuántos cubos a presión has utilizado?
2. ¿Cuál es la longitud de arista del cubo que has construido?
3. ¿Cuál es el área de cada cara del cubo construido? Razona.
4. ¿Cuál es el volumen del cubo construido? Muestra tu razonamiento.
1. 27
2. 3 unidades
3. 9 unidades cuadradas
4. 27 unidades cúbicas ERRORES ANTICIPADOS
Es posible que los estudiantes no escriban las unidades de longitud o área y que necesiten que se les recuerde hacerlo.
Al determinar el área, los estudiantes pueden multiplicar un lado por dos en lugar de elevarlo al cuadrado. Al determinar el volumen, pueden multiplicar un lado por tres en lugar de elevarlo al cubo. Si esto ocurre, pídeles que cuenten los cuadrados individuales para que puedan ver que hay un error en su razonamiento.
Grado 6 . Matemáticas . Unidad 1

Centre el debate de toda la clase en las formas en que los estudiantes calcularon los volúmenes de los dos cubos que construyeron. Selecciona a estudiantes previamente identificados para que compartan sus enfoques empezando por el menos eficiente (contar cubos individuales) hasta el más eficiente (multiplicar longitudes laterales).
Subraya cómo la longitud lateral de un cubo determina su volumen, y específicamente que el número 27 es 3 ⋅ 3 ⋅ 3. Si algún grupo construye un cubo con 64 cubos de presión, señale que el número 64 es 4 ⋅ 4 ⋅ 4. Estas observaciones preparan a los estudiantes para pensar sobre los cubos perfectos en la siguiente actividad y sobre una expresión general para el volumen de un cubo más adelante en la lección.
¿Estás listo para más?
Este applet tiene un total de 64 cubos a presión. Construye el cubo más grande que puedas.
1. ¿Cuántos cubos a presión has utilizado?
2. ¿Cuál es la longitud de las aristas del nuevo cubo que has construido?
3. ¿Cuál es el área de cada cara de este cubo construido? Muestra tu razonamiento.
4. ¿Cuál es el volumen de este cubo construido? Muestra tu razonamiento.
"¿Estás preparado para más?" Respuesta de los estudiantes
1. 64
2. 4 unidades
3. 16 unidades cuadradas
4. 64 unidades cúbicas
10 minutos
Rutinas instructivas
MLR8: Apoyos para la discusión
Pensar Compartir
Anteriormente, los estudiantes vieron ejemplos y no ejemplos de cuadrados perfectos. En esta actividad, piensan en ejemplos y no ejemplos de cubos perfectos y hallan los volúmenes de los cubos dadas las longitudes de sus aristas. Los estudiantes ven que la longitud de las aristas de un cubo determina su volumen, se fijan en las expresiones numéricas que se pueden escribir al calcular volúmenes y escriben una expresión general para hallar el volumen de un cubo (MP8).
Puede que algunos estudiantes se sientan incómodos escribiendo simbólicamente la respuesta a la última pregunta porque implica una variable y prefieran escribir una explicación verbal. Esto está bien; la notación exponencial que sigue será de gran ayuda.
Di a los estudiantes: "Algunos números se llaman cubos perfectos. Por ejemplo, 27 es un cubo perfecto". Exponga un cubo como éste para que todos lo vean:

Organice a los estudiantes en grupos de 2. Dé a los estudiantes unos minutos para pensar en silencio y otro minuto para discutir sus respuestas con su compañero.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

Apoyo para estudiantes de inglés
Hablar, representar: MLR8 Apoyos para el debate. A medida que los estudiantes trabajan en parejas para dar sentido a los cubos perfectos, anime a pensar en voz alta, revoicing, y presionar para obtener detalles (por ejemplo, "¿Cómo sabes que _____ es (o no es) un cubo perfecto?" "Cuéntame más sobre..."). El uso práctico de cubos a presión ayudará a los estudiantes a ver ejemplos y no ejemplos de cubos perfectos y a reconocer que la longitud de las aristas de un cubo determina su volumen.
Principio(s) de diseño: Apoyar la creación de sentido; Maximizar la objetivoconciencia
Apoyo para estudiantes con discapacidad
Procesamiento conceptual: Manipulativos. Proporcionar manipulativos (por ejemplo, fichas de una pulgada) para ayudar a los estudiantes que se benefician de las actividades prácticas.
1. El número 27 es un cubo perfecto.. Encuentra otros cuatro números que sean cubos perfectos y dos números que no sean cubos perfectos.
2. Un cubo tiene una longitud de lado de 4 cm. ¿Cuál es su volumen?
3. Un cubo tiene una longitud de lado de 10 pulgadas. ¿Cuál es su volumen?
4. Un cubo tiene una longitud de lado de s unidades. ¿Cuál es su volumen?

1. Las respuestas varían: 1, 8, 64, 125, 216, 1,000. No cubos: 2, 3, 4.
2. 4 ⋅ 4 ⋅ 4 or 64 centímetros cúbicos
3. 10 ⋅ 10 ⋅ 10 or 1,000 pulgadas cúbicas
4. s ⋅ s ⋅ s unidades cúbicas
Esté atento a si los estudiantes usan unidades cuadradas en lugar de cúbicas. Recuérdeles que el volumen es una medida del espacio dentro del cubo y se mide en unidades cúbicas. Los estudiantes pueden multiplicar por 3 para calcular el volumen de un cubo en lugar de multiplicar tres longitudes de aristas (que son el mismo número). Asimismo, podrían pensar que un cubo perfecto es un número multiplicado por 3. Sugiérales que dibujen o construyan un cubo con esa longitud de arista y cuenten el número de cubos unitarios. O pídales que piensen en cómo calcular el volumen de un prisma cuando las longitudes de aristas son diferentes (por ejemplo, un prisma que mide 1 unidad por 2 unidades por 3 unidades).
Después de las conversaciones en parejas, invite a los estudiantes a compartir cómo pensaron en la primera pregunta y decidieron si un número es o no un cubo perfecto. Resalte la idea de que multiplicar tres longitudes de arista nos permite determinar el volumen eficientemente, y que determinar si un número es un cubo perfecto implica pensar si es un producto de tres veces el mismo número. Si un estudiante pregunta si el 0 es un cubo perfecto, espere hasta el final de la lección, cuando se introduce la notación exponencial. El 0 es un cubo perfecto porque 03 = 0
Asegúrese de que los estudiantes vean las respuestas a las últimas tres preguntas escritas como expresiones.:
Grado 6 . Matemáticas . Unidad 1
EXPONENTES
15 minutos
Rutinas instructivas
MLR3: Aclarar, Criticar, Corregir
Esta actividad presenta a los estudiantes los exponentes de 2 y 3 y el lenguaje que utilizamos para hablar de ellos. Los estudiantes utilizan e interpretan esta notación en el contexto de los cuadrados geométricos y sus áreas, y de los cubos geométricos y sus volúmenes. Es probable que los estudiantes hayan visto la notación de exponentes para 103 en su trabajo sobre los valores posicionales en 5º curso. Esa experiencia sería útil, pero no es necesaria.
Tenga en cuenta que el término "exponente" deliberadamente no se define de manera más general en este momento. Los estudiantes trabajarán con exponentes en mayor profundidad en una unidad posterior.
Mientras los estudiantes trabajan, observe cómo abordan las dos últimas preguntas. Identifique a un par de estudiantes que aborden la cuarta pregunta de forma diferente para que puedan compartirla más tarde. Observe también si los estudiantes incluyen unidades apropiadas, escritas usando exponentes, en sus respuestas.
Pregunte a los estudiantes si han visto antes una expresión como 103 . Diga a los estudiantes que en esta expresión, el 3 se llama exponente. Explique el uso de exponentes de 2 y 3:
• "Cuando multiplicamos dos del mismo número juntos, como 5 ⋅ 5, decimos que estamos elevando el número al cuadrado. Podemos escribir la expresión como 52 Porque 5 ⋅ 5 es 25, podemos escribir 52 = 25, y decimos: '5 al cuadrado es 25.' También podemos decir que 25 es un cuadrado perfecto. El elevado 2 en 52 se llama exponente."

• "Cuando multiplicamos tres del mismo número juntos como 4 ⋅ 4 ⋅ 4, decimos que estamos cubicando el número. Podemos escribirlo así: 43 Porque 4 ⋅ 4 ⋅ 4 es 64, podemos escribir 43 = 64, y decimos, '4 elevado al cubo es 64.' También decimos que 64 es un cubo perfecto. El elevado 3 en 43 se llama exponente."
Explica que también podemos usar exponentes como una forma abreviada de las unidades usadas para el área y el volumen:
• Un cuadrado con longitud de lado 5 pulgadas tiene un área de 25 pulgadas cuadradas, que podemos escribir como 25 en2
• Un cubo con longitud de arista 4 centímetros tiene un volumen de 64 centímetros cúbicos, que podemos escribir como 64 cm3 .
Pida a los estudiantes que lean algunas áreas y volúmenes en diferentes unidades (por ejemplo, 100 pies2 se lee "100 pies cuadrados" y 125 yd3 se lee "125 yardas cúbicas").
Mantenga a los estudiantes en grupos de 2. Dé a los estudiantes 3-4 minutos de silencio para completar la actividad y un minuto para discutir su respuesta con su compañero. Pida a sus compañeros que anoten cualquier desacuerdo para poder discutirlo.
Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (por ejemplo, cuadrado, cubo, exponente) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para referencia futura.
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus compañeros tutores previamente
Asegúrate de incluir las unidades de medida correctas en cada respuesta.
1. Un cuadrado tiene 10 cm de lado. Usa un exponente para expresar su área.
2. El área de un cuadrado es de 72 pulgadas cuadradas. ¿Cuál es la longitud de su lado?
3. El área de un cuadrado es de 81 m². Usa un exponente para expresar esta área.
4. Un cubo tiene 5 pulgadas de arista. Usa un exponente para expresar su volumen.
5. El volumen de un cubo es de 63 cm³. ¿Cuál es la longitud de su arista?
6. Un cubo tiene 5 unidades de arista. Usa un exponente para escribir una expresión para su volumen.
Nation California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTASS
ERRORES ANTICIPADOS
1. 102 cm2
2. 7 pulgadas
3. 92 m2
4. 53 en3
5. 6 cm
6. s3 unidades3 o s3 unidades cúbicas
Al ver 63 en la cuarta pregunta, es posible que algunos estudiantes no sepan interpretar la pregunta, calculen automáticamente 6 ⋅ 6 ⋅ 6, y concluyan que la longitud de la arista es 216 cm. Pídales que comprueben su respuesta hallando el volumen de un cubo con longitud de arista 216 cm.
SÍNTESIS DE LA ACTIVIDAD
Pida a los compañeros que compartan los desacuerdos en sus respuestas, si los hubiera. A continuación, centre el debate de toda la clase en las dos últimas preguntas. Seleccione a un par de estudiantes previamente identificados para que compartan sus interpretaciones de la cuarta pregunta. Destaque que un cubo con un volumen de 63 unidades cúbicas tiene una longitud de arista de 6 unidades, porque sabemos que hay 6 ⋅ 6 ⋅ 6 unidades cúbicas en un cubo con esa longitud de arista. En otras palabras, podemos expresar el volumen de un cubo utilizando un número (216), un producto de tres números (6 ⋅ 6 ⋅ 6), o una expresión con exponente (63). Esta idea puede extenderse a todos los cubos. El volumen de un cubo con arista de longitud s es: s ⋅ s ⋅ s s3 Los estudiantes tendrán más oportunidades de generalizar las expresiones para el volumen de un cubo en la próxima lección.
Apoyo a los estudiantes de inglés
Conversing: MLR3 Aclarar, Criticar, Corregir. Presente una respuesta incorrecta del tipo: "Si el volumen de un cubo es 63 cm3, entonces la longitud de la arista es 216 cm porque 6 x 6 x 6 es 216." Pida a los estudiantes que identifiquen el error y ofrezcan un argumento correcto para determinar la longitud de arista del cubo. Esto ayudará a los estudiantes a utilizar el lenguaje matemático y a reflexionar sobre su trabajo y el de los demás.
Principio(s) de diseño: Optimizar el resultado (para la justificación); Maximizar la objetivoconciencia
¿Estás preparado para más?
Encuentra algunos números que sean a la vez cuadrados perfectos y cubos perfectos, y escríbelos utilizando la notación. Por ejemplo, 1 es a la vez un cuadrado perfecto porque 1 ⋅ 1=1 y un cubo perfecto porque 1 ⋅ 1 ⋅ 1=1, y podemos escribirlo así: 1=12 1=13
"¿Estás preparado para más?" Respuesta del estudiante
Los ejemplos más pequeños son 0, 1, 64, y 729.
5 minutos
Repase el lenguaje y la notación para elevar al cuadrado y elevar al cubo un número. Recuerda a los estudiantes que también utilizamos esta notación para las unidades cuadradas y cúbicas.
Grado 6 . Matemáticas . Unidad 1
• Cuando multiplicamos dos números iguales como 10 ⋅ 10 decimos que estamos elevando al cuadrado el número. Escribimos, por ejemplo, 102 = 100 y decimos: "Diez al cuadrado son cien."
• Cuando multiplicamos tres del mismo número juntos como 10 ⋅ 10 ⋅ 10, decimos que estamos cubicando el número. Escribimos, por ejemplo, 103 = 1.000 y decimos: "Diez elevado al cubo es mil."
• Los exponentes se usan para escribir unidades cuadradas y cúbicas. El área de un cuadrado de lado 7 km es 72 km2. El volumen de un cubo de lado 2 milímetros es 23 mm3 .
5 minutos

DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
1. ¿Cuál es mayor, 52 o 33?
2. Un cubo tiene una longitud de arista de 21 cm. Utiliza un exponente para expresar su volumen.
FALTAS ANTICIPADAS
1. 33=27 y 52=25, por lo que 33 es mayor que 52.
2. 213 cm3 o 213 centímetros cúbicos
Los estudiantes pueden realizar cálculos en la segunda pregunta, lo cual no es necesario ya que el objetivo es una expresión con exponente.
PROBLEMA 1
¿Cuál es el volumen de este cubo?
Posibles soluciones
8 cm cúbicos (2⋅2⋅2=8)

California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

PROBLEMA 2
A. Decide si cada número de la lista es un cuadrado perfecto 16 125 20 114 25 225 100 10.000
B. Escribe una frase que explique tu razonamiento.
PROBLEMA 3
A. Decide si cada número de la lista es un cubo perfecto. 1 27 3 64 8 100 9 125
B. Explica qué es un cubo perfecto.
PROBLEMA 4
A. Un cuadrado tiene de lado 4 cm. ¿Cuál es su área?
B. El área de un cuadrado es 49m2. ¿Cuál es su longitud lateral?
C. Un cubo tiene de arista 3 pulg. ¿Cuál es su volumen?
PROBLEMA 5
Del Grado 6, Unidad 1, Lección 16
El prisma A y el prisma B son prismas rectangulares.
• El prisma A mide 3 pulgadas por 2 pulgadas por 1 pulgadas.
• El prisma B mide 1 pulgadas por 1 pulgadas por 6 pulgadas.
Selecciona todas las afirmaciones que sean ciertas sobre los dos prismas.
Tienen el mismo volumen.
Tienen el mismo número de caras.
En el prisma A caben más cubos de pulgadas que en el prisma B.
Los dos prismas tienen la misma superficie.
La superficie del prisma B es mayor que la del prisma A.
Posibles soluciones
A. Todos estos números, excepto 20 y 125, son cuadrados perfectos.
B. Las respuestas varían. Ejemplo de respuesta: Los cuadrados perfectos se pueden encontrar multiplicando un número entero por sí mismo.
Posibles soluciones
A. Todos los números excepto 3, 9, y 100 son cubos perfectos.
B. Las respuestas varían. Ejemplo de respuesta: Los cubos perfectos se pueden encontrar multiplicando números enteros por sí mismos tres veces.
Posibles soluciones
A. 16 cm2
B. 7 m
C. 27 pulg3
Posibles soluciones
Tienen el mismo volumen.
Tienen el mismo número de caras.
Se pueden empaquetar más cubos de una pulgada en el Prisma A que en el Prisma B.
Los dos prismas tienen la misma superficie.
La superficie del Prisma B es mayor que la del Prisma A.
Grado 6 . Matemáticas . Unidad 1

PROBLEMA 6
Del Grado 6, Unidad 1, Lección 14
A. ¿Qué poliedro se puede ensamblar a partir de esta red?
B. ¿Qué información necesitarías para hallar su área superficial? Sea específico y etiquete el diagrama según sea necesario.
Posibles soluciones
A. Prisma triangular
B. Longitud y anchura de cada cara rectangular (como se muestra en el diagrama), así como la altura de las caras triangulares
PROBLEMA 7
Del Grado 6, Unidad 1, Lección 15
Encuentre el área de la superficie de este prisma triangular. Todas las medidas están en metros.
Posibles soluciones
4,8 metros cuadrados. Ejemplo de razonamiento:
• Hay dos caras triangulares con un área de 0,48 metros cuadrados cada una.
1 2 ⋅ (1,2) ⋅ (0,8) = 0,48

• Hay dos caras rectangulares con un área de 1,2 metros cuadrados cada una. 1 ⋅ (1.2) = 1.2
• Hay una cara rectangular con un área de (1.2) ⋅ (1.2) = 1.44 metros cuadrados.
• 2 ⋅ (0.48) + 2 ⋅ (1.2) + (1.44) = 4.8, o 4.8 metros cuadrados.
Reflexiones:
Math Nation California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados

• Redes y superficie
• Generalizar con representaciones múltiples
ALINEACIÓN
Abordar
6.EE.1 Escribir y evaluar expresiones numéricas que involucren exponentes de números enteros.
6.EE.2a Escribir expresiones que registren operaciones con números y con letras que representen números.
Alineación de estándares y principios de California
6.G.2 Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V=lwh y V=bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.
6.G.4 Representar figuras tridimensionales utilizando redes formadas por rectángulos y triángulos, y utilizar las redes para hallar la superficie de estas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.
Enfocar SMPs
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.3
I.B.7
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .
dan sentido al mundo e influyen en el futuro
buscan y expresan regularidades en razonamientos repetidos desmontando enteros, juntando piezas y descubriendo la forma y el espacio.
OBJETIVO(S) DE APRENDIZAJE
• Escribamos una fórmula para hallar el área de la superficie de un cubo.
OBJETIVO(S)
• Puedo escribir y explicar la fórmula para el área de la superficie de un cubo.
• Cuando conozco la longitud de la arista de un cubo, puedo hallar su área de superficie y expresarla usando las unidades apropiadas.
OBJETIVOS DE APRENDIZAJE PARA
• Generalizar un proceso para hallar la superficie de un cubo y justificar (oralmente) por qué se puede abstraer como 6⋅s2 .
• Interpretar (oralmente) expresiones que incluyan sumas repetidas, multiplicaciones, multiplicaciones repetidas o exponentes.
• Escribir expresiones, con o sin exponentes, para representar la superficie de un cubo dado.
Rutinas instructivas
MLR7: Comparar y conectar
Pensar, compartir en parejas
Anticipar, supervisar, seleccionar, secuenciar, conectar
MLR3: Clarificar, Criticar, Corregir
Anticipar, Monitorizar, Seleccionar, Secuenciar, Conectar
Materiales necesarios
Enfriamiento
geometry toolkits (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
En esta lección, los estudiantes practican el uso de exponentes de 2 y 3 para expresar productos y escribir unidades cuadradas y cúbicas. Además, buscan y utilizan la estructura de las expresiones numéricas (MP7). También buscan y expresan regularidades en razonamientos repetidos (MP8) para escribir la fórmula de la superficie de un cubo. Los estudiantes continuarán este trabajo más adelante en el curso, en la unidad sobre expresiones y ecuaciones.
Nota: Los estudiantes deberán traer con antelación una colección personal de 10-50 pequeños objetos para la primera lección de la siguiente unidad. Por ejemplo, piedras, conchas, cromos o monedas.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 5 min. Los estudiantes comparan expresiones sin hacer cálculos para determinar qué expresión tiene un valor mayor.
Actividad de exploración En parejas 20 min. Los estudiantes dibujan redes, escriben expresiones y encuentran áreas de superficie y volúmenes de diferentes cubos.
Actividad de exploración Independiente 10 min. Los estudiantes generalizan una expresión para el área de la superficie y el volumen de un cubo.
Síntesis Todo el grupo 5 min. Los estudiantes resumen las fórmulas derivadas para el volumen y el área de la superficie de los cubos.
Enfriamiento Independiente 5 min. Los estudiantes escriben y usan expresiones para el volumen y el área de la superficie de cubos.
Práctica Independiente 8-10 min. El componente de práctica independiente incluye 3 problemas de repaso de la lección y 3 problemas de repaso en espiral.

California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
5 minutos
En este calentamiento, los estudiantes comparan pares de expresiones numéricas e identifican la expresión con el valor mayor. La tarea permite a los estudiantes repasar lo aprendido sobre exponentes y les incita a buscar y utilizar la estructura de las expresiones numéricas (MP7).
Los estudiantes deben realizar estas preguntas sin calculadora y sin calcular, aunque está bien que comprueben sus respuestas con una calculadora.

Apoyo a los estudiantes con discapacidad
Lenguaje receptivo/expresivo: Tiempo de procesamiento. Lea todos los enunciados en voz alta. Los estudiantes que escuchen y lean la información se beneficiarán de un tiempo de procesamiento adicional.
Seleccione la expresión mayor de cada par sin calcular el valor de cada expresión. Prepárate para explicar tus elecciones.
• 10 ⋅ 3 o 103
• 132 o 12 ⋅ 12
• 97 + 97 + 97 + 97 + 97 + 97 o 5⋅97 POSIBLES RESPUESTASS
• 103 es mayor porque es 1.000.
• 132 es mayor porque es 13 ⋅ 13, y ésta será mayor que 12 ⋅ 12.
• 97 + 97 + 97 + 97 + 97 + 97 es mayor porque es 6 ⋅ 97, que es mayor que 5 ⋅ 97
Cuando se les da una expresión con exponente, los estudiantes pueden interpretar erróneamente la base y el exponente como factores y multiplicar los dos números. Recuérdeles el significado de la notación de exponente. Por ejemplo, demuestre que 5 ⋅ 3 = 15, que es mucho menor que 5 ⋅ 5 ⋅ 5, que es igual a 125
Grado 6 . Matemáticas . Unidad 1

Pida a uno o más estudiantes que expliquen su razonamiento para cada elección. Si no se menciona en las explicaciones de los estudiantes, destaque las estructuras de las expresiones que nos permiten evaluar cada una sin realizar ningún cálculo.
Señale, por ejemplo, que como sabemos que 103 significa 10 ⋅ 10 ⋅ 10, podemos decir que es mucho mayor que 10 ⋅ 3
Para la última pregunta, recuerde a los estudiantes que podemos pensar en la suma repetida en términos de grupos múltiples (es decir, que la suma de seis 97s puede verse como seis grupos de 97 o 6 ⋅ 97). La idea de utilizar grupos para escribir expresiones equivalentes ayudará a los estudiantes a escribir expresiones para la superficie de un cubo más adelante en la lección (p. ej, escribir las áreas de todas las caras cuadradas de un cubo como 6s2)
20 minutos
Rutinas instructivas
MLR7: Comparar y conectar
Pensar, compartir en parejas
Anticipar, controlar, seleccionar, secuenciar, conectar
Esta actividad contiene dos conjuntos de problemas. En el primero se realizan cálculos con números sencillos y debe resolverse numéricamente. Utilice el trabajo de los estudiantes aquí para comprobar que dibujan correctamente una red.
El segundo conjunto anima a los estudiantes a escribir expresiones en lugar de simplificarlas mediante cálculos. El objetivo es preparar a los estudiantes para las reglas generales s3 y 6s2, que se entienden más fácilmente a través de un paso intermedio que implica números.
Tenga en cuenta que los estudiantes conocerán la idea de que 5 ⋅ x significa lo mismo que 5x en una unidad posterior, así que espere que escriban 6 ⋅ 172 en lugar de 6(172). No es fundamental que entiendan que un número y una variable (o un número y una expresión entre paréntesis) colocados uno al lado del otro significa que se están multiplicando.
A medida que los estudiantes trabajen en el segundo conjunto, controle las formas en que escriben sus expresiones para superficie y volumen. Identifica aquellas cuyas expresiones incluyan :
• productos (por ejemplo, 17 ⋅ 17 o 17 ⋅ 17 ⋅ 17),
• sumas de productos (por ejemplo, (17 ⋅ 17) + (17 ⋅ 17) +...),
• combinación de términos semejantes (por ejemplo, 6 ⋅ (17 ⋅ 17)),
• exponentes (por ejemplo, 172 + 172 + ...) o 173), y
• cálculo completado (por ejemplo, 289).
Seleccione a estos estudiantes para compartir su trabajo más tarde. Fíjese en la longitud de las expresiones y ordene sus explicaciones, desde la expresión más larga a la más sucinta.
Organizar a los estudiantes en grupos de 2. Dé a los estudiantes acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y 8-10 minutos de tiempo de trabajo tranquilo. Pide a los estudiantes que intenten responder a las preguntas sin utilizar la calculadora. Pídeles que después compartan sus respuestas con su compañero.
Apoyo a estudiantes con discapacidad
Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten cómo dibujar cada red según sea necesario.
©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSSIBLE RESPONSES
A. Un cubo tiene una longitud de arista de 5 pulgadas.
B. Dibuja el desarrollo de este cubo y etiqueta sus lados con las medidas.
C. ¿Cuál es la forma de cada cara?
D. ¿Cuál es el área de cada cara?
E. ¿Cuál es el área de la superficie de este cubo?
F. ¿Cuál es el volumen de este cubo?
G. Un segundo cubo tiene una longitud de arista de 17 unidades.
H. Dibuja el desarrollo de este cubo y etiqueta sus lados con las medidas.
I. Explica por qué el área de cada cara de este cubo es de 172 unidades cuadradas. ¿Cuál es el área de cada cara?
J. Escribe una expresión para el área de la superficie, en unidades cuadradas.
K. Escribe una expresión para el volumen, en unidades cúbicas.
1. Para el cubo con una longitud de arista de 5:
A. Los dibujos varían. Son posibles 11 desarrollos únicos::
B. Cuadrado
C. 25 pulgadas cuadradas
D. 150 pulgadas cuadradas
E. 125 pulgadas cúbicas
2. Para el cubo que tiene una longitud de arista de 17:
A. Los dibujos varían, pero deben ser una de las 11 redes mostradas en el problema anterior.

B. Las respuestas varían. Ejemplo de explicación: La longitud del lado de cada cara cuadrada es de 17 unidades, por lo que su área es 17 × 17 o 172 unidades cuadradas.
C. 6 ⋅ 172 (o equivalente)
D. 173 (o equivalente)
Los estudiantes podrían pensar que el área superficial es (17 ⋅ 17)6. Indíqueles que escriban cómo calcularían el área superficial paso a paso, antes de intentar resumir sus pasos en una expresión. Indíqueles que no usen calculadora en los dos últimos problemas y asegúreles que construir una expresión no requiere cálculos extensos. Los estudiantes podrían pensar que abstenerse de usar calculadora significa realizar todos los cálculos, incluidos los de números grandes, en papel o mentalmente, especialmente si no tienen claro el significado del término "expresión". Pídales que consulten las expresiones del ejercicio de calentamiento o que compartan ejemplos de expresiones en diferentes formas para ayudarlos a ver cómo el área superficial y el volumen se pueden expresar sin cálculos.
Tras las conversaciones en parejas, seleccione a un par de estudiantes para que presenten las soluciones al primer conjunto de preguntas, que deben ser sencillas. Luego, invite a los estudiantes previamente identificados a compartir sus expresiones para las dos últimas preguntas. Si es posible, organice su presentación en el siguiente orden. Si falta alguna expresión, pero es necesaria para ilustrar la idea de escribir expresiones concisas, añádala a las listas. Superficie:
• (17 ⋅ 17) + (17 ⋅ 17) + (17 ⋅ 17) + (17 ⋅ 17) + (17 ⋅ 17) + (17 ⋅ 17)
• 172 + 172 + 172 + 172 + 172 + 172
• 6 ⋅ (17 ⋅ 17)
• 6 ⋅ (172)
• 6 ⋅ (289)
• 1,734
Volumen:
• 17 ⋅ 17 ⋅ 17
• 173
• 4,913
ACTIVIDAD SÍNTESIS CONTINUACIÓN

Grado 6 . Matemáticas . Unidad 1
Discute cómo la multiplicación puede simplificar expresiones que implican sumas repetidas y cómo los exponentes pueden hacer lo mismo con multiplicaciones repetidas. Aunque la última expresión de cada conjunto anterior es la más sencilla de escribir, llegar a ella requiere bastantes cálculos. Destaca 6 ⋅ 172 y 173 como formas eficientes de expresar la superficie y el volumen del cubo.
Mientras la clase discute las diferentes expresiones, considera dirigir la atención de los estudiantes a las unidades de medida. Recuerda a los estudiantes que, en lugar de escribir 6 ⋅ (172) unidades cuadradas, podemos escribir 6 ⋅ (172) unidades2, y en lugar de 173 unidades cúbicas, podemos escribir 173 unidades2. Las notaciones de unidades volverán a aparecer más adelante en el curso, así que esto también puede reforzarse más adelante.
Si los estudiantes aún no están preparados para la fórmula general, que viene a continuación, ofrezca otro ejemplo. Por ejemplo, diga: "Un cubo tiene de arista 38 cm. ¿Cómo podemos expresar su superficie y su volumen?"
Ayude a los estudiantes a ver que su superficie es 6 ⋅ (382) cm2 y su volumen es 382 cm3. El número grande desalentará el cálculo y centrará a los estudiantes en la forma de las expresiones que están construyendo y en el uso de exponentes.
Representar, conversar: MLR7 Comparar y conectar. Mientras los estudiantes participan en sus discusiones por parejas sobre los dos cubos, pregunte "¿Qué es igual y qué es diferente?" en los cálculos de la superficie (y el volumen) de cada cubo respectivo. Esto ayuda a los estudiantes a establecer y describir las conexiones entre los cálculos, independientemente de la longitud de las aristas del cubo.
Principio(s) de diseño: Cultivar la conversación; Maximizar la objetivoconciencia
ENTERO 5 minutos
Rutinas didácticas
MLR3: Clarificar, Criticar, Corregir
Anticipar, Supervisar, Seleccionar, Secuenciar, Conectar
En esta actividad, los estudiantes se basan en lo aprendido anteriormente y desarrollan las fórmulas para el área de la superficie y el volumen de un cubo en términos de una longitud de arista variable s.
Anime a los estudiantes a referirse a su trabajo en la actividad anterior tanto como sea posible y a generalizar a partir de él. Como en el caso anterior, observe las distintas formas de escribir las expresiones para la superficie y el volumen. Identifique a los estudiantes cuyo trabajo incluya lo siguiente:
• productos (por ejemplo, s ⋅ s, o s ⋅ s ⋅ s),
• sumas de productos (por ejemplo, (s ⋅ s) + (s ⋅ s) +...),
• combinación de términos semejantes (por ejemplo, 6 ⋅ (s ⋅ s)), y
• exponentes (por ejemplo, s2 + s2+..., o s3).
Seleccione a estos estudiantes para compartir su trabajo más tarde. Una vez más, fíjese en la longitud de las expresiones y ordene sus explicaciones, desde la expresión más larga a la más sucinta.
INSTRUCCIÓN
Dé a los estudiantes acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) y 7-8 minutos de tiempo para pensar en silencio. Diles que responderán a las mismas preguntas que antes, pero con una variable para la longitud del lado. Anímales a que se ayuden del trabajo que han hecho antes.
Nation California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten cómo dibujar cada red según sea necesario.
POSIBLES RESPUESTASS

ERRORES ANTICIPADOS
Un cubo tiene aristas de longitud s.
1. Dibuja una red para el cubo.
2. Escribe una expresión para el área de cada cara. Etiqueta cada cara con su área.
3. Escribe una expresión para el área de la superficie.
4. Escribe una expresión para el volumen.
1. Los dibujos varían. Aquí tienes una posible red etiquetada (cada cara es un cuadrado cuyas longitudes laterales son s):
2. El área de cada cara es s2
3. El área de la superficie es 6 ⋅ s2
4. El volumen es s3 .
Si los estudiantes no tienen claro o no están seguros sobre el uso de la variable s, explíqueles que estamos buscando una expresión que funcione para cualquier longitud de arista, y que una variable, como s, puede representar cualquier número. Para relacionar el trabajo de los estudiantes con ejemplos anteriores, señale el cubo con la longitud de arista 17 unidades de la actividad anterior. Pregunte: "Si antes escribiste el área de la superficie como 6 ⋅ 172, ¿cuál debería ser ahora?"
Mientras los estudiantes trabajan, anime a aquellos que se sientan más cómodos utilizando símbolos de multiplicación a que utilicen exponentes siempre que sea posible.
Discuta los problemas de forma similar a como se hizo en la actividad anterior con un cubo de aristas 17 unidades. Esto permite a los estudiantes ver la estructura de las expresiones (MP7) y generalizar mediante razonamientos repetidos (MP8).
Seleccione a los estudiantes previamente identificados para que compartan sus respuestas con la clase. Si es posible, secuencie su presentación en el siguiente orden para ayudar a los estudiantes a ver cómo se producen las expresiones 6 ⋅ s2 y s3. Si falta alguna expresión pero es necesaria para ilustrar la idea de escribir expresiones sucintas, añádela a las listas.
Superficie:
• (s ⋅ s) + (s ⋅ s) + (s ⋅ s) + (s ⋅ s) + (s ⋅ s) + (s ⋅ s)
• s2 + s2 + s2 + s2 + s2 + s2
• 6(s ⋅ s)
• 6 ⋅ (s2) o 6 ⋅ s2
Grado 6 . Matemáticas . Unidad 1

ACTIVIDAD SÍNTESIS CONTINUACIÓN
Volumen:
• s ⋅ s ⋅ s
• s2
Vuelve a consultar el ejemplo de la longitud lateral numérica (un cubo con arista de longitud 17 unidades) si los estudiantes tienen problemas para entender de dónde sale la expresión más concisa de superficie. Presenta la superficie como 6 ⋅ s2. Puedes optar por escribirla también como 6s2
Conversing: MLR3 Aclarar, Criticar, Corregir. Presente una respuesta incorrecta del tipo: "Si el cubo tiene arista de longitud s, entonces el área de cada cara es 2s porque "s × s=2s.". Pida a los estudiantes que identifiquen el error y que ofrezcan un argumento correcto para escribir una expresión para el área de cada cara. Esto ayudará a los estudiantes a utilizar representaciones simbólicas mientras generalizan cálculos relacionados con el área de la superficie.
Principio(s) de diseño: Optimizar el resultado (para la generalización); Maximizar la objetivoconciencia
5 minutos
Repasa las fórmulas para el volumen y la superficie de un cubo.
• El volumen de un cubo con longitud de arista s es s3
• Un cubo tiene 6 caras que son todas cuadrados idénticos. La superficie de un cubo de arista s es 6 ⋅ s2
CARA DEL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
5 minutos
1. Un cubo tiene una longitud de arista 11 pulgadas. Escribe una expresión para su volumen y otra para su área superficial.
2. Un cubo tiene un volumen de 73 centímetros cúbicos. ¿Cuál es su área superficial?
1. Volumen: 113 o 11 ⋅ 11 ⋅ 11. Superficie: 6 ⋅ (11 ⋅ 11) (o equivalente).
2. La superficie es 6 ⋅ 72, lo que equivale a 294 centímetros cuadrados.
California - Grado 6 ©Accelerate Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1
PROBLEMA 1
A. ¿Cuál es el volumen de un cubo de arista 8 in?
B. ¿Cuál es el volumen de un cubo de arista 1 3 cm?
C. Un cubo tiene un volumen de 8 ft3. ¿Cuál es la longitud de sus aristas?
PROBLEMA 2
A. ¿Qué figura tridimensional se puede montar a partir de esta red?

B. Si cada cuadrado tiene una longitud lateral de 61 cm, escribe una expresión para el área superficial y otra para el volumen de la figura.
PROBLEMA 3
A. Dibuja una red para un cubo con longitud de arista x cm.
B. ¿Cuál es el área de la superficie de este cubo?
C. ¿Cuál es el volumen de este cubo?

Posibles soluciones
A. 512 cu in (8 ⋅ 8 ⋅ 8 = 512)
B. 1 27 cu cm ( 1 3 ⋅ 1 3 ⋅ 1 3 = 1 27 )
C. 2 ft (2 ⋅ 2 ⋅ 2 = 8)
Posibles soluciones
A. Cubo
B. El área de la superficie es 6 ⋅ 612 cm2, y el volumen es 613 cm2.
Posibles soluciones
A.
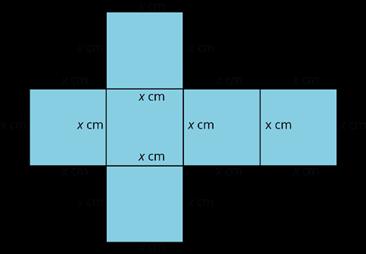
B. 6x2 cm2 (o equivalente)
C. x ⋅ x ⋅ x cu cm (o equivalente)
PROBLEMA 4
Del Grado 6, Unidad 1, Lección 14
Aquí tienes una red para un prisma rectangular que no se dibujó con precisión.
Learning Inc. - Todos los derechos reservados
Grado 6 . Matemáticas . Unidad 1

A. Explica qué falla en la red.
B. Dibuja una red que pueda ensamblarse en un prisma rectangular.
C. Crea otra red para el mismo prisma.
Posibles soluciones
A. Cuando se dobla la forma, los dos cuadrados pequeños no tienen el tamaño adecuado para cerrar la figura tridimensional. Los cuadrados pequeños pueden sustituirse por rectángulos como en la figura, o los cuadrados grandes pueden tener el mismo tamaño y forma que los dos rectángulos (no cuadrados) de la red.
B. C.
PROBLEMA 5
Del 6º curso, Unidad 1, Lección 13
Di si cada figura es un poliedro. Explica cómo lo sabes.
Posibles soluciones

La figura A no es un poliedro. Tiene una superficie curva y hay caras que no son polígonos. La figura B es un poliedro. Está compuesto de polígonos y cada lado de cada polígono se une a un lado de otro polígono.
PROBLEMA 6
Del Grado 6, Unidad 1, Lección 12
Aquí está el trabajo de Elena para encontrar el área de la superficie de un prisma rectangular que mide 1 pie por 1 pie por 2 pies.
Llegó a la conclusión de que la superficie del prisma es 296 pies cuadrados. ¿Estás de acuerdo con su conclusión? Explica tu razonamiento.
Posibles soluciones
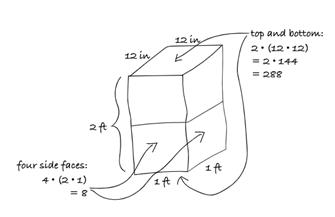
En desacuerdo. Ejemplo de razonamiento: Elena calculó el área de las caras superior e inferior en pulgadas cuadradas pero el área de las caras laterales en pies cuadrados. El área combinada de las caras superior e inferior es 2 pies cuadrados, por lo que la superficie correcta es 10 pies cuadrados.
Nation California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados

• Redes y superficie
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
6.G.1 Encuentra el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplica estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
6.G.4 Representa figuras tridimensionales usando redes hechas de rectángulos y triángulos, y usa las redes para encontrar el área de la superficie de estas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.
Enfocar SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP4 Modelar con matemáticas.
MP5 Usar herramientas apropiadas estratégicamente.
Estándares ELD de California
I.A.4
II.A.1
California EP&Cs
4.B 5.A
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
impactan en el futuro
modelan con las matemáticas
OBJETIVO(S) DE APRENDIZAJE
• Vamos a diseñar unas tiendas de campaña.
OBJETIVO(S) DE APRENDIZAJE
desmontando enteros, juntando piezas y descubriendo la forma y el espacio.
• Puedo aplicar lo que sé sobre el área de los polígonos para hallar el área de la superficie de objetos tridimensionales.
• Puedo utilizar el área de la superficie para razonar sobre objetos del mundo real.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Aplicar la comprensión de la superficie para estimar la cantidad de tela de una tienda de campaña y explicar (oralmente y por escrito) la estrategia de estimación.
• Comparar y contrastar (oralmente) diferentes diseños de tiendas de campaña.
• Interpretar información (presentada por escrito y a través de otras representaciones) sobre tiendas de campaña y sacos de dormir.
Rutinas instructivas
MLR5: Preguntas y problemas de elaboración conjunta
MLR7: Comparar y conectar
Preparación requerida
Prepare una copia del esquema para cada estudiante.
Materiales necesarios
Lápiz negro para la actividad 19.1
Copias del lápiz negro
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Grado 6 . Matemáticas . Unidad 1
Narrativa de la lección
En esta lección culminante, los estudiantes utilizan lo que han aprendido en esta unidad para diseñar una tienda de campaña y determinar cuánta tela se necesita para la tienda. La tarea lleva a los estudiantes a modelizar una situación con las matemáticas que conocen, hacer suposiciones y planificar un camino para resolver un problema (MP4). También permite a los estudiantes elegir herramientas de forma estratégica (MP5) y elaborar un argumento lógico para apoyar su razonamiento (MP3).
La lección consta de dos partes. En la primera parte, los estudiantes aprenden sobre la tarea, recopilan información y comienzan a diseñar. La introducción es importante para garantizar que todos los estudiantes entienden el contexto. A continuación, tras responder a algunas preguntas preparatorias en grupos y como clase, los estudiantes trabajan individualmente para diseñar y dibujar sus tiendas. Utilizan sus conocimientos sobre el área y la superficie para calcular y justificar una estimación de la cantidad de tela necesaria para su diseño.
La segunda parte consiste en la reflexión y el debate sobre el trabajo de los estudiantes. Los estudiantes explican su trabajo a un compañero o a un pequeño grupo, discuten y comparan sus diseños y consideran el impacto de las decisiones de diseño en las áreas superficiales de sus tiendas.
Dependiendo de las opciones pedagógicas elegidas, esta lección podría llevar una o más sesiones de clase. Las estimaciones de tiempo se han dejado en blanco intencionadamente, ya que el tiempo necesario variará en función de las decisiones pedagógicas que se tomen. Puede depender de:
• si los estudiantes utilizan la información proporcionada sobre tiendas de campaña y sacos de dormir o si investigan esta información.
• si se proporciona la Hoja de planificación del diseño de la tienda de campaña o si los estudiantes organizan su trabajo con más autonomía.
• expectativas en torno a la redacción, la revisión y el producto final.
• cómo se comparte finalmente el trabajo de los estudiantes con la clase (nada en absoluto, de manera informal o con presentaciones formales).
Nota: Los estudiantes tendrán que traer una colección personal de 10-50 objetos pequeños con antelación para la primera lección de la siguiente unidad. Por ejemplo, piedras, conchas, cromos o monedas.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento En parejas

Actividad de exploración Grupos reducidos
El tiempo depende de las opciones didácticas elegidas por el maestro.
Ver la Narrativa de la Lección.
Los estudiantes diseñan y dibujan una tienda de acampada con adaptaciones específicas para estimar la cantidad de tela necesaria para construirla.
Los estudiantes explican y comparan sus diseños de tienda de campaña y los cálculos de la tela.
Esta tarea podría ampliarse como una oportunidad para establecer conexiones con lo que se tiene en cuenta a la hora de tomar decisiones sobre los recursos y los sistemas naturales y el efecto de la producción textil en la contaminación del medio ambiente.
Esta tarea también podría ampliarse como una oportunidad para debatir cómo los sistemas naturales no tienen límites impermeables que impidan los efectos de los seres humanos al acampar; por lo tanto, deben tomarse consideraciones para evitar los efectos negativos en los sistemas naturales de las alteraciones o subproductos causados por los seres humanos.
Síntesis Todo el grupo
California - Grado 6
Los estudiantes demuestran su comprensión de las aplicaciones del área y la superficie en el mundo real mediante debates o presentaciones.
Learning Inc. - Todos los derechos reservados


• Tutores compañeros: Procesamiento Conceptual/Funcionamiento Ejecutivo/Memoria-Esta actividad integra múltiples habilidades y comprensiones y los estudiantes pueden necesitar ayuda extra para acceder al aprendizaje y organizarlo de forma clara para poder realizar esta tarea.
• Reducir Barreras: Aprendizaje basado en la fuerza-Muchos estudiantes que pueden tener dificultades en el diseño brillarán en la construcción de la tienda.
• Tabletas: Habilidades motoras finas/Procesamiento visual-espacial-Utilizar el lápiz óptico para el diseño y el zoom para mayor claridad y reducción de distracciones extrañas.
• Ayudas visuales: Procesamiento Conceptual-Tener especificaciones de altura en la pizarra para apoyo permanente y referencia mientras se crea la carpa.
• Progresiones deTrabajo en Grupo: Lenguaje Expresivo y Receptivo-Para la segunda parte, organice la puesta en común del trabajo de manera que el estudiante con discapacidad pueda sumarse a la discusión, ya sea para compartir primero o para tener un complemento claro a la idea de otro estudiante, de manera que su idea no sea tomada por otro, perdiendo su oportunidad de
Rutinas instructivas
MLR5: Preguntas y problemas para trabajar juntos

Materiales necesarios
Maestro de línea negra
Esta actividad consta de dos partes: una introducción a la tarea y un tiempo de trabajo individual. En la primera parte, los estudiantes leen el problema de diseño y hacen preguntas aclaratorias, y luego trabajan con uno o dos compañeros para ver diseños y especificaciones de tiendas de campaña. A continuación, trabajan individualmente para diseñar una tienda de campaña, crear las representaciones necesarias de la misma, calcular su superficie y estimar la cantidad de tela necesaria para construirla.
Mientras los estudiantes trabajan individualmente, circule y centre sus observaciones en dos objetivos principales:
1. Observe las estrategias y las ideas matemáticas que utilizan los estudiantes para completar la tarea. ¿Los estudiantes:
• descomponen o reorganizan partes del diseño de su tienda para hallar el área? ¿Cómo?
• ¿dibujan una red de su diseño?
• ¿etiquetan sus dibujos con medidas?
• ¿calculan el área con precisión?
• ¿utilizan las fórmulas que han aprendido en esta unidad? ¿Cómo?
• ¿contabilizando las áreas de todas las superficies de su diseño de tienda?
• ¿utilizando unidades cuadradas para las medidas de área?
2. Registra los tamaños (en términos de número de personas alojadas) y las formas de los diseños individuales de tienda. Utiliza esta información para organizar a los estudiantes en grupos por tamaño de tienda en la siguiente actividad.
Recoge el trabajo de los estudiantes al final de la sesión. Disponga que trabajen juntos los estudiantes de 2-3 que tengan tiendas con capacidad para el mismo número de personas pero diseños diferentes (por ejemplo, dos estudiantes diseñaron tiendas para tres personas, pero uno diseñó un prisma triangular y el otro un prisma pentagonal). Reúna sus trabajos para comenzar la segunda sesión.
Dé a los estudiantes 1-2 minutos para leer el enunciado de la tarea individualmente y hacer cualquier pregunta aclaratoria. En este punto, los estudiantes sólo tienen que entender que las tiendas deben alojar sacos de dormir del mismo tamaño y que no hay una única forma correcta de diseñarlas.
A continuación, organice a los estudiantes en grupos de 2. Conceda a los grupos unos 15 minutos para examinar y debatir los posibles diseños de tiendas, las especificaciones de las tiendas y la información sobre los sacos de dormir. Diga a los estudiantes que los diseños se proporcionan como inspiración y referencia, pero que no están limitados a ellos.
INSTRUCCIÓN CONTINUACIÓN

Grado 6 . Matemáticas . Unidad 1
Después de las discusiones en parejas, entrega a cada estudiante una copia de la Hoja de planificación del diseño de la tienda de campaña de la hoja maestra. Concede a los estudiantes un tiempo de reflexión tranquilo para que esbocen el diseño de su tienda, creen los dibujos necesarios, calculen la superficie y justifiquen su estimación. Proporcione papel en blanco para que los estudiantes dibujen sus diseños y acceso a sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). (Tenga en cuenta que un dibujo a escala no es una expectativa; el factor de escala es un estándar de 7º grado).
Apoyo para estudiantes
Hablar, escuchar: MLR5 Co-Craft Preguntas. Utilice esta rutina para ayudar a los estudiantes a identificar lo que será importante tener en cuenta a la hora de diseñar sus tiendas de campaña. Muestre sólo las imágenes de las tiendas de campaña, sin la información restante de la tarea. Pida a los estudiantes que trabajen con un compañero para crear una lista de preguntas matemáticas que podrían plantearse sobre las tiendas. Invite a las parejas a compartir sus preguntas con la clase. Esto ofrece a los estudiantes la oportunidad de comprometerse con el contexto de la tarea antes de considerar lo que se les pregunta.
Principio(s) de diseño: Optimizar el rendimiento (para la explicación); Cultivar la conversación; Maximizar la objetivoconciencia
Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus compañeros tutores previamente identificados.
Lenguaje receptivo/expresivo:Tiempo de procesamiento. Los estudiantes que se benefician de un tiempo de procesamiento adicional también se verían favorecidos por la MLR6.
¿Has ido alguna vez de acampada?
Puede que sepas que los sacos de dormir tienen todos más o menos el mismo tamaño, pero las tiendas de campaña tienen formas y tamaños muy variados.
Tu tarea consiste en diseñar una tienda de campaña para alojar hasta cuatro personas y calcular la cantidad de tela necesaria para fabricarla. Tu diseño y tu estimación deben basarse en la información proporcionada y tener una justificación matemática.
En primer lugar, observa estos ejemplos de tiendas, las especificaciones medias de una tienda de acampada y las medidas estándar de los sacos de dormir. Habla con un compañero sobre:
• Similitudes y diferencias entre las tiendas de campaña
• Información que será importante en tu proceso de diseño
• Los pros y los contras de los distintos diseños
Estilos de tiendas de campaña
California - Grado 6
©Accelerate Learning Inc. - Todos los derechos reservados


6 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS
Especificaciones de altura de la tienda
Altura Descripción Altura de la tienda Notas
Altura para sentarse 3 pies
Altura para arrodillarse 4 pies
Altura para agacharse 5 pies
Altura de pie 6 pies
Altura ambulante 7 pies
Medidas del saco de dormir
Los campistas pueden sentarse, tumbarse o gatear dentro de la tienda.
Los campistas pueden arrodillarse dentro de la tienda. Se encuentra principalmente en tiendas para 3-4 personas.
Los campistas pueden moverse de pie dentro de la tienda, pero la mayoría no podrán mantenerse erguidos.
La mayoría de los campistas adultos pueden mantenerse erguidos dentro de la tienda.
Los campistas adultos pueden mantenerse erguidos y caminar dentro de la tienda.
1. Crea y bosqueja el diseño de tu tienda. La tienda debe incluir un suelo.
2. ¿Qué decisiones fueron importantes a la hora de elegir el diseño de tu tienda?
3. ¿Cuánta tela calculas que será necesaria para hacer tu tienda? Muestra tu razonamiento y proporciona una justificación matemática.
Las respuestas varían.
ERRORES PREVISTOS
A algunos estudiantes puede resultarles difícil desarrollar y representar un objeto tridimensional en papel. Pregúnteles qué podría ayudarles a crear o transmitir su diseño. A algunos les puede resultar útil pensar en términos bidimensionales y empezar dibujando una red. A otros les puede interesar construir un modelo físico de su diseño a partir de papel u otro material flexible, o utilizar una herramienta de dibujo digital. Anime a los estudiantes a considerar las herramientas que tienen a su disposición y a elegir las que les permitan completar la tarea (MP5). SÍNTESIS
Después de que los estudiantes completen la tarea, entable un debate con toda la clase. Pregunte a los estudiantes: "¿Qué cosas importantes tuvisteis que pensar en vuestro diseño?"
Recoja el trabajo de los estudiantes al final de la sesión.
Disponga que los estudiantes que tengan tiendas para el mismo número de personas pero con diseños diferentes trabajen juntos (por ejemplo, dos estudiantes diseñaron tiendas para tres personas, pero uno diseñó un prisma triangular y el otro un prisma pentagonal). Junta sus trabajos para empezar la segunda sesión. Diga a los estudiantes que seguirán pensando en el problema y en su propuesta de solución en la siguiente actividad.
Grado 6 . Matemáticas . Unidad 1
Rutinas instructivas
MLR7: Comparar y conectar
Esta actividad da a los estudiantes la oportunidad de explicar y reflexionar sobre su trabajo. En grupos de 2-3, comparten los dibujos del diseño de su tienda, una estimación de la cantidad de tela necesaria y la justificación. Comparan sus creaciones con uno o varios compañeros. Los estudiantes debaten no sólo sobre la cantidad de tela necesaria, sino también sobre los efectos que los diferentes diseños tienen sobre dicha cantidad.
Antes de la sesión, identifique a los estudiantes de 2-3 que tengan tiendas con capacidad para el mismo número de personas pero con diseños diferentes (por ejemplo, dos estudiantes diseñan cada uno una tienda 3 para una persona, pero uno diseña un prisma triangular y el otro un prisma pentagonal). Junta los trabajos de la parte 1.
Mientras los estudiantes discuten en grupos, fíjate en cómo razonan y comunican su trabajo.
• ¿Proporcionan una justificación de sus medidas y elecciones?
• ¿Explican claramente su proceso de cálculo de la superficie?
• ¿Ven cómo el tipo de diseño afecta a la cantidad de tela?
• ¿Comparan sus tiendas en términos de las diferencias en las medidas de la base y la altura de la tienda?

Diga a los estudiantes que ahora reflexionarán y discutirán sobre sus tiendas con otro estudiante que diseñó una tienda para el mismo número de personas pero de forma diferente. Organice a los estudiantes en los grupos predeterminados de 2-3 y devuélvales los juegos de papeles preseleccionados.
Apoyo a los estudiantes de inglés
Conversing: MLR7 Comparar y conectar. Mientras los estudiantes comparan diseños en los que cabe el mismo número de personas pero que difieren en superficie, llame su atención sobre el modo en que la utilización de diferentes polígonos para crear cada tienda influye en la superficie. Pida a los estudiantes que comparen su diseño con el que utiliza menos tela. Discuta si su conocimiento del área de los polígonos puede influir en sus decisiones de diseño y en la cantidad de tela utilizada, y de qué manera.
Principio(s) de diseño: Optimizar el resultado (para la justificación); Cultivar la conversación; Maximizar la TAREAS PARA EL ESTUDIANTE
1. Explícales a tus socios el diseño de tu tienda y el presupuesto de tela. Asegúrate de explicar por qué elegiste este diseño y cómo calculaste el presupuesto de tela.
2. Comparen la cantidad estimada de tela necesaria para cada tienda de campaña de su grupo. Analicen las siguientes preguntas:
• ¿Qué diseño de tienda usó menos tela? ¿Por qué?
• ¿Qué diseño de tienda usó más tela? ¿Por qué?
• ¿Qué cambio de diseño influyó más en la cantidad de tela necesaria para la carpa? ¿Por qué?
Learning Inc. - Todos los derechos reservados


Grado 6 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
Las respuestas varían.
Gran parte del debate tendrá lugar dentro de los grupos. Una vez que los grupos hayan tenido la oportunidad de compartir sus diseños, reúnanse de nuevo como clase. Una idea sería exponer los diseños de tiendas que hayan utilizado más y menos tela. Considera también la posibilidad de pedir a los estudiantes que reflexionen sobre las siguientes preguntas:
• ¿Qué opciones de diseño llevan a utilizar menos tela?
• ¿Qué opciones de diseño llevan a utilizar más tela?
• ¿De qué maneras las tiendas diseñadas para albergar el mismo número de personas pueden utilizar cantidades muy diferentes de tela?
• Al calcular la superficie de tu tienda, ¿qué técnicas de esta unidad te han resultado útiles?
Esta lección culminante podría concluirse de varias maneras, dependiendo del tiempo disponible y de sus objetivos y expectativas. Puede optar por un sencillo debate de conclusión o pedir a los estudiantes que elaboren una presentación más elaborada del diseño de su tienda de campaña con carteles o modelos tridimensionales de sus tiendas.
Reflexiones:
