MN CA Seventh Grade Spanish Unit Sample by acceleratelearning

POR ACCELERATE LEARNING

Grado 7

Muestra de la edición para el maestro

Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).

La plataforma de recursos curriculares en línea que se ofrece en "mathnation.com", incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.

La marca comercial "Math Nation" es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.

Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.

UNIDAD 1

DIBUJOS A ESCALA

UNIDAD NARRATIVA

El trabajo con dibujos a escala en 7.º grado se basa en el trabajo previo con geometría y medidas geométricas. Los estudiantes comenzaron a aprender sobre las formas bidimensionales y tridimensionales en el jardín de infancia y continuaron este trabajo en los grados 1 y 2, componiendo, descomponiendo e identificando formas. El trabajo de los estudiantes con las medidas geométricas comenzó con la longitud y continuó con el área. Los estudiantes aprendieron a estructurar el espacio bidimensional, es decir, a ver un rectángulo con longitudes laterales enteras como un conjunto de cuadrados unitarios, o filas o columnas de cuadrados unitarios. En 3.º grado, los estudiantes distinguen entre perímetro y área. Relacionaron el área de un rectángulo con la multiplicación, entendiendo por qué (para longitudes laterales enteras) multiplicando las longitudes laterales de un rectángulo se obtiene el número de cuadrados unitarios que forman el rectángulo. Utilizaron diagramas de área para representar casos de la propiedad distributiva. En 4.º grado, los estudiantes aplicaron las fórmulas de área y perímetro de rectángulos para resolver problemas matemáticos y de la vida real y aprendieron a utilizar transportadores. En 5.º grado, los estudiantes ampliaron la fórmula del área de un rectángulo para incluir rectángulos con lados de longitud fraccionaria. En 6.º grado, los estudiantes se basaron en sus conocimientos de geometría y medidas geométricas para elaborar fórmulas para las áreas de paralelogramos y triángulos, utilizando estas fórmulas para hallar las áreas superficiales de los poliedros. En esta unidad, los estudiantes estudian copias a escala de imágenes y figuras planas y luego aplican lo que han aprendido a dibujos a escala, por ejemplo, mapas y planos de plantas. Esto proporciona una preparación geométrica para el trabajo de 7.º grado sobre relaciones proporcionales, así como para el trabajo de 8.º grado sobre dilataciones y semejanzas.

Los estudiantes comienzan observando copias de una imagen, algunas de las cuales están a escala y otras no. Utilizan sus propias palabras para describir en qué se diferencian las copias a escala de las que no lo están. A medida que avanza la unidad, los estudiantes aprenden que todas las longitudes de una copia a escala se multiplican por un factor de escala y que todos los ángulos son iguales. Dibujan copias a escala de figuras. Aprenden que si el factor de escala es mayor que 1, la copia será mayor, y si el factor de escala es menor que 1, la copia será menor. Estudian cómo cambia el área en las copias a escala de una imagen.

A continuación, los estudiantes estudian los dibujos a escala. Comprueban que los principios y estrategias que utilizaron para razonar sobre copias a escala de figuras se pueden utilizar con dibujos a escala. Interpretan y dibujan mapas y planos. Trabajan con escalas que incluyen unidades (por ejemplo: 1 cm representa 10 km) y escalas que no incluyen unidades (por ejemplo: La escala e des 1 a 100). Aprenden a expresar escalas con unidades como escalas sin unidades y viceversa. Comprenden que las longitudes reales son productos de un factor de escala y las longitudes correspondientes en el dibujo a escala, por lo que las longitudes en el dibujo son el producto de las longitudes reales y el recíproco de ese factor de escala. Estudian la relación entre regiones y longitudes en los dibujos a escala. A lo largo de la unidad, discuten sus ideas matemáticas y responden a las ideas de los demás (MP3, MP6). En la lección culminante de esta unidad, los estudiantes realizan un plano de su aula o de alguna otra habitación o espacio de su centro escolar. Esta es una oportunidad para que apliquen lo que han aprendido en la unidad a la vida cotidiana (MP4).

En la unidad, varios planes de clase sugieren que cada estudiante tenga acceso a un juego de herramientas de geometría. Cada kit contiene papel de calco, papel cuadriculado, lápices de colores, tijeras, una regla centimétrica, un transportador (se recomiendan los transportadores transparentes sin agujeros que muestran líneas radiales) y una ficha para utilizar como regla o para marcar ángulos rectos. Proporcionar a los estudiantes estos juegos de herramientas les da la oportunidad de desarrollar habilidades para seleccionar las herramientas adecuadas y utilizarlas estratégicamente para resolver problemas (MP5). Tenga en cuenta que incluso los estudiantes en un aula mejorada digitalmente deben tener acceso a este tipo de herramientas; aplicaciones y simulaciones deben ser consideradas adiciones a sus juegos de herramientas, no sustitutos de las herramientas físicas.

Tenga en cuenta que el estudio de las copias a escala se limita a pares de figuras que tienen la misma rotación y orientación especular (es decir, que no son rotaciones o reflexiones entre sí), porque la unidad se centra en la escala, factores de escala y dibujos a escala. En 8.º grado, los estudiantes ampliarán sus conocimientos sobre copias a escala cuando estudien traslaciones, rotaciones, reflexiones y dilataciones.

Grado 7 . Matemáticas . Unidad 1

Progresión del lenguaje disciplinario

En esta unidad, los maestros pueden anticipar que los estudiantes utilizarán el lenguaje con fines matemáticos, como representar, generalizar y explicar. A lo largo de la unidad, los estudiantes se beneficiarán de rutinas diseñadas para desarrollar un lenguaje disciplinar sólido, tanto para su propia creación de sentido como para construir un entendimiento compartido con sus compañeros. Los profesores pueden evaluar formativamente cómo los estudiantes utilizan el lenguaje de estas maneras, en particular cuando los estudiantes utilizan el lenguaje para:

Representar

• una copia a escala para un factor de escala dado (lecciones 3 y 5)

• distancias con diferentes escalas (lección 11)

• características relevantes de un aula con un dibujo a escala (lección 13)

Generalizar

• sobre distancias y ángulos correspondientes en copias a escala (lección 4)

• sobre factores de escala mayores que, menores que, e igual a 1 (lección 5)

• sobre factores de escala y área (lecciones 6 y 10)

• sobre factores de escala con y sin unidades (lección 12)

Explicar

• cómo usar dibujos a escala para encontrar distancias reales (lecciones 7 y 11)

• cómo usar dibujos a escala para encontrar distancias reales, velocidad y tiempo transcurrido (lección 8)

• cómo usar dibujos a escala para encontrar áreas reales (lección 12)

Además, se espera que los estudiantes describan características de copias a escala, justifiquen y critiquen razonamientos sobre copias a escala y comparen cómo las diferentes escalas afectan a los dibujos. A lo largo de la unidad, los maestros pueden apoyar la comprensión matemática de los estudiantes ampliando (no simplificando) el lenguaje utilizado para todos estos propósitos a medida que los estudiantes demuestran y desarrollan ideas.

La tabla muestra las lecciones en las que se introduce nueva terminología por primera vez, incluido cuándo se espera que los estudiantes comprendan la palabra o frase de forma receptiva y cuándo se espera que los estudiantes produzcan la palabra o frase en su propia expresión oral o escrita. Los términos del glosario aparecen en negrita. Los maestros deben seguir apoyando el uso por parte de los estudiantes de un término nuevo en las lecciones siguientes a aquella en la que se introdujo por primera vez.

Lección

Receptiva

7.1.1 copia a escala original polígono

7.1.2 correspondiente factor de escala figura segmento

Nueva terminología

Productiva

7.1.4 cuadrilátero medida distancia correspondiente factor de escala original

7.1.5 recíproco

7.1.6 área unidimensional bidimensional al cuadrado

7 . Matemáticas . Unidad 1

7.1.7

dibujo a escala escala representar real tridimensional copia a escala

7.1.8 estimar viajar velocidad constante escala

7.1.9 plano de planta 1.9 plano

7.1.10 apropiado dimensión real representar

7.1.11 escala sin unidades a escala dibujo

7.1.12 escalas equivalentes a

IDEAS FUNDAMENTALES Y ESTÁNDARES

Enfoque en ideas fundamentales

• Dibujos a escala

• Formas en el mundo ESTÁNDARES POR LECCIÓN

Lección

7.1.1

7.1.2

7.1.3

Estándar(es) abordado(s)

7.G.1

7.1.4 7.G.1

7.1.5 7.G.1

7.1.6

7.G.1, 7.G.6

7.1.7 7.G.1

7.1.8 7.G.1

7.1.9 7.G.1

7.1.10 7.G.1

7.1.11 7.G.1

7.1.12 7.G.1

7.1.13 7.G.1

LECCIÓN 1

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

7.G.1 Resolver problemas que involucren dibujos a escala de figuras geométricas, incluyendo el cálculo de longitudes y áreas reales a partir de un dibujo a escala y la reproducción de un dibujo a escala a una escala diferente.

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.C.12

II.B.5

¿QUÉ SON LAS COPIAS A ESCALA?

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo

atienden a la precisión y buscan y hacen uso de la estructura

META(S) DE APRENDIZAJE

• Exploremos las copias a escala.

META(S) DE APRENDIZAJE

descubriendo la forma y el espacio y explorando las cantidades cambiantes.

• Puedo describir algunas características de una copia a escala.

• Puedo decir si una figura es o no una copia a escala de otra figura.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente) las características de las copias a escala y sin escala.

• Identificar copias a escala de una figura y justificar (oralmente y por escrito) que se trata de una copia a escala.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR2: Recopilar y mostrar

Piensa en pareja, comparte

MLR1: Cada vez más fuerte y claro

MLR8: Apoyo para la discusión

Tomar turnos

Materiales necesarios

Maestra de línea negra para la Actividad 1.3

Enfriamiento

Hojas preimpresas, recortadas de copias de la maestra de línea negra

Preparación necesaria

Para esta lección necesitarás el patrón de líneas negras de Pares de polígonos a escala. Imprime y recorta las láminas

A-J para la actividad Pares de polígonos a escala. Prepare 1 copia para cada 2 estudiantes. Si es posible, copie cada juego completo en un color diferente de papel, de modo que cualquier hoja extraviada pueda volver a colocarse rápidamente en su lugar.

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

Esta lección introduce a los alumnos en la idea de copia a escala de un dibujo o una figura. Los alumnos aprenden a distinguir las copias a escala de las que no lo son, primero de manera informal y, después, cada vez con mayor precisión. Pueden empezar diciendo que las copias a escala tienen la misma forma que la figura original, o que no parecen estar distorsionadas en modo alguno, aunque puedan tener un tamaño diferente. A continuación, observan que las longitudes de los segmentos de una copia a escala varían con respecto a las longitudes de la figura original de manera uniforme. Por ejemplo, si un segmento de una copia a escala tiene la mitad de longitud que su homólogo en el original, todos los demás segmentos de la copia tienen también la mitad de longitud que sus homólogos originales. Los alumnos trabajan para articular cuantitativamente las características de las copias a escala (por ejemplo, "todos los segmentos son el doble de largos", "todas las longitudes se han reducido en un tercio" o "todos los segmentos son un cuarto del tamaño de los segmentos en el original"), articulando las relaciones cuidadosamente (MP6) a lo largo del camino.

La lección está diseñada para ser accesible a todos los alumnos, independientemente de sus conocimientos previos, y para animar a los alumnos a dar sentido a los problemas y perseverar en su resolución (MP1) desde el principio del curso.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Se presenta a los estudiantes el término copia a escala mientras consideran este concepto utilizando varias copias diferentes de un retrato.

Calentamiento Parejas 10 min.

Actividad de exploración Parejas 10 min.

Actividad de exploración Pares 15 min.

Hay disponible un applet digital interactivo para permitir a los estudiantes explorar las copias a escala utilizando la tecnología.

Los alumnos examinan los dibujos con más detenimiento para identificar las características distintivas que separan las copias a escala de los dibujos no dibujados a escala, lo que les permite comprender mejor una copia a escala.

Existe un applet digital interactivo que permite a los alumnos explorar el dibujo de copias a escala utilizando la tecnología.

Para ayudar a los estudiantes a refinar su comprensión de las copias a escala, los estudiantes examinan copias a escala de figuras más complejas a través de una actividad de emparejamiento de tarjetas.

Un applet digital interactivo está disponible para permitir a los estudiantes practicar el dibujo de copias a escala utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las propiedades que hacen que los polígonos sean copias a escala unos de otros.

Síntesis Grupo completo 3-5 min. Utilizando las actividades de la lección, los estudiantes sacan conclusiones sobre las copias a escala.

Enfriamiento Independiente 5 min. Los estudiantes identifican y justifican qué figuras son copias a escala de la figura original.

Práctica Independiente 5 min. El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso.

de 7º grado . Unidad 1

CALENTAMIENTO | IMPRESIÓN DE RETRATOS 10 minutos

Rutinas didácticas

MLR2: Colecciona y exhibe

Piensa, empareja y comparte

Esta tarea inicial introduce el término copia a escala. Pide a los alumnos que observen varias copias de un dibujo, distingan visualmente las copias a escala de las que no lo están y expresen las diferencias con sus propias palabras. Además de permitir a los alumnos mantener una conversación matemática sobre las propiedades de las figuras, proporciona una entrada accesible en el concepto y brinda la oportunidad de escuchar el lenguaje y las ideas que los alumnos asocian con las figuras a escala.

Es probable que los alumnos tengan alguna intuición sobre el término "a escala", ya sea por trabajos anteriores en 6.º curso (por ejemplo, escalar una receta, o escalar una cantidad hacia arriba o hacia abajo en una recta numérica doble) o fuera del aula. Esta intuición puede ayudarles a identificar copias a escala.

Espere que utilicen adjetivos como "estirado", "aplastado", "sesgado", "reducido", etc., de forma imprecisa. Esto está bien, ya que la definición intuitiva de los alumnos de copias a escala se refinará a lo largo de la lección. A medida que los alumnos discutan, observe la variedad de descripciones utilizadas. Observe a los alumnos cuyas descripciones apoyen especialmente la idea de que las longitudes de una copia a escala se obtienen multiplicando las longitudes originales por el mismo valor. Invítelos a compartir sus respuestas más tarde.

LANZAMIENTO

Organizar a los estudiantes en grupos de 2. Dar a los estudiantes 2-3 minutos de tiempo para pensar en silencio y un minuto para compartir su respuesta con su compañero.

Si se utiliza la actividad digital, hacer que los estudiantes trabajen en grupos de 2-3 para completar la actividad. Deben disponer de tiempo de silencio, además del tiempo para compartir, mientras resuelven el problema y desarrollan el lenguaje para describir el escalamiento.

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Tecnología de apoyo. Proporcione acceso a la versión digital de esta actividad.

He aquí el retrato de un alumno.

1. Observa los retratos A-E. ¿En qué se parece o en qué se diferencia cada uno del retrato original del alumno?

Matemáticas de 7º grado . Unidad 1

1. Algunos de los retratos A–E son copias a escala del retrato original. ¿Cuáles crees que son copias a escala? Explica tu razonamiento.

2. ¿Qué crees que significa «copia a escala»?

POSIBLES RESPUESTAS

• Las respuestas varían. Ejemplo de respuesta:

• Similitudes: Las imágenes A–E se basan en el mismo retrato original. Todas muestran al mismo niño con camisa azul y cabello castaño. Todas tienen el mismo fondo blanco.

• Diferencias: Todas tienen tamaños diferentes; algunas tienen formas diferentes. Las imágenes A, B y E se han estirado o distorsionado de alguna manera. C y D no están estiradas ni distorsionadas, pero cada una tiene un tamaño diferente al original.

• C y D son copias a escala. Ejemplo de explicación:

• A, B y E no son copias a escala porque han cambiado de forma en comparación con el retrato original. El retrato A se estira verticalmente, por lo que el lado vertical ahora es mucho más largo que el horizontal. El retrato B se estira lateralmente, por lo que los lados horizontales ahora son más largos que los verticales. El retrato E parece tener sus esquinas superior izquierda e inferior derecha estiradas en direcciones opuestas. El retrato ya no es un rectángulo.

• C es una copia más pequeña y D es una copia más grande del original, pero sus formas siguen siendo las mismas.

• Las respuestas varían. Ejemplos de definiciones:

• Una copia a escala es una copia de una imagen que cambia de tamaño, pero no de forma.

• Una copia a escala es un duplicado de una imagen sin ninguna distorsión, aunque puede ser más grande, más pequeña o del mismo tamaño.

• Una copia a escala es una copia de una imagen que se ha ampliado o reducido, pero que no ha sufrido cambios en ningún otro aspecto.

Seleccione a algunos estudiantes para que compartan sus observaciones. Registre y muestre las explicaciones de los estudiantes para la segunda pregunta. Considere organizar las observaciones en términos de cómo ciertas imágenes están o no distorsionadas. Por ejemplo, los estudiantes podrían decir que C y D son copias a escala porque cada una es una versión más grande o más pequeña de la imagen, pero la cara (o la manga, o el contorno de la imagen) no ha cambiado de forma. Podrían decir que A, B y E no son copias a escala porque algo más que el tamaño ha cambiado. Si no se mencionó ya en la discusión, guíe a los estudiantes para que vean las características de C y D que las distinguen de A, B y E.

Invite a un par de estudiantes a compartir su definición práctica de copias a escala. Algunas descripciones de los estudiantes pueden no ser completamente precisas. Esto es apropiado para esta lección, ya que el objetivo es desarrollar y refinar este lenguaje en el transcurso de las próximas lecciones hasta que los estudiantes tengan una noción más precisa de lo que significa que una imagen o figura sea una copia a escala.

ACTIVIDAD DE EXPLORACIÓN | ESCALA F

10 minutos

Rutinas didácticas

Piensa, comparte y comparte

MLR1: Cada vez más fuerte y claro

de 7º grado . Unidad 1

Esta tarea permite a los alumnos describir con mayor precisión las características de las copias a escala y precisar el significado del término. Los alumnos observan copias de un dibujo lineal en una cuadrícula y se fijan en cómo se comparan las longitudes de los segmentos lineales y los ángulos formados por ellos con los del dibujo original.

En esta tarea, los alumnos se implican en el MP7 de múltiples maneras. Identificar los rasgos distintivos de las copias a escala significa encontrar similitudes y diferencias en las formas. Además, el hecho de que las partes correspondientes aumenten en el mismo factor de escala es una propiedad estructural vital de las copias a escala.

Para la primera pregunta, espere que los alumnos expliquen sus elecciones de copias a escala en términos intuitivos y cualitativos. Para la segunda pregunta, los alumnos deben empezar a distinguir entre copias escaladas y no escaladas de forma más específica y cuantificable. Si a los alumnos no se les ocurre fijarse en las longitudes de los segmentos, sugiérales que lo hagan.

A medida que los alumnos trabajen, observe si se fijan en los siguientes aspectos de las figuras. Sin embargo, no se espera que los estudiantes utilicen estos términos matemáticos en este momento.

• El dibujo original de la letra F y sus copias a escala tienen proporciones equivalentes de ancho a alto.

• Podemos utilizar un factor de escala (o un multiplicador) para comparar las longitudes de diferentes figuras y ver si son copias a escala del original.

• La figura original y las copias a escala tienen ángulos correspondientes que tienen la misma medida.

Mantenga a los estudiantes en los mismos grupos. Deles 3-4 minutos de tiempo de trabajo en silencio, y luego 1-2 minutos para compartir sus respuestas con su compañero. Diga a los alumnos que la forma en que decidan si cada uno de los siete dibujos es una copia a escala puede ser muy diferente de la forma en que decida su compañero. Anime a los alumnos a escuchar atentamente los planteamientos de los demás y a estar preparados para compartir sus estrategias. Utilice gestos para obtener de los alumnos las palabras "horizontal" y "vertical" y pida a los grupos que acuerden internamente términos comunes para referirse a las partes de la F (por ejemplo, "tallos horizontales").

Apoyo para estudiantes de inglés

Speaking: Rutina del Lenguaje Matemático 1 Cada vez más fuerte y claro. Esta es la primera vez que se sugiere la Rutina 1 del Lenguaje Matemático como apoyo en este curso. En esta rutina, a los estudiantes se les da una pregunta o un estímulo que les haga pensar y se les pide que creen un primer borrador de respuesta por escrito. Los estudiantes se reúnen con 2-3 compañeros para compartir y refinar su respuesta a través de la conversación. Durante la reunión, los oyentes hacen preguntas como: "¿Qué querías decir con . . .?" y "¿Puedes decirlo de otra manera?". Por último, los alumnos escriben un segundo borrador de su respuesta en el que reflejan las ideas de los compañeros y las mejoras de sus ideas iniciales. El propósito de esta rutina es ofrecer una oportunidad estructurada e interactiva para que los alumnos revisen y perfeccionen sus ideas por medios verbales y escritos.

Principio(s) de diseño: Optimizar el resultado (para la explicación)

Cómo se lleva a cabo:

1. Utilice esta rutina para proporcionar a los estudiantes una oportunidad estructurada de refinar sus explicaciones para la primera pregunta: "Identifica todos los dibujos que son copias a escala del dibujo original de la letra F. Explica cómo lo sabes". Explica cómo lo sabes". Conceda a los estudiantes 2-3 minutos para crear individualmente un primer borrador de respuestas por escrito.

2. Invite a los estudiantes a reunirse con 2-3 otros compañeros para recibir sus comentarios. Indique al orador que empiece compartiendo sus ideas sin mirar su borrador escrito, si es posible. Proporcione al oyente las siguientes sugerencias para que su interlocutor refuerce sus ideas y aclare su lenguaje: "¿Qué quieres decir con ....?", "¿Puedes describirlo de otra manera?", "¿Cómo sabes que es una copia a escala?", "¿Podrías justificarlo de otra manera?". Asegúrate de que los socios cambian de papel. Conceda 1-2 minutos para debatir.

3. Indique a los alumnos que pasen al siguiente compañero y repitan esta reunión estructurada.

4. Cierre las conversaciones por parejas e invite a los alumnos a revisar y perfeccionar su redacción en un segundo borrador.

Matemáticas de 7º grado . Unidad 1

Apoyo para estudiantes que aprenden inglés Continuación

Proporcione estos marcos de oraciones para ayudar a los estudiantes a organizar sus pensamientos de manera clara y precisa: "El dibujo es una copia a escala del original, y lo sé porque....", "Cuando miro las longitudes, me doy cuenta de que....", y "Cuando miro los ángulos, me doy cuenta de que...."

He aquí un ejemplo de un segundo borrador:

"El dibujo 7 es una copia a escala del original, y lo sé porque está ampliado uniformemente en las direcciones horizontal y vertical. No parece desigual ni estirado de forma diferente en una dirección. Cuando miro la longitud del segmento superior, es 3 veces más grande que el original, y los demás segmentos hacen lo mismo. Además, cuando miro los ángulos, me doy cuenta de que todos son ángulos rectos tanto en el original como en la copia a escala."

5. Si el tiempo lo permite, haz que los alumnos comparen su primer y segundo borrador. Si no, haz que los alumnos continúen trabajando en los siguientes problemas.

Apoyo para estudiantes con discapacidades

Habilidades motoras finas:

• Tutores compañeros. Empareje a los alumnos con sus compañeros tutores previamente identificados y permita que los alumnos que tienen dificultades con la motricidad fina dicten copias a escala de los dibujos según sea necesario.

• Tecnología de apoyo. Proporcione acceso a la versión digital de esta actividad.

Aquí tienes un dibujo original de la letra F y otros dibujos.

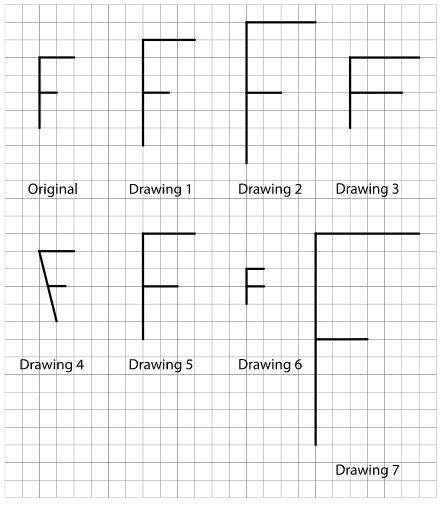
1. Identifica todos los dibujos que son copias a escala del dibujo original de la letra F. Explica cómo lo sabes.

2. Examina todas las copias a escala más de cerca, específicamente, las longitudes de cada parte de la letra F. ¿Cómo se comparan con el original? ¿Qué observas?

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA CONTINUACIÓN

POSIBLES RESPUESTAS

de 7º grado . Unidad 1

3. En la cuadrícula, dibuja una copia a escala diferente de la letra F original.

1. Los dibujos 1, 2 y 7 son copias a escala del dibujo original. Las explicaciones varían. Ejemplo de explicación: Lo sé porque no están ampliados de manera diferente en una dirección. Están ampliados uniformemente en ambas direcciones, vertical y horizontal.

2. Las respuestas varían. Ejemplos de respuestas:

• En las copias a escala, cada segmento es el mismo número de veces más largo que el segmento correspondiente en el dibujo original.

• En las copias a escala, todos los segmentos mantienen las mismas relaciones que en el original. El dibujo original de F mide 4 unidades de alto. Su segmento horizontal superior es 2 unidades de ancho y el segmento horizontal más corto es 1 unidad. En el dibujo 1, la F mide 6 unidades de alto y 3 unidades de ancho; en el dibujo 2, mide 8 unidades de alto y 4 unidades de ancho, y en el dibujo 7, mide 8 unidades de alto y 4 unidades de ancho. En cada copia a escala, la anchura es la mitad de la altura, igual que en el dibujo original de F, y el segmento horizontal más corto es la mitad del más largo.

3. Los dibujos varían. Respuesta de muestra:

Los alumnos pueden tomar decisiones "a ojo" en lugar de observar las longitudes de los lados y los ángulos. Anímeles a buscar pruebas cuantificables y a fijarse en las longitudes y los ángulos.

Algunos pueden pensar que los vértices deben estar en las intersecciones de las líneas de la cuadrícula (por ejemplo, pueden decir que el dibujo 4 no es una copia a escala porque los puntos extremos del segmento horizontal más corto no están en las intersecciones de la cuadrícula). Aborde esta cuestión durante el debate de toda la clase, después de que los alumnos hayan tenido la oportunidad de compartir sus observaciones sobre las longitudes de los segmentos.

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Muestre las siete copias de la letra F para que todos las vean. Para cada copia, pida a los alumnos que indiquen si creen que cada una es una copia a escala de la F original. Registre y muestre los resultados para que todos los vean. En el caso de los dibujos dudosos, pida a los alumnos 1-2 que expliquen brevemente por qué los han descartado.

Discuta las copias a escala y sin escala identificadas.

• ¿Qué características tienen en común las copias a escala? (Asegúrese de invitar a los alumnos que estaban pensando en factores de escala y medidas de ángulos a que compartan sus ideas).

• ¿Cómo es que las otras copias no muestran estas características? (A veces las longitudes de los lados en la copia usan multiplicadores diferentes para lados diferentes. A veces los ángulos en la copia no coinciden con los ángulos en el original).

Si existe la idea errónea de que las copias a escala deben tener vértices en las intersecciones de las líneas de la cuadrícula, utilice Dibujo 1 (o un dibujo relevante de un estudiante) para discutir cómo no es el caso.

Algunos estudiantes pueden no estar familiarizados con palabras como "dos veces", "doble" o "triple". Aclare los significados diciendo "dos veces más" o "tres veces más".

ACTIVIDAD DE EXPLORACIÓN | PARES DE POLÍGONOS A ESCALA

15 minutos

Rutinas didácticas

MLR8: Apoyos para la discusión

Turnos

Materiales necesarios

Patrón de líneas negras

En esta actividad, los alumnos perfeccionan su comprensión de las copias a escala trabajando con figuras más complejas. Los alumnos trabajan con un compañero para emparejar pares de polígonos que son copias a escala. Los polígonos parecen comparables entre sí, por lo que los alumnos tienen que fijarse muy bien en todas las longitudes de los lados de los polígonos para saber si son copias a escala.

Mientras los alumnos hablan entre sí, fíjese en cómo buscan la correspondencia. Observe a los estudiantes que utilizan un lenguaje preciso (MP6) para articular su razonamiento (por ejemplo, "El lado superior de A es la mitad de largo que el lado superior de G, pero los lados verticales de A son un tercio de largos que los de G.").

Para esta actividad necesitará el patrón de líneas negras de Pares de polígonos a escala.

Demuestre cómo preparar y realizar la actividad de emparejamiento. Elige a un alumno como compañero. Mezcla las tarjetas y colócalas boca arriba. Diles que cada polígono tiene una y sólo una correspondencia (es decir, para cada polígono, hay una y sólo una copia a escala del polígono). Selecciona dos tarjetas y explica a tu compañero por qué crees que coinciden o no. Demuestre formas productivas de estar de acuerdo o en desacuerdo (por ejemplo, explicando su pensamiento matemático, haciendo preguntas aclaratorias, etc.).

Organice a los estudiantes en grupos de 2. Entregue a cada grupo un conjunto de 10 fichas recortadas del patrón de líneas negras. Anima a los alumnos a consultar una lista de enunciados y diagramas para refinar su lenguaje y sus explicaciones sobre cómo saben que una figura es una copia a escala de la otra.

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyo a la conversación. Use esta rutina para apoyar la conversación cuando los estudiantes emparejan pares de polígonos que son copias a escala uno del otro. Muestre los siguientes marcos de frases: " coincide con porque ." y "Estoy de acuerdo/en desacuerdo porque ."

Principio(s) de diseño: Apoyar la creación de sentido; Optimizar la salida (para la explicación)

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de Procesamiento. Comenzar con una demostración de un partido, que proporcionará acceso a los estudiantes que se benefician de instrucciones claras y explícitas. Habilidades motoras finas:

• Tecnología de apoyo. Proporcione acceso a la versión digital de esta actividad.

Tu maestro te dará un juego de tarjetas con polígonos dibujados en una cuadrícula. Mezcla las tarjetas y colócalas todas boca arriba.

1. Túrnate con tu compañero para emparejar un par de polígonos que sean copias a escala el uno del otro.

2. Cuando estéis de acuerdo en todos los emparejamientos, comprobad vuestras respuestas con la clave de respuestas. Si hay algún error, discute por qué y revisa tus emparejamientos.

3. Selecciona un par de polígonos para examinarlos más a fondo. Dibuja ambos polígonos en la cuadrícula. Explique o muestre cómo sabe que un polígono es una copia a escala del otro.

1. Los siguientes polígonos son versiones a escala uno del otro:

• A y C

POSIBLES RESPUESTAS

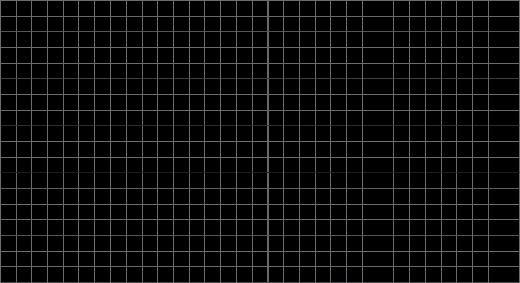
• B y D

• E e I

• F y G

• H y J

2. No se necesita respuesta.

3. Las respuestas varían. Ejemplo de explicación para A y C: Todas las longitudes de los lados de C son el doble de largas que las longitudes de los lados coincidentes de A.

Algunos alumnos pueden pensar que una figura tiene más de una coincidencia. Recuérdales que sólo hay una copia a escala de cada polígono y pídeles que vuelvan a comprobar todas las longitudes de los lados.

Algunos alumnos pueden pensar que los vértices deben estar en las intersecciones de las líneas de la cuadrícula y concluir que, por ejemplo, G no puede ser una copia de F porque no todos los vértices de F están en dichas intersecciones. Pídeles que piensen cómo cambiaría un segmento de 1 de longitud si se redujera a la mitad de su tamaño original. ¿Dónde debe caer uno o los dos vértices?

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

El objetivo de este debate es extraer métodos concretos para decidir si dos polígonos son o no copias a escala uno del otro y, en particular, comprender que no basta con mirar a simple vista para ver si se parecen o no para determinar que son copias a escala.

Muestra la imagen de todos los polígonos. Pida a los alumnos que compartan sus emparejamientos y guíe un debate sobre cómo hicieron para encontrar las copias a escala. Formule preguntas como las siguientes:

• Cuando observaste otro polígono, ¿qué comprobaste o buscaste exactamente? (Forma general, longitud de los lados)

• ¿Cuántos lados comparaste antes de decidir que el polígono era o no una copia a escala? (Dos lados pueden ser suficientes para saber que los polígonos no son copias a escala; se necesitan todos los lados para asegurarse de que un polígono es una copia a escala).

• ¿Alguien comprobó los ángulos de los polígonos? ¿Por qué sí o por qué no? (No; los lados de los polígonos siguen todos las líneas de la cuadrícula.)

Si los alumnos no se ponen de acuerdo sobre algunos emparejamientos después de la discusión, pide a los grupos que expliquen su caso y discutan cuál de los emparejamientos es el correcto. Destaque el uso de descriptores cuantitativos como "la mitad de largo" o "tres veces más largo" en la discusión. Asegúrese de que los alumnos vean que cuando una figura es una copia a escala de otra, todos sus segmentos son el mismo número de veces más largos que los segmentos correspondientes en la otra.

¿Estás preparado para más?

¿Es posible dibujar un polígono que sea una copia a escala tanto del Polígono A como del Polígono B? Dibuja tal polígono o explica cómo sabes que esto es imposible.

"¿Estás listo para más?" Respuesta del alumno

Es imposible dibujar un polígono que sea una copia a escala tanto del Polígono A como del Polígono B. Ejemplos de explicaciones:

• Si dibujo un polígono que sea una copia a escala de A, todas las longitudes de los lados serían el mismo número de veces mayores o menores que A, pero no serán el mismo número de veces mayores o menores que B.

• A y B no son copias a escala el uno del otro, así que si dibujo una copia a escala de uno, no será una copia a escala del otro.

SÍNTESIS DE LA LECCIÓN

3-5 minutos

En esta lección, hemos visto copias de una figura a escala y sin escala. Hemos visto diferentes versiones de un retrato de un alumno y de una letra F, así como una variedad de polígonos que tenían algunas cosas en común.

En cada caso, hemos decidido que unos eran copias a escala de otros y otros no. Considera preguntar a los alumnos:

• ¿Qué es una copia a escala?

• ¿Cuáles son algunas características de las copias a escala? ¿En qué se diferencian de las figuras que no son copias a escala?

• ¿Qué información específica buscabais para determinar si algo era una copia a escala de un original?

Aunque las respuestas iniciales no tienen por qué ser especialmente precisas en esta fase de la unidad (por ejemplo, "las copias a escala parecen iguales pero tienen un tamaño diferente"), oriente el debate hacia la formulación de afirmaciones cuidadosas que se puedan poner a prueba. Las longitudes de los segmentos de una copia a escala se relacionan con las longitudes de la figura original de forma coherente. Por ejemplo, si un segmento de una copia a escala tiene la mitad de longitud que su homólogo en el original, entonces todos los demás segmentos de la copia tienen también la mitad de longitud que sus homólogos originales. Podríamos decir: "Todos los segmentos miden el doble" o "Todos los segmentos miden un tercio de lo que miden los segmentos del original".

Matemáticas de 7º grado . Unidad 1

ENFRIAMIENTO | ESCALADO L 5 minutos DE CARA AL ALUMNO ENUNCIADO DE LA TAREA

¿Alguna de las figuras B, C o D son copias a escala de la figura A? Explica cómo lo sabes.

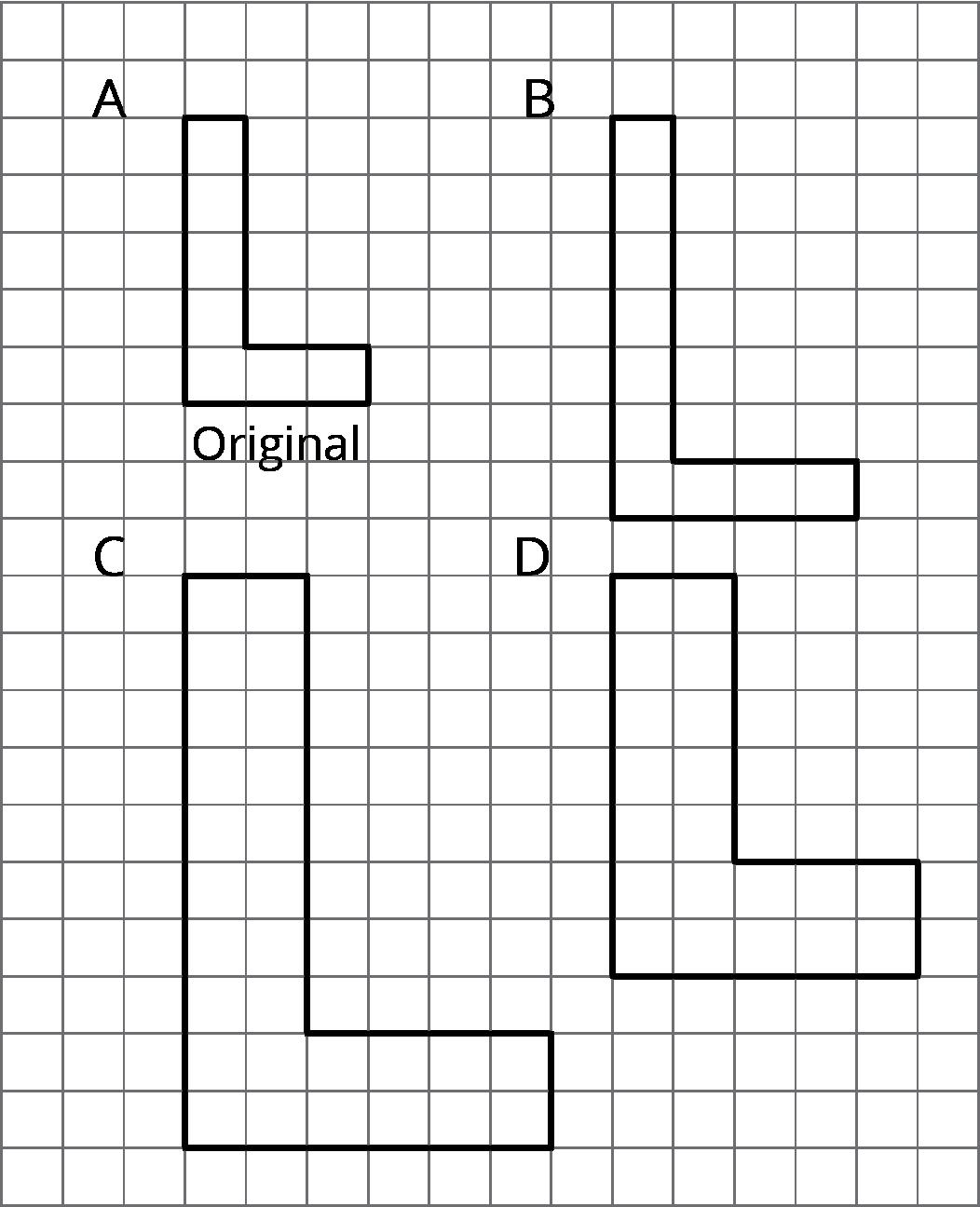
POSIBLES RESPUESTAS

Sólo la figura C es una copia a escala de la figura A. Ejemplo de explicación: En la figura C, la longitud de cada segmento de la letra L es el doble de la longitud del segmento correspondiente en A. En B, ninguno de los segmentos tiene el doble de longitud. En la figura D, algunos segmentos tienen el doble de longitud y otros no. Por lo tanto, las letras mayúsculas de B y D no se agrandan uniformemente.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

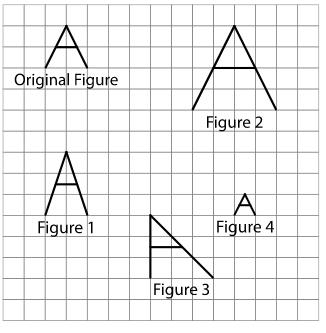
Aquí hay una figura que se parece a la letra A, junto con varias otras figuras. ¿Qué figuras son copias a escala de la A original? Explica cómo lo sabes.

Posibles soluciones

Las figuras 2 y 4 son copias a escala. Ejemplos de explicaciones:

• La A original cabe dentro de un cuadrado. El segmento horizontal está a la mitad de la altura del cuadrado. La punta de la A está en el punto medio del lado horizontal del cuadrado.

• La figura 1 está dentro de un rectángulo, no de un cuadrado, por lo que no es una copia a escala. La figura 3 encaja dentro de un cuadrado, pero la forma es diferente a la de la letra A original, ya que una de las patas de la A en la figura 3 es ahora vertical, por lo que tampoco es una copia a escala.

• La figura 2 es el doble de alta y el doble de ancha que la A original, y la figura 4 es la mitad de alta y de ancha, pero en ambas figuras las ubicaciones del segmento horizontal y la punta de la letra A siguen coincidiendo con el original.

Matemáticas de 7º grado . Unidad 1

PROBLEMA 2

Tyler dice que la Figura B es una copia a escala de la Figura A porque todos los picos son la mitad de altos. ¿Estás de acuerdo con Tyler? Explica tu razonamiento.

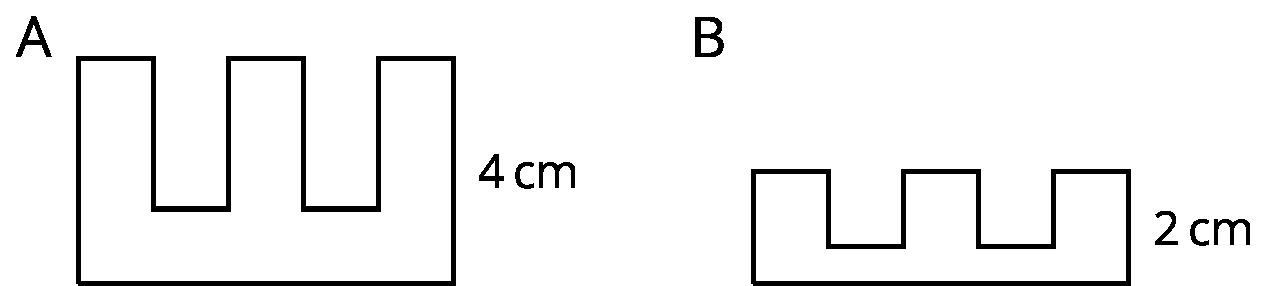
Posibles soluciones

No. Para que la figura más pequeña sea una copia a escala, la figura también tendría que ser la mitad de ancha.

PROBLEMA 3

Aquí hay una imagen del estadio Rose Bowl en Pasadena, CA.

Aquí hay algunas copias de la imagen. Selecciona todas las imágenes que son copias a escala de la imagen original.

Posibles soluciones

A y D. B está comprimida horizontalmente, y C está comprimida verticalmente.

PROBLEMA 4

Completa cada ecuación con un número que la haga verdadera.

1. 5 ⋅ = 15

2. 4 ⋅ = 32

3. 6 ⋅ = 9

4. 12 ⋅ = 3

Posibles soluciones

1. 3 2. 8

3. 1.5, 3 2 , o equivalente

4. 0.25, 1 4 , o equivalente

LECCIÓN 2

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

7.G.1 Resolver problemas que involucren dibujos a escala de figuras geométricas, incluyendo calcular longitudes y áreas reales a partir de un dibujo a escala y reproducir un dibujo a escala a una escala diferente.

Construir

5.NF.4

Construir

7.RP.2

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de CaliforniaD

I.B.5

I.C.12

II.C.6

PARTES CORRESPONDIENTES Y FACTORES SCALE

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo y predicen lo que podría ocurrir buscan estructuras y expresan regularidades en razonamientos repetidos descubren la forma y el espacio y exploran cantidades cambiantes.

META(S) DE APRENDIZAJE

• Describamos las características de las copias a escala.

META(S)

DE APRENDIZAJE

• Puedo describir qué tiene que ver el factor de escala con una figura y su copia a escala.

• En un par de figuras, puedo identificar puntos correspondientes, segmentos correspondientes y ángulos correspondientes.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender la frase "factor de escala" y explicar (oralmente) cómo se relacionan las longitudes correspondientes de una figura y su copia a escala.

• Explicar (oralmente) qué significa decir que una parte de una figura "corresponde" a una parte de otra figura.

• Identificar y describir (oralmente y por escrito) puntos correspondientes, segmentos correspondientes o ángulos correspondientes en un par de figuras.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Hablar de números

MLR8: Apoyos para la discusión

Notar y maravillarse

MLR3: Aclarar, Criticar, Corregir

Piensa, Comparte

Materiales necesarios

Enfriamiento

Kits de herramientas de geometría (papel de calco, papel milimetrado, lápices de colores, tijeras y una ficha)

Preparación necesaria

Prepárese para mostrar las imágenes de la señal de cruce de ferrocarril para la actividad Partes correspondientes. Asegúrate de que los alumnos tengan acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), especialmente papel de calco y papel cuadriculado.

Matemáticas de 7º grado . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

Esta lección desarrolla el vocabulario para hablar de la escala y de las copias a escala con mayor precisión (MP6), y para identificar las estructuras en común entre dos figuras (MP7).

En concreto, los alumnos aprenden a utilizar el término correspondiente para referirse a un par de puntos, segmentos o ángulos en dos figuras que son copias a escala. Los alumnos también empiezan a describir la relación numérica entre las longitudes correspondientes en dos figuras utilizando un factor de escala . Observan que cuando dos figuras son copias a escala una de otra, el mismo factor de escala relaciona sus longitudes correspondientes. Practican la identificación de los factores de escala.

Aquí también comienza el estudio de los ángulos de las copias a escala. Los alumnos utilizan papel de calco para trazar y comparar los ángulos de una figura original y sus copias. Observan que en las copias a escala las medidas de los ángulos correspondientes son iguales.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento Independiente 5 min. Los estudiantes repasan estrategias para multiplicar números racionales.

Los estudiantes son introducidos a las partes correspondientes de las figuras, incluyendo puntos, segmentos y ángulos.

Actividad de exploración Pares 15 min.

Actividad de exploración Grupo pequeño 15 min.

Síntesis Grupo completo 5 min.

Enfriamiento Independiente 5 min.

Un applet digital interactivo está disponible para permitir a los estudiantes explorar los tamaños de las partes correspondientes de las figuras usando la tecnología.

Los estudiantes identifican las partes correspondientes en triángulos a escala antes de descubrir el factor de escala a través de patrones numéricos.

Hay disponible una extensión de exploración para desarrollar una comprensión más profunda de las longitudes de los lados correspondientes de copias a escala.

Los estudiantes establecen conexiones entre las longitudes de las partes correspondientes de figuras a escala y el factor de escala.

Los estudiantes identifican las partes correspondientes y determinan el factor de escala de una copia a escala.

Práctica Independiente 5-7 min. El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

CHARLA SOBRE NÚMEROS: MULTIPLICAR POR UNA FRACCIÓN UNITARIA 5

minutos

Rutinas didácticas

Hablar de números

MLR8: Apoyos para la discusión

Esta charla numérica permite a los alumnos repasar las estrategias de multiplicación, refrescando la idea de que multiplicar por una fracción unitaria es lo mismo que dividir por su recíproco entero. Anima a los alumnos a utilizar la estructura de los números de base diez y las propiedades de las operaciones para hallar el producto de dos números enteros (MP7). Por ejemplo, un alumno puede hallar 72 ⋅ 1 9 (o 72 ÷ 9) y luego desplazar el decimal un lugar a la derecha para evaluar (7.2) ⋅ 1 9 . Cada problema se eligió para obtener diferentes enfoques, así que cuando los estudiantes compartan los suyos, pregúnteles cómo influyeron los factores de cada problema en sus estrategias.

Antes de que los estudiantes comiencen, considere establecer una pequeña y discreta señal con la mano (como un pulgar hacia arriba) que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar razonando. Una señal discreta es una forma rápida de que los maestroes recojan información sobre el momento oportuno. También evita que los estudiantes se distraigan o se apresuren con las manos levantadas alrededor de la clase.

INTRODUCCIÓN

Muestre un problema a la vez. Dé a los estudiantes hasta 1 minuto de tiempo para pensar en silencio por problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. Continúe con un breve debate con toda la clase.

Apoyo a los estudiantes con discapacidad

Memoria: Tiempo de procesamiento. Proporcione notas adhesivas o minipizarras para ayudar a los alumnos con dificultades de memoria de trabajo.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Encuentra mentalmente cada producto.

1 4 ⋅ 32

(7.2) ⋅ 1 9

1 4 ⋅ (5.6)

1. 1 4 ⋅ 32 = 8. Posible estrategia: 32 ÷ 4 = 8

2. (7.2) ⋅ 1 9 = 0.8. Estrategia posible: 72 ÷ 9 = 8 entonces (7,2) ÷ 9 = 0,8

3. 1 4 ⋅ (5,6) = 1,4. Posible estrategia: (5,6) ÷ 4 = 1,4

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Pida a los alumnos que compartan sus estrategias para cada problema. Anote y muestre sus explicaciones para que todos puedan verlas. Si los alumnos expresan sus estrategias en términos de división, pregúnteles si esa estrategia funcionaría para cualquier problema de multiplicación que incluya fracciones. Destaque que estos problemas sólo incluyen fracciones unitarias y que la división por el denominador es una estrategia que funciona cuando se multiplica por una fracción unitaria.

Para involucrar a más estudiantes en la conversación, considere preguntar:

• ¿Quién puede replantear el razonamiento de de una manera diferente?

• ¿Alguien resolvió el problema de la misma manera pero lo explicaría de forma diferente?

• ¿Alguien resolvió el problema de una manera diferente?

• ¿Alguien quiere agregar algo a la estrategia de ?

• ¿Están de acuerdo o en desacuerdo? ¿Por qué?

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyos para el debate. Proporcione marcos oracionales para ayudar a los estudiantes a explicar sus estrategias. Por ejemplo, "I noticed that , so I ." o "First, I because .". Cuando los alumnos compartan sus respuestas con un compañero, pídales que ensayen lo que dirán cuando lo compartan con todo el grupo. Ensayar les brinda la oportunidad de aclarar sus ideas.

Principio(s) de diseño: Optimizar el resultado (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | PARTES CORRESPONDIENTES

15 minutos

Rutinas didácticas

MLR8: Apoyos para la discusión

Notar y maravillarse

Esta actividad introduce un lenguaje importante que los alumnos aplicarán para describir copias a escala. En particular, introduce la importante idea de las partes correspondientes. Los alumnos ya han analizado los lados correspondientes en las figuras. Aquí comenzarán a examinar también explícitamente los ángulos, comprendiendo que los ángulos correspondientes en una figura y en su copia a escala tienen la misma medida.

Diga a los alumnos que en esta lección observarán más de cerca las copias de figuras y describirán partes específicas en ellas. Muestre los diseños (las tres imágenes en el enunciado de la actividad) y las siguientes descripciones para que todos los vean. Pregunte a los alumnos qué observan y qué se preguntan. Tras el debate, explique que el diseño original y sus dos copias tienen partes que se corresponden entre sí. Señale algunas de sus partes correspondientes:

• El patrón en X que atraviesa cada figura

• El contorno curvo de cada figura

• Los puntos �� en el cartel original, �� en la Copia 1, y �� en la Copia 2

Organice a los estudiantes en grupos de 2 y facilíteles el acceso a sus kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) (especialmente el papel de calco). Dé a los alumnos 2-3 minutos para responder a las dos primeras preguntas y otros 2 minutos para comentar sus respuestas con su compañero. Pida a los alumnos que hagan una pausa en su trabajo para mantener un rápido debate en clase después. Pida a algunos alumnos que nombren un conjunto de puntos, segmentos y ángulos correspondientes.

A continuación, pida a los alumnos que indiquen si creen que alguna de las copias es una copia a escala. Invita a un par de alumnos a compartir su razonamiento. Cuando la clase llegue a un acuerdo sobre si la Copia 1 es una copia a escala y la Copia 2 no lo es, pida a los alumnos que completen las preguntas restantes individualmente y que utilicen papel de calco como herramienta.

Matemáticas de 7º grado . Unidad 1

INICIO CONTINUACIÓN

Considere la posibilidad de demostrar a la clase cómo utilizar el papel de calco para comparar ángulos. Diga o muestre a los alumnos que los segmentos de línea que forman un ángulo pueden extenderse para facilitar el trazado y la comparación.

Para las aulas que utilicen la versión digital de la actividad, el applet tiene una herramienta de ángulos móvil para comparar los ángulos de las copias con los ángulos del original.

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyos para la Discusión. Utilice esta rutina para ampliar los usos matemáticos del lenguaje para comunicarse sobre puntos, segmentos y ángulos correspondientes. Cuando los estudiantes compartan lo que notaron entre las tres imágenes, revoque sus afirmaciones usando el término "correspondiente". A continuación, invite a los alumnos a utilizar el término "correspondiente" cuando describan lo que han observado. Algunos alumnos pueden beneficiarse de repetir a coro las frases que incluyen la palabra "correspondiente" en el contexto.

Principio(s) de diseño: Optimizar la salida (para la explicación)

Aquí tienes una figura y dos copias, cada una con algunos puntos etiquetados.

1. Completa esta tabla para mostrar las partes correspondientes en las tres figuras.

Original Copia 1 Copia 2 punto �� segmento �� segmento �� punto ��

ángulo ��

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la repasen antes de realizar esta actividad.

Funcionamiento ejecutivo: Ayudas visuales. Cree un gráfico de anclaje (es decir, ejemplos de puntos, segmentos de línea y ángulos correspondientes) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para referencia futura.

ángulo ��

2. ¿Es alguna de las copias una copia a escala de la figura original? Explica tu razonamiento.

3. Utiliza papel de calco para comparar el ángulo �� con sus ángulos correspondientes en la Copia 1 y la Copia 2. ¿Qué observas?

4. Utiliza papel de calco para comparar el ángulo �� con sus ángulos correspondientes en la Copia 1 y la Copia 2. ¿Qué observas? ¿Qué observas?

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Original Copia 1 Copia 2

punto �� punto �� punto ��

segmento �� segmento �� segmento ��

segmento �� segmento �� segmento �� punto �� punto �� punto ��

ángulo �� ángulo �� ángulo ��

2. La copia 1 es una copia a escala, pero la copia 2 no lo es. Ejemplo de explicación: El signo original es un círculo. La copia 1 también es un círculo, pero más pequeño. La copia 2 ha sido estirada lateralmente y encogida verticalmente; su forma ha cambiado a un óvalo, por lo que no es una copia a escala.

3. El ángulo �� de la copia 1 corresponde y tiene el mismo tamaño que el ángulo ��. El ángulo �� en la Copia 2 también corresponde al ángulo �� pero tiene un tamaño menor que el ángulo original.

4. El ángulo �� en la Copia 1 corresponde y tiene el mismo tamaño que el ángulo ��. El ángulo �� en la Copia 2 también corresponde al ángulo �� pero es más grande en tamaño que el ángulo original.

Seleccione a algunos alumnos para que compartan sus observaciones sobre los ángulos. Discuta el tamaño de los ángulos correspondientes en las figuras que son copias a escala y en las que no lo son. Haga preguntas como:

• En la copia a escala, Copia 1, ¿cambió el tamaño de algún ángulo en comparación con su ángulo correspondiente en el signo original? (No)

• En la copia 2, ¿cambió el tamaño de algún ángulo en relación con su ángulo correspondiente en el signo original? (Sí) ¿Cuáles? (El ángulo �� tiene una medida diferente que el ángulo ��, por ejemplo.)

• ¿Qué puedes decir sobre los ángulos correspondientes en dos figuras que son copias a escala una de otra? (Tienen la misma medida.)

• ¿Qué puedes decir sobre los ángulos correspondientes en dos figuras que no son copias a escala? (Puede que no tengan la misma medida.)

ACTIVIDAD DE

EXPLORACIÓN

| TRIÁNGULOS A ESCALA

15 minutos

Rutinas didácticas

MLR3: Clarificar, Criticar, Corregir

Piensa en pareja y comparte

En esta actividad, los estudiantes continúan practicando la identificación de las partes correspondientes de las copias a escala. Al organizar las longitudes correspondientes en una tabla, los alumnos ven que hay un único factor que relaciona cada longitud en el triángulo original con su longitud correspondiente en una copia (MP8). Aprenden que este número se llama factor de escala .

Mientras los estudiantes trabajan en la primera pregunta, escuche cómo razonan sobre qué triángulos son copias a escala. Identifique los grupos que utilizan las longitudes de los lados y los ángulos como base para decidir. (No se espera que los alumnos razonen formalmente todavía, pero deben empezar a buscar pistas en las longitudes y los ángulos).

Mientras los alumnos identifican los lados correspondientes y sus medidas en la segunda y tercera preguntas, preste atención a la confusión sobre las partes correspondientes. Observe cómo los alumnos deciden qué lados de los triángulos rectángulos se corresponden.

Si los alumnos aún tienen acceso al papel de calco, observe si los alumnos utilizan esta herramienta de forma estratégica (MP5).

California - Grado 7

de 7º grado . Unidad 1 INTRODUCCIÓN

Organice a los estudiantes en grupos de 4. Asigne a cada estudiante uno de los siguientes pares de triángulos de la primera pregunta.

• �� y ��

Dé a los estudiantes 2 minutos de tiempo de reflexión en silencio para determinar si sus triángulos asignados son copias a escala del triángulo original. Dales otros 2-3 minutos para que discutan sus respuestas y completen la primera pregunta en grupos.

Discute brevemente en clase qué triángulos son copias a escala y selecciona un par de grupos que hayan razonado en términos de longitudes y ángulos para que expliquen su razonamiento. Algunas preguntas orientadoras:

• ¿Qué información utilizaste para distinguir las copias a escala de las que no lo son?

• ¿Cómo pudiste darte cuenta de inmediato de que algunas figuras no son copias a escala?

Da a los estudiantes un tiempo de trabajo tranquilo para completar el resto de la tarea después de que la clase reconozca que ��, ��, ��, y �� no son copias a escala.

Apoyo para estudiantes de inglés

Writing: MLR3 Aclarar, Criticar, Corregir. Circule y escuche mientras los estudiantes discuten sus triángulos asignados, luego presente una explicación incorrecta que refleje un concepto erróneo común. Por ejemplo, "El triángulo �� no puede ser una copia a escala del triángulo ��, porque las longitudes de los lados son las mismas que las del original" o "El triángulo �� es una copia a escala del triángulo ��, porque la longitud de cada lado se incrementa en 3". Pida a los alumnos que identifiquen el error (por ejemplo, pregúnteles: "¿Estáis de acuerdo con la afirmación?" "¿Por qué sí o por qué no?") y, a continuación, escriba una versión correcta de la afirmación. Esto ayuda a los estudiantes a evaluar y mejorar los argumentos matemáticos escritos por otros. Principio(s) de diseño: Maximizar la metaconciencia

He aquí el triángulo ��, seguido de otros triángulos.

Apoyo a los alumnos con discapacidad

Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (es decir, información necesaria para determinar copias a escala) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para futuras consultas.

Procesamiento conceptual: Tiempo de procesamiento. Comience con una demostración de la coincidencia de una copia a escala, que proporcionará acceso a los estudiantes que se benefician de instrucciones claras y explícitas. ENUNCIADO

Matemáticas de 7º grado . Unidad 1

DE TAREA PARA EL ESTUDIANTE

ENUNCIADO

POSIBLES RESPUESTAS

Su maestro les asignará dos de los triángulos para que los observen.

1. Para cada uno de los triángulos asignados, ¿es una copia a escala del Triángulo ��? Prepárense para explicar su razonamiento.

2. En grupo, identifiquen todas las copias a escala del triángulo �� de la colección. Discutid vuestras ideas. Si no están de acuerdo, trabajen para llegar a un acuerdo.

3. Enumera todos los triángulos que son copias a escala en la tabla. Registre las longitudes de los lados que corresponden a las longitudes de los lados del triángulo �� que aparecen en cada columna.

Triángulo �� 3 4 5

4. Explique o muestre cómo se ha escalado cada copia del original (triángulo ��).

1. Las respuestas varían dependiendo del par de triángulos que tengan los estudiantes. Los triángulos ��, ��, ��, y �� son copias a escala.

2. Los triángulos ��, ��, ��, y �� son copias a escala. Ejemplo de razonamiento: ��, ��, ��, y �� no han cambiado de forma (siguen siendo triángulos rectángulos). Cada uno de sus lados es el mismo número de veces más largo que los lados correspondientes del triángulo original. Los triángulos �� y �� no tienen la misma forma que el triángulo �� (sus ángulos son todos diferentes), por lo que no son copias a escala. Los triángulos ��, ��, y �� son triángulos rectángulos, pero sus lados no son el mismo número de veces más largos que los lados correspondientes del triángulo original.

3. Triángulo

4. Las explicaciones varían. Ejemplos de explicaciones:

• El triángulo �� es una copia del original del mismo tamaño. Todas las longitudes son iguales.

• En el triángulo ��, todas las longitudes son la mitad de las originales.

• En el triángulo ��, todos los lados duplican su longitud.

• En el triángulo ��, las longitudes son 2 3 veces las longitudes correspondientes en el triángulo original. ERRORES PREVISTOS

Los alumnos pueden pensar que el triángulo �� es una copia a escala porque, al igual que en el triángulo 34 - 5, los lados también son tres números enteros consecutivos.

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Muestre la imagen de todos los triángulos e invite a un par de estudiantes a compartir cómo supieron a qué lados de los triángulos corresponden. A continuación, muestre la tabla completada en la tercera pregunta para que todos la vean. Pide a cada grupo que presente sus observaciones sobre un triángulo y cómo se ha escalado el triángulo respecto al original. Anima a los alumnos a utilizar el término "correspondiente" en sus explicaciones. A medida que los estudiantes presentan, registre o ilustre su razonamiento en la tabla, por ejemplo, dibujando flechas entre las filas y anotando con la operación que los estudiantes están describiendo, como se muestra aquí.

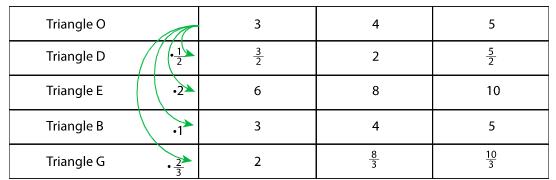
Utilice el lenguaje que los estudiantes utilizan para describir las longitudes de los lados y las relaciones numéricas en la tabla para guiar a los estudiantes hacia factor de escala. Por ejemplo: "Explicaste que las longitudes en el Triángulo �� son todas el doble de las del triángulo original, así que podemos escribirlas como "2 veces" los números originales. Las longitudes del triángulo �� son la mitad de las del original; podemos escribir " 1 2 veces" los números originales. Llamamos a estos multiplicadores - 2 y 1 2 - factores de escala. Decimos que escalar el triángulo �� por un factor de escala de 2 produce el triángulo ��, y que escalar el triángulo �� por 1 2 produce el triángulo ��."

¿Estás preparado para más?

Elige uno de los triángulos que no sea una copia a escala del triángulo ��. Describe cómo podrías cambiar al menos un lado para hacer una copia a escala, dejando al menos un lado sin cambiar.

"¿Estás listo para más?" Respuesta del alumno

Las respuestas varían. Ejemplo de respuesta: en el triángulo ��, el lado de longitud 7 podría ampliarse para tener una longitud 10

SÍNTESIS DE LA LECCIÓN

5 minutos

• ¿Qué entendemos por partes correspondientes?

• ¿Qué es un factor de escala? ¿Cómo funciona?

Los alumnos pueden utilizar un lenguaje informal para describir las partes correspondientes y reconocer un factor de escala como un cociente común entre las longitudes de los lados correspondientes. En la figura, el triángulo �� es una copia a escala del triángulo ��. Llamamos partes correspondientes a las que tienen la misma posición dentro de cada figura. Por ejemplo, nos referimos al vértice �� en el triángulo �� y al vértice �� en el triángulo �� como puntos correspondientes; al segmento �� y segmento �� como segmentos correspondientes; y ángulo �� (o ángulo ��) y ángulo �� (o ángulo ��) como ángulos correspondientes.

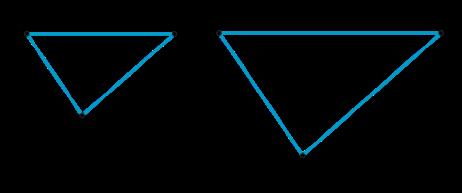
Los segmentos de una copia a escala son siempre un cierto número de veces más largos que los segmentos correspondientes de la figura original. Llamamos a ese número el factor de escala . Por ejemplo, el factor de escala entre �� y su triángulo copia �� es 3 2 o 1,5 porque todas las longitudes del triángulo �� son 1.5 veces mayores que las longitudes correspondientes en el triángulo ��

de 7º grado . Unidad 1

ENFRIAMIENTO | COMPARACIÓN DE POLÍGONOS ABCD Y PQRS

5 minutos

Polígono �� es una copia a escala del polígono ��.

1. Nombre el ángulo en la copia a escala que corresponde al ángulo ��

2. Nombre el segmento en la copia a escala que corresponde al segmento ��

3. ¿Cuál es el factor de escala del polígono �� al polígono ��?

1. El ángulo �� corresponde al ángulo ��.

2. El segmento �� corresponde al segmento ��

3. El factor de escala es 3 2 ya que �� = 3 y �� = 2

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

El segundo �� polígono es una copia a escala del primero.

A. Muestra un par de puntos correspondientes y dos pares de lados correspondientes en el polígono original y su copia. Considera usar lápices de colores para resaltar las partes correspondientes o etiquetar algunos de los vértices.

B. ¿Qué factor de escala lleva el polígono original a su copia más pequeña? Explica o muestra tu razonamiento.

Posibles soluciones

A. Las respuestas varían. Ejemplo de marcas:

B. 1 4 o 0.25. Ejemplo de explicación: Los lados que miden 4 unidades de longitud en el polígono original miden 1 unidad de longitud en la copia, que es una cuarta parte de la longitud original.

PROBLEMA 2

La figura �� es una copia a escala de la figura ��. Seleccione todas las afirmaciones que deben ser verdaderas:

La figura �� es mayor que la figura ��

La figura �� tiene el mismo número de aristas que la figura ��

La figura �� tiene el mismo perímetro que la figura ��

La figura �� tiene el mismo número de ángulos que la figura ��

La figura �� tiene ángulos con las mismas medidas que la figura ��

Posibles soluciones

La figura �� es mayor que la figura ��

La figura �� tiene el mismo número de aristas que la figura ��

La figura �� tiene el mismo perímetro que la figura ��

La figura �� tiene el mismo número de ángulos que la figura ��

La figura �� tiene ángulos con las mismas medidas que la figura ��

Matemáticas de 7º grado . Unidad 1

PROBLEMA 3

El polígono �� es una copia a escala del polígono ��.

A. ¿Cuál es el factor de escala del polígono �� al polígono ��? Explica tu razonamiento.

B. Halla la longitud que falta de cada lado marcado con ? en el Polígono ��.

C. Determina la medida de cada ángulo marcado con ? en el Polígono ��

Posibles soluciones

A. 2 porque el lado horizontal superior tiene una longitud 2,5 unidades en el Polígono �� y 5 unidades en el Polígono ��

B. Todos los lados escalan por el mismo factor de 2, por lo que el lado que es 2.5 unidades en el Polígono �� es 5 unidades en la copia, y el 1.5-unidades de largo es 3 unidades en la copia

C. 53° y 82° porque las copias a escala tienen los mismos ángulos correspondientes

PROBLEMA 4

Completa cada ecuación con un número que la haga verdadera.

1. 8 ⋅ = 40

2. 8 + = 40

3. 21 ÷ = 7

4. 21 - = 7

5. 21 ⋅ = 7

Reflexiones:

Posibles soluciones

Math Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

6.NS.3

Construir

7.RP.2

Enfoque SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.3

I.C.11

II.C.6

LECCIÓN 3 HACER COPIAS A ESCALA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

dar sentido al mundo e influir en el futuro

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

construir argumentos viables y criticar el razonamiento de los demás

META(S) DE APRENDIZAJE

• Dibujemos copias a escala.

META(S) DE APRENDIZAJE

descubrir la forma y el espacio y explorar las cantidades cambiantes.

• Puedo dibujar una copia a escala de una figura usando un factor de escala dado.

• Sé qué operación usar en las longitudes de los lados de una figura para producir una copia a escala.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Criticar (oralmente y por escrito) diferentes estrategias (expresadas con palabras y a través de otras representaciones) para crear copias a escala de una figura.

• Dibujar una copia a escala de una figura dada utilizando un factor de escala dado.

• Generalizar (oralmente y por escrito) que la relación entre las longitudes de los lados de una figura y su copia a escala es multiplicativa, no aditiva.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR1: Más fuerte y más claro cada vez

Pensar, compartir en parejas

Anticipar, controlar, seleccionar, secuenciar, conectar

MLR3: Clarificar, Criticar, Corregir

MLR7: Comparar y Conectar

MLR2: Recoger y Mostrar

Materiales necesarios

Enfriamiento

Juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)

Preparación necesaria

Asegúrate de que los alumnos tienen acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), especialmente papel de calco y fichas.

de 7º grado . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

En la lección anterior, los alumnos aprendieron que podemos utilizar factores de escala para describir la relación entre las longitudes correspondientes en figuras a escala. Aquí aplican esta idea para dibujar copias a escala de figuras simples dentro y fuera de una cuadrícula. También refuerzan su comprensión de que la relación entre copias a escala es multiplicativa, no aditiva. Los alumnos argumentan cuidadosamente sobre el proceso de escalado (MP3) y tienen la oportunidad de utilizar herramientas como el papel de calco o las fichas de forma estratégica (MP5).

A medida que los alumnos dibujan copias a escala y analizan las relaciones de escala con más detenimiento, anímeles a seguir utilizando los términos factor de escala y correspondiente en sus razonamientos.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento Independiente 5 min. Los estudiantes razonan sobre los productos de decimales y generalizan sobre su tamaño sin hacer cálculos reales.

Actividad de exploración opcional

Actividad de exploración

Pares 10 min.

Los estudiantes dibujan dos copias geométricas a escala en una cuadrícula, una con un factor de escala mayor que 1 y la otra con un factor de escala menor que 1

Existe un applet digital interactivo que permite a los estudiantes dibujar copias a escala de figuras utilizando la tecnología.

Pares 10 min. Al comparar y contrastar el trabajo de muestra de los estudiantes, éstos descubren que existe una relación multiplicativa entre las copias a escala.

Los estudiantes dibujan copias a escala sin una cuadrícula para reforzar el concepto de que las copias a escala tienen una relación multiplicativa.

Actividad de exploración Pares 10 min.

Síntesis Grupo completo 2 min.

Enfriamiento Independiente 5 min.

Hay disponible una extensión de exploración para desarrollar conexiones más profundas entre las relaciones multiplicativas de las longitudes de los lados correspondientes en cualquier figura a escala.

Los estudiantes repasan y justifican cómo dibujar copias a escala.

Los estudiantes practican cómo dibujar una copia a escala y determinan las posibles longitudes de los lados de una copia a escala.

Práctica Independiente 5-10 min. El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.

de 7º grado . Unidad 1

CALENTAMIENTO | ¿MÁS O MENOS? 5

minutos

En este calentamiento se pide a los alumnos que utilicen lo que saben sobre los números y la multiplicación para razonar sobre los cálculos decimales. Los problemas están diseñados para obtener una respuesta muy cercana a las opciones dadas, por lo que los alumnos deben ser más precisos en su razonamiento que simplemente redondear y calcular.

Mientras que una charla sobre números suele presentar una expresión numérica y pedir a los alumnos que expliquen estrategias para evaluarla, esta actividad plantea una cuestión ligeramente distinta, ya que los alumnos no tienen que evaluar necesariamente la expresión. En cambio, se les pide que juzguen si la expresión es mayor o menor que un valor dado. Aunque esta actividad no es exactamente lo mismo que una charla sobre números, la discusión puede sonar bastante similar.

INTRODUCCIÓN

Muestre los problemas para que todos los vean. Dé a los alumnos 2 minutos de tiempo para pensar en silencio. Diga a los alumnos que no tienen que calcular, sino que pueden razonar utilizando lo que saben sobre los números y la operación de cada problema. Pida a los alumnos que hagan una señal cuando tengan una respuesta y una estrategia para cada problema.

Apoyo a los alumnos con discapacidad

Procesamiento conceptual: Ayudas visuales. Incluir imágenes que representen "más" y "menos" (por ejemplo, flechas hacia arriba y hacia abajo), lo que ayudaría a los alumnos que se benefician de múltiples vías para el procesamiento del lenguaje.

Para cada problema, selecciona la respuesta de entre las dos opciones.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. El valor de 25 ⋅ (8,5) es:

A. Mayor que 205

B. Menor que 205

2. El valor de (9.93) ⋅ (0.984) es:

A. Mayor que 10

B. Menor que 10

3. El valor de (0.24) ⋅ (0.67) es:

A. Mayor que 0.2

B. Menor que 0.2 POSIBLES RESPUESTASS

1. Mayor que 205. Como 8 ⋅ 25 = 200 y 0.5 ⋅ 25 = 12.5, entonces el producto debe ser mayor que 205

2. Menor que 10. Como 9.93 ⋅ 1 = 9.93 y 0.9 es menor que 1, entonces el producto debe ser menor que 10.

3. Menor que 0.2. Como 0,24 es menor que 1 4 y 0,68 es menor que 0,8, el producto debe ser menor que 0,2 que es 1 4 de 0,8.

Los alumnos pueden decir que hay más superficie cubierta por el color que ven más en cada imagen, diciendo, por ejemplo: "Parece que hay más rojo". Pregunte a estos alumnos si hay alguna forma de demostrar sus observaciones.

de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Discuta cada problema de uno en uno con esta estructura:

• Pida a los alumnos que indiquen con qué opción están de acuerdo.

• Si todos están de acuerdo en una respuesta, pida a algunos estudiantes que compartan su razonamiento, registrándolo para que todos lo vean.

• Si hay desacuerdo en una respuesta, pida a los estudiantes con respuestas diferentes que expliquen su razonamiento y lleguen a un acuerdo sobre una respuesta.

OPCIONAL ACTIVIDAD DE EXPLORACIÓN | DIBUJAR

COPIAS A ESCALA

10 minutos

Materiales para reunir

MLR1: Cada vez más fuerte y más claro

Pensar Compartir en pareja

Los alumnos siguen trabajando con copias a escala de figuras geométricas sencillas, esta vez sobre una cuadrícula. Al intentar escalar segmentos no horizontales ni verticales, los alumnos pueden pensar en utilizar papel de calco o una regla para medir longitudes y un transportador para medir ángulos. Asegúrate de que tienen la oportunidad de ver cómo la estructura de la cuadrícula puede ser útil para escalar las longitudes de segmentos no verticales y no horizontales. Para crear copias a escala, los alumnos deben prestar atención a todas las partes de la figura original, ya que, de lo contrario, la copia no se escalará correctamente. El uso de la cuadrícula para escalar segmentos no horizontales y no verticales es un buen ejemplo de uso estratégico de las herramientas (MP5).

Mientras los alumnos trabajan, vigile si encuentran una forma de escalar correctamente las longitudes de los segmentos pero olvidan tener en cuenta el tamaño de los ángulos correspondientes (especialmente al hacer una copia de las figuras B y D).

LANZAR

Dar a los estudiantes 3 minutos de tiempo tranquilo para dibujar y otros 3 minutos para compartir sus dibujos con un compañero, comprobar el trabajo de los demás y hacer revisiones. Facilítales sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Apoyo para estudiantes de inglés

Hablar, representar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para apoyar la discusión productiva cuando los estudiantes comparten sus dibujos con un compañero. Dé a los estudiantes tiempo para reunirse con 2-3 partners, para compartir y obtener comentarios sobre sus copias a escala. Proporcione a los estudiantes sugerencias que ayuden a sus compañeros a reforzar sus ideas y aclarar sus dibujos (por ejemplo, "¿Cómo supiste la longitud de cada lado?", "¿Cómo mediste cada ángulo?", "¿Cómo utilizaste la cuadrícula para crear tu copia a escala?"). Los alumnos pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar su trabajo. De este modo, los alumnos tienen la oportunidad de producir lenguaje matemático verbal al servicio del perfeccionamiento de sus ideas y sus dibujos.

Principio(s) de diseño: Optimizar el resultado (para justificarlo)

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Tecnología de apoyo. Proporcione acceso a la versión digital de esta actividad.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTAS

ERRORES PREVISTOS

1. Dibuje una copia a escala de la Figura A o B utilizando un factor de escala de 3.

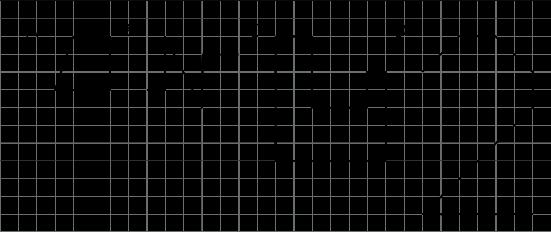
2. Dibuje una copia a escala de la Figura C o D utilizando un factor de escala de 1 2

Algunos estudiantes pueden pensar que la Figura C no se puede escalar por un factor de 1 2 porque algunos vértices no caerán en las intersecciones de las líneas de la cuadrícula. Aclare que la cuadrícula nos ayuda a ver las longitudes en unidades enteras, pero que los segmentos que dibujamos en ellas no están limitados a unidades enteras de longitud. SÍNTESIS

Invite a los alumnos a compartir sus estrategias sobre cómo utilizaron la cuadrícula (u otras herramientas) para asegurarse de que sus dibujos eran copias a escala. Considere hacer preguntas como:

• ¿Cómo supiste cuánto medir cada lado en tu copia a escala?

• ¿Cómo supiste cuánto medir cada ángulo en tu copia a escala?

• Si cometiste un error al dibujar tu copia a escala, ¿cómo te diste cuenta?

Modele, estimule y escuche el lenguaje que usan los estudiantes para distinguir entre figuras a escala y no a escala. Haga hincapié en la utilidad de la cuadrícula para dibujar y comprobar ángulos rectos, y para dibujar y comprobar longitudes de segmentos. Todas las respuestas correctas tendrán el mismo tamaño y la misma forma, pero podrían dibujarse en diferentes posiciones en la cuadrícula.

de 7º grado . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | ¿QUÉ OPERACIONES?

(PARTE 1) 10

minutos

Materiales para reunir

Anticipar, controlar, seleccionar, secuenciar, conectar

Pensar en pareja Compartir

MLR3: Clarificar, Criticar, Corregir

El objetivo de esta actividad es contrastar los efectos de multiplicar las longitudes laterales frente a sumarlas cuando se crean copias de un polígono. Para encontrar las longitudes laterales correspondientes en una copia a escala, las longitudes laterales de una figura se multiplican (o dividen) por el mismo número. Sin embargo, los alumnos suelen pensar erróneamente que sumando o restando el mismo número a todas las longitudes laterales también se creará una copia a escala. Cuando los alumnos reconocen que existe una relación multiplicativa entre las longitudes de los lados en lugar de una aditiva, están buscando y haciendo uso de la estructura (MP7).

Supervise a los alumnos que:

• se dan cuenta de que la copia de Diego ya no es un polígono mientras que la de Jada sigue siéndolo

• se dan cuenta de que las relaciones entre las longitudes de los lados en la copia de Diego han cambiado (por ejemplo, El lado 1 es el doble de largo que el lado 2 en el original, pero no es el doble de largo que el lado 2 en la copia), mientras que en la copia de Jada no lo han hecho

• observa que todos los ángulos correspondientes tienen medidas iguales (es decir, 90 o 270 grados)

• describe la copia de Jada como si todas las longitudes de los lados estuvieran divididas por 3

• describe la copia de Jada como si todas las longitudes de los lados tuvieran un tercio de sus longitudes originales

• describe la copia de Jada como si tuviera un factor de escala de 1 3

INTRODUCCIÓN

Dar a los estudiantes 2-3 minutos de tiempo para pensar en silencio, y luego 2 minutos para compartir su pensamiento con un compañero.

Apoyo a los alumnos con discapacidad

Lenguaje receptivo/expresivo: Tiempo de Procesamiento. Los estudiantes que se benefician de tiempo de procesamiento adicional también serían ayudados por MLR3 Aclarar, Criticar, Corregir. ENUNCIADO DE TAREA PARA

Diego y Jada quieren escalar este polígono de modo que el lado que corresponde a 15 unidades en el original sea 5 unidades en la copia a escala

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA DEL ESTUIDIANTE CONTINUACIÓN

Diego y Jada utilizan cada uno una operación diferente para encontrar las nuevas longitudes de los lados. Aquí están sus dibujos terminados.

1. ¿Qué operación crees que usó Diego para calcular las longitudes de su dibujo?

2. ¿Qué operación crees que usó Jada para calcular las longitudes de su dibujo?

3. ¿Cada método produjo una copia a escala del polígono? Explica tu razonamiento.

POSIBLES RESPUESTASS

1. Puesto que podemos llegar de 15 a 5 restando 10, Diego puede haber restado 10 unidades de la longitud de cada lado. Restando 10 de la longitud de cada lado en el original se obtiene la imagen de Diego.

2. Jada pasó de 15 a 5 multiplicando por 1 3 o dividiendo por 3. Multiplicando cada lado por 1 3 en el original se obtiene la imagen de Jada.

3. No, sólo el método de Jada produce una copia a escala. Ejemplo de explicación: Restar 10 de cada longitud no funcionó porque ahora la figura ya no es un polígono. Hay un gran hueco entre los dos lados que deberían encontrarse. Para crear una copia a escala, cada longitud debe multiplicarse (o dividirse) por el mismo número.

SÍNTESIS DE LA ACTIVIDAD

Invite a los alumnos previamente seleccionados a compartir sus respuestas y razonamientos. Secuencie sus explicaciones de la más general a la más técnica.

Antes de pasar a la siguiente actividad, considere la posibilidad de hacer preguntas como las siguientes:

• ¿Cuál es el factor de escala utilizado para crear el dibujo de Jada? ¿Y para el dibujo de Diego? ( 1 3 para el de Jada; no lo hay para el de Diego, porque no es una copia a escala.)

• ¿Qué puedes decir sobre los ángulos correspondientes en los dibujos de Jada y Diego? (Todos son iguales, aunque uno sea una copia a escala y el otro no.)

• La resta de las longitudes de los lados (normalmente) no produce copias a escala. ¿Crees que la suma funcionaría? (Las respuestas varían.)

Nota: Hay casos raros en los que sumar o restar la misma longitud de cada lado de un polígono (y mantener los ángulos iguales) producirá una copia a escala, concretamente si todas las longitudes de los lados son iguales. Si los alumnos no lo mencionan, no es importante discutirlo en este punto.

Apoyo para estudiantes de inglés

Representar, escribir y hablar: Rutina del Lenguaje Matemático 3 Aclarar, Criticar, Corregir. Esta es la primera vez que se sugiere la Rutina del Lenguaje Matemático 3 como apoyo en este curso. En esta rutina, los estudiantes reciben un trabajo matemático incorrecto o incompleto. Puede ser en forma de enunciado escrito, dibujo, pasos de resolución de problemas u otra representación matemática. Los alumnos analizan, reflexionan y mejoran el trabajo escrito corrigiendo errores y aclarando el significado. Las preguntas típicas son: "¿Hay algo poco claro?" y/o "¿Hay algún error de razonamiento?". El objetivo de esta rutina es que los alumnos analicen el pensamiento matemático que no es el suyo y que consoliden sus conocimientos mediante la comunicación sobre errores conceptuales y ambigüedades en el lenguaje.

Principio(s) de diseño: Apoyar la creación de sentido; Optimizar el resultado (para el razonamiento)

de 7º grado . Unidad 1

Apoyo para estudiantes que aprenden inglés Continuación

Cómo sucede:

1. Haga el papel de Diego y presente a la clase la siguiente afirmación junto con su dibujo defectuoso. "Yo utilicé un factor de escala de menos 10, y Jada utilizó un factor de escala de un tercio. Así que mi dibujo es una copia a escala diferente de la de Jada".

Pregunte a los alumnos: "¿Qué pasos siguió Diego para hacer el dibujo?" y "¿Creó una copia a escala? ¿Cómo lo sabes?"

2. Conceda a los alumnos 1 minuto de reflexión en silencio para analizar el enunciado y, a continuación, 3 minutos para trabajar en la mejora del enunciado con un compañero.

Mientras discuten en parejas, proporcione estos marcos de frases para el andamiaje: "Creo que Diego creó el dibujo porque .", "Diego creó/no creó una copia a escala. Lo sé porque .", "No puedes porque .". Anime al oyente a hacer preguntas aclaratorias refiriéndose al enunciado y a los dibujos. Permita que cada pareja se turne como hablante y oyente.

Escuche si los alumnos identifican el tipo de operación utilizada y la justificación de haber realizado o no un dibujo a escala. Haga que las parejas lleguen a un entendimiento mutuo y a un acuerdo sobre una afirmación correcta acerca del dibujo de Diego.

3. Invite a las parejas 3 o 4 a presentar su afirmación mejorada a la clase, tanto oralmente como por escrito. . Pida a los alumnos que presten atención a las palabras de transición de orden/tiempo (primero, después, luego, etc.) y a cualquier elemento de justificación (por ejemplo, Primero, porque .).

He aquí dos ejemplos de enunciados mejorados:

"He restado 10 de la longitud de cada lado y Jada ha utilizado un factor de escala de un tercio. Así que mi dibujo no es una copia a escala y el de Jada sí. El de Jada es una copia a escala porque sé que multiplicando -no restando- se crea una copia a escala. Su dibujo creó un polígono sin huecos."

"Resté 10 de cada lado, pero debería haberme dado cuenta de que para escalar 15 unidades en el original hasta 5 unidades en la copia, tienes que dividir por 3. Jada utilizó un factor de escala de un tercio, que es lo mismo que dividir por 3. Mi dibujo no es una copia a escala y el de Jada sí lo es porque el suyo no es un polígono sin huecos, y restar 10 no es un factor de escala".

Llame la atención sobre las afirmaciones que generalizan que el método para hallar las longitudes de los lados de una copia a escala es multiplicando o dividiendo, no sumando o restando. Revoque las ideas de los estudiantes haciendo hincapié en saber si crearon o no un polígono a escala.

4. Cierre la conversación sobre el dibujo de Diego, discuta la exactitud de la copia a escala de Jada y luego pase a la siguiente actividad de la lección.

ACTIVIDAD DE EXPLORACIÓN | ¿QUÉ OPERACIONES?

(PARTE 2) 10 minutos

Materiales a reunir

MLR7: Comparar y conectar

MLR2: Colecciona y exhibe

Piensa, empareja y comparte

En la actividad anterior, los alumnos vieron que restar el mismo valor a todas las longitudes de los lados de un polígono no producía una copia a escala (más pequeña). Esta actividad demuestra que sumar el mismo valor a todas las longitudes tampoco produce una copia a escala (mayor), reforzando la idea de que la escala implica multiplicación.

Esta actividad ofrece a los alumnos la oportunidad de dibujar una copia a escala sin cuadrícula y de utilizar el papel como herramienta de medición. Para crear una copia utilizando un factor de escala de 2, los alumnos tienen que marcar la longitud de cada segmento original y transferirla dos veces a su superficie de dibujo, reforzando de forma táctil el significado del factor de escala. Los ángulos del polígono son ángulos rectos (y un 270 ángulo de un grado en un caso) y pueden formarse utilizando la esquina de una ficha.

Algunos alumnos pueden tener dificultades para averiguar cómo utilizar una ficha o una hoja de papel para medir longitudes. Antes de hacer la demostración, anímales a pensar en cómo copiar una longitud del polígono en una ficha y utilizarla como incremento para medir. Si es necesario, muestre cómo marcar la 4 unidad de longitud a lo largo del borde de una tarjeta y cómo utilizar la marca para determinar las longitudes necesarias para la copia.

INTRODUCCIÓN

Pida a los alumnos que lean el enunciado de la tarea y comprueben que entienden qué lado del polígono quiere André que tenga 8 unidades de longitud en su dibujo. Proporcione acceso a fichas para que los alumnos puedan utilizarlas como herramienta de medición. Considere la posibilidad de no dirigir explícitamente a los alumnos en cuanto a su uso para darles la oportunidad de utilizar las herramientas de forma estratégica (MP5). Conceda a los estudiantes 5-6 minutos de tiempo de trabajo tranquilo y, a continuación, 2 minutos para compartir su trabajo con un compañero.

Apoyo a los alumnos con discapacidad

Lenguaje receptivo/expresivo: Tiempo de Procesamiento. Los alumnos que se benefician de un tiempo de procesamiento adicional también se verían favorecidos por la MLR2 (Recoger y mostrar).

DE TAREA PARA EL ESTUDIANTE

Andre quiere hacer una copia a escala del dibujo de Jada para que el lado que corresponde a 4 unidades en el polígono de Jada sea 8 unidades en su copia a escala.

ENUNCIADO

1. Andre dice "Me pregunto si debería agregar 4 unidades a las longitudes de todos los segmentos de ". ¿Qué le responderías a André? Explica o muestra tu razonamiento.

2. Crea la copia a escala que quiere André. Si te atascas, considera usar el borde de una ficha o papel para medir las longitudes necesarias para dibujar la copia.

1. Las respuestas varían. Ejemplo de razonamiento: Sumar 4 unidades no funcionaría porque la forma de la copia sería diferente de la forma del original. Por ejemplo, en el dibujo original, el segmento horizontal superior es 12 unidades y los dos segmentos horizontales inferiores (5 unidades y 7 unidades) también suman 12 unidades. Si añadimos 4 unidades a cada segmento, el segmento horizontal superior tendrá 16 unidades, y los dos segmentos horizontales inferiores serán 9 unidades y 11 unidades, o un total de 20 unidades. Habrá un hueco donde deberían encontrarse dos segmentos, o si hacemos que los dos extremos se encuentren, los ángulos dejarán de ser ángulos rectos. Véase la figura de la izquierda.

2. Véase la figura de la derecha.

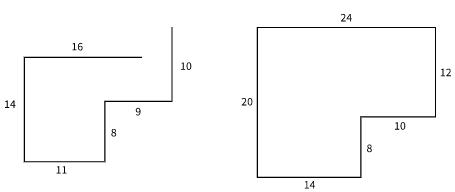
Matemáticas de 7º grado . Unidad 1

ERRORES PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Puede que algunos alumnos no estén convencidos de que hacer cada segmento 4 unidades más largo no funcione. Para demostrar que añadir 4 unidades funcionaría, podrían simplemente volver a dibujar el polígono y escribir las longitudes de los lados que son 4 unidades más largas, independientemente de si los números coinciden con las longitudes reales. Pídeles que comprueben las longitudes de los lados midiéndolas. Explícales (o muéstrales, si es necesario) cómo la longitud de 4 unidades del dibujo de Jada podría utilizarse como unidad de medida y añadirse a todos los lados. Otros alumnos podrían añadir 4 unidades a todos los lados y conseguir formar un polígono, pero cambiando los ángulos por el camino. Si los alumnos lo hacen para argumentar que la copia no se escalará, plantéate compartir sus ilustraciones con la clase, ya que pueden ayudar a contrarrestar la idea de que "escalar implica sumar". Si, por el contrario, los alumnos lo hacen para demostrar que la suma de 4 unidades alrededor sí funciona, aborde la idea errónea. Pídales que recuerden el tamaño de los ángulos correspondientes en las copias a escala, o recuérdeles que los ángulos en una copia a escala tienen el mismo tamaño que sus homólogos en la figura original.

El propósito de la actividad es señalar explícitamente un posible malentendido sobre cómo funcionan los factores de escala, haciendo hincapié en que los factores de escala funcionan multiplicando las longitudes de los lados existentes por un factor común, en lugar de añadir una longitud común a cada uno.

Invite a un par de estudiantes a compartir sus explicaciones o ilustraciones de que añadir 4 unidades a la longitud de cada segmento no funcionaría (por ejemplo, la copia ya no es un polígono, o la copia tiene ángulos diferentes a los de la figura original). A continuación, selecciona a un par de alumnos para que muestren sus copias a escala y compartan cómo las han creado. Pregunte:

• ¿Qué factor de escala utilizaste para crear tu copia? ¿Por qué?

• ¿Cómo utilizaste una ficha (o una hoja de papel) para medir las longitudes de la copia?

• ¿Cómo mediste los ángulos de la copia?

Apoyo para estudiantes de inglés

Speaking: Rutina del Lenguaje Matemático 7 Compara y Conecta. Esta es la primera vez que se sugiere la Rutina 7 del Lenguaje Matemático como apoyo en este curso. En esta rutina, se da a los estudiantes un problema que puede abordarse utilizando múltiples estrategias o representaciones, y se les pide que preparen una muestra visual de su método. A continuación, los alumnos investigan las estrategias (mediante un recorrido guiado por el maestro, un intercambio entre compañeros, una presentación en grupo, etc.), comparan enfoques e identifican correspondencias entre distintas representaciones. Un tema de debate típico es "¿Qué es lo mismo y qué es diferente?", comparando su propia estrategia con las demás. El propósito de esta rutina es permitir a los estudiantes dar sentido a las estrategias matemáticas identificando, comparando, contrastando y conectando otros enfoques con los suyos, y desarrollar la conciencia de los estudiantes sobre el lenguaje utilizado a través de conversaciones constructivas.

Principio(s) de diseño: Maximizar la metaconciencia

Cómo se lleva a cabo:

1. Utilice esta rutina para comparar y contrastar diferentes métodos para crear copias a escala del dibujo de Jada. Antes de seleccionar a los alumnos para que expongan su método a toda la clase, déles primero la oportunidad de hacerlo en un grupo de 3-4. Invite a los alumnos a investigar en silencio el trabajo de los demás. Pídales que piensen en lo que es igual y lo que es diferente en cada exposición. Invite a los alumnos a explicar paso a paso su método utilizando este marco de frases: "Para crear la copia, primero .... A continuación, .... Después, .... Por último,....". Conceda 1-2 minutos a cada exposición y señale cuándo es el momento de cambiar.

2. A continuación, dé a cada alumno la oportunidad de añadir detalles a su propia exposición durante 1-2 minutos. Mientras los alumnos trabajan en sus exposiciones, circule por la sala para identificar al menos dos métodos diferentes o dos formas distintas de representar un método. Busque también métodos que sólo hayan tenido un éxito parcial.

3. Considere la posibilidad de seleccionar a 1-2 estudiantes para que compartan los métodos que sólo hayan tenido un éxito parcial en la producción de copias a escala. A continuación, seleccione a un par de alumnos para que expongan los métodos que sí produjeron copias a escala.

Llame la atención de los alumnos sobre los enfoques utilizados en cada dibujo (por ejemplo, sumar el mismo valor a la longitud de cada lado, no prestar atención a los ángulos, multiplicar por un factor común, no crear un polígono, etc.). Pregunte a los alumnos: "¿Con este método se ha creado una copia a escala? ¿Por qué sí o por qué no?"

4. Después de que los alumnos preseleccionados hayan terminado de compartir con toda la clase, dirija un debate en el que se comparen, contrasten y conecten los diferentes enfoques y representaciones.

En este debate, demuestre el uso del lenguaje matemático "factor de escala", "correspondiente" y "multiplicativo" para ampliar el lenguaje de los alumnos.

Considere la posibilidad de utilizar las siguientes indicaciones:

• "¿Cómo apareció el factor de escala en cada método?",

• "¿Por qué los diferentes enfoques condujeron al mismo resultado?",

• "¿Qué funcionó bien en el enfoque/representación de ? ¿Qué no funcionó bien?", y

• "¿Qué papel desempeña la multiplicación en cada enfoque?"

5. Cierre el debate invitando a 3 alumnos a que repitan el método incorrecto para crear un dibujo a escala y, a continuación, invite a 3 alumnos diferentes a que repitan el método correcto para crear un dibujo a escala. A continuación, vuelva a la síntesis de la lección y al enfriamiento.

Apoyo a los alumnos con discapacidad

Lenguaje receptivo/expresivo: Tiempo de Procesamiento. Los alumnos que se benefician de un tiempo extra de procesamiento también se verían favorecidos por la RML8 (Apoyos a la Discusión).

¿Estás listo para más?

Las longitudes de los lados del Triángulo �� son todas 5 más que las longitudes de los lados del Triángulo ��. ¿Puede el Triángulo �� ser una copia a escala del Triángulo ��? Explica tu razonamiento.

"¿Estás preparado para más?" Respuesta del alumno

Sí, si el triángulo �� es equilátero entonces las longitudes de sus lados son todas iguales. Añadiendo 5 a cada lado, las longitudes seguirán siendo las mismas, por lo que el triángulo �� también será equilátero.

Si el triángulo �� no es equilátero, entonces el triángulo �� no será una copia a escala del triángulo ��. Para ver por qué, observa que añadiendo 5 a un lado de 5 se duplica la longitud del lado. Añadir 5 a una longitud lateral mayor que 5 cambia el lado en un factor de escala menor que 2 mientras que añadir 5 a una longitud lateral menor que 5 cambia la longitud lateral en un factor de escala menor que 2. Por tanto, si una longitud lateral del triángulo �� es 5, todas las longitudes laterales tienen que ser 5 o, de lo contrario, el triángulo �� no será una copia a escala del triángulo ��. Este razonamiento funciona para longitudes de lado distintas de 5. En general, al añadir 5 a una longitud lateral mayor se utiliza un factor de escala menor.

SÍNTESIS DE LA LECCIÓN

2 minutos

• ¿Cómo dibujamos una copia a escala de una figura?

• ¿Podemos crear copias a escala sumando o restando el mismo valor a todas las longitudes? ¿Por qué sí o por qué no?

La escala es un proceso multiplicativo. Para dibujar una copia a escala de una figura, tenemos que multiplicar todas las longitudes por el factor de escala. En la lección vimos que sumar o restar el mismo valor a todas las longitudes no creará copias a escala.

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

ENFRIAMIENTO | MÁS COPIAS A ESCALA 5 minutos

1. Crea una copia a escala de �� utilizando un factor de escala de 4

2. Triángulo �� es una copia a escala de Triángulo ��.

Seleccione todos los conjuntos de valores que podrían ser las longitudes de los lados del triángulo ��.

8, 11, y 14.

10, 17.5, y 25

6, 9, y 11

6, 10.5, y 15.

8, 14, y 20

POSIBLES RESPUESTASS

8, 11, y 14.

10, 17.5, y 25

6, 9, y 11.

6, 10.5, y 15.

8, 14, y 20

Matemáticas de 7º grado . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Aquí hay 3 polígonos.

Dibuja una copia a escala del Polígono �� utilizando un factor de escala de 2

Dibuja una copia a escala del Polígono �� utilizando un factor de escala de 1 2

Dibuja una copia a escala del Polígono �� usando un factor de escala de 3 2

Posibles soluciones

PROBLEMA 2

El cuadrilátero �� tiene longitudes laterales 6, 9, 9, y 12. El cuadrilátero �� es una copia a escala del cuadrilátero ��, con su lado más corto de longitud 2. ¿Cuál es el perímetro del cuadrilátero ��?

Posibles soluciones

El factor de escala es 1 3 , por lo que las longitudes de los lados del cuadrilátero �� son 2, 3, 3, y 4 . Sumando estos cuatro números se obtiene el perímetro de 12

PROBLEMA 3

He aquí un polígono en una cuadrícula.

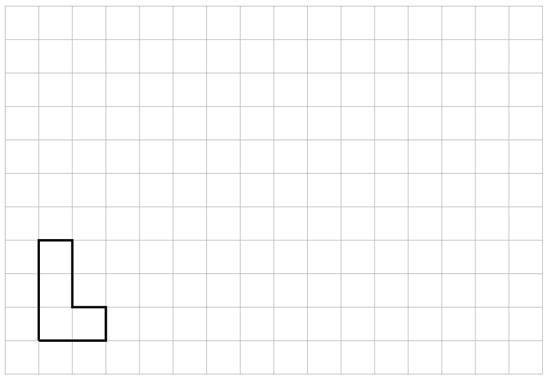
Dibuja una copia a escala de este polígono que tenga un perímetro de 30 unidades. ¿Cuál es el factor de escala? Explica cómo lo sabes.

A. B.

Matemáticas de 7º grado . Unidad 1

Posibles soluciones

El perímetro del polígono original es 10 unidades. Dado que el perímetro de una copia a escala se multiplica por el factor de escala, es necesario aplicar un factor de escala de 3 para obtener una copia con un perímetro de 30

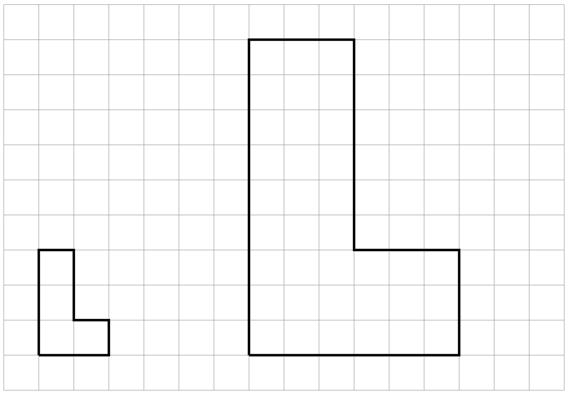
PROBLEMA 4

Del 7º curso, Unidad 1, Lección 1 Priya y Tyler están discutiendo las figuras que se muestran a continuación. Priya piensa que ��, ��, y �� son copias a escala de ��. Tyler dice que �� y �� son copias a escala de ��. ¿Estás de acuerdo con Priya o con Tyler? Explica tu razonamiento.

Posibles soluciones

Las respuestas varían. Ejemplo de respuesta: No estoy de acuerdo con ninguna de las dos. Sólo �� es una copia a escala de ��. En ��, la longitud de cada segmento del signo más es el doble de los segmentos coincidentes en ��. En �� y ��, algunos segmentos tienen el doble de las longitudes coincidentes en �� pero otros no.

Reflejos:

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Enfoque SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.3

II.C.6

II.C.7

LECCIÓN 4 RELACIONES A ESCALA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo e inciden en el futuro

hacen uso de la estructura y construyen argumentos viables exploran cantidades cambiantes y descubren la forma y el espacio.

META(S) DE APRENDIZAJE

• Encontremos relaciones entre copias a escala.

META(S)

DE APRENDIZAJE

• Puedo usar distancias correspondientes y ángulos correspondientes para decir si una figura es una copia a escala de otra.

• Cuando veo una figura y su copia a escala, puedo explicar lo que es cierto acerca de los ángulos correspondientes.

• Cuando veo una figura y su copia a escala, puedo explicar lo que es cierto acerca de las distancias correspondientes.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Explicar (oralmente y por escrito) que los ángulos correspondientes en una figura y sus copias a escala tienen la misma medida.

• Identificar (oralmente y por escrito) las distancias o ángulos correspondientes que pueden mostrar que una figura no es una copia a escala de otra.

• Reconocer que las distancias correspondientes en una figura y su copia a escala están relacionadas por el mismo factor de escala que los lados correspondientes.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Notar y maravillarse

MLR7: Comparar y conectar

MLR1: Cada vez más fuerte y más claro

MLR8: Apoyos a la discusión

Anticipar, controlar, seleccionar, secuenciar, conectar

Materiales necesarios

Enfriamiento

Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)

de 7º grado . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación necesaria

Asegúrese de que los estudiantes tienen acceso a sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), especialmente reglas y transportadores.

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

En lecciones anteriores, los alumnos observaron la relación entre una figura y una copia a escala encontrando el factor de escala que relaciona las longitudes de los lados y utilizando papel de calco para comparar los ángulos. Esta lección lleva ambas comparaciones un paso más allá.

• Los alumnos estudian las distancias correspondientes entre puntos que no están conectados por segmentos, tanto en copias a escala como sin escala. Observan que cuando una figura es una copia a escala de otra, las distancias correspondientes que no están conectadas por un segmento también están relacionadas por el mismo factor de escala que los lados correspondientes.

• Los alumnos utilizan transportadores para comprobar sus observaciones sobre los ángulos correspondientes. Verifican en varios conjuntos de ejemplos que los ángulos correspondientes en una figura y sus copias a escala tienen el mismo tamaño.

Los alumnos utilizan ambas observaciones -sobre ángulos y distancias entre puntos- para argumentar si una figura es o no una copia a escala de otra (MP3). La práctica con el uso de transportadores ayudará a desarrollar el sentido de la precisión en las mediciones, y cómo sacar conclusiones a partir de dichas mediciones, a la hora de determinar si dos ángulos son iguales o no.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Descripción breve

Calentamiento Independiente 5 min. Los estudiantes conjeturan y luego verifican las medidas de los ángulos correspondientes de figuras a escala.

Actividad de exploración Pares 10 min.

Actividad de Exploración Pares 10 min.

Usando las mismas figuras del Calentamiento, los estudiantes comparan las distancias correspondientes en copias a escala y hacen conexiones con lados o segmentos correspondientes y factores de escala.

Los estudiantes usan lados correspondientes, distancias, medidas de ángulos y factores de escala para verificar si un cuadrilátero es una copia a escala de otro.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las propiedades que deben cumplirse para que un polígono sea una copia a escala de otro.

Actividad de exploración opcional Grupos reducidos 10 min.

Los alumnos aplican sus conocimientos sobre las relaciones de escala para fundamentar, con pruebas, si una imagen no es una copia a escala de otra imagen. Hay disponible un applet digital interactivo que permite a los alumnos explorar las relaciones de escala en la imagen utilizando herramientas geométricas basadas en la tecnología.

Síntesis Todo el grupo 5 min. Los estudiantes repasan los criterios que se pueden utilizar para determinar si las imágenes o figuras son copias a escala unas de otras.

Enfriamiento Independiente 5 min. Los estudiantes explican si un polígono es una copia a escala de otro.

Práctica Independiente 5-8 min. El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

CALENTAMIENTO | TRES CUADRILÁTEROS (PARTE 1) 5

minutos

Rutinas didácticas

Notar y preguntarse

Este calentamiento da a los estudiantes la oportunidad de practicar la identificación de los ángulos correspondientes de copias a escala, medir ángulos usando un transportador y probar su conjetura anterior de que los ángulos correspondientes tienen la misma medida.

Haz que los estudiantes observen las figuras de la actividad y pregúntales "¿Qué notas? ¿Qué se preguntan?

Haga preguntas concretas sobre los ángulos de las figuras (por ejemplo, si los correspondientes tienen la misma medida). Diga a los alumnos que van a comprobar su observación anterior sobre los ángulos de las figuras a escala, esta vez utilizando transportadores en lugar de papel de calco.

Facilite el acceso a los transportadores. Se recomiendan los transportadores transparentes sin agujeros y con líneas radiales impresas. Algunos ángulos pueden ser difíciles de medir debido al tamaño de los polígonos. Si los estudiantes encuentran que los lados de un polígono no son lo suficientemente largos para acomodar las mediciones de ángulos, sugiérales que extiendan las líneas o demuéstreles cómo hacerlo (especialmente si los transportadores disponibles son opacos con agujeros en el centro).

Apoyo a los estudiantes con

discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.

Cada uno de estos polígonos es una copia a escala de los otros.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTAS

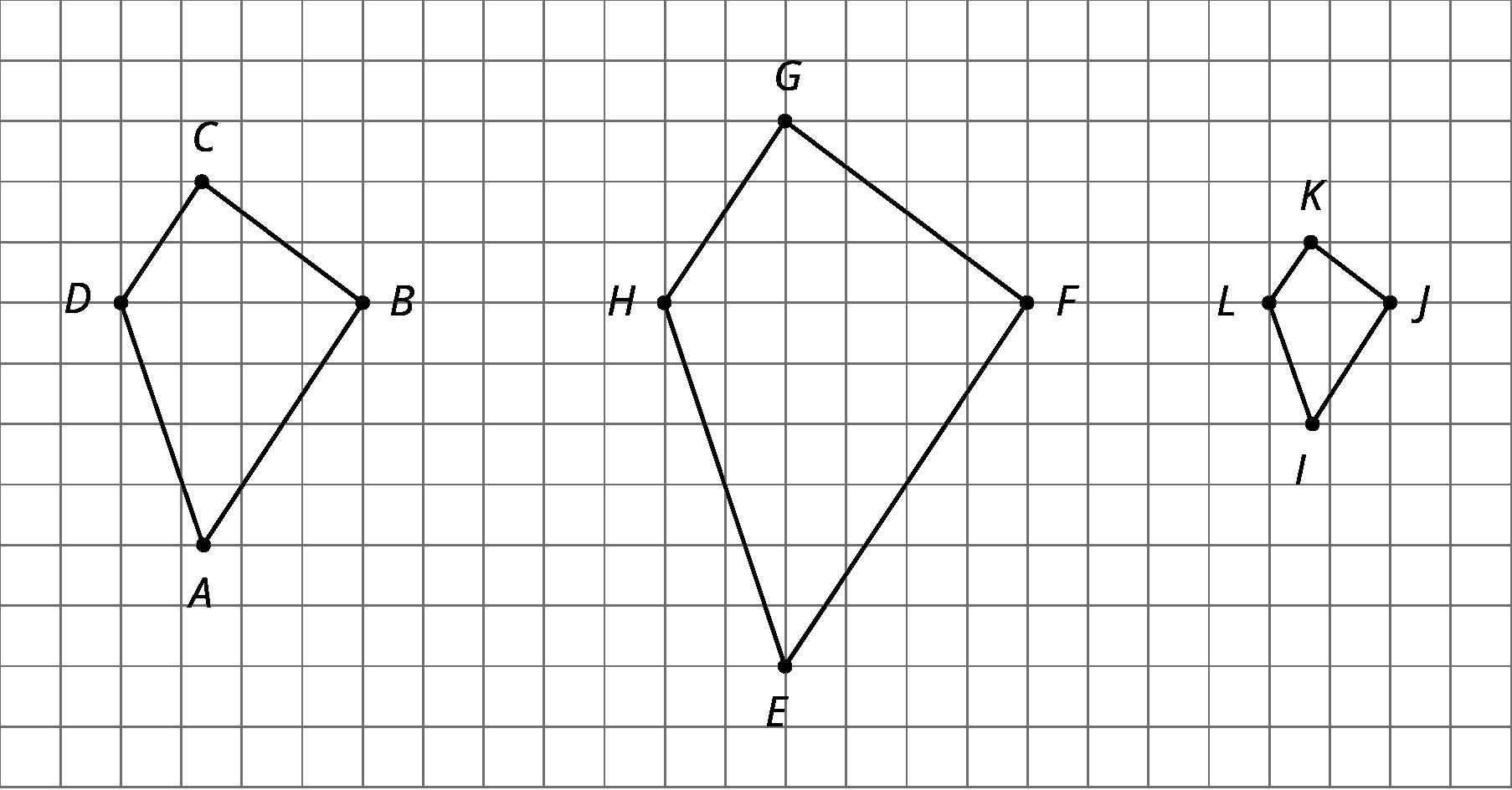
1. Nombra dos pares de ángulos correspondientes. ¿Qué puedes decir sobre los tamaños de estos ángulos?

2. Comprueba tu predicción midiendo al menos un par de ángulos correspondientes utilizando un transportador. Registra tus mediciones con una aproximación de 5°

1. Las respuestas varían. Ejemplo de respuesta:

• Ángulos �� y �� (a.k.a. ángulos �� y ��)

Los ángulos correspondientes de los polígonos serán del mismo tamaño.

2. Al menos dos ángulos de una de estas listas:

• Los ángulos ��, ��, y �� miden cada uno aproximadamente 50°

• Los ángulos ��, ��, y �� miden cada uno aproximadamente 95°

• Los ángulos ��, ��, y �� miden cada uno alrededor de 90°

• Los ángulos ��, ��, y �� miden cada uno alrededor de 125°

de 7º grado . Unidad 1

Algunos estudiantes pueden leer el número equivocado en el transportador, moviéndose hacia abajo desde la marca 180° en lugar de hacia arriba desde la marca 0°, o leyendo la medida fuera de una de las líneas que forman el ángulo en lugar de entre las dos líneas. Aclara el ángulo que se está midiendo, cómo alinear el transportador o cómo leer las marcas correctamente.

Selecciona a algunos alumnos para que compartan sus mediciones de ángulos y sondea brevemente a la clase para ver si hay acuerdo o desacuerdo. Discute las principales discrepancias, si las hay. Los estudiantes deben ser capaces de confirmar que todos los ángulos correspondientes en los polígonos a escala son iguales. Si lo desea, pregunte a los estudiantes si sería adecuado registrar los ángulos con una precisión de 1 grados: en general, el grosor de los segmentos de línea y las marcas del transportador limitan la precisión, por lo que es adecuado informar con una precisión de 5 grados (siempre que ninguno de los ángulos esté demasiado cerca de la mitad de dos incrementos).

ACTIVIDAD DE EXPLORACIÓN | TRES CUADRILÁTEROS

(PARTE 2)

10 minutos

Rutinas didácticas

MLR7: Comparar y conectar

Los alumnos han visto que las longitudes de los segmentos correspondientes en una figura y su copia a escala varían por el mismo factor de escala. Aquí, aprenden que en ese par de figuras, cualquier distancia correspondiente -no limitada a longitudes de lados o segmentos- está relacionada por el mismo factor de escala. Las longitudes de los lados de los polígonos de esta tarea no pueden determinarse fácilmente, por lo que los alumnos deben buscar otras distancias para comparar.

Los alumnos deben tener cuidado cuando identifiquen los vértices y las distancias correspondientes. A medida que los alumnos trabajen, insístales en que presten atención al orden en que se enumeran los puntos o segmentos.

Si los alumnos no están seguros de qué sacar de los valores de la tabla (para la segunda pregunta), anímeles a considerar las distancias correspondientes de dos figuras a la vez. Por ejemplo, pregunte: ¿Qué observan en las distancias verticales correspondientes en �� y ��? ¿Qué pasa con las distancias horizontales correspondientes en esas dos figuras?

Organice a los estudiantes en grupos de 2. Pregúnteles si pueden decir las longitudes de los segmentos �� o �� a partir de la cuadrícula (sin usar reglas). Explíqueles que van a explorar otra forma de comparar medidas de longitud en copias a escala.

Dé a los alumnos 2-3 minutos de tiempo de trabajo tranquilo para las dos primeras preguntas, y 1 minuto para discutir sus respuestas con un compañero antes de continuar con la última pregunta.

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.

Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una pregunta a la vez), lo que ayudará a los estudiantes que se benefician del apoyo con habilidades de organización en la resolución de problemas.

Matemáticas de 7º grado . Unidad 1

POSIBLES RESPUESTAS

Cada uno de estos polígonos es una copia a escala de los demás. Ya revisaste sus ángulos correspondientes.

1. Las longitudes de los lados de los polígonos son difíciles de determinar en la cuadrícula, pero existen otras distancias correspondientes que son más fáciles de comparar. Identifica las distancias en los otros dos polígonos que corresponden a �� y ��, anótalas en la tabla.

Cuadrilátera

Distancia que corresponde a ��

�� = 4 �� = 6

2. Observa los valores en la tabla. ¿Qué observas?

3. Haz una pausa para que tu maestro pueda revisar tu trabajo.

4. La figura más grande es una copia a escala de la figura más pequeña.

1. Si �� = 4,¿cuál es la distancia correspondiente en la primera figura? Explica o muestra tu razonamiento.

2. Si �� = 5, ¿cuál es la distancia correspondiente en la primera figura? Explica o muestra tu razonamiento.

1. Cuadrilátera

Distancia que corresponde a �� Distancia que corresponde a ��

= 4

= 6

= 2

= 6

= 9

= 3

Matemáticas de 7º grado . Unidad 1

POSIBLES RESPUESTASS CONTINUACIÓN

1. Estas distancias correspondientes están relacionadas por el mismo factor de escala aunque no sean longitudes de lado.

1. �� = 10. Ejemplo de explicación: 15 ÷6 = 2,5, por lo que la segunda figura está relacionada con la primera por un factor de escala de 2,5 �� es la distancia correspondiente a �� y también está relacionada por un factor de 2,5 (2,5) ⋅ 4 = 10

2. �� = 2. Explicación de ejemplo: El factor de escala de la figura pequeña a la copia más grande es 2,5, por lo que dividiendo �� entre 2,5 se obtiene la distancia correspondiente en la figura original. 5 ÷ 2,5 = 2

Los alumnos pueden enumerar los vértices correspondientes a las distancias en el orden equivocado. Por ejemplo, en lugar de escribir �� como la distancia correspondiente a ��, pueden escribir ��. Recuerde a los alumnos los puntos correspondientes preguntándoles: "¿Qué vértice de �� corresponde a ��? ¿Cuál corresponde a ��?" y pídeles que hagan coincidir el orden de los vértices en consecuencia.

SÍNTESIS

DE LA ACTIVIDAD

Muestra las tablas completadas para que todos las vean. Para destacar cómo todas las distancias en una copia a escala (no sólo las longitudes de los lados de la figura) están relacionadas por el mismo factor de escala, discute:

• ¿Cómo se compara la distancia vertical en �� con la de ��? Cómo se comparan las distancias horizontales en los dos polígonos? ¿Comparten los pares de distancias verticales y horizontales el mismo factor de escala?

• ¿Cómo se comparan las distancias verticales en �� y ��? Qué pasa con las distancias horizontales? ¿Existe un factor de escala común? ¿Cuál es ese factor de escala?

• ¿Qué factor de escala relaciona las longitudes y distancias correspondientes en los dos dibujos de la letra ��?

Apoyo a los estudiantes de inglés

Speaking: MLR7 Comparar y conectar. Utilice esta rutina para llamar la atención sobre las diferentes formas en que los alumnos pueden identificar los factores de escala. Muestre los siguientes enunciados: "El factor de escala de �� a �� es 3," y "El factor de escala de �� a �� es 1 2 ." Conceda a los alumnos 2 minutos de tiempo de reflexión en silencio para leer y considerar si una o ambas afirmaciones son correctas. Invite a los alumnos a compartir su reflexión inicial con un compañero antes de seleccionar 2-3 alumnos para compartirla con la clase. En esta discusión, escuche y amplíe los comentarios que hagan referencia al orden de la figura original y su copia a escala, así como los que identifiquen los vértices y las distancias correspondientes. Llame la atención de los alumnos sobre las distintas formas de describir las relaciones entre las copias a escala y la figura original.

Principio(s) de diseño: Maximizar la metaconciencia

ACTIVIDAD DE EXPLORACIÓN | ¿A ESCALA O SIN ESCALA?

10 minutos

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

El objetivo de esta actividad es que los alumnos determinen que las figuras no son copias a escala, aunque tengan ángulos correspondientes con medidas iguales o distancias correspondientes multiplicadas por el mismo factor de escala. Esto demuestra que,

California - Grado 7

para determinar si una figura es una copia a escala de otra, tenemos que comprobar tanto los ángulos correspondientes como las distancias correspondientes.

Mientras los alumnos trabajan, controle si tienen argumentos convincentes sobre por qué un polígono es o no una copia a escala del otro. Pídeles que expongan sus argumentos durante el debate de toda la clase. A medida que presenten y analicen diferentes argumentos sobre las figuras en la discusión, los estudiantes participarán en MP3.

Mantenga a los estudiantes en los mismos grupos. Proporcione acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Dé a los estudiantes 6-7 minutos de tiempo de trabajo en silencio.

Apoyo para estudiantes de inglés

Escribir, hablar y representar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para ayudar a los alumnos a refinar sus justificaciones sobre si están de acuerdo con Mai o con Noah. Dé tiempo a los estudiantes para que se reúnan con sus compañeros de 2-3 y compartan sus respuestas. Anima a los oyentes a insistir en los detalles y la claridad, según proceda, en función de lo que diga cada orador. Proporcione a los alumnos indicaciones que les ayuden a reforzar sus ideas y a aclarar su lenguaje (por ejemplo, "¿Por qué has...?", "¿Puedes aclarar cómo...?", etc.). Los alumnos pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar su producto final.

Principio(s) de diseño: Optimizar el resultado (para la justificación)

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA DEL ESTUDIANTE CONTINUACIÓN

Aquí hay dos cuadriláteros.

1. Mai dice que el Polígono �� es una copia a escala del Polígono ��, pero Noah no está de acuerdo. ¿Estás de acuerdo con alguno de ellos? Explica o muestra tu razonamiento.

2. Anota las distancias correspondientes en la tabla. ¿Qué observas?

Cuadrilátero Distancia Horizontal Distancia Vertical

3. Mide al menos tres pares de ángulos correspondientes en �� y �� utilizando un transportador. Anota tus medidas con una aproximación de 5°. ¿Qué observas?

4. ¿Cambian estos resultados tu respuesta a la primera pregunta? Explícalo.

Aquí tienes otros dos cuadriláteros.

5. Kiran dice que el polígono �� es una copia a escala de ��, pero Lin no está de acuerdo. ¿Estás de acuerdo con alguno de ellos? Explica o muestra tu razonamiento.

Matemáticas de 7º grado . Unidad 1

1. Las respuestas varían. Ejemplo de respuesta: Noé es correcto, porque los ángulos correspondientes no son iguales. Mai puede haber notado que las distancias correspondientes se multiplican por 3 2 y pensó que esto significaba que los polígonos eran similares.

2. Cuadrilátero Distancia horizontal Distancia vertical

�� = 6 �� = 9

�� = 4 �� = 6

3. Los ángulos correspondientes no son todos del mismo tamaño. Redondeadas a la unidad más cercana 5°, las medidas son:

��

ángulo �� medidas 100° ángulo �� medidas 125°

ángulo �� medidas 40° ángulo �� medidas 40°

ángulo �� medidas 75° ángulo �� medidas 75°

ángulo �� medidas 140° ángulo �� medidas 115°

4. Puesto que los ángulos correspondientes no son iguales, los polígonos definitivamente no son copias a escala unos de otros.

5. Las respuestas varían. Ejemplo de respuesta: Lin es correcto, porque las distancias correspondientes no se multiplican por el mismo número (en comparación con ��, el lado superior en �� es la mitad de largo, mientras que el lado inferior es dos tercios de largo). Kiran puede haber notado que los ángulos correspondientes son iguales y pensó que esto significaba que los polígonos son similares. Me he dado cuenta de que los factores de escala de los lados correspondientes no son iguales. �� y �� están relacionados por un factor de escala de 2 3 , pero �� y �� están relacionados por un factor de escala de 1 2 . ERRORES PREVISTOS

Es posible que los alumnos se basen en la apariencia de las figuras en lugar de analizar la información dada para sacar conclusiones sobre el escalado. Pídales que busquen información sobre distancias y ángulos (y que piensen qué herramientas podrían ayudarles a encontrar dicha información) para apoyar su argumento. Algunos alumnos pueden tener dificultades para comparar los ángulos correspondientes en el primer par de figuras. Recuérdales las herramientas que tienen a su disposición y que, si es necesario, pueden ampliar los lados de los polígonos para que les resulte más fácil medir los ángulos.

El objetivo de esta discusión es dejar claro que tanto las medidas de los ángulos como las distancias son importantes a la hora de decidir si dos polígonos son copias a escala. Para poner de relieve los diferentes argumentos sobre si un polígono es una copia a escala de otro, considere la posibilidad de realizar un juego de rol. Pide a cuatro alumnos que asuman los papeles de los cuatro personajes -Mai y Noah en la primera pregunta, y Kiran y Lin en la segunda- y que argumenten brevemente por qué creen que una figura es una copia a escala de la otra en cada caso. Sondee a la clase después de presentar cada par de casos y averigüe con quién están de acuerdo los estudiantes.

¿Estás preparado para más?

Matemáticas de 7º grado . Unidad 1

Todas las longitudes de los lados del cuadrilátero �� son 2, y todas las longitudes de los lados del cuadrilátero �� son 3 ¿Tiene que ser �� una copia a escala de ��? Explica tu razonamiento.

"¿Estás preparado para más?" Respuesta del alumno

No. �� podría ser un cuadrado y �� podría ser un rombo que no es un cuadrado. Como los ángulos son diferentes, �� no es una copia a escala de ��

OPCIONAL ACTIVIDAD DE EXPLORACIÓN | COMPARACIÓN DE IMÁGENES DE PÁJAROS

Rutinas didácticas

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyo a la discusión. Dé a los estudiantes tiempo adicional para asegurarse de que todos en su grupo pueden explicar o justificar por qué la copia del pájaro no es una copia a escala. A continuación, varíe a quién le toca representar las ideas de cada grupo. Esta rutina preparará a los alumnos para el papel de representante del grupo y para apoyarse mutuamente para asumir ese papel.

Principio(s) de diseño: Optimizar el rendimiento (para la explicación)

MLR8: Apoyos para el debate

Anticipar, supervisar, seleccionar, secuenciar, conectar

10 minutos

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la repasen antes de realizar esta actividad. Lenguaje expresivo: Eliminar Barreras. Proporcione marcos de oraciones para que los estudiantes expliquen su razonamiento (por ejemplo, Esta no es una copia a escala porque .).

En esta actividad, los alumnos utilizan lo que saben sobre longitudes y ángulos correspondientes para demostrar que una imagen de un pájaro no es una copia a escala de la otra. A diferencia de las tareas anteriores, en este caso el andamiaje es mínimo, por lo que los alumnos deben decidir qué pruebas son necesarias para explicar o demostrar la ausencia de escala. A medida que los alumnos trabajan, observe las diferentes formas en que utilizan las longitudes y los ángulos correspondientes para pensar en la escala.

Identificar una medida específica en una imagen y las medidas correspondientes en la otra (que muestran que una no es una copia a escala de la otra) requiere pensar en la estructura de las imágenes (MP7).

Supervise a los alumnos en busca de diferentes enfoques para demostrar que una imagen no es una copia a escala de la otra:

• Identificando los ángulos correspondientes en las dos imágenes que tienen diferentes medidas

• Identificando dos pares de segmentos correspondientes en las imágenes con diferentes factores de escala

Seleccione a los alumnos que utilicen estos métodos y pídales que presenten sus enfoques, en esta secuencia, durante la discusión.

California - Grado 7

de 7º grado . Unidad 1

INTRODUCCIÓN

Organice a los estudiantes en grupos de 3-4. Proporcione a los estudiantes herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Conceda a los estudiantes 2 minutos de tiempo de trabajo en silencio seguidos de 1-2 minutos para discutir en grupos cómo encontrar pruebas de que una imagen no es una copia a escala de la otra. A continuación, discute brevemente en clase las ideas de los alumnos. Considere la posibilidad de hacer una lista de las ideas para que todos puedan verlas y discutir cuáles son las más eficaces.

Si las ideas de los alumnos se desvían del dibujo de puntos y segmentos correspondientes y de la comparación de distancias y ángulos, guíelos con algunas indicaciones. Por ejemplo:

• Elija un punto fácilmente referenciable (por ejemplo, la punta de un ala) en un dibujo. Pregunte cuál es el punto correspondiente en la otra.

• Pregunte si ese par de puntos correspondientes podría ayudarles a determinar si una imagen está a escala de la otra. Si no es así, pregunta qué más se podría necesitar.

• Añade otro punto y un segmento que conecte los dos puntos. Pregunte si el segmento podría ayudar o cómo, y así sucesivamente. ENUNCIADO

Aquí hay dos fotos de un pájaro. Encuentra pruebas de que una imagen no es una copia a escala de la otra. Prepárate para explicar tu razonamiento.

Matemáticas de 7º grado . Unidad 1

POSIBLES RESPUESTAS

ERRORES PREVISTOS

Las respuestas varían. Ejemplo de razonamiento:

• Los ángulos correspondientes no coinciden, por lo que una imagen no puede ser una copia a escala de la otra.

• Las longitudes de los segmentos correspondientes no están relacionadas por el mismo factor de escala, por lo que una imagen no puede ser una copia a escala de la otra.

Los estudiantes pueden dibujar dos segmentos que no compartan un punto, o elegir puntos y segmentos que no coincidan en las dos figuras. Remita a los alumnos a trabajos anteriores sobre polígonos y señale los pares de distancias que podrían utilizarse para la comparación y los que no. Recuérdales que sólo podemos comparar las partes correspondientes, no dos partes cualesquiera.

DE LA ACTIVIDAD

SÍNTESIS

Invite a algunos alumnos a compartir su razonamiento. Pregúnteles cómo supieron que determinados pares de puntos de las imágenes eran puntos correspondientes. Los alumnos podrían identificar una característica única, como los ojos o la punta del ala. Asegúrese de que los alumnos entienden que:

• Los ángulos correspondientes en una imagen y en una copia a escala tienen la misma medida

• Los segmentos correspondientes en una imagen y en una copia a escala están relacionados por el mismo factor de escala

Para concluir que una imagen no es una copia a escala de otra, basta con encontrar un par de medidas de ángulos correspondientes que sean diferentes o un par de segmentos correspondientes con longitudes diferentes.

SÍNTESIS DE LA LECCIÓN

5 minutos

• ¿Afecta un factor de escala a otras medidas que no sean las longitudes de los segmentos?

• ¿Cómo podemos estar seguros de que una figura es una copia a escala? ¿Qué características comprobamos?

Cuando se crea una copia a escala a partir de una figura, sabemos que:

• Las distancias entre dos puntos cualesquiera de la figura original, incluso los que no están conectados por segmentos, se escalan con el mismo factor de escala.

Matemáticas de 7º grado . Unidad 1

• Los ángulos correspondientes en la figura original y en las copias a escala son congruentes. Los polígonos son un contexto perfecto en el que aplicar estas dos ideas, ya que están formados por segmentos de recta que se encuentran en ángulos. Así que podemos utilizar estas observaciones para comprobar si un polígono es realmente una copia a escala de otro. Si todos los ángulos correspondientes son del mismo tamaño y todas las distancias correspondientes están escaladas por el mismo factor, entonces podemos concluir que es una copia a escala del otro.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES

ENFRIAMIENTO | POLÍGONOS CORRESPONDIENTES

5 minutos

Proporcionar acceso a juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Aquí hay dos polígonos en una cuadrícula.

¿Es �� una copia a escala de ��? Explica tu razonamiento.

No. Ejemplo de explicación: �� no es una copia a escala de �� porque necesitamos utilizar diferentes factores de escala al comparar las longitudes correspondientes (1 para los segmentos correspondientes �� y �� y 2 para los segmentos correspondientes �� y ��). Además, no todos sus ángulos correspondientes tienen el mismo tamaño. El ángulo �� y el ángulo �� no tienen el mismo tamaño.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Selecciona todas las afirmaciones que deben ser ciertas para cualquier copia a escala �� de Polígono ��

A. Las longitudes de los lados son todas números enteros.

B. Las medidas de los ángulos son todas números enteros.

C. �� tiene exactamente 1 ángulo recto.

D. Si el factor de escala entre �� y �� es 1 5 , entonces cada longitud lateral de �� se multiplica por 1 5 para obtener la longitud lateral correspondiente de ��

E. Si el factor de escala es 2, cada ángulo en �� se multiplica por 2 para obtener el ángulo correspondiente en ��

F. �� tiene 2 ángulos agudos y 3 ángulos obtusos.

Posibles soluciones

B, C, D, F

PROBLEMA 2

Aquí está el cuadrilátero ��

Cuadrilátero �� es una copia a escala de Cuadrilátero �� El punto �� corresponde a ��, �� a ��, �� a ��, y �� a ��.

Si la distancia de �� a �� es 3 unidades, ¿cuál es la distancia de �� a ��?

Explique su razonamiento.

Posibles soluciones

Dado que las longitudes de �� y �� son 6, y �� corresponde a ��, el factor de escala debe ser 1 2. Como �� corresponde a ��, �� debe ser también 3 unidades de longitud.

PROBLEMA 3

La Figura 2 es una copia a escala de la Figura 1.

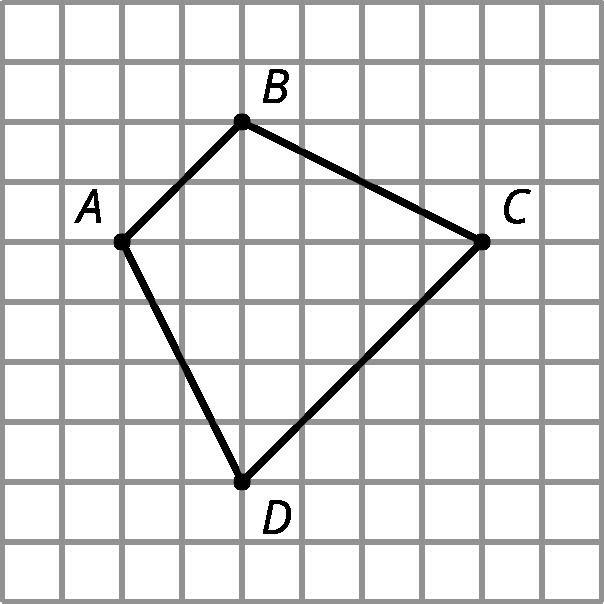
de 7º grado . Unidad 1

1. Identifique los puntos de la Figura 2 que se corresponden con los puntos �� y �� la Figura 1. Rotúlelos �� . Etiquétalos como �� y ��. ¿Cuál es la distancia entre ��

2. Identifica los puntos de la Figura 1 que corresponden a los puntos �� y �� en Figura 2. Etiquétalos como �� y ��. ¿Cuál es la distancia entre �� y ��?

3. ¿Cuál es el factor de escala que lleva la Figura 1 a la Figura 2?

4. �� y �� son dos puntos de la Figura 1, pero no se muestran. La distancia entre �� y �� es 1. ¿Cuál es la distancia entre los correspondientes puntos de la Figura 2?

Posibles soluciones

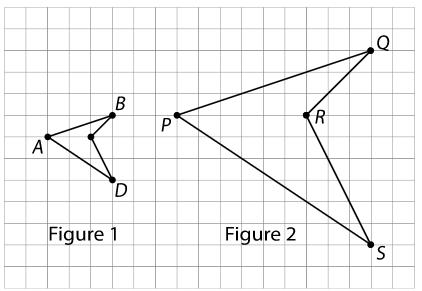
1. 6 unidades

2. 3 unidades

3. 3 porque las distancias entre los puntos de la Figura 2 son tres veces las distancias correspondientes en la Figura 1

4. 3 unidades porque el factor de escala es 3

- Grado 7

LECCIÓN 5

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

5.NF.5

Construir

7.RP.2

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de CaliforniaD

I.C.11

I.C.12

II.C.7

EL TAMAÑO DEL FACTOR DE ESCALA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

dan sentido al mundo e inciden en el futuro

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

utilizan herramientas apropiadas para buscar y hacer uso de la estructura

META(S) DE APRENDIZAJE

• Veamos los efectos de diferentes factores de escala.

META(S) DE APRENDIZAJE

exploran cantidades cambiantes y descubren la forma y el espacio.

• Puedo describir el efecto en una copia a escala cuando uso un factor de escala que es mayor que 1, menor que 1, o igual a 1

• Puedo explicar cómo el factor de escala que lleva la Figura A a su copia Figura B está relacionado con el factor de escala que lleva la Figura B a la Figura A.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente y por escrito) cómo los factores de escala de 1, menor que 1, y mayor que 1 afectan al tamaño de las copias a escala.

• Explicar y mostrar (oralmente y por escrito) cómo recrear la figura original dada una copia a escala y su factor de escala.

• Reconocer (oralmente y por escrito) que la relación entre el factor de escala de una copia a escala y su figura original es el "recíproco" del factor de escala de la figura original y su copia a escala.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Hablar de números

MLR8: Apoyos para el debate

MLR3: Aclarar, Criticar, Corregir

Anticipar, Monitorear, Seleccionar, Secuenciar, Conectar

Pensar, Emparejar, Compartir

Materiales necesarios

Patrón de líneas negras para la Actividad 5.2

Patrón de líneas negras para la Actividad 5.3

Enfriamiento

Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)

Fichas preimpresas, recortadas de copias del patrón de líneas negras.

Matemáticas de 7º grado . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación necesaria

Imprima y recorte los juegos de fichas para la actividad de clasificación del patrón de la línea negra de Clasificación de tarjetas de copias a escala. Haga suficientes copias para que cada grupo de 3-4 estudiantes tenga un juego. Si es posible, copie cada juego completo en un color de papel diferente, de modo que las fichas que se pierdan puedan volver a colocarse rápidamente en su lugar.

Imprima y recorte las piezas del rompecabezas y los cuadrados en blanco para la actividad Escalar un rompecabezas del patrón de líneas negras Escalar un rompecabezas. Haz suficientes copias para que cada grupo de 3 estudiantes tenga 1 rompecabezas original y 6 cuadrados en blanco.

Asegúrate de que los estudiantes tengan acceso a sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), especialmente reglas y transportadores.

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

En esta lección, los estudiantes profundizan su comprensión de los factores de escala de dos maneras:

1. Clasifican los factores de escala por tamaño (menor que 1, exactamente 1, y mayor que 1) y observan cómo cada clase de factores afecta a las copias a escala (MP8), y

2. Ven que el factor de escala que lleva una figura original a su copia y el que lleva la copia al original son recíprocos (MP7). Esto significa que el proceso de escala es reversible, y que si la Figura B es una copia a escala de la Figura A, entonces la Figura A es también una copia a escala de la Figura B.

Los alumnos también continúan aplicando los factores de escala y lo que han aprendido sobre las distancias y ángulos correspondientes para dibujar copias a escala sin cuadrícula.

Dos de las actividades, Escalar un puzzle y Falta figura, factor o copia, son opcionales. En Escalar un puzzle, los alumnos escalan las 6 piezas de un puzzle individualmente y luego las ensamblan para hacer una copia escalada del puzzle. Las piezas individuales son rectangulares con segmentos de línea que las dividen en regiones. Los alumnos tienen que pensar estratégicamente qué medidas tomar para escalar las piezas con precisión. En Figura, factor o copia que falta, los alumnos adquieren soltura al tratar los distintos aspectos de las copias a escala, aportando la información que falta en cada caso.

LECCIÓN

DE UN VISTAZO

Componente de la Lección Estructura Tiempo Descripción breve

Calentamiento Independiente 10 min.

Actividad de exploración

Grupos pequeños 15 min.

Los estudiantes resuelven mentalmente ecuaciones de multiplicación que conducen a aquellas que involucran coeficientes fraccionarios y discuten las estrategias utilizadas.

Los estudiantes utilizan una clasificación de tarjetas para descubrir cómo el tamaño de un factor de escala en relación con 1 afecta a la copia a escala y cómo la aplicación de un factor de escala o su recíproco afecta al tamaño de las imágenes a escala.

Hay disponible una extensión de exploración para desarrollar conexiones más profundas entre el tamaño de un factor de escala y la imagen a escala.

Actividad de exploración opcional

Grupos pequeños 15 min.

Nation California - Grado 7

Sin una cuadrícula, los estudiantes utilizan factores de escala, longitudes y ángulos para crear copias a escala de las piezas de un puzzle. Al examinar las piezas resultantes, los estudiantes profundizan su comprensión de los factores de escala.

de 7º grado . Unidad 1

RESUMEN DE LA LECCIÓN CONTINUACIÓN

Componente de la lección

Actividad de exploración opcional

Estructura Tiempo

En parejas 10 min.

Síntesis Todo el grupo 5 min.

Enfriamiento Independiente 5 min.

Descripción breve

Los estudiantes examinan dos piezas de información sobre las copias a escala (imagen original, imagen a escala y factor de escala) y determinan la tercera pieza.

Los estudiantes discuten cómo el tamaño del factor de escala afecta a la copia escalada y cómo invertir la escala para volver a la imagen original.

Los estudiantes escalan un rectángulo y aplican el factor recíproco para invertir la escala.

Práctica Independiente 5-10 min. El componente de práctica independiente incluye 3 problemas de repaso de la lección y 2 problemas de repaso en espiral.

CALENTAMIENTO | CHARLA SOBRE NÚMEROS: FACTOR

FALTANTE 10 minutos

Rutinas didácticas

Charla sobre números

MLR8: Apoyos para la discusión

Esta charla numérica anima a los estudiantes a utilizar la estructura y la relación entre la multiplicación y la división para resolver mentalmente problemas que implican fracciones. Incita a los alumnos a pensar en cómo el tamaño de los factores influye en el tamaño del producto. Repasa la idea de los factores recíprocos como preparación para el trabajo de la lección.

INTRODUCCIÓN

Pregunta a los estudiantes qué operación se entiende cuando un número y una variable se colocan uno al lado del otro en una ecuación. (Multiplicación)

Mostrar un problema a la vez. Conceda a los alumnos 1 minuto de tiempo de reflexión por problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. A continuación, discuta el problema con toda la clase.

Apoyo a los alumnos con discapacidad

Memoria: Tiempo de procesamiento. Proporcione notas adhesivas o minipizarras para ayudar a los alumnos con dificultades de memoria de trabajo. ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Resuelva cada ecuación mentalmente.

16 �� = 176

16�� = 8

16�� = 1

1 5 �� = 1

2 5 �� = 1

Matemáticas de 7º grado . Unidad 1

POSIBLES RESPUESTASS

ERRORES ANTICIPADOS

1. 11. Posible estrategia: 16 ⋅ 10 = 160 y 16 ⋅ 1 = 16, por lo que 16 ⋅ 11 = 176

2. 1 2 o equivalente. Posible estrategia: 16 dividido por 2 es 8, y dividiendo por 2 es lo mismo que multiplicando por 1 2 .

3. 1 16 . Posible estrategia: Se necesita 16 de 1 16 para hacer 1

4. 5. Estrategia posible: Hay 5 copias de 1 5 en 1, por lo que 5 ⋅ 1 5 = 1.

5. 5 2 o equivalente. Posible estrategia: 5 grupos de 2 3 5 5 hacen 2, por lo que 5 2 grupos de 2 5 hacen 1

Los alumnos pueden pensar que un producto no puede ser menor que uno de los factores, sin darse cuenta de que uno de los factores puede ser una fracción. Utilice ejemplos con números más pequeños y conocidos para recordarles que es posible. Pregunte, por ejemplo: "¿Cuántas veces 10 es 5?"

SÍNTESIS DE LA ACTIVIDAD

Pida a los alumnos que compartan sus estrategias para cada problema. Grabe y muestre sus explicaciones para que todos puedan verlas. Para implicar a más alumnos en la conversación, pregunte:

• ¿Quién puede replantear el razonamiento de de otra forma?

• ¿Alguien ha resuelto el problema de la misma forma pero lo explicaría de otra manera?

• ¿Alguien ha resuelto el problema de otra forma?

• ¿Alguien quiere añadir algo a la estrategia de ?

• ¿Estás de acuerdo o en desacuerdo? ¿Por qué?

Resalta que multiplicar un factor por una fracción menor que 1 da como resultado un producto que es menor que uno de los factores, y que dos factores que se multiplican para ser 1 son recíprocos.

Apoyo para estudiantes de inglés

Speaking: MLR 8 Discussion Supports. Proporcione marcos oracionales para ayudar a los estudiantes a explicar sus estrategias. Por ejemplo, "I noticed that , so I ." o "First, I because .". Cuando los alumnos compartan sus respuestas con un compañero, pídales que ensayen lo que dirán cuando lo compartan con todo el grupo. Ensayar les brinda la oportunidad de aclarar sus ideas.

Principio(s) de diseño: Optimizar el resultado (para la explicación)

de 7º grado . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | CLASIFICACIÓN DE TARJETAS DE COPIAS A ESCALA 15

Rutinas didácticas

MLR3: Clarificar, Criticar, Corregir Anticipar, Supervisar, Seleccionar, Secuenciar, Conectar

minutos

Materiales requeridos

Fichas preimpresas, recortadas de las copias del patrón de líneas negras

Los alumnos han estudiado muchos ejemplos de copias a escala y saben que las longitudes correspondientes en una figura y su copia a escala están relacionadas por el mismo factor de escala. El objetivo de esta actividad es que los alumnos examinen cómo el tamaño del factor de escala está relacionado con la figura original y la copia a escala. La actividad tiene varios propósitos:

1. Reforzar la conciencia de los alumnos sobre los factores de escala

2. Llamar la atención sobre cómo se comportan las copias a escala cuando el factor de escala es 1, menor que 1, y mayor que 1; y

3. Ayudar a los alumnos a darse cuenta de que los factores de escala recíprocos invierten la escala. Para esta actividad necesitará el máster en línea negra Ordenar tarjetas de copias a escala. Aquí tiene una imagen de las tarjetas para su referencia y planificación.

Supervise a los alumnos que agrupan las tarjetas en términos de:

• Factores de escala específicos (por ejemplo, 2, 3, 1 2 , etc.)

• Rangos de factores de escala que producen determinados efectos (por ejemplo, factores que producen copias mayores, iguales o menores)

• Factores de escala recíprocos (por ejemplo, un factor escala la Figura A a B, y su recíproco invierte la escala)

Seleccione grupos que utilicen cada uno de estos enfoques (y cualquier otro) y pídales que compartan durante la discusión.

Organice a los estudiantes en grupos de 3-4 personas. Distribuya un juego de fichas a cada grupo. Conceda a los alumnos 7-8 minutos de trabajo en grupo, seguidos de un debate con toda la clase.

Apoyo a estudiantes con discapacidad

Procesamiento conceptual: Eliminar barreras. Demuestre los pasos de la actividad o juego haciendo que un grupo de alumnos y el personal jueguen una ronda de ejemplo mientras el resto de la clase observa.

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Tu maestro te dará un conjunto de tarjetas. En cada tarjeta, la Figura A es el original y la Figura B es una copia a escala.

1. Clasifica las tarjetas en función de sus factores de escala. Prepárate para explicar tu razonamiento.

2. Examina más detenidamente las tarjetas 10 y 13. ¿Qué observas en las formas y tamaños de las figuras? ¿Qué observas en los factores de escala?

3. Examina más detenidamente las tarjetas 8 y 12. ¿Qué observas en las figuras? ¿Qué observas en los factores de escala?

POSIBLES RESPUESTAS

1. Las categorías de agrupación varían. Ejemplos de categorías:

• Factor de escala de 2: Tarjetas 1 y 9

• Factor de escala de : Tarjetas 1 2 3, 7, y 11.

• Factor de escala de 3: Tarjetas 2, 5, y 10

• Factor de escala de : Tarjetas 1 3 4, 6, y 13

• Factor de escala de 1: Tarjetas 8 y 12.

2. Las respuestas varían. Ejemplo de respuesta: Las formas de ambas tarjetas son iguales, pero en la Tarjeta 10, la copia a escala es mayor y el factor de escala es 3. En la Tarjeta 13, la copia a escala es menor y el factor de escala es 1 3 .

3. Las respuestas varían. Respuesta de ejemplo: El original y la copia tienen el mismo tamaño en las Tarjetas 8 y 12

La copia es idéntica al original. El factor de escala es 1.

Los alumnos pueden ordenar por los tipos de figuras en lugar de por cómo se escala la segunda figura de cada par con respecto a la primera. Recuerde a los alumnos que deben ordenar basándose en cómo se escala la Figura A para crear la Figura B.

Los alumnos pueden pensar en el cambio de longitudes entre las Figuras A y B en términos de suma o resta, en lugar de multiplicación o división. Recuerde a los alumnos una lección anterior en la que exploraron el efecto de restar la misma longitud a cada lado de un polígono para escalarlo. ¿Qué ocurrió con la copia? (No terminó siendo un polígono y no era una copia a escala del original).

Es posible que los alumnos no tengan claro cómo describir cuánto más grande o más pequeña es una figura, o que no recuerden el significado de factor de escala. Pídeles que comparen las longitudes de cada lado de la figura. ¿Cuál es el factor común por el que se multiplica cada lado?

Seleccione grupos para que expliquen sus decisiones de clasificación siguiendo la secuencia indicada en la Descripción de la actividad. Si ningún grupo ordenó en términos de rangos de factores de escala (menor que 1, exactamente 1, y mayor que 1) o de escala recíproca, pregunte:

• ¿Qué podemos decir acerca de los factores de escala que producen copias más grandes? ¿Copias más pequeñas? ¿Copias del mismo tamaño?

• Algunas tarjetas tenían el mismo par de figuras, sólo que en orden inverso (es decir, los pares #1 y 7, #10 y 13). ¿Qué observa en sus factores de escala?

Destaque las dos ideas principales de la lección: 1) los efectos de los factores de escala mayores que 1, exactamente 1, y menores que 1; y 2) la reversibilidad de la escala. Señale que si la figura B es una copia a escala de la figura A, entonces A es también una copia a escala de B. En otras palabras, A y B son copias a escala la una de la otra, y sus factores de escala son recíprocos. Sugiera a los alumnos que añadan estas observaciones a su respuesta a la última pregunta.

de 7º grado . Unidad 1

Apoyo a los estudiantes que aprenden inglés

Writing: MLR3 Aclarar, Criticar, Corregir. Presente una afirmación incorrecta que refleje un posible malentendido de la clase para la última indicación. Por ejemplo: "El factor de escala de las tarjetas 8 y 12 es 0 porque las formas son las mismas y no hubo cambios". Pida a los alumnos que identifiquen el error (por ejemplo, pídales que piensen si están de acuerdo o en desacuerdo con la afirmación y por qué) y, a continuación, escriban una versión correcta. En este debate, destaque el uso del lenguaje disciplinario revocando las ideas de los alumnos. Esto ayuda a los estudiantes a evaluar y mejorar los argumentos matemáticos escritos de los demás.

Principio(s) de diseño: Maximizar la metaconciencia

¿Estás preparado para más?

El Triángulo B es una copia a escala del Triángulo A con un factor de escala 1 2

1. ¿Cuántas veces mayores son las longitudes de los lados del Triángulo B en comparación con el Triángulo A?

2. Imagina que escalas el Triángulo B por un factor de escala de 1 2 para obtener el Triángulo C. ¿Cuántas veces mayores serán las longitudes de los lados del Triángulo C en comparación con el Triángulo A?

3. El Triángulo B se ha escalado una vez. El triángulo C se ha escalado dos veces. Imagina que escalas el triángulo A n veces para obtener el Triángulo N, utilizando siempre un factor de escala de 1 2 . ¿Cuántas veces mayores serán las longitudes laterales del Triángulo N cuando se comparan con las del Triángulo A?

"¿Estás preparado para más?" Respuesta del alumno

1. 1 2

2. 1 4

OPCIONAL ACTIVIDAD DE EXPLORACIÓN | ESCALAR UN

PUZZLE

15 minutos

Rutinas didácticas

MLR8: Apoyos para la discusión

Materiales necesarios

Juegos de herramientas de geometría

Fichas preimpresas, recortadas de copias del patrón de líneas negras

Esta actividad da a los alumnos la oportunidad de aplicar lo que saben sobre factores de escala, longitudes y ángulos y crear copias a escala sin el apoyo de una cuadrícula. Los alumnos trabajan en grupos de 3 para completar un rompecabezas, cada miembro del grupo escala 2 piezas no adyacentes de un rompecabezas de 6 piezas con un factor de escala de 1 2 . A continuación, el grupo ensambla las piezas escaladas y examina la exactitud de su rompecabezas escalado. Considere la posibilidad de que los alumnos utilicen un color en lugar del rayado en cruz.

A medida que los alumnos trabajan, observe cómo miden las distancias y si tienen en cuenta los ángulos. Dependiendo de cómo determinen los alumnos las distancias a escala, puede que no necesiten transferir los ángulos. Esté atento a los alumnos que miden sólo las longitudes de los segmentos dibujados en lugar de las distancias, por ejemplo, entre la esquina de un cuadrado y donde comienza un segmento. Sugiérales que consideren otras medidas que podrían ayudarles a localizar el comienzo y el final de un segmento.

Para esta actividad necesitará el patrón de líneas negras Escalar un rompecabezas.

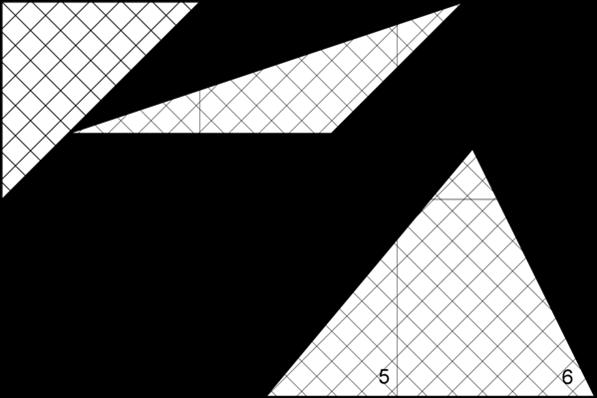
Matemáticas de 7º grado . Unidad 1

Organice a los alumnos en grupos de 3. Entregue los cuadrados precortados del puzzle 1 y 5 a un alumno del grupo, los cuadrados 2 y 6 a un segundo alumno, y los cuadrados 3 y 4 al tercero. Después de que los alumnos hayan respondido a la primera pregunta, entregue a cada alumno 2 cuadrados en blanco cuyos lados sean la mitad de la longitud lateral de los cuadrados del puzzle. Proporcione herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Apoyo para estudiantes de inglés

Speaking: MLR 8 Apoyo al debate. Proporcione marcos de oraciones para ayudar a los estudiantes a producir respuestas a la pregunta: "Si dibujaras copias a escala de las piezas de tu rompecabezas utilizando un factor de escala de 1 2 , ¿serían más grandes o más pequeñas que las piezas originales? ¿Cómo lo sabes?" Por ejemplo: "La pieza del puzzle sería (más grande/ pequeña) porque ."

Principio(s) de diseño: Apoyar la creación de sentido, Optimizar la salida (para comparación)

Tu maestro te dará 2 piezas de un 6-puzzle.

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Tutores compañeros Empareje a los estudiantes con sus tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina les dicten cómo armar los rompecabezas según sea necesario.

1. Si dibujaras copias a escala de las piezas de tu puzzle utilizando un factor de escala de 1 2 , ¿serían más grandes o más pequeñas que las piezas originales? ¿Cómo lo sabes?

2. Crea una copia a escala de cada pieza del rompecabezas en un cuadrado en blanco, con un factor de escala de 1 2

3. Cuando todos los miembros de tu grupo hayan terminado, junta todas las 6 piezas originales del rompecabezas de esta manera:

4. A continuación, junta todas las 6 copias a escala. Compara tu puzzle a escala con el puzzle original. ¿Qué partes parecen estar escaladas correctamente y cuáles no? ¿Qué puede haber causado que esas partes estén mal?

5. Revisa cualquiera de las copias a escala que pueda haber sido dibujada incorrectamente.

6. Si perdieras una de las piezas del rompecabezas original, pero aún tuvieras la copia a escala, ¿cómo podrías recrear la pieza perdida?

1. Serían más pequeñas porque 1 2 < 1.

2. Copias de las piezas del rompecabezas a escala 1 2

3. Las respuestas varían dependiendo de cómo dibujó cada estudiante sus piezas.

4. Copias revisadas de las piezas del rompecabezas.

5. Usa la copia y un factor de escala de 2 para recrear la pieza original del rompecabezas. Explicación de ejemplo: 2 es el recíproco de 1 2 , por lo que volvería a escalar la copia hasta el original.

Matemáticas de 7º grado . Unidad 1

ERRORES ANTICIPADOS

Los alumnos pueden incorporar el factor de escala al escalar segmentos de recta, pero no lo hacen al escalar distancias entre dos puntos no conectados por un segmento. Recuérdeles que todas las distancias se escalan con el mismo factor.

Es posible que los alumnos no recuerden comprobar que los ángulos de sus copias deben seguir siendo los mismos que los del original. Pídales que se fijen en los ángulos y que recuerden lo que ocurre con los ángulos cuando una figura es una copia a escala.

SÍNTESIS DE LA ACTIVIDAD

Gran parte de las conversaciones sobre la creación de copias a escala precisas se habrán producido entre compañeros, pero considere la posibilidad de reunirse como clase para reflexionar sobre las diferentes formas en que trabajaron los alumnos. Formule preguntas como:

• ¿Por qué esta tarea es más difícil que crear copias a escala de polígonos en una cuadrícula?

• Además de las distancias o longitudes, ¿qué le ayudó a crear una copia exacta?

• ¿Cómo supo o decidió qué distancias medir?

• Antes de montar sus dibujos, ¿cómo comprobó si eran correctos?

Las respuestas de los alumnos a estas preguntas pueden variar: por ejemplo, para la pieza 6, las dos líneas se pueden dibujar midiendo distancias en el borde de la pieza del puzzle; los ángulos se calculan correctamente de forma automática. Para la pieza 2, sin embargo, para que las tres líneas que se unen en un punto en el centro de la pieza queden bien, los alumnos pueden medir ángulos o extender esos segmentos de línea hasta que se encuentren con el borde de la pieza (y luego medir distancias).

OPCIONAL ACTIVIDAD DE EXPLORACIÓN | FIGURA, FACTOR O COPIA QUE FALTAN

10 minutos

Rutinas didácticas

Piensa, comparte, en pareja

MLR8: Apoyos para el debate

En esta actividad, los alumnos investigan diferentes aspectos del trío figura, copia a escala y factor de escala. Dados dos cualquiera de estos tres, podemos encontrar el tercero. Los alumnos trabajan con estos diferentes escenarios en una cuadrícula, tratando con factores de escala mayores que 1, menores que 1, e iguales a 1. Además, crean una copia a escala de una figura no poligonal fuera de una cuadrícula.

Tanto dentro como fuera de una cuadrícula, los alumnos deben decidir qué herramientas utilizar (MP5) para medir los ángulos y las longitudes de los lados con el fin de producir las copias a escala.

Distribuye a los estudiantes en grupos de 2. Proporciona acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a los alumnos 3-4 minutos de trabajo en silencio, seguidos de 2 minutos de debate en grupo y, a continuación, debate en toda la clase.

Matemáticas de 7º grado . Unidad 1

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Tutores compañeros. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten copias a escala de dibujos según sea necesario.

Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una pregunta a la vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.

1. ¿Cuál es el factor de escala del triángulo original a su copia? Explica o muestra tu razonamiento.

3. El factor de escala de la figura original a su copia es 32. Dibuja la figura original.

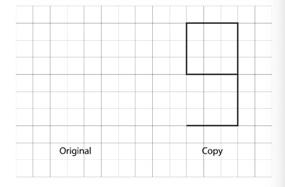
2. El factor de escala del trapecio original a su copia es 2. Dibuja la copia a escala.

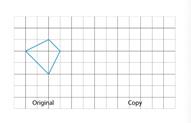
4. ¿Cuál es el factor de escala de la figura original a la copia? Explica cómo lo sabes.

5. El factor de escala de la figura original a su copia a escala es 3. Dibuja la copia a escala.

1. Factor de escala: 1 5 ya que los lados vertical y horizontal en el original tienen 5 unidades de cuadrícula de longitud y los lados correspondientes en la copia tienen 1 unidad de cuadrícula de longitud.

3. Figura original:

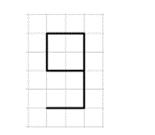
- Grado

2. Copia a escala:

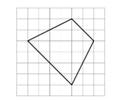
4. Factor de escala: 1 ya que la figura y la copia tienen el mismo tamaño.

SÍNTESIS DE LA ACTIVIDAD

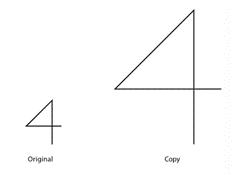
El objetivo de este debate es garantizar que los alumnos comprendan las conexiones entre la figura original, la copia a escala y el factor de escala: si se les da dos de los tres, deben comprender un método para encontrar el tercero.

Pregunte a los alumnos cómo resolvieron las tres primeras preguntas. ¿Cuál fue la más difícil? ¿Por qué? Es probable que las respuestas individuales varíen, pero la pregunta en la que falta la figura original merece especial atención. Esto requiere ir hacia atrás, ya que tenemos la copia a escala y el factor de escala. Este escenario también refuerza que la forma de "deshacer" el factor de escala de 3 2 que se ha aplicado para producir la copia es aplicar un factor de escala de 2 3

Para el último problema, pregunte a los alumnos cómo utilizaron las longitudes de los segmentos y los ángulos de la figura original. Es posible que hayan dibujado la copia sin comprobar los ángulos. Pregúnteles por qué es importante medir los ángulos.

Apoyo para estudiantes de inglés

Listening, Representing: MLR 8 Discussion Supports. Al comienzo de la síntesis, proporcione los siguientes marcos de oraciones para que los estudiantes los completen y luego los compartan en la discusión: "La estrategia más exitosa que utilicé para crear copias a escala fue , porque..." y "Esta tarea fue más/menos desafiante para mí porque...". Esto ayudará a los alumnos a organizar sus ideas y reflexionar sobre su trabajo antes de participar en el debate con toda la clase.

Principio(s) de diseño: Maximizar la metaconciencia

LECCIÓN SÍNTESIS

• ¿Qué le ocurre a la copia cuando se crea con un factor de escala mayor que 1? ¿Inferior a 1? ¿Exactamente 1?

• ¿Cómo podemos invertir la escala para volver a la figura original cuando tenemos una copia escalada?

Cuando el factor de escala es mayor que 1, la copia escalada es mayor que el original. Cuando es menor que 1, la copia es menor que el original. Un factor de escala de exactamente 1 produce una copia del mismo tamaño.

La escala puede invertirse utilizando factores recíprocos. Si escalamos la figura A en un factor de 4 para obtener la figura B, podemos volver a escalar B a A utilizando un factor de 1 4 . Esto significa que si B es una copia escalada de A, A también es una copia escalada de B; son copias escaladas la una de la otra.

de 7º grado . Unidad 1

ENFRIAMIENTO | ESCALANDO UN RECTÁNGULO

5 minutos

Un rectángulo que mide 2 pulgadas por 3 pulgadas ha sido escalado por un factor de 7

1. ¿Cuáles son las longitudes de los lados de la copia escalada?

2. Supón que quieres volver a escalar la copia a su tamaño original. ¿Qué factor de escala deberías utilizar?

1. 14 pulgadas por 21 pulgadas, porque 2 ⋅ 7 = 14 y 3 ⋅ 7 = 21

2. 1 7 , porque es el recíproco de 7

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Los rectángulos P, Q, R, y S son copias a escala uno del otro. Para cada par, decide si el factor de escala de uno a otro es mayor que 1, igual a 1, o menor que 1

1. de P a Q

2. de P a R

3. de Q a S

4. de Q a R

5. de S a P

6. de R a P

7. de P a S

Posibles soluciones

1. Mayor que que 1

2. Mayor que 1

3. Menor que 1

4. Mayor que 1

5. Igual que 1

6. Menor que 1

7. Igual que 1

Matemáticas de 7º grado . Unidad 1

PROBLEMA 2

El triángulo S y el triángulo L son copias a escala uno del otro.

1. ¿Cuál es el factor de escala de S a L?

2. ¿Cuál es el factor de escala de L a S?

3. Triángulo M es también una copia a escala de S. El factor de escala de S a M es 3 2 . ¿Cuál es el factor de escala de M a S?

Posibles soluciones

1. 2

2. 1 2

3. 2 3 . Los dos factores de escala son recíprocos entre sí.

PROBLEMA 3

¿Son dos cuadrados con las mismas longitudes de lado copias a escala uno del otro? Explica tu razonamiento.

Posibles soluciones

Sí. Hay un factor de escala de 1 entre ellos.

PROBLEMA 4

Del Grado 7, Unidad 1, Lección 2

Cuadrilátero A tiene longitudes laterales 2, 3, 5, y 6. El cuadrilátero B tiene longitudes laterales 4, 5, 8, y 10. ¿Podría uno de los cuadriláteros ser una copia a escala del otro? Explica.

Posibles soluciones

No. Para que los lados más cortos coincidan, el factor de escala de A a B tendría que ser 2. Pero escalar el lado de A de longitud 3 por un factor de 2 daría un lado de longitud 6, que no coincide con ninguna de las longitudes de los lados de B

PROBLEMA 5

Del 6º curso, Unidad 2, Lección 5

Selecciona todos los cocientes que sean equivalentes al cociente 12:3. Explica cómo lo sabes.

A. 6:1

B. 1:4

C. 4:1

D. 24:6

Posibles soluciones

E. 15:6

F. 1.200:300

G. 112:13

C, D y F. Para C, 3 ⋅ 4 = 12 y 3 ⋅ 1 = 3. Para D, 2 ⋅ 12 = 24 y 2 ⋅ 3 = 6. Para F, 100 ⋅ 12 = 1,200 y 100 ⋅ 3 = 300. Para A, B, E y G, no hay ningún número por el que pueda multiplicar 12 y 3 para obtener este par de números.

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Abordar

LECCIÓN 6 ESCALA Y ÁREA

ENFOQUE EN IDEAS FUNDAMENTALES

Alineación de estándares y principios de California

7.G.6 Resolver problemas matemáticos y del mundo real que involucren el área, el volumen y la superficie de objetos bidimensionales y tridimensionales compuestos de triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

Construir

6.G.1

Construir

7.G.4 7.RP.2a Enfoque SMPs

MP7 Buscar y hacer uso de la estructura.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.A.1

II.C.6

II.C.7

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

dan sentido al mundo e inciden en el futuro

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

buscan y expresan regularidades en razonamientos repetidos

META(S) DE APRENDIZAJE

descubren la forma y el espacio y exploran cantidades cambiantes.

• Construyamos figuras a escala e investiguemos sus áreas.

META(S) DE APRENDIZAJE

• Puedo describir cómo el área de una copia a escala está relacionada con el área de la figura original y el factor de escala que se utilizó.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Calcular y comparar (oralmente y por escrito) las áreas de múltiples copias a escala de la misma figura.

• Generalizar (oralmente) que el área de una copia a escala es el producto del área de la figura original y el "cuadrado" del factor de escala.

• Reconocer que un atributo bidimensional, como el área, se escala a un ritmo diferente que los atributos unidimensionales, como la longitud y la distancia.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Anticipar, supervisar, seleccionar, secuenciar, conectar

MLR8: Apoyos para el debate

MLR7: Comparar y conectar

Pensar, compartir en parejas

Materiales necesarios

Patrón de líneas negras para la Actividad 6.3

Enfriamiento

Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)

Bloques de patrones

Fichas preimpresas, recortadas a partir de copias del patrón de líneas negras.

Matemáticas de 7º grado . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación requerida

Prepárate para distribuir los bloques de patrones, al menos 16 rombos azules, 16 triángulos verdes, 10 trapecios rojos y 7 hexágonos amarillos por grupo de 3-4 estudiantes.

Copia y recorta el patrón de líneas negras Área de paralelogramos y triángulos a escala para que cada grupo de 2 alumnos pueda obtener 1 de las 2 formas.

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

Esta lección es opcional. En esta lección, los estudiantes aprenden cómo el área de una copia a escala se relaciona con el área de la figura original. Los estudiantes se basan en su trabajo de grado 6 con exponentes para reconocer que el área aumenta por el cuadrado del factor de escala por el que aumentaron los lados. Los alumnos continuarán trabajando con el área de formas a escala más adelante en esta unidad y en unidades posteriores de este curso. Aunque la lección es opcional, será especialmente útil para los alumnos haber tenido ya esta introducción cuando estudien el área de los círculos en una unidad posterior.

En dos de las actividades de esta lección, los alumnos construyen copias a escala utilizando bloques patrón como unidades de área. Este trabajo con manipulativos ayuda a acostumbrar a los alumnos a un patrón que muchos encuentran contraintuitivo al principio (MP8). (Es una suposición común pero falsa que el área de las copias a escala aumenta por el mismo factor de escala que los lados). Después, los alumnos calculan el área de copias a escala de paralelogramos y triángulos para aplicar los patrones que descubrieron en las actividades prácticas (MP7).

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Grupos pequeños 10 min.

Actividad de exploración opcional Grupos pequeños 10 min.

Actividad de exploración opcional

En parejas 15 min.

Síntesis Todo el grupo 3 min.

Descripción breve

Hay disponible un applet digital interactivoAl construir copias a escala con bloques de patrones, los estudiantes descubren que el área de una copia a escala está relacionada con el factor de escala al cuadrado. que permite a los estudiantes explorar el área al escalar bloques de patrones utilizando la tecnología.

Los estudiantes amplían el concepto descubierto en el calentamiento escalando formas de bloques patrón que contienen más de 1 bloque

Los applets digitales interactivos están disponibles para permitir a los estudiantes explorar el área al escalar formas de bloques utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda del área al escalar formas de bloques de patrones.

Los grupos de estudiantes comparan cómo el factor de escala afecta a las dimensiones de una figura dada y a su área para desarrollar una conjetura sobre la relación entre el factor de escala y las áreas de copias a escala de una figura.

Los estudiantes hacen generalizaciones sobre cómo las áreas de las copias a escala están relacionadas con el área de la copia original de una figura.

Enfriamiento Independiente 5 min. Los estudiantes determinan las áreas de las copias a escala de varios objetos.

Práctica Independiente 5-10 min. El componente de práctica independiente incluye 3 en la lección y 2 problemas de repaso en espiral.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

CALENTAMIENTO | ESCALANDO UN BLOQUE PATRÓN 10 minutos

A estas alturas, los estudiantes entienden que las longitudes en una copia escalada están relacionadas con las longitudes originales por el factor de escala. Aquí ven que el área de una copia a escala está relacionada con el área original por el cuadrado del factor de escala.

Los alumnos construyen copias a escala de un único bloque patrón, utilizando bloques de la misma forma para hacerlo. Determinan cuántos bloques se necesitan para crear una copia a cada factor de escala especificado. Cada bloque patrón sirve como unidad informal de área. Como cada forma original tiene un área de 1 bloque, el (factor de escala)2 patrón para el área de una copia a escala es más fácil de reconocer.

Los alumnos utilizan el mismo conjunto de factores de escala para construir copias de tres formas diferentes (un rombo, un triángulo y un hexágono). Se dan cuenta de la regularidad en su razonamiento repetido y utilizan sus observaciones para predecir el número de bloques necesarios para construir otras copias a escala (MP8).

Organizar a los estudiantes en grupos de 3-4. Distribuya los bloques patrón y pida a los alumnos que los utilicen para construir copias a escala de cada forma, tal y como se describe en la tarea. Cada grupo necesitará como máximo 16 bloques del triángulo verde, el rombo azul y el trapecio rojo. Si no hay suficientes para que cada grupo tenga un juego completo con 16 cada uno de los bloques verde, azul y rojo, considere la posibilidad de rotar los bloques de cada color entre los grupos, o que los estudiantes comiencen con 10 bloques de cada uno y pidan más según sea necesario.

Dé a los estudiantes 6-7 minutos para colaborar en la tarea y siga con una discusión de toda la clase. Asegúrese de que todos los alumnos entienden que "el doble de largo" significa "2 veces más largo".

Es preferible utilizar bloques con patrones reales, pero la Actividad digital puede sustituir a los manipulativos si no se dispone de ellos.

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Compañeros tutores. Empareje a los alumnos con sus compañeros tutores previamente identificados y permita a los alumnos que tienen dificultades con la motricidad fina dictar la construcción de copias a escala según sea necesario.

Tu maestro te dará algunos bloques patrón. Trabaja con tu grupo para construir las copias a escala descritas en cada pregunta.

1. ¿Cuántos rombos azules se necesitan para construir una copia a escala de la figura A:

1. en la que cada lado sea el doble de largo?

2. en la que cada lado sea 3 veces más largo?

3. en la que cada lado sea 4 veces más largo?

2. ¿Cuántos bloques triangulares verdes se necesitan para construir una copia a escala de la figura B:

1. Donde cada lado es el doble de largo?

2. Donde cada lado es 3 veces más largo?

3. Utilizando un factor de escala de 4?

3. ¿Cuántos bloques trapezoidales rojos se necesitan para construir una copia a escala de la figura C:

1. Utilizando un factor de escala de 2?

2. Utilizando un factor de escala de 3?

3. Utilizando un factor de escala de 4?

4. Haz una predicción: ¿Cuántos bloques harían falta para construir copias a escala de estas figuras utilizando un factor de escala de 5? Utilizando un factor de escala de 6? Prepárate para explicar tu razonamiento.

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

Para ayudar a los alumnos a notar, ampliar y generalizar el patrón de la tabla, guíe una discusión utilizando preguntas como éstas:

• En la tabla, ¿cómo se relaciona el número de bloques con el factor de escala? ¿Existe algún patrón?

• ¿Cuántos bloques se necesitan para construir copias a escala utilizando factores de escala de 5 o 10? ¿Cómo lo sabes?

• ¿Cuántos bloques se necesitan para construir una copia a escala utilizando cualquier factor de escala s?

• Si queremos una copia a escala en la que cada lado sea la mitad de largo, ¿cuántos bloques se necesitarían? ¿Cómo se sabe? ¿Sigue siendo válida la misma regla?

Si los alumnos no lo han mencionado, subraya el hecho de que el número de bloques necesarios para construir cada forma a escala es igual al factor de escala multiplicado por sí mismo, independientemente de la forma (mira la fila de la tabla correspondiente a s). Esta regla se aplica a cualquier factor, incluidos los que son menores que 1.

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | ESCALAR MÁS

BLOQUES DE PATRONES 10 minutos

Rutinas didácticas

Anticipar, supervisar, seleccionar, secuenciar, conectar

MLR8: Apoyos para el debate

Esta actividad amplía el trabajo conceptual de la anterior añadiendo una capa de complejidad. Aquí, las formas originales están compuestas por más de 1 bloques, por lo que el número de bloques necesarios para construir sus copias a escala no es simplemente (factor de escala)2, sino n×(factor de escala)2, donde n es el número de bloques de la forma original. Los alumnos empiezan a pensar en cómo se relaciona el área escalada con el área original, que ya no es 1 unidad de área. Observan que el patrón (factor de escala)2 se presenta en el factor por el que ha cambiado el número original de bloques, más que en el número total de bloques de la copia.

Al igual que en la tarea anterior, los alumnos observan la regularidad en el razonamiento repetido (MP8), y se dan cuenta de que, independientemente de las formas, si se parte de n bloques patrón y se escala por s se utilizan ns2 bloques patrón.

También como en la tarea anterior, la forma compuesta por trapezoides puede ser más difícil de escalar que las compuestas por rombos y triángulos. Prepárese para ayudar a los alumnos a escalar la forma roja ofreciéndoles alguna orientación o tiempo adicional, si es posible.

Mientras los alumnos trabajan, observe si hay grupos que se dan cuenta de que el patrón de factores de escala al cuadrado se sigue dando aquí, y que es evidente si se tiene en cuenta el número original de bloques. Selecciónelos para compartirlos durante la discusión en clase.

Mantenga a los estudiantes en los mismos grupos, o forme grupos combinados si no hay suficientes bloques. Asigne una forma para que cada grupo la construya (o deje que los grupos elijan una forma, siempre que todas 3 las formas estén representadas por igual). Para construir una copia de cada forma utilizando un factor de escala de 2, los grupos necesitarán 12 rombos azules, 8 trapezoides rojos o 16 triángulos verdes. Para construir completamente una copia de cada forma dada con un factor de escala de 3, necesitarían 27 rombos azules, 18 trapecios rojos y 36 triángulos verdes; sin embargo, la tarea les pide que dejen de construir cuando sepan cuál será la respuesta. Dé a los alumnos 6-7 minutos para construir sus figuras y completar la tarea. Recuérdeles que utilicen los mismos bloques que en la forma original y que comprueben las longitudes de los lados de cada forma construida para asegurarse de que se han escalado correctamente. Es preferible utilizar bloques con patrones reales, pero la Actividad digital puede sustituir a los manipulativos si no están disponibles.

de 7º grado . Unidad 1

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita a los estudiantes que tienen dificultades con las habilidades motoras finas dictar la construcción de copias a escala según sea necesario.

Funcionamiento Ejecutivo: Organizadores gráficos. Proporcione un diagrama de Venn con el que comparar las similitudes y diferencias entre los patrones de la actividad anterior y ésta.

Tu maestro asignará a tu grupo una de estas figuras.

ENUNCIADO DE TAREA

POSIBLES RESPUESTAS

1. Construye una copia a escala de la figura asignada utilizando un factor de escala de 2. Utiliza la misma forma de bloques que en la figura original. ¿Cuántos bloques se necesitan?

2. Tu compañero de clase piensa que las copias a escala del problema anterior necesitarán 4 bloques cada una para construirlas. ¿Estás de acuerdo o no? Explica tu razonamiento.

3. Comienza a construir una copia a escala de la figura asignada utilizando un factor de escala de 3 Detente cuando puedas decir con seguridad cuántos bloques se necesitarían. Registra tu respuesta.

4. ¿Cuántos bloques se necesitarían para construir copias a escala de tu figura utilizando los factores de escala 4, 5, y 6? Explica o muestra tu razonamiento.

5. ¿En qué se parece el patrón de esta actividad al patrón que viste en la actividad anterior? ¿En qué se diferencia?

1. 12 rombos azules, 8 trapezoides rojos, o 16 triángulos verdes.

2. Las respuestas varían. Posible explicación: Esta vez, la figura original estaba formada por más de un bloque.

3. 27 rombos azules, 18 trapezoides rojos, o 36 triángulos verdes.

4. Rombos azules necesarios para copias a escala de la corona azul: 3

Trapecios rojos necesarios para las copias a escala de la mariposa roja:

72. Triángulos verdes necesarios para las copias a escala del chevron verde:

62 = 144

5. A primera vista, el patrón no parece el mismo porque las respuestas no son 4 y 9. Sin embargo, cada bloque individual se escala en 4 y luego en 9, por lo que hay que multiplicarlo por el número de bloques de la forma original para obtener el número de bloques de la copia a escala.

Los alumnos pueden olvidarse de comprobar que se han escalado las longitudes de todos los lados de su forma y terminar con un recuento inexacto de los bloques del patrón. Recuérdales que todos los segmentos deben escalarse por el mismo factor.

de 7º grado . Unidad 1

El objetivo de este debate es que los alumnos comprendan que el patrón para el número de bloques en las copias a escala depende tanto del factor de escala como del número de bloques en el patrón. Muestra una tabla con sólo los encabezados de las columnas rellenados. Pregunta a la clase cuántos bloques les llevó construir cada copia a escala utilizando los factores de 2 y 3. Registre sus respuestas en la tabla.

Factor de escala

SÍNTESIS DE LA ACTIVIDAD

Número de bloques para construir la figura D

Número de bloques para construir la figura E

Número de bloques para construir la figura F

Considere la posibilidad de mostrar las figuras construidas o imágenes de las mismas para que todos las vean.

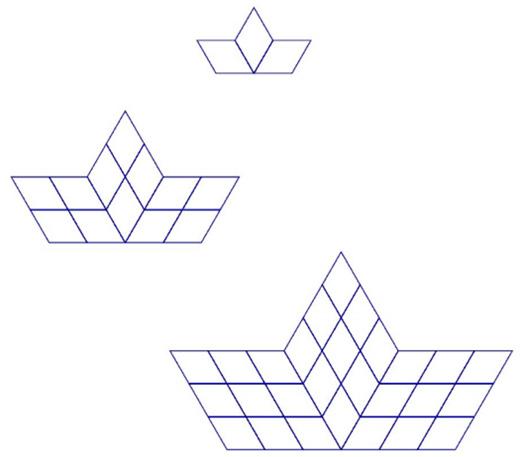
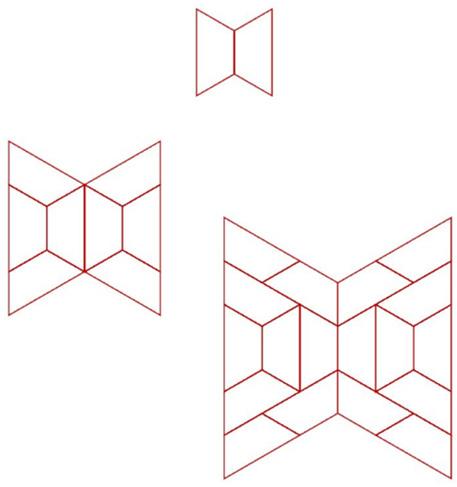
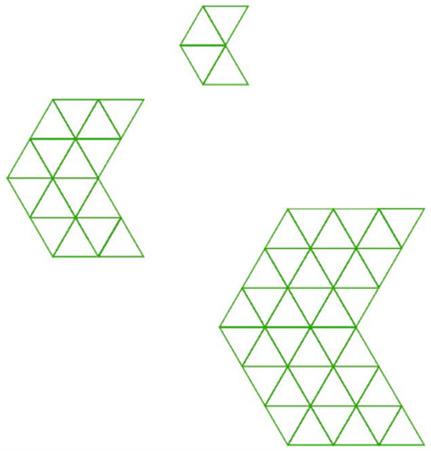
Invite a los alumnos seleccionados a compartir el patrón que sus grupos observaron y utilizaron para predecir el número de bloques necesarios para las copias con factores de escala 4, 5, y 6. Anota sus predicciones en la tabla. Debate:

• ¿Cómo se compara el patrón del número de bloques de esta actividad con el patrón de la actividad anterior? ¿Están relacionados? ¿Cómo?

• Para cada figura, ¿cuántos bloques se necesitan para construir una copia utilizando cualquier factor de escala ��?

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyos para el debate. Dé a los estudiantes tiempo adicional para asegurarse de que todos en el grupo pueden describir los patrones que notaron y las formas en que predijeron el número de bloques necesarios para las copias con factores de escala 4, 5, y 6. Varía a quién se llama para que represente las ideas de cada grupo. Esta rutina proporcionará a los estudiantes oportunidades adicionales para preparar y compartir su pensamiento públicamente. Principio(s) de diseño: Optimizar la producción (para la explicación)

¿Estás preparado para más?

1. ¿Cuántos bloques crees que harían falta para construir una copia a escala de un hexágono amarillo en el que cada lado fuera el doble de largo? ¿Tres veces más largo?

2. Busca la forma de construir estas copias a escala.

3. ¿Ves algún patrón en el número de bloques utilizados para construir estas copias a escala? Explica tu razonamiento.

Matemáticas de 7º grado . Unidad 1

"¿Estás listo para más?" Respuesta del estudiante

1. Debería tomar 4 bloques y 9 bloques siguiendo el patrón para las otras formas.

2. Las respuestas varían. Ejemplo de respuesta: aquí tienes una forma de construir las copias a escala utilizando hexágonos amarillos y rombos azules:

3. El patrón no funciona si sólo cuentas el número de bloques; sin embargo, sí funciona si tienes en cuenta el tamaño de cada bloque que se utiliza. El primer hexágono necesitó 6 bloques para construirse: 3 hexágonos amarillos y 3 rombos azules, pero 3 rombos azules cubren la misma superficie que 1 hexágono amarillo, por lo que el tamaño de la copia a escala equivale a 4 hexágonos amarillos, porque 3 + 3 3 = 4. Del mismo modo, el tamaño total de la copia a escala con factor de escala 3 es equivalente a 9 hexágonos amarillos.

OPCIONAL ACTIVIDAD DE EXPLORACIÓN | ÁREA DE PARALELOGRAMOS Y TRIÁNGULOS A ESCALA

15 minutos

Rutinas didácticas

MLR7: Comparar y conectar

Anticipar, monitorear, seleccionar, secuenciar, conectar

Pensar Compartir en parejas

En esta actividad, los alumnos transfieren lo aprendido con los bloques de patrones para calcular el área de otras formas a escala (MP8). En grupos de 2, los alumnos dibujan copias a escala de un paralelogramo o un triángulo y calculan sus áreas. Después, cada grupo compara sus resultados con los de un grupo que trabajó con la otra forma. Comprueban que las áreas a escala de las dos figuras son iguales (aunque las figuras de partida sean diferentes y tengan medidas distintas) y lo atribuyen al hecho de que las dos figuras tenían la misma área original y se escalaron utilizando los mismos factores de escala.

Aunque no se pide a los alumnos que razonen sobre las áreas a escala mediante mosaicos (como habían hecho en las actividades anteriores), cada copia a escala se puede embaldosar para ilustrar cómo se han escalado las medidas de longitud y cómo ha cambiado el área original. Algunos alumnos pueden optar por dibujar copias a escala y pensar en áreas a escala de esta manera.

Mientras los alumnos encuentran las áreas de copias con factores de escala 5 y 3 5 sin dibujar (para la última pregunta), controle estos métodos, dependiendo de su comprensión o comodidad con el patrón (factor de escala)2:

• Escalando la base y la altura originales y luego multiplicando para encontrar el área

• Multiplicando el área original por el cuadrado del factor de escala

Seleccione alumnos que utilicen cada enfoque. Invítelos a compartir su razonamiento, secuenciado en este orden, durante la discusión.

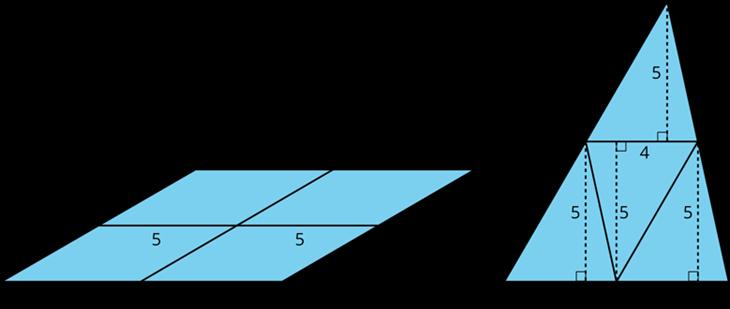
Para esta actividad necesitará el patrón de líneas negras Área de paralelogramos y triángulos escalados.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

Organice a los estudiantes en grupos de 2. Proporcione acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Distribuya fichas que muestren el paralelogramo a la mitad de los grupos y el triángulo a los demás. Conceda a los alumnos 1 un minuto de tiempo de trabajo tranquilo para la primera pregunta y, a continuación, tiempo para completar el resto de la tarea con su compañero.

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita a los estudiantes que tienen dificultades con la motricidad fina dictar copias a escala de dibujos según sea necesario.

Funcionamiento ejecutivo: Organizadores gráficos. Proporcione un diagrama de Venn con el que comparar las similitudes y diferencias entre los dibujos a escala de los alumnos.

1. Tu maestro te dará una figura con medidas en centímetros. ¿Cuál es el área de tu figura? ¿Cómo lo sabes?

2. Trabaja con tu compañero para dibujar copias a escala de tu figura, utilizando cada factor de escala de la tabla. Completa la tabla con las medidas de tus copias a escala.

Factor de escala

Base (cm)

Altura (cm) Área (cm2)

3. Compara tus resultados con un grupo que trabajó con una figura diferente. ¿En qué coinciden tus respuestas? ¿Cuál es la diferencia?

4. Si dibujaras copias a escala de tu figura con los siguientes factores de escala, ¿cuáles serían sus áreas? Discute tus ideas. Si no estáis de acuerdo, tratad de llegar a un acuerdo. Prepárate para explicar tu razonamiento.

Factor de escala

Área (cm2)

1. El área de cualquiera de las dos figuras es 10 unidades cuadradas, porque 5 ⋅ 2 = 10 y 1 2 ⋅ 4 ⋅ 5 = 10

Matemáticas de 7º grado . Unidad 1

SÍNTESIS

POSIBLES

1. Para el paralelogramo:

escala

Para el triángulo:

2. Las áreas son las mismas para cada factor de escala, aunque las dimensiones sean diferentes. En concreto, las bases de los paralelogramos son iguales a las alturas de los triángulos.

Es posible que los alumnos no recuerden cómo calcular el área de paralelogramos y triángulos. Asegúrate de que tienen el área correcta de 10 unidades cuadradas para su forma original antes de que calculen el área de sus copias a escala. Al dibujar sus copias a escala, puede que algunos alumnos no se centren en que los ángulos correspondientes sean iguales. Mientras escalen la base y la altura de su polígono correctamente, esto no afectará a sus cálculos de área. Sin embargo, si el tiempo lo permite, pídeles que comprueben sus ángulos utilizando papel de calco o un transportador. Algunos alumnos podrían centrarse innecesariamente en medir las longitudes de otros lados de su polígono, en lugar de prestar atención sólo a la base y la altura. Si el tiempo es limitado, anímales a escalar la base y la altura con cuidado y a comprobar o medir los ángulos en su lugar.

Invite a los alumnos seleccionados a compartir sus soluciones. A continuación, centre el debate en clase en dos temas: cómo se comparan los valores de las tablas de las dos formas y cómo determinaron los alumnos las áreas a escala para los factores de escala 5 y 3 5 . Haga preguntas como:

• ¿Qué notaron cuando compararon sus respuestas con las de otro grupo que trabajó con la otra figura? (Cuando los factores de escala son los mismos, las áreas a escala son las mismas, aunque las bases y las alturas sean diferentes.)

California - Grado 7

Matemáticas de 7º grado . Unidad 1

DE LA ACTIVIDAD CONTINUACIÓN

• ¿Cómo encontraste las áreas escaladas para factores de escala de 5 y 3 5 ? (Escalando la base y la altura originales y multiplicando las medidas escaladas; multiplicando el área original por (factor de escala)2.)

SÍNTESIS

• ¿En qué se parece y en qué se diferencia el proceso para hallar el área a escala de las actividades anteriores con bloques patrón? (Las unidades de área son diferentes; el patrón de elevar al cuadrado el factor de escala es el mismo).

• Resalta la conexión entre las dos formas de hallar áreas a escala. Señale que cuando en multiplicamos la base y la altura por el factor de escala y luego multiplicamos los resultados, esencialmente estamos multiplicando las longitudes originales por el factor de escala dos veces. El efecto de este proceso es el mismo que multiplicar el área original por (factor de escala)2

Apoyo para estudiantes de inglés

Representar, hablar y escuchar: MLR7 Comparar y conectar. Invite a los estudiantes a preparar un visual que muestre su enfoque para encontrar las áreas de los factores de escala de 5 y 3 5 . Pida a los alumnos que investiguen cómo abordaron el problema otros estudiantes, en busca de un método diferente al suyo. Pida a los alumnos que describan por qué los distintos enfoques dan lugar a las mismas respuestas. Durante el debate de toda la clase, haga hincapié en el lenguaje utilizado para explicar las diferentes estrategias, especialmente las frases relacionadas con "elevar al cuadrado" y "multiplicar un número por sí mismo". Esto reforzará el uso del lenguaje matemático de los alumnos y el razonamiento basado en la relación entre los factores de escala y el área.

Principio(s) de diseño: Maximizar la metaconciencia

SÍNTESIS DE LA LECCIÓN

• Si todas las dimensiones de una copia a escala son el doble que en la forma original, ¿será el área de la copia a escala el doble de grande? (No)

• ¿Por qué no? (Tanto la longitud como la anchura se multiplican por 2, por lo que el área se multiplica por 4.)

• Si el factor de escala es 5, ¿cuántas veces mayor será el área de la copia a escala? (25 veces mayor)

ENFRIAMIENTO | ÁREAS AMPLIADAS

5 minutos

La primera pregunta sólo da a los estudiantes el área de la forma original -pero no las dimensiones- para animarles a encontrar el área de la copia a escala multiplicando por el (factor de escala)2; sin embargo, los estudiantes también pueden elegir una longitud y una anchura para el rectángulo que daría el área original correcta, y luego escalar esas dimensiones por el factor de escala para calcular el área. La segunda pregunta sólo pide a los alumnos que encuentren el (factor de escala)2, pero no que se multipliquen por él.

1. Lin tiene un dibujo con un área de 20 en2. Si aumenta todos los lados en un factor de escala de 4, ¿cuál será la nueva área?

2. Noah amplió una fotografía en un factor de escala de 6. El área de la foto ampliada es ¿cuántas veces mayor que el área de la original?

Matemáticas de 7º grado . Unidad 1

POSIBLES RESPUESTASS

1. 320 en2, Posibles estrategias:

• 20 ⋅ 42 = 320

• Si el rectángulo es 4 pulgadas por 5 pulgadas, la copia a escala será 4 ⋅ 4 pulgadas por 4 ⋅ 5 pulgadas y

(4 ⋅ 4) ⋅ (4 ⋅ 5) = 16 ⋅ 20 = 320

• Si el rectángulo mide 2 pulgadas por 10 pulgadas, la copia a escala será 4 ⋅ 2 pulgadas por 4 ⋅ 10 pulgadas y (4 ⋅ 2) ⋅ (4 ⋅ 10) = 8 ⋅ 40 = 320

2. 36 veces más grande, porque 62 = 36.

Algunos estudiantes pueden multiplicar el área de la forma original sólo por el factor de escala, en lugar de por el (factor de escala)2, obteniendo 80 en2. Los alumnos que no entiendan la regla generalizada de cómo afecta la escala al área podrían responder correctamente a la primera pregunta. Podrían asumir algunas dimensiones para el rectángulo original que le darían un área de 20 en2, escalar esas dimensiones por el factor de escala dado, y luego multiplicar esas dimensiones escaladas para encontrar la nueva área.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

En la cuadrícula, dibuja una copia a escala del Polígono Q utilizando un factor de escala de 2. Compare el perímetro y el área del nuevo polígono con los de Q.

Posibles soluciones

El perímetro de Q es 20 unidades, y el área de Q es 16 unidades cuadradas. El perímetro de la copia a escala es 40 unidades, y su área es 64 unidades cuadradas. El perímetro se multiplica por el factor de escala de 2, y el área se multiplica por el cuadrado del factor de escala, que es 4

California - Grado 7

Matemáticas de 7º grado . Unidad 1

PROBLEMA 2

Un triángulo rectángulo tiene un área de 36 unidades cuadradas. Si dibujas copias a escala de este triángulo utilizando los factores de escala de la tabla, ¿cuáles serán las áreas de estas copias a escala? Explica o muestra tu razonamiento.

Factor de escala Área (unidades2) 1 36 2 3 5 1 2 2 3

PROBLEMA 3

Diego dibujó una versión a escala de un Polígono P y lo etiquetó Q.

Posibles soluciones

El área de cada triángulo a escala es la misma que el área del triángulo original (36 unidades cuadradas) multiplicada por el cuadrado del factor de escala:

de escala Área2)

Si el área del polígono P es 72 unidades cuadradas, ¿qué factor de escala utilizó Diego para pasar de P a Q? Explica tu razonamiento.

Posibles soluciones

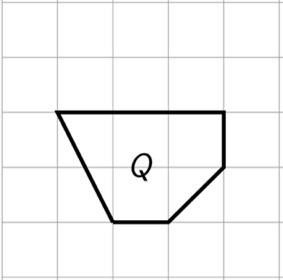
1 4 . El área de Q es 4 5 unidades cuadradas (3 unidades cuadradas enteras, un 2-unidad-por-1-unidad triángulo rectángulo, y un 1-unidad-por-1-unidad triángulo rectángulo). Esta área es 1 16 del área de P. Esto significa que el factor de escala es

PROBLEMA 4

Del Grado 7, Unidad 1, Lección 2 Aquí hay un polígono sin etiquetar, junto con sus copias a escala Polígonos A-D. Para cada copia, determina el factor de escala. Explica cómo lo sabes.

Posibles soluciones

1. 1 2 porque el lado vertical en la copia es 1 2 la longitud del lado vertical en el original.

2. 2 porque el lado vertical de la copia es el doble de largo que el lado vertical del original.

3. 3 2 porque el lado vertical de la copia es 3 2 de largo que el lado vertical del original.

4. 1 porque el original y la copia tienen el mismo tamaño.

PROBLEMA 5

Del Grado 7, Unidad 1, Lección 5

Resuelve cada ecuación mentalmente.

1. 1 7 ⋅ �� = 1

2. �� ⋅ 1 11 = 1

3. 1 ÷ 1 5 = ��

Soluciones posibles

1. �� = 7

2. �� = 11

3. �� = 5

Math Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Alineación de estándares y principios de Abordar

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.B.5

EP&Cs de CA

2.A 2.C

LECCIÓN 7 DIBUJOS A ESCALA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo e influyen en el futuro

buscan y hacen uso de la estructura

OBJETIVO(S) DE APRENDIZAJE

• Exploremos los dibujos a escala.

OBJETIVO(S) DE APRENDIZAJE

II.B.5

descubren la forma y el espacio y exploran las cantidades cambiantes.

• Puedo explicar qué es un dibujo a escala y qué significa su escala.

• Puedo usar un dibujo a escala y su escala para encontrar distancias reales.

• Puedo usar distancias reales y una escala para encontrar distancias a escala.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente) qué es un "dibujo a escala".

• Explicar (oralmente y por escrito) cómo utilizar escalas y dibujos a escala para calcular distancias reales y a escala.

• Interpretar la "escala" de un dibujo a escala.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR1: Más fuerte y más claro cada vez

MLR8: Apoyos para el debate

Anticipar, controlar, seleccionar, secuenciar, conectar

Materiales necesarios

Lápiz negro para la actividad 7.2

Enfriamiento

Copias del lápiz negro

Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Matemáticas de 7º grado . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación necesaria

Prepárese para exponer los ejemplos y no ejemplos de dibujos a escala para que todos los vean. Considere agregar a la colección un mapa local que muestre la ruta real de una línea de tren o autobús (ejemplo de dibujo a escala) y un mapa de tránsito diagramático (no ejemplo).

Asegúrese de que los estudiantes tengan acceso a los kits de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una tarjeta de índice), especialmente reglas centimétricas y tarjetas de índice o papel para usar como herramienta de medición.

Para esta lección necesitará el patrón de líneas negras Dimensionar una cancha de baloncesto. Prepara una copia por alumno.

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

Hasta este punto, los alumnos han estado explorando copias a escala, o imágenes bidimensionales que han sido recreadas a determinados factores de escala. En esta lección, comienzan a observar dibujos a escala, o representaciones bidimensionales a escala de objetos o lugares reales. Los alumnos ven que, aunque los dibujos a escala capturan objetos o lugares tridimensionales, muestran medidas a escala sólo en dos de las dimensiones, y que toda la información se proyecta sobre un plano.

En esta lección y en las siguientes, los alumnos ven que los principios y estrategias que utilizaron para razonar sobre copias a escala son aplicables a los dibujos a escala (MP7). Por ejemplo, antes veían el factor de escala como un número que describe cómo las longitudes en una figura se corresponden con las longitudes en una copia de la figura (y viceversa). Ahora ven que scale tiene un propósito similar: describe cómo las longitudes en un objeto real están relacionadas con las longitudes en una representación dibujada del mismo. Aprenden que la escala puede expresarse de varias maneras y utilizan la escala y los dibujos a escala para encontrar longitudes reales y a escala.

Los alumnos empiezan interpretando dibujos a escala dados. En lecciones posteriores, crearán o reproducirán dibujos a escala a escalas especificadas, así como determinarán las escalas apropiadas a utilizar, dadas las restricciones en el tamaño del dibujo.

LECCIÓN DE UN VISTAZO

Componente de lección

Estructura Tiempo

Calentamiento Pares 5 min.

Actividad de exploración

Parejas 15 min.

Parejas o Grupos pequeños 15 min.

Nation California - Grado 7

Descripción breve

Los estudiantes comparan imágenes de dibujos a escala con imágenes similares no dibujadas a escala para definir dibujo a escala

Esta tarea podría ampliarse como una oportunidad para establecer conexiones con el modo en que la expansión y el crecimiento de las poblaciones humanas afectan negativamente a los sistemas naturales, centrándose en cómo el transporte público puede reducir estos efectos.

Los alumnos miden un dibujo a escala para explorar el significado y la aplicación de escala en el mundo real. Después, aplican la misma escala a otros objetos.

Los alumnos utilizan medidas e interpretan las escalas proporcionadas para objetos del mundo real para aproximarse a las medidas de los objetos en el mundo real. Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la relación entre las medidas del mundo real y las del dibujo a escala.

RESUMEN DE LA LECCIÓN CONTINUACIÓN

Componente de la lección

Estructura Tiempo

Síntesis Grupo completo 5 min.

Enfriamiento Independiente 5 min.

Práctica Independiente 10-15 min.

Descripción breve

Los estudiantes repasan cómo utilizar dibujos a escala bidimensionales para encontrar distancias del mundo real.

Los estudiantes definen formalmente dibujo a escala y escala mientras hacen referencia a ejemplos del mundo real en los que se puede utilizar un dibujo a escala.

Los estudiantes aplican dimensiones a escala para encontrar medidas de objetos del mundo real.

El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.

CALENTAMIENTO | ¿QUÉ ES UN DIBUJO A ESCALA?

5 minutos

Esta actividad anima a los alumnos a fijarse en las características de los dibujos a escala observando ejemplos y contraejemplos, y a articular qué es un dibujo a escala. Aunque no se espera que los alumnos den definiciones precisas, es probable que puedan intuir que los dibujos a escala son representaciones bidimensionales exactas de lo que representan, en el sentido de que todas las formas, disposiciones de las piezas y tamaños relativos coinciden con los de los objetos reales.

Espere que las observaciones de los alumnos sobre los dibujos a escala sean informales y no matemáticas. Por ejemplo, pueden decir que un dibujo a escala se parece al objeto que representa, que las piezas que aparecen tienen el tamaño correcto y están en los lugares adecuados del dibujo. O que en un dibujo a escala, una parte más pequeña en el objeto real no acaba siendo más grande en el dibujo. Como cualquier modelo matemático de una situación real, un dibujo a escala capta algunos aspectos importantes del objeto real e ignora otros aspectos. Puede que a los alumnos no les resulte evidente que los dibujos a escala dan prioridad a las características de un plano del objeto (y a veces a las características de otros planos paralelos a él) e ignoran otras superficies y dimensiones. Fíjese en los alumnos que muestren percepciones sobre esta idea para que puedan compartirlas más tarde.

INTRODUCCIÓN

Organice a los alumnos en grupos de 2. Antes de que los alumnos vean los materiales, sondee a la clase para averiguar quién ha visto dibujos a escala. Pide a algunos alumnos que estén familiarizados con ellos que den un par de ejemplos de dibujos a escala que hayan visto. A continuación, dé a los alumnos 2 minutos para que observen los ejemplos y contraejemplos de dibujos a escala y discutan en grupos qué creen que es un dibujo a escala.

Apoyo a los alumnos con discapacidad

Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (es decir, un muro de palabras) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para referencia futura.

Matemáticas de 7º grado . Unidad 1 ENUNCIADO DE TAREA

POSIBLES RESPUESTAS

Aquí tienes algunos dibujos de un autobús escolar, una moneda de 25 centavos y las líneas de metro de los alrededores de Boston, Massachusetts. Los tres primeros dibujos son dibujos a escala de estos objetos.

Los tres dibujos siguientes no son dibujos a escala de estos objetos.

Comenta con tu compañero qué es un dibujo a escala.

Las respuestas varían. Ejemplos de descripciones:

• Un dibujo a escala es un dibujo que muestra el objeto con precisión y todas las partes del dibujo coinciden con las partes del objeto real.

• Ninguna parte de un dibujo a escala está distorsionada.

• Un dibujo a escala es como una copia a escala de un objeto real, pero es un dibujo que muestra una superficie plana del objeto.

ERRORES PREVISTOS

Si los alumnos tienen dificultades para caracterizar los dibujos a escala, ofrezca indicaciones para animarles a mirar más de cerca. Por ejemplo, pregunte: "¿Cómo se comparan las formas y tamaños de los objetos de los dibujos con los de los objetos reales?". Los alumnos pueden decir que los tamaños de los objetos de los dibujos a escala son más pequeños que los de los objetos reales. Pregúnteles si alguna parte de los dibujos a escala está distorsionada, en comparación con el objeto real; pídales que se centren en las dos imágenes de la moneda de 25 centavos, una de las cuales tiene forma circular, mientras que la otra no.

Pida a algunos alumnos que compartan lo que han observado sobre las características de los dibujos a escala y que comparen y contrasten las copias a escala y los dibujos a escala. Discuta cuestiones como las siguientes. Anote los temas comunes y las descripciones útiles.

• ¿Qué tienen o muestran los ejemplos que no tengan los contraejemplos?

• ¿En qué se parecen los dibujos a escala a las copias a escala que vieron en lecciones anteriores? ¿En qué se diferencian de las copias a escala?

• ¿Qué aspectos del autobús, de la moneda y de la ciudad de Boston muestran los dibujos a escala? ¿Qué aspectos de los objetos reales no muestran los dibujos a escala? Observe los conceptos erróneos, pero no es necesario abordarlos de inmediato, ya que la comprensión de los alumnos se formará en esta lección y en las siguientes. Diga a los alumnos que seguirán analizando los dibujos a escala y revisando sus definiciones en las próximas actividades.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | DIMENSIONAR UNA CANCHA DE BALONCESTO

15 minutos

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

Materiales necesarios

En esta actividad introductoria, los alumnos exploran el significado de escala. Ellos comienzan a ver que una escala comunica la relación entre las longitudes en un dibujo y las longitudes correspondientes en los objetos que representan, y aprenden algunas formas de expresar esta relación:

• "a unidades en el dibujo representan b unidades de longitud real"

• "a una escala de a unidades (en el dibujo) a b unidades (reales)"

• "a unidades (en el dibujo) por cada b unidades (reales)"

Los alumnos miden longitudes en un dibujo a escala y utilizan una escala dada para encontrar longitudes correspondientes en una cancha de baloncesto (MP2).

Dado que los alumnos miden con una precisión de una décima de centímetro, algunas de las medidas reales que calculen no tendrán la precisión de las medidas oficiales . Por ejemplo, la medida oficial de �� es 0,9 m.

Para esta actividad necesitará el patrón de líneas negras Dimensionar una cancha de baloncesto.

INTRODUCCIÓN

Pregunte a los alumnos si alguna vez han jugado al baloncesto o han visto una cancha de baloncesto. Si es así, ¿dónde? Si algunos alumnos han jugado al baloncesto o han visto una cancha de baloncesto, pregúntales si podrían lanzar una pelota de baloncesto a lo ancho de una cancha de baloncesto. ¿Y a lo largo de toda la cancha?

Organice a los alumnos en grupos de 2. Distribuya una copia del patrón de líneas negras y una regla a cada alumno. Conceda a los alumnos 6-7 minutos de tiempo de trabajo tranquilo para responder a las tres primeras preguntas. Pídeles que compartan sus respuestas con sus compañeros antes de completar las preguntas restantes.

Apoyo para estudiantes de inglés

Escribir, hablar, escuchar: MLR1 Cada vez más fuerte y más claro. Después de que los estudiantes hayan completado las tres primeras preguntas, deles la oportunidad de refinar su razonamiento para la tercera pregunta. Pida a cada estudiante que se reúna con 2-3 otros compañeros en fila para recibir comentarios. Proporcione a los alumnos indicaciones que les ayuden a reforzar sus ideas y a aclarar su lenguaje (por ejemplo, "¿Cómo has utilizado la escala en tus cálculos?", "¿Por qué has multiplicado cada medida del dibujo por 2?", etc.). Los alumnos pueden tomar prestadas las ideas y el lenguaje de cada compañero para perfeccionar y aclarar su explicación original. Esto ayudará a los alumnos a perfeccionar su propia explicación y a conocer otras formas de hallar las medidas reales utilizando las medidas de un dibujo a escala.

Principios de diseño: Optimizar el resultado (para la explicación); Maximizar la meta-conciencia

Matemáticas de 7º grado . Unidad 1

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual:Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la repasen antes de realizar esta actividad.

Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus compañeros tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten medidas según sea necesario.

Tu maestro te dará un dibujo a escala de una cancha de baloncesto. El dibujo no tiene ninguna medida etiquetada, pero dice que 1 centímetro representa 2 metros.

1. Mide las distancias en el dibujo a escala que están etiquetadas a-d a la décima más cercana de un centímetro. Registra tus resultados en la primera fila de la tabla.

2. La afirmación "1 cm representa 2 m" es la escala del dibujo. También puede expresarse como "1 cm a 2 m," o "1 cm por cada 2 m". ¿Qué crees que nos dice la escala?

3. ¿Qué longitud tendría cada medida de la primera pregunta en una cancha de baloncesto real? Explica o muestra tu razonamiento. (a)

Longitud de la cancha (b) Anchura de la cancha (c) De aro a aro

(d)

3 Línea de puntos a la línea lateral

Dibujo a escala

Cancha real

4. En una cancha de baloncesto real, el área de los banquillos suele medir 9 metros.

1. Sin medir, determina cuánto debería medir el área de los banquillos en el dibujo a escala.

2. Comprueba tu respuesta midiendo el área de los banquillos en el dibujo a escala. ¿Coincide tu predicción con tu medición?

1. 14 cm, 7.5 cm, 12,4 cm, 0,5 cm, aunque los alumnos pueden redondear las medidas de forma diferente.

2. Las respuestas varían. Ejemplos de respuestas:

• La escala nos indica cómo se comparan las longitudes del dibujo con las longitudes reales.

• La escala nos indica cómo utilizar las medidas del dibujo para encontrar las medidas reales.

3. Ejemplos de razonamiento: Como cada centímetro representa 2 metros, multipliqué cada medida del dibujo por 2 para encontrar la medida real en metros. (a)

Longitud de la cancha (b)

Ancho de la cancha (c) De aro a aro (d) 3 Punto de línea a línea lateral

Dibujo a escala

Cancha real 28 m

4. 4,5 cm. Las respuestas varían.

En lugar de utilizar la escala para hallar las medidas reales, los alumnos pueden intentar convertir las distancias en centímetros a metros (14 cm es 0,14 m). Explique que las distancias que midieron en papel podrían convertirse a metros, pero entonces los resultados seguirían siendo longitudes en papel, sólo que expresadas en metros, en lugar de las medidas de la cancha de baloncesto real. Llame la atención de los alumnos sobre la afirmación "1 cm representa 2 m" en el dibujo a escala y pídales que piensen en cómo utilizarla para hallar medidas reales.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Antes de informar a la clase, muestre la tabla que muestra sólo las distancias a escala para que los alumnos puedan hacer una comprobación rápida de sus medidas (que pueden redondear de forma diferente).

Explique a los alumnos que las distancias en un dibujo a escala suelen denominarse "distancias a escala". Las distancias en la cancha de baloncesto, en este caso, se denominan distancias reales.

Centre el debate en el significado de escala y en cómo utilizaron los alumnos la escala dada para hallar las distancias reales. Invite a algunos alumnos a compartir sus respuestas a la segunda y tercera preguntas. Para que los alumnos comprendan mejor la escala, discuta:

• ¿Significa "1 cm por cada 2 m" que la distancia real es el doble de la que aparece en el dibujo? ¿Por qué sí o por qué no?

• ¿Qué partes de la pista deben dibujarse utilizando la regla "1 cm por cada 2 m"?

• ¿Podemos invertir el orden en el que enumeramos las distancias reales y a escala? Por ejemplo, ¿podemos decir "2 m de distancia real a 1 cm en el dibujo" o "2 m a 1 cm"?

Tenga en cuenta que la distancia a escala se indica convencionalmente en primer lugar, pero la distancia real representada también podría ir en primer lugar siempre que quede claro por el contexto.

Si es necesario, un breve debate sobre la precisión de las medidas en el dibujo a escala podría destacar algunas posibles fuentes de error de medición, entre ellas:

• No medir en línea recta.

• Las líneas en el dibujo a escala tienen anchura, y esto podría contribuir a un pequeño error dependiendo de si la medición es desde el interior o el exterior de las líneas.

OPCIONAL ACTIVIDAD DE EXPLORACIÓN | ESTRUCTURAS DE GRAN ALTURA

15 minutos

Rutinas didácticas

• MLR8: Apoyos a la discusión

• Anticipar, Monitorizar, Seleccionar, Secuenciar, Conectar

Esta actividad introduce a los estudiantes a las escalas gráficas. Los alumnos las interpretan, las utilizan para encontrar medidas reales (alturas de edificios altos) y las expresan de forma no gráfica. En lecciones anteriores, los alumnos utilizaron marcas en una ficha u hoja de papel para medir un dibujo y crear copias a escala. Aquí, vuelven a utilizar herramientas de medición no estándar para resolver problemas (MP5). Los alumnos hacen marcas en una regla sin marcar para medir longitudes a escala en un dibujo y, a continuación, utilizan la escala dada para determinar las longitudes reales. Esta estrategia de medición se basa en el trabajo de los estudiantes con la medición en los grados 1 y 2 (es decir, la colocación de varias copias de un objeto más corto extremo a extremo y la expresión de longitudes en términos del número de objetos).

A medida que los estudiantes trabajan, anímelos a ser lo más precisos posible al hacer sus marcas y en la estimación de longitudes que son menos de 1 escala-segmento de largo. La mayoría de las distancias que los alumnos miden aquí no son segmentos de recta, sino distancias entre un punto (la punta de un edificio) y una recta (el suelo).

Supervise las distintas formas en que los alumnos razonan sobre las distancias a escala y las reales. A continuación se presentan dos enfoques probables para encontrar la diferencia entre el Burj Khalifa y la Torre Eiffel (la segunda pregunta):

• Encuentre la altura real de cada torre y luego encuentre su diferencia.

• Encuentre la diferencia de alturas a escala y luego utilice la escala para encontrar la diferencia de alturas reales.

Seleccione a los estudiantes que utilizan estos enfoques para compartirlos durante la discusión de toda la clase en esta secuencia.

Matemáticas de 7º grado . Unidad 1

INTRODUCCIÓN

Muestre el dibujo a escala de las estructuras. Antes de comenzar la tarea, es posible que los alumnos estén interesados o deseosos de compartir la ubicación de las estructuras. Tómese unos minutos para preguntarles qué saben o muestre un mapamundi en el que aparezcan las ubicaciones de las estructuras. Pregunte a los alumnos qué puede significar el segmento marcado con "0 m" y "100 m". Es probable que algunos alumnos digan que también transmite una escala. Verifique que, efectivamente, una escala puede comunicarse gráficamente; una distancia real no está representada por una medida numérica, sino más bien, por la longitud del segmento.

Proporcione acceso a fichas u hojas de papel que los alumnos puedan utilizar para medir. Diga a los alumnos que comprueben sus respuestas a la primera pregunta con un compañero. Dígales que discutan lo necesario hasta llegar a un acuerdo antes de proceder a trabajar en el resto de los problemas. Dé a los estudiantes 4-5 minutos de tiempo de trabajo en silencio y de discusión por parejas.

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.

Habilidades motoras finas: Tutores compañeros. Empareje a los estudiantes con sus compañeros tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten medidas según sea necesario.

ENUNCIADO DE TAREA PARA

EL ESTUDIANTE

1. Aquí tienes un dibujo a escala de algunas de las estructuras más altas del mundo.

2. ¿Aproximadamente cuánto mide la Torre Willis?

¿Aproximadamente cuánto mide la Gran Pirámide? Prepárate para explicar tu razonamiento.

3. ¿Aproximadamente cuánto más alto es el Burj Khalifa que la Torre Eiffel?

4. Explica o muestra tu razonamiento.

5. Mide el segmento de línea que muestra la escala, redondeándolo a la décima de centímetro más cercana. Expresa la escala del dibujo con números y palabras.

POSSIBLE

RESPONSES

• La Torre Willis mide poco más de 500 m de altura. Se necesitan aproximadamente 5 segmentos para medir su altura. La Gran Pirámide mide aproximadamente 150 m. Su altura equivale aproximadamente a un segmento.

• El Burj Khalifa es aproximadamente 550 m más alto que la Torre Eiffel.

Matemáticas de 7º grado . Unidad 1

ERRORES PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Es posible que los alumnos no midan las alturas de los edificios en ángulo recto desde la línea del suelo. Recuerde a los alumnos que las alturas deben medirse perpendicularmente al suelo o a la línea de base. Si es necesario, demuestre cómo utilizar el borde de una hoja de papel o una ficha para medir longitudes en un dibujo a escala con una escala gráfica.

Sondee a la clase para conocer sus respuestas a la primera pregunta. Pregunta cuáles podrían ser algunas fuentes de discrepancias. En este caso, el principal problema es el error de medición, pero también existen diferentes métodos para realizar las mediciones y estimar las alturas de los edificios. Dos métodos para estimar las alturas de los edificios (y sus limitaciones) son:

• Estima cuántas veces "más alto" es cada edificio en comparación con el segmento de línea que da la escala. A continuación, multiplica este número por 100 m. En este caso, la precisión no es muy buena a menos que, por ejemplo, la altura del edificio esté muy cerca de ser un número entero veces la longitud de la escala.

• Mide el segmento que da la escala (en centímetros, por ejemplo) y, a continuación, expresa la escala utilizando centímetros (por ejemplo, 0,7 cm representa 100 m). A continuación, mide cada edificio y utiliza la escala para hallar la altura real. Será necesario realizar estimaciones y redondeos al medir la escala y al medir los edificios.

Pida a los alumnos previamente seleccionados y secuenciados que destaquen los diferentes enfoques para comparar las alturas del Burj Khalifa y de la Torre Eiffel. La principal diferencia entre las dos estrategias es el orden aritmético. Tomar la diferencia de las alturas reales de los edificios significa multiplicar primero las alturas a escala y luego restar. Tomar la diferencia de las alturas a escala y luego aplicar el factor de escala significa restar primero las alturas a escala y luego multiplicar por el factor de escala.

Si el tiempo lo permite, discuta más ampliamente el dibujo a escala de las torres. Pregunte:

• Además de la información sobre la altura, ¿qué otra información sobre las torres muestra el dibujo? (La anchura de los edificios y sus formas generales.)

• ¿Qué información no muestra? (La profundidad de cada edificio, cualquier saliente o protuberancia, las formas de las diferentes partes de los edificios, etc.)

• ¿En qué se parece este dibujo a escala al de la cancha de baloncesto? (Ambos muestran información en un solo plano y están dibujados a escala.) ¿En qué se diferencian? (La cancha de baloncesto es una superficie plana, como el dibujo de la cancha. El dibujo de las torres es una vista lateral o frontal; los objetos reales representados no son en realidad objetos planos).

Apoyo para estudiantes de inglés

Hablar: MLR8 Apoyo a la discusión. Utilice esta rutina para apoyar la discusión de toda la clase. Para cada respuesta u observación que se comparta, pida a los alumnos que repitan o vuelvan a expresar lo que han oído utilizando un lenguaje matemático preciso. Considere la posibilidad de dar tiempo a los alumnos para que repitan lo que han oído a un compañero, antes de seleccionar a uno o dos alumnos para que lo compartan con la clase. Pregunte al orador original si su compañero ha sido capaz de repetir su pensamiento con precisión. Llame la atención de los alumnos sobre las palabras o frases que hayan ayudado a aclarar la afirmación original. De este modo, más alumnos tendrán la oportunidad de producir lenguaje al interpretar el razonamiento of otros.

Principio(s) de diseño: Apoyar la creación de sentido

Matemáticas de 7º grado . Unidad 1

¿Estás preparado para más?

La montaña más alta de Estados Unidos, el monte Denali en Alaska, mide aproximadamente 6.190 m. Si esta montaña se mostrara en el dibujo a escala, ¿cómo se compararía su altura con las alturas de las estructuras? Explica o muestra tu razonamiento.

"¿Estás preparado para más?" Respuesta del alumno

El monte Denali será mucho más alto (unas 7,5 veces más alto) que el Burj Khalifa. Ejemplos de explicaciones:

• He averiguado que el Burj Khalifa mide unos 830 m. El monte Denali mide 6.190 m, y 6.190 dividido por 830 es aproximadamente 7.5, por lo que la montaña será unas 7,5 veces más alta que el Burj Khalifa.

• Se necesitan unas 62 de los 100-m segmentos para medir la montaña (6, 190 ÷ 100 = 61,9). Se necesitan unos 8 1 4 de los 100-m segmentos para medir el Burj Khalifa. Esto significa que la montaña es unas 7,5 veces más alta que el Burj, ya que 62 dividido por 8 1 4 es aproximadamente 7,5

SÍNTESIS DE LA LECCIÓN

• ¿Qué es un dibujo a escala?

5 minutos

• ¿Cómo podemos describir la escala de un dibujo a escala?

• ¿Cómo encontramos distancias utilizando un dibujo a escala?

Un dibujo a escala es una representación a escala de un objeto. La escala nos dice cómo se relacionan las longitudes en el dibujo con las longitudes en el objeto real. Por ejemplo, en la actividad de la cancha de baloncesto, vimos que 1 centímetro en el dibujo representaba 2 metros de distancia real en la cancha real.

Si tenemos un dibujo a escala, podemos usar la escala para encontrar longitudes en el objeto real. Por ejemplo, si un segmento de línea en el dibujo a escala de la cancha de baloncesto es 5 cm, entonces representa un segmento de línea 10 m en una cancha real, porque 2 ⋅ 5 = 10. Es importante recordar que un dibujo a escala muestra medidas a escala en sólo dos dimensiones, es decir, las medidas de una superficie concreta de un objeto y las que se han proyectado sobre un plano concreto. Por ejemplo, el dibujo de la cancha de baloncesto no muestra la altura de los aros de baloncesto.

5 minutos INTRODUCCIÓN

ENFRIAMIENTO | LONGITUD DE UN AUTOBÚS Y ANCHURA DE UN LAGO

Si lo desea, proporcione acceso a calculadoras de cuatro funciones.

1. Un dibujo a escala de un autobús escolar tiene una escala de 1 2 pulgadas a 5 pies. Si la longitud del autobús escolar es 4 1 2 pulgadas en el dibujo a escala, ¿cuál es la longitud real del autobús? Explica o muestra tu razonamiento.

2. Un dibujo a escala de un lago tiene una escala de 1 cm a 80 m. Si la anchura real del lago es 1.000 m, ¿cuál es la anchura del lago en el dibujo a escala? Explica o muestra tu razonamiento.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

1. 45 pies. Ejemplo de explicación: Hay 9 grupos de 1 2 en 4 1 2 . Si 1 2 pulgadas representa 5 pies, entonces 4 1 2 pulgadas representa 9 ⋅ 5 o 45 pies.

2. 12,5 cm. Ejemplo de razonamiento: Como cada 80 m está representado por 1 cm, 1.000 m está representado por 1.000 ÷ 80 o 12,5 cm.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

El Westland Lysander fue un avión utilizado por la Royal Air Force en la década de 1930. Aquí hay algunos dibujos a escala que muestran las vistas superior, lateral y frontal del Lysander.

Utilice las escalas y los dibujos a escala para aproximar las longitudes reales de:

1. la envergadura del avión, al pie más cercano

2. la altura del avión, al pie más cercano

3. la longitud del Lysander Mk. I, al metro más cercano

Posibles soluciones

1. 46 pies

2. 12 pies

3. 9 metros

PROBLEMA 2

El plano de un edificio incluye una habitación rectangular que mide 3 pulgadas de largo y 5,5 pulgadas de ancho. La escala del plano dice que 1 pulgada en el plano equivale a 10 pies en el edificio real. ¿Cuáles son las dimensiones de esta habitación rectangular en el edificio real?

Posibles soluciones

30 pies de largo y 55 pies de ancho

PROBLEMA 3

Este es un plano a escala de Lafayette Square, un jardín rectangular al norte de la Casa Blanca.

1. La escala se muestra en la esquina inferior derecha. Halla las longitudes reales de los lados de Lafayette Square en pies.

2. Utiliza una regla de pulgadas para medir el segmento de línea de la escala gráfica. ¿Aproximadamente cuántos pies representa una pulgada en este mapa?

Posibles soluciones

1. Aproximadamente 800 pies por 500 pies

2. Las respuestas varían según el tamaño de la escala impresa. Ejemplo de respuesta: 1 pulgada representa 300 pies.

de 7º grado . Unidad 1

PROBLEMA 4

Del 7º Grado, Unidad 1, Lección 6

Aquí está el Triángulo A. Lin creó una copia a escala del Triángulo A con un área de 72 unidades cuadradas.

1. ¿Cuántas veces mayor es el área de la copia a escala comparada con la del Triángulo A?

2. ¿Qué factor de escala aplicó Lin al Triángulo A para crear la copia?

3. ¿Cuál es la longitud del lado inferior de la copia a escala?

Posibles soluciones

1. 16 veces mayor (72 ÷ 4,5 = 16)

2. 4

3. 12 unidades

Reflexiones:

Nation California - Grado 7

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

6.NS.2 6.RP.3b

Construir

7.RP.2b

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP2 Razonar abstracta y cuantitativamente.

MP4 Representar con matemáticas.

Estándares ELD de California

I.A.1

II.C.6

LECCIÓN 8 DIBUJOS A ESCALA Y MAPAS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo modelan con matemáticas descubriendo la forma y el espacio y explorando las cantidades cambiantes.

OBJETIVO(S) DE APRENDIZAJE

• Utilicemos dibujos a escala para resolver problemas.

OBJETIVO(S) DE APRENDIZAJE

• Puedo utilizar un mapa y su escala para resolver problemas sobre viajes.

OBJETIVOS DE

APRENDIZAJE PARA EL MAESTRO

• Justificar (oralmente y por escrito) cuál de dos objetos se movía más rápido.

• Utilizar un dibujo a escala para estimar la distancia recorrida por un objeto, así como su velocidad o el tiempo transcurrido, y explicar (oralmente y por escrito) el método de solución.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR7: Comparar y conectar

Anticipar, supervisar, seleccionar, secuenciar, conectar

Pensar, compartir en parejas

Materiales necesarios

Enfriamiento

Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)

Preparación requerida

Asegúrese de que los estudiantes tienen acceso a juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Matemáticas de 7º grado . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

Esta lección es opcional. En esta lección, los estudiantes aplican lo que han aprendido sobre dibujos a escala para resolver problemas que involucran velocidad constante (MP1, MP2). A los estudiantes se les da un mapa con escala, así como un punto de partida y un punto final. Además, o bien se les da el tiempo que dura el viaje y se les pide que estimen la velocidad, o bien se les da la velocidad y se les pide que estimen cuánto dura el viaje. En ambos casos, tendrán que hacer un uso estratégico del mapa y la escala y estimar las distancias porque las carreteras no son rectas.

En sexto curso, los alumnos han examinado muchos contextos que implican viajar a velocidad constante. Si un coche viaja a 30 mph, existe una relación entre el tiempo de viaje y la distancia recorrida. Esto se puede representar en una tabla de proporciones, o en un gráfico, o con una ecuación. Si �� es la distancia recorrida en millas, y �� es la cantidad de tiempo en horas, entonces viajar a 30 mph puede representarse mediante la ecuación �� = 30��. Los alumnos pueden o no utilizar esta representación mientras trabajan en las actividades de esta lección. Pero se familiarizarán más con este importante contexto que examinarán en mayor profundidad cuando estudien las razones y el razonamiento proporcional en séptimo grado, a partir de la próxima unidad.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento Independiente 5 min. Los alumnos analizan y comparan las velocidades de un coche y un tren para determinar cuál viaja más rápido en la misma distancia.

Actividad de exploración opcional Por parejas 15 min.

Actividad de exploración opcional Pares 10 min.

A partir de un mapa y su escala, los alumnos exploran las relaciones entre la distancia recorrida, el tiempo y la velocidad de los diferentes medios de transporte. Un applet digital interactivo está disponible para permitir a los estudiantes medir la distancia en el gráfico utilizando la tecnología.

Los alumnos estiman la distancia y el tiempo que se tardará en viajar en bicicleta entre dos ciudades utilizando el mapa dado y su escala.

Hay disponible una extensión de exploración para desarrollar una comprensión más profunda de los mapas dibujados a escala y no dibujados a escala.

Síntesis Independiente 5 min. Los alumnos generalizan la relación entre distancia, tiempo y velocidad al viajar entre dos puntos.

Enfriamiento Independiente 5 min.

Los estudiantes aplican la relación entre distancia, tiempo y velocidad para determinar valores desconocidos utilizando un mapa y su escala.

Práctica Independiente 10 min. El componente de práctica independiente incluye 2 problemas de la lección.

Matemáticas de 7º grado . Unidad 1

CALENTAMIENTO | UN TREN Y UN COCHE

5 minutos

Este calentamiento tiene dos propósitos. Refresca el concepto de distancia, velocidad y tiempo de viaje del 6º curso, preparando a los alumnos para utilizar dibujos a escala para resolver problemas relacionados con la velocidad. También permite a los estudiantes estimar los cálculos decimales.

Es probable que los estudiantes aborden la pregunta de diferentes maneras. A medida que los estudiantes trabajan, observe que utilizan cada estrategia.

• Encontrando o estimando la velocidad del tren en millas por hora y comparándola con la velocidad del coche

• Encontrando la distancia que recorre el coche en 4 horas y comparándola con la distancia que recorre el tren en 4 horas

Dé a los alumnos 3 minutos de tiempo para pensar en silencio. Pida a los alumnos que calculen la respuesta mentalmente y que hagan una señal cuando tengan una respuesta y una explicación. Continúe con un debate con toda la clase.

Apoyo para estudiantes con discapacidad

Memoria: Tiempo de procesamiento. Después de calcular mentalmente, proporcione notas adhesivas o minipizarras para ayudar a los alumnos con dificultades de memoria de trabajo.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTAS

Dos ciudades están a 243 millas de distancia.

• Un tren tarda 4 horas en viajar entre las dos ciudades a una velocidad constante.

• Un coche viaja entre las dos ciudades a una velocidad constante de 65 millas por hora.

¿Cuál viaja más rápido, el coche o el tren? Prepárese para explicar su razonamiento.

El coche viaja más rápido. Ejemplo de estrategia: la velocidad del tren en millas por hora es 243 ÷ 4. Esto es (240 ÷ 4) + (3 ÷ 4) = 60 3 4 , y eso es más lento que el coche. Alternativamente, en 4 horas, el coche recorrería 4 ⋅ 65 o 260 millas, y eso es más lejos que la distancia entre las ciudades. Así que, de nuevo, la conclusión es que el coche viaja más rápido.

Invite a los estudiantes a compartir sus estrategias. Asegúrese de destacar las diferentes estrategias, como calcular la velocidad del tren a partir de la información y calcular la distancia que recorrería el coche en 4 horas.

Grabe y muestre las explicaciones de los alumnos para que todos puedan verlas. Para que más alumnos participen en la conversación, pregúntales:

• ¿Alguien ha resuelto el problema de otra manera?

• ¿Alguien quiere añadir algo a la estrategia de ?

• ¿Estás de acuerdo o en desacuerdo? ¿Por qué?

de 7º grado . Unidad 1

ACTIVIDAD

DE EXPLORACIÓN OPCIONAL | CONDUCIR POR

LA I-90 15 minutos

Rutinas didácticas

MLR7: Comparar y conectar

Anticipar, monitorear, seleccionar, secuenciar, conectar

Aquí, los alumnos utilizan una escala y un dibujo a escala para responder a una pregunta relacionada con la velocidad. La tarea implica al menos un par de pasos más allá de hallar la distancia recorrida y puede abordarse de varias maneras. Aquí se ofrece un andamiaje mínimo, lo que permite a los alumnos representar con las matemáticas de forma más independiente (MP4).

A medida que los alumnos trabajan, observe los diferentes enfoques que utilizan para hallar la distancia real y para determinar si el conductor iba a gran velocidad. Algunas variaciones probables:

• Comparar la velocidad en millas por minuto (calcular la velocidad del coche en millas por minuto y convertir el límite de velocidad en millas por minuto).

• Comparar la velocidad en millas por hora (encontrar la velocidad del coche en millas por minuto y convertirla en millas por hora para poder compararla con el límite de velocidad en millas por hora).

• Comparar el tiempo que se tardaría en recorrer la misma distancia a dos velocidades diferentes (la del coche y la límite).

• Comparar la distancia recorrida en la misma cantidad de tiempo a dos velocidades diferentes (la del coche y la límite).

Identificar a los estudiantes que utilizan cada método para que puedan compartirlo más tarde.

INTRODUCCIÓN

Diga a los alumnos que ahora utilizarán un dibujo a escala (un mapa) para resolver un problema sobre la velocidad de desplazamiento. Pregunte a la clase si están familiarizados con los viajes por carretera y los límites de velocidad. Si algunos estudiantes no están familiarizados con los límites de velocidad, pida a los que sí lo están que se lo expliquen.

Organice a los estudiantes en grupos de 2 y facilíteles acceso a los juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Dé a los estudiantes 5 minutos para trabajar en el problema, ya sea individualmente o con su compañero.

En la Actividad Digital, los estudiantes tienen opciones sobre el número de puntos a trazar a lo largo de la ruta y si quieren o no dibujar segmentos. Los alumnos deben prestar atención a la leyenda del mapa; activar la cuadrícula les ayuda a ver que una unidad en la cuadrícula equivale a 0,5 millas.

Apoyo para estudiantes con discapacidades

Habilidades motoras finas: Tutores. Empareje a los estudiantes con sus compañeros tutores previamente identificados y permita a los estudiantes que tienen dificultades con la motricidad fina dictar medidas según sea necesario.

Motricidad fina: Tecnología de apoyo. Proporcione acceso a la versión digital de esta actividad.

1. Un conductor viaja a velocidad constante por la interestatal 90 a las afueras de Chicago. Si viajó del Punto A al Punto B en 8 minutos, ¿obedeció el límite de velocidad de 55 millas por hora? Explique su razonamiento.

2. Un helicóptero de tráfico voló directamente del Punto A al Punto B en 8 minutos. ¿Viajó el helicóptero más rápido o más lento que el conductor? Explica o muestra tu razonamiento.

Matemáticas de 7º grado . Unidad 1

POSIBLES RESPUESTASS

1. No, no lo hizo. Ejemplos de explicaciones:

• Utilizando la escala y el papel, descubrí que la distancia del Punto A al Punto B es aproximadamente 8,5 veces la escala que representa 1 milla, o 8,5 millas. Si viajara a 55 millas por hora, tardaría aproximadamente 0,15 hora o 9 minutos en recorrer 8,5 millas, ya que 8,5 ÷ 55 ≈ 0,15. Como llegó de A a B en 8 minutos, debe haber ido más rápido que el límite de velocidad.

• La distancia entre A y B es aproximadamente 8,5 veces la longitud del segmento que representa 1 milla, por lo que la distancia es aproximadamente 8,5 millas. Recorrió 8,5 millas en 8 minutos, por lo que su velocidad fue de aproximadamente 1,06 millas por minuto. La velocidad de 55 millas por hora es aproximadamente 0.917 millas por minuto, así que el conductor no obedeció el límite de velocidad.

2. El helicóptero viajó más lento, ya que la distancia directa (en línea recta) es más corta que la distancia a lo largo de la autopista. Dado que tardó la misma cantidad de tiempo en recorrer una distancia más corta, el helicóptero viajó más despacio.

Es posible que los alumnos no se den cuenta de que necesitan comparar dos cantidades (ya sea dos velocidades, dos distancias recorridas en la misma cantidad de tiempo o dos duraciones de viaje) para responder a la pregunta sobre el exceso de velocidad. Recuérdeles que hay dos situaciones posibles: que el conductor respete el límite de velocidad o que no lo respete.

Una vez que los alumnos hayan comprobado que la distancia entre A y B es de aproximadamente 8,5 millas, podrían inclinarse por dividir 55 entre 8,5 simplemente porque 55 es un número mayor. Puede ser útil utilizar líneas numéricas dobles o una tabla para mostrar la relación entre las millas recorridas y el número de horas, así como utilizar ejemplos más amistosos de distancias (por ejemplo, "¿Cuánto tiempo se tardaría en recorrer 110 millas? 11 millas?").

SÍNTESIS DE LA ACTIVIDAD

Pida a los alumnos que indiquen si creen que el conductor iba con exceso de velocidad o no. Invite a los alumnos que abordaron la tarea de diferentes maneras a compartirla, destacando los métodos que se centran en:

• Calcular o estimar la velocidad a la que viaja el conductor (en millas por minuto o millas por hora)

• Averiguar cuánto tiempo se tardaría en hacer el viaje a la velocidad límite

• Averiguar qué distancia recorrería el conductor en 8 minutos yendo a la velocidad límite

Mostrar su trabajo o registrarlo o resumirlo para que todos lo vean.

Pregunte a los alumnos si creen que algún método parece más eficiente que otros y por qué. Destaque que todos los métodos implicaban hallar la distancia recorrida, y que el dibujo a escala y la escala nos permitían hallar esa distancia. Un método para resolver este problema que evita los decimales que aproximan las cantidades fraccionarias es observar que 55 millas por hora es lo mismo que 55 millas en 60 minutos, por lo que es menos de una milla por minuto. Por lo tanto, se tardará más de 8,5 minutos en recorrer 8,5 millas a 55 millas por hora, y el conductor debe haber ido con exceso de velocidad.

Apoyo para estudiantes de inglés

Speaking: Representar: MLR7 Comparar y conectar. Utilice esta rutina para que los alumnos compartan sus representaciones visuales de diferentes enfoques para determinar si el conductor iba a gran velocidad. Invite a los estudiantes a crear y luego compartir sus presentaciones con un compañero antes de seleccionar 2-3 estudiantes para compartir con la clase. En este debate, escuche y amplíe las diferentes formas de hacer comparaciones (por ejemplo, comparar la velocidad del conductor con el límite de velocidad utilizando millas por minuto o millas por hora; comparar el tiempo que se tardaría en recorrer la misma distancia a dos velocidades diferentes; comparar la distancia recorrida en el mismo tiempo a dos velocidades diferentes, utilizando millas por minuto o millas por hora; y comparar cuánto tiempo se tardaría en hacer el viaje al límite de velocidad con la distancia que recorrería el conductor en 8 minutos viajando al límite de velocidad).

Principio(s) de diseño: Maximizar la metaconciencia; Optimizar el resultado (comparación).

Matemáticas de 7º grado . Unidad 1

ACTIVIDAD DE EXPLORACIÓN OPCIONAL |

EN BICICLETA

POR KANSAS

10 minutos

Rutinas didácticas

MLR7: Comparar y conectar

Pensar Compartir

En la actividad anterior, los alumnos recibieron un mapa con una escala y la cantidad de tiempo que se tardaba en llegar de un lugar a otro. A partir de ahí, calculan la velocidad del trayecto. En esta actividad, los alumnos trabajan con la velocidad y un mapa con escala para encontrar la cantidad de tiempo que tardará un viaje.

La estrategia principal que se espera es medir la distancia entre los dos lugares en el mapa y utilizar la escala para convertirla en la distancia entre las ciudades reales. A continuación, los alumnos pueden calcular cuánto tiempo tardarán a 15 mph.

INTRODUCCIÓN

Diga a los estudiantes que ahora utilizarán un dibujo a escala (un mapa) para resolver un problema diferente sobre viajes, esta vez centrándose en cuánto tiempo tardarán. Pregunte a los alumnos cuál es el trayecto más largo que han recorrido en bicicleta. ¿Cuánto tardaron? ¿Conocen a alguien que haya ido más lejos o durante más tiempo? Si es así, ¿qué distancia y cuánto tiempo?

Mantén a los alumnos en los mismos grupos. Conceda a los alumnos 4-5 minutos de tiempo de trabajo en silencio, seguidos de un debate por parejas y con toda la clase.

Apoyo para alumnos con discapacidad

POSSIBLE RESPONSES

Un ciclista circula a una velocidad constante de 24 kilómetros por hora. A esta velocidad, ¿cuánto tardaría aproximadamente en recorrer el trayecto de Garden City a Dodge City, Kansas?

Procesamiento conceptual: Eliminar el tiempo de procesamiento. Proporcione la imagen del mapa a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad. ENUNCIADO

Las respuestas varían. Ejemplo de respuesta 1: Usando la escala, parece que hay unas 50 millas desde Garden City. En 3 horas, el ciclista recorrería 45 millas, y las 5 millas restantes le tomarían una hora o 20 minutos. El ciclista tardaría unas 3 horas y 20 minutos.

Ejemplo de respuesta 2: 15 mph son 15 millas en 60 minutos o 1 milla cada 4 minutos. Por lo tanto, 4 millas tardan 16 minutos. La escala (4 millas) encaja un poco más de 12 veces, lo que significa que el viaje durará un poco más de 12 × 16 minutos. Eso es 192 minutos o 3 horas y 12 minutos.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

ERRORES PREVISTOS

La carretera de Garden City a Dodge City tiene muchas curvas. Es posible que los alumnos no estén seguros de cómo tratarlas. Diles que hagan su mejor estimación. Medir muchos segmentos pequeños de la carretera tendrá la ventaja de que esos segmentos cortos son rectos, pero lleva mucho tiempo. Una buena estimación será suficiente en este caso.

SÍNTESIS DE LA ACTIVIDAD

En primer lugar, pida a los alumnos que comparen las respuestas con un compañero y discutan su razonamiento hasta llegar a un acuerdo.

A continuación, invite a los alumnos a compartir cómo estimaron la distancia entre las dos ciudades (y cuánto tarda el ciclista en recorrer esta distancia). Pida a los alumnos que piensen en las diferentes distancias que han calculado para el trayecto. ¿Cuáles son las razones de estas diferencias? Las posibles explicaciones incluyen:

• Error de medición

• El camino no es recto y, por lo tanto, debe ser aproximado

• Para los estudiantes que trazan la escala una y otra vez para cubrir la distancia, es difícil estimar la fracción de la escala en el último paso

Debido a estas diferentes fuentes de inexactitud, informar la distancia como 50 millas es razonable; informarla como 52 millas requeriría mucho tiempo y mediciones; e informarla como 516 millas no es razonable con la escala y el mapa dados.

Apoyo para estudiantes de inglés

Speaking: Listening: MLR7 Comparar y conectar. Mientras los estudiantes trabajan para determinar la duración del viaje de Garden City a Dodge City, busque estudiantes con diferentes estrategias para estimar la distancia entre las dos ciudades. A medida que los estudiantes investigan el trabajo de los demás, pídales que compartan lo que funcionó bien en un enfoque particular. Durante esta discusión, preste atención a cualquier comentario que haga que la estimación de la distancia sea más precisa. A continuación, anime a los alumnos a establecer conexiones entre los distintos usos de la velocidad constante para calcular la duración del viaje. Amplíe el lenguaje que utilizan los alumnos para dar sentido a la velocidad constante del ciclista y cómo podría representarse en el mapa. Esto apoyará conversaciones constructivas mientras los alumnos comparan estrategias para calcular la duración de un viaje y establecen conexiones entre la cantidad y las representaciones visuales de la velocidad constante en el mapa. Principio(s) de diseño: Cultivar la conversación; Maximizar la metaconciencia

¿Estás listo para más?

Jada encuentra un mapa que dice: "Nota: Este mapa no está a escala". ¿Qué crees que significa? ¿Por qué es importante esta información?

"¿Estás preparado para más?" Respuesta del alumno

Las respuestas varían. Ejemplo de respuesta: significa que no hay un factor de escala que relacione las distancias en el mapa con las distancias en el lugar representado por el mapa. Algunas distancias están distorsionadas. Si Jada utilizara su mapa para calcular cuánto tardaría en viajar de un punto a otro del mapa, su predicción podría ser inexacta.

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA LECCIÓN

5 minutos

Un mapa con escala ayuda a estimar la distancia entre dos lugares midiendo la distancia en el mapa y utilizando la escala para encontrar la distancia real. Una vez conocida la distancia entre dos lugares:

• Si conocemos la duración del viaje, podemos calcular la velocidad hallando el cociente entre la distancia y el tiempo.

• Si conocemos la velocidad, podemos calcular la duración del viaje hallando el cociente entre la distancia y la velocidad.

En ambos casos, hay que tener cuidado con las unidades. Por ejemplo, si un viaje de 130 millas a una velocidad constante dura dos horas, entonces la velocidad es 65 millas por hora, porque 130 ÷ 2 = 65. Un viaje de 35 millas a 70 millas por hora toma 1 2 hora, porque 35 ÷ 70 = 1 2

INTRODUCCIÓN

EL ESTUDIANTE

ENUNCIADO DE TAREA PARA

ENFRIAMIENTO | CAMINANDO ALREDEDOR DEL JARDÍN BOTÁNICO

5 minutos

Proporcione acceso a los juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Asegúrate de que los estudiantes sepan dónde están los límites del Jardín Botánico en el mapa.

Piensa en tu trabajo de hoy y escribe tu mejor definición de área. Aquí tienes un mapa del Jardín Botánico de Missouri . Clara caminó alrededor de todo el jardín.

1. ¿Cuál es la distancia real alrededor del jardín? Muestra tu razonamiento.

2. Clare tardó 30 minutos en dar la vuelta al jardín a velocidad constante. ¿A qué velocidad caminaba? Muestra tu razonamiento.

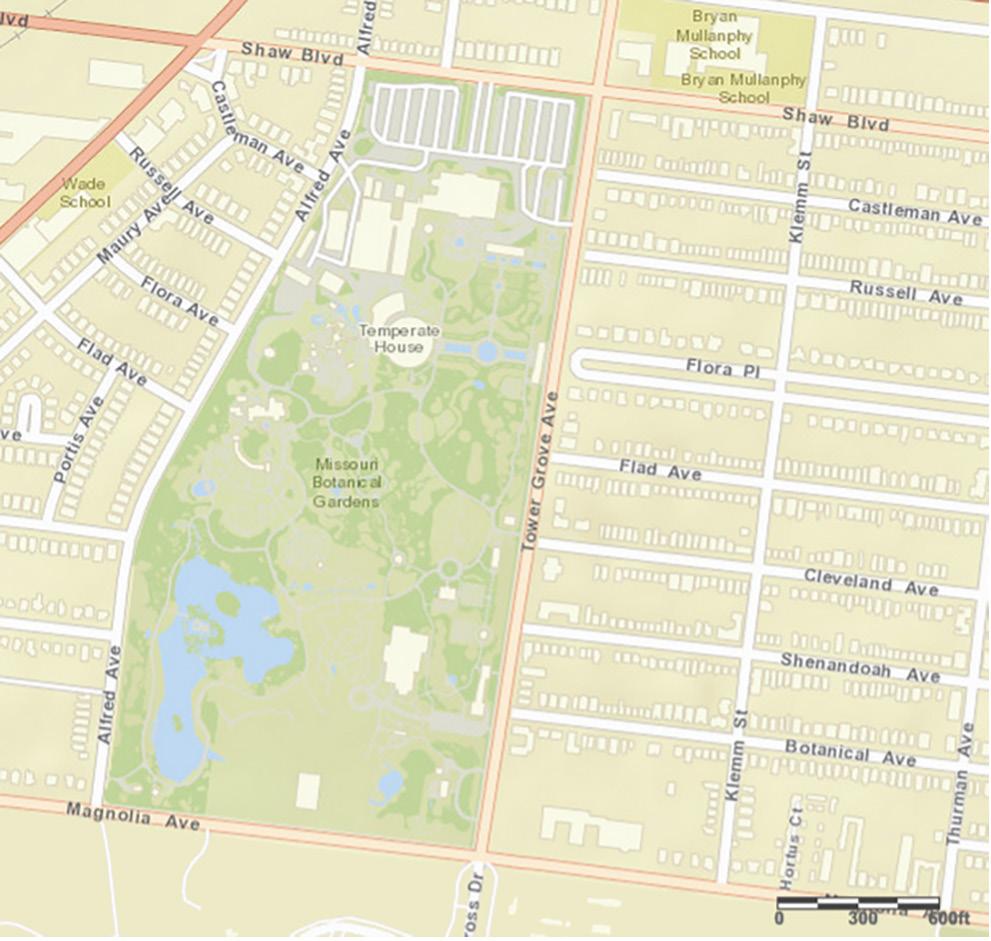
1. Se necesitan unos 14 segmentos de la escala para medir el perímetro del jardín, y 14 ⋅ 600 = 8.400. Así que la distancia alrededor es de unos 8.400 pies.

2. Si camina durante 30 minutos, significa que lo hace a unos 280 pies por minuto (8.400 ÷ 30 = 280), o a unos 16.800 pies por hora (280 ⋅ 60 ≈ 16.800).

California - Grado 7

Matemáticas de 7º grado . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Aquí hay un mapa que muestra partes de Texas y Oklahoma.

1. ¿Qué distancia hay aproximadamente de Amarillo a Oklahoma City? Explica tu razonamiento.

2. Conduciendo a una velocidad constante de 70 millas por hora, ¿será posible hacer este viaje en 3 horas? Explique cómo lo sabe.

Posibles soluciones

1. Aproximadamente 260 millas (pero la carretera no es recta, por lo que es difícil saber la distancia exacta a partir del mapa)

2. No, un viajero sólo puede recorrer 210 millas en 3 horas, y la distancia entre las ciudades es definitivamente mayor que eso.

PROBLEMA 2

Un parque local tiene forma de cuadrado. Se hace un mapa del parque local con la escala 1 pulgada a 200 pies.

1. Si el parque se muestra como un cuadrado en el mapa, cada lado del cual mide un pie, ¿cuánto mide cada lado del parque cuadrado?

2. Si un camino recto en el parque mide 900 pies, ¿qué longitud tendría el camino representado en el mapa?

Posibles soluciones

1. 2.400 pies

2. 4,5 pulgadas

Reflexiones:

Math Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

LECCIÓN

9

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Alineación de estándares y principios de Abordar

Enfoque SMPs

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.B.5

II.C.6

CREACIÓN DE DIBUJOS A ESCALA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo buscan y utilizan la estructura descubren la forma y el espacio y exploran las cantidades cambiantes.

META(S) DE APRENDIZAJE

• Vamos a crear nuestros propios dibujos a escala.

META(S) DE APRENDIZAJE

• Puedo determinar la escala de un dibujo a escala cuando conozco las longitudes en el dibujo y las longitudes reales correspondientes.

• Sé cómo afectan las diferentes escalas a las longitudes en el dibujo a escala.

• Cuando conozco las medidas reales, puedo crear un dibujo a escala a una escala dada.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comparar y contrastar (oralmente) diferentes dibujos a escala del mismo objeto, ay describir (oralmente) cómo afecta la escala al tamaño del dibujo.

• Crear un dibujo a escala, dadas las dimensiones reales del objeto y la escala .

• Determinar la escala utilizada para crear un dibujo a escala y generar múltiples formas de expresarlo (por escrito).

LESSON PREPARATION

Instructional Routines

Charla numérica

MLR8: Apoyo para la discusión

Piensa, empareja y comparte

MLR7: Compara y conecta

Observa y reflexiona

MLR3: Clarificar, Criticar, Corregir

Materiales necesarios

Enfriamiento

Juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)

Preparación necesaria

Asegúrese de que los estudiantes tienen acceso a los juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).

Matemáticas de 7º grado . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

En lecciones anteriores, los alumnos han utilizado dibujos a escala para calcular distancias reales. Esta es la primera lección en la que los alumnos utilizan la distancia real para calcular la distancia a escala y crear sus propios dibujos a escala. Observan cómo se pueden crear diferentes dibujos a escala de la misma cosa real, utilizando diferentes escalas. También ven cómo la elección de la escala influye en el dibujo. Por ejemplo, un dibujo a escala con una escala de 1 cm a 5 m será más pequeño que un dibujo a escala del mismo objeto con una escala de 1 cm a 2 m (since cada cm representa una distancia mayor, se necesitan menos cm para representar el objeto). Esto les prepara para futuras lecciones en las que recrearán un dibujo a una escala determinada a una escala diferente.

Notar cómo cambian los dibujos a escala con la elección de la escala desarrolla una importante comprensión estructural de los dibujos a escala (MP7).

LECCIÓN DE UN VISTAZO

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento Independiente 5 min. Los estudiantes comparan los cocientes de diferentes pares de números sin realizar los cálculos.

Después de considerar un croquis de una habitación no dibujado a escala, los estudiantes consideran cómo crear un plano de planta que sea un dibujo a escala utilizando una escala para determinar longitudes desconocidas.

Actividad de exploración Pares 10 min.

Un applet digital interactivo está disponible para permitir a los estudiantes explorar las escalas apropiadas utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de dar sentido a las escalas apropiadas.

Actividad de exploración Independiente 15 min. Los estudiantes crean y comparan diferentes dibujos a escala del estado de Utah.

Síntesis Todo el grupo 5 min.

Los estudiantes generalizan cómo una escala grande o pequeña afectaría al dibujo a escala y dan sentido a escribir una escala equivalente utilizando diferentes valores.

Enfriamiento Independiente 5 min. Los estudiantes hacen un dibujo a escala de una piscina utilizando una escala dada.

Práctica Independiente 10 min. El componente de práctica independiente incluye 2 problemas de la lección y 2 problemas en espiraleview.

Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

CALENTAMIENTO | HABLAR DE NÚMEROS: ¿CUÁL ES

MAYOR? 5 minutos

Rutinas didácticas

Charla numérica

MLR8: Apoyo a la discusión

En esta charla sobre números, los alumnos comparan cantidades que implican la división con números enteros, decimales y fracciones. En cada caso, existe una estrategia que no requiere calcular las cantidades. Cuando las cantidades son complejas, se motiva el uso de lae estructura de las expresiones a comparar (MP7) ya que los cálculos reales consumirían más tiempo.

INTRODUCCIÓN

Mostrar un problema a la vez. Dé a los estudiantes 2 minutos de tiempo para pensar en silencio por problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. A continuación, discute con toda la clase.

Apoyo a los estudiantes con discapacidad

Memoria: Tiempo de procesamiento. Proporcione notas adhesivas o minipizarras para ayudar a los alumnos con dificultades de memoria de trabajo.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Sin calcular, decide qué cociente es mayor.

11 ÷ 23 o 7 ÷ 13

0.63 ÷ 2 o 0.55 ÷ 3

15 ÷ 1 3 o 15 ÷ 1 4 POSIBLES RESPUESTASS

1. 7 ÷ 13 es mayor, porque es mayor que 1 2 mientras que 11 23 es menor que 1 2 .

2. 0,63 ÷ 2 es mayor que 0,55 ÷ 3 ya que 0,63 > 0,55 y 0,63 está siendo dividido por 2, mientras que 0.55 se está dividiendo en partes más iguales (3).

3. 15 ÷ 1 4 es mayor que 15 ÷ 1 3 ya que 1 4 es menor que 1 3 , y al dividir por una fracción (unidad) menor se obtiene un cociente mayor. ERRORES ANTICIPADOS

Los alumnos pueden interpretar erróneamente la última pregunta como 15 ⋅ 1 3 o 15 ⋅ 1 4

.Señale que una forma de interpretar la primera expresiónes "¿Cuántos tercios hay en 15?"

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Asegúrese de presentar diferentes enfoques para comparar las cantidades, evitando el cálculo directo cuandosea posible:

• 7 13 y 11 23 pueden compararse con 12, o los estudiantes pueden encontrar un numerador o denominador común, pero esto requiere más cálculos.

• 0.63 es mayor que 0.55, y 2 es menor que 3, o los alumnos pueden observar que 0.63 ÷ 2 es mayor que 0.3 while 0.55 ÷ 3 es menor que 0.2

• Dividir por 1 4 equivale a multiplicar por 4 mientras que dividir por 1 3 equivale a multiplicar por 3, so 15 ÷ 1 4 es mayor que 15 ÷ 1 3 .

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyos para el debate. Proporcione marcos de frases para ayudar a los alumnos a explicar sus estrategias. Fo ejemplo, "I noticed that , so I ." o "First, I because ." Cuando los alumnos compartan su respuestas con un compañero, pídales que ensayen lo que dirán cuando lo compartan con todo el grupo. Ensayar les brinda la oportunidad de aclarar sus ideas.

Principio(s) de diseño: Optimizar el resultado (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | PLANO DEL DORMITORIO

10 minutos

Rutinas didácticas

Pensar Compartir en Pareja

MLR7: Comparar y Conectar

En lecciones anteriores de esta unidad, los alumnos han investigado el significado de los dibujos a escala y los han utilizado para resolver problemas. El objetivo de esta actividad es preparar a los alumnos para crear su propio dibujo a escala. El debate pone de relieve que una escala puede expresarse de diferentes maneras, o que pueden utilizarse diferentes pares de números para mostrar la misma relación. Por ejemplo, una escala de 4 cm a 1 m es equivalente a una escala de 1 cm a 0,25 m.

A medida que los alumnos trabajen, fíjese en aquellos que utilicen el lenguaje de la escala adecuadamente, por ejemplo diciendo que "cada 4 cm en el dibujo representats 1 m", o "cada 0,25 m aparece como 1 cm en el dibujo". Fíjese también en los que prestan o no atención a la relación entre las longitudes reales y a escala a la hora de encontrar las medidas que faltan.

Explique a los alumnos que un plano de planta es un dibujo de vista superior que muestra la distribución de una habitación o de un edificio. Los planos de planta suelen ser dibujos a escala. Explique que a veces no se especifica la escala de un dibujo, pero que aún así podemos saber la escala si conocemos tanto la longitud a escala como la longitud real. Organice a los estudiantes en grupos de 2. Dé a los estudiantes 4-5 minutos de tiempo de trabajo en silencio y de discusión por parejas.

Para los alumnos que utilicen la Actividad Digital, los maestroes pueden permitir la exploración con el applet durante el tiempo de reflexión.

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.

Habilidades motoras finas: Tecnología de apoyo. Proporcione acceso a la versión digital de esta actividad. Lenguaje expresivo: Ayudas visuales. Revisar la tabla de anclaje (es decir, el muro de palabras) que muestra públicamente definiciones, reglas, fórmulas o conceptos importantes para ayudar en las explicaciones y el razonamiento.

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTASS

Noah ha hecho un boceto de la distribución de su habitación (no es un dibujo a escala).

1. Noah quiere crear un plano de planta que sea un dibujo a escala. La longitud real de la Pared C es 4 m. Noah dibuja un segmento 16 cm de largo para representar la Pared C. ¿Qué escala está utilizando? Explica o muestra tu razonamiento.

2. Busca otra forma de expresar la escala.

3. Haz una pausa y comenta tus respuestas con un compañero. ¿Cómo se comparan tus escalas?

4. Las longitudes reales del Muro A, el Muro B y el Muro D son 2,5 m, 2,75 m y 3,75 m. Determine qué longitud tendrán estas paredes en el plano a escala de Noé.

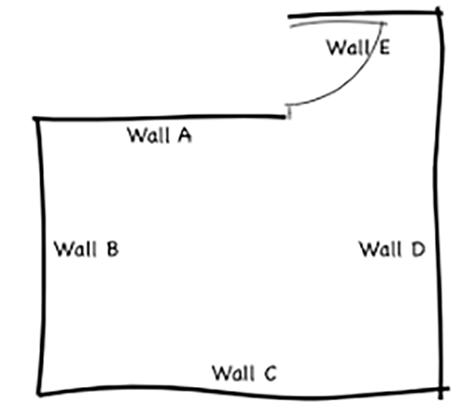
1. 4 cm a 1 m; 1 cm a 0,25 m; o 16 cm a 4 m. Ejemplo de explicación: Como 16 cm representa una longitud real de 4 m, entonces 1 cm debe representar 1 16 de 4 m, que es 0,25 m.

2. Las respuestas varían en función de la respuesta a la primera pregunta.

3. Las respuestas varían.

4. Pared A: 10 cm. Pared B: 11 cm. Pared D: 15 cm. Ejemplos de explicaciones:

• Como cada 1 m se muestra como 4 cm en el dibujo, he multiplicado las longitudes reales por 4

• Como cada 1 cm representa 0.25 m, dividí las longitudes reales por 0,25.

ERRORES ANTICIPADOS

Los alumnos pueden ver que un valor es 4 veces el otro y escribir la escala al revés, como "1 cm a 4 m". Pida a los alumnos que presten atención a las unidades y al significado de cada número.

SÍNTESIS

Centre el debate en clase en dos aspectos:

1. Diferentes formas de expresar la misma escala

2. La relación entre las longitudes a escala y las reales

Invite a un par de alumnos a compartir cómo determinaron la escala del dibujo. Es probable que los alumnos propongan diversas variaciones, por ejemplo, 4 cm a 1 m, 1 cm a 0,25 m, 16 cm a 4 m, etc. Discuta cómo todas ellas expresan la misma relación y, por tanto, son equivalentes, especialmente cómo 4 cm a 1 m es equivalente a 1 cm a 0,25 m (o 1 cm a 1 4 m).

Explique que, aunque podemos expresar una escala de formas múltiples pero equivalentes, 1) las escalas se simplifican a menudo para mostrar la distancia real para 1 unidad a escala, y 2) es habitual expresar al menos una distancia (usualmentelly la distancia a escala) como un número entero o una fracción de referencia (por ejemplo, 1 4 1 2 ) o un punto de referencia decimal (p. ej., 0,25, 0,5, 0,75).

Dado su trabajo sobre copias a escala, los alumnos pueden inclinarse a decir que las longitudes a escala y reales están relacionadas por un factor de escala de 4. Pregunte: "¿Son las longitudes reales cuatro veces las longitudes del dibujo? ¿Por qué sí o por qué no? Señale que, como las unidades de las dos cantidades son diferentes, al multiplicar una longitud a escala en centímetros (por ejemplo, 2,5 cm) por 4 se obtendrá otra longitud en centímetros (10 cm), que no es la longitud real. No es esencial que los estudiantes sepan que el factor de escala aquí es 250. Ese trabajo se explorará en una próxima lección .

Matemáticas de 7º grado . Unidad 1

Apoyo para estudiantes de inglés

Speaking, Listening: MLR7 Comparar y conectar. Mientras los alumnos preparan una exposición visual de cómo han creado el plano, busque alumnos que hayan expresado la escala de formas diferentes. Mientras los estudiantes investigan el trabajo de los demás, pídales que compartan lo que está especialmente claro sobre un enfoque en particular. A continuación, anime a los alumnos a explicar por qué hay varias formas, aunque equivalentes, de expresar la escala, como 4 cm a 1 m y 1 cm a 0,25 m. Haga hincapié en el lenguaje utilizado para dar sentido a las distintas formas de expresar la misma escala (por ejemplo, Dado que 4 cm en el plano representa 1 m en la habitación real, entonces 1 cm en el plano representa 14 de 1 m, que es 0,25 m.) Esto reforzará el uso por parte de los alumnos del lenguaje matemático relacionado con las escalas equivalentes.

Principios de diseño: Cultivar la conversación; Maximizar la metaconciencia

¿Estás preparado para más?

Si Noé quisiera dibujar otro plano en el que la Pared C midiera 20 cm, ¿sería 1 cm a 5 m la escala correcta a utilizar? Exexplica tu razonamiento.

"¿Estás preparado para más?" Respuesta del alumno

No. Ejemplos de explicaciones:

• Si utilizó 1 cm a 5 m, la Pared C, que mide 4 m, será menos de 1 cm en el dibujo-mucho más pequeña de lo que él quería.

• Si utilizara 1 cm para 5 m, un segmento de 20-cm representaría un muro de 100-m de largo, que no es la longitud del Muro C.

ACTIVIDAD DE EXPLORACIÓN | DOS MAPAS DE

UTAH 15 minutos

Rutinas didácticas

Notar y maravillarse

MLR3: Clarificar, Criticar, Corregir

En la actividad anterior, los estudiantes calcularon las distancias a escala que necesitarían para crear un dibujo a escala, pero no crearonte el dibujo a escala. En esta actividad, crean dos dibujos a escala diferentes del estado de Utah y observan cómo la escala afectacts al dibujo. Una de las razones por las que la elección de una escala es importante es que queremos ver el nivel apropiado de detalle dentro de un espacio fijo. INTRODUCCIÓN

Mostrar el esquema de Utah y preguntar a los alumnos "¿Qué notáis?

¿Qué te llama la atención?"

Pide a los estudiantes que describan la forma: un rectángulo con un rectángulo más pequeño eliminado en la esquina superior derecha.

Da a los estudiantes 5-6 minutos de tiempo de trabajo en silencio seguidos de discusión en clase.

Apoyo a estudiantes con discapacidad

Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores compañeros previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten dibujos a escala según sea necesario.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

CONCEPTOS

POSIBLES RESPUESTAS

Un rectángulo alrededor de Utah mide aproximadamente 430 kilómetros de ancho y 560 kilómetros de alto. La esquina superior derecha que falta mide aproximadamente 177 kilómetros de ancho y 112 kilómetros de alto.

Haz un dibujo a escala de Utah donde 1 centímetro represente 80 kilómetros.

Haz un dibujo a escala de Utah donde 1 centímetro represente 120 kilómetros.

¿Cómo se comparan los dos dibujos? ¿Cómo influye la elección de la escala en el dibujo?

1. Un rectángulo de aproximadamente 5,4 centímetros de ancho y 7 centímetros de alto, al que le falta la esquina superior derecha, que mide aproximadamente 2,2 centímetros de ancho y 1,4 centímetros de alto.

2. Un rectángulo de aproximadamente 3,6 centímetros de ancho y 4,7 centímetros de alto, al que le falta la esquina superior derecha, que mide aproximadamente 1,5 centímetros de ancho y 1 centímetro de alto.

3. Las medidas en los dibujos a escala de 1 cm a 50 millas son mayores que las medidas en el dibujo a escala de 1 cm a 75 millas. Esto tiene sentido, ya que cuando 1 centímetro representa 50 millas, se necesitan 1,5 centímetros para representar 75 millas.

Algunos estudiantes pueden obtener una figura que no sea cerrada o que no tenga ángulos rectos si no midieron con suficiente cuidado. Anímelos a que revisen la medida de un lado específico del estado si puede identificar fácilmente qué lado está mal dibujado.

Los estudiantes pueden pensar que una escala de 1 centímetro por 50 millas producirá un dibujo a menor escala que una escala de 1 centímetro por 75 millas (porque 50 es menor que 75). Pregúnteles cuántos centímetros se necesitan para representar 75 millas si 1 centímetro representa 50 millas (1.5) y cuántos centímetros se necesitan para representar 75 millas si 1 centímetro representa 75 millas (1).

SÍNTESIS

Pregunte a los estudiantes qué tienen en común los dos dibujos a escala. Las respuestas incluyen: ambos representan a Utah, ambos tienen la misma forma y ambos pueden usarse para medir distancias en el estado de Utah.

Pregunte a los estudiantes en qué se diferencian los dos dibujos a escala. El que tiene una escala de 1 centímetro por 50 millas es más grande que el que tiene una escala de 1 centímetro por 75 millas.

Algunos estudiantes pueden notar que el dibujo a escala de 1 centímetro por 75 millas es en realidad una copia a escala del otro dibujo, con un factor de escala de 1,5. De ser así, pídales que compartan su observación relacionando los dibujos a escala con las copias a escala.

Matemáticas de 7º grado . Unidad 1

Apoyo para estudiantes de inglés

Reading, Speaking: MLR3 Aclarar, Criticar, Corregir. Antes de presentar los dibujos a escala correctos de Utah, presentar un dibujo incorrecto y una explicación escrita. Por ejemplo, presentar un rectángulo de aproximadamente 5,4 cm de ancho y 7 cm de alto al que le falta una esquina superior derecha que mide aproximadamente 1,4 cm de ancho y 2,2 cm de alto, y proporcionar la afirmación: "Como 1 cm representa 50 millas, dividí 110 y 70 cada uno por 50, y obtuve 2,2 y 1,4 El pequeño rectángulo que falta mide 2,2 cm de alto y 1,4 cm de ancho". Pida a los alumnos que identifiquen el error, critiquen el razonamiento y revisen el enunciado para que el dibujo sea un dibujo a escala de Utah. Esto recordará a los alumnos las características de los dibujos a escala que se trataron en lecciones anteriores y cómo determinar si un dibujo puede considerarse un dibujo a escala de un objeto real.

Principio(s) de diseño: Optimizar la salida (para la explicación); Maximizar la metaconciencia

SÍNTESIS DE LA LECCIÓN

5 minutos

El tamaño de la escala determina el tamaño del dibujo. Se pueden tener dibujos a escala de diferentes tamaños del mismo objeto real, pero tel tamaño del objeto real no cambia.

• "Supongamos que hay dos dibujos a escala de la misma casa. Uno utiliza la escala de 1 cm a 2 m, y el otro utiliza la scale 1 cm a 4 m. ¿Qué dibujo es más grande? ¿Por qué?" (El que tiene la escala de 1 cm a 2 m es más grande, porque se necesitan 2 cm en tel dibujo para representar 4 m de longitud real.)

• "Otro dibujo a escala de la casa utiliza la escala de 5 cm a 10 m. ¿Cómo se compara su tamaño con los otros dos?" (Tiene el mismo tamaño que el dibujo con la escala de 1 cm a 2 m.)

A veces dos escalas diferentes son en realidad equivalentes, como 5 cm a 10 m y 1 cm a 2 m. Es habitual escribir una escala de modo queen ella te indique lo que representa una unidad en el dibujo a escala (por ejemplo, 1 cm a 2 m).

ENUNCIADO DE TAREA PARA

ENFRIAMIENTO | DIBUJAR UNA PISCINA

5 minutos

Una piscina rectangular mide 50 metros de largo y 25 metros de ancho. 1. Haz un dibujo a escala de la piscina en el que 1 centímetro represente 5 metros. 2. ¿Cuál es la longitud y la anchura de tu dibujo a escala?

California - Grado 7

de 7º grado . Unidad 1

PROBLEMAS PRÁCTICOS

PROBLEMA 1

La imagen de un libro que aparece en un sitio web mide 1,5 pulgadas de ancho y 3 pulgadas de alto en el monitor de un ordenador. El libro real mide 9 pulgadas de ancho.

1. ¿Qué escala se está usando para la imagen?

2. ¿Qué altura tiene el libro real?

Posibles soluciones

1. 1 pulgadas a 6 pulgadas

2. 18 pulgadas

PROBLEMA 2

La bandera de Colombia es un rectángulo que mide 6 pies de largo con tres franjas horizontales.

• La franja superior mide 2 pies de alto y es amarilla.

• La franja del medio mide 1 ft y es azul.

• La franja inferior también mide 1 ft y es roja.

1. Crea un dibujo a escala de la bandera colombiana con una escala de 1 cm a 2 ft.

2. Crea un dibujo a escala de la bandera de Colombia con una escala de 2 cm a 1 ft.

Posibles soluciones

1. La bandera medirá 3 cm de largo y 2 cm de alto. El rectángulo amarillo mide 1 cm de alto y los rectángulos rojo y azul miden 0,5 cm de alto cada uno.

2. La bandera medirá 12 cm de largo y 8 cm de alto. El rectángulo amarillo mide 4 cm y los rectángulos rojo y azul miden 2 cm cada uno.

PROBLEMA 3

Estos triángulos son copias a escala unos de otros. Para cada par de triángulos enumerados, el área del segundo triángulo es ¿cuántas veces mayor que el área del primero?

1. Triángulo G y Triángulo F 4. Triángulo F y Triángulo H

2. Triángulo G y Triángulo B 5. Triángulo G y Triángulo H Triángulo G y Triángulo H

3. Triángulo B y Triángulo F 6. Triángulo H y Triángulo B Triángulo H y Triángulo B

Posibles soluciones

1. 4

2. 1 4

3. 16

Matemáticas de 7º grado . Unidad 1

PROBLEMA 4

Del Grado 7, Unidad 1, Lección 3

Aquí hay un rectángulo sin etiquetar, seguido de otros cuadriláteros que están etiquetados.

1. Selecciona todos los cuadriláteros que son copias a escala del rectángulo sin etiqueta. Explica cómo lo sabes.

2. En papel cuadriculado, dibuja una versión a escala diferente del rectángulo original.

Posibles soluciones

1. C, D, E y H. Ejemplo de explicación: La longitud y la anchura de cada copia están relacionadas con la longitud y la anchura del original por el mismo factor y los ángulos correspondientes no cambian.

2. Los dibujos varían. Ejemplo de respuesta:

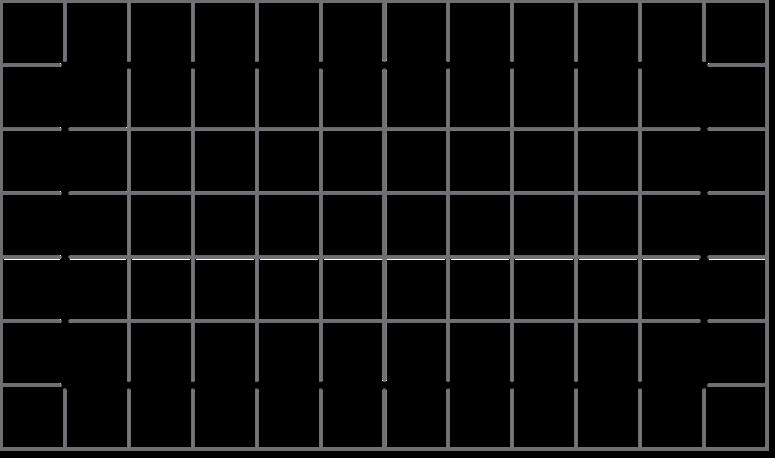
Reflejos:

LECCIÓN 10

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

Construir

6.G.1

Construir

7.G.6 7.RP.3

Enfoque SMPs

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

CA EP&Cs

3.B

I.A.3

II.C.6

CAMBIO DE ESCALAS EN LOS DIBUJOS DE SCALE

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo buscan y utilizan la estructura descubren la forma and sritmo y exploran las cantidades cambiantes.

META(S) DE APRENDIZAJE

• Exploremos diferentes dibujos a escala de la misma cosa real.

META(S) DE APRENDIZAJE

• Dado un dibujo a escala, puedo crear otro dibujo a escala que muestre la misma cosa a una escala diferente.

• Puedo usar un dibujo a escala para encontrar áreas reales.

• OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Determinar cuánta superficie real representa una unidad cuadrada en un dibujo aescala.

• Generalizar (oralmente) que a medida que aumenta la distancia real representada por una unidad en el dibujo aescala, disminuye el tamaño del dibujo a escala.

• Reproducir un dibujo a escala a una escala diferente y explicar (oralmente) el método desolución.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR2: Recoger y Mostrar

MLR7: Comparar y Conectar

Anticipar, Controlar, Seleccionar, Secuenciar, Conectar

Lápiz negro para la actividad 10.2

Enfriamiento

Herramientas de geometría (papel de calco, lápices de colores, tijeras y una ficha)Materiales necesarios

Láminas preimpresas, recortadas de las copias deLápiz negroLápiz negro para la actividad 10.2

Matemáticas de 7º grado . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación requerida

Imprime y recorta las escalas para la actividad de la misma parcela, diferentes dibujos del patrón de líneas negras (1 juego de escalas por grupode 5-6 estudiantes).

Asegúrate de que los estudiantes tengan acceso a sus juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una tarjeta de índice), especialmente las reglas centimétricas.

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

En la lección anterior, los estudiantes crearon múltiples dibujos a escala utilizando diferentes escalas. En esta lección, los alumnos reciben un dibujo a escala y se les pide que lo recreen a una escala diferente. Dos posibles estrategias para producir estos dibujos son:

• Calcular las longitudes reales y luego usar la nueva escala para encontrar las longitudes en el nuevo dibujo a escala.

• Relacionar las dos escalas y calcular las longitudes para el nuevo dibujo a escala usando las longitudes correspondientes en el ala given dra.

Además, los estudiantes vieron previamente que el área de una copia a escala se puede encontrar multiplicando el área de la figura original por (scale factor)2. En esta lección, amplían este trabajo de dos maneras:

• Comparan áreas de dibujos a escala del mismo objeto con diferentes escalas.

• Examinan cuánta área, en el objeto real, está representada por 1 centímetro cuadrado en el dibujo a escala.Por ejemplo, si la escala dees de 1 cm a 50 m, entonces 1 cm2 representa 50 ⋅ 50, o 2.500 m2

A lo largo de esta lección, los alumnos observan y explican la estructura (MP7), tanto cuando reproducen un dibujo a escala a unale aescala diferente como cuando estudian cómo el área de un dibujo a escala depende de la escala.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Descripción breve

Calentamiento En parejas 5 min. Los estudiantes aproximan las longitudes de los pies utilizando una regla proporcionada.

Los estudiantes aplican diferentes escalas para determinar las longitudes a escala y el área de un plote de terreno.

Actividad de exploración Grupos pequeños 15 min.

Esta tarea podría ampliarse como una oportunidad para establecer conexiones con las prácticas humanas que dependen de los ciclos que operan dentro de los sistemas naturales y cómo se construyen las carreteras en una ciudad para dar cabida a los espacios verdes naturales.

Se dispone de una extensión de exploración para desarrollar una comprensión más profunda de la comparación de escalas en los dibujos a escala.

Actividad de exploración Grupos reducidos 15 min. A partir de un dibujo a escala, los estudiantes crean y comparan dibujos utilizando diferentesescalas.

Síntesis Todo el grupo 5 min. Los alumnos relacionan las longitudes y las áreas de los dibujos creados a diferentes escalas y cómo el cambio de escala afecta a lo que transmite el dibujo.

Enfriamiento Independiente 5 min. Los estudiantes crean un dibujo a escala utilizando una escala diferente a la original.

Práctica Independiente 5 min. El componente de práctica independiente incluye 3 en-lección y 2 rev espiraliew problemas.

Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

CALENTAMIENTO | MEDIDAS APROPIADAS

5 minutos

Este calentamiento anima a los alumnos a prestar atención a la precisión en las medidas, que será importante en el próximo trabajo.

PUESTA

EN MARCHA

Organice a los alumnos en grupos de 2. Conceda a los alumnos 1 minuto de tiempo de reflexión en silencio para estimar el tamaño de su propio pie en centímetros o pulgadas, y un momento para compartir su estimación con un compañero. A continuación, pídales que completen la tarea.

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los alumnos que se benefician de un tiempo de procesamiento adicional para que la repasen antes de realizar esta actividad.

Lenguaje expresivo: Eliminar Barreras. Proporcione marcos de oraciones para que los estudiantes expliquen su razonamiento (por ejemplo, es una medida apropiada porque .).

1. Si un estudiante usa una regla como esta para medir la longitud de su pie, ¿qué opciones serían las medidas adecuadas? Seleccione todas las que correspondan. Prepárese para explicar su razonamiento.

ENUNCIADO DE TAREA PARA

POSSIBLE RESPONSES

A. 9 1 4 inches

B. 9 5 64 inches

C. 23.47659 centimeters

D. 23.5 centimeters

E. 23.48 centimeters

2. Aquí hay un dibujo a escala del pie de un estudiante promedio de séptimo grado junto a un dibujo a escala del pie de la persona con los pies más grandes del mundo. Calcula la longitud del pie más grande.

1. A y D serían las únicas medidas apropiadas según las marcas de la regla dada.

1. Dado que la regla solo está marcada en 1 8 pulgadas y 1 10 centímetro, no pudimos obtener medidas tan precisas como B, C o E.

2. The largest foot in the world is about 1.5 times as long as the average seventh grader's foot. My foot is about 10 inches long, so the largest foot is about 15 inches or 1 foot and 3 inches long.

Matemáticas de 7º grado . Unidad 1

ERRORES PREVISTOS

Es posible que algunos alumnos digan que el pie grande mide aproximadamente 3 1 2 pulgadas o unos 9 centímetros, porque suponenque laregla mostrada en la primera pregunta está a la misma escala que los pies mostrados en la segunda pregunta.

SÍNTESIS DE LA ACTIVIDAD

Seleccione a algunos estudiantes para que compartan las medidas que creen que serían apropiadas basándose en la regla dada. Considera la posibilidad de exponer la imagen de la regla para que todos la vean y anota en ella las respuestas de los alumnos. Después de cada respuesta, pregunta a la clase si están de acuerdo o en desacuerdo.

Si los alumnos consideran que B, C o E es una medida apropiada, pídeles que compartan cómo se consigue ese nivel de precisión en la regla. Asegúrese de que los alumnos entienden que no sería apropiado informar de las medidas con una precisión de 1 64 of una pulgada o de las cienmilésimas de centímetro (es decir, demuestre que la regla no permite estos niveles de precisión).

La opción E de 23,48 cm puede merecer una atención específica. Con la regla, es posible adivinar que la centésima es un 8. Esto puede ser incluso correcto. El problema de comunicar la medida de esta forma es que alguien que la vea podría malinterpretarla e imaginar que se utilizó un aparato de medición extremadamente preciso para medir el pie, en lugar de esta regla. La forma en que se comunica una medida refleja cómo se tomó.

A continuación, invite a los alumnos a compartir sus estimaciones sobre la longitud del pie grande. Dado que es difícil medir la longitud de estos pies con mucha precisión, estas medidas no deben ser reportadas con un alto nivel de precisión; el centímetro más cercano sería lo apropiado.

ACTIVIDAD

DE EXPLORACIÓN

| MISMO GRÁFICO, DIBUJOS DIFERENTES

15 minutos

Rutinas didácticas

MLR2: Recoger y Mostrar

Esta actividad tiene varias finalidades: permitir a los alumnos practicar la creación de dibujos a escalas dadas, llamar la atención sobre la sización del dibujo a escala cuando cambia uno de los valores de la escala, y explorar más a fondo la relación entre el área a escala y el área real.Explique que las imágenes están dibujadas a escalas diferentes.

Cada miembro del grupo utiliza una escala diferente para calcular las longitudes a escala de la misma parcela de terreno, dibujar un dibujo a escala y calcular su área a escala. A continuación, el grupo ordena los distintos dibujos y los analiza. Piensan cuántos metros cuadrados de superficie real representa un centímetro cuadrado en cada dibujo. Es probable que los alumnos determinen este valor de dos maneras:

• Visualizando lo que representa un cuadrado de 1 × 1 centímetro a una escala determinada (por ejemplo, a una escala de 1 cm a 5 m, cada 1 cm2 representa 5 ⋅ 5, o 25 m2).

• Dividiendo el área real representada por el dibujo a escala por el área de sus dibujos a escala.

Las relaciones entre la escala, las longitudes en los dibujos a escala y el área en los dibujos a escala son ejemplos importantes de la estructura matemática (MP7) de los dibujos a escala.

Para esta actividad necesitará el patrón de líneas negras Mismo plano, diferentes dibujos.

Matemáticas de 7º grado . Unidad 1

INTRODUCCIÓN

Muestre este mapa de un barrio de Filadelfia para que todos lo vean. Diga a los alumnos que van a reproducir un mapa del terreno triangular a una escala diferente.

Diga a los alumnos que la base real del triángulo es 120 m y su altura real es 90 m. Pregunte: "¿Cuál es la superficie del terreno?". (5400 metros cuadrados -la mitad de la base por la altura del triángulo.)

Organice a los estudiantes en grupos de 5-6 y facilíteles acceso a papel milimetrado. Asigne a cada estudiante de un grupo una escala diferente (del patrón de líneas negras) para que la utilice para crear un dibujo a escala. Dé a los estudiantes 3-4 minutos de tiempo de trabajo en silencio para responder a las primeras 3 preguntas, y luego 1-2 minutos para trabajar en la última pregunta en sus grupos.

Recuerde a los alumnos que incluyan las unidades en sus medidas.

Apoyo

a estudiantes con discapacidad

Aquí tienes un mapa que muestra un terreno en forma de triángulo rectángulo.

1. Tu maestro te asignará una escala para que la utilices. En papel milimetrado , haz un dibujo a escala del terreno. Asegúrate de escribir la escala en el dibujo.

2. ¿Cuál es el área del triángulo que has dibujado? Explica o muestra tu razonamiento.

3. ¿Cuántos metros cuadrados representa 1 centímetro cuadrado en tu dibujo?

4. Cuando todos los miembros de tu grupo hayan terminado, ordena los dibujos a escala de mayor a menor. ¿Qué notas acerca de las escalas cuando tus dibujos están colocados en este orden?

1. Triángulos rectángulos de varios tamaños:

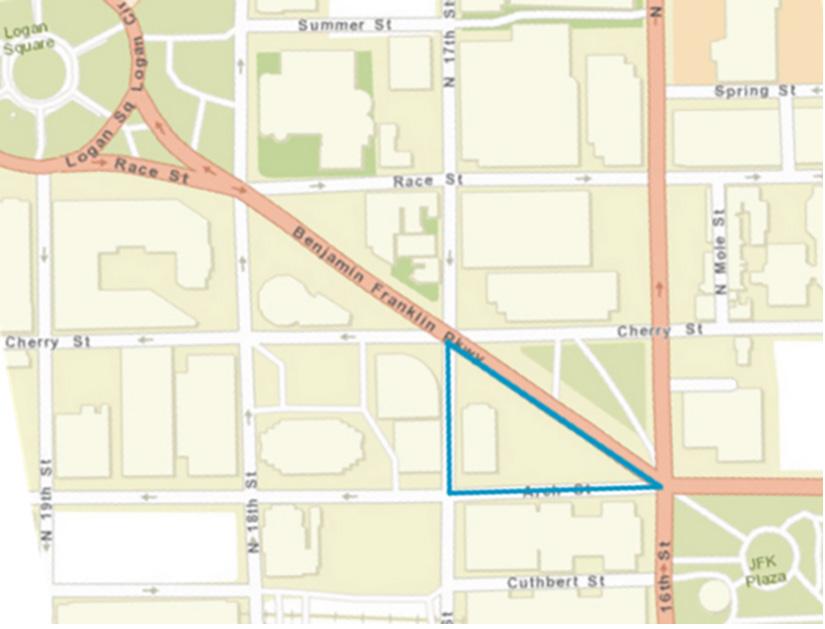
POSIBLES RESPUESTAS

2. Las respuestas varían dependiendo de la escala asignada. Posibles soluciones:

• 216 cm2, porque 1 2 - 24 ⋅ 18 = 216

• 54 cm2, porque 1 2 ⋅ 12 ⋅ 9 = 54

• 24 cm2, porque 1 2 ⋅ 8 ⋅ 6 = 24.

• 13.5 cm2, porque 1 2 ⋅ 6 ⋅ (4.5) = 13.5

• 6 cm2, porque 1 2 ⋅ 4 ⋅ 3 = 6

• 2.16 cm2, porque 1 2 ⋅ (2.4) ⋅ (1.8) = 2.16.

Matemáticas de 7º grado . Unidad 1

POSIBLES RESPUESTASS CONTINUACIÓN

SÍNTESIS DE LA ACTIVIDAD

1. Las respuestas varían en función de la escala asignada. Posibles soluciones:

• 25 m2, porque 5400 ÷ 216 = 25.

• 100 m2, porque 5400 ÷ 54 = 100

• 225 m2, porque 5400 ÷ 24= 225

• 400 m2, porque 5400 ÷ 13,5 = 400.

• 900 m2, porque 5400 ÷ 6 = 900

• 2.500 m2, porque 5400 ÷ 2.16 = 2500.

2. Cuanto menor sea el número de metros representados por un centímetro, mayor será el dibujo a escala.

Centre el debate en los patrones o características que los alumnos hayan observado en los diferentes dibujos a escala.

• ¿Cómo influye el cambio de escala en el tamaño de los dibujos?

• (A medida que aumenta la longitud representada por 1 cm, disminuye el tamaño del dibujo.)

• ¿Cómo se comparan las longitudes del dibujo a escala en el que 1 cm representa 5 metros con las longitudes del dibujo a escala en el que Formule preguntas como las siguientes:1 cm representa 15 metros? (Son tres veces más largas.)

• ¿Cómo se comparan las longitudes del dibujo a escala donde 1 cm representa 5 metros con las longitudes odel dibujong donde 1 cm representa 50 metros? (Son diez veces más largos.)

• ¿Cómo se compara el área del dibujo a escala donde 1 cm representa 5 metros con el área del dibujo donde 1 cm representa 15 metros? (Es 9 veces mayor.)

• ¿Cómo se compara el área del dibujo a escala donde 1 cm representa 5 metros con el área del dibujo donde 1 cm representa 50 metros? (Es 100 veces mayor.)

Ayude a los alumnos a observar y formular estos patrones:

• A medida que aumenta el número de metros representados por un centímetro, disminuyen las longitudes en el dibujo a escala.

• A medida que aumenta el número de metros representados por un centímetro, el área del dibujo a escala also dedisminuye, pero disminuye por el cuadrado del factor de las longitudes (porque hallar el área significa multiplicar la longitud y el ancho, los cuales disminuyen por el mismo factor).

Apoyo

para estudiantes de inglés

Conversar, leer: Rutina del Lenguaje Matemático 2 Recoger y Mostrar. Esta es la primera vez que se sugiere la Rutina 2 del Lenguaje Matemático como apoyo en este curso. En esta rutina, el maestro circula y escucha la conversación de los estudiantes mientras anota las palabras, frases, dibujos o escritos que los estudiantes utilizan. El lenguaje recogido se expone visualmente para que toda la clase pueda utilizarlo a lo largo de la lección y de la unidad. Por lo general, la exposición contiene diferentes ejemplos de alumnos que utilizan características de las funciones lingüísticas disciplinares, como interpretar, justificar o comparar. El propósito de esta rutina es capturar una variedad de palabras y frases de los estudiantes en una pantalla a la que los estudiantes puedan referirse, sobre la que puedan basarse o con la que puedan establecer conexiones durante futuras discusiones, y aumentar la conciencia de los estudiantes sobre el lenguaje utilizado en las conversaciones sobre matemáticas.

Principio(s) de diseño: Apoyar la creación de sentido; Maximizar la metaconciencia

Cómo sucede:

1. A medida que los estudiantes comparten sus ideas en sus grupos sobre lo que notan en los dibujos a escala, anote el lenguaje que utilizan para describir cómo la escala afecta al tamaño del dibujo a escala. Escuche el lenguaje que utilizan los alumnos para comparar las longitudes y las áreas de los dibujos a escala con diferentes escalas.

Para apoyar el debate, proporcione estos marcos de frases: "A medida que aumenta el valor de la escala, el tamaño del dibujo porque .", "Cuando comparo las longitudes de (elija dos dibujos a escala), me doy cuenta de que .", y "Cuando comparo las áreas de (elija dos dibujos a escala), me doy cuenta de que ."

2. Cuando los grupos terminen su conversación, muestre el lenguaje recopilado para que todos puedan consultarlo.

3. A continuación, facilite un debate con toda la clase animando a los alumnos a hacer y responder preguntas aclaratorias sobre el significado de una palabra o frase de la pantalla.

Para suscitar el debate, pregunte a los alumnos: "¿Qué palabra o frase no está clara? De la lengua que he recogido, ¿qué parte no tiene sentido para vosotros?".

He aquí un ejemplo:

Alumno A: La frase "el triángulo es 9 veces mayor" no me queda clara. No estoy seguro de lo que significa 9 veces mayor.

Maestro: [Señala la frase en la pantalla] ¿Puede alguien aclarar esta frase con detalles específicos?

Alumno B: El área del triángulo con una escala de 1 cm a 5 m es 9 veces mayor que el área del triángulo con una escala de 1 cm a 15 m.

Maestro: (pide más detalles) ¿Por qué es 9 veces mayor? ¿Puede alguien diferente explicar o ilustrar qué significa 9 veces mayor en este caso?

Alumno C: [El alumno añade un croquis de ambos triángulos a la pantalla junto a la frase; el maestro añade etiquetas/flechas/ cálculos al croquis mientras el alumno C explica] Es 9 veces mayor porque 15 m dividido por 5 m es 3, y como estamos hablando de área, entonces calculas 3 por 3 para obtener 9

4. Si el tiempo lo permite, continúa esta discusión hasta que se hayan abordado todas las preguntas. Si no ha surgido a través de las preguntas y respuestas de los alumnos, ayúdeles a generalizar que, a medida que aumenta el número de metros representados por one centimetro, disminuyen las longitudes y áreas del dibujo a escala. Si los alumnos tienen dificultades, considere la posibilidad de utilizar varios ejemplos de la actividad para llegar a la generalización. Puede decir: "Veamos el caso en el que estamos comparando...." o "¿Alguien puede demostrar tos steps que tomaron para comparar...?"

5. Cierre esta conversación colocando la pantalla en la parte delantera del aula para que los alumnos puedan consultarla durante el resto de la lección y, a continuación, haga que los alumnos pasen a la siguiente actividad.

¿Estás preparado para más?

Noé y Elena hacen cada uno un dibujo a escala del mismo terreno triangular, utilizando las siguientes escalas. Haz una predicción sobre ele tamaño de cada dibujo. ¿Cómo se compararían con los dibujos a escala realizados por tu grupo?

1. Noé utiliza la escala 1 cm a 200 m.

2. Elena utiliza la escala 2 cm a 25 m.

"¿Estás preparado para más?" Respuesta del alumno

1. El dibujo de Noé será más pequeño que todos los demás dibujos. La escala que creó el dibujo más pequeño hasta ahora fue 1 cm a 50 m. Cada longitud en un dibujo hecho a 1 cm a 200 m será 4 veces más pequeña que en el dibujo hecho a 1 cm a50 m porque cada centímetro representa 4 veces más longitud.

2. La escala 2 cm a 25 m es equivalente a 1 cm a 12.5 m, por lo que el dibujo de Elena será mayor que el de 1 cm a 15 m pero menor que el de 1 cm a 10 m.

ACTIVIDAD DE EXPLORACIÓN | UN NUEVO DIBUJO DE TTHE PLAYGROUND

15 minutos

Rutinas didácticas

MLR7: Comparar y conectar

Anticipar, controlar, seleccionar, secuenciar, conectar

Anteriormente, los alumnos crearon dibujos a escala a partir de las dimensiones reales y de diferentes escalas. En esta actividad, en lugar de darles las dimensiones reales, se les da un dibujo a escala para que lo reproduzcan a una escala diferente.

Matemáticas de 7º grado . Unidad 1

Los alumnos pueden aplicar dos tipos diferentes de razonamiento. Supervise a los estudiantes que:

• Utilicen el dibujo a escala para encontrar las dimensiones del patio de recreo real de la escuela y luego utilicen esas medidas para encontrar las dimensiones del nuevo dibujo a escala.

• Observe que en el dibujo dado, 1 centímetro representa 30 m, y en el nuevo dibujo, 1 centímetro representa 20 m.

Estot significa que cada centímetro en el nuevo dibujo representa 2 3 centímetros en el dado. Por tanto, en el nuevo dibujo, lae longitud de cada lado debe multiplicarse por un factor de 3 2

Seleccione a los alumnos que utilicen cada estrategia para compartirla durante la discusión, secuenciados en este orden.

INICIO

Diga a los alumnos que van a reproducir un dibujo a escala utilizando una escala diferente. La escala del dibujo dado es de 1 cm a 30 metros, y van a hacer un nuevo dibujo a escala de 1 cm a 20 metros. Pregúnteles si creen que el nuevo dibujo será más grande o más pequeño que el anterior.

Disponga a los alumnos en grupos de 3. Asegúrese de que disponen de sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a los estudiantes 5 minutos de trabajo en silencio, seguidos de 3 minutos de discusión en grupo.

Apoyo a estudiantes con discapacidad

Procesamiento conceptual: Eliminar Barreras. Permita que los alumnos utilicen calculadoras para garantizar una participación inclusiva en la actividad.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Este es un dibujo a escala de un parque infantil.

La escala es de 1 centímetro a 30 metros.

1. Haz otro dibujo a escala del mismo parque infantil a una escala de 1 centímetro a 20 metros.

2. ¿Cómo se comparan los dos dibujos a escala? POSIBLES RESPUESTASS

1. Copia a escala del dibujo donde cada borde es 1,5 veces más largo que en el dibujo.

2. El nuevo dibujo es más grande. Ejemplo de explicación: Cuando 1 cm representa 20 m, se necesita 1,5 cm para representar 30 m. Por lo tanto, las medidas de longitud en la escala de 1 cm a 20 m son 1,5 veces más largas de lo que son con la escala de 1 cm a 30 m. Las medidas del área son 2,25 (1,5 ⋅ 1,5) veces más grandes.

Puede que algunos alumnos no sepan cómo empezar la tarea. Indícales que empiecen calculando la longitud real de cada lado del patio.

California - Grado 7

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Invite a los alumnos seleccionados a compartir su trabajo de elaboración del nuevo dibujo a escala. Pregunte a los alumnos cómo se comparan los dos dibujos a escala. Asegúrese de que reconocen que las formas son las mismas (ambas representan el mismo parque infantil) pero los tamaños son diferentes.

Pregunte a los alumnos si su predicción sobre qué dibujo a escala sería más grande era correcta.y el dibujo a escala de 1 cm a 20 m es mayor que el dibujo a escala de 1 cm a 30 m.

La idea importante aquí es que cuando Pídales que expliquen por qué1 cm en el dibujo a escala representa una distancia mayor, se necesitan pocoser de esos centímetros para describir el objeto. Por lo tanto, el dibujo a escala de 1 cm a 30 m es más pequeño queel dibujo a escala dee a escala de 1 cm a 20 m.

Considere hacer una demostración en la que amplíe un mapa mostrando la escala.

Para animar a los alumnos a pensar en las áreas de los dibujos a escala como hicieron en la actividad anterior, considere hacer preguntas como las siguientes:

• "En el mapa original con la escala de 1 cm a 30 m, ¿cuánta área representa un centímetro cuadrado?" (900 cm2)

• "En el nuevo mapa con la escala de 1 cm a 20 m, ¿cuánta superficie representa un centímetro cuadrado?" (400 cm2)

• "¿Cuántas veces más grande que el mapa original es el nuevo mapa?" (1,5 veces para la longitud de los lados; 1,5 ⋅ 1,5, o 2.25, veces para el área)

Apoyo para estudiantes de inglés

Speaking, Listening: MLR7 Comparar y conectar. Pedir a los alumnos que establezcan conexiones entre las distintas estrategias deo para elaborar el nuevo dibujo a escala del parque infantil. Algunos estudiantes pueden encontrar las dimensiones del parque infantil real y luego utilizar esas medidas para encontrar las dimensiones del nuevo dibujo a escala. Otros pueden razonar que cuando 1 cm representa 20 m, se necesitan 1,5 cm para representar 30 m. Por lo tanto, las medidas de longitud en la escala de 1 cm a 20 m son 1.5 veces más largas de lo que son con la escala de 1 cm a 30 m. Anime a los alumnos a pensar por qué ambos métodos resultanlt en el mismo dibujo a escala. Esto fomentará el uso del lenguaje matemático por parte de los alumnos a medida que establezcan conexiones entre las distintas formas de reproducir un dibujo a escala a una escala diferente.

Principios de diseño: Cultivar la conversación; Maximizar la metaconciencia

SÍNTESIS DE LA LECCIÓN

5 minutos

A veces tenemos un dibujo a escala y queremos reproducirlo a una escala diferente. Dos enfoques comunes son:

1. Usar el dibujo a escala original para calcular las longitudes reales y luego usar las longitudes reales y la nueva escala para calcular las longitudes correspondientes en el nuevo dibujo.

2. Escalar las longitudes en el dibujo a escala original por un factor que relacione las escalas de los dos dibujos.

Supón que tienes un mapa que utiliza la escala 1 cm a 200 m. Dibujas un nuevo mapa del mismo lugar utilizando la escala 1 cm a 20 m.

• ¿Cómo se compara tu nuevo mapa con tu mapa original? (Las longitudes son 10 veces más largas y el área es 100 veces más grande.)

• ¿Cuánta área real representa 1 cm2 en tu nuevo mapa? (400 m2)

• ¿Cuánta superficie real representaba 1 cm2 en tu mapa original? (40.000 m2)

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTAS

ENFRIAMIENTO | MARCO DE VENTANA

5 minutos

Aquí hay un dibujo a escala de un marco de ventana que utiliza una escala de 1 cm a 6 pulgadas.

Crea otro dibujo a escala del marco de ventana que utiliza una escala de 1 cm a 12 pulgadas.

Copia a escala del dibujo donde cada longitud es la mitad que en el original.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Aquí hay un dibujo a escala de una piscina donde 1 cm representa 1 m.

1. ¿Qué longitud y anchura tiene la piscina real?

2. ¿Un dibujo a escala donde 1 cm representa 2 m será mayor o menor que este dibujo?

3. Haz un dibujo a escala de la piscina donde 1 cm representa 2 m.

Posibles soluciones

1. Las respuestas varían. Ejemplo de respuesta: El dibujo a escala mide 10 cm de largo y 5 cm de ancho, por lo que la piscina real mide 10 m de largo ay 5 m de ancho.

2. Será más pequeña. Cada centímetro representará una distancia mayor, por lo que se necesitarán menos centímetros para representar la anchura yd longitud de la piscina.

3. Las respuestas varían. Ejemplo de respuesta: La longitud y la anchura serán cada una la mitad del dibujo a escala dado. Así que el nuevo dibujo a escala de la piscina será 5 cm de largo y 2.5 cm de ancho.

PROBLEMA 2

Un mapa de un parque tiene una escala de 1 pulgadas a 1,000 pies. Otro mapa del mismo parque tiene una escala de 1 pulgada a 500 pies. ¿Qué mapa es más grande? Explica o muestra tu razonamiento.

Posibles soluciones

El mapa con una escala de 1 pulgadas a 500 pies. Se necesita el doble de unidades en este mapa para representar la misma distancia real recorrida por el otro mapa. Por ejemplo, en el mapa 1 pulgadas a 1.000 pies, se necesita 1 pulgadas para representar 1.000 pies en el parque real. En el mapa 1 pulgadas a 500 pies, se necesitan 2 pulgadas para representar los mismos 1.000 pies en el parque.

Matemáticas de 7º grado . Unidad 1

PROBLEMA 3

En un mapa con una escala de 1 pulgadas a 12 pies, el área de un restaurante es 60 en2. Han dice que la superficie real del restaurante es 720 pies2. ¿Estás de acuerdo o en desacuerdo? Explica tu razonamiento.

Posibles soluciones

No estoy de acuerdo. Ejemplo de razonamiento: A la escala de 1 pulgada a 12 pies, cada 1 pulgada cuadrada representa 144 pies cuadrados, ya que 12 ⋅ 12 = 144. El área real del restaurante debe ser 8,640 pies cuadrados, porque 60 ⋅ 144 = 8,640

PROBLEMA 4

Del Grado 7, Unidad 1, Lección 3

Si el cuadrilátero Q es una copia a escala del cuadrilátero P creado con un factor de escala de 3, ¿cuál es el perímetro de Q?

Posibles soluciones

186

PROBLEMA 5

Del 7º curso, Unidad 1, Lección 2

El triángulo DEF es una copia a escala del triángulo ABC. Para cada una de las siguientes partes del triángulo ABC, identifique el correspondiente parte del triángulo DEF

• ángulo ABC

• ángulo BCA

• segmento AC

• segmento BA

Posibles Soluciones

• ángulo DEF

• ángulo EFD

• segmento DF

• segmento ED

Reflexiones:

Math Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Alineación de estándares y principios de Abordar

Enfoque SMPs

MP6 Atender a la precisión.

MP7 Buscar y utilizar estructuras.

Estándares ELD de California

I.A.1

CA EP&Cs

4.C

I.A.4

I.B.5

LECCIÓN 11 ESCALAS SIN UNIDADES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo buscan y hacen uso de la estructura

OBJETIVO(S) DE APRENDIZAJE

• Exploremos una forma diferente de expresar las escalas.

OBJETIVO(S) DE APRENDIZAJE

descubriendo la forma y el espacio y explorando cantidades cambiantes.

• Puedo explicar el significado de las escalas expresadas sin unidades.

• Puedo utilizar escalas sin unidades para hallar distancias a escala o distancias reales.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Explicar (oralmente y por escrito) cómo utilizar escalas sin unidades para determinar distancias a escala o reales.

• Interpretar escalas expresadas sin unidades, por ejemplo, "1 a 50," (en lenguaje oral y escritotten).

PREPARACIÓN DE LA LECCIÓN

Materiales necesarios

Pensar, Compartir, Compartir en parejas

Anticipar, Controlar, Seleccionar, Secuenciar, Conectar

MLR8: Apoyos para el debate

Materiales necesarios

Lápiz negro para la actividad 11.2

Enfriamiento

Copias del lápiz negro

Reglas

Preparación necesaria

Para esta lección necesitará el Apollo Lunar Module blackline master. Prepara una copia por estudiante.

Asegúrate de que los estudiantes tengan acceso a los kits de herramientas de geometría (papel de calco papel cuadriculado, lápices de colores, tijeras, yy una ficha), especialmente reglasay papel cuadriculado.

de 7º grado . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

En lecciones anteriores, los alumnos trabajaron con escalas que asociaban dos medidas distintas: una para la distancia en un dibujo yd otra para la distancia real. Las unidades utilizadas en las dos medidas suelen ser diferentes (centímetro y metro, pulgada y pie, etc.). En esta lección, los alumnos ven que una escala puede expresarse sin unidades. Por ejemplo, considere la escala 1 a 60. Esto significa quet cada unidad de longitud en el dibujo a escala representa una longitud real que es 60 veces su tamaño, cualquiera que sea la unidad (inches, centímetros, etc.).

Expresar la escala como 1 a 60 resalta el factor de escala que relaciona el dibujo a escala con el objeto real. Cada medida del dibujo a escala se multiplica por 60 para encontrar la medida correspondiente en el objeto real. Esto guarda una estrecha relación con las copias a escala que se examinaron anteriormente en la unidad, en las que cada copia se relacionaba con el original mediante un factor de escala. Los alumnos comprenden mejor tanto las copias a escala como los dibujos a escala, ya que comprenden la estructura subyacente común (MP7).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento En parejas 5 min. Los estudiantes razonan sobre la escala de un mapa sin unidades dadas.

Los estudiantes analizan un dibujo a escala de un objeto del mundo real y, dada una escala, encuentran la longitud real del objeto.

Actividad de exploración Por parejas 15 min.

Actividad de exploración Independiente 15 min.

Síntesis Grupo completo 5 min.

Enfriamiento Independiente 5 min.

Esta tarea podría ampliarse como una oportunidad para hacer conexiones entre los sistemas naturales y las sociedades humanas en la Tierra y los recursos naturales que están disponibles en otros planetas a través de la exploración espacial.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda del uso de escalas sin unidades para resolver diferentes escenarios del mundo real.

Los estudiantes exploran las conexiones entre escalas con y sin unidades para crearte dibujos a escala.

Los estudiantes describen cómo una escala sin unidades y una escala con unidades pueden expresarse como una relación y utilizarse para resolver problemas.

Los estudiantes encuentran medidas reales utilizando un dibujo a escala y proporcionando una escala sin unidades.

Práctica Independiente 15 min. El componente de práctica independiente incluye 3 en-lección y 3 problemas en espiral revista.

CALENTAMIENTO | DE UNO A CIEN 5

minutos

Rutinas didácticas

Pensar Compartir en pareja

Este calentamiento presenta a los estudiantes una escala sin unidades y les invita a interpretarla utilizando lo que han aprendido sobre escalases hasta ahora.

A medida que los estudiantes trabajan y discuten, observe aquellos que interpretan la escala sin unidades como números que tienen las mismas unidades, así como aquellos que ven "1 a 100" como comparable a utilizar un factor de escala de 100. Invítelos a compartir su pensamiento más tarde.

INTRODUCCIÓN

Recuerde a los alumnos que, hasta ahora, hemos trabajado con escalas que especifican dos unidades cada una: una para el dibujo y otra para el objeto que representa. Diga a los estudiantes que a veces las escalas se dan sin unidades.

Organice a los estudiantes en grupos de 2. Dé a los estudiantes 2 minutos para pensar en silencio y otro minuto para discuss their thinking with a partner.

Apoyo a estudiantes con discapacidad

Funcionamiento socioemocional: Tutores. Emparejar a los estudiantes con sus tutores previamente identificados.

Un mapa de un parque dice que su escala es de 1 a 100.

1. ¿Qué crees que significa eso?

2. Da un ejemplo de cómo esta escala podría informarnos sobre las medidas en el parque.

1. Las respuestas varían. Ejemplos de respuestas:

• Las distancias en el parque son 100 veces mayores que las distancias correspondientes en el mapa.

• Una unidad en el mapa representa 100 unidades de distancia en el parque.

2. Las respuestas varían. Ejemplos de respuestas:

• Si un camino tiene 6 pulgadas de largo en el mapa, entonces podríamos decir que el camino real tiene 600 pulgadas de largo.

• Podríamos usar la escala para decir el tamaño del parque. Por ejemplo, si el parque mide 20 pulgadas de ancho on tel mapa, podemos decir que el parque real mide 2.000 pulgadas de ancho.

Los alumnos pueden pensar que, cuando no se dan unidades, podemos elegir las nuestras, utilizando unidades diferentess para tel 1 y el 100. Esta es una interpretación natural, dado el trabajo de los alumnos hasta ahora. Tome nota de estas malaconcepción, pero aborde la cuestión sólo si persiste más allá de la lección.

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Solicite a los alumnos ideas sobre el significado de la escala y pídales algunos ejemplos de lo que podría decirnos sobre las medidas en el parque. Si los alumnos aún no lo han mencionado, señale que una escala escrita sin unidades simplemente nos dice cuántas veces más grande o más pequeña es una medida real en comparación con lo que aparece en el dibujo. En este ejemplo, una distancia en el parque sería 100 veces la distancia correspondiente en el mapa, por lo que una distancia de 12 cm en el mapa significaría 1.200 cm o 12 m en el parque.

Explique que las distancias podrían estar en cualquier unidad, pero como una se expresa como un número multiplicado por la otra, la unidad es la misma para ambas.

Diga a los alumnos que exploraremos este tipo de escala en esta lección.

ACTIVIDAD DE EXPLORACIÓN | MÓDULO LUNAR

APOLO 15 minutos

Rutinas didácticas

Anticipar, Supervisar, Seleccionar, Secuenciar, Conectar

MLR8: Apoyos para el debate

En esta actividad, los alumnos utilizan un dibujo a escala y una escala expresada sin unidades para calcular longitudes reales. Los alumnos tendrán que elegir qué unidades utilizar, y algunas opciones facilitan el trabajo más que otras.

Observe los distintos caminos que pueden tomar los alumnos para determinar las alturas reales de los objetos del dibujo. Su elección de unidades podríad influir en el número de conversiones necesarias y en la eficiencia de sus caminos (como se muestra en las respuestas de muestra de los estudiantes). Seleccione estudiantes con los siguientes enfoques, secuenciados en este orden, para compartirlos durante la discusión.

• Medir en cm, encontrar los cm para la nave espacial real, luego convertir a m

• Medir en cm, convertir a m para el dibujo a escala, luego encontrar la medida de la nave espacial en m

Otro enfoque que los estudiantes pueden utilizar es medir el dibujo a escala utilizando una regla de pulgadas. Esto conlleva una conversión adicional de pulgadas a centímetros o metros. Pídales que consideren la unidad de interés. Discuta y destaque las elecciones estratégicas de unidades durante la sesión informativa para toda la clase.

Para esta actividad necesitará el esquema del módulo lunar Apollo.

Diga a los alumnos que Neil Armstrong y Buzz Aldrin fueron las primeras personas que caminaron sobre la superficie de la Luna. El Módulo Lunar Apolo fue la nave espacial utilizada por los astronautas cuando aterrizaron en la Luna en 1969. Considere la posibilidad de mostrar una imagen del módulo de aterrizaje como ésta. Explique a los alumnos que el módulo de aterrizaje formaba parte de una nave espacial más grande que se lanzó desde la Tierra.

Pida que hagan conjeturas sobre el tamaño de la nave espacial y sobre cómo podría compararse la altura de una persona con ella. Explique a los alumnos que van a utilizar un dibujo a escala del módulo lunar Apolo para averiguarlo.

Organice a los alumnos en grupos de 2. Entregue a cada alumno un dibujo a escala del módulo lunar Apolo (de la hoja maestra). Proporcione reglas en centímetros y pulgadas. Dé a los alumnos 3-4 minutos para responder a las dos primeras preguntas. Pídales que hagan una breve pausa y discutan sus respuestas con su compañero antes de completar el resto de las preguntas.

Se pide a los estudiantes que encuentren las alturas de las personas si están dibujadas "a escala". Explique que la frase significa "a la misma escala" o "a la escala especificada".

Apoyo a los estudiantes con discapacidad

Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen maestra de la línea negra a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.

Tu maestro te dará un dibujo del módulo lunar Apolo. Está dibujado a una escala de 1 a 50

1. Las "patas" de la nave espacial son su tren de aterrizaje. Utiliza el dibujo para calcular la longitud real de cada pata en los laterales. Escribe tu respuesta con una aproximación de 10 centímetros. Explica o muestra tu razonamiento.

2. Utiliza el dibujo para calcular la altura real del módulo lunar Apolo con una aproximación de 10 centímetros. Explica o muestra tu razonamiento.

3. Neil Armstrong medía 71 pulgadas cuando salió a la superficie de la Luna en el Módulo Lunar Apolo. ¿Qué altura tendría en el dibujo si se dibujara con su altura a escala? Demuestra tu razonamiento.

4. Dibuja una figura de palo que te represente de pie junto al módulo lunar Apolo. Asegúrate de que la altura de la figura está a escala. Muestra cómo determinaste tu altura en el dibujo.

1. La pata de la nave espacial mide aproximadamente 350 cm si sólo incluyes un segmento recto. Ejemplo de razonamiento:

• La pata mide unos 7 cm en el dibujo, así que la longitud real es 7 ⋅ 50 o 350 cm.

POSIBLES RESPUESTAS:

• Lapata mide unos 2,75 pulgadas en el dibujo, así que la longitud real es 137,5 pulgadas. (2,75) ⋅ 50 = 137,5. Multiplicando 137,5 por 2,54 se obtiene la longitud en centímetros. (137,5) ⋅ (2,54) = 349,5; esto es 350 cm redondeado a los 10 cm más cercanos.

2. El Módulo Lunar medía unos 7 metros de altura. Explicaciones de ejemplo:

• La nave espacial mide unos 14 cm de altura en el dibujo. La altura real es 50 veces 14 cm, lo que es 700 cm. 700 cm es 7 m.

• 14 cm es 0,14 m, porque 14 ÷ 100 = 0,14, y (0,14) ⋅ 50 = 7, así que la nave mide aproximadamente 7 m.

• La nave mide aproximadamente 5,5 pulgadas en el dibujo. (5,5) ⋅ 50 = 275. La altura real es de unas 275 pulgadas, lo que equivale a 698,5 cm. 275 ⋅ (2,54) = 698.5. 698.5 cm es 6.985 m, o aproximadamente 7 m. (No resaltesight esta solución en la discusión en clase.)

3. Neil Armstrong mediría aproximadamente 1.4 pulgadas en el dibujo a escala. Ejemplo de razonamiento: 71 ÷ 50 ≈ 1,4

4. Los dibujos varían en función de la estatura del alumno. Ejemplo de razonamiento:

• Mi altura es 5 pies y 2 pulgadas, lo que equivale a 62 pulgadas. (5 ⋅ 12) + 2 = 62. Mi altura en el dibujo es de aproximadamente 114 pulgadas, ya que 62 ÷ 50 ≈ 1,24

• Mido 155 cm. 155 ÷ 50 = 3,1. Mi altura es 3,1 cm en el dibujo.

Si los alumnos no están seguros de cómo empezar a averiguar la longitud real del tren de aterrizaje o la altura real de la nave espacial, sugiérales que primero averigüen la longitud en el dibujo.

Los alumnos pueden medir la altura de la nave espacial en centímetros y luego simplemente convertirla a metros sin utilizar la escala. Pida a los alumnos que consideren lo razonable de su respuesta (que probablemente esté en torno a 0,14 m) y recuérdeles que deben tener en cuenta la escala.

SÍNTESIS DE LA ACTIVIDAD

Matemáticas de 7º grado . Unidad 1

Invite a los alumnos seleccionados que midieron con una regla centimétrica a compartir sus estrategias y soluciones para las dos primeras preguntas. Considere la posibilidad de registrar sus razonamientos para que todos puedan verlos. Destaque la multiplicación de las medidas a escala por 50 para hallar las medidas reales. Por ejemplo, la altura de cada pierna esut 350 cm porque 50 ⋅ 7 = 350

Discute si importan o no las unidades en problemas que impliquen escalas sin unidades:

• ¿Importa qué unidad usamos para medir el dibujo? ¿Por qué sí o por qué no?

• ¿Qué unidad es más eficaz para medir la altura del módulo lunar en el dibujo: pulgadas o centímetros? (Dado que la pregunta pide una altura en metros, los centímetros serían más eficientes, ya que implican menos conversiones. Si la pregunta pide la altura real en pies, las pulgadas serían una unidad máse estratégica).

Pide a otros alumnos que compartan sus respuestas a las dos últimas preguntas. Selecciona a aquellos que hayan dado sus alturas en unidades diferentes para que compartan sus soluciones al último problema. Subraye que, independientemente de la unidad de partida, encontrar la longitud en el dibujo a escala implica dividir la medida real por 50. In otras palabras, las medidas reales pueden traducirse a medidas a escala

con un factor de escala de 1 50 .

Si el tiempo lo permite, considere la posibilidad de mostrar una fotografía de uno de los astronautas junto al módulo lunar, stal como shpropio aquí, como una forma de comprobar visualmente la razonabilidad de las soluciones de los alumnos.

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyo a la discusión. Utilice esta rutina para apoyar la discusión de toda la clase. Para cada respuesta u observación que se comparta, pida a los alumnos que repitan o vuelvan a expresar lo que han oído utilizando un lenguaje matemático preciso. Considere la posibilidad de dar tiempo a los alumnos para que repitan lo que han oído a un compañero, antes de seleccionar a uno o dos alumnos para que lo compartan con la clasee . Pregunte al orador original si su compañero ha sido capaz de expresar su pensamiento con precisión. Llame la atención de los alumnos sobreny palabras o frases que hayan ayudado a aclarar la afirmación original. De este modo, más alumnos tendrán la oportunidad deo producir lenguaje al interpretar el razonamiento de otros.

Principio(s) de diseño: Apoyar la creación de sentido

¿Estás preparado para más?

La tabla muestra la distancia entre el Sol y 8 planetas de nuestro sistema solar.

1. Si quisieras crear un modelo a escala del sistema solar que pudiera caber en algún lugar de tu escuela, ¿qué escala utilizarías?

2. El diámetro de la Tierra es de aproximadamente 8.000 millas. ¿Cuál sería el diámetro de la Tierra en tu maqueta?

planeta distancia media (millones de millas)

Mercurio 35

Venus 67

Tierra 93

Marte 142

Júpiter 484

Saturno 887

Urano 1.784

Neptuno 2.795

Matemáticas de 7º grado . Unidad 1

"¿Estás preparado para más?" Respuesta del alumno

Las respuestas varían. Ejemplo de respuesta:

1. El gimnasio tiene un espacio de unos 100 pies por 100 pies. La mayor distancia que necesitamos representar es entre el sun y Neptuno y esto es aproximadamente 2800 millones (o 3 billones) de millas. Así que si 1 pie representa unos 30 millones de millas, el sistema solar cabrá.

2. 8000 millas es una milésima parte de 8 millones de millas y una millonésima parte de 8000 millones de millas. Así pues, el diámetro de la Orejath será aproximadamente 3 millonésima parte de la distancia de Neptuno al Sol. Esta distancia está representada por unos 100 pies en tel scale model, por lo que el diámetro de la tierra será de unos 3 millonésimas de 100 pies. Esto es aproximadamente 1 2500 de pulgada. Esto es¡más grande que un grano fino de arena!

ACTIVIDAD DE EXPLORACIÓN | MISMO DIBUJO, DIFERENTES

ESCALAS

15 minutos

Rutinas didácticas

MLR8: Apoyos a la discusión

En esta actividad, los alumnos exploran la conexión entre una escala con unidades y otra sin unidades. Se les dan dos escalas equivalentes (una con unidades y otra sin ellas) y se les pide que expliquen por qué las dos pueden dar las mismas medidas a escala de un objeto real. También aprenden a reescribir una escala con unidades como una escala sin unidades.

Los alumnos tendrán que prestar atención a la precisión (MP6) mientras trabajan simultáneamente con escalas con unidades y sin unidades. Una escala de 1 pulgada a 16 pies es muy diferente de una escala de 1 a 16, y los estudiantes tienen múltiples oportunidades para abordar esta sutileza en la actividad.

A medida que los estudiantes trabajan, identifique los grupos que son capaces de razonar claramente acerca de por qué las dos escalas producen el mismo dibujo a escala.

• Utilizar las dos escalas y las dimensiones dadas del aparcamiento para calcular y verificar los cálculos de los estudiantes.

• Pensar en el significado de las escalas, es decir, en cada caso, las medidas reales son 180 veces las medidas en el dibujo a escala.Los dos tipos de razonamiento que se pueden esperar son:

Pregunte a los estudiantes: "¿Es posible expresar la escala 1 a 50 del Módulo Lunar como una escala con unidades? En caso afirmativo, ¿qué unidades utilizaríamos?". Solicite algunas ideas. Es probable que los alumnos digan "1 pulgadas a 50 pulgadas", y "1 cm a 50 cm". También pueden surgir otras unidades. Sin resolver las preguntas, explique a los alumnos que su siguiente tarea es explorar cómo una escala sin unidades y una con unidades podrían expresar la misma relación entre longitudes a escala y longitudes reales.

Mantenga a los alumnos en los mismos grupos. Proporcione reglas. Conceda a sus compañeros 3-4 minutos para responder a la primera preguntat question y otros 3-4 minutos de trabajo tranquilo para las dos últimas preguntas.

Apoyo a los alumnos con discapacidad

Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando la situación de una persona a la vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Un estacionamiento rectangular mide 36,5 metros de largo y 22,8 metros de ancho.

2. Lin hizo un dibujo a escala del estacionamiento de 2,54 cm por 4,56 metros. El dibujo mide 20,32 cm por 12,76 cm.

3. Diego hizo otro dibujo a escala del estacionamiento de 1 a 180, también de 20,32 cm por 12,76 cm.

4. Explica o muestra cómo cada escala daría como resultado un dibujo de 20,32 cm por 12,76 cm.

5. Haz otro dibujo a escala del mismo estacionamiento de 2,54 cm por 6,16 metros. Prepárate para explicar tu razonamiento.

6. Expresa la escala de 2,54 cm por 6,16 metros como una escala sin unidades. Explica tu razonamiento.

POSSIBLE RESPONSES

CONCEPTOS ERRÓNEOS ANTICIPADOS

Las respuestas varían. Ejemplos de explicaciones:

En el caso de Lin, 1 pulgada representa 15 pies, por lo que 120 pies son 8 pulgadas (120 ÷ 15 = 8) y 75 pies son 5 pulgadas (75 ÷ 15 = 5).

En el caso de Diego, 1 unidad en el dibujo representa 180 de la misma unidad en la distancia real, por lo que 1 pulgada representa 180 pulgadas. 180 pulgadas es igual a 15 ft (180 ÷ 12 = 15). Since the scale here is also 1 in to 15 ft, the drawing will also be 8 in by 5 in. 120 ft is 1,440 in (120 ⋅ 12 = 1,440) and 75 ft is 900 in (75 ⋅ 12 = 900). If the scale is 1 to 180, the sides of the parking lot will be 1,440 ÷ 180 and 900 ÷ 180, or 8 in and 5 in, respectively. El dibujo debe mostrar un rectángulo de 6 pulgadas por 3 3/4 pulgadas. Ejemplo de razonamiento: 120 ÷ 20 = 6. 75 ÷ 20 = 3 3 4 . 1 a 240.

Ejemplo de explicación: 20 pies son 240 pulgadas, por lo que 1 pulgada en el dibujo representa 240 pulgadas de distancia real.

Algunos estudiantes pueden tener dificultades para empezar. Sugiérales que empiecen por analizar cada escala por separado y que descubran, por ejempo, cómo una escala de 2,5 cm por 4,5 m produce un dibujo de 20 cm por 12,5 cm.

Seleccione un par de grupos previamente identificados para compartir sus respuestas a la primera pregunta y un par de grupos más para las otras preguntas.

Resalte cómo las longitudes escaladas y las longitudes reales están relacionadas por un factor de 180 en ambas escalas, y que este factor se muestra explícitamente en una escala pero no en la otra.

• En el caso de 1 a 180, sabemos que las longitudes reales son 180 veces más largas que las longitudes escaladas (o las longitudes escaladas son 1 180 de longitudes reales).

Si las longitudes a escala se dan en pulgadas, podemos usarlas para hallar las longitudes reales en pulgadas y, si se desea, convertirlas posteriormente a pies, y viceversa.

En el caso de 1 pulgada a 15 pies, aunque sabemos que las medidas reales no son 15 veces más largas que sus medidas correspondientes en un dibujo (porque 15 pies no es 15 veces más grande que 1 pulgada), no es inmediatamente evidente qué factor relaciona ambas medidas. Convertir las unidades nos ayuda a ver el factor de escala. Dado que 1 pie equivale a 12 pulgadas y 15 × 12 = 180, la escala de 1 pulgada a 15 pies es equivalente a la escala de 1 pulgada a 180 pulgadas, o de 1 a 180.

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyo a la discusión. Proporcionar marcos de oraciones para apoyar a los estudiantes en la producción de declaraciones sobre cómo se relacionan las longitudes a escala y las longitudes reales. Algunos ejemplos son: "Cuando el factor de escala es a , las longitudes reales son veces más largas que las longitudes a escala", o "Si el factor de escala es a , puedes encontrar la longitud a escala/real mediante ."

Principio(s) de Diseño: Apoyar la creación de sentido, Optimizar la salida (para explicación)

SÍNTESIS DE LA LECCIÓN

5 minutos

• ¿Qué significa que la escala de un dibujo a escala no indique ninguna unidad?

• ¿En qué se diferencia una escala sin unidades de una escala con unidades?

• ¿Cómo puede utilizarse una escala sin unidades para calcular distancias a escala o reales?

Cuando una escala no indica unidades, se utiliza la misma unidad tanto para la distancia a escala como para la distancia real. Por ejemplo, una escala de 1 a 500 significa que 1 pulgada en el dibujo representa 500 pulgadas en la distancia real, y 10 mm en un dibujo representa 5.000 mm en la distancia real. En otras palabras, la distancia real es 500 veces la distancia en el dibujo, y la distancia a escala es 1 500 de la distancia real. Para calcular las distancias reales, podemos multiplicar todas las distancias del dibujo por el factor 500, independientemente de la unidad que elijamos o nos den. Del mismo modo, para encontrar distancias a escala, multiplicamos las distancias reales por 1 500 , independientemente de la unidad utilizada. 500 y 1 500 son factores de escala que relacionan las dos medidas (real y a escala).

ENFRIAMIENTO | DIBUJOS DE PATIOS A ESCALA

5 minutos

André dibujó un plano de un patio a escala de 1 a 60. En su dibujo, un lado del patio mide 2.75 pulgadas.

1. ¿Cuál es la medida real de ese lado del patio? Expresa tu respuesta en pulgadas yen pies.

2. Si André hiciera otro dibujo a escala del patio a una escala de 1 a 12, ¿sería este dibujo más pequeñoo más grande que el primer dibujo? Explica tu razonamiento.

1. 165 pulgadas, que son 13,75 pies. Ejemplo de razonamiento: 2,75 ⋅ 60 = 165. 165 ÷ 12 = 13,75.

2. Sería más grande. Ejemplo de explicación: Una escala de 1 a 12 significa que la longitud en papel es 1 12 de la longitud original (o 10 pulgadas por 13,75 pulgadas), por lo que el dibujo sería mayor que uno dibujado a 1 60 la longitud original.

Matemáticas de 7º grado . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Un dibujo a escala de un coche se presenta en las tres escalas siguientes. Ordena los dibujos a escala de menor a mayor. Explica tu razonamiento. (Hay aproximadamente 1,1 yardas en un metro, y 2,54 cm en una pulgada.)

1. 1 in to 1 ft

2. 1 in to 1 m

3. 1 in to 1 yd

Posibles soluciones

b, c, a. Las explicaciones varían. Ejemplos de respuestas:

• De las tres unidades, 1 ft es la unidad más pequeña, y 1 m es la más grande. Por lo tanto, un dibujo con escala 1 in a 1 ft requerirá la mayor cantidad de unidades numéricas (la mayor), y un dibujo con escala 1 in a 1 m requerirá la menor (la menor).

• Cada escala se convirtió en una escala sin unidades. 1 in a 1 ft equivale a 1 a 12 1 in a 1 m equivale a 2.54 cm a 100 cm, lo que equivale aproximadamente a 1 a 39. Y 1 pulg. a 1 yd. equivale a 1 a 36

PROBLEMA 2

¿Qué escalas equivalen a 1 pulg. a 1 pie? Seleccione todas las que correspondan.

1. 1 a 12

2. 1 12 a 1

3. 100 a 0,12

Posibles soluciones

A, B, D, F

PROBLEMA 3

4. 5 a 60 5. 36 a 3 6. 9 a 108

Un aeromodelo se construye a una escala de 1 a 72. Si el modelo de avión mide 8 pulgadas, ¿cuántos pies mide el avión real?

Posibles soluciones

48 pies. El avión real mide 72 veces la longitud de la maqueta. 8 ⋅ 72 = 576 576 pulgadas son 48 pies, ya que 576 ÷ 12 = 48

PROBLEMA 4

Del Grado 7, Unidad 1, Lección 3

El cuadrilátero A tiene longitudes laterales 3, 6, 6, y 9. El cuadrilátero B es una copia a escala de A con una longitud lateral más corta igual a 2. Jada dice, "Puesto que las longitudes laterales disminuyen en 1 en esta escala, el perímetro disminuye en 4 en total." ¿Estás de acuerdo con Jada? Explica tu razonamiento.

Posibles soluciones

No. Las longitudes laterales de B no son cada 1 menos que las de A. Las longitudes laterales de B son 2 3 de las de A, por lo que deben ser 2, 4, 4, y 6. El perímetro de A es 24 y el perímetro de B es 16, lo que es 8 menos en total.

Matemáticas de 7º grado . Unidad 1

PROBLEMA 5

Del Grado 7, Unidad 1, Lección 6

El polígono B es una copia a escala del polígono A usando un factor de escala de 5. ¿El área del polígono A es qué fracción del área del polígono B?

Posibles soluciones

1 25

PROBLEMA 6

Del 7º Grado, Unidad 1, Lección 5

Las figuras R, S y T son copias a escala una de otra.3. La figura T es una copia a escala de S

La figura S es una copia a escala de R usando un factor de escala de usando un factor de escala de 2. Encuentra los factores de escala para cada una de las siguientes:

1. De T a S

2. De S a R

3. De R a T

4. De T a R

Posibles soluciones

Reflexiones:

Math Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

LECCIÓN

12

GRANDES IDEAS)

• Dibujo a escala

• Formas del mundo

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

Construir

6.RP.3d

Enfoque SMPs

MP7 Buscar y utilizar estructuras.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.A.1

I.C.12

II.C.6

UNIDADES EN DIBUJOS A ESCALA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo

buscan y hacen uso de la estructura

OBJETIVO(S) DE APRENDIZAJE

descubriendo la forma y el espacio y explorando cantidades cambiantes.

• Utilicemos diferentes escalas para describir el mismo dibujo.

OBJETIVO(S)

DE APRENDIZAJE

• Sé decir si dos escalas son equivalentes.

• Puedo escribir escalas con unidades como escalas sin unidades.

• Comprender que la frase "escalas equivalentes" se refiere a diferentes escalas que tienen el mismo factor de escala.Metas de aprendizaje para el docente

• Generar una escala sin unidades que sea equivalente a una escala dada con unidades, or vice versa.

• Justificar (oralmente y por escrito) que las escalas son equivalentes, incluyendo escalas conay sin unidades.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Turnos de palabra

MLR8: Apoyos para el debate Pensar en pareja Compartir

MLR5: Preguntas y problemas elaborados conjuntamente

Notar y maravillarse

Required Materials

Patrón de líneas negras para la Actividad 12.2

Patrón de líneas negras para la Actividad 12.4

Enfriamiento

Copias del patrón de líneas negras

Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras yuna ficha)

Tablas de conversión de unidades métricas y habituales

Fichas preimpresas, recortadas de las copias del patrón de líneas

negrasMateriales necesarios

Matemáticas de 7º grado . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación necesaria

Nota: Esta lección contiene actividades opcionales. Decida qué actividades va a realizar antes de preparar los materiales.

• Para la actividad de clasificación de tarjetas de escalas, imprima y recorte las fichas del patrón de líneas negras, de modo que cada grupo de 3-4 estudiantes tenga un juego completo. Si es posible, copie cada juego completo en un color de papel diferente, de modo que las fichas que se pierdan puedan volver a colocarse rápidamente en su sitio.

• Para la actividad de los estanques de reflexión, prepare una copia del patrón de líneas negras para cada estudiante.

Asegúrese de que los estudiantes tengan acceso a los juegos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). También se recomienda proporcionar una tabla de conversión de unidades de longitud métricas y consuetudinarias mientras los alumnos trabajan en las actividades de esta lección.

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

En lecciones anteriores, los alumnos aprendieron a expresar escalas cono sin unidades que pueden ser iguales o diferentes. En esta lección, analizan varias escalas y descubren que a veces es útil reescribir escalas con unidades como escalas sin unidades para poder compararlas. Ven que las escalas equivalentes relacionan las medidas escaladas y las reales mediante el mismo factor de escala, aunque las escalas puedan expresarse de forma diferente. Por ejemplo, la escala 1 pulgada a 2,5 pies es equivalente a la escala 5 m a 150 m, porque ambas son unat a escala de 1 a 30

Esta lección es también la culminación del trabajo de los alumnos sobre escalas y áreas. Los estudiantes han visto muchos ejemplos de la relación entre el área a escala y el área real, y ahora deben utilizar esta comprensión para encontrar el área de una piscina de forma irregular (MP7, MP8).

A continuación se presentan algunos factores de conversión que los estudiantes pueden querer consultar durante estas actividades.

RESUMEN

DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento Independiente 5 min.

Actividad de exploración opcional Grupos pequeños 15 min.

Actividad Exploratoria Grupos Pequeños 15 min.

Nation California - Grado 7

Los estudiantes identifican una expresión equivalente que representa una conversión de unidades.

Los estudiantes clasifican las tarjetas en grupos de escalas equivalentes identificando los grupos que tienen el mismo factor de escala.

Dada una escala, los estudiantes encuentran las dimensiones que faltan de una bandera y su modelo a escala. Después, determinan y comparan las áreas de las dos banderas.

de 7º grado . Unidad 1

LECCIÓN A SIMPLE VISTA CONTINUACIÓN

Componente de la lección

Actividad de exploración opcional

Estructura Tiempo

En parejas 10 min.

Síntesis Todo el grupo 5 min.

Enfriamiento Independiente 5 min.

Práctica Independiente 5-10 min.

Descripción breve

Los estudiantes calculan la escala de un plano de un centro recreativo para hallar las áreas de las piscinas rectangular y en forma de riñón.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la determinación de las áreas de copias a escala.

Los alumnos discuten cómo se pueden utilizar las escalas de un dibujo para determinar la longitud real o el área de una figura.

Los estudiantes reescriben las escalas dadas sin unidades para determinar qué escala drawing es mayor.

El componente de práctica independiente incluye 3 problemas en la clase y 3 problemas en espiralw.

CALENTAMIENTO | CENTÍMETROS EN UNA MILLA

5 minutos

El objetivo de este calentamiento es repasar expresiones en el contexto de las conversiones. Esta lección examinará en profundidad las escalas equivalentes, es decir, las escalas que conducen a un dibujo a escala del mismo tamaño. Comprobar si dos escalas son o no equivalentes suele implicar la conversión de cantidades a unidades comunes.

Apoyo a estudiantes con discapacidad

Procesamiento conceptual: Eliminar Barreras. Permita que los alumnos utilicen calculadoras para garantizar una participación inclusiva en la actividad.

Hay 2,54 cm en una pulgada, 12 pulgadas en un pie y 5280 pies en una milla. ¿Qué expresión representa la cantidad de centímetros en una milla? Explica tu razonamiento.

A. 2.54 12 · 5,280

B. 5,280 ⋅ 12 ⋅ (2.54)

C. 1 5280 · 12 · (2.54)

D. 5,280 + 12 + 2.54

E. 5280 ⋅ 12 2.54 POSSIBLE RESPONSES B

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Pide a uno o varios alumnos que expliquen su razonamiento para la elección correcta 5.280 ⋅ 12 ⋅ (2,54). Hay 2,54 centímetros en una pulgada y 12 pulgadas en un pie, lo que significa que hay 12 ⋅ (2,54) centímetros en un pie. Entonces hay 5.280 pies en una milla, así que eso hace 5.280 ⋅ 12 ⋅(2,54) centímetros en una milla. Los alumnos también pueden usar el sentido común sobre las medidas. Un centímetro es una unidad de medida pequeña, mientras que una milla es bastante grande, así que tiene que haber muchos centímetros en una milla. Asegúrese de preguntar a los alumnos qué representa la opción C, 1 5280 - 12 - (2.54) en este escenario. (El factor de escala para convertir de millas a centímetros.)

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | CLASIFICACIÓN DE TARJETAS DE ESCALAS

15 minutos

Rutinas didácticas

Toma turnos

MLR8: Apoyos para la discusión

El propósito de esta actividad es dar a los estudiantes más práctica en la identificación de escalas equivalentes, incluyendo algunas expresadas sin unidades y otras con unidades. Los alumnos trabajan con su grupo para clasificar las fichas en grupos de escalas equivalentes y explicar su razonamiento. Una clave envista para descubrir aquí es que, al comparar escalas, puede ser útil convertirlas en escalas equivalentes en un formato determinado (por ejemplo, sin unidades o utilizando las mismas unidades).

Para esta actividad necesitarás el patrón de líneas negras Ordenar tarjetas de escalas.

INTRODUCCIÓN

Demuestre cómo preparar y realizar la actividad de emparejamiento. Elige a un alumno como compañero. Mezcla el resto de las tarjetas y colócalas boca arriba. Elige dos tarjetas y explica a tu compañero por qué crees que las tarjetas coinciden o no. Demuestra formas productivas de estar de acuerdo o en desacuerdo (por ejemplo, explicando tu pensamiento matemático, haciendo preguntas aclaratorias, etc.).

Organiza a los estudiantes en grupos de 4. Si lo deseas, organiza a los estudiantes en grupos de 4-6 en dos dimensiones. (Asigne a cada estudiante a un grupo y luego a una etiqueta dentro de él, de modo que puedan formarse más tarde nuevos grupos -compuestos por un estudiante de cada uno de los grupos originales).

Dé a los estudiantes 5-6 minutos para clasificar las fichas, y otros 2-3 minutos para comprobar el trabajo de otro grupo, seguido de un debate de toda la clase.

Apoyo para estudiantes de inglés

Listening, Representing: MLR8 Apoyos para el debate. To aumentar la metaconciencia de los alumnos, piense en voz alta mientras demuestra el juego con un alumno. Mientras habla, modele el uso del lenguaje matemático y destaque la relación entre las escalas equivalentes.

Principio(s) de diseño: Maximizar la metaconciencia

Apoyo a estudiantes con discapacidad

Procesamiento conceptual: Eliminar barreras. Demuestre los pasos de la actividad o juego, haciendo que un grupo de alumnos y el personal jueguen una ronda de ejemplo mientras el resto de la clase observa.

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Tu maestro te dará unas tarjetas con una escala en cada tarjeta.

1. Ordena las tarjetas en conjuntos de escalas equivalentes. Prepárate para explicar cómo sabes que las escalas de cada conjunto son equivalentes. Cada grupo debe tener al menos dos tarjetas.

2. Cambia de grupo y comprueba el trabajo de los demás. Si no están de acuerdo sobre cómo deben ordenarse las escalas, trabajen para llegar a un acuerdo.

Hagan una pausa aquí para que su maestro pueda revisar su trabajo.

3. A continuación, registren uno de los conjuntos con tres escalas equivalentes y expliquen por qué son equivalentes.

POSIBLES RESPUESTASS

FALTAS PREVISTAS

• 1 centímetro a 1 metro, y 1 a 100

• 1 centímetro a 1 kilómetro, 1 2 cm a 500 m, y 1 a 100.000

• 1 pulgada a 8 pies, 1 8 pulgada a 1 pie, y 1 a 96

• 1 centímetro a 10 metros, 1 pulgada a 1.000 pulgadas, y 1 milímetro a 1 metro

• 1 pie a 1 milla, y 1 a 5.280

• 1 pulgada a 1 milla, y 1 a 63.360

2. No es necesario responder.

3. Las respuestas varían. Respuesta de ejemplo: En un kilómetro hay 100.000 centímetros. Además, 100.000 grupos de 1 2 centímetros son 50.000 centímetros. Esta es la misma longitud que 500 metros, porque 50,000 ÷ 100 = 500. Esto significa que las escalas 1 cm a 1 km y 1 2 cm a 500 m son ambas equivalentes a la escala 1 a 100.000.

Si los grupos tienen problemas para empezar, anímeles a pensar en diferentes formas de expresar una escala, tanto con unidades como sin ellas.

Los alumnos pueden clasificar las tarjetas por tipos (métrica o consuetudinaria; con unidades o sin unidades) en lugar de mediante factores de escala comunes. Recuerde a los alumnos que las escalas que son equivalentes tienen el mismo factor que relaciona sus longitudes escaladas con las longitudes reales.

Los alumnos pueden pensar que las escalas en unidades métricas y las que están en unidades consuetudinarias no pueden ser equivalentes. Por ejemplo, pueden pensar que "1 pulgadas a 1.000 pulgadas" pertenece a un grupo y "1 cm a 10 m" pertenece a otro. Si surge este malentendido y no se resuelve en las discusiones de grupo, aborde la cuestión durante la síntesis de la actividad.

Gran parte de la discusión se producirá en y entre los grupos pequeños, por lo que puede ser necesaria una reunión de toda la clase sólo para atar los cabos sueltos. Invite a algunos alumnos a compartir cómo razonó su grupo sobre un par de escalas (por ejemplo, de 1 2 cm a 500 m, de 1 mm a 1 m).

Aborde cualquier duda que haya surgido durante la clasificación, los conceptos erróneos comunes o los desacuerdos no resueltos entre los grupos. Por ejemplo, es posible que los alumnos aún no tengan claro si las escalas en unidades consuetudinarias y métricas pueden ser equivalentes. (Por ejemplo, ¿pueden ir en el mismo grupo "1 pulgadas a 1.000 pulgadas" y "1 centímetros a 10 metros"? ¿Por qué sí o por qué no?) Ayude a los alumnos a ver que, mientras las dos escalas representen el mismo factor de escala, son equivalentes y producirán el mismo dibujo a escala.

Si dispone de tiempo, pida a los alumnos que ordenen sus grupos de escalas equivalentes, empezando por las que producirían el dibujo más pequeño de la misma cosa real hasta las que producirían el dibujo más grande. Invite a los alumnos a explicar su razonamiento.

Matemáticas de 7º grado . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | LA BANDERA MÁS

GRANDE DEL MUNDO 15 minutos

Rutinas didácticas

MLR8: Apoyos para la discusión

Piense, comparta en parejas

En esta actividad, los alumnos utilizan una escala sin unidades para encontrar distancias reales y a escala que implican un rango más amplio de números, desde 0.02 hasta 2.000. También vuelven a pensar en cómo el área de un dibujo a escala se relaciona con el área de la cosa real.

Es probable que los estudiantes encuentren longitudes a escala de una de estas dos maneras: 1) convirtiendo primero la medida en metros a centímetros y dividiendo después por 2.000; o 2) dividiendo la medida por 2.000 y convirtiendo después el resultado a centímetros. Para hallar las longitudes reales, es probable que se sigan los mismos caminos, salvo que los alumnos multiplicarán por 2.000 e invertirán la conversión de unidades. Identifique a los estudiantes queho uutilizan diferentes enfoques para que puedan compartirlos más tarde.

INTRODUCCIÓN

Haga que los estudiantes cierren sus libros o dispositivos. Muestre una imagen de la bandera de Túnez. Explica que Túnez tiene el récord mundial de la versión más grande de la bandera de un país. La bandera récord mide casi cuatro campos de fútbol. Pida a los alumnos que adivinen la escala adecuada para crear un dibujo a escala de la bandera en una hoja de papel. Si se lo piden, indique la longitud de la bandera (396 m) y el tamaño del papel (ter tamaño: 8 1 2 pulgadas por 11 pulgadas, o aproximadamente 21,5 cm por 28 cm).

Después de escuchar algunas conjeturas, explique a los alumnos que ahora van a resolver problemas sobre la escala y elcale drawing de la gigantesca bandera tunecina.

Apoyo a los alumnos con discapacidad

Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (por ejemplo, un gráfico de conversión de unidades) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para futuras consultas.

Procesamiento conceptual: Eliminar Barreras. Permita que los alumnos utilicen calculadoras para garantizar una participación inclusiva en la actividad.

A partir de 2016, Túnez ostenta el récord mundial de la versión más grande de una bandera nacional. Era casi tan larga como cuatro campos de fútbol. La bandera tiene un círculo en el centro, una luna creciente dentro del círculo y una estrella dentro de la luna creciente. 1. Completa la tabla. Explica o muestra tu razonamiento.

Longitud de la bandera Altura de la bandera Altura de la luna creciente

TAREA PARA

ESTUDIANTE CONTINUACIÓN

1. Completa cada escala con el valor que la hace equivalente a la escala de 1 a 2.000.

Explica o muestra tu razonamiento.

A. 1 cm a cm

B. 1 cm a m

C. 1 cm a km

D. 2 m a m

E. 5 cm a m

F. cm a 1.000 m

G. mm a 20 m

POSIBLES RESPUESTASS

A. ¿Cuál es el área de la bandera grande?

B. ¿Cuál es el área de la bandera más pequeña?

C. El área de la bandera grande es ¿cuántas veces el área de la bandera más pequeña?

Longitud de la bandera

Altura de la bandera

Altura de la media luna

Ejemplo de razonamiento:

• Longitud de la bandera: 396 ÷ 2.000 = 0,198 0,198 m es 19,8 cm.

• Altura de la bandera: (13,2)⋅2.000=26.400. 26.400 cm es 264 m.

• Altura de la media luna en la bandera: 99 ÷ 2.000 = 0,0495. 0,0495 m es 4,95 cm.

A. 1 cm a 2.000 cm. 2.000 veces 1 cm es 2.000 cm.

B. 1 cm a 20 m. He convertido 2.000 cm a m. 2.000 ÷ 100 = 20

C. 1 cm a 0,02 km. He convertido 2000 cm a km. 2.000 ÷ 100.000 = 0,02.

D. 2 m a 4.000 m. 2.000 veces 2 m es 4.000 m.

E. 5 cm a 100 m. Sé que 1 cm representa 20 m, por lo que 5 cm representa 5 ⋅ 20

F. 50 cm a 1.000 m. He dividido 1.000 m por 2.000, lo que es 0,5 m o 50 cm.

G. 10 mm a 20 m. Sé que 1 cm representa 20 m y 1 cm es 10 mm, por lo que 10 mm representa 20 m.

A. La bandera grande mide 396 m por 264 m, por lo que su área es 104.544 m2

B. La bandera pequeña mide 19,8 cm por 13,2 cm, por lo que su área es 261,36 cm2 .

C. El factor de escala para la altura es 2.000 y el factor de escala para la longitud es 2.000, por lo que el área de la bandera real es 2.000 ⋅ 2.000, o 4.000.000 veces el área del dibujo a escala.

Los alumnos pueden confundirse sobre si multiplicar o dividir por 2.000 (o multiplicar por 2.000 o por 1 2000 ) al encontrar las longitudes que faltan. Anime a los alumnos a articular lo que significa una escala de 1 a 2.000, o recuérdeles que es una forma abreviada de decir "1 unidad en un dibujo a escala representa 2.000 ode las same unidades en el objeto que representa". Pídales que piensen cuál de las dos longitudes -real o a escala- es 2.000 veces la otra y cuál es 1 2000 de la otra.

Para la tercera pregunta, que relaciona el área de la bandera real con el modelo a escala, si los alumnos se quedan atascados, anímeles a que calculen las dimensiones de cada uno explícitamente y a que utilicen esto para calcular el factor de escala entrelas áreas.

Matemáticas de 7º grado . Unidad 1

DE LA ACTIVIDAD

SÍNTESIS

Selecciona a algunos alumnos con distintas vías de solución para que compartan sus respuestas a la primera pregunta. Registre y muestre sus razonamientos para que todos puedan verlos. Destaque dos formas diferentes de abordar las conversiones de unidades. Por ejemplo, para encontrar longitudes a escala, primero se puede convertir la longitud real en metros a centímetros y luego multiplicar por 1 2000 , o multiplicar primero por 1 2000 , y luego convertir el cociente en centímetros.

Invite a los estudiantes previamente identificados a mostrar y compartir sus respuestas para los subproblemas de la segunda pregunta. Después de que cada persona comparta, solicite preguntas o comentarios de la clase. Haga hincapié en que todas las escalas son equivalentes porque en cada escala, un factor de 2.000 relaciona las distancias a escala con las distancias reales.

Reitere el hecho de que una escala no tiene por qué expresarse en términos de 1 unidad a escala, como se muestra en las last three sub-preguntas, sino que 1 se elige a menudo porque hace que el factor de escala sea más fácil de ver y puede hacer que los cálculos sean más eficientes.

Asegúrese de que los alumnos entienden por qué el factor de escala para el área de las dos banderas es 4.000.000 (Tanto la longitud como la altura de la bandera grande son 2.000 veces la longitud y la altura de la bandera pequeña. Por tanto, el área de la bandera grande es 2.000 ⋅ 2.000 veces el área de la bandera pequeña. Alternativamente, hay 10.000 centímetros cuadrados en un metro cuadrado, así que en centímetros cuadrados, el área de la bandera grande es 1.053.360.000. Dividiendo esto por el área de la bandera pequeña en centímetros cuadrados, 261,36, también se obtiene 4.000.000.)

Apoyo para estudiantes de inglés

Speaking: MLR8 Apoyos a la Discusión. Durante la explicación de sus caminos de solución, proporcione a los estudiantes un marco de frases como: "Primero yo , porque ". Esto reforzará el uso del lenguaje matemático y el razonamiento de los alumnos cuando describan estrategias para utilizar una escala sin unidades para encontrar distancias reales y a escala.

Principio(s) de diseño: Maximizar la metaconciencia; Optimizar el resultado (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | PONDERING POOLS

10 minutos

Rutinas didácticas

MLR5: Preguntas y problemas de elaboración conjunta

Observar y maravillarse

Anteriormente, cada vez que se pedía a los alumnos que utilizaran un dibujo a escala para calcular el área de una región real, podían hallar las dimensiones de la región real como paso intermedio. Cada vez, se pedía a los alumnos que se dieran cuenta de que el área real estaba relacionadad con el área a escala por el (factor de escala)2. Es posible que algunos alumnos ya se sientan cómodos utilizando esta relación para calcular el área real directamente a partir del área a escala, sin necesidad de calcular las dimensiones reales como paso intermedio.

El propósito de esta actividad es ayudar a todos los alumnos a interiorizar este método más eficiente. La pregunta sobre la piscina rectangular can puede resolverse de cualquier forma, pero para la pregunta sobre la piscina con forma de riñón, los alumnos deben basarse en la relación entre el área a escala y el área real.

Mientras los alumnos trabajan, observe si expresan la escala del dibujo de formas diferentes pero equivalentes (por ejemplo, 2,8 cm a 14 m, 1 cm a 5 m, 28 cm a 140 m). Supervise también las diferentes formas en que los estudiantes hallan el área de la gran piscina rectangular:

• Hallando primero las longitudes laterales reales de la piscina en metros y multiplicándolas después

• Calculando el área a escala en centímetros cuadrados y multiplicándola por 25 (o 52)

Para esta actividad necesitará el patrón de líneas negras Pondering Pools.

Nation California - Grado 7

de 7º grado . Unidad 1 INTRODUCCIÓN

Entregue a cada alumno una copia del esquema. Invite a los alumnos a compartir lo que les llama la atención y lo que se preguntan sobre el plano del centro acuático.

Algunas cosas que les pueden llamar la atención son:

• Hay tres piscinas diferentes en el plano.

• Este plano tiene más detalles que otros con los que han trabajado anteriormente, como escaleras y puertas.

Algunas cosas que podrían preguntarse son:

• ¿Cuál es la escala de este dibujo?

• ¿Qué profundidad tienen estas piscinas?

• ¿Dónde está situado este centro acuático?

• ¿Cuánto cuesta utilizar estas piscinas?

Proporcione acceso a reglas centimétricas. Conceda a los alumnos un tiempo de trabajo tranquilo de 4 a 5 minutos, seguido de un debate con toda la clase.

Apoyo para estudiantes de inglés

Representar, Conversar, Escribir: Rutina del Lenguaje Matemático 5: Co-Craft Questions. Esta es la primera vez que se sugiere la Rutina 5 del Lenguaje Matemático como apoyo en este curso. En esta rutina, se da a los estudiantes un contexto o situación, a menudo en forma de raíz de problema con o sin valores numéricos. Los alumnos elaboran preguntas matemáticas que pueden plantearseed abfuera de la situación. Una pregunta típica es: "El objetivo de esta rutina es permitir a los alumnos entender el contexto antes de sentirse presionados para dar respuestas y desarrollar su conciencia del lenguaje utilizado en los problemas matemáticos.

Principio(s) de diseño: Fomentar la conversación; Apoyar la adquisición de sentido

Cómo se lleva a cabo:

1. Entregue a cada alumno una copia del plano del centro acuático. No permita que los alumnos vean las preguntas de seguimiento de esta situación.

Pregunte a los alumnos: "¿Qué preguntas matemáticas podríais hacer sobre esta situación?"

2. Conceda a los alumnos 1 minuto de tiempo individual para tomar algunas notas y, a continuación, 3 minutos para compartir ideas con un compañero.

Mientras discuten en parejas, ayude a los estudiantes a utilizar las habilidades de conversación para generar y refinar sus preguntas de forma colaborativa buscando claridad, remitiéndose a las notas escritas de los estudiantes y repitiendo las respuestas orales según sea necesario. Preste atención a la forma en que los alumnos se refieren a la escala del dibujo y hablan del área en su debate.

3. Pida a cada pareja de alumnos que aporte una pregunta escrita a un cartel, a la pizarra o a la proyección digital. Ctodos on 2-3 parejas de estudiantes para que presenten su pregunta a toda la clase, e invite a la clase a hacer comparaciones entre las preguntas compartidas y sus propias preguntas. Preste atención a las preguntas que pretendan indagar sobre la escala del plano y las superficies de las piscinas, y tome nota de las que utilicen unidades y las que no las utilicen.n diferentespero equivalentes, así como en los distintos métodos para hallar las áreas de las piscinas, siempre quet serves para aclarar una pregunta.

4. Presente las tres preguntas de seguimiento para esta situación y dé a los alumnos un par de minutos para compararlas con laspropias y con las de sus compañeros. Identifique las similitudes y las diferencias. Vuelva a analizar las ideas de los alumnos haciendo hincapié en las escalas

Considere la posibilidad de dar estas indicaciones: "¿Cuál de tus preguntas es más parecida/diferente a las que se proporcionan? ¿Por qué?", "¿Hay algún concepto matemático principal que esté presente tanto en tus preguntas como en las proporcionadas? Si es así, descríbalo", y "¿Cómo se relacionan sus preguntas con uno de los objetivos de la lección de comprender escalas equivalentes?"

5. Invite a los estudiantes a elegir una pregunta para responder (de la clase o del plan de estudios), y luego haga que los estudiantespasen a los siguientes problemas.

Matemáticas de 7º grado . Unidad 1

Apoyo a los alumnos con discapacidad

Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una pregunta a la vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.

Procesamiento conceptual: Tiempo de procesamiento. Compruebe la comprensión de cada uno de los alumnos según sea necesario en cada paso de la actividad.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Tu maestro te dará un plano de planta de un centro recreativo.

1. ¿Cuál es la escala del plano de planta si la longitud real del lado de la piscina cuadrada es 14 m?

EjPresiona tu respuesta tanto como escala con unidades como sin unidades.

2. Encuentra el área real de la gran piscina rectangular. Muestra tu razonamiento.

3. La piscina en forma de riñón tiene un área de 3,2 cm2 en el dibujo. ¿Cuál es su área real?

Explain o muestra tu razonamiento.

POSIBLES RESPUESTASS

1. La escala es 1 a 500, que también podría expresarse como 1 cm a 5 m o 2,8 cm a 14 m. Muestra tu razonamiento: La longitud lateral de la piscina cuadrada es 14 m. En el dibujo, la longitud lateral mide 2.8 cm. La escala es 2,8 cm a 14 m, o 1 cm a 5 m. Hay 500 cm en 5 m.

2. Sobre 385 m2. Explicaciones de ejemplo:

• En el dibujo, la piscina mide aproximadamente 5,5 cm por 2,8 cm. Las medidas reales de la piscina son 27,5 m por 14 m. Su área es 385 m2, porque (27,5) ⋅ 14 = 385.

• En el dibujo, la piscina mide aproximadamente 5,5 cm por 2,8 cm, por lo que su área es aproximadamente 15,4 cm2. Si 1 cm representa 5 m, 1 cm2 es 25 m2 en área real, por lo que el área es 385 m2, porque (15,4) ⋅ 25 = 385.

3. Sobre 80 m2. Ejemplo de explicación: Sé que 1 cm2 representa 25 m2, así que he multiplicado 3,2 cm2 por 25. (3,2) ⋅ 25 = 80.

Los alumnos pueden multiplicar el área a escala por 5 en lugar de por 52. Recuérdeles que consideren lo que representa 1 centímetro cuadrado, en lugar de lo que representa 1 centímetro.

Los alumnos pueden pensar que no se puede responder a la última pregunta porque no se da suficiente información. Anímeles a revisar su trabajo anterior sobre cómo se relaciona el área a escala con el área real.

Los objetivos de este debate son reforzar que hay más de una forma de expresar la escala de un dibujo a escala y ver que, para un problema determinado, una forma de expresar la escala puede ser más útil que otra.

En primer lugar, invite a los alumnos a compartir las escalas que escribieron para la primera pregunta. Anota las respuestas para que todos las vean. Para cada respuesta, pregunte a la clase si están de acuerdo en que la escala es equivalente.

A continuación, pida a los alumnos seleccionados que compartan cómo resolvieron las preguntas sobre el área de las piscinas. Debate:

• ¿Fue más fácil utilizar alguna de estas escalas para hallar el área real? ¿Alguna era más difícil? ¿Cuáles?

• ¿Cuáles podrían ser las ventajas de utilizar un método en lugar de otro para hallar el área real?

Matemáticas de 7º grado . Unidad 1

¿Estás preparado para más?

1. El cuadrado A es una copia a escala del cuadrado B con un factor de escala 2. Si el área del cuadrado A es 10 unidades2, ¿cuál es el área del cuadrado B?

2. El cubo A es una copia a escala del cubo B con factor de escala 2. Si el volumen del Cubo A es 10 unidades3, ¿cuál es el volumen del Cubo B?

3. El Hipercubo A de cuatro dimensiones es una copia a escala del Hipercubo B con factor de escala 2. Si el "volumen" del Hipercubo A es 10 unidades4, ¿cuál crees que es el "volumen" del Hipercubo B?

"¿Estás listo para más?" Respuesta del estudiante

1. 10 22

2. 10 23

3. ¡La respuesta a esto depende de lo que signifique escalar un hipercubo en 4 dimensiones! Asumiendo que el patrón que vemos en 2 y 3 dimensiones se mantiene, podríamos sospechar que la respuesta es . Eso podría incluso ayudarnos a pensar en cómo definir el escalado en 10 24 cuatro dimensiones. Si usamos coordenadas y pensamos en escalar por un factor de 2 como multiplicar todas las coordenadas por un factor de 2, entonces, de hecho, funciona como pensamos que debería basándonos en el patrón de las dimensiones 2 y 3

SÍNTESIS DE LA LECCIÓN

5 minutos

Las escalas pueden expresarse de muchas maneras diferentes, incluyendo el uso de diferentes unidades o el no uso de ninguna unidad.

• ¿Cómo podemos expresar la escala 1 pulgada a 5 millas sin unidades? (Puesto que hay 12 pulgadas en un pie y 5.280 pies en una milla, tsu es lo mismo que 1 pulgadas a 63.360 pulgadas, o 1 a 63.360.)

Una escala nos dice cómo una distancia en un dibujo a escala corresponde a una distancia real, y también puede decirnos cómo un área en un dibujo corresponde a un área real.

Si un mapa utiliza la escala 1 pulgada a 5 millas:

• ¿Cómo podemos encontrar el área real de una región representada en el mapa? (Encuentra el área en el mapa en pulgadas cuadradas y multiply por 25, porque 1 pulgada cuadrada representa 25 millas cuadradas.)

• ¿Cómo podemos encontrar el área a escala de una región si conocemos su área real? (Multiplica el área de la región real por 1 25 )

ENFRIAMIENTO | DIBUJANDO EL PATIO TRASERO

5 minutos

Lin y su hermano crearon cada uno un dibujo a escala de su patio trasero, pero a diferentes escalas. Lin utilizó una escalaale de 1 pulgadas a 1 pies. Su hermano utilizó una escala de 1 pulgadas a 1 yardas.

1. Expresa las escalas de los dibujos sin unidades.

2. ¿De quién es el dibujo más grande? ¿Cuántas veces más grande es? Explica o muestra tu razonamiento.

Matemáticas de 7º grado . Unidad 1

1. La escala de Lin de 1 pulgada a 1 pie se puede escribirte La escala de su hermano de Recuerde que 1 pulgada a 1 yarda puede escribirse como 1 a 36

2. El dibujo de Lin es más grande. Explicaciones de ejemplo:

• Las longitudes en el plano de Lin son 3 veces las longitudes correspondientes en el dibujo de su hermano. El área del dibujo de Lin es 9 veces el área del dibujo de su hermano.

• Dado que 1 yarda equivale a 3 pies, la escala del dibujo del hermano de Lin equivale a 1 pulgada a 3 pies. Each inch en su dibujo representa una distancia mayor que en el dibujo de Lin, por lo que su dibujo requerirá menos espacio en el papel.

• En 1 pulgada a 1 pie, el dibujo de Lin mostrará 1 12 de reales las distancias. En 1 pulgada a 1 yarda, o 1 pulgada a 3 feet, el dibujo de su hermano mostrará 1 36 de las distancias reales. Como 1 12 es mayor que 1 36 , su dibujo será mayor.

PROBLEMAS PRÁCTICOS

PROBLEMA 1

El Empire State Building de Nueva York tiene unos 1.450 pies de altura (incluida la antena de la parte superior) y 400 pies de ancho. Andre quiere hacer un dibujo a escala de la vista frontal del Empire State Building en un trozo de papel de 8 1 2 -pulgadas por11pulgadas. Eligela escala que consideres más adecuada para el dibujo a escala. Explica tu razonamiento.

A. 1 pulgada a 1 pie

B. 1 pulgada a 100 pies

C. 1 pulgada a 1 milla

Posibles soluciones

D. 1 centímetro a 1 metro

E. 1 centímetro a 50 metros

F. 1 centímetro a 1 kilómetro

E, o 1 cm a 50 m, serían las más apropiadas. Las explicaciones varían. Ejemplo de explicación: Con A, B y D, la imagen escalada no cabrá en la página. Con C y F, la imagen será demasiado pequeña. La opción E es la correcta porque de 1 cm a 50 m, la altura del edificio es de unos 10 cm, y la anchura es de unos 3 cm.

PROBLEMA 2

Elena encuentra que el área de una casa en un dibujo a escala es 25 pulgadas cuadradas. El área real de la casa es 2,025 pies cuadrados.

¿Cuál es la escala del dibujo?

Posibles soluciones

1 pulgada a 9 pies

PROBLEMA 3

¿Cuál de estas escalas equivale a 3 cm a 4 km? Seleccione todas las que correspondan. 1 pulgada equivale a 2,54 centímetros.

A. 0,75 cm a 1 km

B. 1 cm a 12 km

C. 6 mm a 2 km

Posibles soluciones

A, D

California - Grado 7

D. 0,3 mm a 40 m

E. 1 pulgada a 7,62 km

Matemáticas de 7º grado . Unidad 1

PROBLEMA 4

Del Grado 7, Unidad 1, Lección 6

Estos dos triángulos son copias a escala uno del otro. El área del triángulo más pequeño es 9 unidades cuadradas. ¿Cuál es el área del triángulo mayor?

Explica o muestra cómo lo sabes.

Posibles soluciones

36 unidades cuadradas. Cuando las longitudes de una copia a escala son 2 veces las de la figura original, el área de la copia es 4 veces ladel área original: 4 ⋅ 9 = 36

PROBLEMA 5

Del Grado 6, Unidad 2, Lección 8

El agua cuesta 1,25 $ por botella. A este precio, ¿cuál es el coste de:

1. 10 botellas?

2. 20 botellas?

PROBLEMA 6

Del Grado 6, Unidad 2, Lección 11

3. 50 botellas?

Soluciones posibles

1. $12.50 (porque 10 ⋅ 1.25 = 12.5)

2. $25 (porque 20 ⋅ 1.25 = 25)

3. $62.50 (porque 50 ⋅ 1.25 = 62.5)

La primera fila de la tabla muestra la cantidad de detergente y agua necesaria para hacer una solución jabonosa.

1. Completa la tabla para 2, 3, y 4 lotes.

2. ¿Cuánta agua y detergente se necesita para 8 lotes? Explica tu razonamiento.

Número de lotes

Posibles soluciones

1. Número de lotes

2. 48 tazas de agua y 8 tazas de detergente para vajilla. Las explicaciones varían. Respuesta de ejemplo: 8 tazas es 2 veces 4 tazas. Si se duplican 24 se obtienen 48 y si se duplican 4 se obtienen 8

Math Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1

GRANDES IDEAS)

• Dibujos a escala

• Formas del mundo

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP4 Representar con matemáticas.

Estándares ELD de California

I.A.1

I.A.4

LECCIÓN 13 DIBÚJALO A ESCALA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dan sentido al mundo modelan con matemáticas descubriendo la forma y el espacio y explorando las cantidades cambiantes.

OBJETIVO(S) DE APRENDIZAJE

• Vamos a dibujar un plano.

OBJETIVO(S) DE APRENDIZAJE

• Puedo crear un dibujo a escala de mi aula.

• Cuando se me dan requisitos de tamaño de dibujo, puedo elegir una escala apropiada para representar un objeto real.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comparar, contrastar y criticar (oralmente) dibujos a escala del aula.

• Generar una escala apropiada para representar una distancia real en un dibujo de tamaño limitado y explicar (oralmente) el razonamiento.

• Hacer suposiciones simplificadoras y determinar qué información se necesita para crear un dibujo a escala del aula.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR8: Apoyos para el debate

Piensa, comparte, en parejas

MLR2: Recopila y exhibe

MLR1: Cada vez más fuerte y claro

Presentaciones en Grupo

Materiales necesarios

Papel en blanco

Papel milimetrado

Instrumentos de medida

Matemáticas de 7º grado . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación necesaria

Pon a disposición cualquier herramienta de medición lineal disponible, que podría incluir reglas, varas de medir y cintas métricas, en centímetros y pulgadas.

Prepara al menos tres tipos diferentes de papel para cada grupo, que podrían incluir:

• 8 1 2 × 11 papel para impresora

• 11 × 17 papel para impresora

• Papel milimetrado

• 1 4 papel milimetrado

• 1 5 papel milimetrado

INFORMACIÓN DE LA LECCIÓN

Narrativa de la lección

Esta lección culminante es opcional. Los alumnos utilizan lo que han aprendido en esta unidad para crear un plano a escala de su aula.

La lección está organizada en tres partes principales:

• Parte 1. Planificar y medir: Planificar y medir. Cada alumno dibuja un plano aproximado de la clase. En grupos, deciden qué medidas es necesario tomar, planifican los pasos y las herramientas para medir y llevan a cabo su plan (MP1).

• Parte 2: Calcular y dibujar. Los alumnos seleccionan el papel que utilizarán para dibujar, deciden la escala y trabajan individualmente para crear sus dibujos. Eligen su escala y método estratégicamente, dadas sus medidas y las limitaciones de su papel.

• Parte 3: Reflexionar y debatir. En pequeños grupos, los alumnos explican su trabajo, discuten y comparan sus planos (MP3) y evalúan las decisiones que tomaron al crear el dibujo a escala (MP4). Como clase, reflexionan sobre cómo la elección de la escala, las unidades y el papel afectaron al proceso de dibujo y a los planos de planta creados.

Dependiendo de las opciones pedagógicas elegidas, esta lección podría requerir una o más sesiones de clase. La cantidad de tiempo necesaria para cada parte podría variar en función de factores como:

• El tamaño y la complejidad del aula, y si la medición requiere preparación o pasos adicionales (por ejemplo, mover muebles, tomar turnos, etc.).

• Lo que la clase o los estudiantes individuales decidan incluir en los planos.

• Cuánto apoyo organizativo se da a los estudiantes.

• Cómo se comparte finalmente el trabajo de los estudiantes con la clase (nada en absoluto, informalmente o con presentaciones formales).

Considere la posibilidad de definir mejor el alcance del trabajo de los alumnos y de establecer un límite de tiempo para cada parte de la actividad, a fin de centrar el trabajo de los alumnos y optimizar el tiempo de clase.

Esta actividad puede modificarse para que los alumnos dibujen planos de diferentes partes de la escuela -la cafetería, el gimnasio, los terrenos de la escuela, etc.- y sus dibujos puedan ensamblarse posteriormente como un plano a escala de la escuela. Si se elige esta versión, coordina la escala utilizada por todos los alumnos antes de que empiecen a dibujar.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Independiente 5 min.

Actividad de exploración opcional

Grupos pequeños 15 min.

Independiente 15 min.

Actividad de exploración opcional

Grupos reducidos 15 min.

Descripción breve

Los alumnos crean una lista de medidas importantes y de las características necesarias para crear un plano del aula a escala.

Los estudiantes crean un boceto de un plano del aula, incluyendo las características clave; planifican cómo medir el aula; y luego utilizan herramientas para tomar medidas precisas.

Los alumnos utilizan diferentes tipos de papel, las medidas de la actividad anterior y una escala elegida para crear un plano del aula a escala.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la aplicación de dibujos a escala para resolver problemas del mundo real.

Los alumnos comparten sus planos a escala y estrategias con otros grupos, intercambian opiniones y revisan su trabajo basándose en los debates.

CALENTAMIENTO | ¿QUÉ MEDIDAS SON IMPORTANTES?

5 minutos

Este calentamiento prepara a los alumnos para crear un plano del aula a escala. Los alumnos hacen una lluvia de ideas y una lista de los aspectos del aula que deben incluirse en el plano y las medidas que deben tomarse.

Es probable que los alumnos tomen nota de los elementos empotrados, como paredes, ventanas y puertas, como componentes importantes que deben medirse. También pueden incluir objetos móviles como muebles. A medida que los alumnos trabajen, identifique a aquellos que enumeren las posiciones de los objetos (por ejemplo, dónde está una pizarra en una pared, a qué distancia está el escritorio del maestro de la puerta, etc.). Invítelos a compartir más tarde.

Diga a los alumnos que van a crear un dibujo a escala del aula. Su primera tarea es pensar qué partes del aula van a medir para el dibujo. Conceda a los alumnos 2 minutos de reflexión en silencio para hacer una lista, seguidos de 3 minutos de debate con toda la clase. Pide a los alumnos que especifiquen las medidas que incluirían en la lista.

Apoyo para estudiantes con discapacidades

Enfoque basado en fortalezas:

• Esta actividad aprovecha muchas fortalezas naturales de los estudiantes con TDAH, LD y otros aprendices concretos en términos de su integración del contexto del mundo real y el interés personal del estudiante.

• Esta puede ser una oportunidad para que el maestro destaque esta fortaleza en clase y permita que un individuo con discapacidad dirija las interacciones/discusiones de los compañeros, aumentando la aceptación.

Funcionamiento ejecutivo: Ayudas visuales. Cree un gráfico de anclaje (por ejemplo, medidas del aula) que muestre públicamente definiciones, reglas, fórmulas o conceptos importantes para referencia futura.

Matemáticas de 7º grado . Unidad 1

ENUNCIADO DE TAREA PARA

POSIBLES RESPUESTAS

DE LA ACTIVIDAD

SÍNTESIS

¿Qué medidas necesitarías para dibujar un plano a escala de tu aula? Enumere qué partes del aula mediría e incluiría en el dibujo. Sea lo más específico posible.

Las respuestas varían. Ejemplos de respuestas:

• La longitud de las paredes

• El tamaño y la ubicación de las ventanas y puertas

• El tamaño y la ubicación de los muebles fijos y móviles

• Las medidas de los diferentes materiales del suelo del aula

Invite a los alumnos a compartir sus respuestas con la clase, especialmente aquellos que incluyeron medidas entre objetos en sus listas. Registre y muestre las respuestas de los alumnos para que todos las vean y sirvan de referencia durante la actividad principal. Considere la posibilidad de organizar las respuestas de los alumnos por tipo en lugar de por objetos (por ejemplo, enumerando "muebles" en lugar de "sillas", "escritorios", etc.). Algunas preguntas orientativas:

• ¿Qué partes del aula deben incluirse en un plano a escala? ¿Qué partes son menos importantes?

• ¿Qué medidas necesitamos?

• Además de las longitudes de las paredes y los objetos, ¿qué más sería útil? (Si nadie ha mencionado las posiciones de los objetos, pregunta cómo sabemos dónde colocar determinados objetos en el dibujo).

• ¿Debemos incluir medidas verticales? ¿Por qué sí o por qué no?

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | CREACIÓN DE UN PLANO DE PLANTA (PARTE 1)

15 minutos

Rutinas didácticas

MLR8: Apoyos para el debate

Pensar Compartir Compartir

El objetivo de esta actividad es que los alumnos hagan los preparativos para crear sus dibujos a escala. Esbozan un plano aproximado del aula. En grupos, planifican los pasos para realizar las mediciones y, a continuación, llevan a cabo su plan.

Algunos aspectos a tener en cuenta mientras los alumnos trabajan:

• Mientras dibujan sus bocetos, anímeles a centrarse en los elementos generales y no en los detalles. No es importante que el boceto sea nítido o elaborado. Lo que importa más es que no omita elementos importantes como la puerta.

• Cuando hagan planes para medir y registrar, anímales a trabajar sistemáticamente para minimizar las omisiones y los errores.

• Insta a los alumnos a medir dos veces y registrar una vez. Es mejor tomarse un poco más de tiempo para volver a comprobar las medidas que descubrir durante el dibujo que están mal tomadas.

Matemáticas de 7º grado . Unidad 1

INTRODUCCIÓN

Conceda a los alumnos 1-2 minutos para leer individualmente el enunciado de la tarea y formular cualquier pregunta aclaratoria. Considere la posibilidad de mostrar un croquis del plano de otra habitación del centro. Haga hincapié en que el croquis tiene una función similar a la de un esquema escrito. No es necesario que sea a escala, preciso o elaborado, pero debe mostrar todas las piezas importantes en los lugares adecuados para que pueda servir de referencia a la hora de crear el dibujo a escala.

Organice a los alumnos en grupos de 2-4. Los grupos más pequeños permiten que cada alumno participe más en el proceso de medición, lo cual es una ventaja, pero ten en cuenta que también puede hacer que el proceso de medición lleve más tiempo (ya que implicaría más grupos moviéndose en un espacio reducido).

Distribuya papel en blanco y dé a los alumnos 4-5 minutos para dibujar un boceto y compartirlo con un compañero. Proporcione acceso a herramientas de medición. Dé a los alumnos otros 4-5 minutos para planificar en grupos y, a continuación, tiempo para medir (que puede variar en función del tamaño del aula y de otros factores).

Apoyo para estudiantes con discapacidades

Funcionamiento ejecutivo: Eliminar barreras. Proporcione una lista de verificación de tareas que explicite todos los componentes necesarios de la actividad.

Habilidades motoras finas: Tutores. Emparejar a los alumnos con sus tutores compañeros previamente identificados y permitir que los alumnos que tienen dificultades con la motricidad fina dicten dibujos o bocetos según sea necesario.

1. En una hoja de papel en blanco, haga un esbozo de un plano del aula. Incluye las partes del aula que la clase haya decidido incluir o que a ti te gustaría incluir. La precisión no es importante en este esbozo, pero ten cuidado de no omitir elementos importantes, como una puerta.

2. Intercambia los esbozos con un compañero y revisa el trabajo de cada uno. En concreto, comprueba si falta alguna pieza o si está mal colocada. Devuélveles su trabajo y revisa tu boceto si es necesario.

3. Discute con tu grupo un plan de medición. Trabajen para llegar a un acuerdo sobre:

• Qué características del aula deben medirse y cuáles son opcionales.

• Las unidades que se utilizarán.

• Cómo registrar y organizar las mediciones (en el croquis, en una lista, en una tabla, etc.).

• Cómo compartir el trabajo de medición y registro (o el papel que desempeñará cada miembro del grupo).

4. Reúnan sus herramientas, tomen sus mediciones y regístrenlas según lo planeado. Asegúrate de volver a comprobar tus mediciones.

5. Haz tu propia copia de todas las mediciones que haya recogido tu grupo, si aún no lo has hecho. Las necesitarás para la siguiente actividad.

POSIBLES RESPUESTAS

Las respuestas varían.

Matemáticas de 7º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Cuando los grupos terminen de medir, pídales que se aseguren de que todos los miembros del grupo tienen una copia de las mediciones antes de pasar a la siguiente parte.

Considere la posibilidad de debatir brevemente lo que supuso un reto a la hora de realizar las mediciones. Algunas cuestiones importantes que pueden surgir son:

• Asegurarse de que el dispositivo de medición se mantiene en línea recta.

• Es difícil ser preciso cuando el dispositivo de medición debe utilizarse varias veces para encontrar la longitud de algo largo, como una pared.

• Turnarse con otros grupos que intentan medir lo mismo.

• Las mediciones no son exactas y deben redondearse.

Apoyo a los Estudiantes de Inglés

Speaking: MLR8 Apoyo a la discusión. A medida que los estudiantes describen su proceso para medir las características de la habitación, presione para obtener detalles en las explicaciones de los estudiantes solicitando que los estudiantes cuestionen una idea, elaboren una idea o den un ejemplo de su proceso de medición. Proporcione un marco de frases como: "Fue un reto medir ______ porque _______". Esto ayudará a los alumnos a producir y dar sentido al lenguaje necesario para comunicar sus propias ideas.

Principio(s) de diseño: Apoyar la creación de sentido; Optimizar el resultado (para la explicación)

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | CREACIÓN DE UN PLANO DE PLANTA (2ª PARTE)

15 minutos

Rutinas didácticas

MLR2: Recoger y exponer

En esta actividad, los alumnos utilizan las medidas que acaban de recoger para crear sus planos a escala. Cada estudiante selecciona una de las opciones de papel, decide la escala que va a utilizar y trabaja individualmente para crear sus dibujos.

Apoye a los estudiantes mientras razonan sobre la escala, las longitudes a escala y cómo proceder para crear el dibujo. Anima a todos a prestar atención a las unidades cuando calculen las longitudes a escala. Pide a los alumnos que piensen en las distintas formas en que podemos escribir una escala. Si tienen dificultades, recuérdeles que una escala puede escribirse en diferentes unidades o sin unidades.

Apoyo a los alumnos con discapacidad

Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, una sección de la habitación a la vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.

Habilidades motoras finas: Tutores. Emparejar a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que luchan con las habilidades motoras finas dictar dibujos o bocetos según sea necesario.

Matemáticas de 7º grado . Unidad 1

INTRODUCCIÓN

Distribuya al menos tres tipos diferentes de papel para cada grupo, que podrían incluir:

• 8 1 2 × 11 papel de impresora

• 11 × 17 papel de impresora

• Papel milimetrado

• 1 4 papel milimetrado

• 1 5 papel milimetrado

Pida a cada miembro del grupo que seleccione un papel para su dibujo. Anime a los participantes a elegir papeles diferentes. Explíqueles que deben elegir una escala adecuada en función del tamaño de su papel, del tamaño del aula y de las unidades de medida que hayan elegido. Esto significa que el plano debe caber en el papel y no ser demasiado pequeño (por ejemplo, si el papel es 11 × 17 pulgadas, el plano no debe tener el tamaño de una postal).

Dé a los alumnos tiempo suficiente para crear su plano. Si la distribución del aula es bastante compleja, considere la posibilidad de pedir a los alumnos que hagan una pausa después de haber completado una determinada parte del dibujo (por ejemplo, las paredes principales del aula) para poder comprobar su trabajo.

También puede darles un minuto para que compartan su dibujo con un compañero y discutan cualquier problema.

Apoyo para estudiantes de inglés

Conversar, representar: MLR2 Recoger y mostrar. Mientras los estudiantes trabajan, circule y escuche a los estudiantes hablar, y tome notas sobre frases comunes o importantes (por ejemplo, escala, tamaño, unidades, etc.), junto con bocetos o diagramas útiles. Preste especial atención al modo en que los alumnos determinan las escalas para sus planos. Anote las palabras y los dibujos de los alumnos en una pantalla visual para consultarlos durante los debates de toda la clase a lo largo de esta lección y del resto de la unidad. Esto ayudará a los alumnos a utilizar el lenguaje matemático durante sus debates en grupo y en clase.

Principio(s) de diseño: Optimizar el resultado (para la explicación)

Su maestro le dará varias opciones de papel para su plano a escala.

1. Determine una escala apropiada para su dibujo basándose en sus medidas y en el papel elegido. Tu plano debe caber en el papel y no resultar demasiado pequeño.

2. Utiliza la escala y las medidas que tu grupo ha tomado para dibujar un plano a escala del aula. Asegúrate de:

• Mostrar la escala de tu dibujo.

• Etiquetar las partes clave de tu dibujo (las paredes, las aberturas principales, etc.) con sus medidas reales.

• Mostrar tu pensamiento y organizarlo para que pueda ser seguido por otros. POSIBLES RESPUESTAS

Las respuestas varían.

Matemáticas de 7º grado . Unidad 1

ERRORES PREVISTOS

Es posible que algunos alumnos elijan una escala y empiecen a dibujar sin tener en cuenta el tamaño que tendrá su plano terminado. Anima a los alumnos a que tengan en cuenta el tamaño de su papel para determinar una escala adecuada antes de empezar a dibujar.

En la siguiente actividad se realizarán reflexiones en pequeños grupos y en toda la clase.

SÍNTESIS

¿Estás preparado para más?

1. Si el material del suelo de tu aula se va a sustituir por baldosas de 10-pulgadas por 10-pulgadas, ¿cuántas baldosas harían falta para cubrir toda la habitación? Utiliza tu dibujo a escala para calcular aproximadamente el número de baldosas necesarias.

2. ¿Cómo cambiaría el número de baldosas necesarias si se utilizaran 20-pulgadas por 20-pulgadas (en lugar de 10-pulgadas por 10-pulgadas)? Explica tu razonamiento.

"¿Estás preparado para más?" Respuesta del alumno

1. Las respuestas varían.

2. Reduciría el número de baldosas. Cada 20-por-20 baldosa cubre 4 veces el área de cada 10-por-10 baldosa, por lo que se necesitaría aproximadamente 1 4 el mismo número de baldosas.

OPCIONAL ACTIVIDAD DE EXPLORACIÓN | CREACIÓN DE UN PLANO DE PLANTA (PARTE 3)

15 minutos

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

Presentaciones en grupo

En la fase final del proyecto de dibujo, los alumnos reflexionan y revisan su trabajo. Los estudiantes que eligieron la misma opción de papel se reúnen en pequeños grupos para analizar y comparar sus planos. Discuten sus decisiones, evalúan la precisión de sus dibujos y los revisan si es necesario.

Después de la revisión, los estudiantes se reúnen en clase y discuten cómo la elección de la escala, las unidades y el papel afectaron al proceso de dibujo y a los planos que crearon.

Matemáticas de 7º grado . Unidad 1

INTRODUCCIÓN

Organice en pequeños grupos a los alumnos que utilicen el mismo tipo y tamaño de papel. Deles 8-10 minutos para compartir y explicar sus dibujos. Exponga y lea en voz alta preguntas como las siguientes. Pida a los alumnos que las utilicen para orientar su debate.

• ¿Qué escala has utilizado? ¿Cómo decidisteis la escala?

• ¿Parecen exactas las medidas a escala de cada dibujo? ¿Representan correctamente las medidas reales?

• ¿Te pareció adecuada la escala para el papel elegido? ¿Por qué sí o por qué no?

• ¿Qué fue lo primero que dibujaste en tu dibujo? ¿Por qué?

• ¿Cómo decidiste los objetos que mostrarías en tu dibujo?

• ¿Qué aspectos de tus dibujos son diferentes?

• ¿Cómo podría revisarse cada plano para representar mejor el aula?

Apoyo para estudiantes con discapacidades

Lenguaje receptivo/expresivo: Tiempo de procesamiento. Los alumnos que necesitan más tiempo de procesamiento también se beneficiarían de MLR1 (Stronger and Clearer Each Time).

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTAS

SÍNTESIS DE LA ACTIVIDAD

1. Intercambia los planos con otro alumno que haya utilizado el mismo tamaño de papel que tú. Comenta tus observaciones y reflexiones.

2. Intercambia planos con otro estudiante que haya utilizado un tamaño de papel diferente al tuyo. Discuta sus observaciones y pensamientos.

3. Basándose en sus discusiones, anote ideas sobre cómo podría mejorarse su plano.

Las respuestas varían.

Antes de informar a la clase, dé a los alumnos entre 4 y 5 minutos de silencio para reflexionar. Pídales que anoten ideas para revisar su plano y estrategias para crear dibujos a escala precisos basándose en su conversación.

Aunque gran parte del debate tendrá lugar dentro de los grupos, informe a la clase para que los alumnos puedan ver planos creados a distintas escalas y en distintos tipos o tamaños de papel. Exponga una serie de dibujos a escala para que todos los vean y debatan las siguientes preguntas. (Otra posibilidad es exponer todos los trabajos de los alumnos en una galería y pedirles que reflexionen sobre estas cuestiones).

• ¿Qué diferencias hay entre estos dibujos?

• ¿Cómo influyeron las diferentes escalas en el dibujo final?

• ¿Cómo influyó el tamaño del papel en la elección de la escala?

• ¿Qué elecciones fueron realmente importantes a la hora de crear el dibujo a escala?

• ¿Serían estas elecciones las mismas si estuvieras haciendo una sala diferente de la escuela? ¿O en otro edificio?

Math Nation California - Grado 7

Matemáticas de 7º grado . Unidad 1