




Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).
La plataforma de recursos curriculares en línea que se ofrece en "mathnation.com", incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.
La marca comercial "Math Nation" es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.
Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.
Objetivos de aprendizaje de la unidad
• Los estudiantes representan y resuelven problemas de historias dentro de 20 a través del contexto de gráficos de imágenes y barras que representan datos categóricos. Los alumnos adquieren fluidez en la suma y la resta.
En esta unidad, los estudiantes comienzan el trabajo de un año para desarrollar fluidez con sumas y diferencias dentro de 20, construyendo sobre conceptos de suma y resta de 1er grado. Aprenden nuevas formas de representar y resolver problemas que involucran sumas, restas y datos categóricos.
SSSSS, SSSSSS S SSSSSSSS
SSS SSSSS
En primer grado, los estudiantes sumaron y restaron dentro de 20 utilizando estrategias basadas en las propiedades de la suma y el valor posicional. Desarrollaron fluidez con sumas y diferencias dentro de 10. Los alumnos también adquieren experiencia en la recogida, organización y representación de datos categóricos.
Aquí, los alumnos se inician en los gráficos de imágenes y de barras como forma de representar datos categóricos. Formulan y responden preguntas sobre situaciones descritas por los datos. La estructura de los gráficos de barras allana el camino para una nueva representación, el diagrama de cinta.
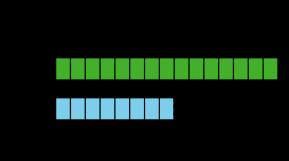

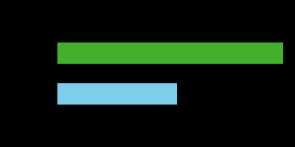
Los alumnos aprenden que los diagramas de cinta pueden utilizarse para representar y dar sentido a problemas que implican la comparación de dos cantidades. Los diagramas también ayudan a profundizar la comprensión de los estudiantes de la relación entre la suma y la resta.
Esta unidad de apertura también ofrece oportunidades para introducir rutinas matemáticas y estructuras para los centros, y para desarrollar una comprensión compartida de lo que significa hacer matemáticas y ser parte de una comunidad matemática.
Sección A: Sumar y restar dentro de 20
Alineación de estándares
Abordando
• 2.NBT.5
• 2.OA.2
Sección Objetivos de aprendizaje
• Adquirir fluidez para sumar dentro de 100
• Adquirir fluidez para restar dentro de 20.
Esta sección inicial ofrece a los profesores la oportunidad de evaluar la fluidez de los alumnos con las operaciones de suma y resta hasta el 10 y cómo abordan la suma y la resta. Las primeras lecciones se centran en la formación de una decena como estrategia para sumar y restar, lo que ayuda a los alumnos a adquirir fluidez con las operaciones hasta el 20 y refuerza el trabajo con números mayores (como la composición y la descomposición de números como forma de sumar y restar). En la última lección de la sección, los alumnos utilizan las estrategias aprendidas en 1.er grado para sumar hasta el 50.
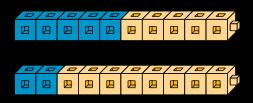

10 − 5 = _______
5 + ________ = 10
2 + _______ = 10
10 − 8 = _______
Algunas actividades se llevan a cabo en centros, lo que permite a los profesores también introducir rutinas y estructuras mientras ayudan a los estudiantes a desarrollar estrategias mentales para sumar y restar.
PLC: Lección 2, Activity 2, Sums of 10
Sección B: Formas
Alineaciones de estándares
Direccionamiento
• 2.MD.10
• 2.NBT.5
• 2.OA.2
Objetivos de aprendizaje de la sección
• Interpretar imágenes y gráficos de barras.
• Representar datos mediante imágenes y gráficos de barras.
• Resolver problemas de uno y dos pasos utilizando sumas y restas hasta 20.
En esta sección, los estudiantes exploran situaciones y problemas que involucran datos categóricos y aprenden nuevas formas de representarlos. Comienzan representando datos de su clase de forma que tengan sentido. Luego, se les presentan las gráficas de imágenes y las gráficas de barras. Los estudiantes aprenden las convenciones de estas gráficas a medida que las crean. Analizan los tipos de preguntas que pueden formularse y responderse con las gráficas, incluyendo aquellas que requieren combinar y comparar diferentes categorías.

PLC: Lección 9, Actividad 1, Opciones de excursión
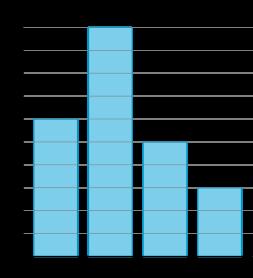


Alineaciones de estándares
Direccionamiento
• 2.MD.10
• 2.NBT.2
• 2.NBT.5
• 2.OA.1
• 2.OA.2
Objetivos de aprendizaje de la sección
• Comprender e interpretar diagramas de cinta.
• Representar y resolver problemas de comparación con incógnitas en todas las posiciones hasta 100.
Los estudiantes ya han representado y razonado cantidades en problemas de texto. En 1.er grado, compararon cantidades mediante diagramas con particiones discretas. En la sección anterior, razonaron cantidades en gráficos de barras. Aquí, aprenden a usar diagramas de cinta como otra forma de comprender la relación entre dos cantidades y entre la suma y la resta.
Los estudiantes exploran problemas de comparación con una diferencia desconocida, un número mayor desconocido o un número menor desconocido. Los diagramas de cinta ayudan a los estudiantes a visualizar estas estructuras y los apoyan en el razonamiento sobre estrategias para resolver problemas, como contar hacia adelante o hacia atrás. La tabla destaca los diferentes tipos de problemas en esta sección.
diferencia desconocida desconocido más grande Más pequeño desconocido
Lin contó 28 barcos. Diego contó 32. ¿Cuántos barcos más contó Diego?

Lin encontró 28 conchas más que Diego. Diego encontró 32 conchas. ¿Cuántas conchas encontró Lin?

Lin vio 32 estrellas de mar. Diego vio 28 estrellas de mar menos que Lin. ¿Cuántas estrellas de mar vio Diego?

Los estudiantes también escriben ecuaciones para razonar sobre preguntas que preguntan "¿cuántos más?" y "¿cuántos menos?". Reconocen que se pueden usar diferentes ecuaciones y diagramas para representar la misma diferencia entre dos números.
PLC: Lección 14, Actividad 1, Hora de fiesta (Parte 1)

Días estimados:14−18
Centrarse en las grandes ideas
• Estrategias numéricas
• Representar datos
ESTÁNDARES POR LECCIÓN
LECCIÓN

Norma(s) abordadas
2.1.1 2.OA.2
2.1.2 2.OA.2
2.1.3 2.OA.2
2.1.4 2.OA.2
2.1.5 2.NBT.5
2.1.6 2.NBT.5, 2.OA.2
2.1.7 2.MD.10
2.1.8 2.MD.10
2.1.9 2.MD.10
2.1.10 2.MD.10
2.1.11 2.MD.10, 2.OA.2
2.1.12
2.MD.10, 2.NBT.5, 2.OA.2
2.1.13 2.MD.10, 2.OA.2
2.1.14 2.MD.10
2.1.15 2.OA.1, 2.OA.2
2.1.16 2.OA.1, 2.OA.2
2.1.17
2.1.18
2.MD.10, 2.NBT.2, 2.NBT.5
2.MD.10, 2.OA.1, 2.OA.2

IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Abordando
Estándares y principios de CA Alineación
2.OA.2 Sumar y restar con fluidez dentro de 20 usando estrategias mentales. Al final del segundo grado, sabe de memoria todas las sumas de dos números de un dígito.
Building On
1.OA.6
Enfocar SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
CA ELD Standards
I.A.3
I.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . . dar sentido al mundo
construir argumentos viables y criticar el razonamiento de los demás desmontar el todo, unir las partes.
OBJETIVO(S) DE APRENDIZAJE
• Sé sumar y restar números dentro de 10
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Sé sumar y restar dentro de 10
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
¿Qué es lo que más te gusta de las matemáticas? ¿Cómo compartes esa alegría con tus alumnos y les animas a pensar en lo que les gusta de las matemáticas?
PREPARACIÓN DE LA LECCIÓN
Rutinas instructivas
¿Qué sabes sobre ?
(Calentamiento)
Materiales para reunir
Cubos o fichas para conectar
Materiales para copiar
Tarjetas numéricas (0-10)
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 1:
Cree un juego de tarjetas numéricas para cada grupo de 2
Las tarjetas numéricas se utilizarán en las próximas lecciones y a lo largo del año. Considera la posibilidad de copiar las tarjetas en cartulina o plastificarlas para utilizarlas en el futuro .
Crea el póster de la comunidad matemática para exponerlo en la síntesis de la lección.
Matemáticas de 2º grado . Unidad 1
• Sumemos y restemos dentro de 10
Narrativa de la lección
El objetivo de esta lección es que los estudiantes sumen y resten dentro de 10
Los estudiantes desarrollan fluidez con sumas y restas dentro de 10 en el grado 1. Esta lección ofrece una oportunidad para evaluar la fluidez de los estudiantes en 10, incluyendo el reconocimiento de sumas con un valor de 10. A lo largo de la lección, observe las formas en que los estudiantes encuentran los valores de sumas y diferencias y cómo describen sus métodos a los demás. Puede haber sumas y diferencias que los alumnos digan que "simplemente saben". En este caso, no exija a los alumnos que expliquen cómo han obtenido su respuesta cada vez, y tome nota de las expresiones que muchos alumnos ya se saben de memoria. Se deben poner a disposición de los alumnos contadores o cubos de conexión para que los utilicen; no obstante, anime a los alumnos a no utilizarlos si no los necesitan.
Comunidad matemática
En la síntesis de la lección, los alumnos debaten sobre lo que significa formar parte de una comunidad matemática. Prepare un espacio, por ejemplo una cartulina, con el título "Comunidad matemática" y un gráfico en forma de T con el encabezamiento "Hacer matemáticas" y "Normas". Divide las columnas en dos secciones: alumnos y profesor. Las dos secciones animan a los alumnos y al profesor a ser conscientes de que ambas partes son responsables de la forma en que se hacen las matemáticas en el aula. En la síntesis de esta lección, los alumnos añadirán sus ideas a la sección "Haciendo matemáticas". En las lecciones siguientes, los estudiantes completarán y revisarán sus aportaciones, incluida la redacción de las normas del aula.
Comunidad matemática
Hacer matemáticas
Normas Alumnos Alumnos
Profesor

Profesor
LECCIÓN DE UN VISTAZO
Componente de la Lección Estructura Tiempo Breve Descripción
Calentamiento Independiente 15 min. Los estudiantes describen lo que saben sobre matemáticas.
Actividad de Exploración 1 Pares 20 min. Usando dos tarjetas de números etiquetadas 0-10, los estudiantes escriben una expresión de suma o resta para encontrar un valor listado en una tabla.
Actividad de Exploración 2 Pares 10 min.
Los estudiantes emparejan expresiones de suma y resta dentro de 10 con su suma o diferencia y luego exploran patrones de expresiones con una suma de 10.
Síntesis Todo el grupo 10 min. Los alumnos reflexionan y describen acciones como parte de una comunidad matemática.
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
Componente de la lección Estructura Tiempo

Breve descripción
Enfriamiento Independiente 5 min. Los estudiantes encuentran el valor de expresiones que contienen la suma o diferencia de números enteros dentro de 10 y luego identifican expresiones que suman 10
Centro(s) sugerido(s) Grupos pequeños Opcional
Apoyo:
• Rompecabezas numéricos: Suma y resta (1-4), Etapa 1: Dentro de 10
Rutinas instructivas
¿Qué sabes sobre ?
15 minutos
El propósito de esta actividad es obtener ideas que los estudiantes tienen sobre cómo hacer matemáticas. Los estudiantes aprenden la rutina ¿Qué sabes de matemáticas? ? que se utilizará durante todo el año. Esta rutina proporciona una oportunidad para que todos los alumnos contribuyan a la conversación y para que el profesor escuche los conocimientos que los alumnos ya tienen. Como se trata del primer calentamiento del año, asignamos 15 minutos, en lugar de 10, para establecer la estructura de una rutina.
Para todas las rutinas, considere la posibilidad de establecer una pequeña y discreta señal con la mano que los alumnos puedan mostrar para indicar que tienen una respuesta que pueden apoyar con un razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, u otra señal sutil. Es una forma rápida de ver si los alumnos han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se apresuren por las manos que se levantan alrededor de la clase.
• Mostrar la pregunta.
LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
• "¿Qué sabes sobre matemáticas?"
• 1 minuto: tiempo para pensar en silencio
• Registrar las respuestas.
¿Qué sabes sobre las matemáticas?
SÍNTESIS DE LA ACTIVIDAD
Ejemplos de respuestas:
• Las matemáticas usan números.
• Sumas y restas en matemáticas.
• Trabajas con formas en matemáticas.
• Las matemáticas están en todas partes.
• "Hoy, podrás hacer matemáticas de diferentes maneras".
Matemáticas de 2º grado . Unidad 1
Materiales para reunir
Conectar cubos o fichas

Materiales para copiar
Tarjetas numéricas (0-10)
Preparación necesaria
Cree un conjunto de tarjetas numéricas para cada grupo de 2
Las tarjetas numéricas se utilizarán en las próximas lecciones y durante todo el año. Considere la posibilidad de copiar las tarjetas en cartulina o plastificarlas para utilizarlas en el futuro.
Cree el póster de la comunidad matemática para exponerlo en la síntesis de la lección.
El objetivo de esta actividad es que los alumnos demuestren los métodos que tienen para sumar y restar dentro de 10. En esta actividad, los alumnos dibujan 2 tarjetas y piensan cómo podrían sumar o restar los números para crear un valor que coincida con uno de los números objetivo (0-10). Escuche cómo piensan los alumnos para hallar el valor de sumas y diferencias, incluidas las sumas y diferencias que se saben de memoria, y cómo comparten su pensamiento con su compañero. Si los alumnos no están de acuerdo sobre el valor de una suma o diferencia, anímelos a discutir su razonamiento y a llegar a un acuerdo (MP3).
Los alumnos pueden escribir expresiones de resta que no coincidan con su cálculo (por ejemplo, los alumnos escriben 2 - 4 en lugar de 4 - 2). Pídales que utilicen fichas o cubos para representar la resta. Subraye que empezaron con 4 y quitaron 2 y pídales que relacionen esta acción con la expresión. Para mantener la coherencia matemática con lo que los estudiantes aprenderán en grados posteriores sobre las operaciones con números racionales, evite el lenguaje que sugiere que los estudiantes sólo pueden restar un número menor de un número mayor.
MLR8 Apoyos para el debate. Ofrezca a todos los estudiantes la oportunidad de expresarse verbalmente. Invite a los estudiantes a leer cada expresión que creen a su compañero. Amplifique palabras y frases como: add, addition, sum, take away, difference, value y expression.
Avances: Hablar, escuchar, representar
Representación: Acceso para la percepción. Algunos alumnos pueden beneficiarse de una demostración de cómo jugar al juego utilizando los cubos o fichas de conexión disponibles.
Apoya la accesibilidad para: Procesamiento conceptual, Procesamiento visual-espacial
LANZAMIENTO
Math
Nation California - Grado 2
• Grupos de 2
• Dé a cada grupo un juego de tarjetas numéricas.
• Dé a los estudiantes acceso a cubos o fichas de conexión.
• "Vamos a jugar a Comprobar: Sumar o restar dentro de 10. El objetivo es ser la primera persona en escribir la expresión para cada número". El objetivo es ser la primera persona en escribir una expresión para cada número".
• "Voy a elegir dos tarjetas. (Muestra 10 y 7.) Tengo que decidir si quiero sumar o restar. No quiero un valor mayor que 10, así que voy a restar."
• Escribe 10 - 7.
• "¿Cuál es el valor de la diferencia?"
• 30 segundos: tiempo para pensar en silencio
• Comparte las respuestas.
• "Anoto la expresión que he hecho en mi hoja de registro junto al valor de la diferencia y marco el número. Ahora es el turno de mi compañero".
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

LANZAMIENTO CONTINUACIÓN
ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• "Elige tarjetas por turnos, haz una expresión de suma o resta, encuentra el valor de la suma o diferencia y muestra a tu compañero cómo lo sabes."
• "Si te quedas sin tarjetas antes de que alguien marque todos los números, baraja y vuelve a empezar."
• 10-15 minutos: tiempo de trabajo en pareja
1. Elige 2 tarjetas y encuentra el valor de la suma o la diferencia.
2. Marque el número que haya encontrado y escriba la expresión.
3. Gana la persona que marque más números.
¡Lo encontré! Expresión
POSIBLES RESPUESTAS
Las respuestas varían. Ejemplo de respuesta:
Lo encontré! Expresión
Learning Inc. - Todos los derechos reservados
Las respuestas varían. Ejemplo de respuesta: ¡Lo encontré!
Matemáticas de 2º grado . Unidad 1

POSIBLES RESPUESTAS CONTINUACIÓN
SÍNTESIS DE LA ACTIVIDAD
• "¿Escribiste alguna expresión que coincidiera con el mismo valor? ¿Qué número era? ¿Cuáles eran las expresiones?"
• "¿Hubo algún valor que tú y tu compañero no encontrasteis? ¿Cuáles son algunas expresiones que podrían coincidir con estos números?"
• Si es necesario, pregunte,
• "¿Qué expresiones obtuviste para 5?"
• (Las respuestas variarán. Ejemplo de respuesta: Encontré 10 - 5 y 3 + 2.)
• "¿Qué expresiones obtuviste para 0?"
• (Las respuestas variarán. Respuesta de ejemplo: Encontré 9 - 9 y 0 + 0.)
• "¿Qué expresiones obtuviste para 10?"
• (Las respuestas variarán. Ejemplo de respuesta: Encontré 3 + 7 y 10 + 0.)
Materiales a reunir
Cubos conectores o contadores
10 minutos
El propósito de la actividad es que los estudiantes practiquen la búsqueda del valor de sumas y diferencias dentro de 10. Los estudiantes también identifican expresiones de suma que tienen un valor de 10. Los alumnos trabajarán más con sumas de 10 en la próxima lección. Esta actividad ofrece la oportunidad de observar cómo los alumnos encuentran sumas y diferencias dentro de 10, incluidas las que se saben de memoria.
LANZAMIENTO
ACTIVIDAD
• Grupos de 2
• Dar a los estudiantes acceso a los cubos conectores o contadores.
• Lea el enunciado de la tarea.
• 6 minutos: tiempo de trabajo independiente
• "Comparte tu pensamiento y tus respuestas con un compañero."
• 1 minuto: discusión en pareja
Math
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
1. Empareje cada expresión con el valor de la suma o la diferencia.
• 5 • 9
• 3 - 1 • 3
• 10 - 1
• 4 + 5
• 6 + 3
• 6 - 5
• 1 + 6
• 9 - 5
• 8 - 5
• 3 + 6
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
8
7
1
4
2
2. Encierra en un círculo todas las expresiones de suma que tengan un valor de 10

3. ¿Qué patrones ves en los números de las expresiones que tienen+ 3
1. Rodea correctamente cada expresión.
2. Rodea 10 + 0, 9 + 1, 8 + 2, 7 + 3, 6 + 4, 5 + 5,
3. Ejemplos de respuestas:
+
, y 0 + 10
,
• Cuando uno de los números aumenta, el otro disminuye.
• Veo 3 + 7 y 4 + 6. El 3 cambia a 4 sumando 1 por lo que el otro número necesita restar 1 por lo que pasa de 7 a 6.
• Pide a los alumnos que compartan las respuestas al problema 3.
• Registra las respuestas.
10 minutos
"Hoy, has jugado a un juego de matemáticas y has sumado y restado dentro de 10. Vamos a hacer una tabla. Vamos a hacer una tabla para describir lo que tú haces y yo hago en nuestra comunidad matemática."
Muestra el póster de la comunidad matemática.
©Accelerate Learning Inc. - Todos los derechos reservados
Nation California - Grade 2
Matemáticas de 2º grado . Unidad 1
"¿Cómo es y cómo suena hacer matemáticas juntos como una comunidad matemática?". (Hablamos entre nosotros y con el profesor. Tuvimos un rato de silencio para pensar. Compartimos nuestras ideas. Pensamos en las ideas y palabras matemáticas que conocíamos. Escribías nuestras respuestas. Esperabas a que diéramos las respuestas.)
Compartir y anotar las respuestas.
minutos
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA 1. 4 + 2 = 2. 9 - 3 = 3. Encierra en un círculo las expresiones que tienen un valor de 10
POSIBLES RESPUESTAS
Reflexiones:

Math Nation California - Grado 2
6
6
Círculos 4 + 6, 5 + 5, y 7 + 3
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Abordando
Estándares y principios de CA Alineación
2.OA.2 Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del segundo grado, saber de memoria todas las sumas de dos números de un dígito.
Construyendo Hacia
1.OA.1
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP4 Modelar con matemáticas.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1
I.B.8 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
dan sentido al mundo modelan con matemáticas desmontando enteros, juntando partes.
• Puedo determinar el número desconocido en ecuaciones de adición y sustracción.
• Puedo escribir ecuaciones de adición y sustracción que involucren 10
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Encontrar el número que hace que las ecuaciones dentro de 20 sean verdaderas.
• Escribir ecuaciones con sumandos desconocidos y sumas de 10 y sus ecuaciones de sustracción relacionadas.
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
¿Cómo facilita la creación de una comunidad matemática productiva? ¿Dónde puede señalar pruebas de ello para que las vean los alumnos?
DE LA
Rutinas instructivas
¿Qué sabes sobre _____?
(Calentamiento)
Materiales a reunir
Conectar cubos
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales para copiar
¿Qué hay detrás de mi espalda? Etapa 2 Hoja de grabación Grado 1
Preparación necesaria
Actividad 1:
Reúne una torre de 10 cubos de conexión para utilizar en el lanzamiento.
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Pensemos en la relación entre la suma y la resta.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes encuentren el número que hace verdaderas las ecuaciones y escriban ecuaciones de suma y resta relacionadas dentro de 10
En grados anteriores, los estudiantes aprendieron a encontrar el número que hace 10 cuando se suma a un número dado y a hacer una decena para sumar dentro de 20 y 100. La capacidad de buscar y utilizar sumas que tienen un valor de 10 es una habilidad fundamental para el punto de referencia del grado 2 de fluidez dentro de 20 y para sumar y restar dentro de 1,000 utilizando métodos basados en el valor posicional.
En esta lección, los estudiantes retoman una actividad del centro, Qué hay detrás de mi espalda, y utilizan cubos de conexión para obtener su comprensión de sumas que tienen un valor de 10 y la relación entre la suma y la resta. Los estudiantes continuarán practicando el reconocimiento y el uso de estas sumas en las actividades de la lección a lo largo de la unidad.
Comunidad matemática
Diga a los estudiantes que tendrán la oportunidad de revisar sus ideas de comunidad matemática al final de esta lección, por lo que mientras trabajan hoy deben pensar en las acciones que pueden faltar en la lista actual.
Actividad 2: Sumas de 10
LESSON-AT-A-GLANCE
Componente de la lección Estructura Tiempo

Breve descripción
Calentamiento Independiente 10 min. Los estudiantes identifican los datos que conocen sobre el número 10.
Actividad de Exploración 1 Pares 20 min.
Actividad de exploración 2 Pares 15 min.
Síntesis Grupo completo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Math Nation California - Grado 2
Los estudiantes determinan ecuaciones o diagramas de suma y resta para representar el número desconocido de cubos conectores (de 10) que están detrás de la espalda de un estudiante.
Los alumnos escriben ecuaciones de suma y resta formadas por dos cubos de conexión de colores diferentes que forman un grupo de 10 y luego completan las ecuaciones con un valor que las haga verdaderas.
Los estudiantes reflexionan sobre las acciones matemáticas que realizaron durante la lección y luego las agregan a la tabla de la Comunidad Matemática.
Los estudiantes seleccionan ecuaciones de suma y resta que representan cubos de conexión de colores de 10
Apoyo:
• Rompecabezas numéricos: Suma y resta (1-4), Etapa 1: Dentro de 10
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
Rutinas instructivas
¿Qué sabes sobre _____?

10 minutos
El objetivo de esta actividad es suscitar las ideas que los alumnos tienen sobre el número 10. Esta rutina ofrece una oportunidad para que todos los alumnos contribuyan a la conversación y para que el profesor escuche los conocimientos que los alumnos ya tienen. Cuando los alumnos comparten dónde ven 10 en el mundo real, demuestran su capacidad para contextualizar los números (MP2). Cuando los estudiantes comparten sobre los números que están cerca de 10 al contar, relacionan 10 unos con la unidad diez, y suman y diferencian con el valor de 10, muestran lo que saben sobre la estructura de los números enteros, el valor posicional y las propiedades de las operaciones (MP7).
LANZAMIENTO
ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
• Mostrar el número.
• "¿Qué sabes sobre 10?"
• 1 minuto: tiempo para pensar en silencio
• Registrar las respuestas.
¿Qué sabes de 10?
SÍNTESIS DE LA ACTIVIDAD
Ejemplos de respuestas:
• 10 es 5 y 5
• Hay 10 contadores en un 10-marco.
• Tengo 10 dedos.
• 10 es uno más que 9
• 10 es parte de los números adolescentes.
• Si es necesario, "¿Cómo podríamos representar el número 10?"
Materiales para reunir
Cubos de conexión
Materiales para copiar
Lo que hay detrás de mi espalda Hoja de registro de la Etapa 2 Grado 1
20 minutos
Preparación necesaria
Reúna una torre de 10 cubos de conexión para usar en el lanzamiento.
El propósito de esta actividad es que los estudiantes revisen la etapa 2 del centro Lo que hay detrás de mi espalda, que se introdujo por primera vez en el primer grado. Los alumnos comienzan con una torre de 10 cubos de conexión. Desmontan la torre y representan las dos partes con un dibujo y una expresión. A lo largo de la actividad, los alumnos practican utilizando lo que saben sobre sumas de 10 y la relación entre suma y resta para encontrar sumandos desconocidos. Los alumnos explican a su compañero su razonamiento sobre cómo saben cuántos cubos faltan (MP3). Mientras los estudiantes discuten, preste atención a las formas en que los estudiantes muestran cómo buscan y utilizan la secuencia de conteo, las propiedades de las operaciones o la relación entre la suma y la resta (MP7).
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1

Apoyo para estudiantes de inglés
MLR8 Apoyos de discusión. Hacer visibles las conexiones entre las representaciones. Pensar en voz alta, usar gestos y una pantalla etiquetada para mostrar las conexiones entre las partes de la ecuación y los cubos que son visibles y los que están ocultos.
Avances: Escuchar, Representar
LANZA
ACTIVIDAD
SÍNTESIS DE LA ACTIVIDAD
• Grupos de 2
• Reparte a cada grupo 10 cubos de conexión.
• "Vamos a jugar a un juego al que puede que hayáis jugado en primer curso llamado ¿Qué hay detrás de mi espalda?"
• Muestra a los alumnos una torre de 10 cubos. Coloca la torre detrás de tu espalda. Rompe 4 cubos, y muestra el resto de la torre.
• "¿Cuántos cubos hay detrás de mi espalda? ¿Cómo lo sabes?" (4 porque hay 6 y 4 más hacen 10. Lo sé porque 10 - 4 = 6.)
• 30 segundos: tiempo para pensar en silencio
• 1 minuto: discusión por parejas
• Comparte las respuestas.
• "Después de que un compañero haya escondido los cubos, cambiad los papeles."
• 10 minutos: tiempo de trabajo por parejas
• Pida a un estudiante que juegue una ronda del juego con la clase.
• Mientras el estudiante muestra la torre, escriba en la pizarra la ecuación de adición relacionada con un sumando desconocido. (por ejemplo, si un estudiante muestra 2 bloques, escriba 2 + ____ = 10.)
• "¿Cómo representa esta ecuación el juego?"
• "¿Qué número hace que la ecuación sea verdadera?"
• "¿Cómo podemos representar el juego con una ecuación de resta?"
(10 - 2 = 8 o 10 - 8 = 2)
• Si es necesario, pida a los alumnos que muestren cómo los números de las ecuaciones de suma y resta representan los cubos de la ronda.
15 minutos
El propósito de la actividad es que los estudiantes practiquen su fluidez con sumas de 10 a medida que encuentran los números que hacen que las ecuaciones sean verdaderas. En esta actividad, los alumnos representan imágenes de torres de cubos conectadas con ecuaciones y emparejan ecuaciones con un número desconocido con estas imágenes (MP2). En la síntesis, los estudiantes explican cómo sus ecuaciones coinciden con las imágenes (MP6).
Apoyo a los estudiantes con discapacidad
Acción y Expresión: Desarrolla la Expresión y la Comunicación. Dar a los alumnos acceso a un marco de diez y cubos conectores o fichas para recrear las ecuaciones.
Apoya la accesibilidad para: Organización, Procesamiento Conceptual
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

LANZAMIENTO
ACTIVIDAD
• Grupos de 2
• "Mira la torre de cubos A en tu libro."
• "Escribe tantas ecuaciones como se te ocurran que representen la torre."
• 2 minutos: tiempo de trabajo en pareja
• Comparte las respuestas.
• "Continúa escribiendo ecuaciones para cada torre de cubos. Escribe tantas ecuaciones como se te ocurran para cada torre. Puedes escribir ecuaciones de suma y resta."
• 5 minutos: tiempo de trabajo en pareja
• "Ahora mira las ecuaciones de la tabla. Algunas de las ecuaciones pueden coincidir con las ecuaciones que escribiste debajo de las torres cúbicas."
• "Encuentra el número que hace que cada ecuación sea verdadera. Luego escribe la letra de la torre de cubos que representa la ecuación."
• 5 minutos: tiempo de trabajo en pareja
1. Para cada torre de cubos, escribe tantas ecuaciones como se te ocurran que representen los cubos.

DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA




2. Encuentra el número que hace que cada ecuación sea verdadera. Luego escribe la letra de la torre de cubos que representa la ecuación.
3 + _____ = 10 Letra: _____ 10 - 7 = _____ Letra: _____ 10 - 5 = _____ Letra: _____ 2 + _____ = 10 Letra: _____ 10 - 1 = _____ Letra: _____ 10 - 2 = _____ Letra: _____ _____ + 6 = 10 Letra: _____ _____ + 9 = 10 Letra: _____
5 + _____ = 10 Letra: _____ 10 - _____ = 4 Letra: _____
Matemáticas de 2º grado . Unidad 1

POSIBLE RESPUESTAS
3 + 7 = 10
10 - 7 = 3
10 - 5 = 5
2 + 8 = 10
10 - 1 = 9
10 - 2 = 8
4 + 6 = 10
1 + 9 = 10
5 + 5 = 10
10 - 6 = 4
• Mostrar 10 - 7 = _____
SÍNTESIS DE LA ACTIVIDAD
Letra: C
Letra: C
Letra: A
Letra: D
Letra: E
Letra: D
Letra: B
Letra: E
Letra: A
Letra: B
• "¿Qué torre de cubos representa esta ecuación?" (C)
• "¿Dónde ves cada parte de la ecuación en la torre? (Hay 10 cubos en total. 7 cubos son amarillos y el número desconocido de cubos es azul.)
• "¿Cómo puede ayudarnos la torre a encontrar el número desconocido?" (Te ayuda ver que hay 10 cubos y 7 amarillos y 3 azules harían 10. Si quitamos el 7 amarillo, vemos que el número desconocido es 3.)
Comunidad matemática
"Volvamos a ver nuestra tabla de Comunidad matemática".
Muestra la tabla.
10 minutos
"Basándonos en lo que hemos hecho hoy, ¿qué podemos añadir a "Haciendo matemáticas"?
ENUNCIADO DE LA TAREA PARA EL ALUMNO
POSIBLES RESPUESTASS
Math Nation California - Grado 2
5 minutos
Encierra en un círculo las 2 ecuaciones que representan los cubos.
7 + _____ = 10
10 + 3 = _____
3 + _____ = 7
10 - 3 = _____

Los estudiantes rodean 7 + _____ = 10 y 10 - 3 = _____
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Alineación
Estándares y principios de CA
Abordando
2.OA.2 Sumar y restar con fluidez dentro de 20 usando estrategias mentales. Al final del Grado 2, sabe de memoria todas las sumas de dos números de un dígito.
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP4 Modelar con matemáticas.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.2
I.B.5 II.C.7
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
predecir lo que podría ocurrir buscar y utilizar la estructura desmontar el todo, unir las partes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo encontrar un número dentro de 20 que hace que una ecuación de suma o resta sea verdadera.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Encuentra el número que hace que las ecuaciones dentro de 20 sean verdaderas utilizando la relación entre suma y resta.
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
¿Qué hace que alguien sea bueno en matemáticas? ¿De qué manera estás haciendo suposiciones sobre cuáles de tus alumnos son buenos en matemáticas?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Hablar de números (calentamiento)
Materiales a reunir
Conectar cubos
Materiales para copiar
What's Behind My Back Stage 3 Recording Sheet
Objetivos de aprendizaje para el estudiante
• Encontremos el número que hace verdaderas las ecuaciones con 20
Narrativa de la lección
El objetivo de esta lección es que los estudiantes encuentren el número que hace verdaderas las ecuaciones con 20
©Accelerate Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
En esta lección, los estudiantes aplican el razonamiento que utilizaron en lecciones anteriores con los sumandos que hacen 10 para encontrar el número que hace verdadera una ecuación que incluye el número 20. En la primera actividad, los estudiantes aprenden la etapa 3 del centro Qué hay detrás de mi espalda en la que trabajan con 20 cubos, organizados en dos torres de 10 cubos. En la segunda actividad, los alumnos encuentran el número que hace verdaderas diferentes ecuaciones con expresiones de suma y resta.
A lo largo de la lección, los alumnos tienen la oportunidad de utilizar lo que saben sobre la estructura de los números enteros y la relación de la suma y la resta para encontrar los números desconocidos y explicar sus métodos (MP3, MP7).
Math Community
En la síntesis de la lección, los alumnos utilizan su póster de la comunidad matemática para crear normas para el aula.
Componente de lección

Estructura Tiemp
Calentamiento Independiente 10 min.
Actividad de exploración 1 Pares 20 min.
Actividad de exploración 2 Pares 15 min.
Síntesis Todo el grupo 10 min.
Descripción breve
Los estudiantes evalúan expresiones de suma y resta que contienen números enteros dentro de 10.
Los estudiantes determinan cuántos cubos de 20 conexión hay detrás de la espalda de un estudiante y luego escriben las ecuaciones correspondientes.
Los estudiantes determinan el valor desconocido para completar ecuaciones de suma y resta de números enteros dentro de 20
Los estudiantes discuten las normas del grupo para la exhibición del póster de la Comunidad Matemática de la clase.
Enfriamiento Independiente 5 min. Los estudiantes completan ecuaciones de suma y resta de números enteros dentro de 20 para encontrar los valores faltantes.
Centro(s) sugerido(s) Grupos pequeños Opcional
Apoyo:
• Rompecabezas numéricos: Suma y resta (1-4), Etapa 1: Dentro de 10
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos
Rutinas instructivas
Conversación sobre números
Esta charla sobre los números anima a los alumnos a pensar en la relación entre la suma y la resta para resolver problemas mentalmente. Se basa en el trabajo de la lección anterior, en la que los alumnos utilizaron la relación entre la suma y la resta para encontrar números desconocidos en ecuaciones. La comprensión obtenida aquí será útil más adelante en la lección cuando los estudiantes encuentren el valor para que una ecuación sea verdadera.
LANZAMIENTO

ACTIVIDAD
DE CARA AL ESTUDIANTE
ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• Muestra una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste."
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada expresión.
• 7 + 3
• 10 - 7
• 10 - 2
• 10 - 4
• 10: Ya lo sé.
• 3: si 7 + 3 es 10, entonces 10 - 7 es 3
• 8: he vuelto a contar 2
• 6: Sé 6 + 4 es 10
• "¿Cómo te ayudó a restar el pensar en la suma?" (Pensé en qué número podría sumar al 4 para hacer 10. Como sé 4 + 6 = 10 entonces supe 10 - 4 = 6)
• Si es necesario, utilice cubos conectores para representar el pensamiento de los alumnos.
Materiales para reunir
Cubos conectores
20 minutos
Materiales para copiar
Lo que hay detrás de mi espalda Hoja de registro de la Etapa 3
En esta actividad, los alumnos aprenden la etapa 3 del centro Lo que hay a mis espaldas. En esta nueva etapa, llamada 20 cubos, los alumnos trabajan con 20 cubos, organizados en dos torres de 10 cubos. Un compañero rompe la torre y coloca una parte detrás de su espalda y muestra la otra parte a su compañero. El otro compañero calcula cuántos cubos hay detrás de la espalda de su compañero. Los alumnos escriben una ecuación de suma con un espacio en blanco para representar los cubos que faltan. Los alumnos pueden escribir ecuaciones con el espacio en blanco como primer o segundo sumando. Pida a los alumnos que expliquen qué representa cada número y cada espacio en blanco de la ecuación en el contexto de la actividad del centro (MP2).
Apoyo para estudiantes de inglés
MLR7 Comparar y conectar. Síntesis: Invite a los estudiantes a discutir las conexiones entre los diferentes enfoques. Pregunte: "¿Qué tenían en común estas estrategias? ¿En qué se diferenciaban?"
Avances: Representar, Conversar

Matemáticas de 2º grado . Unidad 1
Apoyo a los alumnos con discapacidad
Representación: Interiorizar Comprender. Síntesis: Invite a los alumnos a identificar a qué detalles era importante o más útil prestar atención. Muestre el marco de la frase: "Para averiguar cuántos cubos hay a la espalda de mi compañero, puedo...".
Apoya la accesibilidad para: Procesamiento visualespacial
ACTIVIDAD
SÍNTESIS DE LA ACTIVIDAD
• Grupos de 2
• Entrega a cada grupo 20 cubos conectores y una hoja de registro.
• "Vamos a jugar a Qué hay detrás de mi espalda, esta vez con 20 cubos"
• "¿Cómo averiguaste cuántos cubos conectores había detrás de la espalda de tu compañero la última vez?" (Pensé en una expresión de suma que diera 10.
• Resté lo que me mostraron de 10.)
• "Juguemos una ronda con 20."
• Muestra a los alumnos 2 torres de 10 cubos. Coloque las torres a sus espaldas. Separe y muestre 8 de los cubos.
• "Esta vez, cuando jueguen, van a registrar una ecuación de suma con un espacio en blanco para representar los cubos que faltan, antes de averiguar cuántos hay detrás de la espalda de su compañero. ¿Qué ecuación debemos registrar?" (8 + = 20)
• 30 segundos: tiempo para pensar en silencio
• Comparte las respuestas.
• "¿Cuántos cubos hay detrás de mi espalda? ¿Cómo lo sabes?" (12 porque 2 más hacen 10 y luego aquí hay otra torre de 10.)
• 30 segundos: tiempo para pensar en silencio
• 30 segundos: discusión en pareja
• "Juega con tu pareja. No olvides anotar una ecuación en cada ronda."
• 10 minutos: tiempo de trabajo en pareja
• Muestra 9 cubos.
• "¿Qué ecuación de suma puedo escribir para representar el número de cubos que sabes y el número de cubos que necesitas averiguar?" (9 + = 20)
• "Dile a tu compañero cómo puedes averiguar cuántos cubos faltan"
• Monitorea a los estudiantes que hablan de hacer un 10 y saber que hay un más 10.
• Comparte las respuestas.
ECUACIÓN SEA CIERTA 15 minutos
Materiales para reunir
Conectar cubos
California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
El propósito de esta actividad es que los estudiantes encuentren el valor que hace verdadera una ecuación de suma o resta, con totales de 20. Los alumnos pueden utilizar el método que les parezca más adecuado. En el lanzamiento, los estudiantes trabajan con un nuevo compañero y completan el sumando desconocido en las ecuaciones de su hoja de registro de la Actividad 1.
• Grupos de 2: diferente a la actividad anterior
• Dar a los grupos acceso a los cubos de conexión.

LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• "Vas a encontrar el número que hace que cada ecuación sea verdadera. Cambia las hojas de registro con alguien con quien no hayas jugado a ¿Qué hay a mis espaldas? Escribe el número que hace que cada ecuación sea verdadera. Prepárate para compartir con tu compañero cómo encontraste cada número".
• 3 minutos: tiempo de trabajo independiente
• "Comparte tu trabajo con tu compañero. Escoge una ecuación y explícale cómo encontraste el número que la hace verdadera."
• 3 minutos: discusión en parejas
• "Trabaja en tu libro para encontrar el número que hace verdadera cada ecuación."
• 5 minutos: tiempo de trabajo independiente
• Monitorea a los estudiantes que buscan maneras de hacer 10.
Encuentra el número que hace verdadera cada ecuación.
1. 4 + = 20
2. 20 - = 4
3. 6 + = 20
4. 20 - = 10
5. + 3 = 20
6. 20 - 15 =
7. 20 - = 18
8. Si tienes tiempo: - 5 = 20
1. 16. Ejemplo de respuesta: 4 + 6 = 10, 10 + 10 = 20, 6 + 10 = 16
2. 16. Ejemplo de respuesta: Si 4 + 16 = 20 entonces 20 - 16 = 4
3. 14. Ejemplo de respuesta: 6 + 4 = 10, 10 + 10 = 20, 4 + 10 = 14
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
4. 10. Ejemplo de respuesta: He utilizado 2 torres de 10. Tengo que quitar 1 para que me queden 10 cubos.
5. 17. Respuesta de muestra: 20 - 3 = 17
6. 5. Ejemplo de respuesta: Empecé con 2 decenas. Quité 1 decena y 5 cubos de la otra torre. Me quedaban 5 cubos.
7. 2. Respuesta de ejemplo: Conté hacia atrás 2 para llegar a 18
8. 25. Ejemplo de respuesta: 20 + 5 = 25
• Invite a los alumnos seleccionados a mostrar su pensamiento para + 3 = 20 y 20 - = 18.
• "¿Cómo les ayudó pensar en una decena a encontrar su respuesta?". (Sabían que 20 son 2 decenas, así que utilizaron 1 de las decenas para facilitar los problemas).
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1

10 minutos
"Hoy, encontramos el número desconocido en las ecuaciones que las hace verdaderas."
Comunidad matemática
Muestre el póster Comunidad matemática. Explique a los estudiantes que las normas son expectativas que ayudan a que todos en el salón se sientan seguros, cómodos y productivos haciendo matemáticas juntos.
"Vamos a hacer una lista de normas sobre cómo hacemos matemáticas juntos. Un ejemplo de norma es 'Escuchar cuando los demás comparten sus ideas'. ¿Qué otras normas deberíamos establecer para nuestra clase?"
Compartir y anotar las respuestas.
VERDADERAS? 5 minutos
Encuentra el número que hace que cada ecuación sea verdadera.
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
Reflexiones:
1. + 17 = 20
2. 20 - 9 = 3. + 5 = 20 4. 20 - = 8
1. 3. Ejemplo de respuesta: 18, 19, 20. Conté 3 más.
2. 11. Respuesta de muestra: 9 + 1 = 10, 10 + 10 = 20, 10 + 1 = 11
3. 15. Ejemplo de respuesta: 5 + 5 = 10, 10 + 10 = 20, 10 + 5 = 15
4. 12. Ejemplo de respuesta: 8 + 2 = 10, 10 + 10 = 20, 10 + 2 = 12
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Estándares y principios de CA Alineación Abordar
2.OA.2 Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del segundo grado, saber de memoria todas las sumas de dos números de un dígito.
Enfoque SMPs
MP6 Prestar atención a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.2
I.B.5
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
predicen lo que podría ocurrir atienden a la precisión desmontando enteros, juntando piezas.
OBJETIVO(S) DE APRENDIZAJE
• Sé sumar y restar números dentro de 20
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Sé sumar y restar dentro de 20 de una forma que tenga sentido para ellos.
PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO
Al final del segundo grado, los estudiantes deben saber sumar y restar con fluidez dentro de 20, incluyendo saber de memoria todas las sumas de 2 números de un dígito. ¿Qué aprendió sobre sus alumnos durante las actividades de hoy que lo ayudará a preparar a todos los alumnos para cumplir con este estándar?
PREPARACIÓN DE LA LECCIÓN
Rutinas instructivas
Conversación sobre números (calentamiento)
Materiales para reunir
Cubos para conectar
Tarjetas numéricas 0-10
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales para copiar
¿A qué distancia? Hoja de registro de la Etapa 1
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Sumemos y restemos dentro de 20
Narrativa de la lección
El objetivo de esta lección es que los estudiantes sumen y resten dentro de 20 de una manera que tenga sentido para ellos.
El trabajo en esta lección se basa en el grado 1, donde los estudiantes suman y restan dentro de 20 con diferentes estrategias. Esta es una oportunidad para evaluar formativamente cómo los estudiantes encuentran sumas y diferencias en este rango. Los cubos de conexión organizados en torres de 10 y sencillos deben estar disponibles para que los estudiantes los usen, sin embargo, anime a los estudiantes a no usarlos si no los necesitan. Al final del segundo grado, los estudiantes deben sumar y restar con fluidez dentro de 20
Comunidad matemática
Diga a los estudiantes que, al final de la lección, se les pedirá que identifiquen ejemplos específicos de normas que experimentaron mientras hacían matemáticas.
LECCIÓN DE UN VISTAZO
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 10 min. Los estudiantes evalúan sumas de dos números enteros de un dígito.
Actividad de exploración 1 En parejas 20 min.
Actividad de exploración 2 En parejas 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes eligen tres números enteros de un dígito cuya suma sea lo más cercana posible a 20 y luego escriben una ecuación que represente la suma.
Los estudiantes utilizan diferentes estrategias para evaluar expresiones de suma y resta dentro de 20
Los estudiantes añaden o revisan las normas del aula al póster Comunidad matemática.
Los estudiantes encuentran el valor de expresiones que contienen la suma o la diferencia de números enteros dentro de 20
Apoyo: • Rompecabezas numéricos: Suma y resta (1-4), Etapa 1: Dentro de 10

Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
minutos

Rutinas instructivas
Hablar de números
El propósito de esta Charla sobre números es obtener estrategias y comprensiones que los estudiantes tienen para hacer una decena para sumar. Cuando los alumnos buscan formas de descomponer un sumando para formar 10, buscan y utilizan la estructura de los números y las propiedades de las operaciones (MP7). Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de sumar dentro de 20
• Mostrar una expresión.
LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste."
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra el valor de cada suma mentalmente.
• 8 + 2
• 8 + 3
• 8 + 5
• 7 + 6
• 10: Simplemente lo sé.
• 11: 8 + 2 = 10 y 8 + 3 es sólo 1 más.
• 13: 5 puede descomponerse en 2 y 3 8 + 2 = 10 y 10 + 3 = 13
• 13: 7 + 3 = 10 y 10 + 3 = 13
• "¿Cómo ayuda hacer 10 a encontrar el valor de las sumas?" (Me ayudó porque pude usar hechos que ya conozco. Sé que 7 + 3 = 10 y sé que 10 + 3 = 13.)
CERCA? 20 minutos
Materiales para reunir
Tarjetas numéricas 0-10
Materiales para copiar
¿Qué tan cerca? Etapa 1 Hoja de registro
El propósito de esta actividad es que los estudiantes revisen la etapa 1 del centro Qué tan cerca, que se introdujo por primera vez en el primer grado. Los estudiantes eligen las tarjetas de dígitos 5 y luego eligen 3 para hacer una expresión que tenga un valor lo más cercano posible al número objetivo, que es 20 en la etapa 1. Los alumnos pueden utilizar diversas estrategias, como hacer un 10 para sumar dos números o utilizar la relación entre la suma y la resta para elegir estratégicamente 3 números (MP7).
Apoyo para estudiantes de inglés
MLR2 Recoger y mostrar. Circule y recoja el lenguaje que utilizan los alumnos mientras juegan y comparan ecuaciones. En una pantalla visible, anote palabras y frases como: hacer diez, sumar, adición, suma, quitar, diferencia, valor y ecuación. Invite a los alumnos a tomar prestado el lenguaje del expositor según sea necesario y actualícelo a lo largo de la lección.
Avances: Conversar, leer

LANZAMIENTO
ACTIVIDAD
ENUNCIADO DE LA TAREA PARA EL ESTUDIANTE SÍNTESIS DE LA ACTIVIDAD
Matemáticas de 2º grado . Unidad 1
California - Grado 2
Apoyo a los estudiantes con discapacidad
Acción y Expresión: Desarrollar la expresión y la comunicación. Proporcione acceso a diez marcos o cubos de conexión. Los alumnos pueden utilizar dos colores diferentes para representar los dos sumandos o el minuendo.
Apoya la accesibilidad para: Organización, Procesamiento Conceptual
• Grupos de 2
• Entregue a cada grupo un juego de tarjetas. Pídales que retiren las tarjetas del número 10.
• Muestre las tarjetas de dígitos en la parte superior de la página del alumno.
• "Vamos a jugar a un juego llamado Cuán cerca. Vamos a jugar 1 ronda juntos".
• "Mira las 5 tarjetas. Piensa qué 3 tarjetas elegirías para sumar y acercarte a 20."
• 1 minuto: tiempo para pensar en silencio
• 2-3 minutos: tiempo de trabajo en pareja
• Comparte las respuestas.
• "Después de elegir tus 3 tarjetas, escribirás una ecuación que muestre la suma."
• Demuestra cómo escribir una ecuación para mostrar la suma de las 3 tarjetas que más se acercan a 20.
• "Cuando tengas tu ecuación escrita, compárala con la de tu compañero para ver quién encontró una suma más cercana a 20."
• "Luego reemplazarás las cartas que usaste y volverás a jugar."
• "Ahora juega a Qué tan cerca con tu compañero."
• 10 minutos: tiempo de trabajo en pareja
• Controle a los estudiantes que:
• intentan hacer 10 y luego le suman el mayor número posible
• suman los 2 mayores números y luego buscan el otro número necesario para
• hacer 20





• "¿Qué métodos usaste para encontrar una suma cercana a 20?
• Invite a los alumnos previamente seleccionados a compartir sus estrategias.
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
Materiales para reunir
Cubos de conexión
El objetivo de esta actividad es que los alumnos sumen y resten dentro de 20 utilizando cualquier método que tenga sentido para ellos. En la actividad anterior, los alumnos compartieron los métodos que utilizaron para sumar dentro de 20. Esta actividad ofrece a los alumnos la oportunidad de probar algunos de los métodos que comentaron. En esta actividad, los estudiantes también restan dentro de 20 y discutirán sus métodos en la síntesis.
• Grupos de 2
• Dé a los estudiantes acceso a los cubos de conexión.

LANZAMIENTO
ACTIVIDAD
• "Ahora vamos a sumar y restar dentro de 20. Piensa cómo mostrar tu pensamiento. Piensa en cómo puedes mostrar tu pensamiento para que otros puedan entenderlo"
• "Tienes tiempo para trabajar de forma independiente antes de compartir tu pensamiento con un compañero"
• 5 minutos: tiempo de trabajo independiente
• 5 minutos: discusión en parejas
• Vigila los diferentes métodos utilizados para encontrar el valor de 17 - 9
• Por ejemplo:
• sumar para obtener 10 (9 + 1, 10 + 17, 1 + 7 = 8)
• descomponer un número para llegar primero a 10 (17 - 7 = 10, 10 - 2 = 8)
Encontrar el valor de cada expresión.
Muestra tu razonamiento utilizando dibujos, números o palabras.
1. 4 + 9
ENUNCIADO DE LA TAREA PARA EL ALUMNO
POSIBLES RESPUESTAS
2. 15 - 3
3. 7 + 6
4. 17 - 9
5. 14 + 5
6. 12 - 4
7. 6 + 12
8. 16 - 5
1. 13. Ejemplo de respuesta: 9 + 1 = 10, 10 + 3 = 13
2. 12. Respuesta de muestra: He vuelto a contar 14, 13, 12
3. 13. Respuesta de muestra: 7 + 7 = 14, 14 - 1 = 13
4. 8. Respuesta de muestra: 9 + 1 = 10, 10 + 7 = 17, 1 + 7 = 8
5. 19. Respuesta de muestra: 4 + 5 = 9 entonces 14 + 5 = 19
6. 8. Respuesta de muestra: Lo sé 8 + 4 = 12
7. 18. Respuesta de muestra: 6 + 2 = 8 entonces 6 + 1 2 = 18
8. 11. Respuesta de muestra: 6 - 5 = 1 entonces 16 - 5 = 11
Learning Inc. - Todos los derechos reservados
AVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD

Matemáticas de 2º grado . Unidad 1
Si los estudiantes están contando todos los cubos de 1 en 1 o trabajando con cubos sueltos, considere preguntar: "¿Cómo podrían usar torres de 10 para ayudarse a encontrar las sumas o diferencias?"
• Despliegue 17 - 9
• Seleccione estudiantes previamente identificados para compartir sus estrategias.
10 minutos
"Hoy trabajamos con un compañero para jugar un juego sobre sumar y restar dentro de 20."
Comunidad matemática
Muestre el póster Comunidad matemática.
Pregunte a los estudiantes si desean agregar o revisar sus normas de comunidad matemática.
Comparta y registre las respuestas.
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
Reflexiones:
5 minutos
Encuentre el valor de cada expresión. Muestre su razonamiento utilizando dibujos, números o palabras.
1. 8 + 6
2. 13 - 5
3. 16 - 4
1. 14. Ejemplo de respuesta: 8 + 2 = 10, 10 + 4 = 14
2. 8. Respuesta de ejemplo: 13 - 3 = 10, 10 - 2 = 8
3. 12. Respuesta de muestra: Acabo de restar los 6 - 4 = 2
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Abordando
Estándares y principios de CA Alineación
2.NBT.5 Sumar y restar con fluidez dentro de 100 utilizando estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta.
Construyendo sobre
1.NBT.4
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1
I.A.4
I.B.8
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
dan sentido al mundo
dan sentido a los problemas y perseveran en su resolución desmontando enteros, juntando piezas.
OBJETIVO(S) DE APRENDIZAJE
• Puedo sumar números enteros dentro de 50.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Sumar dentro de 50 de una forma que tenga sentido para ellos.
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
¿En qué aspectos va bien la comunidad matemática que está trabajando para fomentar? ¿Qué medidas puede tomar para seguir construyendo la comunidad?
PREPARACIÓN DE LA LECCIÓN
Rutinas instructivas
Hablar de números (Calentamiento)
Materiales a reunir
Cubos de conexión: Actividad 2
Tarjetas numéricas 0-10: Actividad 1
Materiales para copiar
¿Cómo de cerca? Hoja de registro de la Etapa 3 (grupos de 1): Actividad 1
Objetivos de aprendizaje para el alumno
• Sumemos dentro de 50.
Narrativa de la lección
El objetivo de esta lección es que los alumnos sumen dentro de 50. Los estudiantes encuentran el valor de las sumas dentro de 50 de cualquier manera que tenga sentido para ellos.
©Accelerate Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
Los alumnos sumaron dentro de 100 en primer curso. Esta lección sirve como evaluación formativa de cómo los estudiantes encuentran el valor de sumas con sumandos mayores. A lo largo de la lección, controle que los estudiantes busquen y utilicen la estructura del valor posicional para sumar decenas con decenas y unidades con unidades (MP7).
Comunidad de matemáticas
Diga a los estudiantes que, al final de la lección, se les pedirá que reflexionen sobre las normas y que pueden agregar normas sobre el trabajo con un compañero.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 10 min.
Actividad de exploración 1 Pares 20 min.
Actividad de exploración 2 Por parejas 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes determinan la suma de números enteros de uno y dos dígitos dentro de 50
Los estudiantes eligen cuatro tarjetas para hacer 2 números enteros de dos dígitos cuya suma sea lo más cercana posible a 50 y luego escriben una ecuación que muestre la suma.
Los estudiantes evalúan expresiones de suma de números enteros de una y dos cifras cuya suma se aproxime a 50
Los estudiantes reflexionan sobre varias normas utilizadas en el trabajo independiente y por parejas y luego las añaden al póster de la Comunidad matemática.
Los estudiantes calculan el valor de expresiones de suma de números enteros con una suma dentro de 50
Apoyo:
• Rompecabezas numéricos: Suma y resta (1-4), Etapa 1: Dentro de 10

Math
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos

Rutinas instructivas
Conversación sobre números
El propósito de esta Conversación sobre números es obtener estrategias y conocimientos que los estudiantes tienen para sumar un número de un dígito a un número de dos dígitos. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de sumar dentro de 50
LANZA
ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• Muestra una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste."
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo a la vista.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada suma.
• 16 + 3
• 16 + 5
• 26 + 5
• 38 + 6
• 19: 3 + 6 = 9 entonces 13 + 6 = 19
• 21: 16 + 4 = 20 y 1 más es 21
• 31: 26 + 4 = 30 y 1 más es 31
• 44: 6 puede dividirse en 2 y 4 38 + 2 = 40 y 40 + 4 = 44
• "¿Cómo ayuda buscar formas de hacer 10 para encontrar el valor de la suma con números más grandes?" (Puedes hacer una decena con las unas y luego volver a sumar las otras decenas. 38 + 6, 8 + 2 = 10, 10 + 30 + 4 = 44.)
Materiales para reunir
20 minutos
Materiales para copiar
Tarjetas numéricas 0-10 ¿Cuánto falta? Hoja de registro de la Etapa 3 (grupos de 1)
El propósito de esta actividad es que los estudiantes aprendan la etapa 3 del centro Qué tan cerca que se introdujo en el primer grado. En esta etapa, cada estudiante toma 7 tarjetas y elige 4 de ellas para crear 2 números de dos dígitos. Cada alumno suma los números y el alumno cuya suma sea más cercana a 100 gana un punto para la ronda. Se recomienda que, en este momento del año, los alumnos comiencen con un número objetivo de 50 en lugar de 100 en esta etapa.
Si los alumnos aún no son capaces de hacer 2 números que se acerquen a 50, anímelos a elegir 2 tarjetas, hacer un 2 número de dos cifras y representar el número con cubos. A continuación, determine cuántos cubos más necesitan para llegar a 50 y elija las tarjetas 2 que más se acerquen a ese número.
Matemáticas de 2º grado . Unidad 1

Apoyo a los alumnos con discapacidad
Representación: Interiorizar la comprensión. Comience preguntando: "¿Recuerdan el juego 'Qué tan cerca'?". Invite a los alumnos a recordar las estrategias que les ayudaron a trabajar dentro de 20. Pídales que piensen en cómo cambiará el juego cuando el objetivo sea 50.
Apoya la accesibilidad para: Memoria, Atención, Organización
• Grupos de 2
• Entregue un juego de tarjetas de dígitos a cada grupo.
• "Hoy vamos a jugar a otro juego de Qué tan cerca. Esta vez jugaremos a Qué tan cerca de 50."
• Muestre las tarjetas de dígitos en la parte superior de la página del alumno.
• "Comenzamos con 7 tarjetas de nuevo. Piensa qué tarjetas elegirías para hacer 2 números de dos dígitos que tengan una suma cercana a 50."
• 1 minuto: tiempo para pensar en silencio
• 2-3 minutos: tiempo para trabajar en pareja
• Comparte las respuestas.
• "Después de hacer tus números de dos dígitos, escribirás una ecuación que muestre la suma"
• Haz una demostración de cómo escribir una ecuación en la hoja de registro.
• "Ahora, vemos de quién es la suma más cercana a 50. Habla con tu compañero sobre cómo podrías calcularlo". (Puedes contar hacia arriba o hacia atrás desde 50 y ver de quién es el número que está más cerca.)
• 30 segundos: tiempo para pensar en silencio
• 1 minuto: discusión en pareja
• "Luego, reemplazarás las tarjetas que usaste y volverás a jugar."
• "Ahora juega a Qué tan cerca con tu compañero."
ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• 10 minutos: tiempo de trabajo en pareja







SÍNTESIS DE LA ACTIVIDAD
Math Nation California - Grado 2
• Muestra las tarjetas de dígitos de la página del alumno.
• "Diego hizo el número 38. ¿Qué número podría hacer Diego a continuación para acercarse a 50?"
©Accelerate Learning Inc. - Todos los derechos reservados


50 15 minutos
Materiales para reunir

Preparación necesaria
Cubos de conexión Cree cubos de conexión en torres de 10 y sencillos.
En esta actividad, los alumnos encuentran el valor de sumas con números más grandes utilizando cualquier método que tenga sentido para ellos. Pueden representar su pensamiento utilizando cubos de conexión, dibujos, ecuaciones o palabras. Controle las formas en que los alumnos utilizan métodos basados en el valor posicional, incluido el lenguaje que utilizan para describir la composición de una decena al sumar decenas y decenas y unidades y unidades (MP3, MP6).
MLR8 Discussion Supports. Síntesis: Después de presentar una estrategia a la clase, invite a los alumnos a que se dirijan a un compañero y repitan lo que han oído con sus propias palabras. Anime a los estudiantes a tomar prestado el lenguaje de una pantalla con palabras y frases recogidas de lecciones anteriores.
Avances: Escuchar, hablar
2 Matemáticas de 2º grado . Unidad 1
INICIAR
ACTIVIDAD
ENUNCIADO DE LA TAREA
ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA
ACTIVIDAD
Learning Inc. - Todos los derechos reservados
• Grupos de 2
• Dar a los alumnos acceso a cubos de conexión en torres de 10 y sencillos.
• "Ahora vamos a sumar números más grandes. Piensa en cómo puedes mostrar tu pensamiento para que los demás puedan entenderlo"
• "Tienes tiempo para trabajar de forma independiente antes de compartir tu pensamiento con un compañero."
• 5 minutos: tiempo de trabajo independiente
• 5 minutos: discusión por parejas
• Supervise a los estudiantes que:
• Suman por valor posicional (27 + 15, 20 + 10 = 30, 7 + 5 = 12, 30 + 12 = 42)
• Descomponen 1 número para hacer un 10, luego suma el resto (27 + 15, 27 + 3 = 30, 30 + 12 = 42)
Encuentra el valor de cada suma. Muestra tu razonamiento utilizando dibujos, números o palabras.
1. 37 + 8
2. 24 + 23
3. 16 + 30
4. 39 + 11
5. 27 + 15
1. 45. Ejemplo de respuesta: 37 +3 = 40, 40 + 5 = 45
2. 47. Respuesta de muestra: 20 + 20 = 40, 4 + 3 = 7, 40 + 7 = 47
3. 46. Ejemplo de respuesta: 30 + 10 = 40, 40 + 6 = 46
4. 50. Respuesta de muestra: 39 + 1 = 40, 40 + 10 = 50
5. 42. Ejemplo de respuesta: 20 + 10 = 30, 7 + 5 = 12, 30 + 12 = 42
• Mostrar 27 + 15.
• Seleccionar a los alumnos previamente identificados para compartir.
-
Matemáticas de 2º grado . Unidad 1
10 minutos
"Hoy hemos jugado a otro juego con un compañero. También hemos resuelto algunos problemas de forma independiente antes de compartir nuestras ideas con los demás. Vamos a añadir a nuestra tabla de ayer."
Muestra la tabla de la lección anterior y lee las normas a los alumnos.
"¿Qué normas os gustaría añadir?"
CONTROL 5 minutos
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
Reflexiones:

Math Nation California - Grado 2
Encuentra el valor de cada suma. Muestra tu pensamiento usando dibujos, números o palabras.
• 26 + 6
• 32 + 17
• 28 + 14
32. Ejemplo de respuesta: 26 + 4 = 30, 30 + 2 = 32
49. Respuesta de muestra: 30 + 10 = 40, 2 + 7 = 9, 40 + 9 = 49
42. Ejemplo de respuesta: 28 + 14 = 30 + 12 = 42
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Abordando
Alineación
Estándares y principios de CA
2.NBT.5 Sumar y restar con fluidez dentro de 100 utilizando estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta.
2.OA.2 Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del 2do grado, saber de memoria todas las sumas de dos números de un dígito.
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en resolverlos.
MP4 Modelar con matemáticas.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares CA ELD
I.A.1 I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
predicen lo que podría ocurrir buscan y expresan regularidad en razonamientos repetidos desmontando enteros, juntando partes.
OBJETIVO(S) DE APRENDIZAJE
• Sé sumar y restar números enteros dentro de 20
• Sé sumar números enteros dentro de 50
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Aprender la estructura de las lecciones del día del centro.
• Practicar la suma y la resta dentro de 10 o 20
• Practicar la suma dentro de 50
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
¿Cómo puedes utilizar lo que has aprendido hoy sobre tus alumnos y la estructura de los centros para poner en práctica los centros en tus próximas clases?
PREPARACIÓN DE LA LECCIÓN
Rutinas instructivas
Hablar de números (Calentamiento)
Materiales a reunir
Tarjetas numéricas 0-10: Actividad 2
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales para copiar
Rompecabezas numéricos Suma y resta
Etapa 2 Tablero de juego (grupos de 1): Actividad 1
Rompecabezas numéricos Tarjetas con dígitos
(grupos de 2): Actividad 1
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Sumemos y restemos en actividades de centro.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes practiquen la suma y la resta dentro de 10, 20, o 50
Esta lección es opcional porque es una oportunidad de práctica extra que no todas las clases pueden necesitar. En ambas actividades, los alumnos pueden elegir entre 2 centros introducidos en lecciones anteriores. Los alumnos eligen el centro en el que les gustaría participar y trabajan con un compañero en esa actividad. Utilice esta lección como una oportunidad para establecer las estructuras de los centros para el año, por ejemplo, cómo se organizarán los materiales, cuántos estudiantes trabajarán en cada centro, cómo los estudiantes harán la transición de un centro a otro y cómo los estudiantes trabajarán juntos con sus compañeros en cada centro.
Comunidad de matemáticas
Diga a los estudiantes que reflexionarán sobre sus normas identificadas al final de esta lección.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 10 min.
Actividad de Exploración 1 Pares 15 min.

Centros Parejas o Grupos pequeños 25 min.
Los estudiantes identifican el valor de expresiones que contienen la suma de números enteros dentro de 50
Los estudiantes usan tarjetas de dígitos para hacer ecuaciones de suma y resta dentro de 20
Los estudiantes eligen entre los centros para practicar la suma y la resta de números enteros dentro de 50 Centros sugeridos:
• Qué hay a mis espaldas, Etapas 2 y 3
• Qué tan cerca, Etapas 1-3
• Rompecabezas numéricos, Etapas 1 y 2
Síntesis Todo el grupo 10 min.
Los estudiantes resumen las normas que funcionan bien y las normas que se pueden mejorar.
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos

Rutinas instructivas
Conversación sobre números
El propósito de esta Conversación sobre números es obtener las estrategias y comprensiones que los estudiantes tienen sobre las estrategias para sumar basadas en el valor posicional. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten poder sumar 2 números de dos dígitos dentro de 50, y a lo largo del año a medida que los estudiantes desarrollen fluidez para sumar dentro de 100
• Muestra una expresión.
LANZA
ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• "Hacedme una señal cuando tengáis una respuesta y podáis explicar cómo la habéis obtenido".
• 1 minuto: tiempo para pensar en silencio
• Registrar las respuestas y la estrategia.
• Mantener las expresiones y el trabajo mostrados.
• Repetir con cada expresión.
Encontrar mentalmente el valor de cada expresión.
• 14 + 22
• 19 + 22
• 15 + 25
• 17 + 25
• 36: 14 + 20 = 34, 34 + 2 = 36
• 41: 19 + 1 = 20, 20 + 21 = 41
• 40: 15 + 25 = 25 + 10 = 35, 35 + 5 =40
• 42: 17 + 3 = 20, 20 + 22 = 42
• "Hemos visto muchas formas diferentes de encontrar la suma de 2 números de dos dígitos. Habrá más oportunidades para probar diferentes métodos mientras trabajamos en centros hoy".
Materiales para copiar
Rompecabezas numéricos Tablero de juego de sumas y restas Etapa 2 (grupos de 1), Rompecabezas numéricos Tarjetas de dígitos (grupos de 2)
15 minutos
Preparación necesaria
Crea un conjunto de tarjetas de dígitos a partir del patrón de líneas negras para cada grupo de 2
El propósito de esta actividad es que los estudiantes revisen la etapa 2 del centro de Acertijos numéricos que se introdujo por primera vez en el primer grado. Los alumnos trabajan juntos para usar tarjetas de dígitos para hacer que las ecuaciones de suma y resta dentro de 20 sean verdaderas. Cada tarjeta de dígitos sólo puede usarse una vez en una página.
LANZAMIENTO

ACTIVIDAD
SÍNTESIS DE LA ACTIVIDAD
• Grupos de 2
• Entregue a cada grupo un juego de tarjetas de dígitos y tableros de juego.
• "Vamos a jugar un juego que quizás hayan jugado en primer grado llamado Rompecabezas de Números"
• "En este juego, se usan tarjetas de dígitos para hacer que cada ecuación sea verdadera. Sólo puedes usar cada tarjeta de dígitos una vez en el tablero de juego.
• 10 minutos: tiempo de trabajo en el centro
• Rompecabezas de visualización 1
• "¿Con qué ecuación empezarías? ¿Por qué comenzarías allí?"
25 minutos
Materiales para reunir
Tarjetas numéricas 0-10
Preparación requerida
Reúne materiales de:
• Qué hay detrás de mi espalda, Etapas 2 y 3
• Qué tan cerca, Etapas 1-3
• Rompecabezas numéricos, Etapas 1 y 2
El propósito de esta actividad es que los estudiantes vuelvan a elegir entre actividades que se centran en sumar o restar.
Los estudiantes eligen entre cualquier etapa de los centros previamente introducidos.
• ¿Qué hay detrás de mi espalda?
• ¿Qué tan cerca?
• Rompecabezas numéricos
LANZA
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
Math Nation California - Grado 2
• "Ahora puedes elegir un centro diferente."
• Muestre las opciones de centros en el libro del alumno.
• "Piensen en qué centro les gustaría trabajar ahora."
• 30 segundos: tiempo para pensar en silencio
• Invite a los alumnos a trabajar en el centro de su elección.
• 10 minutos: tiempo de trabajo en el centro
• "Elige lo que te gustaría hacer a continuación."
• 10 minutos: tiempo de trabajo en el centro
Elige un centro.
¿Qué hay a mi espalda? ¿Qué tan cerca?


Rompecabezas numéricos

©Accelerate Learning Inc. - Todos los derechos reservados Matemáticas de 2º grado . Unidad 1


Matemáticas de 2º grado . Unidad 1
SÍNTESIS DE LA ACTIVIDAD

• "¿Qué es una cosa que aprendiste o mejoraste al trabajar en la actividad que elegiste?"
10 minutos
"Hoy elegimos actividades para trabajar y trabajamos con un compañero durante el tiempo de centro."
Comunidad matemática
Muestre la tabla de la lección anterior y lea las normas a los estudiantes.
"¿Qué salió bien? En qué podemos seguir trabajando?"
Reflexiones:
©Accelerate Learning Inc. - Todos los derechos reservados
Nation California - Grade 2


IDEA(S) PRINCIPAL(ES)
• Representar datos
ALINEACIÓN
Abordaje
Estándares y principios de CA Alineación
2.MD.10 Dibujar un gráfico y un gráfico de barras (con escala de una unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando información presentada en una gráfica de barras.
Enfocar SMPs
MP4 Modelar con matemáticas.
MP5 Usar herramientas apropiadas estratégicamente.
CA ELD Standards
I.A.2 I.C.9
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . . dar sentido al mundo
utilizar las herramientas adecuadas para razonar estratégicamente con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo organizar y representar datos de diferentes maneras.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Aprender la estructura de las lecciones del día del centro.
• Practicar la suma y la resta dentro de 10 o 20
• Practicar la suma dentro de 50
En el primer curso, los alumnos organizaron y representaron los datos con un máximo de tres categorías. ¿Cómo vio u oyó a los estudiantes demostrar su comprensión de las diferentes formas de organizar los datos?
Rutinas instructivas
MLR7 Comparar y conectar (Actividad 2)
Notar y maravillarse (Calentamiento)
Materiales para copiar
Cómo llegamos a la escuela (grupos de 1): Actividad 1
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales a reunir
Papel milimetrado: Actividad 1
Pegamento: Actividad 2
Rotuladores: Actividad 2
Materiales de una actividad anterior: Actividad 2
Tijeras: Actividad 1, Actividad 2
Pegatinas: Actividad 2
Cinta adhesiva: Actividad 1, Actividad 2
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Organicemos los datos y compartámoslos con los demás.
Narrativa de la lección
El objetivo matemático de esta lección es obtener y construir sobre los conocimientos y experiencias previas de los estudiantes con la organización y representación de datos
En primer grado, los estudiantes recolectaron datos y los representaron de diferentes maneras. En esta lección, los estudiantes recopilan datos sobre su clase, responden preguntas, discuten la necesidad de representar los datos de forma organizada y crean sus propias representaciones de sus datos. A lo largo de la lección, observe las distintas formas que eligen los alumnos para organizar y representar los datos y pregúnteles por las decisiones que toman. En próximas lecciones, los alumnos aprenderán a interpretar y representar los datos utilizando gráficos de imágenes y de barras.
En esta lección, los alumnos recopilan datos sobre la pregunta "¿Cómo llegamos a la escuela?". Si esta pregunta no es relevante para tu clase, elige otra pregunta de la encuesta o cambia las categorías para que sean más relevantes para tus alumnos.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento En parejas 10 min.
Actividad de exploración 1 Independiente 15 min.
Actividad de exploración 2 Por parejas 20 min.
Los estudiantes hacen observaciones sobre imágenes de diferentes tipos de transporte.
Los estudiantes construyen una tabla de datos de la clase seleccionando una imagen de transporte de cómo llegan a la escuela.
Los alumnos definen los datos y después organizan los datos de transporte de la clase de varias formas.
Síntesis Grupo completo 10 min. Los alumnos reflexionan sobre las formas de organizar y representar los datos.
Enfriamiento Independiente 5 min. Los alumnos comparan y contrastan dos representaciones de los mismos datos.
Abordaje:
Centro(s) sugerido(s) Grupos pequeños Opcional

Math Nation California - Grado 2
• ¿Cómo de cerca? (1-5), Etapa 3: Añadir a 100
Apoyo:
• Ordenar y mostrar (1-3), Etapa 1: De cualquier manera
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
ALLÁ 10 minutos
Rutinas didácticas
Observación y asombro
El objetivo de este calentamiento es invitar a los alumnos a observar y asombrarse con las imágenes de los medios de transporte que se utilizarán más adelante en la clase. Pueden darse cuenta de que todos los dibujos son medios de transporte que la gente de la comunidad utiliza para desplazarse. Esto conduce a la siguiente actividad, en la que los alumnos recopilan datos sobre cómo llegan a la escuela.
• Grupos de 2
• Muestre la imagen.
LANZAMIENTO

ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• "¿Qué observas? ¿Qué te preguntas?"
• 1 minuto: tiempo para pensar en silencio
• "Comenta lo que has pensado con tu compañero."
• 1 minuto: debate en pareja
• Comparte y anota las respuestas.
¿Qué observas? ¿Qué te preguntas?




POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
Learning Inc. - Todos los derechos reservados
Ejemplos de respuestas:
• Hay un coche.
• Todas son formas de desplazarse.
• Muchas de ellas tienen ruedas.
• ¿Por qué hay una persona con estas imágenes?
• "Vamos a seguir pensando en estas formas de desplazarse en nuestra primera actividad de hoy."
Matemáticas de 2º grado . Unidad 1
Materiales para reunir
Materiales para copiar Preparación necesaria
Papel milimetrado, tijeras, cinta adhesiva Cómo llegamos a la escuela (grupos de 1)
Cree un gráfico titulado "Cómo llegamos hoy a la escuela" para exhibirlo en la puesta en marcha.
Cada estudiante necesita un par de tijeras y acceso a cinta adhesiva.
Tenga a mano copias adicionales del patrón de líneas negras.
El objetivo de esta actividad es que los alumnos recojan datos y los representen para crear una exposición en clase. En esta actividad, se hace una pregunta a los alumnos y éstos eligen una imagen para representar su respuesta. Cuando se invite a los alumnos a añadir su imagen a la exposición de la clase, no les dé más indicaciones sobre el aspecto que debe tener la exposición. Los alumnos pueden elegir añadir su foto junto a otras fotos iguales o junto a las fotos de su compañero o de otros amigos sin prestar atención a la categoría. No pasa nada si la exposición parece desorganizada. En la síntesis, los alumnos responden a preguntas sobre los datos y pueden ver que sería más fácil responder a estas preguntas si los datos estuvieran representados de forma más organizada.
Representación: Acceso para la percepción. Proporcionar acceso a objetos concretos, como cubos de conexión, que los alumnos puedan utilizar para representar y organizar cada punto de datos.
Apoya la accesibilidad para: Procesamiento conceptual, Organización

LANZAMIENTO
ACTIVIDAD
DECLARACIÓN DE TAREAS PARA EL ESTUDIANTE
• Grupos de 2
• Expongan el papelógrafo titulado “Cómo llegamos a la escuela hoy”.
• Entreguen a cada estudiante unas tijeras, una copia del original y cinta adhesiva.
• “¿Cuáles son algunas de las diferentes maneras de llegar a nuestra escuela? ¿De qué otras maneras se puede llegar a la escuela en otros lugares?”
• “Elige la imagen que muestra cómo llegaste a la escuela hoy”.
• “Escribe tu nombre en la imagen”.
• Invita a los estudiantes a agregar su imagen a la tabla.
Elige la imagen que muestra cómo llegaste a la escuela hoy. Escribe tu nombre en la imagen.
POSIBLES RESPUESTAS Los gráficos variarán según el aula.
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• "¿Cómo podríamos averiguar cuántos alumnos de nuestra clase han cogido hoy el autobús para ir al colegio?" (Podríamos contar todas las fotos de autobuses.)
• "¿Qué otras preguntas podríamos hacer sobre cómo hemos llegado hoy al colegio basándonos en nuestra tabla?" (¿Cuántos alumnos han ido andando al colegio? ¿Cuántos alumnos han ido en coche?)
• "¿Es fácil responder a estas preguntas a partir de nuestra tabla con sólo mirarla? ¿Por qué sí o por qué no? (No, los dibujos están por todas partes, podrías perder la cuenta. Sería más fácil si estuvieran en filas o juntas. Sí, puedes contar cada imagen.)
20 minutos
Rutinas instructivas Materiales para reunir Preparación necesaria
MLR7 Comparar y conectar Pegamento, rotuladores, materiales de una actividad anterior, tijeras, pegatinas, cinta
Cada grupo de 2 necesita tener acceso a copias extra del patrón de líneas negras de la actividad anterior, pegamento, rotuladores, tijeras, cinta adhesiva y pegatinas.
El propósito de esta actividad es que los estudiantes representen los datos de una manera organizada. En el grado 1, los estudiantes fueron introducidos a cada una de las representaciones que se muestran en la sección Respuestas de los estudiantes a continuación.
Los estudiantes deben tener acceso a herramientas que puedan ayudarles a representar los datos (por ejemplo, copias adicionales de las imágenes de la Actividad 1, tijeras, pegamento o cinta adhesiva, marcadores o pegatinas). A lo largo de la actividad, los alumnos toman sus propias decisiones sobre qué utilizar para representar los datos y reflexionan sobre sus elecciones (MP5). La actividad puede servir como evaluación formativa para ver lo que los alumnos ya saben sobre la representación de datos. Durante la síntesis de la lección, los estudiantes ven diferentes representaciones y discuten las similitudes y diferencias de cada una.
Esta actividad utiliza MLR7 Comparar y conectar. Avances: representar, conversar.
LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• Grupos de 2
• Dar a cada grupo acceso a rotuladores, pegatinas, pegamento y cinta adhesiva.
• "Organiza y representa los datos que hemos recogido en una muestra visual"
• "Los datos son información sobre las cosas o las personas de un grupo"
• "Piensa en cómo puedes representar los datos de forma que tengan sentido para otras personas"."
• 8 minutos: tiempo de trabajo independiente
• Supervisar a los estudiantes que:
• organizan las imágenes en grupos
• utilizan marcas de conteo u otros símbolos
• 5 minutos: recorrido por la galería
Learning Inc. - Todos los derechos reservados
Organizar y representar los datos sobre cómo nuestra clase llega a la escuela.

Math Nation California - Grado 2
Ejemplos de respuestas:
1. Organiza las imágenes
Matemáticas de 2º grado . Unidad 1

2. Hace listas
autobús coche paseo tren
Serafina Liam Lune Thai Arjun Carrie Carlos Aishlinn
Xander Nia Elijah Paul
Lisa Jareb
Somari
Dougie Micah Beverly Rand Mandy
Dina Otis
Gary
3. Utiliza tally marks
• auto IIIIIII
• autobús IIIII
• paseo III
• tren IIIIII
4. Escribe números en una tabla
auto 7
autobús 5 paseo 3 tren 8
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
MLR7 Comparar y conectar
• Mostrar la representación de un alumno que utilizó dibujos y la representación de un alumno que utilizó marcas u otros símbolos.
• "¿En qué se parecen y en qué se diferencian estas representaciones?"
• 30 segundos tiempo de reflexión en silencio
• 1 minuto: discusión por parejas
• "¿Qué sugerencias tienes para _____ hacer su representación más clara?" (_____ podría contar las marcas y poner cuántas en total para cada grupo.)
10 minutos
"Hoy, vimos que hay diferentes maneras de representar datos en forma organizada."
Muestre 2 representaciones en las que los estudiantes agruparon imágenes o símbolos para representar cada categoría de diferentes maneras.
"¿Cómo te ayuda cada representación a ver cuántos estudiantes tomaron el autobús?" (Pude ver que hay 5 autobuses porque están alineados en una fila. Veo el número 5 junto a la palabra autobús. Veo que hay 5 cuentas junto a la palabra autobús.)
"¿Qué hace que una visualización de datos sea organizada y clara de leer?" (Es más fácil de leer si las cosas que se parecen están juntas. Puedes agrupar las cosas que se parecen. Puedes usar palabras y números para etiquetar las cosas.)
Comparte las respuestas.
5 minutos
Mai y Priya mostraron cómo los alumnos de su clase viajaban a la escuela.
La manera de Mai
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA CONTINUACIÓN

POSIBLES RESPUESTAS
Reflexiones:
Math Nation California - Grado 2
Matemáticas de 2º grado . Unidad 1
La manera de Priya
¿En qué se parecen la manera de Mai y la de Priya? ¿En qué se diferencian?
Ejemplos de respuestas:
• Ambas utilizan imágenes. Mai agrupó las imágenes.
• Ambas tienen el mismo número de imágenes. Mai utiliza palabras y agrupa las imágenes.
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Representar datos
ALINEACIÓN
Abordaje
Estándares y principios de CA Alineación
2.MD.10 Dibuja un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando información presentada en una gráfica de barras.
Construyendo sobre
1.OA.5
Enfocar SMPs
MP2 Razonar abstracta y cuantitativamente.
MP4 Modelar con matemáticas.
MP7 Buscar y hacer uso de la estructura.
CA ELD Standards
I.A.2 I.B.8 II.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . . dan sentido al mundo modelan con matemáticas razonan con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo interpretar datos representados en un gráfico de imagen.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Responder a preguntas basadas en un gráfico de imagen.
• Determinar si una pregunta puede responderse mediante un gráfico de imagen dado.
• Interpretar datos representados en un gráfico de imagen.
PREGUNTA DE REFLEXIÓN PARA EL PROFESOR
Reflexiona sobre quién ha participado hoy en la clase de matemáticas. ¿Qué suposiciones estás haciendo sobre los que no participaron? ¿Cómo puedes aprovechar las ideas de cada uno de tus alumnos para ayudarles a ser vistos y escuchados en la clase de matemáticas de mañana?
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
¿Cuántos ves? (Calentamiento)
Objetivos de aprendizaje para el alumno
• Vamos a responder preguntas basadas en gráficos de imágenes.
Narrativa de la lección
El objetivo de esta lección es que los alumnos lean e interpreten un gráfico de imágenes, que es una forma estándar de representar datos.
©Accelerate Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
En la lección anterior, los alumnos estudiaron distintas formas de organizar los datos para facilitar la formulación y respuesta de preguntas sobre ellos. En esta lección, se presenta a los alumnos un gráfico como forma de representar datos. A lo largo de la lección, los alumnos comprenden la estructura y las características de un gráfico de imágenes, consideran lo que pueden aprender de un gráfico de imágenes y los tipos de preguntas que pueden y no pueden responder con un gráfico de imágenes. Utilizan los gráficos para responder a preguntas sobre cuántos hay en una categoría, así como a preguntas en las que se les pide que combinen o comparen categorías.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura
Calentamiento Parejas 10 min.
Actividad de exploración 1 Parejas 20 min.
Actividad de exploración 2 Parejas 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.

Centro(s) sugerido(s) Grupos pequeños Opcional
Breve descripción
Los estudiantes cuentan objetos en una imagen dispuestos de diferentes maneras.
Los estudiantes analizan y responden preguntas sobre datos del mundo real presentados en gráficos de imágenes.
Los alumnos identifican qué preguntas sobre datos del mundo real pueden responderse a partir de un gráfico y, a continuación, responden a las preguntas.
Los alumnos discuten cómo pueden utilizarse los gráficos para responder a preguntas utilizando datos.
Los estudiantes determinan qué preguntas sobre datos del mundo real pueden responderse con un gráfico y luego explican por qué algunas preguntas no pueden responderse.
Abordaje:
• ¿Qué tan cerca? (1-5), Etapa 3: Add to 100
Apoyo:
• Sort and Display (1-3), Etapa 1: Any Way
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10
10 minutos
Rutinas instructivas
¿Cuántos ves?
El propósito de este calentamiento es que los estudiantes utilicen estrategias de agrupamiento para describir las imágenes que ven. Esta es la primera experiencia de los alumnos con la rutina "¿Cuántos ves?" en 2º curso. Pueden utilizar sus conocimientos de las operaciones de suma o estrategias mentales para determinar el número total de puntos. Cuando los estudiantes notan y usan la estructura de 5 puntos para describir cómo ven las imágenes, buscan y hacen uso de la estructura (MP7).
• Grupos de 2
• "¿Cuántos ves? ¿Cómo los ves?"

LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• Imagen flash.
• 30 segundos: tiempo para pensar en silencio
• Muestra la imagen.
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Registra las respuestas.
• Repite para cada imagen.
¿Cuántos ves? ¿Cómo los ves?



POSIBLES RESPUESTAS
©Accelerate Learning Inc. - Todos los derechos reservados
• 7 puntos: Veo 5 en la parte inferior y 2 más en la parte superior.
• 10 puntos: Veo 5 en la parte superior y luego hay 5 más en la parte inferior (5 + 5 = 10).
• 9 puntos: Vi el 9 porque había un 5 y un 4 (5 + 4 = 9).
SÍNTESIS DE LA ACTIVIDAD

Matemáticas de 2º grado . Unidad 1
• "¿Cómo permaneció igual o cambió su método en cada imagen?" (Para la primera imagen conté con 5, 6, 7. Para la segunda imagen conté 5 + 5 = 10. Para la última imagen alejé 1 de 10.)
• Establezcan conexiones entre las representaciones visuales y las ecuaciones que podrían representarlas al registrar sus respuestas.
AMAR 20 minutos
Materiales para reunir
Materiales para copiar Preparación necesaria
Papel milimetrado, tijeras, cinta adhesiva Cómo llegamos a la escuela (grupos de 1)
Elabore un cuadro titulado "Cómo llegamos hoy a la escuela" para exhibirlo en el lanzamiento.
Cada estudiante necesita un par de tijeras y acceso a cinta adhesiva. Tenga a mano copias adicionales del patrón de líneas negras.
El objetivo de esta actividad es que los alumnos aprendan una nueva forma de organizar los datos: un gráfico de imágenes. En la puesta en marcha, los alumnos entablan un debate sobre lo que observan en el gráfico y sobre cómo un gráfico de imágenes facilita la interpretación de los datos. Después de que los alumnos discutan el gráfico y piensen qué pueden aprender de él, concluya con la siguiente pregunta: "¿Cuál es el número total de niños a los que les gustan las espinacas o el maíz?". Esta pregunta utiliza "o" para indicar la suma de las dos categorías. Esta formulación puede ser nueva para los alumnos.
Apoyo para estudiantes de inglés
MLR8 Discussion Supports. Invite a los estudiantes a nombrar las verduras que ven en el gráfico de imágenes. Algunos estudiantes pueden beneficiarse de ver fotografías de verduras con las que no están familiarizados. Si es necesario, discuta el significado de la palabra "veggie".
Avances: Hablar, conversar
• Grupos de 2
• Mostrar el gráfico "Las verduras que les gustan a los niños", pero tapando el título.
• "Clare hizo este gráfico para compartir los datos que recopiló"
• "¿Qué podría representar este gráfico?"
• 30 segundos: tiempo de reflexión en silencio
• Compartir las respuestas.
• "Clare preguntó a los niños de su clase qué verdura les gustaba"
• "Hizo un gráfico para mostrar sus respuestas"
• "Un gráfico es una forma de mostrar cuántos hay en cada grupo o categoría utilizando imágenes de los objetos o símbolos" "¿Qué aprendes con este gráfico?"
• "¿Qué puedes aprender sobre las verduras que les gustan a los niños a partir de su gráfico?" (La verdura con más votos es la zanahoria. A muchos niños no les gustan las espinacas).)
• 1 minuto: tiempo de reflexión en silencio
• 2 minutos: debate por parejas
• Anota las respuestas de los alumnos con frases completas.
• "¿Cuál es el número total de niños a los que les gustan las espinacas o el maíz?" (6 niños. A dos les gustan las espinacas y a 4 el maíz.)
• 30 segundos: tiempo de reflexión en silencio
• Comparte las respuestas
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• "Ahora puedes responder algunas preguntas basándote en un gráfico que muestra datos sobre las verduras que les gustan a los adultos de la escuela."
• 6 minutos: tiempo de trabajo independiente
• "Comparte con un compañero el dato que escribiste para la tercera pregunta."
• 3 minutos: discusión en parejas
Clare preguntó a un grupo de niños: "¿Qué verduras te gustan?".. Sus respuestas se muestran en este gráfico

¿Qué puedes aprender sobre las verduras que les gustan a los niños a partir del gráfico de Clare?
Se preguntó a un grupo de adultos: "¿Qué verduras te gustan?". Sus respuestas se muestran en este gráfico.

Responde a las preguntas basándote en el gráfico.
1. ¿A cuántos adultos les gustan las espinacas?
2. ¿Cuál es el número total de adultos a los que les gustan las zanahorias o el maíz? Demuestra lo que piensas con dibujos, números o palabras.
3. Escribe un dato que hayas aprendido sobre las verduras que les gustan a los adultos basándote en los datos representados en el gráfico.
©Accelerate Learning Inc. - Todos los derechos reservados
Nation California - Grade 2
Matemáticas de 2º grado . Unidad 1

POSIBLES RESPUESTASS
ADEVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
• 2 a los adultos les gustan las espinacas.
• 13 a los adultos les gustan las zanahorias o el maíz. Respuesta de muestra: 8 + 5 = 13
• Respuestas de muestra: Sólo A 5 adultos les gusta el maíz. A 3 adultos les gusta el brócoli. 8 adultos a los que les gustan las zanahorias.
Si la respuesta de los estudiantes para el número de adultos a los que les gustan las zanahorias o el maíz no refleja claramente las categorías combinadas, considere preguntar:
• "¿Puedes explicar cómo encontraste el número total de adultos a los que les gustan las zanahorias o el maíz?"
• "¿Dónde lo ves en el gráfico?"
• Muestra el gráfico “Vegetales que aman los adultos”.
• "¿A cuántos adultos más les gustan las zanahorias que las espinacas? Explica cómo lo sabes". (6 a más adultos les gustan las zanahorias que las espinacas. Vi que había 2 para las espinacas, así que conté las zanahorias por encima de 2. Hice 8 - 2 = 6 porque había 8 votos para las zanahorias y 2 para las espinacas.)
• 30 segundos: tiempo para pensar en silencio
• Compartir y anotar las respuestas
RESPUESTA 15 minutos
El objetivo de esta actividad es que los alumnos interpreten los datos representados en un gráfico ilustrado. Los alumnos dan sentido a las preguntas relacionadas con el contexto y deciden si las preguntas pueden responderse con los datos. Este tipo de razonamiento ayuda a los alumnos a dar sentido a los elementos matemáticos de un contexto y a interpretar y utilizar los datos presentados en el gráfico para responder a las preguntas (MP4). Cuando los alumnos leen el gráfico y utilizan métodos basados en el uso de sumas y restas o los basados en contar hacia delante o hacia atrás a partir de las imágenes del gráfico, razonan de forma abstracta y cuantitativa (MP2).
Representación: Interiorizar Comprender. Síntesis: Invite a los alumnos a identificar a qué detalles era importante prestar atención. Considere la posibilidad de utilizar el marco de la frase: "La próxima vez que responda a una pregunta sobre un gráfico ilustrado, buscaré en ...". "
Apoya la accesibilidad para: Procesamiento conceptual
LANZAMIENTO
• Grupos de 2
• "Algunas preguntas pueden responderse utilizando un gráfico de imágenes, pero otras no."
• "Encierra en un círculo cualquier pregunta que pueda responderse utilizando el gráfico."
• "A continuación, utiliza el gráfico de imágenes para responder a las preguntas."
• 8 minutos: tiempo de trabajo independiente
• Compara tus respuestas con un compañero.
ACTIVIDAD
Math Nation California - Grado 2
• 2 minutos: discusión en parejas
• Supervise a los estudiantes que explican cómo:
• contaron para hallar la suma de dos categorías
• contaron para hallar cuántos más
• contaron el número de dibujos en cada categoría y usaron la suma o la resta
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
Se preguntó a un grupo de niños: "¿Qué alimentos te gusta comer?". Sus respuestas se muestran en este gráfico.
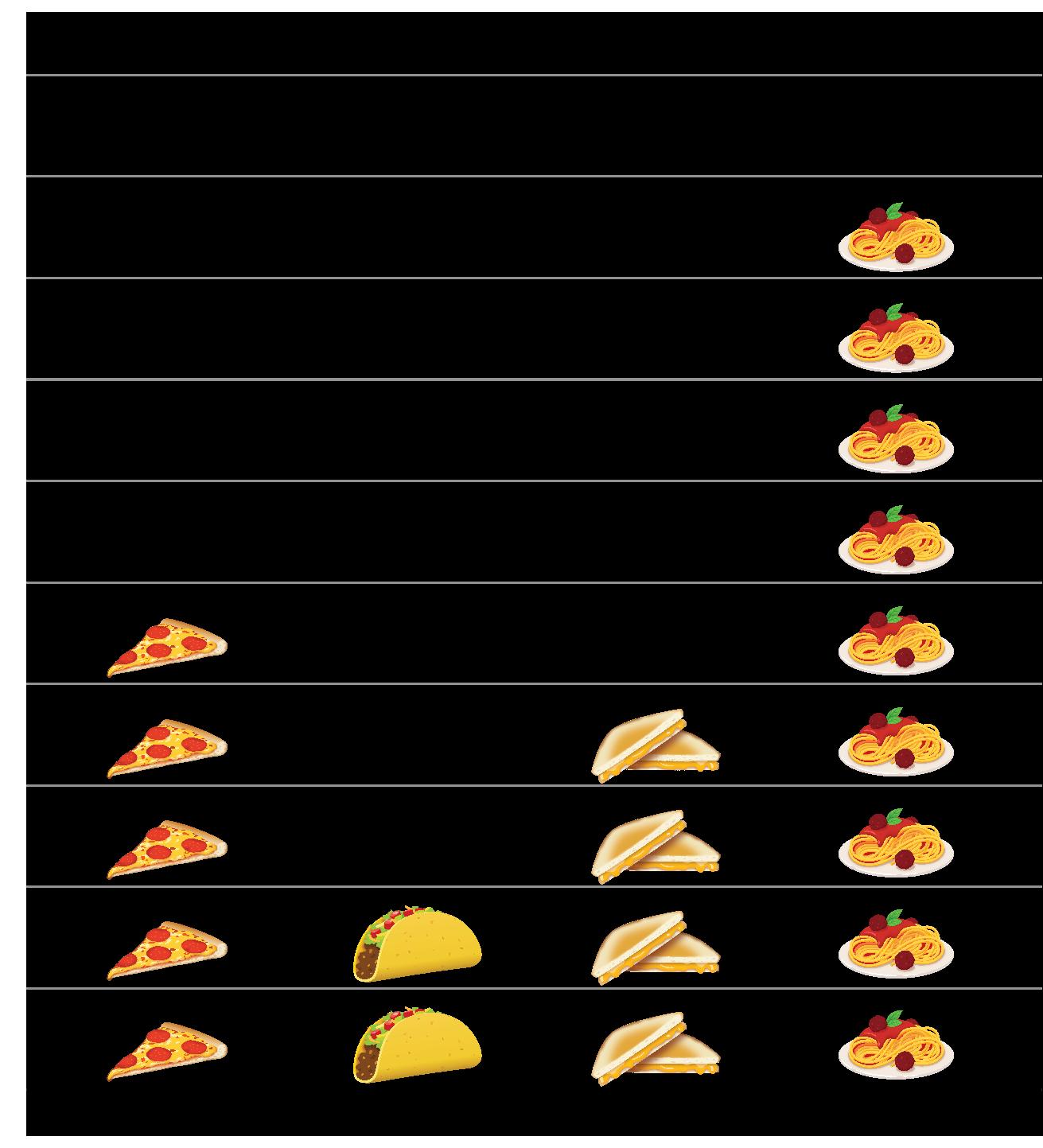
1. Encierra en un círculo las 4 preguntas que se pueden responder utilizando el gráfico.
A. ¿Cuántos niños eligieron pizza?
B. ¿Cuántos eligieron tacos o queso a la parrilla?
C. ¿Por qué tantos niños eligieron espaguetis?
D. ¿Cuántos niños más eligieron pizza que tacos?
E. ¿Cuál es el número total de niños que eligieron espaguetis o pizza?
2. Responda a cada pregunta que rodeó con un círculo.
1. a, b, d y e
2.
POSIBLES RESPUESTAS
ADEVANCE STUDENT THINKING
ACTIVIDAD
A. 5 niños eligieron pizza.
B. 6 niños eligieron tacos o queso a la plancha. Ejemplo de respuesta: 2 + 4 = 6
C. No sabemos por qué les gustan tanto los espaguetis.
D. 3 más niños eligieron pizza que tacos. Respuesta de muestra: 5 - 2 = 3
E. 14 niños eligieron espaguetis o pizza. Respuesta de muestra: 9 + 5 = 14
Si los estudiantes combinan categorías cuando deberían encontrar la diferencia entre ellas, considere preguntar:
• "¿Cómo decidiste combinar estos dos grupos?"
• "¿Cómo podría el gráfico ayudarte a pensar sobre cuántos más eligieron pizza?"
• "¿Cómo coincide esto con la pregunta?"
• "¿Qué pregunta decidiste que no podía responderse? Explícala". (No sabemos por qué tantos niños eligieron espaguetis. El gráfico muestra cuántos, pero no sus razones.)
• Invite a los alumnos previamente identificados a compartir las respuestas para las preguntas que les pedían combinar categorías o comparar categorías.
Matemáticas de 2º grado . Unidad 1
10 minutos
"Hoy has aprendido sobre los gráficos de imágenes , que es una forma de representar datos. ¿Qué aprendiste acerca de cómo los gráficos pueden ayudar a responder preguntas sobre datos? "
5 minutos
Se preguntó a un grupo de estudiantes: "¿Cuál es tu mascota favorita?". Sus respuestas se muestran en este gráfico.

DE CARA AL ESTUDIANTE
ENUNCIADO DE LA TAREA

1. Encierra en un círculo las 2 preguntas que pueden responderse con el gráfico.
A. ¿Cuántos estudiantes eligieron un gato como su mascota favorita?
B. ¿A cuántos estudiantes les gustan más los conejos que los perros?
C. ¿Quién tiene un lagarto?
D. ¿Cuántos estudiantes más eligieron gatos que perros?
E. ¿Por qué no les gustan los perros a más estudiantes?
2. Elige una pregunta que no pueda responderse con los datos del gráfico. Explica por qué no se puede responder.
1. A, D
2. Para B, el gráfico no nos dice el número de conejos.
POSIBLES RESPUESTAS
Math Nation California - Grado 2
Para C, el gráfico no nos dice los nombres de los dueños.
Para E, el gráfico no nos dice por qué los estudiantes eligen sus mascotas.
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Representar datos
ALINEACIÓN
Abordaje
Estándares y principios de CA Alineación
2.MD.10 Dibujar un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando información presentada en una gráfica de barras.
Enfocar SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
Estándares CA ELD
I.A.1 I.B.5 II.B.2
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . . dar sentido al mundo y predecir lo que podría ocurrir
razonar abstracta y cuantitativamente razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo interpretar y responder a preguntas sobre datos representados en un gráfico de barras.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Responder a preguntas basadas en un gráfico de barras.
• Interpretar datos representados en un gráfico de barras.
PREGUNTA DE REFLEXIÓN DEL PROFESOR
La escala del gráfico de barras será importante a medida que los estudiantes resuelvan problemas basados en datos. ¿Cómo has visto que los alumnos han utilizado hoy la escala del gráfico de barras?
PREPARACIÓN DE LA LECCIÓN
Rutinas instructivas
MLR6 Tres lecturas (Actividad 2)
Notar y maravillarse (Calentamiento)
Objetivos de aprendizaje para el estudiante
• Interpretemos datos en gráficos de barras.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes interpreten datos en un gráfico de barras para responder preguntas.
©Accelerate Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
En lecciones anteriores, los alumnos aprendieron a interpretar datos categóricos representados en gráficos de imágenes y otras representaciones. En esta lección, se presentan los gráficos de barras como otra forma de representar datos categóricos. Los alumnos comparan las características de los gráficos de barras con las de los gráficos de imágenes y utilizan las características únicas de los gráficos de barras para interpretar los datos y responder a las preguntas. Cuando los alumnos relacionan los datos con el contexto que representan e interpretan cuidadosamente los elementos de un gráfico, razonan de forma abstracta y cuantitativa y prestan atención a la precisión (MP2, MP6).
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Parejas 10 min.
Actividad de exploración 1 Grupos pequeños 15 min.
Actividad de exploración 2 Parejas 20 min.
Síntesis Grupo completo 10 min.
Enfriamiento Independiente 5 min.

Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes hacen observaciones sobre datos del mundo real mostrados como un gráfico de imagen y un gráfico de barras.
Los estudiantes interpretan y comparan datos del mundo real en gráficos de barras escribiendo afirmaciones verdaderas.
Los estudiantes interpretan y responden preguntas sobre un conjunto de datos del mundo real representados en un gráfico de barras.
Los estudiantes comparan y contrastan representaciones de datos en gráficos de imágenes y gráficos de barras.
Los estudiantes responden preguntas sobre un conjunto de datos del mundo real representados en un gráfico de barras.
Abordaje:
• ¿Qué tan cerca? (1-5), Etapa 3: Añadir a 100
Apoyo:
• Ordenar y mostrar (1-3), Etapa 1: De cualquier manera
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos
Rutinas didácticas
Notar y preguntarse
El objetivo de este calentamiento es que los alumnos establezcan conexiones entre los gráficos de barras y los gráficos de imágenes. Aunque los alumnos pueden notare y preguntarse muchas cosas sobre estos gráficos, centra la síntesis en cómo los gráficos representan los mismos datos de diferentes maneras. Esta conversación conduce directamente a la siguiente actividad, en la que los alumnos leerán e interpretarán los datos representados en gráficos de barras.
• Grupos de 2
• Muestre la imagen.
LANZAMIENTO

ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• "¿Qué notan? ¿Qué te sorprende?"
• 1 minuto: tiempo para pensar en silencio
• "Comenta lo que has pensado con tu compañero."
• 1 minuto: debate entre compañeros
• Comparte y anota las respuestas.
¿Qué te llama la atención? ¿Qué te preguntas?

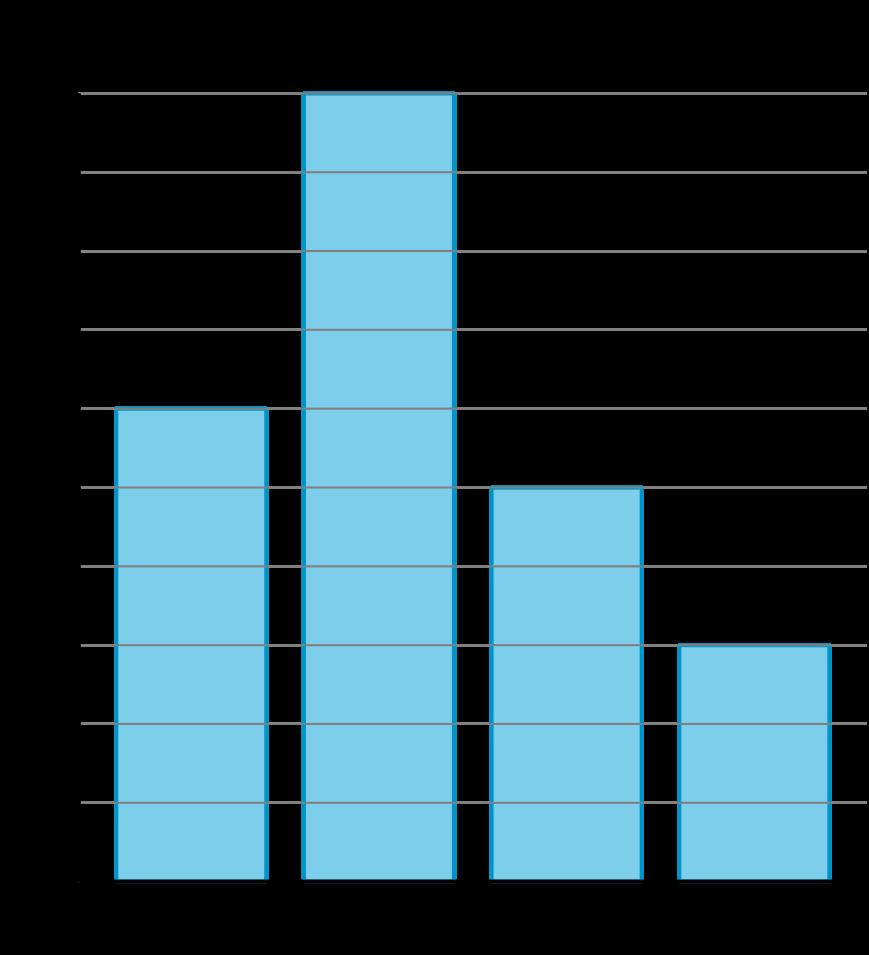
Los alumnos pueden notar:
• Uno tiene dibujos.
• Tienen los mismos animales.
POSIBLES RESPUESTAS
• Los perros son los que más aparecen en ambos gráficos.
Los alumnos pueden preguntarse:
• ¿Son iguales?
• ¿Por qué el segundo no muestra los animales?
SÍNTESIS DE LA ACTIVIDAD
• "El gráfico de la derecha se llama gráfico de barras . Un gráfico de barras es una forma de mostrar cuántos hay en cada grupo o categoría utilizando la longitud de los rectángulos."
• "¿En qué se diferencian los datos representados en el gráfico de barras en comparación con el gráfico de imágenes?" (El número de objetos se muestra en la escala de la izquierda en lugar de en imágenes. No hay que contar).
Matemáticas de 2º grado . Unidad 1
15 minutos
El objetivo de esta actividad es que los alumnos exploren y utilicen cubos de conexión. Los alumnos tienen la oportunidad de explorar los cubos conectores antes de que se les pida que los utilicen para representar situaciones matemáticas en lecciones posteriores. A medida que los alumnos trabajan, observe si ordenan, cuentan o utilizan lenguaje de comparación mientras trabajan con los cubos de conexión. Los alumnos tendrán la oportunidad de seguir explorando los cubos de conexión en los centros en futuras lecciones. Esta es la etapa 1 del centro de Cubos Conectores.
Apoyo a los estudiantes con discapacidad
Acción y expresión: Desarrollar la expresión y la comunicación. Proporcione acceso a cubos de conexión de diferentes colores tque losudiantes puedan utilizar para representar los datos al responder a las preguntas. Esto ofrece una representación concreta de los dos puntos de datos en los que centrar la atención.
Apoya la accesibilidad para: Procesamiento conceptual, Organización, Atención

LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• Grupos de 3
• Asigne a cada grupo un gráfico para interpretar.
• "Con su grupo, escriba tantas afirmaciones como pueda para mostrar lo que se puede aprender sobre las elecciones de excursiones de los estudiantes a partir de su gráfico."
• "Compartiremos las afirmaciones que escribas con la clase para ver si pueden adivinar qué gráfico has interpretado".
• 8 minutos: tiempo de trabajo en pequeños grupos
• Supervise a los estudiantes que crean una variedad de afirmaciones diferentes, incluidas las que combinan o comparan categorías, para compartirlas durante la síntesis de la actividad. Elija al menos 1 grupo para cada gráfico.
Se preguntó a grupos de alumnos de diferentes clases: "¿Adónde te gustaría ir en nuestra excursión?". Sus respuestas se muestran en los gráficos de barras a continuación.

Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

CONTINUACIÓN
Escriba tantas afirmaciones como pueda para mostrar lo que se puede aprender sobre laselecciones de excursiones de los alumnos a partir del gráfico de barras.De cara al alumno Enunciado de la tarea

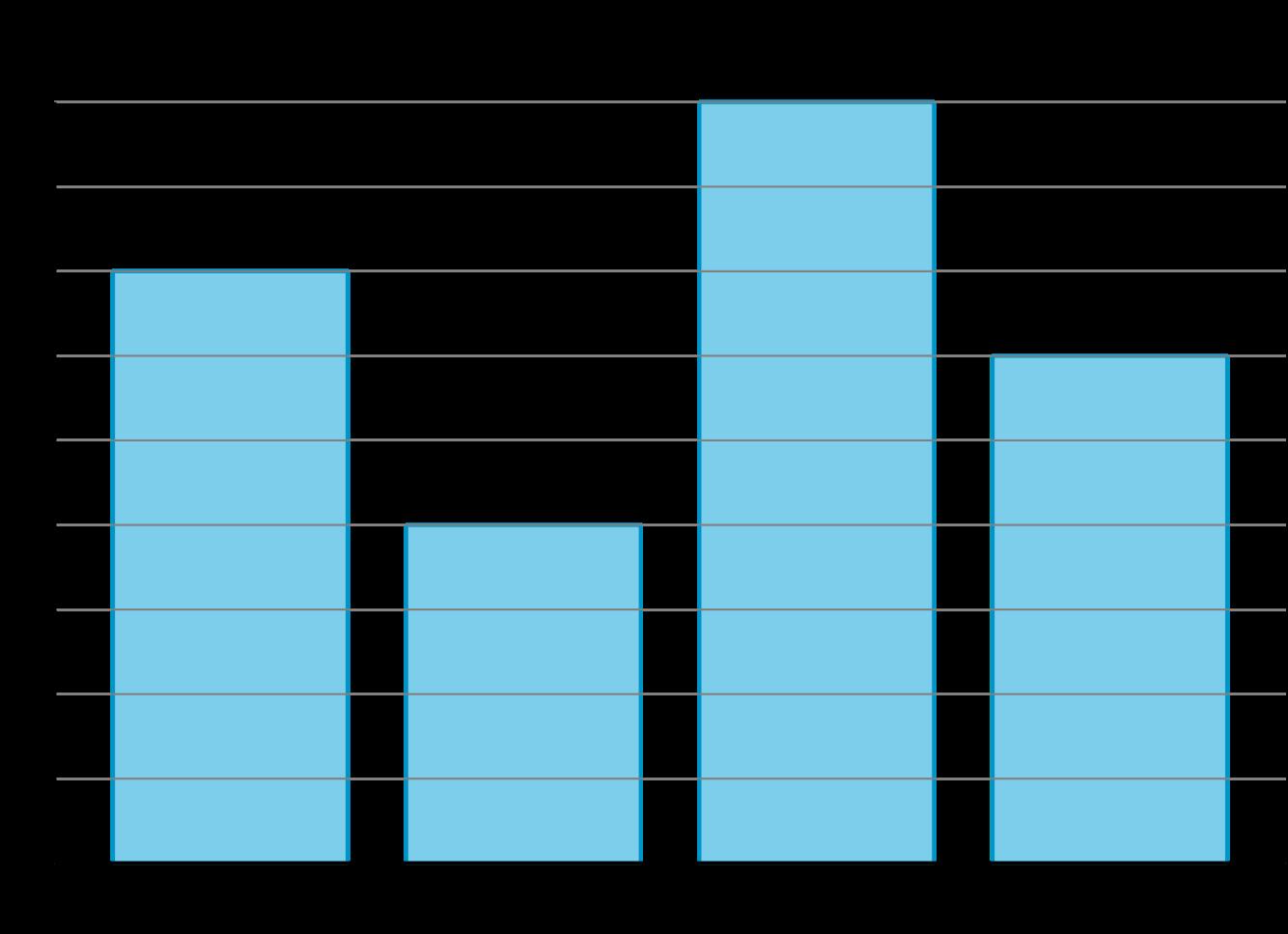
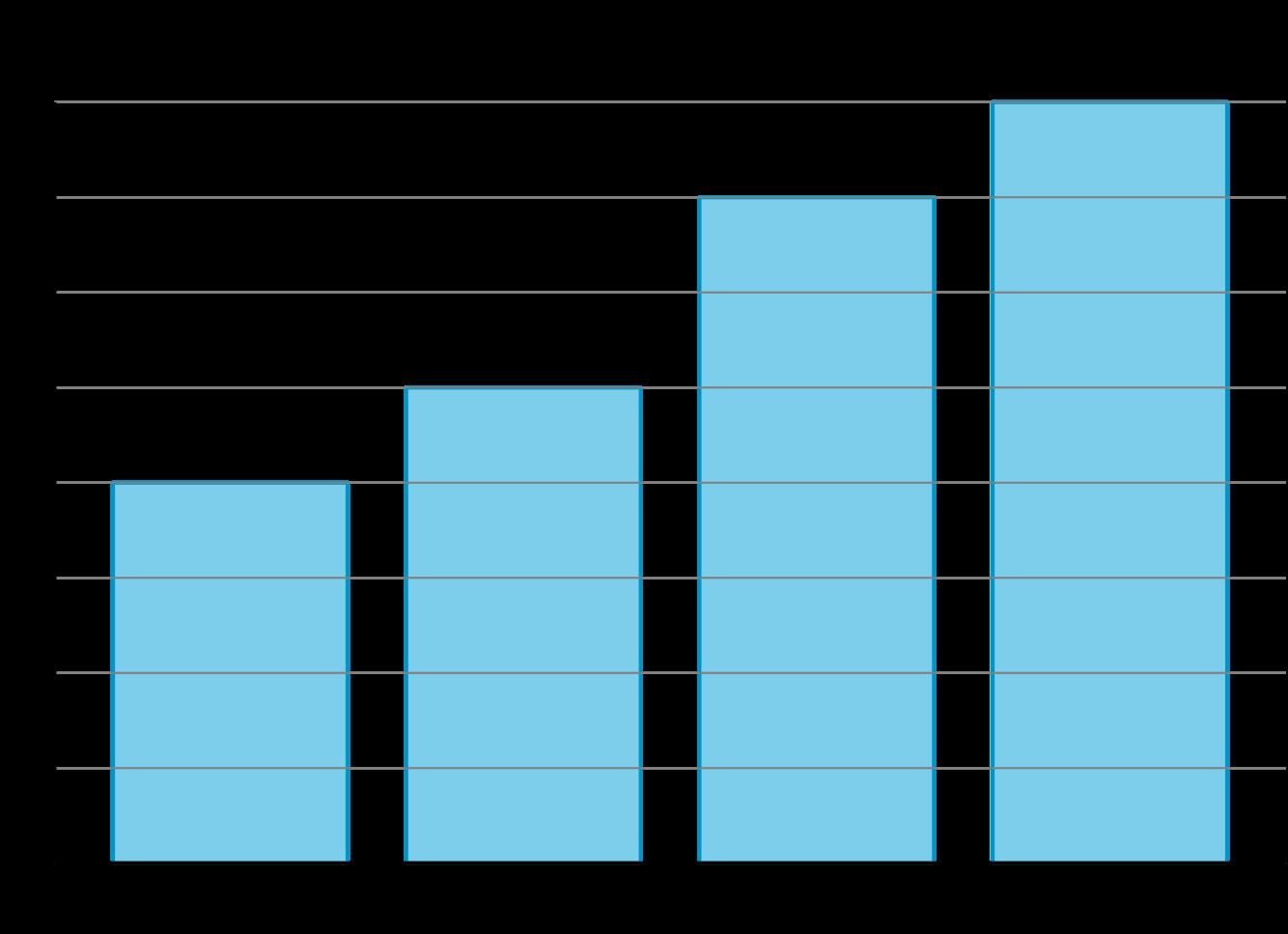
Ejemplos de respuestas para la clase 1:
1. 25 alumnos votaron.
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
2. 11 estudiantes votaron por el museo infantil o el zoológico.
3. La estación de bomberos obtuvo 3 menos votos que el museo infantil.
• Invite a uno de los grupos previamente identificados a compartir 2-3 de sus afirmaciones.
• "¿Qué gráfico interpretó este grupo? ¿Cómo lo sabe?"
• Repita, variando los grupos que interpretaron gráficos diferentes, según el tiempo lo permita.
©Accelerate Learning Inc. - Todos los derechos reservados Math Nation California - Grade 2
Matemáticas de 2º grado . Unidad 1
20 minutos
Rutinas instructivas
MLR6 Three Reads
El objetivo de esta actividad es que los alumnos interpreten los datos representados en un gráfico de barras y respondan a preguntas sobre los datos. En trabajos anteriores con gráficos de imágenes, los alumnos tenían que contar las imágenes para responder a preguntas del tipo "cuántas". Durante esta actividad, identifique a los estudiantes que reconocen que pueden utilizar la escala (números en el lateral) en lugar de contar cada línea o sección de lae barra. Pida a estos alumnos que compartan durante la síntesis. Es importante que los estudiantes consideren los beneficios de utilizar un gráfico de barras en comparación cono un gráfico de imágenes.
Esta actividad utiliza MLR6 Three Reads. Avances: leer, escuchar, representar
LANZAMIENTO

Math
ACTIVIDAD
• Grupos de 2
• Mostrar el gráfico de barras Our Favorite Seasons, sin revelar las preguntas.
MLR6 Three Reads
• "Aquí hay un gráfico de barras que muestra los datos recogidos sobre las estaciones favoritas de los estudiantes. Vamos a leer este gráfico 3 veces."
• 1ª Lectura: "Tómate un momento para leer los datos que muestra este gráfico."
• "¿De qué trata este gráfico?"
• 1 minuto: discusión en parejas
• Escucha y aclara cualquier pregunta sobre el contexto.
• 2ª Lectura: "Lee e interpreta el gráfico de barras por segunda vez. ¿Qué se puede contar o medir en esta situación?". (número de alumnos que han votado por cada estación, número de alumnos que han votado)
• 30 segundos: tiempo para pensar en silencio
• 2 minutos: discusión en parejas
• Registrar las cantidades en una pantalla para que todos las vean.
• 3ª Lectura: Lea las preguntas en voz alta.
• "¿Cómo podemos utilizar el gráfico de barras para responder a estas preguntas?"
• 30 segundos: tiempo para pensar en silencio
• 1-2 minutos: discusión por parejas
• "Utilice el gráfico de barras para responder a las preguntas.
• 7 minutos: tiempo de trabajo independiente
• Vigile a los estudiantes que:
• cuentan cada sección de las barras
• utilizan la escala
• crean ecuaciones para registrar cómo combinan las categorías
• Si algunos estudiantes terminan antes, puede pedirles que escriban afirmaciones sobre clo que se puede aprender u otras preguntas que se pueden hacer sobre los datos del gráfico de barras."
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
Se preguntó a un grupo de estudiantes: "¿Cuál es tu estación favorita?". Sus respuestas se muestran en el gráfico de barras.
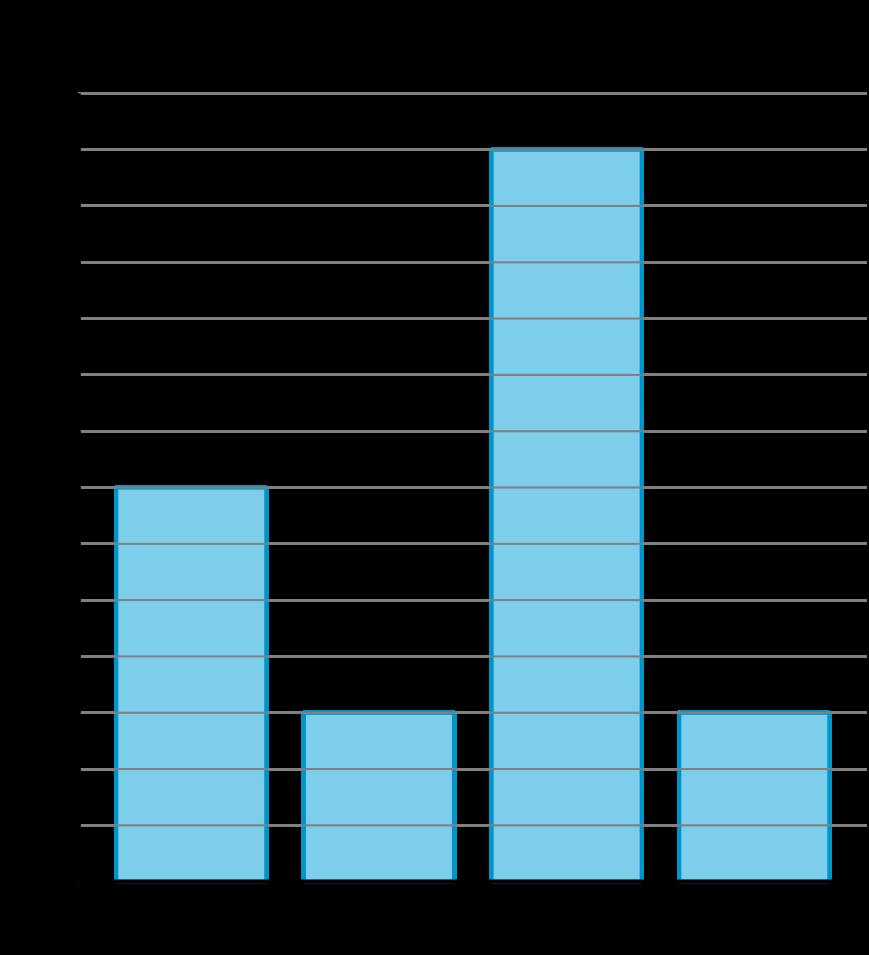
Responde a las preguntas utilizando el gráfico.
1. ¿Cuántos estudiantes votaron por el verano?
2. ¿Cuál es el número total de estudiantes que votaron por el otoño o la primavera?
3. ¿Qué dos estaciones tienen un total de 10 votos?
4. ¿Cuántos estudiantes votaron?
1. 13.
2. 6 estudiantes votaron por primavera u otoño.
3. Invierno y primavera tienen un total de 10 votos.
4. 26 estudiantes votaron.
• Invita a los estudiantes previamente identificados a compartir cómo usaron el gráfico de barras para encontrar cuántos estudiantes votaron por el verano.
• Invita a los estudiantes previamente identificados a compartir cómo encontraron el número totalde estudiantesque votaron.
10 minutos
"Hoy hemos interpretado datos representados en un gráfico de barras. Usar un gráfico de barras es un poco diferente a usar un gráfico de imágenes para responder preguntas"
"¿En qué se diferencian las formas en que usaste un gráfico de barras para responder preguntas de cómo usaste los gráficos de imágenes?" (Los gráficos de barras tienen una escala que te ayuda a ver cuántos hay en cada grupo sin tener que contar cada uno. asegurarte de que estabas contando lo correcto porque no había dibujos que correspondieran a cada grupo.)Realmente tenías que leer los gráficos de barras para m
"¿En qué se parecen?" (Ambos muestran un número en cada grupo. Puedes contar cada imagen en un gráfico de imágenes y puedes contarnt cada parte de la barra en un gráfico de barras.)
Matemáticas de 2º grado . Unidad 1
Un cuidador de zoo contó el número de leones, guepardos, monos y cebras que había en el zoo. Los datos del cuidador se muestran en este gráfico de barras.

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
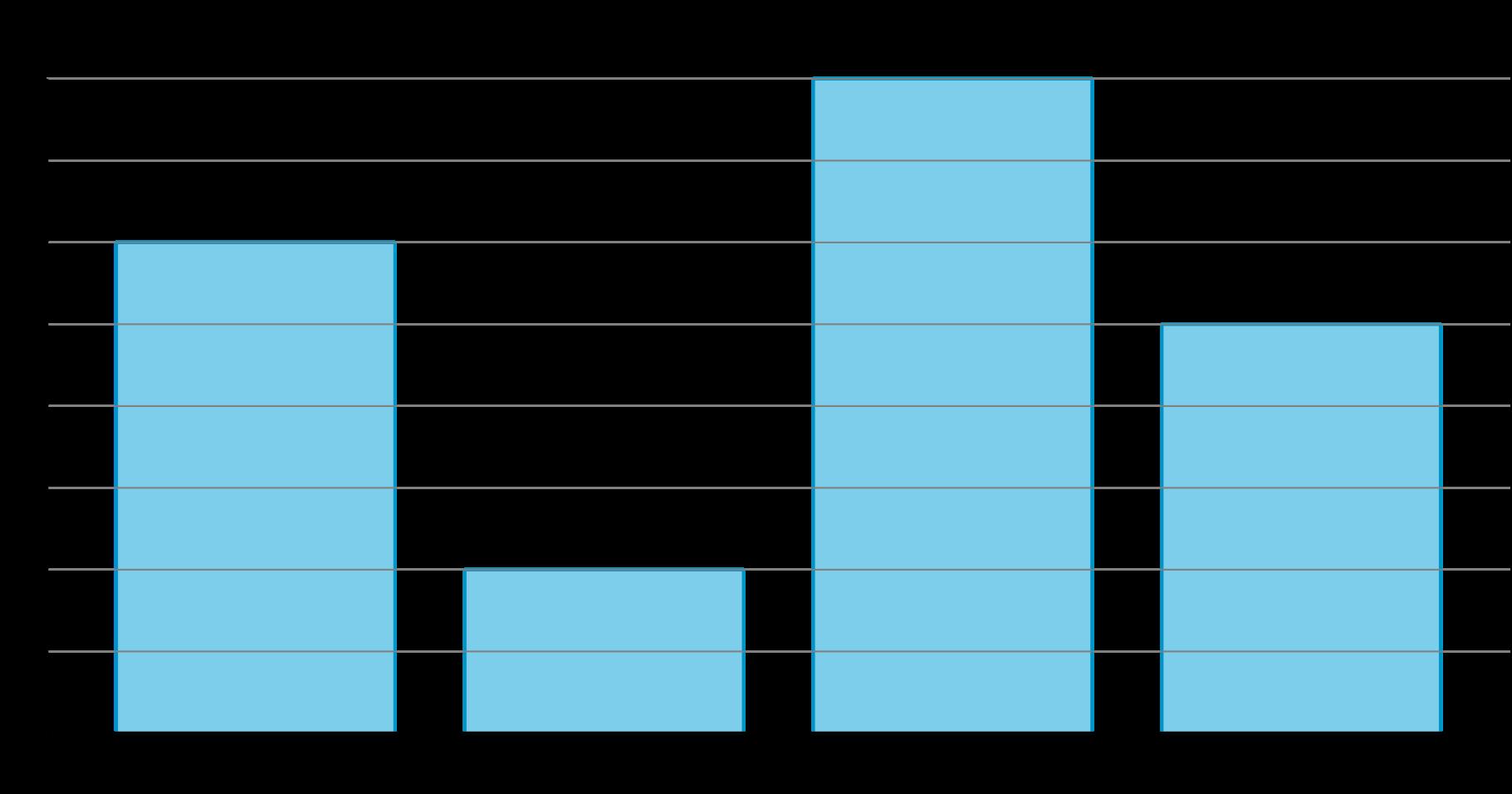
1. ¿Cuántos monos había en el zoo?
2. ¿Cuántos leones había en el zoo?
3. 3. ¿Cuál es el número total de guepardos y cebras?
POSIBLES RESPUESTAS
Reflexiones:
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Representar datos
ALINEACIÓN
Abordaje
Alineación
Estándares y principios de CA
2.MD.10 Dibujar un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando información presentada en una gráfica de barras.
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP4 Modelar con matemáticas.
MP6 Atender a la precisión.
Estándares CA ELD
I.A.2
I.B.8 I.C.12
DATOS
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
predicen lo que podría ocurrir modelan con matemáticas razonan con datos.
• Puedo explicar cómo se pueden utilizar los gráficos de imágenes, los gráficos de barras y las tablas para representar los mismos datos.
• Puedo crear un gráfico de imágenes y un gráfico de barras utilizando datos del mundo real.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Explicar cómo los gráficos de imágenes, los gráficos de barras y las tablas representan los mismos datos.Objetivo(s) de aprendizaje
• Representar datos utilizando un gráfico de imágenes y un gráfico de barras.ar.
¿Cuál ha sido la mejor pregunta que has hecho hoy a los alumnos? ¿Por qué la consideras la mejor basándote en lo que han dicho o hecho los alumnos?
Rutinas instructivas
MLR8 Apoyos para la discusión (Actividad 1)
¿Cuál no pertenece? (Calentamiento)
Materiales a Reunir
Materiales de una actividad anterior: Actividad 2
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales para copiar
Tablas de datos (grupos de 6): Actividad 1
Plantilla de dibujos y gráficos de barras (grupos de 1): Actividad 1
Plantilla de dibujos y gráficos de barras (grupos de 1): Actividad 2
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el alumno
• Vamos a hacer nuestros propios gráficos de imágenes y gráficos de barras.
Narrativa de la lección
El objetivo de esta lección es que los alumnos presten atención a las características de los gráficos de imágenes y los gráficos de barras al representar un conjunto dado de datos categóricos en gráficos de imágenes y bar gráficos.
En la primera actividad, se presenta a los alumnos la idea de utilizar un símbolo en un gráfico de imágenes en lugar de un dibujo basado en la categoría. Puede que les resulte más fácil y eficaz utilizar un símbolo al dibujar sus gráficos. En la segunda actividad, los alumnos prestan atención a las características de los gráficos de barras mientras dibujan un gráfico de barras para representar un conjunto dado de datos categóricos. El trabajo de esta lección conecta con las lecciones siguientes, ya que los alumnos pasan de una representación discreta de números con el gráfico de dibujos a una representación continua de números con el gráfico de barras. A partir de ahí, los estudiantes utilizan los gráficos de barras para ayudarles a entender los diagramas de cinta en lecciones posteriores. Los estudiantes utilizan los gráficos que crean en esta lección en la lección siguiente.
Componente de lección Estructura Tiempo

Descripción breve
Calentamiento Pares 10 min. Los estudiantes examinan imágenes de datos en gráficos de barras, gráficos de imágenes y tablas para explicar cuáles no pertenecen.
Actividad de exploración 1 Pares 20 min. Los estudiantes crean un gráfico de imágenes para representar datos del mundo real.
Actividad de exploració 2 Pares 15 min. Los estudiantes crean un gráfico de barras para representar datos del mundo real.
Síntesis Todo el grupo 10 min. Los estudiantes discuten las estrategias para representar datos en un gráfico de imágenes o un gráfico de barras.
Enfriarse Independiente 5 min. Los estudiantes completan un gráfico de imágenes y un gráfico de barras con los mismos datos del mundo real.
Direccionamiento:
Centro(s) sugerido(s) Grupos pequeños Opcional
• Agitar y derramar (K–2), Etapa 5: Cubrir (hasta 20)
Secundario:
• Ordenar y mostrar (1–3), Etapa 1: Cualquier forma
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
Rutinas instructivas
¿Cuál no pertenece?
El objetivo de este calentamiento es que los alumnos comparen cuatro representaciones de datos. Los alumnos utilizan y revisan su lenguaje para describir claramente las características de cada representación de datos y explicar en qué se parecen y en qué se diferencian (MP6). Los alumnos show entienden que los datos representan un contexto cuando razonan sobre si los gráficos representan contextos iguales o diferentes (MP2). Los alumnos han visto datos categóricos representados de cada una de estas formas, excepto en el gráfico de barras horizontales. Permita que los estudiantes discutan lo que piensan de esa representación.
• Grupos de 2
• Muestre la imagen.
LANZAMIENTO

ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• "Elija uno que no pertenezca. Prepárate para compartir por qué no pertenece."
• 1 minuto: tiempo para pensar en silencio
• "Discute tu pensamiento con tu compañero."
• 2-3 minutos: discusión en pareja
• Comparte y anota las respuestas.
¿Cuál no pertenece?
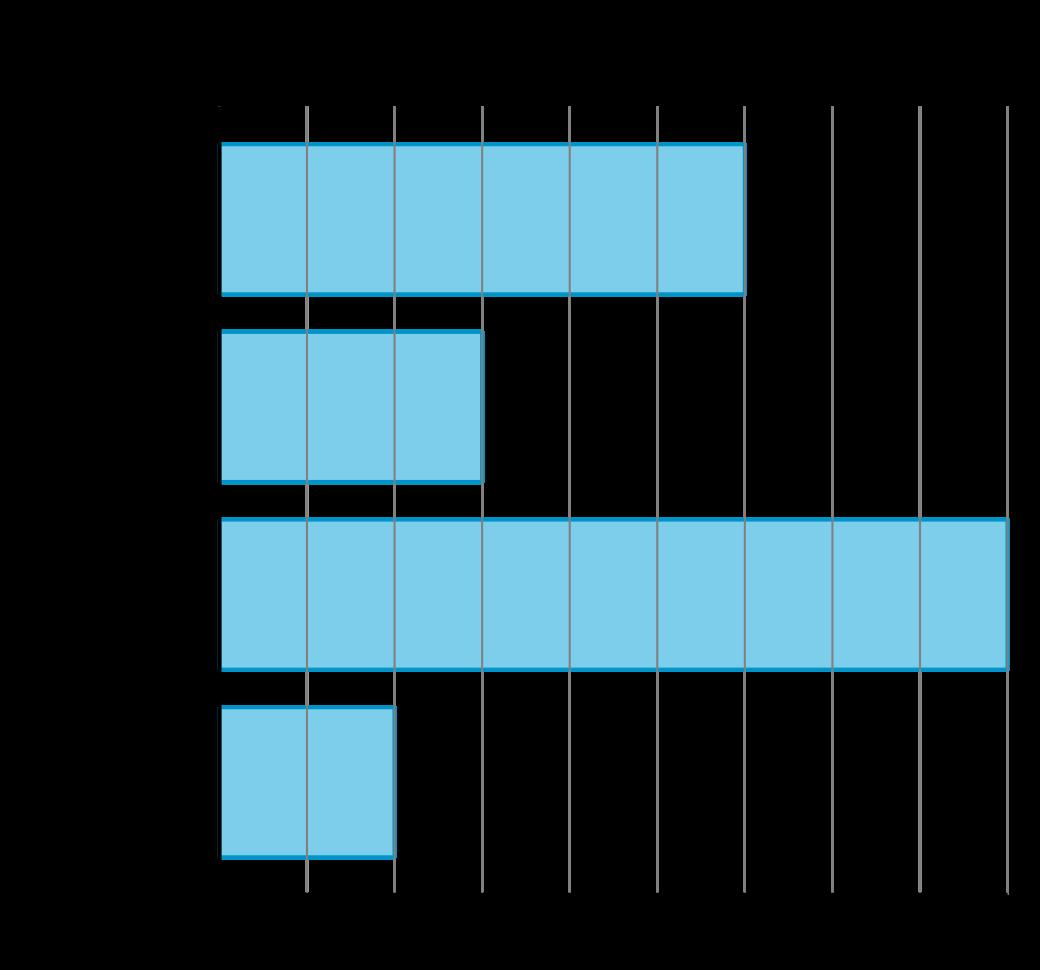
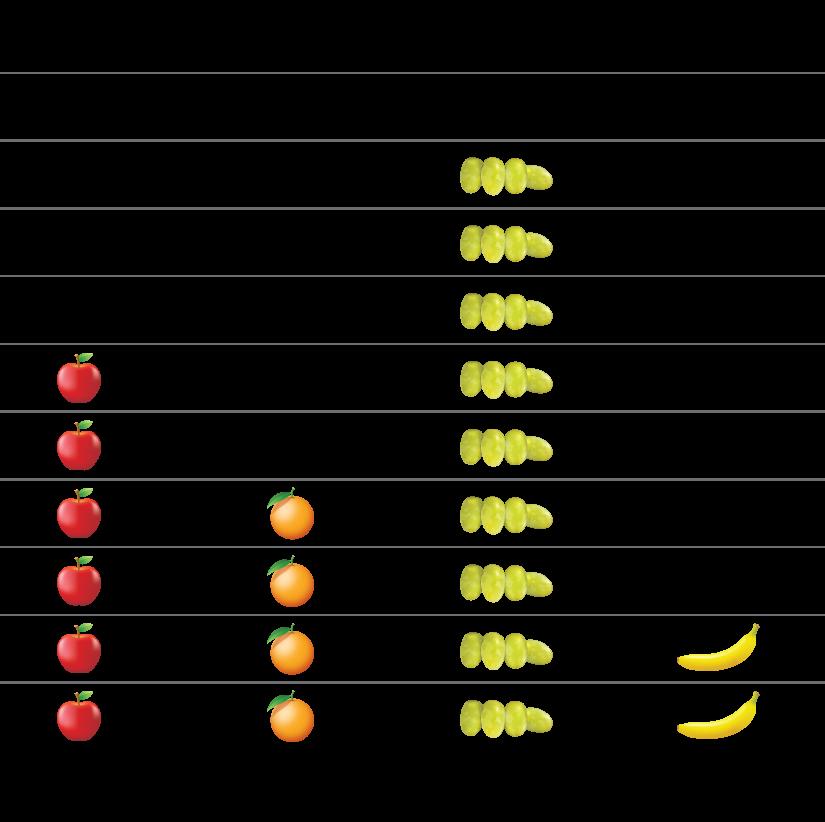

POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD

Matemáticas de 2º grado . Unidad 1
• A es la única representación que no va de arriba abajo (vertical). Está de lado.
• B es la única representación que no muestra un total de 2 plátanos.
• C es la única representación que no muestra un total de 3 naranjas.
• D es la única representación que no es un gráfico.
• "¿En qué se diferencia el gráfico A de otros gráficos que hemos visto? ¿En qué se parece?"
Rutinas instructivas Materiales para copiar
MLR8 Discussion Supports Tablas de datos (grupos de 6)
Plantilla de imagen y gráfico de barras (grupos de 1)
20 minutos
Preparación necesaria
Cada estudiante necesita 1 tabla de datos del patrón de líneas negras. Cada estudiante de un grupo de 2 puede recibir diferentes tablas de datos.
El propósito de esta actividad es que los estudiantes dibujen sus propios gráficos para representar los datos dados. Cada alumno recibe una tabla de datos para utilizar . Después de dibujar sus propias gráficas, las comparten con un compañero y reciben comentarios sobre lo que está claro y lo que podrían mejorar. A medida que los alumnos representan los datos y comparten sus gráficos con los demás, observan y describen las características de los gráficos que facilitan la comprensión de los demás (MP3, MP6). Mientras los alumnos hacen sus gráficos, vigile cualquier característica que muchos alumnos omitan (por ejemplo, títulos o etiquetas de categorías) para destacarla al compartirla en la síntesis.
Las tablas de datos se volverán a utilizar en la siguiente actividad.
Esta actividad utiliza MLR8 Discussion Supports. Avances: leer, escribir y conversar.
• Grupos de 2
• Muestra el gráfico "Deportes favoritos de los alumnos de 2º grado".
Math Nation California - Grado 2
• "¿Qué puedes aprender sobre los deportes favoritos de los alumnos de 2º grado a partir de este gráfico?"
• "¿Cuáles son algunas características de este gráfico que nos ayudan a entender los datos?"
• Comparte las respuestas.
• Subraya las características importantes (título, etiquetas e imágenes o símbolos).
• "Ahora vas a crear tu propio gráfico con imágenes."
• Entrega a cada alumno 1 tabla de datos y una plantilla de gráfico del patrón de líneas negras.
• "Escribe el número de la tabla de datos en tu página.
• "Este gráfico utiliza caritas sonrientes, pero puedes elegir algo diferente cuando hagas tu gráfico."
• "Piensa qué imagen vas a utilizar, luego representa los datos que se muestran en tu tabla en un gráfico.""
• 10 minutos: tiempo de trabajo independiente
• Supervisa a los estudiantes que utilizan símbolos que son fáciles de dibujar.
• "Cambia los gráficos con tu compañero."
• "Dile a tu compañero 1 cosa que crees que hicieron realmente bien y 1 cosa sobre la que todavía tienes una pregunta."
MLR8 Apoyos para la discusión
• Mostrar marcos de oraciones.
• "Lo hiciste realmente bien en tu gráfico."
• "¿Por qué hiciste . . .
• "¿Puedes decir algo más sobre...? ?"
• 5 minutos: tiempo de trabajo en pareja
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
Se preguntó a un grupo de alumnos de 2º curso: "¿Cuál es tu deporte favorito?". Sus respuestas se muestran en este gráfico.
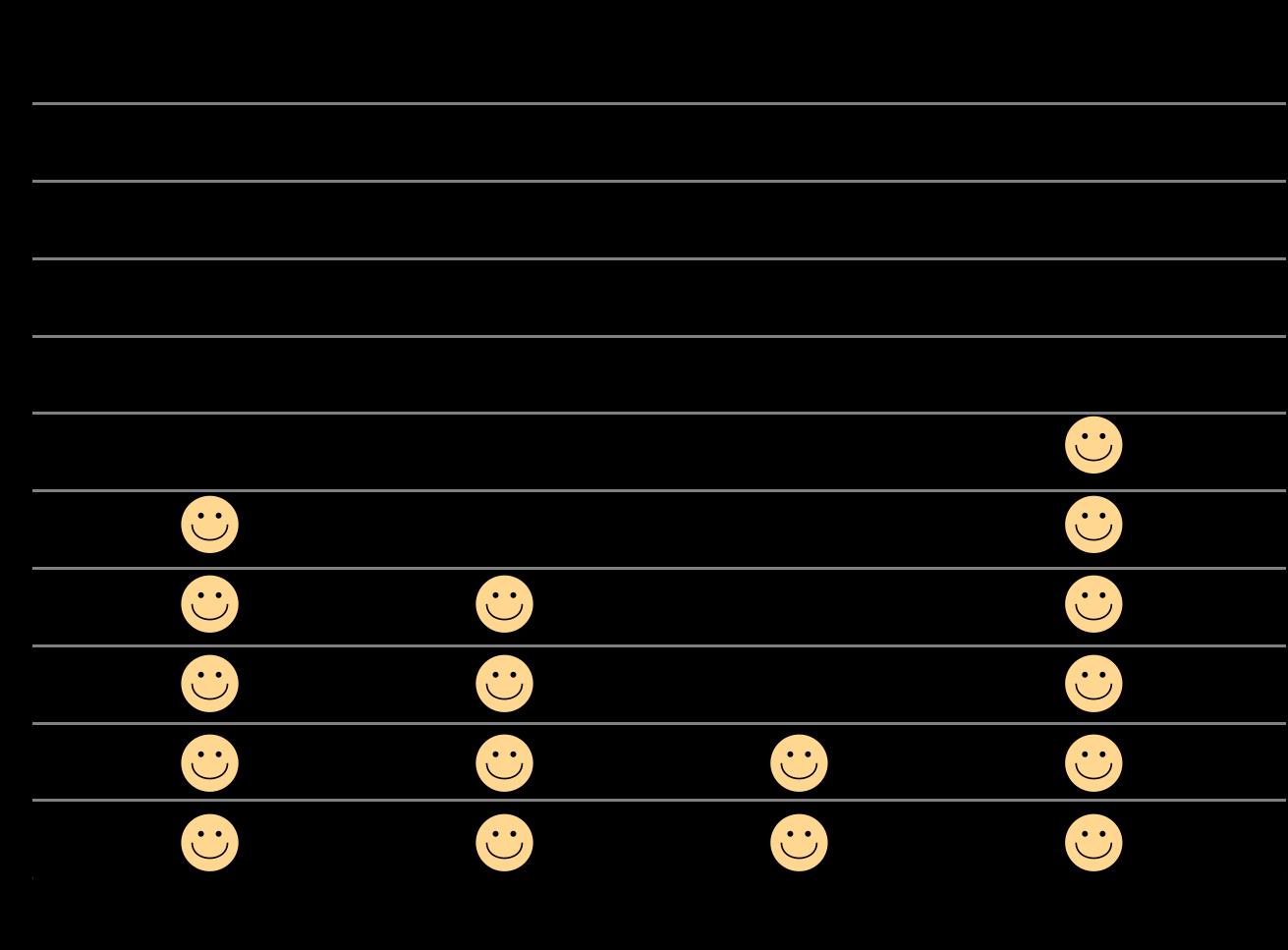
Represente los datos de su tabla en un gráfico.
Tabla #
POSIBLES RESPUESTAS

• Muestre los gráficos de los estudiantes seleccionados previamente.
• "¿Qué hay de igual en estos gráficos?
• 1 minuto: tiempo para pensar en silencio
SÍNTESIS DE LA ACTIVIDAD
• 1-2 minutos: discusión en parejas
• Comparta las respuestas.
• Considere preguntar a los estudiantes seleccionados:
• "¿Por qué elegiste ese símbolo?"
• "¿Qué otras características agregaste a tu gráfico para ayudar a los demás a entenderlo?"¿Qué es diferente?"
Matemáticas de 2º grado . Unidad 1
15 minutos
Materiales para reunir
Materiales de una actividad anterior

Materiales para copiar
Plantilla de gráfico de imágenes y de barras (grupos de 1)
El objetivo de esta actividad es que los alumnos representen los datos en un gráfico de barras. Los alumnos utilizan las mismas tablas de datos de la Actividad 1, pero cambian con un compañero para asegurarse de que tienen datos nuevos. En la síntesis, los alumnos repasan las similitudes y diferencias entre las características de los gráficos de imágenes y los gráficos de barras describiendo cómo fue dibujar cada tipo de gráfico. Al igual que en la actividad anterior, los alumnos comparten sus gráficos con los demás y comparan las diferentes características que incluyen para que sus datos sean claros para los demás (MP3, MP6).
Apoyo a los estudiantes con discapacidad
Compromiso: Proporcione acceso captando el interés. Utilice un temporizador para ayudar a los estudiantes a anticiparse y prepararse para las transiciones. Un temporizador programado para un tiempo de trabajo específico, antes de compartir el trabajo con un compañero, ayudará a los estudiantes a mantenerse concentrados. Cuando el temporizador is arriba, los estudiantes compartirán su trabajo.
Apoya la accesibilidad para: Atención, Organización
• Grupos de 2
• Mostrar el gráfico de barras "Fruits We Love" con las categorías cubiertas.
• "¿Qué crees que son las etiquetas de la parte inferior? ¿Por qué?"
• 2 minutos: discusión por parejas
LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
Math Nation California - Grado 2
• Compartir y anotar las respuestas.
• "¿Cuáles son algunas características de este gráfico que nos ayudan a entender los datos?"
• Compartir las respuestas.
• Resaltar las características importantes (título, etiquetas, números/escala).
• Entregar a cada alumno una copia de la plantilla del gráfico.
• Pedir a los alumnos que intercambien las tablas de datos con su compañero u otro alumno.
• "Cuando hagáis vuestro propio gráfico de barras, utilizad la cuadrícula para dibujar un gráfico de barras que represente los datos de vuestra tabla de datos."
• "Escribid el número de la tabla de datos en vuestra página."
• "Después de haber hecho vuestro gráfico de barras, comparadlo con un compañero."
• 10 minutos: tiempo de trabajo independiente
Se preguntó a un grupo de alumnos: "¿Qué fruta te gusta comer?". Sus respuestas se muestran en este gráfico de barras.

©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA CONTINUACIÓN
Representa los datos de tu tabla en un gráfico de barras.
Tabla #

Los gráficos de los alumnos varían en función de sus tablas de datos. Todos los gráficos deben incluir un título, etiquetas, números a los lados y barras para representar sus datos.
Ejemplo de respuesta:
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
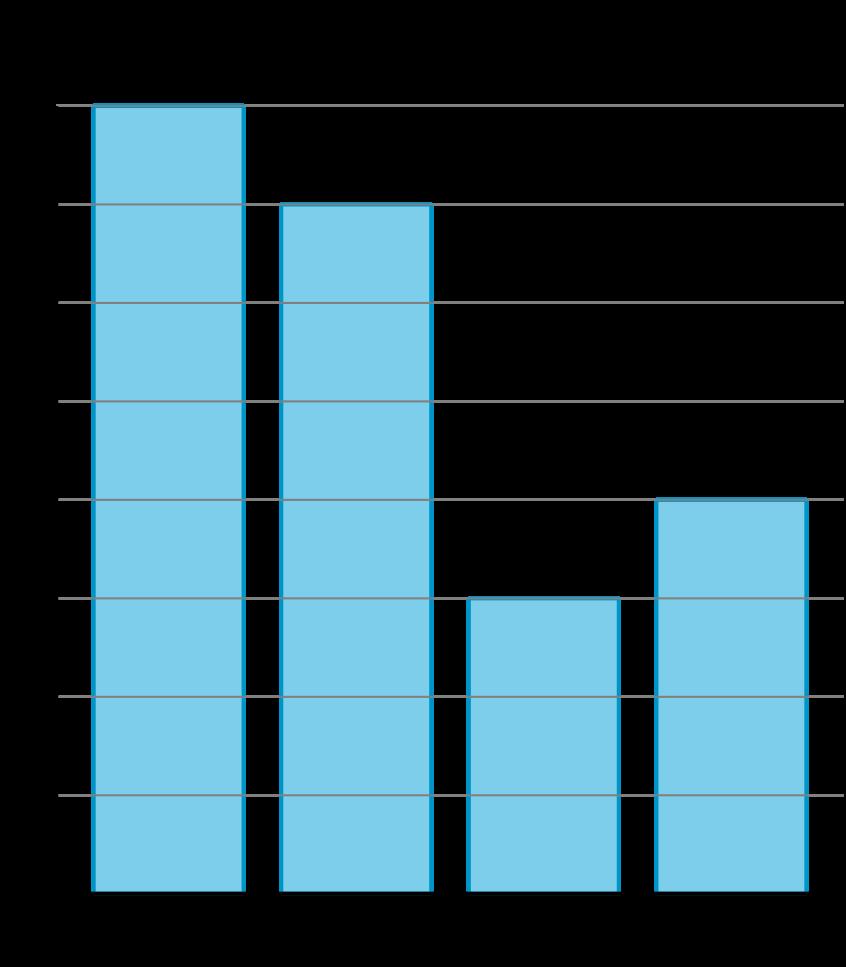
• "¿Cómo supiste qué altura darle a cada barra de tu gráfico?" (Sabía que 8 a la gente le gustaban más las matemáticas, así que encontré 8 al lado y sombreé desde esa línea hacia abajo.)
• "¿En qué se pareció dibujar un gráfico de barras a dibujar un gráfico de imágenes? ¿En qué se diferenciaba? (Al igual que en los gráficos, teníamos que usar etiquetas y títulos y asegurarnos de que los números coincidían. Era diferente porque no teníamos que hacer dibujos diferentes, sólo podíamos usar la escala y dibujar torres que coincidieran. En un gráfico de barras túu have to write the numbers on the side).
10 minutos
"Hoy hiciste gráficos de imágenes y gráficos de barras para representar datos."
"¿Qué es algo nuevo sobre gráficos que aprendiste hoy?"
"¿Qué es algo nuevo que aprendiste al trabajar con tu compañero?"
"¿Cómo revisaste tu gráfico de hoy para facilitarle a otra persona la comprensión de los datos?"
"Mañana usarás tus gráficos para escribir preguntas para que tus compañeros las respondan y tendrás la oportunidad de responder a sus preguntastiones based en los gráficos."
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
5 minutos
El Sr. Green preguntó al equipo de fútbol: "¿Qué frutas os gusta comer?"
Mai y Lin utilizaron los datos que recogió para hacer gráficos.
Mai empezó un gráfico de imágenes. Lin comenzó un gráfico de barras.
Completa cada gráfico.
Mai's Graph Lin's Graph

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA


POSSIBLE RESPONSES Los estudiantes muestran 6 fresas, 5 uvas, 3 naranjas, y 6 manzanas en cada gráfico.
Reflections:
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados

GRANDES IDEAS)
• Representar datos
• Estrategias numéricas
ALINEACIÓN
Abordaje
Alineación
Estándares y principios de CA
2.MD.10 Dibujar un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar utilizando la información presentada en un gráfico de barras.
2.OA.2 Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del Grado 2, saber de memoria todas las sumas de dos números de un dígito.
Construyendo sobre
1.OA.6
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP4 Modelar con matemáticas.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.2
I.B.7
I.C.11
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
predecir lo que podría ocurrir y repercutir en el futuro razonar abstracta y cuantitativamente razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo generar y responder preguntas sobre datos representados en gráficos de imágenes y gráficos de barras.
OBJETIVOS DE APRENDIZAJE
• Generar y responder preguntas sobre datos representados en gráficos de imágenes y gráficos de barras.
¿Qué aspectos de la lección de hoy han permitido a cada uno de tus alumnos verse a sí mismos como razonadores matemáticos productivos??
Rutinas didácticas
Hablar de números (calentamiento)
Materiales Para reunir
Materiales de una lección anterior: Actividad 1, Actividad 2
Objetivos de aprendizaje para el alumno
• Vamos a responder preguntas utilizando gráficos de imágenes y de barras.
Narrativa de la lección
El objetivo de esta lección es que los alumnos formulen y respondan preguntas sobre un conjunto dado de datos categóricos representados en gráficos de imágenes y de barras.
©Accelerate Learning Inc. - Todos los derechos reservados

Matemáticas de 2º grado . Unidad 1
En lecciones anteriores, los alumnos interpretaron gráficos de imágenes y de barras y respondieron a preguntas utilizando los datos presentados en los gráficos. En esta lección, los alumnos generan sus propias preguntas sobre los datos representados en los gráficos que crearon en la lección anterior. Utilizan los gráficos y los diagramas de barras de sus compañeros de clase para responder a las preguntas queent-generan sobre los datos. A lo largo de la lección, los alumnos tienen la oportunidad de compartir y revisar su trabajo con diferentes compañeros. Estas conversaciones les ayudan a profundizar en su comprensión de la estructura de los gráficos de barras e imágenes y de las características que ayudan a comunicar los datos con claridad (MP3, MP6). Cuando los alumnos formulan sus propias preguntas y responden a preguntas sobre los datos, prestan atención a las características de lose graph y al significado de estas características dentro del contexto (MP2).
Esta lección tiene un Resumen de la Sección del Alumno.
LESSON-AT-A-GLANCE
Componente de la lección
Estructura
Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 Por parejas 15 min.
Actividad de exploración 2 Por parejas 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Centro(s) sugerido(s) Grupos pequeños Opcional
Breve descripción
Los estudiantes calculan el valor de expresiones numéricas que contienen la suma de números enteros dentro de 20
Los alumnos escriben preguntas sobre datos del mundo real representados en gráficos de imágenes y de barras de la lección anterior.
Los estudiantes responden preguntas creadas por sus compañeros utilizando datos del mundo real.
Los estudiantes discuten cómo crearon y respondieron preguntas sobre datos representados en gráficos.
Los estudiantes responden preguntas sobre datos del mundo real representados en gráficos de imágenes y gráficos de barras.
Abordaje:
• Agitar y derramar (K-2), Etapa 5: Cubrir (hasta 20)
Apoyo:
• Ordenar y mostrar (1-3), Etapa 1: De cualquier manera
Math
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
CON 10 minutos
Rutinas instructivas
Hablar de números
El propósito de esta Charla sobre números es estimular a los estudiantes a usar su comprensión de las propiedades de las operaciones y la estructura de los números enteros para sumar dentro de 20 (MP7). Cada expresión está diseñada para animar a los alumnos a buscar formas de sumar diez buscando dos sumandos que sepan que suman diez o descomponiendo un sumando para sumar diez con otro. La capacidad de encontrar maneras de formar una decena ayudará a los estudiantes a desarrollar fluidez dentro de 20 y será útil más adelante en esta lección y en lecciones posteriores cuando los estudiantes sumen y resten dentro de 20
• Mostrar una expresión.
LANZAMIENTO

ACTIVIDAD
DE CARA AL ESTUDIANTE
ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste.
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra mentalmente el valor de cada suma.
• 3 + 7
• 3 + 7 + 2
• 5 + 7
• 2 + 4 + 8
• 10: 3 + 7 = 10
• 12: 3 + 7 = 10 y 2 más es 12
• 12: Descompuse el 5 en 3 y 2 3 + 7 = 10 y 10 + 2 = 12
• 14: 2 + 8 = 10 y 10 + 4 = 14
• "¿Cómo la búsqueda de formas de hacer una decena facilita encontrar los valores de estas expresiones?"
BASED EN GRAFOS 15 minutos
Materiales a reunir
Materiales de una lección anterior
Preparación necesaria
Cada alumno necesita el gráfico de imagen y el gráfico de barras que crearon en la lección anterior.
El objetivo de esta actividad es que los alumnos formulen preguntas que puedan responderse sobre un conjunto dado de datos categóricos representados en gráficos de imágenes y de barras. Los alumnos decidirán qué gráfico se puede utilizar para responder a cada pregunta, por lo que se les debe animar a que mezclen el orden de las preguntas.
Matemáticas de 2º grado . Unidad 1

Apoyo para estudiantes de inglés
MLR7 Comparar y conectar. Síntesis: Registre las preguntas que comparten los estudiantes en una pantalla. Pregunte: "¿Qué tienen en común estas preguntas? ¿En qué se diferencian?" Amplifique las respuestas de los alumnos que llamen la atención sobre el lenguaje de las preguntas matemáticas.
Avances: Representar, conversar
LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• Grupos de 2
• Entrega a cada alumno sus gráficos de la lección anterior o pide a los alumnos que recuperen sus gráficos.
• "Ahora escribiréis preguntas que podríais hacer sobre los datos de ynuestros gráficoshs."
• "Escribe 2 preguntas para cada gráfico, pero no las pongas todas en orden."
• "Tus compañeros tendrán que pensar qué gráfico utilizar para responder a tus preguntas."
• "Escribe al menos 1 pregunta que requiera que alguien combine o compare dos categorías."
• 8 minutos: tiempo de trabajo independiente
• Vigila la variedad de preguntas que creen los estudiantes y que requieran combinar o comparar dos o más categorías."
• "Cambia las preguntas con un compañero. Asegúrate de tener preguntas que puedan responderse con los gráficos".
• 4 minutos: discusión por parejas
Escribe 4 preguntas que podrías hacer sobre los datos de tus gráficos. Asegúrate de tenere 2 para cada gráfico.
1. 2. 3. Pregunta extra:
POSIBLES RESPUESTAS

Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


de 2º grado . Unidad 1

POSIBLES RESPUESTAS CONTINUACIÓN
1. ¿Qué opción de almuerzo obtuvo más votos?
2. ¿Cuántas personas eligieron macarrones con queso?
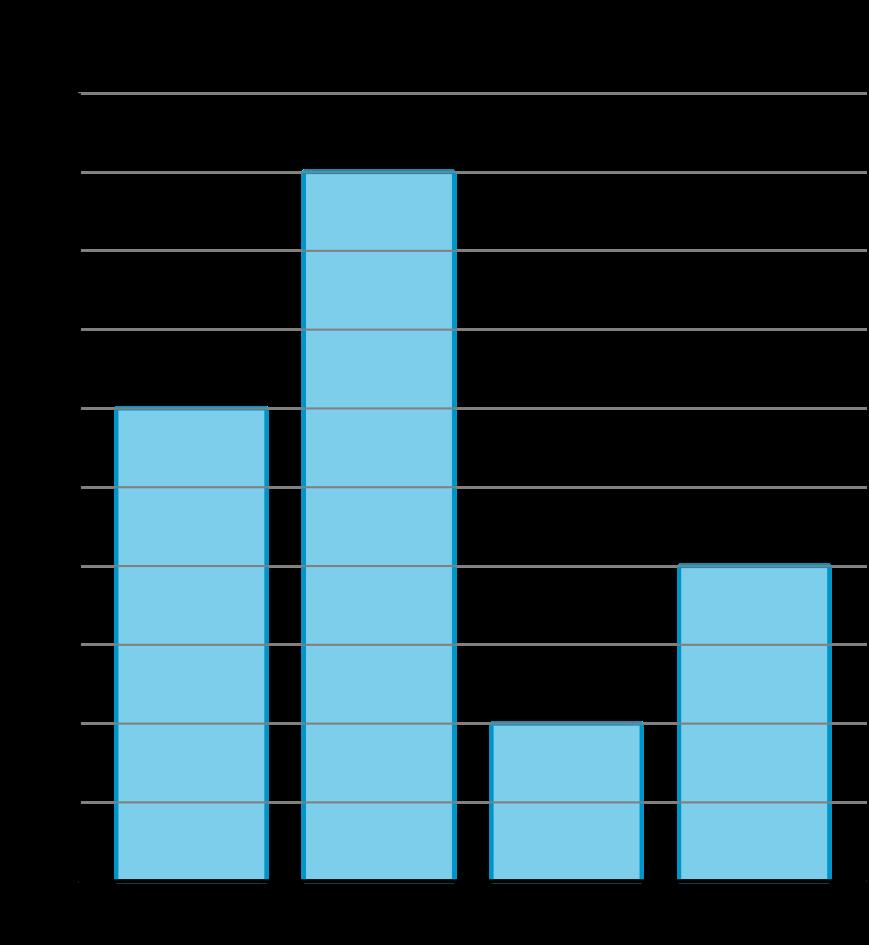
3. ¿A cuántos estudiantes más les gusta el helado que las galletas?
4. ¿Cuál es el número total de estudiantes a los que les gustan más los brownies o el pastel?. ¿Cuál es el número total de estudiantes a los que les gustan más los brownies o las tartas?
Si los estudiantes sólo escriben preguntas que piden a otros que respondan cuántos hay en una categoría, considera preguntar:
ADEVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
SÍNTESIS DE LA ACTIVIDAD
• "¿Cuántas categorías necesitaría mirar alguien para responder a tu(s) pregunta(s)?"
• "¿Cuál es una pregunta que podrías escribir que pida a alguien que compare dos categorías en tu gráfico?
• "¿Cuál es la pregunta que podrías escribir para que alguien encuentre el total de dos o más categorías en tu gráfico?""
• Invite a los estudiantes previamente identificados a compartir las preguntas que crearon y que requerirían combinar o comparar dos categorías más.
• "¿Cómo saben que estas preguntas requerirán que alguien combine o compare los totales de dos o más categorías?" (Las preguntas preguntan sobre dos o más categorías. No sólo piden decir cuántos hay en una categoría o qué categoría tenía más. Veo palabras como "cuántos más" o "cuántos menos")
• "Si quieres, puedes revisar tus preguntas o añadir una pregunta extra"
Materiales a reunir
Materiales de una lección anterior
20 minutos
Preparación necesaria
Cada estudiante necesita el gráfico de dibujos y el gráfico de barras que crearon en la lección anterior.
El objetivo de esta actividad es que los alumnos respondan preguntas sobre los datos representados en sus gráficos de imágenes y de barras. Los alumnos cambian de cuaderno con un nuevo compañero, lo que les da la oportunidad de ver el trabajo de los demás y ver diferentes representaciones de los datos. Mientras los alumnos responden a las preguntas basadas en los distintos gráficos, identifique las preguntas que les resultan más difíciles de responder. Estas preguntas pueden discutirse en la síntesis de la lección. En las próximas lecciones, los estudiantes tendrán más oportunidades de trabajar con preguntas que requieran comparar categorías.
Matemáticas de 2º grado . Unidad 1
Representación: Interiorizar Comprender. Síntesis: Invite a los alumnos a identificar a qué detalles era importante o más útil prestar atención. Muestre el marco de la frase: "La próxima vez que responda a preguntas sobre un gráfico, yo..."
Apoya la accesibilidad para: Procesamiento conceptual, Memoria
LANZAMIENTO

ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• Grupos de 2: compañero diferente al de la actividad anterior
• "Arranquen la página de sus libros titulada 'Respondiendo preguntas usando gráficas'"
• "Ahora van a responder preguntas que un compañero diferente ha escrito sobre sus gráficas"
• "Escriban su nombre y el de su compañero en la parte superior de la página"
• "Intercambien gráficas y preguntas con su compañero. Contesta a cada una de las preguntas que ha escrito tu compañero."
• 6 minutos: tiempo de trabajo independiente
• "Discute las preguntas y respuestas con tu compañero para ver si estáis de acuerdo."
• 6 minutos: discusión entre compañeros
• Vigila a los alumnos que mencionen las características de los gráficos, como el título o las etiquetas, al responder: "¿Cómo supiste dónde encontrar la respuesta a cada pregunta?"
Contesta a las preguntas de tu compañero de la Actividad 1 utilizando los gráficos.
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
Math Nation California - Grado 2
5. ¿Cómo supiste dónde encontrar la respuesta a cada pregunta?
Las respuestas varían. Ejemplos de respuestas:
• 7 a más alumnos les gusta el helado que las galletas.
• 4 la gente eligió macarrones con queso.
• 10 a los alumnos les gustan más los brownies o la tarta.
• Los nuggets de pollo fueron los más votados.
• Seleccione 2-3 estudiantes identificados para que compartan una pregunta que hayan respondido y cómo supieron dónde encontrar la respuesta.
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos
"Hoy has formulado y respondido preguntas basadas en datos representados en gráficos de imágenes y gráficos de barras."
"¿Qué tipo de preguntas eran más fáciles de responder? ¿Qué tipo de preguntas fueron más difíciles de responder?"
"¿Dónde miraste en cada gráfico para encontrar las respuestas a las preguntas?"
5 minutos
Se preguntó a los alumnos: "¿Cuál es tu deporte favorito para jugar?" y "¿A qué recess game de interior te gusta jugar?". Sus respuestas se muestran en el gráfico and bar gráfico.

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA

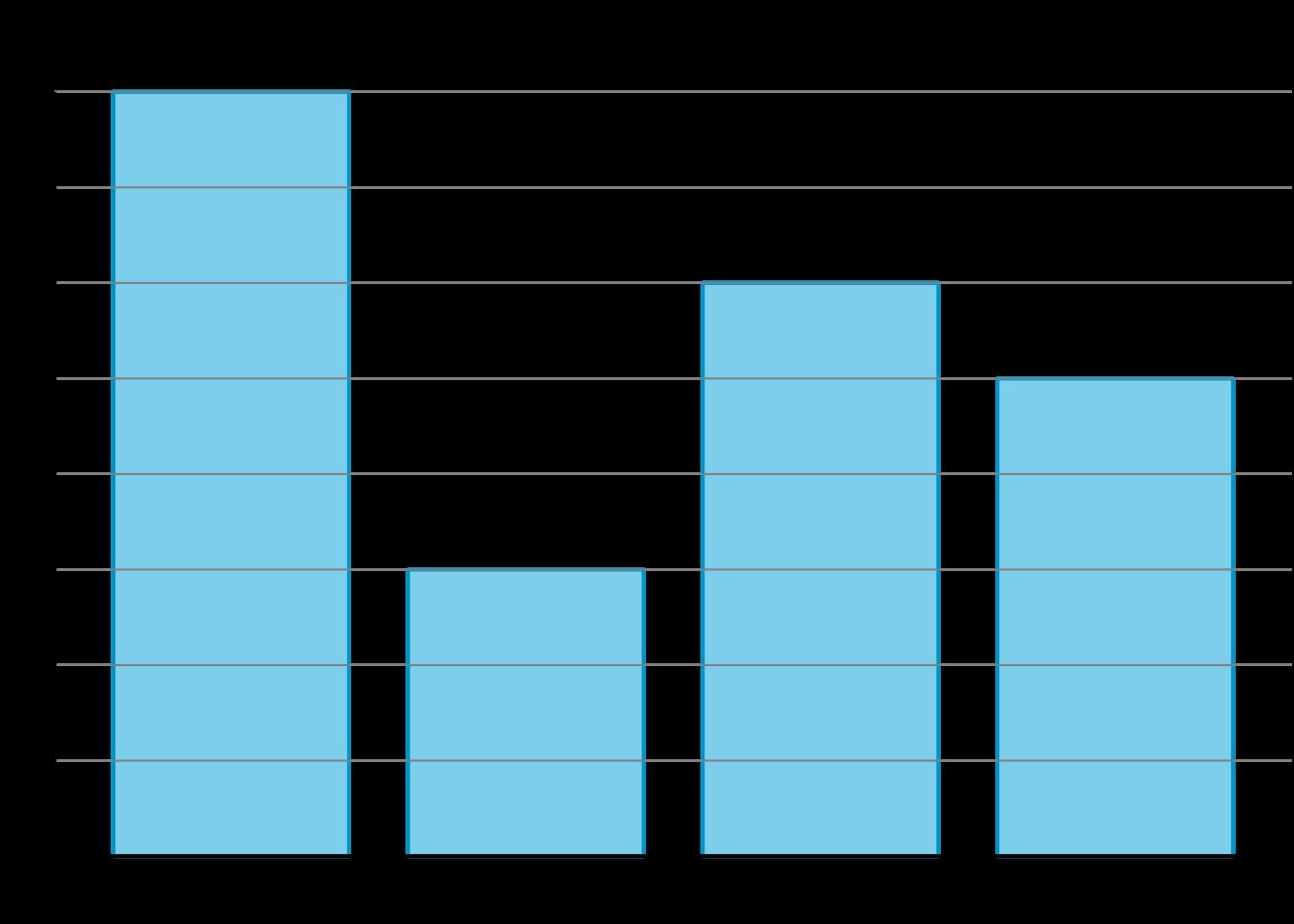
1. ¿A cuántos alumnos les gusta jugar al fútbol?
2. 2. ¿A cuántos alumnos les gusta jugar a juegos de mesa?
3. ¿Qué gráfico se utilizó para representar el número de alumnos a los que les gusta el baloncesto?
Encierra uno en un círculo:
Gráfico de imagen
Gráfico de barras
4. ¿Qué gráfico trata de los juegos de interior? ¿Qué gráfico se refiere a los juegos de interior? Encierra en un círculo:
Gráfico de imagen
POSIBLES RESPUESTAS
Reflexiones:
Gráfico de barras
1. 6 a los estudiantes les gusta jugar al fútbol.
2. 8 a los estudiantes les gusta jugar a juegos de mesa.
3. gráfico de imagen
4. gráfico de barras


GRANDES IDEAS)
• Representar datos
• Estrategias numéricas
ALINEACIÓN
Abordaje
2.MD.10 Dibujar un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando información presentada en una gráfica de barras.
Alineación
Estándares y principios de CA
2.NBT.5 Sumar y restar con fluidez dentro de 100 usando estrategias basadas en el valor posicional, propiedades de las operaciones y/o la relación entre suma y resta.
2.OA.2 Sumar y restar con fluidez dentro de 20 usando estrategias mentales. Al final del Grado 2, saber de memoria todas las sumas de dos números de un dígito.
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP2 Razonar abstracta y cuantitativamente.
MP4 Modelar con matemáticas.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.4 I.C.12 II.C.7
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
repercuten en el futuro
dan sentido a los problemas y perseveran en su resolución
OBJETIVO(S) DE APRENDIZAJE
• Puedo sumar y restar números enteros dentro de 50
desmontando enteros, juntando piezas y razonando con datos.
• Puedo representar datos utilizando dibujos y gráficos de barras.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Practicar la suma y la resta dentro de 10 or 20
• Practicar la suma dentro de 50
• Representar datos utilizando dibujos y gráficos de barras.
PREGUNTA DE REFLEXIÓN PARA EL PROFESOR
Reflexione sobre lo cómodos que se sienten sus alumnos haciéndole preguntas a usted y entre ellos. ¿Qué puede hacer para animar a los alumnos a hacer preguntas?
PREPARACIÓN DE LA LECCIÓN
Rutinas instructivas
Hablar de números (calentamiento)
Materiales para reunir
Colecciones de objetos: Actividad 1
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales Para copiar
Clasificar y mostrar Hoja de registro de la Etapa 2 (grupos de 1): Actividad 1

Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Vamos a ordenar una colección y hacer gráficos para representarla.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes practiquen la organización de datos y el uso de gráficos para representarlos. Los estudiantes también practican la suma y la resta dentro de 10, 20, o 50
Esta lección es opcional porque es una oportunidad de práctica extra que no todas las clases pueden necesitar. En la Actividad 1, los alumnos aprenden la etapa 2 del centro Ordenar y mostrar, que se introdujo por primera vez en el primer curso. En esta nueva etapa, llamada Gráfico de barras o de imágenes, los alumnos clasifican 20-30 objetos en 3 categorías y hacen un dibujo o gráfico de barras que muestra cómo los clasificaron. En la Actividad 2, los alumnos eligen entre dos centros previamente introducidos centrados en la suma y la resta.
LECCIÓN DE UN VISTAZO
Componente de lección Estructura Tiempo
Descripción breve
Calentamiento Independiente 10 min. Los estudiantes evalúan expresiones numéricas de resta de números enteros hasta 20.
Actividad de exploración 1 Pares 20 min.
Centros Parejas o Grupos pequeños 20 min.
Utilizando el centro Clasificar y mostrar, los estudiantes clasifican objetos en categorías, representan los datos en un gráfico de imágenes o de barras y crean preguntas sobre los datos.
Los estudiantes suman y restan números enteros dentro de 50 Centros sugeridos:
• ¿Qué hay a mis espaldas? Etapas 2 y 3
• ¿Qué tan cerca?, Etapas 1-3
• Rompecabezas numéricos, Etapas 1 y 2
Síntesis Grupo completo 10 min. Los alumnos reflexionan sobre las normas del aula para las actividades de centro que funcionan bien y las normas que pueden mejorarse.
Math
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos
Rutinas instructivas
Hablar de números
El propósito de esta Charla sobre números es obtener las estrategias y comprensiones que los alumnos tienen para restar un número de un dígito de un número de dos dígitos utilizando una decena. Cuando los alumnos descomponen un número para llegar a una decena, buscan y utilizan la estructura de números enteros y las propiedades de las operaciones (MP7).
LANZAMIENTO

ACTIVIDAD
DE CARA AL ESTUDIANTE
ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
• Mostrar una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste."
• 1 minuto: tiempo para pensar en silencio
• Registrar las respuestas y la estrategia.
• Mantener las expresiones y el trabajo mostrados.
• Repetir con cada expresión.
Encontrar el valor de cada expresión mentalmente.
• 17 - 7
• 17 - 9
• 15 - 5
• 15 - 8
• 10: 17 es 1 diez y 7 unos, así que quité los unos.
• 8: Sabía que 17 - 7=10, y entonces quité 2 más.
• 10: Sé que 10 + 5 es 15, así que quité los 5
• 7: Quité 5 y volví a contar 3 más.
• "¿Cómo podemos usar la primera expresión para encontrar el valor de la segunda?" (Yo sabía que 17 - 7=10, y luego saqué 2 más.)
Materiales para reunir
Colecciones de objetos
20 minutos
Materiales para copiar
Clasificar y mostrar Hoja de registro de la Etapa 2 (grupos de 1)
Preparación necesaria
Cada grupo de 2 necesita una colección de 20-30 objetos que puedan clasificarse en al menos 3 categorías. Ejemplos: bloques de patrones, cubos, juegos de libros o una combinación de bloques, cubos y fichas.
El propósito de esta actividad es que los alumnos aprendan la etapa 2 del centro Ordenar y Mostrar. Los alumnos clasifican 20-30 objetos en 3 categorías y hacen un dibujo o gráfico de barras que muestre cómo han clasificado. A continuación, plantean a su compañero 2 preguntas que pueden responder basándose en su gráfico. Los alumnos tienen la oportunidad de ordenar los objetos, representar cómo los han ordenado y crear preguntas que se pueden hacer sobre los datos de su representación (MP2, MP6).
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
Para conectar este centro con Lengua y Literatura Inglesas, los alumnos podrían utilizar libros para buscar una colección. Los alumnos miran la portada de un libro y eligen 3 palabras o 3 imágenes que creen que aparecerán con más frecuencia en la historia y explican por qué a su compañero. Los compañeros anotan estas elecciones como categorías iniciales. A continuación, los alumnos leen u hojean el libro juntos, exploran su predicción y deciden juntos si quieren revisar sus categorías basándose en lo que han leído. En la segunda lectura, recogen y registran los datos de sus categorías revisadas. Por último, los alumnos crean representaciones basadas en sus datos y escriben 2 preguntas del tipo "¿Cuántos?" que pueden hacerse sobre los datos de sus representaciones.
• Grupos de 2
• Entregue a cada alumno una hoja de registro.
• "Hay un nuevo centro llamado "Clasificar y mostrar".
• Lea las instrucciones en voz alta a los alumnos.

LANZAMIENTO
ACTIVIDAD
SÍNTESIS DE LA ACTIVIDAD
• "Elija una colección para clasificar. Clasifícala en 3 categorías. Representa los datos en un gráfico que muestre cuántos hay en cada categoría."
• "Después de que hayas hecho tu representación, tú y un compañero debéis haceros preguntas sobre los datos de tu gráfico."
• 12-15 minutos: tiempo de trabajo en pareja
• Monitoriza para 1-2 gráficos para compartir en la síntesis de la actividad.
• Muestre la representación de los estudiantes.
• "¿Qué preguntas podemos hacer sobre la representación de cómo clasificaron?"
20 minutos
Preparación requerida
Reúna los materiales de :
• Qué hay detrás de mi espalda, Etapas 2 y 3
• Qué tan cerca, Etapas 1-3
• Rompecabezas numéricos, Etapas 1 y 2
El propósito de esta actividad es que los estudiantes elijan entre actividades que se centren en sumar o restar.
Los estudiantes eligen entre cualquier etapa de los centros presentados previamente.
• ¿Qué hay detrás de mi espalda?
• ¿Qué tan cerca?
• Rompecabezas numéricos
LANZAMIENTO
ACTIVIDAD
Math Nation California - Grado 2
• "Ahora elegirán de los centros que ya hemos aprendido que se enfocan en sumar y restar."
• Muestre las opciones de centros en el libro del alumno.
• "Piensen qué les gustaría hacer primero."
• 30 segundos: tiempo para pensar en silencio
• Invite a los alumnos a trabajar en el centro de su elección.
• 15 minutos: tiempo de trabajo en el centro
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
Elija un centro.
¿Qué hay a mis espaldas? ¿Qué tan cerca?


Rompecabezas numéricos

SÍNTESIS DE LA ACTIVIDAD • "¿Qué actividad elegiste? ¿Qué te gustó de la actividad que elegiste?"
10 minutos
"Hoy hemos elegido actividades para trabajar y hemos trabajado con un compañero durante el tiempo de centro."
Comunidad matemática
Muestre la tabla de la lección anterior y lea las normas a los alumnos.
"¿Qué ha ido bien? ¿En qué podemos seguir trabajando?"
Reflexiones:


IDEA(S) PRINCIPAL(ES)
• Representar datos
Abordaje
Alineación
Estándares y principios de CA
2.MD.10 Dibujar un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar utilizando la información presentada en un gráfico de barras.
2.OA.2 Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del Grado 2, saber de memoria todas las sumas de dos números de un dígito.
Enfocar SMPs
MP2 Razonar abstracta y cuantitativamente.
MP5 Usar herramientas apropiadas estratégicamente.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1 I.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . . dar sentido al mundo utilizar las herramientas adecuadas para razonar estratégicamente con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo resolver Problemas de comparación con una diferencia desconocida dentro de 20
• Puedo escribir ecuaciones para representar Problemas de comparación.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Puedo resolver Problemas de comparación con una diferencia desconocida dentro de 20
• Puedo escribir ecuaciones para representar Problemas de comparación.
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
En futuras lecciones, los alumnos darán sentido a los diagramas de cinta para representar problemas de comparación.

¿Cómo ayuda el trabajo de hoy con los gráficos de barras a que los alumnos comprendan este diagrama más abstracto?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Verdadero o falso (calentamiento)
©Accelerate Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1

Objetivos de aprendizaje para el estudiante
• Utilicemos gráficos de barras para resolver problemas de comparación.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes comprendan y resuelvan problemas de comparación utilizando la estructura de un gráfico de barras y ecuaciones. Información de la lección
En primer grado, los estudiantes utilizan la relación entre la suma y la resta para resolver y representar problemas de comparación. Crean diagramas y escriben ecuaciones para representar cómo piensan sobre las cantidades dentro de los problemas de comparación. En esta lección, los alumnos interpretan gráficos de barras y utilizan su estructura visual para comparar cantidades. Escriben ecuaciones para representar comparaciones y relacionan estas ecuaciones con la estructura del gráfico de barras (MP2). En las próximas lecciones, los alumnos utilizarán los gráficos de barras para dar sentido a los diagramas de cinta que representan los problemas de comparación.
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Independiente 10 min.
Actividad de exploración 1
Pares 15 min.
Actividad de exploración 2 Pares 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.
Los estudiantes explican si las ecuaciones de suma que involucran números enteros dentro de 20 son verdaderas.
Los estudiantes comparan categorías representadas en gráficos de barras y luego aplican diferentes estrategias para representar y resolver el problema del mundo real.
Los estudiantes completan enunciados de comparación entre dos categorías representadas en un gráfico de barras. Después, escriben ecuaciones de suma y resta para representar los problemas.
Los estudiantes reflexionan sobre cómo se pueden utilizar los gráficos de barras para comparar datos.
Los estudiantes resuelven un problema de comparación a partir de datos en un gráfico de barras y luego escriben una ecuación para representar el problema.
Abordaje:
Centro(s) sugerido(s) Grupos pequeños Opcional
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de barras o imágenes
Apoyo:
• Agitar y derramar (K-2), Etapa 5: Cubrir (hasta 20)
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
CON 9 10 minutos
Rutinas instruccionales
Verdadero o falso
El propósito de este calentamiento es activar las experiencias previas de los estudiantes en las que buscaron formas de hacer diezespecíficamente, cuando un sumando es 9. La habilidad de hacer diez ayudará a los estudiantes a desarrollar fluidez dentro de 20 y será útil más adelante en esta lección y en lecciones posteriores cuando los estudiantes sumen y resten dentro de 20
Cuando los estudiantes buscan formas de formar una decena y notan similitudes en los sumandos y valores en cada una de las expresiones, buscan y hacen uso de la estructura de los números enteros y las propiedades de las operaciones (MP7).
• Muestre un enunciado.
LANZAMIENTO

ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• "Hazme una señal cuando sepas si el enunciado es verdadero y puedas explicar cómo lo sabes"
• 1 minuto: tiempo para pensar en silencio
• Comparte y registra las respuestas y la estrategia.
• Repite con cada enunciado.
Decide si cada enunciado es verdadero o falso. Prepárate para explicar tu razonamiento.
• 9 + 4 = 9 + 1 + 3
• 9 + 4 = 10 + 3
• 9 + 5 = 10 + 6
• Verdadero: ambos lados tienen 9 y 4, porque 4 se puede descomponer en 1 + 3
• Verdadero: si tomo 1 del 4 y se lo doy al 9, entonces tengo 10 y 3, que es lo que hay en el otro lado.
• Falso: si quiero hacer un 10, necesito tomar 1 del 5 y dárselo al 9. Eso haría un 10, pero entonces sólo quedaría 4. Así que sería 10 + 4 y 10 + 6, y no son lo mismo.
• "¿Cómo puedes justificar tu respuesta sin sumar?" (Veo que 9 + 4 y 9 + 1 + 3 son iguales porque 1 + 3 = 4.)
15 minutos
El objetivo de esta actividad es que los alumnos utilicen un gráfico de barras para comparar dos cantidades y describan los métodos que utilizan para hallar la diferencia desconocida. Observe si los alumnos dibujan en el gráfico y describen formas de hallar la diferencia contando hacia delante o hacia atrás. Si los alumnos dibujan en su gráfico o no discuten ambos métodos de conteo durante la actividad, elabore y muestre el trabajo para que cada método pueda ser discutido durante la síntesis. Los segmentos discretos del gráfico de barras se utilizan para obtener estos métodos de recuento (MP5); sin embargo, algunos alumnos pueden utilizar la suma o la resta, incluidas sumas conocidas, para hallar la diferencia. Anime a estos estudiantes a conectar sus métodos con los métodos de conteo compartidos en la síntesis.
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
MLR8 Apoyos para el debate. Ofrezca a todos los estudiantes la oportunidad de hablar y de practicar el uso de enunciados comparativos. Invite a los alumnos a repetir a coro enunciados que utilicen "más" y "menos" al unísono 1-2 veces.
Avances: Hablar, escuchar

LANZAR
ACTIVIDAD
ENUNCIADO DE LA TAREA PARA EL ESTUDIANTE
Math Nation California - Grado 2
• Grupos de 2
• Mostrar la imagen (gráfico sin escala).
• "Se preguntó a un grupo de alumnos de tercer grado: '¿Qué mascotas tienes?' Sus respuestas se muestran en el gráfico de barras. Sus respuestas se muestran en el gráfico de barras."
• "¿Qué observas en los datos del gráfico? ¿Qué se preguntan?"
• 1 minuto: tiempo para pensar en silencio
• 1 minuto: discusión por parejas
• Monitoree para que los estudiantes digan: "Hay más estudiantes que tienen gatos que que tienen conejos", o se pregunten: "¿Cuántos estudiantes más tienen gatos que tienen conejos?"
• Comparta y registre las respuestas de los estudiantes.
• Si los estudiantes no hacen afirmaciones usando "más" o "menos", muestre:
• "Hay más que ."
• "Hay menos que ."
• "¿Cómo podrías completar las frases para convertirlas en afirmaciones verdaderas sobre el gráfico?"
• 1 minuto: tiempo para pensar en silencio
• 1 minuto: debate en parejas
• Comparte las respuestas.
• "Te has dado cuenta de que hay más estudiantes con gatos que con conejos. Ahora tienes que averiguar cuántos alumnos más tienen gatos que conejos. Piensa en dos formas diferentes de hallar la respuesta y anótalas"
• 3-4 minutos: tiempo de trabajo independiente
• 2-3 minutos: discusión en parejas
• Vigila si hay un estudiante que utiliza el método de contar hacia delante y otro que utiliza el método de contar hacia atrás.
Se preguntó a un grupo de estudiantes de tercer grado: "¿Qué mascotas tienes?" Sus respuestas se muestran en el gráfico de barras.
¿Qué notas? ¿Qué te preguntas?
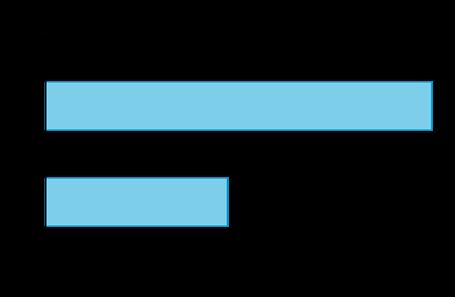
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ALUMNO ENUNCIADO DE LA TAREA CONTINUACIÓN
Sus respuestas también se muestran en este gráfico de barras.
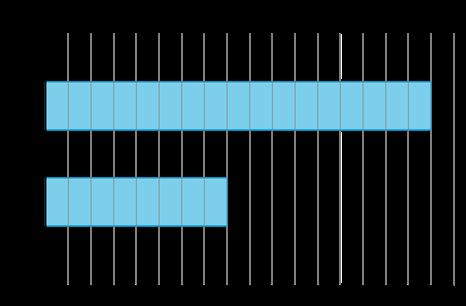
¿Cuántos alumnos más tienen gatos que conejos? Muestre dos maneras de hallar la diferencia.
• 9. Ejemplos de respuestas:
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
• Los alumnos muestran o describen la cuenta regresiva desde 8 hasta 17 en el gráfico (8 + ? = 17, 8 + 9 = 17).
• Los alumnos muestran o describen la cuenta regresiva desde 17 hasta 8 en el gráfico (17 -? = 8,
• 17 - 9 = 8).
• Invite a los estudiantes previamente identificados a compartir cómo encontraron la diferencia. Si los métodos sólo se explican verbalmente, considere preguntar: "¿Puedes mostrarnos en el gráfico de barras cómo podrías contar hacia adelante (o hacia atrás) para encontrar cuántos más?"
• Registre los métodos de los estudiantes con una ecuación. Por ejemplo, en el caso de los alumnos que describan cómo contar, escriba "8 + 9 = 17."
• "¿En qué se parecen sus métodos? ¿En qué se diferencian sus métodos?" (Un método comienza con el número menor de mascotas y sigue contando hasta el número mayor, como añadir 9 más. El otro comienza con el número mayor de mascotas y cuenta hacia atrás hasta el número menor, como restando 9.)
PARQUE 20 minutos
El propósito de esta actividad es que los alumnos utilicen gráficos para hacer afirmaciones de comparación y resolver problemas de comparación. Los alumnos representan sus comparaciones con ecuaciones. En la síntesis, los estudiantes conectan el gráfico, sus enunciados de comparación y sus ecuaciones.
Cuando los estudiantes describen cómo ven sus ecuaciones en el gráfico y cómo sus ecuaciones se relacionan con el contexto, piensan de manera abstracta y cuantitativa (MP2).
Apoyo a los estudiantes con discapacidad
Representación: Acceso para la percepción. Muestra la información en un formato flexible para facilitar las comparaciones. Crea una visualización del gráfico con barras separables, de modo que los tipos de perros que no aparecen uno junto al otro en el gráfico original puedan compararse más fácilmente. Por ejemplo, número de caniches y número de carlinos.
Apoya la accesibilidad para: Procesamiento visual-espacial, Procesamiento conceptual
LANZA

ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• Grupos de 2
• Muestra el gráfico Perros en el parque.
POSIBLES RESPUESTAS
ADVANZAR EL PENSAMIENTO DE LOS ESTUDIANTES
Nation California - Grado 2
Matemáticas de 2º grado . Unidad 1
• "¿Qué afirmación puedes hacer que compare el número de huskies con el número de bulldogs?" (Hay más bulldogs que huskies. Hay menos huskies que bulldogs. Hay 6 más bulldogs que huskies.)
• 1 minuto: discusión por parejas
• 1 minuto: discusión con toda la clase
• Comparte enunciados que utilicen "más" y "menos".
• "Ahora vas a escribir algunos enunciados utilizando "más" y "menos" y escribirás ecuaciones para mostrar cómo encontrar la diferencia."
• 5 minutos: tiempo de trabajo independiente
• "Ahora comprueba con tu compañero. ¿Son ciertas sus afirmaciones?"
• 3 minutos: discusión por parejas
• Vigila las diferentes ecuaciones que los estudiantes utilizan para cada comparación.
Kiran y Lin contaron los tipos de perros que vieron en un parque. Sus datos se muestran en el gráfico de barras.
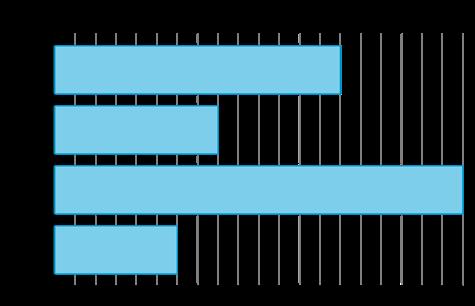
1. Haga que esta afirmación sea verdadera: Hay más que .
2. Escriba una ecuación de suma y resta para mostrar cuántos más hay.
3. Haga que esta afirmación sea verdadera: Hay menos que .
4. Escriba una ecuación de suma y resta para mostrar cuántos menos hay.
• Ejemplo de respuesta: Hay más bulldogs que huskies.
• Respuesta de ejemplo: 6 más. 20 - 14 = 6, 14 + 6 = 20
• Respuesta de ejemplo: Hay menos caniches que carlinos.
• Respuesta de muestra: 8 - 6 = 2, 6 + 2 = 8
Si los estudiantes escriben afirmaciones que no son ciertas, considere preguntar:
• "¿Cómo decidiste qué grupo tenía menos?"
• "¿Dónde ves esto en el gráfico?"
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• Invite a 1-2 estudiantes previamente identificados a compartir sus afirmaciones usando menos y una ecuación. (Ejemplo de respuesta: Hay menos carlinos que bulldogs. Hay 12 menos. 8 + 12 = 20)
• Registre la ecuación.
• "¿Qué otras ecuaciones podríamos escribir para mostrar cuántos menos para el enunciado de 's?" (Ejemplo de respuesta: Podríamos usar la resta. 20 - 12 = 8 muestra que puedes contar hacia atrás 12 desde 20 para llegar a 8.)
• Registre las ecuaciones.
• Para cada ecuación, pregunte: "¿Qué representa cada número en la ecuación?". (20 representa el número de bulldogs. 8 representa el número de carlinos. 12 representa cuántos carlinos menos).
10 minutos
"Hoy hemos aprendido que hay diferentes formas en las que podemos hablar de comparaciones y escribir ecuaciones para representarlas"
Muestre el gráfico de la Actividad 2.

Muestre: 14 + 6 = 20
"6 es la respuesta. ¿Cuál es la pregunta?" (Ejemplo de respuesta: ¿Cuántos bulldogs más hay que huskies?")
Considere preguntar: "¿Cómo has utilizado el gráfico? ¿Qué has buscado?"
Si el tiempo lo permite (o si 14 + 6 = 20 se discutió en la Actividad 2 Síntesis):
Muestra: 8 - 2 = 6
"2 es la respuesta. ¿Cuál es la pregunta?" (Ejemplo de respuesta: ¿Cuántos caniches menos hay que carlinos?)
Considera preguntar: "¿Cómo has utilizado el gráfico? ¿Qué buscaste?"
Matemáticas de 2º grado . Unidad 1
La escuela recopiló datos de asistencia para ver cuántos alumnos de segundo grado estuvieron ausentes cada mes desde septiembre hasta diciembre. Los datos se muestran en este gráfico de barras.

DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
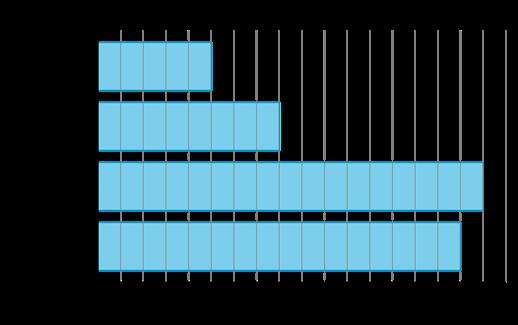
1. ¿Cuántos alumnos menos faltaron en octubre que en noviembre? Muestra tu razonamiento usando dibujos, números o palabras.
2. Escribe una ecuación que muestre cómo encontraste la diferencia. ¿Puedes escribir otra ecuación que muestre cómo hallar la diferencia?
1. 9 menos estudiantes estuvieron ausentes en octubre que en noviembre. Ejemplos de respuestas:
• Primero divide 8 en 7 y 1. Luego resta 17 - 7 = 10 y 10 - 1 = 9.
• El estudiante muestra contando desde 8 a 17 y etiquetando 9 menos estudiantes.
POSIBLES RESPUESTAS
Reflexiones:
2. Ejemplos de respuestas:
• 17 - 8 = 9
• 8 + 9 = 17
• 8 + ? = 17
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Representar datos
ALINEACIÓN
Abordando
Alineación
Estándares y principios de CA
2.MD.10 Dibuja un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando información presentada en una gráfica de barras.
Construyendo hacia
2.OA.1
Enfocar SMPs
MP2 Razonar abstracta y cuantitativamente.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.4
I.B.8
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
dar sentido al mundo buscar y utilizar la estructura razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo hacer conexiones entre gráficos de barras y diagramas de cinta.
• Puedo usar un diagrama de cinta para representar problemas de historias.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Resolver Comparar problemas con una diferencia desconocida dentro de 20
• Usar la comprensión de los gráficos de barras para dar sentido a los diagramas de cinta.
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
La relación entre la suma y la resta es importante a medida que los estudiantes desarrollan fluidez dentro de 20 en el grado 2. ¿Cómo utilizó el diagrama de cinta para ayudar a los estudiantes a construir esta comprensión?
PREPARACIÓN DE LA LECCIÓN
Materiales a reunir
Pegamento o cinta adhesiva
Tijeras
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales para copiar
Hora de fiesta
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Utilicemos gráficos de barras y diagramas para resolver problemas de Comparación.
Narrativa de la lección
En esta lección, los estudiantes utilizan su comprensión de los gráficos de barras para dar sentido a una nueva representación, el diagrama de cinta. El diagrama de cinta es una representación que pueden usar los estudiantes para representar problemas de historias. Los estudiantes usarán diagramas de cinta en segundo grado y a lo largo de la primaria, secundaria y preparatoria.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento Parejas 10 min.
Actividad de exploración 1 Grupos pequeños 20 min.
Actividad de exploración 2 Parejas 15 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.

Math
Centro(s) sugerido(s) Grupos pequeños Opcional
Los estudiantes hacen observaciones sobre datos del mundo real mostrados en un gráfico de barras y en un diagrama de cinta.
Los estudiantes crean diagramas de cinta para comparar dos categorías de datos mostrados en un gráfico de barras y luego escriben frases de comparación utilizando los datos.
Los estudiantes completan diagramas de cinta para comparar dos categorías de datos mostrados en un gráfico de barras y luego escriben enunciados y ecuaciones explicando la comparación.
Los estudiantes crean un contexto del mundo real representado por un diagrama de cinta.
Los estudiantes completan un diagrama de cinta y lo utilizan para comparar dos categorías de datos mostrados en un gráfico de barras.
Abordaje:
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de imagen o de barras
Apoyo:
• Agitar y derramar (K-2), Etapa 5: Cubrir (hasta 20)
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos

Rutinas instructivas
Notar y preguntarse
El propósito de este calentamiento es suscitar la idea de que los diagramas de cinta son similares a los gráficos de barras y pueden utilizarse para representar los mismos datos, lo que será útil cuando los alumnos den sentido al diagrama de cinta a lo largo de esta sección. Aunque los estudiantes pueden notar y preguntarse muchas cosas sobre estas imágenes, reconocer que los diagramas de cinta pueden mostrar comparaciones como un gráfico de barras es el punto de discusión importante.
Cuando los estudiantes hacen conexiones entre las diferentes formas en que las representaciones representan las mismas categorías y cantidades, razonan abstracta y cuantitativamente y buscan y hacen uso de la estructura (MP2, MP7).
• Grupos de 2
• Mostrar imagen.
LANZAMIENTO
ACTIVIDAD
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• "¿Qué notas? ¿Qué te llama la atención?"
• 1 minuto: tiempo para pensar en silencio
• "Comenta lo que has pensado con tu compañero"
• 1 minuto: debate entre compañeros
• Comparte y anota las respuestas.
¿Qué te llama la atención? ¿Qué te preguntas?
Matemáticas de 2º grado . Unidad 1

POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
Los estudiantes pueden notar:
• Todos tienen manzana y uva.
• Los números son los mismos.
• Los de abajo no tienen todas las barras.
Los estudiantes pueden preguntarse:
• ¿Por qué los dos de abajo no tienen todos los sabores?
• ¿Es este un nuevo tipo de gráfico?
• ¿Por qué hay uno sin secciones?
• "Las imágenes 2 de la parte inferior se llaman diagramas."
• "¿Qué crees que representan 15 y 8 en los diagramas de la parte inferior?" (El número de estudiantes que eligieron zumo de manzana y el número de estudiantes que eligieron zumo de uva.)
• "¿Qué representa el signo de interrogación en el diagrama?" (La diferencia entre el número de estudiantes que eligieron zumo de manzana y de uva, cuántos estudiantes más eligieron zumo de manzana que de uva, cuántos estudiantes menos eligieron zumo de uva que de manzana.)
20 minutos
Materiales para reunir
Pegamento o cinta adhesiva
Tijeras
Materiales para copiar
Hora de la fiesta
El propósito de esta actividad es que los alumnos utilicen su comprensión de los gráficos de barras para dar sentido a los diagramas de cinta. Los alumnos crean físicamente un diagrama de cinta a partir de un gráfico de barras y comparan dos de las categorías. Los alumnos reconocen que, incluso sin una escala determinada, pueden utilizar esta estructura visual para comparar cantidades y razonar sobre la diferencia entre ambas (MP2).
Los alumnos repasan el significado de diagrama: un dibujo o imagen que representa cantidades.
Apoyo para estudiantes de inglés
MLR2 Recopilar y mostrar. Recopile el lenguaje que utilizan los alumnos cuando hacen afirmaciones comparativas. Muestre palabras y frases usadas para comparar datos como "menos", "menos", "menos", "mayor", "más" y "más". Durante la síntesis, invite a los alumnos a sugerir formas de actualizar la lista: "¿Qué otras palabras o frases de comparación deberíamos incluir?". Invite a los alumnos a tomar prestado lenguaje de la pantalla según sea necesario.
Avances: Conversar, leer
Nation California - Grado 2
Apoyo a los estudiantes con discapacidad
Representación: Acceso para la percepción. Proporcionar adaptaciones y apoyos adecuados a la lectura para garantizar el acceso de los alumnos a los problemas de palabras y otros contenidos basados en texto.
Apoya la accesibilidad para: Lenguaje, Procesamiento visual-espacial, Atención
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

LANZAMIENTO
• Grupos de 3-4
• Muestre el gráfico de barras de la hora de la fiesta del patrón de líneas negras.
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
• "¿Qué podemos aprender de este gráfico?"
• Comparta las respuestas.
• "Un equipo de fútbol está celebrando una fiesta. El entrenador preguntó a los jugadores si querían perritos calientes, hamburguesas o pizza. Sus respuestas se muestran en este gráfico de barras."
• Entrega a cada alumno una copia del patrón de líneas negras, tijeras y cinta adhesiva o pegamento.
• "Recorta cada una de las barras del gráfico y coloca las tiras una al lado de la otra. ¿Qué afirmaciones comparativas puedes hacer sobre las barras?"
• 5 minutos: tiempo de trabajo en pequeños grupos
• "¿Qué afirmaciones comparativas has hecho sobre los datos? ¿Alguien se ha confundido sobre lo que representa cada barra? ¿Alguien se confundió sobre cuántos hay en cada barra?"
• 3-4 minutos: discusión en clase
• "Podemos usar las barras para hacer un diagrama, como el que vimos en el calentamiento. Un diagrama puede servirnos para representar y comparar cantidades. Al igual que los gráficos, los diagramas necesitan etiquetas para que podamos entender lo que representan. Utiliza tus barras para crear un diagrama que compare el número de alumnos que querían perritos calientes con los que querían hamburguesas. Cuando termines, escribe dos afirmaciones diferentes que comparen los perritos calientes con las hamburguesas."
• 5 minutos: tiempo de trabajo independiente
• Controla a los alumnos que etiquetan las categorías y las cantidades.
• Pega las dos barras que comparan el número de alumnos que eligieron perritos calientes con el número que eligió hamburguesas.
• Escriba dos enunciados que comparen el número de estudiantes que eligieron perros calientes con el número que eligió hamburguesas.
1. Ejemplo de respuesta:
POSIBLES RESPUESTAS
2. Respuestas de muestra:
• Hay más perritos calientes que hamburguesas.
• Hay menos hamburguesas que perritos calientes
SÍNTESIS DE LA ACTIVIDAD

Matemáticas de 2º grado . Unidad 1
• Mostrar el diagrama de cinta completado de un alumno.
• "¿Cómo facilita tu diagrama ver qué alimentos recibieron más votos?". (Escribimos etiquetas para mostrar qué barra corresponde a cada alimento.)
• "¿Qué necesitas añadir a las barras para responder a preguntas como "¿Cuántos alumnos más eligieron perritos calientes que hamburguesas?"". (Etiqueta qué número representa la barra.)
• 1 minuto: tiempo para pensar en silencio
• 1 minuto: discusión en parejas
• Comparte las respuestas.
• Según sea necesario, dibuja un diagrama que se parezca al diagrama de cinta del calentamiento.
• "Los diagramas pueden ayudar a representar Problemas de comparación. Puedes usar rectángulos como las barras en un gráfico de barras para representar la cantidad mayor, la cantidad menor y la diferencia"
15 minutos
El objetivo de esta actividad es que los alumnos completen un diagrama de cinta y describan las características de los diagramas de cinta. A lo largo de la actividad, los alumnos utilizan lo que saben sobre los gráficos de barras para dar sentido a lo que representa cada número en un diagrama de cinta y el papel del signo de interrogación. También relacionan la estructura del diagrama de barras con ecuaciones que representan la comparación de dos cantidades (MP2). A medida que los alumnos relacionan las etiquetas del diagrama de cinta con la pregunta, las características del gráfico y el contexto, prestan atención a la precisión y razonan de forma abstracta y cuantitativa (MP6).
LANZAMIENTO • Grupos de 2
• "Ahora vas a usar los datos del gráfico de la hora de la fiesta para completar algunos diagramas más."
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• 3 minutos: tiempo de trabajo en silencio
• 6 minutos: discusión por parejas
1. Utiliza los datos del gráfico de barras para completar el diagrama.
Math Nation California - Grado 2
2. ¿Cuántos estudiantes más eligieron pizza que hamburguesas? Escribe una ecuación para mostrar cómo has hallado la diferencia.
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

1. Utiliza los datos del gráfico de barras para completar el diagrama.
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA CONTINÚA
2. Escribe un enunciado que compare los votos de los estudiantes en el diagrama.
1. Rotula los diagramas de cinta para que coincidan con el gráfico.
POSIBLES RESPUESTASS
2. 19 - 8 = 11 o 8 + 11 = 19 11 más jugadores eligieron pizza que hamburguesas. Respuesta de ejemplo: 8 + (2 + 9) = 19 o (8 + 2) + 9 = 19
3.
SÍNTESIS DE LA ACTIVIDAD
4. Más alumnos eligieron pizza que perritos calientes.
• "¿Cómo averiguaste qué comida se comparaba con la pizza?" (Buscamos la comida que eligieron 14 estudiantes.)
• "¿Qué representa el signo de interrogación en el diagrama?" (Muestra la diferencia entre los perritos calientes y la pizza. Muestra cuántos alumnos más necesitarían elegir perritos calientes para ser el mismo que el número de alumnos que eligieron pizza.)
• Señala los guiones que representan la diferencia, pero no una cantidad real.
• "¿Qué ecuación podríamos escribir para representar esta diferencia?" (19 -? = 14, 14 + ? = 19)
• Anote las respuestas.
• "¿Cómo ves representado cada número en el diagrama?" (19 muestra cuántos eligieron pizza, 14 muestra cuántos eligieron perritos calientes. El signo de interrogación muestra la diferencia).
Matemáticas de 2º grado . Unidad 1
10 minutos
"Hoy hemos aprendido sobre diagramas que pueden representar problemas en los que comparamos dos cantidades."
Muestra el diagrama de cinta adhesiva del calentamiento:

"Cuenta a tu compañero una historia que esté representada por este diagrama." (Ejemplo de respuesta: Ocho alumnos votaron por el zumo de uva. 15 alumnos votaron por el zumo de manzana. ¿Cuántos estudiantes más votaron por el zumo de manzana?)
5 minutos
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
Estas dos representaciones muestran los mismos datos sobre perros en una tienda de mascotas.
1. Utiliza el gráfico de barras para rellenar las casillas del diagrama.
2. ¿Cuántos perros blancos hay más que perros marrones? Muestra tu pensamiento usando dibujos, números o palabras.
1.
POSIBLES RESPUESTAS
Math Nation California - Grado 2
2. Ejemplo de respuesta: Hay 4 perros blancos más que perros marrones. 8 + 4 = 12
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Abordando
Alineación
Estándares y principios de CA
2.OA.1 Usar la suma y la resta dentro de 100 para resolver problemas de palabras de uno y dos pasos que involucren situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones.
2.OA.2 Sumar y restar con fluidez dentro de 20 usando estrategias mentales. Al final del 2do Grado, saber de memoria todas las sumas de dos números de un dígito.
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en resolverlos.
MP2 Razonar abstracta y cuantitativamente.
MP4 Modelar con matemáticas.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.B.7
I.C.11 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
dar sentido al mundo y predecir lo que podría ocurrir
dar sentido a los problemas y perseverar en su resolución desmontar el todo, unir las partes.
• Puedo interpretar diagramas de cinta que representan Problemas de comparación dentro de 100
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Puedo interpretar diagramas de cinta que representan Problemas de comparación, con incógnitas en todas las posiciones dentro de 100
Mientras los alumnos trabajaban hoy en sus pequeños grupos, ¿las ideas de quién fueron escuchadas, valoradas y aceptadas? ¿Cómo puedes ajustar la estructura de los grupos en futuras lecciones para garantizar que las ideas de cada alumno formen parte del aprendizaje colectivo?
PREPARACIÓN DE LA LECCIÓN
Materiales para copiar
Cart Sort: En la playa
Preparación necesaria
Actividad 2:
Crea un juego de tarjetas a partir del patrón de líneas negras para cada grupo de 2
©Accelerate Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Conectemos los problemas de comparación con los diagramas.
Narrativa de la lección
En esta lección, los estudiantes continúan dándole sentido a los diagramas de cinta al conectarlos con los problemas de la historia. Los problemas de esta lección incluyen problemas de comparación con una diferencia desconocida, un número mayor desconocido o un número menor desconocido. Debido a que estos tipos de problemas son familiares desde el primer grado, los estudiantes también comienzan a trabajar con números dentro de 100 en esta lección. Esto les da a los estudiantes la oportunidad de notar cómo el diagrama de cinta puede usarse para visualizar rápidamente problemas de historias con cantidades más grandes. Los alumnos utilizan los diagramas de cinta para dar sentido a los problemas de Comparar. Cuando los estudiantes conectan situaciones, diagramas de cinta y ecuaciones, profundizan su comprensión del tipo de problema y desarrollan estrategias que pueden utilizar para dar sentido y perseverar en la resolución de estos problemas en futuras lecciones (MP1, MP2).
Componente de lección Estructura Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 Por parejas 15 min.
Actividad de exploración 2 Por parejas 20 min.
Síntesis Todo el grupo 10 min.
Enfriamiento Independiente 5 min.

Math
Centro(s) sugerido(s) Grupos pequeños Opcional
Descripción breve
Los estudiantes aplican la estrategia de sumar hasta 10 para evaluar expresiones numéricas que contienen la suma de números enteros dentro de 20..
Cuando se les da un problema con un valor desconocido más pequeño, los estudiantes completan un diagrama de cinta y escriben una ecuación para representar la situación.
Los estudiantes utilizan una clasificación de tarjetas para emparejar diagramas de cinta, ecuaciones y problemas. Luego, explican su razonamiento y estrategias.
Los estudiantes discuten cómo usar los diagramas de cinta para representar Problemas de comparación con una diferencia desconocida, un número mayor desconocido o un número menor desconocido.
Los estudiantes seleccionan el diagrama de cinta que representa un problema de historia y explican su razonamiento.
Abordaje:
• Rompecabezas numéricos: Suma y resta (1-4), Etapa 2: Dentro de 20
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de imagen o de barras
Apoyo:
• Agitar y derramar (K-2), Etapa 5: Cubrir (hasta 20)
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
MÁS 10 minutos
Rutinas instructivas
Conversación sobre números
El propósito de esta Charla sobre números es obtener estrategias y conocimientos que los estudiantes tienen para hacer 10 al sumar. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez con las operaciones dentro de 20
Cuando los estudiantes buscan formas de reorganizar y descomponer números para hacer 10, notan y hacen uso de la estructura de las expresiones y los números enteros (MP7).
LANZAMIENTO

ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• Muestre una expresión.
• "Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste".
• 1 minuto: tiempo para pensar
• Registra respuestas y estrategias.
• Mantén las expresiones y el trabajo desplegados.
• Repite para cada expresión.
Encuentra mentalmente el valor de cada suma.
• 4 + 8 + 2
• 4 + 5 + 3 + 2
• 9 + 3 + 1
• 9 + 5
• 14: 8 + 2 = 10 y 10 + 4 = 14
• 14: 5 + 3 = 8 y 8 + 2 = 10, así que es como la primera. 10 + 4 = 14
• 13: 9 + 1 = 10 y 10 + 3 = 13
• 14: Sé que 5 es 1 + 4, así que 9 + 1 = 10 y 10 + 4 = 14
• "¿Cómo ayudó hacer una decena al encontrar las sumas?"
15 minutos
El propósito de esta actividad es que los estudiantes interpreten un problema de Comparación con la incógnita del valor más pequeño y conecten el problema con un diagrama de cinta. La puesta en marcha de la actividad es una oportunidad para que los alumnos compartan sus experiencias y hagan preguntas sobre una playa para asegurarse de que cada alumno tiene acceso al contexto. Si resulta útil, muestre algunas imágenes de playas de distintas zonas del mundo. El problema de la historia se presenta sin números para que los alumnos puedan considerar la relación entre las cantidades. Los alumnos consideran quién tiene más o menos, lo que apoya su interpretación del diagrama de cinta. Si es necesario para ayudar a los estudiantes a conectar el diagrama de cinta con la ecuación de la resta, muestre a los estudiantes que si miran el rectángulo de Diego y tapan la parte de abajo que muestra 20, será igual al rectángulo de Lin.
Al comienzo de esta actividad, asegúrese de que los estudiantes aún no tengan abierto su cuaderno de trabajo
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
Acción y Expresión: Desarrollar la Expresión y la Comunicación. Dar a los alumnos acceso a cubos de conexión para construir la comparación con un manipulativo concreto. Los números del problema se muestran exactamente, con la diferencia muy aparente también. Esto apoya las imágenes pictóricas de los diagramas de cinta.
Apoya la accesibilidad para: Procesamiento conceptual, Organización

LANZAMIENTO
ACTIVIDAD
• Grupos de 2
• "Voy a contarles una historia rápida sobre dos estudiantes que visitaron una playa. Pero antes de hacerlo, cuéntenle a su compañero algo que sepan o preguntas que tengan sobre una playa"
• Compartan las respuestas.
• "Ahora, nuestra historia: Diego tiene algunas conchas. Lin tiene menos conchas."
• "Habla con tu compañero sobre cuántas conchas podría tener Diego y cuántas podría tener Lin."
• Comparte las respuestas. Subraye que Diego tiene más y pregúnteles cómo saben que debería tener más.
• 1 minuto: discusión en parejas
• Registre las respuestas.
• "Diego tiene 55 conchas y Lin tiene 20 menos conchas que Diego."
• Muestre el diagrama parcialmente etiquetado.
• "Este diagrama muestra algunas partes del problema de la historia que acaban de leer, pero le faltan algunas etiquetas."
• "Etiquete el diagrama para que muestre cuántas conchas tiene Diego y cuántas tiene Lin. Luego escribe una ecuación para mostrar cómo podrías hallar la parte desconocida. Usa un signo de interrogación para mostrar la incógnita."
• 2 minutos: tiempo de trabajo independiente
• 3 minutos: discusión en parejas
• Monitorea a los estudiantes que explican cómo cada parte del diagrama y la ecuación se conectan con el problema de la historia.
Diego tiene 55 conchas. Lin tiene 20 conchas menos que Diego. 1. Usa el problema de la historia para completar el diagrama.
A LA VISTA DEL ESTUDIANTE ENUNCIADO DE LA TAREA
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA CONTINUACIÓN
1. Escribe una ecuación para mostrar cómo podrías encontrar el número desconocido de conchas. Utiliza un signo de interrogación para representar la incógnita.

1.
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
2. Ejemplos de respuestas: 55 - 20 = ? O ? + 20 = 55
• Invite a los estudiantes previamente identificados a explicar cómo rotularon el diagrama de cinta.
• Considere preguntar:
• "¿Qué parte representa las conchas de Diego? ¿Cómo lo sabes?"
• "¿Qué parte representa las conchas de Lin? ¿Cómo lo sabes?"
• "¿Qué parte muestra la diferencia entre la cantidad de conchas que tiene cada estudiante?"
• "¿Alguien podría explicar cómo decidió rotular el diagrama con sus propias palabras?"
• Invite a los estudiantes previamente identificados a compartir la ecuación que usaron para representar el problema de la historia.
• "¿Cómo usaste el diagrama para escribir tu ecuación?" (El diagrama me ayudó a ver que podía empezar con 55 y quitar 20 para encontrar las conchas de Lin. El diagrama me ayudó a ver que las conchas de Lin y 20 más serían lo mismo que 55.)
• Considera pedir a los estudiantes que describan lo que representan los números y símbolos en la ecuación, como lo hicieron para el diagrama.
20 minutos
Rutinas instructivas
Ordenar carritos
Materiales para copiar
Ordenar carritos: En la playa
Preparación requerida
Crea un conjunto de tarjetas a partir del patrón de líneas negras para cada grupo de 2
El propósito de esta actividad es que los estudiantes conecten Comparar problemas, diagramas de cinta y ecuaciones con incógnitas en todas las posiciones. Ayude a los alumnos a interpretar "más" o "menos" en el contexto del problema de la historia animándoles a explicar qué cantidad debería ser la mayor y cuál la menor. Pídales que describan lo que buscan en
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
un diagrama o una ecuación para asegurarse de que coincide con un problema de la historia. Cuando los alumnos analizan y relacionan las cantidades y las estructuras en los problemas de la historia, los diagramas y las ecuaciones, piensan de forma abstracta y cuantitativa (MP2) y hacen uso de la estructura (MP7).
Si los alumnos aún no leen de forma independiente, considere la posibilidad de leer un problema de la historia a la vez y dar tiempo a los alumnos para encontrar de forma independiente sus coincidencias. Se recomienda leer los problemas de la historia en orden empezando por el problema de la historia A si se facilita de esta manera.
Apoyo para estudiantes de inglés
MLR8 Discussion Supports. Para apoyar a los estudiantes mientras se turnan para encontrar una coincidencia y explicar su razonamiento, muestre los siguientes marcos de oraciones para que todos los vean: "Me fijé en , así que emparejé...". Anime a los alumnos a desafiarse unos a otros cuando no estén de acuerdo.
Avances: Hablar, conversar

LANZAMIENTO
ACTIVIDAD
A CARGO DEL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
• Grupos de 2
• Entregue a cada grupo un juego de tarjetas del patrón de líneas negras.
• "Lin y Diego quieren comparar otras cosas que recolectaron e hicieron en la playa"
• "Encuentren un diagrama y una ecuación que coincidan con un problema de la historia. Puede haber más de una ecuación que coincida con cada problema de la historia."
• "Tomen turnos para leer un problema de la historia. Después de que un compañero lea, trabajen juntos para encontrar otras tarjetas que coincidan. Cuando crean que han encontrado una coincidencia, expliquen a su compañero por qué las tarjetas coinciden"
• "Si les sirve de ayuda, pueden rotular los diagramas para explicar sus coincidencias"
• Según sea necesario, haga una demostración de la actividad con un estudiante voluntario.
• 8 minutos: tiempo de trabajo en parejas
• Supervise a los estudiantes que explican cómo cada diagrama y ecuación coincide con las cantidades en el contexto del problema de la historia.
• "Comparen sus coincidencias con las coincidencias de otro grupo. Si las coincidencias son diferentes, trabajen juntos para explicar a qué grupo pertenecen las tarjetas o por qué una tarjeta podría pertenecer a grupos diferentes."
• 4 minutos: tiempo de trabajo en grupos pequeños
• Lea una tarjeta con un problema de la historia.
• Encuentre las tarjetas que coincidan con el problema de la historia
• Explique por qué coinciden las tarjetas.
Ejemplos de respuestas:
• A-K-Q
• B-G-O-M
• C-I-M-O
• D-J-N-P
• E-L-R
• F-H-P-N
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

SÍNTESIS DE LA ACTIVIDAD
• Invitar a 2-3 grupos de estudiantes a compartir sus coincidencias. Considere seleccionar grupos para que compartan sus coincidencias para los problemas de la historia A, B y C.
• Considere preguntar:
• "¿Cómo sabes que el diagrama coincide con el problema de la historia?"
• "¿Cómo coincide tu ecuación con el problema de la historia?"
• "¿Hay otra ecuación que podría coincidir con tu problema de la historia? ¿Cómo lo sabes?"
10 minutos
"Hoy hemos trabajado más con diagramas para representar problemas de Comparar historias. Los diagramas pueden ayudar a mostrar si necesitamos encontrar el número más grande, el número más pequeño o la diferencia"
Pantalla: Tarjeta H, J y L de la Actividad 2. H J L
"¿Qué diagrama muestra que estás buscando el número más grande? ¿Cómo lo sabes?" (L porque la barra más grande tiene un signo de interrogación.)
"¿Qué diagrama muestra que estás buscando el número más pequeño? ¿Cómo lo sabes? (Diagrama J, porque la barra más pequeña tiene un signo de interrogación.)
5 minutos
Los niños encontraron conchas y rocas en la playa. Encontraron 8 conchas más que rocas. Encontraron 19 rocas. ¿Cuántas conchas encontraron los niños?
1. Encierra en un círculo el diagrama que corresponda al problema de la historia.
DE CARA AL ALUMNO ENUNCIADO DE LA TAREA
2. Explica cómo sabes que el diagrama coincide con la historia.
POSIBLES RESPUESTAS
©Accelerate Learning Inc. - Todos los derechos reservados
1. Rodea con un círculo la opción de la izquierda.
2. Ejemplo de respuesta: El diagrama coincide porque muestra que habrá más conchas que rocas. No dice cuántas conchas, por eso tiene un ?
California - Grade 2


IDEA(S) PRINCIPAL(ES)
• Estrategias numéricas
ALINEACIÓN
Abordando
Alineación
Estándares y principios de CA
2.OA.1 Usar la suma y la resta dentro de 100 para resolver problemas de palabras de uno y dos pasos que involucren situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones.
2.OA.2 Sumar y restar con fluidez dentro de 20 usando estrategias mentales. Al final del segundo grado, saber de memoria todas las sumas de dos números de un dígito. Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP2 Razonar abstracta y cuantitativamente.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares CA ELD
I.A.1 I.B.5 II.C.7
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
predecir lo que podría ocurrir razonar de forma abstracta y cuantitativa descomponer, unir y razonar con datos.
OBJETIVO(S) DE APRENDIZAJE
• Puedo representar y resolver Comparar problemas utilizando el valor posicional.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Resolver Comparar problemas con incógnitas en todas las posiciones dentro de 100
PREGUNTA PARA LA REFLEXIÓN DEL PROFESOR
¿Qué conexiones establecieron los alumnos entre los contextos de los problemas de las historias y la colocación del signo de interrogación en los diagramas de cinta? ¿Cómo utilizan los alumnos los diagramas de cinta para dar sentido a los problemas de Compare?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Verdadero o falso (calentamiento)
MLR6 Tres lecturas (Actividad 2)
Objetivos de aprendizaje para el estudiante
• Resolvamos problemas de comparación.
Narrativa de la lección
Las opciones numéricas en los problemas de comparación de esta lección alientan a los estudiantes a usar métodos basados en el valor posicional para encontrar el valor desconocido. Los estudiantes pueden buscar maneras de componer una decena o restar múltiplos de diez al encontrar valores desconocidos dentro de 100. Los estudiantes restarán números que no sean múltiplos de diez dentro de 100 en lecciones futuras. Anime a los alumnos a utilizar un diagrama de cinta para dar sentido al problema si les resulta útil.
©Accelerate Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
Componente de lección Estructura Tiempo
Calentamiento Independiente 10 min.
Actividad de exploración 1 En parejas 20 min.
Actividad de exploración 2 En parejas 20 min.
Síntesis Grupo completo 10 min.
Enfriamiento Independiente 5 min.

Centro(s) sugerido(s) Grupos pequeños Opcional
Math Nation California - Grado 2
Descripción breve
Los estudiantes explican si las ecuaciones de suma de números enteros son verdaderas.
Los estudiantes etiquetan diagramas de cinta para un problema de historia y los utilizan para resolver problemas de comparación.
Los estudiantes crean diagramas de cinta para representar y resolver problemas de comparación del mundo real.
Los estudiantes discuten y registran sus estrategias para resolver problemas de comparación utilizando diagramas de cinta y valores posicionales.
Utilizando un diagrama de cinta o una ecuación, los estudiantes resuelven un problema de comparación del mundo real.
Abordaje:
• Rompecabezas numéricos: Suma y resta (1-4), Etapa 2: Dentro de 20
• Ordenar y mostrar (1-3), Etapa 2: Gráficos de imagen o de barras
Apoyo:
• Agitar y derramar (K-2), Etapa 5: Cubrir (hasta 20)
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos
Rutinas instructivas
Verdadero o falso
El propósito de este Verdadero o Falso es obtener estrategias y conocimientos que los estudiantes tienen para componer una decena cuando suman dentro de 100. Esto será útil en la lección cuando los estudiantes sumen dentro de 100 para encontrar valores desconocidos en problemas de comparación. También ayuda a los estudiantes a desarrollar fluidez con la adición dentro de 100 y profundiza su comprensión de las propiedades de las operaciones y la estructura de los números enteros (MP7).
• Mostrar una expresión.
LANZAMIENTO

ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• "Hazme una señal cuando sepas si la expresión es verdadera y puedas explicar cómo lo sabes."
• 1 minuto: tiempo para pensar
• Comparte y registra las respuestas y la estrategia.
• Repite con cada expresión.
Decide si cada expresión es verdadera o falsa. Prepárate para explicar tu razonamiento.
• 18 + 5 = 18 + 2 + 3
• 28 + 5 = 30 + 3
• 38 + 4 = 40 + 3
• Verdadero: 2 + 3 = 5, por lo que 18 + 2 + 3 tiene el mismo valor que 18 + 5. La respuesta en ambos lados sería 23
• Verdadero: 28 + 2 = 30 y 5 - 2 = 3, por lo que 28_5 tiene el mismo valor que 30 + 3
• Falso: 38 + 2 = 40, por lo que no sobraría 3 de 4, sólo 2.
• "¿Cómo podrías cambiar 28 + 5 para que sea 30 + 3?" (Podría tomar 2 de 30 y agregar a 3.)
BIBLIOTECA 20 minutos
El propósito de esta actividad es que los estudiantes representen y resuelvan problemas de Comparar historias. Los alumnos rotulan un diagrama de cinta basado en la información dada y representan la incógnita con un signo de interrogación. Cuando los alumnos conectan el problema de la historia y el diagrama, buscan y dan sentido a la estructura del problema (MP2).
Al iniciar la actividad, puede ser útil pedir a los estudiantes que compartan lo que saben o tienen preguntas sobre una biblioteca para asegurarse de que todos los estudiantes tienen acceso al contexto y entienden que los libros se sacan y se devuelven.
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
MLR8 Discussion Supports. Síntesis: Dé a los estudiantes 2-3 minutos para planificar lo que van a decir y practicar con un compañero antes de presentarlo a la clase. Anímeles a que se hagan preguntas unos a otros utilizando marcos oracionales como "¿Puedes decirnos más sobre...?" y "¿Por qué...?". . . ?"
Avances: Hablar, conversar, representar

Engagement: Proporcionar acceso captando el interés. Ofrezca opciones. Invita a los alumnos a decidir en qué orden completar los problemas. Permita que los alumnos elijan por dónde empezar.
Apoya la accesibilidad para: Atención, Funcionamiento socioemocional
LANZAMIENTO
ACTIVIDAD
• Grupos de 2
• Lee la primera parte del enunciado de la tarea.
• "¿Quién devolvió más libros?"
• 1 minuto: tiempo para pensar en silencio
• Comparte las respuestas.
• "¿Cómo lo sabes?"
• "Vas a seguir trabajando en este problema y a resolver otro igual. Hay un diagrama para representar cada problema. Pueden elegir etiquetar el diagrama primero o responder las preguntas y luego completar el diagrama."
• 10 minutos: tiempo de trabajo independiente
• Controle que los estudiantes que comenzaron con el diagrama de cinta en cada problema compartan durante la síntesis.
• Si los estudiantes terminan antes, pregúnteles si pueden escribir su propio problema que pueda ser representado por un diagrama.
1. Priya y Andre devolvieron libros a la biblioteca. Priya devolvió 29 libros. Andre devolvió 8 libros más que Priya.
A. ¿Quién devolvió más libros?
B. Utiliza el problema de la historia para completar el diagrama.
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
C. ¿Cuántos libros devolvió Andre?
2. Andre leyó 45 páginas de su libro anoche. Priya leyó 20 páginas menos de su libro que Andre.
A. ¿Quién leyó más libros?
B. Utiliza el problema de la historia para completar el diagrama.
Nation California - Grado 2
C. ¿Cuántas páginas leyó Priya?
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

POSIBLES RESPUESTASS 1.
A. André devolvió más libros. B.
C. Devolvió 37 libros. 29 + 8 = 37 2.
A. Andre leyó más páginas. B.
SÍNTESIS DE LA ACTIVIDAD
C. Priya leyó 25 páginas. 45 - 20 = 25
• Mostrar el trabajo de los estudiantes para el primer problema.
• Los estudiantes explican su trabajo, describiendo cómo usaron el diagrama de cinta.
• "¿Alguien tiene una pregunta para sobre su pensamiento o trabajo?"
• "¿Cómo supiste dónde poner los números y el signo de interrogación en este problema?"
• Repetir para el segundo problema.
20 minutos
Rutinas instructivas
MLR6 Tres lecturas
Esta actividad comienza con el uso de la Rutina del Lenguaje Matemático de las Tres Lecturas. Esta rutina ayuda a los estudiantes a practicar una forma de dar sentido a un problema y perseverar en su resolución (MP1). El propósito de esta actividad es que los estudiantes analicen y resuelvan una variedad de problemas de Comparación. Los estudiantes pueden utilizar diagramas de cinta o cualquier otro método que tenga sentido para ellos para resolver cada problema de la historia. Observe los diferentes métodos que utilizan los estudiantes, incluidos los dibujos que no sean diagramas de cinta y el uso de ecuaciones. Observe también cómo los alumnos calculan y describen sus cálculos cuando encuentran los valores desconocidos. Preste atención a los métodos basados en el valor posicional y en la multiplicación por diez.
Los alumnos comienzan la actividad mirando el primer problema de la historia expuesto, en lugar de en sus libros. Al final del lanzamiento, los alumnos abren sus libros y trabajan en los problemas de la historia. Si los estudiantes no muestran su razonamiento utilizando un diagrama de cinta y su ecuación no coincide con el problema de la historia, pídales que describan las matemáticas del problema de la historia explicando lo que representa cada cantidad en el contexto de la historia. Si es necesario, dibuje un diagrama de cinta sin etiquetar para apoyar el pensamiento de los estudiantes.
Esta actividad utiliza MLR6 Three Reads. Avances: leer, escuchar, representar.
©Accelerate Learning Inc. - Todos los derechos reservados

Matemáticas de 2º grado . Unidad 1
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS:
• Grupos de 2
MLR6 Tres lecturas
• Mostrar sólo la raíz del problema de la historia para la pregunta 1, sin revelar la pregunta.
• "Vamos a leer este problema de la historia 3 veces."
• 1st leer: "Jada leyó 10 páginas menos que Noah. Noah leyó 27 páginas."
• "¿De qué trata esta historia?"
• 1 minuto: discusión por parejas.
• Escuche y aclare cualquier duda sobre el contexto.
• 2nd read: "Jada leyó 10 páginas menos que Noah. Noah leyó 27 páginas."
• "¿Cuáles son todas las cosas que podemos contar en
• esta historia?" (Podríamos contar las páginas que leyó Jada, los libros, las páginas que leyeron juntos.)
• 30 segundos: tiempo para pensar en silencio
• 2 minutos: discusión en parejas
• Compartir y registrar todas las cantidades.
• Revelar la(s) pregunta(s)
• 3rd lectura: Leer todo el problema, incluida la pregunta, en voz alta.
• "¿Cuáles son las diferentes formas en que podemos resolver este problema?" (Podríamos hacer un diagrama de cinta. Podríamos escribir ecuaciones.)
• 30 segundos: tiempo para pensar en silencio
• 1-2 minutos: discusión por parejas
• "Hoy vas a resolver problemas con tu compañero. Mostrad lo que pensáis utilizando dibujos, números, palabras o una ecuación."
• "Recordad haceros preguntas mientras dais sentido al problema y creáis representaciones."
• 12 minutos: tiempo de trabajo en pareja
• A medida que los estudiantes trabajan, controle si hay diferentes representaciones para compartir durante la síntesis:
• diagramas de cinta
• ecuaciones
• otros dibujos o diagramas etiquetados.
1. Jada leyó 10 páginas menos que Noah. Noah leyó 27 páginas. ¿Cuántas páginas leyó Jada?
2. Noah pasó 25 minutos leyendo. Jada pasó 30 minutos más leyendo que Noah. ¿Cuántos minutos pasó Jada leyendo?
3. Jada leyó 47 páginas del libro. Noah leyó 20 páginas del libro. ¿Cuántas páginas menos leyó Noah?
4. Noah apiló 14 libros más que Jada. Jada apiló 28 libros. ¿Cuántos libros apiló Noé?
1. Jada leyó 17 páginas. Ejemplo de respuesta: 27 - 10 = 17
Math Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

POSIBLES RESPUESTAS CONTINUACIÓN
1. Jada pasa 55 minutos leyendo: Ejemplo de respuesta: 25 + 30 = 55
2. Noah leyó 27 menos páginas del libro. Respuesta de muestra: 47 - 20 = 27
3. Noah apiló 42 libros. Respuesta de muestra: 28 + 14 = 42
SÍNTESIS DE LA ACTIVIDAD
• Muestra el trabajo de los estudiantes que muestra diferentes formas de representar cuántos minutos más pasó Jada leyendo.
• "¿Qué hay de igual en sus representaciones? ¿Qué es diferente?"
• 1 minuto: tiempo para pensar en silencio
• 1 minuto: discusión en parejas
• "¿Cómo te ayudó tu representación a decidir si sumar o restar?"
• Si hay tiempo, discute las estrategias de cálculo:
• sumar y restar decenas con decenas (problemas 2 y 3)
• descomponer para hacer una decena (problema 4)
10 minutos
"Hoy hemos dado sentido y resuelto muchos problemas de Compara. ¿Qué hiciste para averiguar cómo resolver estos problemas?".
(Lee el problema detenidamente y varias veces para averiguar quién hizo más, quién hizo menos y la diferencia. Haz un diagrama para mostrar toda la información.)
Comparte y registra las estrategias para que todos las vean.
Learning Inc. - Todos los derechos reservados
Matemáticas de 2º grado . Unidad 1
minutos

DE CARA AL ALUMNO
ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
Jada leyó 17 páginas. Noah leyó 9 páginas más que Jada. ¿Cuántas páginas leyó Noah?
Muestra tu razonamiento mediante dibujos, números, palabras o una ecuación. Si te ayuda, puedes usar el diagrama.
Noah leyó 26 páginas.
Ejemplos de respuestas: 17 + 9 = ?
16 + 1 + 9 = 26
Resumen de la sección del estudiante
En esta sección de la Unidad 1, aprendimos cómo representar y resolver problemas de Comparación. Primero, usamos gráficos de barras para hallar la diferencia entre dos categorías.
FRENTE AL ESTUDIANTE
ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
Math
Nation California - Grado 2
¿Cuántos estudiantes más tienen gatos que tienen conejos? Muestra dos formas de hallar la diferencia.
Aprendimos sobre una nueva representación llamada diagrama. Nos ayuda a dar sentido a los problemas de una historia. Podemos usar diagramas para mostrar qué parte de una comparación necesitamos encontrar.
Jada leyó 47 páginas del libro. Noah leyó 20 páginas del libro. ¿Cuántas páginas menos leyó Noé?
En este problema, estamos hallando la diferencia. Sabemos cuántas páginas leyeron Noah y Jada, así que ? representa la diferencia.
©Accelerate Learning Inc. - Todos los derechos reservados

GRANDES IDEAS)
• Representar datos
• Estrategias numéricas
ALINEACIÓN
Abordaje
Alineación
Estándares y principios de CA
2.MD.10 Dibujar un gráfico y un gráfico de barras (con escala de una unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando información presentada en un gráfico de barras.
2.NBT.2 Contar dentro de 1000; omitir el conteo por 2s, 5s, 10s, y 100s.
2.NBT.5 Sumar y restar con fluidez dentro de 100 usando estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta.
Enfocar SMPs
MP4 Modelar con matemáticas.
MP7 Buscar y hacer uso de la estructura.
CA ELD Standards
I.A.4
I.C.12
II.C.7
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los alumnos . . . (CC) ¿Qué? . . . mientras . .
repercuten en el futuro
buscarán y utilizarán la estructura
OBJETIVO(S) DE APRENDIZAJE
• Puedo contar grandes colecciones de objetos hasta 120
• Puedo sumar y restar números enteros dentro de 50
desmontando enteros, juntando partes y razonando con datos.
• Puedo representar datos utilizando gráficos de imágenes y de barras.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Contar grandes colecciones de objetos.
• Practicar la suma dentro de 50
• Representar datos utilizando gráficos de imágenes y de barras.
PREGUNTA DE REFLEXIÓN PARA EL PROFESOR
¿Qué le han demostrado los alumnos que entienden sobre el valor posicional en la lección de hoy? ¿Cómo puedes utilizar lo que aprendiste hoy sobre tus estudiantes en tus próximas lecciones?
PREPARACIÓN DE LA LECCIÓN
Materiales para reunir
Contar colecciones
Materiales de los centros anteriores
Materiales para copiar
Contar colecciones Hoja de registro de la Etapa 3
10-Marco estándar
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Actividad 1:
Cada grupo de 2 necesita una colección de 100-120 objetos.
Actividad 2:
Reúna materiales de:
• Lo que hay a mis espaldas, Etapas 2 y 3
• Qué tan cerca, Etapas 1-3
• Rompecabezas numéricos, Etapas 1 y 2
• Clasificar y mostrar, Etapa 2

Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el estudiante
• Contemos grandes grupos de objetos y juguemos para practicar la adición y la creación de gráficos.
Narrativa de la lección
Esta lección es opcional porque es una oportunidad para la práctica adicional que no todas las clases pueden necesitar. En la Actividad 1, los alumnos revisan la etapa 3 de las Colecciones de conteo, que se introdujo por primera vez en Kindergarten. En esta etapa, llamada Estimar y contar hasta 120, los alumnos cuentan colecciones de hasta 120 objetos y representan cómo contaron. En la Actividad 2, los alumnos eligen entre dos centros previamente introducidos centrados en sumar y restar dentro de 50 o representar datos con gráficos.
LECCIÓN DE UN VISTAZO
Componente de lección
Estructura Tiempo
Descripción breve
Calentamiento Independiente 10 min. Los estudiantes calculan el valor de expresiones numéricas que contienen la suma de múltiplos de decenas y números enteros.
Exploration Activity 1 Pairs 20 min.
Centros Parejas o Grupos pequeños 25 min.
Utilizando el centro Contar colecciones, los estudiantes identifican diferentes estrategias para contar una gran colección de objetos y demuestran cómo llevan la cuenta y los cuentan.
Los estudiantes trabajan en centros centrados en la suma y la resta de números enteros dentro de 50 y en la clasificación y representación de datos.
Centros sugeridos:
• ¿Qué hay a mi espalda? Etapas 2 y 3
• ¿Qué tan cerca?, Etapas 1-3
• Rompecabezas numéricos, Etapas 1 y 2
• Clasificar y mostrar, Etapa 2
Síntesis Grupo completo 10 min.
Los estudiantes reflexionan sobre las actividades que completaron en esta lección y luego discuten las normas que funcionan bien y las normas que se pueden mejorar.
Math
Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
Rutinas instructivas
Charla de números
El propósito de esta Charla sobre números es obtener estrategias y conocimientos de los alumnos para contar de diez en diez y sumar por valor posicional. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes desarrollen maneras de contar eficientemente grandes colecciones de objetos. Los estudiantes demuestran su comprensión del valor posicional cuando observan que las sumas tienen el mismo dígito en el lugar de las unidades pero cambia el dígito en el lugar de las decenas (MP7).
LANZAMIENTO

ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTASS
SÍNTESIS DE LA ACTIVIDAD
• Muestra una expresión.
• Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste"
• 1 minuto: tiempo para pensar en silencio
• Registra las respuestas y la estrategia.
• Mantén las expresiones y el trabajo desplegados.
• Repite con cada expresión.
Encuentra el valor de cada suma mentalmente.
• 27 + 10
• 27 + 10 + 10
• 27 + 30
• 37 + 30
• 37: Empecé en 27 y añadí una decena más.
• 47: Empecé en 27 y conté de diez en diez. 27, 37, 47
• 57: Añadí tres decenas a 27 3 decenas + 2 decenas es 5 decenas.
• 67: 3 decenas + 3 decenas = 6 decenas. 6 decenas 7 unidades = 67
• "¿Cómo has utilizado lo que sabes sobre el valor posicional para hallar las sumas?". (Sabía que podía empezar en 27 y contar de diez en diez. Sabía que 30 es lo mismo que 3 decenas. Sé que podría sumar las decenas de cada número y las unidades.)
Materiales para reunir
Contar colecciones
20 minutos
Materiales para copiar
Contar colecciones Etapa 3 Hoja de registro
10- Marco estándar
Preparación necesaria
Cada grupo de 2 necesita una colección de 100-120 objetos
El objetivo de esta actividad es que los alumnos repasen la etapa 3 del centro de Colecciones de conteo. Los alumnos reciben una colección de hasta 120 objetos. Anotan una estimación de cuántos objetos creen que hay en su colección. A continuación, trabajan con un compañero para averiguar cuántos objetos hay en su colección y cada compañero anota cuántos hay. Los alumnos pueden hacer dibujos, escribir números o ecuaciones, o utilizar representaciones en base diez para mostrar su colección. Los grandes grupos de objetos animan a los alumnos a utilizar más
Matemáticas de 2º grado . Unidad 1
Métodos de recuento sofisticados, como agrupar y contar de dos en dos, de cinco en cinco o de diez en diez. Observe si los alumnos agrupan objetos, cuentan de diez en diez y justifican su total relacionándolo con el número de decenas y unidades que han contado. 10-los marcos se proporcionan en forma de esquema. Los alumnos seguirán utilizándolos a lo largo del curso. Considere la posibilidad de copiarlos en cartulina o plastificarlos y mantenerlos organizados para utilizarlos repetidamente. Las bolsas de objetos deben guardarse para usarlas en lecciones posteriores.
• Grupos de 2
• Entregue a cada grupo una colección de 100-120 objetos.

LANZAMIENTO
ACTIVIDAD
SÍNTESIS DE LA ACTIVIDAD
• "Vamos a volver a visitar un centro al que quizás hayan jugado en el jardín de infantes o en primer grado. Tú y tu compañero recibirán una colección de objetos. Tu trabajo es averiguar cuántos objetos hay en tu colección y mostrar cómo contaste."
• 8 minutos: tiempo de trabajo en pareja
• Si es necesario:
• "¿Cómo vas a contar tu colección?"
• "¿Cuántos objetos había en tu colección? ¿Puedes demostrármelo?"
• "¿Puedes hacer un dibujo para mostrar cómo has contado?"
• Supervise a los estudiantes que organizan sus objetos en grupos de 10 mientras cuentan y crean una representación con dibujos o números.
• Seleccione estudiantes previamente identificados para compartir.
• "¿Cómo mantuvieron la cuenta mientras contaban?"
• "¿Cómo representaron cómo contaban?"
25 minutos
Materiales para reunir
Materiales de centros anteriores
Preparación requerida
Reúna materiales de:
• Qué hay detrás de mi espalda, Etapas 2 y 3
• Qué tan cerca, Etapas 1-3
• Rompecabezas numéricos, Etapas 1 y 2
• Ordenar y mostrar, Etapa 2
El propósito de esta actividad es que los estudiantes elijan entre actividades que se centran en sumar y restar o en ordenar y representar datos. Los estudiantes eligen entre cualquier etapa de los centros introducidos previamente.
• ¿Qué hay detrás de mi espalda?
• ¿Qué tan cerca?
• Number Puzzles
• Sort and Display
LANZAMIENTO
Math
Nation California - Grado 2
• "Hoy elegirán entre los centros que ya hemos aprendido."
• Mostrar las opciones de centros en el libro del alumno.
• "Piensa en lo que te gustaría hacer primero"
• 30 segundos: tiempo para pensar en silencio
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1

ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• Invite a los estudiantes a trabajar en el centro de su elección.
• 10 minutos: tiempo de trabajo en el centro
• "Elijan lo que les gustaría hacer a continuación"
• 10 minutos: tiempo de trabajo en el centro
Elijan un centro.
¿Qué hay detrás de mi espalda? ¿Qué tan cerca?


Rompecabezas numéricos Ordenar y mostrar


SÍNTESIS DE LA ACTIVIDAD
• "¿Qué actividad elegiste? ¿Qué te ha gustado de la actividad que has elegido?"
10 minutos
"Hoy elegimos actividades para trabajar y trabajamos con un compañero durante el tiempo de trabajo en el centro."
Comunidad matemática
Muestre la tabla de las secciones anteriores y lea las normas a los estudiantes.
"¿Qué salió bien? ¿En qué podemos seguir trabajando?"
Reflexiones:
©Accelerate Learning Inc. - Todos los derechos reservados


IDEA(S) PRINCIPAL(ES)
• Representar datos
ALINEACIÓN
Abordaje
Alineación
Estándares y principios de CA
2.MD.10 Dibujar un gráfico de imagen y un gráfico de barras (con escala de una sola unidad) para representar un conjunto de datos con hasta cuatro categorías. Resolver problemas sencillos de armar, desarmar y comparar usando la información presentada en un gráfico de barras.
2.OA.1 Usar la suma y la resta dentro de 100 para resolver problemas de palabras de uno y dos pasos que involucren situaciones de sumar a, quitar de, armar, desarmar y comparar, con incógnitas en todas las posiciones.
2.OA.2 Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del segundo grado, saber de memoria todas las sumas de dos números de un dígito.
Enfoque SMPs
MP4 Modelar con matemáticas.
MP5 Usar herramientas apropiadas estratégicamente.
Estándares CA ELD
I.A.2 I.C.11 II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .
repercuten en el futuro utilizan las herramientas adecuadas para razonar estratégicamente con datos.
• Puedo recopilar, organizar, representar e interpretar datos de preguntas de encuestas.
• Puedo crear y responder preguntas utilizando los datos recopilados.
OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR
• Recopilar, organizar y representar datos de preguntas de encuestas.
• Crear preguntas relacionadas con datos de encuestas.
• Interpretar los resultados de una encuesta y representar los hallazgos.
Reflexiona sobre cómo puedes reforzar el trabajo realizado en la lección de hoy fuera de la clase de matemáticas. ¿Cuándo puedes hacer preguntas a los alumnos que impliquen organizar o interpretar datos categóricos? ¿Cómo puedes incorporar este trabajo a otras asignaturas, como ciencias o estudios sociales?
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
¿Qué sabes de ?
Materiales a reunir
Lápiz de color
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales para copiar
Picture and Bar Graph Template
Matemáticas de 2º grado . Unidad 1
Objetivos de aprendizaje para el alumno
• Vamos a crear nuestras propias encuestas para conocer mejor a nuestros compañeros
Narrativa de la lección
El objetivo de esta lección es que los alumnos utilicen lo que han aprendido sobre datos, gráficos de barras y diagramas de cinta para crear una encuesta y organizar, recopilar y representar datos. Los alumnos utilizan sus conocimientos sobre sumas y restas para formular y responder preguntas relacionadas con los datos.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento En parejas 10 min. Los estudiantes explican su comprensión de los gráficos de barras.
Actividad de exploración 1 En parejas 30 min.
Actividad de Exploración 2 Grupos Pequeños 15 min.
Actividad de Exploración 3 Pares 15 min.
Síntesis Todo el Grupo 10 min.
Los alumnos crean una encuesta a partir de una lista de temas, recopilan y organizan los datos y luego los representan en un gráfico de imagen o de barras.
Los estudiantes crean y responden preguntas sobre los datos de la encuesta de la actividad anterior.
Los estudiantes crean un diagrama para comparar dos categorías a partir de los datos y luego escriben una ecuación para representar la comparación.
Los estudiantes hacen conexiones entre gráficos de barras, gráficos de imágenes y diagramas de cinta.

Nation California - Grado 2
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
10 minutos

Rutinas instructivas
¿Qué sabes sobre ?
El propósito de este ¿Qué sabes sobre ? es invitar a los estudiantes a compartir lo que han aprendido sobre los gráficos de barras y cómo pueden usarlos.
LANZAMIENTO
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
• "¿Qué sabes sobre los gráficos de barras?"
• 1 minuto: tiempo para pensar en silencio
• "Discute tu pensamiento con tu compañero."
• 1 minuto: discusión en pareja
• Comparte y registra las respuestas.
SÍNTESIS DE LA ACTIVIDAD
¿Qué sabes acerca de los gráficos de barras?
• Muestra cuántos hay en cada grupo.
• Es un gráfico con una barra.
• Hay números en una escala en el lado izquierdo.
• "¿Cuál es un ejemplo de cómo podríamos utilizar un gráfico de barras?" (Puedes utilizarlo para mostrar datos que hayas recogido después de hacer una pregunta o contar cosas. Podrías mostrar los sabores favoritos de helado o cuántos animales de cada tipo vimos en el zoológico).
• "¿De qué otras formas puedes representar los datos?" (gráficos de imágenes, listas, recuentos, tablas)
30 minutos
Materiales para reunir
Lápices de colores
Materiales para copiar
Plantilla de imagen y gráfico de barras
El propósito de esta actividad es que los estudiantes creen una encuesta, recopilen y organicen sus datos y los representen como una imagen o un gráfico de barras.
Para añadir movimiento a esta actividad, considera un paseo por la galería para que los alumnos vean y comparen las diferentes representaciones de sus datos.
Apoyo para estudiantes de inglés
MLR7 Comparar y conectar. Síntesis: Mostrar una selección de preguntas de la encuesta. Invite a los alumnos a reflexionar sobre lo que observan en el lenguaje de las preguntas de la encuesta. Ampliar las observaciones relacionadas con la estructura de las preguntas, incluyendo palabras y frases comunes.
Avances: Leer, representar

Matemáticas de 2º grado . Unidad 1
Nation California - Grado 2
Apoyo a los estudiantes con discapacidad
Engagement: Proporciona acceso captando el interés. Utiliza temporizadores visibles o alertas sonoras para ayudar a los alumnos a controlar su progreso y asegúrate de que tienen tiempo suficiente para encuestar a todos sus compañeros.
Apoya la accesibilidad para: Atención, Organización
• Grupos de 2
• "Estos son algunos temas que exploramos en lecciones anteriores."
• Muestre la lista de temas:
• Cómo llegamos a la escuela
• Deporte favorito
• Estación favorita
• Elección de excursión
• Actividad de recreo
• Mascota favorita
• Comida para una fiesta
• Frutas que nos gustan
• Verduras que nos gustan
• "Con tu compañero, haz una lluvia de ideas sobre otras cosas que quieras aprender sobre tus compañeros de clase."
• 2 minutos: debate por parejas.
• Invita a algunos alumnos a compartir y anota las respuestas.
• "Mira las dos listas de posibles temas para encuestar a nuestros compañeros de clase. Con tu compañero, elige un tema y escribe una pregunta para la encuesta. Decide las posibles respuestas para tu pregunta de la encuesta: 3 o 4."
• "Por turnos, formula tu pregunta de la encuesta a tu compañero y registra las respuestas de ambos en tu cuaderno de trabajo."
• "Ahora harás tu pregunta de la encuesta a otros estudiantes de nuestra clase y registrarás los datos que recopiles."
• 5 minutos: tiempo de trabajo en pareja
• Supervisa para asegurarte de que los estudiantes han recopilado suficientes datos.
• Mientras los estudiantes hacen la encuesta, entrega a cada estudiante la plantilla de gráfico y acceso a lápices de colores.
• "Utiliza tus datos para crear un dibujo o un gráfico de barras. "
• 10 minutos: tiempo de trabajo en parejas.
• Supervise a los estudiantes que creen:
• un gráfico que utilice imágenes que representen cada categoría (por ejemplo, dibujar cada tipo de animal para una encuesta sobre mascotas)
• un gráfico que utilice la misma imagen abstracta para cada categoría (por ejemplo, dibujar un círculo para representar cada mascota en una encuesta sobre mascotas)
• un gráfico de barras con un título claro, escala y etiquetas de categoría.
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
LOS ESTUDIANTES DECLARACIÓN DE TAREAS

POSIBLES RESPUESTAS
1. ¿Cuál es la pregunta de la encuesta?
2. ¿Cuáles son sus categorías?
• Categoría 1:
• Categoría 2:
• Categoría 3:
• Categoría 4:
3. Registra los datos.
4. Organizar y representar los datos en un gráfico o en un diagrama de barras.
Ejemplo de respuesta:
• ¿Cuál es tu mascota favorita?
• gato, perro, pez, hámster
• Los alumnos pueden registrar los datos recogidos en una tabla utilizando números o cuentas.
• Los alumnos crean un diagrama de barras con un título, categorías y escala. O crean un gráfico con estrellas para representar cada voto o puntos.
• Invite a los estudiantes previamente seleccionados a compartir sus gráficos.
SÍNTESIS DE LA ACTIVIDAD
• "¿En qué se parecen estos gráficos? ¿En qué se diferencian? (El gráfico de barras tiene números, pero los gráficos de imágenes no. Algunos tienen 3 y otros tienen 4 diferentes respuestas. Algunos son de arriba abajo y otros de lado a lado.)
• "¿Qué opciones tomaron estos matemáticos con sus gráficos?" (Tuvieron que decidir qué tipo de gráfico hacer, un título, en qué dirección mostrar las barras cómo representar sus datos para que quede claro con un título, etiquetas o dibujos.)
15 minutos
El propósito de esta actividad es que los estudiantes creen sus propias preguntas matemáticas relevantes y utilicen su comprensión de la suma y la resta para responder a preguntas sobre sus propios datos de la encuesta y los de sus compañeros.
LANZA
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
• Combina las parejas en grupos de 4
• "Cambia de gráfico. Utiliza los enunciados o crea tus propias preguntas sobre los gráficos del otro grupo."
• 1-2 minutos: tiempo de trabajo independiente
• 4 minutos: tiempo de trabajo en pareja.
• "Turnaos para haceros las preguntas que se os ocurrieron y utilizad vuestro propio gráfico para responder."
• "Cuando sea posible, escriban una ecuación para mostrar su razonamiento."
• 5 minutos: discusión en grupo.
• Supervise a los estudiantes que escriben ecuaciones para mostrar las categorías que combinan o comparan cuando responden a las preguntas de sus compañeros.
1. Intercambien gráficos. Crear preguntas sobre el gráfico del otro grupo. Tallos de frases:
¿Cuántos alumnos eligieron y juntos?
¿Cuántos estudiantes más eligieron que ?
2. Túrnense para hacer y responder preguntas. Respuesta de los alumnos
Matemáticas de 2º grado . Unidad 1

POSIBLES RESPUESTAS
1. Ejemplos de respuestas:
• ¿Cuántos alumnos eligieron gatos y perros juntos?
• ¿Cuántos más eligieron perros que hámsters?
2. Ejemplos de respuestas:
• 14 alumnos eligieron gatos y perros. 5 + 9 = 14
• 5 más alumnos eligieron perros que hámsters. 9 - 4 = 5
• Invite a los estudiantes previamente seleccionados a compartir.
• "¿Dónde vemos las ecuaciones en su gráfico? ¿Qué significa la ecuación?"
• "¿Cuál es la diferencia entre responder las preguntas de un gráfico de barras y responderlas de un gráfico de imágenes?"
CON
15 minutos
El objetivo de esta actividad es que los alumnos analicen lo que han aprendido a partir de los datos y las representaciones de las actividades anteriores y compartan sus conclusiones. En esta actividad, los alumnos seleccionan dos cosas que han aprendido y las ilustran utilizando un diagrama de cinta.
Supervise los diagramas de cinta que se pueden mostrar durante la síntesis de la lección y compararlos con el gráfico de barras seleccionado en una actividad anterior. Aunque el gráfico y el diagrama no tienen por qué ser del mismo par, sería útil que los alumnos vieran datos de la misma encuesta mostrados con representaciones diferentes.
Para añadir movimiento a esta actividad, considere la posibilidad de realizar un recorrido por la galería. Los alumnos pueden hacer sus diagramas en papel de póster. A medida que los estudiantes caminan por la sala, seleccionan algunos diagramas y determinan qué información aprenden sobre su clase basándose en el diagrama y la ecuación.
• Grupos de 2
• "Tú y tu compañero van a dibujar un diagrama. Tu diagrama debe comparar dos hechos que has aprendido de tu encuesta."
ACTIVIDAD
DE CARA AL ESTUDIANTE ENUNCIADO DE LA TAREA
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
Math Nation California - Grado 2
• "Decide con tu compañero qué 2 hechos quieres compartir con la clase y cómo vas a comparar los dos hechos."
• 1 minuto: discusión por parejas.
• 5 minutos: tiempo de trabajo independiente
• Los alumnos comprueban con sus compañeros que sus representaciones tienen sentido y son precisas.
• 3 minutos: discusión por parejas
• Supervise algunos ejemplos de diagramas de cinta y ecuaciones precisas.
1. Dibuje un diagrama. Tu diagrama debe comparar dos hechos que aprendiste de tu encuesta.
2. Escriba una ecuación que represente la comparación.
1. Un diagrama de cinta que refleje los datos que los estudiantes recopilaron.
2. Una ecuación de suma o resta que represente el diagrama de cinta.
• Muestre el trabajo seleccionado de los estudiantes.
• "¿Qué información nos dice este diagrama o ecuación sobre nuestros compañeros de clase?"
• "¿Dónde ves esta ecuación en el diagrama?"
©Accelerate Learning Inc. - Todos los derechos reservados


Matemáticas de 2º grado . Unidad 1
"Hoy hemos tenido la oportunidad de aprender más unos de otros recopilando datos y representándolos de múltiples maneras."
Muestre un gráfico de barras o de imágenes generado por el estudiante y el diagrama de cinta uno al lado del otro.
Considere preguntar:
• "¿En qué se parecen estas representaciones?" (Provienen de la misma encuesta.)
• "¿Qué información podemos ver en el gráfico de barras o de imagen que no vemos en el diagrama?" (Todas las personas que fueron encuestadas.)
• "¿Qué información podemos ver en el diagrama que no vemos en la imagen/gráfico de barras?" (Es más fácil comparar dos de los grupos en el diagrama que en el gráfico.)
Reflexiones:

Learning Inc. - Todos los derechos reservados
