MN CA Geometry Spanish Unit Sample by acceleratelearning

Muestra de la edición para el maestro

POR ACCELERATE LEARNING

Geometría

Muestra de la edición para el maestro

Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).

La plataforma de recursos curriculares en línea que se ofrece en «mathnation.com», incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.

La marca comercial «Math Nation» es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.

Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.

UNIT 1

CONSTRUCTIONS AND RIGID TRANSFORMATIONS

UNIT NARRATIVE

In grade 8, students determine the angle-preserving and length-preserving properties of rigid transformations experimentally, mostly with the help of a coordinate grid. Students have previously studied angle properties, including the Triangle Angle Sum Theorem, but no formal proofs have been required. In this unit, students create rigid motions using construction tools with no coordinate grid. This leads to more rigorous definitions of rotations, reflections, and translations. Students begin to explain and prove angle relationships like the Triangle Angle Sum Theorem using these rigorous definitions and a few assertions.

In previous courses, students developed their understanding of the concept of functions. In this unit, the concept of a transformation is made somewhat more formal using the language of functions. While students do not use function notation, they do move away from describing transformations as “moves” that act on figures and towards describing them as taking points in the plane as inputs and producing points in the plane as outputs.

Constructions play a significant role in the logical foundation of geometry. A focus of this unit is for students to explore properties of shapes in the plane without the aid of given measurements. At this point, students have worked so much with numbers, equations, variables, coordinate grids, and other quantifiable structures, that it may come as a surprise just how far they can push concepts in geometry without measuring distances or angles. Constructions are used throughout several lessons to introduce students to reasoning about distances, generating conjectures, and attending to the level of precision required to define rigid motions later in the unit. The definition of a circle is an important foundation for concepts in this unit and throughout the course.

Then, students learn rigorous definitions of rigid motions without reference to a coordinate grid. In subsequent units, they use those definitions to prove theorems. To prepare students for future congruence proofs, students start to come up with a systematic, pointby-point sequence of transformations that will work to take any pair of congruent polygons onto one another. This point-by-point perspective also illustrates the transition from thinking about transformations as “moves” on the grid to thinking about transformations as functions that take points as inputs and produce points as outputs. Students also examine the rigid transformations that take some shapes to themselves, otherwise known as symmetries. The concept of transformations as functions is developed further in a later unit that explores coordinate geometry.

In the final lessons of the unit, students learn ways to express their reasoning more formally. Students create conjectures about angle relationships and prove them using what they know about rigid transformations. As a tool for communicating more precisely, students begin to label and mark figures to indicate congruence. In the culminating lesson of the study of constructions, students build on their experiences with perpendicular bisectors to answer questions about allocating resources in a real-world situation.

A blank reference chart is provided for students, and a completed reference chart for teachers. The purpose of the reference chart is to be a resource for students to reference as they make formal arguments. Students will continue adding to it throughout the course. Refer to About These Materials in the Geometry course for more information.

Students have the opportunity to choose appropriate tools (MP5) in nearly every lesson as they select among the options in their geometry toolkit as well as dynamic geometry software. For this reason, this math practice is only highlighted in lessons where it's particularly salient.

BIG IDEAS AND STANDARDS

Focus On Big Ideas

• Points and Shapes

• Transformations

• Triangle Problems

STANDARDS BY LESSON

Lesson

G.1.1

G.1.2

G.1.3

G.1.4

• Circle Relationships

• Geometric Models

Standard(s) Addressed

G-CO.1, G-CO.12

G-CO.12, G-CO.13

G.1.5 G-CO.12

G.1.6

G-CO.1, G-CO.12

G.1.7 G-CO.13

G.1.8

G.1.9

G.1.10

G.1.11

G-CO.1, G-CO.12, G-CO.13

G-CO.12, G-MG.3

G-CO.2, G-CO.5

G-CO.2, G-CO.4

G.1.12 G-CO.4

G.1.13

G-CO.1, G-CO.2, G-CO.5

G.1.14 G-CO.4

G.1.15

G-CO.2, G-CO.3

G.1.16 G-CO.3

G.1.17

G.1.18

G-CO.2, G-CO.5

G.1.19 G-CO.9

G.1.20

G.1.21

G-CO.1, G-CO.2, G-CO.9

G-CO.9, G-CO.10

G.1.22 G-GMD.6

G.1.23

G-CO.12, G-CO.13

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

ALINEACIÓN

Abordar

G-CO.1 Conocer definiciones precisas de ángulo, círculo, línea perpendicular, línea paralela y segmento de línea, basadas en las nociones indefinidas de punto, línea, distancia a lo largo de una línea y distancia alrededor de un arco circular.

Alineación de estándares y principios de California

G-CO.12 Hacer construcciones geométricas formales con una variedad de herramientas y métodos (compás y regla, cuerda, dispositivos reflectantes, plegado de papel, programa geométrico dinámico, etc.). Copiar un segmento; copiar un ángulo; bisecar un segmento; bisecar un ángulo; construir líneas perpendiculares, incluyendo la bisectriz perpendicular de un segmento de línea; y construir una línea paralela a una línea dada a través de un punto que no está en la línea.

Construir

G-CO.13

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.1 II.B.5

LECCIÓN 1

CONSTRÚYELO

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué?

Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo, atienden a la precisión descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Sé crear diagramas utilizando una regla.

• Sé utilizar un compás para construir un círculo.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender que los compases crean círculos y pueden utilizarse para transferir distancias a través de una construcción.

• Crear diagramas utilizando una regla para producir una línea o segmento a través de dos puntos.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Constrúyelo

MLR1: Cada vez más fuerte y más claro

Preparación requerida

Crea una muestra de los movimientos de la regla y el compás que permanecerá expuesta para que todos la vean a lo largo Unidad. Véase un ejemplo en la síntesis de calentamiento.

Reunir los conjuntos de herramientas de geometría. Lo mejor sería que los estudiantes tuvieran acceso a estos juegos de herramientas en todo momento a lo largo Unidad.

Materiales necesarios

Conjunto de herramientas de geometría (preparatoria)

Fichas para usar como reglas, compás, papel de calco, papel en blanco, lápices de colores y tijeras

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Utilicemos herramientas para crear formas con precisión.

Narrativa de la lección

Esta lección establece los movimientos de la regla y el compás que los estudiantes utilizarán para realizar varias construcciones. Los estudiantes construyen sobre su comprensión previa de círculos como un conjunto de puntos todos equidistantes del centro y segmentos de línea como un conjunto de puntos en una línea con dos puntos finales. Las construcciones se utilizan en lecciones posteriores para introducir a los estudiantes en el razonamiento sobre distancias, generando conjeturas y atendiendo al nivel de precisión requerido para definir movimientos rígidos más adelante en la unidad. Los estudiantes atienden a la precisión cuando discuten por qué los movimientos con regla y compás comunican información geométrica de forma consistente, en contraposición a la observación a ojo (MP6).

Estos materiales utilizan palabras en lugar de notación simbólica para permitir a los estudiantes centrarse en el contenido. Al utilizar palabras, los estudiantes no necesitan traducir el significado del símbolo mientras leen. Para aumentar la exposición a las diferentes notaciones, las imágenes con información dada marcadas con marcas de verificación, marcas de ángulo recto o flechas también tienen una leyenda con la notación simbólica (AB ≌ AC, AB ⟂ AC o AB ∥ AC). No dudes en utilizar la notación simbólica cuando registres las respuestas de los estudiantes, ya que es un uso apropiado de la taquigrafía.

En esta lección y en las siguientes de esta sección, todas las construcciones son accesibles utilizando reglas físicas y compases rígidos. Si los estudiantes tienen acceso a materiales digitales en clase, pueden optar por realizar alguna o todas las actividades de construcción con la herramienta de construcción de GeoGebra accesible en las herramientas matemáticas o disponible en geogebra.org/m/VQ57WNyR. El calentamiento de la lección opcional «Uso de la tecnología para construcciones» es una buena introducción a la herramienta de construcción de GeoGebra. Realice ese calentamiento con los estudiantes antes de comenzar esta lección si los estudiantes van a utilizar la herramienta digital en lugar de herramientas físicas. Si los estudiantes no tienen acceso a esta herramienta digital en clase, considere el uso de la herramienta de construcción GeoGebra para demostrar construcciones durante la actividad o las síntesis de la lección.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 10 min

Actividad de Exploración En parejas 15 min

Actividad de Exploración En parejas 10 min

Síntesis Todo el grupo 5 min

Descripción breve

Los estudiantes exploran el uso de una regla y un compás para practicar el dibujo de círculos y segmentos de línea.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar el dibujo de círculos y segmentos de línea utilizando la tecnología.

Los estudiantes descubren cómo las herramientas de construcción pueden ser utilizadas para transferir distancias a través de una construcción.

Los estudiantes utilizan una regla y un compás para construir un hexágono regular y justifican cómo saben que las longitudes de los lados son iguales.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la construcción de un hexágono utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la repetición en las construcciones.

Los estudiantes definen los términos geométricos y discuten los términos indefinidos implicados en las construcciones realizadas durante la lección.

RESUMEN DE LA LECCIÓN, CONTINUACIÓN

Componente de la lección

Estructura Tiempo

Descripción breve

Enfriamiento Independiente 5 min Los estudiantes utilizan herramientas de construcción para construir un círculo con un radio dado.

Práctica Independiente 5-8 min El componente de práctica independiente incluye 4 problemas de la lección.

CALENTAMIENTO | LA HERRAMIENTA ADECUADA

(10 minutos)

El propósito de este calentamiento es que los estudiantes se familiaricen con la regla y el compás.

Aprenderán a:

• dibujar un círculo

• dibujar un segmento de línea

• transferir una distancia

INTRODUCCIÓN

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Dé a los estudiantes 2 minutos de tiempo de trabajo tranquilo.

Haz una pausa en la clase para:

• demostrar cómo usar un compás marcando un punto y creando un círculo centrado en ese punto

• demostrar cómo usar una regla marcando un punto en el círculo y conectándolo al centro para hacer un radio

• anotar que el segmento PQ es la parte de la recta que pasa por P y Q que tiene los puntos extremos P y Q

• observar que la longitud PQ es la distancia desde el punto P hasta el punto Q

Invite a los estudiantes a utilizar sus herramientas para completar las preguntas restantes.

1. Copie esta figura utilizando solo un lápiz y ninguna otra herramientas.

2. Familiarízate con tu regla y tu compás dibujando algunos círculos de diferentes tamaños, algunos segmentos de línea de diferentes longitudes y extendiendo algunos de esos segmentos de línea en ambas direcciones.

3. Completa estos pasos con una regla y un compás:

A. Dibuja un punto y etiquétalo como A

B. Dibuja un círculo centrado en el punto A con un radio de longitud PQ

C. Marca un punto en el círculo y etiquétalo como B

D. Dibuje otro círculo centrado en el punto B que pase por el punto A

E. Dibuje un segmento de línea entre los puntos A y B

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

La figura creada al completar los pasos debe ser idéntica a la figura dada, excepto que los dos puntos etiquetados se etiquetan como A y B.

Si se utilizan reglas como reglas, es posible que algunos estudiantes deseen utilizar la regla para medir la longitud de PQ. Enfatice que nuestra regla solo puede usarse para crear líneas o segmentos de línea entre dos puntos marcados, pero que su compás puede ajustarse a la longitud entre dos puntos y luego moverse para crear un círculo con ese radio en cualquier punto marcado.

SÍNTESIS DE LA ACTIVIDAD

El objetivo es asegurarse de que los estudiantes comprenden los movimientos de la regla y el compás que se permitirán durante las actividades que impliquen construcciones y por qué es importante ponerse de acuerdo sobre los movimientos de construcción estándar. Pregunte a los estudiantes: «¿Cuál es la diferencia entre tu intento en la primera pregunta y lo que se te ocurrió usando la regla y el compás?». (Ejemplo de respuesta: Sin las herramientas, era difícil hacer círculos y líneas rectas. El compás hace que sea más fácil hacer círculos y la regla hace que sea más fácil hacer líneas rectas).

Haz una exposición en clase que incorpore todos los movimientos válidos. Esta exposición se colocará en el aula durante el resto de las lecciones de esta unidad. Debe incluir:

• Si partes de un espacio en blanco, empieza marcando dos puntos.

• Puedes crear una línea o segmento de línea entre dos puntos marcados.

• Puedes crear un círculo centrado en un punto marcado que pase por otro punto marcado.

• Puede ajustar su compás a la longitud entre dos puntos marcados y crear un círculo con ese radio centrado en cualquier punto marcado.

• Puede marcar puntos de intersección.

• Puede marcar un punto en un círculo.

• Puede marcar un punto en una línea o segmento de línea.

Diga a los estudiantes que el uso de estos movimientos garantiza una construcción precisa. Por el contrario, mirar a ojo dónde debe ir un punto o segmento significa que no hay garantía de que alguien sea capaz de reproducirlo con precisión.

ACTIVIDAD DE EXPLORACIÓN | LA CONSTRUCCIÓN ILEGALUCCIÓN SE MUEVE

(15 minutos)

Rutinas didácticas

Constrúyelo

El propósito de esta actividad es que los estudiantes exploren por qué las construcciones con regla y compás pueden utilizarse para comunicar información geométrica de forma precisa y coherente.

Identifique a un estudiante que sitúe el punto C más cerca del punto A y a otro estudiante que sitúe el punto C más cerca del punto B para comparar durante la discusión.

INTRODUCCIÓN

Organiza a los estudiantes en grupos de 2.

Para los estudiantes que utilicen la herramienta digital Construcciones, recomienda que empiecen dibujando un segmento AB

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Mantenga un despliegue de términos y vocabulario importantes. Durante el Introducciónmiento, tome tiempo para repasar los siguientes términos de grados anteriores a los que los estudiantes necesitarán acceder para esta actividad: segmento, punto medio, círculo, radio y triángulo.

Apoya la accesibilidad para: Memoria; lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

1. Crea un círculo centrado en A con radio AB.

2. Estima el punto medio del segmento AB y etiquétalo como C.

3. Crea un círculo centrado en B con radio BC. Esto crea 2 puntos de intersección. Etiqueta el que está hacia la parte superior de la página como D y el que está hacia la parte inferior como E.

4. Usa tu regla para conectar los puntos A, D y E para formar el triángulo ADE y sombrea ligeramente con tu lápiz.

Ejemplo de respuesta:

CONCEPTOS ERRÓNEOS PREVISTOS

Si los estudiantes no recuerdan cómo encontrar un punto medio, descomponga la palabra y explique que se trata de un punto en medio del segmento.

El punto clave para la discusión es que con las construcciones es posible investigar la geometría sin números. En su lugar, los estudiantes pueden utilizar herramientas de construcción para transferir distancias sin medir.

Pida a los estudiantes que tracen el triángulo ADE en papel de calco y que comparen su triángulo con el de sus compañeros. Aaquí hay algunas preguntas para el debate:

• «¿Qué pasos de las instrucciones hicieron posible que estos triángulos tuvieran un aspecto tan diferente?». (Estimar la ubicación del punto medio).

• «¿Qué es idéntico en cada diagrama?». (El primer círculo).

SÍNTESIS DE LA ACTIVIDAD

• «Escribir AD = AE significa que la longitud del segmento AD es igual a la longitud del segmento AE. ¿Es cierto?». (Sí, ambos son radios del mismo círculo).

• «Escribir AB = 2AC significa que la longitud del segmento AB es igual al doble de la longitud del segmento AC. ¿Es eso cierto?». (Parece que podría serlo, pero hemos estimado el punto medio, así que no necesariamente).

• «¿Por qué los movimientos válidos de regla y compás garantizan que todos producirán la misma construcción?». (Nunca hay que hacer estimaciones ni mirar a ojo).

Si la pregunta 2 se sustituyera por un método para encontrar el punto medio de forma precisa con una regla y un compás, entonces el triángulo ADE estaría garantizado para ser consistente independientemente del estudiante que lo construyera, hasta el pequeño error permitido por las herramientas. Para estar seguro de que una construcción es válida, no debe incluir ninguna estimación o cálculo a ojo.

ACTIVIDAD DE EXPLORACIÓN | ¿PUEDES HACER UNA COPIA

PERFECTA?

(10 minutos)

Rutinas didácticas

Constrúyelo

MLR1: Cada vez más fuerte y más claro

El objetivo de esta actividad es que los estudiantes determinen cómo utilizar los movimientos de la regla y el compás para construir un hexágono regular con precisión. Los estudiantes deben jugar con los movimientos de construcción hasta alcanzar su objetivo en lugar de seguir una demostración explícita de los pasos de construcción. Aunque el término regular aparece en la tarea, no es importante que los estudiantes conozcan la definición precisa de polígono regular en este momento.

Identifique a los estudiantes cuyas explicaciones de que los lados son congruentes utilizan papel de calco o comparan los radios de los diferentes círculos de la construcción. El papel de calco conecta con la idea de movimientos rígidos, mientras que la comparación de radios hace referencia a la definición precisa de círculo, que los estudiantes utilizarán a lo largo de esta unidad y de las siguientes.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Proporcione acceso al papel de calco. Dé a los estudiantes 10 minutos de tiempo de trabajo seguidos de un debate con toda la clase.

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Fomente y apoye las oportunidades de interacción entre compañeros. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen sus razonamientos. Por ejemplo: «Cada uno de los lados de la figura que he construido tiene la misma longitud porque...».

Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales; procesamiento conceptual

Aquí hay un hexágono con todos los ángulos y lados congruentes (llamado hexágono regular).

1. Dibuja una copia del hexágono regular usando solo lápiz y sin otras herramientas. Calca tu copia en papel de calco. Intenta doblarla por la mitad. ¿Qué sucedió?

2. Aquí hay una figura que muestra los primeros pasos para construir el hexágono regular. Usa regla y compás para terminar de construir el hexágono regular. Calca la copia en papel de calco y comprueba que, al doblarla por la mitad, los bordes queden alineados.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

3. ¿Cómo sabes que todos los lados de la figura tienen la misma longitud? Explica tu razonamiento.

RESPUESTAS POSIBLES

1. Las respuestas varían. Es probable que los estudiantes dibujen una figura con 6 lados, pero los lados tendrán longitudes ligeramente diferentes y no serán perfectamente rectos, y los ángulos interiores no serán congruentes.

2. Ejemplo de construcción:

3. Cada círculo de la construcción tiene el mismo radio, que es también la longitud de cada lado del hexágono regular.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Si los estudiantes pasan más de unos minutos sin avanzar significativamente, dígales que el segmento dado en la figura es uno de los 6 lados del hexágono. Invite a los estudiantes a comparar el hexágono dado con el inicio de la construcción. A continuación, pregúnteles si pueden dibujar otro segmento para formar un lado adyacente del hexágono.

El objetivo de este debate es avanzar hacia el concepto de demostración pidiendo a los estudiantes que expliquen de manera informal por qué un hecho sobre un objeto geométrico debe ser cierto. Pida a los estudiantes previamente identificados que compartan sus respuestas a«¿Cómo sabes que cada uno de los lados de la figura tiene la misma longitud?»..

Apoyo para estudiantes que aprenden el idioma inglés

Escribir, hablar, conversar: MLR 1 Cada vez más fuerte y más claro. Utilícelo con sucesivas puestas en común por parejas para dar a los estudiantes una oportunidad estructurada de revisar y perfeccionar su respuesta a «¿Cómo sabes que cada uno de los lados de la figura tiene la misma longitud?». Pida a cada estudiante que se reúna con otros 2 ó 3 compañeros en fila para recibir comentarios. Proporcione a los estudiantes sugerencias que les ayuden a reforzar sus ideas y a aclarar su lenguaje. Por ejemplo: «¿Puedes explicar cómo...?», «¿Cómo ayudan los círculos a la construcción?», «¿Qué sabes sobre los radios que ayude aquí?» o «¿Qué quieres decir con...?». Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar su explicación final.

Principio(s) de diseño: Optimizar el resultado (para la justificación); apoyar la creación de sentido

¿Estás preparado para más?

¿Por qué la construcción termina donde empezó? Es decir, ¿cómo sabemos que los ángulos centrales dan exactamente 360 grados a la redonda?

Respuesta

del estudiante

Ejemplo de respuesta: Nuestra construcción se hizo realizando repetidamente los primeros pasos mostrados en la actividad. Si nos referimos a los centros de las dos circunferencias como los puntos A y B y al punto de intersección como C, entonces sabemos que AB = AC y AB = CB, ya que son radios de las mismas circunferencias. De ello se deduce que ABC es un triángulo equilátero y m∠CAB = 60∘. Cuando aplicamos este razonamiento a los seis segmentos construidos y sus ángulos relacionados, tenemos un total de 360 grados.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Señale de nuevo la visualización de los movimientos de la regla y el compás. Pida a los estudiantes que identifiquen y definan los términos geométricos que aparecen en la pantalla.

• Si se parte de un espacio en blanco, comience marcando 2 puntos.

• Cree una línea o segmento de línea entre 2 puntos marcados.

• Cree un círculo centrado en un punto marcado que pase por otro punto marcado.

• Ajuste tu compás a la longitud entre 2 puntos marcados y crea un círculo con ese radio centrado en cualquier punto marcado.

• Marque los puntos de intersección

• Marque un punto en un círculo.

• Marque un punto en una línea o segmento de línea.

Después de que varios estudiantes compartan, diga a la clase que punto, línea y distancia (o longitud) son términos indefinidos. Podemos utilizar estos términos indefinidos para definir otros términos. Es importante saber que:

• Los puntos son infinitesimales.

• Las rectas son infinitamente largas y se extienden en ambas direcciones.

• Parte de una recta con un extremo se llama semirrecta y se extiende en una dirección.

• Parte de una recta con dos extremos se llama segmento y tiene una longitud medible.

• Una circunferencia está formada por todos los puntos a una distancia determinada de un punto.

• El punto se llama centro y la distancia determinada se llama radio.

Diga a los estudiantes que, en este curso, se basarán en su comprensión previa de estos términos y otros para utilizar definiciones precisas para describir figuras geométricas.

ENFRIAMIENTO | CONSTRÚYELO

(5 minutos)

Este enfriamiento evalúa si los estudiantes son capaces de usar herramientas de construcción para transferir distancias y crear líneas a través de dos puntos.

Aquí está el segmento AB y un punto C:

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Crea un círculo centrado en C cuyo radio sea la longitud de AB. Marca un punto en el círculo y etiquételo como D. Traza la línea CD y etiqueta su otra intersección con el círculo como el punto E.

RESPUESTAS POSIBLES

Las respuestas varían. Un estudiante debe usar un compás para transferir la distancia AB para crear un círculo de radio AB centrado en C y luego construir una línea a través del centro del círculo.

CONCEPTOS ERRÓNEOS PREVISTOS

Los estudiantes pueden dibujar solamente el segmento CD y afirmar que no hay otro punto de intersección. Recuerda a estos estudiantes que las líneas se extienden infinitamente en ambas direcciones.

Resumen de la lección para el estudiante

Para construir figuras geométricas, utilizamos una regla y un compás. Estas herramientas nos permiten crear dibujos precisos que otra persona podría copiar exactamente.

• Usamos la regla para dibujar un segmento de línea, que es un conjunto de puntos en una línea con 2 puntos extremos.

• Nombramos un segmento por sus puntos extremos. Aquí está el segmento AB, con puntos extremos A y B

• Usamos el compás para dibujar un círculo, que es el conjunto de todos los puntos a la misma distancia del centro.

• Describimos una circunferencia nombrando su centro y su radio. Aquí está el círculo centrado en F con radio FG

Los primeros matemáticos se dieron cuenta de que ciertas propiedades de las formas eran ciertas independientemente de lo grandes o pequeñas que fueran. Las construcciones se usaron como una forma de investigar lo que tiene que ser cierto en geometría sin referirse a números o medidas directas.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Aquí hay un diagrama de una construcción con regla y compás. C es el centro de una circunferencia y B es el centro de la otra. Explica por qué la longitud del segmento BD es la misma que la longitud del segmento AB

Soluciones posibles

Los dos segmentos deben tener la misma longitud ya que ambos son radios del mismo círculo centrado en B

PROBLEMA 2

Clara usó un compás para hacer un círculo con radio de la misma longitud que el segmento AB. Ella etiquetó el centro como C. ¿Cuál afirmación es verdadera?

Soluciones posibles

PROBLEMA 3

El diagrama se construyó con herramientas de regla y compás. Los puntos A, B, C, D y E están todos en el segmento de línea CD Nombra un segmento de línea que tenga la mitad de la longitud de CD. Explica cómo lo sabes.

PROBLEMA 4

Este diagrama se construyó con herramientas de regla y compás. A es el centro de un círculo y C es el centro del otro.

A. Los 2 círculos se intersecan en el punto B. Etiqueta el otro punto de intersección como E

B. ¿Cómo se compara la longitud del segmento CE con la longitud del segmento AD?

Soluciones posibles

Reflexiones:

Soluciones posibles

Ejemplo de respuesta: CB. Los segmentos de línea CA, AB, BE y ED tienen todos la misma longitud. Un segmento de recta compuesto por dos de estos segmentos tiene la mitad de la longitud de CD

B. Ejemplo de respuesta: La longitud del segmento CE es la mitad de la longitud del segmento AD porque es un radio del círculo C y el segmento de línea AD es un diámetro del mismo círculo.

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Relaciones entre círculos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

G-CO.13

Enfoque SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.3

I.C.12

II.B.5

LECCIÓN 2

CONSTRUIR PATRONES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo y predicen lo que podría ocurrir,

OBJETIVO(S)

atienden a la precisión y utilizan las herramientas adecuadas de forma estratégica

DE APRENDIZAJE

• Puedo seguir instrucciones para crear una construcción.

descuben la forma y el espacio.

• Puedo utilizar un lenguaje matemático preciso para describir una construcción.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Crear una construcción a partir de instrucciones (en lenguaje escrito).

• Describir (por escrito) los pasos de la construcción con precisión.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyos para el debate

Constrúyelo

Materiales necesarios

Juegos de herramientas de geometría (HS)

Fichas para usar como rectas, compases, papel de calco, papel en blanco, lápices de colores y tijeras.

Nota: El «papel de calco» es más fácil de usar cuando tiene un tamaño más pequeño. El «papel de calco» comercial mide 5 pulgadas por 5 pulgadas y es ideal para esto. Si utilizas hojas de papel de calco más grandes, considera la posibilidad de recortarlas para uso de los estudiantes.

INFORMACIÓN

DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Usemos construcciones con compás y regla para hacer patrones.

Narrativa de la lección

El propósito de esta lección es que los estudiantes practiquen escribiendo y siguiendo instrucciones precisas con movimientos de regla y compás mientras crean diseños interesantes. En la lección anterior, los estudiantes aprendieron a usar la regla y el compás. En las lecciones siguientes, los estudiantes utilizarán las propiedades de las construcciones para elaborar argumentos. En esta lección, los estudiantes atienden a la precisión cuando se refieren a figuras en su construcción utilizando términos matemáticos y puntos etiquetados (MP6).

En el enfriamiento, los pasos que los estudiantes siguen construirán una línea paralela. Este es el primer conjunto de instrucciones que ven para líneas que no se cruzan, pero los estudiantes idearán otra construcción para crear líneas que sean paralelas después de que hayan aprendido a construir líneas perpendiculares.

Los patrones de la introducción de la actividad «Haz tu propia construcción» se utilizan con permiso del autor.

Si los estudiantes tienen acceso a materiales digitales en clase, pueden optar por realizar todas las actividades de construcción con la herramienta de construcción GeoGebra accesible en las herramientas matemáticas o disponible en https://www.geogebra.org/m/ VQ57WNyR

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de Exploración Independiente 10 min

Actividad de exploración Por parejas 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 10 min

Descripción breve

Los estudiantes analizan una imagen de una construcción y justifican cómo las afirmaciones dadas sobre la construcción son ciertas.

Los estudiantes usan herramientas de construcción para crear su propio patrón usando un círculo y un radio como punto de partida y luego registran cada movimiento que hacen en su patrón.

Una extensióndeexploración está disponible para desarrollar una comprensión más profunda del uso de herramientas de construcción para crear un patrón.

Los estudiantes descubren la importancia de las instrucciones claras y precisas siguiendo las instrucciones creadas por su compañero para reproducir su patrón.

Los estudiantes discuten las dificultades que surgen cuando las instrucciones para las construcciones no son claras y sugieren cambios que harían en sus instrucciones.

Los estudiantes utilizan herramientas de construcción y siguen instrucciones para crear una línea paralela a una línea dada a través de un punto dado.

Práctica Independiente 5-8 min El componente de práctica independiente incluye 2 de la lección y 2 problemas de repaso en espiral.

CALENTAMIENTO |

CHARLA

DE MATEMÁTICAS: ¿POR QUÉ ES VERDAD? (5 minutos)

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyo para el debate

Esta es la primera actividad de conversación matemática del curso. Vea el Introducción para instrucciones extendidas para facilitar esta actividad con éxito. El propósito de esta charla de matemáticas es obtener estrategias y entendimientos que los estudiantes tienen para justificar afirmaciones basadas en una figura geométrica. Por ejemplo, los estudiantes pueden notar que los dos círculos tienen el mismo radio y usar ese hecho para explicar por qué el segmento CD se corta en tres segmentos congruentes. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles en temas futuros como las pruebas y el razonamiento formal.

Cuando los estudiantes se dan cuenta de que dos círculos tienen el mismo radio y utilizan ese hecho para razonar sobre otras distancias, se dan cuenta y hacen uso de la estructura (MP7). Los estudiantes también construyen argumentos viables y critican el razonamiento de otros cuando explican por qué una afirmación sobre el diagrama dado es verdadera o participan en el cuestionamiento de la explicación de otro estudiante (MP3).

INTRODUCCIÓN

Esta es la primera vez que los estudiantes realizan la rutina didáctica de la conversación de matemáicas, por lo que es importante explicar cómo funciona antes de comenzar. Explicar la rutina de la conversación de matemáicas: Se muestra un problema a la vez. Para cada problema, los estudiantes disponen de unos minutos para pensar en silencio y dar una señal cuando tengan una respuesta y una estrategia. El maestro selecciona a los estudiantes para que compartan diferentes estrategias para cada problema y puede hacer preguntas como «¿Quién lo ha pensado de otra manera?». El maestro anota las explicaciones de los estudiantes para que todos las vean. Se puede pedir a los estudiantes que den más detalles sobre por qué decidieron abordar un problema de una determinada manera. Puede que no sea posible compartir todas las estrategias posibles dado el tiempo limitado de que se dispone; puede que el maestro solo recoja dos o tres estrategias distintivas por problema. Considere la posibilidad de establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con un razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, u otra señal sutil. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evite que los estudiantes se distraigan o se precipiten al levantar las manos por toda la clase. Exponga un problema cada vez. Conceda a los estudiantes un tiempo de reflexión tranquilo para cada problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. Mantenga todos los problemas expuestos durante la charla. Continúe con un debate de toda la clase.

Aquí hay 2 círculos con centros A y B

Basándote en el diagrama, explica cómo sabes que cada afirmación es cierta.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

La longitud del segmento EA es igual a la longitud del segmento EB

El triángulo ABF es equilátero.

AB = 1 3 CD

CB = DA

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

• Ejemplo de respuesta: EA = EB porque ambos segmentos son radios de círculos con el mismo radio, AB.

• Ejemplo de respuesta: Debido a que FB y AB son ambos radios del mismo círculo centrado en B, FB = AB. Del mismo modo, FA y AB son ambos radios del mismo círculo centrado en A, por lo que FA = AB. Esto significa que el triángulo ABF es equilátero.

• Ejemplo de respuesta: CA y AB son cada uno un radio del círculo centrado en A, por lo que tienen la misma longitud. Del mismo modo, AB y BD son cada uno un radio del círculo centrado en B. Así que AB, CA y BD son todos de la misma longitud. Observa también que C, A, B y D se encuentran sobre la misma línea que pasa por los centros de los dos círculos.

Así que CD = CA + AB + BD = 3AB. En otras palabras, AB = 1 3 CD

• Ejemplo de respuesta: CB = DA porque CB y DA son diámetros de circunferencias del mismo radio.

Pida a los estudiantes que compartan sus estrategias para cada problema. Registre y muestre sus respuestas para que todos puedan verlas. Para implicar a más estudiantes en la conversación, puede preguntar:

• «¿Quién puede replantear el razonamiento de de otra manera?»..

• «¿Alguien tenía la misma estrategia pero la explicaría de otra manera?»..

• «¿Alguien resolvió el problema de otra manera?»..

• «¿Alguien quiere añadir algo a la estrategia de ?»..

• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?»..

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: MLR8 Apoyos para el debate. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «Primero porque...» o «Noté , así que...». Algunos estudiantes pueden beneficiarse de la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.

Principio(s) de diseño: Optimizar la salida (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | CREA TU PROPIO

10 minutos

Rutinas didácticas

Constrúyelo

En esta actividad, los estudiantes crean un diseño original con simetría séxtuple o triple. A medida que crean su diseño, anotan los pasos que han dado con el compás y la regla. En la siguiente actividad, los estudiantes intercambiarán sus instrucciones con un compañero e intentarán recrear el diseño del compañero siguiendo los pasos escritos. Sus instrucciones deben ser lo suficientemente precisas como para que otra persona pueda replicar su diseño basándose en la descripción.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

El problema «¿Estás preparado para más?». contiene un video creado por Samira Mian, utilizado con permiso.

INTRODUCCIÓN

Muestra estos patrones de muestra para que todos los vean:

Diga a los estudiantes que cada uno de estos patrones parte de la construcción de un hexágono regular, aunque no tienen por qué limitarse a este tipo de patrón. Mientras utilicen movimientos de regla y compás y registren sus movimientos para que otra persona pueda entenderlos, pueden hacer cualquier patrón que elijan. Comparte algunos consejos útiles:

• Las construcciones más grandes son más fáciles de recrear con precisión.

• Si alguna parte de la construcción implica dibujo a mano alzada en lugar de movimientos con regla y compás, no será posible recrearla con precisión. Para los estudiantes que utilicen la herramienta digital de construcciones, recomiéndeles que empiecen dibujando un círculo y un radio.

Apoyo para estudiantes con discapacidad

Participación: Desarrollar el esfuerzo y la persistencia. Fomente y apoye las oportunidades de interacción entre compañeros. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Además de mostrar los movimientos de construcción, muestre marcos de frases para apoyar a los estudiantes cuando describan su proceso. Por ejemplo, «Primero, porque.... Después, yo ....».

Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Utiliza movimientos de regla y compás para construir tu propio patrón utilizando el círculo y el radio como punto de partida. A medida que construyas tu patrón, anota cada movimiento en una hoja de papel en blanco. Utiliza un vocabulario preciso para que alguien pueda hacer una copia perfecta sin ver el original. Incluye instrucciones sobre cómo sombrear o colorear tu patrón.

RESPUESTAS POSIBLES Las respuestas varían. Cualquier patrón que incluya movimientos con regla y compás es aceptable.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Si a los estudiantes les cuesta empezar, diríjalos a la pantalla de movimientos de construcción para recordarles sus opciones.

Pida a los estudiantes que predigan lo bien que se reproducirá su patrón basándose en las instrucciones que dieron.

. Matemáticas . Unidad 1

¿Estás preparado para más?

Si alguna vez has visitado una mezquita, una madraza u otro lugar donde se practique la religión del Islam, habrás visto paredes decoradas con intrincados motivos geométricos. A lo largo de la historia, artistas y artesanos han desarrollado estos patrones que se basan en construcciones con compás y regla.

Puedes encontrar muchos tutoriales en línea para crear estos hermosos diseños. Aquí tienes un ejemplo para probar.

El video «Fes Design» está disponible aquí: https://player.vimeo.com/video/736665153

Respuestas de los estudiantes

Las respuestas varían.

ACTIVIDAD DE EXPLORACIÓN | HACER EL DE OTRA

PERSONA

(15 minutos)

Rutinas didácticas

Constrúyelo

MLR8: Apoyos para el debate

El objetivo de esta actividad es que los estudiantes sigan instrucciones precisas para reproducir un patrón y analicen qué tipo de instrucciones son claras y precisas, y qué tipo de instrucciones son ambiguas o difíciles de seguir. Identifique a los estudiantes que utilizan palabras como círculo, línea, segmento de línea, punto o etiquetan figuras con letras.

Poner a disposición de los estudiantes software de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Invite a los estudiantes a intercambiar instrucciones con un compañero. Lo mejor sería que los compañeros no hayan visto aún el diseño final.

Para los estudiantes que utilicen la herramienta digital de construcciones, recomiende que los estudiantes comiencen dibujando un círculo y un radio.

Apoyo para estudiantes con discapacidad

Representación: Acceso para la percepción. Pide a los estudiantes que lean en voz alta cada paso de las instrucciones a su compañero. Los estudiantes que escuchen y lean la información a la vez se beneficiarán de un tiempo de procesamiento adicional.

Apoyos a la accesibilidad para: Lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Siga las instrucciones con precisión para recrear el patrón.

RESPUESTAS POSIBLES Las respuestas varían.

SÍNTESIS DE LA ACTIVIDAD

Muestre varios pares de patrones originales junto a las recreaciones. Pregunte:

• «¿Qué había en las instrucciones que las hacía claras y fáciles de entender?». (Si las instrucciones eran paso a paso con etiquetas).

• «¿Qué había en las instrucciones que podría haber sido más preciso?». (Utilizando palabras de vocabulario o puntos etiquetados).

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Cuando los estudiantes describan qué aspectos de las instrucciones eran más o menos claros, insista en los detalles de las explicaciones de los estudiantes pidiéndoles que profundicen en una idea o den un ejemplo. Si es necesario, proporcione a los estudiantes fragmentos de oraciones, como por ejemplo «_____ era (claro / no claro) porque _____...». A medida que los estudiantes compartan sus ideas, revoque sus ideas para representarel uso del lenguaje matemático aplicando el lenguaje apropiado, como círculo, recta, segmento de recta y punto. Esto ayudará a los estudiantes a producir y dar sentido al lenguaje necesario para comunicar sus propias ideas. Principio(s) de diseño: Apoyar la adquisición de sentido

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Pregunte a los estudiantes:

• «¿Qué fue difícil al seguir las instrucciones de alguien?». (A veces era difícil cuando las instrucciones eran ambiguas. Sería fácil hacer una figura que se viera diferente si los puntos no estuvieran etiquetados o si las instrucciones fueran imprecisas).

• «¿Qué cambios harías en la forma en que escribiste las instrucciones para describir figuras en geometría?». (Las instrucciones serían más fáciles de entender si etiquetaran los puntos, usaran palabras como segmento, centro, radio, círculo, recta, semirrecta y otras).

• «¿Hubo alguna figura o patrón que te sorprendió que se pudiera hacer con movimientos de regla y compás?»..

. Matemáticas . Unidad 1

ENFRIAMIENTO

| CONSTRUIR UNA RECTA

PARALELA

(10 minutos)

Aquí está el punto A en la recta ℓ y el punto B que no está en ℓ.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Utiliza estos movimientos de regla y compás para crear una recta paralela a la recta dada que pase por el punto B:

1. Crea una recta que pase por A y B que se extienda en ambas direcciones. Etiqueae esta recta como p.

2. Cree un círculo centrado en A con radio AB. Este círculo se interseca con la línea ℓ en 2 lugares. Etiqueta el punto de intersección a la derecha de A como C.

3. Crea un círculo centrado en B con radio BA. Este círculo interseca con la línea p en A y 1 otro punto. Etiqueta el nuevo punto de intersección como D

4. Crea un círculo centrado en D con un radio de longitud BC. Este círculo se interseca con el círculo centrado en B en 2 lugares. Etiqueta el punto de intersección a la derecha de B como E.

5. Utilizando un lápiz de otro color, crea una línea a través de B y E que se extienda en ambas direcciones.

Resumen de la lección para el estudiante

Podemos utilizar los movimientos de la regla y el compás para construir patrones interesantes. ¿Qué pasa si otra persona quiere hacer el mismo patrón? Necesitamos comunicar cómo reproducir el patrón con precisión. Compara estos conjuntos de instrucciones:

1. Empieza con una línea y 2 puntos.

2. Crea una línea.

3. Crea un círculo.

4. Crea un círculo.

5. Crea un círculo.

6. Crea una línea.

. Matemáticas . Unidad 1

1. Comienza con una recta ℓ, punto A en la recta l y punto B no en la recta ℓ

2. Crea una recta a través de A y B que se extienda en ambas direcciones. Etiqueta esta recta como p

3. Crea un círculo centrado en A con radio AB. Este círculo se interseca con la recta ℓ en 2 lugares. Etiqueta el punto de intersección a la derecha de A como C

4. Crea un círculo centrado en B con radio BA. Este círculo interseca con la línea p en A y 1 otro punto. Etiqueta el nuevo punto de intersección como D.

5. Crea un círculo centrado en D con un radio de longitud BC. Este círculo se interseca con el círculo centrado en B en 2 lugares. Etiqueta el punto de intersección a la derecha de B como E

6. Crea una recta a través de B y E extendiéndose en ambas direcciones.

Es importante etiquetar puntos y segmentos, como punto A o segmento AB, para comunicar con precisión.

Estas son instrucciones para construir una recta paralela a una recta dada. Decimos que 2 rectas son paralelas si no se cruzan. También decimos que 2 segmentos son paralelos si se extienden en rectas paralelas.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Este diagrama fue creado comenzando con los puntos A y B y usando solo regla y compás para construir el resto. Todos los pasos de la construcción son visibles. Describa con precisión los movimientos de regla y compás necesarios para construir la línea CD en este diagrama.

Soluciones posibles

Ejemplo de respuesta:

A. Utiliza un compás para crear un círculo centrado en A que pase por B

B. Utiliza un compás para crear un círculo centrado en B que pase por A

C. Marca los dos puntos de intersección entre las dos circunferencias como C y D

D. Utiliza una regla para crear una recta que pase por C y D

PROBLEMA 2

En la construcción, A es el centro de una circunferencia y B es el centro de la otra. Identifiqua todos los segmentos que tengan la misma longitud que el segmento AB segmento AC segmento AE segmento BC segmento CD segmento DE

Soluciones posibles

segmento AC segmento AE segmento BC segmento CD segmento DE

PROBLEMA 3

(Unidad 1, lección 1).

Este diagrama se construyó con herramientas de regla y compás. A es el centro de un círculo y C es el centro del otro. Selecciona todos los segmentos de línea que deben tener la misma longitud que el segmento AB

AB AC

Soluciones posibles

AB AC

PROBLEMA 4

(Unidad 1, lección 1).

Clare usó un compás para hacer un círculo con radio de la misma longitud que el segmento AB Ella etiquetó el centro C. ¿Qué afirmación debe ser verdadera?

A. AB = CD

B. AB = CE

C. AB = CF

D. AB = EF

Soluciones posibles

Reflexiones:

Geometría . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Problemas de triángulos

• Relaciones entre círculos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

G-CO.4 G-CO.9

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1 II.C.6

LECCIÓN 3

TÉCNICAS DE CONSTRUCCIÓN 1: BISECTRICES PERPENDICULARES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo y predicen lo que podría ocurrir, utilizan las herramientas adecuadas de forma estratégica descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Sé construir una mediatriz.

• Comprendo qué tiene de especial el conjunto de puntos que equidistan de dos puntos dados.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender que una mediatriz es el conjunto de puntos que equidistan de dos puntos dados.

• Construir una mediatriz.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

Anticipar, supervisar, seleccionar, secuenciar, conectar

Constrúyelo

MLR8: Apoyos para el debate

Preparación necesaria

Para la mediatriz humana, marca dos puntos en el suelo del salón de clases a dos metros de distancia, utilizando cinta adhesiva. Deja un espacio amplio alrededor y entre los dos puntos marcados.

Materiales necesarios

Juegos de herramientas de geometría (HS)

Fichas para usar como rectas, compases, papel de calco, papel en blanco, lápices de colores y tijeras.

Cinta adhesiva

Cintas métricas

INFORMACIÓN DE LA LECCIÓN

Metas de aprendizaje para el estudiante

• Exploremos las distancias iguales.

Narrativa de la lección

El propósito de esta lección es sentar las bases para entender la bisectriz perpendicular de un segmento tanto como una recta perpendicular a un segmento que pasa por su punto medio (por definición) y el conjunto de puntos equidistantes a los puntos extremos. El segundo hecho se demostrará en la siguiente unidad. La mediatriz desempeña un papel clave en la definición de reflexión más adelante en esta unidad y en la demostración del teorema de congruencia del triángulo lado-lado-lado en la próxima unidad.

Esta lección continúa el tema de preguntarse cuánto se puede aprender sin utilizar números para medir la distancia, así como la construcción de la comprensión de los estudiantes de ángulo y perpendicular de los grados anteriores. Los estudiantes buscan y hacen uso de la estructura cuando piensan dónde deben colocarse sus compañeros durante la Bisectriz perpendicular humana para estar a la misma distancia de dos puntos dados (MP7). Cuantos más estudiantes se coloquen correctamente, más evidente será la estructura. Una vez que los estudiantes determinan la estructura, la registran como una conjetura. Una conjetura se define como una suposición razonable que los estudiantes intentan demostrar o refutar.

Si los estudiantes tienen acceso a materiales digitales en clase, pueden optar por realizar todas las actividades de construcción con la herramienta de construcción de GeoGebra accesible en las herramientas matemáticas o disponible en https://www.geogebra.org/m/ VQ57WNyR

RESUMEN DE LA LECCIÓN

Componente de la lección

Calentamiento

Estructura Tiempo

Independiente 5 min

Actividad de exploración Todo el grupo 15 min

Actividad de exploración

Independiente 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 5-8 min

Descripción breve

Los estudiantes utilizan la definición de un círculo para explorar puntos que son equidistantes de 2 puntos dados.

Los estudiantes exploran el concepto de una bisectriz perpendicular encontrando un punto en el aula que sea equidistante de 2 puntos en el suelo y dibujan un diagrama para representar lo sucedido.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de los puntos equidistantes en el espacio tridimensional.

Los estudiantes descubren diferentes métodos para construir la mediatriz de un segmento de recta dado.

Los estudiantes resumen las propiedades de las bisectrices perpendiculares y discuten formas de determinar si los puntos son equidistantes de 2 puntos sin medir con una regla.

Los estudiantes demuestran su comprensión contextual de una bisectriz perpendicular y usan una regla y un compás para construir una.

El componente de práctica independiente incluye 2 en la lección y 3 problemas de repaso en espiral.

CALENTAMIENTO | ¡ENCUENTRA TODOS LOS PUNTOS! (5

minutos)

El propósito de este calentamiento es aplicar la definición precisa de un círculo para explorar puntos que son equidistantes de dos puntos.

Aquí hay 2 puntos etiquetados como A y B y un segmento de recta CD:

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Marca 5 puntos que están a una distancia CD del punto A. ¿Cómo podrías describir todos los puntos que están a una distancia CD del punto A?

2. Marca 5 puntos que están a una distancia CD del punto B. ¿Cómo podrías describir todos los puntos que están a una distancia CD del punto B?

3. Marca con otro color todos los puntos que estén a una distancia CD tanto de A como de B al mismo tiempo.

1. Cualquiera 5 puntos del círculo. El círculo con radio CD y centro A

2. Cualquiera 5 puntos en el círculo. El círculo con radio CD y centro B

3. Los dos puntos donde los círculos se intersecan.

RESPUESTAS POSIBLESS

El propósito de la discusión es enfatizar la definición de un círculo. He aquí algunas preguntas a considerar:

• «¿Por qué todos los puntos crean un círculo?». (Un círculo es el conjunto de puntos que están a la misma distancia del centro).

SÍNTESIS DE LA ACTIVIDAD

• «¿Qué observas en los puntos que están a la misma distancia, CD, tanto de A como de B?». (Los puntos que están a la misma distancia, CD, tanto de A como de B son los dos puntos de intersección de los círculos).

• «¿Podría haber 3 puntos que estén todos a la misma distancia, CD, de A y B?». (No. Los puntos del círculo centrado en B que están dentro del otro círculo están más cerca de A que de B y el resto de los puntos están más lejos de A que de B).

. Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | BISECTRIZ

PERPENDICULAR HUMANA (15 minutos)

Rutinas didácticas

Observar y preguntarse

El propósito de esta actividad es que los estudiantes desarrollen la intuición de que el conjunto de puntos equidistantes a dos puntos dados forma una bisectriz perpendicular pidiéndoles que hagan el papel de los puntos. Los estudiantes formalizarán esta conjetura en la síntesis de la lección y la demostrarán en una lección posterior.

Localice un área en el saló de clases o cerca a donde varios estudiantes puedan estar juntos y ser vistos por todos los estudiantes. Marque dos puntos en el suelo a unos 2 metros de distancia con cinta adhesiva y despeje un espacio entre los puntos y alrededor de ellos. Marque un punto A y un punto B. Invite a un estudiante a colocarse en A y a otro en B

Diga a los estudiantes: «El siguiente voluntario se colocará a la misma distancia de A y de B. Levanten la mano cuando tengan una idea de dónde se colocará».

INTRODUCCIÓN

Seleccione a un estudiante cuya mano se haya levantado para que se coloque en el lugar que haya elegido. Pregunte a la clase: «¿Están a la misma distancia de A que de B? ¿Cómo podemos comprobarlo?». Compruebe las distancias utilizando los métodos que sugieran los estudiantes.

Diga a los estudiantes: «El siguiente voluntario también se colocará de forma que su distancia de A sea la misma que su distancia de B. No pueden colocarse en el mismo lugar que . Levanten la mano cuando tengan una idea de dónde se colocarán». Continúe pidiendo voluntarios para que se coloquen, comprobando sus distancias y pidiendo nuevos voluntarios hasta que los estudiantes no duden en buscar un nuevo lugar y se coloquen en línea recta perpendicular al segmento AB. En este punto, pida a los estudiantes que vuelvan a sus asientos y dibujen un diagrama de lo que acaba de ocurrir.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Su maestro marcará los puntos A y B en el suelo. Decide dónde colocarte de manera que estés a la misma distancia del punto A que del punto B. Piensa en otro lugar donde podrías colocarte en caso de que alguien ya haya ocupado ese lugar. Después de que todos se sienten, dibuja un diagrama de lo sucedido.

Un bosquejo de un segmento y una línea perpendicular a través del punto medio.

El propósito de la discusión es establecer la conjetura de que la mediatriz de un segmento es el conjunto de puntos que están a la misma distancia de cada punto extremo.

Invite a los estudiantes a observar su bosquejo de los puntos cuya distancia de A es la misma que su distancia de B. Pregúnteles qué observan en los puntos. Pregúnteles qué se preguntan sobre los puntos.

Cosas que los estudiantes pueden observar:

• Todos los puntos equidistantes forman una recta.

• La recta pasa por el punto medio del segmento AB.

• La recta es perpendicular al segmento AB

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

¿Estás preparado para más?

Cosas que los estudiantes pueden preguntarse:

• ¿Será esto siempre cierto?

• ¿Por qué la recta es perpendicular al segmento AB?

• ¿Tiene nombre esta recta?

Pida a los estudiantes que compartan las cosas que notaron y se preguntaron. Registre y muestre sus respuestas para que todos las vean. Una vez registradas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que se estén preguntando ahora?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria.

Explique a los estudiantes que, en matemáticas, las cosas que la gente se pregunta suelen denominarse conjeturas. Una conjetura es una afirmación que nos preguntamos si es cierta. Pida a los estudiantes que hagan una conjetura sobre el conjunto de todos los puntos cuya distancia desde A es la misma que su distancia desde B y seleccione 2 o 3 para compartir.

En esta actividad, hemos pensado en el conjunto de puntos del suelo —un plano bidimensional— que equidistan de dos puntos dados A y B. ¿Qué pasaría si no nos limitáramos al suelo? Partimos de dos puntos A y B en el espacio tridimensional. ¿Qué aspecto tendría el conjunto de puntos equidistantes de A y B?

Respuesta del estudiante

Sería un plano que es la mediatriz del segmento AB en el espacio tridimensional.

ACTIVIDAD DE EXPLORACIÓN | ¿HASTA QUÉ PUNTO PUEDES HACER PARTES?

(15 minutos)

Rutinas didácticas

Anticipar, supercisar, seleccionar, secuenciar, conectar

Construirlo

MLR8: Apoyos para el debate

El objetivo de esta actividad es utilizar lo que los estudiantes saben sobre los puntos equidistantes a dos puntos dados para desarrollar la construcción de la mediatriz utilizando una regla y un compás.

Supervise a los estudiantes que utilicen estos métodos:

• plegado de papel

• dibujo a mano alzada

• construcción con compás y regla

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Definir la bisectriz perpendicular como una recta que pasa por el punto medio de un segmento y que es perpendicular a ese segmento. Informalmente, explica que bi significa dos y sect significa cortan, y así una mediatriz es literalmente una línea perpendicular a un segmento que lo corta en dos trozos congruentes.

INTRODUCCIÓN CONTINUACIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Geometría . Matemáticas . Unidad 1

Muestre estas dos figuras y pida a los estudiantes que expliquen por qué cada línea discontinua no es una bisectriz perpendicular del segmento que interseca.

Los estudiantes podrían señalar que en una, los ángulos no son rectos; por lo tanto, las rectas no son perpendiculares. En el otro, los estudiantes podrían afirmar que las rectas son perpendiculares, pero que el segmento FG no es bisectriz ya que H no es el punto medio de FG

Utilice las herramientas disponibles para hallar la mediatriz del segmento PQ.

Después de idear un método, haz una copia del segmento PQ en papel de calco y busca otro método para hallar su mediatriz.

Ejemplos de respuestas:

Dobla el papel de modo que P quede encima de Q. El pliegue es la bisectriz perpendicular. Utiliza el compás y la regla para construir:

Si a los estudiantes les cuesta empezar, dirígelos a su diagrama del calentamiento. ¿Cómo podrían construir ese diagrama?

El objetivo de este debate es comparar diferentes métodos para dibujar una mediatriz, destacando los pros y los contras de cada uno.

Invite a un alumno que haya utilizado el plegado de papel a hacer una demostración primero. Muestre dos copias del segmento PQ para que todos lo vean. Explique que los segmentos mostrados no se pueden plegar. Invite a un alumno que haya hecho un dibujo a mano alzada a hacer una demostración a continuación. Siga con un estudiante que usó un compás y una regla para hacer una construcción.

Discuta cómo verificar la exactitud de una mediatriz. La discusión puede incluir:

• medir para ver si la mediatriz pasa por el punto medio del segmento PQ y forma un ángulo 90∘ con el segmento PQ

• seleccionar un punto de la mediatriz y medir para ver si está a la misma distancia de P y Q, repitiendo para varios puntos

• utilizar el compás para ver si los puntos de la mediatriz están a la misma distancia de P y Q

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

Si ningún alumno utiliza un compás para construir o comprobar, anime a la clase a plantearse cómo utilizar esa herramienta. Muestre de nuevo la imagen del calentamiento e invite a los estudiantes a explicar cómo utilizar esa construcción para hallar una mediatriz. Haga hincapié en que tanto el plegado de papel como la construcción con compás y regla son métodos válidos y precisos, pero la construcción a mano alzada solo sirve para un bosquejo. La elección de uno u otro dependerá del problema y de las herramientas disponibles.

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Use esta rutina para ayudar a los estudiantes a producir enunciados que describan los pasos a seguir para construir la mediatriz usando una regla y un compás en sus grupos. Proporcione marcos de oraciones para que los estudiantes utilicen, tales como: «Primero, necesitamos porque ».

Esto ayudará a los estudiantes a producir y dar sentido al lenguaje necesario para comunicar sus propias ideas al describir construcciones geométricas.

Principio(s) de diseño: Apoyar la creación de sentido

SÍNTESIS DE LA LECCIÓN

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen sus estrategias e ideas. Por ejemplo: «Primero, porque . Después, » y «Este método funciona/no funciona porque....».

Apoya la accesibilidad para: Lenguaje; Organización

(5 minutos)

Muestre una imagen de una bisectriz perpendicular para que todos la vean.

AB ⟂ CD, AE = EB

Enseñe a los estudiantes la notación para segmentos congruentes, rectas perpendiculares y ángulos rectos. Recuérdeles que pueden encontrar esta notación en los pies de imagen.

• AB ⟂ CD

• m∠AEC = 90°

• AE = EB

Recuerde a los estudiantes que una conjetura es una afirmación que ellos piensan que podría ser cierta. Muestre la conjetura de que la mediatriz de un segmento es el conjunto de puntos que están a la misma distancia de los puntos extremos de dicho segmento. Aquí hay algunas preguntas para el debate:

• «¿Cómo sabíamos que un punto estaba a la misma distancia de los dos puntos dados sin medir con una regla?». (Lo sabíamos porque utilizábamos círculos. Si el punto estaba en la intersección de dos círculos centrados en cada uno de los puntos dados y los dos círculos eran del mismo tamaño, entonces sabíamos que el punto tenía que estar a la misma distancia de cada centro).

• «¿Qué es exactamente un círculo? ¿Cómo usamos los círculos para razonar sobre distancias sin usar una regla?». (Un círculo es el conjunto de puntos que están a una distancia determinada del centro. Utilizamos los círculos para comparar distancias porque si un punto está en un círculo, significa que está a una distancia determinada del centro del círculo).

Diga a los estudiantes que demostrarán que esta conjetura es cierta en una lección posterior.

ENFRIAMIENTO | CAMINAR POR LA LÍNEA

(5 minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Aquí hay un pasillo con láseres:

Imagina que debes cruzar el pasillo manteniéndote a la misma distancia de cada láser. Si te acercas más a un láser que al otro, este te disparará. Utiliza una brújula y una regla para trazar un camino seguro a través del pasillo.

Resumen de la lección para el estudiante

Una bisectriz perpendicular de un segmento es una recta que pasa por el punto medio del segmento y que es perpendicular a él. Recuerda que un ángulo recto es el ángulo que se forma cuando dividimos un ángulo recto en 2 ángulos congruentes. Las rectas que se cruzan en ángulos rectos se llaman perpendiculares.

Una conjetura de es una suposición que aún no se ha demostrado. Conjeturamos que la mediatriz del segmento AB es el conjunto de todos los puntos que están a la misma distancia de A que de B. Esto resulta ser cierto. La mediatriz de cualquier segmento se puede construir encontrando los puntos que están a la misma distancia de los extremos del segmento. La intersección de círculos centrados en cada punto final del segmento se puede utilizar para encontrar puntos que estén a la misma distancia de cada punto final, porque los círculos muestran todos los puntos que están a una distancia dada de su punto central.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Este diagrama es una construcción con regla y compás. A es el centro de un círculo y B es el centro del otro. Selecciona todas las afirmaciones verdaderas.

La recta CD es perpendicular al segmento AB.

El punto M es el punto medio del segmento AB.

La longitud AB es igual a la longitud CD

Segmento AM es perpendicular al segmento BM.

CB + BD > CD

Soluciones posibles

La recta CD es perpendicular al segmento AB.

El punto M es el punto medio del segmento AB.

La longitud AB es igual a la longitud CD

El segmento AM es perpendicular al segmento BM.

CB + BD > CD

PROBLEMA 2

En este diagrama, el segmento CD es la mediatriz del segmento AB. Supongamos que es cierta la conjetura de que el conjunto de puntos equidistantes de A y B es la mediatriz de AB. ¿Está el punto E más cerca del punto A, más cerca del punto B o hay la misma distancia entre los puntos? Explica cómo lo sabes.

AB ⊥ CD

Soluciones posibles

Ejemplo de respuesta: E está más cerca del punto A porque está en el mismo lado de la mediatriz que A.

PROBLEMA 3

(Unidad 1, lección 2).

Partiendo de 2 puntos marcados, A y B, describe con precisión los movimientos de regla y compás necesarios para construir el triángulo ABC en este diagrama.

Soluciones posibles

Ejemplo de respuesta:

A. Utilice un compás para crear un círculo centrado en A que pase por B.

B. Utilice un compás para crear un círculo centrado en B que pase por A

C. Marque un punto de intersección entre los dos círculos como C

D. Utilice una regla para crear los segmentos AB, AC, y BC

PROBLEMA 4

(Unidad 1, lección 2).

Este diagrama fue creado comenzando con los puntos C y D y usando solo regla y compás para construir el resto. Todos los pasos de la construcción son visibles. Selecciona todos los pasos necesarios para producir este diagrama.

Construye un círculo centrado en A

Construye un círculo centrado en C

Construye un círculo centrado en D

Etiqueta los puntos de intersección de los círculos A y B

Dibuja la recta que pasa por los puntos C y D

Dibuja la recta que pasa por los puntos A y B

Soluciones posibles

Construye una circunferencia centrada en A.

Construir una circunferencia centrada en C

Construir una circunferencia centrada en D

Señalar los puntos de intersección de las circunferencias A y B

Trazar la recta que pasa por los puntos C y D

Dibuja la línea que pasa por los puntos A y B

PROBLEMA 5

(Unidad 1, lección 1).

Este diagrama se construyó con herramientas de regla y compás. A es el centro de un círculo y C es el centro del otro. todas las afirmaciones verdaderas.

AB = BC

AB = BD

AD = 2AC

BC = CD

BD = CD

Soluciones posibles

AB = BC

AB = BD

AD = 2AC

BC = CD

BD = CD

Selecciona

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Problemas de triángulos

• Relaciones entre círculos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.12 Realizar construcciones geométricas formales con una variedad de herramientas y métodos (compás y regla, cuerda, dispositivos reflectantes, plegado de papel, programa geométrico dinámico, etc.). Copiar un segmento; copiar un ángulo; bisecar un segmento; bisecar un ángulo; construir rectas perpendiculares, incluida la mediatriz de un segmento de recta; y construir una recta paralela a una recta dada que pase por un punto que no esté en la recta.

G-CO.13 Construir un triángulo equilátero, un cuadrado y un hexágono regular inscrito en un círculo.

Construir

G-CO.3

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su solución.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

Estándares ELD de California

I.A.3 I.B.5

LECCIÓN 4

TÉCNICAS DE CONSTRUCCIÓN 2: TRIÁNGULOS EQUILÁTEROS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo y predecir lo que podría ocurrir, utilizan las herramientas adecuadas de forma estratégica descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo construir un triángulo equilátero.

• Puedo identificar segmentos congruentes en figuras y explicar por qué son congruentes.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Construir un triángulo equilátero.

• Utilizar círculos en una construcción para razonar (utilizando palabras y otras representaciones) sobre longitudes en figuras.

PREPARACIÓN

DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

Anticipar, supervisar, seleccionar, secuenciar, conectar

Construirlo

MLR8: Apoyos para el debate

Materiales necesarios

Conjunto de herramientas de geometría (HS)

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Identifiquemos qué formas son posibles dentro de la construcción de un hexágono regular.

Narrativa de la lección

Esta lección permite a los estudiantes determinar un proceso para construir un triángulo equilátero encontrando las formas posibles dentro de la construcción de un hexágono regular. Hay una oportunidad para practicar el vocabulario de polígonos más allá de los triángulos equiláteros durante la primera actividad. Los estudiantes continúan practicando las técnicas de construcción con regla y compás, así como justificando afirmaciones relativas a la distancia. Los estudiantes presentan argumentos y critican el razonamiento de los demás cuando discuten afirmaciones sobre la distancia utilizando círculos (MP3).

Una conjetura que se basa en lecciones posteriores sobre la prueba a través del movimiento rígido es el uso de la rotación por 120 grados para demostrar que la construcción del triángulo equilátero produce un triángulo con todos los ángulos congruentes y todos los lados congruentes. Los estudiantes son introducidos a la palabra inscrito para describir una situación en la que un polígono se encuentra dentro de un círculo con todos los vértices en el círculo.

Si los estudiantes tienen acceso a materiales digitales en clase, pueden optar por realizar todas las actividades de construcción con la herramienta de construcción GeoGebra accesible en las herramientas de matemáticas o disponible en https://www.geogebra.org/m/ VQ57WNyR

RESUMEN DE LA LECCIÓN

Componente de lección

Calentamiento

Actividad de exploración

Estructura Tiempo

En pareja 5 min

Independiente 15 min

Actividad de exploración Independiente 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes analizan una imagen de una construcción geométrica compuesta por círculos e identifican las cosas que notan y se preguntan.

Los estudiantes exploran cómo la construcción de un hexágono regular inscrito en un círculo puede utilizarse para construir otros polígonos.

La actividad requiere el uso de un aplicación digital interactiva para que los estudiantes puedan construir polígonos inscritos en un círculo utilizando la tecnología.

Los estudiantes utilizan una regla y un compás para construir triángulos equiláteros de diferentes tamaños.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las construcciones que involucran triángulos equiláteros y otras figuras.

Los estudiantes revisan la construcción geométrica del calentamiento e identifican cualquier forma adicional que no hayan notado antes.

Los estudiantes construyen un triángulo equilátero inscrito en un círculo utilizando una regla y un compás.

El componente de práctica independiente incluye 3 problemas de repaso de la lección y 6 problemas de repaso de la espiral.

CALENTAMIENTO | OBSERVAR Y MARAVILLARSE: CÍRCULOS CÍRCULOS

(5 minutos)

Rutinas didácticas

Observar y preguntarse

Este es la primera actividad de «Observar y preguntarse» del curso. Se muestra a los estudiantes una construcción geométrica compuesta por siete círculos. Se les pregunta: «¿Qué te llama la atención? ¿Qué te sorprende?». Se les da unos minutos para que escriban las cosas que les llaman la atención y las cosas que les asombran. Después de que los estudiantes hayan tenido la oportunidad de escribir sus respuestas, pida a varios estudiantes que compartan las cosas que notan y las cosas que se preguntan; anótelas para que todos las vean. A menudo, el objetivo es dirigir la conversación hacia las preguntas sobre algo matemático en lo que la clase está a punto de centrarse. El propósito es hacer que una tarea matemática sea accesible a todos los estudiantes con estas dos preguntas abordables. Al pensar en ellas y responder, los estudiantes se introducen en el contexto y puede que les pique la curiosidad.

El objetivo de este calentamiento es suscitar la idea de que pueden surgir muchas formas dentro de la construcción del hexágono regular, lo que será útil cuando los estudiantes razonen sobre otras formas y construyan triángulos equiláteros en una actividad posterior. Si bien los estudiantes pueden notar y preguntarse muchas cosas sobre esta imagen, nombrar los polígonos que los estudiantes podrían dibujar es el punto de discusión importante.

Este calentamiento incita a los estudiantes a dar sentido a un problema antes de resolverlo, familiarizándose con un contexto y las matemáticas que podrían estar involucradas (MP1).

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Muestre la imagen para que todos la vean. Pida a los estudiantes que piensen en al menos una cosa que les llame la atención y en al menos una cosa que les sorprenda. Conceda a los estudiantes 1 minuto de tiempo para pensar en silencio y, a continuación, 1 minuto para comentar con su compañero las cosas que observan y se preguntan, seguido de un debate con toda la clase.

¿Qué observas? ¿Qué te preguntas?

RESPUESTAS POSIBLES

Cosas que los estudiantes pueden observar:

• Algunos puntos de intersección están marcados y otros no.

• Hay 7 círculos superpuestos.

• Hay una figura que parece una 6 flor con pétalos en el círculo central.

Cosas que los estudiantes pueden preguntarse:

• ¿Todos los círculos tienen el mismo tamaño?

• ¿Cuántos tipos de formas hay en la imagen?

• Si conectáramos otros puntos de intersección, ¿qué tipos de formas podríamos hacer?

SÍNTESIS DE LA ACTIVIDAD

Pida a los estudiantes que compartan las cosas que notaron y se preguntaron. Anote y muestre sus respuestas para que todos las vean. Si es posible, anote los razonamientos pertinentes en la imagen o cerca de ella. Una vez registradas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que se pregunten ahora?».

Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria. Si la conexión de puntos de intersección para formar polígonos no surge durante la conversación, pida a los estudiantes que discutan esta idea.

ACTIVIDAD

DE EXPLORACIÓN | ¿QUÉ POLÍGONOS

PUEDES ENCONTRAR?

(15 minutos)

Rutinas didácticas

Anticipar, supervisar, seleccionar, secuenciar, conectar

Construirlo

El objetivo de esta actividad es que los estudiantes piensen qué otras formas son posibles dentro de la construcción del hexágono regular. Esto conduce a la siguiente actividad sobre la construcción de un triángulo equilátero.

Identifica a los estudiantes que encuentran varias formas para compartirlas durante la discusión. Por ejemplo, triángulos rectángulos, triángulos equiláteros de varios tamaños, rombos, paralelogramos, rectángulos, trapecios isósceles, hexágonos regulares y otros. Vigile también a los estudiantes cuyas conjeturas solo impliquen afirmaciones sobre la distancia. Estas son las conjeturas más apropiadas para justificar durante la discusión, porque todos los círculos tienen el mismo radio.

Muestre una imagen de un hexágono inscrito en un círculo para que todos lo vean.

INTRODUCCIÓN

Recuerde a los estudiantes que en una lección anterior construyeron un hexágono regular dentro de un círculo. Explica que cuando una figura cabe dentro de un círculo y todos los vértices del polígono están en el círculo, decimos que la figura está inscrita en el círculo. Diga a los estudiantes que la palabra inscribir se divide en partes: in, que significa dentro, y escribir, que significa dibujado o escrito, por lo que la palabra significa literalmente dibujado dentro.

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre fragmentos de oraciones para apoyar a los estudiantes cuando expliquen sus ideas. Por ejemplo, «Me doy cuenta de que », «Lo sé porque » y «Eso podría / no podría ser cierto porque....».

Apoya la accesibilidad para: Lenguaje; organización

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Aquí tienes una construcción con regla y compás de un hexágono regular inscrito en un círculo justo antes del último paso de dibujar los lados:

1. Utiliza la herramienta polígono (la que parece un triángulo) para dibujar al menos 2 polígonos en la figura. Los vértices de tus polígonos deben ser puntos de intersección en la figura. Sombrea tus polígonos utilizando diferentes colores para que sean más fáciles de ver. Utiliza la barra de estilo para cambiar el color. Este es el aspecto de la barra de estilo.

2. Escribe al menos 2 conjeturas sobre los polígonos que has hecho.

1. Ejemplo de respuesta:

CONCEPTOS ERRÓNEOS PREVISTOS

2. Respuesta de ejemplo: Una conjetura sería que el triángulo es un triángulo equilátero. Otra conjetura sería que el área del triángulo es mayor que la mitad del área de uno de los círculos.

Algunos estudiantes pueden centrarse solo en los polígonos cuyos vértices están marcados en el diagrama. Indíqueles que busquen otros puntos de intersección que puedan utilizarse como vértices.

El propósito de esta discusión es ilustrar que muchas conjeturas, aunque parezcan obvias, son difíciles de justificar con la única información de que todos los círculos tienen el mismo radio. Exponga varias respuestas de los estudiantes para que todos las vean, a fin de destacar las enormes posibilidades que permite esta sencilla construcción.

Aquí hay algunas preguntas para el debate:

• «¿Todos los círculos tienen el mismo tamaño?». (Sí. Al unir los centros de cualquier par de círculos adyacentes se demuestra que tienen el mismo radio. La comparación de pares sucesivos muestra que todos tienen la misma longitud de radio).

SÍNTESIS DE LA ACTIVIDAD

• «¿Para cuál de estas conjeturas podemos dar una explicación convincente de por qué es cierta?».

• «¿Para cuál de estas conjeturas no sabemos todavía lo suficiente como para explicarla?»..

Si es necesario, basándose en el diagnóstico previo a la unidad, utilice las distintas formas que los estudiantes generaron para repasar el vocabulario.

• «¿Cómo se llama cuando un triángulo tiene dos lados congruentes?». (Triángulo isósceles).

• «¿Cómo se llama el cuadrilátero que tiene dos lados paralelos? ¿Y si dos de sus lados son congruentes?». (Trapecio, trapecio isósceles).

• «¿Cómo se llama el cuadrilátero que tiene dos pares de lados paralelos? ¿Y si todos 4 sus lados son congruentes?». (Paralelogramo, rombo).

ACTIVIDAD

DE EXPLORACIÓN | BUSCA EL EQUILÁTERO

(15 minutos)

Rutinas didácticas

Constrúyelo

MLR8: Apoyos para el debate

El objetivo de esta actividad es que los estudiantes comparen las posibles formas de construir triángulos equiláteros. Busca trabajos de los estudiantes que ilustren una variedad de métodos y tamaños de triángulos.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Anime a los estudiantes a construir los triángulos equiláteros usando diferentes métodos en lugar de repetir el mismo método dos veces.

Usa movimientos de regla y compás para construir al menos 2 triángulos equiláteros de diferentes tamaños.

Ejemplo de respuesta:

RESPUESTAS POSIBLES

¿Estás listo para más?

1. Examina la figura cuidadosamente. ¿De qué formas diferentes está compuesta? Especifica.

2. Averigua cómo construir la figura con un compás y una regla.

3. Después, recórtala y comprueba si puedes doblarla en un recipiente como este.

Respuestas posibles

1. Triángulos equiláteros, un hexágono regular y 1 6 sectores de un círculo. 2.

3. Una vez que la figura está construida correctamente y recortada, crear el recipiente es cuestión de hacer pliegues precisos de «montaña» y «valle».

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Si los estudiantes se atascan, pídales que consulten el calentamiento para ver si pueden detectar triángulos equiláteros. A continuación, anímales a realizar los movimientos de compás y regla necesarios para formar esos triángulos equiláteros.

Muestre varias respuestas de los estudiantes para que todos las vean. Pida a los estudiantes que expliquen sus métodos para producir triángulos equiláteros y que justifiquen cómo saben que cada triángulo es equilátero. Si los estudiantes no lo mencionan, conjeture que, en algunas de estas construcciones, toda la construcción permanece igual incluso cuando se gira 1 3 de una vuelta completa (120 grados) alrededor del centro. Esto significa que cada lado se puede girar sobre los demás lados, y cada ángulo se puede girar sobre los demás ángulos. Esto nos da ideas sobre la simetría que exploraremos en lecciones posteriores.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar y representar: MLR8 Apoyos para el debate. Utilice esta rutina para ayudar a los estudiantes a prepararse para la discusión de toda la clase. Organice a los estudiantes en grupos de 2. Invite a los estudiantes a que se turnen para explicar su método para construir triángulos equiláteros de diferentes tamaños. Esto proporcionará a todos los estudiantes oportunidades adicionales para aclarar su pensamiento y producir lenguaje.

Principio(s) de diseño: Apoyar la creación de sentido; cultivar la conversación

SÍNTESIS DE LA LECCIÓN

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia y sus ideas. Por ejemplo, «Primero, yo porque . Luego, yo....» y «Yo sé porque....».

Apoya la accesibilidad para: Lenguaje; organización

(5 minutos)

Vuelve a mostrar la imagen del calentamiento para que todos la vean. Pregunte a los estudiantes si son capaces de encontrar ahora alguna forma que no hayan visto al principio de la clase. Pide a algunos estudiantes que muestren sus respuestas. Invite a los estudiantes a hacer conjeturas sobre su forma y a justificar sus afirmaciones.

ENFRIAMIENTO | ESTOY ATRAPADO EN UN CÍRCULO (5

minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Utiliza los movimientos de la regla y el compás para crear un triángulo equilátero. Sombrea ligeramente el triángulo para que sea más fácil de ver.

Cualquier triángulo equilátero es aceptable; no es necesario que esté inscrito en el círculo dado. Ejemplo de respuesta:

Resumen de la lección para el estudiante

La regla nos permite construir líneas y segmentos de línea y el compás nos permite hacer círculos con un radio específico. Con estas herramientas, podemos razonar sobre las distancias para explicar por qué ciertas formas tienen determinadas propiedades. Por ejemplo, cuando construimos un hexágono regular utilizando círculos del mismo radio, sabemos que todos los lados tienen la misma longitud porque todos los círculos son del mismo tamaño. El hexágono se llama inscrito porque cabe dentro del círculo y cada vértice del hexágono está en el círculo.

Del mismo modo, podríamos utilizar la misma construcción para hacer un triángulo inscrito. Si conectamos cada otro punto alrededor del círculo central, se forma un triángulo equilátero. Podemos conjeturar que este triángulo tiene 3 lados congruentes y 3 ángulos congruentes porque toda la construcción parece permanecer exactamente igual siempre que se gira 1 3 de una vuelta completa alrededor del centro.

. Matemáticas . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Este diagrama es una construcción con regla y compás. A es el centro de un círculo y B es el centro del otro. Explica cómo sabemos que el triángulo ABC es equilátero.

Soluciones posibles

Ejemplo de respuesta: El segmento AB tiene la misma longitud que el segmento AC porque ambos son radios del mismo círculo centrado en el punto A AB tiene la misma longitud que el segmento BC porque ambos son radios del mismo círculo centrado en el punto B. Por lo tanto, los tres lados tienen la misma longitud.

PROBLEMA 2

A, B, y C son los centros de los círculos 3. ¿Cuántos triángulos equiláteros hay en este diagrama?

Soluciones posibles 5

PROBLEMA 3

Este diagrama es una construcción con regla y compás. A es el centro de un círculo y B es el centro del otro. Selecciona todas las afirmaciones verdaderas.

AC = BC

AC = BD

Soluciones posibles

AC = BC

AC = BD

CD = AB ABCD es un cuadrado.

ABD es un triángulo equilátero.

CD = AB + AB

ABD es un triángulo equilátero.

CD = AB + AB

. Matemáticas . Unidad 1

PROBLEMA 4

El segmento de recta CD es la mediatriz del segmento de recta AB. ¿Es el segmento de recta AB la mediatriz del segmento de recta CD?

Soluciones posibles

No necesariamente y no en este caso. La recta segmento AB es perpendicular a la recta segmento CD. Pero para ser la mediatriz, M debe ser el punto medio de CD. Esta información no se da y en este caso el segmento CM es más largo que el segmento DM

PROBLEMA 5

Aquí hay 2 puntos en el plano.

A. Usando solo una regla, ¿puedes encontrar puntos en el plano que estén a la misma distancia de los puntos A y B? Explica tu razonamiento.

B. Utilizando solo un compás, ¿puedes encontrar puntos en el plano que estén a la misma distancia de los puntos A y B?

Explica tu razonamiento.

PROBLEMA 6

Soluciones posibles

A. Ejemplo de respuesta: No. Con una regla podrías construir el segmento de recta AB, pero necesitarías un compás para localizar los puntos que están a la misma distancia de un punto dado.

B. Respuesta de ejemplo: Sí. Construye la circunferencia centrada en A que pase por B. Construye la circunferencia centrada en B que pase por A. Los puntos de intersección de estas dos circunferencias están a la misma distancia de A y B porque se encuentran en circunferencias con radios de la misma longitud.

En este diagrama, la recta segmento CD es la mediatriz de la recta segmento AB. Supongamos que es cierta la conjetura de que el conjunto de puntos que equidistan de A y B es la mediatriz de AB. Selecciona todas las afirmaciones que deben ser ciertas.

AB ⊥ CD

AM = BM

CM = DM

Soluciones posibles

AM = BM

CM = DM

EA = EM

EA < EB

AM < AB

EA = EM

EA < EB

AM > BM

AM < AB

AM > BM

Geometría . Matemáticas . Unidad 1

PROBLEMA 7

El diagrama se construyó con herramientas de regla y compás. Nombra todos los segmentos que tengan la misma longitud que el segmento AC

Soluciones posibles

AB, BE, CA, ED (o equivalente)

PROBLEMA 8

Partiendo de 2 puntos marcados, A y B, describe con precisión los movimientos de regla y compás necesarios para construir el cuadrilátero ABCD en este diagrama.

Soluciones posibles

Ejemplo de respuesta:

A. Usa un compás para crear un círculo centrado en A que pase por B

B. Usa un compás para crear un círculo centrado en B que pase por A

C. Marca los puntos de intersección entre los dos círculos C y D

D. Utilice una regla para crear los segmentos AC, CB, BD y DA

PROBLEMA 9

En la construcción, A es el centro de un círculo y B es el centro del otro. ¿Qué segmento tiene la misma longitud que AB?

A. CB

B. CD

C. CE

D. CA

Soluciones posibles

Reflexiones:

Geometría . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Relaciones entre círculos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.12 Realizar construcciones geométricas formales con una variedad de herramientas y métodos (compás y regla, cuerda, dispositivos reflectantes, plegado de papel, Programa geométrico dinámico, etc.). Copiar un segmento; copiar un ángulo; bisecar un segmento; bisecar un ángulo; construir líneas perpendiculares, incluyendo la bisectriz perpendicular de un segmento de línea; y construir una línea paralela a una línea dada a través de un punto que no está en la línea.

Construir

G-CO.1

Construir

G-CO.9 G-CO.12

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su solución.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California I.C.11 II.C.6

LECCIÓN 5

TÉCNICAS DE CONSTRUCCIÓN 3: LÍNEAS PERPENDICULARES Y ÁNGULO BISECTOR

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES

INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir buscan y hacen uso de la estructura descubren la forma y el espacio.

OBJETIVO(S)

DE APRENDIZAJE

• Puedo construir una recta que sea perpendicular a una recta dada a través de un punto de la recta.

• Puedo construir una bisectriz de un ángulo.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Construir una recta perpendicular a una recta dada que pase por un punto dado de la recta.

• Construir una bisectriz de un ángulo.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Pensar, girar y compartir

Constrúyelo

MLR3: Clarificar, criticar, corregir

Tomar turnos

Materiales necesarios

Conjunto de herramientas de geometría (HS)

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Utilicemos herramientas para resolver algunos desafíos de construcción.

Narrativa de la lección

En esta lección, los estudiantes aprenden dos construcciones:

• una recta perpendicular a una recta dada a través de un punto en la recta

• una bisectriz de ángulo

Para la construcción de la recta perpendicular, los estudiantes se basan en su experiencia con la construcción de la mediatriz. La construcción bisectriz de ángulo se conecta entonces a la construcción de la recta perpendicular con la observación de que construir una recta perpendicular es lo mismo que bisecar un ángulo recto. Los estudiantes hacen uso de la estructura cuando deciden cómo aplicar lo que ya saben sobre construcciones para construir rectas perpendiculares y bisectrices de ángulos (MP7). Es probable que los estudiantes tengan dificultades para hacerlo; esta es una oportunidad para animarles a perseverar en la resolución de problemas (MP1).

Existe una conexión significativa entre la bisectriz del ángulo y la perpendicular en triángulos que se realiza en esta lección y se desarrolla en la siguiente unidad. Para los triángulos isósceles, en particular, el ángulo bisectriz del vértice entre los lados congruentes es el mismo que la mediatriz del lado opuesto a ese vértice. Esta conexión es esencial para demostrar que la mediatriz y el conjunto de puntos equidistantes a 2 puntos dados son el mismo conjunto.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento En parejas 5 min

Actividad de exploración Independiente 10 min

Actividad de Exploración En parejas 20 min

Los estudiantes analizan una imagen de una construcción y crean una conjetura sobre la relación entre los segmentos de línea en la construcción.

Los estudiantes utilizan una regla y un compás para construir una línea perpendicular a una línea dada que pasa por un punto específico.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la construcción de líneas perpendiculares utilizando la tecnología.

Los estudiantes exploran el uso de la regla y el compás para construir un ángulo bisector.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la construcción de bisectrices de ángulos usando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las herramientas usadas para las construcciones.

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Los estudiantes hacen conexiones entre la construcción de 2 círculos y las construcciones de líneas perpendiculares y bisectrices de ángulos.

Los estudiantes construyen una bisectriz de ángulo utilizando herramientas de construcción.

El componente de práctica independiente incluye 2 problemas de repaso de la lección y 6 problemas de repaso de la espiral.

CALENTAMIENTO | DOS CÍRCULOS

(5 minutos)

Rutinas didácticas

Pensar, girar y compartir

El propósito de esta actividad es preparar a los estudiantes para la construcción de una línea perpendicular a través de un punto en la recta. Esta figura de dos círculos del mismo radio que se intersecan también juega un papel importante en la construcción de la bisectriz de un ángulo más adelante en la lección.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2. Después, de un tiempo de trabajo en silencio, pida a los estudiantes que comparen sus conjeturas con las de sus compañeros y decidan si ambas son correctas, aunque sean diferentes. A continuación, discuta con toda la clase.

Los puntos �� y �� se encuentran cada uno en los centros de círculos de radio ��

1. Compara la distancia �� con la distancia �� Prepárate para explicar tu razonamiento.

2. Compara la distancia �� con la distancia �� Prepárate para explicar tu razonamiento.

3. Dibuja la recta �� y escribe una conjetura sobre su relación con el segmento ��.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

1. �� = ��, porque ambas distancias son iguales a la distancia ��, el radio de ambos círculos.

2. �� = ��, porque ambas distancias son iguales a la distancia ��, radio de ambos círculos.

3. La recta �� es perpendicular al segmento �� y lo biseca.

El objetivo de esta discusión es conectar este diagrama con las rectas perpendiculares. Pide a los estudiantes que compartan sus conjeturas. Conecte estas ideas con la actividad anterior, «La mediatriz humana», en la que los estudiantes conjeturaron que el conjunto de puntos situados a la misma distancia de los puntos �� y �� es la mediatriz del segmento ��. En este caso, eso significaría que la recta �� sería la mediatriz del segmento ��

ACTIVIDAD DE EXPLORACIÓN | HAZLO BIEN

(10 minutos)

Rutinas didácticas

Constrúyelo

Esta actividad invita a los estudiantes a jugar con los movimientos de la regla y el compás para construir una recta perpendicular a una recta dada que pase por un punto de la recta dada. Esto conduce a la siguiente lección en la que los estudiantes ampliarán esta habilidad para construir un cuadrado inscrito en un círculo.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

. Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience con una demostración física para recordar a los estudiantes los movimientos válidos de la regla y el compás. Por ejemplo, demuestre cómo crear un círculo centrado en un punto marcado que pase por otro punto marcado. Pregunte a los estudiantes cómo se podría utilizar este movimiento de regla y compás para construir una línea perpendicular a ℓ que pase por ��

Apoya la accesibilidad para: Procesamiento conceptual; procesamiento visual-espacial

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Aquí hay una línea ℓ con un punto etiquetado como ��. Utiliza movimientos de regla y compás para construir una línea perpendicular a ℓ que pase por ��.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS

DE LA ACTIVIDAD

Algunos estudiantes pueden quedarse atascados durante más tiempo del que sería productivo. Pida a estos estudiantes que piensen cómo podrían usar sus herramientas para construir los puntos �� y �� como en el calentamiento.

El objetivo de esta discusión es establecer un método para construir una recta perpendicular. Pida a 2 o 3 estudiantes que expliquen cómo han podido construir una recta perpendicular. Conecte estos métodos con la figura que los estudiantes exploraron en el calentamiento (dos círculos donde cada centro está en el otro círculo).

ACTIVIDAD DE EXPLORACIÓN | BISECAR ESTO

Rutinas didácticas

Constrúyelo

MLR3: Clarificar, criticar, corregir

Tomar turnos

(20 minutos)

En esta actividad, los estudiantes se turnan utilizando una regla y un compás para construir una bisectriz de ángulo. Los estudiantes intercambian papeles, explicando su pensamiento y escuchando, lo que les da la oportunidad de explicar su razonamiento y criticar el razonamiento de los demás (MP3).

Poner a disposición de los estudiantes un programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Explíqueles que practicarán su técnica de construcción dibujando y bisecando más ángulos una vez que hayan bisecado el ángulo ��. Señale que las instrucciones para «crear una semirrecta que divida el ángulo �� en 2 ángulos congruentes» son instrucciones para bisecar ese ángulo. Anime a los estudiantes a dibujar ángulos que parezcan diferentes del ángulo dado cuando estén practicando.

Apoyo para estudiantes que aprenden el idioma inglés

Leer, hablar: MLR3 Aclarar, criticar, corregir. Presente un primer borrador de una explicación de cómo bisecar otro ángulo: «Hice tres círculos y luego tracé una línea por el medio». Promueva el debate preguntando: «¿Cuáles fueron los pasos que siguió el autor?». Pida a los estudiantes que aclaren y corrijan el enunciado. Las afirmaciones mejoradas deben incluir algunos de los siguientes datos: el centro y el radio de los círculos construidos, dos puntos específicos que se utilizaron para construir una recta, el orden o las palabras de transición temporal (primero, después, luego, etc.) y las razones de las decisiones tomadas durante los pasos. Esto ayudará a los estudiantes a desarrollar y comprender las explicaciones sobre cómo llevar a cabo las construcciones.

Principio(s) de diseño: Maximizar la metaconciencia; optimizar el resultado (para la explicación)

Apoyo para estudiantes con discapacidad

Compromiso: Interiorizar la autorregulación. Demostrar dar y recibir retroalimentación constructiva. Utilizar un proceso estructurado y mostrar marcos de frases para apoyar la retroalimentación productiva. Por ejemplo, «Este método funciona / no funciona porque...», «Podemos estar de acuerdo en que...» y «La idea de me recuerda a....».

Apoya la accesibilidad para: Habilidades socioemocionales; organización; lenguaje

Aquí hay un ángulo:

1. Estima la ubicación de un punto �� de modo que el ángulo �� sea aproximadamente congruente con el ángulo ��.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

2. Usa movimientos de compás y regla para crear una semirrecta que divida el ángulo �� en 2 ángulos congruentes. ¿Qué tan cerca está la semirrecta de pasar por tu punto ��?

3. Túrnate con tu compañero para dibujar y bisecar otros ángulos.

• Para cada ángulo que dibujes, explica a tu compañero cómo cada movimiento de la regla y el compás te ayuda a bisecarlo.

• Para cada ángulo que dibuje tu compañero, escucha atentamente su explicación. Si no estás de acuerdo, hablen sobre sus ideas y trabajen para llegar a un acuerdo.

. Matemáticas . Unidad 1

RESPUESTAS POSIBLES

1. Las respuestas varían.

2. Ejemplo de respuesta:

3. Ejemplo de respuesta: Dibujo un círculo centrado en �� para encontrar dos puntos en el ángulo que estén a la misma distancia de ��. Luego puedo dibujar el segmento que une esos dos puntos y construir la mediatriz de ese segmento usando otras dos circunferencias. Esa recta tendrá que pasar por ��, ya que todos los puntos de una mediatriz están a la misma distancia de los puntos extremos.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Algunos estudiantes pueden quedarse atascados más tiempo del productivo. Pregunta a estos estudiantes cómo podrían utilizar sus herramientas para construir un segmento que saben cortar por la mitad como hicieron en el calentamiento y en la última actividad. Si necesitan más ayuda, pídales que construyan una circunferencia centrada en �� y subraye el segmento que se crea al unir los dos puntos de intersección.

El propósito de esta discusión es conectar la construcción anterior de una línea perpendicular con la construcción de una bisectriz de ángulo. Seleccione 2 o 3 estudiantes para que muestren sus respuestas a la vista de todos. Pídales que expliquen cómo pudieron construir una semirrecta que divide el ángulo en dos partes congruentes. Presente el término bisectriz de ángulo. Recuerde que «bi» significa «dos» y «sector» significa «cortar», por lo que bisetcar un ángulo significa literalmente cortar el ángulo en dos ángulos congruentes. Considere hacer una conexión con la actividad anterior demostrando la construcción utilizando el programa de geometría y aumentando la medida del ángulo hasta que alcance 180 grados. Si el tiempo lo permite, pide a los estudiantes que tracen el ángulo junto con su punto de estimación �� y superpongan varios papeles de calco para mostrar un grupo de puntos. Compara la estimación de la clase con la bisectriz del ángulo.

¿Estás preparado para más?

Durante miles de años, desde que los antiguos griegos empezaron a jugar con construcciones con regla y compás, la gente se esforzó por encontrar una construcción para triseccionar un ángulo arbitrario en tres ángulos iguales. Muchos afirmaban haber encontrado tal construcción, pero siempre había algún fallo en su razonamiento. Finalmente, en 1837, Pierre Wantzel utilizó un nuevo campo de las matemáticas para demostrar que era imposible, lo que no impidió que algunos afirmaran haber encontrado una construcción. Sin embargo, si utilizamos otras herramientas además de la regla y el compás, es posible. Por ejemplo, prueba este método de usar origami (plegado de papel) para trisecar un ángulo.

El video Trisecar un ángulo con origami está disponible en https://player.vimeo.com/video/298418799

Respuestas posibles

Las respuestas varían.

SÍNTESIS DE LA LECCIÓN (5

minutos)

El propósito de esta discusión es conectar la construcción básica de dos círculos que pasan uno por el centro del otro con las construcciones de una recta perpendicular a una recta dada y una bisectriz de un ángulo. Muestre imágenes de las construcciones de cada actividad para que todos las vean. Pregunte a los estudiantes:

• «¿Cuál fue el primer paso en cada una de estas construcciones?». (En cada construcción, el primer paso fue crear un círculo que intersecara la línea o el ángulo dado en dos lugares).

• «El primer círculo crea dos puntos que están a la misma distancia del centro. Ahora, ¿dónde ves los dos círculos que pasan por el centro del otro en cada una de las construcciones?». (En cada construcción, los 2 puntos creados a partir del primer paso se convierten en centros de círculos que pasan uno por el centro del otro).

Resalte los 2 puntos creados a partir del primer paso de cada construcción y luego resalte los 2 círculos que pasan uno por el centro del otro en el segundo paso.

Expliqie que cada construcción es en realidad una bisectriz perpendicular. En el caso de la bisectriz de un ángulo, la conexión de los dos puntos equidistantes forma un triángulo isósceles. Esto establece una conexión sorprendente e importante. La bisectriz de un ángulo de un triángulo isósceles parece ser también la mediatriz de la base. Diga a los estudiantes que, de momento, se trata solo de una conjetura, pero que esta conexión entre la mediatriz de un triángulo isósceles y la mediatriz de su base desempeñará un papel importante en la próxima unidad.

ENFRIAMIENTO | BISECTRIZ QUE... (5

minutos)

Aquí hay un ángulo:

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Usa movimientos de compás y regla para construir la bisectriz del ángulo para el ángulo ��. En otras palabras, crea una semirrecta que divida el ángulo �� en 2 ángulos congruentes.

Geometría . Matemáticas . Unidad 1

Resumen de la lección

Podemos construir una recta que sea perpendicular a una línea dada. También podemos bisecar un ángulo dado usando solo una regla y un compás. La recta que biseca un ángulo se llama bisectriz de ángulo. Ambas construcciones utilizan 2 círculos que pasan por el centro de cada uno:

Para la recta perpendicular, empiece por encontrar 2 puntos de la recta a la misma distancia del punto dado. Luego cree los 2 círculos que pasen por sus centros. Una los puntos de intersección de esos círculos para dibujar una línea perpendicular.

Para la bisectriz de un ángulo, empiece encontrando 2 puntos en las semirrectas a la misma distancia del vértice. Luego cree los 2 círculos que pasen por los centros de cada uno. Conecte los puntos de intersección de esos círculos para dibujar la bisectriz del ángulo.

De hecho, ¡podemos pensar en crear una recta perpendicular como bisecar un ángulo de 180 grados!

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Este diagrama es una construcción con regla y compás de una línea perpendicular a la línea �� que pasa por el punto ��. Explica por qué fue útil construir los puntos �� y �� para que estuvieran a la misma distancia de ��

Soluciones posibles

Ejemplo de respuesta: Fue útil construir �� para que estuviera a la misma distancia de �� que A porque esto hace que �� sea el punto medio del segmento ��. Así que la mediatriz de �� funciona para crear una línea perpendicular al segmento ��, que pasaría por ��

Math Nation California . Geometría

. Matemáticas . Unidad 1

PROBLEMA 2

Este diagrama es una construcción de regla y compás. Selecciona todas las afirmaciones verdaderas.

Soluciones posibles

La línea �� es la bisectriz del ángulo ��

La recta �� es la mediatriz del segmento ��

La línea �� es la mediatriz del segmento ��

La recta �� es paralela a la recta ��

La recta �� es la bisectriz del ángulo ��

La recta �� es la mediatriz del segmento ��

La línea �� es la mediatriz del segmento ��

La línea �� es paralela a la línea ��

PROBLEMA 3

Este diagrama es una construcción con regla y compás. �� es el centro de una circunferencia y �� es el centro de la otra. Un rombo es un cuadrilátero con 4 lados congruentes. Explica por qué el cuadrilátero �� es un rombo.

Soluciones posibles

Ejemplo de respuesta: El segmento �� tiene la misma longitud que el segmento �� porque ambos son radios del círculo centrado en el punto ��. El segmento �� tiene la misma longitud que el segmento �� porque ambos son radios del círculo centrado en el punto ��. Ambas circunferencias pasan por el centro de la otra circunferencia por lo que sus radios tienen la misma longitud. Esto significa que los cuatro segmentos son congruentes entre sí.

PROBLEMA 4

��, �� y �� son centros de las tres circunferencias.

¿Qué segmento de recta es congruente con ��?

A. ��

B. ��

C. ��

D. ��

Soluciones posibles C

PROBLEMA 5

En la construcción, �� es el centro de una circunferencia y �� es el centro de la otra. Explica por qué el segmento �� tiene la misma longitud que el segmento ��

Soluciones posibles

Ejemplo de respuesta: �� y �� son ambos radios de círculos con un radio común. La circunferencia centrada en �� pasa por �� y la circunferencia centrada en �� pasa por �� por lo que cualquier radio de cualquiera de las dos circunferencias tendrá la misma longitud.

PROBLEMA 6

En este diagrama, el segmento de recta �� es la mediatriz del segmento de recta �� Supongamos que es cierta la conjetura de que el conjunto de puntos que equidistan de �� y �� es la mediatriz de ��. ¿Está el punto �� más cerca del punto ��, más cerca del punto �� o a la misma distancia de ambos puntos? Explica cómo lo sabes.

Soluciones posibles

Ejemplo de respuesta: El punto �� está a la misma distancia de ambos puntos porque se encuentra en la mediatriz del segmento ��

PROBLEMA 7

Una hoja de papel con los puntos �� y �� está doblada de modo que �� y �� coinciden entre sí.

Explica por qué el pliegue de la hoja de papel es la mediatriz del segmento ��. (Supongamos que es cierta la conjetura de que el conjunto de puntos equidistantes de �� y �� es la mediatriz del segmento ��).

PROBLEMA 8

Soluciones posibles

Si �� es un punto del pliegue del papel doblado, se puede dibujar un segmento que una simultáneamente �� con �� y �� mientras el papel sigue doblado. Es el mismo segmento por lo que esto significa que la distancia de �� a �� es la misma que la distancia de �� a ��. Como cada punto del pliegue es equidistante de �� y ��, el pliegue es la mediatriz del segmento ��

Aquí hay un diagrama de una construcción con regla y compás. �� es el centro de una circunferencia y �� es el centro de la otra. Explica por qué la longitud del segmento �� es la misma que la longitud del segmento ��

Soluciones posibles

Ejemplo de respuesta: Los dos segmentos deben tener la misma longitud ya que ambos son radios del mismo círculo centrado en ��.

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Relaciones entre círculos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Copiar un segmento; copiar un ángulo; bisecar un segmento; bisecar un ángulo; construir líneas perpendiculares, incluyendo la bisectriz perpendicular de un segmento de línea; y construir una línea paralela a una línea dada a través de un punto que no está en la línea.

Construir

8.G.2

Construir

G-CO.2 G-CO.4

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.A.1

II.B.5

II.C.6

LECCIÓN 6

TÉCNICAS DE CONSTRUCCIÓN 4: LÍNEAS PARALELAS Y PERPENDICULARES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir, buscan y hacen uso de la estructura descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo construir una recta paralela que pase por un punto dado.

• Puedo construir una recta perpendicular que pase por un punto dado.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Construye una recta paralela a una recta dada que pase por un punto que no esté en la recta dada.

• Construye una recta perpendicular a una recta dada que pase por un punto que no esté en la recta dada.

PREPARACIÓN DE LECCIONES

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyos para el debate

Constrúyelo

MLR1: Cada vez más sólido y claro

Pensar, girar y compartir

Materiales necesarios

conjunto de herramientas de geometría (HS)

Preparación necesaria

Para la charla de matemáticas: Transformaciones. Puede utilizar GeoGebra para realizar y mostrar las transformaciones de los estudiantes. También puedes preparar varias copias de las imágenes y anotar la estrategia de cada alumno en una copia diferente.

Cree una pantalla que haga un inventario de las figuras que los estudiantes saben construir para «De pie sobre los hombros de los gigantes».

INFORMACIÓN

DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Utilicemos herramientas para dibujar líneas paralelas y perpendiculares con precisión.

Narrativa de la lección

En esta lección, los estudiantes utilizan construcciones previas para crear nuevas construcciones. Esto proporciona un ejemplo de un tema más general del aprendizaje: que los descubrimientos se construyen unos sobre otros y sientan las bases para nuevos conocimientos. Las secciones y unidades subsiguientes guiarán a los estudiantes a través de un proceso de establecimiento de una base teórica y de construcción de nuevos conocimientos sobre sí mismos en el marco de la geometría transformacional. Los estudiantes hacen uso de la estructura de que dos circunferencias del mismo radio que pasan por el centro de la otra pueden utilizarse para construir rectas perpendiculares para pensar estratégicamente sobre cómo construir una recta perpendicular a una recta dada que pase por un punto dado que no está en la recta (MP7). A medida que los estudiantes continúan aplicando el método para construir una línea perpendicular para construir una línea paralela, están participando en el razonamiento repetido (MP8).

En el calentamiento, los estudiantes identifican los movimientos rígidos como una revisión de su estudio de la congruencia en el grado 8. En el enfriamiento, los estudiantes utilizan una construcción para reflejar un punto a través de una recta —aunque puede que no se den cuenta de que eso es lo que han hecho— como avance de las lecciones posteriores.

Si los estudiantes tienen acceso a materiales digitales en clase, pueden elegir realizar todas las actividades de construcción con la herramienta de construcción de GeoGebra accesible en las herramientas de matemáticas o disponible en https://www.geogebra. org/m/VQ57WNyR

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 10 min

Actividad de Exploración En pareja 10 min

Actividad de exploración Independiente 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Descripción breve

Los estudiantes identifican una transformación o una secuencia de transformaciones que lleva una figura a otra figura.

Los estudiantes descubren cómo construir una recta perpendicular a través de un punto que no está en la recta.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la construcción de rectas perpendiculares utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las bisectrices perpendiculares.

Los estudiantes aplican conocimientos previos de construcciones para construir una recta paralela que pase por un punto, no sobre la recta.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la construcción de rectas paralelas usando la tecnología.

Los estudiantes resumen las diferentes figuras que pueden construir usando una regla y un compás.

Los estudiantes construyen un segmento de rectas perpendicular a la recta que lo biseca.

Práctica Independiente 5-8 min El componente de práctica independiente incluye 2 en la lección y 6 problemas de repaso en espiral.

CHARLA DE MATEMÁTICAS: TRANSFORMACIONES

(10 minutos)

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyo para el debate

El propósito de esta charla de matemáticas es obtener estrategias y entendimientos que los estudiantes tienen para las transformaciones rígidas. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta unidad cuando los estudiantes necesiten ser capaces de definir transformaciones rigurosamente y usar transformaciones en pruebas. Al participar en esta actividad, los estudiantes deben ser precisos en la elección de palabras y en el uso del lenguaje (MP6). Los estudiantes continuarán desarrollando vocabulario de transformaciones a lo largo Unidad, no es necesario que los estudiantes utilicen frases como segmento de recta dirigida en este momento. Está bien si no hay suficiente tiempo para discutir todos los 4 problemas.

INTRODUCCIÓN

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Muestre un problema a la vez. Conceda a los estudiantes un tiempo de reflexión tranquilo para cada problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. Mantenga todos los problemas expuestos durante la charla. Continúe con un debate de toda la clase.

Cada par de figuras es congruente. Identifica mentalmente una transformación o secuencia de transformaciones que podrían llevar una forma a la otra.

• Respuesta de ejemplo: Trasladar el círculo centrado en el punto P por el segmento de recta dirigida que va de P a Q.

• Respuesta de ejemplo: Trasladar el segmento AB por el segmento de recta dirigida desde A hasta C

RESPUESTAS POSIBLES

• Respuesta de ejemplo: Trasladar el triángulo DEF por el segmento de recta dirigida desde F hasta L. Rotar el triángulo D'E'F' usando el centro L por el ángulo E'LK. Reflejar el triángulo D''E''F'' sobre la recta LK.

• Ejemplo de respuesta: trasladar el segmento ST por el segmento de línea dirigida de S a M. Gire el segmento S'T' en sentido antihorario alrededor del centro M hasta que T'' aterrice en N.

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

El objetivo de esta discusión es identificar líneas paralelas. Pide a los estudiantes que compartan sus estrategias para cada problema. Anote y muestre sus respuestas para que todos puedan verlas. Para involucrar a más estudiantes en la conversación, considere preguntar:

• «¿Quién puede replantear el razonamiento de de una manera diferente?».

• «¿Alguien tenía la misma estrategia pero la explicaría de otra manera?».

• «¿Alguien resolvió el problema de una manera diferente?».

• «¿Alguien quiere agregar algo a la estrategia de ?».

• «¿Están de acuerdo o en desacuerdo? ¿Por qué?».

Si los estudiantes no mencionan las líneas paralelas, pregunte: «¿Por qué no necesitamos usar una rotación para este par?». (Las líneas son paralelas).

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «Primero, yo porque...» o «Noto , así que...». Algunos estudiantes pueden beneficiarse de la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.

Principio(s) de diseño: Optimizar la salida (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | DE PIE SOBRE LOS HOMBROS DE GIGANTES

(10 minutos)

Rutinas didácticas

Constrúyelo

MLR1: Más fuerte y más claro cada vez

Pensar, girar y compartir

El propósito de esta actividad es extender lo que los estudiantes saben sobre la construcción de una recta perpendicular a través de un punto en la recta dada a una nueva situación en la que la recta perpendicular construida pasa por un punto que no está en la recta dada.

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

Organice a los estudiantes en grupos de 2. Muestre la imagen para que todos la vean:

Recuerde a los estudiantes que en la lección anterior utilizaron movimientos de regla y compás para crear una línea perpendicular a ℓ que pasa por el punto B, que estaba en la línea ℓ. Ahora muestre una imagen de la construcción de una recta perpendicular que pase por B para que todos la vean a lo largo de la actividad:

INTRODUCCIÓN

INTRODUCCIÓN CONTINUACIÓN

Muestre una lista de las construcciones que los estudiantes ya conocen. Esta lista se colocará en el salón de clases durante el resto de las lecciones de esta unidad. Debería ser algo así (ahora solo incluya las primeras 6 construcciones):

• círculos de cierto radio

• rectas y segmentos de recta que pasan por dos puntos

• hexágonos regulares

• triángulos equiláteros

• una mediatriz de un segmento dado

• una recta perpendicular que pasa por un punto de la recta dada

• una recta perpendicular que pasa por un punto que no está en la recta dada (añadida en esta lección)

• una recta paralela que pasa por un punto que no está en la recta dada (añadida en esta lección)

Después de un tiempo de trabajo en silencio, pida a los estudiantes que comparen sus respuestas con las de sus compañeros y decidan si ambas son correctas, aunque sean diferentes. Continúe con un debate con toda la clase.

Apoyo para estudiantes que aprenden el idioma inglés

Escribir, hablar, conversar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para dar a los estudiantes una oportunidad estructurada de revisar y refinar el razonamiento utilizado para crear su construcción. Pida a cada estudiante que se reúna con 2-3 otros compañeros seguidos para recibir comentarios. Proporcione a los estudiantes indicaciones que les ayuden a reforzar sus ideas y a aclarar su lenguaje. Por ejemplo: «¿Puedes explicar cómo...?»., «¿Por qué elegiste construir un círculo ahí?»., «¿Qué sabes sobre radios que te ayude aquí?». o «¿Qué quieres decir con...?». Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar su explicación final.

Principio(s) de diseño: Optimizar el resultado (para la justificación); apoyar la creación de sentido

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Apoyo para estudiantes con discapacidad

Acción y expresión: Proporcionar acceso para la acción física. Proporciona acceso a herramientas y tecnologías de apoyo como el programa de geometría dinámica.

Apoya la accesibilidad para: Procesamiento visual-espacial; procesamiento conceptual; organización

RESPUESTAS POSIBLES

Aquí hay una recta m y un punto C que no está en la recta. Utiliza movimientos de regla y compás para construir una recta perpendicular a la recta m que pase por el punto C. Prepárate para compartir tu razonamiento.

Ejemplos de respuestas:

• La construcción anterior comenzó creando un círculo centrado en el punto dado. Eso produjo dos puntos que estaban a la misma distancia del punto dado. Entonces, pudimos construir la mediatriz entre esos dos puntos. En esta construcción, necesitamos crear esos dos puntos para un punto dado NO sobre la recta. Probamos a hacer un círculo centrado en el punto dado y a utilizar los dos puntos de intersección con la recta dada, y aún así funcionó.

RESPUESTAS POSIBLES CONTINUACIÓN

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

¿Estás preparado para más?

• Elija dos puntos cualesquiera de la recta y cree círculos centrados en esos puntos que pasen por C. Si une los dos puntos de intersección de esos círculos, se crea una recta perpendicular que pasa por C

Algunos estudiantes pueden esforzarse más de lo que es productivo. Pídales que dibujen un segmento de recta y construyan su mediatriz. En esa construcción, la mediatriz pasará por un punto de intersección de dos circunferencias. Pregunte: «¿Qué ocurre si creamos una circunferencia centrada en ese punto de intersección que pase por un extremo del segmento? ¿Por qué ocurre esto? ¿Cómo puedes utilizar esta idea en esta nueva actividad?»..

Concéntrese en el proceso de utilizar una construcción previa para generar nuevas construcciones. Aquí hay algunas preguntas para el debate:

• «¿En qué se diferenciaba esta construcción de las construcciones de líneas perpendiculares que has hecho antes? ¿Cómo te ayudó el pensar en las diferencias a planificar qué hacer?». (No tenía un segmento para bisecar, porque el punto no estaba en la recta. Me di cuenta de que aún podía hacer un segmento usando el nuevo punto).

• «¿Cómo te ayuda saber algunas construcciones a hacer otras más complicadas?». (Puedo usar los mismos movimientos, pero cambiándolos un poco).

1. El segmento de recta AB tiene una longitud de 1 unidad. Construye su mediatriz y dibuja el punto donde esta recta corta a nuestro segmento original AB. ¿A qué distancia está este nuevo punto de A?

2. Ahora tenemos dibujados 3 puntos. Utiliza un par de puntos para construir una nueva mediatriz que aún no se ha dibujado y marca su intersección con el segmento AB. ¿A qué distancia se encuentra este nuevo punto de A?

3. Si repites este proceso de trazar nuevas mediatrices perpendiculares y consideras a qué distancia se encuentra tu punto de A, ¿qué puedes decir de todas las distancias?

Respuesta posibles

1. 1 2 unidad

2. O 1 4 de unidad o 3 4 de unidad, dependiendo de qué puntos se elijan.

3. Respuesta de ejemplo: Todas las distancias podrían escribirse como a 2n unidad para algunos enteros positivos a y n

ACTIVIDAD DE

EXPLORACIÓN

| DESAFÍO DE CONSTRUCCIONES PARALELAS (15 minutos)

El propósito de esta actividad es que los estudiantes piensen estratégicamente sobre cómo aplicar construcciones previas a una nueva construcción.

No se espera que los estudiantes utilicen ningún otro método que no sean dos rectas perpendiculares consecutivas, pero si a los estudiantes se les ocurren otros métodos, considere discutir esos métodos durante la síntesis de la lección.

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

INTRODUCCIÓN

Apoyo para estudiantes

Añada un elemento adicional al inventario de las diferentes construcciones que los estudiantes han aprendido.

• Una recta perpendicular que pase por un punto de la recta dada Recuerde a los estudiantes que pueden utilizar este inventario para pensar en cómo utilizar las construcciones que conocen para construir algo nuevo.

con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Divida esta tarea en partes más manejables para apoyar a los estudiantes con habilidades organizativas en la resolución de problemas. Por ejemplo, primero invite a los estudiantes a construir una línea perpendicular a la línea m que pase por el punto C. Luego, pida a los estudiantes que consideren la relación entre la línea perpendicular a m y la línea paralela a la línea m. Finalmente, pida a los estudiantes que construyan una línea paralela a la línea m que pase por el punto C

Apoya la accesibilidad para: Organización; atención

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Aquí hay una recta m y un punto C que no está en la recta. Utiliza movimientos de regla y compás para construir una recta a la recta m que pase por el punto C.

Ejemplo de respuesta: Construir una recta perpendicular a la recta dada que pase por el punto dado y luego una perpendicular a esa recta que pase por el punto dado.

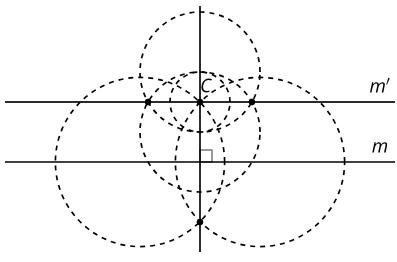
CONCEPTOS ERRÓNEOS ANTICIPADOS

ACTIVIDAD SÍNTESIS

Algunos estudiantes pueden esforzarse más de lo que es productivo. Píaeles que consideren lo que acaban de aprender para construir a partir del punto y la recta. (Una recta perpendicular). Invíteles a considerar la relación entre la recta que podrían construir y la recta paralela que quieren construir. (También son perpendiculares).

El propósito de la discusión es centrarse en el proceso de utilizar construcciones previas para generar nuevas construcciones. Pregunte a los estudiantes: «¿De qué manera conocer algunas construcciones te ayuda a hacer otras más complicadas?». (En esta construcción, repetí dos veces una construcción que ya conocía).

Agregue un elemento adicional a la lista de construcciones que los estudiantes ya conocen:

• Una recta paralela que pasa por un punto que no está en la recta dada

SÍNTESIS DE LA LECCIÓN (5

minutos)

Haga referencia a la muestra de figuras que los estudiantes saben construir. Invite a los estudiantes a debatir qué otras figuras podrían dibujar utilizando este inventario. (Cuadriláteros con lados paralelos o ángulos rectos incluyendo trapecios, paralelogramos, rectángulos y cuadrados).

ENFRIAMIENTO | ENCUENTRA EL PUNTO FINAL QUE FALTA

(5 minutos)

RESPUESTAS POSIBLES

La recta ℓ es la mediatriz del segmento PS. Desafortunadamente, S se perdió.

1. Usa movimientos de regla y compás para construir una recta perpendicular a ℓ que pase por P. 2. Marca el punto S. Explica o muestra tu razonamiento.

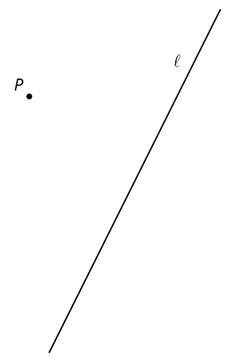
Ejemplo de respuesta: Un diagrama claramente etiquetado es suficiente.

Posible explicación: La recta ℓ debe pasar por el punto medio de PS y encontrarse con PS en un ángulo recto para ser la mediatriz. En primer lugar, construir una recta a través de P perpendicular a ℓ. Entonces S debe estar a la misma distancia de ℓ que P, así que construye el círculo centrado en el punto de intersección a través de P

Resumen de la lección para el estudiante

Cuando escribimos las instrucciones para una construcción, podemos usar una construcción anterior como uno de los pasos. Ahora conocemos 2 nuevas construcciones que están formadas por una secuencia de movimientos.

• Las rectas perpendiculares son rectas que se encuentran en un ángulo de 90 grados.

• Las rectas paralelas son líneas que no se cruzan. Una forma de hacer líneas paralelas es dibujar 2 rectas perpendiculares a la misma recta.

. Matemáticas . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

¿Cuál de las siguientes construcciones ayudaría a construir una recta que pasa por el punto C que es perpendicular a la recta AB?

A. Construcción de un triángulo equilátero de un lado AB

B. Construcción de un hexágono de un lado BC

Soluciones posibles

PROBLEMA 2

Dos rectas distintas, ℓ y m, son perpendiculares a la misma recta n. Selecciona todas las afirmaciones verdaderas.

Las rectas ℓ y m son perpendiculares.

Las rectas ℓ y n son perpendiculares.

Las rectas m y n son perpendiculares.

Las rectas ℓ y m son paralelas.

Las rectas ℓ y n son paralelas.

Las rectas m y n son paralelas.

PROBLEMA 3

Geometría, unidad 1, lección 5

C. Construcción de una mediatriz que pase por C

D. Construcción de un cuadrado de un lado AB

Soluciones posibles

Las rectas ℓ y m son perpendiculares.

Las rectas ℓ y n son perpendiculares.

Las rectas m y n son perpendiculares.

Las rectas ℓ y m son paralelas.

Las rectas ℓ y n son paralelas.

Las rectas m y n son paralelas.

Este diagrama es una construcción con regla y compás de la bisectriz del ángulo BAC. Solo se da el ángulo BAC. Explica los pasos de la construcción en orden. Incluya un paso para cada nuevo círculo, línea y punto.

Soluciones posibles

Ejemplo de respuesta. Primero, dibuje el círculo con centro A a través de B. Este interseca el segmento AC en D. Luego, dibuje un círculo con centro B que contenga D y un círculo con centro D que contenga B. Estos dos círculos se encuentran en los puntos E y F. A continuación, dibuje una recta que pase por los puntos A, E, y F

PROBLEMA 4

Unidad 1, lección 5

Este diagrama es una construcción con regla y compás de una línea perpendicular a la línea AB que pasa por el punto C. ¿Qué segmento tiene la misma longitud que segmento EA?

A. EC B. ED

Soluciones posibles B

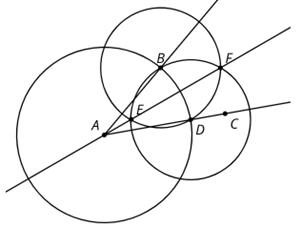
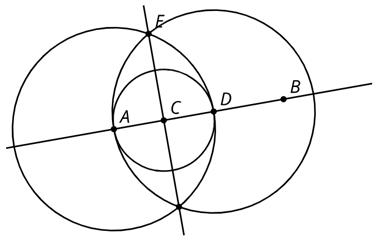
PROBLEMA 5

Unidad 1, lección 4

Este diagrama es una construcción con regla y compás. ¿Qué triángulo es equilátero? Explica cómo lo sabes.

Soluciones posibles

El triángulo VWZ es equilátero. Cada lado de este triángulo está formado por dos radios que tienen la misma longitud. El triángulo STU no es equilátero. Dos lados son radios del círculo T pero el tercer lado, el segmento SU, no es un radio de ningún círculo mostrado en el diagrama.

PROBLEMA 6

Unidad 1, lección 2

En la construcción, A es el centro de un círculo y B es el centro del otro. Nombra los segmentos del diagrama que tienen la misma longitud que el segmento AB

Soluciones posibles

AC, AD, BC, BD

PROBLEMA 7

Unidad 1, lección 3

Este diagrama es una construcción con regla y compás. A es el centro de un círculo y B es el centro del otro.

A. Nombra un par de segmentos de recta perpendiculares.

B. Nombra un par de segmentos de recta con la misma longitud.

Soluciones posibles

Ejemplos de respuestas:

A. Los segmentos de recta AB y CD son perpendiculares.

B. Los segmentos de línea AM y BM tienen la misma longitud.

PROBLEMA 8

Unidad 1, lección 4

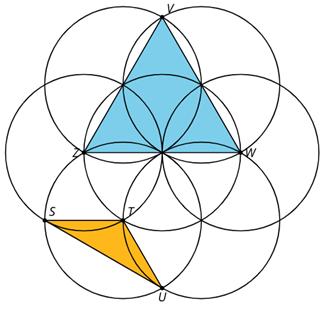
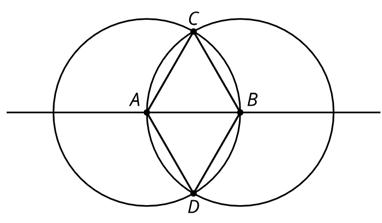
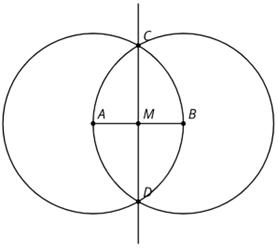
A, B, y C son los centros de los 3 círculos. Seleccione todos los segmentos que son congruentes con AB.

Soluciones posibles

LECCIÓN 7

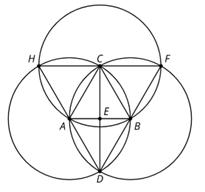
IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Relaciones entre círculos

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

G-CO.13 Construye un triángulo equilátero, un cuadrado y un hexágono regular inscrito en un círculo.

Construir

G-CO.1 G-CO.12

Construir

G-CO.3

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.B.7

I.C.12

TÉCNICAS DE CONSTRUCCIÓN 5: CUADRADOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir,

OBJETIVO(S)

utilizan las herramientas adecuadas de forma estratégica descubren la forma y el espacio.

DE APRENDIZAJE

• Puedo construir un cuadrado inscrito en un círculo.

• Puedo construir un cuadrado utilizando un segmento dado para uno de sus lados.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Construir un cuadrado.

• Describir (oralmente y por escrito) las diagonales de un cuadrado y utilizar estas conjeturas para construir un cuadrado inscrito en un círculo.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

¿Cuál no pertenece?

Constrúyalo

MLR1: Cada vez más fuerte y más claro

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Usemos movimientos de regla y compás para construir cuadrados.

Narrativa de la lección

En esta lección, los estudiantes aplican sus conocimientos sobre la construcción de rectas perpendiculares y la transferencia de distancias para construir cuadrados —primero un cuadrado con un lado dado y luego un cuadrado inscrito en un círculo —. Los estudiantes deberán reconocer la estructura de las partes perpendiculares (lados o diagonales) para identificar una técnica de construcción adecuada (MP7).

En el calentamiento, los estudiantes identifican atributos pertenecientes a categorías de figuras bidimensionales para repasar la definición de cuadrado. La construcción del cuadrado inscrito en un círculo proporciona la oportunidad de previsualizar la idea de simetría que se desarrolla más adelante en la unidad. Los estudiantes también aprenden el término polígono regular para describir formas que son a la vez equiláteras y equiángulas, incluidos los cuadrados.

Si los estudiantes tienen acceso a materiales digitales en clase, pueden optar por realizar todas las actividades de construcción con la herramienta de construcción GeoGebra, accesible en las herramientas matemáticas o disponible en https://www.geogebra.org/m/ VQ57WNyR

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Grupos pequeños 5 min

Actividad de exploración Independiente 15 min

Actividad de Exploración Independiente 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 5-8 min

Descripción breve

Los estudiantes analizan 4 polígonos e identifican cuál no pertenece.

Los estudiantes aplican movimientos de regla y compás para construir un cuadrado, dada una longitud de lado.

Un aplicación digital interactiva está disponible para permitir a los estudiantes explorar la construcción de un cuadrado utilizando la tecnología.

Los estudiantes descubren cómo construir un cuadrado inscrito en un círculo utilizando herramientas de construcción.

Un aplicación digital interactiva está disponible para permitir a los estudiantes explorar la construcción de un cuadrado inscrito en un círculo utilizando la tecnología.

Una extensió de exploración está disponible para desarrollar una comprensión más profunda de un círculo inscrito en un cuadrado.

Los estudiantes discuten técnicas de construcción que son beneficiosas cuando se construye un polígono regular inscrito en un círculo.

Los estudiantes construyen un cuadrado usando un lado de un triángulo dado como la longitud del lado del cuadrado.

El componente de práctica independiente incluye 2 problemas de repaso de la lección y 5 problemas de repaso en espiral.

CALENTAMIENTO

| CUÁL NO PERTENECE:

POLÍGONOS

(5 minutos)

Rutinas didácticas

¿Cuál no pertenece?

Esta es la primera rutina «¿Cuál no pertenece?» del curso. En esta rutina, se presentan a los estudiantes cuatro figuras, diagramas, gráficos o expresiones con la pregunta «¿Cuál no pertenece?». Normalmente, cada una de las cuatro opciones «no pertenece» por una razón diferente y las similitudes y diferencias son matemáticamente significativas. Se pide a los estudiantes que expliquen su razonamiento para decidir que una opción no pertenece y se les da la oportunidad de precisar su razonamiento.

Este calentamiento pide a los estudiantes que comparen cuatro polígonos. Da a los estudiantes un motivo para utilizar el lenguaje con precisión (MP6). Da al maestro la oportunidad de escuchar cómo los estudiantes utilizan la terminología y hablan de las características de los elementos en comparación con los demás.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2-4. Exponga los polígonos para que todos los vean. Dé a los estudiantes 1 minuto de tiempo para pensar en silencio y luego tiempo para compartir su pensamiento con su pequeño grupo. En sus pequeños grupos, pida a cada estudiante que comparta su razonamiento de por qué un elemento en particular no pertenece y, juntos, encuentren al menos una razón por la que cada elemento no pertenece.

¿Cuál no pertenece?

RESPUESTAS POSIBLES

Ejemplos de respuestas:

A no pertenece porque:

• no tiene una longitud de lado de 1

• está sombreado en

B no pertenece porque:

• no es equilátero

• no está sombreado en negro

C no pertenece porque:

• no es equiangular

• no tiene un perímetro de 8

D no pertenece porque:

• no es un cuadrilátero

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

Durante el debate, pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como nombres de formas, regular, equilátero o equiangular. Además, presione a los estudiantes sobre las afirmaciones sin fundamento.

ACTIVIDAD DE EXPLORACIÓN | ES GENIAL SER CUADRADO (15 minutos)

Rutinas didácticas

Constrúyelo

MLR1: Cada vez más fuerte y más claro

En esta actividad, los estudiantes construyen un cuadrado, dado un lado. Esto es similar a cómo los estudiantes construyeron una recta paralela con dos rectas perpendiculares sucesivas, excepto que también tienen que prestar atención a marcar distancias iguales a lo largo de las líneas perpendiculares.

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Sugiera a los estudiantes que utilicen un lápiz para dibujar ligeramente los movimientos de la regla y el compás y, a continuación, que utilicen un lápiz de color para resaltar los lados del cuadrado.

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience con una demostración física de la construcción de una recta perpendicular a través de un punto en la recta dada, para apoyar las conexiones entre las nuevas situaciones y los conocimientos previos. Pregunte a los estudiantes cómo podría utilizarse la construcción de una recta perpendicular para construir un cuadrado.

Apoya la accesibilidad para: Procesamiento conceptual; procesamiento visual-espacial

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTAS

Utilice movimientos de regla y compás para construir un cuadrado con el segmento AB como uno de los lados.

A continuación se presenta una respuesta parcial: Se construye una perpendicular a la recta AB a través del punto A y luego se interseca con el círculo centrado en A de radio AB para encontrar un punto D. Repitiendo este proceso con una perpendicular a AB a través del punto B se obtiene un punto C tal que el cuadrilátero ABCD es un cuadrado.

RESPUESTAS POSIBLES CONTINUACIÓN

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Es posible que algunos estudiantes se esfuercen más de lo productivo. Pregunte a estos estudiantes qué saben sobre cuadrados y qué técnicas de construcción previas podrían utilizar para abordar este problema.

Pregunte a los estudiantes: «¿Cómo sabes que lo que has construido es un cuadrado?». (Por la construcción de rectas perpendiculares, sabemos que la forma tiene 4 ángulos rectos. Por el compás, sabemos que los 4 lados tienen longitud AB).

Apoyo para estudiantes que aprenden el idioma inglés

Escribir, conversar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para preparar a los estudiantes para el debate de toda la clase proporcionándoles múltiples oportunidades para aclarar sus explicaciones a través de la conversación. Antes de que comience la discusión de toda la clase, dé tiempo a los estudiantes para que se reúnan con 2-3 compañeros para compartir su respuesta a la pregunta: «¿Cómo sabes que lo que construiste es un cuadrado?». Invite a los oyentes a hacer preguntas para aclarar y razonar y a insistir en los detalles y el lenguaje matemático.

Principio(s) de diseño: Optimizar el resultado (para la explicación); cultivar la conversación

ACTIVIDAD DE EXPLORACIÓN | TRATAR DE CIRCUNSCRIBIR

UN CUADRADO (15 minutos)

Rutinas didácticas

Constrúyelo

El propósito de esta actividad es que los estudiantes construyan un cuadrado inscrito en un círculo. Al igual que la construcción del triángulo equilátero inscrito en un círculo, esta construcción proporciona una oportunidad para previsualizar la simetría de rotación.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

Dé a los estudiantes 5 minutos para responder a las preguntas sobre el cuadrado ABCD y luego haga una pausa en la clase para una breve discusión de toda la clase.

INTRODUCCIÓN

Los estudiantes deben llegar a dos conjeturas clave:

• Las diagonales de un cuadrado son bisectrices perpendiculares entre sí.

• Para inscribir un cuadrado en un círculo, las diagonales deben ser diámetros del círculo.

Dé a los estudiantes 5 minutos para terminar la actividad y continúe con un debate de toda la clase.

. Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad

Acción y Expresión: Interiorizar las funciones ejecutivas. Divida esta tarea en partes más manejables para ayudar a los estudiantes que se benefician del apoyo con habilidades organizativas en la resolución de problemas. Por ejemplo, presente una pregunta cada vez y asegúrece de que los estudiantes completen cada paso correctamente antes de pasar al siguiente.

Apoya la accesibilidad para: Organización; atención

1. Aquí está el cuadrado ABCD con la diagonal BD dibujada:

A. Construya un círculo centrado en A con radio AD

B. Construya un círculo centrado en C con radio CD.

C. Dibuje la diagonal AC y escriba una conjetura sobre la relación entre las diagonales BD y AC

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

D. Etiquete la intersección de las diagonales como el punto E y construya un círculo centrado en E con radio EB ¿Cómo se relacionan las diagonales con este círculo?

2. Utiliza tu conjetura y los movimientos de regla y compás para construir un cuadrado inscrito en un círculo.

RESPUESTAS POSIBLES

A. El resultado debería ser un círculo centrado en A que pase por los puntos B y D.

B. El resultado debería ser un círculo centrado en C que pase por los puntos B y D

C. Respuesta de ejemplo: Las diagonales del cuadrado son bisectrices perpendiculares entre sí.

D. El círculo centrado en E de radio EB pasa por todos los puntos del cuadrado, haciendo que las diagonales sean ambos diámetros del círculo.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

¿Estás listo para más?

Algunos estudiantes pueden tener dificultades con el hecho de que, al empezar con el círculo, no tenemos dos puntos marcados ni para construir una recta ni para establecer un radio para un círculo. Pregúntales cómo podemos marcar nuevos puntos que puedan utilizarse en nuestra construcción.

«¿En qué se diferenciaba esta construcción del cuadrado de la actividad anterior?». (Yo empecé con la diagonal en lugar de con un lado).

Conjetura que toda la construcción sigue siendo la misma incluso cuando se rota 1 4 de una vuelta completa (90 grados) alrededor del centro. Esto significa que cada lado se puede girar sobre los otros lados y cada ángulo se puede girar sobre los otros ángulos.

Utiliza movimientos de regla y compás para construir un cuadrado que encaje perfectamente fuera del círculo, de modo que el círculo quede inscrito en el cuadrado. ¿Cómo se comparan las áreas de estos 2 cuadrados?

Respuestas posibles

El área del cuadrado más grande es el doble del área del cuadrado más pequeño.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Recuerda a los estudiantes que ya han construido un triángulo equilátero, un hexágono regular y un cuadrado, cada uno inscrito en un círculo. Cada uno de ellos es un ejemplo de polígono regular, que es un polígono con todos los lados congruentes y todos los ángulos congruentes. Pregunte a los estudiantes: «Partiendo de cualquiera de estas formas, ¿qué técnicas de construcción os ayudarían a hacer otros polígonos regulares inscritos en circunferencias?». (Partiendo de cualquiera de ellos, podemos hacer el doble de lados bisecando los ángulos y marcando los puntos donde las bisectrices de los ángulos se cruzan con el círculo. Podríamos repetir este proceso).

ENFRIAR | CONSTRUIR UNA CASA

(5 minutos)

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Lea el título de esta actividad en voz alta. Dibuje un bosquejo de una casa (cuadrado con un triángulo en la parte superior) para demostrar la expectativa sin revelar ninguna de las marcas de construcción.

Usa el compás y los movimientos de la regla para construir un cuadrado con el segmento BC como uno de los lados.

RESPUESTAS POSIBLES

. Matemáticas . Unidad 1

Respuesta de ejemplo: Construir una recta perpendicular a BC que pase por B. La intersección de la recta con la circunferencia de radio BC centrada en B da un tercer vértice del cuadrado. Repitiendo esta construcción análogamente en C se obtiene el último vértice. Construir el cuadrado de forma que el triángulo quede dentro también es una solución válida.

Resumen de la lección para el estudiante

Podemos usar lo que sabemos sobre líneas perpendiculares y segmentos congruentes para construir muchos objetos diferentes. Un cuadrado está formado por 4 segmentos congruentes que crean 4 ángulos rectos. Un cuadrado es un ejemplo de polígono regular ya que es equilátero (todos los lados son congruentes) y equiángulo (todos los ángulos son congruentes). Aquí hay algunos polígonos regulares inscritos dentro de círculos:

PROBLEMAS

DE PRÁCTICA

PROBLEMA 1

¿Cuál de estas afirmaciones es cierta?

A. Todos los rectángulos son polígonos regulares.

B. Todos los cuadrados son polígonos regulares.

C. Todos los rombos son polígonos regulares.

D. Todos los paralelogramos son polígonos regulares.

Soluciones posibles

Geometría . Matemáticas . Unidad 1

PROBLEMA 2

Este diagrama es una construcción con regla y compás de un cuadrado BACD (no se muestran todas las marcas). La construcción siguió estos pasos:

1. Empezar con dos puntos marcados A y B

2. Usar una regla para construir la recta AB

3. Usar una construcción previa para construir una recta perpendicular a AB que pase por A

4. Usar una construcción previa para construir una recta perpendicular a AB que pase por B

5. Usar un compás para construir un círculo centrado en en A que pase por B

6. Etiquete un punto de intersección de ese círculo y la recta del paso 3 como C

7. Use una construcción previa para construir una recta paralela a AB que pase por C

8. Etiquete la intersección de esa recta y la recta del paso 4 como D

9. Use una regla para construir los segmentos AC, CD y DB

Explica por qué necesitas construir un círculo en el paso 5.

Soluciones posibles

Ejemplo de respuesta: Necesito asegurarme de que AC tiene la misma longitud que AB

PROBLEMA 3

Para construir una recta que pase por el punto C que sea paralela a la recta AB, el primer paso es crear una recta que pase por C perpendicular a AB. ¿Cuál es el siguiente paso?

A. Construir un triángulo equilátero de lado CD

B. Construir una recta que pase por el punto B perpendicular a AB

C. Construir un segmento de igual longitud que AB con extremo C

D. Construye una recta que pase por el punto C perpendicular a CD

Soluciones posibles

PROBLEMA 4

Jada quería construir una recta perpendicular a la recta l que pasara por el punto C. El diagrama muestra su construcción. ¿Cuál fue su error?

Soluciones posibles

Jada construyó una mediatriz en lugar de una recta perpendicular que pasa por el punto C La recta que dibujó es perpendicular a l, pero no pasa por el punto C

PROBLEMA 5

Noé intenta bisecar el ángulo BAC. Dibuja círculos del mismo radio con centros B y C y luego utiliza uno de los puntos de intersección para su semirrecta. ¿Qué error ha cometido Noé en su construcción?

Soluciones posibles

Los segmentos AB y AC tienen longitudes diferentes. La construcción de la bisectriz del ángulo BAC comienza dibujando una circunferencia con centro A y luego utiliza los puntos donde esa circunferencia interseca a las dos semirrectas del ángulo BAC. Esos dos puntos son equidistantes de A. Si usamos puntos que no son equidistantes de A para el resto de la construcción, entonces no biseca el ángulo como muestra la construcción de Noé.

PROBLEMA 6

Aquí hay una construcción con regla y compás. Usa una regla para dibujar un triángulo equilátero en la figura. Explica cómo sabes que el triángulo es equilátero.

Soluciones posibles

Ejemplo de respuesta: El triángulo es equilátero porque todos los círculos de esta construcción tienen radios de la misma longitud. Cada lado está compuesto por dos radios, lo que significa que todos los lados tienen la misma longitud.

PROBLEMA 7

Aquí hay 2 puntos en el plano. Explica cómo construir un segmento de recta que sea la mitad de la longitud del segmento AB

Soluciones posibles

Ejemplo de respuesta: Utiliza una regla para dibujar el segmento AB. Dibuja una circunferencia con centro A que pase por B. Dibuja una circunferencia con centro B que pase por A. Dibuja la recta que pasa por los puntos de intersección de las dos circunferencias. Marca el punto donde esta línea interseca al segmento AB y etiquétalo como C. El segmento AC es la mitad de la longitud de AB

Reflexiones:

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Problemas de triángulos

• Relaciones entre círculos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.12 Hacer construcciones geométricas formales con una variedad de herramientas y métodos (compás y regla, cuerda, dispositivos reflectantes, plegado de papel, programa geométrico dinámico, etc.). Copiar un segmento; copiar un ángulo; bisecar un segmento; bisecar un ángulo; construir rectas perpendiculares, incluida la mediatriz de un segmento de recta; y construir una recta paralela a una recta dada que pase por un punto que no esté en la recta.

G-CO.13 Construir un triángulo equilátero, un cuadrado y un hexágono regular inscrito en un círculo.

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

Estándares ELD de California

I.A.2

I.B.5

I.C.12

LECCIÓN 8

USO DE LA TECNOLOGÍA PARA

CONSTRUCCIONES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

impactar el futuro, dan sentido a los problemas y perseveran en su resolución

OBJETIVO(S) DE APRENDIZAJE

descubren la forma y el espacio.

• Puedo utilizar la tecnología para ayudarme a construir diagramas específicos.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Coordinar (oralmente) herramientas tecnológicas con herramientas de papel y lápiz para construir un diagrama.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Dibújalo

Constrúyelo

MLR8: Apoyos para el debate

Materiales necesarios

Software de geometría dinámica

Preparación necesaria

Adquirir dispositivos que puedan ejecutar GeoGebra (recomendado) u otra tecnología de geometría dinámica. Lo ideal es que cada pareja de estudiantes disponga de un dispositivo. (La aplicación de construcción GeoGebra y la aplicación de geometría están disponibles en las herramientas matemáticas).

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Usemos la tecnología para construir un diagrama.

Narrativa de la lección

Esta lección es opcional.

En esta lección, los estudiantes que no han tenido la oportunidad de involucrarse con la tecnología de geometría dinámica pueden aprender a usarla para hacer un diagrama con herramientas de construcción digital que son análogas a un compás y una regla. Los estudiantes repasan las construcciones que han hecho en papel y avanzan hacia construcciones más complejas facilitadas por la tecnología. El trabajo de esta lección se conecta con el trabajo futuro porque los estudiantes tendrán la oportunidad de utilizar esta tecnología a lo largo del curso. La actividad Brújula digital y construcción con regla se deja abierta y sin estructurar intencionadamente para que los estudiantes tengan la oportunidad de dar sentido a los problemas (MP1).

Anime a los estudiantes a que terminen una actividad antes para jugar, hacer una figura compuesta o recrear un diseño de una lección anterior.

LECCIÓN DE UN VISTAZO

Componente de lección

Estructura Tiempo

Calentamiento En parejas 10 min

Actividad de Exploración Independiente 15 min

Actividad de Exploración Independiente 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Descripción breve

Los estudiantes se familiarizan con las herramientas de construcción dinámica utilizadas para realizar construcciones con tecnología digital.

La actividad requiere el uso de una aplicación digital interactiva para que los estudiantes puedan realizar construcciones utilizando la tecnología.

Los estudiantes realizan una o más construcciones utilizando herramientas digitales.

La actividad requiere el uso de una aplicación digital interactiva para que los estudiantes puedan realizar construcciones utilizando tecnología.

Los estudiantes utilizan la herramienta de recta paralela y la herramienta de recta perpendicular para construir figuras utilizando tecnología digital.

La actividad requiere el uso de una aplicación digital interactiva para que los estudiantes puedan realizar construcciones usando tecnología.

Los estudiantes resumen cómo se puede usar la tecnología para realizar construcciones y discuten los beneficios de usar tecnología.

Los estudiantes analizan los pasos digitales tomados para construir un cuadrilátero e identifican la forma que fue construida.

Práctica Independiente 8-10 min El componente de práctica independiente incluye 9 problemas de la lección.

CALENTAMIENTO | ¿CÓMO FUNCIONAN LAS HERRAMIENTAS DIGITALES

DE CONSTRUCCIÓN? (10 minutos)

Rutinas didácticas

Dibújalo

El propósito de esta actividad es familiarizarse con las herramientas de construcción dinámica para que los estudiantes puedan realizar construcciones utilizando tecnología digital. La aplicación de construcción GeoGebra incluye 9 herramientas de construcción, que pueden replicar todos los movimientos que se pueden hacer con un lápiz, una regla y un compás. También hay 5 herramientas de edición.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2. Proporciona a cada pareja acceso a la tecnología de geometría dinámica. Si los estudiantes utilizan la versión digital de los materiales, muéstreles cómo abrir la aplicación de construcción GeoGebra en las herramientas matemáticas. No es necesario que los estudiantes escriban las respuestas a las preguntas de esta tarea. Deben discutirlas con su compañero.

Abre la aplicación de construcción en las herramientas matemáticas (o en ggbm.at/C9acgzUx).

Prueba todas las herramientas del espacio de trabajo.

1. Encuentra el botón «Deshacer». Deshacer

2. Haz clic en la imagen de 3 segmentos apilados, el menú principal, para guardar su trabajo o ir a una nueva página. Menú principal

3. ¿Qué herramientas hacen el mismo trabajo que una regla?

4. La aplicación de construcción tiene 3 herramientas para hacer un punto. Para conocerlas, abra la aplicación en ggbm.at/cuupdskk. En esta aplicación, se han utilizado todas las 3 herramientas de puntos.

A. Arrastra cada punto y cada recta para ver qué ocurre en la vista «Álgebra» de la derecha.

B. Observa cómo se definen los puntos en la vista «Álgebra» de la izquierda.

C. Explica cómo se relaciona cada definición con el comportamiento del punto correspondiente.

5. Hay varias formas de utilizar la herramienta compás. Primero, configura un espacio de trabajo que se parezca a la imagen:

A. Abre una nueva página en blanco en la aplicación de construcción.

B. Dibuja el círculo A a través del punto B

C. Dibuja el segmento CD que no intersecte el círculo centrado en A

D. Dibuja el punto E que no intersecte el círculo centrado en A o el segmento CD

6. Selecciona la herramienta compás y haz clic en el segmento CD. ¿Qué ocurre?

7. Ahora haz clic en el punto E. ¿Qué ocurre?

8. Haz un nuevo segmento EF que tenga la misma longitud que CD

9. Haz un círculo con el mismo radio que el círculo centrado en A.

10. Explica en qué se parece y en qué se diferencia la herramienta compás digital de un compás físico.

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

Invite a los estudiantes a compartir lo que aprendieron. Si los estudiantes no lo mencionan, señale estos consejos:

• Si se intenta hacer un punto libre muy cerca de un objeto, GeoGebra puede encajar ese punto en el objeto. El punto A en la aplicación fue hecho en un espacio vacío y arrastrado a la recta. Por eso sigue libre.

• La herramienta compás digital puede usarse para dibujar un círculo o para transferir una longitud. Cuando copias una longitud, en realidad estás copiando el radio de un círculo. La herramienta compás te permite definir un radio seleccionando dos puntos, un segmento o incluso otro círculo. Entonces la herramienta arrastrará ese círculo hasta que selecciones un punto para que sea su centro.

ACTIVIDAD DE EXPLORACIÓN | COMPÁS DIGITAL Y CONSTRUCCIÓN CON REGLA

(15 minutos)

Rutinas didácticas

Constrúyelo

MLR8: Apoyos para el debate

En esta actividad, los estudiantes recrean construcciones conocidas utilizando herramientas digitales.

INTRODUCCIÓN

Recuerda a los estudiantes que han hecho cada una de estas construcciones con papel, un lápiz, un compás y una regla en lecciones anteriores. El objetivo es recrear la construcción utilizando las nuevas herramientas. La aplicación de construcción se puede encontrar en ggbm.at/C9acgzUx

Apoyo para estudiantes con discapacidad

Acción y Expresión: Interiorizar las funciones ejecutivas. Comience con una demostración para grupos pequeños o para toda la clase y piense en voz alta en la primera construcción para recordar a los estudiantes cómo construir una mediatriz de un segmento de recta utilizando un compás y una regla. Mantenga la construcción a la vista para que los estudiantes puedan consultarla mientras trabajan. Favorece la accesibilidad para: Memoria; procesamiento conceptual

• Usa la aplicación de construcción del conjunto de herramientas de matemáticas para crear una o más de estas figuras:

• una bisectriz perpendicular del segmento AB

• un triángulo equilátero

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

• un hexágono regular

• un cuadrado

• un cuadrado inscrito en una circunferencia

• dos triángulos rectángulos congruentes que no comparten un lado

Para que tu construcción sea correcta, debe ser imposible arruinarla arrastrando un punto. Asegúrate de probar tus construcciones.

• bisectriz perpendicular https://ggbm.at/x45Q3nQV

• triángulo equilátero https://ggbm.at/mjPd29JZ

• hexágono regular https://ggbm.at/eh9r32hw

• cuadrado https://ggbm.at/gemq2d9f

. Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Invite a algunos estudiantes a compartir sus construcciones. Utilice la prueba de arrastre para demostrar que cada una de ellas es una construcción y no un dibujo basado en una estimación.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: MLR8 Apoyos para el debate. Utilice esta rutina para apoyar la discusión de toda la clase. Para cada construcción que se comparta, pida a los estudiantes que repitan lo que han oído utilizando un lenguaje matemático preciso. Considere dar tiempo a los estudiantes para que repitan lo que han oído a un compañero antes de seleccionar a uno o dos estudiantes para que lo compartan con la clase. Pregunte al orador original si su compañero ha sido capaz de repetir su proceso con precisión. Llame la atención de los estudiantes sobre cualquier palabra o frase que haya ayudado a aclarar la declaración original. De este modo, más estudiantes tienen la oportunidad de producir lenguaje mientras interpretan el razonamiento de otros.

Principio(s) de diseño: Apoyar la creación de sentido

ACTIVIDAD DE EXPLORACIÓN | HERRAMIENTAS DIGITALES MÁS ÚTILES

(10 minutos)

En esta actividad, los estudiantes aprenden a construir más figuras utilizando las herramientas disponibles en un programa completo de geometría dinámica.

«¿Cuántos pasos se necesitarían para construir líneas perpendiculares o paralelas utilizando solo las herramientas digitales que imitan un lápiz, un compás y una regla?». (¡Muchos!). Anime estas construcciones con el botón Reproducir/Pausar en la parte inferior de la aplicacion:

• rectas perpendiculares ggbm.at/AggMCCCc

INTRODUCCIÓN

• rectas paralelas ggbm.at/FbjY5DTr

«Las herramientas de geometría dinámica se han ampliado para construir estos pasos en comandos simples. La aplicación de geometría de GeoGebra (geogebra. org/geometry) tiene comandos para rectas perpendiculares, rectas paralelas y más. Cuando la abra, verá algunas herramientas básicas y en la parte inferior, hay un lugar para hacer clic para MÁS».

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience con una demostración física de la herramienta de línea perpendicular y la herramienta de línea paralela utilizando el programa de geometría dinámica, que proporcionará acceso a los estudiantes para ver las conexiones entre las nuevas situaciones y los conocimientos previos. Pregunta a los estudiantes cómo estas herramientas digitales podrían ayudarles a construir un paralelogramo, un rectángulo, un rombo o un cuadrado.

Apoya la accesibilidad para: Procesamiento conceptual; procesamiento visual-espacial

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Cuando abras la aplicación de geometría de GeoGebra geogebra.org/geometry, verás algunas herramientas básicas. Haz clic en la palabra «MÁS» y verás algunas categorías de herramientas, incluidas las de «Construir».

Herramienta recta perpendicula Herramienta recta paralela

. Matemáticas . Unidad 1

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACIÓN

CONCEPTOS ERRÓNEOS ANTICIPADOS

SÍNTESIS DE ACTIVIDAD

1. Construye una recta o un segmento de recta y un punto adicional que no esté en ella. Luego, prueba las herramientas de recta perpendicular y recta paralela. Usa la herramienta «Mover» para arrastrar algunos puntos y observa qué sucede.

2. Usa cualquiera de las herramientas digitales para crear una o más de estas figuras. Pon a prueba tus construcciones arrastrando un punto.

A. Paralelogramo

B. Rectángulo

C. Rombo

D. Cuadrado

Si los estudiantes están atascados, invítelos a construir la figura en papel o buscar una construcción similar en papel como referencia.

Invite a algunos estudiantes a compartir sus construcciones. Usa la prueba de arrastre para demostrar que cada una es una construcción y no un dibujo basado en una estimación.

SÍNTESIS DE LA LECCIÓN

(5 minutes)

El objetivo de esta lección es que los estudiantes utilicen herramientas tecnológicas para construir un diagrama. Aquí hay algunas preguntas para debatir:

• ¿Cómo se construye un círculo usando tecnología? (Se trazan dos puntos y se usa la herramienta «Círculo» con centro en el punto, o se elige la herramienta «Compás», se define un radio y luego se elige un punto para su centro).

• ¿Cuáles son algunas ventajas de usar tecnología para hacer construcciones geométricas? (Precisión y la capacidad de ver cambios en la construcción al cambiar un elemento, como en la prueba de arrastre).

• ¿Cuándo crees que es apropiado usar tecnología para hacer construcciones geométricas? (Para comprobar una conjetura con un modelo dinámico y ver si siempre es cierta. También sería útil al hacer una construcción muy precisa).

ENFRIARSE | ¿ES UN RECTÁNGULO?

(5 minutes)

A continuacion se presenta una construccion que se puede utilizar para facilitar la disusion en clase1 https://ggbm.at/eZ7NbQxR

Tyler hizo un cuadrilátero siguiendo estos pasos. Cree que parece un rectángulo. Cuando Andre tomó el punto A y lo movió, el cuadrilátero ya no parece un rectángulo.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

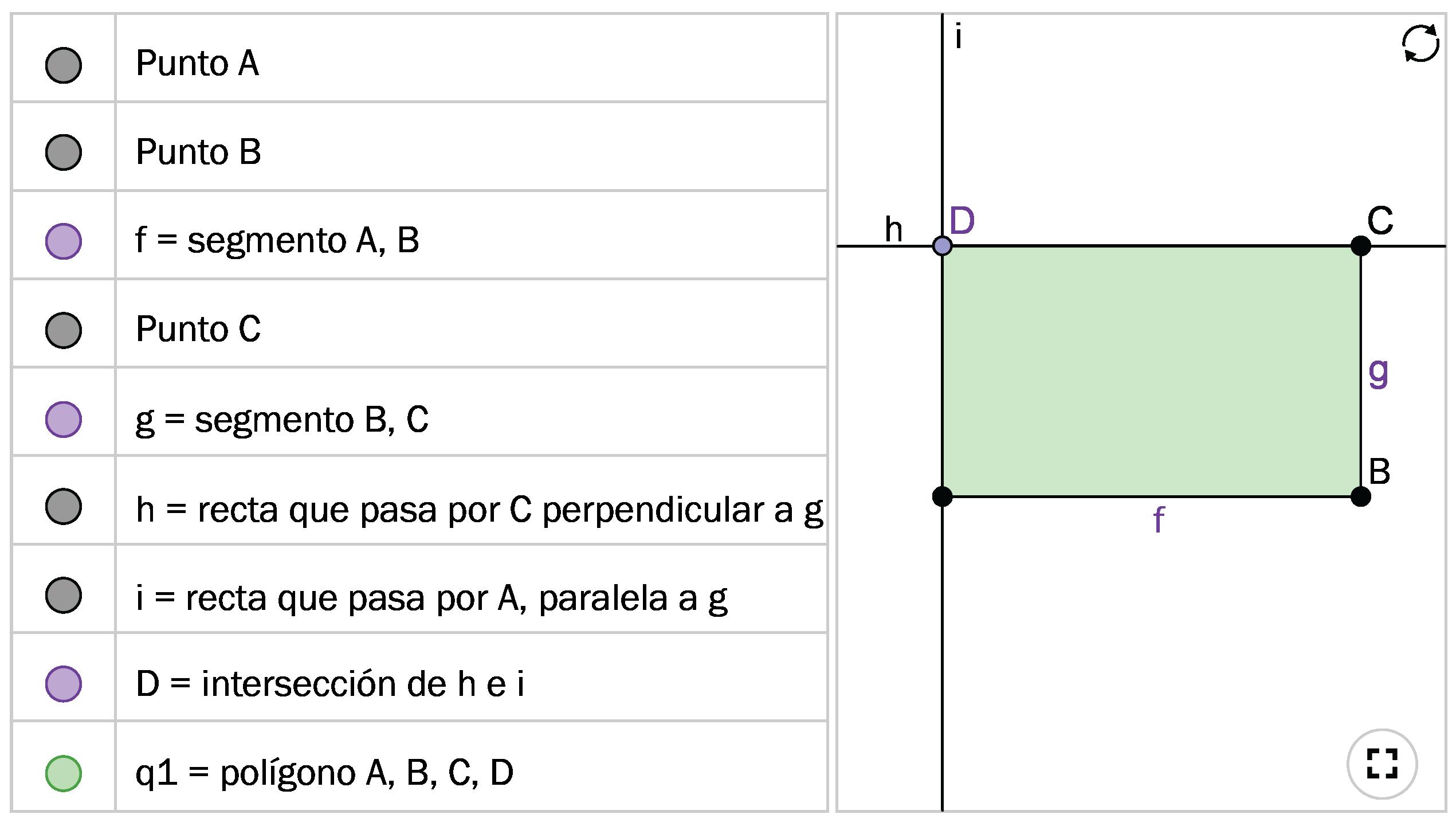
¿Qué figura hizo Tyler? Explica cómo lo sabes.

POSIBLES RESPUESTAS

ABCD es un trapezoide. Las rectas g e i son paralelas, pero las rectas f y h no lo son necesariamente.

. Matemáticas . Unidad 1

Resumen de la lección para el estudiante

Comenzaremos con un pequeño conjunto de herramientas. La aplicación de construcción GeoGebra se encuentra en https://ggbm.at/C9acgzUx. Estas son las herramientas de GeoGebra que realizan las mismas funciones que un lápiz, un compás y una regla.

Tres herramientas lápiz:

Punto libre

Punto trazado sobre objeto

Punto de intersección de objetos

Cuatro herramientas regla: Recta Segmento

Semirrecta

Polígono

Dos herramientas compás:

Círculo con centro a través del punto

Compás

La aplicación GeoGebra Geometría se encuentra en https://www.geogebra.org/geometry. Haz clic en «MÁS» para ver las categorías ocultas de herramientas. En lugar de realizar cada paso de una construcción, GeoGebra Geometría realizará todos los pasos de las construcciones de nuestro inventario. Tiene comandos para líneas perpendiculares, líneas paralelas ¡y más!

Herramienta de recta perpendicular

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Seleccionar todas de las herramientas digitales de construcción que hacen el mismo trabajo que un lápiz solo (sin regla ni compás).

Punto trazado sobre un objeto

Polígono

Círculo con centro a través de punto

Punto de intersección

Recta

PROBLEMA 2

Herramienta de recta paralela

Soluciones posibles

Punto trazado sobre un objeto

Polígono

Círculo con centro a través de punto

Punto de intersección

Recta

¿Cómo puedes comprobar si un diagrama realizado con herramientas digitales es una construcción o solo un dibujo basado en una estimación?

Soluciones posibles

Arrastra un punto libre para ver si cambia la construcción.

. Matemáticas . Unidad 1

PROBLEMA 3

Han pensó que había construido un rectángulo utilizando herramientas digitales. Cuando movió el punto A la pantalla tenía este aspecto. ¿Qué hizo mal Han?

Soluciones posibles

Ejemplo de respuesta: Han usó la herramienta polígono para dibujar un cuadrilátero que parece un rectángulo en lugar de usar herramientas de construcción como el compás, la rectaparalela y la recta perpendicular.

PROBLEMA 4

Selecciona todas las herramientas de construcción digital que hacen el mismo trabajo que una regla.

Círculo con centro a través de punto

Punto trazado sobre un objeto

Punto de intersección

Segmento

Recta

PROBLEMA 5

Soluciones posibles

Círculo con centro a través de punto

Punto trazado sobre un objeto

Punto de intersección

Segmento

Recta

¿Qué herramienta de construcción digital realiza la misma función que un compás?

A. Punto

B. Recta

C. Polígono

D. Círculo con centro a través del punto

Soluciones posibles

PROBLEMA 6

Este diagrama se realizó utilizando herramientas de construcción digital. Uno de estos triángulos se hizo con la herramienta polígono y el otro con la herramienta polígono regular. Explica qué podrías hacer para diferenciarlas.

Soluciones posibles

Ejemplo de respuesta: Arrastra un punto libre en cada figura. En un polígono regular, todos los puntos de vértice se mueven para mantener ángulos congruentes y lados congruentes. En un polígono, solo se moverá el punto arrastrado.

Geometría . Matemáticas . Unidad 1

PROBLEMA 7

¿Qué herramienta de construcción digital le ayudaría a determinar si el punto C o el punto D es el punto medio del segmento AB?

A. Bisectriz del ángulo

B. Bisectriz perpendicular

C. Recta perpendicular

D. Recta paralela

Soluciones posibles

PROBLEMA 8

Aquí se muestra una construcción de un hexágono regular inscrito en un círculo. No se muestran todas las partes de la construcción. Explique cómo construir un triángulo equilátero inscrito en el círculo centrado en A utilizando herramientas de construcción digital

Soluciones posibles

Ejemplo de respuesta: Utiliza la herramienta polígono para construir un polígono con los vértices B, D y F

PROBLEMA 9

A continuación se muestra la construcción de un hexágono regular inscrito en una circunferencia. No se muestran todas las partes de la construcción. Explique cómo construir un polígono regular de 12 lados inscrito en el círculo centrado en A utilizando herramientas de construcción digital

Soluciones posibles

Ejemplo de respuesta: Construye las mediatrices de los lados del hexágono BCDEFG. Marca los puntos de intersección de las mediatrices con la circunferencia. Utiliza la herramienta polígono para dibujar un polígono que conecte los doce puntos marcados en el círculo centrado en A

Reflexiones:

Math Nation California . Geometría

Geometría . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Puntos y formas

• Modelos geométricos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-MG.3 Aplicar métodos geométricos para resolver problemas de diseño.

Construir

N-Q.2 N-Q.3

Enfoque SMPs

MP4 Representar con matemáticas.

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.B.5

I.C.11

II.C.6

LECCIÓN 9

ENTREGA

RÁPIDA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

repercutir en el futuro, representan con las matemáticas descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo construir bisectrices perpendiculares para ayudar a resolver problemas.

• Puedo utilizar mis conocimientos de geometría para resolver problemas.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Elegir métodos geométricos para resolver problemas de diseño.

• Construir bisectrices perpendiculares y explicar (por escrito) cómo se utilizan para resolver problemas.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

Aspectos de la representación matemática

Dibújalo

MLR5: Preguntas de co-elaboración

Materiales necesarios

Copias del original

Programa de geometría dinámico

Preparación necesaria

Adquirir ordenadores o tabletas que puedan ejecutar GeoGebra Geometry de las herramientas matemáticas, con uno por cada 2-3 estudiante. Se recomienda la versión digital para todas las clases en lugar de la versión de papel y lápiz.

Asegúrese de que los estudiantes tengan al menos 4 colores en sus conjuntos de herramientas si van a hacer la versión de papel y lápiz de «¿Quién está más cerca?».

. Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Usemos bisectrices perpendiculares.

Narrativa de la lección

En esta lección, los estudiantes se basan en sus experiencias con bisectrices perpendiculares para responder preguntas sobre la asignación de recursos en una situación del mundo real (MP4). Para completar más pasos en el ciclo de modelización matemática, utiliza la actividad opcional ¿Ahora quién está más cerca? A continuación, los estudiantes estudian una teselación (una disposición de figuras que cubren todo el plano), crean un diagrama de Voronoi aplicando bisectrices perpendiculares y conjeturan que el diagrama de Voronoi de una teselación también es una teselación.

Algunas de las actividades de esta lección funcionan mejor cuando cada estudiante tiene acceso a GeoGebra Geometry from Math Tools, porque los estudiantes están utilizando bisectrices perpendiculares para determinar qué regiones de un mapa están más cerca de determinados puntos. En «¿Quién está más cerca?», hacen esto con 3 y 4 puntos, pero hacerlo con más en «¿Ahora quién está más cerca?» requerirá ayuda de la tecnología.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento En parejas 5 min

Actividad de exploración

En parejas o en pequeños grupos 15 min

Actividad de Exploración En parejas o en pequeños grupos 20 min

Actividad de exploración Independiente 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 5-8 min

Descripción breve

Los estudiantes analizan una imagen de un rectángulo dividido con puntos etiquetados e identifican las cosas que observan y se preguntan.

Los estudiantes utilizan bisectrices perpendiculares para determinar cuál es la mejor manera de dividir un cuadrado que representa una situación del mundo real.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la partición de un cuadrado utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda del uso de la geometría para resolver problemas del mundo real.

Los estudiantes representan datos utilizando la tecnología y el comando Voronoi y explican los beneficios de los resultados de sus datos.

La actividad requiere el uso del programa de geometría, que está disponible en la edición digital del estudiante.

Los estudiantes utilizan bisectrices perpendiculares para mejorar el diseño de una teselación.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la mejora de teselaciones utilizando la tecnología.

Los estudiantes revisan el cuadrado en el calentamiento y discuten en qué contextos del mundo real la partición tendría sentido y cuándo sería injusta.

Los estudiantes explican el diagrama que construyeron en una actividad anterior.

El componente de práctica independiente incluye 4 problemas de repaso de la lección y 3 problemas de repaso en espiral.

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE: PUNTOS EN UN CUADRADO

(5 minutos)

Rutinas didácticas

Observar y preguntarse

En esta actividad, los estudiantes observan y se preguntan sobre una imagen similar a otras que utilizarán a lo largo de esta lección. Cuando los estudiantes expresan lo que observan y se preguntan sobre la imagen, tienen la oportunidad de prestar atención a la precisión del lenguaje que utilizan para describir lo que ven (MP6). Podrían proponer primero un lenguaje menos formal o impreciso y, a continuación, reformular su observación con un lenguaje más preciso para comunicarse con mayor claridad. Los estudiantes examinarán una versión simplificada de este diagrama en la siguiente actividad y después tendrán la oportunidad de interactuar con una versión aún más compleja en la actividad opcional «¿Ahora quién está más cerca?».

INTRODUCCIÓN

Muestre la imagen para que todos la vean. Pida a los estudiantes que piensen en al menos una cosa que les llame la atención y en al menos una cosa que les asombre. Conceda a los estudiantes 1 minuto para pensar en silencio y, a continuación, 1 minuto para comentar con su compañero las cosas que han observado, seguido de un debate con toda la clase.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Proporcionar a los estudiantes una tabla para anotar lo que notan y se preguntan antes de que se espere que compartan estas ideas con los demás.

Apoya la accesibilidad para: Lenguaje; organización

¿Qué observas? ¿Qué te preguntas?

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Cosas que los estudiantes pueden observar:

• Hay 9 puntos en el interior

• El rectángulo grande está dividido en 3 rectángulos más pequeños

• Hay 3 puntos en cada rectángulo pequeño

Cosas que los estudiantes pueden preguntarse:

• ¿Qué representan los puntos?

• ¿Por qué los rectángulos pequeños no son del mismo tamaño?

• ¿Es esta una forma justa de descomponer el espacio?

SÍNTESIS DE LA ACTIVIDAD

Pide a los estudiantes que compartan las cosas que notaron y se preguntaron. Registra y muestra sus respuestas para que todos puedan verlas. Si es posible, anota el razonamiento pertinente en la imagen o cerca de ella. Una vez grabadas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que os estéis preguntando ahora?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria.

ACTIVIDAD DE EXPLORACIÓN | ¿QUIÉN ESTÁ MÁS CERCA?

(15 minutos)

Rutinas didácticas

Aspectos de la representación matemática

Dibújalo

En esta actividad, los estudiantes desarrollan habilidades que les ayudarán en la representación matemática (MP4). Se proporciona el método de representar las tiendas de una ciudad con puntos en un cuadrado, pero los estudiantes tienen que darse cuenta de que pueden utilizar bisectrices perpendiculares para determinar qué tiendas deben responsabilizarse de qué partes de la ciudad. Los estudiantes también tienen que decidir cómo asignar los 100 empleados. Se espera que los estudiantes que no utilicen herramientas digitales para medir áreas aproximen áreas utilizando técnicas de descomposición y estimación. Es probable que los estudiantes que trabajen en papel no tengan tiempo para el análisis de la cuarta tienda; los estudiantes no necesitan ver esta pregunta para participar en la discusión.

Esta actividad funciona mejor cuando cada estudiante tiene acceso a GeoGebra Geometry de las herramientas matemáticas porque llevaría demasiado tiempo hacerlo de otra manera. Si los estudiantes no tienen acceso individual, sería útil proyectar GeoGebra Geometry durante la síntesis.

INTRODUCCIÓN

Invite a los estudiantes a utilizar diferentes colores para sombrear el cuadrado. «Elige 1 color para el punto ��. Sombrea cualquier punto que sepas que está más cerca de �� que de los puntos �� o ��. Repite utilizando un nuevo color para cada uno de los otros 2 puntos». Diga a los estudiantes que ahora examinarán una situación en la que podría aplicarse este sombreado.

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Relacione un concepto nuevo con otro con el que los estudiantes hayan tenido éxito. Por ejemplo, recuerde a los estudiantes la construcción de una mediatriz de un segmento de recta y pregúnteles cómo esta construcción podría ayudarles a dividir la ciudad entre las tres tiendas.

Apoya la accesibilidad para: Habilidades socioemocionales; procesamiento conceptual

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Aquí hay una cuidad con 3 ubicaciones de la misma tienda.

1. La empresa quiere dividir la ciudad en regiones para que, cuando alguien haga un pedido desde una dirección, este se envíe a la tienda más cercana. Te han contratado para decidir cómo dividir la ciudad entre las tres tiendas. Explica o muestra tu razonamiento..

2. Si hay 100 empleados, ¿cómo deberían distribuirse entre las 3 ubicaciones?

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES

1. ¿Hay algún lugar en la ciudad que tenga la misma distancia a todas las 3 tiendas? 2. Ahora se abre una cuarta tienda. Vuelve a dividir la ciudad.

CONCEPTOS ERRÓNEOS PREVISTOS

1. https://www.geogebra.org/m/k8gk6fvz

3. Sí, la intersección de las bisectrices perpendiculares.

SÍNTESIS DE LA ACTIVIDAD

2. El área alrededor del punto �� es aproximadamente 28 % del área total, así que aproximadamente 28 trabajadores. El área alrededor del punto �� es aproximadamente 40 % del área total, así que aproximadamente 40 trabajadores. Esto deja la tienda en el punto �� con aproximadamente 32 trabajadores.

Si a un estudiante le cuesta empezar, pídale que piense qué pasaría si solo hubiera 2 tiendas. Pídales que piensen en su experiencia de las lecciones sobre técnicas de construcción y si pueden encontrar una manera de separar los puntos que están más cerca de una de las dos tiendas de los puntos que están más cerca de la otra tienda. Si un estudiante está atascado encontrando el área en papel, anímele a dividir las formas en piezas más simples o a estimar, dependiendo del tiempo. Si un estudiante se atasca para encontrar el área en la aplicación, muéstrele la herramienta de área en el menú de medidas (busque el icono del ángulo).

El propósito de esta discusión es destacar el nivel de confianza de los estudiantes en la exactitud del modelo. Pide a los estudiantes que compartan cómo decidieron dividir la ciudad y cómo utilizaron esa información para decidir cuántos empleados colocar en cada tienda.

. Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

CONTINUACIÓN

Si los estudiantes no lo plantean, pregunte si sería apropiado asignar 28.2 trabajadores a un lugar. (No, dos décimos de persona no tiene sentido. Sí, si alguien pasara parte de su semana en un lugar y parte en otro distinto).

Si los estudiantes no lo plantean, mencione que utilizar el área para asignar los 100 trabajadores supone que la población de la ciudad está distribuida uniformemente dentro de sus límites. Pregunte a los estudiantes cómo cambiarían su forma de pensar si supieran que los barrios más cercanos a la esquina superior izquierda son los más densamente poblados de la ciudad.

¿Estás preparado para más?

En 1854, hubo un brote de cólera en Londres. Un médico llamado John Snow pensó que el suministro de agua podía ser el responsable. Hizo un mapa que mostraba la ubicación de todas las bombas de agua de la ciudad y las ubicaciones de todas las muertes por cólera en la ciudad. ¿Cómo podría haber utilizado las ideas de esta actividad para ayudar a aislar la causa del brote?

Los diagramas que hiciste en la actividad y que hizo Snow se llaman diagramas de Voronoi y siguen siendo estudiados activamente por los matemáticos.

Respuestas de los estudiantes

Ejemplo de respuesta: Podría haber dividido la ciudad según qué regiones estaban más cerca de qué bombas de agua. Entonces podría haber observado que casi todas las muertes se produjeron en la región más cercana a una bomba de agua en particular.

ACTIVIDAD DE EXPLORACIÓN | ¿AHORA QUIÉN ESTÁ MÁS

CERCA?

(20 minutos)

Rutinas didácticas

Aspectos de la representación matemática

Dibújalo

MLR5: Preguntas Co-Craft

Esta actividad es opcional porque solo se ofrece en formato digital.

En esta actividad, los estudiantes continúan desarrollando habilidades que les ayudarán en la modelización matemática (MP4). Los estudiantes tienen la oportunidad de elegir los datos que les gustaría modelizar. A continuación, se les encomienda la tarea de explicar a alguien interesado en los datos lo que significan los resultados de su diagrama.

Una buena fuente de mapas para esta actividad es la página web de un municipio o estado. La mayoría de los municipios tienen un SIG, un Sistema de Información Geográfica, con mapas de diversas características de la región. Para el ejemplo siguiente, se han utilizado los lugares de aterrizaje del Life Star (helicóptero de emergencia) en una pequeña ciudad. Los estudiantes deben guardar sus imágenes como archivos jpg o png para GeoGebra Geometry.

Demuestre cómo utilizar el comando Voronoi en la aplicación GeoGebra Classic en el conjunto dehHerramientas matemáticas o en geogebra.org/classic. Comienza importando la imagen con la Herramienta Imagen, situada en el menú desplegable con el icono del deslizador.

INTRODUCCIÓN

INTRODUCCIÓN CONTINUACIÓN

GeoGebra asignará los puntos �� y �� como las posiciones inferior izquierda y derecha de la imagen. Desplázate y haz zoom para colocar y dimensionar el mapa de forma que quepa en la pantalla.

Ahora utiliza la herramienta de punto para marcar cada punto de interés en el mapa. Esta técnica de partición es tan común que GeoGebra tiene una función incorporada para ello. Se llama así por Georgy Voronoi, el matemático ucraniano del siglo XIX que definió este proceso.

Antes de que podamos usar el comando Voronoi, necesitamos poner nuestros puntos de interés en una lista. En la barra de entrada, escriba «list1={» y comience a enumerar los puntos de su mapa, sin incluir los dos puntos que mantienen la imagen en su lugar. Probablemente tendrá una lista que comienza con el punto ��. Escriba el resto de sus puntos, separados por comas, y cierre el «}» para terminar la lista.

Luego, en la barra de entrada, escriba, «Voronoi[list1]» e ingrese.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar, leer: MLR5 Preguntas Co-Craft. Utilice esta rutina para crear un espacio para que los estudiantes produzcan el lenguaje de las preguntas matemáticas sobre mapas. Antes de demostrar cómo utilizar el comando Voronoi, muestre un mapa local (o el ejemplo de Life Star) y pida a los estudiantes que escriban posibles preguntas matemáticas que podrían hacerse sobre el mapa. Invite a los estudiantes a comparar sus preguntas antes de continuar con el resto de la actividad. Principio(s) de diseño: Maximizar la metaconciencia; apoyar la creación de sentido

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

1. Utiliza el programa de geometría dinámica para crear un diagrama de Voronoi a partir de un mapa.

2. ¿A quién podría interesar esta información?

3. Escribe una carta a la persona u organización, explicando lo que el diagrama les dice sobre el mapa que elegiste.

RESPUESTAS POSIBLES CONTINUACIÓN

SÍNTESIS DE LA ACTIVIDAD

1. Pilotos de helicópteros de emergencia

2. Estimados pilotos de helicópteros de emergencia, he elaborado un diagrama que muestra los puntos de aterrizaje Life Star más cercanos a cualquier punto de la ciudad. Para utilizar este diagrama, busque su ubicación en el mapa. El punto de aterrizaje más cercano es el que se encuentra en el mismo polígono que su ubicación actual. Si se encuentra en un borde, hay dos puntos de aterrizaje igualmente cercanos. Si su ubicación está en un vértice, hay tres o más sitios igual de cerca, así que elija el que más le guste. Espero que este mapa sea útil la próxima vez que necesites aterrizar en algún sitio rápidamente!

Pida a los estudiantes que compartan sus respuestas y muéstrelas a la vista de todos. Pregunte a los estudiantes:

• «¿En qué se parece esta actividad a la anterior?». (Seguimos dividiendo el mapa en las regiones más cercanas a los puntos de interés dados).

• «¿En qué se diferencia?». (Hay muchos más puntos. Los puntos representan algo diferente).

ACTIVIDAD DE EXPLORACIÓN | OTRA CAPA

(15 minutos)

Rutinas didácticas

Dibújalo

Esta actividad se basa en la actividad «Quién está más cerca» empleando la misma técnica de encontrar las regiones que están más cerca de ciertos puntos y decorar esas regiones para crear patrones nuevos e interesantes.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Entregue a cada estudiante un teselado de la plantilla maestra. Diga a los estudiantes que un teselado es un patrón regular repetido de una o más formas que cubren todo el plano. Diga a los estudiantes que, para ahorrar tiempo, está bien que utilicen papel plegado o que hagan estimaciones en lugar de utilizar técnicas formales de construcción con regla y compás para hacer bisectrices perpendiculares.

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience con una demostración física de la técnica de plegado de papel para construir bisectrices perpendiculares, a fin de establecer conexiones superficiales entre situaciones nuevas y conocimientos previos. Pregunte a los estudiantes cómo esta técnica de plegado de papel podría ayudarles a definir las regiones más cercanas a cada uno de los puntos de intersección del teselado.

Apoya la accesibilidad para: Procesamiento conceptual; procesamiento visual-espacial

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Tu maestro te dará un teselado.

1. Marca los puntos de intersección en el teselado.

2. Imagina que cada punto es una tienda de la actividad «¿Quién está más cerca?». Repite el proceso que utilizaste allí para definir las regiones más cercanas a cada uno de los puntos.

3. Utiliza el color o el sombreado para realzar tu diseño.

RESPUESTAS POSIBLES

Ejemplo de respuesta: (A partir del teselado de octógonos y cuadrados)

SÍNTESIS DE LA ACTIVIDAD

Muestre las respuestas de los estudiantes para que todos las vean. Invite a los estudiantes a debatir si su nuevo diagrama es un teselado.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Muestre de nuevo la imagen del calentamiento. Invite a los estudiantes a pensar en qué contextos tendría sentido la partición actual del cuadrado. (Si la mayoría de la gente vive en el centro de la ciudad, entonces tendría sentido que los puntos del centro sirvieran a una zona más pequeña. Por ejemplo, podrían ser lugares de votación y todo el mundo tiene una opción algo cerca, pero dividen el centro de la ciudad, por lo que en ningún sitio habría una cola demasiado larga). A continuación, invite a los estudiantes a debatir en qué contextos esa división sería injusta. (Si la gente está repartida por igual, entonces es injusto que algunas personas tengan que ir a un colegio electoral lejano solo porque su colegio más cercano está al otro lado de la línea divisoria).

ENFRIAMIENTO | ESCRIBIR UNA CARTA

(5 minutos)

Los estudiantes que no tuvieron la oportunidad de escribir una carta en «Ahora, ¿quién está más cerca?» pueden hacerlo en esta actividad.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Escribe una carta al propietario de la empresa que tiene 4 tiendas en la ciudad. Explícale lo que les dice el diagrama que has dibujado. Pídele toda la información que necesites para decidir cómo distribuir 100 los empleados entre las 4 tiendas.

Estimado propietario de la empresa, El mapa de la ciudad le muestra qué tienda está más cerca de cada parte de la ciudad. Cuando reciba un pedido, busque la dirección en el mapa. Habrá una tienda en la misma región que la dirección, sin que el repartidor cruce ningún segmento. Si la dirección está en un borde, entonces hay dos tiendas a la misma distancia y cualquiera de ellas puede entregarlo.

Para saber cuál es la mejor forma de distribuir los 100 empleados, necesito información sobre qué región tiene el mayor número de clientes. Cuantos más pedidos procedan de una determinada sección del mapa, más personas deberán trabajar en la tienda de esa sección.

Resumen de la lección para el estudiante

Un teselado es una disposición de figuras que cubre todo el plano sin huecos ni superposiciones. Un ejemplo sencillo es una cuadrícula cuadrada. Esto significa que el papel cuadriculado es una teselación. Aquí tienes otra teselación hecha de cuadriláteros. ¿Puedes ver cómo repitiendo este patrón se podría cubrir todo el plano?

Una forma de dibujar un nuevo teselado es descomponer el plano en las regiones más cercanas a cada vértice. Este método utiliza bisectrices perpendiculares y se denomina diagrama de Voronoi. También es un teselado. ¿Qué aspecto tendría este patrón cuando se extiende para cubrir todo el plano?

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

¿Qué construcción se puede utilizar para determinar si el punto �� está más cerca del punto �� o del punto ��?

A. Construir el triángulo ��

B. Construir una recta perpendicular al segmento AB que pase por el punto ��

C. Construir la bisectriz del ángulo ��

D. Construir la mediatriz del segmento ��

PROBLEMA 2

Soluciones posibles D

El diagrama es una construcción con regla y compás. Las rectas ℓ, �� y �� son las bisectrices perpendiculares de los lados del triángulo ��. Selecciona todas las afirmaciones verdaderas.

El punto �� está más cerca del punto �� que del punto ��

El punto �� está más cerca del punto �� que del punto �� o del punto ��

Soluciones posibles

El punto �� está más cerca del punto �� que del punto ��

El punto �� está más cerca del punto �� que del punto �� o del punto ��

. Matemáticas . Unidad 1

PROBLEMA 3

Descompón la figura en las regiones más próximas a cada vértice. Explica o muestra tu razonamiento.

Soluciones posibles

Para dividir los triángulos en estas regiones, construye la mediatriz de cada segmento. Las mediatrices se cruzan y dividen cada triángulo en tres regiones. Los puntos de cada región son los más cercanos al vértice de esa región.

PROBLEMA 4

¿Qué construcción podría utilizarse para construir un triángulo isósceles �� dado el segmento de recta ��?

A. Marcar un tercer punto �� que no esté en el segmento ��. Dibujar los segmentos �� y ��

B. Marcar un punto �� en el segmento �� y construir una recta perpendicular a �� que pase por el punto ��. Dibujar los segmentos �� y ��

C. Construir la mediatriz del segmento ��. Marcar la intersección de esta recta con �� y etiquetar ��. Dibuja los segmentos �� y ��

D. Construir la mediatriz del segmento ��. Marcar cualquier punto �� en la mediatriz excepto donde interseca ��. Dibujar los segmentos �� y ��

Soluciones posibles

PROBLEMA 5

Selecciona todas las afirmaciones verdaderas sobre polígonos regulares.

Todos los ángulos son rectos.

Todos los ángulos son congruentes.

Todas las longitudes de los lados son iguales.

Hay exactamente 4 lados.

Hay al menos 3 lados

Soluciones posibles

Todos los ángulos son rectos.

Todos los ángulos son congruentes.

Todos los lados son iguales.

Hay exactamente 4 lados.

Hay al menos 3 lados

PROBLEMA 6

Este diagrama muestra el principio de la construcción de un rectángulo con regla y compás. La construcción siguió estos pasos:

A. Empezar con dos puntos marcados �� y ��

B. Usar una regla para construir la línea ��

C. Usar una construcción previa para construir una línea perpendicular a �� que pase por ��

D. Utilizar una construcción anterior para construir una recta perpendicular a �� que pase por ��

E. Marcar un punto �� en la recta perpendicular a �� que pase por �� Explica los pasos necesarios para completar esta construcción.

Soluciones posibles

Ejemplo de respuesta: Construir una recta perpendicular a �� que pase por el punto ��. Marcar el punto de intersección de esta recta con la recta perpendicular a �� que pasa por �� y etiquetarlo como ��. Dibujar los segmentos ��, �� y ��

PROBLEMA 7

Este diagrama es una construcción con regla y compás. ¿Es importante que la circunferencia con centro �� pase por �� y que la circunferencia con centro �� pase por ��? Muestra o explica tu razonamiento.

Soluciones posibles

Ejemplo de respuesta: No, podría cambiar el radio de estos círculos para que el de centro �� no contenga �� y el de centro �� no contenga ��. Es importante que estos círculos tengan el mismo radio. También es importante que el radio sea lo suficientemente grande como para que los dos círculos se encuentren en un par de puntos.

Reflexiones:

LECCIÓN 10

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.2 Representar transformaciones en el plano; describir transformaciones como funciones que toman puntos en el plano como entradas y dan otros puntos como salidas. Comparar transformaciones que preservan distancia y ángulo con aquellas que no lo hacen.

G-CO.5 Dada una figura geométrica y una rotación, reflexión o traslación, dibujar la figura transformada. Especificar una secuencia de transformaciones que llevarán una figura dada a otra.

Construir

8.G.2

Enfoque SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

Estándares ELD de California

I.A.3

I.B.5 I.C.12

TRANSFORMACIONES RÍGIDAS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

predecir lo que podría ocurrir,

(SMPs) ¿Cómo? ... los estudiantes...

construyen argumentos viables y criticar el razonamiento de los demás

OBJETIVO(S) DE APRENDIZAJE

(CC) ¿Qué? ... mientras...

desmontar enteros, unir partes y descubrir la forma y el espacio.

• Dada una figura y la descripción de una transformación, puedo dibujar la imagen de la figura después de la transformación.

• Puedo describir la secuencia de transformaciones necesarias para llevar una figura a otra figura.

• Sé que las transformaciones rígidas dan como resultado figuras congruentes.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender que las transformaciones rígidas producen figuras congruentes preservando la distancia y los ángulos.

• Dibujar el resultado de una transformación (en lenguaje escrito) de una figura dada.

• Explicar (oralmente y por escrito) una secuencia de transformaciones para llevar una figura dada a otra.

PREPARACIÓN DE LECCIONES

Rutinas didácticas

Observar y preguntarse

Conjunto de herramientas de geometría (HS)

Dibujar

MLR3: Aclarar, criticar, corregir Piensa, haz coincidir, comparte

Materiales necesarios

Conjunto de herramientas de geometría (HS)

. Matemáticas . Unidad 1

PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN

Preparación requerida

Cada estudiante necesitará 4 colores diferentes para «¿Qué es lo mismo?», así que asegúrese de que los juegos de herramientas de geometría tengan suficientes lápices de colores.

Cree una exhibición de la tabla de referencia para que todos la vean. Deberá permanecer expuesta durante el resto del año. Antes de esta lección, la tabla de referencia estará en blanco. La tabla de referencia en blanco se incluye como un patrón de línea negra, así como una copia para el maestro de una versión completada. El objetivo del cuadro de referencia es que los estudiantes lo utilicen como referencia a la hora de elaborar argumentos formales. A lo largo del curso, los estudiantes irán añadiendo elementos. Cada afirmación que hagan debe estar respaldada por referencias a afirmaciones, definiciones o teoremas de la tabla de referencia.

Si imparte varias secciones de este curso, considere la posibilidad de ocultar las entradas del cuadro de referencia de la clase y mostrarlas en el momento oportuno, en lugar de mostrarlas varias veces.

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje del estudiante

• Vamos a dibujar algunas transformaciones.

Narrativa de la lección

Esta lección se basa en los conocimientos previos sobre congruencia para reforzar la idea de que los movimientos rígidos, traslaciones, reflexiones, y rotaciones conservan las distancias y los ángulos. Estos movimientos y las secuencias de los movimientos, llamados transformaciones rígidas, afectan a todo el plano, pero los estudiantes se centran generalmente en una sola figura y su imagen (el resultado de una transformación). Los estudiantes también recuerdan que la definición de congruente son dos figuras cualesquiera en las que existe una secuencia de traslaciones, rotaciones y reflexiones que lleva la primera figura a la segunda. En esta lección, los estudiantes estudian las transformaciones sobre una cuadrícula y, en lecciones posteriores de esta unidad, aprenden definiciones precisas de los movimientos rígidos que se aplican fuera de la cuadrícula. El estudio de la geometría de coordenadas se reserva para una unidad posterior. Los estudiantes trabajan en una cuadrícula isométrica para empujarlos hacia la necesidad de definiciones precisas.

Durante esta lección, los estudiantes se centran en las traslaciones y las reflexiones. Aunque los estudiantes pueden mencionarlas, las rotaciones no se definen hasta una lección posterior. Los estudiantes determinan que diferentes secuencias de movimientos rígidos pueden dar como resultado la misma imagen y que cuando las secuencias se reordenan, a veces no dan como resultado la misma imagen. Esta idea refuerza el concepto de transformaciones como funciones, al tiempo que prepara a los estudiantes para razonar sobre secuencias de transformaciones, además de sobre movimientos individuales. Los estudiantes presentan argumentos y critican los argumentos de otros cuando comparan estrategias para encontrar secuencias de transformaciones rígidas que llevan una figura sobre otra (MP3).

En este punto, los estudiantes toman como definición la distancia entre un punto y una recta como la distancia a lo largo de la perpendicular. En una unidad posterior, los estudiantes demostrarán que el camino más corto entre un punto y una recta es a lo largo de la perpendicular.

La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes elijan usar la tecnología apropiada para resolver problemas. Recomendamos que la tecnología esté disponible.

LECCIÓN DE UN VISTAZO

Componente de lección Estructura Tiempo

Calentamiento En parejas 10 min

Actividad de exploración Independiente 15 min

Actividad de Exploración En parejas 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 5-8 min

Descripción breve

Los estudiantes analizan una imagen de formas que representan una secuencia de transformaciones e identifican cosas que notan y se preguntan.

Los estudiantes activan sus conocimientos previos sobre transformaciones dibujando y comparando transformaciones rígidas.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la realización de transformaciones rígidas utilizando la tecnología.

Los estudiantes descubren cómo el orden de una secuencia de transformaciones puede afectar a la imagen resultante.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar secuencias de transformaciones rígidas usando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda del orden de una secuencia de transformaciones rígidas.

Los estudiantes resumen sus ideas de transformaciones rígidas y registran las definiciones para transformación rígida y congruente

Los estudiantes dibujan la imagen resultante de reflejar la figura original sobre una línea.

El componente de práctica independiente incluye 3 problemas de repaso de la lección y 3 problemas de repaso de la espiral.

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE:

TRANSFORMADO (10 minutos)

Rutinas didácticas

Observar y preguntarse

El propósito de este calentamiento es provocar la idea de que algunas formas pueden describirse como transformaciones de otras formas, lo que será útil cuando los estudiantes especifiquen secuencias de transformaciones rígidas que llevan una figura sobre otra en las siguientes actividades. Aunque los estudiantes pueden fijarse y preguntarse muchas cosas sobre estas imágenes, el punto de discusión importante es que las transformaciones rígidas llevan lados a lados de la misma longitud y ángulos a ángulos de la misma medida.

INTRODUCCIÓN

Muestre la imagen para que todos la vean. Pida a los estudiantes que piensen en al menos una cosa que noten y en al menos una cosa que se pregunten. Conceda a los estudiantes 1 minuto de tiempo para pensar en silencio y, a continuación, 1 minuto para comentar las cosas que observan con su compañero, seguido de un debate con toda la clase.

100

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Proporcione a los estudiantes una tabla para anotar lo que notan y se preguntan antes de que se espere que compartan estas ideas con los demás.

Apoya la accesibilidad para: Lenguaje; organización

¿Qué observas? ¿Qué te preguntas?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Cosas que los estudiantes pueden observar:

• El paralelogramo S puede reflejarse en el otro paralelogramo M

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

• Los paralelogramos S y M son congruentes.

• El punto A está a 2 espacios tanto del punto O como del punto E.

• Hay puntos A, B, C y D

• Hay puntos A', B', C' y D'.

Cosas que los estudiantes pueden preguntarse:

• ¿Qué transformaciones utilizaron?

• ¿Es D similar a S?

• ¿Tienen las formas la misma área?

• ¿Son iguales las longitudes de los lados?

• ¿Cómo se pronuncia A'?

• ¿Por qué se utilizan las mismas letras dos veces?

Pida a los estudiantes que compartan las cosas que notaron y se preguntaron. Registre y muestre sus respuestas para que todos puedan verlas. Si es posible, anota el razonamiento pertinente en la imagen o cerca de ella. Una vez grabadas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que se pregunten ahora?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones y señalar información contradictoria.

Si las secuencias de transformaciones rígidas o las medidas correspondientes no surgen durante la conversación, pida a los estudiantes que discutan esta idea. Refuerce que debido a que los tamaños, las formas y los ángulos no cambiaron de la Figura S a la Figura M, esa transformación se llama una transformación rígida. Pero la transformación de la figura S a la figura D no es una transformación rígida porque el tamaño cambió.

Si la diferencia entre A y A' no surge durante la conversación, pida a los estudiantes que discutan esta idea y dígales que A' se pronuncia «A prima». Explique que ABCD se llama la figura original y A'B'C'D' se llama la imagen de la transformación.

ACTIVIDAD DE

EXPLORACIÓN | ¿QUÉ ES LO

MISMO?

(15 minutos)

Rutinas didácticas

Herramientas de geometría (HS)

El objetivo de esta actividad es activar los conocimientos previos de los estudiantes sobre las transformaciones rígidas. Los estudiantes también ven que la imagen de un polígono viene determinada por las imágenes de cada uno de sus vértices. Los estudiantes construyen hacia el concepto de que las transformaciones son funciones que toman puntos como entradas y producen puntos como salidas de manera que las distancias y los ángulos se conservan.

Dé a los estudiantes 3 minutos de tiempo tranquilo para trabajar, luego haga una pausa para una breve discusión de toda la clase.

INTRODUCCIÓN

Invite a un estudiante a demostrar cómo utilizar papel de calco para traducir. Recomiende a los estudiantes que empiecen con los bordes del papel de calco paralelos a los lados del papel para que puedan ver si inclinan accidentalmente el papel de calco mientras traducen. Invite a los estudiantes a definir traslación (Una traslación tiene una distancia y una dirección. Desplaza todos los puntos de una figura a la distancia y en la dirección indicadas).

Muestre la imagen del ejercicio de calentamiento con marcas de construcción. Invite a los estudiantes a definir reflexión. (Cada punto de la figura termina al otro lado de la línea de reflexión y a la misma distancia de la línea). Si los estudiantes no lo mencionan, señale que las marcas de construcción son líneas perpendiculares a la línea de reflexión.

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Mantenga a la vista términos y vocabulario importantes. Durante el lanzamiento, dedique tiempo a repasar los siguientes términos de lecciones anteriores a los que los estudiantes necesitarán acceder para esta actividad: transformación rígida, imagen, traslación, reflejo y congruente.

Apoya la accesibilidad para: Memoria; lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Dibuja cada transformación rígida en un color diferente.

1. Traslada figura S a lo largo del segmento de recta en la dirección indicada por la flecha.

Color:

2. Refleja la figura S a lo largo de la recta y

Color:

3. Refleja la figura S a lo largo de la recta m

Color:

4. Traslada la figura S a lo largo del segmento de recta w en la dirección mostrada por la flecha. Refleja esta imagen a través de la recta y.

Color:

5. ¿En qué se parecen las imágenes? ¿En qué se diferencian?

Los colores varían.

1. Verde

2. Rojo

3. Rojo claro

4. Verde claro (la imagen intermedia es amarilla)

5. Respuesta de ejemplo: Todas las imágenes son congruentes. Las imágenes reflejadas tienen una orientación diferente.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Algunos estudiantes pueden tener problemas para reflejar en la cuadrícula isométrica. Pida a estos estudiantes que utilicen papel de calco para doblar a través de la línea de reflexión y encontrar la imagen.

Si los estudiantes están atascados en cuanto a cómo traducir cuando w no está conectado a un vértice de la figura, recuerde a los estudiantes que w les está diciendo la dirección y la distancia, pero la ubicación no importa.

La idea importante para la discusión es que las transformaciones rígidas preservan las distancias y los ángulos. Muestre el trabajo de un estudiante para que todos lo vean y pregunte:

• Para la reflexión de S a través de la recta y, ¿cómo se comparan las longitudes laterales de S con las longitudes laterales correspondientes en su imagen? (Las longitudes son iguales).

• ¿Cuáles son las medidas del ángulo en la esquina superior izquierda de S? ¿Cómo se compara con la medida del ángulo correspondiente en cualquiera de las imágenes de S? (Este ángulo y todas sus imágenes miden 120 grados).

ACTIVIDAD DE EXPLORACIÓN | ¿IMPORTA EL ORDEN?

(10 minutos)

Rutinas Instruccionales

Dibújalo

MLR3: Aclarar, criticar, corregir

Piensa, haz coincidir, comparte

El propósito de esta actividad es observar que el orden de las transformaciones en una secuencia de transformaciones puede tener un efecto en la imagen.

Monitoree a los estudiantes que definen una secuencia que funciona incluso cuando se invierte el orden para compararla con los estudiantes cuyas secuencias no funcionan cuando se invierte el orden durante la discusión.

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Recuerde a los estudiantes que si hay una secuencia de transformaciones rígidas que lleva una figura sobre otra, las figuras se llaman congruentes. Diga a los estudiantes que hay muchas respuestas posibles para las preguntas. Después de un tiempo de trabajo en silencio, pida a los estudiantes que comparen sus respuestas con las de sus compañeros y decidan si ambas son correctas, aunque sean diferentes. Continúe con un debate con toda la clase. Si los estudiantes tienen dificultades después de varios minutos, invítelos a compartir los movimientos rígidos que necesitarán. (Reflexión porque la figura B tiene forma de L y la figura C se puede girar para que parezca una L, pero la figura A no). Sugiéreles que empiecen cada secuencia con una reflexión y que luego utilicen una traslación.

Apoyo para estudiantes que aprenden el idioma inglés

Leer, escribir: MLR3 Aclarar, criticar, corregir. Presente un primer borrador de la descripción de una secuencia de transformaciones que llevarán la figura A a la figura B: «Le di la vuelta y la deslicé». Promueva el debate preguntando: «¿Cuáles fueron los pasos que dio el autor?». Pida a los estudiantes que aclaren y corrijan el enunciado. Los enunciados mejorados deben incluir algunos de los siguientes elementos: una distancia dirigida para una traslación, especificar qué punto se lleva a qué punto como resultado de una traslación, las palabras «traslación» y «reflexión», la recta sobre la que se refleja la figura A. Esto ayudará a los estudiantes a desarrollar descripciones de transformaciones.

Principio(s) de diseño: Maximizar la metaconciencia; optimizar la salida (para la explicación)

Apoyo para estudiantes con discapacidad

Comprimiso: Interiorizar la autorregulación. Demostrar que da y recibe comentarios constructivos. Utilizar un proceso estructurado y mostrar marcos de frases para apoyar la retroalimentación productiva. Por ejemplo, «Este método funciona / no funciona porque...», «Otra estrategia sería porque...» y «¿Hay otra manera de decir/hacer...?». Apoya la accesibilidad para: Habilidades socioemocionales; organización; lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Aquí hay 3 formas congruentes L en una cuadrícula.

1. Describe una secuencia de transformaciones que lleve la figura A a la figura B.

2. Si inviertes el orden de tu secuencia, ¿seguirá llevando la secuencia inversa A a B?

3. Describe una secuencia de transformaciones que lleve la figura A a la figura C

4. Si inviertes el orden de tu secuencia, ¿seguirá la secuencia inversa llevando A a C?

1. Ejemplo de respuesta: Refleja a través de la recta ℓ (dibujada en el diagrama), luego traslada a la izquierda 2 unidades.

2. Ejemplo de respuesta: Sí

3. Ejemplo de respuesta: Refleja a través de la línea m (dibujada en el diagrama), luego traslada por v (dibujada en el diagrama).

4. Ejemplo de respuesta: No.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

¿Estás listo para más?

Invertir la secuencia significa utilizar los mismos pasos, pero el paso 2 se convierte en el paso 1. Por ejemplo, (1) reflejar a través de la recta ℓ; luego (2) trasladar a la izquierda 2 unidades se convertiría en (1) trasladar a la izquierda 2 unidades luego (2) reflejar a través de la recta ℓ

Seleccione estudiantes previamente identificados para que compartan sus respuestas. Resalte que invertir los pasos en una secuencia de transformaciones a veces da como resultado la misma transformación y a veces da como resultado una transformación diferente.

1. Construye algunos ejemplos de secuencias de dos transformaciones rígidas que lleven la figura A a una nueva figura D donde invertir el orden de la secuencia también lleve la figura A a la figura D

2. Haz algunas conjeturas sobre cuándo invertir el orden de una secuencia de dos transformaciones rígidas sigue llevando una figura al mismo lugar.

Posibles respuestas

1. Ejemplo de respuesta: Traslada 5 unidades a la izquierda. Luego traslada 2 unidades a la derecha.

2. Respuestas de ejemplo: Si cada transformación es una traslación; si cada transformación es una rotación a través del mismo punto; si cada transformación es una reflexión y las dos rectas de reflexión son perpendiculares; si una transformación es una reflexión en una recta y la otra es traslación por un segmento dirigido en una dirección paralela a la recta.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Pregunte a los estudiantes: «¿Qué ideas importantes aprendiste sobre las transformaciones rígidas?». (El resultado se denomina imagen. La imagen es congruente con la figura original).

Muestre el cuadro de referencia en blanco para que todos lo vean y entregue 1 copia de la plantilla maestra del cuadro de referencia en blanco a cada estudiante. Explica que, para escribir argumentos convincentes, deben apoyar sus afirmaciones con hechos. La tabla de referencia es una forma de llevar un registro de esos hechos para poder consultarlos en el futuro cuando intenten demostrar nuevos hechos. Pida a los estudiantes que añadan una afirmación y una definición a sus tablas de referencia mientras usted las añade a la tabla de referencia de la clase:

Una transformación rígida es una traslación, reflexión, rotación o cualquier secuencia de las tres.

Las transformaciones rígidas llevan las rectas a rectas, los ángulos a ángulos de la misma medida y los segmentos a segmentos de la misma longitud.

(Afirmación)

Una figura es congruente con otra si existe una secuencia de traslaciones, rotaciones y reflexiones que lleva la primera figura exactamente a la segunda figura.

La segunda figura se denomina imagen de la transformación rígida.

(Definición)

Cada entrada del cuadro de referencia incluye una afirmación, un diagrama y un tipo. Los tipos serán aserciones, definiciones y teoremas. Explica que una afirmación es una observación que parece ser cierta, pero que no está demostrada. El hecho de que las transformaciones rígidas siempre llevan rectas a rectas, ángulos a ángulos de la misma medida y segmentos a segmentos de la misma longitud parece ser cierto, pero no hay forma de demostrarlo o refutarlo. Así que, avanzando, pueden afirmar que las transformaciones rígidas tienen estas propiedades y averiguar qué se deduce de ese punto de partida. Recuerde a los estudiantes que antes conjeturaron que la mediatriz de un segmento es el conjunto de puntos que están a la misma distancia de cada extremo. Ellos podrían escribir esto como una afirmación basada en sus experimentos, pero verán en la próxima unidad que en realidad es posible demostrar que es cierto basándose en la afirmación que acaban de hacer sobre las transformaciones rígidas. La geometría suele ser más interesante cuando se intenta conectar el mayor número posible de ideas con unas pocas afirmaciones de partida.

ENFRIAMIENTO | ¿CÓMO SE LLEGA HASTA ALLÍ?

(5 minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Refleja el cuadrilátero ABCD a través de la recta f

RESPUESTAS POSIBLES

. Matemáticas . Unidad 1

Resumen de la lección para el estudiante

Una figura se llama congruente con otra figura si existe una secuencia de traslaciones, rotaciones y reflexiones que lleva una de las figuras a la otra. Esto se debe a que las traslaciones, rotaciones y reflexiones son movimientos rígidos. Cualquier secuencia de movimientos rígidos se llama transformación rígida . Una transformación rígida es una transformación que no cambia las medidas de ninguna figura. Con una transformación rígida, figuras como los polígonos tienen lados correspondientes de la misma longitud y ángulos correspondientes de la misma medida.

El resultado de cualquier transformación se llama imagen. Los puntos de la figura original son las entradas de la secuencia de transformación y se nombran con letras mayúsculas. Los puntos de la imagen son las salidas y se nombran con mayúsculas y un apóstrofo, que se denomina «prima». Hay muchas formas de demostrar que 2 figuras son congruentes, ya que muchas secuencias de transformaciones llevan una figura a la misma imagen. Sin embargo, el orden importa en un conjunto de instrucciones. A veces podemos cambiar 2 pasos en una secuencia y obtener el mismo resultado, pero otras veces, cambiando 2 pasos se obtiene una imagen diferente. Estas 2 secuenciases de transformaciones tienen los puntos A, B y C como entradas y los puntos A″, B″ y C″ como salidas. Cada paso en las secuencias de transformaciones rígidas crea un triángulo que es congruente con el triángulo ABC

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Aquí hay 4 triángulos que han sido transformados cada uno por una transformación diferente. ¿Qué transformación no es una transformación rígida?

Soluciones posibles

Geometría . Matemáticas . Unidad 1

PROBLEMA 2

¿Cuál es la definición de congruencia?

A. Si dos figuras tienen la misma forma, entonces son congruentes.

B. Si dos figuras tienen la misma área, entonces son congruentes.

C. Si hay una secuencia de transformaciones que llevan una figura a otra, entonces son congruentes.

D. Si hay una secuencia de rotaciones, reflexiones y traslaciones que llevan una figura a la otra, entonces son congruentes.

Soluciones posibles

PROBLEMA 3

Hay una secuencia de transformaciones rígidas que lleva A a A', B a B' y C a C'. La misma secuencia lleva D a D'. Dibuja y etiqueta

D':

PROBLEMA 4

Soluciones posibles

Tres escuelas están situadas en los puntos A, B y C. El distrito escolar quiere situar su nuevo estadio en un lugar que esté aproximadamente a la misma distancia de todas las 3 escuelas. ¿Dónde deberían construir el estadio? Explica o muestra tu razonamiento.

Soluciones posibles

Ejemplo de respuesta: Construir el estadio lo más cerca posible de la intersección de las mediatrices de los lados del triángulo ABC Dibuja el triángulo ABC. Construye la mediatriz de cada lado del triángulo. Estas rectas se intersecan en un punto que está a la misma distancia de cada vértice del triángulo.

PROBLEMA 5

Para construir una recta que pase por el punto C y que sea paralela a la recta AB, Han construyó la mediatriz de AB y luego trazó la recta CD

¿Está garantizado que CD es paralela a AB? Explica cómo lo sabes.

Soluciones posibles

No. Ejemplo de respuesta: Las líneas de Han solo parecen paralelas. Nada en esta construcción garantiza que las líneas no se crucen. Una forma de construir una recta paralela a AB, es empezar con una recta que pase por C que sea perpendicular a AB. Entonces se garantiza que una recta perpendicular a esa recta es paralela a la recta AB

PROBLEMA 6

Este diagrama es una construcción con regla y compás de una recta perpendicular a la recta AB que pasa por el punto C todas las afirmaciones que deben ser ciertas.

AD = BD

EC = AD

AC = DC

EA = ED

ED = DB

CB = AD

Soluciones posibles

AD = BD

EC = AD

AC = DC

EA = ED

ED = DB

CB = AD

Reflexiones:

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.4 Desarrollar definiciones de rotaciones, reflexiones y traslaciones en términos de ángulos, círculos, líneas perpendiculares, líneas paralelas y segmentos de línea.

Construir

8.G.1 G-CO.1 G-CO.12

Construir

G-CO.9 G-CO.10

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.1

I.C.12

II.C.6

LECCIÓN 11

DEFINICIÓN DE LOS REFLEJOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir

atienden a la precisión, construyen argumentos viables y critican el razonamiento de los demás

OBJETIVO(S) DE APRENDIZAJE

desmontan enteros, juntan piezas y descubren la forma y el espacio.

• Puedo describir una reflexión especificando la línea de reflexión.

• Puedo dibujar reflexiones.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender que el término «reflexión» (en lenguaje escrito y oral) requiere especificar una línea de reflexión.

• Determinar si una figura es reflexión de otra.

• Dibujar reflexiones de figuras.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

¿Cuál no pertenece?

MLR4: Tarjetas de brechas informativas

Dibújalo

Material necesario

Recortes preimpresos, recortados a partir de copias de la plantilla maestra.

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Reflejemos algunas figuras.

Narrativa de la lección

En grados anteriores, los estudiantes han verificado experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones. En esta lección, los estudiantes se basan en estas experiencias y en sus construcciones con regla y compás para definir rigurosamente reflexiones como transformaciones que llevan cada punto de una figura a un punto directamente opuesto a él al otro lado de la línea de reflexión y a la misma distancia de la línea de reflexión. En una lección anterior, los estudiantes conjeturaron que la mediatriz de un segmento es igual al conjunto de puntos que equidistan de los extremos del segmento. Esta conjetura se utiliza para motivar la definición de reflexión. Los estudiantes utilizarán la definición de reflexión para demostrar teoremas en esta unidad y en las siguientes. Cuando los estudiantes analizan un error sobre reflexiones, están criticando el razonamiento de otros y elaborando sus propios argumentos viables (MP3).

La actividad de la brecha de información podría tomar más tiempo de lo esperado ya que es la primera del curso, en cuyo caso, esta lección podría abarcar dos días.

LECCIÓN DE UN VISTAZO

Componente de lección Estructura Tiempo

Calentamiento Grupos pequeños 5 min

Actividad de exploración En parejas 20 min

Actividad de Exploración Independiente 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Descripción breve

Los estudiantes observan 4 figuras de un segmento y una línea que se intersecan y razonan cuál no corresponde.

Los estudiantes piden y proporcionan la información necesaria para resolver problemas que involucran reflexiones.

Los estudiantes usan herramientas de construcción para reflejar con precisión puntos e imágenes a través de una línea sin usar una cuadrícula de coordenadas.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar las propiedades de las reflexiones usando la tecnología.

Los estudiantes discuten la definición de una reflexión y cómo la definición puede ser usada para probar conjeturas hechas previamente.

Los estudiantes analizan una muestra estudiantil de una reflexión para identificar y corregir el error o errores cometidos.

Práctica Independiente 8-10 min El componente de práctica independiente incluye 3 problemas de repaso en clase y 4 problemas de repaso en espiral.

. Matemáticas . Unidad 1

CALENTAMIENTO | ¿CUÁL NO PERTENECE? CRUZANDO LA LÍNEA

(5 minutos)

Rutinas didácticas

¿Cuál no pertenece?

Este calentamiento pide a los estudiantes que comparen cuatro cifras. Da a los estudiantes un motivo para utilizar el lenguaje con precisión (MP6). Ofrece al maestro la oportunidad de escuchar cómo los estudiantes utilizan la terminología y hablan de las características de los elementos en comparación con los demás.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTEA

Organice a los estudiantes en grupos de 2-4. Exponga las cifras para que todos las vean. Conceda a los estudiantes 1 un minuto de reflexión en silencio y, a continuación, un tiempo para compartir sus ideas con su pequeño grupo. En sus pequeños grupos, pida a cada estudiante que comparta su razonamiento de por qué un elemento en particular no pertenece, y juntos, encuentren al menos una razón por la que cada elemento no pertenece.

¿Cuál no pertenece?

Figura 1

Figura 2

Figura 3

Figura 4

RESPUESTAS POSIBLES

Ejemplos de respuestas:

La figura 1 no pertenece porque:

• El segmento que cruza la recta ℓ no es perpendicular a ℓ

La figura 2 no pertenece porque:

• Las distancias a ambos lados de ℓ no son iguales.

• No hay marcas de graduación.

La figura 3 no pertenece porque:

• Los puntos están etiquetados C y C'

La figura 4 no pertenece porque:

• La longitud total del segmento que cruza ℓ no es 10 unidades.

SÍNTESIS DE LA ACTIVIDAD

Pida a cada grupo que comparta una razón por la que un elemento en particular no pertenece. Registre y muestre las respuestas para que todos las vean. Después de cada respuesta, pregunta a la clase si están de acuerdo o en desacuerdo. Dado que no hay una única respuesta correcta a la pregunta cuál no pertenece, atienda a las explicaciones de los estudiantes y asegúrese de que las razones dadas sean correctas. Durante el debate, pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como «reflexión». Además, presione a los estudiantes sobre las afirmaciones sin fundamento.

ACTIVIDAD DE EXPLORACIÓN | BRECHA INFORMATIVA: ¿QUÉ SENTIDO TIENE? REFLEXIONES (20 minutos)

Rutinas didácticas

MLR4: Tarjetas de brecha de información

Esta es la primera actividad de brecha informativa del curso. Consulte la introducción para obtener instrucciones ampliadas para facilitar esta actividad con éxito.

Esta actividad de brecha informativa ofrece a los estudiantes la oportunidad de explorar las propiedades de las reflexiones antes de definirlas oficialmente.

La estructura de la brecha informativa requiere que los estudiantes den sentido a los problemas determinando qué información es necesaria y, a continuación, pidan la información que necesitan para resolverlo. Esto puede requerir varias rondas de discusión si sus primeras peticiones no aportan la información que necesitan (MP1). También les permite refinar el lenguaje que utilizan y hacer preguntas cada vez más precisas hasta que obtienen la información que necesitan (MP6).

A continuación se presenta el texto de las tarjetas para referencia y planificación:

Diga a los estudiantes que continuarán estudiando las transformaciones, solo que ahora sin una cuadrícula.

Esta es la primera vez que los estudiantes hacen la rutina de instrucción Tarjetas de brecha de información, por lo que es importante demostrar la rutina en una discusión de toda la clase antes de que hagan la rutina entre ellos.

INTRODUCCIÓN CONTINUACIÓN

Explique la rutina de la brecha informativa: los estudiantes trabajan con un compañero. Un compañero recibe una tarjeta de problema con una pregunta que no tiene suficiente información dada y el otro compañero recibe una tarjeta de datos con información relevante para la tarjeta de problema. Los estudiantes se hacen preguntas como «¿Qué información necesitas?». y se espera que expliquen lo que harán con la información. Una vez que el compañero con la tarjeta del problema tiene suficiente información para resolver el problema, ambos compañeros pueden mirar la tarjeta del problema y resolver el problema de forma independiente. Este gráfico ilustra un marco para la rutina:

Diga a los estudiantes que, en primer lugar, se realizará una demostración con toda la clase. Como clase, ellos desempeñan el papel de la persona con la tarjeta de problema mientras que usted desempeña el papel de la persona con la tarjeta de datos. Explique a los estudiantes que es tarea de la persona con la tarjeta de problema (en este caso, toda la clase) pensar qué información necesitan para responder a la pregunta. Muestre una imagen del enunciado de la tarea (la colección de puntos, junto con los pasos para la persona con la tarjeta del problema y la tarjeta de datos) junto con la pregunta:

Se ha reflejado el triángulo TDG de modo que los vértices de la imagen estén etiquetados como puntos. ¿Cuál es la imagen del triángulo TDG?

Pregunte a los estudiantes: «¿Qué información específica necesitas para averiguar cuál es la imagen del triángulo?». Seleccione a los estudiantes para que formulen sus preguntas. Responda a cada pregunta con: «¿Por qué necesitas esa información?». Una vez que los estudiantes justifiquen su pregunta, solo responda a las preguntas si pueden responderse utilizando estos datos.

• La imagen de A es G y la imagen de G es A.

• La imagen de D es D.

• La imagen de N es N.

• La imagen de V es I y la imagen de I es V.

• La imagen de L es Q y la imagen de Q es L.

INTRODUCCIÓN CONTINUACIÓN

. Matemáticas . Unidad 1

Explique que si la persona de la tarjeta del problema pide información que no está en la tarjeta de datos (¡incluida la respuesta!), entonces la persona de la tarjeta de datos debe responder: «No tengo esa información». Pida a los estudiantes que expliquen a su compañero (usted) cómo han utilizado la información para resolver el problema. (Como D y N se llevan a sí mismas por la reflexión, la recta ND debe ser la recta de reflexión. Puesto que la imagen de T es un punto etiquetado, el punto J es el único punto que tiene sentido como su imagen cuando se refleja a través de ND. La imagen del triángulo TDG cuando se refleja a través de la recta ND es el triángulo JDA). El hecho de que la imagen y la figura original se solapen puede resultar confuso para los estudiantes. Si los estudiantes no lo mencionan, pídales que reflejen cada punto individualmente y luego observen el resultado final. Organice a los estudiantes en grupos de 2. En cada grupo, distribuya una tarjeta de problema a un estudiante y una tarjeta de datos al otro. Después de revisar su trabajo en el primer problema, entrégueles las tarjetas para un segundo problema e indíqueles que cambien los papeles. Anima a los estudiantes a que anoten su diagrama.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: Esta actividad utiliza la «Brecha de información» MLR4 para dar a los estudiantes un propósito para discutir la información necesaria para resolver problemas que implican . Muestre preguntas o iniciadores de preguntas para los estudiantes que necesiten un punto de partida como: «¿Puedes decirme...? (dato concreto)» y «¿Por qué necesitas saber... (esa información)».

Principio(s) de diseño: Cultivar la conversación

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Muestre o proporcione a los estudiantes una copia física de las instrucciones escritas. Compruebe la comprensión invitando a los estudiantes a reformular las instrucciones con sus propias palabras. Mantenga las instrucciones visibles durante toda la actividad.

Favorece la accesibilidad para: Memoria; organización

Tu maestro te dará una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu compañero.

Si tu maestro te da la tarjeta de datos:

1. Lee en silencio la información de tu tarjeta.

2. Pregunta a tu compañero «¿Qué información específica necesitas?». y espera a que tu compañero te pida información. Da solo la información que aparece en tu tarjeta. (¡No averigües nada por tu compañero!).

3. Antes de dar la información a tu compañero, pregúntale «¿Por qué necesitas saber (ese dato)?».

4. Lee la tarjeta del problema y resuelve el problema.

Lee la tarjeta del problema y resuélvelo de forma independiente.

5. Comparte la tarjeta de datos y discute tu razonamiento.

Si tu maestro te da la tarjeta del problema:

1. Lee en silencio tu tarjeta y piensa qué información necesitas para responder a la pregunta.

2. Pide a tu compañero la información específica que necesitas.

3. Explica a tu compañero cómo estás utilizando la información para resolver el problema.

4. Cuando tengas suficiente información, comparte la tarjeta del problema con tu compañero y resuelve el problema de forma independiente.

5. Lee la tarjeta de datos y discute tu razonamiento.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Problema 1: La imagen del triángulo GEN es el triángulo GJU

Problema 2: La línea de reflexión es ND.

El propósito de la discusión es enfatizar que la recta de reflexión parece ser la bisectriz perpendicular de los segmentos que conectan la figura original con la imagen. Muestre la conjetura de que el conjunto de puntos que están a la misma distancia de dos puntos dados es la mediatriz del segmento que une esos dos puntos. Pregunte: «¿Qué deberíamos esperar ver si hiciéramos segmentos que conectaran los puntos con sus imágenes?». (Deberíamos esperar ver que la recta de reflexión es la mediatriz de todos los segmentos que conectan puntos con imágenes). Pida a los estudiantes que lo comprueben experimentalmente dibujando segmentos que conecten puntos con imágenes a partir de su tarjeta de datos y de la recta de reflexión. Aquí tiene algunas preguntas adicionales para debatir. Elija en función del tiempo y de la comprensión de los estudiantes de la lección anterior:

• «¿Qué tipo de preguntas fueron las más útiles de hacer?». (¿Cuál es la imagen de este punto? ¿Qué puntos no se mueven?).

• «¿Hubo alguna pregunta que no estaba seguro de cómo responder?». (¿Cuál es la recta de reflexión? No tenía esa información exacta, pero podía deducirla a partir de los puntos que no se movían). Tenga en cuenta que la persona con la tarjeta de datos solo debe proporcionar información, no hacer suposiciones. Pero está bien ayudar diciendo: «Yo no tengo esa información; solo tengo información sobre las imágenes de los puntos».

• «¿Cómo sabes si un punto está en la línea de reflexión?». (Las reflexiones dejan los puntos sobre la recta de reflexión fijos donde están).

• «¿Qué notas sobre los puntos y sus imágenes?». (El punto original y la imagen están en lados opuestos de la recta a la misma distancia. Si un punto se lleva a otro punto, entonces el segundo punto también se lleva al primer punto).

• «¿Cómo puedes comprobar si un punto y su imagen están a la misma distancia de la línea de reflexión?». (Si construimos una circunferencia centrada en cualquier punto de la recta de reflexión que pase por el punto original, también debería pasar por la imagen).

. Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | TRIÁNGULO EN EL

ESPEJO

(15 minutos)

Rutinas didácticas

Dibújalo

En esta actividad, los estudiantes utilizan lo que saben sobre la construcción de rectas perpendiculares para determinar dónde debe tomar un punto una reflexión. Esta actividad refuerza la comprensión de los estudiantes sobre las reflexiones sin referencia a una cuadrícula de coordenadas. Reconocer que la reflexión lleva un punto a otro punto situado a la misma distancia de la recta y que la distancia entre un punto y una recta se mide sobre la recta perpendicular, conduce a una definición rigurosa de las reflexiones que utilizarán para demostrar teoremas en las siguientes lecciones. Vigila las estrategias que utilizan los estudiantes para determinar la imagen del punto C, incluyendo:

• Construir círculos centrados en 2 o más puntos en m que pasen por el punto C. El punto C' será la intersección común de todos estos círculos porque los puntos de m están cada uno a la misma distancia de C que de C'

• Construir una línea perpendicular a m que pase por C y luego marcar un punto que esté a la misma distancia de m que C

Poner a disposición de los estudiantes un programade geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Si los estudiantes tienen acceso a un programa de geometría dinámico, sugiérales que podría ser una herramienta útil en esta actividad. Pide a los estudiantes que utilicen la herramienta de construcción GeoGebra, o navega en esta URL: https://www.geogebra.org/m/VQ57WNyR. Dado que el propósito de esta actividad es explorar las propiedades de las reflexiones, GeoGebra Geometry no es una herramienta apropiada, mientras que GeoGebra Constructions sí lo es.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Divida esta tarea en partes más manejables para apoyar a los estudiantes que se benefician del apoyo con habilidades organizativas en la resolución de problemas. Por ejemplo, presente una pregunta cada vez y asegúrese de que los estudiantes completan cada paso correctamente antes de pasar al siguiente. Apoya la accesibilidad para: Organización; atención

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Kiran empezó reflejando el triángulo CDE a través de la línea m. Hasta ahora, sabe que la imagen de D es D' y la imagen de E es E'. 1. Anota el diagrama para mostrar cómo reflejó el punto D. 2. Usa movimientos de regla y compás para determinar la ubicación de C'. Luego sombrea ligeramente el triángulo C'D'E'. 3. Escribe un conjunto de instrucciones sobre cómo reflejar cualquier punto P a través de una recta dada ℓ.

Geometría . Matemáticas . Unidad 1

ENUNCIADO DE TAREA DEL ESTUDIANTE CONTINUACIÓN

1. Elena encontró C' incorrectamente. Elena está convencida de que el triángulo C'D'E' «se ve bien». Explica a Elena por qué su C' no es un reflejo del punto C a través de la línea m Diagrama de Kiran Diagrama de Elena

1. Respuesta de muestra:

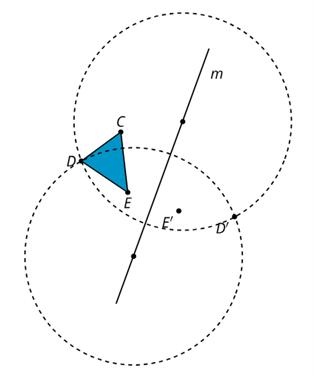
2. Respuesta de muestra:

RESPUESTAS POSIBLES

3. Ejemplos de respuestas:

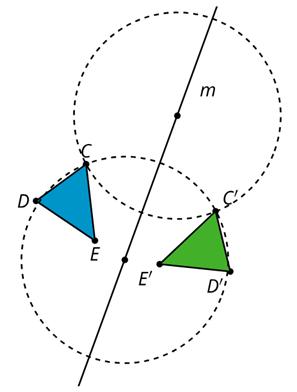
• Cualquier punto de ℓ estará a la misma distancia de P que P'. Elige dos puntos A y B en la línea ℓ y usa un compás para hacer círculos centrados en A y B con radios AP y BP. Los dos puntos de intersección de estos círculos son P y P'

• La recta ℓ es un conjunto de puntos que están a la misma distancia de P que de P'. Esto significa que ℓ es la mediatriz de PP'. Construya una recta perpendicular a ℓ que pase por P y llámela n. Etiquete el punto de intersección de ℓ y n como M. Utilice un compás para crear un círculo centrado en M de radio MC. Los puntos de intersección de este círculo con n son P y P'.

Nation California . Geometría

. Matemáticas . Unidad 1

RESPUESTAS POSIBLES CONTINUACIÓN

CONCEPTOS ERRÓNEOS PREVISTOS

1. Ejemplos de respuestas:

• Utilizando movimientos de regla y compás para construir una recta perpendicular a m que pase por el punto C muestra que C' de Elena no es un reflejo de C

• Utilizando un compás, los puntos de m no están a la misma distancia de C' de Elena que de C

• Dibuja el segmento entre C y C' de Elena y usa papel de calco para mostrar que los ángulos formados donde el segmento CC' se encuentra con m no son todos congruentes y, por lo tanto, no 90 grados.

Si un estudiante tiene problemas para empezar, sugiérale que conecte E con E' y pregúntele qué nota sobre las distancias a la línea. Si siguen atascados, pídales que marquen algún punto en la recta de reflexión y piensen en la distancia desde ese punto a E y E'.

SÍNTESIS DE LA ACTIVIDAD

La idea importante para la discusión es que la línea m es la mediatriz de los segmentos que conectan cada punto de la figura original con su imagen. Recuerde a los estudiantes que la distancia entre un punto y una recta es la distancia perpendicular, por lo que para que una reflexión dé puntos a la misma distancia, necesitan utilizar una perpendicular.

Pida a los estudiantes que compartan sus estrategias para localizar C'. Si los estudiantes no lo mencionan, discuta la estrategia de construir una recta perpendicular a m que pase por C' y marque el punto que está a la misma distancia de m que C

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Explique a los estudiantes que han utilizado herramientas para explorar las reflexiones, pero que para poder demostrar si las conjeturas que han hecho son ciertas, necesitan tener una definición precisa de reflexión. Esta definición les ayudará a explicar por qué una reflexión garantiza que un punto se traslade a otro. Pida a los estudiantes que añadan esta definición a su tabla de referencia al mismo tiempo que usted la añade a la tabla de referencia de la clase:

Reflexión A a través de la recta m.

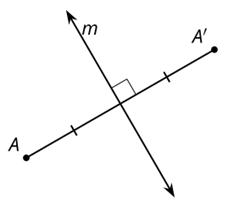
Reflexión es una transformación rígida que lleva un punto a otro punto que está a la misma distancia de la recta dada, se encuentra al otro lado de la recta dada y de modo que el segmento que va del punto original a la imagen es perpendicular a la recta dada.

Reflejar (objeto) a través de la recta (nombre)

. Matemáticas . Unidad 1

ENFRIAMIENTO | ¿QUÉ SALIÓ MAL? REFLEXIÓN (5 minutos)

Lin intentó reflejar el triángulo ABC a través de la recta t. Ella sabe que algo salió mal porque la imagen no es congruente con la figura original.

1. ¿Cuál es una idea que Lin probablemente entiende acerca de las reflexiones?

2. ¿Cuál es una idea que Lin no entiende acerca de las reflexiones?

3. Reflejar el triángulo ABC correctamente.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

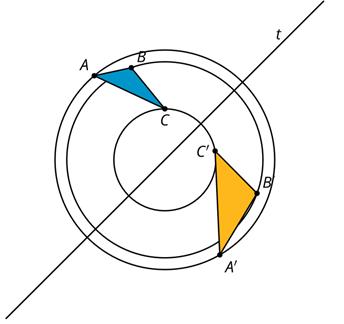
1. Lin probablemente entiende que la imagen debe estar a la misma distancia de la recta que la figura original.

2. Ejemplos de respuestas:

• Lin no entiende que la imagen debe estar a la misma distancia de todos los puntos de la recta, no solo de uno.

• Lin no entiende que los segmentos que conectan la figura original con la imagen deben ser perpendiculares a la línea.

RESPUESTAS POSIBLES

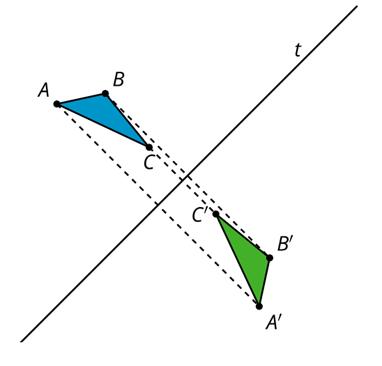
Geometría . Matemáticas . Unidad 1

Resumen de la lección para el estudiante

Piensa en reflejar el punto A a través de la recta ℓ:

La imagen A' está en algún lugar al otro lado de ℓ desde A. La línea ℓ es el límite entre todos los puntos que están más cerca de A y todos los puntos que están más cerca de A'. En otras palabras, ℓ es el conjunto de puntos que están a la misma distancia de A que de A'. En una lección anterior, conjeturamos que el conjunto de puntos que están a la misma distancia de A que de A' es la mediatriz del segmento AA'. Utilizando una técnica de construcción de una lección anterior, podemos construir una recta perpendicular a ℓ que pase por A:

A' se encuentra sobre esta nueva recta a la misma distancia de ℓ que A:

Definimos la reflexión a través de la recta ℓ como una transformación que lleva cada punto A a un punto A' como sigue: A' se encuentra en la recta que pasa por A que es perpendicular a ℓ, está al otro lado de ℓ y está a la misma distancia de ℓ que A. Si A resulta estar en la recta ℓ, entonces A y A' se encuentran en el mismo lugar (ambos están a una distancia de cero de la recta ℓ).

Nation California . Geometría

. Matemáticas . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

¿Cuál de estas construcciones formaría una recta de reflexión que llevase el punto A al punto B?

A. Construir la mediatriz del segmento AB

B. Construir una recta que pase por B perpendicular al segmento AB

C. Construir la recta que pasa por A y B

D. Construir una recta paralela a la recta AB

PROBLEMA 2

Un punto P permanece en el mismo lugar cuando se refleja sobre la recta ℓ

¿Qué puedes concluir acerca de P?

PROBLEMA 3

Las rectas ℓ y m son perpendiculares con punto de intersección P

Soluciones posibles A

Soluciones posibles

El punto P debe estar sobre la recta ℓ porque de lo contrario se mueve de un lado de ℓ al otro.

Noah dice que una rotación de 180 grados, con centro P, tiene el mismo efecto sobre los puntos del plano que la reflexión sobre la recta m. ¿Estás de acuerdo con Noah? Explica tu razonamiento.

Soluciones posibles

Ejemplo de respuesta 1: Noah no está en lo cierto. Para un punto Q en la recta ℓ, girar 180 grados con centro P tiene el mismo efecto que reflejar sobre la línea m. Pero si Q se encuentra en m pero no en ℓ, entonces la reflexión sobre la recta m deja Q en el mismo lugar mientras que la rotación de 180 grados con centro P lleva Q al otro lado de la recta ℓ

Respuesta de ejemplo 2: Noah no es correcta. La reflexión sobre la recta m lleva una recta con pendiente positiva por P a una recta con pendiente negativa. La rotación por 180 grados con centro P lleva estas líneas de vuelta a sí mismas. m ⊥ ℓ

Geometría . Matemáticas . Unidad 1

PROBLEMA 4

Geometría, unidad 1, lección 10

Aquí hay 4 triángulos que han sido transformados cada uno por una transformación diferente. ¿Qué transformación no es una transformación rígida?

Soluciones posibles

PROBLEMA 5

Geometría, unidad 1, lección 4

Hay una secuencia de transformaciones rígidas que lleva A a A', B a B' y C a C'. La misma secuencia lleva D a D'

Dibuje y etiquete D':

Nation California . Geometría

Soluciones posibles

C. D.

Geometría . Matemáticas . Unidad 1

PROBLEMA 6

Geometría, unidad 1, lección 9

Aquí hay 3 puntos en el plano. Explica cómo determinar si el punto C está más cerca del punto A o del punto B

PROBLEMA 7

Geometría, unidad 1, lección 7

Soluciones posibles

Ejemplo de respuesta: Utiliza una regla para trazar el segmento de recta AB. Construye la mediatriz de AB. Si el punto C se encuentra en la mediatriz, está a la misma distancia de los puntos A y B. Si el punto C se encuentra en el mismo lado de la mediatriz que el punto B, entonces está más cerca del punto B. En caso contrario está más cerca de punto A

Diego dice que un cuadrilátero con 4 lados congruentes es siempre un polígono regular. Mai dice que nunca lo es. ¿Estás de acuerdo con alguno de ellos?

Soluciones posibles

No. Ambos están equivocados. Si un cuadrilátero con 4 lados congruentes también tiene 4 ángulos rectos, entonces será un polígono regular.

Reflexiones:

Geometría . Matemáticas . Unidad 1

LECCIÓN 12

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.4 Desarrollar definiciones de rotaciones, reflexiones y traslaciones en términos de ángulos, círculos, líneas perpendiculares, rectas paralelas y segmentos de recta.

Construir

8.G.1 8.G.3

Construir

G-CO.9

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

Estándares ELD de California

I.A.1

I.A.3

II.C.6

DEFINICIÓN DE TRADUCCIONES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

dar sentido al mundo y predecir lo que podría ocurrir,

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

construyen argumentos viables y criticar el razonamiento de otros

OBJETIVO(S) DE APRENDIZAJE

desmontan enteros, unen partes y descubren la forma y el espacio.

• Puedo describir una traslación indicando el segmento de recta dirigido.

• Puedo dibujar traslaciones.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender que el término «traslación» (en lenguaje escrito y hablado) requiere especificar un segmento de línea dirigido.

• Determinar si una figura es traslación de otra.

• Dibujar traslaciones de figuras.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

Dibújalo

MLR8: Apoyos para el debate

Piensa, comparte en parejas

. Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Traduzcamos algunas figuras.

Narrativa de la lección

Esta lección continúa el tema de revisar las transformaciones rígidas que los estudiantes exploraron en cuadrículas de coordenadas en grados anteriores y refinar su comprensión para definir esas transformaciones de manera más general sin cuadrículas de coordenadas. Se introduce el concepto de segmento de recta dirigido para dar a los estudiantes un lenguaje que describa eficientemente la dirección y longitud de una traslación. Los estudiantes conocen el término segmento de recta, por lo que la frase segmento de recta dirigido se basa en un concepto que ya conocen y lo conecta con el concepto de traslaciones. La palabra vector se evita a propósito porque la interpretación geométrica de un vector debe surgir como consecuencia del trabajo futuro con vectores, no como definición. Los estudiantes argumentan y critican el razonamiento de los demás cuando explican por qué la traslación de un segmento de recta da como resultado un paralelogramo (MP3). Este argumento conduce al Postulado del Paralelogramo.

La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes elijan utilizar la tecnología apropiada para resolver los problemas. Recomendamos que la tecnología esté disponible.

LECCIÓN DE UN VISTAZO

Componente de lección

Estructura Tiempo

Descripción breve

Calentamiento En parejas 5 min Los estudiantes analizan una imagen de dos triángulos y una flecha y comentan lo que observan y se preguntan.

Actividad de exploración

Independiente 15 min

Actividad de exploración En parejas 15 min

Los estudiantes analizan e identifican traslaciones de puntos para escribir y verificar conjeturas sobre traslaciones sin una cuadrícula de coordenadas.

Los estudiantes traducen triángulos y segmentos de recta usando segmentos de recta dirigidos y razonan sobre las longitudes, distancias y formas creadas por las traslaciones.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar traslaciones usando tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la conexión entre traslaciones y rectas paralelas.

Síntesis Todo el grupo 5 min Los estudiantes resumen la relación entre traslaciones y rectas paralelas.

Enfriamiento Independiente 5 min Los estudiantes explican y corrigen el(los) error(es) cometido(s) en una traducción.

Práctica Independiente 8-10 min El componente de práctica independiente incluye 3 sobre la lección y 4 problemas de repaso en espiral.

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE: ¿DOS TRIÁNGULOS Y UNA FLECHA? (5 minutos)

Rutinas didácticas

Observar y preguntarse

El objetivo de este calentamiento es provocar la idea de que una traslación lleva a cada punto en la misma dirección por la misma distancia, lo que será útil cuando los estudiantes investiguen las traslaciones a lo largo de esta lección. Aunque los estudiantes pueden fijarse y preguntarse muchas cosas sobre estas imágenes, la «flecha» y su relación con los triángulos es el punto de discusión importante. Al entablar un debate y reflexionar sobre las matemáticas relacionadas con la «flecha», los estudiantes dan sentido al problema (MP1).

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Muestre la imagen para que todos la vean. Pida a los estudiantes que piensen en al menos una cosa que noten y en al menos una cosa que se pregunten. Conceda a los estudiantes 1 minuto para pensar en silencio y, a continuación, 1 minuto para comentar las cosas que observan con su compañero, seguido de un debate con toda la clase.

¿Qué observas? ¿Qué te preguntas?

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Cosas que los estudiantes pueden observar:

• Hay dos triángulos.

• Hay letras para algunos puntos, pero no para todos.

• Hay una flecha.

• Los lados correspondientes de los triángulos parecen ser paralelos.

Cosas que los estudiantes pueden preguntarse:

• ¿Cómo se relaciona la flecha con los dos triángulos?

• ¿Son congruentes los dos triángulos?

• ¿Cabe esa flecha entre los tres pares de puntos correspondientes?

Pida a los estudiantes que compartan las cosas que notaron y se preguntaron. Registra y muestra sus respuestas para que todos las vean. Si es posible, anote el razonamiento pertinente en la imagen o cerca de ella. Una vez registradas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que se pregunten ahora?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria. Si la conexión de los puntos de un triángulo con sus correspondientes puntos en el otro no surge durante la conversación, pida a los estudiantes que discutan esta idea.

. Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | ¿QUÉ SENTIDO TIENEN?

TRASLACIONES

(15 minutos)

En esta actividad, los estudiantes exploran las traslaciones sin una cuadrícula de coordenadas identificando y describiendo transformaciones. Supervise a los estudiantes que noten rectas paralelas formadas por segmentos de rectas dirigidas o formadas por puntos y sus imágenes.

INTRODUCCIÓN

Sugiera a los estudiantes que utilicen papel de calco o dos colores diferentes para diferenciar claramente las dos transformaciones.

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen sus ideas. Por ejemplo: «Yo me di cuenta , así que yo...» y « podría / podría no ser cierto porque...».

Apoya la accesibilidad para: Lenguaje; organización

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Tras una traslación, la imagen de V es W. Encuentra al menos otros 3 puntos que dicha traslación lleve a un punto etiquetado.

Escribe al menos una conjetura sobre las traslaciones.

En una nueva traslación, la imagen de V es Z. Encuentra al menos otros 3 puntos que la nueva traslación lleve a un punto etiquetado.

¿Siguen siendo válidas tus conjeturas para la nueva traslación?

RESPUESTAS POSIBLES

Observa la imagen:

Respuesta de ejemplo: Las traslaciones convierten las líneas en líneas paralelas. Los segmentos de línea dirigidos forman líneas paralelas.

RESPUESTAS POSIBLES CONTINUACIÓN

CONCEPTOS ERRÓNEOS PREVISTOS

Observa la imagen:

SÍNTESIS DE LA ACTIVIDAD

Las respuestas varían.

Puede que sea necesario recordar a los estudiantes las herramientas que tienen en su caja de herramientas de geometría, como el papel de calco, las reglas y los compases.

Invite a los estudiantes a compartir lo que conjeturaron.

Destaque para los estudiantes que conectar cada punto original con cada imagen da como resultado flechas que son todas de la misma longitud y van en la misma dirección. Diga a los estudiantes que llamamos a estas flechas segmentos de recta dirigidos. En otras palabras, un segmento de recta dirigido es un segmento de recta con una dirección. Un segmento de recta dirigida transmite la dirección y la distancia a la que se traslada cada punto.

Si ningún estudiante hace conjeturas sobre la traslación de rectas a paralelas, muestre las imágenes de las soluciones de los estudiantes con las rectas dibujadas. Habrá tiempo en actividades subsiguientes para explorar esta idea más a fondo; los estudiantes solo están conjeturando en este punto.

ACTIVIDAD DE EXPLORACIÓN | TRASLACIÓN DE TRIÁNGULOS

(15 minutos)

Rutinas didácticas

Dibújalo

MLR8: Apoyos para el debate

Piensa, haz coincidir y comparte

Esta actividad pone de relieve que las traslaciones llevan las rectas a rectas paralelas y los segmentos a segmentos de la misma longitud. Ambas propiedades se utilizarán en futuras lecciones para demostrar teoremas. La actividad también anticipa una demostración del Teorema de la suma de ángulos de triángulos más adelante en esta unidad.

Observa las diferentes formas en que los estudiantes justifican sus afirmaciones sobre líneas paralelas y distancias iguales. No se espera que los estudiantes presenten argumentos rigurosos y formales en este punto, pero es importante animarlos a justificar sus ideas como una forma de transición a argumentos más formales.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Después de un tiempo de trabajo en silencio, pida a los estudiantes que comparen sus respuestas con las de sus compañeros y decidan si ambas son correctas, aunque sean diferentes. A continuación, debate con toda la clase.

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Para apoyar a los estudiantes en la producción de afirmaciones sobre las propiedades de las figuras traducidas, proporcione fracciones de oraciones para que los estudiantes utilicen tales como: «BC y B'C' son porque ».o«FormaEDD'E'esuna porque ».

Principio(s) de diseño: Apoyar la creación de sentido; optimizar la salida (para la comparación)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

. Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidades

Compromiso: Interiorizar la autorregulación. Demostrar que da y recibe comentarios constructivos. Utilice un proceso estructurado y mostrar fracciones de frases para apoyar la retroalimentación productiva. Por ejemplo: «Este método funciona / no funciona porque...», «Otra estrategia sería porque...» y «¿Hay otra manera de decir/hacer...?».

Apoya la accesibilidad para: Habilidades socioemocionales; organización; lenguaje

1. Traduzca el triángulo ABC por el segmento de línea dirigida de A a C

A. ¿Cuál es la relación entre la línea BC y la línea B'C'? Explica tu razonamiento.

B. ¿Cuál es la relación entre la longitud del segmento BC y la longitud del segmento B'C'? Explica tu razonamiento.

2. Traslada el segmento DE por el segmento de recta dirigida w. Etiqueta los nuevos puntos extremos D' y E'.

A. Conecta D a D' y E a E'.

B. ¿Qué tipo de figura has dibujado? ¿Qué propiedades tiene? Explica tu razonamiento.

A. Las rectas BC y B'C' son paralelas porque la traslación llevó a cada punto del segmento BC la misma distancia en la misma dirección.

B. Los segmentos BC y B'C' tienen la misma longitud porque si no tuvieran la misma longitud, entonces A, C, y C' no estarían sobre la misma línea, o el segmento B'B' no sería paralelo al segmento AC

RESPUESTAS POSIBLES

A. Ver la imagen.

B. Ejemplos de respuestas: La forma parece un paralelogramo. El segmento EE' es paralelo al segmento DD' porque ambos son paralelos a la recta dirigida segmento w. Sabemos que la recta ED es paralela a la recta E'D' ya que la traslación lleva a cada punto de ED la misma distancia en la misma dirección. El segmento EE' tiene la misma longitud que el segmento DD' porque ambos tienen la misma longitud que el segmento de recta dirigida w. El segmento ED tiene la misma longitud que E'D', pero no hay forma de demostrarlo con seguridad.

SÍNTESIS DE LA ACTIVIDAD

El propósito de esta discusión es resaltar el hecho de que las traslaciones llevan las rectas a rectas paralelas y los segmentos a segmentos de igual longitud. Esta síntesis es intencionadamente corta para dar más tiempo a la síntesis de la lección. Aquí hay algunas preguntas para la discusión:

• «¿Cómo sabes que las rectas BC y B'C' son paralelas?». (Las rectas BC y B'C' son paralelas porque la traslación llevó a cada punto del segmento BC la misma distancia en la misma dirección. Una forma de pensar en lo que hace que las rectas sean paralelas es que todos los pares de puntos correspondientes están a la misma distancia).

• «¿Cómo sabes que los segmentos BC y B'C' tienen la misma longitud?». (Como afirmación, las traslaciones son transformaciones rígidas que llevan segmentos a segmentos de igual longitud).

¿Estás preparado para más?

1. Sobre el triángulo ABC de la tarea, construye con regla y compás la recta que pasa por A y es perpendicular a AC. Etiqueta ℓ A continuación, construye la mediatriz de AC y etiqueta como m. Dibuja la reflexión de ABC a través de la recta ℓ. Como la etiqueta A'B'C' ya se ha utilizado, etiquétala en su lugar DEF

2. ¿Cuál es la reflexión de DEF a través de la recta m?

3. Explica por qué es genial.

Respuestas de los estudiantes

2. Es la misma A'B'C' que ya se había dibujado.

3. ¡Una traslación puede hacerse como dos reflexiones en rectas perpendiculares al segmento de recta dirigida donde la distancia entre ellas es la mitad de la longitud del segmento!

SÍNTESIS DE LA LECCIÓN

(5 minutos)

El propósito de esta discusión es recapitular las ideas de la clase y agregarlas al cuadro de referencia. Elija cuántos detalles incluir en función del tiempo.

Explique a los estudiantes que hay dos hechos relacionados con las traslaciones y las rectas paralelas que aparecerán varias veces en futuras lecciones y unidades:

• Dada una recta y un punto fuera de la recta, hay una única recta paralela que pasa por el punto.

• Las traslaciones llevan rectas a rectas paralelas o a sí mismas.

Muestre una recta ℓ y un punto que no está en la recta, B. Pregunte a los estudiantes: «¿Cuáles son las posibles rectas que pasan por B? ¿Cuántas de ellas son paralelas a ℓ?». (Infinitas rectas pasan por B, pero solo una es paralela a ℓ). Diga a los estudiantes que la idea de que hay una única recta paralela a ℓ que pasa por B se denomina postulado de las paralelas. Es una observación que parece cierta, pero no hay forma de demostrarla o refutarla. Lo tomaremos como una afirmación.

Explique a los estudiantes que las traslaciones no tienen sentido sin el Postulado Paralelo porque la definición de traslacionar un punto A por un segmento de recta dirigido t supone que solo hay una recta que pasa por A que es paralela a t.

Recuerde a los estudiantes que en la actividad anterior propusieron explicaciones de por qué las traslaciones llevan segmentos a segmentos paralelos. Si dispone de tiempo, demuestre una prueba de una idea similar, en concreto, que las traslaciones llevan a las rectas hacia sí mismas o hacia rectas paralelas:

• Suponga que una recta ℓ es trasladada por un segmento de recta dirigido v.

• La imagen de ℓ es paralela o existe al menos un punto de intersección. Supongamos que hay un punto de intersección y lo llamamos A

• Eso significa que hay algún otro punto en l que fue llevado a A. Etiquete el punto llevado a A como P

• Eso significa que el segmento de línea dirigida original, v, tiene la misma dirección y longitud que el segmento de línea dirigida fde P a A

Por lo tanto, cuando la imagen de una recta no es paralela a la figura original, es porque el segmento de recta dirigida ha desplazado todos los puntos a lo largo de la recta. Otra forma de decir esto es que los segmentos de recta dirigidos trasladan puntos sobre una recta dada a puntos fuera de la recta dada, a menos que el segmento de recta dirigido comenzara paralelo a la recta dada en primer lugar. En ese caso, traslada todos los puntos a lo largo de la recta en esa dirección. Este es un ejemplo de simetría de traslación. Los estudiantes explorarán otros tipos de simetría en una lección posterior.

Pida a los estudiantes que añadan estas definiciones, afirmaciones y teoremas a sus tablas de referencia a medida que usted las añade a la tabla de referencia de la clase:

Traslación es una transformación rígida que lleva un punto a otro punto de modo que el segmento de recta dirigido desde el punto original a la imagen es paralelo al segmento de recta dado y tiene la misma longitud y dirección.

Traducir (objeto) por el segmento de línea dirigido (nombre o de [punto] a [punto]).

(Definición)

Postulado Paralelo: Dada una recta (m) y un punto (A) que no está en m, hay exactamente una recta que pasa por A que es paralela a m

(Afirmación)

Traducir A por el segmento de línea dirigido v.

Las traslaciones llevan rectas a rectas paralelas o a sí mismas.

(Teorema) m ∥ m'

ENFRIAMIENTO | ¿QUÉ FALLÓ? TRASLACIÓN

(5 minutos)

Priya intentó trasladar el triángulo ABC por el segmento de recta dirigida desde D hasta E. Ella sabe que algo salió mal porque la imagen no es congruente con la figura original.

1. ¿Cuál es una idea que Priya probablemente entiende sobre traslaciones?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

2. ¿Cuál es una idea que Priya no entiende acerca de las traslaciones?

3. Traslada el triángulo ABC por el segmento de línea dirigida de D a E.

1. Priya sabe que las traslaciones llevan puntos a un nuevo punto a la misma distancia.

2. Priya no entiende que los movimientos tienen que ser en la misma dirección y que todos los segmentos deben ser paralelos.

RESPUESTAS POSIBLES

Resumen de la lección para el estudiante

Una traslación desliza una figura en una dirección dada para una distancia dada sin rotación. La distancia y la dirección están dadas por un segmento de línea dirigida. La flecha del segmento de línea dirigida especifica la dirección de la traslación y la longitud del segmento de línea dirigida especifica cuánto se traslada la figura.

Más concretamente, una traslación de un punto A a lo largo de un segmento de recta dirigida t es una transformación que lleva A a A' de modo que el segmento de recta dirigida AA' es paralelo a t, va en la misma dirección que t y tiene la misma longitud que t.

Geometría . Matemáticas . Unidad 1

Aaquí hay una traslación de 3 puntos. Observa que los segmentos de recta dirigida CC', DD' y EE' son paralelos a v, van en la misma dirección que v y tienen la misma longitud que v

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Haz coincidir el segmento de recta dirigida con la imagen del polígono P que se transforma en el polígono Q por traslación por ese segmento de recta dirigida.

Traslación 1

Soluciones posibles

A: i, B: iv, C: iii, D: ii

Traslación 2

Traslación 3

i. Traslación 1

ii. Traslación 2

iii. Traducción 3

iv. Traslación 4

Traslación 4

Geometría . Matemáticas . Unidad 1

PROBLEMA 2

Dibuja la imagen del cuadrilátero ABCD cuando es trasladado por el segmento de recta dirigida v. Etiqueta la imagen de A como A', la imagen de B como B', la imagen de C como C' y la imagen de D como D'

Soluciones posibles

PROBLEMA 3

¿Qué afirmación es cierta sobre una traslación?

A. Una traslación lleva una recta a una recta paralela o a sí misma.

B. Una traslación lleva una recta a una recta perpendicular.

C. Una traslación requiere un centro de traslación.

D. Una traslación requiere una recta de traslación.

Soluciones posibles

PROBLEMA 4

Selecciona todos los puntos que permanecen en el mismo lugar después de ser reflejados a través de la recta ℓ

Soluciones posibles

PROBLEMA 5

Las rectas ℓ y m son perpendiculares. Un punto Q tiene esta propiedad: girar Q 180 grados usando el centro P tiene el mismo efecto que reflejar Q sobre la recta m

A. Da dos posibles ubicaciones de Q.

B. ¿Tienen esta propiedad todos los puntos del plano?

Soluciones posibles

A. Ejemplo de respuesta: Dos puntos cualesquiera de la recta ℓ

B. No, solo los puntos de ℓ

PROBLEMA 6

Existe una secuencia de transformaciones rígidas que lleva A a A', B a B' y C a C'. La misma secuencia lleva D a D'. Dibuja y etiqueta

D':

Soluciones posibles

PROBLEMA 7

Dos rectas distintas, ℓ y m, son perpendiculares a la misma recta n.

A. ¿Cuál es la medida del ángulo donde la recta ℓ se encuentra con la recta n?

B. ¿Cuál es la medida del ángulo donde la recta m se encuentra con la recta n?

Soluciones posibles

A. 90 grados

B. 90 grados

Reflexiones:

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

G-CO.1 Conocer definiciones precisas de ángulo, círculo, recta perpendicular, recta paralela y segmento de recta, basadas en las nociones indefinidas de punto, línea, distancia a lo largo de una línea y distancia alrededor de un arco circular.

Alineación de estándares y principios de California

G-CO.5 Dada una figura geométrica y una rotación, reflexión o traslación, dibujar la figura transformada. Especificar una secuencia de transformaciones que llevarán una figura dada a otra.

Construir

N-Q.3

Construir

G-CO.6

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.B.5

I.C.11

II.C.6

LECCIÓN 13

INCORPORACIÓN DE ROTACIONES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

dar sentido al mundo y predecir lo que podría ocurrir,

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

atienden a la precisión y utilizan las herramientas adecuadas de forma estratégica

OBJETIVO(S) DE APRENDIZAJE

descubren la forma y el espacio.

• Dada una figura y la descripción de una transformación, puedo dibujar la imagen de la figura después de la transformación.

• Puedo describir la secuencia de transformaciones necesarias para llevar una figura a otra figura.

• Sé que las transformaciones rígidas dan como resultado figuras congruentes.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender que las transformaciones rígidas producen figuras congruentes preservando la distancia y los ángulos.

• Dibujar el resultado de una transformación (en lenguaje escrito) de una figura dada.

• Explicar (oralmente y por escrito) una secuencia de transformaciones para llevar una figura dada a otra.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Dibújalo

MLR8: Apoyos para el debate

Materiales necesarios

Juegos de herramientas de geometría

Transportadores

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Dibujemos algunas transformaciones.

Narrativa de la lección

Esta lección continúa construyendo sobre el conocimiento previo acerca de la congruencia para reforzar la idea de que los movimientos rígidos, las traslaciones, las reflexiones y las rotaciones preservan las distancias y los ángulos. En esta lección, los estudiantes vuelven a estudiar las transformaciones sobre una cuadrícula, ya que se encuentran con las rotaciones por primera vez en este curso. En las siguientes lecciones de esta unidad, los estudiantes aprenden una definición precisa de rotación que se aplica fuera de la cuadrícula.

En una actividad, los estudiantes completan una secuencia de traslación, reflexión y rotación en la que cada movimiento rígido alinea un par de puntos en un par de triángulos congruentes. Esta secuencia de transformación punto por punto será la base de la prueba de congruencia de triángulos en una unidad posterior. Los estudiantes prestan atención a la precisión cuando determinan las piezas necesarias de información para describir una rotación, así como cuando determinan los niveles apropiados de confianza al medir con un transportador (MP6).

Tenga en cuenta que estos materiales utilizan la convención de que todos los ángulos nombrados se supone que miden menos de 180 grados, a menos que se especifique lo contrario.

La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes opten por utilizar la tecnología apropiada para resolver problemas. Recomendamos que la tecnología esté disponible.

LECCIÓN DE UN VISTAZO

Componente de lección Estructura Tiempo

Descripción breve

Calentamiento Independiente 10 min Los estudiantes describen las rotaciones representadas en las imágenes.

Los estudiantes realizan rotaciones de polígonos en una cuadrícula rectangular y en una cuadrícula isométrica.

Actividad de Exploración Independiente 15 min

Actividad de Exploración En parejas o grupos pequeños 10 min

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar las rotaciones utilizando la tecnología

Los estudiantes dibujan cada imagen en una secuencia de transformaciones en una cuadrícula isométrica e identifican el grado de rotación en la secuencia.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la realización de una secuencia de transformaciones utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las rotaciones.

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Los estudiantes solidifican su comprensión de las transformaciones actuando o dibujando diferentes transformaciones rígidas.

Los estudiantes determinan una secuencia de transformaciones que lleva una figura a otra figura.

El componente de práctica independiente incluye 2 en la lección y 5 problemas de repaso en espiral.

CALENTAMIENTO | DE IZQUIERDA A DERECHA (10 minutos)

En esta actividad, los estudiantes describen rotaciones. Durante la discusión, los estudiantes trabajan juntos para determinar que una descripción completa de una rotación incluye un centro, una dirección y un ángulo. Los estudiantes también practican la medición de ángulos con transportadores para prepararse para una lección posterior en la que tendrán que utilizar transportadores para dibujar rotaciones con una medida de ángulo dada.

Muestra esta imagen y explica que la gente utiliza banderas para señalar mensajes con el alfabeto del semáforo.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Proporciona acceso a los transportadores.

El alfabeto del semáforo es una forma de utilizar banderas para señalar mensajes. Aquí está cómo señalar las letras

Z y J. Para cada una, describa con precisión una rotación que llevaría la bandera de la mano izquierda a la bandera de la mano derecha.

Z: Gira la bandera de la mano izquierda 45 grados en el sentido de las agujas del reloj alrededor del punto de intersección de los brazos.

J: Gira la bandera de la izquierda 90 grados en el sentido contrario a las agujas del reloj alrededor del punto de intersección de los brazos.

El propósito de esta discusión es identificar las características de una rotación y practicar el uso de transportadores. Invite a los estudiantes a compartir sus descripciones. Registre sus respuestas para que todos puedan verlas. Anote las imágenes a medida que los estudiantes comparten. Demuestre cómo usar un transportador para medir los ángulos. Invite a los estudiantes a practicar con sus transportadores. Los estudiantes pueden obtener medidas de ángulos que varían ligeramente. Discuta las limitaciones de medir con un transportador. Cuando el diagrama está etiquetado, podemos saber la medida exacta; de lo contrario, tenemos que estimar utilizando cualquier herramienta disponible. Muestre la imagen con marcas de construcción.

SÍNTESIS DE LA ACTIVIDAD

CONTINUACIÓN

Invite a los estudiantes a definir rotación. (Cada punto de una figura se mueve en un círculo alrededor del centro. Tiene que haber una dirección, en el sentido de las agujas del reloj o en sentido contrario, y un ángulo). Si los estudiantes no lo mencionan, señale que la marca de construcción es un círculo, lo que significa que la distancia desde el centro permanece constante.

ACTIVIDAD DE EXPLORACIÓN | GIRAR EN UNA CUADRÍCULA

(15 minutos)

Rutinas didácticas

Dibújalo

En esta actividad, los estudiantes giran imágenes tanto en una cuadrícula rectangular como en una cuadrícula isométrica para practicar la rotación en una variedad de ángulos. Practicarán considerando todos los aspectos de una rotación: centro, ángulo y dirección de rotación.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

INTRODUCCIÓN

Dé a los estudiantes 3 minutos de tiempo tranquilo para trabajar y, a continuación, haga una pausa para un breve debate con toda la clase. Invite a un estudiante a demostrar cómo utilizar el papel de calco para rotar. Recomiende a los estudiantes que utilicen el lápiz para sujetar el papel vegetal en el centro de rotación y que giren el papel alrededor de ese punto.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Divida esta tarea en partes más manejables para apoyar a los estudiantes que se benefician del apoyo con habilidades organizativas en la resolución de problemas. Por ejemplo, presente una pregunta a la vez y asegúrese de que los estudiantes completen cada rotación correctamente antes de pasar a la siguiente rotación.

Apoya la accesibilidad para: Organización; atención

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Rota �� 90 grados en el sentido de las agujas del reloj alrededor de ��

2. Rota �� 180 grados alrededor de R.

3. Rotr �� 120 grados en el sentido de las agujas del reloj alrededor de ��

4. Gira �� 60 grados en sentido antihorario alrededor de ��.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Transformaciones rotacionales.

El propósito de esta discusión es solidificar los aspectos de una rotación.

«¿Qué información necesitas para hacer una rotación?». (Centro, ángulo y dirección de rotación).

«¿Por qué no necesitas saber la dirección de rotación cuando el ángulo de rotación es 180 grados?». (Tanto en sentido horario como antihorario caen en el mismo lugar ya que 180 grados es la mitad de un círculo.)

ACTIVIDAD DE EXPLORACIÓN | TRASLACIÓN, ROTACIÓN, REFLEXIÓN

(10 minutos)

Rutinas didácticas

Dibújalo

MLR8: Apoyos para el debate

Los estudiantes practican el dibujo de transformaciones siguiendo las instrucciones de un personaje. Esta es la primera vez que los estudiantes ven las transformaciones punto por punto que utilizarán en una unidad posterior para demostrar que los triángulos son congruentes.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Fomente y apoye las oportunidades de interacción entre compañeros. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «Primero, porque Después, yo...», «¿Cómo sabes que...?» y «Este método funciona / no funciona porque....».

Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Mai sospecha que el triángulo �� es congruente con el triángulo ��. Piensa que estos pasos funcionarán para demostrar que existe una transformación rígida de �� a ��

• Traslada por el segmento de recta dirigida ��

• Gira la imagen grados en el sentido de las agujas del reloj alrededor del punto ��

• Refleja esa imagen sobre la línea �� Dibuja cada imagen y determina el ángulo de rotación necesario para que estos pasos lleven �� a ��

El ángulo de rotación es 120 grados.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Si los estudiantes tienen dificultades para identificar el ángulo de rotación, pídales que encuentren y tracen el ángulo que une un punto, su imagen y el centro de rotación. A continuación, ofrezca dos opciones. Pueden usar un transportador para medir un ángulo o pueden usar las propiedades de la cuadrícula para calcular la medida de un ángulo.

El propósito de esta discusión es enfatizar que las figuras son congruentes si existe una transformación rígida que lleva una a la otra. He aquí algunas preguntas para la discusión:

• «¿Cuál es la definición de congruente?». (Hay una transformación rígida que lleva una figura a la otra).

• «Tenemos una transformación que lleva el triángulo �� al triángulo ��. ¿Qué nos dice eso?». (La secuencia incluye una traslación, una reflexión y una rotación. Cada uno de ellos es un movimiento rígido, por lo que las medidas del triángulo �� deben coincidir con las medidas del triángulo ��. Son iguales, solo que en lugares diferentes).

Apoyo para estudiantes que aprenden el idioma inglés

Hablar y representar: MLR8 Apoyos para el debate. Utilice esta rutina para ampliar los usos matemáticos del lenguaje para describir rotaciones. Después de que un estudiante hable, invítelo a repetir su razonamiento utilizando lenguaje matemático relevante para la lección, como: centro, ángulo, sentido de rotación, sentido horario, sentido antihorario y «alrededor del punto X». Considere invitar a los estudiantes restantes a repetir estas frases para proporcionar oportunidades adicionales para que todos los estudiantes produzcan este lenguaje.

Principio(s) de diseño: Apoyar la creación de sentido; optimizar el resultado (para la explicación)

Geometría . Matemáticas . Unidad 1

¿Estás listo para más?

Los primeros 2 pasos de Mai podrían combinarse en una sola rotación.

1. Encuentra el centro y el ángulo de esta rotación.

2. Describe un procedimiento general para encontrar un centro de rotación.

Respuestas de los estudiantes

1. 120 grados en el sentido de las agujas del reloj.

2. Respuesta de ejemplo: Une un punto con su imagen. Halla la mediatriz de ese segmento. Repite para otro punto de la figura. La intersección de las dos mediatrices es el centro de rotación.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Invite a los estudiantes a dibujar o representar (utilizando los brazos y el papel como banderas) algunas transformaciones. Para representar las letras, indique a los estudiantes la posición inicial de su bandera izquierda.

• Gira 135 grados en el sentido de las agujas del reloj. (Semáforo letra S).

• Refleja sobre una recta vertical. (Semáforo letra N).

• Trasládate a la izquierda, luego gira 45 grados en el sentido de las agujas del reloj. (Semáforo letra O).

S N O

ENFRIAMIENTO | ENCUENTRA UNA SECUENCIA

5 minutos

Describe una secuencia de reflexiones, rotaciones y traslaciones que tome �� en

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Geometría . Matemáticas . Unidad 1

Respuesta de ejemplo: Gire 120 grados en el sentido de las agujas del reloj alrededor de ��, luego refléjelo sobre la línea vertical ��.

Resumen de la lección para el estudiante

Los 3 movimientos rígidos son reflejar, trasladar y rotar. Cada uno de estos movimientos rígidos puede aplicarse a cualquier figura para crear una imagen que sea congruente. Para hacer una rotación, necesitamos saber 3 cosas: el centro, la dirección y el ángulo.

Gira ABCD 90 grados en el sentido de las agujas del reloj alrededor del punto P

Gira EFG 120 grados en el sentido contrario a las agujas del reloj alrededor del punto W

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Aquí hay 2 polígonos:

Selecciona todas las secuencias de traslaciones, rotaciones y reflexiones de abajo que llevarían el polígono �� al polígono ��

Rotar 180° alrededor del punto ��

Rotar 60° en sentido antihorario alrededor del punto �� y luego reflejar sobre la línea �� Trasladar de modo que �� se lleve a ��. Luego reflejar sobre la línea ��

Reflejar sobre la línea �� y luego trasladar por el segmento de línea dirigido �� Reflejar sobre la línea �� y luego rotar 60° en sentido antihorario alrededor del punto ��

Soluciones posibles

Rotar 180° alrededor del punto ��

Rotar 60° en sentido antihorario alrededor del punto �� y luego reflejar sobre la línea ��

Trasladar de modo que �� se lleve a ��. Luego reflejar sobre la línea ��

Reflejar sobre la línea �� y luego trasladar por el segmento de línea dirigido ��

Reflejar sobre la línea �� y luego rotar 60° en sentido antihorario alrededor del punto ��

PROBLEMA 2

El alfabeto semáforo es una forma de usar banderas para señalar mensajes. He aquí cómo señalar la letra Q. Describe una transformación que lleve la bandera de la izquierda a la bandera de la derecha.

Soluciones posibles

Gira la figura �� 135 grados en sentido antihorario alrededor del punto de intersección de los brazos. Refleja a través del brazo derecho.

PROBLEMA 3

(Unidad 1, lección 12)

Haz coincidir el segmento de recta dirigida con la imagen del polígono �� que se transforma en el polígono �� por traslación mediante ese segmento de recta dirigida.

Traducción 1

Traducción 3

Soluciones posibles

A. ii

B. iii

C. iv

D. i

PROBLEMA 4

(Unidad 1, lección 12)

Dibuja la imagen del cuadrilátero �� cuando es trasladado por el segmento de recta dirigido v. Etiqueta la imagen de �� como ��′, la imagen de �� como ��′, la imagen de �� como ��′ y la imagen de �� como ��′

Traducción 2

Traducción 4

i. Traslación 1

ii. Traslación 2

iii. Traslación 3

iv. Traslación 4

Soluciones posibles

A. B.

. Matemáticas . Unidad 1

PROBLEMA 5

(Unidad 1, lección 11)

Aquí hay una recta ℓ

Traza 2 puntos, �� y ��, que permanecen en el mismo lugar cuando se reflejan sobre ℓ. Traza otros 2 puntos, �� y ��, que se mueven cuando se reflejan sobre ℓ

PROBLEMA 6

(Unidad 1, lección 9)

Soluciones posibles

Ejemplo de respuesta:

Aquí hay 3 puntos en el plano. Selecciona todas las construcciones de regla y compás necesarias para localizar el punto que está a la misma distancia de todos 3 los puntos.

Construir la bisectriz del ángulo ��

Construir la mediatriz del ángulo ��

Construir la mediatriz de ��

Construir una recta perpendicular a �� que pase por el punto ��.

Construir una recta perpendicular a �� que pase por el punto ��

Soluciones posibles

Construir la bisectriz del ángulo ��

Construir la mediatriz del ángulo ��

Construir la mediatriz de ��

Construir una recta perpendicular a �� que pase por el punto ��

PROBLEMA 7

(Unidad 1, lección 7)

Esta construcción con regla y compás muestra el cuadrilátero ��. ¿Es �� un rombo? Explica cómo lo sabes.

Soluciones posibles

Ejemplo de respuesta: La longitud del segmento �� es la misma que la longitud del segmento �� ya que ambos son radios del mismo círculo. Análogamente los segmentos �� y �� tienen la misma longitud. La longitud del segmento �� es la misma que la longitud del segmento �� ya que ambos son radios del mismo círculo. Esto significa que los segmentos ��, ��, �� y �� tienen todos la misma longitud por lo que el cuadrilátero �� es un rombo.

Geometría . Matemáticas . Unidad 1

LECCIÓN 14

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.4 Desarrollar definiciones de rotaciones, reflexiones y traslaciones en términos de ángulos, círculos, rectas perpendiculares, rectas paralelas y segmentos de recta.

Construir

8.G.1 N-Q.3

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.1

I.A.3

I.C.12

DEFINICIÓN DE ROTACIONES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir,

atienden a la precisión, dan sentido a los problemas y perseveran en su resolución descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo describir una rotación indicando el centro y el ángulo de rotación.

• Puedo dibujar rotaciones.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender que el término «rotación» (en lenguaje escrito y hablado) requiere varios descriptores, incluyendo ángulo, centro y dirección.

• Determinar si una figura es una rotación de otra.

• Dibujar rotaciones de figuras.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyos para el debate

MLR4: Tarjetas de información

Dibuja

Materiales necesarios

Conjunto de herramientas de geometría (HS)

Tarjetas preimpresas, recortadas a partir de copias de la plantilla maestra

Transportadores

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Rotemos formas con precisión.

Narrativa de la lección

El propósito de esta lección es desarrollar una definición rigurosa de rotación, partiendo de lo que los estudiantes saben de cursos anteriores. Los estudiantes primero se enfocan en qué información es importante para definir una rotación y luego determinan las propiedades de las rotaciones rotando segmentos para formar triángulos isósceles. Los estudiantes prestan atención a la precisión cuando aclaran qué información necesitan para determinar de forma única una rotación dada (MP6).

La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes elijan utilizar la tecnología apropiada para resolver problemas. Recomendamos que la tecnología esté disponible.

LECCIÓN DE UN VISTAZO

Componente de la lección Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración En parejas 15 min

Actividad de exploración Independiente 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes analizan y comparan conjuntos de figuras con ángulos para determinar qué par de ángulos parecen congruentes.

Los estudiantes reciben tarjetas de referencia y luego piden y proporcionan la información necesaria para describir rotaciones y determinar puntos de la imagen después de una rotación sin cuadrícula.

Los estudiantes crean triángulos rotando segmentos de recta, identifican los triángulos y describen sus propiedades.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda del uso de rotaciones para crear polígonos regulares.

Los estudiantes registran la definición de rotación y discuten lo que es necesario al describir o realizar una rotación.

Los estudiantes identifican y corrigen el(los) error(es) cometido(s) en la rotación de un triángulo.

El componente de práctica independiente incluye 3 en la lección y 4 problemas de repaso en espiral.

CHARLA DE MATEMÁTICAS: COMPARACIÓN DE ÁNGULOS

(5 minutos)

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyo para el debate

El propósito de esta charla de matemáticsa es obtener estrategias y conocimientos que los estudiantes tienen para usar herramientas para comparar ángulos. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de comparar o reproducir con precisión ángulos para dibujar figuras rotadas.

INTRODUCCIÓN

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Para cada figura, ¿qué par de ángulos parece congruente? ¿Cómo podrías comprobarlo?

Figura 1

Figura 3

Figura 4

Figura 2

• ∠ABC y ∠GHL

• ∠RSL y ∠PBK

• ∠DVG y ∠LJX

RESPUESTAS POSIBLES

• ∠LHG y ∠DEF

Ejemplos de respuestas: Utilizar papel de calco para trazar un ángulo y comprobar si se puede alinear exactamente con uno de los otros dos ángulos. Utiliza un transportador para medir cada ángulo. Si los círculos son congruentes, mide las longitudes de las cuerdas.

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

• «¿Quién puede replantear el razonamiento de de otra manera?».

• «¿Tenía alguien más la misma estrategia, pero la explicaría de otra manera?».

• «¿Resolvió alguien el problema de otra manera?».

• «¿Quiere alguien añadir algo a la estrategia de ?».

• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?».

Ten en cuenta que medir ángulos no es lo mismo que demostrar que son congruentes, debido a la limitación de las herramientas de medición. Asegúrese de que todos los estudiantes se sienten cómodos utilizando un transportador para medir ángulos.

Si los estudiantes no lo mencionan, no es necesario mencionar los arcos, las cuerdas o los triángulos congruentes. Si los estudiantes miden cuerdas o longitudes de arco para comparar ángulos, haga hincapié en que los círculos utilizados para definir los arcos o las cuerdas deben ser del mismo tamaño.

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo, «Primero, yo porque...» o «Noté , así que yo...». A algunos estudiantes les puede venir bien tener la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.

Principio(s) de diseño: Optimizar la salida (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | BRECHA INFORMATIVA: CUÁL ES EL PUNTO: ROTACIONES

(15 minutos)

Rutinas didácticas

MLR4: Fichas de vacío de información

Esta actividad de brecha informativa ofrece a los estudiantes la oportunidad de determinar y solicitar la información necesaria para definir una rotación.

La estructura de brecha informativa requiere que los estudiantes den sentido a los problemas determinando qué información es necesaria y, a continuación, pidan la información que necesitan para resolverlo. Esto puede requerir varias rondas de discusión si sus primeras peticiones no aportan la información que necesitan (MP1). También les permite refinar el lenguaje que utilizan y hacer preguntas cada vez más precisas hasta que obtienen la información que necesitan (MP6).

Busque estudiantes que no especifiquen el ángulo de rotación, la dirección de rotación o el centro de rotación para comparar con rotaciones correctas durante la discusión.

Aquí está el texto de las tarjetas para referencia y planificación:

Tarjeta de problema 1

El triángulo DCI ha sido rotado de manera que los vértices de su imagen están etiquetados como puntos. ¿Cuál es su imagen?

Tarjeta de datos 1

• El ángulo de rotación es HLI

• La rotación es en sentido contrario a las agujas del reloj.

• El centro de rotación es L

• La imagen de C es G

• La imagen de I es H

• La imagen de L es L

• La imagen de U es C

• La imagen de V es D

Tarjeta de problema 2

Se han rotado varios puntos alrededor de un punto etiquetado. Describa con precisión la rotación.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: Esta actividad utiliza la brecha informativa MLR4 para dar a los estudiantes la oportunidad de determinar y solicitar la información necesaria para definir una rotación. Muestre preguntas o iniciadores de preguntas para los estudiantes que necesiten un punto de partida como: «¿Puedes decirme... (dato concreto)?» y «¿Por qué necesitas saber... (esa información)?»..

Principio(s) de diseño: Cultivar la conversación

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Tarjeta de datos 2

• El ángulo de rotación es HNW

• El centro de rotación es N

• La imagen de F es H.

• La imagen de H es W

• La imagen de J es B

• La imagen de N es N

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Muestre o proporcione a los estudiantes una copia física de las instrucciones escritas. Compruebe la comprensión invitando a los estudiantes a reformular las instrucciones con sus propias palabras. Mantén las instrucciones visibles durante toda la actividad.

Favorece la accesibilidad para: Memoria; organización

Tu maestro te dará una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu compañero.

Si tu maestro te da la tarjeta de datos:

1. Lee en silencio la información de tu tarjeta.

2. Pregunta a tu compañero «¿Qué información específica necesitas?» y espera a que tu compañero te pida información. Da solo la información que aparece en tu tarjeta. (¡No averigües nada por tu compañero!).

3. Antes de dar la información a tu compañero, pregúntale «¿Por qué necesitas saber (ese dato)?».

4. Lee la tarjeta del problema y resuelve el problema.

Lee la tarjeta del problema y resuélvelo de forma independiente.

5. Comparte la tarjeta de datos y discute tu razonamiento.

Si tu maestro te da la tarjeta del problema:

1. Lee en silencio tu tarjeta y piensa qué información necesitas para responder a la pregunta.

2. Pide a tu compañero la información específica que necesitas.

3. Explica a tu compañero cómo estás utilizando la información para resolver el problema.

4. Cuando tengas suficiente información, comparte la tarjeta del problema con tu compañero y resuelve el problema de forma independiente.

5. Lee la tarjeta de datos y discute tu razonamiento.

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Ficha de problema 1: Después de una rotación en sentido antihorario alrededor del centro L por el ángulo HLI, la imagen del triángulo DCI es el triángulo BGH. Ficha de problema 2: La rotación es en sentido horario utilizando el centro N y el ángulo HNW

Es posible que los estudiantes necesiten que se les recuerden las herramientas que tienen en su caja de herramientas de geometría, como el papel de calco, las reglas y los compases.

Es posible que los estudiantes intenten calcular la medida del ángulo de rotación. Recuérdeles que pueden nombrar un ángulo con 3 letras.

El propósito de la discusión es enfatizar que un ángulo, una dirección y un centro de rotación son necesarios para describir con precisión una rotación. Si hubo respuestas que utilizaron el centro de rotación o la dirección de rotación incorrectos, muéstrelos junto a las respuestas correctas. Sin revelar quién está en lo correcto, pida a los estudiantes de estos grupos que reconcilien estas diferencias.

ACTIVIDAD DE EXPLORACIÓN | ROTACIÓN EN TRIÁNGULOS

(15 minutos)

Rutinas didácticas

Dibújalo

El objetivo de esta actividad es practicar la aplicación de la definición de rotación. En esta actividad, los estudiantes rotan un segmento alrededor de su extremo para crear un triángulo isósceles. Al rotar un segmento alrededor de un extremo, los estudiantes pueden observar que la distancia entre el centro de rotación y un punto es la misma que la distancia entre el centro de rotación y la imagen de ese punto. Esta observación se recoge posteriormente en la definición formal de rotación.

Poner a disposición de los estudiantes software de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Demuestre brevemente cómo crear un ángulo de una medida dada con un transportador y pida a los estudiantes que usen sus transportadores junto con usted. Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5). Puede demostrar el uso de GeoGebra Geometry en las herramientas matemáticas.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Divida esta tarea en partes más manejables para ayudar a los estudiantes que se benefician del apoyo con habilidades organizativas en la resolución de problemas. Por ejemplo, presente una pregunta cada vez y asegúrese de que los estudiantes completan cada paso correctamente antes de pasar al siguiente.

Apoya la accesibilidad para: Organización; atención

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS

POSIBLES

1. Dibuja un segmento. Etiqueta los puntos extremos A y B.

A. Rota el segmento AB en el sentido de las agujas del reloj alrededor del centro B en 90 grados. Etiqueta el nuevo punto final A'.

B. Conecta A a A' y sombrea ligeramente el triángulo resultante.

C. ¿Qué tipo de triángulo has dibujado? ¿Qué otras propiedades observas en la figura? Explica tu razonamiento.

2. Dibuja un segmento. Etiqueta los puntos extremos C y D

A. Rota el segmento CD en sentido antihorario alrededor del centro D en 30 grados. Etiqueta el nuevo punto final C'

B. Rota el segmento C'D en sentido antihorario alrededor del centro D en 30 grados. Etiqueta el nuevo punto final C″

C. Conecta C a C″ y sombrea ligeramente el triángulo resultante.

D. ¿Qué tipo de triángulo has dibujado? ¿Qué otras propiedades observas en la figura? Explica tu razonamiento.

1. El resultado debe ser un segmento etiquetado AB

A. El resultado debe ser un nuevo segmento de línea BA' tal que el ángulo ABA' mida 90 grados.

B. Se debe dibujar el segmento AA' y sombrear ligeramente el triángulo resultante.

C. Es un triángulo isósceles rectángulo. Es un triángulo rectángulo porque el ángulo de rotación fue 90 grados. Es isósceles porque una rotación es una transformación rígida por lo que el segmento AB es congruente con el segmento A'B Los ángulos base parecen congruentes.

2. El resultado debería ser un segmento etiquetado CD

A. El resultado debería ser un nuevo segmento de recta DC' tal que el ángulo CDC' mida 30 grados.

B. El resultado debe ser un nuevo segmento de recta DC″ tal que el ángulo C'DC″ mide 30 grados.

C. El resultado debe ser un triángulo equilátero DCC″

D. Es un triángulo equilátero porque dos lados son iguales y el ángulo es 60 grados. El segmento C'D es un ángulo bisectriz debido a la construcción. El segmento C'D es una bisectriz perpendicular (los estudiantes conocen varias formas de comprobarlo).

CONCEPTOS ERRÓNEOS PREVISTOS

Es posible que los estudiantes no observen ninguna otra propiedad aparte de que la rotación conserva las distancias al centro de rotación. Anime a estos estudiantes a utilizar papel de calco para hacer otras conjeturas sobre las longitudes de los lados o los ángulos.

Muestra un triángulo isósceles ABC con base BC

Aquí hay algunas conjeturas y observaciones clave con las que los estudiantes deberían salir de la discusión:

• Las rotaciones conservan la distancia al centro de rotación.

SÍNTESIS DE LA ACTIVIDAD

• La mediatriz del ángulo A es también la mediatriz de la base (BC) de un triángulo isósceles.

• Los dos ángulos de la base (ángulo B y ángulo C) de un triángulo isósceles son congruentes.

• Un triángulo isósceles en el que el ángulo A es 60 grados también es equilátero.

No es necesario en este momento formalizar el lenguaje de estas ideas. Esto se hará más adelante, cuando los estudiantes demuestren algunas de estas afirmaciones en una unidad posterior.

. Matemáticas . Unidad 1

¿Estás preparado para más?

Has construido un triángulo equilátero girando un segmento dado alrededor de uno de sus extremos con una medida de ángulo específica. Un triángulo equilátero es un ejemplo de polígono regular: un polígono con todos los lados congruentes y todos los ángulos interiores congruentes. Intenta construir otros polígonos regulares con este método.

Posibles respuestas

Ejemplo de respuesta: Se puede construir un cuadrado empezando con un segmento, girándolo 90 grados alrededor de uno de sus extremos y repitiendo el proceso con los nuevos segmentos 2 veces más.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Explique a los estudiantes que han desarrollado conjeturas sobre rotaciones, pero que para poder demostrar si las conjeturas que han hecho son ciertas, necesitan ponerse de acuerdo en una definición de rotación. Esta definición les ayudará a explicar por qué una rotación garantiza que un punto se lleve a otro.

Recuerde a los estudiantes que para describir una rotación, necesitan especificar un centro, un ángulo y una dirección (en el sentido de las agujas del reloj o en sentido contrario). Pida a los estudiantes que añadan la definición a sus tablas de referencia al mismo tiempo que usted la añade a la tabla de referencia de la clase:

Rotación es una transformación rígida que lleva un punto a otro punto de la circunferencia pasando por el punto original con el centro dado. Los dos radios al punto original y la imagen hacen el ángulo dado.

Rota (un objeto) (en sentido horario o antihorario) (ángulo o medida de ángulo) usando el centro (punto) (Definición)

Rotar P en sentido antihorario por a° usando centro C

El ángulo PCP' mide a° y P' es antihorario alrededor del círculo desde P. Si la dirección fuera en el sentido de las agujas del reloj, entonces P' sería en el sentido de las agujas del reloj alrededor del círculo desde P. Observe que si P = C, entonces la rotación envía P a P' en el círculo de radio cero y así los puntos P, C y P' están en el mismo lugar antes y después de la rotación.

Pregunte a los estudiantes: «Esta definición menciona un círculo, pero en realidad no hay ningún círculo en la imagen». (Las distancias CP y CP' son iguales, por lo que cada una es un radio para un círculo centrado en C).

ENFRIAMIENTO | ¿QUÉ SALIÓ MAL? ROTACIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

(5 minutos)

Andre intentó rotar el triángulo ABC 45 grados en sentido contrario a las agujas del reloj. Él sabe que algo salió mal porque la imagen no parece ser congruente con la figura original.

1. ¿Cuál es una idea que Andre probablemente entiende sobre rotaciones?

2. ¿Cuál es una idea que Andre no entiende sobre rotaciones?

3. Rota el triángulo ABC en 45 grados en sentido antihorario, evitando el error de Andre.

. Matemáticas . Unidad 1

ENUNCIADO DE TAREA DEL ESTUDIANTE CONTINUACIÓN

Paso 1 de Andre

Paso 3 de Andre

RESPUESTAS POSIBLES

Paso 2 de Andre

Tu turno

1. Andre utilizó círculos y rotó los tres puntos con el mismo ángulo.

2. Andre no dijo cuál era el centro de rotación. Tiene que elegir un centro para los tres puntos.

3. El triángulo A'B'C' será congruente con el triángulo ABC y debe haber evidencia de un centro y marcas de ángulo.

Resumen de la lección para el estudiante

Una rotación es una transformación con un centro, un ángulo y una dirección (en el sentido de las agujas del reloj o en sentido contrario).

Aquí está cómo una rotación con un punto central C, un ángulo que mide t grados y una dirección contraria a las agujas del reloj transforma un punto P:

• La rotación envía el punto P a un punto P' en el círculo de radio CP

• El ángulo PCP' mide t grados y P' gira en el sentido contrario a las agujas del reloj alrededor del círculo de P

Si en cambio el sentido fuera el de las agujas del reloj, entonces P' giraría en el sentido de las agujas del reloj alrededor del círculo de radio CP. Si P y C están en el mismo lugar, entonces la rotación envía P a P' en el círculo de radio cero,y así los puntos P, C y P' están todos en el mismo lugar.

PROBLEMAS

DE PRÁCTICA

PROBLEMA 1

Dibuja la imagen del cuadrilátero ABCD al girarlo 120° en sentido antihorario alrededor del punto D

PROBLEMA 2

Hay un triángulo equilátero, ABC, inscrito en una circunferencia con centro D. ¿Cuál es el ángulo más pequeño que se puede girar el triángulo ABC alrededor D de modo que la imagen de A sea B?

A. 60°

B. 90°

C. 120°

D. 180°

PROBLEMA 3

¿Qué segmento es la imagen de AB cuando se gira 90° en sentido antihorario alrededor del punto P?

Soluciones posibles

Soluciones posibles C

Soluciones posibles FG

. Matemáticas . Unidad 1

PROBLEMA 4

(Unidad 1, Lección 13.)

El alfabeto del semáforo es una forma de utilizar banderas para señalar mensajes. He aquí cómo señalar la letra Q. Describe una transformación que llevaría la bandera de la derecha a la bandera de la izquierda. Q

Soluciones posibles

Gira la figura R 135 grados en el sentido de las agujas del reloj alrededor del punto de intersección de los brazos. Refleja a través del brazo izquierdo.

PROBLEMA 5

(Unidad 1, lección 13)

Aquí hay 2 polígonos:

Selecciona todas las secuencias de traslaciones, rotaciones y reflexiones de abajo que llevarían el polígono P al polígono

Rota 180° alrededor del punto A

Traslada de modo que A se lleve a J. Luego refleja sobre la recta BA

Rota 60° en sentido antihorario alrededor del punto A y luego refleje sobre la recta FA

Refleja sobre la recta BA y luego rota 60° en sentido antihorario alrededor del punto A

Refleja sobre la recta BA y luego trasladar por el segmento de rectadirigida BA

Soluciones posibles

Rotar 180° alrededor del punto A

Traslada de manera que A se lleve a J. Luego refleja sobre la recta BA

Rota 60° en el sentido contrario a las agujas del reloj alrededor del punto A y luego reflejar sobre la recta FA

Refleja sobre la recta BA y luego rota 60° en el sentido contrario a las agujas del reloj alrededor del punto A

Refleja sobre la recta BA y luego traslada por el segmento de recta dirigida BA

PROBLEMA 6

(Unidad 1, lección 12)

A. Dibuja la imagen de la figura ABC cuando es trasladada por el segmento de recta dirigida u. Etiqueta la imagen de A como A', la imagen de B como B' y la imagen de C como C'.

B. Explica por qué la recta que contiene AB es paralela a la recta que contiene A'B'

Soluciones posibles

B. Las rectas son paralelas porque una traslación lleva una recta a una recta paralela o a sí misma. Como el segmento de recta dirigido no estaba en la recta que contiene al segmento AB ni era paralelo a él, la imagen de AB es una recta paralela.

PROBLEMA 7

(Unidad 1, lección 10)

Existe una secuencia de transformaciones rígidas que lleva A a A', B a B' y C a C'. La misma secuencia lleva D a D'

Dibuja y etiqueta D':

Reflexiones:

Soluciones posibles

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.2 Representar transformaciones en el plano; describir transformaciones como funciones que toman puntos en el plano como entradas y dan otros puntos como salidas. Comparar las transformaciones que preservan la distancia y el ángulo con las que no lo hacen.

G-CO.3 Dado un rectángulo, paralelogramo, trapezoide o polígono regular, describir las rotaciones y reflexiones que lo llevan sobre sí mismo.

Construir

8.G.1 G-CO.4

Enfoque SMPs

MP7 Buscar y utilizar estructuras.

Estándares ELD de California

I.B.7

I.C.9

I.C.11

LECCIÓN 15 SIMETRÍA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir, buscan y hacen uso de la estructura descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo describir las reflexiones que toma una figura sobre sí misma.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente y por escrito) los reflejos que toma una figura sobre sí misma.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

Materiales necesarios

Copias de la plantilla maestra

Conjunto de herramientas de geometría (HS)

Notas adhesivas

Herramientas para crear una presentación visual

Preparación necesaria

Imprima y recorte las fichas de la plantilla maestra. El esquema de esta lección contiene 8 figuras diferentes. Cada grupo de 2-4 estudiantes investigará una figura. Prepara suficientes copias del esquema para que cada estudiante de cada grupo tenga una copia de la figura que su grupo investigará. (Nota: Los estudiantes repetirán este proceso para la simetría de rotación en la próxima lección; puede ser más fácil preparar el doble de figuras una vez en lugar de repetir el proceso).

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Vamos a describir algunas simetrías de figuras.

Narrativa de la lección

En esta lección y en la siguiente, los estudiantes determinan los casos en los que aplicar un cierto movimiento rígido a una figura no la cambia. Esta es la idea de simetría. Se dice que una figura tiene simetría si existe una transformación rígida que lleva la figura a sí misma. Los estudiantes estudian primero simetría de reflexión utilizando líneas de simetría y luego estudian simetría de rotación en una lección posterior. La simetría de traslación no se menciona explícitamente, pero los estudiantes han sido expuestos a la idea de que una línea tiene simetría de traslación en una lección anterior. Los estudiantes aplican sus conocimientos sobre transformaciones rígidas para identificar figuras en las que existe una línea de simetría que refleja la figura sobre sí misma, satisfaciendo así la definición de simetría de reflexión. El hecho de que la reflexión de un segmento a través de su bisectriz perpendicular intercambie sus puntos extremos resultará útil en la próxima unidad, cuando los estudiantes estudien la congruencia de los triángulos.

En una actividad, se asigna a cada grupo una figura diferente. Los estudiantes hacen uso de la estructura cuando discuten qué líneas de simetría se aplican a un tipo de figura en general, en lugar de limitar su pensamiento a un ejemplo dado (MP7).

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración Grupos pequeños 20 min

Actividad de exploración Independiente 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Descripción breve

Los estudiantes identifican transformaciones rígidas que resultan con una imagen en el mismo lugar que la preimagen.

Dada una figura, los estudiantes exploran la simetría de reflexión mediante la creación de una pantalla que identifica y describe sus líneas de simetría, incluyendo un no ejemplo.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las líneas de simetría.

Los estudiantes utilizan las propiedades de la reflexión para justificar si las diagonales de una cometa son líneas de simetría.

Los estudiantes dibujan figuras para hacer conexiones entre las líneas de simetría y las líneas de reflexión.

Los estudiantes demuestran su comprensión de las líneas de simetría en un rectángulo.

Práctica Independiente 8-10 min El componente de práctica independiente incluye 2 en la lección y 5 problemas de repaso en espiral.

CALENTAMIENTO | VOLVER AL PRINCIPIO 5

minutos

Este calentamiento invita a los estudiantes a visualizar diferentes secuencias de transformaciones que tomarán un segmento sobre sí mismo. Esta idea se ampliará en actividades posteriores en las que los estudiantes determinarán las líneas de simetría y los ángulos de rotación que crean simetría para diversas figuras. El hecho de que reflejar un segmento a través de su bisectriz perpendicular intercambia sus puntos extremos será útil en la próxima unidad cuando los estudiantes estudien la congruencia de triángulos.

Aquí hay un segmento AB:

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

ACTIVIDAD SÍNTESIS

Si trasladas el segmento hacia arriba 5 unidades y luego hacia abajo 5 unidades, se ve igual que como se veía originalmente.

1. ¿Qué otras transformaciones rígidas crean una imagen que se ajusta exactamente sobre el segmento original?

2. ¿Hay algún movimiento rígido simple que haga lo mismo?

1. Ejemplos de respuestas:

• cualquier transformación seguida de una transformación que la deshaga (por ejemplo, reflejar a través de una línea dada dos veces)

• traslación a lo largo del segmento de A a B y luego rotar 180 grados usando A' como centro

• reflexión a través de una recta perpendicular al segmento que pasa por B seguida de una traslación a lo largo del segmento de recta dirigida de A' a B'

2. Ejemplos de respuestas:

• rotación de 180 grados (en cualquier dirección) utilizando el punto medio del segmento como centro

• reflexión a través de la mediatriz del segmento

• reflexión a través de la recta AB

Seleccione a un estudiante para que comparta una única reflexión que lleve el segmento sobre sí mismo, y a otro estudiante para que comparta una única rotación que lleve el segmento sobre sí mismo. Diga a los estudiantes que si existe una transformación rígida que toma una figura sobre sí misma, se dice que la figura tiene simetría. Explique que cuando una sola reflexión toma una figura sobre sí misma, la figura tiene simetría de reflexión y la línea de reflexión se llama línea de simetría de la figura. Diga también a los estudiantes que cuando una sola rotación estrictamente entre 0 y 360 grados toma una figura sobre sí misma, la figura tiene simetría de rotación

ACTIVIDAD DE EXPLORACIÓN | AUTORREFLEXIÓN

(20 minutos)

En esta actividad, los estudiantes trabajan juntos para investigar líneas de simetría y comunicar su pensamiento en una muestra visual. Mientras supervisa, pregunte a los grupos si han encontrado todas las líneas de simetría posibles y que expliquen cómo saben que todas las figuras de ese tipo tienen esa misma simetría.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2-4. Proporcione a cada grupo las herramientas para crear una presentación visual.

Asigne una figura diferente de la plantilla maestra a cada grupo y proporcione suficientes copias de esa figura para cada estudiante de cada grupo. Tenga en cuenta que el enfriamiento utiliza un rectángulo, por lo que puede optar por asignar el rectángulo a un grupo de estudiantes que necesiten más tiempo de procesamiento.

Dé a los estudiantes 5 minutos de tiempo de trabajo seguidos de 5 minutos para montar su presentación visual. Explíqueles que no dispondrán de tiempo suficiente para que la presentación visual sea perfecta, por lo que el objetivo es que plasmen sus ideas de forma organizada.

Determina todas las líneas de simetría de la figura que te asigne tu maestro. Crea una presentación visual de tu figura. Incluye estas partes en tu presentación:

• el nombre de tu figura

• la definición de tu figura

• dibujos de cada línea de simetría

• una descripción en palabras de cada línea de simetría

• un no ejemplo en un color diferente (una descripción y dibujo de una reflexión no sobre una línea de simetría)

Ejemplo de respuesta:

• rectángulo

• un cuadrilátero con 4 ángulos rectos

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

• Los dibujos deben incluir las dos rectas que pasan por el centro del rectángulo y que son perpendiculares a sus lados.

• Si el rectángulo está orientado de forma que sus lados son verticales y horizontales, las líneas que pasan vertical y horizontalmente por el centro son líneas de simetría.

• Las diagonales no son líneas de simetría a menos que el rectángulo sea también un cuadrado.

Los estudiantes pueden pensar que cualquier línea que divida el área de una figura por la mitad, como una diagonal de un rectángulo no cuadrado, es una línea de simetría. Pida a los estudiantes que se reflejen a través de estas líneas para ver que las figuras no están tomadas sobre sí mismas.

El objetivo de este debate es identificar qué tipos de figuras tienen simetría de reflexión. Pida a los grupos que expongan sus representaciones visuales en el aula para que todos las vean en orden del número de líneas de simetría que tiene su figura. Tendrán que comunicarse con otros grupos para conseguirlo.

SÍNTESIS DE LA ACTIVIDAD

Invite a los estudiantes a hacer un «paseo por la galería» en el que dejen comentarios escritos en notas adhesivas para los demás grupos. A continuación se ofrece una guía sobre el tipo de comentarios que los estudiantes deben darse unos a otros:

• ¿Hubo algo en la organización de la presentación visual que aclarara especialmente las ideas? ¿Hay algún aspecto de la organización que pueda mejorarse?

• ¿Hay algún aspecto de la explicación de las ideas que las haya hecho especialmente claras? ¿Hay algún aspecto de las explicaciones que pueda mejorarse?

• ¿Hay alguna línea de simetría que el grupo haya pasado por alto?

• ¿Hay alguna línea de simetría que no funcione para todas las figuras del tipo dado?

ACTIVIDAD SÍNTESIS CONTINUACIÓN

Después del recorrido por la galería, pida a los estudiantes que compartan sus observaciones sobre las simetrías de reflexión de las diferentes figuras. Pregunte:

• «¿Qué figuras tienen menos líneas de simetría? ¿Cuál tiene más?». (El paralelogramo que no es un rombo no tiene ninguna línea de simetría. El círculo es el que más tiene, ya que tiene infinitas).

• «¿Hubo alguna línea que pensaste que serían líneas de simetría, pero cuando intentaste reflejar, resultó que no lo eran?». (La diagonal de un paralelogramo que no es un rombo parecía que sería una línea de simetría, pero no lo es).

• «Describe una figura que no tenga líneas de simetría». (Un triángulo escaleno no tiene líneas de simetría).

Guarde las representaciones visuales si es posible para compararlas con las representaciones de ángulos de rotación que crean simetría en una lección posterior.

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Divida la clase en pequeños grupos de debate e invite a un representante de cada grupo a informar a toda la clase.

Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales; atención

¿Estás listo para más?

Mira todas las figuras que exploró la clase y enfócate en aquellas que tenían más de una línea de simetría.

1. ¿Qué es cierto para todas las líneas de simetría en estas figuras?

2. Da un ejemplo de una figura que tenga dos o más líneas de simetría que no se crucen en el mismo punto.

3. ¿Qué pasaría si hicieras una secuencia de dos reflexiones diferentes a través de líneas de simetría para las figuras que exploraste en clase?

Respuestas de los estudiantes

1. Todas las líneas se intersecan en el mismo punto.

2. Una línea tiene simetría de reflexión en todas las líneas que son perpendiculares a ella.

3. Obtendrías una rotación centrada en el punto de intersección que lleva la figura hacia sí misma.

ACTIVIDAD DE EXPLORACIÓN | DIAGONALES DIABÓLICAS

(10 minutos)

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

Esta actividad invita a los estudiantes a aplicar la definición de reflexión cuando escriben una justificación de por qué una línea es o no una línea de simetría en una cometa.

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Mantenga a la vista términos y vocabulario importantes. Durante el lanzamiento, tome tiempo para repasar los siguientes términos de lecciones anteriores a los que los estudiantes necesitarán acceder para esta actividad: cometa, diagonal, línea de simetría, reflexión, congruente.

Apoya la accesibilidad para: Memoria; lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS ANTICIPADOS

SÍNTESIS DE ACTIVIDAD

. Matemáticas . Unidad 1

Kiran cree que ambas diagonales de una cometa son ejes de simetría. Tyler cree que solo una diagonal es un eje de simetría. ¿Quién tiene razón? Explica cómo lo sabes.

Tyler tiene razón.

Ejemplo de repsuesta: Un eje de simetría refleja la cometa sobre sí misma. Las reflexiones convierten segmentos en segmentos congruentes. Una cometa tiene dos pares de lados contiguos que son congruentes. Por lo tanto, en la cometa ABCD, AB ≅ AD y BC ≅ DC. Usando la diagonal AC como eje de simetría, la reflexión convierte el lado AB en el lado AD y el lado BC en el lado DC, lo cual funciona. Pero al reflejar sobre la diagonal BD, intentaría convertir el lado AB en el lado CB y esos lados no son necesariamente congruentes, por lo que no es necesariamente un eje de simetría.

Si los estudiantes tienen dificultades para comenzar, pídales que consulten sus tablas de referencia: «¿Qué información es útil?». (La definición de reflexión).

Si los estudiantes no conocen la definición de cometa, proporcióneles una: Un cuadrilátero con dos lados congruentes, uno al lado del otro y donde los otros dos lados también lo son.

El propósito de esta discusión es reforzar el uso de definiciones para justificar una respuesta. Invite a algunos estudiantes a compartir sus respuestas con la clase. Si un estudiante usó un diagrama bien etiquetado en su explicación, resalte esa estrategia. Si no lo mencionan, pregunte si un diagrama sería útil. (Sí, es más fácil hablar de puntos etiquetados que describir un lado genérico).

Apoyo para estudiantes que aprenden el idioma inglés

Escribir y hablar: MLR1 Cada vez más fuerte y más claro. Utilícelo con sucesivas puestas en común por parejas para dar a los estudiantes una oportunidad estructurada de revisar y perfeccionar su respuesta a «¿Quién tiene razón? Explica cómo lo sabes». Pida a cada estudiante que se reúna con 2-3 otros compañeros en fila para recibir comentarios. Muestre indicaciones para la retroalimentación que ayuden a los equipos a reforzar sus ideas y aclarar su lenguaje. Por ejemplo: «¿Puedes explicar cómo...?», «Deberías ampliar...», etc. Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar el producto final.

Principio(s) de diseño: Optimizar el resultado (para la generalización)

SÍNTESIS DE LA LECCIÓN

(5 minutos)

La idea principal a extraer de esta lección es la relación entre la definición de reflexión y la simetría de reflexión. Pregunte a los estudiantes cuándo una línea de reflexión es también una línea de simetría. (Esto ocurre cuando la reflexión lleva la figura hacia sí misma).

Invite a los estudiantes a dibujar figuras que tengan las siguientes simetrías y a escribir un enunciado de transformación para cada una de ellas. Sugiera a los estudiantes que miren el marco de la frase en la definición de reflexión en su cuadro de referencia si se atascan.

• Exactamente 1 línea de simetría

• Al menos 2 líneas de simetría

• Exactamente 5 líneas de simetría

ENFRIAMIENTO | ENTRECRUZADO (5 minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

¿Qué le ocurre a la diagonal de un rectángulo cuando el rectángulo se refleja a través de una línea de simetría? ¿Qué sugiere esto sobre las diagonales de los rectángulos?

Ejemplo de respuesta: Reflejar un rectángulo a través de una de sus líneas de simetría lleva una diagonal a la otra, por lo que deben tener la misma longitud.

Resumen de la lección para el estudiante

Una figura tiene simetría si existe una transformación rígida que crea una imagen que se ajusta exactamente sobre la figura original. Una figura tiene simetría de reflexión si hay una reflexión que lleva la figura hacia sí misma y la línea de reflexión en este caso se llama línea de simetría. Un hexágono regular tiene muchas líneas de simetría. Aquí tienes 2 de ellas. ¿Qué otras líneas crean una reflexión en la que la imagen es la misma que la figura original?

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Para cada figura, identifica cualquier línea de simetría que tenga la figura.

Soluciones posibles

• Yin-yang: ninguna

• Bandera: simetría de reflexión a través de líneas horizontales y verticales que pasan por el centro

• Figura de tres pies: ninguna

PROBLEMA 2

En el cuadrilátero BADC, AB = AD y BC = DC. La recta AC es una recta de simetría para este cuadrilátero.

A. Basándose en la línea de simetría, explica por qué las diagonales AC y BD son perpendiculares.

B. Basándose en la línea de simetría, explica por qué los ángulos ABC y ADC tienen la misma medida.

Soluciones posibles

A. Respuesta de ejemplo: La línea de simetría AC es una línea de reflexión que lleva B a D y por tanto es por definición la mediatriz de BD

B. Ejemplo de respuesta: La reflexión utilizando la línea de simetría AC fija los puntos A y C y lleva B a D. Por tanto, lleva el ángulo ABC a ADC y las reflexiones conservan la medida del ángulo.

PROBLEMA 3

(Unidad 1, lección 14)

Tres segmentos de recta forman la letra Z. Gira la letra Z en sentido contrario a las agujas del reloj alrededor del punto medio del segmento BC en 180 grados. Describe el resultado.

PROBLEMA 4

(Unidad 1, lección 14)

Hay un cuadrado, ABCS, inscrito en un círculo con centro D ¿Cuál es el ángulo más pequeño que podemos girar alrededor de D para que la imagen de A sea B?

A. 45°

B. 60°

C. 90°

D. 180°

PROBLEMA 5

(Unidad 1, lección 9)

Los puntos A, B, C y D son vértices de un cuadrado. El punto E está dentro del cuadrado. Explica cómo saber si el punto E está más cerca de A, B, C o D

Soluciones posibles

La imagen es la misma letra Z.

Soluciones posibles C

Soluciones posibles

Ejemplo de respuesta: Construye las mediatrices de los 4 lados del cuadrado. Las bisectrices perpendiculares dividen el cuadrado en 4 regiones. El punto E y el vértice más cercano se encuentran en la misma región. Si el punto E está en una arista o punto de intersección de las mediatrices, entonces está a la misma distancia de varios vértices.

PROBLEMA 6

(Unidad 1, lección 11)

Las rectas ℓ y m son perpendiculares.

A veces reflejar un punto sobre m tiene el mismo efecto que rotar el punto 180 grados usando el centro P. Selecciona todos los puntos etiquetados que tienen la misma imagen para ambas transformaciones.

. Matemáticas . Unidad 1

Soluciones posibles

PROBLEMA 7

(Unidad 1, lección 13)

Aquí está el triángulo POG. Haz coincidir la descripción de la rotación con la imagen de POG bajo esa rotación.

A. Rota 60 grados en el sentido de las agujas del reloj alrededor de O

B. Rota 120 grados en el sentido de las agujas del reloj alrededor de O

C. Rota 60 grados en el sentido contrario a las agujas del reloj alrededor de O

D. Rota 60 grados en el sentido de las agujas del reloj alrededor de P

Soluciones posibles

A. iv

B. ii C. i D. iii

Geometría . Matemáticas . Unidad 1

IIDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

G-CO.3 Dado un rectángulo, paralelogramo, trapezoide o polígono regular, describir las rotaciones y reflexiones que lo llevan sobre sí mismo.

Construir

G-CO.1 G-CO.4

Enfoque SMPs

MP6 Atender a la precisión.

Estándares ELD de California

I.B.8 I.C.9 I.C.12

LECCIÓN 16 MÁS SIMETRÍA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir, atienden a la precisión descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo describir las rotaciones que toma una figura sobre sí misma.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente y por escrito) las rotaciones que toma una figura sobre sí misma.

PREPARACIÓN

DE LA LECCIÓN

Rutinas didácticas

¿Cuál no pertenece?

MLR7: Comparar y conectar

MLR1: Cada vez más fuerte y más claro

Materiales necesarios

Plantillas maestras para el maestro

Conjunto de herramientas de geometría (HS)

Notas adhesivas

Herramientas para crear una presentación visual

Preparación necesaria

Si no hay suficientes figuras sobrantes de la lección anterior, prepara más copias de la plantilla maestra de «Autorreflexión» para que cada estudiante de cada grupo tenga copias de la figura que su grupo investigará en «Autorreflexión».

. Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Describamos más simetrías de figuras.

Narrativa de la lección

En esta lección, los estudiantes continúan examinando casos en los que aplicar un cierto movimiento rígido a una figura no la cambia, y esta vez, los estudiantes estarán observando simetría de rotación. Para que una figura tenga simetría de rotación, debe haber un ángulo para el que la rotación lleve a la figura hacia sí misma. Los estudiantes tienen la oportunidad de utilizar un lenguaje preciso en el calentamiento cuando identifican los diferentes tipos de simetría (MP6). Los estudiantes siguen utilizando un lenguaje preciso en sus justificaciones de la simetría a lo largo de las actividades.

RESUMEN DE LA LECCIÓN

Componente de lección Estructura Tiempo Descripción breve

Calentamiento Grupos pequeños 5 min Los estudiantes observan y comparan 4 figuras para determinar cuál figura no pertenece.

Actividad de Exploración Grupos pequeños 20 min

Dada una figura, los estudiantes exploran la simetría de rotación creando un despliegue visual que identifique y describa todas las rotaciones de la figura que crean simetría, incluyendo un no ejemplo.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de los tipos de simetría.

Actividad de Exploración Independiente 10 min Los estudiantes determinan y describen la simetría rotacional de un paralelogramo.

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Los estudiantes dibujan figuras que tienen simetría de rotación para varios grados de rotación.

Los estudiantes aplican sus conocimientos de simetría de reflexión y rotación para identificar un cuadrilátero que tenga ambas.

El componente de práctica independiente incluye 3 problemas de repaso de la lección y 4 problemas de repaso en espiral.

. Matemáticas . Unidad 1

CALENTAMIENTO | ¿CUÁL NO PERTENECE?: SIMETRÍA

(5 minutos)

Rutinas didácticas

¿Cuál no pertenece?

Este calentamiento pide a los estudiantes que comparen cuatro imágenes. Da a los estudiantes un motivo para utilizar el lenguaje con precisión (MP6). Da al maestro la oportunidad de escuchar cómo los estudiantes utilizan la terminología y hablan de las características de los elementos en comparación unos con otros.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2-4. Exponga las imágenes para que todos las vean. Conceda a los estudiantes 1 un minuto de reflexión en silencio y, a continuación, un tiempo para compartir sus ideas con su pequeño grupo. En sus pequeños grupos, pida a cada estudiante que comparta su razonamiento de por qué un elemento en particular no pertenece y, juntos, encuentren al menos una razón por la que cada elemento no pertenece.

¿Cuál no pertenece?

Ejemplos de respuestas:

A no pertenece porque:

• Tiene dos tipos de simetría (reflexión y rotación).

• Es curvo, no está hecho de líneas rectas y ángulos.

B no pertenece porque:

• Solo tiene simetría de reflexión.

• Tiene marcas de graduación.

RESPUESTAS POSIBLES

C no pertenece porque:

• Solo tiene simetría de rotación.

• Las letras van en el sentido de las agujas del reloj.

D no pertenece porque:

• No tiene ninguna simetría.

• Está sombreado.

• No tiene un punto A.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Geometría . Matemáticas . Unidad 1

A algunos estudiantes les puede preocupar que al girar el paralelogramo se invierta la dirección de las flechas. Haga hincapié en que las flechas son marcas para indicar que los segmentos son paralelos, pero que en realidad no forman parte del paralelogramo en sí.

Pida a cada grupo que comparta una razón por la que un elemento en particular no pertenece. Anote y muestre las respuestas para que todos las vean. Después de cada respuesta, pregunte a la clase si están de acuerdo o en desacuerdo. Dado que no hay una única respuesta correcta a la pregunta de cuál no pertenece, preste atención a las explicaciones de los estudiantes y asegúrese de que las razones dadas son correctas.

Durante el debate, pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como línea de simetría o diagonal. Además, presione a los estudiantes sobre las afirmaciones sin fundamento.

ACTIVIDAD DE EXPLORACIÓN | AUTOROTACIÓN (20

minutos)

Rutinas didácticas

MLR7: Comparar y conectar

En esta actividad, los estudiantes trabajan juntos para investigar la simetría de la rotación y comunicar su pensamiento en una presentación visual. Mientras supervisa, pregunte a los grupos si han encontrado todos los ángulos de rotación posibles que producen simetría y que expliquen cómo saben que estos ángulos se aplican a todas las figuras de ese tipo.

Organice a los estudiantes en los mismos grupos que la clase anterior. Proporcione a cada grupo herramientas para crear una presentación visual. Asigna a cada grupo una figura diferente de la «Autoreflexión» y proporciona suficientes copias de la figura para todos en el grupo.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Da a los estudiantes 5 minutos de tiempo de trabajo seguidos de 5 minutos para armar su exhibición visual. Explíqueles que no dispondrán de tiempo suficiente para que la presentación visual sea perfecta, por lo que el objetivo es que plasmen sus ideas aproximadas de forma organizada.

Determina todos los ángulos de rotación que crean simetría para la figura que te asigne tu maestro. Crea una presentación visual de tu figura. Incluye estas partes en tu presentación:

• el nombre de tu figura

• la definición de tu figura

• dibujos de cada rotación que crea simetría

• una descripción en palabras de cada rotación que crea simetría, incluyendo el centro, ángulo y dirección de rotación

• un no ejemplo (una descripción y dibujo de una rotación que no resulta en simetría)

Ejemplo de respuesta:

• Triángulo equilátero

• Un triángulo con 3 lados congruentes

RESPUESTAS POSIBLES

• Los dibujos deben mostrar rotaciones de 60 grados y rotaciones de 120 grados

• Rota el triángulo 60 grados alrededor del centro, en sentido horario o antihorario

• Un no-ejemplo sería una rotación de 30 grados

El objetivo de este debate es identificar qué tipos de figuras tienen simetría de rotación.

Pide a los grupos que expongan sus presentaciones visuales en el aula para que todos las vean en orden del número de ángulos de rotación que crean simetría para su figura. Para ello tendrán que comunicarse con otros grupos. Si es posible, muestre las representaciones visuales de simetría de reflexión de la clase anterior para compararlas.

Invite a los estudiantes a hacer un «recorrido por la galería» en el que dejen comentarios escritos en notas adhesivas para los otros grupos. A continuación se ofrece una guía sobre el tipo de comentarios que los estudiantes deben darse entre sí:

• ¿Hubo algo en la organización de la presentación visual que aclarara especialmente las ideas? ¿Hay algún aspecto de la organización que pueda mejorarse?

• ¿Hay algún aspecto de la explicación de las ideas que las haya hecho especialmente claras? ¿Hay algún aspecto de las explicaciones que podría mejorarse?

• ¿Hay algún ángulo de rotación que cree simetría y que el grupo no haya visto?

SÍNTESIS DE LA ACTIVIDAD

• ¿Hay algún ángulo de rotación que no cree simetría para todas las figuras del tipo dado?

Después del recorrido por la galería, pida a los estudiantes que compartan sus observaciones sobre la simetría de rotación. Pregunte:

• «¿Qué figuras tienen menos ángulos de rotación que crean simetría? ¿Cuál tiene más?». (El trapecio isósceles no tiene simetría de rotación porque las únicas rotaciones que lo llevan a sí mismo son 0 grados o 360 grados. Para el círculo, cualquier ángulo de rotación crea simetría).

• «¿Qué notas sobre el orden de las figuras en términos de simetría de reflexión versus el orden de las figuras en términos de simetría de rotación?». (El círculo es el que tiene más líneas de simetría y más ángulos de rotación que crean simetría. Parece ser la figura más simétrica en general. El paralelogramo que no es un rombo tiene 180 grados de simetría de rotación, pero no tiene líneas de simetría; pero el rombo tiene 180 grados de simetría de rotación y 2 líneas de simetría).

Si surgen preguntas sobre rotaciones de 0 o 360 grados, explica que todas las figuras, por extrañas que sean, tienen el mismo aspecto cuando se rotan 0 grados o 360 grados. Si estas rotaciones son las únicas que llevan la figura a sí misma, entonces se considera que no tiene simetría de rotación.

Apoyo para estudiantes que aprenden el idioma

inglés

Hablar: MLR 7 Comparar y conectar. Utilice esta rutina cuando los estudiantes presenten sus categorías y su secuencia de rotaciones, traslaciones y reflexiones para llegar de la figura original a la imagen. Pida a los estudiantes que consideren qué es igual y qué es diferente en las secuencias de transformaciones. Llame la atención de los estudiantes sobre el modo en que se describen las transformaciones con precisión (es decir, orden, números, palabras). Estos intercambios refuerzan el uso del lenguaje matemático de los estudiantes y su razonamiento sobre las transformaciones.

Principio(s) de diseño: Maximizar la metaconciencia

Apoyo a los estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Divide la clase en pequeños grupos de debate e invita a un representante de cada grupo a informar a toda la clase.

Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales; Atención

¿Estás preparado para más?

Las figuras finitas, como las que hemos visto en clase, no pueden tener simetría de traslación. Pero con un patrón que continúe eternamente, sí es posible. Los patrones como este que tienen simetría de traslación en una sola dirección se llaman patrones de friso

1. ¿Cuáles son las líneas de simetría de este patrón?

2. ¿Qué ángulos de rotación producen simetría para este patrón?

3. ¿Qué traslaciones producen simetría para este patrón si lo imaginamos extendiéndose horizontalmente para siempre?

Respuestas de los estudiantes

1. Hay una línea de simetría horizontal que pasa por el centro de la imagen y una línea de simetría vertical que pasa por el centro de cada octógono y por el centro de cada cuadrado entre los octógonos.

2. El punto donde se encuentran cada línea vertical y horizontal es el centro de una rotación de 180 grados que crea simetría.

3. La traslación por cada segmento de línea dirigida desde el centro de cualquier octógono al centro de otro crea simetría.

ACTIVIDAD DE EXPLORACIÓN | SIMETRÍA DEL

PARALELOGRAMO (10 minutos)

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

En esta actividad, los estudiantes escriben una descripción de la simetría de rotación de un paralelogramo. Esto invita a los estudiantes a aplicar la definición de rotación.

Apoyo para estudiantes con discapacidad

Representación: Acceso para la percepción. Lea la situación en voz alta. Los estudiantes que escuchen y lean a la vez la información se beneficiarán de un tiempo de procesamiento adicional.

Apoya la accesibilidad para: Lenguaje

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Clare dice: «En la clase pasada pensé que el paralelogramo tendría simetría de reflexión. Intenté usar una diagonal como eje de simetría, pero no funcionó. Así que ahora dudo que tenga simetría de rotación».

Lin dice: «Yo también lo pensé al principio, pero ahora creo que un paralelogramo sí tiene simetría de rotación. Mira esto».

¿Cómo podría Lin describirle a Clare la simetría que ve?

Respuesta de ejemplo: El diagrama muestra que los vértices opuestos están a la misma distancia del centro. Clare pudo ver la trayectoria de cada vértice durante una rotación de 180 grados. Lin pudo describir con precisión la rotación que, según ella, lleva al paralelogramo hacia sí mismo, indicando el centro, el ángulo y la dirección de la rotación. El centro del paralelogramo ABCD es la intersección de las diagonales AC y BD. Llamemos a este punto E. Al girar ABCD 180 grados en sentido horario alrededor del centro E, AB se convierte en DC y BC en DA.

. Matemáticas . Unidad 1

CONCEPTOS ERRÓNEOS ANTICIPADOS

SÍNTESIS DE LA ACTIVIDAD

Dirija a los estudiantes a sus tablas de referencia. ¿Qué información es útil? (La definición de rotación).

El propósito de esta discusión es reforzar el uso de definiciones para justificar una respuesta. Invite a algunos estudiantes a compartir sus respuestas con la clase. Destaque cualquier mejora respecto a las justificaciones anteriores, como el buen uso de un diagrama bien etiquetado.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

La idea principal a extraer de esta lección es la relación entre la definición de rotación y la simetría de rotación. Pregunta a los estudiantes cuándo una rotación muestra que una figura tiene simetría de rotación. (Esto ocurre cuando la rotación lleva la figura hacia sí misma).

Apoyo para estudiantes que aprenden el idioma inglés

Escribir, hablar MLR 1 Cada vez más fuerte y más claro. Utilice esto con sucesivas comparticiones por parejas para dar a los estudiantes una oportunidad estructurada de revisar y refinar su respuesta a «¿Cómo podría Lin describir a Clare la simetría de rotación que ve?». Pida a cada estudiante que se reúna con 2-3 otros compañeros en fila para recibir comentarios. Muestre indicaciones para la retroalimentación que ayuden a los equipos a reforzar sus ideas y aclarar su lenguaje. Por ejemplo: «¿Puedes explicar cómo...?», «Deberías ampliar...», etc. Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar el producto final.

Principio(s) de diseño: Optimizar el resultado (para la generalización)

Invite a los estudiantes a dibujar figuras para las que los siguientes ángulos de rotación creen simetría y a escribir un enunciado de transformación para cada una de ellas. Sugiera a los estudiantes que miren el marco de la oración en la definición de rotación en su tabla de referencia si se atascan.

• 180 grados

• 90 grados

• 45 grados

ENFRIAMIENTO | CUADRILÁTERO MISTERIOSO

(5 minutos)

En esta actividad, los estudiantes combinan sus conocimientos de simetría de reflexión y rotación para identificar un cuadrilátero con ambos tipos.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

El cuadrilátero ABCD tiene simetría de reflexión y rotación. ¿Qué tipo de cuadrilátero podría ser ABCD? Muestra o explica tu razonamiento.

RESPUESTAS POSIBLES

Ejemplos de respuestas: Podría ser un rombo, que tiene simetría de reflexión utilizando una diagonal como línea de simetría y simetría de rotación de 180 grados. Podría ser un rectángulo, que tiene simetría de reflexión usando un segmento que une puntos medios opuestos como línea de simetría y simetría de rotación de 180 grados.

Resumen de la lección

Una figura tiene simetría de rotación si hay una rotación entre 0 y 360 grados que lleva la figura hacia sí misma. Un hexágono regular tiene muchos ángulos que funcionan para crear simetría de rotación. Aquí tienes uno de ellos. ¿Qué otros ángulos crearían una rotación donde la imagen es la misma que la figura original?

¿Puedes pensar en una figura que tenga simetría de traslación?

No hay polígonos con simetría de traslación, pero una figura infinita como una línea puede trasladarse de tal manera que la traslación lleve la línea hacia sí misma.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Para cada figura, identifica cualquier ángulo de rotación que cree simetría.

Soluciones posibles

• Yin-yang: Rotando 180 grados alrededor del centro del círculo se crea simetría ignorando los colores. No hay simetría incluyendo los colores.

• Bandera: Rotando 180 grados alrededor del centro de la figura se crea simetría.

• Figura de tres patas: Rotando 120 y 240 grados alrededor del centro de la figura se crea simetría.

PROBLEMA 2

Un triángulo tiene simetría de rotación que puede llevar cualquiera de sus vértices a cualquiera de sus otros vértices. Selecciona todas las conclusiones a las que podemos llegar a partir de esto.

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida.

Todas las rotaciones llevan una mitad del triángulo a la otra mitad del triángulo.

PROBLEMA 3

Soluciones posibles

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida. Todas las rotaciones llevan una mitad del triángulo a la otra mitad del triángulo.

Selecciona todos los ángulos de rotación que producen simetría para esta flor.

45 grados

90 grados

135 grados

180 grados

225 grados

270 grados

. Matemáticas . Unidad 1

Soluciones posibles

45 grados

90 grados

135 grados

180 grados

225 grados

270 grados

PROBLEMA 4

(Unidad 1, lección 15)

Identifica cualquier línea de simetría que tenga la figura.

PROBLEMA 5

(Unidad 1, lección 15)

Un triángulo tiene una línea de simetría. Selecciona todas las conclusiones que deben ser ciertas.

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida.

Ningún lado del triángulo tiene la misma longitud.

Ningún ángulo del triángulo tiene la misma medida.

Dos lados del triángulo tienen la misma longitud.

Dos ángulos del triángulo tienen la misma medida.

PROBLEMA 6

(Unidad 1, lección 10)

Soluciones posibles

Simetría de reflexión a través de líneas horizontales y verticales que pasan por el centro.

Soluciones posibles

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida.

Ningún lado del triángulo tiene la misma longitud.

Ningún ángulo del triángulo tiene la misma medida.

Dos lados del triángulo tienen la misma longitud.

Dos ángulos del triángulo tienen la misma medida.

Aquí hay 4 triángulos que han sido transformados cada uno por una transformación diferente. ¿Qué transformación no es una transformación rígida?

A. B.

Soluciones posibles A

PROBLEMA 7

(Unidad 1, lección 12)

Haz coincidir cada segmento de recta dirigida con la traslación del polígono P al polígono Q por ese segmento de recta dirigida.

Traslación 1 Traslación 2

Soluciones posibles

A: iv, B: ii, C: iii, D: i

Math Nation California . Geometría

Traslación 3

Traslación 4

C. D.

A. i. Traslación 1

B. ii. Traslación 2

C. iii. Traslación 3

D. iv. Traslación 4

LECCIÓN 17

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.5 Dada una figura geométrica y una rotación, reflexión o traslación, dibujar la figura transformada. Especificar una secuencia de transformaciones que llevarán una figura dada a otra.

Construir

8.G.2 G-CO.4

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1 I.C.12 II.C.6

TRABAJAR CON TRANSFORMACIONES RÍGIDAS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir, buscar y hacer uso de la estructura descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo describir una transformación que lleva puntos dados a otro conjunto de puntos.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comparar y contrastar (oralmente) diagramas de transformaciones.

• Comprender que la notación A' representa la imagen del punto A.

• Explicar (oralmente y por escrito) una secuencia de transformaciones que llevan puntos dados a otro conjunto de puntos.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyo para el debate

Clasificación de tarjetas

MLR7: Comparar y conectar

Dibújalo

Materiales necesarios

Conjunto de herramientas de geometría (HS)

Tarjetas preimpresas, recortadas a partir de copias de la plantilla maestra

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Comparemos figuras transformadas.

Narrativa de la lección

En grados anteriores, los estudiantes describen una secuencia de transformaciones rígidas que exhibe la congruencia entre dos figuras. Para preparar a los estudiantes para futuras pruebas de congruencia, esta lección pide a los estudiantes que ideen una secuencia sistemática, punto por punto, de transformaciones que funcionen para llevar cualquier par de polígonos congruentes uno sobre otro. A medida que el enfoque se desplaza a las secuencias de transformaciones entre figuras con características más generales en lugar de medidas específicas, anime a los estudiantes a explicar cómo saben que sus secuencias harán que ciertos puntos o líneas coincidan. Cuando los estudiantes consideran cómo de generalizable es una estrategia para definir secuencias de transformaciones rígidas, están buscando las estructuras de pares de figuras congruentes (MP7).

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración En parejas 20 min

Actividad de exploración Independiente 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes identifican mentalmente las transformaciones rígidas que llevan un punto a otro.

Los estudiantes clasifican las tarjetas que muestran las transformaciones en categorías de su elección y luego escriben una secuencia de transformaciones para describir cada transformación rígida.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las transformaciones rígidas.

Los estudiantes explican cómo determinar la línea de reflexión en una transformación dada.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la identificación de la línea de reflexión utilizando la tecnología.

Los estudiantes discuten cómo diferentes secuencias de transformaciones producen imágenes en diferentes posiciones.

Los estudiantes describen una secuencia de transformaciones rígidas que podrían mapear 1 triángulo sobre otro.

El componente de práctica independiente incluye 3 problemas de repaso de la lección y 6 problemas de repaso de la espiral.

CALENTAMIENTO | CHARLA DE MATEMÁTICAS: DE AQUÍ PARA ALLÁ (5

minutos)

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyos para el debate

El propósito de este calentamiento es obtener estrategias y conocimientos que los estudiantes tienen para usar movimientos rígidos punto por punto sin una cuadrícula. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de armar transformaciones rígidas que lleven un polígono a otro sin hacer referencia a una cuadrícula. Mientras participan en esta actividad, los estudiantes necesitan ser precisos en la elección de palabras y en el uso del lenguaje (MP6) porque los movimientos rígidos solo pueden definirse en referencia a puntos etiquetados.

INTRODUCCIÓN

Muestre el diagrama y un problema cada vez. Conceda a los estudiantes un tiempo de reflexión para cada problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. Mantenga todos los problemas expuestos durante la charla. Continúe con un debate con toda la clase.

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Para apoyar la memoria de trabajo, proporcione a los estudiantes notas adhesivas o minipizarras.

Apoya la accesibilidad para: Memoria; organización

El segmento CD es la mediatriz del segmento AB. Encuentra mentalmente cada transformación.

Una transformación que lleva de A a B

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Una transformación que lleva de B a A

Una transformación que lleva de C a D

Una transformación que lleva de D a C

• Ejemplos de respuestas:

• Traslación por el segmento AB. Reflexión en CD. Rotación de 180 grados alrededor del centro M.

• Traslación por el segmento BA. Reflexión en CD. Rotación de 180 grados alrededor del centro M.

• Traslación por el segmento CD. Reflexión en la mediatriz de CD.

• Traslación por el segmento DC. Reflexión en la mediatriz de CD.

CONCEPTOS ERRÓNEOS PREVISTOS

. Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Algunos estudiantes pueden pensar que C puede reflejarse sobre la línea AB en D. Pregúnteles qué necesitaríamos saber para que eso funcione.

• «¿Quién puede replantear el razonamiento de de otra manera?».

• «¿Tenía alguien la misma estrategia pero la explicaría de otra manera?».

• «¿Resolvió alguine el problema de otra manera?».

• «Quiere alguien añadir algo a la estrategia de ?».

• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?».

Si ningún estudiante saca el tema, pregunte a los estudiantes cómo puede utilizarse una rotación para llevar A a B

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «Primero, yo porque...» o «Noté que , así que yo...». Algunos estudiantes pueden beneficiarse de la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.

Principio(s) de diseño: Optimizar la salida (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | CLASIFICACIÓN DE TARJETAS: ¿CÓMO LLEGÓ ESTO HASTA AQUÍ?

(20 minutos)

Rutinas didácticas

Clasificación de tarjetas

MLR7: Comparar y conectar

El objetivo de esta actividad es activar los conocimientos previos de los estudiantes sobre las transformaciones rígidas y no rígidas. Pedir a los estudiantes que elijan sus propias categorías les invita a determinar qué características podrían ser importantes para fijarse en ellas. Los estudiantes también empiezan a practicar la habilidad de definir una transformación rígida que lleva una figura a la otra sin utilizar una cuadrícula para estimar o definir centros, ángulos, líneas de reflexión o segmentos de recta dirigidos.

Los estudiantes pueden tener dificultades para describir la ubicación de la línea de reflexión. No hay necesidad de abordar esto durante esta actividad, ya que se cubrirá en una actividad posterior.

Monitoree a los estudiantes que primero se trasladan para alinear un par de vértices correspondientes y luego giran para la tarjeta con el triángulo ABC

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Distribuya las tarjetas precortadas. Dé a los estudiantes 3 minutos para clasificar y luego haga una pausa para debatir. Pida a algunos grupos que expliquen cómo clasificaron sus tarjetas.

Invite a los estudiantes a escribir las transformaciones y a continuación discuta con toda la clase.

. Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

1. Tu maestro te dará un conjunto de tarjetas que muestran transformaciones de figuras. i. Clasifica las tarjetas en las categorías que elijas. Prepárate para explicar el significado de tus categorías.

ii. A continuación, ordena las tarjetas en categorías de otra manera. Prepárate para explicar el significado de tus nuevas categorías.

2. Para cada tarjeta con una transformación rígida: escribe una secuencia de rotaciones, traslaciones y reflexiones para llegar de la figura original a la imagen. Sé preciso.

1. Ejemplos de respuestas: congruentes vs. no congruentes, cuadriláteros vs. triángulos vs. otros polígonos.

2. Ejemplos de respuestas:

Traslada el triángulo ABC por el segmento de recta dirigido desde C hasta C'. Gira la imagen en el sentido de las agujas del reloj alrededor del centro C' por el ángulo XC'A'. (Ver imagen).

Traslada el rectángulo GHIJ por el segmento de recta dirigido desde J a J'

Refleja RSTU a través de la bisectriz perpendicular de R y R'.

Traslada VWXYZ por el segmento de línea dirigida de W a W'. Luego gira la imagen en el sentido de las agujas del reloj alrededor del centro W' por el ángulo V'W'B. (Ver imagen). (Los estudiantes no deben describir las transformaciones no rígidas).

Un propósito de la discusión es volver a enfatizar que las traslaciones, rotaciones y reflexiones son transformaciones rígidas, que mantienen el tamaño y la forma de los polígonos mientras que otras transformaciones no lo hacen. Recuerde a los estudiantes que las figuras se llaman congruentes cuando hay una secuencia de transformaciones rígidas que lleva una figura sobre otra.

El segundo propósito de la discusión es ayudar a los estudiantes a identificar lo que es difícil de definir de las transformaciones rígidas fuera de la cuadrícula. Si los estudiantes tienen dificultades para definir con precisión las transformaciones rígidas, existe una lección opcional sobre transformaciones punto por punto para utilizar además de esta discusión.

SÍNTESIS DE LA ACTIVIDAD

Considere la tarjeta con los triángulos ABC y A'B'C'. Si algún estudiante ha realizado primero la traslación para alinear un par de vértices correspondientes y luego ha girado, pídale que comparta su método. Si no, discuta la dificultad de estimar dónde colocar el centro de rotación para que una sola rotación alinee definitivamente los tres puntos. Demuestre a los estudiantes cómo se puede trasladar por el segmento de línea dirigida desde C hasta C' y, luego, rotar por el ángulo formado en el vértice C

Si ningún estudiante ha utilizado un método punto por punto, anímeles a que vuelvan a mirar la tarjeta con VWXYZ e intenten utilizar un método punto por punto para definir movimientos rígidos que lleven la figura original a la imagen sin estimar las ubicaciones de ninguna línea o punto nuevos.

Espere a discutir en detalle la transformación de la tarjeta con RSTU, ya que será el tema central de la siguiente actividad.

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR7 Comparar y conectar. Utilice esta rutina cuando los estudiantes presenten sus categorías y su secuencia de rotaciones, traslaciones y reflexiones para llegar de la figura original a la imagen. Pida a los estudiantes que consideren qué es igual y qué es diferente en las secuencias de transformaciones. Llame la atención de los estudiantes sobre la precisión con que se describen las transformaciones. Estos intercambios refuerzan el uso del lenguaje matemático y el razonamiento de los estudiantes sobre las transformaciones.

Principio(s) de diseño: Maximizar la metaconciencia

¿Estás listo para más?

Diego observa que, aunque a menudo era más fácil usar una secuencia de reflexiones, rotaciones y traslaciones para describir las transformaciones rígidas de las tarjetas, cada una de ellas podía hacerse con una sola reflexión, rotación o traslación. Sin embargo, Priya dibuja su propia tarjeta, que se muestra, que según ella no se puede hacer como una sola reflexión, rotación o traslación.

1. Para cada transformación rígida de la clasificación de tarjetas, escribe la transformación como una sola reflexión, rotación o traslación.

2. Justifica por qué la transformación de Priya no se puede escribir como una sola reflexión, rotación o traslación.

Posibles

respuestas

3. El rectángulo y el trapecio ya se describen como tales en la respuesta del estudiante para la actividad. El triángulo puede girarse 90 grados en el sentido de las agujas del reloj alrededor de un punto que sea la intersección de las mediatrices de los segmentos que unen cada punto y su imagen. El pentágono se puede girar 135 grados en el sentido de las agujas del reloj alrededor de un punto que es la intersección de las bisectrices perpendiculares de los segmentos que conectan cada punto y su imagen.

4. Ejemplo de respuesta: Dado que ABC se produce en el sentido contrario a las agujas del reloj y A'B'C' en el sentido de las agujas del reloj es imposible que una rotación o traslación lleve ABC a A'B'C'. Una reflexión simple tampoco puede funcionar ya que la mediatriz de AA' no es la misma que la mediatriz de BB'

ACTIVIDAD DE EXPLORACIÓN | REFLEXIÓN SOBRE LA REFLEXIÓN

(10 minutos)

Rutinas didácticas

Dibújalo

En esta actividad, los estudiantes determinan si una reflexión puede llevar una figura a otra y cómo encontrar la línea de reflexión precisa para figuras disjuntas.

Poner a disposición de los estudiantes un programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5). Si se lleva a cabo utilizando material impreso, indique a los estudiantes que consulten la ficha de la actividad anterior con la figura RSTU.

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Fomente y apoye las oportunidades de interacción entre compañeros. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo, «Sé porque...», «Primero, porque . Después, yo...» y «Este método funciona / no funciona porque....».

Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales

. Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Diego dice: «Veo por qué una reflexión podría llevar RSTU a R'S'T'U', pero no estoy seguro de dónde está la línea de reflexión. Solo adivinaré».

1. ¿Cómo podría Diego ver que una reflexión podría funcionar sin saber dónde está la línea de reflexión?

2. ¿Cómo podría Diego encontrar una línea de reflexión exacta que funcionara?

Ejemplos de respuestas:

1. Los vértices RSTU aparecen en el orden de las agujas del reloj alrededor del cuadrilátero, pero su imagen R'S'T'U' aparece en el orden contrario a las agujas del reloj.

2. La línea de reflexión debe ser la mediatriz de RR' que también debe ser la mediatriz de SS', TT' y UU'

El propósito de esta discusión es reforzar el uso de definiciones para justificar una respuesta. Invite a algunos estudiantes a compartir sus respuestas con la clase. Destaque las mejoras respecto a las justificaciones anteriores, como el buen uso de un diagrama bien etiquetado.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Muestra dos triángulos congruentes para que todos los vean:

Pregunta a los estudiantes:

• ¿Qué triángulo es el original y cuál es la imagen? (El triángulo de la derecha es el original y el de la izquierda es la imagen. La notación prima en las etiquetas de los vértices lo indica).

• ¿Cuál sería la secuencia de transformaciones que llevaría el triángulo ABC al triángulo A'B'C'? Explica cómo sabes que la imagen de A coincide con A'. (Traslada B sobre B' y luego gira hasta que la imagen de A caiga sobre A'. Las transformaciones mantienen las distancias iguales, de modo que la imagen de A está en el semirrecta B'A' a una distancia de B'A'. Eso significa que la imagen de A tiene que aterrizar en A').

• ¿Funcionaría esa secuencia solo para este par de triángulos congruentes, o funcionaría también para otros pares de triángulos congruentes? (Esta secuencia funcionará para cualquier par de triángulos congruentes, siempre que no haya una reflexión implicada).

Muestre otra imagen para que todos la vean.

Pregunte a los estudiantes:

• ¿Qué tiene de diferente este caso del anterior? (El caso anterior no implica una reflexión).

• ¿Qué ocurre si intentamos la misma secuencia de transformaciones de la última vez? (Si trasladamos B sobre B' y luego rotamos hasta que la imagen de A caiga sobre A', entonces los triángulos compartirán lado A'B', pero la imagen de C estará en el lado opuesto de la línea A'B' como C').

• ¿Qué tenemos que añadir a la secuencia para llevar el triángulo ABC al triángulo A'B'C'? (Una reflexión sobre la recta A'B' llevará la imagen de C a C').

Diga a los estudiantes que definir estas secuencias y observar los resultados es suficiente para conjeturar que las secuencias llevan una figura a otra. Para ser convincente, es necesario poder explicar por qué cada vértice cae exactamente donde creemos que debería caer. Explicar por qué cada punto cae exactamente donde debería es algo en lo que trabajarán con el tiempo.

Geometría . Matemáticas . Unidad 1

ENFRIAMIENTO | LLEGA HASTA AQUÍ

(5 minutos)

Encuentra una secuencia de movimientos rígidos para llevar cada vértice del triángulo ABC al vértice correspondiente del triángulo A'B'C'

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Trasladar el triángulo ABC por el segmento de recta dirigida que va de A a A'. Reflejar la imagen del triángulo ABC a través de la recta A'B'.

Resumen de la lección para el estudiante

Si 2 figuras son congruentes, siempre podemos encontrar una transformación rígida que lleve una sobre la otra.

Observa las figuras congruentes ABC y DEF. Parece que DEF podría ser una reflexión y traslación de ABC. Pero ¿hay alguna forma de describir una secuencia de transformaciones sin adivinar dónde podría estar la línea de reflexión?

Nuestro objetivo es tomar la imagen de E sobre B. Luego queremos tomar la imagen de D sobre A sin mover E y B. Finalmente, necesitamos tomar la imagen de F sobre C sin mover ninguno de los puntos coincidentes.

Podemos empezar con la traslación: Trasladar el triángulo DEF por el segmento de recta dirigida que va de E a B

Nation California . Geometría

. Matemáticas . Unidad 1

Ahora, un par de puntos correspondientes coinciden. ¿Hay alguna transformación que podamos usar para llevar D' a A que deje B y E' en su lugar? Las rotaciones tienen un punto fijo, así que rota el triángulo D' E' F' por el ángulo D' BA usando el punto B como centro.

Ahora, 2 pares de puntos correspondientes coinciden. La reflexión a través de la recta AB llevará D″ E″ F″ a ABC, que es lo que intentábamos hacer. Sabemos que D″ y E″ no se moverán, ya que los puntos sobre la línea de reflexión no se mueven. ¿Cómo sabemos que F″ acabará en C? Puesto que los triángulos son congruentes, F″ y C están a la misma distancia de la línea de reflexión.

Siempre es posible describir transformaciones utilizando puntos, ángulos y segmentos existentes. Puede llevar un paso extra, pero podemos estar seguros de que las transformaciones funcionan si no adivinamos dónde puede estar la línea de reflexión o el centro de rotación.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

El cuadrilátero ABCD es congruente con el cuadrilátero A'B'C'D'. Describe una secuencia de movimientos rígidos que lleve A a A', B a B', C a C' y D a D'

Soluciones posibles

Ejemplo de respuesta: Traslada el cuadrilátero ABCD por el segmento de línea dirigido BB'. Gira la imagen utilizando el centro B' hasta que la imagen de C coincida con C'

PROBLEMA 2

Selecciona todas las transformaciones que deben llevar cualquier punto A a cualquier punto B

Rotación de 180° alrededor de A

Rotación de 180° alrededor de B

Rotación de 180° alrededor del punto medio del segmento AB

Reflexión sobre la recta AB

Reflexión sobre la mediatriz del segmento AB

Traslación por el segmento de recta dirigida AB

Traslación por el segmento de recta dirigida BA

Soluciones posibles

Rotación de 180° alrededor de A

Rotación de 180° alrededor de B

Rotación de 180° alrededor del punto medio del segmento AB

Reflexión sobre la recta AB

Reflexión sobre la mediatriz del segmento AB

Traslación por la recta segmento dirigido AB

Traslación por la recta segmento dirigido BA

PROBLEMA 3

El triángulo ABC es congruente con el triángulo A'B'C'. Describe una secuencia de movimientos rígidos que lleve A a A', B a B' y C a C'

PROBLEMA 4

(Unidad 1, lección 16)

Matemáticas . Unidad 1

Soluciones posibles

Ejemplo de respuesta: Traslada el triángulo ABC por el segmento de recta dirigido AA'. Gira la imagen usando el centro A' hasta que la imagen de B coincida con B'

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida.

Todas las rotaciones llevan una mitad del triángulo a la otra mitad del triángulo.

Es un triángulo rectángulo.

Ninguno de los lados del triángulo tiene la misma longitud.

Ninguno de los ángulos del triángulo tiene la misma medida.

Soluciones posibles

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida.

Todas las rotaciones llevan una mitad del triángulo a la otra mitad del triángulo.

Es un triángulo rectángulo.

Ninguno de los lados del triángulo tiene la misma longitud.

Ninguno de los ángulos del triángulo tiene la misma medida.

PROBLEMA 5

(Unidad 1, lección 16)

Selecciona todos los ángulos de rotación que producen simetría para esta flor.

. Matemáticas . Unidad 1

PROBLEMA 6

(Unidad 1, lección 15)

Un triángulo rectángulo tiene una línea de simetría. Selecciona todas las conclusiones que deben ser ciertas.

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida.

Dos lados del triángulo tienen la misma longitud.

Dos ángulos del triángulo tienen la misma medida.

Ningún lado del triángulo tiene la misma longitud.

Ningún ángulo del triángulo tiene la misma medida.

PROBLEMA 7

(Unidad 1, lección 15)

Soluciones posibles

Todos los lados del triángulo tienen la misma longitud.

Todos los ángulos del triángulo tienen la misma medida.

Dos lados del triángulo tienen la misma longitud.

Dos ángulos del triángulo tienen la misma medida.

Ningún lado del triángulo tiene la misma longitud.

Ningún ángulo del triángulo tiene la misma medida.

En el cuadrilátero BADC, AB = AD y BC = DC. La recta AC es una recta de simetría para este cuadrilátero. Basándote en la línea de simetría, explica por qué los ángulos ACB y ACD tienen la misma medida.

Soluciones posibles

Ejemplo de respuesta: La reflexión usando la línea de simetría AC fija los puntos A y C y lleva B a D. Por lo tanto, lleva el ángulo ACB a ACD y las reflexiones conservan la medida del ángulo.

PROBLEMA 8

(Unidad 1, lección 11)

¿Cuál de estas construcciones formaría una recta de reflexión que lleva el punto A al punto B?

A. Construir el punto medio del segmento AB

B. Construir la mediatriz del segmento AB

C. Construir una recta tangente a la circunferencia A de radio AB

D. Construir una recta vertical que pase por el punto A y una recta horizontal que pase por el punto B

Soluciones posibles

PROBLEMA 9

(Unidad 1, lección 13)

Aquí está el triángulo POG. Haz coincidir la descripción de la rotación con la imagen de POG bajo esa rotación.

A. Rota 300 grados en el sentido de las agujas del reloj alrededor de O

B. Rota 60 grados en el sentido de las agujas del reloj alrededor de O

C. Rotar 60 grados en el sentido de las agujas del reloj alrededor de P

D. Rotar 240 grados en el sentido contrario a las agujas del reloj alrededor de O

Soluciones posibles

Nation California . Geometría

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.5 Dada una figura geométrica y una rotación, reflexión o traslación, dibujar la figura transformada. Especificar una secuencia de transformaciones que llevarán una figura dada a otra.

Construir

8.G.2

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.B.5 II.C.6

LECCIÓN 18

PRACTICAR TRANSFORMACIONES PUNTO POR PUNTO

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientra...

predecir lo que podría ocurrir y repercutir en el futuro, atienden a la precisión descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Dada una figura y la descripción de una transformación, puedo dibujar la imagen de la figura después de la transformación.

• Puedo describir una transformación que lleva puntos dados a otro conjunto de puntos.

OBJETIVOS DE APRENDIZAJE PARA EL PROFESOR

• Dibujar el resultado de una transformación (en lenguaje escrito) de una figura dada.

• Explicar (oralmente y por escrito) una secuencia de transformaciones para llevar una figura dada a otra.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

Dibújalo

Anticipar, controlar, seleccionar, secuenciar, conectar

MLR7: Comparar y conectar

Materiales necesarios

Conjunto de herramientas de geometría (HS)

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Vamos a resolver algunas transformaciones.

Narrativa de la lección

Esta lección es opcional.

Esta lección proporciona a los estudiantes más práctica para definir secuencias de transformaciones en términos de puntos etiquetados en la figura. Será especialmente útil si los estudiantes tuvieron dificultades con la lección anterior. La primera actividad de la carrera de obstáculos incluye una cuadrícula para proporcionar algún tipo de andamiaje, pero anima a los estudiantes a pensar en las transformaciones en términos de los puntos etiquetados. En la segunda actividad, la cuadrícula se elimina por completo para preparar las lecciones siguientes.

El objetivo es que los estudiantes empiecen a desarrollar una secuencia sistemática, punto por punto, de transformaciones que funcionen para llevar cualquier par de polígonos congruentes uno sobre otro. Esto es especialmente importante porque cuando las transformaciones se utilizan en las pruebas de congruencia de triángulos en una lección posterior, los estudiantes estarán justificando cómo saben que una determinada transformación llevará un triángulo sobre otro.

Los estudiantes practican la atención a la precisión (MP6) cuando describen las transformaciones paso a paso.

La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes opten por utilizar la tecnología adecuada para resolver los problemas. Recomendamos que la tecnología esté disponible.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento En parejas 5 min

Actividad de exploración Independiente 15 min

Actividad de exploración En parejas o grupos pequeños 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes analizan una figura y sus líneas en una cuadrícula de puntos isométrica e identifican las cosas que observan y se preguntan.

Los estudiantes determinan una secuencia de traslaciones y rotaciones para mapear una figura sobre otra figura con restricciones.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar traslaciones y rotaciones utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las secuencias de transformaciones.

Los estudiantes identifican múltiples secuencias de transformaciones rígidas para mapear una figura sobre otra sin una cuadrícula.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar secuencias de transformaciones rígidas utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las transformaciones de figuras tridimensionales.

Los estudiantes esbozan ejemplos de transformaciones a partir de descripciones escritas de movimientos.

Los estudiantes describen una secuencia de transformaciones rígidas para llevar un triángulo a la parte superior de un cuadrado.

El componente de práctica independiente incluye 3 en la lección y 6 problemas de repaso en espiral.

. Matemáticas . Unidad 1

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE: OBSTÁCULOS

(5 minutos)

Rutinas didácticas

Observar y preguntarse

El objetivo de este calentamiento es que los estudiantes comprendan la idea en la que se basa la actividad «Carrera de obstáculos» de esta lección. Los estudiantes imaginan que todos los movimientos rígidos se realizan físicamente en el plano, por lo que no se les permite realizar una traslación o rotación en la que el movimiento físico llevaría a la figura a través de un obstáculo sólido. Aunque los estudiantes pueden notar y preguntarse muchas cosas sobre este diagrama, la idea de que fueron necesarias dos traslaciones para evitar el obstáculo es el punto de discusión más importante. Este calentamiento anima a los estudiantes a dar sentido a un problema antes de resolverlo, familiarizándose con un contexto y con las matemáticas que podrían estar implicadas (MP1).

INTRODUCCIÓN

Muestre el diagrama para que todos lo vean. Pida a los estudiantes que piensen en al menos una cosa que observen y en al menos una cosa que se pregunten. Conceda a los estudiantes 1 minuto de tiempo para pensar en silencio y, a continuación, 1 minuto para comentar las cosas que observan con su compañero, seguido de un debate con toda la clase.

Apoyo para estudiantes con discapacidad

Apoya la accesibilidad para: Lenguaje; organización

¿Qué notas? ¿Qué te preguntas?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Cosas que los estudiantes pueden observar:

• Hay una figura discontinua que se parece a �� y ��.

• Hay un hexágono sólido.

RESPUESTAS POSIBLES

• Las figuras �� y �� parecen congruentes.

• Los puntos de la cuadrícula en filas alternas no se alinean como nuestros puntos de cuadrícula habituales.

Cosas que los estudiantes pueden preguntarse:

• ¿Qué representa la figura discontinua?

• ¿Por qué hay un hexágono sólido en el diagrama?

• Si las figuras verdes son imágenes de la figura azul, ¿cómo podríamos describir la transformación?

SÍNTESIS DE LA ACTIVIDAD

Pida a los estudiantes que compartan las cosas que notaron y se preguntaron. Registre y muestre sus respuestas para que todos puedan verlas. Si es posible, anote el razonamiento pertinente en el diagrama o cerca de él. Una vez registradas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que se pregunten ahora?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria. Si la pregunta sobre por qué la figura �� no se tradujo directamente a �� no surge durante la conversación, pida a los estudiantes que discutan esta idea.

ACTIVIDAD DE EXPLORACIÓN | CARRERA DE OBSTÁCULOS

(15 minutos)

Rutinas didácticas

Dibújalo

El objetivo de esta actividad es dar a los estudiantes la oportunidad de practicar la concentración en puntos individuales cuando escriben y dibujan una secuencia de rotaciones y traslaciones. Esto les ayudará en la siguiente unidad cuando trabajen en demostrar que los triángulos son congruentes.

Para el segundo obstáculo, los estudiantes tendrán que girar la figura, realizar una secuencia de traslaciones y, a continuación, volver a girar la figura. Esta idea de transformar un problema, trabajar con el problema transformado y luego volver a transformarlo es muy poderosa en matemáticas. Por ejemplo, con las coordenadas, si sabemos cómo dilatar usando el origen como centro pero no desde otro punto, podemos trasladar el centro al origen, dilatar la imagen y volver a trasladar.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

Apoyopar a estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Mantenga un despliegue de términos y vocabulario importantes. Durante el lanzamiento tómese tiempo para repasar los siguientes términos de lecciones anteriores a los que los estudiantes necesitarán acceder para esta actividad: traslación, segmento de recta dirigida, rotación, centro de rotación, ángulo de rotación, sentido horario y antihorario.

Apoya la accesibilidad para: Memoria; lenguaje

Para cada diagrama, encuentra una secuencia de traslaciones y rotaciones que lleven la figura original a la imagen, de modo que si se hiciera físicamente, la figura no tocaría ninguno de los obstáculos sólidos y no saldría del diagrama. Comprueba tu secuencia dibujando la imagen de cada paso.

1. Toma �� a ��

2. Toma �� a ��.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

. Matemáticas . Unidad 1

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

¿Estás preparado para más?

1. Ejemplo de respuesta: Traslada por el segmento de recta dirigida ��. A continuación, gira en sentido antihorario alrededor de �� por el ángulo ��.

2. Respuesta de ejemplo: Rota en el sentido de las agujas del reloj alrededor de �� por 60 grados. A continuación, traslada por el segmento de recta dirigida ��′. A continuación, traslada por segmento de recta dirigida ��′��. A continuación, gira en sentido contrario a las agujas del reloj alrededor de �� en 60 grados.

Si los estudiantes se quedan atascados con la idea de trasladar la segunda figura y no están seguros de qué hacer, pregúnteles por qué no funciona trasladar (los obstáculos están en medio) y qué otra transformación podría ayudar (girar para que quepa entre los obstáculos).

Invite a algunos estudiantes a compartir sus respuestas con la clase. Muestre cada imagen intermedia de la secuencia y pida a los demás estudiantes que expliquen lo que esa única traslación o rotación ayudó a conseguir. El propósito de esta discusión es resaltar los beneficios de pensar en un punto a la vez cuando se establece una secuencia de transformaciones para llevar una figura a otra.

Crea tu propia carrera de obstáculos con una figura original, una imagen y al menos un obstáculo. Asegúrate de que es posible resolverlo. Reta a un compañero a resolver tu carrera de obstáculos.

Respuestas de los estudiantes

Las respuestas varían.

ACTIVIDAD DE EXPLORACIÓN | PUNTO POR PUNTO

(15 minutos)

Rutinas didácticas

Anticipar, monitorear, seleccionar, secuenciar, conectar

Dibújalo

MLR7: Comparar y conectar

El objetivo de esta actividad es que los estudiantes comiencen a desarrollar una secuencia sistemática, punto por punto, de transformaciones que funcionarán para llevar cualquier par de polígonos congruentes uno sobre otro. Esto es especialmente importante porque cuando las transformaciones se utilicen en las pruebas de congruencia de triángulos en una lección posterior, los estudiantes tendrán que justificar cómo saben que una determinada transformación llevará un triángulo sobre otro. Encontrar una única transformación que lleve cada vértice de un triángulo a cada vértice correspondiente de otro no puede generalizarse porque es específica de un par de triángulos congruentes. En una demostración, los estudiantes deben definir secuencias de transformaciones rígidas que lleven un triángulo dado a cualquier triángulo con partes correspondientes congruentes y justificar por qué se garantiza que esa secuencia lleva cada vértice a su vértice correspondiente.

Supervise a los estudiantes que:

• Encuentren una única transformación independiente que lleve �� a ��′ y B a ��′, de modo que cuando �� vaya a ��′, �� ya no permanezca en ��′.

• Busquen una única transformación que lleve el cuadrilátero �� al cuadrilátero ��′��′��′��′ de una sola vez.

• Alineen uno o dos puntos y luego te quedas atascado.

• Alineen sistemáticamente pares de puntos correspondientes y luego usa transformaciones con puntos fijos para alinear bordes. Puede encontrar estudiantes que utilicen la traslación, luego la rotación, luego la reflexión, así como estudiantes que utilicen reflexiones a través de bisectrices perpendiculares y luego bordes.

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

. Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Conecte un concepto nuevo con otro con el que los estudiantes hayan tenido éxito. Por ejemplo, recuerde a los estudiantes la secuencia de traslaciones y rotaciones que llevan �� a �� en la actividad anterior. Pregunte a los estudiantes cómo pueden utilizar la misma idea para describir la secuencia de traslaciones y rotaciones que lleva el paralelogramo �� a ��′��′��′��′

Apoya la accesibilidad para: Habilidades socioemocionales; procesamiento conceptual

Para cada pregunta, describe una secuencia de traslaciones, rotaciones y reflexiones que lleven al paralelogramo �� al paralelogramo ��′��′��′��′. 1. 2.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Ejemplo de respuesta: Traslada el paralelogramo �� por el segmento de recta dirigido desde �� hasta ��′. Rota la imagen usando el centro ��′ hasta que la imagen de �� caiga sobre ��′.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

2. Respuesta de ejemplo: Traslada el paralelogramo �� por el segmento de recta dirigido desde �� hasta ��′. Gira la imagen utilizando el centro ��′ hasta que la imagen de �� aterrice en ��′. Refleja la nueva imagen a través de ��′��′.

Selecciona estudiantes previamente identificados para compartir en este orden:

• Busca una única transformación que mueva todos los puntos a la vez.

• Alinea uno o dos puntos y luego quédate atascado.

• Alinea sistemáticamente pares de puntos correspondientes y, a continuación, utilice transformaciones con puntos fijos para alinear los bordes.

Para cada estrategia compartida, céntrese en qué pregunta ayuda a responder esa estrategia o qué tiene de único y valioso esa estrategia.

• Si un estudiante que comparte buscó una única transformación, concéntrese en la elegancia de encontrar un único movimiento rígido, e invite al estudiante a compartir lo que le resultó difícil de su estrategia.

• Si un estudiante que comparte se quedó atascado, destaque la elección estratégica de intentar alinear solo uno o dos puntos a la vez y por qué eso podría ser más fácil que encontrar una o dos transformaciones más complicadas.

• Si un estudiante que comparte alineó sistemáticamente un punto cada vez utilizando transformaciones con puntos fijos para asegurarse de que los puntos previamente alineados no se movieran, haga hincapié en por qué esta estrategia podría utilizarse para muchas condiciones de partida diferentes.

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR7 Comparar y conectar. Utilice esta rutina cuando los estudiantes presenten su secuencia de traslaciones, rotaciones y reflexiones que llevarán el paralelogramo �� al paralelogramo ��′��′��′��′. Pida a los estudiantes que piensen en lo que es igual y lo que es diferente en las secuencias de transformaciones. Llame la atención de los estudiantes sobre la forma en que se describen las transformaciones con precisión (es decir, orden, números, palabras). Estos intercambios refuerzan el uso del lenguaje matemático de los estudiantes y su razonamiento sobre las transformaciones.

Principio(s) de diseño: Maximizar la metaconciencia

¿Estás preparado para más?

En esta unidad nos hemos centrado en las transformaciones rígidas en dos dimensiones. Pensando detenidamente en definiciones precisas, podemos extender muchas de estas ideas a las tres dimensiones. ¿Cómo podrías definir las rotaciones, reflexiones y traslaciones en tres dimensiones?

Respuestas de los estudiantes

Ejemplo de respuesta: En tres dimensiones, el centro de una rotación podría ser una línea en lugar de un punto. En lugar de reflejar a través de una línea que es la bisectriz perpendicular del segmento entre un punto y su imagen, podríamos reflejar a través de un plano que es la bisectriz perpendicular del segmento entre un punto y su imagen. Podríamos seguir trasladando por segmentos dirigidos.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Invite a los estudiantes a dibujar un ejemplo que corresponda a cada descripción:

• Un par de figuras que podría llevar una a la otra con un movimiento rígido. (Cualquier figura congruente en la que el estudiante pueda nombrar la transformación).

• Un par de figuras que puedas llevar de una a otra con más de un movimiento rígido. (Cualquier figura congruente).

• Un par de figuras que no podrías llevar una a la otra, sin importar cuántos movimientos rígidos. (Cualquier figura que no sea congruente).

ENFRIAMIENTO | CONSTRUYE OTRA CASA

(5 minutos)

Este enfriamiento da a los estudiantes la oportunidad de practicar la escritura de una secuencia de una traslación y una rotación para alinear segmentos congruentes.

Encuentra una secuencia de traslaciones, rotaciones y reflexiones que transformen el triángulo �� de manera que su imagen descanse sobre el cuadrado �� para formar juntos un dibujo simple de una casa.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Ejemplo de respuesta: Traslada por el segmento de línea dirigida �� . A continuación, gira en sentido antihorario utilizando �� como centro por el ángulo ��′ ��

Geometría . Matemáticas . Unidad 1

Resumen de la lección

A veces no es difícil encontrar una transformación que lleve todos los puntos de una figura directamente a todos los puntos de su imagen. Aquí, parece que hay una rotación de 90 grados que llevará la figura ABCD a la figura EFGH. Sin embargo, no es obvio dónde estaría el centro de rotación. En su lugar, podríamos describir la transformación en 2 pasos. Primero, trasladamos la figura ABCD por el segmento de línea dirigida AE. Después, rota la imagen de ABCD en el sentido de las agujas del reloj por el ángulo B' EF usando el centro E. Parece que esta es una rotación de 90 grados, pero podemos estar seguros de que la rotación funcionará si usamos las etiquetas para definir la rotación en lugar de una medida de ángulo. Este método de emparejar 1 punto a la vez hasta que toda la figura haya sido llevada a la imagen funcionará para cualquier transformación, incluyendo aquellas en las que es difícil ver una única transformación de una figura a la otra.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Las figuras son congruentes. Selecciona todas las secuencias de transformaciones que llevarían la figura 1 a la figura 2.

Trasladar por el segmento de recta dirigida ��

Rotar 180 grados alrededor del punto ��

Trasladar por el segmento de recta dirigida �� y reflejar respecto a ��

Trasladar por el segmento de recta dirigida �� y rotar 90 grados en sentido antihorario alrededor del punto ��

Rotar 180 grados alrededor del punto ��, trasladar por el segmento de recta dirigida �� y reflejar a través del segmento ��

Reflejar a través del segmento ��, rotar en el sentido de las agujas del reloj en el ángulo �� utilizando el centro �� y luego reflejar a través del segmento ��

Soluciones posibles

Trasladar por el segmento de recta dirigida ��

Rotar 180 grados alrededor del punto ��

Trasladar por el segmento de recta dirigida �� y reflejar respecto a ��

Trasladar por el segmento de recta dirigida �� y rotar 90 grados en sentido antihorario alrededor del punto ��

Rotar 180 grados alrededor del punto ��, trasladar por el segmento de recta dirigida �� y reflejar a través del segmento ��

Reflejar a través del segmento ��, rotar en el sentido de las agujas del reloj en el ángulo �� utilizando el centro �� y luego reflejar a través del segmento ��

PROBLEMA 2

A. Dibuja la imagen de la figura �� después de una rotación en el sentido de las agujas del reloj alrededor del punto �� utilizando el ángulo �� y luego una traslación por el segmento de recta dirigida ��

B. Describa otra secuencia de transformaciones que dé como resultado la misma imagen.

Soluciones posibles

B. Ejemplo de respuesta: Traslada por el segmento de recta dirigida ��. Rota en el sentido de las agujas del reloj alrededor de la imagen del punto �� por ángulo ��

. Matemáticas . Unidad 1

PROBLEMA 3

Dibuje la imagen del triángulo �� después de esta secuencia de transformaciones rígidas.

• Refleja a través del segmento de recta ��

• Traslada por el segmento de recta dirigida ��

PROBLEMA 4

(Unidad 1, lección 17)

Describe una transformación que lleve cualquier punto �� a cualquier punto ��

Soluciones posibles

Ejemplos de respuestas:

• Rotar 180 grados usando el punto medio del segmento �� como centro

• Reflexión a través de la mediatriz del segmento ��

• Traslación por el segmento de recta dirigida ��

PROBLEMA 5

(Unidad 1, lección 17)

Triángulo �� es congruente con el triángulo ��′��′��′. Describe una secuencia de movimientos rígidos que lleve �� a ��′, �� a ��′ y �� a ��′.

Soluciones posibles

Respuesta de ejemplo: Traslada el triángulo �� por el segmento de recta dirigida ��′ Gira la imagen utilizando el centro ��′ hasta que la imagen de �� coincida con ��′. Luego refleja a través de la recta ��′��′

PROBLEMA 6

(Unidad 1, lección 16)

Un cuadrilátero tiene simetría de rotación que puede llevar cualquiera de sus vértices a cualquiera de sus otros vértices. Selecciona todas las conclusiones a las que podemos llegar a partir de esto.

Todos los lados del cuadrilátero tienen la misma longitud.

Todos los ángulos del cuadrilátero tienen la misma medida.

Todas las rotaciones llevan una mitad del cuadrilátero a la otra mitad del cuadrilátero.

Soluciones posibles

Todos los lados del cuadrilátero tienen la misma longitud.

Todos los ángulos del cuadrilátero tienen la misma medida.

Todas las rotaciones llevan una mitad del cuadrilátero a la otra mitad del cuadrilátero.

PROBLEMA 7

(Unidad 1, lección 15)

Un cuadrilátero tiene una línea de simetría. Selecciona todas las conclusiones que deben ser ciertas.

Todos los lados del cuadrilátero tienen la misma longitud.

Todos los ángulos del cuadrilátero tienen la misma medida.

Dos lados del cuadrilátero tienen la misma longitud.

Dos ángulos del cuadrilátero tienen la misma medida.

Ningún lado del cuadrilátero tiene la misma longitud.

Ningún ángulo del cuadrilátero tiene la misma medida.

PROBLEMA 8

(Unidad 1, lección 14)

¿Qué segmento es la imagen de �� cuando se gira 90° en el sentido de las agujas del reloj alrededor del punto ��?

PROBLEMA 9

(Unidad 1, lección 12)

¿Qué afirmación es cierta sobre una traslación?

A. Una traslación rota una recta.

B. Una traslación lleva una recta a una recta paralela o a sí misma.

C. Una traslación lleva una recta a una recta perpendicular.

D. Una traslación dilata una recta.

Reflexiones:

Soluciones posibles

Todos los lados del cuadrilátero tienen la misma longitud.

Todos los ángulos del cuadrilátero tienen la misma medida.

Dos lados del cuadrilátero tienen la misma longitud.

Dos ángulos del cuadrilátero tienen la misma medida.

Ningún lado del cuadrilátero tiene la misma longitud.

Ningún ángulo del cuadrilátero tiene la misma medida.

Soluciones posibles ��

Soluciones posibles B

LECCIÓN

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.9 Demostrar teoremas sobre líneas y ángulos. Los teoremas incluyen: los ángulos verticales son congruentes; cuando una transversal cruza líneas paralelas, los ángulos interiores alternativos son congruentes y los ángulos correspondientes son congruentes; los puntos en una bisectriz perpendicular de un segmento de línea son exactamente aquellos equidistantes de los puntos extremos del segmento.

Construir

7.G.5 G-CO.1

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.3

I.B.7

I.C.12

19 EVIDENCIA, ÁNGULOS Y PRUEBA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo, construyen argumentos viables y critican el razonamiento de otros descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo etiquetar y hacer conjeturas a partir de diagramas.

• Puedo demostrar que los ángulos verticales son congruentes.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Etiquetar diagramas y explicar conjeturas (oralmente y por escrito).

• Demostrar (por escrito) que los ángulos verticales son congruentes.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyo para el debate

MLR1: Cada vez más sólido y claro

Observar y preguntarse

Anticipar, monitorear, seleccionar, secuenciar, conectar

Piensa, haz coincidir y comparte

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Hagamos explicaciones convincentes.

Narrativa de la lección

En grados anteriores, los estudiantes utilizaron datos sobre ángulos suplementarios, complementarios, verticales y adyacentes para resolver problemas. En lecciones anteriores, los estudiantes hicieron conjeturas, desarrollaron definiciones de los movimientos rígidos básicos y explicaron por qué creen que ciertas afirmaciones son verdaderas o falsas. En las próximas lecciones, los estudiantes aprenderán a expresar sus razonamientos de manera más formal. En esta lección, los estudiantes crean conjeturas sobre relaciones angulares y las demuestran utilizando lo que saben sobre transformaciones rígidas. Los estudiantes empiezan a etiquetar y marcar figuras para indicar la congruencia, lo que les ayuda a comunicarse con mayor precisión. Se pide a los estudiantes que presenten argumentos viables y critiquen el razonamiento de los demás cuando escriban explicaciones convincentes de por qué los ángulos verticales son congruentes (MP3).

Todas las pruebas de estos materiales están escritas en forma narrativa. El formato narrativo coincide con la discusión que los estudiantes podrían tener para convencer a su compañero y también coincide con la forma en que los matemáticos escriben las pruebas. Aunque los estudiantes pueden utilizar otros formatos para apoyar su organización, es importante que puedan ver el flujo de razonamiento que existe en una demostración bien escrita. Una demostración a dos columnas puede considerarse como el esquema de una redacción. Los esquemas ayudan a organizar las ideas, pero son menos persuasivos que una redacción bien escrita. Los estudiantes deben aprender a escribir una justificación bien redactada en forma de prueba narrativa. Esta es una oportunidad para que den sentido a los problemas y perseveren en su resolución (MP1).

La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes decidan utilizar la tecnología adecuada para resolver los problemas. Recomendamos que la tecnología esté disponible.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración En parejas o grupos pequeños 15 min

Actividad de exploración En parejas 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes calculan mentalmente las medidas de los ángulos que faltan en 4 figuras.

Los estudiantes validan una conjetura dada sobre las bisectrices de ángulos de un par lineal de ángulos que forman un ángulo recto.

Los estudiantes escriben sus propias conjeturas sobre la relación entre ángulos verticales y explican su razonamiento.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la demostración de la validez de las conjeturas.

Los estudiantes discuten sus diferentes explicaciones de por qué los ángulos verticales son congruentes a partir de la «Actividad de exploración 2».

Los estudiantes escriben una explicación para mostrar cómo 2 los ángulos verticales son congruentes.

El componente de práctica independiente incluye 3 en la lección y 5 problemas de repaso en espiral.

. Matemáticas . Unidad 1

CALENTAMIENTO | CHARLA DE MATEMÁTICAS: ÁNGULOS

SUPLEMENTARIOS (5 minutos)

Rutinas de instrucción

Charla de matemáticas

MLR8: Apoyo para el debate

El propósito de esta charla de matemáticas es obtener estrategias y entendimientos que los estudiantes tienen para determinar las medidas de ángulos en pares de líneas que se intersectan o para pares de ángulos que forman un ángulo recto. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de explicar por qué los ángulos verticales son congruentes. En esta actividad, los estudiantes tienen la oportunidad de notar y hacer uso de la estructura (MP7) cuando identifican ángulos suplementarios.

INTRODUCCIÓN

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Para apoyar la memoria de trabajo, proporcione a los estudiantes notas adhesivas o minipizarras.

Apoya la accesibilidad para: Memoria; organización

Evalúa mentalmente todas las medidas de ángulo que faltan en cada figura.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Figura A: m∠DAE = 130°, m∠EAB = 180°

RESPUESTAS POSIBLES

• Figura B: m∠FEI = 150°, m∠HEI = 30°, m∠HEG = 150°

• Figura C: m∠ECF = 115°, m∠FCD = 180°

• Figura D: m∠BAD = 135°, m∠EAD = 45°, m∠BAC = 45°

Figura

Figura C

Figura D.

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

• «¿Quién puede replantear el razonamiento de de otra manera?».

• «¿Tenía alguien más la misma estrategia, pero la explicaría de otra manera?».

• «¿Resolvió alguien el problema de otra manera?».

• «¿Quiere alguien añadir algo a la estrategia de ?».

• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?».

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo, «Primero, yo porque...» o «Noté que , así que yo...». A algunos estudiantes les puede venir bien tener la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.

Principio(s) de diseño: Optimizar la salida (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | ¿NO PUEDE SER CIERTO, VERDAD?

(15 minutos)

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

Observar y preguntarse

El propósito de esta actividad es que los estudiantes tomen una conjetura informal y la describan con mayor precisión etiquetando una figura. Los estudiantes comienzan describiendo tres ejemplos de bisectrices de ángulos y formando una conjetura. Al dar un paso atrás y familiarizarse con el contexto y las matemáticas que pueden estar implicadas, los estudiantes dan sentido a los problemas (MP1). Cuando los estudiantes empiezan a etiquetar el diagrama, pueden utilizar diversos métodos para dar sentido y explicar. Las formas en que los estudiantes intentan formular la conjetura con mayor precisión se refinarán en la discusión.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

Muestre tres ejemplos de bisectrices de ángulos de pares lineales para que todos los vean:

INTRODUCCIÓN

Preguntar a los estudiantes: «¿Qué observan? ¿Qué se preguntan?».

Cosas que los estudiantes pueden observar:

• Hay líneas sólidas y discontinuas.

• Hay una línea horizontal en las tres.

• Los dos ángulos sólidos forman un par lineal.

Cosas que los estudiantes pueden preguntarse:

• ¿Son las líneas discontinuas bisectrices de ángulos?

• ¿Forman las líneas discontinuas un ángulo recto?

. Matemáticas . Unidad 1

INTRODUCCIÓN CONTINUACIÓN

Pida a los estudiantes que compartan las cosas que notaron y se preguntaron. Registre y muestre sus respuestas para que todos puedan verlas. Si es posible, anote los razonamientos pertinentes en la imagen o cerca de ella. Si la conjetura de que el ángulo entre los bisectores de ángulos es siempre un ángulo recto no surge durante la conversación, pida a los estudiantes que discutan esta idea.

Si los estudiantes tienen acceso a GeoGebra Geometry de las herramientas de matemáticas, sugiera que podría ser una herramienta útil en esta actividad.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Proporcione a los estudiantes una tabla para anotar lo que observan y se preguntan antes de que se espere que compartan estas ideas con los demás.

Apoya la accesibilidad para: Lenguaje; organización

Aquí hay una figura en la que el semirrecta r se encuentra con la línea ℓ. Los semirrectas discontinuos son bisectrices de ángulos.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Diego hizo la conjetura: «El ángulo formado entre las bisectrices de ángulos es siempre un ángulo recto, sea cual sea el ángulo entre r y ℓ». Es difícil decir específicamente a qué ángulos se refiere Diego en su conjetura. Etiqueta el diagrama y reformula la conjetura de Diego de forma más precisa utilizando tus etiquetas.

2. ¿Es cierta la conjetura? Explica tu razonamiento.

1. Ejemplo de respuesta:

RESPUESTAS POSIBLES

Con estas etiquetas, la conjetura de Diego puede reformularse como: «Dado que la semirrecta CE biseca el ángulo ACD en dos ángulos congruentes que miden a° y que la semirrecta CF biseca el ángulo BCD en dos ángulos congruentes que miden b°, entonces el ángulo ECF es un ángulo recto. En otras palabras, a + b = 90»

2. Ejemplo de respuesta: Sí, la conjetura de Diego es cierta. El ángulo ACB forma una recta, por lo que mide 180 grados. Eso significa 2a + 2b = 180. Dividiendo cada lado por 2, tenemos a + b = 90. La expresión a + b puede interpretarse como la medida del ángulo ECF, por lo que el ángulo ECF es un ángulo recto. Este argumento funciona sin importar los valores particulares de a y b, siempre que dichos valores tengan sentido con las restricciones de la figura.

CONCEPTOS ERRÓNEOS ANTICIPADOS

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

Si los estudiantes se atascan, pídales que estimen la medida de un ángulo y luego hagan argumentos basados en la medida del ángulo como en el calentamiento. Si el tiempo lo permite, invite a los estudiantes a generalizar.

El propósito de esta discusión es introducir el concepto de marcar ángulos como congruentes, etiquetar puntos y etiquetar ángulos.

Pida a los estudiantes que compartan argumentos convincentes de por qué la conjetura de Diego es verdadera o falsa. Rotule una imagen expuesta a la vista de todos con la información que aporten. No es necesario que los estudiantes escriban una prueba formal en este punto, pero anímelos a reformularla utilizando un lenguaje más preciso.

Aproveche las ideas que los estudiantes han compartido sobre cómo etiquetaron la figura para introducir convenciones sobre cómo marcar ángulos como congruentes, etiquetar puntos y etiquetar medidas variables de ángulos. Para ver un ejemplo de una forma de marcar la figura, consulte la respuesta de muestra del estudiante.

Apoyo para estudiantes que aprenden el idioma inglés

Escribir y hablar: MLR 1 Cada vez más fuerte y más claro. Use esto con parejas sucesivas para dar a los estudiantes una oportunidad estructurada de revisar y refinar su respuesta a «Para cada par de ángulos congruentes que encuentres, explica a tu compañero cómo sabes que los ángulos son congruentes». Pida a cada estudiante que se reúna con 2-3 otros compañeros en una fila para recibir comentarios. Proporcione a los estudiantes indicaciones que les ayuden a reforzar sus ideas y a aclarar su lenguaje (por ejemplo: «¿Puedes explicar cómo...?», «Deberías ampliar...», etc.). Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar el producto final. Principio(s) de diseño: Optimizar el resultado (para la generalización)

ACTIVIDAD DE EXPLORACIÓN | CONVÉNCEME

(15 minutos)

Rutinas instruccionales

Anticipar, monitorear, seleccionar, secuenciar, conectar

Pensar y compartir

El propósito de esta actividad es que los estudiantes prueben que los ángulos verticales son congruentes y trabajen hacia una manera más formal y rigurosa de expresarse al dar argumentos basados en transformaciones rígidas. A medida que los estudiantes trabajan, recuérdeles que etiqueten los puntos y hagan marcas en el diagrama para ayudar en el proceso de explicar sus ideas.

Monitoree los argumentos basados en:

• transformaciones

• ángulos suplementarios

INTRODUCCIÓN

Muestre dos líneas de intersección para que todos las vean. Recuerda a los estudiantes que los pares de ángulos opuestos al punto de intersección se llaman ángulos verticales. Organice a los estudiantes en grupos de 2. Diga a los estudiantes que hay muchas respuestas posibles para las preguntas. Después de un tiempo de trabajo en silencio, pida a los estudiantes que comparen sus respuestas con las de sus compañeros y decidan si ambas son correctas, aunque sean diferentes. A continuación, debate con toda la clase.

Apoyo para estudiantes con discapacidad

Compromiso: Interiorizar la autorregulación. Demostrar dar y recibir retroalimentación constructiva. Utilizar un proceso estructurado y mostrar marcos de frases para apoyar la retroalimentación productiva. Por ejemplo: «¿Cómo sabes...?», «Eso podría / podría no ser cierto porque...» y «Podemos estar de acuerdo en que...».

Apoya la accesibilidad para: Habilidades socioemocionales; organización; lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Aquí hay 2 líneas de intersección que crean 2 pares de ángulos verticales:

1. ¿Cuál es la relación entre los ángulos verticales? Escribe una conjetura. Etiqueta el diagrama para que te sea más fácil escribir tu conjetura con precisión.

2. ¿Cómo sabes que tu conjetura es cierta para todos los pares posibles de ángulos verticales? Explica tu razonamiento.

RESPUESTAS POSIBLES

1. Los ángulos verticales son congruentes. El ángulo AED es congruente con el ángulo BEC.

2. Ejemplo de respuesta:

Rota la figura 180 grados alrededor del punto E. Entonces el semirrecta EA va al semirrecta EB y el semirrecta ED va al semirrecta EC. Esto significa que la rotación lleva el ángulo AED al ángulo BEC y así ∠AED ≅ ∠BEC. Ninguna de esas afirmaciones es específica de esos ángulos concretos. Si los tamaños de los ángulos cambiaran, nada cambiaría en el razonamiento.

CONCEPTOS ERRÓNEOS PREVISTOS

Si los estudiantes se atascan, sugiérales que etiqueten uno de los ángulos agudos como x° Pregunte qué más pueden etiquetar o deducir basándose en esa información.

SÍNTESIS DE LA ACTIVIDAD

El propósito de la discusión es refinar los argumentos de los estudiantes para convertirlos en pruebas convincentes. Con la ayuda de los estudiantes, etiquete los puntos de la figura para que todos puedan debatir sobre los mismos objetos de forma coherente. Pida a los estudiantes previamente identificados que compartan su argumento de transformación. A continuación, invite a los estudiantes previamente identificados a compartir su argumento de los ángulos suplementarios.

Pregunte si alguno de los argumentos se basó en las características específicas de los ángulos particulares dados. Diga a los estudiantes que una demostración tiene que funcionar para cualquier medida de ángulo, de lo contrario es un ejemplo.

Los estudiantes escribirán una explicación de que los ángulos verticales son congruentes en el enfriamiento, así que asegúrese de que los estudiantes entienden al menos uno de estos argumentos.

. Matemáticas . Unidad 1

¿Estás listo para más?

Una de las razones por las que a los matemáticos les gusta tener pruebas rigurosas incluso cuando las conjeturas parecen ser ciertas es que a veces las conjeturas que se hacen resultan no ser ciertas. Aquí hay un ejemplo famoso. Si dibujamos n puntos en un círculo y conectamos cada par de puntos, ¿en cuántas regiones se divide el círculo? Si dibujamos solo 1 punto no hay segmentos de línea para conectar y por lo tanto solo 1 región en el círculo. Si dibujamos 2 puntos que están conectados por un segmento de línea que divide el círculo en 2 regiones.

1. Si dibujamos 3 puntos en un círculo y conectamos cada par de puntos con un segmento de recta, ¿cuántas regiones obtenemos en nuestro círculo?

2. Si dibujamos 4 puntos en un círculo y conectamos cada par de puntos con un segmento de recta, ¿cuántas regiones obtenemos en nuestro círculo?

3. Si dibujamos 5 puntos en un círculo y unimos cada par de puntos con un segmento de recta, ¿cuántas regiones obtendremos en nuestro círculo?

4. Haz una conjetura sobre cuántas regiones obtendremos si dibujamos n puntos en un círculo y unimos cada par de puntos con un segmento de recta.

5. Comprueba tu conjetura con 6 puntos en un círculo. ¿Cuántas regiones obtenemos?

Posibles respuestas

1. 4

2. 8

3. 16

4. Ejemplo de respuesta: 2n-1

5. 31

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Diga a los estudiantes: «En la vida cotidiana, a menudo es complicado comprender todas las razones por las que las afirmaciones son verdaderas o falsas. Por ejemplo, piense en el sistema económico, las relaciones internacionales o la historia de un país. En geometría, los objetos de estudio no son tan complejos: ángulos, rectas, puntos, triángulos, etc. De este modo, la geometría es un gran campo de entrenamiento para comprender las razones por las que las ideas son ciertas y comunicar esas razones a los demás».

En la actividad anterior, los estudiantes propusieron diferentes explicaciones de por qué los ángulos verticales son congruentes. Discuta la diferencia entre argumentos basados en la medida del ángulo y argumentos basados en transformaciones. Pregunte a los estudiantes lo siguiente:

• «¿Qué argumento tiene más sentido para ustedes, las transformaciones rígidas que llevan un ángulo vertical sobre el otro, o usar ángulos rectos para ver sumas de 180 grados?». (Las transformaciones tienen más sentido porque es posible ver cómo un ángulo se traslada al otro. Me gusta más el álgebra, así que prefiero las sumas de 180 grados).

• «¿Cuál es la diferencia entre ángulo y la medida de un ángulo?». (Es como la diferencia entre un segmento y su longitud. Los segmentos y los ángulos son figuras geométricas, pero las longitudes y las medidas de los ángulos son números que se utilizan para describir lo grandes o pequeños que son los segmentos y los ángulos).

Pida a los estudiantes que añadan este teorema a sus tablas de referencia al mismo tiempo que usted lo añade a la tabla de referencia de la clase:

Los ángulos verticales son congruentes.

(Teorema)

Proporcione el consejo: Busque ángulos verticales siempre que dos líneas se crucen.

ENFRIAMIENTO | ARGUMENTAR SU CASO (5

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

minutos)

Dé la explicación más convincente que pueda de por qué a = c

RESPUESTAS POSIBLES

Ejemplo de respuesta: a + b = 180 y b + c = 180 por lo que 180 - b = a y 180 - b = c. Por lo tanto, a = c.

Resumen de la lección para el estudiante

En muchas situaciones, es importante comprender las razones por las que una idea es cierta. Aquí hay algunas preguntas para hacer cuando tratamos de convencernos a nosotros mismos o a otros de que una afirmación es verdadera:

• ¿Cómo sabemos que esto es verdad?

• ¿Convencerían estas razones a alguien que no pensara que es verdad?

• ¿Es esto verdad siempre o solo en ciertos casos?

• ¿Podemos encontrar alguna situación en la que esto sea falso?

En esta lección, razonamos que pares de ángulos verticales son siempre congruentes entre sí:

Vimos esto etiquetando el diagrama y haciendo argumentos precisos que tienen que ver con transformaciones o relaciones de ángulos. Por ejemplo, etiquetamos el diagrama con puntos:

Rotamos la figura 180 grados alrededor del punto E. Entonces la semirrecta EA pasa a la semirrecta EB y la semirrecta ED pasa a la semirrecta EC. Esto significa que la rotación lleva el ángulo AED al ángulo BEC y entonces el ángulo AED es congruente con el ángulo BEC.

Muchas afirmaciones verdaderas tienen múltiples explicaciones. Otra línea de razonamiento utiliza las relaciones entre ángulos. Observa que los ángulos AED y AEC juntos forman la recta CD. Esto significa que �� + �� = 180. Del mismo modo, �� + �� = 180. Esto significa que tanto �� como �� son iguales a 180 - ��, por lo que son iguales entre sí. Como el ángulo AED y el ángulo CEB tienen la misma medida en grados, deben ser congruentes.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

¿Cuál es la medida del ángulo ABE?

Soluciones posibles

40 grados

PROBLEMA 2

Seleccione todas las afirmaciones verdaderas sobre la figura.

c + b = d + c

d + b = 180

Gira en el sentido de las agujas del reloj el ángulo ABC utilizando el centro B. Entonces el ángulo CBD es la imagen del ángulo ABE

Rota 180 grados usando el centro B. Entonces el ángulo CBD es la imagen del ángulo EBA

Se refleja a través de la bisectriz del ángulo ABC. Entonces el ángulo CBD es la imagen del ángulo ABE

Se refleja a través de la recta CE. Entonces el ángulo CBD es la imagen del ángulo EBA.

Soluciones posibles

c + b = d + c

d + b = 180

Gira en el sentido de las agujas del reloj el ángulo ABC utilizando el centro B. Entonces el ángulo CBD es la imagen del ángulo ABE

Rota 180 grados usando el centro B. Entonces el ángulo CBD es la imagen del ángulo EBA

Se refleja a través de la bisectriz del ángulo ABC. Entonces el ángulo CBD es la imagen del ángulo ABE

Se refleja a través de la recta CE. Entonces el ángulo CBD es la imagen del ángulo EBA.

PROBLEMA 3

El punto D se gira 180 grados usando B como centro. Explica por qué la imagen de D debe estar en la semirrecta BA

Soluciones posibles

Ejemplo de respuesta: Por la definición de rotación, la imagen de D debe ser un punto D' de modo que el ángulo DBD' sea 180 grados. Eso significa que esos tres puntos deben formar una línea recta y D' debe estar en el lado opuesto de B como D. Así que D' debe estar en la semirrecta BA

PROBLEMA 4

(Unidad 1, lección 18)

Dibuja el resultado de esta secuencia de transformaciones.

A. Gira ABCD en el sentido de las agujas del reloj el ángulo ADC usando el punto D como centro.

B. Traslada la imagen por el segmento de recta dirigido DE

Soluciones posibles

PROBLEMA 5

(Unidad 1, lección 17)

El cuadrilátero ABCD es congruente con el cuadrilátero A'B'C'D'. Describe una secuencia de movimientos rígidos que lleve A a A', B a B', C a C', y D a D'.

Soluciones posibles

Ejemplo de respuesta: Traslada el cuadrilátero ABCD por el segmento de recta dirigida BB'. Gira la imagen usando el centro B' hasta que la imagen de C coincida con C'

PROBLEMA 6

(Unidad 1, lección 17)

El triángulo ABC es congruente con el triángulo A'B'C'. Describe una secuencia de movimientos rígidos que lleve A a A', B a B' y C a C'.

Soluciones posibles

Ejemplo de respuesta: Traslade el triángulo ABC por el segmento de recta dirigida AA'. Gira la imagen usando el centro A' hasta que la imagen de B coincida con B'

PROBLEMA 7

(Unidad 1, lección 15)

En el cuadrilátero BADC, AB = AD y BC = DC. La recta AC es una recta de simetría para este cuadrilátero.

A. Con base en la línea de simetría, explica por qué las diagonales AC y BD son perpendiculares.

B. Con base en la línea de simetría, explica por qué los ángulos ACB y ACD tienen la misma medida.

Soluciones posibles

A. Respuesta de ejemplo: La línea de simetría AC es una línea de reflexión que lleva B a D y por tanto es por definición la mediatriz de BD

B. Ejemplo de respuesta: La reflexión usando la línea de simetría AC fija los puntos A y C y lleva B a D. Por lo tanto, lleva el ángulo ACB a ACD y las reflexiones conservan la medida del ángulo.

PROBLEMA 8

(Unidad 1, lección 13)

Aquí hay 2 polígonos:

. Matemáticas . Unidad 1

Selecciona todas las secuencias de traslaciones, rotaciones y reflexiones de abajo que llevarían el polígono P al polígono Q

Reflejar sobre la línea BA y luego trasladar por el segmento de recta dirigida CB

Trasladar por segmento de recta dirigida BA y luego refleja sobre recta BA

Girar 60° en el sentido de las agujas del reloj alrededor del punto B y trasladar mediante el segmento de recta dirigida CB

Trasladar de modo que E se lleve a H. Luego gírar 120° en el sentido de las agujas del reloj alrededor del punto H

Trasladar de modo que A se lleve a J. Luego reflejar sobre la recta BA

Soluciones posibles

Reflejar sobre la línea BA y luego trasladar por el segmento de recta dirigida CB

Trasladar por segmento de recta dirigida BA y luego refleja sobre recta BA

Girar 60° en el sentido de las agujas del reloj alrededor del punto B y trasladar mediante el segmento de recta dirigida CB

Trasladar de modo que E se lleve a H. Luego gírar 120° en el sentido de las agujas del reloj alrededor del punto H

Trasladar de modo que A se lleve a J. Luego reflejar sobre la recta BA

Reflexiones:

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

G-CO.1 Conocer definiciones precisas de ángulo, círculo, línea perpendicular, recta paralela y segmento de recta, basadas en las nociones indefinidas de punto, línea, distancia a lo largo de una recta y distancia alrededor de un arco circular.

Alineación de estándares y principios de California

G-CO.9 Demostrar teoremas sobre líneas y ángulos. Los teoremas incluyen: los ángulos verticales son congruentes; cuando una transversal cruza líneas paralelas, los ángulos interiores alternativos son congruentes y los ángulos correspondientes son congruentes; los puntos en una bisectriz perpendicular de un segmento de recta son exactamente aquellos equidistantes de los puntos extremos del segmento.

Construir

8.G.5 G-CO.4

Construir

G-CO.10

LECCIÓN 20

TRANSFORMACIONES, TRANSVERSALES Y PRUEBA

ALINEACIÓN, CONTINUCIÓN

Alineación de estándares y principios de California

Enfoque SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares CA ELD

I.B.8 I.C.11

II.B.5

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo,

atienden a la precisión, construyen argumentos viables y critican el razonamiento de otros

OBJETIVO(S)

DE APRENDIZAJE

descubren la forma y el espacio.

• Puedo demostrar que los ángulos interiores alternos son congruentes.

• Puedo demostrar que los ángulos correspondientes son congruentes.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Demostrar (por escrito) que cuando una transversal cruza rectas paralelas, los ángulos interiores alternos son congruentes.

• Demostrar que cuando una transversal cruza rectas paralelas, los ángulos correspondientes son congruentes.

PREPARACIÓN DE LA LECCIÓN

Rutinas de Instrucción

Charla de matemáticas

MLR8: Apoyo para el debate

Dibuja

MLR1: Cada vez más fuerte y claro

Tomen turnos

Materiales requeridos

Copias de las hojas maestras conjunto de herramientas de geometría (HS)

INFORMACIÓN

Preparación necesaria

Prepare copias adicionales de la tabla de referencia en blanco (a doble cara, 1 por estudiante). Los estudiantes pueden grapar la nueva tabla a la completa, ya que necesitarán seguir consultando todo el paquete.

DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Demostremos afirmaciones sobre rectas paralelas.

Narrativa de la lección

En esta lección, los estudiantes usan transformaciones rígidas para comprender las relaciones angulares formadas por rectas paralelas y una transversal. Este es el comienzo de la demostración de transformaciones, un tema importante de las unidades siguientes. Al formar rectas paralelas con una traslación, los estudiantes ven que los ángulos correspondientes son congruentes. Luego forman rectas paralelas con una rotación de 180 grados y ven que los ángulos interiores alternos son congruentes. Estas experiencias preparan a los estudiantes para elegir una traslación o rotación sensata cuando prueben que las rectas paralelas cortadas por una transversal tienen ángulos interiores alternos que son congruentes y ángulos correspondientes que son congruentes en el enfriamiento. Los estudiantes prestan atención a la precisión cuando utilizan las definiciones, teoremas y afirmaciones sobre traslaciones y rotaciones para explicar por qué las imágenes de ciertos objetos están garantizadas para coincidir con otros objetos (MP6).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración

En parejas 15 min

Descripción breve

Los estudiantes determinan mentalmente las medidas de los ángulos que faltan en 4 figuras de rectas paralelas y transversales.

Los estudiantes trasladan una línea para crear 2 rectas paralelas intersecadas por una transversal y luego justifican todos los pares de ángulos congruentes.

Los estudiantes rotan una recta para crear 2 rectas paralelas cortadas por una transversal y luego determinan todos los pares de ángulos congruentes.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las transformaciones con rectas paralelas.

RESUMEN DE LA LECCIÓN, CONTINUACIÓN

Componente de la lección

Estructura Tiempo

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 10 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes discuten formalmente el teorema del ángulo interior alterno y el teorema del ángulo correspondiente.

Los estudiantes usan transformaciones para probar el teorema del ángulo interior alterno y el teorema del ángulo correspondiente.

El componente de práctica independiente incluye 2 en la lección y 8 problemas de repaso en espiral.

CHARLA DE MATEMÁTICAS: RELACIONES ANGULARES

(5 minutos)

Rutinas de instrucción

Charla de matemáticas

MLR8: Apoyo para el debate

El propósito de esta charla de matemática es obtener estrategias y conocimientos de los estudiantes sobre las relaciones angulares en líneas paralelas cortadas por una transversal. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten ser capaces de probar estas relaciones usando argumentos transformacionales. En esta actividad, los estudiantes tienen la oportunidad de notar y hacer uso de la estructura (MP7) a medida que identifican pares de ángulos congruentes formados por rectas paralelas cortadas por una transversal.

INTRODUCCIÓN

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Para apoyar la memoria de trabajo, proporcione a los estudiantes notas adhesivas o minipizarras.

Apoya la accesibilidad para: Memoria; organización

Las rectas ℓ y m son paralelas. Evalúa mentalmente la medida x en cada figura.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Figura

Figura B

Figura C

Figura D

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACI Ó N

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

• Figura A: x = 40

• Figura B: x = 61

• Figura C: x = 82

• Figura D: x = 125

Pida a los estudiantes que compartan sus estrategias para cada problema. Registre y muestre sus respuestas para que todos puedan verlas. Anime a los estudiantes a utilizar un lenguaje preciso para expresar sus ideas. Si los estudiantes no recuerdan frases como ángulos interiores alternos, ese lenguaje puede esperar hasta la síntesis de la actividad siguiente.

Para implicar a más estudiantes en la conversación, considere preguntar:

• «¿Quién puede replantear el razonamiento de de una forma diferente?».

• «¿Tenía alguien más la misma estrategia, pero la explicaría de forma diferente?».

• «¿Resolvió alguien el problema de una forma diferente?».

• «¿Quiere alguien añadir algo a la estrategia de ?».

• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?».

Apoyo para estudiantes que aprenden el idioma inglés

Principio(s) de diseño: Optimizar la salida (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | ¿HACER UNA MARCA?

DA UNA RAZÓN.

(15 minutos)

Rutinas didácticas

Dibújalo

MLR1: Más fuerte y más claro cada vez

Toma turnos

En esta actividad, los estudiantes trasladan una recta de un par de rectas que se intersecan para crear rectas paralelas cortadas por una transversal. Utilizando la definición y las propiedades de las traslaciones, los estudiantes concluyen que los pares de ángulos correspondientes son congruentes. Los estudiantes trabajan con un compañero e intercambian papeles explicando su pensamiento y escuchando, proporcionando oportunidades para explicar su razonamiento y criticar el razonamiento de los demás (MP3).

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2. Pida a los estudiantes que se turnen para marcar los ángulos como congruentes. El primer compañero identifica un par de ángulos congruentes y explica por qué cree que los ángulos son congruentes mientras el otro escucha y se esfuerza por entender. A continuación, cambian los papeles.

Considere la posibilidad de proporcionar iniciadores de frases como: El ángulo es congruente con el ángulo porque

Aquí se cruzan las rectas AE y CD.

1. Traslada las rectas AE y CD por el segmento de recta dirigida desde B hasta C. Etiqueta las imágenes de A, B, C, D, E como A', B', C', D', E'

2. ¿Qué hay de cierto en las rectas AE y A'E'? Explica tu razonamiento.

3. Por turnos, identifica con tu compañero los ángulos congruentes.

A. Para cada par de ángulos congruentes que encuentres, explica a tu compañero cómo sabes que los ángulos son congruentes.

B. Para cada pareja que encuentre tu compañero, escucha atentamente su explicación. Si no estás de acuerdo, discute tu pensamiento y trabaja para llegar a un acuerdo.

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

2. Las rectas AE y A'E' son paralelas porque las traslaciones llevan las rectas a rectas paralelas.

3. Ejemplos de respuestas:

• Los ángulos verticales son congruentes, así que marca el ángulo ABC congruente con el ángulo EBD y el ángulo ABD congruente con el ángulo EBC.

• La traslación lleva el ángulo EBD al ángulo E'CB, así que son congruentes. Del mismo modo, el ángulo EBC es congruente con el ángulo E'CC', el ángulo ABD es congruente con el ángulo A'CB y el ángulo ABC es congruente con el ángulo A'CC'.

• Ahora todos los ángulos se han marcado como congruentes con el ángulo ABD o congruentes con el ángulo ABC.

Algunos estudiantes pueden tener dificultades para dibujar una imagen razonablemente precisa de la figura. Recuérdeles las herramientas de geometría que tienen a su disposición, como el papel de calco y la regla.

SÍNTESIS DE LA ACTIVIDAD

Geometría . Matemáticas . Unidad 1

El objetivo del debate es perfeccionar las explicaciones de los estudiantes con un lenguaje más formal.

Pida a los estudiantes que compartan sus respuestas. Mientras los estudiantes comparten, registre lo que dicen escribiendo una afirmación de congruencia (∠ABC ≅ EBD) y marcando la figura. Insista en que siempre que la figura esté marcada con una congruencia, los estudiantes tienen que escribir un enunciado de congruencia y dar una razón que haga referencia a una definición o a propiedades de las traslaciones. Si los estudiantes se atascan al justificar los enunciados de congruencia, pídales que busquen las propiedades de las traslaciones en sus tablas de referencia para obtener ayuda.

Si los estudiantes no lo mencionan, introduzca el vocabulario de ángulos interiores alternos y ángulos correspondientes.

Apoyo para estudiantes que aprenden el idioma inglés

Escribir y hablar: MLR 1Más fuerte y más claro cada vez. Use esto con sucesivas comparticiones en parejas para dar a los estudiantes una oportunidad estructurada de revisar y refinar su respuesta a «Para cada par de ángulos congruentes que encuentres, explica a tu compañero cómo sabes que los ángulos son congruentes». Pida a cada estudiante que se reúna con 2-3 otros compañeros en una fila para recibir comentarios. Proporcione a los estudiantes indicaciones que les ayuden a reforzar sus ideas y a aclarar su lenguaje (por ejemplo: «¿Puedes explicar cómo...?», «Deberías ampliar...»). Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar el producto final.

Principio(s) de diseño: Optimizar el resultado (para la generalización)

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Demuestre y anime a los estudiantes a utilizar códigos de colores y anotaciones para resaltar las conexiones entre las representaciones de un problema. Por ejemplo, escriba el enunciado de congruencia ∠ABC ≅ EBD y marque los ángulos de la figura, ∠ABC y ∠EBD, del mismo color.

Apoya la accesibilidad para: Procesamiento visual-espacial

ACTIVIDAD DE EXPLORACIÓN | UNA EXPLICACIÓN

ALTERNATIVA (15 minutos)

Rutinas didácticas

Dibújalo

Toma turnos

En esta actividad, los estudiantes rotan una recta de un par de rectas que se intersecan en 180 grados para crear rectas paralelas cortadas por una transversal. Utilizando la definición y las propiedades de las rotaciones, los estudiantes concluyen que los pares de ángulos correspondientes son congruentes. Los estudiantes trabajan con un compañero e intercambian papeles explicando su pensamiento y escuchando, proporcionando oportunidades para explicar su razonamiento y criticar el razonamiento de los demás (MP3).

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Diga a los estudiantes que van a ver un montaje similar al de en la actividad anterior, pero que en su lugar van a hacer una rotación de 180 grados. Enfatice que una propiedad importante de las rotaciones de 180 grados es que llevan las rectas hacia sí mismas si el centro de rotación está sobre la recta o hacia rectas paralelas si el centro de rotación está fuera de la recta. Los estudiantes pueden verificar esto experimentalmente usando papel de calco para rotar la recta CD en 180 grados alrededor de varios puntos en la recta AE, incluyendo B, luego trasladando a lo largo de la recta AE hasta que la recta regrese a donde comenzó.

Pida a los estudiantes que agreguen esto como una afirmación en sus tablas de referencia mientras usted lo agrega a la tabla de referencia de la clase: La rotación en 180 grados lleva las rectas a rectas paralelas o a sí mismas.

Aquí se cruzan las rectas AE y CD:

1. Rota la recta AE en 180 grados alrededor del punto C. Etiquete las imágenes de A, B, C, D, E como A’, B’, C’, D’, E’.

2. ¿Qué hay de cierto en las líneas AB y A'B'? Explica tu razonamiento.

3. Túrnate con tu compañero para identificar ángulos congruentes.

A. Por cada par de ángulos congruentes que encuentres, explica a tu compañero cómo sabes que los ángulos son congruentes.

B. Para cada par que encuentre tu compañero, escucha atentamente su explicación. Si no estás de acuerdo, discute tu pensamiento y trabaja para llegar a un acuerdo.

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

2. Las rectas AB y A'B' son paralelas porque una rotación de 180 grados lleva las rectas a rectas paralelas.

3. Ejemplo de respuesta: La rotación lleva el ángulo ABC al ángulo A'B'C y por tanto esos ángulos son congruentes. Del mismo modo, el ángulo EBC es congruente con el ángulo E'B'C, el ángulo DBA es congruente con el ángulo D'B'A', y el ángulo DBE es congruente con el ángulo D'B'E'.

Si los estudiantes tienen dificultades para estimar visualmente el resultado de la rotación de 180 grados, invíteles a trazar la recta BC en papel de calco y pregúnteles cómo sabrán cuándo han girado 180 grados. A continuación, pueden trazar todo el diagrama y repetir el proceso.

SÍNTESIS

DE LA ACTIVIDAD

El propósito de la discusión es refinar las explicaciones de los estudiantes de que los ángulos interiores alternos son congruentes con un lenguaje más formal. Pida a los estudiantes que compartan sus respuestas. Mientras los estudiantes comparten, registre lo que dicen usando símbolos de congruencia y marcando la figura. Insista en que siempre que la figura esté marcada con una congruencia, los estudiantes deben escribir una afirmación de congruencia y dar una razón que haga referencia a la definición y las propiedades de las traslaciones. Pregunte a los estudiantes en qué se diferencia esta actividad de la anterior. (En la actividad anterior se utilizaba la traslación, pero en ésta se utiliza la rotación).

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Demuestre y anime a los estudiantes a utilizar códigos de colores y anotaciones para resaltar las conexiones entre las representaciones de un problema. Por ejemplo, escriba el enunciado de congruencia ∠ABC ≅ ∠EBD y marque los ángulos de la figura, ∠ABC y ∠A'B'C, del mismo color.

Apoya la accesibilidad para: Procesamiento visual-espacial

¿Estás preparado para más?

1. Demuestra que las rotaciones de 180 grados llevan a las rectas que no pasan por el centro de rotación a rectas paralelas.

2. ¿Cuál es la imagen de una recta que se rota 180 grados alrededor de un punto de la recta?

Respuesta del estudiante

1. Ejemplo de respuesta: Etiqueta el centro de rotación O de modo que la recta l no pase por O. Etiqueta la imagen de ℓ bajo la rotación ℓ'. Queremos demostrar que ℓ y ℓ' deben ser paralelas. Si no fueran paralelas, habría un punto Q en ambas rectas. Como Q está en ℓ' debe ser imagen de algún punto P en ℓ. Como la rotación es 180 grados debemos tener P, O y Q en la misma recta. Sin embargo, ℓ ya es la única línea que pasa por P y Q, así que eso significa que ℓ también tendría que pasar por O. Como eso no ocurre, debe ser imposible que ℓ y ℓ' se crucen, por lo que son paralelas.

2. La recta en sí.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Durante la lección, los estudiantes utilizaron transformaciones para crear rectas paralelas y luego observaron qué ángulos son congruentes. Pero ¿y si empezaran con rectas paralelas? Muestre una imagen de dos rectas paralelas con los ángulos correspondientes destacados:

Diga a los estudiantes que las rectas AI y GJ son paralelas y que la recta FE es una transversal que las interseca. He aquí algunas preguntas para el debate:

• «¿Qué transformación llevaría el ángulo EBI al ángulo BCJ?». (Traslación).

• «¿Cómo sabemos que una traslación a lo largo del segmento de recta dirigida de B a C lleva la recta AI a la recta GJ?». (Las traslaciones llevan las rectas a rectas paralelas y B se lleva a C, por lo que la recta AI se lleva a una recta paralela que pasa por C. Solo hay una recta de este tipo, que es la recta GJ).

Los estudiantes completarán el resto de la demostración en su enfriamiento. También tendrán la oportunidad de demostrar las conversiones en problemas de práctica. Los enunciados inversos se estudian en una lección posterior. Por ahora, señale que los dos enunciados están relacionados pero tienen información dada diferente.

Distribuya nuevas copias de la tabla de referencia en blanco. Informe a los estudiantes que seguirán necesitando la primera página junto con esta, por lo que deben mantener las páginas juntas.

Pida a los estudiantes que agreguen estos teoremas a sus tablas de referencia a medida que usted los agrega a la tabla de referencia de la clase:

Teorema del ángulo interior alterno: Si dos rectas paralelas son cortadas por una transversal, entonces los ángulos interiores alternos son congruentes.

A la inversa, si dos rectas son cortadas por una transversal y los ángulos interiores alternos son congruentes, entonces las rectas tienen que ser paralelas.

(Teorema)

Teorema del ángulo correspondiente: Si dos rectas paralelas son cortadas por una transversal, entonces los ángulos correspondientes son congruentes.

A la inversa, si dos rectas son cortadas por una transversal y los ángulos correspondientes son congruentes, entonces las rectas tienen que ser paralelas.

(Teorema)

ENFRIAMIENTO | TRANSFORMACIONES EN RECTAS

PARALELAS

(10 minutos)

Los estudiantes escribirán pruebas en esta actividad. No se espera que los estudiantes demuestren un dominio completo del lenguaje o justificaciones perfectamente sólidas en este momento. Es probable que los estudiantes se limiten a describir cómo las transformaciones actúan sobre los semirrectas relevantes, pero que no justifiquen por qué los semirrectas se llevan donde deben. Habrá muchas más oportunidades para que los estudiantes desarrollen esa habilidad.

En cada pregunta, las rectas AI y GJ son paralelas y están intersecadas por la recta transversal FE.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Los ángulos EBI y BCJ son ángulos correspondientes. Usa una transformación que lleve el ángulo EBI al ángulo BCJ para probar que los ángulos correspondientes son congruentes.

2. Los ángulos ABC y BCJ son ángulos interiores alternos. Usa una transformación que lleve el ángulo ABC al ángulo BCJ para probar que los ángulos interiores alternos son congruentes. Rotula cualquier otro punto de la figura que ayude a definir una transformación.

RESPUESTAS POSIBLES

1. Ejemplo de respuesta: Traslada a lo largo del segmento de recta dirigida de B a C. El semirrecta BE se toma al semirrecta CB. La recta AI se lleva a una recta paralela que pasa por C. Solo hay una recta de este tipo, y es GJ. Por tanto, la semirrecta BI se lleva a la semirrecta CJ. Como la semirrecta BE se lleva a la semirrecta CB y la semirrecta BI se lleva a la semirrecta CJ, eso significa que el ángulo EBI se lleva al ángulo BCJ

2. Respuesta de ejemplo: Etiqueta el punto medio del segmento BC como M y rote 180 grados alrededor de M. Una rotación 180 grados alrededor de un punto en la línea FE lleva la recta FE a sí misma. Los puntos B y C están sobre la misma recta y equidistan de M, por lo que B se lleva a C y C se lleva a B Por lo que la semirrecta BC se lleva a la semirrecta CB. La rotación de 180 grados de lleva la recta AI a una recta paralela que pasa por C. Solo hay una recta de este tipo y es GJ. Así que la semirrecta BA se lleva a la semirrecta CJ. Como la semirrecta BA se lleva a la semirrecta CJ y la semirrecta BC se lleva a la semirrecta CB, eso significa que el ángulo ABC se lleva al ángulo BCJ

. Matemáticas . Unidad 1

Resumen de la lección para el estudiante

A menudo hay varias formas diferentes de explicar por qué las afirmaciones son verdaderas. Comparar las distintas formas puede conducir a nuevos conocimientos o a una comprensión más flexible. Considera los ángulos que se forman cuando 2 las rectas paralelas ℓ y m son cortadas por una transversal:

Supón que queremos explicar por qué el ángulo ABE es congruente con el ángulo GCF. Etiqueta el punto medio de BC como M. Rotando 180 grados alrededor de M lleva el ángulo ABE al ángulo GCF. ¿Por qué?

Pues bien, B y C son equidistantes de M, de modo que la rotación lleva B a C. Además, lleva la transversal a sí misma, de modo que lleva la semirrecta BE a la semirrecta CF. Finalmente, la rotación lleva la recta l a la recta m porque las rotaciones de 180 grados llevan las rectas a rectas paralelas y m es la única recta paralela a ℓ que también pasa por C

Una explicación diferente puede demostrar el mismo hecho usando una traslación y la idea de que los ángulos verticales son congruentes. Intenta pensar en esa explicación tú mismo.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Priya: Apuesto a que si los ángulos interiores alternos son congruentes, entonces las rectas tendrán que ser paralelas.

Han: ¿En serio? Sabemos que si las rectas son paralelas entonces los ángulos interiores alternos son congruentes, pero no sabía que funcionara en ambos sentidos.

Priya: Bueno, creo que sí. ¿Y si el ángulo ABC y el ángulo BCJ son ambos 40 grados? Si trazo una recta perpendicular a la recta AI a través del punto B, obtengo este triángulo. El ángulo CBX sería 50 grados porque 40 + 50 = 90. Y como los ángulos de un triángulo suman 180 grados, el ángulo CXB es 90 grados. ¡También es un ángulo recto!

Han: ¡Oh! Entonces la recta AI y la recta GJ son ambas perpendiculares a la misma recta. Así es como construimos rectas paralelas, haciendo que ambas sean perpendiculares a la misma recta. Así que las rectas AI y GJ deben ser paralelas.

A. Etiqueta el diagrama basándote en la conversación de Priya y Han.

B. ¿Hay algo especial en 40 grados? ¿Serán paralelas 2 rectas cualesquiera cortadas por una transversal con ángulos interiores alternos congruentes?

Soluciones posibles

A. Diagrama con el ángulo CBX etiquetado 50 grados y el ángulo CXB etiquetado 90 grados.

B. Ejemplo de respuesta: No 40 grados no es especial, esto siempre funcionará. El argumento podría repetirse con una variable en lugar de 40 grados para demostrarlo en general.

PROBLEMA 2

Demuestra que las rectas AI y GJ son paralelas. Soluciones posibles

El ángulo ABC tiene medida a° debido a los ángulos verticales. El ángulo CBX tiene medida (90 - a)° porque es complementario del ángulo ABC. Por suma de ángulos triangulares, el ángulo CXB debe medir 90 grados. Por tanto, BX es perpendicular a ambas rectas AI y GJ, por lo que son paralelas.

Geometría . Matemáticas . Unidad 1

PROBLEMA 3

(Unidad 1, lección 18)

¿Cuál es la medida del ángulo ABE?

PROBLEMA 4

(Unidad 1, lección 19)

Las rectas AB y BC son perpendiculares. Los semirrectas discontinuos bisecan los ángulos ABD y CBD. Explica por qué la medida del ángulo EBF es 45 grados.

Soluciones posibles

50 grados

PROBLEMA 5

(Unidad 1, lección 18)

Identifica una figura que no sea la imagen del cuadrilátero ABCD después de una secuencia de transformaciones. Explica cómo lo sabes.

Soluciones posibles

Puesto que las rectas AB y BC son perpendiculares, esto significa que la medida de ∠ABC es 90 grados. Los ángulos ABE y EBD tienen la misma medida que los ángulos DBF y FBC.

Soluciones posibles

Cuadrilátero DJMA. El lado más largo de ABCD es AD. El lado más largo de DJMA es JM. Estos lados tienen longitudes diferentes. Si las figuras no son congruentes, entonces no hay una secuencia de transformaciones que lleve una figura a la otra.

. Matemáticas . Unidad 1

PROBLEMA 6

(Unidad 1, lección 17)

El cuadrilátero ABCD es congruente con el cuadrilátero A'B'C'D'

Describe una secuencia de movimientos rígidos que lleve A a A', B aB', C a C', y D a D'

PROBLEMA 7

(Unidad 1, lección 17)

El triángulo ABC es congruente con el triángulo A'B'C'. Describe una secuencia de movimientos rígidos que lleve A a A', B a B', y C a C'

Soluciones posibles

Ejemplo de respuesta: Traslade el cuadrilátero ABCD por el segmento de recta dirigida BB'. Gira la imagen usando el centro B' hasta que la imagen de A coincida con A'

Soluciones posibles

Ejemplos de respuestas: Traslade el triángulo ABC por el segmento de recta dirigida AA'. Rota la imagen usando el centro A' hasta que la imagen de B coincida con B'

PROBLEMA 8

(Unidad 1, lección 16)

Identifica cualquier ángulo de rotación que cree simetría.

Soluciones posibles

Rota 120 y 240 grados alrededor del centro de la figura crea simetría.

PROBLEMA 9

(Unidad 1, lección 16)

Selecciona todos los ángulos de rotación que producen simetría para esta flor.

Geometría . Matemáticas . Unidad 1

PROBLEMA 10

(Unidad 1, lección 14)

Tres segmentos de recta forman la letra N. Gira la letra N en el sentido de las agujas del reloj alrededor del punto medio del segmento BC en 180 grados. Describe el resultado.

Soluciones posibles

La imagen es la misma letra N.

Reflexiones:

Nation California . Geometría

Math Nation California . Geometría

Geometría . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Transformaciones

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.9 Demostrar teoremas sobre líneas y ángulos. Los teoremas incluyen: los ángulos verticales son congruentes; cuando una transversal cruza rectas paralelas, los ángulos interiores alternativos son congruentes y los ángulos correspondientes son congruentes; los puntos en una bisectriz perpendicular de un segmento de recta son exactamente los que equidistan de los puntos extremos del segmento.

G-CO.10 Demostrar teoremas sobre triángulos. Los teoremas incluyen: las medidas de los ángulos interiores de un triángulo suman 180°; los ángulos de las bases de los triángulos isósceles son congruentes; el segmento que une los puntos medios de dos lados de un triángulo es paralelo al tercer lado y tiene la mitad de la longitud; las medianas de un triángulo se encuentran en un punto.

Construir

8.G.5 G-CO.1 G-CO.2 G-CO.4

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y usar estructuras.

Estándares ELD de California

I.B.5

I.C.12

II.C.6

LECCIÓN 21

CIENTO OCHENTA

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo, buscan y utilizan la estructura descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo demostrar que la suma de los ángulos de un triángulo es 180 grados.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Demostrar (por escrito) que la suma de las medidas de los ángulos de un triángulo es 180 grados.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Piensa, haz coincidir y comparte

Dibújalo

MLR8: Apoyos para el debate

Toma turnos

. Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Demostremos el teorema de la suma de triángulos.

Narrativa de la lección

Los estudiantes se basan en las relaciones de ángulos que establecieron en lecciones anteriores para demostrar que la suma de las medidas de los ángulos en un triángulo es 180 grados. En octavo grado, los estudiantes usaron argumentos informales para demostrar el teorema de la suma de ángulos de triángulos. Esta lección retoma ese trabajo y lo lleva más lejos utilizando definiciones más rigurosas y razonamientos más cuidadosos. Los estudiantes continuarán desarrollando sus habilidades para escribir pruebas en unidades posteriores.

Los estudiantes trabajan en dos pruebas. Al igual que en la lección anterior, una prueba utiliza una rotación de 180 grados y la otra utiliza traslaciones. Los estudiantes hacen uso de la estructura cuando comparan varios triángulos y observan que los mismos argumentos funcionan para demostrar el teorema de la suma de ángulos de triángulos sin importar con qué triángulo comiencen (MP7).

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Grupos pequeños 10 min

Actividad de exploración En parejas o grupos pequeños 15 min

Actividad de exploración En parejas o Grupos pequeños 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes analizan una prueba para determinar qué afirmaciones son verdaderas con respecto a 2 rectas intersecadas por una transversal.

Los estudiantes utilizan transformaciones para crear rectas paralelas y transversales para demostrar el teorema de la suma de ángulos de triángulos.

La actividad requiere el uso del programa de geometría, que está disponible en la edición digital para estudiantes.

Los estudiantes aplican traslaciones de triángulos para probar el teorema de la suma de ángulos de triángulos.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda del teorema de la suma de ángulos de triángulos.

Los estudiantes resumen los 2 diferentes métodos usados para probar el teorema de la suma de ángulos de triángulos.

Los estudiantes completan una prueba usando rotaciones de triángulos para probar el teorema de la suma de ángulos de triángulos.

El componente de práctica independiente incluye 2 en la lección y 7 problemas de repaso en espiral.

CALENTAMIENTO | ¿QUÉ FALLÓ? (10 minutos)

Rutinas didácticas

Piensa, haz coincidir y comparte

El propósito de esta actividad es que los estudiantes analicen una prueba y decidan si cada paso tiene sentido. Al encontrar el error en esta prueba, los estudiantes refuerzan su comprensión de que los ángulos correspondientes solo son congruentes cuando las rectas dadas son paralelas.

INTRODUCCIÓN

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 4 y asigna una afirmación diferente a cada estudiante en un grupo. Conceda a los estudiantes un tiempo de trabajo tranquilo para decidir si su afirmación es cierta. A continuación, invite a los estudiantes a compartir sus respuestas con su grupo antes de discutir las circunstancias que hacen que los ángulos correspondientes sean congruentes. Continúe con un debate para toda la clase.

Aquí hay 2 rectas ℓ y m que no son paralelas que han sido cortadas por una transversal.

Tyler piensa que el ángulo EBF es congruente con el ángulo BCD porque son ángulos correspondientes y una traslación a lo largo del segmento de recta dirigida de B a C llevaría un ángulo al otro. He aquí sus razones.

• La traslación lleva a B sobre C, de modo que la imagen de B es C

• La traslación lleva a E a algún punto del semirrecta CB porque necesitaría trasladarse una distancia mayor que BC para caer al otro lado de C

• La imagen de F tiene que aterrizar en algún punto de la recta m porque las traslaciones llevan las rectas a paralelas y la recta m es la única paralela a ℓ que pasa por B'

• La imagen de F, llámala F', tiene que aterrizar en el lado derecho de la línea BC o de lo contrario la recta FF' no sería paralela al segmento de recta dirigida que va de B a C

1. Tu maestro te asignará una de las afirmaciones de Tyler para que reflexiones sobre ella. ¿Es cierta la afirmación? Explica tu razonamiento.

2. ¿En qué circunstancias son congruentes los ángulos correspondientes? Prepárate para compartir tu razonamiento.

1. Las afirmaciones 1, 2 y 4 son verdaderas, mientras que la afirmación 3 es falsa.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

2. Los ángulos correspondientes solo son congruentes si las rectas cortadas por la transversal son paralelas.

El propósito de la discusión es destacar el hecho de que el teorema del ángulo correspondiente solo es verdadero cuando las rectas dadas son paralelas. Pida a los estudiantes que señalen exactamente dónde se rompe el argumento en la situación en la que las dos rectas dadas no son paralelas (tercera afirmación de Tyler). Pida a los estudiantes que expongan en qué circunstancias los ángulos correspondientes son congruentes y que expliquen su razonamiento. (Solo las rectas paralelas con una transversal producen ángulos correspondientes congruentes, como vimos con las pruebas de rotación y transformación).

. Matemáticas . Unidad 1

ACTIVIDAD

DE EXPLORACIÓN | SOMA DE LOS ÁNGULOS DE UN TRIÁNGULO EN UNA DIRECCIÓN

(15 minutos)

Rutinas didácticas

Dibújalo

MLR8: Apoyos para el debate

Toma turnos

En octavo grado, los estudiantes utilizaron argumentos informales para demostrar el teorema de la suma de ángulos de triángulos. Esta actividad retoma ese trabajo y lo lleva más lejos utilizando definiciones más rigurosas y razonamientos más cuidadosos. Los estudiantes deben hacer uso de sus tablas de referencia.

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

INTRODUCCIÓN

Recuerde a los estudiantes el significado del teorema de la suma de ángulos de triángulos mostrando un triángulo grande en papel de calco con las medidas de los ángulos etiquetadas a°, b° y c° para que todos lo vean. Arranca los ángulos y reordénalos para formar una línea recta. Pregunta cuál es la suma de las medidas de los tres ángulos, dado que forman una línea recta. (180 grados).

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience la actividad con contextos concretos o familiares. Por ejemplo, proporcione a los estudiantes un triángulo que tenga medidas de ángulos conocidas como 50°, 60°, y 70°. Pida a los estudiantes que completen la tarea con este triángulo. A continuación, pida a los estudiantes que consideren la relación entre los ángulos formados por las rectas paralelas y cada transversal.

Apoya la accesibilidad para: Procesamiento conceptual; memoria

1. Utiliza la tecnología para crear un triángulo. Utiliza la herramienta de texto para etiquetar los 3 ángulos interiores como a, b, y c.

2. Marca los puntos medios de 2 de los lados.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

3. Extiende el lado del triángulo sin el punto medio en ambas direcciones para formar una línea.

4. Utiliza lo que sabes sobre rotaciones para crear una recta paralela a la recta que has hecho que pase por el vértice opuesto.

5. ¿Cuál es el valor de a + b + c? Explica tu razonamiento.

Los estudiantes crean un triángulo y forman un par de rectas paralelas para las que dos lados del triángulo son transversales. Utilizando el hecho de que los ángulos interiores alternos son congruentes cuando las rectas son paralelas, los ángulos forman una recta y así a + b + c = 180

CONCEPTOS ERRÓNEOS PREVISTOS

Algunos estudiantes pueden atascarse a la hora de encontrar las medidas de los ángulos que faltan. Dirija a esos estudiantes a sus tablas de referencia.

La idea importante es que, sin importar con qué triángulo comenzaron los estudiantes, la suma de las medidas de los tres ángulos siempre es 180 grados. Selecciona varias respuestas de los estudiantes para mostrarlas a todos. Aquí hay algunas preguntas para el debate:

SÍNTESIS DE LA ACTIVIDAD

Apoyo para estudiantes

• «¿Qué hay de igual en estas figuras? ¿Qué es diferente?». (El etiquetado particular de los puntos y las medidas de los ángulos puede ser diferente, pero el resultado es siempre el mismo. Los ángulos forman una línea recta y, por tanto, las medidas de los ángulos suman 180 grados).

• «¿Cómo has creado una segunda línea paralela a la primera?». (Girando 180 grados alrededor de cualquiera de los puntos medios creados se lleva la primera recta a la segunda recta).

• «¿Por qué girando 180 grados alrededor de un punto medio se crea la misma recta que girando alrededor del otro?». (Ambas rectas son paralelas a la recta dada y ambas rectas pasan por el vértice opuesto a la recta dada. El Postulado Paralelo dice que hay una única recta paralela a la recta dada que pasa por el punto en cuestión, por lo que las dos rectas deben ser la misma recta).

que aprenden el idioma inglés

Hablar y representar: MLR8 Apoyos para el debate. Utilice esta rutina para apoyar el debate de toda la clase. Después de que cada estudiante comparta, proporcione a la clase los siguientes fragmentos de oraciones para ayudarles a responder: «Estoy de acuerdo porque ....» o «No estoy de acuerdo porque ....». Si es necesario, revoque las ideas de los estudiantes para demostrar el uso del lenguaje matemático replanteando una afirmación como pregunta con el fin de aclarar, aplicar un lenguaje apropiado e implicar a más estudiantes.

Principio(s) de diseño: Apoyar la adquisición de sentido

ACTIVIDAD DE EXPLORACIÓN | SUMA DE TRIÁNGULOS DE OTRA FORMA

(15 minutos)

Rutinas didácticas

Dibújalo

En esta actividad, los estudiantes demuestran el teorema de la suma de ángulos de triángulos utilizando traslaciones.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Comience con una demostración en pequeños grupos o para toda la clase y piense en voz alta en la primera pregunta para recordar a los estudiantes cómo trasladar un triángulo a lo largo de un segmento de recta dirigido. Mantén a la vista la traslación realizada para que los estudiantes puedan consultarla mientras trabajan.

Apoya la accesibilidad para: Memoria; Procesamiento conceptual

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

. Matemáticas . Unidad 1

Aquí está el triángulo ABC con medidas de ángulo a°, b° y c°. Cada lado se ha extendido a una recta.

RESPUESTAS POSIBLES

1. Traslada el triángulo ABC a lo largo del segmento de recta dirigida desde B hasta C para formar el triángulo A'B'C'. Etiqueta las medidas de los ángulos en el triángulo A'B'C'

2. Traslada el triángulo A'B'C' a lo largo del segmento de recta dirigida de A' a C' para formar el triángulo A''B''C''. Etiqueta las medidas de los ángulos del triángulo A''B''C''

3. Etiqueta las medidas de los ángulos que se encuentran en el punto C. Explica tu razonamiento. ¿Cuál es el valor de a + b + b? Explica tu razonamiento.

CONCEPTOS ERRÓNEOS PREVISTOS

1. Ver imagen (triángulo de la derecha)

2. Ver imagen (triángulo de abajo)

3. Puesto que los ángulos verticales son congruentes, el ángulo BCB'' también mide b°. Del mismo modo, el ángulo ACA' mide a° y el ángulo C'CC'' mide c°.

4. Ejemplo de respuesta: Tres ángulos adyacentes cualesquiera en el punto C forman una línea recta y miden a° + b° + c°. Por lo tanto a + b + c =180.

Algunos estudiantes pueden tener dificultades para dibujar una imagen razonablemente precisa de la figura bajo la traslación. Recuérdales las herramientas de geometría que tienen a su disposición, como el papel de calco, las reglas y los compases.

Algunos estudiantes pueden atascarse a la hora de encontrar las medidas de los ángulos que faltan. Dirígelos a sus tablas de referencia.

. Matemáticas . Unidad 1

¿Estás

SÍNTESIS DE LA ACTIVIDAD

listo para más?

Aquí tienes algunas preguntas para debatir:

• «¿Cómo has encontrado las medidas de los otros ángulos en el punto C?». (Algunos de los ángulos son imágenes del triángulo original después de una transformación rígida. Deben tener la misma medida que el triángulo original. Puedo encontrar las otras medidas de ángulos usando propiedades de ángulos verticales).

• «¿Cómo sabes que el punto C'' cae sobre la recta AC?». (Las traslaciones llevan rectas a rectas paralelas y A' se lleva a C, por lo que el segmento A'C''' tiene que llevarse a una recta paralela que pase por C. Solo hay una recta de este tipo, que es la recta AC. Así que C'' cae en algún lugar de la recta AC. Para que C'C'' sea paralela a la recta A'C, tendría que aterrizar en la recta AC a la derecha de C).

Una razón por la que a los matemáticos les gusta tener pruebas rigurosas incluso cuando las conjeturas parecen ser ciertas es que pueden ayudar a revelar qué afirmaciones se utilizaron. Esto puede abrir nuevas áreas que explorar si cambiamos esas suposiciones. Por ejemplo, nuestras dos pruebas de que las medidas de los ángulos de un triángulo suman 180 degree basaban en transformaciones rígidas que llevan las rectas a líneas paralelas. Si nuestras suposiciones sobre las rectas paralelas cambiaran, también lo harían las consecuencias sobre las sumas de los ángulos de los triángulos. Cualquier estudio de la geometría en el que cambien estos supuestos se denomina geometría no euclidiana. En algunas geometrías no euclidianas, las rectas en la misma dirección pueden intersecarse, mientras que en otras no. En la geometría esférica, que estudia superficies curvas como la superficie de la Tierra, las rectas en la misma dirección siempre se cruzan. Esto tiene consecuencias sorprendentes para los triángulos. Imaginemos un triángulo que une el polo norte, un punto del ecuador y un segundo punto del ecuador situado a una cuarta parte de la distancia entre el primero y la Tierra. ¿Cuál es la suma de los ángulos de este triángulo?

Respuesta del estudiante

270 grados

SÍNTESIS DE LA LECCIÓN

(5 minutos)

En esta lección, los estudiantes exploraron dos pruebas diferentes del teorema de la suma de ángulos de Triángulos. Pida a los estudiantes que agreguen este teorema a sus tablas de referencia mientras usted lo agrega a la tabla de referencia de la clase: Teorema de la suma de ángulos de triángulos: Las medidas de los tres ángulos de cualquier triángulo siempre suman 180 grados. (Teorema)

a + b + c = 180

Aquí hay algunas preguntas para el debate:

• «Repasa las dos pruebas del teorema de la suma de ángulos triangulares. ¿Hay alguna parte del argumento que dependa de las medidas particulares de tu triángulo, o habrían funcionado los mismos argumentos con otros tipos de triángulos?». (El mismo argumento valdría para cualquier triángulo. Las medidas particulares no importan).

• «¿En qué se diferencian las pruebas de 2 del teorema de la suma de ángulos de triángulos? ¿En qué son iguales?». (Ambas actividades usan transformaciones para colocar los tres ángulos adyacentes para hacer una línea recta. Las pruebas son diferentes porque en la primera se utilizaron rotaciones de 180 grados, mientras que en la segunda se utilizaron traslaciones).

ENFRIAMIENTO | SUMA DE TRIÁNGULOS DE UNA TERCERA MANERA

(5 minutos)

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Elena quiere demostrar que las medidas de los 3 ángulos de un triángulo siempre suman 180 grados. Comienza usando movimientos rígidos para rotar el triángulo 180 grados alrededor de 2 puntos medios.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACIÓN

Explica cómo Elena etiquetó su diagrama para terminar su prueba. RESPUESTAS POSIBLES

Elena giró el triángulo ABC 180 grados usando el punto medio de AB como centro. Eso lleva el ángulo ABC al ángulo DAB por lo que Elena etiquetó el ángulo DAB como b°. También giró el triángulo ABC 180 grados usando el punto medio de AC como centro. Eso lleva el ángulo ACB al ángulo EAC por lo que Elena etiquetó el ángulo EAC como c°. Ahora tres ángulos que miden a°, b° y c° son adyacentes y parecen formar una recta.

Dado que los segmentos AD y AE son ambos rotaciones de 180 grados del segmento, BC ambos deben ser paralelos a BC. Esto significa que AD y AE están en la misma recta ya que ambos pasan por A. Los tres ángulos forman una recta. Así que a + b + c = 180 grados.

Resumen de la lección para el estudiante

Usando rotaciones y rectas paralelas, podemos entender por qué los ángulos en un triángulo siempre suman 180 grados. Aquí está el triángulo ABC

Rota el triángulo ABC 180 grados alrededor del punto medio del segmento AB y etiqueta la imagen de C como D. Luego, rota el triángulo ABC 180 grados alrededor del punto medio del segmento AC y etiqueta la imagen de B como E

Observa que cada rotación de 180 grados lleva a la recta BC a una recta paralela. Así que la recta DA es paralela a BC y la recta AE es también paralela a BC. Solo hay una recta paralela a BC que pase por el punto A, por lo que las rectas DA y AE son la misma recta. Como la recta DE es paralela a la recta BC, sabemos que los ángulos interiores alternos son congruentes. Eso significa que el ángulo BAD también mide b∘ y el ángulo CAE también mide c∘

Como DE es una recta, las medidas de los ángulos 3 en el punto A deben sumar 180 grados. Así que a + b + c = 180. Este argumento no depende del triángulo con el que empezamos, por lo que demuestra que la suma de las 3 medidas angulares de cualquier triángulo es siempre 180 grados.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Cada uno de los triángulos de aquí se obtiene aplicando movimientos rígidos al triángulo 1.

A. ¿Qué triángulos son traslaciones del triángulo 1? Explica cómo lo sabes.

B. ¿Qué triángulos no son traslaciones del triángulo 1? Explica cómo lo sabes.

Soluciones posibles

A. Los triángulos impares son traslaciones del triángulo 1. Tienen la misma orientación en el plano. Tienen la misma orientación en el plano y requieren una traslación vertical (y a veces) horizontal.

B. Los triángulos pares no son traslaciones del triángulo 1 porque el lado más largo está en la «parte superior» y no en la «parte inferior». Los triángulos pares son, sin embargo, traslaciones unos de otros.

PROBLEMA 2

El cuadrilátero es un paralelogramo. Halla la medida de los ángulos 1, 2 y 3.

Soluciones posibles

El ángulo 1 mide 100°, el ángulo 2 mide 80° y el ángulo 3 mide 100°

. Matemáticas . Unidad 1

PROBLEMA 3

(Unidad 1, lección 20)

En la figura mostrada, las rectas f y g son paralelas. Selecciona el ángulo que es congruente con unngulo 1.

A. Ángulo 2

B. Ángulo 6

Soluciones posibles

PROBLEMA 4

(Unidad 1, lección 20)

C. Ángulo 7

D. Ángulo 8

El ángulo BDE es congruente con el ángulo BAC. Nombra otro par de ángulos congruentes. Explica cómo lo sabes.

Soluciones posibles

Los ángulos BED y BCA son congruentes. La recta m debe ser paralela a la recta l porque estas rectas son cortadas por la transversal AB y los ángulos correspondientes BDE y BAC son congruentes. Los ángulos correspondientes BED y BCA también son congruentes porque están formados por rectas paralelas cortadas por la transversal BC

PROBLEMA 5

(Unidad 1, lección 20)

A. Describe una transformación que podría usarse para demostrar que los ángulos correspondientes son congruentes.

B. Describe una transformación que podría usarse para mostrar que los ángulos interiores alternos son congruentes.

Soluciones posibles

A. Ejemplo de respuesta: Trasladar un ángulo a su ángulo correspondiente.

B. Ejemplo de respuesta: Rotar un ángulo sobre su ángulo interior alterno.

PROBLEMA 6

(Unidad 1, lección 19)

Las rectas AD y EC se encuentran en el punto B ¿Cuál de estas debe ser verdadera? Selecciona todas las que correspondan.

Una rotación de 180 grados en el sentido de las agujas del reloj usando el centro B lleva D a A

La imagen de D después de una rotación de 180 grados usando el centro B se encuentra en la semirrecta BA

Si una rotación 180 grados con centro B lleva C a E entonces también lleva E a C

El ángulo ABC es congruente con el ángulo DBE

El ángulo ABE es congruente con el ángulo ABC

Soluciones posibles

Una rotación de 180 grados en el sentido de las agujas del reloj usando el centro B lleva D a A

La imagen de D después de una rotación de 180 grados usando el centro B se encuentra en la semirrecta BA

Si una rotación 180 grados con centro B lleva C a E entonces también lleva E a C

El ángulo ABC es congruente con el ángulo DBE

El ángulo ABE es congruente con el ángulo ABC

Geometría . Matemáticas . Unidad 1

PROBLEMA 7

(Unidad 1, lección 19)

Los puntos E, B y C son colineales. Explica por qué los puntos A, B y D son colineales.

Soluciones posibles

Rote la recta EC en el sentido de las agujas del reloj 30 grados usando el centro B. El semirrecta BE lleva al semirrecta BA y el semirrecta BC lleva al semirrecta BD. Las rotaciones llevan rectas a rectas por lo que los puntos A, B y D deben ser colineales.

PROBLEMA 8

(Unidad 1, lección 18)

A. Dibuja la imagen de la figura ACTS después de una rotación en el sentido de las agujas del reloj alrededor del punto C utilizando el ángulo CTS y después una traslación por el segmento de recta dirigido CT

B. Describe otra secuencia de transformaciones que dé como resultado la misma imagen.

Soluciones posibles

B. Ejemplo de respuesta: Traslación por el segmento de línea dirigida CT. Rotar en el sentido de las agujas del reloj alrededor de la imagen del punto C por el ángulo CTS

PROBLEMA 9

(Unidad 1, lección 17)

El triángulo ABC es congruente con el triángulo A'B'C'. Describe una secuencia de movimientos rígidos que lleve A a A', B a B' y C a C'

Soluciones posibles

Ejemplo de respuesta: Traslada el triángulo ABC por el segmento de recta dirigida BB'. Gira la imagen utilizando el centro B' hasta que la imagen de C coincida con C'. Luego refleja a través de la recta B'C'

Reflexiones:

Geometría . Matemáticas . Unidad 1

LECCIÓN 22

IDEA(S) FUNDAMENTAL(ES)

• Problemas de triángulos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-GMD.6 Verificar experimentalmente que en un triángulo, los ángulos opuestos a los lados más largos son más grandes, los lados opuestos a los ángulos más grandes son más largos, y la suma de dos longitudes laterales cualesquiera es mayor que la longitud lateral restante; aplicar estas relaciones para resolver problemas matemáticos y del mundo real.

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

II.B.5

II.C.6

RELACIONES DE ÁNGULOS Y LADOS EN TRIÁNGULOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo y predecir lo que podría ocurrir

buscan y hacen uso de la estructura descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo verificar experimentalmente el teorema de la desigualdad de los triángulos.

• En un triángulo, puedo verificar experimentalmente que los lados opuestos a ángulos mayores son más largos y que los ángulos opuestos a lados mayores son mayores.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Demostrar que la suma de las longitudes de dos lados de un triángulo debe ser mayor que el tercer lado del triángulo.

• Comparar las medidas de los ángulos y las longitudes de los lados de un triángulo para determinar cuál es mayor o menor que.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Sondear a la clase

MLR8: Apoyos para el debate

MLR1: Cada vez más fuerte y más claro

Materiales necesarios

Papel de calco

Copias de la plantilla maestra

Conjunto de herramientas de geometría (HS)

. Matemáticas . Unidad 1

INFORMACIÓN

DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Comparemos las medidas de los ángulos y las longitudes de los lados de los triángulos.

Narrativa de la lección

Los estudiantes experimentan con triángulos para verificar el teorema de desigualdad del triángulo y la relación entre la longitud del lado de un triángulo y la medida del ángulo opuesto al lado. Los estudiantes analizan las medidas y reconocen patrones para crear conjeturas sobre las longitudes de los lados y las medidas de los ángulos de los triángulos (MP7).

Aunque no es necesario para esta lección, se recomienda poner la tecnología a disposición de los estudiantes, ya que hay oportunidades para que utilicen la tecnología y las herramientas adecuadas para resolver problemas (MP5).

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración En parejas 15 min

Actividad de exploración En parejas o en grupos pequeños 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Descripción breve

Los estudiantes justifican por qué los tres ángulos de un triángulo pueden disponerse en una línea con los tres vértices en un punto.

Los estudiantes determinan si un triángulo puede estar formado por conjuntos de longitudes laterales y luego analizan las longitudes laterales que pueden formar triángulos para verificar el teorema de la desigualdad de los triángulos.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar el teorema de la desigualdad de triángulos utilizando la tecnología.

Los estudiantes registran las medidas de los ángulos y las longitudes de los lados de varios triángulos para descubrir que el lado más largo es opuesto al ángulo más grande.

Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar la relación entre las longitudes de los lados y las medidas de los ángulos utilizando la tecnología.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la relación entre el ángulo más grande y el lado más largo.

Los estudiantes consolidan su comprensión mediante la creación de una representación visual del teorema de la desigualdad del triángulo y la relación entre el ángulo mayor y el lado más largo.

Los estudiantes utilizan las relaciones descubiertas en esta lección para identificar los enunciados de comparación verdaderos para un triángulo dado.

Práctica Independiente 8-10 min El componente de práctica independiente incluye 7 problemas de la lección y 1 problema de repaso en espiral.

CALENTAMIENTO | SUMA DE ÁNGULOS DE TRIÁNGULOS

(5 minutos)

Los estudiantes activan sus conocimientos previos sobre el teorema de la suma de triángulos. Vigile las diferentes estrategias que pueden utilizar los estudiantes, como medir los ángulos con un transportador, utilizar papel de calco para trazar cada ángulo y luego reordenar los ángulos en la recta, o construir una copia de cada ángulo en la recta utilizando el punto X como vértice de cada ángulo.

Poner a disposición de los estudiantes herramientas de geometría les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Disponga de herramientas de geometría si los estudiantes las piden. Conceda a los estudiantes unos minutos de trabajo en silencio, seguidos de un debate con toda la clase.

Se muestra el triángulo WHN.

Los tres ángulos del triángulo WHN se muestran en la tabla.

Ángulo H Ángulo N Ángulo W

1. Explica por qué es posible reorganizar los tres ángulos del triángulo WHN de manera que los lados de cada ángulo se alineen con la recta o con el ángulo o ángulos adyacentes a él, mientras que los tres vértices se alinean con el punto X de la recta mostrada.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

1. Ejemplo de respuesta: Puedo medir cada ángulo para demostrar que los tres ángulos del triángulo suman 180°. Como la medida de un ángulo recto también es 180°, los ángulos H, N y W pueden colocarse uno al lado del otro para crear el ángulo recto.

Invite a los estudiantes previamente identificados a compartir sus respuestas y estrategias con la clase. Diga a la clase que los estudiantes pueden tener diferentes enfoques para este problema, pero la constante en estos enfoques es que los tres ángulos del triángulo se pueden disponer a lo largo de la recta porque tienen una suma de 180°.

ACTIVIDAD DE EXPLORACIÓN | CREACIÓN DE TRIÁNGULOS (15 minutos)

Rutinas didácticas

Sondear a la clase

MLR 8: Apoyos para el debate

Los estudiantes comprueban el teorema de la desigualdad de los triángulos. Los estudiantes crean triángulos utilizando conjuntos de longitudes laterales y exploran si se puede construir un triángulo a partir de las longitudes laterales dadas. Si los estudiantes son capaces de crear un triángulo, identifican el tipo de triángulo que han creado. Los estudiantes escriben una conjetura sobre cómo determinar si un conjunto de longitudes laterales puede utilizarse para construir triángulos. Esta actividad puede implementarse con herramientas digitales o prácticas.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2. Deles acceso a una copia de la plantilla maestra y papel de calco. Diga a los estudiantes que trazarán las longitudes de los lados para determinar si se puede crear un triángulo. Considere la posibilidad de mostrar la primera fila de la tabla, demostrando cómo utilizar el papel de calco para trazar cada longitud lateral y determinar si se puede crear un triángulo. Pida a los estudiantes que completen la tabla con sus compañeros, animándoles a que se turnen para trazar las longitudes laterales y justificar si las longitudes laterales pueden crear un triángulo. A continuación, debate con toda la clase. La aplicació de la edición digital para el estudiante puede utilizarse en lugar del esquema y el papel de calco. Si se utiliza la aplicación, anime a los estudiantes a completar la tabla individualmente y luego completar el problema 2 con sus compañeros.

1. Determina si cada conjunto de longitudes laterales dadas puede utilizarse para crear un triángulo. A continuación, completa la tabla.

Longitudes laterales

11, 12, 17

8, 8, 17

8, 15, 17

9, 9, 24

9, 9, 18

9, 9, 16

5, 12, 15

4, 12, 15

¿Pueden las longitudes laterales crear un triángulo?

Sí No

En caso afirmativo, ¿qué tipo de triángulo se creó?

. Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACI Ó N

Longitudes de los lados

3, 12, 15

2, 12, 15

¿Pueden las longitudes de los lados crear un triángulo?

Sí

En caso afirmativo, ¿qué tipo de triángulo se ha creado?

RESPUESTAS POSIBLES

1. Haz una conjetura sobre cómo determinar si un conjunto de longitudes de lado puede usarse para construir un triángulo sin dibujarlo.

SÍNTESIS DE LA ACTIVIDAD

Longitudes laterales

11, 12 , 17

8, 8, 17

8, 15, 17

9, 9, 24

9, 9, 18

9, 9, 16

5, 12, 15

4, 12, 15

3, 12, 15

2, 12, 15

¿Pueden las longitudes laterales crear un triángulo?

Sí

En caso afirmativo, ¿qué tipo de triángulo se creó?

Escaleno y triángulo obtusángulo

Escaleno y triángulo rectángulo

Sí Triángulo isósceles y obtuso

Sí

Triángulo escaleno y obtuso

Sí Triángulo escaleno y obtuso

2. Respuesta de ejemplo: La suma de las dos longitudes laterales más cortas debe ser mayor que la tercera longitud lateral.

Cuando revise las respuestas para el problema 1, considere usar la rutina instructiva «Sondear a la clase». Muestre cada conjunto de longitudes laterales de uno en uno y pida a los estudiantes que anoten sus respuestas en una minipizarra. Cuando dé una señal, pida a los estudiantes que levanten sus respuestas. Si no hay pizarras blancas disponibles, considere la posibilidad de que los estudiantes levanten un pulgar hacia arriba para decir «sí» o pulgar hacia abajo para decir «no». Seleccione 1-2 estudiantes por problema para que compartan sus procesos de pensamiento y estrategias.

Invita a algunos estudiantes a compartir sus conjeturas con la clase. Mientras los estudiantes comparten sus respuestas, considere hacer las siguientes preguntas:

• «¿Estás de acuerdo con la conjetura de ______?».

• «¿Puedes pensar en un contraejemplo para la conjetura?».

• «¿Funcionará siempre esta conjetura?».

• «¿Se puede formar un triángulo si la suma de 2 longitudes de los lados es igual a la longitud del tercer lado? Explícalo».

. Matemáticas . Unidad 1

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Para apoyar a los estudiantes en la producción de una conjetura sobre las longitudes de los lados de los triángulos, proporcionar estructuras de oraciones como las siguientes: «Me he dado cuenta de que , por lo tanto ». «Estamos de acuerdo en que _________». «_______ es similar o diferente de porque ».

Principios de diseño: Apoyar la creación de sentido; optimizar la salida (para la comparación)

ACTIVIDAD DE EXPLORACIÓN | LONGITUDES DE LOS LADOS Y MEDIDAS DE LOS ÁNGULOS

(15 minutos)

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

Los estudiantes establecen conexiones entre las longitudes de los lados y las medidas de los ángulos en un triángulo. Miden las longitudes de los lados y las medidas de los ángulos de varios triángulos. A continuación, los estudiantes analizan estas medidas para descubrir que el ángulo más grande es el que atraviesa el lado más largo y el ángulo más pequeño es el que atraviesa el lado más corto.

A medida que los estudiantes miden, deben registrar las medidas con precisión para ayudarles a ver la relación entre las longitudes de los lados y las medidas de los ángulos (MP6). Esta actividad puede implementarse con herramientas digitales o prácticas.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2 o 4. Deles acceso a reglas y transportadores. Considere la posibilidad de que cada pareja dibuje y mida dos triángulos o que cada miembro de un grupo de 4 dibuje y mida un triángulo. Dé tiempo a los estudiantes para que anoten sus resultados y los de su grupo. Pida a los estudiantes que completen los problemas 2 y 3 con su pareja o grupo, seguido de un debate con toda la clase.

Hay un aplicación disponible para esta actividad en la edición digital para estudiantes. Si utiliza la aplicación, organice a los estudiantes por parejas. Pida a cada estudiante que anote las medidas de cuatro triángulos antes de comparar las medidas y completar los problemas 2 y 3 con su compañero o grupo.

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Algunos estudiantes pueden beneficiarse de tener los triángulos ya dibujados con sus medidas proporcionadas, lo que les dará más tiempo para hacer conexiones entre las longitudes de los lados y las medidas de los ángulos de un triángulo.

Apoya la accesibilidad para: Procesamiento conceptual

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Crea cuatro triángulos con diferentes longitudes de lado. Etiqueta los vértices de cada triángulo como A, B y C y cada lado como a, b y c de modo que el lado a sea opuesto al ángulo A, el lado b sea opuesto al ángulo B y el lado c sea opuesto al ángulo C. Mide y anota en la tabla las longitudes de los lados y las medidas de los ángulos. Después, completa la tabla.

Longitudes de los lados

Medidas de los ángulos ¿Qué lado es el más largo? ¿Qué ángulo es el mayor? a

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

2. Compara las longitudes de los lados y las medidas de los ángulos que has anotado con las longitudes de los lados y las medidas de los ángulos que ha anotado tu compañero. ¿Qué observas?

3. Haz una conjetura sobre la relación entre la longitud del lado de un triángulo y la medida del ángulo opuesto a ese lado.

1. Las respuestas varían.

2. Ejemplo de respuesta: Observo que el ángulo más grande está opuesto al lado más largo y el ángulo más pequeño está opuesto al lado más corto.

3. Ejemplos de respuestas:

• En un triángulo, el lado más largo está enfrente del ángulo más grande.

• En un triángulo, el ángulo más grande está enfrente del lado más largo.

• Si dos lados de un triángulo son desiguales en longitud, entonces el ángulo opuesto al lado más largo tiene la medida mayor.

• Si dos ángulos de un triángulo son desiguales en medida, entonces el lado opuesto al ángulo con la medida mayor es el lado más largo.

Invite a algunos estudiantes a compartir las medidas de uno de los triángulos que han creado. Luego, pregunte a la clase qué observan en las medidas. Anote las respuestas de los estudiantes. Pida a algunos estudiantes que compartan con la clase sus conjeturas del problema 3. Considere hacer las siguientes preguntas:

• «¿Funcionará esta conjetura para cualquier triángulo?».

• «¿Puedes pensar en un contraejemplo para esta conjetura?».

• «Si un triángulo tiene 2 ángulos congruentes, ¿qué puedes determinar acerca de las longitudes de los lados opuestos a los ángulos congruentes?». (Las longitudes de los lados opuestos a los ángulos congruentes también serán congruentes).

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

. Matemáticas . Unidad 1

Considera la posibilidad de mostrar las distintas variaciones de la relación entre la longitud del lado de un triángulo y la medida del ángulo opuesto al lado. Subraye las que no se hayan mencionado en clase.

• En un triángulo, el lado más largo está enfrente del ángulo más grande.

• En un triángulo, el ángulo más grande está enfrente del lado más largo.

• Si dos lados de un triángulo son desiguales en longitud, entonces el ángulo opuesto al lado más largo tiene la medida mayor.

• Si dos ángulos de un triángulo son desiguales en medida, entonces el lado opuesto al ángulo con la medida mayor es el lado más largo.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para ayudar a los estudiantes a mejorar sus respuestas escritas. Dé tiempo a los estudiantes para reunirse con 2-3 compañeros para compartir y recibir comentarios sobre sus respuestas. Invite a los estudiantes a volver atrás y revisar o perfeccionar sus respuestas escritas basándose en los comentarios de sus compañeros.

Principio(s) de diseño: Optimizar la producción (para la generalización); maximizar la metaconciencia

¿Estás preparado para más?

1. Las medidas de los ángulos del triángulo HTR son m∠R = 57°, m∠T = 62° y m∠H = 61°. ¿Qué lado del triángulo HTR tiene mayor longitud?

2. Las longitudes laterales del triángulo DWN son DN = 6,2, DW = 4,5 y WN = 5,4. ¿Qué ángulo del triángulo DWN es el mayor?

3. El triángulo MPK es un triángulo isósceles, donde MK = PK. Discute con tu compañero en qué circunstancias la medida del ángulo K sería mayor que la medida del ángulo M y la medida del ángulo P. Resume tu discusión.

Posibles respuestas

1. Longitud lateral HR

2. Ángulo W

3. Ejemplo de respuesta: Si la medida del ángulo K es mayor que 90°, entonces el ángulo será mayor que la medida de los ángulos M y P. Si MP > MK y/o MP > PK, entonces m∠K >90°

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Los estudiantes exploraron los criterios para las longitudes de los lados que podrían utilizarse para construir un triángulo, incluido el reconocimiento de cuándo no podían formar un triángulo. Los estudiantes también descubrieron la relación entre las longitudes de los lados de un triángulo y las medidas de los ángulos opuestos a los lados.

Considere la posibilidad de que los estudiantes trabajen en pequeños grupos para crear una presentación visual sobre el teorema de desigualdad del triángulo y la relación entre las longitudes de los lados de un triángulo y las medidas de los ángulos opuestos a los lados. Si es posible, pida a los estudiantes que incluyan ejemplos y contraejemplos.

Si el tiempo lo permite, cuelgue las exposiciones por el salón e invite a los estudiantes a realizar un recorrido por la galería, en el que dejarán comentarios en notas adhesivas para otros grupos. Oriente a los estudiantes sobre el tipo de comentarios que deben darse unos a otros. Considere la posibilidad de plantear las siguientes preguntas:

• «¿Hay algo en la organización de la exposición visual que aclare especialmente las ideas? ¿Hay algo en la organización que pueda mejorarse?»..

• «¿Hay algo en la forma de explicar las ideas que las haga especialmente claras? ¿Hay algo en las explicaciones que podría mejorarse?»..

• «¿Estás de acuerdo con los ejemplos? ¿Y con los contraejemplos?».

ENFRIAMIENTO | COMPARACIÓN DE LONGITUDES DE LADOS Y MEDIDAS DE ÁNGULOS (5

minutos)

Se muestra el triángulo XYZ, donde m∠Y = 97°

1. Seleccione todas las afirmaciones que deben ser verdaderas.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

+ XY > ZY

+ YZ > ZX

2. Explica cómo saber que m∠Y = 97° es suficiente información para determinar cuál lado del triángulo XYZ es el más largo

1. Selecciona todas las afirmaciones que deben ser ciertas.

RESPUESTAS POSIBLES

2. Respuesta de ejemplo: Saber que m∠Y = 97° es suficiente porque la suma del ángulo X y el ángulo Z es 83°, por lo que el ángulo Y es el ángulo mayor y la longitud del lado XZ es el lado mayor.

Resumen de la lección para el estudiante

Se pueden crear triángulos a partir de un conjunto de tres longitudes de lados si cumplen ciertos criterios.

• Se puede crear un triángulo si la suma de las longitudes de dos lados cualesquiera de un triángulo es mayor que la longitud del tercer lado.

• Si tres segmentos tienen longitudes tales que la suma de dos cualesquiera es mayor que la del tercero, entonces se puede construir un triángulo a partir de los segmentos.

Se muestra el triángulo FYB, donde las longitudes de los lados están en unidades.

Si se aplican las relaciones descubiertas en la lección, entonces estas relaciones para el triángulo FYB son verdaderas.

FB + YB > FY

FB + FY > YB

FY + YB > FB

. Matemáticas . Unidad 1

Las longitudes de los lados de cualquier triángulo tendrán las relaciones que se muestran. a + b > c

Estas relaciones se conocen como teorema de la desigualdad de los triángulos

b + c > a

a + c > b

El teorema de la desigualdad de los triángulos establece que la suma de las longitudes de dos lados cualesquiera de un triángulo debe ser mayor que el tercer lado.

La inversa del teorema de la desigualdad de los triángulos establece que si los valores positivos a, b y c satisfacen las desigualdades a + b > c, b + c > a y a + c > b, entonces los tres valores se pueden utilizar como longitudes de los lados para crear un triángulo.

La relación entre la longitud del lado de un triángulo y la medida del ángulo opuesto a ese lado se puede describir como se muestra.

• En un triángulo, el lado más largo está enfrente del ángulo más grande.

• En un triángulo, el ángulo mayor está enfrente del lado mayor.

• Si dos lados de un triángulo son desiguales en medida, entonces el ángulo opuesto al lado más largo tiene la medida mayor.

• Si dos ángulos de un triángulo son desiguales en medida, entonces el lado opuesto al ángulo con la medida mayor es el lado más largo.

Todas estas afirmaciones están sacando esencialmente la misma conclusión sobre los ángulos de un triángulo.

Se muestra el triángulo ABC, donde c > b > a

Porque c > b > a, las siguientes relaciones son ciertas.

• m∠B > m∠A

• m∠C > m∠A

• m∠C > m∠B

• AC > BC

• AB > BC

• AB > AC

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Selecciona todos los conjuntos de longitudes de lado que se pueden utilizar para crear un triángulo.

8, 5, 4

4, 4, 10

13, 17, 9

8.2, 7.3, 16.1

18.3, 10.5, 29.1

Soluciones posibles

8, 5, 4

4, 4, 10 13, 17, 9

8.2, 7.3, 16.1

, 10.5, 29.1

• Segmento AB es el lado más largo.

Geometría . Matemáticas . Unidad 1

PROBLEMA 2

Las longitudes laterales del triángulo LNB son BN = 8,6, LB = 11,3 y LN = 7,9. ¿Qué ángulo del triángulo LNB es el mayor?

Posible solución

Ángulo N

PROBLEMA 3

Las longitudes laterales del triángulo GRN son RN = 28,4, GR = 19,2 y GN = 23,5. Enumera los ángulos en orden de menor a mayor.

Posible solución

Ángulo N, ángulo R, ángulo G

PROBLEMA 4

Las medidas de los ángulos del triángulo TWK son m∠T = 57°, m ∠ W = 88° y m∠K = 35°. Enumera las longitudes de los lados ordenadas de menor a mayor.

Posible solución

Longitud lateral TW, longitud lateral KW, longitud lateral TK

PROBLEMA 5

Se muestra el triángulo XHT

Completa cada enunciado utilizando > o <.

PROBLEMA 6

Dos de las longitudes laterales del triángulo KZN son KN = 34,5 y ZN = 24.8

Selecciona todos los valores que podrían ser la longitud del lado KZ

Soluciones posibles

Nation California . Geometría

PROBLEMA 7

Un ranchero está construyendo una valla que encierra un área triangular. Utiliza el diagrama del triángulo RMW, donde m∠M = 100°, para ayudarle a considerar diferentes longitudes de lado.

Selecciona todas las longitudes de lado, en pies, que el ranchero podría utilizar para construir la valla.

WR = 65 pies, MW = 47 pies y MR = 55 pies

MW = 105 pies, WR = 250 pies y MR = 140 pies

MW = 86.1 pies, RM = 92.8 pies y WR = 193.5 pies

RW = 218,7 pies, RM = 119,1 pies y WM = 99,8 pies

MR = 112,4 pies, WR = 112,4 pies y MW = 98,1 pies

RM = 179,4 pies, MW = 105.6 pies y RW = 164.9 pies

Soluciones posibles

WR = 65 pies, MW = 47 pies y RM = 55 pies

MW = 105 pies, WR = 250 pies y RM = 140 pies

MW = 86.1 pies, RM = 92,8 pies y WR = 193,5 pies

RW = 218,7 pies, RM = 119,1 pies y WM = 99.8 pies

MR = 112,4 pies, WR = 112,4 pies y MW = 98,1 pies

RM = 179,4 pies, MW = 105,6 pies y RW = 164.9 pies

PROBLEMA 8

(Unidad 1, lección 21)

Se muestran las rectas paralelas MR y CW, donde m∠MKH = 136° y m∠RYH = 92°. ¿Cuál es la medida del ángulo KHY?

Soluciones posibles

m∠KHY = 48°

Reflexiones:

IDEA(S) PRINCIPAL(ES)

• Puntos y formas

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

G-CO.13 Construir un triángulo equilátero, un cuadrado y un hexágono regular inscrito en un círculo.

Construir

G-CO.1

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.C.12

II.B.3

LECCIÓN 23

¿Y AHORA QUÉ PUEDES

CONSTRUIR?

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

repercutir en el futuro,

(SMPs) ¿Cómo? ... los estudiantes...

(CC) ¿Qué? ... mientras...

utilizan las herramientas adecuadas de forma estratégica y atienden a la precisión descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo seguir instrucciones para construir un patrón.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Crear un nuevo patrón geométrico utilizando técnicas de construcción.

• Crear un patrón a partir de instrucciones (en lenguaje escrito).

• Describir (por escrito) cómo recrear un patrón.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

MLR8: Apoyos para el debate

Materiales necesarios

Copias de los patrones

Herramientas de geometría (HS)

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Construyamos algunas formas creativas.

Narrativa de la lección

Esta lección es opcional porque va más allá de la profundidad de comprensión requerida para abordar los estándares.

Hacia el comienzo Unidad, los estudiantes tuvieron la oportunidad de crear sus propios patrones y reproducir los patrones de otros. Ahora que tienen más experiencia con las construcciones con regla y compás, pueden tener nuevas ideas sobre la creación de diseños. Esta sería una buena oportunidad para comparar el trabajo de los estudiantes de una lección anterior con el fin de mostrar su progreso. Cuando los estudiantes escriban sus propias instrucciones, tendrán que prestar atención a la precisión (MP6).

Los diseños de esta lección se han utilizado con permiso del autor.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento En parejas 5 min

Actividad de exploración opcional

En parejas 15 min

Independiente 15 min

En parejas 15 min

Síntesis Todo el grupo 5 min

Práctica Independiente 8-10 min

Descripción breve

Los estudiantes observan diseños con formas e identifican las cosas que notan y se preguntan.

Los estudiantes recrean un diseño hecho con un hexágono regular y luego escriben instrucciones para explicar cómo construir el diseño.

Los estudiantes usan herramientas de construcción para crear sus propios diseños y escriben instrucciones para que otros los repliquen.

Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la construcción de diseños.

Los estudiantes siguen las instrucciones dadas por un compañero para recrear su diseño e identificar formas congruentes.

Los estudiantes observan los diseños creados por sus compañeros y anotan las instrucciones para recrear los diseños si así lo desean.

El componente de práctica independiente incluye 2 problemas de repaso de la lección y 8 problemas de repaso de la espiral.

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE

(5 minutos)

Rutinas didácticas

Observar y preguntarse

El propósito de este calentamiento es provocar la idea de que los diseños se construyen a partir de muchas formas más pequeñas, lo que será útil cuando los estudiantes construyan sus propios diseños en una actividad posterior. Aunque los estudiantes pueden observar y preguntarse muchas cosas sobre estas imágenes, las líneas perpendiculares, las líneas paralelas y las formas que saben construir son los puntos de discusión importantes. Este ejercicio ofrece a los estudiantes la oportunidad de ver y utilizar las estructuras (MP7). Las estructuras específicas que podrían observar son las líneas perpendiculares y otras formas de construcciones que han realizado a lo largo de la sección.

INTRODUCCIÓN

Muestre la imagen para que todos la vean. Pida a los estudiantes que piensen en al menos una cosa que les llame la atención y en al menos una cosa que les asombre. Conceda a los estudiantes 1 minuto para pensar en silencio y, a continuación, 1 minuto para comentar las cosas que observan con su compañero, seguido de un debate con toda la clase.

Apoyo para estudiantes con discapacidad

Apoya la accesibilidad para: Lenguaje; organización

¿Qué observas? ¿Qué te preguntas?

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Cosas que los estudiantes pueden observar:

• Círculos congruentes

• Dos figuras tienen simetría de reflexión

• Dos figuras tienen simetría de rotación

• Rectas perpendiculares

• Rectas paralelas

• Hexágonos

Cosas que los estudiantes pueden preguntarse:

• Cómo construir

• Cómo inventar su propio patrón.

• ¿Es un cubo en la esquina de la habitación o un cubo con una esquina recortada?

SÍNTESIS DE LA ACTIVIDAD

. Matemáticas . Unidad 1

Pida a los estudiantes que compartan las cosas que notaron y se preguntaron. Registre y muestre sus respuestas para que todos puedan verlas. Si es posible, anote el razonamiento pertinente en la imagen o cerca de ella. Una vez registrada todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que se pregunten?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria. Si los hexágonos no surgen durante la conversación, pida a los estudiantes que discutan dónde ven un hexágono.

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | DUPLICAR DISEÑO

(15 minutos)

Rutinas didácticas

MLR8: Apoyos para el debate

Los estudiantes comienzan examinando un diseño. A continuación, trabajan para recrearlo y anotan las instrucciones para que otro estudiante lo haga mientras ellos trabajan. Esto proporciona oportunidades para que los estudiantes practiquen sus técnicas de construcción mientras identifican las figuras geométricas y sus propiedades.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

Distribuya copias de la plantilla maestra. Dé a los estudiantes acceso a papel en blanco para crear sus diseños.

INTRODUCCIÓN

Si los estudiantes tienen acceso a el programa de geometría dinámica, sugiera que GeoGebra Geometry de las herramientas de matemáticas podría ser útil en esta actividad.

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience con una demostración física de la construcción de un hexágono regular, que proporcionará a los estudiantes acceso para ver las conexiones entre las nuevas situaciones y las comprensiones previas. Pregunte a los estudiantes cómo la construcción de un hexágono regular podría ayudarles a recrear el diseño.

Apoya la accesibilidad para: Procesamiento conceptual; procesamiento visual-espacial

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Tu maestro te dará una colección de diseños que parten de la construcción de un hexágono regular. Elige uno para utilizarlo.

1. Anota cualquier movimiento rígido (rotación, reflexión o traslación) que veas en el diseño.

2. Utiliza movimientos de regla y compás para recrear el diseño.

3. Escribe las instrucciones para construirlo.

RESPUESTAS POSIBLES Las respuestas varían.

. Matemáticas . Unidad 1

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Para los estudiantes que tengan problemas para empezar, considere la posibilidad de dirigirlos hacia la visualización de las técnicas de construcción. Dígales que cada patrón comienza con un hexágono regular o un triángulo y que, a partir de ahí, pueden utilizar las diagonales para encontrar diferentes puntos de intersección alrededor de los cuales centrar los círculos.

Invite a algunos estudiantes a compartir su diseño y a explicar qué construcciones utilizaron para realizarlo.

Apoyo para estudiantes que aprenden el idioma inglés

Representar y conversar: MLR8 Apoyos para el debate. Organice a los estudiantes en grupos de 2. Invite a los estudiantes a que, por turnos, lean las instrucciones en voz alta. Si el tiempo lo permite, el oyente puede intentar crear el diseño siguiendo las instrucciones a medida que se leen. Anime a los estudiantes a presionarse unos a otros para obtener instrucciones detalladas que utilicen lenguaje matemático. Dé a los estudiantes la oportunidad de revisar y perfeccionar sus instrucciones escritas.

Principio(s) de diseño: Optimizar el resultado (para la explicación); cultivar la conversación

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | CREA TU PROPIO DISEÑO

(15 minutos)

Esta actividad invita a los estudiantes a utilizar lo que han aprendido sobre construcciones para crear su propio diseño. No es necesario que los estudiantes partan de la construcción de un hexágono regular, pero puede ser un buen punto de partida para los estudiantes que tengan problemas para empezar.

Poner a disposición de los estudiantes el programa de geometría dinámica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Relacione un concepto nuevo con otro con el que los estudiantes hayan tenido éxito. Por ejemplo, recuerde a los estudiantes la construcción de un triángulo equilátero y la construcción de un hexágono regular. Pregunte a los estudiantes cómo estas construcciones podrían ayudarles a crear su propio diseño.

Apoya la accesibilidad para: Habilidades socioemocionales; procesamiento conceptual

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Utiliza los movimientos de la regla y el compás para crear un nuevo diseño. Escribe los movimientos que has seguido en la misma hoja de papel para que otra persona pueda recrear tu diseño.

POSIBLES RESPUESTAS Las respuestas varían.

ERRORES PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Si los estudiantes no están seguros de por dónde empezar, sugiérales que repasen todas las construcciones que han hecho hasta ahora para inspirarse.

Si los estudiantes no van a completar la actividad Haz su diseño: Invite a algunos estudiantes a compartir su diseño y a explicar qué construcciones utilizaron para realizarlo.

¿Estás preparado para más?

Construye un teselado con simetría de rotación, reflexión y traslación.

Respuestas de los estudiantes

Ejemplo de respuesta: Una rejilla rectangular

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | CREA SU DISEÑO

(15 minutos)

Los estudiantes tienen la oportunidad de practicar la construcción, la identificación de partes congruentes y la justificación de su pensamiento siguiendo las instrucciones del diseño de otro estudiante.

Invite a los estudiantes a intercambiar instrucciones con alguien que no sea su compañero manteniendo el diseño en secreto.

INTRODUCCIÓN

Poner a disposición el programa de geometría dinámica da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

Apoyo para estudiantes con discapacidad

Representación: Acceso para la percepción. Pida a los estudiantes que lean en voz alta cada paso de las instrucciones a su compañero. Los estudiantes que escuchen y lean la información a la vez se beneficiarán de un tiempo de procesamiento adicional.

Apoyos a la accesibilidad para: Lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Sigue las instrucciones para hacer un diseño. 2. Enumera todo lo que es congruente en el diseño. Explica cómo lo sabes.

RESPUESTAS POSIBLES Las respuestas varían.

Pida a los estudiantes que comparen su diseño con el de la persona de la que recibieron las instrucciones.

SÍNTESIS DE LA ACTIVIDAD

Invite a los estudiantes a compartir qué hizo que las instrucciones fueran más fáciles o más difíciles de seguir. (Es más fácil cuando cada paso está escrito y hay etiquetas que me ayudan a orientarme. Es más difícil cuando todos los pasos están juntos en una larga lista sin etiquetas ni puntos de parada).

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Recoge los diseños de los estudiantes para decorar el salón de clases. Dígales que todos los diseños vienen con instrucciones, así que pueden anotar esas instrucciones y recrear los diseños para sus propios proyectos artísticos si lo desean.

Recrear estos diseños o crear otros nuevos podría ser una actividad continua para los estudiantes cuando necesiten algo tranquilo que hacer por sí mismos, después de una evaluación, por ejemplo.

. Matemáticas . Unidad 1

Resumen de la lección para el estudiante

Existe una profunda conexión entre la geometría y el arte. Utilizando sencillas herramientas de construcción, es posible crear bellos patrones. Registrar con precisión las instrucciones de un patrón permite a otras personas hacer el mismo patrón y disfrutarlo por sí mismas. Estas mismas ideas pueden aplicarse en el espacio tridimensional para crear los objetos que utilizamos y apreciamos cada día.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Este diseño partió de la construcción de un hexágono regular. Nombra 2 pares de figuras congruentes.

Soluciones posibles

Ejemplos de respuestas: El triángulo EHF es congruente con el triángulo BGC. Triángulo AHF es congruente con triángulo DGC. El triángulo AFE es congruente con el triángulo DCB. El segmento AB es congruente con el segmento DE

PROBLEMA 2

Este diseño partió de la construcción de un hexágono regular. Describe un movimiento rígido que lleve la figura hacia sí misma.

Soluciones posibles

Gira 180 grados alrededor del centro del hexágono.

PROBLEMA 3

Unidad 1, lección 21

Noah comienza con el triángulo ABC y hace 2 nuevos triángulos trasladando B a A y trasladando B a C. Noah piensa que el triángulo DCA es congruente con el triángulo BAC. ¿Estás de acuerdo con Noah? Explica tu razonamiento.

Soluciones posibles

Noah tiene razón. Ejemplos de respuestas: La recta AD es paralela a la recta BC porque es una traslación de la recta BC. Por ángulos interiores alternos, ∠DAC ≅ ∠BCA. Análogamente, ∠ADC ≅ ∠DCE y ∠DCE ≅ ∠ABC ya que el triángulo DCE es una traslación del triángulo ABC. Por lo tanto por el teorema de la suma de ángulos de triángulos todos los 3 ángulos son congruentes. La traslación también preserva la longitud por lo que los lados del triángulo DCA son congruentes con los lados del triángulo BAC y los triángulos son congruentes.

La recta AD es paralela a la recta BC porque es una traslación de la recta BC. Si rotamos el triángulo ABC en 180 grados usando el punto medio del segmento AC como centro, esto llevará BC a AD. Del mismo modo, AB es paralelo a DC y la misma rotación llevaría a AB a DC. Por último, si se gira AC 180 grados alrededor de su punto medio, AC pasará a AC, por lo que los triángulos deben ser congruentes.

PROBLEMA 4

Unidad 1, lección 21

En la imagen, el triángulo ABC es congruente con el triángulo BAD y el triángulo CEA. ¿Cuáles son las medidas de los 3 ángulos del triángulo CEA? Muestra o explica tu razonamiento.

PROBLEMA 5

Unidad 1, lección 20

Soluciones posibles

La medida del ángulo ACE es 75 grados ya que el triángulo CEA es congruente al triángulo ABC y la medida del ángulo CAB es 75 grados. La medida del ángulo EAC es 45 grados porque corresponde al ángulo D del triángulo BAD. Como la suma de los ángulos del triángulo CEA es 180 grados, esto significa que la medida del ángulo CEA es 60 grados.

En la figura mostrada, el ángulo 3 es congruente con el ángulo 6. Selecciona todas las afirmaciones que deben ser ciertas.

Las rectas f y g son paralelas.

El ángulo 2 es congruente con el ángulo 6.

El ángulo 2 y el ángulo 5 son suplementarios.

El ángulo 1 es congruente con el ángulo 7.

El ángulo 4 es congruente con el ángulo 6.

Soluciones posibles

Las rectasf y g son paralelas.

El ángulo 2 es congruente con el ángulo 6.

El ángulo 2 y el ángulo 5 son suplementarios.

El ángulo 1 es congruente con el ángulo 7.

El ángulo 4 es congruente con el ángulo 6.

PROBLEMA 6

Unidad 1, lección 20

En este diagrama, el punto M es el punto medio del segmento AC y B′ es la imagen de B mediante una rotación de 180° alrededor de M

A. Explica por qué la rotación de 180° usando el centro M lleva A a C

B. Explica por qué los ángulos BAC y B′CA tienen la misma medida.

Soluciones posibles

A. Si A' es la imagen de A al girar 180° alrededor de M, entonces sabemos AMA′ debe ser un ángulo 180°. Así que A′ debe estar en la semirrecta MC. También sabemos que las rotaciones preservan la distancia, así que la imagen de A debe ser C

B. La rotación lleva B a B', A a C y C a A, así que lleva el ángulo BAC al ángulo B'CA. Como la rotación conserva las medidas de los ángulos, estos ángulos deben tener la misma medida.

Geometría . Matemáticas . Unidad 1

PROBLEMA 7

Las rectas AB y BC son perpendiculares. Los semirrectas discontinuos bisecan los ángulos ABD y CBD.

Seleccione todas las afirmaciones que deben ser ciertas:

El ángulo CBF es congruente con el ángulo DBF.

El ángulo CBE es obtuso.

El ángulo ABC es congruente con el ángulo EBF.

El ángulo DBC es congruente con el ángulo EBF.

El ángulo EBF es 45 grados.

Soluciones posibles

Ángulo CBF es congruente con el ángulo DBF.

Ángulo CBE es obtuso.

Ángulo ABC es congruente con el ángulo EBF.

Ángulo DBC es congruente con el ángulo EBF.

Ángulo EBF es 45 grados.

PROBLEMA 8

Unidad 1. lecciones 19 y 20, lección 19

Las rectasAD y EC se encuentran en el punto B

Dé un ejemplo de una rotación usando un ángulo mayor que 0 grados y menor que 360 grados, que lleve ambas líneas a sí mismas. Explique por qué su rotación funciona.

Soluciones posibles

A 180 grados de rotación usando el centro B. Esto lleva la recta AD a la recta AD y la recta EC a la recta EC

PROBLEMA 9

Unidad 1, lección 18

Dibuja la imagen del triángulo ABC después de esta secuencia de transformaciones rígidas.

A. Refleja a través del segmento de recta AB

B. Trasladar por el segmento de rectadirigido u

PROBLEMA 10

Unidad 1, lección 18

Soluciones posibles

A. Dibuja la imagen de la figura CAST después de una rotación en sentido horario alrededor del punto T usando el ángulo CAS y luego una traslación por el segmento de recta dirigida AS

B. Describe otra secuencia de transformaciones que dé como resultado la misma imagen.

Soluciones posibles

B. Ejemplo de respuesta: Traslade por el segmento de recta dirigida AS. Rota en el sentido de las agujas del reloj alrededor de la imagen del punto T por el ángulo CAS

Reflexiones: