MN CA Fourth Grade Spanish Unit Sample by acceleratelearning

POR ACCELERATE LEARNING

Grado 4

Muestra de la edición para el maestro

Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).

La plataforma de recursos curriculares en línea que se ofrece en «mathnation.com», incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.

La marca comercial «Math Nation» es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.

Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.

UNIDAD 1 FACTORES Y MÚLTIPLOS

NARRATIVA DE LA UNIDAD

Objetivos de aprendizaje de la unidad

• Los estudiantes aplican su comprensión de la multiplicación y el área para trabajar con factores y múltiplos.

En esta unidad, los estudiantes amplían sus conocimientos sobre la multiplicación, la división y el área de un rectángulo para profundizar su comprensión de los factores y aprender sobre los múltiplos.

En tercer grado, los estudiantes aprendieron que pueden multiplicar las dos longitudes laterales de un rectángulo para encontrar su área, y dividir el área por una longitud lateral para encontrar la otra longitud lateral.

Para representar estas ideas, utilizaron diagramas de área, escribieron expresiones y ecuaciones, y aprendieron los términos «factores» y «productos». En esta unidad, los estudiantes retoman el concepto de área para dar sentido a los factores y múltiplos de números. Dado un rectángulo con un área determinada, los estudiantes encuentran tantos pares de longitudes laterales de números enteros como pueden. Consideran esas longitudes laterales como pares de factores del área del número entero y el área como múltiplo de cada longitud lateral.

Los estudiantes también aprenden que un número puede clasificarse como primo o compuesto en función del número de pares de factores que tenga.

A lo largo de la unidad, los estudiantes se encuentran con diversos contextos relacionados con la escuela, las reuniones y las celebraciones. Su objetivo es invitar a los estudiantes a conversar sobre sus vidas y experiencias. Considérelos como oportunidades para aprender sobre los estudiantes como individuos, para fomentar una comunidad de aprendizaje positiva y para dar forma a cada lección con base en las percepciones sobre los estudiantes.

Sección A: Comprender factores y múltiplos

Alineación de estándares

Abordar

• 4.OA.4

Sección de los objetivos de aprendizaje

• Determinar si un número es primo o compuesto.

• Explicar lo que significa ser un factor o un múltiplo de un número entero.

• Relacionar las longitudes de los lados y el área de un rectángulo con factores y múltiplos.

En esta sección, los estudiantes retoman las ideas de área y factores del tercer grado y encuentran la idea de múltiplos. Empiezan construyendo rectángulos con longitudes de lado específicas e identificando posibles áreas cuando solo se conoce la longitud de un lado. Los estudiantes utilizan fichas y diagramas para mejorar su comprensión antes de aprender nueva terminología.

A continuación, construyen rectángulos a partir de un área determinada. Observan que las longitudes de los lados de los rectángulos representan los pares de factores del valor del área dada. Los estudiantes también observan la propiedad conmutativa de la multiplicación cuando ven que los rectángulos con el mismo par de longitudes laterales tienen la misma área, independientemente de su orientación.

Grado 4 . Matemáticas . Unidad 1

Construye 5 rectángulos diferentes con la anchura dada. Registra el área de cada rectángulo en la tabla.

Área del rectángulo

2 fichas cuadradas de ancho

3 fichas cuadradas de ancho

4 fichas cuadradas de ancho

Los estudiantes descubren que para algunos valores de área en números enteros, solo se puede construir un rectángulo, y para otros valores, es posible construir más de un rectángulo. Del mismo modo, algunos números solo tienen un par de factores (el propio número y 1) y otros números tienen más de un par de factores. Los estudiantes aprenden que a los primeros los llamamos «números primos» y a los segundos «números compuestos».

La sección termina con un día de juego opcional, que es una oportunidad para comprobar la fluidez de los estudiantes con la multiplicación y la división dentro de 100

PLC: Lección 1, actividad 2: ¿Qué áreas puedes construir?

Sección B: Encontrar pares de factores y múltiplos

Alineación con estándares

Abordar

• 4.OA.3

• 4.OA.4

Sección de los objetivos de aprendizaje

• Aplicar la fluidez de la multiplicación dentro de 100 y la relación entre la multiplicación y la división para encontrar pares de factores y múltiplos.

En esta sección, los estudiantes aplican y profundizan su comprensión de las ideas de factores y múltiplos mientras juegan y resuelven problemas en contexto. Las actividades incitan a los estudiantes a buscar patrones en factores, múltiplos y números primos y compuestos, y a utilizarlos para hacer predicciones y generalizar sus observaciones.

Veinte estudiantes juegan un juego con 20 taquillas en fila. El primer estudiante empieza por la primera taquilla y abre todas las taquillas.

El segundo empieza por la segunda taquilla y cierra todas las demás. El tercer estudiante se detiene en cada tercera taquilla y la abre si está cerrada o la cierra si está abierta.

¿Qué números de taquilla le toca el tercer estudiante?

¿Cuántos estudiantes les toca la taquilla 17?

En la última lección, los estudiantes tienen la oportunidad de utilizar las ideas de esta unidad para crear arte geométrico.

PLC: Lección 6, actividad 1: Taquillas cuestionables

Math

Nation California . Grado 4

Días estimados: 6-8

Grado 4 . Matemáticas . Unidad 1

IDEAS FUNDAMENTALES Y ESTÁNDARES

Enfoque en ideas fundamentales

• Factores y modelos de área

• Resolución de problemas conectados

ESTÁNDARES POR LECCIÓN

Lección

Estándar(es) abordado(s)

4.1.1 4.OA.4

4.1.2 4.OA.4

4.1.3 4.OA.4

4.1.4 4.OA.4

4.1.5 4.OA.3, 4.OA.4

4.1.6 4.OA.4

4.1.7 4.OA.4

4.1.8 4.OA.4

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

4.OA.4 Encontrar todos los pares de factores para un número entero en el rango 1-100. Reconocer que un número entero es múltiplo de cada uno de sus factores. Determinar si un número entero dado en el rango 1-100 es múltiplo de un número dado de una cifra. Determinar si un número entero dado en el rango 1-100 es primo o compuesto.

Construir

3.MD.7a

Enfoque SMPs

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.A.3

LECCIÓN 1

MÚLTIPLOS DE UN NÚMERO

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo y predecir lo que podría ocurrir

buscan y hacen uso de la estructura y atienden a la precisión exploran cantidades que cambian.

OBJETIVO(S)

DE APRENDIZAJE

• Puedo encontrar posibles áreas para un rectángulo cuando se conoce la medida de 1 la longitud del lado.

• Puedo relacionar múltiplos de números con longitudes de lados y áreas de rectángulos.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Encontrar áreas de diferentes rectángulos con una longitud de lado dada.

• Entender que el área de un rectángulo es un múltiplo de cada una de las longitudes de sus lados.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO

En tercer curso, los estudiantes multiplicaban y dividían con fluidez dentro de 100 y relacionaban el área con la multiplicación y la suma. ¿De qué manera ese conocimiento previo ayuda a los estudiantes a comprender los múltiplos en esta lección?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

¿Cuál no pertenece? (Calentamiento)

Materiales para reunir

fichas cuadradas de una pulgada: Actividad 1, actividad 2

Materiales para copiar

Papel cuadriculado en centímetro: Estándar (grupos de 2), actividad 2

Grado 4 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Construyamos algunos rectángulos.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes apliquen su comprensión del área para explorar los múltiplos.

En tercer grado, los estudiantes aprendieron cómo encontrar el área de un rectángulo mediante la formación de mosaicos y descubrieron que multiplicando las longitudes de los lados se obtiene el mismo resultado.

El propósito de esta lección es que los estudiantes apliquen su comprensión del área y la multiplicación para construir rectángulos y encontrar su área. A medida que los estudiantes consideran el área decomo de rectángulos con una longitud lateral dada, exploran la idea de múltiplos. Los estudiantes aprenden que un múltiplo de un número es el resultado de multiplicar ese número entero por otro.

Aunque los estudiantes se familiarizan con el término múltiplo en esta lección, trabajan más con it en lecciones posteriores. No es necesario que tengan una comprensión formal del término en esta lección. En las próximas lecciones, los estudiantes también explorarán y aprenderán el par terms factor y factor. En esta lección, se refieren a ellos como longitudes de lado dentro dele contexto del área.

RESUMEN

DE LA LECCIÓN

Componente de lección Estructura Tiemp

Calentamiento En pareja 10 min

Actividad de exploración 1 En pareja 20 min

Actividad de exploración 2 En pareja 15 min

Síntesis Todo el grupo 10 min

Descripción breve

Los estudiantes examinan imágenes de polígonos y justifican por qué un polígono no pertenece.

Los estudiantes construyen diferentes rectángulos de anchuras dadas, determinan las áreas de esos rectángulos y luego hacen predicciones sobre el área de un rectángulo adicional para cada anchura dada.

Los estudiantes exploran los múltiplos de un número dibujando rectángulos de una anchura determinada y una posible área y, a continuación, hacen conexiones y conjeturas basadas en sus resultados.

Los estudiantes reflexionan sobre su trabajo para consolidar su comprensión de un múltiplo de un número.

Enfriamiento Independiente 5 min Los estudiantes determinan tres posibles áreas de un rectángulo de un ancho específico.

Abordar:

• ¿Puedes construirlo? (3-5), Etapa 2: Rectángulos múltiples

Enfriamiento Grupos pequeños Opcional

Apoyo:

• ¿Puedes construirlo? (3-5). Etapa 1: Rectángulos

• Captura cuadrados (1-3). Etapa 7: Multiplicar con 6-9

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

Comunidad matemática

Prepara un espacio, como un pedazo de papel afiche, titulado «Comunidad matemática» y una tabla T con los encabezados «Haciendo Matemáticas» y «Normas» como se muestra aquí.

Comunidad matemática

Haciendo matemáticas

Estudiantes

Maestro

Norma

Estudiantes

Maestro

Las dos secciones animan a los estudiantes y al maestro a ser conscientes de que ambas partes respectivas son responsables de la forma en que se hacen las matemáticas en el salón de clases.

CALENTAMIENTO | CUÁL NO PERTENECE: TODOS LOS TIPOS DE ÁREA

(10 minutos)

Rutinas didácticas

¿Cuál no pertenece?

Este calentamiento anima a los estudiantes a analizar y comparar cuidadosamente el área de diferentes figuras. Al hacer las comparaciones, los estudiantes tienen un motivo para utilizar el lenguaje con precisión (MP6) al describir el área de diferentes figuras. También permite al maestro escuchar la terminología que conocen los estudiantes y cómo hablan de las características de las figuras que les ayudan a encontrar áreas diferentes.

Para todas las rutinas de calentamiento, considere la posibilidad de establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con un razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, o una señal sutil diferente. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se precipiten al levantar las manos por toda la clase.

Comunidad matemática

• Después del calentamiento, pide a los estudiantes que reflexionen sobre las acciones individuales y de grupo mientras se plantean las siguientes preguntas: «¿Qué aspecto tiene y cómo suena hacer matemáticas juntos como una Comunidad matemática? ¿Qué hago yo? ¿Qué haces tú?»..

• Registra y muestra sus respuestas en el apartado «Haciendo matemáticas». Los estudiantes pueden mencionar cosas como: hablamos entre nosotros y con el maestro, tuvimos tiempo tranquilo para pensar, compartimos nuestras ideas, pensamos en las ideas y palabras matemáticas que sabíamos, estabas escribiendo nuestras respuestas, estabas esperando hasta que diéramos las respuestas.

• Grupos de 2

INSTRUCCIÓN

ACTIVIDAD

• Muestra la imagen.

• «Elige uno que no pertenezca. Prepárate para compartir por qué no pertenece».

• 1 minuto: tiempo para pensar en silencio

• «Discute tu pensamiento con tu compañero».

• 2-3 minutos: Debate en pareja

• Comparte y registra las respuestas.

Grado 4 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

¿Cuál no pertenece?

A B C D

Ejemplos de respuestas:

• A es la única figura que no tiene un lado horizontal de 4 unidades. Es la única cuyos lados verticales no son más largos que el lado horizontal.

• B es la única que no tiene etiquetadas las longitudes de los lados.

• C es la única que no tiene un área de 20 unidades cuadradas.

• D es la única figura que no tiene exactamente cuatro lados o no es un rectángulo.

• «¿Cómo podríamos determinar el área de cada figura?».. (Podemos usar la multiplicación para la mayoría de ellas o contar las unidades en una de ellas).

• Considere decir: «Encontremos al menos una razón por la que cada una no pertenece».

EXPLORACIÓN ACTIVIDAD 1 | CONSTRUIR RECTÁNGULOS Y HALLAR EL ÁREA

(20 minutos)

Materiales para reunir

Fichas cuadradas de una pulgada

Preparación necesaria

Cada grupo de 2 necesita al menos 36 fichas cuadradas

El objetivo de esta actividad es que los estudiantes hallen el área de un rectángulo mediante la colocación de fichas cuadradas y recuerden que el área también se puede hallar multiplicando las longitudes de los lados. Los estudiantes construyen rectángulos con una longitud de lado dada y calculan el área de esos rectángulos. Trabajan juntos para comparar y explicar las estrategias utilizadas para hallar el área de los rectángulos y establecer conexiones entre ellas. Los estudiantes observan cómo varía el área de rectángulos con una anchura dada a medida que cambia la longitud y hacen predicciones sobre qué áreas son posibles con las anchuras dadas (MP7).

Apoyo para estudiantes que aprenden el idioma inglés

MLR8 Apoyos para el debate. Los estudiantes deben buscar por turnos una correspondencia y explicar su razonamiento a su compañero. Muestre los siguientes marcos de frases para que todos los vean: «Me fijé en , así que hice coincidir..». Anime a los estudiantes a desafiarse mutuamente cuando no estén de acuerdo.

Avances: Conversar, representar

INSTRUCCIÓN

Math Nation California . Grado 4

• Muestra el rectángulo en el libro.

• «Mira el rectángulo en tu página y descríbelo a un compañero». (Tiene 6 unidades. Hay 2 filas y 3 columnas».

• Reparte a cada grupo 10 fichas.

• «Construye todos los rectángulos que puedas utilizando las 10 fichas. Descríbelos a un compañero».

• 2 minutos: Debate en parejas

• «¿Quién tiene un rectángulo que tenga 2 fichas cuadradas de ancho, 5 fichas cuadradas de ancho, 10 fichgas cuadradas de ancho?»..

• Dibuja cada rectángulo mientras los estudiantes comparten sus respuestas.

Grado 4 . Matemáticas . Unidad 1

ACTIVIDAD

• Entrega a los estudiantes más fichas cuadradas de una pulgada.

• «Ahora construye cinco rectángulos diferentes que tengan cada uno 2 fichas cuadradas de ancho. Anota el área de cada rectángulo en la tabla».

• «Repite con rectángulos que tengan cada uno 3 fichas y 4 fichas cuadradas de ancho».

• 5-7 minutos: Tiempo de trabajo en parejas

• Supervise a los estudiantes que:

• construyen una fila o columna y repiten el mismo número de fichas cuadradas una y otra vez para construir el área

• cuentan salteado o multiplican para determinar el área de cada rectángulo

• combinan el contar salteado con otra estrategia de conteo

1. Construye 5 rectángulos diferentes con cada uno de los anchos dados. Registra el área de cada rectángulo en la tabla.

Área del rectángulo

2 fichas de ancho

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

3 fichas de ancho

4 fichas de ancho

2. Comenta con un compañero lo que observas sobre las áreas en cada fila de la tabla.

3. Predice el área de otro rectángulo que tenga cada anchura. Explica tu razonamiento.

• 2 fichas cuadradas:

• 3 fichas cuadradas:

• 4 fichas cuadradas:

1. Ejemplos de respuestas: Área del rectángulo

2 fichas de ancho 12 6 8 4 10

3 fichas de ancho 6 18 12 15 9

4 fichas de ancho 8 12 20 24 16

2. Podemos contar por el ancho para obtener el área.

DESARROLLAR EL PENSAMIENTO DEL ESTUDIANTE

• 2 fichas cuadradas de ancho: 16. Añadí 4 al área más grande que encontré antes.

• 3 fichas cuadradas de ancho: 24. Si construyo 3 filas de 8, el rectángulo tendría 24 cuadrados.

• 4 fichas cuadradas de ancho: 40. Sé que 4 × 10 es 40.

Los estudiantes pueden contar las fichas por 1 para determinar el área de los rectángulos que construyen. Considere preguntar: «¿Ves grupos de fichas cuadradas que podrían ayudarte a contar?».

SÍNTESIS DE LA ACTIVIDAD

Grado 4 . Matemáticas . Unidad 1

• Recoge predicciones para áreas de rectángulos con una anchura de 2. (18, 14, 20, 30)

• «Para rectángulos que tienen 2 de ancho, ¿cómo podemos saber si nuestras predicciones de área son ciertas sin construir cada rectángulo?».. (Cada área es un número par. Es lo que decimos cuando contamos por 2 o multiplicamos por 2).

• «¿Cómo podemos comprobar nuestras predicciones para rectángulos que tienen 3 o 4 fichas cuadradas de ancho». (Las predicciones son números que obtenemos cuando multiplicamos un número por 3 o 4).

ACTIVIDAD DE EXPLORACIÓN 2 | ¿QUÉ ÁREAS PUEDES

CONSTRUIR? (15 minutos)

Materiales para reunir

Fichas cuadradas de una pulgada

Materiales para copiar

Papel cuadriculado en centímetros:

Estándar (grupos de 2)

Preparación necesaria

Cada grupo de 2 necesita al menos 36 fichas cuadradas de la actividad anterior

El propósito de esta actividad es que los estudiantes exploren la idea de múltiplos a través de un contexto de áreas. Los estudiantes aprenden que un múltiplo de un número es el resultado de multiplicar cualquier número entero por otro número entero. A medida que los estudiantes construyen y encuentran el área de rectángulos dada una longitud lateral, ven que cada área es un múltiplo de cada una de las longitudes laterales de un rectángulo.

Apoyo para estudiantes

con discapacidad

Representación: Desarrollar el lenguaje y los símbolos. Síntesis: Mantenga una pantalla visible para registrar el vocabulario nuevo. Invite a los estudiantes a sugerir detalles (palabras, imágenes o ecuaciones) que les ayuden a recordar el significado de los términos. En esta lección, incluya los términos «multipla», «par» e «impar». A lo largo de la unidad, añada los términos «factor», «par de factores», «compuesto» y «primo».

Apoya la accesibilidad para: Lenguaje, memoria

• Grupos de 2

• Da a cada grupo fichas de pulgadas y acceso al papel cuadriculado.

INSTRUCCIÓN

ACTIVIDAD

Math Nation California . Grado 4

• «Estoy pensando en un rectángulo que tiene 2 fichas de ancho. ¿Cuál podría ser el área de mi rectángulo?»..

• 1 minuto: Debate en parejas

• Compartir y anotar las respuestas.

• «¿Cómo sabemos que todas estas son áreas posibles?». (Podemos multiplicar otro número por 2 para obtener esos números).

• «En esta actividad, vamos a pensar cuál podría ser el área de un rectángulo si solo conociéramos la longitud de un lado. Trabaja con tu compañero para responder a estas preguntas».

• 5-7 minutos: Tiempo de trabajo en pareja

• Vigila a los estudiantes que se den cuenta de que las áreas que puedes construir son el resultado de multiplicar 3 por otra longitud lateral posible.

Grado 4 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Elena está construyendo rectángulos con una anchura de 3 unidades y un área de 30 unidades cuadradas o menos.

A. Construye los rectángulos que Elena podría hacer y dibuja los rectángulos en papel cuadriculado. Rotula el área y las longitudes de los lados de cada rectángulo.

B. ¿Cuál es el área de cada rectángulo que construiste?

C. ¿Qué notas acerca de las áreas?

2. ¿Por qué 28 unidades cuadradas no es un área posible para un rectángulo con un ancho de 3 unidades?

3. Si el área del rectángulo puede ser mayor que 30 unidades cuadradas, encuentra 2 otras áreas que podría tener. Explica o muestra tu razonamiento.

4. ¿Qué área no es posible para un rectángulo con un ancho de 3 unidades?

Exexplique o muestre su razonamiento.

RESPUESTAS POSIBLESS

SÍNTESIS DE LA ACTIVIDAD

A. Hay diez rectángulos posibles, cada uno de los cuales tiene una longitud lateral que es 3 unidades y la otra longitud lateral es un número entero comprendido entre 1 y 10

B. 3, 6, 9, 12, 15, 18, 21, 24, 27, y 30 unidades cuadradas

C. Respuestas de ejemplo:

• Las áreas aumentaron en 3 para cada rectángulo cuando añadimos un número ta la length.

• Las áreas se alternaban: par, impar, impar, par.

2. Ejemplo de respuesta: No hay ningún número por el que podamos multiplicar 3 para obtener 28.

3. Respuestas de ejemplo:

• 33 unidades cuadradas, ya que 33 ÷3 = 11.

• 45 unidades cuadradas, ya que 15 × 3 = 45

• 75 unidades cuadradas, ya que 3 × 25 = 75.

4. Respuestas de ejemplo:

• 16 unidades cuadradas. No podemos multiplicar ningún número por 3 para obtener 16.

• 35 unidades cuadradas. No podemos multiplicar ningún número por 3 para obtener 35.

• Muestre un conjunto de áreas generadas por los estudiantes que sean menores a 30 unidades cuadradas.

• «¿Qué notaron acerca de las áreas que encontraron?».

• Pida a los estudiantes que expliquen por qué el rectángulo no podría tener un área de 28 unidades cuadradas.

• «Para las dos últimas preguntas, ¿cómo supiste si un rectángulo con un ancho de 3 unidades podría tener esa área?».

• «Podemos tener un área de 12 unidades cuadradas cuando el ancho del rectángulo es 3 unidades. Esto se debe a que 12 es múltiplo de 3».

• «Un múltiplo de un número es el resultado de multiplicar un número por un número entero».

• «Vuelve a mirar tu trabajo y coméntalo con tu compañero: ¿Qué números son múltiplos de 3?». (3, 6, 9, 12, 15, 18, 21, 24, 27 y 30)

• «¿Qué números no son múltiplos de 3?». (29, 28, 26, 25, 23, 22, 20, 19, 17, 16, 14, 13, 11, 10, 8, 7, 5, 4, 2, 1).

• 2 minutos: Debate en parejas

Grado 4 . Matemáticas . Unidad 1

SÍNTESIS DE LA LECCIÓN

(10 minutos)

«Hoy construimos rectángulos y aprendimos sobre los múltiplos de un número. Un múltiplo de un número es el resultado de multiplicar ese número por un número entero».

«¿Cómo decidirías si 28 es múltiplo de 4?». (Pienso si hay un número por el que pueda multiplicar 4 para obtener 28).

«¿Cuál es un número que no sería múltiplo de 4? ¿Cómo lo sabes?». (Veinticinco no es múltiplo de 4 porque no puedo multiplicar 4 por ningún número entero para obtener 25).

Comunidad matemática

Después del enfriamiento, revise la lista de acciones «Haciendo matemáticas». Pide a los estudiantes que discutan con un compañero dónde vieron pruebas de las acciones durante el resto de la lección. En grupo, añade las acciones que falten y revisa las ideas anteriores.

ENFRIAMIENTO | ÁREA Y MÚLTIPLOS

ENUNCIADO DE TAREA PARA EL ESTUDIANTEA

RESPUESTAS POSIBLES

Reflexiones:

Math Nation California . Grado 4

(5 minutos)

Si un rectángulo tiene 6 fichas cuadradas de ancho, ¿cuál podría ser su área? Nombra tres posibilidades. Explica o muestra tu razonamiento.

Ejemplo de respuesta: 12, 18 y 24, porque 6 × 2 = 12, 6 × 3 = 18 y 6 × 4 = 24.

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

3.MD.7a

Enfoque SMPs

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.A.1

I.A.2

II.C.6

LECCIÓN 2

PARES DE FACTORES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo y predecir lo que podría ocurrir

buscnr y hacen uso de la estructura y utilizan las herramientas adecuadas de forma estratégica

OBJETIVO(S) DE APRENDIZAJE

exploran cantidades que cambian.

• Puedo determinar las posibles longitudes de los lados de un rectángulo cuando se me da su área.

• Puedo identificar pares de factores de un número entero.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Encontrar las longitudes de los lados de diferentes rectángulos con un área dada.

• Entender que cada longitud de ladoe de un rectángulo es un factor de su área.

PREGUNTA DE REFLEXIÓN DEL MAESTRO

¿Qué pregunta formulada durante la síntesis aportó más información sobre la comprensión por parte de los estudiantes del objetivo de aprendizaje de la lección? ¿Qué has oído o visto que te ha hecho pensar así?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR7 Comparar y conectar (actividad 1, actividad 2)

Hablar de números (Calentamiento)

Materiales a reunir

Pegamento o cinta adhesiva: Actividad 1

Fichas de una pulgada: Actividad 1

Tijeras: Actividad 1

Herramientas para crear una presentación visual: Actividad 1

Materiales para copiar

Papel cuadriculado en centimetro: Estándar (grupos de 2), actividad 1

Grado 4 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Aprendamos sobre pares de factores.

Narrativa de la lección

El propósito de esta lección es que los estudiantes aprendan el significado de pares de factores construyendo rectángulos con un área específica.

En tercer grado, los estudiantes aprendieron que un factor es un número que se multiplica por otro número. Por ejemplo, cuando multiplicamos 3 y 5 para encontrar el total en 3 grupos de 5, o para encontrar el área de un rectángulo que es 3 unidades por 5 unidades, el 3 y 5 son factores. En esta lección, los estudiantes aprenden que un par factor de un número n es un par de números enteros que se multiplican para dar como resultado n. Por ejemplo: 3 y 5 un par factor de 15

Anteriormente, los estudiantes dieron sentido a los múltiplos de un número en el contexto del área: construyeron y dibujaron rectángulos con una longitud lateral dada y razonaron sobre su área. Aquí, utilizan el mismo contexto para dar sentido a los pares de factores. Los estudiantes construyen y dibujan rectángulos con un área dada y razonan sobre sus longitudes laterales. A continuación, los estudiantes analizan los rectángulos que la clase ha dibujado en un recorrido por la galería. Hacen observaciones sobre las longitudes de los lados de los rectángulos y consideran si se han dibujado todos los rectángulos posibles para cada área. En estas actividades, un rectángulo con 3 filas y 2 columnas se considera igual que un rectángulo con 2 filas y 3 columnas.

Comunidad matemática

Diga a los estudiantes que tendrán la oportunidad de revisar sus ideas de «Comunidad matemática» al final de esta lección, por lo que mientras trabajan hoy deben pensar en acciones que puedan faltar en la lista actual.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Independiente 10 min

Actividad de exploración 1 En parejas 20 min

Actividad de exploración 2 En parejas 15 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Math

Enfriamiento Grupos pequeños Opcional

Nation California . Grado 4

Descripción breve

Los estudiantes calculan mentalmente productos de números de un solo dígito en los que el segundo factor es siempre el mismo valor.

Los estudiantes dibujan y etiquetan las longitudes de los lados de todos los rectángulos posibles para áreas dadas.

Los estudiantes observan los rectángulos creados por los estudiantes para explorar el significado de los pares de factores.

Los estudiantes solidifican el significado de los pares de factores proporcionando ejemplos y luego discuten estrategias para encontrar todos los pares de factores posibles de números enteros.

Los estudiantes demuestran su comprensión encontrando todas las posibles longitudes de los lados de los rectángulos dadas sus áreas.

Abordar:

• ¿Puedes construirlo? (3-5). Etapa 2: Rectángulos múltiples

Apoyo:

• ¿Puedes construirlo? (3-5). Etapa 1: Rectángulos

• Captura cuadrados (1-3). Etapa 7: Multiplicar con 6-9

Grado 4 . Matemáticas . Unidad 1

CHARLA SOBRE NÚMEROS: MULTIPLICACIÓN (10

minutos)

Rutinas didácticas

Charla sobre números

El propósito de esta charla sobre números es obtener estrategias y conocimientos que los estudiantes tienen para multiplicar números de un solo dígito. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes encuentren pares de factores de números.

A medida que los estudiantes usan problemas anteriores para encontrar los nuevos productos, buscan y hacen uso de la estructura (MP7) y usan reas repetidasoning (MP8).

• Muestre una expresión.

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTEA

RESPUESTAS POSIBLESS

SÍNTESIS DE LA ACTIVIDAD

• «Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste».

• 1 minuto: Tiempo para pensar en silencio

• Registra las respuestas y la estrategia.

• Mantén las expresiones y el trabajo desplegados.

• Repite con cada expresión.

Encuentra mentalmente el valor de cada expresión.

• 2 × 7

• 4 × 7

• 3 × 7

• 7 × 7

• 14: Simplemente lo sé. Es 2 grupos de 7

• 28: Cuatro es doble 2, entonces 4 × 7 es doble 2 × 7 o doble 14, que es 28

• 21: Es un grupo menos de 7 que 4 × 7 o 7 menos que 28.

• 49: Siete es 4 + 3, así que podría sumar las respuestas a los dos problemas anteriores: 28 + 21 =49.

• «¿Cómo te ayudaron las tres primeras expresiones a encontrar 7 × 7?». (El 7 se descompone into 3 y 4, por lo que pude multiplicar en partes y sumarlas).

• Considera preguntar:

• «¿Quién puede replantear el razonamiento de de una manera diferente?».

• «¿Tuvo alguien la misma estrategia, pero la explicaría de otra manera?».

• «¿Planteó alguien la expresión de una manera diferente?».

• «¿Quiere alguien añadir algo a la estrategia de ?».

Grado 4 . Matemáticas . Unidad 1

ACTIVIDAD

DE EXPLORACIÓN 1 | ¿CUÁNTOS

RECTÁNGULOS?

(20 minutos)

Rutinas didácticas Materiales para reunir Materiales para copiar Preparación necesaria

MLR7 Comparar y conectar

Pegamento o cinta adhesiva, fichas cuadradas de una pulgadas, tijeras, herramientas para crear una presentación visual

Papel cuadriculado en centímetro: Estándar (grupos de 2)

Cada uno de los 8 grupos necesitas aols para crear una presentación visual.

El objetivo de esta actividad es que los estudiantes encuentren todos los pares posibles de longitudes de lados enteros dada el área de un rectángulo. A cada grupo se le asignan 2 áreas para las que encuentran todos los rectángulos posibles. Dibujan y recortan los rectángulos posibles con esa área. En la siguiente actividad, expondrán los rectángulos en un paseo por la galería. Para encontrar todos los rectángulos posibles con un área determinada, los estudiantes pueden utilizar fichas, pero también pueden empezar a observar patrones como, por ejemplo, si hay un número par de filas, entonces el número de fichas del rectángulo es un número par (MP7).

Áreas a asignar (en unidades cuadradas):

Grupo A: 11, 27

Grupo B: 25, 5

Grupo C: 16, 8

Grupo D: 9, 18

Grupo E: 24, 12

Grupo F: 14, 28

Grupo G: 15, 30

Grupo H: 19, 20

Esta actividad utiliza MLR7 Comparar y conectar. Avances: Representar, conversar.

Apoyo para estudiantes con discapacidad

Compromiso: Proporcionar acceso captando el interés. Los estudiantes pueden beneficiarse de 2-3 minutos de tiempo de trabajo independiente para dar sentido y comenzar la tarea antes de unirse a un grupo.

Apoya la accesibilidad para: Procesamiento conceptual, procesamiento visual-espacial

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Math Nation California . Grado 4

• 8 grupos

• Dar a cada grupo acceso a fichas cuadradas de una pulgadas, papel cuadriculado, cartulina para hacer un cartel, tijeras y pegamento

MLR7 Comparar y conectar

• «Se les darán 2 números. Cada número representa el área de un rectángulo. Con tu grupo, dibuja todos los rectángulos posibles con esa área y crea un cartel para cada área. Las ficha cuadradas de una pulgadas están disponibles si te resultan útiles».

• «Tu cartel debe mostrar los rectángulos con cada una de las áreas asignadas. Incluye detalles como el área y la longitud de los lados para ayudar a los demás a entender tu pensamiento».

• Asigna a cada grupo 2 valores de área.

• (15 minutos): Tiempo de trabajo en grupos pequeños

«Tu maestro asignará 2 números a tu grupo. Cada número representa el área de un rectángulo». 1. En papel cuadriculado:

• «Dibuja todos los rectángulos posibles que tengan el área dada».

• «Etiqueta el área y las longitudes de los lados».

• «Usa cada par de longitudes de lado solo una vez. (Por ejemplo, si dibujas un rectángulo con 4 unidades a lo ancho y 6 unidades a lo bajo, no necesitas dibujar también un rectángulo con 6 unidades a lo ancho y 4 unidades a lo bajo porque tienen el mismo par de longitudes laterales)».

Grado 4 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN

1. Cuando creas que has dibujado todos los rectángulos posibles para ambas áreas, recorta tus rectángulos y colócalos en un cartel para cada área que se te asignó.

2. Muestra tu cartel para que todos lo vean.

RESPUESTAS POSIBLES

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD

Las respuestas varían. Los estudiantes crean afiches que muestran cada rectángulo posible para sus áreas dadas con las longitudes de los lados y las áreas etiquetadas.

Los estudiantes pueden enumerar solo algunos de los pares de factores para un número dado. Considere preguntar: «¿Hay algún otro rectángulo que puedas dibujar?» o «¿Cómo puedes estar seguro de que has dibujado todos los rectángulos posibles?».

• «Antes de dar una vuelta y mirar todos los carteles, tómate un minuto para reflexionar sobre lose números con los que has trabajado. ¿Qué notaste y te preguntaste mientras trabajabas en esta actividad?».

• 1-2 minutos: Tiempo para pensar en silencio

ACTIVIDAD DE EXPLORACIÓN 2 | CUÁNTOS RECTÁNGULOS: PASEO POR LA GALERÍA

(15 minutos)

Rutinas didácticas

MLR7 Comparar y conectar

En esta actividad, los estudiantes examinan los rectángulos dibujados por sus compañeros y aprenden el término pares de factores Los estudiantes reconocen las longitudes de los lados de cada rectángulo como un par de factores de su área.

Esta actividad utiliza MLR7 Compare and Connect. Avances: representar, conversar

INSTRUCCIÓN • Grupos de 2

• 5-7 minutos: paseo por la galería

ACTIVIDAD

• Monitorear las diferentes explicaciones que los estudiantes ofrecen sobre cómo saben si se han encontrado todos los rectángulos posibles con un área dada.

Grado 4 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLESS

SÍNTESIS DE LA ACTIVIDAD

Al visitar cada cartel, discute con tu compañero:

1. ¿Qué observas? Usa los siguientes fragmentos de oraciones cuando compartas:

A. «Observo que algunos de los carteles..».

B. «Observo que los carteles de los números y son iguales porque..».

2. ¿Cómo sabes que se encontraron todos los rectángulos posibles para el área dada?

1. Ejemplos de respuestas:

A. Observo que algunos carteles solo tienen 2 rectángulos.

B. Observo que los carteles de los números pares son iguales porque cada uno tiene 2 como longitud lateral .

2. Ejemplo de respuesta: Sabemos que no hay más rectángulos para un área dada porque no hay más números que se multipliquen juntos para dar esa área como su producto.

MLR7 Comparar y conectar

• «¿Qué es igual y qué es diferente entre los rectángulos de los carteles?».

• 30 segundos: Tiempo para pensar en silencio

• 1 minuto: Debate en parejas

• «¿Cómo sabes que se han encontrado todos los rectángulos posibles para el área dada?». (No pudimos encontrar ningún otro número que se multiplique para hacer el área).

• Muestra los rectángulos para 21: 1 por 21 y 3 por 7

• «¿Hay más rectángulos que podamos dibujar? ¿Por qué sí o por qué no?». (No, no hay más factores de números enteros de 21 21 solo podemos multiplicar 1 y 21, 3 y 7, 7 y 3, y 21 y 1).

• Llamamos 1 y 21 a un par de factores de 21 porque cada uno de ellos es un factor de 21 y al multiplicarlos obtenemos 21. El otro factor par de 21 es 3 y 7».

• «Trabaja con tu compañero para escribir los pares de factores de las áreas que se te asignaron».

• 2 minutos: Tiempo de trabajo del compañero

SÍNTESIS DE LA LECCIÓN

(10 minutos)

«Hoy aprendimos que un par de factores de un número entero es un par de números enteros que se multiplican para dar como resultado ese número. Por ejemplo: 5 y 4 son un par de factores de 20».

«¿Cuáles son los pares de factores de 24?». (1 y 24, 2 y 12, 3 y 8 y 4 y 6).

«¿Cómo sabemos si hemos encontrado todos los pares de factores de 24?». (Fuimos por orden. Cuando llegamos a 4 y 6, no hay más pares entre 4 y 6, así que podemos parar allí. O usamos la multiplicación para ver cuántos hechos podríamos emparejar para hacer 24 O usamos la división y estos eran todos los números que podíamos dividir por igual).

«¿Puedes usar las mismas estrategias para encontrar todos los pares de factores de 45?». (Sí, 1 y 45, 3 y 15, 5 y 9. No hay más factores entre 5 y 9, así que he encontrado todos los pares de factores).

«¿Puedes utilizar estas estrategias para encontrar los pares de factores de cualquier número entero?».

Comunidad matemática

Después del enfriamiento, da a los estudiantes 2-3 minutos para discutir cualquier revisión de las acciones «Haciendo matemáticas» en pequeños grupos. Comparte las ideas con todo el grupo y anota las revisiones.

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

ENFRIAMIENTO | LA LONGITUD DE LOS LADOS DE LOS RECTÁNGULOS

(5 minutos)

TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Reflexiones:

1. ¿Cuáles son todas las posibles longitudes de los lados de un rectángulo con un área de 21 unidades cuadradas?

2. ¿Cuáles son todas las longitudes laterales posibles de un rectángulo con un área de 50 unidades cuadradas?

1. 1 y 21, 3 y 7

2. 1 y 50, 2 y 25 y 5 y 10

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

3.MD.7a

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.B.5 I.C.12

LECCIÓN 3

NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

dar sentido al mundo y predecir lo que podría ocurrir

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

buscan y expresan regularidad en razonamientos repetidos exploran cantidades que cambian.

OBJETIVO(S) DE APRENDIZAJE

• Puedo determinar si un número entero hasta 100 es primo o compuesto.

• Puedo identificar los pares de factores de números enteros hasta 100.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Determinar si un número entero dado en el rango 1-100 es primo o compuesto.

• Encontrar los pares de factores de un número entero dadober 1-100

PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO

¿Qué voces no se han escuchado hoy en clase de matemáticas? ¿Cómo podrías aprovecharge las ideas de cada estudiante y contribuir a que se oigan y se vean enn la clase de mañana?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Clasificación de tarjetas (actividad 1)

Conteo coral (Calentamiento)

Materiales a reunir

Papel cuadriculado: Actividad 1, actividad 2

Fichas de una pulgada: Actividad 1, actividad 2

Materiales para copiar

Clasificación de tarjetas. Área (grupos de 2): Actividad 1

Grado 4 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Identifiquemos números primos y compuestos.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes identifiquen pares de factores y determinen si un número entero dado en el rango 1-100 es primo o compuesto.

En lecciones anteriores, los estudiantes conocieron los términos «múltiplos» y «pares de factoress». En esta lección, aprenden que los números enteros pueden clasificarse como primos o compuestos en función del número de pares de factores que tengan.

Los estudiantes razonan sobre estos números en términos del área y de los pares de longitudes de los lados de rectángulos. Aprenden que un número primo tiene exactamente 1 par de factores —1 y el propio número— y que un número compuesto tiene más de 1 par de factores. Relacionan «primo» con un número que podría representar el área de un solo rectángulo (con un solo par de longitudes de lado) y «compuesto» con un número que podría representar el área de múltiples rectángulos (con múltiples pares de longitudes de lado).

Comunidad matemática

Dile a los estudiantes que, al final de la lección, se les pedirá que identifiquen acciones específicas que experimentaron personalmente de su lista «Haciendo matemáticas» (tanto de la sección del maestro como de la sección del estudiante).

Esta lección tiene un resumen de la sección del estudiante.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Independiente 10 min

Actividad de exploración 1 En parejas 15 min

Actividad de exploración 2 En parejas 20 min

Síntesis Todo el grupo 10 min

Descripción breve

Los estudiantes cuentan en coro por 2 y por 5 y luego observan patrones dentro y entre los conteos.

Los estudiantes toman conciencia de los números primos y compuestos clasificando las tarjetas por áreas y creando un rectángulo adicional para cada área, si es posible.

Los estudiantes determinan cuántos rectángulos se pueden hacer para un área dada y luego dicen si el valor del área es un número primo o un número compuesto.

Los estudiantes explican la conexión entre las áreas de los rectángulos y si los números son primos o compuestos.

Enfriamiento Independiente 5 min Los estudiantes justifican si los números son primos o compuestos.

Abordar:

• Encontrar el número (4). Etapa 1. Factores

Enfriamiento Grupos pequeños Opcional

Math

Nation California . Grado 4

Apoyo:

• Cinco en una fila: Multiplicación (3-5). Etapa 1: Factores 1-5 y 10

Grado 4 . Matemáticas . Unidad 1

CALENTAMIENTO | CONTEO CORAL: DOS Y CINCOS

(10 minutos)

Rutinas didácticas

Conteo coral

El propósito de este conteo coral es invitar a los estudiantes a practicar el conteo de 2 y 5 y a notar patrones en el conteo. Esta comprensión ayuda a los estudiantes a desarrollar fluidez y será útil más adelante cuando los estudiantes encuentren pares de factores.

Cuando los estudiantes predicen múltiplos comunes para 2 y 5 basándose en los números registrados del conteo y en lo que saben sobre multiplicación, buscan y expresan regularidad en el razonamiento repetido (MP8).

INSTRUCCIÓN

ACTIVIDAD

RESPUESTAS POSIBLES

• «Contar de 2 en 2, comenzando en 0».

• Anotar mientras los estudiantes cuentan.

• Detenga el conteo y el registro en 30.

• «Cuente de 5 en 5, comenzando en 0».

• Anote a medida que los estudiantes cuentan.

• Detenga el conteo y el registro en 75.

• «¿Qué patrones ven en los conteos individuales?».

• 1-2 minutos: Tiempo para pensar en silencio

• Registre las respuestas.

• «¿Qué patrones observas entre los dos recuentos?».

• 1-2 minutos: Tiempo para pensar en silencio

• Registra las respuestas.

RESPUESTAS POSIBLES CONTINUACIÓN

Grado 4 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Ejemplos de respuestas:

• Patrón en el conteo de 2 en 2:

• Los dígitos en el lugar de los unos se repiten 2, 4, 6, 8, 0, 2, 4, 6, 8, 0.

• Patrón en el conteo de 5 en 5:

• Los dígitos en el lugar de los unos se alternan 5, 0, 5, 0.

• Patrones entre las dos cuentas:

• Algunos números están en ambas listas, como 10 y 20.

• Se necesitan 5 dos para llegar a 10 y 2 cincos para llegar a 10

• Entre las columnas añadimos 3 (2 + 3 = 5), luego 6 (4 + 6 = 10), luego 9 (6 + 9 = 15), y así sucesivamente. El número añadido sigue subiendo en 3 por cada fila.

• Si no aparece en las respuestas de los estudiantes, pregunte: «¿Cuántos dos se necesitaron para llegar a 10? ¿Cuántos cincos se necesitaron para llegar a 10?». (Hicieron falta 5 de dos en dos y 2 de cinco en cinco para llegar a 10).

• «Diez es múltiplo de 2 y 5. ¿Observas algún otro múltiplo tanto de 2 como de 5?». (20 y 30 están en ambas listas).

• 1 minuto: Debate en parejas

• Registra las respuestas.

• «Si los conteos continúan, ¿qué otros números verías que son múltiplos tanto de 2 como de 5?». (Creo que 40 sería el siguiente múltiplo común porque los múltiplos están subiendo por 10. Creo que 100 sería un múltiplo común porque 2 × 50 = 100 y 5 × 20 = 100).

• 2 minutos: Debate en parejas

• Registrar las respuestas.

ACTIVIDAD DE EXPLORACIÓN 1 | CLASIFICACIÓN DE TARJETAS: ÁREA

(15 minutos)

Rutinas didácticas Materiales para reunir Materiales para copiar Preparación necesaria

Clasificación de tarjetas Papel cuadriculado, fichas cuadrdas de una pulgadas

Clasificación de tarjetas: Área (grupos de 2)

Crea un conjunto de tarjetas las plantillas maestras para cada grupo de 2.

El objetivo de esta actividad es que los estudiantes aprendan sobre números primos y números compuestos. Se entrega a los estudiantes un conjunto de tarjetas con rectángulos. Clasifican los rectángulos por áreas y luego intentan dibujar un rectángulo adicional para cada categoríay y un rectángulo.

Durante la síntesis, subraye que las longitudes laterales de cada rectángulo representan un par de factores (cada par de longitudes laterales debe utilizarse una sola vez), y que el área de cada rectángulo representa un múltiplo de cada longitud lateral. Los estudiantes aprenden que un número observan que algunas áreas pueden representarse con más de un rectángulo y que otras solo pueden representarse un factor par —1 y el propio número— es un número primo y que un número con más de un par de factores es un número compuesto.

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

Aquí tiene una imagen de las tarjetas como referencia.

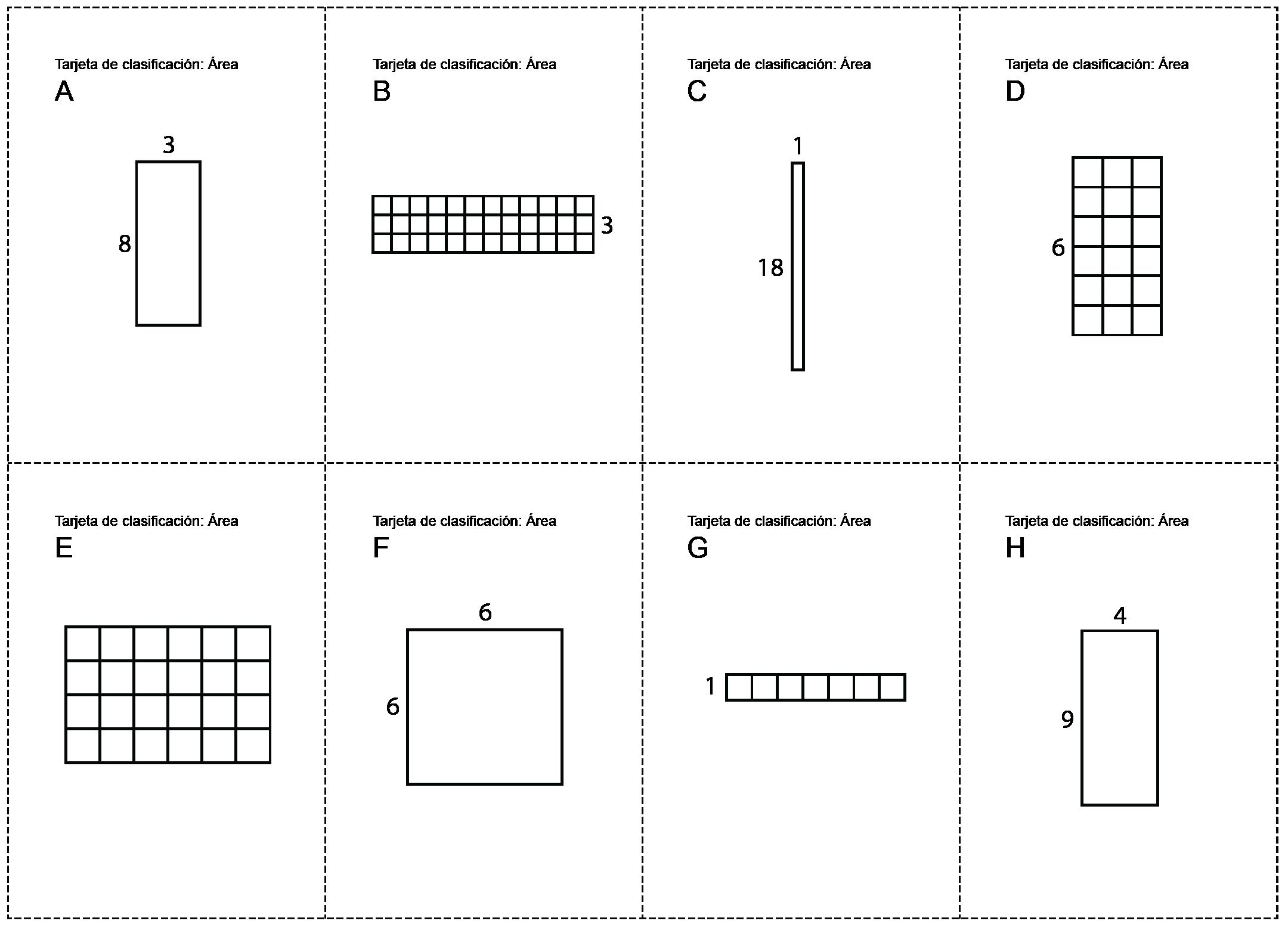
Apoyo para estudiantes que aprenden el idioma inglés

MLR8 Apoyos para el debate. Invite a los estudiantes a que, por turnos, seleccionen un rectángulo y expliquen a su compañero cómo deben clasificarlo. Muestre los siguientes fragmentos de oraciones: «Este rectángulo pertenece a , porque..». Anime a los estudiantes a debatir cuando no estén de acuerdo.

Avances: Conversar, representar

INSTRUCCIÓN

Apoyo para estudiantes con discapacidades

Compromiso: Desarrollar el esfuerzo y la persistencia. Divida esta tarea en partes manejables para apoyar las habilidades organizativas en la resolución de problemas. Algunos estudiantes pueden beneficiarse de una orientación explícita sobre cómo empezar. Por ejemplo, antes de clasificar, los estudiantes pueden encontrar el área de cada rectángulo.

Apoya la accesibilidad para: Procesamiento conceptual, Procesamiento visual-espacial, organización

ACTIVIDAD

• Grupos de 2

• Entregue a cada grupo un conjunto de tarjetas del patrón de líneas negras.

• «Clasifiquen las tarjetas en categorías de cualquier manera que tenga sentido para ustedes».

• 2 minutos: Tiempo de trabajo en parejas

• Pida a los estudiantes que compartan las formas en que clasificaron.

• «Si aún no lo hicieron, clasifiquen los rectángulos por su área».

• 3-5 minutos: Tiempo de trabajo en parejas

• Pida a los estudiantes que comprueben su trabajo con otro grupo para asegurarse de que las tarjetas de cada categoría coinciden.

• «Ahora, cred al menos un rectángulo para añadir a cada categoría de tu clasificación de tarjetas».

• 3-5 minutos: Tiempo de trabajo en parejas

• Observe los rectángulos que los estudiantes añaden a cada categoría. Vigile a los estudiantes que noten que no se pudieron dibujar nuevos rectángulos para el área de 7 unidades cuadradas.

Nation California . Grado 4

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Grado 4 . Matemáticas . Unidad 1

Tu maestroa te dará un conjunto de tarjetas para ordenar.

1. Clasifica las tarjetas por área. Anota los resultados. Prepárate para explicar tus elecciones.

2. Para cada grupo de tarjetas ordenadas, piensa en al menos un rectángulo más. Indica su longitud y ancho. Prepárate para explicar tu razonamiento.

RESPUESTAS POSIBLES

• Área de 24 unidades cuadradas: A and E

• Área de 36 unidades cuadradas: B, F y H

• Área de 18 unidades cuadradas: C y D

• Área de 7 unidades cuadradas: G

2. Sample responses:

• Área de 24 unidades cuadradas: 1 por 24 o 2 por 12

• Área de 36 unidades cuadradas: 1 por 36, 2 por 18

• Área de 18 unidades cuadradas: 9 por 2

• Área de 7 unidades cuadradas: ninguna

• Seleccione de 2 a 3 estudiantes para que compartan los rectángulos que agregaron a cada categoría.

• «¿Por qué pudieron crear más rectángulos para algunas áreas y no para otras?». (Algunos números tenían más pares de factores. Para algunos números, solo había un par de factores posible).

SÍNTESIS DE ACTIVIDAD

• Repita el razonamiento de los estudiantes. «Solo se puede formar un rectángulo para el área de 7. Números como este se llaman primos. Los números primos solo tienen un par de factores: 1 y sí mismo».

• «¿Con qué otros números compuestos trabajaron? ¿Cómo saben que son compuestos?». (Veinticuatro es un número compuesto porque puedo formar dos filas de 12 o cuatro filas de 6. Dieciocho es compuesto porque tiene pares de factores de 2 y 9 y 3 y 6).

ACTIVIDAD DE EXPLORACIÓN 2| PRIMO O

COMPUESTO? (20 minutes)

Materiales para reunir

Papel cuadriculado, fichas cuadradas de una pulgadas

En esta actividad, los estudiantes usan el área de rectángulos para hallar todos los pares de factores de un número entero dado y determinar si el número es primo o compuesto. La síntesis se centra en hallar todos los rectángulos posibles para un área dada como estrategia para hallar todos los pares de factores de un número. Los estudiantes pueden notar que no necesitan hallar todos los rectángulos posibles para determinar si un número es primo o compuesto.

Math

Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Grupos de 2

• Dé a cada grupo acceso a fichas cuadradas de una pulgada y papel cuadriculado.

• «Si te dieran un número que es el área del rectángulo, ¿cómo podrías averiguar cuántos rectángulos con esa área se pueden hacer?». (Pruébalo con fichas. Piensa en pares de factores para el número).

• 1 minuto: Debate en parejas

• Comparte y anota las respuestas.

• «Trabaja con tu pareja para completar esta tabla. Las fichas cuadradas de una pulgada y el papel cuadriculado están disponibles si los deseas».

• (10 minutos): Tiempo de trabajo en pareja

• Vigila las diferentes formas en que los estudiantes encuentran el número de rectángulos, tales como:

• construir los rectángulos con fichas cuadradas de una pulgada

• dibujar rectángulos en papel cuadriculado

• dibujar rectángulos sin regla

• enumerar los pares de factores del número y saber que un rectángulo corresponde a cada par

La tabla muestra diferentes áreas. ¿Cuántos rectángulos se pueden hacer para cada área?

Completa la tabla y prepárate para explicar o mostrar tu razonamiento.

Los rectángulos con el mismo par de longitudes laterales deben contarse una sola vez. Por ejemplo: Si cuentas un rectángulo con 4 unidades a lo ancho y 6 unidades hacia abajo, no necesitas contar también un rectángulo con 6 unidades a lo ancho y 4 unidades hacia abajo.

Área ¿Cuántos rectángulos? ¿Primo o compuesto?

2 unidades cuadradas

10 unidades cuadradas

48 unidades cuadradas

11 unidades cuadradas

21 unidades cuadradas

23 unidades cuadradas

60 unidades cuadradas

32 unidades cuadradas

42 unidades cuadradas

31 unidades cuadradas

56 unidades cuadradas

RESPUESTAS POSIBLES

Grado 4 . Matemáticas . Unidad 1

Área ¿Cuántos rectángulos? ¿Primo o compuesto?

2 unidades cuadradas 1 primo

10 unidades cuadradas 2 compuesto 48 unidades cuadradas 5 compuesto 11 unidades cuadradas 1 primo 21 unidades cuadradas 2 compuesto

23 unidades cuadradas 1 primo 60 unidades cuadradas 6 compuesto

32 unidades cuadradas 3 compuesto

42 unidades cuadradas 4 compuesto 31 unidades cuadradas 1 primo

56 unidades cuadradas 4 compuesto

• Invita a los grupos 3-4 a compartir su estrategia para encontrar el número de rectángulos para un área dada.

• «¿Cómo se relaciona el número de pares de factores con el número de rectángulos?». (La longitudes de los lados de cada rectángulo es un par de factores. Así que encontrar todos los rectángulos nos daría todos los pares de factores. O bien, encontrar todos los pares de factores del número nos diría cuántos rectángulos tienen ese número como área).

SÍNTESIS DE LA ACTIVIDAD

• «¿Cuáles son todos los números primos de nuestra lista? ¿Cómo sabemos que son primos?». (2, 23, 31. Cada uno de ellos solo tiene un conjunto de longitudes laterales, 1 y el propio número).

• «¿Qué observas en los números primos?». (Son números impares excepto el número 2).

• «¿Cuál es el número primo más pequeño de nuestro conjunto? ¿Es el número primo más pequeño?». (2. No lo sé. ¿Es 1 un número primo?).

• Visualiza un rectángulo con un área de 1 unidad cuadrada.

• «¿Cuáles son las longitudes de los lados de un rectángulo con un área de 1 unidad cuadrada?». (1 y 1)

• "Como 1 solo tiene 1 factor, no tiene ningún par de factores, por lo que no es ni primo ni compuesto».

• «¿Cuáles son todos los números compuestos de nuestro conjunto? ¿Cómo sabemos que no son primos?». (10, 48, 21, 60, 32, 42, 56. Cada uno tiene más de 1 par de factores).

SÍNTESIS DE LA LECCIÓN

(10 minutos)

«Hoy aprendimos sobre los números primos y compuestos».

«¿Cómo encontrar todos los rectángulos con una determinada área nos dice si el valor del área es primo o compuesto?». (Las longitudes de los lados de cada rectángulo son un par de factores del área. Si podemos encontrar más de un rectángulo con esa área, significa que el número tiene más de un par de factores y es compuesto. Si solo podemos encontrar un rectángulo, el número es primo).

«¿Qué preguntas tienes todavía sobre este tipo de números?».

California . Grado 4

Grado 4 . Matemáticas . Unidad 1

ENFRIAMIENTO | ¿PRIMO O COMPUESTO? (5 minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

A. ¿Cuáles son los pares de factores de 40?

B. ¿Es 40 un número primo o compuesto? Explica o muestra tu razonamiento.

2. ¿Es 17 un número primo o compuesto? Explica o muestra tu razonamiento.

RESPUESTAS POSIBLES

A. 1 y 40, 2 y 20, 4 y 10, 5 y 8.

B. Compuesta, porque tiene más de 1 par de factores.

2. Primo, porque solo tiene un par de factores, 1 y 17

Resumen de la sección del estudiante

En esta sección, usamos nuestra comprensión del área de rectángulos para aprender sobre factores, múltiplos, pares de factores, números primos y números compuestos.

Si conocemos la longitud lateral de un rectángulo, podemos encontrar las áreas que el rectángulo podría tener. Por ejemplo, un rectángulo con una longitud lateral de 3 podría tener un área de 3, 6, 9, 12, 15, u otros números que resulten de multiplicar un número entero y 3. Llamamos a estos números múltiplos de 3

Si conocemos el área de un rectángulo, podemos hallar las longitudes de los lados que podría tener. Por ejemplo, un rectángulo con un área de 24 unidades cuadradas puede tener longitudes laterales de 1 y 24, 2 y 12, 3 y 8 o 4 y 6. Llamamos a estos posibles pares de longitudes de lado los factores pares de 24

También hemos aprendido que un número que solo tiene un par de factores —1 y el propio número— se llama número primo. Por ejemplo: 5 es primo porque su único par de factores es 1 y 5

Un número que tiene dos o más pares de factores es un número compuesto. Por ejemplo: 15 es compuesto porque sus pares de factores son 1 y 15 y 3 y 5.

Reflexiones:

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

3.OA.7

Enfoque SMPs

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.B.5

II.B.7

LECCIÓN 4 MULTIPLICACIÓN PRÁCTICA (OPCIONAL)

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo buscan y hacen uso de la estructura exploran cantidades que cambian.

OBJETIVO(S) DE APRENDIZAJE

• Puedo multiplicar factores de productos hasta 100

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Practicar la multiplicación dentro de 100

PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO

¿Qué nuevos conocimientos has obtenido sobre cómo piensan o se reasgieren los estudiantes al realizar una multiplicación? ¿Cómo podrías utilizar lo que has aprendido sobre estos estudiantes en la clase de mañana?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Charla sobre números (Calentamiento)

Materiales para reunir

Cubos de centímetros: Actividad 2

Materiales para copiar

Clasificación de tarjetas. Multiplicación (grupos de 2): Actividad 1

Tablero de juego e instrucción para el centro «Encuentra el número» de la etapa 1 (grupos de 2): Actividad 2

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Practiquemos la multiplicación.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes practiquen la multiplicación dentro de 100

Grado 4 . Matemáticas . Unidad 1

En tercer grado, los estudiantes multiplican y dividen con fluidez dentro de 100, incluyendo recordar de memoria operaciones de multiplicación de un solo dígito. El propósito de esta lección opcional es que los estudiantes practiquen la multiplicación dentro de 100 y repasen estrategias para encontrar productos que no conocen.

Comunidad matemática

Antes de la lección, explique a los estudiantes que las normas son expectativas que ayudan a que todos en el salón se sientan seguros, cómodos y productivos haciendo matemáticas juntos. Diga a los estudiantes: «Algunas de estas normas pueden aplicarse tanto a ti como a mí, sin embargo, puede haber cosas que necesites que yo haga para apoyarte al hacer matemáticas cada día». Ofrezca un ejemplo, como por ejemplo «Puede ayudarnos a compartir nuestras ideas como toda la clase si tenemos la norma 'Escuchar mientras los demás comparten sus ideas'». Diga a los estudiantes que hará una pausa en dos momentos diferentes de la lección para identificar normas que ayuden a todos a hacer matemáticas.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Independiente 10 min

Actividad de exploración 1

Actividad de exploración 2

En parejas 15 min

En parejas 20 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Enfriamiento Grupos pequeños Opcional

Descripción breve

Los estudiantes calculan mentalmente expresiones de multiplicación en las que un factor es mayor o igual que 10

Los estudiantes clasifican tarjetas de expresiones de multiplicación en grupos dependiendo de si conocen el valor de inmediato, pueden encontrarlo rápidamente o aún no lo conocen.

Los estudiantes juegan a un juego para practicar la fluidez de la multiplicación identificando múltiplos para valores desde 1 hasta 36

Los estudiantes reflexionan y discuten estrategias para multiplicar números enteros de productos desde 1 hasta 100

Los estudiantes reflexionan sobre su comprensión y estrategias de las operaciones de multiplicación.

Abordar:

• Encuentra el número (4). Etapa 1: Factores

• Cinco en una fila. Multiplicación (3-5), etapa 2: Factores 1-9

Apoyo:

• Fracción secreta (3), Etapa 1: Construcción de fracciones no unitarias

Math

Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

CALENTAMIENTO | CHARLA SOBRE NÚMEROS: FACTORES ARRIBA DE DIEZ

(10 minutos)

Rutinas didácticas

Charla sobre números

El propósito de esta charla sobre números es obtener estrategias y conocimientos que los estudiantes tienen para multiplicar dentro de 100 con un factor mayor que 10. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles cuando los estudiantes encuentren pares de factores de números más adelante en la lección.

En esta actividad, los estudiantes tienen la oportunidad de buscar y hacer uso de la estructura (MP7) a medida que usan una combinación de productos de factores más pequeños para encontrar productos de factores más grandes.

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLESS

SÍNTESIS DE LA ACTIVIDAD

• Mostrar una expresión.

• «Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste».

• 1 minuto: Tiempo para pensar en silencio

• Registrar respuestas y estrategia.

• Mantener las expresiones y el trabajo mostrados.

• Repetir con cada expresión.

Encontrar el valor de cada expresión mentalmente.

• 10 × 6 • 13 × 6

• 3 × 6 • 12 × 4

• 60: Simplemente lo sé. Es 10 grupos de 6

• 18: Simplemente lo sé.

• 78: 10 × 6 = 60 y 3 × 6 = 18, así que simplemente puedo sumar 60 + 18 = 78, ya que es 13 grupos de 6.

• 48: Sé que 10 × 4 = 40 y 2 × 4 = 8, por lo que es 40 + 8 = 48. Sé que 12 × 2 = 24 y puedo duplicarlo.

• «¿Cómo puede ayudarte conocer el valor de las dos primeras expresiones a encontrar el valore de la tercera expresión?». (Puedo multiplicar por partes y sumar las partes más pequeñas para hallar un producto mayor).

ACTIVIDAD DE EXPLORACIÓN 1 | CLASIFICACIÓN DE TARJETAS: MULTIPLICACIÓN

Materiales para copiar

(15 minutos)

Preparación necesaria

Clasificación de tarjetas: Multiplicación (grupos de 2) Crea un conjunto de tarjetas de multiplicación de fluidez con las plantillas maestras para cada grupo de 2

El objetivo de esta actividad es que los estudiantes autoevalúen su propia fluidez con las operaciones de multiplicación y practiquen las que les resulten menos familiares. Los estudiantes reciben un conjunto de expresiones. Las clasifican en categorías de «lo saben enseguida», «pueden encontrarlo rápidamente» o «aún no lo saben». A continuación, identifican los productos que todavía no conocen (o que no conocen bien), discuten estrategias para encontrar esos productos y practican el uso de esas estrategias.

Apoyo para estudiantes que aprenden el idioma inglés

MLR8 Apoyso para el debate. Los estudiantes que están trabajando en la producción verbal pueden beneficiarse del acceso a minipizarras, notas adhesivas o papel de repuesto para escribir y mostrar sus respuestas a su compañero.

Avances: Escribir, representar

Grado 4 . Matemáticas . Unidad 1

Apoyo para los estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Divida esta tarea en partes más manejables. Dé a los estudiantes un subconjunto de tarjetas para empezar e introduzca lase reprincipales tarjetas una vez que los estudiantes hayan completado su conjunto Instrucciónl.

Apoya la accesibilidad para: Memoria, funcionamiento compañeroemocional

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

• Grupos de 1-2

• Entrega a cada grupo un conjunto de tarjetas de fluidez.

• «Tómate tu tiempo para clasificar las tarjetas en uno de los tres grupos».

• 3-5 minutos: Tiempo de trabajo en parejas

• «Compartamos estrategias para encontrar productos que aún no conocemos y practiquemos con ellos».

• «Elige 5 operaciones de multiplicación que aún no conozcas y anota las expresiones. Estos son los productos que practicarás encontrar».

• 1 minuto:Ttiempo de trabajo independiente

• «Ahora, comparte tu lista con tu compañero. Comenta algunas estrategias que podrías utilizar para encontrar los productos rápidamente. Después, tómate un tiempo para practicar cómo encontrar los productos que elegiste».

• 3-5 minutos) tiempo de trabajo en pareja

Por turnos, clasifica las expresiones de multiplicación en uno de estos grupos:

• lo sé de inmediato

• puedo encontrarlo rápidamente

• aún no lo sé

Expresiones de multiplicación que voy a practicar:

RESPUESTAS POSIBLES Las respuestas varían.

PROMOVER EL PENSAMIENTO ESTUDIANTIL

SÍNTESIS DE LA ACTIVIDAD

Nation California . Grado 4

Para ayudar a los estudiantes a relacionar las operaciones de multiplicación que conocen con las que todavía están aprendiendo, puede preguntarles: «¿Qué te llama la atención de los números? ¿Qué notas acerca de los números en las operaciones de multiplicación que aún estás trabajando?» o «¿Puedes pensar en una operación de multiplicación relacionada que podría ser útil?».

• «¿Cuáles son algunas estrategias útiles para encontrar productos que aún no conocía?». (Piense en un producto que ya conozca y utilícelo para encontrar el que aún no conocía. Imagina grupos de igual tamaño. Divide las expresiones en números más pequeños, encuentra esos productos y luego súmalos).

Grado 4 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN 2 | INTRODUCIR ENCONTRAR EL NÚMERO, FACTORES

Materiales para reunir

Cubos centímetros

(20 minutos)

Materiales para copiar

Tablero de juego e instrucción para el centro «Encuentra el número» de la etapa 1 (grupos de 2)

El propósito de esta actividad es que los estudiantes apliquen la fluidez de la multiplicación dentro de 100 para encontrar factores de múltiplos dentro del rango of 1-36. Este juego es la etapa 1 del centro «Encuentra el número». En esta etapa, los estudiantes encuentran todos los factores de un número dado.

Un jugador elige un número en el tablero de juego (1-36) y obtiene esa cantidad de puntos. El segundo jugador cubre todos los factores de ese número. La puntuación del segundo jugador es la suma de todos los factores cubiertos.

Los jugadores eligen por turnos el número Instrucciónl. El jugador que elija un número sin ningún factor sin cubrir pierde su siguiente turno. Cuando no queden números con factores sin cubrir, gana el jugador con más puntos.

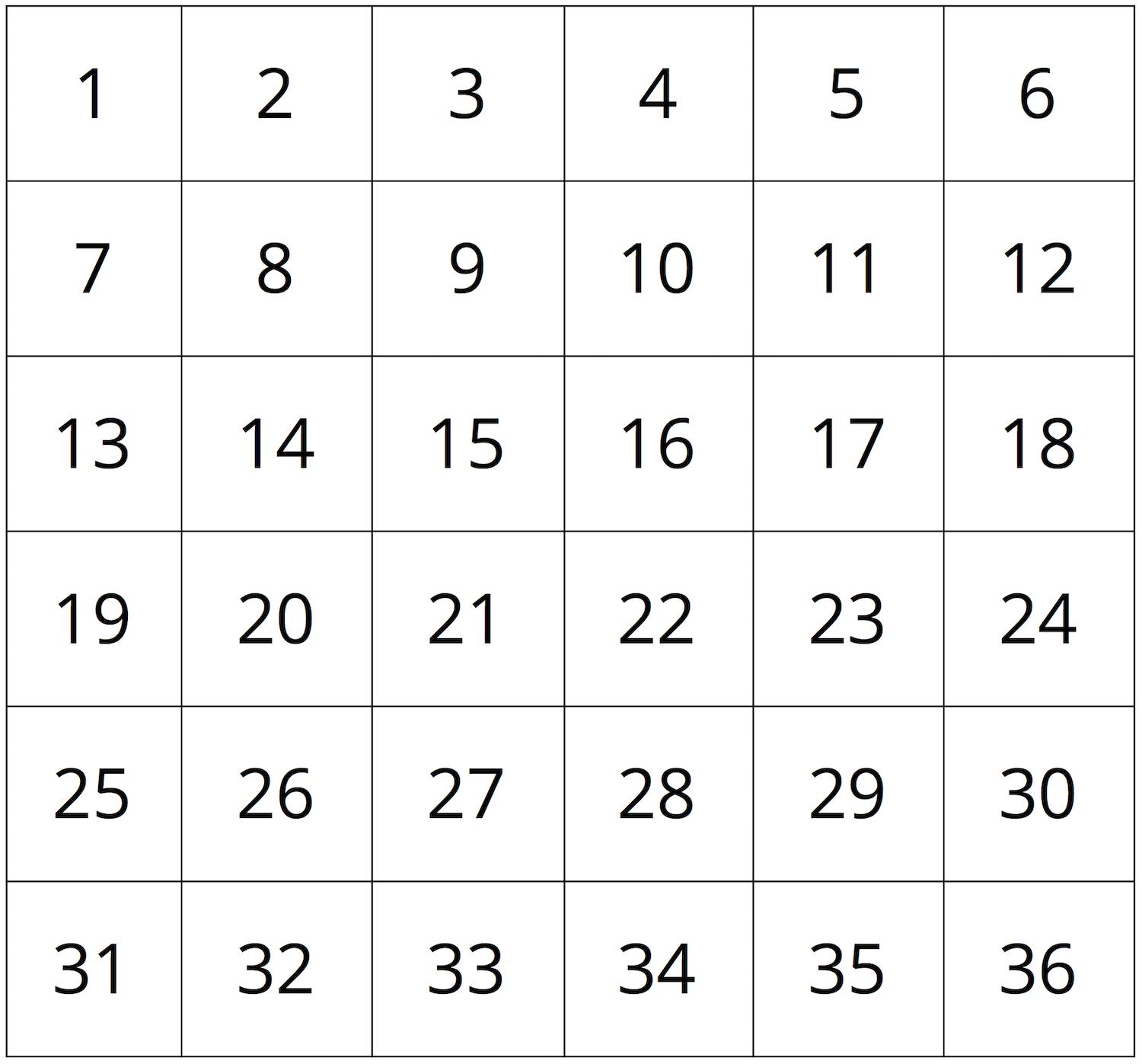
• Grupos de 2

• Entrega a cada grupo una copia del patrón de líneas negras y cubos centímetros.

• «Vamos a jugar un juego Encuentra el número Tómense unos minutos para leer las Instrucción de».

INSTRUCCIÓN

ACTIVIDAD

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

• 2 minutos: Tiempo de trabajo independiente

• «¿Qué preguntas tienen sobre el juego?».

• Considere jugar una ronda de demostración o hacer preguntas como:

• «Si yo cubriera el número 9, ¿qué factores cubrirías tú?». (1, 3)

• «¿Cuál sería tu puntuación?». (4)

• «¿Cuál sería mi puntuación?». (9)

• 10-15 minutos: Tiempo de juego en parejas

Ejemplos de respuestas:

• El compañero A cubre 4 para una puntuación de 4 puntos. El compañero B cubre 1 y 2 para una puntuación de 3.

• El compañero B cubre 6 para una puntuación de 6. El compañero A solo cubre 3, porque 1 y 2 ya estaban cubiertos, para una puntuación de 3.

• «¿Qué estrategias fueron útiles para el juego?». (Elige números con menos factores para mantener baja la puntuación de tu oponente).

Grado 4 . Matemáticas . Unidad 1

SÍNTESIS DE LA LECCIÓN

(10 minutos)

«Hoy hemos practicado la multiplicación».

«¿Qué estrategias recuerdas del tercer gardo? ¿Qué nueva estrategia aprendiste hoy?».

Comunidad matemática

Pida a los estudiantes que reflexionen sobre las acciones individuales y grupales y que consideren la pregunta: En la medida que hicimos matemáticas en nuestra comunidad matemática, ¿qué normas, o expectativas, tuvimos en cuenta?». Registre y muestre sus respuestas bajo el encabezado «Normas».

ENFRIAMIENTO | REFLEXIONAR SOBRE LA MULTIPLICACIÓN AY STRATEGIAS

(5 minutos)

1. ¿Qué operaciones de multiplicación quieres seguir practicando?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLESS

Reflexiones:

Math Nation California . Grado 4

2. Describe una estrategia que puedas utilizar en el futuro para multiplicar dos números enteros.

Ejemplo de respuesta:

1. Quiero seguir practicando los productos de 7 y 9 porque todavía no los sé y me lleva más tiempo encontrarlos.

2. Cuando multiplico, puedo ver si hay datos que conozco que me ayudarían a averiguar el producto en el que estoy trabajando.

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

• Resolución de problemas conectados

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

4.OA.3 Resolver problemas de palabras de varios pasos planteados con números enteros y que tengan respuestas de números enteros utilizando las cuatro operaciones, incluyendo problemas en los que se deban interpretar los restos. Representar estos problemas mediante ecuaciones con una letra que represente la incógnita. Evaluar la razonabilidad de las respuestas utilizando el cálculo mental y estrategias de estimación, incluido el redondeo.

4.OA.4 Hallar todos los pares de factores de un número entero en el intervalo 1-100 Reconocer que un número entero es múltiplo de cada uno de sus factores. Determinar si un número entero dado en el rango 1-100 es múltiplo de un número dado de una cifra. Determinar si un número entero dado en el rango 1-100 es primo o compuesto.

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP2 Razonar abstracta y cuantitativamente.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP4 Representar las matemáticas.

Estándares ELD de California

I.A.1 I.C.11

LECCIÓN 5 MÁS MÚLTIPLOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

dar sentido al mundo e influir en el futuro

representan las matemáticas para dar sentido a los problemas y perseveran en su resolución

OBJETIVO(S) DE APRENDIZAJE

exploran cantidades que cambian y descubren la forma y el espacio.

• Puedo razonar con múltiplos de 1-9 para resolver problemas del mundo real.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Aplicar la comprensión de la multiplicación y los múltiplos en el range 1-100 para resolver problemasdel mundo real.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO

¿Qué estrategias utilizan los estudiantes con más frecuencia para decidir si un número es múltiplo de un número entero dado?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Estimación de la exploración (Calentamiento)

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Resolvamos problemas que involucran factores y múltiplos.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes utilicen múltiplos de números de un solo dígito para resolver problemas del mundo real. Esto incluye situaciones con soluciones múltiples y situaciones sin soluciones.

Grado 4 . Matemáticas . Unidad 1

En lecciones anteriores, los estudiantes usaron el área de rectángulos para desarrollar una comprensión de factores y múltiplos. También trabajaron en su fluidez con las operaciones de multiplicación.En esta lección, aplican estos conocimientos para resolver problemas.

En algunos problemas, las soluciones son resultados de multiplicar o dividir números enteros. Fo ejemplo: Si los huevos vienen en paquetes de 12, ¿cuántos huevos hay en 5 paquetes? (60 huevos). Pero en otras, los estudiantes necesitan dar sentido a los productos o cocientes en función de la situación. Por ejemplo: ¿Cuántos paquetes debemos comprar si necesitamos exactamente 50 huevos? Los estudiantes razonan que es imposible conseguir exactamente 50 huevos, ya que hay 48 huevos en 4 paquetes y 60 huevos en 5 paquetes.

A medida que examinan los números en estas situaciones, incluida la interpretación de los restos en los problemas de división, los estudiantes dan sentido a los problemas y perseveran en su resolución (MP1) y razonan cuantitativa y abstractamente (MP2).

Comunidad de matemáticas

Diga a los estudiantes que, al final de la lección, se les pedirá que identifiquen ejemplos específicos de normas mientras hacían matemáticas.

RESUMEN DE LA LECCIÓN

Componente de lección Estructura Tiempo

Calentamiento En parejas 10 min

Actividad de exploración 1 En parejas 20 min

Actividad de exploración 2 Grupos pequeños 15 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Math

Enfriamiento Grupos pequeños Opcional

Descripción breve

Los estudiantes observan una fotografía para hacer estimaciones de varios niveles de precisión.

Los estudiantes razonan con múltiplos de dos números para determinar las mejores soluciones a problemas del mundo real.

Los estudiantes determinan múltiplos compartidos de dos números para identificar opciones razonables al resolver problemas del mundo real.

Los estudiantes revisan el contenido de la lección estableciendo expectativas con una mentalidad de crecimiento para su comunidad matemática.

Los estudiantes demuestran comprensión del uso de múltiplos para resolver problemas del mundo real.

Abordar:

• ¿Puedes Construirlo? (3-5). Etapa 2: Rectángulos múltiples

• Encontrar el número (4). Etapa 2: Factores y múltiplos

• Cinco en una fila: Multiplicación (3-5). Etapa 2: Factores 1-9

Apoyo:

• Fracción secreta (3). Etapa 1: Construcción de fracciones no unitarias

Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

CALENTAMIENTO | EXPLORACIÓN DE ESTIMACIONES:

ASIENTOS DEL BANQUETE (10

minutos)

Rutinas didácticas

Exploración de estimaciones

El objetivo de una exploración de estimaciones es practicar la habilidad de estimar una respuesta razonable basándose en la experiencia y en la información conocida. Ofrece a los estudiantes una oportunidad poco arriesgada de compartir una afirmación matemática y el razonamiento que la sustenta. Por ejemplo, los estudiantes pueden razonar que hay 10 sillas en cada mesa y luego hacer una estimación del número de mesas (MP3). Preguntarse: «¿Tiene esto sentido?». es un componente de la comprensión de los problemas y hacer una estimación o un rango de respuestas razonables con información incompleta es una parte de la modelización con matemáticas (MP4).

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Grupos de 2

• Muestra la imagen.

• «¿Qué es una estimación demasiado alta? ¿Demasiado baja? ¿Más o menos correcto?».

• 1 minuto: Tiempo para pensar en silencio

• 1 minuto: Debate en parejas

• Registra las respuestas.

¿Cuántas sillas hay en la habitación?

Registre una estimación que sea:

Demasiado bajo Más o menos correcto Demasiado alto

• Demasiado bajas: 200

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

• Demasiado altas: 500

• Más o menos correctas: 300-400

• «¿Qué parte de la imagen utilizaste para hacer tu estimación?». (El número de asientos de una mesa. El número de filas y de mesas en cada fila).

• «¿Qué estimaciones habrían sido poco razonables?». (353, 22 o 198 y otros números que no terminen en cero. Como hay diez sillas en una mesa, el número total tiene que ser múltiplo de 10 y terminar en un 0).

Grado 4 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN 1 | ELEGIR LAS MESAS CORRECTAS

(20 minutos)

El propósito de esta actividad es encontrar múltiplos de dos números diferentes en contexto. Los estudiantes deciden el posible tamaño de las mesas para una fiesta en función de si un número determinado de personas es o no múltiplo de 6, 8, ambos o ninguno. En situaciones en las que un número dado no es múltiplo de 6 o 8, razonan sobre lo que significa en el contexto (MP2).

Centrar la síntesis en cómo el número de asientos en los dos tamaños de mesa se relaciona con la multiplicación y qué significa cuando el número de personas no es múltiplo del número de asientos en una mesa.

Apoyo para estudiantes que aprenden el idioma inglés

MLR2 Recopilar y mostrar. Recopilar el lenguaje que utilizan los estudiantes cuando discuten las diferentes opciones para las mesas. Muestre palabras y frases como: no hay asientos vacíos, 6 veces un número, 8 veces un número, multiplicado por, múltiplos de 6 u 8, y × 6 sumado a × 8 para combinaciones de tamaños de mesas. Durante la síntesis, solicite formas de actualizar la visualización: «¿Qué otras palabras o frases deberíamos incluir?»., etc. Invite a los estudiantes a tomar prestado lenguaje de la visualización según sea necesario.

Avances: Conversar

Apoyo para estudiantes con discapacidad

Representación: Acceso para la percepción. Proporcione acceso a materiales que ayuden a los estudiantes a representar el problema, como fichas cuadradas de una pulgada, cubosconectables un diagrama de conjuntos en blanco o parcialmente completado y un diagrama de cintas en blanco o parcialmente completado. Invite a los estudiantes a identificar correspondencias entre estas representaciones, ecuaciones de multiplicación y el término «múltiplo» a lo largo de la lección.

Apoya la accesibilidad para: Procesamiento conceptual, procesamiento visual-espacial

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Math Nation California . Grado 4

• Grupos de 2

• «Trabaja con tu compañero para elegir un tipo de mesa para sentar a diferentes grupos of estudiantes».

• 8-10 minutos): Tiempo de trabajo en pareja

• Supervise a los estudiantes que:

• hacen dibujos para resaltar por qué el número de estudiantes en las mesas de 6 es múltiplo de 6 y el de las mesas de 8 es múltiplo de 8

• enumeran los múltiplos de 6 y los múltiplos de 8 para determinar qué mesa utilizar

• utilizan operaciones de multiplicación para explicar su razonamiento

Los estudiantes se están preparando para una fiesta. La escuela tiene mesas en las que se pueden sentar

6 personas y mesas en las que se pueden sentar 8 personas.

Los estudiantes solo pueden elegir un tipo de mesa y quieren evitar que haya empidad de asientos.

Grado 4 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES

1. La clase de Jada tiene 18 estudiantes. ¿Qué mesas elegiría para la clase de Jada? Explique o muestre su razonamiento.

2. La clase de Noah tiene 30 estudiantes. ¿Qué tablas elegirías para la clase de Noah? Explica o muestra tu razonamiento.

3. ¿Qué tablas elegirías para las clases de Noah y Jada juntas? ¿Puedes encontrar más de una opción? Explica o muestra tu razonamiento.

4. Si también quieres sitios para que se sienten el maestro de Noah y de Jada, ¿qué mesas elegirías? Explica o muestra tu razonamiento.

1. 3 mesas en las que se sientan 6 estudiantes, porque 3 × 6 = 18.

2. 5 mesas en las que se sientan 6 estudiantes, porque 5 × 6 = 30

3. 6 mesas en las que se sientan 8, o 8 mesas en las que se sientan 6, porque 8 × 6 = 48 y tanto 6 como 8 son factores de 48.

4. Ningún conjunto de mesas tendría exactamente suficientes asientos para 31 o 19, porque ni 31 ni 19 son múltiplos de 6 o 8.

• Invite a los estudiantes que utilizaron dibujos, la idea de múltiplos o las operaciones de multiplicación a compartir mientras discuten las siguientes preguntas.

• «¿La clase de Noah puede caber exactamente en las tablas de 6? ¿Cómo lo sabes?». (Sí. 30 = 5 × 6, así que la clase de Noah llenará exactamente las tablas de 5).

SÍNTESIS DE LA ACTIVIDAD

• «¿Puede la clase de Noah caber exactamente en las tablas de 8? ¿Cómo lo sabes?». (No, 30 no es múltiplo de 8. Necesitarían al menos 4 mesas pero eso son demasiados asientos, así que 2 de los asientos estarían vacíos).

• «¿Cómo nos ayudan a pensar en este problema las operaciones de multiplicación o la idea de múltiplos?». (Sabemos que 24 y 32 son productos de 8 y otro número, pero 30 no lo es).

• «Para el problema con las dos clases y los maestros, ¿podrían caber todos en mesas de 6? ¿Por qué sí o por qué no?». (Sí, podrían caber 9 mesas de 6, pero habrá 4 asientos vacíos. Si no quieren asientos vacíos, las mesas de 6 no funcionarán ya que 50 es no un múltiplo de 6).

• «¿Podrían caber todos en mesas de 8? ¿Por qué sí o por qué no?». (Sí, podrían caber 7 en mesas de 8, pero habrá 6 asientos vacíos. Si no quieren asientos vacíos, las mesas de 8 no funcionarán, ya que 50 no es múltiplo de 8).

ACTIVIDAD DE EXPLORACIÓN 2 | HOT DOGS Y PANECILLOS

(15 minutos)

En esta actividad, los estudiantes resuelven problemas que consisten en encontrar múltiplos compartidos por dos números diferentes: el número de hot dogs en un paquete y el número de panecillos de perritos calientes en un paquete. Razonan sobre cuántos panecillos de cada paquete hay que obtener para make un certo número de raciones de perritos calientes. Como cabe esperar múltiples respuestas, la atención se centra en explicar por qué las soluciones tienen sentido (MP3).

Para resolver los problemas, los estudiantes pueden descontextualizar la situación y razonar sobre factores y múltiplos, y luego recontextualizar las soluciones en términos de raciones de perritos calientes. Al hacerlo, practican el razonamiento cuantitativo y abstracto (MP2). Durante la síntesis, analice las diferentes soluciones y discuta por qué los números que son múltiplos tanto de 8 como de 10 son útiles en esta situación.

Grado 4 . Matemáticas . Unidad 1

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Grupos de 2-4

• Lee el párrafo Instrucciónl como clase.

• «¿Qué preguntas podrías hacer sobre la situación?».

• 1 minuto: Tiempo para pensar en silencio

• Compartir las respuestas.

• «Vamos a resolver problemas sobre hot dogs y panecillos para hot dogs, que vienen en paquetesde diferentes tamañod».

• «Para cada problema, busca los posibles números de paquetes que se necesitan para servir hot dogs en una merienda campestre».

• «Tómate un minuto para leer los problemas y pensar cómo los resolverías».

• 1 minuto: Tiempo para pensar en silencio

• «Ahora trabaja con tu grupo para resolver estos problemas».

• 8-10 minutos: Tiempo de trabajo en grupo

• Vigile a los estudiantes que:

• utilicen el término «múltiple» en sus explicaciones

• prueben diferentes posibilidades para el número de paquetes a comprar

• intenten encontrar números de paquetes que den el número exacto (o cercano a lo exacto) de raciones

Cada paquete de perritos calientes tiene 10 hot dogs. Cada paquete de panecillos para hot dogs tiene 8 panecillos.

1. Lin espera necesitar 50 hot dogs para una campestre de la clase.

a. ¿Cuántos paquetes de hot dogs debería comprar Lin? Explica o muestra tu razonamiento.

b. ¿Puede Lin conseguir exactamente 50 panecillos de hot dogs? ¿Cuántos paquetes de panecillos de hot dogs debe comprar Lin? Explica o muestra tu razonamiento.

2. Diego espera necesitar 72 hot dogs para una merienda campestre de la clase.

a. ¿Cuántos paquetes de hot dogs debería comprar Diego? Explica o muestra tu razonamiento.

b. ¿Cuántos paquetes de panecillos de hot dogs debería comprar Diego? Explica o muestra tu razonamiento.

3. ¿Es posible comprar exactamente el mismo número de hot dogs y de panecillos? Si es así, ¿cuál sería ese número? Si no es así, explique tu razonamiento.

1. Ejemplos de respuestas:

a. 5, porque 5 grupo de 1 0hot dogs es 50 hot dogs.

b. No, porque 50 no es múltiplo de 8. si recibe 7 paquetes de panecillos, eso es 7 × 8 o 56 panecillos, así que si necesita 50 panecillos, tendrá suficientes.

2. Ejemplos de respuestas:

RESPUESTAS POSIBLESS

Math Nation California . Grado 4

a. 7 paquetes serían 70 hot dogs, que se acerca a 72 pero no es suficiente. 8 paquetes serían 80, que son demasiados.

b. 9 paquetes serían 72 panecillos, así que es perfecto, pero si consigue 8 paquetes de hot dogs necesitará 10 paquetes de panecillos para tener un panecillo para cada hot dogs.

3. Ejemplo de respuesta: 40 hot dogs es 4 paquetes de 10 y 40 panecillos es 5 paquetes de 8. 80 hot dogs es 8 paquetes de 10 y 80 panecillos es 10 paquetes de 8

Grado 4 . Matemáticas . Unidad 1

FOMENTAR EL PENSAMIENTO DE LOS ESTUDIANTES

Si los estudiantes utilizan el método de adivinar y comprobar, pregúnteles: «¿Cómo eliges qué número probar?» o «¿Cómo puede ayudarte a resolver el problema pensar en los múltiplos?».

• Invite a los estudiantes a compartir sus respuestas al problema sobre 72 hot dogs, incluyendo a aquellos que obtienen 70 hot dogs y 72 panecillos o 80 hot dogs y 80 panecillos. Anime a los estudiantes a destacar cómo están utilizando múltiplos en su razonamiento.

SÍNTESIS DE LA ACTIVIDAD

• «¿Por qué hay diferentes respuestas a esta pregunta?». (Los números no salen exactamente para obtener 72 hot dogs y 72 panecillos, así que tenemos que buscar diferentes alternativas).

• «¿Es posible comprar exactamente el mismo número de hot dogs y de panecillos? En caso afirmativo, ¿cuántos de cada uno?». (Sí, 40, 80).

• «¿Por qué es posible comprar exactamente el mismo número d ehot dogs y panecillos cuando los paquetes son diferente?». (Algunos múltiplos de 10 son también múltiplos de 8, como 40 y 80).

SÍNTESIS DE LA LECCIÓN

(10 minutos)

Comunidad matemática

Crea un gráfico en forma de T titulado «Maneras de discrepar» y dos columnas etiquetadas como «suena como» y «parece como». Revise la lista de lo que usted está haciendo y lo que los estudiantes están haciendo en la clase de matemáticas.

«¿Cometer errores forma parte de la clase de matemáticas y de hacer matemáticas juntos?». (Sí).

«¿Qué sientes cuando alguien te señala un error o no está de acuerdo con tu idea?». (Es vergonzoso. Hiere mis sentimientos).

«¿Cómo sería o cómo sonaría desafiar las ideas de los demás sin herir sentimientos?». (Hacer preguntas para entender mejor, decir «no estoy de acuerdo», preguntar «¿puedes explicar qué quieres decir con...?»).

ENFRIAMIENTO | FIESTA DE CUARTO GRADO

(5 minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Todas las clases de cuarto curso se reúnen para celebrar una fiesta. Tienen mesas en las que 6 se puede sentar la gente y mesas en las que 8 se puede sentar la gente. Habrá 72 estudiantes que necesitan asientos.

Si solo pudieras utilizar un tipo de mesa, ¿qué tipo de mesa elegirías? Explique o muestre su razonamiento.

Ejemplos de respuestas:

• Elegiría las mesas en las que se sientan 8 porque 72 es múltiplo de 8 y 8 × 9 = 72

• Elegiría las mesas en las que se sientan 8 porque 72 es un número que digo cuando me salto la cuenta por 8

• Elegiría 12 las mesas que sientan 6 porque 12 × 6 = 72.

• Elegiría las mesas que sientan 6 porque 72 es un número que digo cuando me salto la cuenta por 6.

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

LECCIÓN 6

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP4 Representar con las matemáticas.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.A.1

I.B.5

II.C.6

EL PROBLEMA DEL ARMARIO

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

dar sentido al mundo y predecir lo que podría ocurrir

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

hacen sentido de los problemas y perseveran en su resolución al representrarlos con las matemáticas exploran cantidades que cambian.

OBJETIVO(S) DE APRENDIZAJE

• Puedo razonar con factores, múltiplos y números primos y compuestos para resolver problemas del mundo real.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Aplicar la comprensión de factores, múltiplos y números primos y compuestos para resolver problemas.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO

Mientras los estudiantes trabajaban hoy en sus pequeños grupos, ¿las ideas de quién fueron escuchadas, valoradas y aceptadas? ¿Cómo puedes ajustar la estructura del grupo mañana para garantizar que las ideas de cada estudiante formen parte del aprendizaje colectivo?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Conteo coral (calentamiento)

Materiales para reunir

Monedas: Actividad 1

Fichas de notas: Actividad 1

Papel: Actividad 1

Fichas de dos colores: Actividad 1

Grado 4 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Vamos a averiguar qué sucede en un juego sobre casilleros.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes examinen factores de números desde 1 to 20 y los utilicen para resolver problemas.

En lecciones anteriores, los estudiantes usaron múltiplos para resolver problemas sobre grupos de igual tamaños (Las tablas acomodan cierto número de asientos y paquetes que contienen cierto número de artículos). En esta lección, los estudiantes aplican sus conocimientos sobre factores, múltiplos, números primos y números compuestos para resolver problemas sobre un juego que consiste en abrir y cerrar taquillas. Los estudiantes buscan patrones en los factores or múltiplos de números y los usan para hacer predicciones sobre los casilleros que hanhan sido tocados después de que todos 20 los jugadores del juego tengan un turno.

Comunidad matemática

Diga a los estudiantes que reflexionarán sobre las normas que identificaron al final de esta lección.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Todo el grupo 10 min

Actividad de Exploración 1 Grupos pequeños 10 min

Actividad de Exploración 2 Grupos pequeños 25 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Enfriamiento Grupos pequeños Opcional

Descripción breve

Los estudiantes cuentan en coro por 2 y por 4 y luego observan patrones dentro y entre los conteos.

Los estudiantes crean representaciones de un problema del mundo real que involucra factores de números desde 1 hasta 20

Los estudiantes usan su representación de la actividad anterior para justificar respuestas sobre el contexto usando factores y múltiplos de números desde 1 hasta 20.

Los estudiantes vuelven a examinar el problema del mundo real de la lección para establecer conexiones con las soluciones que implican factores, múltiplos, números primos y números compuestos.

Los estudiantes reflexionan sobre las estrategias y los procesos de pensamiento que utilizaron para encontrar soluciones a los problemas de la lección.

Abordar:

• Encuentra el número (4). Etapa 2: Factores y múltiplos

• Cinco en una fila: Multiplicación (3-5). Etapa 2: Factores 1-9

Apoyo:

• Fracción secreta (3). Etapa 1: Construcción de fracciones no unitarias

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

CALENTAMIENTO | CONTEO CORAL: DOS Y CUATRO (10

minutos)

Rutinas didácticas

Conteo coral

El propósito de este conteo coral es que los estudiantes practiquen contar por 2 y 4 y noten los múltiplos comunes de los dos números in el conteo. Los estudiantes pueden notar que el conteo por 4 es uno de cada dos números en el conteo por 2. La relación entre los dos conteoso también se puede describir usando la multiplicación y este es el objetivo de la síntesis.

INSTRUCCIÓN

ACTIVIDAD

RESPUESTAS POSIBLES

• «Cuenta de 2 en 2, comenzando en 0»

• Anote mientras los estudiantes cuentan.

• Detenga el conteo y el registro en 30

• Cuente de 4 en 4, comenzando en 0

• Anote mientras los estudiantes cuentan.

• Detenga el conteo y el registro en 60

• «¿Qué patrones ves?».

• 1-2 minutos: Tiempo para pensar en silencio

• Registra las respuestas.

Ejemplos de respuestas:

• Patrón en el conteo de 2 en 2:

• Los números en el lugar de las unidades se repiten 2, 4, 6, 8, 0, 2, 4, 6, 8, 0

• Patrón en el conteo de 4 en 4:

• Los números en el lugar unos se repiten 4, 8, 2, 6, 0, 4, 8, 2, 6, 0

• Patrones entre los dos conteos:

• La segunda lista está incluida en la primera lista.

• Todos los demás números de la primera lista están en la segunda lista.

• Cada número de la segunda lista es el doble del número correspondiente de la primera lista..

• Cada número de la primera lista es la mitad del número correspondiente de lasegunda lista.

SÍNTESIS DE LA ACTIVIDAD

• «¿Cómo puedo obtener el número de la segunda lista a partir del número correspondiente de la primera lista?». (Duplícalo sumándolo a sí mismo o multiplica el número por 2).

• «¿Cómo puedo obtener el número de la primera lista a partir del número correspondiente de la segunda lista?». (Puedo sacar la mitad o dividir el número por 2).

ACTIVIDAD DE EXPLORACIÓN 1 | CASILLEROS

DUDOSOS (10 minutos)

Materiales a reunir

Monedas, fichas de notas, papel, fichas de dos colores

El propósito de esta actividad es que los estudiantes visualicen y den sentido al contexto de los problemas que resolverán en la siguiente actividad. También considerarán las representaciones que se pueden utilizar para representar las cantidades y acciones de la situación (MP4) e intentarán crearlas. Los estudiantes no tendrán tiempo de hacer una representación completa, por lo que se centrarán en dar sentido a la situación yd perseverar en la búsqueda de representaciones eficaces (MP1).

Grado 4 . Matemáticas . Unidad 1

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Grupos de 3 o 4

• Muestre la imagen de las taquillas.

• «En tu grupo pequeño habla de lo que observas y te preguntas sobre la imagen»

• 1 minuto: Tiempo para pensar en silencio

• 1 minuto: Debaten en grupo

• Compartir y anotar las respuestas. Si los estudiantes no están familiarizados con las taquillas, explíqueles que en algunas escuelas se utilizan para guardar los abrigos, los libros y las mochilas de los estudiantes.

• Lea el problema en voz alta a los estudiantes.

• «Tómense un tiempo para entender el problema. Tal vez quieran intentar visualizarlo o releer el problema».

• 2 minutos: Tiempo para pensar en silencio

• Dé a los estudiantes acceso a fichas de dos colores, fichas, monedas y otros materiales que puedan serles útiles.

• «Con base en lo que saben, creen una representación del problema».

• (5 minutos): Tiempo de trabajo independiente

• Supervise y seleccione 3 diferentes representaciones que:

• representen las taquillas de diferentes maneras

• muestren instancias de contacto con las taquillas (o de apertura y cierre)

• muestren la correspondencia entre cada estudiante y las taquillas tocadas

La imagen muestra taquillas en un pasillo de la escuela.

Los 20 estudiantes de la clase de cuarto grado de Tyler juegan en un pasillo que tiene 20 casilleros en fila.

• El primer estudiante comienza con el primer casillero y avanza por el pasillo y abre todos los casilleros.

• El segundo estudiante comienza con el segundo casillero y avanza por el pasillo y cierra todos los demás casilleros.

• El tercer estudiante se detiene en cada tercer casillero y abre el casillero si está cerrado o cierra el casillero si está abierto. Este proceso continúa hasta que todos los 20 estudiantes de la clase hayan tocado los casilleros.

Crea una representación para mostrar lo que entiendes sobre este problema. Considere:

• ¿Cómo muestra su representación los casilleros?

• ¿Cómo mantiene su representación un registro de los estudiantes que tocan los casilleros?

• ¿Cómo muestra su representación qué casilleros están abiertos o cerrados?

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Los estudiantes pueden:

• poner los números 1-20 en fichas

• usar fichas de dos colores y marcos de 10

• usar las caras de la cara y del canto de las monedas

• usar símbolos o colores para indicar si una taquilla está cerrada o abierta, por ejemplo X o O

• lista de los números de cada estudiante por fila y una indicación de cómo su acción change los símbolos o colores

• Mientras se discute cada representación, pregunte a los estudiantes:

• «¿Dónde están las taquillas en esta representación?». (Números o dibujos utilizados para indicar las taquillas).

• «¿Cómo podemos saber si una taquilla está abierta o cerrada en esta representación?». (Símbolos o colores utilizados para indicar abierto o cerrado).

• «¿Cómo muestra esta representación qué estudiante está tocando las taquillas?». (Los estudiantes y sus acciones se enumeran en una tabla o un gráfico en T).

• «En la siguiente actividad, responderás a preguntas sobre el juego. Puedes usar tu representación o la que compartió un compañero para ayudarte a pensar en los problemas».

ACTIVIDAD DE EXPLORACIÓN 2 | UN CASO ABIERTO Y CERRADO

(25minutos)

El objetivo de esta actividad es que los estudiantes resuelvan problemas sobre un juego de taquillas utilizando las ideas de factores y múltiplos y observando patrones en los números. La situación ofrece muchas posibilidades de exploración, pero las preguntas sobre qué taquillas se tocan y por cuántas personas están diseñadas para que los estudiantes comprendan la multiplicación.

La discusión sobre qué taquillas se abrirán o cerrarán o por quién se abrirán probablemente alejará a los estudiantes de la reflexión sobre factores y múltiplos y no debería ser el objetivo. La pregunta final desafía a los estudiantes que están preparados para más a buscar patrones adicionales y generalizar sus observaciones. No se espera que todos los estudiantes la completen. Los estudiantes que estén preparados pueden simular la apertura dey el cierre de las taquillas de diferentes maneras, como por ejemplo:

• utilizando taquillas reales, si están disponibles

• utilizando un conjunto impreso de cuadrados etiquetados 1 a 20

• utilizando fichas de dos colores y marcos de 10, si están disponibles

• utilizando las caras de la cara y del canto de las monedas

Apoyo para estudiantes que aprenden el idioma inglés

MLR7 Comparar y conectar. Invite a los grupos a preparar una presentación visual que muestre la estrategia que utilizaron para determinar qué casilleros estarán abiertos. Anime a los estudiantes a incluir detalles que ayuden a otros a interpretar su pensamiento. Por ejemplo, lenguaje específico, uso de diferentes colores, sombreado, flechas, etiquetas, notas, diagramas o dibujos. Dé tiempo a los estudiantes para que investiguen el trabajo de los demás. Durante el debate de toda la clase, pregunte a los estudiantes: «¿Qué estudiantes abren o cierran la taquilla 10? ¿Y la taquilla 20? ¿Qué patrones observáis sobre el número de factores para un número de taquilla y si está abierta or cerrada?».

Avances: Representar, conversar

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Ayude a los estudiantes a transferir sus conocimientos a un nuevo contexto. Comience preguntando: «¿Este problema le recuerda a alguien los conceptos que hemos estado estudiando?». Invite a los estudiantes a hacer referencia a la visualización del vocabulario y continúe remitiéndoles a ella a lo largo de la lección.

Apoya la accesibilidad para: Procesamiento conceptual, lenguaje, atención

Grado 4 . Matemáticas . Unidad 1

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Grupos de 3-4

• «Vamos a resolver algunos problemas sobre un juego que leíste antes, en el que los estudiantes se turnan para abrir y cerrar los casilleros».

• «Lee en silencio y piensa en cada pregunta».

• 1 minuto: Tiempo para pensar en silencio

• «Trabaja en tu grupo para responder cada pregunta».

• 15-20 minutos: Tiempo de trabajo en grupo

• Monitoree a los estudiantes que:

• representan cada contacto con los casilleros de manera sistemática

• representan los casilleros abiertos y cerrados de varias maneras

• razonan sobre factores y múltiplos y usan el vocabulario en sus explicaciones

• Anime a los estudiantes que usan un patrón para responder la pregunta final a compartir su explicaciónación. Invítelos a considerar una situación con más casilleros tales Consideren las representaciones que crearon o vieron antes para ayudarlos a pensar en los problemas como 50 o 100.

Los 20 estudiantes de la clase de cuarto grado de Tyler juegan en un pasillo con 20 casilleros en fila.

Su objetivo es averiguar cuáles casilleros serán tocados a medida que todos 20 los estudiantes turnan tocando los casilleros.

1. ¿Qué números de taquilla toca el 3.º estudiante?

2. ¿Qué números de taquilla toca el 5.º estudiante?

3. ¿Cuántos estudiantes tocan la taquilla 17? Explique o muestre cómo lo sabe.

4. ¿Qué taquillas solo tocan 2 los estudiantes? Explique o muestre cómo lo sabe.

5. ¿Qué taquillas tocan solo 3 estudiantes? Explique o muestre cómo lo sabe.

6. ¿Qué taquillas se tocan más? Explica o muestra cómo lo sabes.

Si tienes tiempo: ¿Qué taquillas siguen abiertas al final del partido? Explica o muestra cómo lo sabes.

Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES

1. 3, 6, 9, 12, 15, 18

2. 5, 10, 15, 20

3. 2. Respuestas de ejemplo:

• Hice un diagrama y vi que los únicos estudiantes que tocan taquilla 17 son 1 y 17.

• No dije 17 cuando estaba contando por cualquier número que no fuera 1 o 17

4. 2, 3, 5, 7, 11, 13, 17, 19. Respuesta de ejemplo: Cada uno de estos números solo tiene 2 factores, uno de los cuales es 1

5. 4, 9. Ejemplo de respuesta: Estos números tienen 3 factores. Los factores de 4 son 1, 2, and 4. Los de 9 son 1, 3 y 9

6. 12, 18 y 20 son tocados cada uno por 6 estudiantes diferentes. También son los números que tienen más factores.

Si tienes tiempo: Las taquillas que están abiertas son 1, 4, 9 y 16. Respuestas de ejemplo:

• Estos números tienen un número impar de factores, por lo que las taquillas cambiaron un número impar de veces. Cuando enumeramos sus pares de factores, un par es el mismo número dos veces. Por ejemplo: 4 = 1 × 4 y 4 = 2 × 2, por lo que 4 tiene tres factores: 1, 2, 4. Así los primeros, segundos y cuartos estudiantes tocan el número de casillero 4 y el patrón es abrir-cerrar-abrir. Para 16, que tiene cinco factores, el patrón es abrir -cerrar-abrir-cerrar-abrir.

• Todos los demás números tienen un número par de factores, por lo que las taquillas se cerrarán porque se tocan un número par de veces (abrir-cerrar-abrir-cerrar...).

• «Tómense unos minutos para compartir sus respuestas con los estudiantes de un grupo diferente».

SÍNTESIS DE LA ACTIVIDAD

• Invite a los estudiantes a compartir cómo llevaron la cuenta del número de toques para cada casillero.

• Ver la síntesis de la lección.

SÍNTESIS DE LA LECCIÓN

(10 minutos)

«Hoy hemos visto un juego sobre taquillas que se abren y se cierran».

«¿Qué taquillas solo han tocado 2 estudiantes? ¿Qué tienen en común esos números?». (2, 3, 5, 7, 11, 13, 17, 19. Todos son números primos).

«¿Qué taquillas solo han tocado 3 estudiantes? ¿Qué tienen en común esos números?». (4, 9, 16. Todos tienen un número impar de factores. Uno de sus pares de factores incluye el mismo número, como 3 y 3 o 4 y 4).

«¿Cómo se relacionan los problemas de hoy con lo que hemos estado estudiando?». (Los factores de los números de taquilla nos dicen cuántos y qué estudiantes tocarían la taquilla. Si el número del casillero es un número compuesto, sabemos que más de 2 estudiante tocarían la taquilla).

Comunidad matemática

Después del enfriamiento, pida a los estudiantes que reflexionen individualmente sobre la siguiente pregunta: «¿Cuál de las normas te ha parecido más importante en tu trabajo de hoy y por qué?». Los estudiantes pueden escribir sus respuestas en la parte inferior de su papel de enfriamiento, en una hoja separada o en un diario de matemáticas.

Diga a los estudiantes que a medida que su comunidad matemática trabaje junta en el transcurso del año, el grupo continuamente agregará y revisará sus acciones y expectativass «Haciendo Matemáticas» y «Normas».

Grado 4 . Matemáticas . Unidad 1

ENFRIAMIENTO | REFLEXIONAR SOBRE LA RESOLUCIÓN DE PROBLEMAS (5 minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Reflexiones:

Math Nation California . Grado 4

Reflexionen sobre su trabajo de hoy. ¿Cómo has organizado tu pensamiento? ¿Cómo ajustaste tu trabajo y tu pensamiento a lo largo del proceso? ¿Qué les resultó útil?

Ejemplo de respuesta: Empecé intentando escribir todo en un solo color, pero luego vi que si utilizaba diferentes colores, era más fácil seguir la pista.

LECCIÓN

7

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Enfoque SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.1

I.A.3

II.C.6

HALLAR FACTORES Y MULTIPLOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

impactar en el futuro

construyen argumentos viables y critican el razonamiento de otros mientras atienden a la precisión y exploran cantidades que cambian.

OBJETIVO(S) DE APRENDIZAJE

• Puedo determinar factores y múltiplos de números enteros 1-100

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Determinar si un número de 1-100 es múltiplo de otro número.

• Encontrar todos los pares de factores de un número entero dado de 1-100

PREGUNTA DE REFLEXIÓN PARA EL MAESTRO

Al terminar esta sección, reflexione sobre las normas y actividades que han apoyado a cada estudiante en el aprendizaje de las matemáticas. ¿Cómo has visto crecer a cada estudiante como joven matemático a lo largo de este trabajo? ¿Cómo te has visto crecer a ti mismo como maestro?

PREPARACIÓN

DE LA LECCIÓN

Rutinas didácticas

Charla sobre números (calentamiento)

Materiales para reunir

Cubos de centímetros: Actividad 2 Materiales Para copiar

Tablero de jueog e instrucción de «Encuentra el número» de la etapa 2 (grupos de 2): Actividad 2

Grado 4 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Encontremos factores y múltiplos de números enteros de 1-100

Narrativa de la lección

El objetivo de esta lección es que los estudiantes encuentren factores y múltiplos de un número entero dado de 1-100

En lecciones anteriores, los estudiantes aprendieron sobre pares de factores, múltiplos y números primos y compuestos.

El objetivo de esta lección es que los estudiantes utilicen el lenguaje de factores y múltiplos para describir números dentro de 100

Los estudiantes buscan todos los factores de los números y deciden si un número dado es primo o compuesto. Se anima a los estudiantes a encontrar patrones en los números compuestos que les ayuden a identificar un factor. Por ejemplo, si el último dígito de un número es 0 entonces 2, 5 y 10 son todos factores de ese número.

Esta lección tiene un resumen de la sección del estudiante.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Descripción breve

Calentamiento Independiente 10 min Los estudiantes calculan mentalmente cuatro expresiones de división con el mismo divisor.

Actividad de exploración 1

Actividad de exploración 2

En parejas 15 min Los estudiantes completan enunciados identificando factores y múltiplos de diferentes números y luego justifican su razonamiento.

En parejas 20 min Los estudiantes juegan a un juego en el que se turnan para tapar factores o múltiplos de números 1-100

Síntesis Todo el grupo 10 min

Los estudiantes identifican y resumen sus observaciones sobre los múltiplos y factores de 1, 2, 5 y 10

Enfriamiento Independiente 5 min Los estudiantes demuestran su comprensión identificando factores y múltiplos de números.

Abordar:

• Cinco en una fila: Multiplicación (3-5). Etapa 2: Factores 1-9

Enfriamiento Grupos pequeños Opcional

Apoyo:

• Fracción secreta (3). Etapa 1: Construcción de fracciones no unitarias

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

CALENTAMIENTO | CHARLA SOBRE NÚMEROS: DIVISIÓN

(10 minutos)

Rutinas didácticas

Charla sobre números

El propósito de esta charla sobre Números es obtener estrategias y conocimientos que los estudiantes tienen para dividir entre 100. Estos conocimientos ayudan a los estudiantes a desarrollar fluidez en las divisiones. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes encuentren pares de factores de números.

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLESS

SÍNTESIS DE LA ACTIVIDAD

• Muestra una expresión.

• «Hazme una señal cuando tengas una respuesta y puedas explicar cómo la obtuviste».

• 1 minuto: Tiempo para pensar en silencio

• Registra las respuestas y la estrategia.

• Mantén las expresiones y el trabajo desplegados.

• Repite para cada expresión.

Encuentra el valor de cada expresión mentalmente.

• 2 ÷ 3

• 30 ÷ 3

• 60 ÷ 3

• 72 ÷ 3

• 4. Sé que 4 grupos de 3 es 12

• 10. Sé que 10 grupos de 3 es 30.

• 20. Sé que 20 × 3 = 60

• 24 72 es 60 y 12 por lo que es 20 y 4 grupos o 24 grupos de 3

• «¿Cómo te ayuda conocer el primer y el tercer cociente a encontrar el último cociente?».. (Como 12 + 60 = 72, podemos sumar las respuestas a esos cocientes para obtener la respuesta al último problema).

• Considere preguntar:

• «¿Quién puede replantear el razonamiento de una manera diferente?».

• «¿Tuvo alguien la misma estrategia, pero la explicaría de otra manera?».

• «¿Planteó alguien la expresión de una manera diferente?».

• «¿Quiere alguien añadir algo a la estrategia de ?».

EXPLORACIÓN ACTIVIDAD 1 | ENUNCIADOS DE FACTORES Y MÚLTIPLOS

(15 minutos)

El propósito de esta actividad es que los estudiantes encuentren factores y múltiplos de un número dado y hagan enunciados que utilicen los términos «factores» y «múltiplos». Este trabajo anima a los estudiantes a utilizar el lenguaje con precisión (MP6).

Los estudiantes pueden generar muchos enunciados diferentes para cada número y utilizar el número dado en cualquiera de los dos espacios en blanco de la raíz de la frase. A continuación, comparten sus enunciados con su compañero y explican por qué sus frases tienen sentido. Al hacerlo, los estudiantes practican la construcción de argumentos viables y la atención al razonamiento de los demás (MP3).

Grado 4 . Matemáticas . Unidad 1

Apoyo para estudiantes que aprenden el idioma inglés

MLR8 Apoyos para el debates. Utilizar ejemplos multimodales para mostrar el significado de factor y múltiple. Invite a los estudiantes a usar descripciones verbales junto con gestos, dibujos u objetos concretos para mostrar factores de 10 y múltiplos de 10

Avances: Escuchar, representar

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Grupos de 2

• «Vamos a practicar el uso de las palabras 'factor' y 'múltiple' como preparación para un juego que vamos a jugar. Tómate un tiempo para completar los enunciados por tu cuenta».

• 3-5 minutos): Tiempo de trabajo independiente

• «Ahora comparte tus enunciados con tu compañero. Asegúrate de hacerte preguntas mientras explicas tus enunciados».

• 3-5 minutos): Debate en parejas

1. Completa un enunciado usando la palabra «factor». Completa un enunciado usando la palabra «factor» y un enunciado usando la palabra «múltiplo» para cada número.

Número Factor Múltiplo

10 es un factor de porque... es un múltiplo de porque...

7 es un factor de porque... es un múltiplo de porque...

50 es un factor de porque... es un múltiplo de porque...

16 es un factor de porque... es un múltiplo de porque...

número factor múltiplo

35 es un factor de porque... es un múltiplo de porque...

20 es un factor de porque... es un múltiplo de porque...

19 es un factor de porque... es un múltiplo de porque...

6 es un factor de porque... es un múltiplo de porque...

2. Mientras comparas los enunciados con tu compañero, comenta una cosa que notes and one cosa que te preguntes.

1. Ejemplos de respuestas:

RESPUESTAS POSIBLES

Math Nation California . Grado 4

• 10 es un factor de 20 porque 10 × 2 = 20. 10 es un múltiplo de 5 porque podemos count por 5 y decir 10.

• 5 es un factor de 10 porque 5 × 2 = 10. 30 es múltiplo de 10 porque 10 × 3 = 30.

Grado 4 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES CONTINUACIÓN

SÍNTESIS DE LA ACTIVIDAD

2. Los estudiantes pueden darse cuenta de que:

• Si un número fuera mayor, podríamos pensar entre qué lo dividiríamos para encontrar factores del número.

• Si el número era más pequeño, lo multiplicábamos por otro número para hallar un múltiplo.

• Los números primos como 7 y 19 solo tienen 2 factores.

• 10 es factor de un número y un número es múltiplo de 10 cuando last digit del numero es 0

• 5 es factor de un número y un número es múltiplo de 5 cuando last dígito del número es 5 o 0

• Los números pares son múltiplos de 2 Los estudiantes pueden preguntarse:

• ¿Es todo número factor o múltiplo de otro número?

• ¿Es 1 factor de todo número?

• «¿Cuál fue tu frase favorita? ¿Por qué fue tu favorita?».

• «¿Qué notaron y se preguntaron tú y tu compañero acerca de esta actividad?».

EXPLORACIÓN ACTIVIDAD 2 | INTRODUCIR ENCONTRAR EL NÚMERO, FACTORES Y MÚLTIPLOS

(20 minutos)

Materiales para reunir

Cubos centímetros

El objetivo de esta actividad es que los estudiantes practiquen cómo encontrar factores y múltiplos de números y utilicen el vocabulario. Los estudiantes pueden jugar varias rondas del juego según el tiempo disponible y se les debe animar a que utilicen las ideas de la actividad anterior, si es necesario. Este juego de es la etapa 2 del centro «Encuentra el número». En esta etapa, los estudiantes encuentran los factores y múltiplos de un número dado. Ele tablero de juego es una cuadrícula cuadrada con los números 1-100

Para empezar, un jugador elige un número par menor que 50. El otro jugador elige un factor o múltiplo de ese número. Por turnos, los estudiantes cubren un múltiplo o un factor del número anterior. Cuando no quedan factores o múltiplos por cubrir, el jugadorr que cubrió el último número obtiene un punto. Los estudiantes eligen por turnos el número Instrucciónl. Los estudiantes juegan 10 rondas, o tantas rondas como permita el tiempo. El jugador con más puntos gana.

Grado 4 . Matemáticas . Unidad 1

INSTRUCCIÓN

ACTIVIDAD

RESPUESTAS POSIBLESS

SÍNTESIS DE LA ACTIVIDAD

• Grupos de 2

• Entrega a cada grupo de 2 estudiantes el patrón de líneas negras y los cubos centímetros.

• "Vamos a jugar a un juego llamado Encuentra el número. Tómense unos minutos para leer las Instrucción».

• 2 minutos: Tiempo de trabajo independiente

• «¿Qué preguntas tienen sobre el juego?».

• Si es necesario, jueguen una ronda de ejemplo.

• 10-15 minutos: Tiempo de juego en parejas

• Vigile a los estudiantes que eligen estratégicamente los números para ganar la ronda.

Ejemplo de ronda:

• El compañero A elige cubrir 24.

• El compañero B cubre 12, porque 12 es un factor de 24

• El compañero A cubre 60, porque 60 es un múltiplo de 12.

• El compañero B cubre 10, porque 10 es un factor de 60.

• El compañero A cubre 5, porque 5 es un factor de 10

• El compañero B afirma que no se pueden cubrir otros números.

• El compañero A no está de acuerdo y dice: «Podríamos elegir 15, 20, 25 u otros múltiplos de 5 o podría elegir 1 porque es un factor de 5».

• El compañero A gana un punto para la ronda.

• «¿Cuál fue tu estrategia para elegir los números mientras jugabas?». (Intentaba que la ronda durara el mayor tiempo posible, así que me gustaba elegir números que supiera que tenían muchos factores. Traté de encontrar un número que fuera primo y que pudiera usar para que a mi compañero le costara más trabajo elegir un número).

SÍNTESIS DE LA LECCIÓN

(10 minutos)

«En la lección de hoy hemos utilizado los términos factores y múltiplos para describir números comprendidos entre 100».

Muestre las siguientes indicaciones:

• «¿Cómo sabes si es un factor de un número?».

• «¿Cómo sabes si un número es múltiplo de ?».

«Con tu compañero, túrnense usando cada número 1, 2, 5 y 10 para preguntar y responder las indicaciones. Por ejemplo: El primer compañero pregunta: "¿Cómo sabes si 2 es factor de un número?" y el segundo compañero responde. A continuación, el segundo compañero pregunta: "¿Cómo sabesw si un número es múltiplo de 2?" y el primer compañero responde».

Comparta y anote las respuestas. Subraye estas observaciones:

• El número 1 es factor de todo número y todo número es múltiplo de 1

• El número 2 es factor de todo número par y todo número par es múltiplo de 2.

• Un número es múltiplo de 5 cuando la última cifra del número es 5 o 0

• El número 10 es factor de un número cuando la última cifra del número es 0

• Un número es múltiplo de 10 si su última cifra es 0

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

ENFRIARSE | LAS SEMILLAS DE JADA (5 minutos)

Completa los enunciados para cada número. número factor múltiplo

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

11 es un factor de porque... es un múltiplo de porque...

24 es un factor de porque... es un múltiplo de porque...

Ejemplos de respuestas: número factor múltiplo

11 11 es un factor de 55 porque 11 × 5= 55

24 8 es un factor de 24 porque 8 × 3 = 24.

Resumen de la sección del estudiante

11 es un múltiplo de 1 porque 11 × 1 = 11

24 es un múltiplo de 8 porque 8 × 3 = 24.

En esta sección, usamos lo que aprendimos sobre factores, múltiplos y números primos y compuestos entre 1-100 para jugar y resolver problemas.

Aprendimos que los números pueden compartir factores y múltiplos. Por ejemplo:

• El número 2 es un factor de 6 y también un factor de 8

• El número 24 es un múltiplo 6 y también un múltiplo de 8

Saber sobre factores y múltiplos nos ayudó a responder preguntas como:

• «¿Podemos poner 24 sillas en 6 filas iguales? ¿Y 7 filas iguales o 8 filas iguales?».

• «Si hay 20 taquillas en fila y un estudiante toca una de cada cuatro taquillas, ¿cuántas taquillas tocaría? ¿Quénúmero de taquilla tocaría?».

Reflexiones:

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Factores y modelos de área

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

Enfoque SMPs

MP4 Representar con matemáticas.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.2

II.C.6

LECCIÓN 8

ARTE MONDRIANO (OPCIONAL)

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

impactar el futuro representan con las matemáticas y atienden a la precisión exploran cantidades que cambian.

OBJETIVO(S)

DE APRENDIZAJE

• Puedo crear un diseño geométrico formado por rectángulos con diferentes áreas aplicando el conocimiento de factores, múltiplos y números primos y compuestos.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Aplicar la comprensión de factores, múltiplos y números primos y compuestos para crear un diseño geométrico.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTRO

¿Qué ideas matemáticas de la lección de hoy ha sido la más difícil para los estudiantes?

¿Te ha sorprendido o era lo que esperabas?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse (Calentamiento)

Materiales a reunir

Lápices de colores, crayones o marcadores: Actividad 1, actividad 2

Pegamento o cinta adhesiva: Actividad 2

Reglas o reglas: Actividad 1

Notas adhesivas: Actividad 2

Materiales para copiar

Papel cuadriculado centímetro. Estándar (grupos de 2): Actividad 1

Grado 4 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Hagamos arte con rectángulos.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes apliquen su comprensión del área de rectángulos y pares de factores para crear y analizar arte inspirado en Mondrian.

Esta lección es opcional porque no aborda nuevos estándares de contenido matemático. Ofrece a los estudiantes la oportunidad de desarrollar habilidades de representar las matemática mientras aplican las ideas de área, factores, múltiplos, números primos y números compuestos.

Los estudiantes crean una obra de arte basada en el área de rectángulos y las operaciones de multiplicación dentro de 100. Empiezan aprendiendo sobre Piet Mondrian y analizando algunos de sus cuadros abstractos. Reconocen que los cuadros están compuestos por rectángulos, algunos con la misma área y otros con áreas diferentes.

A continuación, los estudiantes esbozan su propia composición, dividiendo una cuadrícula 18 por24 en espacios rectangulares con determinados requisitos. A continuación, los estudiantes examinan la obra de un compañero. Identifican rectángulos con áreas iguales y aquellos que representan números primos o compuestos.

Cuando los estudiantes aíslan y describen los elementos matemáticos en el arte y se adhieren a restricciones matemáticas para crear arte, representan con las matemáticas (MP4).

Esta lección puede durar más de 60 minutos, ya que los estudiantes pueden necesitar tiempo adicional para colorear, analizar y presentar sus diseños. Considere la posibilidad de modificar las actividades o ampliar la lección a lo largo de 2 días para satisfacer las necesidades de los estudiantes y cualquier limitación de tiempo.

RESUMEN DE LA LECCIÓN

Componente de lección Estructura Tiempo

Calentamiento En parejas 10 min

Actividad de exploración 1 En parejas 20 min

Actividad de exploración 2 En parejas 20 min

Síntesis Todo el grupo 10 min

Enfriamiento Grupos pequeños Opcional

Math

Nation California . Grado 4

Descripción breve

Los estudiantes observan patrones geométricos y colores en una muestra de arte de Piet Mondrian y discuten lo que notan y se preguntan como preparación para crear sus propias versiones del arte de Mondrian.

Los estudiantes crean una obra de arte de estilo Mondrian formada por rectángulos con parámetros específicos para sus áreas.

Los estudiantes analizan las obras de arte de los demás para identificar y describir las áreas de los rectángulos de la actividad anterior.

Los estudiantes participan en un recorrido por la galería y luego reflexionan sobre las conexiones entre las matemáticas que aprendieron a lo largo de la unidad y la actividad de arte.

Abordar:

• Cinco en una fila: Multiplicación (3-5). Etapa 2: Factores 1-9

Apoyo:

• Fracción secreta (3). Etapa 1: Construcción de fracciones no unitarias

Grado 4 . Matemáticas . Unidad 1

CALENTAMIENTO | OBSERVA Y PREGUNTARSE: EL

ARTE DE PIET MONDRIAN

(10 minutos)

Rutinas didácticas

Observa y preguntarse

El objetivo de esta tarea es presentar a los estudiantes la obra de arte de Piet Mondrian. Los estudiantes se darán cuenta de que sus cuadros están compuestos por rectángulos de varios tamaños. Los estudiantes crearán sus propias versiones del arte de Mondrian en la primera actividad.

Para mostrar a los estudiantes otras obras de arte de Mondrian, considere la posibilidad de visitar una instalación virtual de la obra de Piet Mondrian en el sitio web del Museo de Arte Moderno (MoMA) o visitar el sitio web de la Tate Gallery.

• Grupos de 2

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Muestra las imágenes.

• «¿Qué observas? ¿Qué te llama la atención?».

• 1 minuto: Tiempo para pensar en silencio

• «Comenta lo que has pensado con tu compañero».

• 1 minuto: Debate entre compañeros

• Comparte y anota las respuestas.

¿Qué te llama la atención? ¿Qué se preguntan?

Los estudiantes pueden notar:

• Muchos rectángulos.

• Los rectángulos son todos de diferentes tamaños.

• Las pinturas no eran de nada.

• Solo hay 3 o 4 colores.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

• Hay líneas negras alrededor de todos los rectángulos.

El estudiante puede preguntarse:

• ¿Alguno de los rectángulos es del mismo tamaño?

• ¿Cuál es el área de los rectángulos blancos?

• ¿Qué colores llenan más espacio en los cuadros?

• «Éstas son copias digitales de cuadros famosos de un artista holandés llamado Piet Mondrian. Vivió desde 1872 hasta 1944. Hace poco más de 100 años, se hizo conocido por pintar en un estilo que se relaciona con las matemáticas que hemos estado estudiando. Muchos de sus cuadros están expuestos en museos de todo el mundo».

Grado 4 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

CONTINUACIÓN

• «¿Qué relación crees que tiene su arte con lo que hemos estado estudiando? ¿Por qué lo estamos viendo durante la clase de matemáticas?». (Utiliza muchos rectángulos. Su obra parece muy precisa. Parecía haber planeado que los rectángulos tuvieran ciertas longitudes de lado).

• Si los estudiantes no lo mencionan, destaque que algunas de las líneas van de borde a borde del cuadro mientras que otras son más cortas, y que algunos rectángulos parecen tener la misma área.

• Considere mostrar a los estudiantes otras obras de Mondrian.

ACTIVIDAD DE EXPLORACIÓN | MI ESQUEMA

MONDRIAN (20 minutos)

Materiales a Reunir

Lápices de colores, crayones o marcadores, reglas o bordes rectos

Materiales a Copiar

Papel cuadriculado en centímetro: Estándar (grupos de 2)

Preparación Requerida

Cada estudiante necesitará un marcador negro o crayón.

El objetivo de esta actividad es que los estudiantes creen un esquema para su obra de arte. En esta actividad, los estudiantes dibujan líneas en papel cuadriculado, marcando áreas rectangulares que serán la base de su obra de arte inspirada en Mondrian.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Compruebe la comprensión invitando a los estudiantes a reformular las Instruccióncon sus propias palabras. Mantener una muestra de los cuadros de Mondrian visible durante toda la actividad.

Apoya la accesibilidad para: Memoria, organización

• «Vamos a crear nuestras propias obras de arte inspiradas en la obra de Mondrian».

• Lea el enunciado de la actividad en clase.

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

• Seleccione a un estudiante para que explique la tarea con sus propias palabras. Invite a la clase a hacer preguntas aclaratorias.

• Entregue a los estudiantes una copia del patrón de líneas negras, una regla y marcadores negroso lápices de colores.

• «Utiliza la regla y el lápiz para dividir tu cuadrícula. Intenta al menos uno de los retos».

• «Una vez que estés satisfecho con tu diseño, trázalo con un marcador negro o un crayón».

• 13-15 minutos): Tiempo de trabajo independiente

• Supervisa a los estudiantes que intenten o logren uno o más de los retos.

Crea un esquema de arte al estilo Mondrian, comenzando con una cuadrícula 18 por 24

Tu obra de arte debe:

• estar dividida en al menos 12 rectángulos

• incluir dos rectángulos diferentes que tengan la misma área

• incluir al menos un rectángulo cuya área sea un número primo

Intenta al menos uno de estos desafíos. Haz un diseño en el que:

• todos menos dos de los rectángulos tengan un número primo para su área

• no haya dos rectángulos que compartan un lado por completo

RESPUESTAS POSIBLES Las respuestas varían.

Math Nation California . Grado 4

Grado 4 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

• «Compara tu trabajo con un compañero. ¿En qué se parecen o en qué se diferencian vuestros esquemas?». (Son parecidos porque solo muestran rectángulos, pero la forma en que están dispuestos y sus tamaños son diferentes).

• «¿Cómo puedes determinar si alguno de los rectángulos tiene la misma área?». (Observa si los lados son pares de factores del mismo número. Usa las longitudes de los lados y multiplícalas para ver si el producto es el mismo número).

ACTIVIDAD DE EXPLORACIÓN | ANALIZAR LOS RECTÁNGULOS (20 minutos)

Materiales a reunir

Lápices de colores, crayones o marcadores, pegamento o cinta adhesiva, notas adhesivas

En esta actividad, los estudiantes utilizan sus conocimientos sobre pares de factores, números primos y compuestos para analizar las ilustraciones de sus compañeros. Buscan rectángulos que tengan la misma área y aquellos que tengan un número primo o un número compuesto para su área. Los estudiantes practican la comunicación con precisión a medida que identifican los rectángulos y cómo saben que los rectángulos cumplen estas condiciones (MP6).

Después de que los estudiantes compartan sus análisis con su compañero y de un breve debate en clase, déles tiempo para colorear sus obras de arte y prepararlas para exponerlas.

Apoyo para los estudiantes que aprenden inglés

MLR8 Apoyos para el debate. Síntesis: Muestre los siguientes fragmentos de oraciones para apoyar la discusión de toda la clase: «Para encontrar rectángulos con la misma área busqué..». «Para encontrar rectángulos con un área que es primo, busqué..»., y «Para encontrar rectángulos con un área que es compuesta, busqué..».

Avances: Hablar, representar

INSTRUCCIÓN

ACTIVIDAD

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• Grupos de 2

• «Cambia de ilustración con tu compañero».

• «Observa el trabajo de tu compañero e intenta encontrar tres tipos de rectángulos: rectángulos con la misma área, rectángulos con un área que sea un número primo y rectángulos con un área que sea un número compuesto».

• «Luego, si su compañero completó un desafío de la primera actividad, vea cuál hicieron».

• 5-7 minutos: Tiempo de trabajo independiente

• 2-3 minutos: Debate en pareja

• Monitoree a los estudiantes que consideran pares de factores de un número mientras buscan rectángulos con la misma área en la obra de arte de su compañero.

Intercambia ilustraciones con tu compañero.

Utilizando las ilustraciones de tu compañero, busca y describe cada uno de los siguientes elementos:

1. Rectángulos que tienen la misma área

2. Rectángulos con un área que es un número primo

3. Rectángulos con un área que es un número primo

4. Qué reto completaron

Grado 4 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Ejemplos de respuestas:

1. Hay un rectángulo que mide 3 unidades por 10 unidades y otro que mide 6 unidades por 5 unidades. El área de ambos es 30 unidades cuadradas.

2. Hay un rectángulo que es 11 unidades por 1 unidad. El área es 11 unidades cuadradas.

3. Hay muchos rectángulos con un número compuesto para el área: 18 unidades cuadradas, 12 unidades cuadradas, 21 unidades cuadradas y más.

4. No hay dos rectángulos que compartan un lado por completo.

• Invite a 1-2 estudiantes previamente seleccionados a compartir cómo encontraron rectángulos con la misma área. (Los lados son pares de factores del mismo número).

• «Ahora, tómate un momento para colorear tu obra de arte con 3-4 colores. Más tarde, expondrás tu trabajo para que lo vean los demás».

• Entregue a los estudiantes lápices de colores, ceras o marcadores.

• 8-10 minutos: Tiempo de trabajo independiente

• Entregue a los estudiantes los materiales necesarios para el recorrido por la galería: pegamento o cinta adhesiva para exponer sus obras de arte y notas adhesivas para escribir comentarios o preguntas.

SÍNTESIS DE LA LECCIÓN

(10 minutos)

Pida a los estudiantes que expongan sus obras de arte para que todos las vean.

«Ahora van a dar una vuelta y mirar las obras de arte que ha hecho la clase. Mientras lo hacen, piensen en las preguntas que podrían hacer a los artistas sobre su diseño. Elige al menos una obra de arte y escribe una pregunta sobre ella en una nota adhesiva».

5-6 minutos: Paseo por la galería

Observa si hay preguntas relacionadas con la intención del artista o con las matemáticas en el diseño. Invite a un par de estudiantes a los que se dirijan esas preguntas a responder sobre su obra de arte.

«Hoy has tenido la oportunidad de crear una obra de arte y exponerla como en una galería de arte».

«¿Cuál ha sido la parte más difícil de crear la obra de arte?». (Yo estaba limitado a utilizar solo rectángulos. Tenía que asegurarme de que dos rectángulos tuvieran la misma área).

«¿Qué conexiones ves entre las matemáticas y el arte que hemos experimentado hoy?». (El arte que hicimos utiliza rectángulos. Podemos utilizar la multiplicación para averiguar si las áreas son iguales o diferentes. Teníamos los mismos requisitos, pero nuestro arte era diferente porque elegimos diferentes longitudes de lado).

Reflexiones:

Math Nation California . Grado 4