Issuu

POR ACCELERATE LEARNING

Grado 5

Muestra de la edición para el maestro

Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).

La plataforma de recursos curriculares en línea que se ofrece en "mathnation.com", incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.

La marca comercial "Math Nation" es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.

Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.

UNIDAD 1 HALLAR EL VOLUMEN

NARRATIVA DE LA UNIDAD

Objetivos de aprendizaje de la unidad

• Los estudiantes hallan el volumen de prismas rectangulares rectos y de figuras sólidas compuestas por dos prismas rectangulares rectos.

Esta unidad introduce a los estudiantes al concepto de volumen basándose en su comprensión del área y la multiplicación.

En tercer grado, los estudiantes aprendieron que el área de una figura bidimensional es el número de unidades cuadradas que la cubren sin huecos ni superposiciones. Primero hallaron las áreas contando cuadrados y empezaron a intuir que el área es aditiva. Más tarde, reconocen que el área de un rectángulo es el producto de las longitudes de sus lados y calculan el área de figuras más complejas compuestas por rectángulos.

Aquí, los estudiantes aprenden que el volumen de una figura sólida es el número de cubos unitarios que la llenan sin huecos ni superposiciones. En primer lugar, miden el volumen contando cubos unitarios y observan su naturaleza aditiva. También aprenden que diferentes figuras sólidas pueden tener el mismo volumen.

A continuación, se centran en los prismas rectangulares: los construyen utilizando cubos unitarios, analizan su estructura y calculan su volumen. Escriben expresiones numéricas para representar sus estrategias de razonamiento y trabajan con representaciones cada vez más abstractas de los prismas.

Más adelante, los estudiantes generalizan que el volumen de un prisma rectangular puede hallarse multiplicando las medidas de sus lados (longitud × anchura × altura), o multiplicando el área de la base y su altura (área de la base × altura). A medida que analizan, escriben y evalúan diferentes expresiones que representan el volumen del mismo prisma, los estudiantes revisan propiedades familiares de operaciones de grados anteriores.

Más adelante en la unidad, los estudiantes aplican estos conocimientos para encontrar el volumen de figuras sólidas compuestas por dos prismas rectangulares no superpuestos y resolver problemas del mundo real que involucran tales figuras. Al hacerlo, también pasan de utilizar cubos a utilizar unidades estándar para medir el volumen.

Grado 5 . Matemáticas . Unidad 1

Sección A: Cubos unitarios y volumen

Alineación de estándares

Abordar

• 5.MD.3a

• 5.MD.3b

• 5.MD.4

• 5.MD.5a

• 5.OA.2

Sección: Objetivos de aprendizaje

• Describir el volumen como el espacio que ocupa un objeto sólido.

• Medir el volumen de un prisma rectangular hallando el número de cubos unitarios necesarios para llenarlo.

• Utilizar la estructura en capas de un prisma rectangular para hallar el volumen.

En esta sección, los estudiantes dan sentido al volumen como medida de figuras tridimensionales construyendo objetos con cubos unitarios y contando los cubos. Experimentan con diferentes figuras hechas con el mismo número de cubos y consideran que tienen el mismo volumen.

A continuación, los estudiantes construyen prismas rectangulares rectos y analizan imágenes de prismas construidos con cubos unitarios. Para hallar el volumen de estos sólidos, los estudiantes observan su estructura y relacionan el número de capas horizontales y verticales con el número total de cubos (MP7). Se comprometen con las propiedades conmutativas y asociativas de la multiplicación a medida que razonan sobre el volumen de prismas rectangulares que están orientados de diferentes maneras.

PLC: Lección 4, Actividad 1, Capas en prismas rectangulares

Sección B: Expresiones para hallar el volumen

Alineación con estándares

Abordar

• 5.MD.4

• 5.MD.5a

• 5.MD.5b

• 5.OA.1

• 5.OA.2

Sección: Objetivos de aprendizaje

• Describir los cálculos de la sección anterior como longitud × anchura × altura o área de la base × altura

• Hallar el volumen usando longitud × anchura × altura o área de la base × altura

En este apartado, los estudiantes siguen trabajando con prismas rectangulares y relacionando las medidas de los lados con el volumen. Observan que multiplicando el número de capas de cubos de un prisma por el número de cubos de una capa se obtiene su volumen. También ven que el número de cubos de una capa es, en esencia, el área de un rectángulo.

A continuación, los estudiantes generalizan el volumen de un prisma rectangular recto como el producto de las longitudes de sus lados, longitud × anchura × altura y como el producto del área de su base y su altura, área de la base × altura

Grado 5 . Matemáticas . Unidad 1

Para promover el uso flexible de las medidas y el sentido común a la hora de hallar el volumen, los estudiantes conectan estos términos matemáticos con expresiones numéricas que representan el volumen, en lugar de basarse en fórmulas algebraicas. Este trabajo refuerza la propiedad asociativa de la multiplicación y destaca que el volumen de un prisma rectangular puede representarse con expresiones de multiplicación equivalentes.

PLC: Lección 5, Actividad 2, Prisma en crecimiento

Sección C: Volumen de figuras sólidas

Alineación de estándares

Abordar

• 5.MD.5a

• 5.MD.5b

• 5.MD.5c

• 5.OA.1

• 5.OA.2

Sección: Objetivos de aprendizaje

• Hallar el volumen de una figura compuesta por prismas rectangulares.

En esta sección, los estudiantes aplican su comprensión del volumen para resolver problemas matemáticos y del mundo real. Se encuentran con figuras sólidas compuestas por dos o más prismas rectangulares rectos, lo que refuerza su comprensión de la naturaleza aditiva del volumen. Los estudiantes también exploran las relaciones multiplicativas en contextos geométricos. Analizan la relación entre las longitudes laterales y los perímetros de los cuadriláteros, realizando conversiones de unidades.

Los estudiantes también trabajan con longitudes laterales mayores que las de secciones anteriores, lo que les lleva a activar estrategias de multiplicación de grados anteriores. El trabajo recuerda a los estudiantes que pueden descomponer factores de varios dígitos por valor posicional para encontrar su producto, allanando el camino hacia el algoritmo estándar para la multiplicación en una unidad posterior.

PLC: Lección 10, Actividad 2, Hallar el volumen de diferentes maneras

Días estimados: 11-12

IDEAS FUNDAMENTALES Y ESTÁNDARES

Enfoque en ideas fundamentales

• Capas de cubos

• Modelado

• Factores y grupos

• Ver división

ESTÁNDARES POR LECCIÓN

Lección

5.1.1

5.1.2

Estándar(es) abordado(s)

5.MD.3a, 5.MD.3b

5.MD.3a, 5.MD.3b, 5.MD.4

5.1.3 5.MD.4

5.1.4

5.MD.5a, 5.OA.2

5.1.5 5.MD.5b

5.1.6

5.MD.5a, 5.MD.5b, 5.OA.1, 5.OA.2

5.1.7 5.MD.4

5.1.8 5.MD.5c

5.1.9

5.1.10

5.1.11

5.1.12

5.MD.5c, 5.OA.2

5.MD.5c, 5.OA.1, 5.OA.2

5.MD.5a, 5.MD.5b, 5.MD.5c

5.MD.5a, 5.MD.5c

IDEAS FUNDAMENTALES

• Capas de cubos

• Ver la división

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

5.MD.3a Se dice que un cubo con una longitud lateral de 1 unidad, llamado "cubo unitario", tiene "una unidad cúbica" de volumen, y se puede utilizar para medir el volumen.

5.MD.3b Se dice que una figura sólida que se puede empaquetar sin huecos ni solapamientos utilizando n cubos unitarios tiene un volumen de n unidades cúbicas.

Enfocar SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP5 Utilizar estratégicamente las herramientas adecuadas.

MP6 Atender a la precisión.

Estándares ELD de California

I.B.5

I.C.11

II.B.5

LECCIÓN 1

¿QUÉ ES EL VOLUMEN?

ENFOQUE EN LAS IDEAS

FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

utilizar estratégicamente las herramientas adecuadas y construir argumentos viables y criticar el razonamiento de los demás

OBJETIVO(S) DE APRENDIZAJE

desmontar enteros, unir piezas y descubrir la forma y el espacio.

• Puedo comparar el tamaño de objetos hechos con cubos unitarios conectados.

OBJETIVOS DE APRENDIZAJE

PARA EL MAESTO

• Explora el volumen construyendo objetos con cubos unitarios y comparándolos.

PREGUNTA DE REFLEXIÓN PARA EL MAESTO

¿Quién ha participado hoy en clase de matemáticas? ¿Qué suposiciones estás haciendo sobre los que no participaron? ¿Cómo puedes aprovechar las ideas de cada uno de tus estudiantes para ayudarles a ser vistos y escuchados en la clase de matemáticas de mañana?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

¿Cuál no pertenece?

(Calentamiento)

Materiales para copiar

Estándar de papel de puntos isométricos: Actividad 2

Materiales a Reunir

Conectando cubos: Actividad 2

Preparación necesaria

Actividad 2:

Cada grupo de 2 necesita 24 cubos de conexión.

Disponga de copias de papel de puntos centimétricos para los estudiantes que quieran intentar dibujar sus objetos.

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Construyamos y comparemos objetos hechos de cubos.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes comprendan que los objetos sólidos tienen atributos medibles. El volumen es uno de estos atributos y se define como la cantidad de espacio que ocupa un objeto.

En grados anteriores, los estudiantes aprendieron que pueden contar el número de fichas cuadradas que cubren una forma plana sin huecos ni superposiciones para hallar el área de la forma. En esta lección, los estudiantes exploran el concepto de volumen mientras construyen y comparan objetos hechos con cubos. Los estudiantes aprenden que los objetos pueden tener formas diferentes pero ocupar la misma cantidad de espacio y que llamamos a esta cantidad el volumen de un objeto.

En la siguiente lección, los estudiantes aprenden que el volumen se mide en unidades cúbicas y utilizan cubos unitarios para hallar el volumen de diferentes objetos. Este trabajo construye una comprensión conceptual del volumen antes de la introducción de formas formales de calcular el volumen de prismas rectangulares.

En las lecciones con imágenes de objetos formados por cubos, los estudiantes pueden preguntarse si a los objetos les faltan cubos que no pueden ver. En estos casos, diga a los estudiantes que asuman que los objetos, incluidos los prismas, están completamente llenos de cubos.

Considere la posibilidad de dar un paseo por la comunidad y fijarse en los edificios y objetos que tienen forma de prismas rectangulares en la comunidad en la que viven sus estudiantes. En futuras lecciones, puede exponer una lista de estos edificios y objetos y pedir a los estudiantes que la completen.

Comunidad matemática

Prepare un espacio, como un trozo de papel de póster, titulado "Comunidad matemática" y un gráfico en forma de T con los encabezamientos "Haciendo matemáticas" y "Normas". Divide cada una de las columnas en dos secciones: estudiantes y maesto. Las dos secciones animan a los estudiantes y al maesto a ser conscientes de que ambas partes son responsables de la forma en que se hacen las matemáticas en el aula.

Comunidad matemática

Haciendo matemáticas

Estudiantes

Normas

Estudiantes

Maesto Maesto

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Breve descripción

Calentamiento Pares 10 min

Actividad de exploración 1 Pares 15 min

Math Nation California - Grado 5

Los estudiantes observan las diferencias entre las figuras tridimensionales hechas de cubos unitarios.

Los estudiantes comparan las imágenes de un par de figuras tridimensionales hechas de cubos unitarios y explican cuál es más grande.

Grado 5 . Matemáticas . Unidad 1

RESUMEN DE LA LECCIÓN CONTINUACIÓN

Componente de la lección Estructura Tiempo

Actividad de exploración 2 Grupos pequeños 20 min

Síntesis Grupo completo 10 min

Enfriamiento Independiente 5 min

Prácticas Grupos pequeños Opcional

Breve descripción

Los estudiantes construyen objetos en 3-D utilizando cubos de conexión con volúmenes similares y diferentes.

Los estudiantes explican cómo comparar objetos 3-D con formas diferentes pero igual volumen.

Los estudiantes determinan qué objeto 3-D mostrado usando cubos unitarios tiene mayor volumen.

Abordar:

• ¿Puedes construirlo? (3-5), Etapa 3: Prismas rectangulares

Apoyo:

• ¿Puedes construirlo? (3-5), Etapa 2: Rectángulos múltiples

• Capturar cuadrados (1-3), Multiplicar con 6-9

CALENTAMIENTO | ¿CUÁL NO PERTENECE? OBJETOS HECHOS

Rutinas instructivas

¿Cuál no pertenece?

DE CUBOS

10 minutos

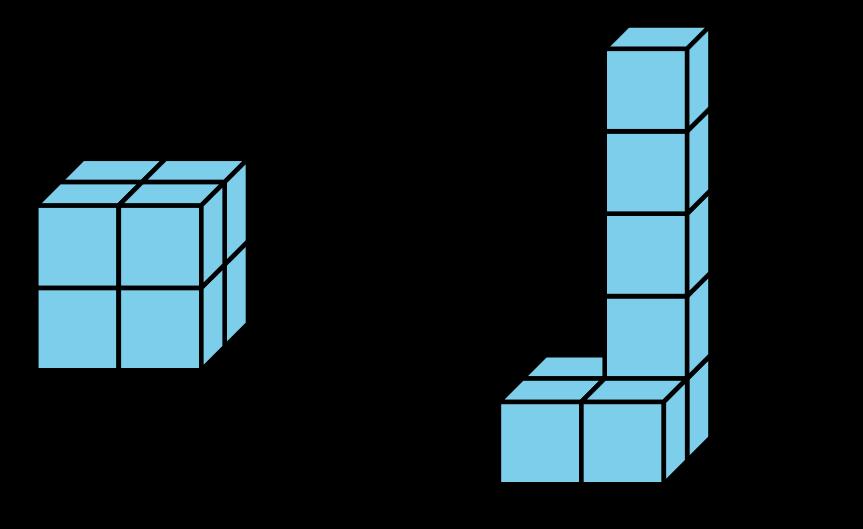
El objetivo de este calentamiento es que los estudiantes comparen cuatro objetos hechos de cubos y razonen sobre su configuración. Las respuestas relacionadas con la orientación del objeto y el número de cubos de cada uno serán aplicables a las actividades siguientes.

Para todas las rutinas de calentamiento, considere la posibilidad de establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con el razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, o una señal sutil diferente. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se precipiten al levantar las manos por toda la clase.

Comunidad matemática

• Después del calentamiento, pide a los estudiantes que reflexionen sobre las acciones individuales y de grupo mientras se plantean la pregunta "¿Qué aspecto tiene y qué sonido tiene hacer matemáticas juntos como una comunidad matemática? ¿Qué hago yo? ¿Qué haces tú?"

• Registra y muestra sus respuestas bajo el encabezamiento "Hacer matemáticas". Los estudiantes podrían mencionar cosas como: hablamos entre nosotros y con el maesto; tuvimos tiempo tranquilo para pensar; compartimos nuestras ideas; pensamos en las ideas y palabras matemáticas que sabíamos; estabas escribiendo nuestras respuestas; estabas esperando hasta que diéramos las respuestas.

• Grupos de 2

• Mostrar imagen

INSTRUCCIONES

ACTIVIDAD

• "Elige uno que no pertenezca. Prepárate para compartir por qué no pertenece."

• 1 minuto: tiempo para pensar en silencio

• 2-3 minutos: discusión por parejas

• Comparte y anota las respuestas.

Nation California - Grade 5

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

SÍNTESIS DE LA ACTIVIDAD

¿Cuál no pertenece?

Ejemplos de respuestas:

Grado 5 . Matemáticas . Unidad 1

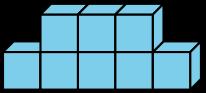
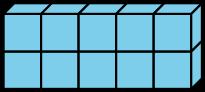
• A es el único que no tiene 1 capa de cubos.

• B es el único que no tiene el mismo número de cubos en cada fila.

• C es el único que no tiene 2 cubos de altura.

• D es el único que no tiene 8 cubos.

• "¿Qué tienen en común los objetos A, C y D?" (Cada lado o cara de las formas es un rectángulo. Todas están hechas de cubos del mismo tamaño).

ACTIVIDAD DE EXPLORACIÓN | CONSTRUIR OBJETOS

CON

CUBOS

15 minutos

El propósito de esta actividad es que los estudiantes reconozcan que los objetos con el mismo volumen ocupan la misma cantidad de espacio. La palabra más grande es intencionadamente vaga para suscitar ideas sobre longitud, anchura y altura y animar a los estudiantes a razonar sobre el número de cubos.

Preste atención al lenguaje que utilizan los estudiantes para explicar sus elecciones, como más largo, más ancho, más alto o referencia al número de cubos. Los estudiantes pueden optar por utilizar cubos de conexión para construir los objetos con el fin de comparar y aclarar sus argumentos (MP5). A medida que los estudiantes discuten y justifican sus decisiones, tienen la oportunidad de crear argumentos viables y criticar el razonamiento de los demás (MP3). La discusión y comparación de los argumentos de los estudiantes ayuda a ilustrar la necesidad de un vocabulario matemático preciso y prepara a los estudiantes para aprender el significado de volumen (MP6).

Apoyo para estudiantes de inglés

MLR2 Recoger y mostrar. Recopilar y registrar el lenguaje que utilizan los estudiantes para comparar objetos. Mostrar palabras y frases como: "más grande", "más largo", "más ancho", "más alto", "más bajo", "cuántos", "más que", "menos que".

Durante la síntesis, invite a los estudiantes a sugerir formas de actualizar la pantalla.

Avances: Escuchar, hablar

California - Grado 5

Grado 5 . Matemáticas . Unidad 1

INSTRUCCIONES

ACTIVIDAD

• Grupos de 2

• "Ahora compararéis objetos para determinar cuál es más grande, incluyendo algunos del calentamiento."

• 5 minutos: tiempo de trabajo individual

• 5 minutos: tiempo de trabajo en pareja

• Mientras los estudiantes trabajan, vigile a los estudiantes que hablan de "más grande" en términos del número de cubos.

1. ¿Cuál es más grande?

¿Cuál es más grande? Explica o muestra tu razonamiento. A.

2. ¿Cuál es mayor?

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

SÍNTESIS DE LA ACTIVIDAD

¿Cuál es más grande? Explica o muestra tu razonamiento. A.

3. ¿Cuál es más grande?

¿Qué significa que un objeto sea "más grande"?

1. A es más ancho, pero ambos tienen el mismo tamaño. A es más ancho, pero tienen la misma cantidad de cubos.

2. B es más alto, pero tienen la misma cantidad de cubos.

3. Tiene más cubos.

• Comparte las respuestas para ambos problemas. Anima a los estudiantes que elijan diferentes opciones a que expliquen su razonamiento.

• Muestre la primera pareja de objetos.

• "¿Cómo describirías la cantidad de espacio que ocupa cada objeto?" (Es la misma para ambas formas. Están hechas de 8 cubos individuales.)

• "Llamamos a la cantidad de espacio que ocupa un objeto su volumen."

• Muestra el segundo par de objetos.

• "¿Qué objeto tiene mayor volumen?" (Son iguales. Ambos están hechos de 8 cubos.)

• "¿En qué se diferencian los dos objetos?" (Uno es un cubo y el otro no. Uno es más alto que el otro).

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | CONSTRUIR Y ORDENAR

Materiales para reunir

Cubos de conexión

10 minutos

Materiales para copiar

Preparación necesaria

Papel de puntos isométricos Estándar Cada grupo de 2 necesita 24 cubos de conexión.

Tenga copias de papel de puntos centimétricos disponibles para los estudiantes que quieran intentar dibujar sus objetos.

El propósito de esta actividad es que los estudiantes construyan objetos sólidos y los comparen por su volumen. Los estudiantes cuentan el número de cubos de cada objeto y pueden reconocer que la forma y la orientación del objeto no importan a la hora de comparar volúmenes. Anime a los estudiantes a construir cualquier objeto en el que se conecten los cubos, no sólo prismas rectangulares.

Si disponen de tiempo extra, los estudiantes podrían intentar dibujar sus objetos en papel de puntos (patrón de líneas negras). No se espera que los estudiantes usen el papel de puntos, pero a algunos les puede gustar intentar representar sus objetos con él.

Apoyo a los estudiantes con discapacidad

Representación: Acceso para la percepción. Lea las instrucciones en voz alta. Los estudiantes que escuchan y leen a la vez la información se beneficiarán de un tiempo de procesamiento adicional.

Apoya la accesibilidad para: Lenguaje, Atención

• Grupos de 4

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Entrega a cada grupo una pila de cubos de conexión.

• 10 minutos: tiempo de trabajo en grupo

• Mientras los estudiantes trabajan, recoge los objetos de un grupo que tengan todos un volumen de 9 unidades pero que tengan diferentes disposiciones.

1. Cada miembro del grupo:A. Coge un puñado de cubos de conexión. B. Construye un objeto. Cada miembro del grupo:

A. Coge un puñado de cubos de conexión.

B. Construye un objeto.

2. Ordena los objetos por volumen.

3. Repite.

4. Cada miembro del grupo:

A. Toma 9 cubos de conexión.

B. Construye un objeto.

5. Ordena los objetos por volumen. Ordenar los objetos por volumen

POSIBLES RESPUESTAS

Math Nation California - Grado 5

1 y 2: Ejemplos de respuestas. Los estudiantes pueden construir algunos objetos con el mismo volumen o todos 4 los objetos pueden tener volúmenes diferentes.

4 y 5: Todos los objetos tienen el mismo volumen, pero pueden tener formas diferentes.

Grado 5 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

• Muestre 3 o 4 objetos construidos con 9 cubos.

• "¿Qué es igual? ¿Qué es diferente?" (Algunos de los objetos son más altos, otros más bajos. Algunos objetos son más anchos. Todos están hechos con 9 cubos).

• "¿Cómo se comparan los volúmenes de estos objetos? ¿Cómo lo sabes?" (Todos son iguales porque cada objeto ocupa la misma cantidad de espacio o tiene el mismo número de cubos.)

• "¿Cuánto espacio ocupa cada objeto?" (9 cubos)

SÍNTESIS DE LA LECCIÓN

10 minutos

"Hoy hemos construido objetos con cubos y los hemos comparado por la cantidad de espacio que ocupan. A esto lo llamamos volumen de un objeto".

Muestra las imágenes de la actividad o los objetos hechos con cubos.

"¿En qué se parecen los dos objetos?". (Ambos están hechos de 8 cubos. Hay cuatro cubos uno al lado del otro en la capa inferior.)

"¿En qué se diferencian los dos objetos?" (Uno de ellos es un cubo y el otro parece una torre. Uno de ellos es más alto que el otro.)

"Estos dos objetos parecen diferentes, pero ocupan la misma cantidad de espacio, es decir, tienen el mismo volumen."

Comunidad matemática

Después del enfriamiento, vuelve a revisar la lista de acciones "Haciendo matemáticas". Pide a los estudiantes que discutan con un compañero dónde vieron evidencias de las acciones durante el resto de la lección del día. En grupo, añade las acciones que falten y revisa las ideas anteriores.

ENFRIAMIENTO | ¿QUÉ TIENE MÁS VOLUMEN?

5 minutos

¿Qué objeto tiene un volumen mayor? Explica o muestra tu razonamiento.

ENUNCIADO DE LA TAREA

POSIBLES

RESPUESTASS

A. B.

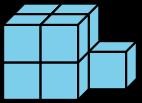
B, está hecho de 9 cubos y A está hecho de 8 cubos.

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

IDEAS FUNDAMENTALES

• Capas de cubos

• Modelado

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

5.MD.3a Se dice que un cubo con longitud lateral de 1 unidad, llamado "cubo unitario", tiene "una unidad cúbica" de volumen, y puede usarse para medir el volumen.

5.MD.3b Se dice que una figura sólida que se puede empaquetar sin huecos ni solapamientos utilizando n cubos unitarios tiene un volumen de n unidades cúbicas.

5.MD.4 Mide volúmenes contando cubos unitarios, usando cm cúbicos, pulg cúbicos, pies cúbicos y unidades improvisadas

Enfocar SMPs

MP6 Atiende a la precisión.

MP7 Busca y hace uso de la estructura.

Estándares CA ELD

I.A.1

I.A.4

II.C.6

LECCIÓN 2

MEDIR EL VOLUMEN

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

dar sentido al mundo y predecir lo que podría ocurrir buscar y hacer uso de la estructura explorar cantidades cambiantes y descubrir sha pe y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo determinar el volumen de figuras tridimensionales utilizando cubos unitarios.

• Puedo describir y construir un prisma rectangular utilizando cubos unitarios.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTO

• Encontrar el volumen de figuras sólidas, incluyendo prismas rectangulares, en cubos unitarios, de una manera que tenga sentido para ellos.

• Entender que el volumen se mide en cubos unitarios.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

¿Qué entendían los estudiantes sobre el volumen de los objetos sólidos al comenzar la lección? ¿De qué manera cambió su comprensión del volumen al finalizar la lección?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

¿Cuál no pertenece? (Calentamiento)

MLR2 Recoger y exponer (Actividad 2)

Materiales a reunir

Cubos de conexión

Preparación necesaria

Actividad 1:

Cada grupo de 2 necesita 24 cubos de conexión.

Actividad 2:

Cada grupo de 2 necesita 16-24 cubos de conexión.

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Contemos cubos.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes comprendan que el volumen es la cantidad de cubos unitarios que llenan un espacio.

Los estudiantes son introducidos a prismas rectangulares mientras comienzan a usar informalmente la estructura de los prismas rectangulares para encontrar el número de cubos en el prisma. En grados anteriores, los estudiantes aprendieron a medir el área contando cuadrados unitarios, descompusieron una región rectangular en filas y columnas y multiplicaron el número de cuadrados unitarios de una fila por el número de filas o el número de cuadrados unitarios de una columna por el número de columnas. Del mismo modo, en esta lección, los estudiantes aprovechan la estructura en capas de un prisma rectangular para contar los cubos de una forma más sistemática (MP7). Los estudiantes tendrán muchas oportunidades de contar el número de cubos en prismas rectangulares en las lecciones 3 y 4 antes de la introducción de fórmulas en la lección 5.

Math Community

Diga a los estudiantes que tendrán la oportunidad de revisar sus ideas de "Comunidad matemática" al final de esta lección, por lo que mientras trabajan hoy deben pensar en las acciones que pueden faltar en la lista actual.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Parejas 10 min

Actividad de exploración 1 Parejas 15 min

Actividad de exploración 2 En parejas 20 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Prácticas Grupos pequeños Opcional

Breve descripción

Los estudiantes explican a qué figura tridimensional de cubos unitarios apilados no pertenecen.

Los estudiantes construyen objetos tridimensionales utilizando cubos unitarios basándose en las descripciones dadas para desarrollar estrategias sobre cómo contar eficientemente el número de cubos de cada objeto.

Los estudiantes utilizan la definición de prisma rectangular para construir y describir prismas utilizando cubos unitarios.

Los estudiantes discuten cómo describir prismas rectangulares y cómo medir su volumen utilizando cubos unitarios.

Los estudiantes determinan el volumen de un prisma rectangular en términos de cubos unitarios.

Abordar:

• ¿Puedes construirlo? (3-5), Etapa 3: Prismas rectangulares

Apoyo:

• ¿Puedes construirlo? (3-5), Etapa 2: Rectángulos múltiples

• Capturar cuadrados (1-3), Etapa 7. Multiplicar con 6-9 Multiplica con 6-9

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | ¿CUÁL NO PERTENECE? CUBOS 10

minutos

Rutinas instructivas

¿Cuál no pertenece?

El objetivo de este calentamiento es que los estudiantes comparen objetos sólidos. Los estudiantes pueden utilizar un lenguaje informal para describir la estructura y la orientación de los objetos. Más adelante, los estudiantes tendrán la oportunidad de relacionar su lenguaje informal con un vocabulario matemático más formal. Durante la síntesis, conecta las descripciones de los objetos por parte de los estudiantes con las estrategias que utilizarían para contar el número de cubos de cada objeto. Da a los estudiantes una razón para utilizar el lenguaje con precisión (MP6). Da al maesto la oportunidad de escuchar cómo los estudiantes utilizan la terminología al describir la estructura y la orientación de los objetos tridimensionales. Durante la síntesis, pide a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como volumen.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Grupos de 2

• Muestra la imagen.

• "Elige uno que no pertenezca. Prepárense para compartir por qué no pertenece."

• 1 minuto: tiempo para pensar en silencio

• 2-3 minutos: discusión en parejas

• Compartir y registrar las respuestas.

¿Cuál no pertenece?

POSIBLES RESPUESTAS

SÍNTESIS DE LA ACTIVIDAD

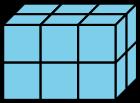
• A no pertenece porque es el único que no es un solo objeto.

• B no pertenece porque es el único que no usa 12 cubos.

• C no pertenece porque es el único que no tiene 2 cubos de profundidad.

• D no pertenece porque es el único que no tiene 3 cubos de altura.

• "Podemos contar el número de cubos unitarios que hay en un objeto para medir su volumen."

• "¿Cuántos cubos hay en el objeto D? ¿Cómo los has contado?" (12, hay 6 en la parte inferior y 6 en la parte superior)

• "¿Qué estrategia utilizarías para contar los cubos de los otros objetos?" (En objeto A, también puedo ver 2 grupos de 6. En el objeto B, puedo ver 2 grupos de 6 menos 1. En el objeto C, sólo hay un grupo de 6 y luego hay 4 cubos y 2 cubos).

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | ENCONTRAR EL VOLUMEN

15 minutos

Preparación requerida

Cada grupo de 2 necesita 24 cubos de conexión.

El propósito de esta actividad es que los estudiantes construyan cualquier objeto que deseen. En la siguiente actividad, los estudiantes se centrarán únicamente en los prismas rectangulares. Cuando los estudiantes cuenten, tendrán que asegurarse de contar cada cubo una y sólo una vez. Controle estas estrategias:

• Toque cada cubo mientras lo cuenta

• Cuente los cubos por capa (incluso cuando haya diferentes números de cubos en cada capa)

• Use la suma o la multiplicación cuando los cubos estén organizados en capas

• Grupos de 2

• Entregar 24 cubos de conexión a cada grupo.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

• "En esta actividad, utilizarán cubos unitarios para construir objetos y describir cómo medirían el volumen"

• 10 minutos: tiempo de trabajo en parejas

• Mientras los estudiantes trabajan, controle si hay estudiantes que construyen prismas rectangulares para compartir durante la síntesis.

1. Pareja A: Construye un objeto utilizando . Compañero A: Construye un objeto usando entrega el objeto al Compañero B.

2. Compañero B: Explica cómo construirías un prisma rectangular. contarías el número de cubos en el objeto.

3. Compañero A: Explica si contarías los cubos en la misma manera o de una manera diferente.

4. Cambia los papeles y repite.

5. ¿Qué objetos fueron más fáciles de contar? ¿Por qué?

SÍNTESIS DE LA ACTIVIDAD

Math Nation California - Grado 5

5. Los que tenían estructura como capas, filas iguales o columnas iguales fueron los más fáciles de contar porque no tuve que contar cada cubo individualmente.

Si los estudiantes están contando todos los cubos de a uno por vez, pregunte: "¿dónde ven cubos que podrían contarse como un grupo?"

• Discuta las respuestas al último problema.

• "¿Cuáles fueron los objetos más difíciles de contar?" (Objetos en los que tenía que contar cada cubo individualmente porque tenía una forma rara.)

• "¿Qué objetos eran los más sencillos de contar?" (Formas organizadas como torres, rectángulos, cubos o cajas.)

• Invite a los estudiantes seleccionados a compartir los prismas rectangulares que construyeron y cómo contaron el número de cubos.

• "¿Cómo contaste los cubos?" (Sabía que había 4 cubos en cada capa y 2 capas así que eso es 8 cubos.)

• "Llamamos a estos objetos prismas rectangulares. ¿Cuáles fueron algunas de las formas que utilizaste para contar los cubos en prismas rectangulares?" (Conté los cubos en grupos y luego salté la cuenta. Utilicé la multiplicación para hallar el total).

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | ADIVINA MI

PRISMA

Rutinas instructivas

MLR2 Collect and Display

20 minutos

Preparación necesaria

Cada grupo de 2 necesita 16-24 cubos de conexión.

En la actividad anterior, los estudiantes describieron cómo contar el número de cubos unitarios de un objeto y observaron que, en el caso de una forma especial llamada prisma rectangular, los cubos están organizados en una estructura que hace que contarlos sea más sistemático. El objetivo de esta actividad es que los estudiantes sigan explorando los prismas rectangulares, en particular su estructura. A medida que los estudiantes describen los prismas, comunican sus ideas con claridad y precisión (MP6). Describir un objeto requiere que los estudiantes identifiquen las características clave del objeto y las comuniquen de forma inequívoca a su compañero.

Esta actividad utiliza MLR2 Recoger y mostrar. Avances: lectura, escritura

Apoyo a los estudiantes con discapacidad

Representación: Interiorizar la Comprensión. Utiliza múltiples ejemplos y no ejemplos para enfatizar los atributos de un prisma rectangular identificado en la actividad anterior.

Apoya la accesibilidad para: Memoria, Procesamiento Conceptual INSTRUCCIONES

• Grupos de 2

• Visualización de imágenes.

• "¿Qué es lo mismo? ¿Qué es diferente?" (Hay 6 cubos de cada forma. Cada objeto mide 2 cubos de ancho y 3 cubos de largo. Un objeto está de pie sobre un lado de 2 cubos y el otro está tumbado sobre un lado de 6 cubos.)

• "En esta actividad, construirás y describirás prismas rectangulares."

• Entrega a cada estudiante 16-24 cubos de conexión.

• Considere la posibilidad de sentar a los estudiantes espalda con espalda o con un objeto entre ellos que obstruya la vista, como una carpeta.

MLR2 Recoger y mostrar

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Circule, escuche y recoja el lenguaje que los estudiantes utilizan para comparar cantidades. Escuche: capas, filas, columnas, longitud, anchura, altura, arriba, abajo o lado.

• Registre las palabras y frases de los estudiantes en una pantalla visual y actualícela durante el resto de la lección.

¿Qué es lo mismo? ¿Qué es diferente?

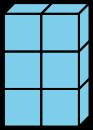
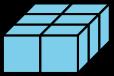
1. El objetivo del juego es conseguir que tu compañero construya el mismo prisma.

• Compañero A: Utiliza 16-24 cubos para construir un prisma. Descríbelo a tu compañero.

• Compañero B: Construye el prisma que te describe tu compañero.

2. Coloca los dos prismas uno al lado del otro y discute qué tienen de igual y de diferente.

3. Cambia los papeles y repite.

Grado 5 . Matemáticas . Unidad 1

Ejemplos de respuestas:

1. El socio A construye:

El compañero A describe: "He utilizado 12 cubos para construir mi prisma. Tiene 2 capas. Cada capa tiene 6 cubos".

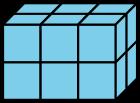
POSIBLES RESPUESTASS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

El compañero B construye:

2. ¿Qué es lo mismo en sus prismas?

• Ambos prismas tienen 12 cubos.

• Ambos prismas tienen 2 capas con 6 cubos en cada capa.

• Ambos prismas tienen 3 capas con 4 cubos en cada capa.

¿En qué se diferencian? El mío era más alto y el de mi compañero más largo.

Si los estudiantes no ven que dos prismas son iguales cuando están orientados de forma diferente, pídales que describan un prisma, cambie la orientación del prisma y pídales que vuelvan a describirlo. Haga hincapié en que el número total de cubos sigue siendo el mismo, pero el prisma tiene un aspecto diferente.

• Invita a los compañeros que construyeron prismas diferentes a compartir sus prismas y descripciones.

• "¿Qué lenguaje utilizó tu compañero que te resultó más útil para entender el prisma que querían que construyeras?" (Mi compañero dijo que había 6 cubos en la parte inferior y 6 más en la parte superior. Así que hice una fila de 6 cubos y puse otra fila encima. Pero mi compañero tenía dos filas de 3 en lugar de una fila de 6.)

SÍNTESIS DE LA ACTIVIDAD

• Utiliza esta discusión para actualizar la visualización, añadiendo (o eliminando) lenguaje, diagramas o anotaciones.

• Invita a los grupos que construyeron los mismos prismas a compartir.

• "¿Cómo describiste tu prisma a tu compañero?"(Yo dije cuántos cubos había en el fondo y qué altura tenía el prisma).

• Utilice este debate para actualizar la presentación, añadiendo (o eliminando) lenguaje, diagramas o anotaciones.

• Muestre cualquier prisma que haya hecho un estudiante.

• "¿Cómo podemos describir este prisma utilizando el lenguaje de nuestra presentación?". (Destaque el uso de lenguaje sobre capas o pilas).

SÍNTESIS DE LA LECCIÓN

10 minutos

"Hoy hemos descrito prismas rectangulares y medido sus volúmenes".

Pida a un estudiante que no haya compartido en actividades anteriores que muestre un prisma que haya construido.

Pregunte a la clase: "¿Cómo podemos hallar el volumen de este prisma rectangular?". (Encuentre el número de cubos en una capa y multiplique ese número por cuántas capas hay.)

"¿Cómo podemos describir este prisma rectangular para que nuestro compañero pueda construir el mismo?" (Describe los cubos de la parte inferior y cuántas capas hay.)

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

Comunidad Matemática

Después del enfriamiento, dé a los estudiantes 2-3 minutos para discutir cualquier revisión a las acciones de "Haciendo Matemáticas" en pequeños grupos. Comparta las ideas con todo el grupo y registre las revisiones.

ENFRIAMIENTO | VOLUMEN DE UN PRISMA

RECTANGULAR 5 minutos

Encuentre el volumen del prisma rectangular. Explica o muestra tu razonamiento.

ENUNCIADO DE LA TAREA

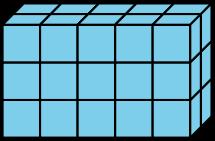
POSIBLES RESPUESTAS • El volumen es 30 cubos. Ejemplos de respuestas: 5 × 6 = 30, 5 × 3 = 15 y 15 × 2 = 30, o 3 × 2 = 6 y 6 × 5 = 30

Reflexiones:

Nation California - Grade 5

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

LECCIÓN 3

IDEAS FUNDAMENTALES

• Capas de cubos

• Modelado

ALINEACIÓN

Alineación de estándares y principios de California

Abordando

5.MD.4 Mide volúmenes contando cubos de unidades, usando cm cúbicos, pulg cúbicos, pies cúbicos y unidades improvisadas.

Construyendo Sobre

3.OA.7

Construyendo Hacia

5.MD.5

Enfocar SMPs

MP2 Razonar abstracta y cuantitativamente.

MP7 Buscar y hacer uso de la estructura.

Estándares CA ELD

I.A.4

I.C.10 II.A.1

VOLÚMENES DE DIBUJOS DE PRISMAS

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

dan sentido al mundo y predicen lo que podría ocurrir

razonan abstracta y cuantitativamente exploran cantidades cambiantes y descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo utilizar las capas de cubos de un prisma rectangular para hallar su volumen.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTO

• Hallar el volumen de un prisma rectangular utilizando su estructura en capas.

PREGUNTA PARA LA REFLEXIÓN

DEL MAESTO

¿Qué conexiones establecieron los estudiantes entre las distintas estrategias que utilizaron para construir los prismas y determinar el volumen? ¿Qué preguntas hiciste para ayudar a que las conexiones fueran más visibles?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

Hablar de números (Calentamiento)

Materiales para reunir

Conectar cubos: Actividad 1, Actividad 2

Materiales para copiar

Clasificar tarjetas Prisma rectangular: Actividad 1

Materiales necesarios

Actividad 1:

Cada uno Crea un conjunto de tarjetas del patrón de líneas negras para cada grupo de 4

Cada grupo de 2 necesita 48 cubos de conexión.

Actividad 2:

Da a los estudiantes acceso a los cubos de conexión.

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Usemos capas para encontrar el volumen.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes encuentren el volumen de un prisma rectangular usando su estructura en capas. Información de la lección

En lecciones anteriores, los estudiantes construyeron objetos, incluyendo prismas rectangulares, con cubos unitarios y contaron el número de cubos. En esta lección, los estudiantes siguen contando el número de cubos unitarios necesarios para construir un prisma rectangular, pero ahora se les presentan imágenes de prismas en lugar de los propios objetos. Para animar a los estudiantes a desarrollar una forma sistemática de contar los cubos, se les muestran prismas formados por un mayor número de cubos. A medida que los estudiantes utilizan capas horizontales o verticales para medir el volumen, hacen uso de la estructura en capas de los prismas (MP7).

Comunidad Matemática

Diga a los estudiantes que, al final de la lección, se les pedirá que identifiquen acciones específicas de su lista "Haciendo matemáticas" (tanto de la sección del maesto como de la del estudiante) que hayan experimentado personalmente.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 10 min

Actividad de exploración 1

En parejas 20 min

Actividad de exploración 2 En parejas 15 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Prácticas Grupos pequeños Opcional

Breve descripción

Los estudiantes evalúan expresiones numéricas mentalmente.

Los estudiantes usan cubos unitarios para construir y encontrar el volumen de prismas rectangulares mostrados en imágenes de una clasificación de tarjetas.

Los estudiantes relacionan las capas de cubos unitarios de un prisma rectangular con el volumen del prisma.

Los estudiantes discuten e identifican estrategias para determinar el volumen de prismas formados por cubos.

Los estudiantes seleccionan una imagen de un prisma rectangular hecho de cubos utilizando una descripción escrita y luego encuentran su volumen.

Abordar:

• ¿Puedes construirlo? (3-5), Etapa 3: Prismas rectangulares

Apoyo:

• Cinco en raya: Multiplicación (3-5), Etapa 3: Factores de dos cifras

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | CHARLA SOBRE NÚMEROS: MULTIPLICACIÓN

10 minutos

Rutinas instructivas

Charla sobre números

El propósito de esta Charla sobre números es que los estudiantes multipliquen tres factores. Las estrategias para multiplicar tres factores serán útiles cuando los estudiantes encuentren el volumen de prismas rectangulares en esta lección y en las lecciones siguientes. Como el primer problema es sólo 2 factores, no es importante reunir múltiples estrategias para dejar más tiempo para los otros problemas. Los estudiantes pueden relacionar el tercer factor de los tres últimos problemas con "añadir otra capa de cubos" en un prisma al hallar el volumen. Invite a estos estudiantes a compartir sus observaciones durante la síntesis.

• Muestre un problema.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

SÍNTESIS DE LA ACTIVIDAD

• "Háganme una señal cuando tengan una respuesta y puedan explicar cómo la obtuvieron."

• 1 minuto: tiempo de pensamiento individual

• Registrar respuestas y estrategia.

• Mantener expresiones y trabajo desplegados.

• Repetir con cada expresión

Encontrar mentalmente el valor de cada expresión.

• 6 × 4

• 3 × 2 × 4

• 3 × 2 × 5

• 3 × 2 × 6

• 24: Simplemente lo sé, 6 × 2 = 12 y 12 × 2 = 24

• 24: Es igual a la primera, pero en lugar de 6 dice 3 × 2

• 30: 6 × 5 = 30, 10 × 3 = 30

• 36: Acabo de añadir otro 3 × 2 o 6, 6 × 6 = 36

• "¿Cómo afectó al producto el cambio de uno de los factores?" (El aumento de uno de los factores hizo que el producto aumentara en 6.)

• Considere preguntar:

• "¿En qué se parecen los problemas 2-4 al trabajo que hicimos ayer con los prismas?"

• "¿Quién puede replantear 'el razonamiento de otra manera?"

• "¿Alguien tuvo la misma estrategia pero la explicaría de otra manera?"

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | CONSTRUIR PRISMAS

RECTANGULARES 20 minutos

Materiales para reunir

Cubos conectores

Materiales para copiar

Clasificación de tarjetas Tarjetas de prismas rectangulares

Preparación necesaria

Crea un conjunto de tarjetas a partir del patrón de líneas negras para cada grupo de 4

Cada grupo de 2 necesita 48 cubos conectores.

El propósito de esta actividad es que los estudiantes construyan y determinen el volumen de prismas rectangulares a partir de imágenes. En la síntesis de la actividad, los estudiantes observan dos prismas relacionados para alentarlos a pensar en 8 cubos como una capa.

Apoyo para estudiantes de inglés

MLR8 Apoyos de discusión. Durante la discusión en pequeños grupos, invite a los estudiantes a compartir sus respuestas por turnos. Pida a los estudiantes que repitan lo que han oído utilizando un lenguaje matemático preciso y sus propias palabras. Muestre el marco de frases: "Te he oído decir...". Los interlocutores originales pueden estar de acuerdo o aclarar para su compañero.

Avances: Escuchar, hablar

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

Math Nation California - Grado 5

• Grupos de 2

• Dar a los estudiantes acceso a los cubos de conexión.

• "Vais a construir los prismas rectangulares que aparecen en las tarjetas. Antes de mirar las tarjetas, ¿qué información de la imagen os ayudará a construir el prisma?" (El número de cubos en cada capa y el número de capas.)

• Comparte las respuestas.

• "Ahora, cada uno elegirá una tarjeta, construirá el prisma y hallará su volumen. Expliquen a su compañero cómo encontraron el volumen y luego elijan otra tarjeta."

• Observe si los estudiantes discuten:

• cuántos cubos hay en cada capa.

• cómo están dispuestos los cubos en cada capa.

• cuántas capas hay en el prisma.

• Comunidad matemática: Mientras los estudiantes trabajan, monitoree si hay ejemplos de las acciones "Haciendo Matemáticas".

Los prismas de las tarjetas están completamente llenos de cubos unitarios.

1. Escoge una tarjeta. Escoge una tarjeta.

2. Construye el prisma rectangular.

3. Halla el volumen. Explica a tu compañero cómo has hallado el volumen

4. Repite.

Grado 5 . Matemáticas . Unidad 1

RESPUESTAS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

Algunos estudiantes pueden seguir contando cada cubo individual para determinar el volumen del prisma. Pregunte: "¿Cuántos cubos hay en cada capa? ¿Cuántas capas hay?"

• Mostrar Tarjeta E

• "¿Cómo construiste este prisma rectangular?" (Conté 8 cubos y luego hice una pila de 8 cubos.)

SÍNTESIS DE LA ACTIVIDAD

• "¿Cuál es el volumen de este prisma rectangular? ¿Cómo lo sabes?" (8 cubos porque conté 8 cubos.)

• Muestra la tarjeta A

• "¿Cómo construiste este prisma rectangular?" (Vi que hay 8 cubos arriba y abajo en 2 filas de 4. Luego lo construí hasta que tuvo 3 cubos de alto.)

• "¿Cuál es el volumen de este prisma rectangular? ¿Cómo lo sabes?" (24 cubos porque hay 3 conjuntos de 8 cubos y 3 × 8 - 24)

ACTIVIDAD DE EXPLORACIÓN | CAPAS, CAPAS Y MÁS CAPAS

15 minutos

Materiales para reunir

Cubos para conectar

Preparación necesaria

Da a los estudiantes acceso a cubos para conectar.

El propósito de esta actividad es que los estudiantes encuentren el volumen de prismas rectangulares más grandes mostrados en imágenes. En lecciones anteriores, los estudiantes construyeron prismas rectangulares con cubos y contaron los cubos para determinar el volumen de los prismas rectangulares. En esta actividad, los prismas se eligieron intencionadamente para animar a los estudiantes a utilizar la estructura en capas del prisma para determinar su volumen (MP7). Cuando los estudiantes conectan esta estructura con la operación de multiplicación y utilizan expresiones y ecuaciones para hallar el volumen, descontextualizan la estructura geométrica para resolver los problemas (MP2).

Apoyo a los estudiantes con discapacidad

Representar el compromiso: Desarrollar el Esfuerzo y la Persistencia. Invite a los estudiantes a identificar correspondencias entre la representación visual y el prisma formado por cubos de conexión. Haz visibles las conexiones entre las representaciones mediante gestos o etiquetados.

Apoya la accesibilidad para: Procesamiento visual-espacial, Procesamiento conceptual

Grado 5 . Matemáticas . Unidad 1

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Grupos de 2

• Muestra el primer prisma.

• "¿Cómo describirías este prisma?" (Hay 5 capas y cada capa tiene 8 cubos o hay 2 capas y cada capa tiene 20 cubos en ella.)

• Dar a los estudiantes acceso a los cubos de conexión.

• 10 minutos: tiempo de trabajo independiente

• 2 minutos: discusión por parejas

• Supervise a los estudiantes que utilizan la estructura de capas para determinar el volumen.

Los prismas están completamente llenos de cubos unitarios. Determine el volumen de cada prisma. Explique o muestre su razonamiento.

POSIBLES RESPUESTAS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD

1. 40 cubos: 5 × 4 × 2, 20 × 2, 8 × 5

2. 60 cubos: 20 × 3, 15 × 4

3. prismas:

80 cubos: 20 × 4, 16 × 5

Si los estudiantes no se dan cuenta de que cada prisma tiene una capa más de 20 cubos, plantéate preguntar: "¿Qué hay de igual en cada uno de estos prismas? ¿Qué es diferente?"

• Invita a los estudiantes a compartir cómo encontraron el volumen de los prismas rectangulares.

• Muestra la imagen del primer prisma.

• "La expresión 5 × 8 representa el volumen del prisma. ¿Dónde ves 5 grupos de 8 cubos en este prisma?" (La parte superior e inferior son 2 por 4 por lo que hay 8 cubos en la parte superior e inferior. Hay 5 de esas capas por lo que es 5 × 8.)

• "¿Qué tienen en común estos prismas rectangulares?" (Todos tienen 5 cubos de altura. Todos se pueden dividir en 5 capas o grupos iguales. También todos tienen un lado que mide 4 cubos de largo. Todos pueden romperse en capas con 20 cubos.)

• Si el tiempo lo permite, pregunte: "¿Quién vio las capas de forma diferente?". (Para el primer prisma, utilicé la capa lateral de 10 cubos. Multipliqué 10 por 4 capas para obtener 40.)

SÍNTESIS DE LA LECCIÓN

10 minutos

Tema de debate o de diario: "¿Qué sabes sobre cómo hallar el volumen de un prisma formado por cubos después de las actividades de hoy? ¿Hay algo sobre lo que tengas preguntas?"

Comparte las respuestas o lee los diarios después de clase.

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

Comunidad matemática

• Después del enfriamiento, pide a los estudiantes que reflexionen individualmente sobre la pregunta "¿Qué acción de "Hacer matemáticas" te ha parecido más importante en tu trabajo de hoy y por qué?". Pida a los estudiantes que escriban sus respuestas en la parte inferior de su papel "Cool-down", en una hoja aparte o en un diario de matemáticas.

• Recoja y lea sus respuestas después de clase. Estas respuestas le darán una idea de cómo se sienten los estudiantes acerca de su propio trabajo matemático y le ayudarán a establecer conexiones personales con las normas que crearán durante los días 4-6

ENFRIAMIENTO | EL PRISMA DE JADA

5 minutos

El prisma de Jada tiene 4 capas y cada capa tiene 9 cubos.

1. Encierra en un círculo el prisma que es Jada. Encierra en un círculo el prisma de Jada.

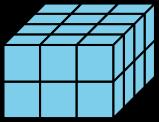
ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

Reflejos:

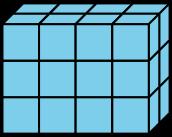
2. Halla el volumen del prisma de Jada. Explica o muestra tu razonamiento.

1. Encierra en un círculo el prisma de Jada. B

2. 36 cubos. Hay 4 capas con 9 cubos en cada capa por lo que hay 36 cubos, 4 × 9 = 36

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

LECCIÓN 4

IDEAS FUNDAMENTALES

• Factores y grupos

• Capas de cubos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

5.MD.5a Hallar el volumen de un prisma rectangular recto con longitudes laterales de números enteros empaquetándolo con cubos unitarios, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de las aristas, equivalentemente multiplicando la altura por el área de la base. Representar productos de tres números enteros como volúmenes.

5.OA.2 Escribir expresiones sencillas que registren cálculos con números, e interpretar expresiones numéricas sin evaluarlas.

Enfocar SMPs

MP2 Razonar abstracta y cuantitativamente.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP4 Modelar con matemáticas.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.3

I.B.5 I.C.11

UTILIZAR CAPAS PARA DETERMINAR EL VOLUMEN

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

dar sentido al mundo y predecir lo que podría ocurrir

construir argumentos viables y criticar el razonamiento de otros y buscar y hacer uso de la estructura

OBJETIVO(S) DE APRENDIZAJE

explorar cantidades cambiantes y descubrir la forma y el espacio.

• Puedo utilizar capas de cubos en un prisma rectangular para explicar expresiones de volumen y multiplicación.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTO

• Describir y representar el volumen de un prisma rectangular como el producto del número de cubos en una capa y el número de capas.

• Escribir e interpretar expresiones y ecuaciones en el contexto del volumen de prismas rectangulares.

PREGUNTA

PARA LA REFLEXIÓN DEL MAESTO

Mientras los estudiantes compartían sus ideas hoy, ¿cómo te aseguraste de que las voces de todos los estudiantes fueran escuchadas y valoradas como una parte importante del aprendizaje colectivo?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

Exploración de la estimación (Calentamiento)

Materiales a reunir

Cubos de conexión: Actividad 1, Actividad 2

Preparación necesaria

Actividad 1:

Disponga de cubos de conexión para los estudiantes que los necesiten.

Actividad 2:

Disponga de cubos de conexión para los estudiantes que los necesiten.

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Relacionemos la multiplicación con la forma en que usamos las capas para encontrar el volumen.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes apliquen su comprensión de la estructura en capas de los prismas rectangulares para encontrar el volumen de un prisma cuando no pueden ver todos los cubos.

En lecciones anteriores, los estudiantes usaron la estructura en capas para determinar el volumen de prismas rectangulares que estaban llenos de cubos. El objetivo de esta lección es ampliar su comprensión de la estructura de los prismas rectangulares conceptualizando una capa base en un prisma rectangular y utilizándola para hallar el volumen en un prisma lleno total o parcialmente. Los estudiantes conectan la estructura en capas con la multiplicación cuando escriben e interpretan expresiones que representan el volumen de prismas rectangulares (MP2, MP7). Esta es una forma conceptual para que los estudiantes den sentido a la propiedad asociativa de la multiplicación. Sin embargo, no es necesario que los estudiantes nombren o identifiquen la propiedad.

Actividad 1: Capas en prismas rectangulares

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Parejas 10 min

Actividad de exploración 1 Parejas 20 min

Actividad de exploración 2 En parejas 15 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Prácticas Parejas o Grupos pequeños Opcional

Breve descripción

Los estudiantes calculan el número de cubos utilizados para construir un prisma que se muestra en una imagen.

Los estudiantes razonan sobre el número de cubos de una capa y la altura de un prisma para determinar su volumen.

Los estudiantes analizan cómo diferentes expresiones de multiplicación representan el volumen de prismas rectangulares formados por cubos apilados.

Los estudiantes explican cómo las capas de un prisma rectangular pueden utilizarse para crear diferentes expresiones de multiplicación para hallar el volumen del prisma.

Los estudiantes aplican su comprensión de las capas de cubos en un prisma rectangular para determinar su volumen y describir cómo una expresión de multiplicación representa el volumen.

Abordar:

• ¿Puedes construirlo? (3-5), Etapa 3: Prismas rectangulares

Apoyo:

• Cinco en raya: Multiplicación (3-5), Etapa 3: Factores de dos cifras

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | EXPLORACIÓN DE ESTIMACIONES: ¿CUÁNTOS CUBOS?

10 minutos

Rutinas instructivas

Exploración de estimaciones

El propósito de este calentamiento es que los estudiantes consideren la información que necesitan para hallar el volumen de un prisma rectangular y utilicen la estructura de un prisma rectangular para pensar en una estimación razonable. Los estudiantes pueden ver los 9 cubos de la capa frontal, pero es difícil ver cuántas capas hay.

El propósito de una Exploración de estimaciones es pensar en lo razonable basándose en la experiencia y en la información conocida. Ofrece a los estudiantes una oportunidad poco arriesgada de compartir una afirmación matemática y el pensamiento que la sustenta (MP3). Hacer una estimación o un rango de respuestas razonables con información incompleta es parte del modelado con matemáticas (MP4).

• Grupos de 2

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Mostrar imagen

• "¿Qué es una estimación demasiado alta?" "¿Demasiado baja?" "¿Más o menos?"

• 1 minuto: tiempo para pensar en silencio

• 1 minuto: discusión en parejas

• Compartir y registrar las respuestas

Aproximadamente, ¿cuántos cubos se utilizaron para construir este prisma?

Registre una estimación que sea:

Demasiado bajo Más o menos correcto

Ejemplos de respuestas:

POSIBLES RESPUESTAS

• demasiado bajo: 30 o menos

• más o menos correcto: 60 a 100

• demasiado alto: 200 a 300

Demasiado alto

Grado 5 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

• "¿Por qué los múltiplos de 9 son buenas estimaciones?" (Podemos ver la capa de 9.)

• "¿Qué información te ayudaría a encontrar el número exacto de cubos del prisma?" (Cuántas capas de 9 cubos hay. Qué profundidad tiene el prisma.)

• "Basándose en esta discusión, ¿alguien quiere revisar su estimación?"

• Opcional: Muestre un dibujo que muestre el número de capas, 10.

Comunidad matemática

• Pida a los estudiantes que reflexionen sobre las acciones individuales y de grupo mientras consideran la pregunta "¿Qué normas, o expectativas, teníamos en cuenta mientras hacíamos matemáticas juntos en nuestra comunidad matemática?"

• Registre y muestre sus respuestas bajo el encabezado "Normas".

ACTIVIDAD DE EXPLORACIÓN | CAPAS EN PRISMAS RECTANGULARES

20 minutos

Materiales para reunir

Cubos para conectar

Preparación necesaria

Tenga cubos para conectar disponibles para los estudiantes que los necesiten.

En la lección anterior, los estudiantes razonaron de forma abstracta sobre el volumen de los prismas rectangulares cuando consideraron el volumen en términos de capas o grupos iguales de cubos unitarios. Esta actividad continúa desarrollando la idea de descomponer los prismas rectangulares en capas. Los estudiantes multiplican explícitamente el número de cubos de una capa base por el número de capas. Los estudiantes pueden utilizar cualquier capa del prisma como capa base siempre que la altura sea el número de esas capas base.

Apoyo a los estudiantes con discapacidad

Acción y Expresión: Interiorizar las Funciones Ejecutivas. Síntesis: Invite a los estudiantes a planificar una estrategia, incluyendo las herramientas que utilizarán, para encontrar el volumen de prismas parcialmente llenos. Si el tiempo lo permite, invite a los estudiantes a compartir su plan con un compañero antes de empezar.

Apoya la accesibilidad para: Procesamiento conceptual, Memoria

Math

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Grupos de 2

• Mostrar la primera imagen del cuaderno de trabajo del estudiante

• "¿Qué sabes sobre el volumen de este prisma?"

• "¿Qué necesitarías averiguar para encontrar el volumen exacto de este prisma?"

• "En esta actividad vas a trabajar con prismas que sólo están parcialmente llenos"."

• Dé a los estudiantes acceso a los cubos de conexión.

• 5 minutos: tiempo de trabajo independiente

• 5 minutos: tiempo de trabajo en pareja

• Mientras los estudiantes trabajan, observe:

• estudiantes que se dan cuenta de que los prismas A y D y los prismas B y C son "iguales" pero están asentados sobre caras diferentes, por lo que las capas podrían contarse de formas diferentes.

• estudiantes que razonan sobre los prismas parcialmente llenos refiriéndose a los cubos de una capa que verían si se mostraran todos los cubos.

• estudiantes que reconocen que hay varias capas diferentes que pueden utilizar para determinar el volumen de un prisma, y que todas ellas dan como resultado el mismo volumen.

1. Completa la tabla. Prepárate para explicar tu razonamiento.

Prisma Número de cubos en una capa Número de capas Volumen

Prisma A

Prisma B

Prisma C

Prisma D

Grado 5 . Matemáticas . Unidad 1

2. Halla el volumen de cada prisma. Explica o muestra tu razonamiento.

Prisma D

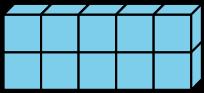
ENUNCIADO DE LA TAREA CONTINUACIÓN

POSIBLES RESPUESTAS

SÍNTESIS DE ACTIVIDAD

Math Nation California - Grado 5

Prisma F

3. ¿Cómo puedes encontrar el volumen de cualquier prisma rectangular?

Prisma Número de cubos en una capa

Número de capas Volumen

A 6, 8, o 12 4, 3, o 2 24 cubos

B 15, 6, o 10 2, 5, o 3 30 cubos

C 6, 15, o 10 5, 2, o 3 30 cubos

D 8, 6, o 12 3, 4, o 2 24 cubos

2. Prisma E: 10 cubos. 2 × 5 = 10

Prisma F: 84 cubos. Hay 2 columnas de 6 (o 6 filas de 2) en una capa vertical. Hay 7 capas, es decir, 2 × 6 × 7. Hay 14 cubos en una capa horizontal. Hay 6 capas en total, es decir, 6 × 14. Hay 7 columnas de 6 en una capa y puedo multiplicar eso por las 2 capas, es decir, 7 × 6 × 2.

3. Multiplica la cantidad de cubos en una capa por la altura con esa capa como base.

• Mostrar las expresiones:

• 2 × 12

• 3 × 8

• ¿Cómo representan estas expresiones el volumen del prisma A? (Hay dos capas de 12. También podemos ver tres capas de 8).

• ¿Cómo nos ayuda pensar en capas a encontrar el volumen de los prismas que no están completamente llenos? (Sé que todas las capas tienen el mismo número de cubos, aunque no se muestren).

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | ENCONTRAR EL VOLUMEN DE DIFERENTES

Materiales a reunir

Cubos conectores

MANERAS

20 minutos

Preparación requerida

Tenga cubos conectores disponibles para los estudiantes que los necesiten.

En la actividad anterior, los estudiantes vieron que un prisma rectangular está compuesto de capas y que hay diferentes maneras de descomponer un prisma en capas, dependiendo de cómo los estudiantes vean el prisma y descompongan el prisma. Los estudiantes reconocen que el volumen sigue siendo el mismo, independientemente de la orientación del prisma. El objetivo de esta actividad es que los estudiantes identifiquen cómo diferentes expresiones representan el volumen de un mismo prisma y se corresponden con la organización de las capas. Los estudiantes han trabajado con paréntesis en grados anteriores, por lo que la síntesis de la lección proporciona una oportunidad para que los estudiantes revisen las expresiones con paréntesis. Los estudiantes tendrán más experiencia con la evaluación de expresiones con símbolos de agrupación en lecciones futuras. Los estudiantes van y vienen entre expresiones numéricas y un objeto geométrico cuyo volumen está representado por la expresión (MP2).

Apoyo para estudiantes de inglés

MLR7 Comparar y conectar. Síntesis: Preguntar: "¿qué hay de igual y de diferente en las estrategias utilizadas para calcular el volumen del prisma rectangular?". Añadir etiquetas o anotaciones a una pantalla visible para apoyar las conexiones entre enfoques, y para amplificar lenguaje como capas, horizontal, vertical, volumen y expresión.

Avances: Representar, conversar

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Grupos de 2

• "Vais a analizar diferentes formas de hallar el volumen de un prisma rectangular."

• Dar a los estudiantes acceso a los cubos de conexión.

• 5 minutos: tiempo de trabajo independiente

• 5 minutos: tiempo de trabajo en grupo

• Monitoree a los estudiantes que identifican el factor 5 o 6 como el número de capas y el segundo factor es entonces el número de cubos en cada capa.

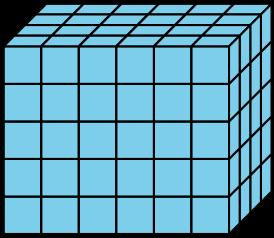
1. Explica o muestra cómo la expresión 5 × 24 representa el volumen de este prisma rectangular.

2. Explica o muestra cómo la expresión 6 × 20 representa el volumen de este prisma rectangular.

3. 3. Encuentra otra forma de calcular el volumen de este prisma rectangular. Explica o muestra tu razonamiento.

4. Escribe una expresión que represente la forma en que calculaste el volumen.

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTASS

AVANZAR EN EL PENSAMIENTO DEL ESTUDIANTE

SÍNTESIS DE LA ACTIVIDAD

• La expresión muestra 5 capas horizontales de cubos en el prisma. Hay 24 o 6 × 4 cubos en cada capa, lo que hace 5 × 24 cubos en el prisma.

• La expresión muestra 6 capas verticales de cubos en el prisma. Cada capa tiene 4 × 5 o 20 cubos en ella, lo que hace 6 × 20 cubos en el prisma.

• Respuesta de ejemplo: 4 × 30 porque hay 4 capas y cada capa tiene 30 cubos

• Respuesta de ejemplo: 4 × 30

Si los estudiantes no explican cómo la expresión representa el volumen del prisma, pregunte: "¿Puedes explicar cómo hallarías el volumen de este prisma?".

A continuación, relacione la descripción del estudiante con los números de las expresiones.

• "¿Cómo 5 × 24 representa el volumen del prisma?" (Hay 5 capas si corto el prisma horizontalmente y cada capa tiene 24 cubos en ella.)

• Muestra la expresión: 5 × (4 × 6)

• "¿Cómo representa esta expresión el volumen del prisma?" (Muestra las 5 capas y los 24 cubos como 4 filas de 6 cubos en cada capa.)

• "¿Cómo representa 6 × 20 el volumen del prisma?" (Hay 6 capas si corto verticalmente a lo largo de la cara frontal. Cada capa tiene 5 filas de 4 o 20 cubos.)

• Visualiza la expresión: 6 × (4 × 5).

• "¿Cómo representa esta expresión el volumen del prisma?" (Muestra las 6 capas y 4 columnas de 5 cubos en cada capa.)

SÍNTESIS DE LA LECCIÓN

10 minutos

Muestre la imagen del calentamiento que muestra todas las capas del prisma.

"Describe las capas del prisma a un compañero. ¿Cuál es la expresión de multiplicación que representaría el volumen del prisma? ¿Cómo representa la expresión el volumen del prisma?". (10 × 9, hay 9 cubos en cada capa y puedo ver 10 capas.)

Comunidad matemática

Revise la lista de "Normas". Pida a los estudiantes que comenten con un compañero cuándo una norma les resultó útil mientras hacían matemáticas. Agregue cualquier idea que falte o revise las anteriores.

ENFRIAMIENTO | USAR EXPRESIONES

1. Si el prisma rectangular se llenara completamente, ¿cuántos cubos podría contener?

ENUNCIADO DE LA TAREA

Math Nation California - Grado 5

5 minutos

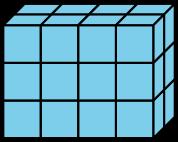
2. Explica o muestra cómo la expresión 3 × 8 representa el volumen del prisma.

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS

1. El volumen es de 60 cubos.

2. Una de las capas tiene 8 cubos en ella y hay 3 de esas capas.

Resumen de la sección del estudiante

Llamamos volumenEl volumen es a la cantidad de espacio que ocupa un objeto. Este prisma tiene un volumen de 120 cubos.

ENUNCIADO DE LA TAREA

Para hallar el volumen de cualquier prisma, podemos hallar el número de cubos en una capa y multiplicar ese número por el número de capas. Podemos describir este prisma como si tuviera

6 capas de 20 cubos, 4 capas de 30 cubos, o 5 capas de 24 cubos. Podemos utilizar todas estas expresiones para representar el volumen del prisma:

5 × 24, 5 × (6 × 4)

6 × 20, 6 × (5 × 4)

4 × 30, 4 × (5 × 6)

Reflexiones:

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

LECCIÓN 5

IDEAS FUNDAMENTALES

• Modelado

• Capas de cubos

• Ver la división

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

5.MD.5b Aplicar las fórmulas �� = �� × �� × h y �� = �� × h para prismas rectangulares para hallar volúmenes de prismas rectangulares rectos con longitudes de arista de números enteros en el contexto de la resolución de problemas matemáticos y del mundo real.

Enfocar SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP2 Razonar abstracta y cuantitativamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.1

I.C.12

II.B.5

LONGITUDES LATERALES DE PRISMAS RECTANGULARES

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . . .

dar sentido al mundo y predecir lo que podría ocurrir

razonar de forma abstracta y cuantitativa

OBJETIVO(S) DE APRENDIZAJE

separar enteros, unir partes y descubrir la forma y el espacio.

• Puedo describir las longitudes de los lados de un prisma rectangular y encontrar su volumen multiplicando el área de la base por la altura.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir prismas rectangulares en términos de sus longitudes de los lados.

• Encontrar el volumen de un prisma rectangular derecho multiplicando las longitudes de los lados y conectarlo con encontrar el volumen multiplicando el área de la base por la altura.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

Mientras los estudiantes trabajaban hoy en sus pequeños grupos, ¿las ideas de quién fueron escuchadas, valoradas y aceptadas? ¿Cómo puedes ajustar la estructura del grupo mañana para garantizar que las ideas de cada estudiante formen parte del aprendizaje colectivo?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

Observa y maravíllate (Calentamiento)

Materiales a reunir

Cubos de conexión: Actividad 1, Actividad 2

Materiales de una actividad anterior

Preparación necesaria

Actividad 1:

Disponga de cubos de conexión para los estudiantes que los necesiten.

Actividad 2:

Disponga de cubos de conexión para los estudiantes que los necesiten.

Grado 5 . Matemáticas . Unidad 1

Objetivos de aprendizaje para el estudiante

• Describamos las longitudes de los lados de un prisma y hallemos su volumen.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes formalicen el lenguaje que utilizan para describir las longitudes de los lados de un prisma rectangular. Información de la lección

En lecciones anteriores, los estudiantes utilizaron la estructura de un prisma rectangular, es decir, las capas, para hallar su volumen. En esta lección, los estudiantes describen el número de capas y el número de cubos de cada capa en función de la longitud, la anchura y la altura del prisma (MP6). Los estudiantes eligen una base para el prisma y reconocen que el número de cubos de cada capa es el producto de la longitud y la anchura de la base elegida. También reconocen que la altura que corresponde a la base elegida representa el número de capas del prisma. Relacionan esta relación con el producto de la longitud, la anchura y la altura de un prisma. Con esta comprensión de cómo hallar el volumen de un prisma rectangular, los estudiantes no siempre necesitan ver los cubos individuales que componen el prisma. El póster de una lección anterior que muestra el lenguaje que los estudiantes utilizaron mientras construían y describían prismas se revisará en esta síntesis de la lección para incluir los términos longitud, anchura, altura y área de una base.

Comunidad matemática

Diga a los estudiantes que, al final de la lección, se les pedirá que identifiquen ejemplos específicos de normas que experimentaron mientras hacían matemáticas.

Actividad 2: Prisma creciente

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Parejas 10 min

Actividad de exploración 1 Parejas 10 min

Actividad de exploración 2 Parejas 15 min

Actividad de Exploración 3 Parejas 10 min

Síntesis Todo el Grupo 10 min

Enfriamiento Independiente 5 min

Prácticas Parejas o Grupos pequeños Opcional

Math Nation California - Grado 5

Breve descripción

Los estudiantes hacen observaciones sobre figuras bidimensionales y tridimensionales hechas con cubos unitarios.

Los estudiantes emparejan prismas con sus bases rectangulares para determinar el volumen de cada figura.

Los estudiantes calculan el volumen de prismas con la base rectangular dada. Hacen conexiones sobre cómo los cambios en la altura afectan al volumen del prisma.

Los estudiantes trabajan hacia atrás para determinar las preguntas que se hacen sobre un prisma rectangular con la base dada.

Los estudiantes discuten la información necesaria para determinar el volumen de un prisma rectangular.

Los estudiantes determinan el volumen de un prisma cuando se les da la base rectangular y la medida de la altura.

Abordar:

• ¿Puedes construirlo? (3-5), Etapa 3: Prismas rectangulares

• Cinco en raya: Multiplicación (3-5), Etapa 4: Tres factores

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | OBSERVA Y MARAVÍLLATE: PRISMA

IMPRIMIR 10 minutos

Rutinas instructivas

Observar y preguntarse

El objetivo de este calentamiento es que los estudiantes se den cuenta de que cada cara de un prisma puede ser la base, lo que será útil cuando los estudiantes utilicen la base de un prisma para hallar el volumen del prisma en una actividad posterior. Aunque los estudiantes pueden observar y preguntarse muchas cosas sobre estas imágenes, la relación entre las imágenes del prisma y las imágenes de los rectángulos son los puntos de discusión importantes.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Tamaño del grupo: 2

• Muestre las imágenes para que todos las vean.

• Pida a los estudiantes que piensen en al menos una cosa que observan y al menos una cosa que se preguntan.

• 1 minuto: tiempo para pensar en silencio

• 2 minuto: discusión por parejas

• Compartir y anotar las respuestas.

¿Qué observas?

¿Qué te preguntas?

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS

SÍNTESIS DE LA ACTIVIDAD

Los estudiantes pueden observar:

• Todos los prismas tienen un volumen de 12 cubos.

• Los prismas coinciden con los rectángulos.

• El prisma de la izquierda mide 2 cubos y lo mismo ocurre con el rectángulo que tiene debajo.

Los estudiantes pueden preguntarse:

• ¿Son todos el mismo prisma?

• ¿Se supone que el prisma se mueve?

• ¿Caben los prismas encima de los rectángulos?

• "Estos rectángulos muestran diferentes caras de los prismas. Cualquier cara de un prisma puede ser una base. Vamos a aprender más sobre esto en las actividades."

• "¿Dónde vemos cada base en el prisma?"

ACTIVIDAD DE EXPLORACIÓN | TODO SOBRE ESA

BASE 10 minutos

Materiales a reunir

Cubos de conexión

Preparación necesaria

Ten cubos de conexión disponibles para los estudiantes que los necesiten.

El objetivo de esta actividad es que los estudiantes reconozcan que la base de un prisma es un rectángulo bidimensional y que cualquier cara de un prisma puede ser una base. Los estudiantes pueden empezar con una posible base rectangular e intentar visualizar qué cara de un prisma dado coincide con la base o pueden empezar con el prisma, estudiar las caras e intentar encontrar una base adecuada que coincida. En cualquier caso, deben perseverar y pensar sistemáticamente en todas las bases posibles de cada prisma para resolver este problema (MP1).

Apoyo a los estudiantes con discapacidad

Engagement: Proporcionar acceso captando el interés. Ofrecer opciones y autonomía. Proporcione acceso a diversas herramientas que puedan utilizarse para resolver el problema. Por ejemplo, se pueden utilizar cubos de conexión para construir los prismas y lápices de colores para sombrear las caras de cada prisma.

Apoya la accesibilidad para: Procesamiento visual-espacial, Procesamiento conceptual

INSTRUCCIONES

ACTIVIDAD

Math Nation California - Grado 5

• Grupos de 2

• Dar a los estudiantes acceso a los cubos de conexión.

• 4 minutos: tiempo de trabajo independiente

• 2 minutos: discusión en parejas

• Monitorear a los estudiantes que:

• Emparejan cada prisma con un rectángulo que representa la base sobre la que el prisma está descansando.

• Reconocer que el 4 por 3 rectángulo representa una base en cada uno de los prismas.

Grado 5 . Matemáticas . Unidad 1

Aquí hay 3 prismas rectangulares. 1 2 3

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD

Estos rectángulos representan las bases de los prismas.

1. Empareja cada prisma con un rectángulo que represente su base. Nota: Algunos prismas pueden coincidir con más de 1 base rectangular.

2. Halla el volumen de cada prisma. Explica o muestra tu razonamiento.

1. El prisma 1 coincide con la base B, el prisma 2 coincide con las bases A y B, el prisma 3 coincide con las bases B y C.

2. Prisma 1 tiene 48 cubos. Ejemplo de respuesta: La base tiene 12 cubos y hay 4 capas.

3. El prisma 2 tiene 72 cubos. Ejemplo de respuesta: La base tiene 18 cubos y hay 4 capas.

El prisma 3 tiene 60 cubos. Ejemplo de respuesta: La base tiene 15 cubos y hay 4 capas.

Si los estudiantes no emparejan correctamente los prismas con las bases, pídales que construyan cada prisma y describan cómo una cara determinada coincide o no con cada base que está representada con los rectángulos A, B y C.

• Invite a los estudiantes previamente identificados a compartir.

• Muestre el trabajo de los estudiantes que muestra que es posible que el rectángulo B sea una base para cualquiera de los prismas.

• "¿Dónde vemos este rectángulo como base en cada prisma?". (Si giramos cada prisma para que descanse sobre la cara que está mirando hacia nosotros, cada prisma descansaría sobre la base B.)

• "Si el prisma 2 descansara sobre la base 4 por 3 , ¿cuántas capas de altura tendría el prisma?" (6 capas)

• "Podemos utilizar la palabra altura para describir lo alto que es un prisma."

• "Si el prisma 3 estuviera apoyado sobre la 4 por 3 base, ¿cuál sería la altura del prisma?" (5 cubos)

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | PRISMA CRECIENTE

15 minutos

Materiales a reunir

Cubos de conexión

Preparación necesaria

Tenga cubos de conexión disponibles para los estudiantes que los necesiten.

El objetivo de esta actividad es que los estudiantes describan la estructura en capas de los prismas rectangulares utilizando las longitudes de los lados del prisma. En lugar de diagramas de prismas rectangulares construidos a partir de cubos, se muestra a los estudiantes un diagrama de una de las bases de un prisma y se les pide que encuentren el volumen del prisma con diferentes alturas. Los estudiantes pueden seguir utilizando un lenguaje informal, como el de las capas, para describir los prismas y hallar su volumen. Durante la síntesis de la lección, conecte su lenguaje informal con el lenguaje matemático más formal de longitud, anchura, altura y área de la base.

Apoyo para estudiantes de inglés

MLR2 Recoger y mostrar. Amplificar palabras y frases como: largo, ancho, más alto, patrón, base, número de capas.

Avances: Conversar, Leer

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Grupos de 2

• Dar a los estudiantes acceso a los cubos de conexión.

• 2 minutos: tiempo de trabajo independiente

• 10 minutos: tiempo de trabajo en pareja

• A medida que los estudiantes trabajan, monitoree a los estudiantes que:

• describen y utilizan las capas del prisma.

• multiplican 40 por la altura del prisma para determinar el volumen de los prismas.

Aquí se muestra la base de un prisma rectangular.

1. Completa la tabla para los volúmenes de prismas rectangulares con esta base y diferentes alturas.

Expresión de multiplicación para Representar el volumen

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

Ejemplos de respuestas: 1.

Altura

POSIBLES RESPUESTAS

Expresión de multiplicación para Representar el volumen

SÍNTESIS DE LA ACTIVIDAD

• Pida a los estudiantes previamente seleccionados que compartan sus soluciones para el primer problema.

• Muestre una tabla completada o utilice la que se da en las soluciones de los estudiantes:

Altura

Expresión de multiplicación para Representar el volumen

25 4 × 10 × 25 o 40 × 25 1,000 cubos

• "¿Cómo cambia el volumen del prisma en la tabla?" (El volumen aumenta en 40 cubos por cada capa que se añade al prisma.)

• "¿Cómo se representa el cambio de volumen en las expresiones de multiplicación de cada fila?" (Las expresiones de cada fila muestran más grupos de 40.)

• Muestra la expresión 3 × 40.

• "¿Cómo representa la expresión el volumen del prisma?" (Hay 40 cubos en la capa base del prisma o 4 filas de 10 cubos. Entonces hay 3 de estas capas.)

ACTIVIDAD DE EXPLORACIÓN | ¿CUÁL ES LA PREGUNTA?

10 minutos

Esta actividad ofrece a los estudiantes la oportunidad de interpretar un cálculo en el contexto de la situación (MP2) cuando se plantea un escenario con una ecuación que muestra soluciones a incógnitas. Los estudiantes tienen que interpretar las ecuaciones y formular la pregunta cuya respuesta se da. Los números se eligen específicamente para incitar a los estudiantes a considerar la estructura de los prismas rectangulares.

INSTRUCCIONES

ACTIVIDAD

• Grupos de 2

• 2 minutos: tiempo de reflexión en silencio

• 4 minutos: tiempo de trabajo en pareja

• Vigilar a los estudiantes que:

• utilicen un lenguaje informal, como capas.

• utilizan los términos longitud, anchura, altura y base en sus preguntas.

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

SÍNTESIS DE ACTIVIDAD

Grado 5 . Matemáticas . Unidad 1

Esta es la base de un prisma rectangular que tiene una altura de 5 cubos.

Estas son respuestas a preguntas sobre el prisma. Lee cada respuesta y determina qué pregunta responde sobre el prisma.

1. 3 es la respuesta. ¿Cuál es la pregunta?

2. 5 es la respuesta. ¿Cuál es la pregunta?

3. 3 × 4 = 12. La respuesta es 12. ¿Cuál es la pregunta?

4. 12 × 5 = 60. La respuesta es 60 cubos. ¿Cuál es la pregunta?

5. 3 x 4 x 5 es la respuesta. ¿Cuál es la pregunta?

1. ¿Cuál es el ancho del prisma?

2. ¿Cuál es la altura del prisma?

3. ¿Cuál es el volumen de una capa de cubos? ¿Cuál es el área de la base?

4. ¿Cuál es el volumen de todo el prisma?

5. ¿Cuáles son la longitud, el ancho y la altura del prisma?

• Pida a los estudiantes previamente seleccionados que compartan sus soluciones.

• Relacione el lenguaje informal con los términos matemáticos longitud, ancho, altura y área de una base.

• "¿Cómo representa la expresión 3 × 4 × 5 el prisma descrito en la segunda pregunta?" (El área de la base es 3 × 4 = 12 y la altura es 5; por lo tanto, 3 × 4 × 5 representa el producto de longitud, ancho y altura).

SÍNTESIS DE LECCIONES

Muestre el póster con el texto de una lección anterior.

10 minutos

"¿Qué información se necesita para medir el volumen de cualquier prisma rectangular?" (Necesitamos saber el área de una base y su altura con esa base, o bien, el largo, el ancho y la altura).

A medida que los estudiantes compartan sus respuestas, actualice el póster añadiendo (o reemplazando) texto, diagramas o anotaciones.

"¿Qué texto podemos añadir a nuestro póster para explicar cómo hallar el volumen de un prisma cuando no podemos ver los cubos?" (Podemos multiplicar el área de la base por la altura. Podemos multiplicar el largo, el ancho y la altura).

"¿Cuál es la relación entre el número de capas y la altura del prisma?" (El número de capas es el número de cubos de altura, o la altura).

Actualice el póster.

Comunidad Matemática

Después de la sesión de enfriamiento, dé a los estudiantes de 2 a 3 minutos para discutir en grupos pequeños las revisiones de la sección "Normas".

Recopile y registre las revisiones.

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

ENFRIAR | DETERMINAR EL VOLUMEN 5

ENUNCIADO DE LA TAREA

minutos

He aquí la base de un prisma rectangular.

¿Cuál es el volumen del prisma si tiene una altura de 3?

POSIBLES RESPUESTAS • 36 cubos

Reflexiones:

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

IDEAS FUNDAMENTALES

• Modelado

• Capas de cubos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

5.MD.5b Aplicar las fórmulas �� = �� × �� × h y �� = �� × h para prismas rectangulares para hallar volúmenes de prismas rectangulares rectángulos con longitudes de arista de números enteros en el contexto de la resolución de problemas matemáticos y del mundo real.

5.OA.1 Utilizar paréntesis, corchetes o llaves en expresiones numéricas y evaluar expresiones con estos símbolos.

5.OA.2 Escribir expresiones simples que registren cálculos con números, e interpretar expresiones numéricas sin evaluarlas.

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.4

I.C.11

II.C.6

LECCIÓN 6

EXPRESIONES DE VOLUMEN

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

dan sentido al mundo e influyen en el futuro buscan y hacen uso de la estructura exploran cantidades cambiantes y descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo escribir expresiones numéricas para representar el volumen de un prisma rectangular.

• Puedo determinar el volumen de un prisma rectangular.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Encontrar el volumen de un prisma rectangular derecho multiplicando las longitudes de los lados y conectar eso con encontrar el volumen multiplicando el área de la base por la altura.

• Escribir e interpretar expresiones numéricas en el contexto del volumen de un prisma rectangular.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

Cuando los estudiantes han emparejado hoy expresiones con imágenes de prismas, ¿qué pruebas has visto de que están ampliando sus conocimientos sobre la estructura de los prismas rectangulares?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

Verdadero o falso (Calentamiento)

Clasificación de tarjetas (Actividad 1)

Materiales para reunir

Cubos para conectar: Actividad 1

Materiales Para copiar

Prismas y expresiones coincidentes: Actividad 1

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Escribamos expresiones para el volumen de prismas rectangulares.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes utilicen su comprensión de la estructura de los prismas rectangulares para encontrar el volumen y escribir expresiones numéricas para representar el volumen.

En una lección anterior los estudiantes aprendieron a encontrar el volumen de un prisma rectangular multiplicando el número de cubos en una capa base por el número de capas. Relacionaron este conocimiento con la multiplicación de la longitud, la anchura y la altura para hallar el volumen. También utilizaron una representación bidimensional de una base y su altura correspondiente para hallar el volumen de un prisma rectangular.

En esta lección los estudiantes escriben e interpretan expresiones numéricas que representan el volumen de prismas rectangulares. Los estudiantes utilizan lo que saben sobre los prismas rectangulares para razonar si una expresión representa o no su volumen. Durante la siguiente lección, los estudiantes describirán qué unidad cúbica estándar utilizarían para medir el volumen de objetos que tienen forma de prisma rectangular. Considere qué objetos de los que los estudiantes ven habitualmente en sus comunidades tienen forma de prisma rectangular y traiga fotos de esos objetos para mostrárselas a los estudiantes durante la próxima lección. Si es posible, considere la posibilidad de realizar una búsqueda del prisma por la comunidad antes de la próxima lección.

Comunidad Matemática

Diga a los estudiantes que reflexionarán sobre las normas que han identificado al final de esta lección.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento Independiente 10 min

Actividad de exploración 1

Pares 15 min

Actividad de exploración 2 Parejas 10 min

Actividad Exploratoria Opcional 3 Pares 10 min

Síntesis Grupo Completo 10 min

Enfriamiento Independiente 5 min

Math Nation California - Grado 5

Breve descripción

Los estudiantes explican si cada ecuación numérica es verdadera utilizando propiedades algebraicas.

Los estudiantes emparejan y escriben expresiones numéricas que se pueden utilizar para representar el volumen de prismas rectangulares.

Los estudiantes establecen conexiones entre expresiones de volumen que implican el área de la base y la altura y expresiones de volumen que utilizan la longitud, la anchura y la altura.

Los estudiantes escriben ecuaciones que representan y no representan el volumen de diferentes prismas.

Los estudiantes discuten expresiones para representar el volumen de un prisma dado y cómo usar paréntesis y factores para representar el área de la base.

Los estudiantes seleccionan todas las expresiones posibles que se pueden usar para determinar el volumen de un prisma rectangular dado.

Grado 5 . Matemáticas . Unidad 1

LECCIÓN (CONTINUACIÓN)

Componente de la lección

Estructura Tiempo

Prácticas Parejas o Grupos pequeños Opcional

Breve descripción

Abordar:

• Cinco en raya: Multiplicación (3-5), Etapa 4: Tres factores

Apoyo:

• Captar cuadrados (1-3), Etapa 7: Multiplicar con 6-9

CALENTAMIENTO | VERDADERO O FALSO: PARÉNTESIS O SIN

PARÉNTESIS

Rutinas instruccionales

Verdadero o falso

10 minutos

El propósito de este Verdadero o Falso es que los estudiantes demuestren las estrategias y comprensiones que tienen para determinar la equivalencia de expresiones numéricas. Estos conocimientos ayudan a los estudiantes a profundizar su comprensión de las propiedades de las operaciones y son útiles cuando los estudiantes interpretan expresiones de volumen. En esta actividad, los estudiantes tienen la oportunidad de notar y hacer uso de la estructura (MP7) cuando utilizan las propiedades de las operaciones para determinar la equivalencia sin tener que calcular.

• Muestre una afirmación.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

SÍNTESIS DE LA ACTIVIDAD

• "Háganme una señal cuando sepan si el enunciado es verdadero y puedan explicar cómo lo saben."

• 1 minuto: tiempo para pensar en silencio

• Compartan y registren las respuestas y la estrategia.

• Repitan con cada enunciado.

Decidan si cada enunciado es verdadero o falso. Prepárate para explicar tu razonamiento.

• (4 × 2) × 5 = 4 × (2 × 5)

• (2 × 5) × 4 = 2 × 20

• 5 × 4 × 2 = 10 × 40

• Verdadero porque se están multiplicando los mismos números pero agrupados de forma diferente.

• Verdadero porque 2 × (5 × 4) = 2 × 20, (2 × 5) × 4 = 2 × 20; ambos lados son iguales a 40

• Falso porque 5 × 2 es 10 pero un lado está multiplicando ese 10 por 4 y el otro lado por 40

• Pregunta de enfoque: "¿Cómo puedes justificar tu respuesta sin evaluar ambos lados?". (Pude ver en la primera ecuación que todos los factores son iguales, por lo que es verdadera.)

• Considera preguntar:

• "¿Quién puede replantear el razonamiento de _________ de una manera diferente?"

• "¿Alguien quiere agregar algo al razonamiento de _________?"

• "¿Podemos hacer alguna generalización basada en los enunciados?"

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | CLASIFICACIÓN DE TARJETAS: EMPAREJA LA EXPRESIÓN 15

Rutinas instructivas Materiales para reunir

minutos

Materiales para copiar Preparación necesaria

Clasificación de tarjetas Cubos conectores Prismas y expresiones relacionadas

Cree un conjunto de tarjetas a partir del patrón de líneas negras para cada grupo de 2

Tenga cubos conectores disponibles para los estudiantes que los necesiten.

El objetivo de esta actividad es que los estudiantes interpreten expresiones que representan el volumen de un prisma rectangular. Los estudiantes relacionan la estructura de los prismas rectangulares con los símbolos de las expresiones relacionadas (MP2, MP7). Si dispone de tiempo y desea añadir movimiento a los estudiantes, pídales que hagan un póster para exponer las tarjetas clasificadas. Los estudiantes pueden caminar y agregar expresiones adicionales a otros carteles para representar el volumen del prisma.

Apoyo para estudiantes de inglés

MLR8 Apoyos de discusión. Invite a los estudiantes a que se turnen para encontrar una coincidencia y explicar su razonamiento. Muestre los siguientes marcos de oraciones para que todos los vean: "Me fijé en __________ , así que emparejé..." y "__________ y __________ coinciden/no coinciden porque...". Anime a los estudiantes a rebatirse cuando no estén de acuerdo.

Avances: Conversar, representar

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

Math Nation California - Grado 5

• Grupos de 2

• Distribuye un juego de tarjetas precortadas a cada grupo de estudiantes.

• "¿Qué observas en los prismas de estas tarjetas?". (No tienen cubos, dice "unidades".)

• "Cuando las medidas están en unidades, los cubos que usamos para llenar el prisma se llaman unidades cúbicas".

• "En esta actividad, clasificarás algunas tarjetas en las categorías que elijas. Cuando clasifiques las tarjetas, deberás trabajar con tu compañero para establecer las categorías."

• 4 minutos: tiempo de trabajo por parejas

• Selecciona grupos para que compartan sus categorías y cómo clasificaron sus tarjetas.

• "Ahora trabaja con tu compañero para emparejar cada prisma con las expresiones que representan el volumen."

• 3 minutos: tiempo de trabajo por parejas

1. Empareja cada prisma rectangular con la(s) expresión(es) que representa(n) su volumen en unidades cúbicas. Prepárate para explicar tu razonamiento.

2. Para cada prisma escribe una expresión adicional, no en la clasificación de tarjetas, que represente su volumen en unidades cúbicas.

Grado 5 . Matemáticas . Unidad 1

POSIBLE RESPUESTAS

AVANCE EN EL PENSAMIENTO DEL ESTUDIANTE

1. Coincide:

A. El prisma A coincide con (6 × 5) × 3, 15 × 6, 6 × (5 × 3)

B. El prisma B coincide con 2 × 12, 24 × 1

C. El prisma C coincide con 3 × 7 × 4, (7 × 4) × 3

D. El prisma D coincide con 3 × 8 × 3, 24 × 3, 9 × 8

2. Expresiones adicionales:

A. Prisma A: 18 × 5, 30 × 3, 3 × 5 × 6 en cualquier orden

B. El prisma B coincide con 2 × 12 × 1 en cualquier orden

C. El prisma C coincide con 21 × 4, 12 × 7, 28 × 3, 7 × 4 × 3 en cualquier orden

D. El prisma D coincide con 8 × 3 × 3 en cualquier orden

Si los estudiantes no emparejan correctamente las expresiones con los prismas, pregunte:

"¿Cómo podemos utilizar los cubos de conexión para ayudaros a emparejar las expresiones con los prismas?"

• Seleccione grupos para que compartan sus emparejamientos.

• Muestre el Prisma A:

SÍNTESIS DE LA ACTIVIDAD

• "¿Cómo representan el volumen estas expresiones?"

• 6 × (5 × 3)

• (6 × 5) × 3

• 15 × 6

• Muestre:

• (5 × 3) × 6 = 15 × 6

• "¿Cómo se relaciona la ecuación con el Prisma A?" (Ambas expresiones muestran que el prisma tiene una altura de 6. Una expresión muestra las longitudes de los lados de la base. La otra expresión muestra el área de la base).

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | HISTORIA DE DOS TABLAS

10 minutos

El objetivo de esta actividad es que los estudiantes comparen y contrasten dos formas diferentes de calcular el volumen de un prisma rectangular: multiplicando el área de la base y su altura correspondiente, y multiplicando las tres longitudes de los lados. Los estudiantes comprueban que ambas estrategias dan como resultado el mismo volumen. Es una convención considerar base de un prisma la cara sobre la que se apoya, sin embargo, al calcular el volumen de un prisma rectangular, cualquier cara del prisma puede considerarse base siempre que se multiplique por la altura correspondiente. Del mismo modo, al calcular el volumen de un prisma rectangular, cualquier arista puede considerarse longitud, anchura o altura.

Apoyo a los estudiantes con discapacidad

Compromiso: Proporcionar acceso captando el interés. Ofrecer opciones y autonomía. Proporcione acceso a diversas herramientas que puedan utilizarse para resolver el problema. Por ejemplo, se pueden utilizar lápices de colores para sombrear la base y las diferentes capas de los prismas.

Apoya la accesibilidad para: Procesamiento visual-espacial, Procesamiento conceptual

INSTRUCCIONES

ACTIVIDAD

• Grupos de 2

• 1 minuto: tiempo de trabajo independiente

• 8 minutos: tiempo de trabajo en pareja

1. Trabaja con tu compañero para completar las tablas. Trabaja con tu compañero para completar las tablas. Un compañero completa la Tabla 1 y el otro la Tabla 2.

Prisma A Prisma B

Tabla 1

ENUNCIADO DE LA TAREA

Longitud (unidades)

Anchura (unidades)

Altura (unidades)

Prisma A

Prisma B

Tabla 2

área de la base (unidades cuadradas)

Prisma A

Prisma B

Math Nation California - Grado 5

Altura (unidades)

Volumen (unidades cúbicas)

Grado 5 . Matemáticas . Unidad 1

ENUNCIADO DE LA TAREA CONTINUADO

POSIBLES RESPUESTAS

2. Comparen sus tablas y discutan: A. Compare sus tablas y discuta:

A. ¿Qué tienen en común las tablas?

B. ¿En qué se diferencian las tablas?

1. Tabla 1: La longitud, la altura y la anchura del prisma A son 6 unidades, 4 unidades y 3 unidades enumeradas en cualquier orden. El volumen del prisma A es 72 unidades cúbicas. La longitud, altura y anchura del prisma B son 8 unidades, 5 unidades y 4 unidades enumeradas en cualquier orden. El volumen del prisma B es 160 unidades cúbicas.

Área de la base (unidades cuadradas)

Altura (unidades)

AVANCE EN EL PENSAMIENTO DEL ESTUDIANTE

SÍNTESIS DE LA ACTIVIDAD

Volumen (unidades cúbicas)

Prisma A 18 o 12 o 24 4 o 6 o 3 72

Prisma B 40 o 20 o 32 4 o 8 o 5 160

A. Hallamos el volumen de los mismos prismas. Obtenemos el mismo volumen. Usamos la altura para hallar el volumen. El área de la base se halla usando la longitud y el ancho, así que usamos la misma información (o números, o longitudes de los lados).

B. Uno tiene longitud y ancho y el otro usa la base. Los números son diferentes. El orden de nuestros números es diferente.

Si un estudiante no escribe la altura correspondiente correcta para una base dada, pregunte: "¿Qué relación tienen los números de la tabla con el prisma?" o "¿Cómo decidiste qué números escribir en la tabla?"

• Pida a los estudiantes que compartan las respuestas al segundo problema. Muestre la expresión: 6 × 3 × 4

• "¿Cómo representa esta expresión el volumen del prisma A?" (Las longitudes de los lados del prisma son 6, 4, y 3 y las multiplico para hallar el volumen.)

• Muestra la expresión: (6 × 3) × 4

• "¿Cómo representa esta expresión el volumen del prisma A?" (Una base tiene una longitud de 6 unidades y una anchura de 3 unidades y la altura es 4 unidades.)

• "¿Qué expresión podrías usar para hallar el volumen usando la base 3 unidades por 4 unidades?" (Podríamos utilizar (3 × 4) × 6 o 6 × (3 × 4). Son iguales y ambas representan el volumen del prisma.

• Visualiza la ecuación: (6 × 3) × 4 = (3 × 4) × 6

• "¿Cómo sabes que la ecuación es cierta?" (Ambas expresiones representan el volumen del prisma y podemos ver ambas expresiones en el prisma. Una de ellas representa una base con las longitudes laterales 6 y 3 y una altura de 4. La otra expresión representa una base con las longitudes laterales 3 y 4 cubos y una altura de 6).

Tabla 2

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | DOS VERDADES Y UNA MENTIRA [OPCIONAL

10 minutos

Esta actividad es opcional si los estudiantes necesitan práctica adicional escribiendo expresiones para representar el volumen de un prisma rectangular. Esta actividad también ayuda a los estudiantes a identificar la información que necesitan para representar el volumen. Los estudiantes tienen la oportunidad de escribir e interpretar expresiones que muestren que el volumen es el mismo al multiplicar las longitudes de las aristas o al multiplicar el área de la base y la altura. En la segunda parte de la actividad, los estudiantes razonan abstracta y cuantitativamente cuando interpretan el significado de expresiones en el contexto del volumen (MP2).

• Grupos de 2

• "Tú y tu compañero vais a jugar a 2 verdades y una mentira con prismas rectangulares."

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• "Cada uno de vosotros escribirá expresiones, 2 verdaderas y una falsa, para representar el volumen de dos prismas y luego intercambiaréis para responder a algunas preguntas."

• "Un compañero escribe 2 verdades y una mentira para los prismas A y C y el otro compañero escribe sobre los prismas B y D."."

• 5 minutos: tiempo de trabajo independiente (crear expresiones)

• "Cambia de papel con tu compañero y comprueba si puedes averiguar la expresión que es una mentira para cada uno de sus prismas."

• 5 minutos: tiempo de trabajo independiente sobre los problemas de los compañeros (analizar expresiones)

Tu maesto te asignará a ti y a tu compañero dos prismas.

Para cada uno de los prismas asignados:

• Escribe 2 expresiones que representen el volumen en unidades cúbicas.

• Escribe 1 expresión que NO represente el volumen en unidades cúbicas.

Entrega tus expresiones a tu compañero:

1. Para cada prisma, ¿qué expresión no representa su volumen en unidades cúbicas? ¿Cómo lo sabes?

2. ¿Qué otras expresiones representan el volumen de este prisma en unidades cúbicas?

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTASS

AVANCE EN EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD

Ejemplos de respuestas:

• Prisma A Verdad: 3 × 4 × 5, 12 × 5. Mentira: 20 × 5

• Prisma B Verdad: 4 × 4 × 4, 4 × 16. Mentira: 4 × 4 × 4 × 4 × 4 × 4

• Prisma C Verdad: 60 × 3, 18 × 10. Mentira: 10 × 10 × 6

• Prisma D Verdad: 8 × 10, 2 × 40. Mentira: 14 × 2

Si los estudiantes no escriben ninguna expresión correcta que represente el volumen del prisma, refiérase a una expresión que sí represente el volumen del prisma y pregunte: "¿Pueden explicar cómo esta expresión representa el volumen del prisma?"

• Muestre cada uno de los prismas.

• "¿Qué expresiones representan el volumen del prisma en unidades cúbicas? ¿Cuáles no?"

• "¿Cómo decidiste las expresiones que no representaban el volumen de un prisma rectangular?" (Observando las diferentes bases y alturas y experimentando con las expresiones. Hallando el producto y comprobando que no coincide con el volumen de ninguno de los prismas).

SÍNTESIS DE LA LECCIÓN

Muestre el prisma C de la actividad 1:

10 minutos

"¿Qué expresiones podríamos escribir para representar el volumen de este prisma en unidades cúbicas?"

Para cada expresión, pida a los estudiantes que expliquen cómo representa el volumen del prisma. Mientras los estudiantes explican, anota las expresiones en un póster para que todos las vean. Utilice paréntesis para mostrar qué factores representan el área de una base y qué factor representa la altura correspondiente. Si los estudiantes no mencionan estas expresiones, muéstrelas y coméntelas.

• (7 × 4) × 3

• 28 × 3

• (7 × 3) × 4

• 21 × 4

• 7 × (3 × 4)

• 7 × 12

Comunidad matemática

Después del enfriamiento, pida a los estudiantes que reflexionen individualmente sobre la siguiente pregunta: "¿Cuál de las normas te ha parecido más importante en tu trabajo de hoy y por qué?". Los estudiantes pueden escribir sus respuestas en la parte inferior de su papel de enfriamiento, en una hoja separada o en un diario de matemáticas.

Diga a los estudiantes que, a medida que su comunidad matemática trabaje junta en el transgrado del año, el grupo agregará y revisará continuamente sus acciones y expectativas de "Hacer matemáticas" y "Normas".

Grado 5 . Matemáticas . Unidad 1

ENFRIAMIENTO | ESCOGE LA EXPRESIÓN

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

Reflexiones:

5 minutos

1. ¿Cuál de estas expresiones no representa el volumen del prisma rectangular en unidades cúbicas? Explica o muestra tu razonamiento.

4 × 5 × 8 × 4 20 × 8 (4 × 5) × 8 4 × 40

2. Elige una de las expresiones anteriores y explica por qué representa el volumen del prisma en unidades cúbicas.

1. 4 × 5 × 8 × 4 porque una vez hallada el área de la base (4 × 5), sólo hay que multiplicarla por la altura, 8.

2. Elige una de las expresiones anteriores y explica por qué representa el volumen del prisma en unidades cúbicas. Ejemplos de respuestas: 20 × 8 porque 20 representa el área de una base y 8 es la altura del prisma con esa base. (4 × 5) × 8 porque 4 × 5 son las longitudes de los lados de una base y 8 es la altura del prisma con esa base. 4 × 40 porque 40 es el área de una de las bases y 4 es la altura del prisma con esa base.

IDEAS FUNDAMENTALES

• Capas de cubos

• Modelado

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

5.MD.4 Medir volúmenes contando cubos unitarios, usando cm cúbicos, pulg. cúbicos, pies cúbicos y unidades improvisadas.

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en resolverlos.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP4 Modelar con matemáticas.

MP6 Atender a la precisión.

Estándares CA ELD

I.A.1

I.C.12

II.B.6

LECCIÓN 7

UNIDADES DE MEDIDA CÚBICAS

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

dar sentido al mundo y predecir lo que podría ocurrir

dar sentido a los problemas y perseverar en su resolución y atender a la precisión

OBJETIVO(S) DE APRENDIZAJE

explorar cantidades cambiantes y descubrir la forma y el espacio.

• Puedo explicar qué unidades cúbicas son las más apropiadas para describir el volumen de diferentes prismas.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTO

• Halla el volumen de prismas rectangulares con unidades de medida estándar multiplicando la base por la altura o multiplicando la longitud por la anchura por la altura.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

Durante la lección de hoy, los estudiantes han descrito qué unidad de medida cúbica estándar utilizarían para medir el volumen de objetos con forma de prisma rectangular. Piense qué objetos de los que los estudiantes ven habitualmente en sus comunidades tienen forma de prisma rectangular. ¿Cómo incorporó estos objetos a la lección para ayudar a los estudiantes a conectar su experiencia vivida con el desarrollo de su identidad matemática?

¿Cómo puede incorporar estos objetos en futuras lecciones?

PREPARACIÓN DE LA LECCIÓN

Rutinas Instructivas

Notar y Preguntarse (Calentamiento)

MLR4 Brecha de Información (Actividad 2)

Materiales a Reunir

Reglas (centímetros): Actividad 1

Reglas (pulgadas): Actividad 1

Varas de medir: Actividad 1

Materiales para copiar

Fichas de volumen de la brecha informativa: Actividad 2

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Usemos unidades cúbicas de diferentes tamaños para medir el volumen.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes encuentren el volumen de prismas rectangulares en centímetros cúbicos, pulgadas cúbicas y pies cúbicos.

En lecciones anteriores, los estudiantes usaron cubos unitarios con una longitud lateral de 1 unidad para determinar el volumen de prismas rectangulares rectos. En esta lección, las unidades son ahora una unidad de medida específica. En 5º grado, los estudiantes usan palabras, no exponentes, cuando registran la unidad de medida cúbica, como "centímetros cúbicos (cm)", "pies cúbicos (ft)" o "pulgadas cúbicas (in)". Los exponentes en 5º grado se limitan a potencias de 10, que se abordarán en una unidad posterior.

En esta lección, los estudiantes distinguen entre diferentes unidades de medida estándar de volumen. Examinan la distinción entre cm cúbicos, pulg cúbicos y pies cúbicos. A lo largo de la lección, los estudiantes comparten sus razones para elegir una unidad para medir objetos específicos del mundo real y aprenden la importancia de identificar la unidad de medida al encontrar el volumen de un objeto (MP6).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Breve descripción

Calentamiento En parejas 10 min

Actividad de exploración 1 En parejas 10 min

Actividad de Exploración 2 Parejas 25 min

Síntesis Todo el Grupo 10 min

Los estudiantes hacen observaciones sobre las características de cubos de diferentes tamaños.

Los estudiantes razonan sobre el tamaño de la unidad de medida para diferentes objetos del mundo real.

Los estudiantes recopilan información a través de preguntas generadas por los estudiantes para determinar el volumen de un objeto del mundo real.

Los estudiantes discuten cómo decidir qué medida es la más apropiada para encontrar el volumen en diferentes escenarios

Enfriamiento Independiente 5 min Los estudiantes determinan el volumen de un prisma usando una descripción escrita.

Abordar:

• Cinco en Raya: Multiplicación (3-5), Etapa 4: Tres Factores

Prácticas Grupos Pequeños Opcional

Apoyo:

• Capturar Cuadrados (1-3), Etapa 7. Multiplicar con Multiplicar con 6-9

Math

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | OBSERVA Y PREGUNTA: DOS PRISMAS

Rutinas instructivas

Notar y preguntarse

10 minutos

El objetivo de este calentamiento es que los estudiantes se den cuenta de que existen unidades cúbicas de diferentes tamaños. Esto será útil cuando los estudiantes utilicen unidades estándar para medir los volúmenes de prismas rectangulares en las próximas actividades. Aunque los estudiantes pueden notar y preguntarse muchas cosas sobre estos cubos, las características de un cubo y el tamaño de los cubos son los puntos de discusión importantes.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Grupos de 2

• Muestra la imagen.

• "¿Qué notas? ¿Qué te sorprende?"

• 1 minuto: tiempo para pensar en silencio

• 1 minuto: debate en parejas

• Compartir y anotar las respuestas.

¿Qué observas?

¿Qué te sorprende?

Los estudiantes pueden observar:

• Parecen cubos.

• Son de diferentes tamaños.

• Uno de los cubos es más alto que el niño.

POSIBLES RESPUESTAS

SÍNTESIS DE LA ACTIVIDAD

Los estudiantes pueden preguntarse:

• ¿Qué tamaño tienen esos cubos?

• ¿Para qué sirven esos cubos?

• ¿Cuántos de los cubos pequeños caben dentro del cubo grande?

• "El cubo pequeño representa un pie cúbico. El cubo grande representa una yarda cúbica. Aproximadamente, ¿cuántos de los cubos grandes cabrían en nuestra clase?". (Las respuestas varían. Si el tiempo lo permite, mide la longitud y la anchura del aula, redondéalas a la yarda más cercana y comprueba si las estimaciones son razonables).

• "Hemos estado utilizando unidades cúbicas para medir el volumen, pero no hemos definido el tamaño de la unidad. La elección de la unidad depende del tamaño del objeto."

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD

UNIDADES?

DE EXPLORACIÓN 1 | ¿QUÉ SON LAS

10 minutos

Materiales a reunir

Reglas (centímetros)

Reglas (pulgadas)

Varas de medir

El propósito de esta actividad es que los estudiantes consideren cómo el tamaño de un objeto influye en la unidad que usamos para medir el volumen de ese objeto. Dado que ésta es la primera experiencia de los estudiantes con estas unidades de medida cúbicas, puede resultarles útil ver la longitud real de un centímetro, una pulgada y un pie. Disponga de reglas o cubos como apoyo adicional para visualizar el tamaño de las unidades de medida cúbicas. Dado que no hay respuestas matemáticamente correctas o incorrectas, esta actividad proporciona una rica oportunidad para que los estudiantes discutan y defiendan diferentes puntos de vista (MP3).

El instrucciones de la actividad es una oportunidad para que los estudiantes compartan sus experiencias y hagan preguntas sobre los objetos para asegurarse de que cada estudiante tiene acceso al contexto. Si resulta útil, muestre imágenes de los objetos para que los estudiantes puedan consultarlos.

• Grupos de 2

• Escribe la lista de objetos (camión de mudanzas, congelador, etc. ....) en un expositor para que la vean todos los estudiantes.

• "Tómate un minuto para leer esta lista. ¿Qué sabes de estos objetos?

• ¿Qué te preguntas?"

• 3 minutos: debate por parejas

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Comparte algunas respuestas.

• Muestra la imagen del calentamiento.

• "En esta actividad vamos a considerar el uso de diferentes unidades cúbicas de medida para encontrar el volumen de objetos de diferentes tamaños. No hay respuestas correctas o incorrectas en estas preguntas, pero prepárense para explicar su elección"

• Dé a los estudiantes acceso a reglas y varas de medir.

• 2 minutos: tiempo de trabajo independiente

• 5 minutos: discusión en parejas

• Mientras los estudiantes trabajan, controle si hay estudiantes que discuten cuán grande o pequeño es el objeto al elegir el tamaño de la unidad de medida. Pida a estos estudiantes que compartan durante la síntesis.

• Si los estudiantes terminan antes, pídales que busquen otros objetos cuyo volumen medirían utilizando las diferentes unidades de medida cúbicas. Si los objetos están en la sala, podrían estimar y comprobar sus estimaciones.

Para cada objeto, elige la unidad cúbica que utilizarías para medir el volumen: centímetro cúbico, pulgada cúbica o pie cúbico.

Objeto

el volumen de un camión de mudanzas

el volumen de un congelador

el volumen de una caja de zumo

el volumen de un aula

el volumen de un contenedor de basura

el volumen de una fiambrera

Unidad que utilizarías

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS

Objeto Unidad que utilizarías el volumen de un camión de mudanzas pies cúbicos

el volumen de un congelador

pies cúbicos, pulgadas cúbicas (dependiendo del tipo) el volumen de una caja de zumo cm cúbicos el volumen de un aula pies cúbicos el volumen de un contenedor de basura pies cúbicos el volumen de una fiambrera pulgadas cúbicas

• "¿Cómo decidiste qué unidades tenían sentido?" (Intenté elegir una unidad que no fuera ni mucho más pequeña ni mucho más grande que el objeto que se estaba midiendo).

SÍNTESIS DE LA ACTIVIDAD

• "¿Qué pasaría si sólo escribiera 24 como volumen para el congelador? ¿Qué preguntas te harías?" (Me preguntaría 24 ¿qué? Si no conocemos la unidad de medida, no sabemos lo grande que es realmente el congelador.)

• Visualiza: 24 centímetros cúbicos, 24 pulgadas cúbicas, 24 yardas cúbicas

• "¿Qué es lo mismo en estas medidas?" (Todas son 24 unidades. Todas son unidades cúbicas.)

• "¿Qué tienen de diferente estas medidas?" (Son tamaños diferentes. Los centímetros cúbicos y las pulgadas cúbicas son mucho más pequeños que las yardas cúbicas.)

ACTIVIDAD DE EXPLORACIÓN 2 | BRECHA DE INFORMACIÓN: DIMENSIONAR UNIDADES CÚBICAS

Rutinas instructivas

MLR4 Brecha de información

25 minutos

Materiales para copiar

Brecha de información Tarjetas de volumen

Esta actividad de la Brecha de Información ofrece a los estudiantes la oportunidad de determinar y solicitar la información necesaria para medir el volumen de prismas rectangulares utilizando unidades de diferentes tamaños.

La rutina Info Gap requiere que los estudiantes den sentido a los problemas determinando qué información es necesaria y, a continuación, pidan la información que necesitan para resolverlos. Esto puede requerir varias rondas de discusión si sus primeras peticiones no aportan la información que necesitan (MP1). También les permite perfeccionar el lenguaje que utilizan y formular preguntas cada vez más precisas hasta obtener la información que necesitan (MP6). Dado que ésta es la primera experiencia de los estudiantes con la rutina de la brecha informativa, el instrucciones ofrece la oportunidad de ensayar la rutina juntos.

Apoyo a los estudiantes con discapacidad

Representación: Acceso para la percepción. Proporcionar adaptaciones y apoyos adecuados a la lectura para garantizar el acceso de los estudiantes a instrucciones escritas, problemas de palabras y otros contenidos basados en texto.

Apoya la accesibilidad para: Lenguaje, Procesamiento conceptual

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

Grado 5 . Matemáticas . Unidad 1

Nation California - Grado 5

• Grupos de 2

• Muestra una tarjeta de problema de muestra del cuaderno de trabajo del estudiante.

• "Este es un diagrama de un congelador. ¿Cuál es el volumen del congelador?"

• Lea el problema en voz alta.

• Escuche y aclare cualquier pregunta sobre el contexto.

• "Falta parte de la información que necesitas para resolver este problema, y yo la tengo aquí. Con tu compañero, decidid qué información necesitáis para resolver el problema y cread una lista de preguntas que podéis hacer para averiguarla."

• 1-2 minutos: tiempo para pensar en silencio

• 2-3 minutos: debate en parejas

• Invite a los estudiantes a compartir 1 pregunta cada vez.

• Registre cada pregunta en una pantalla y responda: "¿Por qué necesitas saber _____ [reitere la información solicitada]?". Los estudiantes deben justificar cómo utilizarán la información antes de revelarla. Por ejemplo, si los estudiantes preguntan: "¿Cuál es la anchura del congelador?", responda con: "¿Por qué necesitan saber la anchura del congelador?"

• Responda a las preguntas utilizando únicamente la información que figura en la Tarjeta de datos de muestra a continuación (no la revele):

• La anchura del congelador es 2 pies.

• La longitud del congelador es 4 pies.

• Registre la información que se comparte en la pantalla. Dé tiempo a los estudiantes para decidir si tienen suficiente información para resolver el problema.

• Repita hasta que los estudiantes decidan que tienen suficiente información para resolver.

• 2-4 minutos: tiempo de trabajo independiente

• En cada grupo, distribuya una tarjeta de problema a un estudiante y una tarjeta de datos al otro.

• Después de revisar su trabajo en el primer problema, entrégueles las tarjetas para un segundo problema e indíqueles que cambien los papeles.

Este es un diagrama de un congelador.

¿Cuál es el volumen del congelador?

Grado 5 . Matemáticas . Unidad 1

ENUNCIADO DE LA TAREA CONTINUACIÓN

POSIBLES RESPUESTASS

SÍNTESIS DE LA ACTIVIDAD

Problema 1:

• El compañero A tiene la tarjeta del problema.

• El compañero B tiene la tarjeta de datos.

Problema 2:

• El compañero B tiene la tarjeta del problema.

• El compañero A tiene la tarjeta de datos.

Tu maesto te dará una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu compañero.

Haz una pausa aquí para que tu maesto pueda revisar tu trabajo. Pide a tu maesto un nuevo juego de tarjetas y repite la actividad, intercambiando los papeles con tu compañero.

• Problema 1: Como 2 yardas son 6 pies, el volumen del contenedor es 20 × 6 × 8 = 960; 960 pies cúbicos.

• Problema 2: Cada caja mide 5 × 4 × 9 = 180; es decir 180 centímetros cúbicos por cada caja de zumo. 180 × 100 = 1.800 centímetros cúbicos. Jada no puede meter las diez cajas porque 1.800 centímetros cúbicos es mayor que los 1.500 centímetros cúbicos de espacio que le quedan a Jada en la mochila.

• Comparte las respuestas correctas, incluyendo las unidades, y pide a los estudiantes que discutan el proceso de resolución de los problemas.

• "¿Qué preguntas hiciste para ayudarte a encontrar el volumen?" (¿Cuál es la altura del contenedor? ¿Cuánto espacio tiene Jada en su mochila?)

• "¿Qué unidades se utilizaron para cada problema? ¿Tenían sentido esas unidades?" (Pies cúbicos y centímetros cúbicos. Sí, porque un contenedor de basura es grande y una caja de zumo es relativamente pequeña).

Grado 5 . Matemáticas . Unidad 1

SÍNTESIS DE LA LECCIÓN

Muestra la imagen de notice/wonder.

10 minutos

Escribe las palabras cubic inches (pulgadas cúbicas), cubic feet (pies cúbicos), cubic yards (yardas cúbicas) para que todos las vean.

"Hoy hemos trabajado con estas unidades cúbicas de diferentes tamaños. Voltéate y habla con tu compañero y trata de pensar en un objeto para el cual usarías cada unidad de medida para hallar el volumen."

Discusión entre compañeros

"Ahora, escoge una de las cosas que discutiste y explícale a tu compañero cómo hallarías el volumen de ese objeto." (Yo multiplicaría el área de una base por la altura correspondiente o Yo multiplicaría las longitudes de los tres lados.)

ENFRIAMIENTO | ENCONTRAR EL VOLUMEN

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

5 minutos

La familia de Priya alquiló un camión de mudanzas para trasladar sus pertenencias a su nueva casa. El espacio dentro de la parte trasera del camión de mudanzas mide 15 pies de largo, 5 pies de ancho y 8 pies de alto.

¿Cuál es el volumen de la parte trasera del camión de mudanzas? Explica o muestra tu razonamiento. (Recuerda incluir la unidad de medida cúbica.)

El volumen del camión de mudanzas es 600 pies cúbicos.

Respuesta de ejemplo: 8 × 5 × 15 = 40 × 15 = (40 × 10) + (40 × 5) = 400 + 200 = 600

Resumen de la sección del estudiante

Encontramos el volumen de un prisma rectangular derecho multiplicando las longitudes de los lados o multiplicando el área de una base por la altura correspondiente.

4 × (5 × 3)

(4 × 5) × 3

15 × 4

Cada una de estas expresiones representa el volumen de este prisma. El volumen de este prisma rectangular es 60 unidades cúbicas.

Podemos usar unidades cúbicas de diferentes tamaños para medir el volumen de objetos de diferentes tamaños.

En esta sección, usamos pulgadas cúbicas, pies cúbicos, yardas cúbicas y centímetros cúbicos.

Math Nation California - Grado 5

LECCIÓN 8

IDEAS FUNDAMENTALES

• Capas de cubos

• Modelado

ALINEACIÓN

Abordando

Alineación de estándares y principios de California

5.MD.5c Reconocer el volumen como aditivo. Hallar volúmenes de figuras sólidas compuestas por dos prismas rectangulares rectos no superpuestos sumando los volúmenes de las partes no superpuestas, aplicando esta técnica para resolver problemas del mundo real.

Construyendo sobre

5.MD.5a

Enfocar SMPs

MP6 Prestar atención a la precisión.

MP7 Buscar y hacer uso de la estructura.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares CA ELD

I.A.2

I.C.12

II.C.6

FIGURAS FORMADAS POR PRISMAS

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

predicen lo que podría ocurrir y repercutir en el futuro buscan y expresan regularidades en razonamientos repetidos

exploran cantidades cambiantes y descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo encontrar el volumen de figuras, en cubos unitarios, compuestas de prismas rectangulares.

OBJETIVOS DE APRENDIZAJE

PARA EL MAESTO

• Explicar que el volumen de una figura compuesta de prismas rectangulares es la suma de los volúmenes de los prismas.

• Encontrar el volumen de una figura compuesta de prismas rectangulares en la que los cubos unitarios son visibles.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

¿Qué lenguaje utilizaron los estudiantes para demostrar que comprendían que las figuras con las que trabajaron hoy estaban compuestas por prismas rectangulares?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

¿Cuál no pertenece?

(Calentamiento)

Materiales a Reunir

Conectar cubos: Actividad 1

Preparación necesaria

Actividad 1:

Cada grupo de 2 necesita al menos 30 cubos de conexión.

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Vamos a hallar el volumen de figuras formadas por prismas.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes reconozcan la estructura de una figura sólida formada por dos prismas rectangulares rectos no superpuestos y comprendan que su volumen es la suma de los volúmenes de los dos prismas rectangulares.

En lecciones anteriores, los estudiantes hallaron el volumen de prismas rectangulares rectos representados en imágenes donde se mostraban o no los cubos. En esta lección, construyen prismas rectangulares separados y los juntan para enfatizar la relación entre el volumen de los prismas individuales más pequeños y el volumen de la figura completa. A continuación, hallan los volúmenes de figuras formadas por dos prismas rectangulares sin construir primero cada parte. Los estudiantes reconocen que cuando se da la figura compuesta por dos prismas rectangulares, hay diferentes formas de descomponer la figura, lo que conduce a diferentes cálculos del mismo volumen.

LECCIÓN DE UN VISTAZO

Componente de la lección Estructura Tiempo Breve Descripción

Calentamiento Pares 10 min

Actividad de exploración 1 Por parejas 20 min

Actividad de exploración 2 Por parejas 15 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Math

Prácticas Grupos pequeños Opcional

Los estudiantes examinan imágenes de figuras tridimensionales compuestas por cubos unitarios para explicar qué figura no pertenece.

Los estudiantes construyen un prisma rectangular utilizando cubos de conexión y determinan el volumen de prismas rectangulares compuestos.

Los estudiantes determinan el volumen de figuras compuestas por prismas rectangulares formados por cubos unitarios.

Los estudiantes describen cómo encontrar el volumen de figuras tridimensionales formadas por dos o más prismas rectangulares.

Los estudiantes calculan el volumen de una figura 3-D compuesta por varios prismas rectangulares.

Abordar:

• Cinco en raya: Multiplicación (3-5), Etapa 4: Tres factores

Apoyo:

• Capturar cuadrados (1-3), Etapa 7: Multiplicar con 6-9

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO

| CUÁL NO PERTENECE:

FIGURAS DIFERENTES

Rutinas instructivas

¿Cuál no pertenece?

10 minutos

Este calentamiento lleva a los estudiantes a analizar y comparar cuidadosamente las características de figuras construidas a partir de prismas rectangulares. Al hacer las comparaciones, los estudiantes tienen un motivo para utilizar el lenguaje con precisión (MP6) y referirse a las diferentes medidas de las figuras, su volumen u otras características.

• Grupos de 2

• Muestre la imagen.

INSTRUCCIONES

ACTIVIDAD

• "Elija uno que no pertenezca. Prepárate para compartir por qué no pertenece."

• 1 minuto: tiempo para pensar en silencio

• "Discute tu pensamiento con tu compañero."

• 2-3 minutos: discusión en pareja

• Comparte y registra las respuestas.

¿Cuál no pertenece?

ENUNCIADO DE LA TAREA

POSIBLE RESPUESTAS

• A no pertenece porque no está organizado, no se puede cortar en dos capas iguales y no se puede cortar en dos prismas rectangulares.

• B no pertenece porque es el único prisma rectangular. No tiene piezas que sobresalgan.

• C no pertenece porque no tiene 3 cubos de altura.

• D no pertenece porque no tiene un volumen de 12 cubos.

SÍNTESIS DE LA ACTIVIDAD

Grado 5 . Matemáticas . Unidad 1

• Consulte la figura C. "Hoy vamos a hallar el volumen de figuras formadas por dos o más prismas rectangulares. ¿Dónde vemos dos prismas rectangulares en la Figura C?"

• Si es posible, dibuje sobre la imagen mientras los estudiantes explican dónde ven los dos prismas.

• Si nadie lo menciona, muestre dos formas diferentes en que la Figura C puede descomponerse en dos prismas rectangulares rectos, es decir, cortando vertical u horizontalmente.

EXPLORACIÓN ACTIVIDAD 1 | JÚNTALO

Materiales a reunir

Cubos de conexión

20 minutos

Preparación necesaria

Cada grupo de 2 necesita al menos 30 cubos de conexión.

El propósito de esta actividad es que los estudiantes combinen prismas rectangulares para hacer una nueva figura y comprendan que el volumen de la nueva figura es la suma de los volúmenes de los dos prismas rectangulares. Esto será cierto independientemente de cómo junten los dos prismas rectangulares.

Apoyo a los estudiantes con discapacidad

Engagement: Desarrollar el Esfuerzo y la Persistencia. Invite a los estudiantes a elaborar una lista de expectativas compartidas para el trabajo en grupo. Registre las respuestas en un cartel y manténgalo visible durante la actividad.

Apoya la accesibilidad para: Atención, Funcionamiento socioemocional

• Grupos de 2

• "Vamos a construir diferentes prismas rectangulares y a unirlos".

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

Math Nation California - Grado 5

• "Compañero A, construye un prisma rectangular con 12 cubos. Compañero B, construye un prisma rectangular con 10 cubos."

• 10 minutos: tiempo de trabajo de los compañeros construyendo prismas y encontrando el volumen.

• 2 minutos: tiempo de discusión por parejas

• Supervisa a los estudiantes que construyen una figura a partir de dos prismas rectangulares de diferentes maneras.

1. Compañero A, construye un prisma rectangular con 12 cubos.

2. Compañero B, construye un prisma rectangular con 10 cubos.

3. Junta tus dos prismas rectangulares para hacer una figura. ¿Cuál es el volumen de la nueva figura? Explica o muestra tu razonamiento.

4. Diego y Jada juntaron dos prismas rectangulares para hacer esta figura:

A. ¿Cuál es el volumen de la figura que hicieron Diego y Jada?

B. ¿Qué prismas rectangulares podrían haber construido Diego y Jada? Explica o muestra tu razonamiento. Organízalo para que pueda ser seguido por otros.

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTASS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

1. Las respuestas de muestra incluyen prismas rectangulares construidos con 12 cubos.

2. Las respuestas de muestra incluyen prismas rectangulares construidos con 10 cubos.

3. Ejemplo de respuesta: El volumen es 22 unidades cúbicas porque una parte tiene 10 unidades cúbicas y la otra parte tiene 12.

4. A. 30 unidades cúbicas

B. Jada podría haber hecho el prisma 2 por 3 por 4 en la parte inferior, y Diego podría haber hecho el prisma 2 por 3 por 1 en la parte superior.

Si los estudiantes no ven dos prismas rectangulares que componen la figura, pídeles que construyan la figura con cubos y que muestren cómo podrían descomponer la figura en dos prismas rectangulares.

• Pida a los estudiantes previamente identificados que compartan los prismas individuales que construyeron y cómo los juntaron.

SÍNTESIS DE LA ACTIVIDAD

• "¿Cuál fue el volumen de la forma que hiciste cuando juntaste tus prismas? ¿Cómo lo sabes?" (22 unidades cúbicas porque yo usé 12 cubos y mi compañero usó 10 cubos, así que son 22 cubos en total.)

• Resalte que las diferentes figuras que hicieron los estudiantes tienen todas un volumen de 22 unidades cúbicas.

• Muestre la figura que hicieron Diego y Jada.

• "¿Cuál es el volumen de la figura que hicieron Diego y Jada? ¿Cómo lo sabes?" ("30 unidades cúbicas. La partí en dos prismas y hallé sus volúmenes y los sumé")

ACTIVIDAD DE EXPLORACIÓN 2 | VEO DOS PRISMAS

15 minutos

El objetivo de esta actividad es que los estudiantes encuentren el volumen de una figura compuesta por dos prismas rectangulares y reconozcan que el volumen es aditivo. En la actividad anterior, los estudiantes juntaron físicamente dos prismas rectangulares y luego descompusieron una figura en dos prismas rectangulares. En esta actividad, se les da una imagen de una figura compuesta por dos prismas rectangulares y se les pide que encuentren el volumen. Pueden hacerlo de muchas maneras. Durante la síntesis, relacione las diferentes estrategias que los estudiantes utilizaron con la descomposición de la figura en dos prismas rectangulares.

A medida que los estudiantes experimentan con diferentes formas de agrupar los cubos para contarlos eficientemente, aplicando lo que ya saben sobre el volumen de los prismas rectangulares, están buscando y haciendo uso de la estructura de los objetos geométricos (MP7). A medida que los estudiantes comienzan a generalizar la idea de que el volumen es aditivo, están buscando y expresando regularidad en razonamientos repetidos (MP8).

Apoyo para estudiantes de inglés

MLR7 Comparar y conectar. Síntesis: Invite a los estudiantes a preparar una presentación visual que muestre la estrategia que utilizaron para hallar el volumen de cada figura. Anime a los estudiantes a incluir detalles que ayuden a los demás a interpretar su pensamiento; por ejemplo, utilizando un lenguaje específico, o usando diferentes colores, sombreados o flechas. Dé tiempo a los estudiantes para que investiguen el trabajo de los demás.

Avances: Representación de

Grado 5 . Matemáticas . Unidad 1

INSTRUCCIONES • Grupos de 2

• 5 minutos: tiempo de trabajo individual

• 5 minutos: discusión en parejas

• Mientras los estudiantes trabajan, controle si hay estudiantes que:

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD

Nation California - Grado 5

• encuentran dos (o más) prismas rectangulares que se pueden juntar para hacer la figura y sumar sus volúmenes.

• encuentran el número de cubos de una capa base y multiplican por el número de capas, aunque la capa base no sea un rectángulo (figura d).

Encuentra el volumen de cada figura. Explica o muestra tu razonamiento. a.

a. 46 unidades cúbicas. Ejemplo de respuesta: Hay un prisma rectangular de 3 por 3 por 5, así que son 45 cubos y hay un cubo más, así que son 46. b. 50 unidades cúbicas. Respuesta de ejemplo: Hay un prisma de 3 por 3 por 5 como en el primer problema, así que son 45 cubos y hay una fila de 5 más, así que son 50. c. 60 unidades cúbicas. Respuesta de ejemplo: Hay un prisma de 3 por 3 por 6, así que son 54 cubos y hay una fila de 6, así que son 60. d. 57 unidades cúbicas. Respuesta de muestra: Hay un prisma de 3 por 3 por 5, así que son 45 cubos y luego un prisma de 2 por 2 por 3, así que son 12 más.

Si los estudiantes no descompusieron las figuras en prismas rectangulares, anímelos a construir las figuras con cubos de conexión y pregúnteles: "¿cómo pueden descomponer la figura en dos prismas rectangulares?"

• Muestre las figuras c y d.

• Pida a los estudiantes seleccionados que compartan su manera de dividir cada figura.

• "¿Quién dividió la figura de la misma manera? ¿Quién la partió de otra manera?"

• "¿Se les ocurren otras formas de partir estas figuras?" (Puedo cortarlas en varias capas-3 capas horizontales para c, y 5 capas verticales para d. Cada capa es un prisma rectangular.

Grado 5 . Matemáticas . Unidad 1

SÍNTESIS DE LA LECCIÓN

10 minutos

"Hoy hemos averiguado el volumen de las figuras construidas a partir de 2 o más prismas rectangulares. Cuando una figura se construye a partir de 2 o más prismas rectangulares, su volumen se puede hallar sumando los volúmenes de esos prismas rectangulares."

"¿Dónde usaste la multiplicación en tu trabajo de hoy? ¿Dónde has utilizado la suma?" (Usé la multiplicación cuando hallé el volumen de un prisma. Usé la suma cuando sumé los cubos en las diferentes partes en las que dividí la figura.)

ENFRIAMIENTO | VOLUMEN DE UNA FIGURA HECHA DE PRISMAS

5 minutos

Halla el volumen de la figura. Explica o muestra tu razonamiento.

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

Reflexiones:

56 unidades cúbicas

Ejemplo de respuesta: Corto la forma horizontalmente para hacer un conjunto de cubos 2 por 2 por 4 y un conjunto de cubos 4 por 2 por 5. Así que son 16 y 40 más, haciendo 56 cubos en total.

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

LECCIÓN 9

IDEAS FUNDAMENTALES

• Capas de cubos

• Factores y grupos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

5.OA.2 Escribir expresiones sencillas que registren cálculos con números , e interpretar expresiones numéricas sin evaluarlas.

Construyendo hacia

5.NBT.2

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.4

I.C.12

II.C.7

MEDIR FIGURAS HECHAS CON PRISMAS

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

dan sentido al mundo e inciden en el futuro razonan de forma abstracta y cuantitativa exploran cantidades cambiantes y descubren la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo encontrar el volumen de una figura compuesta de prismas rectangulares.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTO

• Encuentra el volumen de una figura compuesta de prismas rectangulares en la que no se muestran cubos unitarios.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

¿Qué conexiones establecieron los estudiantes entre las distintas estrategias compartidas? ¿Qué preguntas formuló para ayudar a que las conexiones fueran más visibles?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Hablar de números (calentamiento)

Materiales Para Copiar

Isometric Dot Paper Standard: Actividad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Vamos a encontrar el volumen de más figuras.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes encuentren el volumen de figuras compuestas por dos prismas rectangulares rectos no superpuestos sumando los volúmenes de las partes no superpuestas.

Grado 5 . Matemáticas . Unidad 1

En la lección anterior, las figuras con las que trabajaron los estudiantes mostraban los cubos unitarios, lo que les brindó la oportunidad de visualizar el número de cubos unitarios y encontrar el volumen de diversas maneras. En esta lección, las figuras compuestas por dos prismas rectangulares rectos no superpuestos no muestran los cubos individuales. Esto anima a los estudiantes a aplicar las fórmulas de volumen y a establecer conexiones entre las expresiones y la forma en que se pueden descomponer las figuras. Dada una expresión y una figura sólida compuesta por dos prismas rectangulares, los estudiantes determinan cómo descomponer la figura para que coincida con la expresión dada (MP2, MP7).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Breve descripción

Calentamiento Independiente 10 min Los estudiantes evalúan expresiones numéricas de multiplicación.

Actividad de exploración 1 Pares 20 min Los estudiantes aplican diferentes estrategias de descomposición para determinar el volumen de prismas.

Actividad de exploración 2 Parejas 15 min Los estudiantes explican cómo las expresiones que implican multiplicación y suma representan el volumen de figuras compuestas formadas por prismas rectangulares.

Síntesis Todo el grupo 10 min Los estudiantes crean expresiones numéricas para el volumen de un prisma descomponiendo la forma utilizando diferentes estrategias.

Enfriamiento Independiente 5 min

Math

Prácticas Grupos pequeños Opcional

Los estudiantes determinan el volumen de un prisma aplicando una estrategia de descomposición.

Dirección:

• Cinco en raya: Multiplicación (3-5), Etapa 4: Tres factores

Apoyo:

• Rodar para fracciones (3-5), Etapa 1: Fracciones equivalentes

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | CONVERSACIÓN NUMÉRICA: DIEZ

VECES

Rutinas instructivas

10 minutos

Conversación sobre números

El propósito de esta Charla sobre Números es que los estudiantes razonen sobre las relaciones de valor posicional y las propiedades de la multiplicación. Las comprensiones y estrategias obtenidas serán útiles en lecciones y unidades posteriores cuando multipliquen números grandes. En esta unidad, los estudiantes producen e interpretan expresiones de multiplicación en términos de volumen.

• Mostrar una expresión.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• "Háganme una señal cuando tengan una respuesta y puedan explicar cómo la obtuvieron".

• 1 minuto: tiempo para pensar en silencio

• Registrar las respuestas y la estrategia.

• Mantener las expresiones y el trabajo mostrados.

• Repetir con cada expresión.

Encontrar el valor de cada expresión mentalmente.

• 6 × 2

• 6 × 2 × 10

• 6 × 20 × 10

• 60 × 20 × 10

POSIBLES RESPUESTASS

SÍNTESIS DE LA ACTIVIDAD

• 12: Simplemente lo sé.

• 120: 60 × 2 = 120, 12 × 10 = 120

• 1,200: 200 × 6 = 1.200, 120 × 10 = 1.200

• 12,000: 200 × 10 × 6 = 12.000, Va a ser 10 veces más que el producto anterior.

• "¿Qué patrones observas en los problemas que hemos resuelto?" (Hay un 6 y 2 en cada producto. También hay factores de 10, y los 6 y 2 a veces se multiplican por un factor de 10.)

• Considera preguntar:

• "¿Quién puede replantear el razonamiento de de una manera diferente?"

• "¿Alguien tenía la misma estrategia pero la explicaría de otra manera?"

• "¿Alguien enfocó el problema de una manera diferente?"

EXPLORACIÓN ACTIVIDAD 1 | HALLAR EL VOLUMEN DE FIGURAS

20 minutos

Material para copiar

Grado 5 . Matemáticas . Unidad 1

Papel de puntos isométricos Estándar

El objetivo de esta actividad es que los estudiantes hallen el volumen de figuras compuestas por dos prismas rectangulares rectángulos no superpuestos sumando los volúmenes de las partes no superpuestas. Hay diferentes formas de descomponer las figuras. Vigile a los estudiantes que descomponen las figuras de forma diferente y encuentran el mismo volumen total. Para reforzar

el trabajo previo con unidades de medida cúbicas, pregunte a los estudiantes por la unidad de medida en su respuesta si indican el volumen sólo como un número (MP2). Si los estudiantes terminan antes, entrégueles papel cuadriculado isométrico para que dibujen una figura compuesta por dos prismas rectangulares para que su compañero encuentre el volumen.

Apoyo para estudiantes con discapacidad

Representación: Interiorizar Comprender. Síntesis: Invite a los estudiantes a identificar qué detalles fueron necesarios para resolver el problema. Muestre el marco de la oración: "La próxima vez que necesite encontrar el volumen de una figura compuesta por dos prismas rectangulares, voy a...".

Apoya la accesibilidad para: Procesamiento conceptual, Organización, Memoria

• Grupos de 2

• Muestra la imagen del cuaderno del estudiante con las longitudes de los lados que faltan.

• "¿Cómo podemos encontrar las longitudes de los lados que faltan?"

INSTRUCCIONES

• 1 minuto: tiempo para pensar en silencio

• 2 minutos: discusión por parejas

• Comparte y anota las respuestas en la imagen de la figura. (Podemos restar 5 de 7 en ambos casos.)

• "Ahora, cada compañero hallará el volumen de una de las figuras y luego cambiará de papel. Su trabajo consiste en encontrar el volumen utilizando una estrategia de descomposición diferente a la de su compañero."

ACTIVIDAD

• Si hay tiempo, los grupos de 2 pueden hacer grupos de 4 y compartir respuestas y estrategias.

• 10 minutos: tiempo de trabajo independiente con discusión por parejas

• Dar a los estudiantes acceso a papel de puntos isométricos para dibujar las figuras si terminan antes.

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

Compañero A: Halla el volumen de la Figura 1.

Figura 1

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

Compañero B: Halla el volumen de la Figura 2.

Figura 2

• Ejemplo de respuesta 1: Cortando la figura verticalmente se obtiene un prisma 7 por 2 por 2 a la izquierda, y un prisma 5 por 5 por 2 a la derecha. El volumen total es (2 × 2 × 7) + (5 × 2 × 5) pies cúbicos, que son 28 + 50 o 78 pies cúbicos.

• Cortando la figura horizontalmente se obtiene un prisma de 2 pies por 2 pies por 2 pies en la parte superior, y un prisma de 7 pies por 2 pies por 5 pies en la parte inferior. El volumen es (2 × 2 × 2) + (7 × 2 × 5) pies cúbicos, que es 8 + 70 o 78 pies cúbicos.

Figura 2

• Ejemplo de respuesta 1: Cortando verticalmente se obtiene un prisma rectangular de 3 pulgadas por 4 pulgadas por 7 pulgadas y un prisma rectangular de 5 pulgadas por 5 pulgadas por 7 pulgadas. El volumen es (3 × 4 × 7) + (5 × 5 × 7) pulgadas cúbicas, que es 84 + 175 o 259 pulgadas cúbicas.

• Respuesta de ejemplo 2: Cortando horizontalmente se obtiene un prisma rectangular de 3 pulgadas por 9 pulgadas por 7 pulgadas y un prisma rectangular de 2 pulgadas por 5 pulgadas por 7 pulgadas. El volumen es (3 × 9 × 7) + (2 × 5 × 7) pulgadas cúbicas, lo que equivale a 189 + 70 o 259 pulgadas cúbicas.

Si los estudiantes no encuentran el volumen correcto de la figura, pregúnteles: "¿Dónde ven prismas rectangulares en esta figura?"

Grado 5 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

• Visualizar: Figura 2

• "¿Cómo rompiste esta forma para encontrar el volumen?" (Corté la pieza que sobresale verticalmente para hacer dos prismas rectangulares. Corto la pieza inferior sobre la que se apoya la figura, horizontalmente).

• "¿Cómo has encontrado las longitudes de los lados de los prismas rectangulares?". (Algunas de las longitudes vienen dadas, y las otras las hallé restando.)

• "¿Obtuviste el mismo volumen cuando descompusiste la figura de manera diferente? ¿Por qué?" (Sí. Los cálculos fueron diferentes pero ambos me dicen cuántas pulgadas cúbicas se necesitan para llenar la figura.)

ACTIVIDAD DE EXPLORACIÓN 2 | EXPRESIONES

PARA EL

VOLUMEN DE FIGURAS

15 minutos

El objetivo de esta actividad es representar expresiones como descomposiciones de una figura formada por dos prismas rectangulares rectos no superpuestos. Esto da a los estudiantes la oportunidad de interpretar los paréntesis en las expresiones, a la vez que comprueban su comprensión de las diferentes formas de representar el volumen de un prisma rectangular; a saber, longitud por anchura por altura y área de una base por la altura correspondiente.

Los estudiantes trabajan de forma abstracta y cuantitativa en este problema (MP2) a medida que relacionan expresiones abstractas con descomposiciones de figuras compuestas por dos prismas rectangulares.

• Grupos de 2

• "Mira la primera figura y piensa cómo podrías descomponerla en 2 prismas."

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• 1 minuto: tiempo para pensar en silencio

• "Ahora considerarás cómo diferentes expresiones pueden representar el volumen de figuras."

• 5 minutos: tiempo de trabajo independiente

• 5 minutos: tiempo de discusión por parejas

• Supervise a los estudiantes que

• utilizan los números de las expresiones para determinar cómo descomponer la figura

• descomponer la figura y utilizan esto para identificar las expresiones.

1. Explica cómo cada expresión representa el volumen de la figura. Muestra tu razonamiento. Organízalo para que pueda ser seguido por otros.

A. ((2 × 3) × 4) + ((3 × 3) × 2)

B. (5 × 6) + (3 × 4)

2. ¿Cómo representa cada expresión el volumen del prisma? Explica o muestra tu razonamiento. Organízalo para que pueda ser seguido por otros.

A. (5 × 8 × 6) + (5 × 4 × 9) pulgadas cúbicas

B. (5 × 4 × 3) + (5 × 12 × 6) pulgadas cúbicas

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

Cada explicación de los estudiantes muestra que la figura está compuesta por 2 prismas rectangulares con las propiedades descritas. 1.

A. Un prisma tiene una base que es 2 pulgadas por 3 pulgadas y una altura de 4 pulgadas y el otro prisma tiene una base de 3 pulgadas por 3 pulgadas y una altura de 2 pulgadas.

POSIBLES RESPUESTAS

AVANZAR EN EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD

B. Un prisma tiene una base que tiene área 6 pulgadas cuadradas y la altura para esa base es 5 pulgadas. El otro prisma tiene una base con área 4 pulgadas cuadradas y la altura para esa base es 3 pulgadas. 2.

A. Un prisma tiene una base que es 8 pulgadas por 6 pulgadas y una altura de 5 pulgadas y el otro prisma tiene una base que es 4 pulgadas por 9 pulgadas y una altura de 5 pulgadas.

B. Un prisma tiene una base que es 4 pulgadas por 3 pulgadas y una altura de 5 pulgadas y el otro prisma tiene una base que es 12 pulgadas por 6 pulgadas y una altura de 5 pulgadas.

Si los estudiantes no describen cómo las expresiones representan el volumen de la figura, muéstreles parte de la expresión, los números dentro de los paréntesis, por ejemplo, y pídales que expliquen qué parte de la figura está representada.

• Invite a los estudiantes a compartir cómo las expresiones para el primer prisma representan su volumen.

• "¿Por qué hay 3 factores en la expresión (2 × 3) × 4 pero sólo 2 factores en la expresión (5 × 6)?" (Los 2, 3, y 4 son la longitud, la anchura y la altura del prisma de atrás. El 5 es la altura del prisma de abajo cuya área de la base es 6.)

• "En la expresión (3 × 3) × 2, ¿qué te dicen los paréntesis?". (Me dicen que primero multiplique 3 por 3, lo que me da el área de la base, y luego multiplique eso por 2 para obtener el volumen del prisma).

SÍNTESIS DE LA LECCIÓN

10 minutos

"Hoy hemos representado con expresiones los volúmenes de figuras formadas por prismas rectangulares."

Muestre la imagen de la primera actividad:

"Esta es una de las figuras con las que hemos trabajado hoy."

Muestre la expresión: 3 × 7 × 9 pulgadas cúbicas.

"¿Qué parte de la figura está representada por esta expresión? ¿Cómo lo sabes?" (El prisma rectangular de la parte superior de la figura. Mide 3 pulgadas de alto, 9 pulgadas de ancho, y 7 pulgadas de profundidad, así que su volumen es 3 × 7 × 9 pulgadas cúbicas.)

Dibuja una línea para mostrar el prisma.

Grado 5 . Matemáticas . Unidad 1

"¿Cuál es el volumen del otro prisma rectangular? ¿Cómo lo sabes?" (2 × 5 × 7 pulgadas cúbicas, ya que tiene 2 pulgadas de alto, 5 pulgadas de ancho y 7 pulgadas de profundidad.)

Muestra la expresión: (3 × 7 × 9) + (2 × 5 × 7) pulgadas cúbicas

"¿Cómo representa esta expresión el volumen de la figura?" (Muestra la suma de los volúmenes de los dos prismas rectangulares de los que está hecha la figura).

ENFRIAMIENTO | ENCONTRAR EL VOLUMEN DE UNA FIGURA

5 minutos

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

Halla el volumen de la figura. Explica o muestra tu razonamiento.

Ejemplo de respuesta 1: Al cortar la figura verticalmente se obtiene un prisma 5 por 2 por 1 a la izquierda y un prisma 4 por 2 por 1 a la derecha. El volumen total es (5 × 2 × 1) + (4 × 2 × 1) pies cúbicos, que es 10 + 8 o 18 pies cúbicos.

Respuesta de ejemplo 2: Al cortar la figura horizontalmente se obtiene un prisma de 3 pies por 2 pies por 1 pies en la parte superior y un prisma de 6 pies por 2 pies por 1 pies en la parte inferior. El volumen es (3 × 2 × 1) + (6 × 2 × 1) pies cúbicos, que es 6 + 12 o 18 pies cúbicos.

Math Nation California - Grado 5

LECCIÓN 10

IDEAS FUNDAMENTALES

• Capas de cubos

• Factores y grupos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

5.OA.1 Usar paréntesis, corchetes o llaves en expresiones numéricas, y evaluar expresiones con estos símbolos.

5.OA.2 Escribir expresiones simples que registren cálculos con números, e interpretar expresiones numéricas sin evaluarlas.

Enfocar SMPs

MP2 Razonar abstracta y cuantitativamente.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.3

I.C.11

II.C.6

REPRESENTAR EL VOLUMEN CON EXPRESIONES

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

influyen en el futuro

construyen argumentos viables y critican el razonamiento de los demás

OBJETIVO(S) DE APRENDIZAJE

exploran el cambio de cantidades y descubren la forma y el espacio.

• Puedo escribir expresiones numéricas para representar el volumen de una figura descompuesta de diferentes maneras.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTO

• Escribir e interpretar expresiones numéricas para representar el volumen de una figura descompuesta de diferentes maneras.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

¿Cómo ha sentado el trabajo de las secciones anteriores de la unidad las bases para que los estudiantes tengan éxito en esta lección?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

Notar y maravillarse (Calentamiento)

5 Prácticas (Actividad 2)

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Escribamos expresiones para el volumen de figuras.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes escriban, interpreten y evalúen expresiones numéricas que representen el volumen de figuras sólidas compuestas por dos prismas rectangulares rectos.

En lecciones anteriores, los estudiantes usaron fórmulas para encontrar el volumen de prismas rectangulares rectos. También aprendieron a aplicar estas fórmulas para encontrar los volúmenes de figuras formadas por dos prismas rectangulares no superpuestos. En esta lección, los estudiantes usan lo que han aprendido para escribir e interpretar expresiones numéricas en el contexto de hallar el volumen de figuras compuestas por prismas rectangulares (MP2).

Los estudiantes reconocen que la resta se puede usar para hallar el volumen de figuras compuestas por dos prismas rectangulares no superpuestos.

Actividad 2: Hallar el volumen de diferentes maneras

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Breve descripción

Calentamiento Parejas 10 min Los estudiantes hacen observaciones sobre un prisma descompuesto de formas diferentes.

Actividad de exploración 1 Parejas 10 min

Actividad de exploración 2 Parejas 25 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Prácticas Grupos pequeños Opcional

Los estudiantes escriben y comparan expresiones para el volumen de una figura tridimensional formada por cubos unitarios.

Los estudiantes determinan el volumen de una figura tridimensional descomponiéndola de diferentes maneras e interpretan una expresión para el volumen del prisma utilizando la resta.

Los estudiantes discuten diferentes estrategias para descomponer figuras 3D de diferentes maneras para determinar su volumen.

Los estudiantes escriben y evalúan una expresión para el volumen de una figura 3D.

Abordando:

• Cinco en raya: Multiplicación (3-5), Etapa 4: Tres factores

Apoyando:

• Rodando por fracciones (3-5), Etapa 1: Fracciones equivalentes

Math

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | NOTAR Y MARAVILLARSE: PIEZAS DE PRISMA

10 minutos

Rutinas instructivas

Conversación sobre números

El objetivo de este calentamiento es que los estudiantes se den cuenta de que las figuras compuestas por dos prismas rectangulares rectos pueden descomponerse de diferentes maneras, lo que será útil cuando los estudiantes encuentren el volumen de figuras compuestas por dos prismas rectangulares rectos en una actividad posterior. Aunque los estudiantes pueden observar y preguntarse muchas cosas sobre estas imágenes, la comparación de las longitudes de los lados de las dos figuras es el punto de discusión importante.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

SÍNTESIS DE LA ACTIVIDAD

• Grupos de 2

• Muestre la imagen.

• "¿Qué observas? ¿Qué te preguntas?"

• 1 minuto: tiempo para pensar en silencio

• 1 minuto: discusión en parejas

• Compartir y registrar las respuestas.

¿Qué notas?

¿Qué te preguntas?

Los estudiantes pueden notar:

• Algunas de las longitudes de los lados son iguales para las dos figuras.

• Hay un prisma azul y un prisma naranja en ambas figuras.

• El prisma azul es más corto en la figura de la izquierda.

• El prisma naranja es más largo en el prisma de la izquierda.

Los estudiantes pueden preguntarse:

• ¿Son la misma figura?

• ¿Cuál es el volumen de las figuras?

• "¿Crees que las imágenes muestran la misma figura? ¿Por qué sí o por qué no?" (Sí, parecen iguales. Sí, puedo usar las longitudes de los lados dadas para calcular que son iguales.)

ACTIVIDAD DE EXPLORACIÓN 1 | COMPARAR EXPRESIONES

10 minutos

El propósito de esta actividad es que los estudiantes encuentren el volumen de una figura de diferentes maneras. La figura dada se puede descomponer de dos maneras en prismas rectangulares haciendo diferentes cortes. Sin embargo, también se puede hallar

Grado 5 . Matemáticas . Unidad 1

utilizando un único prisma rectangular más grande eliminando un prisma rectangular más pequeño. Esto brinda la oportunidad de expresar su volumen como diferencia de volúmenes de prismas rectangulares. Los estudiantes pueden fijarse en esta característica, que se destaca en la síntesis de la actividad.

Cuando los estudiantes deciden si tienen o no las mismas expresiones, tienen que razonar cuidadosamente sobre lo que significa "lo mismo". Consideran si el orden de los factores es diferente, es la misma expresión y si el orden de los sumandos es diferente, es la misma expresión. Los estudiantes utilizan lo que saben sobre volumen, figuras geométricas y las propiedades de las operaciones para justificar la equivalencia de las expresiones y criticar el razonamiento de sus compañeros (MP2, MP3, MP7).

Apoyo para estudiantes de inglés

MLR8 Apoyos de discusión. Mostrar marcos de frases para apoyar la discusión entre compañeros: "En primer lugar, yo porque . . ." , " y son iguales porque . . .", " y son diferentes porque . . ."

Avances: Conversar, Representar

INSTRUCCIONES

ACTIVIDAD

Math

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

AVANCES EN EL PENSAMIENTO DE LOS ESTUDIANTES

SÍNTESIS DE LA ACTIVIDAD

Nation California - Grado 5

• Grupos de 2

• "Vais a buscar diferentes expresiones para calcular el volumen de una figura."

• 5 minutos: tiempo de trabajo en parejas

• Vigilar a los estudiantes que dibujan una línea vertical para mostrar dónde descomponen la figura para compartirla durante la síntesis.

1. Escribe una expresión para representar el volumen de la figura en cubos unitarios.

2. Compara las expresiones con tu compañero.

A. ¿En qué se parecen?

B. ¿En qué se diferencian?

3. Si son iguales, intenta encontrar otra forma de representar el volumen.

• Ejemplos de respuestas: (5 × 2 × 5) + (3 × 3 × 5), (3 × 5 × 5) + (2 × 2 × 5), (5 × 5 × 5) - (2 × 3 × 5)

• Ejemplo de respuesta: Las expresiones tienen el mismo valor pero son diferentes.

• Las respuestas varían.

Si los estudiantes no vieron la figura como un cubo al que le falta un prisma rectangular, pídales que construyan la figura y la pieza que falta y que se puede agregar para convertirla en un cubo.

• Invite a los estudiantes a compartir diferentes expresiones para el volumen de la figura.

• Muestre la expresión: (3 × 5 × 5) + (2 × 2 × 5)

• "¿Cómo representa la expresión el volumen de la figura?" (3 × 5 × 5 representa el prisma que mide 3 por 5 por 5 cubos de alto y el 2 × 2 × 5 representa el prisma que mide 2 por 2 por 5 cubos de alto.)

• Si ningún estudiante escribió la expresión (5 × 5 × 5) - (2×3×5), muestra esta expresión.

• "¿Cómo muestra la expresión el volumen de la figura en unidades cúbicas?" (Hay un cubo de 5 por 5 por 5 y se le ha quitado un trozo. La pieza que se quita mide 2 cubos por 3 cubos por 5 cubos.)

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN 2 | HALLAR EL VOLUMEN DE

DIFERENTES MANERAS 25

minutos

Rutinas instructivas

5 Prácticas

El objetivo de esta actividad es que los estudiantes escriban expresiones equivalentes para hallar el volumen de una figura compuesta por dos prismas rectangulares derechos. Los estudiantes descomponen la figura de dos formas diferentes y escriben expresiones equivalentes para hallar el volumen. Como apoyo adicional, proporcione a los estudiantes lápices de colores para que sombreen las dos partes del prisma antes de encontrar las longitudes de los lados que necesitan para calcular el volumen. Supervise y seleccione a un estudiante con cada una de las siguientes estrategias para compartir en la síntesis:

• descompuso la figura en un prisma con las longitudes laterales 4 pies por 4 pies por 3 pies y un prisma con las longitudes laterales 10 pies por 4 pies por 3 pies y escribió esta expresión (o una escrita en un orden diferente) para representar el volumen: (4 × 4 × 3) + (10 × 4 × 3)

• descompuso la figura en un prisma con las longitudes laterales 4 pies por 8 pies por 3 pies y un prisma con las longitudes laterales 6 pies por 4 pies por 3 pies y escribió esta expresión (o una escrita en otro orden) para representar el volumen: (4 × 8 × 3 ) + (6 × 4 × 3)

Apoyo a estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Invite a los estudiantes a planificar una estrategia, incluyendo las herramientas que utilizarán, para encontrar el volumen de las figuras. Si el tiempo lo permite, invite a los estudiantes a compartir su plan con un compañero antes de empezar.

Apoya la accesibilidad para: Organización, Memoria, Atención

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

• Grupos de 2

• 10 minutos: tiempo de trabajo individual

• 5 minutos: discusión por parejas

• Mientras los estudiantes trabajan, considera preguntar, "¿Por qué elegiste descomponer el prisma de esa manera?"

1. Halla el volumen de la figura descomponiéndola de 2 formas diferentes. Muestra tu razonamiento. Organízalo de manera que pueda ser seguido por otros.

2. Para cada forma en que descompusiste la figura, escribe una expresión que represente el volumen.

ENUNCIADO DE LA TAREA CONTINUACIÓN

Grado 5 . Matemáticas . Unidad 1

3. Mai utilizó esta expresión para hallar el volumen de la figura: (10 × 8 × 3) - (6 × 4 × 3). Utiliza el diagrama para interpretar la expresión de Mai. Muestra tu razonamiento. Organízalo para que pueda ser seguido por otros.

POSIBLES RESPUESTASS 1.

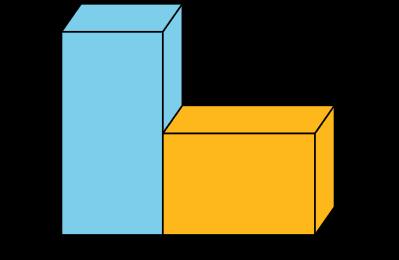
2. (4 × 4 × 3) + (10 × 4 × 3) pies cúbicos, (4 × 8 × 3) + (6 × 4 × 3) pies cúbicos, y (10 × 8 × 3) - (6 × 4 × 3) pies cúbicos

3. La figura es un 10 pie por 8 pie por 3 pie prisma rectangular y luego se ha eliminado un 6 pie por 4 foot por 3 pie prisma. Así que su volumen es (10 × 8 × 3) - (6 × 4 × 3) pies cúbicos.

• Pide a los dos estudiantes seleccionados que muestren sus trabajos uno al lado del otro para que todos los vean.

• "¿En qué se parecen los diagramas? ¿En qué se diferencian?"

SÍNTESIS DE LA ACTIVIDAD

• "¿Cómo se relacionan las expresiones con los diagramas?"

• Muestra: (10 × 8 × 3) - (6 × 4 × 3)

• "¿Cómo representa esta expresión el volumen del prisma?" (El prisma rectangular más grande tiene de lado 10 × 8 × 3 pies cúbicos. Podemos restar un prisma rectangular con las longitudes laterales 6 × 4 × 3 pies cúbicos.)

• "¿Cuál es el valor de (10 × 8 × 3) - (6 × 4 × 3)?" (168)

SÍNTESIS DE LA LECCIÓN

10 minutos

"Hoy hemos descompuesto la misma figura de diferentes maneras y hemos escrito expresiones para representar el volumen".

"¿Qué estrategia de descomposición preferiste utilizar? ¿Por qué?" (Depende de los números. Descompongo la figura de la manera que me da los números más amigables.)

"¿Obtienes las mismas expresiones usando cualquiera de las dos descomposiciones? ¿Por qué?" (No, porque la figura se descompone en prismas rectangulares con diferentes longitudes de lado.)

"Las expresiones son diferentes, dependiendo de cómo descompusimos la forma, pero el volumen es el mismo. ¿Por qué?" (El volumen no cambia. Sólo descomponemos la figura de distintas maneras. Las expresiones son iguales).

Math

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

ENFRIAMIENTO | EXPRESIONES COMO VOLUMEN 5 minutos

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

Reflexiones:

1. Escribe una expresión para representar el volumen de la figura en pies cúbicos. 2. Halla el volumen de la figura.

1. (4 × 8 × 2) + (2 × 3 × 2) o (4 × 5 × 2) + (6 × 3 × 2) (o equivalente)

2. 76 pies cúbicos

Nation California - Grade 5

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

IDEAS FUNDAMENTALES

• Capas de cubos

• Modelado

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

5.MD.5a Hallar el volumen de un prisma rectangular recto con longitudes laterales de números enteros empaquetándolo con cubos unitarios , y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de las aristas, equivalentemente multiplicando la altura por el área de la base. Representar productos de tres números enteros como volúmenes.

5.MD. Aplicar las fórmulas �� = �� × �� × ℎ y �� = �� × ℎ para prismas rectangulares para hallar volúmenes de prismas rectangulares rectos con longitudes de arista de números enteros en el contexto de la resolución de problemas matemáticos y del mundo real.

5.MD.5c Reconocer el volumen como aditivo. Encontrar volúmenes de figuras sólidas compuestas de dos prismas rectangulares rectos no superpuestos sumando los volúmenes de las partes no superpuestas, aplicando esta técnica para resolver problemas del mundo real.

Enfocar SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP6 Atender a la precisión.

Estándares ELD de California

I.B.6

I.C.11

II.C.6

LECCIÓN 11

PRISMAS DE TODO TIPO

ENFOQUE EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

repercuten en el futuro

dan sentido a los problemas y perseveran en su resolución explorando cantidades cambiantes y descubriendo la forma y el espacio.

OBJETIVO(S) DE APRENDIZAJE

• Puedo encontrar el volumen de prismas tridimensionales en situaciones matemáticas y del mundo real.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Resolver problemas matemáticos y del mundo real que involucren volumen.

PREGUNTA DE REFLEXIÓN PARA EL MAESTO

Al finalizar esta unidad, reflexione sobre las normas y actividades que han apoyado a cada estudiante en el aprendizaje de las matemáticas. ¿Cómo has visto crecer a cada estudiante como joven matemático a lo largo de este trabajo? ¿Cómo te has visto crecer a ti mismo como maesto? ¿Qué vas a seguir haciendo y qué vas a mejorar en la Unidad 2?

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

¿Cuál no pertenece? (Calentamiento)

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Vamos a encontrar el volumen de todos los diferentes tipos de prismas.

Narrativa de la lección

El objetivo matemático de esta lección es que los estudiantes apliquen lo que han aprendido acerca de encontrar los volúmenes de prismas rectangulares rectos y figuras compuestas de prismas rectangulares rectos para resolver problemas del mundo real.

En lecciones anteriores, los estudiantes aprendieron a encontrar el volumen de un prisma rectangular recto multiplicando el número de cubos en una capa por el número de capas. Hallaron los volúmenes de prismas rectangulares con y sin los cubos unitarios mostrados. Han utilizado la propiedad asociativa de la multiplicación para representar productos triples de números enteros como volúmenes y han aprendido a hallar el volumen de prismas rectangulares con longitudes laterales de números enteros multiplicando la longitud por la anchura por la altura y multiplicando el área de la base por la altura. También entienden el volumen como aditivo. Han hallado los volúmenes de figuras sólidas compuestas por dos prismas rectangulares rectos no superpuestos sumando los volúmenes de las partes no superpuestas. En esta lección, los estudiantes aplican estos conocimientos para resolver problemas del mundo real.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Breve descripción

Calentamiento En parejas 10 min Los estudiantes observan las diferencias entre prismas tridimensionales.

Actividad de exploración 1 En parejas 20 min

Actividad de exploración 2 Parejas 15 min

Síntesis Todo el grupo 10 min

Enfriamiento Independiente 5 min

Math

Prácticas Grupos pequeños Opcional

Los estudiantes calculan el volumen de prismas presentados en situaciones reales utilizando figuras sólidas dadas y contextos descriptivos.

Los estudiantes analizan un prisma dado, representan su volumen utilizando una expresión matemática y crean una nueva figura sólida con el mismo volumen pero diferentes dimensiones.

Los estudiantes resumen sus conocimientos sobre el volumen de los prismas rectangulares con y sin cubos unitarios.

Los estudiantes aplican sus conocimientos sobre los prismas tridimensionales para determinar el volumen de un objeto del mundo real.

Abordar:

• Cinco en raya: Multiplicación (3-5), Etapa 4: Tres factores

Apoyo:

• Rodar para fracciones (3-5), Etapa 2: Multiplicar una fracción por un número entero

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | CUÁL NO PERTENECE: MUCHOS PRISMAS 10

minutos

Rutinas instructivas

¿Cuál no pertenece?

Este calentamiento pide a los estudiantes que comparen cuatro imágenes. Da a los estudiantes una razón para utilizar el lenguaje con precisión (MP6). Ofrece al maesto la oportunidad de escuchar cómo los estudiantes utilizan la terminología y hablan de las características de los elementos en comparación unos con otros. Durante la síntesis, pide a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como volumen, base, altura, longitud y anchura.

Grupos de 2

INSTRUCCIONES

ACTIVIDAD

• Muestre la imagen.

• "Elija uno que no pertenezca. Prepárense para compartir por qué no pertenece."

• 1 minuto: tiempo para pensar en silencio

• 2-3 minutos: discusión en parejas

• Compartir y registrar las respuestas.

¿Cuál no pertenece?

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTASS

SÍNTESIS DE LA ACTIVIDAD

Ejemplos de respuestas:

A. B. C.

• A no pertenece porque no es más alto que ancho o largo.

• B no pertenece porque no muestra ningún cubo individual.

• C no pertenece porque no se puede saber cuánto mide.

• D no pertenece porque no es un prisma rectangular.

• "¿Qué tienen en común las figuras A, C y D?" (Todas muestran cubos individuales. Todos tienen 5 como una de las longitudes de sus lados.)

ACTIVIDAD DE EXPLORACIÓN 1 | PRISM PALOOZA

20 minutos

El propósito de esta actividad es que los estudiantes practiquen cómo encontrar el volumen de prismas rectangulares en un contexto del mundo real. El primer problema proporciona un diagrama como el que los estudiantes han visto en lecciones anteriores para ilustrar el contexto. En los demás problemas no se proporciona ninguna imagen, por lo que los estudiantes tendrán que visualizar o dibujar un esquema de la situación. Pasar de las palabras del problema a una imagen mental y a una estrategia de solución son todos aspectos importantes para dar sentido y resolver un problema (MP1).

Grado 5 . Matemáticas . Unidad 1

Como se trata de problemas del mundo real, cada prisma rectangular se asienta sobre una base natural. Vigila a los estudiantes que utilicen esta estructura y utiliza la fórmula que relaciona el volumen con el área de la base y la altura relativa a esa base.

Apoyo

para estudiantes de inglés

MLR6 Tres lecturas. Mantenga los libros o dispositivos cerrados. Muestre sólo la raíz del problema y la imagen, sin revelar la pregunta. "Vamos a leer esta pregunta 3 veces". Después de la 1primera lectura: "Dile a tu compañero de qué trata esta situación". Después de la 2nd Lea: "Enumera las cantidades. ¿Qué se puede contar o medir?". Revela la pregunta. Después del 3rd Lee: "¿Qué estrategias podemos utilizar para resolver este problema?"

Avanza: Leer, Representar

INSTRUCCIONES

Math

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

• Grupos de 2

• 8 minutos: tiempo de trabajo individual

• 2 minutos: discusión por parejas

• Monitorea a los estudiantes que encuentran el volumen de diferentes maneras, ya sea usando diferentes bases o usando 3 medidas para la longitud, el ancho y la altura.

Para cada problema, explique o muestre su razonamiento.

1. Han está llenando una caja con cubos. Abajo hay un diagrama de la caja. ¿Cuántos cubos caben en la caja si Han la llena completamente, sin huecos entre cubos?

2. Clare compró un contenedor de almacenamiento para sus materiales de arte. El contenedor mide 4 pies de ancho, 9 pies de largo y 5 pies de alto. ¿Cuál es el volumen de su contenedor?

3. El nuevo dormitorio de Mai tiene un vestidor con un suelo que mide 30 pies cuadrados. El techo del armario está a 9 pies del suelo. ¿Cuál es el volumen de su armario?

1. 300 cubos. Ejemplo de respuesta: hay 6 × 10 o 60 cubos en una capa y hay 5 capas así que 5 × 60 = 300

2. 180 pies cúbicos. Respuesta de muestra: 4 × 5 = 20 y 20 × 9 = 180.

3. 270 pies cúbicos. Respuesta de muestra: 30 × 9 = 270

• Pide a los estudiantes seleccionados que compartan sus soluciones para el segundo problema.

SÍNTESIS DE LA ACTIVIDAD

Nation California - Grado 5

• "¿En qué son iguales las estrategias? ¿En qué se diferencian?" (Ambos obtuvieron la misma solución, pero una persona multiplicó 4 × 9 para obtener el área de la base y luego multiplicó el resultado por 5, pero la otra persona eligió multiplicar primero 4 × 5.)

• "¿En qué se diferencia el tercer problema de los dos primeros?" (No nos da la longitud ni la anchura del armario. Sólo nos da el área del suelo.)

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN 2

| RESOLUCIÓN

DE PROBLEMAS CON FIGURAS

15 minutos

El propósito de esta actividad es que los estudiantes resuelvan un problema del mundo real que implica encontrar el volumen de una figura compuesta por dos prismas rectangulares derechos. A diferencia de muchas otras figuras que han visto los estudiantes, ésta sólo puede descomponerse en dos prismas rectangulares de una manera. Los estudiantes pueden reorganizar los dos prismas para formar un único prisma rectangular alargado.

Apoyo a estudiantes con discapacidad

Acción y Expresión: Desarrollar la expresión y la comunicación. Dar a los estudiantes acceso a papel cuadriculado o cubos de conexión como herramientas para diseñar su propio jardín.

Apoya la accesibilidad para: Procesamiento Visual-Espacial, Procesamiento Conceptual, Organización

• Muestra la imagen del jardín del cuaderno del estudiante:

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

• "Este tipo de jardín se llama jardín de camas elevadas porque las plantas no están en el suelo."

• "Si plantáramos un jardín en nuestro colegio, ¿qué hortalizas te gustaría cultivar?"

• 5 minutos: tiempo de trabajo individual

• 5 minutos: discusión por parejas

• Supervise a los estudiantes que dividen el jardín en dos prismas rectangulares, hallando el volumen de cada uno, y a los estudiantes que los juntan para formar un único prisma rectangular.

La escuela primaria va a construir un jardín de bancales elevados como el de la imagen, pero utilizarán un diseño diferente. Aquí tienes un diagrama que muestra las longitudes de los lados del huerto que construirá la escuela.

1. ¿Cuál es el volumen del huerto? Explica o muestra tu razonamiento.

2. Escribe una expresión para representar el volumen del jardín.

3. Noah quiere diseñar un jardín con el mismo volumen pero diferentes longitudes laterales. ¿Cuáles podrían ser las longitudes laterales de su jardín?

4. ¿Qué diseño de jardín te gusta más? Explica tu razonamiento.

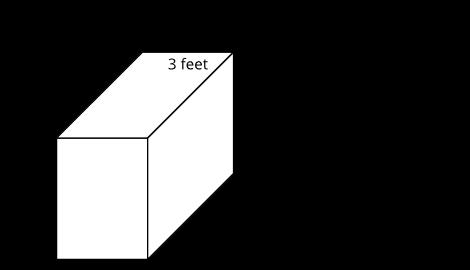
1. 216 pies cúbicos (3 × 8 × 4) + (3 × 10 × 4) = 96 + 120 = 216

2. (3 × 8 × 4) + (3× 10 × 4) con factores en cualquier orden

3. Respuesta de ejemplo: 3 × 4 × 18

4. Respuesta de ejemplo: Me gusta más mi jardín porque se parece más a un cuadrado.

Grado 5 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

• Muestre el diagrama del jardín de la tarea.

• Invite a los estudiantes a compartir cómo encontraron su volumen.

• "¿Qué tienen en común las dos partes del jardín?" (Ambas tienen 4 pies de alto y 3 pies de ancho.)

• "¿Qué tienen de diferente las dos partes del jardín?" (La longitud. Una pieza mide 10 pies de largo y la otra 8 pies de largo.)

• "¿Cómo podrías unir las piezas para formar un único prisma rectangular?" (Los lados que miden 3 pies por 4 pies encajan y la longitud sería 18 pies.)

SÍNTESIS DE LA LECCIÓN

10 minutos

"En esta unidad, has trabajado mucho con prismas y volumen. ¿Qué cosas sabes sobre el volumen y los prismas rectangulares?"

Comparte y anota las respuestas de los estudiantes.

Muestra estas imágenes de la unidad:

"Habla con tu vecino. Comenta qué parte de la unidad te ha gustado más y por qué. ¿Cómo te ayudó el trabajo con los cubos con el resto del trabajo de volumen de la unidad?"

ENFRIAMIENTO | EL VOLUMEN DE UN ARENERO

5 minutos

Un preescolar está construyendo un arenero. Abajo hay un diagrama que muestra las longitudes de los lados del arenero.

¿Cuál es el volumen del arenero? Explique o muestre su razonamiento.

ENUNCIADO DE LA TAREA

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS

El volumen del arenero es 124 pies cúbicos. Ejemplo de respuesta: Es un prisma de 10 pies por 5 pies por 2 pies y un prisma de 6 pies por 2 pies por 2 pies, así que es (10 × 5 × 2) + (6 × 2 × 2) pies cúbicos.

Resumen de la sección del estudiante

ENUNCIADO DE LA TAREA

Reflexiones:

Algunas figuras están hechas de dos prismas rectangulares. Podemos descomponer estas figuras y hallar el volumen de cada prisma. Luego, sumamos los volúmenes de los dos prismas para hallar el volumen total de la figura. A menudo hay más de una manera de descomponer figuras hechas de 2 prismas rectangulares. Estas expresiones pueden utilizarse para hallar el volumen de la figura:

(3 × 3 × 5) + (5 × 2 × 5)

(3 × 5 × 5) + (2 × 2 × 5)

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

IDEAS FUNDAMENTALES

• Factores y grupos

• Capas de cubos

• Modelización

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Enfocar SMPs

MP1 Dar sentido a los problemas y perseverar en resolverlos.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP4 Modelar con matemáticas.

Estándares ELD de California

I.A.1

II.A.2

California EP&Cs

4.A

I.B.8

LECCIÓN 12

MONTONES Y MONTONES DE BASURA (OPCIONAL)

ENFOQUE

EN LAS IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué?

Para . . . (SMPs) ¿Cómo? . . . los estudiantes . . . (CC) ¿Qué? . . . mientras . .

predecir lo que podría ocurrir y repercutir en el futuro

dar sentido a los problemas y perseverar en su resolución y modelizar con matemáticas

OBJETIVO(S) DE APRENDIZAJE

dar sentido a los problemas y perseverar en su resolución y modelizar con matemáticas

• Puedo encontrar el volumen de un prisma rectangular en una situación del mundo real usando cubos de unidades.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Encuentra el volumen de prismas rectangulares con unidades de medida estándar multiplicando la base por la altura o multiplicando el largo por el ancho por la altura.

PREGUNTA PARA LA REFLEXIÓN DEL MAESTO

¿Quién ha podido hacer matemáticas hoy en clase y cómo lo sabes? Identifica las normas o rutinas que permitieron a esos estudiantes dedicarse a las matemáticas. ¿Cómo puede ajustar estas normas y rutinas para que todos los estudiantes hagan matemáticas mañana?

PREPARACIÓN DE LA LECCIÓN

Rutinas instructivas

Observa y maravíllate (Calentamiento)

Materiales a reunir

Cubos de conexión: Actividad 1

Papel Patty: Actividad 1

Herramientas para crear una muestra visual: Actividad 1

Preparación necesaria

Actividad 1:

Cada grupo de 2 necesita al menos 20 cubos de conexión.

Grado 5 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Investiguemos qué le sucede a la basura.

Narrativa de la lección

El objetivo de esta lección es que los estudiantes utilicen su comprensión del volumen de prismas rectangulares para resolver un problema del mundo real. Los estudiantes hacen un modelo para visualizar grandes cantidades de basura.

Esta lección es opcional porque no aborda ningún nuevo estándar de contenido matemático. Esta lección sí brinda a los estudiantes la oportunidad de aplicar habilidades pregradoras de la modelación matemática.

En lecciones anteriores, los estudiantes calcularon volúmenes. Colocaron cubos unitarios dentro de cajas y hallaron el volumen de la caja multiplicando las longitudes de los lados de la caja. En esta lección, investigarán un problema del mundo real utilizando esas ideas.

En el calentamiento, los estudiantes leen un breve párrafo de un artículo sobre la exportación de basura. Se pide a los estudiantes que visualicen 3.300 toneladas o 60 contenedores de basura. Matematizar el mundo reconociendo las matemáticas en la vida cotidiana es un paso importante de la modelización matemática.

En la primera actividad, los estudiantes encuentran diferentes disposiciones de 60 contenedores de transporte, suponiendo que son cubos. Aunque los contenedores reales no son cubos, podemos simplificar la situación utilizando figuras con las que sea más fácil trabajar. Este paso de hacer suposiciones simplificadas es una parte importante de la modelización matemática. Se pide a los estudiantes que dibujen un diagrama de una de sus disposiciones.

En la segunda actividad, los estudiantes estiman el número de contenedores de un buque de carga completamente cargado a partir de una imagen. Cuando los estudiantes estiman cantidades y hacen suposiciones, modelizan con matemáticas. Los estudiantes vuelven a la cuestión de la basura calculando juntos cuánta basura cabría en un carguero completamente cargado. Cuando los estudiantes trasladan una respuesta matemática a la situación del mundo real, modelizan con matemáticas (MP4).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Breve descripción

Calentamiento En parejas 10 min Los estudiantes hacen observaciones sobre un camión de basura.

Los estudiantes crean diferentes expresiones para modelizar el volumen de prismas rectangulares apilados.

Math

Actividad de exploración 1 En parejas o En pequeños grupos 25 min

Esta tarea podría ampliarse como una oportunidad para establecer conexiones con los efectos de las actividades humanas que están directamente relacionadas con las cantidades de regrados consumidos y las oportunidades para que los seres humanos minimicen los residuos en todo el mundo.

Actividad de exploración 2 En parejas 20 min Los estudiantes estiman y razonan sobre el volumen de cubos apilados en diferentes escenarios.

Síntesis Todo el grupo 10 min Los estudiantes establecen conexiones entre un escenario del mundo real que modela el volumen y cómo afecta a sus vidas cotidianas.

Abordar:

• Cinco en raya: Multiplicación (3-5), Etapa 4: Tres factores

Prácticas Grupos pequeños Opcional

Nation California - Grado 5

Apoyo:

• Rodar para fracciones (3-5), Etapa 2: Multiplicar una fracción por un número entero

Grado 5 . Matemáticas . Unidad 1

CALENTAMIENTO | CONVERSACIÓN NUMÉRICA: CAMIÓN DE LA BASURA

10 minutos

Rutinas instructivas

Notar y preguntarse

El propósito de este calentamiento es que los estudiantes discutan cuánto espacio ocupa una tonelada de basura, lo que será útil cuando los estudiantes consideren 3.300 toneladas de basura plástica en contenedores de transporte en una actividad posterior. Puede que algunos estudiantes no conozcan la definición exacta de tonelada. Anime a los estudiantes a visualizar qué aspecto podrían tener 2.000 libras de basura. La síntesis da a los estudiantes la oportunidad de considerar el tipo y la cantidad de basura que se produce en su comunidad.

• Grupos de 2

• Muestre la imagen.

INSTRUCCIONES

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

• "¿Qué notan? ¿Qué te sorprende?"

• 1 minuto: tiempo para pensar en silencio

• "Comenta lo que has pensado con tu compañero."

• 1 minuto: debate en pareja

• Comparte y anota las respuestas.

¿Qué observas?

¿Qué te sorprende?

SÍNTESIS DE LA ACTIVIDAD

Los estudiantes pueden observar:

• Hay un camión de la basura.

• El camión parece estar aparcado o esperando en un semáforo.

• Parece que el camión está cerca de un parque.

Los estudiantes pueden preguntarse:

• ¿Qué hay en el camión?

• ¿Cuánta basura hay en el camión?

• ¿Dónde está el camión de la basura?

• "El camión de la basura medio puede contener 12-14 toneladas de basura."

• Si es necesario, "1 tonelada es lo mismo que 2.000 libras."

• "Si este camión recoge la basura sólo de nuestro colegio (o barrio) ¿con qué tipo de cosas podría llenarse el camión?"

• "¿Cuánto tiempo crees que tardaría nuestro colegio (o barrio) en llenar completamente el camión?"

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN 1 | 60 CONTENEDORES

25 minutos

Materiales a reunir

Cubos de conexión

Papel patty

Herramientas para crear una exhibición visual

Preparación requerida

Cada grupo de 2 necesita al menos 20 cubos de conexión.

En esta actividad los estudiantes encuentran diferentes maneras de ordenar 60 contenedores de transporte. Deciden qué disposición es la mejor en el contexto del transporte de 3.300 toneladas de basura.

Apoyo para estudiantes de inglés

MLR7 Comparar y conectar. Síntesis: Después de que se hayan presentado todas las estrategias, dirija una discusión comparando, contrastando y conectando los diferentes enfoques. Pregunte: "¿Qué tenían en común las representaciones?", "¿En qué se diferenciaban?" y "¿Alguien resolvió el problema de la misma manera, pero lo explicaría de forma diferente?".

Avances: Representar, conversar

Apoyo a los estudiantes con discapacidad

Compromiso: Facilitar el acceso captando el interés. Utiliza temporizadores visibles o alertas sonoras para ayudar a los estudiantes a controlar su progreso y asegúrate de que tienen tiempo suficiente para crear una visualización.

Apoya la accesibilidad para: Atención, Organización

INSTRUCCIONES

• Grupos de 2 o 4

• "He aquí un breve párrafo de un artículo de periódico de 2018."

• Mostrar "Malasia planea enviar de vuelta aproximadamente 3,300 toneladas de basura plástica a países como Estados Unidos y Canadá."

• "¿Cuáles son algunas preguntas que tienes después de leer esto?" (¿Dónde está Malasia? ¿Por qué la devuelve Malasia? ¿Por qué los países envían su basura a lugares como Malasia? ¿A qué otros lugares va nuestra basura?)

• Si es necesario, muestra a los estudiantes Malasia en un mapa.

• "La basura cabe en 60 contenedores marítimos y será devuelta en un gran carguero sobre el agua."

• "¿Qué aspecto tiene un contenedor marítimo?"

• Muestra la imagen de un contenedor marítimo.

• Da acceso a cubos de conexión, papel para carteles, cartulina y herramientas de escritura a cada grupo.

Math

Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1

ACTIVIDAD

ENUNCIADO DE LA TAREA

POSIBLES RESPUESTAS

• 1 minuto: tiempo de trabajo independiente.

• 15 minutos: tiempo de trabajo en parejas

• A medida que los estudiantes trabajan, controle si utilizan diferentes disposiciones.

1. Encuentre al menos 5 formas diferentes de organizar 60 recipientes. Represente cada disposición con una expresión.

2. Cree una presentación visual para mostrar cuál es la mejor disposición para enviar las 3.300 toneladas de basura.

• 1 × 1 × 60, 1 × 2 × 30, 1 × 3 × 20, 1 × 4 × 15, 1 × 5 × 12, 1 × 6 × 10, 2 × 15 × 2, 2 × 3 × 10, 2 × 5 × 6, 3 × 4 × 5

• Los estudiantes pueden hacer cualquier modelo visual que tenga sentido para ellos.

• Invite a los estudiantes previamente seleccionados a compartir su presentación visual.

• "¿Qué disposición representa la presentación visual de este grupo? ¿Por qué podrían pensar que ésta es la mejor disposición?"

SÍNTESIS DE LA ACTIVIDAD

• "¿Qué puedes decirle a este grupo que podría hacerles cambiar su decisión?" (Es demasiado alto y podría empezar a caer al agua. Es demasiado ancho y podría no caber. Es demasiado ancho y podría no dejar espacio para nada más.)

• Considera preguntar "¿Cuánta basura crees que hay en cada uno de los contenedores?". (Los estudiantes pueden hacer una estimación o una conjetura.)

ACTIVIDAD DE EXPLORACIÓN 2 | ¿CUÁNTOS

CONTENEDORES EN

EL BARCO?

20 minutos

El objetivo de esta actividad es que los estudiantes calculen el número de contenedores que hay en un buque de carga completamente cargado. A continuación, hacen muchas suposiciones sobre la disposición de los contenedores en el barco para llegar a una estimación mejor.

• Grupos de 2

• Muestra la imagen.

• "¿Cuántos contenedores hay en el carguero?"

INSTRUCCIONES

• "¿Qué estimación es demasiado alta?" "¿Demasiado bajo?" "¿Más o menos?"

• 1 minuto: tiempo para pensar en silencio

• Registrar las respuestas.

ACTIVIDAD

Grado 5 . Matemáticas . Unidad 1

• "Un carguero puede contener muchos más de 60 contenedores. La segunda imagen muestra un carguero completamente cargado."

• 5 minutos: tiempo de trabajo independiente

• "Discute tus estimaciones y suposiciones con tu compañero."

• 2 minutos: discusión en parejas

• Vigila a los estudiantes que hagan suposiciones diferentes:

• El barco está completamente cargado.

• Parte del espacio está ocupado por estructuras.

• Hay más contenedores debajo de la cubierta que no podemos ver.

• Todos los contenedores tienen el mismo tamaño.

• las longitudes de los lados específicos de los contenedores de carga

1. ¿Cuántos contenedores hay en el buque de carga?

Registre una estimación que sea: Demasiado bajo Más o menos correcto Demasiado alto

ENUNCIADO DE LA TAREA

2. ¿Cuántos contenedores hay en el buque de carga?

Registre una estimación que sea: Demasiado bajo Más o menos correcto Demasiado alto

Math Nation California - Grado 5

3. ¿Qué suposiciones estaba haciendo cuando llegó a sus estimaciones?

Grado 5 . Matemáticas . Unidad 1

POSIBLES RESPUESTAS

1. Ejemplos de respuestas:

• Demasiado bajo: 0-200

• Más o menos: 1.000-1.500

• Demasiado alto: 5.000-6.000

2. Ejemplos de respuestas:

• Demasiado bajo: 1.000-2.000

• Más o menos correcto: 4.000-5.000

• Demasiado alto: 10.000-12.000

3. Supuestos:

• El barco está completamente cargado.

• Parte del espacio está ocupado por estructuras.

• Hay más contenedores bajo cubierta que no podemos ver.

• Todos los contenedores tienen el mismo tamaño.

• Invita a los estudiantes a compartir sus estimaciones y cualquier suposición que hayan hecho.

SÍNTESIS DE LA ACTIVIDAD

• "¿Cómo podrías mejorar tu estimación?" (Recrea el barco utilizando una maqueta. Comprueba la altura, la anchura y la longitud de la disposición de los contenedores. Comprueba cuántos hay en un lado del barco y multiplícalo para obtener una estimación más aproximada.)

SÍNTESIS DE LA LECCIÓN

10 minutos

"Hemos utilizado las matemáticas para investigar una situación del mundo real en la que cada ciudad y cada país tienen que pensar: qué hacer con su basura." Pida a los estudiantes que escriban una respuesta en su diario a algunas de las siguientes preguntas.

• "¿Cuánta basura crees que produce nuestra comunidad y a dónde crees que va?"

• "¿Dónde pueden poner los EE.UU. y Canadá las 3.300 toneladas de basura devueltas desde Malasia?"

• "¿Cuáles son algunos de los retos de hacerse cargo de las 3.300 toneladas de basura y ponerlas en algún lugar de EE.UU. o Canadá?"

• "¿Cuáles son algunos de los retos de enviar la basura a otra ciudad o país?"

Reflexiones:

Math Nation California - Grado 5

Grado 5 . Matemáticas . Unidad 1