Grado 8
Muestra de la edición para el maestro
Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).
La plataforma de recursos curriculares en línea que se ofrece en «mathnation.com», incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.
La marca comercial «Math Nation» es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.
Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.
UNIDAD 1 TRANSFORMACIONES RÍGIDAS Y CONGRUENCIA
UNIDAD NARRATIVA
El trabajo con las transformaciones de las figuras planas en el grado 8 se basa en el trabajo anterior con la geometría y la medición geométrica. Los estudiantes comenzaron a aprender sobre las formas bidimensionales y tridimensionales en el jardín de infancia y continuaron este trabajo en los grados 1 y 2, componiendo, descomponiendo e identificando figuras. El trabajo de los estudiantes con las medidas geométricas comenzó con la longitud y continuó con el área. Los estudiantes aprendieron a estructurar el espacio bidimensional, es decir, a ver un rectángulo con longitudes laterales de números enteros como compuesto por un conjunto de cuadrados unitarios o compuesto por filas iteradas o columnas iteradas de cuadrados unitarios. En 3.º grado, los estudiantes distinguen entre perímetro y área. Relacionaron el área de un rectángulo con la multiplicación, entendiendo por qué (para longitudes laterales enteras) multiplicando las longitudes laterales de un rectángulo se obtiene el número de cuadrados unitarios que forman el rectángulo. Utilizaron diagramas de área para representar casos de la propiedad distributiva. En 4.º grado, los estudiantes aplicaron las fórmulas de área y perímetro de rectángulos para resolver problemas matemáticos y de la vida real y aprendieron a utilizar transportadores. En 5.º grado, los estudiantes amplían la fórmula del área de rectángulos a rectángulos con lados de longitud fraccionaria. En 6.º grado, los estudiantes combinaron sus conocimientos de geometría y medidas geométricas para elaborar fórmulas de áreas de paralelogramos y triángulos y las utilizaron para hallar áreas de superficies de poliedros. En 7.º grado, los estudiantes trabajaron con copias a escala y dibujos a escala, aprendiendo que las medidas de los ángulos se conservan en las copias a escala, pero que las áreas aumentan o disminuyen proporcionalmente al cuadrado del factor de escala. Su estudio de las copias a escala se limitó a pares de figuras con la misma rotación y orientación especular. Visto desde la perspectiva del grado 8, una copia a escala es una dilatación y traslación, no una rotación o reflexión, de otra figura.
En el grado 8, los estudiantes extienden su razonamiento a figuras planas con diferentes orientaciones de rotación y espejo.
A través de actividades diseñadas y secuenciadas para permitir a los estudiantes dar sentido a los problemas y perseverar en su resolución (MP1), los estudiantes utilizan y amplían sus conocimientos de geometría y medidas geométricas. Comienzan la unidad observando pares de dibujos animados, cada uno de los cuales ilustra una traslación, rotación o reflexión. Los estudiantes describen con sus propias palabras cómo mover una figura de dibujos animados sobre otra. A medida que avanza la unidad, consolidan su comprensión de estas transformaciones, aumentan la precisión de sus descripciones (MP6) y empiezan a utilizar la terminología asociada, reconociendo qué determina cada tipo de transformación, por ejemplo, dos puntos determinan una traslación. En las primeras lecciones, los estudiantes se encuentran con ejemplos de transformaciones en el plano, sin la estructura añadida de una cuadrícula o coordenadas. La razón de esta elección es evitar limitar el esquema de los estudiantes mostrando los ejemplos menos restrictivos de transformaciones. En concreto, los estudiantes ven ejemplos de traslaciones en cualquier dirección, rotaciones por cualquier ángulo y reflexiones sobre cualquier línea arbitraria. A través de estos ejemplos, empiezan a comprender las características de estas transformaciones sin que su comprensión se limite, por ejemplo, a traslaciones horizontales o verticales o rotaciones solo de 90 o 180 grados. Además, mediante el uso de transparencias, la comprensión inicial de las transformaciones por parte de los estudiantes implica mover todo el plano, en lugar de solo mover una figura determinada. Puesto que todas las transformaciones son transformaciones del plano, es preferible que los estudiantes encuentren primero ejemplos que impliquen mover todo el plano .
Identifican y describen traslaciones, rotaciones y reflexiones y secuencias de éstas. Al describir imágenes de figuras bajo transformaciones rígidas dentro y fuera de cuadrículas y del plano de coordenadas, los estudiantes utilizan los términos «puntos correspondientes», «lados correspondientes» e «imagen». Los estudiantes aprenden que los ángulos y las distancias se conservan mediante cualquier secuencia de traslaciones, rotaciones y reflexiones y que dicha secuencia se denomina «transformación rígida». Aprenden la definición de «congruente»: se dice que dos figuras son congruentes si existe una transformación rígida que lleva una figura a la otra. Los estudiantes comprueban experimentalmente las propiedades de las traslaciones, rotaciones y reflexiones y utilizan estas propiedades para razonar sobre figuras planas, comprendiendo argumentos informales que demuestran que los ángulos interiores alternos cortados por una transversal tienen la misma medida y que la suma de los ángulos de un triángulo es 180°. Este último se utilizará en una unidad posterior de 8.º grado sobre semejanza y dilataciones. A lo largo de la unidad, los estudiantes discuten sus ideas matemáticas y responden a las ideas de los
demás (MP3, MP6).
Grado 8 . Matemáticas . Unidad 1
En muchas de las lecciones de esta unidad se pide a los estudiantes que trabajen con figuras geométricas que no están situadas en un contexto real. Esta elección de diseño respeta el importante trabajo intelectual que supone razonar sobre el área. Las tareas en contextos reales son a veces artificiosas y dificultan la comprensión en lugar de ayudarla. Además, los contextos matemáticos son contextos legítimos que merecen ser estudiados. En la unidad, los estudiantes tienen la oportunidad de abordar aplicaciones del mundo real. En la actividad culminante de la unidad, los estudiantes examinan y crean diferentes patrones formados por figuras planas. Esta es una oportunidad para que apliquen lo que han aprendido en la unidad (MP4).
En esta unidad, varios planes de clase sugieren que cada estudiante tenga acceso a un juego de herramientas de geometría. Estos contienen papel de calco, papel cuadriculado, lápices de colores, tijeras, regla, transportador y una ficha para utilizar como regla o para marcar ángulos rectos, dando a los estudiantes la oportunidad de desarrollar sus habilidades para seleccionar las herramientas adecuadas y utilizarlas estratégicamente para resolver problemas (MP5). Tenga en cuenta que incluso los estudiantes en un aula mejorada digitalmente deben tener acceso a este tipo de herramientas; las aplicaciones y simulaciones deben considerarse adiciones a sus juegos de herramientas, no sustitutos de las herramientas físicas.
Progresión del lenguaje disciplinario
En esta unidad, los maestros pueden anticipar que los estudiantes utilicen el lenguaje con fines matemáticos, tales como describir, generalizar y justificar. A lo largo de la unidad, los estudiantes se beneficiarán de rutinas diseñadas para desarrollar un lenguaje disciplinar sólido, tanto para su propia construcción de sentido como para construir un entendimiento compartido con sus compañeros. Los maestros pueden evaluar formativamente cómo los estudiantes utilizan el lenguaje de estas maneras, en particular cuando los estudiantes utilizan el lenguaje para:
Describir
• movimientos de figuras (lecciones 1 y 2)
• observaciones sobre la transformación de líneas paralelas (lección 9)
• transformaciones com puntos correspondientes, segmentos de línea y ángulos (lección 10)
• observaciones sobre mediciones de ángulos (lección 16)
• transformaciones encontradas en teselaciones y en diseños con simetría rotacional (lección 17)
Generalizar
• sobre categorías para el movimiento (lección 2)
• sobre segmentos de línea en rotación (lección 8)
• sobre la relación entre ángulos verticales (lección 9)
• sobre transformaciones y congruencia (lección 12)
• sobre segmentos correspondientes y longitud (lección 13)
• sobre ángulos interiores alternos (lección 14)
• sobre la suma de ángulos en un triángulo (lección 16)
Justifica
• si las transformaciones rígidas pueden o no producir una imagen (lección 7)
• si las formas son o no congruentes (lección 11)
• si los polígonos son congruentes o no (lección 12)
• si los óvalos son congruentes o no (lección 13)
• si se pueden crear triángulos a partir de medidas de ángulos dadas (lección 15)
Además, se espera que los estudiantes expliquen e interpreten instrucciones para transformar figuras y cómo aplicar transformaciones para encontrar imágenes específicas. También se les pide que utilicen el lenguaje para comparar rotaciones de un segmento de recta y comparar perímetros y áreas de rectángulos. A lo largo de la unidad, los profesores pueden apoyar la comprensión matemática de los estudiantes ampliando (no simplificando) el lenguaje utilizado para todos estos propósitos a medida que los estudiantes demuestran y desarrollan ideas.
La tabla muestra las lecciones en las que se introduce por primera vez nueva terminología, incluido cuándo se espera que los estudiantes comprendan la palabra o frase de forma receptiva y cuándo se espera que los estudiantes produzcan la palabra o frase en su propia expresión oral o escrita. Los términos del glosario aparecen en negrita. Los maestros deben seguir ayudando a los estudiantes a utilizar un término nuevo en las lecciones siguientes a aquella en la que se introdujo por primera vez.
California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Lección
Nueva terminología Receptivo Productivo
8.1.1 vértice plano medida dirección giro de deslizamiento
8.1.2
8.1.3 imagen ángulo de rotación centro (de rotación) línea de reflexión vértice 3
sentido horario sentido antihorario reflexión rotación traslación opuesto
imagen
ángulo de rotación centro (de rotación) línea de reflexión vértice
8.1.4 secuencia de transformaciones distancia
8.1. 51.5
plano de coordenadas punto segmento coordenadas eje �� eje ����
8.1.6 polígono 1.6 polígono
sentido horario sentido antihorario reflejar rotar trasladar
ángulo de rotación centro (de rotación) línea de reflexión
8.1.7 transformación rígida correspondiente medidas conservar reflexión rotación traslación medida punto
8.1.8 punto medio segmento
8.1.99 ángulos verticales paralelos intersecan distancia
8.1.10
8.1. congruentes11 congruente perímetro área
8.1.12
imagen transformación rígida punto medio paralelo
ángulo recto eje �� eje ���� área
8.1.13 correspondiente
Learning Inc. - Todos los derechos reservados
8.1.14
ángulos interiores alternos transversal
8.1.15 ángulo recto
8.1.16
8.1.17 teselado simetría
Grado 8 . Matemáticas . Unidad 1
ángulos verticales congruente ángulos suplementarios
ángulos interiores alternos transversal ángulo recto
IDEAS FUNDAMENTALES Y ESTÁNDARES
Enfoque en ideas fundamentales
• Geometría transformacional
ESTÁNDARES POR LECCIÓN
Lección
8.1.1
8.1.2
8.1.3
8.1.4
8.1.5
8.1.6
8.1.7
8.1.8
8.1.9
8.1.10
8.1.11
Estándar(es) abordado(s)
8.G.1
8.G.1a, 8.G.1b
8.G.1a, 8.G.1b
8.G.1a, 8.G.1b
8.G.3
8.G.1a, 8.G.1b, 8.G.3
8.G.1a, 8.G.1b
8.G.1a, 8.G.1b
8.G.1a, 8.G.1b, 8.G.1c
8.G.1a, 8.G.1b
8.G.1a, 8.G.1b, 8.G.2
8.1.12 8.G.2
8.1.13
8.1.14
8.1.15
8.1.16
8.1.17
8.G.1a, 8.G.2
8.G.1c, 8.G.5
8.G.2, 8.G.5
8.G.5
8.G.2, 8G.5
IDEA(S) FUNDAMENTAL(ES
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1 Verificar experimentalmente las propiedades de rotaciones, reflexiones y traslaciones.
Enfoque SMPs
MP5 Usar herramientas apropiadas estratégicamente.
MP6 Atender a la precisión.
Estándares ELD de California
I.A.4
II.B.3
LECCIÓN 1 MOVERSE EN EL PLANO
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo, atienden a la precisión descubren la figura y el espacio.
METAS(S) DE APRENDIZAJE
• Describamos las formas en que las figuras pueden moverse en el plano.
META(S) DE APRENDIZAJE
• Puedo describir cómo una figura se mueve y gira para llegar de una posición a otra.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Describir (oralmente y por escrito) una traslación o rotación de una forma utilizando un lenguaje informal, por ejemplo, «deslizar», «girar a la izquierda», etc.
• Identificar ángulos y rayos que no pertenecen a un grupo y justificar (oralmente) por qué el objeto no pertenece.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Pensar, girar y compartir
¿Cuál no pertenece?
MLR8: Apoyos para el debate
Requerimientos necesarios
Para esta lección necesitará el patrón de plantillas maestras del «Baile del cuadrado y del triángulo». Haga 1 copia de las 3 páginas por cada 2 estudiantes.
Reúne los conjuntos de herramientas de geometría. Lo mejor sería que los estudiantes tuvieran acceso a estos juegos de herramientas en todo momento a lo largo de la unidad. Los juegos de herramientas incluyen papel de calco, papel cuadriculado, lápices de colores, tijeras, regla, transportador y una ficha para utilizar como regla o para marcar ángulos rectos. En esta unidad es especialmente importante disponer de papel de calco. Lo mejor es utilizar papel de calco cortado a un tamaño más o menos pequeño (aproximadamente 5″ por 5″); el «papel de hamburguesa» disponible en el mercado es ideal para ello. Si utiliza hojas de papel de calco más grandes, como 8,5″ por 11″, corte cada hoja en cuartos.
Grado 8 . Matemáticas . Unidad 1
PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN
Preparación necesaria
Enfriamiento
Copias de los patrones de plantillas maestras
Conjunto de herramientas de geometría
Para el grado 6: papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha para usar como regla o para marcar ángulos rectos.
Para los grados 7 y 8: todo lo del grado 6, más una regla y un transportador. Se recomiendan los transportadores transparentes sin agujeros y con líneas radiales impresas.
Notas: (1) El «papel de calco» es más fácil de usar cuando tiene un tamaño más pequeño. El «papel para hamburguesas» disponible comercialmente es de 5 pulgadas por 5 pulgadas e ideal para esto. Si utilizas hojas de papel de calco más grandes, considera la posibilidad de recortarlas para uso de los estudiantes. (2) Cuando se exigen compases en los grados 6 a 8, se incluyen como material obligatorio aparte.
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
El propósito de esta lección es introducir a los estudiantes a las traslaciones y rotaciones de figuras planas y hacer que describan estos movimientos en lenguaje cotidiano. Se espera que los estudiantes utilicen palabras como «deslizar» y «girar». En la próxima lección, se les presentarán los términos matemáticos. El término «transformación» aún no se utiliza y se introducirá en una lección posterior. En todas las lecciones de esta unidad, los estudiantes deben tener acceso a sus conjuntos de herramientas de geometría, que deben contener papel de calco, papel cuadriculado, lápices de colores, tijeras, regla, transportador y una ficha. Para esta unidad, es especialmente importante disponer de papel de calco y de una regla. Es posible que los estudiantes no necesiten todas (o ninguna) de estas herramientas para resolver un problema concreto. Sin embargo, para tomar decisiones estratégicas sobre cuándo utilizar qué herramientas (MP5), los estudiantes necesitan tener la oportunidad de tomar esas decisiones. Las aplicaciones y las simulaciones deben complementar y no sustituir a las herramientas físicas.
LECCIÓN DE UN VISTAZO
Componente de lección
Estructura Tiempo
Descripción breve
Calentamiento En parejas o grupos pequeños 10 min Los estudiantes observan cuatro imágenes de ángulos y justifican cuál no pertenece.
Se presenta informalmente a los estudiantes las traslaciones (deslizamientos) y rotaciones (giros) de diferentes figuras.
Actividad de exploración En parejas 20-25 min
Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar las traslaciones y rotaciones utilizando la tecnología.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las traslaciones y rotaciones.
Síntesis Grupo completo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Nation California . Grado 8
Los estudiantes discuten ejemplos adicionales de transformaciones utilizando un lenguaje informal.
Los estudiantes describen informalmente los cambios en las figuras utilizando los términos diapositiva y giro
El componente de práctica independiente incluye 3 problemas de la lección.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | ¿CUÁL NO PERTENECE?
DIAGRAMAS
(10 minutos)
Rutinas didácticas
Pensar, girar y compartir
¿Cuál no pertenece?
Este calentamiento pide a los estudiantes que comparen cuatro imágenes. Anima a los estudiantes a explicar sus razonamientos y a mantener conversaciones matemáticas. Te da la oportunidad de escuchar cómo utilizan la terminología y hablan de las características de las imágenes en comparación unas con otras. Para que todos los estudiantes puedan acceder a la actividad, cada imagen tiene una razón obvia por la que no pertenece. Anime a los estudiantes a encontrar razones basadas en propiedades matemáticas (por ejemplo, la figura B es el único ángulo recto). Durante la discusión, preste atención a las ideas importantes y a la terminología que será útil en los próximos trabajos de la unidad. La actividad también ofrece a los estudiantes la oportunidad de encontrar herramientas útiles en su caja de herramientas de geometría.
Antes de que los estudiantes comiencen, considere la posibilidad de establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con un razonamiento. Esta señal podría ser un pulgar hacia arriba, o los estudiantes podrían mostrar el número de dedos que indican el número de respuestas que tienen para el problema. Esta es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema y evita que se distraigan o se precipiten al levantar las manos por toda la clase.
A medida que los estudiantes comparten sus respuestas, preste atención a las ideas importantes y a la terminología que será útil en el próximo trabajo de la unidad, como la referencia a los ángulos y sus medidas.
INTRODUCCIÓN
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organice a los estudiantes en grupos de 2-4 y proporcione acceso a los conjuntos de herramientas de geometría. Exponga las figuras para que todos las vean. Pida a los estudiantes que indiquen cuándo se han dado cuenta de que hay una que no encaja y que expliquen por qué. Conceda a los estudiantes 1 minuto de reflexión en silencio y, a continuación, tiempo para compartir sus ideas con su pequeño grupo. En sus pequeños grupos, pida a cada estudiante que comparta su razonamiento de por qué una pregunta en particular no pertenece. Juntos, encuentren al menos una razón por la que cada pregunta no pertenece.
¿Cuál no pertenece?
Las respuestas varían. Ejemplos de respuestas:
A no pertenece porque:
• Los rayos apuntan en direcciones opuestas.
• No es posible formar un triángulo uniendo los puntos de los rayos.
B no pertenece porque:
• Forman un ángulo recto.
• Ambos rayos están a la derecha del vértice.
C no pertenece porque:
• Es un ángulo agudo.
• Ambos rayos apuntan hacia abajo.
D no pertenece porque:
• Es un ángulo obtuso (mide menos de 180 grados).
• El rayo largo apunta a la izquierda del rayo corto.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Pide a cada grupo que comparta una razón por la que una determinada imagen no pertenece al grupo. Anota y muestra las respuestas para que todos las vean. Después de cada respuesta, pregunta a la clase si están de acuerdo o en desacuerdo. Dado que no hay una única respuesta correcta a la pregunta de cuál no pertenece, preste atención a las explicaciones de los estudiantes y asegúrese de que las razones dadas son correctas.
Durante el debate, pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como rayo, grado o ángulo agudo. Presione también a los estudiantes sobre las afirmaciones sin fundamento. Por ejemplo, un estudiante puede hacer afirmaciones sobre las medidas de los ángulos. Pregúnteles cómo saben la medida y demuéstreles cómo pueden utilizar el papel de calco o la regla de la caja de herramientas para comprobarlo.
ACTIVIDAD DE EXPLORACIÓN | BAILE DEL CUADRADO Y DEL TRIÁNGULO
(25 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
El objetivo de esta actividad es que los estudiantes empiecen a observar y describir traslaciones y rotaciones. En grupos de 2, describen uno de los 3 posibles bailes, presentado en forma de viñeta, y el compañero identifica qué baile se está describiendo. Identificar a los estudiantes que utilizan un lenguaje específico y detallado para describir la danza y seleccionarlos para compartir durante la discusión en clase.
Aunque no se espera que los estudiantes utilicen un lenguaje preciso todavía, esta actividad proporciona tanto la necesidad intelectual de ponerse de acuerdo sobre un lenguaje común como dar a los estudiantes la oportunidad de experimentar con diferentes formas de describir algunos movimientos en el plano (MP6).
INTRODUCCIÓN
Organice a los estudiantes en grupos de 2 y entregue una copia de todas las hojas de 3 plantillas maestras a cada grupo. Explique que cada hoja es un dibujo animado con 6 marcos que muestran los movimientos realizados por las figuras que bailan. Pida a los estudiantes que coloquen las tres hojas boca arriba y dígales que, por turnos, seleccionen un baile y se lo describan a su compañero, sin revelar qué baile han seleccionado. El otro estudiante identifica la danza que está describiendo. En una pantalla, anote el lenguaje que utilizan los estudiantes para describir el movimiento de las formas para después agruparlo y conectarlo con un lenguaje más formal como «rotación» y «traslación». Dé a los estudiantes 15 minutos para trabajar en sus grupos, seguidos de un debate con toda la clase.
Si utiliza la actividad digital, pida a los estudiantes que cierren sus dispositivos. Distribuya las hojas y repase las reglas del juego para asegurarse de que los estudiantes comprenden la tarea. Dé a los estudiantes unos 10 minutos para jugar. Después de 10 minutos, invite a los estudiantes a abrir sus dispositivos y a observar cómo las aplicaciones corresponden a los tres bailes. Dé a los estudiantes otros 5 minutos para llegar a un consenso sobre la mejor manera de describir los movimientos con sus propias palabras antes de un debate con toda la clase.
Apoyo para estudiantes que aprenden el idioma inglés
Representación: MLR8 Apoyos para el debate. Para ayudar a los estudiantes a comprender el lenguaje de la pantalla, invítelos a «representar» cada uno de los diferentes tipos de movimientos. Incluya diagramas o imágenes en la pantalla para que los estudiantes recuerden visualmente el significado de cada término. Por ejemplo, dibuje flechas para ilustrar la dirección. Recuerde a los estudiantes que tomen prestado el lenguaje de la pantalla cuando sea necesario.
Principio(s) de diseño: Apoyar la adquisición de sentido
Apoyo para estudiantes con discapacidad
Representación: Proporcione acceso para la percepción. Muestre o proporcione a los estudiantes una copia física de las instrucciones escritas y léalas en voz alta. Compruebe la comprensión invitando a los estudiantes a reformular las instrucciones con sus propias palabras. Considera la posibilidad de mantener las instrucciones visibles durante toda la actividad.
Favorece la accesibilidad para: Lenguaje; memoria
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Su maestro les dará tres imágenes. Cada una de ellas muestra una serie de movimientos de baile diferentes.
DE TAREA PARA EL ESTUDIANTE
ENUNCIADO
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS PREVISTOS
1. 1. Coloca los tres dibujos de forma que tanto tú como tu compañero los veáis bien. 2. Elige quién empezará el juego.
• El jugador que empieza elige mentalmente A, B o C y describe el baile al otro jugador.
• El otro jugador identifica de qué baile se está hablando: A, B o C.
2. Después de una ronda, intercambien los papeles. Cuando hayas descrito los tres bailes, ponte de acuerdo sobre las palabras que utilizas para describir los movimientos de cada baile.
3. Con tu compañero, escribe una descripción de los movimientos de cada baile.
Las respuestas varían. Ejemplo de respuesta:
A. Muévete a la derecha, gira 90° en el sentido de las agujas del reloj, muévete hacia arriba, muévete a la izquierda y gira 90° en el sentido contrario a las agujas del reloj.
B. Muévete a la derecha, gira 90° en el sentido de las agujas del reloj, muévete a la izquierda, muévete hacia arriba y gira 90° en el sentido contrario a las agujas del reloj.
C. Muévete a la derecha, gira 90° en el sentido contrario a las agujas del reloj, muévete a la izquierda, muévete hacia arriba y gira 90° en el sentido de las agujas del reloj.
Los términos izquierda, derecha y arriba en esta respuesta son desde el punto de vista de un observador que mira el baile. Como alternativa, los estudiantes podrían ponerse en el lugar de los triángulos y describir las cosas en términos de izquierda, derecha, arriba y abajo del triángulo. Los estudiantes pueden utilizar otras palabras, como «desplazamiento» y «paso» para las traslaciones y «giro» y «rotar» para los giros. Podrían describir los giros 90° como «cuartos de vuelta».
Algunos estudiantes pueden interpretar direcciones como «izquierda» y «derecha» de forma diferente a como lo hizo su pareja, dependiendo de si están pensando desde el punto de vista de un observador que ve el baile o si se ponen en el baile y describen las cosas en términos de izquierda, derecha, arriba y abajo del triángulo. Esté atento a este tipo de malentendidos, señale que ninguna de las dos perspectivas es errónea y anime a los estudiantes a ser más precisos en su lenguaje.
A menudo, los estudiantes confunden o no están seguros del significado de los términos «en el sentido de las agujas del reloj» y «en sentido contrario a las agujas del reloj». Comente con ellos (y demuéstreles, si es posible) cómo giran las agujas de un reloj, haciendo hincapié en el sentido de la rotación. Los estudiantes también pueden tener dudas sobre cómo describir la cantidad de rotación. Considere la posibilidad de pedir a un estudiante que exprese las medidas angulares en términos de grados que explique cómo lo ve.
Seleccione a un estudiante para que comparta su descripción para cada una de las páginas y muestre el lenguaje que observó y registró durante la actividad para los diferentes tipos de movimientos. Organice las palabras en dos grupos, las que describen traslaciones y las que describen rotaciones (pero no utilice estos términos). Póngase de acuerdo sobre una palabra para cada tipo y discuta qué palabras adicionales son necesarias para especificar exactamente la transformación (por ejemplo, mover a la derecha, girar en el sentido de las agujas del reloj 90°).
Considere la posibilidad de preguntar a los estudiantes qué es lo que les resulta más difícil a la hora de describir los bailes: entre las respuestas esperadas se incluye ser lo más preciso posible sobre los diferentes movimientos (por ejemplo, describir si la forma gira en el sentido de las agujas del reloj o en sentido contrario). También se puede preguntar a los estudiantes si a veces son capaces de identificar el baile antes de que su compañero termine de describir todos los movimientos. Los tres bailes comienzan moviéndose hacia la derecha, pero en el segundo paso, los bailes A y B giran 90 grados en el sentido de las agujas del reloj, mientras que el baile C gira 90 grados en sentido contrario a las agujas del reloj. (Así que si el segundo movimiento fue rotar 90 grados en sentido contrario a las agujas del reloj, esta debe ser el baile C). Los bailes A y B divergen en el deslizamiento 4.
Grado 8 . Matemáticas . Unidad 1
¿Estás listo para más?
Podríamos pensar en cada baile como un nuevo baile ejecutándola en sentido inverso, comenzando en el 6.º marco y trabajando hacia atrás hasta el primero.
1. Elige un baile y describe con palabras una de estas danzas invertidas.
2. ¿Cómo se comparan las direcciones para ejecutar tu danza en sentido directo y en sentido inverso?
«¿Estás listo para más?». Respuesta del estudiante
1. Las respuestas varían. Ejemplo de respuesta: A: girar 90° en el sentido de las agujas del reloj, moverse a la derecha, moverse hacia abajo, girar 90° en el sentido contrario a las agujas del reloj, moverse a la izquierda; B: girar 90° en el sentido de las agujas del reloj, moverse hacia abajo, moverse a la derecha, girar 90° en el sentido contrario a las agujas del reloj, moverse a la izquierda; C: girar 90° en el sentido contrario a las agujas del reloj, moverse hacia abajo, moverse a la derecha, girar 90° en el sentido de las agujas del reloj, moverse a la izquierda.
2. Los pasos se enumeran en orden inverso. Los pasos se indican en orden inverso. La derecha se sustituye por la izquierda y la izquierda por la derecha y las agujas del reloj se sustituyen por las agujas del reloj y viceversa.
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Hemos empezado a razonar sobre lo que significa mover una figura en el plano. Muestra dos figuras que muestren claramente un deslizamiento y dos figuras que muestren claramente un giro.
Ejemplo de un deslizamiento:
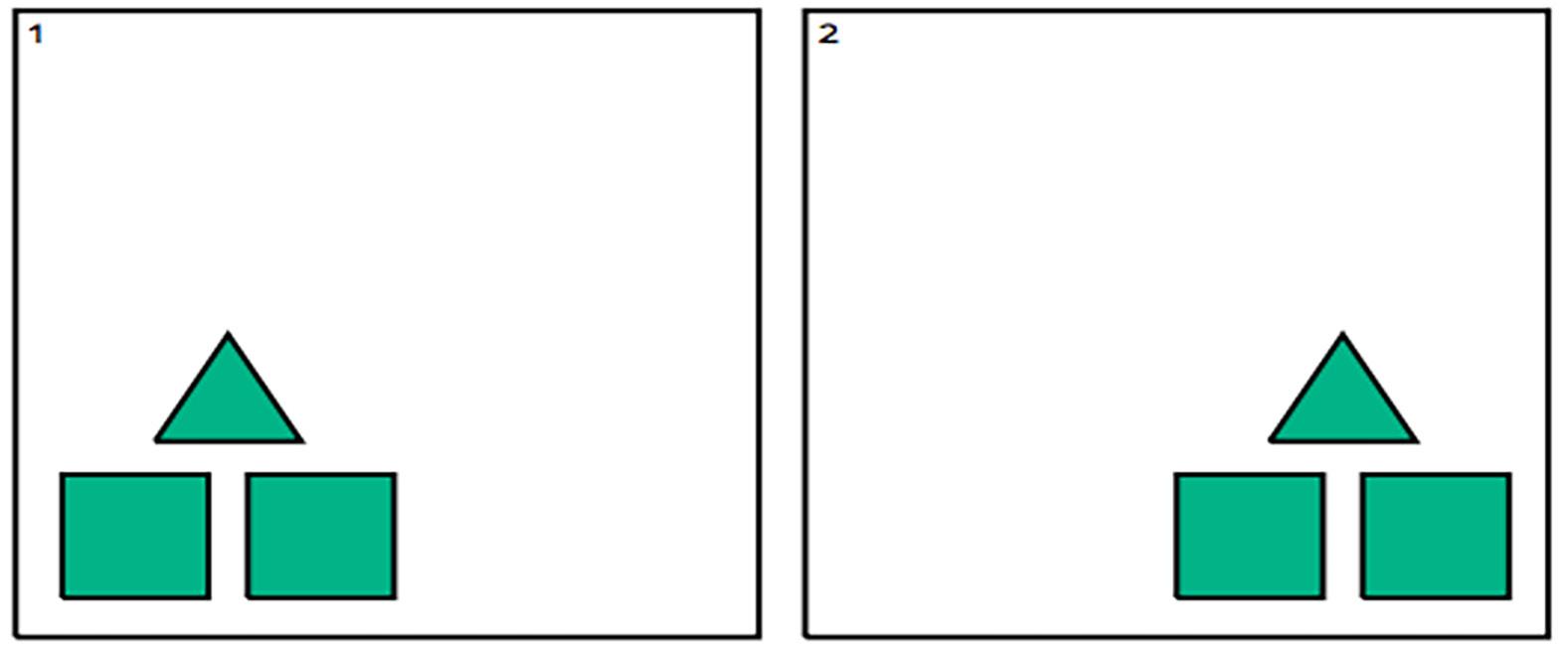
Ejemplo de un giro:
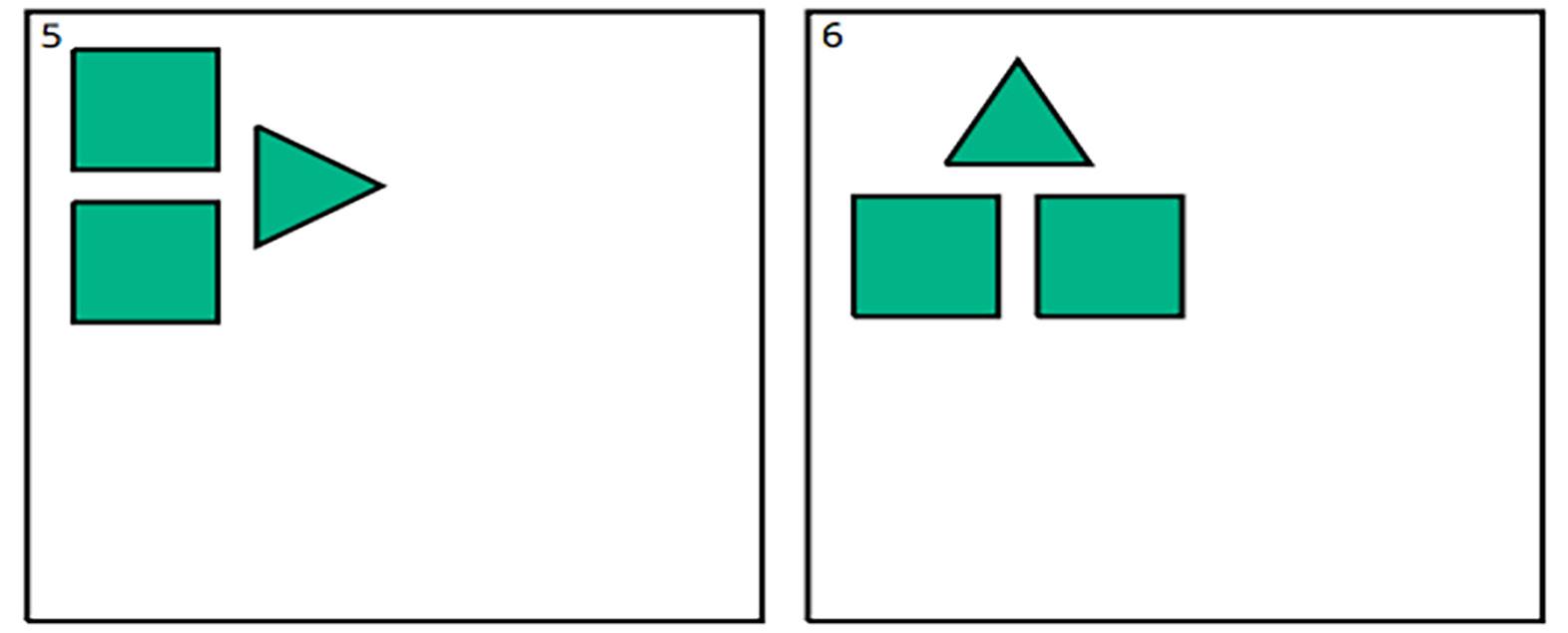
Invite a los estudiantes a compartir el lenguaje que utilizarían para describirlas: por ejemplo, «mover» o «deslizar» para las traslaciones y «girar» para las rotaciones. Pregunte a los estudiantes cómo podrían cuantificar cada movimiento, por ejemplo con una distancia y una dirección para los deslizamientos y un centro y un ángulo de rotación para los giros. Diles que seguiremos estudiando estos movimientos con más detalle en futuras lecciones.
ENFRIAMIENTO | MARCO A MARCO
Aquí están las posiciones sucesivas de una figura.
Describe cómo se mueve la figura de:
1. Marco 1 al marco 2.
2. Marco 2 al marco 3.
3. Marco 3 a marco 4.
(5 minutos)
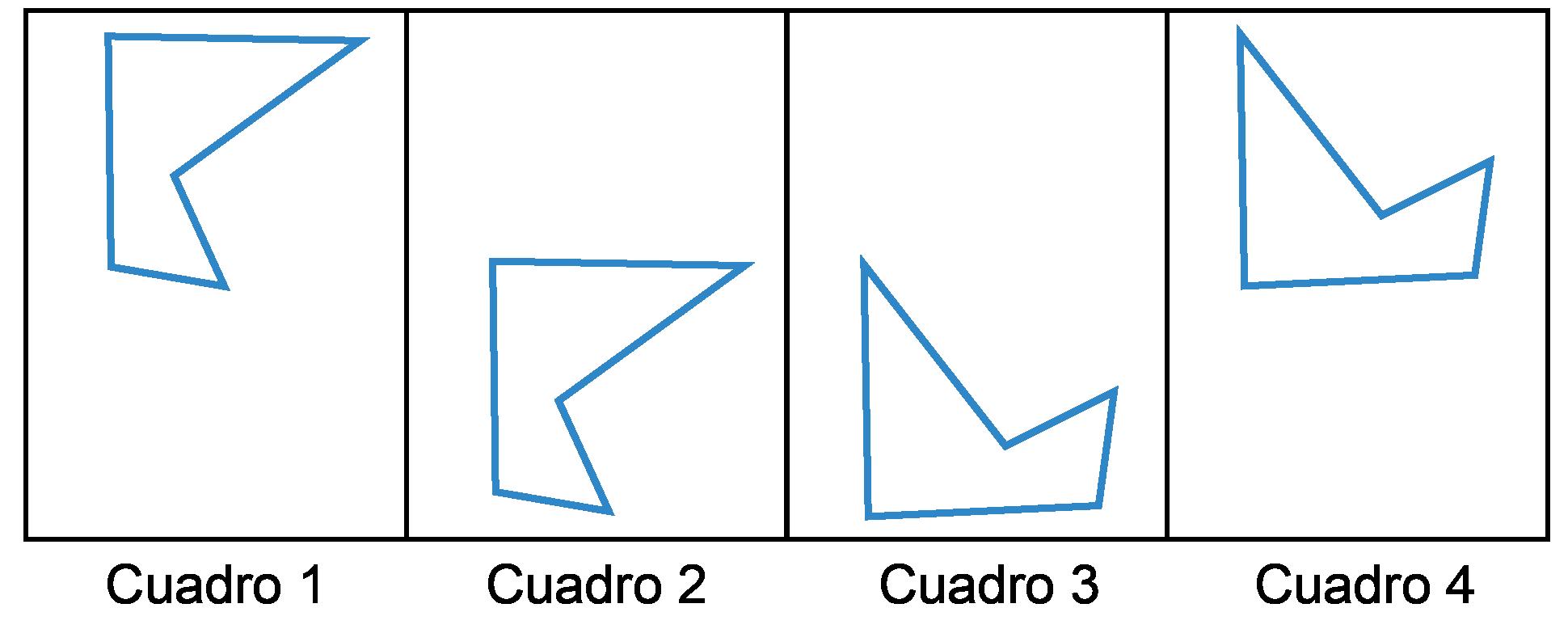
1. Deslícese hacia abajo.
2. Gire hacia la izquierda 90 grados (o un cuarto de vuelta completa).
3. Deslícese hacia arriba.
Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Los seis marcos muestran las diferentes posiciones de una figura.
Describe cómo se mueve la figura para llegar de su posición en cada marco al siguiente.
Soluciones posibles
Para llegar de la posición 1 a la posición 2, la figura se mueve hacia arriba. Para ir de la posición 2 a la posición 3, la figura gira 90 grados en el sentido contrario a las agujas del reloj. Para ir de la posición 3 a la posición 4, la figura se mueve hacia abajo y a la derecha. Para ir de la posición 4 a la posición 5 la figura gira 90 grados en el sentido de las agujas del reloj. Para ir de la posición 5 a la posición 6, la figura se mueve hacia la izquierda.
Nota: 90 grados en el sentido contrario a las agujas del reloj es lo mismo que 270 grados en el sentido de las agujas del reloj y de forma similar, 90 grados en el sentido de las agujas del reloj es lo mismo que 270 grados en el sentido contrario a las agujas del reloj.
PROBLEMA 2
Estos cinco marcos muestran las diferentes posiciones de una figura.
Describe cómo se mueve la figura para llegar de su posición en cada marco al siguiente.
Soluciones posibles
Para llegar de la posición 1 a la posición 2, la figura se mueve hacia la derecha. Para llegar de la posición 2 a la posición 3, la forma rota 90 grados en el sentido de las agujas del reloj. Para ir de la posición 3 a la posición 4, la figura se mueve hacia abajo. Para llegar de la posición 4 a la posición 5, la figura gira 180 grados.
PROBLEMA 3
Diego comenzó con esta figura.
Diego mueve la figura hacia abajo, la gira 90 grados en el sentido de las agujas del reloj y luego mueve la figura hacia la derecha. Dibuja la ubicación de la figura después de cada movimiento.
Soluciones posibles
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas son llevadas a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos son llevados a ángulos de la misma medida. Enfoque SMPs
MP3 Construye argumentos viables y critica el razonamiento de otros.
Estándares ELD de California
I.A.3
I.C.12
LECCIÓN 2 NOMBRAR LOS MOVIMIENTOS
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo y predecir lo que podría ocurrir,
construyen argumentos viables y criticar el razonamiento de los demás descubren la figura y el espacio.
METAS(S) DE APRENDIZAJE
• Seamos más precisos al describir movimientos de figuras en el plano.
META(S) DE APRENDIZAJE
• Puedo identificar los puntos correspondientes antes y después de una traslación.
• Conozco la diferencia entre traslaciones, rotaciones y reflexiones.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comprender que el término «imagen» se refiere a una figura después de que se haya producido una transformación (por ejemplo, La figura �� es la imagen de la figura ��) y el término «puntos correspondientes» se refiere a un punto que está en la misma parte de la figura tanto en la figura original como en la imagen.
• Describir (oralmente y por escrito) el movimiento de las figuras de manera informal y formal utilizando los términos «en el sentido de las agujas del reloj», «en el sentido contrario», «traslaciones», «rotaciones» y «reflexiones» de las figuras.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Pensar, girar y compartir
MLR8: Apoyos para el debate
Toma turnos
Materiales necesarios
Lápiz negro para la actividad 2.3
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Fichas preimpresas, recortadas a partir de copias del lápiz negro.
Grado 8 . Matemáticas . Unidad 1
PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN
Preparación necesaria
Impriae y recorte las tarjetas del patrón de la línea negra «Traslados, rotaciones y reflejos». Prepare 1 copia para cada 3 estudiantes.
Asegúrese de que los estudiantes tienen acceso a los elementos de sus conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) a para utilizar como regla o para marcar ángulos rectos.
El acceso al papel de calco es particularmente importante. Cada estudiante necesitará unas 10 hojas pequeñas de papel de calco (lo ideal es utilizar papel de estraza). Si utiliza hojas grandes de papel de calco, por ejemplo de 8,5 por 11 pulgadas, corte cada hoja en cuartos.
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
En esta lección, los estudiantes comienzan a describir una traslación, rotación o reflexión dada con mayor precisión y se les presentan los términos traslación, rotación y reflexión. Los términos colectivos «transformación» y «transformación rígida» no se utilizan hasta lecciones posteriores. Los estudiantes conocen los términos imagen y puntos correspondientes. Utilizan los términos sentido horario y sentido antihorario. A continuación, los estudiantes utilizan este lenguaje para identificar los movimientos individuales en varias figuras.
Los estudiantes participan en el MP6 mientras experimentan con formas de describir los movimientos con la precisión suficiente para que otro entienda su significado.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo
Descripción breve
Calentamiento En parejas o grupos pequeños 10 min Los estudiantes aproximan el ángulo de rotación que mapea un cuadrilátero a otro.
Actividad de exploración En parejas o grupos pequeños 10 min
Actividad de exploración Grupos equeños 15 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Los estudiantes describen informalmente las transformaciones (movimientos) de un marco a otro a medida que se les presentan las reflexiones.
Los estudiantes trabajan con sus compañeros para completar una clasificación de tarjetas de transformación antes de utilizar formalmente el vocabulario apropiado para describir las transformaciones.
Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar las transformaciones rígidas utilizando la tecnología.
Los estudiantes describen transformaciones utilizando nuevo vocabulario académico (traslación, rotación, reflexión, imagen, puntos correspondientes) con ejemplos adicionales.
Los estudiantes identifican y explican qué transformación puede usarse para mapear una figura en otra.
El componente de práctica independiente incluye 2 problemas de la lección y 1 problema de repaso en espiral.
Nation California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | UN PAR DE CUADRILÁTEROS
(10 minutos)
Rutinas didácticas
Pensar, girar y compartir
Los estudiantes estiman un ángulo de rotación. Aunque no es necesario que utilicen un transportador, un transportador es una herramienta ideal y les permite estimar la medida del ángulo con mayor precisión. Controle cómo los estudiantes informan la medida del ángulo: ¿redondean al grado más cercano, a los 5 grados más cercanos?
ÓN
Organice a los estudiantes en grupos de 2-4. Proporcione herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Exponga las dos figuras de cuadriláteros para que todos las vean. (Pida a los estudiantes que hagan una señal discreta con la mano cuando tengan una estimación del ángulo de rotación. Conceda a los estudiantes 2 minutos de reflexión en silencio y, a continuación, tiempo para compartir sus ideas con su grupo antes de un debate con toda la clase.
Apoyo para estudiantes con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la repasen antes de realizar esta actividad.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
El cuadrilátero �� puede rotarse hasta la posición del cuadrilátero ��.
Estime el ángulo de rotación.
Las respuestas varían. Ejemplo de respuesta: Alrededor de 120 grados (en sentido contrario a las agujas del reloj)
Esta figura no tiene por qué formar parte de las respuestas de los estudiantes, sino que se proporciona como ejemplo de un ángulo entre dos segmentos que podría medirse para hallar el ángulo de rotación de �� a ��
Grado 8 . Matemáticas . Unidad 1
CONCEPTOS ERRÓNEOS PREVISTOS
Los estudiantes pueden no estar seguros de qué ángulo medir. Pueden medir el ángulo agudo entre la figura �� y la figura ��. Pida a estos estudiantes que tracen la figura �� en papel de calco y la giren ese ángulo para comprobar que no se obtiene la figura ��
SÍNTESIS DE LA ACTIVIDAD
Invite a los estudiantes a compartir sus estimaciones sobre el ángulo de giro. Pregunte a los estudiantes cómo supieron, por ejemplo, que el ángulo es más que 90 grados (porque el ángulo es obtuso) pero menos que 180 grados (porque el ángulo es menor que una línea recta).
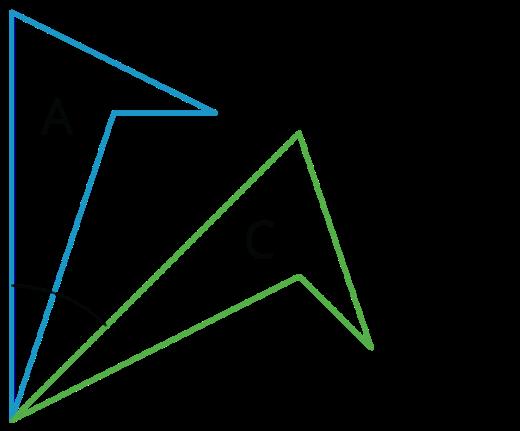
Presente o reitere el lenguaje de sentido de las agujas del reloj (para girar en la dirección en que se mueven las agujas de un reloj) y sentido contrario a las agujas del reloj (para girar en la dirección opuesta). En este caso, no se especifica el sentido de la rotación, pero es natural ver la figura �� girando en sentido contrario a las agujas del reloj sobre la figura ��. Asegúrese de introducir el lenguaje del centro de rotación (el vértice compartido por �� y �� es el centro de rotación) y diga a los estudiantes que llamamos a la figura �� la imagen de la figura �� para la rotación.
Puede ser útil mostrar la imagen del enunciado de la tarea para apoyar esta discusión y, si es posible, mostrar dinámicamente el giro 120° en el sentido contrario a las agujas del reloj.
ACTIVIDAD DE EXPLORACIÓN | ¿CÓMO SE HIZO
QUE SE MUEVE?
(10 minutos)
Rutinas didácticas
Pensar, girar y compartir
MLR8: Apoyos para el debate
Esta actividad introduce informalmente las reflexiones, que aparecen además de algunas traslaciones y rotaciones (que se introdujeron informalmente en la lección anterior). Se entrega a los estudiantes un dibujo animado de 6 cuadros que muestra el cambio de posición de un polígono. Como en la lección anterior, describen los movimientos, pero esta vez hay reflexiones, que pueden parecer imposibles como movimientos físicos a menos que se permita que la forma salga del plano. Los estudiantes identifican los nuevos movimientos e intentan describirlos.
Al final de esta actividad, se habrán introducido los tres movimientos básicos y en la siguiente actividad se introducirán sus nombres (traslaciones, rotaciones y reflexiones).
Mantenga a los estudiantes en los mismos grupos y mantenga el acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a los estudiantes 5 minutos de tiempo de trabajo en silencio y, a continuación, invíteles a compartir sus respuestas con su grupo. A continuación, discuta con toda la clase. Diga a los estudiantes que van a describir movimientos como lo hicieron en la lección anterior, pero que esta vez hay un nuevo movimiento en el que deben fijarse. Recuerde las palabras que utilizó la clase para describir los toboganes y los giros.
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes con discapacidad
Procesamiento conceptual: Eliminar barreras. Demostrar los pasos de la actividad o juego, en el que un grupo de estudiantes y el personal juegan una ronda de ejemplo mientras el resto de la clase observa.
Funcionamiento ejecutivo: Organizadores gráficos. Proporcione un diagrama de Venn con el que comparar las similitudes y diferencias entre las rotaciones y los reflejos.
DE TAREA PARA EL ESTUDIANTE
NUNCIADO
A continuación, se presenta otra serie de movimientos de baile.
1. Describe cada movimiento o di si es un movimiento nuevo.
A. Cuadro 1 a cuadro 2
B. Cuadro 2 a cuadro 3
C. Cuadro 3 a cuadro 4
D. Cuadro 4 a cuadro 5
E. Cuadro 5 a cuadro 6
2. ¿Cómo describirísa el nuevo traslado?
RESPUESTAS POSIBLES
Las respuestas varían. Ejemplo de respuesta:
1.
A. Cuadro 1 a cuadro 2: Desplazamiento a la derecha
B. Cuadro 2 a cuadro 3: Nuevo movimiento
C. Cuadro 3 a cuadro 4: Gira 90° en el sentido de las agujas del reloj
D. Cuadro 4 a cuadro 5: Desplazamiento hacia arriba
E. Cuadro 5 a cuadro 6: Nuevo movimiento
2. El nuevo movimiento es como convertirse en su imagen reflejada a través de un espejo colocado en el centro del cuadro. Para el segundo movimiento, el espejo es vertical y para el último movimiento es horizontal.
Los estudiantes pueden ver un reflejo como una traslación, especialmente porque las figuras no están en el mismo marco. Pida a estos estudiantes que tracen el cuadro 2 en papel vegetal. ¿Hay alguna forma de convertirlo en el cuadro 3 deslizándolo? ¿Qué tienen que hacer para convertirlo en el cuadro 3? (Tienen que darle la vuelta al papel vegetal, por lo que se trata de un nuevo tipo de movimiento).
Al describir las reflexiones, los estudiantes pueden confundir los términos horizontal y vertical. Considere colocar los términos horizontal y vertical con ejemplos en su salón.
SÍNTESIS DE LA ACTIVIDAD
Grado 8 . Matemáticas . Unidad 1
El propósito de esta discusión es una comprensión inicial de que hay un tercer tipo de movimiento que es fundamentalmente diferente de los movimientos encontrados en la lección anterior, porque invierte las direcciones. Algunas posibles preguntas de debate para ayudarles a identificarlo son:
• «¿En qué se diferencia el movimiento del panel 2 al panel 3 de los que discutimos ayer?».
• «¿Hay algún otro movimiento en este dibujo animado?».
• «¿Qué características de la imagen nos ayudan a ver que se está produciendo este movimiento?».
Para ayudar a responder a estas preguntas, diga a los estudiantes que presten atención a la dirección en la que apunta el «pico» del polígono, izquierda o derecha. Dibuje una línea vertical punteada en el centro del cuadro 2 y diga: «Aquí hay un espejo. El polígono en el cuadro 3 es lo que el polígono en el cuadro 2 ve cuando se mira en el espejo».
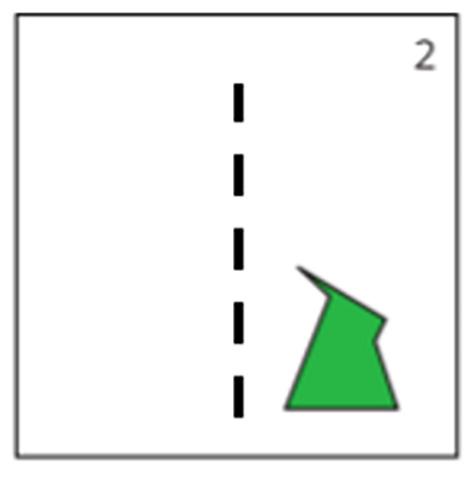
Demuéstrelo usando papel de calco o transparencias para mostrar que son imágenes especulares. A continuación, pregunte a los estudiantes si hay otras líneas especulares en otros cuadros. Para el segundo reflejo, del cuadro 5 al cuadro 6, señale que la línea de espejo es ahora una línea horizontal: en el cuadro 5 el pico apunta hacia abajo y en el cuadro 6 el pico apunta hacia arriba, con la cabeza a la derecha del cuerpo en ambos casos. Esto contrasta con una rotación de 180 grados, que situaría la cabeza a la izquierda del cuerpo.
Apoyo para estudiantes que aprenden el idioma inglés
Representar y conversar: MLR8 Apoyos para el debate. Utilice esta rutina para invitar a los estudiantes a representar o mostrar los movimientos del polígono para ayudarles a describir su movimiento. Después de que los estudiantes hayan completado los dos problemas, deben describir las diferencias en los movimientos con un compañero. Anime a los estudiantes a mostrar lo que saben haciendo una de las siguientes cosas: crear un movimiento de baile sencillo y mostrar con su cuerpo cómo cambiaría de un cuadro a otro, dibujar la forma en una pequeña pizarra y mostrar con flechas cómo gira o se mueve o dibujar la forma en papel y recortarla. Si los estudiantes dibujan y recortan la forma, deben deslizarla, girarla o rotarla físicamente. Recuerde a los estudiantes que utilicen términos como horizontal y vertical, deslizar a izquierda/derecha o girar.
Principio(s) de diseño: Apoyar la creación de sentido; cultivar la conversación
ACTIVIDAD
DE EXPLORACIÓN
| CLASIFICACIÓN DE CARTAS DE MOVIMIENTO
(15 minutos)
Rutinas didácticas
Turnos
MLR8: Apoyos para el debate
El objetivo de esta actividad de ordenación de tarjetas es que los estudiantes practiquen más la identificación de traslaciones, rotaciones y reflexiones y, en el debate posterior a la realización de la tarea, introduzcan estos términos. En grupos de 3 clasifican las tarjetas 9 en categorías. Hay 3 traslaciones, 3 rotaciones y 3 reflexiones. Los estudiantes explican sus categorías y llegan a un acuerdo sobre ellas.
En realidad, en el esquema hay 12 tarjetas. Las tres últimas muestran movimientos algo más complicados que las primeras 9. Estas pueden retenerse, al principio, y utilizarse si el tiempo lo permite.
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Los estudiantes podrían identificar solo las categorías 2, poniendo las reflexiones con las traslaciones (en el caso de la tarjeta 3) o las rotaciones (en el caso de la tarjeta 5). Mientras los estudiantes trabajan, observe si los grupos han clasificado las tarjetas en traslaciones, rotaciones y reflexiones (aunque no necesariamente utilizando esas palabras). Observe también si hay descripciones de los puntos correspondientes, como «estos puntos van juntos» o «aquí hay puntos anteriores y posteriores»
Organice a los estudiantes en grupos de 3 y facilite el acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Entrega a cada grupo las primeras 9 fichas. Reserve las últimas 3 tarjetas para utilizarlas si el tiempo lo permite.
Diga a los estudiantes que su trabajo consiste en clasificar las tarjetas en categorías según el tipo de movimiento que muestren. Después de llegar a un consenso sobre qué categorías utilizar, se turnan para colocar una tarjeta en una categoría y explicar por qué creen que su tarjeta va en esa categoría. Cuando no es su turno, su trabajo consiste en escuchar el razonamiento de su compañero y asegurarse de que lo ha entendido. Considere la posibilidad de hacer una breve demostración con un estudiante de formas productivas de comunicarse durante esta actividad. Por ejemplo, muéstrele cómo es esperar su turno, explicar lo que piensa y escuchar lo que piensa su compañero.
Dé a los estudiantes unos (10 minutos) para clasificar las tarjetas. No indique explícitamente a los estudiantes al principio que utilicen las palabras traslaciones, rotaciones y reflexiones. Vigile si hay algún grupo que utilice estas categorías, aunque las denominen de forma diferente. Si el tiempo lo permite, distribuya las tarjetas 3 restantes. Continúe con un debate para toda la clase.
Si utiliza la actividad digital, pida a los estudiantes que cierren sus dispositivos, al principio. Una vez que hayan llegado a un acuerdo sobre cómo clasificar sus tarjetas, pueden abrir sus dispositivos y utilizar las aplicaciones para ayudarles a perfeccionar la forma en que describen los movimientos.
Apoyo para estudiantes con discapacidad
Funcionamiento socioemocional: Tutores. Junte a los estudiantes con sus tutores previamente identificados.
Traducciones: 1, 7, 8, 10
Rotaciones: 2, 6, 9, 12
Reflexiones: 3, 4, 5, 11
Tu maestro te dará un conjunto de tarjetas. Ordena las tarjetas en categorías según el tipo de movimiento que muestren. Prepárate para describir cada categoría y por qué es diferente de las demás. RESPUESTAS POSIBLES
Para detectar si una figura es una traslación de otra, fíjate si sigue sentada exactamente igual, por ejemplo, las dos figuras tienen la misma orientación y están sentadas sobre la misma base. Para detectar si una figura es una rotación de otra, fíjate si una figura no está de pie exactamente igual que la otra, sino que parece estar girada. Las reflexiones pueden confundirse tanto con traslaciones (si las dos figuras siguen sobre la misma base) como con rotaciones (si parecen estar giradas). La forma de detectar un reflejo en estos ejemplos es elegir una característica de la figura que exista en un lado de la misma pero no en el otro (por ejemplo, las «orejas de conejo» puntiagudas de esta actividad) y ver si apunta hacia la izquierda en una figura y hacia la derecha en la otra. (Alternativamente, hacia arriba y hacia abajo si la línea de reflexión es horizontal). INTRODUCCIÓN
Grado 8 . Matemáticas . Unidad 1
CONCEPTOS ERRÓNEOS PREVISTOS
Los estudiantes pueden tener dificultades para diferenciar entre los tres movimientos, confundiendo las reflexiones con traslaciones o rotaciones. Después de que tomen su mejor decisión, anime a estos estudiantes a utilizar papel de calco para justificar su respuesta. En la ficha 10, los estudiantes pueden confundirse cuando la figura traducida se superpone a la original. En la tarjeta 4, los estudiantes pueden pensar primero que se trata de una rotación (al igual que en las tarjetas 6 y 9). Anime a estos estudiantes a utilizar papel de calco para comprobar sus respuestas.
Seleccione uno o varios grupos para que compartan los nombres de sus categorías. Selecciona uno o más grupos para que compartan cómo clasificaron las tarjetas en las categorías. Pregunte a la clase si no están de acuerdo con alguna de las opciones y dé a los estudiantes la oportunidad de justificar su razonamiento (MP3).
Presente los términos traducción, rotación, y reflexión. Puede ser útil mostrar un ejemplo de cada uno para facilitar el debate:
DE LA ACTIVIDAD
SÍNTESIS
Alternativamente, puede mostrar las aplicaciones de geogebra utilizados en la versión digital de los materiales del estudiante para facilitar el debate:
• Traducción: ggbm.at/bndgwbqu
• Rotación: ggbm.at/acp9xpz6
• Reflexión: ggbm.at/ah8qgabm
(Para acceder a los enlaces a estos recursos y a otros, visite la unidad 1, lección 2, en el «Área del maestro en línea»).
Señale formas de identificar de qué tipo de movimiento se trata. Los traslados son un deslizamiento sin giro. Las rotaciones son un giro. Las reflexiones son en la dirección opuesta. Introducir el término puntos correspondientes. Si vemos las figuras como conejos, entonces las puntas de las orejas en la figura original y las puntas de las orejas en su imagen son puntos correspondientes, por ejemplo. Introduzca también el término imagen para una figura después de aplicar una transformación: para cada una de las tarjetas, una figura es la imagen de la otra figura después de aplicar una traslación, rotación o reflexión.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos para el debate. Utilice este apoyo para ampliar los usos matemáticos del lenguaje para comunicarse sobre rotaciones, reflexiones y traslaciones. Mientras los grupos comparten cómo clasificaron y ordenaron las formas, revoque sus ideas usando los términos «traslación», «rotación», «reflexión», «imagen» y «puntos correspondientes». A continuación, invite a los estudiantes a utilizar los términos al describir sus categorías y estrategias de clasificación. Algunos estudiantes pueden beneficiarse de repetir a coro las frases que incluyen los términos «traslación», «rotación», «reflexión», «imagen» y «puntos correspondientes» en contexto. Principio(s) de diseño: Optimizar la salida (para explicación)
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Preguntas para el debate:
• «Hemos encontrado un nuevo tipo de movimiento diferente al de ayer. ¿Qué puedes contarme sobre él?». (Es como una imagen especular, no puedes hacer el movimiento deslizando o girando, la figura mira en la dirección opuesta).
• «Hemos dado nombres matemáticos a los tres tipos de movimientos que hemos visto. ¿Cómo se llaman?». (El «deslizamiento» se llama traslación, el «giro» se llama rotación y la imagen especular se llama reflexión).
• «¿Qué entendemos por puntos correspondientes?».. (Un punto que está en la misma parte de la figura tanto en la figura original como en la imagen).
• «¿Qué entendemos por imagen de una figura?». (La figura resultante después de haber realizado un movimiento).
Considere la posibilidad de crear una pantalla semipermanente que muestre estos tres términos y sus defInstrucciónnes como referencia a lo largo de la unidad.
Una traslación desliza una figura sin girarla. Cada punto de la figura recorre la misma distancia en la misma dirección. Por ejemplo, la figura �� se traslada hacia abajo y hacia la izquierda, como muestran las flechas. La figura �� es una traslación de la figura ��
Una rotación gira una figura alrededor de un punto, llamado centro de la rotación. Cada punto de la figura gira en círculo alrededor del centro y forma el mismo ángulo. La rotación puede ser en el sentido de las agujas del reloj, yendo en la misma dirección que las agujas de un reloj, o en el sentido contrario, yendo en la otra dirección. Por ejemplo, la figura �� se giró 45° en el sentido de las agujas del reloj alrededor de su vértice inferior. La figura �� es una rotación de la figura ��
Una reflexión coloca puntos en el lado opuesto de una línea de reflexión. La imagen reflejada es una copia al revés de la figura original. La línea de reflexión muestra dónde debe situarse el espejo. Por ejemplo, la figura �� se refleja a través de la línea de puntos. La figura �� es un reflejo de la figura ��
Grado 8 . Matemáticas . Unidad 1
ENFRIAMIENTO | ¿ES UN REFLEJO? (5
minutos)
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
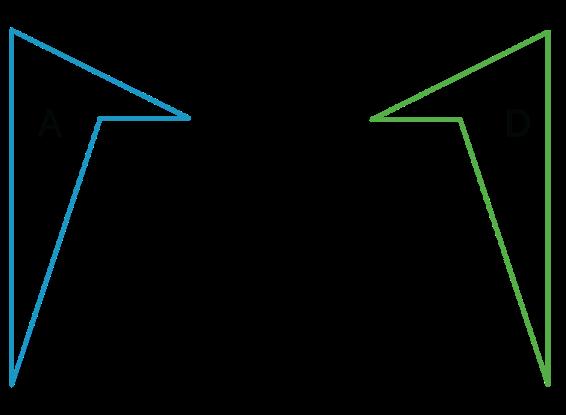
¿Qué tipo de movimiento lleva la figura �� a la Figura ��?
Explica tu razonamiento.
Las respuestas varían. Ejemplo de respuesta: Se trata de una rotación. Si la figura �� se gira alrededor del punto compartido por las figuras �� y ��, puede aterrizar en la figura ��.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Cada una de las seis tarjetas muestra una forma.
A. ¿Qué par de tarjetas muestra una forma y su imagen después de una rotación?
B. ¿Qué par de tarjetas muestra una figura y su imagen después de una reflexión?
Soluciones posibles
A. Tarjetas 1 y 4
B. Tarjetas 3 y 5
PROBLEMA 2
Los cinco cuadros muestran las diferentes posiciones de una figura.
Describa cómo se mueve la figura para ir de su posición en cada cuadro a el siguiente.
Soluciones posibles
Para ir de la posición 1 a la posición 2, la figura se mueve hacia la derecha. Para obtener de la posición 2 a la posición 3, la forma se voltea sobre una línea horizontal. Para obtener desde la posición 3 a la posición 4, la forma se mueve a la izquierda. Para ir de la posición 4 a la posición 5, la figura vuelve a pasar por encima de una línea horizontal. La forma ha vuelto entonces a su posición original en la posición 1
Alternativamente, para ir de la posición 1 a la posición 2 o de la posición 3 a la posición 4, la forma puede voltear sobre una línea vertical. Como la forma es simétrica, un giro tiene el mismo aspecto que un desplazamiento. Para ir de la posición 2 a la posición 3 o de la posición 4 a la posición 5, la forma se puede rotar 180 grados alrededor de un punto que no esté en el polígono.
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 3
Grado 8, unidad 1, lección 1
El rectángulo visto en el cuadro 1 es rotado a una nueva posición, vista en el Cuadro 2.
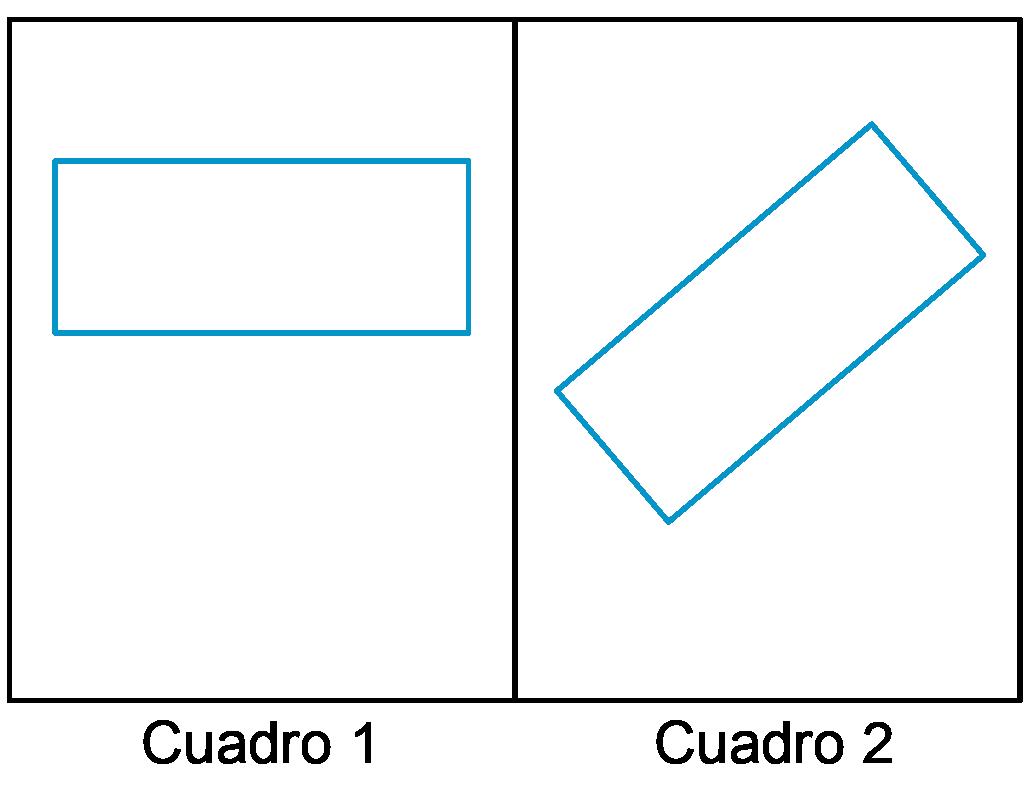
Selecciona todas las formas en que el rectángulo podría haber sido rotado para llegar del cuadro 1 al cuadro 2.
40 grados en el sentido de las agujas del reloj
40 grados en sentido contrario a las agujas del reloj
90 grados en el sentido de las agujas del reloj
90 grados en sentido contrario a las agujas del reloj
140 grados en el sentido de las agujas del reloj
140 grados en sentido contrario a las agujas del reloj
Reflexiones:
Soluciones posibles
40 grados en el sentido de las agujas del reloj
40 grados en sentido contrario a las agujas del reloj
90 grados en el sentido de las agujas del reloj
90 grados en sentido contrario a las agujas del reloj
140 grados en el sentido de las agujas del reloj
140 grados en sentido contrario a las agujas del reloj
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas son llevadas a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos son llevados a ángulos de la misma medida. Enfoque SMPs
MP5 Usa herramientas apropiadas estratégicamente.
MP6 Atiende a la precisión.
MP7 Busca y usa estructuras.
Estándares ELD de California
I.A.1
II.B.3
LECCIÓN 4 HACER LOS MOVIMIENTOS
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predecir lo que podría ocurrir atienden a la precisión descubren la figura y el espacio.
METAS(S) DE APRENDIZAJE
• Dibujemos y describamos traslaciones, rotaciones y reflexiones.
META(S) DE APRENDIZAJE
• Puedo utilizar los términos traslación, rotación y reflexión para describir con precisión las transformaciones.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comprender que una «transformación» es una traslación, rotación, reflexión o una combinación de ellas.
• Dibujar una transformación de una figura utilizando información dada oralmente.
• Explicar (oralmente) la «secuencia de transformaciones» que «lleva» una figura a su imagen.
• Identificar (oralmente y por escrito) las características que determinan una traslación, rotación o reflexión.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR7: Comparar y conectar
MLR1: Cada vez más fuerte y más claro
MLR2: Recopilar y mostrar
Anticipar, monitorear, seleccionar, secuenciar y conectar
Preparación requerida
Impriama y recorte las tarjetas de laplantilla maestra «Haz ese movimiento». Prepare 1 conjunto de tarjetas por cada 4 estudiantes.
Materiales necesarios
Lápiz negro para la actividad 4.2
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Fichas preimpresas, recortadas a partir de copias del lápiz negro
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
En la lección anterior, los estudiantes conocieron los términos «traslación», «rotación» y «reflexión». En esta lección, los estudiantes comprenden que:
• Una traslación está determinada por dos puntos que especifican la distancia y la dirección de la traslación.
• Una rotación está determinada por un punto, un ángulo de rotación y una dirección de rotación.
• Una reflexión está determinada por una línea.
Estos movimientos se llaman transformaciones por primera vez y los estudiantes dibujan imágenes de figuras bajo estas transformaciones. También estudian dónde van las figuras bajo secuencias de estas transformaciones e identifican los pasos de una secuencia de transformaciones que lleva una figura a otra. Observa el sutil cambio de lenguaje. En la lección anterior, una figura «se desplaza» a la otra, como si la figura original fuera la que se desplaza. En esta lección, la transformación «lleva» una forma a la otra forma: esta elección lingüística centra la transformación en sí misma como objeto de estudio.
Los estudiantes que utilicen la versión impresa pueden utilizar papel de calco para experimentar el movimiento de las formas. Los estudiantes que utilicen la versión digital tienen acceso a las aplicaciones de Geogebra para realizar transformaciones. Siempre que los estudiantes decidan utilizar una herramienta adecuada, estarán participando en el MP5. También es probable que los estudiantes empiecen a pensar estratégicamente qué transformaciones llevarán una figura a otra, identificando propiedades de las formas que indiquen si una traslación, rotación, reflexión o secuencia de estas logrará este objetivo (MP7).
LECCIÓN DE UN VISTAZO
Componente de la lección Estructura Tiempo Descripción breve
Los estudiantes crean una imagen después de una reflexión de un triángulo dado y comparten las estrategias que utilizaron.
Calentamiento Independiente 5 min
Actividad de Exploración En parejas 15 min
Actividad de Exploración En parejas 15 min
Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar las transformaciones utilizando la tecnología.
Los estudiantes dibujan una transformación basándose en una descripción dada por su compañero.
Una aplicación digital interactiva está disponiblepara permitir a los estudiantes explorar transformaciones en una cuadrícula utilizando la tecnología.
Los estudiantes exploran secuencias de transformaciones describiendo primero la transformación de la figura A a la figura B y después nombrando la transformación de la figura B a la figura C. A continuación, los estudiantes nombran una secuencia de transformaciones que lleva de la figura A a la figura C.
Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar secuencias de transformaciones utilizando la tecnología.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las secuencias de transformaciones.
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-8 min
Los estudiantes discuten diferentes maneras de describir una traslación, rotación y reflexión y definen formalmente las transformaciones y la secuencia de transformaciones.
Los estudiantes identifican la información necesaria para realizar cada transformación.
El componente de práctica independiente incluye 1 problema de la lección y 2 problemas de repaso en espiral.
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | REFLEJO IMAGEN RÁPIDA (5
minutos)
Rutinas didácticas
MLR7: Comparar y conectar
MLR1: Cada vez más fuerte y más claro
En este calentamiento, se pide a los estudiantes que dibujen un reflejo de un triángulo dado y expliquen las estrategias que utilizaron. El objetivo es que los estudiantes se den cuenta de que pueden utilizar la ubicación de un único punto y el hecho de que la imagen es un reflejo del triángulo para dibujar la imagen. Para animar a los estudiantes a utilizar lo que saben sobre reflexiones y no contar cada línea de la cuadrícula, esta imagen se muestra durante unos segundos y luego se oculta. Se muestra una vez más para que los estudiantes comprueben su pensamiento.
INTRODUCCIÓN
Antes de empezar, asegúrese de que los estudiantes tienen sus libros o dispositivos abiertos en la página correcta. Diga a los estudiantes que les mostrará una imagen de un reflejo del triángulo ������ durante 3 segundos. Su tarea consiste en dibujar la imagen y explicar las estrategias que hayan utilizado.
Para las clases que utilicen la versión digital de los materiales, muestre la aplicación y demuestre el uso de las distintas herramientas. Dé a los estudiantes uno o dos minutos para probarlas. Pídales que reinicien la aplicación antes de comenzar la actividad.
Muestre la imagen completada durante 3 segundos y luego ocúltela. Haga esto dos veces. Dé a los estudiantes 1 minuto de tiempo de trabajo tranquilo después de cada destello de la imagen. Anima a los estudiantes a que piensen en los atajos que han utilizado para dibujar la imagen reflejada.
Apoyo para estudiantes con discapacidad
Memoria: Tiempo de procesamiento. Esta rutina de instrucción puede ser muy exigente para la memoria de trabajo del estudiante. Para los estudiantes con dificultades en esta área, muestre la imagen durante un período de tiempo más largo o repita el flash de la imagen según sea necesario. Los estudiantes también se benefician si se les dice explícitamente que busquen estructuras útiles dentro de la imagen.
Lenguaje receptivo/expresivo: Tiempo de procesamiento. Los estudiantes que se benefician de un tiempo de procesamiento adicional también se verían favorecidos por MLR1 («Más fuerte y más claro cada vez»).
Aquí tienes una imagen incompleta. Tu maestro mostrará la imagen completa dos veces. Tu tarea consiste en completar la imagen en tu copia.
POSIBLES
Grado 8 . Matemáticas . Unidad 1
Las respuestas varían. Posible respuesta: El primer destello mostraba dónde poner ��′ y el segundo destello dónde poner ��′. Una vez colocados éstos, solo había un lugar donde ��′ podía ir, debajo del segmento ��′��′, de modo que △��′��′��′ es una imagen reflejada de △������
SÍNTESIS DE LA ACTIVIDAD
Los estudiantes pueden tener dificultades para dibujar la imagen bajo transformación a partir de los destellos rápidos de la imagen porque están intentando contar la cantidad de espacios que se mueve cada vértice. Anime a estos estudiantes a utilizar la línea de la imagen para ayudarles a reflejar la imagen.
Seleccione a algunos estudiantes para que compartan las estrategias que utilizaron al dibujar su figura. Considere la posibilidad de formular algunas de las siguientes preguntas:
• «¿Qué fue importante a la hora de crear tu boceto (qué necesitabas)?»..
• «¿Qué buscaste en el primer destello? ¿En el segundo?»..
• «¿Qué permaneció igual y qué es diferente en la figura y su imagen?»..
• «¿Cómo decidiste dónde colocar los vértices de la imagen?»..
• «¿Cómo decidiste la longitud de los lados?»..
ACTIVIDAD DE EXPLORACIÓN | HAZ ESE
MOVIMIENTO (15 minutos)
Rutinas didácticas
MLR2: Recopilar y mostrar
El objetivo de esta actividad es que los estudiantes den descripciones precisas de traslaciones, rotaciones y reflexiones. Al final de la lección anterior, los estudiantes han identificado y esbozado estas transformaciones a partir de indicaciones escritas, pero no han utilizado este lenguaje más preciso para describir los tres movimientos. Las imágenes de esta actividad se presentan en cuadrículas para permitir y animar a los estudiantes a describir la transformación en términos de puntos, líneas o ángulos concretos. Describir los movimientos con precisión y claridad requerirá que los estudiantes realicen MP6
Hay cuatro tarjetas de transformación diferentes que los estudiantes utilizan en esta actividad: 1A, 1B, 2A, y 2B. Cada tarjeta contiene la imagen original y la imagen sometida a una transformación. Los estudiantes se organizan en grupos de 2 y cada uno recibe una tarjeta de transformación diferente: algunas parejas reciben las tarjetas 1A y 1B, mientras que otras parejas reciben 2A y 2B. Cada tarjeta A es una traslación, mientras que las tarjetas B muestran una rotación o una reflexión.
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
A medida que los estudiantes describen sus transformaciones y dibujan sus imágenes bajo transformación, vigile que los estudiantes utilicen descripciones precisas a su compañero en términos de puntos, líneas o ángulos específicos.
Introducir la palabra transformación: Esta es una palabra para un movimiento (como la reflexión en el calentamiento) o para una secuencia de movimientos. Es una palabra matemática que se utilizará en lugar de «movimiento», que se ha utilizado hasta ahora.
Organice a los estudiantes en grupos de 2. Muestra la imagen original que cada estudiante tiene también delante. Entregue a cada estudiante una de las cuatro tarjetas de transformación y papel de calco; asegúrese de que los estudiantes sepan no que deben mostrar su tarjeta a su compañero. Diga a los estudiantes que dibujarán una transformación basándose en las instrucciones que les dé un compañero.
Los compañeros tienen las tarjetas 1A y 1B o las tarjetas 2A y 2B. Diga a los estudiantes que, en la primera ronda, los que tengan las tarjetas A den a su compañero una descripción precisa de la transformación que aparece en su tarjeta. Sus compañeros pueden utilizar papel de calco para producir la imagen bajo transformación en la cuadrícula con la imagen original. En los salones de clase digitales, los estudiantes tienen acceso a aplicaciones que pueden utilizar para transformar la figura. Cuando el boceto está completo, el estudiante que describe la transformación revela su tarjeta y, juntos, los estudiantes deciden si el boceto es correcto. En la segunda ronda, se invierten los papeles. Los estudiantes con las tarjetas B describen su transformación mientras su compañero dibuja.
El estudiante que describe la transformación puede repetir, revisar o añadir cualquier información importante mientras su compañero dibuja, pero no puede decirle que arregle nada hasta que haya terminado. El estudiante que dibuja no debe hablar, solo dibujar. (Recuerde a los estudiantes que deben utilizar el lenguaje geométrico para describir reflexiones, rotaciones y traslaciones que se utilizó en la lección anterior.
Apoyo para estudiantes que aprenden el idioma inglés
Escuchar y hablar: Rutina del lenguaje matemático 2 «Comparar y conectar» Esta es la primera vez que se sugiere la rutina 2 del lenguaje matemático como apoyo en este curso. En esta rutina, el maestro circula y escucha la conversación de los estudiantes mientras anota las palabras, frases, dibujos o escritos que utilizan. El lenguaje recogido se expone visualmente para que toda la clase pueda utilizarlo a lo largo de la lección y de la unidad. Por lo general, la exposición contiene diferentes ejemplos de estudiantes que utilizan características de las funciones lingüísticas disciplinares, como interpretar, justificar o comparar. El propósito de esta rutina es capturar una variedad de palabras y frases de los estudiantes en una pantalla a la que los estudiantes puedan referirse, sobre la que puedan construir o con la que puedan hacer conexiones durante futuras discusiones, y aumentar la conciencia de los estudiantes sobre el lenguaje utilizado en las conversaciones sobre matemáticas.
Principio(s) de diseño: Optimizar la salida (para la explicación); maximizar la metaconciencia
Cómo sucede
1. Los estudiantes describen la transformación de un triángulo en un triángulo. Mientras los estudiantes describen la transformación del triángulo ������ a su compañero, escuche y recoja el vocabulario y las frases que los estudiantes utilizan para describir los movimientos. Concéntrese en captar a los estudiantes que utilizan el lenguaje geométrico para describir reflexiones, rotaciones y traslaciones.
Si el interlocutor se queda atascado, plantéele estas preguntas «¿cómo se transformó el punto �� en ��′?». «Elije uno de los puntos, rectas o ángulos y describa cómo cambió y en general, «¿parece que el nuevo triángulo es una traslación, rotación o reflexión del original?». Si utiliza la aplicación, compruebe la precisión y las etiquetas a medida que los estudiantes colocan la nueva imagen bajo la transformación.
2. Escriba las palabras de los estudiantes en una visualización. Divida la pantalla en 3 secciones. Agrupe el lenguaje sobre las tarjetas 1A y 2A en el lado izquierdo de la pantalla, el lenguaje sobre la tarjeta 1B en el centro y el lenguaje sobre la tarjeta 2B en el lado derecho.
Anote todo el lenguaje (ya sea preciso, ambiguo, correcto o incorrecto) en la columna correspondiente según lo descrito por los estudiantes.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma inglés, continuación
3. Organice a los estudiantes en grupos de 2, e invite a sus compañeros a debatir qué palabras o frases les llaman la atención. Pregunte a los estudiantes: «¿Hay alguna palabra o frase que os llame la atención o que no esté en una columna concreta? ¿Por qué?». De nuevo, camine por la clase y recoja las palabras, frases y dibujos adicionales en la pantalla. Los estudiantes deben notar que el lado izquierdo consiste en lenguaje que describe traslaciones, el medio consiste en lenguaje que describe reflexiones y el lado derecho consiste en lenguaje que describe rotaciones.
4. Seleccione 3-4 grupos para formar un grupo. Seleccione 3-4 grupos para que compartan sus ideas con la clase. Invite a los estudiantes a demostrar su razonamiento con la aplicación o el papel de calco y asegúrese de modificar la pantalla en consecuencia. Utilice este debate para aclarar, revisar y mejorar la forma de comunicar y representar las ideas. Si los estudiantes siguen utilizando palabras vagas (por ejemplo, mover, voltear, imagen especular, etc.), refuerce los términos geométricos precisos (por ejemplo, transformación, traslación, rotación, reflexión, etc.). Pregunte a los estudiantes: «¿Hay alguna otra forma de decir esto? o ¿alguien puede ayudar a aclarar este lenguaje?».
5. Cierre esta conversación colocando la pantalla en la parte delantera del salón de clases para que los estudiantes puedan consultarla durante el resto de la lección y asegúrese de actualizar la pantalla durante el resto de la lección.
Apoyo para estudiantes con discapacidad
Funcionamiento socioemocional: Tutores. Agrupe a los estudiantes con sus tutores previamente identificados.
Funcionamiento ejecutivo: Ayudas visuales. Cree un gráfico de anclaje (es decir, un muro de palabras) que muestre públicamente defInstrucciónnes, reglas, fórmulas o conceptos importantes para referencia futura.
Su compañero describirá la imagen de este triángulo después de una determinada transformación. Dibújela aquí.
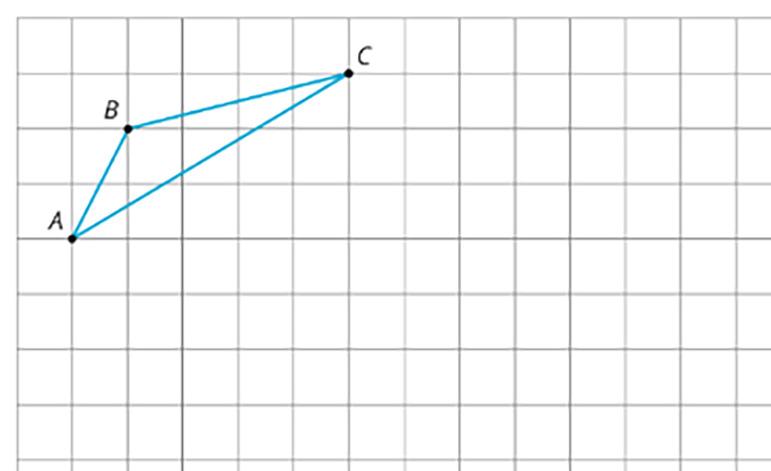
Las transformaciones correctas se muestran en las tarjetas.
Los estudiantes pueden atascarse pensando que necesitan utilizar los términos precisos para la transformación en su descripción. Anima a estos estudiantes a describirla de una manera que tenga sentido para ellos y a buscar cosas que sepan sobre los puntos, las rectas o los ángulos específicos de su tarjeta para ayudarles.
California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Muestre las siguientes preguntas para que todos las vean y da a los grupos 2 minutos para debatir:
• ¿Qué partes de la descripción de tu compañero te resultaron útiles a la hora de dibujar?
• ¿Qué partes te resultaron difíciles de explicar a tu compañero? Señala ejemplos concretos en tus tarjetas.
• Cuando estabas dibujando, ¿qué preguntas habría sido útil poder hacer al descriptor?
Pide a los estudiantes seleccionados a los que observaste utilizar descripciones precisas y dibujar con base en esas descripciones que expliquen por qué utilizaron la información que utilizaron y cómo fue útil para dibujar. Concéntrese en:
• la dirección y la distancia de una traslación
• el centro y la medida de una rotación
• la línea de una reflexión
Si hay tiempo, pida a los estudiantes que usaron y no usaron papel de calco que expliquen su proceso.
• Refuerce el término transformación como un término que abarca traslaciones, rotaciones y reflexiones. Diles que hay otros tipos de transformaciones, pero que por ahora nos centraremos en estos tres tipos.
ACTIVIDAD DE EXPLORACIÓN | A A B A C
(15 minutos)
Rutinas didácticas
MLR7: Comparar y conectar
Anticipar, controlar, seleccionar, secuenciar y conectar
Los estudiantes han visto imágenes que muestran una secuencia de transformaciones en la primera lección de esta unidad, sin embargo no han oído el término secuencia de transformaciones. Tampoco se les ha pedido que describan las transformaciones de la secuencia utilizando un lenguaje preciso. La introducción de esta actividad introduce este término y da a los estudiantes la oportunidad de describir la secuencia de más de una transformación.
Para el segundo problema, anime a los estudiantes a encontrar una secuencia de transformaciones diferente de la que se muestra en la imagen. Cada vez que se mencione una reflexión, pregunte a los estudiantes dónde se encuentra la línea de reflexión y cuando se mencione una rotación, pregunte por el centro de la rotación y la cantidad de grados. Controle si los estudiantes aplican transformaciones diferentes (o aplican transformaciones en un orden diferente).
Organice a los estudiantes en grupos de 2, y proporcione acceso a sus conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Muestre la imagen para que todos la vean. Pregunte a los estudiantes si pueden imaginar una sola traslación, rotación o reflexión que lleve un pájaro a otro. Después de un minuto, compruebe que no es posible.
Pida a los estudiantes que describan cómo podríamos utilizar traslaciones, rotaciones y reflexiones para llevar un pájaro a otro. Recoja algunas respuestas diferentes. (Una forma sería tomar el pájaro de la izquierda, trasladarlo hacia arriba y luego reflejarlo sobre una línea vertical). Diga a los estudiantes que cuando hacemos una o más transformaciones seguidas para llevar una figura a otra, se llama secuencia de transformaciones. Si utiliza la actividad digital, puede repasar las herramientas de transformación en la aplicación. (Las instrucciones se repiten en la actividad para referencia de los estudiantes).
Dé a los estudiantes 2 minutos de tiempo de trabajo tranquilo para realizar la tarea, seguidos de 3 minutos para discutir sus respuestas con un compañero y completar las preguntas que hayan quedado pendientes. Continúe con un debate de toda la clase.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de poner en práctica esta actividad.
Funcionamiento socioemocional: Compañeros tutores. Junte a los estudiantes con sus compañeros tutores previamente identificados.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Aquí hay algunas figuras en una cuadrícula isométrica.
1. Nombra una transformación que lleve la figura �� a la figura �� Nombra una transformación que lleva la figura �� a la figura ��
2. ¿Cuál es una secuencia de transformaciones que lleva la figura �� a la figura ��? Explica cómo lo sabes.
RESPUESTAS POSIBLES
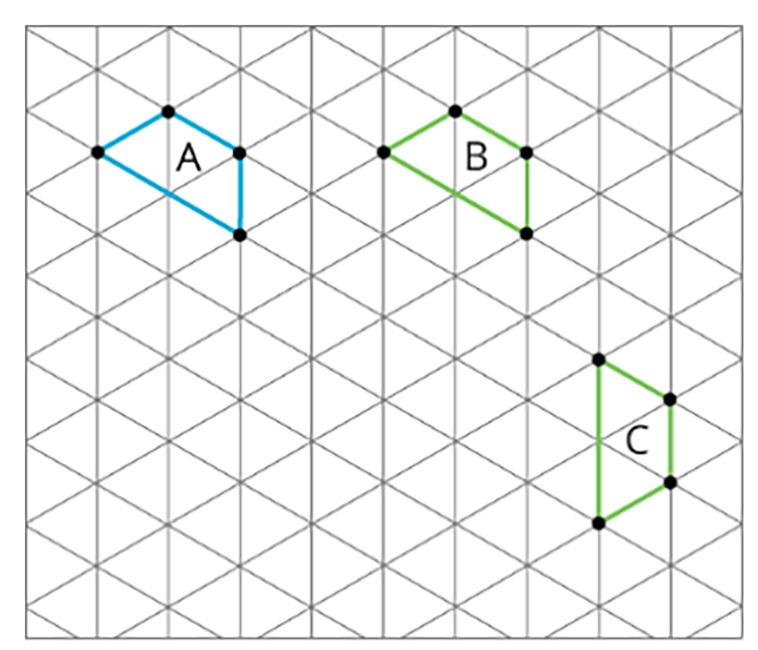
1. Hay muchas formas de describir la traslación que lleva �� a ��: Cualquier par de puntos correspondientes sirve. En la figura, se muestran dos puntos correspondientes �� y ��. Hay dos maneras de llevar �� a �� con una sola transformación. Una es una reflexión con línea de reflexión ℓ (mostrada). La otra es una rotación 60° en el sentido de las agujas del reloj alrededor del punto �� en la línea ℓ
2. Las respuestas varían. Ejemplo de respuesta: Utilizando las transformaciones del problema 1, aplique primero una traslación de modo que �� pase a �� y después una reflexión llevando �� a ��
Seleccione a los estudiantes con diferentes respuestas correctas para que muestren sus soluciones. Asegúrese de destacar al menos una rotación. Si ningún estudiante lo menciona, demuestre una forma de llevar A a C que implique una rotación. Tanto si los estudiantes utilizan la aplicación de Geogebra como si no, puede ser útil mostrar la aplicación para facilitar la discusión: ggbm.at/zjtya9qs (para enlaces a este recurso y más, visite la unidad 1, lección 4, en el «Área del maestro en línea»).
Haga hincapié en que hay muchas maneras de describir la traslación que lleva la figura �� a la figura ��. Todo lo que se necesita es identificar un par de puntos correspondientes y nombrarlos en el orden correcto (y utilizar la palabra «trasladar»).
SÍNTESIS
Para los estudiantes que utilizaron una reflexión para llevar �� a ��, haga hincapié en que las reflexiones están determinadas por líneas y que debemos nombrar la línea cuando queremos comunicarnos sobre ella.
Después de que un estudiante o el maestro utilicen una rotación, haga hincapié en que una rotación está definida por un punto central y un ángulo (con una dirección). Es necesario nombrar el punto central y la medida del ángulo o un ángulo con la medida correcta (al igual que la dirección). Refuerce con los estudiantes que cuando hacemos más de una transformación seguida, la llamamos secuencia de transformaciones.
.
8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: Rutina del lenguaje matemático 7 «Comparar y conectar». Esta es la primera vez que se sugiere la rutina del lenguaje matemático 7 como apoyo en este curso. En esta rutina, se da a los estudiantes un problema que puede abordarse utilizando múltiples estrategias o representaciones y se les pide que preparen una muestra visual de su método. A continuación, los estudiantes investigan las estrategias (mediante un recorrido guiado por el maestro, un intercambio entre compañeros, una presentación en grupo, etc.), comparan enfoques e identifican correspondencias entre diferentes representaciones. Un tema de debate típico es: «¿Qué es lo mismo y qué es diferente?» en relación con su propia estrategia y la de los demás. El propósito de esta rutina es permitir a los estudiantes dar sentido a las estrategias matemáticas identificando, comparando, contrastando y conectando otros enfoques con el suyo propio y desarrollar la conciencia de los estudiantes sobre el lenguaje utilizado a través de conversaciones constructivas.
Principio(s) de diseño: Maximizar la metaconciencia: apoyar la creación de sentido
Cómo se lleva a cabo
1. Comparar y contrastar diferentes enfoques.Utilice esta rutina para comparar y contrastar diferentes estrategias para transformar la figura �� en la figura ��. Invite a los estudiantes a crear una presentación visual que muestre cómo entendieron el problema y por qué su solución tiene sentido para transformar la figura �� en la figura ��
Los estudiantes deben incluir estas características en su exposición:
• un esquema de las figuras (no es necesario si se utiliza la aplicación)
• un esquema de las figuras después de cada transformación (no es necesario si se utiliza la aplicación)
• una secuencia escrita de las transformaciones con una explicación
2. Antes de seleccionar a los estudiantes para que muestren sus soluciones a la clase, dé primero a los estudiantes la oportunidad de hacerlo en un grupo de 3-4. Pida a los estudiantes que intercambien e investiguen el trabajo de los demás. Conceda 1 minuto a cada exposición y señale cuándo es el momento de cambiar.
Mientras investigan el trabajo de los demás, pida a los estudiantes que piensen en lo que es igual y lo que es diferente en cada enfoque. A continuación, dé a cada estudiante la oportunidad de añadir detalles a su propia presentación durante 1-2 minutos.
3. Mientras los grupos realizan sus presentaciones, vaya por el salón de clases y seleccione 2-3 estudiantes para que compartan su secuencia de transformaciones desde la figura �� hasta la figura ��. Asegúrese de seleccionar una variedad de enfoques, incluido uno que implique una rotación.
Llame la atención de los estudiantes sobre las diferentes formas en que se transformaron las figuras (por ejemplo, rotaciones, reflexiones y traslaciones) y cómo se expresa la secuencia de transformación en su explicación. Asimismo, utilice las viñetas «Síntesis de la actividad» para hacer hincapié en las características específicas de las traslaciones, reflexiones y rotaciones. 4. Una vez que los estudiantes seleccionados hayan terminado de compartir con toda la clase, dirija un debate en el que se comparen, contrasten y conecten los diferentes enfoques.
Considera la posibilidad de utilizar estas indicaciones para ampliar el lenguaje de los estudiantes mientras comparan y contrastan los distintos enfoques: «¿Por qué los enfoques condujeron al mismo resultado?, ¿qué funcionó bien en el enfoque de ?, ¿qué no funcionó bien? y ¿qué haría que la estrategia de fuera más completa o fácil de entender?».
Considera la posibilidad de utilizar estas indicaciones para ampliar el lenguaje de los estudiantes a la vez que conectas los distintos enfoques: «¿Qué papel desempeña la traducción en cada enfoque?, ¿es posible utilizar los tres tipos de transformaciones? y ¿qué transformación ves presente en todas las estrategias?».
5. Cierra el debate invitando a los estudiantes a 3 volver a expresar las estrategias utilizadas en las presentaciones y, a continuación, pasa de nuevo a la síntesis y enfriamiento de la lección.
¿Estás preparado para más?
Experimenta con otras formas de llevar la figura �� a la figura ��. Por ejemplo: ¿puedes hacerlo...
• sin rotaciones?
• sin reflexiones?
• sin traslaciones?
«¿Estás listo para más?». Respuesta del estudiante
Las respuestas varían. Ejemplo de respuesta sin reflexión: Primero traslada �� a �� y luego rota 60 grados en el sentido de las agujas del reloj.
Respuesta de muestra sin rotación: Traslada �� a �� y luego refleja sobre una línea de cuadrícula para hacer que las figuras se alineen.
Ejemplo de respuesta sin reflexión: Traslada �� a �� y luego gira alrededor de �� para que las figuras se alineen.
Ejemplo de respuesta sin traslación: Reflexione a través de la recta ��, tomando �� hasta �� y luego gire alrededor de �� para que las figuras se alineen.
SÍNTESIS DE LA LECCIÓN
(5 minutos)
8 . Matemáticas . Unidad 1
El objetivo de esta lección es que los estudiantes comiencen a identificar las características que determinan una traslación, rotación o reflexión. Para ello, consulte la visualización permanente realizada en una lección anterior. Para destacar las características específicas de cada tipo de transformación, considere formular las siguientes preguntas:
• «Si quieres describir una traslación, ¿qué información importante debes incluir?». (Una traslación está determinada por dos puntos que especifican la distancia y la dirección de la traslación).
• «Si quieres describir una rotación, ¿qué información importante necesitas incluir?». (Una rotación está determinada por un punto central y un ángulo con una dirección).
• «Si quieres describir una reflexión, ¿qué información importante necesitas incluir?». (Una reflexión viene determinada por una línea).
• «¿Qué significa la palabra transformación ?». (Traslados, rotaciones y reflexiones, o cualquier combinación de ellas).
• «¿Qué significa secuencia de transformaciones?». (Más de una aplicada una tras otra).
ENFRIAMIENTO | ¿QUÉ SE NECESITA?
(5 minutos)
1. 1. Si tuvieras que describir una traslación del triángulo ������, ¿qué información tendrías que incluir en tu descripción?
2. Si tuvieras que describir una rotación del triángulo ������, ¿qué información tendrías que incluir en tu descripción?
3. Si tuvieras que describir una rotación del triángulo ������, ¿qué información tendrías que incluir en tu descripción?.
1. La distancia y la dirección de la traslación. Una forma de hacerlo sería eligiendo un punto en el triángulo (��, por ejemplo) y luego mostrando dónde va este punto (��′ en el triángulo trasladado).
2. Un punto central, un ángulo y una dirección (en el sentido de las agujas del reloj o en sentido contrario).
3. Una línea.
Grado 8 . Matemáticas . Unidad 1
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Para cada par de polígonos, describe una secuencia de traslaciones, rotaciones y reflexiones que lleve el polígono �� al polígono ��
Soluciones posibles
A. B. C.
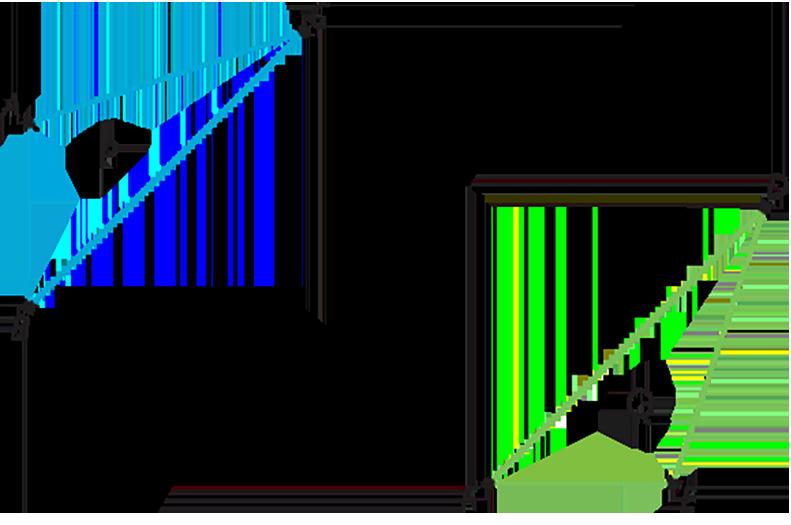
A. Ejemplo de respuesta: �� se traslada a ��, seguido de una rotación 60 grados en el sentido de las agujas del reloj con centro ��
B. Ejemplo de respuesta: El polígono ���������� se refleja sobre la recta ���� �� se traslada entonces a �� y se aplica una rotación de 60 grados en el sentido de las agujas del reloj con centro ��
C. Ejemplo de respuesta: �� se traslada a ��, luego se aplica una rotación con centro �� de modo que �� caiga encima de ��. Finalmente el polígono se refleja sobre la recta ����
PROBLEMA 2
Grado 8, unidad 1, lección 2
Aquí está el cuadrilátero �������� y la recta ℓ
Dibuja la imagen del cuadrilátero �������� después de reflejarlo a través de la recta ℓ
Soluciones posibles
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 3
Grado 8, unidad 1, lección 2
Aquí está el cuadrilátero ��������
Dibuja la imagen del cuadrilátero �������� después de cada rotación usando �� como centro.
A. 90 grados en el sentido de las agujas del reloj
B. 120 grados en el sentido de las agujas del reloj
C. 30 grados en el sentido contrario a las agujas del reloj
Soluciones posibles
Reflexiones:
Math Nation California . Grado 8
Learning Inc. - Todos los derechos reservados
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.3 Describir el efecto de dilataciones, traslaciones, rotaciones y reflexiones en figuras bidimensionales usando coordenadas.
Construir
8.G.1
Enfoque SMPs
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.C.12
II.C.6
LECCIÓN 5 MOVIMIENTOS DE COORDENADAS
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
dar sentido al mundo y predicen lo que podría ocurrir,
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
buscan y utilizan la estructura descubren la forma y el espacio.
METAS(S) DE APRENDIZAJE
• Transformemos algunas figuras y veamos qué sucede con las coordenadas de points.
META(S) DE APRENDIZAJE
• Puedo aplicar transformaciones a puntos de una cuadrícula si conozco sus coordenadas.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Dibujar y etiquetar un diagrama de un segmento de línea girado 90 grados en sentido horario o antihorario alrededor de un centro dado.
• Generalizar (oralmente y por escrito) el proceso para reflejar cualquier punto en el plano catesiano.
• Identificar (oralmente y por escrito) coordenadas que representan una transformación de una figura a otra.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR7: Comparar y conectar
MLR8: Apoyos para el debate
Materiales necesarios
Enfriamiento
Conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE
LA LECCIÓN
Narrativa de la lección
Los estudiantes continúan investigando los efectos de las transformaciones. La novedad de esta lección es el plano catesiano. En esta lección, los estudiantes usan coordenadas para describir figuras y sus imágenes bajo transformaciones en el plano catesiano. Las reflexiones sobre los ejes X y Y tienen una estructura muy agradable capturada por coordenadas. Cuando reflejamos un punto como (2, 5) sobre el eje ��, la distancia desde el eje �� sigue siendo la misma, pero en lugar de estar 5 unidades por encima del eje ��, la imagen se encuentra 5 unidades por debajo del eje ��. Esto significa que la imagen de (2, 5) cuando se refleja sobre el eje �� es (2, -5). Del mismo modo, cuando se refleja sobre el eje ��, (2, 5) va a (-2, 5), el punto 2 unsu a la izquierda del eje ��
Usar las coordenadas para ayudar a entender las transformaciones implica MP7 (descubrir los patrones que obedecen las coordenadas cuando se aplican transformaciones).
RESUMEN
DE LA LECCIÓN
Componente de la lección
Estructura Tiempo
Descripción breve
Calentamiento Independiente 5 min Los estudiantes determinan qué secuencia de traslaciones puede usarse para mapear una figura sobre otra en un plano catesiano.
Los estudiantes reflejan pares ordenados en el plano catesiano sobre los ejes �� y ��
Actividad de exploración Independiente 15 min
Actividad de exploración Independiente 15 min
Una aplicación digital interactivaLos estudiantes desarrollan conjeturas sobre cómo cambian los puntos de las coordenadas después de aplicar diferentes reflexiones. está disponible para permitir a los estudiantes explorar reflexiones en un plano catesiano utilizando la tecnología.
Los estudiantes exploran rotaciones de un segmento de línea en diferentes direcciones alrededor de varios centros de rotación en un plano catesiano.
Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar rotaciones en un cplano catesiano usando la tecnología.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las secuencias de transformaciones.
Síntesis Todo el grupo 5 min
Los estudiantes explican las transformaciones rígidas en el plano catesiano, incluyendo cómo cada transformación puede impactar los pares ordenados de los puntos correspondientes.
Enfriamiento Independiente 5 min Dado un plano catesiano con tres figuras, los estudiantes identifican las imágenes creadas usando una rotación y una reflexión.
Práctica Independiente 5 min El componente de práctica independiente incluye 1 en la lección y 2 problemas de repaso en espiral.
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | TRASLACIÓN DE COORDENADAS (5 minutos)
El propósito de este calentamiento es recordar a los estudiantes cómo funciona el plano catesiano y darles la oportunidad de ver cómo se puede describir una traslación cuando la figura se representa en el plano catesiano.
Hay muchas maneras de expresar una traslación porque una traslación está determinada por dos puntos �� y �� una vez que sabemos que �� está trasladado a ��. Hay muchos pares de puntos que expresan la misma traslación. Esto es diferente de las reflexiones que están determinadas por una línea única y las rotaciones que tienen un centro único y un ángulo de rotación específico.
INTRODUCCIÓN
Pregunte a los estudiantes cómo describen una traducción. ¿Hay más de una forma de describir la misma traducción? Después de que hayan reflexionado durante un minuto, concédales 2 minutos de trabajo en silencio, seguidos de un debate en clase.
Apoyo para estudiantes
con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen del gráfico a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Seleccione todas las traducciones que llevan Triángulo �� a Triángulo ��. Puede haber más de una respuesta correcta.
1. Traduzca (-3, 0) a (1, 2)
2. Traduzca (2, 1) a (-2, -1).
3. Traduzca (-4, -3) a (0, -1)
4. Traduzca (1, 2) a (2, 1) POSIBLES RESPUESTAS
Ambas son correctas: (-3, 0) a (1, 2) y (-4, -3) a (0, -1)
CONCEPTOS ERRÓNEOS PREVISTOS
Los estudiantes pueden pensar que necesitan más información para determinarine la traducción. Recuérdeles que especificar un punto le indica la distancia y la dirección a la que se mueven todos los demás puntos en una traslación.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Recuerde a los estudiantes que una vez que nombra un punto inicial y un punto final, eso determina completamente una traslación porque especifica una distancia y una dirección para todos los puntos del plano. Recurrir a sus experiencias con el papel de calco puede ayudar. En este caso, podríamos describir esa distancia y dirección diciendo «todos los puntos van hacia arriba 2 unidades y hacia la derecha 4 unidades». Dibuje la flecha para las dos descripciones correctas y una tercera que no esté en la lista, así: Señala que cada flecha, de hecho, sube 2 y 4 a la derecha.
ACTIVIDAD DE EXPLORACIÓN | PUNTOS REFLEJADOS EN EL PLANO CARTESIANO
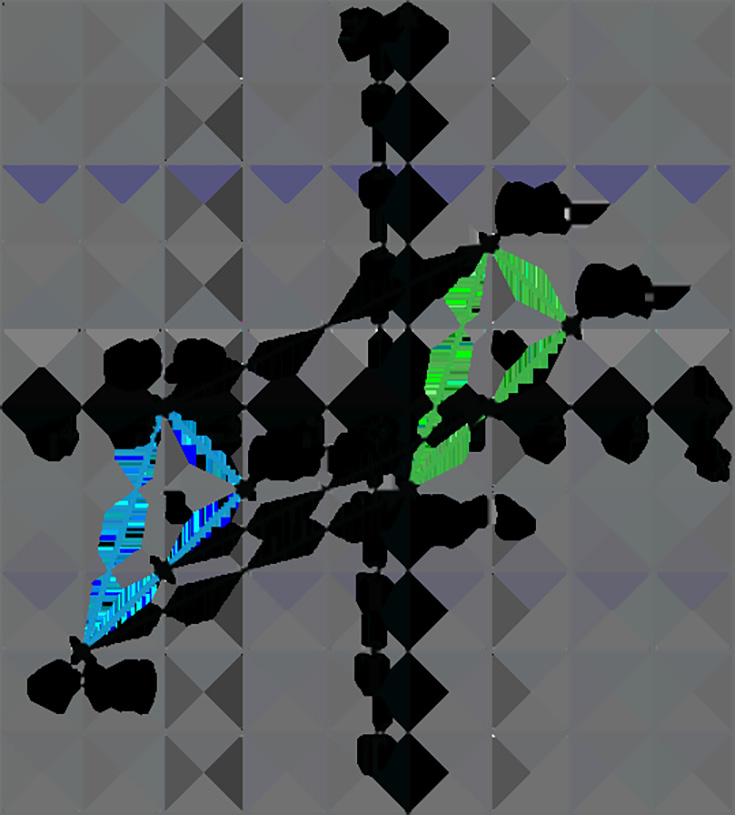
(15 minutos)
Rutinas didácticas
MLR7: Comparar y conectar
Mientras que el calentamiento se centra en el estudio de las traslaciones utilizando una cuadrícula de coordenadas, el objetivo de esta actividad es que los estudiantes trabajen a través de múltiples ejemplos de puntos específicos reflejados sobre el eje �� y luego generalicen para describir dónde una reflexión toma cualquier punto (MP8). También consideran las reflexiones sobre el eje �� con un poco menos de andamiaje. En la siguiente actividad, los estudiantes estudiarán rotaciones de 1 grado en una cuadrícula de coordenadas, completando esta investigación preliminar sobre cómo funcionan las transformaciones en la cuadrícula de coordenadas.
Preste atención a los estudiantes que identifiquen pronto el patrón de cómo las reflexiones sobre el eje �� o el eje �� influyen en las coordenadas de un punto. Asegúrese de que se centran en explicar por qué el patrón se mantiene, ya que el objetivo aquí es comprender mejor las reflexiones utilizando la cuadrícula de coordenadas. La regla es menos importante que entender cómo es esencial ver la cuadrícula de coordenadas y enunciar la regla.
Diga a los estudiantes que dispondrán de (5 minutos) de tiempo de reflexión en silencio para trabajar en la actividad y dígales que hagan una pausa después de la segunda pregunta.
Seleccione 2-3 estudiantes para que compartan sus estrategias para las primeras 2 preguntas. Puede empezar con estudiantes que midan las distancias de los puntos desde el eje �� o que cuenten la cantidad de cuadrados que hay entre un punto y el eje �� y luego cuenten la misma cantidad para encontrar el punto reflejado. Estas estrategias funcionan, pero pasan por alto la estructura del plano catesiano. Para ayudar a señalar el papel del plano catesiano, seleccione a un estudiante que haya observado el patrón de cambio de signo de la coordenada �� al reflejar sobre el eje ��
Después de esta discusión inicial, dé a 2-3 minutos de tiempo de trabajo tranquilo para las preguntas restantes, en las que se les pide que generalicen cómo reflejar un punto sobre el eje ��
Las clases que utilizan la versión digital tienen una aplicación para representar gráficamente y etiquetar los puntos.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR7 Comparar y conectar. Utilice esta rutina cuando los estudiantes presenten sus estrategias para reflejar puntos utilizando el eje �� como línea de reflexión antes de continuar. Pida a los estudiantes que consideren en qué coinciden y en qué difieren las estrategias. Llame la atención de los estudiantes sobre las distintas formas en que razonaron para hallar las coordenadas reflejadas. Estos intercambios refuerzan el uso del lenguaje matemático de los estudiantes y el razonamiento de las reflexiones a lo largo del eje �� y del eje ��.
Principio(s) de diseño: Maximizar la metaconciencia
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes con discapacidades
Habilidades motoras finas:
• Tutores compañeros. Junte a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que luchan con las habilidades motoras finas dictar transformaciones según sea necesario.
• Tecnología de asistencia. Proporcione acceso a la versión digital de esta actividad.
Funcionamiento ejecutivo: Eliminar las barreras. Divida esta actividad en partes más manejables (por ejemplo, presentando una pregunta a la vez), lo que ayudará a los estudiantes que se benefician del apoyo con habilidades de organización en la resolución de problemas.
1. Aquí hay una lista de puntos. �� = (0.5, 4) �� = (-4, 5) �� = (7, -2) �� = (6, 0) �� = (0, -3)
En el plano catesiano:
A. Traza cada punto y etiquete cada uno con sus coordenadas.
B. Utilizando el eje �� como línea de reflexión, traza la imagen de cada punto.
C. Etiqueta la imagen de cada punto con sus coordenadas.
D. Incluye una etiqueta utilizando una letra. Por ejemplo, la imagen de punto �� debería etiquetarse ��′.
2. Si el punto (13, 10) se reflejara utilizando el eje �� como línea de reflexión, ¿cuáles serían las coordenadas de la imagen? ¿Y (13, -20)? (13, 570)? Explica cómo lo sabes.
3. El punto �� tiene coordenadas (3, 2)
A. Sin graficar, predice las coordenadas de la imagen del punto �� si el punto �� fuera reflejado usando el eje �� como línea de reflexión.
B. Compruebe su respuesta encontrando la imagen de �� en el gráfico.
C. Etiqueta la imagen del punto �� como ��′
D. ¿Cuáles son las coordenadas de ��′?
4. Supón que refleja un punto utilizando eleje �� como línea de reflexión. ¿Cómo describirías su imagen?
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS PREVISTOS
Grado 8 . Matemáticas . Unidad 1
1. La imagen muestra los puntos ��, ��, ��, ��, �� y también sus reflexiones sobre el eje ��: ��′ = (0.5, -4), ��′ = (-4, -5), ��′ = (7, 2), ��′ = (6, 0), ��′ = (0, 3).
2. Utilizando el eje �� como línea de reflexión, la reflexión de (13, 10) es (13, -10), la reflexión de (13, -20) es (13, 20) y la reflexión de (13, 570) es (13, -570). Utilizar el eje �� como línea de reflexión no desplaza horizontalmente los puntos, pero sí desplaza verticalmente los puntos que no están en el eje ��. En coordenadas, la coordenada �� del punto permanece igual mientras que la coordenada �� cambia de signo.
3. Usando el eje �� como línea de reflexión no mueve puntos verticalmente, pero sí mueve puntos que no están en el eje �� horizontalmente. En coordenadas, la coordenada �� del punto permanece igual mientras que la coordenada �� cambia de signo. El punto �� tiene coordenadas (3, 2). Cuando lo reflejo sobre el eje �� pasará a (-3, 2): la coordenada �� cambia de signo, pero la coordenada �� permanece igual.
4. El punto tendrá la misma coordenada ��, pero la coordenada �� cambiará de signo. La distancia desde el eje �� no cambia y la coordenada �� no cambia.
Si algún estudiante tiene dificultades para empezar porque no sabe dónde trazar los puntos, remítale a la actividad de calentamiento y practique con él el trazado de algunos puntos de ejemplo.
Para facilitar la discusión, muestre una cuadrícula de coordenadas en blanco. Preguntas para la discusión:
• «Cuando tienes un punto y un eje de reflexión, ¿cómo encuentras la reflexión del punto?».
• «¿Cómo puedes usar las coordenadas de un punto para ayudar a encontrar la reflexión?».
• «¿Algunos puntos son más fáciles de reflejar que otros? ¿Por qué?».
• «¿Qué patrones has visto en estas reflexiones de puntos en la cuadrícula de coordenadas?».
El objetivo de la actividad no es crear una regla que los estudiantes memoricen. El objetivo al es que los estudiantes se den cuenta del patrón de reflexión sobre un eje que cambia el signo de la coordenada (sin tener que graficar). La cuadrícula de coordenadas puede ser a veces una herramienta poderosa para comprender y expresar la estructura, y esto es cierto para las reflexiones sobre los ejes X y Y
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
ACTIVIDAD DE EXPLORACIÓN | TRANSFORMACIONES DE UN SEGMENTO
(15 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
Esta actividad concluye viendo cómo se comportan las diferentes transformaciones básicas (traslaciones, rotaciones y reflexiones) cuando se aplican a puntos en una cuadrícula de coordenadas. En general, es difícil utilizar coordenadas para describir rotaciones. Pero cuando el centro de la rotación es (0, 0) y la rotación es 90 grados (en el sentido de las agujas del reloj o en sentido contrario), hay una descripción directa de las rotaciones utilizando coordenadas.
A diferencia de las traslaciones y reflexiones sobre el eje �� o ��, es más difícil visualizar dónde una rotación de 90 grados lleva a un punto. El papel de calco es una herramienta útil, al igual que una ficha.
INTRODUCCIÓN
Demuestre cómo utilizar el papel de calco para realizar una rotación de 90 grados. Es útil poner un pequeño conjunto de ejes perpendiculares ( �� + signo) en el trozo de papel de calco y colocar su punto de intersección en el centro de rotación. Uno de los pequeños ejes puede alinearse con el segmento que se está rotando y entonces la rotación se completa cuando el otro pequeño eje se alinea con el segmento. Un método alternativo para realizar rotaciones sería con la esquina de una ficha, que forma parte del Conjunto de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Los estudiantes que utilicen la versión digital verán cómo el ordenador rota el segmento a medida que manipulan los controles deslizantes.
Apoyo para estudiantes con discapacidad
Habilidades motoras finas: Tutores compañeros. Junte a los estudiantes con sus tutores compañeros previamente identificados y permitir que los estudiantes que tienen dificultades con la motricidad fina dicten las rotaciones según sea necesario.
Aplica cada una de las siguientes transformaciones al segmento ����.
1. Gira el segmento ���� 90 grados en sentido antihorario alrededor del centro ��. Etiqueta la imagen de �� como ��. ¿Cuáles son las coordenadas de ��?
2. Gira el segmento ���� 90 grados en sentido antihorario alrededor del centro ��. Etiqueta la imagen de �� como ��. ¿Cuáles son las coordenadas de ��?
3. Gira el segmento ���� 90 grados en el sentido de las agujas del reloj alrededor de (0, 0). Etiqueta la imagen de �� como �� y la imagen de �� como ��. ¿Cuáles son las coordenadas de �� y ��?
4. Compare las dos rotaciones de 90 grados en sentido antihorario del segmento ����. ¿Qué es lo mismo en las imágenes de estas rotaciones? ¿Qué es diferente?
Grado 8 . Matemáticas . Unidad 1
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
1. �� = (3, -2)
2. �� = (1, 7)
3. �� = (3, 0), �� = (2, -4)
4. Las respuestas varían. Respuesta de ejemplo. Las dos rotaciones en sentido antihorario de ���� están en lugares diferentes. Los puntos �� y �� se mueven diferentes distancias con las diferentes rotaciones. Una rotación se puede mapear a la otra mediante una traslación.
Pida a los estudiantes que describan o demuestren cómo encontraron las rotaciones del segmento ����. Asegúrese de destacar estas estrategias:
• Utilizar papel de calco para representar una rotación a través de un ángulo de 90 grados.
• Utilizar una ficha: Coloque la esquina de la tarjeta en el centro de rotación, alinea un lado con el punto que se va a rotar y encuentra la ubicación del punto rotado a lo largo de un lado adyacente de la tarjeta. (La distancia de cada punto a la esquina debe ser igual).
• Utilizar la estructura de la cuadrícula de coordenadas: Todas las líneas de la cuadrícula son perpendiculares, por lo que una rotación de 90 grados con centro en la intersección de dos líneas de la cuadrícula llevará las líneas horizontales de la cuadrícula a las líneas verticales de la cuadrícula y las líneas verticales de la cuadrícula a las líneas horizontales de la cuadrícula.
La tercera estrategia solo debe resaltarse si los estudiantes se dan cuenta o la utilizan para ejecutar la rotación, con o sin papel de calco. Este último método es el más preciso porque no requiere ninguna tecnología para ejecutarse, sino que se basa en la estructura de la cuadrícula de coordenadas.
Si algunos estudiantes observan que las tres rotaciones del segmento ���� son todas paralelas, esto también debe resaltarse.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyo para el debate. Para ayudar a los estudiantes a explicar las similitudes y diferencias de las rotaciones de segmentos de la última pregunta, proporcione marcos de oraciones para que los estudiantes los usen cuando comparen segmentos, puntos y rotaciones. Por ejemplo, « es similar a porque .» o « es diferente a porque ». Revoque las ideas de los estudiantes utilizando el lenguaje matemático según sea necesario.
Principio(s) de diseño: Apoyar la creación de sentido; optimizar la salida para (comparación)
¿Estás preparado para más?
Supongamos que ���� y ���� son segmentos de línea de la misma longitud. Describe una secuencia de transformaciones que traslade ���� a ����
«¿Estás listo para más?»: Respuesta del estudiante
Las respuestas varían. Por ejemplo, traslada ���� de modo que �� caiga sobre �� y luego gira ���� con centro �� hasta que (la imagen de) �� caiga sobre ��
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Llegados a este punto, los estudiantes deberían empezar a sentirse seguros aplicando traslaciones, reflexiones sobre cualquiera de los ejes y rotaciones de 90 grados en el sentido de las agujas del reloj o en sentido contrario a las agujas del reloj a un punto o forma en el plano catesiano.
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Cuando los estudiantes estén trabajando en el plano catesiano al hacer transformaciones, pregunte:
• «¿Cuáles son algunas de las ventajas de conocer las coordenadas de los puntos al hacer transformaciones?».
• «¿Qué cambios observamos al reflejar puntos sobre el eje ��? ¿Y sobre el eje ��?».
• «¿Cómo se realiza una rotación de 90 grados en el sentido de las agujas del reloj de un punto con centro (0, 0)?».
Si el tiempo lo permite, pida a los estudiantes que apliquen algunas transformaciones a un punto. Por ejemplo, ¿dónde va (1, 2) cuando...
• se refleja sobre el eje ��? (1, -2)
• reflejado sobre el eje ��? (-1, 2)
• se gira 90 grados en el sentido de las agujas del reloj con centro (0, 0)? (2, -1)
ENFRIAMIENTO | ROTACIÓN O REFLEXIÓN
(5 minutos)
ENUNCIADO DE TAREA PARA EL ESTUDIANTE Uno de los triángulos representados es una rotación del triángulo ������ y uno de ellos es una reflexión.
POSIBLES RESPUESTAS
1. Identifica el centro de rotación y etiqueta la imagen rotada ������
2. Identifica la línea de reflexión y etiqueta la imagen reflejada ������.
1. El centro de la rotación lleva △������ a △������ es (0, 0), y la rotación es 90 grados en una dirección contraria a las agujas del reloj.
2. Una reflexión sobre el eje �� lleva △������ a △������
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
A. Aquí hay algunos puntos.
¿Cuáles son las coordenadas de ��, �� y �� después de una traslación a la derecha por 4 unidades y arriba 1 unidad? Traza estos puntos en la cuadrícula y etiquétalos ��′, ��′ y ��′
B. Aquí tienes algunos puntos.
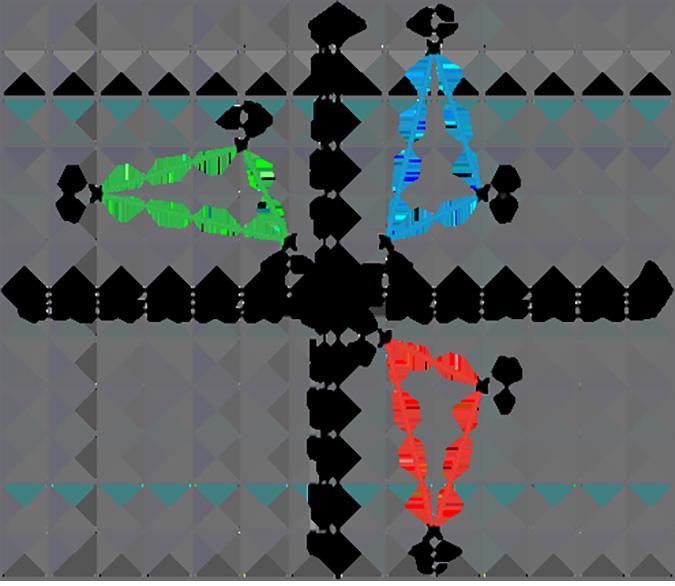
¿Cuáles son las coordenadas de ��, �� y �� tras una reflexión sobre el eje ��? Traza estos puntos en la cuadrícula y etiquételos ��′, ��′ y ��′
A. Aquí tienes algunos puntos.
Grado 8 . Matemáticas . Unidad 1
¿Cuáles son las coordenadas de ��, �� y �� después de una rotación alrededor de (0, 0) en 90 grados en el sentido de las agujas del reloj? Traza estos puntos en la cuadrícula y etiquétalos ��′, ��′ y ��′
Soluciones posibles
A. ��′ = (-2, 6), ��′ = (7, 3), ��′ = (4, 0)
C. ��′ = (3, 1), ��′ = (0, 4), ��′ = (-2, -3)
B. ��′ = (3, 3), ��′ = (-5, 0), ��′ = (-2, -2)
PROBLEMA 2
Grado 8, unidad 1, lección 4
Describe una secuencia de transformaciones que lleve el trapecio �� al trapecio ��
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta: Traslada �� hacia arriba, luego gíralo 60 grados en sentido contrario a las agujas del reloj (con centro de rotación el vértice inferior) y luego trasládalo hacia la izquierda.
PROBLEMA 3
Grado 8, unidad 1, lección 3
Refleja el polígono �� usando la recta ℓ
Reflexiones:
Learning Inc. - Todos los derechos reservados
Soluciones posibles
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas son llevadas a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos son llevados a ángulos de la misma medida.
8.G.3 Describir el efecto de dilataciones, traslaciones, rotaciones y reflexiones en figuras bidimensionales usando coordenadas.
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
Estándares ELD de California
I.B.5 I.A.3
LECCIÓN 6
DESCRIPCIÓN DE LAS TRANSFORMACIONES
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predecir lo que podría ocurrir,
dan sentido a los problemas y perseverar en resolverlos descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Vamos a transformar algunos polígonos en el plano de coordenadas.
META(S) DE APRENDIZAJE
• Puedo aplicar transformaciones a un polígono en una cuadrícula si conozco las coordenadas de sus vértices.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Crear un dibujo en una cuadrícula de coordenadas de un objeto transformado utilizando descripciones verbales.
• Identificar qué información se necesita para transformar un polígono. Hacer preguntas para obtener esa información.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Pensar, girar y compartir
MLR4: Brecha de información
Preparación necesaria
Imprima 1 copia de la plantilla maestra para cada 2 estudiantes. Recórtalas con anticipación.
De los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), el papel cuadriculado y el papel de calco son especialmente útiles.
Materiales necesarios
Lápiz negro para la actividad 6.2
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Láminas preimpresas, recortadas de las copias del lápiz negro.
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE
LA LECCIÓN
Narrativa de la lección
Antes de esta lección, los estudiantes han estudiado y clasificado diferentes tipos de transformaciones (traslaciones, rotaciones, reflexiones). Han practicado la aplicación de transformaciones individuales y secuencias de transformaciones a figuras tanto dentro como fuera de una cuadrícula de coordenadas. En esta lección, se centran en comunicar con precisión la información necesaria para aplicar una secuencia de transformaciones a un polígono en la cuadrícula de coordenadas. Deben pensar detenidamente qué información necesitan (MP1) y solicitar esta información a su compañero de forma clara y precisa. También explican por qué necesitan cada dato (MP3). La cuadrícula de coordenadas desempeña un papel fundamental en este trabajo, ya que permite a los estudiantes comunicar con precisión la ubicación de los polígonos y cómo se transforman.
LECCIÓN DE UN VISTAZO
Componente de lección Estructura Tiempo
Calentamiento En parejas 5 min
Actividad de exploración En parejas 30 min
Síntesis Grupo completo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Descripción breve
Los estudiantes utilizan la preimagen y la imagen de una figura rotada para determinar el centro de rotación.
Los estudiantes trabajan con un compañero para aplicar una secuencia de transformaciones en una figura dada en un plano de coordenadas.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda mediante la comparación de transformaciones individuales con secuencias de transformaciones que describen el mismo movimiento.
Los estudiantes identifican qué transformación rígida prefieren y explican su razonamiento a sus compañeros antes de compartir sus respuestas con la clase.
Los estudiantes explican qué información se necesita para describir una traslación y a reflexión sin una imagen o preimagen dada.
El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.
California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | ENCONTRAR UN CENTRO DE ROTACIÓN
(5 minutos)
Rutinas didácticas
Pensar, girar y compartir
A veces es fácil olvidar comunicar toda la información vital sobre una transformación. En este caso, el centro de una rotación se deja sin especificar. Los estudiantes no necesitan desarrollar un método general para encontrar el centro de rotación, dado un polígono y su imagen rotada. Identifican el centro en una situación y esto puede hacerse mediante intuición geométrica y un poco de ensayo y error.
INTRODUCCIÓN
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
André realiza una rotación de 90 grados en sentido antihorario del polígono �� y obtiene el polígono ��′, pero no dice cuál es el centro de la rotación. ¿Puedes encontrar el centro?
Organice a los estudiantes en grupos de 2 y facilite el acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Diga a los estudiantes que tienen un diagrama de una figura y su imagen rotada y que necesitan identificar el centro de rotación. Concédales 2 minutos de tiempo de trabajo en silencio y la oportunidad de compartir con un compañero, seguido de un debate con toda la clase. ENUNCIADO DE TAREA
La rotación lleva el lado horizontal de �� al lado vertical de ��′ y el centro de rotación es la intersección de las líneas de la cuadrícula que contienen estos dos lados.
Grado 8 . Matemáticas . Unidad 1
Los estudiantes pueden tener problemas para empezar. Sugiérales que tracen �� en papel de calco e intenten girarlo 90°. ¿Cómo deben girarlo para que caiga sobre ��′? ¿Dónde está el centro del «giro»?
CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
Haga hincapié en que es importante comunicarse con claridad. Cuando realizamos una transformación, debemos proporcionar la información necesaria para que los demás entiendan lo que hemos hecho. Para una rotación, esto significa comunicar:
• el centro de la rotación
• la dirección de la rotación (sentido horario o antihorario)
• el ángulo de rotación
La cuadrícula proporciona una estructura adicional que ayuda a identificar estas tres partes de la rotación. Invite a los estudiantes a compartir cómo identificaron el centro de rotación. Los métodos pueden incluir:
• experimentar con papel de calco
• entender que la rotación no cambia la distancia entre el centro de rotación y cada vértice, por lo que el centro debe estar a la misma distancia de cada vértice y su imagen
ACTIVIDAD DE EXPLORACIÓN | BRECHA DE INFORMACIÓN: INFORMACIÓN DE TRANSFORMACIÓN
(30 minutos)
Rutinas didácticas
MLR4: Brecha de información
Esta actividad de brecha de información da a los estudiantes la oportunidad de determinar y solicitar la información necesaria para realizar una transformación en el plano de coordenadas. Un par de tarjetas de muestra tiene el siguiente aspecto:
8 . Matemáticas . Unidad 1
Los estudiantes probablemente necesiten varias rondas para determinar la información que necesitan.
• Necesitan saber qué transformaciones se aplicaron (es decir, traslación, rotación o reflexión).
• Necesitan determinar el orden en que se aplicaron las transformaciones.
• Necesitan recordar qué información se necesita para describir una traslación, rotación o reflexión.
Controle a los estudiantes que determinan o recuerdan con éxito cada una de estas tres piezas importantes de información, así como a los estudiantes que han resuelto el problema parcialmente, pero no por completo. Los estudiantes pueden no darse cuenta de que el orden en que se aplican las transformaciones es importante y esto debe abordarse en la síntesis.
La estructura de la brecha de información requiere que los estudiantes den sentido a los problemas determinando qué información es necesaria y luego pedir la información que necesitan para resolverlo. Esto puede requerir varias rondas de discusión si sus primeras peticiones no aportan la información que necesitan (MP1). También les permite refinar el lenguaje que utilizan y hacer preguntas cada vez más precisas hasta que obtienen la información que necesitan (MP6).
INSTRUCCIÓN
Diga a los estudiantes que continuarán describiendo transformaciones utilizando coordenadas. Explique la estructura de la brecha de información y considere la posibilidad de demostrar el protocolo si los estudiantes no están familiarizados con él.
Organice a los estudiantes en grupos de 2. Proporcione acceso a papel cuadriculado. En cada grupo, distribuya una tarjeta de problema a un estudiante y una tarjeta de datos al otro. Después de revisar su trabajo en el primer problema, dele las tarjetas para un segundo problema e indíqueles que cambien los papeles.
Apoyo para estudiantes que aprenden el idioma inglés
Conversación: Esta actividad utiliza la Brecha de Información MLR4 para dar a los estudiantes un propósito para discutir la información necesaria para resolver problemas que implican la descripción de transformaciones.
Principio(s) de Diseño: Cultivar la conversación
Apoyo para estudiantes con discapacidades
Procesamiento Conceptual: Eliminar barreras. Muestre los pasos para la actividad o el juego, en el que un grupo de estudiantes y el personal juegan una ronda de ejemplo mientras el resto de la clase observa.
Tu maestro te dará una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu compañero.
Si tu maestro te da la tarjeta de problema:
1. Lee en silencio tu tarjeta y piensa qué información necesitas para responder a la pregunta.
2. Pide a tu compañero la información específica que necesitas.
3. Explica a tu compañero cómo estás utilizando la información para resolver el problema.
4. Resuelve el problema y explica tu razonamiento a tu compañero.
Si tu maestro te da la tarjeta de datos:
1. Lee en silencio la información de tu tarjeta.
2. Pregunta a tu compañero «¿qué información específica necesitas?» y espera a que tu compañero te pida información. Solo da la información que está en tu tarjeta. (¡No descubras nada para tu compañero!).
3. Antes de dar la información a tu compañero, pregúntale «¿por qué necesitas esa información?».
4. Después de que tu compañero resuelva el problema, pídele que explique su razonamiento y escucha su explicación.
Haz una pausa aquí para que tu maestro pueda revisar tu trabajo. Pide a tu maestro un nuevo juego de tarjetas y repite la actividad, intercambiando los papeles con tu compañero.
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS PREVISTOS
Grado 8 . Matemáticas . Unidad 1
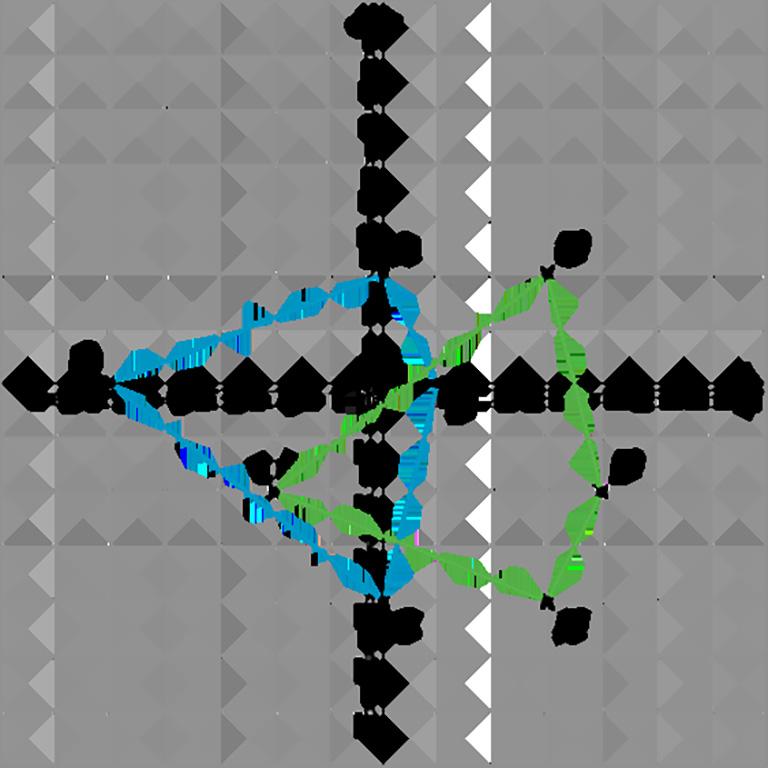
Los estudiantes pueden tener dificultades para pedir a su compañero toda la información que necesitan o pueden hacer una pregunta que no sea lo suficientemente precisa, como «¿cuáles son las transformaciones?». Pregunte a estos estudiantes con qué tipos de transformaciones han trabajado. ¿Qué información se necesita para realizar una traslación? ¿Y para una rotación o una reflexión? Anímeles a que averigüen qué transformaciones necesitan realizar (¿hay una translación?, ¿hay una rotación?) y, a continuación, averigüen la información que necesitan para cada transformación.
DE LA ACTIVIDAD
SÍNTESIS
Una vez que los estudiantes hayan terminado su trabajo, comparta las respuestas correctas y pida a los estudiantes que discutan el proceso de resolución de los problemas. Algunas preguntas orientadoras:
• «¿Cómo ayudó el uso de coordenadas al hablar del problema?».
• «¿Fue importante el orden en que se aplicaron las transformaciones? ¿Por qué?».
• "Si este mismo problema fuera una imagen en una cuadrícula sin coordenadas, ¿cómo hablarías de los puntos?».
Resalte para los estudiantes que una ventaja del plano de coordenadas es que nos permite comunicar información sobre transformaciones con precisión. Esto es lo que se necesita para cada tipo de transformación (considere mostrar un ejemplo de cada una mientras repasa las diferentes transformaciones):
• Para una traslación, la distancia de las componentes vertical y horizontal
• Para una rotación, el centro de rotación, la dirección de rotación y el ángulo de rotación
• Para una reflexión, la línea de reflexión
¿Estás listo para más?
A veces dos transformaciones, una realizada después de la otra, tienen una bonita descripción como una sola transformación. Por ejemplo, en lugar de trasladar 2 unidades hacia arriba seguido de trasladar 3 unidades hacia arriba, podríamos simplemente trasladar 5 unidades hacia arriba. En lugar de rotar 20 grados en el sentido contrario a las agujas del reloj alrededor del origen, seguido de rotar 80 grados en el sentido de las agujas del reloj alrededor del origen, podríamos simplemente rotar 60 grados en el sentido de las agujas del reloj alrededor del origen.
¿Puede encontrar una descripción sencilla de la reflexión a través del eje �� seguida de la reflexión a través del eje ��?
«¿Estás preparado para más?». Respuesta del estudiante
Reflexionar sobre el eje �� seguido de reflexionar sobre el eje �� es lo mismo que girar 180 grados (en cualquier dirección) alrededor del origen.
Learning Inc. - Todos los derechos reservados
8 . Matemáticas . Unidad 1
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Pida a los estudiantes que elijan cuál de las tres transformaciones que han estudiado hasta ahora (traslación, reflexión, rotación) es su favorita y dé 2-3 minutos para que los estudiantes escriban unas frases explicando por qué. Pida a los estudiantes que primero compartan sus explicaciones con un compañero y luego invítelos a compartir su favorita con la clase.
ENFRIAMIENTO | DESCRIBIR UNA SECUENCIA DE TRANSFORMACIONES
(5 minutos)
Los estudiantes describen qué información se requiere para realizar una traslación y qué información se requiere para realizar una reflexión. También necesitan pensar en el orden en el que se aplican las dos transformaciones ya que acaban de ver que cambiar el orden puede afectar al resultado.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Jada aplica dos transformaciones a un polígono en el plano de coordenadas. Una de las transformaciones es una translación y la otra es una reflexión. ¿Qué información necesita proporcionar Jada para comunicar las transformaciones que ha utilizado?
Para la traslación, Jada necesita proporcionar la distancia y dirección del desplazamiento vertical y la distancia y dirección del desplazamiento horizontal. Para la reflexión, Jada debe indicar la línea de reflexión. También es importante que Jada comunique el orden en que se aplican las transformaciones.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Aquí está el trapezoide �� en el plano cartesiano:
A. Dibuja el polígono ��, imagen de ��, utilizando el eje �� como línea de reflexión.
B. Dibuja el polígono ��, imagen de ��, utilizando el eje �� como línea de reflexión.
C. Dibuja el polígono ��, imagen de ��, utilizando el eje �� como línea de reflexión.
Grado 8 . Matemáticas . Unidad 1
Soluciones posibles
El polígono �� es el mismo que ��: reflejar un polígono dos veces sobre el eje �� lo devuelve a su posición original.
PROBLEMA 2
El punto (–4, 1) se gira 180 grados en sentido antihorario usando el centro (-3, 0). ¿Cuáles son las coordenadas de la imagen?
A. (–5, –2)
B. (–4, –1)
C. (–2, –1)
D. (4, –1)
Soluciones posibles
C
PROBLEMA 3
Describe una secuencia de transformaciones para la cual el triángulo �� es la imagen del triángulo ��
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta: �� es la imagen de �� bajo una reflexión sobre el eje ��, luego una traslación 2 unidades a la derecha y 2 unidades hacia arriba.
Math Nation California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 4
Grado 8, unidad 1, lección 2
Aquí está el cuadrilátero ��������
Dibuja la imagen del cuadrilátero �������� después de cada transformación.
A. La traslación que lleva �� a ��
B. La reflexión sobre el segmento ����
C. La rotación sobre el punto �� por el ángulo ������, en sentido contrario a las agujas del reloj.
Soluciones posibles
A. Imagen del trapecio desplazada hacia la izquierda de forma que �� se alinee con ��
B. Imagen del trapecio compartiendo segmento ���� con ��������
C. Imagen del trapezoide girada de modo que el lado correspondiente a ���� forme ahora parte del segmento ����
Reflexiones:
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas se toman a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos se toman como ángulos de la misma medida. Enfoque SMPs
MP5 Usa herramientas apropiadas estratégicamente.
MP7 Busca y usa estructuras.
Estándares ELD de California
I.B.5
II.B.5
I.A.1
LECCIÓN 7
SIN FLEXIONES NI ESTIRAMIENTOS
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
dar sentido al mundo,
META(S)
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
utilizan las herramientas adecuadas de forma estratégica descubren la figura y el espacio.
DE APRENDIZAJE
• Comparemos medidas antes y después de traslaciones, rotaciones y reflexiones.
META(S) DE APRENDIZAJE
• Puedo describir los efectos de una transformación rígida sobre las longitudes y ángulos en un polígono.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comprender que la frase «transformación rígida» se refiere a una transformación en la que todos los pares de medidas de «distancias correspondientes» y «ángulos correspondientes» en la figura y su imagen son iguales.
• Dibujar y etiquetar un diagrama de la imagen de un polígono bajo una transformación rígida, incluyendo el cálculo de las longitudes de los lados y las medidas de los ángulos.
• Identificar (oralmente y por escrito) una secuencia de transformaciones rígidas usando el dibujo de una figura y su imagen.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR8: Apoyos para el debate
Anticipar, supervisar, seleccionar, secuenciar, conectar
MLR2: Recopilar y mostrar
Materiales necesarios
Enfriamiento
Conjuntos de herramientas de geometría (papel de calco, papel milimetrado, lápices de colores, tijeras y una ficha)
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE LA
LECCIÓN
Narrativa de la lección
En esta lección, los estudiantes comienzan a ver que las traslaciones, rotaciones y reflexiones preservan longitudes y medidas de ángulos, y por primera vez las llaman transformaciones rígidas. En lecciones anteriores, los estudiantes hablaron de los puntos correspondientes bajo una transformación. Ahora hablarán de lados correspondientes y ángulos correspondientes de un polígono y su imagen.
A medida que los estudiantes experimentan con la medición de lados y ángulos correspondientes en un polígono y su imagen, necesitarán usar la estructura de la cuadrícula (MP7) así como la tecnología apropiada, incluyendo transportadores, reglas y papel de calco.
RESUMEN DE LA LECCIÓN
Componente de la lección
Estructura Tiempo
Calentamiento Independiente 5 min
Actividad de Exploración Independiente 15 min
Actividad de exploración En parejas 10 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Descripción breve
Los estudiantes usan reglas para medir y aproximar las longitudes de segmentos de línea con diferentes niveles de precisión.
Los estudiantes realizan transformaciones en figuras dadas en una cuadrícula usando papel de calco o una ficha. A continuación, los estudiantes determinan las medidas de los ángulos de la figura transformada.
Existen aplicación digital interactiva que permiten a los estudiantes realizar transformaciones en las figuras dadas utilizando la tecnología.
Los estudiantes determinan qué imagen puede crearse mediante una transformación rígida y, a continuación, describen una secuencia de transformaciones rígidas que podrían utilizarse para mapear la preimagen a la imagen.
Existe una aplicación digital interactiva que permite a los estudiantes explorar una secuencia de transformaciones rígidas utilizando la tecnología.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las transformaciones rígidas en términos de longitudes de los lados con conexiones al perímetro.
Los estudiantes formalizan el significado de transformaciones rígidas con un enfoque en las longitudes de los lados correspondientes y las medidas de los ángulos correspondientes.
Los estudiantes identifican los vértices correspondientes de una figura transformada y determinan todas las posibles longitudes de los lados y medidas de los ángulos.
El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | MEDICIÓN DE SEGMENTOS
(5 minutos)
En este calentamiento, los estudiantes miden cuatro segmentos de recta. Debaten los distintos aspectos de la realización y el registro de mediciones precisas. Es importante destacar las marcas fraccionarias y los equivalentes fraccionarios y decimales utilizados mientras los estudiantes explican cómo determinaron la longitud del segmento.
INTRODUCCIÓN
Dé a los estudiantes 2 minutos de tiempo de trabajo tranquilo seguido de un debate en clase.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual:Tiempo de procesamiento. Proporcione las imágenes a los estudiantes que se benefician de un tiempo de procesamiento adicional para que las revisen antes de realizar esta actividad.
Para cada pregunta, la unidad está representada por las marcas grandes con números enteros.
1. Encuentre la longitud de este segmento a la 1 8 más cercana de una unidad.
2. Encuentre la longitud de este segmento a la 0.1 más cercana de una unidad.
3. Estime la longitud de este segmento a la 1 8 más cercana de una unidad.
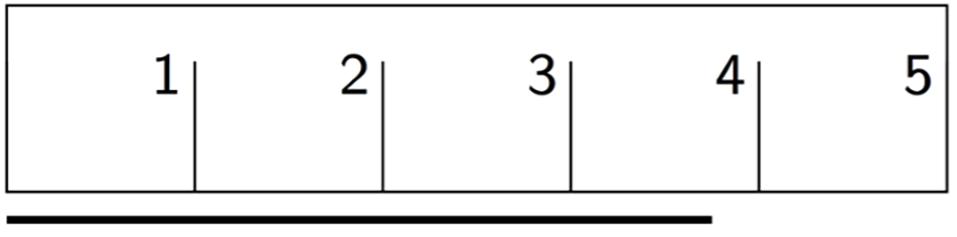
4. Estime la longitud del segmento en la pregunta anterior a la 0.1 más cercana de una unidad.
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS PREVISTOS
1. 4 5 8 unidades
2. 4,7 unidades
3. 3 3 4 �o 3 6 8 unidades�
4. 3.7 unidades (o 3.8 unidades)
Los estudiantes pueden tener dificultades con la regla que no está preparticionada en unidades fraccionarias. Anime a estos estudiantes a utilizar lo que saben sobre octavos y décimos para particionar la regla y estimar su respuesta.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Invite a los estudiantes a compartir sus respuestas y anótelas para que todos las vean. Pregunte a la clase si están de acuerdo o en desacuerdo con cada respuesta. Cuando haya desacuerdo, pida a los estudiantes que discutan las posibles razones de las diferentes medidas. Es probable que los estudiantes tengan respuestas diferentes para su medida del tercer segmento. La regla que se muestra no es tan precisa como requiere la pregunta, ya que no se ha dividido previamente en unidades fraccionarias. Pida a los estudiantes de 2-3 con respuestas diferentes que compartan sus estrategias para medir el tercer segmento. Habrá oportunidades para que los estudiantes utilicen estrategias de medición más adelante en esta lección.
Apoyo para los estudiantes
con discapacidad
Lenguaje expresivo: Eliminar barreras. Proporcione marcos oracionales para que los estudiantes expliquen su razonamiento (por ejemplo: Estoy de acuerdo o en desacuerdo porque ).
ACTIVIDAD DE EXPLORACIÓN | LADOS Y ÁNGULOS
(15 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
El propósito de esta actividad es que los estudiantes vean que las traslaciones, rotaciones y reflexiones preservan las longitudes y medidas de los ángulos. Los estudiantes pueden utilizar papel de calco para dibujar las figuras y hacer observaciones sobre la conservación de las longitudes de los lados y las medidas de los ángulos en las transformaciones. Mientras que la cuadrícula ayuda a medir longitudes de segmentos horizontales y verticales, los estudiantes pueden necesitar más orientación cuando se les pide que midan longitudes diagonales. Es importante que en la presentación demuestre a los estudiantes cómo utilizar el papel de calco o una ficha para marcar las longitudes unitarias utilizando la cuadrícula (MP5).
Dado que los estudiantes están creando su propia herramienta de medición, solo pueden dar una estimación, y debe permitirse cierta flexibilidad en la respuesta. Durante el debate, destaque las diferentes respuestas razonables que los estudiantes encuentren para las longitudes que no sean números enteros.
Mientras los estudiantes trabajan individualmente, monitorice y pídales que expliquen cómo están realizando sus transformaciones y encontrando las longitudes de los lados y las medidas de los ángulos. Durante la discusión, seleccione a los estudiantes que mencionen los lados y ángulos correspondientes, que aprendieron en 7.º grado al hacer copias a escala, para que los compartan. Seleccione también a los estudiantes que hayan calculado correctamente las longitudes de los lados de la figura C utilizando el papel de calco o la ficha.
Diga a los estudiantes: «En esta actividad realizarás transformaciones. Puedes utilizar papel de calco para ayudaros a dibujar las imágenes de las figuras o para comprobar tu trabajo». Señale a los estudiantes la figura �� y dígales: «Cuando se les pida que midan las longitudes de los lados aquí, tendrás que hacer una regla en papel de calco o en el borde en blanco de una ficha de notas». Esto refuerza las estrategias y estimaciones que los estudiantes hicieron en el calentamiento. Dé a los estudiantes 3 minutos de tiempo para pensar en silencio. Asegúrate de reservar al menos (5 minutos) para el debate.
Para las aulas que utilicen la versión digital de la actividad, las aplicaciones digitales contienen herramientas para las tres transformaciones rígidas que necesitan los estudiantes. Tienen que elegir qué herramienta utilizar en cada problema. Advierta a los estudiantes de que un clic rápido es todo lo que necesitan para seleccionar una figura. Si alejan el cursor y la imagen no aparece «resaltada», es probable que hayan seleccionado y deseleccionado la figura.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes con discapacidades
Procesamiento conceptual: Tiempo de procesamiento. Compruebe con cada estudiante, según sea necesario, si ha comprendido cada paso de la actividad.
1. Traslada el polígono �� de modo que el punto �� vaya al punto ��′. En la imagen, escribe la longitud de cada lado, en unidades de cuadrícula, junto al lado.
2. Gira el triángulo �� 90° en el sentido de las agujas del reloj usando �� como centro de rotación. En la imagen, escribe la medida de cada ángulo en su interior.
3. Refleja el pentágono �� a través de la línea ℓ
A. En la imagen, escribe la longitud de cada lado, en unidades de cuadrícula, junto al lado. Puede que necesites hacer tu propia regla con papel de calco o una ficha en blanco.
B. En la imagen, escribe la medida de cada ángulo en el interior.
1. Las longitudes de los lados se miden en unidades donde una unidad es la longitud del lado del cuadrado en la cuadrícula.
2.
3. Las longitudes se miden en unidades de la cuadrícula. Los lados no son enteros los números se han redondeado a la décima más cercana.
Grado 8 . Matemáticas . Unidad 1
CONCEPTOS ERRÓNEOS PREVISTOS
Los estudiantes pueden intentar contar los cuadrados de la cuadrícula en las longitudes de los lados diagonales. Recuérdeles que midan estas longitudes con su papel de calco o ficha de notas. Los estudiantes también pueden tener dificultades para estimar las longitudes de los lados diagonales en su ficha o papel de calco. Recuerde a los estudiantes cómo estimaron las longitudes para las preguntas del calentamiento en las que la regla no estaba marcada.
ACTIVIDAD SÍNTESIS
Pida a los estudiantes seleccionados que compartan cómo realizaron la transformación dada para cada pregunta. Después de cada explicación, pregunte a la clase si están de acuerdo o en desacuerdo. Presente a los estudiantes la idea de lados correspondientes y ángulos correspondientes. Pida a los estudiantes que identifiquen los ángulos correspondientes en la primera pregunta y las longitudes de los lados correspondientes en la segunda, ya que no se les preguntó por estos atributos la primera vez. No se trata de encontrar los valores reales, sino de comprobar que las medidas correspondientes son iguales. Dado que a veces no es posible medir con exactitud los ángulos o las longitudes de los lados, las estimaciones de los estudiantes para estos valores (tanto los lados como los ángulos correspondientes) pueden ser ligeramente diferentes.
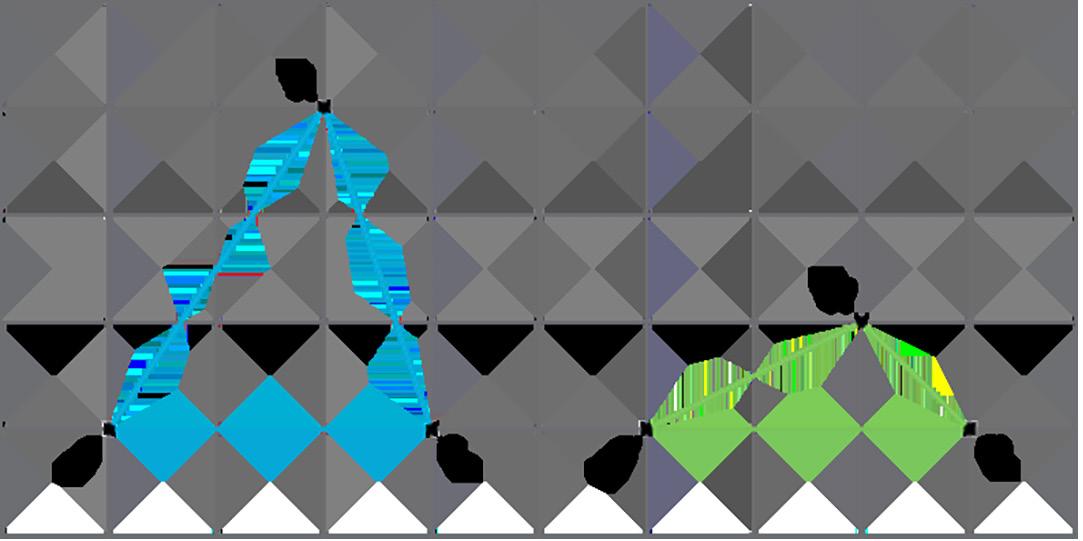
Señale que para cada una de las transformaciones de esta actividad, las longitudes de los lados de la figura original son iguales a las longitudes de los lados correspondientes en la imagen, y las medidas de los ángulos en la figura original son iguales a las medidas de los ángulos correspondientes en la imagen. Por esta razón, llamamos a estas transformaciones transformaciones rígidas: se comportan como si estuviéramos moviendo las formas sin estirarlas, doblarlas o romperlas. Un ejemplo de transformación no rígida es la que comprime una figura verticalmente, así:
Dígales que una transformación rígida es una transformación en la que todos los pares de distancias y medidas de ángulo correspondientes en la figura y su imagen son iguales. Resulta que las traslaciones, las reflexiones y las rotaciones son los componentes básicos de todas las transformaciones rígidas.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR 8 Apoyos para el debate. A medida que los estudiantes describen sus enfoques, insista en los detalles de las explicaciones de los estudiantes pidiéndoles que cuestionen una idea, que elaboren una idea o que den un ejemplo de su proceso. Conecte los términos lados correspondientes y ángulos correspondientes a las explicaciones de los estudiantes multimodalmente utilizando diferentes tipos de aportaciones sensoriales, como demostrando la transformación o invitando a los estudiantes a hacerlo, utilizando las imágenes y utilizando gestos. Esto ayudará a los estudiantes a producir y dar sentido al lenguaje necesario para comunicar sus propias ideas.
Principio(s) de diseño: Optimizar la salida (para la explicación)
ACTIVIDAD DE EXPLORACIÓN | ¿CUÁL?
(10 minutos)
Rutinas didácticas
Anticipar, monitorear, seleccionar, secuenciar, conectar
MLR2: Recopilar y mostrar
El propósito de esta actividad es decidir si existe una secuencia de traslaciones, rotaciones y reflexiones que lleven una figura a otra y, en caso afirmativo, producir una de tales secuencias. Para decidir si tal secuencia es posible o no, se utiliza el conocimiento de que las
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
traslaciones, rotaciones y reflexiones no cambian las longitudes de los lados ni las medidas de los ángulos. Los triángulos ������ y ������ forman parte de un gran patrón de imágenes del triángulo ������ que se examinará más detenidamente en futuras lecciones. Vigile a los estudiantes que utilizan diferentes transformaciones para llevar el triángulo ������ al triángulo ������ y selecciónelos para compartirlos durante la discusión. (Hay dos secuencias posibles en la sección respuestas posibles, pero no son las dos únicas).
INTRODUCCI
Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Dé a los estudiantes 4 minutos de tiempo de trabajo en silencio, 2 minutos para discutir con el compañero y luego tiempo para una discusión con toda la clase. Si utiliza la actividad digital, tenga una breve discusión de la actividad anterior para resaltar las transformaciones que los estudiantes utilizaron. A continuación, conceda a los estudiantes 4 minutos de trabajo individual, 2 minutos para debatir con un compañero y, a continuación, tiempo para un debate de toda la clase.
Apoyo para estudiantes que aprenden el idioma inglés
Conversar: MLR2 Recoger y mostrar. Mientras los estudiantes discuten su trabajo con un compañero, escuche y recoja el lenguaje que los estudiantes usan para describir cada transformación. Registre las palabras y frases de los estudiantes en una pantalla visual (por ejemplo: «Rotar el triángulo ������ 90 grados en sentido contrario a las agujas del reloj alrededor del punto ��. Trasladar el triángulo ������ 7 unidades a la derecha, etc.».) y actualícela durante el resto de la lección. Recuerde a los estudiantes que tomen prestado el lenguaje de la pantalla cuando sea necesario. Esto ayudará a los estudiantes a leer y utilizar el lenguaje matemático durante los debates en parejas y en grupo. Principio(s) de diseño: Optimizar el resultado (para la explicación); maximizar la metaconciencia
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Aquí hay una cuadrícula que muestra el triángulo ������ y otros dos triángulos. Puedes usar una transformación rígida para llevar el triángulo ������ a uno de los otros triángulos.
1. ¿Cuál? Explica cómo lo sabes.
2. Describe una transformación rígida que lleve ������ al triángulo que has seleccionado.
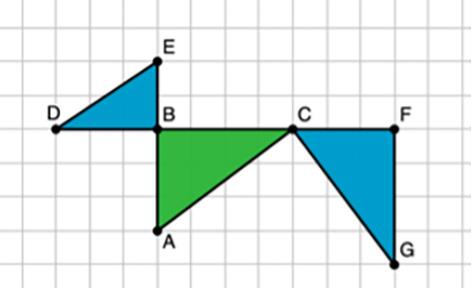
1. Es el triángulo ������. El triángulo ������ es más pequeño que △������ por lo que ninguna secuencia de transformaciones rígidas llevará △������ al triángulo ������
2. Las respuestas varían. Aquí hay dos secuencias posibles:
• Traslada el triángulo ������ 7 unidades a la derecha de modo que �� coincida con ��. A continuación, gire 90 grados en el sentido de las agujas del reloj alrededor de ��:
• Gira el triángulo ������ 90 grados en sentido contrario a las agujas del reloj alrededor del punto ��, luego gira 180 grados alrededor del punto medio de �� del segmento ����:
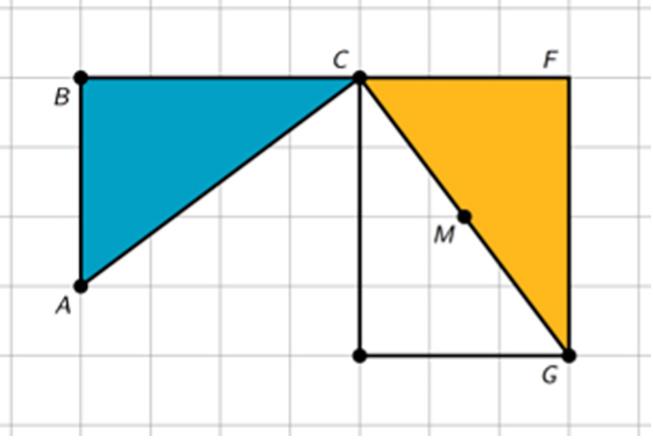
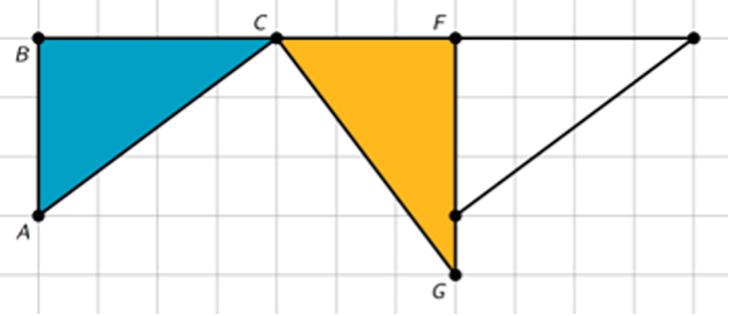
Grado 8 . Matemáticas . Unidad 1
DE LA ACTIVIDAD
SÍNTESIS
Pida a un estudiante que explique por qué el triángulo ������ no puede llevarse al triángulo ������. (solo estamos utilizando transformaciones rígidas y por tanto las longitudes correspondientes tienen que ser iguales y no lo son). Si un estudiante saca a colación que cree que el triángulo ������ es un dibujo a escala de ������En lugar de hablar de cómo o por qué el triángulo ������ no es en realidad un dibujo a escala de ������.
Ofrezca tantos métodos de transformación del triángulo ������ como el tiempo lo permita, seleccionando a estudiantes previamente identificados para que compartan sus métodos. Incluya al menos dos secuencias diferentes de transformaciones. Asegúrese de que los estudiantes prestan atención a especificar cada transformación con el nivel de precisión necesario. Por ejemplo, para una rotación, que especifiquen el centro de rotación, la dirección y el ángulo de rotación.
Si el tiempo lo permite, considere hacer las siguientes preguntas:
• «¿Se puede llevar el triángulo ������ al triángulo ������ con solo una traslación?». (No, ya que ������ está rotado).
• «¿Y con solo una reflexión?». (No, porque tienen la misma orientación).
• «¿Y con una sola rotación?». (La respuesta es sí, pero no es necesario responder a esta pregunta ahora, ya que los estudiantes tendrán la oportunidad de investigarlo más a fondo en una lección futura).
¿Estás preparado para más?
Un cuadrado está formado por una región en forma de L y tres transformaciones de la región. Si el perímetro del cuadrado es 40 units, ¿cuál es el perímetro de cada región en forma de L?
«¿Estás listo para más?». Respuesta del estudiante
25 unidades
SÍNTESIS DE LA LECCIÓN
(5 minutos)
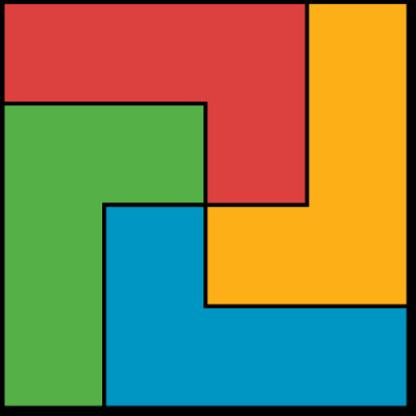
Recuerde a los estudiantes que una transformación rígida es una transformación para la cual todos los pares de correspondientes longitudes y medidas de ángulos en la figura original y su imagen son iguales. Las traslaciones, rotaciones y reflexiones tienen esta propiedad, por lo que son transformaciones rígidas. Las secuencias de éstas también lo son; por ejemplo, si trasladas una figura y luego reflejas la imagen, las longitudes de los lados y las medidas de los ángulos permanecen iguales.
Pide a los estudiantes que piensen en formas en las que podrían mirar dos figuras y decir que una no es la imagen de la otra bajo una transformación rígida. Concédales un momento para pensar en silencio y, a continuación, invite a los estudiantes a compartir sus ideas (Si dos figuras tienen longitudes laterales o medidas de ángulos diferentes, entonces no existe una transformación rígida que lleve una figura a la otra).
Cuando existe una transformación rígida que lleva una figura a otra, hay muchas formas de hacerlo. Pregunte a los estudiantes:
• «¿Cuáles son algunas buenas maneras de saber si una figura puede ser llevada a otra con una secuencia de transformaciones rígidas?». (Mida todas las longitudes de los lados y la medida de los ángulos y asegúrese de que las medidas correspondientes son iguales. Utiliza papel de calco para ver si una forma coincide exactamente con la otra).
• «¿Cuáles son los tres tipos básicos de transformaciones rígidas?». (Rotaciones, traslaciones y reflexiones).
ENFRIAMIENTO | TRAPEZOIDE TRASLADADO
(5 minutos)
Los estudiantes utilizan las propiedades clave que definen a las transformaciones rígidas, a saber, que preservan las longitudes de los lados y las medidas de los ángulos, para calcular las longitudes de los lados y las medidas de los ángulos en un polígono y su imagen bajo una transformación rígida.
Grado 8 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Trapezoide ��′��′��′��′ es la imagen del trapezoide �������� bajo una transformación rígida.
1. Etiqueta todos los vértices del trapezoide ��′��′��′��′.
2. En ambas figuras, etiqueta todas las longitudes de los lados conocidas y las medidas de los ángulos.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
¿Existe una transformación rígida que lleve el rombo �� al rombo ��? Explique cómo lo sabe.
PROBLEMA 2
Soluciones posibles
No, porque las medidas de los ángulos de los dos polígonos son diferentes, y una transformación rígida debe preservar todas las longitudes y angle medidas.
Describa una transformación rígida que lleve triángulo �� a triángulo ��
Soluciones posibles
Traslade tres unidades a la derecha y dos unidades hacia arriba.
PROBLEMA 3
¿Existe una transformación rígida que lleve rectángulo �� a rectángulo ��? Explica cómo lo sabes.
Soluciones posibles
No, porque las longitudes de los lados de los dos rectángulos son diferentes, y una transformación rígida debe preservar todas las longitudes y medidas de los ángulos.
Learning Inc. - Todos los derechos reservados
PROBLEMA 4
Grado 8, unidad 1, lección 4
Para cada forma, dibuja su imagen después de realizar la transformación. Si te atascas, considera usar papel de calco.
A. Traslada la figura de modo que �� pase a ��′
B. Gira la figura 180 grados en sentido antihorario alrededor de ��
C. Refleja la figura sobre la línea mostrada.
Reflexiones:
Grado 8 . Matemáticas . Unidad 1
Soluciones posibles
Math Nation California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas se toman a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos se toman como ángulos de la misma medida. Construir
8.G.1c
Enfoque SMPs
MP7 Busca y hace uso de la estructura.
MP8 Busca y expresa regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.3
I.C.11
LECCIÓN 8
PATRONES
DE ROTACIÓN
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predecir lo que podría ocurrir, buscan y utilizan la estructura descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Vamos a rotar figuras en un plano.
META(S) DE APRENDIZAJE
• Puedo describir cómo mover una parte de una figura a otra usando una transformación rígida.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Dibujar y etiquetar rotaciones de 180 grados de un segmento de línea desde los centros del punto medio, un punto en el segmento y un punto fuera del segmento.
• Generalizar (oralmente y por escrito) el resultado al rotar un segmento de línea 180 grados.
• Identificar (oralmente y por escrito) las transformaciones rígidas que pueden construir un diagrama a partir de una figura inicial.
PREPARACIÓN
DE LA LECCIÓN
Rutinas didácticas
Pensar, girar y compartir
MLR8: Apoyos para el debate
Materiales necesarios
Enfriamiento
Conjuntos de herramientas de geometría (papel de calco, papel milimetrado, lápices de colores, tijeras y una ficha)
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE
LA LECCIÓN
Narrativa de la lección
En esta lección, se aplican transformaciones rígidas a segmentos de recta y triángulos. En el caso de los segmentos de recta, los estudiantes examinan el impacto de una rotación de 180 grados. Este es un importante trabajo preparatorio para el estudio de las rectas paralelas y las transformaciones rígidas, tema de la próxima lección. En el caso de los triángulos, los estudiantes estudian una serie de transformaciones en las que las rotaciones de 90 grados y 180 grados vuelven a ser el centro de atención. Este trabajo y los patrones que construyan los estudiantes serán importantes más adelante, cuando estudien el teorema de Pitágoras.
A lo largo de la lección, los estudiantes utilizan las propiedades de las transformaciones rígidas (no cambian las distancias ni los ángulos) para sacar conclusiones sobre los objetos que están transformando (MP7).
LECCIÓN DE UN VISTAZO
Componente de la lección
Estructura Tiempo
Calentamiento Independiente 5 min
Actividad de exploración En pareja 15 min
Actividad de Exploración Grupos Pequeños 10 min
Síntesis Grupo Entero 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Descripción breve
Los estudiantes describen una figura que se puede formar después de realizar una secuencia de rotaciones.
Los estudiantes exploran rotaciones de segmentos de línea 180° en cualquier dirección.
La actividad requiere el uso de una aplicación digital interactiva para que los estudiantes puedan aplicar una secuencia de transformaciones en una cuadrícula de coordenadas utilizando la tecnología.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la rotación de segmentos de rectas.
Los estudiantes describen transformaciones rígidas de triángulos inscritos en un cuadrado.
Una aplicación digital interactiva está disponible para que los estudiantes puedan explorar una secuencia de transformaciones usando la tecnología.
Los estudiantes discuten los resultados de un segmento de línea rotado en diferentes direcciones con diferentes centros de rotación.
Los estudiantes explican si los dos triángulos dados pueden ser mapeados uno sobre el otro a través de una rotación.
El componente de práctica independiente incluye 2 en la lección y 2 problemas de repaso en espiral.
California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | CONSTRUIR UN CUADRILÁTERO (5 minutos)
Los estudiantes giran cuatro veces una copia de un triángulo isósceles rectángulo para construir un cuadrilátero. Resulta que el cuadrilátero es un cuadrado. No se pide ni se espera que los estudiantes lo justifiquen, pero puede abordarse en el debate. La cuarta pregunta sobre la simetría rotacional del cuadrilátero ayudará a los estudiantes a concluir que es un cuadrado.
Hay muchas más oportunidades de construir figuras utilizando transformaciones rígidas en otras lecciones.
INTRODUCCIÓN
Proporcionar acceso a conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), en particular papel de calco.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
He aquí un triángulo isósceles rectángulo:
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
1. Gira el triángulo ������ 90 grados en el sentido de las agujas del reloj alrededor de ��.
2. Girar el triángulo ������ 180 grados en el sentido de las agujas del reloj alrededor de ��.
3. Girar el triángulo ������ 270 grados en el sentido de las agujas del reloj alrededor de ��.
4. ¿Qué aspecto tendría al girar los cuatro triángulos 90 grados en el sentido de las agujas del reloj alrededor de ��? 180 grados? ¿270 grados en el sentido de las agujas del reloj?
1.
2.
3.
4. Estas rotaciones intercambian los 4 triángulos.
Pregunta a los estudiantes qué observan y qué se preguntan sobre el cuadrilátero que han construido. Entre las respuestas más probables se incluyen:
• Parece un cuadrado.
• Al girarlo 90 grados en el sentido de las agujas del reloj o en sentido contrario, se intercambian los 4 ejemplares del triángulo ������
• Continuando con el patrón de rotaciones, la siguiente colocará ������ de nuevo en su posición original. Pregunte a los estudiantes cómo saben que los cuatro triángulos encajan sin huecos ni solapamientos para formar un quadrilátero. Aquí el punto clave es que el triángulo es isósceles, por lo que las rotaciones hacen coincidir perfectamente estos lados. Los cuatro ángulos rectos forman un completp de 360 grados, por lo que la forma es realmente un cuadrilátero. El hecho de que el cuadrilátero es un cuadrado puede deducirse del hecho de que se traza sobre sí mismo mediante una rotación de 90 grados, pero no es necesario recalcar ni tratar este punto.
Grado 8 . Matemáticas . Unidad 1
ACTIVIDAD DE EXPLORACIÓN | ROTAR UN SEGMENTO
(15 minutos)
Rutinas didácticas
Pensar, girar y compartir
MLR8: Apoyos para el debate
El propósito de esta actividad es permitir a los estudiantes explorar casos especiales de rotación de un segmento de recta 180°. En general, al rotar un segmento 180° se obtiene un segmento paralelo de la misma longitud que el original. Esta actividad también trata dos casos especiales:
Cuando el centro de rotación es el punto medio, el segmento rotado es el mismo segmento que el original, excepto que los vértices están intercambiados.
Cuando el centro de rotación es un punto final, el segmento junto con su imagen forman un segmento dos veces más largo que el original.
A medida que los estudiantes tratan de hacer afirmaciones generales sobre lo que ocurre cuando un segmento de línea se rota 180° se involucran en el MP8. Están experimentando con un segmento de recta en particular, pero las conclusiones que sacan, especialmente en el último problema, son para cualquier segmento de recta.
Observe cómo los estudiantes explican que la rotación 180° del segmento ���� en la segunda parte de la pregunta es paralela a ���� Algunos estudiantes pueden decir que «parecen paralelas», mientras que otros pueden intentar razonar utilizando la estructura de la cuadrícula. Diles que lo investigarán más a fondo en la próxima lección.
INTRODUCCIÓN
Organice a los estudiantes en grupos de 2. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda 3 minutos de tiempo de trabajo en silencio, seguido de una puesta en común con un compañero y un debate con toda la clase.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Comience con una demostración de la primera rotación, que proporcionará acceso a los estudiantes que se benefician de instrucciones claras y explícitas.
Crear un segmento ���� y un punto �� que no esté en el segmento ����
1. Rotar el segmento ���� 180° alrededor del punto ��.
ENUNCIADO DE
2. Gira el segmento ���� 180° alrededor del punto 1. Construye el punto medio del segmento ���� con la herramienta de punto medio.
3. Gira el segmento ���� 180° alrededor de su punto medio. ¿Cuál es la imagen de ��?
4. ¿Qué sucede cuando se rota un segmento 180°?
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Las respuestas varían. Ejemplo de respuesta: 1. 2.
RESPUESTAS POSIBLES
3. La imagen del segmento se alinea consigo misma, pero los puntos extremos se intercambian. �� está ahora donde estaba �� y �� está donde estaba ��.
4. El nuevo segmento puede cambiar su ubicación, pero sigue teniendo la misma longitud. El nuevo segmento es paralelo al segmento original. Cuando el punto de rotación es el punto medio del segmento, entonces el segmento rotado es el mismo que el original (los puntos extremos intercambian lugares) y cuando el punto de rotación es un punto final del segmento, la imagen se conecta con el original para formar un segmento el doble de largo.
CONCEPTOS ERRÓNEOS PREVISTOS
Los estudiantes pueden confundirse al rotar alrededor del punto medio porque piensan que la imagen no puede ser el mismo segmento que el original. Asegure a los estudiantes que esto puede ocurrir y destaque ese punto en la discusión.
Pregunte a los estudiantes por qué no es necesario especificar la dirección de una rotación de 180 grados (porque una rotación de 180 grados en el sentido de las agujas del reloj alrededor del punto �� tiene el mismo efecto que una rotación de 180 grados en el sentido contrario a las agujas del reloj alrededor de ��).
Invite a los grupos a compartir sus respuestas. Pregunte a la clase si están de acuerdo o en desacuerdo con cada respuesta. Cuando haya desacuerdo, pida a los estudiantes que discutan las posibles razones de las diferencias.
Tres ideas importantes que surgen en la discusión son:
• Rotar un segmento 180° alrededor de un punto que no está en la recta segmento original produce un segmento paralelo de la misma longitud que el original.
• Cuando el centro de rotación es el punto medio, el segmento rotado es el mismo segmento que el original, excepto que los vértices están intercambiados.
• Cuando el centro de rotación es un punto final, el segmento junto con su imagen forman un segmento el doble de largo.
Si alguna de las ideas anteriores no es planteada por los estudiantes durante la discusión en clase, asegúrese de darla a conocer.
Todas estas ideas pueden ser enfatizadas dinámicamente llevando a cabo una rotación especificada en el applet y luego moviendo el centro de rotación o un punto final del segmento de línea original. Incluso si los estudiantes no están utilizando la versión digital de la actividad, puede que desee mostrar y demostrar con la aplicación.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos para el debate. Utilice esta rutina para apoyarel debate de toda la clase cuando los estudiantes discutan si es necesario especificar la dirección de una rotación de 180 grados. Después de que un estudiante hable, pida a los estudiantes que vuelvan a decir y/o repetir lo que se compartió utilizando lenguaje matemático (por ejemplo, rotación, segmento derecta, punto medio, etc.). Esto proporcionará a más estudiantes la oportunidad de producir lenguaje mientras exploran casos especiales de rotación de un segmento derecta de 180°.
Principio(s) de diseño: Apoyar la creación de sentido; maximizar la metaconciencia
¿Estás preparado para más?
Aquí hay dos segmentos de recta. ¿Es posible girar un segmento de recta con respecto al otro?
Si es así, encuentra el centro de dicha rotación. Si no, explica por qué no.
«¿Estás listo para más?». Respuesta del estudiante
Sí
ACTIVIDAD DE EXPLORACIÓN | UN PATRÓN DE CUATRO TRIÁNGULOS
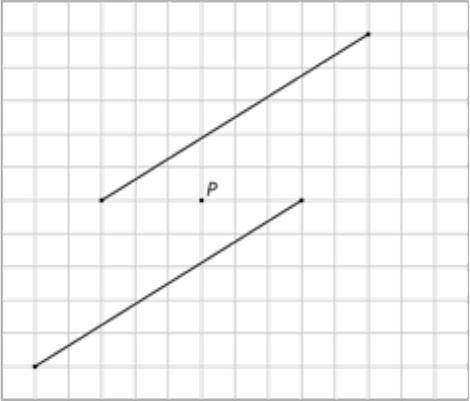
(10 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
En esta actividad, los estudiantes usan rotaciones para construir un patrón de triángulos. En la lección anterior, los estudiantes examinaron un triángulo rectángulo y una transformación rigida del triángulo. En esta actividad, varias transformaciones rígidas del triángulo forman un patrón interesante.
El triángulo ������ puede mapearse a cada uno de los otros tres triángulos del patrón con una sola rotación. Mientras los estudiantes trabajan en las tres primeras preguntas, observe si alguno ve que una sola rotación puede llevar el triángulo ������ a ������. El centro para la rotación no está dibujado en el diagrama: es la intersección del segmento ���� y el segmento ����. Para los estudiantes que terminan temprano, guíelos para que busquen una single transformación que lleva ������ a cada uno de los otros triángulos.
Este patrón jugará un papel importante más adelante cuando los estudiantes usen esta forma para entender una demostración del teorema de Pitágoras.
Identifique a los estudiantes que notan que ya han resuelto la primera pregunta en una actividad anterior. Esté atento a los estudiantes que piensen que �������� es un cuadrado y dígales que esto se tratará en una lección futura. Sin embargo, anímeles a pensar en lo que concluyen sobre �������� ahora. Observe también a los estudiantes que repiten los mismos pasos para demostrar que ������ puede asignarse a cada uno de los otros tres triángulos.
California . Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Ó N Organice a los estudiantes en grupos de 2-4. Proporcione a los estudiantes herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
INTRODUCCI
Si utiliza la actividad digital, dé a los estudiantes un tiempo de trabajo individual antes de permitirles conversar con un partner.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual: Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
He aquí un diagrama construido con tres transformaciones rígidas diferentes del triángulo ������.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Utilice el aplicación digital para responder las preguntas. Puede ser útil reiniciar la imagen después de cada pregunta.
1. Describa una transformación rígida que lleve el triángulo ������ al triángulo ������.
2. Describir una transformación rígida que lleve el triángulo ������ al triángulo ������.
3. Describir una transformación rígida que lleve el triángulo ������ al triángulo ������.
4. ¿Tienen los segmentos ����, ����, ���� y ���� todos la misma longitud? Explica tu razonamiento.
POSIBLES
RESPUESTAS
1. Las respuestas varían. Ejemplos de respuestas:
• Traslada el punto �� al punto ��, luego rota 90 grados en el sentido de las agujas del reloj usando �� como centro.
• Gira en sentido contrario a las agujas del reloj usando �� como centro hasta que el segmento ���� coincida perfectamente con el segmento ����, luego gira 180 grados usando el punto medio del segmento ���� como centro.
2. Las respuestas varían. Ejemplos de respuestas:
• Traslada �� a �� y luego rota 180 grados con centro ��
• Traducir de modo que el segmento ���� coincida con el segmento ���� y luego rotar 180 grados con el punto medio del segmento ���� como centro de rotación.
3. Las respuestas varían. Ejemplos de respuestas:
• Trasladar �� a �� y luego rotar 90 grados en sentido antihorario con centro ��
• Gire con centro �� para que el segmento ���� coincida con el segmento ���� y luego gire 180 degrees con el punto medio del segmento ���� como centro.
4. Sí, porque el tamaño y la forma del triángulo ������ no cambiaron bajo la transformación rígida. El segmento ���� se puede alinear exactamente con los segmentos ����, ���� y ���� por lo que las longitudes de estos segmentos son todas iguales.
Puede que algunos estudiantes no reconozcan en qué se parece este trabajo al de la actividad anterior. Para estos estudiantes, pídales que den un paso atrás y consideren solo los triángulos ������ y ������, quizás cubriendo la mitad inferior del diagrama.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Seleccione a un estudiante previamente identificado que haya notado cómo la primera pregunta se relaciona con una actividad anterior para que comparta su observación. Discuta aquí cómo el trabajo previo puede ser útil en el nuevo trabajo, ya que es posible que los estudiantes no estén buscando activamente estas conexiones. Las siguientes preguntas son como la primera, pero los triángulos tienen una orientación diferente y se necesitan transformaciones diferentes. Discuta las transformaciones rígidas. Concéntrate especialmente en la pregunta sobre longitudes. Un concepto clave en esta sección es la idea de que las longitudes y las medidas de los ángulos se conservan bajo transformaciones rígidas. Algunos estudiantes pueden afirmar que �������� es un cuadrado. Si esto surge, déjalo como pregunta abierta por ahora. Esta cuestión se retomará al final de esta unidad, una vez conocida la suma de ángulos en un triángulo. La última pregunta establece que �������� es un rombo.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos para el debate. Conceda a los estudiantes más tiempo para asegurarse de que todos los miembros de su grupo pueden explicar si los segmentos ����, ����, ���� y ���� tienen todos la misma longitud. A continuación, varía a quién se llama para representar las ideas de cada grupo. Esta rutina preparará a los estudiantes para el papel de representante del grupo y para apoyarse mutuamente para asumir ese papel.
Principio(s) de diseño: Optimizar el rendimiento (para la explicación)
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Pida a los estudiantes que describan los posibles resultados cuando un segmento de línea ���� se gira 180 grados.
• ���� se mapea a sí mismo, cuando el centro de rotación es el punto medio del segmento
• ���� se mapea a otro segmento colineal con el primero, cuando el centro de rotación es �� o �� (o cualquier otro punto del segmento ����)
• ���� se mapea a un segmento paralelo, cuando el centro de rotación no está en la línea ����
ENFRIAMIENTO | ¿ES UNA ROTACIÓN?
(5 minutos)
Después de haber estudiado en detalle las rotaciones a lo largo de esta lección, los estudiantes observan un triángulo y su imagen después de una transformación rígida. Deciden si una es o no una rotación de la otra. Resulta que es una reflexión y no una rotación. Los estudiantes pueden usar papel de calco para verificar sus conjeturas, pero en este punto deberían empezar a tener una intuición de los efectos de una rotación frente a una reflexión.
Disponga de papel de calco.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Aquí hay dos triángulos. ¿Es el triángulo �� una rotación del triángulo ��? Explica tu razonamiento.
No, el triángulo �� es una reflexión del triángulo �� sobre la línea ℓ. Se puede utilizar una rotación para hacer coincidir dos lados de los triángulos, pero no hará que uno coincida perfectamente con el otro.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Para la figura que se muestra aquí,
A. Rota el segmento ���� 180° alrededor del punto ��
B. Rotar el segmento ���� 180° alrededor del punto ��
C. Rotar el segmento ���� 180° alrededor del punto ��
PROBLEMA 2
He aquí un triángulo rectángulo isósceles: Dibuja estas tres rotaciones del triángulo ������ juntas.
A. Gira el triángulo ������ 90 grados en el sentido de las agujas del reloj alrededor de ��
B. Gira el triángulo ������ 180 grados alrededor de ��
C. Girar el triángulo ������ 270 grados en el sentido de las agujas del reloj alrededor de ��
Learning Inc. - Todos los derechos reservados
Soluciones posibles
A. El segmento está unido en el punto �� y es una prolongación del segmento ����
B. El segmento está por encima del punto �� y es paralelo a segmento ����
C. El segmento es idéntico al segmento ����
Soluciones posibles
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 3
Grado 8, unidad 1, lección 5
Cada gráfico muestra dos polígonos �������� y ��′��′��′��′. En cada caso, describa una secuencia de transformaciones que lleve �������� a ��′��′��′��′. A. B.
Soluciones posibles
A. Reflejar �������� sobre el eje Y y luego trasladar hacia abajo 1.
B. Gire �������� 90 grados en el sentido de las agujas del reloj con centro �� = (–1, 0) y luego traslade (–1, 0) a (3, 1)
PROBLEMA 4
Grado 8, unidad 1, lección 4
Lin dice que puede trazar el polígono �� al polígono �� usando solo reflexiones. ¿Estás de acuerdo con Lin? Explica tu razonamiento.
Reflexiones:
Soluciones posibles
Estoy de acuerdo con Lin. Si el polígono �� se refleja primero sobre la línea vertical ℓ y luego sobre la línea horizontal ��, esto lleva al polígono 1 al polígono ��
Nation California . Grado 8
Learning Inc. - Todos los derechos reservados
LECCIÓN 9
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas se toman a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos se toman a ángulos de la misma medida.
8.G.1c Verificar experimentalmente las propiedades de rotaciones, reflexiones y traslaciones: Las líneas paralelas se llevan a líneas paralelas.
Construir
7.G.5
Enfoque SMPs
MP7 Busca y utiliza estructuras.
Estándares ELD de California
I.C.9 II.C.6
MOVIMIENTOS EN PARALELO
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
impactar en el futuro, buscan y hacen uso de la estructura descubren la forma y el espacio.
META(S) DE APRENDIZAJE
• Transformemos algunas rectas.
META(S) DE APRENDIZAJE
• Puedo describir los efectos de una transformación rígida sobre un par de rectas paralelas.
• Si tengo un par de ángulos verticales y conozco la medida del ángulo de uno de ellos, Puedo encontrar la medida del ángulo del otro.
METAS DE APRENDIZAJE PARA EL MAESTRO
• Comprender que una rotación de 180 grados alrededor de un punto de dos líneas que se intersectan mueve cada ángulo al ángulo que es vertical a él.
• Describir (oralmente y por escrito) observaciones de líneas y líneas paralelas bajo transformaciones rígidas, incluyendo líneas que son llevadas a líneas y líneas paralelas que son llevadas a líneas paralelas.
• Dibujar y rotular transformaciones rígidas de una recta y explicar la relación entre una recta y su imagen bajo la transformación.
• Generalizar (oralmente) que los «ángulos verticales» son congruentes usando argumentos informales sobre 180 rotaciones de grados de rectas.
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
MLR1: Cada vez más fuerte y más claro
MLR7: Comparar y conectar
Materiales necesarios
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
La lección anterior examina el impacto de las rotaciones sobre los segmentos de recta y los polígonos. Esta lección se centra en los efectos de las transformaciones rígidas sobre las rectas. En particular, los estudiantes ven que las rectas paralelas se llevan a las rectas paralelas y que una 180° rotación sobre un punto de la recta lleva a la recta a sí misma. En el grado 7, los estudiantes descubrieron que los ángulos verticales tienen la misma medida, y lo justifican aquí usando una rotación 180°
Al investigar cómo las rotaciones de 180° influyen en las rectas paralelas y en las rectas que se intersecan, los estudiantes observan ejemplos específicos, pero sus conclusiones son válidas para todos los pares de rectas paralelas o que se intersecan. No se utilizan propiedades especiales de las dos rectas que se intersecan, por lo que la rotación 180° mostrará que los ángulos verticales tienen la misma medida para cualquier par de ángulos verticales.
LECCIÓN DE UN VISTAZO
Componente de la lección
Estructura Tiempo
Descripción breve
Calentamiento Independiente 5-10 min Los estudiantes describen una transformación rígida que puede ser usada para mapear una línea a otra línea en una cuadrícula.
Actividad de Exploración Grupos Pequeños 10-15 min
Actividad de Exploración Independiente 15 min
Síntesis Grupo Completo 3-5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Los estudiantes exploran cómo diferentes transformaciones rígidas afectan la relación entre líneas paralelas.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las figuras formadas a través de transformaciones de líneas paralelas.
Los estudiantes exploran rotaciones de figuras alrededor de diferentes puntos del centro e identifican relaciones formadas entre partes de las figuras al aplicar dichas transformaciones.
Los estudiantes resumen las relaciones observadas a través de las exploraciones de esta lección en líneas paralelas y transformaciones rígidas. Los estudiantes revisan el concepto de ángulos verticales de 7º grado a través de transformaciones.
Los estudiantes identifican y encuentran medidas de ángulos verticales en una figura formada por rotaciones.
El componente de práctica independiente incluye 3 problemas de repaso de la lección y 2 problemas de repaso en espiral.
California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | LA LÍNEA SE MUEVE
(10 minutos)
En este calentamiento, los estudiantes continúan su trabajo con las transformaciones pasando de aplicar transformaciones rígidas a las formas a aplicarlas específicamente a las líneas. Cada imagen de esta actividad tiene la misma línea de partida y se pide a los estudiantes que nombren la traslación, rotación o reflexión que lleva esta línea a la segunda línea marcada. Debido a su naturaleza infinita y simétrica, las diferentes transformaciones de las rectas tienen el mismo aspecto a menos que se marquen puntos específicos, por lo que se marcan 1-2 puntos en cada línea.
Aunque los estudiantes tienen experiencia en la transformación de diversas figuras, esta actividad les brinda la oportunidad de utilizar un lenguaje preciso al describir las transformaciones de las rectas, a la vez que exploran cómo a veces diferentes transformaciones pueden dar como resultado las mismas figuras finales. Durante la actividad, anime a los estudiantes a buscar más de una forma de transformar la línea original.
Ó N Proporcione acceso a papel de calco. Conceda a los estudiantes 2 minutos de tiempo de trabajo en silencio, seguidos de un debate con toda la clase.
Apoyo para estudiantes con discapacidades
Funcionamiento ejecutivo: Organizadores gráficos. Proporcione una red de palabras para las transformaciones. Los estudiantes deben enlazar la información importante para futuras consultas (por ejemplo, vocabulario, reglas y procedimientos).
Para cada diagrama, describa una traslación, rotación o reflexión que lleve la línea ℓ a la línea ℓ′. Luego traza y etiqueta ��′ y ��′, las imágenes de �� y ��.
1.
2.
RESPUESTAS POSIBLES
1. Las respuestas varían. Respuestas posibles:
• Traducción en muchas direcciones posibles, por ejemplo, hacia abajo 3 unidades
• Reflexión sobre una línea paralela a ℓ a medio camino entre ℓ y ℓ′
• Rotación utilizando un punto a medio camino entre ℓ y ℓ′ como centro de rotación y un ángulo de 180°
2. Las respuestas varían. Respuestas posibles:
• Reflexión a través de la línea vertical que pasa por el punto ��
• Reflexión a través de la línea horizontal que pasa por el punto ��
• Rotación en sentido contrario a las agujas del reloj sobre el punto �� por el ángulo obtuso cuyo vértice está en ��
• Rotación en sentido de las agujas del reloj sobre el punto �� por el ángulo agudo cuyo vértice está en ��
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Invite a los estudiantes a compartir las transformaciones que eligieron para cada problema. Cada diagrama tiene más de una transformación posible que daría como resultado la figura final. Si la clase solo encontró una, haga una pausa durante 2-3 minutos y anime a los estudiantes a ver si pueden encontrar otra. Para el primer diagrama, busque una sola traslación, una sola rotación y una sola reflexión que funcionen. Para el segundo diagrama, busca una sola rotación y una sola reflexión.
• «¿Funcionará una traslación para el segundo diagrama? Explica tu razonamiento». (Una traslación no funcionará. Dado que las traslaciones no incorporan un giro, las traslaciones de una recta son paralelas a la recta original o son la misma recta).
ACTIVIDAD DE EXPLORACIÓN | LÍNEAS PARALELAS (15 minutos)
Rutinas didácticas
MLR1: Cada vez más fuerte y más claro
En esta actividad, los estudiantes investigarán la pregunta «qué les ocurre a las líneas paralelas bajo transformaciones rígidas?». realizando tres transformaciones diferentes sobre un conjunto de líneas paralelas. Después de aplicar cada transformación, anotarán lo que observan respondiendo a las preguntas correspondientes a cada una de las transformaciones enumeradas.
A medida que los estudiantes resuelven estos problemas, pueden recordar características esenciales de las rectas paralelas (no se encuentran, permanecen a la misma distancia). Las transformaciones rígidas no cambian ninguna de estas características, lo que significa que la imagen de un conjunto de líneas paralelas después de una transformación rígida es otro conjunto de líneas paralelas (MP7).
Identifique a los estudiantes que vieron que la orientación de las líneas cambia, pero las líneas permanecen paralelas entre sí a pesar de todo y selecciónelos para compartir durante la discusión.
INTRODUCCIÓN
Antes de comenzar, repase con los estudiantes lo que sucede cuando realizamos una transformación rígida. Haga una demostración moviendo el papel de calco sobre la imagen para reproducir un ejemplo de transformación (por ejemplo, rotación de las líneas en el sentido de las agujas del reloj 90° alrededor del centro ��). Diga a los estudiantes que el objetivo de esta actividad es investigar: «¿Qué les ocurre a las rectas paralelas cuando realizamos transformaciones rígidas sobre ellas?».
Organice a los estudiantes en grupos de 3. Facilite papel de calco. Cada estudiante del grupo realiza uno de los problemas y luego el grupo discute sus conclusiones.
Apoyo para estudiantes con discapacidad
Habilidades motoras finas:Tutores compañeros. Agrupe a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que tienen dificultades con la motricidad fina dictar transformaciones de trazado según sea necesario.
Utiliza un trozo de papel de calco para trazar las rectas �� y �� y el punto ��
A continuación, utiliza ese papel de calco para dibujar las imágenes de las rectas bajo las tres transformaciones diferentes enumeradas.
Mientras realizas cada transformación, piensa en la pregunta:
¿Cuál es la imagen de dos rectas paralelas bajo una transformación rígida?
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
1. Traduzca las líneas �� y �� 3 unidades hacia arriba y 2 unidades hacia la derecha.
A. ¿Qué observa en los cambios que se producen en las líneas �� y �� después de la traducción?
B. ¿Qué es lo mismo en el original y en la imagen?
2. Gira las líneas �� y �� en sentido contrario a las agujas del reloj 180 grados usando �� como centro de rotación.
A. ¿Qué observa en los cambios que se producen en las líneas �� y �� después de la rotación?
B. ¿Qué es lo mismo en el original y en la imagen?
3. Refleje las líneas �� y �� a través de la línea ℎ
A. ¿Qué observas en los cambios que se producen en las líneas �� y �� después de la reflexión?
B. ¿Qué es lo mismo en el original y en la imagen?
1. Traducción: 3 unidades cuadradas hacia arriba y 2 unidades cuadradas hacia la derecha
Las respuestas varían. Ejemplos de respuestas:
A. Todas las 4 rectas, ��, ��, ��′ y ��′ son paralelas. Las rectas ��′ y ��′ se parecen a �� y �� pero desplazadas hacia arriba.
B. El par de rectas permanecen paralelas. La distancia entre las rectas no cambió.
2. Rotación alrededor de ��
Las respuestas varían. Ejemplos de respuestas:
A. El nuevo par de rectas ��′ y ��′ son paralelas a las rectas originales �� y ��.
B. Las rectas ��′ y ��′ siguen siendo paralelas y están a la misma distancia que �� y ��.
3. Reflexió sobre la línea ℎ.
Las respuestas varían. Ejemplos de respuestas:
A. La recta �� está por encima de la recta �� mientras que la recta ��′ está por encima de la recta ��′.
B. Las rectas ��′ y ��′ siguen siendo paralelas y están a la misma distancia que las rectas �� y ��. Las cuatro rectas son paralelas entre sí.
Los estudiantes no pueden realizar las transformaciones encima de la imagen original. Pida a estos estudiantes que coloquen las rectas trazadas sobre el original y realicen cada transformación a partir de ahí.
Pida a los estudiantes previamente seleccionados que vieron que las imágenes de las rectas paralelas eran paralelas al original en los tres casos que compartan cómo responderían a la pregunta principal «¿cuál es la imagen de dos rectas paralelas bajo una transformación rígida?». Asegúrese de que los estudiantes entienden que, en general, si ℓ y m son rectas paralelas y ℓ′ y ��′ son sus imágenes bajo una transformación rígida, entonces:
• ℓ′ y ��′ son paralelas.
• ℓ y �� son no necesariamente paralelas a ℓ′ y ��′ (consulte la rotación de 90 grados mostrada durante la introducción).
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS
LA ACTIVIDAD CONTINUACIÓN
Además de que las rectas paralelas permanecen paralelas entre sí cuando se realizan transformaciones rígidas, la distancia entre las rectas permanece invariable. Lo que puede cambiar es la posición de las rectas en el plano, en términos relativos (es decir, qué recta está «encima») o en términos absolutos (es decir, si una recta contiene un punto concreto del plano).
Da a los estudiantes 1-2 minutos de silencio para que escriban una respuesta a la pregunta principal: «¿Cuál es la imagen de dos rectas paralelas bajo una transformación rígida?».
Apoyo para estudiantes que aprenden el idioma inglés
Escribir, hablar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para ayudar a los estudiantes a refinar una explicación escrita sobre lo que le sucede a dos líneas paralelas bajo una transformación rígida. Dé tiempo a los estudiantes para que se reúnan con sus compañeros de 2-3 , para compartir y recibir comentarios sobre su escritura. Anime a los oyentes a insistir en los detalles y la claridad, según proceda, en función de lo que produzca cada orador. Muestre indicaciones para recibir comentarios que ayuden a cada uno a reforzar sus ideas y aclarar su lenguaje, como por ejemplo: «¿Puedes dar o dibujar un ejemplo?, ¿cuándo las líneas son paralelas o se cruzan? y ¿qué cambia en una transformación rígida?». Conceda a los estudiantes 2-3 minutos para revisar su redacción con base en los comentarios que reciban. Principio(s) de diseño: Optimizar la salida (para la explicación)
¿Estás preparado para más?
Cuando giras dos rectas paralelas, a veces las dos rectas originales intersecan sus imágenes y forman un cuadrilátero. ¿Qué es lo más concreto que puedes decir de este cuadrilátero? ¿Puede ser un cuadrado? ¿Un rombo? ¿Un rectángulo que no es un cuadrado? Explica tu razonamiento.
«¿Estás preparado para más?». Respuesta del estudiante
El cuadrilátero es siempre un rombo. Puede ser un cuadrado si los dos pares de rectas paralelas son perpendiculares. No puede ser un rectángulo que no sea un cuadrado porque la distancia entre los dos pares de rectas paralelas es la misma.
ACTIVIDAD DE EXPLORACIÓN | HAGAMOS ALGUNAS
180'S (15 minutos)
Rutinas didácticas
MLR7: Comparar y conectar
En esta actividad, los estudiantes aplican sus conocimientos sobre las propiedades de las transformaciones rígidas a 180° rotaciones de una recta alrededor de un punto de la recta para establecer el teorema del ángulo vertical. Es probable que los estudiantes ya hayan utilizado este teorema en el grado 7, pero esta lección demuestra informalmente por qué el teorema es verdadero. La demostración del teorema del ángulo vertical explota la estructura de las rectas paralelas y las propiedades tanto de las 180 rotaciones de grado (estudiadas en la lección anterior) como de las transformaciones rígidas. Esta lección es un buen ejemplo de MP7, investigando la estructura de diferentes objetos matemáticos.
Los estudiantes comienzan la actividad rotando una recta con puntos marcados 180° alrededor de un punto de la recta. A diferencia del ejemplo de toda la clase discutido en la introducción, esta recta contiene puntos marcados distintos del centro de rotación. A continuación, los estudiantes giran un ángulo 180° alrededor de un punto de la recta para sacar conclusiones sobre longitudes y ángulos. Finalmente, se pide a los estudiantes que consideren la intersección de dos rectas, los ángulos que se forman y cómo las medidas de esos ángulos pueden deducirse usando una rotación 180° sobre la intersección de las rectas, que es el teorema del ángulo vertical.
Mientras los estudiantes trabajan, aliente el uso de papel de calco para mostrar las transformaciones directamente sobre la imagen original con el fin de ayudar a los estudiantes a no perder de vista lo que sucede con las rectas en cada rotación 180°
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
INTRODUCCIÓN
Las rotaciones requieren que los estudiantes piensen en rotar una figura entera. Sería bueno recordar a los estudiantes esto antes de comenzar esta actividad. Esto podría ayudar a los estudiantes a ver mejor lo que ocurre en la primera pregunta. Antes de que los estudiantes lean la actividad, dibuje una línea ℓ con un punto marcado �� para que todos la vean.
Pida a los estudiantes que imaginen cómo es la figura girada 180° alrededor del punto �� . Tras un minuto de reflexión en silencio, invite a los estudiantes a compartir el aspecto que creen que tendría la figura transformada. Asegúrese de que todos los estudiantes están de acuerdo en que ℓ′ tiene «el mismo aspect» que la original. Si ningún estudiante lo menciona en sus explicaciones, pida sugerencias de características que permitirían distinguir rápidamente la diferencia entre ℓ′ y ℓ, como otro punto o si la línea fuera de distinto color a cada lado del punto ��
Proporcione acceso a papel de calco.
Apoyo para estudiantes con discapacidad
Habilidades motoras finas:Tutores compañeros. Agrupe a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que luchan con las habilidades motoras finas dictar transformaciones según sea necesario.
1. El diagrama muestra una línea con puntos etiquetados ��, ��, �� y ��.
A. En el diagrama, dibuje la imagen de la línea y los puntos ��, �� y �� después de que la línea haya girado 180 grados alrededor de punto ��
B. Rotula las imágenes de los puntos ��′, ��, y ��′.
C. ¿Cuál es el orden de los siete puntos? Explica o muestra tu razonamiento.
2. El diagrama muestra una recta con los puntos �� y �� sobre la recta y un segmento ���� donde �� no está sobre la recta.
A. Gira la figura 180 grados alrededor del punto ��. Etiqueta la imagen de �� como ��′ y la imagen de �� como ��′.
B. ¿Qué sabes de la relación entre el ángulo ������ y el ángulo ����′��′? Explique o muestre su razonamiento.
3. El diagrama muestra dos rectas ℓ y �� que se cruzan en un punto �� con punto �� en ℓ y punto �� en ��.
A. Gire la figura 180 grados alrededor de ��. Etiqueta la imagen de �� como ��′ y la imagen de �� como ��′
B. ¿Qué sabes de la relación entre los ángulos de la figura? Explica o muestra tu razonamiento.
1. ��, ��, ��′, ��, ��, ��′, ��.′
2. Las longitudes del segmento ���� y del segmento ����′ son iguales, las longitudes del segmento ���� y del segmento ��′��′ son iguales, y los ángulos ������ y ����′��′ tienen la misma medida porque tanto las distancias como las medidas de los ángulos se conservan bajo transformaciones rígidas.
1. Respuestas posibles: Los ángulos ������ y ��′����′ tienen la misma medida . Los ángulos ������′ y ��′���� tienen la misma medida.
Grado 8 . Matemáticas . Unidad 1
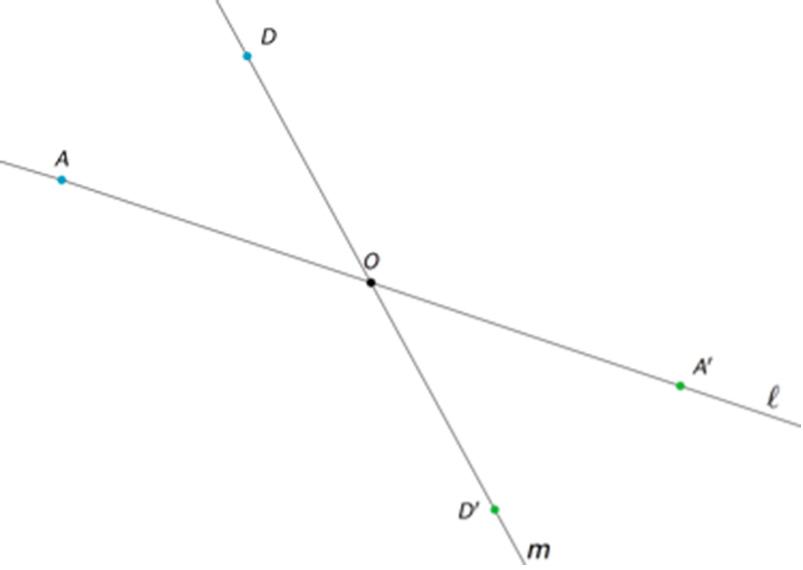
En la segunda pregunta, es posible que los estudiantes no entiendan que la rotación de la figura incluye tanto el segmento ���� como el segmento ���� , ya que han estado trabajando con la rotación de un segmento cada vez. Explique a estos estudiantes que la figura se refiere a ambos segmentos. Anímelos a utilizar papel de calco para ayudarles a visualizar la rotación.
SÍNTESIS DE LA ACTIVIDAD
El foco de la discusión debe comenzar con las relaciones que los estudiantes encuentran entre las longitudes de los segmentos y las medidas de los ángulos y luego pasar al problema final, que establece el teorema del ángulo vertical tal como se entiende a través de las transformaciones rígidas. Las preguntas para conectar la discusión incluyen:
• «¿Qué relaciones entre las longitudes encontramos después de realizar las transformaciones?». (Son iguales).
• «¿Qué relaciones entre las medidas de los ángulos encontramos después de realizar las transformaciones?». (Son iguales).
• «¿Qué prueba informalmente esta transformación?». (Los ángulos verticales son congruentes). Si el tiempo lo permite, considere discutir cómo se abordó el teorema del ángulo vertical en el grado 7, es decir, buscando pares de ángulos suplementarios. Los pares de ángulos verticales tienen la misma medida porque ambos son suplementarios del mismo ángulo. El argumento utilizando rotaciones de 180 grados es diferente porque no es necesario hacer referencia al ángulo suplementario. La rotación 180 grados muestra que ambos pares de ángulos verticales tienen la misma medida directamente al mapearlos entre sí.
Apoyo para estudiantes que aprenden el idioma inglés
Representar, hablar: MLR7 Comparar y conectar. Utilice esta rutina cuando los estudiantes compartan lo que notaron sobre las relaciones entre las medidas de los ángulos. Pida a los estudiantes que consideren qué cambia y qué permanece igual cuando se aplican transformaciones rígidas a líneas y segmentos. Llame la atención de los estudiantes sobre las asociaciones entre la transformación rígida, las longitudes de los segmentos y las medidas de los ángulos. Estos intercambios refuerzan el uso del lenguaje matemático de los estudiantes y el razonamiento basado en las transformaciones rígidas de rectas y conducirán al argumento informal del teorema del ángulo vertical.
Principio(s) de diseño: Maximizar la metaconciencia
SÍNTESIS DE LA LECCIÓN
En esta lección, los estudiantes aplican diferentes transformaciones rígidas a rectas, centrándose en las rectas paralelas. Deberán ser capaces de articular lo que le sucede a las rectas paralelas cuando se realiza una transformación rígida sobre ellas. Además, los estudiantes adquieren una mejor comprensión de por qué el teorema del ángulo vertical que aprendieron en el grado 7 es cierto.
. Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Para destacar cómo afectan las transformaciones a las rectas paralelas, pregunte a los estudiantes:
• "Cuando realizamos transformaciones rígidas en rectas paralelas, ¿qué sabemos sobre su imagen?».
• «¿Cambia la distancia entre las rectas?».
Para ayudar a los estudiantes a establecer una conexión con cómo afectan las rotaciones a las rectas en la segunda actividad, pregunte:
• «Cuando rotamos una recta 180° alrededor de un punto de la recta, ¿dónde cae la recta?».
• «¿Cómo afecta la rotación a las medidas de los ángulos de un par de rectas que se intersecan?».
• «¿Cómo nos ayuda esto a demostrar el teorema del ángulo vertical?».
Los estudiantes deben ver que una rotación de dos rectas que se intersecan alrededor del punto de intersección en 180° mueve cada ángulo al ángulo que le es vertical. Como la rotación es una transformación rígida, los ángulos verticales deben tener la misma medida. En general, las transformaciones rígidas nos ayudan a ver que cuando transformamos rectas puede cambiar la orientación pero las rectas mantienen sus propiedades originales.
ENFRIAMIENTO | ENCONTRAR LAS MEDIDAS QUE
FALTAN
(5 minutos)
Constuyendo directamente en la actividad anterior, los estudiantes completan las medidas que faltan utilizando su comprensión tanto de las transformaciones rígidas como del teorema del ángulo vertical.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Los puntos ��′, ��′ y ��′ son las imágenes de rotaciones de 180 grados de �� y ��, respectivamente, alrededor del punto ��
Contesta a cada pregunta y explica tu razonamiento sin medir segmentos o ángulos.
1. Nombra un segmento cuya longitud sea la misma que segmento ����.
2. ¿Cuál es la medida del ángulo ��′����′?
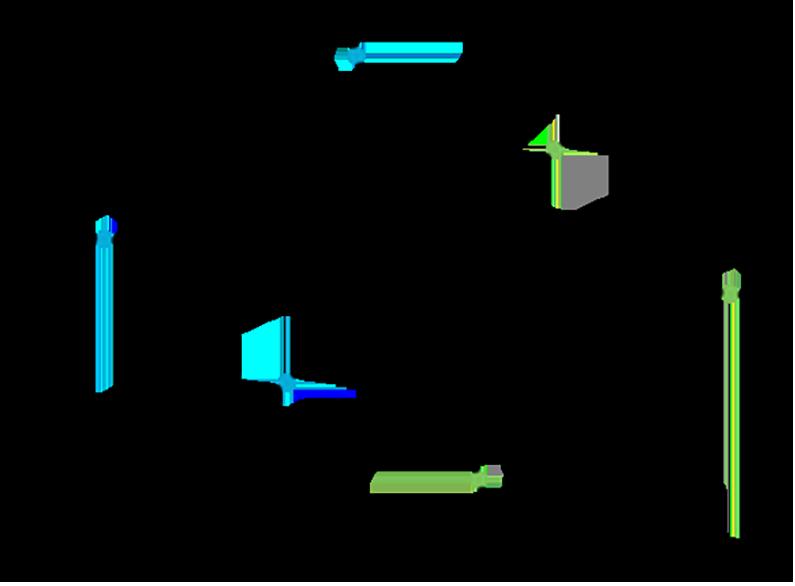
1. Segmento ��′��, porque ��′ es la imagen de �� después de una rotación de 180 grados con centro en �� Esta rotación preserva las distancias y lleva el segmento ���� al segmento ��′��.
2. 79 grados, la misma medida que ∠������, porque la rotación 180 grados con centro en �� lleva ∠������ a ∠��′����′. La rotación conserva las medidas angulares.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
A. Dibuja rectas paralelas ���� y ����
B. Elige un punto cualquiera ��. Gira ���� 90 grados en el sentido de las agujas del reloj alrededor de ��
C. Gira ���� 90 grados en el sentido de las agujas del reloj alrededor de ��
D. ¿Qué observas?
Soluciones posibles
A. Las respuestas varían.
B. Las respuestas varían. La nueva línea debe ser perpendicular a ����
C. Las respuestas varían. La nueva línea debe ser perpendicular a ���� y paralela a ��′��′
D. Las respuestas varían. Ejemplo de respuesta: las dos nuevas líneas rotadas son paralelas.
PROBLEMA 2
Utiliza el diagrama para hallar las medidas de cada ángulo. Explica tu razonamiento.
A. ��∠������
B. ��∠������
C. ��∠������
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 3
Los puntos �� y �� están trazados sobre una recta.
Soluciones posibles
A. 130 grados. ∠������ y ∠������ forman una línea, por lo que suman 180 grados.
B. 130 grados. ∠������ y ∠������ forman una línea, por lo que suman 180 grados.
C. 50 grados. ∠������ y ∠������ forman una recta, por lo que suman 180 grados.
A. Encontrar un punto �� de modo que una rotación 180-grado con centro �� envía �� a �� y �� a ��
B. Hay más de un punto �� que funcione para la parte a?
Soluciones posibles
A. Si. �� es el punto medio del segmento ����, entonces una rotación de 180 grados con centro �� envía �� a �� y �� a ��
B. No. (El punto medio de ���� es el único punto que funciona. 180 rotaciones con cualquier otro centro no envían �� a �� o �� a ��).
PROBLEMA 4
Grado 8, unidad 1, lección 7
En la imagen el triángulo ��′��′��′ es una imagen del triángulo ������ después de una rotación. El centro de rotación es ��
A. ¿Cuál es la longitud del lado ��′��′? Explica cómo lo sabes.
B. ¿Cuál es la medida del ángulo ��? Explica cómo lo sabes.
C. ¿Cuál es la medida del ángulo ��? Explica cómo lo sabes.
Soluciones posibles
A. 4 unidades. Las rotaciones conservan las longitudes de los lados y el lado ��′��′ corresponde al lado ���� bajo esta rotación.
B. 52 grados. Las rotaciones conservan las medidas de los ángulos y los ángulos �� y ��′ se corresponden bajo esta rotación.
C. 50 grados. Las rotaciones conservan las medidas de los ángulos y los ángulos �� y ��′ se corresponden entre sí bajo esta rotación.
PROBLEMA 5
Grado 8, unidad 1, lección 6
El punto (–4, 1) se rota 180 grados en sentido antihorario usando el centro (0, 0). ¿Cuáles son las coordenadas de la imagen?
A. (– 1, – 4)
B. (– 1, 4)
C. (4, 1)
D. (4, – 1)
California . Grado 8
Soluciones posibles
Learning Inc. - Todos los derechos reservados
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas se toman a rectas y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos se toman como ángulos de la misma medida.
Enfoque SMPs
MP6 Prestar atención a la precisión.
MP7 Buscar y hacer uso de la estructura.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.3 I.C.11
LECCIÓN 10 COMPOSICIÓN DE FIGURAS
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predecir lo que podría ocurrir, buscan y hacen uso de la estructura descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Usemos el razonamiento sobre transformaciones rígidas para encontrar medidas sin medir.
META(S) DE APRENDIZAJE
• Puedo encontrar longitudes de lados o medidas de ángulos faltantes usando propiedades de transformaciones rígidas.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Dibujar y etiquetar imágenes de triángulos bajo transformaciones rígidas y luego describir (oralmente y por escrito) propiedades de la figura compuesta creada por las imágenes.
• Generalizar que las medidas de longitudes y ángulos se conservan bajo cualquier transformación rígida.
• Identificar longitudes de lados y ángulos que tienen medidas equivalentes en figuras compuestas y explicar (oralmente y por escrito) por qué son equivalentes.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Pensar, girar y compartir
MLR1: Cada vez más fuerte y más claro
MLR3: Clarificar, criticar, corregir
MLR7: Comparar y conectar
Materiales necesarios
Enfriamiento
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN
DE LA LECCIÓN
Narrativa de la lección
En esta lección, los estudiantes crean formas compuestas utilizando traslaciones, rotaciones y reflexiones de polígonos y continúan observando que las longitudes de los lados y las medidas de los ángulos no cambian. Utilizan este conocimiento para sacar conclusiones sobre las formas compuestas. Más adelante, utilizarán estas habilidades para construir argumentos informales, por ejemplo, sobre la suma de los ángulos de un triángulo.
Cuando los estudiantes giran alrededor de un vértice o se reflejan a través del lado de una figura, es fácil perder la pista del centro de rotación o de la línea de reflexión, puesto que ya forman parte de la figura. También puede ser un reto nombrar los puntos, segmentos y ángulos correspondientes cuando una figura y su transformación comparten un lado. Los estudiantes prestan atención a estos detalles cuidadosamente en esta lección (MP6).
Considere la posibilidad de utilizar la actividad opcional si necesita reforzar la creencia de los estudiantes de que las transformaciones rígidas conservan las distancias y las medidas de los ángulos después de las actividades principales.
RESUMEN DE LA LECCIÓN
Componente de la lección
Estructura Tiempo
Calentamiento Independiente 10 min
Actividad de exploración En parejas 10 min
Actividad de Exploración En parejas 15 min
Actividad de Exploración Opcional Independiente 10 min
Síntesis Todo el grupo 3-5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Descripción breve
Los estudiantes aplican dos transformaciones rígidas diferentes a un triángulo y comparan las medidas de los ángulos en las imágenes resultantes.
Los estudiantes aplican transformaciones rígidas a un triángulo para formar un cuadrilátero.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las conexiones entre las áreas de paralelogramos y triángulos.
Los estudiantes continúan describiendo transformaciones rígidas de triángulos en una cuadrícula. Luego, identifican y justifican las partes de las figuras que tienen longitudes iguales o medidas de ángulos iguales.
Los estudiantes exploran las relaciones entre las longitudes de los lados y las medidas de los ángulos de las imágenes después de aplicar transformaciones rígidas a un triángulo isósceles. Los estudiantes hacen conjeturas sobre los posibles patrones que ocurren cuando la misma transformación se aplica varias veces.
Los estudiantes repasan la idea de que las transformaciones rígidas preservan las longitudes de los lados y las medidas de los ángulos a través de ejemplos adicionales.
Los estudiantes determinan las longitudes de los lados y las medidas de los ángulos que faltan en las figuras transformadas.
El componente de práctica independiente incluye 2 en la lección y 3 problemas de repaso en espiral.
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | ÁNGULOS DE UN TRIÁNGULO ISÓSCELES
(10 minutos)
Los triángulos isósceles son triángulos con (al menos) un par de lados congruentes. Los triángulos isósceles también tienen (al menos) un par de ángulos congruentes. En este calentamiento, los estudiantes muestran por qué esto es así usando movimientos rígidos explotando el hecho de que los movimientos rígidos del plano no cambian las medidas de los ángulos (MP7).
Ó N Da a los estudiantes 3 minutos de tiempo de trabajo tranquilo seguido de una discusión en clase.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual:Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Aquí hay un triángulo.
1. Reflejar el triángulo ������ sobre la línea ����. Etiqueta la imagen de �� como ��′
2. Gira el triángulo ������′ alrededor de �� de modo que ��′ coincida con ��
3. Qué puedes decir de las medidas de los ángulos �� y ��?
RESPUESTAS POSIBLES 1.
SÍNTESIS DE LA ACTIVIDAD
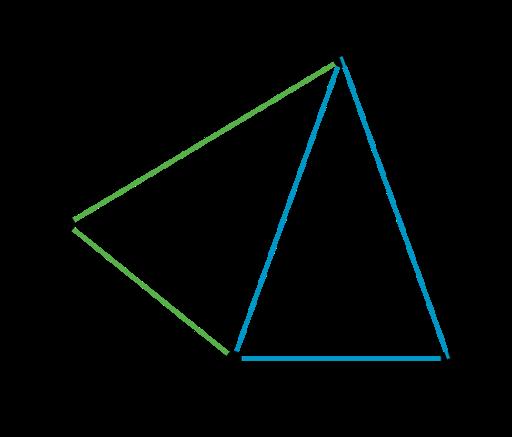
2. Al rotar ������′ como se ha descrito, se devuelve ������′ al triángulo original.
3. Las medidas de los ángulos �� y �� son iguales. Ni la rotación ni la reflexión cambian las medidas de los ángulos, por lo que como estas transformaciones llevan el ángulo en �� al ángulo en ��, deben tener la misma medida.
Asegúrate de que los estudiantes son precisos en su respuesta a la tercera pregunta, indicando tanto el centro del giro como el ángulo de giro.
Si el tiempo lo permite, menciona que también es cierto que cuando un triángulo tiene dos ángulos con la misma medida entonces los lados opuestos a esos ángulos tienen la misma longitud (es decir, el triángulo es isósceles). Esto también se puede demostrar con transformaciones rígidas; refleje primero el triángulo y luego alinee los lados que contienen los pares de ángulos con la misma medida.
Grado 8 . Matemáticas . Unidad 1
ACTIVIDAD DE EXPLORACIÓN | TRIÁNGULO MÁS
UNO (10 minutos)
Rutinas didácticas
Pensar, girar y compatir
MLR1: Cada vez más fuerte y más claro
El propósito de esta tarea es utilizar transformaciones rígidas para describir una imagen importante que los estudiantes han visto en el grado 6 cuando desarrollaron la fórmula para el área de un triángulo. Primero hallaron que el área de un paralelogramo es base ⋅ altura y luego, para hallar 1 2 base ⋅ altura para el área de un triángulo, «compusieron» dos copias de un triángulo para hacer un paralelogramo. El lenguaje «componer» es una forma apropiada para el grado 6 de hablar de una rotación de 180° . El objetivo de esta actividad es desarrollar este lenguaje preciso para describir una situación geométrica familiar.
Los estudiantes deben recordar y utilizar una propiedad importante de las rotaciones de 180 grados, a saber, que la imagen de una recta después de una rotación de 180 grados es paralela a esa recta. Esto es lo que les permite llegar a la conclusión de que la forma que han construido es un paralelogramo (MP7).
INTRODUCCIÓN
Organiza a los estudiantes en grupos de 2. Proporciona acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Unos minutos de trabajo en silencio, seguidos de una puesta en común con un compañero y un debate con toda la clase.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual:Tiempo de procesamiento. Compruebe con cada estudiante, según sea necesario, si ha comprendido cada paso de la actividad.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
Aquí está el triángulo ������.
1. Dibuja el punto medio �� del lado ����
2. Gira el triángulo ������ 180 grados usando el centro �� para formar el triángulo ������. Dibuja y rotula este triángulo.
3. ¿Qué tipo de cuadrilátero es ��������? Explica cómo lo sabes.
1.
2.
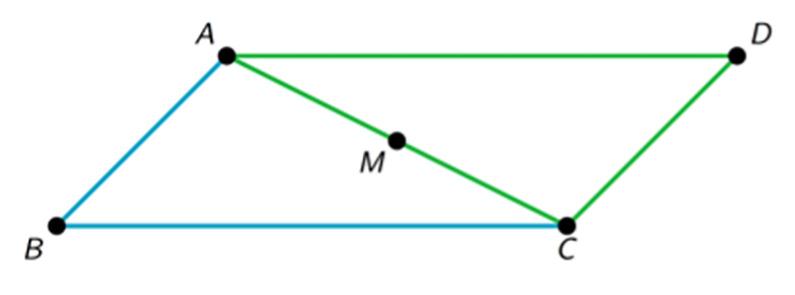
3. Un paralelogramo. La rotación de 180 grados alrededor de �� lleva la línea ���� a la línea ���� por lo que éstas son paralelas. También lleva línea ���� a línea ���� por lo que estas líneas también son paralelas. Eso significa que �������� es un paralelogramo.
California . Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CONCEPTOS ERRÓNEOS PREVISTOS
Los estudiantes pueden tener dificultades para ver la rotación 180° utilizando el centro ��. Esto puede deberse a que no entiendan que �� es el centro de rotación o a que les cueste visualizar una rotación 180° . Ofrezca a estos estudiantes cartulina, una transparencia o la superposición de rotación de antes en esta unidad para ayudarles a ver el triángulo rotado.
SÍNTESIS DE LA ACTIVIDAD
Inicie el debate preguntando: «¿Qué les ocurre a los puntos �� y �� bajo la rotación?». (Terminan en �� y ��, respectivamente). Este tipo de rotación y análisis ocurrirá varias veces en próximas lecciones.
A continuación, pregunta: «¿Cómo sabes que las rectas que contienen lados opuestos de �������� son paralelas?». (Se llevan entre sí mediante una rotación de 180 grados). Como se vio en la lección anterior, la imagen de una rotación de 180° de una línea ℓ es paralela a ℓ. Los estudiantes también vieron que cuando se aplicaban rotaciones de 180° a un par de rectas paralelas se obtenía un (a veces) nuevo par de rectas paralelas que también son paralelas a las rectas originales. La lógica aquí es la misma, salvo que solo se rota una recta 180° en lugar de un par de rectas. No es necesario mencionar esto a menos que los estudiantes lo planteen.
Por último, pregunte a los estudiantes «¿Cómo se relaciona el área del paralelogramo �������� con el área del triángulo ������?». (El área del paralelogramo �������� es el doble del área del triángulo ������ porque está formado por ������ y ������ que tiene la misma área que ������). Más adelante en esta unidad se estudiará más a fondo el área de las formas y sus imágenes bajo transformaciones rígidas.
Apoyo para estudiantes que aprenden el idioma inglés
Escribir, hablar: Rutina 1 del lenguage matemático: Cada vez más fuerte y claro. Esta es la primera vez que se sugiere la rutina 1 de Lenguaje matemático como apoyo en este curso. En esta rutina, los estudiantes reciben una pregunta o un estímulo que les hace reflexionar y se les pide que creen un primer borrador de respuesta. Los estudiantes se reúnen con 2-3 compañeros para compartir y refinar su respuesta a través de la conversación. Mientras se reúnen, los oyentes hacen preguntas como: «¿Qué querías decir con...? y ¿puedes decirlo de otra manera?». Por último, los estudiantes escriben un segundo borrador de su respuesta en el que reflejan las ideas de los compañeros y las mejoras de sus ideas iniciales. El propósito de esta rutina es ofrecer una oportunidad estructurada e interactiva para que los estudiantes revisen y perfeccionen sus ideas por medios verbales y escritos.
Principio(s) de diseño: Optimizar la salida (para la justificación)
Cómo sucede:
1. Utilice esta rutina para proporcionar a los estudiantes una oportunidad estructurada para refinar su justificación para la pregunta «¿Qué tipo de cuadrilátero es ��������? Explica cómo lo sabes». Dé a los estudiantes 2-3 minutos para crear individualmente un primer borrador de respuestas por escrito.
2. Invite a los estudiantes a reunirse con 2-3 otros compañeros para recibir sus comentarios.
Indique al orador que empiece compartiendo sus ideas sin mirar su borrador escrito, si es posible. Los oyentes deben insistir en los detalles y la claridad.
Proporcione a los estudiantes las siguientes sugerencias para que cada uno refuerce sus ideas y aclare su lenguaje: «¿Qué quieres decir cuando dices...?, ¿puedes describirlo de otra manera?, ¿cómo sabes que las rectas son paralelas?, ¿qué les ocurre a las rectas bajo rotaciones?». Asegúrate de que las parejas cambian de papel. Conceda 1-2 minutos para debatir.
3. Indique a los estudiantes que pasen al siguiente compañero y repitan esta reunión estructurada.
Grado 8 . Matemáticas . Unidad 1
1. Cierre las conversaciones por parejas e invite a los estudiantes a revisar y perfeccionar sus escritos en un segundo borrador. Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar el producto final.
Proporcione estos fragmentos de oraciones para ayudar a los estudiantes a organizar sus pensamientos de forma clara y precisa: «El cuadrilátero �������� es un porque...» y «Otra forma de comprobarlo es....».
He aquí un ejemplo de un segundo borrador:
«�������� es un paralelogramo, lo sé porque una rotación de 180 grados crea nuevas líneas que son paralelas a las líneas originales. En esta figura, la rotación 180 grados lleva la línea ���� a la línea ���� y la línea ���� a la línea ����. Lo he comprobado copiando el triángulo en papel de estraza y girándolo 180 grados. Esto significa que la nueva forma tendrá dos pares de lados paralelos. Los cuadriláteros que tienen dos pares de lados paralelos se llaman paralelogramos».
2. Si el tiempo lo permite, haz que los estudiantes comparen su primer y segundo borrador. Si no, que los estudiantes continúen comentando otros aspectos de la actividad.
¿Estás listo para más?
En la actividad, hicimos un paralelogramo tomando un triángulo y su imagen bajo una rotación de 180 grados alrededor del punto medio de un lado. Esta imagen te ayuda a justificar una fórmula muy conocida para el área de un triángulo. ¿Cuál es la fórmula y cómo ayuda la figura a justificarla?
«¿Estás preparado para más?». Respuesta del estudiante
La fórmula para el área de un triángulo es �� = 1 2 ��ℎ, donde �� es la base del triángulo y ℎ la altura correspondiente. En la imagen hemos añadido �� y ℎ al paralelogramo, y marcado dos triángulos de interés con líneas discontinuas. Como los triángulos izquierdo y derecho tienen la misma área, el área del paralelogramo mostrado es la misma que la de un rectángulo con altura ℎ y base ��, es decir, un área de ��ℎ. Como el área de cada triángulo es la mitad del área del paralelogramo, cada triángulo tiene un área �� = 1 2 ��ℎ
ACTIVIDAD
DE EXPLORACIÓN
| TRIÁNGULO MÁS
DOS (15 minutos)
Rutinas didácticas
MLR3: Clarificar, criticar, corregir
Esta actividad continúa la anterior, construyendo esta vez una forma más compleja añadiendo una copia adicional del triángulo original. La imagen de los tres triángulos del enunciado de la tarea será importante más adelante en esta unidad, cuando los estudiantes demuestren que la suma de los tres ángulos de un triángulo es 180°. Para ello, anime a los estudiantes a observar que los puntos ��, �� y �� se encuentran sobre una recta.
Como en muchas de las lecciones en las que se aplican transformaciones para construir formas, los estudiantes utilizan constantemente sus propiedades estructurales (MP7) para sacar conclusiones sobre sus formas. Específicamente, que las transformaciones rígidas preservan los ángulos y las longitudes de los lados.
INTRODUCCIÓN
Mantener a los estudiantes en los mismos grupos. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda unos minutos de trabajo en silencio, seguidos de una puesta en común con un compañero y un debate con toda la clase.
Apoyo para estudiantes con discapacidad
Funcionamiento socioemocional: Tutores. Agrupe a los estudiantes con sus tutores previamente identificados.
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS PREVISTOS
La imagen muestra 3 triángulos. El triángulo 2 y el triángulo 3 son imágenes del triángulo 1 bajo transformaciones rígidas.
1. Describe una transformación rígida que lleve el triángulo 1 al triángulo 2. ¿Qué puntos del triángulo 2 corresponden a los puntos ��, ��, y �� del triángulo original?
2. Describa una transformación rígida que lleva el triángulo 1 al triángulo 3. ¿Qué puntos del triángulo 3 corresponden a los puntos ��, �� y �� del triángulo original?
3. Encuentra dos pares de segmentos de recta en el diagrama que tengan la misma longitud y explica cómo sabes que tienen la misma longitud.
4. Encuentra dos pares de ángulos en el diagrama que tengan la misma medida y explica cómo sabes que tienen la misma medida.
1. Las respuestas varían. Ejemplo de respuesta: Una rotación de 180 grados usando el punto medio del lado ���� como centro. En el triángulo 2, el punto �� corresponde a �� en el original, �� corresponde a �� en el original y �� corresponde a �� en el original.
2. Las respuestas varían. Ejemplos de respuestas: Una rotación de 180 grados usando el punto medio del lado ���� como centro o una rotación de 180 grados usando el punto medio del segmento ���� como centro seguida de una traslación llevando �� a ��. En el triángulo 3, el punto �� corresponde a �� en el original, �� corresponde a �� en el original y �� corresponde a �� en el original.
3. Las respuestas varían. Ejemplo de respuesta: El segmento ���� y el segmento ���� tienen la misma longitud y los segmentos ���� y ���� también tienen la misma longitud. Esto es cierto porque una transformación rígida no cambia las longitudes de los lados de una figura.
4. Las respuestas varían. Ejemplo de respuesta: ∠�� y ∠������ tienen la misma medida y también ∠�� y ∠������. Esto es cierto porque una transformación rígida no cambia las medidas de los ángulos de una figura.
Los estudiantes pueden tener problemas para entender qué pares de puntos se corresponden en las dos primeras preguntas, en particular el hecho de que el punto �� de un triángulo puede no corresponderse con el punto A de otro. Utiliza papel de calco para crear una transparencia del triángulo ������, con sus puntos etiquetados, y deja que los estudiantes realicen su transformación rígida. Deberían ver ��, �� y �� encima de los puntos del nuevo triángulo.
Pida a los estudiantes que enumeren tantos pares diferentes de segmentos de recta coincidentes como puedan encontrar. A continuación, haz lo mismo con los ángulos. Anótelos para que todos puedan verlos. Los estudiantes pueden preguntarse por qué hay menos pares de segmentos de recta: esto se debe a los lados compartidos ���� y ����. Si no preguntan, no hay razón para sacar el tema. Si creas una representación visual de estos pares, quédate con la información sobre los ángulos que tienen la misma medida. El mismo diagrama aparece más adelante en esta unidad y se utiliza para una demostración sobre la suma de las medidas de los ángulos en un triángulo.
Después de esta actividad, pide a los estudiantes que resuman lo que han entendido sobre longitudes y medidas de ángulos bajo transformaciones rígidas. Si los estudiantes no lo dicen directamente, usted debería hacerlo: «Bajo cualquier transformación rígida, las longitudes y las medidas de los ángulos se conservan».
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma inglés
Escribir: Rutina 3 del lenguaje matemático: Aclarar, criticar, corregir. Esta es la primera vez que se sugiere la rutina 3 del lenguaje matemático como apoyo en este curso. En esta rutina, los estudiantes reciben un trabajo matemático incorrecto o incompleto. Puede ser en forma de enunciado escrito, dibujo, pasos de resolución de problemas u otra representación matemática. Por parejas, los estudiantes analizan, reflexionan y mejoran el trabajo escrito corrigiendo los errores y aclarando el significado. Las preguntas típicas son: «¿Hay algo que no esté claro? o ¿hay algún error de razonamiento?». El propósito de esta rutina es que los estudiantes analicen el pensamiento matemático que no es el suyo y consoliden sus conocimientos mediante la comunicación sobre errores conceptuales y ambigüedades en el lenguaje.
Principio(s) de diseño: Maximizar la metaconciencia
Cómo sucede:
1. En la discusión en clase para esta actividad, presente esta descripción incompleta de una transformación rígida que lleva el Triángulo 1 al Triángulo 2:
«���� y ���� son iguales porque se gira ������».
Pida a los estudiantes que identifiquen la ambigüedad de esta respuesta. Pregunte a los estudiantes: «¿Qué crees que intenta decir esta persona? ¿Qué es lo que no está claro?».
2. Conceda a los estudiantes 1 minuto de tiempo individual para responder a las preguntas por escrito y, a continuación, 3 minutos para debatir con un compañero.
Mientras discuten en parejas, proporcione estos fragmentos de oraciones para el andamiaje: «Creo que lo que el autor quiso decir con 'girar ������' fue...» , «La parte que me resulta más confusa es... porque...» y «Creo que lo que esta persona está intentando decir...». Anime al oyente a insistir en los detalles haciendo preguntas de seguimiento para aclarar el significado de la afirmación. Permita que cada miembro de la pareja actúe por turnos como hablante y oyente.
Escuche si los estudiantes utilizan términos geométricos adecuados, como «transformación» y «rotación», para explicar por qué los dos lados son equivalentes.
3. A continuación, pida a los estudiantes que escriban una versión más precisa y expliquen su razonamiento por escrito con su compañero. Las respuestas mejoradas deben incluir para cada paso una explicación, palabras de transición de orden/tiempo (primero, después, luego, etc) y/o razones de las decisiones tomadas durante los pasos.
He aquí dos ejemplos de respuestas mejoradas:
«Primero, utilicé papel de calco para crear una copia del triángulo ������ porque quería transformarlo en el nuevo triángulo.
A continuación, he marcado los vértices en el papel de calco. A continuación, utilizando el punto medio del lado ���� como centro, giré el papel de calco 180 grados, porque así encajaba encima del triángulo 2. Así, los lados ���� y ���� son equivalentes».
o
«Primero, accedí a mi herramienta tecnológica de geometría para crear el dibujo solo del triángulo 1 y 2. A continuación, probé diferentes transformaciones del triángulo 1 para hacer que los puntos ��, �� y �� cayeran encima de los puntos del triángulo 2. El que funcionó fue girar el triángulo 1 180 grados usando el punto medio del lado ����. Finalmente, sé que los lados ���� y ���� son equivalentes porque el triángulo 1 está exactamente encima del triángulo 2».
4. Pida a cada pareja de estudiantes que aporte su respuesta mejorada en un póster, la pizarra o la proyección digital. Pida a las parejas de estudiantes 2-3 que presenten su respuesta a toda la clase e invite a la clase a hacer comparaciones entre las respuestas compartidas y sus propias respuestas.
Escuche las respuestas que identifiquen el par correcto de lados equivalentes y expliquen cómo lo saben. En esta conversación, dé también a los estudiantes la oportunidad de nombrar otros lados y ángulos equivalentes.
5. Cierre la conversación con la generalización de que las medidas de las longitudes y los ángulos se conservan bajo cualquier transformación rígida y, a continuación, pase a la siguiente actividad de la lección.
8 . Matemáticas . Unidad 1
ACTIVIDAD DE EXPLORACIÓN OPCIONAL | TRIÁNGULO UNO MÁS
(10 minutos)
Rutinas didácticas
MLR7: Comparar y conectar
Esta actividad se basa en las ideas de la anterior. Esta vez se construye un patrón a partir de un único triángulo mediante reflexiones y el objetivo es estudiar los ángulos y las longitudes de los lados en este patrón a medida que crece. Si construyen el patrón con cuidado, los estudiantes pueden darse cuenta, después de juntar los triángulos 6 , como en la actividad anterior, de que dos de los lados de los triángulos (un lado del original y un lado del 6) están sobre la misma línea. El patrón del triángulo 6 puede reflejarse sobre esta línea para hacerlo «completo» con 12 copias del triángulo original. Alternativamente, los estudiantes pueden fijarse en el ángulo recto formado por 3 triángulos y razonar que pueden completar un círculo con 4 ángulos rectos. Ambos argumentos son buenos ejemplos de MP8. En lugar de repetir el procedimiento de reflexión 12 veces, es posible utilizar la estructura de lo que han aprendido a lo largo del camino para predecir con precisión cuántas copias hacen un círculo.
INTRODUCCIÓN
Proporcionar acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda 8 minutos de tiempo de trabajo y, a continuación, un breve debate con toda la clase.
Apoyo para estudiantes con discapacidad
Habilidades motoras finas:Tutores compañeros. Agrupe a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que tienen dificultades con la motricidad fina dictar reflexiones según sea necesario.
ENUNCIADO DE TAREA
He aquí un triángulo isósceles ������. Sus lados ���� y ���� tienen longitudes iguales. El ángulo
30 grados. La longitud de ���� es 5 unidades.
1. Reflejar el triángulo ������ a través del segmento ����. Rotula el nuevo vértice ��.
2. ¿Cuál es la medida del ángulo ������?
3. ¿Cuál es la medida del ángulo ������?
4. Refleja el triángulo ������ a través del segmento ����. Etiqueta el punto que corresponde a �� como ��
5. ¿Cuánto mide ����? ¿Cómo lo sabes?
6. ¿Cuál es la medida del ángulo ������?
7. Si continúas reflejando cada nuevo triángulo de esta manera para hacer un patrón, ¿cómo será el patrón? RESPUESTAS POSIBLESS
1. 2. 30° porque las medidas de los ángulos son las mismas después de aplicar una transformación rígida y el ángulo ������ se convierte en el ángulo ������ después de la reflexión.
1. 60° porque ∠������ se obtiene juntando ∠������ y ∠������ y ambos son ángulos de 30 grados. 2.
RESPUESTAS POSIBLES CONTINÚA
Grado 8 . Matemáticas . Unidad 1
3. El segmento ���� mide 5 unidades porque es la imagen del segmento ���� después de una reflexión por lo que tiene la misma longitud que el segmento ����.
4. 90° un ángulo recto porque ∠������ mide 60° y ∠������ mide 30°. Como ∠������ se obtiene juntando ∠������ y ∠������ entonces es un ángulo de 90 grados.
5. Las respuestas varían. Una posible descripción: Eventualmente el punto �� estará completamente rodeado de triángulos, con el 12triángulo tocando ���� de nuevo. Hay 4 ángulos rectos en un círculo completo y cada ángulo recto tiene 3 copias del triángulo original. CONCEPTOS ERRÓNEOS PREVISTOS
Si los estudiantes se atascan con la primera reflexión, sugiérales que utilicen papel de calco. Si es necesario, muéstreles el primer triángulo reflejado y, a continuación, pídales que continúen respondiendo a los problemas y que hagan la siguiente reflexión por su cuenta.
Algunos estudiantes pueden tener dificultades con la longitud de ����, ya que utiliza la información inicial de que el triángulo ������ es isósceles (en caso contrario, ���� no está marcado). Pregunte a los estudiantes qué otra información se da y si pueden utilizarla para averiguar la longitud que falta.
SÍNTESIS DE LA ACTIVIDAD
El objetivo principal de esta actividad es aplicar y reforzar la creencia de los estudiantes de que las transformaciones rígidas conservan las distancias y las medidas de los ángulos. Observa y asegúrate de que los estudiantes lo están haciendo bien. Si no es así, refuerce el concepto. Es fundamental que los estudiantes lo comprendan antes de seguir adelante.
Identifique a algunos estudiantes, cada uno con una respuesta diferente, para que compartan su descripción del patrón que vieron en la última pregunta. La forma en que cada estudiante visualiza y explica esta forma puede dar una idea de las diferentes estrategias utilizadas para crear el patrón final.
Nota: No es importante ni obligatorio que los estudiantes sepan o entiendan cómo encontrar las medidas de los ángulos de la base de los triángulos isósceles o incluso que los ángulos de la base tengan la misma medida (aunque los estudiantes estudian esto en el calentamiento). Más adelante en esta unidad, los estudiantes aprenderán y demostrarán que la suma de las medidas de los ángulos de un triángulo es 180 grados.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR7 Comparar y conectar. Utilice esta rutina cuando los estudiantes describan el patrón que vieron al reflejar el triángulo varias veces. Pida a los estudiantes que consideren qué es igual y qué es diferente en cada descripción. Llame la atención de los estudiantes sobre las diferentes formas en que se explica el patrón. Algunos estudiantes pueden beneficiarse del uso de gestos para apoyar su comprensión de las descripciones. Estos intercambios pueden reforzar el uso del lenguaje matemático y el razonamiento de los estudiantes para dar sentido a las estrategias utilizadas para crear formas compuestas.
Principio(s) de diseño: Maximizar la metaconciencia
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Repasa brevemente las propiedades de las transformaciones rígidas (conservan las longitudes y las medidas de los ángulos). Repasa algunos ejemplos de lados y ángulos correspondientes en figuras que comparten puntos. Por ejemplo, hable sobre qué lados y ángulos se corresponden si esta imagen se encuentra reflejando �������� a través de la línea ����
Señale a los estudiantes que los lados en una línea de reflexión no se mueven, por lo que son su propia imagen cuando reflejamos a través de un lado. Asimismo, el centro de rotación no se mueve, por lo que es su propia imagen cuando giramos a su alrededor. Todos los puntos se mueven con una traslación.
ENFRIARSE | ENCONTRAR MEDIDAS FALTANTES
(5 minutos)
Los estudiantes aplican el hecho de que los movimientos rígidos preservan las longitudes de los lados y los ángulos. Se les presenta una figura y dos imágenes transformadas, y utilizan lo que saben para hallar las longitudes de los lados y los ángulos de las figuras transformadas.
A continuación se muestra un diagrama que muestra el triángulo ������ y algunas transformaciones del triángulo ������
En el lado izquierdo del diagrama, el triángulo ������ ha sido reflejado a través de la línea ���� para formar el cuadrilátero ��������. En la parte derecha del diagrama, el triángulo ������ se ha girado 180 grados utilizando el punto medio �� como centro para formar el cuadrilátero ��������
Utilizando lo que sabes sobre transformaciones rígidas, longitudes laterales y medidas de ángulos, etiqueta tantas longitudes laterales y medidas de ángulos como puedas en los cuadriláteros �������� y ��������
RESPUESTAS POSIBLES
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Este es el diseño de la bandera de Trinidad y Tobago.
Describe una secuencia de traslaciones, rotaciones y reflexiones que lleven el triángulo inferior izquierdo al triángulo superior derecho.
Grado 8 . Matemáticas . Unidad 1
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta: 180 grados de rotación alrededor del punto central de la bandera. Otra Ejemplo de respuesta: El triángulo inferior izquierdo se traslada primero a la derecha de modo que comparta una arista con el triángulo superior derecho. Luego se rota 180 grados alrededor del punto medio del lado común.
PROBLEMA 2
Aquí se muestra una imagen de una versión antigua de la bandera de Gran Bretaña. Hay una transformación rígida que lleva el triángulo 1 al triángulo 2, otra que lleva el triángulo 1 al triángulo 3, y otra que lleva el triángulo 1 al triángulo 4
A. Mide las longitudes de los lados de los triángulos 1 y 2. ¿Qué observas?
B. ¿Cuáles son las longitudes de los lados del Triángulo 3? Explica cómo lo sabes.
C. ¿Tienen los ocho triángulos de la bandera la misma área? Explica cómo lo sabes.
Soluciones posibles
A. Las respuestas varían. Las longitudes laterales de los dos triángulos son iguales.
B. Las longitudes laterales serán las mismas que las del triángulo 1, porque hay una transformación rígida que lleva el triángulo 1 al triángulo 3
C. No. Los cuatro triángulos sin etiquetas numéricas son más grandes, por lo que no tendrán la misma área que los triángulos etiquetados más pequeños.
PROBLEMA 3
Grado 8, unidad 1, lección 9
A. ¿Cuál de las líneas de la imagen es paralela a la línea ℓ? Explique cómo lo sabe.
B. Explique cómo trasladar, rotar o reflejar la línea ℓ para obtener la línea ��
C. Explique cómo trasladar, rotar o reflejar la línea ℓ para obtener la línea ��
Soluciones posibles
A. ��. Estas dos rectas no se cruzan por mucho que se extiendan.
B. La recta �� puede obtenerse trasladando la línea ℓ
C. La recta �� puede obtenerse rotando la línea ℓ
La imagen de abajo muestra cómo trasladar ℓ para obtener �� y cómo rotar ℓ para obtener ��
California . Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 4
Grado 8, unidad 1, lección 6
El punto �� tiene coordenadas (3,4). Después de una traslación 4 unidades a la izquierda, una reflexión a través del eje �� y una traslación 2 unidades hacia abajo, ¿cuáles son las coordenadas de la imagen?
PROBLEMA 5
Grado 8, unidad 1, lección 8
Aquí está el triángulo ������:
Dibuja estas tres rotaciones del triángulo ������ juntas.
A. Gira el triángulo ������ 90 grados en el sentido de las agujas del reloj alrededor de ��
B. Gira el triángulo ������ 180 grados alrededor de ��
C. Rotar el triángulo ������ 270 grados en el sentido de las agujas del reloj alrededor de ��
Reflexiones:
Soluciones posibles (-1, -6)
Soluciones posibles
Cada rotación comparte vértice �� con el triángulo ������. Los cuatro triángulos juntos parecen un molinete.
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas se toman a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
Alineación de estándares y principios de California
8.G.1b Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Los ángulos se toman como ángulos de la misma medida.
8.G.2 Comprender que una figura bidimensional es congruente con otra si la segunda puede obtenerse a partir de la primera mediante una secuencia de rotaciones, reflexiones y traslaciones; dadas dos figuras congruentes, describir una secuencia que muestre la congruencia entre ellas.
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Prestar atención a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.3 I.C.12 II.C.6
LECCIÓN 11 ¿QUÉ ES LO MISMO?
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo y predecir lo que podría ocurrir,
buscan y hacen uso de la estructura descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Decidamos si las figuras son iguales.
META(S) DE APRENDIZAJE
• Puedo decidir visualmente si dos figuras son o no congruentes.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Compara y contrasta (oralmente y por escrito) longitudes laterales, medidas de ángulos y áreas utilizando transformaciones rígidas para explicar por qué una figura es o no congruente con otra.
• Comprende que las figuras congruentes tienen longitudes laterales, medidas de ángulos, y áreas correspondientes iguales.
• Describe (oralmente y por escrito) como «congruentes» dos figuras que pueden moverse una hacia la otra utilizando una secuencia de transformaciones rígidas.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Pensar, girar t compartir
MLR7: Comparar y conectar
MLR2: Recopilar y mostrar
Anticipar, monitorera, seleccionar, secuenciar, conectar
MLR1: Cada vez más fuerte y claro
Materiales necesarios
Enfriamiento
Conjuntos de herramientas de geometría (papel de calco, papel milimetrado, papel de colores)
Materiales necesarios
Se supone que los lápices de colores son una parte habitual del conjunto de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), pero se piden aquí porque en una actividad se pide a los estudiantes que sombreen rectángulos utilizando diferentes colores.
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN
DE LA LECCIÓN
Narrativa de la lección
En esta lección, los estudiantes exploran lo que significa que las figuras sean «iguales» y aprenden que el término congruente es una forma matemática de hablar de figuras iguales que tiene un significado preciso. En concreto, aprenden que dos figuras son congruentes si existe una secuencia de traslaciones, rotaciones y reflexiones que traslada una a la otra. Aprenden que las figuras que son congruentes pueden tener orientaciones diferentes, pero las longitudes y medidas de los ángulos correspondientes son iguales. Acordar y formular la definición de congruencia requiere un uso cuidadoso de un lenguaje preciso (MP6) y se basa en todas las experiencias de los estudiantes hasta el momento en esta unidad, moviendo figuras y tratando de hacerlas coincidir.
Mientras trabajan para decidir si los pares de figuras son o no congruentes, los estudiantes aplicarán el MP7. Para las formas que no son congruentes, ¿qué propiedad se puede identificar en una que no sea compartida por la otra? Puede ser la medida de un ángulo, la longitud de un lado o el tamaño de la forma. Para las formas que son congruentes, ¿hay alguna forma de saberlo aparte de experimentar con papel de calco? En algunos casos, como el de los rectángulos, los estudiantes descubren que basta con mirar la longitud y la anchura para decidir si son congruentes.
En los cursos de primaria, decidir si dos formas son «iguales» suele implicar asegurarse de que tienen la misma forma general (por ejemplo, triángulos o círculos) y de que el tamaño es el mismo. A medida que las formas se hacen más complejas y desarrollamos nuevas formas de medirlas (los ángulos, por ejemplo), se necesita algo más preciso. La definición de congruencia dice que dos figuras son congruentes si existe una secuencia de traslaciones, rotaciones y reflexiones que hace que una figura coincida exactamente con la otra. Esta definición tiene muchas ventajas:
• No requiere medir todas las longitudes de los lados o los ángulos.
• Se aplica igualmente bien a todas las formas, no solo a los polígonos.
• Es precisa e inequívoca: se permiten ciertos movimientos y dos formas son congruentes cuando una se puede mover para alinearse exactamente con la otra.
El material tratado aquí se retomará en secundaria (G-CO.B) desde un punto de vista más abstracto. En 8.º grado, es esencial que los estudiantes adquieran experiencia ejecutando movimientos rígidos con diversas herramientas (papel de calco, coordenadas, tecnología) para desarrollar la intuición que necesitarán cuando estudien estos movimientos (o transformaciones) con mayor profundidad más adelante.
RESUMEN DE LA LECCIÓN
Componente de la lección
Estructura Tiempo
Calentamiento En parejas 5 min
Actividad de Exploración Independiente 15 min
Actividad de Exploración En parejas 10 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Descripción breve
Los estudiantes determinan qué imágenes son una imagen especular de una figura dada.
Los estudiantes determinan informalmente si pares de figuras son congruentes identificando si las figuras son o no iguales.
Los estudiantes establecen conexiones entre el área y el perímetro de rectángulos y si las figuras son congruentes.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la aplicación de la congruencia a situaciones únicas y novedosas.
Los estudiantes discuten la definición de congruente y resumen las formas de determinar si dos figuras son congruentes.
Los estudiantes explican si dos figuras formadas por una reflexión son congruentes.
El componente de práctica independiente incluye 4 problemas de repaso de la lección y 2 problemas de repaso en espiral.
California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | ENCUENTRA LAS MANOS CORRECTAS
(5 minutos)
Rutinas didácticas
Pensar, girar y compartir
En esta actividad, los estudiantes reciben su primera introducción formal a la idea de la orientación en el espejo, a veces llamada «lateralidad» porque las manos izquierda y derecha son reflejos una de la otra. La forma más fácil de decidir cuáles son las manos correctas es levantar las manos y girarlas hasta que coincidan con una figura determinada (o no). Esto les prepara para un debate sobre si las figuras con diferente orientación especular son iguales o no. INTRODUCCIÓN
Organice a los estudiantes en grupos de 2 y proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda 2 minutos de trabajo en silencio, seguidos de tiempo para compartir con un compañero y un debate con toda la clase.
Muestre a los estudiantes esta imagen o levante ambas manos y señale que nuestras manos son imágenes especulares la una de la otra. Estas manos se muestran por detrás. Si es necesario, aclare a los estudiantes que todas las manos de la tarea se muestran por detrás.
Apoyo para los estudiantes con discapacidad
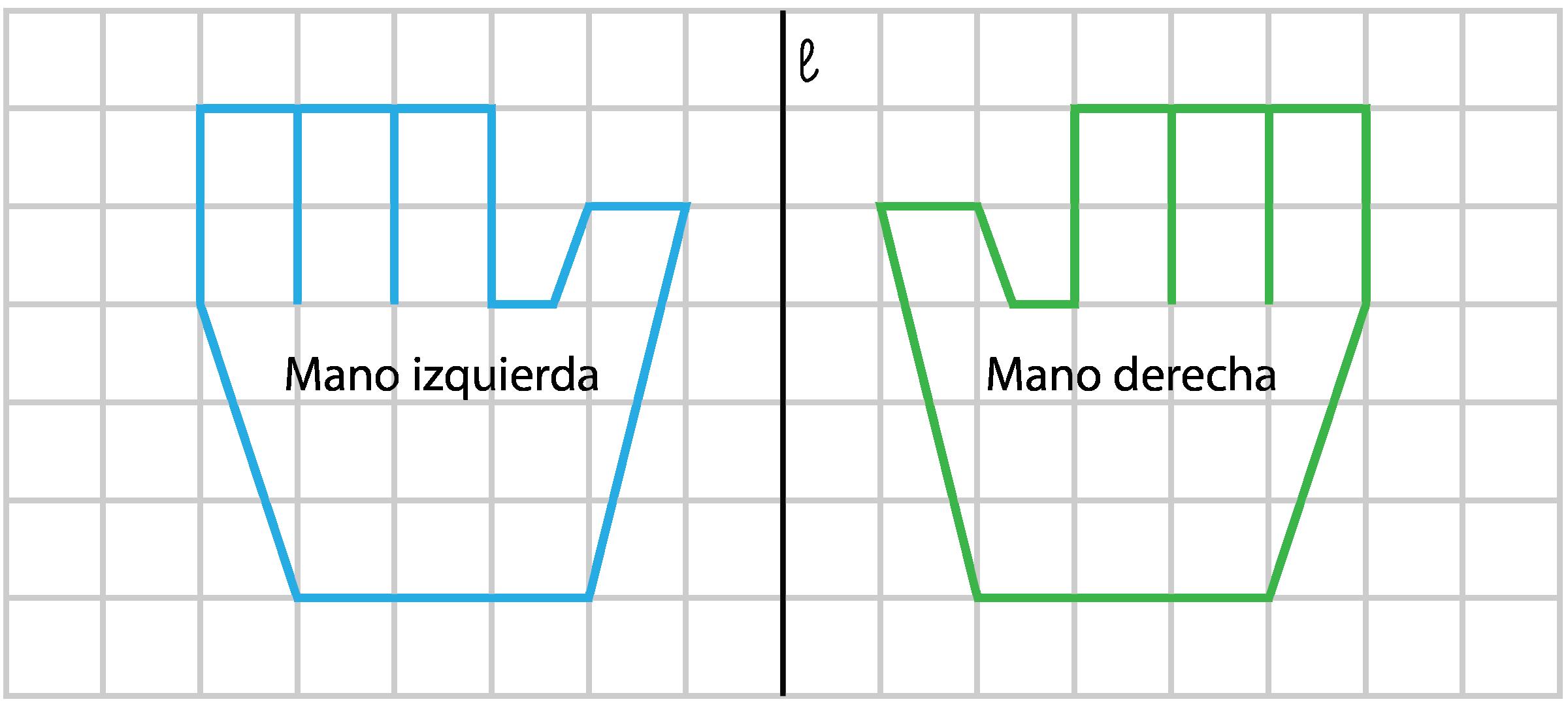
Procesamiento conceptual:Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
Las manos de una persona son imágenes especulares una de otra. En el diagrama, la mano izquierda está marcada. Sombrea todas las manos derechas .
RESPUESTAS
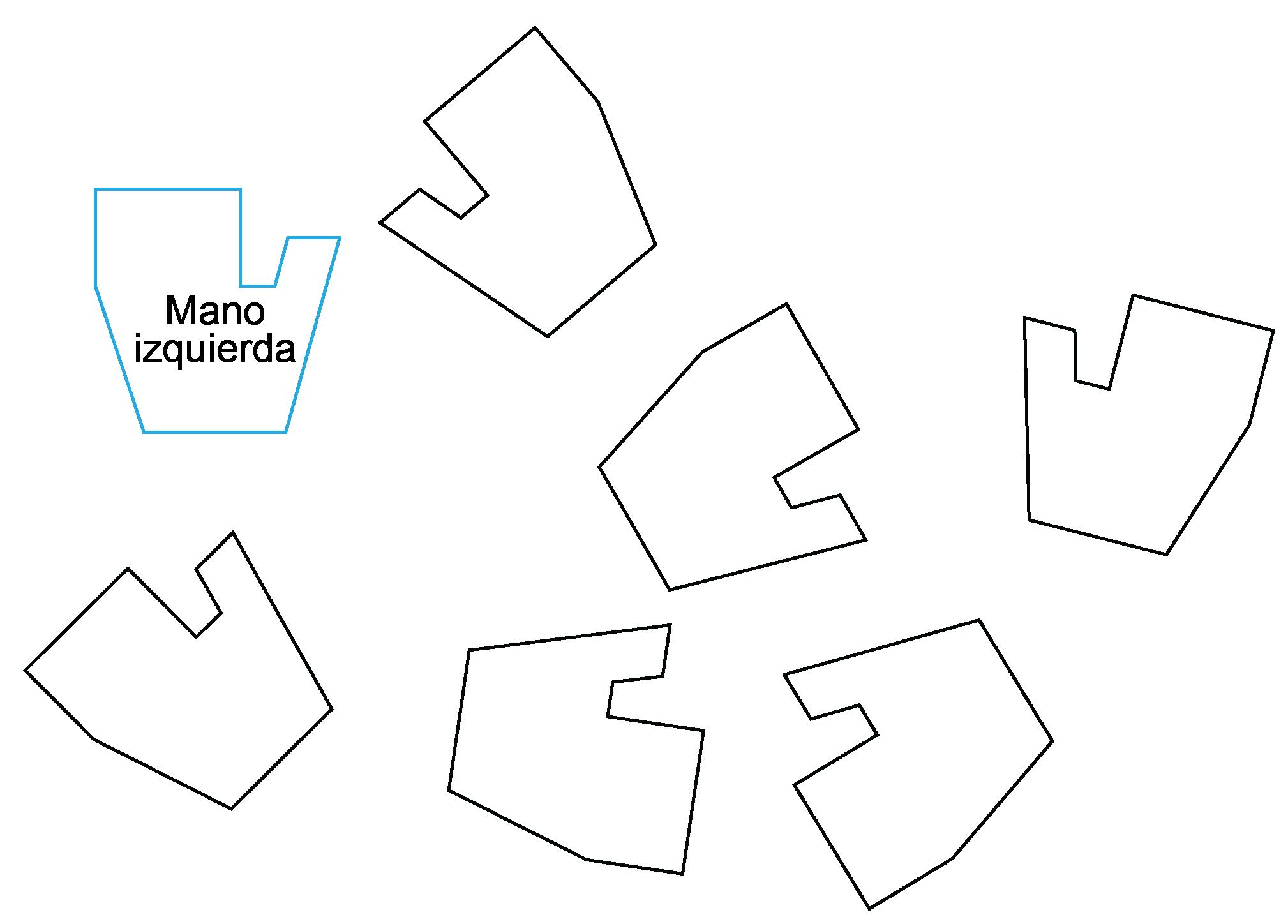
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Pida a los estudiantes que piensen en las formas en que las manos izquierda y derecha son iguales, y en las formas en que son diferentes.
Algunas formas en que son iguales incluyen:
• Las longitudes de los lados y los ángulos de las manos izquierda y derecha coinciden entre sí.
• Si se voltea una mano izquierda, puede coincidir perfectamente con una mano derecha (y viceversa).
Algunas formas en que son diferentes incluyen:
• No pueden alinearse entre sí sin voltear una de las manos.
• No es posible hacer que una mano izquierda y una derecha físicas se alineen entre sí, excepto como «imágenes especulares».
ACTIVIDAD DE EXPLORACIÓN | ¿SON IGUALES? (15 minutos)
Rutinas didácticas
MLR7: Comparar y conectar
MLR2: Recopilar y mostrar
Anticipar, monitorear, seleccionar, secuenciar, conectar
En el trabajo anterior, los estudiantes aprendieron a identificar traslaciones, rotaciones y reflexiones. Empezaron a estudiar qué les ocurre a diferentes formas cuando se aplican estas transformaciones. Utilizaron secuencias de traslaciones, rotaciones y reflexiones para construir nuevas figuras y estudiar configuraciones complejas para comparar, por ejemplo, ángulos verticales formados por un par de rectas que se cruzan. A partir de esta lección, las transformaciones rígidas se utilizan para formalizar lo que significa que dos formas sean iguales, una noción que los estudiantes han estudiado y aplicado desde los primeros cursos de primaria.
En esta actividad, los estudiantes expresan lo que significa que dos formas sean iguales considerando ejemplos cuidadosamente elegidos. Los estudiantes trabajan para decidir si los distintos pares de formas son iguales o no. A continuación, la clase discute sus conclusiones y llega a un consenso sobre lo que significa que dos formas sean iguales: la palabra «iguales» se sustituye por «congruentes» en adelante.
Puede haber discusiones en las que se requiera una reflexión para emparejar una forma con la otra. Los estudiantes pueden discrepar sobre si deben considerarse iguales o no, por lo que debe fomentarse el debate. Esta actividad fomenta el MP3, ya que los estudiantes deben explicar por qué creen que un par de figuras son iguales o no.
Vigile a los estudiantes que utilicen estos métodos para decidir si las formas son iguales o no e invíteles a compartirlos durante el debate:
• Observación (a menudo es suficiente para decidir que no son iguales): Anime a los estudiantes a articular qué característica o características de las formas les ayudan a decidir que no son iguales.
• Medir las longitudes de los lados con una regla o los ángulos con un transportador: A continuación, utilice las diferencias entre estas medidas para argumentar que dos formas no son iguales.
California . Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
• Recortar una forma e intentar colocarla encima de la otra: Una variante de esto sería separar las dos imágenes y luego intentar poner una encima de la otra o utilizar papel de calco para trazar una de las formas. Se trata de una versión de de la aplicación de transformaciones estudiada ampliamente antes de esta lección.
INTRODUCCIÓN
Conceda (5 minutos) de tiempo de trabajo tranquilo seguido de un debate con toda la clase. Proporcione acceso a las herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Apoyo para estudiantes que aprenden el idioma inglés
Conversar, representar: MLR2 Recopilar y mostrar. Mientras los estudiantes trabajan comparando formas, camine y escuche a los estudiantes hablar. Anote las frases comunes o importantes (por ejemplo, longitud del lado, girado, reflejado, etc.), junto con los bocetos o diagramas útiles en una pantalla. Preste especial atención a la forma en que los estudiantes utilizan el lenguaje de transformación al determinar si las formas son iguales. Anote las palabras y los dibujos de los estudiantes en una pantalla para consultarlos durante los debates de toda la clase a lo largo de esta lección y del resto de la unidad. Esto ayudará a los estudiantes a utilizar el lenguaje matemático durante sus debates en grupo y en clase.
Principio(s) de diseño: Apoyar la adquisición de sentido
Apoyo para estudiantes con discapacidad
Funcionamiento socioemocional: Tutores. Agrupe a los estudiantes con sus tutores previamente identificados.
Para cada par de formas, decide si son iguales o no.
1. Las dos formas son iguales. Al girar la forma de la izquierda (180 grados) alrededor del punto superior y moverla hacia abajo y a la derecha, se ajusta perfectamente a la forma de la derecha.
2. No son iguales. Posible estrategia: Los lados de las figuras son iguales, pero los ángulos no. La figura de la derecha está más compacta (y tiene menos área), así que no son iguales.
3. Las dos formas son iguales. Al girar la forma de la izquierda (180 grados) alrededor del punto superior y moverla hacia abajo y a la derecha, se ajusta perfectamente a la forma de la derecha.
4. No son iguales. Posible estrategia: Los lados de las figuras son iguales, pero los ángulos no. La figura de la derecha está más compacta (y tiene menos área), así que no son iguales.
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
RESPUESTAS POSIBLES CONTINUACIÓN
1. Son iguales. Posible estrategia: Las dos formas son flechas rizadas y parece que tienen el mismo tamaño. Reflexionando sobre una recta vertical a medio camino entre las dos figuras, parece que coinciden perfectamente entre sí. O bien, no son iguales. Posible estrategia: La flecha rizada de la izquierda se mueve en el sentido de las agujas del reloj, mientras que la de la derecha lo hace en sentido contrario.
2. No son iguales. Posible estrategia: Las formas generales son iguales y los ángulos coinciden, pero las longitudes de los lados son diferentes. La figura de la izquierda es más grande que la de la derecha.
3. No son iguales. Posible estrategia: La parte que sobresale del lado derecho está más alta en la primera pieza y más baja en la segunda. Construyendo un rompecabezas, ambas formas no encajarían en el mismo sitio.
Los estudiantes pueden pensar que todas las formas son iguales porque tienen la misma forma general a primera vista. Pide a estos estudiantes que busquen las diferencias que puedan encontrar entre los pares de formas.
Para cada par de formas, sondea a la clase. Cuenta cuántos estudiantes decidieron que cada par era igual o no. A continuación, para cada par de formas, selecciona al menos a un estudiante para que defienda su razonamiento. (Si hay acuerdo unánime sobre alguno de los pares de formas, éstos pueden tratarse rápidamente, pero permita que la clase escuche al menos un argumento para cada par de figuras).
Secuencie estas explicaciones en el orden sugerido en la narración de la actividad: observaciones generales, toma de medidas y aplicación de transformaciones rígidas con ayuda de papel de calco.
El más general y preciso de estos criterios es el tercero, que constituye el fundamento de la definición matemática de congruencia: Los otros dos son consecuencias. Los movimientos permitidos por las transformaciones rígidas no cambian la forma, el tamaño, las longitudes de los lados ni las medidas de los ángulos.
Puede haber desacuerdo sobre si incluir o no las reflexiones a la hora de decidir si dos formas son iguales. He aquí algunas razones para incluir reflexiones:
• Una figura y su imagen reflejada pueden coincidir perfectamente (usando una reflexión).
• Los ángulos correspondientes y las longitudes laterales de una figura y su imagen reflejada son iguales.
Y he aquí algunas razones en contra de incluir reflexiones:
• Un pie izquierdo y un pie derecho (por ejemplo) no funcionan exactamente igual. Si tuviéramos literalmente dos pies izquierdos, ¡sería difícil funcionar con normalidad!
• Las traslaciones y rotaciones pueden realizarse, por ejemplo, colocando una hoja de papel vegetal encima de otra y trasladándola o rotándola físicamente. En el caso de un reflejo, la forma típica de hacerlo es levantar una de las hojas y darle la vuelta.
Si no surge este desacuerdo, pida a los estudiantes que piensen por qué alguien podría llegar a la conclusión de que el par de figuras de C no son iguales. Explique a los estudiantes que la gente en el mundo puede querer decir muchas cosas cuando dice que dos cosas son «iguales». En matemáticas a menudo es necesario ser más preciso, y un tipo de «lo mismo» es congruente. (Dos figuras son congruentes si una es reflejo de la otra, pero, si se quisiera, se podría definir un término diferente, un tipo diferente de «lo mismo», en el que no se permitiera la inversión).
Explica que la figura A es congruente con la figura B si existe una secuencia de traslaciones, rotaciones y reflexiones que hacen que la figura A coincida exactamente con la figura B.
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
DE LA ACTIVIDAD CONTINUACIÓN
SÍNTESIS
Combinando esto con la discusión anterior, algunas observaciones generales sobre figuras congruentes incluyen
• Los lados correspondientes de figuras congruentes son congruentes.
• Los ángulos correspondientes de figuras congruentes son congruentes.
• El área de figuras congruentes es igual.
¿Qué puede ser «diferente» en dos figuras congruentes? La ubicación (no tienen que estar una encima de la otra) y la orientación (se requiere una reflexión para mover una a la otra) pueden ser diferentes.
Apoyo a los estudiantes de inglés
Hablar: MLR7 Comparar y conectar. Para apoyar a los estudiantes en la explicación de cada par de formas, pedirles que consideren por qué una forma es igual o diferente de otra. Llame la atención de los estudiantes sobre la asociación entre las observaciones generales, la toma de medidas y la aplicación de transformaciones rígidas para utilizarlas en la comparación de segmentos, ángulos, reflexiones y rotaciones ( por ejemplo, pregunte: «Para iguras que no son congruentes, ¿qué propiedad se puede identificar en una que no comparta la otra? o para las formas que son congruentes, ¿hay alguna manera de saberlo aparte de experimentar con papel de calco?»). Estos intercambios reforzarán en los estudiantes el uso del lenguaje matemático y el razonamiento basado en transformaciones rígidas.
Principio(s) de diseño: Apoyar la creación de sentido
ACTIVIDAD DE EXPLORACIÓN | ÁREA, PERÍMETRO, Y CONGRUENCIA
(10 minutos)
Rutinas didácticas
Pensar, girar y compartir
MLR1: Cada vez más fuerte y más claro
A veces la gente caracteriza la congruencia como «mismo tamaño, misma forma». El problema con esto es que no está claro qué queremos decir con «misma forma». Todas las figuras de esta actividad tienen la misma forma porque todas son rectángulos, pero no todas son congruentes. Los estudiantes examinan un conjunto de rectángulos y los clasifican según su área y su perímetro. A continuación, identifican cuáles son congruentes. Como las formas congruentes tienen la misma longitud de lado, los rectángulos congruentes tienen el mismo perímetro. Pero los rectángulos con el mismo perímetro son no siempre congruentes. Las formas congruentes, incluidos los rectángulos, también tienen la misma área. Pero los rectángulos con la misma área no son siempre congruentes. Resaltar las características importantes, como el perímetro y el área, que pueden utilizarse para establecer rápidamente que dos figuras no son congruentes desarrolla el MP7, identificando las propiedades fundamentales compartidas por cualquier par de figuras congruentes.
Diga a los estudiantes que investigarán más a fondo cómo encontrar el área y el perímetro de una figura puede ayudar a demostrar que dos figuras no son congruentes. Puede que haya pasado algún tiempo desde que los estudiantes pensaron en los términos área y perímetro. Si es necesario, para recordar a los estudiantes qué significan estas palabras y cómo se pueden calcular, muestra un rectángulo como éste para que todos lo vean. Pida a los estudiantes que expliquen qué significa perímetro y cómo pueden hallar el perímetro y el área de este rectángulo.
Organice a los estudiantes en grupos de 2. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) (se piden específicamente lápices de colores). Conceda 2 minutos para trabajar en silencio y, a continuación, comparta con un compañero y discuta con toda la clase.
Grado 8 . Matemáticas . Unidad 1
Apoyo para los estudiantes con discapacidad
Funcionamiento ejecutivo: Organizadores gráficos. Proporcionar un diagrama de Venn con el que comparar las similitudes y diferencias entre los rectángulos.
1. ¿Cuál de estos rectángulos tiene la misma área que el rectángulo R pero diferente perímetro?
2. ¿Qué rectángulos tienen el mismo perímetro pero diferente área?
3. ¿Cuáles tienen la misma área y el mismo perímetro?
4. Usa materiales del kit de herramientas de geometría para decidir qué rectángulos son congruentes. Sombrea los rectángulos congruentes con el mismo color.
RESPUESTAS POSIBLESS
El perímetro del rectángulo R es 10 unidades ya que 3 + 2 + 3 + 2 = 10 mientras que su área es 6 unidades cuadradas ya que 2 ⋅ 3 = 6. Todos los rectángulos de la figura comparten al menos una de estas propiedades (el perímetro o el área), pero solo los rectángulos 2 unidades por 3 unidades comparten ambas:
1. Los rectángulos B y C tienen la misma área (6 unidades cuadradas) pero diferente perímetro (14 unidades)
2. Los rectángulos D y F tienen el mismo perímetro (10 unidades) pero diferente área (4 unidades cuadradas)
3. Los rectángulos A y E tienen la misma área y perímetro: solo su posición y orientación en la página es diferente.
4. Los rectángulos 2 por 3 son congruentes con el rectángulo R. En cada caso, el rectángulo R se puede trasladar y girar para que coincida perfectamente con el rectángulo 2 por 3 . El mismo argumento demuestra que los rectángulos B y C son congruentes al igual que los rectángulos D y F.
Vigila a los estudiantes que piensan en la pregunta final en términos de «misma forma y tamaño». Recuérdales la definición de congruencia introducida en la última actividad.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Invite a los estudiantes que utilizaron el lenguaje de las transformaciones para responder a la pregunta final a que describan cómo determinaron que un par de rectángulos son congruentes.
El perímetro y el área son dos formas diferentes de medir el tamaño de una forma. Pregunta a los estudiantes:
• «¿Tienen los rectángulos congruentes el mismo perímetro? Explica tu razonamiento». (Sí. Los movimientos rígidos no cambian las distancias, por lo que los rectángulos congruentes tienen el mismo perímetro).
• «¿Tienen los rectángulos congruentes la misma área? Explica tu razonamiento». (Sí. Los movimientos rígidos no cambian el área o los movimientos rígidos no cambian las distancias y por tanto no cambian la longitud por la anchura en un rectángulo).
• «¿Son siempre congruentes los rectángulos con el mismo perímetro?». (No. Los rectángulos D y F tienen el mismo perímetro pero no son congruentes).
• «¿Son siempre congruentes los rectángulos con la misma área?». (No. Los rectángulos B y C tienen la misma área pero no son congruentes).
Una lección importante es que medir el perímetro y el área es un buen método para demostrar que dos figuras no son congruentes si estas medidas difieren. Cuando las medidas son las mismas, se necesita más trabajo para decidir si dos figuras son o no congruentes.
Un riesgo de utilizar rectángulos es que los estudiantes pueden llegar a la conclusión errónea de que si dos figuras tienen la misma área y el mismo perímetro, entonces son congruentes. Si esto ocurre, reta a los estudiantes a pensar en dos figuras que tengan la misma área y el mismo perímetro, pero que no sean congruentes. He aquí un ejemplo:
Apoyo para estudiantes que aprenden el idioma inglés
Escribir, hablar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina con sucesivos intercambios de parejas para dar a los estudiantes una oportunidad estructurada de revisar sus estrategias escritas para decidir qué rectángulos son congruentes. Pida a cada estudiante que se reúna con 2-3 otros compañeros en una fila para recibir comentarios. Proporcione a los estudiantes indicaciones que les ayuden a reforzar sus ideas y a clarificar su lenguaje (por ejemplo: «¿Cómo se utilizó una secuencia de transformaciones para...?, ¿qué propiedades comparten las formas?, ¿qué era diferente y qué era igual en cada par?», etc.). Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar su producto final.
Principio(s) de diseño: Optimizar el resultado (para la explicación)
¿Estás listo para más?
En el cuadrado ��������, los puntos ��, ��, �� y �� son puntos medios de sus lados respectivos. ¿Qué fracción del cuadrado �������� está sombreada? Explica tu razonamiento.
«¿Estás listo para más?». Respuesta del estudiante
1 5 del cuadrado �������� está sombreado. El razonamiento varía. Ejemplo de razonamiento: Transformar las piezas sin sombrear en cuatro cuadrados congruentes que lo sean cada uno con el cuadrado sombreado.
Es interesante generalizar este problema de modo que los puntos ��, ��, �� y �� dividan los lados de �������� en una proporción distinta de 1: 1
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Pida a los estudiantes que expongan su mejor definición de congruente. (Dos formas son congruentes cuando hay una secuencia de traslaciones, rotaciones y reflexiones que llevan una forma a la otra).
Algunos conceptos importantes para discutir:
• «¿Cómo puedes comprobar si dos formas son congruentes?». (Para los rectángulos, la longitud de los lados es suficiente. Para formas más complejas, es necesario experimentar con transformaciones).
• «¿Son congruentes una forma y su imagen especular?». (Sí, porque un reflejo lleva una forma a su imagen especular).
• «¿Cuáles son algunas formas de saber que dos formas no son congruentes?». (Dos formas no son congruentes si tienen áreas, longitudes de lados o ángulos diferentes).
• «¿Cuáles son algunas propiedades que comparten las formas congruentes?». (Tienen el mismo número de lados, lados de la misma longitud, los mismos ángulos, la misma área).
ENFRIARSE | IMÁGENES ESPECULARES
(5 minutos)
A lo largo de esta unidad, los estudiantes han utilizado traslaciones, rotaciones y reflexiones para mover figuras en el plano. En esta lección, los estudiantes han aprendido que la figura A es congruente con la figura B cuando hay una secuencia de traslaciones, rotaciones y reflexiones que llevan la figura A a la figura B. Aquí aplican esto a dos figuras no poligonales, una de las cuales es un reflejo de la otra.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
La figura B es la imagen de la figura A cuando se refleja a través de la línea ℓ. ¿Son congruentes la figura A y la figura B? Explica tu razonamiento.
Sí, son congruentes. Existe una transformación rígida que lleva una figura a la otra, por lo que son congruentes.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Si dos rectángulos tienen el mismo perímetro, ¿tienen que ser congruentes? Explica cómo lo sabes.
Soluciones posibles
No. Dos rectángulos no congruentes pueden tener el mismo perímetro. Por ejemplo, un rectángulo con longitudes laterales 3 pulgadas y 4 pulgadas no es congruente con un rectángulo con longitudes laterales 2 pulgadas y 5 pulgadas. Aunque los ángulos de todos los rectángulos tienen la misma medida, cuando dos figuras son congruentes todas las longitudes de los lados y las medidas de los ángulos son iguales.
Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 2
Dibuja dos rectángulos que tengan la misma área, pero que no sean congruentes.
PROBLEMA 3
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta: un rectángulo 2 por 6 o y un rectángul 3 por 4
Para cada par de figuras, decide si parece o no que las dos figuras son congruentes. Explica tu razonamiento.
A. B.
Soluciones posibles
A. Parece que son congruentes. Si se traza la figura de la derecha, se puede desplazar y parece que coincide perfectamente con la figura de la izquierda. Esto se puede hacer con una rotación (90 grados en el sentido de las agujas del reloj) y luego una traslación.
B. Parecen congruentes. Si �������������� se refleja sobre una línea vertical y luego se traslada, parece caer encima de ��������������
PROBLEMA 4
A. Refleje el cuadrilátero A sobre el eje ��. Etiqueta la imagen como cuadrilátero B. Refleje el cuadrilátero B sobre el eje ��. Etiqueta la imagen C.
Soluciones posibles
B. ¿Son congruentes los cuadriláteros A y C? Explica cómo sabe.
A. B. Sí, porque existe una transformación rígida que lleva �� a ��, las dos figuras son congruentes.
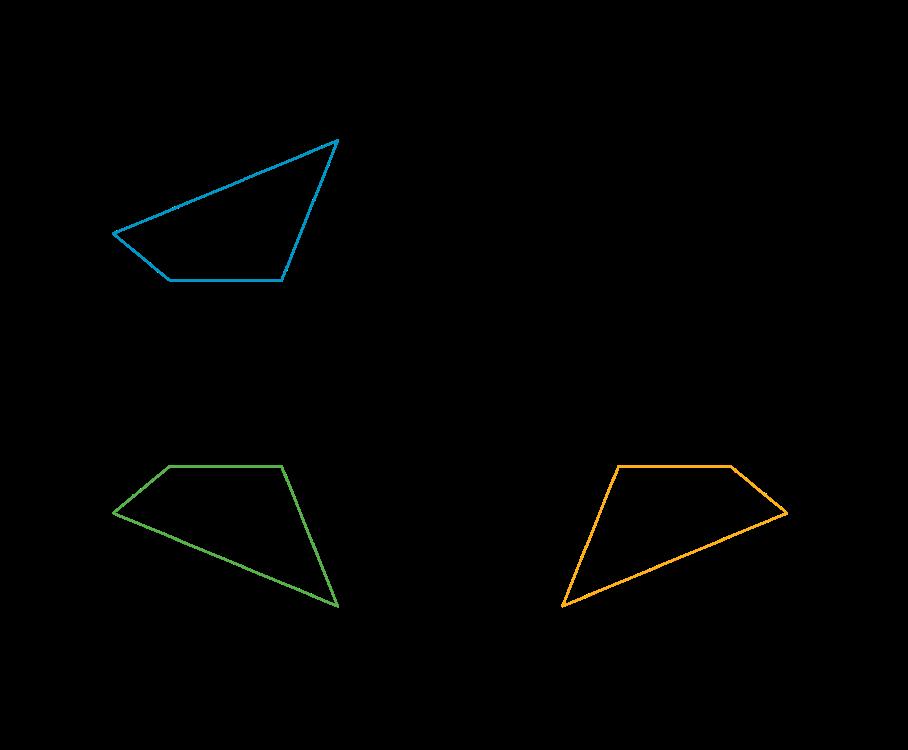
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 5
Grado 8, unidad 1, lección 6
El punto (–2, –3) se gira 90 grados en sentido antihorario con centro (0, 0). ¿Cuáles son las coordenadas de la imagen?
A. (–3, – 2) B. (– 3, 2) C. (3, – 2) D. (3, 2)
Soluciones posibles
C
PROBLEMA 6
Grado 8, unidad 1, lección 7
Describa una transformación rígida que lleve el polígono A al polígono B.
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta: Rotar el polígono A 180 grados alrededor de (0, 0).
Reflexiones:
Math Nation California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.2 Entender que una figura bidimensional es congruente con otra si la segunda se puede obtener a partir de la primera mediante una secuencia de rotaciones, reflexiones y traslaciones; dadas dos figuras congruentes, describir una secuencia que muestre la congruencia entre ellas.
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP5 Usar herramientas apropiadas estratégicamente.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1 I.B.5
LECCIÓN 12 POLÍGONOS CONGRUENTES
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo
construyen argumentos viables y critican el razonamiento de otros
META(S) DE APRENDIZAJE
• Decidamos si dos figuras son congruentes.
META(S) DE APRENDIZAJE
descubriendo la forma y el espacio.
• Puedo decidir visualmente si dos figuras son congruentes o no.
OBJETIVOS DE APRENDIZAJE PARA
EL MAESTRO
• Comprender que figuras con la misma área y perímetro pueden o no ser congruentes.
• Criticar argumentos (oralmente) de que dos figuras con lados correspondientes congruentes pueden ser figuras no congruentes.
• Justificar (oralmente y por escrito) que dos polígonos en una cuadrícula son congruentes usando la definición de congruencia en términos de transformaciones.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR7: Comparar y conectar
Anticipar, monitorear, seleccionar, secuenciar, conectar
Turnarse
MLR8: Apoyos para el debate
Materiales necesarios
Enfriamiento
Conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Preparación necesaria
Si decide que los estudiantes realicen la actividad opcional, tenga preparados conjuntos de objetos para que los estudiantes construyan cuadriláteros. Cada pareja de estudiantes necesita 12 objetos (como palillos, lápices o popotes) para utilizarlos como lados de los cuadriláteros: 8 objetos de una longitud y 4 objetos de otra longitud.
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
En esta lección, los estudiantes encuentran transformaciones rígidas que demuestran que dos figuras son congruentes y argumentan por qué dos figuras no son congruentes. Aprenden que, para muchas figuras, el simple hecho de que las longitudes de los lados correspondientes sean iguales no garantiza que las figuras sean congruentes.
En la lección anterior, los estudiantes definieron lo que significa que dos figuras sean congruentes y comenzaron a aplicar la definición para determinar si un par de figuras es congruente. En la primera parte de esta lección, los estudiantes siguen determinando si los pares de figuras son o no congruentes, pero aquí cuentan con la estructura adicional de una cuadrícula. Con esta estructura adicional, los estudiantes utilizan MP6 (prestar atención a la precisión) al describir traslaciones, reflexiones y rotaciones. Por ejemplo:
• En lugar de «traslada hacia abajo y hacia la izquierda», los estudiantes pueden decir «traslada 3 unidades hacia abajo y 2 unidades hacia la izquierda».
• En lugar de «refleja la figura», los estudiantes pueden decir «refleja la figura sobre esta línea vertical».
Además, los estudiantes tienen que tener cuidado al nombrar los polígonos congruentes, asegurándose de que los vértices correspondientes aparecen en el orden correcto.
Una parte opcional de la lección comienza a examinar los criterios para decidir cuándo dos formas son congruentes. Si dos formas son congruentes, entonces sus lados y ángulos correspondientes son congruentes. ¿Es cierto que basta con que los lados (o los ángulos) sean iguales para determinar si dos figuras son congruentes? Los estudiantes investigan esta cuestión para cuadriláteros en dos situaciones diferentes:
• 4 longitudes de lado congruentes.
• 2 pares de longitudes de lado congruentes donde los pares son de diferente longitud.
RESUMEN DE LA LECCIÓN
Componente de la lección
Estructura Tiempo
Calentamiento Independiente 5 min
Actividad de Exploración Independiente 12-15 min
Actividad de Exploración En parejas 10-15 min
Actividad de Exploración Opcional En parejas 10 min
Síntesis Todo el Grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
. Grado 8
Descripción breve
Los estudiantes reconocen qué triángulos congruentes son imágenes de un triángulo dado bajo una traslación.
Los estudiantes usan una secuencia de transformaciones rígidas para justificar si pares de figuras mostradas en un plano de coordenadas son congruentes.
Los estudiantes identifican y explican si los pares de polígonos mostrados en un plano de coordenadas son congruentes.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la congruencia creando polígonos que satisfagan condiciones dadas.
Los estudiantes crean cuadriláteros a partir de objetos dados y verifican si su compañero creó una figura congruente a la suya.
Los estudiantes discuten las características de los polígonos que son congruentes y no congruentes usando ejemplos de la lección.
Los estudiantes describen una secuencia de transformaciones rígidas para demostrar que una figura es congruente con otra.
El componente de práctica independiente incluye 2 en la lección y 2 problemas de repaso en espiral.
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | IMÁGENES TRADUCIDAS (5 minutos)
Esta tarea ayuda a los estudiantes a pensar estratégicamente sobre qué tipo de transformaciones podrían utilizar para demostrar que dos figuras son congruentes. Ser capaz de reconocer cuando dos figuras tienen una orientación especular o rotacional es útil para planificar una secuencia de transformaciones.
INTRODUCCIÓN
Proporcionar acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda 2 minutos de tiempo de trabajo en silencio seguidos de un debate con toda la clase.
Todos estos triángulos son congruentes. A veces podemos llevar una figura a otra con una traslación. Sombrea los triángulos que son imágenes del triángulo ������ bajo una traslación. RESPUESTAS
Si algún estudiante afirma que un triángulo es una traslación cuando en realidad no lo es, pídele que utilice papel de calco para demostrar cómo trasladar el triángulo original para aterrizar en él. Inevitablemente, tendrán que girar o voltear el papel. Recuérdales que una traslación consiste únicamente en deslizar el papel vegetal sin girarlo ni voltearlo.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Señale a los estudiantes que si nos limitamos a trasladar una figura, la imagen acabará apuntando en la misma dirección. (Más formalmente, la figura y su imagen tienen la misma orientación especular y rotacional). Las rotaciones y reflexiones generalmente (pero no siempre) cambian la orientación de una figura.
Para un par de triángulos que no son traslaciones de la figura dada, pregunte qué secuencia de transformaciones mostraría que son congruentes, y demuestre cualquier rotación o reflexión requerida.
ACTIVIDAD DE EXPLORACIÓN | PARES CONGRUENTES
(PARTE 1) (15
minutos)
Rutinas didácticas
MLR7: Comparar y conectar
Anticipar, monitorear, seleccionar, secuenciar, conectar
En la lección anterior, los estudiantes formularon una definición matemática precisa de congruencia y comenzaron a aplicarla para determinar si pares de figuras son o no congruentes. Esta actividad es una continuación directa de ese trabajo con la estructura adicional de una cuadrícula cuadrada. La cuadrícula cuadrada puede ser una estructura útil para describir las distintas transformaciones de forma precisa. Por ejemplo, con las traslaciones podemos hablar de traslación hacia arriba o hacia abajo o hacia la izquierda o la derecha en un número determinado de unidades. Del mismo modo, podemos reflejar fácilmente sobre líneas horizontales y verticales y realizar algunas rotaciones sencillas. Los estudiantes pueden utilizar papel de calco para realizar estas transformaciones. Elegir un método apropiado para demostrar que dos figuras son congruentes anima a MP5.
Se dan a los estudiantes varios pares de figuras en cuadrículas y se les pide que determinen si las figuras son congruentes. Las figuras congruentes se eligen deliberadamente para que sea necesaria más de una transformación para demostrar la congruencia. En estos casos, es probable que los estudiantes encuentren diferentes formas de demostrar la congruencia. Observe si hay diferentes secuencias de transformaciones que muestren la congruencia. Por ejemplo, para el primer par de cuadriláteros, algunas formas diferentes son:
• Traslada �������� 1 unidad a la derecha, y luego rota su imagen 180° alrededor de (0,0).
• Reflejar �������� sobre el eje ��, luego reflejar su imagen sobre el eje ��, y luego trasladar esta imagen 1 unidad a la izquierda.
Para los pares de figuras que no son congruentes, los estudiantes tienen que identificar una característica de una figura que no comparta la otra para argumentar que no es posible mover una forma encima de otra con movimientos rígidos. En esta fase inicial, los argumentos pueden ser informales. Vigile estas situaciones:
• Las longitudes de los lados son diferentes, por lo que no es posible hacerlas coincidir.
• Los ángulos son diferentes, por lo que no es posible hacer coincidir las dos formas.
• Las áreas de las formas son diferentes.
Ó N Proporcionar acceso a conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda 5-10 minutos de tiempo de trabajo en silencio seguido de un debate con toda la clase.
Apoyo para estudiantes con discapacidad
Funcionamiento socioemocional: Tutores. Agrupe a los estudiantes con sus tutores previamente identificados.
Grado 8 . Matemáticas . Unidad 1
Para cada uno de los siguientes pares de formas, decide si son o no congruentes. Explica tu razonamiento.
1. Son congruentes. Ejemplo de respuesta: Gira el cuadrilátero �������� alrededor de �� en 180 grados, y luego trasládalo hacia la izquierda 3 unidades y hacia abajo 2 unidades. Coincide perfectamente con ��������.
2. No son congruentes. Ejemplo de ejemplo 1: Ambos son pentágonos, pero ���������� tiene un par de lados opuestos paralelos mientras que ���������� no. Ejemplo de respuesta 2: El ángulo �� en ���������� mide más de 180 grados, mientras que todos los ángulos en ���������� miden menos de 180 grados. Ejemplo de respuesta 3: El lado ���� mide una unidad de longitud, mientras que todos los lados de ���������� miden más de 1 unidad de longitud.
3. Son congruentes. Ejemplo de ejemplo: Gira el triángulo ������ alrededor de (0, 0) en el sentido contrario a las agujas del reloj 90 grados, y luego trasládalo hacia abajo 2 unidades y hacia la izquierda 3 unidades. Coincide perfectamente con el triángulo ������ .
4. No son congruentes. Ejemplo de respuesta: Ambos son octógonos regulares, pero ���������������� es mayor que ����������������. Esto puede verse comparando las imágenes o mirando los lados ���� y ����. El lado ���� tiene 2 unidadess de longitud, mientras que el lado ���� tiene menos de 2 unidades de longitud.
Es posible que los estudiantes quieran determinar visualmente la congruencia cada vez o explicar la congruencia diciendo: «Parecen iguales». Anime a esos estudiantes a explicar la congruencia en términos de traslaciones, rotaciones, reflexiones y longitudes de los lados. Para los estudiantes que se centran en las características de las figuras, como las longitudes de los lados y los ángulos, pregúnteles cómo podrían demostrar que las longitudes de los lados o las medidas de los ángulos son iguales o diferentes utilizando la cuadrícula o el papel de calco.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Sondee a la clase para que identifique qué figuras son congruentes (A y C) y cuáles no lo son (B y D). Para las figuras congruentes, pregunte qué movimientos (traslaciones, rotaciones o reflexiones) utilizaron los estudiantes y seleccione a estudiantes previamente identificados para que muestren diferentes métodos. Ordene los métodos de mayor a menor número de pasos cuando sea posible.
Para las figuras que son no congruentes, invite a los estudiantes a identificar las características que utilizaron para demostrarlo y pregúnteles si intentaron mover una forma encima de la otra. En caso afirmativo, ¿qué ocurrió? Es importante que los estudiantes relacionen las diferencias entre identificar figuras congruentes y no congruentes.
El objetivo de la discusión es que comprendan que cuando dos figuras son congruentes, existe una transformación rígida que hace coincidir perfectamente una figura con la otra. Elegir la secuencia correcta requiere práctica. Hay que animar a los estudiantes a experimentar, utilizando la tecnología y el papel de calco cuando esté disponible. Cuando dos figuras no son congruentes, no existe una transformación rígida que haga coincidir perfectamente una figura con la otra. No es posible realizar todas las posibles secuencias de transformaciones en la práctica, por lo que para demostrar que una figura es no congruente con otra, identificamos una propiedad de una figura que no es compartida por la otra. Para las figuras de este conjunto de problemas, los estudiantes pueden centrarse en las longitudes laterales: para cada par de figuras no congruentes, una figura tiene una longitud lateral que no comparte la otra. Como las transformaciones no cambian las longitudes de los lados, esto es suficiente para concluir que las dos figuras no son congruentes.
Apoyo para estudiantes que aprenden el idioma inglés
Representar, conversar, escuchar: MLR7 Comparar y conectar. Mientras los estudiantes preparan sus trabajos para la discusión, busque enfoques que se centren en determinar visualmente la congruencia y en enfoques que se centren en características de las formas como longitudes de los lados y ángulos. Anime a los estudiantes a explicar la congruencia en términos de traslaciones, rotaciones, reflexiones y longitudes de los lados y a mostrar representaciones físicas de la congruencia de las longitudes de los lados y las medidas de los ángulos utilizando cuadrículas o papel de calco. Enfatizar el lenguaje transformacional utilizado para dar sentido a las estrategias para identificar figuras congruentes y no congruentes.
Principio(s) de Diseño: Maximizar la metaconciencia; apoyar la creación de sentido
ACTIVIDAD DE EXPLORACIÓN | PARES CONGRUENTES (PARTE 2)
(15 minutos)
Rutinas didácticas
Toma turnos
MLR8: Apoyos para el debate
Los estudiantes se turnan con un compañero para afirmar que dos polígonos dados son o no congruentes y explicar su razonamiento. El trabajo del compañero consiste en escuchar para comprender y rebatir a su compañero si su razonamiento es incorrecto o incompleto. Esta actividad ofrece a los estudiantes la oportunidad de justificar su razonamiento y criticar el de los demás (MP3). Esta actividad continúa investigando la congruencia de polígonos en una cuadrícula. A diferencia de la actividad anterior, los pares de polígonos no congruentes comparten las mismas longitudes de los lados.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Organice a los estudiantes en grupos de 2, y facilíteles acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Diga a los estudiantes que se turnarán en cada pregunta. En la primera pregunta, el estudiante A debe decir si las figuras son congruentes o no. Si el estudiante A afirma que son congruentes, debe describir una secuencia de transformaciones para demostrar la congruencia, mientras que el estudiante B comprueba la afirmación realizando las transformaciones. Si el estudiante A afirma que las formas no son congruentes, debe apoyar esta afirmación con una explicación para convencer al estudiante B de que no lo son. Para cada pregunta, los estudiantes intercambian los papeles.
Pida a un estudiante voluntario que le ayude a demostrar este proceso utilizando el par de figuras que aparecen aquí.
A continuación, los estudiantes realizan este mismo proceso con sus propios compañeros en las preguntas de la actividad.
Apoyo para estudiantes con discapacidad
Funcionamiento socioemocional: Tutores. Agrupe a los estudiantes con sus tutores previamente identificados.
Enunciado de la tarea para cada par de figuras, decide si la figura A es o no congruente con la figura B. Explica cómo lo sabes. 1. 2. 3.
Grado 8 . Matemáticas . Unidad 1
CONCEPTOS ERRÓNEOS PREVISTOS
1. Sí, son congruentes. Ejemplo de respuesta: Gira el Hexágono �� 90 grados en el sentido de las agujas del reloj con centro (0, 0), y luego trasládalo 7 unidades a la derecha. Coincide perfectamente con el hexágono ��.
2. No, no son congruentes. Ejemplo de respuesta: El hexágono �� tiene mayor área (8 unidades cuadradas) que el hexágono �� (6 unidades cuadradas). No son congruentes porque las traslaciones, rotaciones y reflexiones no cambian el área de una figura.
3. Sí, son congruentes. Ejemplo de respuesta: Refleja el cuadrilátero �� sobre el eje ��, y luego trasládalo una unidad a la derecha y una unidad hacia abajo. Coincide perfectamente con el cuadrilátero ��
4. No, no son congruentes. Ejemplo de respuesta: Ambas formas son cuadriláteros y las longitudes de los lados parecen tener todas 5 unidades de longitud. Pero los ángulos no son iguales. El cuadrilátero �� es un cuadrado con 4 ángulos rectos. El cuadrilátero �� es un rombo. Los ángulos �� y �� son agudos mientras que los ángulos �� y J son obtusos. Puesto que las traslaciones, rotaciones y reflexiones no cambian las medidas de los ángulos, no hay forma de igualar ninguno de los ángulos de estos cuadriláteros.
5. No, no son congruentes. Ejemplo de respuesta 1: Rota el cuadrilátero �� alrededor de �� en 45 grados en sentido contrario a las agujas del reloj y luego trasládalo hacia la izquierda en 7 unidades. El ángulo ������ coincide con el ángulo ������, pero los lados del cuadrilátero �� son un poco más cortos que los del cuadrilátero ��, por lo que las dos formas no son congruentes. Ejemplo de respuesta 2: El área del cuadrilátero cuadrado �� es 9 unidades cuadradas. El área del cuadrilátero �� (que también es un cuadrado) es 8 unidades cuadradas porque contiene 4 cuadrados de unidades enteras y luego 8 cuadrados de medias unidades que hacen 4 cuadrados de unidades más. Las figuras congruentes tienen la misma área, por lo que estas dos figuras no son congruentes.
Para el problema 5, los estudiantes pueden estar en lo cierto al decir que las figuras no son congruentes, pero por una razón equivocada. Pueden decir que una es un 3 por 3 cuadrado y la otra es un 2 por 2 cuadrado, contando las longitudes de los lados diagonales como una unidad. Si es así, pídeles que comparen las longitudes marcándolas en el borde de una tarjeta o midiéndolas con una regla.
Al discutir la congruencia para el problema 4, los estudiantes pueden decir que el cuadrilátero �������� es congruente con el cuadrilátero ��������, pero esto no es correcto. Después de aplicar un conjunto de transformaciones al cuadrilátero ��������, corresponde al cuadrilátero ��������. Los vértices deben enumerarse en este orden para comunicar con precisión la correspondencia entre los dos cuadriláteros congruentes.
Para poner de relieve el razonamiento y el uso del lenguaje de los estudiantes, invita a los grupos a responder a las siguientes preguntas:
• «¿Para qué figuras fue más fácil dar indicaciones a tu compañero? ¿Fueron algunas transformaciones más difíciles de describir que otras?».
• «Para los pares de formas que no eran congruentes, ¿cómo convenciste a tu compañero? ¿Utilizaste transformaciones o te centraste en algunas características distintivas de las formas?».
• «¿Utilizaste alguna medida (longitud, área, medidas de ángulo) para ayudar a decidir si los pares de figuras son congruentes o no?».
Para practicar más la articulación de por qué dos figuras son o no congruentes, selecciona estudiantes con diferentes métodos para que compartan cómo demostraron la congruencia (o no). Si la actividad anterior ha proporcionado suficientes oportunidades, puede que esto no sea necesario.
Apoyo para estudiantes que aprenden el idioma inglés
Escuchar, representar: MLR8 Apoyos para el debate. Durante la discusión final, revoque las ideas de los estudiantes para demostrar el uso del lenguaje matemático replanteando una afirmación como una pregunta con el fin de clarificar, aplicar el lenguaje apropiado e involucrar a más estudiantes.
Principio(s) de Diseño: Maximizar la metaconciencia
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
¿Estás listo para más?
Un polígono tiene 8 lados: cinco de longitud 1, dos de longitud 2 y uno de longitud 3. Todos los lados se encuentran en las líneas de la cuadrícula. (Puede ser útil usar papel cuadriculado cuando trabajes en este problema).
1. Encuentra un polígono con estas propiedades.
2. ¿Existe un segundo polígono, no congruente con el primero, con estas propiedades?
«¿Estás listo para más?». Respuesta del estudiante
Aquí hay dos formas no congruentes que cumplen las condiciones.
ACTIVIDAD DE EXPLORACIÓN OPCIONAL | CONSTRUYENDO CUADRILÁTEROS
(10 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
En actividades anteriores, los estudiantes vieron que dos polígonos congruentes tienen las mismas longitudes de lado en el mismo orden. También han visto que los polígonos congruentes tienen ángulos correspondientes con las mismas medidas. En esta actividad, los estudiantes construyen cuadriláteros que contienen lados congruentes e investigan si forman o no cuadriláteros congruentes.
Además de construir una intuición sobre cómo las longitudes de los lados y las medidas de los ángulos influyen en la congruencia, los estudiantes también tienen la oportunidad de revisar la taxonomía de los cuadriláteros a medida que estudian qué tipos de cuadriláteros son capaces de construir con longitudes de lado especificadas. Esta visión de alto nivel de los diferentes tipos de cuadriláteros es un buen ejemplo de ver y comprender la estructura matemática (MP7).
Observe a los estudiantes que construyen tanto paralelogramos como cometas con los dos pares de lados de longitudes diferentes. Invítelos a compartir durante la discusión.
Hay dos juegos de materiales de construcción. Cada juego contiene 4 longitudes de lado. El conjunto A contiene 4 longitudes laterales del mismo tamaño. El conjunto B contiene 2 longitudes laterales de un tamaño y 2 longitudes laterales de otro tamaño.
Divida la clase en dos grupos. A un grupo se le asignará trabajar con el conjunto A y al otro con conjunto B. Dentro de cada grupo, los estudiantes trabajan en parejas. A cada pareja se le dan dos del mismo conjunto de materiales de construcción. Cada estudiante utiliza el conjunto de longitudes de lado para construir un cuadrilátero al mismo tiempo. Cada vez que se crea un nuevo conjunto de cuadriláteros, las parejas comparan los dos cuadriláteros creados y determinan si son congruentes o no. Dé a los estudiantes (5 minutos) para trabajar con su compañero y, a continuación, discuta con toda la clase.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes con discapacidad
Habilidades motoras finas: Compañeros tutores. Agrupe a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que luchan con las habilidades motoras finas dictar hacer cuadriláteros según sea necesario.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Tu maestro te dará un conjunto de cuatro objetos.
1. Haz un cuadrilátero con tus cuatro objetos y anota lo que has hecho.
2. Compara tu cuadrilátero con el de tu compañero. ¿Son congruentes? Explica cómo lo sabes.
3. Repite los pasos 1 y 2, formando cuadriláteros diferentes. Si tus primeros cuadriláteros no eran congruentes, ¿puedes construir un par que sí lo sea? Si tus primeros cuadriláteros eran congruentes, ¿puedes construir un par que no lo sea? Explica.
CONCEPTOS ERRÓNEOS PREVISTOS
Debería haber una variedad de rombos y cuadrados del conjunto A y paralelogramos y cometas del conjunto B. Es posible construir polígonos congruentes y no congruentes a partir de ambos conjuntos de objetos.
Para iniciar el debate, pregunte:
• «¿Eran siempre congruentes los cuadriláteros que construiste? ¿Cómo lo comprobaste?».
• «¿Fue posible construir cuadriláteros congruentes? ¿En qué partes era importante tener cuidado al construirlos?».
Los estudiantes deben reconocer que hay tres preocupaciones importantes a la hora de crear polígonos congruentes: lados congruentes, ángulos congruentes y el orden en que se ensamblan.
Diga a los estudiantes que, en realidad, basta con garantizar la congruencia entre dos polígonos si se cumplen esos tres criterios. Es decir, «Dos polígonos son congruentes si tienen lados correspondientes que son congruentes y ángulos correspondientes que son congruentes».
Los estudiantes pueden suponer que cuando se construyen cuadriláteros con un conjunto de objetos de la misma longitud, las formas resultantes son congruentes. Pueden pensar que dos figuras son congruentes porque pueden manipularlas físicamente para hacerlas congruentes. Pídeles que primero construyan su cuadrilátero y luego lo comparen con el de su compañero. El objetivo no es asegurarse de que los dos son congruentes, sino decidir si tienen que ser congruentes. SÍNTESIS DE
Destaque también el hecho de que con dos pares de lados congruentes diferentes se pueden construir dos tipos diferentes de cuadriláteros: cometas (los pares de lados congruentes son adyacentes) y paralelogramos (los pares de lados congruentes son opuestos entre sí). Cuando todos los 4 lados son congruentes, los cuadriláteros que se pueden construir son todos rombos.
. Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos para el debate. Dé a los estudiantes tiempo extra para asegurarse de que cada pareja puede explicar o justificar cada paso o parte del problema. Repita las ideas de los estudiantes para representar el uso del lenguaje disciplinario cuando usted insista en los detalles. Asegúrate de variar a quién se pide que represente el trabajo durante el debate para que los estudiantes se acostumbren a prepararse mutuamente para desempeñar ese papel. Esto preparará a los estudiantes para el papel de representante del grupo y para apoyarse mutuamente para asumirlo.
Principio(s) de diseño: Apoyar la creación de sentido
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Los puntos principales a destacar en la conclusión de la lección son:
• Dos figuras son congruentes cuando hay una secuencia de traslaciones, rotaciones y reflexiones que hacen coincidir perfectamente una figura con la otra (esto es de la lección anterior pero es vital para el pensamiento en esta lección también).
• Cuando mostramos que dos figuras son congruentes en una cuadrícula, usamos la estructura de la cuadrícula para describir cada movimiento rígido. Por ejemplo, las traslaciones pueden describirse indicando cuántas unidades de cuadrícula hay que mover a la izquierda o a la derecha y cuántas unidades de cuadrícula hay que mover hacia arriba o hacia abajo. Las reflexiones pueden describirse indicando la línea de reflexión (un eje o una línea particular de la cuadrícula son fácilmente disponibles).
• Dos figuras son no congruentes si tienen diferentes longitudes de lado, diferentes ángulos o diferentes áreas.
• Incluso si dos figuras tienen las mismas longitudes de lado, pueden no ser congruentes. Con cuatro lados de la misma longitud, por ejemplo, podemos hacer muchos rombos diferentes que no son congruentes entre sí porque los ángulos son diferentes.
ENFRIAMIENTO | PASANDO A LA CONGRUENCIA
(5 minutos)
Los estudiantes describen transformaciones explícitas que llevan un polígono a otro. Hay varias soluciones posibles. Aunque los estudiantes pueden utilizar papel de calco para ayudar a visualizar las diferentes transformaciones, en este punto deben ser capaces de articular el movimiento de forma abstracta utilizando el lenguaje de las traslaciones, rotaciones y reflexiones.
Describa una secuencia de reflexiones, rotaciones y traslaciones que demuestre que el cuadrilátero �������� es congruente con el cuadrilátero ��������.
Las respuestas varían. Ejemplo de respuesta: Traslade �������� hacia abajo 1 y 5 hacia la derecha. Luego reflejar sobre la línea ����
Grado 8 . Matemáticas . Unidad 1
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
A. Demuestra que los dos pentágonos son congruentes.
B. Encuentra las longitudes de los lados de ���������� y las medidas de los ángulos de ����������
PROBLEMA 2
Para cada par de formas, decide si las dos figuras son o no congruentes. Explica tu razonamiento.
Soluciones posibles
A. Después de realizar una rotación de 90 grados en el sentido de las agujas del reloj con centro ��, luego trasladar 3 unidades hacia abajo y 6 unidades hacia la derecha, ���������� coincide perfectamente con ���������� La rotación y la traslación no cambian las longitudes de los lados ni las medidas de los ángulos.
��∠�� = 162°.
Soluciones posibles
1. No son congruentes. El segmento ���� del polígono �������� es más largo que cualquiera de los lados del polígono �������� ��, �� y �� pueden coincidir con los vértices ��, �� y ��, pero �� no coincide con ��
2. Congruente. Si ������������ se gira 90 grados en el sentido de las agujas del reloj alrededor de �� y luego se mueve 4 unidades a la derecha y 1 unidad hacia arriba, coincide perfectamente con ������������
3. Congruente. Si el círculo de arriba a la izquierda se traslada hacia la derecha 8 unidades y hacia abajo 3 unidades, cae encima del otro círculo.
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 3
Grado 8, unidad 1, lección 8
A. Dibujar el segmento ����
B. Cuando ���� se gira 180° alrededor del punto ��, el segmento resultante es el mismo que ����. ¿Dónde podría estar situado el punto �� ?
PROBLEMA 4
Grado 8, unidad 1, lección 10 Aquí está el trapezoide ��������
Usando transformaciones rígidas en el trapezoide, construye un patrón. Describe algunas de las transformaciones rígidas que utilizaste.
Reflexiones:
Soluciones posibles
A. Las respuestas varían.
B. �� debe ser el punto medio de ����
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta: Rotaciones en el sentido de las agujas del reloj, centradas en el vértice del ángulo 60°, de 60°, 120°, 180°, 240° y 300° hacer una figura tipo «molino de viento» con copias del trapezoide.
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
IDEA(S) FUNDAMENTAL(ES)
• Geometría transfiguracional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1a Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas se llevan a rectas, y los segmentos de recta a segmentos de recta de la misma longitud.
8.G.2 Comprender que una figura bidimensional es congruente con otra si la segunda puede obtenerse a partir de la primera mediante una secuencia de rotaciones, reflexiones y traslaciones; dadas dos figuras congruentes, describir una secuencia que exhiba la congruencia entre ellas.
Enfoque SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Prestar atención a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.3 II.C.7
LECCIÓN 13 CONGRUENCIA
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo buscan y utilizan la estructura descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Encontremos figuras de probar la congruencia de figuras interesantes.
META(S) DE APRENDIZAJE
• Puedo usar distancias entre puntos para decidir si dos figuras son congruentes.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Determinar si las figuras son congruentes midiendo los puntos correspondientes.
• Dibujar y etiquetar los puntos correspondientes en figuras congruentes.
• Justificar (oralmente y por escrito) que las figuras congruentes tienen distancias correspondientes iguales entre pares de puntos.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Pensar, girar y compartir
MLR5: Preguntas y problemas elaborados conjuntamente
MLR7: Comparar y conectar
MLR8: Apoyos para el debate
Materiales necesarios
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Grado 8 . Matemáticas . Unidad 1
INFIGURACIÓN DE LA LECCIÓN
Narrativa de la lección
Hasta ahora, hemos estudiado principalmente la congruencia de los polígonos. Los polígonos son especiales porque están determinados por segmentos de rectas. Estos segmentos de recta dan a los polígonos distancias y ángulos fácilmente definibles para medir y comparar. Para una figura más compleja con lados curvos, la situación es un poco diferente (a menos que la figura tenga propiedades especiales como ser un círculo). Aquí nos centramos en el hecho de que la distancia entre cualquier par de puntos correspondientes de figuras congruentes debe ser la misma. Dado que hay demasiados pares de puntos a considerar, éste es principalmente un criterio para demostrar que dos figuras no son congruentes: es decir, si hay un par de puntos en una figura que están a una distancia diferente de los puntos correspondientes en otra figura, entonces esas figuras son no congruentes.
Una de las prácticas matemáticas que toma protagonismo en esta lección es MP6. Para figuras congruentes construidas a partir de varias partes diferentes (por ejemplo, un conjunto de círculos) las distancias entre todos los pares de puntos deben ser las mismas. No basta con que las partes constituyentes (círculos, por ejemplo) sean congruentes: también deben estar en la misma configuración, a la misma distancia. Esto se deduce de la definición de congruencia: los movimientos rígidos no modifican las distancias entre los puntos, de modo que si la figura 1 es congruente con la figura 2 entonces la distancia entre cualquier par de puntos de la figura 1 es igual a la distancia entre el par de puntos correspondiente de la figura 2
RESUMEN DE LA LECCIÓN
Componente de la lección
Estructura Tiempo
Calentamiento Independiente 5 min
Actividad de exploración
En parejas 8-10 min
Actividad de exploración En parejas 15 min
Actividad de exploración En parejas 10 min
Síntesis Todo el grupo 3-5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Descripción breve
Los estudiantes encuentran los puntos correspondientes entre dos trapezoides figurados por una traslación.
Los estudiantes comienzan a explorar la congruencia en figuras curvas identificando y explicando qué óvalos son congruentes.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la congruencia de polígonos en una cuadrícula de coordenadas.
Los estudiantes dibujan puntos correspondientes en dos figuras congruentes para demostrar que la distancia entre pares de puntos correspondientes en figuras congruentes es la misma.
Los estudiantes determinan si dos caras mostradas en una cuadrícula son congruentes mostrando si los pares de puntos correspondientes en las dos imágenes están a la misma distancia.
Los estudiantes discuten las diferencias entre figuras congruentes y no congruentes y cómo la distancia entre pares de puntos correspondientes en figuras congruentes es la misma.
Los estudiantes determinan y explican si los dos óvalos mostrados en una cuadrícula son congruentes.
El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | NO SOLO LOS VÉRTICES
(5 minutos)
Pos polígonos son figuras especiales porque una vez que conocemos los vértices, listados en orden, podemos unirlos mediante segmentos de rectas para producir el polígono. Esto es importante cuando realizamos transfiguraciones rígidas. Dado que las transfiguraciones rígidas llevan segmentos de rectas a segmentos de rectas, una vez que sabemos dónde van los vértices de un polígono, podemos unirlos en el orden correcto con segmentos para encontrar la imagen del polígono.
In este calentamiento, los estudiantes comienzan a explorar esta estructura, encontrando los puntos correspondientes en polígonos congruentes que son no vértices.
Dé a 3 minutos de tiempo para pensar en silencio, seguidos de 2 minutos para una discusión de toda la clase.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLESS
Los trapecios �������� y ��′��′��′��′ son congruentes.
• Dibuja y rotula los puntos de ��′��′��′��′ que corresponden a �� y ��.
• Dibuja y etiqueta los puntos de �������� que corresponden a ��′ y ��′.
• Dibuja y etiqueta al menos otros tres pares de puntos correspondientes.
Las respuestas varían. He aquí algunas posibilidades:
Los estudiantes pueden tener dificultades para encontrar puntos correspondientes que no sean vértices. Sugiérales que utilicen papel de calco o la estructura de la cuadrícula para ayudarles a identificar estos puntos correspondientes.
Recuerde a los estudiantes que cuando dos figuras son congruentes, cada punto de una figura tiene un punto correspondiente en la otra figura.
Pregunte a los estudiantes qué métodos utilizaron para encontrar sus puntos correspondientes. Entre las Respuestas posibles se incluyen:
• Utilizar la cuadrícula y los vértices correspondientes para llevar la cuenta de las distancias y colocar el punto correspondiente en el lugar correcto
• Utilizar papel de calco y movimientos rígidos llevando un polígono al otro.
Grado 8 . Matemáticas . Unidad 1
ACTIVIDAD DE EXPLORACIÓN | ÓVALOS CONGRUENTES
(10 minutos)
Rutinas didácticas
Pensar, girar y compartir
MLR5: Problemas y preguntas del trabajo colaborativo
Esta actividad inicia una secuencia que examina figuras que no son polígonos. Desde el punto de vista de la congruencia, los polígonos son figuras especiales porque están completamente determinadas por el conjunto de vértices. En el caso de las figuras curvas, normalmente no podemos comprobar que son congruentes examinando unos pocos puntos privilegiados, como los vértices de los polígonos. Podemos comprobar que no son congruentes identificando una característica de una figura que no comparte la otra (por ejemplo, este óvalo tiene 3 unidades de ancho mientras que éste solo tiene 2 1 2 unidades de ancho). Pero para demostrar que dos figuras curvas son congruentes, tenemos que aplicar la definición de congruencia e intentar mover una figura para que coincida exactamente con la otra después de algunas traslaciones, rotaciones y reflexiones. En esta actividad, los estudiantes empiezan a explorar las sutilezas de la congruencia para las figuras curvas. Asegúrese de que los estudiantes proporcionan un argumento matemático sólido para las figuras que son congruentes, más allá de decir que parecen iguales. Proporcionar un argumento viable, MP3, requiere pensar cuidadosamente sobre el significado de congruencia y la estructura de las figuras. Observe a los grupos que utilizan un lenguaje preciso de transfiguraciones cuando intentan mover un óvalo trazado para que coincida perfectamente con otro. Invíteles a compartir su razonamiento durante el debate. Vigile también los argumentos basados en la medida para explicar por qué ninguno de los óvalos superiores puede ser congruente con ninguno de los inferiores.
INTRODUCCIÓN
Organice a los estudiantes en grupos de 2. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a los estudiantes 3 minutos de tiempo de trabajo en silencio y, a continuación, invíteles a compartir sus razonamientos con un compañero, seguido de un debate con toda la clase.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: Rutina 5 del lenguaje matemático 5: Preguntas del trabajo colaborativo. Esta es la primera vez que se sugiere la rutina 5 del lenguaje matemático como apoyo en este curso. En esta rutina, se da a los estudiantes un contexto o situación, a menudo en figura de raíz de problema con o sin valores numéricos. Los estudiantes elaboran preguntas matemáticas que pueden plantearse sobre la situación. Una pregunta típica es «¿qué preguntas matemáticas podrías hacer sobre esta situación?». El propósito de esta rutina es permitir a los estudiantes dar sentido a un contexto antes de sentirse presionados para producir respuestas y desarrollar la conciencia de los estudiantes sobre el lenguaje utilizado en los problemas de matemáticas.
Principio(s) de diseño(s): Cultivar conversaciones; maximizar la metaconciencia
Cómo sucede
1. Muestre las cuatro imágenes de los óvalos sin las instrucciones.
Pregunte a los estudiantes: «¿Qué preguntas matemáticas podrían hacerse sobre esta situación?».
2. Conceda a los estudiantes 1 minuto de tiempo individual para tomar algunas notas y, a continuación, 3 minutos para compartir ideas con un compañero.
Mientras discuten en parejas, ayude a los estudiantes a utilizar las habilidades de conversación para generar y refinar sus preguntas de figura colaborativa, buscando claridad, remitiéndose a las notas escritas de los estudiantes y repitiendo las respuestas orales, según sea necesario. Preste atención a cómo los estudiantes utilizan el lenguaje sobre transfiguraciones y/o se refieren a las medidas de las figuras al hablar de los polígonos curvos.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma
inglés, continuación
3. Pida a cada pareja de estudiantes que contribuya con una pregunta escrita en un póster, en la pizarra o en la proyección digital. Pida a 2-3 parejas de estudiantes que presenten su pregunta a toda la clase e invite a la clase a hacer comparaciones entre las preguntas compartidas y sus propias preguntas.
Preste atención a las preguntas que comparan diferentes características de los óvalos para determinar la congruencia, especialmente las que utilizan las distancias entre los puntos correspondientes. Repita las ideas de los estudiantes haciendo hincapié en las medidas siempre que sirva para aclarar una pregunta.
4. Presente la pregunta «¿alguno de los óvalos es congruente con otro?» y dé a los estudiantes un par de minutos para compararla con su propia pregunta y las de sus compañeros. Identifique similitudes y diferencias.
Considere la posibilidad de dar estas indicaciones: «¿Cuál de tus preguntas es más parecida/diferente de la que se proporciona? ¿Por qué?, ¿Hay algún concepto matemático principal que esté presente tanto en tu pregunta como en la que se ha proporcionado? Si es así, descríbalo y ¿cómo se relacionan sus preguntas con uno de los objetivos de la lección de medir los puntos correspondientes para determinar la congruencia?».
5. Invite a los estudiantes a elegir una pregunta para responder (de la clase o del plan de estudios) y, a continuación, pídales que pasen a la Síntesis de la actividad.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual:Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la repasen antes de realizar esta actividad.
Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus tutores pares previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten la superposición de figuras según sea necesario.
¿Alguno de los óvalos es congruente entre sí? Explica cómo lo sabes.
Ejemplo de respuesta: Las cuatro figuras son óvalos. Las dos figuras superiores pueden estar rodeadas por rectángulos que midan 3 unidades por 2 unidades. Las dos figuras inferiores miden aproximadamente 2 1 2 (posiblemente un poco menos) unidades por 2 unidades. Esto significa que las figuras superiores no son congruentes con las inferiores. Las dos figuras superiores y las dos inferiores tienen la misma anchura y altura (aunque la orientación es diferente). Sin embargo, hace falta algo más paradeterminar si los dos óvalos superiores (y los dos inferiores) son o no congruentes. Para ello, podemos trazar uno de los dos óvalos superiores en papel de calco y comprobar que puede colocarse encima del otro y lo mismo para el par de óvalos inferior. Esto se puede hacer, por ejemplo, con una rotación de 90 grados en el sentido de las agujas del reloj con centro en el punto que se muestra aquí:
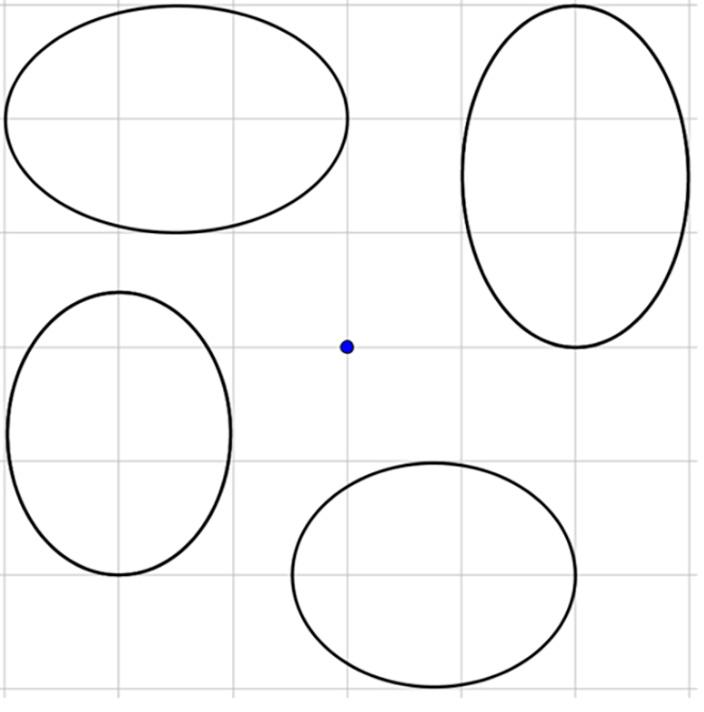
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Invite a los grupos a explicar cómo determinaron que los óvalos superiores no son congruentes con los inferiores, con al menos una explicación centrada en atributos medibles diferentes (por ejemplo, longitud y anchura). Invite también a los grupos previamente seleccionados a mostrar cómo demostraron que los dos óvalos superiores (y los dos inferiores) son congruentes, centrándose en el lenguaje preciso de las transfiguraciones.
Haga hincapié en que para demostrar que dos óvalos son congruentes es necesario utilizando la definición de congruencia: ¿Es posible mover una figura para que coincida perfectamente con la otra utilizando únicamente transfiguraciones rígidas?
La experimentación con transfiguraciones es esencial para demostrar que dos óvalos coinciden porque, a diferencia de los polígonos, estas figuras no están determinadas por una lista finita de vértices y longitudes laterales.
Los estudiantes han visto que los rectángulos que tienen las mismas longitudes laterales son congruentes y más adelante encontrarán criterios para determinar cuándo dos triángulos son congruentes. Para figuras curvas más complejas, se requiere la definición de congruencia.
¿Estás listo para más?
Puedes usar 12 palillos para crear un polígono con un área de cinco palillos cuadrados, así:
¿Puedes usar exactamente 12 palillos para crear un polígono con un área de cuatro palillos cuadrados?
«¿Estás listo para más?». Respuesta del estudiante
Hay más de una solución, pero aquí tienes una aproximación. La primera figura tiene un perímetro de 10 unidades y un área de 4 unidades cuadradas. Para meter dos palillos más sin cambiar el área, se puede poner una hendidura en un lado que se equilibra con la parte que «sobresale» del otro lado:
ACTIVIDAD
DE EXPLORACIÓN
| PUNTOS
CORRESPONDIENTES EN
FIGURAS
CONGRUENTES (15 minutos)
Rutinas didácticas
MLR7: Comparar y conectar
MLR8: Apoyos para el debate
Los lados correspondientes de polígonos congruentes tienen la misma longitud. Para figuras como los óvalos, examinados en la actividad anterior, no hay «lados». Sin embargo, si los puntos �� y �� de una figura corresponden a los puntos ��′ y ��′ de una figura congruente, entonces la longitud del segmento ���� es igual a la longitud del segmento ��′��′ porque las traslaciones, rotaciones y reflexiones no cambian las distancias entre puntos. Los estudiantes han visto y trabajado con esta idea en el contexto de los polígonos y sus lados. Esto sigue siendo cierto para otras figuras también.
Debido a que los movimientos rígidos no cambian las distancias entre los puntos, los puntos correspondientes en figuras congruentes (¡incluso figuras con figuras extrañas!) están a la misma distancia. Este es otro buen ejemplo MP7 ya que la propiedad matemática fundamental de los movimientos rígidos es que no cambian las distancias entre los puntos correspondientes: esta idea es válida para cualquier punto en cualquier figura congruente.
Hay dos estrategias probables para identificar los puntos correspondientes en las dos figuras correspondientes:
• Buscar las partes correspondientes de las figuras, como los segmentos de rectas
• Realizar movimientos rígidos con papel de calco para emparejar las figuras
Ambas son importantes. Observe si los estudiantes utilizan cada técnica e invíteles a compartirlas durante el debate.
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1 INTRODUCCI
Ó N Mantenga a los estudiantes en los mismos grupos. Conceda (5 minutos) de tiempo de trabajo en silencio, seguido de una puesta en común con un compañero y un debate con toda la clase. Proporcione herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha) (para esta actividad se necesitan reglas).
Apoyo para estudiantes con discapacidad
Habilidades motoras finas: Compañeros tutores. Agrupe a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que luchan con las habilidades motoras finas dictar puntos de dibujo y segmentos de rectas según sea necesario. ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Aquí hay dos figuras congruentes con algunos puntos correspondientes etiquetados.
1. Dibuja los puntos correspondientes a ��, �� y �� y etiquétalo ��′, ��′ y ��′.
2. Dibuja los segmentos de rectas ���� y ��′��′ y mídelos. Haz lo mismo con los segmentos ���� y ��′��′ y con los segmentos ���� y ��′��′. ¿Qué observas?
3. ¿Crees que podría haber un par de segmentos correspondientes con longitudes diferentes? Explica.
RESPUESTAS POSIBLESS
SÍNTESIS DE LA ACTIVIDAD
1.
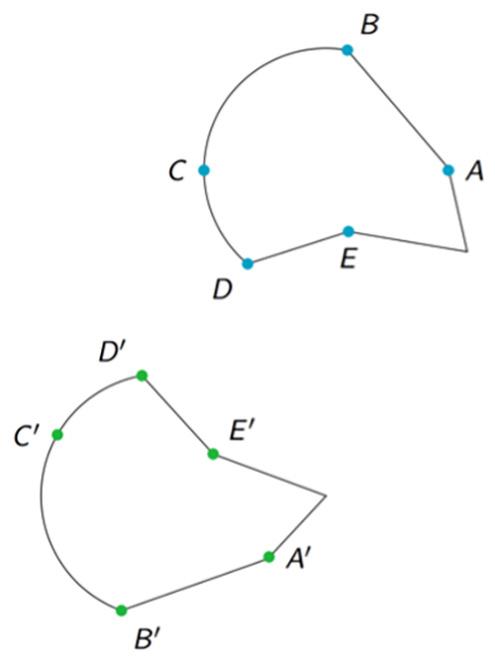
2. Las longitudes son iguales. Las transfiguraciones rígidas del plano utilizadas para mostrar la congruencia de estas figuras no cambian las distancias entre los puntos. Así, la distancia entre �� y ��, por ejemplo, es la misma que la distancia entre ��′ y ��′
Lo mismo ocurre con los demás pares de puntos correspondientes. Los segmentos que conectan estos puntos se muestran aquí:
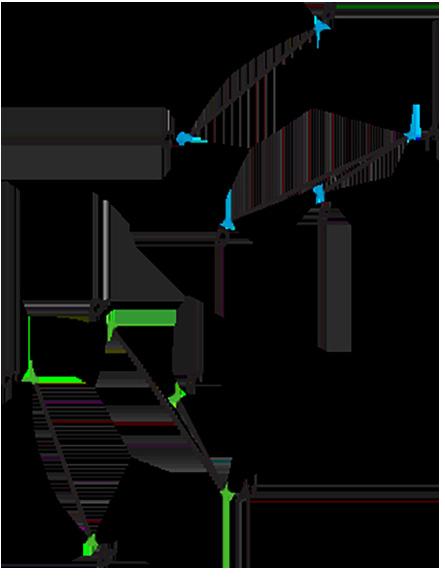
3. Ejemplo de respuesta: No, las transfiguraciones rígidas no cambian las distancias entre puntos. Los segmentos correspondientes en las dos figuras congruentes deben tener la misma longitud.
Pida a los estudiantes seleccionados que muestren cómo determinaron los puntos correspondientes a ��, ��, y ��, destacando diferentes estrategias (identificar características clave de las figuras y realizar movimientos rígidos). Pregunte a los estudiantes si estas estrategias funcionarían para encontrar ��′ si no se hubiera marcado. Realizar movimientos rígidos encaja perfectamente las figuras, por lo que este método nos permite encontrar el punto correspondiente para cualquier punto de la figura. La identificación de rasgos clave solo funciona para puntos como ��, ��, �� y ��, que son esencialmente como vértices y pueden identificarse por las partes de las figuras que están «unidas» en ese punto.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN
Aunque es difícil comprobar «a ojo» si figuras complejas como éstas son o no congruentes, el significado matemático de la palabra «congruente» es el mismo que con los polígonos: dos figuras son congruentes cuando hay una secuencia de traslaciones, reflexiones y rotaciones que hacen coincidir exactamente una figura con la otra. Dado que las traslaciones, reflexiones y rotaciones no cambian las distancias entre los puntos, cualquier par de segmentos correspondientes en figuras congruentes tendrá la misma longitud. Si el tiempo lo permite, pida a los estudiantes que utilicen papel de calco para hacer una nueva figura que sea congruente con la figura de la actividad o ligeramente diferente. Exponga varias para que todos las vean y sondee a la clase para ver si los estudiantes piensan que la figura es congruente o no. Comprueba cómo lo ha hecho la clase alineando la nueva figura con una de las originales. El trabajo con estas figuras complejas es importante porque tendemos a confiar mucho en la intuición visual para comprobar si dos polígonos son o no congruentes. Esta intuición suele ser fiable a menos que los polígonos sean complejos o presenten diferencias muy sutiles que no puedan apreciarse fácilmente. El significado de congruencia en términos de movimientos rígidos y nuestra intuición visual de congruencia pueden reforzarse mutuamente de figura efectiva:
• Si las figuras parecen congruentes, entonces podemos usar esta intuición para encontrar los movimientos correctos del plano para demostrar que son congruentes.
• Experimentando con movimientos rígidos, aumentamos nuestra intuición visual sobre qué figuras son congruentes.
Apoyo para estudiantes que aprenden el idioma inglés
Representar, conversar, escuchar: MLR7 Comparar y conectar. Mientras los estudiantes trabajan, observe si realizan movimientos rígidos con papel de calco para comprobar la congruencia de dos figuras. Llame la atención de los estudiantes sobre las diferentes figuras de emparejar figuras para identificar los puntos correspondientes, y sobre las diferentes figuras en que estas operaciones se hacen visibles en cada representación (por ejemplo, las longitudes de segmentos que son iguales, las traslaciones, rotaciones y reflexiones no cambian las distancias entre puntos). Enfatizar y ampliar el lenguaje matemático que utilizan los estudiantes cuando determinan si dos figuras son congruentes.
Principio(s) de diseño: Maximizar la metaconciencia; apoyar la creación de sentido
ACTIVIDAD DE
ASOMBRADAS
Rutinas didácticas
MLR8: Apoyos para el debate
Apoyo para estudiantes con discapacidad
Lenguaje receptivo/expresivo:Tiempo de procesamiento. Los estudiantes que se benefician de un tiempo de procesamiento adicional también se verían favorecidos por MLR8 (Apoyos para el debate). Utilizar «modelos de pensamiento en voz alta» para concretar la intuición visual.
EXPLORACIÓN | CARAS
(10 minutos)
Hasta ahora, los estudiantes han trabajado sobre todo con figuras simples, es decir, figuras individuales y completas que no se dividen de figura natural en partes. En esta actividad, los estudiantes examinan dos figuras figuradas por piezas disjuntas: el contorno de una cara, dos ojos y una boca. Las piezas disjuntas son congruentes entre sí si se consideran aisladamente. Pero no son congruentes tomadas como un todo colectivo porque las posiciones relativas de los ojos, la boca y el contorno de la cara son diferentes en las dos imágenes.
Esta actividad refuerza un objetivo de la actividad anterior. Para que dos figuras sean congruentes, todos los pares de puntos correspondientes en las dos imágenes deben estar a la misma distancia. Para el ejemplo estudiado aquí, esto es cierto para muchos pares de puntos. Por ejemplo, si elegimos un par de puntos en una boca y el correspondiente par de puntos en la otra boca, estarán a la misma distancia el uno del otro.
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Lo mismo ocurre si elegimos un par de puntos en el ojo de una figura y el correspondiente par de puntos en un ojo de la otra figura. Pero si elegimos un punto en cada ojo o un punto en la boca y un punto en un ojo, las distancias cambian. Seleccionar estratégicamente puntos correspondientes cuya distancia no sea la misma en las dos figuras es MP7, ya que requiere una sólida comprensión del significado de congruencia y partes correspondientes. Observe a los estudiantes que:
• Identifican que las partes (contorno de la cara, ojos, boca) de las dos caras son congruentes.
• Identifican que la posición relativa de las partes en las dos caras no es la misma.
Elija a los estudiantes para que compartan estas observaciones al comienzo de la discusión.
Ó N
Organice a los estudiantes en grupos de 2. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda (5 minutos) de trabajo en silencio, seguidos de tiempo para compartir sus resultados y razonamientos con su compañero y, a continuación, un debate con toda la clase.
Si lo desea, proporcione papel de calco. Sin embargo, en este caso, se debe animar a los estudiantes a buscar otras figuras de saber que las figuras no son congruentes, además de decir que no coinciden cuando los estudiantes intentan colocar una encima de la otra.
Apoyo para los estudiantes con discapacidad
Funcionamiento ejecutivo: Eliminar barreras. Divida esta tarea en partes más manejables (por ejemplo, presentando una sección de la cara a la vez), lo que ayudará a los estudiantes que se benefician de apoyo con habilidades de organización en la resolución de problemas.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Aquí hay dos caras, Max y Frankie. ¿Son congruentes estas caras? Explica tu razonamiento.
No. Ejemplo de respuesta: Las caras no son congruentes aunque las partes de las caras (contorno, ojos, boca) son congruentes tomadas una a una. Los dos contornos ovalados de las caras se sitúan en rectángulos de 8 unidades por 10 unidades y son congruentes como puede verse trasladando el contorno de la cara izquierda 10 unidades a la derecha (o reflejando sobre la línea vertical central en la cuadrícula). Todos los 4 ojos de las dos caras también son congruentes: Esto puede demostrarse utilizando traslaciones horizontales. Las dos bocas son congruentes, también usando una traslación, pero esta vez la traslación tiene un componente horizontal (10 unidades a la derecha) y un componente vertical (aproximadamente media unidad hacia abajo). Mientras que las partes individuales son congruentes, las caras en su conjunto no lo son. En la figura de la izquierda, los ojos están separados por una unidad. En la figura de la derecha están separados por casi 2 unidades. La boca de la izquierda está aproximadamente una unidad por debajo de cada ojo, mientras que la boca de la derecha está más de una unidad por debajo de cada ojo. La boca de la derecha también está más cerca del contorno de la cara que la boca de la izquierda. En cada caso, hay un par de puntos correspondientes en las dos figuras cuyas distancias son diferentes. Esto significa que las figuras no son congruentes.
Grado 8 . Matemáticas . Unidad 1
CONCEPTOS ERRÓNEOS PREVISTOS
Los estudiantes pueden pensar que las dos caras son congruentes si todas las piezas de las caras coinciden, sin embargo las traslaciones para que cada una coincida son diferentes. Esto puede ocurrir cuando los estudiantes utilizan papel de calco para probar cada pieza individual. Pide a los estudiantes que encuentren la distancia entre un par de puntos correspondientes que no sea la misma en las dos caras. Por ejemplo, pídales que midan la distancia entre un punto del ojo izquierdo y un punto del ojo derecho y la distancia correspondiente en la segunda cara.
SÍNTESIS
Pregunte a los estudiantes seleccionados si los contornos de las caras son congruentes. ¿Y los ojos? ¿Las bocas? Pídales que compartan su método de comprobación, haciendo hincapié en un lenguaje preciso que utilice movimientos rígidos (las traslaciones son todo lo que se necesita).
Pregunte a los estudiantes seleccionados si las dos caras, tomadas en su conjunto, son congruentes. ¿Qué puntos correspondientes fueron capaces de identificar que no estuvieran a la misma distancia en las dos caras? La distancia entre los ojos, de los ojos a la boca, de los ojos al contorno de la cara o de la boca al contorno de la cara son todas respuestas válidas.
Aunque las partes individuales de las dos caras son congruentes, las dos caras son no congruentes. Podríamos encontrar una traslación que llevara el contorno de una cara al contorno de la otra y, de figura similar, podríamos encontrar una traslación que llevara el ojo izquierdo, el ojo derecho y la boca de una figura al ojo izquierdo, el ojo derecho y la boca de la otra. Pero estas traslaciones son diferentes. Para que dos figuras sean congruentes, debe haber una secuencia de transfiguraciones que haga coincidir perfectamente todas las partes de una figura con la otra.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR 8 Apoyos para el debate. Amplifique el uso que hacen los estudiantes del lenguaje matemático para comunicarse sobre las transfiguraciones rígidas. Mientras las parejas comparten sus resultados y razonamientos, revoque sus ideas utilizando los términos «figuras congruentes», «componente vertical» y «componente horizontal». A continuación, invite a los estudiantes a utilizar los términos al describir sus resultados y estrategias para determinar la congruencia. Algunos estudiantes pueden beneficiarse de repetir a coro las frases que incluyen los términos «figuras congruentes«, «componente vertical» y «componente horizontal» en contexto.
Principio(s) de diseño: Optimizar el rendimiento (para la explicación)
SÍNTESIS DE LA LECCIÓN
(3-5 minutos)
Esta lección concluye el trabajo sobre la congruencia. Los puntos importantes a destacar incluyen:
• Dos figuras son congruentes cuando hay una secuencia de traslaciones, rotaciones y reflexiones que hacen coincidir una figura con la otra.
• Para demostrar que dos figuras son no congruentes basta con encontrar puntos correspondientes en las figuras que no estén a la misma distancia o ángulos correspondientes que tengan diferente medida.
• La distancia entre pares de puntos correspondientes en figuras congruentes es la misma (esto dice que las longitudes de los lados correspondientes en polígonos tienen la misma longitud pero se aplica también a figuras curvas o a cualquier par de puntos, no necesariamente vértices, en polígonos)
• Algunas figuras están figuradas por varias partes. Por ejemplo, estos dos diseños están figurados cada uno por tres círculos:
• Los seis círculos son congruentes (como podríamos comprobar utilizando papel de calco). Pero en el diseño de la izquierda, cada círculo toca a los otros dos, pero esto no ocurre en el diseño de la derecha. Las distancias entre dos centros de círculo cualesquiera en un diseño serán diferentes de las distancias entre dos centros de círculo cualesquiera en el otro diseño.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
ENFRIAMIENTO | EXPLICACIÓN DE LA CONGRUENCIA
(5 minutos)
Los estudiantes deciden si dos óvalos son o no congruentes. Estos óvalos en particular son visualmente muy distintos, por lo que se espera que los estudiantes utilicen uno de estos métodos:
• Identificar una distancia en un óvalo que sea diferente de la distancia correspondiente en el otro óvalo.
• Trazar uno de los óvalos y observar que no coincide con el otro.
Poner a disposición papel de calco.
RESPUESTAS POSIBLES
¿Son congruentes las figuras �� y ��? Explica tu razonamiento.
Las respuestas varían. Ejemplo de respuesta: Estas figuras no son congruentes porque si lo fueran, las distancias horizontales más largas entre dos puntos serían iguales. Sin embargo, para �� es menor que 4 unidades, y para �� es aproximadamente 4 unidades.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
¿Cuál de estas cuatro figuras es congruente con la figura superior?
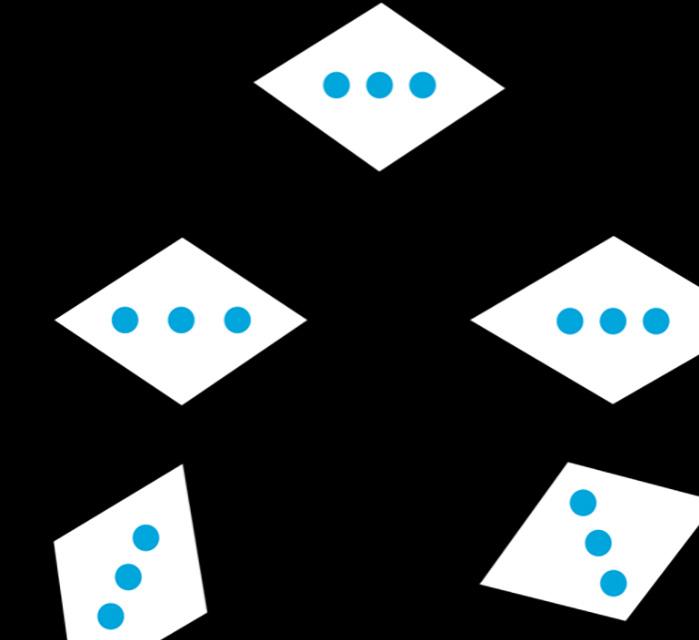
Soluciones posibles
B
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 2
Estas dos figuras son congruentes, con los puntos correspondientes marcados.
A. ¿Son congruentes los ángulos ������ y ��′��′��′? Explica tu razonamiento.
B. Mide los ángulos ������ y ��′��′��′ para comprobar tu respuesta.
Soluciones posibles
A. Sí, son ángulos figurados por puntos correspondientes de figuras congruentes, por lo que son congruentes.
B. Ambos ángulos miden aproximadamente 110 grados.
PROBLEMA 3
Aquí hay dos figuras.
Demuestra, usando medidas, que estas dos figuras son no congruentes.
Soluciones posibles
Las respuestas varían. Ejemplo de respuesta: Los puntos más a la derecha y más a la izquierda de la figura �� están más separados que cualquier par de puntos de la figura ��. Así que estos dos puntos no pueden corresponder a ningún par de puntos de la figura �� y las dos figuras no son congruentes.
PROBLEMA 4
Grado 8, unidad 1, lección 3
Cada dibujo muestra dos polígonos, uno etiquetado polígono �� y otro etiquetado polígono ��. Describa cómo mover el polígono �� a la posición del polígono �� utilizando una transfiguración.
Soluciones posibles
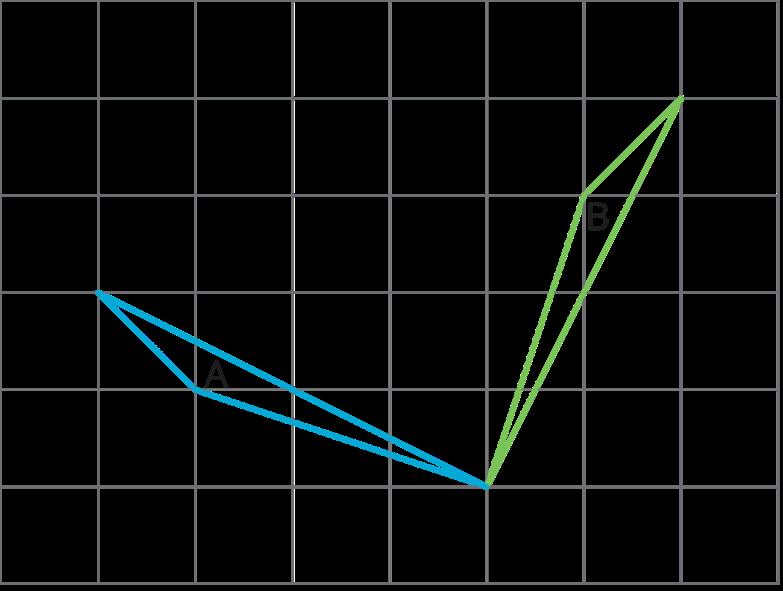
A. Voltee A sobre la línea vertical que pasa por el vértice compartido por �� y ��
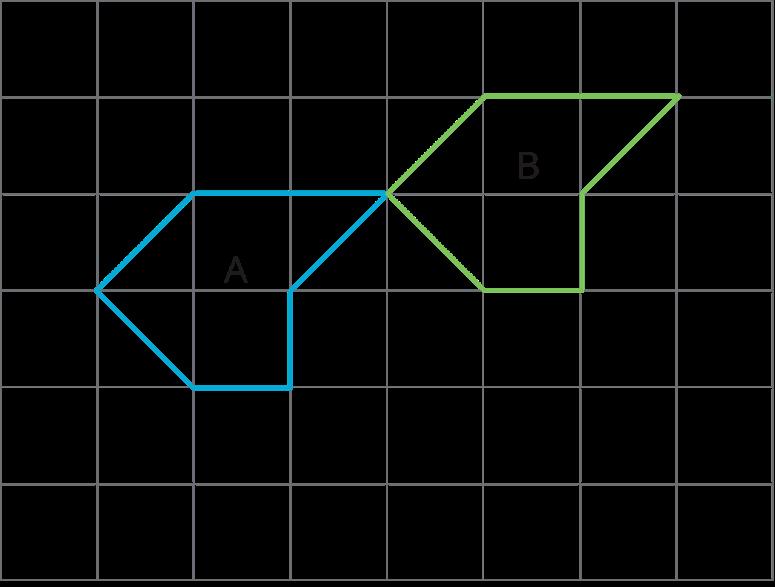
B. Gira �� en el sentido de las agujas del reloj alrededor del vértice compartido por los dos polígonos.
C. Traslada �� hacia arriba y a la derecha. Tiene que subir una unidad y a la derecha 3 unidades.
Reflexiones:
California . Grado 8
Learning Inc. - Todos los derechos reservados
A.
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.1c Verificar experimentalmente las propiedades de las rotaciones, reflexiones y traslaciones: Las rectas paralelas se llevan a rectas paralelas.
8.G.5 Usar argumentos informales para establecer hechos sobre la suma de ángulos y el ángulo exterior de triángulos, sobre los ángulos creados cuando rectas paralelas son cortadas por una transversal, y el criterio ángulo-ángulo para la semejanza de triángulos.
Construir
7.G.5
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP5 Usar herramientas apropiadas estratégicamente.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
Estándares ELD de California
I.A.1
I.C.12
II.C.6
LECCIÓN 14 ÁNGULOS INTERIORES ALTERNOS
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dan sentido al mundo, dan sentido a los problemas y perseveran en su resolución descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Exploremos por qué algunos ángulos son siempre iguales.
META(S) DE APRENDIZAJE
• Si tengo dos rectas paralelas cortadas por una transversal, puedo identificar ángulos interiores alternos y usar eso para encontrar medidas de ángulos faltantes.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Calcular medidas de ángulos utilizando ángulos interiores alternos, adyacentes, verticales y suplementarios para resolver problemas.
• Justificar (oralmente y por escrito) que los «ángulos interiores alternos» formados por una «transversal» que une dos rectas paralelas son congruentes utilizando propiedades de los movimientos rígidos.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Pensar, girar y compartir
MLR2: Recopilar y mostrar
MLR8: Apoyos para el debate
Materiales necesarios
Enfriamiento
Conjuntos de herramientas de geometría (papel de calco, papel milimetrado, lápices de colores, tijeras y una ficha)
Preparación necesaria
Los estudiantes necesitan reglas y papel de calco de los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
En esta lección, los estudiantes justifican que los ángulos interiores alternos son congruentes, y usan esto y el teorema del ángulo vertical, previamente justificado, para resolver problemas.
Hasta ahora en esta unidad, los estudiantes han estudiado diferentes tipos de movimientos rígidos, usándolos para examinar y construir diferentes figuras. Este trabajo continúa aquí, haciendo hincapié en el examen de los ángulos. En una lección anterior, Se emplearon rotaciones de 180 grados para demostrar que los ángulos verticales, formados por rectas que se cruzan, son congruentes. El calentamiento recuerda hechos anteriores sobre ángulos formados por rectas que se intersecan, incluyendo ángulos verticales y adyacentes. A continuación se añade una tercera recta paralela a una de las dos rectas que se cruzan. Ahora hay 8 ángulos, 4 cada uno en los dos puntos de intersección de las rectas. En cada vértice, los ángulos verticales y adyacentes se pueden utilizar para calcular todas las medidas angulares una vez que se conoce un ángulo. Pero, ¿cómo se comparan las medidas de los ángulos en los dos vértices? Resulta que cada ángulo en un vértice es congruente con el ángulo correspondiente (vía traslación) en el otro vértice y esto se puede ver utilizando movimientos rígidos: las traslaciones y rotaciones de 180 grados son particularmente efectivas para revelar las relaciones entre las medidas de los ángulos.
Una práctica matemática que es particularmente relevante para esta lección es MP8. Los estudiantes se darán cuenta, a medida que calculan ángulos, de que utilizan repetidamente ángulos verticales y adyacentes y de que, a menudo, pueden elegir qué método aplicar. También se darán cuenta de que los ángulos formados por rectas paralelas cortadas por una transversal son iguales y esta observación es la estructura clave de esta lección.
LECCIÓN DE UN VISTAZO
Componente de lección Estructura Tiempo
Calentamiento En parejas 5 min
Actividad de exploración En parejas 10-15 min
Actividad de Exploración Independiente 15 min
Síntesis Grupo completo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
. Grado 8
Descripción breve
Los estudiantes aplican el conocimiento previo de los ángulos suplementarios y verticales para encontrar los ángulos faltantes formados por líneas que se intersecan.
Los estudiantes exploran las relaciones angulares formadas por dos rectas cortadas por una transversal utilizando diferentes ejemplos con rectas paralelas y no paralelas.
Se dispone de una extensión de exploración para desarrollar una comprensión más profunda de las medidas angulares formadas por dos rectas paralelas cortadas por dos transversales.
Los estudiantes hacen conexiones entre los movimientos rígidos y las medidas angulares formadas por líneas paralelas y no paralelas cortadas por una transversal, enfocándose específicamente en los ángulos interiores alternos.
Los estudiantes revisan un ejemplo de dos líneas paralelas cortadas por una transversal y las diferentes relaciones angulares encontradas entre pares de ángulos interiores alternos, verticales y suplementarios.
Los estudiantes determinan las medidas de los ángulos faltantes formados por dos rectas intersecadas por una transversal.
El componente de práctica independiente incluye 2 en la lección y 2 problemas de repaso en espiral.
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | PARES DE ÁNGULOS (5 minutos)
Esta tarea está diseñada para que los estudiantes recuerden su trabajo previo con ángulos suplementarios. Si bien han visto este material en el grado 7, esta es la primera vez que aparece explícitamente en el grado 8. A medida que los estudiantes trabajan en la tarea, escuche sus conversaciones específicamente en busca del uso de vocabulario como ángulos suplementarios y verticales. Si ningún estudiante utiliza este lenguaje, explicite estos términos en la discusión.
Slgunos estudiantes pueden utilizar transportadores, ya sea para comprobar el trabajo o para investigar las diferentes medidas de los ángulos. Este es un uso apropiado de la tecnología (MP5), pero pregunte a estos estudiantes qué otros métodos podrían utilizar en su lugar.
INTRODUCCIÓN
Proporcione acceso a conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Antes de que los estudiantes empiecen a trabajar, asegúrate de que están familiarizados con la convención para nombrar un ángulo utilizando tres puntos, donde la letra del medio denota el vértice del ángulo.
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual:Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la revisen antes de realizar esta actividad.
Habilidades finas motoras: Compañeros tutores. Agrupe a los estudiantes con sus tutores pares previamente identificados y permita que los estudiantes que tienen dificultades con las habilidades motoras finas dicten el uso de transportadores según sea necesario.
1. Encuentra la medida del ángulo ������. Explica o muestra tu razonamiento.
2. Encuentra y etiqueta un segundo ángulo 30° en el diagrama. Encuentra y rotula un ángulo congruente con el ángulo ������.
1. 150°. Ejemplo de respuesta: En el diagrama, el ángulo 30° dado y el ángulo ������ son suplementarios, por lo que suman 180°.
2. Los ángulos se etiquetan como se muestra usando razonamiento sobre ángulos verticales o suplementarios.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
Muestre la imagen para que todos la vean. Invite a los estudiantes a compartir sus respuestas, añadiendo a la imagen lo que sea necesario para ayudar a aclarar el pensamiento de los estudiantes. Si los estudiantes no lo mencionan, asegúrese de resaltar el término ángulos suplementarios para describir, por ejemplo, los ángulos ������ y ������, y ángulos verticales para describir, por ejemplo, los ángulos ������ y ������
ACTIVIDAD DE EXPLORACIÓN | CORTAR RECTAS
PARALELAS CON UNA TRANSVERSAL
(15 minutos)
Rutinas didácticas
Pensar, girar y compartir
MLR2: Recopilar y mostrar
En esta tarea, los estudiantes exploran la relación entre los ángulos que se forman cuando dos rectas paralelas son cortadas por una transversal. Los estudiantes investigan si conocer la medida de un ángulo es suficiente para averiguar todas las medidas de los ángulos en esta situación. También se plantean si las relaciones que han encontrado son válidas para dos rectas cualesquiera cortadas por una transversal.
Las dos últimas preguntas de esta actividad son optativas y pueden completarse si el tiempo lo permite. Asegúrate de dejar tiempo suficiente para la siguiente actividad, «Los ángulos interiores alternos son congruentes».
A medida que los estudiantes trabajan con sus compañeros, empiezan a completar los ángulos suplementarios y los ángulos verticales. Para hallar las medidas de los interiores correspondientes y alternos, los estudiantes pueden utilizar papel de calco y algunas de las estrategias encontradas anteriormente en la unidad. Por ejemplo, pueden utilizar papel de calco para trasladar el vértice �� al vértice ��. Podrían intentar trasladar ��′ a ��′ en la segunda imagen y observar que los ángulos en esos dos vértices no son congruentes. Del mismo modo, para hallar las medidas de los ángulos verticales los estudiantes pueden utilizar una rotación 180° como hicieron anteriormente en esta unidad al demostrar que los ángulos verticales son congruentes. Vigile a los estudiantes que utilicen estas diferentes estrategias y selecciónelos para compartirlas durante la discusión.
Para los estudiantes que terminen antes, pídales que piensen en diferentes métodos que podrían utilizar para determinar los ángulos: Por ejemplo, se puede demostrar que todos los ángulos congruentes lo son con transformaciones.
Una transversal (o línea transversal) para un par de líneas paralelas es una línea que se encuentra con cada una de las líneas paralelas exactamente en un punto. Presente esta idea y proporcione una imagen como la siguiente, en la que la recta �� es una transversal para las líneas paralelas ℓ y ��:
Organice a los estudiantes en grupos de 2. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a los estudiantes 1 un minuto de tiempo de reflexión en silencio para planificar cómo encontrar las medidas de los ángulos en la imagen y, a continuación, tiempo para compartir su plan con su compañero. Dé a sus compañeros tiempo para el resto de la tarea, seguido de un debate con toda la clase. Indique a los estudiantes que paren después de la tercera pregunta si ha decidido saltarse las dos últimas.
Apoyo para los estudiantes con discapacidad
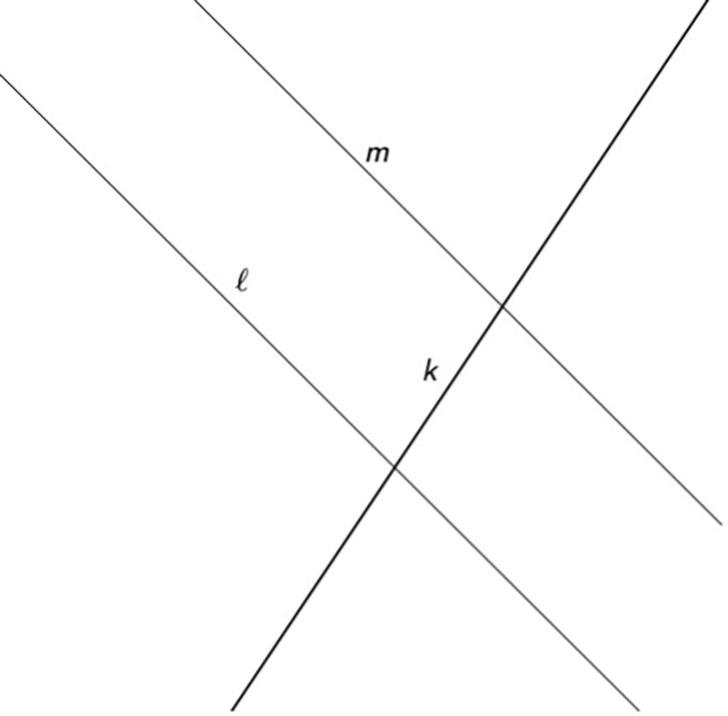
Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (es decir, un muro de palabras) que muestre públicamente defInstrucciónnes, reglas, fórmulas o conceptos importantes para referencia futura.
©Accelerate Learning Inc. - Todos los derechos reservados
DE TAREA PARA EL ESTUDIANTE
Grado 8 . Matemáticas . Unidad 1 ENUNCIADO
Las líneas ���� y ���� son paralelas. Están cortadas por transversal ����.
1. Con tu compañero, encuentra las siete medidas de ángulo desconocidas en el diagrama. Explica tu razonamiento.
2. ¿Qué observas en los ángulos con vértice �� y en los ángulos con vértice ��?
3. Utilizando lo que has observado, halla las medidas de los cuatro ángulos en el punto �� del segundo diagrama. Las líneas ���� y ���� son paralelas.
4. El siguiente diagrama se parece al primero, pero las líneas forman ángulos ligeramente diferentes. Trabaja con tu compañero para encontrar los seis ángulos desconocidos con vértices en los puntos �� y ��
5. ¿Qué notas acerca de los ángulos en este diagrama en comparación con el diagrama anterior? ¿En qué se diferencian los dos diagramas? ¿En qué se parecen?
RESPUESTAS POSIBLES
Grado 8 . Matemáticas . Unidad 1
1. Las explicaciones varían. Ejemplo de estrategia 1: El papel de calco ayudó a encontrar los tres ángulos de 117 grados. Cada uno de los otros cuatro ángulos es suplementario a un ángulo 117 grados, así que todos son ángulos 63 grados. Ejemplo de estrategia 2: El uso de pares de ángulos verticales muestra que el ángulo ������ es un 63
2. Las respuestas varían. Ejemplo de respuesta: Los ángulos en el mismo lugar respecto a la transversal tienen la misma medida.
3. Las respuestas varían. Ejemplo de respuesta: El ángulo ������ es un ángulo 34 grados porque forma un par vertical con el ángulo marcado 34 grados después de trasladar �� a ��. El ángulo ������ es un ángulo 146 grados porque es suplementario al ángulo 34 grados encontrado al trasladar �� a ��
4.
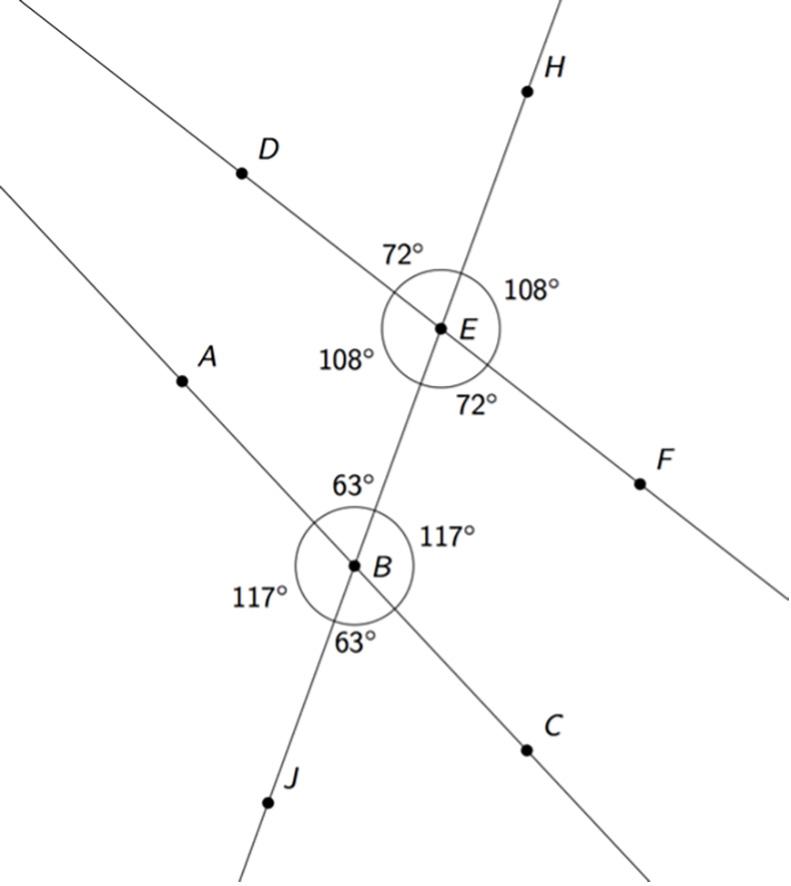
5. Las respuestas varían. Ejemplo de respuesta: En ambas figuras, los dos pares de ángulos verticales en cada vértice son congruentes. También los ángulos adyacentes en cada vértice son suplementarios. En la primera imagen, las medidas de los ángulos en los dos vértices son iguales mientras que en la segunda imagen son diferentes.
En la primera imagen, los estudiantes pueden completar las medidas de los ángulos congruentes basándose en el argumento de que parecen de la misma medida. Pregunte a los estudiantes cómo pueden estar seguros de que los ángulos no difieren en medida en 1 grado. Anímales a que expliquen cómo podemos saber con seguridad que los ángulos miden exactamente lo mismo.
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD
El objetivo de este debate es asegurarse de que los estudiantes se han dado cuenta de las relaciones entre los ángulos que se forman cuando dos rectas paralelas son cortadas por una transversal e introducir a los estudiantes el término ángulos interiores alternos. Muestre las imágenes del Enunciado de la tarea para que todos las vean de una en una e invite a los grupos a compartir sus respuestas. Anime a los estudiantes a utilizar vocabulario preciso, como ángulos suplementarios y verticales, cuando describan cómo han calculado las diferentes medidas de los ángulos. Después de que los estudiantes señalen los ángulos coincidentes en los dos vértices, defina el término ángulos interiores alternos y pida a algunos estudiantes que identifiquen algunos pares de ángulos de la actividad. Considere hacer algunas de las siguientes preguntas:
• «¿Cuáles fueron algunas de las herramientas que utilizaste para encontrar o confirmar las medidas de los ángulos?». (Papel de calco, transportador, transformaciones).
• «¿Cuáles fueron algunas relaciones entre ángulos que utilizaste para encontrar las medidas que faltaban?». (Ángulos verticales, ángulos suplementarios).
• «¿Qué notas acerca de los ángulos en el vértice �� en comparación con los ángulos en el vértice ��?». (Tienen las mismas medidas angulares para ángulos en la misma posición relativa a la transversal).
• «¿Qué relaciones angulares eran ciertas para las tres imágenes? ¿Cuáles eran verdaderas solo para una o dos de las imágenes?». (Los ángulos congruentes verticales y suplementarios alrededor de un vértice eran siempre verdaderos. Los ángulos congruentes en posiciones correspondientes en los dos vértices solo eran ciertos en las dos primeras imágenes, que tenían líneas paralelas).
Apoyo para estudiantes que aprenden el idioma inglés
Conversar, representar: MLR2 Recopilar y mostrar. Mientras los estudiantes trabajan, escuche y recoja el lenguaje que utilizan los estudiantes para describir las relaciones que observan entre los ángulos que se forman cuando dos rectas paralelas son cortadas por una transversal. Registre las palabras y frases de los estudiantes en una presentación visual y actualícela a lo largo de la lección. También puede ser útil incluir esquemas o diagramas. Presta atención a cómo utilizan los estudiantes el lenguaje matemático cuando trabajan juntos para determinar la congruencia de los ángulos. Esto ayudará a los estudiantes a utilizar el lenguaje matemático durante los debates en pequeños grupos y en toda la clase.
Principio(s) de diseño: Apoyar la creación de sentido
¿Estás preparado para más?
Las rectas paralelas ℓ y m están cortadas por dos transversales que se intersecan ℓ en el mismo punto. En la figura se marcan dos ángulos. Halla la medida �� del tercer ángulo.
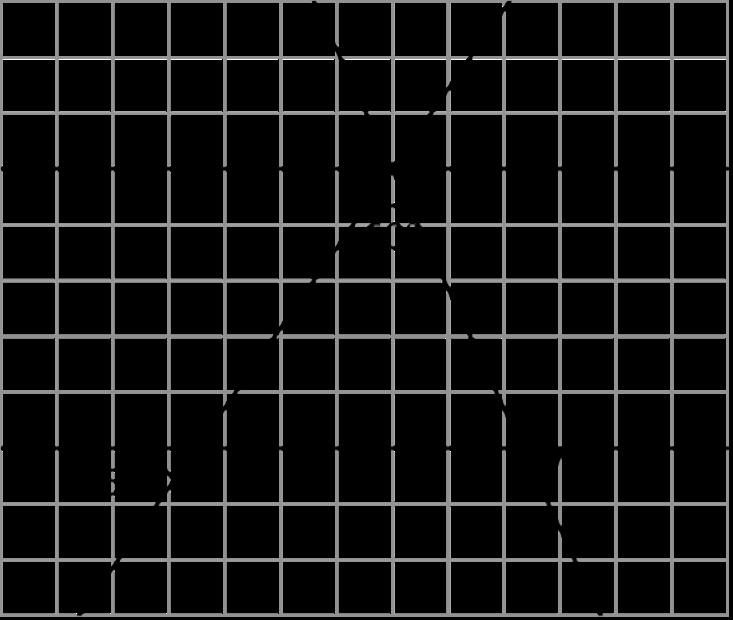
«¿Estás preparado para más?». Respuesta del estudiante
�� = 65°
Añadiendo dos ángulos interiores alternos, vemos que los ángulos
marcados 55°, 60° y ��° forman un ángulo recto, por lo que 55 + 60 + �� = 180
Grado 8 . Matemáticas . Unidad 1
ACTIVIDAD DE EXPLORACIÓN OPCIONAL | LOS ÁNGULOS
INTERIORES ALTERNOS SON CONGRUENTES (15
minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
El objetivo de esta tarea es experimentar con movimientos rígidos para ayudar a visualizar por qué los ángulos interiores alternos (formados por una transversal que une dos rectas paralelas) son congruentes. Este resultado se utilizará en una lección futura para establecer que la suma de los ángulos de un triángulo es 180 grados. La segunda pregunta es opcional si el tiempo lo permite. Esto proporciona una comprensión más profunda de la relación entre los ángulos formados por un par de rectas (no necesariamente paralelas) cortadas por una transversal.
Espera argumentos informales, ya que los estudiantes solo están empezando a desarrollar una comprensión formal de las rectas paralelas y los movimientos rígidos. Sin embargo, han estudiado la idea de rotaciones de 180 grados en una lección anterior en la que utilizaron esta técnica para demostrar que un par de ángulos verticales formados por rectas que se cruzan son congruentes. Considere la posibilidad de recordar esta técnica especialmente a los estudiantes que se atascan y sugerirles el uso de papel de calco. Teniendo en cuenta el diagrama, el papel de calco y lo que han aprendido en esta unidad, los estudiantes deben buscar formas de demostrar que los ángulos interiores alternos son congruentes utilizando transformaciones. Tome nota de las diferentes estrategias (incluidas las diferentes transformaciones) que utilizan los estudiantes para demostrar que los ángulos son congruentes e invítelos a compartir sus estrategias durante la discusión. Los enfoques podrían incluir:
• Una rotación de 180 grados sobre ��
• Primero trasladando �� a �� y luego aplicando una rotación de 180 grados con centro ��
INTRODUCCIÓN
Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Diga a los estudiantes que en esta actividad trataremos de averiguar por qué vimos todos los ángulos iguales que vimos en la última actividad.
Apoyo para estudiantes
con discapacidad
Habilidades motoras finas:Tutores compañeros. Agrupe a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que luchan con las habilidades motoras finas dictar el uso de reglas y papel de calco según sea necesario.
1. Las líneas ℓ y �� son paralelas y �� es una transversal. El punto �� es el punto medio del segmento ����
Encuentra una transformación rígida que demuestre que los ángulos ������ y ������ son congruentes.
2. En esta imagen, las rectas ℓ y �� ya no son paralelas. �� sigue siendo el punto medio del segmento ����
¿Se aplica en esta situación tu argumento del problema anterior? Explícalo.
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
RESPUESTAS POSIBLESS
1. Gire la imagen 180° con centro ��.
Como 180 grados es la mitad de un círculo, esto lleva cada punto del círculo a su "opuesto». El punto �� mapea al punto �� y �� mapea a ��. Por tanto, la rotación de 180 grados de a intercambiará �� y ��. La rotación intercambia las líneas ℓ y �� y también los ángulos ������ y ������ por lo que los ángulos son congruentes.
2. Si ℓ y m no son paralelos, una rotación de 180 grados alrededor de �� sigue llevando �� a �� y �� a ��. El problema es que no toma ℓ a ��, y no toma �� a ℓ porque m no es paralelo a ℓ. Así que esta rotación no lleva el ángulo ������ al ángulo ������ y viceversa. El argumento de 1 no se aplica a menos que ℓ y �� sean paralelos.
DE LA ACTIVIDAD
SÍNTESIS
Seleccione a los estudiantes para que compartan sus explicaciones. Preste mucha atención a qué transformaciones utilizan los estudiantes en la primera pregunta y asegúrese de destacar las distintas posibilidades si se presentan. Pida a los estudiantes que describan y demuestren las transformaciones que utilizaron para demostrar que los ángulos interiores alternos son congruentes. Destaque el hecho de que los estudiantes están utilizando muchas de las transformaciones de secciones anteriores de esta unidad. El argumento aquí es especialmente parecido al utilizado para demostrar que los ángulos verticales formados por rectas que se cruzan son congruentes. En ambos casos una rotación 180 grados intercambia pares de ángulos. Para los ángulos verticales, el centro de rotación es el punto común de las rectas que se intersecan. Para ángulos interiores alternos, el centro de rotación es el punto medio de la transversal entre las dos rectas paralelas. Pero la estructura de estos argumentos es idéntica.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos para el debate. Utilice esta rutina para ampliar los usos matemáticos del lenguaje de los estudiantes cuando describan y demuestren las transformaciones utilizadas para demostrar que los ángulos interiores alternos son congruentes. Después de que un estudiante comparta su respuesta, invite a otro estudiante a repetir el razonamiento utilizando lenguaje matemático (por ejemplo: «ángulos verticales», «180 grados de rotación», «centro de rotación», «líneas de intersección», «punto medio», «rectas paralelas, etc). Invite a todos los estudiantes a repetir a coro las frases que incluyan estas palabras en su contexto.
Principio(s) de diseño: Apoyar la creación de sentido, optimizar la salida (para la explicación)
SÍNTESIS DE LA LECCIÓN
(5 minutos)
Muestre la imagen de dos rectas paralelas cortadas por una transversal. Diga a los estudiantes que, en casos como éste, las traslaciones y rotaciones pueden ser especialmente útiles para calcular las medidas de los ángulos, ya que los desplazan a nuevas posiciones, pero la medida del ángulo no cambia.
Pida a los estudiantes que señalen ejemplos de ángulos interiores alternos, verticales y suplementarios en la imagen. También deben ser capaces de articular qué ángulos son congruentes entre sí y dar un ejemplo de transformación rígida que explique por qué.
En particular, asegúrese de que los estudiantes pueden articular:
• �� = 60 porque es la medida de un ángulo que forma un ángulo interior alterno con el ángulo dado de 60 grados.
• �� = �� = 120 porque también son ángulos interiores alternos, cada uno suplementario de un ángulo de 60 grados.
• El resto de las medidas de ángulos se pueden encontrar usando ángulos verticales o suplementarios.
Grado 8 . Matemáticas . Unidad 1
ENFRIAMIENTO | TODO LO DEMÁS (5 minutos)
Los estudiantes utilizan lo que han aprendido sobre ángulos verticales y ángulos interiores alternos en esta lección y en lecciones anteriores, aplicándolo a un diagrama para completar las medidas de los ángulos sin necesidad de medir. ENUNCIADO DE TAREA PARA
El diagrama muestra dos rectas paralelas cortadas por una transversal. Se muestra una medida de ángulo. Encuentre los valores de ��, ��, ��, ��, ��, �� y ��. RESPUESTAS POSIBLES ��: 126, ��: 54, ��: 126, ��: 54, ��: 126, ��: 54, ��: 126
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Grado 8, unidad 1, lección 9
Utiliza el diagrama para hallar las medidas de cada ángulo. Explica tu razonamiento.
A. ��∠������
B. ��∠������
C. ��∠������
Soluciones posibles
A. 130 grados. ∠������ y ∠������ forman una línea, por lo que suman 180 grados.
B. 130 grados. ∠������ y ∠������ forman una línea, por lo que suman 180 grados.
C. 50 grados. ∠������ y ∠������ forman una línea, por lo que suman 180 grados.
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 2
Las líneas �� y ℓ son paralelas, y la medida del ángulo ������ es 19 grados.
A. Explique por qué la medida del ángulo ������ es 19 grados. Si te atascas, considera trasladar la línea ℓ moviendo �� a ��
B. ¿Cuál es la medida del ángulo ������? Explique.
Soluciones posibles
A. Si ℓ se traslada de modo que �� va a ��, entonces �� va a �� porque �� es paralelo a ℓ. El ángulo ������ coincide con el ángulo ������ después de esta traslación, por lo que ������ (y ������) es también un ángulo 19 grados.
B. Los ángulos ������ y ������ son congruentes porque son ángulos verticales. Como el ángulo ������ es un ángulo de 19 grados, también lo es el ángulo ������
PROBLEMA 3
El diagrama muestra tres rectas con algunas medidas de ángulo marcadas.
Encuentra las medidas de ángulo que faltan marcadas con signos
PROBLEMA 4
Las dos figuras son copias a escala una de la otra.
A. ¿De qué manera se puede saber que son copias a escala?
B. ¿Cuál es el factor de escala que lleva la Figura 1 a la Figura 2?
C. ¿Cuál es el factor de escala que lleva la Figura 2 a la Figura 1?
Soluciones posibles
Soluciones posibles
A. Las respuestas varían.
B. 3
C. 1 3
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.2 Entender que una figura bidimensional es congruente con otra si la segunda se puede obtener a partir de la primera mediante una secuencia de rotaciones, reflexiones y traslaciones; dadas dos figuras congruentes, describir una secuencia que exhiba la congruencia entre ellas.
8.G.5 Utilizar argumentos informales para establecer hechos sobre la suma de ángulos y el ángulo exterior de triángulos, sobre los ángulos creados cuando líneas paralelas son cortadas por una transversal, y el criterio ángulo-ángulo para la semejanza de triángulos.
Construir
7.G.2
Enfoque SMPs
MP7 Buscar y hacer uso de la estructura
Estándares ELD de California
I.C.9 II.C.6
LECCIÓN 15 SUMA DE LOS ÁNGULOS EN UN TRIÁNGULO
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
dar sentido al mundo
buscan y utilizan la estructura descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Exploremos los ángulos en triángulos.
META(S) DE APRENDIZAJE
• Si conozco 2 de las medidas de ángulos en un triángulo, puedo encontrar la medida del tercer ángulo.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comprender que un ángulo recto puede descomponerse en 3 ángulos para construir un triángulo.
• Justificar (oralmente y por escrito) que la suma de los ángulos de un triángulo es 180 grados utilizando propiedades de los movimientos rígidos.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR8: Apoyos para el debate
MLR7: Comparar y conectar
Presentaciones en grupo
Materiales necesarios
Plantillas maestras para la actividad 15.2
Plantillas maestras para la actividad 15.3
Enfriamiento
Copias de las plantillas maestras
Conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Fichas preimpresas, recortadas de las copiaslas plantillas maestras
Grado 8 . Matemáticas . Unidad 1
PREPARACIÓN DE LA LECCIÓN, CONTINUACIÓN
Preparación requerida
Imprima copias de la plantilla maestra de «Romperlo». Prepara 1 copia para cada grupo de 4 estudiantes. De la caja de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), los estudiantes necesitarán tijeras. Si va a realizar la actividad opcional «Buscar los tres», prepare 1 copia del esquema para cada 15 estudiantes. Córtelas con antelación.
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
En esta lección nos centramos en los ángulos interiores de un triángulo. ¿Qué podemos decir de los tres ángulos interiores de un triángulo? ¿Tienen propiedades especiales?
La lección comienza con una actividad opcional en la que se estudian diferentes tipos de triángulos, con especial atención a las combinaciones de ángulos de triángulos agudos, rectángulos y obtusos específicos. Tras recibir un triángulo, los estudiantes forman grupos de 3 identificando a otros dos estudiantes con un triángulo congruente con el suyo. Tras recoger algunos datos de clase sobre todos los triángulos y sus ángulos, descubren que la suma de las medidas de los ángulos en todos los triángulos resulta ser 180 grados.
En la siguiente actividad, los estudiantes observan que si un ángulo recto se descompone en tres ángulos, parece que los tres ángulos pueden utilizarse para crear un triángulo. Juntas, las actividades proporcionan pruebas de una estrecha conexión entre tres números positivos que suman 180 y tener un triángulo con esos tres números como medidas de los ángulos.
Se necesita un nuevo argumento para justificar esta relación entre tres ángulos que forman una recta y tres ángulos que son los ángulos de un triángulo. Este es el tema de la siguiente lección.
LECCIÓN DE UN VISTAZO
Componente de lección
Estructura Tiempo
Descripción breve
Calentamiento Pares 5-10 min Los estudiantes crean triángulos con diferentes propiedades y determinan si es imposible.
Actividad de exploración Grupos pequeños 15 min Los estudiantes utilizan su comprensión de las transformaciones y las medidas de los ángulos correspondientes para encontrar triángulos congruentes.
Actividad de Exploración Grupos Pequeños 20-25 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Nation California . Grado 8
A través de una investigación informal, los estudiantes descubren que si la suma de las medidas de tres ángulos es 180°, esos ángulos pueden usarse para crear un triángulo.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de la suma de las medidas de los ángulos interiores de un cuadrilátero.
Los estudiantes establecen conexiones entre tres ángulos que pueden usarse para crear un ángulo recto y la suma de las medidas de los ángulos interiores de un triángulo.
Los estudiantes aplican su comprensión de la suma de las medidas de los ángulos interiores de un triángulo para determinar posibles medidas de ángulos desconocidos.
El componente de práctica independiente incluye 3 problemas de la lección y 2 problemas de repaso en espiral.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | ¿PUEDES DIBUJARLO? (10 minutos)
Los estudiantes intentan dibujar triángulos que satisfagan diferentes propiedades. Completan la tabla y después comprueban con un compañero si están o no de acuerdo en que los dibujos son correctos o en que no se puede dibujar un triángulo así. Los objetivos de este calentamiento son:
• Repasar diferentes propiedades y tipos de triángulos.
• Centrarse en las medidas individuales de los ángulos en los triángulos como preparación para estudiar su suma.
Note que utilizamos la definición inclusiva de triángulo isósceles que tiene al menos dos lados congruentes. Es posible que en experiencias anteriores los estudiantes hayan aprendido que un triángulo isósceles tiene exactamente dos lados congruentes. Es posible que ni siquiera se plantee esta cuestión, pero tenga en cuenta que los estudiantes pueden estar trabajando con una definición de isósceles diferente de la que aparece en el enunciado de la tarea.
ó N Distribuya a los estudiantes en grupos de 2. Tiempo de trabajo en silencio durante 3 minutos para completar la tabla, seguido de un debate por parejas y con toda la clase.
Apoyo para los estudiantes con discapacidad
Funcionamiento ejecutivo: Ayudas visuales. Crear un gráfico de anclaje (es decir, la tabla triangular) que muestre públicamente defInstrucciónnes, reglas, fórmulas o conceptos importantes para referencia futura.
• Completa la tabla dibujando un triángulo en cada celda que tenga las propiedades indicadas para su columna y fila. Si crees que no puedes dibujar un triángulo con esas propiedades, escribe «imposible» en la celda.
EL ESTUDIANTE
RESPUESTAS
POSIBLES
• Comparte tus dibujos con un compañero. Intercambien ideas. Si no están de acuerdo, trabajen para llegar a un acuerdo.
Agudo (todos los ángulos) Derecho (tiene un ángulo recto) Obtuso (tiene un ángulo obtuso)
Escaleno (longitudes de lados diferentes)
Isósceles (al menos dos lados tienen la misma longitud)
Equilátero (tres lados con la misma longitud)
Respuesta de muestra:
Aguda (todos los ángulos agudos)
Escaleno (longitudes de lados diferentes)
Derecha (tiene un ángulo recto) Obtuso (tiene un ángulo obtuso)
SÍNTESIS DE LA ACTIVIDAD
TRES
Isósceles (al menos dos longitudes de lado son iguales)
Grado 8 . Matemáticas . Unidad 1
Agudo (todos los ángulos son agudos) Recto tTiene un ángulo recto) Obtuso (tiene un ángulo obtuso)
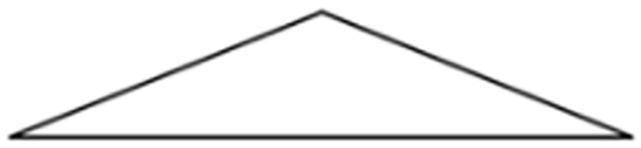
Equilátero (tres longitudes de lado Iguales) Imposible Imposible
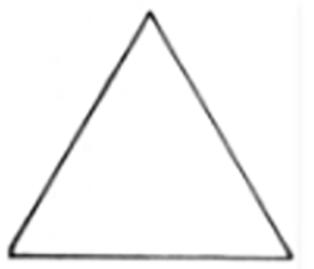
Invite a los estudiantes a compartir algunos triángulos que pudieron dibujar como:
• Recto e isósceles
• Equilátero y agudo
Pida a los estudiantes que compartan qué triángulos no pudieron dibujar y por qué. Por ejemplo, no hay triángulo equilátero rectángulo ni equilátero obtuso porque el lado opuesto al ángulo recto (u obtuso) es más largo que cualquiera de los otros dos lados.
ACTIVIDAD DE EXPLORACIÓN | ENCUENTRA LOS
(15 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
Se trata de una actividad de relacionar en la que cada estudiante recibe una tarjeta que muestra un triángulo y trabaja para formar un grupo de tres. Cada tarjeta muestra un triángulo con la medida de uno solo de sus ángulos. Los estudiantes utilizan lo que saben sobre transformaciones y estimaciones de las medidas de los ángulos para encontrar compañeros con triángulos congruentes con los suyos. A continuación, se muestran los tres ángulos interiores de cada triángulo. Los estudiantes observan que la suma de las medidas de los ángulos de cada triángulo es 180 grados.
Durante esta actividad, los estudiantes pueden utilizar MP7, pensando en aplicar movimientos rígidos a su triángulo para ver si podría coincidir con el triángulo de otro estudiante. O pueden identificar que su triángulo es agudo, recto u obtuso y usar esto como criterio cuando busquen una copia congruente (también MP7).
Necesitará el patrón de líneas negras Encuentra los tres para esta actividad.
INTRODUCCIÓN
Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Distribuya una tarjeta a cada estudiante, asegurándose de que se hayan distribuido las tres tarjetas para cada triángulo. (Si el número de estudiantes en su clase no es múltiplo de tres, puede que uno o dos estudiantes se apropien de dos tarjetas que muestran triángulos congruentes). Explique que hay otros dos estudiantes que tienen un triángulo congruente con el suyo, que ha sido reorientado en el plano de coordenadas mediante combinaciones de traslaciones, rotaciones y reflexiones. Indique a los estudiantes que observen el triángulo en su tarjeta y estimen las medidas de los otros dos ángulos. Con estas estimaciones y su triángulo en mente, los estudiantes buscan los dos triángulos congruentes con el suyo que tengan uno de los ángulos faltantes etiquetado.
California . Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
INTRODUCCIÓN CONTINUACIÓN
Prepara y muestra una tabla para que todos la vean con las columnas ángulo 1, ángulo 2, ángulo 3 y una fila para cada grupo de tres estudiantes. Debería tener este aspecto: Grupos de estudiantes Ángulo �� Ángulo �� Ángulo ��
Una vez que los tres compañeros estén juntos, completan una fila en la tabla expuesta para las medidas de los ángulos de sus triángulos. A continuación, debate en clase.
Los estudiantes pueden preguntar si pueden utilizar papel de calco para encontrar triángulos congruentes. Pregunte cómo lo utilizarían y escuche si comprenden las transformaciones para comprobar la congruencia. Responda que parece una buena idea.
Apoyo para estudiantes con discapacidad
Procesamiento conceptual: Eliminar barreras. Demuestre los pasos de la actividad o juego, en el que un grupo de estudiantes y el personal juegan una ronda de ejemplo mientras el resto de la clase observa.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Tu maestro te dará una tarjeta con la imagen de un triángulo.
1. La medida de uno de los ángulos está etiquetada. Estima mentalmente las medidas de los otros dos ángulos.
2. Encuentra a otros dos estudiantes con triángulos congruentes al tuyo pero con un ángulo diferente etiquetado. Confirma que los triángulos son congruentes, que cada tarjeta tiene etiquetado un ángulo diferente y que las medidas de los ángulos tienen sentido.
3. Introduce las tres medidas de los ángulos de tu triángulo en la tabla que tu maestro ha colocado.
Las combinaciones de ángulos son: 40, 50, 90; 40, 60, 80; 50, 50, 80; 20, 20, 140; 20, 40, 120
Comienza el debate preguntando a los estudiantes:
• «¿Qué pensabas mientras buscaba a tu compañero?».
• «¿Cómo sabías que habías encontrado al compañero correcto?».
Espere que los estudiantes discutan las estimaciones de las medidas de los ángulos y su experiencia sobre cómo influyen las diferentes transformaciones en la posición y el aspecto de un polígono.
A continuación, mire la tabla de ángulos de triángulos y pregunte a los estudiantes:
• «¿Notas algo en las combinaciones de las tres medidas de ángulos?».
• «¿Hay algo en común en cada fila?».
Guíe a los estudiantes para que noten que la suma en cada fila es la misma, 180 grados. Pregúnteles si creen que esto es siempre cierto para cualquier triángulo. Explique a los estudiantes que en la siguiente actividad se plantearán si este resultado es válido para todos los triángulos.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos para el debate. Utilice esta rutina para apoyar el debate con toda la clase. Muestre fragmentos de oraciones para que los estudiantes los usen cuando discutan las relaciones entre los tres ángulos. Por ejemplo: «Sabemos que nuestros triángulos son congruentes porque...» y amplíe el uso del lenguaje matemático en las explicaciones de los estudiantes (por ejemplo, transformaciones, tipos de triángulos, estimaciones de las medidas de los ángulos, etc). Esto ayudará a los estudiantes a explicar su razonamiento sobre las combinaciones de ángulos de los triángulos agudos, rectángulos y obtusos.
Principio(s) de diseño: Apoyar el razonamiento; optimizar el resultado (para la explicación)
ACTIVIDAD OPCIONAL
DE EXPLORACIÓN |
ROMPERLO
2(5 minutos)
EnRutinas estructurales
MLR7: Comparar y conectar
Presentaciones en grupo
En la actividad opcional, los estudiantes comprobaron que la suma de los ángulos de todos los triángulos de las tarjetas era 180 grados y se preguntaron si todos los triángulos tienen la misma suma de ángulos. En esta actividad, los estudiantes experimentan con la inversa: Si sabemos que las medidas de tres ángulos suman 180 grados, ¿pueden estos tres ángulos ser los ángulos interiores de un triángulo?
Los estudiantes recortan tres ángulos que forman una línea y luego intentan utilizar estos tres ángulos para formar un triángulo. Los estudiantes también pueden crear sus propios tres ángulos a partir de una línea y comprobar si pueden construir un triángulo con sus ángulos.
Observa a los estudiantes que consiguen hacer triángulos con cada conjunto de ángulos y selecciónalos para compartirlos (tanto el producto acabado como la forma en que trabajaron para disponer los ángulos) durante el debate. Observa también cómo los estudiantes dividen la línea en blanco en ángulos. Es útil que todos los rayos tengan más o menos la misma longitud que en los ejemplos prefabricados.
Organice a los estudiantes en grupos de 4. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), especialmente las tijeras. Distribuya 1 copia de la plantilla maestra a cada grupo.
Indique a los estudiantes que recorten las cuatro imágenes individuales de la plantilla maestra. Cada estudiante trabajará con uno de ellos. Indique al estudiante con la copia en blanco que utilice una regla para dividir la línea en tres ángulos (diferentes de los tres ángulos que tienen los demás estudiantes del grupo). Muestre cómo hacerlo si es necesario.
Si es necesario, puede demostrar la parte de la actividad «hacer un triángul»" para que los estudiantes entiendan la intención. Con tres ángulos recortados de 60 grados, por ejemplo, se puede construir un triángulo equilátero. A continuación se muestra un dibujo en el que aparecen tres ángulos de 60 grados dispuestos de manera que puedan unirse para formar los tres ángulos de un triángulo equilátero. Los estudiantes tendrán que colocar los ángulos con cuidado, y puede que necesiten utilizar una regla para añadir las líneas de puntos para unir los ángulos y crear un triángulo.
Apoyo para estudiantes con discapacidad
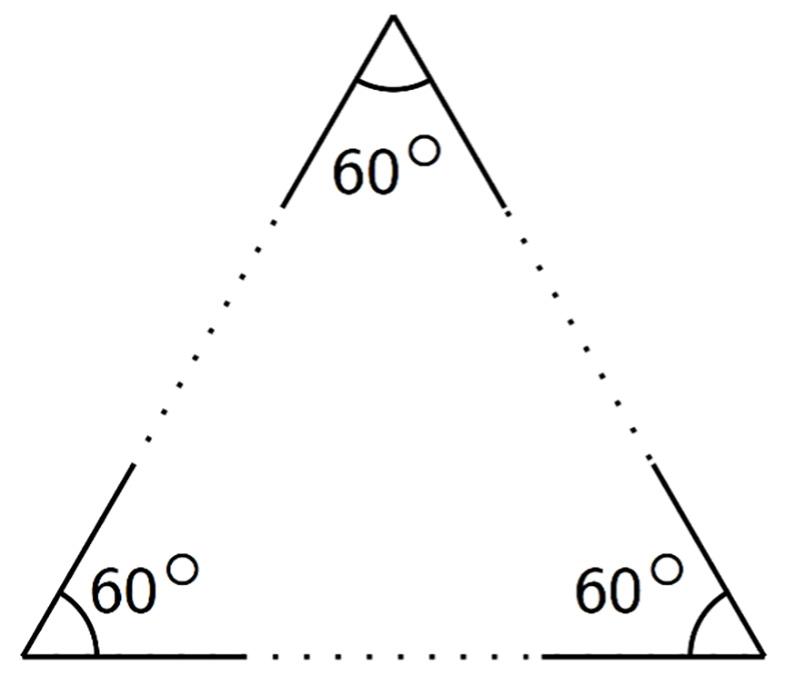
Habilidades motoras finas:Tutores compañeros. Agrupa a los estudiantes con sus tutores compañeros previamente identificados y permitir a los estudiantes que luchan con las habilidades motoras finas dictar triángulos de corte según sea necesario.
Grado 8 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
Tu maestro te dará una página con tres conjuntos de ángulos y un espacio en blanco. Recorta cada conjunto de tres ángulos. ¿Puedes formar un triángulo con cada conjunto que tenga los mismos tres ángulos?
Las respuestas varían. Ejemplo de respuesta: Todos pudimos construir triángulos con los conjuntos de ángulos dados. Uno es rectángulo, otro acutángulo y otro obtusángulo. Los tres ángulos que elegimos también formaban un triángulo.
SÍNTESIS DE ACTIVIDAD
Si el tiempo lo permite, pida a los estudiantes que hagan un recorrido por la galería al comienzo de la discusión. Pídales que comparen el triángulo que formaron con los demás triángulos formados con los mismos ángulos y que estén preparados para compartir lo que observaron. (Por ejemplo, podrían notar que todos los demás triángulos formados con sus ángulos eran prácticamente iguales, pero de diferentes tamaños). Si no lo mencionan, pídales que se den cuenta de que todos los estudiantes del grupo «crea tres ángulos propios» lograron formar un triángulo, no solo los que tenían los ángulos ya formados.
• Pida a los estudiantes previamente seleccionados que compartan sus triángulos y expliquen cómo los formaron. Para formar los triángulos, se requiere ensayo y error. Un método básico consiste en alinear los segmentos de recta de dos ángulos (para obtener un lado del triángulo) y luego intentar colocar el tercer ángulo de manera que se alinee con los rayos que provienen de los dos ángulos ya existentes. Dependiendo de la longitud de las semirrectas, estos pueden superponerse o quizás sea necesario separar los ángulos. Haga preguntas para asegurarse de que los estudiantes comprendan la importante conexión:
• «¿Cómo sabes que los tres ángulos que te dieron suman 180 grados?». (Estaban adyacentes entre sí a lo largo de una línea).
• «¿Cómo sabes que estos pueden ser los tres ángulos de un triángulo?». (Pudimos hacer un triángulo usando estos tres ángulos).
• «¿Qué sabes sobre los tres ángulos del triángulo que formaste y por qué?». (Sus medidas suman 180 porque eran los mismos tres ángulos que formaban una línea).
Pregunte a los estudiantes si creen que pueden formar un triángulo con cualquier conjunto de tres ángulos que formen una línea y pregunte a la clase si la respuesta es afirmativa o negativa. Indíqueles que investigarán esto en la siguiente lección y enfatice que, si bien los experimentos pueden llevarnos a creer que esta afirmación es verdadera, los métodos utilizados no son muy precisos y solo se aplicaron a unos pocos conjuntos de ángulos.
Si el tiempo lo permite, realice una demostración de lo contrario: comience con un triángulo, corte sus tres esquinas y demuestre que estos tres ángulos, cuando se colocan adyacentes entre sí, suman una línea.
Apoyo para estudiantes que aprenden el idioma inglés
Representar, conversar, escuchar: MLR7 Comparar y conectar. Mientras los estudiantes preparan sus trabajos para la discusión, busque a aquellos que construyen triángulos con éxito a partir de cada conjunto de ángulos y a aquellos que crean sus propios tres ángulos a partir de una línea y crean triángulos. Anime a los estudiantes a explicar cómo han trabajado para ordenar los ángulos. Haga hincapié en el lenguaje utilizado para dar sentido a las estrategias empleadas para averiguar que la suma de los ángulos de un triángulo es 180 grados.
Principio(s) de diseño: Maximizar la metaconciencia, apoyar la creación con sentido
Grado 8 . Matemáticas . Unidad 1
¿Estás preparado para más?
1. Dibuja un cuadrilátero. Recórtalo, arranca sus ángulos y alínealos. ¿Qué observas?
2. Repite esta operación con varios cuadriláteros más. ¿Tienes alguna conjetura sobre los ángulos?
«¿Estás preparado para más?». Respuesta del estudiante
La suma de los ángulos interiores de cualquier cuadrilátero es 360°. Esto está bastante claro con los rectángulos. Los paralelogramos tienen 2 pares de ángulos suplementarios iguales, así que también funcionan. De hecho, funciona con cualquier cosa, incluso con cuadriláteros no convexos.
SÍNTESIS DE LA LECCIÓN
(5 minutos)
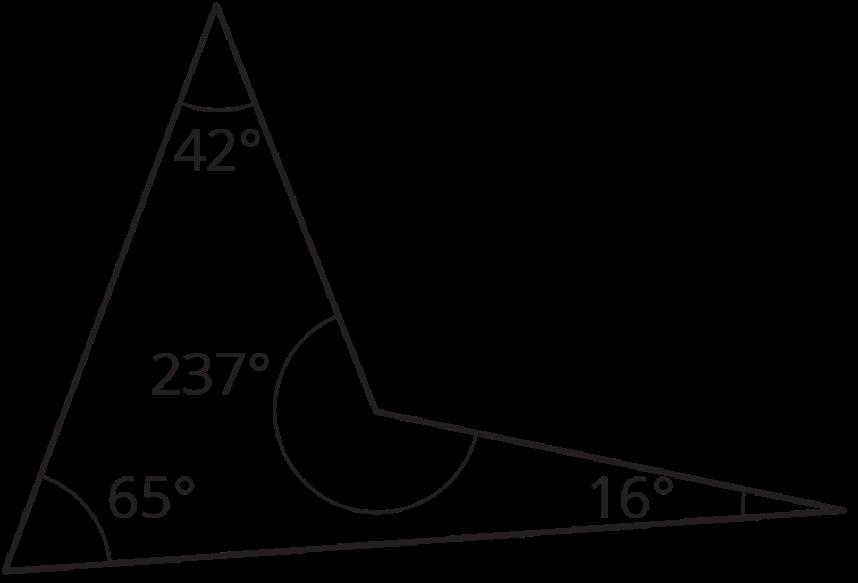
Algunas preguntas guía para la discusión incluyen:
• «¿Qué observamos sobre la suma de los ángulos dentro de un triángulo?». (La suma de los ángulos dentro de un triángulo parece sumar siempre 180 grados).
• «Cuando conoces dos ángulos dentro de un triángulo, ¿cómo puedes encontrar el tercer ángulo?». (Si los tres ángulos suman 180 grados, entonces restando dos de los ángulos de 180 obtendrás la medida del tercer ángulo).
• «¿Hay pares de ángulos que no pueden usarse para formar un triángulo?». (Sí. Sí los dos ángulos son mayores o iguales que 90 grados, entonces no se puede formar un triángulo).
Enfatice que pudimos ver para múltiples triángulos que la suma de sus ángulos es 180° y que usando varios conjuntos de tres ángulos que suman 180° pudimos construir triángulos con esos ángulos. En la próxima lección investigaremos y explicaremos esta interesante relación.
ENFRIAMIENTO | MEDIDAS DE ÁNGULOS QUE
FALTAN (5 minutos)
Los estudiantes han experimentado para ver que la suma de los ángulos de un triángulo es de ������ grados. Aunque demostrarán esto en la próxima lección, aquí aplican el concepto para dar ejemplos de diferentes tipos de triángulos con una medida de ángulo dada.
Si es necesario, diga a los estudiantes que usen su conjetura de que la suma de los ángulos en un triángulo es siempre 180 grados mientras trabajan en estos problemas.
En el triángulo ������, la medida del ángulo �� es 50 grados.
1. Dar los posibles valores de las medidas de los ángulos �� y �� si ������ es un triángulo acutángulo.
2. Dar los posibles valores de las medidas de los ángulos �� y �� si ������ es un triángulo obtusángulo.
3. Dar los posibles valores de las medidas de los ángulos �� y �� si ������ es un triángulo rectángulo.
. Grado 8 ©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
RESPUESTAS POSIBLES
Las respuestas varían. Ejemplos de respuestas:
1. Para formar un triángulo agudo, los otros dos ángulos deben medir menos de 90 grados (por ejemplo: 60, 70).
2. Para formar un triángulo obtuso, uno de los dos ángulos debe medir más de 90 grados (100, 30).
3. Solo hay una forma de formar un triángulo rectángulo (90, 40).
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
En el triángulo ������, la medida del ángulo �� es 40°
A. Dar las posibles medidas de los ángulos �� y �� si el triángulo ������ es isósceles.
B. Dar las posibles medidas de los ángulos �� y �� si el triángulo ������ es rectángulo.
PROBLEMA 2
Para cada conjunto de ángulos, decide si existe un triángulo cuyos ángulos tengan estas medidas en grados:
A. 60, 60, 60
B. 90, 90, 45
C. 30, 40, 50
D. 90, 45, 45
E. 120, 30, 30
Si te atascas, considera hacer un segmento de recta. A continuación, utilice un transportador para medir ángulos con las dos primeras medidas de ángulos.
PROBLEMA 3
Soluciones posibles
A. Hay dos posibilidades: Los ángulos �� y �� miden cada uno 70°, o uno de los ángulos �� y �� mide 40° y el otro mide 100°.
B. Uno de los ángulos �� y �� mide 50° y el otro ángulo mide 90°
Soluciones posibles
Se pueden formar triángulos con los conjuntos de ángulos en ��, ��, y �� pero no con ��, y ��
El ángulo �� en el triángulo ������ es obtuso. ¿Puede ser obtuso el ángulo �� o el ángulo ��? Explica tu razonamiento.
Soluciones posibles
No, un triángulo no puede tener dos ángulos obtusos. Si los ángulos obtusos estuvieran en los vértices �� y ��, por ejemplo, entonces esos ángulos no se encuentran en ningún punto ��
Grado 8 . Matemáticas . Unidad 1
PROBLEMA 4
Grado 8, unidad 1, lección 3
Para cada par de polígonos, describa la transformación que podría aplicarse al polígono �� para obtener el polígono ��
A. B. C.
Soluciones posibles
A. Traslación hacia abajo 3 unidades y hacia la derecha 6 unidades
B. Reflexión con una línea vertical de reflexión a mitad de camino entre los dos polígonos
C. Rotación de 90 grados en sentido antihorario con el vértice compartido por los dos polígonos como centro de rotación
PROBLEMA 5
Grado 8, unidad 1, lección 14
En la cuadrícula, dibuje una copia a escala del cuadrilátero �������� utilizando un factor de escala de 1 2
Soluciones posibles
Las respuestas varían. Cada lado es 1 2 la longitud del lado correspondiente en ��������. Por ejemplo, si ��′��′ en la copia a escala corresponde a ����, entonces ��′ debería estar abajo 1 cuadrícula y a la derecha 2 cuadrículas de ��′. Lo mismo debería ser cierto para todos los demás lados: esto garantiza que los ángulos correspondientes tendrán la misma medida.
Reflexiones:
Nation California . Grado 8
Learning Inc. - Todos los derechos reservados
IDEA(S) FUNDAMENTAL(ES)
• Geometría transformacional
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.5 Usar argumentos informales para establecer hechos sobre la suma de ángulos y el ángulo exterior de triángulos, sobre los ángulos creados cuando líneas paralelas son cortadas por una transversal, y el criterio ángulo-ángulo para la semejanza de triángulos.
Construir
8.G.1b
Construir
8.G.6
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP7 Buscar y utilizar estructuras.
Estándares ELD de California
I.A.1
II.B.5
LECCIÓN 16
LÍNEAS PARALELAS Y LOS ÁNGULOS EN UN TRIÁNGULO
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
repercutir en el futuro, dan sentido a los problemas y perseveran en su resolución descubrir la figura y el espacio.
META(S) DE APRENDIZAJE
• Veamos por qué los ángulos de un triángulo suman 180 grados.
META(S) DE APRENDIZAJE
• Puedo usar imágenes para explicar por qué la suma de los ángulos de cualquier triángulo es 180 grados.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Crear diagramas usando rotaciones de 180 grados de triángulos para justificar (oralmente y por escrito) que la medida de los ángulos en un triángulo suman 180 grados.
• Generalizar el Teorema de la Suma de Triángulos usando transformaciones rígidas o la congruencia de ángulos interiores alternos de líneas paralelas cortadas por una transversal.
PREPARACIÓN DE LA LECCIÓN
Rutinas de instrucción
MLR8: Apoyos para el debate
MLR5: Preguntas y problemas de elaboración conjunta
Materiales necesarios
Enfriamiento
Herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Grado 8 . Matemáticas . Unidad 1
INFORMACIÓN DE LA LECCIÓN
Narrativa de la lección
Anteriormente en esta unidad, los estudiantes aprendieron que cuando se aplica una rotación de 180° a una línea ℓ, la línea resultante es paralela a ℓ. A continuación se muestra una imagen con la que los estudiantes trabajaron anteriormente en la unidad:
La imagen se creó aplicando rotaciones de 180° a △������ con centros en los puntos medios de los segmentos ���� y ����. Obsérvese que ��, ��, y �� se encuentran en la misma línea de cuadrícula que es paralela a la línea ����. En este caso, tenemos la estructura de la cuadrícula para ayudar a ver por qué esto es cierto. Este argumento exhibe un aspecto de MP7, usando la estructura de la cuadrícula para ayudar a explicar por qué los tres ángulos en este triángulo suman 180 grados.
En esta lección, los estudiantes comienzan examinando el argumento usando las líneas de la cuadrícula descrito anteriormente. Luego examinan un triángulo fuera de la cuadrícula, ������. Aquí una recta auxiliar hace el papel de las rectas de la cuadrícula: la recta paralela a la recta ���� que pasa por el vértice opuesto ��
Los tres ángulos que comparten el vértice �� forman una recta y así suman 180 grados. Utilizando lo que han aprendido anteriormente en esta unidad (ya sea ángulos interiores alternos congruentes para rectas paralelas cortadas por una transversal o aplicando transformaciones rígidas explícitamente), los estudiantes argumentan que la suma de los ángulos del triángulo ������ es igual a la suma de los ángulos que se encuentran en el vértice ��. Esto demuestra que la suma de los ángulos en cualquier triángulo es 180 grados. La idea de utilizar una recta auxiliar en una construcción para resolver un problema se expone explícitamente en MP7.
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo
Descripción breve
Calentamiento Independiente 5 min Los estudiantes verifican si las ecuaciones numéricas dadas son verdaderas.
Actividad de exploración En parejas o en grupos pequeños 15 min
Actividad de exploración En parejas o en grupos pequeños 15 min
Actividad de exploración opcional Independiente 5 min
Nation California . Grado 8
Los estudiantes aplican transformaciones rígidas sobre un triángulo para crear un trapecio. Después, los estudiantes analizan las relaciones angulares formadas usando rotaciones y traslaciones.
Una aplicación digital interactiva está disponible para permitir a los estudiantes explorar las transformaciones rígidas de un triángulo utilizando la tecnología.
Los estudiantes utilizan sus conocimientos sobre las rectas paralelas cortadas por una transversal y las medidas de los ángulos en los triángulos para establecer conexiones y desarrollar conjeturas entre los ángulos rectos y la suma de las medidas de los ángulos interiores en un triángulo.
Una extensión de exploración está disponible para desarrollar una comprensión más profunda de las conexiones entre las medidas de ángulos en triángulos y cuadriláteros.
Los estudiantes vuelven a visitar un cuadrado familiar con triángulos formados por transformaciones. Aplican sus conocimientos sobre medidas de ángulos en triángulos y transformaciones rígidas para determinar medidas de ángulos desconocidos en la figura.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
RESUMEN DE LA LECCIÓN, CONTINUACIÓN
Componente de la lección
Estructura Tiempo
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5 min
Descripción breve
Los estudiantes repasan diferentes propiedades de los triángulos, incluyendo la suma de los ángulos interiores de un triángulo, triángulos rectángulos y triángulos equiláteros.
Los estudiantes dibujan triángulos para satisfacer diferentes condiciones dadas.
El componente de práctica independiente incluye 4 problemas de la lección y 1 problema de repaso en espiral.
CALENTAMIENTO | VERDADERO O FALSO: RELACIONES
COMPUTACIONALES (5 minutos)
Este calentamiento anima a los estudiantes a razonar algebraicamente sobre diversas relaciones y patrones computacionales. Aunque los estudiantes pueden evaluar cada lado de la ecuación para determinar si es verdadera o falsa, anímelos a pensar en las propiedades de las operaciones aritméticas en su razonamiento.
Ver la estructura que hace que las ecuaciones sean verdaderas o falsas desarrolla MP7
INTRODUCCIÓN
Muestre un problema a la vez. Diga a los estudiantes que hagan una señal cuando tengan una respuesta y una estrategia. Después de cada problema, conceda a los estudiantes 1 minuto de reflexión en silencio y, a continuación, organice un debate con toda la clase.
Apoyo para los estudiantes con discapacidad
Memoria:Tiempo de procesamiento. Proporcione notas adhesivas o minipizarras para ayudar a los estudiantes con dificultades de memoria de trabajo.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE ¿Es cada ecuación verdadera o falsa?
62 - 28 = 60 - 30
3 ⋅ -8 = (2 ⋅ -8) - 8
16 2 + 24 2 = 40 2 RESPUESTAS POSIBLESS
• Falso. Las explicaciones varían. Posible respuesta: Piensa en una recta numérica. La diferencia entre los números es la distancia que los separa. 62 y 28 están más separados que 60 y 30
• Verdadero. Las explicaciones varían. Posible respuesta: Reescribe (3 ⋅ -8) como (2 ⋅ -8) + (1 ⋅ -8).
• Verdadero. Las explicaciones varían. Posible respuesta: Como 16 + 24 = 40 ambos lados de la ecuación son iguales a 40 2 .
Grado 8 . Matemáticas . Unidad 1 CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
En la primera pregunta, los estudiantes pueden pensar que se pueden redondear o ajustar los números en un problema de resta del mismo modo que en los problemas de suma. Por ejemplo, al sumar 62 + 28, tomar 2 del 62 y sumarlo al 28 no cambia la suma. Sin embargo, utilizando esa misma estrategia al restar, la distancia entre los números en la recta numérica cambia y la diferencia no permanece igual.
Pida a los estudiantes que compartan sus estrategias para cada problema. Registre y muestre sus explicaciones para que todos puedan verlas. Pregunte a los estudiantes cómo decidieron una estrategia. Para involucrar a más estudiantes en la conversación, pregunte:
• ¿Estás de acuerdo o en desacuerdo? ¿Por qué?
• ¿Quién puede reformular el razonamiento de de otra manera?
• ¿Alguien quiere añadir algo al razonamiento de ?
Después de cada ecuación verdadera, pregunte a los estudiantes si podrían basarse en el razonamiento utilizado en el problema dado para pensar o resolver otros problemas de tipo similar. Después de cada ecuación falsa, pregunte a los estudiantes cómo podríamos hacer que la ecuación fuera verdadera.
ACTIVIDAD DE EXPLORACIÓN | ÁNGULO MÁS DOS
(15 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
En la lección anterior, los estudiantes conjeturaron que las medidas de los ángulos interiores de un triángulo suman 180 grados. El objetivo de esta actividad es explicar esta estructura en algunos casos. Los estudiantes aplican 180° rotaciones a un triángulo para calcular la suma de sus tres ángulos. Anteriormente ya habían aplicado estas transformaciones en el contexto de la construcción de figuras mediante transformaciones rígidas. Aquí aprovechan la estructura de la cuadrícula de coordenadas para ver en un caso particular que la suma de los tres ángulos de un triángulo es 180 grados. La siguiente actividad elimina las líneas de la cuadrícula y ofrece un argumento que se aplica a todos los triángulos.
Organice a los estudiantes en grupos de 2-3. Proporcione acceso a los conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Conceda a (5 minutos) de trabajo para construir el diagrama y medir los ángulos. A continuación, permita que toda la clase realice una breve comprobación sobre el error en la medición de ángulos y, después, dé tiempo a los estudiantes para que completen la tarea.
Nota importante para las clases que utilicen la actividad digital: La aplicación mide ángulos en la dirección estándar, en sentido contrario a las agujas del reloj. Los estudiantes deben seleccionar los puntos en orden. Por ejemplo, para medir el ángulo ������ en este triángulo, los estudiantes seleccionarían la herramienta de medida de ángulos y luego harían clic en ��, después en �� y luego ��. Si hacen clic en ��, �� y luego ��, obtienen el ángulo reflejo.
Apoyo para estudiantes con discapacidades
Habilidades motoras finas:
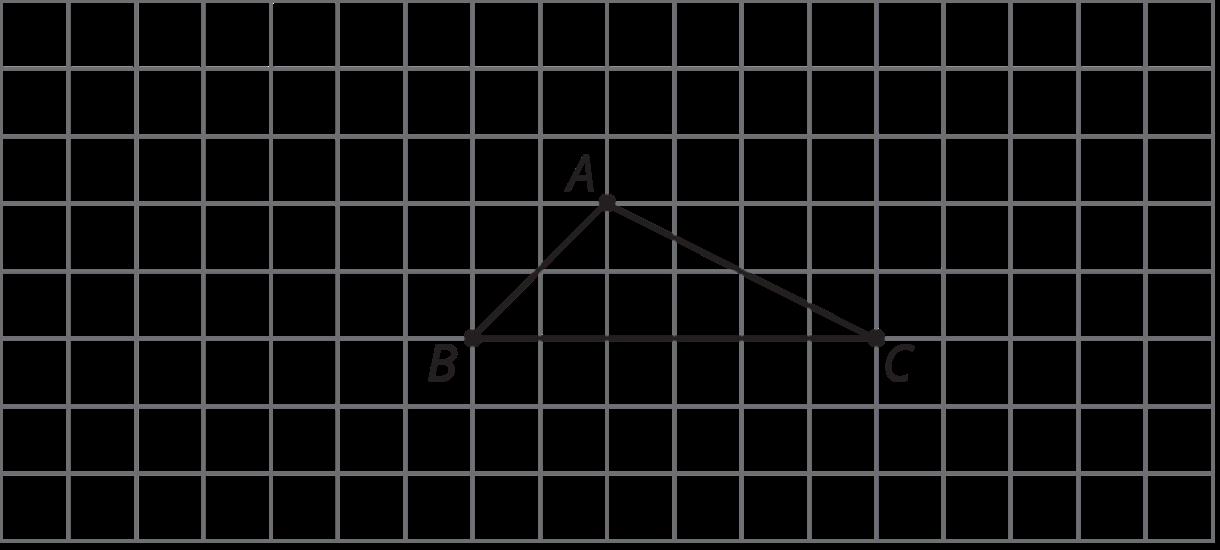
• Tutores compañeros. Agrupe a los estudiantes con sus compañeros tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten las rotaciones y las medidas según sea necesario.
• Tecnología de apoyo. Proporcione acceso a la versión digital de esta actividad.
Grado 8 . Matemáticas . Unidad 1
DE TAREA PARA
ENUNCIADO
EL ESTUDIANTE
RESPUESTAS POSIBLESS
Aquí está el triángulo ������.
1. Gira el triángulo ������ 180° alrededor del punto medio del lado ����. Haga clic con el botón derecho en el punto y seleccione Renombrar para etiquetar el nuevo vértice ��.
2. Gire el triángulo ������ 180° alrededor del punto medio del lado ����. Haz clic con el botón derecho en el punto y selecciona Renombrar para etiquetar el nuevo vértice ��
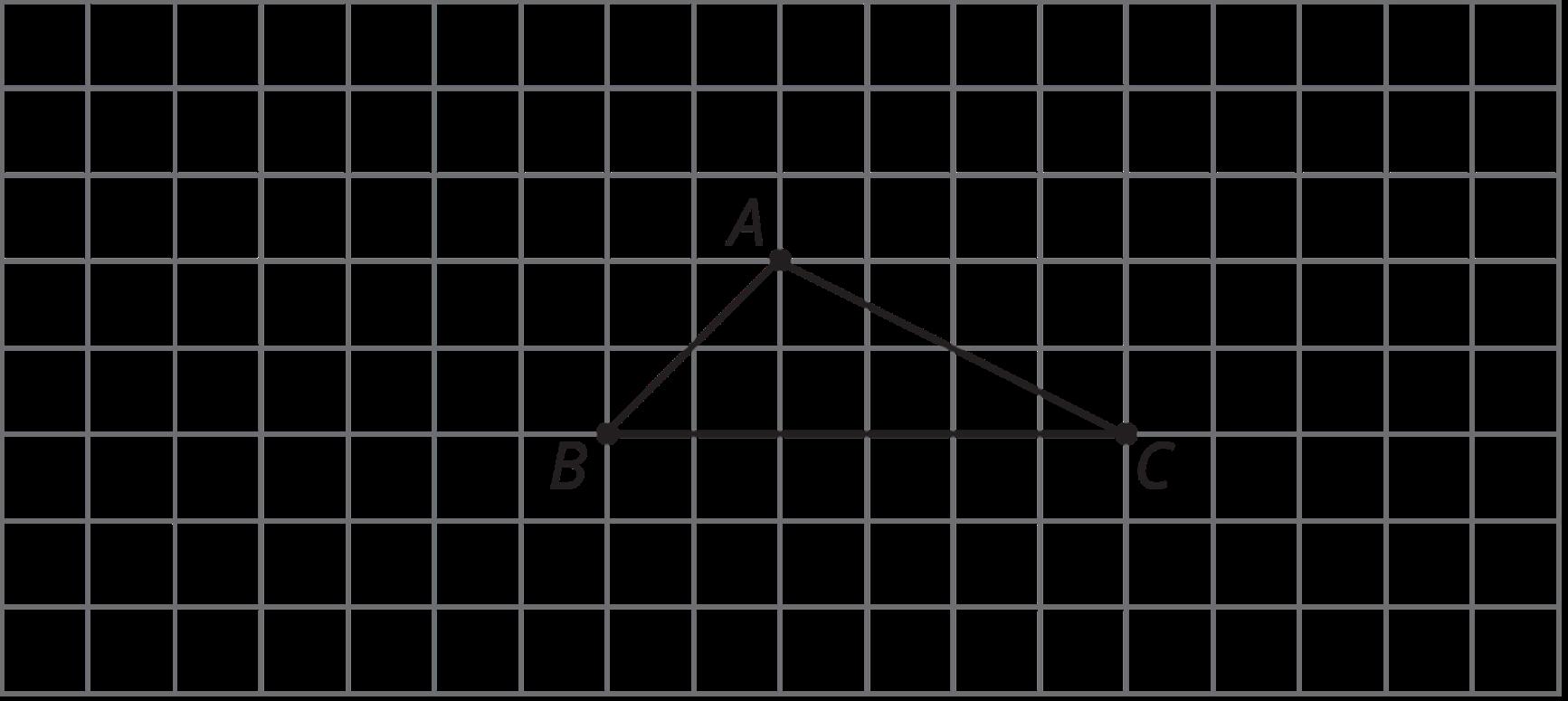
3. Observa los ángulos ������, ������ y ������. Sin medir, escribe cuál crees que es la suma de las medidas de estos ángulos. Explica o muestra tu razonamiento.
4. ¿Es la medida del ángulo ������ igual a la medida de cualquier ángulo del triángulo ������? Si es así, ¿cuál? Si no es así, ¿cómo lo sabes?
5. ¿Es la medida del ángulo ������ igual a la medida de cualquier ángulo del triángulo ������? Si es así, ¿cuál? Si no, ¿cómo lo sabes?
6. ¿Cuál es la suma de las medidas de los ángulos ������, ������, y ������?
1. Cuando giro 180° alrededor del punto medio del segmento ����, �� y �� intercambian lugares y �� va al nuevo punto etiquetado �� en la imagen.
2. Cuando giro 180° alrededor del punto medio del segmento ����, los puntos �� y �� se intercambian y �� va al nuevo punto etiquetado �� en la imagen.
3. Parece que sumarán 180°, porque parecen formar un ángulo recto y hay 180° en un ángulo recto.
4. Sí, el ángulo ������. Lo sé porque cuando giré el triángulo ������ en 180 grados con centro el punto medio del segmento ����, ∠������ va a ∠������
5. Sí, el ángulo ������. Lo sé porque cuando giré el triángulo ������ en 180 grados con centro el punto medio del segmento ����, ∠������ va a ∠������.
6. La medida total de estos ángulos debe ser 180°, porque es la misma que la medida total de los ángulos ������, ������, y ������ y estos ángulos suman 180°.
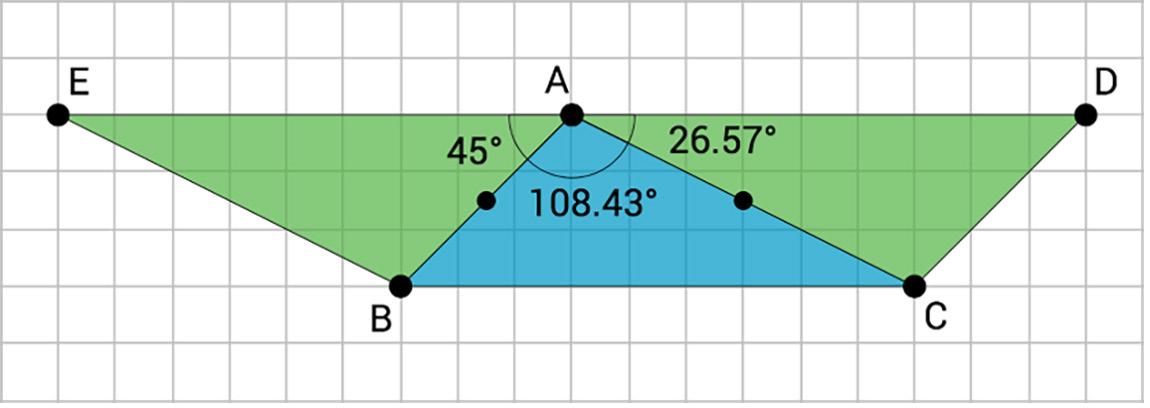
Algunos estudiantes pueden tener problemas con las rotaciones. Si tienen dificultades, recuérdeles un trabajo similar que hicieron en una lección anterior. Ayúdeles con la primera rotación y permítales que realicen la segunda rotación por su cuenta.
Pregunte a los estudiantes cómo las líneas de la cuadrícula les ayudaron a demostrar que la suma de los ángulos de este triángulo es 180 grados. Entre las ideas importantes a destacar se incluyen:
• Una 180 rotación de una línea ���� (con centro el punto medio de ���� o el punto medio de ����) es paralelo a la línea ���� y se encuentra sobre la línea horizontal de la cuadrícula en la que está el punto ��.
• Las líneas de la cuadrícula son paralelas, por lo que los ángulos girados se encuentran en la (misma) línea de la cuadrícula.
Grado 8 . Matemáticas . Unidad 1
SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN
Considere la posibilidad de preguntar a los estudiantes: «¿Es siempre cierto que la suma de los ángulos de un triángulo es 180°?». (Asegúrese de que los estudiantes entienden que el argumento no se aplica a la mayoría de los triángulos, ya que se basa en gran medida en el hecho de que ���� se encuentra en una recta cuadriculada, lo que significa que sabemos que las imágenes de ����, ���� y ����, también se encuentran en la recta cuadriculada en la que está el punto ��).
Resulta que la clave para mostrar el resultado más general está en estudiar las rotaciones que se utilizaron para generar la imagen de los tres triángulos. Esta investigación es el tema de la siguiente actividad.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos para el debate. Utilice esta rutina para apoyarel debate de toda la clase. Para cada observación que se comparta, pida a los estudiantes que repitan y/o vuelvan a expresar lo que han oído utilizando el lenguaje matemático. Considere dar tiempo a los estudiantes para que repitan lo que han oído a un compañero, antes de seleccionar a uno o dos estudiantes para que lo compartan con la clase. Pregunte al orador original si su compañero ha sido capaz de expresar correctamente su pensamiento. Llame la atención de los estudiantes sobre las palabras o frases que hayan ayudado a aclarar la afirmación original. De este modo, más estudiantes tendrán la oportunidad de producir un lenguaje sobre las transformaciones.
Principio(s) de diseño: Apoyar la creación de sentido
ACTIVIDAD DE EXPLORACIÓN | CADA TRIÁNGULO EN EL MUNDO
(15 minutos)
Rutinas didácticas
MLR5: Preguntas y problemas de trabajo colaborativo
La actividad anterior recuerda las rotaciones 180° utilizadas para crear un importante diagrama. Este diagrama muestra que la suma de los ángulos de un triángulo es 180° si el triángulo se encuentra en una cuadrícula con un lado horizontal. El objetivo de esta actividad es proporcionar un argumento completo, que no dependa de la cuadrícula, de por qué la suma de los tres ángulos de un triángulo es 180°
En esta actividad, en lugar de construir una forma compleja a partir de un triángulo y sus rotaciones, los estudiantes empiezan con un triángulo y una recta paralela a la base que pasa por el vértice opuesto:
En esta imagen, las rectas ���� y ���� son paralelas. La ventaja de esta situación es que sabemos que los puntos ��, ��, y �� se encuentran sobre una recta. Para calcular los ángulos ������ y ������, los estudiantes pueden utilizar la idea de rotación de la actividad anterior o la congruencia de ángulos interiores alternos de rectas paralelas cortadas por una transversal. En cualquiera de los dos casos, tienen que analizar las restricciones dadas y decidir qué camino seguir para demostrar la congruencia de los ángulos. A continuación, los estudiantes concluyen, a partir del hecho de que ��, �� y �� se encuentran sobre la misma recta, que �� + �� + �� = 180
Hay una sutil distinción en la lógica entre esta lección y la anterior. La lección anterior sugiere que la suma de los ángulos de un triángulo es 180° utilizando medidas directas de un triángulo en una cuadrícula. Esta actividad demuestra que es así utilizando un triángulo genérico y razonando sobre rectas paralelas cortadas por una transversal. Pero, para ello, necesitábamos saber que hay que trazar la recta paralela a la recta ���� a través de �� y que esta idea surgió experimentando con triángulos giratorios.
INTRODUCCIÓN
Mantén a los estudiantes en los mismos grupos. Diga a los estudiantes que van a trabajar en esta actividad sin el conjunto de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha de notas).
En caso de que los estudiantes no hayan visto esta notación antes, explique que ��∠������ es la abreviatura de «la medida del ángulo ������».
Comience con (5 minutos) de tiempo de trabajo tranquilo. Da tiempo a los grupos para que comparen sus argumentos y, a continuación, discute con toda la clase.
California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma inglés
Conversar, representar, escribir: MLR 5 Preguntas de trabajo colaborativo. Muestre solola imagen y la primera línea de esta tarea (por ejemplo: «Aquí está el triángulo ������. La línea ���� es paralela...». Pida a los estudiantes que, por parejas, escriban posibles preguntas matemáticas sobre la representación. A continuación, invite a las parejas a compartir sus respuestas con la clase. Escuche a los estudiantes que hablan de las relaciones entre la suma de ángulos en un triángulo y en un ángulo recto. Esto ayudará a los estudiantes a producir el lenguaje de las preguntas matemáticas antes de que se les pida que analicen el razonamiento de otro para la tarea.
Principio(s) de diseño: Cultivar la conversación; apoyar la creación con sentido
Apoyo para estudiantes con discapacidades
Funcionamiento socioemocional: Tutores. Agrupe a los estudiantes con sus tutores previamente identificados.
ACTIVIDAD DE EXPLORACIÓN | CADA TRIÁNGULO EN EL MUNDO
(15 minutos)
Rutinas didácticas
MLR5: Preguntas y problemas de trabajo colaborativo
La actividad anterior recuerda las rotaciones 180° utilizadas para crear un importante diagrama. Este diagrama muestra que la suma de los ángulos de un triángulo es 180° si el triángulo se encuentra en una cuadrícula con un lado horizontal. El objetivo de esta actividad es proporcionar un argumento completo, que no dependa de la cuadrícula, de por qué la suma de los tres ángulos de un triángulo es 180°.
En esta actividad, en lugar de construir una forma compleja a partir de un triángulo y sus rotaciones, los estudiantes empiezan con un triángulo y una recta paralela a la base que pasa por el vértice opuesto:
En esta imagen, las rectas ���� y ���� son paralelas. La ventaja de esta situación es que sabemos que los puntos ��, ��, y �� se encuentran sobre una recta. Para calcular los ángulos ������ y ������, los estudiantes pueden utilizar la idea de rotación de la actividad anterior o la congruencia de ángulos interiores alternos de rectas paralelas cortadas por una transversal. En cualquiera de los dos casos, tienen que analizar las restricciones dadas y decidir qué camino seguir para demostrar la congruencia de los ángulos. A continuación, los estudiantes concluyen, a partir del hecho de que ��, �� y �� se encuentran sobre la misma recta, que �� + �� + �� = 180
Hay una sutil distinción en la lógica entre esta lección y la anterior. La lección anterior sugiere que la suma de los ángulos de un triángulo es 180° utilizando medidas directas de un triángulo en una cuadrícula. Esta actividad demuestra que es así utilizando un triángulo genérico y razonando sobre rectas paralelas cortadas por una transversal. Pero, para ello, necesitábamos saber que hay que trazar la recta paralela a la recta ���� a través de �� y que esta idea surgió experimentando con triángulos giratorios.
INTRODUCCIÓN
Mantén a los estudiantes en los mismos grupos. Diga a los estudiantes que van a trabajar en esta actividad sin el Conjunto de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha).
En caso de que los estudiantes no hayan visto esta notación antes, explique que ��∠������ es la abreviatura de «la medida del ángulo ������».
Comience con (5 minutos) de tiempo de trabajo tranquilo. Da tiempo a los grupos para que comparen sus argumentos y, a continuación, debate con toda la clase.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
Aquí está △������. La línea ���� es paralela a la línea ����.
1. ¿Qué es ��∠������ + �� + ��∠������? Explique cómo lo sabe.
2. Utilice su respuesta para explicar por qué �� + �� + �� = 180.
3. Explique por qué su argumento funcionará para cualquier triángulo: es decir, explique por qué la suma de las medidas de los ángulos en cualquier triángulo es 180°
Grado 8 . Matemáticas . Unidad 1
1. Los ángulos ������, ������, y ������ forman una recta. Por lo tanto, la suma de las medidas de sus ángulos es 180°.
2. Los ángulos ������ y ������ son congruentes porque son ángulos interiores alternos para las rectas paralelas ���� y ���� con transversal ����. Los ángulos ������ y ������ son congruentes porque son ángulos interiores alternos para las rectas paralelas ���� y ���� con transversal ����. Los ángulos ������, ������, y ������ forman una recta, por lo que sus medidas angulares suman 180°. Entonces �� + �� + �� = 180
3. Para cualquier triángulo, dibuje una línea paralela a un lado, que contenga el vértice opuesto:
Con este dibujo, utilice el mismo argumento para demostrar que la suma de los tres ángulos del triángulo es 180°. Esto funciona para todos los triángulos
Algunos estudiantes pueden decir que ��, �� y �� son los tres ángulos de un triángulo, por lo que suman 180. Asegúrese de que estos estudiantes entienden que el objetivo de esta actividad es explicar por qué esto debe ser cierto. Anímeles a utilizar su respuesta a la primera pregunta y a pensar en lo que saben sobre los diferentes ángulos del diagrama. Para la última pregunta, los estudiantes pueden no entender por qué su trabajo en la pregunta anterior solomuestra �� + �� + �� = 180 para un triángulo en particular. Considere la posibilidad de dibujar un triángulo diferente (sin la línea paralela a una de las bases), etiquetando las tres medidas de ángulo ��, ��, ��, y preguntando al estudiante por qué �� + �� + �� = 180 para este triángulo.
Pregunta a los estudiantes en qué se diferencia esta actividad de la anterior, en la que △������ tenía un lado horizontal situado sobre una línea de cuadrícula. Subraya que:
• Este argumento se aplica a cualquier triángulo ������
• El argumento anterior se basa en tener líneas de cuadrícula y que la base del triángulo esté sobre una línea de cuadrícula.
• Este argumento se basa en gran medida en tener dibujada la línea paralela a ���� a través de �� , algo que siempre podemos añadir a un triángulo.
La inspiración clave en esta actividad es poner la línea ���� a través de �� paralela a ����. Una vez trazada esta recta, los resultados anteriores sobre rectas paralelas cortadas por una transversal nos permiten ver por qué la suma de los ángulos de un triángulo es 180°. Diga a los estudiantes que la recta ���� suele denominarse «construcción auxilia» porque estamos intentando demostrar algo sobre △������ y resulta que esta recta es muy útil para conseguir ese objetivo. A menudo hace falta experiencia y creatividad para dar con la construcción auxiliar adecuada cuando se trata de demostrar cosas en matemáticas.
¿Estás preparado para más?
1. Con una regla, crea unos cuantos cuadriláteros. Utiliza un transportador para medir los cuatro ángulos dentro del cuadrilátero. ¿Cuál es la suma de las medidas de estos cuatro ángulos?
2. Inventa una explicación de por qué todo lo que observas debe ser cierto (pista: dibuja una diagonal en cada cuadrilátero).
Grado 8 . Matemáticas . Unidad 1
Apoyo para los estudiantes con discapacidad
Procesamiento conceptual:Tiempo de procesamiento. Proporcione la imagen a los estudiantes que se benefician de un tiempo de procesamiento adicional para que la repasen antes de realizar esta actividad.
Habilidades motoras finas: Compañeros tutores. Empareje a los estudiantes con sus compañeros tutores previamente identificados y permita que los estudiantes que tienen dificultades con la motricidad fina dicten medidas según sea necesario.
«¿Estás listo para más?». Respuesta del estudiante
1. La suma de las medidas de los ángulos interiores en cualquier cuadrilátero es 360°. Ten en cuenta que, dado que los transportadores son imprecisos, las medidas físicas pueden distar unos grados de este valor.
2. En cualquier cuadrilátero, puedes dibujar una diagonal que divida el cuadrilátero en dos triángulos. La suma de las medidas de los ángulos de cada triángulo es 180°, y los seis ángulos de los dos triángulos comprenden todos los ángulos del cuadrilátero.
ACTIVIDAD DE EXPLORACIÓN OPCIONAL | LOS CUATRO TRIÁNGULOS REVISITADOS
(5 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
Esta actividad revisa una imagen que los estudiantes han visto anteriormente y que volverán a ver más adelante cuando investiguen el teorema de Pitágoras. Los cuatro triángulos rectángulos que rodean el límite forman en su interior un cuadrilátero que resulta ser un cuadrado. Como los cuatro triángulos que rodean el cuadrilátero interior son congruentes por construcción, la forma interior es un rombo. Los cálculos de ángulos que los estudiantes hacen aquí justifican por qué es en realidad un cuadrado. El hecho de que el cuadrilátero �������� sea un cuadrado no se pide en la actividad, pero si algún estudiante se da cuenta de ello, anímale a compartir sus observaciones y razonamientos.
Los estudiantes hacen uso de la estructura (MP7) a lo largo de esta actividad, sobre todo:
• Usando el hecho de que los triángulos congruentes tienen ángulos congruentes.
• Usando el hecho de que las medidas de los ángulos que forman una recta suman 180 grados.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR 8 Apoyos para el debate. Para ayudar a los estudiantes a producir enunciados sobre cómo encontrar los ángulos desconocidos en el diagrama, proporcione marcos de oraciones como: «Saber , me ayuda a encontrar porque » o «El ángulo corresponde al ángulo porque ».
Principio(s) de diseño: Optimizar la salida (para la explicación); apoyar la creación de sentido
ó N Proporcione 3 minutos de tiempo de trabajo seguidos de un debate con toda la clase.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Grado 8 . Matemáticas . Unidad 1
Este diagrama muestra un cuadrado �������� que ha sido formado por imágenes del triángulo ������ bajo transformaciones rígidas.
Dado que el ángulo ������ mide 53 grados, encuentra tantas otras medidas de ángulos como puedas.
RESPUESTAS
POSIBLESS
SÍNTESIS
DE LA ACTIVIDAD
Todos los demás ángulos se pueden determinar a partir de la única medida dada.
Los ángulos ������, ������ y ������ miden todos 53° porque la medida de ∠������ es 53°. Estos tres ángulos corresponden a ∠������ bajo un movimiento rígido de △������. Para encontrar los ángulos ������, ������, ������ y ������, observa que todos ellos son congruentes porque corresponden a ∠������ de △������ bajo un movimiento rígido. El ángulo ������ mide 37° porque los ángulos de un triángulo suman 180°. Un ángulo en △������ mide 53°, y otro mide 90°, por lo que el tercer ángulo mide 180° – 53° – 90° = 37°.
Los ángulos ������, ������, ������ y ������ miden todos 90. He aquí un argumento para ∠������: Sabemos que el ángulo ������ mide 37° y el ángulo ������ mide 53°. Entonces, el ángulo ������ debe medir 90° porque forma una recta junto con ∠������ y ∠������
Muestra la imagen de los 4 triángulos para que todos la vean. Invite a los estudiantes a compartir cómo calcularon uno de los otros ángulos desconocidos de la imagen, añadiendo a la imagen hasta completar todos los ángulos desconocidos.
Para terminar, observe que los ángulos ������, ������, ������ y ������ son todos ángulos rectos. Todavía no es necesario mostrar o decir a los estudiantes que �������� es un cuadrado. Este diagrama se utilizará para establecer el teorema de Pitágoras más adelante en el curso, así que es un buen lugar para terminar.
SÍNTESIS DE LA LECCIÓN
(10 minutos)
Repase los pasos básicos de la demostración que demuestra que la suma de los ángulos de un triángulo es 180°. Considera la posibilidad de pedir a un estudiante que haga un triángulo que puedas exponer para que todos lo vean y que lo añada mostrando cada paso.
• Teníamos un triángulo y una recta que pasaba por un vértice paralelo al lado opuesto.
• Sabíamos que los tres ángulos con sus vértices en la recta sumaban 180°
• Sabíamos que dos de estos ángulos eran congruentes con los ángulos correspondientes del triángulo y que el tercero estaba dentro del triángulo.
• Por tanto, los tres ángulos del triángulo también deben sumar 180°
Di a los estudiantes que éste es uno de los resultados más útiles de la geometría y que podrán utilizarlo una y otra vez en el futuro.
ENFRIAMIENTO | TAMAÑOS DE ÁNGULOS
(5 minutos)
Los estudiantes dibujan diferentes triángulos y enumeran las posibilidades de ángulos. Sabiendo que la suma de los ángulos de un triángulo es 180 grados se establece que cada ángulo de un triángulo equilátero mide 60 grados.
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
POSSIBLE RESPONSES
1. En un triángulo equilátero, todos los lados y los ángulos son iguales. Dibuja un triángulo equilátero. ¿Cuáles son las medidas de sus ángulos?
2. En un triángulo isósceles, que no es equilátero, dos lados y dos ángulos son iguales. Dibuja tres triángulos isósceles diferentes.
3. Indica dos posibilidades para las medidas de los ángulos de un triángulo isósceles.
1. Las medidas de los tres ángulos deben sumar 180°, pero todas deben ser iguales. Por lo tanto, cada medida es 60°, desde 60 = 1 3 ⋅ 180.
2. Las respuestas varían. Los triángulos deben tener dos lados de la misma longitud, pero no tres..
3. Las respuestas varían. Ejemplos de respuestas: 70°, 70°, 40° y 30°, 30°, 120°.
PROBLEMAS DE PRÁCTICA
PROBLEMA 1
Para cada triángulo, encuentra la medida del ángulo que falta.
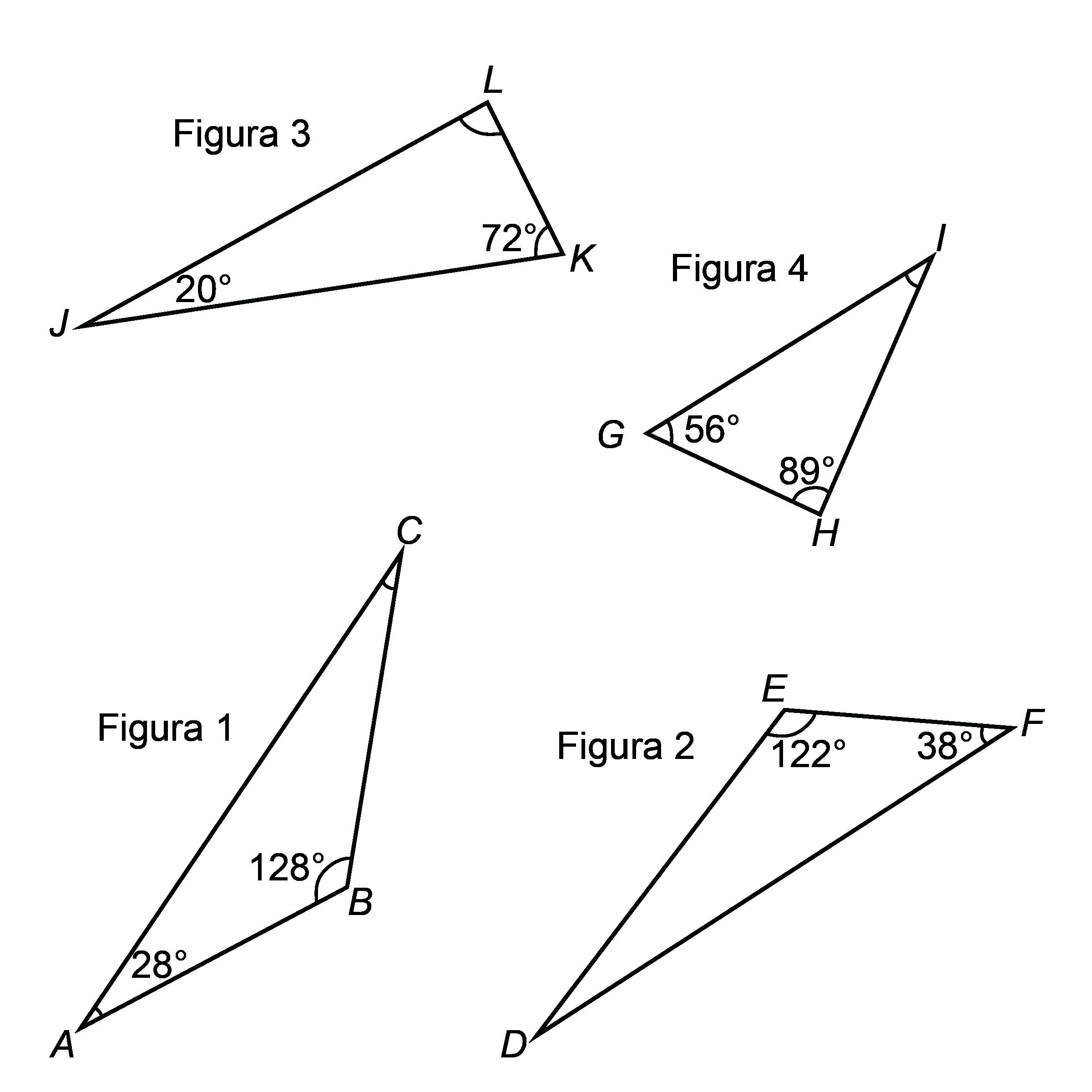
PROBLEMA 2
¿Existe un triángulo con dos ángulos rectos? Explica tu razonamiento.
Soluciones posibles
A. 24 grados(24 + 28 + 128 = 180)
B. 20 grados (20 + 38 + 122 = 180)
C. 88 grados (88 + 20 + 72 = 180)
D. 35 grados (35 + 56 + 89 = 180)
Soluciones posibles
No, los tres ángulos de un triángulo suman 180 grados. Dos ángulos rectos ya sumarían 180 grados, por lo que el tercer ángulo del triángulo tendría que ser de 0 grados; esto no es posible.
PROBLEMA 3
En este diagrama, las líneas ���� and ���� son paralelas Ángulo ������ mide 35° y el ángulo ������ mide 115°
A. ¿Qué es ��∠������?
B. ¿Qué es ��∠������?
C. ¿Qué es ��∠������?
Soluciones posibles
A. 115°
B. 35°
C. 30°
PROBLEMA 4
He aquí un diagrama del triángulo ������
A. Encuentre las medidas de los ángulos ��, �� y ��
B. Encuentre la suma de las medidas de los ángulos ��, �� y ��
C. ¿Qué observa en estos tres ángulos?
Soluciones posibles
A. �� = 100, �� = 135, �� = 125
Grado 8 . Matemáticas . Unidad 1
Grado 8 . Matemáticas . Unidad 1
B. �� + �� + �� = 360
C. Las respuestas varían. Ejemplo de respuesta: Esos tres ángulos juntos dan una vuelta completa a un círculo o 360 grados. Si una persona empieza a caminar en el centro del segmento ���� hacia ��, luego gira y camina hacia ��, gira de nuevo y camina hacia ��, y gira una vez más para volver al lugar de partida, acaba mirando en la misma dirección en la que empezó.
PROBLEMA 5
Grado 8, unidad 1, lección 13
Las dos figuras son congruentes.
A. Etiqueta los puntos ��′, ��′ y ��′ que corresponden a ��, �� y �� en la figura de la derecha.
B. Si el segmento ���� mide 2 cm, ¿cuánto mide el segmento ��′��′? Explica.
C. El punto �� se muestra además de �� y ��. Cómo puedes encontrar el punto ��′ que corresponde a ��? Explica tu razonamiento.
Reflexiones:
Soluciones posibles
A.
B. 2 cm. Las figuras son congruentes, y los segmentos correspondientes de figuras congruentes son congruentes.
C. Dado que las figuras son congruentes, el punto ��′ estará en el lado correspondiente y estará a la misma distancia de ��′ que �� está de �� �� puede encontrarse buscando el punto en el segmento que va hacia abajo y a la derecha desde ��′ que esté a la distancia adecuada desde ��′
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
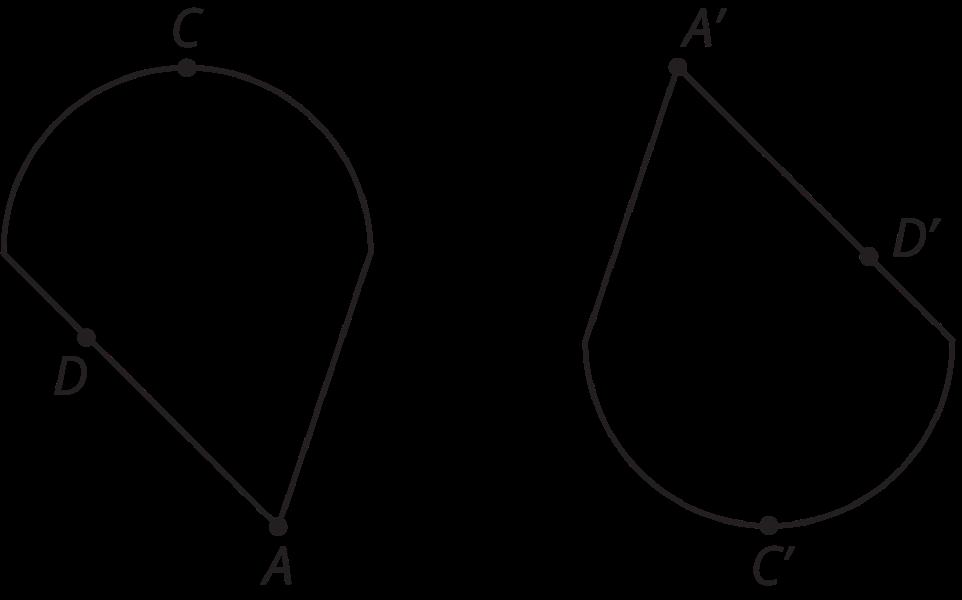
IDEA(S) FUNDAMENTAL(ES)
• Graficar relaciones
• Tasas unitarias en el mundo
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
8.G.2 Entender que una figura de dos dimensiones es congruente con otra si la segunda se puede obtener a partir de la primera mediante una secuencia de rotaciones, reflexiones y traslaciones; dadas dos figuras congruentes, describir una secuencia que exhiba la congruencia entre ellas.
8.G.5 Utilizar argumentos informales para establecer hechos sobre la suma de ángulos y el ángulo exterior de triángulos, sobre los ángulos creados cuando líneas paralelas son cortadas por una transversal, y el criterio ángulo-ángulo de semejanza de triángulos.
Construir
7.G.5
Enfoque SMPs
MP2 Razonar abstracta y cuantitativamente.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.4
I.C.9
II.B.5
LECCIÓN 17 ROTAR Y TESELAR
ENFOQUE EN IDEAS FUNDAMENTALES
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
repercutir en el futuro, razonan abstracta y cuantitativamente descubren la figura y el espacio.
META(S) DE APRENDIZAJE
• Hagamos patrones complejos usando transformaciones.
META(S)
DE APRENDIZAJE
• Puedo usar repetidamente transformaciones rígidas para hacer patrones repetitivos interesantes de figuras.
• Puedo usar propiedades de sumas de ángulos para razonar sobre cómo encajarán las figuras.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Crear teselados y diseños con simetría rotacional utilizando transformaciones rígidas.
• Explicar (oralmente y por escrito) las transformaciones rígidas necesarias para mover un teselado o diseño con simetría rotacional sobre sí mismo.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR8: Apoyos para el debate
MLR1: Cada vez más fuerte y más claro
Presentaciones en grupo
MLR2: Recopilación y presentación
Materiales requeridos
Plantillas maestras para la actividad 17.1
Papel en blanco
Copiasde las plantillas maestras
Conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha)
Papel cuadriculado
Papel cuadriculado isométrico
Grado 8 . Matemáticas . Unidad 1
PREPARACIÓN DE LA LECCIÓN CONTINUACIÓN
Preparación requerida
Imprime la plantilla maestra titulada «Deducir las medidas de ángulos». Prepara 1 copia para cada 2 estudiantes. Corta las copias por la mitad, de modo que haya suficientes copias para que cada estudiante reciba media hoja. Si es posible, haga estas copias en cartulina para que a los estudiantes les resulte más fácil calcar las formas después de recortarlas. Si están disponibles, los bloques de patrones también funcionan bien para esto.
Los estudiantes pueden beneficiarse del uso de papel cuadriculado y papel cuadriculado isométrico, pero estos materiales son opcionales.
INFORMACIÓN
Narrativa de la lección
DE LA LECCIÓN
En esta unidad, los estudiantes han aprendido a nombrar diferentes tipos de movimientos rígidos del plano y han estudiado cómo mover diferentes figuras (líneas, segmentos de línea, polígonos y formas más complejas). También han utilizado los movimientos rígidos para definir lo que significa que las figuras sean congruentes y han utilizado los movimientos rígidos para investigar la suma de los ángulos de un triángulo. En esta lección, los estudiantes utilizan el lenguaje de las transformaciones para producir, describir e investigar patrones en el plano. Se trata de una extensión directa del trabajo anterior con triángulos
• se dispusieron tres triángulos en el plano para demostrar que la suma de los ángulos de un triángulo es 180 grados
• se dispusieron cuatro copias de un triángulo en un cuadrado grande, recortando un cuadrado más pequeño en el centro
Aquí el enfoque es más creativo. Los estudiantes examinarán y crearán diferentes patrones de formas, incluyendo teselaciones (patrones que llenan todo el plano) y diseños complejos que muestran simetría rotacional (es decir, el diseño es congruente consigo mismo mediante varias rotaciones). Dependiendo del tiempo disponible, los estudiantes pueden trabajar en ambas actividades o elegir una de las dos.
Como en muchas de las actividades de esta lección, MP7 es fundamental, ya que los estudiantes utilizan la estructura de un conjunto dado de polígonos para producir una teselación. Las longitudes de los lados y los ángulos de los polígonos son restricciones y, a través de la experimentación y el razonamiento abstracto, los estudiantes descubren un patrón de repcomer (MP2).
RESUMEN DE LA LECCIÓN
Componente de la lección
Estructura Tiempo
Calentamiento En parejas 5-10 min
Actividad de exploración En parejas 35 min
Actividad Exploratoria En parejas 35 min
Descripción breve
Los estudiantes repasan los conocimientos previos rotando copias de polígonos alrededor de un vértice singulo para determinar las medidas de los ángulos de las figuras rotadas.
Los estudiantes aplican sus conocimientos sobre la suma de ángulos interiores de figuras y transformaciones rígidas para crear una teselación utilizando traslaciones.
Los estudiantes aplican sus conocimientos sobre la suma de ángulos interiores de figuras y transformaciones rígidas para crear una teselación usando rotaciones.
. Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
CALENTAMIENTO | DEDUCCIÓN DE MEDIDAS DE ÁNGULOS
(10 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
A lo largo de esta lección, los estudiantes construyen diferentes patrones con copias de algunos polígonos. En esta actividad, hacen algunas copias de cada polígono y las disponen en círculo. Calculan algunos de los ángulos de los polígonos a la vez que intuyen cómo encajan los polígonos entre sí. Éstas son las figuras incluidas en el esquema:
Los estudiantes pueden utilizar un transportador para medir ángulos, pero las medidas de todos los ángulos también pueden deducirse. En la primera pregunta de la tarea, se pide a los estudiantes que ajusten las copias de un triángulo equilátero alrededor de un único vértice. Caben seis copias, lo que les lleva a deducir que cada ángulo mide 60° porque 360 ÷ 6 = 60
Para las otras formas, pueden razonar sobre ángulos que suman 360°, ángulos que suman una recta y ángulos que suman un ángulo conocido.
Ó N Proporcionar acceso a conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Distribuya una media hoja (que contenga 7 formas) a cada estudiante. Puede ser conveniente demostrar cómo utilizar el papel de calco para colocar y trazar copias del triángulo alrededor de un único vértice, tal como se describe en la primera pregunta.
INTRODUCCI
Apoyo para los estudiantes con discapacidad
Lenguaje receptivo/expresivo: Tiempo de procesamiento. Los estudiantes que se benefician de un tiempo extra de procesamiento también se verían favorecidos por la RML8 (Apoyos para el debate).
Tu maestro te dará algunas formas.
1. ¿Cuántas copias del triángulo equilátero puedes encajar alrededor de un solo vértice, de modo que los bordes de los triángulos no tengan huecos ni se superpongan? ¿Cuál es la medida de cada ángulo en estos triángulos?
2. ¿Cuáles son las medidas de los ángulos en el...
A. cuadrado?
B. hexágono?
C. paralelogramo?
1. 6, 60°
2. Medidas de los ángulos:
A. Cuadrado: 90°
B. Hexágono: 120°
C. Paralelogramo: 120° y 60°
D. triángulo rectángulo?
E. octógono?
F. pentágono?
D. Triángulo rectángulo: 45° y 90°
E. Octógono: 135°
F. Pentágono: 90°, 120°, y 150°
Grado 8 . Matemáticas . Unidad 1
CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS
DE LA ACTIVIDAD
Al deducir las medidas de los ángulos, es importante saber que los ángulos «que rodean» un vértice suman 360°. También es importante saber que los ángulos que forman una recta cuando son adyacentes suman 180°. Vigila a los estudiantes que necesiten que se les recuerden estos datos.
Para el resto de la lección, no es tan importante que se conozcan las medidas en grados de los ángulos, así que no te enfoques en las respuestas. Selecciona a algunos estudiantes que hayan deducido las medidas de los ángulos encajando piezas para que presenten su trabajo. Asegúrate de que los estudiantes vean muchos ejemplos de formas que encajan como piezas de recompenzas. Recuerda de la lección anterior que los 3 ángulos congruentes de un triángulo equilátero forman una línea o ángulo de 180 grados, por lo que tiene sentido que 6 copias de este ángulo formen un círculo completo.
ACTIVIDAD DE EXPLORACIÓN | TESELA ESTO
(35 minutos)
Rutinas didácticas
MLR1: Cada vez más fuerte y más claro Presentaciones en grupo
Cada actividad de clase de esta lección (ésta, la creación de una teselación, y la siguiente, la creación de un diseño con simetría rotacional) podría fácilmente llevar todo un período de clase o más. Considera la posibilidad de dejar que los estudiantes elijan realizar una de las dos actividades.
Una teselación del plano es un patrón regular repetido de una o más formas que cubre todo el plano. Algunos de los ejemplos más conocidos de teselaciones son los azulejos del baño y la cocina. Las baldosas (para suelos, techos, baños, cocinas) suelen estar compuestas por copias de las mismas formas porque necesitan encajar y extenderse siguiendo un patrón regular para cubrir una gran superficie.
Comparta con los estudiantes una definición de teselación, del tipo: «Una teselación del plano es un patrón regular repetido de una o más formas que cubre todo el plano». Muestre varios ejemplos de teselaciones. Una teselación verdadera cubre todo el plano: Aunque es imposible de mostrar, podemos identificar un patrón que se repite eternamente en todas direcciones. Esto es importante cuando pensamos en teselaciones y simetría. Una definición de simetría es: «Puedes agarrarlo y ponerlo de otra forma y parece exactamente igual». En una teselación, puedes realizar una traslación y la imagen se ve exactamente igual. En el ejemplo de este teselado, la traslación que lleva el punto �� al punto �� da como resultado una figura que se ve exactamente igual que con la que empezaste. Lo mismo ocurre cones la traslación que lleva �� a ��. La descripción de una de estas traslaciones demuestra que esta figura tiene simetría traslacional. Proporcione acceso a conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Sugiera a los estudiantes que si recortan una forma, es fácil hacer muchas copias de la misma calcándola. Anime a los estudiantes a utilizar las formas de la actividad anterior (o los bloques de patrones, si están disponibles) y a experimentar uniéndolos. No es necesario que utilicen todas las formas, así que si tienen dificultades, sugiérales que prueben a utilizar copias de un par de las formas más sencillas.
California . Grado 8
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes con discapacidad
Procesamiento conceptual: Manipulativos. Proporcione manipulativos (por ejemplo, bloques de patrones o recortes de figuras) para ayudar a los estudiantes que se benefician de las actividades prácticas.
1. Diseña tu propio teselado. Tendrás que decidir qué formas quieres utilizar y hacer copias. Recuerda que una teselación es un patrón que se repite hasta llenar todo el plano.
2. Busca un compañero e intercambia imágenes. Describe una transformación del dibujo de tu compañero que lleve el patrón a sí mismo. ¿Cuántas transformaciones diferentes puedes encontrar que lleven el patrón a sí mismo? Considera traslaciones, reflexiones y rotaciones.
3. Si tienes tiempo, colorea y decora tu teselación.
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS PREVISTOS
1. Las respuestas varían.
2. Las respuestas varían. Por ejemplo, en el teselado anterior, podríamos reflejarnos a través de la línea discontinua o rotar 90 grados en el sentido de las agujas del reloj alrededor del punto marcado con ��.
Cuidado con los estudiantes que eligen figuras que casi encajan, pero no completamente. Reitere que el patrón tiene que continuar siempre; a menudo, los pequeños huecos o solapamientos se hacen más evidentes cuando se intenta continuar el patrón.
SÍNTESIS DE LA ACTIVIDAD
Invite a los estudiantes a compartir sus diseños y también a describir una transformación que lleve el diseño a sí mismo. Considera la posibilidad de decorar tu habitación con sus productos acabados.
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes que aprenden el idioma inglés
Escribir, hablar, escuchar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina con sucesivos intercambios de parejas para dar a los estudiantes una oportunidad estructurada de revisar su explicación inicial para crear sus teselaciones. Después de escribir una explicación inicial, pida a los estudiantes que se reúnan con 2-3 otros compañeros en fila para recibir comentarios. Ofrezca a los estudiantes sugerencias para que refuercen sus ideas y aclaren su lenguaje (por ejemplo: «¿Puedes explicar cómo has creado tu teselación?», «¿Cuántas transformaciones rígidas llevará el patrón a sí mismo?», etc).. Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar la explicación final. A continuación, pueden volver a sus asientos y escribir su descripción revisada del teselado.
Principio(s) de diseño: Optimizar la salida (para la generalización)
ACTIVIDAD DE EXPLORACIÓN | GIRA ESO
(35 minutos)
Rutinas didácticas
MLR2: Recopilar y mostrar
Presentaciones en grupo
Cada actividad de la clase de esta lección (la anterior, crear una teselación, y de esta, crear un diseño con simetría rotacional) podría llevar fácilmente un período de la clase o más. Considera la posibilidad de dejar que los estudiantes elijan una de las dos actividades. En esta actividad, utilizando sus herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha), los estudiantes pueden crear su propio diseño con simetría rotacional. A continuación, comparten los diseños y encuentran las diferentes rotaciones (y posiblemente reflexiones) que hacen que la forma coincida consigo misma.
INTRODUCCIÓN
Pregunte a los estudiantes qué transformación podrían realizar en la figura para que coincida con su posición original. Hay varias rotaciones utilizando A como centro que funcionarían: 72° o cualquier múltiplo de 72°. Asegúrate de que los estudiantes entienden que los triángulos 5 de este patrón son congruentes y que 5 ⋅ 72 = 360: Por eso los múltiplos de 72° con centro A son congruentes con esta figura. Deben tener cuidado al seleccionar los ángulos de las figuras de su patrón. Si tienen dificultades, pídales que utilicen fichas de patrones o copias de las figuras de la actividad anterior para ayudarles a construir un patrón.
Si es posible, muestre a los estudiantes varios ejemplos de figuras que tengan simetría rotacional.
Proporcione acceso a conjuntos de herramientas de geometría (papel de calco, papel cuadriculado, lápices de colores, tijeras y una ficha). Si es posible, proporcione papel cuadriculado o papel cuadriculado isométrico.
Apoyo para estudiantes que aprenden el idioma inglés
Conversar, representar: MLR2 Recopilar y mostrar. Camine y escuche a los estudiantes hablar sobre sus teselaciones durante el trabajo en parejas o en grupo, y tomar notas sobre palabras y frases comunes o importantes (por ejemplo, reflejar, rotar, centrar, grados, múltiplos), junto con bocetos o diagramas útiles. Escriba las palabras y los esquemas de los estudiantes en una pantalla para consultarlos durante los debates de toda la clase a lo largo de la lección. Esto ayudará a los estudiantes a utilizar un lenguaje matemático y de transformación al describir sus diseños de simetría rotacional.
Principio(s) de diseño: Apoyar la creación de sentido; maximizar la metaconciencia
Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1
Apoyo para estudiantes con discapacidad
Procesamiento conceptual: Manipulativos. Proporcione manipulativos (por ejemplo, bloques de patrones o recortes de formas) para ayudar a los estudiantes que se benefician de las actividades prácticas.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. Crea un diseño con simetría rotacional.
2. Busca un compañero que también haya creado un diseño. Intercambien diseños y encuentren una transformación del diseño de tu compañero que lo adapte a sí mismo. Considera rotaciones, reflexiones y traslaciones.
3. Si tienes tiempo, colorea y decora tu diseño.
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS ANTICIPADOS
Las respuestas varían. A continuación se muestra un ejemplo de forma.
Hasta ahora, los estudiantes podrían pensar que la simetría de reflexión es el único tipo de simetría. Por ello, podrían crear un diseño con simetría de reflexión, pero no rotacional. Oriente a los estudiantes en la dirección correcta pidiéndoles que realicen una rotación que lleve la figura hacia sí misma. Reconozca que la simetría de reflexión es un tipo de simetría, pero la tarea aquí es crear un diseño con simetría rotacional.
Invita a los estudiantes a compartir sus diseños y a describir una transformación que los transforme. Considera decorar tu habitación con sus productos terminados.
Math Nation California . Grado 8
©Accelerate Learning Inc. - Todos los derechos reservados
Grado 8 . Matemáticas . Unidad 1