



Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).
La plataforma de recursos curriculares en línea que se ofrece en "mathnation.com", incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.
La marca comercial "Math Nation" es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.
Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.
En Álgebra 1, los estudiantes estudiaron varias familias de funciones. Se centraron en las funciones lineales, exponenciales y cuadráticas y sus características clave. También conocieron las funciones de valor absoluto y las secuencias. Para repasar y construir sobre este aprendizaje, Álgebra 2 comienza con esta unidad centrada en las ideas generales fundamentales para el estudio de las funciones. Los temas explorados en esta unidad pueden ampliarse a lo largo del año escolar en unidades que profundizan en tipos específicos de funciones y a medida que se introducen nuevos tipos de funciones.
En esta unidad, los estudiantes consideran las funciones, ecuaciones y desigualdades como un todo. Los conceptos que exploran incluyen la revisión de funciones principales clave y la introducción de algunos tipos de funciones que estudian por primera vez en este grado. Además, los estudiantes exploran la tasa media de cambio, secuencias y series, y ecuaciones y desigualdades de valor absoluto. Los estudiantes también revisan los sistemas de inecuaciones a medida que desarrollan una comprensión de la representación de restricciones en el contexto de la representación con las matemáticas (MP4). Los estudiantes analizan gráficos, tablas, ecuaciones y contextos a medida que trabajan para conectar las representaciones y comprender la estructura de las diferentes relaciones (MP7).
Los estudiantes comienzan la unidad con un repaso de los tipos de función en los que se centraron en Álgebra 1 (lineal, cuadrática y exponencial) y revisa algunas de las características clave de estas relaciones. A continuación, repasan el concepto de razón media de cambio. Estos conceptos están integrados en la primera unidad para proporcionar la oportunidad de centrarse en los fundamentos del curso.
A continuación, los estudiantes exploran las secuencias y series, primero van a repasan el aprendizaje previo relacionado con las secuencias aritméticas y geométricas. Luego, se encuentran con algunas situaciones en las que tiene sentido calcular la suma de una secuencia finita con estrategias eficientes en lugar de la suma incremental. El desarrollo de una fórmula para tal suma de términos en una secuencia se produce en una unidad futura.
La unidad pasa entonces a ecuaciones, desigualdades y sistemas. Los estudiantes amplían sus conocimientos previos para escribir y resolver ecuaciones y desigualdades de valor absoluto en contextos matemáticos y reales. Luego, revisan los sistemas de inecuaciones, lo que conduce al estudio de las restricciones en contextos de representación. Utilizan sistemas de ecuaciones y desigualdades para representar restricciones que surgen en una situación del mundo real, un concepto que volverán a tratar a lo largo del curso en varios contextos de representación.
©Accelerate Learning Inc. - Todos los derechos reservados
2 . Matemáticas . Unidad 1
Enfoque en ideas fundamentales
• Analizar funciones
• Representar con funciones
• Ecuaciones para predecir y representar
ESTÁNDARES POR LECCIÓN
Lección
A2.1.1

Estándar(es) abordado(s)
Prerrequisito para F-IF.7c, F-BF.3
A2.1.2 F-IF.6
A2.1.3 F-IF.6
A2.1.4 F-IF.4; F-IF.9
A2.1.5 Prerrequisito para A-SSE.4
A2.1.6 A-SSE.4
A2.1.7
A2.1.8
A2.1.9
A-REI.3.1; A-CED.1
A-REI.3.1; A-CED.1
A-CED.3; F-IF.5
A2.1.10 A-CED.3
Nation California . Algebra 2
Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Analizar funciones
Abordar
Alineación de estándares y principios de California
F-IF.7c Graficar funciones expresadas simbólicamente y mostrar las características clave de la gráfica, a mano en casos sencillos y con tecnología para casos más complicados. Graficar funciones polinómicas identificando los ceros cuando se dispone de factorizaciones adecuadas y mostrando el comportamiento final.
F-BF.3 f(x) por f(x) + k, kf(x), f(kx), y f(x + k) para valores específicos de k (tanto positivos como negativos); hallar el valor de k dados los gráficos. Experimentar con casos e ilustrar una explicación de los efectos en la gráfica con tecnología. Identificar el efecto en la gráfica de sustituir
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.4
I.C.9
II.B.5
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
comprender al mundo, buscarán y harán uso de la estructura exploran cantidades cambiantes.
• Puedo reconocer tipos de funciones con gráficas, ecuaciones o tablas de valores.
• Puedo determinar un tipo de función que podría representar una transformación de una función principal.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comprender que las funciones pueden representarse con gráficas, ecuaciones o tablas de valores.
• Determinar la función principal de diferentes representaciones de funciones transformadas.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
¿Cuál no pertenece?
Sondear a la clase
Pensar, girar y compartir
MLR1: Cada vez más fuerte y más claro
Tomar turnos
©Accelerate Learning Inc. - Todos los derechos reservados
Materiales necesarios
Plantilla maestra para la actividad de exploración (1 juego por cada 2 estudiantes)
Imprime y recorta las plantillas maestras de la actividad de exploración.
Álgebra 2 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Reconozcamos diferentes tipos de funciones a partir de varias representaciones.
Narrativa de la lección
Los estudiantes activan sus conocimientos previos sobre los tipos de funciones. Primero exploran diferentes representaciones de funciones lineales, cuadráticas y exponenciales con las que deben estar familiarizados de Álgebra 1 e identifican sus características clave. Los estudiantes también identifican los tipos de funciones a partir de una tabla de valores y repasan las diferentes formas de cada tipo de función.
A medida que la lección continúa, los estudiantes determinan los tipos de funciones para incluir funciones cúbicas, de valor absoluto y de raíz cuadrada. Amplían sus conocimientos sobre la determinación y el reconocimiento de tipos de funciones con gráficas, ecuaciones o tablas de valores para determinar tipos de funciones que podrían representar una transformación de una función principal (MP1).
El principal resultado del aprendizaje en esta lección es que los estudiantes revisen y amplíen sus conocimientos previos sobre los tipos de funciones y sus representaciones como ecuaciones, gráficas y tablas de valores antes de profundizar en los conceptos básicos de funciones explorados a lo largo de esta unidad (MP7).
Componente de la lección

Estructura Tiempo
Calentamiento Grupos pequeños 5 min
Actividad de Exploración En parejas 15 min
Actividad de exploración Grupos pequeños 10 min
Síntesis Grupo el grupo 5 min
Enfriamiento Independiente 5 min
Descripción breve
Los estudiantes hacen observaciones sobre las gráficas de cuatro funciones para determinar cuál no pertenece y explican su razonamiento.
Los estudiantes hacen conexiones entre gráficas, tablas y diferentes formas de ecuaciones de funciones familiares, como lineal, exponencial y cuadrática.
Los estudiantes utilizan una clasificación de tarjetas para hacer coincidir el nombre de la función, la ecuación de la función principal, el gráfico, la tabla de valores y la característica clave de varias funciones conocidas y nuevas.
Los estudiantes reflexionan sobre qué representaciones de funciones son más útiles para identificar características clave específicas, así como qué funciones son más fáciles de identificar en comparación con otras.
Los estudiantes utilizan diferentes representaciones de funciones para determinar las ecuaciones de las funciones padre.
Práctica Independiente 10 min El componente de práctica independiente incluye 3 problemas de la lección y 1 problema de repaso en espiral.
. Algebra 2 ©Accelerate Learning Inc. - Todos los derechos reservados


(5 minutos)

Rutinas didácticas
¿Cuál no pertenece?
Sondear a la clase
Los estudiantes ven 4 gráficos y deben elegir cuál no pertenece. A continuación, explican su razonamiento para decidir que 1 opción no pertenece y tienen la oportunidad de precisar más su razonamiento. No hay una única respuesta correcta. Los estudiantes obtienen un punto de entrada a la lección y usted puede escuchar parte de la terminología y conceptos que los estudiantes han retenido de Álgebra 1.
INSTRUCCIÓN
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
Organice a los estudiantes en grupos de 2-4. Muestre las 4 gráficas de las funciones para que todos las vean. Dé a los estudiantes 1 minuto (min) de tiempo para pensar en silencio y pídales que indiquen cuándo han decidido que 1 gráfico no pertenece y pueden explicar por qué. Anímeles a pensar en más de 1 posibilidades. Cuando se acabe el minuto, dé a los estudiantes 2 minutos para compartir sus respuestas con sus grupos y luego pídales que trabajen juntos para encontrar al menos 1 razón, si es posible, por la que cada gráfica no pertenece.
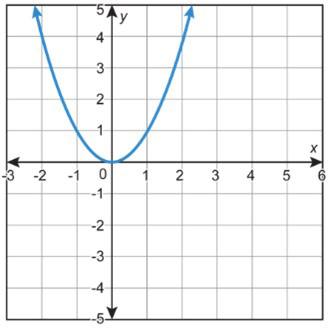
Se muestran las gráficas de 4 funciones.
Función A
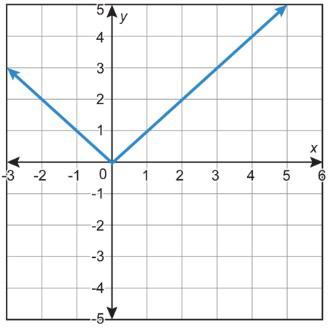
Función C
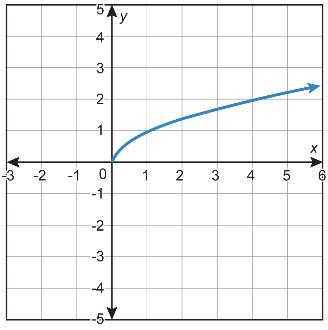
1. ¿Qué función no pertenece?
2. Explique tu razonamiento.
Función B
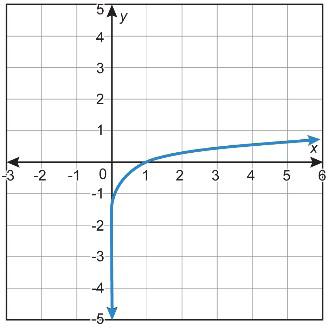
Función D
RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD
Álgebra 2 . Matemáticas . Unidad 1
Las respuestas variarán. Ejemplos de respuestas:
• La función A es la única función que no es curva. La función A es la única gráfica con el punto (2, 2). La función A es la única función con valor absoluto.
• La función B es la única función que tiene valores negativos de la función. La función B es la única gráfica que no incluye el punto (1, 1). La función B es la única gráfica con un comportamiento final que se aproxima a -∞
• La función C es la única función que no tiene un dominio de (-∞, ∞). La función C es el único gráfico que incluye el punto (4, 2). La función C es la única gráfica que incluye solo valores positivos X y Y.
• La función D es la única función cuadrática. La función D es la única gráfica que incluye el punto (2, 4). La función D es la única gráfica con forma de U.
Después de que los estudiantes compartan sus observaciones en grupos, invite a cada grupo a compartir 1 la razón por la que una gráfica concreta de una función podría no pertenecer a un grupo. Registre y muestre las respuestas. Después de cada respuesta, sondee al resto de la clase para ver si otros han hecho la misma observación. Dado que no hay una única respuesta correcta a la pregunta de qué gráfica de una función no pertenece, preste atención a las explicaciones de los estudiantes y asegúrese de que las razones dadas son correctas. Pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como dominio, rango, interceptos, intervalos positivo/negativo y creciente/decreciente, y que fundamenten sus afirmaciones.
(15 minutos)
Rutinas didácticas
Pensar, girar y compartir
MLR1: Cada vez más fuerte y más claro
Los estudiantes trabajan en colaboración con un compañero para revisar las representaciones de funciones lineales, cuadráticas y exponenciales que aprendieron en Álgebra 1. La actividad proporciona a los estudiantes un repaso de los conceptos clave del curso anterior, al tiempo que le da la oportunidad de ver lo que los estudiantes recuerdan y lo que no recuerdan del curso anterior antes de planificar el resto de la unidad. Los estudiantes volverán a tratar las relaciones lineales, cuadráticas y exponenciales en futuras lecciones y unidades, por lo que no es necesario dedicar tiempo extra a esta lección o a esta actividad, ya que el dominio no es todavía el objetivo.
Esta actividad le permite establecer normas para este tipo de actividad en el aula. Considere la posibilidad de establecer normas para el aprendizaje colaborativo antes de empezar.
INSTRUCCIÓN
Organice a los estudiantes en grupos de 2. Proporcione a los estudiantes 2-3 minutos de tiempo de trabajo tranquilo para trabajar en el problema 1 y sus partes. A continuación, dé a los estudiantes 1-2 minutos para que discutan sus respuestas con sus compañeros. Continúe este proceso a través de los problemas 2-3 antes de terminar con un debate en grupo sobre las cosas que han aprendido o redescubierto en esta actividad.
©Accelerate Learning Inc. - Todos los derechos reservados


Apoyo para estudiantes que aprenden el idioma inglés
Hablar, representar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para apoyar una discusión productiva. Dé tiempo a los estudiantes para que se reúnan con 2-3 compañeros para compartir y recibir comentarios. Proporcióneles indicaciones para recibir comentarios que ayuden a sus compañeros a fortalecer y aclarar sus ideas (por ejemplo: «¿Cómo conseguiste esa coincidencia?«
«¿Cómo determinaste la X o intercepción Y?» y «¿Cómo determinaste qué ecuación coincide»). De este modo, los estudiantes tienen la oportunidad de producir lenguaje matemático verbal al servicio del perfeccionamiento de sus ideas y sus dibujos.
Principio(s) de diseño: Optimizar la salida (para la justificación)

Apoyo a estudiantes con discapacidad
Representación: Manipulativos. Para los estudiantes que se benefician de las actividades prácticas, considere la posibilidad de recortar los gráficos, ecuaciones y tablas de valores para hacer tarjetas para los estudiantes. Proporcione a cada estudiante o pareja de estudiantes una bolsa de tarjetas. Pida a los estudiantes que hagan coincidir o agrupen las tarjetas que representan la misma función. En lugar de anotar qué tabla y qué ecuaciones corresponden a un gráfico concreto, los estudiantes pueden ver el gráfico, la ecuación y la tabla de valores al mismo tiempo y hacer coincidirlos según corresponda.
Apoya la accesibilidad para: Procesamiento visual-espacial, procesamiento conceptual
Trabaja con tu compañero para completar lo siguiente.
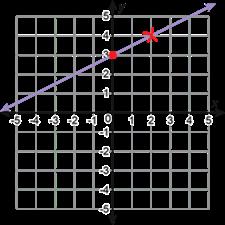
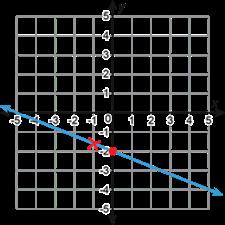
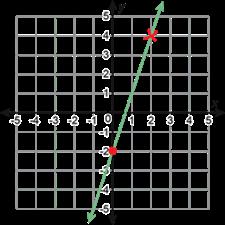
1. Se muestran las gráficas de tres funciones lineales.
Función lineal
Gráfica
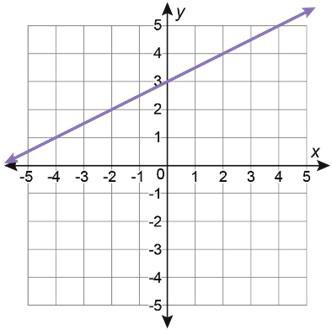
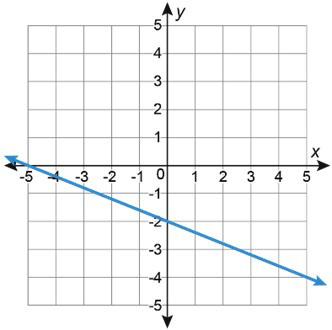
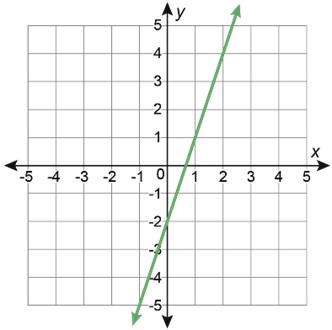
Tabla de valores
A. Escribe el número de la tabla en la fila vacía de la tabla anterior para hacer coincidir cada tabla de valores con la gráfica a la que corresponde.
Tabla de valores 1 Tabla de valores 2 Tabla de valores 3
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
CONTINUACIÓN

California . Algebra 2
Álgebra 2 . Matemáticas . Unidad 1
A. Cada función lineal también puede representarse mediante ecuaciones lineales de diferentes formas. Haz coincidir cada gráfica con un conjunto de ecuaciones escribiendo la letra de la gráfica en la columna vacía de abajo.
Forma estándar Forma pendienteintercepto Forma punto-pendiente Gráfica
3x - y = 2 y = 3x - 2 (y - 4) = 3(x - 2) x - 2y = -6 y = 1 2 x + 3 (y - 4) = 1 2 (x - 2) 2x + 5y = -10 y =2 5 x - 2 (y + 1.6) = - 2 5 (x + 1)
B. En cada gráfica, dibuja una X en la coordenada que se usó para crear la forma punto-pendiente de la ecuación en la tabla. Luego, encierra en un círculo las coordenadas del punto en la tabla de valores.
C. Traza un punto en la intercepción Y de cada gráfica. Después, subraya el valor de la intercepción Y en la ecuación de la recta que la revela. 1. Se muestran las gráficas de tres funciones cuadráticas.
Función cuadrática D E F Gráfica
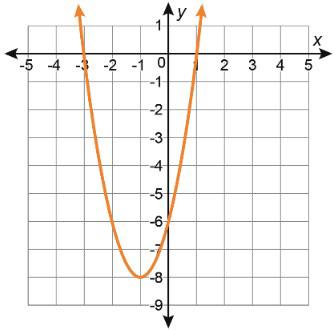
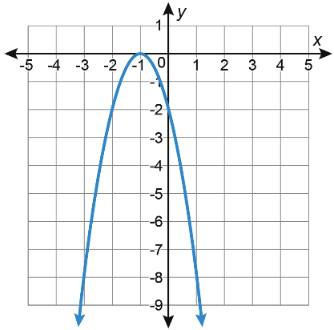
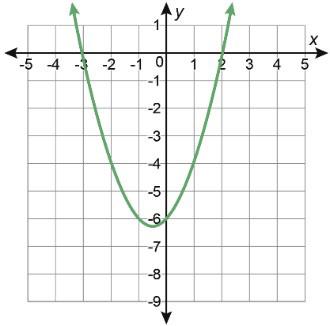
Tabla de valores
A. Haz coincidir cada tabla de valores con la parábola a la que corresponde escribiendo el número de la tabla en la fila vacía de la tabla anterior.
Tabla de valores 4
Tabla de valores 5 Tabla de valores 6
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN
A. Cada función cuadrática también puede representarse con ecuaciones de diferentes formas. Escribe la letra de la gráfica en la columna vacía de abajo para hacer coincidir cada gráfica con un conjunto de ecuaciones.
Gráfica Ecuaciones Forma
f(x) = x2 + x - 6 Estándar
f(x) = (x - 2)(x + 3) Factorizada
f(x) = (x + 1 2 )2 - 6.25 Vértice
f(x)= -2x2 - 4x - 2 Estándar
f(x) = -2(x + 1)(x + 1) Factorizada
f(x) = -2(x + 1)2 Vértice
f(x) = 2x2 + 4x - 6 Estándar
f(x) = 2(x + 3)(x - 1) Factorizada
f(x)=2(x + 1)2 - 8 Vértice
B. Dibuja una X en cada gráfica en el vértice de la parábola. Luego, subraya los valores que pueden usarse para determinar el vértice en la ecuación que lo reve .
C. Traza un punto en la(s) intercepción(es) X de cada gráfica. Luego, encierra con un círculo la forma de las ecuaciones que pueden usarse para revelarlas.
D. Subraya el valor de la intercepción Y en la ecuación que la revela.
1. Se muestran las gráficas de dos funciones exponenciales. Función exponencial G H
Gráfica
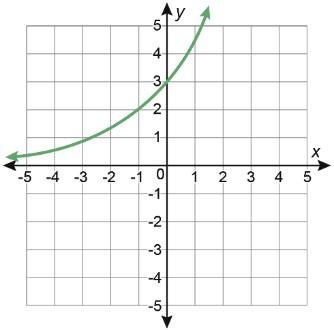
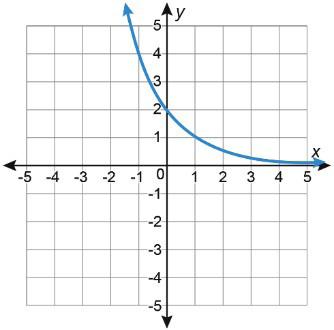
Tabla de valores
A. Escribe el número en la fila vacía de la tabla anterior para hacer coincidir cada tabla de valores con la gráfica exponencial a la que corresponde. Tabla de valores 7 Tabla de valores 8
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES
1.
California . Algebra 2
Álgebra 2 . Matemáticas . Unidad 1
A. Cada función exponencial también puede representarse mediante ecuaciones de diferentes formas. Haz coincidir cada gráfica con su correspondiente conjunto de ecuaciones escribiendo la letra de la gráfica en la última columna.
Funciones exponenciales Gráfico
f(x) = 3(1.5)x f(x) = 3(1 + 1 2 )x
f(x) = 2(0.5)x f(x) = 2(1 - 1 2 )x
B. Traza un punto en la intercepción Y de cada gráfica. Luego, subraya el valor de la intercepción Y en cada ecuación.
C. Ambas funciones exponenciales tienen una asíntota horizontal en y = 0. Explica lo que esto significa en términos de la gráfica.
A. Función lineal A: Tabla de valores 2
Función lineal B: Tabla de valores 1
Función lineal C: Tabla de valores 3 B. Formulario estándar Forma pendienteintersección Forma punto-pendiente Gráfico 3x − y = 2 y = 3x − 2 (y − 4) = 3(x − 2) C x − 2y = −6 y = 1 2 x + 3 (y − 4) = 1 2 (x − 2) A 2x + 5y = −10 y =
D. La respuesta se muestra en las tablas anteriores.
©Accelerate Learning Inc. - Todos los derechos reservados


2 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES CONTINUACIÓN 1.
A. Función cuadrática D: Tabla de valores 5 Función cuadrática E : Tabla de valores 4 Función cuadrática F : Tabla de valores 6 B.
Gráfico Ecuaciones Forma
f(x) = x2 + x − 6 Estándar
f(x) = (x − 2)(x + 3) Factorizada
f(x) = (x + 1 2 )2 − 6.25 Vértice
f(x)= −2x 2 − 4x − 2 Estándar
f(x) = −2(x + 1)(x + 1) Factorizada
f(x) = −2(x + 1)2 Vértice
f(x) = 2x2 + 4x − 6 Estándar
f(x) = 2(x + 3)(x − 1) Factorizada
f(x)=2(x + 1)2 − 8 Vértice C. Función cuadrática D E F
Gráfico
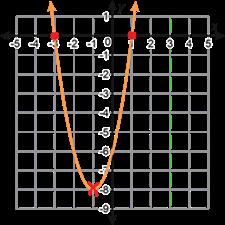
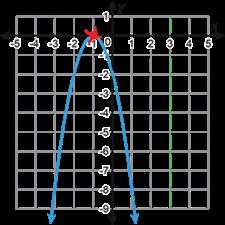
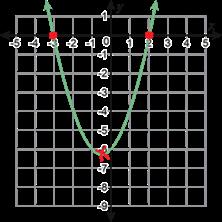
Tabla de valores 5 4 6
D. Véanse las tablas de los problemas 2b y 2c. E. Véase la tabla del problema 2b. 2.
A. La función exponencial G concuereda con la tabla de valores 8. La función exponencial H concuerda con la tabla de valores 7. B.
Funciones exponenciales Gráfica
f(x) = 3(1.5)x f(x) = 3(1 + )x G
f(x) = 2(0.5)x f(x) = 2(1 - )x H
RESPUESTAS POSIBLES CONTINUACIÓN

CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
2 . Matemáticas . Unidad 1
Función exponencial G H
Gráfico
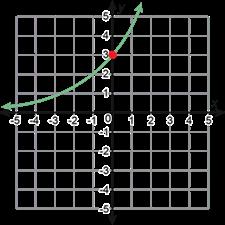
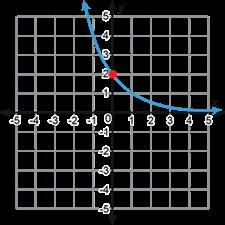
Tabla de valores 8 7
B. Ejemplo de respuesta: La gráfica de la función continúa acercándose a y = 0 (el eje x) a medida que x se hace más grande (gráfica H) o a medida que x se hace más pequeña (gráfica G), pero la gráfica nunca tocará o intersectará el eje x
Los estudiantes pueden confundir la intercepción X y la intercepción Y en la gráfica. Considera proporcionarles un ejemplo donde los interceptos estén etiquetados con sus coordenadas para usarlos como referencia.
Los estudiantes pueden confundir los signos cuando escriben el vértice de la forma de vértice de una función cuadrática. Por ejemplo, los estudiantes pueden escribir el vértice como (−2, −1) para la función en forma de vértice, f(x) = a(x - 2)2 -1.
Esta actividad repasa 3 de los tipos de función con los que los estudiantes trabajaron a lo largo de Algebra 1. Refresca a los estudiantes en cada tipo de función, sus gráficos y algunas características clave. Considera facilitar una discusión en clase usando las preguntas que se muestran:
• «¿Cómo puede usarse la forma de vértice para encontrar el vértice de una función cuadrática?».
• «¿Alguna de las funciones exponenciales G o H cruza alguna vez el eje X? ¿Por qué sí o por qué no?».
• «¿Es posible elevar un número a una potencia, digamos 2x y obtener 0? Es decir, ¿es posible que 2x = 0».
• «¿Cuál es la relación entre las formas 2 de una función exponencial?».
Rutinas didácticas
Por turnos
(10 minutos)
Materiales necesarios
Plantilla maestra (1 juego de recortables por cada 2 estudiantes)
Los estudiantes trabajan con un compañero o grupo para hacer coincidir las funciones padre (y los tipos de función correspondientes) con sus gráficas, tablas de valores y características clave para 8 diferentes tipos de función.
INSTRUCCIÓN
Los estudiantes necesitan tener acceso a las tarjetas plantillas maestras recortables. Prepárelas con antelación y organícelas en grupos para facilitar su distribución al comienzo de la actividad. Organice a los estudiantes en grupos de 2-4. En cada grupo, los estudiantes colocan todas las tarjetas y se turnan para hacer coincidir el gráfico, la tabla de valores y las características clave con una función principal. Cada estudiante hace coincidir 1 a la vez. El otro compañero o compañeros deben escuchar la explicación del estudiante y hacer preguntas de sondeo o aclaración. Dado que es la primera vez que los estudiantes realizan una clasificación por tarjetas, considere la posibilidad de demostrar a la clase cómo debe desarrollarse la discusión en cada grupo.

eje x) pequeña
Considera para
vértice (−2, algunas por posible

Compromiso: Tutores compañeros. Asigna a los estudiantes con sus compañeros tutores previamente identificados.
Apoya la accesibilidad para: Funcionamiento socioemocional

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. Trabaja con tu compañero para clasificar las tarjetas de modo que coincidan con la ecuación, la gráfica, la tabla de valores y las características clave de la función principal para cada tipo de función. La ecuación de cada función principal se corresponde con el tipo de función correspondiente en la tabla. Escribe la letra de la gráfica, la tabla de valores y el conjunto de características clave de cada función principal para completar la tabla.
Tipo de función Función principal Gráfico
Lineal y = x
Cuadrática y = 2
Cúbica y = x3
Crecimiento exponencial y = (2)x
Decaimiento exponencial y = ( 1 2 )x
Valor absoluto y = |x|
Raíz cuadrada y = √x
Raíz cúbica y = ∛x
Tipo de función
Función principal
Gráfica
Tabla de valores
Características principales
RESPUESTAS POSIBLES
Tabla de valores
Características clave
Lineal y = x U V N
Cuadrática y = x2 P C S o Z
Cúbica y = x3 W D K o T
Crecimiento exponencial y = (2)x Y R H
Decaimiento exponencial y = ( 1 2 )x E Q
Valor absoluto y = |x|
Raíz cúbica y = ∛x L F
CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD
Los estudiantes pueden confundir las gráficas de las funciones cúbica y raíz cúbica. Considere proporcionarles ejemplos de cada función y resalte las áreas que hacen que los gráficos y las funciones sean diferentes.
Facilite un debate en clase después de que los estudiantes hayan terminado la actividad. Considere el uso de las siguientes preguntas para estimular la discusión.
• «¿Cómo determinaste qué gráfica, tabla de valores y características clave iban con cada función principal?».
• «¿Qué estrategias usaste?».
• «¿Cómo sabes que tus respuestas son correctas?».
(5 minutos)
Los estudiantes revisaron el conocimiento previo de las funciones padre aprendido en Álgebra 1, que es parte de los fundamentos de Álgebra 2, donde también aprenderán tipos de funciones adicionales. Formule a los estudiantes las siguientes preguntas:
• «¿Qué representaciones creen que facilitan la identificación de una función principal? ¿Por qué?».
• «¿Qué representaciones de una función te parecieron más difíciles de hacer coincidir con sus funciones padre? ¿Por qué?».
Consulte la sección «Resumen de la lección para el estudiante» para repasar formalmente los nuevos términos de vocabulario introducidos en esta lección. Anime a los estudiantes a crear diagramas, ejemplos, no ejemplos y explicaciones de cada uno de los términos estudiados en esta lección. Considere la posibilidad de crear un esquema de anclaje o un diagrama de los diferentes tipos de funciones matrices con sus ecuaciones, gráficos, tablas de valores y características clave. Los estudiantes pueden usar esto como referencia a lo largo del curso a medida que construyen sobre esta base
(5 minutos)
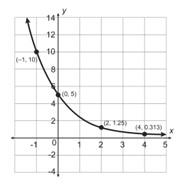
1. La tabla muestra representaciones de transformaciones de diferentes funciones madre. Determina a qué familia de funciones pertenece cada transformación. Representación de la transformación Ecuación de la función principal
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


RESPUESTAS POSIBLES

• y = |x|
• y = ( 1 2 )x
• y = x2
Resumen de la lección para el estudiante
Esta lección es la introducción al estudio de las funciones en este curso. Una familia de funciones comparte las mismas características y forma general. La más básica de ellas se llama función principal. Se pueden aplicar transformaciones a la función principal función para crear otros miembros de la familia de funciones que comparten características similares. Conocer información sobre una función principal es útil para identificar transformaciones de esa función principal.
A lo largo de este curso, explorarás una variedad de funciones padre y sus gráficas. Algunas de las funciones madre ya deben ser familiares, como las funciones lineales, cuadráticas, de valor absoluto y exponenciales. El resto de las funciones madre exploradas en esta lección (y algunas funciones adicionales) se estudiarán en detalle en lecciones futuras.
PROBLEMA 1
En la tabla se muestran representaciones de transformaciones de diferentes funciones principales. Determina a qué familia de funciones pertenece cada transformación.
Representación de la transformación Ecuación de la función principal
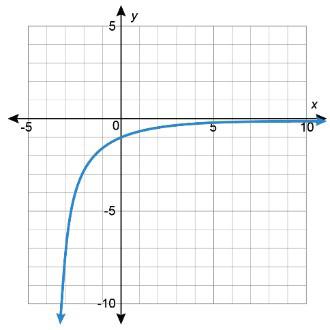
y = x y = x2 y = x3 y = |x|
y = √x y = 2x
y = ( 1 2 )x x −2 −1
y = x y = x2 y = x3 y = |x|
y = |x + 5|
y = x y = x2 y = x3 y = |x|
y = x y = x2 y = x3
y = |x|
y = √x y = 2x y = ( 1 2 )x
y = √x y = 2x
y = ( 1 2 )x
y = √x y = 2x
y = ( 1 2 )x
Soluciones posibles
• y = ( 1 2 )x
• y = x
• y = |x|
• y = 2x
2 . Matemáticas . Unidad 1

PROBLEMA 2
En la tabla se muestran representaciones de transformaciones de diferentes funciones padre. Determine a qué familia de funciones pertenece cada transformación.
Representación de la transformación Ecuación de la función principal
x −2 −1 0 1 2 y 6 3 0 3 6
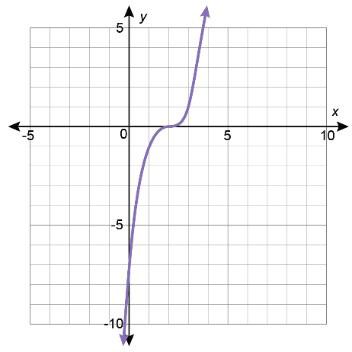
f(x) = ( 1 2 )x− 5
y = x y = x2 y = x3 y = |x|
y = √x y = 2x y = ( 1 2 )x
y = x y = x2 y = x3 y = |x| y = √x y = 2x y = ( 1 2 )x
y = x y = x2 y = x3 y = |x|
y = √x y = 2x y = ( 1 2 )x
Soluciones posibles
• y = |x|
• y = x3
• y = ( 2 )x
PROBLEMA 3
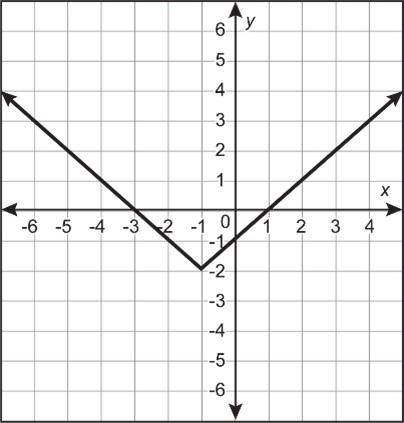
Se muestra la gráfica de una función principal transformada.
Daniel identificó la familia de funciones de la gráfica como cuadrática, pero cometió un error.
A. Explica por qué Daniel está equivocado.
B. Identifica la función principal correcta para la gráfica.
Soluciones posibles
A. Ejemplo de respuesta: Una función cuadrática tiene forma parabólica (U), pero esta gráfica tiene forma de V.
B. Esta gráfica pertenece a la familia del valor absoluto.
Math Nation California . Algebra 2 ©Accelerate Learning Inc. - Todos los derechos reservados


PROBLEMA 4
(De Álgebra 1, unidad 2, lección 7).
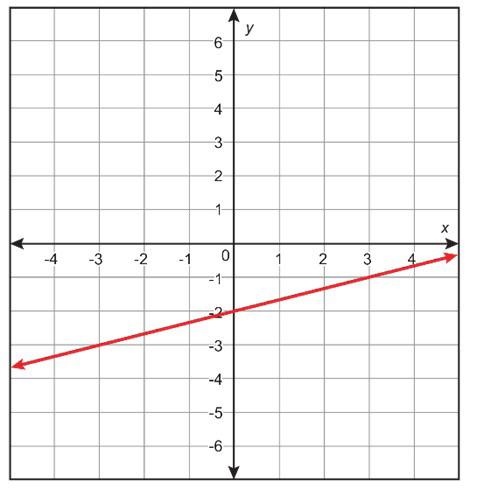
Considera la función lineal y = 1 3 x − 2.
A. Determina la pendiente y el intercepto en Y de la función lineal.
B. Grafica la función lineal en el plano de coordenadas.
Soluciones posibles
A. Pendiente = 1 3 , y el inntercepto en Y (0, −2)
B.

Reflexiones:
©Accelerate Learning Inc. - Todos los derechos reservados
Nation California . Algebra 2 Álgebra 2 . Matemáticas . Unidad 1


IDEA(S) FUNDAMENTAL(ES)
• Representar con funciones
ALINEACIÓN
Alineación de estándares y principios de Californian
Abordar
F-IF.6 Calcular e interpretar la tasa de cambio promedio de una función (presentada simbólicamente o como una tabla) en un intervalo específico. Estimar la tasa de cambio con una gráfica. Enfocar SMPs
MP4 Representar con matemáticas.
MP8 Buscar y expresar regularidad en razonamientos repetidos.
CA ELD Standards
I.A.2
I.B.8
II.C.7
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
comprender al mundo, buscarán y expresarán regularidades en razonamientos repetidos
analizan los datos y exploraran cantidades cambiantes.
OBJETIVO(S)
• Puedo calcular la tasa de cambio promedio de una función dada en forma gráfica, simbólica y numérica.
• Calcular la tasa de variación media de una función representada de diferentes formas.
Rutinas didácticas
Pensar, girar y compartir
Anticipar, supervisar, seleccionar, secuenciar, conectar
MLR7: Comparar y conectar
MLR3: Clarificar, criticar, corregir
©Accelerate Learning Inc. - Todos los derechos reservados
Álgebra 2 Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Calculemos la tasa de cambio promedio de diferentes funciones.
Narrativa de la lección
Los estudiantes aprenden a calcular la tasa de cambio promedio para diferentes problemas matemáticos y del mundo real representados gráficamente, algebraicamente o en una tabla de valores.
A lo largo de la lección, los estudiantes utilizan funciones conocidas (lineal, cuadrática y exponencial) y desconocidas (raíz cuadrada). El tipo de función en sí no importa para desarrollar una comprensión de la tasa de cambio promedio entre 2 puntos de la función.
La fórmula con la que los estudiantes determinan la tasa de cambio promedio utiliza la forma general de cambio en y sobre el cambio en x, lo que permite a los estudiantes hacer conexiones entre pendientes de cursos anteriores y conduce a la definición formal de una derivada en cálculo. Esta lección está diseñada para animar a los estudiantes a demostrar un pensamiento profundo y flexible en torno a las relaciones matemáticas (MP4).
Componente de la lección

Estructura Tiempo
Calentamiento En parejas 5 min
Actividad de Exploración En parejas 10 min
Actividad de Exploración Grupos pequeños 15 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Descripción breve
Los estudiantes evalúan expresiones algebraicas con dos variables.
Los estudiantes determinan la tasa de cambio promedio en diferentes intervalos de funciones que están representadas en gráficas, tablas de valores y ecuaciones.
Los estudiantes utilizan la tasa de cambio promedio para comparar funciones lineales, exponenciales y cuadráticas a través del tiempo en un contexto del mundo real.
Los estudiantes discuten las diversas estrategias que utilizaron para determinar la tasa de cambio promedio de funciones que se muestran como gráficas, ecuaciones o tablas de valores.
Los estudiantes razonan sobre el trabajo de estudiantes de muestra para identificar el error en la determinación de la tasa de cambio promedio usando una gráfica de una función.
El componente de práctica independiente incluye 3 problemas de repaso en la lección y 2 problemas de repaso en espiral.
Nation California - Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


minutos)

Rutinas didácticas
Pensar, girar y compartir
Los estudiantes sustituyen los valores de x y y en una expresión para evaluar, lo que les da la oportunidad de utilizar informalmente la fórmula de la pendiente en una expresión parcialmente completa, centrándose primero sólo en el cálculo.
INTRODUCCIÓN
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organice a los estudiantes en grupos de 2. Dé a los estudiantes 2-3 minutos (min) de tiempo de trabajo tranquilo y luego otro minuto para compartir su respuesta con sus compañeros. Continúe con un debate con toda la clase.
Evalúe cada una de las expresiones cuando x = 2 y y = -2
SÍNTESIS DE LA ACTIVIDAD
Invite a los estudiantes a compartir sus pasos y los valores que determinaron para cada paso. Hable de cómo la evaluación de las expresiones puede ser similar a otros cálculos con los que pueden estar familiarizados, tales como encontrar la pendiente de una recta.
(10 minutos)
Rutinas didácticas
Anticipar, supervisar, seleccionar, secuenciar, conectar
MLR7: Comparar y conectar
Los estudiantes determinan la tasa de cambio promedio en intervalos especificados para funciones dadas como un gráfico, una tabla de valores y una ecuación.
Esta actividad proporciona oportunidades para que los estudiantes trabajen de forma independiente, en colaboración y con orientación estructurada, según sea necesario. La idea de la tasa de cambio promedio es mostrar el cambio general en valores de y de la función a medida que x aumenta en un intervalo específico.

Álgebra 2 Matemáticas . Unidad 1
Organice a los estudiantes en grupos de 2. Dé a los estudiantes 1-2 minutos para que discutan cómo hallarían la tasa media de cambio entre 2 puntos del gráfico. A continuación, pídales que compartan sus respuestas con sus compañeros y que continúen el debate con toda la clase. Durante la discusión en cada representación, aclare que los valores entre los puntos finales del intervalo no importan porque no buscan cada tasa de cambio entre los puntos del intervalo, sino la media entre los puntos finales de 2. Remita a los estudiantes a la definición formal de tasa media de cambio en la sección «Glosario de la edición digital para el estudiante.
En cada representación, es probable que los estudiantes observen los siguientes conceptos:
• La tasa media de cambio se determina con la fórmula de la pendiente y1 - y2 x1 - x2 entre los 2 puntos (x1, y1 ) y (x2, y2 ) que son los puntos extremos del intervalo. La determinación de la tasa de variación media mediante una gráfica puede mostrar que el valor puede ser positivo o negativo, dependiendo de si la gráfica aumenta o disminuye a lo largo de ese intervalo.
• Cuando se utiliza una ecuación, los estudiantes primero tienen que determinar las coordenadas de los puntos extremos del intervalo dado antes de calcular la tasa de variación media.
Durante la discusión, anime a los estudiantes a trazar una línea entre los puntos 2. Llámela recta secante. Álgebra 1 introdujo a los estudiantes a la tasa de cambio promedio, pero dependiendo de las discusiones al inicio de la actividad, considere mostrar el primer par de preguntas antes de liberar el siguiente conjunto de preguntas a los estudiantes.
Representar, conversar: MLR7: Comparar y conectar. En esta rutina, usted debe demostrar el pensamiento en voz alta (por ejemplo, comparar cómo encontrar la tasa media de cambio en diferentes representaciones de funciones) y los estudiantes deben reflexionar y responder. Esta rutina apoya la conciencia metacognitiva y metalingüística y también apoya las conversaciones matemáticas.
Principio(s) de diseño: Cultivar la conversación
Ayudas visuales. Los estudiantes que se benefician de la representación concreta pueden entender el concepto de tasa de cambio promedio analizando los gráficos de cada función y conectando los 2 puntos finales con una regla. Considere la posibilidad de proporcionar gráficos de cada función con los puntos finales marcados en el gráfico para que los estudiantes puedan utilizar una regla para conectar los puntos. La representación física puede ayudar a los estudiantes a comprender que la tasa de variación media será positiva o negativa.
Apoya la accesibilidad para: Procesamiento visualespacial; organización
California - Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE
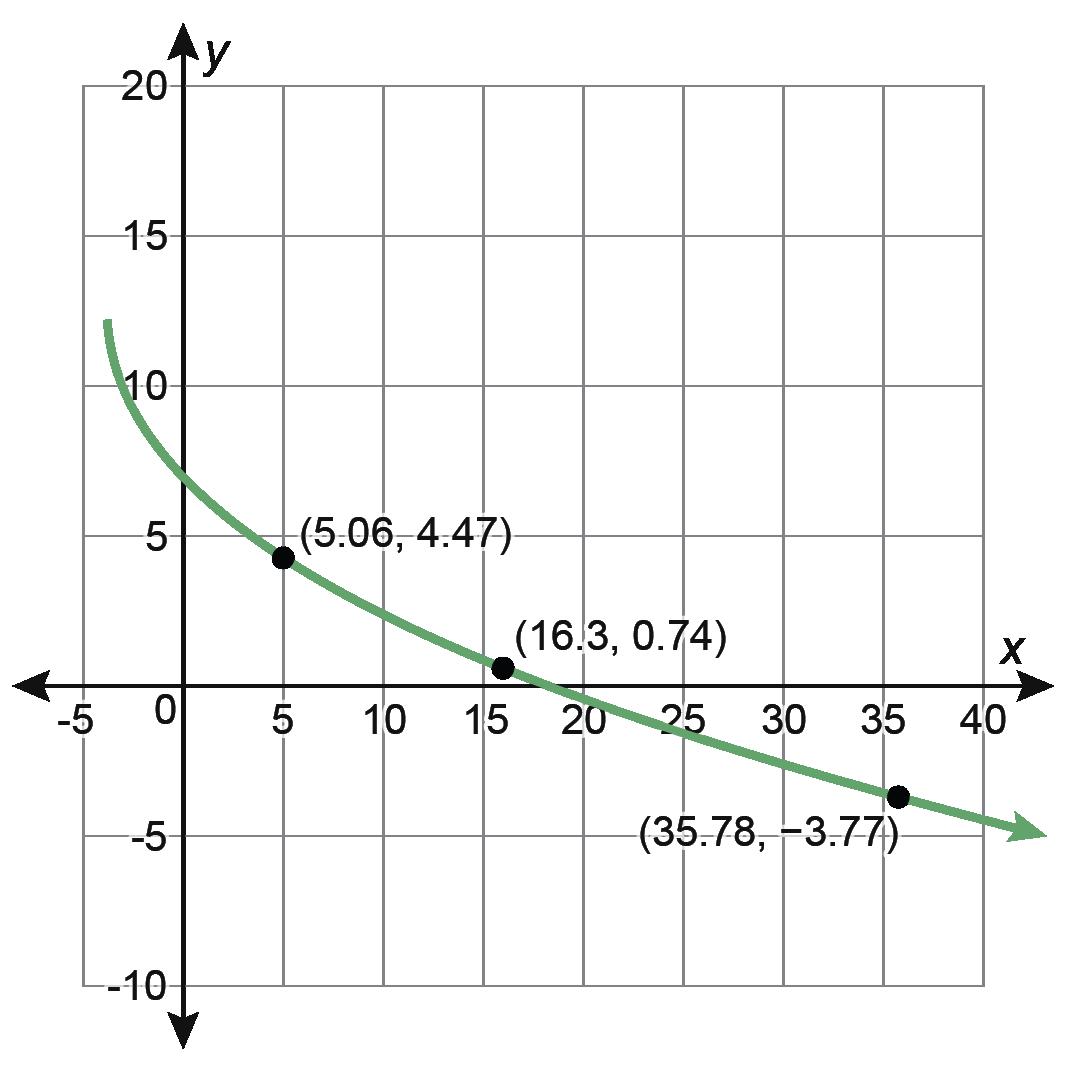
1. Se muestra la gráfica de una función. Se indican las coordenadas de 3 puntos de la gráfica.
A. Comenta con tu compañero cómo se puede usar una recta secante para hallar la tasa de cambio promedio entre 2 puntos cualesquiera de la gráfica.
B. ¿Cuál es la tasa de cambio promedio entre (5.06, 4.47) y (16.3, 0.74)?
C. ¿Cuál es la tasa de cambio promedio entre (5.06, 4.47) y (35.78, −3.77)?
2. Se muestra una tabla de valores para la función g.
3. Determine la tasa de cambio promedio en el intervalo [−2, 3].
4. Determine la tasa de cambio promedio en el intervalo [−1, 1].
5. Determine la tasa de cambio promedio en el intervalo [2, 5].
6. Determine la tasa de cambio promedio en el intervalo [−1, 5, 2, 4] para la función f(x) = 3x² − 4x + 2.
1.
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS PREVISTOS
2.
SINTESIS DE LA ACTIVIDAD
A. No se espera respuesta por escrito. Ejemplo de discusión: La tasa de cambio promedio entre dos puntos cualesquiera debería ser la pendiente de la línea que los une. Según la gráfica, la tasa de cambio promedio debería ser negativa, pero no parece que sea el mismo valor entre dos puntos cualesquiera.
B. Aproximadamente −0.332
C. Aproximadamente −0.268
A. 0
B. −11
C. 54
3. −1.3
Los estudiantes pueden determinar la pendiente con una fórmula incorrecta de cambio en x cambio en y , Lo cual es un error común en el desarrollo de la comprensión de la tasa de cambio por parte de los estudiantes. Considere revisar la gráfica y la ecuación de una recta para mostrarles la conexión entre el valor de la pendiente en la ecuación y la gráfica, y así recordarles que la tasa de cambio promedio de cualquier función es cambio en y cambio en x entre los 2 puntos finales del intervalo.
Los estudiantes pueden determinar la pendiente con una fórmula incorrecta cambio en x cambio en y , lo cual es un error común en el desarrollo de la comprensión de la tasa de cambio por parte de los estudiantes. Considere revisar la gráfica y la ecuación de una recta para mostrarles la conexión entre el valor de la pendiente en la ecuación y la gráfica, y así recordarles que la tasa de cambio promedio de cualquier función es cambio en y cambio en x entre los 2 puntos finales del intervalo.
SÍNTESIS DE LA ACTIVIDAD
CONTINUADA

Álgebra 2 Matemáticas . Unidad 1
Haga las preguntas como las siguientes.
• «¿Es la tasa de cambio promedio siempre positiva o siempre negativa para cada función?». (No necesariamente porque algunas funciones pueden pasar de crecientes a decrecientes o viceversa)
• «¿Será la tasa de variación media la misma para cualquier conjunto de puntos de cada función?». (No, la tasa de cambio promedio es diferente entre diferentes conjuntos de puntos en el gráfico y la tabla, por lo que la tasa de cambio promedio no es siempre la misma a menos que's una función lineal. Nótese que este concepto será explorado con mayor detalle en la siguiente actividad).
(15 minutos)
Rutinas didácticas
MLR3: Aclarar, criticar, corregir
Los estudiantes comparan las tasas de cambio promedio sobre los mismos intervalos para diferentes funciones para llegar a la idea de que la tasa de cambio promedio es constante para una función lineal pero no es constante en cualquier otro tipo de función.
INTRODUCCIÓN
Organice a los estudiantes en grupos de 3. Considere diferentes formas de trabajar esta actividad. Dependiendo de la estructura de los grupos, considere pedir a cada miembro del grupo que determine primero la tasa media de cambio para el mismo intervalo y compare sus resultados antes de pasar al siguiente intervalo. Alternativamente, considere asignar a cada miembro del grupo una empresa diferente para explorar.
Dé a los estudiantes 1-2 minutos para que discutan cómo encontrarían la tasa media de cambio entre los puntos 2 utilizando los gráficos que representan a cada empresa. A continuación, pida a los estudiantes que determinen el intervalo medio para cada intervalo dado para su empresa. Anime a los estudiantes a trazar una línea entre cada uno de los 2 puntos de cada intervalo.
Reading, Writing, Speaking: MLR3 Aclarar, Criticar, Corregir. Antes de que los estudiantes compartan las similitudes entre las 3 empresas' ventas, pida a los estudiantes que expliquen cómo determinaron la tasa media de cambio para cada empresa. Mientras discuten con sus compañeros, preste atención a los estudiantes que justifican por qué la tasa media de variación no es la misma para cada una de las empresas. Invite a los estudiantes a compartir sus críticas con la clase. Escuche y amplíe el lenguaje que utilizan para describir lo que ocurre con la tasa media de cambio de las empresas 3 y cómo los valores aumentan más rápido, más despacio o de forma constante.
Principio(s) de diseño: Optimizar el resultado (para la explicación); Maximizar la metaconciencia
Apoyo a los estudiantes con discapacidad
Representación: Interiorizar la comprensión. Divida esta tarea en partes más manejables para diferenciar el grado de dificultad o complejidad comenzando sólo con el primer intervalo. Por ejemplo, dé a los estudiantes 1-2 min. para determinar la tasa media de cambio del intervalo [2,4] primero, y luego pídales que comparen la tasa media de cambio de su empresa seleccionada con las empresas de los miembros de su grupo'. A continuación, dé a los estudiantes 3-4 min. para que determinen la tasa media de cambio de los intervalos restantes.
Apoya la accesibilidad para: Procesamiento conceptual; Organización
California - Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. Se muestran las ventas totales de tres empresas' a lo largo de 10 semanas, en miles de dólares.
Empresa A Empresa B Empresa C
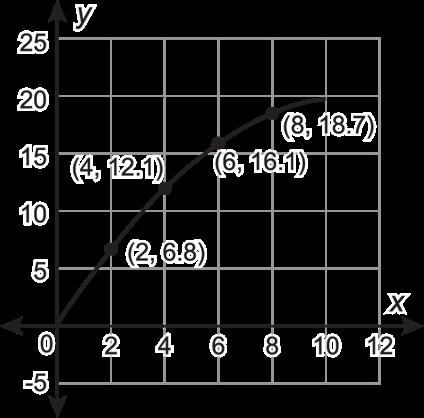
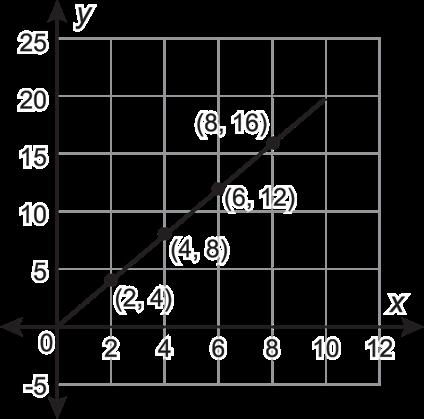
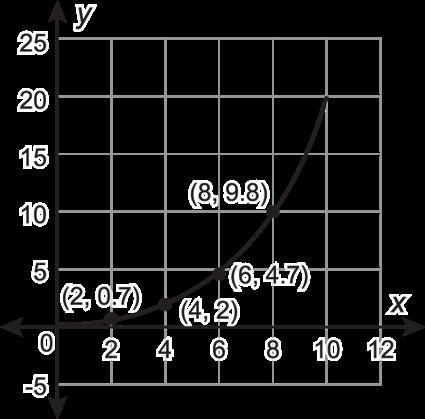
A. Completa la tabla determinando la tasa media de cambio para cada una de las funciones a lo largo de los intervalos dados. Redondea a la décima más cercana.
Intervalo
[2, 4]
[4, 6]
[6, 8]
[2, 8]
Empresa A Empresa B Empresa C
B. Habla con tu compañero de las similitudes entre las 3 empresas de ventas a lo largo de las 10 semanas.
C. ¿Por qué la tasa media de variación es diferente para las empresas A y C que para la empresa B?
2. ¿Qué función tendrá una tasa media de variación constante?
A. y = 3x2 + 2x − 5
B. y = 4|x - 2| + 3
C. y = -2(3)x + 5
D. 3x - 5y = 4
RESPUESTAS POSIBLES 1. A.
Intervalo Empresa A
B. No se espera una respuesta escrita. Ejemplo de discusión: La empresa A cambia en 0.7 en cada intervalo y sigue disminuyendo, la tasa media de cambio de la empresa B no cambia en ninguno de los intervalos y la tasa media de cambio de la empresa C aumenta en cada intervalo creciente.
C. Las respuestas variarán. La tasa media de cambio es la misma para la empresa B porque es una función lineal.
2. D
CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD
Álgebra 2 Matemáticas . Unidad 1
Los estudiantes pueden pensar que el valor de la tasa de cambio promedio es cuánto cambia la función en cualquier intervalo dado. Pida a los estudiantes que comparen la tasa de cambio promedio de las diferentes compañías para ver si siempre tienen la misma tasa de cambio.
Los estudiantes determinan que la tasa de cambio promedio es diferente para todos los intervalos en diferentes funciones, excepto para una función lineal. Los estudiantes generalizan que la tasa de cambio promedio de una función lineal es la misma que la pendiente de una función lineal y siempre constante. Utilice sus observaciones de esta actividad para determinar si la estructura de la Síntesis de la lección debe modelar ejemplos de pensamiento en voz alta o discusión con preguntas guía. Si los estudiantes necesitan ejemplos concretos, la síntesis de la lección y el resumen de la lección para el estudiante ofrecen oportunidades adicionales.
(5 minutos)
Considere usar el resumen de la lección del estudiante para recapitular lo aprendido en esta lección y use el ejemplo proporcionado de determinar la tasa de cambio promedio dadas las diferentes representaciones de la misma función.
Si los estudiantes necesitan ejemplos adicionales, entonces considere mostrar las siguientes ecuaciones:
y = x y = 2x y = 3 − 5x y = 2x2 - 8 y = ( 1 2 )x y = 4
Haga a los estudiantes las siguientes preguntas.
• «¿Qué ecuación(es) tiene(n) una tasa de cambio promedio constante?».
• «¿Qué ecuación(es) tiene(n) una tasa de cambio promedio positiva en cualquier intervalo?».
• «¿Qué ecuación(es) tiene(n) una tasa de cambio promedio negativa en cualquier intervalo?».
• Explique por qué algunas ecuaciones no son las respuestas a ninguna de las preguntas anteriores.
Asegúrese de que los estudiantes ven los siguientes conceptos:
• No todas las funciones tienen una tasa de cambio promedio positiva o negativa para cualquier intervalo. Algunas, como las funciones cuadráticas (y otras que los estudiantes verán a lo largo de este curso), tienen una tasa de cambio promedio diferente dependiendo del intervalo.
• Las funciones lineales tienen una tasa de cambio promedio constante.
• La función exponencial y = ( 1 2 )x tiene una tasa de cambio promedio negativa a pesar de que los valores en la ecuación son todos positivos.
(5 minutos)
Se muestra la gráfica de una función. Las coordenadas de 4 puntos en la gráfica están etiquetadas.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
California - Algebra 2
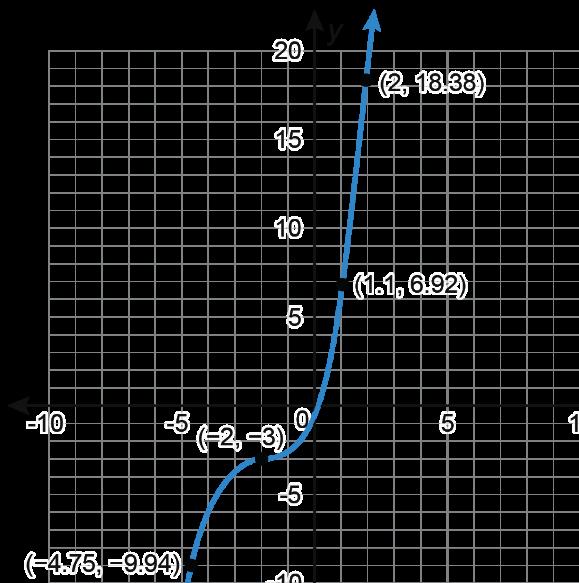
©Accelerate Learning Inc. - Todos los derechos reservados


ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES
Misty y Serena están determinando la tasa de cambio promedio entre (1.1, 6.92) y (2, 18.38). Se muestra su trabajo. El trabajo de Misty
de Serena
1. ¿Qué estudiante está en lo correcto?
2. Escribe una nota al estudiante cuyo trabajo es incorrecto y explícale el error que cometió y cómo puede evitarlo en el futuro.
1. Serena
2. Las respuestas variarán. Ejemplo de respuesta: Misty, cuando calculaste la tasa de cambio promedio, pusiste los valores x en el numerador de la fracción en lugar de poner los valores y en el numerador. Recuerda, la tasa de cambio promedio es el cambio en y sobre el cambio en x
Se puede trazar una línea para conectar cualesquiera 2 puntos en un gráfico. Esta línea se llama línea secante y puede usarse para determinar la tasa promedio de cambio entre cualesquiera 2 puntos en una gráfica.
La tasa de cambio promedio puede usarse para resumir el cambio general de una función en un intervalo específico. La tasa de cambio promedio es diferente entre cualquier 2 punto en una curva para todas las funciones excepto para una función lineal. Las funciones lineales siempre tienen una tasa de cambio promedio constante, que es equivalente a la pendiente de la línea.
Se muestran tres representaciones diferentes de f(x)
Gráfica
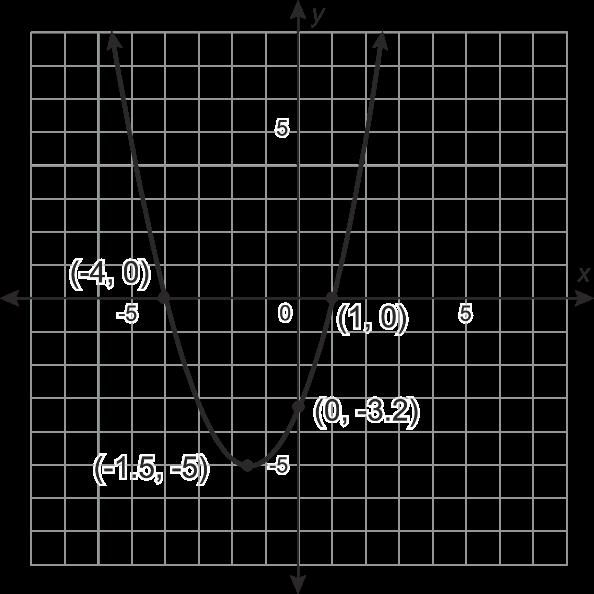
Tabla Ecuación
La tasa de cambio promedio de f(x) sobre el intervalo [−1.5, 1] es f(b) − f(a) b − a = f(1) − f(−1.5) 1−(−1.5) = 0 + 5 2.5 = 2
2 Matemáticas . Unidad 1
PROBLEMA 1
En la tabla se muestran seis funciones, representadas de diferentes maneras.
Función A y = 3x - 5
Función C
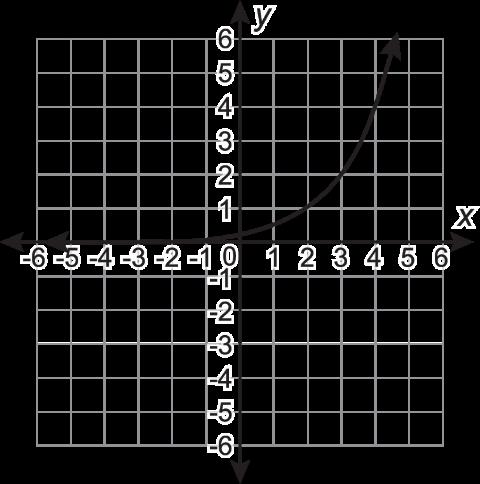

Función B y = x2 + 4
Función D
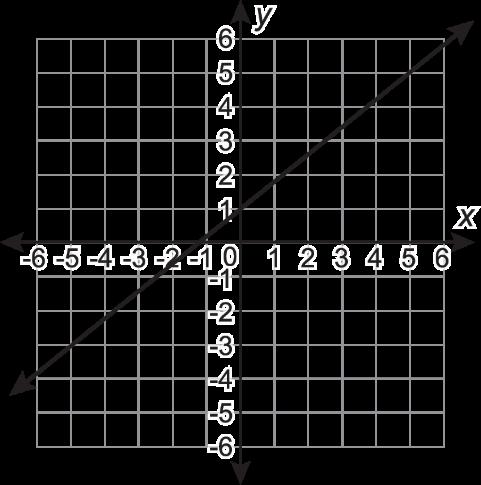
Seleccione todas las funciones que tengan una tasa de variación media constante.
Función A
Función B
Función C
Función D
Función E
Función F
Soluciones posibles
Función A
Función B
Función C
Función D
Función E
Función F
Math Nation California - Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


2 Matemáticas . Unidad 1
PROBLEMA 2
Shirana y Madelin emanejan en bicicleta para practicar para una carrera. Se muestran gráficos que representan la distancia, en millas (mi), que cada ciclista recorrió durante los primeros 10 minutos (min) de su recorrido.
Shirana
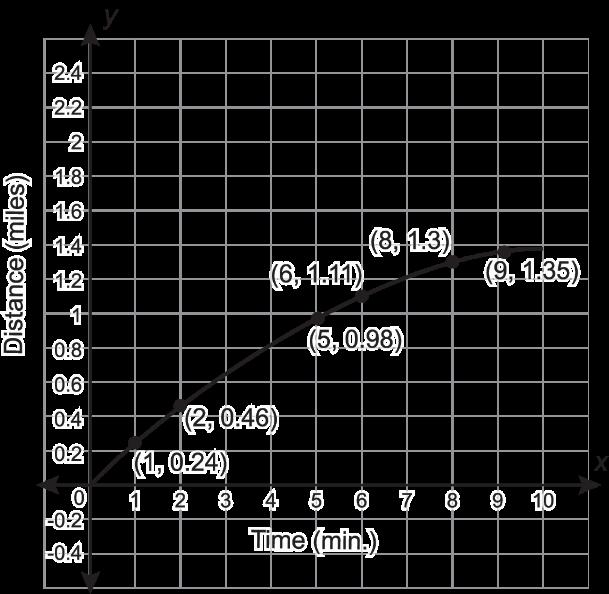

Madeline
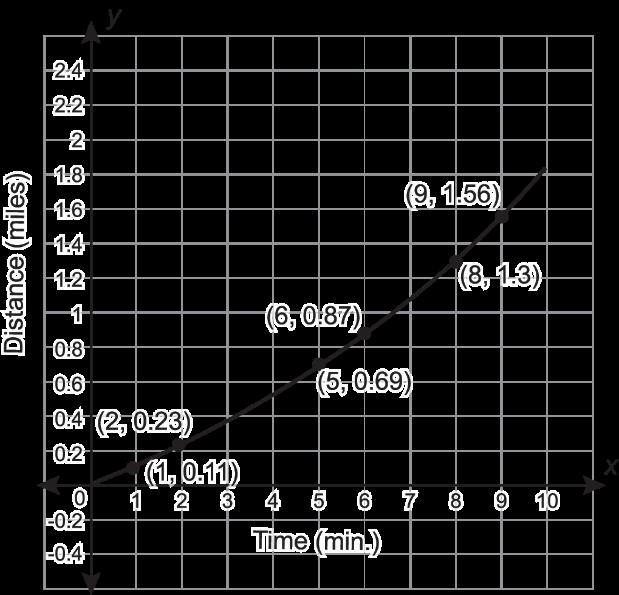
A. Determinando la tasa media de cambio para cada ciclista en cada intervalo dado para completar la tabla. Redondea a la centésima más cercana, si es necesario.
Intervalo Shirana Madeline
[1, 2]
[2, 5]
[5, 6]
[8, 9]
B. Explica qué indican los índices de cambio promedio sobre los 2 ciclistas.
Soluciones posibles
A. Intervalo
9]
B. Las respuestas variarán. Ejemplo de respuesta: Shirana va más despacio durante el período de 10 minutos, mientras que Madeline va más rápido.
©Accelerate Learning Inc. - Todos los derechos reservados Math Nation California - Algebra 2
Álgebra 2 Matemáticas . Unidad 1

PROBLEMA 3
Determinar la tasa de variación media de la función f(x) = 2x2 − x + 1 en cada intervalo.
A. [0, 1 2 ]
B. [−1, 2]
C. [−3.1,−-3]
PROBLEMA 4
(De Álgebra 1, unidad 7, lección 9).
Grafica la función cuadrática y = −2(x + 1)(x − 3) en el plano de coordenadas.
PROBLEMA 5
(De Álgebra 1, unidad 2, lección 17).
Soluciones posibles
A. 0
B. 1
C. −13.2
Soluciones posibles
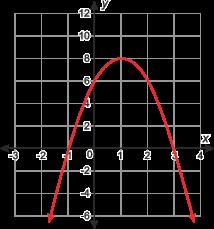
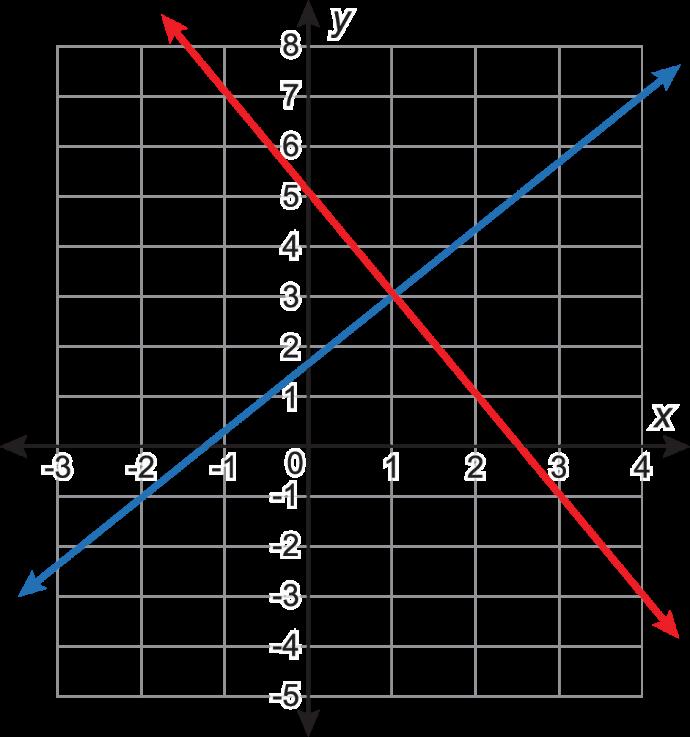
El sistema de euaciones { 2x + y = 5 −4x + 3y = 5 se representa gráficamente en el plano de coordenadas .
Usa la gráfica para determinar la solución del sistema de ecuaciones.
Soluciones posibles (1, 3)
Reflexiones:
Math Nation California - Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Representar con funciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
F-IF.6 Calcular e interpretar la tasa de cambio promedio de una función (presentada simbólicamente o como una tabla) en un intervalo especificado. Estimar la tasa de cambio a partir de un gráfico.
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP2 Razonar abstracta y cuantitativamente.
MP4 Representar con matemáticas.
Estándares ELD de California
I.B.6
I.C.12
EP&Cs de California
4.C
II.A.1
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
comprender al mundo e influir en el futuro,
darán sentido a los problemas y perseverar en su resolución analizan los datos y exploran cantidades cambiantes.
• Puedo calcular la tasa media de cambio de una situación del mundo real representada gráfica, numérica o simbólicamente a lo largo de un intervalo especificado.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Calcular la tasa media de cambio de una situación del mundo real a partir de diferentes representaciones.
Rutinas didáctitas
Pensar, girar y compartir
Anticipar, supervisar, seleccionar, secuenciar, conectar
MLR8: Apoyos para el debate
MLR5: Preguntas de elaboración conjunta
©Accelerate Learning Inc. - Todos los derechos reservados
2 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Determinemos e interpretemos la tasa de cambio promedio de diferentes funciones en situaciones del mundo real.
Narrativa de la Lección
Los estudiantes continúan su estudio de la tasa de cambio promedio y aplican su comprensión de la tasa de cambio promedio en situaciones del mundo real.
Los estudiantes trabajan dando sentido a problemas en contexto tanto para determinar como para interpretar la tasa de cambio promedio dentro de situaciones del mundo real (MP1). La información del mundo real presentada de diversas formas hace que los estudiantes exploren las relaciones de las funciones matemáticas (MP4).
Componente de la lección Estructura Tiempo Breve descripción
Calentamiento En parejas 5 min.

Actividad de exploración Grupos pequeños 10 min.
Los estudiantes utilizan una ecuación de una función para determinar la tasa media de cambio a lo largo de un intervalo, e identifican un intervalo en el que la tasa media de cambio es positiva.
Los estudiantes razonan sobre los patrones de cambios en la población a lo largo de diferentes intervalos de tiempo, presentados en una tabla de valores, aplicando e interpretando la tasa media de cambio dentro del contexto del mundo real.
Esta tarea podría ampliarse como una oportunidad para debatir sobre la capacidad de la población de rinocerontes blancos para adaptarse a las alteraciones causadas por el hombre. Los estudiantes pueden establecer conexiones entre los cambios en la población de rinocerontes blancos durante los últimos 100 años y las diferentes protecciones y prácticas de caza durante el mismo período de tiempo.
Actividad de exploración Grupos pequeños 15 min.
Síntesis Todo grupo 5 min.
Enfriamiento Independiente 5 min.
Práctica Independiente 10 min.
Los estudiantes determinan e interpretan la tasa media de cambio de varias funciones que modelan situaciones del mundo real y diferentes intervalos de tiempo.
Los estudiantes reflexionan sobre las estrategias más eficientes para determinar la tasa media de cambio de funciones mostradas en diferentes representaciones.
Los estudiantes determinan e interpretan la tasa de cambio promedio de funciones que representan diferentes escenarios.
El componente de práctica independiente incluye 5 problemas de la lección y 1 problema de repaso en espiral.
California . Algebra 2 ©Accelerate Learning Inc. - Todos los derechos reservados



Rutinas didáctitas
Pensar, girar y compartir
Anticipar, supervisar, seleccionar, secuenciar, conectar
Los estudiantes determinan y analizan la tasa de variación media dada una ecuación de una función a lo largo de diferentes intervalos.
Antes de empezar, considere la posibilidad de establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con un razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen, u otra señal sutil. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se apresuren por las manos que se levantan alrededor de la clase.
INTRODUCCIÓN
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organice a los estudiantes en grupos de 2. Dé a los estudiantes 1 minuto (min) de tiempo para pensar en silencio, y pídales que indiquen cuándo tienen un plan de cómo resolver las 2 preguntas. Cuando se acabe el minuto, dé a los estudiantes 2 minutos para que compartan su respuesta con sus compañeros y, a continuación, trabajen juntos para encontrar las soluciones.
Considere una función con una ecuación de �� = -��2 − 3 ��.
1. ¿Cuál es la tasa media de cambio en el intervalo [−2.1, 1.6]?
2. ¿Qué intervalo tiene una tasa de variación positiva?
A. [1, 2]
B. [−3, 0]
C. [−2, 0]
D. [−2, −4]
1. − 2.5
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
2. D
Después de que los estudiantes compartan sus observaciones en parejas, invite a algunos de los grupos a compartir sus estrategias o sus soluciones a la pregunta con toda la clase. Explique a los estudiantes que la tasa de variación media es la pendiente de la recta secante de la función. Tenga en cuenta que recta secante es un término de vocabulario introducido en la lección anterior pero que no tiene una importancia significativa hasta que los estudiantes pasen a futuros cursos de matemáticas. Destaque el pensamiento de los estudiantes para identificar el intervalo con una tasa de cambio positiva. Los estudiantes pueden tener diferentes estrategias para identificar este intervalo, que pueden incluir la determinación de los valores y de los 2 puntos finales, la representación gráfica de la función, o el uso de la fórmula para la tasa de cambio promedio ��( ��) - ��( ��) �� - �� . Considere la posibilidad de mostrar la gráfica de la función en una calculadora gráfica para concluir la discusión, destacando cada uno de los intervalos discutidos y relacionando la tasa media de cambio con la gráfica.
REAL 10 minutos
Rutinas didácticas
MLR8: Apoyos para la discusión
Los estudiantes determinan la tasa media de cambio de una tabla de valores que representa una situación del mundo real. Es de esperar que algunos estudiantes tengan dificultades para ver las conexiones entre la tasa media de cambio y el contexto de la población de rinocerontes. A lo largo de esta actividad, los estudiantes repasan cómo determinar la tasa media de cambio y se les introduce a la interpretación de la tasa media de cambio en el contexto.
Tenga en cuenta que esta actividad de exploración está diseñada para aclarar las ideas clave y confirmar la comprensión de los estudiantes antes de permitirles trabajar en colaboración sin tanta orientación en la siguiente actividad.
Organice a los estudiantes en grupos de 2-4 personas. Explique que los estudiantes deben considerar la tasa media de cambio en el contexto. Presente el contexto y la tabla, y pregunte a los estudiantes cómo utilizar la tabla para determinar en qué año aparece cada población en la tabla.

INSTRUCCIÓN
Después de esta discusión inicial, dé a los estudiantes la oportunidad de familiarizarse con el contexto. Permítales 1-2 min. para anotar el año encima de cada par de valores dados en la tabla y para generar respuestas iniciales a la parte a antes de la discusión de toda la clase. Utilice las partes b y v para comprobar que los estudiantes comprenden cómo determinar e interpretar la tasa media de variación en este contexto. Antes de dejar que los estudiantes trabajen en sus grupos durante el resto de la actividad, considere la posibilidad de mostrar cómo se trabaja en cada una de estas partes. Dé a los estudiantes 5 minutos de tiempo para trabajar en las partes e y f. Mientras tanto, controle la discusión de los estudiantes para identificar grupos/pares que compartan su pensamiento y enfoque con toda la clase.
Durante las discusiones en parejas, controle si hay grupos que discutan las siguientes ideas para que puedan compartirlas más tarde, en esta secuencia:
• Patrones generales de aumento de la población y disminución de la población
• Como 0 no forma parte de la tabla, no conocemos la población del rinoceronte en 1929.
• Hubo un gran cambio entre 1993 y 2007, por lo que la tasa media de cambio será significativamente mayor que en cualquier otro intervalo.
• La tasa media de cambio entre 1948 y 2021 es 216.3, y la tasa media de cambio entre 1991 y 2007 es 744.
Hablar: MLR8 Apoyos para la discusión. Proporcione marcos de oraciones para apoyar a los estudiantes en la producción de afirmaciones que describan las similitudes y diferencias entre la población de rinocerontes blancos durante diferentes intervalos. Por ejemplo: «No estoy de acuerdo porque...», «Podemos estar de acuerdo en que...» y «Lo que diferencia a de es ».
Principio(s) de diseño: Apoyar la creación de sentido; optimizar el resultado (para la comparación)
Compromiso: Desarrollar el esfuerzo y la persistencia. Fomente y apoye las oportunidades de interacción entre iguales. Invite a los estudiantes a comentar sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «En primer lugar, porque...», «Me fijé en , así que...» o «¿Cómo conseguiste...?».
Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales
Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1



ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. A lo largo del siglo XX, la intensa protección del rinoceronte blanco del sur ha dado lugar a un aumento significativo de su población. Sin embargo, en los últimos años, el aumento de la caza furtiva ha provocado un nuevo descenso de su población.
La tabla muestra el tamaño estimado de la población del rinoceronte blanco del sur desde 1929 hasta 2021.
Años
desde 1929 19 55 62 64 78 83 86 92
Tamaño de la población
A. Describe el patrón del tamaño de la población del rinoceronte desde 1929 hasta 2021.
B. Encuentra la tasa media de cambio para el período de tiempo de 1991 a 2007.
C. Interpreta la tasa media de cambio hallada en la parte B en función del contexto.
D. Habla con tu compañero por qué la tasa de cambio promedio para el período de 1991 a 2007 no describe con exactitud el cambio poblacional del rinoceronte de 1929 a 2021.
E. Encuentre la tasa de cambio promedio para el período de 2012 a 2021.
F. Interprete la tasa de cambio promedio encontrada en la parte E en términos del contexto.
RESPUESTAS POSIBLES
CONCEPTOS ERRÓNEOS
PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
1.
A. Las respuestas pueden variar. El tamaño de la población comienza a crecer lentamente y luego aumenta más rápidamente hasta que vuelve a disminuir después de 2012.
B. Aproximadamente 744
C. Las respuestas variarán. La población de rinocerontes aumentó a un ritmo de aproximadamente 744 rinocerontes por año entre 1991 y 2007.
D. No se espera ninguna respuesta escrita. Ejemplo de debate: La tasa media de cambio entre 1948 y 2021 es 216,3, y la tasa media de cambio entre 1991 y 2007 es 744.
E. Aproximadamente −597
F. Las respuestas variarán. La población de rinocerontes disminuyó a un ritmo de aproximadamente 597 rinocerontes por año desde 2012 hasta 2021.
Los estudiantes pueden calcular la tasa media de cambio incorrectamente encontrando el recíproco de la fórmula como cambio en �� sobre cambio en �� en lugar de ��1 − ��2 ��1 − ��2
Considere la posibilidad de utilizar un gráfico para mostrar a los estudiantes que la tasa de variación media es el cambio vertical sobre el cambio horizontal.
Los estudiantes pueden tener dificultades para interpretar la tasa de variación media en el contexto. Recuérdeles que interpreten el valor con las unidades de �� por ��. En este caso, el valor es el cambio en la cantidad de rinocerontes por año.
Invite a los estudiantes a compartir sus ideas discutidas en la parte d antes de pedir a algunos estudiantes que compartan sus respuestas e interpretaciones para las partes e y f. Utilice las estrategias identificadas en el introducción para determinar a qué estudiantes invitar a compartir sus soluciones. Al debatir las soluciones a las preguntas de este componente, concéntrese en formular las respuestas en el contexto del cambio de la población de rinocerontes. Los estudiantes que tengan dificultades con los cálculos matemáticos podrán comprender mejor la tasa media de cambio en una situación contextual.
Como posible opción, considere la posibilidad de trazar los puntos en un gráfico para que los estudiantes puedan visualizar mejor los cambios en la población de rinocerontes.
Álgebra 2 . Matemáticas . Unidad 1
(15 minutos)
Rutinas didáctitas
Anticipar, supervisar, seleccionar, secuenciar, conectar
MLR5: Preguntas de elaboración conjunta
Los estudiantes determinan e interpretan la tasa de cambio promedio de modelos matemáticos representados de diferentes maneras, como una ecuación o una descripción verbal (MP4). Se proporcionan andamios a los estudiantes a través de interacciones para completar oraciones y preguntas guiadas a medida que continúan desarrollando una comprensión de la tasa de cambio promedio. Esta actividad identifica las diferentes formas en que la tasa de cambio promedio se puede utilizar en contextos del mundo real y en modelos matemáticos. Algunos estudiantes pueden ser capaces de comparar y contrastar la tasa de cambio promedio en estas situaciones fácilmente porque tiene sentido contextual para ellos. Otros estudiantes pueden necesitar apoyo adicional en la lectura del escenario para la información importante (MP2).

Organizar a los estudiantes en grupos de 2-4. Considere la posibilidad de utilizar la estrategia de las tres lecturas para ayudar a los lectores con dificultades a comprender el contexto y a identificar la información adecuada para determinar e interpretar la tasa media de cambio. Dé a los grupos 5 minutos para completar el problema 1 juntos. Aproveche este tiempo para supervisar la discusión de los estudiantes sobre estrategias acertadas y posibles conceptos erróneos. Informe a toda la clase antes de permitir que los estudiantes trabajen en el resto de la actividad.
Apoyo para estudiantes para aprender el idioma inglés
Expresión oral, lectura: MLR5 Preguntas de elaboración conjunta. Utilice esta rutina para ayudar a los estudiantes a interpretar el lenguaje de la tasa de cambio promedio y para aumentar la conciencia del lenguaje utilizado para hablar de modelos matemáticos. Muestre solo la primera frase del problema 2 (En la primera mitad de una temporada de jóquey, un jugador marcó un total de 34 goles en los 15 partidos que jugó). Pida a los estudiantes que escriban posibles preguntas matemáticas que podrían hacerse sobre la situación. Invíteles a comparar sus preguntas antes de revelar el resto de la pregunta. Escuche y amplíe cualquier pregunta que implique modelar los datos con funciones.
Principio(s) de diseño: Maximizar la metaconciencia; apoyar la creación de sentido
Compromiso: Desarrollar el esfuerzo y la persistencia. Fomente y apoye las oportunidades de interacción entre compañeros. Invite a los estudiantes a comentar sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «En primer lugar, porque...», «Me fijé en , así que...» o «¿Cómo conseguiste...?» o «¿Cómo conseguiste...?».
Apoya la accesibilidad para: Lenguaje; Habilidades socioemocionales
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. La función P( ��) = 2,639(1.1075)x representa el crecimiento de la población de Queen Creek, Arizona, desde 1990 hasta 2021, donde �� es el número de años transcurridos desde 1990.
A. Comenta con tu compañero cómo utilizar la función para determinar la tasa media de cambio en un intervalo especificado.
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN
A. Completa los enunciados. Para calcular la tasa media de cambio dada una función, determina primero el valores x valores y intervalo con base en la información dada. Sustituye el en la función para determinar el correspondiente de los valores x valores y valores x valores y 2 puntos distintos usados para calcular la tasa de cambio promedio.
B. ¿Cuál es la tasa de cambio promedio para el período de tiempo de 1990 a 2002? Incluya las unidades.
C. ¿Cuál es la tasa de variación media para el período comprendido entre 1998 y 2017? Incluye las unidades.
D. Discute con tu compañero qué te dicen las pendientes sobre si el gráfico está aumentando o disminuyendo en un intervalo dado. Resume tu discusión.
1. En la primera mitad de una temporada de jóquey, un jugador marcó un total de 34 goles en los 15 partidos que jugó. En la segunda mitad de la temporada, el mismo jugador marcó un total de 54 goles en los 36 partidos que jugó. ¿Cuál es la tasa media de variación de la cantidad de goles por partido del jugador entre la primera y la segunda mitad de la temporada? Redondee a la centésima más cercana.
2. La temperatura alta media en grados Fahrenheit (℉), por mes, en una ciudad de Carolina del Sur puede mostrar mediante la función t( ��) = −0.9 ��2 + 13 �� + 43, donde �� es el mes del año.
A. ¿Cuál es la tasa media de cambio de la temperatura alta de la ciudad para el intervalo entre marzo y mayo?
B. ¿Cuál es la tasa media de variación de la temperatura máxima de la ciudad para el intervalo entre agosto y noviembre?
C. Interprete las tasas medias de variación halladas en las partes A y B en este contexto.
RESPUESTAS POSIBLES
1.
A. No se espera ninguna respuesta escrita. Ejemplo de discusión: Para determinar la tasa media de cambio en el intervalo de 1990 a 2021, sustituya �� = 0 y �� = 31 en la expresión para P( ��) para determinar los correspondientes valores y. A continuación, calcule ��
para hallar la tasa media de cambio.
B. Valores x; valores x; valores y
C. Aproximadamente 529 personas al año
D. Aproximadamente 1,873 personas al año
E. Las respuestas variarán. Ejemplo de respuesta: Si la tasa media de cambio es positiva, entonces el gráfico es creciente en ese intervalo. Si la tasa media de cambio es negativa, entonces el gráfico está disminuyendo en ese intervalo.
2. 0.95 goles/partido
3.
A. Aumento de 5.8 ℉ por mes
B. Disminución de 4.1 ℉ por mes
C. Las respuestas variarán. La temperatura tiende a aumentar entre marzo y mayo, y a disminuir entre agosto y noviembre.
SÍNTESIS DE LA ACTIVIDAD

Álgebra 2 . Matemáticas . Unidad 1
Analice las preguntas restantes pidiendo a los estudiantes previamente identificados que compartan su pensamiento, estrategias e interpretaciones utilizadas en los problemas 2 y 3. Concéntrese en ampliar el lenguaje de los estudiantes que incluye la interpretación de cada respuesta en el contexto del escenario en lugar de solo el valor. Consulte el resumen de la lección del estudiante para resumir cómo abordar la tasa de cambio promedio utilizando diversas representaciones de situaciones del mundo real.
(5 minutos)
Resuma las diferentes representaciones de las funciones (gráficas, ecuaciones, tablas y descripciones escritas) y cómo determinar la tasa de cambio promedio a partir de cada representación. Considere formular preguntas orientadoras como las siguientes.
• «Cuando una función se presenta como una gráfica, ¿cómo se determina la tasa de cambio promedio a lo largo de un intervalo?». (Identifique las coordenadas de los 2 puntos finales del intervalo con la gráfica y, a continuación, encuentre la pendiente de la recta secante que une esos 2 puntos).
• «Cuando una función se presenta como una tabla de valores, ¿cómo determina la tasa media de cambio a lo largo de un intervalo?». (Utilice los valores �� del intervalo, determine los valores �� correspondientes y, a continuación, calcule la pendiente entre los 2 puntos).
• «¿Qué unidades se utilizan para interpretar una tasa media de cambio?». (Unidades de �� por unidad de ��)
• «¿Qué tipos de funciones tienen una tasa de cambio media que es constante?». (Lineal).
(5 minutos)
1. Determine la tasa de variación media para la función ��( ��) = ��3 − 1 2 �� en el intervalo [2, 5]
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
2. Flynn opera un negocio de viajes compartidos. Registra el número de millas (mi), ��, que conduce cada día, ��, durante la primera semana del mes. �� 1 2 3 4 5 6 7 �� 65 25 30 42 51 65 12
A. ¿Qué intervalo tiene una tasa de variación media de 0?
B. Seleccione todos los intervalos que tienen una tasa de variación positiva. [1, 2] [3, 6]
[2, 4] [6, 7]
[4, 5] [1, 7]
2.
RESPUESTAS POSIBLES 1. 38.5
A. [1, 6]
B.
[1, 2] [3, 6]
[2, 4] [6, 7]
[4, 5] [1, 7]
©Accelerate Learning Inc. - Todos los derechos reservados


La tasa de cambio promedio puede determinarse usando una gráfica, una tabla o una ecuación que modele situaciones del mundo real. La pendiente entre cualquier punto de 2 una función puede usarse para determinar la razón promedio de cambio sobre ese intervalo. En situaciones del mundo real, por ejemplo, la tasa de cambio promedio a menudo se determina entre el principio y el final de un período de tiempo, como un año o una década.
La tasa de cambio promedio de una función lineal es constante y a menudo se denomina simplemente tasa de cambio o tasa de cambio constante, porque el valor será el mismo entre cualesquiera 2 puntos de la línea. La tasa de cambio de una función lineal es la pendiente.
PROBLEMA 1
El uso de teléfonos móviles como forma de comunicación ha crecido exponencialmente desde 1976. La tabla muestra el número de suscripciones a teléfonos móviles, en millones, desde 1976 hasta 2020.
Considere el intervalo de 1976 a 1979.
A. Encuentre la tasa media de cambio en este intervalo.
B. Interprete la tasa media de cambio para este intervalo en términos del contexto. Incluya las unidades.
Soluciones posibles
A. 0
B. Las respuestas pueden variar. De 1976 a 1979, no hubo cambios en el número de suscripciones a teléfonos móviles.
PROBLEMA 2

Años desde 1976 Abonos a teléfonos móviles (en millones)
¿Cuál es la tasa media de cambio, en millones de suscripciones a teléfonos móviles por año, para el período de 1992 a 2003?
Soluciones posibles
Acerca de 102 millones de suscripciones por año
PROBLEMA 3
¿Cuál es la tasa media de cambio, en millones de suscripciones a teléfonos móviles por año, para el período de 2003 a 2018?
Soluciones posibles
Sobre 447 millones de suscripciones al año
PROBLEMA 4
¿Por qué cree que la tasa media de cambio de 2003 a 2018 es mayor que la tasa media de cambio de 1992 a 2003?
Soluciones posibles
Las respuestas variarán. La tasa media de cambio es mayor de 2003 a 2018 porque más personas se suscribieron a teléfonos móviles durante ese período de tiempo que de 1992 a 2003. Los teléfonos móviles se hicieron más comunes con el tiempo.
Álgebra 2 . Matemáticas . Unidad 1

PROBLEMA 5
Interprete la tasa de cambio promedio para el intervalo 2003 a 2018 en términos del contexto.
Soluciones posibles
Las respuestas variarán. El número de suscripciones a teléfonos móviles aumentó en alrededor de 447 millones de suscripciones por año desde 2003 hasta 2018.
PROBLEMA 6
(De Álgebra 1, unidad 2, lección 19).
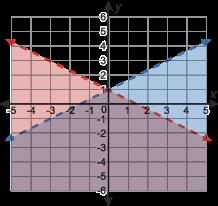
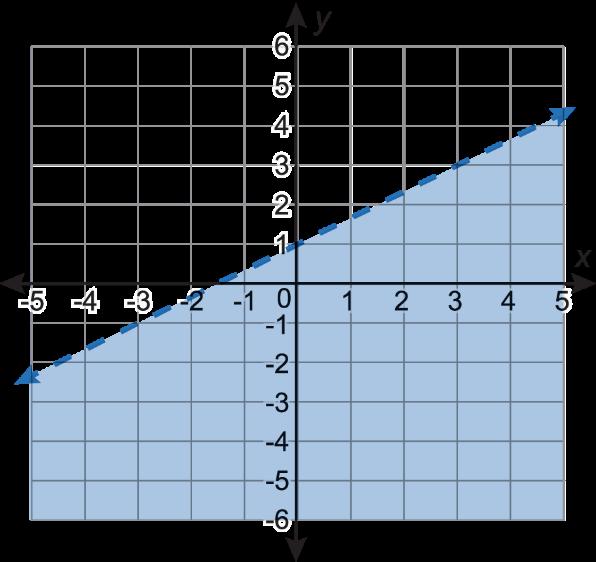
Sergio graficó la desigualdad lineal �� <− 2 3 �� + 1, pero cometió un error. Se muestra su gráfico.
A. Explique el error de Sergio.
B. Grafique la desigualdad lineal �� <− 2 3 �� + 1 en el plano de coordenadas.
Soluciones posibles
A. Las respuestas pueden variar. Sergio utilizó la pendiente de 2 3 en lugar de 2 3
B.
Reflexiones:
Math Nation California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados

IDEA(S) FUNDAMENTAL(ES)
• Analizar funciones
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
F-IF.4 Para una función que represente una relación entre dos cantidades, interpretar características clave de gráficas y tablas en términos de las cantidades, y bosquejar gráficas que muestren características clave dada una descripción verbal de la relación.
F-IF.9 Comparar propiedades de dos funciones cada una representada de manera diferente (algebraicamente, gráficamente, numéricamente en tablas o por descripciones verbales).
Enfocar SMPs
MP2 Razonar abstracta y cuantitativamente.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP6 Atender a la precisión.
Estándares ELD de Californi
I.A.3
I.B.5
II.B.5
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predicen lo que podría ocurrir, razonarán abstracta y cuantitativamente exploran cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo comparar las características clave de dos funciones representadas de formas diferentes.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Comparar características clave de funciones representadas de diferentes maneras.
Rutinas didácticas
Sondear a la clase
Observar y pre
MLR2: Recopilar y mostrar
MLR3: Aclarar, criticar, corregir
©Accelerate Learning Inc. - Todos los derechos reservados
2 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Comparemos las características clave de las funciones.
Narrativa de la lección
Los estudiantes revisan tipos de funciones familiares representadas mediante ecuaciones, tablas de valores y gráficas. Identifican características clave de funciones para comparar sus interceptos, comportamiento final, valores máximos o mínimos e intervalos crecientes o decrecientes. Los estudiantes se basan en su comprensión de las funciones que se representan de diferentes maneras para hacer las comparaciones y justificar su razonamiento. A lo largo de la lección, se anima a los estudiantes a razonar de forma abstracta y cuantitativa para comparar las distintas funciones (MP2).
Componente de la lección Estructura Tiempo Descripción breve
Calentamiento En parejas 5 min
Actividad de Exploración En parejas 20 min
Actividad de Exploración En parejas 10 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Los estudiantes identifican características clave de una función cuadrática y de valor absoluto representadas de diferentes maneras.
Los estudiantes exploran diferentes representaciones de funciones para identificar y comparar características clave.
Los estudiantes utilizan gráficas de tres funciones presentadas en diferentes ventanas para comparar sus comportamientos finales.
Los estudiantes discuten las diferentes estrategias que utilizaron para identificar y comparar las características clave de las funciones presentadas como una ecuación, un gráfico o una tabla de valores.
Los estudiantes usan diferentes representaciones de cuatro funciones para determinar y explicar cuál excederá a todas las demás a medida que x se acerca al infinito.
El componente de práctica independiente incluye 2 problemas de repaso de la lección y 2 problemas de repaso en espiral.

California . Algebra 2 ©Accelerate Learning Inc. - Todos los derechos reservados


(5 minutos)
Rutinas didácticas
Sondear a la clase
Este calentamiento pide a los estudiantes que identifiquen las características clave de las funciones representadas de diferentes maneras. Les da una razón para utilizar el lenguaje con precisión al identificar cada característica (MP6). El objetivo de esta actividad es que los estudiantes empiecen a pensar en cómo se pueden identificar y comparar las características dede funciones a partir de diferentes representaciones.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organizar a los estudiantes en grupos de 2. Darles tiempo para trabajar en silencio y luego tiempo para compartir sus respuestas y estrategias con sus compañeros. Continúe con un debate con toda la clase.
1. Se muestran dos funciones que usan diferentes representaciones.
Función R
Función T ��( ��) = −( �� + 1)( �� - 3)
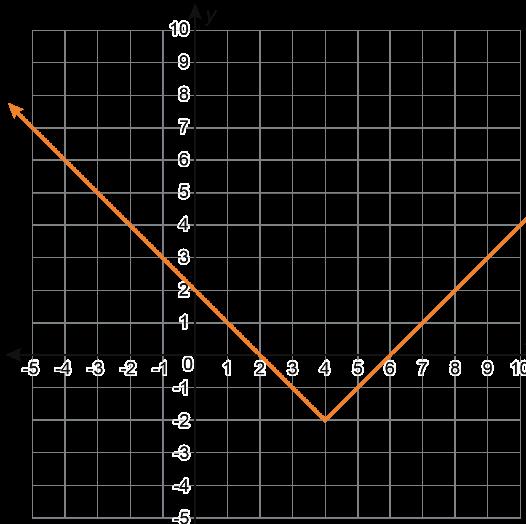
Completa la tabla determinando las características clave de cada función.
Característica clave
intercepto(s) ��
intercepto ��
Vértice
Característica clave
RESPUESTAS POSIBLES
Función R Función T
Función R Función T
intercepto(s) �� (−1, 0), (3, 0) (2, 0), (6, 0)
intercepto �� (0, 3) (0, 2)
Vértice (1, 4) (4, −2)
SÍNTESIS DE LA ACTIVIDAD

Álgebra 2 . Matemáticas . Unidad 1
Utilice la rutina de sondear la clase cuando revise las respuestas de los estudiantes. Muestre una función clave cada vez y pida a los estudiantes que anoten sus respuestas en un trozo de papel o en una minipizarra. A su señal, pídales que levanten sus respuestas. Seleccione 1-2 estudiantes por característica clave para que compartan sus procesos de pensamiento y estrategias para identificarla a partir de cada representación.
(20 minutos)
Rutinas didácticas
Observar y preguntarse
MLR2: Recopilar y mostrar
En esta actividad, los estudiantes aplican lo que saben sobre funciones lineales, cuadráticas y exponenciales de Álgebra 1 para identificar y comparar características clave con diferentes representaciones. Se pide a los estudiantes que aborden las diferentes representaciones con flexibilidad explorando características clave como X y los interceptos de Y, comportamiento de los extremos y valores máximos y mínimos. A medida que los estudiantes dan sentido a las diferentes representaciones de las funciones practican el razonamiento cuantitativo y abstracto (MP2).
INTRODUCCIÓN
Organice a los estudiantes en grupos de 2. Muestre las dos funciones lineales de la edición para estudiantes. Dé a los estudiantes 1-2 minutos (min. para escribir algunas cosas que observen en las gráficas. Pídales que compartan sus observaciones con sus compañeros y luego invítelos a compartirlas con la clase. Solicite a los estudiantes algunas ideas sobre las dos funciones lineales y anote lo que compartan. Deles otros 3-4 minutos para completar los problemas 2-4 antes de facilitar un breve debate con toda la clase. Céntrese en las características clave que los estudiantes identifican con las tablas de valores. Concluya las comparaciones de funciones lineales y muestre la respuesta al problema 6 con estrategias de pensamiento en voz alta. Dé a los estudiantes 1-2 minutos para conversar y resumir su debate en el problema 7.
Explique a los estudiantes que se pueden hacer comparaciones similares entre funciones cuadráticas y exponenciales. Deles 4-5 minutos para completar los problemas 8-11 y luego invíteles a compartir sus respuestas con la clase durante la síntesis de la actividad.
Apoyo para estudiantes con discapacidad
Representación: Interiorizar la comprensión. Utilice el códugi de colores y anotaciones para resaltar las conexiones entre las representaciones en un problema. Por ejemplo, demuestre resaltando la intercepción y en una gráfica, en una tabla de valores o en la ecuación de la función.
Proporcione marcadores fluorescentes y anime a los estudiantes a anotar las funciones de forma similara para comprobar que comparan las características correctas.
Apoya la accesibilidad para: Procesamiento visualespacial
Principio de diseño: Maximizar la metaconciencia
.
Apoyo para estudiantes que aprendenel idioma inglés
Lectura: MLR2 Recopilar y mostrar. Mientras los estudiantes comparten sus observaciones sobre lo que notan en las gráficas, tablas y ecuaciones de las funciones, escuche y registre el lenguaje que usan para describir las conexiones entre las diferentes representaciones. Escriba sus palabras y frases en un cartel visual y llame su atención sobre el lenguaje que compara las diferentes representaciones. Recuerde a los estudiantes que tomen prestado el lenguaje de la pantalla cuando lo necesiten. Esto les ayudará a utilizar el lenguaje matemático cuando comparen las características de las funciones.
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Se grafican dos funciones lineales en una cuadrícula de coordenadas. Las funciones se muestran con 2 ventanas diferentes. La línea morada es la función lineal T y la línea naranja es la función lineal W.
1
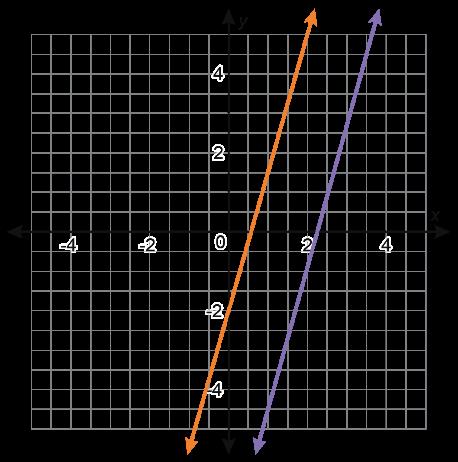
1. ¿Qué observas en las gráficas?
2
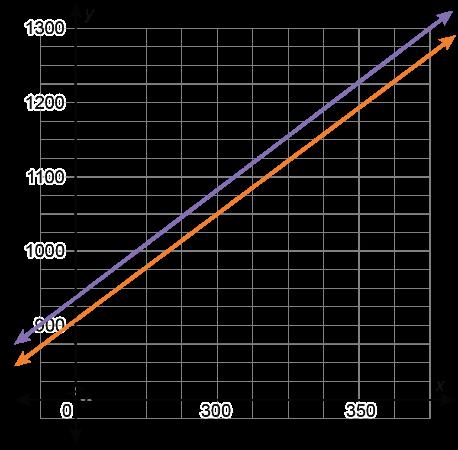
Las mismas 2 funciones lineales se muestran con diferentes representaciones.
Representación
2. Habla con tu compañero acerca de qué representación —ventana 1, ventana 2, las tablas de valores o las ecuaciones— proporciona la mejor información sobre qué función aumenta a mayor tasa. Resume el debate.
3. Usa las ecuaciones para determinar los valores que faltan en cada tabla.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN

. Algebra 2
Álgebra 2 . Matemáticas . Unidad 1
4. Debate con tu compañero lo que estos valores revelan sobre las 2 funciones lineales. Resume tu debate.
5. Vuelve a escribir las ecuaciones en forma pendiente-intersección. Muestra tu trabajo.
6. Completa los enunciados.
A. La forma pendiente-intersección de la función lineal W es .
B. La forma pendiente-intersección de la función lineal T es
7. Debate con tu compañero qué característica de la forma pendiente-intersección sería útil para determinar por qué en la ventana 1, la función lineal W parece aumentar a un ritmo más rápido como �� → ∞, pero la ventana 2 muestra que la función lineal T aumenta a un ritmo más rápido como �� → ∞. Resuma su debate.
8. Se muestran dos funciones cuadráticas.
Función cuadrática H Función cuadrática K
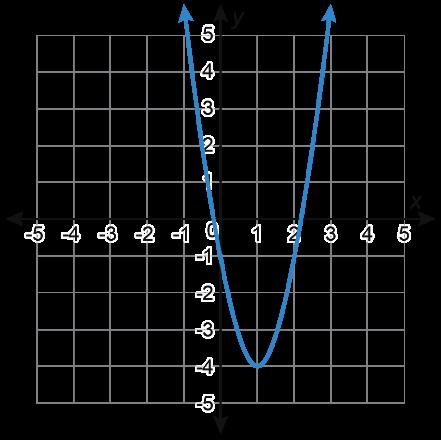
A. ¿Qué función cuadrática tiene el mínimo más pequeño?
B. ¿Qué función cuadrática tiene el intercepto �� más grande?
C. A medida que �� → ∞, los valores de �� de qué función cuadrática aumentan más rápidamente?
9. Se muestran dos funciones exponenciales.
Función exponencial N Función exponencial R �� = 4( 1 2 )�� + 3
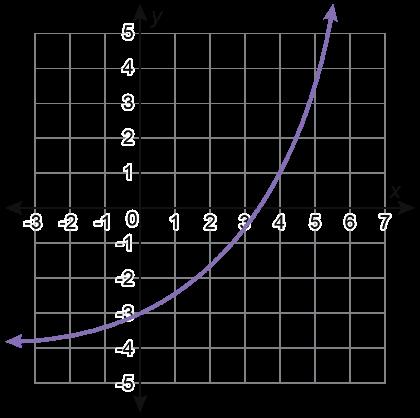
A. ¿Qué función exponencial tiene la mayor intercepción ��?
B. ¿Qué función exponencial superará finalmente a la otra a medida que �� → ∞?
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN
10. Se muestran la función cuadrática H y la función lineal T.
cuadrática H
RESPUESTAS POSIBLES
Habla con tu compañero sobre qué función superará finalmente a la otra como �� → ∞. Explica tu elección para resumir tu debate.
11. Se muestran la función cuadrática H y la función exponencial N.
exponencial N
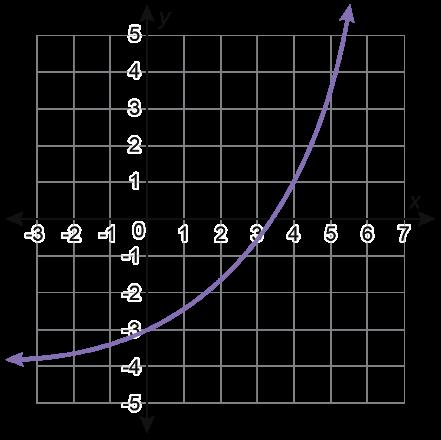
Habla con tu compañero sobre qué función acabará superando a la otra como �� → ∞. Explica tu elección para resumir tu debate.
1. Las respuestas variarán. Tanto para la línea naranja como para la línea morada, como �� → ∞, �� → ∞. En la ventana 1, los valores �� de la línea naranja están por encima de los valores �� de la línea morada, pero en la ventana 2, la línea morada está por encima de la línea naranja.
2. Las respuestas variarán. La ecuación de cada función puede reescribirse en forma pendiente-intercepto para identificar qué ecuación tiene la mayor pendiente. Los estudiantes podrían usar la tabla de valores para determinar la pendiente de cada función e identificar la mayor tasa de cambio.
RESPUESTAS POSIBLES CONTINUACIÓN 3.
4. Las respuestas variarán. A medida que �� aumenta, los valores de y de la función lineal T aumentan más rápido que la función lineal W.
5. Función lineal T Función Lineal W −18 �� + 5 �� = −40
�� − 2 �� = 4 5 �� = 18 �� − 40
�� = −7 �� + 4 �� = 18 5 �� − 8 Función Lineal T �� − 2
6. A. �� = 3.5 �� − 2 B. �� = 18 5 �� − 8
7. Las respuestas pueden variar. Los estudiantes pueden notar que una línea con una pendiente positiva mayor incrementará más rápido.
8.

SÍNTESIS DE LA ACTIVIDAD
. Algebra 2 ©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1
9.
A. Función cuadrática H
B. Función cuadrática H
C. Función cuadrática K
A. Función exponencial R
B. Función exponencial N
10. Función cuadrática H. Las explicaciones variarán.
11. Función exponencial N. Las explicaciones variarán.
Seleccione a los estudiantes para que compartan sus respuestas y estrategias para los problemas 8-11 con la clase. Mientras comparten, considere hacer las siguientes preguntas:
• «¿Tuvi alguien la misma respuesta, pero la explicaría de manera diferente?».
• «¿Qué representación fue la más útil para responder la pregunta?».
• «¿Usó alguien una representación diferente?».
• «¿Quiere alguien agregar algo a la estrategia de ?».
• «¿Están de acuerdo o en desacuerdo? ¿Por qué?».
Durante la discusión, considere la posibilidad de retomar el concepto de qué función (lineal, cuadrática o exponencial) crecerá más rápido que las demás a medida que �� → ∞. Los estudiantes han trabajado esta idea en Álgebra 1 y pueden basarse en las características clave de las distintas funciones para razonar sobre cómo crecen y actúan los distintos tipos de funciones para valores extremadamente grandes.


(10 minutos)

Rutinas didácticas
MLR3: Clarificar, criticar, corregir
En esta actividad, los estudiantes comparan la rapidez con la que crecen las funciones lineales, exponenciales y cuadráticas a medida que sus valores �� se acercan al infinito. Ellos construyen argumentos viables y critican el razonamiento de los demás mientras predicen qué funciones excederán a otras funciones usando el comportamiento final (MP3).
INTRODUCCIÓN
Organice a los estudiantes en grupos de 2 y pídales que trabajen en silencio durante unos minutos antes de compartir su pensamiento con sus compañeros. Escuche el debate sobre el problema 3 para identificar los razonamientos de los estudiantes que se deben destacar durante la síntesis de la actividad.
Apoyo para estudiantes con discapacidad
Representación: Acceso para la percepción. Lea los enunciados de los problemas en voz alta y anime a los estudiantes a participar en el problema anotando mientras escuchan. Los estudiantes que escuchen y lean la información se beneficiarán del tiempo de procesamiento adicional.
Favorece la accesibilidad para: Lenguaje; procesamiento conceptual
La función lineal T, la función cuadrática H y la función exponencial N se muestran en diferentes ventanas gráficas.
Ventana A Ventana B Ventana C
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
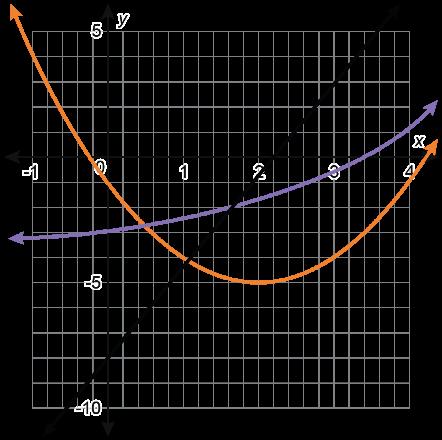
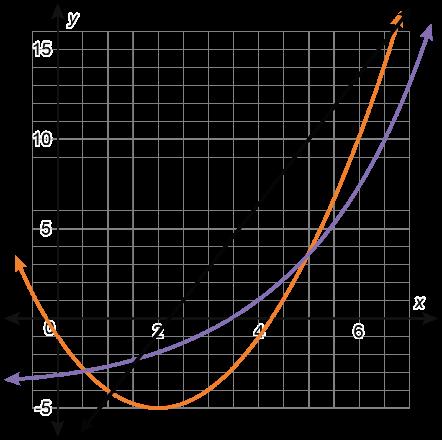
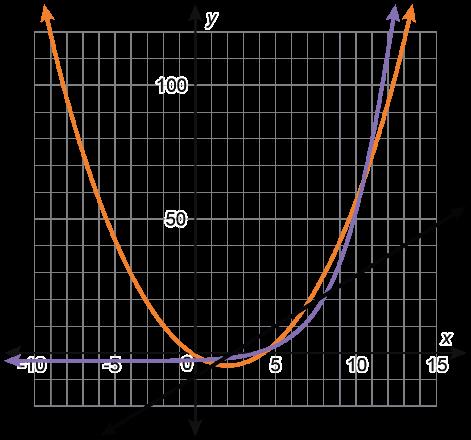
1. Complete los enunciados.
A. La ventana A parece mostrar que
función lineal T función cuadrática H función exponencial N supera a las otras como �� → ∞
B. La ventana B parece mostrar que
función lineal T función cuadrática H función exponencial N supera a las otras como �� → ∞.
Álgebra 2 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN
C. La ventana C parece mostrar que
función lineal T función cuadrática H función exponencial N supera a las otras como �� → ∞
1. Habla con tu compañero sobre si la función exponencial R de la actividad anterior superará a la función lineal T o a la función cuadrática H como �� → ∞. Resume el debate.
2. ¿Qué tipo de funciones exponenciales siempre excederán a una función lineal con pendiente positiva y a una función cuadrática con un valor a mayor que 0?
1.
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
A. Función lineal T
B. Función cuadrática H
C. Función exponencial N
2. Las respuestas variarán. Los estudiantes deben tener en cuenta que la Función Exponencial R es una función de decaimiento exponencial, por lo que no superará a las otras 2 funciones como �� → ∞
3. Las respuestas variarán. Las funciones exponenciales en las que 1 + �� es mayor que 1 crecerán exponencialmente como �� → ∞, por lo que siempre superarán a las funciones lineales con pendiente positiva y a las funciones cuadráticas con un ��-valor mayor que 0
Pida a algunos estudiantes que compartan y expliquen sus respuestas a cada problema. Anote y muestre sus explicaciones. Al discutir el problema 3, haga preguntas aclaratorias para resaltar el razonamiento sobre las relaciones entre las funciones lineal, cuadrática y exponencial. Pida a los estudiantes que generen ecuaciones de ejemplo para cada función a fin de explorar sus hipótesis para el problema 3.
Apoyo para estudiantes que aprenden el idioma inglés
Conversar: MLR3 Aclarar, criticar, corregir. Presente una respuesta incorrecta para el problema 1. Pida a los estudiantes que identifiquen el error y que ofrezcan una vía de solución correcta. Esto les ayudará a generalizar estrategias para operaciones con funciones en escenarios del mundo real.
Principio(s) de diseño: Optimizar el resultado (para la generalización); maximizar la metaconciencia
(5 minutos)
Ayude a los estudiantes a reflexionar sobre las ideas clave de la lección debatiendo, primero en clase o en parejas, preguntas como las siguientes:
• «¿Cómo determinaste qué tipo de función estaba representada en cada gráfica?». (Busqué características clave como una tasa de cambio constante, un vértice o una asíntota).
• «¿Qué tipo de función exponencial no superará finalmente a una función lineal o cuadrática a medida que �� → ∞?». (Una función de decaimiento exponencial no superará a una función lineal con pendiente positiva ni a una cuadrática con coeficiente principal positivo).
• «¿Qué características clave se pueden utilizar para determinar qué tipo de función está representada por una tabla de valores?». (Las funciones lineales tienen una tasa de cambio constante, las funciones cuadráticas aumentan y luego disminuyen o disminuyen y luego aumentan, las funciones cuadráticas también tienen una segunda diferencia común y las funciones exponenciales tienen una tasa de cambio porcentual constante).
• «¿Qué características clave se pueden utilizar para determinar qué tipo de función está representada por una ecuación?» (Las funciones lineales solo tienen variables elevadas a la primera potencia, las funciones cuadráticas tienen un término ��2, y las funciones exponenciales tienen una variable en el exponente).
.
©Accelerate Learning Inc. - Todos los derechos reservados


Se muestran cuatro funciones con diferentes representaciones.
Y

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
RESPUESTAS POSIBLES
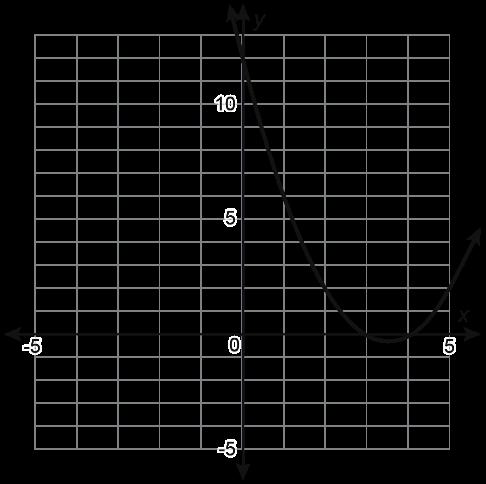
1. ¿Qué función superará finalmente a todas las demás funciones como �� → ∞?
2. Explique su razonamiento.
1. Función K
2. Las respuestas variarán. Una función de crecimiento exponencial acabará superando a las funciones que aumentan lineal o cuadráticamente a medida que �� aumenta. Las funciones de decaimiento exponencial como la función F disminuyen a medida que �� aumenta.
Las características clave de las funciones pueden incluir interceptos, comportamiento final, valores máximos o mínimos, intervalos crecientes y decrecientes, dominio y rango. Las funciones pueden representarse mediante ecuaciones, gráficas, tablas de valores o descripciones verbales. Al comparar funciones, identifique las características clave para la comparación con las representaciones proporcionadas.
Las funciones B, S y H se muestran en la tabla.
Función B
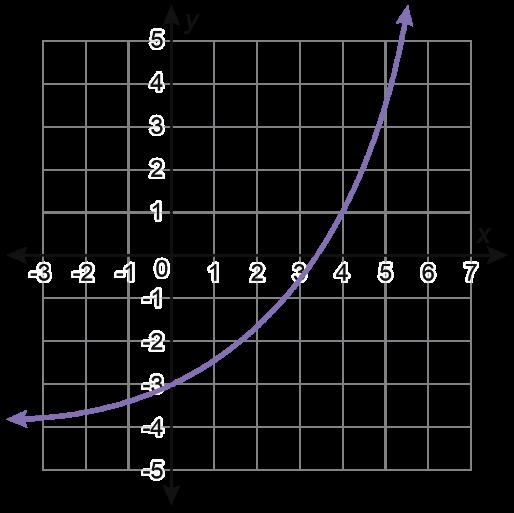
Función S Función H
Observa que para algunas representaciones de funciones es más fácil identificar algunas características clave que otras. Considere los ejemplos descritos.
• Mientras que la intercepción �� de la función B es fácil de identificar a partir del gráfico, la intercepción �� no es tan clara a partir de esta representación.
• Determinar los intercepto ��- y �� de la función H requiere trabajo adicional. Sin embargo, determinar la forma y el comportamiento final de la función H es posible extendiendo el patrón de la tabla, asumiendo que es una función continua.
• La ecuación de la función S define una función lineal donde la intercepto Y y la pendiente de la gráfica pueden determinarse fácilmente. Se pueden determinar características clave adicionales con la ecuación.
2 . Matemáticas . Unidad 1
PROBLEMA 1
Se muestran las funciones L, Z y R.
Función L
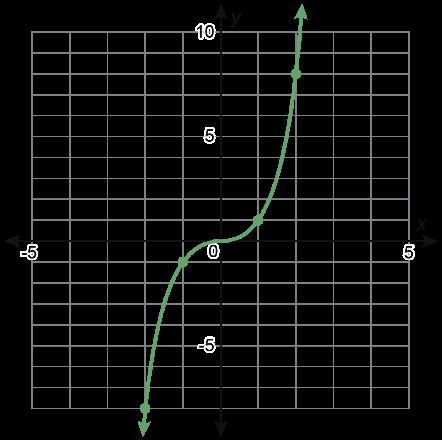

Función Z
Función R
A. ¿Qué función tiene la intercepción �� más pequeña? Explique su razonamiento.
B. ¿Qué función superará finalmente a las otras a medida que �� → ∞? Explica tu razonamiento.
Soluciones posibles
A. Función L. Ejemplo de respuesta: La función L tiene intercepto �� en �� = 0, mientras que las funciones Z y R tienen interceptos �� de �� = 2 y �� = 1, respectivamente.
B. Función Z. Ejemplo de respuesta: La función Z crece por factores iguales en intervalos iguales, por lo que es una función de crecimiento exponencial. Las funciones de crecimiento exponencial superan finalmente a las funciones cuadráticas (función R) y cúbicas (función L) a medida que �� → ∞
PROBLEMA 2
Se muestran las funciones K y M.
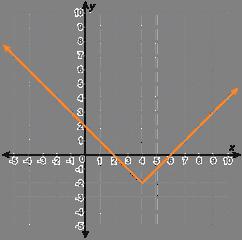
A. ¿Qué función tiene la intercepción �� mayor?
B. ¿Qué función es creciente en el intervalo −4 < �� < 4?
C. ¿Qué función tiene el menor valor cuando �� = −1?
Nation California . Algebra 2
Learning Inc. - Todos los derechos reservados


Soluciones posibles
A. Función K
B. Función M
C. Función M
PROBLEMA 3
(De la unidad 1, lección 2).
Determine la tasa de cambio promedio de la función ��( ��) = ��3 - 3 �� + 4 en cada intervalo.
A. [−1, 3]
B. [1, 4]
C. [−3 2 , 0]
PROBLEMA 4
(De la unidad 1, lección 2).
¿Qué función tiene una tasa de variación media constante?
A. �� (��) = 3 ��2 − 4
B. ��( ��) = -2| �� + 1|
C. ��( ��) = 4 + 5 2 ��
D. ��( ��) = (2)-�� + 1 2
Reflexiones:

Soluciones posibles
A. 4 B. 18 C. 3 4
Soluciones posibles C


BIG IDEA(S)
• Ecuaciones para predecir y modelar
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
A-SSE.4 Derivar la fórmula para la suma de una serie geométrica finita (cuando la razón común no es 1), y usar la fórmula para resolver problemas.
Construyendo Sobre
F-IF.3 F-BF.2 F-LE.2
Enfocar SMPs
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP5 Utilizar estratégicamente las herramientas adecuadas.
Estándares ELD de California
I.A.3
I.B.5
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predecir lo que podría ocurrir,
construiráb argumentos viables y criticarán el razonamiento de otros exploran cantidades cambiantes.
OBJETIVO(S) DE APRENDIZAJE
• Puedo representar una secuencia de diferentes maneras.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRP
• Crear una tabla, gráfico o definición recursiva de una secuencia a partir de una información dada.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
Encaja
Observar y preguntarse
Materiales necesarios
Papel milimetrado
©Accelerate Learning Inc. - Todos los derechos reservados

Objetivos de aprendizaje para el estudiante
• Veamos diferentes formas de representar una secuencia.
Narrativa de la lección
El objetivo de la lección es que los estudiantes practiquen la interpretación y escritura de definiciones recursivas de funciones, a la vez que representan funciones de diferentes maneras. Los estudiantes hacen coincidir secuencias y definiciones recursivas en una actividad de pareo, dándoles la oportunidad de explicar su razonamiento y criticar el razonamiento de los demás (MP3). Una parte importante de las actividades es dar tiempo a los estudiantes para que compartan y expliquen sus estrategias para crear diferentes representaciones. Esto ayuda a poner de relieve que a menudo hay más de una forma de abordar los problemas. También ayuda a establecer que compartir estrategias y aprender de otros estudiantes son normas del aula.
La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes elijan utilizar la tecnología apropiada para resolver problemas. Recomendamos poner la tecnología a disposición de los estudiantes (MP5).
Componente de la lección Estructura Tiempo Descripción breve
Calentamiento Independiente 5 min. Los estudiantes determinan el factor de crecimiento o la tasa de cambio para secuencias dadas en varias representaciones.
Actividad de exploración En parejas 15 min. Los estudiantes relacionan secuencias de números con sus definiciones de funciones recursivas y explican su razonamiento.
Actividad de exploración En parejas 15 min.
Síntesis Todo el grupo 5 min.
Enfriamiento Independiente 5 min.
Dado un patrón geométrico, los estudiantes escriben una función recursiva para la secuencia; grafican los pasos 1 a 7; y explican si la secuencia es geométrica, aritmética o ninguna de las dos.
Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de la determinación de un patrón basado en una descripción geométrica.
Los estudiantes revisan un resumen de secuencias aritméticas y geométricas para crear un gráfico y un patrón visual para una secuencia asignada.
Los estudiantes escriben y grafican los primeros cinco términos de una secuencia dada una definición recursiva.
Práctica Independiente 10 min. El componente de práctica independiente incluye 2 en lección y 4 problemas de repaso en espiral.
California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


(5 minutos)
El objetivo de este calentamiento es que los estudiantes recuerden algunas de las formas en que se pueden representar las funciones, como tablas, gráficas, ecuaciones y descripciones. Nos centraremos en las funciones exponenciales y lineales, y en la identificación de la tasa de cambio o el factor de crecimiento. Los estudiantes continuarán con esta habilidad más adelante en la unidad cuando revisen la escritura de ecuaciones explícitas para situaciones exponenciales y lineales.
Para cada secuencia mostrada, encuentre el factor de crecimiento o la tasa de cambio. Prepárate para explicar tu razonamiento.
1. 5, 15, 25, 35, 45,...
2. Empezar en 10, cada nuevo término es 5 2 menor que el término anterior.
3.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
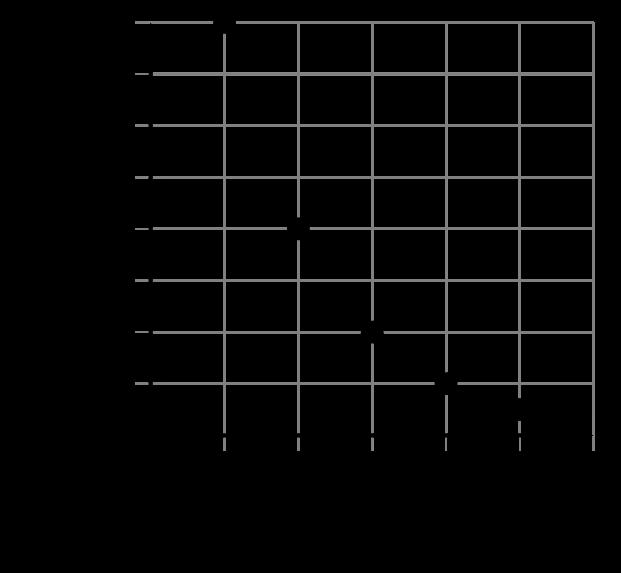
4. ��(1) = −5, ��( ��) = ��( �� − 1) ⋅ −2 para �� ≥ 2
5.
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
1. La tasa de variación es 10
2. La tasa de variación es 5 2
3. El factor de crecimiento es 0.5
4. El factor de crecimiento es −2
5. La tasa de cambio es 0.1
Muestre las preguntas para que todos las vean durante la discusión. Para cada problema, seleccione estudiantes para que compartan cómo identificaron el factor de crecimiento o la tasa de cambio. Destaque cualquier comentario que vincule estas secuencias con funciones lineales o exponenciales, como que la tasa de cambio sería la pendiente de la recta en la que se encuentran los términos de la secuencia cuando se representan gráficamente.
Álgebra 2 . Matemáticas . Unidad 1
(15 minutos)
En esta actividad por parejas, los estudiantes se turnan parahacer coincidir una secuencia con una definición. A medida que los estudiantes intercambian papelse, explican su pensamiento y escuchan,lo que les da la oportunidad de explicar su razonamiento y criticar el razonamiento de los demás (MP3).
Una secuencia y una definición no tienen correspondencia. Se pide a los estudiantes que escriban la correspondencia.
Compruebe si los estudiantes utilizan un razonamiento claro mientras crean una definición recursiva para la secuencia 18, 20, 22, 24 para compartirla durante el debate .
Disponer de una hoja de cálculo ofrece a los estudiantes la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).
INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Diga a los estudiantes que, para cada secuencia, un compañero encuentra la definición recursiva que corresponde y explica por qué cree que corresponde. El trabajo del compañero es escuchar y asegurarse de que están de acuerdo. Si no lo están, hablen hasta llegar a un acuerdo. Para la siguiente secuencia, los estudiantes intercambian los papeles. Si es necesario, haga una demostración de este protocolo antes de que los estudiantes empiecen a trabajar.
Asegúrese de que los estudiantes se dan cuenta de que una secuencia y una definición no tienen correspondencias, y de que tienen la tarea de escribir la correspondencia para cada una.
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyo a la discusión. Utilice esta rutina para apoyar la discusión en pequeños grupos, ya que los estudiantes deben turnarse para encontrar un par. Muestre los siguientes fragmentos de oraciones para que todos los vean: «La secuencia y la definición coinciden porque...» y «Me di cuenta , así que hice coincidir...». Anime a los estudiantes a que se desafíen mutuamente cuando no estén de acuerdo y que presionen por un lenguaje matemático preciso. Esto ayudará a los estudiantes a aclarar su razonamiento sobre cada correspondencia.
Principio(s) de diseño: Apoyar la creación de sentido; maximizar la metaconciencia
Apoyo a los estudiantes con discapacidad
Engagement: Facilitar el acceso despertando el interés. Aproveche la elección en torno al reto percibido. Invite a grupos de estudiantes a encontrar coincidencias para al menos 4 de las secuencias. La división de esta tarea en partes más manejables también puede ayudar a los estudiantes que necesitan más tiempo de procesamiento.
Apoya la accesibilidad para: Organización; Atención; Habilidades socioemocionales
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
California . Algebra 2
Túrnase con tu compañero para hacer coincidir una secuencia con una definición recursiva. Puede ser útil averiguar primero si la secuencia es aritmética o geométrica.
• Para cada correspondencia que encuentres, explica a tu compañero cómo sabes que es una correspondencia.
• Para cada correspondencia que encuentre tu compañero, escucha atentamente su explicación. Si no estás de acuerdo, hable de sus ideas y traten de llegar a un acuerdo.
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN
Hay una secuencia y una definición que no tienen pares. Crea su par correspondiente.
Secuencias:
1. 3, 6, 12, 24
2. 18, 36, 72, 144
3. 3, 8, 13, 18
4. 18, 13, 8, 3
5. 18, 9, 4,5, 2.25
6. 18, 20, 22, 24
Definiciones:
• G(1) = 18, G( ��) = 1 2 ⋅ G( �� − 1), �� ≥ 2
• H(1) = 3, H( ��) = 5 ⋅ H( �� − 1), �� ≥ 2
• J(1) = 3, J( ��) = J( �� − 1) + 5, �� ≥ 2
• K(1) = 18, K( �� K( �� - 1) − 5, �� ≥ 2
• L(1) = 18, L( ��) = 2 ⋅ L( �� − 1), �� ≥ 2
• M(1) = 3, M(��) = 2 ⋅ M(�� − 1), �� ≥ 2
Partidos:
• 1 y M (geométrica)
• 2 y L (geométrica)
• 3 y J (aritmética)
POSIBLES RESPUESTAS
• 4 y K (aritmética)
• 5 y G (geométrica)
La definición de 6 es ��(1) = 18, ��( ��) = ��( �� − 1) + 2, �� ≥ 2 o equivalente (aritmética).
La secuencia para H es 3, 15, 75, 375, (geométrica).
CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
Algunos estudiantes pueden no estar seguros de cómo empezar a relacionar los términos de una secuencia con una definición. Anímeles a empezar eligiendo una definición y calculando los primeros términos de la secuencia que representa.
Una vez que todos los grupos hayan completado el pareo, pregunte «¿Cómo decidisteis qué definiciones hacer coincidir con la secuencia 3, 6, 12, 24 y la secuencia 18, 36, 72, 144 cuando ambas implican duplicar?». (Ambas son geométricas con un factor de crecimiento de 2, pero como los términos primeros son diferentes puedes usarlos para hacer coincidir las secuencias con M y L).
Luego, invita a los estudiantes previamente identificados a compartir la definición recursiva que crearon para la secuencia 18, 20, 22, 24 y su estrategia para escribirla. Si el tiempo lo permite y los estudiantes necesitan práctica extra graficando funciones, asigna a los estudiantes una función a cada uno del enunciado de la tarea para que dibujen una gráfica. Después del tiempo de trabajo, seleccione a los estudiantes para que compartan sus bosquejos, mostrándolos para que todos los vean y comparen.
Álgebra 2 . Matemáticas . Unidad 1
(15 minutos)
Rutinas didácticas
Encájalo
Observar y preguntarse
El propósito de esta tarea es que los estudiantes escriban una definición recursiva para una secuencia que represente un contexto matemático y creen otras representaciones de la secuencia.
Vigile a los grupos que crean sus definiciones recursivas de diferentes maneras para compartirlas durante la discusión de toda la clase. Por ejemplo, algunos estudiantes pueden crear primero una tabla que muestre el número de pasos y los valores asociados, mientras que otros pueden dibujar pasos adicionales.
Permita a los estudiantes utilizar papel cuadriculado para dibujar sus gráficos si es necesario. Poner a disposición de los estudiantes la tecnología gráfica les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

Muestre la imagen para que todos la vean. Pide a los estudiantes que piensen en al menos una cosa que les llame la atención y en al menos una cosa que les haga dudar. Conceda a los estudiantes 1 un minuto de reflexión en silencio y, a continuación, pídales que compartan lo que han observado y lo que se preguntan. Registre y muestre sus respuestas para que todos puedan verlas. Si es posible, anota el razonamiento pertinente en la imagen o cerca de ella. Una vez registradas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista que te preguntes ahora?». Anime a los estudiantes a que discrepen respetuosamente, pidan aclaraciones o señalen información contradictoria. Si no lo plantean los estudiantes, pregunte «¿Cómo describirías la cantidad total de cuadrados del paso 3 comparado con la cantidad total de cuadrados pequeños del paso 2?». (Hay 9 o 32, más cuadrados en el paso 4 que en el paso 3).
Organice a los estudiantes en grupos de 2. Anímelos a que se comuniquen con su compañero con frecuencia mientras realizan la tarea.
Apoyo para estudiantes con discapacidad
Acción y expresión: Interiorizar las funciones ejecutivas. Proporcionar a los estudiantes cuadrícula o papel cuadriculado para organizar su trabajo con representaciones de secuencias geométricas y aritméticas.
Apoya la accesibilidad para: Lenguaje; organización
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
Aquí hay un patrón en el que la cantidad de cuadrados pequeños aumenta con cada nuevo paso.

1. Escribe una definición recursiva para la cantidad total de cuadrados pequeños S(��) en el paso ��.
2. Esboza una gráfica de S que muestre los pasos 1 al 7.
3. ¿Es esta secuencia geométrica, aritmética o ninguna de las dos? Prepárate para explicar cómo lo sabes.
©Accelerate Learning Inc. - Todos los derechos reservados



RESPUESTA POSIBLES
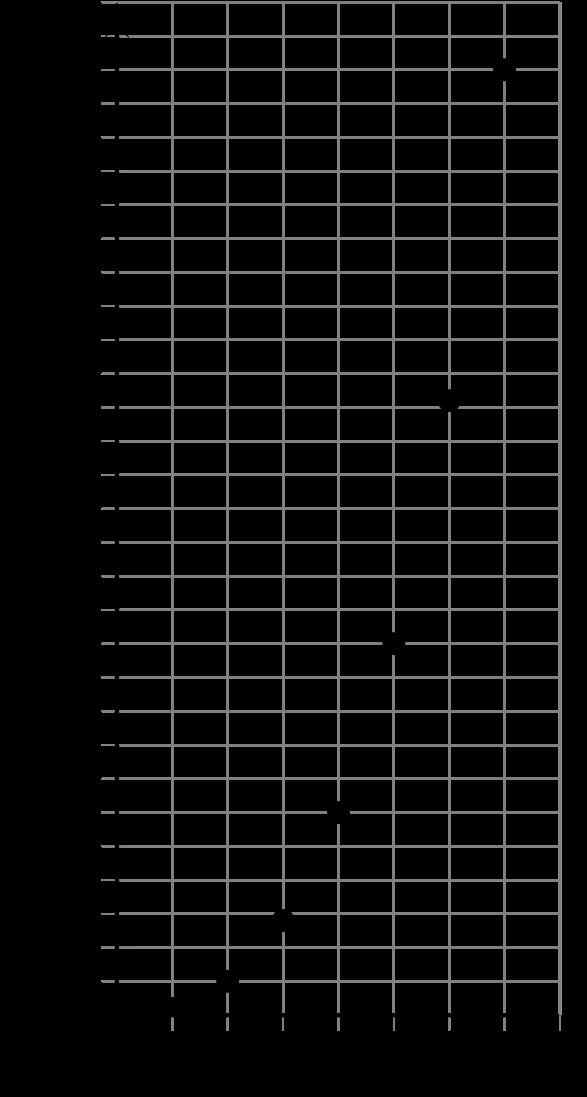
3. Tampoco. Ejemplo de respuesta: La secuencia no es geométrica ni aritmética porque no hay una tasa de cambio constante ni un factor de crecimiento para los términos.
CONCEPTOS ERRÓNEOS PREVISTOS
Es posible que los estudiantes no estén seguros de por dónde empezar con el gráfico, ya que en el enunciado de la tarea no se proporcionan ejes. Anima a estos estudiantes a que primero averigüen qué valores necesitan graficar antes de dibujar, escalar y etiquetar sus ejes.
SÍNTESIS DE LA ACTIVIDAD
El objetivo de esta discusión es que los estudiantes compartan cómo razonaron sobre una definición recursiva para S y cómo crearon su gráfico para los pasos 1 a 7. Invite a los grupos previamente identificados a compartir cómo crearon sus definiciones, asegurándose de mostrar a todos las representaciones adicionales que utilizaron para ayudar a su pensamiento. Después de que estos estudiantes hayan compartido, pregunte: «¿Utilizó alguien una estrategia diferente para escribir su definición?» e invite a cualquier estudiante nuevo a compartir su pensamiento. Concluya el debate revisando las estrategias de graficación. Seleccione a los estudiantes de 2-4 para que compartan cómo crearon su bosquejo de S. En particular, concéntrese en cómo se eligió la escala en cada eje.
¿Estás listo para más?
Comienza con un círculo. Si haces 1 recorte, tienes 2 partes. Si haces 2 recortes, puedes tener un máximo de 4 partes. Si haces 3 recortes, puedes tener un máximo de 7 partes.
1. Haz un dibujo para mostrar cómo 3 recortes pueden dar 7 partes.
2. Encuentra la cantidad máxima de partes que puedes obtener de 4 recortes.
3. De 5 recortes.
4. ¿Puedes encontrar una función que dé la máximacantidad de partes a partir de n cortes?
1. Un dibujo de un círculo con 3 recortes y divide el círculo en 7 partes.
2. 11
3. 16
4. Cualquiera de las dos fórmulas o equivalente:
A. Cerrado: 1 2 ( ��2 + �� + 2)
B. Recursivo: ��(0) = 1, ��( ��) = ��( �� − 1) + �� �� − 1)

5 minutos
Haga un póster de clase para las secuencias geométricas y otro para las secuencias aritméticas para resumir el repaso de las secuencias. Este póster puede utilizarse en la siguiente lección, cuando los estudiantes continúen trabajando con secuencias. También puede revisarse cuando los estudiantes profundicen en las series geométricas al final de la Unidad 3. Se muestra un ejemplo de secuencias que pueden utilizarse para crear las visualizaciones de clase.
Secuencias geométricas y aritméticas
Secuencia geométrica (función exponencial)
Multiplique cada término consecutivo por el factor de crecimiento.
Secuencia de ejemplo: 2, 6, 18, 54, . . .
Factor de crecimiento: 3
Recursiva: ��(1) = 2, ��( ��) = 3 ⋅ ��( �� - 1), �� ≥ 2
��th término: ��(��) = 2 ⋅ 3 �� - 1, �� ≥ 1
Secuencia de ejemplo: 160, 40, 10, 2.5, . . .
Factor de crecimiento: 1 4
Recursivo: h(1) = 160, h( ��) = 1 4 ⋅ h( �� - 1), �� ≥ 2
��th término: h( ��) = 160 ⋅ ( 1 4 ) �� - 1 , �� ≥ 1
Secuencia aritmética (función lineal)
Añada la tasa de cambio a cada término consecutivo.
Secuencia ejemplo: 2, 7, 12, 17, . . .
Tasa de cambio: 5
Recursiva: ��(1) = 2, ��( ��) = 5 + ��( �� - 1), �� ≥ 2
��th término: ��( ��) = 2 + 5( �� - 1), �� ≥ 1
Secuencia ejemplo: 9, 5, 1, -3, . . .
Tasa de cambio: -4
Recursivo: ��(1) = 9, ��( ��) = -4 + ��( �� - 1), �� ≥ 2
��th término: ��( ��) = 9 - 4( �� - 1), �� ≥ 1
Organice a los estudiantes en grupos de 3-4 y asigne a cada grupo una de las secuencias de ejemplo. Diga a los grupos que creen un gráfico y un patrón visual que muestre los cinco primeros valores de su secuencia. Después del tiempo de trabajo, invite a los grupos a compartir sus representaciones. Añádalas al póster para futuras referencias.
ENUNCIADO DE LA TAREA
ENUNCIADO DE LA TAREA
RESPUESTAS POSIBLES
5 minutos
Una secuencia tiene la definición recursiva ��(1) = 2 3 , ��( ��) = ��( �� - 1) ⋅ 3 2 para �� ≥ 2.
1. Escriba los cinco primeros términos de la sucesión. 2. Trace un gráfico de los cinco primeros términos de la sucesión.
1. 2 3 , 1, 3 2 , 9 4 , 27 8
2. Respuesta de ejemplo:
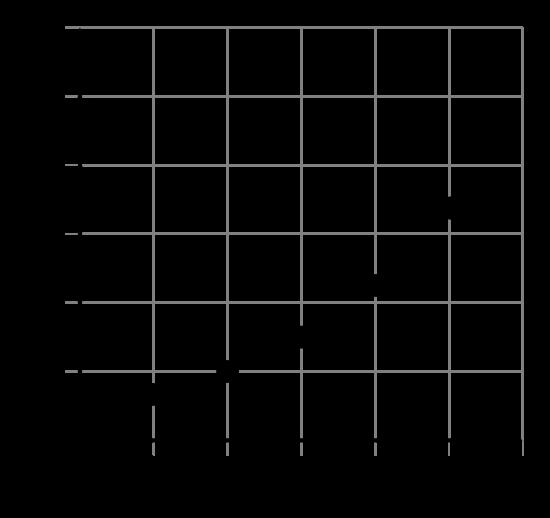
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


He aquí algunas formas de representar una secuencia. Cada representación da una visión diferente de la misma secuencia.
• A lista de términos. He aquí una lista de términos para una secuencia aritmética D: 4, 7, 10, 13, 16, . . . Podemos demostrar que esta secuencia es aritmética observando que la diferencia entre términos consecutivos es siempre 3, por lo que podemos decir que esta secuencia tiene una tasa de cambio de 3
• A tabla. Una tabla lista el número de término �� y el valor de cada término D( ��). A veces puede ser más fácil detectar o analizar patrones cuando se utiliza una tabla.

• A gráfico. La gráfica de una sucesión es un conjunto de puntos, porque una sucesión es una función cuyo dominio es una parte de los números enteros. Para una secuencia aritmética, estos puntos se encuentran en una recta, ya que las secuencias aritméticas son un tipo de función lineal.
• Una ecuación . Podemos definir secuencias recursivamente usando la notación de función para hacer una ecuación. Fo la secuencia 4, 7, 10, 13, 16, . . ., el término inicial es 4 y la tasa de cambio es 3, por lo que D(1) = 4, D( ��) = D( �� - 1) + 3 para �� ≥ 2. Este tipo de definición nos dice cómo encontrar cualquier término si conocemos el término anterior. No es tan útil para calcular términos que están lejos como D(100). Algunas secuencias no tienen definiciones recursivas, pero las secuencias geométricas y aritméticas siempre las tienen.
PROBLEMA 1
Una secuencia aritmética �� empieza 2, 5, . . .
A. Escribe una definición recursiva para esta secuencia usando notación de función.
B. Use su definición para hacer una tabla de valores para ��(��) y encuentre ��(6)
Posibles soluciones
Ejemplo de respuesta:
A. , ��(��) = ��(�� - 1) + 3 para �� ≥ 2 o equivalente
B.
Álgebra 2 . Matemáticas . Unidad 1

PROBLEMA 2
Una secuencia geométrica �� comienza 1, 3, . . .
A. Escriba una definición recursiva para esta secuencia utilizando la notación de funciones.
B. Dibuje un gráfico de los primeros 5 términos de ��
C. Explique cómo utilizar la definición recursiva para determinar ��(30). (No determine realmente el valor).
Posibles soluciones
A. ��(1) = 1, ��(��) = 3 ⋅ ��(�� - 1), �� ≥ 2 o equivalente
B. Ejemplo de respuesta:
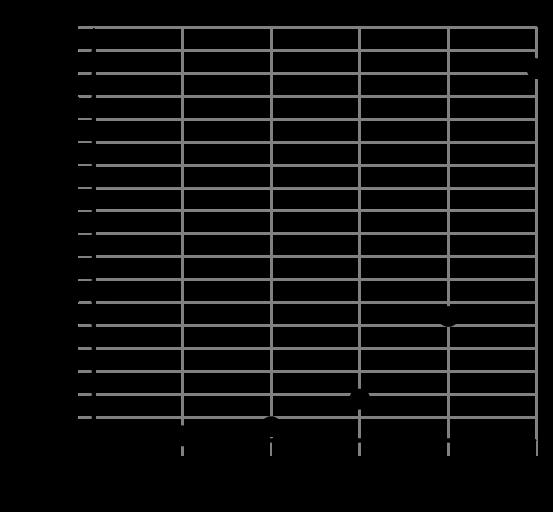
C. Ejemplo de respuesta: Para encontrar ��(30), comience en ��(0) y multiplique por 3 repetidamente.
PROBLEMA 3
(De Álgebra 1, Unidad 9, Lección 4).
Empareje cada secuencia con una de las definiciones recursivas. Observa que sólo se da la parte de la definición que muestra la relación entre el término actual y el anterior para no desvelar las soluciones.
A. 3, 15, 75, 375
B. 18, 6, 2, 2 3
C. 1, 2, 4, 7
D. 17, 13, 9, 5
Posibles soluciones
A. iii
B. i
PROBLEMA 4
(De Álgebra 1, Unidad 9, Lección 4).)
Escribe los cinco primeros términos de cada sucesión.
A. ��(1) = 1, ��( ��) = 3 ⋅ ��( �� - 1), �� ≥ 2
B. ��(1) = 1, ��( ��) = -2 + ��( �� - 1), �� ≥ 2
C. ��(1) = 1, ��( ��) = 2 ⋅ ��( �� - 1) + 1, �� ≥ 2
D. ��(1) = 1, ��( ��) = ��( �� - 1)2 + 1, �� ≥ 2
E. ��(1) = 1, ��( ��) = ��( �� - 1) + 2 �� - 2, �� ≥ 2
California . Algebra 2
i. ��( ��) = 1 3 ⋅ ��( �� - 1)
ii. ��( ��) = ��( �� - 1) - 4
iii. ��( ��) = 5 ⋅ ��( �� - 1)
iv. ��( ��) = ��( �� - 1) + �� - 1
C. iv
D. ii
Posibles soluciones
A. 1, 3, 9, 27, 81
B. 1, -1, -3, -5, -7
C. 1, 3, 7, 15, 31
D. 1, 2, 5, 26, 677
E. 1, 3, 7, 13, 21
©Accelerate Learning Inc. - Todos los derechos reservados


2 . Matemáticas . Unidad 1
PROBLEMA 5
(De Álgebra 1, Unidad 9, Lección 4).
Una secuencia tiene ��(1) = 120, ��(2) = 60
A. Determine los 2 términos siguientes si se trata de una secuencia aritmética, luego escriba una definición recursiva que coincida con la secuencia en la formae ��(1) = 120, ��( ��) = ��( �� - 1) + para �� ≥ 2
B. Determine los 2 términos siguientes si se trata de una secuencia geométrica, luego escriba una definición recursiva que coincida con la secuencia de la forma ��(1) = 120, ��( ��) = ⋅ ��( �� - 1) para �� ≥ 2
Posibles soluciones
A. 0, -60, ��( ��) = ��( �� - 1) - 60
B. 30, 15, ��( ��) = 1 2 ⋅ ��( �� - 1)
PROBLEMA 6
(De Álgebra 1, Unidad 9, Lección 2. Una hora después de la administración de un antibiótico, la población de una bacteria es) 1.000.000. Cada hora siguiente, disminuye en un factor de 1 2
A. Completa la tabla con la población de bacterias en los momentos dados.
B. ¿Las poblaciones de bacterias forman una secuencia geométrica? Explica cómo lo sabes.
Número de horas Población

Posibles soluciones
A. Completa la tabla con la población de bacterias a las horas dadas.
Número de horas Población
B. Sí. Respuesta de ejemplo: La secuencia de poblaciones comienza en 1.000.000 y hay un factor de crecimiento de . 1 2
Reflexiones:


IDEA(S) FUNDAMENTAL(ES)
• Ecuaciones para predecir y modelizar
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
A-SSE.4 Derivar la fórmula para la suma de una serie geométrica finita (cuando la razón común no es 1) y usar la fórmula para resolver problemas.
Construir
F-LE.2 F-BF.1a F-BF.2 Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en resolverlos.
MP7 Buscar y utilizar estructuras.
Estándares CA ELD
I.A.4
I.C.9
II.C.6
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predecir lo que podría ocurrir,
OBJETIVO(S)
darán sentido a los problemas y perseverarán en su resolución exploran cantidades cambiantes.
• Puedo determinar la suma de una secuencia que representa una situación.
• Calcular la suma de una secuencia geométrica simple que describa una situación sin utilizar una fórmula.
Rutinas didácticas
Charla de matemáticas
MLR8: Apoyo para el debate
Materiales necesarios
Papel en blanco
Tijeras
©Accelerate Learning Inc. - Todos los derechos reservados
Preparación necesaria
Proporcione 1 trozo de papel en blanco y 1 par de tijeras por cada 4 estudiantes para representar la situación en la actividad «Rastro de papel»

Objetivos de aprendizaje para el estudiante
• Veamos las secuencias y las sumas de sus términos.
Narrativa de la lección
El objetivo de esta lección es que los estudiantes se encuentren con varias situaciones en las que tiene sentido hallar la suma de una secuencia, definida aquí como la suma del valor de los términos de la secuencia. En este punto, el número de términos que los estudiantes deben sumar es reducido, ya que la suma se realiza a mano. En una unidad futura, los estudiantes utilizarán las identidades polinómicas para desarrollar una fórmula para sumar los primeros �� términos de cualquier secuencia geométrica.
Las actividades principales de esta lección están pensadas para ser relativamente sencillas, dando a los estudiantes la oportunidad de dar sentido a los problemas utilizando las herramientas con las que han trabajado a lo largo de esta unidad, como tablas, gráficas y ecuaciones (MP1).
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo
Calentamiento Independiente 5 min
Actividad de exploración Grupos pequeños 15 min
Actividad de exploración Grupos pequeños 15 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 5-10 min
California . Algebra 2
Descripción breve
Los estudiantes determinan las sumas de varias fracciones que no tienen denominador común.
Los estudiantes exploran las secuencias que se forman al cortar un trozo de papel en trozos iguales y distribuirlos entre diferentes números de personas.
Los estudiantes razonan sobre la secuencia formada por el copo de nieve de Koch, incluido la función que se puede utilizar para representar la secuencia y la suma de los términos.
Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de los patrones formados por figuras geométricas y la suma de los términos en una secuencia.
Usar las exploraciones de la lección, los estudiantes discuten posibles estrategias para determinar la suma de los términos en una secuencia.
Los estudiantes crean una secuencia para representar un escenario del mundo real y usan la secuencia para determinar la suma de los términos.
El componente de práctica independiente incluye 2 en la lección y 6 problemas de repaso en espiral.
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


(5 minutos)
Rutinas didácticas
Charla de matemáticas
MLR8: Apoyos para el debate
Esta es la primera actividad de charla de matemáticas del curso. Vea la sección de intr para instrucciones extendidas para facilitar esta actividad exitosamente.
El propósito de esta charla de matemáticas es obtener estrategias y entendimientos que los estudiantes tienen para sumar fracciones. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten sumar y restar fracciones.
Esta es la primera vez que los estudiantes realizan la rutina de Introducción charla de matemáticas, por lo que es importante explicar cómo funciona antes de comenzar.

INTRODUCCIÓN
Explique la rutina de charla de matemáticas: se muestra un problema a la vez. Para cada problema, los estudiantes disponen de unos minutos para pensar en silencio y hacer una señal cuando tengan una respuesta y una estrategia. El maestro selecciona a los estudiantes para que compartan diferentes estrategias para cada problema y puede hacer preguntas como: «¿Quién lo ha pensado de otra manera?». El maestro anota las explicaciones de los estudiantes para que todos las vean. Se puede pedir a los estudiantes que den más detalles sobre por qué decidieron abordar un problema de una determinada manera. Puede que no sea posible compartir todas las estrategias posibles en el tiempo limitado de que se dispone; puede que el maestro solo recoja dos o tres estrategias distintivas por problema.
Considere la posibilidad de establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con un razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen u otra señal sutil. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se apresuren al levantar la mano por toda la clase. Exponga un problema cada vez. Conceda a los estudiantes un tiempo de reflexión tranquilo para cada problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. Mantenga todos los problemas expuestos durante la charla. A continuación, debate con toda la clase.
Representación: Interiorizar la comprensión. Para apoyar la memoria de trabajo, proporciona a los estudiantes notas adhesivas o minipizarras.
Apoya la accesibilidad para: Memoria; Organización
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Evaluar mentalmente. 1 2 + 1 4 1 2 + 1 4 + 1 8 1 2 + 1 4 + 1 8 + 1 16 3 2 + 3 4 + 3 8 + 3 16
RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD
Pida a los estudiantes que compartan sus estrategias para cada problema. Anote y muestre sus respuestas para que todos puedan verlas. Para involucrar a más estudiantes en la conversación, considere preguntar:
• «¿Quién puede replantear el razonamiento de [nombre del estudiante] de una manera diferente?».
• «¿Tenía alguien la misma estrategia, pero la explicaría de manera diferente?».
• «¿Resolvió alguien el problema de una manera diferente?».
• «¿Quiere alguien agregar algo a la estrategia de [nombre del estudiante]?».
• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?».
Apoyo para estudiantes de inglés
Hablar: MLR8 Apoyos para el debate. Muestrefragmentos de frases para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «Primero, porque...» o «Noto así que...». Algunos estudiantes pueden beneficiarse de la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.
Principio(s) de diseño: Optimizar la salida (para la explicación)
(15 minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
El objetivo de esta actividad es que los estudiantes representen una situación con una secuencia en la que tenga sentido sumar los términos de la secuencia para responder a una pregunta sobre la situación. Esta situación se eligió por su naturaleza práctica para ayudar a los estudiantes a entender por qué necesitaríamos sumar términos en una secuencia. Los estudiantes continuarán con este tipo de pensamiento en la siguiente actividad, en la que trabajarán con una famosa forma matemática: el copo de nieve de Koch.
INTRODUCCIÓN
Organice a los estudiantes en grupos de 4. Puede resultar útil asignar a un estudiante para que sea «Tyler» y lleve a cabo las acciones descritas en la tarea a modo de demostración para la clase. A los estudiantes les puede resultar útil doblar y desplegar el papel primero para tener líneas de pliegue que seguir al hacer los cortes. Proporcione a los grupos papel y tijeras.
Apoyo para estudiantes con discapacidad
Representación: Acceso para la percepción. Lea en voz alta el enunciado de la tarea del estudiante. Los estudiantes que escuchen y lean a la vez la información se beneficiarán de un tiempo de procesamiento adicional.
Apoya la accesibilidad para: Lenguaje
.
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


ENUNCIADO DE TAREA
PARA EL ESTUDIANTE

RESPUESTAS POSIBLES
1. Tyler tiene un trozo de papel y lo comparte con Elena, Clare y Andre. Corta el papel para crear cuatro trozos iguales, luego entrega un trozo a cada uno de los otros y se queda con uno para él. ¿Qué fracción del trozo de papel original tiene cada persona?
2. A continuación, Tyler agarra el papel que le queda y vuelve a hacerlo. Corta el papel para crear cuatro trozos iguales, luego entrega un trozo a cada uno de los otros y se queda con uno para él. ¿Qué fracción del trozo de papel original tiene ahora cada persona?
3. Luego, Tyler agarra el papel que le queda y vuelve a hacerlo. ¿Qué fracción del papel original tiene ahora cada persona? ¿Qué ocurre después de más pasos del mismo proceso?
1. Cada uno de ellos tiene 1 4 del papel original.
2. Tyler tiene ahora 1 16 del papel original. Cada uno de los otros tiene 1 4 + 1 16 = 5 16 .
3. Tyler tiene ahora 1 64 del documento original. Los demás tienen cada uno 5 16 + 1 64 = 21 64 Ejemplo de respuesta: Tyler casi se quedará sin papel y los otros tendrán cada uno aproximadamente 1 3 del papel original.
CONCEPTOS ERRÓNEOS PREVISTOS
Haga hincapié en que Tyler regala trozos de su hoja de papel original mientras que los otros 3 estudiantes toman los trozos de Tyler. Esto ayudará a los estudiantes a reconocer que la cantidad de papel que tiene Tyler disminuye mientras que la cantidad de papel que tienen los otros estudiantes aumenta. Teniendo esto en cuenta, los estudiantes pueden entender mejor por qué sumar la secuencia de Tyler no tiene sentido mientras que sumar la secuencia que representa a los otros trozos de papel sí lo tiene.
Comience el debate y muestre la tabla que se muestra aquí para que todos la vean: Cantidad de recortes �� �� �� ��
SÍNTESIS DE LA ACTIVIDAD
Invite a los grupos a explicar de dónde salieron los valores para Tyler y del otro miembro del grupo. Destaque a los estudiantes que razonen sobre el tamaño del papel de Tyler utilizando una ecuación como ��(��) = 1 ⋅ � 1 4 � �� . Si ningún estudiante utiliza una ecuación para dar sentido al documento de Tyler, pídales que lo hagan y, tras un breve tiempo de trabajo, invite a los estudiantes a compartir sus ecuaciones. Una conexión importante para que los estudiantes hagan es que mientras que una cantidad de papel en la mano de Tyler está representada por la secuencia �� con los términos 1, 1 4 , 1 16, 1 64 la cantidad de papel en las manos de uno de los otros miembros del grupo en cada paso es la suma de los términos de la secuencia de Tyler a partir de ��(1) = 1 4 . Si el tiempo lo permite, demuestre con ayuda de la tecnología que esta suma se aproxima a 1 3 a medida que aumenta el número de pasos, y que si sigue sumando términos adicionales se acerca cada vez más a 1 3 . Esto coincide con la intuición de que cada persona acabaría sosteniendo muy cerca de 1 3 del trozo de papel original después de varias rondas de corte y distribución de papel.
Álgebra 2 . Matemáticas . Unidad 1

Apoyo para estudiantes que aprenden el idioma inglés
Hablar, representar: MLR8 Apoyos a la discusión. Dar a los estudiantes tiempo adicional para asegurarse de que todos en su grupo pueden explicar sus soluciones y las relaciones entre las cantidades representadas. Invite a los grupos a ensayar lo que dirán cuando lo compartan con toda la clase. Ensayar proporciona a los estudiantes oportunidades adicionales para hablar y aclarar su pensamiento, y mejorará la calidad de las explicaciones compartidas durante el debate con toda la clase.
Principio(s) de diseño: Optimizar la producción (para la explicación)
Esta actividad es una oportunidad para contrastar cuándo tiene y cuándo no tiene sentido sumar una secuencia. Esta tarea es relativamente sencilla en comparación con lecciones anteriores, dando a los estudiantes la oportunidad de dar sentido al problema, por ejemplo, dibujando el paso 2 u organizando los datos en una tabla (MP1).
Si lo desea, comparta con los estudiantes que esta forma es conocida en matemáticas como el copo de nieve de Koch.
Diga a los estudiantes que cierren sus libros o dispositivos. Dibuje y etiquete un triángulo equilátero como Paso 0. A su lado, dibuje y etiquete Step 1, partiendo de un triángulo equilátero y borrando el centro 1 3 de cada lado y dibujando dos segmentos adicionales que salgan de cada lado (como se muestra en el enunciado de la tarea).
INTRODUCCIÓN
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Invite a los estudiantes a describir con sus propias palabras cómo se ha dibujado el segundo triángulo y a decir cuántos lados tienen los pasos 0 y 1 .
Organice a los estudiantes en grupos de 2-4. Dé tiempo a los grupos para que trabajen y, a continuación, discuta con toda la clase .
Aquí hay una forma geométrica construida por etapas.
• La etapa 0 es un triángulo equilátero.
• Para pasar de la etapa 0 a la etapa 1, toma todas las aristas de la etapa 0 y sustituya su tercio central por un triángulo equilátero orientado hacia el exterior.
• Para ir del paso 1 al paso 2, toma cada arista del paso 1 y reemplaza su tercio medio con un triángulo equilátero hacia afuera.
• Este proceso puede continuar para crear cualquier paso del diseño.
1. Encuentra una ecuación para representar la función ��, donde ��(��) es el número de lados en el paso ��. ¿Qué es ��(2)?
2. Consideremos una función diferente ��, donde ��(��) es el número de nuevos triángulos añadidos al dibujar el paso ��. Sea ��(0) = 1. ¿Cuántos triángulos nuevos hay en los pasos 1, 2 y 3? Explica cómo lo sabes.
3. ¿Cuál es la cantidad total de triángulos utilizados en la construcción del paso 3?
©Accelerate Learning Inc. - Todos los derechos reservados


RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS
1. ��(2) = 48. Ejemplo de respuesta: Recursiva: ��(0) = 3, ��(��) = 4 ⋅ ��(�� − 1) para �� > 0, el término enésimo (n): ��(��) = 3 ⋅ 4 �� para �� ≥ 0 o equivalente. 2. Ejemplo de respuesta: La cantidad de triángulos nuevos en el paso �� es el mismo que la cantidad de lados en el paso �� − 1, porque cada segmento genera un triángulo nuevo.
SÍNTESIS DE LA ACTIVIDAD
Si los estudiantes tienen problemas para encontrar una regla para la función ��, sugiérales que dibujen el paso 2 y, a luego, creen una tabla que relacione cada paso con la cantidad de lados del copo de nieve en ese paso.
El objetivo de esta discusión es que los estudiantes compartan las diferentes formas en que representaron y calcularon los valores de ��(��) y ��(��). Comienza la discusión pidiendo a los estudiantes que expliquen cómo han encontrado los términos a sumar para hallar el número total de triángulos utilizados en la construcción del Paso 3. (Sumando los términos de ��(��) desde �� = 0 hasta �� = 3). Habla de cualquier idea cuando compara los datos de ��(��) y ��(��) y diga por qué ��(��) = ��(�� − 1)
Pida a los estudiantes que expliquen qué significaría sumar los términos en la secuencia �� desde �� = 0 hasta �� = 3 para concluir el debate? (Esta suma no representa nada significativo en esta situación, excepto quizás la cantidad total de lados que tendría que dibujar para realizar ambos pasos). Contrasta esto con encontrar la suma de los términos a través del paso 3 de ��, que representa la cantidad total de triángulos en el copo de nieve del paso 3
¿Estás preparado para más?
Supongamos que el triángulo del paso 0 tiene un área de 1 unidad cuadrada. Completa la tabla. ¿Qué patrones observas?
Ejemplo de respuesta: En cada paso sucesivo, se añade un nuevo triángulo a cada segmento del perímetro y su área es 1 9 el área del triángulo precedente. Así que en el paso 1 obtenemos 3 nuevos triángulos cada uno con área 1 9 unidad cuadrada. Después del primer paso, el área de cada triángulo disminuye en un factor de 1 9 pero el número de triángulos nuevos aumenta en un factor de 4 (cada lado del triángulo antiguo se sustituye por 4 lados nuevos).
Álgebra 2 . Matemáticas . Unidad 1
(10 minutos)
Pida a los estudiantes que consideren lo que significaría encontrar la suma de la secuencia definida por ��(0) = 3 10, ��(��) = 1 10 ⋅ ��(�� − 1) para �� ≥ 1. (La suma de los términos de ��(��) parece acercarse cada vez más a 1 3 cuantos más términos se suman). Después de un rato de trabajo en silencio, seleccione a los estudiantes para que compartan su pensamiento, anotando sus ideas para que todos las vean. Destaque en particular a cualquier estudiante que conecte de nuevo con la actividad «Rastro de papel», en la que la suma de las fracciones que tiene cada persona también parece acercarse cada vez más a 1 3 cuantas más veces recorta y reparte Tyler trozos de su hoja de papel original.
ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES
(5 minutos)
Lin pasó 80 minutos haciendo los deberes el lunes. Cada día, de martes a viernes, Lin pasó la mitad de tiempo haciendo los deberes que el día anterior. ¿Cuánto tiempo total pasó Lin haciendo los deberes, de lunes a viernes? Explica cómo lo sabes.
155 minutos. Ejemplo de respuesta: Lin pasó 155 minutos, porque
80 + 40 + 20 + 10 + 5 = 155
Resumen de la lección para el estudiante
La suma de una secuencia es la suma de sus términos.
Por ejemplo, supón que te dieron $1 el primer día, luego $2 el segundo día, luego $4 el tercer día y se duplicó cada día durante siete días. Después de hallar cada término de la sucesión, puedes hallar la suma: 1 + 2 + 4 + 8 + 16 + 32 + 64 = 127
Para estos siete días, la cantidad total de dinero es $127. En una unidad posterior, aprenderás un método para hallar la suma de una sucesión geométrica de manera más eficiente.
PROBLEMA 1
Halla la suma de la sucesión:
Posibles soluciones
Nation California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


2 . Matemáticas . Unidad 1
PROBLEMA 2
Priya camina por un pasillo largo. Recorre la mitad del camino y se detiene. Luego, camina la mitad de la distancia restante y se detiene de nuevo. Continúa deteniéndose cada vez que recorre la mitad de la distancia restante.
A. ¿Qué fracción de la longitud del pasillo habrá recorrido Priya después de comenzar y detenerse dos veces?
B. ¿Qué fracción de la longitud del pasillo habrá recorrido Priya después de comenzar y detenerse cuatro veces?
C. ¿Llegará Priya alguna vez al final del pasillo, comenzando y deteniéndose repetidamente en la mitad de la distancia restante? Explica tu razonamiento.
PROBLEMA 3
De Álgebra 1, unidad 9, lección 6.

Posibles soluciones
A. 1 2 + 1 4 = 3 4
B. 1 2 + 1 4 + 1 8 +
C. Las explicaciones varían.
Una secuencia geométrica ℎ comienza con 10, 5,... Explica cómo calcularías el valor del término 100
Posibles soluciones
Ejemplo de respuesta: Con una hoja de cálculo, pondría 10 en la celda A1 y = A1 ∗ 0,5 en la celda A2. A continuación, utilizaría la función de relleno para calcular los valores de ℎ hasta ℎ(100)
PROBLEMA 4
De la unidad 1, lección 5
He aquí un gráfico de la secuencia ��. Define �� recursivamente con notación de función.
Posibles soluciones
��(1) = 1, ��(��) = ��(�� − 1) ⋅ 2 para �� ≥ 2 o equivalente
PROBLEMA 5
De Álgebra 1, unidad 9, lección 7
Un trozo de papel desplegado tiene 0.05 mm de grosor.
A. Completa la tabla con el grosor del trozo de papel ��(��) después de doblarlo por la mitad �� veces.
B. Defina �� para el enésimo término (��)
C. ¿Cuál es un dominio razonable para la función ��? Explique cómo lo sabe.
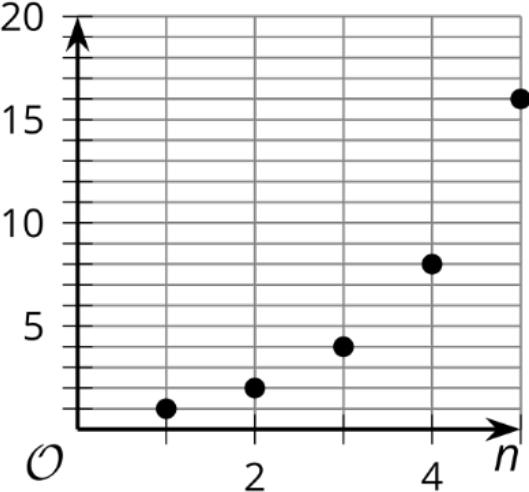
Posibles soluciones
B. ��(��) = 0,05 ⋅ 2 �� para �� ≥ 0
C. Ejemplo de respuesta: porque el papel es demasiado pequeño y demasiado grueso para doblarlo más.
PROBLEMA 6
De Álgebra 1, unidad 9, lección 7
Un trozo de papel tiene 0.05 mm de grosor.
A. Completa la tabla con el grosor del papel ��(��), en mm, después de que haya sido doblado �� veces.
B. ¿Tiene sentido ��(0.5)? Explica cómo lo sabes.

PROBLEMA 7
De Álgebra 1, unidad 9, lección 8
Una secuencia aritmética �� empieza 84, 77, . . .
A. Define �� recursivamente.
B. Defínase �� para el enésimo término (n)
PROBLEMA 8
Del Álgebra 1, unidad 9, lección 8
Aquí hay un patrón de rectángulos crecientes:
A. Describe cómo crece el rectángulo desde el paso 0 hasta el paso 2.
B. Escribe una ecuación para la secuencia ��, de modo que ��(��) sea el número de cuadrados en el paso ��
C. ¿Es �� una secuencia geométrica, una secuencia aritmética o ninguna de las dos? Explica cómo lo sabes.
Posibles soluciones
California . Algebra 2
B. No. Ejemplo de respuesta: El papel solo puede doblarse un número entero de veces.
Posibles soluciones
A. ��(0) = 84, ��(��) = ��(�� − 1) − 7 para �� ≥ 1 o equivalente.
B. ��(��) = 84 - 7�� para �� ≥ 0 o equivalente.
Posibles soluciones
A. Ejemplo de response: De un paso a otro, se añaden 3 nuevas filas y 1 columna.
B. Ejemplo de respuesta: ��(0) = 3, ��(��) = ��(�� - 1) + 3(�� + 1) + 3��, para �� ≥ 1 o ��(��) = 3(�� + 1)2 para �� ≥ 0 o equivalente.
C. Ejemplo de respuesta: �� no es geométrico ni aritmético, porque sus términos no se pueden formar multiplicando repetidamente por el mismo número, ni sumando repetidamente el mismo número.
Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)
• Ecuaciones para predecir y representar
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
A-CED.1 Crear ecuaciones e inecuaciones en una variable incluido aquellas con valor absoluto y usarlas para resolver problemas. Incluir ecuaciones que surjan de funciones lineales y cuadráticas y de funciones racionales y exponenciales sencillas.
A-REI.3.1 Resolver ecuaciones e inecuaciones de una variable en las que intervenga el valor absoluto, representar gráficamente las soluciones e interpretarlas en su contexto.
Enfoque SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP3 Construir argumentos viables y criticar el razonamiento de otros.
MP4 Representar con matemáticas.
MP7 Buscar y utilizar estructuras.
Estándares ELD de California
I.A.2
I.A.3
II.B.5
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
predecir lo que podría ocurrir, buscarán y harán uso de la estructura exploran cantidades cambiantes.
• Puedo escribir una ecuación de valor absoluto para representar un contexto del mundo real.
• Puedo resolver una ecuación de valor absoluto.
• Crear ecuaciones de valor absoluto para representar contextos del mundo real.
• Resolver ecuaciones de valor absoluto gráfica y algebraicamente.
Rutinas didácticas
Sondear a la clase
Pensar, girar y completar
MLR1: Cada vez más fuerte y más claro
MLR3: Aclarar, criticar, corregir
©Accelerate Learning Inc. - Todos los derechos reservados
Álgebra 2 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Resolvamos ecuaciones de valor absoluto.
• Creemos ecuaciones de valor absoluto para representar escenarios del mundo real.
Narrativa de la lección
Los estudiantes aplican sus conocimientos sobre el uso de gráficas para resolver ecuaciones con el fin de resolver ecuaciones de valor absoluto. Comienzan haciendo conexiones entre soluciones de ecuaciones de valor absoluto y puntos de intersección en una gráfica. A continuación, los estudiantes pasan a resolver ecuaciones de valor absoluto algebraicamente mediante la exploración de diversas estrategias y la identificación de estructuras coherentes que conducen a vías de solución equivalentes (MP1). A lo largo de la lección, los estudiantes exploran la razonabilidad de sus soluciones dentro de contextos matemáticos y del mundo real (MP4).
RESUMEN DE LA LECCIÓN
Componente de la lección

Estructura Tiempo
Calentamiento Independiente 5 min
Actividad de Exploración
En pareja 10 min
Actividad Exploratoria
En pareja 10 min
Actividad de exploración En pareja 10 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Descripción breve
Los estudiantes utilizan la gráfica de una función de valor absoluto para determinar los valores de expresiones dadas.
Los estudiantes dan sentido a la tolerancia en diferentes contextos del mundo real representados por ecuaciones de valor absoluto con valores máximos y mínimos aceptables.
Los estudiantes resuelven ecuaciones de valor absoluto tanto algebraicamente como utilizando una gráfica de la función de valor absoluto. También exploran el proceso de reescritura de ecuaciones de valor absoluto como dos ecuaciones lineales separadas.
Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de las conexiones entre la resolución de ecuaciones de valor absoluto gráfica y algebraicamente.
Los estudiantes dan sentido a varios métodos de solución algebraica para resolver ecuaciones de valor absoluto. En el proceso, aplican sus conocimientos sobre la reescritura de expresiones de valor absoluto como expresiones lineales equivalentes.
Los estudiantes comparan diferentes métodos para resolver ecuaciones de valor absoluto para determinar cuál es el más estratégico y eficiente.
Los estudiantes resuelven una ecuación de valor absoluto algebraicamente.
Práctica Independiente 5-10 min El componente de práctica independiente incluye 5 problemas de la lección y 1 problema de repaso en espiral.
Nation California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


(5 minutos)

Rutinas didácticas
Sondeo de la clase
Este calentamiento pide a los estudiantes que usen la gráfica de una función de valor absoluto para determinar los valores de X y Y Esta actividad está diseñada para hacerlos pensar acerca de encontrar soluciones usando gráficas en lugar de algebraicamente para que esas conexiones se puedan hacer a lo largo del resto de la lección.
INTRODUCCIÓN
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Dé a los estudiantes 2-3 minutos de tiempo de trabajo tranquilo para completar la actividad. Continúe con un debate con toda la clase.
La gráfica de la función absoluta y = f(x) se muestra en la cuadrícula de coordenadas.
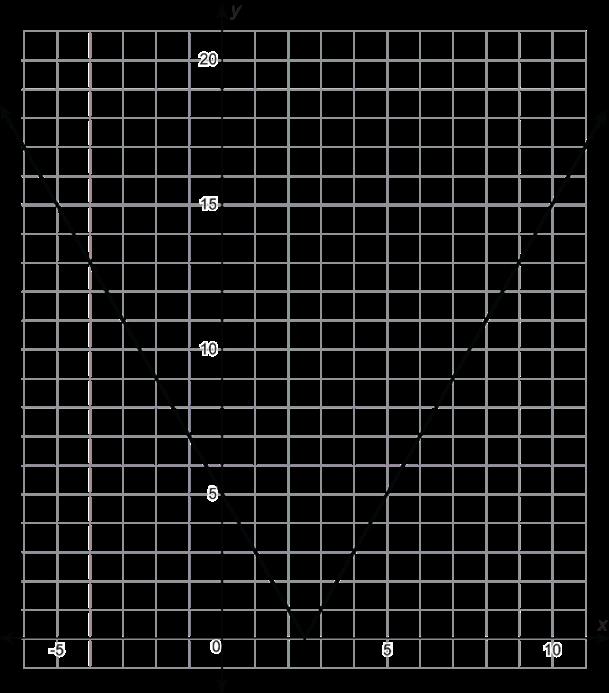
1. Determina el valor de cada expresión.
A. f(0)
B. f(-4)
C. f(7)
2. Determina el valor de x en cada ecuación.
A. f(x) = -2
B. f(x) = 7
C. f(x) = 0
1.
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
2.
A. 5
B. 13
C. 9
A. Sin solución
B. x = -1 y x = 6
C. x = 2,5
Utilice la rutina de sondear a la clase cuando revise las respuestas de los estudiantes. Muestre una pregunta cada vez y pida a los estudiantes que anoten sus respuestas en una hoja de papel o en una minipizarra. A su señal, pídales que levanten sus respuestas. Seleccione 1-2 estudiantes por pregunta para que compartan sus procesos de pensamiento y estrategias para determinar el valor de la expresión.
Álgebra 2 . Matemáticas . Unidad 1
(10 minutos)

INTRODUCCIÓN
Organice a los estudiantes en grupos de 2. Presénteles el concepto de tolerancia en la fabricación antes de dejar que los compañeros trabajen en el problema 1. Considere la posibilidad de guiar a los estudiantes en la primera parte de esta actividad con una técnica de pensamiento en voz alta para explicar su pensamiento y razonamiento a medida que trabaja con las partes del problema 1. Deje que trabajen el resto de la actividad con sus compañeros.
Apoyo para estudiantes con discapacidad
Lenguaje receptivo/expresivo: Tutores. Agrupe a los estudiantes con sus tutores compañeros previamente identificados para ayudar en la comprensión y expresión de la comprensión.
Apoya la accesibilidad para: Habilidades socioemocionales
Tolerancia describe la desviación de un componente fabricado con respecto a algún valor especificado. Un componente fabricado puede necesitar tener una longitud de 3 pulgadas, pero debido al proceso de fabricación, la longitud puede ser ligeramente más corta o ligeramente más larga. Si un componente está fuera de la tolerancia aceptada, entonces el componente no cumple las normas.
1. El gráfico representa las longitudes variables de un componente fabricado con la longitud objetivo de 3 pulgadas. Las longitudes mínima y máxima están etiquetadas.
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
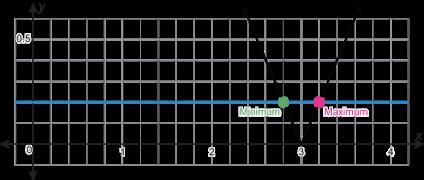
A. Determine la longitud mínima aceptable del componente.
B. Determine la longitud máxima aceptable del componente.
C. ¿Cuál es el nivel de tolerancia para este componente fabricado?
D. Complete la ecuación que representa las longitudes mínima y máxima del componente, x, como se muestra en el gráfico.
|x − 3| =
2. Un componente fabricado necesita tener una longitud de 17 pulgadas con una tolerancia de 0.5 pulgadas. Escriba una ecuación absoluta que pueda utilizarse para determinar las longitudes mínima y máxima.
3. Un restaurante indica el número de calorías de una comida que incluye filete como 645 calorías. El número real de calorías puede variar en 60 calorías en función del tamaño del filete. Escribe una ecuación de valor absoluto que pueda usarse para determinar el número mínimo y máximo de calorías de la comida.
©Accelerate Learning Inc. - Todos los derechos reservados


POSIBLES RESPUESTAS

SÍNTESIS DE LA ACTIVIDAD
1.
A. 2.8 pulgadas
B. 3.2 pulgadas
C. 0.2 pulgadas
D. |x − 3| = 0.2
2. |x - 17| = 0.5
3. |x - 645| = 60
Seleccione a los estudiantes para compartir sus respuestas y estrategias para los problemas 2-3 con la clase. Mientras comparten, considere hacer las siguientes preguntas:
• «¿Tuvo alguien la misma respuesta, pero la explicaría de manera diferente?».
• «¿Tuvo alguien una respuesta diferente que piensa que también es correcta?».
• «¿Quiere alguien agregar algo a la estrategia de _____?».
• «¿Están de acuerdo o en desacuerdo? ¿Por qué?».
Durante el debate, considere revisar el concepto de ecuaciones de valor absoluto y la idea de que las expresiones de valor absoluto representan distancias desde 0. En casos contextuales, la distancia que miden las expresiones de valor absoluto no siempre es desde 0 sino desde un valor objetivo especificado en el contexto.
(10 minutos)
Rutinas didácticas
Pensar, girar y compartir
MLR3: Aclarar, criticar, corregir
En esta actividad, los estudiantes utilizan una gráfica para resolver ecuaciones de valor absoluto más complicadas y de varios pasos. Exploran la estructura algebraica de reescribir ecuaciones de valor absoluto como dos ecuaciones lineales con soluciones diferentes. Los estudiantes también se basan en su comprensión de los gráficos de valor absoluto para determinar los valores que darían lugar a una ecuación que no tiene solución.
INTRODUCCIÓN
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organice a los estudiantes en grupos de 2. Deles un tiempo de trabajo tranquilo para responder a los problemas 1-4. Después, dé a los estudiantes otros 2-3 minutos para hablar de sus soluciones y trabajar con sus compañeros. Una vez que los compañeros estén de acuerdo con las soluciones deben continuar con el resto de la actividad.
La gráfica de la ecuación y = |−3x − 9| −5 se muestra.
1. Use la gráfica para encontrar la solución a |−3x − 9| − 5 = 10
2. Usa la gráfica para encontrar la solución a |−3x − 9| − 5 = −2.
3. Usa la gráfica para encontrar la solución de |−3x − 9| − 5 = −5.
4. Trabaja con tu compañero para escribir una ecuación que no tenga solución con la expresión |−3x − 9| − 5.
5. Resuelve -3x - 9 - 5 = 10. Muestra tus pasos.
6. Habla con tu compañero por qué |−3x − 9| − 5 = 10 tiene dos soluciones y −3x − 9 − 5 = 10 tiene una solución. Resume el debate.

Álgebra 2 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
1. x = 2 y x = -8
2. x = -2 y x = -4
3. x = -3
4. Las respuestas variarán. Cualquier ecuación |−3x − 9| − 5 = a donde a < −5 no tendrá solución.
5. x = −8
6. Las respuestas variarán. Ejemplos de respuestas pueden incluir la comparación de las soluciones de las gráficas de y = |−3x − 9| − 5 y y = −3x − 9 − 5
El propósito de esta discusión es que los estudiantes articulen diferentes escenarios que darían como resultado una ecuación de valor absoluto sin solución, con una solución o con dos soluciones. Comience seleccionando a los estudiantes previamente identificados para que compartan sus respuestas a los problemas 1-3. Destaque cómo se puede utilizar el gráfico para determinar los valores, así como el proceso para resolver las ecuaciones algebraicamente. Invite a varios estudiantes a compartir las ecuaciones que crearon para el problema 4 y solicite ideas a la clase sobre lo que las ecuaciones tienen en común (a < −5, lo que resultaría en que la expresión del valor absoluto fuera igual a un valor negativo). Por último, muestra gráficamente cómo la solución del problema 5 solo se refiere a la parte de la gráfica del valor absoluto con pendiente positiva. Esta es la razón por la que, al resolver ecuaciones de valor absoluto algebraicamente, deben plantearse y resolverse dos ecuaciones.
Apoyo para estudiantes que aprenden el idioma inglés
Hablae: MLR3 Aclarar, criticar, corregir. Presente una respuesta incorrecta para los problemas 1-3 y pida a los estudiantes que identifiquen el error y ofrezcan una vía de solución correcta. Esto les ayudará a generalizar estrategias para operaciones con funciones en escenarios del mundo real.
Principio(s) de Diseño: Optimizar el resultado (para la generalización); aximizar la metaconciencia ¿Estás preparado para más?
1. ¿Para qué valores de x es |x| = 8?
2. ¿Cómo crees que podría reescribirse la ecuación |x| = 8 para determinar los valores de x algebraicamente?
3. y = |−2x − 7| y y = 5
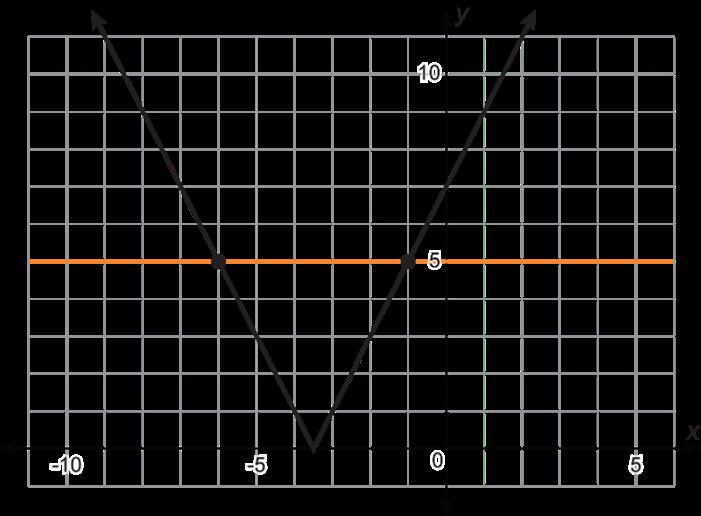
Las gráficas muestran que |−2x − 7| = 5 tiene dos soluciones, x = −6 y x = −1
La solución de la ecuación−2x − 7 = 5 is x = −6 Determine algebraicamente cómo encontrar la otra solución de |−2x − 7| = 5
California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


Posibles respuestas
1. x = 8 y x = -8
2. x = 8 y -x = 8 3. -2x - 7 = -5 x = -1
minutos)

Rutinas didácticas
MLR1: Cada vez más fuerte y más claro
En esta actividad, los estudiantes resuelven ecuaciones de valor absoluto de varios pasos con un coeficiente inicial delante de la expresión de valor absoluto o delante de x. Exploran varias formas de resolver la misma ecuación de valor absoluto para identificar estructuras que sean aplicables y matemáticamente correctas al reescribir ecuaciones de valor absoluto en los trozos positivo y negativo (MP7). Los estudiantes evalúan el trabajo de otros estudiantes para identificar posibles errores en las vías de solución y hacer sugerencias para enfoques más eficientes o consistentes para resolver ecuaciones de valor absoluto (MP3).
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organizar a los estudiantes en grupos de 2. Darles 2 minutos para responder al problema 1 con sus compañeros. Escuche las conversaciones para destacar el razonamiento de los estudiantes y compartirlo con la clase durante un breve debate. Concéntrese en las estrategias que abordan el problema con métodos gráficos y algebraicos. Guíe a los estudiantes a través del método de solución del problema 2 antes de dejarles trabajar en colaboración en el resto de la actividad.
1. Las dos soluciones de la ecuación |−2x + 11| = 29 son x = −9 y x = 20. Escribe las dos ecuaciones que se pueden utilizar para determinar las soluciones.
2. Resuelve |3x + 23| = 5.
3. Las soluciones de la ecuación |−3x − 9| − 5 = 10 son x = −7 y x = 2. En la tabla se muestran los trabajos parciales de dos estudiantes.
Charlotte
|−3x − 9| − 5 = 10
−3x − 9 − 5 = 10 y
−3x − 9 + 5 = −10
−3x − 14 = 10 y
−3x − 4 = 10
Dominic
|−3x − 9| − 5 = 10
|−3x − 9| = 15
−3x − 9 = 15 y
−3x − 9 = −15
A. ¿El trabajo de qué estudiante conducirá a las soluciones correctas?
B. Comenta con tu compañero el error en el trabajo del otro estudiante. Escribe una breve explicación que pueda ayudar a otros estudiantes a evitar este error.
4. Resuelve |5x − 20| + 18 = 83
5. Habla con tu compañero si las soluciones de |5x − 20| + 18 = 83 son las mismas que las soluciones de 5|x − 4| + 18 = 83
6. Resuelve |−2x + 12| − 19 = −5
7. Habla con tu compañero si las soluciones de |−2x + 12| − 19 = −5 son las mismas que las soluciones de −2|x − 6| −19 = − 5. Resume el debate.
8. Usa tus respuestas a los problemas 5 y 7 para explicar por qué distribuir un valor negativo a la expresión dentro del valor absoluto tiene un efecto diferente que distribuir un valor positivo a la expresión dentro del valor absoluto.
RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD
Álgebra 2 . Matemáticas . Unidad 1
1. −2x + 11 = 29 y -2x + 11 = −29 (o 2x − 11 = 29)
2. x = −6 y x = −9.3
3. A. Dominic
B. Las respuestas variarán. Algunos ejemplos de respuestas pueden ser los siguientes Al resolver ecuaciones de valor absoluto, una de las ecuaciones solución debe incluir el negativo de todos los términos que no sean la expresión dentro del valor absoluto.
4. x = 17 y x =−9
5. Ejemplo de respuesta del estudiante: Ambas ecuaciones tienen las mismas soluciones de x = 17 y x = −9
6. x = −1 y x = 13
7. Respuesta de muestra del estudiante: Las dos ecuaciones no tienen las mismas soluciones.
8. Ejemplo de respuesta del estudiante: Al distribuir el negativo dentro de la expresión del valor absoluto, su valor cambia. Esto no ocurre con un valor positivo.
Invite a los estudiantes a compartir sus respuestas a los problemas 2-6. Anímelos a hacerse preguntas y a cuestionar las estrategias de los demás. El objetivo de la discusión debe ser que los estudiantes busquen una estructura matemática en la resolución de ecuaciones de valor absoluto de varios pasos. Al discutir las soluciones de los problemas 7 y 8, considere la posibilidad de mostrar las gráficas de las ecuaciones. Grafique y = −2|x − 6| − 19 y y = |−2x + 12| − 19 y pregunte a los estudiantes qué observan y qué se preguntan. Deberían ver que las dos gráficas no son equivalentes. Los estudiantes encontrarán sentido a esta diferencia en unidades futuras, cuando exploren cómo las diferentes transformaciones afectan a las gráficas de las funciones madre. En esta discusión, concéntrese en la idea de que −2(x 6) = −2x + 12 (los componentes positivos de la ecuación,) pero −2(x + 6) ≠ 2x − 12 (los componentes negativos de la ecuación).
Escribir, escuchar, conversar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para ayudar a los estudiantes a mejorar sus respuestas escritas para los problemas 5, 7 y 8. Deles tiempo para reunirse con 2-3 compañeros para compartir y recibir comentarios sobre sus respuestas. Invite a los estudiantes a revisar o perfeccionar sus respuestas escritas con base en los comentarios de sus compañeros. Esto les ayudará a justificar por qué los problemas 5 y 7 no tienen la misma vía de solución.
Principio(s) de diseño: Optimizar el resultado (para la justificación); cultivar la conversación
(10 minutos)
Las ecuaciones de valor absoluto pueden no tener solución, tener una solución o tener dos soluciones. Un ejemplo de ecuación de valor absoluto que no tiene solución es |x + 6| = −19 porque la distancia no puede ser un valor negativo.
Explique a los estudiantes que existen dos métodos principales para resolver ecuaciones de valor absoluto. Muestre ambos métodos y dé a los estudiantes 2-3 minutos para que comparen los dos métodos y expliquen a sus compañeros por qué son matemáticamente equivalentes.
California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados



Método A
2 |11− 4x| −19 = 51
2 |11 − 4x| −19 + 19 = 51 + 19
2 |11 − 4x| =70
2 |11 − 4x| 2 = 70 2 |11 − 4x| = 35
11 − 4x = 35 y 11 − 4x = −35
11 − 4x − 11 = 35 − 11 y
11 − 4x − 11 = −35 − 11
−4x = 24 y −4x = −46 x = −6 y x = 11.5
Método B
2 |11 − 4x| −19 = 51
2(11 − 4x) −19 = 51 y 2(−11 + 4x) −19 = 51
22 − 8x−- 19 = 51 y -22 + 8x 5
-8x + 3 = 51 y 8xm − 41 = 51
−8x + 3 − 3 = 51 − 3 y 8x − 41 + 41 = 51 + 41
−8x = 48 y 8x = 92 x = −6 y x = 11.5
Invite a los estudiantes a compartir sus observaciones y comparaciones de los dos métodos. Si el tiempo lo permite, pida a los estudiantes que utilicen ambos métodos para resolver algunas de las ecuaciones de las actividades de la lección y comparen cuál les resulta más intuitivo o eficiente.
Un método, mostrado en la tabla como método A, aísla la expresión del valor absoluto y luego establece la expresión del valor absoluto igual al valor positivo y negativo de la expresión del otro lado. El método B escribe la expresión dentro del valor absoluto como una ecuación y escribe el opuesto de todos los términos de la expresión dentro del valor absoluto como la otra ecuación. El método A aplica la comprensión de que el valor de x en |x| = 8 podría ser ±8, mientras que el método B aplica la comprensión de que la variable x podría ser ±x
Como descubrieron los estudiantes en las actividades de la lección, el método B a veces puede dar lugar a respuestas incorrectas cuando el coeficiente del valor absoluto es negativo. Aunque el método B es viable para muchos casos, puede dar lugar a más errores que el método A.
ABSOLUTO (5 minutos)
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE Resuelva |−10x − 19| + 24 = 193 para x.
RESPUESTAS POSIBLES x = −18.8 y x = 15
Resolver una ecuación de valor absoluto significa determinar la distancia desde un punto hasta un valor objetivo. Esta es la razón por la que, en muchos casos, hay dos soluciones para una ecuación de valor absoluto. La gráfica de una ecuación de valor absoluto consiste en dos rectas, una con pendiente negativa y otra con pendiente positiva. Dado que la distancia es siempre positiva, es posible determinar dos lugares donde la distancia desde un valor x es la misma.
La ecuación |x| = 5 esencialmente pide los valores x en la gráfica que tienen una distancia horizontal de 5 unidades desde el valor x de 0, que se encuentra en el vértice. El gráfico muestra una distancia de 5 desde 0 al valor x de -5 y al valor x de 5
Álgebra 2 . Matemáticas . Unidad 1
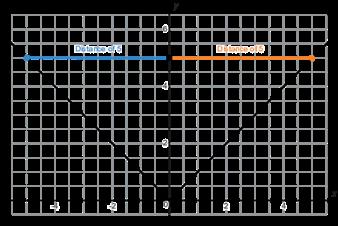
La ecuación |x − 2| =3 esencialmente pide los valores x en la gráfica que tienen una distancia horizontal de 3 unidades del valor x de 2
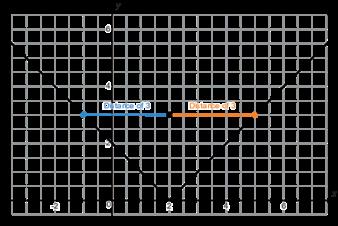
Como la distancia se expresa como un valor positivo, la expresión dentro del valor absoluto puede ser igual al valor positivo y al valor negativo. Como se ilustra en las gráficas, una de las soluciones está en la recta que tiene pendiente negativa y una de las soluciones está en la recta con pendiente positiva.
Las ecuaciones de valor absoluto tienen tres tipos de soluciones: ninguna solución, una solución o dos soluciones.
• La ecuación |x + 6| = 2 tiene dos soluciones. La distancia entre x y −6 es 2 unidades para dos valores diferentes, cuando x = −8 y cuando x = −4
• La ecuación |x + 6| = 0 tiene una solución. La distancia entre x y −6 es 0 unidades para un valor, cuando x = −6
• La ecuación |x + 6| = −19 no tiene solución. La distancia entre x y −6 no puede ser un valor negativo. Por lo tanto, esta ecuación no tiene solución.
PROBLEMA 1
Una pelota de béisbol de la Nippon Professional Baseball (NPB) es ligeramente más pequeña que la utilizada en las Grandes Ligas de Béisbol. La pelota de béisbol para la NPB tiene una circunferencia de 9 pulgadas con una tolerancia de 0.125 pulgadas. Escribe una ecuación absoluta que pueda usarse para determinar las circunferencias mínima y máxima.
Solución posible
|x − 9| = 0.125
Math
Nation California . Algebra 2

©Accelerate Learning Inc. - Todos los derechos reservados


Álgebra 2 . Matemáticas . Unidad 1
PROBLEMA 2
Según una encuesta, el64 % de los habitantes de la ciudad estaban en contra de la construcción de una nueva autopista. El servicio de sondeos declaró que esta encuesta tenía una precisión de 3 %. Escriba una ecuación de valor absoluto que pueda usarse para encontrar los porcentajes mínimo y máximo de residentes de la ciudad que están en contra de la construcción de una nueva autopista.
Solución posible
|x − 64| = 3
PROBLEMA 3
Seleccione todas las ecuaciones que darían como resultado una de las soluciones de |3x − 7| = 12
3x + 7 = 12
3x − 7 = 12
3x + 7 = −12
-3x + 7 = 12
3x − 7 = −12
-3x + 7 = −12
PROBLEMA 4
Resuelva |−4x + 13| −19 = 30 para x
PROBLEMA 5
Determine las soluciones de -7|2x − 3| − 1 = −64
PROBLEMA 6
(De la unidad 1, lección 2)
Encuentre la tasa de cambio promedio de la función f(x) = x2 − 6 sobre el intervalo [−2, −1]
Reflexiones:

Learning Inc. - Todos los derechos reservados
Solución posible
3x + 7 = 12
3x − 7 = 12
3x + 7 = −12
-3x + 7 = 12
3x - 7 = −12
-3x + 7 = −12
Solución posible
x = 15,5 y x = −9
Solución posible
x = −3 y x = 6
Solución posible
−3


IDEA(S) FUNDAMENTAL(ES)
• Ecuaciones para predecir y representar
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
A-REI.3.1 Resolver ecuaciones e desigualdades de una variable que involucren valor absoluto, graficar las soluciones e interpretándolas en contexto.
A-CED.1 Crear ecuaciones e desigualdades en una variable incluyendo aquellas con valor absoluto y usarlas para resolver problemas. Incluir ecuaciones que surjan de funciones lineales y cuadráticas, y funciones racionales y exponenciales simples.
Enfocar SMPs
MP1 Dar sentido a los problemas y perseverar en su resolución.
MP4 Representar con matemáticas.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.1
I.B.7
II.B.5
RESOLVER DESIGUALDADES DE VALOR ABSOLUTO EN CONTEXTO DEL MUNDO REAL
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
comprender al mundo y prededir lo que podría ocurrir,
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
representarán con matemáticas exploran cantidades cambiantes.
• Puedo resolver desigualdades de valor absoluto de una variable en un contexto del mundo real.
• Puedo representar soluciones a desigualdades de valor absoluto de una variable algebraica y gráficamente.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Crear y resolver desigualdades de valor absoluto de una variable en contextos del mundo real.
• Graficar e interpretar soluciones de desigualdades de valor absoluto de una variable en escenarios del mundo real.
Rutinas didácticas
Pensar, girar y compartir
MLR2: Recopilar y mostrar
MLR6: Tres lecturas
Anticipar, supervisar, seleccionar, secuenciar, conectar
©Accelerate Learning Inc. - Todos los derechos reservados
Objetivos de aprendizaje para el estudiante
• Creemos y resolvamos desigualdades de valor absoluto de una variable en escenarios del mundo real.
Narrativa de la lección
Los estudiantes trabajan con desigualdades de valor absoluto representando e interpretando contextos del mundo real que tratan con restricciones de una variable (MP4, MP1). Esto construye un puente entre las soluciones algebraicas con las que trabajaron en el pasado y su trabajo futuro con el margen de error y el dominio y rango de funciones periódicas (MP7).
RESUMEN DE LA LECCIÓN
Componente de la lección Estructura Tiempo Descripción breve
Calentamiento En parejas 5 min
Actividad de exploración Grupos pequeños 15 min
Actividad de Exploración Independiente 15 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min

Nation California . Algebra 2
Los estudiantes comparan valores en un escenario del mundo real con una desigualdad compuesta.
Los estudiantes resuelven, grafican e interpretan soluciones a desigualdades de valor absoluto de una variable qu emuestran escenarios del mundo real.
Los estudiantes crean, resuelven e interpretan soluciones a desigualdades de valor absoluto en contextos del mundo real.
Los estudiantes debaten las estrategias que utilizaron para crear desigualdades de valor absoluto y cómo interpretar las soluciones a las desigualdades en diferentes contextos.
Los estudiantes determinan e interpretan la solución de una desigualdad de valor absoluto de una variable en un contexto del mundo real.
El componente de práctica independiente incluye 3 problemas de la lección y 2 problemas de repaso en espiral.
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


Rutinas didácticas
Pensar, girar y compartir
INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Asigne a los estudiantes grupos de 2. Dé 1 minuto (min) de tiempo de trabajo en silencio y luego un minuto adicional para discutir sus soluciones con sus compañeros.
Olivia planea pintar su dormitorio. Calcula que necesitará entre 2 y 3 galones (gal) de pintura para cubrir todas las paredes de su dormitorio. La tabla muestra el precio por galón de los diferentes tipos de pintura que Olivia compara.
Tipo de Pintura Coste por galón Coste por 2 galón Coste por 3 galón
Plana
RESPUESTAS POSIBLES
SÍNTESIS DE LA ACTIVIDAD
Escriba una desigualdad compuesta para representar cuánto dinero, ��, Olivia debe presupuestar para este proyecto.
Las respuestas variarán. Cualquier respuesta en la que 49.90 < �� < 116.85 sea aceptable.
Invite a varios grupos a compartir sus respuestas. Algunos grupos pueden tener un rango de valores ligeramente diferente al de otros. Anima a los estudiantes a debatir por qué ha ocurrido esto y si las desigualdades compuestas que han creado siguen cumpliendo los requisitos del problema.
REAL (15 minutos)
Rutinas didácticas
MLR2: Recopilar y mostrar
Los estudiantes resuelven problemas del mundo real y los representan con desigualdades de valor absoluto. A través de esta exploración, construyen una comprensión del valor absoluto como un rango aceptable en un escenario específico.
INICIO

Álgebra 2 . Matemáticas . Unidad 1
Organice a los estudiantes en grupos de 2-3. Muestre la introducción y, a continuación, dé a los estudiantes 1 minutos de tiempo de reflexión en silencio para responder al problema 1. Formule las siguientes preguntas antes de invitar a los estudiantes a compartir sus respuestas:
• «¿Cuál es el tiempo más lento del equipo?». (22.35 − 3.61 = 18.74)
• «¿Cuál es el tiempo más rápido para el equipo?». (22,35 + 3,61 = 25.96)
• «¿Cómo se pueden representar algebraicamente estos tiempos? (18.74 ≤ �� ≤ 25.96)
• «¿Cómo se pueden representar gráficamente estos tiempos?« Dé a los estudiantes 5-7 minutos de tiempo de trabajo en grupo para completar la actividad.
Apoyo para estudiantes que aprenden el idioma inglés
Conversar: MLR2 Recopilar y mostrar. Escuche y registre el lenguaje que utilizan los estudiantes para describir desigualdades de valor absoluto. Registre el lenguaje informal de los estudiantes junto con los términos matemáticos (es mayor que, es menor que, restricción, límite y entre), despliegue y actualícela a lo largo de la lección. Recuerde a los estudiantes que tomen prestado el lenguaje desplegado cuando lo necesiten. De este modo, dispondrán de un recurso al que recurrir durante los debates en pequeños grupos y en grupo.
Principio(s) de diseño: Maximizar la metaconciencia; apoyar la creación de sentido
Apoyo para estudiantes con discapacidad
Representación: Acceso para la percepción. Proporcione un punto de entrada visual a los estudiantes graficando los números de la tabla en una nueva recta numérica. En concreto, utilice el color para demostrar qué valores se encuentran dentro del intervalo de 3.61 minutos de la media. Anime a los estudiantes a trazar los tiempos más lentos y más rápidos.
Los miembros del equipo de campo a través de la escuela se están preparando para correr una carrera de 5k, que es aproximadamente 3.1 millas (mi). El tiempo medio del equipo es 22.35 minutos (min) Los tiempos más rápido y más lento variaron de la media en 3.61 min.
1. Con base en la información dada, ¿cuál es el tiempo de finalización, en minutos, para el equipo que no es probable?
2. Habla con tu compañero acerca de si es posible que un miembro del equipo tuviera un tiempo de 26 minutos. Resume la conversación.
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
3. Trabaja con su compañero para mostrar en la recta numérica todos los tiempos posibles que los miembros del equipo tardaron en completar el 5k. El tiempo promedio de 22.35 ya se muestra en la recta numérica.
Los tiempos sombreados muestran las distancias posibles con respecto al tiempo promedio.
En el contexto del equipo de campo a través, la distancia no se mide desde 0. Más bien, se mide desde el tiempo medio de 22.35 minutos. Si �� es la distancia desde el tiempo promedio, entonces | �� − 22.35| puede representar la distancia en una recta numérica que �� está desde 22.35 minutos.
©Accelerate Learning Inc. - Todos los derechos reservados


2 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN
1. Completa la tabla para determinar si el valor �� dado está dentro del rango de 3.61 minutosdel promedio. �� |x − 22.35| ¿Está dentro de 3.61 minutos del promedio?
2. Resuelve la desigualdad |x − 22.35| ≤ 3.61 3. Grafica el conjunto solución en la recta numérica.
4. Compara la gráfica del conjunto solución de | �� − 22.35| ≤ 3.61 con la gráfica del problema 3. Resuma sus observaciones.
1. Las respuestas variarán: cualquier valor superior a 25.96 min. o inferior a 18.74 min.
2. Ejemplo de respuesta: No. El tiempo más lento varió de la media en 3.61 minutos, por lo que el tiempo más lento fue 22.35 + 3.61 = 25.96 minutos, que es inferior a 26 minutos.
3. 4.
POSIBLES RESPUESTAS
|x − 22.35| ¿Está dentro de 3.61 minutos del promedio?
5. 18,74 ≤ �� ≤ 25,96 6. 7. Las respuestas variarán. Ejemplo de respuesta: Los dos gráficos son iguales. Ambos muestran los tiempos posibles para el equipo.
SÍNTESIS DE LA ACTIVIDAD

Habla de un problema a la vez. Pida a los estudiantes que compartan sus respuestas y razonamientos y que registren y muestren sus explicaciones. Para involucrar a más estudiantes en la conversación, considere hacer estas preguntas:
• «¿Quién puede replantear el razonamiento de de una manera diferente?».
• «¿Quiere alguien añadir algo a la estrategia de ?».
• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?».
Facilite un debate para ayudar a los estudiantes a establecer conexiones entre el escenario del mundo real y la desigualdad de valor absoluto utilizada para representarlo. Use las respuestas compartidas del problema 7 para pedir a los estudiantes que expliquen cómo la desigualdad | �� − 22.25| ≤ 3.61 representa el escenario dado.
(15 minutos)
Rutinas didácticas
MLR6: Tres lecturas
Anticipar, supervisar, seleccionar, secuenciar, conectar
Los estudiantes crean y resuelven desigualdades de valor absoluto presentadas en diversos contextos del mundo real (MP4). Hablan de varias estrategias para crear y resolver las desigualdades e interpretan las soluciones en contexto.
Dé a los estudiantes 1 minuto de tiempo de silencio para leer el escenario del problema 1. Invite a varios voluntarios a generar ideas sobre las diferentes desigualdades posibles que se pueden utilizar para representar el escenario. Considere la posibilidad de crear una tabla de valores para mostrar a los estudiantes cómo cambian los valores en el problema a medida que �� aumenta o disminuye desde el objetivo de 96. Guíeles sobre cómo crear una desigualdad de valor absoluto para representar el escenario y, a continuación, deles 1-2 minutos para resolverlo. Use estrategias de pensamiento en voz alta, muestre cómo resolver la desigualdad, escriba la solución e interprete la solución en el contexto dado.
INTRODUCCIÓN
Dé a los estudiantes 2-3 minutos de tiempo de trabajo tranquilo para intentar el problema 2 por su cuenta. Supervise su trabajo y sus procesos de pensamiento para destacarlos durante la sesión informativa. Identifique a los estudiantes que crean la desigualdad de alguna de las siguientes maneras para discutir durante la síntesis de la actividad:
• Estudiantes que escriben una desigualdad sin valor absoluto: �� − 6 < 0.07
• Estudiantes que escriben una desigualdad compuesta: −0.07 < �� − 6 < 0.07
• Estudiantes que invierten los valores en la desigualdad: | �� − 0.07| < 6
• Estudiantes que escriben la desigualdad en un orden diferente: 6 <
Apoyo para estudiantes que aprenden el idioma inglés
Leer: MLR6 Tres lecturas. Utilice esta rutina para apoyar la comprensión lectora de cada problema. Utilice la primera lectura para orientar a los estudiantes sobre la situación, pidiéndoles que describan de qué trata la situación sin utilizar números (ahorrar dinero en una cuenta cada mes). Utilice la segunda lectura para identificar cantidades y relaciones, preguntando a los estudiantes qué se puede contar o medir sin centrarse en los valores (el objetivo de Imogene de tener cierta cantidad en su cuenta y ahorrar dentro de un intervalo). Después de la tercera lectura, pida a los estudiantes que generen ideas sobre posibles estrategias para responder a esta pregunta: «¿Cuál es la cantidad típica de dinero que Imogene ahorra en su cuenta cada mes?». Esto ayuda a los estudiantes a conectar el lenguaje del problema de palabras con el razonamiento necesario para resolver el problema, manteniendo al mismo tiempo la exigencia cognitiva de la tarea.
Principio de diseño: Apoyar la creación de sentido
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES
1. Imogene se fijó el objetivo personal de ahorrar $96 al mes. Cada mes, ella ha promediado dentro de $8.65 de su meta.
A. Crea una desigualdad que pueda usarse para representar la cantidad de los ahorros mensuales de Imogene, ��.
B. Resuelve la desigualdad.
C. Interpreta la solución de la desigualdad en su contexto
2. La anchura de una matrícula debe ser 6 pulgadas (in). La tolerancia de fabricación está dentro de 0.07 pulgadas.
A. Crea una desigualdad que pueda usarse para representar la anchura aceptable, ��, de una matrícula.
B. Resuelve la desigualdad.
C. Interprete la solución de la desigualdad en su contexto.
1.
2.
CONCEPTOS ERRÓNEOS PREVISTOS
SÍNTESIS DE LA ACTIVIDAD
A. | �� − 96| ≤ 8.65
B. 87.35 ≤ �� ≤ 104.65
C. Los ahorros de Imogene están entre $87.35 y 104.65 $ al mes.
A. | �� − 6| ≤ 0.07
B. 5.93 ≤ �� ≤ 6.07
C. La anchura aceptable de la matrícula está entre 5.93 y 6.07 in.
Los estudiantes pueden resolver correctamente la desigualdad del valor absoluto, pero escribir el intervalo solución sin incluir los puntos extremos. Anímeles a leer para dar sentido al contexto y a la inecuación dada y a verificar si los puntos extremos deben incluirse en estos escenarios.
Comience a discutir el problema 2A invitando a los estudiantes preseleccionados a explicar su razonamiento para crear su desigualdad en 2A. Ayude a los estudiantes a hacer conexiones entre la desigualdad y el escenario con algunas de las siguientes preguntas guía:
• «¿Qué representa el 6 en la desigualdad?». (La anchura objetivo de la matrícula).
• «¿Qué representa el 0.07 en la desigualdad?». (La tolerancia de fabricación).
• «¿Por qué se utiliza el símbolo de comparación ≤?». (Porque la diferencia aceptable entre el blanco y la anchura de la matrícula tiene que ser menor o igual que 0.07).
• «¿Por qué la desigualdad es un valor absoluto en lugar de simplemente �� − 6 ≤ 0.07?». (Porque la matrícula puede ser más larga que 6 in o más corta que 6 in y seguir siendo aceptable)
Invite a 2-3 estudiantes a compartir sus respuestas a los problemas 2B y 2C. Aproveche esta oportunidad para abordar cualquier concepto algebraico erróneo que pueda surgir en el proceso de resolución. Si el tiempo lo permite, considere la posibilidad de mostrar el conjunto de soluciones en una recta numérica para representar todas las soluciones posibles.
(5 minutos)
Los estudiantes profundizaron en la resolución de desigualdades de valor absoluto aplicando su trabajo a escenarios del mundo real. Dieron sentido a las cantidades de las desigualdades e interpretaron las soluciones en los contextos dados. Consulta el resumen de la lección del estudiante para ver ejemplos adicionales de desigualdades de valor absoluto en contextos reales. Use las siguientes preguntas guía para resumir la lección:
• «¿Cómo pueden usarse las desigualdades de valor absoluto para resolver problemas del mundo real?».
• «¿Cómo pueden representarse los problemas del mundo real con desigualdades de valor absoluto?».
• «¿Cómo representas las soluciones de las desigualdades de valor absoluto gráfica y algebraicamente?».
Álgebra 2 . Matemáticas . Unidad 1
ENUNCIADO DE TAREA PARA EL ESTUDIANTE

minutos)
1. El peso objetivo de una moneda de cinco centavos es 0.176 onzas (oz). Para comprobar que hay 40 monedas de cinco centavos en un rollo, el banco pesa el rollo. El envoltorio pesa 0.05 oz. El modelo permite un error de 0.015 oz con una desigualdad: | �� − (40 ⋅ 0.176 + 0.05)| ≤ 0.015.
A. Resuelve la desigualdad de valor absoluto.
B. Interpreta la solución de la desigualdad.
1.
RESPUESTAS POSIBLES
A. 7.075 ≤ �� ≤ 7.105
B. El banco aceptará un rollo de monedas de cinco centavos que pese entre 7.075 y 7.105 oz.
Resolver desigualdades de valor absoluto da como resultado un rango de valores aceptables que se consideran soluciones. A menudo, los contextos del mundo real implican límites o restricciones, como el peso máximo de las maletas al volar, la cantidad máxima de datos utilizados en un plan de telefonía celular o la cantidad mínima de un ingrediente activo en un medicamento. A menudo, en la fabricación o la farmacología, hay un rango de resultados aceptables que se crean utilizando una desigualdad de valor absoluto.
Por ejemplo, en una encuesta para unas próximas elecciones, 38 % de los votantes probables dijeron que planeaban votar por el candidato A. Esta encuesta tiene un margen de error de ±3 %. La desigualdad | �� − 38| ≤ 3 se puede usar para determinar el rango de votantes que probablemente votarán al candidato A.Con la desigualdad, se puede decir que entre 35 % y 41 % de los votantes probables planean votar al candidato A con base en esta encuesta.
PROBLEMA 1
Zahara ensaya para las pruebas de la banda. Para prepararse lo mejor posible, dedica una media de 56 minutos cada día a tocar la flauta. Cada uno de sus tiempos de práctica diarios está dentro de 14 minutos de su media.
A. Crea una desigualdad que pueda usarse para representar el número de minutos, ��, que Zahara practica cada día.
B. Resuelve la desigualdad.
C. Grafica la solución en la recta numérica.
Soluciones posibles
A. | �� − 56| ≤ 14
B. 42 ≤ �� ≤ 70
C.
Nation California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


2 . Matemáticas . Unidad 1
PROBLEMA 2
A Camden le gusta hacer surf. Durante el invierno, alcanzó varias olas con una altura media de 8.1 pies (ft). Todas las olas que surfeó estaban dentro de 3.3 pies de su promedio. La desigualdad |h − 8.1| ≤ 3.3 puede usarse para representar la altura de las olas que surfeó Camden.
Resuelve la desigualdad e interpreta la solución en su contexto.
Soluciones posibles

4.8 ≤ h ≤ 11.4
Ejemplo de interpretación: La altura de las olas osciló entre 4.8 pies y 11.4 pies.
PROBLEMA 3
A Jax le encanta jugar al fútbol. Juega en el equipo de su instituto y promedia 1.2 puntos por partido. Sus partidos con más puntos y con menos puntos estuvieron dentro de 0.45 puntos de su promedio.
A. Crea una desigualdad que pueda usarse para determinar el rango de puntos por partido de Jax, ��
B. Resuelve la desigualdad.
C. Grafique la solución en la recta numérica.
Soluciones posibles
A. | �� − 1.2| ≤ 0.45
B. 0.75 ≤ �� ≤ 1.65
C.
PROBLEMA 4
(De Álgebra 1, unidad 5, lección 9)
La gráfica muestra el número de miligramos (mg) de una sustancia química en el cuerpo d días después de que se midió por primera vez.
A. Explique qué significa el punto (1, 2.5) en esta situación.
B. Marque el punto que representa la cantidad de medicamento que queda en el cuerpo después de 8 horas.
Soluciones posibles
A. Ejemplo de respuesta: Quedaban 2.5 mg de medicamento después de 1 día.
B. Un punto en ( 1 3 , 10)
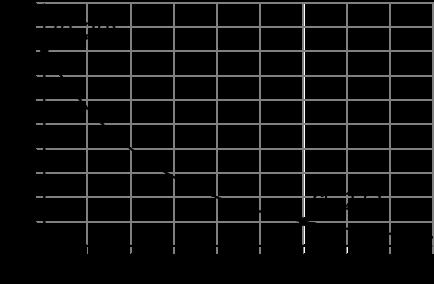

(De Álgebra 1, unidad 5,lLección 5)
Encuentra cada exponente que falta.
A. 10? = 100
B. 10? = 0.01
C. ( 1 10 )? = 1 1,000
D. 2? = 1 2
E. ( 1 2 )? = 2
Soluciones posibles
A. 2
B. −2
C. 3
D. −1
E. −1
Reflexiones:
Math Nation California . Algebra 2 ©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1 98

IDEA(S) FUNDAMENTAL(ES))
• Representar con funciones
ALINEACIÓN
Abordar
Alineación de estándares y principios de California
A-CED.3 Representar restricciones mediante ecuaciones o desigualdades, y mediante sistemas de ecuaciones y/o desigualdades, e interpretar soluciones como opciones viables o no viables en un contexto representado.
F-IF.5 Relacionar el dominio de una función con su gráfica y, en su caso, con la relación cuantitativa que describe.
Enfocar SMPs
MP2 Razonar abstracta y cuantitativamente.
MP4 Representar con matemáticas.
MP6 Atender a la precisión.
MP7 Buscar y hacer uso de la estructura.
Estándares ELD de California
I.A.3
I.B.8
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para...
comprender al mundo
(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
razonarán abstracta y cuantitativamente
analizan los datos y exploran cantidades cambiantes.
• Puedo representar soluciones de sistemas de desigualdades en un plano de coordenadas.
• Puedo identificar restricciones sobre variables en un contexto representado.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Identificar y representar soluciones de sistemas de desigualdades.
• Utilizar e interpretar restricciones en modelos en contextos del mundo real.
PREPARACIÓN DE LA LECCIÓN
Rutinas didácticas
MLR7: Comparar y conectar
MLR8: Apoyos para el debate
©Accelerate Learning Inc. - Todos los derechos reservados
Objetivos de aprendizaje para el estudiante
• Determinemos e interpretemos restricciones en situaciones del mundo real.
• Determinemos soluciones de sistemas de desigualdades.
Narrativa de la lección
Los estudiantes aplican su trabajo previo con desigualdades de dos variables para explorar restricciones en diferentes tipos de funciones en contextos matemáticos y del mundo real. Razonan de forma abstracta y cuantitativa utilizando gráficos, ecuaciones y descripciones verbales de ecuaciones edesigualdades con restricciones para dar sentido a las soluciones y valores que son viables en los escenarios dados (MP2). Los estudiantes exploran modelos utilizando diferentes representaciones para explicar qué tipos de valores son apropiados para el dominio y el rango de las diferentes funciones (MP4).
RESUMEN DE LA LECCIÓN
Componente de la lección

Estructura Tiempo
Calentamiento En pareja 5 min
Actividad de exploración Grupos pequeños 15 min
Actividad de exploración En pareja 15 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
California . Algebra 2
Descripción breve
Los estudiantes analizan gráficas de diferentes funciones para determinar y explicar cuál no pertenece.
Los estudiantes determinan el dominio y el rango de diferentes funciones presentadas como gráficas y con descripciones verbales. Luego, identifican restricciones de modelos de situaciones del mundo real.
Los estudiantes sombrean regiones solución dedesigualdades dadas diferentes restricciones e identifican puntos que son soluciones. Luego, con un escenario del mundo real, determinan las restricciones para el modelo matemático y crean un gráfico de la región solución.
Los estudiantes discuten cómo determinar las restricciones y los puntos de soluciones viables dentro de contextos dados.
Los estudiantes identifican restricciones y soluciones viables para una situación del mundo real.
El componente de práctica independiente incluye 3 en la lección y 2 problemas de repaso en espiral.
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


(5 minutos)
Este calentamiento da a los estudiantes la oportunidad de explorar gráficas de funciones y hacer observaciones sobre sus características o tendencias clave. Les da un motivo para utilizar el lenguaje con precisión al explicar qué gráfica no pertenece al grupo (MP6). Tenga en cuenta que en esta actividad no se proporcionan las ecuaciones de las funciones, lo que permite a los estudiantes centrarse en la comparación de las gráficas en lugar de en las expresiones algebraicas.
Las gráficas de las mismas cuatro funciones se utilizan en la siguiente actividad y en otras partes de la lección para proporcionar apoyos de andamiaje a medida que los estudiantes se involucran con nuevos contenidos.
INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organice a los estudiantes en grupos de 2. Dé un tiempo de trabajo tranquilo y luego tiempo para compartir sus respuestas y razonamientos con sus compañeros. Continúe con un debate con toda la clase.
Se muestran cuatro funciones.
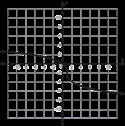
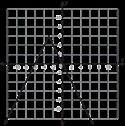
¿Qué función no pertenece?
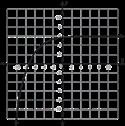

Las respuestas variarán. Ejemplos de respuestas y explicaciones que incluyen lo siguiente:
• ��( ��) no pertenece porque es la única función con un rango de todos los números reales.
RESPUESTAS POSIBLES
• ��( ��) no pertenece porque es la única función que es siempre creciente.
• ��( ��) no pertenece porque es la única función con un máximo.
• ��( ��) no pertenece porque es la única función con un mínimo.
SÍNTESIS DE LA ACTIVIDAD
Invite a los estudiantes que han seleccionado cada función a que razonen su selección. Anote las respuestas de los estudiantes. Resalte el lenguaje de los estudiantes que incluya terminología matemática como dominio, rango, creciente, decreciente, intercepción y vértice. Mantenga expuestas las respuestas de los estudiantes mientras continúan con esta lección.

Álgebra 2 . Matemáticas . Unidad 1
Rutinas didácticas
MLR7: Comparar y conectar
minutos)
En esta actividad, los estudiantes amplían lo que saben sobre el dominio y el rango de las funciones lineales de Álgebra 1 para interpretar las restricciones dentro de contextos del mundo real. Se les pide que den sentido a cómo se puede utilizar un modelo para representar la situación mientras se abordan las restricciones o limitaciones impuestas por el contexto representado (MP4).
INTRODUCCIÓN
Organizar a los estudiantes en grupos de 2-4. Mostrar las cuatro funciones del calentamiento. Dar a los estudiantes 2 minutos para completar el problema 1 de forma independiente antes de discutir sus respuestas con sus grupos. Invíteles a compartir el dominio y el rango de cada función. Siempre que sea posible, destaque el uso que hacen los estudiantes del vocabulario o la terminología matemática. Explique que algunas de las funciones tienen una restricción incorporada en su rango, ya que el rango de las funciones ��( ��), ��( ��) y ��( ��) no son para todos los números reales.
Con estrategias de pensamiento en voz alta, muestre cómo resolver el problema 2 antes de dejar que los estudiantes completen el problema 3 con sus grupos. Supervise las discusiones de los estudiantes en busca de estrategias para destacar durante la síntesis de la actividad.
Apoyo para estudiantes con discapacidades
Acción y expresión: Desarrollar la expresión y la comunicación. Invite a los estudiantes a hablar sobre sus ideas con un compañero antes de escribirlas. Muestre marcos de frases para apoyarles mientras explican sus ideas. Por ejemplo: «Parece que...» y «Tratamos...».
Apoya la accesibilidad para: Lenguaje; organización
ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Apoyo para estudiantes que aprender el idioma
Lectura: MLR7 Comparar y conectar. A medida que los estudiantes comparten sus respuestas y razonamientos con sus grupos, llame su atención sobre las diferentes maneras que sus compañeros han elegido para determinar el dominio y el rango de la función representado en el contexto. Siempre que sea posible, amplíe las palabras y acciones que impliquen el lenguaje de las características clave de las funciones, incluido las siguientes: máximo, mínimo, valores posibles y restricciones.
Principio de diseño: Maximizar la metaconciencia; apoyar la creación de sentido
Se muestran las ecuaciones y gráficos de cuatro funciones.


©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE


1. Completa la tabla identificando el dominio y el rango de cada función. Función
2. Little Theater es un teatro íntimo de 165 butacas en California. El teatro utiliza la función��(��) = 1 8 (1,120 − 16��) para garantizar que cada función genere $1,120 y así cubrir los costos de una producción infantil. La variable �� representa el número de entradas para adultos. La variable y representa el número de entradas para niños.
A. ¿Cuál es el dominio de la función?
B. ¿Cuál es su rango?
C. ¿Qué restricciones, si las hay, son necesarias para la función en el contexto dado?
3. El precio promedio de un galón de jugo de naranja de octubre de 2013 a septiembre de 2014 se puede representar mediante la función h(��) = 6.12 + 0.03��, donde �� representa la cantidad de meses desde octubre de 2013.
A. ¿Cuál es el dominio de la función?
B. ¿Cuál es su rango?
C. ¿Qué restricciones, si las hay, son necesarias para la función en el contexto dado?
1.
Función
��(��)
��(��)
��(��)
��(��)
RESPUESTAS POSIBLES
2.
3.
Dominio
(−∞, ∞)
Rango
(−∞, ∞)
(−∞, ∞) (�� < 6)
(−∞, ∞) (�� ≤ 6)
(−∞, ∞) (�� ≥ 9)
A. Todos los números reales; (−∞, ∞)
B. Todos los números reales; (−∞, ∞)
C. Ambos �� and �� deben ser números enteros.
A. Todos los números reales; (−∞, ∞)
B. Todos los números reales; (−∞, ∞)
C. El valor def �� debe estar entre 0 y 12 porque el modelo solo es apropiado entre octubre de 2013 y septiembre de 2014.
SÍNTESIS DE LA ACTIVIDAD

Álgebra 2 . Matemáticas . Unidad 1
Seleccione a los estudiantes para que compartan sus respuestas y estrategias para el problema 3 con la clase. Mientras comparten, considere hacer las siguientes preguntas:
• «¿Tuvo alguien la misma respuesta, pero la explicaría de manera diferente?».
• «¿Tuvo alguien una respuesta diferente que piensa que también es correcta?».
• «¿Quiere alguien agregar algo a la estrategia de _____?».
• «¿Están de acuerdo o en desacuerdo? ¿Por qué?».
Duranteel debate, considere la posibilidad de mostrar las gráficas de las funciones de los problemas 2 y 3. Explique que su dominio matemático es el mismo que el de las funciones de los problemas 2 y 3. Explique que su dominio matemático y rango son todos números reales porque ambas son funciones lineales; sin embargo, hay restricciones adicionales a las funciones que se usan para representar escenarios del mundo real.
minutos)
Rutinas didácticas
MLR8: Apoyos para el debate
En esta actividad, los estudiantes utilizan desigualdades de dos variables con valor absoluto y ecuaciones cuadráticas de frontera para graficar un conjunto de restricciones. Utilizan la gráfica del sistema de desigualdades para identificar Soluciones posibles antes de aplicar estas estrategias a un problema en un contexto del mundo real (MP7).
INTRODUCCIÓN
Organice a los estudiantes en grupos de 2, y pídales que trabajen en silencio en los problemas 1 y 2 durante unos minutos antes de discutir sus soluciones y reflexiones con sus compañeros. Facilite brevemente un debate de toda la clase invitando a los estudiantes a compartir sus estrategias para sombrear las gráficas de la sdesigualdades no lineales y a identificar la región de solución en el problema 2. Dé a los estudiantes otros 3-4 minutos para trabajar en el problema 3 de forma colaborativa antes de facilitar un debate con toda la clase.
Apoyo para estudiantes con discapacidades
Representación: Acceso para la percepción. Lea en voz alta los enunciados del problema 3 y anime a los estudiantes a participar en el problema haciendo anotaciones mientras escuchan. Los estudiantes que escuchen y lean la información se beneficiarán de un tiempo de procesamiento adicional.
Apoya la accesibilidad para: Lenguaje; procesamiento conceptual
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. La función ��( ��) = −2| �� + 3| + 6 de la actividad anterior puede considerarse una restricción con las desigualdades �� ≤ −2|�� + 3| + 6 y �� ≥ −2|�� + 3| + 6. Complete la gráfica de cada desigualdad sombreando la región apropiada. Desigualdad �� ≤ -2|�� + 3| + 6 �� ≥ -2|�� + 3| + 6

2. Se muestra la gráfica de ��( ��) = ( �� + 1)2 − 9.
A. Sombree la solución al siguiente conjunto de restricciones en ��( ��):
( �� + 1)2 − 9
> 0

B. Seleccione todos los puntos que son soluciones al conjunto de restricciones de la parte A.
(−2, 2)
(0, 0)
(−4, 6)
(0, 10)
(1, −2)
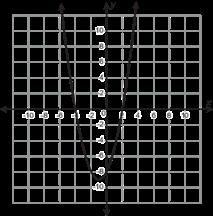
2. Una empresa de alquiler de barcos tiene barcos disponibles con una capacidad máxima de 8 personas y un límite de peso de 850 libras. La empresa utiliza un peso aproximado de 180 libras para cada adulto y 80 libras para cada niño.
A. Habla con tu compañero las restricciones encontradas en este escenario.
B. Seleccione todas las desigualdades que representan restricciones para este escenario, donde X representa la cantidad de adultos y Y representa la cantidad de niños en un barco alquilado.
�� ≥ 0
�� ≥ 0
�� ≤ 180
�� + �� ≤ 8 �� + �� ≤ 850
180 �� + 80 �� ≤ 850
ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN
Math Nation California . Algebra 2 ©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1
A. Grafique las desigualdades que representan las restricciones para este escenario.
B. ¿Qué restricciones adicionales, si las hay, se necesitan para las variables dentro del contexto dado?
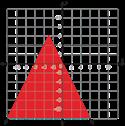

A.
RESPUESTAS POSIBLESS
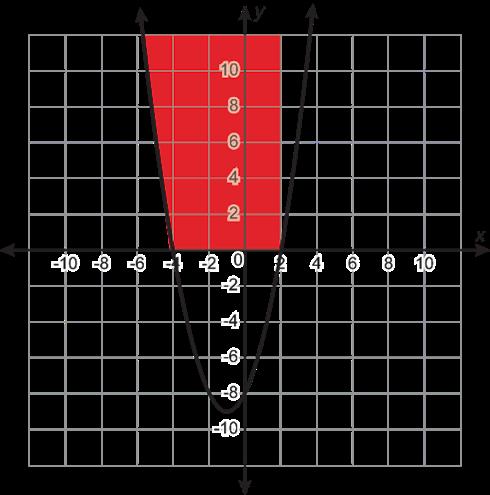
B. (−2, 2) (0, 0) (−4, 6) (0, 10) (1, −2)




RESPUESTAS POSIBLESS CONTINUACIÓN
SÍNTESIS DE LA ACTIVIDAD
1.
A. No se requiere ninguna respuesta por escrito. Las respuestas de debate deben coincidir con la parte B.
B.
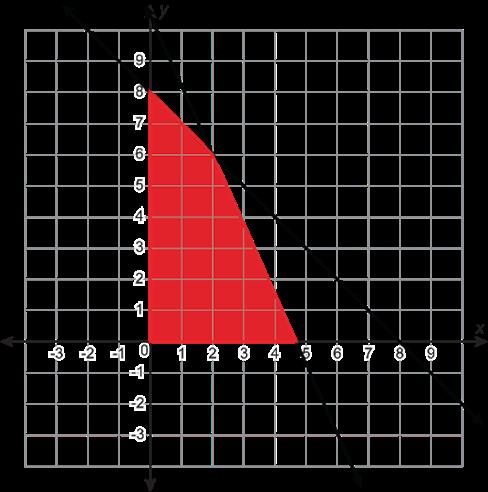
D. Los valores de X y Y deben ser números enteros.
Para cada desigualdad del problema 3B, pida a los estudiantes que expliquen por qué sería una restricción apropiada para representar la situación junto con qué variable se está restringiendo. Centre la conversación en la terminología adecuada resaltando lenguaje como valor máximo, valor mínimo, plausible, no plausible, viable y no viable. Cuando habla del problema 3D, pregunte a los estudiantes qué aspecto tendría el gráfico que representa la restricción de enteros para las variables X y Y (puntos discretos en lugar de una región completamente sombreada).
Apoyo para estudiantes que aprenden el idioma inglés
Hablar: MLR8 Apoyos a al debate. Fomente y apoye las oportunidades de colaboración entre iguales. Cuando los estudiantes compartan su trabajo y estrategias con sus compañeros, muestre estructuras de frases para apoyar su conversación, como las siguientes: «En primer lugar, porque...», «Parece que...», «¿Por qué...» y «Estoy de acuerdo / en desacuerdo porque...».
Principio(s) de diseño: Apoyar la creación de sentido
(5 minutos)
Ayude a los estudiantes a reflexionar sobre las ideas clave de la lección con preguntas guía como las siguientes:
• «¿Cómo se determina una restricción dentro de un contexto dado?». (Razone sobre los valores máximos y mínimos posibles de cada variable. Considera también si la variable podría ser un número decimal, positivo o negativo).
• «¿Cómo decides qué región sombrear al representar una desigualdad en el plano de coordenadas?». (Selecciona puntos de prueba y verifica si hacen que la desigualdad sea verdadera o falsa).
• «¿Cómo determinas si un punto es una solución viable para el conjunto de restricciones?». (Comprueba que el punto es verdadero para todas las restricciones del escenario).
(5 minutos)
1. Una ciudad lleva a cabo una iniciativa para aumentar la cantidad de árboles en una zona urbana. La ciudad dispone de al menos 45,000 pies cuadrados de terreno asignados para los nuevos árboles. Los robles requieren 600 pies cuadrados de espacio. Los arces necesitan 900 metros cuadrados. El presupuesto de la ciudad permite comprar hasta 75 árboles nuevos.
A. Seleccione todas las desigualdades que representan restricciones en este escenario, donde X representa la cantidad de robles plantados y Y representa la cantidad de arces plantados.
600�� + 900 �� ≥ 45.000
�� + ��
ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES
1.
B. Selecciona todas las soluciones viables en este contexto.
(0, 0)
(0, 50)
(75, 0)
(50, 50)
(10, 60)
(20, 20)
C. Interpreta una solución viable de la parte B en este contexto.
A.
600�� + 900 �� ≥ 45.000
�� + ��
(0, 0)
(0, 50)
(75, 0)
(50, 50)
(10, 60)
(20, 20)
C. (10, 60). La ciudad puede plantar 10 robles y 60 arces en el espacio designado.
Las funciones que se utilizan para representar escenarios del mundo real suelen estar limitadas por restricciones como el tiempo, el tamaño o la cantidad de un producto. Las restricciones matemáticas se representan con desigualdades con símbolos, como <, >, ≤, o ≥. Al graficar un modelo con restricciones, se crea una región que representa todos los valores posibles que pueden satisfacer el contexto.
California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


El contexto de los modelos que utilizan desigualdades también podría producir restricciones adicionales sobre los posibles valores de las variables. En algunas situaciones, una cantidad de la relación solo puede representarse con números enteros, números enteros o valores negativos. Es importante dar sentido a la situación para asegurarse de que cualquier punto dentro de la región solución de lasdesigualdades es válido en el contexto dado.
PROBLEMA 1
Se muestra la gráfica de la función ��( ��) = −2∛ �� − 1 − 2
A. Sombree la región solución definida por el siguiente conjunto de restricciones:

B. Selecciona todos los puntos que son soluciones al conjunto de restricciones de la parte A.
(2, 8)
(0, −2)
(−6, 4)
(4, −6)
(−8, 0)
Soluciones posibles
PROBLEMA 2

(0, 0) (2, 8) (0, −2)
(−6, 4) (4, −6) (−8, 0)
Julia planea alquilar una canoa por unas 72 millas de paseo por la ruta de remo del lago Tahoe. El proveedor de la canoa cobra $90 por transportar la canoa y las provisiones hasta el punto de acceso y otros $2.50 por cada milla recorrida por el sendero. La función ��( ��) = 2.5 �� + 90 representa el coste total del viaje después de �� millas recorridas en el sendero. Julia tiene un presupuesto de $200 para este viaje en canoa.
Seleccione todas las desigualdades que muestran restricciones para este escenario.
�� ≥ 0
�� ≥ 0
�� ≤ 72
�� ≥ 200
�� + �� ≤ 90
2.5 �� + 90 ≤ 200
. Algebra 2 Álgebra 2 . Matemáticas . Unidad 1
Learning Inc. - Todos los derechos reservados
Soluciones posibles
�� ≥ 0
�� ≥ 0
�� ≤ 72
�� ≥ 200
�� + �� ≤ 90
2.5 �� + 90 ≤ 200
PROBLEMA 3
Se muestra la gráfica de la función ��( ��) = -� 2 3 �
+ 3 + 6
A. Sombree la región solución definida por el siguiente conjunto de restricciones: �� ≤ −� 2 3 � �� + 3 + 6
≤ 2 �� > -4

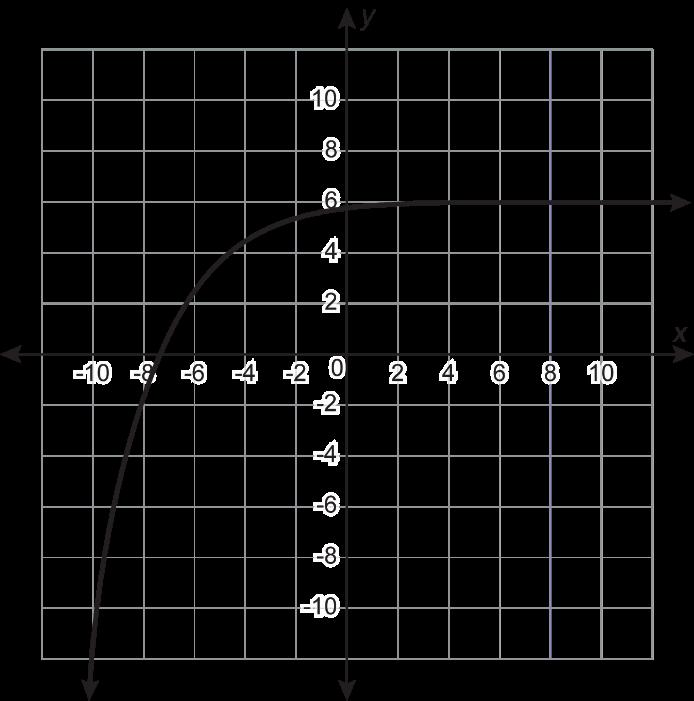
B. Seleccione todos los puntos que son soluciones al conjunto de restricciones de la parte A.
(8, 2)
(−8, 6)
(4, −8)
(-6, −2)
(2, −10)
Soluciones posibles
A. B.
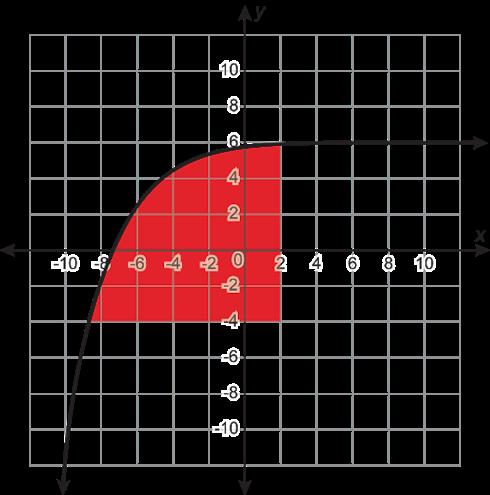
PROBLEMA 4
(De la unidad 1, lección 8)
(0, 0)
(8, 2)
(−8, 6)
(4, −8)
(−6, −2)
(2, −10)
Resuelve y grafica la solución de la desigualdad 1 4 (0, 0) − 4| ≥ 1 en la recta numérica.
Math Nation California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


Soluciones posibles
�� ≤ 0 o �� ≥ 4

PROBLEMA 5
(De la unidad 1, lección 6)
Una sucesión está definida por la función ��( ��) = 8 − 1 2 �� para �� ≥ 1.
A. Escribe los primeros 4 términos de la sucesión.
B. Halla la suma de los primeros 4 términos de la sucesión.
Soluciones posibles
A. 7.5, 7, 6,5, 6
B. 7.5, 14.5, 21, 27
Reflexiones:
Nation California . Algebra 2 Álgebra 2 . Matemáticas . Unidad 1
Learning Inc. - Todos los derechos reservados


IDEA(S) FUNDAMENTAL(ES)
• Modelización con funciones
ALINEACIÓN
Alineación de estándares y principios de California
Abordar
A-CED.3 Representar restricciones mediante ecuaciones o desigualdades, y mediante sistemas de ecuaciones y/o desigualdades, e interpretar soluciones como opciones viables o no viables en un contexto representado.
Enfocar SMPs
MP2 Razonar abstracta y cuantitativamente.
MP4 Representar con matemáticas.
MP6 Atender a la precisión.
Estándares CA ELD
I.A.4
I.B.6
I.C.12
CONEXIONES INTEGRADAS
(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...
prededir lo que podría ocurrir, representarán con matemáticas y atenderán a la precisión exploran cantidades cambiantes.
• Puedo identificar restricciones sobre variables en un contexto representado.
• Puedo interpretar soluciones de sistemas de restricciones en escenarios del mundo real.
OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO
• Identificar e interpretar restricciones en contextos del mundo real.
• Interpretar soluciones de sistemas de restricciones en escenarios representados.
PREPARACIÓN DE LA
Rutinas didácticas
MLR6: Tres lecturas
MLR2: Recopilar y mostrar
©Accelerate Learning Inc. - Todos los derechos reservados
Álgebra 2 . Matemáticas . Unidad 1
Objetivos de aprendizaje para el estudiante
• Determinemos e interpretemos restricciones en situaciones del mundo real.
Narrativa de la lección
Los estudiantes continúan trabajando con restricciones relacionadas con funciones que representan contextos del mundo real. Le dan sentido a diferentes representaciones de contextos, incluido las descripciones verbales, ecuaciones y gráficas para identificar regiones de solución plausibles para varias situaciones. A lo largo de la lección, se anima a los estudiantes a pensar contextualmente y a identificar cualquier restricción en las variables descritas, como situaciones en las que solo números enteros o solo números reales positivos pueden ser plausibles. Mientras representan con matemáticas (MP4), los estudiantes prestan atención a la precisión en la determinación de soluciones viables para el contexto (MP6).
RESUMEN DE LA LECCIÓN
Componente de la lección

Estructura Tiempo
Calentamiento En parejas 5 min
Actividad de exploración
Actividad de exploración
En parejas 20 min
En parejas 10 min
Síntesis Todo el grupo 5 min
Enfriamiento Independiente 5 min
Práctica Independiente 10 min
Descripción breve
Los estudiantes hacen observaciones sobre la construcción de un objeto del mundo real y las restricciones para construirlo.
Los estudiantes crean y utilizan modelos de restricciones para representar situaciones del mundo real, identificar regiones de solución e interpretar los contextos de las soluciones a los escenarios.
Los estudiantes definen variables, escriben inecuaciones con restricciones y grafican sistemas de inecuaciones lineales para situaciones del mundo real.
Los estudiantes generan ejemplos de restricciones en escenarios del mundo real y razonan sobre los valores de las variables dependientes e independientes dentro de varios contextos.
Los estudiantes usan una gráfica de restricciones para identificar qué desigualdades crearían diferentes regiones de solución.
El componente de práctica independiente incluye 2 en la lección y 2 problemas de repaso en espiral.
California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


(5 minutos)
Este calentamiento lleva a los estudiantes a identificar las restricciones en la construcción de una estructura del mundo real. Piensan de forma cuantitativa y abstracta describiendo restricciones matemáticas y del mundo real sin valores numéricos específicos (MP2).
INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
Organice a los estudiantes en grupos de 2. Deles 1-2 minutos (min) de tiempo para pensar en silencio y luego tiempo para compartir sus respuestas al problema 1 con sus compañeros. Continúe con un debate con toda la clase.
1. El acueducto de Pont du Gard cruza el río Garden de Francia. El acueducto se construyó para transportar agua. Como se ve en la imagen, se pueden representar múltiples formas mediante funciones cuadráticas dentro de la estructura.
Cuando construyeron este acueducto, los ingenieros tuvieron que tener en cuenta muchas restricciones a la vez que mantenían la forma de las funciones cuadráticas. Identifica una posible restricción en la creación de la forma del acueducto con funciones cuadráticas.

2. Comenta con tu compañero las limitaciones que has identificado.
POSIBLES RESPUESTAS
SÍNTESIS DE LA ACTIVIDAD
1. Las respuestas pueden variar. El nivel del agua es una restricción para la fila inferior de parábolas. Además, algunas funciones cuadráticas tienen un límite adicional: el acantilado y las rocas. Las filas superiores 2 tienen una restricción de cada fila de cuadráticas por debajo de ellas.
2. No se requiere una respuesta escrita.
Invite a los estudiantes a compartir las restricciones que identificaron en la construcción del acueducto de Pont du Gard. Anote y exponga las ideas compartidas. Anime a los estudiantes a debatir la lista de restricciones y destaque la terminología matemática que surja durante el debate. El objetivo de este debate es permitir que los estudiantes piensen de forma flexible sobre las restricciones, no solo como desigualdades, sino también como el tipo de valor que puede representar una variable.
(20 minutos)
Rutinas didácticas
MLR6: Tres lecturas
Se presenta a los estudiantes el concepto de nanotecnología y cómo afecta a los costes de fabricación de los productos. Observan las restricciones dentro de nuevos contextos y dan sentido a lo que representa cada región creada por las ecuaciones de restricción y las desigualdades.

Álgebra 2 . Matemáticas . Unidad 1
Organice a los estudiantes en grupos de 2 y muestre el párrafo introductorio de la edición para estudiantes. Dé a los estudiantes 2-3 minutos para completar los problemas 1 y 2 de forma independiente antes de discutir sus respuestas con sus compañeros. Luego, pida a los estudiantes 3-4 que compartan sus observaciones con la clase. Aproveche esta conversación para aclarar cualquier duda que tengan sobre la nanotecnología.
Dé a los estudiantes otros 6-8 minutos para que completen los problemas 3 y 4 con sus compañeros. Supervise sus conversaciones en busca de ideas o estrategias que desarrollen para destacarlas durante la síntesis de la actividad. Tenga en cuenta que el problema 4 no incluye una gráfica de la función. Considere la posibilidad de proporcionar tecnología o un gráfico impreso de la función como andamiaje para los estudiantes que puedan necesitar apoyo visual.
Apoyo para estudiantes con discapacidad
Acceso para la percepción. Lea en voz alta los enunciados del problema. Anime a los estudiantes a participar en el problema anotando mientras escuchan. Los estudiantes que escuchen y lean la información se beneficiarán de un tiempo de procesamiento adicional. Si los estudiantes no están seguros de por dónde empezar, pídales que consideren cómo se representan y limitan las variables en cada parte del problema.
Apoya la accesibilidad para: Lenguaje; procesamiento conceptual
Apoyo a los estudiantes que aprenden el idioma inglés
Hablar: MLR6 Tres lecturas. Utilice esta rutina para apoyar la comprensión lectora del párrafo introductorio de esta actividad y del problema 3. Utilice la primera lectura para orientar a los estudiantes sobre la situación, pidiéndoles que describan de qué trata la situación sin utilizar números (una empresa manufacturera está analizando la rentabilidad del uso de la nanotecnología). Utiliza la segunda lectura para identificar cantidades y relaciones, preguntando a los estudiantes qué se puede contar o medir sin centrarse en los valores (el coste de fabricar utilizando nanotecnología y sin utilizar nanotecnología). Después de la tercera lectura, pídeles que hagan una lluvia de ideas sobre posibles estrategias para responder a la siguiente pregunta: «¿Qué representa cada región del gráfico en su contexto?». Esto ayuda a los estudiantes a conectar el lenguaje del problema de palabras con el razonamiento necesario para resolverlo, manteniendo al mismo tiempo la exigencia cognitiva de la tarea.
Principio de diseño: Apoyar la creación de sentido
ESTUDIANTE ENUNCIADO DE LA TAREA
La nanotecnología es una rama de la ciencia y la ingeniería centrada en el diseño y la producción de tecnología en la escala increíblemente pequeña de los nanómetros, donde 1 nanómetro = 0,000000001 metro. Esta tecnología consiste en crear y modificar nanopartículas para satisfacer necesidades específicas en campos como la medicina, la construcción, la agricultura y la electrónica.
1. Comenta con tu compañero qué es una nanopartícula y cómo puede utilizarse en el sector de la construcción.
2. Las empresas de construcción utilizan el análisis de costes para proyectar los costes actuales y futuros como parte del proceso de construcción de un objeto. ¿Por qué es importante que una empresa haga un análisis de costes sobre la producción de un objeto?
©Accelerate Learning Inc. - Todos los derechos reservados



ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. La empresa NT quiere determinar si es más beneficioso construir un objeto con o sin nanotecnología.
El coste para la empresa NT de producir un objeto de forma convencional sin nanotecnología se modela mediante la ecuación y = 0,25x + 3. El coste para la empresa NT de producir un artículo con nanotecnología se calcula mediante la ecuación
y = -0.1(x - 7)2 + 10. Las gráficas de ambas ecuaciones se muestran en el plano de coordenadas.
A. La gráfica del coste utilizando nanotecnología se abre hacia abajo. Discute con tu compañero por qué esto tiene sentido.
B. Explique el significado del punto Q de la gráfica.
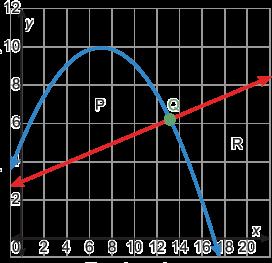
C. Escriba las restricciones del coste mínimo de cada método para iniciar la producción.
D. Explique qué representa la región P.
E. Escriba las desigualdades utilizadas para crear la región R.
F. ¿Cuál es la importancia de las regiones P y R para la empresa NT?
2. Una pequeña ciudad está planeando un espectáculo de fuegos artificiales para una celebración de verano. El ingeniero planea Introducción todos los fuegos artificiales desde una plataforma 29 pies del suelo. La altura de los fuegos artificiales, lanzados con una velocidad inicial de 112 pies por segundo, puede representarse mediante la función h(t) = −16t 2 + 112t + 29, t segundos después del Introducción.
A. Para la seguridad de los espectadores, los fuegos artificiales deben explotar a una altura de al menos y pies. Crea una desigualdad para representar la altura, y, a la que la explosión de los fuegos artificiales puede ocurrir con seguridad.
B. Con base en este escenario, ¿qué valores del conjunto de soluciones no son viables? Explica tu razonamiento.
C. La explosión de los fuegos artificiales no puede comenzar hasta al menos 200 pies sobre el suelo. Crea una desigualdad que pueda representar esta restricción.
D. Utiliza la tecnología gráfica para graficar las desigualdades que creaste en las partes A y C.
E. ¿Cuántos segundos después del Introducción pueden explotar los fuegos artificiales de manera segura?
1. Las respuestas pueden variar. Es una partícula de materia extremadamente pequeña. Puede ser útil en la construcción al reducir el uso de materiales naturales que no están tan fácilmente disponibles o que son caros.
2. Las respuestas pueden variar. Realizar un análisis de costes ayuda a una empresa a determinar si merece la pena invertir en una nueva tecnología. Aunque su uso se abaratará con el tiempo, suele suponer una inversión mayor al principio de un proyecto.
3.
POSIBLES RESPUESTAS
A. Las respuestas variarán. Utilizar nanotecnología tiene muchos costes iniciales que pueden disminuir durante el proyecto.
B. El punto P representa cuándo el coste de utilizar y no utilizar nanotecnología para crear el producto será el mismo.
C. $3 millones si no se utiliza nanotecnología; $5,1 millones si se utiliza nanotecnología
D. Región P representa el momento en que es más eficiente fabricar los productos de forma convencional que con nanotecnología.
E. y ≤ 0.25x + 3 y y ≥ −0,1(x − 7)2 + 10
F. Las regiones P y R pueden utilizarse para determinar el método de producción más rentable en función del tiempo de fabricación del producto.
Álgebra 2 . Matemáticas . Unidad 1

1.
RESPUESTAS POSIBLES CONTINUACIÓNÓN
SÍNTESIS DE LA ACTIVIDAD
A. y ≥ −16t2 + 112t + 29
B. Los valores donde y < 0 o t < 0 no son viables en este escenario.
C. y ≥ 200
D. No se requiere respuesta escrita. Los estudiantes deben ver las gráficas de las inecuaciones de las partes A y C.
E. 2.25 segundos
Hable un problema a la vez y pida a los estudiantes que compartan sus respuestas y razonamientos. Registre y muestre sus explicaciones. Si no se mencionan, pregunte si pudieron escribir inecuaciones para crear regiones específicas en el problema 3 y cómo pudieron resolver la inecuación en el problema 4E. Para involucrar a más estudiantes en la conversación, considere hacer las siguientes preguntas:
• «¿Quién puede replantear el razonamiento de ___ de una manera diferente?».
• «¿Alguien quiere agregar algo a la estrategia de _____?».
• «¿Están de acuerdo o en desacuerdo? ¿Por qué?».
• Si hay tiempo, pida a los estudiantes que compartan sus gráficos del problema 4D y cómo los utilizaron para resolver el problema. Anime a los estudiantes a utilizar su comprensión de la resolución de cuadráticas para resolver el problema algebraicamente a través de la factorización.
(10 minutos)
Rutinas Instructivas
MLR2: Recopilar y mostrar
Los estudiantes definen variables a partir de escenarios del mundo real, escriben inecuaciones con restricciones y grafican los sistemas de inecuaciones lineales creados usando restricciones. Las restricciones en esta actividad no son tan complejas como en los ejemplos anteriores, lo que permite a los estudiantes el andamiaje necesario para crear sus propias ecuaciones e inecuaciones con restricciones a partir del contexto dado.
Organizar a los estudiantes en grupos de 2 y darles 3-4 minutos para completar el problema 1 en colaboración con sus compañeros. Supervise su trabajo y el debate para detectar oportunidades de ampliar el trabajo de los estudiantes durante la reunión de toda la clase. Tome nota de las siguientes estrategias y enfoques para destacarlos en la discusión:
INTRODUCCIÓN
• «¿Cómo seleccionaste las variables para este escenario? ¿Se pueden seleccionar de otra manera?». (En este contexto, cualquiera de las variables puede ser la independiente o la dependiente. La variable x puede representar la cantidad de fotografías o la cantidad de carteles animados creados, mientras que y representan la variable restante).
• «¿Cuántas desigualdades de restricciones identificó? ¿Hay restricciones adicionales que no hayas descubierto?». (Los estudiantes pueden olvidar identificar las restricciones mínimas para X y Y, ya que esos valores no pueden ser negativos. Busca que identifiquen los valores de X y Y como enteros no negativos o números enteros).
©Accelerate Learning Inc. - Todos los derechos reservados


INTRODUCCIÓN CONTINUACIÓNÓN

• «¿Hay más de una manera de representar este escenario en un gráfico?». (Sí, dependiendo de la forma en que se definieron las variables. Los estudiantes también pueden trazar puntos discretos en lugar de sombrear la región de solución para representar el dominio de números enteros y las restricciones de rango).
Después de una discusión de toda la clase del problema 1, dé a los estudiantes 2-3 minutps para completar el problema 2 de forma independiente.
Representación: Desarrollar lenguaje y símbolos. Elabore un cuadro con los aspectos importantes que deben tenerse en cuenta al crear inecuaciones con restricciones, como los valores máximo y mínimo de cada variable dentro del contexto y el tipo de valor que puede tomar cada variable (entero, positivo, negativo, etc). Invite a los estudiantes a sugerir lenguaje o diagramas para incluir que apoyen su comprensión de las restricciones.
Apoya la accesibilidad para: Procesamiento conceptual; lenguaje
1. César tiene un negocio en línea donde vende sus fotografías digitales y carteles animados. César tarda 2 horas en crear 1 cartel animado y 30 minutos en crear 1 fotografía digital. Dedica como máximo 14 horas a la semana a crear carteles animados y fotografías digitales. Para asegurarse de que no tiene demasiadas existencias, César no crea más de 10 artículos por semana.
A. Defina las variables en este escenario.
B. Escriba las desigualdades de restricción para este escenario.
ENUNCIADO DE TAREA
PARA EL ESTUDIANTE
C. Represente gráficamente el sistema de desigualdades lineales definido en la parte B.
2. Un camión de comida local vende nachos y lazo de pan salado. Para obtener beneficios, el camión de comida debe vender al menos 30 platos de nachos, pero no puede preparar más de 70 cada día.
El camión de comida también debe vender al menos 10 lazos de pan salado, pero no puede preparar más de 40 cada día. El camión de comida no puede preparar más de un total de 90 platos de nachos y lazos de pan en total.
A. Defina las variables, X y Y, para este escenario.
B. Escriba las desigualdades de restricción para este escenario.
C. Grafique el sistema de inecuaciones lineales definido en la parte B.
1.
RESPUESTAS POSIBLES
A. Las respuestas variarán. x es el número de fotografías creadas por semana. y es el número de carteles animados creados por semana.
Álgebra 2 . Matemáticas . Unidad 1

1.
RESPUESTAS POSIBLES CONTINUACIÓN
A.
B.
2x + 0.5y ≤ 14
x + y ≤ 10 x ≥ 0 y ≥ 0
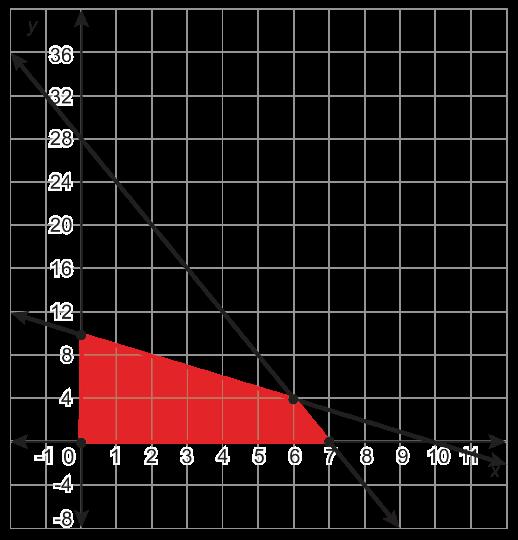
A. Las respuestas variarán. x es la cantidad de platos de nachos. y es la cantidad de lazos de pan salado.
B.
SÍNTESIS DE LA ACTIVIDAD
C.
x + y ≤ 90
x ≥ 30
x ≤ 70
y ≥ 10
y ≤ 40
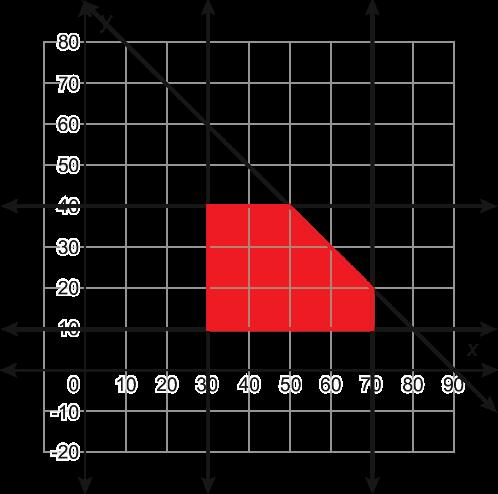
Utilice preguntas orientativas similares a las del Introducción para facilitar un debate de toda la clase sobre el problema 2. Destaque que en el problema 2 se producirían restricciones similares, en las que cualquiera de las variables puede identificarse como dependiente o independiente, y que las variables en el contexto del mundo real serían números enteros.
Apoyo para estudiantes de inglés
Escribir, representar, conversar: MLR2 Recopilar y mostrar. Mientras las parejas de estudiantes trabajan, circule y escúcheles hablar sobre las variables y limitaciones dentro de los contextos dados. En una pantalla visual, anote las frases comunes o importantes que escuche decir a los estudiantes sobre cada escenario. Esto les ayudará a utilizar el lenguaje matemático durante sus debates por parejas y en grupo.
Principio(s) de diseño: Apoyar la creación de sentido; cultivar la conversación
Nation California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados


minutos)
El objetivo de este debate es que los estudiantes den sentido a contextos del mundo real que tienen restricciones adicionales sobre las variables dependiente e independiente. Pídales que propongan ejemplos para cada una de las siguientes situaciones. Registre las respuestas de los estudiantes en una pantalla visual:
• Un escenario en el que solo la variable independiente está restringida a números enteros. (Ejemplo de respuesta: El eje X se mide con valores discretos, como la cantidad de libros en una estantería y el peso de la estantería se mide con valores continuos).
• Un escenario en el que solo la variable dependiente está restringida a números enteros. (Ejemplo de respuesta: El eje X representa la cantidad de espacio disponible para un jardín local y el eje Y representa la cantidad de flores que se plantan).
• Un escenario en el que ninguna de las variables está restringida a números enteros. (Ejemplo de respuesta: El eje Xrepresenta la cantidad de tiempo que una cuenta de ahorros está abierta y el eje y representa cuánto dinero hay en la cuenta).
INTERPRETAR
(5 minutos)
Se muestra un gráfico con seis regiones etiquetadas. Las regiones se formaron con las gráficas de las ecuaciones y = x2 3 + 2x + 3, y = −x + 3 y y = −2

ENUNCIADO DE TAREA PARA EL ESTUDIANTE
1. Complete el conjunto de restricciones que crearían la región solución R. y x2 3 + 2x + 3 y −x + 3 y −2
2. ¿Qué región solución se creó con las restricciones mostradas? y ≥ x2 3 + 2x + 3 y ≤ −x + 3 y ≥ −2
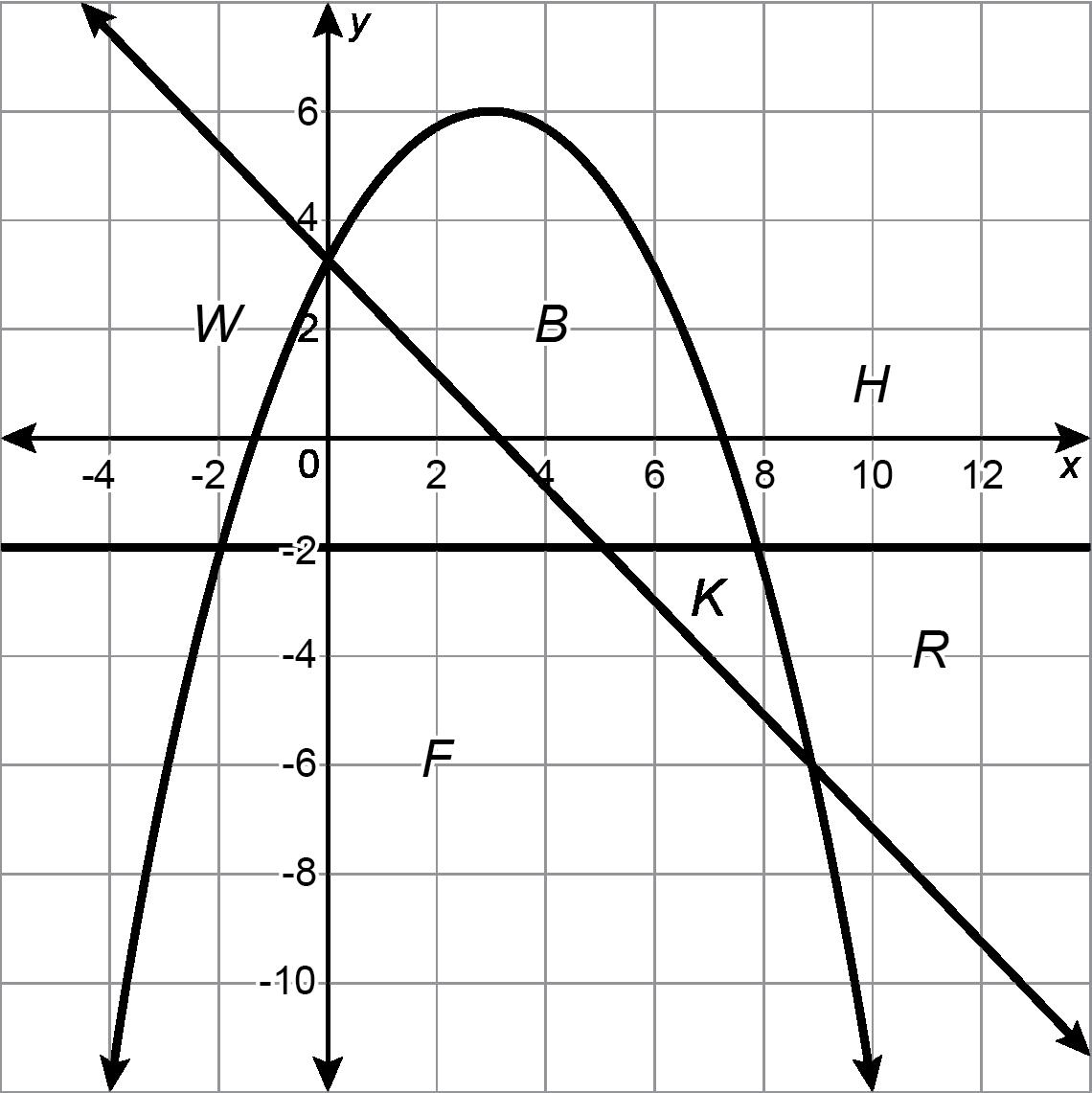
POSIBLES RESPUESTAS
2 2. Región W
Se ha estudido sistemas de desigualdades lineales en cursos y lecciones anteriores, donde la intersección de las inecuaciones representaba la región solución en el escenario. En esta lección, las ecuaciones e inecuaciones lineales y no lineales se usan como restricciones para representar situaciones del mundo real. Cada región que se crea con las restricciones tiene un significado dentro del contexto, por lo que dar sentido a cómo se relacionan las variables con cada región es una parte importante del proceso de modelización. Estas son consideraciones importantes a tener en cuenta al representar con funciones a lo largo del curso.
Cuando las variables no están definidas, es importante identificar cuál representa la variable dependiente y cuál la independiente. En algunos escenarios, las variables dependiente e independiente pueden usarse en cualquier orden, haciendo muy importante la interpretación de la solución de restricciones.
PROBLEMA 1
Una empresa manufacturera ha creado un nuevo proceso que le permite reducir el coste de fabricación de una determinada pieza. El coste máximo de fabricación de la pieza puede representarse con la función C(x) = 602.2(0.8)x, donde x es la cantidad de meses transcurridos desde la implantación del nuevo proceso.
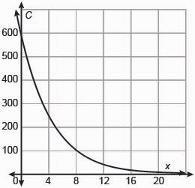
A. Crea una desigualdad para representar el coste, C, de fabricar la pieza x meses después de que se implemente el nuevo proceso.
B. Crea desigualdades de restricción adicionales para este escenario.
C. La empresa identificó como rentable cualquier mes en el que el coste de fabricación sea inferior a $400. Se muestra la gráfica de C(x). Grafica las restricciones en este contexto para determinar la región que resultaría en un mes rentable para la empresa.
PROBLEMA 2

A. C ≤ 602.2(0.8)x
B. Las respuestas variarán: x ≥ 0, C ≥ 0
C.
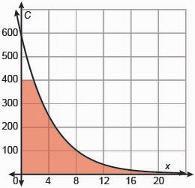
El gerente de un camión de comida sirve hamburguesas y pollo en un evento comunitario. Debido a limitaciones de espacio, el gerente no puede vender más de 70 platos de hamburguesa o 50 platos de pollo. El gerente no puede llevar más de 100 comidas al evento.
A. Defina las variables X y Y en este escenario.
B. Escribe las desigualdades de restricción para este escenario.
C. Grafica el sistema de desigualdades lineales definido en la parte B. Etiqueca la región de solución.
Soluciones posibles
A. Las respuestas variarán. X representa comidas de hamburguesa y Y representa comidas de pollo. Los estudiantes también pueden definir las variables como opuestas.
B. 0 ≤ x ≤ 70, 0 ≤ y ≤ 50, x + y ≤ 100
California . Algebra 2
©Accelerate Learning Inc. - Todos los derechos reservados Álgebra 2 . Matemáticas . Unidad 1


Álgebra 2 . Matemáticas . Unidad 1
A. Se muestran dos gráficas, dependiendo de la cantidad que los estudiantes definan como x
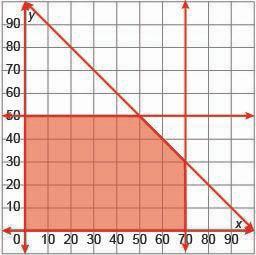
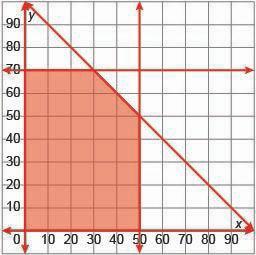
PROBLEMA 3
(De la unidad 1, lección 5)
Una sucesión, f(n), incluye los términos f(3) = 4 y f(5) = 16
A. Escriba una definición para la sucesión si f(n) es aritmética.
B. f(n) es geométrica.
PROBLEMA 4
(De la unidad 1, lección 3)

Soluciones posibles
A. f(n) = −8 + 6(n − 1) para n ≥ 1
B. f(n) = 1(2)n - 1 para n ≥ 1
Una tabla de valores para h(x) ee muestra. Determine la tasa de cambio promedio en los intervalos dados.
A. [2,6]
B. [3.5, 6]
C. [3.3, 7]
Soluciones posibles
A. 3.25
B. 9.2
C. 0
Reflexiones:
