MN CA Algebra 1 Spanish Unit Sample by acceleratelearning

POR ACCELERATE LEARNING

A1ÁLGEBRA

Muestra de la edición para el maestro

POR ACCELERATE LEARNING

ÁLGEBRA 1

Muestra de la edición para el maestro

Math Nation 6-8 fue desarrollado originalmente por Illustrative Mathematics® y tiene derechos de autor de 2019 de Illustrative Mathematics. Tiene la licencia internacional Creative Commons Attribution 4.0 (CCBY 4.0).

La plataforma de recursos curriculares en línea que se ofrece en «mathnation.com», incluidos los videos y las preguntas de práctica, son adiciones al contenido original de Illustrative Mathematics y tiene derechos de autor 2024 de Accelerate Learning, Inc.

La marca comercial «Math Nation» es propiedad de Accelerate Learning, Inc. Todas las demás marcas comerciales y nombres de productos mencionados en el plan de estudios de Math Nation AGA son propiedad de sus respectivos dueños y se utilizan únicamente con fines educativos. A menos que se indique lo contrario, Math Nation no tiene relación con ninguna de las empresas o marcas mencionadas en el plan de estudios y no respalda ni tiene preferencia por ninguna de esas empresas o marcas.

Este plan de estudios incluye imágenes de dominio público o imágenes con licencia abierta que tienen derechos de autor de sus respectivos propietarios. Las imágenes con licencia abierta permanecen bajo los términos de sus respectivas licencias. Consulte la sección de atribución de imágenes para obtener más información.

UNIDAD 1

ESTADÍSTICA DE UNA VARIABLE

UNIDAD NARRATIVA

En los grados 6-8, los estudiantes utilizaron visualizaciones de datos (histogramas, diagramas de puntos y de cajas) como una forma de resumir los datos. Estas visualizaciones de datos se revisan en esta unidad, pero con un enfoque en la interpretación y lo que revelan acerca de los datos, además de la mecánica de la construcción de las visualizaciones de datos.

Los estudiantes fueron introducidos a las medidas de centro (media y mediana) y las medidas de variabilidad (desviación media absoluta y rango intercuartílico) en los grados 6-8. La comprensión de la desviación media absoluta (DMA) y el rango intercuartílico (IQR, por sus siglas en inglés) es una parte importante de esta unidad. La comprensión de la desviación media absoluta (DMA) proporciona una base para la desviación estándar, que es una medida de variabilidad más ampliamente utilizada que se introduce en esta unidad.

Las primeras cinco lecciones de la unidad dan a los estudiantes la oportunidad de revisar ideas de la escuela media mientras profundizan un poco más en el análisis de las visualizaciones de datos. Las lecciones se basan en la comprensión de los estudiantes adquirida en los grados de la escuela media de la variabilidad estadística, la capacidad de describir las distribuciones, y la comparación informal de las distribuciones. Representan e interpretan los datos con representaciones de datos como diagramas de puntos, histogramas y diagramas de cajas. Describen distribuciones con la terminología apropiada como: simétrica, sesgada, uniforme, bimodal y en forma de campana. Crean visualizaciones de datos y calculan estadísticas de resumen con la tecnología, y luego interpretan los valores en su contexto. Reconocen la relación entre la forma de una distribución y la media y la mediana. Comparan conjuntos de datos con diferentes medidas de variabilidad e interpretan conjuntos de datos con mayores DMA o rangos intercuartílicos como si tuvieran mayor variabilidad.

En la edición digital para maestros se incluyen tres lecciones opcionales que pueden utilizarse después de la lección 5 para familiarizar a los estudiantes con las hojas de cálculo y la tecnología que se utilizarán para calcular estadísticas como la media, la mediana, los cuartiles y la desviación estándar, así como para crear visualizaciones de datos. La familiaridad adquirida con la tecnología continuará ayudando a los estudiantes a lo largo de las próximas unidades, ya que utilizan las herramientas para explorar estructuras algebraicas y funciones a lo largo de este curso.

Las hojas de cálculo de Geogebra fueron elegidas por su versatilidad para las matemáticas de nivel en este curso. Aunque otros programas de hojas de cálculo tienen funcionalidades y usos adicionales, están limitados en otros aspectos (como la creación de histogramas, diagramas de puntos o de cajas y el cálculo correcto de cuartiles). Dicho esto, adapte los materiales a las necesidades de sus estudiantes si utiliza estas lecciones opcionales.

En la lección 6, los estudiantes crean e interpretan representaciones de datos como histogramas, diagramas de puntos y diagramas de caja, además de calcular e interpretar medidas de centro (media y mediana) y medidas de variabilidad (rango intercuartílico y desviación media absoluta). Dado que la mayoría de estos conceptos se refieren a ideas de la escuela media, esta unidad no incluye una evaluación intermedia. Los maestros pueden utilizar la información obtenida de los ejercicios de enfriamiento y los problemas de práctica para evaluar informalmente la comprensión de estos conceptos por parte de los estudiantes antes de continuar con las lecciones restantes de la unidad.

Las lecciones 7 a 12 exploran la desviación estándar, los valores atípicos y la comparación de conjuntos de datos con medidas de centro y medidas de variabilidad. Aprenden que la desviación estándar es una medida de variabilidad e interpretan la desviación estándar en contexto. (Obsérvese que esta unidad solo incluye la desviación estándar de la población. La desviació estándar basada en una muestra aparece en una unidad de cursos posteriores). Reconocen los valores atípicos, investigan su origen, toman decisiones sobre su exclusión del conjunto de datos y comprenden cómo la presencia de valores atípicos afecta a las medidas de centro y a las medidas de variabilidad. Comparan las medidas del centro y la desviación estándar y el rango intercuartílico para diferentes conjuntos de datos.

La última lección ofrece a los estudiantes la oportunidad de practicar sus habilidades recopilando datos y analizando los valores. En la actividad culminante, los estudiantes plantean y responden a una pregunta estadística con el diseño de un experimento, la recopilación de datos y el análisis de los datos.

IDEAS FUNDAMENTALES Y ESTÁNDARES

Enfoque en ideas fundamentales

• Investigar datos

ESTÁNDARES POR LECCIÓN

Lección

A1.1.1

Estándar(es) abordado(s)

Prerrequisito para S-ID.1

A1.1.2 S-ID.1

A1.1.3 S-ID.1

A1.1.4 S-ID.1

A1.1.5

Prerrequisito para S-ID.1, S-ID.2

A1.1.6 S-ID.1, S-ID.2

A1.1.7

S-ID.1, S-ID.2, S-ID.3

A1.1.8 S-ID.2

A1.1.9 S-ID.2, S-ID.3

A1.1.10 S-ID.2

A1.1.11 S-ID.2, S-ID.3

A1.1.12 S-ID.1, S-ID.2

A1.1.13

S-ID.1, S-ID.2, S-ID.3

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Alineación de estándares y principios de California

Construir

S-ID.1 Representar datos con gráficas en la recta numérica real ( diagramas de puntos, histogramas y diagramas de cajas).

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su solución.

MP2 Razonar abstracta y cuantitativamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.1

I.A.4

I.B.7

LECCIÓN 1

CONOCERTE

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

comprender al mundo, razonarán abstracta y cuantitativamente analizan los datos.

OBJETIVO(S) DE APRENDIZAJE

• Distingo las preguntas estadísticas de las que no lo son y puedo explicar la diferencia.

• Distingo los datos numéricos de los categóricos.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente y por escrito) la diferencia entre preguntas estadísticas y no estadísticas.

• Describir (oralmente y por escrito) las distinciones entre datos numéricos y categóricos.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

¿Cuál no pertenece?

MLR2: Recopilar y mostrar

Preparación necesaria

Al final de la actividad Representar datos sobre ti y tus compañeros de clase, los estudiantes deberán guardar sus datos para utilizarlos en una lección posterior en la que los estudiantes representarán gráficamente los datos recogidos en esta actividad. Si registran los datos en cuadernos de trabajo, será fácil recuperarlos más tarde. Si los estudiantes registran los datos de otra forma, asegúrese de que su método les permite recuperarlos fácilmente más tarde.

INFORMACIÓN DE LA LECCIÓN

Metas de aprendizaje para el estudiante

• Trabajemos juntos para recolectar datos y explorar preguntas estadísticas.

Narrativa de la lección

El propósito matemático de esta lección es entender qué hace que una pregunta sea estadística y clasificar los datos como numéricos o categóricos. Esta unidad comienza con la creación de visualizaciones de datos y la descripción de distribuciones de datos numéricos. Más adelante en el curso, los estudiantes crean e interpretan tablas de dos vías utilizando datos categóricos Los datos numéricos son respuestas a preguntas que son números que pueden ordenarse de forma natural. Los datos categóricos son respuestas a preguntas que se ajustan a categorías distintas.

Los estudiantes aprenden a reconocer las preguntas estadísticas como preguntas que anticipan la variabilidad en los datos. En esta lección, los estudiantes recuerdan el concepto de variabilidad para discutir la diferencia entre preguntas estadísticas y no estadísticas mientras recogen datos de encuestas de sus compañeros. (Los datos se volverán a utilizar en lecciones posteriores, por lo que deben guardarse en una hoja de cálculo o en una carpeta). Los estudiantes clasifican las preguntas como estadísticas o no estadísticas y clasifican los datos que recogen de las preguntas estadísticas como numéricos o categóricos.

Cuando los estudiantes identifican los datos resultantes de una pregunta estadística como numéricos o categóricos, están participando en el MP2 porque tienen que dar sentido a los datos en relación con la pregunta formulada. Los estudiantes también pasan de un lenguaje informal a otro más preciso, MP6, para varios términos de vocabulario que se utilizarán a lo largo de la unidad.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Descripción breve

Calentamiento En parejas o grupos pequeños 5 min Los estudiantes hacen observaciones sobre preguntas estadísticas y luego explican cuál no pertenece.

Actividad de exploración Grupos pequeños 25 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Los estudiantes recogen respuestas para preguntas de encuesta estadísticas, no estadísticas, categóricas y numéricas.

Hay una extensión de exploración disponible para identificar ejemplos adicionales de preguntas estadísticas en artículos de noticias.

Los estudiantes discuten ejemplos de preguntas estadísticas y no estadísticas y después clasifican los tipos de datos recogidos de cada tipo.

Los estudiantes clasifican y explican si cada pregunta es estadística o no estadística. Si es estadística, determinan si se requieren datos numéricos o categóricos para responderla.

Práctica Independiente 5-8 min El componente de práctica independiente incluye 3 problemas de la lección.

CALENTAMIENTO | CUÁL NO PERTENECE: TIPOS

DE DATOS

(5 minutos)

Rutinas didácticas

¿Cuál no pertenece?

Esta es la primera rutina del curso «¿Cuál no pertenece?«. En esta rutina, se presentan a los estudiantes cuatro figuras, diagramas, gráficos o expresiones con la pregunta «¿Cuál no pertenece?«. Normalmente, cada una de las cuatro opciones de «no pertenece« por una razón diferente, y las similitudes y diferencias son matemáticamente significativas. Se pide a los estiantes que expliquen los motivos por los que han decidido que una opción no pertenece y se les da la oportunidad de precisar sus razones.

En este ejercicio de calentamiento se pide a los estudiantes que comparen cuatro preguntas de una encuesta. Esto le da a los estudiantes una razón para utilizar el lenguaje con precisión (MP6) y le da a usted la oportunidad de escuchar cómo utilizan la terminología y hablan de las características de los artículos en comparación unos con otros.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2-4. Muestra las preguntas de la encuesta para que todos las vean. Concede a los estudiantes 1 un minuto de reflexión en silencio y, a continuación, tiempo para compartir sus ideas con su pequeño grupo. En sus pequeños grupos, diga a cada estudiante que comparta su razonamiento de por qué un artículo en particular no pertenece y que juntos encuentren al menos una razón por la que cada artículo no pertenece.

¿Cuál no pertenece?

Pregunta A: ¿Cuántas papas fritas hay en esta bolsa de papas fritas?

Pregunta B: ¿Cuál es el número típico de papas fritas en una bolsa de papas fritas?

Pregunta C: ¿Qué tipo de papas fritas son estas?

Pregunta D: ¿Qué tipo de papas fritas prefieren los estudiantes de esta clase?

Ejemplos de respuestas:

La pregunta A no pertenece porque...

• solo hay una respuesta correcta a la pregunta y es numérica

La pregunta B no corresponde porque...

• esta es una pregunta estadística y requeriría datsos numéricos para responderla

• necesitaría recopilar datos y encontrar una medida de centro para responder a esta pregunta

RESPUESTAS POSIBLES

La pregunta C no corresponde porque...

• esta no es una pregunta estadística y requeriría datos categóricos para responderla.

• solo hay una respuesta correcta que no es numérica

La pregunta D no pertenece porque...

• esta es una pregunta estadística y requeriría datos categóricos para responderla

• esta pregunta podría responderse cuando observo la respuesta que se repite con más frecuencia en los datos

SÍNTESIS DE LA ACTIVIDAD

Pida a cada grupo que comparta una razón por la que un elemento en particular no pertenece. Registre y muestre las respuestas para que todos las vean. Después de cada respuesta, pregunte a la clase si están de acuerdo o en desacuerdo. Dado que no hay una única respuesta correcta a la pregunta de cuál no pertenece, atienda a las explicaciones de los estudiantes y asegúrase de que las razones dadas son correctas. Durante el debate, pida a los estudiantes que expliquen el significado de cualquier terminología que utilicen, como datos numéricos, datos categóricos o promedio. Asimismo, debata con los estudiantes sobre las afirmaciones sin fundamento.

ACTIVIDAD DE EXPLORACIÓN | REPRESENTAR DATOS

SOBRE TI Y TUS COMPAÑEROS

(25 minutos)

Rutinas didácticas

MLR2: Recopilar y mostrar

En esta actividad, a cada grupo de 4 estudiantes se le asignan tres preguntas. Una de las tres que se les asignan es una pregunta no estadística, otra generaría datos numéricos y otra datos categóricos. Los grupos también generan una cuarta pregunta propia que puede responderse con datos. En primer lugar, el grupo elabora cuatro preguntas de encuesta que pueden plantear a sus compañeros para recopilar datos sobre sus cuatro preguntas de interés. A continuación, recopilan datos de sus compañeros cono las pregunta formuladas de la encuesta. Por último, resumen sus resultados para responder a las cuatro preguntas de interés y reflexionan sobre la naturaleza de las diferentes preguntas que intentaron responder.

En una lección posterior, los estudiantes representarán gráficamente la distribución de los datos recogidos en esta actividad. Si registran los datos en sus cuadernos, será fácil recuperarlos más tarde. Si los estudiantes registran los datos de alguna otra manera, asegúrese de que su método les permita recuperarlos fácilmente más tarde.

Organice a los estudiantes en grupos de 4. Asigne a cada grupo uno de los siguientes conjuntos de tres preguntas.

Conjunto A

1. En promedio, ¿cuántas letras tienen los apellidos de los estudiantes de esta clase?

2. ¿En qué mes hay más cumpleaños de la clase?

3. ¿Cuántos períodos (o bloques) ha habido antes de esta clase de Matemáticas?

Conjunto B

1. En promedio, ¿cuál es la mayor distancia, en millas, que cada estudiante de esta clase ha estado de casa?

2. ¿Preferiría la clase tener un día de nieve o un día de excursión?

3. ¿En qué año se ratificó la 13.ª enmienda?

Conjunto C

1. ¿Cuánto tardaron aproximadamente los estudiantes de esta clase en llegar a la escuela esta mañana?

INTRODUCCIÓN

2. ¿Qué combinación prefiere la clase: mantequilla de cacahuete y plátano o fresa y plátano?

3. ¿Cuál es el elemento más ligero de la tabla periódica?

Set D

1. En promedio, ¿cuántas películas en el cine ha visto cada estudiante de la clase este verano?

2. ¿Prefiere la clase escribir en papel con o sin renglones?

3. ¿Cuántos asientos hay en el aula

Dé a los estudiantes 2 minutos para que escriban una pregunta propia que pueda responderse con los datos de la clase. Después de dar tiempo a los estudiantes para que discutan las preguntas en sus grupos, haga una pausa para debatir con todo el grupo.

Dé a los estudiantes un ejemplo de los tipos de preguntas que deberían hacer a sus compañeros. Por ejemplo, si se les asigna la pregunta: «¿En qué mes hay más cumpleaños de la clase?«, podrían preguntar a sus compañeros: «¿En qué mes es tu cumpleaños?«..

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: MLR 2 Recopilar y mostrar. Mientras los grupos trabajan, camine y escuche a los estudiantes hablar sobre las similitudes y diferencias entre los tipos de datos recogidos. Anote las frases comunes o importantes que escuche decir a los estudiantes sobre cada tipo en una pantalla visual (por ejemplo: «todos estos son números« o «esto solo tiene una respuesta«). Recopile las respuestas en una pantalla visual. A lo largo del resto de la lección, siga actualizando el lenguaje recogido de los estudiantesy recuérdeles que tomen prestado el lenguaje de la pantalla cuando sea necesario. En la síntesis de la lección, una vez introducidos los términos «datos numéricos« y «datos categóricos«, pida a los estudiantes que clasifiquen el lenguaje recogido en dos grupos, uno para cada tipo de datos.

Principio(s) de diseño: Apoyar la creación de sentido; maximizar la metaconciencia.

Apoyo para estudiantes con discapacidad

Representación: Acceso para la percepción. Lee todas las preguntas en voz alta. Los estudiantes que escuchen y lean a la vez la información se beneficiarán de un tiempo de procesamiento adicional.

Apoya la accesibilidad para: Lenguaje

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Tu maestro te asignará un conjunto de 3 preguntas.

• Escribe otra pregunta propia que requiera datos recopilados de la clase para responderla.

• Para cada una de las 4 preguntas, escribe una pregunta de encuesta que te ayude a recopilar datos de la clase que puedan analizarse para responder a la pregunta.

• Haz las 4 preguntas de encuesta a 15 compañeros de clase y registra sus respuestas para recopilar datos.

• Después de recopilar los datos, vuelve a tu grupo.

1. ¿Cuál es la pregunta propia que requerirá datos recopilados de la clase para responder?

2. ¿Cuáles son las 4 preguntas de la encuesta que harás a tus compañeros de clase?

3. Resume los datos de cada pregunta en una o dos frases y comparte los resultados con tu grupo.

4. Con tu grupo, decide qué tienen en común las respuestas de la pregunta número 1. Luego haz lo mismo para las preguntas numeradas 2 y 3

5. ¿Encaja mejor la pregunta que escribiste con las preguntas del número 1, 2 o 3? Explica tu razonamiento.

Nombre de la persona que responde

Respuesta de la pregunta 1

Respuesta de la pregunta 2

Respuesta de la pregunta 3

Respuesta de mi pregunta

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES

Nombre de la persona que responde

Respuesta de la pregunta 1

Respuesta de la pregunta 2

Respuesta de la pregunta 3

Respuesta de mi pregunta

CONCEPTOS ERRÓNEOS PREVISTOS

Ejemplos de respuestas:

1. ¿Cuál es el color favorito más popular entre los estudiantes de esta clase?

2. ¿Cuántas letras tiene su apellido? ¿En qué mes naciste? ¿Cuántos períodos precedieron a esta clase? ¿Cuál es tu color favorito?

3. Los estudiantes de esta clase suelen tener unas cinco o seis letras en su apellido. Febrero es el mes de nacimiento más popular entre los estudiantes de esta clase. Ha habido dos períodos antes de esta clase. El rojo es el color favorito más popular de la clase.

4. Las preguntas del grupo 1 se responden con números y pueden tener diferentes respuestas de diferentes personas. Las preguntas del grupo 2 se responden con palabras o frases y pueden tener diferentes respuestas de diferentes personas. Las preguntas del grupo 3 tienen una única respuesta correcta (aunque la mayoría de las personas no sabían las respuestas).

5. La pregunta: «¿Cuál es el color favorito más popular entre los estudiantes de esta clase?« encaja mejor con las preguntas del grupo 2, ya que hay una variedad de respuestas que se pueden clasificar en categorías, pero que no están relacionadas con números.

Los estudiantes pueden confundir las preguntas estadísticas con las preguntas de una encuesta. Explique que el conjunto de tres preguntas son preguntas estadísticas que pueden responderse con las preguntas de la encuesta. Por ejemplo, los estudiantes pueden pensar que deben preguntar a cada uno de sus compañeros por la distancia promedio que han recorrido desde su casa. Sin embargo, los estudiantes pueden preguntar a cada compañero: «¿Cuál es la distancia más lejana que has recorrido desde casa?« y utilizar colectivamente las respuestas a esta pregunta de la encuesta para responder a la pregunta estadística sobre la distancia promedio que sus compañeros han recorrido desde casa.

SÍNTESIS DE LA ACTIVIDAD

Comparta todas las preguntas con el número 1 de cada conjunto. Pida a los estudiantes que resuman qué tienen en común las respuestas a estas preguntas. (Para responderlas, recopile respuestas que son números).

Repita la operación con las preguntas de los números 2 y 3. (Para responder las preguntas del número 2, se recopilan respuestas que sean palabras descriptivas o características. Las preguntas del número 3 solo tienen una respuesta posible y no tienen ninguna variabilidad en las respuestas).

Diga a los estudiantes que llamamos a los datos recopilados por las preguntas del número 1, datos numéricos, a los datos recopilados por las preguntas del número 2, datos categóricos, y las preguntas del número 3 son preguntas no estadísticas porque no habrá variabilidad en las respuestas. Las preguntas de los números 1 y 2 se denominan preguntas estadísticas ya que requieren la recopilación de datos y se prevé que haya variabilidad en las respuestas.

¿Estás listo para más?

1. Encuentra un artículo de noticias que utilice datos numéricos para hablar sobre una pregunta estadística.

2. Encuentra un artículo de noticias que utilice datos categóricos para hablar sobre una pregunta estadística.

Respuesta del estudiante

Las respuestas varían.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Para promover la comprensión de los estudiantes de las diferencias entre preguntas estadísticas y no estadísticas y la clasificación de datos como numéricos o categóricos, pregunte:

• «¿Qué hace que una pregunta sea estadística?«. (Hay variabilidad en los datos recogidos).

• «¿Cuál es un ejemplo de una pregunta no estadística?«. (¿Qué valor de x hace que la ecuación x + 5 = 7 sea cierta?).

• «¿Cuál es un ejemplo de pregunta estadística que no hemos utilizado en clase?«. (En promedio, ¿cuántas personas desayunan cada día?).

• «¿Qué tipo de datos se recogen para responder a la pregunta estadística: ¿Prefiere la clase pizza o rosquillas?«. (Categórica).

• «¿Cuál es un ejemplo de una pregunta estadística que da como resultado datos numéricos?« (¿Cuál es la superficie estándar de las gránulos de poliestireno?)

Para ayudar a preparar a los estudiantes para la siguiente lección, pregunte:

• «¿Cuáles son algunas formas diferentes de representar datos gráficamente?« (Gráficos de barras, diagramas de puntos, diagramas de cajas, gráficos circulares e histogramas).

ENFRIAMIENTO | CATEGORIZAR PREGUNTAS

(5 minutos)

Clasifique cada una de estas preguntas como uno de estos tipos y, a continuación, explique su razonamiento para colocar la pregunta en esa categoría.

• Pregunta estadística que requiere datos numéricos para responderla

• Pregunta estadística que requiere datos categóricos para responderla

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

• Pregunta no estadística

1. En promedio, ¿cuántos libros lee cada persona en los Estados Unidos cada año?

2. ¿Cuántos actos tiene la obra Romeo y Julieta?

3. ¿Qué libro fue el más leído por los estudiantes de la clase este verano?

4. ¿Cuántos libros hay en el aula en este momento?

RESPUESTAS POSIBLES

1. Pregunta estadística que requiere datos numéricos para responderla. Los datos serán números y tendrán cierta variabilidad.

2. Pregunta no estadística, ya que hay una respuesta correcta a la pregunta.

3. Pregunta estadística que requiere datos categóricos para responderla. Los datos serán palabras o frases y tendrán cierta variabilidad.

4. Pregunta no estadística, ya que hay una respuesta correcta a la pregunta.

Resumen de la lección para el estudiante

La estadística consiste en utilizar datos para resolver problemas o tomar decisiones. Hay dos tipos de datos:

• Los datos numéricos se expresan mediante un número. Por ejemplo, para responder a la pregunta: «¿Cuánto miden los estudiantes de esta clase?« se mediría la altura de cada estudiante, lo que daría como resultado datos numéricos.

• Los datos categóricos se expresan con características. Por ejemplo, para responder a la pregunta: «¿Qué marca de teléfonos utiliza la gente?« se haría una encuesta a varias personas y sus respuestas darían lugar a datos categóricos.

La pregunta que se formula determina el tipo de datos que se recogen y si hay o no variabilidad en los datos recogidos. En cursos anteriores, aprendiste que hay variabilidad en un conjunto de datos si no todos los valores del conjunto de datos son iguales. Estos son ejemplos de preguntas estadísticas porque se responden mediante la recopilación de datos que tienen variabilidad:

• «¿Cuál es el tamaño promedio de la clase en esta escuela?« produciría datos numéricos con cierta variabilidad.

• «¿Cuáles son los colores favoritos de los estudiantes en esta clase?« producirí datos categóricos con cierta variabilidad. Estos son ejemplos de preguntas no estadísticas porque se responden cuando recopilas datos que no varían:

• «¿Cuántos estudiamtes hay en la lista de esta clase?« produciría datos numéricos que no varían. solo hay un valor en el conjunto de datos, por lo que no hay variabilidad.

• «¿De qué color es este marcador?« produciría datos categóricos que no varían. solo hay un valor en el conjunto de datos, por lo que no hay variabilidad..

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Escriba una pregunta de encuesta para la que esperaría recoger datos numéricos..

Soluciones posibles

Ejemplo de respuesta: ¿Cuántos pasos suelo dar al día?

PROBLEMA 2

Escriba una pregunta de encuesta para la que espere recoger datos categóricos.

Soluciones posibles

Ejemplo de respuesta: ¿Cuáles son los equipos deportivos más populares para las personas que cursan noveno grado en mi escuela?

PROBLEMA 3

Seleccione todas las preguntas estadísticas.

¿Cuál es la cantidad estándar de lluvia para el mes de junio en las Islas Galápagos?

¿Cuánto llovió ayer en el Aeropuerto Internacional de la Ciudad de México?

¿Por qué te gusta escuchar música?

¿Cuántas canciones suele escuchar la clase cada día?

¿Cuántas canciones has escuchado hoy?

¿Cuál es la capital de Canadá?

¿Cuánto tiempo suelen tardar los estudiantes de 2.º de primaria en dar una vuelta a la pista?

Soluciones posibles

¿Cuál es la cantidad estándar de lluvia para el mes de junio en las Islas Galápagos?

¿Cuánto llovió ayer en el Aeropuerto Internacional de la Ciudad de México?

¿Por qué te gusta escuchar música?

¿Cuántas canciones suele escuchar la clase cada día?

¿Cuántas canciones has escuchado hoy?

¿Cuál es la capital de Canadá?

¿Cuánto tiempo suelen tardar los estudiantes de 2.º de primaria en dar una vuelta a la pista?

Reflexiones:

Math Nation California . Algebra 1

Álgebra 1 . Matemáticas . Unidad 1

LECCIÓN 2

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

S-ID.1 Representar datos con gráficas en la recta numérica real (gráficas de puntos, histogramas y diagramas de caja).

Construir

S-ID.2

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.3

I.C.12

II.C.6

REPRESENTACIONES DE DATOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES

INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

comprender al mundo, buscan y utilizan la estructura

OBJETIVO(S) DE APRENDIZAJE

analizan los datos y descubren la figura y el espacio.

• Puedo encontrar el resumen de cinco números para los datos.

• Puedo utilizar un diagrama de puntos, un histograma o un diagrama de cajas para representar datos.

OBJETIVOS

APRENDIZAJE PARA EL MAESTRO

• Crear un diagrama de puntos, un histograma y un diagrama de cajas para representar datos numéricos.

• Identificar (por escrito) el resumen de cinco números que describe unos datos estadísticos dados.

• Interpretar un diagrama de cajas que representa un conjunto de datos.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse (Calentamiento)

MLR2: Recopilar y mostrar (Actividad 1)

INFORMACIÓN DE LA LECCIÓN

Metas de aprendizaje para el estudiante

• Representemos y analicemos datos con gráficas de puntos, histogramas y diagrama de cajas.

Narrativa de la lección

Esta lección es opcional porque revisa contenidos por debajo del nivel de grado. Si la evaluación de diagnóstico previa a la unidad indica que sus estudiantes conocen bien las representaciones, esta lección puede omitirse sin problemas.

Álgebra 1 . Matemáticas . Unidad 1

En 6.º grado, los estudiantes representaron datos numéricos en gráficas sobre una recta numérica, las cuales incluían gráficas de puntos, histogramas y diagrama de cajas. Esta lección sirve como un breve repaso del significado de estas representaciones y cómo se crean.

En esta lección, los estudiantes representan datos con histogramas y diagrama de cajas. Calculan valores para el resumen de cinco números y usan esos valores para crear gráficas de puntos. Los estudiantes también crearán dos histogramas diferentes que representen el mismo conjunto de datos con diferentes intervalos en cada uno de los histogramas. Los estudiantes también compararán un diagrama de puntos, un diagrama de cajas y un histograma que representen el mismo conjunto de datos. Cuando los estudiantes identifican la información mostrada por diferentes representaciones gráficas, construyen su conocimiento acerca cuándo utilizar las herramientas apropiadas para que puedan tomar decisiones sobre cómo representar los datos.

Los estudiantes hacen uso de la estructura (MP7) para conectar representaciones visuales de conjuntos de datos y razonan abstracta y cuantitativamente (MP2) con la interpretación de los valores en los contextos dados

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento En parejas 5 min

Actividad de exploración (opcional)

En parejas 15 min

Actividad de exploración (opcional) En parejas 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 10 min

Descripción breve

Los estudiantes hacen observaciones sobre tres presentaciones de datos diferentes y luego hablan de lo que observan y se preguntan..

Los estudiantes crean y comparan dos histogramas que tienen diferentes intervalos para el mismo conjunto de datos.

Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de cómo los rangos de intervalo afectan la forma de la distribución.

Los estudiantes determinan el resumen de cinco números para un conjunto de datos y luego crean una gráfica de caja.

Los estudiantes comparan las fortalezas y debilidades de diferentes visualizaciones de datos, tales como gráficas de puntos, histogramas y diagrama de cajas.

Los estudiantes identifican qué información es fácil de determinar a partir de diferentes representaciones de datos.

El componente de práctica independiente incluye 4 problemas de la lección y 1 problema de repaso en espiral.

Nation California . Algebra 1

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE: DURACIÓN DE LA BATERÍA

(5 minutos)

Rutinas didácticas

Observar y preguntarse

Esta es la primera actividad de «Observar y preguntarse» del curso. Se muestran a los estudiantes tres pantallas estadísticas que representan el mismo conjunto de datos .Las preguntas para los estudiantes deben ser: «¿Qué observas? ¿Qué te preguntas?». Se le debe dar a los estudiantes unos minutos para escribir las cosas que observan y las cosas que se preguntan. Después de que los estudiantes hayan tenido la oportunidad de escribir sus respuestas, pida a varios estudiantes que compartan las cosas que observaron y las cosas que se preguntaron; regístrelas para que todos las vean. A menudo, el objetivo es dirigir la conversación hacia las preguntas sobre algo matemático en lo que la clase está a punto de centrarse. El propósito es hacer que una tarea matemática sea accesible a todos los estudiantes con estas dos preguntas abordables. Al pensar en ellas y responder, los estudiantes se introducen en el contexto y puede que despierten su curiosidad.

El objetivo de este calentamiento es provocar la idea de que los mismos datos pueden mostrarse de diferentes maneras, lo que será útil cuando los estudiantes creen diferentes visualizaciones de datos en una actividad posterior. Aunque los estudiantes pueden observar y preguntarse muchas cosas sobre estas imágenes, la comparación de las tres representaciones y la interpretación de la información en cada representación son los puntos de discusión importantes.

Este estímulo da a los estudiantes la oportunidad de ver y hacer uso de la estructura (MP7). En concreto, podrían utilizar la estructura de las tres representaciones, en particular la estructura de la recta numérica horizontal, para encontrar similitudes importantes desde el punto de vista matemático en la forma en que se representa el mismo conjunto de datos.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Muestre las imágenes para que todos las vean. Pida a los estudiantes que piensen en al menos una cosa que obsevaron y en una pregunta que tengan. Dé a los estudiantes 1 minuto de tiempo para pensar en silencio y luego 1 minuto para hablar de las cosas que observan y se preguntan con su compañero, seguido de una discusión con toda la clase.

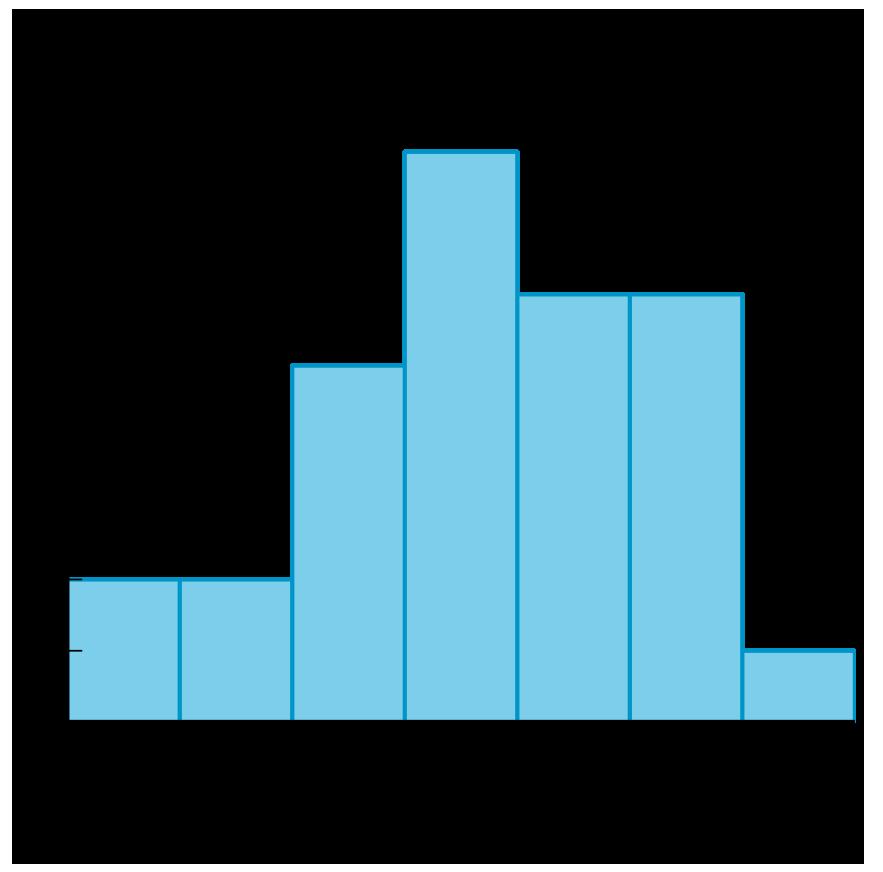
El diagrama de puntos, el histograma y el diagrama de cajas resumen las horas de duración de la batería de 26 los teléfonos móviles que transmiten video constantemente. ¿Qué observas? ¿Qué te preguntas?

7 8 Vida de la batería en horas

RESPUESTAS POSIBLE CONTINUACIÓN

1 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

Cosas que los estudiantes pueden preguntarse:

• Están incluida las 3 horas de duración de la batería en la segunda barra del histograma o en la primera barra?

• ¿Por qué el histograma tiene intervalos de 1 en lugar de 2?

• ¿Cómo se crea un diagrama de caja a partir de los datos?

Pida a los estudiantes que compartan las cosas que observaron y se preguntaron. Registre y muestre sus respuestas para que todos las vean. Si es posible, registre el razonamiento pertinente en la imagen o cerca de ella. Una vez registradas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre algo que te preguntas?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria. El objetivo es ayudar a los estudiantes a recordar diferentes formas de representar distribuciones de datos. Destaque las similitudes entre el diagrama de puntos y el histograma. Diga a los estudiantes que la barra más alta en el histograma se crea con los dos valores de datos en 5 y los seis valores de datos en 5 5 en la gráfica de puntos, y que la barra final se crea con los dos valores de datos en 6 y los dos valores de datos en 6 5 en la gráfica de puntos. Si el tiempo lo permite, haga preguntas como:

• «¿Qué representación(es) muestra(n) todos los valores de los datos?». (El diagrama de puntos muestra todos los valores de los datos).

• «¿Cómo se crea un diagrama de cajas?». (Se calculan los valores del resumen de cinco números y luego se grafican en una recta numérica. El primer cuartil, la mediana y el tercer cuartil se usan para la caja, y el valor mínimo y el valor máximo se usan para los bigotes).

ACTIVIDAD

DE EXPLORACIÓN

OPCIONAL | PLANTAS DE TOMATE: HISTOGRAMA

(15 minutos)

Rutinas didácticas

MLR2: Recopilar y mostrar

El propósito matemático de esta actividad es representar y analizar datos con histogramas. Los estudiantes crearán dos histogramas diferentes a partir del mismo conjunto de datos organizando los datos en diferentes intervalos.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: MLR2 Recopilar y mostrar. Mientras los grupos trabajan, camine y escuche a los estudiantes hablar sobre las similitudes y diferencias entre los tipos de datos recogidos. Anote las frases comunes o importantes que escuche decir a los estudiantes sobre cada tipo en una pantalla visual. Por ejemplo: «todos estos son números» o «esto solo tiene una respuesta». Recoja las respuestas en una pantalla visual. A lo largo del resto de la lección, actualice el lenguaje recopilado de los estudiantes y recuérdeles que tomen prestado el lenguaje de la visualización según sea necesario. En la síntesis de la lección, una vez introducidos los términos «datos numérico» y «datos categóricos», pida a los estudiantes que clasifiquen el lenguaje recogido en dos grupos, uno para cada tipo de datos. Esto ayudará a los estudiantes a organizar los datos a lo largo de la unidad.

Principio(s) de diseño: Apoyar la creación de sentido; maximizar la metaconciencia

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Proporcionar a los estudiantes una cuadrícula o papel cuadriculado para organizar sus dos histogramas con diferente anchura de intervalos.

Apoya la accesibilidad para: Lenguaje; organización

Un histograma puede utilizarse para representar la distribución de datos numéricos.

1. Los datos representan la cantidad de días que tardan las diferentes plantas de tomate en producir tomates. Utiliza la información para completar la tabla de frecuencias.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

2. Utiliza el conjunto de ejes y la información de tu tabla para crear un histograma.

Día para producir fruto

3. El histograma que has creado tiene intervalos de anchura 10 (como 40-50 y 5060). Utiliza el conjunto de ejes y datos para crear otro histograma con un intervalo de anchura 5. ¿En qué se diferencia este histograma del otro?

Día para producir fruto

Álgebra 1 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

3. Ejemplo de respuesta: Este histograma tiene más barras con alturas más cortas. Muestra un poco más de detalle de la forma de la distribución que el histograma con intervalos más grandes.

Los estudiantes pueden tener dificultades para saber cómo colocar los números que se encuentran en el límite entre intervalos. Por ejemplo, es posible que los estudiantes no sepan si un valor como 60 debe incluirse en el intervalo 50-60 o 60-70. Explique a los estudiantes que el valor del límite inferior se incluye en el intervalo y el valor del límite superior no. Por ejemplo, el intervalo 60-70 incluye todos los valores que son mayores o iguales que 60 y menores que 70.

SÍNTESIS DE LA ACTIVIDAD

¿Estás preparado para más?

El propósito de este debate es asegurarse de que los estudiantes saben cómo crear y empezar a interpretar histogramas. He aquí algunas preguntas para la discusión.

• «¿Dónde pusiste el 60? ¿En el intervalo 50-60 o 60-70?». (Diga a los estudiantes que utilizamos la convención de incluir el 60 en el intervalo 60-70. El intervalo 60-70 significa todos los valores mayores o iguales que 60, pero menores que 70. El intervalo 50-60 significa todos los valores mayores o iguales que 50, pero menores que 60).

• «¿Qué información se ve fácilmente en el histograma». (La forma de la distribución, así como estimaciones para la medida del centro y la medida de la variabilidad).

• «Según cada histograma, ¿cuál parece ser el número típico de días que tarda una tomatera en producir tomates?». (Parece que el número típico de días está entre 60 y 80 en el primer histograma. En el segundo histograma, parece que el número típico de días podría estar entre 75 y 80).

• «¿Qué información no se ve en el histograma». (No puedes ver los valores reales. Solo conoces el número de valores dentro de un intervalo y no los valores en sí).

A menudo es necesario jugar un poco con las longitudes de los intervalos para averiguar cuál da la mejor idea de la forma de la distribución.

1. ¿Cuál podría ser el problema de utilizar longitudes de intervalo demasiado grandes?

2. ¿Cuál podría ser el problema de utilizar longitudes de intervalo demasiado pequeñas?

3. ¿Qué otras consideraciones se pueden tener en cuenta a la hora de elegir la longitud de un intervalo?

Respuesta del estudiante

1. Ejemplo de respuesta: Si las longitudes de los intervalos son demasiado grandes, acabaremos teniendo muy pocos intervalos y podrían perderse características importantes dentro de un intervalo. En el caso más extremo, acabaríamos con un único intervalo que lo incluiría todo, lo que no sería muy útil.

2. Ejemplo de respuesta: Si las longitudes de los intervalos son demasiado pequeñas, terminamos con un histograma que es esencialmente lo mismo que un diagrama de puntos. En algunos casos, esto podría ser útil, pero en situaciones en las que cada valor de datos ocurre solo una o dos veces, cada barra tendrá la misma altura no permitiéndonos obtener un buen sentido de la forma de la distribución.

3. Ejemplo de respuesta: Puede haber longitudes de intervalo naturales basadas en el contexto (como 10 décadas de años, rangos de edad comunes o 100 longitudes de yardas). Hay longitudes de intervalo comunes que la gente espera, como 1, 2, 5, 10, 50, 100, etc. Normalmente no tiene sentido tener menos de 5 barras o más de 50 barras en el histograma.

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | PLANTAS DE

TOMATE: DIAGRAMA DE CAJAS

(10 minutos)

El propósito matemático de esta actividad es representar la distribución de datos en la recta numérica real con un diagrama de cajas y ayudar a los estudiantes a pensar informalmente sobre la mediana como medida del centro. Los estudiantes calculan los valores del resumen de cinco números y crean un diagrama de caja. La mediana, los cuartiles y los valores extremos dividen el conjunto de datos en cuatro intervalos con aproximadamente el mismo número de valores de datos en cada uno. Los estudiantes participan en el MP2 cuando interpretan estos valores en el contexto dado. Aunque estos intervalos se denominan a menudo «cuartiles», en estos materiales se utiliza el término «cuartos» para evitar confusiones con los valores de los cuartiles Q1 y Q3.

INTRODUCCIÓN

Mantenga a los estudiantes en grupos de 2. Dé a los estudiantes 5 minutos para trabajar las preguntas. Pídales que comparen sus respuestas con las de su compañero después de cada pregunta.

Álgebra 1 . Matemáticas . Unidad 1

Apoyo para los estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Para apoyar el desarrollo de habilidades organizativas en la resolución de problemas, divida esta tarea en partes más manejables. Por ejemplo, indique a los estudiantes que hagan referencia a sus datos secuenciales, dividan los datos en cuartos y, a continuación, encuentren la mediana, Q1 y Q3.

Apoya la accesibilidad para: Memoria; organización

También se puede utilizar un diagrama de cajas para representar la distribución de datos numéricos.

Mínimo Q1

Mediana Q3 Máximo

1. Con los mismos datos de la actividad anterior para las tomateras, encuentra la mediana y añádala a la tabla. ¿Qué representa la mediana para estos datos?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

2. Encuentra la mediana de los valores 15 mínimos para dividir los datos en el primer y el segundo cuartil. Este valor se denomina primer cuartil. Añade este valor a la tabla bajo Q1. ¿Qué significa este valor en esta situación?

3. Encuentra el valor (el tercer cuartil) que divide los datos en el tercer y cuarto trimestre y añádelo a la tabla bajo Q3. Añade los valores mínimo y máximo a la tabla bajo. Añade los valores mínimo y máximo a la tabla.

4. Utiliza el resumen de cinco números para crear un diagrama de cajas que represente el número de días que tardan estas tomateras en producir tomates.

40 45 50 55 60 65 Tiempo en días 70 75 80 85 90

1. Mediana: 71 días. La mitad (o 15) de las tomateras produjeron tomates en menos o igual a 71 días y la mitad de ellas tardaron al menos 71 días en producir frutos.

2. Q1: 62 días. Aproximadamente una cuarta parte de las tomateras tardaron 62 días o menos en producir tomates y aproximadamente 7 5% de las tomateras tardaron 62 días o más en producir tomates.

3. Q3: 78 días. Mínimo: 47 días. Máximo: 90 días.

CONCEPTOS ERRÓNEOS PREVISTOS

California . Algebra 1

40 45 50 55 60 65 Tiempo en días 70 75 80 85 90

A los estudiantes que tengan dificultades para calcular la mediana, recuérdeles que la mediana es el punto medio de un conjunto de datos secuenciales. Para los estudiantes que tienen dificultad para encontrar Q1 y Q3, pregúnteles cuántos grupos deberíamos tener si dividimos los datos en «cuartos». Los datos deben dividirse en cuatro grupos iguales y la mediana de la mitad inferior de los valores es Q1 y la mediana de la mitad superior de los valores es Q3.

SÍNTESIS DE LA ACTIVIDAD

El objetivo es asegurarse de que los estudiantes entienden el resumen de cinco números y ayudarles a pensar informalmente sobre la mediana como medida del centro. He aquí algunas preguntas para el debate.

• «¿Qué información se ve fácilmente en el gráfico de caja?». (El valor mínimo, los cuartiles, incluida la mediana y el valor máximo. También se destacan el rango intercuartílico y el rango).

• «Según el diagrama de caja, ¿cuál es el número típico de días que tarda una planta de tomate en producir frutos?». (El número típico de días es 71 porque la mediana de los datos es 71 días).

SÍNTESIS DE LA LECCIÓN

(5 minutos)

En esta lección, los estudiantes vieron datos representados mediante diagramas de puntos, histogramas y diagramas de cajas.

• «¿Cuáles son los puntos fuertes de cada una de las representaciones?». (Un diagrama de puntos permite ver todos los datos y cómo se distribuyen. El histograma resume los datos en intervalos que dan lugar a menos columnas. El diagrama de caja muestra gráficamente el resumen de cinco números).

• «¿Cuáles son los puntos débiles de cada una de las representaciones?». (Un diagrama de puntos tiene muchas columnas de puntos que pueden dificultar la determinación de patrones gráficamente. Tanto el histograma como el diagrama de caja no muestran cada valor individual del conjunto de datos, lo que significa que la media no puede calcularse directamente a partir de ninguna de las dos representaciones.

• «¿Cómo se encuentra el valor estándar de un conjunto de datos?». (Puede calcular la media o la mediana o estimar la media o la mediana con una representación gráfica).

ENFRIAMIENTO | RAZONAMIENTO SOBRE REPRESENTACIONES

(5 minutos)

El diagrama de puntos, el histograma y el diagrama de caja representan la distribución de los mismos datos de 3 maneras diferentes.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

1. ¿Qué información se puede ver más fácilmente en el diagrama de puntos?

2. ¿Qué información se puede ver más fácilmente en el histograma?

3. ¿Qué información se puede ver más fácilmente en el diagrama de caja?

Álgebra 1 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES

Ejemplo de respuesta:

1. Los valores reales, la forma de la distribución y el valor más común se ven fácilmente en el diagrama de puntos.

2. La forma de la distribución y el intervalo más común de los datos se ven fácilmente en el histograma.

3. El resumen de cinco números (mínimo, primer cuartil, mediana, tercer cuartil y máximo) se puede ver fácilmente en el diagrama de caja.

Resumen de la lección para el estudiante

La tabla muestra una lista del número de minutos que las personas pueden concentrarse intensamente en una tarea antes de necesitar un descanso. 50 personas de diferentes edades están representadas.

En una situación como ésta, es útil representar los datos gráficamente para observar mejor cualquier patrón u otras características interesantes de los datos. Se puede utilizar un diagrama de puntos para ver la forma y la distribución de los datos.

en minutos

Hubo bastantes personas que perdieron la concentración alrededor de los 3, 7, 13 y 19 minutos y nadie perdió la concentración a los 11, 12, o 15 minutos. Los diagramas de puntos son útiles cuando el conjunto de datos no es demasiado grande y muestra todos los valores individuales del conjunto de datos. En este ejemplo, un diagrama de puntos puede mostrar fácilmente todos los datos. Si el conjunto de datos es muy grande (más de 100 valores, por ejemplo) o si hay muchos valores diferentes que no son exactamente iguales, puede ser difícil ver todos los puntos en un diagrama de puntos.

Un histograma es otra representación que muestra la forma y la distribución de los mismos datos.

La mayoría de las personas perdieron la concentración entre 5 y 10 minutos o entre 15 y 20 minutos, mientras que solo 4 de las 50 personas se distrajeron entre 20 y 25 minutos. Al crear histogramas, cada intervalo incluye el número del extremo inferior del intervalo, pero no el del extremo superior. Por ejemplo, la barra más alta muestra valores que son mayores o iguales a 5 minutos, pero menores que 10 minutos. En un histograma, los valores que se encuentran en un intervalo se agrupan. Aquí se muestra un diagrama de caja que representa los mismos datos.

Tiempo en minutos

Los diagramas de caja se crean utilizando el resumen de cinco números. Para un conjunto de datos, el resumen de cinco números consiste en estos cinco estadísticos: el valor mínimo, el primer cuartil, la mediana, el tercer cuartil y el valor máximo. Estos valores dividen los datos en cuatro secciones, cada una de las cuales representa aproximadamente una cuarta parte de los datos. La mediana de estos datos se indica a 8 minutos y 25 % de los datos cae en el corto segundo cuartil de los datos entre 6 y 8 minutos. Del mismo modo, aproximadamente una cuarta parte de los datos se sitúa entre 8 y 17 minutos. Al igual que el histograma, el diagrama de cajas no muestran valores de datos individuales, pero

Math Nation California . Algebra 1

en minutos

1 . Matemáticas . Unidad 1

otras características como cuartiles, rango y mediana se ven más fácilmente. Las gráficas de puntos, los histogramas y las diagrama de cajas proporcionan 3 diferentes maneras de observar la forma y la distribución, al tiempo que resaltan diferentes aspectos de los datos.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

La gráfica de puntos muestra el cantidad de arbustos en los patios de las casas de un vecindario. ¿Cuál es la mediana?

5 6 7 8 9 10 11 Cantidad de arbustos

PROBLEMA 2

El conjunto de datos representa las tallas de zapatos de 19 estudiantes en una clase de educación física de quinto grado.

4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7 5, 7 5, 8, 8, 8 5, 8 5, 9

Crea un diagrama de cajas para representar la distribución de los datos.

PROBLEMA 3

El conjunto de datos representa el número de páginas del último libro leído por cada uno de 20 estudiantes durante el verano.

163, 170, 171, 173, 175, 205, 220, 220, 220, 253, 267, 281, 305, 305, 305, 355, 371, 388, 402, 431

Crea un histograma para representar la distribución de los datos.

Soluciones posibles 8 arbustos

PROBLEMA 4

Cada conjunto de datos se recopiló de las encuestas para responder a preguntas estadísticas. Seleccione todos los conjuntos de datos que representan datos numéricos.

{1, 1 2, 1 4, 1 4, 1 5, 1 6, 1 8, 1 9, 2, 2, 2 1, 2 5}

{rojo, rojo, amarillo, amarillo, azul, azul, azul}

{45, 60, 60, 70, 75, 80, 85, 90, 90, 100, 100, 100}

{−7, −5, −3, −1, −1, −1, 0}

{98 2, 98 4, 98 4, 98 6, 98 6, 98 6, 98 6, 98 7, 98 8, 98 8}

{sí, sí, sí, sí, tal vez, tal vez, no, no, no}

{A, A, A, B, B, B, C, C, C}

Soluciones posibles 9 Tamaño de zapato 3 4 5 6 7 8 10

Soluciones posibles

{1, 1 2, 1 4, 1 4, 1 5, 1 6, 1 8, 1 9, 2, 2, 2 1, 2 5}

{rojo, rojo, amarillo, amarillo, azul, azul, azul}

{45, 60, 60, 70, 75, 80, 85, 90, 90, 100, 100, 100}

{−7, −5, −3, −1, −1, −1, 0}

{98 2, 98 4, 98 4, 98 6, 98 6, 98 6, 98 6, 98 7, 98 8, 98 8}

{sí, sí, sí, sí, tal vez, tal vez, no, no, no}

{A, A, A, B, B, B, C, C, C}

PROBLEMA 5

(De la unidad 1, lección 1).

¿Es la pregunta: «¿Cuál es la distancia típica que puede recorrer un ciclomotor con un solo depósito de gasolina?» estadística? Explica tu razonamiento.

Soluciones posibles

Ejemplo de respuesta: Sí, es una pregunta estadística porque los datos necesarios para responderla variarían. La distancia recorrida por el ciclomotor dependería probablemente de la rapidez o del número de cuestas.

Reflexiones:

Math Nation California . Algebra 1

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

S-ID.1 Representar datos con gráficas en la recta numérica real (diagramas de puntos, histogramas y diagramas de cajas).

Construir

S-ID.2

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.B.8

II.C.6

LECCIÓN 3 UNA GALERÍA DE DATOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para.... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

comprender al mundo y predecir lo que podría ocurrir,

buscan y hacen uso de la estructura

OBJETIVO(S) DE APRENDIZAJE

analizan los datos y descubren la forma y el espacio.

• Puedo representar gráficamente los datos que he recogido y criticar las representaciones de los demás.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Crear y criticar representaciones gráficas de los datos recogidos por los estudiantes.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

MLR7: Comparar y conectar

Materiales necesarios

Herramientas para crear una exhibición visual.

Cualquier forma para que los estudiantes creen trabajos que puedan ser fácilmente mostrados a la clase. Ejemplos: Papel milimetrado y marcadores, pizarra blanca y marcadores, herramienta de dibujo en línea compartida y acceso a una cámara de documentos.

Preparación necesaria

Los estudiantes necesitarán los datos numéricos que hayan recogido de una pregunta estadística en una lección anterior. Los estudiantes necesitarán herramientas para crear y mostrar un diagrama de puntos y un diagrama de cajas a toda la clase.

INFORMACIÓN DE LA LECCIÓN

Metas de aprendizaje para el estudiante

• Vamos a comparar, interpreta y hacer visualizaciones de datos.

Narrativa de la lección

El propósito matemático de la lección es representar e interpretar datos con visualizaciones de datos de una manera menos andamiada que en la lección anterior. El trabajo de esta lección se conecta con el trabajo previo realizado en sexto grado, donde los estudiantes resumieron y describieron distribuciones. El trabajo de esta lección se conecta con el trabajo futuro porque los estudiantes usarán visualizaciones de datos para describir más formalmente la forma de las distribuciones, y para determinar la medida apropiada del centro y la medida de variabilidad para una distribución dada. Cuando los estudiantes crean e interpretan una visualización de datos, razonan abstracta y cuantitativamente (MP2) porque crean una visualización e interpretan el significado de las cantidades en la visualización. Además, los estudiantes hacen uso de la estructura (MP7) para notar diferencias en distribuciones con la misma forma, pero diferentes centros.

RESUMEN

DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento En parejas 5 min

Actividad de exploración Grupos pequeños 25 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Los estudiantes hacen observaciones sobre dos diagramas de puntos y luego discuten lo que observan y se preguntan.

Los estudiantes crean un diagrama de puntos, un histograma y un diagrama de cajas para una pregunta estadística y luego interpretan los datos.

Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de la recopilación de datos y la interpretación de los resultados de poblaciones de diferentes tamaños.

Los estudiantes hablan de su comprensión e interpretación de las visualizaciones de datos y la información que cada visualización proporciona.

Con los mismos datos, los estudiantes crean visualizaciones de un diagrama de cajas e histogramas y luego hacen comparaciones.

Práctica Independiente 10-15 min El componente de práctica independiente incluye 2 en la lección y 4 problemas de repaso en espiral.

California . Algebra 1

CALENTAMIENTO

| OBSERVAR Y PREGUNTARSE:

DIAGRAMA DE CAJAS

(5 minutos)

Rutinas didácticas

Observar y preguntarse

El propósito de este calentamiento es provocar la idea de que las distribuciones se pueden discutir en términos de forma, lo que será útil cuando los estudiantes describan las visualizaciones de datos en una actividad posterior. Aunque los estudiantes pueden observar y preguntarse muchas cosas sobre estas imágenes, la forma y los valores del eje horizontal son los puntos de discusión importantes. Este estímulo ofrece a los estudiantes la oportunidad de ver y utilizar la estructura (MP7). La estructura específica que pueden observar es que los conjuntos de datos con diferentes valores pueden tener distribuciones con la misma forma si todos los valores en el conjunto de datos se aumentan o disminuyen en el mismo valor.

INTRODUCCIÓN

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Muestre los diagramas de puntos para que todos los vean. Pida a los estudiantes que piensen en al menos una cosa que obsevaron y en una pregunta que tengan. Conceda a los estudiantes 1 minuto para pensar en silencio y, a continuación, 1 minuto para comentar con su compañero las cosas que han observado, seguido de un debate con toda la clase.

Los diagramas de puntos representan la distribución de la cantidad de propinas, en dólares, dejadas en 2 restaurantes diferentes en la misma noche.

¿Qué observas? ¿Qué te preguntas?

0 1 2 3 4 5 6 7 8 9 10 11 Monto de la propina (dólares) 7 8 9 10 11 12 13 14 15 16 17 18 Monto de la propina (dólares)

Cosas que los estudiantes pueden observar:

• La forma de la distribución es la misma.

• El segundo diagrama de puntos son los mismos datos desplazados a $7.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Cosas que los estudiantes pueden preguntarse:

• ¿Qué aspecto tendría un diagrama de cajas de los datos?

• ¿Cuánto costaría una cena con $17 de propina?

Pida a los estudiantes que compartan las cosas que observaron y se preguntaron. Anota y muestra sus respuestas para que todos las vean. Si es posible, anote el razonamiento pertinente en la imagen o cerca de ella. Una vez registradas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre algo que te preguntas?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria. Si la forma de la distribución y los valores del eje horizontal de cada diagrama de puntos no surgen durante la conversación, pida a los estudiantes que hablen de ideas con estas preguntas:

• «¿Qué observan en la forma de cada distribución?». (Los datos se distribuyen exactamente de la misma manera en cada diagrama de puntos).

• «¿Cuál es el valor más frecuente en cada diagrama de puntos?». ($4 y $11).

• «¿Cuál es el valor de la punta más alta en cada diagrama de puntos?». ($10 y $17).

• «¿Cuál es el valor de la punta más baja en cada diagrama de puntos?». ($1 y $8).

• «¿Qué ocurre si se añade $7 a cada una de las puntas del primer diagrama de puntos?». (Se obtiene la distribución de datos en el segundo diagrama de puntos).

1 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | VISUALIZAR DATOS

(25 minutos)

Rutinas didácticas

MLR7: Comparar y conectar

En esta lección, los estudiantes crean y muestran un diagrama de puntos y un diagrama de cajas con datos numéricos que han recogido de una encuesta realizada en una lección anterior. La lección se centra en la creación de visualizaciones gráficas de datos, por lo que los conjuntos de datos apropiados tienen prioridad sobre los datos reales de la clase A continuación se presentan ejemplos de conjuntos de datos para cada una de las cuatro preguntas de la lección anterior.

• En promedio, ¿cuántas letras tienen los apellidos de los estudiantes de esta clase? {4,

8, 9, 10}

• En promedio, ¿cuál es la distancia más lejana, en millas, que cada estudiante de esta clase ha estado de su casa? {50, 50, 50, 100, 200, 200, 250, 250, 300, 300, 300, 500, 500, 500, 500, 500, 500, 800, 1000, 2000}

• ¿Aproximadamente cuánto tiempo tardaron los estudiantes de esta clase en llegar a la escuela esta mañana? {

, 10, 12, 15, 15, 15, 15, 25, 25, 25, 25, 30, 35, 40, 45, 55}

• En promedio, ¿cuántas películas vio cada estudiante de la clase en el cine este verano? {0, 1, 1, 1, 2,

7, 8, 10, 12}

• Luego que los grupos hayan tenido la oportunidad de completar sus trabajos, haga una pausa con la clase para explicar cómo hacer un recorrido por la galería. Provea un ejemplo del trabajo mostrado y pida a los estudiantes que den respuestas a las preguntas de la tarea sobre los ejemplos que ayudan a los estudiantes a entender los tipos de respuestas esperadas.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2-4 y asigne a cada grupo una de las preguntas estadísticas para las que los estudiantes ya hayan recogido datos numéricos. Proporcione a cada grupo las herramientas para crear una representación gráfica. Pida a los estudiantes que hagan una pausa después de la segunda pregunta para el recorrido por la galería.

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre fragmentos de oraciones para apoyar a los estudiantes cuando expliquen sus ideas. Por ejemplo: «Cada estudiante de esta clase...».

Apoya la accesibilidad para: Lenguaje; organización

Tu maestro le asignará a tu grupo una pregunta estadística. En grupo:

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

1. Crea un diagrama de puntos, un histograma y un diagrama de cajas para mostrar la distribución de los datos.

2. Escribe 3 comentarios que interpreten los datos. Cuando visites cada exhibición, escribe una o dos frases que resuman la información de lo mostrado.

Ejemplo de respuesta: Cada estudiante de esta clase vio alrededor de 4 películas este verano. Al menos una persona vio 12 películas y un estudiante vio 0. La mayoría de los datos se agrupan alrededor de 1 a 3 películas con una cola más larga a la derecha.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Es posible que los estudiantes no incluyan los títulos de los ejes y olviden la importancia de construir sus gráficos sobre una recta numérica con intervalos equidistantes. Vigile a los grupos que no recuerden los detalles de la realización de los diferentes tipos de representaciones y sugiérales que se remitan a su trabajo de la lección anterior.

El objetivo es asegurarse de que los estudiantes entienden cómo representar una distribución de datos con un diagrama de puntos, un histograma y un diagrama de cajas y que puedan interpretar cada distribución en el contexto de los datos. El propósito de la discusión es obtener pruebas del pensamiento de los estudiantes sobre las distribuciones. A continuación se presentan algunas preguntas para la discusión:

• «¿De qué maneras resumiste la información en la pantalla?». (Los datos estaban agrupados en torno a un valor. El diagrama de puntos lo muestra, pero el diagrama de cajas no. El diagrama de cajas muestra la mediana como valor típico).

• «Si recopilaras datos de todos los estudiantes de la escuela, en lugar de solo de tus compañeros, ¿qué preferirías crear: un diagrama de puntos o un diagrama de caja? ¿Por qué?». (Un diagrama de cajas porque todo lo que tienes que hacer es encontrar el resumen de cinco números. En un diagrama de puntos, tendrías que trazar cada punto y eso podría ser difícil de hacer con las herramientas que tengo).

• «¿Cuál es la forma de la distribución en tu diagrama de puntos?». (Los datos estaban muy separados).

• «¿Qué información muestra el diagrama de puntos que no muestra el diagrama de cajas?». (El diagrama de puntos muestra todos los valores del conjunto de datos).

• «¿Qué información muestra el diagrama de cajas que no muestra el diagrama de puntos?». (El diagrama de cajas muestra los cuartiles y la mediana).

Apoyo para estudiantes que aprenden el idioma inglés

Hablar, escribir: MLR7 Comparar y conectar. Utilice esta rutina cuando los estudiantes presenten sus representaciones gráficas resumiendo los datos. Pida a los estudiantes que piensen en lo que es igual y lo que es diferente en cada representación. Llame la atención de los estudiantes' sobre las diferentes formas en que se representan los datos (con diagramas de caja, histogramas, diagramas de puntos, etc). y el beneficio de cada representación para la interpretación de los datos. Estos intercambios pueden reforzar el uso del lenguaje matemático y el razonamiento de los estudiantes para dar sentido a las representaciones gráficas de los datos.

¿Estás preparado para más?

Elige una de las preguntas más interesantes que hayas hecho tú o un compañero de clase y recoge datos de un grupo más grande, por ejemplo, de más estudiantes de la escuela. Crea visualizaciones de datos y compara los resultados de los datos recogidos en clase.

Respuesta de los estudiantes

Las respuestas varían.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

En esta lección, los estudiantes crearon dos visualizaciones de datos diferentes con la información que recopilaron en una lección anterior.

• «Cuando observas las dosvisualizaciones de datos que hiciste, ¿qué información te llama la atención?». (El diagrama de puntos muestra la forma de los datos y es fácil ver la frecuencia de cada valor. El diagrama de cajas muestra la mediana y me da una idea del intervalo que contiene el cincuenta por ciento medio de los datos).

RESPUESTAS POSIBLES

Ejemplos de respuestas:

3. El histograma ya que podemos sumar las alturas de las dos últimas barras para obtener la respuesta. No es posible obtener esta información del diagrama de cajas.

Resumen de la lección para el estudiante

Podemos representar una distribución de datos de varias formas diferentes, incluido las listas, diagramas de puntos, histogramas y diagramas de cajas. Una lista muestra todos los valores de un conjunto de datos y puede organizarse de diferentes maneras. Esta lista muestra el pH de 30 diferentes muestras de agua.

He aquí la misma lista organizada en orden de menor a mayor.

8.4 8.4 8.6 6

Con la lista organizada, puedes más fácilmente:

• interpretar los datos

• calcular los valores del resumen de cinco números

• estimar o calcular la media

• crear un diagrama de puntos, un diagrama de cajas o un histograma

Aquí tienes un diagrama de puntos y un histograma que representan la distribución de los datos de la lista.

Un diagrama de puntos se crea cuando colocas un punto para cada valor sobre la posición en una recta numérica. En el diagrama de puntos del pH, hay 2 muestras de agua con un pH de 6.5 y 1 muestra de agua con un pH de 7

Un histograma se hace contando el número de valores del conjunto de datos en un intervalo determinado y dibujando una barra sobre ese intervalo a una altura que coincida con el recuento. En el histograma del pH, hay 5 muestras de agua que tienen un pH entre 6.5 y 7 (incluyendo 6.5, pero no 7). Aquí tienes un diagrama de cajas que representa la distribución de los mismos datos que el diagrama de puntos y el histograma.

Para crear un diagrama de cajas, necesitas encontrar los valores mínimo, primer cuartil, mediana, tercer cuartil y máximo para el conjunto de datos. Estos 5 valores se denominan a veces resumen de cinco números. Cuando dibujas una marca vertical y luego conectas las piezsa, como en el ejemplo, se crea el diagrama de cajas. Para el diagrama de cajas del pH, podemos ver que el mínimo es aproximadamente 5.8, la mediana es aproximadamente 7.4 y el tercer cuartil es aproximadamente 7.9

1 . Matemáticas . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

El diagrama de cajas representa la distribución de rapidez, en millas por hora, de 100 carros a su paso por una intersección muy transitada.

4 8 12 16 20 24

32 36 40 44 48

Rapidez de los carros (millas por hora)

A. ¿Cuál es el valor más pequeño del conjunto de datos? Interpreta este valor en la situación.

B. ¿Cuál es el valor más grande del conjunto de datos? Interpreta este valor en la situación.

C. ¿Cuál es la mediana? Interpreta este valor en la situación.

D. ¿Cuál es el primer cuartil (Q1)? Interpreta este valor en la situación.

E. ¿Cuál es el tercer cuartil (Q3)? Interpreta este valor en la situación.

PROBLEMA 2

El conjunto de datos representa el cantidad de huevos producidos por un pequeño grupo de gallinas cada día durante diez días: 7, 7, 7, 7, 7, 8, 8, 8, 8, 9. Selecciona todos los valores que podrían representar la cantidad típica de huevos producidos en un día.

7.5 huevos

7.6 huevos

7.7 huevos

8 huevos

9 huevos

PROBLEMA 3

(De la unidad 1, lección 2).

Soluciones posibles

A. 8 millas por hora. El carro que pasó más despacio por la intersección iba a 8 millas por hora.

B. 44 millas por hora. El carro que pasó más rápido por el cruce iba a 44 millas por hora.

C. 20 millas por hora. La mitad de los carros pasaron por la intersección a 20 millas por hora o más rápido y la otra mitad pasó por la intersección a 20 millas por hora o más lento.

D. 12 millas por hora. Aproximadamente una cuarta parte de los carros que atravesaban la intersección iban a 12 millas por hora o más despacio.

E. 24 millas por hora. Aproximadamente una cuarta parte de los carros que pasaban por la intersección iban al menos a 24 millas por hora.

Soluciones posibles

7.5 huevos

7.6 huevos

7.7 huevos

8 huevos

9 huevos

El diagrama de puntos muestra las longitudes de los lápices (en pulgadas) utilizados por los estudiantes de una clase. ¿Cuál es la media?

5 5.5 6 6.5 7 Longitud (pulgadas)

Soluciones posibles

. Algebra 1

PROBLEMA 4

(De la unidad 1, lección 2).

El histograma representa las edades de 40 personas en una tienda que vende ropa para niños. ¿Qué intervalo contiene la mediana?

A. El intervalo de 0 a 5 años.

B. El intervalo de 5 a 10 años.

C. El intervalo de 10 a 15 años.

D. El intervalo de 15 a 20 años.

Soluciones posibles

PROBLEMA 5

(De la unidad 1, lección 2).

El conjunto de datos representa las respuestas, en grados Fahrenheit, recogidas para responder a la pregunta: «¿Cuánto calor hace en la acera durante el día escolar?».

, 95, 95, 95, 98, 100, 100, 100, 103, 105,

A. Crea un diagrama de puntos para representar la distribución de los datos.

B. Crea un histograma para representar la distribución de los datos.

C. ¿Qué representación te ofrece una mejor comprensión global de los datos? Explica tu razonamiento.

Soluciones posibles

C. Ejemplo de respuesta: El histograma da una mejor idea de los datos porque muestra que la temperatura de la acera estuvo entre 115 y 120 grados Fahrenheit 12 veces y que la temperatura estuvo entre 90 y 115 grados Fahrenheit el resto del tiempo.

1 . Matemáticas . Unidad 1

PROBLEMA 6

(De la unidad 1, lección 1).

¿Es la pregunta: «¿Cuál es el área del suelo de esta aula?» estadística? Explica tu razonamiento.

Soluciones posibles

Ejemplo de respuesta: No, no es una pregunta estadística porque los datos necesarios no variarían. Solo hay una respuesta.

Reflexiones:

Math Nation California . Algebra 1

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Alineación de estándares y principios de California

Abordar

S-ID.1 Representar datos con gráficas en la recta numérica real ( diagramas de puntos, histogramas y diagramas de cajas).

Construir

S-ID.2

Enfoque SMPs

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.4

I.B.5 I.C.12

LECCIÓN 4

LA FORMA DE LAS

DISTRIBUCIONES

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

impactar el futuro

construirán argumentos viables y criticarán el razonamiento de otros

OBJETIVO(S) DE APRENDIZAJE

analizan los datos y descubren la forma y el espacio.

• Puedo describir la forma de una distribución con los términos simétrica, uniforme, bimodal y en forma de campana

• Puedo utilizar una representación gráfica de datos para sugerir una situación que produjo los datos representados.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente y por escrito) la forma de una distribución con palabras como «simétrica, sesgada, uniforme, bimodal y en forma de campana«.

• Interpretar una representación gráfica para sugerir un posible contexto para los datos.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

¿Cuál no pertenece?

MLR7: Comparar y conectar

Tomar turnos

MLR2: Recopilar y mostrar

Pensar, girar y compartir

Materiales necesarios

Fichas preimpresas, recortes de la plantilla maestra.

Preparación necesaria

Imprima y recorte las fichas de la plantilla maestra. Prepare una copia para cada dos estudiantes.

Álgebra 1 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Exploremos datos y describamos distribuciones.

Narrativa de la lección

El propósito matemático de esta lección es describir distribuciones con la terminología apropiada. Para aprender más sobre los diferentes tipos de distribuciones, una cosa que hacen los estudiantes es inventar contextos razonables para una distribución dada. La terminología que se utiliza se describe aquí.

• En una distribución simétrica, la media es igual a la mediana y hay una línea vertical de simetría en el centro de la visualización de los datos.

• En una distribución sesgada, la media no suele ser igual a la mediana y un lado de la distribución tiene más valores alejados de la mayor parte de los datos que el otro lado.

• Una distribución uniforme tiene los valores de los datos distribuidos uniformemente en todo el rango de los datos.

• Una distribución bimodal tiene dos valores de datos muy comunes que se ven en una diagrama de puntos o histograma como picos distintos.

• Una distribución en forma de campana tiene una diagrama de puntos que toma la forma de una campana con la mayoría de los datos agrupados cerca del centro y menos puntos más alejados del centro.

En el grado 6, los estudiantes pueden haber adquirido algunas formas diferentes de describir distribuciones, aunque no se les exigió aprender la terminología introducida en esta lección. En una lección anterior, los estudiantes crearon visualizaciones de datos. En el trabajo siguiente, los estudiantes utilizarán información sobre la forma de las distribuciones para determinar la medida apropiada del centro. La actividad «Cuál no pertenece« da a los estudiantes un motivo para empezar a utilizar el lenguaje con precisión (MP6) y brinda al maestro la oportunidad de escuchar cómo utilizan la terminología y hablan de las características de los elementos en comparación con los demás. En la clasificación por tarjetas, los estudiantes intercambian papeles, explican su pensamiento y escuchan, lo que les brinda la oportunidad de explicar su razonamiento y criticar el de los demás (MP3).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Grupos pequeños 10 min

Actividad de exploración En parejas 15 min

Actividad de exploración En parejas 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 10 min

Nation California . Algebra 1

Descripción breve

Los estudiantes hacen observaciones sobre cuatro diagramas de puntos y luego explican cuál no pertenece.

Los estudiantes emparejan tarjetas con diferentes representaciones de los mismos conjuntos de datos y luego describen las formas de distribución de las representaciones.

Utilizar un conjunto de datos relacionados de la actividad anterior, los estudiantes escriben una pregunta de encuesta que podría representar los datos. Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de las formas de las distribuciones y cómo interpretarlas.

Los estudiantes hablan de las diferentes formas de las distribuciones y lo que cada forma significa sobre el conjunto de datos.

Los estudiantes describen la forma de cada diagrama de puntos y luego relacionan una representación con un contexto.

El componente de práctica independiente incluye 3 problemas de repaso de la lección y 2 problemas de repaso en espiral.

CALENTAMIENTO | ¿CUÁL NO PERTENECE? FORMA

DE LA DISTRIBUCIÓN

(10 minutos)

Rutinas didácticas

¿Cuál no pertenece?

El propósito matemático de este calentamiento es recoger la terminología informal que los estudiantes puedan utilizar para describir las formas de las distribuciones, así como cualquier forma de describir distribuciones que puedan recordar del trabajo en grados anteriores. Este calentamiento pide a los estudiantes que comparen cuatro distribuciones. Proporciona a los estudiantes una razón para empezar a utilizar el lenguaje con precisión (MP6) y le da a usted la oportunidad de escuchar cómo utilizan la terminología y hablan de las características de los elementos en comparación unos con otros. Escuche a los estudiantes que utilizan el vocabulario estadísticamente correcto, así como a los que utilizan un lenguaje informal para describir las formas.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2-4. Muestre las distribuciones para que todos las vean. Concede a los estudiantes 1 minuto de tiempo para pensar en silencio y luego tiempo para compartir su pensamiento con su pequeño grupo. En sus pequeños grupos, pida a cada estudiante que comparta su razonamiento de por qué un elemento en particular no pertenece y que juntos encuentren al menos una razón por la que cada elemento no pertenece.

¿Cuál no pertenece?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

A. B. C.

Ejemplos de respuestas:

• A no pertenece porque es la única distribución con la mayoría de los datos agrupados cerca del centro. Es la única distribución en forma de campana.

• B no pertenece porque es la única distribución con muy pocos puntos cerca del centro. Es la única distribución bimodal.

• C no pertenece porque es la única distribución que tiene la misma frecuencia para cada valor. Es la única distribución uniforme.

• D no pertenece porque es la única distribución sesgada (o no simétrica). Es la única distribución con un número impar de puntos.

Selecciona los grupos identificados para que compartan su razón por la que un determinado elemento no pertenece, de modo que hablen primero los que tienen un lenguaje informal y les sigan los que tienen una terminología más precisa. Asegúrate de que cada grupo comparta una razón por la que un elemento concreto no pertenece. Registre y muestre las respuestas para que todos las vean. Después de cada respuesta, pregunta a la clase si están de acuerdo o en desacuerdo. Como no hay una respuesta única correcta a la pregunta de cuál no pertenece, atienda a las explicaciones de los estudiantes y asegúrase de que las razones dadas son correctas. Durante el debate, reformule cualquier lenguaje informal que se utilice para describir la forma de cada distribución. Presente y defina los términos simétrica, sesgada, uniforme, bimodal y en forma de campana. Es importante señalar que la distribución en forma de campana también es simétrica.

Álgebra 1 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | PAREO DE DISTRIBUCIONES

(15 minutos)

Rutinas didácticas

MLR7: Comparar y conectar

Tomar turnos

El propósito matemático de esta actividad es dar a los estudiantes la oportunidad de practicar la búsqueda de visualizaciones de datos que representen la distribución del mismo conjunto de datos y utilizar vocabulario preciso para describir la forma de las distribuciones mientras se turnan para hacer coincidir las tarjetas. Los estudiantes intercambian papeles, explican su pensamiento y escuchan, lo que les da la oportunidad de explicar su razonamiento y criticar el razonamiento de los demás (MP3).

Organiza a los estudiantes en grupos de 2. Muestre las imágenes del diagrama de puntos y del histograma. Pregunte a los estudiantes en qué se fijan y qué se preguntan.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Si no surge nada, ayude a los estudiantes a darse cuenta de que estas dos visualizaciones de datos muestran los mismos datos en formatos diferentes. También pueden describirse como sesgados a la derecha.

Entregue a cada grupo un juego de tarjetas recortadas. Explique que un pareo hace coincidir dos visualizaciones diferentes que representan la distribución del mismo conjunto de datos. Pida a los estudiantes que se turnen: el primer compañero identifica un par, explica por qué cree que es una el par corresponde y, a continuación, describe la distribución mientras el otro estudiante escucha y se esfuerza por comprender. Luego cambian los papeles.

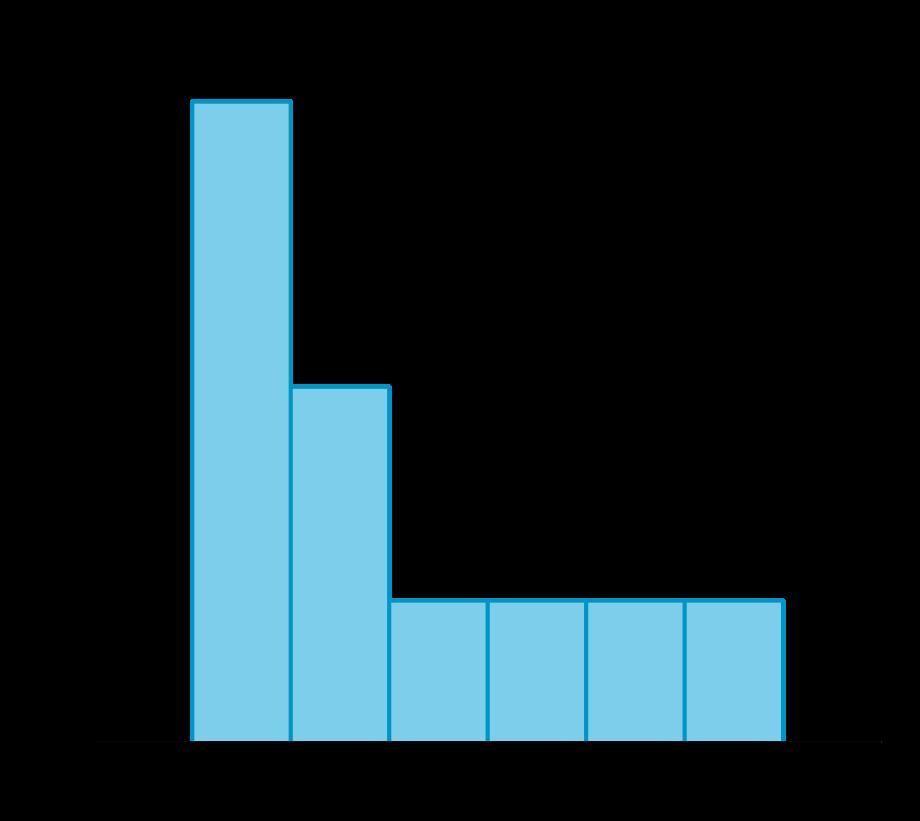
Túrnate con tu compañero para buscar los pares de 2 diferentes visualizaciones de datos que representen la distribución del mismo conjunto de datos.

1. Para cada conjunto que encuentres, explica a tu compañero cómo sabes que es el par.

2. Para cada conjunto que encuentre tu compañero, escucha atentamente su explicación. Si no están de acuerdo, hablen de sus ideas y trabajen para llegar a un acuerdo.

3. Cuando terminen con los diez pares, describan la forma de cada distribución.

La plantilla maestra muestra los pares correctos. Posibles respuestas de los estudiantes que describen la forma de cada distribución:

1. La forma de la distribución parece una campana. Tiene un eje de simetría en el centro.

2. La forma de la distribución tiene forma de campana. Es simétrica.

3. La distribución tiene forma de triángulo reflejado por una línea horizontal en 4.5

4. La distribución es bimodal. Es casi simétrica.

RESPUESTAS POSIBLES

California . Algebra 1

5. La forma de la distribución es una «U« en la que el valor máximo es más frecuente que el valor mínimo.

6. La distribución tiene forma de rectángulo.

7. La forma de la distribución es uniforme.

8. La forma de la distribución es acampanada, pero tiene un valor en el extremo derecho.

9. La forma parece simétrica, excepto en el valor más bajo.

10. La forma parece una horquilla simétrica en torno al valor medio.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Los estudiantes pueden tener dificultades para saber cómo colocar los números que se encuentran en el límite entre intervalos. Por ejemplo, los estudiantes pueden no saber si un valor como 60 debe incluirse en el intervalo 50-60 o 60-70. Explique a los estudiantes que el valor del límite inferior se incluye en el intervalo y el valor del límite superior no. Por ejemplo, el intervalo 60-70 incluye todos los valores que son mayores o iguales que 60 y menores que 70

Una vez que todos los grupos hayan completado el par, comente lo siguiente:

• «¿Qué pares fueron complicados? Explica por qué«. (Las distribuciones uniformes pueden ser difíciles).

• «¿Qué vocabulario fue útil para describir la forma de la distribución?«. (simétrica, sesgada, uniforme, bimodal, en forma de campana).

• «¿Hubo pares que pudieran describirse con más de uno de estos términos de vocabulario?«. (Sí, simétrica o sesgada también se pueden utilizar con algunos de los otros términos para algunas de las distribuciones).

Si es necesario, pida a los estudiantes que vuelvan a expresar descripciones menos formales de la forma de la distribución con un lenguaje formal que incluya:

• distribución simétrica

• distribución sesgada

• distribución uniforme

• distribución bimodal

• distribución en forma de campana

Apoyo para estudiantes que aprenden

el idioma inglés

Discurso, escuchar: MLR7 Comparar y conectar. Pedir a los estudiantes que preparen una presentación visual de sus tarjetas clasificadas. Mientras los estudiantes investigan el trabajo de los demás, pídales que compartan lo que funcionó bien en un planteamiento concreto. Escuche y amplifique cualquier comentario sobre el uso de las palabras simétrico, sesgado, bimodal, acampanado y uniforme para comparar las dos presentaciones diferentes. A continuación, anime a los estudiantes a relacionar las distintas formas de describir las diferentes distribuciones. Repita el lenguaje utilizado por los estudiantes para explicar que las dos representaciones son equivalentes. Esto fomentará la metaconciencia de los estudiantes y apoyará conversaciones constructivas mientras comparan y conectan visualizaciones de datos que representan la misma distribución.

Principio(s) de diseño: Fomentar la conversación; maximizar la metaconciencia

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Proporcionar a los estudiantes un organizador gráfico con la frase «formas de distribuciones« en el centro, conectando a ella todos los conceptos relacionados mencionados durante la discusión.

Apoya la accesibilidad para: Lenguaje; organización

Álgebra 1 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | ¿DE DÓNDE PROCEDE LA DISTRIBUCIÓN? (10 minutos)

Rutinas de Instrucción

MLR2: Recopilar y mostrar Pensar, girar y compartir

El propósito matemático de esta actividad es recordar a los estudiantes la importancia del contexto para la estadística. Aunque algunos análisis se pueden hacer fuera de un contexto, a menudo es útil pensar en las situaciones reales en las que se recogieron los datos para involucrar la intuición y la comprensión de los estudiantes.

INTRODUCCIÓN

Mantenga a los estudiantes en los mismos grupos. Asigne a cada pareja de estudiante suno de los pares completados de la actividad de clasificación de tarjetas. Diga a los estudiantes que hay muchas respuestas posibles para cada representación. Después de 2 minutos de trabajo en silencio, pida a los estudiantes que comparen sus respuestas con las de su compañero y decidan si ambas son razonables. Es posible que tenga que hacer una demostración de esta actividad antes de empezar si cree que los estudiantes pueden tener problemas para empezar. Después de que cada grupo termine con su distribución asignada, asigne al grupo otra distribución a considerar.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar, leer: MLR2 Recopilar y mostrar. Mientras los estudiantes trabajan, camine y escuche la conversación de los estudiantes cuando compartan sus conjeturas sobre la pregunta de la encuesta que produjo los datos para sus pares asignados. Anote las frases comunes o importantes que escuche decir a los estudiantes sobre cada representación, como «eje de simetría«, «en forma de campana«, «sesgada«, «bimodal«, «uniforme«, etc. Escriba las palabras de los estudiantes en una representación visual de las representaciones de los datos. Esto ayudará a los estudiantes a leer y utilizar el lenguaje matemático durante el debate de toda la clase.

Principio(s) de diseño: Apoyar la creación de sentido

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrolla la expresión y la comunicación. Para ayudar a los estudiantes a empezar, muestra fragmentos de oraciones como: «Una pregunta posible de la encuesta que produjo estos datos es porque «.

Apoya la accesibilidad para: Lenguaje, organización

RESPUESTAS POSIBLES

Tu maestro te asignará algunas de las distribuciones pares. Utiliza la información proporcionada en las visualizaciones de datos, haz una conjetura sobre la pregunta de la encuesta que produjo estos datos. Prepárate para compartir tu razonamiento.

Ejemplos de respuestas:

1. ¿A cuántos metros de distancia llegó la pelota cuando Priya intentó lanzarla a un blanco de 6 metros de distancia?

2. ¿A cuántos metros por debajo del nivel del mar nadan los tiburones?

3. ¿Cuántos amigos conociste en la fiesta de cumpleaños?

SÍNTESIS DE LA ACTIVIDAD

Pida a cada grupo que comparta su respuesta para al menos una de las distribuciones que se les asignaron. Después de que cada grupo comparta, pregunte a la clase si su contexto es razonable. He aquí algunas preguntas para la discusión:

• «¿Cómo utilizaste la forma de los datos para llegar a tu pregunta?«. (Como los datos tenían forma de campana, intenté pensar en situaciones en las que la mayoría de los datos fueran similares con algunos puntos un poco alejados de estos valores).

• «¿Esperarías siempre que tu pregunta diera como resultado una distribución [simétrica, sesgada, en forma de campana, etc.]?«. (No necesariamente, pero en la mayoría de los casos sí).

Revele la pregunta real de la encuesta que produjo la distribución. Preguntas reales por fila:

1. ¿Cuántos puntos anotó Kiran en cada uno de sus 22 partidos de esta temporada?

2. ¿Cuáles fueron las temperaturas bajas típicas en una ciudad siberiana durante el mes de enero?

3. En una escala de 1-8, ¿cómo fue el servicio en el restaurante?

4. ¿Cuántas preguntas acertó la gente en el examen de vocabulario la primera semana de clase?

5. ¿Cuántas preguntas acertó la gente en el examen de vocabulario la segunda semana de clase?

6. ¿A cuántos metros de profundidad se tomó cada una de las muestras?

7. ¿Cuántos árboles hay en mi jardín a distintas temperaturas?

8. ¿Cuál fue la suma cuando hiciste girar dos veces una ruleta etiquetada 0 a 5?

9. ¿Cuál fue el peso del cristal que cultivaste en clase de química?

10. ¿Cuántas preguntas acertaron los estudiantes en una prueba de pareo de 10 elementos?

Pida a los estudiantes que compartan lo que han aprendido sobre la distribución ahora que pueden pensar en los datos en una situación real.

¿Estás listo para más?

Esta distribución muestra la longitud en pulgadas de los peces capturados y liberados en un lago cercano.

1. Describe la forma de la distribución.

2. Haz una conjetura sobre qué podría causar que la distribución tenga esta forma.

Respuesta del estudiante

1. Ejemplo de respuesta: La distribución es bimodal. Es aproxiDMAamente simétrica, pero posiblemente ligeramente sesgada a la derecha. La mayoría de los datos no están cerca del centro de la distribución.

2. Ejemplo de respuesta: Podría haber dos tipos diferentes de peces en el lago, uno de los cuales es típicamente más bajo que el otro.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Longitud del pez (pulgadas)

En esta lección, los estudiantes describen la forma de las distribuciones con un lenguaje formal e inventan contextos para distribuciones con diferentes formas. He aquí algunas preguntas para el debate.

• «¿Qué aspecto tiene un conjunto de datos simétrico?«. (Tendrá una línea de simetría en el centro y el lado izquierdo parecerá un reflejo del lado derecho).

• «¿Qué significa decir que la forma de una distribución es uniforme?«. (Habrá un número igual de cada valor de datos y la forma parecerá rectangular).

• «¿Habías oído hablar antes de una curva de campana? ¿Qué relación tiene con una distribución en forma de campana?«. (Sí. He oído hablar de ella en la clase de Ciencias, donde se utilizó una curva de campana para comparar datos en un experimento).

• «¿Cuál es un ejemplo de un contexto en el que esperarías encontrar una distribución bimodal?«. (Podrías encontrarla si midieras el peso de un rebaño de vacas en primavera. Las vacas adultas serían un pico y los terneros serían el otro pico).

Álgebra 1 . Matemáticas . Unidad 1

• «¿Puede una distribución sesgada ser también simétrica? ¿Por qué sí o por qué no?«. (No, porque sesgada significa que un lado del pico de los datos tiene más valores de datos más alejados del pico que el otro lado. No hay línea de simetría).

ENFRIAMIENTO | TIPOS DE DISTRIBUCIÓN

(5 minutos)

Describe cada una de estas distribuciones. Si se aplica más de un término, incluye todos los términos que describen cada distribución. Cuando sea posible, utiliza los términos:

• distribución simétrica

• distribución sesgada

• distribución en forma de campana

• distribución uniforme

• distribución bimodal

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

5. ¿Cuál de estas distribuciones es más probable que muestre los datos recopilados mientras estudias el número de platos que la gente utiliza mientras come en un bufé libre? Explique su razonamiento.

1. simétrica, en forma de campana con centro cerca de 6

2. sesgada a la derecha con centro cerca de 4

3. sesgada a la derecha, bimodal con centro cerca de 6

4. simétrica, uniforme con centro cerca de 6

RESPUESTAS POSIBLES

5. Ejemplo de respuesta: El diagrama de puntos que está sesgado a la derecha, ya que la mayoría de la gente utilizará entre 1 y 3 platos, mientras que en raras ocasiones una persona podría volver una y otra vez a utilizar hasta nueve platos. Las otras distribuciones no tienen mucho sentido para este contexto.

Resumen de la lección para el estudiante

Podemos describir la forma de las distribuciones como simétrica, sesgada, en forma de campana, bimodal o uniforme. A continuación se muestra un diagrama de puntos, un histograma y un diagrama de cajas que representan la distribución del mismo conjunto de datos. Este conjunto de datos tiene una distribución simétrica.

California . Algebra 1

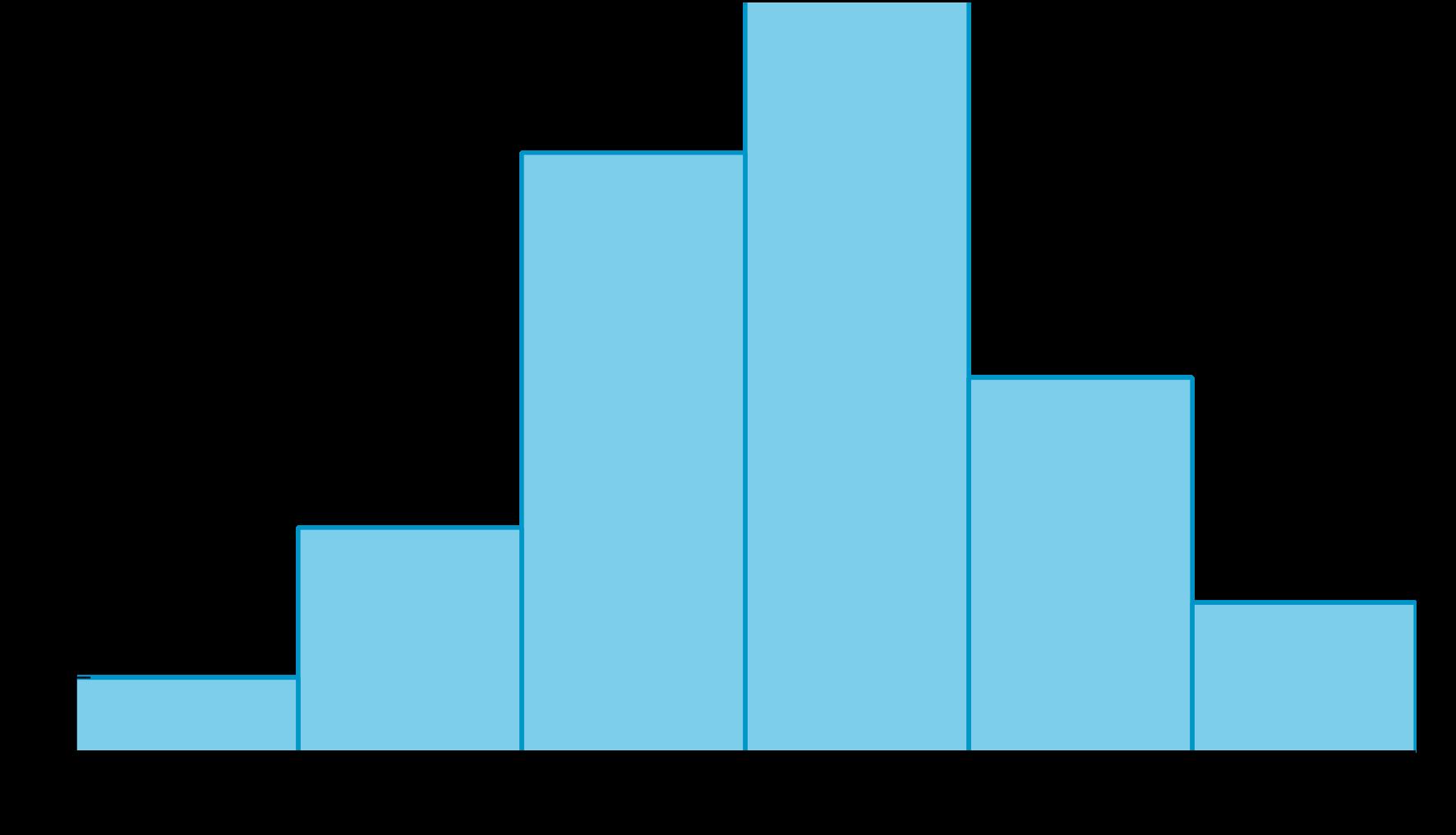
En una distribución simétrica , la media es igual a la mediana y hay una línea vertical de simetría en el centro de la visualización de los datos. Tanto el histograma como el diagrama de cajas agrupan los datos. Dado que los histogramas y los diagramas de cajas no muestran cada valor de los datos individualmente, no proporcionan información sobre la forma de la distribución con el mismo nivel de detalle que un diagrama de puntos. Esta distribución, en particular, también puede denominarse en forma de campana. Una distribución en forma de campana tiene un diagrama de puntos que adopta la forma de una campana con la mayoría de los datos agrupados cerca del centro y menos puntos más alejados del centro. Esto hace que la medida del centro sea una muy buena descripción de los datos en su conjunto. Las distribuciones en forma de campana son siempre simétricas o cercanas a ella.

Aquí se muestra un diagrama de puntos, un histograma y un diagrama de cajas que representan una distribución sesgada.

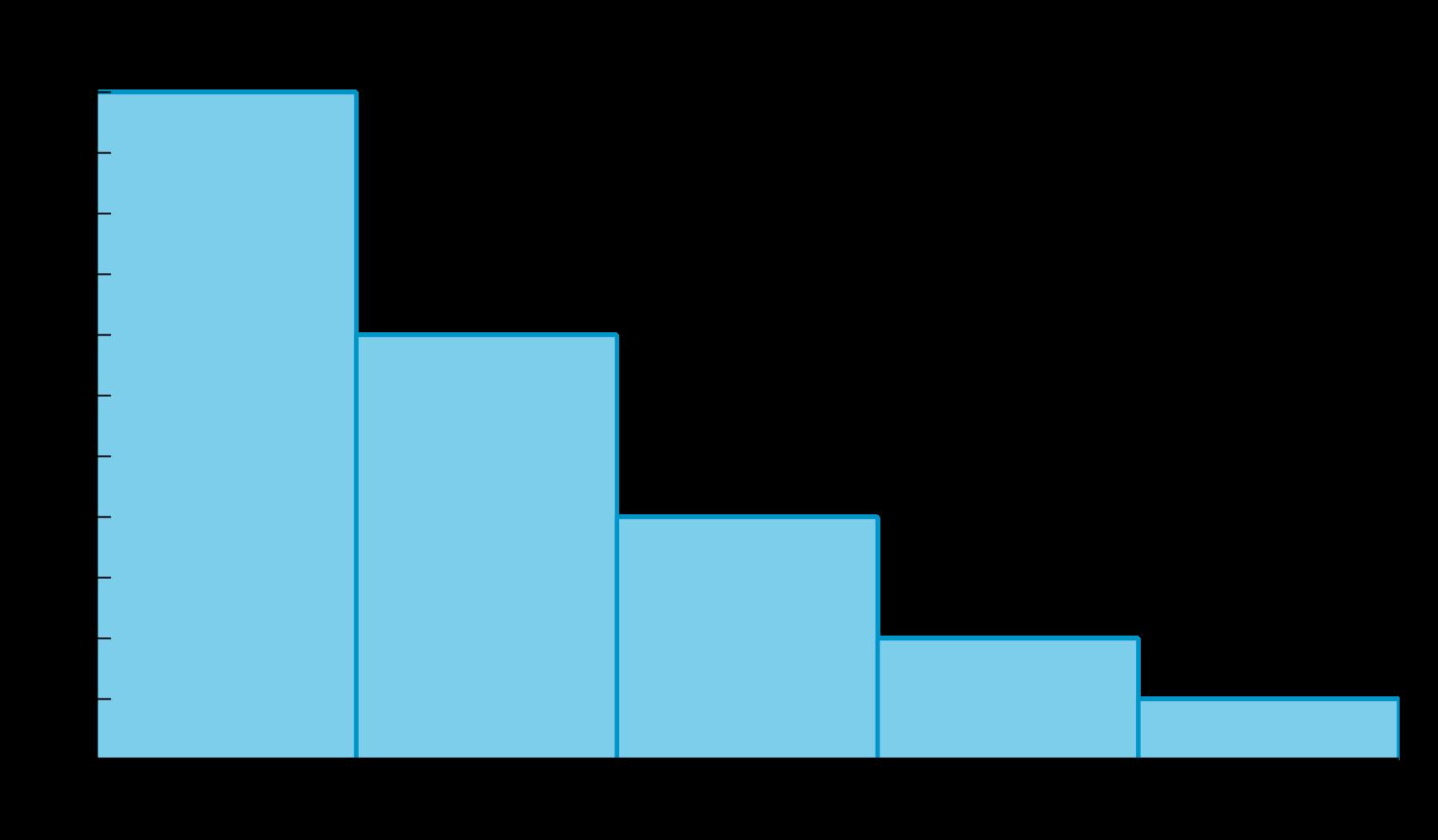
En una distribución sesgada, un lado de la distribución tiene más valores alejados del grueso de los datos que el otro lado. Esto hace que la media y la mediana no sean iguales. En esta distribución sesgada, los datos están sesgados a la derecha porque la mayoría de los datos están cerca del intervalo 8 a 10, pero hay muchos puntos a la derecha. La media es mayor que la mediana. Los grandes valores de datos a la derecha

Álgebra 1 . Matemáticas . Unidad 1

hacen que la media se desplace en esa dirección mientras que la mediana permanece con la mayor parte de los datos, por lo que la media es mayor que la mediana en las distribuciones sesgadas a la derecha. En un conjunto de datos sesgados hacia la izquierda, se produce un efecto similar, pero hacia el otro lado. De nuevo, el diagrama de puntos proporciona un mayor nivel de detalle sobre la forma de la distribución que el histograma o el diagrama de cajas. Una distribución uniforme tiene los valores de los datos distribuidos uniformemente a lo largo del rango de los datos. Esto hace que la distribución parezca un rectángulo.

En una distribución uniforme, la media es igual a la mediana, ya que una distribución uniforme es también una distribución simétrica. El diagrama de cajas no proporciona suficiente información para describir la forma de la distribución como uniforme, aunque la longitud uniforme de cada cuarto sugiere que la distribución puede ser aproxiDMAamente simétrica.

Una distribución bimodal tiene dos valores de datos muy comunes que se ven en un diagrama de puntos o histograma como picos distintos.

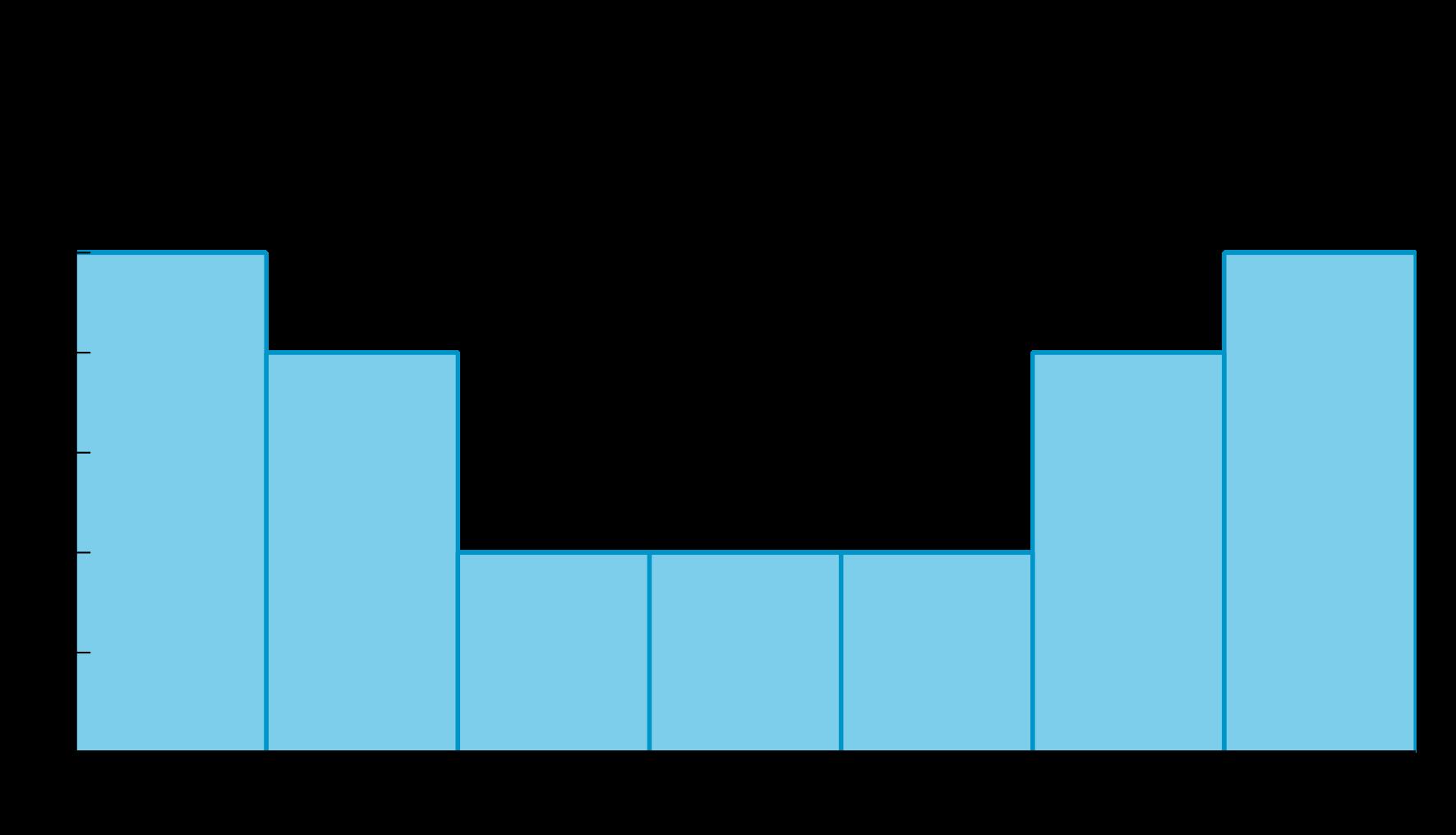
A veces, una distribución bimodal tiene la mayoría de los datos agrupados en el centro de la distribución. En estos casos, el centro de la distribución no describe muy bien los datos. Las distribuciones bimodales no siempre son simétricas. Por ejemplo, los picos pueden no estar igualmente espaciados del centro de la distribución u otros valores de datos pueden romper la simetría.

Math Nation California . Algebra 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

¿Cuál de los diagramas de puntos muestra una distribución simétrica?

PROBLEMA 2

¿Cuál de los diagramas de puntos muestra una distribución sesgada?

Soluciones posibles

B. C.

1 . Matemáticas . Unidad 1

PROBLEMA 3

Crear un diagrama de puntos que muestre una distribución uniforme.

Soluciones posibles

Ejemplo de solución:

PROBLEMA 4

(De la unidad 1, lección 3).

Los datos representan el número de onzas de agua que 26 estudiantes bebieron antes de donar sangre: 8, 8, 8, 16, 16, 16, 32, 32, 32, 32, 32, 32, 64, 64, 64, 64, 64, 64, 64, 64, 80, 80, 80, 80, 88, 88, 88.

A. Crea un diagrama de puntos para los datos.

B. Crea un diagrama de cajas para los datos.

C. ¿Qué información sobre los datos proporciona el diagrama de cajas que no proporciona el diagrama de puntos?

D. ¿Qué información sobre los datos proporciona el diagrama de puntos que no proporciona el diagrama de cajas?

E. Se recomendó que los estudiantes bebieran 48 o más onzas de agua. ¿Cómo podrías utilizar un histograma para mostrar fácilmente el número de estudiantes que bebieron la cantidad recomendada?

PROBLEMA 5

(De la unidad 1, lección 2).

Soluciones posibles

C. Ejemplo de respuesta: El diagrama de cajas muestra la mediana y los cuartiles. Para encontrar esos valores con un diagrama de puntos sería necesario hacer cálculos.

D. Ejemplo de respuesta: El diagrama de puntos muestra todos los datos y puede utilizarse para determinar el valor o los valores más frecuentes.

E. Ejemplo de respuesta: Un histograma con intervalos de 0 a 48 y 48 a 96 mostraría fácilmente esta información.

El diagrama de cajas representa la distribución del número de puntos anotados por un equipo de campo traviesa y en 12 encuentros.

A. Si es posible, encuentra la media. Si no es posible, explica por qué.

B. Si es posible, halla la mediana. Si no es posible, explique por qué no.

C. ¿Alguna vez el equipo de campo traviesa anotó 30 puntos en una competencia?

Soluciones posibles

A. Ejemplo de respuesta: No es posible calcular la media porque el diagrama de cajas no proporciona las 12 puntuaciones. solo proporciona un resumen de las puntuaciones.

B. 34 puntos

C. Ejemplo de respuesta: No es posible saber si obtuvieron 30 puntos. 22 24 26 28 30 32 34 36 38 40 42 Puntos

LECCIÓN 5

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

S-ID.1 Representar datos con gráficas en la recta numérica real (diagramas de puntos, histogramas y diagramas de cajas).

S-ID.2 Usar estadísticas apropiadas a la forma de la distribución de datos para comparar el centro (mediana, media) y la dispersión (rango intercuartil, desviación estándar) de dos o más conjuntos de datos diferentes.

Construir

6.SP.5c

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP4 Representar con matemáticas.

Estándares ELD de California

I.A.3

I.C.12

II.B.5

CÁLCULO DE MEDIDAS DE CENTRO Y VARIABILIDAD

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

comprender al mundo, representan con las matemáticas analizan los datos.

OBJETIVO(S) DE APRENDIZAJE

• Puedo calcular la desviación media absoluta, el rango intercuartílico, la media y la mediana de un conjunto de datos.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Calcular la desviación media absoluta, el rango intercuartílico, la media y la mediana.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR8: Apoyos para el debate

Materiales necesarios

Fichas preimpresas, recortes de la plantilla maestra

Preparación necesaria

Necesitará una vara de medir y 14 monedas de un centavo (u otras pesas pequeñas) para una demostración. Se incluye una plantilla maestra opcional como un organizador gráfico para calcular el rango intercuartílico. Una copia de la plantilla maestra contiene 2 organizadores gráficos.

INFORMACIÓN DE LA LECCIÓN

Metas de aprendizaje para el estudiante

• Calculemos medidas de centro y medidas de variabilidad y sepamos cuáles son las más apropiadas para los datos.

Narrativa de la lección

Esta lección es opcional porque retoma contenidos por debajo del nivel de grado. Si la evaluación diagnóstica previa a la unidad indica que sus estudiantes saben cómo calcular la media, la mediana, la desviación media absoluta (DMA) y el rango intercuartílico (IQR, por sus siglas en inglés), entonces esta lección puede omitirse con seguridad. Esta lección se relaciona con el trabajo siguiente porque los estudiantes interpretarán los datos con medidas de centro y medidas de variabilidad a lo largo de la unidad, por lo que es importante que entiendan lo que significan estos estadísticos. Cuando los estudiantes explican la DMA con el ejemplo de un metro, participan en MP2 porque estaban razonan abstracta y cuantitativamente al interpretar la DMA en contexto.

RESUMEN DE LA LECCIÓN

Componente de lección Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración (opcional) Independiente 10 min

Actividad de exploración (opcional) Independiente 15 min

Síntesis Todo el grupo 5 min

Descripción breve

Los estudiantes determinan qué declaraciones sobre la media y la mediana son verdaderas o falsas y luego justifican su razonamiento..

Los estudiantes determinan la mediana y el rango intercuartílico (IQR) en un conjunto de datos y luego interpretan las medidas de centro y dispersión en diferentes contextos.

Los estudiantes calculan la desviación media absoluta (DMA) con un conjunto de datos del mundo real y, a continuación, la utilizan para explicar la variabilidad de los datos.

Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de la DMA y de cómo se ve afectada por los valores de un conjunto de datos.

Los estudiantes hablan del proceso para calcular el IQR y la DMA y cómo los dos valores se comparan en su medida de variabilidad.

Enfriamiento Independiente 5 min Los estudiantes calculan la DMA y el IQR de un pequeño conjunto de datos.

Práctica Independiente 10 min

El componente de práctica independiente incluye 2 problemas de la lección y 4 problemas de repaso en espiral.

CALENTAMIENTO | CALCULAR CENTROS (5 minutos)

El propósito de este calentamiento es animar a los estudiantes a repasar cómo calcular la media y la mediana.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Mostrar un problema a la vez. Dé a los estudiantes 1 minuto de tiempo para pensar en silencio seguido de una discusión con toda la clase.

Decida si cada situación es verdadera o falsa. Explica tu razonamiento.

1. La media se puede hallar sumando todos los números de un conjunto de datos y dividiendo por el número de números del conjunto de datos.

2. La media de los datos del diagrama de puntos es 4.

3. La mediana del conjunto de datos es 9 para los datos: 4, 5, 9, 1, 10

4. La mediana de los datos en el diagrama de puntos es 3.5.

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

1. Verdadero. Ejemplo de razonamiento: El enunciado es la forma correcta de calcular la media.

2. Falso. Ejemplo de razonamiento: La media es 3.5 porque la suma es 28 y 28 ÷ 8 = 3.5. No redondear a 4.

3. Falso. Ejemplo de razonamiento: Nueve no es la mediana porque los números no están ordenados.

4. Verdadero. Ejemplo de razonamiento: La mediana es 3.5 porque los dos valores del medio son 3 y 4 y su media es 3.5

Algunos estudiantes pueden olvidar ordenar los datos al hallar la mediana. Pregúntales: «¿Qué es la mediana? ¿Qué te dice sobre los datos?». Es posible que algunos estudiantes no recuerden cómo hallar la mediana cuando hay un número par de valores de datos. Pregúntales: «¿Qué te dice la mediana sobre los datos? ¿Cómo podríamos encontrar un número medio entre estos dos valores?».

El objetivo de esta actividad es repasar cómo calcular la media y la mediana e identificar errores comunes en el cálculo de la media y la mediana. En la discusión, pida a los estudiantes que recuerden qué información revelan la media y la mediana sobre los datos.

• «¿Qué te dice la media sobre los datos?». (En promedio, dónde está el centro de los datos).

SÍNTESIS DE LA ACTIVIDAD

• «¿Qué te dice la mediana sobre los datos?». (La mitad de los números son mayores o iguales que la mediana y la otra mitad son menores o iguales que la mediana).

Algunos errores comunes a evitar:

• No poner los números en orden al encontrar la mediana.

• Si hay dos números en el medio, no sumarlos y dividirlos por dos para encontrar la mediana.

• Encontrar el número del medio en el eje horizontal en lugar de en los datos.

• Redondear la media al número entero más cercano.

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | LATIDOS DEL CORAZÓN:

PARTE 1 (10

minutos)

El propósito de esta actividad es que los estudiantes calculen la mediana y el IQR, e investiguen cómo esos valores se ven afectados por los valores atípicos.

Los conjuntos de datos de esta lección son lo suficientemente pequeños como para que no sea necesario encontrar estadísticas de resumen como medidas de centro o medidas de variabilidad. Todo el conjunto de datos podría evaluarse con bastante facilidad y no necesita más análisis. Los conjuntos son pequeños con el fin de practicar el cálculo y la comprensión de los estadísticos. En realidad, la búsqueda de dichas estadísticas es mucho más útil cuando el conjunto de datos es mucho mayor. Por ejemplo, algunos dispositivos encontrarán la frecuencia cardiaca cada 10 minutos, lo que da más de 1,000 valores para una semana que podrían analizarse para determinar información sobre la salud de una persona. Sería difícil entender todos los datos mirando una tabla o incluso una visualización de datos. Disponer de algunos estadísticos de resumen, como la media o la mediana, sería útil para comprender la frecuencia cardíaca de una persona durante la semana.

En esta actividad, se proporciona un organizador gráfico opcional en la plantilla maestra para ayudar a los estudiantes a calcular el rango intercuartílico. Las casillas sombreadas no deben utilizarse y la posición de las casillas abiertas tiene por objeto destacar los datos útiles para calcular el valor de la fila. Por ejemplo, para calcular los primeros cuartiles, los estudiantes utilizan la media de los valores segundo y tercero, por lo que esas casillas se dejan abiertas para indicar que estos datos son útiles.

INTRODUCCIÓN

Dé a los estudiantes 3-5 minutos de tiempo tranquilo para trabajar la primera pregunta y luego haga una pausa para una breve discusión de toda la clase sobre cómo calcular la mediana, los cuartiles y el IQR.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Proporcionar a los estudiantes el organizador gráfico para que organicen su trabajo con el cálculo de la mediana, los cuartiles y el IQR.

Apoya la accesibilidad para: Lenguaje; organización

Las frecuencias cardíacas de ocho estudiantes de secundaria se indican en pulsaciones por minuto:

1. ¿Cuál es el rango intercuartílico?

2. ¿Cuántos valores del conjunto de datos...

A. son menores que el ��1?

B. están entre el ��1 y la mediana?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

C. están entre la mediana y el ��3?

D. son mayores que el ��3?

3. Una manada de delfines contiene 800 delfines de varias edades y longitudes. La longitud media de los delfines de esta manada es 5.8 pies. ¿Qué información le da esto sobre la longitud de los delfines de esta manada?

4. El mismo examen de vocabulario con 50 preguntas se hace a 600 estudiantes de quinto a décimo grado y se recoge el número de respuestas correctas de cada estudiante de este grupo. El rango intercuartílico es 40 respuestas correctas. ¿Qué información le proporciona esto sobre el número de respuestas correctas de los estudiantes que realizan esta prueba?

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

1. 3 pulsaciones por minuto

2. A. 2

B. 2

C. 2

D. 2

3. Ejemplo de respuesta: La mitad de los delfines miden 5.8 pies o más y la otra mitad miden 5.8 pies o menos.

4. Ejemplo de respuesta: Hay mucha variabilidad en el número de respuestas correctas para este grupo. La mitad de los datos abarcó un intervalo de 40 respuestas correctas y, dado que solo hay 50 preguntas, esto indica que hay mucha variabilidad.

Los estudiantes pueden tener dificultades para calcular la mediana de un conjunto de datos con un número par de puntos de datos. Pregúnteles qué representa la mediana para el conjunto de datos y dónde puede estar ese valor. Si siguen teniendo dificultades, recuérdeles que la mediana es la media de los dos números centrales.

El propósito de esta discusión es discutir el método de cálculo de la mediana y el IQR, así como la interpretación de cada uno. He aquí algunas preguntas para la discusión.

SÍNTESIS DE LA ACTIVIDAD

• «¿Qué aspecto tendría un diagrama de cajas para los resultados del examen de vocabulario?». (Dependería de la puntuación alta y baja, pero la caja probablemente empezaría en 5 y llegaría hasta 45 o podría empezar en 10 y llegar hasta 50).

• «¿Qué te dice el IQR sobre un conjunto de datos?». (El IQR es una medida de variabilidad que describe el rango de la mitad media de los datos).

• «¿Cómo dividen los datos la mediana y los cuartiles?». (En cuartiles iguales, de modo que en cada cuartil haya el mismo número de valores).

• «¿Qué proporción de los datos se encuentra entre ��1 y ��3?». (La mitad 50 % de los datos se encuentra entre estos valores).

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | LATIDOS DEL CORAZÓN:

PARTE 2 (15

minutos)

Rutinas didácticas

MLR8: Apoyos para la discusión

El objetivo de esta actividad es que los estudiantes calculen y describan la desviación media absoluta. Se proporciona a los estudiantes un conjunto de datos y un organizador para calcular la desviación absoluta media (DMA). A continuación, se plantean preguntas que pretenden hacerles pensar sobre DMA más conceptualmente como una medida de variabilidad.

INTRODUCCIÓN

Álgebra 1 . Matemáticas . Unidad 1

Ayude a los estudiantes a entender cómo utilizar la tabla mostrándoles la tabla de ejemplo:

Valores de los datos

Desviación de la media (valor de los datos

Esto da como resultado una ��MA de 2.5, ya que

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyo al debate. Utilice esta rutina para ampliar los usos matemáticos del lenguaje para comunicarse sobre valores de datos, medias, desviación de la media y desviaciones absolutas. Invite a los estudiantes a utilizar estas palabras cuando expongan sus ideas. Pida a los estudiantes que repitan a coro las frases que incluyan estas palabras en su contexto.

Principio(s) de diseño: Apoyar la creación con sentido; optimizar el resultado (para la explicación)

1. Calcula la DMA con los mismos datos de la actividad anterior hallando la distancia media de cada valor de los datos a la media. Puede resultarte útil organizar tu trabajo completando la tabla proporcionada.

Valores de los datos Media

Desviación de la media (Valor de los datos

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

��MA:

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES

1. Para otro conjunto de datos, todos los valores están 3 pulsaciones por minuto por encima de la media o 3 pulsaciones por minuto por debajo de la media. ¿Es suficiente información para encontrar el DMA para este conjunto de datos? Si es así, encuentra el DMA. Si no es así, ¿qué otra información se necesita? Explica tu razonamiento.

2. Se colocan varios centavos a lo largo de un metro y se registra la posición en centímetros de cada centavo. La posición media es la marca de 50-centímetros y la DMA es de 10 centímetros. ¿Qué información te da esto sobre la posición de los centavos a lo largo de la vara del metro?

1. 2 pulsaciones por minuto

2. Es suficiente información. La DMA es 3 pulsaciones por minuto, ya que la distancia promedio a la media es 3 pulsaciones por minuto.

3. Respuesta de ejemplo: Los centavos están espaciados de manera que, en promedio, están a unos 10 centímetros de la marca de 50 centímetros.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Vigile a los estudiantes que tienen problemas para encontrar la media o que están usando valores negativos para la distancia a la media. Recuérdeles que el símbolo | ��| representa el valor absoluto. Si es necesario, pídeles que observen una recta numérica y describan la distancia entre dos valores para recordarles que las distancias siempre deben describirse como valores positivos.

Coloca monedas de un centavo en metro de modo que los centros de las monedas estén en {20, 40, 40, 45, 45, 45, 45, 45, 55, 55, 55, 55, 55, 55, 90}. Muestra cómo se equilibra el palito cuando pones el dedo en la marca de 50 centímetros y cómo algunos están más lejos y otros más cerca de 10 centímetros de la media, pero están repartidos de forma que, en promedio, están a 10 centímetros de distancia.

Crea una visualización que incorpore las medidas de centro (media y mediana) y variabilidad (rango intercuartílico y desviación media absoluta) discutidas hasta ahora. Más adelante, se añadirá la desviación típica a la sección de variabilidad. Esta pantalla debe colocarse en el aula durante las lecciones restantes de esta unidad. Debería ser algo parecido a

Mediana: Medida de centro que divide los datos de forma que la mitad de los valores sean mayores que la mediana y la otra mitad menores que la mediana. Las medianas se visualizan con mayor facilidad en un diagrama de cajas.

IQR

0 2 4 6 8 10 12 14 16

Mediana

Media: También llamada promedio, es el valor que se obtiene al sumar todos los valores del conjunto y dividirlo entre los números del conjunto.

Media DMA DMA

0 1.5 2 2.5 3 3.5 4 4.5 5

Rango intercuartil (IQR): Medida de variabilidad determinada por el rango de valores de la mitad central de los datos. Usado a menudo con la mediana, este valor se puede determinar al restar Q3 – Q1. En el cuadro del diagrama que se muestra aquí, el IQR es 5 (ya que 9 – 4 = 5).

Desviación media absoluta (DMA): Medida de variabilidad determinada por la media de las distancias de los puntos de datos a la media de la distribución. Usado a menudo con la media, este valor está relacionado con la dispersión de los datos.

Álgebra 1 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

Aquí hay algunas preguntas para debatir.

• «Si pones centavos a 45, 35 y 70, ¿dónde tienes que poner un centavo para que la metro se equilibre a 50 cm? ¿Cuál es la DMA?». (50 cm, 10 cm)

• «Si pones dos centavos en 60, ¿dónde tienes que poner un centavo para que el metro se equilibre en 50 cm? ¿Cuál es la DMA?». (30 cm, 40 3 cm)

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience con una demostración física del uso de monedas de un centavo en un metro, lo que permitirá a los estudiantes ver las conexiones entre las nuevas situaciones y sus conocimientos previos. Considere la posibilidad de utilizar estas indicaciones: «¿Qué tiene en común esta demostración con las medidas de centro y variabilidad? o ¿Cómo se relaciona el punto de equilibrio con la media o la mediana?».

Apoya la accesibilidad para: Procesamiento conceptual; procesamiento visual-espacial

¿Estás preparado para más?

Supón que hay 6 centavos en un metro de forma que la posición media es la marca 50 centímetros y la DMA es de 10 centímetros.

1. Encuentra posibles ubicaciones para los 6 centavos.

2. Encuentra un conjunto diferente de posibles ubicaciones para los 6 centavos.

Respuesta del estudiante

1. Respuesta de ejemplo: 3 centavos en la marca de 40 centímetros y 3 centavos en la marca de 60 centímetros.

2. Ejemplo de respuesta: 1 centavo en la marca de 35 centímetros, 1 centavo en la marca de 40 centímetros, 1 centavo en la marca de 45 centímetros, 1 centavo en la marca de 55 centímetros, 1 centavo en la marca de 60 centímetros, 1 centavo en la marca de 65 centímetros.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

El objetivo es que los estudiantes sepan calcular la ��MA y �� y que son medidas de variabilidad.

• «¿Cómo se calcula la ��?». (Halla la diferencia entre el valor del tercer cuartil y el del primero).

• «¿Cómo se calcula la DMA?». (Halla la distancia de cada valor a la media. Luego toma la media de esos valores).

• «Un conjunto de datos tiene una �� mayor que otro. Qué significa esto sobre los datos del primer conjunto de datos?».. (Tiene mayor variabilidad. Esto significa que la mitad media de los datos está más separada del centro que la mitad media de los datos del segundo conjunto de datos).

ENFRIAMIENTO | CALVULAR LA DMA Y EL IQR

• 5

• 18

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

California . Algebra 1

(5 minutes)

• 18

• 13

• 6

Media: 12

1. Encuentra la desviación media absoluta de los datos.

2. Encuentae el rango intercuartílico de los datos

1. 5.2

2. 12.5

Resumen de la lección

La desviación media absoluta, o DMA, y el rango intercuartílico, o ��, son medidas de variabilidad. Las medidas de variabilidad indican en qué medida los valores de un conjunto de datos tienden a diferir entre sí. Una medida de variabilidad mayor significa que los datos están más dispersos, mientras que una medida de variabilidad menor significa que los datos son más consistentes y cercanos a la medida del centro.

Para calcular la DMA de un conjunto de datos:

1. Halla la media de los valores del conjunto de datos.

2. Halla la distancia entre cada valor de los datos y la media en la recta numérica: | valor de los datos − media |

3. Halla la media de las distancias. Este valor es el DMA

Para calcular el ��, resta el valor del primer cuartil del valor del tercer cuartil. Recuerda que el primer y tercer cuartil están incluidos en el resumen de cinco números.

PROBLEMAS

DE PRÁCTICA

PROBLEMA 1

El conjunto de datos representa la cantidad de errores en una prueba de mecanografía.

A. ¿Cuál es la mediana? Interpreta este valor en la situación.

B. ¿Cuál es la ��?

Soluciones posibles

A. 9 errores. La mitad de las personas tenían 9 errores o más y la mitad tenían 9 errores o menos.

B. 2 errores

PROBLEMA 2

El conjunto de datos representa las alturas, en centímetros, de diez modelos de puentes hechos para un concurso de ingeniería.

A. ¿Cuál es la media?

B. ¿Cuál es la DMA?

Soluciones posibles

A. 16 centímetros

B. 1.4 centímetros

1 . Matemáticas . Unidad 1

PROBLEMA 3

(De la unidad 1, lección 4).

Describa la forma de la distribución mostrada en el diagrama de puntos. El diagrama de puntos muestra las puntuaciones de un torneo de golf.

PROBLEMA 4

(De la unidad 1, lección 4).

El diagrama de puntos muestra el peso, en gramos, de varias rocas diferentes. Selecciona todos los términos que describen la forma de la distribución.

Soluciones posibles

Sesgado hacia la derecha y centrada cerca de 136 golpes

Soluciones posibles

en forma de campana bimodal sesgada simétrica uniforme

PROBLEMA 5

(De la unidad 1, lección 3).

El diagrama de puntos representa la distribución de los salarios ganados durante un período de una semana por estudiantes universitarios.

A. ¿Cuál es la media? Interpreta este valor con base en la situación.

B. ¿Cuál es la mediana? Interpreta este valor con base en la situación.

C. ¿Le habría permitido un diagrama de caja de los mismos datos encontrar tanto la media como la mediana?

Soluciones posibles

A. $118.25. Ejemplo de la interpretación: Esto significa que si todos los 12 estudiantes juntaran sus ganancias de la semana y luego redistribuyeran el dinero equitativamente, cada persona obtendría $118.25

B. $118. Esto significa que la mitad de los estudiantes ganaron $118 o más, y la mitad ganaron $118 o menos.

C. No, no habría sido posible hallar la media.

1 . Matemáticas . Unidad 1

PROBLEMA 6

(De la unidad 1, lección 2).

El diagrama de cajas muestra la temperatura de las saunas en grados Fahrenheit. ¿Cuál es la mediana?

Grados (Fahrenheit)

Soluciones posibles

118 grados Fahrenheit

Reflexiones:

Math Nation California . Algebra 1

Álgebra 1 . Matemáticas . Unidad 1

LECCIÓN 6

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

S-ID.1 Representar datos con gráficas en la recta numérica real (diagramas de puntos, histogramas y diagramas de cajas).

Construir

S-ID.3

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.B.6

I.C.12

II.C.6

GRAFICADO TECNOLÓGICO

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

predecir lo que podría ocurrir,

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

buscarán y expresarán regularidades en razonamientos repetidos analizan los datos.

OBJETIVO(S) DE APRENDIZAJE

• Puedo crear representaciones gráficas de datos y calcular estadísticas con tecnología.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Utilizar herramientas tecnológicas para representar gráficamente datos y calcular estaística útil.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

Analízalo

MLR2: Recopilar y mostrar

Material Necesario

Estadístico-tecnológico

Preparación requerida

Adquirir dispositivos que puedan ejecutar GeoGebra (recomendado) u otra tecnología de hoja de cálculo. Lo ideal es que cada estudiante tenga su propio dispositivo. (Una hoja de cálculo GeoGebra está disponible en la seccion titulada «Herramientas matemáticas).

Los estudiantes necesitan tener acceso a los datos recogidos de las preguntas de la encuesta en una lección anterior y también a la tecnología de hoja de cálculo. Se recomienda utilizar la hoja de cálculo GeoGebra y la herramienta de estadística de una variable que forma parte de las herramientas de matemáticas proporcionadas con la versión digital de estos materiales y también disponible en https://www.geogebra.org/classic/ spreadsheet. Si opta por utilizar otro tipo de herramienta que pueda encontrar estadísticas resumidas y crear histogramas y diagramas de cajas, es posible que tenga que desarrollar instrucciones tecnológicas alternativas para sus estudiantes.

1 . Matemáticas . Unidad 1

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Usemos la tecnología para representar datos.

Narrativa de la lección

El propósito matemático de esta lección es crear visualizaciones de datos y calcular estadísticas con la tecnología. Los estudiantes se encuentran con el término estadística que es una cantidad que se calcula a partir de datos de muestra. En esta lección los estudiantes introducirán datos en una hoja de cálculo, encontrarán estadísticas y crearán diagramas de cajas con la tecnología. El trabajo de esta lección se conecta con el trabajo previo porque los estudiantes han creado visualizaciones de datos y han interpretado estadísticas sin tecnología. El trabajo de esta lección se relaciona con el trabajo futuro porque los estudiantes tomarán decisiones sobre qué estadísticas son apropiadas después de usar la tecnología para crear visualizaciones de modo que puedan ver la forma de una distribución. Cuando los estudiantes investigan y explican cómo el cambio de valores en un conjunto de datos afecta a la media y a la mediana, estarán trabajando en MP8 porque están buscando y expresando la regularidad en razonamientos repetidos.

RESUMEN DE LA LECCIÓN

Componente de lección

Estructura Tiempo

Calentamiento En pareja 10 min

Actividad de Exploración En pareja 15 min

Actividad de Exploración En pareja 10 min

Síntesis Todo el grupo 5 min

Descripción breve

Los estudiantes introducen datos en una hoja de cálculo y se familiarizan con las posiciones y etiquetas de las celdas.

La actividad requiere el uso de tecnología de hoja de cálculo. Una aplicación digital interactiva está disponible en línea para que los estudiantes puedan utilizar hojas de cálculo para encontrar estadísticas con la tecnología.

Los estudiantes utilizan la hoja de cálculo de la sección «Calentamiento» para calcular las medias y medianas, definidas como estadísticas, del conjunto de datos antes de crear visualizaciones de histogramas.

La actividad requiere el uso de una aplicación digital interactiva para que los estudiantes puedan calcular estadísticas y crear visualizaciones de datos.

Los estudiantes utilizan la pregunta estadística de una lección anterior para calcular estadísticas y luego crear visualizaciones con la tecnología.

La actividad requiere el uso de una aplicación digital interactiva para que los estudiantes calculen estadísticas y creen visualizaciones de datos.

Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de la creación y análisis de visualizaciones de datos con la tecnología.

Los estudiantes reflexionan sobre el proceso de creación de visualizaciones de datos con la tecnología y luego discuten la utilidad de la tecnología para hacerlo.

Enfriamiento Independiente 5 min Los estudiantes interpretan un resumen estadístico de salida de la tecnología.

Práctica Independiente 10 min

El componente de práctica independiente incluye 2 en la lección y 2 problemas de revisión en espiral.

CALENTAMIENTO | TODO COMIENZA CON LOS

DATOS

(10 minutos)

El propósito matemático de esta actividad es familiarizarse con la introducción de datos en una hoja de cálculo y preparar a los estudiantes para la búsqueda de estadísticas con la tecnología.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organizar a los estudiantes en grupos de 2. Si los estudiantes estudian la versión digital de los materiales, mostrarles cómo abrir la aplicación de hoja de cálculo GeoGebra en las herramientas matemáticas. Si los estudiantes usan la versión impresa de los materiales, pueden acceder a la app de la hoja de cálculo GeoGebra en www. geogebra.org/spreadsheet. Si utilizan una tecnología diferente, es posible que deba proporcionarles instrucciones alternativas. Asegúrese de que los estudiantes ingresen los datos en una columna, aunque los datos estén representados en dos columnas en el enunciado de la tarea.

Abre una ventana de hoja de cálculo e ingrese los datos de modo que cada valor esté en su propia celda en la columna A.

1. ¿Cuántos valores hay en la hoja de cálculo? Explica tu razonamiento.

2. Si has introducido los datos en el orden en que aparecen los valores, el número 7 está en la celda en la posición A1 y el número 5 está en la celda A5. Enumere todas las celdas que contienen el número 13

3. En la celda C1 escriba la palabra «Suma», en C2 escriba «Media» y en C3 escriba «Mediana». Puede que desee hacer doble clic o arrastrar la línea vertical entre las columnas C y D para poder ver las palabras completas.

POSIBLES RESPUESTASS

SÍNTESIS DE LA ACTIVIDAD

1. 20, ya que las filas están numeradas y el último valor está junto a 20

2. A4, A12 y A14.

3. No se requiere respuesta.

El objetivo es asegurarse de que los estudiantes sepan cómo escribir datos en una hoja de cálculo y localizar valores en la hoja de cálculo por filas y columnas. Las ubicaciones se referenciarán con funciones de la hoja de cálculo en las próximas actividades. He aquí algunas preguntas para el debate.

• «¿Qué valor hay en la celda A7?». (14)

• «¿Qué ha resultado interesante o desafiante de esta actividad?». (No sabía que podía describir cada celda de la hoja de cálculo con las etiquetas de la fila y columna).

Álgebra 1 . Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | ENCONTRAR ESTADÍSTICAS EN HOJAS DE CÁLCULO

(15 minutos)

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

El propósito matemático de esta actividad es calcular estadísticas, crear visualizaciones de datos e investigar cómo cambian éstos cuando se añaden o eliminan valores del conjunto de datos. Vigila que los estudiantes hablen de la relación entre los valores atípicos y la medida del centro.

Manténga a los estudiantes en los mismos grupos. Seguirán trabajando con la hoja de cálculo que empezaron en la actividad anterior.

Diga a los estudiantes que las estadísticas son valores que se calculan con datos, como la media, la mediana o el rango intercuartílico.

INTRODUCCIÓN

Diga a los estudiantes que después de cambiar el valor en A1 para cambiar la media en la primera serie de preguntas, deben seguir utilizando el valor cambiado para la segunda serie de preguntas en lugar de volver a los valores del calentamiento. Tenga en cuenta que GeoGebra es como cualquier otro programa informático. Necesita instrucciones escritas en una forma específica para que ejecute un comando. Por ejemplo, si los estudiantes olvidan escribire el signo de = o no escriben en mayúscula la palabra «Suma», la fórmula no funcionará. Pida a los estudiantes que hagan una pausa después de escribir las fórmulas y comprueben que las celdas D1, D2 y D3 muestran números para cada estadística. Si no es así, pida a los estudiantes que borren el contenido de la celda y que vuelvan a escribir el signo de = y escriban en mayúsculas «Suma», «Media» y «Mediana».

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para dar a los estudiantes una oportunidad estructurada de revisar su borrador incial de una respuesta a la última pregunta. Pida a cada estudiante que se reúna con 2-3 otros compañeros seguidos para recibir comentarios. Proporcione a los estudiantes indicaciones para la retroalimentación que les ayuden a reforzar sus ideas y a clarificar su lenguaje. Por ejemplo: «¿Puedes explicar cómo cambiaron los valores cuando...?, «Deberías ampliar la relación entre los valores atípicos y....», etc. Después, invite a los estudiantes a ampliar su respuesta, incorporando cualquier comentario que hayan recibido.

Principio(s) de diseño: Fomentar la conversación

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Divide esta tarea en partes más manejables para ayudar a los estudiantes que se benefician de las habilidades organizativas en la resolución de problemas. Por ejemplo, presente un conjunto de preguntas a la vez.

Apoya la accesibilidad para: Organización; atención

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Con los datos del calentamiento, podemos calcular algunas estadísticas y mirar los datos.

• Junto a la palabra «Suma», en la celda D1, escribe = Suma(A1:A20)

• Junto a la palabra «Media», en la celda D2, escribe = Media(A1:A20)

• Junto a la palabra «Mediana», en la celda D3, escribe = Mediana(A1:A20)

1. ¿Cuáles son los valores de cada uno de las estadísticas?

2. Cambia el valor en A1 por 8. ¿Cómo cambia eso las estadísticas?

3. ¿Qué valor se puede poner en A1 para cambiar la media a 10.05 y la mediana a 9?

También podemos usar GeoGebra para crear visualizaciones de datos.

• Haz clic en la letra A de la primera columna para que se resalte toda la columna.

• Haz clic en el botón que parece un histograma para obtener una nueva ventana etiquetada Análisis de una variable

• Haz clic en Analizar para ver un histograma de los datos.

1. Haz clic en el botón Σ �� para ver muchos de los estadísticos.

A. ¿Qué representa el valor de n?

B. ¿Qué representa el valor de Σ ��?

C. ¿Qué otras estadísticas reconoce?

2. Ajuste el control deslizante situado junto a la palabra «Histograma».

3. Haz clic en el botón situado a la derecha del control deslizante para abrir otra ventana con más opciones. A continuación, haz clic en la casilla situada junto a Establecer clases manualmente y establezca el ancho de 5. ¿Qué le hace esto al histograma?

4. Haz clic en la palabra Histograma y observa un diagrama de cajas y un diagrama de puntos de los datos. Cuando miren el diagrama de cajas, observe que hay un �� en el lado derecho del diagrama de caja. Esto representa un punto de datos que se considera un valor atípico

1. La suma es 178, la media es 8.9, la mediana es 8.5

2. La suma es ahora 179, la media es 8.95, la mediana sigue siendo 8.5

3. 30

RESPUESTAS POSIBLES

A. El número de valores analizados.

B. La suma de los valores analizados.

C. Media, mínimo, Q1 (primer cuartil), mediana, Q3 (tercer cuartil), und máximo.

2. Aparece un número a la derecha del deslizador y cambia el número y el tamaño de las barras. 3. Hace que cada barra tenga una anchura de 5.

4. El �� pasa a formar parte del diagrama de cajas. El razonamiento varía. Ejemplo de respuesta: Podría ser útil mostrar los valores atípicos si no estamos seguros del dato extremo y queremos ver qué podría ocurrir si no se incluye ese valor. Podría ser mejor incluir el valor extremo en los datos si no vemos ningún error en los datos y no debemos descartar datos. Si el valor extremo está en duda o si hay una razón para llamar la atención sobre los valores atípicos, podría tener sentido separarlos del diagrama de cajas.

SÍNTESIS DE LA ACTIVIDAD

Álgebra 1 . Matemáticas . Unidad 1

El propósito de esta discusión es que los estudiantes creen visualizaciones de datos con la tecnología y analicen lo que sucede con las visualizaciones y las estadísticas cuando se realizan cambios en el conjunto de datos. Aquí hay algunas preguntas para la discusión.

• «¿Qué pasó con las estadísticas cuando cambiaste el valor de A1 a 8 en la hoja de cálculo». (Cuando se cambió a 8, la media aumentó ligeramente, pero la mediana se mantuvo igual).

• «¿Por qué aumentó la media?|. (La suma de los datos aumentó, pero el número de números se mantuvo igual, por lo que la media tuvo que aumentar).

• «¿Por qué se mantuvo igual la mediana?». (Cambiar un 7 a un 8 en el conjunto de datos no cambió los números medios, 8 y 9, en el conjunto de datos).

• «¿Qué notaste cuando cambiaste el ancho de las clases para el histograma?». (Esto cambió los intervalos para cada barra a un ancho de 5 y los datos fueron reordenados en esos intervalos).

Seleccione a los estudiantes que fueron identificados previamente para discutir la relación entre los valores atípicos y las medidas del centro. Pregunte: «¿cuál es la relación entre los valores atípicos y las medidas del centro?». (Cuando hay valores atípicos, la mediana es la medida de centro preferida porque se ve menos afectada por los valores atípicos que la media).

ACTIVIDAD DE EXPLORACIÓN | CREACIÓN DE VISUALIZACIONES DIGITALES

(10 minutos)

Rutinas didácticas

Analícelo

MLR2: Recopilar y visualizar

El propósito matemático de esta actividad es que los estudiantes creenvisualizaciones de datos y calculen estadísticas con la tecnología. Los estudiantes trazan los datos de la encuesta que recogieron de una pregunta estadística en una lección anterior.

INTRODUCCIÓN

Organice a los estudiantes en grupos de dos. Diles que van a utilizar la tecnología para crear visualizaciones de datos y calcular estadísticas para los datos que recogieron de una pregunta de la encuesta en una lección anterior.

Apoyo para estudiantes que aprenden el idioma inglés

Conversar, representar, escribir: MLR2 Recopilar y visualizar. Mientras las parejas trabajan, escuche y recopile el vocabulario, las frases y los métodos que utilizan los estudiantes para crear diagramas de puntos, diagramas de cajas e histogramas con la tecnología, como conjunto de datos, distribución sesgada, mediana, el diagrama de cajas para el IQR. Considere la posibilidad de agrupar el lenguaje para cada visualización de datos en diferentes áreas y asegúrese de incluir las fórmulas de la hoja de cálculo. Continúe con la actualziación del lenguaje recopilado de los estudiantes a lo largo de toda la actividad y de toda la unidad. Recuerde a los estudiantes que tomen prestado el lenguaje de la visualización según sea necesario. Esto ayudará a los estudiantes a ampliar su notación de definiciones recursivas.

Principio(s) de diseño: Apoyar la creación de sentido; maximizar la metaconciencia

Apoyo para estudiantes con discapacidad

Participación: Desarrollar el esfuerzo y la persistencia. Proporcione avisos, recordatorios, guías, guías de evaluaciones, listas de comprobación que se centren en aumentar la duración de la orientación a la tarea frente a las distracciones. Por ejemplo, crear un diagrama de puntos ejemplar que destaque características específicas, como la escala y las etiquetas, así como los cálculos para la media y la mediana.

Apoya la accesibilidad para: Atención; habilidad socioemocional

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Usa los datos que recopilaste en la pregunta numérica y estadística de una lección anterior. Usa la tecnología para crear un diagrama de puntos, un diagrama de caja y un histograma con tus datos. Luego, calcula la media, la mediana y el rango intercuartil de los datos.

Ejemplo de respuesta:

• Pregunta: En promedio, ¿cuántos libros leyó cada estudiante de la clase este verano?

• Datos:

• La media es 3.65, la mediana es 2 y el IQR es 4.5.

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Los estudiantes podrían perder una visualización de datos cuando comiencen a crear la siguiente. Explíqueles que es importante copiar sus soluciones en un lugar más permanente para que puedan consultarlas más adelante.

El objetivo de esta actividad era que los estudiantes crearan gráficos y hallaran estadísticas con la tecnología. Aquí hay algunas preguntas para debatir.

• «¿Cuáles fueron algunos de los desafíos que enfrentaron al usar la tecnología y cómo los superaron?». (No estaba seguro de qué botones presionar para acceder a la hoja de cálculo. Lo consulté con mi compañero y lo averigüé).

• «¿Qué ancho usaron para su histograma? ¿Por qué?». (Usé 5 porque mi conjunto de datos tiene valores que van del 1 al 42. Podría haber usado 10, pero entonces solo habría tenido 5 barras).

• «¿Cuál es la medida de centro adecuada para su conjunto de datos?». (La mediana fue adecuada porque mi conjunto de datos tiene una distribución asimétrica).

• «¿Qué visualización les permite calcular el IRQ más fácilmente?». (El diagrama de caja porque muestra Q1 y Q3).

• «¿Pueden hallar la mediana con su histograma?|. (No, los datos están agrupados en intervalos, por lo que un histograma no puede usarse para hallar el valor medio de la mediana). •

Álgebra 1 . Matemáticas . Unidad 1

¿Estás listo para más?

Un diagrama de tallo y hojsa es una tabla en la que cada punto de datos se indica cuando se escribe el primer dígito(s) a la izquierda (el tallo) y el último dígito(s) a la derecha (las hojas). Cada tallo se escribe una sola vez y es compartido por todos los puntos de datos con el mismo primer dígito(s). Por ejemplo, los valores 31, 32 y 45 podrían representarse como:

3 1 2

4 5

Clave: 3 | 1 significa 31

Una clase realizó un examen y obtuvo las siguientes puntuaciones: 86, 73, 85, 86, 72, 94, 88, 98, 87, 86, 85, 93, 75, 64, 82, 95, 99, 76, 84, 68

1. Utiliza la tecnología para crear un diagrama de tallo y hojas para este conjunto de datos.

2. ¿Cómo podemos ver la forma de la distribución a partir de este diagrama?

3. ¿Qué información podemos ver en un diagrama de tallo y hojas que no podemos ver en un histograma?

4. ¿Qué podemos controlar mejor en un histograma que en un diagrama de tallo y hojas?

Respuesta del estudiante

1. Clave: 6 | 4 significa 64

6 4 8

7 2 3 5 6

8 2 4 5 5 6 6 6 7 8

9 3 4 5 8 9

2. Ejemplo de respuesta: La longitud de cada hoja es como la altura de una barra en un histograma, excepto que es horizontal en lugar de vertical, por lo que todavía podemos ver los picos y las colas.

3. Podemos ver los valores exactos de cada punto de datos.

4. Un histograma ofrece un control mucho mayor sobre las longitudes de los intervalos utilizados.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

El objetivo de esta lección es que los estudiantes muestren e investiguen datos con la tecnología. Aquí tienes algunas preguntas para debatir.

• «¿Cómo creas visualizaciones de datos utilizando la tecnología?». (Se introducen los datos en la hoja de cálculo y, a continuación, se hace clic en los botones correspondientes).

• «¿Cuáles son algunas de las ventajas de utilizar la tecnología para mostrar datos y calcular estadísticas?». (Puedes cambiar fácilmente entre diferentes visualizaciones de datos y puedes cambiar los intervalos de los histogramas sin tener que volver a ordenar los datos. La ventaja de que la tecnología calcule las estadísticas es que puedo ver cómo cambian las estadísticas a medida que introduzco o hago cambios en los datos).

• «¿Cuándo crees que es apropiado utilizar la tecnología para mostrar datos o calcular estadísticas?». (La tecnología gráfica facilita la determinación de la forma de una distribución. Podría utilizarla para determinar la medida más adecuada del centro de un conjunto de datos. Utilizar la tecnología para calcular estadísticas tiene sentido en la mayoría de las situaciones porque las estadísticas se calculan con algoritmos que pueden complicarse cuando hay muchos valores en el conjunto de datos. La posibilidad de cometer un error al calcular las estadísticas a mano hace que utilizar la tecnología sea una buena opción).

Nation California . Algebra 1

ENFRIAMIENTO | ¿QUÉ SON ESTOS VALORES? (5 minutos)

1. ¿Cuáles es la media y la mediana para los datos?

2. ¿Cuántos valores hay en el conjunto de datos?

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

3. ¿Cuál es el rango intercuartílico para los datos? Explique o muestre su razonamiento.

Mediana Q1 Q3 Máx.

1. Media: 51.68, mediana: 51

2. 100

3. 54, ya que 77 – 23 = 54

Resumen de la lección del estudiante

Las visualizaciones de datos (como histogramas o diagramas de cajas) son muy útiles para comprender rápidamente una gran cantidad de información, pero a menudo lleva mucho tiempo construirlas con precisión con lápiz y papel. La tecnología puede ayudar a crear estas visualizaciones, así como a calcular estadísticas útiles mucho más rápido que haciendo las mismas tareas a mano. Especialmente con conjuntos de datos muy grandes (en algunos experimentos, se recogen millones de datos), la tecnología es esencial para poner la información en formas que sean más fáciles de entender.

Una estadística es una cantidad que se calcula a partir de datos de muestra como medida de una distribución. La media y la mediana son ejemplos de estadísticas que son medidas del centro. La desviación media absoluta (DMA) y el rango intercuartílico (IQR) son ejemplos de estadísticas que son medidas def variabilidad. Aunque la interpretación debe seguir siendo realizada por personas, el uso de las herramientas disponibles puede mejorar la precisión y la velocidad a la hora de realizar cálculos y crear gráficos.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Tecnología necesaria. Los datos representan los puntajes promedios de los clientes para varios artículos vendidos en línea.

A. Utiliza la tecnología para crear un histograma para los datos con intervalos 0-1, 1-2 y así sucesivamente.

B. Describe la forma de la distribución.

C. ¿Qué intervalo tiene la frecuencia más alta?

Soluciones posibles

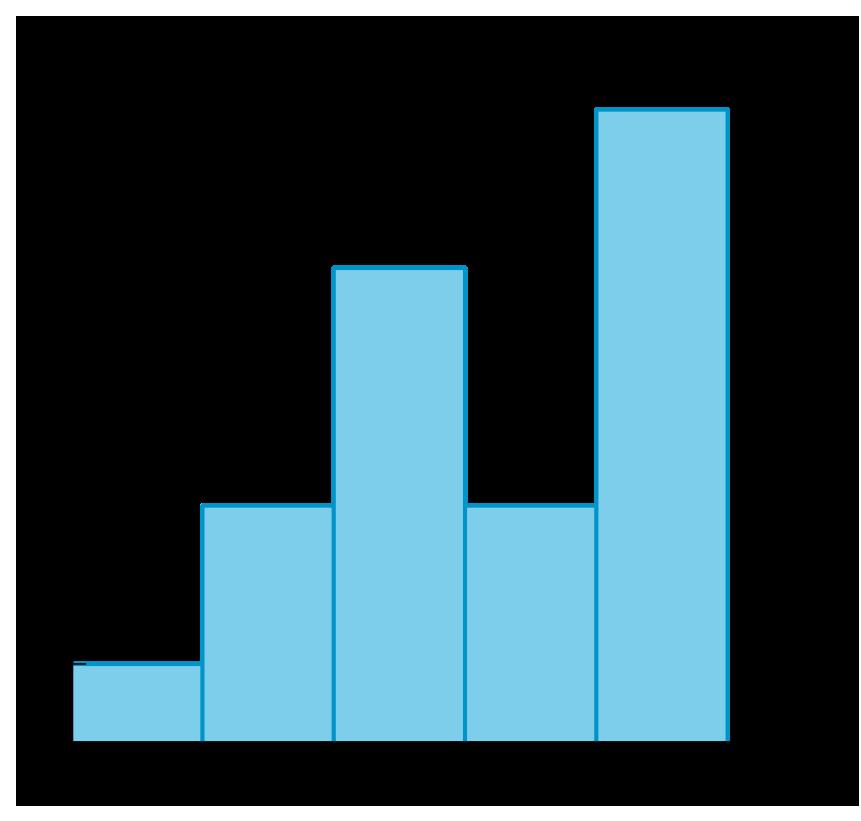
B. La forma está sesgada a la izquierda con un centro cerca de 3 n 100 51.68 29.2957 29.4433 5168 352906 1 23 51 77 105

C. 4 a 5

PROBLEMA 2

Tecnología necesaria. Los datos representan la cantidad de maíz, en fanegas por acre, cosechado en diferentes lugares. 133, 133, 134, 134, 134, 135, 135, 135, 135, 135, 135, 136, 136, 136, 137, 137, 138, 138, 139, 140

A. Utiliza la tecnología para crear un diagrama de puntos y un diagrama de cajas.

B. ¿Cuál es la forma de la distribución?

C. Compara la información mostrada por el diagrama de puntos y el diagrama de cajas.

Soluciones posibles

A. 131 132 133 134 135 136 137 138 139 140 141 Maíz cosechado (fanegas por acre)

B. La distribución está sesgada a la derecha con un centro cerca de 135 fanegas por acre.

C. Ejemplo de respuesta: El diagrama de caja muestra la mediana y los cuartiles y muestra que los datos están sesgados a la derecha. Ambos diagramas muestran el mínimo y el máximo. El diagrama de puntos muestra todos los valores de los datos, pero ninguna medida del centro directamente. El diagrama de puntos muestra la forma de los datos con más precisión que el diagrama de cajas.

PROBLEMA 3

(De la unidad 1, lección 4).

A. Describe la forma de la distribución.

B. ¿Cuántos valores están representados por el histograma?

C. Escribe una pregunta estadística que podría haber producido el conjunto de datos resumido en el histograma.

Soluciones posibles

A. Asimétrica a la derecha con un centro cerca de 9

B. 20

C. Ejemplo de respuesta: ¿Cuál es la longitud típica, en pies, de un mamífero marino?

PROBLEMA 4

(De la unidad 1, lección 3).

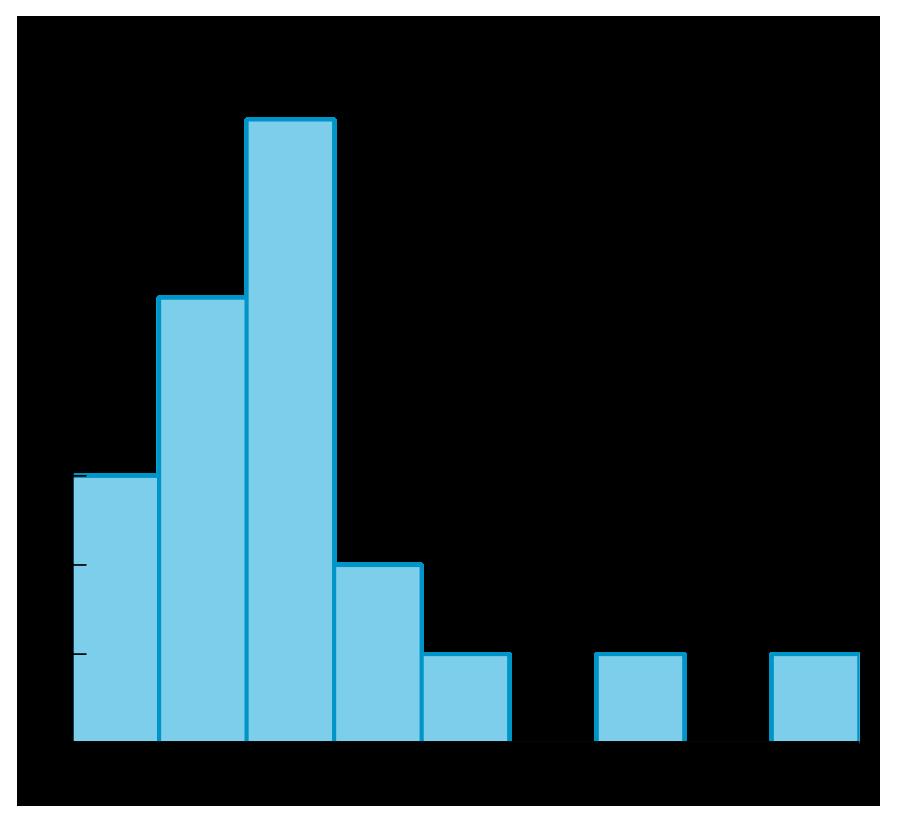
El diagrama de puntos representa la distribución de los índices de satisfacción de una empresa de jardinería en una escala de 1 a 10

Se encuestó a 25 clientes.

Por término medio, ¿cuál fue el grado de satisfacción de la empresa de jardinería?

Soluciones posibles

Ejemplo de respuesta: 8 si se utiliza la mediana o la moda. 7.2 si se utiliza la media.

LECCIÓN 7

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Abordar

S-ID.1 Representar datos con gráficas en la recta numérica real (diagramas de puntos, histogramas y diagramas de cajas).

Alineación de estándares y principios de California

S-ID.3 Interpretar las diferencias en la forma, el centro y la dispersión en el contexto de los conjuntos de datos, teniendo en cuenta los posibles efectos de los puntos de datos extremos (valores atípicos).

Enfoque SMPs

MP4 Representar con matemáticas.

MP5 Usar herramientas apropiadas estratégicamente.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

EL EFECTO DE LOS EXTREMOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predecir lo que podría ocurrir y repercutir en el futuro, representarán con las matemáticas

OBJETIVO(S) DE APRENDIZAJE

analizan los datos y descubren la forma y el espacio.

• Puedo describir cómo un valor extremo afectará a la media y a la mediana.

• Puedo utilizar la forma de una distribución para comparar la media y la mediana.

OBJETIVOS

DE APRENDIZAJE PARA EL MAESTRO

• Reconocer la relación entre la media y la mediana en función de la forma de la distribución.

• Comprender los efectos de los valores extremos en las medidas del centro.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Aspectos para representar las matemática

Analízalo

MLR5: Preguntas de elaboración conjunta

MLR8: Apoyos para el debate

Materiales necesarios

Dispositivo con conexión a Internet

Preparación necesaria

Se requieren dispositivos con acceso a Internet para la versión digital de la actividad «Separado por sesgo».

INFORMACIÓN

DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Veamos cómo cambia la estadística con los datos.

Narrativa de la lección

El propósito matemático de esta lección es reconocer una relación entre la forma de una distribución y la media y la mediana. Los estudiantes usarán diagramas de puntos para investigar esta relación. Anteriormente en esta unidad, los estudiantes crearon visualizaciones de datos para que la forma de la distribución sea clara. Esta lección se conecta con el trabajo siguiente porque los estudiantes utilizarán la forma de la distribución y las medidas del centro para tomar decisiones sobre cómo resumir los datos.

En esta lección, los estudiantes comienzan representando aspectos matemático (MP4) para seleccionar las variables apropiadas para comparar. En otra actividad, los estudiantes hacen uso de la estructura (MP7) y las herramientas apropiadas (MP5) para construir diagramas de puntos de datos que tienen medidas de centro prescritas.

Una de las actividades de esta lección funciona mejor cuando cada estudiante tiene acceso a la tecnología que calcula fácilmente las medidas de centro para producir diagramas de puntos o histogramas, ya que ayudará a los estudiantes a centrarse en la comprensión de la relación entre los valores extremos y la medida de centro sin distraerlos con cálculos largos.

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento En parejas 5 min

Actividad de exploración Grupos pequeños 15 min

Actividad de Exploración Grupos pequeños 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Descripción breve

Los estudiantes analizan una situación y luego consideran cómo comparar diferentes conjuntos de datos.

Los estudiantes crean un diagrama de puntos, calculan medidas de variabilidad y, a continuación, analizan cómo los valores adicionales añadidos al conjunto de datos cambian la variabilidad y la forma de la distribución.

Hay una aplicación digital interactiva disponible que le permite a los estudiantes explorar la creación y análisis de diagramas de puntos con la tecnología.

Los estudiantes crean diferentes diagramas de puntos que cumplen con requisitos específicos de forma y variabilidad y luego discuten sus estrategias.

Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de las relaciones entre las medidas adicionales de variabilidad y puntos de datos extremos.

Los estudiantes discuten la relación entre las medidas del centro y la forma de una distribución.

Los estudiantes comparan las medias y medianas de los diagramas de puntos y relacionan las comparaciones con la forma de cada distribución.

Práctica Independiente 10-15 min El componente de práctica independiente incluye 3 en la lección y 4 problemas de repaso en espiral.

CALENTAMIENTO | BATALLA REAL

(5 minuto)s

Rutinas didácticas

Aspectos para representar las matemáticas

Este calentamiento incita a los estudiantes a pensar en las variables que pueden utilizar para analizar una situación. A continuación, los estudiantes describen visualizaciones de datos que pueden utilizar para comparar dos conjuntos de datos. La elección de variables y la planificación de un proceso para comparar conjuntos de datos involucran a los estudiantes en aspectos de la representación las matemática (MP4).

Preste atención a los grupos que eligen una variable distinta del número de victorias para determinar los mejores jugadores del juego y a los grupos que seleccionan diferentes visualizaciones de datos o formas de comparar conjuntos de datos para compartir con todo el grupo.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2. Diga a los estudiantes que piensen en silencio sobre sus respuestas a las preguntas durante aproximadamente 1 minuto antes de discutirlas con su compañero y luego compartirlas con todo el grupo.

Varios videojuegos se basan en un género llamado «Batalla real» en el que 100 de los jugadores se encuentran en una isla y luchan hasta que solo 1 queda un jugador y es coronado ganador. Este tipo de juego puede jugarse a menudo en modo individual como individuos o en modo por equipos en grupos de 2.

1. ¿Qué información utilizarías para determinar los mejores jugadores de cada modo (individual y por equipos)? Explica tu razonamiento.

2. Una persona afirma que los mejores jugadores en solitario juegan al juego A Otra persona afirma que el juego B tiene mejores jugadores en solitario. ¿Cómo podrías mostrar datos que ayuden a fundamentar su discusión? Explique tu razonamiento.

Ejemplos de respuestas:

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

1. El número de jugadores derrotados en cada modalidad podría ayudar a determinar los mejores jugadores. Aunque también podrían tenerse en cuenta las victorias, es probable que los buenos jugadores derroten a muchos otros jugadores y aun así pierdan contra alguien que estuvo escondido hasta el final de la partida y consiguió una victoria afortunada al final.

2. Yo crearía diagramas de puntos del número de otros jugadores derrotados por los mejores 100 jugadores en cada partida. Luego compararía el centro y la variabilidad de cada distribución.

Seleccione a los estudiantes previamente identificados para que compartan sus soluciones. Si no surge en la discusión, pregunte a los estudiantes cómo podrían interpretar una situación en la que un pequeño grupo de jugadores tiene un número significativamente mayor de victorias o de jugadores derrotados que el resto del grupo. Podría significar que la mayoría de los jugadores no son muy buenos y hay unos pocos que sí lo son o podría significar que hay unos pocos jugadores dominantes que son mucho mejores que los jugadores medios.

ACTIVIDAD DE EXPLORACIÓN | SEPARADOS POR ASIMETRÍA

(15 minutos)

Rutinas didácticas

Analízalo

MLR5: Preguntas de elaboración conjunta

El propósito matemático de esta actividad es ayudar a los estudiantes a entender cómo las medidas del centro para distribuciones con diferentes formas se ven afectadas por los cambios en los datos. Los estudiantes crearán una gráfica de puntos, luego describirán la forma de la distribución y encontrarán las medidas del centro. Investigarán cómo cambian las medidas del centro cuando cambia el conjunto de datos. Los estudiantes crearán e investigarán un conjunto de datos a partir de un conjunto dado de parámetros, incluida la forma de la distribución. Controle que los estudiantes utilicen la terminología correcta para describir la forma de la distribución.

Esta actividad funciona mejor cuando cada estudiante tiene acceso a una tecnología que calcula las medidas del centro y muestra diagramas de puntos o histogramas fácilmente, ya que los estudiantes se beneficiarán de ver la relación de una manera dinámica. Si los estudiantes no tienen acceso individual, proyectar las distribuciones sería útil durante el lanzamiento.

Proporcione acceso a dispositivos que puedan ejecutar GeoGebra u otra tecnología estadística.

Organice a los estudiantes en grupos de 2-4. Después de que hayan completado el problema, pídales que añadan valores a los datos originales, dé a cada grupo una de estas descripciones de distribución:

INTRODUCCIÓN

1. distribución uniforme con datos entre 4 y 12

2. sesgada a la derecha con la mayoría de los valores en 10

3. sesgada a la izquierda con la mayoría de los valores en 10

4. simétrica con la mayoría de los valores en 4 y 16

Recuerde a los estudiantes las palabras utilizadas para describir las formas de las distribuciones: simétrica, sesgada, en forma de campana, uniforme, bimodal.

Apoyo para estudiantes que aprenden el idioma inglés

Escribir: MLR5 Preguntas de elaboración conjunta. Antes de pedir a los estudiantes que respondan a las preguntas dadas, muestre solo los datos y pida a los estudiantes que escriban posibles preguntas matemáticas sobre esta distribución de datos. Tenga en cuenta que no es necesario que los estudiantes respondan a las preguntas que han creado. Invite a los estudiantes a compartir y revisar sus preguntas con un compañero y, a continuación, con toda la clase. Registre las preguntas compartidas con la clase en un espacio público. Esto ayuda a los estudiantes a producir el lenguaje de las preguntas matemáticas a medida que empiezan a razonar sobre la relación entre los valores extremos y la medida del centro.

Principio(s) de diseño: Maximizar la metaconciencia

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Utiliza la tecnología para crear un diagrama de puntos que represente la distribución de los datos y luego describa la forma de la distribución.

2. Encuentra la media y la mediana de los datos.

3. Encuentre la media y la mediana de los datos con 2 valores adicionales incluidos como se describe.

A. Agregue 2 valores al conjunto de datos original que sean mayores que 14.

B. Agregue 2 valores al conjunto de datos original que sean menores que 6.

C. Agregue 1 valor que sea mayor que 14 y 1 valor que sea menor que 6 al conjunto de datos original.

D. Agregue los dos valores, 50 y 100, al conjunto de datos original.

4. Cambia los valores para que la distribución se ajuste a la descripción que te dio tu maestro, luego encuentra la media y la mediana.

5. Busca otro grupo que haya creado una distribución con una descripción diferente. Explica tu trabajo y escucha su explicación; luego, compara tus medidas de centro.

1. La distribución es simétrica y en forma de campana.

2. Media: 10. Mediana: 10.

3. Las respuestas varían. Las respuestas correctas tendrán estas propiedades:

POSIBLES RESPUESTAS

CONCEPTOS ERRÓNEOS PREVISTOS

A. Media mayor que 10. Mediana: 10.

B. Media menor que 10. Mediana: 10.

C. La media dependerá de los valores elegidos. Mediana: 10.

D. Media: 16.5. Mediana: 10.

4. Ejemplos de respuestas:

A. Distribución uniforme: 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10, 11, 11, 12, 12

B. Media: 8. Mediana: 8.

C. Sesgado a la derecha: 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 12, 12, 13, 13, 14, 15, 16 Media: 11.39. Mediana: 11.

D. Sesgado a la izquierda: 11, 11, 11, 10, 10, 10, 10, 10, 9, 9, 9, 8, 8, 7, 7, 6, 5, 4 Media: 8.61. Mediana: 9.

E. Simétrica: 4, 4, 4, 4, 4, 6, 6, 8, 10, 10, 12, 14, 14, 16, 16, 16, 16, 16 Media: 10. Mediana: 10. 5. Ejemplo de respuesta: Cuando la distribución es simétrica o uniforme, la media y la mediana son los mismos valores. La media parece estar más influenciada por los valores extremos en la cola que la mediana.

Los estudiantes podrían tener dificultades para usar la tecnología para crear diagramas de puntos, por lo que podría ser necesario demostrarles cómo usarla. Los estudiantes podrían confundir la media y la mediana. Pídales que consulten trabajos anteriores en los que calcularon cada medida de centro. Después de introducir los valores adicionales según las instrucciones, podrían usar una n incorrecta al calcular la nueva media. Recuérdeles que realicen cálculos detallados.

SÍNTESIS DE LA ACTIVIDAD

El objetivo es asegurarse de que los estudiantes entienden que la mediana es la medida preferida del centro cuando una distribución es asimétrica o si hay valores extremos, y que la media es la medida preferida del centro cuando una distribución es simétrica y no hay valores extremos. He aquí algunas preguntas para el debate.

• «¿Qué notas y te preguntas sobre la media y la mediana de cada una de estas distribuciones?». (Me di cuenta de que a veces la mediana no cambiaba y la media sí. Me pregunté qué pasaría si añadiera un valor de 1,000 al conjunto de datos).

• «¿Para qué distribuciones parece que la media representa mejor lo que es típico en los datos?». (Las distribuciones simétricas).

• «¿Cuándo es la mediana una estadística mejor para describir los valores típicos?». (Las distribuciones sesgadas).

• «¿Por qué la mediana es uan estadística mejor para las distribuciones sesgadas?». (Cuando se añaden valores extremos a un conjunto de datos, estos valores tienden a tener un mayor efecto sobre la media que sobre la mediana).

Apoyo para estudiantes con discapacidad

Compromiso: Desarrollar el esfuerzo y la persistencia. Divida la clase en pequeños grupos de debate e invite a un representante de cada grupo a informar a toda la clase.

Apoya la accesibilidad para: Lenguaje; habilidades socioemocionales; atención

ACTIVIDAD DE EXPLORACIÓN |GRAFICAR MEDIDAS RELACIONADAS

(10 minutos)

Rutinas didácticas

Analízalo

MLR8: Apoyos al debaten

El propósito matemático de esta actividad es reconocer la relación entre las medidas del centro y la forma de la distribución para crear y describir distribuciones con medidas de centro dadas. Escuche a los estudiantes utilizar los términos simétrico, uniforme y sesgado. Cuando los estudiantes crean un diagrama de puntos con una media y mediana dada con la tecnología, participan en el MP7 porque utilizan su comprensión de la estructura de la distribución para ajustar los valores de los datos individuales para cambiar las medidas del centro. Poner a disposición de los estudiantes una hoja de cálculo les da la oportunidad de elegir estratégicamente las herramientas adecuadas (MP5).

INTRODUCCIÓN

Mantener a los estudiantes en sus grupos.

Apoyo para estudiantes con discapacidad

Acción yeExpresión: Interiorizar las funcioneseEjecutivas. Proporcione a los estudiantes cuadrícula o papel cuadriculado para organizar su trabajo con los 3 diagramas de puntos.

Apoya la accesibilidad para: Lenguaje; organización

1 . Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Crea un posible diagrama de puntos con al menos 10 valores para cada una de las condiciones enumeradas. Cada diagrama de puntos debe tener al menos 3 valores que sean diferentes.

1. Una distribución que tenga tanto media como mediana de 10

2. Una distribución que tenga tanto media como mediana de -15

3. Una distribución que tenga una mediana de 2.5 y una media mayor que la mediana

4. Una distribución que tiene una mediana de 5 y una mediana mayor que la media

Ejemplos de respuestas:

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

El propósito de esta discusión es que los estudiantes entiendan por qué la mediana es la medida preferida del centro cuando una distribución es sesgada o si hay valores extremos, y la media es la medida preferida del centro cuando una distribución es simétrica y no hay valores extremos.

Para cada descripción, seleccione 2-3 grupos para compartir sus diagramas de puntos. A continuación se presentan algunas preguntas para la discusión.

• «Para el primer y segundo diagrama de puntos, ¿qué tienen en común las formas de distribución? ¿Por qué elegimos la media como la medida más apropiada del centro?». (Simétrica. La media de un conjunto de datos da la misma importancia a cada valor para encontrar el centro, por lo que es una medida preferida del centro cuando representa con precisión los valores típicos de los datos).

• «¿Qué tienen en común las formas de los diagramas de puntos cuando la media es mayor que la mediana?». (Sesgada a la derecha).

• «¿Qué información te da la forma de las distribuciones sesgadas sobre la mediana y la media?». (Cuando las distribuciones están sesgadas a la derecha, probablemente tendrán una media mayor que la mediana porque los valores de la derecha afectan desproporcionadamente a la media. Cuando las distribuciones están sesgadas a la izquierda es probable que tengan una media menor que la mediana porque los valores situados a la izquierda afectan desproporcionadamente a la media).

¿Estás preparado para más?

La media y la mediana son, con diferencia, las medidas de centro más comunes para datos numéricos. Sin embargo, a veces se utilizan otras medidas. Para cada medida de centro, enumera algunas posibles ventajas y desventajas. Asegúrate de considerar cómo se ve afectada por los extremos.

1. Media intercuartílica: La media de solo aquellos puntos entre el primer cuartil y el tercer cuartil.

2. Media intercuartílica: La media del primer cuartil y el tercer cuartil.

3. Rango medio: La media del valor mínimo y máximo.

4. Trimedia: La media del primer cuartil, la mediana, la mediana de nuevo y el tercer cuartil. Por lo tanto, se promedian cuatro número,s ya que la mediana se cuenta dos veces.

Álgebra 1 . Matemáticas . Unidad 1

Respuesta del estudiante

Ejemplos de respuestas:

1. Una ventaja es que, como la mediana, no se ve muy afectada por los extremos. Una desventaja es que primero tenemos que recortar los datos y luego calcular la media.

2. Una ventaja es que, como la mediana, no se ve muy afectada por los extremos. Sin embargo, este número puede no ser tan diferente de la mediana, que tiene un significado más directo y fácil de entender.

3. Una ventaja es que se puede calcular rápida y fácilmente. Una desventaja es que se vería muy afectada por los extremos.

4. Al igual que la mediana, no se ve muy afectada por los extremos y tiene en cuenta algo más de lo que ocurre en los datos que la mediana. Una desventaja es que es un poco más difícil de calcular y explicar que la mediana.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

He aquí algunas preguntas para extraer la relación entre las medidas del centro y la forma de la distribución.

• «¿Por qué se prefiere la mediana a la media para datos sesgados?». (Los valores situados a la derecha (o a la izquierda) en datos sesgados tienen un mayor efecto sobre la media, por lo que se prefiere la mediana para reflejar mejor los valores típicos).

• «Cuando hay un valor extremo, ¿por qué se prefiere la mediana a la media?». (Los valores extremos tienen un mayor efecto sobre la media que la mediana, por lo que se prefiere la mediana)).

• «Cuando los datos son simétricos o aproximadamente simétricos, ¿por qué se prefiere la media a la mediana?». (La media tiene en cuenta todos los valores de los datos, por lo que es la medida preferida cuando es representativa de lo que es típico para los datos).

ENFRIAMIENTO | FORMA Y ESTADÍSTICA

(5 minutos)

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

1. ¿Es la media mayor, menor, o igual que la mediana? Explica tu razonamiento.

2. ¿Es la media mayor, menor, o igual que la mediana? Explica tu razonamiento.

1. Respuesta de muestra: La media es mayor que la mediana porque los valores más grandes a la derecha hacen que la media sea mayor de lo que sería si la distribución fuera uniforme.

2. Ejemplo de respuesta. La media es igual a la mediana porque los datos son simétricos.

Resumen de la lección

¿Es mejor utilizar la media o la mediana para describir el centro de un conjunto de datos?

La media da la misma importancia a cada valor cuando se encuentra el centro. La media suele representar bien los valores típicos cuando los datos tienen una distribución simétrica. Por otro lado, la media puede verse muy afectada por cambios incluso en un solo valor.

La mediana indica el valor medio del conjunto de datos, por lo que los cambios en un solo valor no suelen afectar mucho a la mediana. Por lo tanto, la mediana es más apropiada para datos que no son muy simétricos.

Podemos observar la distribución de un conjunto de datos y sacar conclusiones sobre la media y la mediana.

Nation California . Algebra 1

Este es un diagrama de puntos que muestra el tiempo que tarda un dardo en dar en la diana en segundos. Los datos producen una distribución simétrica.

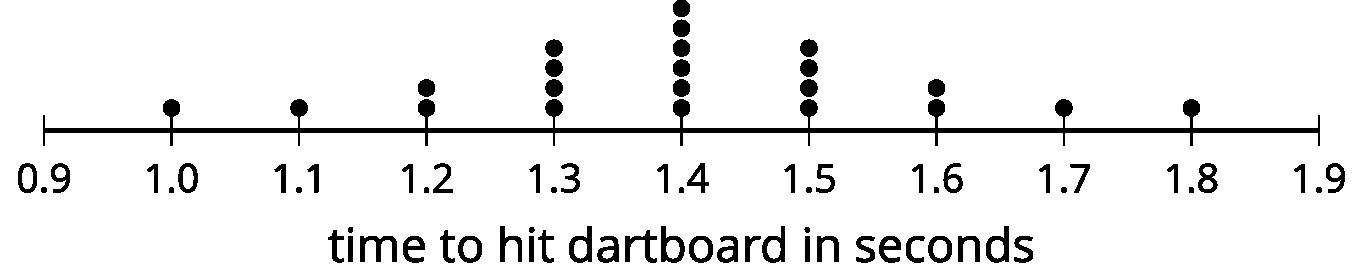
Cuando una distribución es simétrica, tanto la mediana como la media se encuentran en el centro de la distribución. Como la mediana es el valor medio (o la media de los dos valores medios) de un conjunto de datos, puedes utilizar la simetría alrededor del centro de una distribución simétrica para encontrarla fácilmente. Para la media, necesitas saber que la suma de las distancias a la media de los valores mayores que la media es igual a la suma de las distancias a la media de los valores menores que la media. Utilizando la simetría de la distribución simétrica puedes ver que hay cuatro valores 0.1 segundos por encima de la media, dos valores 0.2 segundos por encima de la media, un valor 0.3 segundos por encima de la media, y un valor 0.4 segundos por encima de la media. Del mismo modo, puedes ver que hay el mismo número de valores a las mismas distancias por debajo de la media.

Aquí hay un diagrama de puntos con los mismos datos, pero con dos de los valores cambiados, lo que resulta en una distribución sesgada.

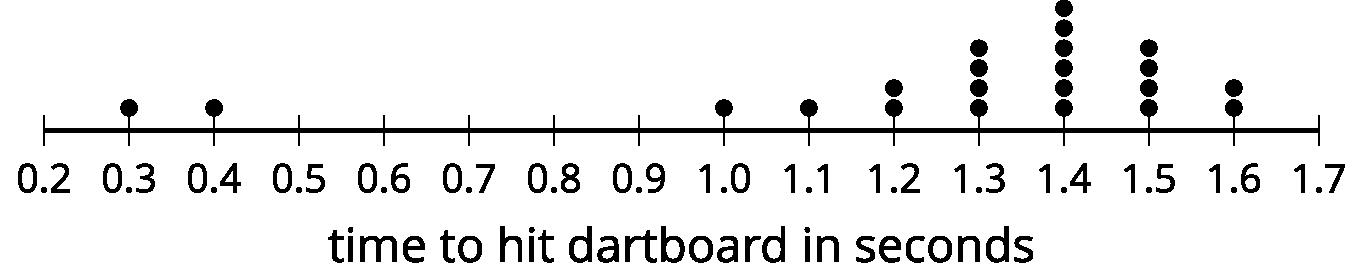
Cuando tienes una distribución sesgada, la distribución no es simétrica, por lo que no puedes usar la simetría para encontrar la mediana y la media. La mediana sigue siendo 1.4 segundos, ya que sigue siendo el valor medio. La media, por otro lado, es ahora de aproximadamente 1.273 segundos. La media es menor que la mediana porque los valores más bajos (0.3 y 0.4) dan como resultado un valor más pequeño para la media.

La mediana suele ser más resistente a los valores extremos que la media. Por esta razón, la mediana es la medida preferida del centro cuando una distribución está sesgada o si hay valores extremos. Cuando se utiliza la mediana, también se utilizaría la IQR como medida preferida de variabilidad. En una distribución más simétrica, la media es la medida preferida del centro y la DMA es la medida preferida de la variabilidad.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Selecciona todas las formas de distribución para las cuales es más apropiado usar la media.

en forma de campana bimodal sesgada simétrica uniforme

PROBLEMA 2

Soluciones posibles

en forma de campana bimodal sesgada simétrica uniforme

¿Para qué forma de distribución suele ser apropiado utilizar la mediana cuando resumes los datos?

A. En forma de campana

B. Sesgada

C. Simétrica

D. Uniforme

Soluciones posibles

PROBLEMA 3

La cantidad de instrumentos de escritura en los escritorios de algunos maestros se muestra en el diagrama de puntos. ¿Cuál es mayor, la media o la mediana? Explica tu razonamiento con la forma de la distribución.

PROBLEMA 4

(De la unidad 1, lección 6).

Un estudiante tiene estas puntuaciones en sus tareas. El maestro considera eliminar la puntuación más baja. ¿Qué efecto tiene eliminar el valor más bajo, 0, del conjunto de datos sobre la media y la mediana?

0, 40, 60, 70, 75, 80, 85, 95, 95, 100

PROBLEMA 5

(De la unidad 1, lección 6).

A. ¿Cuál es el resumen de cinco números para los datos 2, 2, 4, 4, 5, 5, 6, 7, 9, 15?

B. Cuando se elimina el máximo, 15, del conjunto de datos, ¿cuál es el resumen de cinco números?

PROBLEMA 6

(De la unidad 1, lección 4).)

1 . Matemáticas . Unidad 1

Soluciones posibles

La mediana es mayor que la media. Ejemplo de razonamiento: Como la distribución está sesgada a la izquierda, la media será menor que la mediana.

Soluciones posibles

La media aumenta de 70 a aproximadamente 77.78. La mediana aumenta de 77.5 a 80

Soluciones posibles

A. 2, 4, 5, 7, 15 (mínimo, Q1, mediana, Q3, máximo)

B. 2, 3, 5, 6 5, 9 (mínimo, Q1, mediana, Q3, máximo)

El diagrama de cajas resume las puntuaciones de los exámenes de 100 estudiantes:

¿Qué término describe mejor la forma de la distribución?

A. En forma de campana

B. Uniforme

C. SesgadaSsimétrica

Soluciones posibles

PROBLEMA 7

(De la unidad 1, lección 2).

El histograma representa la distribución de longitudes, en pulgadas, 25 de bagre capturados en un lago.

A. Si es posible, halla la media. Si no es posible, explica por qué.

B. Si es posible, halla la mediana. Si no es posible, explique por qué no.

C. ¿Medía alguno de los peces capturados 12 pulgadas?

D. ¿Medía alguno de los peces capturados 19 pulgadas?

Soluciones posibles

A. Ejemplo de respuesta: No es posible hallar la media, porque los valores exactos no se muestran en un histograma.

B. Ejemplo de respuesta: No es posible hallar la mediana, pero sí sabes en qué intervalo se encuentra el número del medio. Está en el intervalo 6 a 9 pulgadas, porque la mediana es el decimotercer valor del conjunto de datos.

C. Ejemplo de respuesta: No hay forma de saber si un pez capturado medía 12 pulgadas con el histograma. Sí sabes que algunos peces estaban en el intervalo de 12 a 15 pulgadas, así que es posible.

D. No

Reflexiones:

Math Nation California . Algebra 1

Álgebra 1 . Matemáticas . Unidad 1

LECCIÓN 8

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

S-ID.2 Utilizar estadísticas apropiadas a la forma de la distribución de datos para comparar el centro (mediana, media) y la dispersión (rango intercuartil, desviación estándar) de dos o más conjuntos de datos diferentes.

Construir

S-ID.1

Construir

S-ID.3

Enfoques SMPs

MP2 Razonar abstracta y cuantitativamente.

MP3 Construir argumentos viables y criticar el razonamiento de otros

MP6 Atender a la precisión.

MP7 Buscar y hacer uso de la estructura.

Estándares ELD de California

I.A.1

I.B.5

I.C.12

COMPARAR Y CONTRASTAR

DISTRIBUCIONES DE DATOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

impactar el futuro

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

razonarán abstracta y cuantitativamente

OBJETIVO(S) DE APRENDIZAJE

analizan los datos y descubren la forma y el espacio.

• Puedo ordenar conjuntos de datos en orden de variabilidad dadas representaciones gráficas.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Interpretar (oralmente) un conjunto de datos con mayor DMA o IQR como si tuviera mayor variabilidad.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyo para la discusión

MLR7: Comparar y conectar

Tomar turnos

MLR2: Recopilar y mostrar

Materiales necesarios

Fichas preimpresas, recortes de la plantilla maestra

Preparación necesaria

Imprima y recorte las fichas de la plantilla maestra. Prepare 1 copia por cada 2 estudiantes.

Álgebra 1 . Matemáticas . Unidad 1

INFORMACIÓN

DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Investigaremos la variabilidad con visualizaciones de datos y estadísticas de resumen.

Narrativa de la lección

El propósito matemático de esta lección es comparar conjuntos de datos con diferentes medidas de variabilidad e interpretar conjuntos de datos con mayor DMA o IQRs como si tuvieran mayor variabilidad. Los estudiantes establecen conexiones entre diferentes visualizaciones de datos y medidas de centro y medidas de variabilidad. Esta lección se basa en el trabajo previo y utiliza lo que los estudiantes han aprendido al crear visualizaciones de datos y determinar qué medida de centro es la adecuada. En las próximas lecciones, los estudiantes utilizarán sus conocimientos de DMA para averiguar el significado de la desviación típica. Cuando los estudiantes emparejan representaciones de datos con descripciones de la forma, medidas del centro o medidas de la variabilidad, están participando en el MP2 porque tienen que dar sentido a la representación de los datos y a la descripción o medida correspondiente. Cuando los estudiantes participan en una charla de matemáticas sobre la determinación de la media, tienen la oportunidad de observar y utilizar la estructura simétrica (MP7) de los valores para determinar la media. Además, los estudiantes deben ser precisos en la elección de palabras y en el uso del lenguaje (MP6). En la actividad por turnos, los estudiantes se intercambian los papeles, explican su pensamiento y escuchan, lo que les da la oportunidad de explicar su razonamiento y criticar el razonamiento de los demás (MP3).

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Descripción breve

Calentamiento Independiente 5 min Los estudiantes calculan mentalmente las medias de cuatro conjuntos de datos.

Actividad de exploración

En parejas 15 min

Actividad de exploración En parejas 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 10-15 min

Los estudiantes hacen coincidir visualizaciones de datos con descripciones de sus formas y medidas de variabilidad o centro. A continuación, determinan qué medida de centro es la más adecuada en función de la forma de la distribución.

Los estudiantes clasifican los diagramas de cajas y de puntos en función de la variabilidad y, a continuación, explican qué medida de centro describe mejor los datos.

Hay una extención de la exploración disponible para profundizar en la comprensión de la relación entre la variabilidad y la forma de una distribución.

Los estudiantes explican cómo determinar y describir la variabilidad en conjuntos de datos que tienen medidas de centro similares.

Los estudiantes utilizan diagramas de puntos dados, las formas de sus distribuciones y sus correspondientes estadísticos de resumen para determinar cuál coincide con las restricciones de un contexto del mundo real.

El componente de práctica independiente incluye 3 problemas de repaso en clase y 4 problemas de repaso en espiral.

California . Algebra 1

CALENTAMIENTO | CHARLA DE MATEMÁTICAS: MEDIA

(5 minuto)s

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyos para la discusión

Esta es la primera actividad de charla de matemática del curso. Vea la intriducción para instrucciones extendidas para facilitar esta actividad exitosamente.

El propósito de esta charla de matemáticas es expandir las estrategias de los estudiantes' para encontrar una media más allá de seguir un algoritmo para razonar que la media de los valores en un conjunto de datos simétricos es el valor medio. El tercer punto está diseñado para ilustrar que esta técnica solo funciona para conjuntos de datos simétricos. Estas comprensiones ayudan a los estudiantes a desarrollar fluidez y serán útiles más adelante en esta lección cuando los estudiantes necesiten usar la simetría para hacer coincidir una media con la distribución.

Esta charla de matemática proporciona una oportunidad para que los estudiantes noten y hagan uso de la estructura simétrica (MP7) de los valores para determinar la media. Mientras participan en estas actividades, los estudiantes deben ser precisos en la elección de palabras y en el uso del lenguaje (MP6).

Monitoree a los estudiantes quienes:

• usan el algoritmo estándar para encontrar la media (sumar y dividir)

• usan la simetría del conjunto de datos

INTRODUCCIÓN

Esta es la primera vez que los estudiantes hacen la rutina de instrucción de la charla de matemáticas, por lo que es importante explicar cómo funciona antes de comenzar. Explique la rutina de la charla de matemática: Se muestra un problema a la vez. Para cada problema, se da a los estudiantes unos minutos para que piensen en silencio y den una señal cuando tengan una respuesta y una estrategia. El maestro selecciona a los estudiantes para que compartan diferentes estrategias para cada problema y puede hacer preguntas como «¿Quién lo ha pensado de otra manera?». El maestro anota las explicaciones de los estudiantes para que todos las vean. Se puede pedir a los estudiantes que den más detalles sobre por qué decidieron abordar un problema de una determinada manera. Puede que no sea posible compartir todas las estrategias posibles en el tiempo limitado de que se dispone; puede que el maestro solo reúna dos o tres estrategias distintivas por problema. Considere la posibilidad de establecer una pequeña y discreta señal con la mano que los estudiantes puedan mostrar para indicar que tienen una respuesta que pueden apoyar con un razonamiento. Esta señal podría ser un pulgar hacia arriba, un número determinado de dedos que indique el número de respuestas que tienen u otra señal sutil. Es una forma rápida de ver si los estudiantes han tenido tiempo suficiente para pensar en el problema. También evita que los estudiantes se distraigan o se apresuren al levantar la mano por toda la clase.

Exponga un problema cada vez. Conceda a los estudiantes un tiempo de reflexión tranquilo para cada problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. Mantenga todos los problemas expuestos durante la charla. A continuación, debate con toda la clase.

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Para apoyar la memoria de trabajo, proporcione a los estudiantes notas adhesivas o minipizarras.

Apoya la accesibilidad para: Memoria; organización

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Álgebra 1 . Matemáticas . Unidad 1

Evalúe mentalmente la media de cada conjunto de datos. 27, 30, 33 61, 71, 81, 91, 101

0, 100, 100, 100, 100 0, 5, 6, 7, 12

• 30

• 81

• 80

• 6

Si los estudiantes tienen dificultades para utilizar la simetría como método para hallar la media, considere pedirles que hallen la media de los valores: 1, 2, 3, 4, 5

Pida a los estudiantes que compartan sus estrategias para cada problema. Registre y muestre sus respuestas para que todos puedan verlas. Para implicar a más estudiantes en la conversación, puede preguntar:

• «¿Quién puede replantear el razonamiento de de otra manera?».

• «¿Tiene alguien la misma estrategia, pero la explicaría de otra manera?».

• «¿Alguien resolvió el problema de otra manera?».

• «¿Alguien quiere añadir algo a la estrategia de ?».

• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?». Aunque todos los métodos correctos para resolver la media son válidos, destaca el uso de la simetría en los datos. En lecciones anteriores, los estudiantes aprendieron que las distribuciones simétricas tienen una media en el centro de los datos. Cuando la simetría está presente, se puede utilizar para descubrir rápidamente la media.

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Muestre fragmentos de oraciones para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «Primero, yo porque... o me di cuenta así que yo...». Algunos estudiantes pueden beneficiarse de la oportunidad de repasar lo que van a decir con un compañero antes de compartirlo con toda la clase.

Principio(s) de diseño: Optimizar el rendimiento (para la explicación)

ACTIVIDAD DE EXPLORACIÓN | DESCRIBIR

DISTRIBUCIONES

DE DATOS

(15 minutos)

Rutinas didácticas

MLR7: Comparar y conectar

Tomar turnos

En esta actividad, los estudiantes se turnan con un compañero para hacer coincidir las visualizaciones de datos con las características de la distribución y determinar qué medida de centro es la más apropiada para los datos. Los estudiantes intercambian papeles, explican su pensamiento y escuchan, lo que les da oportunidades para explicar su razonamiento y criticar el razonamiento de los demás (MP3).

California . Algebra 1

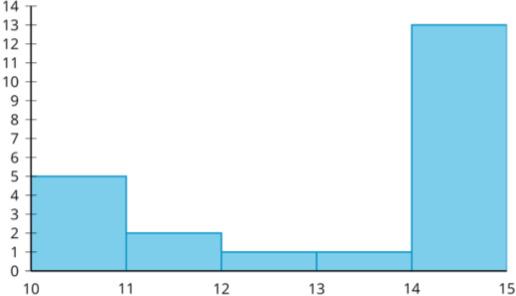
• Sesgada a la derecha

• IQR: 11

• Sesgada a la izquierda • Mediana: 14.5

Mediana: -14

INTRODUCCIÓN

• Sesgada derecha

• Mediana: 11

Organice a los estudiantes en grupos de 2. Muestre cómo establecer y encontrar un compañero. Elige a un estudiante de para que sea su pareja. Mezcla las cartas y colócalas boca arriba. Señale que las tarjetas contienen una visualización de datos o un enunciado escrito. Selecciona una tarjeta de cada tipo y explica a tu compañero por qué crees que las tarjetas coinciden o no. Muestre formas productivas de estar de acuerdo o en desacuerdo, por ejemplo, cuando se explica el pensamiento matemático o se hace preguntas aclaratorias. Entregue a cada grupo un juego de tarjetas recortadas para quelas hagan coincidir. Pida a los estudiantes que hagan una pausa después de completar el pareo para debatirlo con toda la clase. Luego, permita cinco minutos más para que los estudiantes trabajen la segunda pregunta, luego deben pausar para debatir con toda la clase.

Diga a los estudiantes que la medida apropiada del centro puede no ser la que aparece en las tarjetas.

Álgebra 1 . Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad

Participación: Interiorizar la autorregulación. Demostrar que da y recibe comentarios constructivos. Utilizar un proceso estructurado y mostrar fragmentos de frases para apoyar la retroalimentación productiva. Por ejemplo: «Esto coincide porque ». o «Utilizaría media o mediana para el centro de los datos porque __».

Apoya la accesibilidad para: Habilidades socioemocionales; organización; lenguaje

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Tu maestro te dará un juego de tarjetas. Túrnate con tu compañero para hacer coincidir una visualización de datos con un enunciado escrito.

A. Para cada par que encuentres, explica a tu compañero cómo sabes que es un par.

B. Para cada par que encuentre tu compañero, escucha atentamente su explicación. Si no estas de acuerdo, debate tu pensamiento y trabaja para llegar a un acuerdo.

2. Después del pareo, determina si la media o la mediana es más apropiada para describir el centro del conjunto de datos con base en la forma de la distribución. Debate tu razonamiento con tu compañero. Si no se da, calcula (si es posible) o estima la medida apropiada del centro. Prepárate para explicar tu razonamiento.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

California . Algebra 1

A. I

B. L

C. N

D. M

E. J

F. K

G. H

A. Fila 1: media, simétrica, 6

B. Fila 2: media, simétrica, –14

C. Fila 3: media, simétrica, –14

D. Fila 4: mediana, asimétrica, 11

E. Fila 5: mediana, asimétrica, 14.5

F. Fila 6: media, simétrica, –14

G. Fila 7: mediana, asimétrica, 20

Se debate mucho entre compañaeros. Una vez que todos los grupos hayan completado el pareo, debate lo siguiente:

• «¿Qué pares fueron difíciles? Explica por qué». (El diagrama de cajas de la fila 6 fue difícil porque tuve que usar el proceso de eliminación para descubrir que era el uniforme).

• «¿Tuviste que hacer ajustes en tus emparejamientos? ¿Qué podría haber causado un error? ¿Qué ajustes se hicieron?». (Sí. Me di cuenta de que pensaba erróneamente que sesgado a la izquierda significaba que la mayoría de los datos estaban a la izquierda. Sin embargo, aprendí que izquierda sesgada significa que hay datos a la izquierda de donde se encuentra la mayoría de los datos).

• «¿Puedes determinar la mediana utilizando solo un histograma? ¿Por qué sí o por qué no?». (No, pero puedes determinar el intervalo que contiene la mediana).

• «¿Puedes determinar si una distribución es uniforme a partir de un diagrama de caja? ¿Por qué sí o por qué no?». (No. Puedes determinar que los datos podrían ser simétricos con base en la distribución del resumen de cinco números, pero más allá de eso no serías capaz de saber que los datos son uniformes con solo una diagrama de cajas).

El propósito de la segunda parte de la actividad es hablar de la relación entre la media y la mediana con base en la forma de la distribución y hacer la conexión con las medidas de variabilidad. Pregunte:

• «Si la media es la medida apropiada del centro, ¿deberíamos utilizar la DMA o la IQR para medir la variabilidad?». (MAD)

• «Si la mediana es la medida apropiada del centro, ¿deberíamos utilizar el DMA o el IQR para medir la variabilidad?». (IQR) 2.

Apoyo para estudiantes

que aprenden el idioma inglés

Hablar, escuchar: MLR7 Comparar y conectar. Pedir a los estudiantes que preparen por parejas una presentación visual de sus tarjetas clasificadas. Invite a las parejas a investigar el trabajo de los demás' y pida a los estudiantes que compartan lo que funcionó bien en un enfoque concreto. Escuche y amplíe cualquier comentario sobre el uso de datos, medianas y medias para comparar las distintas distribuciones con los enunciados escritos. Anime a los estudiantes a establecer conexiones entre las representaciones y los enunciados. Escuche y amplifique el lenguaje que utilizan los estudiantes para describir la forma de la distribución (sesgada, simétrica o uniforme). Esto fomentará la metaconciencia de los estudiantes' y apoyará las conversaciones constructivas mientras comparan y conectan las visualizaciones de la distribución con las afirmaciones escritas.

Principio(s) de diseño: Fomentar la conversación; maximizar la metaconciencia

INTRODUCCIÓN

ACTIVIDAD DE EXPLORACIÓN | VARIABILIDAD VISUAL Y ESTADÍSTICA

(10 minutos)

Rutinas didácticas

MLR2: Recopilar y mostrar

Esta actividad invita a los estudiantes a comparar la variabilidad en varios conjuntos de datos con el análisis de las distribuciones mostradas en diagramas de cajas y de puntos. Algunos estudiantes pueden razonar sobre la variabilidad cuando observan las formas y características de los datos mostrados. Otros pueden tratar de cuantificar la variabilidad encontrando en el IQR de cada diagrama de caja, o estimando el DMA de cada diagrama de puntos. Busque estudiantes que aborden la tarea cuantitativamente.

INTRODUCCIÓN

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Organice a los estudiantes en grupos de 2. Dé a los estudiantes cinco minutos para trabajar con las preguntas y luego haga una pausa para una discusión con todo el grupo.

Cada diagrama de cajas resume el número de millas conducidas cada día durante 30 días en cada month. Los diagramas de cajas representan, en orden, los meses de agosto, septiembre, octubre, noviembre y diciembre.

1. Los cinco diagramas de cajas tienen la misma mediana. Explica por qué la mediana es más apropiada para describir el centro del conjunto de datos que la media para estas distribuciones.

2. Ordena las diagramas de cajas de menor a mayor variabilidad. Comprueba con otro grupo si están de acuerdo.

Millas manejadas cada

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Nation California . Algebra 1

Álgebra 1 . Matemáticas . Unidad 1

1. Los cinco diagramas de puntos tienen la misma media. Explica por qué la media es más apropiada para describir el centro del conjunto de datos que la mediana. 2. Ordena los puntos de menor a mayor variabilidad. Compruebe con otro grupo si están de acuerdo.

1. Cada una de las distribuciones no es simétrica.

2. E, D y A, C, B o E, A, D, C, B (si A y D se distinguen por el rango)

3. Cada una de las distribuciones es simétrica y no incluye valores atípicos obvios.

4. E, B, A, D, C

Es posible que los estudiantes hayan olvidado qué significa variabilidad o qué estadístico utilizar para determinar la variabilidad de un conjunto de datos. Remítalos a trabajos anteriores o pregúnteles qué medida es útil para determinar la tendencia de un conjunto de datos'a tener valores diferentes.

El objetivo de esta discusión es establecer la conexión entre la forma de la distribución y el uso de IQR o DMA para cuantificar la variabilidad. Otro objetivo es asegurarse de que los estudiantes entienden que un valor mayor de IQR o DMA significa mayor variabilidad. Muestre los diagramas de cajas en orden de variabilidad con el IQR incluido, y luego muestre los diagramas de puntos en orden de variabilidad con el DMA incluido.

IQR: 20

0 10 20 30 40 50

60 70 80 90

Millas manejadas cada día en diciembre

IQR: 40

0 10 20 30 40 50

Millas manejadas cada día en noviembre

SÍNTESIS DE LA ACTIVIDA CONTINUACIÓN

IQR: 40

IQR: 60 0

IQR: 50

DMA: 1.12 DMA: 1.56

DMA: 2.22

DMA: 2.68

La IQR para los datos de las distribuciones A a E son {40, 60, 50, 40, 20} y la DMA para los datos de las distribuciones F a J son aproximadamente {1.56, 1.10, 2.68, 2.22, 0}.

He aquí algunas preguntas para el debate:

• «¿Qué miden IQR y DMA?». (Miden la dispersión o variabilidad de los datos).

• «¿Qué diagramas fueron los más difíciles de organizar?». (Los diagramas de puntos fueron más difíciles porque fue fácil encontrar el IQR para los diagramas de cajas).

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

Álgebra 1 . Matemáticas . Unidad 1

• «¿Coinciden los órdenes dados por los IQR y DMA tu orden?». (Sí, excepto los diagramas de cajas A y D, que tenían el mismo IQR y no'sabía cómo ordenarlos).

• «¿Qué observa en los valores de IQR y DMA?». (Los valores de DMA eran más altos de lo que pensaba, excepto para la distribución J. No sabía que DMA podía ser igual a cero).

• «¿Qué ventajas ofrece el uso de IQR y DMA frente a la inspección visual?».(Los IQR y DMA son valores que pueden ordenarse fácilmente).

Si algunos estudiantes ya han ordenado los gráficos utilizando IQR o DMA , debe preguntarles: «¿Por qué eligiste ordenar los gráficos por IQR o DMA ?« (Yo sabía que IQR y DMA eran medidas de variabilidad, así que las utilicé).

Apoyo para estudiantes que aprenden el idioma inglés

Lectura: MLR2 Recoger y mostrar. Mientras los estudiantes trabajan, camine y escuche la conversación de los estudiantes sobre la conexión entre las formas de la distribución y el uso de IQR o DMA para cuantificar la variabilidad. Después de ordenar los diagramas de cajas y de puntos por orden de variabilidad, anote las frases comunes o importantes que oiga decir a los estudiantes sobre cada representación directamente en esta presentación visual. Capte palabras como «mayor variabilidad, sesgada o dispersión de la fecha». Esto ayudará a los estudiantes a leer y utilizar el lenguaje matemático durante sus debates en parejas y en clase.

Principio(s) de diseño: Apoyar la creación de sentido

Apoyo para estudiantes con

discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Proporcionar a los estudiantes un diagrama de Venn para comparar cómo IQR y DMA son iguales y diferentes.

Apoya la accesibilidad para: Lenguaje; organización

¿Estás preparado para más?

1. Estos dos diagramas de cajas tienen la misma mediana y el mismo IQR. ¿Cómo podríamos comparar la variabilidad de las dos distribuciones?

2. Estos dos diagramas de puntos tienen la misma media y la misma DMA. ¿Cómo podríamos comparar la variabilidad de las dos distribuciones?

Respuesta del estudiante

Ejemplos de respuestas: Podríamos observar el rango y la forma de la distribución para determinar dónde están los valores en la comparación entre sí.

California . Algebra 1

SÍNTESIS DE LA LECCIÓN (5

minutos)

En esta lección, los estudiantes investigaron la variabilidad con visualizaciones de datos y estadísticos de resumen.

• «Un conjunto de datos medida del centro está mejor representado por una mediana de 7 y otro conjunto de datos por una mediana de 10 ¿Cómo determinaría qué conjunto de datos tiene mayor variabilidad?». (Calcula la IQR. La que tenga una IQR mayor es más variable).

• «¿Cómo determinas cuál de dos distribuciones aproximadamente simétricas tiene menos variabilidad?». (Se calcula la DMA. El que tenga una DMA menor tiene menos variabilidad).

• «¿Qué significa decir que un conjunto de datos o distribución tiene más variabilidad que otro?». (La medida apropiada de variabilidad para un conjunto de datos es mayor que el otro. Con una visualización de datos, una distribución está más separada que la otra).

ENFRIAMIENTO | ¿QUÉ MENÚ? (5 minutos)

El propietario de un restaurante cree que es beneficioso tener diferentes elementos de menú con mucha variabilidad para que la gente pueda elegir entre comida cara y barata. Varios chefs ofrecen menús y precios sugeridos para la comida que crean. El propietario crea diagramas de puntos para los precios de los platos del menú y encuentra algunas estadísticas resumidas. ¿Qué menú se ajusta mejor a lo que busca el restaurante? Explique su razonamiento.

Italiano:

Media: $9.03

Mediana: $9

DMA: $2.45 ��: $3.50

Cena:

Media: $3.36

Mediana: $2

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

DMA: $2.12 ��: $4

Japonés:

Media: $10.35

Mediana: $10

DMA: $5.55 ��: $9.50

Asador:

Media: $11.51

Mediana: $10.50

DMA: $3.69 ��: $4.50

Japonés. La variabilidad, ya sea mida con IQR o DMA, es mayor que en cualquiera de los otros menús disponibles.

Álgebra 1 . Matemáticas . Unidad 1

Resumen de la lección

La desviación media absoluta, o DMA, es una medida de variabilidad que se calcula encontrando la distancia media desde la media de todos los puntos de datos. Aquí hay dos diagramas de puntos, cada uno con una media de 15 centímetros, que muestran la longitud de las conchas de vieira en centímetros.

11 12 13 14 15 16 17 18 19

Longitud en centímetros

11 12 13 14 15 16 17 18 19

Longitud en centímetros

Observa que ambos diagramas de puntos muestran una distribución simétrica, por lo que la media y la DMA son opciones apropiadas para describir la variabilidad y el centro. Los datos en el primer diagrama de puntos parecen estar más separados que los datos en el segundo diagrama de puntos, por lo que se puede decir que el primer conjunto de datos parece tener mayor variabilidad que el segundo conjunto de datos. Esto se confirma por el DMA. La DMA del primer conjunto de datos es 1.18 centímetros y el DMA del segundo conjunto de datos es aproximadamente 0.94 cm. Esto significa que los valores del primer conjunto de datos se alejan, por término medio, aproximadamente 1.18 cm de la media y los valores del segundo conjunto de datos se alejan, por término medio, aproximadamente 0.94 cm de la media. Cuanto mayor sea el DMA de los datos, mayor será su variabilidad.

El rango intercuartílico, IQR, es una medida de variabilidad que se calcula restando el valor del primer cuartil, Q1, del valor del tercer cuartil, Q3. Estos dos diagramas de cajas representan las distribuciones de las longitudes en centímetros de un grupo diferente def conchas de vieira, cada una con una mediana de 15 centímetros.

Longitud en centímetros

Observa que ninguno de los diagramas de caja tiene una distribución simétrica. La mediana y el IQR son opciones apropiadas para describir el centro y la variabilidad de estos conjuntos de datos. La mitad central de los datos mostrados en la primera diagrama de cajas parece estar más separada, o mostrar mayor variabilidad, que la mitad central de los datos mostrados en la segunda diagrama de cajas. El IQR de la primera distribución es 14 cm y 10 cm para el segundo conjunto de datos. El IQR mide la diferencia entre la mediana de la segunda mitad de los datos, Q3, y la mediana de la primera mitad, Q1, de los datos, por lo que no se ve afectado por el valor mínimo o máximo del conjunto de datos. Es una medida de la dispersión de la mitad del 50 % de los datos.

La DMA se calcula con todos los valores de los datos, mientras que la IQR se calcula con solo los valores de Q1 y Q3

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

En clase de Ciencias, Clare y Lin estiman la masa de ocho objetos diferentes que en realidad pesan 2,000 gramos cada uno.

Algunos estadísticos de resumen: Clare

• Media: 2,000 gramos

• DMA: 275 gramos

• Mediana: 2,000 gramos

• ��: 500 gramos Lin

• Media: 2,000 gramos

• DMA: 225 gramos

• Mediana: 1,950 gramos

• ��: 350 gramos

¿Qué estudiante estimó mejor la masa de los objetos? Explica tu razonamiento.

Math Nation California . Algebra 1

1 . Matemáticas . Unidad 1

Soluciones posibles

Ejemplo de respuesta: Lin estimaba mejor que Clara porque ambos estudiantes tenían medidas de centro muy cercanas a 2,000 gramos, pero las respuestas de Lin's eran menos variables, como determinan tanto la DMA como la IQR

PROBLEMA 2

Un periodista cuenta el número de veces que un político habla de empleo en sus discursos de campaña. ¿Cuál es la DMA de los datos representados en el diagrama de puntos?

2 3 4 5 6 7 8 9 Número de menciones de «empleos»

A. 1.1 menciones

B. 2 menciones

Soluciones posibles

PROBLEMA 3

C. 2.5 menciones

D. 5.5 menciones

Cuatro minigolfistas aficionados intentan terminar 100 hoyos bajo par varias veces. En cada ronda de 100, se registra el cantidad de hoyos que ellos completan con éxito bajo par. Debido a la presencia de valores extremos, se determinó que los diagramas de cajas eran la mejor representación de los datos. Enumera los cuatro diagramas de cajas en orden de variabilidad de menor a mayor. jugador a

40 43 46 49 52 55

58 61 64 67 70 jugador b

Cantidad de hoyos completos bajo par

58 61 64 67 70 jugador c

40 43 46 49 52 55 Cantidad de hoyos completos bajo par

Soluciones posibles

c, a, b, d

PROBLEMA 4

(De la unidad 1, lección 7).

Selecciona todas las formas de distribución para las que la mediana podría ser mucho menor que la media. simétrica en forma de campana sesgada a la izquierda sesgada a la derecha bimodal

40 43 46 49 52 55

Cantidad de hoyos completos bajo par

58 61 64 67 70 jugador d

40 43 46 49 52 55

58 61 64 67 70

Cantidad de hoyos completos bajo par

Soluciones posibles

simétrica en forma de campana sesgada a la izquierda sesgada a la derecha bimodal

1 . Matemáticas . Unidad 1

PROBLEMA 5

(De la unidad 1, lección 6).

A. ¿Cuál es el resumen de cinco números para los datos 0, 2, 2, 4, 5, 5, 5, 5, 7, 11?

B. ¿Cuándo se elimina el mínimo, 0, del conjunto de datos, ¿cuál es el resumen de cinco números?

Soluciones posibles

0, 2, 5, 5, 11 (mínimo, ��1, mediana, ��3, máximo)

2, 3, 5, 6, 11 (mínimo, ��1, mediana, ��3, máximo)

PROBLEMA 6

(De la unidad 1, lección 6).

¿Qué efecto tiene eliminar el valor más alto, 180, del conjunto de datos sobre la media y la mediana?

25, 50, 50, 60, 70, 85, 85, 90, 90, 180

Soluciones posibles

La media disminuye de 78.5 a aproximadamente 67.22. La mediana disminuye de 77.5 a 70

PROBLEMA 7

(De la unidad 1, lección 3).

El histograma representa la distribución del cantidad de segundos que tardó cada uno de los 50 estudiantes en encontrar la respuesta a una pregunta de trivial con Internet. ¿Qué intervalo contiene la mediana?

A. 0 a 5 segundos

B. 5 a 10 segundos

C. 10 a 15 segundos

D. 15 a 20 segundos

Soluciones posibles

Reflexiones:

California . Algebra 1

LECCIÓN 9

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

S-ID.3 Interpretar las diferencias de forma, centro y dispersión en el contexto de los conjuntos de datos, teniendo en cuenta los posibles efectos de los puntos extremos de los datos (valores atípicos).

Construir

S-ID.1

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP6 Atender a la precisión.

MP8 Buscar y expresar regularidad en razonamientos repetidos.

Estándares ELD de California

I.A.1

I.B.6

II.C.7

DESVIACIÓN ESTÁNDAR

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES

INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

comprender al mundo, razonarán abstracta y cuantitativamente

OBJETIVO(S) DE APRENDIZAJE

analizan los datos y descubren la forma y el espacio.

• Puedo describir la desviación estándar como una medida de variabilidad.

• Puedo utilizar la tecnología para calcular la desviación estándar.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comprender (en lenguaje hablado y escrito) la desviación estándar como medida de variabilidad.

• Utilizar la tecnología para calcular la desviación estándar.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observa y preguntarse

Anticipar, supervisar, seleccionar, secuenciar, conectar

MLR5: Preguntas de elaboración conjunta

MLR1: Cada vez más fuerte y más claro

Materiales necesarios

Estadístico-tecnológico

Preparación necesaria

Los estudiantes deben tener acceso a la tecnología para calcular la desviación estándar y la media. Las actividades opcionales requieren tecnología para crear diagramas de puntos y calcular la desviación estándar, la media y el IQR.

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Aprendamos acerca de la desviación estándar, otra medida de variabilidad

Narrativa de la lección

El propósito matemático de esta lección es introducir la desviación estándar y entender que es una medida de variabilidad. Anteriormente, los estudiantes comprendieron el significado de DMA e IQR; la desviación estándar encaja en su comprensión como otra medida de variabilidad. Las lecciones futuras se basarán en esta lección cuando los estudiantes interpreten la desviación estándar en su contexto. La desviación estándar es una medida de variabilidad que se calcula:

• Hallando el cuadrado de la distancia desde la media a cada valor.

• A continuación, hallando la suma de estas distancias al cuadrado y dividiéndola por n (el número de valores del conjunto de datos).

• Por último, hallando la raíz cuadrada de esta suma.

Cuando los estudiantes manipulan los datos para conseguir varias medidas especificadas de centro o variabilidad están participando en el MP2 porque tienen que hacer uso de la estructura subyacente a la desviación estándar como medida de variabilidad.

Obsérvese que en esta unidad, todas las desviaciones típicas se refieren al cálculo de la desviación estándar poblacional (σ) en lugar de la desviación estándar estándar (s).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración Pares 20 min

Actividad de exploración Independiente 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 10 min

Nation California . Algebra 1

Descripción breve

Los estudiantes hacen observaciones sobr e diagramas de puntos con medias, desviaciones medias absolutas (DMA) y desviaciones estándar dadas.

Los estudiantes calculan las medias y las desviaciones estándar de diferentes diagramas de puntos y hacen comparaciones. Luego, crean conjuntos de datos que cumplen con condiciones específicas y explican su pensamiento.

Hay tecnología opcional está disponible en la edición digital para el maestro.

Los estudiantes analizan los efectos de agregar y quitar valores de los conjuntos de datos en las desviaciones estándar y las medias.

Hay una extensión de exploración disponible para hacer conexiones entre la desviación estándar y la DMA de cualquier conjunto de datos.

Los estudiantes hacen comparaciones entre la desviación estándar y otras medidas de variabilidad y lo que representan en un conjunto de datos.

Los estudiantes explican si las declaraciones sobre la desviación estándar que compara diferentes diagramas de puntos son ciertas.

El componente de práctica independiente incluye 3 problemas de repaso en clase y 4 problemas de repaso en espiral.

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE: MEDIR LA

VARIABILIDAD

(5 minutos)

Rutinas didácticas

Observar y preguntarse

El propósito de este calentamiento es provocar la idea de que calcular la desviación estánda (DE) es muy similar a calcular la DMA, lo que será útil cuando los estudiantes exploren la desviación estándar en una actividad posterior. Mientras que los estudiantes pueden observar y preguntarse muchas cosas acerca de estos diagramas de puntos, las similitudes y diferencias entre la desviación estándar y la DMA como medidas de variabilidad son los puntos importantes de discusión.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Muestre los diagramas de puntos y los estadísticos para que todos los vean. Pida a los estudiantes que piensen en al menos una cosa que observen y que tengan una pregunta. Conceda a los estudiantes 1 minuto de tiempo para pensar en silencio y, a continuación, 1 minuto para comentar las cosas que observan con su compañero, seguido de un debate con toda la clase.

¿Qué observas? ¿Qué te preguntas?

Media: 10, DMA: 1.56, desviación estándar : 2

Media: 10, DMA: 2.68, desviación estándar : 2.92

media: 10, DMA: 2.22, desviación estándar: 2,58

Media: 10, DMA: 1.12, desviación estándar: 1.61

Media: 10, DMA: 2.06, desviación estándar : 2.34

Media: 10, DMA: 0, desviación estándar: 0

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Cosas que los estudiantes pueden observar:

Álgebra 1 . Matemáticas . Unidad 1

• Todos los conjuntos tienen la misma media.

• Tanto la DMA como la desviación estándar son grandes para los mismos diagramas de puntos y pequeñas para los mismos diagramas de puntos.

• La desviación estándar es siempre mayor que la DMA (excepto para el último diagrama donde ambas son cero).

Cosas que los estudiantes pueden preguntarse:

• ¿Son la DMA y la desviación estándar ambas medidas de variabilidad?

• ¿Qué es la desviación estándar?

Pida a los estudiantes que compartan las cosas que observaron y se preguntaron. Registre y muestre sus respuestas para que todos puedan verlas. Si es posible, anota los razonamientos pertinentes en las imágenes o cerca de ellas. Una vez grabadas todas las respuestas sin comentarios ni edición, pregunte a los estudiantes: «¿Hay algo de esta lista sobre lo que os estéis preguntando ahora?». Anime a los estudiantes a discrepar respetuosamente, pedir aclaraciones o señalar información contradictoria. Si el concepto de variabilidad no surge durante la conversación, pida a los estudiantes que hablen de esta idea.

ACTIVIDAD DE EXPLORACIÓN |INVESTIGAR LA DESVIACIÓN ESTÁNDAR

(20 minutos)

Rutinas didácticas

Anticipar, supervisar, seleccionar, secuenciar, conectar

MLR5: Preguntas de elaboración conjunta

El propósito de esta actividad es dejar que los estudiantes investiguen qué sucede con la desviación estándar con diferentes conjuntos de datos. El objetivo es que los estudiantes hagan conjeturas sobre qué mide la desviación estándar y cómo se puede estimar el tamaño relativo de la desviación estándar a partir de la forma de la distribución. En particular, los estudiantes deben reconocer que sumar o restar el mismo valor de cada valor del conjunto de datos cambiará la media en la misma cantidad, pero la desviación estándar permanece invariable. Multiplicar o dividir cada valor del conjunto de datos por el mismo valor aumenta tanto la media como la desviación estándar en el mismo valor.

Supervice a los estudiantes quienes

1. comprueben los valores sin pensar mucho hasta que la media o la desviación estándar sean correctas.

2. utilicen un conjunto inicial de valores y, a continuación, modifiquen algunos de ellos hacia arriba o hacia abajo para que coincidan con las estadísticas dadas.

3. utilicen la simetría para obtener la media correcta.

4. ajusten los datos multiplicando todos los valores por un número para cambiar la dispersión de la distribución y acercarse a la desviación estándar.

Identifique a los estudiantes que crean conjuntos de datos con diferentes tipos de distribuciones para «10 números diferentes que tienen una media de 1» y «10 números diferentes con una desviación estándar tan cercana a 2.5 como se pueda conseguir en un minuto».

INTRODUCCIÓN

Muestre cómo encontrar la desviación estándar y la media con la tecnología disponible. En Álgebra 1, los estudiantes tratan con toda la población y no con el muestra, por lo que se utiliza la desviación estándar de la población.

Abre la herramienta «Hoja de cálculo y estadística»en la sección de «Herramientas de matemáticas» o navega a https://www.geogebra.org/classic/spreadsheet. Introduzca los valores en la columna A. Seleccione toda la columna A y luego elija el botón que parece un histograma y «Análisis de una variable». Haga clic en el botón que dice ∑x. La desviación estándar de la población se etiqueta σ. Además, el comando de la hoja de cálculo = SD(A1:A10) calculará la desviación estándar de la población para los datos de las celdas A1 hasta A10.

Organice a los estudiantes en grupos de 2. Dé tiempo a los estudiantes para que resuelvan las dos primeras preguntas, seguido de un debate con toda la clase.

Apoyo para estudiantes que aprenden el

idioma inglés

Cobversar: MLR5 Preguntas de elaboración conjunta. Muestre solo la primera línea de esta tarea (utiliza la tecnología para hallar la media y la desviación estándar de los datos de los diagramas de puntos) y los diagramas de puntos, y pida a los estudiantes que escriban por parejas posibles preguntas matemáticas sobre las distribuciones. A continuación, invita a las parejas a compartir sus preguntas con la clase. Esto ayuda a los estudiantes a producir el lenguaje de las preguntas matemáticas y a hablar sobre las relaciones entre las dos cantidades de esta tarea (media y desviación estándar).

Principio(s) de diseño: Cultivar la conversación

Usa la tecnología para calcular la media y la desviación estándar de los datos en los diagramas de puntos.

1. ¿Qué observas sobre la media y la desviación estándar que tú y tu compañero hallaron para los tres diagramas de puntos?

2. Inventa datos que se ajusten a las condiciones. Prepárate para compartir tu conjunto de datos y el razonamiento para la elección de los valores.

Compañero 1

Diagramas de puntos:

Compañero 2

Diagramas de puntos:

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Conddiciones:

• 10 números con una desviación estándar igual a la desviación estándar de tu primer diagrama de puntos, con una media de 6.

• 10 números con una desviación estándar tres veces mayor que los datos de la primera fila.

• 10 números diferentes con una desviación estándar lo más cercana a 2 en un 1 minuto.

Conddiciones:

• 10 números con una desviación estándar igual a la desviación estándar de tu primer diagrama de puntos con una media de 12.

• 10 números con una desviación estándar cuatro veces mayor que los datos de la primera fila.

• 10 números diferentes con una desviación estándar lo más cercana a 2 posible en 1 minuto.

RESPUESTAS POSIBLES

Álgebra 1 . Matemáticas . Unidad 1

SÍNTESIS DE LA ACTIVIDAD

1. Estadísticas para los diagramas de puntos.

A. Compañero 1:

• media: 5.5, desviación estándar: 2.87

• media: 30, desviación estándar: 14.14

• media: 2, desviación estándar: 0

B. Compañero 2:

• media: – 4.5, desviación estándar: 2.87

• media: 15, desviación estándar: 7.07

• media: 2, desviación estándar: 5

Ejemplo de respuesta: En el primer diagrama de puntos, la desviación estándar es la misma porque los valores de los datos se distribuyen de la misma manera alrededor de la media. En el segundo diagrama de puntos, la desviación estándar es mayor para el compañero 1 porque los datos están más separados. En el tercer diagrama de puntos, la desviación estándar es mayor para el compañero 2 porque hay alguna variación.

2. Respuestas de muestra para las condiciones:

A. Compañero 1:

• 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5. Para mantener la misma desviación estándar y cambiar la media, los datos deben desplazarse hacia arriba o hacia abajo hasta que tengan la media correcta.

• 3, 6, 9, 12, 15, 18, 21, 24, 27, 30. Para triplicar la desviación estándar, los datos pueden multiplicarse por 3

• 0,7, 1,4, 2,1, 2,8, 3,5, 4,2, 4,9, 5,6, 6,3, 7. Dado que el primer conjunto de datos tenía una desviación estándar de aproximadamente 2.87, dividiendo todos los valores por 2.87 se obtendría un conjunto de datos con una desviación estándar cercana a 1. Multiplicando esos valores por 2 se obtendría un conjunto de datos con una desviación estándar cercana a 2

B. Compañero 2:

• 7,5, 8,5, 9,5, 10,5, 11,5, 12,5, 13,5, 14,5, 15,5, 16,5. Para mantener la misma desviación estándar y cambiar la media, los datos deben desplazarse hacia arriba o hacia abajo hasta que tengan la media correcta.

• - 36, - 32, - 28, - 24, - 20, - 16, - 12, - 8, - 4, 0. Para cuadruplicar la desviación estándar, los datos pueden multiplicarse por 4

• - 6,3, - 5,6, - 4,9, - 4,2, - 3,5, - 2,8, - 2,1, - 1,4, - 0,7, 0. Dado que el primer conjunto de datos tenía una desviación estándar de alrededor de 2.87, dividiendo todos los valores por 2.87 se obtendría un conjunto de datos con una desviación estándar cercana a 1. Multiplicando esos valores por 2 se obtendría un conjunto de datos con una desviación estándar cercana a 2

El propósito de esta discusión es comprender que la desviación estándar es una medida de variabilidad relacionada con la media del conjunto de datos. La discusión también proporciona una oportunidad para que los estudiantes debaten lo que observan y se pregunten acerca de la media y la desviación estándar.

Seleccione a los estudiantes previamente identificados en el orden indicado en la narración para que compartan sus distribuciones y métodos para encontrar los valores que funcionaron. Para el conjunto de datos de al menos un estudiante que tuviera una desviación estándar cercana a 2.5, pregúnteles cómo podrían adaptar los datos para que tuvieran una media de 1 (Desplace los datos hacia arriba o hacia abajo para que tengan una media de 1).

He aquí algunas preguntas para el debate.

• «¿Qué crees que mide la desviación estándar? ¿Por qué lo crees?». (Creo que mide variabilidad porque se comportaba como DMA. Cuando todos los valores eran iguales, era cero).

California . Algebra 1

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

• «¿Por qué la desviación estándar es la misma para {1,

2}?». (Para cada conjunto de datos: 1) los valores a la izquierda de la media están a una distancia de 2 y 1 de la media y los valores a la derecha de la media están a una distancia 2 y 1 de la media, y 2) el valor medio está a 0 de la media. Esto hace que la desviación estándar sea la misma).

• «¿Por qué es diferente la desviación estándar para {- 4,

y {-

1, 0}?». (Los valores del primer conjunto de datos están al doble de distancia de la media que los valores del segundo conjunto de datos. Eso hace que la desviación estándar del primer conjunto sea mayor que la desviación estándar del segundo conjunto de datos).

• «¿Cuándo es igual a cero la desviación estándar?». (Es cero cuando todos los valores son iguales entre sí o cuando no hay variabilidad).

• «¿Fue tu media igual a la media de tu compañero en el quinto partido». (Las respuestas varían. Ejemplo de respuesta: Mi media fue muy diferente a la de mis compañeros. La mía fue 5 y la de ellos fue 10).

• «¿De qué manera el uso de la tecnología ayudó o dificultó tu pensamiento matemático sobre la desviación estándar y la media?». (Realmente me ayudó porque no me atasqué con los cálculos y pude buscar patrones en los datos, las visualizaciones de los datos y las estadísticas. En particular, me ayudó mucho tener que crear mis propios datos y luego ver qué pasaba con las estadísticas).

Apoyo para estudiantes con discapacidades

Acción y expresión: Interiorizar las funciones ejecutivas. Proporciona a los estudiantes un organizador gráfico con la desviación estándar en el centro, conectando a él todos los conceptos relacionados mencionados durante la discusión. Apoya la accesibilidad para: Lenguaje; organización

ACTIVIDAD DE EXPLORACIÓN | INVESTIGAR LA VARIABILIDAD

(10 minutos)

Rutinas didácticas

MLR1: Cada vez más fuerte y más claro

El propósito de esta actividad matemática es que los estudiantes investiguen cómo cambian la desviación estándar y otras medidas de variabilidad cuando se agregan, cambian o eliminan valores en un conjunto de datos. Vigila que los estudiantes mencionen los conceptos de forma, variabilidad y centro. Esta actividad funciona mejor cuando cada estudiante tiene acceso a la tecnología estadística, ya que de lo contrario llevaría demasiado tiempo. Si los estudiantes no tienen acceso individual, proyectar la tecnología estadística sería útil durante el introducción.

INTRODUCCIÓN

Abra la herramienta «Hoja de álculo y estadística» de la sección «Herramientas de matemáticas» o navegue hasta https://www.geogebra.org/classic/spreadsheet Mostrar cómo añadir, cambiar y eliminar puntos de datos de un conjunto de datos con la tecnología. Proporcione acceso a la tecnología estadística. Dé tiempo a los estudiantes para que resuelvan las preguntas y, a continuación, haga una pausa para un breve debate con toda la clase.

Apoyo para estudiantes que aprenden el idioma inglés

Escribir, hablar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para dar a los estudiantes una oportunidad estructurada de revisar y refinar su respuesta a la pregunta: «¿Qué parece cambiar más fácilmente, la desviación estándar o el rango intercuartílico?». Pida a cada estudiante que se reúna con 2-3 compañeros diferentes seguidos para recibir sus comentarios. Proporcione a los estudiantes indicaciones para la retroalimentación que ayuden a los equipos a reforzar sus ideas y aclarar su lenguaje. Por ejemplo: «¿Puedes explicar cómo...? Deberías ampliar ...»., etc. Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para reforzar el producto final.

Principio(s) de diseño: Optimizar el resultado (para la generalización)

Comienza con los datos.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

POSIBLES RESPUESTAS

Álgebra 1 . Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Invite a los estudiantes a hablar de sus ideas con un compañero antes de escribirlas. Muestre fragmentos de frases para apoyar a los estudiantes cuando expliquen sus ideas. Por ejemplo: «Me doy cuenta de que la media se ve afectada cuando...» o «La desviación estándar siempre se verá afectada porque...». Apoya la accesibilidad para: Lenguaje; organización

1, , 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19

1. Usa la tecnología para encontrar la media, la desviación estándar, la mediana y el rango intercuartílico.

2. ¿Cómo cambian la desviación estándar y la media si eliminas el mayor valor del conjunto de datos? ¿Cómo cambian si añades un valor al conjunto de datos que es el doble del valor mayor?

3. ¿Qué predices que ocurrirá con la desviación estándar y la media cuando elimines el menor valor del conjunto de datos? Comprueba si tu predicción es correcta.

4. ¿Qué ocurre con la desviación estándar y la media cuando añades al conjunto de datos un valor igual a la media? Añade un segundo valor igual a la media. ¿Qué ocurre?

5. Añade, cambia y elimina valores del conjunto de datos para responder a la pregunta: ¿Qué parece cambiar más fácilmente, la desviación estándar o el rango intercuartílico? Explica tu razonamiento.

1. Media: 10,5, desviación estándar: 5.77, mediana: 10.5, IQR: 10

2. Ejemplo de respuesta: Tanto la media como la desviación estándar disminuyeron cuando se eliminó el valor más alto. Ambas aumentaron cuando se añadió el valor atípico.

3. Ejemplo de respuesta: La media aumentó y la desviación estándar disminuyó cuando se eliminó el valor menor.

4. Ejemplo de respuesta: La media permaneció igual y la desviación estándar disminuyó ligeramente.

5. Ejemplo de respuesta: La desviación estándar tiende a cambiar más fácilmente. El rango intercuartílico se calcula por la posición de los valores dentro del conjunto de datos ordenados y no por los valores reales en sí, por lo que añadir un valor extremadamente grande adicional tiene el mismo efecto que añadir otro valor igual al valor máximo. Por otro lado, la desviación estándar utiliza la distancia de cada valor a la media, por lo que se ve afectada más fácilmente por la inclusión o eliminación de valores.

California . Algebra 1

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Los estudiantes que calculan una desviación estándar diferente pueden estar utilizando el estadístico de la desviación estándar muestral. Diga a estos estudiantes que utilicen el valor de σ en lugar de s para los cálculos de esta unidad.

El objetivo de esta discusión es hablar de la desviación estándar como medida de variabilidad. El objetivo de esta discusión es asegurarse de que los estudiantes comprendan que la desviación estándar se comporta de manera similar a la DMA y que es una medida de variabilidad que utiliza la media como medida del centro. Discuta cómo la desviación estándar se ve afectada por la adición y eliminación de valores atípicos en el conjunto de datos. La desviación estándar disminuye cuando se eliminan los valores atípicos porque los datos en la distribución muestran menos variabilidad y la desviación estándar aumenta cuando se agregan valores atípicos porque los datos en la distribución muestran más variabilidad.

Agregue la desviación estándar a la presentación de medidas de centro y medidas de variabilidad creadas en una lección anterior.

• Desviación estándar: Una medida de variabilidad utilizada a menudo con la media que describe la dispersión de los datos. Es una medida de variabilidad matemáticamente más útil que la DMA.

• La DMA ya incluida en la visualización del ejemplo es aproxidamente 1.09 y la desviación estándar es 1.194 Aquí hay algunas preguntas para la discusión.

• «¿Qué mide la desviación estándar? ¿Cómo lo sabes?». (Mide la variabilidad. Al igual que la DMA, la desviación estándar aumenta cuando se incluyen valores atípicos en el conjunto de datos).

• «La desviación estándar se calcula utilizando la media, ¿crees que es más apropiado utilizarla con conjuntos de datos simétricos o sesgados?». (Simétricos, porque se calcula con la media).

¿Estás preparado para más?

¿Cómo se calcula la desviación estándar? Hemos visto que la desviación estándar se comporta de forma muy parecida a la desviación media absoluta y eso es porque la idea clave que subyace en ambas es la misma.

1. Con el conjunto de datos original, calcula la desviación de cada punto respecto a la media restando la media de cada punto de datos.

2. Si simplemente intentáramos sacar la media de esas desviaciones, ¿qué obtendríamos?

3. Hay dos formas comunes de convertir valores negativos en valores positivos más útiles: tomar el valor absoluto o elevar el valor al cuadrado. Para hallar la DMA, encontramos el valor absoluto de cada desviación y, a continuación, hallamos la media de esos números. Para hallar la desviación estándar, elevamos al cuadrado cada una de las desviaciones y hallamos la media de esos números. Finalmente, sacamos la raíz cuadrada de esa media. Calcule la DMA y la desviación estándar del conjunto de datos original.

Posibles respuestas

1. {-9.5, -8.5, -7.5,

2. 0

3. DMA: 5, DE: 5.77

Álgebra 1 . Matemáticas . Unidad 1

SÍNTESIS DE LA LECCIÓN

(5 minutos)

He aquí algunas preguntas para el debate.

• «¿Cómo se compara y contrasta la desviación estándar con la DMA y la IQR?« (Al igual que la DMA y la IQR, la desviación estándar es una medida de variabilidad. A diferencia de la IQR, la desviación estándar se basa en la media y no en la mediana. Es muy similar a la DMA porque implica encontrar la diferencia de cada valor y la media, pero luego se realizan diferentes operaciones con esas diferencias).

• «Un conjunto de datos tiene una desviación estándar de 5 y otro conjunto de datos tiene una desviación estándar de 10. ¿Qué te dice esto sobre la distribución de cada conjunto de datos?». (La desviación estándar es una medida de variabilidad, por lo que indica la dispersión de los datos. El segundo conjunto de datos muestra mayor variabilidad que el primero).

ENFRIARSE | VERDADERO O FALSO: RAZONAR CON LA DESVIACIÓN ESTÁNDAR

(5 minutos)

La temperatura baja en grados Celsius para algunas ciudades en los mismos días de marzo se registran en los diagramas de puntos.

bajas de Christchurch, NZ (ºC)

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

bajas de London, UK (ºC)

Decide si cada enunciado es verdadero o falso. Explique tu razonamiento.

1. La desviación estándar de las temperaturas de Christchurch es cero porque los datos son simétricos.

2. La desviación estándar de las temperaturas de San Luis es igual a la desviación estándar de las temperaturas de Chicago.

3. La desviación estándar de las temperaturas de Chicago es menor que la desviación estándar de las temperaturas de Londres.

1. Falso. Ejemplo de respuesta: La desviación estándar es una medida de variabilidad y hay cierta variabilidad en el conjunto de datos.

RESPUESTAS

POSIBLES

2. Verdadero. Ejemplo de respuesta: Las temperaturas de Chicago son las mismas que las de St. Louis, pero 3 grados más frías cada día. Las dos ciudades tienen la misma variabilidad de temperatura y, por tanto, tienen la misma desviación estándar.

3. Verdadero. Ejemplo de respuesta: Londres tiene las mismas temperaturas bajas que Chicago, excepto que el último día, la temperatura de Londres es 3 grados más cálida que la de Chicago. Por lo tanto, las temperaturas de Londres tienen más variabilidad que las de Chicago en esos días.

Resumen de la lección para el estudiante

Podemos describir la variabilidad de una distribución con la desviación estándar. La desviación estándar es una medida de variabilidad que se calcula con un método similar al que se utiliza para calcular la DMA o desviación media absoluta.

California . Algebra 1

Una comprensión más profunda de la importancia de la desviación estándar como medida de variabilidad vendrá con un estudio más profundo de la estadística. Por ahora, sepa que la desviación estándar es matemáticamente importante y se utilizará como la medida apropiada de la variabilidad cuando la media sea una medida apropiada del centro.

Al igual que la DMA, la desviación estándar es grande cuando el conjunto de datos está más disperso, y la desviación estándar es pequeña cuando la variabilidad es pequeña. La intuición que adquirió sobre la DMA también funcionará para la desviación estándar.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Se registran las tallas de todos los pares de zapatos del armario de una persona. 7 7 7 7 7 7 7 7 7 7

A. ¿Cuál es la media?

B. ¿Cuál es la desviación estándar?

PROBLEMA 2

He aquí un conjunto de datos:

1 2 3 3 4 4 4 4 5 5 6 7

A. ¿Qué ocurre con la media y la desviación estándar del conjunto de datos cuando se cambia el 7 por un 70?

B. Para el conjunto de datos con el valor de 70, ¿por qué la mediana sería una mejor opción para la medida del centro que la media?

PROBLEMA 3

Soluciones posibles

A. 7

B. 0

Soluciones posibles

A. La media aumenta de 4 a 9.25 y la desviación estándar aumenta aproximadamente de 1.58 a 18.36

B. La mediana sería una mejor elección, porque el conjunto de datos con el 70 es una distribución sesgada.

¿Cuál de estas estima mejor la desviación estándar de los puntos en un juego de cartas?

A. 5 puntos

B. 20 puntos

C. 50 puntos

D. 500 puntos

Soluciones posibles

PROBLEMA 4

(De la unidad 1, lección 8).

La media del conjunto de datos A es 43.5 y la DMA es 3.7

La media del conjunto de datos B es 12.8 y la DMA es 4.1

A. ¿Qué conjunto de datos muestra mayor variabilidad? Explica tu razonamiento.

B. ¿Qué diferencias esperarías ver al comparar los diagramas de puntos de los dos conjuntos de datos?

Puntos de la tarjeta de juego

Soluciones posibles

A. B muestra mayor variabilidad porque la DMA es mayor que la DMA de A.

B. Ejemplo de respuesta: La gráfica de puntos de A tendrá la mayoría de los datos centrados alrededor de 43.5 con los datos, en promedio, 3.7 unidades por encima o por debajo de 43.5. El diagrama de puntos de B tendrá la mayoría de los datos centrados alrededor de 12.8 con los datos, de media, 4.1 unidades por encima o por debajo de 12.8

PROBLEMA 5

(De la unidad 1, lección 7).

Selecciona todas las formas de distribución para las que la media y la mediana deben ser aproximadamente iguales. formas de campana bimodal sesgada simétrica uniforme

PROBLEMA 6

(De la unidad 1, lección 8).

¿Qué es el IQR?

Soluciones posibles en forma de campana bimodal sesgada simétrica uniforme

1 . Matemáticas . Unidad 1

4 6 8 10 12 14 16 18

Cantidad de ramas en árboles de 10 años

A. 5 ramas

B. 7 ramas

C. 10 ramas

D. 12 ramas

Soluciones posibles

PROBLEMA 7

(De la unidad 1, lección 6).

Los datos representan el número de latas recogidas por diferentes clases para un proyecto de servicio.

12 14 22 14 18 23 42 13 9 19 22 14

A. Encuentra la media.

B. Encuentra la mediana.

C. Elimina el mayor valor, 42, del conjunto de datos. Explica cómo cambian las medidas del centro.

Soluciones posibles

A. 18.5 latas

B. 16 latas

C. La media disminuye a unas 16.36 latas y la mediana disminuye a 14 latas.

IDEA(S) FUNDAMENTAL(ES

• Investigar datos

ALINEACIÓN

Abordar

Alineación

Estándares y Principios de CA

Construir

S-ID.1

Construir

S-ID.3

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP2 Razonar abstracta y cuantitativamente.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.1

I.B.7

EP&Cs de California

II.B.5

5.A

LECCIÓN 10 MÁS DESVIACIÓN ESTÁNDAR

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

comprender al mundo y predicer lo que podría ocurrir, atenderán con precisión

OBJETIVO(S) DE APRENDIZAJE

amalizan los datos y descubren la forma y el espacio.

• Puedo utilizar la desviación típica para decir algo sobre una situación.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente y por escrito) el significado de desviación estándar en su contexto.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyos para el debate

MLR4: Tarjeta de información deficientes

Materiales necesarios

Copias de la plantilla maestra

Fichas para imprimir, recortes de las plantillas maestras

Preparación necesaria

Imprima y recorte las plantillas maestras. Prepare 1 copia por cada 2 estudiantes.

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Sigamos interpretando la desviación estándar.

Narrativa de la lección

Uno de los propósitos de esta lección es introducir a los estudiantes a la rutina «Brecha de informativa (Info Gap)«. Los estudiantes profundizan su comprensión de la desviación estándar interpretándola en varios contextos. Los estudiantes amplían el trabajo de lecciones anteriores al ver la desviación estándar en varios contextos. El trabajo de esta lección se conecta con el trabajo siguiente porque los estudiantes continuarán examinando cómo la variabilidad, junto con el contexto de un problema, puede ayudar a determinar si los datos son valores atípicos y qué hacer con estos valores.

Interpretar la desviación estándar en contexto es evidencia de que los estudiantes razonan abstracta y cuantitativamente (MP2). La actividad de la brecha informativa puede requerir varias rondas de discusión para que los estudiantes encuentren sentido y obtengan la información que necesitan para resolver el problema (MP1). La estructura del vacío de información también les permite refinar el lenguaje que utilizan y formular preguntas cada vez más precisas hasta que obtienen la información que necesitan (MP6).

RESUMEN DE LA LECCIÓN

Componente de lección

Estructura Tiempo

Calentamiento Independiente 5 min

Actividad de exploración

Actividad de Exploración (opcional)

En pareja 30 min

En pareja 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 10 min

California . Algebra 1

Descripción breve

Los estudiantes evalúan mentalmente expresiones numéricas que involucran el orden de las operaciones y luego debaten las estrategias que utilizaron.

Los estudiantes utilizan la rutina de la brecha informativa para hacer y responder preguntas que conducen a la información necesaria para comparar las medias y la variabilidad en dos conjuntos de datos y luego crear un diagrama de puntos.

Esta tarea puede ser una oportunidad para hacer conexiones con los «Principios y conceptos ambientales de California (EP&Cs)« mediante el análisis de los efectos del cautiverio en las poblaciones de elefantes y la toma de decisiones que influyen en los sistemas naturales.

Los estudiantes interpretan y hacen comparaciones entre las medidas de centro y variabilidad en contexto a partir de diagramas de puntos.

Hay una extensión de exploración disponible para desarrollar una comprensión más profunda de la comparación de puntos de datos usando la desviación estándar de un conjunto de datos en contexto.

Los estudiantes debaten cómo usar la desviación estándar para interpretar datos en problemas del mundo real.

Los estudiantes relacionan histogramas con las descripciones de situaciones con las medias y desviaciones estándar dadas.

El componente de práctica independiente incluye 3 problemas de repaso en clase y 4 problemas de repaso en espiral.

1 . Matemáticas . Unidad 1

CHARLA DE MATEMÁTICAS: VALOR ATÍPICO EN MATEMÁTICAS

(5 minutos)

Rutinas didácticas

Charla de matemáticas

MLR8: Apoyo para el debate

El propósito de esta charla de matemáticas es obtener estrategias y conocimientos para calcular valores a partir de expresiones de la forma �� 1.5 ∙ ��. Estos conocimientos serán útiles en una lección posterior, cuando los estudiantes utilicen expresiones como ��1 1.5 ∙ �� para determinar si los valores son valores atípicos.

En esta actividad, los estudiantes tienen la oportunidad de observar y hacer uso de la estructura (MP7) porque están construyendo estrategias que les permitirán tanto multiplicar por 1.5 como restar esa respuesta de otro valor.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Muestre un problema a la vez. Conceda a los estudiantes un tiempo de reflexión tranquilo para cada problema y pídales que hagan una señal cuando tengan una respuesta y una estrategia. Mantenga todos los problemas expuestos durante la charla. Continúe con un debate con toda la clase.

Evalúa mentalmente.

• «¿Quién puede replantear el razonamiento s de otra manera?«.

• «¿Tenía alguien la misma estrategia, pero la explicaría de otra manera?«.

• «¿Alguien resolvió el problema de otra manera?«.

• «¿Alguien quiere añadir algo a la estrategia de s?«.

• «¿Estás de acuerdo o en desacuerdo? ¿Por qué?

Apoyo para estudiantes que aprenden el idioma inglés

Hablar: MLR8 Apoyo de la discusión. Muestre fragmento de oraciones para apoyar a los estudiantes cuando expliquen su estrategia. Por ejemplo: «Primero, porque...« o «Observé así que...«. Algunos estudiantes pueden beneficiarse de la oportunidad de ensayar lo que van a decir con un compañero antes de compartirlo con toda la clase.

Principio(s) de diseño: Optimizar la salida para la explicación

ACTIVIDAD DE EXPLORACIÓN | BRECHA INFORMATIVA: ELEFANTES AFRICANOS Y ASIÁTICOS

(30 minutos)

Rutinas didácticas

MLR4: Tarjetas de la brecha informativa

Álgebra 1 . Matemáticas . Unidad 1

Esta es la primera actividad de brecha informativa del curso. Consulte el lanzamiento para obtener instrucciones ampliadas para facilitar esta actividad con éxito.

Esta actividad de la brecha informativa ofrece a los estudiantes la oportunidad de determinar y solicitar la información necesaria para investigar e interpretar las medidas de centro y variabilidad.

La estructura de brecha informativa requiere que los estudiantes comprendan los problemas determinando qué información es necesaria y, a continuación, soliciten la información que necesitan para resolverlo. Esto puede requerir varias rondas de discusión si sus primeras peticiones no aportan la información que necesitan (MP1). También les permite refinar el lenguaje que utilizan y hacer preguntas cada vez más precisas hasta que obtienen la información que necesitan (MP6).

Aquí está el texto de las tarjetas para referencia y planificación:

INTRODUCCIÓN

Nation California . Algebra 1

Esta es la primera vez en este grado que los estudiantes hacen la rutina instruccional de la tarjeta de brecha informativa, por lo que es importante demostrar la rutina en una discusión de toda la clase antes de que hagan la rutina entre sí. Explicar la rutina de la brecha informativa: Los estudiantes trabajan con un compañero. Un compañero recibe una tarjeta de problema con una pregunta matemática que no tiene suficiente información dada, y el otro compañero recibe una tarjeta de datos con información relevante para la tarjeta de problema. Los estudiantes se hacen preguntas del tipo «¿Qué información necesitas?« y deben explicar lo que harán con la información. Una vez que el compañero con la tarjeta del problema tiene suficiente información para resolver el problema, ambos compañeros pueden mirar la tarjeta del problema y resolver el problema de forma independiente. Este gráfico ilustra el marco de la rutina:

INTRODUCCIÓN CONTINUACIÓN

Diga a los estudiantes que, en primer lugar, se realizará una demostración con toda la clase. Como clase, ellos hacen el papel de la persona con la tarjeta de problema mientras que usted hace el papel de la persona con la tarjeta de datos. Explique a los estudiantes que es tarea de la persona con la tarjeta del problema (en este caso, toda la clase) pensar qué información necesitan para responder a la pregunta.

Muestre este problema para que todos lo vean:

100 se pesan elefantes asiáticos cautivos y 100 elefantes asiáticos salvajes. ¿Existe una diferencia significativa entre los pesos de los dos grupos de elefantes? Explique su razonamiento.

Explique que usted hará el papel de la persona que tiene la tarjeta de datos. Pregunte a los estudiantes: «¿Qué información específica necesitas para averiguar si existe una diferencia significativa entre el peso de los elefantes asiáticos cautivos y salvajes?«. Seleccione a los estudiantes para que formulen sus preguntas. Responda a cada pregunta con: «¿Por qué necesitas esa información?«. Aquí tienes la información de la ficha de datos. Después de este punto, responda a la pregunta solo si estos datos son relevantes:

Tarjeta de datos

• La distribución de pesos para cada conjunto de elefantes es aproximadamente simétrica. Elefantes asiáticos cautivos:

• Peso medio de los elefantes cautivos: 3,073 kg

• Desviación estándar de los pesos de los elefantes cautivos: 282 kg

• Peso medio de los elefantes cautivos: 3,055 kg

• IQR de los pesos de elefantes cautivos: 399 kg

Elefantes asiáticos salvajes:

• Peso medio de los elefantes salvajes: 2.373 kg

• Desviación estándar del peso de los elefantes salvajes: 121 kg

• Mediana del peso de los elefantes salvajes: 2.386 kg

• IQR del peso de los elefantes salvajes: 163 kg

Explique que si la persona de la tarjeta del problema pide información que no está en la tarjeta de datos (¡incluida la respuesta!), entonces la persona de la tarjeta de datos debe responder: «No tengo esa información«. Pida a los estudiantes que expliquen a su compañero (usted) cómo han utilizado la información para resolver el problema. (Hay una diferencia significativa de peso entre los elefantes asiáticos cautivos y salvajes. Como las distribuciones son simétricas, tiene sentido utilizar la media y la desviación típica de los pesos de los dos grupos. La diferencia en las medias de 700 kilogramos es muy diferente, incluso a la luz de las desviaciones estándar para los grupos).

Organice a los estudiantes en grupos de 2. En cada grupo, distribuya una tarjeta de problema a un estudiante y una tarjeta de datos al otro. Después de revisar su trabajo en el primer problema, entrégueles las tarjetas para un segundo problema e indíqueles que cambien los papeles.

Apoyo para estudiantes que aprenden el idioma inglés

Conversación: Esta actividad utiliza la brecha informativa MLR4 para dar a los estudiantes un propósito para discutir la información necesaria para resolver problemas que implican la medida de los centros y la variabilidad. Muestre preguntas o iniciadores de preguntas para los estudiantes que necesiten un punto de partida como: «¿Puedes decirme...? (dato especíﬁco) y ¿Por qué necesitas saber...).

Principio(s) de diseño:) Cultivar la conversación

Álgebra 1 . Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad

Representación: Proporcionar acceso para la percepción. Muestre o proporcione a los estudiantes una copia física de las instrucciones escritas y léalas en voz alta. Compruebe la comprensión invitando a los estudiantes a reformular las instrucciones con sus propias palabras. Considere la posibilidad de mantener las instrucciones visibles durante toda la actividad.

Favorece la accesibilidad para: Lenguaje; memoria

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Tu maestro te dará una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu compañero.

Si tumaestro te da la tarjeta de datos:

1. Lee en silencio la información de tu tarjeta.

2. Pregunta a tu compañero: «¿Qué información específica necesitas?« y espera a que tu compañero te pida información. Da solo la información que aparece en tu tarjeta. (¡No descifres nada para tu compañero!).

3. Antes de dar la información a tu compañero, pregúntale: ¿Por qué necesitas saber (ese dato)?

4. Lee la tarjeta del problema y resuélvelo de forma independiente.

5. Comparte la tarjeta de datos y comenta tu razonamiento.

Tarjeta de problema 1

RESPUESTAS POSIBLES

Si tu maestro te da la tarjeta del problema:

1. Lee en silencio tu tarjeta y piensa qué información necesitas para responder a la pregunta.

2. Pide a tu compañero la información específica que necesitas.

3. Explica a tu compañero cómo estás utilizando la información para resolver el problema.

4. Cuando tengas suficiente información, comparte la tarjeta de problema con tu compañero y resuelve el problema de forma independiente.

5. Lee la tarjeta de datos y discute tu razonamiento.

1. Ejemplo de respuesta: Los pesos típicos de los elefantes de la población A son aproximadamente 300 libras más pesados que los de la población B, con base en la media. Utilicé la media para determinar esto, ya que las distribuciones son simétricas.

2. Ejemplo de respuesta: Los elefantes de la población B tienen una mayor variación de peso, ya que su desviación estándar es aproximadamente 166 libras mayor. La simetría de las distribuciones significa que la desviación estándar es una medida más apropiada de la variabilidad.

Tarjeta de problema 2

Las respuestas varían. Las soluciones correctas deben tener 9 puntos en una distribución simétrica en forma de campana con una media de 8,000 libras y una desviación estándar inferior a 577.35 libras (debe parecer más compacta que el diagrama de puntos dado).

Ejemplo de respuesta:

Peso del elefante asiático (libras)

SÍNTESIS DE LA ACTIVIDAD

Después de que los estudiantes hayan completado su trabajo, comparta las respuestas correctas y pida a los estudiantes que hablen del proceso de resolución de los problemas. A continuación se presentan algunas preguntas para la discusión:

• «¿Qué fue interesante acerca de la tarjeta de problema 1?». (Fue interesante utilizar un contexto real para pensar en la variabilidad).

• «¿Fue más apropiado utilizar la media o la mediana para comparar los pesos típicos para la tarjeta de problema 1? ¿Por qué?». (La media debido a la simetría de los datos).

• «¿Qué medida de variabilidad elegiste para comparar la tarjeta del problema 1? ¿Por qué?». (La desviación estándar, porque utilicé la media y los datos tienen una distribución simétrica).

• «¿Qué fue lo más difícil de la tarjeta del problema 2?». (Fue difícil averiguar cómo hacer el diagrama de puntos sin los datos reales).

• «¿Cómo sabes que tu diagrama de puntos es correcto?». (No hay forma de saberlo, solo se puede aproximar con base en la media, la desviación estándar y la forma aproximada).

Destaque para los estudiantes cómo utilizaron la información sobre el centro, la forma y la variabilidad de la distribución para resolver los problemas.

ACTIVIDAD DE EXPLORACIÓN OPCIONAL | INTERPRETAR

LAS MEDIDAS DE CENTRO Y VARIABILIDAD (10 minutos)

Rutinas didácticas

MLR8: Apoyos para el debate

Esta tarea se proporciona como práctica adicional opcional para comprender la variabilidad en contexto.

El propósito matemático de esta actividad es comparar conjuntos de datos e interpretar las medidas de centro y las medidas de variabilidad en el contexto del problema.

INTRODUCCIÓN

Mantenga a los estudiantes en los mismos grupos. Dar a los estudiantes 5 minutos para trabajar en las preguntas y seguir con una discusión de toda la clase.

Apoyo para estudiantes con discapacidad

Acción y expresión: Desarrollar la expresión y la comunicación. Para ayudar a los estudiantes a empezar, muestre fragmentos de frases como: «En esta situación, un valor mayor/menor para la desviación estándar significa ». o «Ambos gráficos de puntos son diferentes porque...».

Apoya la accesibilidad para: Lenguaje; organización

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Para cada situación, se te proporcionan dos gráficos de datos: una medida de centro y una medida de variabilidad para cada uno.

• Interpreta la medida de centro en función de la situación.

• Interpreta la medida de variabilidad en función de la situación.

• Compara los dos conjuntos de datos.

1 . Matemáticas . Unidad 1

1. Se recogen las alturas de los 40 árboles de cada uno de los dos bosques.

media: 44.8 pies, desviación estándar: 4.2 pies

Altura del árbol en el bosque A (pies)

media: 56.03 pies, desviación estándar: 7.87 pies

Altura del árbol en el bosque B (pies)

2. Se recoge la cantidad de minutos que tardan Lin y Noah en terminar sus exámenes en clase de alemán.

media: 29.48 minutos, desviación típica: 5.44 minutos

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN

media: 28.44 minutos, desviación típica: 7.40 minutos

Tiempo para que Noah termine la prueba (min)

3. Se recoge la cantidad de pasitas en un cereal de marca y la versión genérica del mismo cereal para varias cajas.

media: 289.1 pasitas, desviación típica: 19.8 pasitas

de pasitas en el cereal de marca

media: 249.17 pasitas, desviación típica: 26.35 pasitas

Ejemplos de respuestas:

RESPUESTAS POSIBLES

A. La media nos indica la altura media de los árboles de cada bosque. Algunos serán más altos y otros más bajos.

B. La desviación estándar es una medida de lo variable que es la altura de los árboles. Un valor mayor significa que hay árboles mucho más altos y mucho más bajos que la media, mientras que un valor menor significa que tienen casi la misma altura.

C. Los árboles del bosque B tienden a ser más altos según la media, pero también son más variables, por lo que los árboles del bosque A serán un poco más uniformes que los del bosque B.

A. La media nos indica el número medio de minutos que tarda cada persona en terminar las pruebas de alemán.

B. La desviación estándar representa lo variables que son los tiempos. Un valor mayor significa que a veces la persona termina mucho más lento o más rápido que la media, mientras que un valor menor significa que la persona termina más o menos en el mismo tiempo para cada prueba.

C. Noah es más rápido en terminar las pruebas en promedio, pero Lin es más consistente en sus tiempos de finalización.

A. La media nos dice el cantidad promedio de pasitas en una caja de cereales.

B. La desviación estándar muestra cuán variable es la cantidad de pasitas. Un valor menor significa que las cajas de ese tipo de cereal tienden a ser más consistentes con la cantidad de pasitas en la caja, mientras que un valor mayor significa que hay más variedad en las diferentes cajas del mismo tipo de cereal.

C. El cereal de marca tiene más pasitas en promedio y es más consistente con la cantidad de pasitas en una caja. El cereal genérico tiende a tener menos pasitas, pero también es menos consistente con la cantidad de pasitasen una caja.

CONCEPTOS ERRÓNEOS

PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

Identifique a los estudiantes que tienen dificultades para establecer las conexiones entre los estadísticos resumidos y el contexto del problema. Pregúnteles qué información transmite la desviación estándar. Dígales que se centren menos en el valor real de la desviación estándar y más en cuál de las dos distribuciones tiene una desviación estándar mayor y lo que eso podría significar.

El propósito de esta discusión es que los estudiantes expliquen la media y la desviación estándar en su contexto.

Para cada conjunto de gráficos, seleccione estudiantes que lean sus respuestas para las tres preguntas. Cuando sea necesario, pida a los estudiantes que revisen su lenguaje para incluir los términos forma, medida del centro y variabilidad.

Apoyo para estudiantes que

aprenden el idioma inglés

Hablar: MLR8 Apoyos para el debate. Utilice esta rutina para apoyar el debate de toda la clase. Para cada observación que se comparta, pida a los estudiantes que repitan y/o vuelvan a expresar lo que han oído utilizando un lenguaje matemático preciso (forma, medida del centro y variabilidad). Considere la posibilidad de dar tiempo a los estudiantes para que repitan lo que han oído a un compañero, antes de seleccionar a uno o dos estudiantes para que lo compartan con la clase. Pregunte al orador original si su compañero ha sido capaz de repetir con precisión su pensamiento y, si es necesario, que lo aclare. Llame la atención de los estudiantes sobre las palabras o frases que hayan ayudado a aclarar la afirmación original. De este modo, más estudiantes tendrán la oportunidad de producir lenguaje al explicar la media y la desviación estándar en su contexto.

Principio(s) de diseño: Apoyar la creación de sentido

Álgebra 1 . Matemáticas . Unidad 1

¿Estás preparado para más?

Un uso de la desviación estándar es que proporciona una escala natural de cuánto por encima o por debajo de la media está un punto de datos. Esto es increíblemente útil para comparar puntos de dos distribuciones diferentes.

Por ejemplo, dicen que no se pueden comparar manzanas y naranjas, pero aquí hay una manera. El peso medio de una granny smith es de 128 gramos, con una desviación estándar de unos 10 gramos. El peso medio de una naranja navel es de 140 gramos con una desviación típica de unos 14 gramos. Si tenemos una manzana granny smith de 148 gramos y una naranja navel de 161 gramos, podríamos preguntarnos cuál es más grande para su especie, aunque ambas estén unos 20 gramos por encima de sus respectivas medias. Podríamos decir que la manzana, que está 2 desviaciones estándar por encima de su media, es más grande para su especie que la naranja, que solo está 1.5 desviaciones estándar por encima de su media.

1. ¿Cuántas desviaciones estándar por encima de la altura media de un árbol en el bosque A está su árbol más alto?

2. ¿Cuántas desviaciones estándar por encima de la altura media de un árbol en el bosque B está su árbol más alto?

3. ¿Cuál es el árbol más alto de su bosque?

Posibles respuestas

1. Aproximadamente 2.16 desviaciones típicas.

2. Aproximadamente 1.78 desviaciones típicas.

3. El árbol del bosque A.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

Aquí tienes algunas preguntas para debatir.

• «¿Qué información te da la desviación típica sobre un conjunto de datos?». (Te dice lo variables que son los datos en relación con la media).

• «Dos pilotos de carreras profesionales tienen los mismos tiempos medios por vuelta después de cincuenta vueltas. ¿Qué significa decir que los tiempos por vuelta del primer piloto tienen una desviación estándar mayor que los tiempos por vuelta del segundo piloto?». (Significa que aunque los pilotos tuvieron el mismo tiempo medio por vuelta, el primer piloto mostró una mayor variabilidad en los tiempos por vuelta de las 50 vueltas. El primer conductor tiene tiempos de vuelta que fueron más lentos y más rápidos y menos agrupados cerca de la media que los tiempos de vuelta del segundo conductor).

• «En una clase, los estudiantes tenían una altura media de 68 pulgadas y una desviación estándar de 5 pulgadas. En una segunda clase, los estudiantes tenían una altura media de 67 pulgadas y una desviación estándar de 3.5 pulgadas. ¿Qué diferencias esperarías ver si observaras los gráficos de puntos que representan las distribuciones de datos para cada clase?». (Esperaría que los datos de la primera clase estuvieran más separados y centrados ligeramente a la derecha en comparación con el diagrama de puntos de la segunda clase. Yo esperaría que los valores de los datos de la segunda clase estuvieran más agrupados alrededor de 67 pulgadas que los puntos de la primera clase agrupados alrededor de 68 pulgadas).

ENFRIAMIENTO | ESPECIALIDADES Y SALARIOS

(5 minutos)

Una universidad analiaz los datos de sus graduados universitarios más recientes en función de su especialidad.

• El salario medio de 100 graduados universitarios recientes que se especializaron en ingeniería fue $63,750 con una desviación estándar de $10,020.

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

California . Algebra 1

• El salario medio de 100 recién licenciados en empresariales fue de $52,200 con una desviación típica de $19.400.

• El salario medio de 100 graduados universitarios recientes que se especializaron en ciencias sociales fue de $45.230 con una desviación estándar de $6.750

Relacione cada histograma con las especialidades según la descripción.

• Ingeniería

• Negocios

• Ciencias Sociales

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN

RESPUESTAS POSIBLES

1. Ciencias Sociales

2. Ingeniería

3. Negocios

Resumen de la lección para el estudiante

Cuanta más variación tenga una distribución, mayor será la desviación estándar. Una distribución más compacta tendrá una desviación estándar menor.

El primer diagrama de puntos muestra la cantidad de puntos que un jugador de un equipo de baloncesto hizo durante cada uno de los 15 partidos. El segundo diagrama de puntos muestra la cantidad de puntos anotados por otro jugador durante los mismos 15 partidos.

Puntos para el jugador uno

Puntos para el jugador dos

Los datos del primer diagrama tienen una media de aproximadamente 3.87 puntos y una desviación estándar de aproximadamente 2.33 puntos. Los datos del segundo diagrama tienen una media de aproximadamente 7.73 puntos y una desviación estándar de aproximadamente 4.67 puntos. La segunda distribución tiene mayor variabilidad que la primera porque los datos están más dispersos. Esto se muestra en que la desviación estándar de la segunda distribución es mayor que la desviación estándar de la primera distribución.

La desviación estándar se calcula utilizando la media, por lo que tiene sentido utilizarla como medida de variabilidad cuando es apropiado utilizar la media para la medida del centro. En los casos en los que la mediana es una medida de centro más apropiada, el rango intercuartílico sigue siendo una medida de variabilidad mejor que la desviación estándar.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Tres pilotos compitieron en las mismas quince carreras de aceleración. Se dan la media y la desviación estándar de los tiempos de carrera de cada uno de los pilotos.

El piloto A tuvo un tiempo medio de carrera de 4.01 segundos y una desviación típica de 0.05 segundos.

El piloto B tuvo un tiempo medio de carrera de 3.96 segundos y una desviación típica de 0.12 segundos.

El piloto C tuvo un tiempo medio de carrera de 3.99 segundos y una desviación estándar de 0.19 segundos.

A. ¿Qué piloto tuvo el tiempo típico de carrera más rápido?

B. ¿El tiempo de cuál de los pilotes fueron los de más valor?

C. ¿Qué piloto predices que ganará la próxima carrera de aceleración? Apoya tu predicción con la media y la desviación estándar.

PROBLEMA 2

Soluciones posibles

A. Piloto B

B. Piloto C

C. Ejemplo de respuesta: Predigo que el piloto C ganará. Aunque el tiempo medio de carrera del piloto C está entre los otros dos tiempos medios de carrera, el piloto C muestra más variabilidad. Esto significa que el conductor C a veces es relativamente lento, pero a veces es relativamente rápido. (Tenga en cuenta que también se podría predecir razonablemente que el conductor B ganaría, ya que tiene la media más pequeña y la desviación estándar de sus tiempos de carrera es menor que la del conductor C).

Se recogen las anchuras, en milímetros, de la tela producida en una fábrica de cintas. La media es aproximadamente 23 milímetros y la desviación típica es aproximadamente 0.06 milímetros.

Interpretar la media y la desviación estándar en el contexto del problema.

Soluciones posibles

Ejemplo de respuesta: El ancho de la tela es típicamente 23 milímetros. La desviación estándar de 0.06 milímetros significa que hubo muy poca variabilidad. La anchura de la mayor parte del tejido está entre 22.94 y 23.06 milímetros.

PROBLEMA 3

Seleccione todas las afirmaciones que sean verdaderas sobre la desviación típica.

Es una medida del centro.

Es una medida de variabilidad.

Es lo mismo que la DMA.

Se calcula a partir de la media.

Se calcula con la mediana.

PROBLEMA 4

(De la unidad 1, lección 9).

Se registrala cantidad de especies diferentes de plantas en algunos jardines.

1 2 3 4 4 5 5 6 7 8

A. ¿Cuál es la media?

B. ¿Cuál es la desviación estándar?

California . Algebra 1

Soluciones posibles

Es una medida del centro. Es una medida de variabilidad. Es lo mismo que la DMA.

Se calcula con la media.

Se calcula con la mediana.

Soluciones posibles

A. 4.5 especies

B. Aproximadamente 2.06 especies

Álgebra 1 . Matemáticas . Unidad 1

PROBLEMA 5

(De la unidad 1, lección 9).

Un conjunto de datos tiene diez números. La media de los datos es 12 y la desviación típica es 0. ¿Qué valores podrían componer un conjunto de datos con estos estadísticos?

Soluciones posibles

12, 12, 12, 12, 12, 12, 12, 12, 12, 12

PROBLEMA 6

(De la unidad 1, lección 8).

¿Qué gráfico de caja tiene el mayor rango intercuartílico?

Soluciones posibles

PROBLEMA 7

(De la unidad 1, lección 6)

A. ¿Cuál es el resumen de cinco números para 1, 3, 3, 3, 4, 8, 9, 10, 10, 17?

B. Cuando se elimina el máximo, 17, del conjunto de datos, ¿cuál es el resumen de cinco números?

Soluciones posibles

A. 1, 3, 6, 10, 17 (mínimo, Q1, mediana, Q3, máximo)

B. 1, 3, 4, 9.5, 10 (mínimo, Q1, mediana, Q3, máximo)

Reflexiones:

Math Nation California . Algebra 1

Álgebra 1 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

Construir

S-ID.1

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP4 Representar con las matemáticas.

Estándares ELD de California

I.A.3 I.C.11 II.A.2

LECCIÓN 11

VALORES ATÍPICOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

impactar el futuro, construirán argumentos viables y criticarán el razonamiento de otros analizan los datos.

OBJETIVO(S) DE APRENDIZAJE

• Puedo encontrar valores atípicos, investigar su origen y averiguar qué hacer con ellos.

• Puedo decir cómo afectará un valor atípico a la media, mediana, IQR o desviación estándar.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Describir (oralmente y por escrito) cómo afectan los valores atípicos a la medida del centro y a las medidas de variabilidad.

• Determinar (por escrito) cuándo se consideran valores atípicos, investigar su origen y determinar si deben excluirse de los datos.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Observar y preguntarse

Analízalo

MLR2: Recopilar y mostrar

MLR3: Aclarar, criticar, corregir

Pensar, girar y preguntar

Materiales requeridos

Estadístico-tecnológico

Preparación necesaria

Adquirir dispositivos que puedan ejecutar GeoGebra (recomendado) u otra hoja de cálculo y tecnología estadística. Lo ideal es que cada estudiante disponga de su propio dispositivo. (Una hoja de cálculo GeoGebra está disponible en la sección «Herramientas de matemáticas»).

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Investiguemos los valores atípicos y cómo tratarlos.

Narrativa de la lección

El propósito matemático de la lección es que los estudiantes reconozcan los valores atípicos, investiguen su origen, tomen decisiones acerca de excluirlos del conjunto de datos y comprendan cómo la presencia de valores atípicos afecta las medidas de centro y las medidas de variabilidad. Esta lección se basa en el trabajo de lecciones anteriores en las que los estudiantes encontraron medidas de centro y variabilidad. Esta lección se conecta con el trabajo futuro porque los estudiantes investigarán los valores atípicos al tratar con datos bivariados en otra unidad. Los estudiantes se encuentran con el término «valor atípico», que es un valor de datos que es inusual en el sentido de que difiere bastante de los otros valores en el conjunto de datos.

Cuando los estudiantes tienen que analizar los datos en el contexto de un problema para determinar si excluir o no un valor atípico, están razonando abstracta y cuantitativamente (MP2). Este proceso de razonamiento es también un aspecto de la representación matemática (MP4).

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento Independiente 10 min

Actividad de exploración En parejas 15 min

Actividad de exploración En parejas 10 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 10 min

Los estudiantes determinan un valor atípico en un conjunto de datos mostrado en un diagrama de cajas y un histograma y luego justifican el valor del valor atípico con base en la definición formal.

Los estudiantes utilizan la tecnología para calcular las medidas de centro y variabilidad con y sin el valor atípico. A continuación, razonan sobre cómo afecta el valor atípico a los diferentes estadísticos.

Los estudiantes identifican valores atípicos en conjuntos de datos y, a continuación, determinan si incluirlos o eliminarlos al analizar los datos.

Hay un extensión de exploración para desarrollar una comprensión más profunda de los valores atípicos que pueden producirse en la recopilación de datos y cómo abordarlos al resumir los datos.

Los estudiantes debaten los valores atípicos, cuándo incluirlos en los cálculos estadísticos de resumen y sus efectos en la distribución.

Los estudiantes determinan si un conjunto de datos tiene un valor atípico y cómo la alteración de los valores de los datos puede cambiar las medidas de centro y variabilidad.

El componente de práctica independiente incluye 4 problemas de repaso en clase y 4 problemas de repaso en espiral.

California . Algebra 1

CALENTAMIENTO | OBSERVAR Y PREGUNTARSE: DURACIÓN DE LA BATERÍA

(5 minutos)

Rutinas didácticas

Observar y preguntarse

El propósito de este calentamiento es provocar la idea de que los valores atípicos están a menudo presentes en los datos, lo que será útil cuando los estudiantes investiguen el origen de los valores atípicos y qué hacer con ellos en una actividad posterior.

A medida que los estudiantes trabajan, controle si

• estiman el IQR a partir de los valores del diagrama de cajas

• utilizan una herramienta de medición para determinar el IQR a partir del diagrama de cajas

Se dan a los estudiantes las fórmulas para valores atípicos: se considera que un valor es atípico para un conjunto de datos si es mayor que ��3 + 1.5 - �� o inferior a ��1 − 1,5 − ��. Para encontrar valores extremos, estamos comparando valores muy grandes o pequeños con el grueso de los datos. Esto significa utilizar los cuartiles y el rango intercuartílico para comparar el valor con las distancias típicas al centro de los datos.

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Muestra el histograma y el diagrama de cajas para que todos lo vean. Pida a los estudiantes que piensen en algo que les llame la atención y en algo que les sorprenda de las imágenes. Dé a los estudiantes 1 minuto para pensar en silencio y, a continuación, 1 minuto para comentar con su compañero las cosas que observan. Preste atención a los estudiantes que observen que hay un valor que parece muy diferente del resto de los datos. Seleccione a algunos estudiantes para que compartan las cosas que notan y se pregunten asegurándose de seleccionar al estudiante identificado que note un valor extremo.

El histograma y el diagrama de cajas muestra la cantidad media de dinero, en miles de dólares, gastada en cada persona del país (gasto per cápita) en atención sanitaria en 34 países.

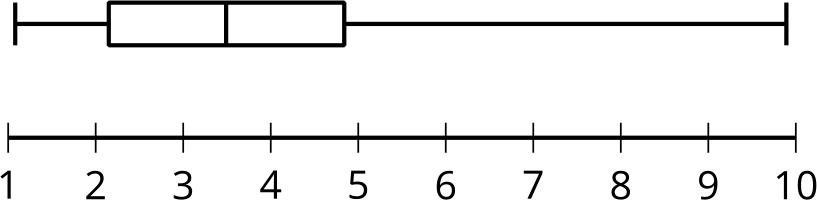
Gasto sanitario per cápita por país (miles de dólares)

1. Un valor del conjunto es un valor atípico. ¿Cuál es? ¿Cuál es su valor aproximado?

2. Según una regla para decidir, un valor es un valor atípico si es más de 1.5 veces el IQR mayor que ��3. Muestre en el diagrama de cajas si su valor cumple o no esta definición de valor atípico.

Álgebra 1 . Matemáticas . Unidad 1

RESPUESTAS POSIBLES

Ejemplos de respuestas:

1. El valor entre 9 y 10 miles de dólares es el valor atípico. 2.

Gasto sanitario per cápita por país (miles de dólares)

Seleccione a los estudiantes previamente identificados en el orden indicado en la narración de la lección para que compartan su método para crear esta visualización de valores atípicos en el diagrama de cajas.

Diga a los estudiantes:

• Los valores de un conjunto de datos que son muy diferentes del resto de los datos se denominan valores atípicos. El significado exacto de muy diferente será diferente para diferentes situaciones. Por ejemplo, una posible diferencia de $4,000 en este gráfico parece mucho, pero si los datos representaran la totalidad de los presupuestos de estos países en miles de millones o billones de dólares (en lugar del gasto en asistencia sanitaria de cada miembro de la población), no sería una gran diferencia.

• El uso de la IQR para determinar los valores atípicos ayuda a ajustar la diferencia a la variabilidad del grueso de los datos medios. Utilizar 1.5 veces el IQR permite considerar habitual cierta variabilidad en los extremos de la distribución.

SÍNTESIS DE LA ACTIVIDAD

• También es posible que haya valores inusualmente bajos en comparación con el resto del conjunto de datos. Considere este diagrama de cajas que muestra ��1 − 1.5 ∙ ��. El valor mínimo de este conjunto de datos debe considerarse un valor atípico.

• A efectos de esta unidad, un valor se considerará atípico para un conjunto de datos si es mayor que ��3 + 1,5 ∙ �� o menor que ��1−1,5 ∙ ��. Estas fórmulas comparan los valores extremos con la mitad central de los datos para determinar si el valor debe considerarse un valor atípico.

Cree una visualización para las fórmulas de valores atípicos de modo que se pueda hacer referencia a ellas durante el resto de la unidad.

ACTIVIDAD DE EXPLORACIÓN | INVESTIGAR VALORES ATÍPICOS

(15 minutos)

Rutinas didácticas

Analícelo

MLR2: Recopilar y mostrar

El propósito matemático de esta actividad es que los estudiantes investiguen el impacto de los valores atípicos en las medidas de centro y variabilidad, y que tomen decisiones sobre si incluir o no valores atípicos en un conjunto de datos.

California . Algebra 1

INTRODUCCIÓN

Organiza a los estudiantes en grupos de 2. Proporciona acceso a dispositivos que puedan ejecutar GeoGebra u otra tecnología estadística. Muestra los datos que muestran el gasto sanitario per cápita por país en 2016 para que todos los vean. Orienta a los estudiantes sobre los datos y explícales que la distribución de este conjunto de datos representa el histograma utilizado en el calentamiento. Asegúrese de que los estudiantes entienden lo que significa per capita. «Gasto sanitario per cápita» significa el gasto sanitario medio por persona. Por ejemplo, Estados Unidos gasta aproximadamente $9,892 en sanidad por cada persona de la población. Recuerde a los estudiantes que clasificaremos un valor de un conjunto de datos como atípico si es mayor que ��3 + 1,5 ∙ �� o menor que ��1 − 1,5 ∙ ��.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Divida esta tarea en partes más manejables para ayudar a los estudiantes que se benefician del apoyo con habilidades organizativas en la resolución de problemas. Por ejemplo, presente una pregunta cada vez.

Apoya la accesibilidad para: Organización; atención

Este es el conjunto de datos utilizado para crear el histograma y el diagrama de cajas del calentamiento.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

1. Utilice la tecnología para hallar la media, la desviación típica y el resumen de cinco números.

2. El valor máximo de este conjunto de datos representa el gasto de Estados Unidos. ¿Debería considerarse el gasto sanitario per cápita de Estados Unidos un valor atípico? Explique su razonamiento.

3. Aunque los valores atípicos no deben eliminarse sin tener en cuenta su causa, es importante ver lo influyentes que pueden ser los valores atípicos para diversas estadísticas. Elimine el valor de Estados Unidos del conjunto de datos.

A. Utilice la tecnología para calcular la nueva media, la desviación estándar y el resumen de cinco números.

B. ¿Cómo se comparan la media, la desviación estándar, la mediana y el rango intercuartílico del conjunto de datos con el valor atípico eliminado con los mismos estadísticos de resumen del conjunto de datos original?

1. Media: 3.7259, desviación típica: 1.827, mínimo: 1.0803, T1: 2.1495, mediana: 3.4904, T3: 4.8398, máximo: 9.8923

2. Sí, ya que 4.84 + 1.5 ∙ 2.69 = 8.875 y 9.89 > 8.875

POSIBLES RESPUESTAS

A. Media: 3.5391, desviación típica: 1.501, mínimo: 1.0803, T1: 2.1253, mediana: 3.3912, T3: 4.7963, máximo: 6.6475

B. La media disminuyó en 0.1868, la desviación estándar disminuyó en 0.326, la mediana disminuyó en 0.0992, y el IQR disminuyó en 0.0193 (el IQR antes de eliminar es 2.6903 y el IQR después de eliminar es 2.671).

CONCEPTOS ERRÓNEOS PREVISTOS

SÍNTESIS DE LA ACTIVIDAD

1 . Matemáticas . Unidad 1

Es posible que los estudiantes calculen incorrectamente la expresión para los valores atípicos. Recuérdeles que utilicen el orden correcto de las operaciones utilizando el calentamiento de la charla de matemáticas de una lección anterior.

El objetivo es asegurarse de que los estudiantes comprendan que los valores atípicos pueden afectar significativamente las medidas del centro y la variabilidad. Hable del impacto del valor atípico en la mediana, la media y la desviación típica y las respuestas de los estudiantes a «¿Crees que 9.8923 debería eliminarse del conjunto de datos?

¿Por qué sí o por qué no?».

Si el tiempo lo permite, haga preguntas como:

• «¿Qué medida del centro se ve más afectada por la inclusión de valores extremos, la media o la mediana? Explique su razonamiento». (La media, ya que utiliza el valor numérico real en lugar de la posición de los valores como hace la mediana).

• «¿Qué medida de variabilidad se ve más afectada por la inclusión de valores extremos, la desviación típica o el rango intercuartílico? Explica tu razonamiento». (La desviación típica, ya que utiliza tanto la media como el valor numérico de cada número del conjunto de datos, mientras que el IQR solo utiliza la posición de la mitad central de los datos).

Apoyo para estudiantes que aprenden el idioma inglés

Escuhar, hablar: MLR2 Recopilar y mostrar. Antes de la discusión de toda la clase, dé a los estudiantes la oportunidad de hablar con su compañero sobre el uso de herramientas estadísticas para calcular y mostrar estadísticas numéricas. Anote las frases comunes o importantes que oiga decir a los estudiantes sobre cada conjunto de datos, como media, mediana, valores atípicos o desviación típica. Escribe las palabras de los estudiantes en una representación visual de los conjuntos de datos de una y dos variables. Continúe ampliando esta presentación durante el resto de la lección. Esto ayudará a los estudiantes a leer y utilizar el lenguaje matemático durante sus discusiones por parejas y con toda la clase mientras toman decisiones sobre si incluir o no los valores atípicos en un conjunto de datos.

Principio(s) de diseño: Apoyar la creación de sentido

ACTIVIDAD DE EXPLORACIÓN | ORÍGENES DE LOS VALORES ATÍPICOS

(10 minutos)

Rutinas didácticas

MLR3: Aclarar, criticar, corregir

Pensar, girar y compartir

El propósito matemático de esta actividad es que los estudiantes reflexionen sobre el origen de los valores atípicos y sobre si es apropiado o no incluirlos al analizar los datos. Es importante subrayar que los datos no deben eliminarse simplemente porque sean atípicos. Si hay alguna duda sobre la razón del valor atípico, los datos deben incluirse en cualquier análisis realizado sobre el conjunto de datos.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Dé a los estudiantes tiempo para pensar tranquilamente y responder a la primera pregunta. Pida a sus compañeros que comparen las respuestas. Continúe con un debate con toda la clase. Pida a los compañeros que respondan y discutan las preguntas restantes.

Apoyo para estudiantes que aprendne el idioma inglés

Leer, escribir: MLR3 Aclarar, criticar, corregir. Presente un enunciado incorrecto o ambiguo para la primera pregunta sobre valores atípicos. Por ejemplo, presente la siguiente afirmación: «593 es un valor atípico ya que lo multipliqué por el IQR y lo encontré». Promueva el debate con la pregunta: «¿Cuáles fueron los pasos que siguió el autor?». Pida a los estudiantes que aclaren y corrijan el enunciado. Las afirmaciones mejoradas deben incluir algo de lo siguiente: explicación de cada paso, palabras de transición de orden/tiempo (primero, luego, entonces, etc.) y/o razones de las decisiones tomadas durante los pasos. Esto ayuda a los estudiantes a evaluar y mejorar los argumentos matemáticos escritos de los demás.

Principio(s) de diseño: Maximizar la metaconciencia

Apoyo para estudiantes con discapacidad

Representación: Interiorizar la comprensión. Activar o aportar conocimientos previos. Permita que los estudiantes utilicen calculadoras para garantizar una participación inclusiva en la actividad.

Apoya la accesibilidad para: Memoria; procesamiento conceptual

1. La cantidad de denuncias de delitos contra la propiedad (como robos) se recoge en 50 colegios de California. Se ofrecen algunas estadísticas resumidas:

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

• 15191.1 informa

• Mínimo: 15 informa

• Q1: 52 informa

• Mediana: 107.5 informes

• Q3: 260 informes

• Máximo: 768 informes

A. ¿Es alguno de los valores atípico? Explica o muestra tu razonamiento.

B. Si hay valores atípicos, ¿por qué crees que pueden existir? ¿Deberían incluirse en un análisis de los datos?

2. Cada una de las situaciones descritas aquí tiene un valor atípico. Para cada situación, ¿cómo determinarías si es apropiado mantener o eliminar el valor atípico al analizar los datos? Habla de tu razonamiento con tu compañero.

A. Un cubo numérico tiene caras etiquetadas como 1-6. Después de lanzar 15 veces, Tyler registra sus datos:

1, 1, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 20

B. El diagrama de puntos representa la distribución de la cantidad de hermanos declarado por un grupo de 20 personas.

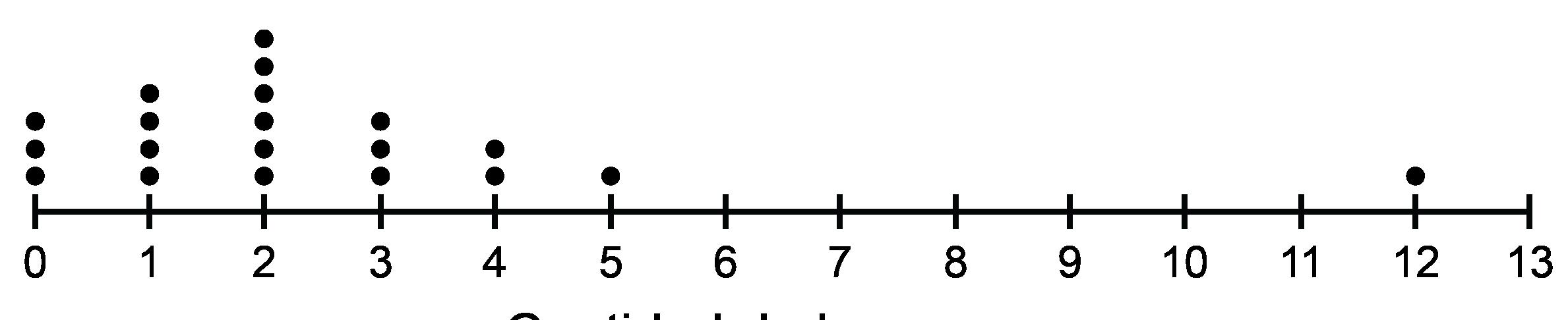
ENUNCIADO DE TAREA PARA EL ESTUDIANTEE CONTINUACIÓN

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Álgebra 1 . Matemáticas . Unidad 1

C. En una clase de Ciencias, 11 grupos de estudiantes están sintetizando biodiésel. Al final del experimento, cada grupo anota la masa en gramos del biodiésel que ha sintetizado. Las masas de biodiésel son: 0, 1.245, 1.292, 1.375, 1.383, 1.412, 1.435, 1.471, 1.482, 1.501, 1.532

Ejemplos de respuesta:

California . Algebra 1

A. Los valores 593, 699 y 768 son valores atípicos, ya que cada uno de estos valores es mayor que 572 (��3 + 1.5 ∙ �� = 206 + 1,5 ∙ 208 que es 572)

B. En California hay pocas universidades grandes y muchas pequeñas. Los datos deben incluirse en un análisis, ya que no se trata de un error de registro o recogida de información.

A. El valor atípico, 20, debe eliminarse porque no es un valor plausible. Es decir, un cubo numérico no puede hacer rodar el número 20.

B. El valor atípico, 12 hermanos, debe investigarse más a fondo para ver si se trata de un error de recogida de datos antes de eliminarlo. Aunque no es habitual que alguien tenga 12 hermanos, sigue siendo posible. Si no se trata de un error o si no puede determinarse, debe conservarse para cualquier análisis posterior.

C. El valor atípico, 0 gramos, debe investigarse más a fondo para ver si el experimento se hizo correctamente o si hubo un error al seguir las instrucciones o los materiales utilizados. Si el experimento se hizo correctamente, los datos deben conservarse, pero si hay un error al seguir las instrucciones o en los materiales utilizados, el 0 podría excluirse.

El propósito de esta discusión es destacar diferentes razones por las que aparecen valores atípicos en los datos. Por ejemplo, podrían ser errores de introducción o recogida de datos, o podrían ser representativos de la muestra. El objetivo es que los estudiantes comprendan que la inclusión de valores atípicos en un conjunto de datos debe evaluarse en el contexto de los datos. En el caso de las tiradas del cubo de números, está claro que los datos no deben utilizarse, ya que es imposible conseguirlo en las circunstancias adecuadas. Para los otros dos escenarios, los estudiantes deben comprender que debe realizarse una investigación más profunda para determinar si el valor atípico debe incluirse y ser capaces de exponer las circunstancias para incluir o excluir el valor atípico en cada contexto.

He aquí algunas preguntas para el debate:

• «¿Por qué es importante analizar el origen de los valores atípicos?». (Para determinar si hay alguna razón para excluir los datos de un análisis).

• «¿Cuáles son las razones para mantener un valor atípico en un conjunto de datos?». (El hecho de que un valor sea extremadamente grande o pequeño no descarta su realidad. Para ser honestos en el análisis, deben incluirse todos los datos válidos).

• «¿Cuáles son las razones para eliminar un valor atípico de un conjunto de datos?». (Si hay un error en la recogida o registro de datos, los datos pueden ser defectuosos y no sería honesto incluir datos que no se ajustan a la pregunta formulada).

• «¿Qué se podría hacer con respecto a los valores atípicos de 3 para los datos de delincuencia universitaria para tener en cuenta el tamaño de la escuela como fuente de los valores atípicos?». (La pregunta podría cambiarse para examinar la delincuencia en las escuelas con una matrícula inferior a cierto nivel. Podría tener más sentido examinar la «tasa de delincuencia» como una medida de delitos por 100 estudiantes o algo similar que tenga en cuenta el tamaño de la escuela en lugar de solo el número de delitos).

• «¿Cómo sabe que un valor es un valor atípico?». (Si es mayor que el tercer cuartil en más de una vez y media el rango intercuartílico o menor que el primer cuartil en la misma cantidad).

1 . Matemáticas . Unidad 1

¿Estás preparado para más?

Repasa algunos de los datos numéricos que tú y tus compañeros recogisteis en la primera lección de esta unidad.

1. ¿Es alguno de los valores atípico? Explica o muestra tu razonamiento.

2. Si hay valores atípicos, ¿por qué crees que pueden existir? ¿Deberían incluirse en un análisis de los datos?

Posibles respuestas

Las respuestas varían.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

El propósito de esta discusión es asegurarse de que los estudiantes sepan qué son los valores atípicos, qué hacer con ellos y cómo afectan a las medidas del centro y a las medidas de variabilidad. He aquí algunas preguntas para la discusión:

• «¿Qué es un valor atípico?». (Un valor de datos que difiere de los demás valores del conjunto de datos. Puede definirse en términos de IQR y cuartiles. Si un valor de datos es 1.5 veces el IQR mayor que el 3.er cuartil o 1.5 veces el IQR menor que el 1.er cuartil, entonces se considera un valor atípico).

• «¿Por qué es importante observar los valores atípicos en un conjunto de datos?». (Pueden indicar un error en el proceso de recopilar datos o un caso interesante para estudiarlo más de cerca. No siempre son representativos de toda la muestra. Su presencia puede afectar desproporcionadamente a los valores de la media, la DMA y la desviación estándar).

• «¿Cómo afectan los valores atípicos a las medidas del centro?». (Los valores atípicos pueden hacer que la media sea mucho más alta o más baja de lo que parece ser estándar dependiendo de si el valor atípico es mucho mayor o mucho menor que la media. Tienen menos efecto sobre la mediana).

• «¿Cómo afectan los valores atípicos a las medidas de variabilidad». (Hacen que la variabilidad sea mayor de lo que sería si los valores atípicos no estuvieran presentes).

• «¿Por qué eliminarías un valor atípico?». (Se eliminarían si son un error o si no son representativos del conjunto de la muestra. Depende del contexto del problema y del proceso de recopilar datos).

ENFRIAMIENTO | ESPERAR VALORES ATÍPICOS

(5 minutos)

Se pide a un grupo de 20 estudiantes que informen de la cantidad de animales domésticos que tienen en su casa. Los resultados son: 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 4, 21

• Media: 2.4 mascotas

• Desviación estándar: 4.47 mascotas

• Q1: 0.5 mascotas

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

• Mediana: 1 mascotas

• Q3: 2.5 mascotas

1. ¿Se consideraría alguno de estos valores atípico? Explique su razonamiento.

2. Después de decirles que no deben contar ningún pez en el informe, el valor de 3 se convierte en 2 y el valor de 21 se convierte en 1. ¿Afectarían estos cambios a la mediana, la media, la desviación estándar o el rango intercuartílico? En caso afirmativo, ¿disminuiría o aumentaría cada medida con respecto a sus valores originales?

1. Sí, 21 mascotas es un valor atípico, ya que es mayor que .,5 = 2,5 + 1,5 ∙ 2

2. La media y la desviación estándar disminuirían con los cambios. La mediana se mantendría igual y el IQR disminuiría ligeramente.

Álgebra 1 . Matemáticas . Unidad 1

Resumen de la lección del estudiante

En estadística, un valor atípico es un valor de datos que es inusual en el sentido de que difiere bastante de los demás valores del conjunto de datos.

Los valores atípicos se producen en los conjuntos de datos por diversas razones, entre las que se incluyen:

• errores en los datos derivados de la recopilación de datos o del proceso de introducción de datos

• resultados en los datos que representan valores inusuales que se producen en la población

Los valores atípicos pueden revelar casos que merece la pena estudiar en detalle o errores en el proceso de recopilación de datos. En general, deben incluirse en cualquier análisis realizado con los datos.

Un valor es un valor atípico si es

• más de 1.5 veces el rango intercuartílico mayor que Q3 (si �� > Q3 + 1,5 ⋅ IQR)

• más de 15 veces el rango intercuartílico menor que Q1 (si �� < Q1 - 1.5 ⋅ IQR)

En este diagrama de cajas, el mínimo y el máximo son al menos dos valores atípicos.

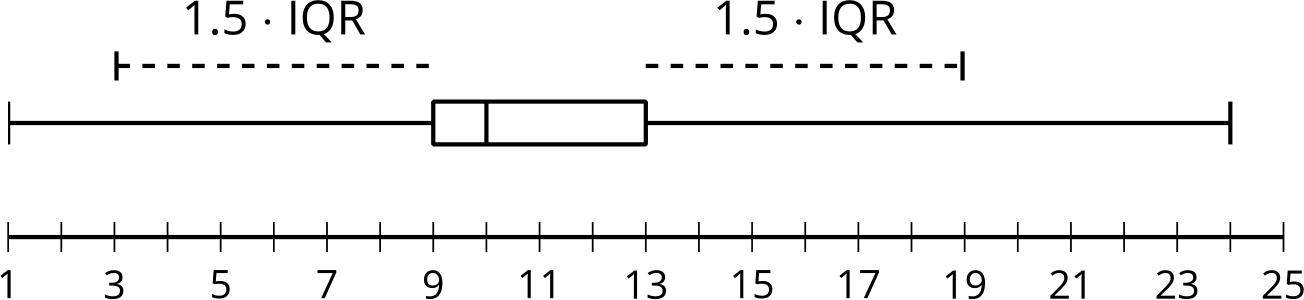
Es importante identificar el origen de los valores atípicos, ya que pueden afectar a las medidas de centro y variabilidad de forma significativa. El diagrama de cajas muestra la frecuencia cardiaca en reposo, en pulsaciones por minuto (ppm), de 50 atletas tomadas cinco minutos después de un entrenamiento.

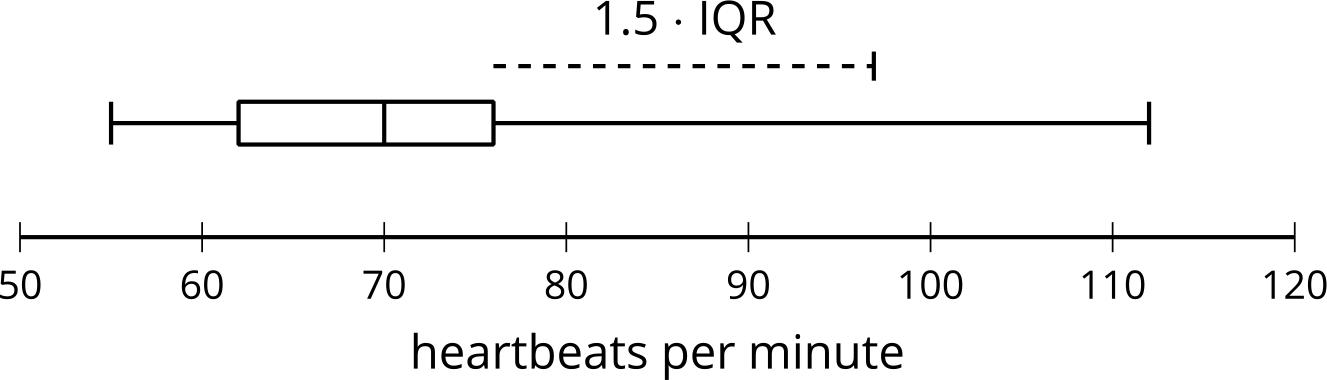
Algunas estadísticas de resumen incluyen:

• Media: 69.78 bpm

• Desviación estándar: 10.71 ppm

• Mínimo: 55pbpm

• Q1: 62 ppm

• Mediana: 70 ppm

• Q3: 76 ppm

• Máximo: 112pbpm

Parece que el valor máximo de 112 ppm puede ser un valor atípico. Dado que el rango intercuartílico es 14 ppm (76 − 62 = 14) y Q3 + 1.5 ⋅ IQR = 97, deberíamos etiquetar el valor máximo como valor atípico. Buscando en el conjunto de datos reales, se puede confirmar que este es el único valor atípico.

Después de revisar el proceso de recogida de datos, se descubre que el atleta con la medición de la frecuencia cardíaca de 112 ppm se tomó un minuto después de un entrenamiento en lugar de cinco minutos después. El valor atípico debe eliminarse del conjunto de datos porque no se obtuvo en las condiciones adecuadas.

Una vez eliminado el valor atípico, el diagrama de cajas y los estadísticos de resumen son:

• Media: 68.92 ppm

• Desviación estándar: 8.9 bpm

• Mínimo: 55 bpm

• Q1: 61 ppm

• Mediana: 70 ppm

• Q3: 75.5 ppm

• Máximo: 85 ppm

La media disminuyó en 0.86 ppm y la mediana se mantuvo igual. La desviación estándar disminuyó en 1.81 ppm, lo que supone aproximadamente 17 % de su valor anterior. Según la desviación estándar, el conjunto de datos con el valor atípico eliminado muestra mucha menos variabilidad que el conjunto de datos original que contiene el valor atípico. Dado que la media y la desviación estándar utilizan todos los valores numéricos, la eliminación de un punto de datos muy grande puede afectar a estas estadísticas de forma importante.

Math Nation California . Algebra 1

1 . Matemáticas . Unidad 1

La mediana se mantuvo igual tras la eliminación del valor atípico y el IQR aumentó ligeramente. Estas medidas de centro y variabilidad son mucho más resistentes al cambio que la media y la desviación típica. La mediana y el IQR miden el centro de los datos basándose en el número de valores y no en los propios valores numéricos reales, por lo que la pérdida de un único valor no suele tener un gran efecto en estas estadísticas.

Siempre debe investigarse el origen de cualquier posible error. Si se comprueba que la medición de 112 pulsaciones por minuto se realizó en las condiciones correctas y solo incluía a un atleta cuya frecuencia cardiaca no disminuyó tanto como la de los demás atletas, no deberá eliminarse para que los datos reflejen las mediciones reales. Si la situación no puede revisarse para determinar el origen del valor atípico, no debe eliminarse. Para evitar la manipulación de los datos e informar de resultados precisos, los valores de los datos no deben eliminarse a menos que pueda confirmarse que se trata de un error en el proceso de recogida o introducción de datos.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Se registra la cnatidad de cartas recibidas por correo durante la semana pasada.

2 3 5 5 5 15

¿Qué valor parece ser un valor atípico?

A. 2

B. 3

C. 5

D. 15

PROBLEMA 2

Elena recoge 112 especímenes de escarabajo y registra sus longitudes para un proyecto de investigación sobre ecología. Cuando vuelve al laboratorio, Elena descubre que registró incorrectamente una de las longitudes de los escarabajos como 122 centímetros (unos 4 pies). ¿Qué debe hacer con el valor atípico, 122 centímetros, cuando analice sus datos?

PROBLEMA 3

Soluciones posibles

Ejemplo de respuesta: Elena debe volver a los 112 especímenes y medirlos de nuevo para encontrar el error. Si no puede hacerlo, debe eliminar el valor atípico de su análisis, ya que se trata de un error de registro.

Mai realizó una encuesta entre los estudiantes de su clase para averiguar cuántas horas dedican a la lectura cada semana. He aquí algunas estadísticas resumidas de los datos que Mai recopiló:

Media: 8.5 horas

Desviación estándar: 5.3 horas

Mediana: 7 horas Q1: 5 horas Q3: 11 horas

A. Pon un ejemplo de un número de horas superior a la mediana que sería un valor atípico. Explica tu razonamiento.

B. ¿Hay valores atípicos por debajo de la mediana? Explique tu razonamiento.

Soluciones posibles

A. Ejemplo de respuesta: 22 horas, ya que Q3 junto con una vez y media el rango intercuartílico es 20

B. No, porque los valores atípicos por debajo de la mediana deben ser menores que −4(5 − 1.5 ∙ (11 − 5) = −4) y no es posible leer para un número negativo de horas.

1 . Matemáticas . Unidad 1

PROBLEMA 4

El diagrama de cajas muestra las estadísticas para el peso, en libras, de algunos perros.

¿Hay algún valor atípico? Explica cómo lo sabes.

PROBLEMA 5

(De la Unidad 1, Lección 10).

La nota media del examen para el primer grupo de veinte examinandos que solicitan un puesto de seguridad es 35.3 con una desviación típica de 3.6

La puntuación media del segundo grupo de veinte examinandos es 34.1 con una desviación típica de 0.5. Ambas distribuciones tienen una forma casi simétrica.

Utilice la media y la desviación típica para comparar las puntuaciones de los dos grupos.

La puntuación mínima necesaria para conseguir una entrevista en persona es de 33. ¿Qué grupo cree que tiene más personas que consiguen entrevistas en persona?

PROBLEMA 6

(De la unidad 1, lección 10).

Se pesa un grupo de peniques fabricados en 2018. La media es aproximadamente 2.5 gramos con una desviación estándar de 0.02 gramos. Interpreta la media y la desviación típica en función del contexto.

PROBLEMA 7

(De la unidad 1, lección 9).

Estos valores representan el número esperado de pinturas que una persona producirá durante los próximos 10 días.

0, 0, 0, 1, 1, 1, 2, 2, 3, 5

A. ¿Cuál es la media y la desviación estándar de los datos?

B. El artista no está satisfecho con estas estadísticas. Si 5 se aumenta a un valor mayor, ¿cómo afecta esto a la mediana, la media y la desviación estándar?

Soluciones posibles

Sí, hay al menos un valor atípico que es demasiado alto. El perro que pesa alrededor de 95 libras es un valor atípico. El IQR es de aproximadamente 20 y 1.5 ∙ 20 = 30. El perro que pesa unas 95 libras está unas 40 libras por encima del tercer cuartil.

Soluciones posibles

Ejemplo de respuesta: El primer grupo obtuvo una puntuación media más alta con base en la media, pero mostró una variabilidad mucho mayor que el segundo grupo, porque el primer grupo tuvo una desviación estándar más alta.

Respuesta de muestra: Creo que más personas del segundo grupo consiguen entrevistas en persona. La puntuación mínima es 33 y tienen una media de 34.1 con una desviación típica de 0.5, por lo que la mayor parte de sus puntuaciones tuvieron que ser superiores a 33. De lo contrario, habrían tenido una desviación típica superior a 1.1

Soluciones posibles

La media de los peniques pesa 2.5 gramos. Hay un poco de variación en los pesos, pero la mayoría de los peniques pesan muy cerca de 2.5, dentro de 0.02 gramos de media según la desviación estándar.

Soluciones posibles

A. Tanto la media como la desviación estándar son 1.5 pinturas.

B. La mediana seguirá siendo 1 pintura. La media aumentará y también la desviación estándar, porque los datos están más dispersos.

1 . Matemáticas . Unidad 1

PROBLEMA 8

(De la unidad 1, lección 8).

Enumera los cuatro gráficos de puntos en orden de variabilidad de menor a mayor.

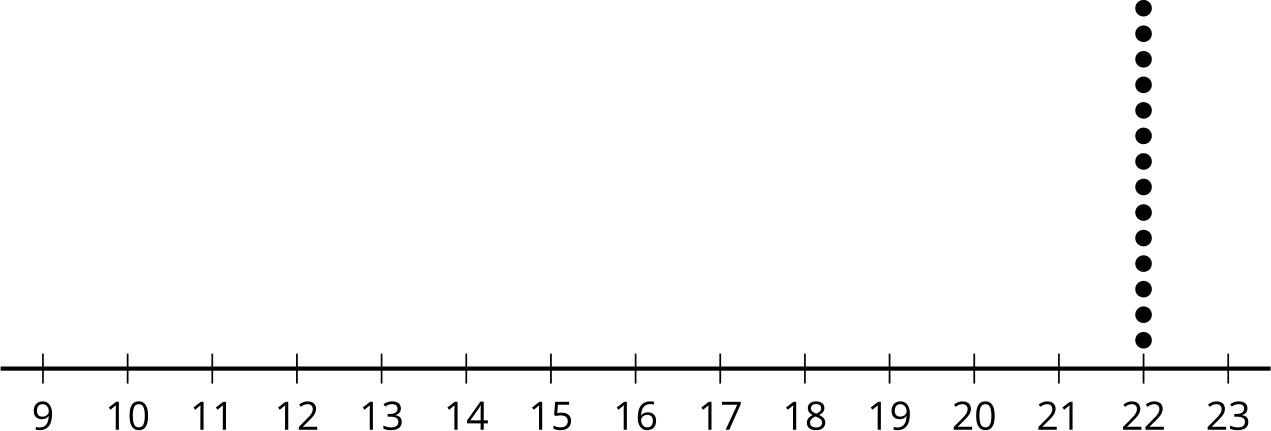
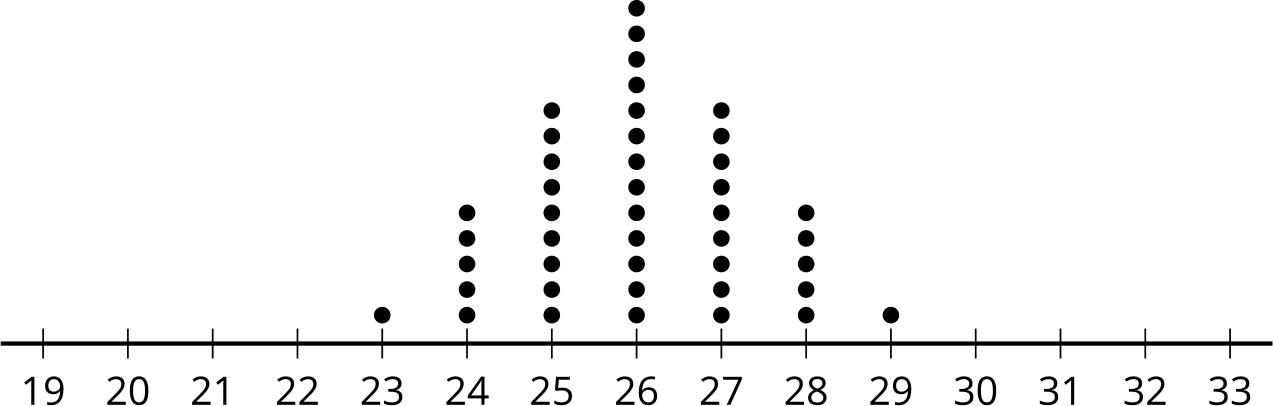
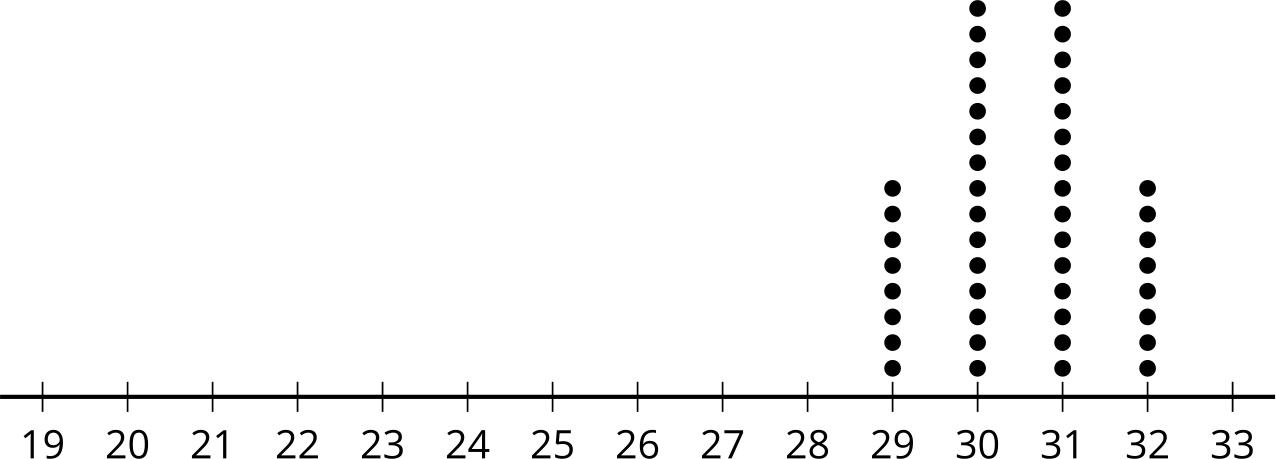
Soluciones posibles

b, d, c, a

Reflexiones:

California . Algebra 1

Math Nation

Math Nation California . Algebra 1

Álgebra 1 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES

• Investigar datos

ALINEACIÓN

Abordar

Alineación de estándares y principios de California

S-ID.1 Representar datos con gráficas en la recta numérica real (diagramas de puntos, histogramas y diagramas de cajas).

Enfoque SMPs

MP2 Razonar abstracta y cuantitativamente.

MP3 Construir argumentos viables y criticar el razonamiento de otros.

MP6 Atender a la precisión.

Estándares ELD de California

I.A.3

I.A.4

II.C.7

LECCIÓN 12 COMPARACIÓN DE CONJUNTOS DE DATOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para...

(SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras...

predicer lo que podría ocurrir e impactar el futuro atenderán con precisión

OBJETIVO(S) DE APRENDIZAJE

analizan los datos y descubren la forma y el espacio.

• Puedo comparar y contrastar situaciones con medidas de centro y medidas de variabilidad.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Comparar y contrastar (oralmente y por escrito) situaciones con medidas de centro y medidas de variabilidad.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Anticipar, supervisar, seleccionar, secuenciar, conectar

MLR5: Preguntas de elaboración conjunta

Turnarse

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Comparemos estadísticas para conjuntos de datos.

Narrativa de la lección

El propósito matemático de esta lección es que los estudiantes comparen las medidas del centro y la desviación estándar y el IQR para diferentes conjuntos de datos. Esta lección proporciona oportunidades para que los estudiantes colaboren, compartan ideas matemáticas y reflexionen sobre su pensamiento matemático acerca de las medidas de centro y las medidas de variabilidad. Esta lección también ofrece a los estudiantes otra oportunidad para comparar medidas de centro y variabilidad, pero ahora utilizando también la desviación estándar y los valores atípicos en las comparaciones. El trabajo de esta lección se conecta con el próximo trabajo porque los estudiantes recogerán y analizarán datos para responder a una pregunta estadística utilizando medidas de centro y medidas de variabilidad. Cuando los estudiantes describen las medidas de centro y las medidas de variabilidad en el contexto del tiempo del maratón razonan abstracta y cuantitativamente (MP2) porque interpretan el significado de su respuesta en el contexto.

RESUMEN DE LA LECCIÓN

Componente de la lección Estructura Tiempo Descripción breve

Calentamiento Grupos pequeños 10 min

Actividad de Exploración Independiente 10 min

Actividad de Exploración En pareja 15 min

Síntesis Todo el grupo 5 min

Enfriamiento Independiente 5 min

Práctica Independiente 10 min

California . AAlgebra 1

Los estudiantes usan histogramas y sus estadísticas resumidas para explicar su razonamiento al seleccionar conjuntos de datos específicos.

Los estudiantes comparan dos conjuntos de datos con medidas de centro, variabilidad y formas de las distribuciones .

Hay una extensión de exploración está disponible para desarrollar una comprensión más profunda del análisis y comparación de conjuntos de datos.

Los estudiantes comparan formas, rangos intercuartílicos (IQR), medidas de centro y desviaciones estándar entre conjuntos de datos mostrados en varias representaciones.

Los estudiantes debaten estrategias que pueden utilizar para comparar las formas, medidas de centro y medidas de variabilidad de múltiples conjuntos de datos.

Los estudiantes comparan dos distribuciones con histogramas y resúmenes estadísticos para responder preguntas sobre el contexto del mundo real.

El componente de práctica independiente incluye 4 problemas de repaso de la lección y 4 problemas de repaso en espiral.

CALENTAMIENTO | COMPAÑEROS DE BOLOS (10 minutos)

El propósito matemático de esta actividad es que los estudiantes comparen diferentes distribuciones con la forma, medidas de centro y medidas de variabilidad. Este calentamiento pide a los estudiantes que comparen cuatro distribuciones que representan puntuaciones recientes de bolos de posibles compañeros de equipo. Proporciona a los estudiantes una razón para utilizar el lenguaje con precisión (MP6) y le da a usted la oportunidad de escuchar cómo utilizan la terminología y hablan sobre las características de las imágenes en comparación con las demás.

INTRODUCCIÓN Organice a los estudiantes en grupos de 2-4

Cada histograma muestra las puntuaciones de bolos de las últimas 25 partidas jugadas por cada persona. Elige 2 de estas personas para formar parte de tu equipo de bolos. Explica tu razonamiento.

Persona A

• Media: 118.96

• Mediana: 111

• Desviación estándar: 32.96

• Rango intercuartílico: 44

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Persona B

• Media: 131.08

• Mediana: 129

• Desviación estándar: 8.64

• Rango intercuartílico: 8

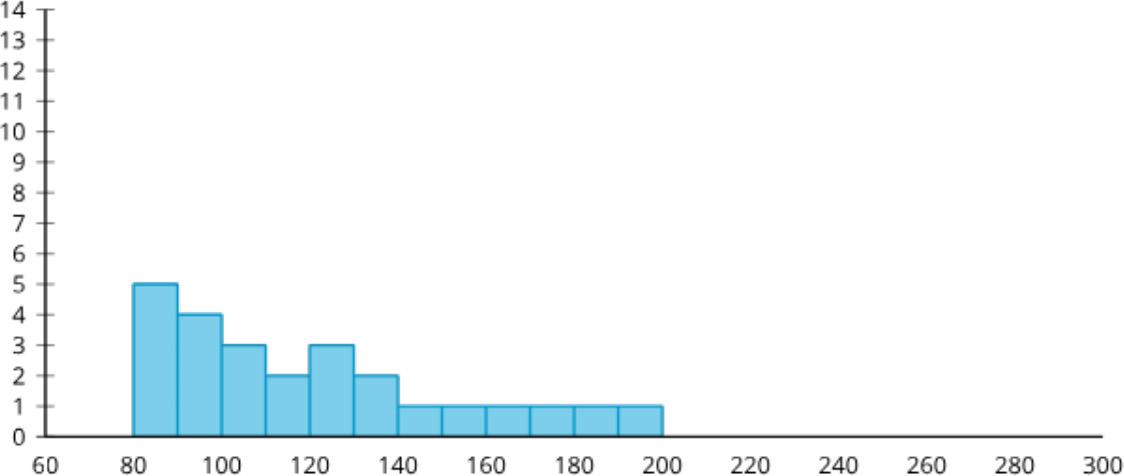
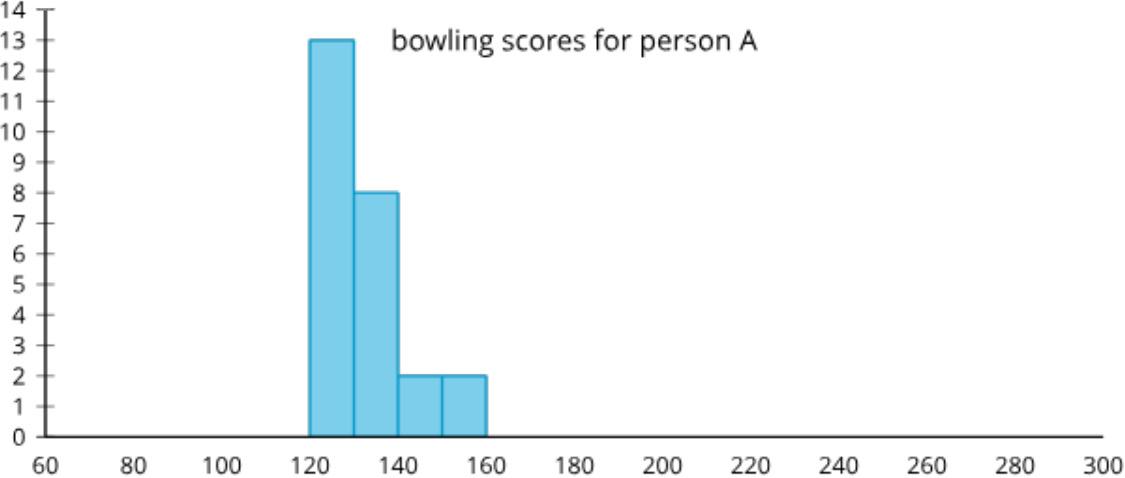
Persona C

• Media: 133.92

• Mediana: 145

• Desviación estándar: 45.04

• Rango intercuartílico: 74

Persona D

• Media: 116.56

• Mediana: 103

• Desviación estándar: 56.22

• Rango intercuartílico: 31.5

Razones para cada jugador de bolos:

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Álgebra 1 . Matemáticas . Unidad 1

1. Aunque la persona A tiene una puntuación media baja, la gran variabilidad significa que esta persona puede puntuar bien a veces. Las puntuaciones de esta persona están repartidas y no es raro que esta persona anote por encima de 140

2. La persona B es muy consistente. Aunque esta persona no tiene grandes partidas como los otros jugadores, su puntuación media está cerca de la cima y obtendrá de forma fiable una puntuación entre 120 y 160

3. La persona C tiene una puntuación media alta, pero también es muy variable. Ha obtenido la puntuación más baja del grupo, pero tiene la mediana más alta. Creo que podríamos entrenar a esta persona para que sea más consistente, así que este comodín podría estar en mi equipo.

4. La persona D tiene la media más baja, pero también es capaz de hacer una partida casi perfecta (dos veces). Esta persona tuvo dos juegos que fueron mucho mejores que los de cualquier otra persona de la lista, así que tal vez lo haga bien cuando cuenta.

Pida a cada grupo que comparta un jugador de bolos que elegiría y su razonamiento. Si ninguno de los grupos selecciona a un determinado jugador, pregunte por qué no se eligió a este jugador o que den razones por las que otro equipo podría querer a este jugador en su equipo. Dado que no hay una única respuesta correcta a la pregunta de cuál no pertenece, atiende a las explicaciones de los estudiantes y asegúrate de que las razones dadas son correctas. Durante el debate, pida a los estudiantes que expliquen cómo han utilizado las estadísticas dadas, así como los histogramas.

ACTIVIDAD DE EXPLORACIÓN | COMPARAR DE TIEMPOS DE MARATÓN

(10 minutos)

Rutinas didácticas

Anticipar, supervisar, seleccionar, secuenciar, conectar

MLR5: Preguntas de elaboración conjunta

El propósito matemático de esta actividad es que los estudiantes comparen medidas de centro y medidas de variabilidad en contexto. Supervise a los estudiantes que:

1. determinen el grupo de edad más lento utilizando una descripción informal del cambio en los datos

2. determinen el grupo de edad más lento utilizando una estimación numérica para la media o la mediana para las medidas del centro

3. determinen la variabilidad a partir del rango de valores

4. utilicen una estimación numérica para el IQR o la desviación estándar como medidas de variabilidad

Apoyo para estudiantes que aprenden el idioma inglés

Conversar: MLR5 Preguntas de elaboración conjunta. Muestre solo la primera línea de esta tarea (Todos los corredores de maratón de cada uno de los dos grupos de edad diferentes tienen sus tiempos finales representados en el diagrama de puntos) y los dos diagramas de puntos, e invite a los estudiantes a escribir en parejas posibles preguntas matemáticas sobre la situación. A continuación, invite a las parejas a compartir sus preguntas con la clase. Esto ayuda a los estudiantes a producir el lenguaje de las preguntas matemáticas y a hablar sobre las relaciones entre los dos conjuntos de datos de esta tarea, las medidas del centro y las medidas de variabilidad, antes de que se les pida que analicen el razonamiento de otro.

Principio(s) de diseño: Cultivar la conversación

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

Todos los corredores de maratón de cada uno de los dos grupos de edad diferentes tienen sus tiempos de llegada a meta representados en el diagrama de puntos.

1. ¿Qué grupo de edad tiende a tardar más en correr el maratón? Explica tu razonamiento.

2. ¿Qué grupo de edad tiene tiempos finales más variables? Explica tu razonamiento.

Ejemplos de respuestas:

1. Los corredores de edades entre 40-49 son más lentos porque tienen una mediana mayor. El centro de los datos está más a la derecha en esta distribución.

2. Los corredores entre 40-49 tienen tiempos más variables porque estos datos están más dispersos a lo largo de la recta numérica que los datos del diagrama de puntos para las edades de 30-39. Tienen un IQR mayor porque la mitad central de los datos parece más dispersa.

El propósito de esta discusión es que los estudiantes comprendan cómo comparar conjuntos de datos con medidas de centro y medidas de variabilidad. Seleccione a los estudiantes para que compartan sus respuestas y razonamientos en una secuencia que vaya de razonamientos menos formales a valores y estadísticas más definidos.

Después de que se mencionen varias estimaciones para la medida del centro y la medida de variación, muestre los valores reales para estos conjuntos de datos.

Edades 30-39

• Media: 294.5 minutos

SÍNTESIS DE LA ACTIVIDAD

• Desviación estándar: 41.84 minutos

• Mediana: 288,5 minutos

• IQR: 65 minutos

• Q1: 260 minutos

• Q3: 325 minutos

Edades 40-49

• Media: 340.6 minutos

• Desviación estándar: 59.93 minutos

• Mediana: 332 minutos

• IQR: 92 minutos

• Q1: 289 minutos

• Q3: 381 minutos

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

Álgebra 1 . Matemáticas . Unidad 1

Haga las siguientes preguntas a los estudiantes:

• «¿Qué medida de centro y qué medida de variabilidad son las más apropiadas para utilizar con las distribuciones? Explica tu razonamiento». (La mediana es la más apropiada porque está más cerca de donde se encuentra la mayoría de los datos. Como he utilizado la mediana como medida del centro, he utilizado la IQR como medida de la variabilidad).

• «¿Qué puntos muestran valores que tienen más probabilidades de ser valores atípicos?». (Los corredores más lentos de cada grupo, en el extremo derecho del diagrama de puntos, podrían ser valores atípicos).

• «Según la información mostrada, ¿hay valores atípicos en estos conjuntos de datos?». (No. Para el grupo de edad 30-39, los valores atípicos deberían ser superiores a 422.5 minutos, pero los tiempos más lentos se sitúan en torno a 380 minutos. Para el grupo de edad 40-49, los valores atípicos tendrían que ser mayores que 534 minutos, pero los tiempos más largos están alrededor de 450 minutos).

¿Estás listo para más?

1. ¿Cómo crees que se compararán los tiempos de llegada a meta para un rango de edad de 20-29 estas dos distribuciones?

2. Encuentra algunos tiempos reales de llegada a meta en maratón para este grupo y haz un diagrama de cajas de tus datos para ayudar a comparar.

Respuestas posibles

Las respuestas varían.

ACTIVIDAD DE EXPLORACIÓN | COMPARAR MEDIDAS

(15 minutos)

Rutinas didácticas

Tomar turnos

En esta actividad, los estudiantes se turnan con un compañero para determinar la mejor medida del centro y la mejor medida de variabilidad para varios conjuntos de datos. Los estudiantes intercambian papeles, explican su pensamiento y escuchan, lo que les da la oportunidad de explicar su razonamiento y criticar el de los demás (MP3). Los estudiantes también determinan qué conjunto de datos tiene una mayor medida de centro y cuál tiene una mayor medida de variabilidad.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Diga a los estudiantes que para cada visualización de datos o descripción de un conjunto de datos en la columna A, un compañero determina la medida apropiada del centro y la medida de variabilidad y explica por qué piensa que es apropiada. El trabajo del compañero es escuchar y asegurarse de que están de acuerdo. Si no están de acuerdo, los compañeros debaten hasta llegar a un acuerdo. Para la siguiente presentación de datos o descripción de un conjunto de datos de la columna B, los estudiantes intercambian los papeles. Si es necesario, demuestre este protocolo antes de que los estudiantes empiecen a trabajar. El último elemento tiene una columna C. Los estudiantes pueden trabajar juntos para determinar las mejores medidas para el conjunto C. Una vez alcanzado un acuerdo para cada grupo de conjuntos de datos, los estudiantes determinarán qué conjunto de datos tiene la mayor medida de centro y qué conjunto de datos tiene la mayor medida de variabilidad.

Álgebra 1 . Matemáticas . Unidad 1

Apoyo para estudiantes con discapacidad

Participación: Interiorizar la autorregulación. Demostrar dar y recibir retroalimentación constructiva. Utilizar un proceso estructurado y mostrar fragmentos de oraciones para apoyar la retroalimentación productiva. Por ejemplo: «Esa medida del centro podría/no podría ser cierta porque...» o «Con base en la forma de la distribución, una mejor elección sería porque...».

Apoya la accesibilidad para: Habilidades socioemocionales; organización; lenguaje

Para cada grupo de conjuntos de datos,

• Determina la mejor medida de centro y medida de variabilidad a utilizar con base en la forma de la distribución.

• Determina qué conjunto tiene la mayor medida de centro.

• Determina qué conjunto tiene la mayor medida de variabilidad.

• Está preparado para explicar su razonamiento.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

ENUNCIADO DE TAREA PARA EL ESTUDIANTE CONTINUACIÓN 4a 4b

RESPUESTAS POSIBLES

Álgebra 1 . Matemáticas . Unidad 1

5a 5b 6a

Un podcast político tiene mayoritariamente críticas que lo aman o lo odian.

Un podcast de cocina tiene críticas que ni lo odian ni lo aman.

En las pruebas de estrés del hormigón de la obra A, todas las 12 muestras se rompen a las 450 libras por pulgada cuadrada (psi, por sus siglas en inglés).

En las pruebas de estrés del hormigón de la obra B, las muestras se rompen cada 10 psi empezando en las 450 psi hasta que el último núcleo se rompe en las 560 psi.

Las pruebas de estrés del hormigón de la obra C hacen que 6 muestras se rompan a 430psi y las otras 6 se rompan a 460 psi

1. La media y la desviación estándar son apropiadas para estas distribuciones, ya que son simétricas. La media de la distribución 1a es mayor porque el centro está a la derecha del centro de la distribución 1b. La desviación estándar de la distribución 1a también es mayor porque la mayoría de los datos están más alejados de la media que en la distribución 1b.

2. La media y la desviación estándar son adecuadas para estas distribuciones porque son simétricas. La media de la distribución 2b es mayor porque el centro está a la derecha del centro de la distribución 2a. La desviación estándar de la distribución 2a es mayor porque los datos están más dispersos en esa distribución.

RESPUESTAS POSIBLES CONTINUACIÓN

1. La mediana y el rango intercuartílico son apropiados para estas distribuciones ya que no son simétricas. La mediana de la distribución 3a es mayor porque el centro está a la derecha del centro de la distribución 3b. El rango intercuartílico es mayor para la distribución 3a ya que los datos están más dispersos en esa distribución.

2. La media y la desviación estándar son apropiadas para estas distribuciones ya que son simétricas. La media de la distribución 4a es mayor porque el centro está a la derecha del centro de la distribución 4b. La desviación estándar de la distribución 4b es mayor, ya que los datos están más dispersos en esa distribución.

3. La mediana y el rango intercuartílico son los más apropiados para estas distribuciones, ya que no son simétricas y el diagrama de caja deja claros estos valores. La mediana para la distribución 5a es mayor ya que la mediana es 700, pero para la distribución 5b es 500. El IQR es mayor para la distribución 5a, ya que es 300, pero solo 200 para la distribución b.

4. La distribución 6a tiene mayor variabilidad ya que los valores se concentrarán en los extremos para el podcast político mientras que el podcast de cocina probablemente tenga valores más agrupados cerca del centro. Las respuestas varían para las otras determinaciones.

5. Dado que las tres distribuciones son simétricas, la media y la desviación estándar son las mejores medidas a utilizar. El sitio B tendrá la mayor media ya que el menor valor para esa distribución es la media para el sitio A (450 psi) y mayor que la media para el sitio C (445 psi). La desviación estándar para el sitio B será la mayor, ya que el sitio A tiene una desviación estándar de 0 psi, el sitio C tiene todos sus datos dentro de 15 psi de la media y el sitio B solo tiene 4 de los valores dentro de 15 psi de la media.

CONCEPTOS ERRÓNEOS ANTICIPADOS

SÍNTESIS DE LA ACTIVIDAD

Para las situaciones descritas en palabras, los estudiantes pueden pensar que no hay suficiente información para responder a la pregunta. Pregunte a estos estudiantes: «¿Cómo crees que podrían ser las distribuciones para las situaciones descritas?». Dígales que utilicen sus distribuciones para responder a la pregunta y que estén preparados para explicar su razonamiento.

Seleccione a los estudiantes para que compartan cómo determinaron si utilizar la media o la mediana y cómo averiguaron qué conjunto de datos mostraba mayor variabilidad.

• «¿Cuáles fueron algunas de las formas en que manejaste los dos últimos problemas?». (Razoné sobre el aspecto que podría tener un diagrama de puntos para imaginar dónde podría estar el centro y qué aspecto podrían tener los datos dispersos).

• «Describe cualquier dificultad que hayas experimentado y cómo la resolviste». (Olvidé qué información contenía un diagrama de caja, así que se lo pregunté a mi compañero).

• «¿Cómo decidiste si utilizar la media o la mediana?». (Recordé lo que había aprendido sobre la forma en la lección anterior. Cuando la distribución era simétrica o cercana a ella, utilicé la media. Cuando era sesgada, utilicé la mediana).

• «¿Cómo decidiste qué conjunto de datos mostraba mayor variabilidad?». (Para el diagrama de caja fue fácil, calculé el IQR. Para los gráficos de puntos, miré cuál estaba más separado. Para los contextos de problemas, traté de ver cuál tendría datos más variados).

SÍNTESIS

DE LA LECCIÓN

(5 minutos)

El propósito de esta discusión es asegurar que los estudiantes sepan cómo comparar conjuntos de datos utilizando medidas de variabilidad, incluida la desviación estándar y medidas de centro. He aquí algunas preguntas para la discusión.

• «¿Cómo se comparan las medidas de variabilidad de un conjunto de datos?». (Puedes calcularlas o estimarlas a partir de una visualización de datos. El conjunto de datos con la medida de variabilidad más alta es más variable).

• «¿Cómo estimas la variabilidad cuando miras las visualizaciones de datos?». (Trata de estimar el centro y, a continuación, el grado de dispersión de los datos).

• «¿Cómo se determina qué medida de centro utilizar para un conjunto de datos?». (Se observa la forma y se utiliza la media cuando es simétrica o muy cercana y la mediana cuando es asimétrica o si hay valores atípicos).

• «¿Por qué la mediana es la medida de centro preferida para distribuciones asimétricas?». (Se prefiere la mediana porque representa con mayor precisión el centro de los datos. Los valores de los datos más alejados del centro afectan menos a la mediana que a la media, por lo que la mediana permanece cerca de los valores típicos).

• «¿Por qué es la media la medida preferida del centro para distribuciones simétricas».« (En una distribución simétrica la media es igual a la mediana. Se prefiere la media porque tiene en cuenta todos los valores del conjunto de datos cuando se calcula).

ENFRIAMIENTO | COMPARAR MASCOTAS

(5 minutos)

Una nueva empresa de comida para mascotas quiere vender su producto en línea y utilizar los medios sociales para promocionarse. Para determinar si utilizar un perro o un gato como mascota, investigan el número de clics en enlaces con una imagen de un perro o un gato.

Media: 1,263.5 clics

Mediana: 1,282 clics

Desviación estándar: 357.4 clics

IQR: 409 clics

ENUNCIADO DE TAREA

PARA EL ESTUDIANTE

Media: 1,105.4 clics

Mediana: 1,125.5 clics

Desviación estándar: 239.3 clics

IQR: 312.5 clics

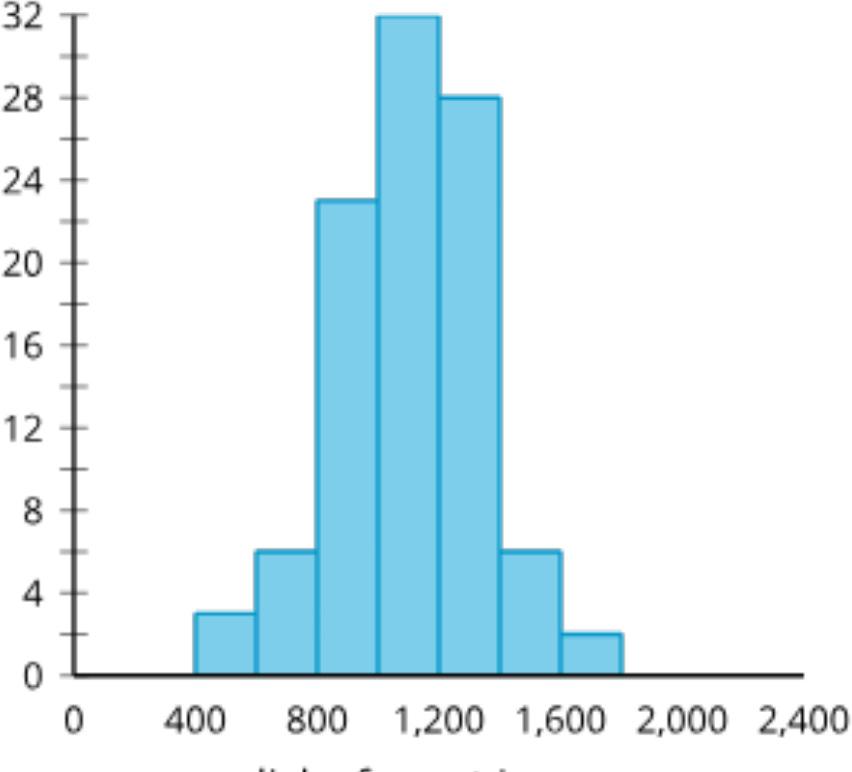
1. Con base en la forma de las distribuciones, ¿qué medida del centro y qué medida de la variabilidad utilizarías para comparar las distribuciones? Explica tu razonamiento.

2. Con base en los datos mostrados aquí, ¿debería la empresa utilizar una mascota de perro o de gato? Explica tu razonamiento.

RESPUESTAS POSIBLES

1. Media y desviación estándar. Dado que las distribuciones son aproximadamente simétricas, la media y la desviación estándar son la mejor opción para representar los datos.

2. Ejemplos de respuestas:

• La empresa debería utilizar una mascota canina, ya que la media es mayor.

• La empresa debería utilizar una mascota felina, ya que la desviación estándar muestra que las imágenes reciben más de 1,000 clics, mientras que las imágenes caninas a veces reciben menos de 200 clics.

Resumen de la lección para el estudiante

Para comparar conjuntos de datos, es útil observar las medidas del centro y las medidas de variabilidad. La forma de la distribución puede ayudar a elegir la medida más útil del centro y la medida de la variabilidad.

Cuando las distribuciones son simétricas o aproximadamente simétricas, la media es la medida preferida del centro y debe emparejarse con la desviación estándar como la medida preferida de la variabilidad. Cuando las distribuciones son asimétricas o cuando hay valores atípicos, la mediana suele ser una mejor medida del centro y debe emparejarse con el rango intercuartílico (IQR) como medida preferida de la variabilidad.

Una vez seleccionadas la medida apropiada del centro y la medida de la variabilidad , estas medidas pueden compararse para conjuntos de datos con formas similares.

Por ejemplo, comparemos el número de segundos que tardan los jugadores de fútbol americano en completar una carrera de 40 yardas en dos posiciones diferentes. En primer lugar, podemos observar un diagrama de puntos de los datos para ver que los tiempos de los extremos cerrados no parecen simétricos, por lo que probablemente deberíamos encontrar la mediana y el IQR de ambos conjuntos de datos para comparar la información.

La mediana y el IQR podrían calcularse a partir de los valores, pero también pueden determinarse a partir de un diagrama de cajas.

Esto muestra que los tiempos de los extremos cerrados tienen una mediana mayor (aproximadamente 4.9 segundos) en comparación con la mediana de los tiempos de los receptores abiertos (aproximadamente 4.5 segundos). El IQR también es mayor para los tiempos de los extremos cerrados (alrededor de 0.5 segundos) en comparación con el IQR para los tiempos de los receptores abiertos (alrededor de 0.25 segundos).

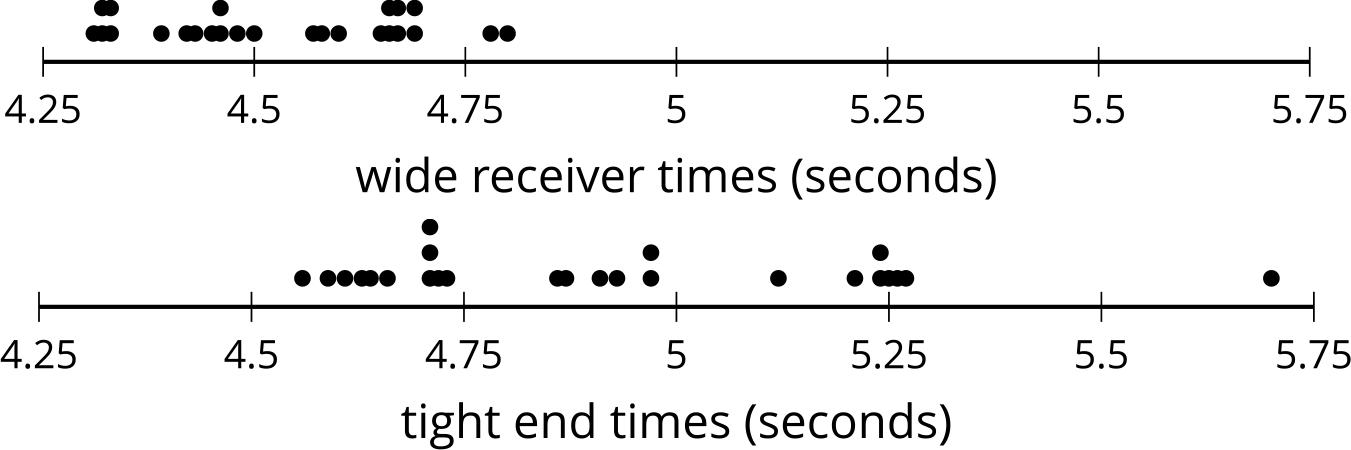
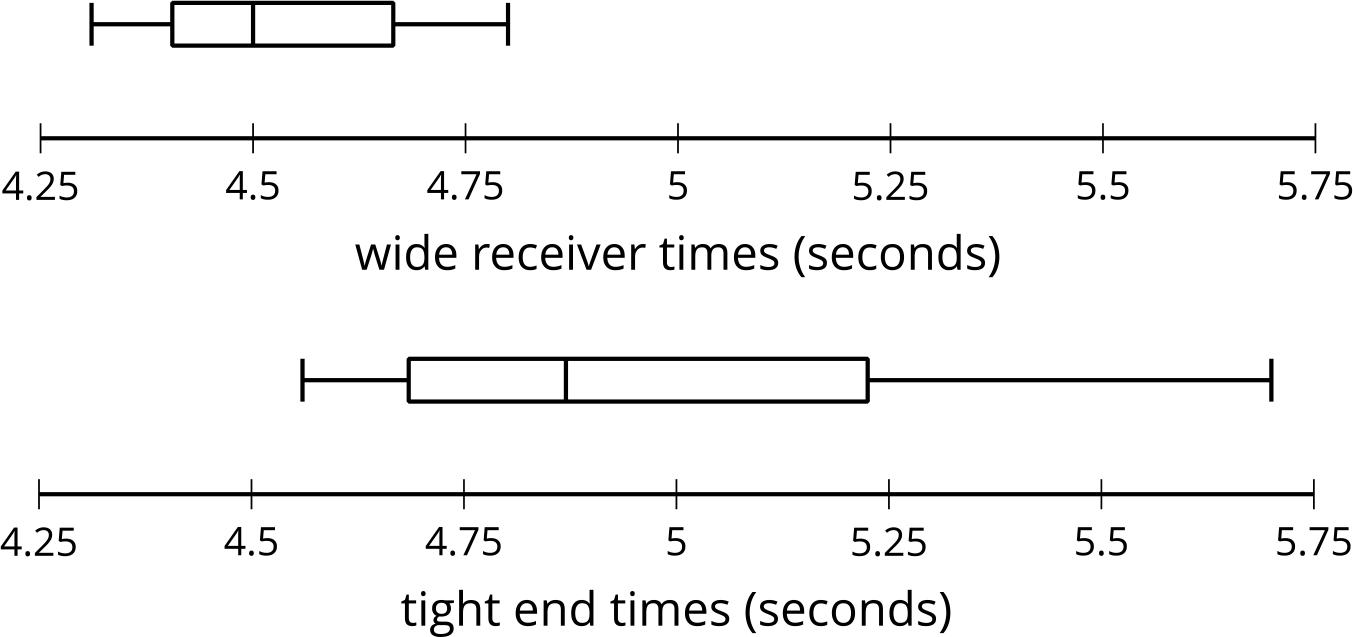
Esto significa que los extremos cerrados tienden a ser más lentos en las carretas de 40 yardas en comparación con los receptores abieros. Los extremos cerrados también tienen una mayor variabilidad en sus tiempos. En conjunto, esto puede interpretarse como que, en general, un receptor abierto típico es más rápido que unextremo cerrado típico, y que los receptores abiertos tienden a tener tiempos más parecidos entre sí que los extremos cerrados.

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

Veinte estudiantes participaron en un experimento psicológico en el que se midió su frecuencia cardiaca en dos situaciones diferentes.

A. ¿Cuáles son las medidas apropiadas de centro y variabilidad para utilizar con los datos? Explica tu razonamiento.

B. ¿Qué situación muestra una mayor frecuencia cardíaca estándar?

C. ¿Qué situación muestra una mayor variabilidad?

1 . Matemáticas . Unidad 1

Soluciones posibles

A. La media y la desviación estándar son adecuadas porque ambas distribuciones son simétricas.

B. La situación A

C. La situación B tiene una desviación estándar mayor.

PROBLEMA 2

A. Inventa dos situaciones que creas que darían lugar a distribuciones con medidas de variabilidad similares. Explica tu razonamiento.

B. Inventa dos situaciones que creas que darían lugar a distribuciones con diferentes medidas de variabilidad. Explica tu razonamiento.

Soluciones posibles

A. Ejemplo de respuesta: Lanzar cubos numéricos con los ojos cerrados y lanzar cubos numéricos con los ojos abiertos. Serían similares porque cerrar los ojos no debería afectar a la suma de los dos cubos numéricos.

B. Respuesta de ejemplo: Las temperaturas máximas diarias de julio y las temperaturas máximas diarias del año. Las temperaturas para el año deberían variar más que las temperaturas para el mes debido al cambio de estaciones.

PROBLEMA 3

Se enumera el conjunto de datos y algunos estadísticos de resumen.

11.5, 12.3, 13.5, 15.6, 16.7, 17.2, 18.4, 19, 19.5, 21.5

• Media: 16.52

• Mediana: 1.,95

• Desviación estándar: 3.11

• IQR: 5.5

A. ¿Cómo afecta a la forma de la distribución añadir 5 a cada uno de los valores del conjunto de datos?

B. ¿Cómo afecta a las medidas del centro añadir 5 a cada uno de los valores del conjunto de datos?

C. ¿Cómo afecta a las medidas de la variabilidad añadir 5 a cada uno de los valores del conjunto de datos?

PROBLEMA 4

Aquí hay dos diagramas de caja:

A. ¿Qué diagrama de caja tiene una mediana mayor?

B. ¿Qué diagrama de caja tiene una medida de variabilidad mayor?

PROBLEMA 5

(De la unidad 1, lección 10).

Soluciones posibles

A. Respuesta de muestra: La forma no cambia; todos los valores se desplazan 5 unidades a la derecha.

B. Respuesta de ejemplo: Ambas medidas del centro aumentarán en 5

C. Respuesta de ejemplo: Añadir 5 no tiene ningún impacto en las medidas de variabilidad.

Soluciones posibles

A. A

B. B

La profundidad de dos lagos se mide en múltiples puntos. Para el primer lago, la profundidad media es de aproximadamente 45 pies con una desviación estándar de 8 feet. Para el segundo lago, la profundidad media es de unos 60 pies con una desviación estándar de 27 pies. Noah dice que el segundo lago es generalmente más profundo que el primero. ¿Estás de acuerdo con Noah?

1 . Matemáticas . Unidad 1

Soluciones posibles

Ejemplo de respuesta: Noah es correcto. La profundidad media del segundo lago es sustancialmente mayor que la profundidad media del primer lago, medida por los valores medios. Por otra parte, hay mucha más variación en la profundidad del segundo lago, por lo que puede haber partes sustanciales del segundo lago que sean poco profundas en comparación con el primer lago.

PROBLEMA 6

(De la unidad 1, lección 9).

Los diagramas de puntos muestran la altura, redondeada al pie más cercano, de los arces de dos granjas diferentes.

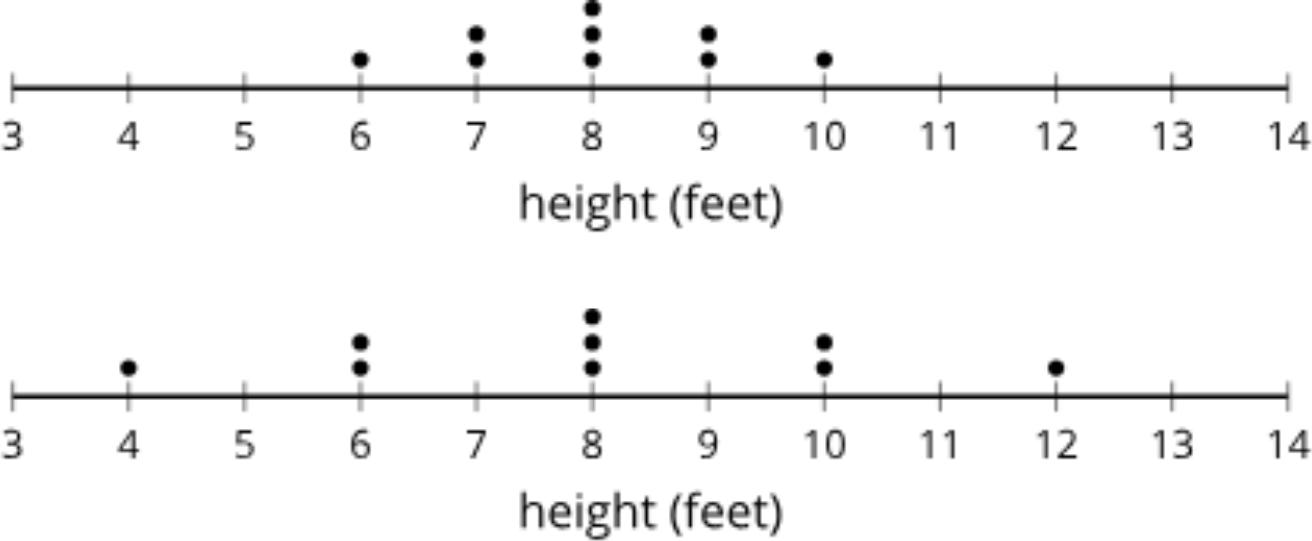
A. Compara la media y la desviación estándar de los dos conjuntos de datos.

B. ¿Qué te dice la desviación estándar sobre los árboles de estas granjas?

PROBLEMA 7

(De la unidad 1, lección 8).

¿Qué diagrama de caja tiene un IQR de 10?

Soluciones posibles C

PROBLEMA 8

(De la unidad 1, lección 6).

Soluciones posibles

A. Las medias de los dos conjuntos de datos son 8 pies. La desviación estándar del primer conjunto de datos es menor que la desviación estándar del segundo conjunto de datos.

B. En la segunda granja, hay un rango más amplio de alturas que en la primera granja, donde las alturas de los árboles están más cerca unas de otras.

¿Qué efecto tiene eliminar el valor más bajo, − 6, del conjunto de datos sobre la media y la mediana? − 6, 3, 3, 3, 3, 5, 6, 6, 8, 10

Soluciones posibles

La media aumenta de 4.1 a aproximadamente 5.22. La mediana aumenta de 4 a 5

Math Nation California . AAlgebra 1

Álgebra 1 . Matemáticas . Unidad 1

IDEA(S) FUNDAMENTAL(ES)

• Investigar datos

ALINEACIÓN

Abordar

S-ID.1 Representar datos con gráficas en la recta numérica real (diagramas de puntos, histogramas y diagramas de cajas).

Estándares y principios de CA Alineación

S-ID.3 Interpretar las diferencias de forma, centro y dispersión en el contexto de los conjuntos de datos, teniendo en cuenta los posibles efectos de los puntos extremos de los datos (outliers).

Enfoque SMPs

MP1 Dar sentido a los problemas y perseverar en su resolución.

MP4 Representar las matemáticas.

MP5 Utilizar estratégicamente las herramientas apropiadas.

Estándares ELD de California

I.A.1

I.C.11

II.B.5

LECCIÓN 13 ANALIZAR DATOS

ENFOQUE EN IDEAS FUNDAMENTALES

CONEXIONES INTEGRADAS

(DI) ¿Por qué? Para... (SMPs) ¿Cómo? ... los estudiantes... (CC) ¿Qué? ... mientras..

impactar el futuro

darán sentido a los problemas y perseverán en su resolución analizan los datos.

OBJETIVO(S) DE APRENDIZAJE

• Puedo recoger datos de un experimento y comparar los resultados utilizando medidas de centro y medidas de variabilidad.

OBJETIVOS DE APRENDIZAJE PARA EL MAESTRO

• Recoger y comparar (utilizando palabras y otras representaciones) conjuntos de datos con diferentes condiciones para un experimento basado en las medidas de centro y medidas de variabilidad.

PREPARACIÓN DE LA LECCIÓN

Rutinas didácticas

Analícelo

MLR1: Cada vez más fuerte y más claro

Aspectos de representar las matemáticas

Materiales necesarios

Reglas

Preparación necesaria

Una regla por cada pareja de estudiantes.

INFORMACIÓN DE LA LECCIÓN

Objetivos de aprendizaje para el estudiante

• Respondamos preguntas estadísticas cuando analizamos datos, comparamos y contrastamos su forma y medidas de centro y variabilidad.

Narrativa de la lección

El propósito matemático de esta actividad es plantear y responder una pregunta estadística diseñando un experimento, recogiendo datos y analizándolos. Los estudiantes determinarán la mejor manera de mostrar los datos, seleccionarán las medidas apropiadas de centro y variabilidad y responderán a una pregunta estadística que involucra dos tratamientos diferentes. El trabajo de esta lección

Álgebra 1 Matemáticas . Unidad 1

se conecta con el trabajo anterior porque los estudiantes aprendieron sobre la forma, las medidas del centro y las medidas de variabilidad para las distribuciones de datos. Esto se conecta con el trabajo futuro porque los estudiantes investigarán datos bivariados con tablas de dos vías, tablas de frecuencia relativa, gráficos de dispersión y líneas de mejor ajuste.

La tecnología no es necesaria para esta lección, pero hay oportunidades para que los estudiantes elijan usar la tecnología apropiada para resolver problemas. Recomendamos que la tecnología esté disponible. Cuando los estudiantes eligen una visualización apropiada para los datos y eligen utilizar la tecnología para calcular estadísticas, utilizan herramientas apropiadas estratégicamente (MP5). Los estudiantes hacen sentido de los problemas y perseveran en su resolución (MP1) porque los estudiantes tienen que dar sentido a la situación para poder plantear una pregunta estadística con sentido. Los estudiantes también deben seleccionar una variable apropiada para analizar la comparación de las alturas de los estudiantes, lo que les involucran los aspectos para representar las matemáticsa (MP4).

RESUMEN DE LA LECCIÓN

Componente de la lección

Estructura Tiempo

Calentamiento En parejas 5 min

Actividad de exploración En parejas 25 min

Actividad de Exploración En parejas 10 min

Descripción breve

Los estudiantes escriben dos preguntas estadísticas que pueden responderse con los datos de un estudio.

Los estudiantes realizan experimentos, recopilan datos, determinan estadísticas resumidos y realizan comparaciones entre los datos. Luego crean una presentación visual para representar la respuesta a su pregunta estadística.

Los estudiantes analizan una gran cantidad de datos y luego hacen comparaciones para determinar si existe una relación entre las variables medidas.

Síntesis Todo el grupo 5 min. Los estudiantes reflexionan sobre los procesos y desafíos que ocurren durante la recolección de datos.

Práctica Independiente 10 min. El componente de práctica independiente incluye 7 problemas de repaso en espiral.

Nation California - Algebra 1

CALENTAMIENTO | CONDICIONES EXPERIMENTALES (5 minutos)

El propósito matemático de esta actividad es que los estudiantes escriban una pregunta estadística para dejar caer y atrapar una regla bajo diferentes condiciones.

Organice a los estudiantes en grupos de 2. Muestre cómo dejar caer la regla y cómo medir la distancia dejada caer. Muestra este video si es necesario. Video Demostración de la caída de la regla disponible en https://player.vimeo.com/video/304121341

INTRODUCCIÓN

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Explique que la regla es sostenida por una persona en la marca de 12 pulgadas y es atrapada por otra persona justo debajo de la marca de 7 pulgadas. La distancia de caída de la regla es de aproximadamente 6 pulgadas. Para los grupos que se esfuerzan por pensar en condiciones que podrían ser interesantes, he aquí algunos ejemplos para ayudarles a empezar:

• De pie y sentado

• Escuchar música y en silencio

• Escuchar una canción favorita y una que sea menos interesante

• Soltar rápidamente después de que estén listos y esperar al menos 3 segundos después de que estén listos antes de soltar

Para probar el tiempo de reacción, la persona que realiza la prueba sostendrá una regla en la marca de 12 pulgadas. La persona cuyo tiempo de reacción se está probando mantendrá el pulgar y el índice abiertos a ambos lados de la parte plana de la regla en la marca de 0 pulgadas del otro lado de la regla. La persona que realiza la prueba dejará caer la regla y la otra persona deberá cerrar los dedos en cuanto note que la regla se mueve para atraparla. La distancia a la que cayó la regla se utilizará como dato para este experimento.

Con su compañero, escriba una pregunta estadística que pueda responderse comparando los datos de dos condiciones diferentes para la prueba.

RESPUESTAS POSIBLES

SÍNTESIS DE LA ACTIVIDAD

Ejemplo de respuesta: ¿Es el tiempo de reacción de mi compañero más rápido si dejo caer la regla mientras mi compañero está parado sobre dos pies o mientras mi compañero está parado sobre un pie?

El objetivo de esta discusión es asegurarse de que todos tengan una pregunta estadística sobre el tiempo de reacción que requiera recolectar datos de dos condiciones diferentes para realizar la prueba.

Revise las preguntas de los estudiantes y ayúdelos a crear una pregunta que cumpla con el requisito. Aquí tienes algunas preguntas para debatir.

• «¿Cuáles son tus dos condiciones?». (De pie sobre un pie y de pie sobre los dos pies).

• «¿Cómo vas a recoger estos datos?». (Sostendré y dejaré caer la regla mientras mi compañero está de pie sobre un pie. Luego lo repetiré mientras él está de pie sobre dos pies).

• «¿Cuántos ensayos crees que deberías hacer en cada condición?». (Al menos diez)

Álgebra 1 Matemáticas . Unidad 1

ACTIVIDAD DE EXPLORACIÓN | DEJAR CAER LA REGLA

(25 minutos)

Rutinas didácticas

Analízalo

MLR1: Cada vez más fuerte y más claro

El propósito matemático de esta actividad es que los estudiantes diseñen un experimento para responder a una pregunta estadística, recopilar datos, analizar los datos utilizando la estadística y comunicar la respuesta a la pregunta estadística utilizando una pantalla. Puede ser útil tener varios grupos combinados para permitir a los estudiantes experimentar las diferentes condiciones para muchos experimentos. Poner a disposición la tecnología estadística da a los estudiantes la oportunidad de elegir estratégicamente las herramientas apropiadas (MP5).

Fíjese en los grupos que crean visualizaciones que comunican su pensamiento matemático con claridad, contienen un error que sería instructivo debatir u organizan la información de manera que sea útil para que todos la vean.

Mantenga a los estudiantes en grupos de 2. Proporcione a cada grupo herramientas para crear una presentación visual. Si los estudiantes tienen acceso a la tecnología estadística, sugiérales que podría ser una herramienta útil en esta actividad.

INTRODUCCIÓN

Explique a los estudiantes que van a recoger y analizar datos utilizando la estadística para responder a su pregunta estadística del calentamiento.

Los estudiantes crearán una visualización que muestre las preguntas estadísticas, los datos, una visualización de datos y una respuesta a la pregunta estadística con cualquier trabajo matemático de apoyo.

Apoyo para estudiantes con discapacidad

Acción y expresión: Interiorizar las funciones ejecutivas. Para apoyar el desarrollo de habilidades organizativas en la resolución de problemas, divida esta tarea en partes más manejables. Por ejemplo, muestre 1-2 características que la visualización debe incluir en lugar de la lista completa. Proporciona a los estudiantes acceso a una cuadrícula o papel cuadriculado para organizar su trabajo matemático de apoyo para la presentación visual.

Apoya la accesibilidad para: Memoria; organización

Anteriormente, tu compañero y tu acordaron una pregunta estadística que puede responderse con los datos recogidos en 2 diferentes condiciones de caída de la regla. Con tu compañero, realiza el experimento para recoger al menos 20 resultados bajo cada condición.

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

Analiza tus 2 conjuntos de datos para comparar la pregunta estadística. A continuación, crea una presentación visual que incluya:

• tu pregunta estadística

• los datos que recogiste

• una presentación de datos

• la medida del centro y la variabilidad que encontraste que son apropiadas para los datos

• una respuesta a la pregunta estadística con cualquier trabajo matemático de apoyo.

RESPUESTAS POSIBLES

Ejemplo de respuesta:

• Condición A: Sobre dos pies 5.5, 6, 6.5,

10, 10, 10.5, 11

Media: 8.18, desviación estándar: 1.44

• Condición B: de pie sobre un pie 5, 6, 6.5,

SÍNTESIS DE LA ACTIVIDAD

, 10.5, 10.5, 10.5, 11, 11.5

1,448.78, desviación estándar 1.72

El tiempo de reacción fue más rápido al estar de pie sobre dos pies. Lo sé porque la distancia media de caída fue 8.18 pulgadas en comparación con 8.78 pulgadas mientras estaba parado sobre un pie. La mayor distancia significa un tiempo de reacción más lento. También me di cuenta de que había una mayor variabilidad en los datos recogidos mientras estaba de pie sobre un pie. Lo supe mirando la desviación estándar. Fue 1.72 pulgadas para los datos de un pie y 1.44 pulgadas para los datos de dos pies. Curiosamente, la distancia más corta fue para los datos de un pie, pero también lo fue la distancia más grande. Decidí utilizar la media y la desviación estándar porque la forma de ambas distribuciones era aproximadamente simétrica.

Selecciona grupos para que compartan sus representaciones visuales. Anima a los estudiantes a hacer preguntas sobre el pensamiento matemático o el enfoque de diseño que se utilizó para crear la presentación. A los estudiantes que hayan tenido un error en su visualización, pregúnteles: «¿Qué error ven en la visualización y cómo lo resolverían». (Las respuestas varían). Ejemplos de respuestas:

• Me he dado cuenta de que han utilizado la media en lugar de la mediana. Yo lo resolvería con la mediana, ya que había un valor atípico

• Me di cuenta de que el IQR se calculó incorrectamente. Yo habría utilizado la tecnología para verificar mis estadísticas).

Aquí hay preguntas para la discusión, si no han sido ya mencionadas por los estudiantes:

• «Una vez que recogiste tus datos, ¿cómo respondiste a tu pregunta estadística?». (Utilicé dos diagramas de puntos diferentes para mostrar mis datos y determiné que la media era la medida más apropiada del centro porque mi diagrama de puntos era aproximadamente simétrico. A continuación, calculé la desviación estándar con la tecnología porque es apropiado utilizarla con la media. A continuación, comparé la media y la desviación estándar de los dos conjuntos de datos y determiné que al estar parado sobre dos pies mi compañero reaccionaba ligeramente más rápido y mostraba menos variabilidad que al estar de pie sobre un pie).

• «¿Cómo elegiste qué medida de centro y qué medida de variabilidad utilizar?« (Utilicé la forma de la distribución para determinar la medida de centro. Mis datos eran asimétricos, así que utilicé la mediana. Utilicé la IQR como medida de variabilidad porque se basa en la mediana. Si hubiera utilizado la media, habría utilizado la desviación estándar).

SÍNTESIS DE LA ACTIVIDAD CONTINUACIÓN

Álgebra 1 Matemáticas . Unidad 1

• «Utilizando el contexto de los dos tratamientos, ¿qué te dijo la medida de variabilidad?». (La medida de la variabilidad me dijo lo separados que estaban los resultados de la medida del centro que elegí. Me permitió saber lo consistente que era el tiempo de reacción para cada tratamiento).

• «Imagina que recoges datos para los mismos tratamientos de todos los estudiantes de la clase. ¿Cómo cambiaría esto la forma de mostrar o analizar los datos». (Habría muchos datos. Probablemente tendría que utilizar la tecnología para encontrar las estadísticas y crear la visualización de los datos. Creo que podría necesitar utilizar un histograma para representar la distribución de los datos).

Apoyo para estudiantes que aprenden el idioma inglés

Escribir, hablar, escuchar: MLR1 Cada vez más fuerte y más claro. Utilice esta rutina para dar a los estudiantes una oportunidad estructurada de revisar y refinar su respuesta a la pregunta estadística elegida anteriormente. Pida a cada estudiante que se reúna con 2-3 otros compañeros en fila para recibir comentarios. Muestre indicaciones para la retroalimentación que ayuden a los equipos a reforzar sus ideas y aclarar su lenguaje. Por ejemplo: «¿Puedes explicar cómo...?», «Deberías ampliar ...», etc. Los estudiantes pueden tomar prestadas ideas y lenguaje de cada compañero para fortalecer el producto final. Esto ayudará a los hablantes a reflexionar sobre lo que han aprendido acerca de la recopilación de datos, el análisis de datos y la respuesta a una pregunta estadística. Principio(s) de diseño: Optimizar el producto (para la generalización)

ACTIVIDAD DE EXPLORACIÓN | ALTURAS Y LATERALIDAD

(10 minutos)

Rutinas didácticas

Aspectos de representar las matemática

En esta actividad, los estudiantes utilizan un gran conjunto de datos para comparar el tamaño de los estudiantes con diferentes manos dominantes. Los estudiantes deben seleccionar una variable que represente mejor el tamaño de los estudiantes y comparar los dos grupos. Al seleccionar la variable relevante para analizar, los estudiantes participan en aspectos de representación matemática (MP4). Además, los estudiantes deben elegir las herramientas adecuadas (MP5) para analizar un gran conjunto de datos como éste.

INTRODUCCIÓN

Organice a los estudiantes en grupos de 2. Distribuya una copia del patrón de líneas negras a cada grupo.

Apoyo a los estudiantes con discapacidad

Representación: Interiorizar la comprensión. Comience la actividad con contextos concretos o familiares. Entablar un debate en clase en el que se preste atención a la relación entre la altura, la longitud de los pies y la envergadura de los brazos de los estudiantes diestros y zurdos de la clase. Esto ayudará a los estudiantes a establecer conexiones entre el gran conjunto de datos y los estudiantes especíﬁcos de la clase.

Apoya la accesibilidad para: Procesamiento conceptual; memoria

California - Algebra 1

1 Matemáticas . Unidad 1

ENUNCIADO DE TAREA PARA EL ESTUDIANTE

RESPUESTAS POSIBLES

¿Existe alguna relación entre la mano dominante de un estudiante y su tamaño? Utilice la tabla de información para comparar el tamaño de los estudiantes con diferentes manos dominantes.

Ejemplo de respuesta:

Con los datos proporcionados, los estudiantes zurdos tienen una altura media de 164.86 cm y una desviación estándar de 25.18 cm, mientras que los estudiantes diestros tienen una altura media de 153.84 cm y una desviación estándar de 41.67 cm. Aunque la estatura media de los estudiantes zurdos es mayor, la gran desviación estándar indica que no hay una gran diferencia entre los grupos.

Sin embargo, si se analizan los datos más detenidamente, hay algunos valores atípicos que no tienen sentido. En concreto, es poco probable que haya estudiantes que midan menos de 100 centímetros (3 pies 3 pulgadas). Es probable que estos estudiantes hayan interpretado erróneamente la pregunta en términos de pulgadas o hayan introducido datos incorrectos. Si se eliminan los valores inferiores a 100 de la información sobre la altura, cambian la media y la desviación estándar. La estatura media de los estudiantes zurdos pasa a ser 169.19 cm con una desviación estándar de 13.86 cm. Para los estudiantes diestros, la nueva altura media es 168.60 cm con una desviación estándar de 10.63 cm.

Con las medias actualizadas, los dos grupos están mucho más cerca y siguen teniendo una desviación estándar relativamente grande, por lo que no parece haber una gran diferencia entre los dos grupos de estudiantes.

SÍNTESIS DE LA ACTIVIDAD

Seleccione a los estudiantes para que compartan su análisis de los datos.

SÍNTESIS DE LA LECCIÓN

(5 minutos)

El propósito de esta discusión es ayudar a los estudiantes a reflexionar sobre lo que han aprendido acerca de la recogida de datos, el análisis de datos y la respuesta a una pregunta estadística. He aquí algunas preguntas para el debate.

• «¿Qué es lo que te ha parecido más difícil de esta lección)». (Fue realmente difícil averiguar qué hacer con los datos que recogí porque no había instrucciones. Tuve que volver a mi pregunta estadística y pensar qué herramientas necesitaría para responderla).

• «¿Qué te ha parecido interesante de esta lección?». (Fue muy interesante poder utilizar las estadísticas que aprendí para responder a una pregunta. Se parecía mucho a cuando hacemos experimentos en clase de Ciencias).

• «¿Qué matemáticas necesitas saber más?« (Sigo teniendo problemas para averiguar la forma de los datos. A veces creo que los datos son aproximadamente simétricos, pero en realidad están sesgados. Me gustaría practicar más la descripción de la forma de las distribuciones).

1 Matemáticas . Unidad 1

PROBLEMAS DE PRÁCTICA

PROBLEMA 1

(De la unidad 1, lección 12).

Aquí están las estadísticas para las altas temperaturas en una ciudad durante octubre:

• Media de 65.3 grados Fahrenheit

• Mediana de 63.5 grados Fahrenheit

• Desviación estándar de 9.3 grados Fahrenheit

• IQR de 7.1 grados Fahrenheit

Recuerda que la temperatura ��, medida en grados Celsius, está relacionada con la temperatura ��, medida en grados Fahrenheit, mediante

�� = 5 9 (�� − 32)

A. Describe cómo cambia el valor de cada estadística cuando 32 se resta de la temperatura en grados Fahrenheit.

B. Describe cómo cambia el valor de cada estadística cuando los nuevos valores se multiplican por 5 9

C. Describe cómo encontrar el valor de cada estadística cuando la temperatura se mide en grados Celsius.

Soluciones posibles

A. Restar 32 a la temperatura en grados Fahrenheit disminuirá la media y la mediana en 32 pero no cambiará la desviación estándar ni la IQR.

B. Multiplicar los nuevos valores (que se han desplazado en 32) por 5 9 multiplicará la media y la mediana por 5 9 . Tanto la desviación estándar como la IQR se multiplican por 5 9

C. Para la media y la mediana, reste 32 de los valores dados y multiplique por 5 9 . Para la desviación estándar y el IQR, multiplique los valores dados por 5 9

PROBLEMA 2

(De la unidad 1, lección 12).

Aquí se muestra un diagrama de caja.

Dé un ejemplo de un diagrama de caja que tenga una mediana y una medida de variabilidad mayor, pero los mismos valores mínimo y máximo.

PROBLEMA 3

(De la unidad 1, lección 11).

Soluciones posibles

El mínimo debe ser 15, el máximo 95, la mediana mayor que 50 y el rango intercuartílico mayor que 15

Ejemplo de respuesta:

El nivel medio de vitamina C para 20 perros era 7.6 miligramos por litro, con una desviación estándar de 2.1 miligramos por litro. El nivel de vitamina C de un perro no estaba dentro del rango normal. Era 0.9 miligramos por litro, que es un nivel muy bajo de vitamina C.

A. Si se elimina el valor 0.9 del conjunto de datos, ¿aumenta o disminuye la media?

B. Si se elimina del conjunto de datos el valor 0.9 , ¿aumenta o disminuye la desviación estándar?

1 Matemáticas . Unidad 1

Soluciones posibles

A. La media aumentará porque 0.9 miligramos por litro está por debajo de la media de 7.6 miligramos por litro.

B. La desviación estándar disminuirá porque 0.9 miligramos por litro está muy lejos de la media, por lo que el nuevo conjunto de datos estará más concentrado alrededor del centro cuando se elimine ese valor.

PROBLEMA 4

(De la unidad 1, lección 11).

El conjunto de datos representa el número de horas que quince estudiantes caminaron durante un período de dos semanas.

La mediana es 10 horas, Q1 es 8, Q3 es 14 y el IQR es de 6 horas. ¿Hay algún valor atípico en los datos? Explique o muestre su razonamiento.

Soluciones posibles

Sí, 30 es un valor atípico, ya que 14 + 1.5 ∙ 6 = 23 y 30 > 23

PROBLEMA 5

(De la unidad 1, lección 11).

A continuación se muestran algunas estadísticas resumidas sobre el número de cuentas que siguen a algunos grupos de música en las redes sociales.

• Media: 15.976 seguidores

• Mediana: 16.432 seguidores

• Desviación estándar: 3.279 seguidores

• Q1: 13.796

• Q3: 19.070

• IQR: 5.274 seguidores

A. Pon un ejemplo del número de seguidores que podría tener un grupo muy popular y que se consideraría un valor atípico para estos datos. Explica o muestra tu razonamiento.

B. Pon un ejemplo del número de seguidores que podría tener un grupo relativamente desconocido y que se consideraría un valor atípico para estos datos. Explique o muestre su razonamiento.

Soluciones posibles

A. Ejemplo de respuesta: 30.000 seguidore,s ya que es un valor atípico si el número de seguidores es mayor que 19.070 + 1.5

5.274, o 26.981 seguidores.

B. Respuesta de ejemplo: 5,000 seguidores ya que es un valor atípico si el número de seguidores es menor que 13.796 − 1.5

5.274 o 5.885 seguidores.

PROBLEMA 6

(De la unidad 1, lección 10).

Los pesos de una población de gorilas de montaña tienen una media de 203 libras y una desviación estándar de 18 libras. Los pesos de otra población de gorilas de montaña tienen una media de 180 libras y una desviación estándar de 25 libras. André dice que las dos poblaciones son similares. ¿Estás de acuerdo? Explica tu razonamiento.

Soluciones posibles

Ejemplo de respuesta: Estoy de acuerdo con Andre. Aunque los pesos de las dos poblaciones tienen medias diferentes, la desviación estándar me permite saber que muchos gorilas de la primera población pesan menos de 203 libras y muchos gorilas de la segunda población pesan más de 180 libras. Las poblaciones tienen pesos que se solapan, así que creo que son similares.

Nation California - Algebra 1

PROBLEMA 7

(De la Unidad 1, Lección 7).

El diagrama de caja representa la distribución de la cantidad de cambio, en centavos, que tenían las 50 personas encuestadas.

El diagrama de caja representa la distribución del mismo conjunto de datos, pero eliminando el máximo, 203

La mediana es 25 céntimos para ambos diagramas. Tras examinar los datos, se elimina el valor 203 , ya que se trata de un error de registro.

A. Explica por qué la mediana sigue siendo la misma al eliminar 203 céntimos del conjunto de datos.

B. Al eliminar 203 céntimos del conjunto de datos, ¿la media sigue siendo la misma? Explica tu razonamiento.

Soluciones posibles

A. La mediana permanece igual porque eliminar un valor extremo de un conjunto de datos tiende a no tener mucho efecto o ningún efecto sobre la mediana. En este caso, puede haber varias personas que lleven 25 céntimos.

B. La media disminuye porque 203 céntimos es mayor que la media del conjunto de datos.

Reflexiones:

Math Nation California - Algebra 1