

“CONSTRUCCIÓN DE MODELOS DE SIMULACIÓN”
PORYURESKIOMAÑA
UNIVERSIDAD BICENTENARIA DE ARAGUA
INTRODUCCION
Los modelos de simulación son herramientas poderosas utilizadas en diversos campos para analizar y predecir el comportamiento de sistemas complejos. Estos modelos permiten a los investigadores y profesionales explorar escenarios hipotéticos, evaluar riesgos y tomar decisiones informadas sin la necesidad de experimentar en sistemas reales.
En el ámbito empresarial y financiero, la simulación de Montecarlo se ha convertido en una técnica particularmente valiosa. Esta metodología utiliza la generación de números aleatorios para crear múltiples escenarios posibles, permitiendo así una evaluación más completa de los resultados potenciales y los riesgos asociados.
Nos centraremos en la construcción de un modelo de simulación de Monte Carlo aplicado a las ventas diarias de un negocio. Utilizando Python y Excel, demostraremos cómo se puede crear un modelo simple pero efectivo para:
Simular el número de clientes diarios 1.
Estimar el gasto por cliente 2.
Calcular las ventas diarias totales 3.
Analizar estadísticas clave como el promedio de ventas y la variabilidad 4. El ejemplo práctico que presentaremos ilustraremos cómo, con unos pocos parámetros iniciales y algunas suposiciones sobre la distribución de los datos, podemos generar insights valiosos sobre el comportamiento esperado de las ventas. Este tipo de simulación puede ser crucial para la planificación financiera, la gestión de inventario y la evaluación de riesgos en un entorno empresarial.
CONSTRUCCION DE MODELOS DE SIMULACION
La construcción de modelos de simulación es el proceso de crear una representación digital o matemática de un sistema real para analizar su comportamiento y prever su desempeño bajo diversas condiciones. Este modelo simulado permite experimentar sin interferir en el sistema real, lo que resulta útil para anticipar resultados y mejorar la toma de decisiones en situaciones donde probar directamente en el sistema es costoso, riesgoso o impracticable.
¿Por qué es útil la construcción de modelos de simulación?
La simulación es valiosa porque permite experimentar con el sistema de manera segura, eficiente y sin afectar su operación real. Los resultados pueden anticipar problemas, identificar oportunidades de mejora y ayudar en la toma de decisiones en áreas como logística, finanzas, fabricación y ciencias de la salud, entre otras.
Tipos de Simulación Comúnmente Utilizados en la Construcción de Modelos
Simulación de Eventos Discretos : Modelo de sistemas que cambian en puntos específicos del tiempo, como el flujo de clientes en un banco.
Simulación Continua : Se utiliza en sistemas que cambian constantemente, como modelos de física o química.
Simulación Montecarlo : Utiliza la aleatoriedad para estimar posibles resultados, siendo útil para problemas financieros o de gestión de inventario.
Simulación Basada en Agentes : Modelo de sistemas complejos como un conjunto de agentes individuales que interactúan entre sí, útiles en ciencias sociales o biológicas.
EJEMPLO DE UNA SIMULACIÓN TIPO MONTECARLO
DESCRIPCIÓN Y CONCEPTUALIZACIÓN DE LA SIMULACIÓN

2. Especificación del objetivo
El objetivo de la simulación es:
Calcular el ingreso promedio diario esperado.
Determinar la variabilidad en las ventas diarias para prevenir las fluctuaciones. Establecer un intervalo de confianza para anticipar el rango de ventas en el que probablemente se encuentre el rendimiento diario.
1. Establecimiento del Problema
La tienda enfrenta incertidumbre diaria en la cantidad de clientes y el gasto promedio por cliente. Estos factores afectan sus ingresos diarios, haciendo difícil prever ingresos futuros, optimizar inventarios y planificar recursos. La simulación se plantea para ayudar a la tienda a estimar un rango razonable de ingresos diarios y ajustar sus estrategias con base en esta variabilidad.
3. Definición de Indicadores
Los principales indicadores definidos son: Ventas Diarias Promedio : Valor esperado de ventas diarias, necesario para el presupuesto.
Desviación Estándar de Ventas Diarias : Variabilidad en las ventas, clave para anticipar las posibles fluctuaciones.
Intervalo de Confianza del 95% para Ventas Diarias : Rango de ventas donde, con un 95% de certeza, se espera que caigan las ventas diarias.
4. Simulación y Determinación de la Muestra
La simulación se ejecuta con 30 días de ventas (una "corrida") y se realiza para: Obtener valores promedio y dispersión de ventas, representantes de un mes. Utilizar distribuciones de Poisson y Normal para reflejar, respectivamente, el número diario de clientes y el gasto de cada cliente. Generar suficientes réplicas (cada día cuenta como una réplica) para obtener una estimación estable.
CARACTERÍSTICAS DE CADA INDICADOR
Ventas diarias Promedio 1.
Argumento de Datos : Generados en la simulación diaria, producto de la cantidad de clientes y el gasto promedio por cliente.
Gráficos : Un histograma muestra la distribución de ventas diarias, mientras una línea en los medios indica el valor promedio.
Estimación de Parámetros : La media (promedio de las ventas diarias) estima la tendencia central del ingreso diario esperado.
2. Desviación Estándar de Ventas Diarias
Argumento de Datos : Calculada sobre las ventas diarias generadas por la simulación.
Gráficos : Un gráfico de dispersión o barra de error ayuda a visualizar la variabilidad en torno al promedio.
Estimación de parámetros : La desviación estándar mide la dispersión, crucial para la planeación del inventario.
3. Intervalo de Confianza del 95% para Ventas Diarias
Argumento de Datos : Calculado usando el promedio y la desviación estándar de ventas diarias.
Gráficos : Un intervalo en el gráfico de barras muestra el rango de confianza.
Estimación de Parámetros : Este intervalo ofrece un rango de valores probables para las ventas diarias, ayudando a predecir ingresos con un nivel de certeza.
EFECTO DE LA VARIABILIDAD EN EL TAMAÑO DE LA SIMULACIÓN
La variabilidad afecta directamente la precisión de los estimadores. Al aumentar el tamaño de la simulación (número de réplicas), la variabilidad relativa disminuye, haciendo que las estimaciones sean más precisas. Por ejemplo, en nuestro caso:
Caso práctico :
EA medida que se aumentan los días simulados (réplicas), el intervalo de confianza se estrecha, mostrando una estimación más confiable del promedio de ventas.
Con 30 días, obtendremos una estimación aproximada, pero una simulación de 90 días produciría un intervalo más estrecho y representativo.
En un sistema de gestión de empleados, puedes tener un objeto "Empleado" que contiene un objeto "Dirección". Si varios empleados comparten la misma dirección (por ejemplo, si trabajan en la misma oficina), no es necesario duplicar los datos de la dirección. Simplemente se crea una instancia única de la clase "Dirección" y se asocia con los empleados correspondientes.
DEFINICIONES CLAVE EN SIMULACIÓN
Réplica : Cada día simulado es una réplica que replica el comportamiento diario de la tienda. Con más réplicas, se mejora la representatividad de los resultados.
Corrida : El conjunto de 30 días simulados conforma una corrida completa de un mes, que permite observar la tendencia y variabilidad.
Estado Transitorio : Los primeros días de ventas podrían mostrar variabilidad inicial hasta que se estabilizan, lo que en otras simulaciones podría descartarse para obtener datos de estado estable.
Estado Estable : Los días en los que el promedio de ventas se estabiliza reflejando el estado estable, donde el comportamiento es predecible.
Condiciones Iniciales : Las condiciones de entrada (media de clientes y gasto por cliente) son constantes, representando el entorno promedio en que opera la tienda.
Reloj de la Simulación : Cada paso diario es el avance en el "reloj" de la simulación, permitiendo ver cómo se comportan las ventas a lo largo del tiempo.

HOJA DE CALCULO DEL EJEMPLO
REALIZADA EN EXCEL
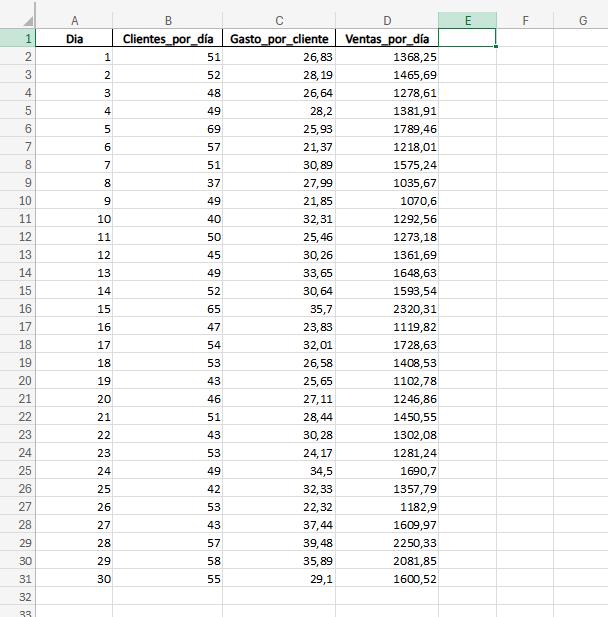
Explicación hoja de calculo
La hoja de calculo realizada en Excel contiene los siguientes elementos:
2.
1. Monto de Venta por Cliente : Valores generados aleatoriamente usando una distribución normal con un gasto promedio de $30 y desviación estándar de $5.
4.
Generación de Clientes Diarios : Valores aleatorios de clientes, con un promedio de 50 clientes por día.
3. Cálculo de Indicadores : Se calcularán el promedio, desviación estándar e intervalo de confianza del 95% para las ventas diarias.
Cálculo de Ventas Diarias : Producto del número de clientes y el gasto por cliente para cada día.
CODIGO QUE REALIZA SIMULACIÓN DEL EJEMPLO
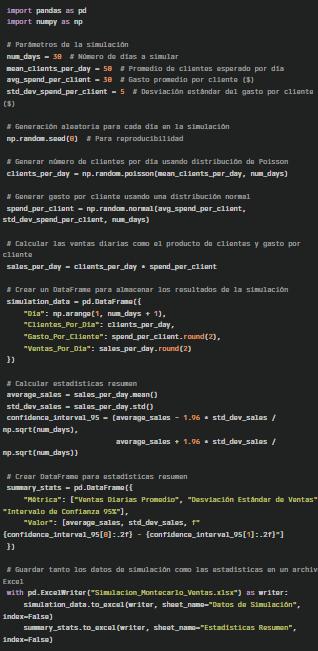
Explicación del codigo:
a continuación, explico de manera concisa el código: Importa pandas y numpy para manejar datos y cálculos.
1.
2.
Definir parámetros de simulación: días, clientes promedio, gasto promedio.
Genera datos aleatorios: 3.
Clientes por día (distribución Poisson)
Gasto por cliente (distribución normal)
4.
Calcula ventas diarias multiplicando clientes por gasto.
5.
Crea marcos de datos:
Uno con datos diarios de simulación.
Otro con estadísticas resumen (promedio, desviación estándar, intervalo de confianza)
6.
Guarde ambos DataFrames en un archivo Excel.
Este código simula las ventas diarias de un negocio, calcula estadísticas clave y exporta los resultados para análisis posterior.
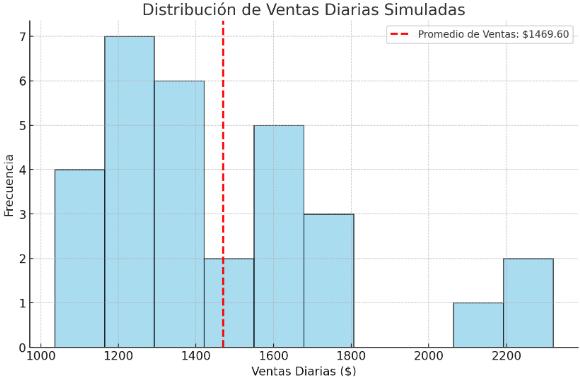
GRAFICO
A continuación, adjunto un gráfico de distribución de ventas diarias generadas por la simulación de Montecarlo. El gráfico incluye:
Un histograma de las ventas diarias para visualizar la frecuencia de cada rango de ingresos.
Una línea vertical en el promedio de ventas, representando el ingreso diario promedio esperado.
CONCLUSION
La construcción de modelos de simulación, especialmente a través de la técnica de Monte Carlo, se ha demostrado como una herramienta invaluable en la toma de decisiones empresariales. A lo largo de este trabajo, hemos explorado cómo un modelo simple puede ofrecer una comprensión profunda del comportamiento de las ventas diarias en un negocio, permitiendo a los profesionales anticipar resultados y gestionar riesgos de manera más efectiva.
El ejemplo práctico presentado, que utiliza Python y Excel para simular el número de clientes y el gasto por cliente, ilustra claramente cómo se pueden aplicar conceptos teóricos en un contexto real. A través de la generación de datos aleatorios y el cálculo de estadísticas clave, hemos podido obtener insights valiosos que pueden guiar la planificación financiera y la estrategia empresarial.
Además, esta simulación no solo proporciona un marco para evaluar el rendimiento esperado, sino que también permite a los gestores explorar diferentes escenarios y ajustar sus estrategias en función de las variaciones en las condiciones del mercado. La capacidad de visualizar el rango potencial de resultados a través del intervalo de confianza fortalece aún más la toma de decisiones informadas.
En resumen, los modelos de simulación son herramientas poderosas que, cuando se utilizan correctamente, pueden transformar la forma en que las organizaciones abordan la incertidumbre y planifican su futuro. La experiencia adquirida a través de este trabajo resalta la importancia de integrar técnicas analíticas avanzadas en la práctica empresarial cotidiana.
REFERENCIAS
IBM. (sf). ¿Qué es la simulación de Montecarlo?
Recuperado de https://www.ibm.com/eses/topics/monte-carlo-simulation
Chicaiza Moncayo, K., Gómez Sánchez, A., Ruiz
Antón, P., & Cevallos-Torres, L. (2019). Modelo de simulación para la optimización del inventario de una distribuidora, basado en Simulación Monte Carlo y Algoritmo Metaheurístico Genético. Revista Ecuatoriana de Ciencias, 3(2), 33-38. http://dx.doi.org/10.46480/esj.3.2.32
