PRUEVA DE HIPOTEISIS : KARLEY CHACON
JULIO 10 del 2025
INTRODUCCIÓN:
En el mundo actual de la estadística inferencial, las pruebas de hipótesis juegan un papel clave cuando se trata de tomar decisiones bien fundamentadas a partir de datos. Este método nos ayuda a responder una pregunta esencial: ¿podemos aceptar o rechazar una afirmación sobre una característica de la población (como la media o la varianza), basándonos en lo que observamos en una muestra?
Para ello, se plantean dos hipótesis enfrentadas: la hipótesis nula y la hipótesis alternativa. Luego, se analizan los datos y se aplican herramientas estadísticas, como la distribución normal o la t de Student, para evaluar cuál de las dos tiene más respaldo en la evidencia. Este enfoque se utiliza en muchísimas áreas desde la medicina y la economía hasta la psicología y la ingeniería, porque proporciona un marco obj ti para confirmar ideas, descubrir ortantes o comparar grupos de forma pre
Prueba de Hipótesis:
Este proceso implica formular dos hipótesis contrapuestas, recolectar datos, calcular un estadístico de prueba y comparar este valor con un valor crítico o un valor p para tomar una decisión. antes de meternos de lleno mostraremos algunos conceptos fundamentales:
Hipótesis Estadística:
Una hipótesis estadística es, en esencia, una idea o suposición que hacemos sobre alguna característica de una población; como un promedio, una proporción o la forma que tiene su distribución. Lo interesante es que estas afirmaciones no se quedan en teoría: se pueden someter a prueba usando datos reales obtenidos a partir de muestras.
Hipótesis Nula (H₀):
La hipótesis nula, representada por H₀, es el punto de partida en cualquier análisis estadístico. Se toma como verdadera hasta que los datos digan lo contrario. Por lo general, implica que no hay diferencias, efectos ni cambios significativos. Siempre incluye un signo de igualdad, como = , ≤ o ≥ porque se busca describir una situación “normal” o esperada.
Hipótesis Alternativa (Ha o H1):
Esta hipótesis es la afirmación que se acepta si la evidencia muestral es suficiente para rechazar la hipótesis nula. Representa lo que el investigador intenta demostrar o lo que se cree que es verdadero si la hipótesis nula es falsa. Siempre excluye el signo de igualdad (<, > , o =).
Prueba de Hipótesis:
¿Errores mas comunes?
Errores en la Prueba de Hipótesis:
Cuando se toman decisiones basadas en datos muestrales, hay que tener en cuenta que no estamos trabajando con toda la población, sino con una parte de ella. Por eso, siempre existe la posibilidad de cometer errores al interpretar los resultados.
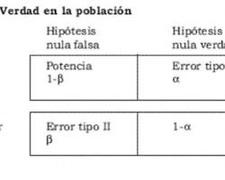
Error Tipo I (α): El falso positivo Este error ocurre cuando se rechaza la hipótesis nula (H₀), aun siendo verdadera. Es como dar por cierto algo que, en realidad, no lo es.
La probabilidad de cometer este error se llama nivel de significancia, y se representa con la letra griega α (alfa).Cuanto más pequeño es el valor de α, menor es la probabilidad de rechazar una hipótesis nula que realmente era correcta.
Error Tipo II (β):
Aquí pasa lo contrario: se acepta la hipótesis nula cuando en realidad es falsa. Es decir, no detectamos un cambio o efecto que sí existe.
1. La probabilidad de cometer este tipo de error se representa con la letra β (beta).
2. La potencia de una prueba, que es 1−β, nos indica qué tan efectiva es para detectar una hipótesis nula falsa. Lo ideal es tener una potencia alta.
Prueba de Hipótesis:
¿Etapas de una prueba de hipótesis?
El proceso de una prueba de hipótesis sigue una secuencia lógica y estructurada de pasos que garantizan la objetividad del análisis.
Cada etapa cumple una función clave para llegar a una conclusión estadísticamente válida. A continuación, se describen las etapas fundamentales:
Planteamiento de las hipótesis (H₀ y H₁): Es el primer y más importante paso. Consiste en establecer: Hipótesis nula (H₀): Representa el estado actual, la ausencia de efecto o diferencia. Siempre contiene un signo de igualdad (ej. μ = μ₀). Hipótesis alternativa (H₁): Propone una diferencia, cambio o efecto. Puede ser:
Unilateral derecha: H₁: μ > μ₀
Unilateral izquierda: H₁: μ < μ₀
Elección del nivel de significancia (α):
Este valor representa la probabilidad de cometer un error tipo I (rechazar H₀ cuando es verdadera). Se fija antes de analizar los datos.
Valores comunes: α = 0.05, 0.01, 0.10
Cuanto más pequeño el α, menor la probabilidad de error tipo I, pero mayor la posibilidad de cometer un error tipo II.
Determinación de la región crítica o cálculo del valor p Región crítica: Se define a partir del nivel de significancia α y la distribución del estadístico. Determina los valores extremos que llevarían al rechazo de H₀.
Valor p: Es la probabilidad de obtener un resultado igual o más extremo que el observado si H₀ fuera verdadera.
Si el valor del estadístico cae en la región crítica → se rechaza H₀. Si valor p ≤ α → se rechaza H₀.
Si valor p > α → no se rechaza H₀.
Prueba de Hipótesis:
Valor p (p-value): El valor p (o p-value) es la probabilidad de obtener un estadístico de prueba tan extremo o más extremo que el observado en la muestra, asumiendo que la hipótesis nula es verdadera.
Regla de Decisión basada en el Valor p:
Si p≤α: Se rechaza la hipótesis nula (H0). Esto indica que la evidencia de la muestra es estadísticamente significativa para apoyar la hipótesis alternativa.
Si p>α: No se rechaza la hipótesis nula (H0). Esto indica que no hay suficiente evidencia estadísticamente significativa para rechazar la hipótesis nula.
Estadístico de Prueba: es un valor numérico calculado a partir de los datos obtenidos en la muestra, utilizado para decidir si se rechaza o no la hipótesis nula dentro de una prueba estadística. Su elección depende del parámetro que se desea evaluar (como la media, la proporción o la varianza), del tipo de datos disponibles (cuantitativos o categóricos), de las características de la población (si se conoce o no su varianza), y del tamaño de la muestra (grande o pequeña).
Región Crítica (Región de Rechazo):
La región crítica es el conjunto de valores del estadístico de prueba que llevarán al rechazo de la hipótesis nula. Estos valores están determinados por el nivel de significancia (α) y la distribución del estadístico de prueba bajo H0. Los valores que caen dentro de la región crítica son considerados "suficientemente extremos" para ser inconsistentes con H0.
Prueba de
Hipótesis
obre una Sola
Media:
¿Qué es ?
Estas pruebas se utilizan para evaluar una afirmación sobre la media (μ) de una única población, utilizando datos de una muestra aleatoria de esa población.
A. Varianza Poblacional Conocida (σ2 Conocida):
Cuando la varianza poblacional (σ2) es conocida (lo cual es raro en la práctica, pero ocurre si se tiene información histórica o de censos completos), y la población es normal o el tamaño de la muestra es grande (n≥30) según el Teorema del Límite Central, se utiliza el estadístico Z. Hipótesis:
H0:μ=μ0
Ha:μ =μ0 (Bilateral), Ha:μ>μ0 (Unilateral Derecha), o Ha :μ<μ0 (Unilateral Izquierda)
B. Varianza Poblacional Desconocida (σ2 Desconocida):
Cuando la varianza poblacional (σ2) es desconocida (lo más común en la práctica) y se debe estimar a partir de la muestra, se utiliza el estadístico t de Student. Esto es aplicable si la población es normal o si el tamaño de la muestra es suficientemente grande (aunque para muestras grandes n≥30, la distribución t se aproxima a la normal, sigue siendo técnicamente más correcto usar la t).
Prueba de Hipótesis obre dos Media:
Estas pruebas se utilizan para comparar las medias de dos poblaciones, basándose en datos de dos muestras independientes tomadas de esas poblaciones. Es fundamental que las muestras sean independientes, es decir, que la selección de elementos en una muestra no afecte la selección de elementos en la otra.
A. Varianzas Poblacionales Conocidas (σ12 y σ22 Conocidas):
Esta situación, aunque poco común, se aplica cuando se tiene información precisa sobre las varianzas de ambas poblaciones (σ12 y σ22). Las poblaciones deben ser normales, o los tamaños de muestra suficientemente grandes (n1≥30 y n2≥30).
B. Varianzas Poblacionales Desconocidas pero Asumidas Iguales (σ12=σ22 Desconocidas):
Esta es una situación común donde no se conocen las varianzas poblacionales, pero hay razones (basadas en conocimiento previo o una prueba preliminar de igualdad de varianzas, como la prueba F) para asumir que son iguales. La distribución t de Student es utilizada. Es esencial que ambas poblaciones sean normales.
Hipótesis:
H0:μ1 μ2=D0
Ha:μ1−μ2 =D0, Ha:μ1−μ2>D0, o Ha:μ1−μ2<D0
¿sabias que? El concepto moderno de prueba de hipótesis fue formalizado en los años 1920 por el estadístico Ronald Fisher, ¡y originalmente no incluía la hipótesis nula! Fue Neyman y Pearson quienes introdujeron ese concepto después, revolucionando cómo se toman decisiones basadas en datos.
¿Qué es CDMA con Salto de Frecuencia?: ¿Que
Es?:
El CDMA (Code Division Multiple Access) es una técnica de acceso múltiple que permite que varios usuarios compartan el mismo canal de comunicación al mismo tiempo y en la misma frecuencia, pero diferenciándose mediante códigos únicos. Cada usuario tiene un código pseudoaleatorio que “firma” su señal, y gracias a eso, el receptor puede identificar y extraer solo la información que le corresponde, ignorando el resto.
Recordemos que, cuando a esta técnica se le añade el salto de frecuencia (lo que se conoce como FH-CDMA, por Frequency Hopping), la señal no solo está codificada, sino que va cambiando de frecuencia constantemente según un patrón conocido por el transmisor y el receptor. Es como si la señal “saltara” de un canal a otro en milisegundos, siguiendo una coreografía secreta.
¿Cómo funciona CDMA?
1.El transmisor modula los datos con un código de expansión.
2.Esta modulación produce una señal de ancho de banda mucho mayor al original (espectro ensanchado).
3.Todas las señales se transmiten simultáneamente en el mismo canal.
4.El receptor usa el mismo código para extraer la señal deseada.
CONCLUSIÓN:
La prueba de hipótesis es una herramienta esencial dentro de la estadística inferencial. Gracias a ella, investigadores y profesionales pueden tomar decisiones fundamentadas sobre una población a partir de datos limitados de muestras. Para que este proceso sea realmente útil, es clave entender bien conceptos como las hipótesis nula y alternativa, los errores tipo I y II, y el valor p, ya que interpretarlos de forma correcta marca la diferencia entre una conclusión confiable y una equivocada. Una elección incorrecta puede hacer que los resultados pierdan sentido. Por eso, antes de aplicar cualquier prueba, es fundamental revisar si sus supuestos se cumplen. Aunque el software estadístico hoy en día hace que el cálculo sea rápido y preciso, entender lo que hay detrás de cada número sigue siendo crucial para darle sentido a los resultados y evitar interpretaciones erróneas. .