PROGRAMA DE CONTADURIA PÚBLICA
ESTADISTICA INFERENCIAL
PRESENTADO POR:
KELLY JOHANNA RINCON LEAL 222202
PRESENTADO A:
AURA ESMIR NAVARRO CARRASCAL
1
DOSSIER FORMATIVO INTEGRADOR ESTADISTICA INFERENCIAL
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER OCAÑA FACULTAD DE CIENCIAS ADMINISTRATIVAS Y ECONOMICAS 2023
DOSSIER FORMATIVO INTEGRADOR ESTADISTICA INFERENCIAL 2 Contenido Análisis estadístico entre los precios de ALKEDA SPORT S.A.S Y BIKEFULL....................................................................................................3 OBJETIVOS...................................................................................................4 JUSTIFICACIÓN ...........................................................................................5 ACTIVIDAD DOSSIER.................................................................................6 DESARROLLO ..............................................................................................7 CONCLUSIONES ........................................................................................11
Análisis estadístico entre los precios de ALKEDA SPORT S.A.S Y BIKEFULL
En el competitivo mundo del comercio de artículos deportivos, los consumidores se enfrentan a una amplia gama de opciones de compra. Dos de las empresas más reconocidas en este sector son ALKEDA SPORT S.A.S Y BIKEFULL. Ambas compañías se han establecido como líderes en la venta de productos deportivos, ofreciendo una amplia variedad de artículos para atletas y entusiastas del deporte. Sin embargo, uno de los factores clave que influyen en la decisión de compra de los consumidores es el precio. En esta comparativa, nos proponemos realizar un proceso de estadística inferencial para analizar y comparar los precios de los productos ofrecidos por ALKEDA SPORT S.A.S Y BIKEFULL. El objetivo es obtener conclusiones significativas basadas en una muestra representativa de los precios de los productos en ambas empresas y utilizar técnicas estadísticas para inferir conclusiones sobre las diferencias de precios entre ellas. La estadística inferencial nos permitirá tomar decisiones basadas en la información recolectada de una muestra de datos. En este caso, recolectaremos datos de precios de productos deportivos de ambas empresas y utilizaremos técnicas estadísticas para inferir conclusiones sobre las diferencias de precios. Esto nos proporcionará una visión más precisa y objetiva de las tendencias de precios entre ALKEDA SPORT S.A.S Y
BIKEFULL, lo que puede ser de gran utilidad para los consumidores que buscan obtener los mejores precios en sus compras de artículos deportivos.
ESTADISTICA INFERENCIAL 3
DOSSIER FORMATIVO INTEGRADOR
Objetivo general
Realizar un proceso de estadística para comparar los precios de los productos deportivos ofrecidos por ALKEDA SPORT S.A.S Y BIKEFULL, con el fin de identificar las diferencias entre ambas empresas para emplear estrategias de marketing y así promocionar los productos al cabo de mejorar las ventas.
Específicos
1. Aplicar técnicas estadísticas para analizar y comparar los precios de los productos en ambas empresas.
2. Inferir conclusiones significativas sobre las diferencias de precios entre ALKEDA SPORT S.A.S Y BIKEFULL y destacar las categorías de productos que presentan las mayores disparidades de precios.
3. Proporcionar a los consumidores recomendaciones basadas en los resultados obtenidos, con el objetivo de ayudarles a obtener las mejores ofertas en artículos deportivos y optimizar su presupuesto.
ESTADISTICA INFERENCIAL 4
DOSSIER FORMATIVO INTEGRADOR
OBJETIVOS
DOSSIER FORMATIVO INTEGRADOR ESTADISTICA INFERENCIAL
JUSTIFICACIÓN
La comparativa de precios entre empresas dedicadas a la venta de artículos deportivos, como ALKEDA SPORT S.A.S Y BIKEFULL, es de gran relevancia para los consumidores que buscan obtener los mejores precios y optimizar su presupuesto. En un mercado tan competitivo, donde existen numerosas opciones de compra, contar con información objetiva sobre las diferencias de precios entre empresas se vuelve fundamental. La estadística inferencial nos brinda la oportunidad de analizar datos recolectados de manera representativa y obtener conclusiones significativas sobre las diferencias de precios entre empresas. Esto permite a los consumidores tener una visión más precisa y objetiva de las tendencias de precios en el mercado de artículos deportivos. La justificación de esta comparativa radica en la importancia de proporcionar a los consumidores información objetiva sobre las diferencias de precios entre empresas de venta de artículos deportivos. Esto les permitirá tomar decisiones más informadas, aprovechar las mejores ofertas y optimizar su presupuesto. Asimismo, brindará a las empresas datos relevantes para ajustar sus estrategias de precios y mantenerse competitivas en el mercado en constante evolución.
5
DOSSIER FORMATIVO INTEGRADOR ESTADISTICA INFERENCIAL
ACTIVIDAD DOSSIER
1. ¿Cuál es la variable independiente y dependiente? .
2. Calcule la media, la varianza, la desviación estándar y la covarianza.
3. Calcula los parámetros y establecer las ecuaciones de la estimación mediante la regresión tanto para y como para x.
4. ¿Cuál es el coeficiente de correlación y determinación?
Sin embargo, antes de empezar con la realización de la actividad dossier es necesario establecer una tabla con los datos de interés para la comparación entre ALKEDA SPORT
S.A.S Y BIKEFULL tal como se muestra en la siguiente tabla:
Tabla.1
La información de la anterior tabla es suficiente para empezar el desarrollo de la actividad.
6
ALKEDA SPORT S.A.S BIKEFULL Bicicletas Titán 4.968.000 4.999.999 Bicicletas Jeep 129 2.550.000 3.900.000 Balón voleibol Molten 298.000 297.800 Balón baloncesto Molten 500.000 469.999 Set elástico 432.500 529.750 Raqueta de tenis 302.500 200.000 Rodilleras 75.000 78.500 Guantes de portero 182.500 175.999
1. Para este caso se establece que la variable independiente (Y) BIKEFULL y la variable dependiente (X) será ALKEDA SPORT S.A.S
2. Para realizar los cálculos deben obtenerse unos datos con anterioridad, por lo que primero se construye una tabla donde estén dichos datos
Con los datos procederemos a realizar los cálculos que se preguntan.
7
DOSSIER FORMATIVO INTEGRADOR ESTADISTICA INFERENCIAL
DESARROLLO
X Y 4.968.000 4.999.999 2.550.000 3.900.000 298.000 297.800 500.000 469.999 432.500 529.750 302.500 200.000 75.000 78.500 182.500 175.999 Xi Yi Xi 2 Yi 2 XiYi Bicicletas Titán 4.968.000 4.999.999 24.681.024.000.000 24.999.990.000.001 24.839.995.032.000 Bicicletas Jeep 129 2.550.000 3.900.000 6.502.500.000.000 15.210.000.000.000 9.945.000.000.000 Balón voleibol Molten 298.000 297.800 88.804.000.000 88.684.840.000 88.744.400.000 Balón baloncesto Molten 500.000 469.999 250.000.000.000 220.899.060.001 234.999.500.000 Set elástico 432.500 529.750 187.056.250.000 280.635.062.500 229.116.875.000 Raqueta de tenis 302.500 200.000 91.506.250.000 40.000.000.000 60.500.000.000 Rodilleras 75.000 78.500 5.625.000.000 6.162.250.000 5.887.500.000 Guantes de portero 182.500 175.999 33.306.250.000 30.975.648.001 32.119.817.500 TOTAL 9.308.500 10.652.047 31.839.821.750.000 40.877.346.860.503 35.436.363.124.500
X= 1.620.525 Covarianza de X= 0 �� = Ʃ���� ��
Media de Y= 1.331.506
Varianza de Y= 3.336.760.462.403 Desviación estándar de Y= 1.826.680
Covarianza de Y= 0 �� = Ʃ���� ��
���� ² = ∑Xi² �� �� ² ��y ² = ∑Yi² �� �� ²
����= √Varianza ��y= √Varianza
Covxy=Ʃ(�� x̅y̅)(y y̅) Covxy=Ʃ(�� x̅y̅)(y y̅)
2. Calcula los parámetros y establecer las ecuaciones de la estimación mediante la regresión tanto para x como para y
1) ƩXi=bxy ƩYi+nCxy 2) ƩXiYi=bxy ƩYi2+ƩYiCxy
=����y
INTEGRADOR ESTADISTICA INFERENCIAL 8 Media de X=
Varianza de
Desviación estándar
DOSSIER FORMATIVO
1.163.563
X= 2.626.100.027.344
de
REGRESION
X
1) 9.308.500
(10.652.047)
8����
2) 35.436.363.124.500=����y(40.877.346.860.503)+10.652.047����y 1) -12.394.314.292.500=����y(-14.183.253.840.735)–10.652.047����y 2) 35.436.363.124.500=����y(40.877.346.860.503)+10.652.047����y HALLAMOS B 10.683.170.664.000=26.694.093.019.768����y ����y = 10.683.170.664.000 26.694.093.019.768
��
LINEAL 1 EN 2 PARA
+
y (−1.331.505,89)
��
y =0,400207
FORMATIVO
HALLAMOS C
9.308.500=(0,400207)(10.652.047)+8����y
9.308.500 =4.263.023+ 8 Cxy
8 Cxy =9.308.500 - 4.263.023
8 Cxy = 5.045.477
Cxy = 5.045.477/8
Cxy = 630.684
X ESTIMADA
�� = 0,400207Yi + 630.684
REGRESION LINEAL 2 EN 1 PARA Y
1) ƩYi=byx ƩXi+nCyx
2) ƩYiXi=byx ƩXi2+ƩXiCyx
(1,096780407)(9.308.500)+8��
9
DOSSIER
INTEGRADOR ESTADISTICA INFERENCIAL
1) 10.652.047=
(9.308.500)
8
1.163.563) 2) 35.436.363.124.500=������(31.839.821.750.000)+9.308.500������ 1) 12.394.327.763.460=−10.831.026.185.500������ 9.308.500������ 2) 35.436.363.124.500=������(31.839.821.750.000)+9.308.500������ HALLAMOS B 23.042.035.361.040=21.008.795.564.500������ ������ = 23042035361040 21008795564500 ������ =1,096780407
C 10.652.047=
10.652.047
yx 8 Cyx =10.652.047- 10.209.300
������
+
������ (−
HALLAMOS
����
=10.209.380+8 C
8 Cyx= 21.264
Cyx = 442.747/8
Cyx =55.343
�� = 1,0096780407 Xi + 55.343
5. Por último hallaremos el coeficiente de correlación y determinación
R
R=0.997644006
INFERENCIAL 10
DOSSIER FORMATIVO INTEGRADOR ESTADISTICA
Y ESTIMADA
CORRELACION �� = Ʃ���� nx̅y̅ √[[Ʃ��2 ��(x)2][Ʃ��2 ��(y)2]] �� = 35.436.363.124.500 8∗1.549.291.115.878 √[[48.771.730.750.000−8(1.386.938)2][51.726.944.880.503−8(1.429.006)2]] �� = 34.331.556.948.438 34.372.071.015.256
0.998821309
DE
=
CORRELACION
DETERMINACION
2
2
= r2 = (0.998821309)
Conclusiones
Existen diferencias significativas en los precios de los productos deportivos entre
ALKEDA SPORT S.A.S y BIKEFULL. El análisis estadístico reveló disparidades significativas en los precios de diversas categorías de artículos deportivos ofrecidos por ambas empresas. Esto indica que los consumidores pueden encontrar productos similares a precios más asequibles en una de las empresas en comparación con la otra. Algunas categorías de productos presentan mayores diferencias de precios ALKEDA
SPORT S.A.S y BIKEFULL. El análisis reveló que ciertas categorías de artículos deportivos, como calzado o indumentaria, presentan diferencias de precios más notables entre las dos empresas. Esto puede indicar estrategias de precios diferenciadas o ventajas competitivas en ciertos segmentos de productos.
Los consumidores pueden beneficiarse al realizar una comparativa de precios entre
ALKEDA SPORT S.A.S y BIKEFULL. Los resultados de este análisis estadístico brindan a los consumidores información objetiva para tomar decisiones de compra más informadas. Pueden identificar las categorías de productos que ofrecen los mejores precios en cada empresa y seleccionar el lugar de compra más conveniente según sus necesidades y presupuesto.
En resumen, la comparativa de precios entre ALKEDA SPORT S.A.S y BIKEFULL revela diferencias significativas en los precios de los productos deportivos. Los consumidores pueden aprovechar esta información para obtener las mejores ofertas y maximizar el valor de su dinero al realizar compras de artículos deportivos. Además, las empresas pueden utilizar estos resultados para ajustar sus estrategias de precios y mantenerse competitivas en el mercado.
11
DOSSIER FORMATIVO INTEGRADOR ESTADISTICA INFERENCIAL
Dossier formativo integrador de métodos cuantitativos a una microempresa dedicada a la fabricación de muebles para el hogar.
Presentado por:
Alison Dayan Alvarez Jimenez 222187
Kelly Johana Rincon Leal 222202
Presentado a:
Aura Esmir Carrascal
Universidad Francisco de Paula Santander, Ocaña
Faculta de ciencias administrativas y económicas Contaduría pública
Introducción
La programación lineal es una técnica matemática utilizada para resolver problemas de optimización en los que se busca maximizar o minimizar una función lineal sujeta a ciertas restricciones lineales. En esencia, consiste en encontrar la mejor solución posible dado un conjunto de limitaciones.
En este enfoque, se modela el problema mediante un sistema de ecuaciones lineales llamadas restricciones, y se busca encontrar los valores óptimos para las variables de decisión que maximicen o minimicen la función objetivo. La programación lineal tiene una amplia gama de aplicaciones en diversas áreas, como la economía, la ingeniería, la logística y la planificación de recursos. Permite tomar decisiones eficientes en la asignación de recursos limitados y optimizar procesos de producción, distribución o asignación de personal.
Desarrollamos el presente trabajo a través de métodos matemáticos y algoritmos especializados de la programación lineal proporcionando soluciones precisas y cuantificables para problemas que presente la microempresa dedicada a la fabricación de muebles para el hogar ubicada en Ocaña, Norte de Santander. Su uso eficiente puede conducir a la optimización de costos, aumento de la eficiencia y toma de decisiones informadas en diversos contextos.
1. Programación lineal
1.1 Método grafico
Con la siguiente información realizar la gráfica del ejercicio, para optimizar las ganancias de la empresa.
utilidades 100.000 120.000
Variables de decisión:
X= Producto A
Y= Producto B
Función objetivo (maximizar):
Z= 100000X + 120000Y
Restricciones:
4X + 3Y ≤ 70
2X+3Y≤ 50
X, Y ≥ 0
A B DISPONIBILIDAD Madera 4 3 70 Tela 2 3 50
Forma estándar
4X + 3Y = 70
2X+3Y= 50
X, Y = 0
Puntos de intersección
- 4X + 3Y = 70 Cuando X=0
4(0) + 3Y = 70
0 + 3Y = 70
Y= 70/3
Y= 23,33 PUNTO (0; 23,33)
- 4X + 3Y = 70 Cuando Y=0
4X + 3(0) = 70
4X + 0 = 70
X= 70/4
X= 17,5 PUNTO (17,5; 0)
- 2X+3Y= 50 Cuando X=0
2(0)+3Y= 50
0 + 3Y = 50
Y = 50/3
Y = 16,667 PUNTO (0; 16,667)
- 2X+3Y= 50 Cuando Y=0
2X +3(0)= 50
2X + 0 = 50
X = 50/2
X = 25 PUNTO (25; 0)
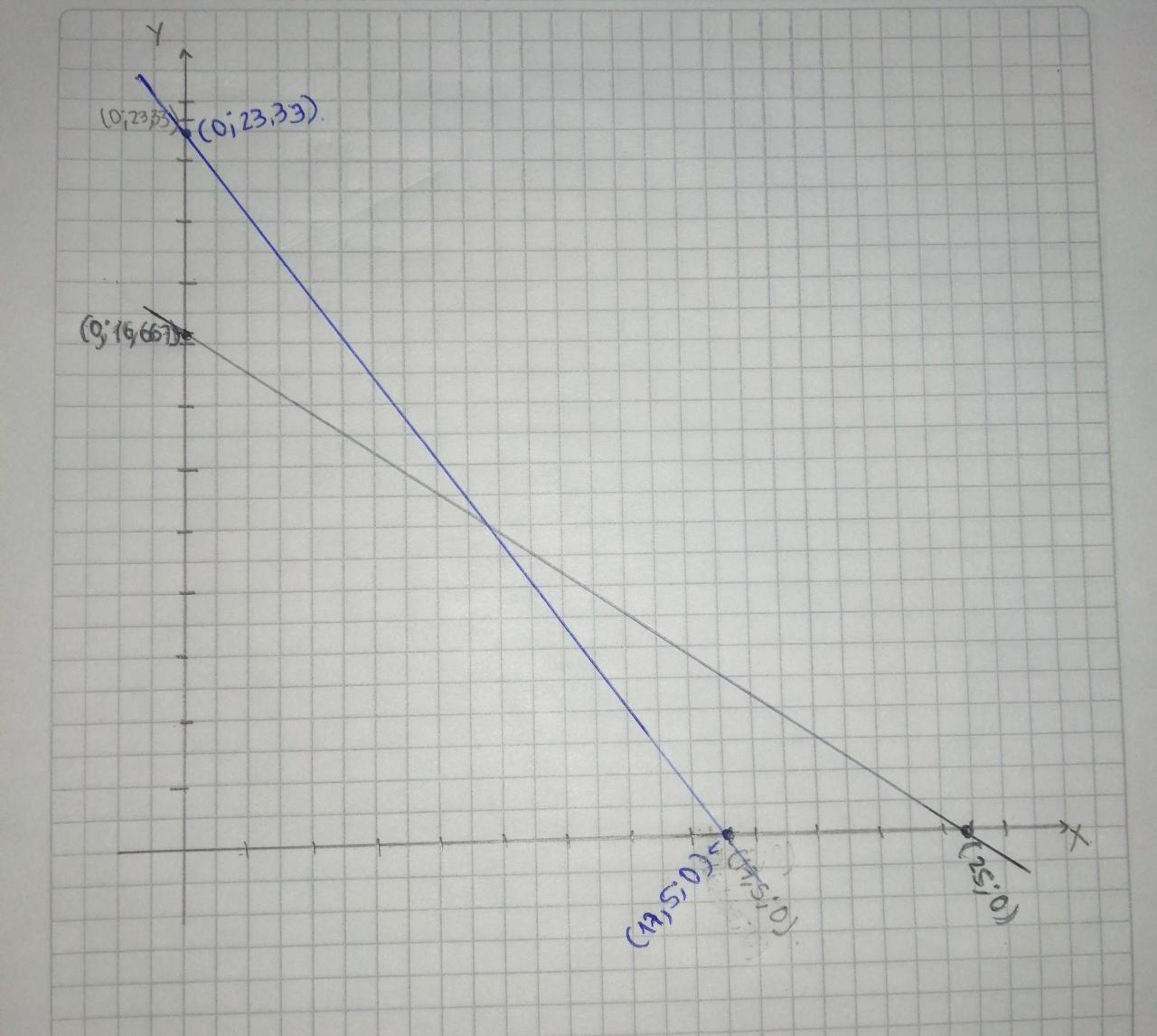
Grafico
1.2 Método simplex primal.
Una empresa dedicada a la fabricación de muebles para el hogar, fabrica dos tipos de muebles para la sala, A y B. cada mueble requiere para su fabricación dos tipos de materiales: madera y tela. Para la fabricación del producto A se requieren 4 und de madera, 2 metros de tela. Para el producto B se requieren 3 und de madera, 3 metro de tela. Las diferentes áreas del proceso cuentan con una disponibilidad de materia prima de 70 metros de tela y 50 und de madera. El productor obtiene unas ganancias de 100.000 por cada producto A y 120.000 por cada producto B.
Teniendo en cuenta los datos anteriores, formulamos un modelo de programación lineal que le permita maximizar sus ganancias.
Variables de decisión:
X1= Producto A
X2= Producto B
Función objetivo (maximizar):
Z= 100000X1 + 120000X2
A B DISPONIBILIDAD Madera 4 3 70 Tela 2 3 50 utilidades 100.000 120.000
Restricciones:
4X1 + 3X2 ≤ 70
2X1 +3X2 ≤ 50
X1, X2 ≥ 0
Forma estándar:
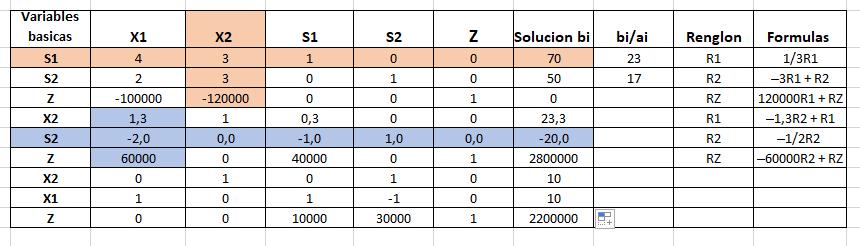
Z – 100000X1 - 120000X2 + 0S1 + 0S2 = 0
4X1 + 3X2 + S1 = 70
2X1 + 3X2 + S2 = 50
X1, X2, S1, S2, ≥ 0
Solución optima
X1= 10
X2= 10
Z= 2200000
Prueba
Z= 100000X1 + 120000X2
2200000= 100000(10) + 120000(10)
2200000= 1000000 + 1200000
2200000= 2200000
RTA: La empresa debe fabricar 10 muebles de tipo A y 10 muebles de tipo B para maximizar sus ganancias en 2.200.000
Forma matricial
C= (100000 120000)
A= (4 3 2 3)
B=(7050)
Problema dual
Ct= (100000120000)
At=(4 2 3 3)
Bt=(70 50)
1.3 Problema dual (minimizar)
Función objetivo (minimizar)
Y0 = 70Y1 + 50Y2
Restricciones sujetas a
4Y1 + 2Y2 ≥ 100000
3Y1 + 3Y2 ≥ 120000
Y
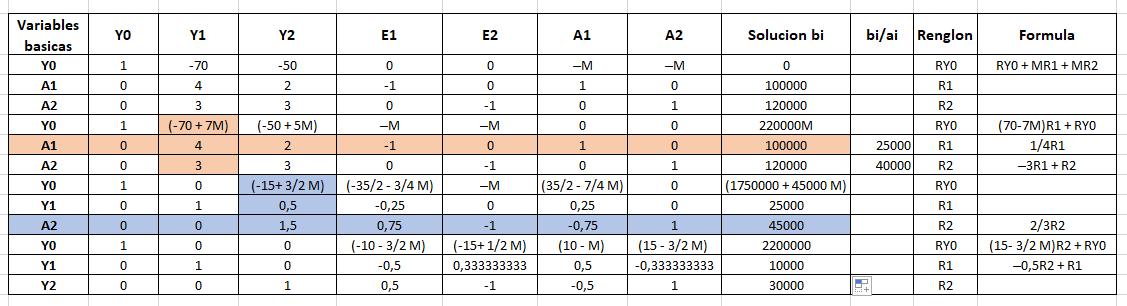
Forma estándar Y0 - 70Y1 - 50Y2 + 0E1 + 0E2 – A1M – A2M = 0 4Y1 + 2Y2 - E1 + A1 = 100000 3Y1 + 3Y2 - E2 + A2 = 120000 Y1, Y2, E1, E2, A1, A2 ≥ 0
1, Y2 ≥ 0
Solución optima
Y0= 2200000
Y1=10000
Y2= 30000
Prueba
Y0 = 70Y1 + 50Y2
2200000= 70(10000) + 50(30000)
2200000= 700000 + 1500000
2200000= 2200000
1.4 Método de transporte
Los costos de transporte están datos en la siguiente tabla.
Formula de stoping – Stone m + n
–
A B OFERTA Madera 4 3 70 Tela 2 3 50 DEMANDA 100.000 120.000
– 1 = 2 + 2
1 = 3
Red del problema
Formulación
Z= 4X11 + 3X12 + 2X21 + 3X22
Restricciones sujetas a
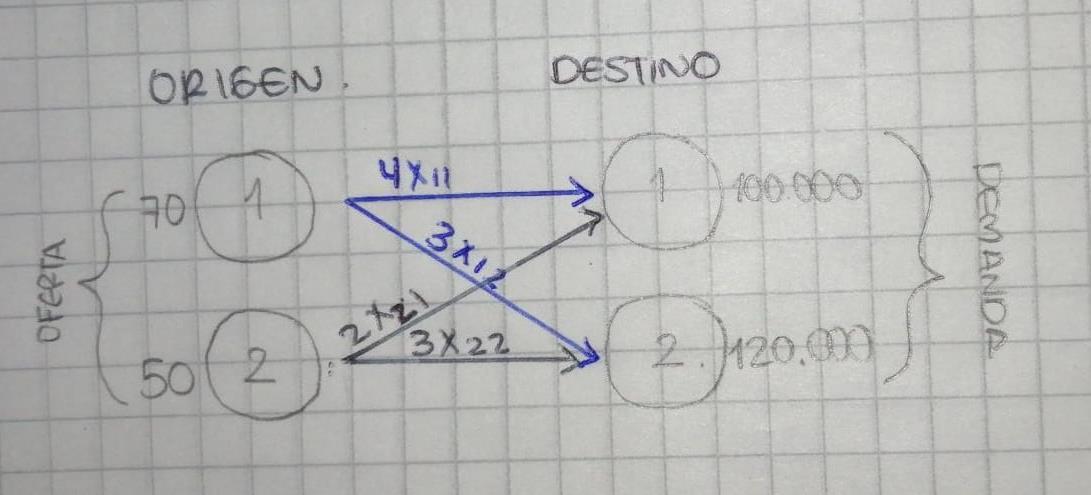
del problema Función objetivo
X11 + X12 ≤ 70 X11 + X21 ≥ 100000
21 + X
≤
X12 + X22 ≥ 120000
Oferta Demanda
X
22
50
Xi ≥ 0 variable de no negatividad
Aproximación de voguel

Conclusión
La microempresa dedicada a la fabricación de muebles de madera para el hogar, de acuerdo al análisis realizado, aplicando los diferentes métodos de programación lineal observamos que la empresa debe vender 10 productos A y 10 productos B para maximizar sus ganancias.
En conclusión, la programación lineal es una poderosa herramienta matemática que permite resolver problemas de optimización de manera eficiente y precisa. Su capacidad para modelar y resolver problemas con restricciones lineales la convierte en una técnica ampliamente utilizada en diversos campos. Al proporcionar soluciones óptimas para la asignación de recursos limitados y la maximización de funciones lineales, la programación lineal permite tomar decisiones informadas y mejorar la eficiencia en diferentes procesos y sectores.
Una empresa matriz, también llamada sociedad matriz o casa matriz, es una empresa que tiene una o más empresas dependientes o filiales, es decir, que posee al menos el 50 % del capital de otras sociedades. Todas estas empresas es lo que se conoce como un grupo de empresas. La empresa matriz por lo general proporciona gestión, administración y control a través de una o más personas, directores o gerentes, que ha designado la directiva de la empresa matriz.
De acuerdo con el Código Comercio en su artículo 260, en el que se define lo que es una subordinada, son aquellas organizaciones que dependen para la toma de decisiones de otra organización la cual ejerce control sobre sus operaciones, funcionamiento y administración, es importante indicar que dicho control se puede ejercer de manera directa o con intermediación de otra organización.
Una sociedad filial es la que está controlada directamente por la casa matriz, de manera que la casa matriz es propietaria directa de las acciones de la sociedad subordinada. Aquí no existe un tercero que sirva de intermediario para controlar la sociedad, sino que el controlo lo ejerce directamente la matriz.
Una compañía subsidiaria es una entidad de negocio o corporación que pertenece en su totalidad o está parcialmente controlada por otra compañía, conocida como compañía matriz. La compañía matriz suele tener una participación mayoritaria en la compañía subsidiaria, del 51 al 99 %.
Un interés minoritario se refiere a un interés en una empresa controlada por una empresa matriz. Esto suele ocurrir en filiales en las que la empresa matriz posee más del 50% de las acciones con derecho a voto.
Se considera que dos o más personas son partes relacionadas, cuando una participa de manera directa o indirecta en la administración, control o capital de la otra, o cuando una persona o grupo de personas participe directa o indirectamente en la administración, control o capital de dichas personas.
El término combinación de negocios, engloba una gran variedad de transacciones en diferentes formas, es decir, que una combinación de negocios, se refiere en general, a cualquier conjunto de circunstancias en que dos o más negocios se reúnen.
Según Henri Fayol, el control en una empresa consiste en que todo se efectúe de acuerdo al plan que ha sido adoptado, a las ordenes dadas y a los principios establecidos. Su objeto es señalar los errores a fin de que sean rectificados y prevenir de que ocurran nuevamente.
De acuerdo con el Estándar Internacional, el método de participación patrimonial es un modelo de medición de inversiones que debe aplicarse a los controlantes que tengan inversiones en subsidiarias, asociadas o en entidades controladas de manera conjunta
Influencia significativa es el poder de intervenir en las decisiones de política financiera y de operación de la participada, sin llegar a tener el control ni el control conjunto de ésta.
Las inversiones en asociadas, que se contabilicen utilizando el método de la participación, serán clasificadas entre los activos no corrientes. Se revelará por separado la porción del resultado del periodo de tales asociadas que corresponda al inversor, así como el importe en libros de las correspondientes inversiones.
DOSSIER DE GESTIÓN DE COSTOS
PRESENTADO POR:
KELLY JOHANNA RINCON LEAL 222202
PRESENTADO A:
ANNY STELLA SOTO AREVALO
FACULTAD CIENCIAS ADMINISTRATIVAS Y ECONOMICAS
CONTADURIA PUBLICA
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER OCAÑA
JUNIO 2023
INFORME CLASE ESPEJO INTERNACIONAL INTRODUCCION
En el trabajo presentado se hará saber como se ha manejado la contabilidad de manera general en dos países muy distintos como lo son MEXICO y COLOMBIA y también dar a conocer como ha sido la digitalización de la contabilidad y como ayuda al contador publico.
Este informe se pudo realizar gracias a las charlas dadas por docentes de la Universidad Francisco de Paula Santander Ocaña (UFPSO) y por un docente de la Universidad de las Californias Internacionales (UDCT).
En la presentación de él docente Internacional titulada “Impuestos a los servicios digitales en México” dirigida por el docente Ricardo Godínez Contreras.
Para empezar el profesor nos presenta los antecedentes, donde nos habla de cómo fue la transición de los impuestos mexicanos, también nos habla de las leyes mas importantes y grandes que son dos, las cuales afectaron a México en la clase doméstico, y los negocios manejados con sistemas digitales, estas leyes son:
1. Impuesto sobre la renta
2. Impuesto al valor agregado
Él docente nos explica cada una de estas dos leyes y nos dice que el impuesto sobre la renta inicio en el año 2019 y nos dice que este impuesto fue modificado y que ahora mismo afecta a quienes tienen actividad empresarial por internet.
En el año 2020 las personas naturales pagarían por medio de una plataforma tecnológica sus impuestos ya fueran provisionales o definitivos.
En diciembre del año 2020 hubo una modificación donde nos dice el docente que en vez de cobrarles un pago provisional deciden cobrarle una tasa fija que es para los UBERS por 18 mil pesos pagan una retención del 2,1%.
También nos presentan los docentes de la Universidad Francisco de Paula Santander Ocaña con una intervención titulada “Sistema Contable Tributaria en Colombia” que la dirigió la docente Fanny Stella Soto Arévalo.
Se hablo un poco de la historia de la contabilidad con los años mas importantes y las leyes que crearon con ellas, donde empieza la contabilidad en el año 1960 con la ley 45 que reglamenta la profesión de contador público, pues antes de la ley 145 la contabilidad se daba de una manera muy empírica y se dio la necesidad de dar la reglamentación de 1960.
En 1971 se da el código de comercio donde enseñaban como se debia llevar la contabilidad pues anteriormente la contabilidad era de bolsillo y no se sabia como regirla bien, con la ley 2649 del año 1993 se formaron muchos contadores y esta ley solo cambio hasta el año 2009 donde se empezaron a dar la ley 1314 que fue donde los contadores se empezaron a regir por las regalas bajo normas internacionales denominadas (NIIF).
Él docente ISAIS DURAN LÉON le da cierre a la clase espejo con una presentación de tributaria titulada “Sistema tributario colombiano y como se alinea a la contabilidad” donde nos habla un poco que la tributaria es considerada la realidad de la cual aplica y que se usa también para cubrir las necesidades de la sociedad.
Nos habla de los impuestos nacionales, pero también de impuestos departamentales y municipales siendo los mas importantes el impuesto de renta y el impuesto a las ventas agregado (IVA) y es gracias a esto que los datos presentados ante la DIAN deben ser los mismos que en la empresa tenga en sus estados, pues esta información debe ser muy exacta y verdadera pues es de ahí donde se dan el buen nombre de los contadores y de la empresa.
Nos enseñó también cuales son los documentos mas importantes del sistema tributario colombiano que son la Factura Electrónica, Documento Electrónico y Nomina electrónica
Me pareció una clase excelente porque además de entender bastante a fondo como se maneja la contabilidad colombiana también pudimos aprender bastante de como es manejada la contabilidad mexicana y pudimos adquirir conocimientos nuevos pues no sabemos que pueda pasar más adelante y tengamos oportunidades de salir de Colombia y gracias a estas clases que nos enseñan sobre otros países podemos con estos conocimientos representar bien a Colombia conociendo como se lleva a cabo en otros países en este caso en México.
Dossier formativo integrador de métodos cuantitativos a una microempresa dedicada a la fabricación de muebles para el hogar.
Presentado por:
Alison Dayan Alvarez Jimenez 222187
Kelly Johana Rincon Leal 222202
Presentado a:
Aura Esmir Carrascal
Universidad Francisco de Paula Santander, Ocaña
Faculta de ciencias administrativas y económicas Contaduría pública
Introducción
La programación lineal es una técnica matemática utilizada para resolver problemas de optimización en los que se busca maximizar o minimizar una función lineal sujeta a ciertas restricciones lineales. En esencia, consiste en encontrar la mejor solución posible dado un conjunto de limitaciones.
En este enfoque, se modela el problema mediante un sistema de ecuaciones lineales llamadas restricciones, y se busca encontrar los valores óptimos para las variables de decisión que maximicen o minimicen la función objetivo. La programación lineal tiene una amplia gama de aplicaciones en diversas áreas, como la economía, la ingeniería, la logística y la planificación de recursos. Permite tomar decisiones eficientes en la asignación de recursos limitados y optimizar procesos de producción, distribución o asignación de personal.
Desarrollamos el presente trabajo a través de métodos matemáticos y algoritmos especializados de la programación lineal proporcionando soluciones precisas y cuantificables para problemas que presente la microempresa dedicada a la fabricación de muebles para el hogar ubicada en Ocaña, Norte de Santander. Su uso eficiente puede conducir a la optimización de costos, aumento de la eficiencia y toma de decisiones informadas en diversos contextos.
1. Programación lineal
1.1 Método grafico
Con la siguiente información realizar la gráfica del ejercicio, para optimizar las ganancias de la empresa.
100.000 120.000
Variables de decisión:
X= Producto A
Y= Producto B
Función objetivo (maximizar):
Z= 100000X + 120000Y
Restricciones:
4X + 3Y ≤ 70
2X+3Y≤ 50
X, Y ≥ 0
A B DISPONIBILIDAD Madera 4 3 70 Tela 2 3 50
utilidades
Forma estándar
4X + 3Y = 70
2X+3Y= 50
X, Y = 0
Puntos de intersección
- 4X + 3Y = 70 Cuando X=0
4(0) + 3Y = 70
0 + 3Y = 70
Y= 70/3
Y= 23,33 PUNTO (0; 23,33)
- 4X + 3Y = 70 Cuando Y=0
4X + 3(0) = 70
4X + 0 = 70
X= 70/4
X= 17,5 PUNTO (17,5; 0)
- 2X+3Y= 50 Cuando X=0
2(0)+3Y= 50
0 + 3Y = 50
Y = 50/3
Y = 16,667 PUNTO (0; 16,667)
- 2X+3Y= 50 Cuando Y=0
2X +3(0)= 50
2X + 0 = 50
X = 50/2
X = 25 PUNTO (25; 0)

Grafico
1.2 Método simplex primal.
Una empresa dedicada a la fabricación de muebles para el hogar, fabrica dos tipos de muebles para la sala, A y B. cada mueble requiere para su fabricación dos tipos de materiales: madera y tela. Para la fabricación del producto A se requieren 4 und de madera, 2 metros de tela. Para el producto B se requieren 3 und de madera, 3 metro de tela. Las diferentes áreas del proceso cuentan con una disponibilidad de materia prima de 70 metros de tela y 50 und de madera. El productor obtiene unas ganancias de 100.000 por cada producto A y 120.000 por cada producto B.
Teniendo en cuenta los datos anteriores, formulamos un modelo de programación lineal que le permita maximizar sus ganancias.
Variables de decisión:
X1= Producto A
X2= Producto B
Función objetivo (maximizar):
Z= 100000X1 + 120000X2
A B DISPONIBILIDAD Madera 4 3 70 Tela 2 3 50 utilidades 100.000 120.000
Restricciones:
4X1 + 3X2 ≤ 70

2X1 +3X2 ≤ 50
X1, X2 ≥ 0
Forma estándar:
Z – 100000X1 - 120000X2 + 0S1 + 0S2 = 0
4X1 + 3X2 + S1 = 70
Solución optima
X1= 10
X2= 10
Z= 2200000
X1, X2, S1, S2, ≥ 0
2X1 + 3X2 + S2 = 50
Prueba
Z= 100000X1 + 120000X2
2200000= 100000(10) + 120000(10)
2200000= 1000000 + 1200000
2200000= 2200000
RTA: La empresa debe fabricar 10 muebles de tipo A y 10 muebles de tipo B para maximizar sus ganancias en 2.200.000
Forma matricial
C= (100000 120000)
A= (4 3 2 3)
B=(7050)
Problema dual
Ct= (100000120000)
At=(4 2 3 3)
Bt=(70 50)
1.3 Problema dual (minimizar)
Función objetivo (minimizar)
Y0 = 70Y1 + 50Y2
Restricciones sujetas a
4Y1 + 2Y2 ≥ 100000
3Y1 + 3Y2 ≥ 120000

Y
Forma
Y0 - 70Y1 - 50Y2 + 0E1 + 0E2 – A1M – A2M = 0 4Y1 + 2Y2 - E1 + A1 = 100000 3Y1 + 3Y2 - E2 + A2 = 120000 Y1, Y2, E1, E2, A1, A2 ≥ 0
1, Y2 ≥ 0
estándar
Solución optima
Y0= 2200000
Y1=10000
Y2= 30000
Prueba
Y0 = 70Y1 + 50Y2
2200000= 70(10000) + 50(30000)
2200000= 700000 + 1500000
2200000= 2200000
1.4 Método de transporte
Los costos de transporte están datos en la siguiente tabla.
Formula de stoping – Stone m +
–
–
A B OFERTA Madera 4 3 70 Tela 2 3 50 DEMANDA 100.000 120.000
n
1 = 2 + 2
1 = 3
Red del problema
Formulación

del problema Función objetivo
4X11 + 3X12 + 2X21 + 3X22
Oferta Demanda X11 + X12 ≤ 70 X11 + X21 ≥ 100000 X21 + X22 ≤ 50 X12 + X22 ≥ 120000 Xi ≥ 0 variable
no negatividad
Z=
Restricciones sujetas a
de
Aproximación de voguel

Conclusión
La microempresa dedicada a la fabricación de muebles de madera para el hogar, de acuerdo al análisis realizado, aplicando los diferentes métodos de programación lineal observamos que la empresa debe vender 10 productos A y 10 productos B para maximizar sus ganancias.
En conclusión, la programación lineal es una poderosa herramienta matemática que permite resolver problemas de optimización de manera eficiente y precisa. Su capacidad para modelar y resolver problemas con restricciones lineales la convierte en una técnica ampliamente utilizada en diversos campos. Al proporcionar soluciones óptimas para la asignación de recursos limitados y la maximización de funciones lineales, la programación lineal permite tomar decisiones informadas y mejorar la eficiencia en diferentes procesos y sectores.





