PROJECTIVE GEOMETREY DIGITAL DRAWING

Motif: Libeskind “Micromegas” Drawing

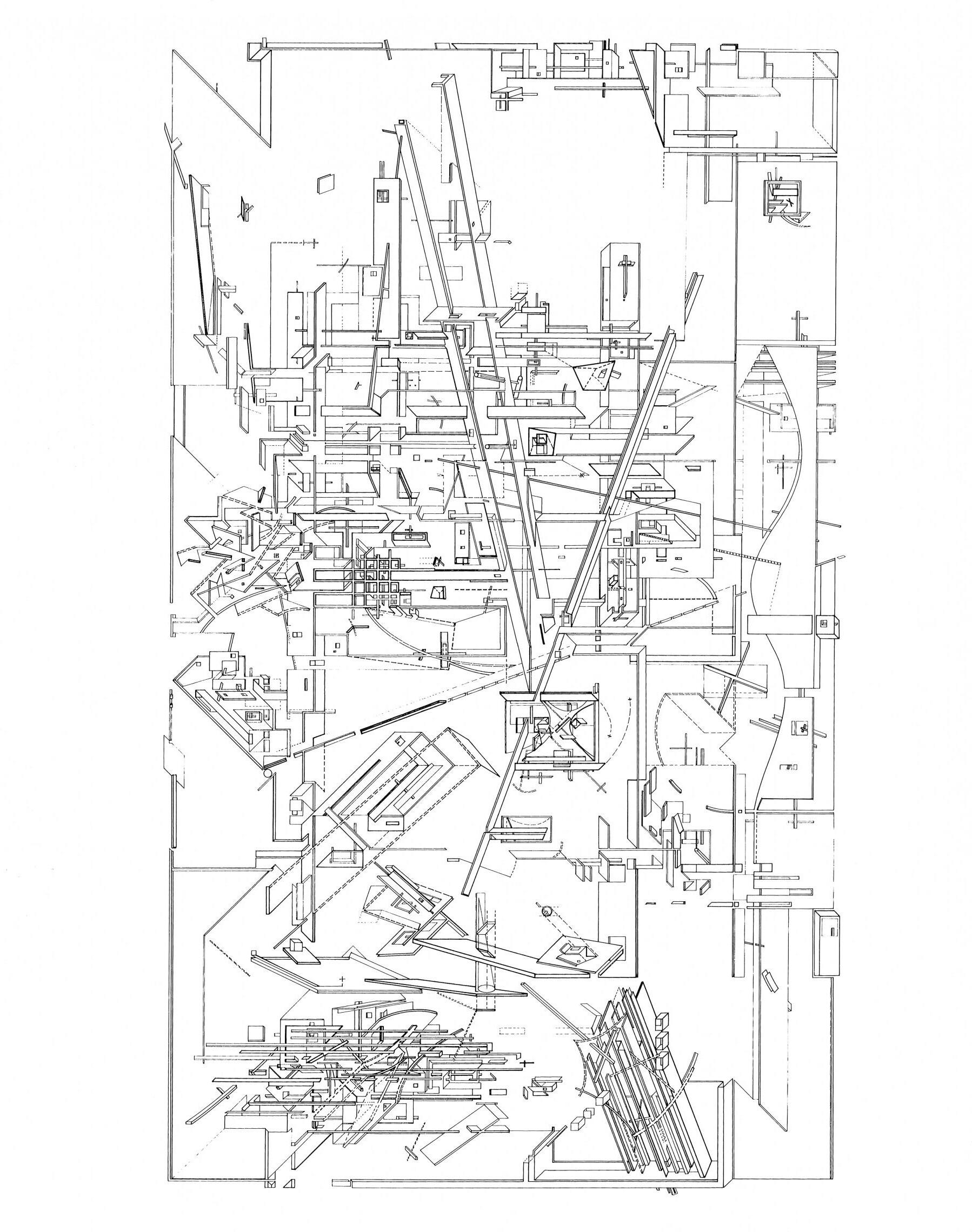
SPACE COMPLEX

Course: Media and Modeling

Instructor: Harris Dimitropoulos

Spring 2020

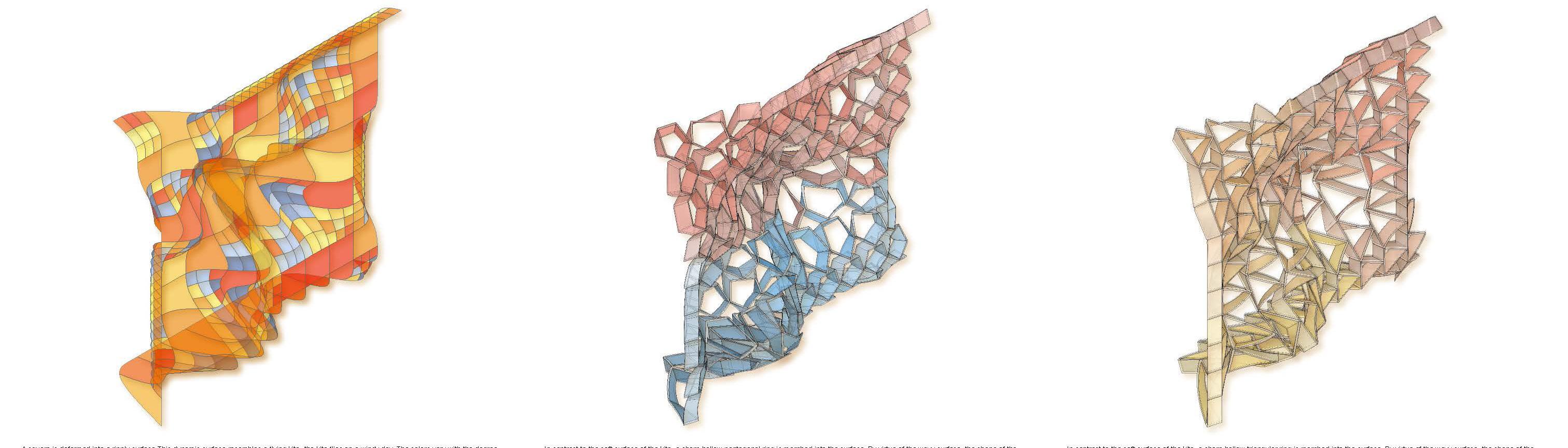
SURFACE CURVATURE ANALYSIS- A FLYING KITE TRIANGULAR WAVING

A square is deformed into a ripply surface.This dynamic surface resembles a flying kite- the kite flies on a windy day. The colors vary with the degree of curvature, and the highest degree of curvature on the kite is colored in blue.

Mathematic Forms I

Course: Media and Modeling II

Instructor: James Park

Spring 2020

In contrast to the soft surface of the kite, a sharp hollow pentagonal ring is morphed into the surface. By virtue of the wavy surface, the shape of the pentagon becomes dutile.The blue and orange seggregate the surface into a “hot zone” and a “cold zone”.

In contrast to the soft surface of the kite, a sharp hollow triangular ring is morphed into the surface. By virtue of the wavy surface, the shape of the triangle becomes dutile. The color gradient from orange to yellow is harmoniously displayed on the structure.

For this assignment, students will work individually to construct a parametric model of morphed tessellations in Grasshopper and generate surface curvature analysis and two design variations using the model. Students will learn fundamental concepts in parametric spatial transformations and how to create a spatial arrangement of a three-dimensional parametric motif specified by the morphing relations from a standard instance of the motif to the subdivisions of a complex surface with varying curvature.

Calla Lily symbolizes magnificant beauty. It is exquisite: even when it is full-blown, its outer petal strives upward.

Construct Point

X: ((a*cos(u))*sin(v))

Y: ((a*sin(u))*sin(v))

Z: (a*(cos(v)+log(tan((0.5*v)))))+(b*u)

This is a Turbo blade spinning in a fluctuating motion. The motion trail of the sharp rim creates a drapery pattern.

Construct Point

X: v*cos(u)

Y: v*sin(u)

Z: a*cos(b*u-v)

Mathematic Forms Ii

Course: Media and Modeling II

Instructor: James Park

Spring 2020

Nature produces elegant and organic geometry. A small creature has a marvelous universe and its center.

Construct Point

X: (1+cos(u/2)*sin(v)-sin(u/2)*sin(2*v))*cos(u)

Y: (1+cos(u/2)*sin(v)- sin(u/2)*sin(2*v))*sin(u)

Z: sin(u/2)*sin(v)+ cos(u/2)*sin(2*v)

For this assignment, students will work individually to construct a parametric model of mathematical surfaces in Grasshopper and generate a set of three variations using the model. Students will learn fundamental concepts of three-dimensional geometries and operations and how to develop a three-dimensional parametric surface specified by mathematical expressions.

Spatial