III
MATEMÁTICAS
Respuestas. a) La rampa 3.
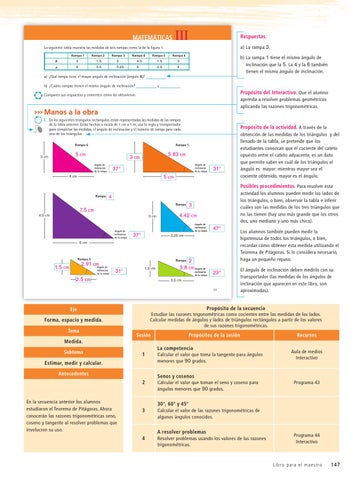
La siguiente tabla muestra las medidas de seis rampas como la de la figura 1.
b a
Rampa 1
Rampa 2
Rampa 3
Rampa 4
Rampa 5
Rampa 6
3
1.5
3
4.5
1.5
3
5
3.5
3.25
6
2.5
4
b) La rampa 1 tiene el mismo ángulo de inclinación que la 5. La 4 y la 6 también tienen el mismo ángulo de inclinación.
a) ¿Qué rampa tiene el mayor ángulo de inclinación (ángulo A)? b) ¿Cuáles rampas tienen el mismo ángulo de inclinación?
y
Propósito del Interactivo. Que el alumno aprenda a resolver problemas geométricos aplicando las razones trigonométricas.
Comparen sus respuestas y comenten cómo las obtuvieron.
Manos a la obra I. En los siguientes triángulos rectángulos están representadas las medidas de las rampas de la tabla anterior. Están hechos a escala de 1 cm a 1 m; usa tu regla y transportador para completar las medidas, el ángulo de inclinación y el número de rampa para cada uno de los triángulos. Rampa 1
Rampa 6
5 cm
3 cm
5.83 cm
3 cm Ángulo de inclinación de la rampa
Ángulo de inclinación de la rampa
37°
31°
5 cm
4 cm
Posibles procedimientos. Para resolver esta actividad los alumnos pueden medir los lados de los triángulos, o bien, observar la tabla e inferir cuáles son las medidas de los tres triángulos que no las tienen (hay uno más grande que los otros dos, uno mediano y uno más chico).
Rampa 6 4 Rampa 63
7.5 cm
4.5 cm
3 cm
Ángulo de inclinación de la rampa
4.42 cm Ángulo de inclinación de la rampa
37°
47°
3.25 cm
6 cm
Rampa 5
2.91 cmÁngulo de
1.5 cm
inclinación de la rampa
Rampa 62
31°
1.5 cm
3.8 cm Ángulo de
inclinación de la rampa
2.5 cm
23°
3.5 cm 131
MAT3 B4 S23.indd 131
Propósito de la actividad. A través de la obtención de las medidas de los triángulos y del llenado de la tabla, se pretende que los estudiantes conozcan que el cociente del cateto opuesto entre el cateto adyacente, es un dato que permite saber en cuál de los triángulos el ángulo es mayor: mientras mayor sea el cociente obtenido, mayor es el ángulo.
Los alumnos también pueden medir la hipotenusa de todos los triángulos, o bien, recordar cómo obtener esta medida utilizando el Teorema de Pitágoras. Si lo considera necesario, haga un pequeño repaso. El ángulo de inclinación deben medirlo con su transportador (las medidas de los ángulos de inclinación que aparecen en este libro, son aproximadas).
12/10/08 6:18:26 PM
Propósito de la secuencia Estudiar las razones trigonométricas como cocientes entre las medidas de los lados. Calcular medidas de ángulos y lados de triángulos rectángulos a partir de los valores de sus razones trigonométricas.
Eje Forma, espacio y medida. Tema
Sesión
Propósitos de la sesión
Recursos
Medida. Subtema
1
La competencia Calcular el valor que toma la tangente para ángulos menores que 90 grados.
2
Senos y cosenos Calcular el valor que toman el seno y coseno para ángulos menores que 90 grados.
3
30°, 60° y 45° Calcular el valor de las razones trigonométricas de algunos ángulos conocidos.
4
A resolver problemas Resolver problemas usando los valores de las razones trigonométricas.
Estimar, medir y calcular. Antecedentes
En la secuencia anterior los alumnos estudiaron el Teorema de Pitágoras. Ahora conocerán las razones trigonométricas seno, coseno y tangente al resolver problemas que involucren su uso.
Aula de medios Interactivo
Programa 43
Programa 44 Interactivo
Li b r o p ara e l maestro
MAT3 B4 S23 maestro.indd 147
147
12/11/08 12:01:36 PM