secuencia 21 Sugerencia didáctica. Asegúrese de que los alumnos hagan esta verificación, para ello pídales que marquen los ángulos internos en cada uno de los polígonos del apartado Consideremos lo siguiente.
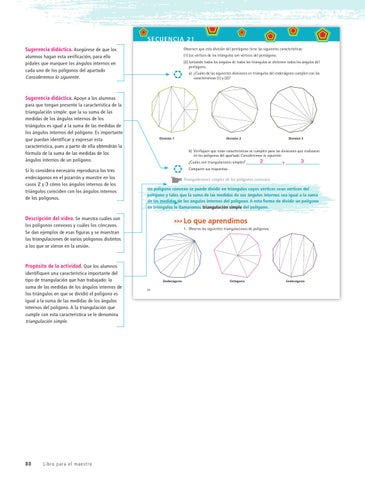
Observen que esta división del pentágono tiene las siguientes características: (1) Los vértices de los triángulos son vértices del pentágono. (2) Juntando todos los ángulos de todos los triángulos se obtienen todos los ángulos del pentágono. a) ¿Cuáles de las siguientes divisiones en triángulos del endecágono cumplen con las características (1) y (2)?
Sugerencia didáctica. Apoye a los alumnos para que tengan presente la característica de la triangulación simple: que la su suma de las medidas de los ángulos internos de los triángulos es igual a la suma de las medidas de los ángulos internos del polígono. Es importante que puedan identificar y expresar esta característica, pues a partir de ella obtendrán la fórmula de la suma de las medidas de los ángulos internos de un polígono. Si lo considera necesario reproduzca los tres endecágonos en el pizarrón y muestre en los casos 2 y 3 cómo los ángulos internos de los triángulos coinciden con los ángulos internos de los polígonos.
División 1
80
División 3
b) Verifiquen que estas características se cumplen para las divisiones que realizaron en los polígonos del apartado Consideremos lo siguiente. ¿Cuáles son triangulaciones simples?
2
y
3
Comparen sus respuestas.
Triangulaciones simples de los polígonos convexos
Un polígono convexo se puede dividir en triángulos cuyos vértices sean vértices del polígono y tales que la suma de las medidas de sus ángulos internos sea igual a la suma de las medidas de los ángulos internos del polígono. A esta forma de dividir un polígono en triángulos le llamaremos triangulación simple del polígono.
Descripción del video. Se muestra cuáles son los polígonos convexos y cuáles los cóncavos. Se dan ejemplos de esas figuras y se muestran las triangulaciones de varios polígonos distintos a los que se vieron en la sesión.
Propósito de la actividad. Que los alumnos identifiquen una característica importante del tipo de triangulación que han trabajado: la suma de las medidas de los ángulos internos de los triángulos en que se dividió el polígono es igual a la suma de las medidas de los ángulos internos del polígono. A la triangulación que cumple con esta característica se le denomina triangulación simple.
División 2
Lo que aprendimos 1. Observa las siguientes triangulaciones de polígonos.
Dodecágono
Octágono
Endecágono
64
MAT2 B3 S21.indd 64
9/10/07 12:33:35 PM
Libro p a ra e l m a e s t r o
MAT2 B3 S21 maestro.indd 80
9/10/07 1:12:02 PM