General Relativity and the Mathematics behind it Aaditya Nandwani

What is the most beautiful Physics theorem of all time? A physicist: if asked this, would find this question notoriously difficult to answer. The 19th and 20th centuries alone; were one of the most influential periods in scientific history; the vaults containing the most fundamental answers to the mechanisms of the universe finally being opened, releasing knowledge about light and EM waves, thermodynamics and quantum mechanics. However, if you were to ask a physicist this question; most of them would mention the theory of General Relativity. Just like Mozart’s requiem or Michelangelo’s Sistine Chapel, many would describe GR as an undying work of art; unifying ideas about space (and its geometry) and finally giving a more precise answer to how the enigmatic “force” of Gravity works. In this article, I hope to explain the development of General Relativity, how it works as well as why its contributions are so important to Physics.

Section 1: The development of General relativity:

An important part of the development of General relativity was the Equivalence principle, which bridged special relativity with General relativity. This principle builds upon the original Newtonian ideas about gravity, acceleration and motion. Newton’s second law states that the acceleration of an object is directly proportional to the net Force acting on the object, which is famously summed up by the equation F=mia (where mi is the mass and a is the acceleration) In this case the mass is known as the inertial mass; and this equation described how an objects motion changes with acceleration. However, he also stated that F=mg, where m is the gravitational mass. This states that if an object is in free fall, it will experience a force equivalent to the mass of the object multiplied by the constant of free fall (which is 9.8 ms-1). Einstein expanded on this and stated that the inertial mass (mass derived from Newton’s second law) is equal to the gravitational mass (derived from the latter equation). This leads us on to Einstein’s well-known elevator thought experiment. He imagined a person in an elevator, and the cables to the elevator snaps. The fate of this person is rather grim and unfortunate! However, he just focused on the period in which the elevator is falling. When the elevator is in free fall, he postulated that it is impossible for the person inside to tell the difference between gravitational effects and acceleration effects.

Einstein then used his thinking and expanded on the equivalence principle. He stated that the effects of acceleration and gravity are “locally indistinguishable”. This word “locally” is significant, it means that in a small region of space, and therefore it is clear that Einstein was starting to make a distinction between the behaviour in small regions of space and larger regions of space. This work was a key milestone in his development of the field equations; the script if you will, for the theory of General Relativity.

Section 2: General Relativity

In the introduction, it was mentioned that General Relativity is the most beautiful theorem of all time; partly due to GR’s ability to uncover and answer previous questions arising from Newton’s work. General Relativity consists of two main ideas: Space-time as a 4 dimensional “fabric” and matters interaction with this Space-time.

Idea 1: Space-time:

Before Einstein’s work, space was described using a different form of Mathematics called Euclidean geometry, which described the topology of space around us using a cartesian co-ordinate system, where, roughly speaking, the position of a point is determined by using two perpendicular lines around it. Space-time, however, is a wildly contrasting idea to this original branch of Mathematics! Originally, as described, space was believed to consist of only 3 dimensions: up and down, forwards and behind, left and right. Early 19th century Mathematicians added on another dimension: time. Therefore, space is no longer a static 3-dimensional structure, but rather a 4 dimensional flexible “fabric”, which consists of the 3 spatial dimensions fused with 1 time dimension. This fascinating addition would allow Einstein to work on geodesic mathematics which would eventually contribute to the final theory of General Relativity; for which he won the Nobel Prize in 1922.

To understand geodesics; it must be made clear that if an object is not accelerating; it will follow the shortest possible path in space-time. An interesting thought experiment can be conducted; imagine two scenarios (both in which there is a pair of people walking together). The first scenario is on a flat plane. If, at the start, their paths are parallel to each other; regardless of how long they walk, it is impossible for their paths to converge. However, now imagine the second scenario; in which they are (hypothetically, of course!), walking on a spherical 3D plane. They are still walking in a straight line; however their paths indeed do converge! This means that all non-accelerating objects will move in straight lines; however, their straight lines are distorted due to warped spacetime.

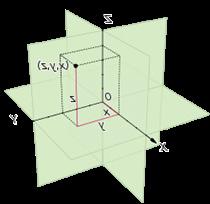
Idea 2: how does matter cause space-time to be warped?

You may be aware of Newton’s gravitational theory; one tied to many myths and mysteries; most commonly regarding the apple! It states that “Every particle attracts every other particle with a

Force that is proportional to the product of their masses and inversely proportional to the square of this distances between their centres” This statement describes a mathematical formula; which summarises Newtonian views about gravity; that it is a non-contact attractive force between objects of mass; and the strength of the force depends on how big the objects are (strictly what their masses are). Although this does work to explain large objects (such as planets orbiting planets) and “ordinary” situations, for example why a ball falls when we drop it; the theory immediately disintegrates when we attempt to explain physics on a microscopic scale or at high speeds near the speed of light. Therefore, Einstein, using features from his Special Relativity theory and the equivalence principle, created a new definition of Gravity. Instead of Gravity as a force (which is described as a mechanical influence which affects the motion of an object); he made a revolutionary observation. Gravity is simply the curvature of space-time. This provided a mechanism for why objects of mass are attracted to each other; and even explains why there is a stronger attraction between objects of larger masses. Einstein described that space-time was flexible (so could be twisted, bent or warped) and therefore a large object such as the Earth causes the space-time around it to be deformed in a way akin to the shape of the Earth. Therefore, the falling of the apple is not explained by a force but instead just geometry. If the apple was on a sheet of completely empty, flat space-time and pushed with a force, it would continue in a straight line. However, when the apple is dropped; the apple follows a geodetic path (as described earlier, due to the original straight line being contorted as a result of flat space-time), and therefore the apple is “attracted” towards the Earth.

Mathematics of General Relativity; section1: Geodesic mathematics:

The first piece of Mathematics which must be tackled in order to understand GR is Geodesic Mathematics. As described earlier; a geodesic is a curve representing the shortest path between two points on a surface. When dealing with the trajectories of objects in curved-space time, we can look at the velocity of the object at a given time and given position and then “transport” this velocity across the trajectory to work out its shape (and therefore the geodesic). This essentially means that the vector of the velocity does not change, therefore the “natural” movement of bodies is non-accelerating. The velocity of the object can be written in the form as shown above: this means that that the vector of the velocity can be written as the sum of the horizontal and vertical components of the vertical vector multiplied by the basis vector. The part in the middle of the derivative (the part in the brackets), is a shorthand version which has been derived from the equation we achieved above. The next part of this includes manipulating derivatives and using a derivative product rule.

We can say that the derivative of the product is equal to the sum of (each term multiplied by the derivative of the other term), which allows us to create the equation above. From the manipulation of the equations above, we now have an equation linking the rate of change of the components of the vector velocity, the rate of change of the basis vector and the actual rate of change of velocity; we can move on to focus on the basis vector.

- The basis of a vector space can be simply described as the set of vectors in that space which can be used as co-ordinates for that vector.

We then can look at the rate of change of the basis vector (The basis vector is represented by e). As seen in the diagram above; we can explore how the base vector (Which is represented by e) can change with respect to x (the change in position of the co-ordinates)

When exploring this; it introduces us to a new tool; the Christoffel symbol; which is crucial to understanding general relativity. It explains how the grid of space-time changes as time progresses.

Finally using the Christoffel symbols; we can use the equation we had earlier to achieve the final Geodetic equation.

That is the beauty of Physics. An equation no longer than a quarter of a line allows us to predict the trajectory of how an object moves in space-time!

Mathematics of General Relativity; Part Two: Einstein Field Equation:

As described earlier; the second great pillar of General Relativity is the Einstein Field Equation. However, for us to understand and manipulate the Einstein Field Equation; each component must first be analysed.

- A tensor can be described as a mathematical object which has “an arbitrary yet defined number of indices”

1. The Ricci Tensor is represented by R mu v (the symbol on the extreme left) and is a tool which allows physicists to represent the difference between volumes in curved space and regular Euclidean space (which was mentioned earlier in the article)

2. The Metric tensor is represented by the symbol g mu v (the symbol on the right of ½) and is a tensor which allows Physicists to calculate small distances between points on a surface

3. The Ricci Scalar (on the right of the metric tensor) characterises the average curvature in all directions

4. The last component we must analyse is the momentum energy tensor which is a tensor which describes the momentum and energy of matter

Through interpretation of the equation, the left side of the equation tells matter how to curve space-time, whereas the right side of the equation tells matter how to move through the curved space-time. In summary; these two equations (the geodesic equation and Einstein’s field equation); have allowed us to model the curvature of space-time and how the space-time is curved!

Applications of General Relativity; Black Holes:

Black Holes are one of the most revered yet mysterious monsters in the Universe, swallowing and consuming any objects unfortunate enough to be within the critical distance. The definition of a Black Hole is a region of space-time in which the gravitational pull is so strong that not even light (which travels at 3 * 10^8 m/s in a vacuum) can escape it. The Black Hole consists of the Event Horizon (which can be thought of as the “mouth of the Black Hole”) its existence initially postulated by a physicist called Karl Schwarzschild. As an object gets closer to the Black Hole; the escape velocity (velocity required for an object to escape the gravitational pull) increases until we get to the Event Horizon (at which the escape velocity is larger than the Speed of Light). As we know from Einstein’s theory of Special Relativity; it is theoretically impossible for any object to travel at a speed exceeding 3 * 108 m/s and thus any objects which find themselves within the escape horizon cannot escape. The Black Hole also consists of the Singularity (which can be thought of as the “Stomach of the Black Hole” where all the matter and energy which falls into the Black Hole accumulates). From General Relativity, we know that matter causes space-time to warp. However, general Relativity also predicts that at the singularity; the space-time is warped to an infinite degree which must mean that the singularity there is an infinite density! Although this may seem slightly counterintuitive and some may therefore disagree with the existence of Black Holes, they have been proven to exist (in 2019 the first ever picture of a black hole was taken by the Event Horizon Telescope!)

What is the Future of General Relativity?

Despite General Relativity being one of the most successful and significant theories in all of Phys- ics (and despite an experiment successfully detecting Gravitational waves in 2016 essentially proving GR) there are still some strands of the story which are incomplete. General Relativity predicts the existence of a singularity at the centre of black holes (an area of infinite density); however, at the singularity, many of the laws of Physics we currently have start to break down. Another example is at the quantum level; where one can only know the probability of an outcome happening, rather than knowledge of a definite outcome. This greatly contradicts general relativity which relies on “continuous” and “deterministic” nature of events; where one event clearly causes another event to take place. Black holes are a perfect case, where these two ideologies dramatically seem to clash. General Relativity states that information can be destroyed in a Black Hole, whereas Quantum Mechanics states that it is impossible for information to be destroyed. So, what does the future hold in place for General Relativity? While some say that GR is incomplete and must be abandoned; there are many who are seeking a theory which elegantly ties together General Relativity and Quantum Mechanics (for example new strides in String Theory seem particularly promising). Therefore, although it seems to be impossible to answer the question of this theory’s future; it is possible to answer an equally important question. Is it the most beautiful theory of all time? Despite its flaws, General Relativity continues to inspire and excite physicists across the world. A theory which initially set out to revolutionise Gravity has managed to establish itself as a backbone of Physics, providing an entirely new and refreshing outlook to the Universe. Herman Bondi albeit, once said, “A theory is only scientific if it can be disproved”. Will this colossal pillar ever be broken? Only time can tell.

Sources and references:

Bibliography: General Relativity article: Hossenfelder, Sabine. “What Is Einstein’s Equivalence Principle?” YouTube, 1 Aug. 2020, www.youtube.com/watch?v=vng2-R64rAY. Accessed 15 Nov. 2022. Helped me to understand the basics of what the Equivalence Principle is.

Possel, Markus. “The Elevator, the Rocket, and Gravity: The Equivalence Principle «Einstein-Online.” Einstein-Online.info, 9 Jan. 2005, www.einstein-online.info/en/spotlight/equivalence_ principle/. Accessed 17 Nov. 2022. Explained what the elevator thought experiment was in more detail and also how it was used to show the equivalence principle.

Arvin Ash. “General Relativity Explained Simply & Visually.” YouTube, 20 June 2020, www. youtube.com/watch?v=tzQC3uYL67U. Accessed 18 Nov. 2022. Gave a basic summary of what space-time was and what General Relativity says about space-time.

Mann, Adam. “What Is Space-Time?” Livescience.com, Live Science, 19 Dec. 2019, www. livescience.com/space-time.html. Accessed 21 Nov. 2022. Helped me to understand what spacetime is and why it is considered as 4 dimensional.

ScienceClic English. “The Maths of General Relativity (3/8)- Geodesics.” YouTube, 8 Dec. 2020, www.youtube.com/watch?v=3NnZzRb7L58. Accessed 22 Nov. 2022. Explained what geodesics are; also provided me with information for the section titled: Mathematics of General Relativity.

Hoang, Lê Nguyên. “Spacetime of General Relativity.” Science4All, 2 June 2013, www. science4all.org/article/spacetime-of-general-relativity/. Accessed 27 Nov. 2022. Explained how space-time is warped (Due to gravity) and also provided basics for the Mathematics of General Relativity.

DeCross, Matt, et al. “General Relativity | Brilliant Math & Science Wiki.” Brilliant.org, brilliant.org/wiki/general-relativity-overview/. Accessed 1 Dec. 2022. Gave an in-depth explanation of the mathematics of the Einstein Field Equation and the Geodesic equation.

ScienceClic English. “Maths of General Relativity (7/8)- the Einstein Equation.” YouTube, 5 Jan. 2021, www.youtube.com/watch?v=PCujLVSRuMk. Accessed 1 Dec. 2022. Provided an explanation of what the Einstein Field Equation is, and what the components of the equation are and their meaning.

Nola Taylor Redd. “Black Holes: Facts, Theory & Definition.” Space.com, Space.com, 11 July 2019, www.space.com/15421-black-holes-facts-formation-discovery-sdcmp.html. Accessed 3 Dec. 2022. Provided a basic description of what Black Holes are.

“Anatomy | Black Holes.” NASA Universe Exploration, universe.nasa.gov/black-holes/anatomy/. Accessed 4 Dec. 2022. Provided an explanation of the parts of a black hole and how they work.

“Unifying Quantum Mechanics with Einstein’s General Relativity.” Research Outreach, 19 Dec. 2019, researchoutreach.org/articles/unifying-quantum-mechanics-einstein-general-relativity/. Accessed 5 Dec. 2022. Provides information whether there have been attempts to combine General Relativity with Quantum Mechanics.

Powell, Corey. “Relativity v Quantum Mechanics – the Battle for the Universe.” The Guardian, 4 Nov. 2015, www.theguardian.com/news/2015/nov/04/relativity-quantum-mechanics-universe-physicists#:~:text=In%20general%20relativity%2C%20events%20are. Accessed 6 Dec. 2022. Shows how General Relativity contradicts with Quantum Mechanics.