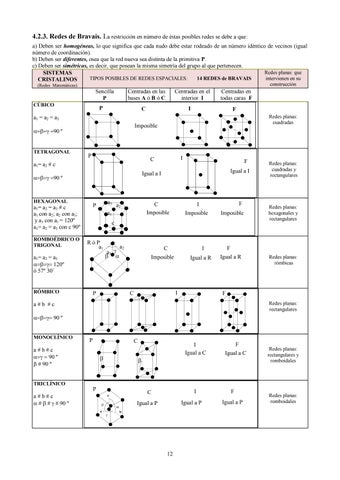
4.2.3. Redes de Bravais. La restricción en número de éstas posibles redes se debe a que: a) Deben ser homogéneas, lo que significa que cada nudo debe estar rodeado de un número idéntico de vecinos (igual número de coordinación). b) Deben ser diferentes, osea que la red nueva sea distinta de la primitiva P. c) Deben ser simétricas, es decir, que posean la misma simetría del grupo al que pertenecen. Redes planas que SISTEMAS TIPOS POSIBLES DE REDES ESPACIALES: 14 REDES de BRAVAIS intervienen en su CRISTALINOS construcción
(Redes Matemáticas)
Sencilla P
Centradas en las bases A ó B ó C
Centradas en el interior I
Centradas en todas caras F
P
C
I
F
CÚBICO
Redes planas: cuadradas
a1 = a2 = a3 Imposible
º
TETRAGONAL
P
F Igual a I
Igual a I
º
HEXAGONAL
a3 a 2 a1
P
a1= a2 = a3 # c a1 con a2; a2 con a3; y a3 con a1 = 120º a1= a2 = a3 con c 90º ROMBOÉDRICO O TRIGONAL
I
C
a1 = a2 # c
F
C Imposible
I Imposible
C
I
F
Imposible
Igual a R
Igual a R
Imposible
c
RóP a1
a1= a2 = a3 º ó 57º 30`
RÓMBICO
a 3
a2
P
I
C
Redes planas: cuadradas y rectangulares
Redes planas: hexagonales y rectangulares
Redes planas: rómbicas
F Redes planas: rectangulares
a#b #c º
MONOCLÍNICO
P
C
a#b#c º º
F
I Igual a C
Igual a C
C
I
F
Igual a P
Igual a P
Igual a P
Redes planas: rectangulares y romboidales
TRICLÍNICO
P a#b#c º
c a
b
12
Redes planas: romboidales