Fenómenos Ondulatorios

PRÁCTICA 10 Fenómenos Ondulatorios

RESUMEN

Con la realización de este trabajo se busca entender y comprender las características que posee los fenómenos ondulatorios. Para esto se a desarrollo 3 experimentos en un simulador, donde se obtuvo la amplitud y con ayuda del simulador se calculó la velocidad, el periodo y la frecuencia. Posteriormente se compararon los resultados teniendo en cuenta unas variaciones en la ejecución de cada experimento y se analizaron con respecto a la teoría de ondas y fenómenos ondulatorios.

INTRODUCCIÓN

En la realización de este laboratorio se tuvieron en cuenta distintos conceptos para entenderlo a detalle y conocer lo que estábamos haciendo, como la perturbación, alteración o trastorno que se produce en el orden o en las características permanentes que conforman una cosa o en el desarrollo normal de un proceso. La longitud de onda que es la distancia real que recorre una perturbación (una onda) en un determinado intervalo de tiempo.

Todas las ondas tienen una velocidad de propagación finita., en cuyo valor influyen las fuerzas recuperadoras elásticas del medio y determinados factores de la masa del medio: la densidad lineal en las cuerdas, la profundidad del agua bajo la superficie, o el coeficiente adiabático, la masa molecular yla temperatura en el caso de la propagación del sonido en un gas

La velocidad de propagación de las ondas superficiales viene dada por: v=g2π+2πptgh 2πh Ecuación número 1.

La dispersión es el fenómeno de separación de las ondas de distinta frecuencia al atravesar un material. Puede ocurrir que en ciertos medios la frecuencia y la longitud de onda sean inversamente proporcionales, de manera que la velocidad es constante (independiente de frecuencia y 2 longitud de onda). En este caso se dice que el medio no presenta dispersión. Por el contrario, cuando la velocidad de propagación depende de la frecuencia decimos que el fenómeno de propagación presenta dispersión o que el medio es dispersivo. Lareflexióneselcambiodedireccióndeunaonda, que,al entraren contacto conlasuperficie de separación entre dos medios cambiantes, regresa al punto donde se originó mientras que la refracción es el cambio de dirección yvelocidad que experimenta una onda al pasar de un medio a otro con distinto índice refractivo. Solo se produce si la onda incide oblicuamente sobre la superficie de separación de los dos medios y si estos tienen índices de refracción distintos.

En la reflexión, una onda que se propaga en el primer medio con velocidad vi y que incide con un ángulo (θi), medido entre la dirección de propagación de la onda y la normal a la superficie que separa los dos medios, es reflejada por la superficie separadora con un Ángulo (θr), de tal manera que se cumple que:

i=r Ecuación número 2.

La fórmula utilizada para calcular el ángulo de refracción de la luz al atravesar la superficie de separación entre dos medios de propagación de la luz (o cualquier onda electromagnética) con índice de refracción distinto es conocida como la Ley de Snell.

vd seni=vi send Ecuación número 3.

MÉTODO EXPERIMENTAL

Termodinámica, Movimiento Armónico, Ondas Parael desarrollo del laboratorio se haceuso de un simuladorllamado fenómeno ondulatorio, en la (Figura 1, 2 y3) se ilustra los distintos fenómenos que se van a utilizaren el laboratorio; luego se realiza un análisis de cada una de las experiencias realizadas en el simulador, se estudiará las ondas en diferentes fenómenos.

Figura 1, en el simulador se seleccionó ondas de agua.

Figura 2, en el simulador se seleccionó ondas de interferencia.

Figura 3, en el simulador se seleccionó ondas de ranuras.

Análisis y resultados:

Seleccionamos agua y se realizó el ajuste de la amplitud y la frecuencia necesarias para observar con mayor claridad la onda generada, de esto se tomaran datos necesarios para calcular la frecuencia y la velocidad de propagación.

Figura 1.1: donde muestra el simulador y la interferencia de onda.

Figura 1.2: se puede observar cómo se tomó la amplitud de onda.

La amplitud de onda en este caso es de 0.9 cm, así como se muestra en la figura 1.2.

Figura 1.3: se puede observar cómo se tomó la longitud de onda.

La longitud de onda en este caso es de 3.4 cm, así como se muestra en la figura 1.3.

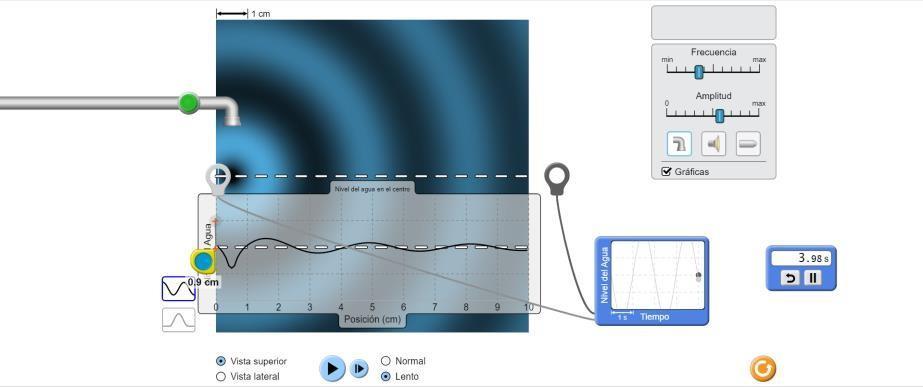
Figura 1.4: se puede observar cómo tomó se el número de onda y tiempo.

Calculo periodo:

�� = ��/�� Donde, n es el numero de crestas y t es el tiempo. T=3.98s/2

T=1,99 s

Cálculo frecuencia:

�� =1/��

Termodinámica, Movimiento Armónico, Ondas f=1/1,99s

f=0,50Hz

Cálculo velocidad:

�� =√��∗ℎ v= √9.8*0,38m

v=1,92 m/s

A continuación, se puede observar la vista lateral:

Figura 1.5: se puede observar cómo se tomó la amplitud de onda.

La amplitud de onda en este caso es de 1.9 cm, así como se muestra en la figura 1.5.

Figura 1.6: se puede observar cómo se tomó la longitud de onda.

La longitud de onda en este caso es de 2.6 cm, así como se muestra en la figura 1.6.

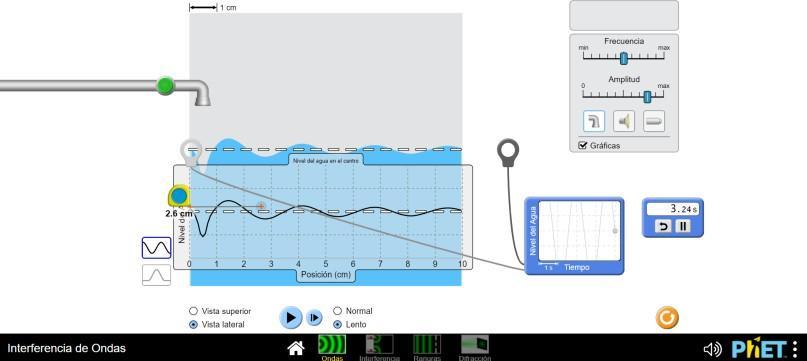
Figura 1.7: se puede observar cómo se tomó el número de onda y tiempo.

Calculo periodo:

�� = ��/�� Donde, n es el número de crestas y t es el tiempo.

T=3.24s/2

T=1,62 s

Cálculo frecuencia:

�� =1/�� f=1/1,62s

Termodinámica, Movimiento Armónico, Ondas f=0,61 Hz

Cálculo velocidad:

�� =√ ��∗ℎ v= √ 9.8*0,38m

v=1,92 m/s

Se pudo analizar que cuando se crea una perturbación en el agua esta viaja trasversalmente, por efectos de amortiguación en el medio se puede observar que las crestas en el extremo opuesto donde se genera la perturbación van disminuyendo en amplitud, si la cubeta fuera infinita llegaría a un punto donde no hubiera crestas, la velocidad en la vista lateral y superior es la misma ya que lo único que afecta a esta en la altura y en ambas es la misma. 2. Seleccionamos el láser y ajustamos la frecuencia y la amplitud necesarias para poder observar las ondas, con esta información calculamos la frecuencia y velocidad de propagación, también observaremos los puntos de interferencia destructiva y constructiva.

Figura 2.1 (Registro toma de datos)

Frecuencia:

�� = 17 31.38 =0,54����

La longitud de onda va a ser igual al valor de la separación dado por el simulador debido a que la longitud de onda coincide con la separación entre dos crestas consecutivas:

λ = 1500nm

Figura 2.2 (Longitud de onda) Ahora calcularemos la velocidad de propagación:

�� =��∗�� �� =(1500����)∗(0.54����)

�� = (1,5��10−6��)∗(0.54����)

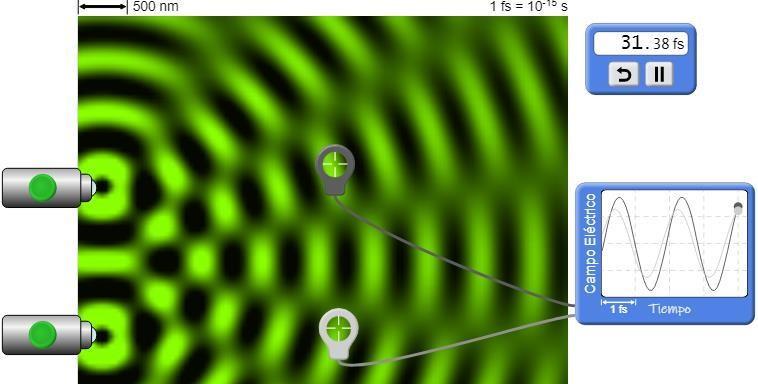
Figura 2.3 (Interferencia de onda)

Constructiva: Se produce cuando las ondas chocan o se superponen en fases, obteniendo una onda resultante de mayor amplitud que las ondas iniciales.

Teniendo en cuenta la información anterior podemos decir que las ondas al producirse al mismo tiempo o en diferente tiempo llegan a un punto de equilibrio en donde tienen valores similares de amplitud, frecuencia y velocidad presentando una Interferencia Constructiva.

Figura 2.4 (Interferencia de onda)

Destructiva: Es la superposición de ondas en antifase, obteniendo una onda resultante de menor amplitud que las ondas iniciales.

Si evaluamos las ondas más suaves podemos encontrar un antifase el cual produce una Interferencia Destructiva, debido a que en este punto se produce una variación en los valores de velocidad, amplitud de onda y frecuencia.

Se pudo analizar que el hacer dos ondas con una frecuencia y amplitud iguales se llega a un punto en el que ambas ondas presentan interferencias que es la superposición donde dependiendo de las longitudes, amplitudes y distancia relativa se pueden presentar dos fenómenos, la interferencia destructiva y la interferencia constructiva.

3. Mediciones de la longitud de la onda ycálculos de frecuencia yvelocidad de propagación. Procedimiento con una ranura, dos y sin barreras.

 Procedimiento con una ranura:

Figura 3.1: Medida de la longitud de onda, procedimiento con una ranura

La longitud de la onda: λ = 43,2 cm λ = 0,432m

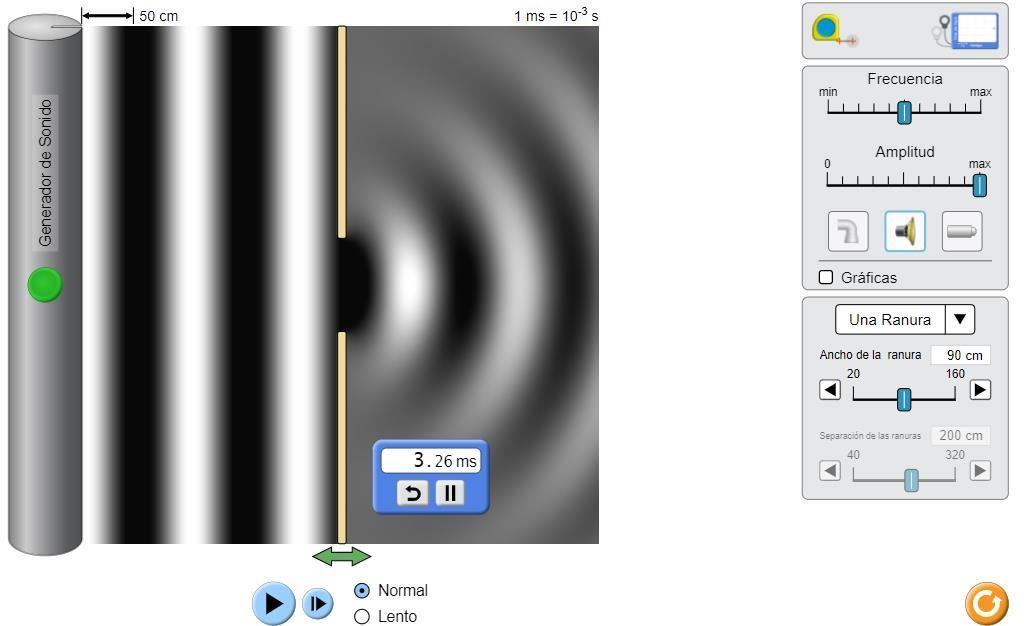
Figura 3.2: Periodo que tarda en repetirse una onda, procedimiento con una ranura

El periodo de la onda es de: 3,26ms = 0,326s

Frecuencia: f = 1/T

f = 1/0,326s f = 3,06s-1

Velocidad de propagación: v = f*λ f = 3,06Hz

v = 3,06Hz*0,432m v = 1,32m/s

 Procedimiento con dos ranuras:

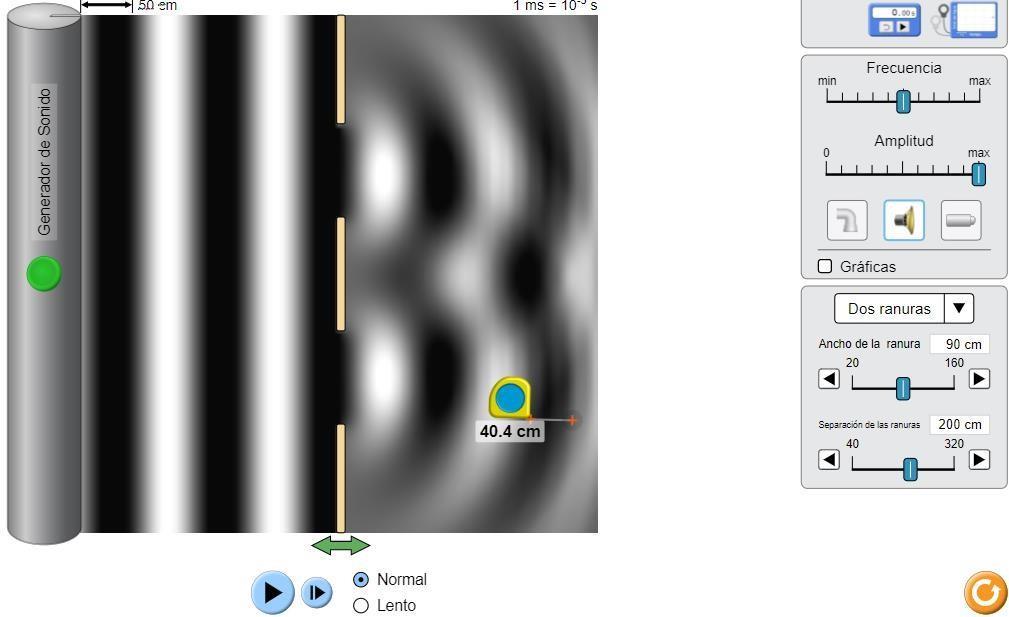
Figura 3.3: Medida de la longitud de onda, procedimiento con dos ranuras

Termodinámica, Movimiento Armónico, Ondas

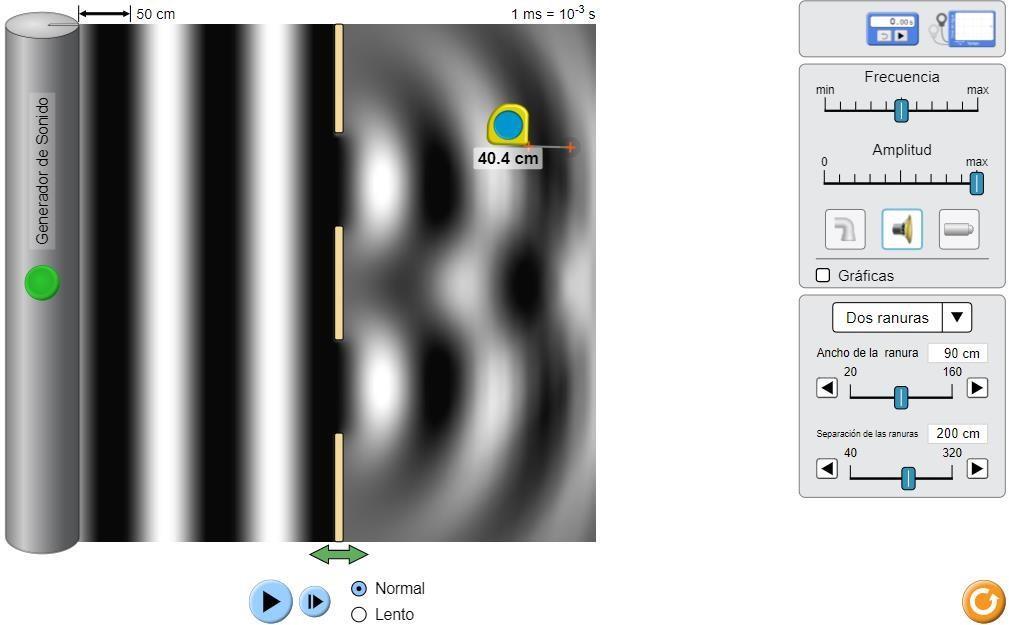
Figura 3.4: Medida de la longitud de onda, procedimiento con dos ranuras

La longitud de la onda: λ = 40,4 cm λ = 0,404m

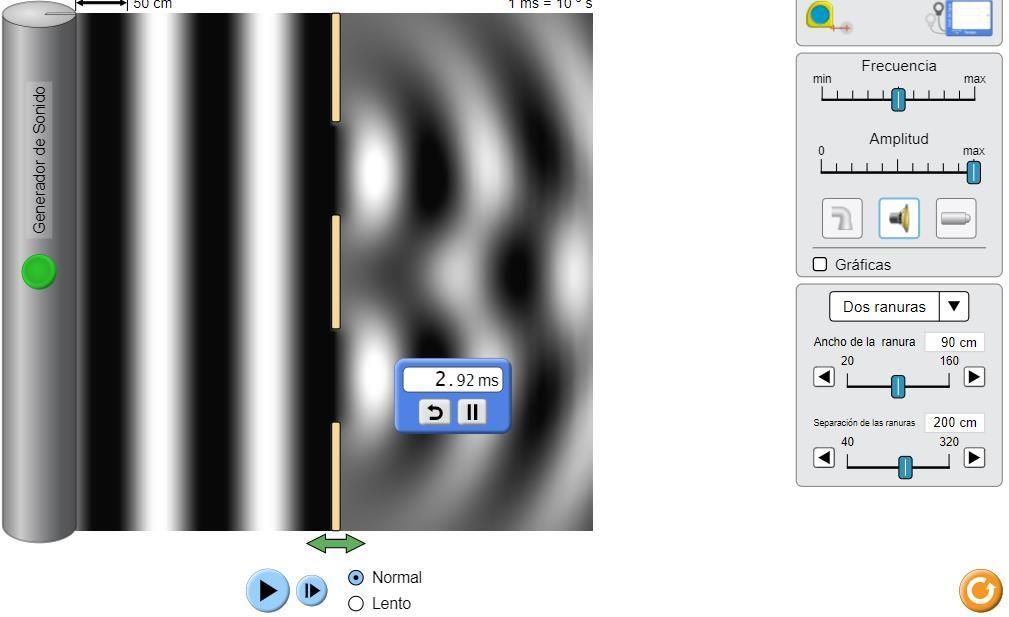
Figura 3.5: Periodo que tarda en repetirse una onda procedimiento con dos ranuras

El periodo de la onda es de: 2,92ms = 0,292s

Frecuencia: f = 1/T

f = 1/0,292s f = 3,42s-1

Velocidad de propagación: v = f*λ v = 3,42Hz*0,404m v = 1,38m/s f = 3,42Hz

 Procedimiento sin barreras:

Figura 3.6: Medida de la longitud de onda, procedimiento sin barreras

Termodinámica, Movimiento Armónico, Ondas La longitud de la onda: λ = 40,3 cm λ = 0,403m

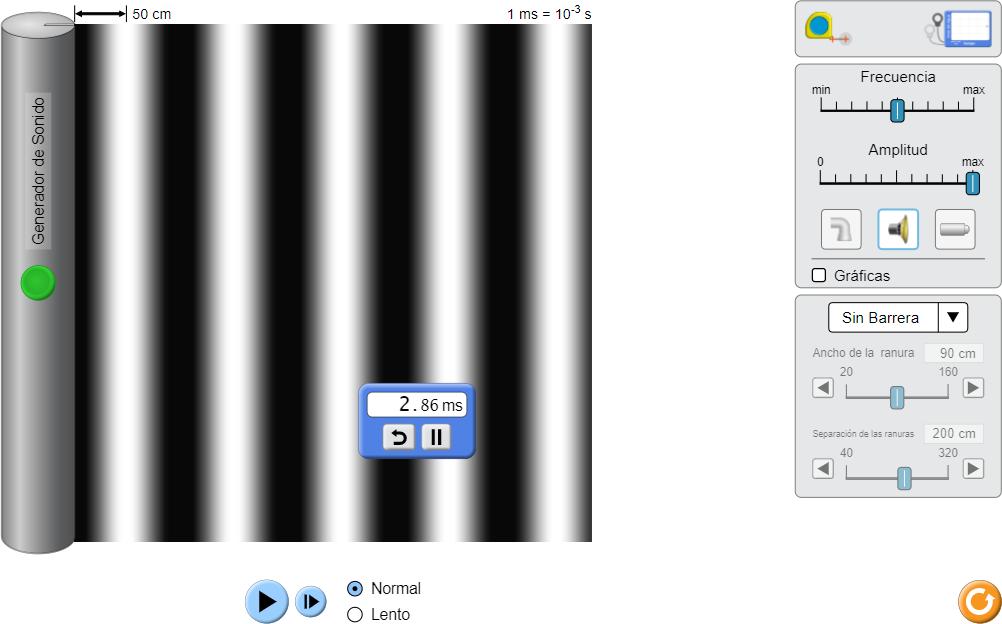
Figura 3.7: Periodo que tarda en repetirse una onda, procedimiento sin barreras.

El periodo de la onda es de: 2,86ms = 0,286s

Frecuencia: f = 1/T

f = 1/0,286s f = 3,49s-1

Velocidad de propagación: v = f*λ f = 3,49Hz

v = 3,49Hz*0,403m v = 1,41m/s

En todas las experiencias trabajadas, nos apoyamos de las herramientas de metro, para medir la longitud de la onda, y del cronómetro para determinar el periodo que tardaba una onda de pasardeunpunto A,aun punto B,todo estotomando los datos gráficos decuando trabajamos con una, dos o sin ranuras. Los valores de periodo de una oscilación fueron necesarios para determinarel valordelafrecuenciacon la cual viajabanuestraondaen estudio, yesteperiodo que obteníamos con el cronómetro del simulador, es inversamente proporcional al valor de la frecuencia. Ahora bien, para el cálculo de la velocidad de propagación desconocíamos una variable para poder despejar en la fórmula, ésta variable era la longitud de onda, la cual pudimos determinar gracias al metro del simulador, teniendo en cuenta que la longitud de la onda debía ser constante cuando se ponían barreras que variaban el paso de las ondas, por tanto debimos ser consientes a la hora de medir, y hacer ciertas predicciones del comportamiento de la onda, así como medir varias veces para obtener un promedio, el promedio encontrado es el que se muestra en cada una de las figuras (3.1 – 3.5), en los cálculos de la velocidad pudimos ver como a mayores escalas de frecuencia y longitud de onda obteníamos mayores valores en la velocidad de propagación, lo cual quiere decir, que la velocidad es directamente proporcional a los valores de frecuencia ylongitud de onda.

4.

Frente de onda: Hace referencia al lugar geométrico en donde los puntos centrales son alcanzados al mismo instante por una onda, está compuesto por todos los puntos que tienen la misma fase, el frente de onda puede ser visto como una superficie que se expande, alejándose del origen y que no se tocan entre sí, podemos observar este comportamiento analizando la imagen 4.1:

Figura 4.1: Ejemplo de frente te onda

Podemos comprender mejor el comportamiento del frente de onda observando la imagen 4.1, corresponde a un frente de onda circular, podemos hacer referencia a que este seria el comportamiento que tendría si se deja caer una piedra en un estanque, donde se empiezan a generar distintos frentes de onda ya que va aumentando su distancia del foco.

Es importante tener en cuenta la forma que toma el frente de la onda, ya que esto nos ayuda a comprender como se comporta la energía, y como se distribuye conforme avanza el movimiento ondulatorio, esta forma varía según el número de dimensiones en la que se propague, para ello es necesario primero saber que este depende de las características que tiene el medio por el cual se propagan, encontramos dos de estos:

 Homogéneos: Hace referencia a un espacio donde sus condiciones físicas y químicas son idénticas en todos los puntos del espacio.  Isótropos: Son en los que las direcciones de propagación son equivalentes, es decir que las propiedades del material no dependen de las direcciones consideradas.

Las ondas se propagan con velocidad constante en los medios homogéneos e independientemente de su dirección en los isótropos.

Conociendo lo anterior es posible hablar de las formas que toma:

 Frentes unidimensionales: Es cuando la onda se genera en un solo foco puntual, un ejemplo de esto es una cuerda vibrando transversalmente, además que sus frentes siempre son simples puntos como se observa en la imagen 4.2:

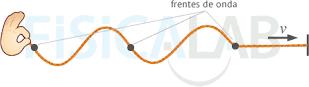
Figura 4.2 Ejemplo de frente unidimensional

 Frente bidimensional: En este caso la onda se propaga en un plano, y tiene su centro en el foco donde se genera la alteración, estos frentes de ondas tienen formas circulares, como se observa en la imagen 4.3:

Figura 4.3 Ejemplo de frente bidimensional

Termodinámica, Movimiento Armónico, Ondas  Frentes tridimensionales: En este caso también tiene su centro en el foco donde se genera la onda, solo que se esparce por todo el espacio creando una esfera como se observa en la imagen 4.4:

Figura 4.4 Ejemplo de frente tridimensional

 Frente plano: Es un tipo de frente tridimensional, donde el frente se encuentra tan alejadodelfocoqueson casiparalelosentresí, comoporejemplolaluz delsolcuando llega a la tierra, podemos observar esto en la imagen 4.5:

Figura 4.5 Ejemplo de frente plano

 Frente cilíndrico: Son frentes tridimensionales, donde el foco no es un simple punto, sino que se parece más a una varilla, generando frente de ondas cilíndricas como se observa en la imagen 4.6:

Figura 4.6 Ejemplo de frente cilíndrico

Cuando hablamos de frente de ondas, es importante también mencionar los rayos, ya que suelen verse dos formas de onda en esto, ya que como se menciona en el frente plano, cuando un frente se aleja mucho del foco se vuelve un frente plano, como se ve en la imagen 4.7:

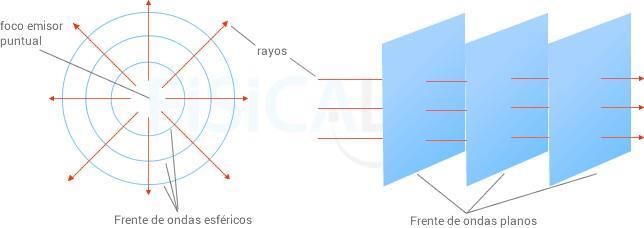
Figura 4.6 Muestra de rayos y sus diferentes formas de frente

Fenómenos ondulatorios:

 Difracción: Fenómeno por el que una onda se reproduce al atravesar una rendija u orificio. sólo se produce si el tamaño de la abertura (d) es del mismo orden que la longitud de onda del movimiento ondulatorio (l) un ejemplo de este es la imagen 4.7:

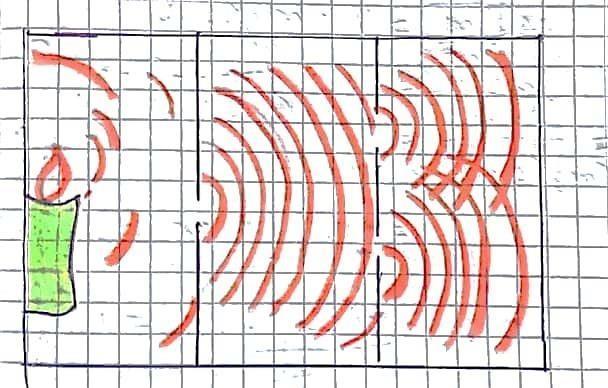
Figura 4.7 Ejemplo de difracción

 Refracción: Ocurretambién cuando laonda se encuentraun obstáculo o borde afilado de tamaño comparable al de su longitud de onda, como se ve en la imagen 4.8:

Figura 4.8 Ejemplo de refracción

 Interferencia:Ocurrecuando dos ondas secombinan al encontrarse enel mismo punto del espacio. Al propagarse dos o más ondas por un medio, la perturbación total resultante es la suma de las perturbaciones de ambas ondas. La interferencia puede

Termodinámica, Movimiento Armónico, Ondas ser constructiva (izquierda) o destructiva (derecha), se puede observar esto en la imagen 4.9:

Figura 4.9 Comportamiento de la interferencia

 Reflexión yrefracción: La reflexión es el cambio de dirección de un rayo o una onda que ocurre en la superficie de separación entre dos medios, de tal forma que regresa al medio inicial. Ejemplos comunes son la reflexión de la luz, el sonido y las ondas en el agua.

La refracción ocurre cuando una onda cambia de dirección al entrar en un nuevo medio en el que viaja a distinta velocidad, esto se puede comprender mejor con un dibujo, como se ve en la imagen 4.10.

Por otro lado, el frente de onda es el lugar geométrico que une todos los puntos en un instante dado y se encuentra en un estado de vibración es decir tiene igual fase.

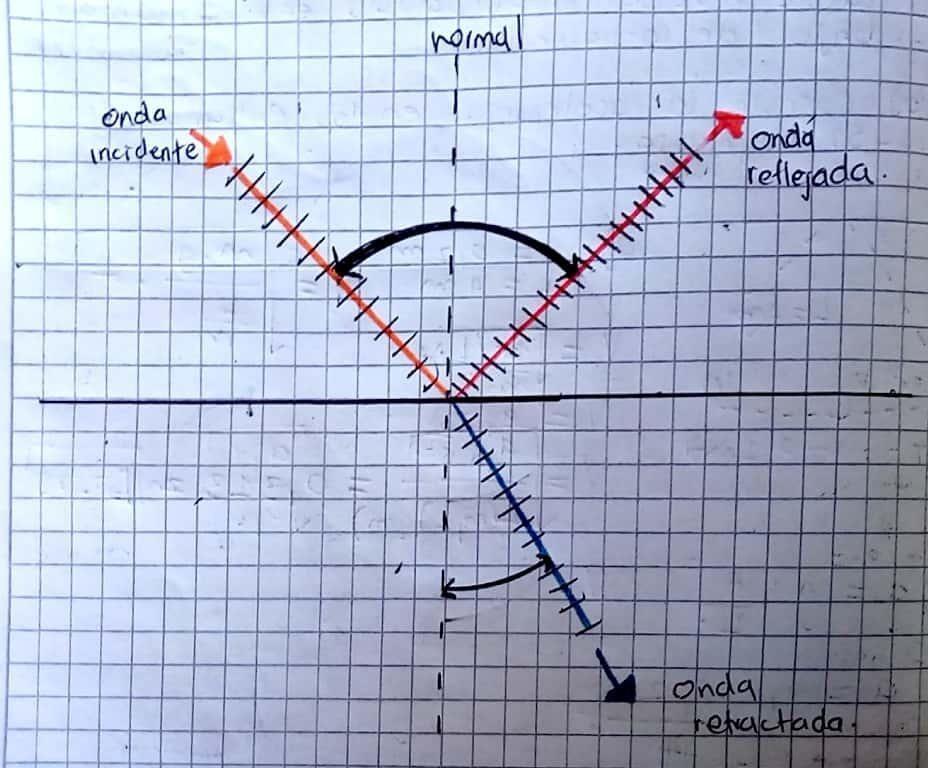
Figura 4.10 Ejemplo gráfico de reflexión y refracción

Diferencias ysimilitudes entre ondas:

El agua sirve como medio de propagación de las ondas, donde los puntos se desplazan de manera vertical, dentro de esta se pueden propagan las ondas de luz y del sonido.

Por otro lado, entre la luz yel sonido existen más similitudes, como quelas dos se comportan como ondas, la frecuencia de estas es fija, solo dependen del calor y del sonido

Termodinámica, Movimiento Armónico, Ondas respectivamente, sin embargo, también tienen diferencias, el sonido es una onda mecánica, mientras que la luz son ondas electromagnéticas, ambas están regidas por las leyes de ondas, como la ley de amortiguación o la ley de reflexión y refracción, además de que la luz puede desplazarse en el vacío, mientras que el sonido no.

Se pudo observar el comportamiento que tiene una onda según varía su frecuencia, donde observamos que la longitud de onda es inversamente proporcional a la frecuencia de esta, por otro lado, se vio que la amplitud no afecta en nada a la longitud de estas, además comprendimos que el agua no genera ondas, sirve como medio de propagación, en cambio la luz y el sonido comparten las leyes que la rigen y varían sus características ya que la luz es un tipo de onda electromagnética y el sonido es una onda mecánica, estas diferencias hacen que viajen de manera distinta, ya que la luz puede desplazarse en el vacío a una velocidad de 300.000kh/s, mientras que el sonido siempre necesita un medio para propagarse, en este caso si estemedio es el aire, tieneunavelocidadde1.200 km/h, unclaro ejemplo delasdiferencias de velocidades son los rayos y los truenos, ya que primero se ve el rayo que sería una onda de luz, y al poco tiempo se escucha el trueno, que es un sonido que viaja considerablemente más lento que la luz.

Adicional a esto pudimos ver características específicas de las ondas como el hecho de que cuando dos ondas están en fase hace referencia a que estas dos coinciden en su elongación y velocidad de movimiento, o las diferencias entre las interferencias constructivas y destructivas,lascuales hacen queaumente la amplitud odisminuyarespectivamente, también vimos que la difracción es un fenómeno que causa la desviación de ondas cuando pasan por un cuerpo opaco, mientras que por otro lado la interferencia es causada cuando dos o más ondas se superponen creando interferencias constructivas o destructivas.

Conclusiones:

 La cantidad de difracción dependerá de que tan grande sea el sitio por donde pueden pasar las ondas, si el sitio es más pequeño que la longitud de onda mayor difracción habrá, en cambio si el sitio es más grande, habrá menos difracción. En caso de que no haya ningún hueco por donde pueda pasar la onda, puede ocurrir la reflexión, donde la onda reflejada sale con el mismo ángulo que con el que había entrado.  Si la onda se encuentra con una superficie y puede atravesar el medio ocurre refracción, y si el medio final es diferente a la inicial, la onda cambiará tanto de dirección como de velocidad para no perder la energía por el camino.  Si tanto la fuente receptora de las ondas, como el receptor, se encuentran en reposo, experimentamos una frecuencia uniforme ya que ninguno de los cuerpos se mueve, pero si en ejemplo la fuente receptora empieza a moverse hacia el receptor, la frecuencia aumentará, ya que se producen las mismas ondas en menos recorrido, esto lo podemos notar en el sonido que se produce pues es más agudo a medida que el espacio es entre los dos cuerposes menor, en cambio si los cuerposse alejan, también la onda se hará más grande, y en caso del sonido se creará un sonido más grave.  Observamos cómo se comportan las ondas dependiendo de los medios en los que se transporta, y en qué dimensión se propaga, además de poder observar el comportamiento que tiene la refracción yla reflexión en estas, y como influyen estas en las ondas.