Ondas en una Cuerda

Termodinámica, Movimiento Armónico, Ondas |exacto − aprox|

exacto

Calculamos el porcentaje de error con la gravedad del planeta Neptuno, ya que era el que tenía la gravedad más parecida a los valores que obtuvimos, tomamos una gravedad de 13.39m/s2 que hace referencia la gravedad promedio de todas las masas, y11.15 m/��2 hace referencia a la gravedad en Neptuno, es el valor exacto es el valor real.

|13.39 − 11.15|

%���������� = 20.08%

Se pudo analizar el tiempo que se demora en hacer una oscilación el péndulo es directamenteproporcional con la amplitud,si la amplitud es pequeña, menor será el periodo o por el contrario si la amplitud es mayor, más grande será el periodo, provocando así un movimiento periódico devaivén,en el queun cuerpo oscilaaun lado ya otro desu posición de equilibrio, en una dirección determinada, y en intervalos iguales de tiempo.

CONCLUSIONES

● El período de un péndulo sólo depende de la longitud de la cuerda y el valor de la gravedad, además la gravedad varía en los planetas y satélites naturales). ● Debido a que el período es independiente de la masa, podemos decir entonces que todos los péndulos simples de igual longitud en el mismo sitio oscilan con períodos iguales. ● La tensión de la cuerda no es constante, sino que varía con la posición angular θ. Su valor máximo se alcanza cuando θ=0, es decir cuando el péndulo pasa por la posición de equilibrio, de la misma forma la velocidad es máxima. Y su valor es mínimo, cuando θ=θ0 en este caso la velocidad es nula. ● Se pudo determinar la dependencia del periodo del péndulo con su longitud, amplitud y la masa pendular. ● Las fuerzas involucradas en un movimiento armónico simple son centrales y por lo tanto conservativas como consecuencia se puede definir un campo escalar llamado energía potencial.

PRÁCTICA 9 Ondas en una cuerda

Resumen

Con la realización de este trabajo se buscó entender y comprender las características que poseen las odas, además de ser capaces de comprender los movimientos de estas aplicando los conocimientos previos dados por el docente.

Para esto se desarrollaron 4 experimentos en un simulador, donde se calculó la velocidad, frecuencia de oscilación, amplitud de onda, distancia y tiempo. Posteriormente se compararon los resultados teniendo en cuenta unas variaciones en la ejecución de cada experimento y se analizaron con respecto a la teoría de las ondas en cuerdas.

Introducción:

Cuando realizamos perturbaciones en una cuerda, observamos como ésta se propaga a través de un medio elástico, es decir que tiene la capacidad de deformarse para luego recuperarse,

Termodinámica, Movimiento Armónico, Ondas en nuestra práctica la perturbación se podía efectuar de tres maneras, manual, mediante oscilación, y mediante pulso, observamos múltiples diferencias a la hora de experimentar la forma de perturbación en la cuerda. Cuando perturbamos el medio, en nuestro caso una cuerda, claramente observamos cómo viajan las partículas transportando energía, pero en ninguno de los casos se transporta masa debido a que las moléculas, están viajando en un medio elástico, en el cual lo único que se transporta es la energía. Cuando hablamos de ondas mecánicas podemos dividirlas en dos tipos, como son las ondas transversales en las cuales las partículas que conforman el medio se mueven de manera perpendicular a la dirección de propagación, y en segundo lugar tenemos las ondas longitudinales, en las que las partículas que conforman el medio se mueven en un va y viene en la misma dirección de propagación. Es importante mencionar las ondas armónicas, en las que las partículas van y vienen como se observó en algunas de las ejecuciones del simulador dado, dado que estas partículas van constantemente en ida y vuelta en una misma dirección, se puede referenciar como un movimiento armónico simple. En la práctica pudimos estudiar magnitudes de gran importancia para el comportamiento de las ondas, las más importantes la longitud de onda, el periodo, el vector de propagación de la onda, la frecuencia angular, el desplazamiento y finalmente el tiempo que tarda en producirse una o varias ondas. El concepto de nodos y antinodos fue de vital importancia a la hora de conocer datos como el número de armónicos, ya que este valor va ser igual al total de antinodos, es decir donde la amplitud de movimiento es máxima para ciertos tiempos. Fue necesaria la utilización de ecuaciones como: v = f λ (1.1), v = ω k (1.2), para el cálculo de la velocidad de onda, y como se observa se tienen en cuenta las magnitudes de, frecuencia angular en la que se tiene en cuenta la dirección en que viaja la onda, el número de onda, la longitud de arco y el periodo.

Para el desarrollo de la práctica se hace uso de las siguientes ecuaciones: �� = ��

Ecuación número 1. Velocidad de transmisión

�� Donde:  �� es distancia, en ocasiones también se representa con la letra ��.  �� es tiempo, esta se mide en ��/��2 .

�� =���� Ecuación número 2. Velocidad de transmisión Donde:  �� es la frecuencia, esta se mide en ���� o ��−1

Método experimental.

Para el desarrollo del laboratorio se hace uso de un simulador de ondas en una cuerda (Figura 1) luego se realiza un análisis de cada una de las experiencias realizadas en el simulador, se estudiará las ondas en una cuerda.

Figura 1. Simulador utilizado para el desarrollo de la práctica.

Análisis y resultados.

Realizamos lamedición dela longitud de onda parauna amplitud de0.57cm yuna frecuencia de 0.45 Hz, como se observa en la Figura 1.1.

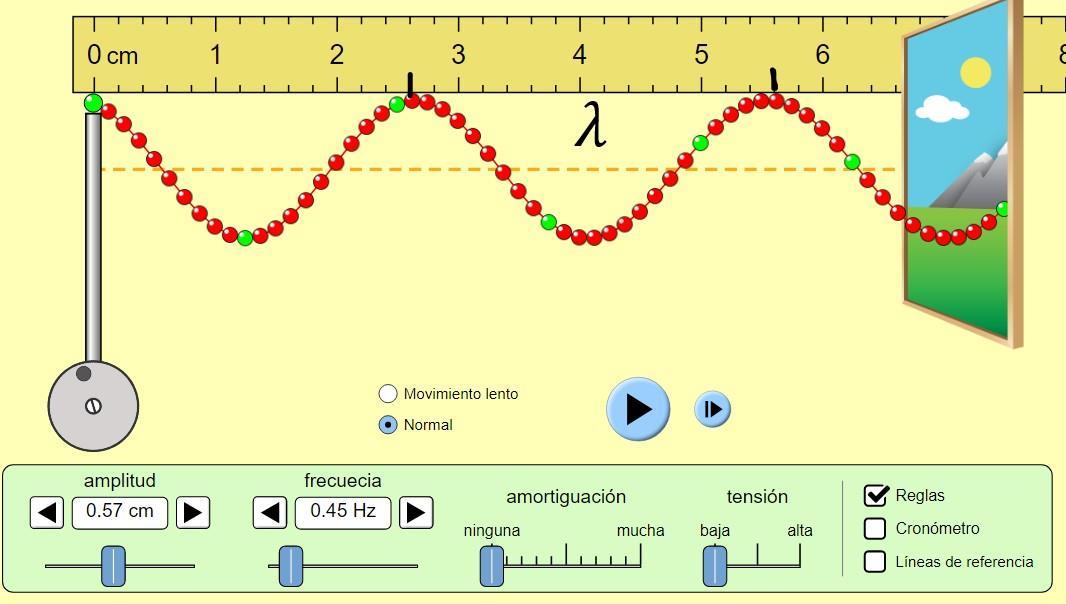
Figura 1.1. correspondiente a la medición de la amplitud de onda.

La medida aproximada para las condiciones, es de 2.7cm como se ve en la figura 1.1.

1. Mantenemos la frecuencia de 0.45 Hz yvariamos la amplitud, en este caso tomamos 0.16cm, y medimos la longitud de onda obteniendo así una longitud aproximada de 2.8 cm, como se muestra en la figura 1.2.

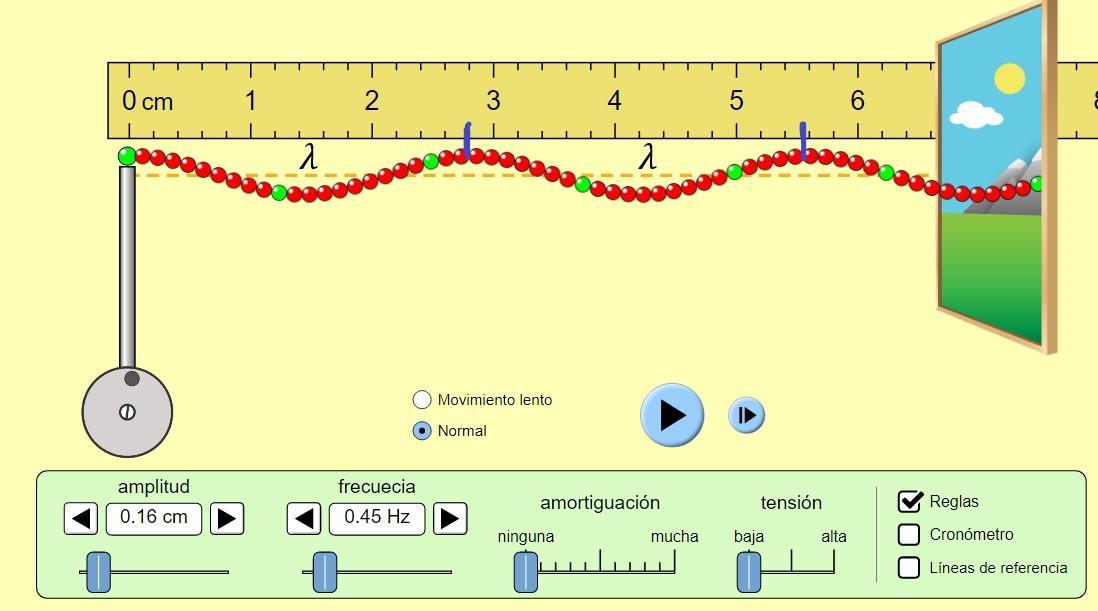
Figura 1.2, toma de la longitud de la onda con una amplitud de 0.16cm y una frecuencia de 0.45 Hz.

Repetimos este procedimiento variando la amplitud obteniendo así la tabla 1.1.

Amplitud(cm) 0.16 0.27 0.48 0.58 0.69 0.83 0.99 1.12 1.25 λ(cm) 2.8 2.7 2.8 2.7 2.7 2.7 2.7 2.8 2.8 Tabla 1.1, donde se muestran los datos obtenidos de las mediciones de la longitud de onda

Si realizamos promedio de los datos obtenidos en la tabla 1.1, podemos obtener una longitud de onda promedio de 2.74444444 cm, esto nos indica que probablemente la longitud correcta sea de 2.7 cm, haciendo de esta manera evidente el hecho de que la amplitud no cambia la longitud de la onda, ya que en la mayoría de los casos nos dio 2.7cm.

2. Experimento realizado manteniendo el valor de la amplitud constante y variando el valor de la frecuencia.

Figura 2.1 (frecuencia utilizada 0,43 Hz)

Figura 2.2 (frecuencia utilizada 0,86 Hz)

Figura 2.3 (frecuencia utilizada 1,29 Hz)

Figura 2.4 (frecuencia utilizada 1,72 Hz)

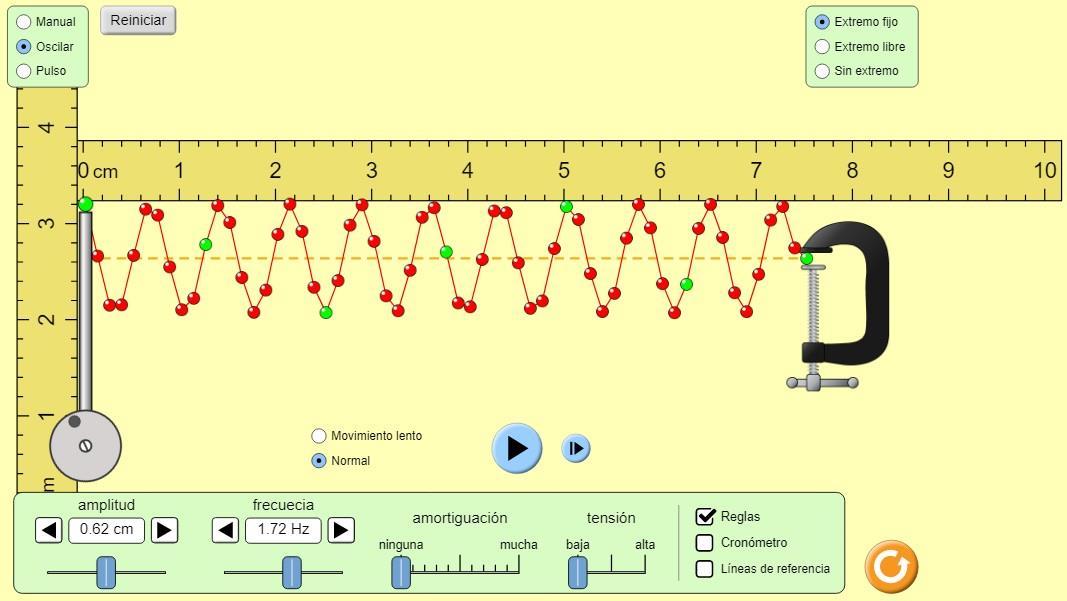
Figura 2.5 (frecuencia utilizada 2,15 Hz)

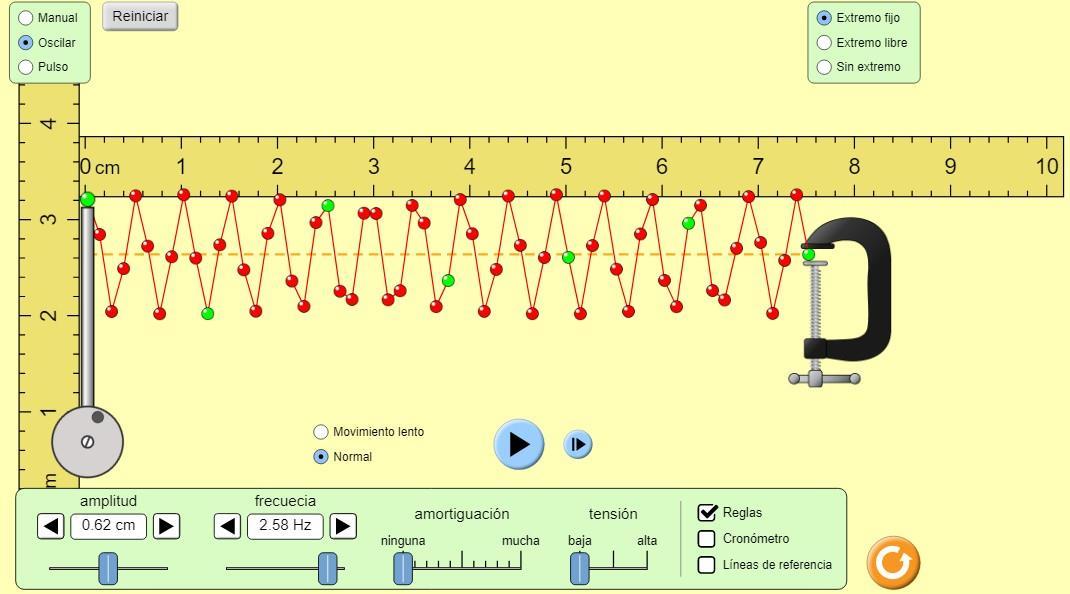
Figura 2.6 (frecuencia Utilizada2,58 Hz)

Figura 2.7 (frecuencia Utilizada 3, 00 Hz)

Repetimos este procedimiento variando frecuencia obteniendo así la tabla 2.

A = 0,62 cm Amortiguación: ninguna Tensión= baja

Frecuencia (Hz) 0,43 0,86 1,29 1,72 2,15 2,58 3,00

λ (mm) 28 mm 14 mm 10 mm 8 mm 6,2 mm 5,9 mm 4 mm Tabla 2. Datos recopilados durante el desarrollo del experimento

Se puede apreciar que a mayor frecuencia menor longitud de onda, debido a que esta se propaga mucho más rápido cada que se aumenta la frecuencia, además la distancia entre cresta y cresta se hace mucho más pequeña y se pueden observar más seguidas. 3. Experimento realizado para calcular la velocidad.

Figura 3.1 (Frecuencia utilizada 1.03 Hz)

Figura 3.2 (Frecuencia utilizada 1.21 Hz).

Figura 3.3 (Frecuencia utilizada 1.52 Hz).

Figura 3.4 (Frecuencia utilizada 1.72 Hz).

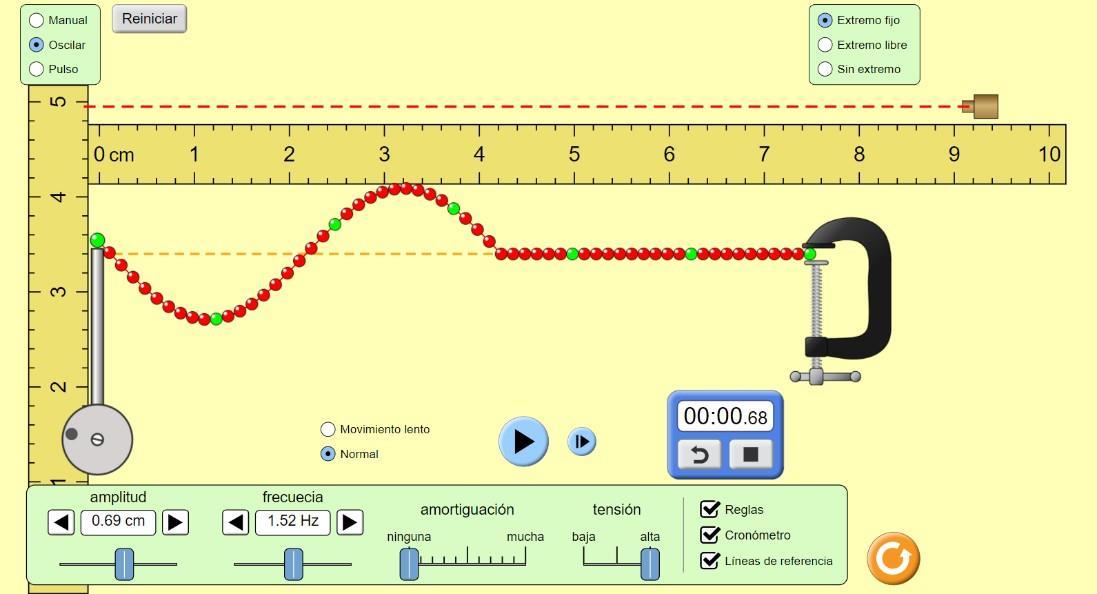
Figura 3.5 (Frecuencia utilizada 2.05 Hz).

Figura 3.6 (Frecuencia utilizada 2.56 Hz).

Para hallar el valor de la velocidad se utilizó la ecuación número 1, remplazamos ytenemos: 7,4���� 00.98�� Donde muestra el resultado obtenido en el simulador y el cálculo de la velocidad.

A: 0,69 cm Amortiguación: ninguna Tensión: alta

X(cm) 7,4 5,4 4,4 3,8 3,2 2,5 t(s) 00.98 00.84 00.68 00.60 00.50 00.40 v(cm/s) 7.55 5,95 6,47 6,33 6,4 6,2 Tabla 3. Datos recopilados durante el desarrollo del experimento

Si realizamos promedio de los datos obtenidos en la tabla 3. podemos obtener una Velocidad de onda promedio de 6,483 centímetros por segundo.

Se pudo analizar que a mayor frecuencia menor longitud de onda ytiempo, debido a que esta se propaga mucho más rápido cada que se aumenta la frecuencia, además se puede observar en las figuras que la distancia entre cresta y cresta se hace mucho más pequeña.

4. Experimento desarrollado manteniendoel valor de laAmplitud constante yvariando el valor de la frecuencia.

A= 0,75cm Amortiguación: Ninguna Tensión: alta

Conocemos el valor de la longitud de onda ysu frecuencia, entonces podemos hallar el valor de la velocidad de trasmisión de cada una de las ondas, entonces remplazamos en la fórmula: �� =����

�� =1,50∗4=6����/��

Termodinámica, Movimiento Armónico, Ondas Repetimos el procedimiento anterior para calcular la velocidad de transmisión según corresponda

F(Hz) 1,50 1,55 1,60 1,65 1,70 1,75 �� (cm) 4 3,6 3,9 3,8 3,7 3,5

V(cm/s) 6 5,58 5,5 6,27 6,29 6,125 Tabla 4. Datos recopilados durante el desarrollo del experimento

Si realizamos promedio de los datos obtenidos en la tabla 4. podemos obtener una Velocidad de onda promedio de 5,960 centímetros por segundo.

Se pudo analizar que las ondas de altas frecuencias tienen longitudes de onda más pequeñas, ya que se repiten muchas veces, en un mismo intervalo de tiempo. También se pudo evidenciar que la velocidad de transmisión de cada onda es independiente de la forma y de energía que transporta cada onda. Con respecto a la velocidad encontrada en la tabla 3, se pudo deducir que la velocidad de transmisión de una onda aumenta si la amplitud aumenta.

5. Identificación de los armónicos que se pueden producir con una cuerda fija en los dos extremos.  Amplitud = 1,25cm Frecuencia= 1,84Hz Amortiguación: ninguna Tensión= alta

Figura No. 5.1, armónicos de una cuerda fija

Numero de armónicos observado = 3

 Amplitud = 1,25cm Frecuencia= 2,09Hz Amortiguación: ninguna Tensión= alta

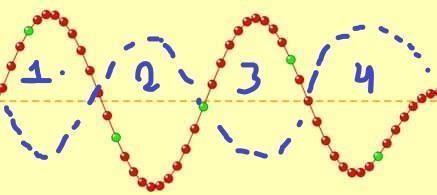
Figura No. 5.2, armónicos de una cuerda fija

Numero de armónicos observado = 4

 Amplitud = 0,88cm Frecuencia= 3,00Hz Amortiguación: ninguna Tensión= alta

Figura No. 5.3, armónicos de una cuerda fija

Numero de armónicos observado = 6

Termodinámica, Movimiento Armónico, Ondas  Amplitud = 0,31cm Frecuencia= 2,45Hz Amortiguación: ninguna Tensión= alta

Figura No. 5.4, armónicos de una cuerda fija

Numero de armónicos observado = 3

 Amplitud = 0,63cm Frecuencia= 1,51Hz Amortiguación: ninguna Tensión= alta

Figura No. 5.5, armónicos de una cuerda fija

Numero de armónicos observado = 3

Pudimos observar como a medida que incrementamos los valores de frecuencia teniendo valores de longitud constantes, este se valor se va incrementar, ya que el número de armónicos lo podemos relacionar con el total de antinodos que se producen al hacer oscilar la cuerda teniendo en cuenta que esta debe estar fija a los dos extremos, por tanto tomando como referencia la figura 2 dada en la guía de laboratorio, podemos darnos cuenta como a medida que el valor de la longitud reduce, el número de armónicos aumenta considerablemente, todo esto pudimos notarlo en el simulador, por lo cual la longitud es inversamente proporcional al número de armónicos que se producen. Por otra parte, cuando incrementamos los valores de frecuencia notamos como crece de manera proporcional el número de antinodos.

Conclusiones:

 Las ondas periódicas realizan movimientos verticales yhorizontales alrededor de sus posiciones de equilibrio, generando un patrón de perturbación ondulatoria y sucesiones simétricas entre crestas y valles, que pueden variar su longitud dependiendo del valor de la frecuencia.  Se pudo determinar la relación entre la cuerda y el número de nodos de la onda estacionaria.  Una perturbación, no va transportar masa, sino que transportará energía, y esto lo podemos aplicar no solo al ejercicio dela cuerda, sino amateriales dediferente estado, como lo pueden ser gases, sólidos o líquidos, la perturbación genera un pulso, y ese pulso a su vez genera una velocidad con la cual viajan las ondas. Por tanto, la velocidad de propagación de las ondas podemos medirla en los diferentes medios como son, gases, sólidos o líquidos, además de diferentes cuerdas donde utilizamos la fuerza de tensión entre la densidad de masa lineal.