Jenna Guo | Capstone Final Project

Detailed Design Report

Stairs Group

Kojo Aduhene, Carmen Andrade, Jenna Guo, Grayce Henderson, David Kim, Oscar Montano, Elisa Pinkowitz

Table of Contents

Executive Summary 3

Problem Definition 3

Components 4

Functions 9

Constraints 9

Preliminary Design Changes 10 Construction Processes 13 Cost Estimation 19 Future Activities 19

Specifications 21

Appendix A: Detailed Design Drawing Set A-1

Appendix B: Calculations B-1

Appendix C: Work Breakdown Structure C-1 References D-1

Executive Summary

Problem Definition

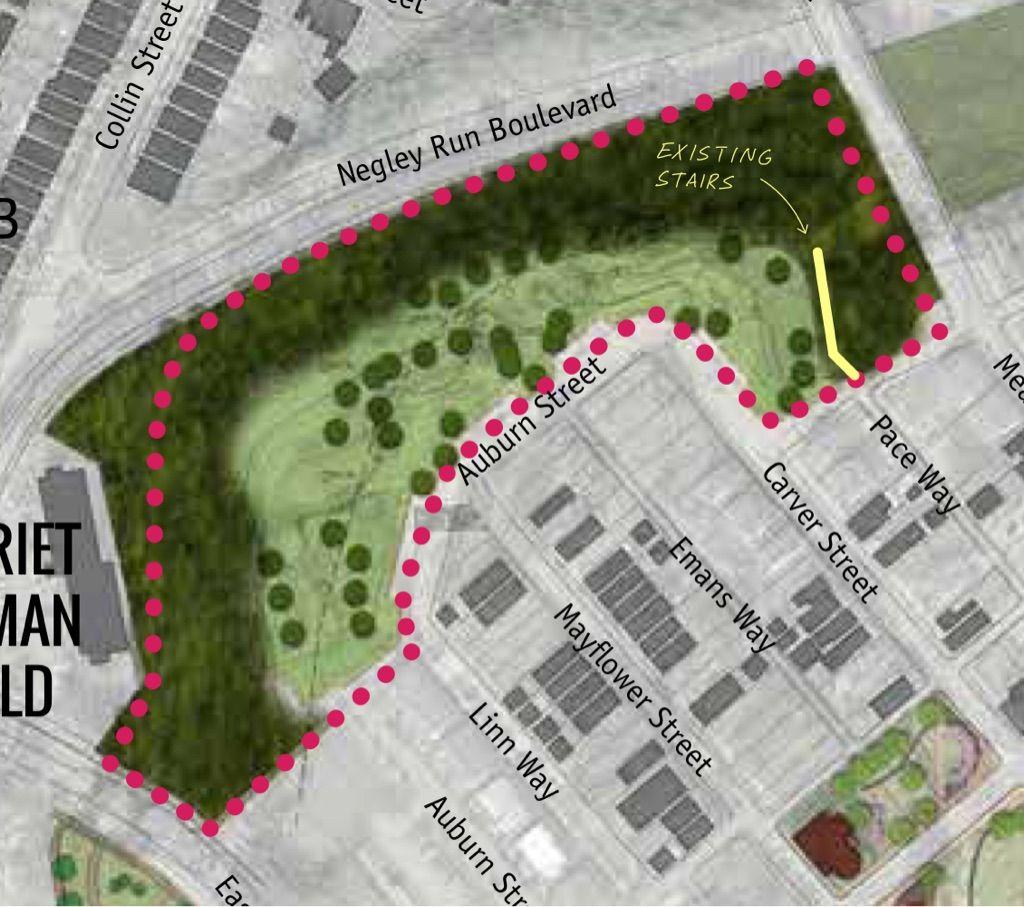
The overall goal of the project is to convey water features and provide an ecological open-space away from the city noise. The Allegheny County Sanitary Authority (ALCOSAN), Pittsburgh Water and Sewer Authority (PWSA), and the Pittsburgh Parks Conservancy (PPC) are among the stakeholders whose utmost priority is the sustainability and economical aspects of the project The land is currently owned by the Housing Authority of the City of Pittsburgh (HACP) The site is a forest flooded by rubbish and altered by landslides. Built decades ago on the site is a deteriorated staircase mostly standing upright on its shallow concrete foundations. Due to the deterioration, the stairway is no longer usable.

The team’s goal is to design a stairway transporting people from Lenora Street down about 340 feet to reach Negley Run Blvd in the valley. The initial step in creating our design alternatives was to define our functions, objectives, and constraints We wanted to create a welcoming space that allowed people to continue their walks or bike rides from the trails to Lenora Street. Our design prioritized minimal damage to the area, interconnectivity, and sustainability. To achieve this, we utilized a combination of above-ground and in-ground stairways.

Components

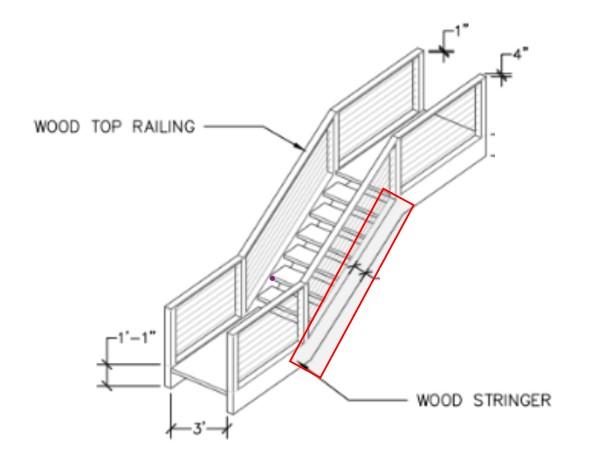
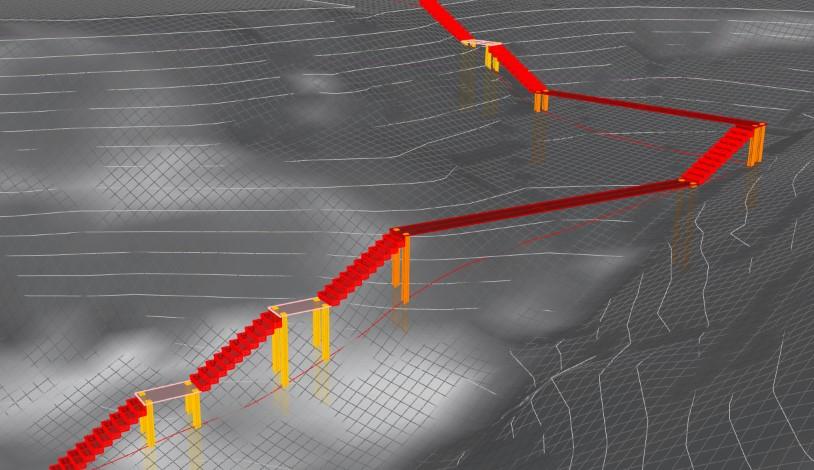
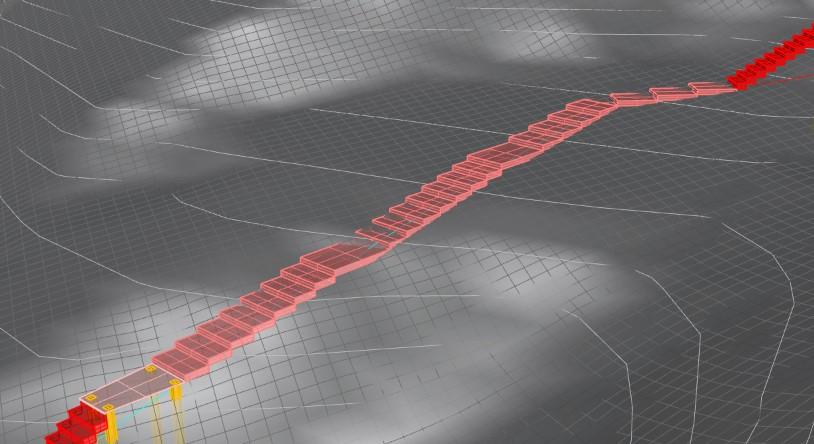
The proposed stairway is split into three sections and comprises two major components: above-ground stairs and in-ground stairs. The first section of the stairs has a length of approximately 82.5 feet with two 10-step above-ground stair flights, a landing in between these stair flights, and a bridge to the first switchback. The second section has a length of approximately 105 5 feet with four 10-step above-ground stair flights, a bridge after the first stair flight, and two landings between three stair flights

Due to the shallow slope at the end of this section, we placed three in-ground steps before the second switchback. The third section spans approximately 95.25 feet with three sets of in-ground stair flights with two landings between each stair flight. This is then followed by four sets of 6-step above-ground stair flights with landings in between each stair flight. This general geometry can be seen below in Figure 1.

Figure 1 | Detailed Design Plan and General Geometry

The above-ground stairs are made up of three subcomponents: landings, stairs, and bridges. The stairs were designed to tackle the significant slope instability present throughout the site while safely transporting pedestrians All subcomponents are elevated and supported by foundation posts with a concrete base The landings and stairs are supported by 6” X 6” (cross-sectional dimension) wooden posts, and the

bridges are supported by A588 steel W12X22 I-beams. Railings are present on each side of the above-ground stairs to keep pedestrians on the stairway at the elevations. Two variations of each subcomponent are used at different points in the bridge to best fit the slope of the terrain.

Landings

The design uses 8 landings composed of wood beams and decks held together by nails, screws, and bolts. All landings in the stairway are the same, with dimensions of 3’ (W) X 6’ (L) X 2” (D), except for one at the transition of the in-ground to the above-ground stairs in the third section; this particular landing has a trapezoidal deck shape instead of a rectangular one to accommodate the width changes between the in-ground stairs to the above-ground stairs The following figure shows these landings, with the typical landing shown on the bottom-left of the figure and the trapezoidal landing shown on the top-right of the figure. Figure 2 | Landings

Above-Ground Stairs

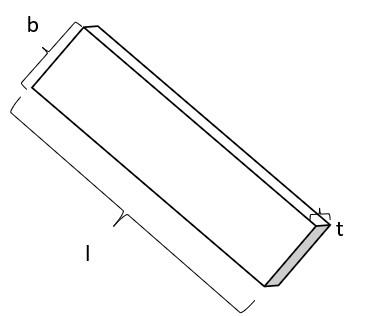
The above-ground stairs are made of two wooden stringers along the stair flight, a set of wooden treads, and galvanized steel connectors There are two stair types in the design, differing only in the number of treads, or length of stair flight. The stairs from the bottom of the valley to the in-ground stairs have 6 steps and 7 rises, shown in Figure 3. The stairs along the top of the valley have 10 steps and 11 rises, shown in Figure 4 An example of a typical stairs-to-landing connection is also shown in Figure 5 below.

Figure 3 | Bottom Stairs (6-Step)

Figure 4 | Top Stairs (10-Step)

Figure 5 | Exploded Axonometric Connection of Landing and Stairs

Bridge

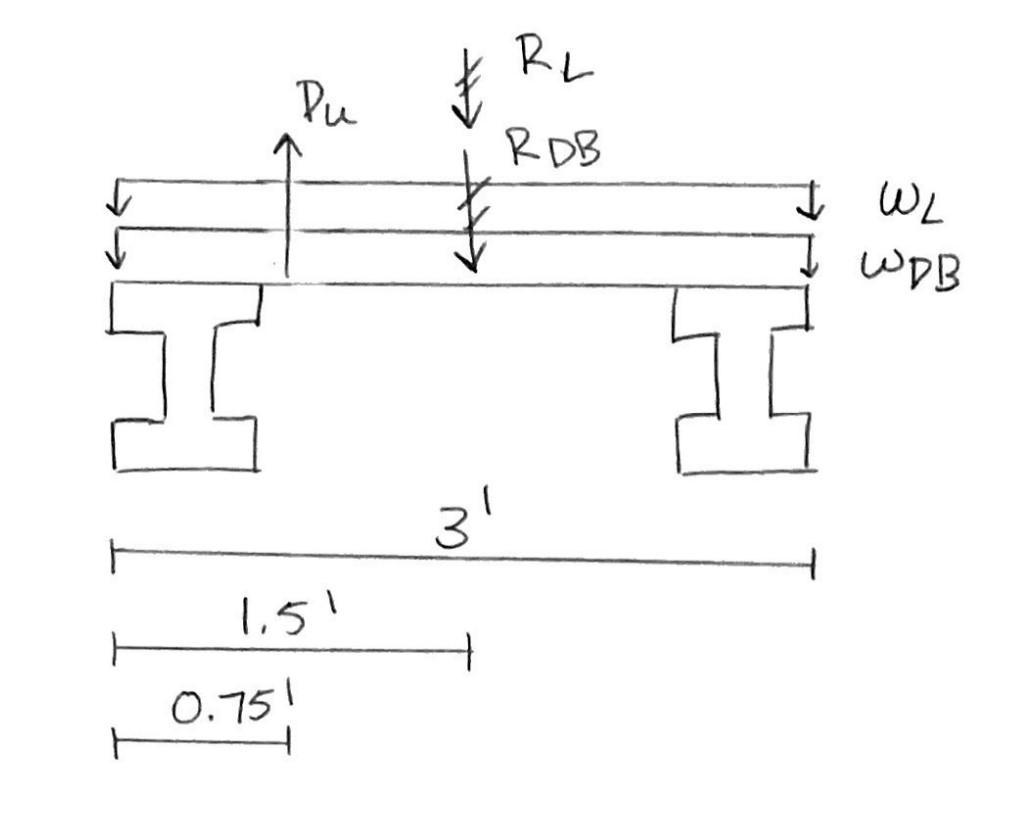
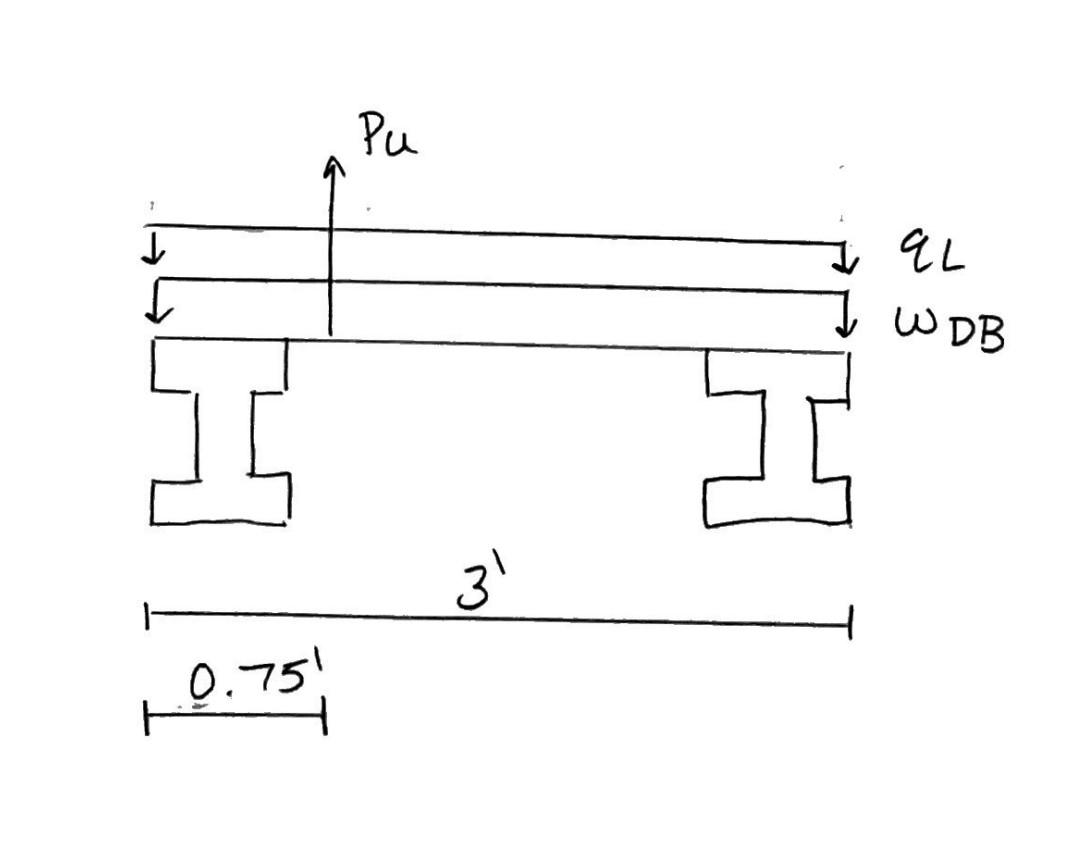
The stairway was designed with two bridges, with one close to the top of the valley spanning 37 feet and the second below spanning 45 feet This design choice was made to accommodate the bioswales which flow underneath these bridges. Along with being rest points and viewpoints, the bridges serve as an educational center that helps explain the various aspects of the Little Negley Run Valley as well as the new stormwater features of the project The two bridges are shown below in Figure 6, with an example of a typical stairs-to-bridge connection in Figure 7.

Figure 6 | Bridges

Figure 7 | Exploded Axonometric Connection of Stairs and Bridge

Railing

The railing along the above-ground stairs uses 4” X 4” wooden posts and 0 25-inch diameter steel wires The top rail is 36 inches above the top of each tread/landing and has a 3” (D) X 4” (W) cross-section. The railing posts are placed at every corner of a landing, which are approximately 5 feet apart; 2 evenly spaced posts are placed between the 10-step stairs; and 1 post is placed in the center of the 6-step stairs This is shown in Figures 3 and 4 on page 6

In-Ground Stairs

The in-ground stairs aim to provide stairs at the shallower sections of the site while minimizing slope disruption and costs The stairs are built with wood, pea gravel (0 75’’ crushed stone), geotextile fabric, rebar, and galvanized spikes (Vermont DEC, 2022). The steps of the stairs are framed by 6’’ X 6’’ (cross-sectional dimension) pieces of timber wood with pea gravel fill to facilitate drainage. Underneath these stairs is a geotextile fabric that helps improve soil stability with rebar that connects adjacent steps This simple design is easily fabricated and was designed to aid drainage in the event of a major rainfall event. There are three different sizes of in-ground stairs used in our design, which can be seen in Figure 8 below; the in-ground stairs along the bottom-left of the figure are 2’ (L) X 4’ (W); the in-ground stairs in the middle of the figure are 3’ (L) X 4’ (W); and the in-ground stairs in the top-right of the figure are 4’ (L) X 4’ (W).

Figure 8 | In-Ground Stairs

Functions

For the stairs of this project, we considered two main functions The first function is to get residents and pedestrians from the road into the valley. This means getting people from Lenora Street into the park via the stairway. A second function is connecting the stairs to the trail. There needs to be cohesion within the park, and this was achieved by having a direct connection between the stairs and the trail system

The stairs we designed clearly met our first function of facilitating walking from Lenora Street to Negley Run Boulevard by creating an accessible design with strong connections to the community and trails in the park along the valley Additionally, we communicated with members of the Larimer community to get feedback on how our designs could be improved and offer more connection to the neighborhood. We also talked with other project teams, especially the Trails Team, to ensure their trail system was well connected The stream and stormwater systems were also investigated to ensure a cohesive entrance and passageway through the park

Constraints

There are a number of constraints that govern our design and decisions. One of the most important constraints that we considered was cost. For our design work, we were not given a specific budget to keep the project within. Cost limited the possibilities of materials we used and created a more efficient design in terms of construction. An overly designed stairway would cost more money than necessary and would increase construction time. Another constraint we considered was location. The existing staircase on the site had to be navigated in our construction plans and was used as a point of reference In our preliminary design, we kept the stairs in the same general area. Additionally, the location of the design was carefully coordinated with all other teams on-site, especially the Trails team to ensure a proper connection. The constraint of location was also considered when looking at site access, as the space is quite tight due to the wooded and steep surrounding areas Equipment, materials, and workers may need to overflow onto Lenora Street, so coordinating that with minimal disruption is essential. The existing soil conditions and geography on-site constrained our designs as well. The steep and landslide-prone areas of our site restrict

construction, so using SlopeGrid is a solution to help keep the slope from moving and failing.

A number of building codes also heavily constrained the design of our stairs. Steps had to follow strict Americans with Disabilities Act (ADA) codes to be compliant. These ADA codes restricted many dimensions including the rise of the steps, tread depths, and nosing lengths Landings were also required at the top and bottom of stair flights, more specifically a landing must be placed at least every 12 feet of vertical rise. We also considered railing regulations and codes. Railings are required to be between 34-38 inches high from the top of each tread. Handrails must also extend horizontally above the landings for a minimum 12 inches At the bottom of stairs, ADA requires handrails to extend at least equal to one tread depth beyond the last riser nosing. Other codes and organizations that constrain our design include the American Institute of Steel Construction (AISC) for the bridge girders and columns, the National Design Specification (NDS) for wood construction (the stair stringer as well as the stair and bridge planks), and the American Association of State Highway and Transportation Officials (AASHTO) for bridge and stair design loads. Citations for all these codes are included in the Reference section and in Appendix B: Calculations.

Preliminary Design Changes

Bridge Abutment Addition

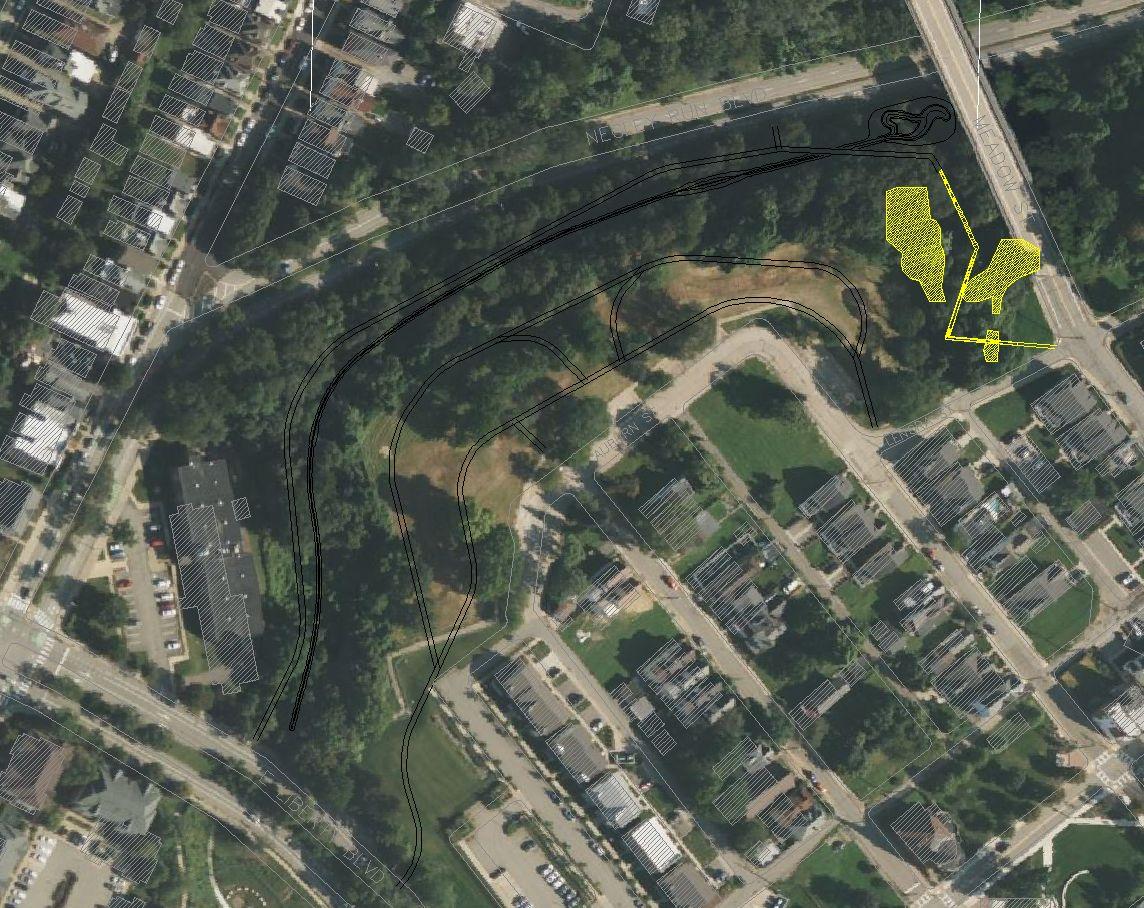
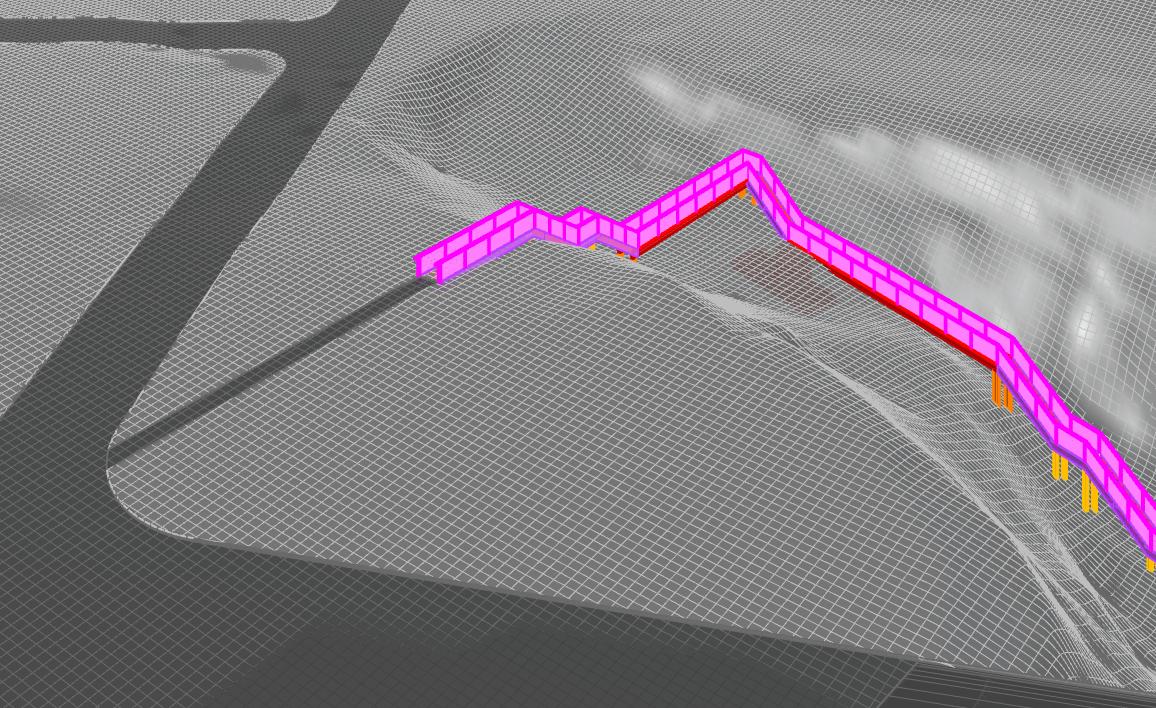
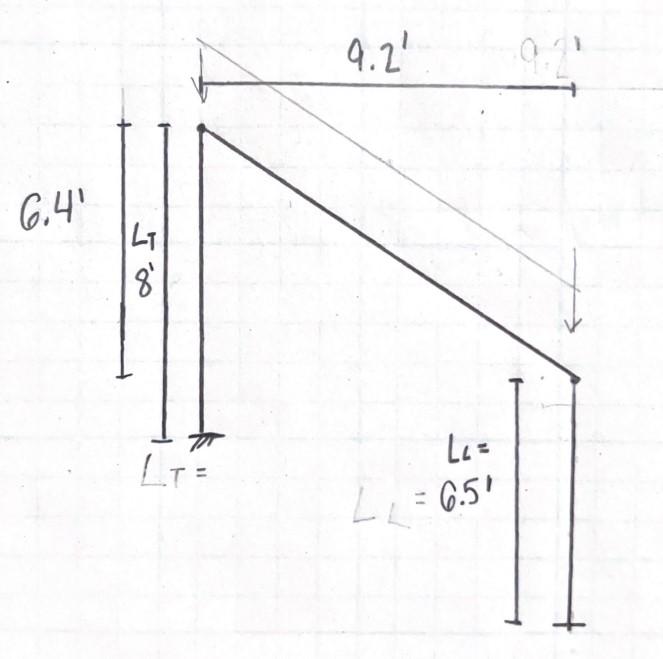
From our preliminary design, we decided to add a few components, along with modifying other elements, based on feedback and additional research. One element we added was an abutment under the lower 45’ long bridge. This abutment is placed on the uphill side of the bridge, as shown in Figure 9 where the bridge abutment is outlined in dark red This retaining wall is used as columns of the bridge Excavating enough to have full columns would not be practical as a small abutment requires much less excavation and would provide much more stability. The abutment will be 6.5’ wide and 19’ into the soil as well as 8’ tall. The soil at the site is rather weak, requiring this large of an abutment This abutment can hold the weight of the bridge, along with preventing the soil from crumbling down the slope.

Entrance Addition

Another element that was added to this detailed design was the entrance to the stairs at the top on the corner of Lenora Street and Meadow Street Before, we had just discussed its existence, but now it is included in our final design. This is an important aspect to include as we are moving the entrance of the stairs from the middle of Lenora Street to the intersection of Lenora Street and Meadow Street. This will allow the park and the stairs to be visible to more people and provide a clear route option from Lenora Street down to the park, providing better accessibility as shown in Figure 10 below

Figure 9 | Wireframe View of Bridge Abutment

Figure 10 | Entrance Trail Along Lenora Street and Meadow Street

Joint Connections Addition

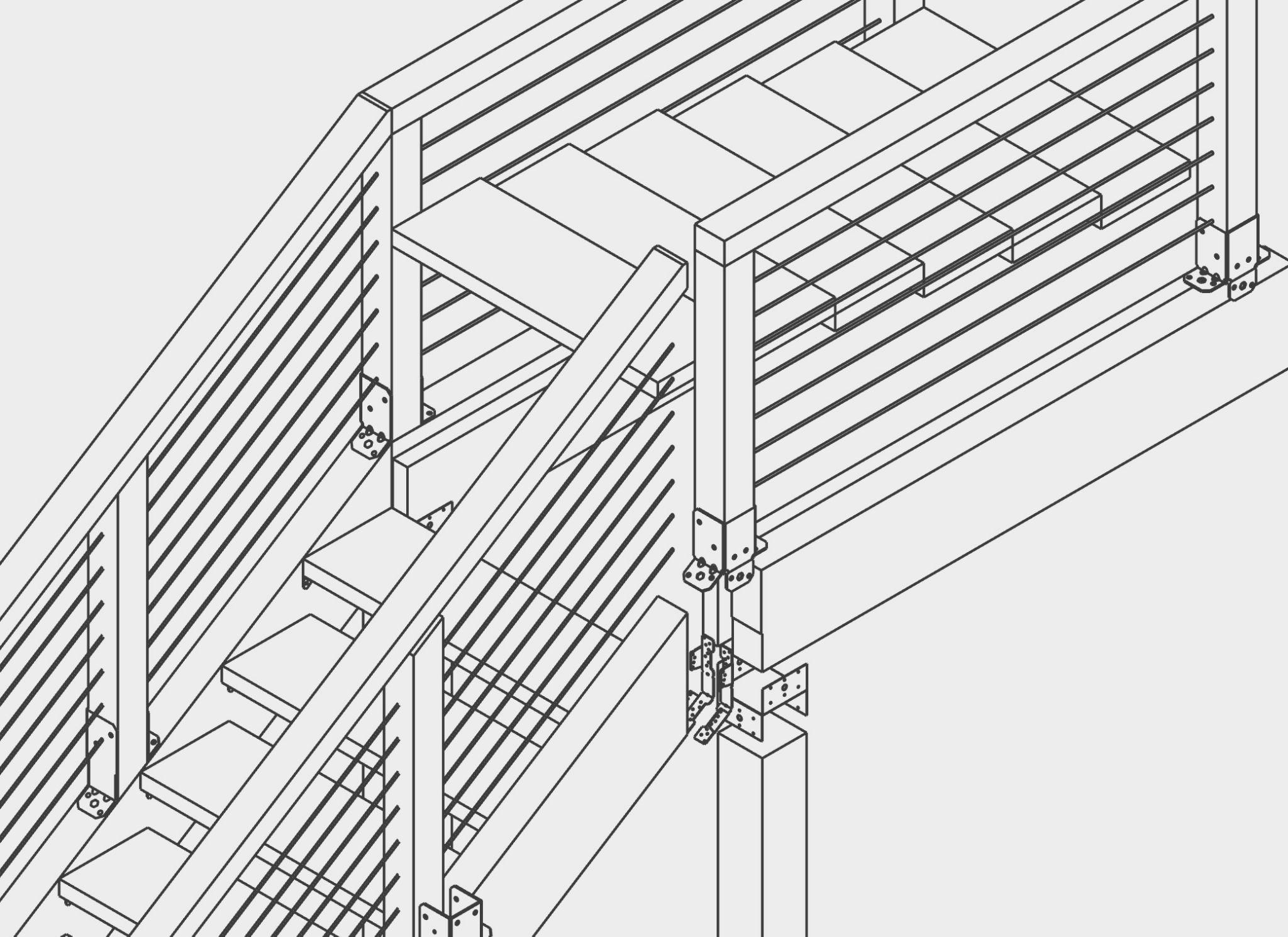
In addition to designing the entrance in more detail, we also included the details of the various connections We used joist hangers, shown in Figure 11 below, of several types to connect and support parts of the stairs. Making sure that these connections were strong enough to support the weight of the wood and people was also an element we looked into and ensured. To facilitate the connection of the railings to the bridge, planks of wood, shown in Figure 12 below, were added on top of the bridge I-beam girders. Connecting the railings and walking planks directly to the steel I-beam would be a difficult task, requiring ample time and tools. Adding these planks of wood along the length of the I-beams makes the connections easier. The planks of wood only need to be attached a few times Screwing wood to wood is a much easier and faster connection than trying to screw wood to steel

Figure 11-12 | Joint Connections

Changes Made

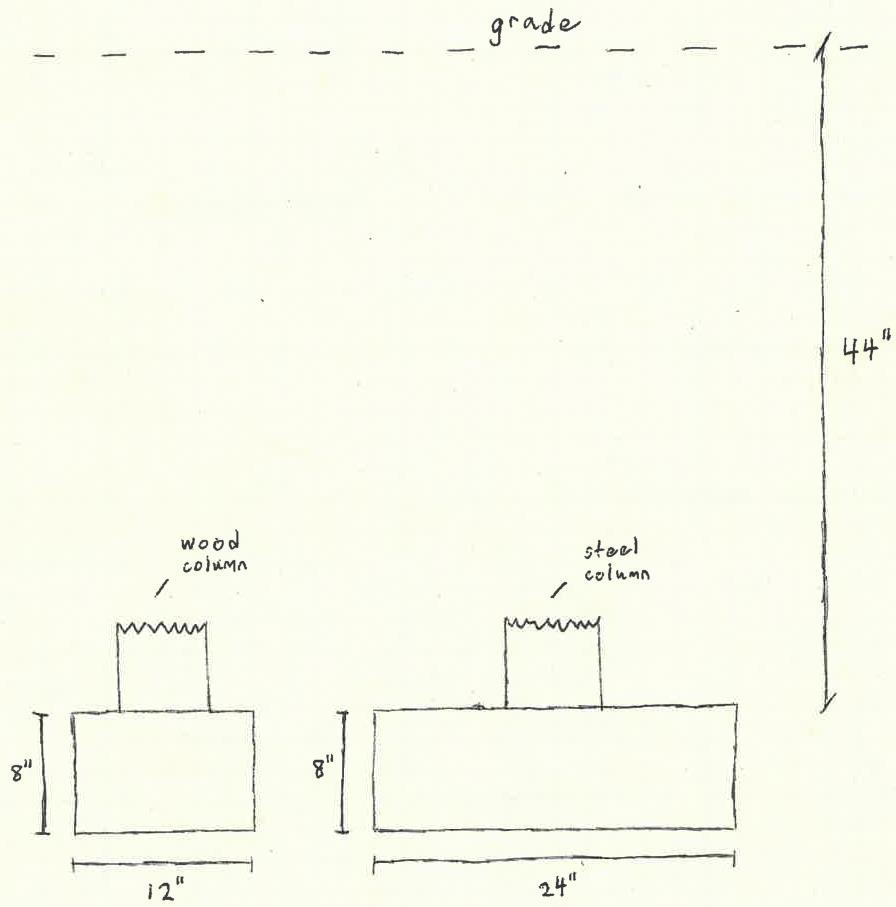
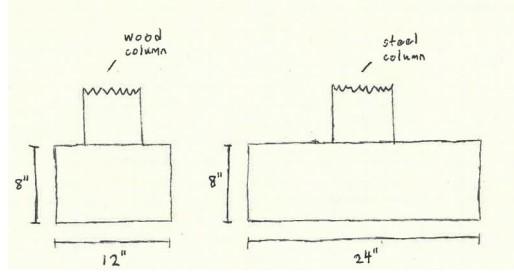
In addition to adding new elements, we changed the dimensions of the railing post spacing to be a maximum of 70 inches along the centers of each post This was necessary because the original spacing caused the railings to bend beyond acceptable limits. The spacing was maximized to save in material cost, while also preventing the lateral loads from bending the railings too much. Furthermore, also due to these bending limits, the railing thickness also had to be increased from one inch to three inches We also changed the dimensions of the foundations to make them larger, so that each wood column had a concrete foundation cross-section of 8” X 12” and that each steel column had a concrete foundation cross-section of 8” X 24”. After looking at our calculations from the preliminary design and hearing feedback, we realized that

our foundations need to be larger in order to support the weight of the bridges and the stairs, as both were originally going to be made out of wood. The foundations also needed to be larger due to the weak and landslide-prone soil on site This landslide-prone soil also caused us to change the depth of our columns, as our columns needed to go deep enough below grade so that the frost line was cleared. Thus, each of our columns, wood and steel, are at least 44 inches below grade.

Construction Processes

The construction process of the stairs will largely depend on the construction process of other systems It will be especially dependent on the construction of the bioswale and the trails. It is dependent on bioswale construction because the bioswale is constructed directly on the path of the old stairs. It is dependent on the trails because the stairs will need to connect to them. The Gantt Chart in Figure 13 describes the general schedule for the stair system The duration of each activity was estimated using the RS Means cost estimate by multiplying the quantity of materials by their labor hours (Gordian, 2022). It is assumed that grubbing and clearing has been completed before the construction of the stairs.

Figure 13 | Gantt Chart

The schedule begins with the demolishing of the old stairs. This is necessary to begin the construction of the bioswale The stairs are also very dilapidated, thus removing them first will remove a safety risk Temporary stabilization will need to be done to minimize the risk of landslides. We will not put the final SlopeGrid stabilization at this point, since it would interfere with the construction equipment mobilization.

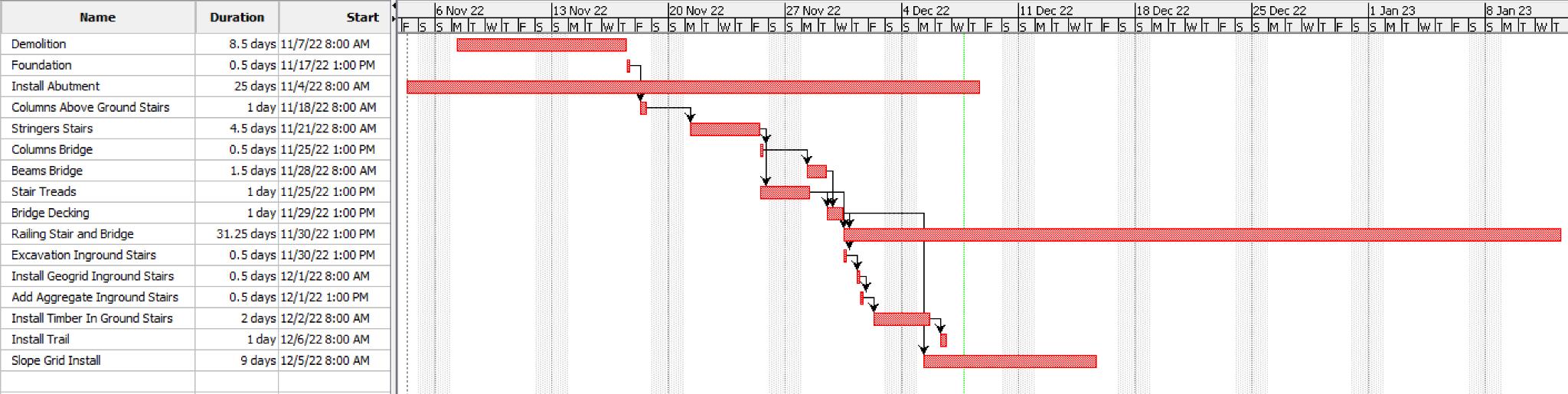
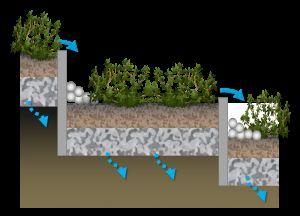
Building the above-ground stairs and bridge is the next step. This is done because the above-ground stairs are connected to the perimeter of the project area. Thus, the above-ground stair construction zone is more accessible The foundations and abutments will be constructed first. After the decking of both the above-ground stairs and bridges is completed, the construction of the in-ground stairs can begin. The team chose to wait until the decking was complete to start the in-ground stair because the in-ground stairs are in the middle of the site and not easily accessible until the above-ground stairs and bridge are complete. While the in-ground stairs are being constructed, the railing of the stairs and bridges is also being completed. Due to the detailing of the railings, this will take quite some time. Thus, working on it concurrently to the in-ground stairs will be the most efficient solution As the railings and in-ground stairs are being constructed, the SlopeGrid will be installed The planned SlopeGrid to be used is sold by the geosynthetic company Cell-Tek. The SlopeGrid should be installed in accordance with the installation instructions found on the manufacturer’s website (Cell-Tek). Figure 14 below shows the general layout for the materials and construction methods for the SlopeGrid

Figure 14 | SlopeGrid General Construction Layout (Cell-Tek).

Once all major components have been finished, the trails connecting the stair system to the streets will be completed. This trail will have the same design as the trails in the rest of the park and include benches to promote community engagement

Some of the major considerations that could impact the safety and timely completion of the work will be demolition and soil stabilization The demolition process will be difficult since the soil is unstable and large equipment will be difficult to use. This means that smaller equipment may need to be used to ease accessibility and avoid landslides, which could lengthen demolition time. Proper soil stabilization during and after construction will be critical for safety. This area is landslide-prone, as can be seen in Figure 15 The angle of the trees clearly indicates that landslides have occurred before. Construction processes and weather conditions could cause further landslides. This will put workers’ safety at risk and increase project duration. Therefore, proper earthwork management is crucial. Finally, another major consideration that could impact safety and time is the construction of the bioswales and bridges happening concurrently. Special consideration will need to be given by project managers to avoid conflicts due to space constraints and equipment, since the bridges are directly above the bioswale. The work on the bioswale should be avoided until the main bridge structure (beams, columns, decking) is completed to avoid falling debris from construction

Figure 15 | Evidence of Previous Landslides

The construction time estimate is 66 days. This estimate includes stops for the weekend and does not include final cleaning or demobilization.

To find equipment and laborers for this project the group used the RS means cost estimate (Gordian, 2022) Table 1 below contains the description of the item, the crew ID, the laborers needed, and the equipment needed. The table does not contain all the materials listed in the estimate since some items were purely material and did not have a quantity attached to them. As can be seen from the table, there is an overlap between many activities’ labor needs It is important to consider these when making a more robust schedule in the detailed design phase. When it came to equipment the major overlap was the need for a crane to assemble the bridge, beams, and columns. In the construction plan, this was considered by making sure the beam and column activities were right after the other This reduces the need to mobilize the crane twice, which will save money and time.

Table 1 | Labor and Equipment Descriptions

Bridge Decking: porch or deck framing, treated lumber, decking

Stair Treads: porch or deck framing, treated lumber, decking

Stair Stringers: Porch or deck framing, treated lumber, stair stringer

Labor Foreman 1 Air Compressor, 250cfm

Demolition: selective concrete demolition B9

2 Breakers, Pavement, 60lb 2-50’ Air Hoses, 1.5” Structural Steel Beam/Girder E2

Laborers

Columns Stairs: 6" x 6" wood, column framing

Column Bridge: column, structural E2

Railings:

1 Truck Driver

1 Roller, Vibratory, 25 tons

1 Truck Tractor, 6x4, 450 HP

1 Water Tank Trailer, 5000 gal

Cost Estimation

Costs were estimated using RS means (Gordian, 2022). The calculations, assumptions, and complete estimates can be found in the calculations section of the report The cost includes labor, material, and equipment for all major components It does not include cost estimates for activities that relate to the entire project, such as site office or clearing and grubbing. The cost was estimated to be around $113,000 dollars. This cost is only preliminary and may change once costs are calculated using quotes for both major components and subcomponents A life cycle cost over 50 years was also calculated Using a 7% real rate of return, maintenance costs, and replacement costs it was estimated that the net present value over 50 years would be $268,000.

Future Activities

In order to transition our detailed design to complete construction documentation, several design tasks will need to be completed. First, our specifications will need to be expanded and completed, covering all elements of the design. For instance, the specification about structure demolition will need to be completed, including the method of demolition along with the required materials. This will help transition our design to construction processes since specific materials will be able to be selected and construction companies can be contacted In addition to

specifications, our drawings will need to be checked and signed off by a professional engineer. The professional engineer will also need to check and sign off on our calculations for all our elements, including the stairs, the bridge, and the railings Having a professional engineer or team of engineers check our design is essential for safety and for turning our design into construction documents. Professional engineers will be able to accurately check over our work and will be able to catch any errors, along with giving specific and constructive feedback on anything that needs to be modified. One final activity that will need to be completed is designing the connection between the retaining wall and the bridge girders. Since the retaining wall was only just added to this iteration of the project, we were not able to design and include connections like we were able to with the stairs, bridge, and railings

Specifications

Specifications Table of Contents

MasterFormat Title MasterFormat Number

Structure Demolition 02 41 16 Wood Treatment 06 05 73 Geogrids for Earthwork 31 05 19 19

Section 1 - 02 41 16 - Structure Demolition

Part 1 - General

1 1 Summary

A. This Section includes: 1. Demolition of existing stairs. 2 Deconstruction of existing stairs

1.2 Definitions

A. Deconstruction: Disassembly of portions of existing stairs for the purpose of recovering materials.

1.3 References

A. ANSI A10.6 - Safety Requirements for Demolition Operations

B Private Demolition Permits - The City of Pittsburgh

1.4 Submittals

A. Demolition Plan: Submit a comprehensive demolition plan, describing the proposed sequence, methods, and equipment for demolition removal of structure; include salvage if required

B. Permits: Submit copies of demolition and debris disposal permits and notices for record purposes

1.5 Quality Assurance

A. All waste to be handled properly and must follow OSHA regulations.

B. All demolition to be inspected by a third party hired by the owner.

Part 2 - Products

2.1 Materials, Equipment, and Facilities

A. The Contractor shall be responsible for the furnishing of all materials, tools, equipment, and services as required for performing demolition

B. Material used for backfill shall conform to backfill requirements and be similar to existing soil on-site

Part 3 - Execution

3.1 Deconstruction

A. Inspect and evaluate for reuse of existing stair structures on site.

B Salvage existing materials for recycling and reuse

3.2 Demolition

A. All stair structures, including superstructure, substructure, foundations and approach structures, shall be completely removed

B. If existing deep foundations exist, they shall be removed to a minimum of 5 feet below the bottom of foundations

3.3 Safety

A. Dispose of removed materials, waste, trash, and debris in a safe, acceptable manner, and in accordance with applicable laws

B. Trash and debris from the site shall be removed in frequent intervals so as not to cause hazardous conditions for workers and the public.

Section 2 - 06 05 73 - Wood Treatment

Part 1 - General

1.1 Summary

A. This Section includes:

1 Wood Treatment

2. Natural Decay.

1.2 Submittals

A Product Data: Submit the following for each treated wood product to be used during the construction process.

1. Sourcing locations. Indicate the location for the extraction and harvesting of the wood.

2. Manufacturing locations. Indicate the location for the manufacturing facility.

B. Letter of Certification for Sustainable Forestry

1 Forest Stewardship Council (FSC) - Provide a letter of certification signed by the lumber supplier.

C Letter of Certification for Pressure Treatment

1. Submit Certification from treating plants stating chemicals and processes used are within specified standards

Part 2 - Products

2.1 Materials

A Preservative Pressure Treatment:

1 Wood products shall be treated with waterborne wood preservatives, excluding those which contain arsenic and/or chromium.

B. Fire Retardant Treatment:

1. Fire-retardant-treated wood products shall be free of halogens, sulfates, ammonium phosphate and formaldehyde

C. Natural Decay and Insect Resistant Wood:

1. Natural decay and insect resistant wood must be sustainably harvested.

Part 3 - Execution

3 1 Inspection

A. Inspect all treated woods for any defects. Properly dispose of wood with defects, do not use it for construction

B Ensure all treated wood for construction does not contain harmful or cancerogenic materials.

3 2 Safety

A. Wear appropriate PPE according to OSHA regulations when working with treated woods that have been deemed to be hazardous.

B Properly and safely dispose of any hazardous treated woods located on the construction site.

Section 3 - 31 05 19.19 - Geogrids for Earthwork

Part 1 - General

1.1 Summary

A. This Section includes:

1 Cellular confinement system, SlopeGrid, for slope protection.

1 2 References

A. Cell-Tek

1. SlopeGrid Technical Data Sheets

B. ASTM

1 ASTM D5199 - Standard Test Method for Measuring the Nominal Thickness of Geosynthetics.

2 ASTM D7328 - Standard Test Method for Effect of Exposure of Unreinforced Polyolefin Geomembrane Using Fluorescent UV Condensation Apparatus.

3. ASTM D1004 - Standard Test Method for Tear Resistance of Plastic Film and Sheeting.

C. Geosynthetic Research Institute

1 GS14 - Standard Test Method for Average Wall Thickness of a Geomembrane-Related Geocell by Indirect Measurement.

1.3 Submittals

A Product Data: Submit the following for each geogrid material to be used.

1 Manufacturer's data sheets

2 Preparation instructions and recommendations

3. Storage and handling requirements.

B. Samples: Submit a representative sample of any material prior to use

C. Provide calculations for the recommended anchor and tendon system

1. Include design conditions and slope stability calculations. Provide all recommended quantities including the number of stakes, anchors, grids, spacing, etc.

Part 2 - Products

2.1 Manufacturers

A. Acceptable Manufacturer: Cell-Tek, which is located at: 809 Barkwood Court; Linthicum, MD 21090; Web: https://wwwcelltekdirect com/

B. Substitutions: Not permitted unless approved by the owner.

2.2 Geogrid System Design

A. Basis of Design: SlopeGrid - SLP-4 - Slope Erosion Control Series as manufactured by Cell-Tek.

1. Cell Depth: 4 in.

2 Nominal Cell Dimensions: 12 in x 12 in x Cell Depth

3. Expanded Grid Dimensions: 8 ft. x 29 ft. (232 sq. ft.).

B. Geocell Stress & Strain Properties

2 3 Anchoring Components

A. Testing: Anchor must have supporting 3rd party testing available that provides pullout resistance in different soil types

2 4 Infill Materials

A. Infill material shall be free of any foreign materials.

B. Clays and organic materials are not acceptable infill material.

C Fill cells with topsoil on site unless otherwise specified

3.1 Installation

A Install geocells in accordance with manufacturer's instructions

B. Remove any of the major vegetation found on the slope that would get in the way of the cell-grid pattern of the fabric

C. Install earth anchors along the top of the slope to fix the fabric in place and prevent further movement

D. Tendons shall be threaded from Earth anchors and through the SlopeGrid to give rigidity

E. J-hooks shall also be installed along these tendons to fix the fabric into the slope

F Vegetation shall be replanted in these cells to improve soil stabilization and reduce risk of erosion.

3 2 Cleaning and Protection

A. Clean and protect all geogrid products in accordance with the manufacturer's recommendations

B. Repair and replace damaged products.

3.3 Safety

A Perform all geogrid work in accordance with OSHA regulations Take necessary precautions when working on steep slopes.

B Perform routine landslide inspections prior to work Stop work and contact the owner if any immediate risks of landslides are present.

Appendix A: Detailed Design Drawing Set

See below for the Detailed Design Drawing Set.

SARARISTIANEE AIRONEEE

SAREAINTEROERTOTEENINEERANNOART TEREOSAEOIEORSEWITOTTEEXRESS WRITTENONSENTOTEENINEER ©ARNEIEEONNIERSIT EARTENTOIIAN ENIRONENTAENINEERIN

920

910

900

890

880

870

860

850

840

830

820

810

ARIERAE&NEERN ARIERARK ITTSRA15206 11042022 REIRAWINSET

2 12072022 ETAIERAWINSET

920

910

900

890

880

870

860

850

840

830

820

930 0+00 1+00 2+00 3+003+12 0+00 1+00 2+00 3+003+12

930 810

SARARISTIANEE AIRONEEE

Appendix B: Calculations

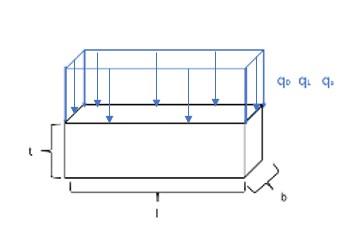
Calculations were made for all major components of the above-ground stairs and bridges. This includes both structural calculations for treads, stringers, beams and columns for the stairs and bridges and geotechnical calculations for abutments and footings It also includes railing calculations Calculations were not done for the in-ground stairs since these do not have any major components that are at risk of failure. In addition to structural and geotechnical calculations, cost calculations were made. These cost calculations include a material take-off, cost estimates using RS means, and a life cycle assessment over 50 years

Stair Calculations

The following pages are preliminary calculations for the stair. This calculation only focuses on the stairs in the top of the project, since these are larger and contain longer columns. Therefore, these set of stairs will face larger forces and are more likely to fail. Since the team is planning to use the same material dimensions for both set of stairs (top and bottom), we believe that if we make sure that the top stair sets are found to be sufficiently strong, the bottom stairs will be acceptable as well. Each of the seven staircases in the top of the system have the same design except for the column lengths. This means treads and stringers only need to be analyzed once. The column are also analyzed in these calculations, the team chose to calculate the staircase with the longest column, since these will face the largest forces.

Calculations will be based on -National Design Specification for Wood Construction (2018) by the American Wood Council -NDS Supplemental (2018)

-ASCE 7 (2022)

-AASHTO Signs (2015) -International Building Code (2021) -Manual for Engineered Wood Construction (2018)

- DCA 6 -Prescriptive Residential Wood Deck Construction Guide (2015) by the American Wood Council

CalculateCapacityofTreads,makesuredimensions chosenareappropriate Non-Commercial Use Only

Ct 1.2 Thermal Factor ASCE 7, Table 7-3

C

I

.9 Terrain B, exposure factor ASCE 7-2

1 Importance Factor ASCE 7, Table 1.5-2

wD = 4.102 lbf ft 0.004 kip ft Dead, based on density of wood (NDS Supplement-Table 1B) pb

T = + wL wD 0.098 kip ft Total Applicable factored load governs with their respective time factor, λ Case Factored Load (ASCE 7, 2.3) λ (NDS 2018, Table N3) 1

wu1 = 1.4⋅wD 0.006 kip ft

λ1 .6 2 ≔ wu2 = + + 1.2⋅wD 1.6⋅wL 0.5⋅ws 0.164 kip ft ≔ λ2 .8 3 ≔ wu3 = + + 1.2⋅wD 1.6⋅ws wL 0.127 kip ft ≔ λ3 .8 ReductionFactors used in this analysis. All from NDS, 2018 Factor Name Source Reasoning

Ci 1 Incising Factor 4.3.8 There are no incisions

CF 1 Size Factor 4.3.6 lumber does not exceed 12" wide and it is not 4" thick

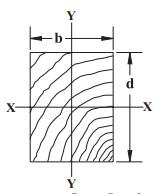
CL 1 Beam Stability Factor 3.3.3 Depth does not exceed breadth (d<b), in flatwise loading

b = bt 0.938 ft

d = tt 1.5 in

Temperature Factor 4.3.4 The structure will not experience sustained exposure of temps above 150F Non-Commercial Use Only

Checkslendernessratio RB Effective length (Table 3.3.3)

Shear

Deflection

Deflection limits (Source IBC Table 1604.3) Deflection Midspan- uniformely loaded

Live Load = lt 240 0.15 in ≔ ΔL = ⎛ ⎝ ⋅ 5⋅wL lt 4 ⎞ ⎠ ⋅ 384⋅E Iyy 0.039 in (M3.5-1)

Total Load = lt 360 0.1 in ≔ ΔT = ⎛ ⎝ ⋅ 5⋅wT lt 4 ⎞ ⎠ ⋅ 384⋅E Iyy 0.04 in

Sincethelimits arelargerthanthedeflections,this is acceptable

CalculateCapacityofStringer,makesuredimensions chosenareappropriate Non-Commercial Use Only

CalculateCapacityofStringer,makesuredimensions chosenareappropriate

Stringer 4inX12in

Standard Dressed Dimensions:

s 3.5 in NDS Supplement (Table 1B)

bs 11.25 in NDS Supplement (Table 1B)

ls 11 ft (estimate, based on preliminary drawings) *Dimensions were first checked with minimum in DCA 6, however, this had too low of a slenderness ratio. Thickness was change to 4 in nominal

The stringer is in red Dimensions of Stringer

Section Properties:

Assuming that the wood is loaded on the narrow face and is dense select structural Property Source

Sxx 73.83 in3 Section Modulus (strong axis) NDS Supplement (Table 1B)

Syy 22.97 in3 Section Modulus (weak axis) NDS Supplement (Table 1B)

Ixx 415.3 in4 Moment of Inertia (strong axis) NDS Supplement (Table 1B)

Iyy 40.20 in4 Moment of Inertia (weak axis) NDS Supplement (Table 1B)

Modulus of Elasticity

Emin 690000 psi Min. Modulus of Elasticity

Comp parallel to grain

Fb 1800 psi Bending design

Southern Pine Dense Select Structural NDS Supplement (Table 4B)

Southern Pine Dense Select Structural NDS Supplement (Table 4B)

Southern Pine Dense Select Structural NDS Supplement (Table 4B)

Southern Pine Dense Select Structural NDS Supplement (Table 4B)

A 39.38 in2 Area of Section NDS Supplement (Table 1B)

Specific Gravity

Southern Pine Dense Select Structural NDS Supplement (Table 4B)

Stair Calculation

w 62.4 lb ft3 Density water = pb 34.353 lb ft3 Density of Southern Pine (NDS Supplement 3.13)

Loads Refer to tread loads, for live and snow load.

Dead Load Need to account for weight of treads and weigth of stringer. Since there are 12 treads, the density of the stringers and treads is the same, and each stringer will carry the weight of half of a tread, the total dead weight will be For a density of the approximate weight is 35 lb ft3

wDt 9.570 lbf ft (NDS Supplement-Table 1B) Assume each stringer carries half the weight of the treads

wD = +

⎛ ⎜ ⎝ ⋅ ⋅ wDt 12 lt 2 ⎞ ⎟ ⎠ ls wDt 0.025 kip ft

Wind Load An additional wind load is also included in calculation. Variables needed to find design wind pressure

Variable Name Source Reasoning

V 100 mph 300-Year MRI Basic Wind Speed AASHTO Signs, 3.8-3b Used map

Kz 1 Height and Exposure Factor AASHTO Signs, 3.8,4-1 Height less than 33 feet

Kd .85 Directionality Factor AASHTO Signs, 3.8,5-1 Assume support type is overhead frame/truss, this is also the lowest factor

G 1.14 Gust Effect Facotor AASHTO Signs, 3.8.6 this is the minimum number

Cd 2.0 Drag Coeffciient AASHTO Signs, 3.8.7 Assume two member or trusses

Wind pressure Equation :Pz

0.00256 Kz Kd G V2 Cd psf mph2 49.613 psf (AASHTO Signs, 3.8.1-1) The wind load will be a force both in the weak and strong axis of the stringer Non-Commercial Use Only

Pz = ⋅

The wind load will be a force both in the weak and strong axis of the stringer

The stringers will face axial compression and bending moment (edwise and flatwise). Thus, need to design for bending in two directions and axial loading

Example of loading on one stringer (SkyCiv)

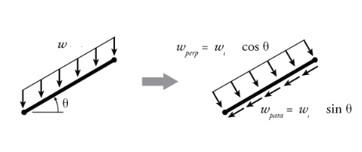
The 4 types of loads will need to be applied to the stringer differently:

Live Load

There is two ways of distributing the force. In the first assume load on the treads is being transferred to stringers. In the second, the loads are assumed to distributed load on both stringers. Tested out both cases in SkyCiv

Load Transferring to stringers

Load distributed on stringers

As can be seen from the two figures the maximum moment is almost the same, so will base calculations on load distributed on stringers This means tributary width will be half the width of tread

TW = .5⋅lt 1.5 ft

Since load causes both axial and bending, need find the axial and bending components. The bending will be in the edgewise case Angle of stairs, the stairs have a rise and run of:

rise 77 in

run 110 in

tan( (θ) ) tan( ( ⋅θ deg) )

Dead Load

Will be just like the live load, since already account for tributary width, I divided weight by TW

Bending:

kip ft

Snow

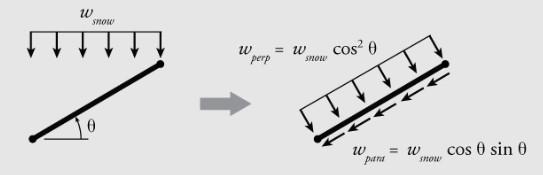
Snow load is along the horizontal projection of the member

kip ft

wS_A = ⋅

qs TW cos( (θ) ) sin( (θ) ) -0.01 kip ft

Wind

Wind will be perpendicular to surface, both causing edgewise and flatwise bending Found the pressure previously, but need to apply this to the surfaces that will be in contact with wind, which in this case includes the railings. The weight of railing is assumed negligible

Edgewise bending

The areas that are considered in edge wise bending is just the area of the tread (12 steps) and stringers

tt lt 12 2

ts ls 5.458 ft2 This means the force due to wind is:

AEdge = +

lbf

Not including torsion in calculation. Will assume this force will be distributed throughout the length of the stringer

ww_edge = Fw ls 0.025 kip ft

Flatwise bending

Flatwise bending

Railings ≔ hr 36 in Railing Height

bp 4 in Post thickness

br 1 in Railing Thickness

Total area that is covered by railing Since there is 4 posts and the length of the top bar is the length of the stringer, the total area covered by the railing is:

Not including torsion in calculation. Will assume this force will be distributed throughout the length of the stringer

ww_flat = Fw ls 0.022 kip ft Now that have all the loads divided in terms of axial and bending can calculate applicable factored loads. Below are factored loads with their respective time factor, λ

Axial Case Factored Load (ASCE 7, 2.3) λ (NDS 2018, Table N3) 1

wu1A = 1.4⋅wD_A -0.015 kip ft

λ1 .6 2

wu2A = + + 1.2⋅wD_A 1.6⋅wL_A 0.5⋅wS_A -0.119 kip ft

λ2 .8 3

wu3A = + + 1.2⋅wD_A 1.6⋅wS_A wL_A -0.092 kip ft

λ3 .8 > > wu2A wu3A wu1A Since case 2 is the larger factored load will be basing calculations on this

Bendingedgewise

Bending

flatwise

Only one case, since the only force is wind

wuF = ww_flat 0.022 kip ft

λ1 1 ReductionFactors used in this analysis. All from NDS, 2018 Factor Name Source Reasoning

CF 1.1 Size Factor 4.3.6 lumber is 4" thick but not more than 12" wide

CLflat 1 Beam Stability Factor 3.3.3 Depth does not exceed breath for flatwise case, refer to tread calc CLedge Beam Stability Factor 3.3.3 Depth exceed breadth (d>b) for edgewise case, need further calculation

Edge wise case Flat wise case

Ct 1 Temperature Factor 4.3.4 The structure will not experience sustained exposure of temps above 150F

CM 0.85 Wet Service Factor, bending Sup. 4B Since stairs outdoor, moisture will exceed 19% for extended periods of time

Stair Groups Stair Calculation

CM 0.85 Since stairs outdoor, moisture will exceed 19% for extended periods of time

CEA R:GAH 12/05/2022 14 of 28

Cr 1 Repetitive Member Factor Sup. 4B stringers are not in contact

Cfuflat 1.2 Flat Use Factor Sup. 4B lumber is used flatwise

Cfuedge 1 Flat Use Factor Sup. 4B luber is used edgewise CP Column stability factor 3.7.1 equation will be below, requires other factors not calculated yet CT Buckling Stiffness Factor 4.4-1 equation will be below, requires other factors not calculated yet

Calculate reduction factors that have not been calculated Buckling Stiffness Factor CT (4.4-1)

Inputs

Assumptions

KM 1200 assuming wood is only partially seasoned

KT 0.59 vissually graded lumber

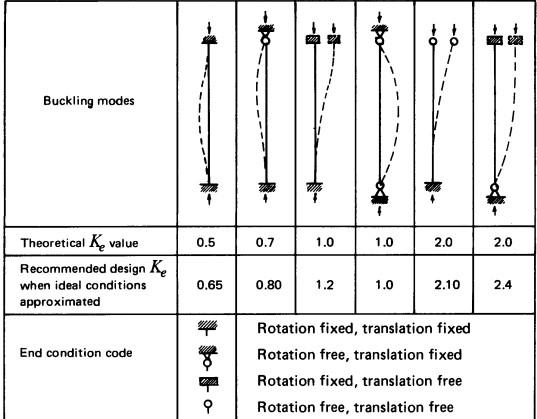
Ke 1 Buckling length coeffcieicent (NDS, 2018 Table G1). Assume rotation is free, but translation is fixed in both flat and narrow face

le1 = ⋅ Ke ls 11 ft Effective column length (3.7.1.2) Since le is greater than 96", then ≔ le1 96 in

⎛ ⎜ ⎝

KM le1 ft ⎞ ⎟ ⎠

CT = 1+

KT E psi

1.01 is unitless CT

Beam stability factor edgewise case CLedge

Distance between supports , will be the distance between treads, since rise and run of lu each step is 7" (rise) by 10" (run). will be lu

lu = ⎛ ⎝ + ( (10 in) ) 2 ( (7 in) ) 2 ⎞ ⎠

1 2 1.017 ft

Effective length for bending, (Table 3.3.3) le Since = lu dE 1.085 < lu dE 7 and assuming single span uniformly loaded

leb = 2.06⋅lu 2.095 ft

Slenderness ratio (3.3-5) RB = dE 11.25 in ≔ RB = ⎛ ⎜ ⎜ ⎝ ⎛ ⎝ ⋅ leb dE⎞ ⎠ bE 2 ⎞ ⎟ ⎟ ⎠

1 2 4.805 Since slenderness ratio does not exceed 50, it is acceptable. This is slenderness of edgeface

Calculate (Table 4.3-1) ′ Emin ≔ Emin ' = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ Emin CM Ct Ci CT ( (1.76) ) ( (0.85) ) ⎛ ⎝8.863⋅105 ⎞ ⎠ psi

Calculate FbE ≔ FbE = 1.2⋅Emin ' RB 2 ⎛ ⎝4.606⋅104 ⎞ ⎠ psi reference bending design value multiplied by all applicable adjustment factors except Fb '' Cfu, and CL (see 2.3) ≔ Fb '' = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ Fb Ci CF Ci Ct CM Cr 2.54 λ2 .85 2.907 ksi

Now can calculate CLedge ≔ CLedge = -

⎛ ⎜ ⎝ 1+ ⎛ ⎜ ⎝ FbE Fb '' ⎞ ⎟ ⎠ ⎞ ⎟ ⎠ 1.9

⎛ ⎜ ⎜ ⎜ ⎝

⎛ ⎜ ⎝ 1+ ⎛ ⎜ ⎝ FbE Fb '' ⎞ ⎟ ⎠ ⎞ ⎟ ⎠ 1.9

⎞ ⎟ ⎟ ⎟ ⎠

2 -

2 ⎛ ⎜ ⎝ FbE Fb '' ⎞ ⎟ ⎠ 0.95 0.997 3.3.3

Column Stability Factor CP (3.7.1) Will be different depending on edgewise or flatwise loading c factor needed in calculation ≔c 0.8 (sawn lumber, 3.7.1)

reference compression design value parallel to grain multiplied by all applicable adjustment Fc '' factors except CP

Fc '' = ⋅ ⋅

Fc CM Ct CF Ci 2.4 0.9 λ2 ⎛ ⎝2.827⋅103 ⎞ ⎠ psi ≔ Emin ' = ⋅ ⋅

Emin CM Ct Ci CT ( (1.76) ) ( (0.85) ) ⎛ ⎝8.863⋅105 ⎞ ⎠ psi Need to see which has the greater slenderness ratio

EdgeWise ≔ le1 = ⋅ Ke ls 11 ft (3.7.1.2) = le1 dE 11.733 (3.7.13) *Note slenderness ratio below 50, so acceptable

FlatWise

Combinedbendingandaxialloading

Since the loads are not completely perpendicular to the stringers, need to look at both bending and axial forces

Main equation + + ⎛ ⎜ ⎝ P P' ⎞ ⎟ ⎠

2 M1 ⋅ M1 ' ⎛ ⎜ ⎝ 1-⎛ ⎜ ⎝ P PE1

⎞ ⎟ ⎠ ⎞ ⎟ ⎠

M2 ⋅ M2 ' ⎛ ⎜ ⎜ ⎝ - 1-⎛ ⎜ ⎝ P PE2

⎞ ⎟ ⎠ ⎛ ⎜ ⎝ M1 ME

⎞ ⎟ ⎠

2 ⎞ ⎟ ⎟ ⎠ (NDS 3.9-1)

= adjusted compression capacity P' =compressive force P =adjusted moment capacity (strong axis) M1 ' =bending moment (strong axis) M1 =ajusted moment capacity (weak axis) M2 ' =bending moment (weak axis) M2 = critical column buckling capacity(strong axis) PE1 =critical column buckling capacity(weak axis) PE2 =critical beam buckling capacity ME

First need moment capacity and buckling capacity related to flat (weak axis) and edgewise case (strong axis). The time factors were chosen previously in the load discussion section λ

= FcE1 5.292 ksi

Calculation CEA R:GAH

< fc FcE1

= fc 0.033 ksi (NDS 3.9.2)

sincethisistruepassescase < fc FcE1

= FcE2 0.512 ksi

= fc 0.033 ksi

< fc FcE2 (NDS 3.9.2)

sincethisistruepassescase < fc FcE2

= FbE 46.057 ksi

= fb1 0.568 ksi

< fb1 FbE (NDS 3.9.2)

sincethisistruepassescase < fb1 FbE

Memberpasses allcases,thedimensions chosenareappropriate

CalculateCapacityofColumn,makesuredimensions chosenareappropriate Non-Commercial Use Only

Southern Pine Dense Select Structural NDS Supplement (Table 4D)

Southern Pine Dense Select Structural NDS Supplement (Table 4D)

Southern Pine Dense Select Structural NDS Supplement (Table 4D) Non-Commercial Use Only

Fb 1750 psi

Fc 1100 psi

Bending design

Comp. parallel to grain

Southern Pine Dense Select Structural NDS Supplement (Table 4D)

Southern Pine Dense Select Structural NDS Supplement (Table 4D)

A 30.25 in2 Area of Section NDS Supplement (Table 1B)

Specific Gravity

Density water

Loads

Southern Pine Dense Select Structural NDS Supplement (Table 4D)

To simplify calculation, since there is 4 columns per stair case will assume that each column will recieve 1/4th of the total load of the stair and 1/4 of the landing loads

ll 6 ft Width of Landing

Length of Landing

wl = lt 3 ft

To do this will make all loads either parallel (acting axially) or perpendicular (bending) on the column

Live and Dead

Live and Dead loads are already parallel with length of column. Therefore can use live and dead loads calculated in stringer calculations. Need to just multiply by the appropriate factor

We know the dead load on each stringer, since there are 2 stringers the total dead load due to stringers is

kip ft

The dead load of each stringer of the landing, since there are 2 stringers the total dead load due to stringers is

ft 6

Dead load on each column, will then be the total dead load times the length of the stringers PD Non-Commercial Use Only

Dead load on each column, will then be the total dead load times the length of the stringers PD ≔ PD = + ⋅ wD_ST ls ⋅ wD_LT ll 4 0.214 kip

Live load will be similar, but using a pressure instead. Multiply pressure by the width of the stair case (width of stair case is the same as width of landing) and the length of stringers (both stringers in the landings and stairs) = qL 0.694 psi Live load on each column, PL ≔ PL = ⋅ qL ⎛ ⎝ + ⋅ lt ls ⋅ ll lt⎞ ⎠ 4 1.275 kip

Snow

Process to make stair stringer snow load parallel to column. In the stringer calculation already did the first step for the stair stringer = wS_B 0.019 kip ft ≔ wS_par = wS_B cos( (θ) ) 0.023 kip ft The landing snow load will be perpendicular to the surface. This was calculated in tread calculation = qs 0.131 psi

Now find point load ≔ PS = + ⋅ ⋅ wS_par ls 2 4 ⎛ ⎝ ⋅ ⋅ qs lt ll⎞ ⎠ 4 0.213 kip

Wind Assume wind is only acting perpendicular to column, thus it is only on the surface area of the column =Pz 0.345 psi ≔ ww = ⋅Pz bC 0.023 kip ft

Now that have all the loads can can calculate applicable factored loads. Below are factored loads with their respective time factor, λ

2018, Table N3)

λ3 .8 Since case 3 is the larger factored load will be basing calculations on this

Pu3A = + + 1.2⋅PD 1.6⋅PS PL 1.873 kip

Bending Only one case, since the only force is wind

λ1 1 ReductionFactors used in this analysis. All from NDS, 2018 Factor Name Source Reasoning

Ci 1 Incising Factor 4.3.8 There are no incisions

CF 1 Size Factor 4.3.6 lumber is more than 5" thick but not more than 12" wide

CL 1 Beam Stability Factor 3.3.3 Depth does not exceed breath for flatwise case, refer to tread calc = bC 0.458 ft = dC 0.458 ft

Ct 1 Temperature Factor 4.3.4 The structure will not experience sustained exposure of temps above 150F

CM 1 Wet Service Factor Sup. 4B Southern Pine use tabulated design values without further adjustment

C

1 Repetitive Member Factor Sup. 4B not applicable to column Non-Commercial Use Only

Combinedbendingandaxialloading

There will be both bending and axial forces on columns. Worst case would be if wind causes bending in two directions

Main equation ≤ + + ⎛ ⎜ ⎝ P P' ⎞ ⎟ ⎠ M1 M1 '⎛ ⎜ ⎝ 1-⎛ ⎜ ⎝ P PE1

⎞ ⎟ ⎠ ⎞ ⎟ ⎠

= adjusted compression capacity P' =compressive force P

M2 Fb2 ' ⎛ ⎜ ⎜ ⎝ - 1-⎛ ⎜ ⎝ P PE2

⎞ ⎟ ⎠ ⎛ ⎜ ⎝ M1 ME

=adjusted moment capacity (strong axis) M1 '

=bending moment (strong axis) M1

=ajusted moment capacity (weak axis) M2 ' =bending moment (weak axis) M2

= critical column buckling capacity(strong axis) PE1

=critical column buckling capacity(weak axis) PE2

=critical beam buckling capacity ME

⎞ ⎟ ⎠

2 ⎞ ⎟ ⎟ ⎠

1 (NDS 3.9-1)

First need moment capacity and buckling capacity. The columns are square, thus there is no strong or weak axis The time factors were chosen previously in the load discussion section λ

Bending ＝λ λ1 ≔ Fb1 ' = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ Fb CM Ct CL CF Cfu Ci Cr 2.54 0.85 λ1 ⎛ ⎝3.778⋅103 ⎞ ⎠ psi (M4.3-1) ≔ M1 ' = ⋅ Fb1 ' Sxx 8.731 ⋅kip ft (M3.3) ≔ FcE1 = ⎛ ⎝0.822⋅Emin '⎞ ⎠ ⎛ ⎜ ⎝ le1 dE

⎞ ⎟ ⎠

2 ⎛ ⎝2.268⋅103 ⎞ ⎠ psi (NDS 3.7) ≔ PE1 = ⋅ FcE1 A ⎛ ⎝6.862⋅104 ⎞ ⎠ lbf (M3.9)

Since there is no strong or weak axis ≔ M2 ' = M1 ' 8.731 ⋅kip ft ≔ FcE2 = FcE1 ⎛ ⎝2.268⋅103 ⎞ ⎠ psi ≔ PE2 = PE1 ⎛ ⎝6.862⋅104 ⎞ ⎠ lbf

Need to calculate slenderness ratio

Distance between supports , will be the length of column lu ≔ lu = lT 8 ft

Effective length for bending, (Table 3.3.3) le Since = lu dC 17.455 > lu dC 7 and assuming single span uniformly loaded ≔ le = + 1.63⋅lu 3⋅dC 14.415 ft

Slenderness ratio (3.3-5) RB

⎝

⎜ ⎜ ⎝

Compression

le dC⎞ ⎠ bC 2 ⎞ ⎟ ⎟ ⎠

RB =

1 2 5.608 Since slenderness ratio does not exceed 50, it is acceptable. This is slenderness of edgeface

Critical buckling capacity ≔ FbE = ⎛ ⎝1.2⋅Emin '⎞ ⎠ RB 2 33.813 ksi (ND7 3.9.2) ≔ ME = ⋅ Sxx FbE 78.136 ⋅kip ft (M3.9)

Now calculate actual compressive force and bending moments Compression ≔P = Pu3A ⎛ ⎝1.873⋅103 ⎞ ⎠ lbf ≔ fc = P A 61.911 psi

Bending- assume simple beam ≔ M1 = ⋅ wuF lT 2 8 0.182 ⋅kip ft (AISC Table 3-23- Aid 1) ≔ fb1 = M1 Sxx 78.722 psi

Same for both sides of column ≔ M2 = M1 0.182 ⋅kip ft ≔ fb2 = fb1 78.722 psi

Checkallcases forBendingandaxialcompression = + + ⎛ ⎜ ⎝ P P' ⎞ ⎟ ⎠

2 M1 ⋅ M1 ' ⎛ ⎜ ⎝ 1-⎛ ⎜ ⎝ P PE1

M2 ⋅ M2 ' ⎛ ⎜ ⎜ ⎝ - 1-⎛ ⎜ ⎝ P PE2

⎛ ⎜ ⎝ fb1 FbE

⎞ ⎟ ⎠

⎞ ⎟ ⎠ ⎞ ⎟ ⎠

⎞ ⎟ ⎠ ⎛ ⎜ ⎝ M1 ME

⎞ ⎟ ⎠

2 ⎞ ⎟ ⎟ ⎠

2 0.027 (NDS 3.9-4)

0.066 (NDS 3.9-1) This is less than1,thus passes case = + fc FcE2

This is less than1,thus passes case = FcE1 2.268 ksi < fc FcE1 = fc 0.062 ksi (NDS 3.9.2) sincethisistruepassescase < fc FcE1

= FcE2 2.268 ksi

= fc 0.062 ksi

< fc FcE2 (NDS 3.9.2)

sincethisistruepassescase < fc FcE2

= FbE 33.813 ksi

= fb1 0.079 ksi

< fb1 FbE (NDS 3.9.2)

sincethisistruepassescase < fb1 FbE

Memberpasses allcases,thedimensions chosenareappropriate

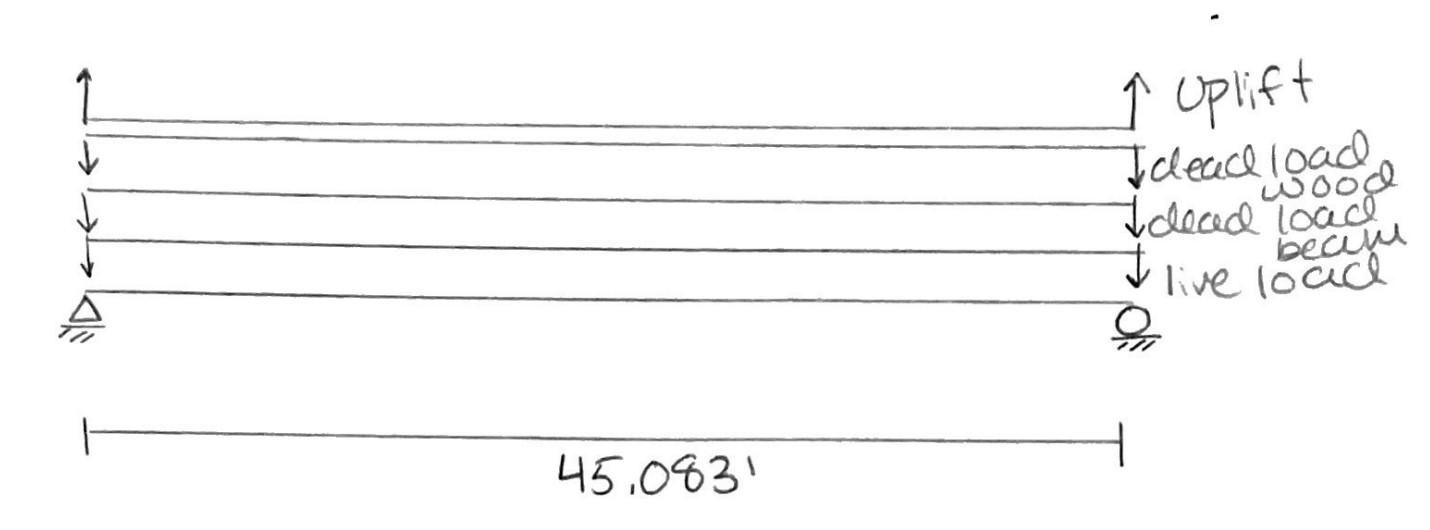
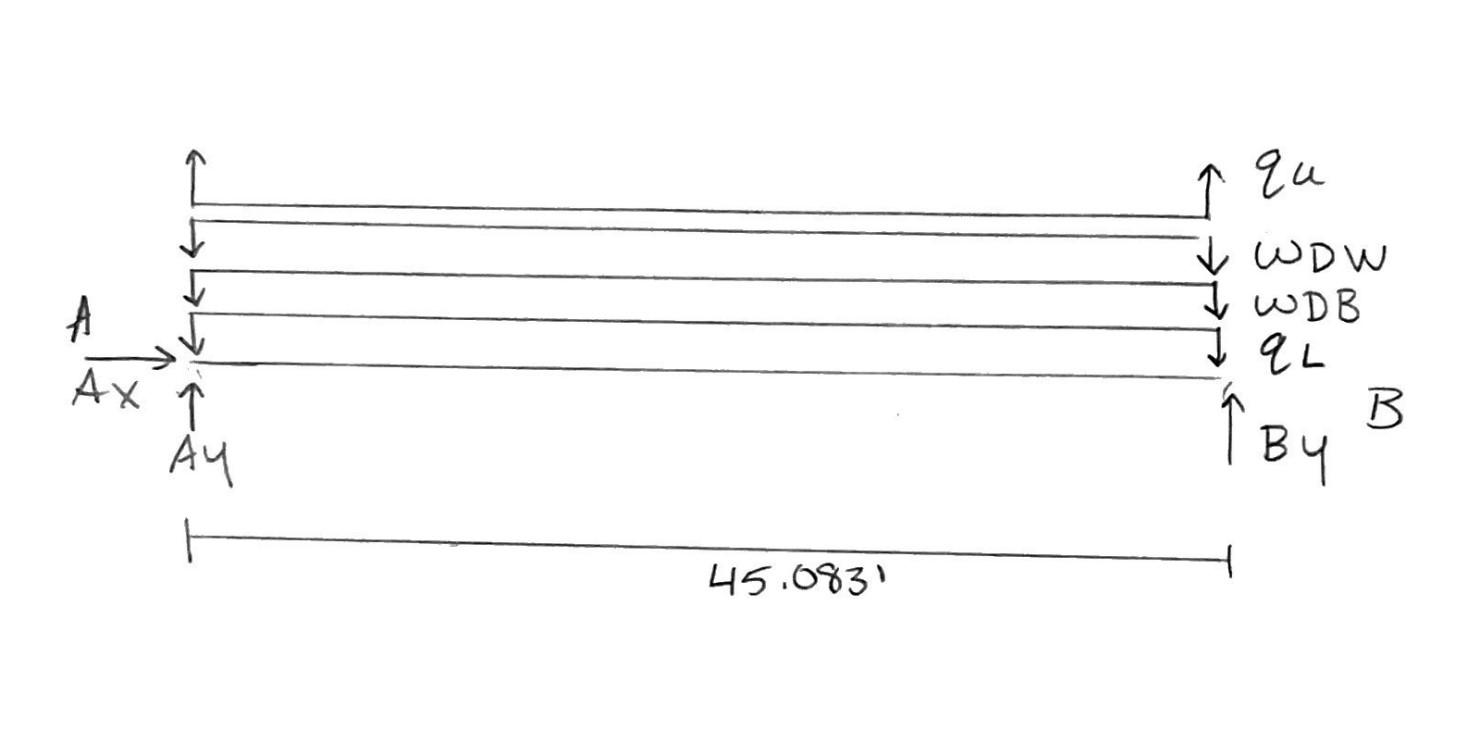
2 Wwood

Wwood 10.665 plf Convert to plf along nominal width, then add weight of 45' wood to support railings Design Aid #1 AISC Table 3.23

DeadLoadBeam

Wi 16 plf AISC Table 1-1 Beam W12x16 =L 45.083 ft Design Aid #1 AISC Table 3.23

Uplift LRFD Guide Specifications for the Design of Pedestrain Bridges (Section 3.4 Wind Loads)

Design Aid #1

AISC Table 3.23

Kd .85 Directionality Factor AASHTO Signs, 3.8,5-1 Assume support type is overhead frame/truss, this is also the lowest factor

G 1.14 Gust Effect Facotor AASHTO Signs, 3.8.6 this is the minimum number

Cd 2.0 Drag Coeffciient AASHTO Signs, 3.8.7 Assume two member or trusses Wind pressure Equation :Pz

CombineDesignAids

Load and Resistance Factor Design (LRFD Method) ≤ Ru φRn AISC 360 Eq. (B3-1)

Ru = required strenth of a member subjected to strength design load combinations = resistance factor φ Rn = nominal strength of the member as determined by the specifcations Rn = design strength φ

CombinationofLoads

Load Combinations Strength II, Strength IV, and Strength V do not need to be considered (LRFD Guide Specifications for the Design of Pedestrian Bridges)

AASHTO Table 3.4.1-1

AASHTO Table 3.4.1-2

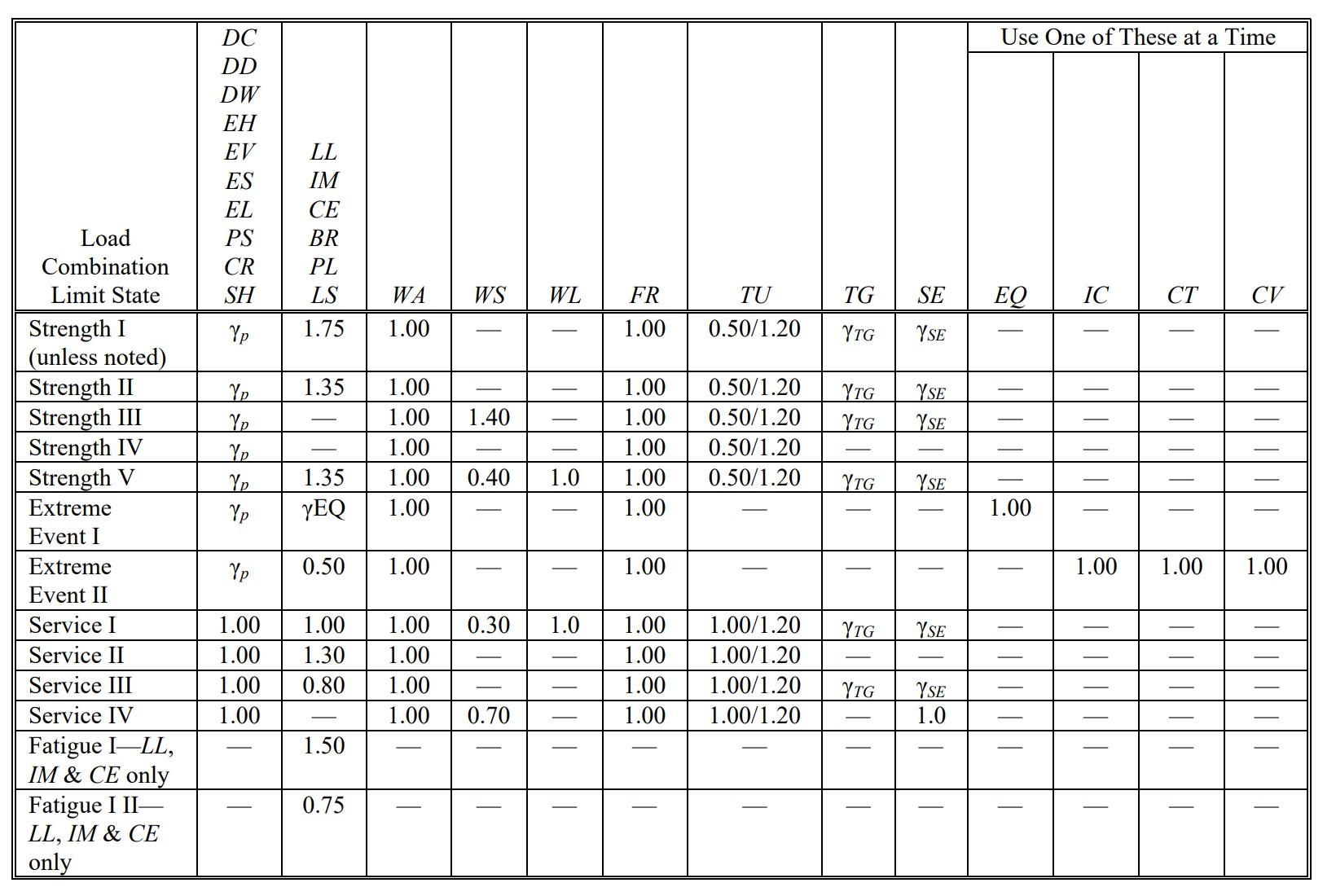
Table 3.4.1-2

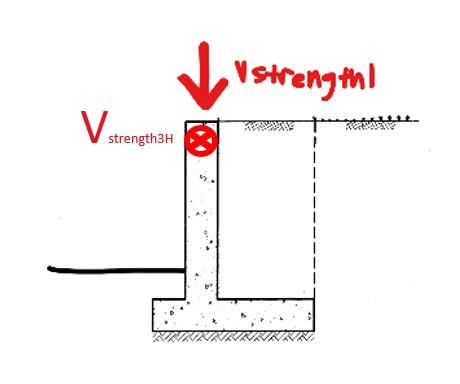
Strength I - Basic load combination relating to the normal use without wind ≔ γp 1.25 vertical: ≤ + ⋅ γp DC 1.75⋅LL φRn shear: ≔ VStrength1 = - + + 1.25⋅VDWmax 1.25⋅VDBmax 1.75⋅VLmax 1.75⋅VUmax 4.893 kip moment: ≔ MStrength1 = - + + 1.25⋅⎛ ⎝MDWmax⎞ ⎠ 1.25⋅MDBmax 1.75⋅MLmax 1.75⋅MUmax 55.152 ⋅kip ft

Strength III - Load combination relating to structure exposed to wind velocity exceeding 55 mph vertical: ≤ ⋅ γp DC φRn shear: ≔ VStrength3V = + 1.25⋅⎛ ⎝VDWmax⎞ ⎠ 1.25⋅VDBmax 0.751 kip moment: ≔ MStrength3V = + 1.25⋅⎛ ⎝MDWmax⎞ ⎠ 1.25⋅MDBmax 8.468 ⋅kip ft horizontal: ≤ 1.4⋅WS φRn shear: ≔ VStrength3H = 1.4⋅VWmax 1.566 kip moment: ≔ MStrength3H = 1.4⋅MWmax 17.646 ⋅kip ft

Service I - Load combination reltaing to the normal operational use of the bridge with a 55 mph wind ≤ + 1.00⋅DC 0.80⋅LL φRn vertical: Non-Commercial Use Only

vertical: ≤ + 1.00⋅DC 0.80⋅LL φRn shear: ≔ VService1V = - + + 1.00⋅⎛ ⎝VDWmax⎞ ⎠ 1.00⋅VDBmax 0.80⋅VLmax 0.8⋅VUmax 2.495 kip moment: ≔ MService1V = - + + 1.00⋅⎛ ⎝MDWmax⎞ ⎠ 1.00⋅MDBmax 0.80⋅MLmax 0.8⋅MUmax 28.116 ⋅kip ft horizontal: ≤ 0.3⋅WS φRn shear: ≔ VService3H = 0.3⋅VWmax 0.336 kip moment: ≔ MService3H = 0.3⋅MWmax 3.781 ⋅kip ft

CheckMaximumShearandMoment

Vertical: > > VStrength1 VService1V VStrength3V > > MStrength1 MService1V MStrength3V ≔ Vu = VStrength1 4.893 kip ≔ Mu = MStrength1 55.152 ⋅kip ft

Horizontal: > VStrength3H VService3H > MStrength3H MService3H ≔ VuH = VStrength3H 1.566 kip ≔ MuH = MStrength3H 17.646 ⋅kip ft

Select Type of Steel Corrosion Resistant Steel needed for outdoors Refer to AISC Table 2-4 Applicable ASTM Specifications for Various Structural Shapes A588Steel is Corrosion Resistant High-Stength Low-Alloy Steel with good Fy and Fu, and can be used in W I beams

Design of Steel Beams in Flexure Find minimum Zx required to withstand moment

Design of Steel Beams for Shear Find minimum Aw required to withstand shear

Look at AISC Table 1-1 W-Shape I-Beams to find beam with minimum Zx and Aw values

Choose smallest beam possible: save weight and money = Zx 14.707 in3 = Aw 0.163 in2

W12x16beam ≔ Zxx 20.1 in3 ≔ tw 0.22 in web thickness ≔d 12 in height ≔ Aw = ⋅ tw d 2.64 in2

Properties of W12x16 beam (AISC Table 1-1) ≔ Abeam 4.71 in2 area ≔d 12 in total height = tw 0.22 in web thickness ≔ bf 3.99 in flange width ≔ tf 0.265 in flange thickness ≔T 10.375 in web height ≔ Ixx 103 in4 moment of inertia about x-axis ≔ Sxx 17.1 in3 elastic section modulus about x-axis ≔ Zxx 20.1 in3 plastic section modulus about x-axis ≔ Iyy 2.82 in4 moment of inertia about y-axis ≔ Syy 1.41 in3 elastic section modulus about y-axis ≔ Zyy 2.26 in3 plastic section modulus about y-axis ≔J 0.103 in4 torsional constnat ≔ Cw 96.9 in6 warping constant

Confirmwoodplankarestructurallysound

Diagram: FBD

CalculateCapacityofTreads,makesuredimensions chosenareappropriate

Dimensions tread:

tt 2 in height

bt 12 in width

lt 3 ft length *Dimensions are based on DCA6 for stair treads

SectionProperties: Assuming that the wood can be considered Decking, since intended for floor use and wide face in contact with supporting members.

Property Source

Syy 4.219 in3 Section Modulus NDS Supplement (Table 1B)

Iyy 3.164 in4 Moment of Inertia NDS Supplement (Table 1B)

E 1900000 psi Modulus of Elasticity Southern Pine No. 2 NDS Supplement (Table 4B) = Fb ⎛ ⎝1.8⋅103 ⎞ ⎠ psi Bending design Southern Pine No. 2 NDS Supplement (Table 4B) = Fv 175 psi Shear Parallel Southern Pine No. 2 NDS Supplement (Table 4B) = Awood 0.117 ft2 Area of Section NDS Supplement (Table 1B)

Pine No. 2 NDS Supplement (Table 4B)

Pine

Supplement

1 Importance Factor ASCE 7, Table 1.5-2

Find distributed loads

wL

qL bt 0.09 kip ft Live

wD = 4.102 lbf ft 0.004 kip ft Dead, based on density of wood (NDS Supplement-Table 1B) pb

ws =

qs bt 0.019 kip ft Snow

wU 0.03 kip ft

wT = + wL wD 0.094 kip ft Total Applicable factored load governs with their respective time factor, λ Case Factored Load (ASCE 7, 2.3) λ (NDS 2018, Table N3) 1

wu1 = 1.4⋅wD 0.006 kip ft

λ1 .6 2

wu2 = + + + 1.2⋅wD 1.6⋅wL 0.5⋅ws 1.2⋅wU 0.194 kip ft

λ2 .8 3

wu3 = + + + 1.2⋅wD 1.6⋅ws wL 1.2⋅wU 0.161 kip ft

λ3 .8 ReductionFactors used in this analysis. All from NDS, 2018 Factor Name Source Reasoning

Ci 1 Incising Factor 4.3.8 There are no incisions

CF 1 Size Factor 4.3.6 lumber does not exceed 12" wide and it is not 4" thick

CL 1 Beam Stability Factor 3.3.3 Depth does not exceed breadth (d<b), in flatwise loading

b = bt 1 ft

d = tt 2 in

Ct 1 Temperature Factor 4.3.4 structure will not experience sustained exposure of temps >150F

CMb 0.85 Wet Service Factor, bending Sup. 4B Since stairs outdoor, moisture will exceed 19% for extended periods of time

CMv 0.97 Wet Service Factor, shear Sup. 4B

Repetitive Member Factor Sup. 4B treads are not in contact Non-Commercial Use Only

Now can calculate M'

Shear

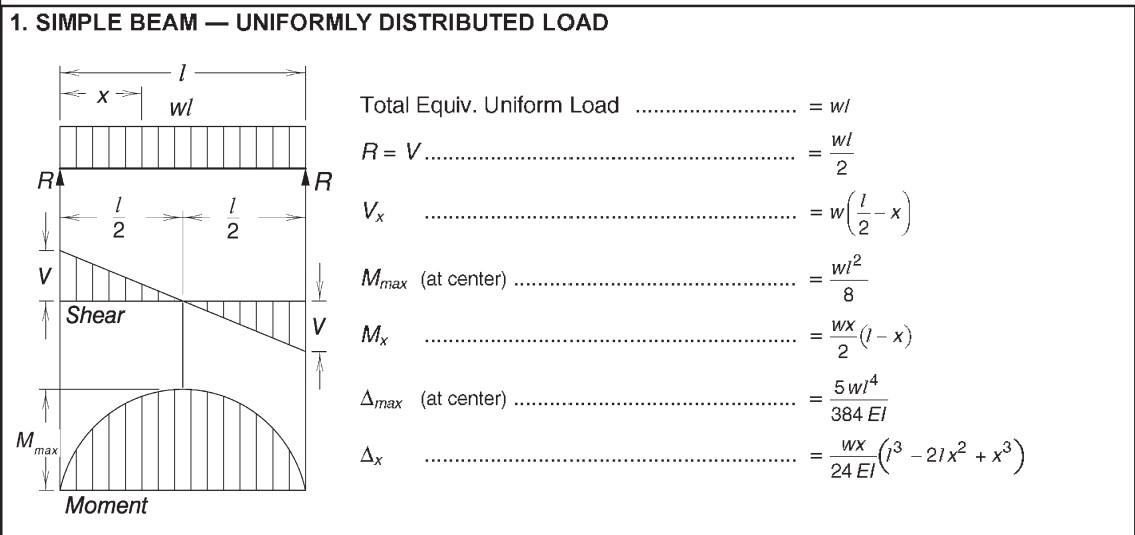
simple beam, AISC Table 3-23- Aid 1)

Deflection

Find

Flexural Buckling of Member without Slender Elements

Vu = VStrength1 4.893 kip check if Pn is greater than Vu

⎛ ⎜ ⎝ Mr MweakMax

⎞ ⎟ ⎠ 0.806 AISC Eq. H1-1b Less than1,thus acceptable

⎞ ⎟ ⎠ 1.0 = + Pr 2⋅Pc Non-Commercial Use Only

⎛ ⎜ ⎝ Mr MweakMax

PropertiesofMaterialsUsed

Type of Steel A588Steel is Corrosion Resistant High-Stength Low-Alloy Steel with good Fy and Fu, and can be used in W I beams

Fy 50⋅ksi minimum yield stress ≔ Fu 70 ksi minimun tensile strength

I-Beam Properties (AISC Table 1-1)

W12x22

Abeam 4.71 in2

W12x22

Abeam 6.48 in2 area

d 12 in ＝d 12.3 in total height ＝ tw 0.22 in ＝ tw 0.26 in web thickness ＝ bf 3.99 in ＝ bf 4.03 in flange width ＝ tf 0.265 in ＝ tf 0.425 in flange thickness

T 10.375 in ＝T 10.375 in web height

Ixx 103 in4

Ixx 156 in4 moment of inertia about x-axis

Sxx 25.4 in3 elastic section modulus about x-axis ＝ rxx 4.67 in ＝ rxx 4.91 in ＝ Zxx 20.1 in3 ＝ Zxx 29.3 in3 plastic section modulus about x-axis

Sxx 17.1 in3

Iyy 2.82 in4

Iyy 4.66 in4 moment of inertia about y-axis

Syy 1.41 in3 ＝ Syy 2.31 in3 elastic section modulus about y-axis

ryy 0.773 in ＝ ryy 0.848 in ＝ Zyy 2.26 in3 ＝ Zyy 3.66 in3 plastic section modulus about y-axis

J 0.103 in4 ＝J 0.293 in4 torsional constnat

Cw 96.9 in6

Syy 4.218 in3

RailingCalculation

These calculations will be based on AASHTO LRFD Bridge Design Specification (2010), pedestrian railings.

Sketch

Dimensions of Railing

Post spacings are different for the landings, the two different stair types, and the bridge. All railings have the same connections and material, thus this calculation will focus on the railing with the largest post spacing. This is because this will lead to the largest live loads. If the railing is sufficient for the area with the largest post spacing, it will also be sufficient for areas with smaller post spacings.

L = 70 in 5.833 ft post spacing

h

36 in Height to top of railing

4 in Railing breadth, nominal

3 in Railing depth, nominal The calculation will be divided into two steps: Longitudinal Elements (the railing) and the posts

d

1.Longitudinal

SectionProperties Property Source

wyL 0.05 kip ft Vertical Distributed Live Load (AASHTO 13.8.2)

2.127 lbf ft Vertical Dead Load for a density of 35 lb ft3 (NDS Supplement-Table 1B)

Cfuflat 1.1 Flat Use Factor Sup. 4B lumber is used flatwise, but the depth is less than 2"

Cfuedge 1 Flat Use Factor Sup. 4B lumber is used edgewise CT Buckling Stiffness Factor 4.4-1 equation will be below, requires other factors not calculated yet Calculate reduction factors that have not been calculated Buckling Stiffness Factor CT (4.4.-1)

Inputs Assumptions

KM 1200 assuming wood is only partially seasoned

KT 0.59 visually graded lumber

Ke 1 Buckling length coefficient (NDS, 2018 Table G1). Assume rotation and translation is fixed in both direction

le =

Ke L 70 in Effective column length (3.7.1.2) (Effective length assumed same in edge and flat wise case) = le dE 20 (3.7.13) *Note slenderness ratio below 50, so acceptable = le dF 28 (3.7.13) *Note slenderness ratio below 50, so acceptable Since le is less than 96", then

Beam stability factor edgewise case CLedge Distance between supports will be the distance between posts

lu =L 5.833 ft = dE 3.5 in Effective length for bending, (Table 3.3.3). Assuming single span with loading conditions not le specified in Table 3.3.3 Since = lu dE 20 and > lu dE 7 ≔ leb = 1.84⋅lu 10.733 ft Slenderness ratio (3.3-5) RB

Slenderness ratio (3.3-5) RB

1 2 8.493 Since slenderness ratio does not exceed 50, it is acceptable. This is slenderness of edgeface Calculate (Table 4.3-1) ′ Emin ≔ Emin ' = ⋅ ⋅

RB = ⎛ ⎜ ⎜ ⎝ ⎛ ⎝ ⋅ leb dE⎞ ⎠ bE 2 ⎞ ⎟ ⎟ ⎠

Emin CM Ct Ci CT ( (1.76) ) ( (0.85) ) 943.151 ksi Calculate FbE ≔ FbE = 1.2⋅Emin ' RB 2 15.691 ksi reference bending design value multiplied by all applicable adjustment factors except Fb '' Cfu, and CL (see 2.3)

⋅

Now can calculate CLedge ≔ CLedge = -

⎛ ⎜ ⎝ 1+ ⎛ ⎜ ⎝ FbE Fb '' ⎞ ⎟ ⎠ ⎞ ⎟ ⎠ 1.9

⎛ ⎜ ⎜ ⎜ ⎝

⎛ ⎜ ⎝ 1+ ⎛ ⎜ ⎝ FbE Fb '' ⎞ ⎟ ⎠ ⎞ ⎟ ⎠ 1.9

⎞ ⎟ ⎟ ⎟ ⎠

2 -

2 ⎛ ⎜ ⎝ FbE Fb '' ⎞ ⎟ ⎠ 0.95 0.984 3.3.3

Now that have all applicable reduction factors can find the design values for combined bending

Combinedbending

Since the loads are both tranverse and vertical to railing need to look at combined bending

Main

Checkallcases forBending = + M1 ⋅ M1 ' ( (1) ) M2 ⋅ M2 ' ⎛ ⎜ ⎜ ⎝ 1⎛ ⎜ ⎝ M1 ME

⎞ ⎟ ⎠

2 ⎞ ⎟ ⎟ ⎠

0.984 (NDS 3.9-1)

This is less than1,thus passes case = ⎛ ⎜ ⎝ fb1 FbE

⎞ ⎟ ⎠

2 0.003 (NDS 3.9-4)

This is less than1,thus passes case = FbE 15.691 ksi < fb1 FbE (NDS 3.9.2) = fb1 0.801 ksi sincethisistruepassescase < fb1 FbE

Memberpasses allcases,thedimensions chosenareappropriate

Applicablefactoredload governs with their respective timefactor, λ (Using NDS and ASCE, because there is bending and axial force) Case Factored Load (ASCE 7, 2.3) λ 1

Puy1 = 1.4⋅PPD 0.017 kip

Pux1 = 1.4⋅0 kip 0 lbf 2

Puy2 = 1.2 PPD 0.015 kip

Pux2 = 1.6⋅PPL 0.787 kip 3

Puy3 = 1⋅PPD 0.012 kip

Pux3 = 1.2⋅PPL 0.59 kip

λ1 .6

λ2 .8

λ3 .8

> Puy1 Puy2 Pu3 Will use case 2, since this has the largest transversal factored load. The vertical load is much smaller, thus it will not affect as much

> Pux2 Pux3 Pux1

Pux = Pux2 0.787 kip ReductionFactors used in this analysis. All from NDS, 2018

Puy = Puy2 0.015 kip Factor Name Source (NDS) Reasoning

Ci 1 Incising Factor 4.3.8 There are no incisions

CF 1 Size Factor 4.3.6 lumber is 4" thick but less than 8" wide

CL 1 Beam Stability Factor 3.3.3 Depth does not exceed breadth (d<b), since it is symmetrical

b = bp 3.5 in

d = dp 3.5 in

Ct 1 Temperature Factor 4.3.4 The structure will not experience sustained exposure of temps above 150F

CM 0.85 Wet Service Factor, bending Sup. 4B Since stairs outdoor, moisture will exceed 19% for extended periods of time

C

1 Repetitive Member Factor Sup. 4B posts are not in contact

Cfu 1 Flat Use Factor Sup. 4B depth and breadth CP Column stability factor 3.7.1 equation will be below CT Buckling Stiffness Factor 4.4-1 equation will be below

Buckling Stiffness Factor CT (NDS 4.4.-1)

≔

KM 1200 assuming wood is only partially seasoned

KT 0.59 visually graded lumber

Ke 2.1 Buckling length coeffcieicent (NDS, 2018 Table G1). Assume rotation fixed and translation free

le =

Ke LP 71.925 in Effective column length (3.7.1.2) (Effective length assumed same in both axis) = le d 20.55 (3.7.13) *Note slenderness ratio below 50, so acceptable = le b 20.55 (3.7.13) *Note slenderness ratio below 50, so acceptable Since le is less than 96", then

Fc '' = ⋅

Fc CM Ct CF Ci 2.4 0.9 λ2 3.011 ksi

KM le 1 in ⎞ ⎟ ⎠

⋅

CT = 1+

KT E psi

Emin CM Ct Ci CT ( (1.76) ) ( (0.85) ) 944.959 ksi Slenderness ratio found for buckling stability factor = le 71.925 in Calculate first Fc

Combinedbending

Since the loads are both tranverse and vertical to railing need to look at combined bending

Main equation

1 ME

2 ⎞

⎠

1 (NDS 3.9-1) = adjusted compression capacity P' =compressive force P =adjusted moment capacity (strong axis) M1 ' =bending moment (strong axis) M1 =ajusted moment capacity (weak axis) M2 ' =bending moment (weak axis) M2 = critical column buckling capacity(strong axis) PE1 =critical column buckling capacity(weak axis) PE2 =critical beam buckling capacity ME

First need moment capacity and buckling capacity, since the post is symmetrical, the moment capacity will be the same for both axis. The time factors were chosen previously in the load λ discussion section

Capaicity

Critical buckling capacity

First need to find slenderness ratio Distance between supports , will be the length of the post, which we will assume is a cantilever l

Effective length for bending, (NDS Table 3.3.3) le Since = lu d 9.786 > lu dE 7 assuming concentrated load at unsupported end

The equation for combined bending considers bending in both axis, since it is symmetrical will calculate main equation considering if moment is the strong or weak axis

Checkallcases forBendingandaxialcompression

If : ＝M M1 ≔ M1 =M 2.245 ⋅ft kip ≔ M2 ⋅ 0 kip ft ≔ fb1 = fb 0.571 ksi ≔ fb2 0 ksi = + + ⎛ ⎜ ⎝ P P' ⎞ ⎟ ⎠

2 M1 ⋅ M1 ' ⎛ ⎜ ⎝ 1-⎛ ⎜ ⎝ P PE1

⎞ ⎟ ⎠ ⎞ ⎟ ⎠

M2 ⋅ M2 ' ⎛ ⎜ ⎜ ⎝ - 1-⎛ ⎜ ⎝ P PE2

⎞ ⎟ ⎠ ⎛ ⎜ ⎝ M1 ME

0.952 (NDS 3.9-1)

⎞ ⎟ ⎠

2 ⎞ ⎟ ⎟ ⎠

This is less than1,thus passes case = + fc FcE2

⎛ ⎜ ⎝ fb1 FbE

⎞ ⎟ ⎠

2 7.35⋅10-4 (NDS 3.9-4)

This is less than1,thus passes case = FbE 66.346 ksi < fb1 FbE (NDS 3.9.2) = fb1 0.571 ksi sincethisistruepassescase < fb1 FbE If : ＝M M2 ≔ M2 =M 2.245 ⋅ft kip ≔ M1 ⋅ 0 kip ft ≔ fb2 = fb 0.571 ksi ≔ fb1 0 ksi =

= FbE 66.346 ksi

= fb1 0 ksi

< fb1 FbE (NDS 3.9.2)

sincethisistruepassescase < fb1 FbE

Other cases to consider

= FcE1 1.839 ksi

< fc FcE1

= fc 0.001 ksi (NDS 3.9.2)

sincethisistruepassescase < fc FcE1

= FcE2 1.839 ksi

= fc 0.001 ksi

< fc FcE2 (NDS 3.9.2)

sincethisistruepassescase < fc FcE2

Memberpasses allcases,thedimensions chosenareappropriate

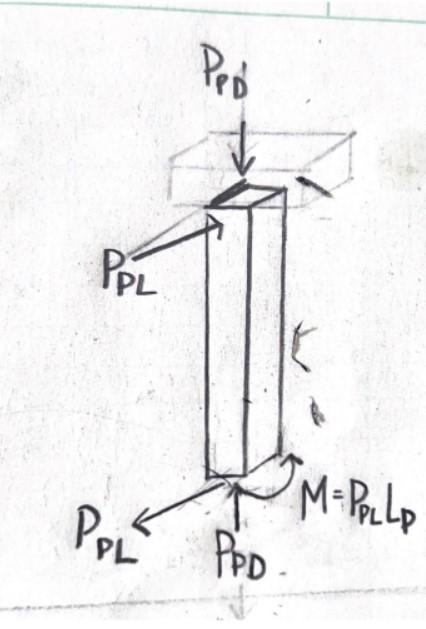
The posts will then be connected to the stringer using the following connection. This connection will need to be able to handle the reactions caused by the loads.

Team Stairs – Geotechnical Engineering Calculations

Soil Assumptions:

UC Davis SoilWeb classifies the soil on-site as Gilpin-Upshur complex.

Figure 1. Soil Classification for Site (UC Davis).

In order to find parameters for the soil on-site, without the ability to take borings, I searched for a geotechnical report on a nearby site with the same classified soil. I was able to find a geotech report for, “Proposed Single Family Residences”, which was prepared by ACA Engineering for MJS Group Ventures in 2019. This site was located at Butler Street, only 1.5 miles from our site, and had the same classified soil of Gilpin-Upshur complex. For all the reasons above, we felt this source was applicable to use for our site and was utilized to determine soil properties.

Figure 2. Site Location of Geotechnical Report, Located 1.5 Miles North From Negley Run (ACA Engineering 2019).

Table 1. Existing Soil Properties for Similar Site and Soil (ACA Engineering 2019).

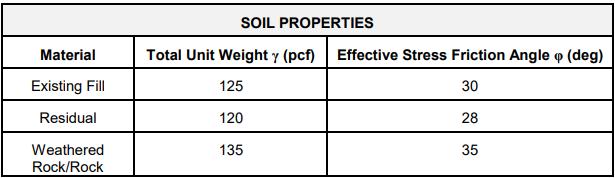
Using the soil properties above, I assumed the soil to have similar properties as the residual soil found at the Butler Street proposed project. The effective friction angle was reduced to 12 degrees to account for poor soil, per the recommendations of Dr. Jim. This is logical since the soil is more cohesive than granular due to the large presence of clay. ����������������ℎ��������������

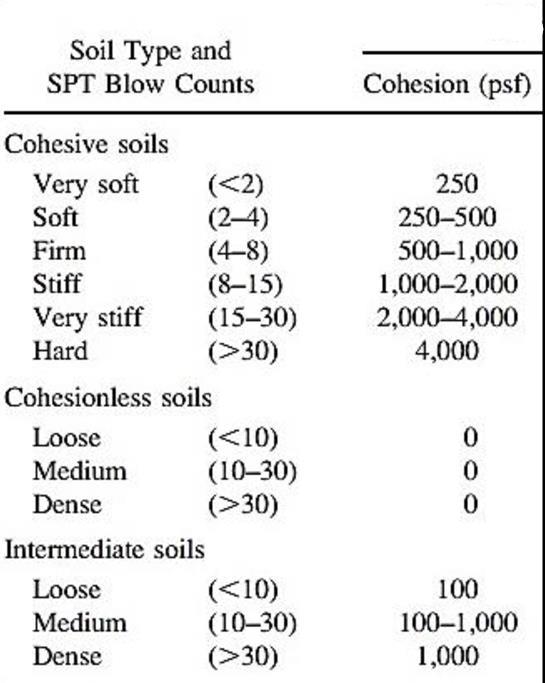
Unfortunately, the tests ran for this geotechnical report did not result in a determination of the cohesion of the clay in this silty clayey soil. This was estimated by using Table 2 below since SPT values were known for the silty clayey layer of the soil on-site. These SPT values averaged ~10 for this layer, as seen in the ACA geotechnical boring logs. The soil on-site classifies as an intermediate soil due to the presence of both silt and clay. Additionally, the water table was stated as being, “more than 80 inches below ground surface” (Negley Run Watershed Task Force 2021), thus not making it a worry when designing foundations since the footing thickness doesn’t reach.

Table 2. Estimates for Cohesion Using SPT Values (Raffek 2016). ����ℎ����������=��′ =100������

Spread

Footings:

Our staircase will sit on square concrete footings which will support wooden and steel columns attached to the stairs. These footings will support portions of the bridges as well. A concrete weight of 150 pcf and compressive strength of 3,500 psi is assumed.

load column concrete footing

Figure 3. Labeled Spread Footing.

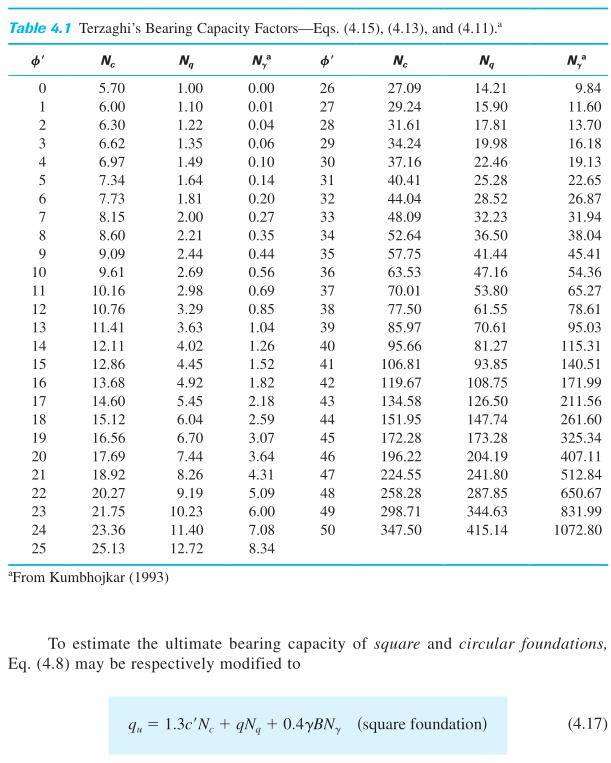
Bearing Capacity using Terzaghi’s Equation: Figure 4. Bearing Capacity Formula & Table for Square Footing (Das 2017).

the capacity factors using effective friction angle determined in soil assumptions. A φ’ of 12° corresponds to the following capacity factors.

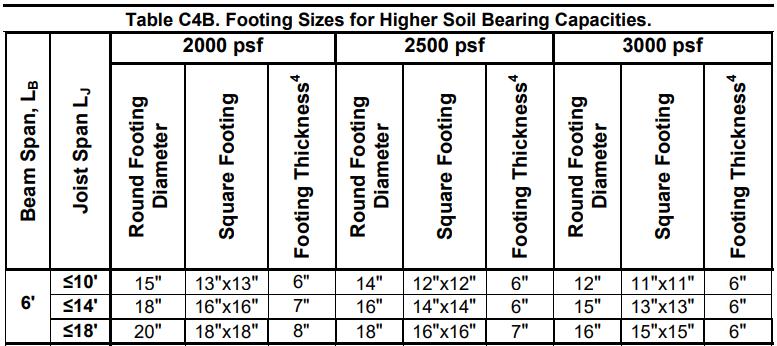
then must assume a width of our foundation to ensure proper capacity. The American Wood Council recommends a square footing size of 13”x13” for our beam and joist spans, and to achieve a safe bearing capacity. I chose to start with 12”x12” and iterate the design until a safe factor of safety is achieved. I also considered the dimensions of the columns which are approximately 6”x6”.

=������

=��������ℎ������������������=��������ℎ���������������������� =44����=3.67����

=12���� =1����

=12���� =1����

=���� =1.3��′���� +������ +0.4��������

=13(100������)(1076)+(120������)(367����)(329)+04(120������)(1����)(085)

���������� =2889������

������������ =1.3(100������)(10.76)+(120������)(3.67����)(3.29)+0.4(120������)(2����)(0.85)

=2929������ The American Wood Council suggests that the soil that these square foundations lay on should have a bearing capacity of 3000 psf on the higher end of their suggested range of soils. This aligns with the calculated values above.

����

������������������ = 2889������ 364������ =79

���� �������������������� = 2929������ 1223������ =24 A factor of safety of 7.9 and 2.4 will be adequate in the design of these foundations. This allows for any errors in our assumed soil assumptions as well. The wood has a large factor of safety due to the area of the column needing to safely fit on the foundation.

Estimated Footing Size using DCA6 – American Wood Council:

The footing size can also be estimated using DCA6 which can confirm that our design calculations above are correct.

Table 4. Estimated Square Footings Sizes (American Wood Council 2015).

Table 4 above shows to achieve a bearing capacity of 3000 psf with a joist span of ~14’ and beam span of 6’, the footing size should be approximately 13”x13”. This corresponds with our chosen footing sizes. The American Wood Council suggests that the soil that these square foundations lay on should have a bearing capacity of 3000 psf on the higher end of their suggested range of soils. This corresponds to our calculated values.

Other Footing Dimensions:

The thickness of our footing can be estimated using Table 4 from the American Wood Council. They recommend a footing thickness of 6” for our existing loads and dimensions. We assumed all of this recommend footing thickness would be below grade. The footings are to be installed below the frost depth after excavation. This excavated area will then be backfilled with existing soil. The Das textbook suggests a minimum footing thickness of 8 inches for footings such as the one we are designing. We chose to go with this number, and it was smaller than our footing widths which is required as well. ����������������ℎ��������������=8����

Figure 5 below shows all of our footing dimensions for clarification.

Figure 5. Square Footing Dimensions.

Settlement: In order to calculate the settlement of my foundations I only looked at primary consolidation due to a lack of known information. I assumed that the existing soil could be classified as a normally consolidated clay since the soil is a silty clay and has most likely not been loaded in the past. Additionally, settlement is most likely not a concern due to the small loads being applied to the foundations.

The in situ void ratio can be determined using this estimated compression index. The compression index for inorganic cohesive soils, silts, silty clays, and clays equation using void ratio was used from Das.

This settlement of 1.2” is generally within the standard tolerance of 1” of settlement in foundation construction. We would hope that the bedrock located directly below the clay layer would help reduce this settlement.

Soil Reinforcement:

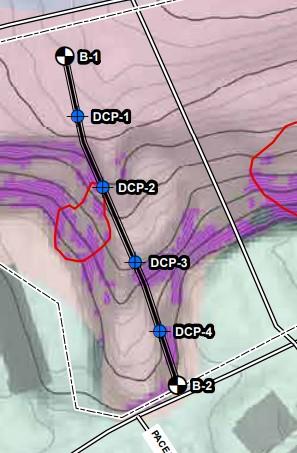
The Implementation Framework outlines evidence of landslide activity on the site and near the existing stairs. They specifically highlight slopes steeper than 1.5H:1V as being landslide prone and should be investigated to help mitigate this danger. In their report they write these slopes, “… have been labeled as slopes with moderate to severe susceptibility to landsliding” (Negley Run Watershed Task Force 2021). We highlighted these landslide prone areas in Figure 7 below.

Figure 7. Hatched Landslide Prone Areas Near Stairs.

To prove these slopes as being unstable and needing additional reinforcement for landslide protection, I calculated the factor of safety of the homogeneous slope. To perform these calculations, I assumed the soil to be homogenous and used the same assumed soil parameters from the previous sections. I used Taylor’s friction circle method of slope stability and the

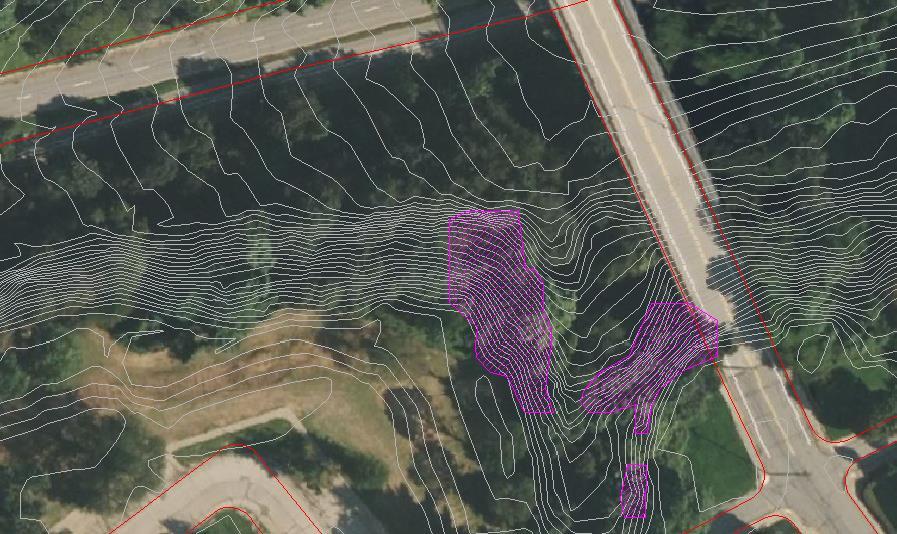
results from Singh (1970) to calculate the factor of safety. The slope stability number is determined as follows below. Additionally, the average height of the slope was calculated using the contour lines from Figure 7, where the top and bottom of the landslide prone slope was at the top and bottom of the two large, hatched areas.

ℎ������ℎ�������������������������������������������� =�� = (890′ 850′)+(900′ 870′) 2 =35���� ����������������������������������������=�� = �� ′ ���� = 100������ 120������∗35���� =0.024

Figure 7. Plot of Stability Number Against FS Based on Singh, 1970 (Das 2017).

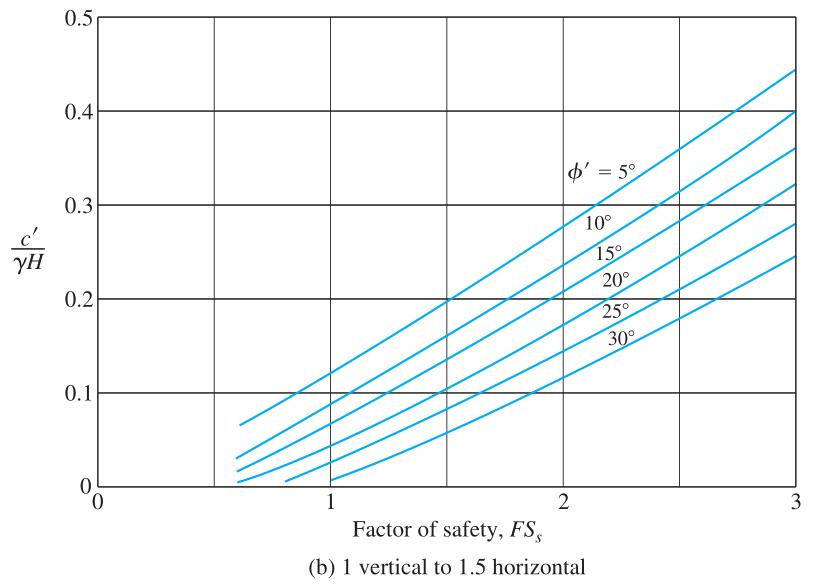
��������������������������������������≈0.8

This small slope factor of safety shows that landslides are a real concern and should be mitigated in a non-invasive and cost-effective manner. Our research showed that a good solution would be the installation of SlopeGrid in these landslide prone areas. SlopeGrid helps reinforce steep slopes by reducing soil sliding and migration, reducing erosion, which is a major cause of landslides, and by minimizing impacts on the slope from water. Additionally, this geotextile fabric is laid on top of the slope surface which doesn’t disrupt the slope. SlopeGrid did not have any definitive engineering calculations to back up their claims. Our research showed that an optimal solution would have anchors that extend beyond the slope failure surface. The longest earth anchor we were able to find in our research was 96”. These would extend through the failure surface in most areas of the slope. ��������ℎ������ℎ��������������ℎ=96����

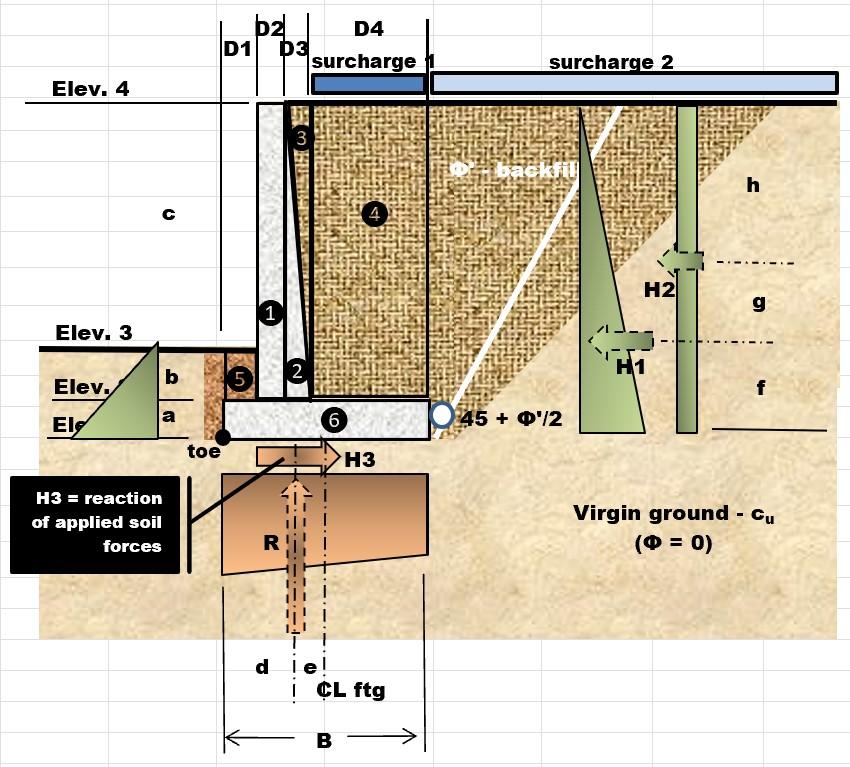
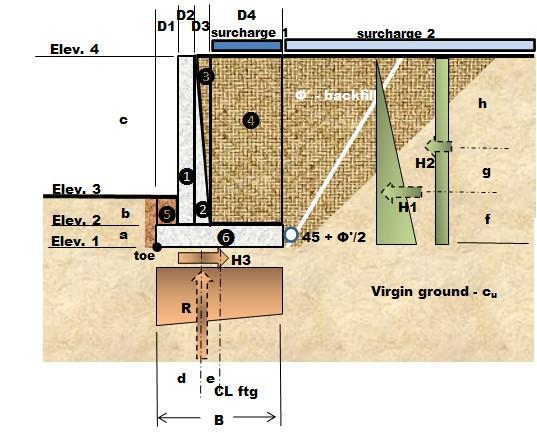
Df = +a b 4.5 ft height for passive pressure

ratio = w hwall 2.235 ratio of base to design height of wall

B = + + + D1 D2 D3 D4 19 ft heel length

SoilProperties - Based on spread footing calculations. Refer to those calculations for assumptions

ϕ' 12⋅

effective internal friction angle for chosen backfill

0.10⋅ksf virgin ground cohesion Given that , the Meyerhof's Bearing Capacity Factors (Das 2017) are

N

0.85

0.15⋅ kip ft3 unit weight of concrete

δ' 22⋅° effective external friction angle for concrete

AASHTOLRFDFactors

R 0.167 resultant location factor AASHTO 11.6.3.3

0.85 sliding factor AASHTO 10.6.3.4 & 10.5.5.2.2

b 0.50 bearing factor AASHTO 10.6.3.3 & 10.5.5.2.2 There is no LRFD Factor for overturning, so the calculation will be done without LRFD factors AASHTO Strength 1 Assumed

DCb 1.25

Vertical Forces & Moment Summation About Toe - Service Loads

W1 = + ⋅ ⋅ ( ( +b c) ) D2 γc V 3.081 klf weight of stem (element 1) and weight from bridge girder

A1 = + D1 D2 2 6.75 ft distance from toe to location where W1 acts

W2 = ⋅ ⋅ ⋅ 1 2 ( ( +b c) ) D3 γc 0.788 klf weight of triangle part of stem (element 2)

A2 = + + D1 D2 D3 3 8 ft distance from toe to location where W2 acts

W3 = ⋅ ⋅ ⋅ 1 2 ( ( +b c) ) D3 γs 0.63 klf weight of triangle area of soil (element 3) ≔ A3 = + + D1 D2 2⋅D3 3 8.5 ft distance from toe to location where W3 acts

W4 = ⋅ ⋅ ( ( +b c) ) D4 γs 8.4 klf weight of soil on top of heel on right side of stem (element 4)

toe to location where W4 acts

of soil on top of heel on left side of stem (element 5)

from toe to location where W5 acts

Demand to Capactiy (D/C) Ratios There is no LRFD for overturning so it will not be included in this section Check that all ratios are less than 1 (a reverse Factor of Safety calculation) D/C for R Location D/C for Bearing

Stringers

2.Decking2x12 2x12 boards will be used for stairs and decking of bridges. All boards will be 3ft long. RS means only has 2x6 so I used that in cost estimating

3 ft width of bridge and stairs

11.25 in nom. width board

BridgeDecking:

Top Bridge

45 ft length bridge Total number of boards top bridge

Lower Bridge

37 ft length bridge Total number of boards bottom bridge

AboveGroundSteps: Top Stairs (shown in picture above)

12 number of 3ft treads in top stairs

ft 6 number of flights of stairs

Total number of top stairs

Lower Stairs

6 number of 3ft treads in top stairs

fl 4 number of flights of stairs

Total number of lower stairs

Landing

7 number of landings

6 ft length of landings

Total number of boards landings

Total square feet of decking stairs Total Number of Boards Non-Commercial Use Only

Total square feet of decking stairs

⎝ + + Nsl Nsl NL⎞ ⎠ w nw 261 ft2

Round up, square feet ≔ DL 270 ft2

Total Number of Boards = ⋅ ⋅

NBT = + + ↲ + + Nsl Nsl NL Nbl Nbt

181

Total square feet of decking bridge = ⋅ ⋅ ⎛ ⎝ + Nbl Nbt⎞ ⎠ w nw 247.5 ft2

Round up, square feet ≔ DL 250 ft2

3.ColumnsWood

There is 9 sets of columns, 7 of these sets will be made of wood, each of the wooden sets has 4 columns. The wooden columns are 6" by 6"

Total amount of wood columns ≔ NCol.W 28

Sum of the height of columns obtained from drawings (rounded to nearest inch). RS mean calculates cost by LF ≔LF = + + + + ↲ + + + + + + + + + + + + ↲ + + + + + + + + + + + 38 in 39 in 29 in 31 in 52 in 52 in 26 in 25 in 37 in 34 in 10 in 2 in 30 in 20 in 15 in 6 in 58 in 50 in 48 in 39 in 99 in 88 in 75 in 65 in 52 in 44 in 11 in 6 in

90 ft

4.ColumnsSteel

There is two columns on the top bridge, since the start of the bridge is in contact with the land. The bottom bridge has 4 columns. Assume the columns are W12x50, which is the lightest column W12 in RS means

Total amount of steel columns ≔ NCol.S 6

LF = + + + + + 83 in 68 in 52 in 48 in 23 in 23 in 25 ft

5.Stringers-Wood

Stringers for stairs will be 4"x12", but RS means only has 2"x12" so estimate will be based on that

Top Stairs

Lower Stairs

Landings

6.Beams-Steel

8.3GalvanizedSpikes

Length ≔L 12 in

According to the manual each step needs 2 spikes, except the first step ≔ Totalspikes = 2⋅( ( -n 1) ) 44

Spikes only cost about 66 cents each in a hardware store (Home Depot,2022), thus their cost was not included into the estimate since they would most likely be even cheaper when a contractor buys them

8.4Geotextile-Ingroundsteps

The geotextile needs to line the area inside each set of timbers, and long enough to extend a few inches up the sides.

Since the timber is 6" assumed that needed the geotextile to extend to 9" ≔SA = ⋅n ⎛ ⎝ + + ⋅ ⋅ ⎛ ⎝ - l4 0.75 ft⎞ ⎠ 0.75 ft 2 ⋅ ⋅ l2 0.75 ft 2 ⋅ ⎛ ⎝ - l4 0.75 ft⎞ ⎠ l2⎞ ⎠ 36.736 yd2

Round up =SA 37 yd2

8.5Crushedstone3/4"

On top of the geotextile goes crushed stone, but it is filled up to 1" below the top.

CYsto = ⋅ ⋅ ⋅n ( ( -w 1 in) ) l2 ⎛ ⎝ - l4 1 ft⎞ ⎠ 2.13 yd3 Round up ≔ CYsto 3 yd3

8.6SoilExcavation

This design requires soil excavation, will base amount on how much soil needs to be removed for each step. Assuming that need to excavate at least a foot deep for each step.

CYexc = ⋅ ⋅ ⋅n l4 ⎛ ⎝ + l2 w⎞ ⎠ 0.75 ft 6.389 yd3 Round up ≔ CYexc 7 yd3

9.Trail

There is a a small trail at the entrance to the stairs that connects to the bigger trail in LarimerPark ≔ Ltrail = 621 in 51.75 ft round up = Ltrail 52 ft

wtrail 3 ft

Atrail = ⋅ Ltrail wtrail 17.25 yd2 round up ≔ Atrail 18 yd2

10.Railings

There will be railings throughout the above-ground stairs and bridges

10.1

WoodRailing

The wood for the railings is 4" by 3" Need to find the linear feet needed of the hand rail.

4"x3"

Railings

Round up: ＝ LR 440 ft The posts (4"x4") are 36" high and on average 70" apart thus the linear feet of the post is

h 36 in 4"x4" Posts

LP 230 ft

10.2steelwires There are 7 wires in each side and they go throughout the length of the stairs and bridge

LR 7 3052 ft Round up

11.GroundStabilization

LT 4000 ft

Total SY of geosynthetic soil stabilization, based on area that needs to be covered that is currently deemed to have very steep slopes Using geotextile as proxy for slopegrid, since no slope grid in in RS means

SY 10000 ft2 =SY 1111.111 yd2 Round up, since this is an estimate

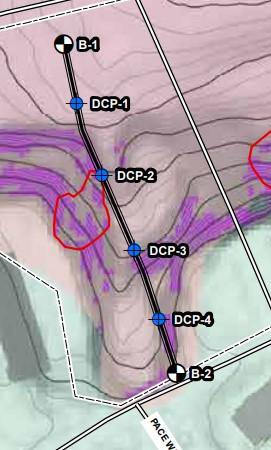
SY 1200 yd2 There will need to be 186 96in earth anchors, since there is no earth anchor in RS means, used GME Supply Co

anchor 186 number of earth anchors

II.LIFECYCLEASSESMENT

Costestimateshowinginitialcapitalcostsandthenetpresentvalueoflifecyclecostsovera 50-yearlifespan

InitialInvestmentandReplacement

The cost estimate of the project can be seen in the RS means report. Total initial capital investment,P was approximately

≔P 113000 dollars

The lifecycle of the abovegroundstairs is estimated to be about 25 years (Traxion, 2021). This means that the stairs will need to be replaced at 25 years. We will assume that the stairs will be replaced with an exact copy, that cost a similar amount. We estimate this cost will be

≔ Fstairs 16000 dollars (this value excludes all costs associated with the inground stairs, bridge, demolition, and slope grid)

Since the deckofbridge is made of wood, it will need to be replaced occasionally. The lifespan of these deck is between 10 to 15 years (TimberTech, 2021). In this analysis we will assume it is 12 years. This means the deck will be replaced 4 times in the 50-year lifespan. Assume to cost of replacing is based on the original cost of the decking

≔ Fdeck 1320 dollars

Steelbridges have a lifespan of over 100 years (US Bridge, 2021). Even though the bridges in this project are not made completely of steel, will assume that the steel components will not be replaced in the next 50 years

We are assuming that the in-groundsteps will never be replaced completely, instead that a few boards will need to be replaced each year

MaintenanceandOperation:

Inspectionofbridgeandstairs-Yearly

The cost of having an inspection is between $0.25 to $2 per squarefoot (Homeadvisor, 2022). Will use the higher number of this range, due to accesability issues.

If assume that the total square feet of project is the slightly more than the square feet of decking, the project has approximately

≔SF 600 ft2 (calculated material takeoff is 510 square feet)

Inspection cost

≔ costinsp = ⋅ 2 ft2 SF 1200 dollars

MaintenanceWorker

Both the inground and above ground stairs will require routine maintenance both due to their location and material. Inground stairs will need to be cleaned out when clogging occurs. Stone, fabric, and wood may need to be replaced. Above ground steps will also have to be replaced occasionally and they will need to be cleaned often to avoid damage. It is hard to predict how many times this will happen and how much it will cost. It is simpler to find the cost of a maintenance worker and assume that their salary will be representative of the cost to maintain the park. Since the stairs are only part of the whole system, will assume that a worker is spending one fourth of their time on the stairs.

Maintenance worker cost ≔W = 39000 4 9750 dollars (salary.com 2022)

Total

Costof

Maintenance ≔M = +W costinsp 10950

For this net present value will use a real rate of return of 7% (Zerbe, 2018). This is the return after inflation, so will not include inflation in analysis. This number is seen as typical for goverment project

Equation for NPV

＝NPV ⋅F ( (1+i) ) -n where F=future cost i=rate of return n=year

Figure that shows all costs over the 50 years

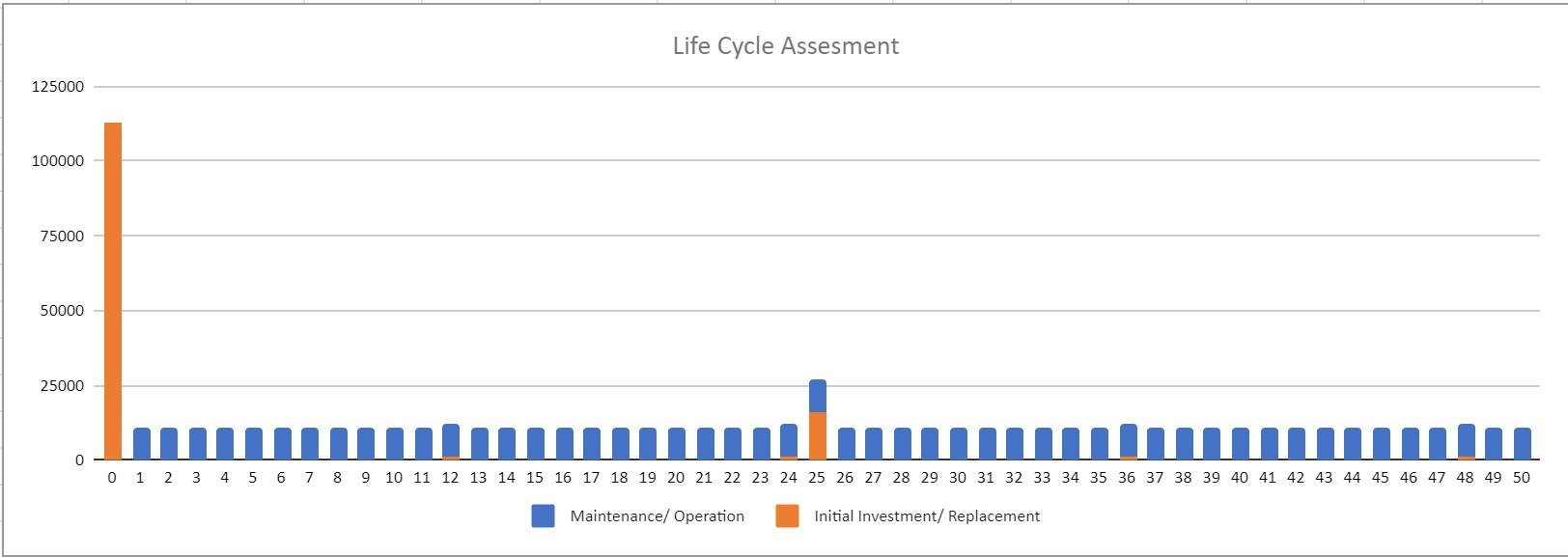
Using excel the NPV of the project was

NPV is then ≔NPV 268000 dollars

Sources:

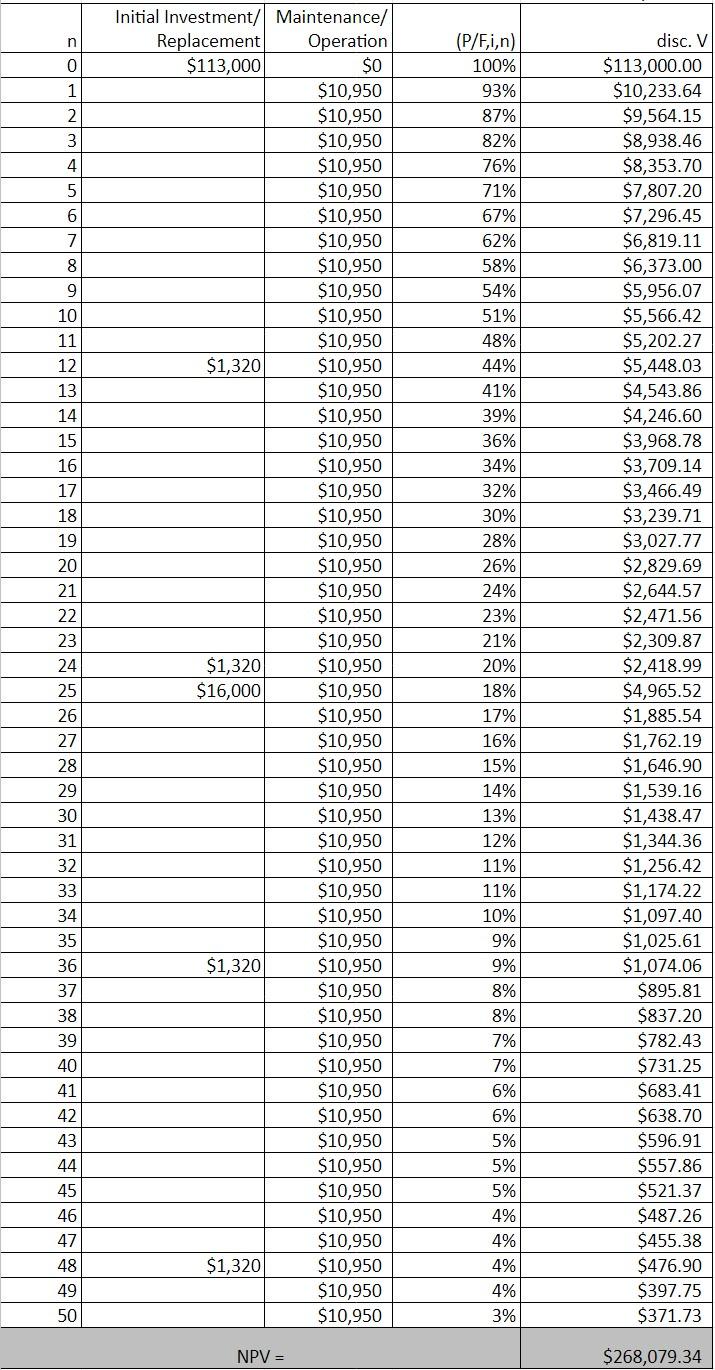
Galvanized Steel Earth Ground Screw Anchor (2022) "GME Supply is North America's Premier Outfitter of fall protection, safety equipment, and gear for at-height workers, industry, and construction." <https:// www.gmesupply.com/galvanized-steel-96-inch-earth-screw-anchor>

HomeAdvisor. (2022). "How Much Does a Structural Engineer Cost?" <https://www.homeadvisor.com/cost/ architects-and-engineers/hire-an-engineer/>

Negley Run Watershed Task Force. (2021). “Implementation Framework Little Negley Run at Larimer Park” <https://www.livingwaterspgh.org/wp-content/uploads/2022/01/LNR-Larimer-Park-ZoneBFINAL-2021-12-03-.pdf>

TimberTech. (2021). "How Long Does Decking Last? It Depends on Your Decking Material." <https:// www.timbertech.com/ideas/how-long-does-decking-last/#:~:text=THE%20AVERAGE%20LIFESPAN%20OF%20A %20WOOD%20DECK%3A%20Typically%2010%20to,with%20wood's%20rigorous%20maintenance% 20schedule.>

Traxion.(2021). "3 Indicators that it's time to repair your outdoor wooden stairs." <https://traxiontreads.com/3indicators-that-its-time-to-repair-your-outdoor-wooden-stairs/>

US Bridge.(2021). "The Lifespan of Structurally Deficient Bridges in America." <https://usbridge.com/thelifespan-of-structurally-deficient-bridges-in-america/>

Vermont Department of Environmental Conservation (Vermont DEC). (2022). “Infiltration Steps.” <https:// dec.vermont.gov/sites/dec/files/wsm/lakes/Lakewise/docs/LP_BMPInfiltrationSteps.pdf>

Zerbe, R. (2014). "What Should Be the Return on Public Investment?" <https://www.cato.org/regulation/ winter-2013-2014/what-should-be-return-public-investment>

Appendix C: Work Breakdown Structure

Updated:

References

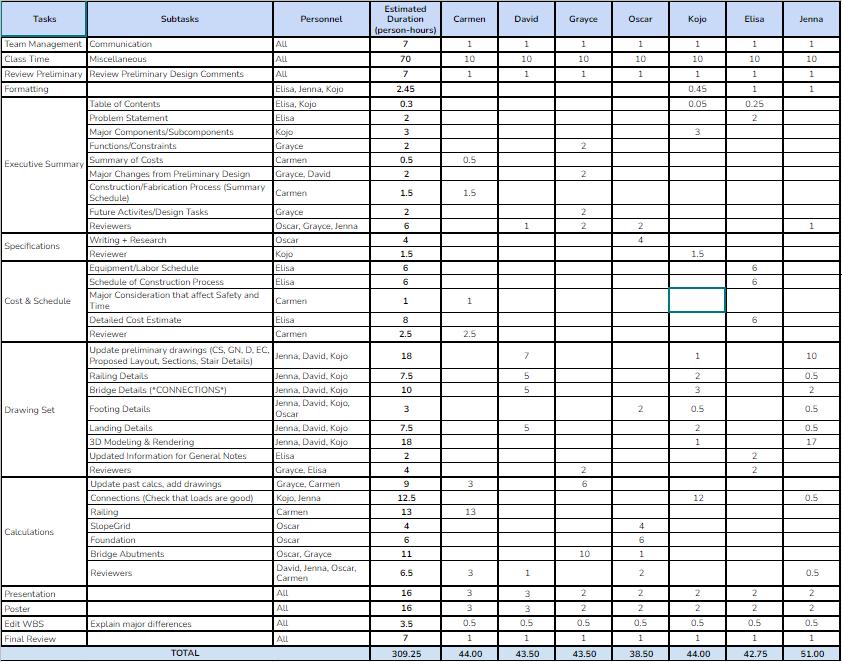
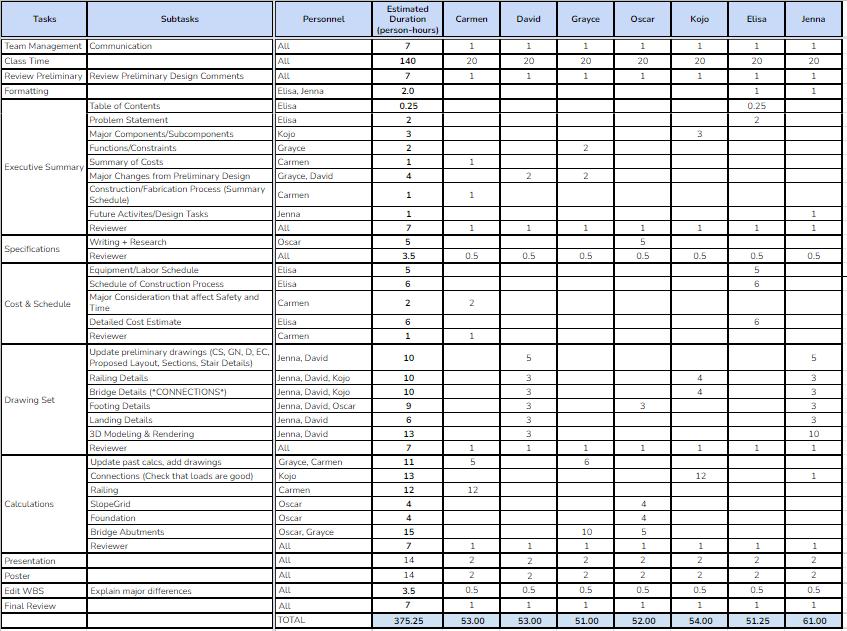
American Association of State Highway and Transportation Officials (AASHTO). (2022) “LRFD Specifications for Structural Supports for Highway Signs, Luminaires, and Traffic Signals (1st Edition), with 2017, 2018, 2019, 2020 Interim Revisions”

ACA Engineering. (2019). “Geotechnical Investigation.” Proposed Single Family Residences - Butler Street, Pittsburgh, PA, <https://images1 loopnet com/d2/-K -AL70Zbk1cvS7wh81q9OxA-gkL0rmY Pbh-gRtzaY/document.pdf>

American Wood Council. (2018). “Manual for Engineered Wood Construction” <https://awc.org/wp-content/uploads/2022/01/AWC-2018-Manual-1810.pd f>

American Wood Council (2018) “National Design Specification for Wood Construction” <https://awc org/publications/2018-nds/>

American Wood Council. (2018). “NDS Supplemental” <https://awc.org/publications/2018-nds-supplement/>

American Wood Council. (2015). “Prescriptive Residential Wood Deck Construction Guide.” Design Code for Acceptance, <https://awc org/wp-content/uploads/2022/02/AWC-DCA62012-DeckGuide -1405.pdf>

ASCE. (2010). ASCE 7 - Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers.

Cell-Tek. (n.d.). “Reinforced Steep Slopes: Cell-Tek.” Cell-Tek Geosynthetics, <https://wwwcelltekdirect com/reinforced-steep-slopes/>

Das, B , and Sivakugan, N (2017) Fundamentals of Geotechnical Engineering Cengage Learning.

GME Supply Co (2022). “Galvanized Steel Earth Ground Screw Anchor.”

<https://www.gmesupply.com/galvanized-steel-96-inch-earth-screw-anch or>

Gordian (2022) RSMeans Data, <https://www rsmeansonline com/>

HomeAdvisor (2022) "How Much Does a Structural Engineer Cost?" <https://www.homeadvisor.com/cost/architects-and-engineers/hire-an-engin eer/>

International Code Council. (2000). International building code. Falls Church, Va.

Negley Run Watershed Task Force. (2021). “Implementation Framework - Little Negley Run at Larimer Park ” <https://www livingwaterspgh org/wp-content/uploads/2022/01/LNR-Larim er-Park-ZoneB-FINAL-2021-12-03-.pdf>

Raffek, M., and Ashnor, M. (2016). “Predicting Standard Penetration Test (SPT-N) Value from Electrical Resistivity Result.” Universiti Teknologi PETRONAS, <http://utpedia utp edu my/17864/1/(1)%20Final%20Dissertation pdf>

TimberTech (2021) "How Long Does Decking Last? It Depends on Your Decking Material." <https://www.timbertech.com/ideas/how-long-does-decking-last/#:~:text=T HE%20AVERAGE%20LIFESPAN%20OF%20A%20WOOD%20DECK%3A

UC Davis. (n.d.). “SoilWeb.” SoilWeb: An Online Soil Survey Browser, <https://casoilresource lawr ucdavis edu/gmap/>

US Bridge.(2021). "The Lifespan of Structurally Deficient Bridges in America."

<https://usbridge.com/the-lifespan-of-structurally-deficient-bridges-in-ameri ca/>

Vermont Department of Environmental Conservation (Vermont DEC). (2022). “Infiltration Steps”

<https://dec vermont gov/sites/dec/files/wsm/lakes/Lakewise/docs/LP_BMPInfi ltrationSteps.pdf>

Zerbe, R (2014) "What Should Be the Return on Public Investment?"

<https://www.cato.org/regulation/winter-2013-2014/what-should-be-return -public-investment>

TEAM STAIRS – GOOGLE DRIVE FOLDER:

https://drive.google.com/drive/u/0/folders/1erMH9tg03JZgg_XMyncSdYgD71s_Eobs