Acción de control proporcional, integral y derivativa

Acción de control proporcional, integral y derivativa

Acción de control proporcional

En este tipo de cotrol, siempre habrá un error en estado estable, denominado offset, para una entrada escalón unitario. Luego, se añade un integrador en la Función de Transferencia directa del sistema para eliminar dicho error. Esta es la misión fundamental de un control PI.

La Función de Transferencia directa de este sistema es:

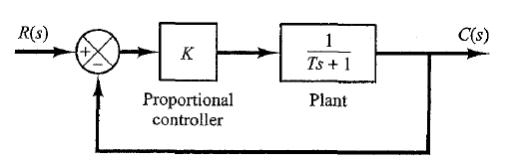
Vamos a obtener el error de estado estable de este sistema para una entrada escalón unitario. Ya que:

El error E(s) está dado por:

Para una entrada escalón unitario R(s) = 1/s, obtenemos:

El error en estado estable es:

Este resultado demuestra que tal sistema, sin un integrador en la ruta de alimentación directa, siempre presentará un error en estado estacionario, denominado Offset, en respuesta a la entrada escalón unitario.

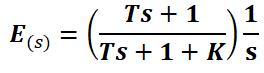
Acción de control integral.

Según lo anterior mencionado, en el control de una planta cuya función de transferencia no posee un integrador 1 / s, se presenta un error en estado estable (offset) en respuesta a una entrada escalón unitario. Tal error se puede eliminar si la acción de control integral está incluida en el controlador. La función principal de la acción integral es asegurarse que la salida del proceso coincide con la señal de referencia en estado estacionario, cosa que se demuestra a continuación.

La función de transferencia directa del sistema anterior es:

Utilizando el mismo razonamiento utilizado para analizar el error del sistema con control proporcional, el error E(s) es:

Suponiendo una entrada escalón unitario:

Aplicando nuevamente el teorema del valor final, determinamos el error en estado estable para una entrada escalón unitario:

Este resultado demuestra que el control integral del sistema elimina así el error de estado estacionario en la respuesta a la entrada escalón unitario. Esta es una mejora importante que se puede sumar al control proporcional para evitar el Offset.

La señal de control u(t) generada por un controlador integral, puede tener un valor distinto de cero cuando la señal de error actuante e(t) es cero. Con acción integral, un pequeño error positivo conducirá siempre a una señal de control creciente, y un error negativo dará una señal de control decreciente sin tener en cuenta lo pequeño que sea el error.

Debe tomarse en cuenta cuenta que la acción de control integral, al eliminar el Offset o el error de estado estable, puede conducir a una respuesta oscilatoria de amplitud decreciente o incluso a una amplitud creciente, ambas de las cuales son por lo general indeseables. Por ello se acostumbra combinarlo con los otros tipos de control.

Acción de control derivativo.

La acción de control derivativo, cuando se agrega a un controlador proporcional, concede un medio para obtener un controlador con alta sensibilidad que responde a la velocidad de cambio del error y puede producir una corrección significativa antes de que la magnitud del error sea demasiado grande. En otras palabras, mejora el amortiguamiento, reduce el sobrepaso en estado estacionario. El control derivado anticipa, pues, el error de accionamiento, inicia una acción correctiva temprana y tiende a aumentar la estabilidad del sistema.

Debido a que el control derivativo opera en la tasa de cambio del error de actuación y no en el error de actuación en sí, este modo nunca se usa solo. Siempre se usa en combinación con una acción de control proporcional o proporcional más integral

Control proporcional de sistemas con carga de inercia.

Considerando los siguientes argumentos:

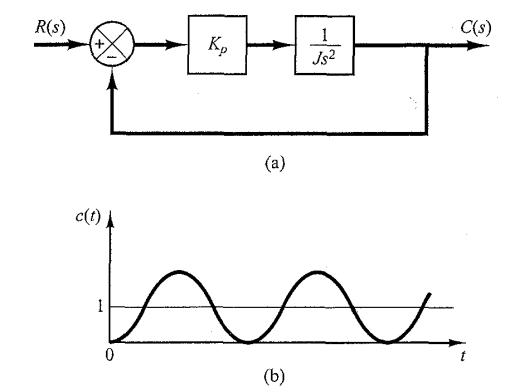
La función de transferencia directa es:

La función de transferencia de lazo cerrado se obtiene mediante:

La ecuación característica es:

Según lo anterior mencionado, las raíces de la ecuación característica son imaginarias, la respuesta a una entrada escalón unitario continúa oscilando indefinidamente. Los sistemas de control que exhiben tales características de respuesta no son deseables. Veremos que la adición de control derivado estabilizará el sistema.

Control Proporcional-Derivativo de un Sistema con Carga Inercial.

Si posee modificaciones el controlador proporcional añadiendo un controlador derivativo, cuya función de transferencia es Kp (1 + Tds). El control derivativo es esencialmente anticipatorio, mide la velocidad de error instantánea y predice un sobrepaso con anticipación. Produce una neutralización adecuada antes de que ocurra un sobrepaso demasiado grande. Considere el sistema que se muestra en la figura 5-47 (a).

La función de transferencia a lazo cerrado de este sistema es:

La ecuación característica es:

Ahora la ecuación característica tiene dos raíces con partes reales negativas para valores positivos de J, Kp y Td. Así, el control derivativo introduce un efecto de amortiguación. Una curva de respuesta típica c(t) a un escalón unitario en la entrada, se muestra en la Figura 5-47 (b). Claramente, la curva de respuesta en este caso muestra una marcada mejora con respecto a la curva de respuesta.