LINTAS BUDAYABAB VIII: MODEL PERSAMAAN STRUKTURAL UNTUK ANALISIS

BAB VIII BAB VIII BAB VIII BAB VIII: : : : MODEL PERSAMAAN STRUKTURAL UNTUK ANALISIS LINTAS MODEL PERSAMAAN STRUKTURAL UNTUK ANALISIS LINTAS MODEL PERSAMAAN STRUKTURAL UNTUK ANALISIS LINTAS MODEL PERSAMAAN STRUKTURAL UNTUK ANALISIS LINTAS BUDAYA BUDAYA BUDAYA BUDAYA

A.

APAKAH MODEL PERSAMAAN STRUKTURAL? pemodelan persamaan struktural adalah teknik multivariat yang menggabungkan (Konfirmasi) pemodelan analisis faktor dari teori psikometri dan pemodelan persamaan struktural yang terkait dengan ekonometrik. Syarat 'Struktural' mengasumsikan bahwa parameter mengungkapkan adanya hubungan kausal. Namun, teknik ini tidak 'menemukan' hubungan kausal. 'Paling-paling, menunjukkan apakah asumsi kausal tertanam dalam model cocok dengan sampel data ‘.

B.

TUJUAN DARI MODEL PERSAMAAN STRUKTURAL Tujuan utama dari SEM adalah untuk menjelaskan pola rangkaian yang saling terkait hubungan ketergantungan secara bersamaan antara satu set laten (teramati) konstruksi, masing masing diukur oleh satu atau lebih manifest (Diamati) variabel.

C.

APLIKASI MODEL PERSAMAAN STRUKTURAL Semua aspek pemodelan SEM harus diarahkan oleh teori, yang penting untuk pengembangan model dan modifikasi. Sebuah penyalahgunaan jelas SEM dapat terjadi ketika data hanya dipasang ke SEM cocok dan teori ini kemudian diperluas dari hasil analisis.

Ada tiga komponen umum model persamaan secara struktural: 1) Analisis jalur; 2) sintesis konseptual variabel laten dan pengukuran model; dan 3) prosedur estimasi umum (Bollen, 1989).

D.

APLIKASI UNTUK PARIWISATA Pemodelan SEM belum banyak digunakan dalam disiplin pariwisata, di luar Amerika Serikat. Namun, penerapan SEM dalam pariwisata penting sebagai alat untuk mempromosikan penelitian kualitas yang lebih baik. peneliti pariwisata yang sering dihadapkan dengan serangkaian pertanyaan yang saling terkait. variabel apa yang menentukan kunjungan wisatawan ke tujuan tertentu? Bagaimana permintaan sebagai laten variabel menggabungkan dengan variabel pasokan untuk mempengaruhi kunjungan wisatawan? Bagaimana permintaan dan penawaran variabel secara simultan mempengaruhi pembelian turis keputusan dan kepuasan liburan? Bagaimana kepuasan liburan

wisata menghasilkan kunjungan yang berulang dan loyalitas untuk tujuan? Banyak yang sama variabel independen mempengaruhi variabel dependen yang berbeda dengan yang berbeda efek. teknik multivariat lainnya tidak menjawab pertanyaan ini dalam metode komprehensif tunggal.

Petrick dan Backman (2002) menemukan bahwa kepuasan golf wisatawan 'keseluruhan ditentukan oleh kepuasan informasi dan kepuasan atribut. Atribut yang berhubungan dengan pengalaman resort memiliki lebih berpengaruh pada kepuasan keseluruhan dari atribut yang berhubungan dengan informasi yang diberikan dan pengalaman emas.

E.

TIPE MODEL LISREL LISREL merupakan singkatan Linear Structural Relationship yang berhubungan dengan komputer. Program untuk analisis struktur kovarians ini pada awalnya diperkenalkan oleh Joreskog dan Van Thillo pada tahun 1972. Model LISREL umum memiliki banyak submodels sebagai kasus khusus. Dalam hal ini, notasi matematika disajikan di halaman berikut, diikuti oleh presentasi dari submodels yang berbeda.

Singkatan :

Submodel 1 adalah model LISREL, yang dirancang untuk mengukur variabel yang diamati. model hanya memiliki x,?, dan? -error variabel. Tidak ada y dan? -variables (Lihat singkatan). Data yang digunakan mengukur hanya korelasi antara konstruk.

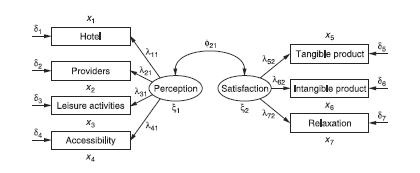
F. TINGKATAN YANG TERDAPAT MODEL PERSAMAAN STRUKTURAL Terdapat delapan tahap yang terlibat dalam proses persamaan struktural pemodelan dan pengujian.

1.

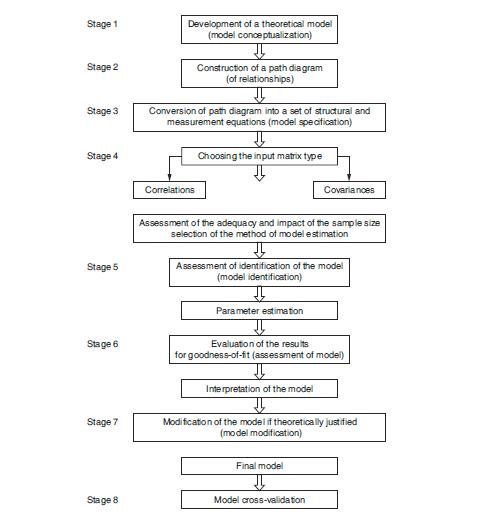
TINGKAT 1 Bagian pertama dari tahap 1 berfokus pada pengembangan teori Model dengan hubungan (relasi didefinisikan) antara konstruk laten dan variabel terukur mereka, mencerminkan hipotesis yang diajukan. Bagian ini merupakan pengembangan dari model struktural.

2.

TINGKAT 2 Tahap 2 melibatkan pembangunan jalur diagram. Untuk memahami simbol geometris diwakili dalam model dan menggambar jalur diagram , LISREL membutuhkan keakraban dengan huruf Yunani yang menggambarkan matriks LISREL. Huruf Yunani yang disajikan sebelumnya.

3. TINGKAT 3

Tahap 3 melibatkan spesifikasi matematika model formal dengan menggambarkan sifat dan jumlah parameter yang akan diestimasi (ukuran variabel yang membangun), menerjemahkan diagram jalur ke serangkaian persamaan linear yang menghubungkan konstruksi, dan menerjemahkan yang ditentukan Model ke dalam bahasa LISREL dalam bentuk matriks, yang menunjukkan korelasi hipotesis antara konstruk atau variabel. Koefisien matriks mewakili jalur dalam model.

4.

TINGKAT 4 Tahap 4 mempertimbangkan apakah varians / kovarians atau matriks korelasi adalah yang akan digunakan sebagai input data, dan ini melibatkan penilaian dari sampel ukuran. Matriks kovarians digunakan ketika tujuannya adalah untuk menguji teori, menyediakan perbandingan antara populasi yang berbeda atau sampel, atau untuk menjelaskan varians total konstruksi yang diperlukan untuk menguji teori. Namun, karena diagonal dari matriks tidak satu, interpretasi hasil lebih sulit karena koefisien harus ditafsirkan dalam hal satuan ukuran untuk konstruksi. Korelasi matriks memungkinkan untuk perbandingan langsung dari koefisien dalam model. Karena itu, itu lebih banyak digunakan. Matriks korelasi juga digunakan untuk memahami pola hubungan antara konstruksi. Hal ini tidak digunakan untuk menjelaskan varians total konstruk yang diperlukan dalam pengujian teori. Dengan demikian, interpretasi hasil dan generalisasi mereka untuk situasi yang berbeda harus dilakukan dengan hati-hati ketika matriks korelasi digunakan.

5.

TINGKAT 5 Tahap 5 alamat isu identifikasi model, yaitu, sejauh mana informasi yang diberikan oleh data yang cukup untuk memungkinkan parameter perkiraan. Jika model tidak diidentifikasi, maka tidak mungkin untuk menentukan parameter model. Sebuah kondisi yang diperlukan untuk identifikasi adalah bahwa jumlah parameter independen kurang dari atau sama untuk jumlah elemen dari matriks sampel covariances antara variabel yang diamati.

6.

TINGKAT 6 Tahap 6 melibatkan penilaian dari model fit menggunakan berbagai langkah-langkah untuk pengukuran dan struktural model (dan mendukung / menolak hipotesis yang diajukan). Namun, sebelum mengevaluasi kebaikan-of-fit antara data dan model beberapa asumsi SEM harus dipenuhi.

7.

TINGKAT 7 Tahap 7 mempertimbangkan apakah modifikasi model harus dibuat di terang hasil yang diperoleh pada tahap sebelumnya. Pada tahap ini analisis menjadi eksplorasi di alam dan hasil dari analisis sebelumnya digunakan untuk mengembangkan model pas lebih baik. Tujuannya adalah untuk mengidentifikasi spesifikasi kesalahan dan memproduksi model baru yang sesuai data yang lebih baik. ini baru Model harus diverifikasi pada sampel independen kedua.

8.

TINGKAT 8 Tahap 8 melibatkan lintas validasi model dengan set data baru. Hal ini dilakukan dengan membagi sampel menjadi dua bagian untuk melakukan validasi uji. Analisis LISREL multisample dapat digunakan untuk tujuan ini. Itu Uji silang validasi dilakukan ketika indeks modifikasi yang digunakan dan model tidak memberikan fit diterima. Tes ini juga harus dilakukan ketika model menunjukkan fit diterima dalam analisis pertama. Selain itu, cross-validasi dapat digunakan untuk membandingkan model bersaing dalam hal validitas prediktif dan memfasilitasi pemilihan model; untuk membandingkan perbedaan antara sampel milik berbeda populasi dan menilai dampak dari variabel moderating (Sharma et al., 1981).