01 Architecture and Symmetry

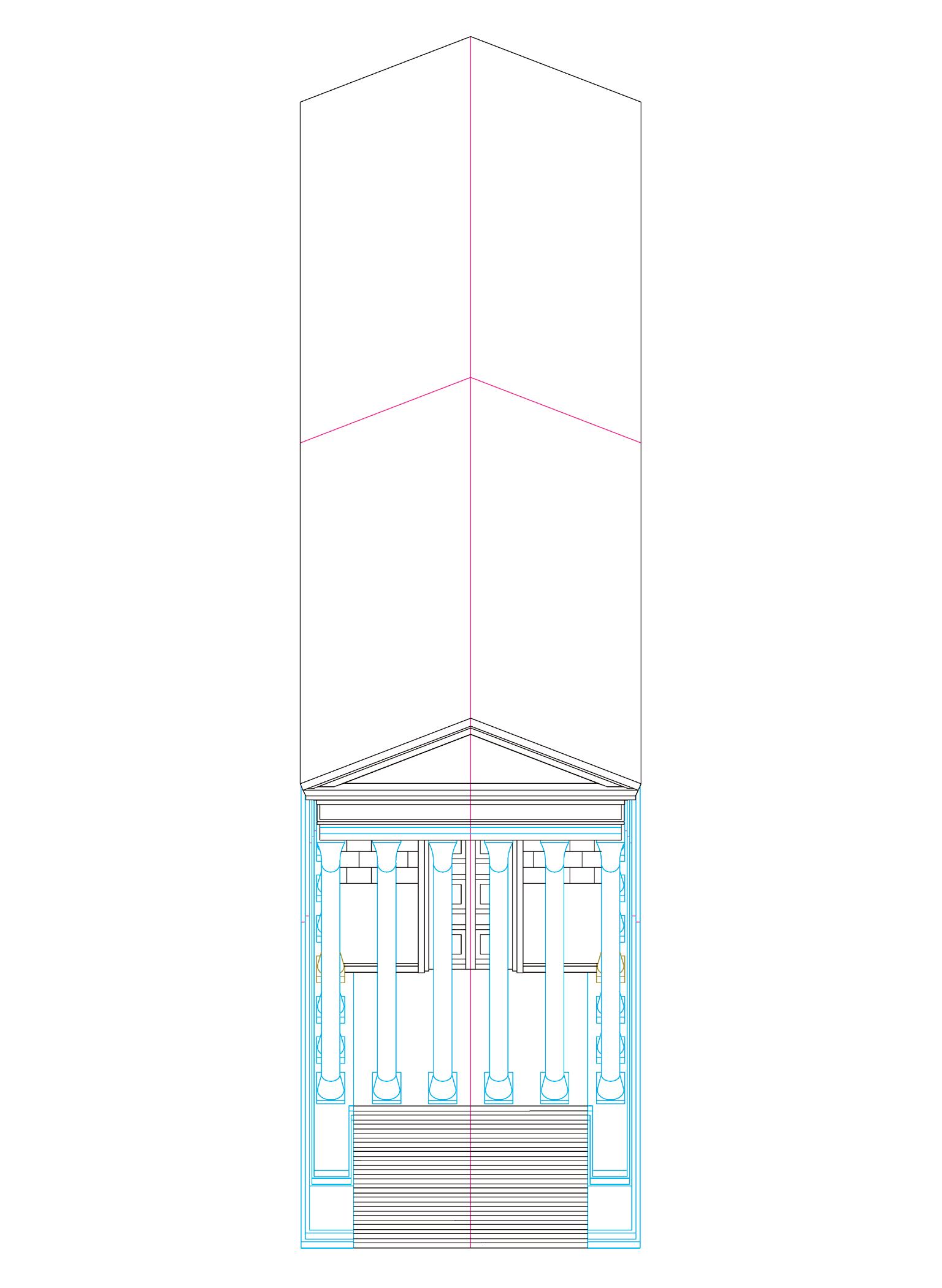
Maison Carrée, Nimes, France. 16 A.C.

Symmetry endures. Symmetry changes. This paradox is evident in the varying definitions and fluctuating influence that symmetry has had on architectural design and discourse for over 2,000 years.1 This chapter outlines symmetry’s consistent presence in Western architectural thought and reveals how it has often been used to establish an objective, quantitative means for creating and evaluating work, while still allowing for subjective innovations within its well-defined limits. In other words, it will examine how symmetry’s disciplinary stability is a function of its flexibility.

Classical Symmetry

The conventional understanding of symmetry is technically defined as reflective symmetry, that is, the relationship between two equal and opposite figures on either side of an axis.2 While the use of this figural trope is indeed ancient, it was not the original definition of symmetry. For the Roman architectural theorist Vitruvius, symmetry described the good and beautiful use of proportions to create a composition, one where the parts were harmoniously related to one another and to the larger whole. Symmetry was not a simple technique; it was a complex method for creating harmony out of a variety of different parts.

The Latin term that Vitruvius used to describe the mathematical relationship between parts and wholes was respondere. The numerical ratios used to create this effect were embodied in the different columnar orders (the Doric, the Ionic, and the Corinthian), and were typically defined by whole-number-based ratios found in the relationship between the width and the height of a column. This ratio, and its sub-ratios, established every dimension found in the design of a truly symmetrical building. While this often resulted in reflective plans and elevations, creating a bilateral image was never an explicit goal and is never mentioned in Vitruvius’ treatise, The Ten Books of Architecture. 3

Medieval Symmetry

Although often defined by its irregularities, medieval architecture also contains multiple symmetries. This is particularly true in the composition of Gothic cathedrals. Symmetry was a requirement for these buildings because of the historical association between, stability, god, and symmetry: “(…) the universe owes its stability to the perfect balance of its elements as instituted by the Creator, a stability that will be denied to any building that does not possess symmetry.”4 Here too, symmetry was a mathematical technique for producing a consistent and underlying objective standard for architecture to conform to.

Symmetry was not limited to the ground plans and elevations of Gothic cathedrals. It helped define the overall geometric relationships between part-to-part and part-to-whole. It also defined the local relationships in structural bays, arches and vaults, and guided the designs of intricately patterned surfaces. Nor was symmetry limited to the bilateral variety. The geometric order found in Gothic architecture contains examples of what 19th century mathematicians would later categorize as the four basic symmetrical operations: reflection, rotation, translation, and glide reflection.5

Renaissance Symmetry

Despite his direct debt to Vitruvius, the term symmetry is absent from Leon Battista Alberti’s 1452 treatise, On the Art of Building. What Alberti does include, which Vitruvius did not, is a description of elements with equal dimensions being identically distributed on either side of a central element. The word Alberti uses to describe this arrangement is respondere. This is the same term Vitruvius used to describe the proportional relationships between parts and wholes within a composition. Alberti does not abandon the idea that beauty requires the use of proportioning systems. He referres to this relationship as concinnitas, and it too is a prerequisite for beauty. In transferring the meaning of respondere, Alberti gives equal value to bilateral symmetry (without using that term) and proportion. While what we now call reflective symmetry was possible in Vitruvius’ theory, it is a requirement of Alberti’s.6

Enlightenment Symmetry

The search for a simple, consistent, underlying logic that explains a large set of phenomena is a hallmark of modern science. In late 17th century France, Claude Perrault attempted to apply this ethos to architecture. After reviewing a variety of architectural treatises and studying the actual measurements of buildings, he came to the conclusion that there was no empirical or theoretical evidence that allowed one to objectively establish one set of proportions as being any better or more beautiful than any other. These empirically established variations led him to the conclusion that proportions were an “arbitrary” or “conventional” standard for producing and evaluating architecture and architectural beauty.7

In contrast, Perrault argued that the size of buildings, the quality of their materials and craftsmanship, and the presence of symmetry were not arbitrary but “positive” and “convincing” sources of architectural beauty. He maintained that these were convincing traits because their “presence in works is bound to please everyone, so easily apprehended are their value and quality.”8 In other words, they are objective. Symmetry could be understood as such because Perrault redefined it as referring exclusively to the reflection of identical parts on either side of an axis. While this trope was not new, Perrault was the first architectural theorist to define symmetry in this way.9

With Perrault, mirror symmetry is established as an objective prerequisite for architectural beauty. It is at this moment that symmetry leaves the realm of opinion and enters the world of reason (something is either symmetrical or it is not). It would take more than a century before the mathematicians Legendre and Galois would establish a similarly central and objective place for symmetry in science and mathematics. Neo-Classical Symmetry

The placement of identical elements on either side of a reflection line would come to define the arrangement and configuration of many monumental buildings in the 18th and 19th century. The organization of circulation and programs astride symmetrical axes became the academic and disciplinary norm in the teachings of J.N.L. Durand at the École Polytechnique and the lecture halls and ateliers of the École des Beaux-Arts, both in Paris. Whether located in buildings with pure geometric envelopes or irregular urban lots, symmetry was used to orient and guide people through a building.10

The Beaux-Arts emphasis on bilateral symmetry was codified by the École’s professor of architectural theory, Julien Gaudet, in his 1901 treatise Eléménts et théorie de l’architecture. These conventions were carried on in 20th century books on architectural composition.11 It was only with the acceptance of the Bauhaus model of basic design, and with Modernism’s emphasis on letting program, structure, and materials directly influence architectural form, that the spell of symmetry was broken.

Modern Symmetry

In 1977, the midst of the postmodern era, architect Thomas Beeby showed how three modernist masters–Frank Lloyd Wright, Le Corbusier and Mies van der Rohe–were all well-versed in the use of symmetry. This skill came not from the study of architecture proper, but from their experience with ornament, especially the intensely symmetrical plates found in Owen Jones’ 1856 book, The Grammar of Ornament. Rather than letting their form follow function, Beeby shows how they distributed structure and space using the four symmetrical operations of reflection, rotation, translation and glide reflection.12

In the 1960s a few architects familiar with the scientific understanding of symmetry attempted to incorporate the new mathematics of symmetry–most notably Alfred Neumann and Anne Tyng–into their work.13 However, the modernist stigma against symmetry, its association with applied ornament, and the radical nature of their work–full of rotations, translations and reflections–kept symmetry out of the spotlight.

Postmodern Symmetry

In his 1982 essay entitled “Fearful Symmetry,” Philip Tabor outlined the historical arguments made for and against architectural symmetry.14 The “fear” in Tabor’s title refers to a poem by William Blake, but it also echoes modernists’ anxiety around the reappearance of bilateral symmetry in the work of postmodern architects like Aldo Rossi in Italy and Michael Graves in the United States.15

Tellingly, Tabor only discusses mirror symmetry. He does not address the other symmetrical operations or the changing uses and definitions of the term in math and science. His emphasis is on what mirror symmetry represents and means. Looking at the history of Western architecture he notes that the arguments made regarding symmetry relate to: “1) bodily experience, 2) the notion of redundancy, and 3) the notion of hierarchy.” The first is related to the empathy humans feel for symmetrical things. We recognize ourselves in these forms. The second category emphasizes the economy of means and ends present in the production and reception of symmetrically composed buildings. They are easier to design and build because they have fewer unique parts. They are easier to understand and remember because they are predictable. Finally, the imposed consistency required with symmetry is often used by and associated with the conformity and authority found in political and religious institutions. In short, symmetry is human, symmetry is quantifiable and easy, and symmetry is powerful.

Contemporary Symmetry

The influence of postmodernism and its use of traditional architectural tropes was challenged in the 1990s by the rise of digital design tools, methods, and forms. Despite the avant-garde stance towards form, the direct rejection of symmetry and the ease with which these tools create asymmetrical forms and patterns, symmetry (especially reflections, rotations, and translations) can still be regularly spotted in the diverse practices of Greg Lynn, FOA, and Norman Foster.16

Even a decade into the 21st century, the four symmetrical operations are still easily found in work done by “postdigital” era architects who are either interested in revisiting postmodernism, or who are importing ideas from the philosophy of Object Oriented Ontology into architectural design and discourse. Despite the oppositional formal and ideological differences of these two trends, in both cases symmetry provides a clear perceptual limit that enables one to grasp what would otherwise be disorienting effects. It is useful but not universal.

To conclude, the constant presence of symmetry should not be mistaken as an architectural essence or prerequisite. Rather, its eternal return reveals that despite the many fluctuations in its status and definition, symmetry endures as a stable reference point for change. In other words, architectural symmetry is itself symmetrical, as its presence has remained consistent despite its definition having been transformed.

1 Giora Hon and Bernard Goldstein, From Summetria to Symmetry: The Making of a Revolutionary Scientific Concept (London: Springer, 2008). 2 Giora Hon and Bernard Goldstein, “From Proportion to Balance: The Background to Symmetry in Science,” Stud. Hist. Phil. Sci. No. 36 (2005): 1-21; Phillip Tabor, “Fearful Symmetry,” Architectural Review No. 1023 (May 1982). 3 Hon and Goldstein, “From Proportion to Balance”, 4-6. 4 Nelly Shafik Ramzy, “The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry,” Perigrinations: The Journal of Medieval Art & Architecture 5, No. 2 (2015), 140. 5 Ibid. 6 Hon and Goldstein, From Summetria to Symmetry. 7 Claude Perrault, Ordonnance for the Five Kinds of Columns after the Method of the Ancients (Santa Monica: Getty Center for the History of Art and the Humanities, 1993). Hon and Goldstein, “From Proportion to Balance”,: 1-21. Perrault’s solution to this problem was not to abandon proportion, but to take the average of the ratios used in the “best” ancient and contemporary buildings, rounding the numbers to the nearest whole number so that they would be easier to remember and use, and then establishing them as a disciplinary standard. 8 Perrault, Ordonnance, 50-52. 9 Hon and Goldstein, “From Proportion to Balance.” 10 Michael Dennis, Court & Garden: From the French Hôtel to the City of Modern Architecture (Cambridge: MIT Press, 1986). 11 Howard Robertson, The Principles of Architectural Composition (London: The Architectural Press, 1942). John F. Harbeson, The Study of Architectural Design, with Special Reference to the Program of the BeauxArts Institute of Design (New York: The Pencil Points Press, 1926). 12 Thomas H. Beeby, “The Grammar of Ornament/Ornament as Grammar,” VIA III (1977), 10-29. 13 George Teyssot, “Toward a Cyborg Architecture,” in A Topology of Everyday Constellations (Cambridge MA: MIT Press, 2013). Ann Tyng. “Geometric Extensions of Consciousness,” Zodiac 19 (1969). Alfred Neumann. “Architecture as Ornament.” Zodiac 19 (1969),: 90-94. 14 Tabor, “Fearful Symmetry.” Tabor’s was one of a few texts at the time that looked at symmetry during the postmodern era, a time when traditional architectural tropes, such as symmetry and ornament, were being reintroduced to the discipline. 15 “The Art of Symmetry,” entire issue. Daidalos 15 (1985). 16 Greg Lynn, “The Renewed Novelty of Symmetry,” Assemblage 26 (1995), 8-37.