02 Science and Symmetry

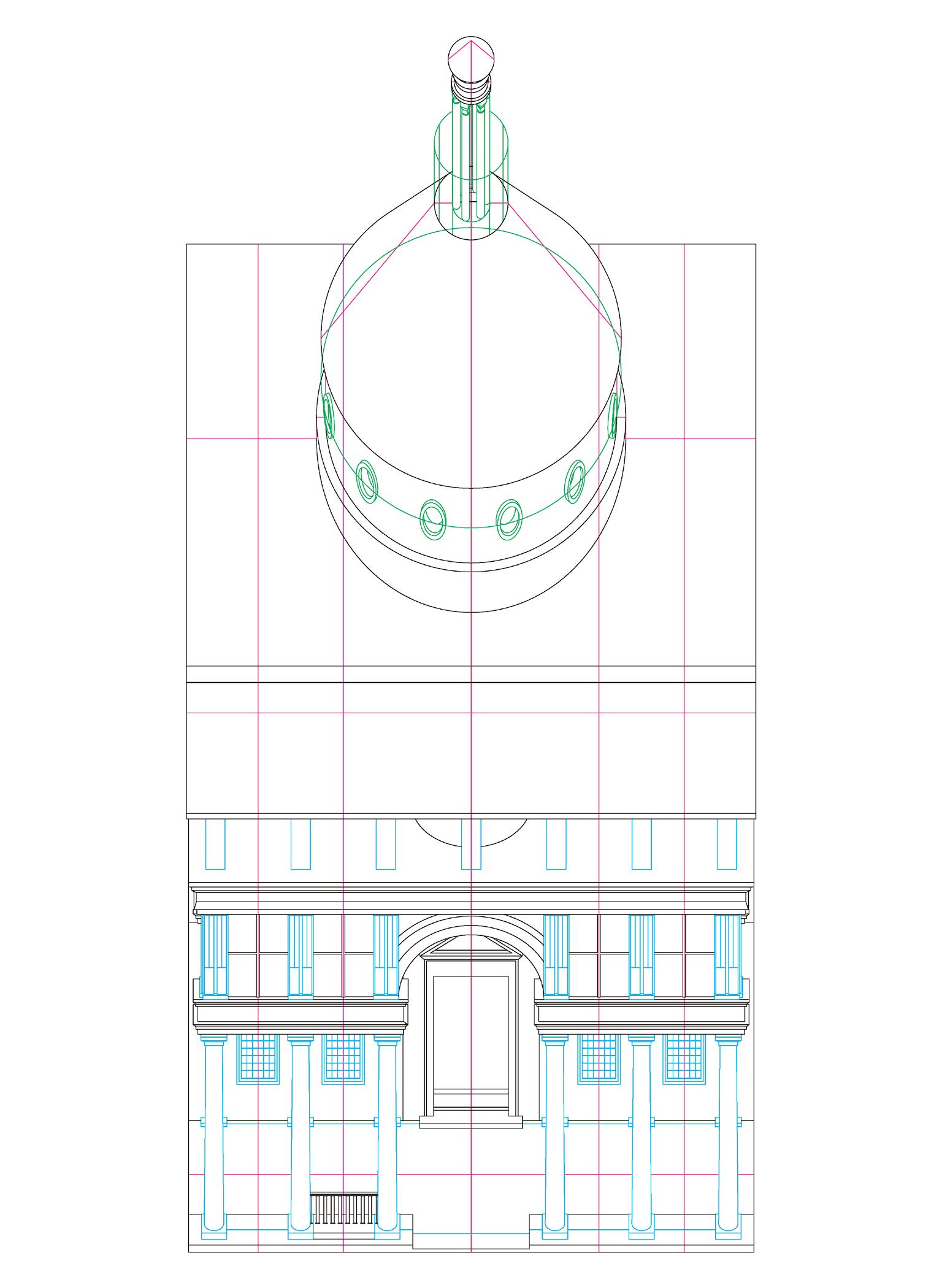
Filippo Brunelleschi, Pazzi Chapel. Firenze, Italy, 1429-1443

Historians Giora Hon and Bernard Goldstein have traced symmetry’s presence in mathematical and aesthetic thought back to ancient Greece.1 The mathematical trajectory begins with it being used to describe proportional relationships. In the aesthetic realm, symmetrical elements served “the function of harmonizing the different elements into a unitary whole.”2 The two were intertwined, as it was the task of the artist to use proportions to create harmonious and pleasing work. However, from these beginnings the understanding of symmetry has changed dramatically. The following brief history of symmetry in math and science shows how its meaning moved from commensurable, to correspondence, to equivalence, to invariance, revealing how these shifts increasingly broadened its predictive and projective powers.3

Ancient Proportions

The mathematical concept of symmetry described in Euclid’s Elements, circa 300 BC, was defined in terms of commensurability. This describes a situation where two objects, magnitudes, or numbers can be described in terms of a third. The numbers 9 and 12 are symmetrical because they can be divided by 3. Or, two pieces of lumber are symmetrical when one has a length of 2 units and a width of 3 units and another has length of 8 and a width of 12. In classical aesthetics, the combination of these differently sized but similarly proportioned elements into a unified whole was a prerequisite for beauty. This was the same definition that Vitruvius gave to symmetry, and it was the one that held sway in architectural theory until the 17th century, and in mathematics until the 19th century. Copernicus, Galileo, Kepler, and Leibniz, all defined symmetry in this classical framing. Copernicus and Kepler even cited Vitruvius’ combination of commensurability and harmony as the source of their astronomical theories of the heavens.4

Symmetrical Operations

Hon and Goldstein credit the mathematician Adrien-Marie Legendre with making symmetry a modern scientific concept. However, his use of the term has its origins in the aesthetic practice of architecture. Legendre was aware of how fellow Frenchman Claude Perrault had redefined architectural symmetry in the 18th century as the correspondence of identical elements equally placed on either side of a central feature in a building’s plan or elevation.5 In other words, he limited its definition to what we now call reflective symmetry. The metaphor Perrault used to describe this situation was a balance. Legendre replaced it with a mirror, and in doing so expanded the concept’s influence.

Legendre was studying the equivalence of solid angles in polyhedra when he used the term symmetry to describe a situation in which two concave solids faced each other. He wrote: “two equal solid angles, which are formed (by the same plane angles) but in the inverse order, will be called (…) symmetrical angles.” The key phrase here is “inverse order.” Before Legendre, this reflected configuration would not have been understood as equivalent or symmetrical. Only objects that were automorphic themselves (i.e. that could be mapped onto themselves without detection), like a rectangle or an equilateral triangle, or the orb of an eye could be. Asymmetrical objects, like human hands, were not.6 However, in Legendre’s new definition, two hands reflected across a line of reflection were symmetrical. The important change is the inclusion of an operation. The hands needed to be understood as having been repeated. After Legendre, symmetry was the result of a process, a very limited process. Only the four rigid movements of reflection, rotation, translation, and glide reflection could produce the symmetrical relationship that he described. These limitations gave symmetry the power of being a clearly defined, objective, measurable, and repeatable quality.

Symmetry Groups

While Legendre’s concept would prove immediately productive in crystallography, the power of symmetry as a set of objectively equivalent phenomena would be made mathematical in the work of Évariste Galois. In his investigations into the algebraic logic of polynomial equations he found that the set (or group) of answers that solved them had a symmetrical structure. That is, they could replace one another without producing a change. Galois discovered this through the use of permutations. For example, according to the rules of multiplication, there are six ways to arrange the variables a, b, and c, with each permutation producing the same result. That is, a*b*c=b*c*a=c*a*b=x. This equivalence is an algebraic automorphism, or symmetry.

In both algebraic and geometrical terms, symmetry could thus be defined as a transformation that preserves structure, or in which its structure is invariant. In the above equation, the structure that is preserved is the transitive property, while the transformation is the order of the variables themselves. In the geometric example of Legendre, the location of the solid angle is changed, but the orientation and angles themselves are preserved.7

By providing an abstract logic to symmetry, Galois made symmetry a generalizable condition. Symmetry could now be understood as any permutation-based process that produces equivalent results. The new mathematics of group theory establishes the structure and notational system for expressing these equivalencies. In other words, it makes them not only analytical but also projective. Galois’ symmetry groups make it possible to predict when symmetry will or will not be present. If Legendre had turned symmetry into an objective geometric property, Galois transformed symmetry from a descriptive to a heuristic process, one that would ultimately be used in a wide variety of scientific fields.

Crystalline Symmetry

The development of the link between symmetrical forms and structures was led by crystallographers in the 19th century. They discovered that the seemingly random forms of crystals were governed by a limited set of underlying symmetries. In 1815, René-Just Haüy was the first to apply symmetry to physical objects. Building on Haüy’s work, and on the mathematical systematization of symmetry, in 1830 Johann Hessel established that there were only thirty-two different combinations of symmetry elements in crystals. In 1848 Auguste Bravais found that there were only fourteen different orientations or lattices in which the symmetrical distribution of molecules within a crystal could be arranged. Finally, in 1891, using these restrictions as a starting point, Evgraf Fedorov and Arthur Schoenflies found that there are 230 ways in which the molecules of a crystal could be symmetrically distributed.8

That same year, 1891, Fedorov established that there were only seventeen possible permutations that will symmetrically distribute elements on a two-dimensional plane and only seven unique ways to symmetrically arrange them in a onedimensional line. The fact that these are commonly referred to as the seventeen wallpaper groups and the seven frieze groups not only recognizes their direct relationship to group theory, but also shows that while it was not until the end of the 19th century that these symmetries were established mathematically, reflections, rotations, translations, and glide reflections had been used in architectural ornament for millennia before that.9

Symmetry and Physics

The notion proposed by crystallographers that there was an underlying symmetrical structure to the physical world was well-established by the time Einstein published his ground-breaking paper on relativity.10 Among the leaps that Einstein took in his essay was making symmetry axiomatic. As Nobel laureate David Green put it, Einstein’s great advance in 1905 was to “put symmetry first,” that is, to regard the symmetry principle as the primary feature of nature that constrains the allowable dynamical laws.11 Thus, the transformation properties of the electromagnetic field were not to be derived from Maxwell’s equations, as Lorenz did, but rather were consequences of relativistic invariance.

By assuming that symmetry not only has a descriptive power, but a predictive one as well,

physicist and mathematician Hermann Weyl extended Einstein’s intuition when he pioneered (with others) the use of symmetry and group theory to understand quantum mechanics. But he took symmetry even further. He held that symmetry, as expressed in group theory, was foundational to the creation and the understanding of a multiplicity of phenomena. In his 1952 book Symmetry, Weyl provides the now common definition of symmetry as any situation in which invariance persists despite a transformation having taken place.12 This is true for physical forces and particle fields, in the positioning of molecules in elements, and in architectural ornaments.

While Weyl argued that symmetry provided the link between a variety of natural and cultural phenomena, it was the mathematics of groups that was at the core of those connections. Central to establishing this relationship is the importance of how multiple scenarios or permutations could produce the same result. That is, far from limiting output to a single outcome, the symmetry of groups allows for multiple (but not an infinite number of) results.

For Weyl, symmetry is both an analytic and a heuristic mechanism, a tool that describes the existing world but can also create new ideas and new worlds. It was expansive not only because it generated form, but also because it established a connection between two ways of knowing— science and art—that were thought to be separate; both having the capacity to reveal and make new (symmetrical) patterns. As in the classical definition, symmetry is a concept in which a unit of different and equal elements are combined. However, because these forms are grounded in the logic of group theory, they were no longer associated with harmony or beauty. Rather, they are presented as an objective, mathematical quality.

Contemporary Symmetry

Symmetry continues to play a central role in physics, particularly in the search for a Grand Unified Theory that will account for all the forces present in the universe. David Green notes that “in the latter half of the 20th century, symmetry has been the most dominant concept in the exploration and formulation of the fundamental laws of physics.”13 Following Weyl, Green emphasizes the conceptual and expansive power of symmetry. Symmetry is an objective, invariant cause (produced by permutations), not an effect.14 It is the source of forms, not their shape.

Despite these changed definitions, the usefulness of symmetry persists. And, no matter its definition, symmetry still represents “a unity.” However, “the way in which this unity is realized (…) and how the equal and different elements are chosen” has changed over time.15 One could again say that symmetry is itself symmetrical, as it retains its invariant presence in art and science, despite the many transformations that have occurred to it as a concept.

1 Giora Hon and Bernard Goldstein, From Summetria to Symmetry: The Making of a Revolutionary Scientific Concept (London: Springer, 2008); A.V. Shubnikov and V.A. Koptsik, Symmetry in Science and Art, translated rrom Russian by G.D. Archard, edited by David Harker (New York: Plenum Press, 1974); Ian Stewart, Why Beauty Is Truth: A History of Symmetry (London: Basic Books, 2007). 2 Katherine Brading and Elena Castellani, “Symmetry and Symmetry Breaking,” The Stanford Encyclopedia of Philosophy (2013). https://plato. stanford.edu/entries/symmetry-breaking/ 3 Ibid; Bas C. Van Fraassen, Laws and Symmetry (Oxford: Clarendon, 1989); Hermann Weyl, Symmetry (Princeton: Princeton University Press, 1952); Shubnikov and Koptsik, Symmetry in Science and Art; Stewart, Why Beauty Is Truth. 4 Hon and Goldstein, From Summetria to Symmetry, 157-177. 5 Claude Perrault. Ordonnance for the Five Kinds of Columns after the Method of the Ancients (Santa Monica: Getty Center for the History of Art and the Humanities, 1993). 6 Hon and Goldstein. From Summetria to Symmetry, 203-219. 7 Stewart, Why Beauty Is Truth, 118-123. 8 Shubnikov and Koptsik, Symmetry in Science and Art. 9 Donald Crowe, “Introduction to the Plane Symmetries,” in Symmetry Comes of Age: The Role of Pattern in Culture, edited by Dorothy K. Washburn and Donald W. Crowe (Seattle: University of Washington Press, 2004), 3-17. 10 Giora Hon and Bernard Goldstein, “Unpacking ‘For Reasons of Symmetry’: Two Categories of Symmetry Arguments,” Philosophy of Science No. 73 (2006), 419-439. 11 Ibid. 425. 12 Weyl, Symmetry. 13 Hon and Goldstein, “Unpacking ‘For Reasons of Symmetry’”, 426. 14 Van Fraassen. Laws and Symmetry; Weyl, Symmetry; Hon and Goldstein, “Unpacking ‘For Reasons of Symmetry’”. 15 Brading and Castellani, “Symmetry and Symmetry Breaking.”