The One and the Many David Salomon

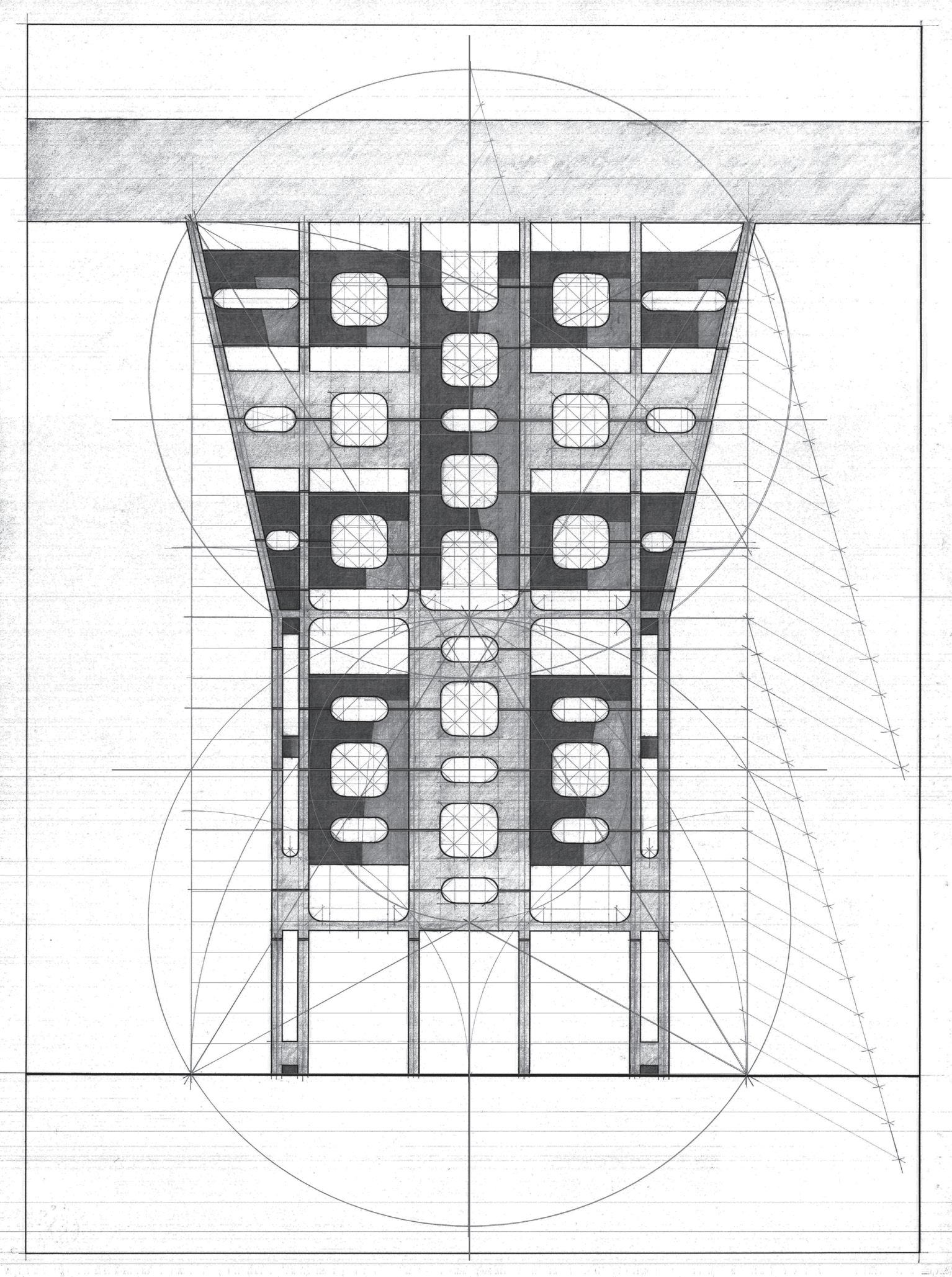
An axis of vertical symmetry determines the proportion of the column by an aureus rectangle, whose side is the maximum width of the column. Two equilateral triangles are defined from the rectangle: the lower horizontal symmetry axis is determined by the proportions of the lower triangle. Estudio CEPRA and Clorindo Testa, Banco de Londres. Buenos Aires, Argentina, 1966. Drawing by Fernando Yabén

Architectural symmetry, we have been told, is obsolete. It is dangerously essentialist and authoritarian. It is superficially applied. Its rigid rules are an indication of indifference—to site, to structure, to use, to climate.1 Symmetry is a problem to overcome, not something to explore. Outside of architecture, however, the opposite is true. At the same time as its architectural relevance was being challenged—at the turn of the 20th century—its importance in math and science increased. Physics, chemistry, and biology recognized the multiple forms and uses of symmetry, and effectively employed it in a variety of contexts.2 A closer look at modern architecture reveals that it never truly abandoned symmetry, it only discursively deserted it. Given the continued presence, even today, of symmetry, this book examines how architecture, math, and science have persistently used it to simultaneously produce specific disciplinary knowledge and establish connections with other fields. But, why revisit symmetry, why now? Because the need for linking diverse ideas and objectives is increasingly crucial today. In a world where the side effects of disciplinary specialization and technological optimization can no longer be solved by more isolation, synthetic modes of inquiry are necessary. Despite its reputation as ideal and autonomous, symmetry has proven to be surprisingly supple and inclusive, and it is worth reexamining it today to see what it can—and what it might already effectively—integrate. In short, given its long history, its covert presence in modernism, and its continued use in contemporary architecture, one must ask if today symmetry still functions as an expression of power and permanence, or if it can be used as an effective device to compare and combine seemingly unlike things. Defining Symmetry Before addressing these issues we need to be clear about what symmetry is. For many, something is symmetrical if it is composed of two equal and identical parts facing each other across an axis. This is typically called mirror or reflective symmetry. The human face is a prime example. However, this is neither the original meaning of symmetry nor its contemporary mathematical use. This phenomenon had not been codified as “symmetry” until the 17th century by the French architect Claude Perrault, and, in the late 18thth, century by the French mathematician Adrien-Marie Legendre.3 An earlier definition of symmetry, which goes back to Vitruvius, defines it as the regular and pleasing harmony that is created by the correct use of proportion. Today, following the findings of group theory in math, symmetry is the quality of anything that remains invariant despite it being transformed.

In all of these definitions, symmetry is plural. For something to be symmetrical there must be more than one element present. But, these elements must be distributed in a particular way. It is a particular kind of pattern, a pattern being defined as an array of elements distributed according to a specific logic or structure.4 Symmetry is a structure that demands a specific kind of equivalence between the parts—the parts of a body, of a formula, of a building, or of anything else.

Formally speaking, an image or object is symmetrical if you can pick it up, move it, then place it back down in a new position without an observer being able to tell it had been moved. Mirroring, or reflection, is one operation that can produce these results. There are three more: translation, rotation, and glide reflection. Mathematicians—building on work done by crystallographers—have proven that there are only seven ways in which these four operations can be used to create one-dimensional patterns (often referred to as frieze patterns). They will also tell you that they can only produce seventeen two-dimensional figures (known as wallpaper patterns) and 230 three-dimensional configurations. Symmetry is by no means infinite, but there is definitely more than one. The Use of Symmetry

While the number of actual permutations possible using the four operations was established mathematically in the 19th century, they had been understood and used for millennia in architecture and design. One could say that symmetry was ornamental before it was mathematical. In other words, traditional symmetrical ornaments are not illustrations of mathematical concepts: they are the engines that produced them. Such knowledge was widespread. In his 1856 book The Grammar of Ornament, Owen Jones attempted to capture how this information was used in every historical era and geographic region in a single volume. At roughly the same time crystallographers and chemists were establishing the symmetrical structures that underlie the appearance of matter. Like Jones, they sought to capture, once and for all, the consistent source of inanimate form.

Thomas Beeby has documented how the foundational work of Frank Lloyd Wright, Le Corbusier, and Mies van der Rohe was directly influenced by the symmetries illustrated by Owen Jones and subsequently described by crystallography.5 All three used symmetry operations to organize and distribute spaces, structural elements, and forms. Symmetry was used as an active organizational and form-making device. It was not just a descriptive idea, but a heuristic, productive device. Meanwhile, in physics and math symmetry became ever more useful in the 20th century; not because of its empirical presence but because of its theoretical value. If in modern architecture symmetry was found in physical objects but was absent from theory, in the natural sciences the opposite was true. Symmetry was a powerful idea, even if it was rarely encountered in its pure state. If symmetry was the rule, then many other phenomena made sense.6

The fact that symmetry is both a property of objects and an underlying concept is also significant. Objects and ideas: for a long time the latter have held sway as the primary source of knowledge production. However, the story of symmetry suggests that this sequence can work in reverse, that aesthetic operations and artifacts can precede and even help produce ideas. This book outlines symmetry’s productive trafficking, especially in the 19th and 20th centuries, between these two ways of knowing. This combination is itself a decidedly architectural move. Architects are alchemists who combine seemingly unrelated parts into complex wholes. Why revisit symmetry now? To examine how this seemingly inevitable architectural trope has and might still effectively integrate a number of architectural ideas and elements with one another.

1 Phillip Tabor, “Fearful Symmetry,” Architectural Review no. 1023 (May, 1982). 2 Giora Hon and Bernard Goldstein, From Summetria to Symmetry: The Making of a Revolutionary Scientific Concept (London: Springer, 2008). 3 Giora Hon and Bernard Goldstein, “Unpacking ‘For Reasons of Symmetry’: Two Categories of Symmetry Arguments,” Philosophy of Science no. 73 (October, 2006), 419-439. 4 Paul Andersen and David Salomon, The Architecture of Patterns (New York: Norton, 2008). 5 Thomas H. Beeby, “The Grammar of Ornament/Ornament as Grammar,” VIA III (1977), 10-29. 6 Giora Hon and Bernard Goldstein, “How Einstein Made Asymmetry Disappear: Symmetry and Relativity in 1905,” Archive for History of Exact Sciences 59, no. 5 (2005), 437-544.

An axis of vertical symmetry determines the geometry of the column by an aureus rectangle, whose side is the maximum width of the column. Estudio CEPRA and Clorindo Testa, Banco de Londres. Buenos Aires, Argentina, 1966. Drawing by Fernando Yabén

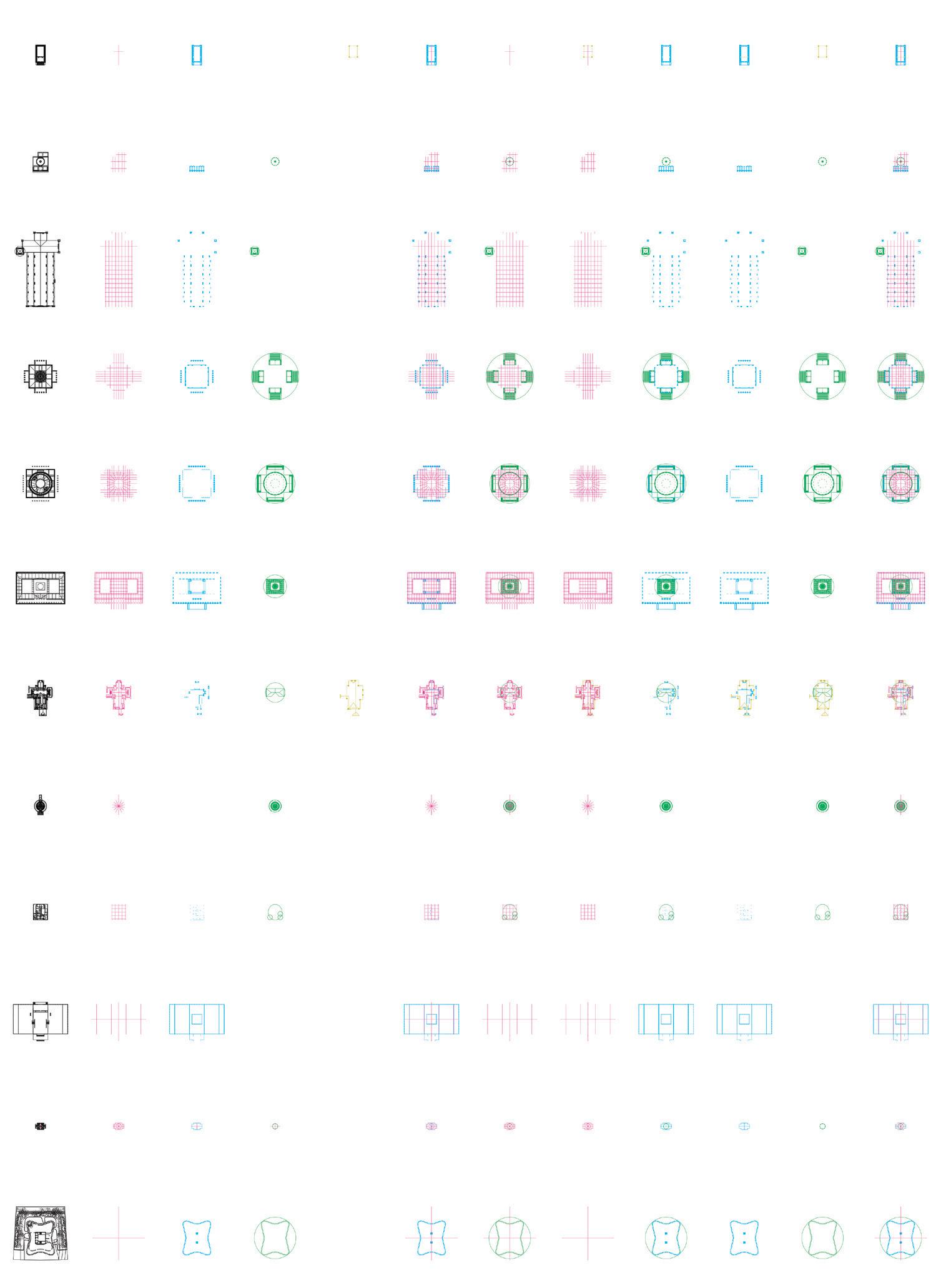
Matrix of symmetry analysis. Plans and axonometries. From top to bottom, one project per row: Maison Carrée, Pazzi Chapel, Santa Maria Novella, Villa Capra, Barrière de la Villete, Altes Museum, Darwin D. Martin House, Glass Pavilion, Villa Savoye, Crown Hall, Teatro del Mondo, O-14. From left to right, one type of symmetry per column: mirror reflections, translations, rotations and glide reflections, and the eight possible combinations between them