DEFINITION AND INTRODUCTION

Background

Definition

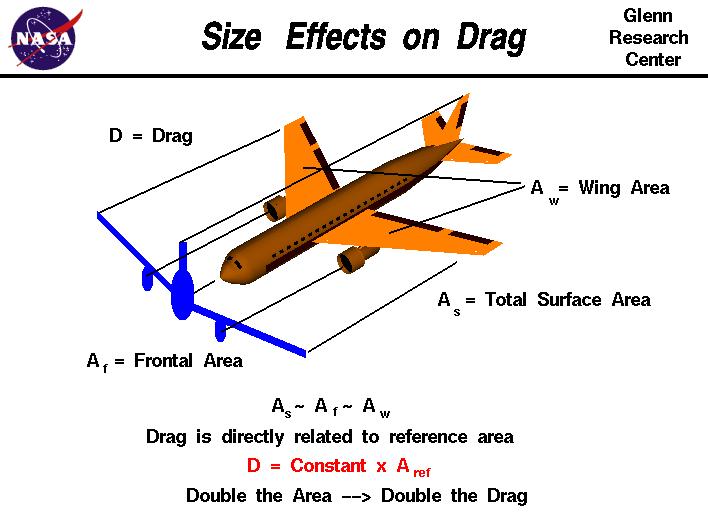
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation in which a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag. The drag coefficient is always associated with a particular surface area.

We can obtain the drag coefficient through the drag equation(F=(1/2)CρSV^2

Basic Principles and Variables:

To make it easier to understand, I split the formula into several parts:

�� and �� are usually affected by the environment, while ���� and A is critical to the measurement of ���� and engineering design.

���� is the drag force, which is by definition the force component in the direction of the flow velocity

�� is the mass density of the fluid

�� is the flow speed of the object relative to the fluid

A is the reference area.

As a result, it is necessary to figure out how those two variables work in the whole formula, especially the ����, drag coefficient. And this is why I decide to put ����, this critical element, to the left of equal sign even if it is not appropriate to interpret in this way. This equation is merely a definition, not a decision.

However we still have some deterministic equations which are related to Reynolds number(Re), dynamic viscosity(��) and Bejan number(Be), flow length(L)

*Bejan number and

Reynold number are widely utilized in thermodynamics and mechanical engineering. I will not include these two numbers in the following presentation.

By analyzing all variables from different formulas…

From this formula, we find that Cd is related to ���� and ����, thatalsoexplainedwhysteamlined bodyoftenhasarelativelysmaller dragcoefficientandairresistense.

D is the equivalent diameter of the object(It is directly related to the shape of the object, we should adopt a method of mathematic analysis to figure it out).

�� is the speed of the object relative to the fluid.

�� is the dynamic viscosity.

L is the contact length between flow and boundaries.

P is pressure drop. Slightly different,

�� in this equation stands for the Kinematic viscosity

We can make a conclusion (in the next page)

Conclusion:

The drag coefficient is basically influenced by two major aspects: the environment(dynamic or kinematic viscosity, changing are pressure) and the shape of the object(retro of wetted area to total area, equivalent diameter)

Although we find a basic conclusion, the variables in the entire formula are various, which means we engineers are required to process those variables in different way in countless situations.

We are able to get this conclusion easily by splitting the sophisticated drag coefficient equation into physical quantities and numbers.

In the next section, we are going to have a general understanding of the practical application of drag coefficient in engineering.