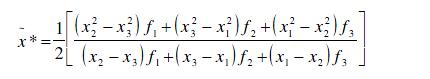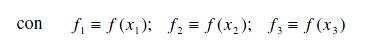
1 minute read
Cuadrática
Métodos de Aproximación Polinómica
Se ha comprobado que los métodos de interpolación polinómica son normalmente ligeramente mejores que el método de la sección áurea.
Advertisement
La interpolación consiste en hallar un dato dentro de un intervalo en el que conocemos los valores en los extremos. La interpolación se dirá lineal cuando sólo se tomen dos puntos y cuadrática cuando se tomen tres.
Interpolación Cúbica
La interpolación cúbica en la búsqueda de un óptimo se basa en la aproximación de la función objetivo por un polinomio de tercer grado dentro del intervalo de interés, y determinar el punto estacionario asociado con el polinomio. Para realizar la interpolación cúbica hacen falta cuatro puntos o dos puntos con sus respectivas derivadas. En el caso de que se evalúen cuatro puntos, tenemos que aparecer un sistema de cuatro ecuaciones lineales con cuatro incógnitas (los coeficientes del polinomio). Sea la matriz X:
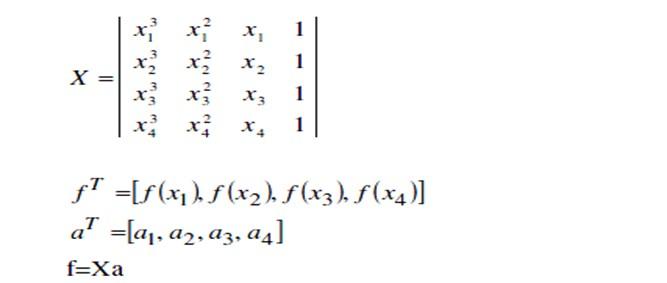
El extremo de f(x) se obtiene igualando la derivada de esta a cero, por lo tanto:
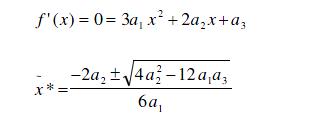
Interpolación Cuadrática
Si comenzamos con tres puntos, por ejemplo x 1 , x 2 , x 3 en orden creciente, y no necesariamente igualmente espaciados, pero contenidos dentro de la zona de búsqueda (a,b), podemos aproximarlos a un polinomio de grado 2, f ( x) = a +bx + cx 2 de tal manera que dicho polinomio pasa exactamente por esos tres puntos y debe presentar un mínimo en: Si suponemos que f(x) se evalúa en los tres puntos, podríamos calcular los valores de a, b, c resolviendo el sistema de tres ecuaciones lineales:
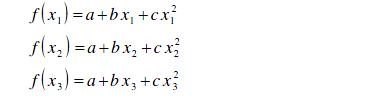
lo que nos lleva a :