Conclusion:MoreThanUnderstanding

Withthehighlyaddictive componentofgaming, genetics,andenvironment playingamajor factorinaddiction,there isampleevidenceto establishthataddiction formanyteenagers inthosecircumstancesis veryprobable.Ifteenagers aremoresusceptible togamingaddiction thanotherdemographics, orifsometeenagersare moresusceptiblethan otherteenagers,isittheir fault?Allthreefactorsof addictioncannotbe controlledbythe individual;whatis society’sduty torecognizethis?With this knowledge,individuals shouldrestructurethe perspective ofunderstanding theaddictedteen.It mustchangefrom blamingtheperson’s identitytounderstanding the combinationofcompone ntsthatresultin addiction.

However,thereis anothersideofpotential ethicalimplicationsthat arisewith theprocessofunderstan ding.Thisresearch wouldserveasatoolfor peopletouseas anexcusefor theiraddiction.Itcan potentiallybe counteractive labeling addictionas“inevitable” willdiscouragepeopleto workoutofit.Inthe scopeofthegenetic factor,individualsmay alsoblameotherpeople fortheiraddiction. Offeringthisideawould takethe responsibilityoffoftheir conscience.

Thus,theactof understandingcan becomeapoison,making itimperative thatwithunderstanding comesaidandgenuine care.Solely understandingis superficial;it iswhatoffersaddictiona scapegoat.“Highly probable”shouldnotbe interpretedasfate,but ratheracallingto recognizethesepeople andsuccorthem,more thanweoriginallyhave.

References

[1] Lenhart, Amanda et al. (16/09/2008). Teens, Video Games, and Civics. Pew Research Center. https://www.pewresearch.org/internet/2008/09/16/. Retrieved: 15/06/2022.

[2] Norcia, Andrea et al. (11/2019). The Impact of Video Games. Sutter Health. https://www.sutterhealth.org/health/parenting-preteens-teens/digital-safety/videogames. Retrieved: 15/06/2022.

[3] (06/01/2021) Is Your Teen Addicted to Games? Latest Research on Teenage Video Game Addiction.

https://www.newportacademy.com/resources/treatment/teenage-video-gameaddiction/. Retrieved: 08/07/2022.

[4] Popescu, Alexandra et al. (23/03/2021). Understanding the genetics and neurobiological pathways behind addiction. Spandidos Publications. https://www.spandidos-publications.com/10.3892/etm.2021.9976. Retrieved: 18/05/2022.

[5] Park, Jooyeon et al. (20/12/2018). Genetic association of human CorticotropinReleasing Hormone Receptor 1 (CRHR1) with Internet gaming addiction in Korean male adolescents. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6302290/ Retrieved: 30/06/2022.

[6] Han, Doug et al. (09/2007). Dopamine genes and reward dependence in adolescents with excessive internet video game play. National Library of Medicine. https://pubmed.ncbi.nlm.nih.gov/21768948/. Retrieved: 30/06/2022.

[7] Mavrikaki, Maria. (28/01/2019). Your genes and addiction. Harvard Health. https://www.health.harvard.edu/blog/your-genes-and-addiction-2019012815730 Retrieved: 25/05/2022.

[8] Can You Pick Your Poison? The Effects of Genetics on Addiction. The Yale Ledger. https://campuspress.yale.edu/ledger/can-you-pick-your-poison-the-effectsof-genetics-on-addiction/. Retrieved: 17/06/2022.

[9] Kim, Yong et al. (14/06/2018). Case Study #1: Computer / Video Game Addiction. NRVIV. https://www.nrviv.org/nrviv-blog/2018/6/12/case-study-1-addand-video-game-addiction. Retrieved: 09/06/2022.

{10] Fields, Douglas. (05/11/2010). Change in the Brain’s White Matter. National Library of Medicine. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3201847/ Retrieved: 09/06/2022.

[11] Lin Fuchun et al. (02/2015). Structural Brain Imaging and Internet Addiction. Research Gate. https://www.researchgate.net/publication/281382444_Structural_Brain_Imaging_an d_Internet_Addiction. Retrieved: 09/06/2022.

[12] Galván, Adriana et al. (13/01/2014). Neural representation of expected value in the adolescent brain. PNAS. https://www.pnas.org/doi/10.1073/pnas.1319762111 Retrieved: 20/06/2022.

[13] Hamilton, Jon. (16/10/2012). Teenage Brains Are Malleable and Vulnerable, Researchers Say. National Public Radio. https://www.npr.org/sections/healthshots/2012/10/16/162997951/teenage-brains-are-malleable-and-vulnerableresearchers-say. Retrieved: 18/06/2022.

[14] Galván, Adriana. (12/02/2010). Adolescent Development of the Reward System. National Library of Medicine. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC. Retrieved: 20/06/2022.

Deciphering The Inscribed Rectangle

What is the problem?

BY GAUTHAM SUBRAMANIAN EDITED BY RYAN MIN

Given any Jordan curve, is it possible to draw a rectangle, such that each of its vertices is on that curve?

A checklist:

That question leaves a lot to be desired: what is a Jordan curve? How does one define a rectangle, in a way helpful to the problem? And, last but not least, how would one even solve something like this?

The first and second questions are fairly simple. A Jordan curve (Image 1) is any squiggly line through space that is continuous, without any gaps, at every point. Another, analogous, term for a Jordan curve is a “closed curve”.

The traditional definition of a rectangle—a quadrilateral with 3 (not 4!) right angles, and parallel sides that are opposite to each other is not very helpful. Another way to define a rectangle is by the properties of its diagonals. Each diagonal of the rectangle must be equal, and the midpoint of one, must be the midpoint of another.

Now onto the last part—how to solve it. Rephrasing the problem would help with that. On any Jordan curve, is it possible to find two pairs of two points on said curve, such that the middle of the line connecting paired points is the same, as well as the distance between paired points? A simple checklist can be used to approach this!

Inscribed Rectangle Problem:

• Is the middle of the lines between paired points the same?

• Is the distance between each pair of points the same?

It might be helpful to find some way to identify the midpoint, therefore, let’s introduce a function. Imagine the Jordan curve on a 2D xy plane. Let’s move the midpoint of each possible diagonal up, on the z-axis, a certain amount, to be able to identify them (Image 2). If the x and y coordinate of any two midpoints match, the first task is complete!

• Is the middle of the lines between paired points the same?

Now, some of you might be wondering how far to move each point up on the z axis. That leads to the second task by moving the midpoints up by the length of the diagonals they are on, the diagonals with the same length will all have the same z-coordinates. Matching z-coordinates represents the completion of the second task, because the corresponding diagonals would be the same length.

• Is the distance between each pair of points the same?

But wait a second. If the x, y and z coordinates are all the same, then all one must find is any point that can be identified by using two different sets of points on the curve. Therefore, all that needs to be done to solve the problem is to plug every possible points into the function, and to find any you can get from two points on the curve.

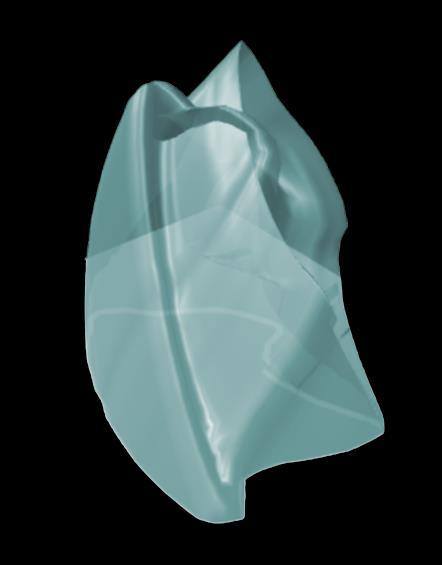
Now, this section’s namesake: the mountain. Applying this function to every point on the Jordan curve moving up the midpoints, by the length of the diagonals they bisect, and plotting that point we get a “mountain” (see image 2).

This mountain is just one way to define the problem. The next section will focus on another, equally useful, way to visualize the problem.

Now, instead of thinking about what happens in 3D, we’ll go down to 1D. How? Scissors!

Let’s take that Jordan curve from earlier and cut it (See image 1). Then, let’s straighten it (See image 3a). On that straight line (think of the number line on the wall of your elementary classroom!), let’s choose a point, and cut it with scissors. Now, instead of an enclosed shape, it is just a curvy line.

This is the confusing part: We can turn this into a straight line by moving each point on the curvy line to a 1D plane, while maintaining the order (See image 3a). The point where the shape was cut will appear twice, at each end of the straight line.

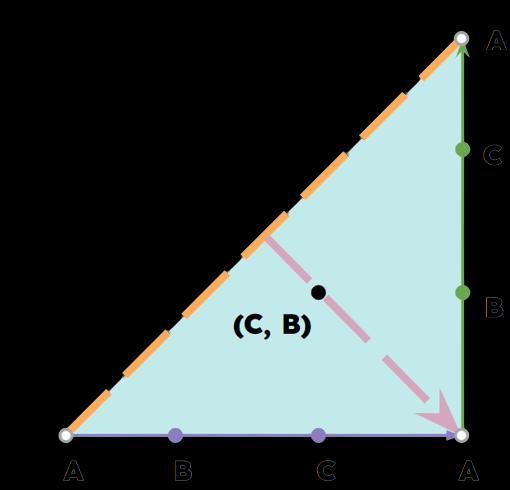
A point on the straight line corresponds to a single one, on the Jordan curve, but there needs to be two points on the Jordan curve to create a rectangle. To solve this, duplicate the straight line to make a square (see image 3b). This square is special, as each point on the square corresponds to a possible rectangle. This can almost be used to compare with our previous, 3D model.

However, another problem arose.

For the sake of objectivity, let’s observe point A and point B, two random points on the shape. On the Jordan curve, any two choices for A and B will result in a single rectangle. However, on the square from earlier, A and B result in two points: (C, B) and (B, C) (see image 3b). Two distinct points on the square will map to the same rectangle. As a side note, if the pair of points on the Jordan curve are the same, the two resulting points on the square will map onto the same point, but that doesn’t matter, due to reasons which will be explained shortly.

Now comes the topology: as long as the overall essence of the shape is preserved, we can draw a number of conclusions. While this may seem broad, imagine you have some paper, scissors and glue; anything you can do to that paper, you can do to this square. The first change to the shape, or transformation, will be to “flip” half of the square onto the other half, in order to remove the second, redundant, ordered pair, turning the square into a triangle with only unordered pairs (see image 3c). Now, there is only a 2D triangle, but two more problems remain!

First, it is only 2D, but it needs to be 3D to compare it to our 3D mountain. We also have to make sure the order of the line is the same, and two points overlap only if they represent the same thing. In other words, we need to make sure the arrows always map onto each other facing in the same direction (See the arrows in image 3c).

There is a solution to both! First, split the triangle in two, based on its altitude (see image 3c). This leaves us with 2 smaller triangles, which account for ¼ of the total area of the original square. By “flipping” one of the triangles and “gluing” it to the next (see image 3d), such that the green line and purple line are coincident, our final 2D polygon is achieved

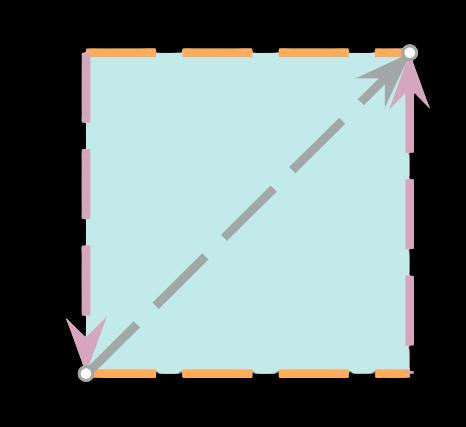
Now, our final step is to make it 3D. Fairly simple: just connect the left and right sides of this smaller square. However, notice that we still have to be careful; the arrows are facing in opposite directions (see image 3d), therefore, they can’t be connected normally. Instead, they have to be “flipped” once more. This will create a Möbius strip (see image 4).

Now the last phase: connecting the pieces.

Connecting the Pieces: the Use of Topology

Both the mountain and the Möbius strip represent the same set of all possible rectangles. Remember, if any point on the mountain is the output of two different pairs of points on the Jordan curve, or a single point on the Möbius strip, the theorem is proved.

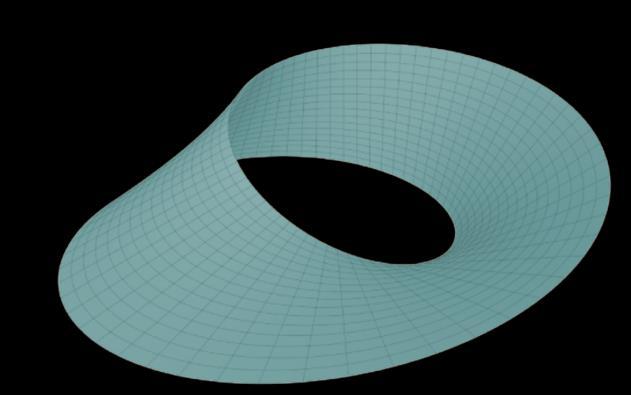
From here, all that is left is proving the Möbius strip cannot map onto the mountain, without intersecting itself. A Möbius strip has a “flip”; it switches direction midway through, creating a 1-sided, yet 3D shape. That flip ensures it cannot map onto the mountain. Try it yourself! Take a piece of paper, flip it once, and connect the two ends. Now see if you can map that onto a rock, such that the rock is completely covered, and the paper never overlaps. And with that, the theorem is proved. The underlying motif throughout this proof was topology: it was used in creating the mountain, creating the Möbius strip, and combining the two shapes. The abstract nature of topology, unbounded by restrictions, such as exact length and angle, can lead to many, otherwise unreachable, conclusions.

Works Cited

Sanderson, Grant. “Who Cares about Topology? (Inscribed Rectangle Problem).” 3Blue1Brown, https://www.3blue1brown.com/lessons/inscribed-rectangle-problem. Ye, Tomáš.“RectanglesInscribedin JordanCurves.” Mathematical Institute of Charles University, Charles University, 2018,pp.2427 https://dspace.cuni.cz/bitstream/handle/20.500.11956/99757/130