GRÁFICOS DE REPRESENTACIÓN

ejemplo

Calcular la moda de la siguiente serie de números:

Solución:

Números en la serie 2 3 4 5 6 8 Repeticiones 2 2 5 6 2 3

El valor más repetido es el número Por lo tanto, la moda es:

En los análisis estadísticos, es frecuente utilizar representaciones visuales complementarias de las tablas que resumen los datos de estudio. Con estas representaciones, adaptadas en cada caso a la finalidad informativa que se persigue, se transmiten los resultados de los análisis de forma rápida, directa y comprensible para un conjunto amplio de personas.

Tipos de representaciones gráficas

Cuando se muestran los datos estadísticos a través de representaciones gráficas, se ha de adaptar el contenido a la información visual que se pretende transmitir. Para ello, se barajan múltiples formas de representación:

Diagramas de barras: muestran los valores de las frecuencias absolutas sobre un sistema de ejes cartesianos, cuando la variable es discreta o cualitativa. Histogramas: formas especiales de diagramas de barras para distribuciones cuantitativas continuas. Polígonos de frecuencias: formados por líneas poligonales abiertas sobre un sistema de ejes cartesianos.

GRÁFICOS DE SECTORES: circulares o de tarta, dividen un círculo en porciones proporcionales según el valor de las frecuencias relativas. PICTOGRAMAS: o representaciones visuales figurativas. En realidad, son diagramas de barras en los que las barras se sustituyen con dibujos alusivos a la variable. CARTOGRAMAS: expresiones gráficas a modo de mapa.

PIRÁMIDES DE POBLACIÓN: para clasificaciones de grupos de población por sexo y edad.

Diagramas de barras e histogramas

Los diagramas de barras se usan para representar gráficamente series estadísticas de valores en un sistema de ejes cartesianos, de manera que en las abscisas se indica el valor de la variable estadística y en las ordenadas se señala su frecuencia absoluta.

Para elaborarlo debemos:

- Utilizar un sistema de coordenadas rectangulares y se llevan al eje de las "x" los valores que toma la variable en estudio y en el eje de las "y" se colocan las frecuencias de cada barra.

- Luego se construyen los rectángulos, tomando como base al eje de las abscisas, cuya altura será igual a cada una de las diferentes frecuencias que presentan las variables en estudio.

23

- La magnitud con que viene expresada la variable se observa en la longitud de las barras (rectángulos). Es importante destacar que solamente la longitud de las barras y no su anchura es lo que denota la diferencia de magnitud entre los valores de la variable. Todas las barras tienen que tener una anchura igual, separadas entre sí, preferiblemente por una longitud igual a la mitad del ancho de estas o distancias iguales entre barras. Las barras se pueden graficar tanto verticalmente como horizontalmente. Se pueden elaborar barras compuestas y barras agrupadas. Este tipo de gráfico se clasifican por:

-BARRAS SIMPLES: Compara valores entre categorías de una variable.

- BARRAS DOBLES: Compara valores entre categorías de dos variables.

- BARRAS MÚLTIPLES: Compara valores entre categorías de dos o más variables.

- BARRAS VERTICALES: Las categorías de la variable deben ubicarse en el eje x.

- BARRAS HORIZONTALES: Las categorías de la variable deben ubicarse en el eje y.

- BARRAS APLICADAS: Compara entre categorías el aporte de cada valor en el total.

Estos gráficos se usan en representación de caracteres cualitativos y cuantitativos discretos. En variables cuantitativas continuas, se emplea una variante de los mismos llamada histograma.

Diagrama de barras.

22

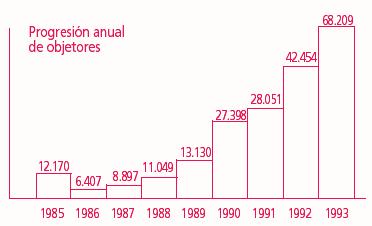
HISTOGRAMA DE FRECUENCIAS: El histograma es un diagrama en forma de columna, muy parecido a los gráficos de barras. Se define como un conjunto de rectángulos paralelos, en el que la base representa la clase de la distribución y su altura la magnitud que alcanza la frecuencia de la clase correspondiente. Son barras rectangulares levantadas sobre el eje de las abscisas del plano cartesiano utilizando escalas adecuadas para los valores que asume la variable en la distribución de frecuencia.

Histograma

El ancho de la base de los rectángulos es proporcional a cada clase de la distribución, de tal manera que, cuando la distribución tiene clases de igual tamaño, el tamaño de todos los rectángulos tendrá bases iguales. Los lados del rectángulo se levantan sobre los puntos del eje de las x que corresponden a los límites de cada clase y la longitud de los mismos será igual a la frecuencia que tenga esa clase, los lados por lo tanto corresponden a la frecuencia de cada clase de la distribución de frecuencia.

Cuando se elaboran gráficas estadísticas en el plano cartesiano es recomendable que en el eje de las ordenadas se representen las frecuencias y el eje de abscisas las variables independientes.

Ejemplo

Una empresa se interesa en el ancho de bloques de madera y ha tomado 100 muestras de la operación de corte. Los datos han sido agrupados en intervalos o rangos y se muestran en el siguiente cuadro:

Del cuadro se puede apreciar que de las 100 muestras de bloques de madera 5 miden de 2 a 13 centésimas de pulgada, 10 miden de 14 a 25 centésimas de pulgada, etc. El mayor número de bloques de madera (34) miden de 28 49 centésimas de pulgada. Podemos representar gráficamente esta información a través del siguiente histograma de frecuencia en el cual la altura de cada barra indica la frecuencia de las observaciones en ese intervalo.

Ejemplos de tipos de representaciones gráficas

Histogramas: Se agrupan los datos en clases, y se cuenta cuántas observaciones (frecuencia absoluta) hay en cada una de ellas. En algunas variables (variables cualitativas) las clases están definidas de modo natural, p.e sexo con dos clases: mujer, varón o grupo sanguíneo con cuatro: A, B, AB, O. En las variables cuantitativas, las clases hay que definirlas explícitamente (intervalos de clase).

Se representan los intervalos de clase en el eje de abcisas (eje horizontal) y las frecuencias, absolutas o relativas, en el de ordenadas (eje vertical).

A veces es más útil representar las frecuencias acumuladas.

O representar simultáneamente los histogramas de una variable en dos situaciones distintas.

Otra forma muy frecuente, de representar dos histogramas de la misma variable en dos situaciones distintas.

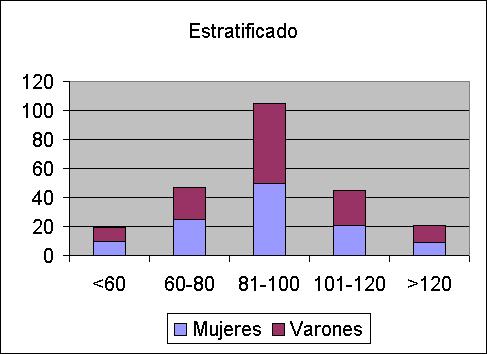
Otra más

En las variables cuantitativas o en las cualitativas ordinales se pueden representar polígonos de frecuencia en lugar de histogramas, cuando se representa la frecuencia acumulativa, se denomina ojiva.

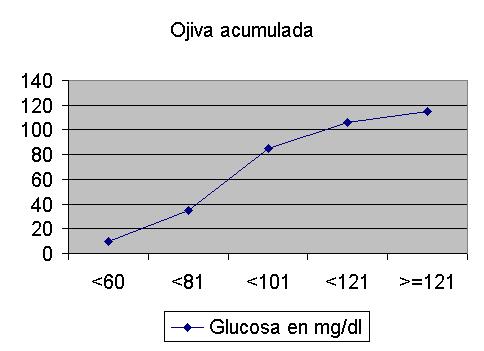
POLÍGONOS DE FRECUENCIAS

Para construir polígonos de frecuencias, se trazan las frecuencias absolutas o relativas de los valores de la variable en un sistema de ejes cartesianos y se unen los puntos resultantes mediante trazos rectos. Con ello se obtiene una forma de línea poligonal abierta.

Los polígonos de frecuencias se utilizan preferentemente en la presentación de caracteres cuantitativos, y tienen especial interés cuando se indican frecuencias acumulativas. Se usan en la expresión de fenómenos que varían con el tiempo, como la densidad de población, el precio o la temperatura. Para construir el polígono de frecuencia se toma la marca de clase que coincide con el punto medio de cada rectángulo de un histograma.

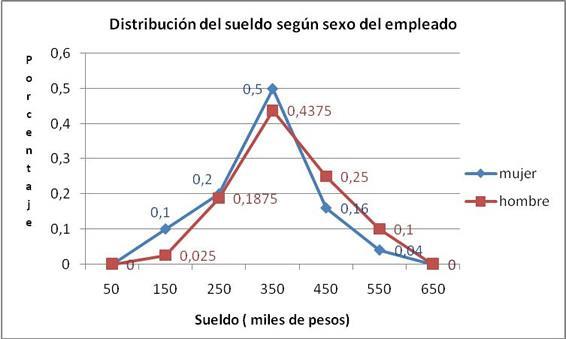
Pasos para elaborar un polígono de frecuencias:

1 - Se dibuja un plano cartesiano.

2- Se traza sobre el eje de las abscisas, a distancias iguales, los puntos medios de las diferentes clases de la distribución de frecuencias.

3- Se levantan perpendiculares por cada una de las marcas de clase, con una longitud igual a la frecuencia de cada una de las clases que integran la distribución de frecuencia. Al final de cada perpendicular se marca un punto.

4- Los puntos resultantes se unen por medio de una línea recta obteniéndose una línea poligonal.

5- Con la finalidad de cerrar la línea poligonal se agrega una clase imaginaria con frecuencia cero a cada extremo de la distribución de frecuencia, por tales motivos ambos extremos del polígono se cortan con el eje de las abscisas.

También se puede elaborar un polígono de frecuencia después de haber graficado un histograma; si se determina el punto medio de cada rectángulo de un histograma y esos puntos medios se unen por medio de segmentos de recta dan como resultado el polígono de frecuencia.

EJEMPLO

Las temperaturas en un día de otoño de una ciudad han sufrido las siguientes variaciones:

HORA TEMPERATURA 6 7º 9 12° 12 14° 15 11° 18 12° 21 10° 24 8°

Gráficos de sectores

En los diagramas de sectores, también llamados circulares o de torta, se muestra el valor de la frecuencia de la variable señalada como un sector circular dentro de un círculo completo. Por ello, resultan útiles particularmente para mostrar comparaciones entre datos, sobre todo en forma de frecuencias relativas de las variables expresadas en forma de porcentaje.

ejemplo

Un compañero de Marta decidió preguntar a sus compañeros por su deporte favorito y obtuvo los datos, que aparecen en la tabla siguiente:

Frec. absoluta Frec. relativa

Danza Fútbol Tenis

5

8

2

Baloncesto

Atletismo

SUMA 3

2

20

0,25 25%

0,4

0,1

0,15

0,1

1

40%

10%

15%

10%

100

Grados del sector

0,25·360º=90º

0,4·360º=144º

0,1·360º=36º

0,15·360º=54º

0,1·360º=36º

360º

GRÁFICO DE LÍNEAS O TENDENCIA: Usado básicamente para mostrar el comportamiento de una variable cuantitativa a través del tiempo. El gráfico de líneas consiste en segmentos rectilíneos unidos entre sí, los cuales resaltan las variaciones de la variable por unidad de tiempo.

Cuando se tienen varias variables a representar, con el fin de establecer comparaciones entre ellas (siempre que su unidad de medida sea la misma); se utiliza plasmarlos en un solo gráfico, el cual es el resultado de representar varias

variables en un mismo plano. A este tipo de gráfico se le llama gráfico de líneas compuesto.

Pictogramas y cartogramas

Para aligerar la presentación de datos estadísticos, con frecuencia se recurre a imágenes pictóricas representativas del valor de las variables. Dos formas comunes de expresión gráfica de los datos son: • Los pictogramas, que muestran diagramas figurativos con figuras o motivos que aluden a la distribución estadística analizada (por ejemplo, una imagen antropomórfica para indicar tamaños, alturas u otros). • Los cartogramas, basados en mapas geográficos que utilizan distintas tramas, colores o intensidades para remarcar las diferencias entre los datos.

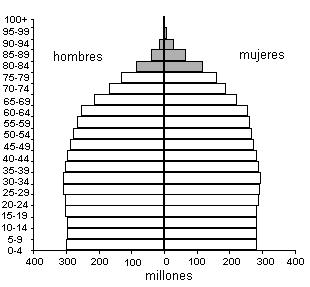
Pirámide de población

Otra forma corriente de presentación visual de datos estadísticos es la llamada pirámide de población. Las pirámides de población se utilizan en la expresión de informaciones demográficas, económicas o sociales, y en ellas se clasifican comúnmente los datos de la población del grupo de muestra considerado en diferentes escalas de edad y diferenciada por sexo.

TIPOS DE PIRÁMIDES DE POBLACIÓN

Existen tres modelos de pirámides de población, que representan diferentes dinámicas demográficas.

PIRÁMIDE ESTABLE: este modelo de pirámide corresponde a poblaciones en las que la natalidad y la mortalidad se mantienen constantes durante un largo periodo de tiempo.

PIRÁMIDE PROGRESIVA: en este modelo de pirámide se observa una base muy ancha y una cima muy angosta. Es típico de poblaciones en las que tanto la natalidad como la mortalidad son altas y la población crece a un ritmo rápido.

PIRÁMIDE REGRESIVA: en este modelo, la base de la pirámide es más pequeña que los escalones siguientes. La pirámide adquiere esta forma en poblaciones cuya natalidad ha descendido en los últimos años y es baja. Este fenómeno genera un envejecimiento de la población.

¿CUAL ES LA UTILIDAD DE ANALIZAR PIRÁMIDES?

Analizando las pirámides de población de diferentes lugares podemos comparar su comportamiento demográfico. Por ejemplo, se puede conocer si la mortalidad y la natalidad han variado en los últimos años.

Por otra parte, analizando varias pirámides de un mismo lugar correspondientes a diferentes momentos históricos, pueden reconstruir su historia demográfica, observando la evolución de los diferentes grupos etarios. Pueden analizar, entre otras cosas, un fenómeno de migración relacionando las pirámides que corresponden al lugar desde donde emigró un grupo de población y al lugar adonde dicha población arriba.

¿Como se construye una pirámide de población?

Para construir una pirámide de población es necesario contar con los datos de la población de una jurisdicción, discriminados por edad y por sexo. Esta información puede ser obtenida a partir de los censos de población.

El gráfico de una pirámide de población se estructura a partir de un eje vertical y otro horizontal.

En el eje vertical de la pirámide se representan los grupos de edades. En general, para la construcción de una pirámide de población se establecen grupos con intervalos de 5 años, de manera que resultan rangos tales como los siguientes: de 0 a 4 años, de 5 a 9 años, de 10 a 14 años, etc. Las edades menores se ubican en la base del gráfico y las mayores, en la cima.

Sobre el eje horizontal se representa la cantidad de población según ambos sexos: hacia la izquierda del eje se ubican los datos correspondientes a los varones y hacia la derecha, la información correspondiente a las mujeres. El eje horizontal puede contener valores absolutos o relativos. La ventaja del uso de valores relativos es que permite realizar comparaciones entre pirámides.

Sobre esta estructura y con los datos de población de un lugar determinado en un momento dado (clasificados según edad y sexo), se construyen las barras horizontales, dispuestas una encima de la otra para cada grupo de edad y sexo.

Las barras horizontales, entonces, indican la cantidad o porcentaje de población por grupo etario. Para construirlas es necesario establecer que cantidad de población le corresponde a cada grupo etario según el sexo al que pertenece y dibujar la barra desde el eje vertical hacia afuera según los valores del eje horizontal. De esta manera se procede con cada grupo etario, y para ambos sexos, hasta completar la serie de edades y, así, terminar la pirámide.

Para construir la pirámide con valores relativos, se requiere calcular previamente el porcentaje que cada grupo etario por sexo representa sobre el total de población.

Un caso curioso es la pirámide de Qatar y otros pequeños países con alto nivel de renta que están atrayendo mucha población emigrante principalmente masculina y en edad adulta por lo que muestran una curiosa deformación.

Pirámide de población mundial en 1998 Pirámide de población mundial estimada para 2050

LINK ESTADISTICA

https://enciclopediaeconomica.com/estadistica/ http://www.hrc.es/bioest/estadis_1.html

GRAFICOS

https://www.portaleducativo.net/primero-medio/50/graficos-estadisticos

http://educativa.catedu.es/44700165/aula/archivos/repositorio/500/546/html/Unidad06/pagina_18.h tml

http://educativa.catedu.es/44700165/aula/archivos/repositorio/500/546/html/Unidad06/pagina_18.h tml

http://www.hrc.es/bioest/Ejemplos_histo.html

MEDIDAS DE TENDENCIA CENTRAL DATOS AGRUPADOS

https://www.superprof.es/apuntes/escolar/matematicas/estadistica/descriptiva/ejerciciosde-la-moda.html

https://www.superprof.es/apuntes/escolar/matematicas/estadistica/descriptiva/mediana.h tml

https://www.lifeder.com/medidas-tendencia-central-datos-agrupados/

https://www.superprof.es/apuntes/escolar/matematicas/estadistica/descriptiva/ejerciciosde-la-media-aritmetica.html

https://www.superprof.es/apuntes/escolar/matematicas/estadistica/descriptiva/mediaaritmetica.html

https://matemovil.com/tablas-de-frecuencias-ejercicios-resueltos/

https://www.portaleducativo.net/primero-medio/50/graficos-estadisticos

https://tratamientodedatos.wordpress.com/2011/03/07/medidas-de-tendencia-central-paradatos-no-agrupados-y-agrupados/

https://www.universoformulas.com/estadistica/descriptiva/

PIRAMIDES

https://www.hiru.eus/es/matematicas/representacion-grafica-de-datos-estadisticos

https://cdn.educ.ar/dinamico/UnidadHtml__get__7c02fdf5-b548-45d3-9b7e4aad848491ae/91686/data/4a0dba4d-7a08-11e1-82fa-ed15e3c494af/index1.htm