Secuenciasdidácticas

A continuación tienes una compilación de secuencias didácticas presentadas porlamaestraHeysihtHernándezylos estudiantes del Seminario Análisis del Conocimiento Matemático

SACM. Secuencias inspiradas en las estrategias de enseñanza aprendizaje centradas en el alumno, como son el Aprendizaje Colaborativo AC y el AprendizajeBasadoenProblemasABP; ademáslasmismassefundamentanen elEsquemaderesolucióndeproblemas de Pólya, la Ingeniería didáctica , las Teorías situacionales y el Constructivismo.

Secuencia 1

Modelo de Secuencia Didáctica de Matemática. SACM

Situación de aprendizaje:

En el planisferio siguiente están representadas las trayectorias parabólicas de dos satélites espaciales. La órbita del satélite meteorológico Aurora viene definida por la función y= , mientras que la órbita del satélite de comunicaciones Radion-3 viene dada por la función y=. En ambos casos es la longitud (el Eje el Ecuador) y y es la latitud (en el Eje del Meridiano de Greenwich).

Colaboración: MaestraIvannovnaCruz. MaestraHeysihtHernández.

Objetivo: Trabajaremos la situación anterior con el objetivo de reconocer el valor numérico de una función.

Metodología: Para trabajar, ya formados en grupos de cuatro, ustedes se dividirán coda uno un rol, de la siguiente manera. Roles de los miembros:

• Lector, quien leerá detenidamente en voz alta para el grupo tanto los problemas como las informaciones recolectadas.

• Sistematizador, quien tomará notas de todas las informaciones relevantes al problema.

•Analista, quien analizará las informaciones y consensuará su relevancia y redactará las conclusiones que el grupo haya acordado, según las informaciones recolectadas.

•Expositor, quien expondrá las informaciones relevantes y conclusiones acordadas.

Reglas de cada grupo:

• Contribuir al logro del objetivo en el grupo. Asumiendo el compromiso de compartir sus conocimientos

• Conocer el objetivo.

• Cooperar responsablemente con la búsqueda de la información que se considere necesaria en los materiales disponibles.

• Interactuar colaborativamente y con comunicación efectiva.

• Seguir procesos valorativos de análisis y síntesis de información

• Respetar los tiempos para coda actividad.

• Autoevaluarse y co-evaluar sinceramente.

Materiales: Fotocopias. Libros. Cuadernos. Lápices. Celulares. Computadoras. Internet. Planisferios. Globos terráqueos.

Secuencia Did Ctica

Centro educativo: Instituto Politécnico Juan Sánchez Ramírez

Asignatura:

Matemática Grado: 5todesecundaria

Tema: Funciones

Docente:

HeysihtHernández

Estrategia: Aprendizaje Basado en Problemas – ABP

Resuelve problemas:

Reconoce el valor numérico de una función.

-Funciones: clasificación.

-Resolución y gráficas de funciones.

Entusiasmo al aplicar las funciones en la resolución de problemas de la cotidianidad.

Astronomía

Geografía

Meteorología

Tecnología

Fotocopias

Libros

Cuadernos

Lápices.

Celulares

Computad oras

Internet

Globos terráqueos.

Planisferio s

Inicio

Desarrollo

La docente formará 8 equipos de estudiantes asignando un número del 1 al 8 a coda estudiante y reuniendo los de igual númeroasignado.

La docente entregará a coda equipo una fotocopia con el problema, los materiales y una ficha con las normas de los grupos, el objetivo, lista de materiales, actividades, productos y coevaluación. Ellos resolverán el problema colaborativamente yrespetando lasreglas.

2clases Por la integración al trabajo en equipos 20%, por la participación en la plenaria 30%, por el trabajo en el cuaderno 50%.

Cierre

Los estudiantes presentarán sus soluciones en sus cuadernos a la docente y en los planisferios o globos terráqueos a todo el curso.

Secuencia 2

Modelo de Secuencia Didáctica de Matemática. SACM

Situación de aprendizaje:

En 1er Grado de Secundaria del CENTRO EDUCATIVO PROF. EUGENIO GENAO REYES deseamos descubrir nuevos procedimientos para extraer raíces cuadradas exactas e inexactas de números enteros. Un estudiante quiso determinar la raíz cuadrada de -64 con una calculadora científica y dio como resultado ERROR en la pantalla. Otra estudiante va en su ayuda y tampoco puede, pero sí pudo determinar la raíz cúbica de -64. Otro alumno sorprendido pregunta: ¿Será que los números negativos no tienen raíz cuadrada?. Preocupados por la situación van y preguntan a la maestra, quien les dice que investiguen el caso para exponerlo en la próxima clase. Buscamos en internet informaciones sobre el tema. Observamos videos en YouTube y anotamos todos los detalles de interés. El día de la plenaria llegamos a la conclusión de que los números negativos no tienen raíz de índice par. Exponemos nuestro trabajo y lo compartimos en las redes sociales contodosnuestroscontactosyconladocente.

Colaboracióndelosmaestrantes: DiosmeryCastroVillaDeGeraldino. YoemilyRodríguezCarrasco. SolennyEspinalMarte. WilmerMarinoNúñezAcosta.

Secuencia 3

Modelo de Secuencia Didáctica de Matemática. SACM

Situación de aprendizaje:

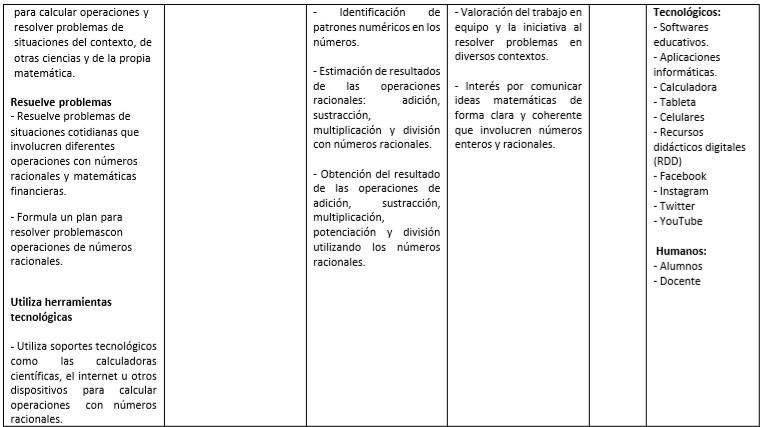
Los estudiantes de 5to del nivel secundario del Liceo Payita ubicado en el municipio de Cabrera muestran preocupación por la baja señal emitida por las compañías telefónicas, lo que dificulta el uso de los medios tecnológicos (celulares, computadoras y Tablets) los cuales son de gran utilidad para la presentación de clases y búsqueda de información para el desarrollo de estas; por tal situación expresaron a su maestro la situación de dificultad que han venido enfrentando. Por lo que acordamos que los estudiantes formaran grupos de 3 para investigar la ubicación de las antenas más cercanas y la altura aproximada. Luego calcularán el radio de la zona afectada y el nivel de la señal emitida por el foco de la antena. Además, enviaran cartas firmadas por personas de la comunidad que también están siendo afectadas a las compañías involucradas. Con esta acción se espera que lascompañías telefónicastrabajen para brindarun servicio de calidad a losresidentesdelacomunidad.

Colaboracióndelosmaestrantes: CandyMaríaRosarioDíaz. LucíaBautistaManzueta. AnyelinaSuárezdelaRosa. JulioAlbertoCastilloGuzmán.

Objetivo:

Utiliza las circunferencias para buscar posibles soluciones a problemáticas del entorno.

Metodología:

Ya formados los grupos de tres estudiantes, se dividirán el trabajo de la siguiente manera:

El primero, buscará utilizando la aplicación de Google map, las ubicaciones de las antenas de la zona y la distancia de estas entre sí.

El segundo, elaborará la carta que se entregará a las compañías. El tercero se encargará de la digitación de todas las informaciones obtenidas. En conjunto saldrán a investigar en las comunidades la potencia de la señal, luego

Calcularán el radio aproximado que abarca la antena en señal.

Reglas de coda grupo:

Se elegirá un estudiante al azar de coda grupo para hacer la presentación correspondiente del trabajo investigado.

Presentaran un manuscrito de la investigación, incluyendo algunas recomendaciones.

Se hará una autoevaluación y coevaluación por grupos.

Lista de cotejo para evaluar exposición y presentación

INDICADORES

Explican de forma clara los conceptos y procedimientos utilizados.

GRUPO1

GRUPO2

GRUPO3

GRUPO4

GRUPO5

Observación

Utilizan tecnología de forma adecuada para la investigación del trabajo propuesto.

Las recomendaciones presentadas se relacionan con las posibles soluciones a la problemática.

Centroeducativo:LiceoPayita

Asignatura:

Matemática

Tema:Lascónicas

Grado:5to

Estrategia:(ABP)aprendizajebasadoenproblemas

Secuenciadid Ctica

Docente:grupo4

•Modelayrepresenta: Representa situaciones desucotidianidadque involucren circunferencia.

Resuelve problemas:

Utiliza las circunferencias para buscar posibles soluciones a problemáticas del entorno.

Circunferencia.

Elementosdelacircunferencia.

Identificación y representación gráfica de la circunferencia.

Calculan el radio de lacircunferencia

Valoración del aporte de las matemáticas en las telecomuni-caciones.

-Sociales

-Español

Mapa de la comunidad.

Compas

Cuaderno de apuntes

Herramienta de Googlemap.

MOMENTO

Inicio

Desarrollo

Protocolodeinicio, Bienvenida,retroalimentacióny verificación de saberes previos.

Presentaalosalumnosel objetivodelaclase. Indagansobrelas conceptualizacionesbásicas propuestas.

Elmaestrodividelosgruposen 3participantesporgrupodeun totalde15estudiantesy orientasobreeltrabajoa realizar.

Actividad2Trabajo deCampo Actividad3 1semana

Los alumnos se reúnen en un lugar previamente acordado.

Protocolodeinicio. Bienvenida,presentacióndel instrumento para la evaluación.

Act.1y3 15minutos

ACT.2

Instrumento de evaluación.

Cierre

Metacognición

¿Quéaprendieron?

¿Cómoloaplicaranaltrabajo?

¿Paraquélessirve?

Los estudiantes ubican las antenas más cercanas utilizando la aplicación Google Map.

Realizan un recorrido por las zonas cercanas tomandoun radio de cobertura de señal.

Organizan el trabajo con los datos encontrados

Organizaneltrabajo conlosdatos encontrado.

Elección de los estudiantes a exponer utilizando una ruletadigital. Exposicióndeltrabajo.

Elaboración de la carta a entregar a la compañía involucradas con la orientacióndelmaestro.

Realizanlaautoevaluacióny coevaluación.

Compartensuexperiencia sobrequéleparecióla clase.

Expresan que aprendieron delaclase.

Secuencia 4

Modelo de Secuencia Didáctica de Matemática. SACM

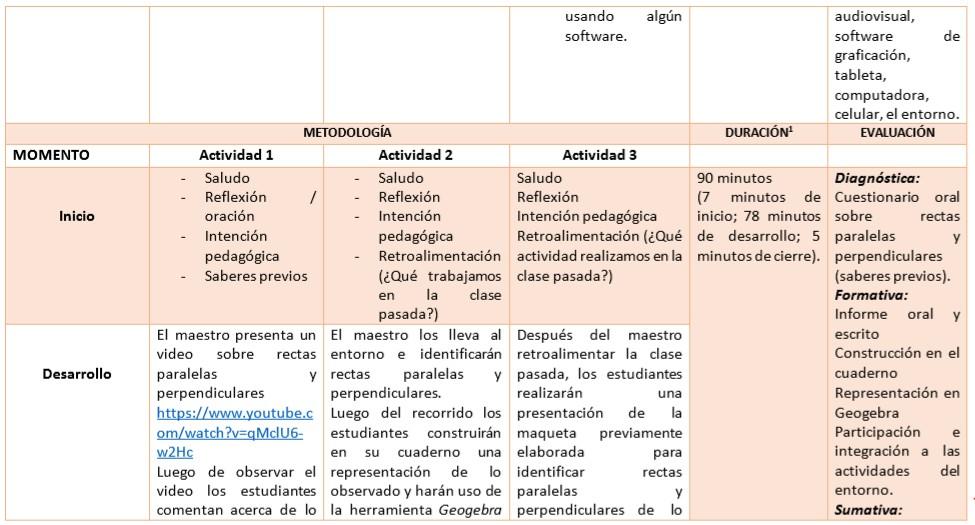
Situación de aprendizaje: Situación de aprendizaje: Los estudiantes del sector Los Castellanos se ausentan al liceo en tiempo de lluvia por el grave deterioro de sus calles, el síndico en busca de solucionar el problema les exige un plano a los moradores de esa comunidad para asfaltarle las calles. ¿Cómo podemos ayudar a los habitantes de esa comunidad? ¿Cuáles tipos de rectas debemos utilizar para elaborar el plano? Los estudiantes de 1ro A del Liceo Olinda Grullón García, con la intención de ayudar a los compañeros que residen en esa comunidad se interesan por las rectas paralelas y perpendiculares. En tal sentido, utilizan la estrategia basada en proyecto, realizan indagaciones en fuentes diversas para luego construir planos, con el objetivo de identificar las calles que son paralelas y perpendiculares de esa comunidad. En nuestro día de intercambio se comunican los hallazgos, auxiliándose de herramientas tecnológicas, elaborando un plano, en la que están en capacidad de distinguir el paralelismo y la perpendicularidad, valorando los aportes de sus compañeros y las aplicaciones en el diseño vial de nuestra comunidad.

Colaboracióndelosmaestrantes: YulennyAltagraciaSantos. MaribelNúñezNúñez.

YeraldyReinoso. CarlaMargaritaMerejo. CarolaGómez.

Fuentes Consultadas

Conant, J. B. (Ed.). (1945).General education in a free society: Report of the Harvard Committee. Harvard UniversityPress.

Godino, J. D., Fernández, T., & Gonzato, M. (2014). Ingeniería didáctica para desarrollar el sentidoalgebraicode maestros en formación.Avances de InvestigaciónenEducaciónMatemática, (5),25-48.

Brousseau, G. (1983). Les obstacles epistemologiques et les problémes en mathematiques. Recherches en Didactique des Mathématiques, Vol. 4, n. 2, pp. 165198.

Castillo, S. (2008). Propuesta pedagógica basada en el constructivismo para el uso óptimo de las TIC en la enseñanza y el aprendizaje de la matemática. Revista latinoamericana de investigación en matemáticaeducativa, 11(2),171-194.

Lovell, K. (1986). Desarrollo de los conceptos básicos matemáticos y científicos enlosniños.EdicionesMorata.

MINERD (2016). Diseño curricular, Primer ciclo (1ero, 2do y 3ero). Recuperado de : RtcE-disenocurricular-del-nivelsecundarioprimerciclopdf.pdf (ministeriodeeduca cion.gob.do)[Consulta22/04/22]

UNESCO (2000). Las aplicaciones en la enseñanza y el aprendizaje de la matemática en la escuela secundaria, recuperado de: https://unesdoc.unesco.org/ark:/48223/pf000 0091571_spa [Consulta11deabril,2022]

Vinacke, W. E. (1952). The psychology of thinking. London: McGrawHill

Dedicamos esta edición a la UTECO, marca patrimonial de la provincia Sánchez Ramírez, dedicatoria especial por su cuadragésimoaniversario.