DIAGRAMA DE ÁRBOL

TIPOS DE TÉCNICAS DE CONTEO

DIAGRAMA DE ÁRBOL

Un diagrama de árbol es una representación gráfica de los posibles resultados de un experimento que tiene varios pasos. Nos permite calcular la probabilidad de que ocurra un evento de una manera muy sencilla.

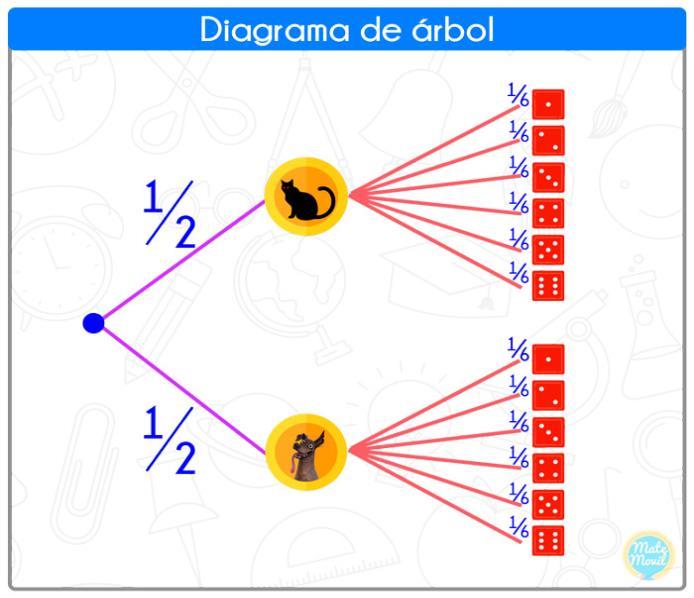
Aquí tenemos un clásico diagrama de árbol, en el cual graficamos los posibles resultados de un experimento que consiste en lanzar una moneda y un dado.

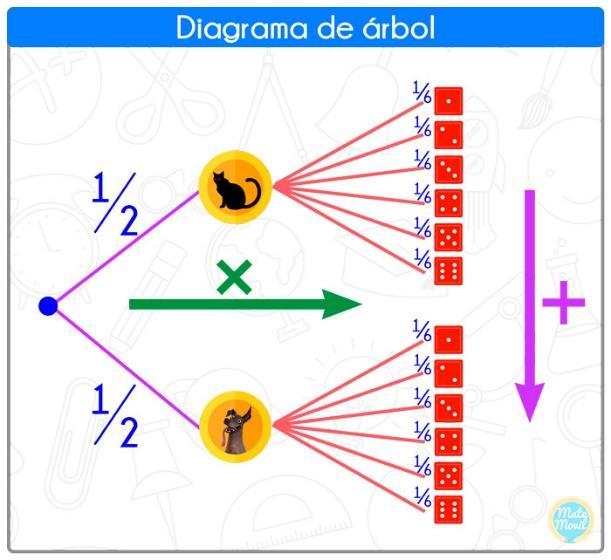
Para el cálculo de las probabilidades, usaremos un truco, si para calcular cierta probabilidad avanzamos hacia la derecha, entonces multiplicamos. Por otro lado, si para calcular cierta probabilidad avanzamos hacia abajo, entonces sumamos.

ELEMENTOS QUE CONFORMAN A UN DIAGRAMA DE ÁRBOL.

RAÍZ: Es el punto en el cuál se origina el árbol. RAMAS: Son las distintas bifurcaciones. NODOS O NUDOS: Son los puntos dónde surgen nuevas bifurcaciones. HOJAS: Son los puntos finales desde los cuales no surgen nuevas bifurcaciones. NIVEL: Es el número de ramas que separa a un nodo u hoja de la raíz. CAMINO: Es cualquier recorrido por las ramas del árbol, desde la raíz hasta algunas de sus hojas.

CARACTERÍSTICAS DE UN DIAGRAMA DE ÁRBOL

Un diagrama de árbol parte de lo general y va hacia lo específico, es decir, la base es el problema y las ramificaciones son los niveles subsecuentes o causas. Un diagrama de árbol es útil en la construcción de agrupación, bien sean combinaciones, variaciones o permutaciones. Se utiliza en diferentes ámbitos, bien sea científico, económico, social incluso puede ser útil en la toma de decisiones a nivel personal. Facilita la toma de decisiones, con el beneficio de que elimina las emociones en la ecuación.

EJEMPLO

Una moneda tiene en sus caras un gato y un perro. Se lanza 2 veces la moneda, calcular:

a) La Probabilidad de obtener 2 gatos. b) La Probabilidad de obtener solo un gato.

SOLUCIÓN

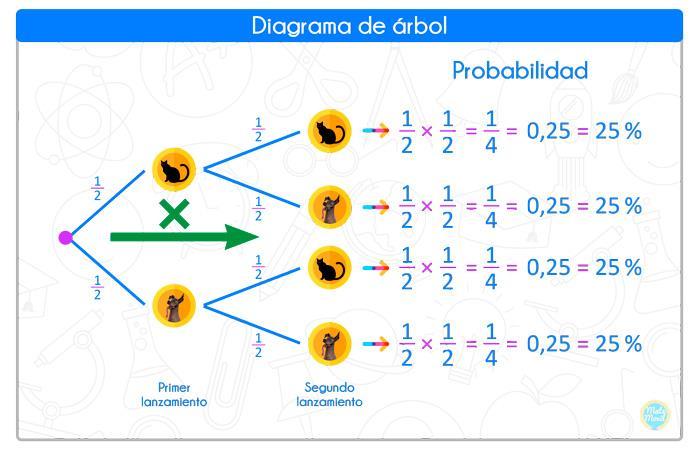
Vamos a elaborar el diagrama de árbol para este experimento. Calculamos la probabilidad para cada uno de los posibles casos, cuando avanzamos a la derecha, multiplicamos.

a) La probabilidad de obtener 2 gatos, la podemos observar en el gráfico.

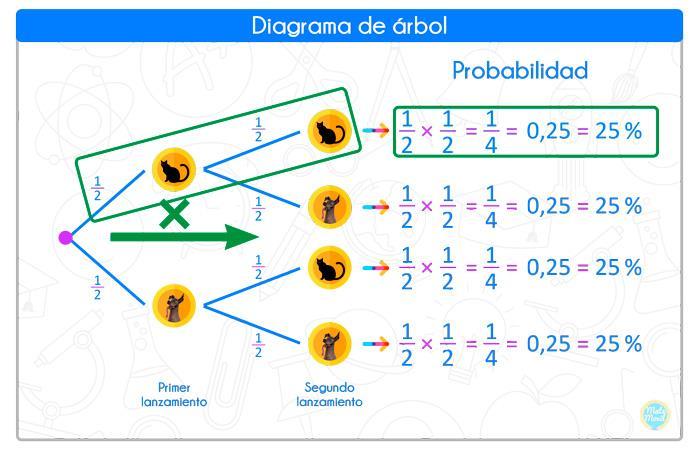
b) La probabilidad de obtener solo 1 gato, se calcula sumando 2 probabilidades, ya que hay 2 maneras de obtener solo 1 gato: • Obtener gato y perro • Obtener perro y gato

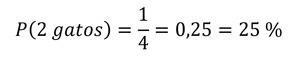
Recuerda que cuando avanzamos hacia abajo, entonces sumamos:

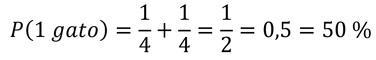
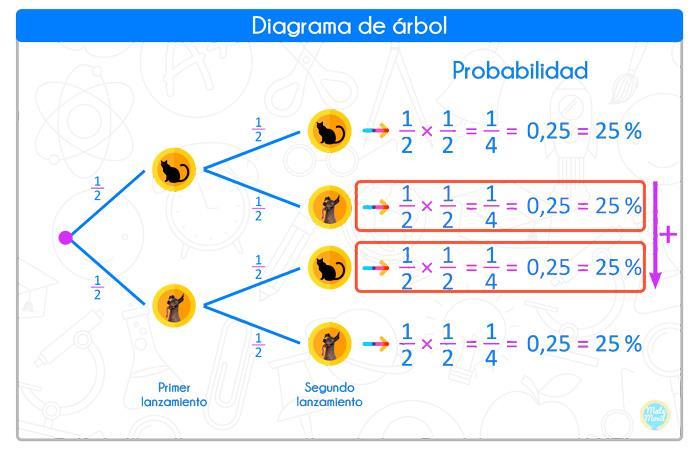
Por lo tanto, la probabilidad de obtener 1 solo gato será: