Bole shape of E. deglupta

Bole shape of E. deglupta

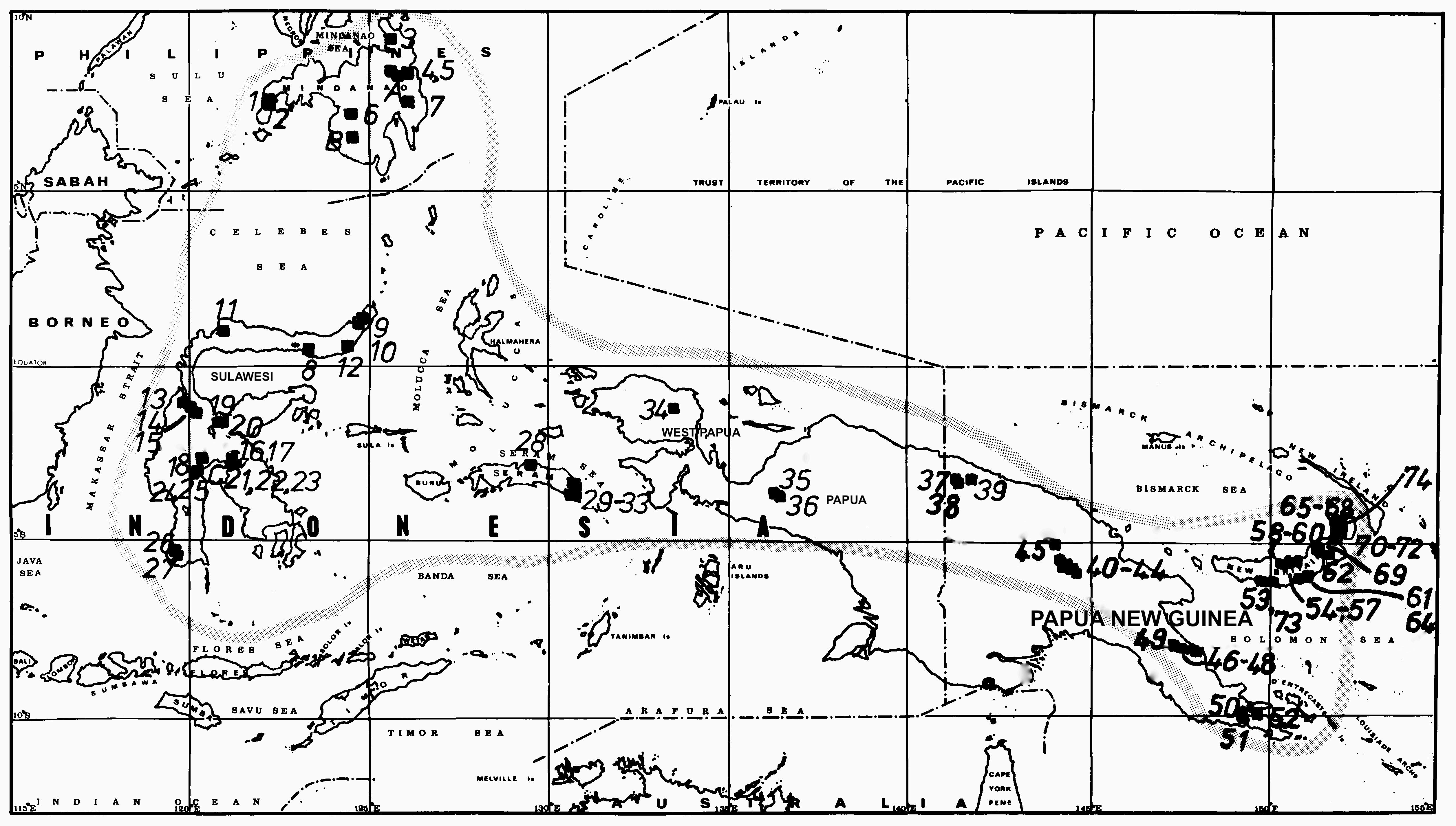
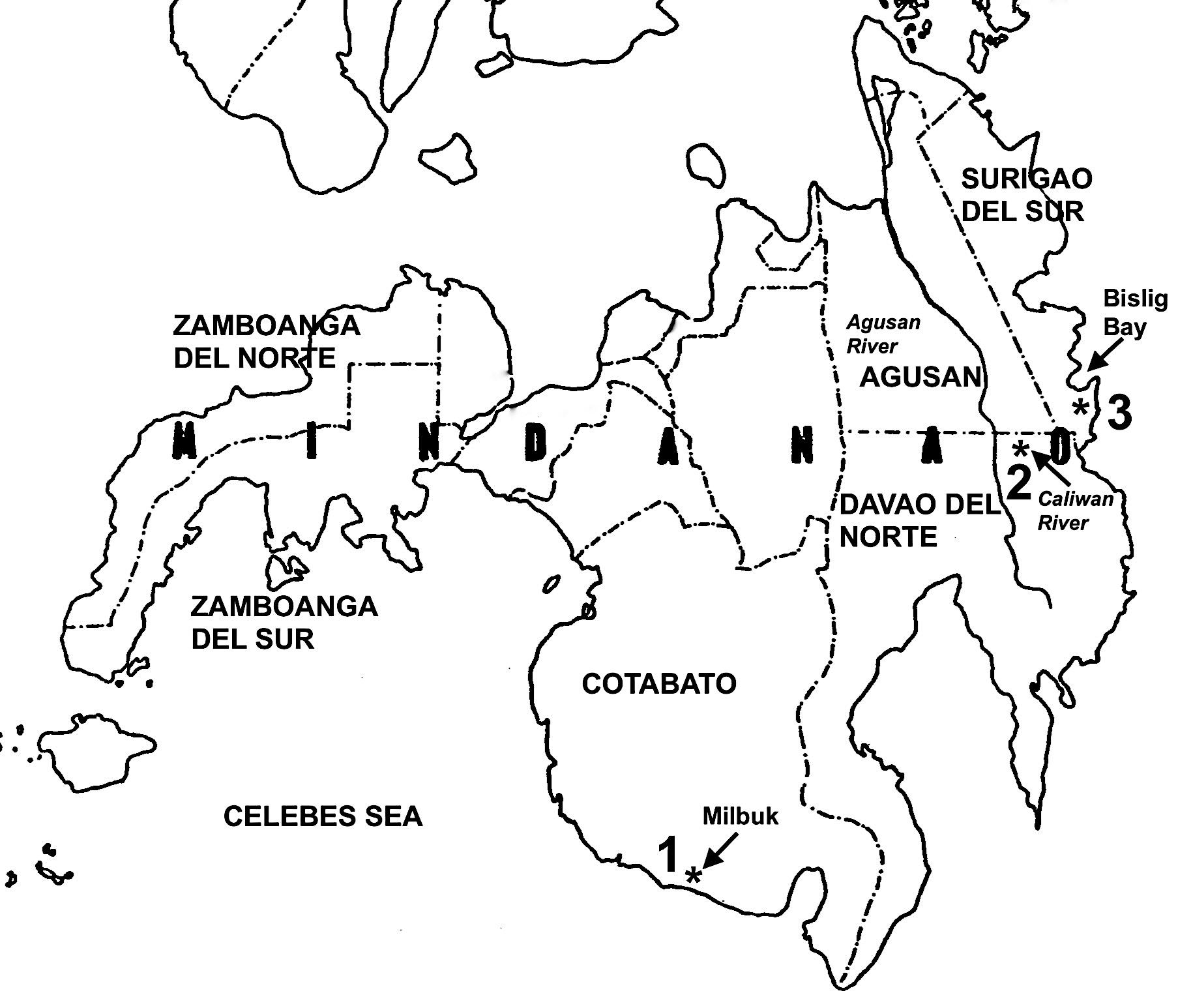
After a database comprising detailed sectional measurements from some 800 trees had been compiled, it was possible to divide the data to study separately the effects of any change in the bole shape on the computation of stand volume tables. Genetic (provenance), environmental (site quality, silvicultural and management practices) and developmental (age and size) effects could be studied on the partitioned data.

If one could determine the shape and rate of taper of a stem, or that part of it of interest, one could derive its volume readily by multiplying the product of the height and sectional area of the base by some factor which would reduce the volume of the cylinder, implied by the product of height and sectional area at the base, to that of the appropriate solid to which the stem is approximated.

The volume (V) of an appropriate cylinder is given by V = π(D/2)

2

H where D = diameter at the base of the cylinder and H = height of the cylinder

or V = (π/4)D

2H ………. (1)

A similar equation is, having the form V = fD

2H ………..….. (2) Where D and H are as given above.

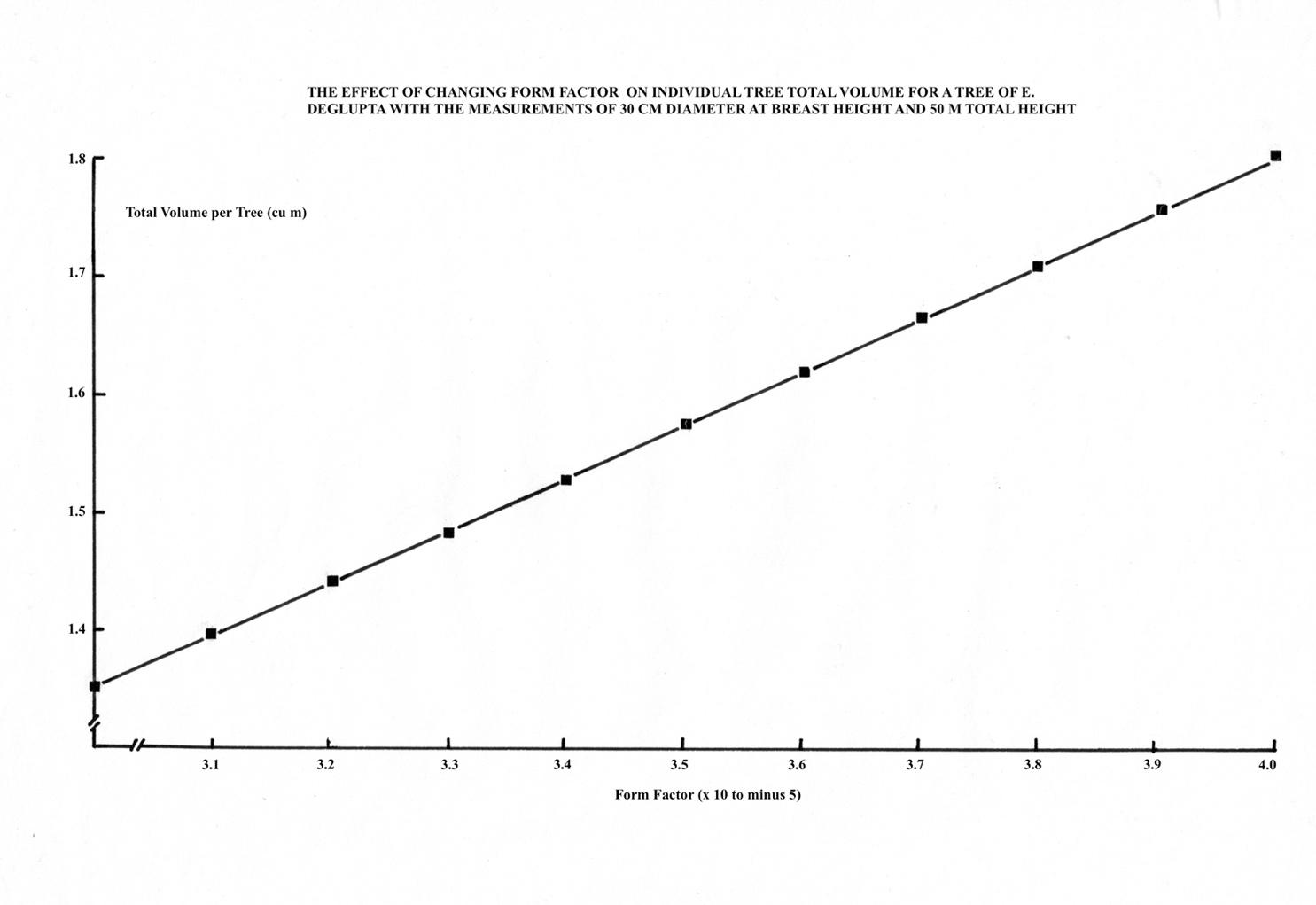
When the factor f in equation 2 incorporates π/4 plus a term for the reduction of the cylinder to the prescribed bole volume it is called a “form factor”. The concept of form factors is a very old one. Some early tree volume tables included an expression of form factor that was assumed appropriate for a particular species.

The form factor was used as a guide to the requirements for volume tables for E. deglupta in PNG. In this sense it was an abstract variable. The form factor was not measured directly on trees but was derived as a regression coefficient relating both diameter at breast height (D) and total height (H) to total volume (V).

Equations showing volume as a function of diameter squared and height were derived by selecting appropriate sums of squares from cross-product matrices and solving the least-square equations.