2 3 3 y 5 6

Cardioide

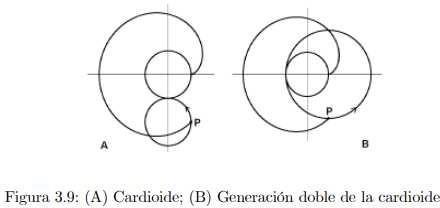
El cardioide es un caso especial del caracol de Pascal estudiado por Etienne Pascal (1588-1640), padre de Blaise Pascal (1623-1662). También es un caso especial de las curvas cicloidales estudiadas por Roemer (1674) en una investigación de la mejor forma de los engranes([3], [7] pp. 34-43, [14] pp. 4-7, [6] pp. 118-120). El nombre de cardioide (del griego cardi, corazón, y eidos, forma) fue usado primero por Johann Castillon (1704-1791) en The Philosophical Transactions of the Royal Society de 1741. Su longitud fue encontrada por Philippe de La Hire (1640-1718) en 1708. El cardioide es la curva que dibuja un punto fijo P en un círculo que rueda sobre el exterior de un círculo fijo de igual tamaño (figura 3.9 A).

(García, 2004)

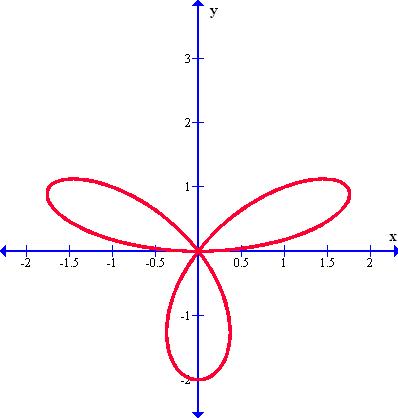
Rosa polar de tres pétalos

Es una curva expresada en coordenadas polares, semejante a una flor de pétalos; fue estudiada por el matemático Luigi Guido Grandi.

(Rojas, 2014)

5

Bibliografía

Berrío, J. G. (2020). Cálculo Vectorial. En J. G. Berrío, Cálculo Vectorial (págs. 21-27). Medellín: Fondo Editorial Pascual Bravo.

Cañestro, I. L. (13 de Julio de 2016). GeoGebra. Obtenido de https://www.geogebra.org/m/UgwgAVFG

García, M. d. (2004). Red Matemática Unam. Obtenido de http://www.redmat.unam.mx/foro/volumenes/vol024/MaterialDeApoyoEnMaple9.pdf

López, J. F. (12 de junio de 2016). GeoGebra. Obtenido de https://www.geogebra.org/m/zYZ59pyY

Rojas, V. (18 de noviembre de 2014). Prezi. Obtenido de https://prezi.com/2-rspedbgx8b/rosapolar/

6