Introducción

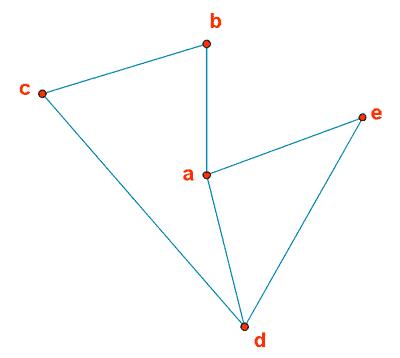
Un grafo es una composición de un conjunto de objetos como nodos que se relacionan con otros nodos a través de un de conexiones conocidas como aristas, estos denominados grafos permiten estudiar las relaciones que existen entre que interactúan con otras. Un grafo está definido por un conjunto de puntos, llamados nodos y un conjunto de pares de vértices denominados aristas

Podemos considerar un grafo con vértices {a, b, c, d, e} y {ab, ad, ae, bc, cd, de} conocidos conjunto

unidades

vértices o o arcos

aristas

Como podemos ver en el ejemplo, los vértices se representan como puntos y cada arista entre dos vértices como una línea que une dichos vértices.

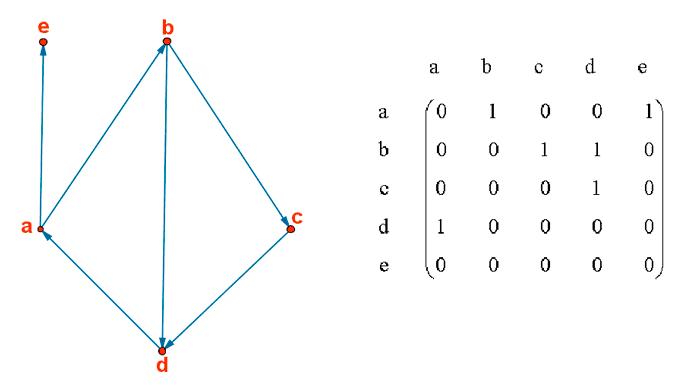
Grafo Dirigido

Un grafo dirigido o dígrafo, es aquel que tiene sus aristas o arcos es decir, sus aristas vienen dadas por pares ordenados.

Podemos considerar un grafo dirigido con vértices { a, b, c, d, e } y { ab, ae, bc, bd, cd, da } orientados,

aristas

En este caso también los vértices se representan como puntos. Las aristas se representan como flechas que parten de un vértice (el primero de cada par) y llegan a otro (el segundo de cada par).

Matriz de adyacencia o asociada

Todo grafo, dirigido o no, puede representarse mediante una matriz cuadrada que tiene como orden el número de vértices del grafo. Esa matriz recibe el nombre de matriz asociada o matriz de adyacencia. Se trata de una matriz cuadrada de n filas x m columnas (siendo n el número de vértices del grafo).

Para construir la matriz de adyacencia, cada elemento ai j vértices i y j. En caso contrario el elemento ai j vale 0. vale 1 cuando haya una arista que una los

La matriz de adyacencia, por tanto, estará formada por ceros y unos.

Para construir las matrices de adyacencia, ordenamos los vértices, por ejemplo

Si tenemos una arista que une los vértices a y b, en la matriz de adyacencia tenemos que poner un 1 tanto en la posición ab como en la posición ba

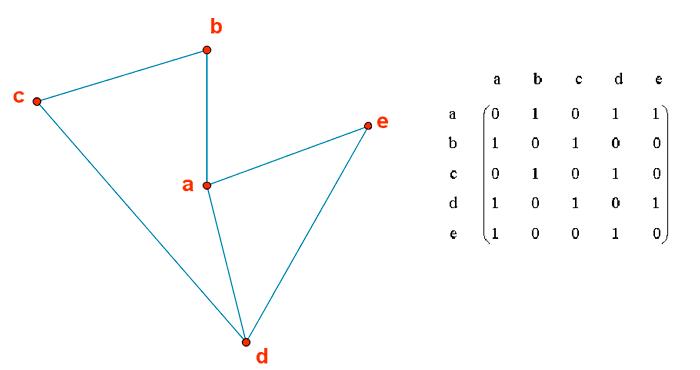
La matriz de adyacencia de los grafos no dirigidos siempre es simétrica.

Para construir las matrices de adyacencia, ordenamos los vértices, por ejemplo:

Si tenemos una flecha que parte del vértice a y llega al vértice e, ponemos un 1 en la posición ae de la matriz de adyacencia. En caso de no tener esa flecha ponemos un 0, una matriz de adyacencia de un grafo no dirigido no tiene por qué ser simétrica.