ÁRBOLES GENERALES

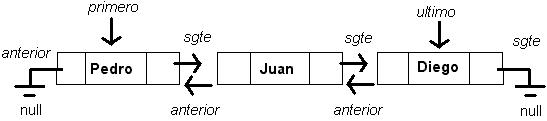
Para invertir el orden de la lista, es decir, que el último elemento de la lista ahora sea el primero, que el penúltimo elemento de la lista ahora sea el segundo, etc..., modificando sólo las referencias y no el contenido de los nodos, es necesario realizar una sola pasada por la lista, y en cada nodo visitado se modifica la referencia siguiente para que apunte al nodo anterior. Es necesario mantener referencias auxiliares para acordarse en donde se encuentra el nodo anterior y el resto de la lista que aún no ha sido modificada:

void invertir(NodoLista lista) {

NodoLista siguiente=lista; NodoLista anterior=null; while(lista!=null) { siguiente=lista.siguiente; lista.siguiente=anterior; anterior=lista; lista=siguiente; } }

La implementación vista de los nodos también se conoce como lista de enlace simple, dado que sólo contiene una referencia al nodo siguiente y por lo tanto sólo puede recorrerse en un solo sentido. En una lista de doble enlace se agrega una segunda referencia al nodo previo, lo que permite recorrer la lista en ambos sentidos, y en general se implementa con una referencia al primer elemento y otra referencia al último elemento.

Árboles

Un árbol se define como una colección de nodos organizados en forma recursiva. Cuando hay 0 nodos se dice que el árbol esta vacío, en caso contrario el árbol consiste en un nodo denominado raíz, el cual tiene 0 o más referencias a otros árboles, conocidos como subárboles. Las raíces de los subárboles se denominan hijos de la raíz, y consecuentemente la raíz se denomina padre de las raíces de sus subárboles. Una visión gráfica de esta definición recursiva se muestra en la siguiente figura:

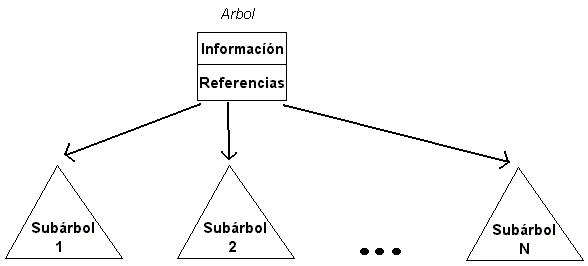
Los nodos que no poseen hijos se denominan hojas. Dos nodos que tienen el padre en común se denominan hermanos.

Un camino entre un nodo n1 y un nodo nk está definido como la secuencia de nodos n1, n2, ..., nk tal que ni es padre de ni+1, 1 <= i < k. El largo del camino es el número de referencias que componen el camino, que para el ejemplo son k-1. Existe un camino desde cada nodo del árbol a sí mismo y es de largo 0. Nótese que en un árbol existe un único camino desde la raíz hasta cualquier otro nodo del árbol. A partir del concepto de camino se definen los conceptos de ancestro y descendiente: un nodo n es ancestro de un nodo m si existe un camino desde n a m; un nodo n es descendiente de un nodo m si existe un camino desde m a n.

Se define la profundidad del nodo nk como el largo del camino entre la raíz del arbol y el nodo nk. Esto implica que la profundidad de la raíz es siempre 0. La altura de un nodo nk es el máximo largo de camino desde nk hasta alguna hoja. Esto implica que la altura de toda hoja es 0. La altura de un árbol es igual a la altura de la raíz, y tiene el mismo valor que la profundidad de la hoja más profunda. La altura de un árbol vacío se define como -1.

Árboles binarios

Un árbol binario es un árbol en donde cada nodo posee 2 referencias a subárboles (ni más, ni menos). En general, dichas referencias se denominan izquierda y derecha, y consecuentemente se define el subárbol izquierdo y subárbol derecho del arbol.

En este caso, la implementacion del nodo de un árbol binario es como sigue:

class NodoArbolBinario {

Object elemento;

NodoArbolBinario izq;

NodoArbolBinario der; }

Los nodos en sí que conforman un árbol binario se denominan nodos internos, y todas las referencias que son null se denominan nodos externos.

Árboles generales

En un árbol general cada nodo puede poseer un número indeterminado de hijos. La implementación de los nodos en este caso se realiza de la siguiente manera: como no se sabe de antemano cuantos hijos tiene un nodo en particular se utilizan dos referencias, una a su primer hijo y otra a su hermano más cercano. La raíz del árbol necesariamente tiene la referencia a su hermano como null.

class NodoArbolGeneral {

Object elemento;

NodoArbolGeneral hijo;

NodoArbolGeneral hermano; }

Nótese que todo árbol general puede representarse como un árbol binario, con la salvedad que el hijo derecho de la raíz es siempre null. Si se permite que la raíz del árbol tenga hermanos, lo que se conoce como bosque, entonces se tiene que el conjunto de los bosques generales es isomorfo al conjunto de los árboles binarios. En efecto, las propiedades vistas en los árboles binarios se siguen cumpliendo en los árboles generales.

NOTA DE CIERRE:

Al ser finalizado esta corta revista, en el contenido que encontraras explicare con detalles los conceptos básicos de árbol binario, Altura, Nivel, grado. Encontraras también tipos de Árboles (Binarios y HEAP), TEOREMAS I, II para arboles binarios y Algoritmos Insertar, Heapify y Estructura de Datos Elementales como sus características que lo conforman.