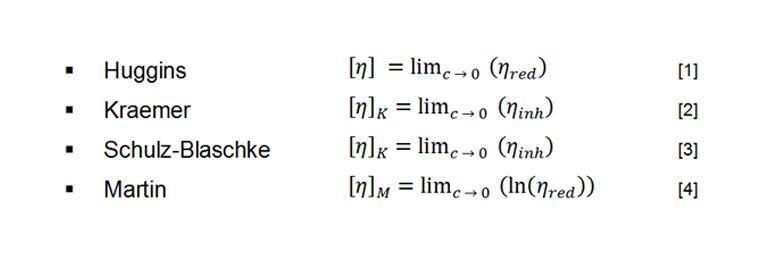
1 minute read
Intrinsic viscosity calculation
The polymer solution’s intrinsic viscosity is the most important characteristic in describing its viscous behaviour. This is because intrinsic viscosity determines a polymer's genuine viscosity-enhancing characteristics regardless of its concentration in solution. It's a term that's used in a variety of sectors to define a product's storage stability and quality. The plastics sector is one example of where intrinsic viscosity is used. In the pharmaceutical sector, however, inherent viscosity is an important testing criterion.
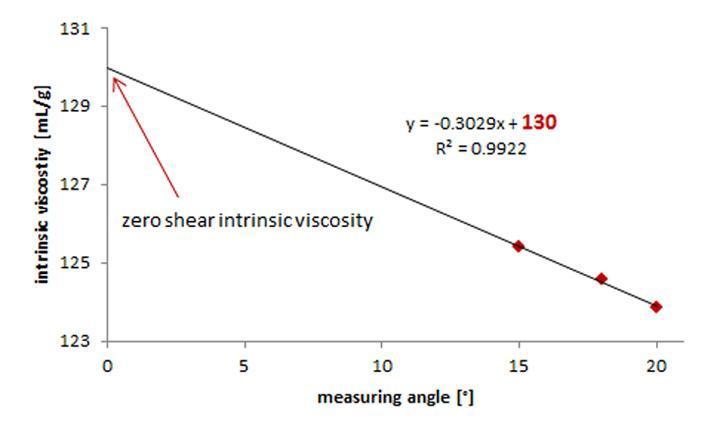
Viscosity measurements for estimating intrinsic viscosity should always be performed at a shear rate close to zero. The viscosity becomes shear-dependent at high shear rates as the polymer solutions begin to exhibit non-Newtonian behaviour, which is not the case at low shear rates (zero-shear viscosity). At various shear rates, polymer solutions can be measured to estimate the intrinsic viscosity at a shear rate approaching zero. The resulting viscosity values are then extrapolated. The intersection determines the zero-shear intrinsic viscosity with the y-axis (Figure 6).
Advertisement
Intrinsic viscosity and molar mass
The Mark-Houwink equation can be used to connect the intrinsic viscosity of a polymer in a given solvent with its molar mass. The intrinsic viscosity formula as per the Mark-Houwink equation is -
[η]=KMa[η] =KMa
[η][η] = intrinsic viscosity
K, a = Mark-Houwink constants
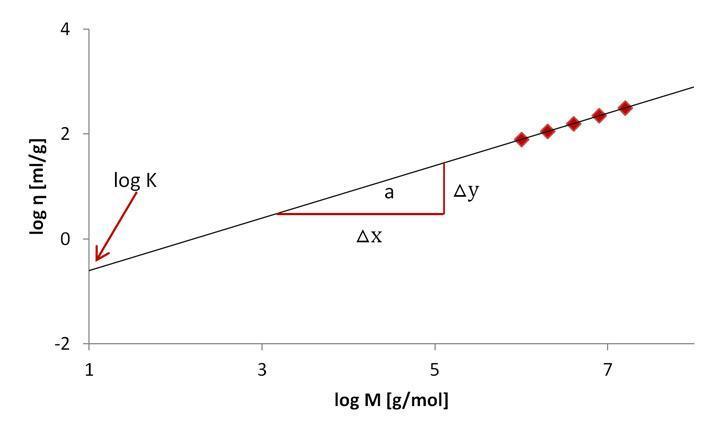
K and a are temperature constants for a particular polymer-solvent combination. If they aren't known from the literature, they must be calculated empirically by charting the logarithm of intrinsic viscosity as a function of logarithmic molar mass (Figure 7). The constant log K is obtained by intersecting the y-axis of a linear fit of data, and the slope of the curve yields the constant “a” (△x/△y).
Figure 7: K and “a” Determination from a linear plot of the intrinsic viscosity against the molar mass
Examples of K and “a” for some polymer-solvent combinations are given in Table 1.