6

А B C

D E

12. Figure out how the order of figures in squares changes. Fill in the blanks in the last square.

13. There are nine dots in this picture. Connect them with eight lines so there are exactly three dots on each line.

14. Every circle should be filled in with one of the colours of the sticks. The arrows point to circles that should be filled in with the same colours as the shorter sticks.

15. Which figure should be the next in line? Circle the correct answer.

а)

d) b)

e) c)

f)

16. Take a look at this row of numbers. In which order have they been assorted?

2, 1, 0, 8, 5, 7, 3, 4, 6

4

Quips

1. How can you get to number 50 by removing 10 out of 40?

2. Two men are standing in the street. One always tells the truth and the other one always tells lies. Ask them a question to which they will both give the same answer.

3. The glass is full of water. How will you get exactly half the amount of water in the glass by only pouring it out? Draw it.

4. Dan and Pete got into an argument about whether this glass is less or more than half full. How can you help them out and give the correct answer to this question without measuring or pouring over the water? Draw it.

5. Two equal, 10-centimeter-tall glasses are shown in the picture. They contain equal amounts of water. How tall is the amount of water in the first glass? cm

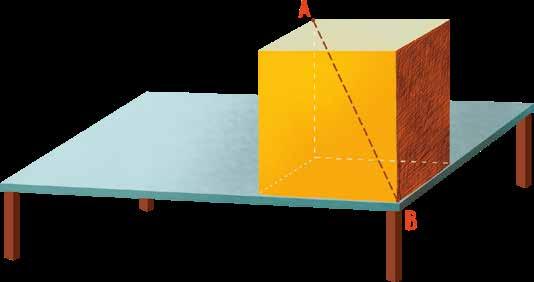
6. There is a cube on this table. How will you measure the length of the AB diagonal with a ruler? Explain your method.

7. The carpenter had four planks. Every plank was several meters long. After cutting all the planks into one-metre pieces, the carpenter had 25 pieces of wood. How many cuts did he have to make with his saw? The planks were cut one at a time.

8. Two fathers, two sons, a grandfather and a grandson – how many people are there in total?

9. Two sons and two fathers split three apples among each other. Each of them got an apple. How is that possible? Explain.

10. Three mothers and three daughters went to the market. There were four of them in total. How is that possible?

Кhis book was intended for fourth-graders who are able to learn faster than their peers. It contains many interesting activities, rarely encountered in your regular maths classes. Dierent problems serve dierent aims: some to promote abstract thinking, others to develop spatial awareness, and some to teach you how to nd your way out of puzzling situations. Many are, simply put, interesting problems, the kind that will make us love maths and drive us to keep practicing it. They are all suitable for discovering and developing mathematical giftedness and promoting creativity. T

9

788652 906864