Lição 1: GANGORRA

A maioria dos playgrounds infantis contém uma gangorra. Você sabia que este jogo divertido e simples é um exemplo perfeito de como uma alavanca funciona? Você pode realizar o próximo experimento e descobrir como uma criança leve pode levantar uma criança mais pesada na gangorra usando o princípio das alavancas!

Materiais Necessários:

» Engino STEM & Robotics Mini.

Vamos aprender:

» Como a força gera momento?

» Como podemos calcular o Momento?

Passo a passo:

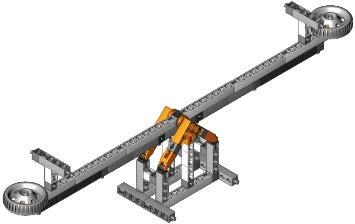
Passo 1: Construa o modelo de gangorra.

Passo 2: Remova uma roda de um lado da gangorra e observe o que acontece.

Passo 3: Use o dedo, apenas de um lado, para restaurar o equilíbrio novamente. Em seguida, mova o dedo lentamente em direção ao meio, tentando diferentes distâncias do centro. Você pode sentir a diferença de esforço?

Passo 4: Deixando apenas uma roda do lado esquerdo da gangorra, tire as rodas restantes da embalagem e tente descobrir quantas rodas você precisa colocar do lado direito para que a gangorra fique equilibrada. À direita, você pode ver 4 casos possíveis para experimentar (exercício 1). Equilibre a gangorra em cada uma empilhando sobre rodas conectadas por roldanas nas posições indicadas. As distâncias do centro para colocação das rodas são: 24, 12, 8 e 6 unidades.

Passo 5: Complete os exercícios 2, 3 e 4.

Exercícios:

Exercício 1: Escreva o número de rodas necessárias para equilibrar a gangorra em cada caso.

1º caso:

Rodas necessárias para equilibrar:

2º caso:

24ª unidades

Rodas necessárias para equilibrar:

12ª unidades

3º caso:

Rodas necessárias para equilibrar:

4º caso:

8ª unidades

Rodas necessárias para equilibrar:

6ª unidades

Exercício 2: Vamos fazer umas contas simples: Multiplique o números de rodas pela distância (quantas unidades) do centro, para cada lado e para cada caso. Que resultados você obteve?

1º caso: Rodas necessárias para equilibrar x 24 unidades = 1 x 24 = 24

2º caso: Rodas necessárias para equilibrar x 12 unidades =

3º caso: Rodas necessárias para equilibrar x 8 unidades =

4º caso: Rodas necessárias para equilibrar x 6 unidades =

Exercício 3: Que conclusão pode ser extraída de suas observações acima, sobre o lado esquerdo e o lado direito?

Exercício 4: Pensando nisso, como uma criança leve consegue equilibrar a gangorra ao brincar com uma criança mais pesada?