Tensor Methods: Revolutionizing Data Science and Machine Learning via Higher-Order Arrays (Campus Feature

Tensor Methods: Revolutionizing Data Science and Machine Learning via Higher-Order Arrays

By Dimitris G. Chachlakis

Modern engineering systems collect large volumes of data measurements across diverse sensing modalities. These measurements can naturally be arranged in higher-order arrays of scalars which are commonly referred to as multi-way arrays or tensors. A 1-way tensor is a standard vector, a 2-way tensor is a standard matrix, and a 3-way array is a data cube of scalars. For higher-order tensors, visualization on paper is a challenging task and is left to the imagination. Tensors find important applications across fields of science and engineering such as data analysis, pattern recognition, computer vison, machine learning, wireless communications, and biomedical signal processing, among others. Data that can be naturally arranged in tensors are, for instance, Amazon reviews in the form of a data cube with modes user-product-word, crime activity of a city in the form of a 4-way array with modes day-hour-community-crime type, Uber pickups across a city in the form of a 4-way tensor with modes date-hour-latitude-longitude, and ratings of Netflix movies in the form of a data cube with modes rating-customer/usermovie title, to name a few.

Fig. 1: Visual illustration of 1-way, 2-way, and 3-way tensors.

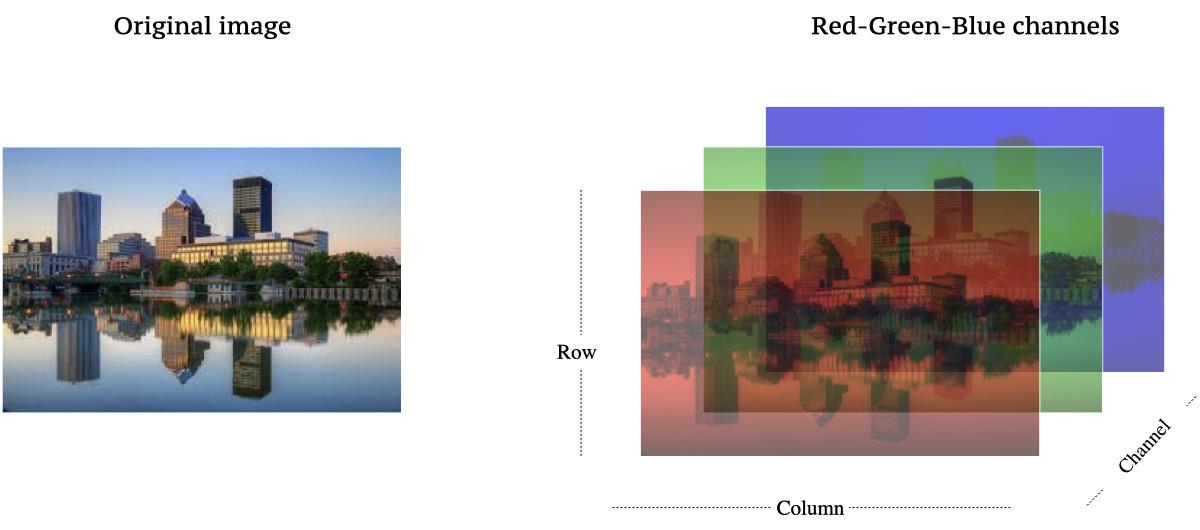
Fig. 2: An image of downtown Rochester stored as a data cube. Original image credit: Patrick Ashley.

Storing, processing, and analyzing tensor data in their natural form enables the discovery of patterns and underlying data structures that would have otherwise stayed hidden. Tensor methods comprise an appealing set of mathematical tools for processing tensor data and are widely considered an extension of the standard matrix methods (e.g., Principal-Component Analysis, Singular Value Decomposition, Independent Component Analysis, etc.) that have been widely used over the past decades. At their core, tensor methods rely on theory of tensor algebra which is also known as multi-linear algebra. Tensor algebra is an extension of the standard matrix algebra (linear algebra). For context, linear algebra operates on matrices and vectors –e.g., operations in the form of matrix-to-matrix product or vector-to-matrix product. Tensor algebra generalizes standard linear algebra and defines operations on tensors –e.g., operations in the form of tensor-to-matrix product and tensor-to-tensor product, to name a few. On one hand, tensor algebra has many similarities with matrix algebra, but on the other hand, it exhibits some notable differences. Despite this fact, tensors and tensor algebra exhibit many meritorious properties and have found applications in a diverse array of applications. For instance, tensor operations are highly parallelizable enabling faster training and inference, they are flexible in the sense that they allow training and inference to be decoupled, and tensors naturally model higher-order relationships in the processed data, to name a few.

At a high level, tensor analysis strives to breaking the processed tensor data down to a sum of (smaller) meaningful parts. In the literature, this process is commonly referred to as tensor decomposition or tensor factorization. After the processed tensor is broken down to a sum of smaller parts, these parts can, in turn, be used for data visualization, model identification, denoising, classification, clustering, filling missing entries, compression and interpretability (e.g., of Deep Neural Networks), or other data analysis/machine learning task per the application’s (of interest) needs. Breaking the processed tensor data down to a sum of smaller parts is often modeled as an optimization problem wherein the objective is to optimize a function of the processed tensor and the unknown smaller parts with respect to some metric (criterion). After a decomposition has been modeled as an optimization problem, then an efficient algorithm is developed which can actually solve the optimization problem (exactly or approximately) and return the smaller parts. In turn, the “learned” smaller parts are used for the data analysis/machine learning task of interest as described above. Popular and widely used tensor decomposition models are the Tucker decomposition, Canonical Polyadic decomposition (CPD), and Tensor-Train decomposition, to name a few.

Fig. 3: Visual illustration of Tucker and Canonical Polyadic Decomposition for 3-way tensors.

Over the past decade, tensors methods have attracted tremendous research interest. As a result, there exists an abundance of tensor decomposition models, formulated based on different criterions, each of which with its own unique properties, strengths, and weaknesses. Accordingly, there exist multiple algorithmic solvers for breaking the processed tensor down to a sum of smaller parts enabling different performance-cost trade-offs and exhibiting different properties. For instance, one criterion may promote sparsity in the smaller parts, another criterion may exhibit robustness against sporadic outliers –i.e., heavily erroneous entries that appear in the processed tensor with low frequency, and another criterion may promote non-negativity. Notably, in the Machine Learning Optimization and Signal Processing (MILOS) Lab of RIT, directed by Prof. P. Markopoulos, our team works on the development of groundbreaking tensor methods for machine learning and data analysis, currently funded by the National Science Foundation, the Air Force Office of Scientific Research, and the National Geospatial-Intelligence Agency.

Fig. 4: Tensor methods lie at the intersection of modern data science, computer science, and machine learning/AI.

To date, tensor methods comprise a set of mathematical tools for storing, processing, and analyzing multi-modal data. Tensor methods lie at the intersection of computer science, data science, and machine learning/AI. Moreover, tensor methods have successfully been applied to diverse modern applications, however, tensor methods for machine learning and data science is a highly active research area and many merits of tensor processing are yet to be revealed by the scientific community. q

Author Bio: Dimitris. G. Chachlakis is a PhD Candidate with the Kate Gleason College of Engineering and a Research Assistant at the MILOS Lab. His research interests include statistical signal processing, machine learning, and data analysis, with a focus on robustness, tensor methods, and sparse array processing.