7 minute read
EULER SYSTEMS
Euler systems can be thought of as a collection of points or cohomology classes attached to an algebraic object, which satisfy some very precise compatibility relations. These systems are very hard to construct, but they have very powerful arithmetic applications, such as proving new cases of the Bloch-Kato conjecture as well as the Birch and Swinnerton-Dyer conjecture, as Professor Sarah Zerbes explains.
64 A collection of cohomology classes for a given algebraic object, the first example of an Euler system was constructed by the Russian mathematician Victor Kolyvagin. While these systems are named after the highly influential 18th century Swiss mathematician Leonhard Euler, they were only introduced relatively recently. “In the case of Kolyvagin’s work, an Euler system is a collection of points on modular elliptic curves,” explains Sarah Zerbes, Professor of Maths at University College London. Euler systems, once constructed, have very powerful applications to some of the central open conjectures in number theory. “Kolyvagin recognised that his Euler system could be used to prove new cases of the conjecture of Birch and Swinnerton-Dyer.” says Professor Zerbes.
These Euler systems are extremely difficult to construct however, and until relatively recently only four were known to exist. Professor Zerbes and her collaborators have since developed a new approach to constructing them. “It started with the Euler system of Beilinson-Flach elements. We found that the method with which we had constructed this system could be applied in great generality, so now we have greatly increased the number of known Euler systems,” she says. As the Principal Investigator of an ERC-funded research project based at UCL, Professor Zerbes is now investigating the arithmetic applications of these systems. “Euler systems are fundamentally geometric constructions. The underlying objects are socalled Shimura varieties, which are algebraic varieties arising in the representation theory of matrix groups,” she outlines.
Euler systems The construction of these systems is based on the use of geometric methods, as well as methods from representation theory and number theory. While researchers were able to construct new examples of Euler systems, it was not initially possible to use them for arithmetic applications. “We constructed these geometric objects, but it was difficult to establish that they were non-zero. We were in the frustrating situation where we

Graphs of the L-functions attached to elliptic curves of ranks 0,1 and 2, respectively.
had many new Euler systems, but we didn’t know that they were non-zero,” explains Professor Zerbes. New results have since emerged which formed the missing piece of the puzzle, enabling Professor Zerbes and her colleagues to give a criterion for the nonvanishing of the Euler systems, and to study the various arithmetical applications. “The way to prove the non-vanishing of an Euler system is by relating it to the value of an L-function. Such a relation is called an explicit reciprocity law.”
This opens up many new exciting avenues of research, with Professor Zerbes particularly interested in proving new cases of the BlochKato conjecture, which predicts that certain values of the L-function govern the size of a Selmer group, attached to the underlying Shimura variety. An Euler system is extremely useful in terms of proving new cases of the conjecture. “Two things can be attached to an Euler system. Firstly, we can attach to it a Selmer group, which is a certain cohomology group. We can also attach to it an L-function, which is a complex analytic function,” outlines Professor Zerbes. This provides the basis for researchers to investigate possible new cases of the Bloch-Kato conjecture. “If the L-function at a certain point does not vanish, then this Selmer group should be zero. This is the case that an Euler system will prove,” continues Professor Zerbes. “We are also interested in the Birch and SwinnertonDyer conjecture. One can think of the BlochKato conjecture as a vast generalisation of the Birch and Swinnerton-Dyer conjecture.”





The Birch and Swinnerton-Dyer conjecture is one of the Clay Millennium Prize Problems; it is concerned with the rational solutions on a so-called elliptic curve, which is an equation in two variables of the form y 2 = f (x) where f is a cubic polynomial with distinct roots. The set of rational points on the curve (together with the point at ∞) forms an abelian group, which is known to be finitely generated; the rank of this group measures the “density” of rational points on the curve – in particular, the rank is 0 if - and only if - the set of rational points is finite.
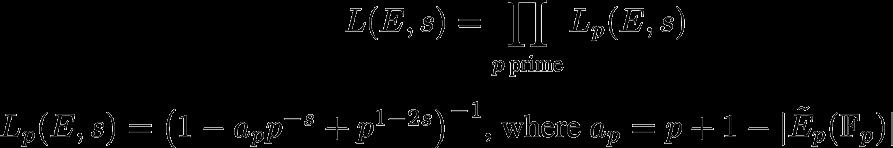
is currently focused on a case where the underlying Shimura variety is a Siegel modular variety. “This is a certain Shimura variety which is attached to the symplectic group GSp (4). We constructed the Euler system, and we are currently proving the explicit reciprocity law,” explains Professor Zerbes. “We are in the process of writing that up, and hopefully it will be available in the next few months. That would have applications to the Birch and SwinnertonDyer conjecture for abelian surfaces.”
We constructed these geometric objects, but it was difficult to establish that they were non-zero. We were in a position where we had lots of new Euler systems, but we didn’t know that any of them were non-trivial.
The Birch-Swinnerton-Dyer conjecture, which was formulated in the 1960s based on extensive numerical computations, relates this quantity to another, very different aspect of the elliptic curve: its L-function. This is a complex-analytic function of a variable s, defined as an infinite product over primes in which the factor for a prime p is determined by counting points on the reduction of the curve modulo p. The conjecture predicts that although this L-function is built up from local data, it encodes global information: the rank of the elliptic curve should be equal to the order of vanishing of the L-function at the point s = 1 (the “analytic rank”).
One specific goal for Professor Zerbes and her colleagues is to prove new cases of a generalisation of the Birch and SwinnertonDyer conjecture for Abelian surfaces. “To do that, we need the Euler system and we need the explicit reciprocity law, which relates the Euler system to the value of the L-function,” she says. A lot of attention Researchers are also continuing to look at other Euler systems, which can be constructed in vastly greater generality than previously possible. Over the next few years the aim is to prove explicit reciprocity laws in all of the cases where Euler systems can be constructed, which can then be used to prove many new cases of the Bloch-Kato conjecture and enable researchers to look towards more ambitious objectives. “The long-term goal would be to prove the Bloch-Kato conjecture in general, or at least for certain Shimura varieties,” says Professor Zerbes. This is a complex and as yet not fully-defined task, however it is a topic that Professor Zerbes is keen to address in her research in future. “The Euler systems give results when the L-function does not vanish at certain points. If it does vanish then everything becomes much more complicated, and at present a strategy for dealing with these cases is not known,” she outlines. “That’s something that my collaborators and I are certainly planning on thinking about in the future.”
EULER SYSTEMS Euler systems and the Birch-Swinnerton-Dyer conjecture Project Objectives To prove new cases of the Bloch—Kato conjecture on special values of L-functions, via a systematic construction and study of so-called Euler systems. In particular, to prove the Birch—Swinnerton-Dyer conjecture for elliptic curves over imaginary quadratic fields in analytic rank 0. Project Funding Funded by the European Research Council - total funding € 1,070,473.
Project Partners The research programme has been developed jointly with Professor David Loeffler (University of Warwick), who is funded by a Royal Society URF. Contact Details Project Coordinator Professor Sarah Livia Zerbes Department of Mathematics University College London Gower Street London WC1E 6BT United Kingdom E: s.zerbes@ucl.ac.uk W: http://www.homepages.ucl. ac.uk/~ucahsze/
Professor Sarah Livia Zerbes
Professor Sarah Zerbes, a German mathematician, completed her undergraduate education at the University of Cambridge in 2002. She then went on to do her doctoral studies under the supervision of Professor John Coates, FRS, receiving her PhD in 2005. She is interested in special values of L-functions and Iwasawa theory, which she investigates together with her husband and close collaborator David Loeffler.











