DẠYKÈMQUYNHƠNOFFICIAL

Trong tam giác AHB , ta có

41 tan 205 AH ABH BH

=== 1119 ABH ′  ≈° .

Suy ra 9011197841 ABC =°−°=°′′ .

Suy ra ( ) 180 5619 ACBBACABC ′ =°−+=°

Áp dụng định lí sin trong tam giác ABC , ta được: sinsin ABCB ACBBAC = .sin 17m sin ABBAC CB ACB  = ≈

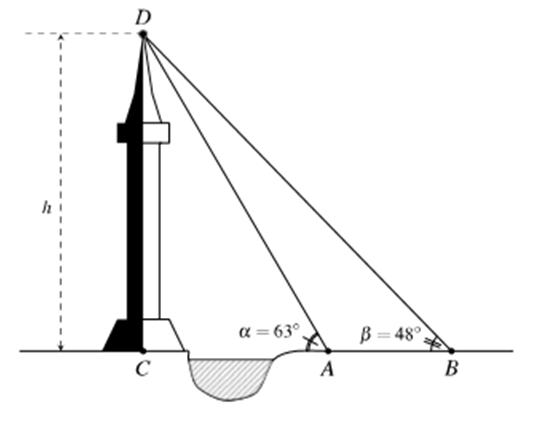
Câu 4: Giả sử CDh = là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A , B trên mặt đất sao cho ba điểm , AB và C thẳng hàng. Ta đo được 24m AB = , 63 CAD =° , 48 CBD =°

. Chiều cao h của tháp gần với giá trị nào sau đây?

Chọn C

Ta có 634815 DD αβαβ =+  =−=°−°=°

Áp dụng định lí sin vào tam giác ABD , ta có

.sin24.sin48 68,91m sinsin15 sinsin ADABAB AD DD β β ° =  ==≈ ° .

Trong tam giác vuông ACD , có .sin68,91mhCDAD α ==≈

Câu 5: Trên nóc một tòa nhà có một cột ăng-ten cao 5m . Từ vị trí quan sát A cao 7m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 050 và 0 40 so với phương nằm ngang. Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?

Vậy 11,9718,9m

CHCDDH=+=+= .

Câu 6: Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng 60m CD = , giả sử chiều cao của giác kế là 1m OC = . Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc

060 AOB = . Chiều cao của ngọn tháp gần với giá trị nào sau đây:

A. 40m B. 114m C. 105m D. 110m Lời giải Chọn C

Tam giác OAB vuông tại B , có tan AB AOB OB = 0 tan60.603mABOB  ==

Vậy chiều cao của ngọn tháp là () 6031105m hABOC=+=+ ≃ .

Câu 7: Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao 70m AB = , phương nhìn AC tạo với phương nằm ngang góc 030 , phương nhìn BC tạo với phương nằm ngang góc 0 1530′ . Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?

A. 135m . B. 234m . C. 165m . D.

Môn học/Hoạt động giáo dục: Toán – Hình học: 10

Thời gian thực hiện: …… tiết

I. MỤC TIÊU

1. Kiến thức:

Nhận biết được giá trị lượng giác của góc từ 00 đến 1800 .

Giải thích được hệ thức liên hệ gi]ã các giá trị lượng giác của 2 góc phụ nhau, bù nhau

Thiết lập được mô hình toán học như các bài toán giải tam giác.

Vận dụng được kiến thức về giải tam giác vào một số bài toán liên quan đến thực tiễn (ví dụ: bài toán xác định khoảng cách giữa hai điểm khi gặp vật cản, xác định chiều cao của vật khi không thể đoa trực tiếp, ...).

2. Về năng lực: Năng lực Yêu cầu cần đạt NĂNG LỰC ĐẶC THÙ

 Giải thích được hệ thức lượng giác của các góc phụ nhau, bù nhau.

Năng lực tư duy và lập luận toán học

 Giải thích được các hệ thức lượng giác cơ bản trong tam giác: Định lí côssin, định lí sin, công thức tính diện tích tam giác.

Năng lực giải quyết vấn đề toán học

Năng lực mô hình hóa toán học.

Năng lực tự chủ và tự học

Năng lực giao tiếp và hợp tác

 Nhận biết được giá trị lượng giác của một góc từ 00 đến 1800. Tính được giá trị lượng giác của một góc từ 00 đến 1800 bằng máy tính cầm tay.

 Mô tả và thực hiện được các cách giải tam giác.

 Xác định khoảng cách giữa hai địa điểm khi gặp vật cản, trong thiết kế, trong xây dựng, xác đinh chiều cao của vật khi không thể đo trực tiếp,....

NĂNG LỰC CHUNG

 Tự giải quyết các bài tập trắc nghiệm ở phần luyện tập và bài tập về nhà.

 Tương tác tích cực của các thành viên trong nhóm khi thực hiện nhiệm vụ hợp tác.

3. Về phẩm chất: Trách nhiệm Có ý thức hỗ trợ, hợp tác với các thành viên trong nhóm để hoàn thành nhiệm vụ

Nhân ái

Có ý thức tôn trọng ý kiến của các thành viên trong nhóm khi hợp tác.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU:

Máy chiếu, phiếu học tập, giấy màu, giấy A0, bút lông, kéo….

III. TIẾN TRÌNH DẠY HỌC:

Hoạt động 1: Ôn tập lại lý thuyết a) Mục tiêu: nh lí sin, giải tam giác và ứng dụng thực

Tạo sự tò mò, gây hứng thú cho học sinh khi giải các bài toán về “Giải tam giác và ứng dụng thực tế”.

Học sinh mong muốn biết thực hiện các bài toán về tam giác, các bài toán thực b) Nội dung:

Hỏi 1: Nêu định lí côsin, định lí sin?

Hỏi 2: Rút ra công thức tính cosA,cosB,cosC , sinA,sinB,sinC ?

Hỏi 3: Nêu các công thức tính diện tích tam giác?

Hỏi 4: c) Sản phẩm:

Định lí côsin 222 222 2cos 2...cos abcbcAhayBCABACABACA =+− =+−

Định lí sin

2. sinsinsin abc R ABC ===

 222 222 222 cos ,cos ,cos 2 2 2 bcaacbbac A B C bc ac ab +− +− +− = = = sinA=,sinB=,sinC= 222 abc RRR

 Diện tích của tam giác: 1111 1

1) 2222...().().. 2 ABCAIBAICBIC SSSScrbrarrcbaabcrpr =++=++=++=++= 111

2)..sin..sin..sin 222 ABC SbcAacBabC ===

3) 4 ABC abc S R =

4)()()() Sppapbpc =−−− , với 2 abc p ++ = d) Tổ chức thực hiện:

Bước 1: Giao nhiệm vụ:

Giáo viên chia lớp thành 4 đội chơi.

Giáo viên phổ biến cách chơi: Giáo viên trình chiếu lần lượt 4 câu hỏi; các đội thảo luận, giơ tay trả lời câu hỏi.

Bước 2: Thực hiện nhiệm vụ:

Các đội giơ tay trả lời các câu hỏi của giáo viên đưa ra.

Bước 3: Báo cáo, thảo luận:

Đội nào có câu trả lời thì giơ tay, đội nào giơ tay trước thì trả lời trước.

Bước 4: Kết luận, nhận định: