DẠYKÈMQUYNHƠNOFFICIAL

Vậy 0 m ≤ thỏa yêu cầu bài toán.

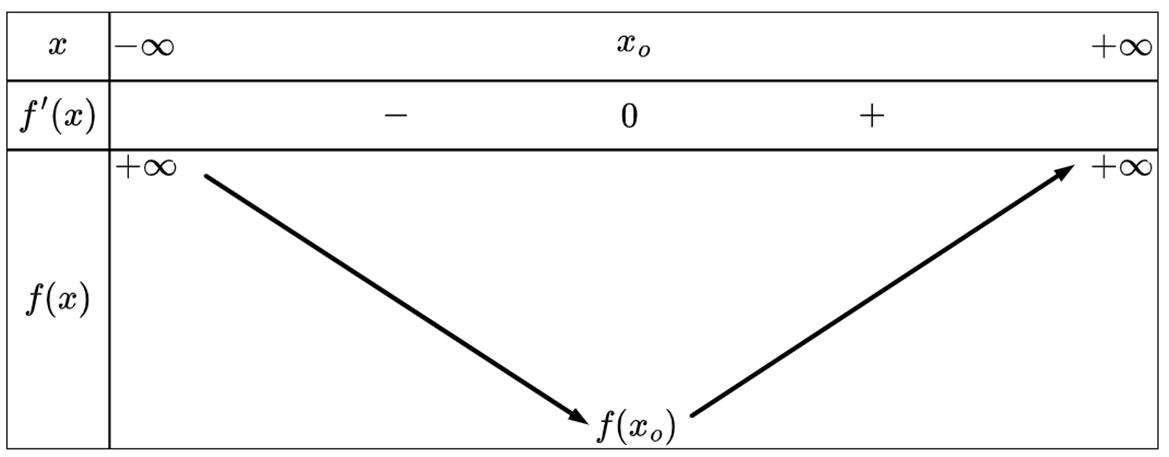
Trường hợp 2: 0 m > . Khi đó () 2 '0logln2 o m fxx=⇔= . Ta có bảng biến thiên của ()fx .

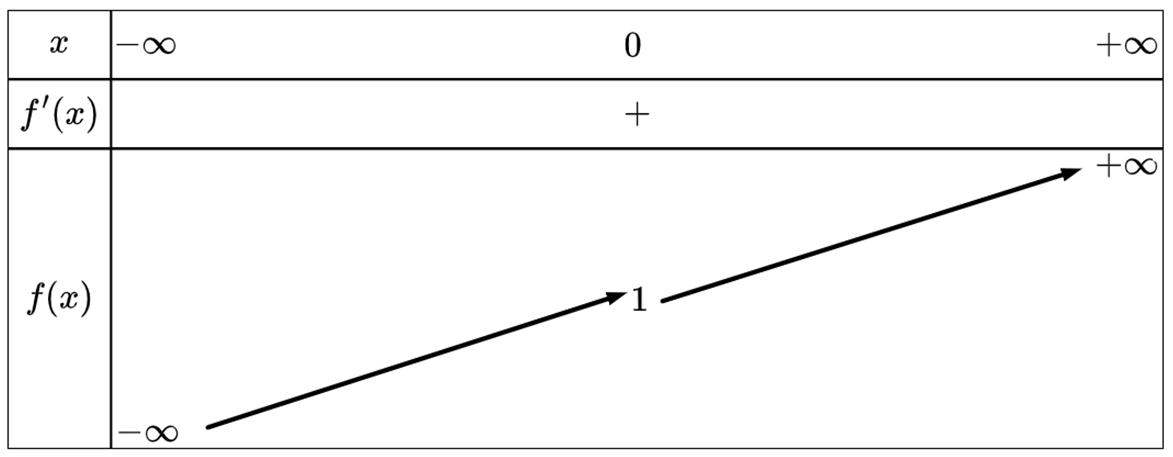
Yêu cầu bài toán () 1 ofx ⇔= . Lại có ()01 f = nên

Tóm lại từ hai trường hợp, ta thấy ph

Câu 47: Cho hàm số ()yfx = liên tục trên ℝ . Bi hinh vể sau: Hàm số

()yfx ′ =

()(13)32023 gxfxxx =+−++ nghịch biến trên khoảng nào sau đây?

3 ;2 2   ời giải Chọn A () 2 ()(13)320233(13)61 gxfxxxgxfxx ′′ =+−++  =+−+ () () 2 0(13)131 3 gxfxx ′′ =⇔+=+− .

(4;1) .

Đặt 31tx=+ ta được phương trình 2 ()1 3 ftt ′ =−