DẠYKÈMQUYNHƠNOFFICIAL

Do đó 08 m ≤≤ . Vậy {} 0;1;2;3;...;16 S = . Suy ra tổng giá trị các phần tử của tập hợp S bằng 136.

Câu 44: Cho phương trình () ()() 3 2 32 2 log3421823 m xxxxm ++++−+=+ , ( m là tham số). Tìm số giá trị nguyên của tham số m để phương trình đã cho có nghiệm duy nhất thuộc [ )2;4 ?

A. 3. B. 4 C. 5. D. 2 Lời giải

Chọn B

Điều kiện 32340xx++>

Ta có () ()() 3 2 32 2 log3421823 m xxxxm ++++−+=+

()() () 3232 2 2 3log34343log22,1 mm xxxx ⇔+++++=+

Xét hàm số () 23log yfttt ==+ với 0 t > có () 1 10,0 .ln2 ftt t ′ =+>∀> nên hàm số () 23log yfttt ==+ đồng biến trên khoảng () 0; +∞

Từ () ()() 32 32 4 2 12343 mm fxxfxx⇔++=⇔ =++ .

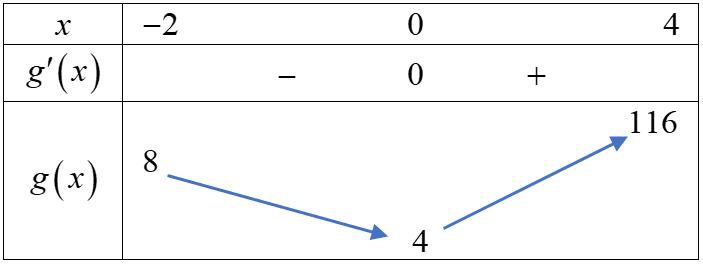
Đặt () 3234gxxx=++ với [ )2;4 x ∈− có